-
PDF
- Split View
-
Views
-
Cite
Cite
Maria Anisimova, Ziheng Yang, Multiple Hypothesis Testing to Detect Lineages under Positive Selection that Affects Only a Few Sites, Molecular Biology and Evolution, Volume 24, Issue 5, May 2007, Pages 1219–1228, https://doi.org/10.1093/molbev/msm042
Close - Share Icon Share
Abstract
Detection of positive Darwinian selection has become ever more important with the rapid growth of genomic data sets. Recent branch–site models of codon substitution account for variation of selective pressure over branches on the tree and across sites in the sequence and provide a means to detect short episodes of molecular adaptation affecting just a few sites. In likelihood ratio tests based on such models, the branches to be tested for positive selection have to be specified a priori. In the absence of a biological hypothesis to designate so-called foreground branches, one may test many branches, but a correction for multiple testing becomes necessary. In this paper, we employ computer simulation to evaluate the performance of 6 multiple test correction procedures when the branch–site models are used to test every branch on the phylogeny for positive selection. Four of the methods control the familywise error rates (FWERs), whereas the other 2 control the false discovery rate (FDR). We found that all correction procedures achieved acceptable FWER except for extremely divergent sequences and serious model violations, when the test may become unreliable. The power of the test to detect positive selection is influenced by the strength of selection and the sequence divergence, with the highest power observed at intermediate divergences. The 4 correction procedures that control the FWER had similar power. We recommend Rom's procedure for its slightly higher power, but the simple Bonferroni correction is useable as well. The 2 correction procedures that control the FDR had slightly more power and also higher FWER. We demonstrate the multiple test procedures by analyzing gene sequences from the extracellular domain of the cluster of differentiation 2 (CD2) gene from 10 mammalian species. Both our simulation and real data analysis suggest that the multiple test procedures are useful when multiple branches have to be tested on the same data set.
Introduction
Genome scans for positive selection are proving useful to further our understanding of gene functions by generating interesting biological hypotheses for experimental ratification (Clark et al. 2003; Nielsen et al. 2005; Arbiza et al. 2006). The rapid accumulation of sequence data has also prompted efforts to develop methods for detecting positive Darwinian selection in protein-coding genes, especially when it affects only a few codons in the gene and a few lineages on the phylogeny (Yang and Nielsen 2002; Forsberg and Christiansen 2003; Bielawski and Yang 2004; Guindon et al. 2004; Yang et al. 2005). In particular, the branch–site models (Yang and Nielsen 2002; Yang et al. 2005) aim to detect episodic positive selection and have recently received much attention (Zhang 2004; Yang et al. 2005; Zhang et al. 2005). These models use the nonsynonymous to synonymous substitution rate ratio (ω) to measure selective pressure on the protein. As they allow the selective pressure indicated by the ω ratio to vary both across sites in the gene and across lineages on the tree, these models have improved power to detect short episodes of positive selection acting on a few amino acids.
However, the initial branch–site methods proposed by Yang and Nielsen (2002) were found to be sensitive to model assumptions and to generate excessive false positives in computer simulations (Zhang 2004). The models were later modified (Yang et al. 2005), and a likelihood ratio test (LRT) based on the modified models was found to have satisfactory accuracy and reasonable power (Zhang et al. 2005). This modified test is used in the present study. As stressed by Yang and Nielsen (2002; see also Yang 1998), the branches to be examined for positive selection in the branch–site test, referred to as the foreground branches, have to be specified a priori. The LRT then compares a branch–site model that allows positive selection on the foreground branches with a simpler model that does not. In some situations, a biological hypothesis may be used to specify the foreground branches in a straightforward manner. For example, to detect positive selection after gene duplication, branches following the duplication event may be designated as foreground branches. However, such a prespecified biological hypothesis may not always be available. For example, when thousands of genes from the genome are scanned automatically for positive selection, it is very unlikely for the same branch to be affected by positive selection in all genes. Similarly, it may be difficult to specify the foreground branch when the functions of the gene under study are poorly understood.
A possible approach then is to test several or all branches on the tree, with every branch treated in turn as the foreground branch. However, in such tests of multiple null hypotheses, the probability of rejecting falsely at least one of them can be high. The family-wise error rate (FWER) or the overall type-I error rate is defined as the probability of false rejection of at least one true null hypothesis in a family of hypotheses. If n independent true null hypotheses are tested, each at the significance level α, the FWER is 1 − (1 − α)n. This is as high as 40% when n = 10 hypotheses are tested at the α = 5% level. Several procedures have been proposed in the statistics literature to correct for multiple testing to ensure that the FWER is ≤α. The simplest is Bonferroni's correction (Miller 1981, p. 67–70), according to which one uses α/n as the significance level to test each of the n hypothesis being tested. This procedure is simple and applicable to most multiple testing situations. However, it is known to be conservative, especially if the multiple hypotheses are strongly correlated. Several modifications were proposed in order to improve the power of the test, including Hochberg's (1988), Hommel's (1988), and Rom's (1990) methods.
In cases where some null hypotheses are expected to be wrong and a small percentage of false rejections are tolerable, it may be too stringent to control the FWER. In this case, a useful concept is the false discovery rate (FDR). A significant result or a rejection of the null hypothesis is called a “discovery,” and the FDR is defined as the expected proportion of falsely rejected hypotheses among all hypotheses that are rejected. The FDR was introduced by Benjamini and Hochberg (1995), and its power has been improved by estimating the number of true null hypotheses (Benjamini and Hochberg 2000; Storey 2002; Storey and Tibshirani 2003). See Manly et al. (2006) for a review of FWER, FDR, and some other criteria useful for multiple test corrections.
We suggest that in tests of positive selection, one normally does not know whether there exists any lineage at all under positive selection and that a false rejection of the null hypothesis of no positive selection on any branch should be considered a serious error, to be avoided. Thus, it appears to us necessary to control the FWER when the branch–site test is applied to multiple branches on the tree. Nevertheless, we include for comparison 2 methods that control the FDR.
In this paper, we use computer simulation to examine the FWER and power of 6 multiple test correction procedures when they are combined with the branch–site test of positive selection to detect episodic selection affecting particular lineages and sites. Four of the procedures control the FWER: 1) Bonferroni's method, 2) Hochberg's (1988) method, 3) Hommel's (1988) method, and 4) Rom's (1990) method, whereas 2 of them control the FDR: 5) method of Benjamini and Hochberg (1995) and 6) an improved version by Storey (2002; Storey and Tibshirani 2003).
We also apply those methods to a real data set, the mammalian immune gene cluster of differentiation 2 (CD2), previously analyzed by Lynn et al. (2005). CD2 is a cell-surface protein expressed in natural killer cells and T-cells, major components in the cell-mediated and innate immune system. Positive selection was detected in this gene by Lynn et al. (2005) using branch and site models that allow variable selective pressures either over branches or over sites, but not over both.
Methods
Branch–Site Test of Positive Selection
The LRT evaluated in this paper is the branch–site test of positive selection of Yang et al. (2005; see also Zhang et al. 2005) based on the so-called branch–site model A (table 1). The phylogenetic tree is assumed known. All branches on the tree are partitioned into 2 categories: the “foreground” branches on which some sites may be under positive selection and the “background” branches on which positive selection is not allowed. Four classes of sites are assumed in the model. Site class 0 includes codons evolving under purifying selection on all branches, with 0 < ω0 < 1. Site class 1 includes codons that are evolving neutrally throughout the tree, with ω1 = 1. Codons in site classes 2a and 2b are conserved or neutral on the background branches but become under positive selection on the foreground branches, with ω2 ≥ 1. The model involves 4 free parameters in the ω distribution to be estimated from the data: p0, p1, ω0, and ω2. This is the alternative hypothesis in the LRT. The null hypothesis is the same model A but with ω2 = 1 fixed. If the null hypothesis is correct, twice the log-likelihood difference between the 2 models (2Δℓ) should follow an asymptotic distribution that is a 1:1 mixture of 0 and , often written as (e.g., Self and Liang 1987; Yang et al. 2005). The critical values of this mixture distribution are 2.71 and 5.41 at the 5% and 1% levels, respectively. To guide against violations of model assumptions, we also use as the null distribution, which is expected to make the test conservative (Zhang et al. 2005). The critical values of the distribution are 3.84 and 5.99 at the 5% and 1% levels, respectively.
| Site Class | Proportion of Sites | Background ω | Foreground ω |
| 0 | p0 | 0 < ω0 < 1 | 0 < ω0 < 1 |
| 1 | p1 | ω1 = 1 | ω1 = 1 |
| 2a | (1 − p0 − p1) p0/(p0 + p1) | 0 < ω0 < 1 | ω2 ≥ 1 |
| 2b | (1 − p0 − p1) p1/(p0 + p1) | ω1 = 1 | ω2 ≥ 1 |
| Site Class | Proportion of Sites | Background ω | Foreground ω |
| 0 | p0 | 0 < ω0 < 1 | 0 < ω0 < 1 |
| 1 | p1 | ω1 = 1 | ω1 = 1 |
| 2a | (1 − p0 − p1) p0/(p0 + p1) | 0 < ω0 < 1 | ω2 ≥ 1 |
| 2b | (1 − p0 − p1) p1/(p0 + p1) | ω1 = 1 | ω2 ≥ 1 |
NOTE.—Model A is the alternative hypothesis for the branch–site test of positive selection. The null model fixes ω2 = 1.
| Site Class | Proportion of Sites | Background ω | Foreground ω |
| 0 | p0 | 0 < ω0 < 1 | 0 < ω0 < 1 |
| 1 | p1 | ω1 = 1 | ω1 = 1 |
| 2a | (1 − p0 − p1) p0/(p0 + p1) | 0 < ω0 < 1 | ω2 ≥ 1 |
| 2b | (1 − p0 − p1) p1/(p0 + p1) | ω1 = 1 | ω2 ≥ 1 |
| Site Class | Proportion of Sites | Background ω | Foreground ω |
| 0 | p0 | 0 < ω0 < 1 | 0 < ω0 < 1 |
| 1 | p1 | ω1 = 1 | ω1 = 1 |
| 2a | (1 − p0 − p1) p0/(p0 + p1) | 0 < ω0 < 1 | ω2 ≥ 1 |
| 2b | (1 − p0 − p1) p1/(p0 + p1) | ω1 = 1 | ω2 ≥ 1 |
NOTE.—Model A is the alternative hypothesis for the branch–site test of positive selection. The null model fixes ω2 = 1.
Corrections for Multiple Testing
Consider testing n null hypotheses H1, H2, …, Hn, with corresponding p values p1, p2, …, pn. The overall null hypothesis H = {H1, H2, …, Hn} is rejected if at least one of the n component hypotheses is rejected. Bonferroni's correction makes use of Bonferroni's inequality, 1 − (1 − α)n ≤ nα, and uses the significance level α/n to test each hypothesis: any hypothesis Hi is rejected if and only if pi ≤ α/n. The FWER is thus ≤α. Bonferroni's procedure strictly controls the FWER but is known to be conservative, especially when many null hypotheses are tested and they are correlated.
Several less-conservative procedures were proposed in the statistics literature, which work as follows. The p values calculated from the data are ranked in ascending order: p(1) ≤ p(2) ≤ ⋯ ≤ p(n), with the corresponding component hypotheses H(1), H(2), …, H(n). The p values are compared with the threshold p values calculated according to a certain procedure. If a component hypothesis with a particular p value is rejected, then all other component hypotheses with smaller p values must also be rejected. Thus, the correction procedures fall into 2 categories. The step-down procedures start with the smallest p value, perform tests in order of increasing p values, and stop as soon as a component hypothesis is not rejected (and then none of the remaining hypotheses, with greater p values, is rejected). In contrast, the step-up procedures start with the largest p value, proceed in order of decreasing p values, and stop as soon as a component hypothesis is rejected (and then all the remaining hypotheses, with smaller p values, are rejected as well).
In Hommel's procedure, H(i) is rejected if p(i) ≤ α/j, where j is the largest number of t = 1, …, n satisfying the inequality p(n − t + k) > kα/t for all k = 1, …, t. If no such j exists, all null hypotheses are rejected.
Benjamini and Hochberg's (1995) procedure controls the FDR. If all null hypotheses are true, it also controls the FWER. This is a step-up procedure and uses the threshold value . It is known to be conservative in controlling FDR when some null hypotheses are false; that is, the FDR achieved by the test is in general lower than the nominal value α (Benjamini and Hochberg 1995). Note that the p value has a uniform U(0, 1) distribution when the null hypothesis is true and the test is exact. If all n null hypotheses are true and all n p values are U(0, 1) variables, a proportion of them will be less than . Thus, is an estimate of the number of false discoveries, and is an estimate of the proportion of false discoveries among the i discoveries when one rejects the first i hypotheses with p values ≤ . The method of Benjamini and Hochberg thus attempts to reject as many hypotheses as possible, subject to the constraint that the estimated FDR is This reasoning, however, assumes that all null hypotheses are true. If some of them are false, will overestimate the number of false discoveries, and it is more appropriate to use , where n0 < n is the number of true null hypotheses (Finner and Roters 2001). Recent methods that improve the power of the procedure of Benjamini and Hochberg attempt to estimate n0 or the proportion of true null hypotheses π0 = n0/n from the observed p values (Benjamini and Hochberg 2000; Storey 2002). Here, we use the R-based program QVALUE, available from http://faculty.washington.edu/∼jstorey/qvalue/, and use the default setting of the program. This uses a cubic-spline smoothing method to estimate π0 for a preset FDR (=5%) (Storey and Tibshirani 2003), with the smoothing parameter λ = 0.0–0.9, at step length 0.01. This is referred to later as Storey's method. Black (2004) demonstrated that the method of Storey (2002) has similar performance to another method due to Benjamini and Hochberg (2000), which uses an alternative method to estimate π0. Note that QVALUE is used here to estimate π0 only to implement an improved FDR procedure. We did not use the positive FDR (or pFDR) or the associated q value of Storey (2002). The pFDR is useful when at least one null hypotheses is known to be wrong, as in some analyses of microarray gene-expression data (Storey and Tibshirani 2003). It is inappropriate for branch–site tests of positive selection, as the error rate (pFDR) is 1 when all null hypotheses are true, that is, when no branch on the tree is under positive selection.
Among the procedures considered here, Bonferroni's correction is the most conservative or least powerful. Theoretical analysis and computer simulations demonstrate that Hommel (1989) and Rom's (1990) procedures are at least as powerful as Hochberg's (1988), but the differences in power are often marginal (e.g., Dunnett and Tamhane 1992; Olejnik et al. 1997). The methods that control the FDR, such as those of Benjamini and Hochberg (1995) and Storey (2002), are expected to have greater power than the methods that control the FWER (e.g., Olejnik et al. 1997). All methods were initially developed under the assumption that the component hypotheses are independent, but simulations suggest that they work reasonably well in many situations with correlated test statistics (e.g., Benjamini and Yekutieli 2001; Storey 2002).
In theory, when their assumptions are satisfied, the multiple test procedures are expected to work well. However, when they are applied to test for positive selection in a phylogenetic analysis, not all the assumptions are met. First, the correction procedures assume that the component null hypotheses are independent and each null hypothesis is tested under the correct model, so that the p values are uniformly distributed. However, the branch–site model partitions branches into the foreground and background categories, and the null hypotheses, which specify different branches as the foreground or background branches, are not independent and are indeed incompatible. Second, the branch–site model makes restrictive assumptions about the selective pressure on lineages and sites, which may be seriously violated in real data. As a result, the p values do not have a uniform distribution, and the standard theory may not apply. In tests of positive selection, the robustness of the test to violations of model assumptions has been considered a very important property (see, e.g., Anisimova et al. 2002; Wong et al. 2004; Zhang 2004; Zhang et al. 2005). We thus use computer simulation to examine the performance of the test, in particular its sensitivity to model violations.
Computer Simulations
Two trees, for 4 and 8 taxa (fig. 1), are used to simulate data sets. The sequence length is 300 codons. The number of replicates is 1000 for the 4-taxa tree and 200 for the 8-taxa tree. The transition/transversion rate ratio is fixed at κ = 2, and the 61 sense codons are assumed to have equal frequencies, except if stated otherwise.
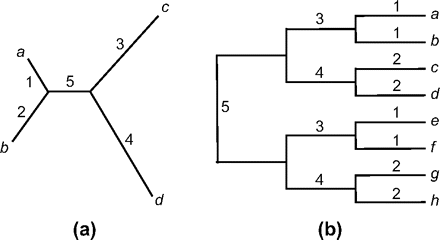
Two unrooted trees for 4 or 8 taxa used to simulate data. (a) In the 4-taxa tree, each of the 5 branches has its own selection regime (table 3) and each is tested as the foreground branch. The tree is represented as “((a: 0.1, b: 0.2): 0.1, c: 0.3, d: 0.4),”where the branch length is measured by the expected number of nucleotide substitutions per codon, averaged over the site classes. (b) In the 8-taxa tree, branches with the same label, such as B1, are assumed to evolve under the same selection regime. When the data are analyzed using the branch–site LRT, each of the 13 branches is used as the foreground branch and tested individually. Results for branches with the same label are expected to be the same, and their averages are presented. All branches have length 0.3 except for branch B5, which has length 0.6.
The 5 branches in the 4-taxa tree are assigned separate selection regimes (ω distribution), whereas the branches with the same label in the 8-taxa tree are assigned the same selection regime. Seven simulation schemes are used: NC1, NC2, NI, SC, SI1, SI2, and SI3 (table 2). Schemes with the abbreviation “N” assume no sites under positive selection along any lineage, whereas “S” means that some sites are under positive selection along certain lineages. The abbreviation “C” means that branch–site model A is used to simulate the data, so that model A is correct when used to analyze the data (at least when one of the branches is being tested), whereas “I” means that the simulation model is more complex and model A is incorrect. In general, we expect the test to perform well when the model assumptions are met, but a good test should be robust to moderate violations of its assumptions.
| Site Class | Proportion | B1 | B2 | B3 | B4 | B5 |
| Scheme NC1 (model A with ω2 = 1 and B5 to be foreground) | ||||||
| Class 0: conserved | 0.6 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| Class 1: neutral | 0.2 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| Class 2a: variable on B5 | 0.15 | 0.3 | 0.3 | 0.3 | 0.3 | 1.0 |
| Class 2b = class 1 | 0.05 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| Scheme NC2 (model A with ω2 = 1 and B1 to be foreground) | ||||||
| Class 0: conserved | 0.6 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| Class 1: neutral | 0.2 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| Class 2a: variable on B1 | 0.15 | 1.0 | 0.3 | 0.3 | 0.3 | 0.3 |
| Class 2b = class 1 | 0.05 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| Scheme NI | ||||||
| Conserved class 1 | 0.3 | 0.0 | 0.0 | 0.1 | 0.2 | 0.3 |
| Conserved class 2 | 0.3 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 |
| Nearly neutral class | 0.2 | 0.7 | 0.8 | 0.9 | 1.0 | 1.0 |
| Relaxed constraint on B1 and B2 | 0.2 | 1.0 | 1.0 | 0.1 | 0.2 | 0.2 |
| Scheme SC | ||||||
| Model A with ω2 = 4 on B5 | ||||||
| Class 0: conserved | 0.6 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| Class 1: neutral | 0.2 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| Class 2a: positive selection | 0.15 | 0.3 | 0.3 | 0.3 | 0.3 | 4.0 |
| Class 2b: positive selection | 0.05 | 1.0 | 1.0 | 1.0 | 1.0 | 4.0 |
| Scheme SI1 | ||||||
| Conserved class 1 | 0.3 | 0.0 | 0.0 | 0.1 | 0.2 | 0.3 |
| Conserved class 2 | 0.3 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 |
| Nearly neutral class | 0.2 | 0.7 | 0.8 | 0.9 | 1.0 | 1.0 |
| Positive selection on B5 | 0.2 | 0.3 | 0.3 | 0.1 | 0.2 | 4.0 |
| Scheme SI2 | ||||||
| Conserved class 1 | 0.3 | 0.0 | 0.0 | 0.1 | 0.2 | 0.3 |
| Conserved class 2 | 0.3 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 |
| Nearly neutral class | 0.2 | 0.7 | 0.8 | 0.9 | 1.0 | 1.0 |
| Positive selection on 5 | 0.1 | 0.3 | 0.3 | 0.1 | 0.2 | 4.0 |
| Positive selection on 1 | 0.1 | 5.0 | 0.3 | 0.1 | 0.2 | 0.3 |
| Scheme SI3 | ||||||
| Conserved class 1 | 0.3 | 0.0 | 0.0 | 0.1 | 0.2 | 0.3 |
| Conserved class 2 | 0.3 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 |
| Nearly neutral class | 0.2 | 0.7 | 0.8 | 0.9 | 1.0 | 1.0 |
| Positive selection on B1-4 | 0.2 | 5.0 | 5.0 | 5.0 | 5.0 | 0.8 |
| Site Class | Proportion | B1 | B2 | B3 | B4 | B5 |
| Scheme NC1 (model A with ω2 = 1 and B5 to be foreground) | ||||||
| Class 0: conserved | 0.6 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| Class 1: neutral | 0.2 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| Class 2a: variable on B5 | 0.15 | 0.3 | 0.3 | 0.3 | 0.3 | 1.0 |
| Class 2b = class 1 | 0.05 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| Scheme NC2 (model A with ω2 = 1 and B1 to be foreground) | ||||||
| Class 0: conserved | 0.6 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| Class 1: neutral | 0.2 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| Class 2a: variable on B1 | 0.15 | 1.0 | 0.3 | 0.3 | 0.3 | 0.3 |
| Class 2b = class 1 | 0.05 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| Scheme NI | ||||||
| Conserved class 1 | 0.3 | 0.0 | 0.0 | 0.1 | 0.2 | 0.3 |
| Conserved class 2 | 0.3 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 |
| Nearly neutral class | 0.2 | 0.7 | 0.8 | 0.9 | 1.0 | 1.0 |
| Relaxed constraint on B1 and B2 | 0.2 | 1.0 | 1.0 | 0.1 | 0.2 | 0.2 |
| Scheme SC | ||||||
| Model A with ω2 = 4 on B5 | ||||||
| Class 0: conserved | 0.6 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| Class 1: neutral | 0.2 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| Class 2a: positive selection | 0.15 | 0.3 | 0.3 | 0.3 | 0.3 | 4.0 |
| Class 2b: positive selection | 0.05 | 1.0 | 1.0 | 1.0 | 1.0 | 4.0 |
| Scheme SI1 | ||||||
| Conserved class 1 | 0.3 | 0.0 | 0.0 | 0.1 | 0.2 | 0.3 |
| Conserved class 2 | 0.3 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 |
| Nearly neutral class | 0.2 | 0.7 | 0.8 | 0.9 | 1.0 | 1.0 |
| Positive selection on B5 | 0.2 | 0.3 | 0.3 | 0.1 | 0.2 | 4.0 |
| Scheme SI2 | ||||||
| Conserved class 1 | 0.3 | 0.0 | 0.0 | 0.1 | 0.2 | 0.3 |
| Conserved class 2 | 0.3 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 |
| Nearly neutral class | 0.2 | 0.7 | 0.8 | 0.9 | 1.0 | 1.0 |
| Positive selection on 5 | 0.1 | 0.3 | 0.3 | 0.1 | 0.2 | 4.0 |
| Positive selection on 1 | 0.1 | 5.0 | 0.3 | 0.1 | 0.2 | 0.3 |
| Scheme SI3 | ||||||
| Conserved class 1 | 0.3 | 0.0 | 0.0 | 0.1 | 0.2 | 0.3 |
| Conserved class 2 | 0.3 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 |
| Nearly neutral class | 0.2 | 0.7 | 0.8 | 0.9 | 1.0 | 1.0 |
| Positive selection on B1-4 | 0.2 | 5.0 | 5.0 | 5.0 | 5.0 | 0.8 |
NOTE.—values of ω greater than 1 are shown in bold.
| Site Class | Proportion | B1 | B2 | B3 | B4 | B5 |
| Scheme NC1 (model A with ω2 = 1 and B5 to be foreground) | ||||||
| Class 0: conserved | 0.6 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| Class 1: neutral | 0.2 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| Class 2a: variable on B5 | 0.15 | 0.3 | 0.3 | 0.3 | 0.3 | 1.0 |
| Class 2b = class 1 | 0.05 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| Scheme NC2 (model A with ω2 = 1 and B1 to be foreground) | ||||||
| Class 0: conserved | 0.6 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| Class 1: neutral | 0.2 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| Class 2a: variable on B1 | 0.15 | 1.0 | 0.3 | 0.3 | 0.3 | 0.3 |
| Class 2b = class 1 | 0.05 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| Scheme NI | ||||||
| Conserved class 1 | 0.3 | 0.0 | 0.0 | 0.1 | 0.2 | 0.3 |
| Conserved class 2 | 0.3 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 |
| Nearly neutral class | 0.2 | 0.7 | 0.8 | 0.9 | 1.0 | 1.0 |
| Relaxed constraint on B1 and B2 | 0.2 | 1.0 | 1.0 | 0.1 | 0.2 | 0.2 |
| Scheme SC | ||||||
| Model A with ω2 = 4 on B5 | ||||||
| Class 0: conserved | 0.6 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| Class 1: neutral | 0.2 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| Class 2a: positive selection | 0.15 | 0.3 | 0.3 | 0.3 | 0.3 | 4.0 |
| Class 2b: positive selection | 0.05 | 1.0 | 1.0 | 1.0 | 1.0 | 4.0 |
| Scheme SI1 | ||||||
| Conserved class 1 | 0.3 | 0.0 | 0.0 | 0.1 | 0.2 | 0.3 |
| Conserved class 2 | 0.3 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 |
| Nearly neutral class | 0.2 | 0.7 | 0.8 | 0.9 | 1.0 | 1.0 |
| Positive selection on B5 | 0.2 | 0.3 | 0.3 | 0.1 | 0.2 | 4.0 |
| Scheme SI2 | ||||||
| Conserved class 1 | 0.3 | 0.0 | 0.0 | 0.1 | 0.2 | 0.3 |
| Conserved class 2 | 0.3 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 |
| Nearly neutral class | 0.2 | 0.7 | 0.8 | 0.9 | 1.0 | 1.0 |
| Positive selection on 5 | 0.1 | 0.3 | 0.3 | 0.1 | 0.2 | 4.0 |
| Positive selection on 1 | 0.1 | 5.0 | 0.3 | 0.1 | 0.2 | 0.3 |
| Scheme SI3 | ||||||
| Conserved class 1 | 0.3 | 0.0 | 0.0 | 0.1 | 0.2 | 0.3 |
| Conserved class 2 | 0.3 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 |
| Nearly neutral class | 0.2 | 0.7 | 0.8 | 0.9 | 1.0 | 1.0 |
| Positive selection on B1-4 | 0.2 | 5.0 | 5.0 | 5.0 | 5.0 | 0.8 |
| Site Class | Proportion | B1 | B2 | B3 | B4 | B5 |
| Scheme NC1 (model A with ω2 = 1 and B5 to be foreground) | ||||||
| Class 0: conserved | 0.6 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| Class 1: neutral | 0.2 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| Class 2a: variable on B5 | 0.15 | 0.3 | 0.3 | 0.3 | 0.3 | 1.0 |
| Class 2b = class 1 | 0.05 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| Scheme NC2 (model A with ω2 = 1 and B1 to be foreground) | ||||||
| Class 0: conserved | 0.6 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| Class 1: neutral | 0.2 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| Class 2a: variable on B1 | 0.15 | 1.0 | 0.3 | 0.3 | 0.3 | 0.3 |
| Class 2b = class 1 | 0.05 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| Scheme NI | ||||||
| Conserved class 1 | 0.3 | 0.0 | 0.0 | 0.1 | 0.2 | 0.3 |
| Conserved class 2 | 0.3 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 |
| Nearly neutral class | 0.2 | 0.7 | 0.8 | 0.9 | 1.0 | 1.0 |
| Relaxed constraint on B1 and B2 | 0.2 | 1.0 | 1.0 | 0.1 | 0.2 | 0.2 |
| Scheme SC | ||||||
| Model A with ω2 = 4 on B5 | ||||||
| Class 0: conserved | 0.6 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| Class 1: neutral | 0.2 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| Class 2a: positive selection | 0.15 | 0.3 | 0.3 | 0.3 | 0.3 | 4.0 |
| Class 2b: positive selection | 0.05 | 1.0 | 1.0 | 1.0 | 1.0 | 4.0 |
| Scheme SI1 | ||||||
| Conserved class 1 | 0.3 | 0.0 | 0.0 | 0.1 | 0.2 | 0.3 |
| Conserved class 2 | 0.3 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 |
| Nearly neutral class | 0.2 | 0.7 | 0.8 | 0.9 | 1.0 | 1.0 |
| Positive selection on B5 | 0.2 | 0.3 | 0.3 | 0.1 | 0.2 | 4.0 |
| Scheme SI2 | ||||||
| Conserved class 1 | 0.3 | 0.0 | 0.0 | 0.1 | 0.2 | 0.3 |
| Conserved class 2 | 0.3 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 |
| Nearly neutral class | 0.2 | 0.7 | 0.8 | 0.9 | 1.0 | 1.0 |
| Positive selection on 5 | 0.1 | 0.3 | 0.3 | 0.1 | 0.2 | 4.0 |
| Positive selection on 1 | 0.1 | 5.0 | 0.3 | 0.1 | 0.2 | 0.3 |
| Scheme SI3 | ||||||
| Conserved class 1 | 0.3 | 0.0 | 0.0 | 0.1 | 0.2 | 0.3 |
| Conserved class 2 | 0.3 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 |
| Nearly neutral class | 0.2 | 0.7 | 0.8 | 0.9 | 1.0 | 1.0 |
| Positive selection on B1-4 | 0.2 | 5.0 | 5.0 | 5.0 | 5.0 | 0.8 |
NOTE.—values of ω greater than 1 are shown in bold.
Schemes NC1 and NC2 conform to the assumptions of branch–site model A, with the foreground branch being branch B5 in NC1 and branch B1 in NC2. In scheme NI, no site evolves with a constant ω ratio throughout the tree, so that assumptions of model A are violated. This is used to evaluate the robustness of the LRT under the null hypothesis of no positive selection.
Schemes SC, SI1, SI2, and SI3 allow positive selection and are used to examine the false-positive rate on branches with no sites under positive selection and the power on branches with some sites under positive selection. Schemes SI1, SI2, and SI3 also serve the purpose of evaluating the robustness of the test when model A is incorrect. SC is the same as NC1 but with ω2 = 4 on branch B5. SI1 is constructed by modifying the last class of scheme NI to incorporate positive selection on branches B5. SI2 is constructed by adding to SI1 another site class with positive selection on branches B1.
Scheme SI3 is a modification of SI1 and is applied to the 4-taxa tree only (fig. 1a). This assumes that all branches have some sites under positive selection except B5, which evolves nearly neutrally. Our interest is on whether the branch–site test is misled into falsely claiming positive selection on branch B5, when some sites are under positive selection on all branches except B5. For this scheme, we also used unequal codon frequencies, estimated from the CD2 data set, to generate data and use the F3 × 4 model of codon usage to analyze them.
From previous studies (e.g., Anisimova et al. 2002), the sequence divergence level is expected to affect the information content in the data and the power of the test. Thus, data sets of lower and higher sequence divergences were simulated under schemes NC1, NI, SC, and SI2 along the 8-taxa tree (fig. 1) but with the branch lengths multiplied by a constant: ¼, ½, 2, or 5. We refer to these data sets as the “¼×,” “½×,” “2×,” and “5×” data sets.
Each simulated data set was analyzed to test for positive selection. The correct tree topology was assumed, whereas branch lengths were estimated under the assumed model by maximizing the log likelihood. Every branch was designated in turn as the foreground branch, and model A was fitted to the data, first with ω2 = 1 fixed and then with ω2 ≥ 1 estimated. The log-likelihood values under the 2 hypotheses were used to calculate the p value for the branch–site test of positive selection on the designated foreground branch using either the mixture distribution or the distribution (Yang et al. 2005; Zhang et al. 2005). Thus, 5 or 13 null hypotheses of no positive selection were tested in every data set for the 4- and 8-taxa trees, respectively. All results are presented for the significance level α = 5%.
All data sets were simulated using the EVOLVER program and analyzed using the CODEML program, both from the PAML package (Yang 1997). As discussed by Yang and Nielsen (2002), the branch–site model sometimes causes the numerical optimization algorithm to fail to converge to the maximum likelihood estimates. We thus ran the same analysis at least twice using different starting values. The results are considered reliable if 2 runs with the highest log-likelihood values produced identical results. Use of good starting values (such as the true parameter values) is found to be very effective.
Results
Accuracy of the LRT in Simulations without Positive Selection
Table 3 presents the results obtained under simulation schemes NC1, NC2, and NI when there is no positive selection. All significant test results are false positives. The columns labeled “B1,” “B2,” etc. show the average false-positive rates for every branch so labeled after applying the multiple test correction. The FWER is the proportion of simulated data sets in which at least one branch was tested significant. For schemes NC1 and NC2, the FWER based on the mixture distribution varied from 4.3% to 5.4%, close to the nominal 5%. For scheme NI, the FWER based on the mixture distribution was close to 5% for 4 taxa but was 8–10% for 8 taxa. Use of the distribution reduced the false-positive rates for all simulation schemes to below 5%.
Percentage (%) of Significant Replicates (Type-I Error Rate) at the 5% Level Based on the Null Mixture Distribution or the Distribution (in parentheses) when Data are Simulated without Positive Selection
| Correction Procedure | s | B1 | B2 | B3 | B4 | B5 | FWER |
| NC1 | |||||||
| B, Hg, Hl, R | 4 | 0.7 (0.2) | 0.7–0.8 (0.5) | 1.2 (0.7) | 0.9 (0.4) | 0.8–0.9 (0.5) | 4.3–4.4 (2.3) |
| B–H, S | 4 | 0.7–1.2 (0.2–0.5) | 0.9–1.3 (0.5–0.7) | 1.3–1.8 (0.7–1) | 0.9–1.3 (0.4–0.5) | 0.9–1.6 (0.5–0.8) | 4.4–6.2 (2.3–3.2) |
| B, Hg, Hl, R | 8 | 0.5 (0.3) | 0.5 (0.3) | 0 (0) | 0.5 (0.3) | 0 (0) | 5 (2.5) |
| B–H, S | 8 | 0.5 (0.3) | 0.5 (0.3) | 0 (0) | 0.5 (0.3) | 0 (0) | 5 (2.5) |
| NC2 | |||||||
| B, Hg, Hl, R | 4 | 1.3 (0.6) | 1.2 (0.4) | 0.7 (0.4) | 1.1 (0.6) | 1.1–1.2 (0.7) | 5.3–5.4 (2.6–2.7) |
| B–H, S | 4 | 1.4–1.9 (0.6–0.9) | 1.2–1.7 (0.4–0.8) | 0.7–1.5 (0.4) | 1.3–2.3 (0.6–0.7) | 1.1–1.7 (0.7–0.8) | 5.4–7.3 (2.6–3.4) |
| B, Hg, Hl, R | 8 | 0.8 (0.5) | 0.3 (0.1) | 0 (0) | 0.3 (0.3) | 0.5 (0.5) | 4.5 (3) |
| B–H, S | 8 | 0.9 (0.5) | 0.3 (0.1) | 0–0.3 (0) | 0.3 (0.3) | 0.5 (0.5) | 4.5–5 (3) |
| NI | |||||||
| B, Hg, Hl, R | 4 | 1.1 (0.3) | 1.5 (1) | 0.8 (0.3) | 1.2 (0.7) | 0.7–0.9 (0.3) | 5.1–5.3 (2.5) |
| B–H, S | 4 | 1.1–1.9 (0.4) | 1.6–2.3 (1–1.1) | 0.9–1.6 (0.3–0.4) | 1.3–2.2 (0.7–0.8) | 0.7–1.6 (0.3–0.4) | 5.2–7.5 (2.5–2.8) |
| B, Hg, Hl, R | 8 | 1.5 (0.9) | 0 (0) | 0.5 (0.3) | 0.3 (0) | 1.5 (0) | 8 (3) |
| B–H, S | 8 | 1.9–2.0 (0.9) | 0 (0) | 0.5–0.8 (0.3) | 0.5 (0) | 1.5 (0) | 9–10 (3) |
| Correction Procedure | s | B1 | B2 | B3 | B4 | B5 | FWER |
| NC1 | |||||||
| B, Hg, Hl, R | 4 | 0.7 (0.2) | 0.7–0.8 (0.5) | 1.2 (0.7) | 0.9 (0.4) | 0.8–0.9 (0.5) | 4.3–4.4 (2.3) |
| B–H, S | 4 | 0.7–1.2 (0.2–0.5) | 0.9–1.3 (0.5–0.7) | 1.3–1.8 (0.7–1) | 0.9–1.3 (0.4–0.5) | 0.9–1.6 (0.5–0.8) | 4.4–6.2 (2.3–3.2) |
| B, Hg, Hl, R | 8 | 0.5 (0.3) | 0.5 (0.3) | 0 (0) | 0.5 (0.3) | 0 (0) | 5 (2.5) |
| B–H, S | 8 | 0.5 (0.3) | 0.5 (0.3) | 0 (0) | 0.5 (0.3) | 0 (0) | 5 (2.5) |
| NC2 | |||||||
| B, Hg, Hl, R | 4 | 1.3 (0.6) | 1.2 (0.4) | 0.7 (0.4) | 1.1 (0.6) | 1.1–1.2 (0.7) | 5.3–5.4 (2.6–2.7) |
| B–H, S | 4 | 1.4–1.9 (0.6–0.9) | 1.2–1.7 (0.4–0.8) | 0.7–1.5 (0.4) | 1.3–2.3 (0.6–0.7) | 1.1–1.7 (0.7–0.8) | 5.4–7.3 (2.6–3.4) |
| B, Hg, Hl, R | 8 | 0.8 (0.5) | 0.3 (0.1) | 0 (0) | 0.3 (0.3) | 0.5 (0.5) | 4.5 (3) |
| B–H, S | 8 | 0.9 (0.5) | 0.3 (0.1) | 0–0.3 (0) | 0.3 (0.3) | 0.5 (0.5) | 4.5–5 (3) |
| NI | |||||||
| B, Hg, Hl, R | 4 | 1.1 (0.3) | 1.5 (1) | 0.8 (0.3) | 1.2 (0.7) | 0.7–0.9 (0.3) | 5.1–5.3 (2.5) |
| B–H, S | 4 | 1.1–1.9 (0.4) | 1.6–2.3 (1–1.1) | 0.9–1.6 (0.3–0.4) | 1.3–2.2 (0.7–0.8) | 0.7–1.6 (0.3–0.4) | 5.2–7.5 (2.5–2.8) |
| B, Hg, Hl, R | 8 | 1.5 (0.9) | 0 (0) | 0.5 (0.3) | 0.3 (0) | 1.5 (0) | 8 (3) |
| B–H, S | 8 | 1.9–2.0 (0.9) | 0 (0) | 0.5–0.8 (0.3) | 0.5 (0) | 1.5 (0) | 9–10 (3) |
NOTE.—s is the number of sequences in the tree, whereas branches B1–5 are labeled as in figure 1. The multiple test correction procedures are as follows: B, Bonferroni; Hg, Hochberg; Hl, Hommel; R, Rom; B–H, Benjamini and Hochberg; and S, Storey. Note that B, Hg, Hl, and R control the FWER, whereas B–H and S control the FDR.
Percentage (%) of Significant Replicates (Type-I Error Rate) at the 5% Level Based on the Null Mixture Distribution or the Distribution (in parentheses) when Data are Simulated without Positive Selection
| Correction Procedure | s | B1 | B2 | B3 | B4 | B5 | FWER |
| NC1 | |||||||
| B, Hg, Hl, R | 4 | 0.7 (0.2) | 0.7–0.8 (0.5) | 1.2 (0.7) | 0.9 (0.4) | 0.8–0.9 (0.5) | 4.3–4.4 (2.3) |
| B–H, S | 4 | 0.7–1.2 (0.2–0.5) | 0.9–1.3 (0.5–0.7) | 1.3–1.8 (0.7–1) | 0.9–1.3 (0.4–0.5) | 0.9–1.6 (0.5–0.8) | 4.4–6.2 (2.3–3.2) |
| B, Hg, Hl, R | 8 | 0.5 (0.3) | 0.5 (0.3) | 0 (0) | 0.5 (0.3) | 0 (0) | 5 (2.5) |
| B–H, S | 8 | 0.5 (0.3) | 0.5 (0.3) | 0 (0) | 0.5 (0.3) | 0 (0) | 5 (2.5) |
| NC2 | |||||||
| B, Hg, Hl, R | 4 | 1.3 (0.6) | 1.2 (0.4) | 0.7 (0.4) | 1.1 (0.6) | 1.1–1.2 (0.7) | 5.3–5.4 (2.6–2.7) |
| B–H, S | 4 | 1.4–1.9 (0.6–0.9) | 1.2–1.7 (0.4–0.8) | 0.7–1.5 (0.4) | 1.3–2.3 (0.6–0.7) | 1.1–1.7 (0.7–0.8) | 5.4–7.3 (2.6–3.4) |
| B, Hg, Hl, R | 8 | 0.8 (0.5) | 0.3 (0.1) | 0 (0) | 0.3 (0.3) | 0.5 (0.5) | 4.5 (3) |
| B–H, S | 8 | 0.9 (0.5) | 0.3 (0.1) | 0–0.3 (0) | 0.3 (0.3) | 0.5 (0.5) | 4.5–5 (3) |
| NI | |||||||
| B, Hg, Hl, R | 4 | 1.1 (0.3) | 1.5 (1) | 0.8 (0.3) | 1.2 (0.7) | 0.7–0.9 (0.3) | 5.1–5.3 (2.5) |
| B–H, S | 4 | 1.1–1.9 (0.4) | 1.6–2.3 (1–1.1) | 0.9–1.6 (0.3–0.4) | 1.3–2.2 (0.7–0.8) | 0.7–1.6 (0.3–0.4) | 5.2–7.5 (2.5–2.8) |
| B, Hg, Hl, R | 8 | 1.5 (0.9) | 0 (0) | 0.5 (0.3) | 0.3 (0) | 1.5 (0) | 8 (3) |
| B–H, S | 8 | 1.9–2.0 (0.9) | 0 (0) | 0.5–0.8 (0.3) | 0.5 (0) | 1.5 (0) | 9–10 (3) |
| Correction Procedure | s | B1 | B2 | B3 | B4 | B5 | FWER |
| NC1 | |||||||
| B, Hg, Hl, R | 4 | 0.7 (0.2) | 0.7–0.8 (0.5) | 1.2 (0.7) | 0.9 (0.4) | 0.8–0.9 (0.5) | 4.3–4.4 (2.3) |
| B–H, S | 4 | 0.7–1.2 (0.2–0.5) | 0.9–1.3 (0.5–0.7) | 1.3–1.8 (0.7–1) | 0.9–1.3 (0.4–0.5) | 0.9–1.6 (0.5–0.8) | 4.4–6.2 (2.3–3.2) |
| B, Hg, Hl, R | 8 | 0.5 (0.3) | 0.5 (0.3) | 0 (0) | 0.5 (0.3) | 0 (0) | 5 (2.5) |
| B–H, S | 8 | 0.5 (0.3) | 0.5 (0.3) | 0 (0) | 0.5 (0.3) | 0 (0) | 5 (2.5) |
| NC2 | |||||||
| B, Hg, Hl, R | 4 | 1.3 (0.6) | 1.2 (0.4) | 0.7 (0.4) | 1.1 (0.6) | 1.1–1.2 (0.7) | 5.3–5.4 (2.6–2.7) |
| B–H, S | 4 | 1.4–1.9 (0.6–0.9) | 1.2–1.7 (0.4–0.8) | 0.7–1.5 (0.4) | 1.3–2.3 (0.6–0.7) | 1.1–1.7 (0.7–0.8) | 5.4–7.3 (2.6–3.4) |
| B, Hg, Hl, R | 8 | 0.8 (0.5) | 0.3 (0.1) | 0 (0) | 0.3 (0.3) | 0.5 (0.5) | 4.5 (3) |
| B–H, S | 8 | 0.9 (0.5) | 0.3 (0.1) | 0–0.3 (0) | 0.3 (0.3) | 0.5 (0.5) | 4.5–5 (3) |
| NI | |||||||
| B, Hg, Hl, R | 4 | 1.1 (0.3) | 1.5 (1) | 0.8 (0.3) | 1.2 (0.7) | 0.7–0.9 (0.3) | 5.1–5.3 (2.5) |
| B–H, S | 4 | 1.1–1.9 (0.4) | 1.6–2.3 (1–1.1) | 0.9–1.6 (0.3–0.4) | 1.3–2.2 (0.7–0.8) | 0.7–1.6 (0.3–0.4) | 5.2–7.5 (2.5–2.8) |
| B, Hg, Hl, R | 8 | 1.5 (0.9) | 0 (0) | 0.5 (0.3) | 0.3 (0) | 1.5 (0) | 8 (3) |
| B–H, S | 8 | 1.9–2.0 (0.9) | 0 (0) | 0.5–0.8 (0.3) | 0.5 (0) | 1.5 (0) | 9–10 (3) |
NOTE.—s is the number of sequences in the tree, whereas branches B1–5 are labeled as in figure 1. The multiple test correction procedures are as follows: B, Bonferroni; Hg, Hochberg; Hl, Hommel; R, Rom; B–H, Benjamini and Hochberg; and S, Storey. Note that B, Hg, Hl, and R control the FWER, whereas B–H and S control the FDR.
Overall, very small differences were found under these simulation schemes among the 4 FWER-controlling procedures examined here: those of Bonferroni, Hochberg (1988), Hommel (1988), and Rom (1990). The 2 FDR-controlling methods (Benjamini and Hochberg 1995; Storey 2002) had slightly higher false-positive rates, but even they produced acceptable FWER.
We also calculated the FWER, that is, the rate of falsely detecting positive selection on at least one branch, when no correction for multiple testing is applied. If the p values for component hypotheses are calculated using the mixture distribution, the FWER is 20–23% among schemes NC1, NC2, and NI for data of 4 taxa and 42–54% for data of 8 taxa. If the distribution is used instead, the FWER is reduced to 11–12% for 4 taxa and 22–30% for 8 taxa. All these error rates are too high compared with the nominal 5%, indicating the importance of correction for multiple testing.
Accuracy and Power of the LRT with Positive Selection
Schemes SC, SI1, SI2, and SI3 involve positive selection on some lineages. The results for those schemes are summarized in table 4. Significant results for foreground branches not under positive selection are false positives, and the frequency of such cases is a measure of the accuracy of the test. Significant results for branches under positive selection are true positives, and the frequency of such cases measures the power of the test.
Percentage (%) of Significant Replicates at the 5% Level Based on the Null Mixture Distribution or the Distribution (in parentheses) when Data are Simulated with Positive Selection
| Correction Procedure | s | B1 | B2 | B3 | B4 | B5 | p1 | FWER | FDR |
| SC | |||||||||
| B, Hg, Hl, R | 4 | 0.5–0.6 (0.2) | 0.7 (0.2) | 1 (0.4) | 0.6 (0.3) | 8.3–8.4 (6–6.2) | 2.6–2.7 (1.1) | 0.7 (0.3) | |
| B–H, S | 4 | 0.6–1.5 (0.2–0.5) | 0.9–2.1 (0.5–0.7) | 1.1–2.2 (0.4–0.7) | 0.8–1.5 (0.3–0.6) | 8.7–11.2 (6–7) | 3.2–5 (1.2–2) | 0.9–1.8 (0.4–0.6) | |
| B, Hg, Hl, R | 8 | 0.3 (0) | 0.3 (0) | 0.5 (0.3) | 0.8 (0.5) | 43–44 (37–37.5) | 4.5 (1.5) | 0.4 (0.1) | |
| B–H, S | 8 | 0.3 (0.1–0.3) | 0.8 (0) | 0.5 (0.5) | 1.5 (0.5) | 43–44 (37.5–39) | 6 (2.5–3) | 0.7 (0.2–0.3) | |
| SI1 | |||||||||
| B, Hg, Hl, R | 4 | 0.6 (0.4) | 1.1–1.2 (0.5) | 0.6–0.7 (0.5) | 1.1 (0.8) | 8.2 (5.2) | 3.3–3.5 (2.1) | 0.9 (0.6) | |
| B–H, S | 4 | 0.6–0.9 (0.5–0.6) | 1.1–1.9 (0.5) | 0.6–1.9 (0.5–0.7) | 1.1–2.3 (0.8–1.1) | 8.2–10.1 (5.3–6.5) | 3.3–5.4 (2.1–2.2) | 0.9–1.8 (0.6–0.7) | |
| B, Hg, Hl, R | 8 | 0.9–1 (0) | 0.3–0.4 (0.3) | 0.5 (0.3) | 0.5 (0.3) | 49.5 (39) | 6.0–7.0 (2.0) | 0.5–0.6 (0.2) | |
| B–H, S | 8 | 1.6 (0.4–0.5) | 0.5–0.6 (0.3–0.4) | 0.8 (0.5) | 0.8–1 (0.3) | 51–52 (40.5–41) | 10–11 (3.5–4.5) | 1 (0.3–0.4) | |
| SI2 | |||||||||
| B, Hg, Hl, R | 4 | 11.2–11.5 (8.1–8.3) | 0.6–0.7 (0) | 1.2 (0.4) | 1.7 (0.8–1) | 5.5–5.7 (3.8–4) | 16.2–16.6 (11.8–12) | 3.3 (0.4–0.5) | 1.2 (1.1–1.2) |
| B–H, S | 4 | 12–15.9 (8.3–9.6) | 0.8–1.6 (0.3–0.5) | 1.4–2.7 (0.6–1.1) | 1.8–2.9 (1.1–1.6) | 6.3–8.9 (4–5.3) | 16.8–21.7 (11.8–13.6) | 3.6–6.1 (0.7–2.7) | 1.3–5.8 (1.2–3.2) |
| B, Hg, Hl, R | 8 | 10–10.6 (6.9–7.1) | 0.3 (0.1) | 0 (0) | 0.5 (0.3) | 23–23.5 (16) | 47.5–48.5 (36.0–36.5) | 2.0 (1.0) | 0.3 (0.1) |
| B–H, S | 8 | 13.6–16.4 (8.9–9.8) | 0.4 (0.3) | 0 (0) | 1.3–1.8 (0.5) | 26–29 (18.5–19) | 50–55.5 (37.5–38.5) | 3.5–4.5 (2.0) | 0.5–0.6 (0.3) |
| SI3 | |||||||||
| B, Hg, Hl, R | 4 | 4.9–5.5 (3.6) | 12–12.5 (8.5–8.6) | 9.3–9.9 (6.3–6.5) | 12.9–13.8 (8.7–8.8) | 1.7–1.8 (0.9) | 34.8–35.3 (24.5–24.6) | 1.7–1.8 (0.9) | 1.7–1.8 (0.9) |
| B–H, S | 4 | 6.8–10.8 (3.8–5.3) | 13.6–17.7 (9.5–11.2) | 12–17.1 (7.1–9.4) | 15.8–21.4 (9.4–11.7) | 2.3–3.9 (1.1–1.4) | 36.2–41.7 (25–28.6) | 2.3–3.9 (1.1–1.4) | 2.3–3.9 (1.1–1.4) |
| Correction Procedure | s | B1 | B2 | B3 | B4 | B5 | p1 | FWER | FDR |
| SC | |||||||||
| B, Hg, Hl, R | 4 | 0.5–0.6 (0.2) | 0.7 (0.2) | 1 (0.4) | 0.6 (0.3) | 8.3–8.4 (6–6.2) | 2.6–2.7 (1.1) | 0.7 (0.3) | |
| B–H, S | 4 | 0.6–1.5 (0.2–0.5) | 0.9–2.1 (0.5–0.7) | 1.1–2.2 (0.4–0.7) | 0.8–1.5 (0.3–0.6) | 8.7–11.2 (6–7) | 3.2–5 (1.2–2) | 0.9–1.8 (0.4–0.6) | |
| B, Hg, Hl, R | 8 | 0.3 (0) | 0.3 (0) | 0.5 (0.3) | 0.8 (0.5) | 43–44 (37–37.5) | 4.5 (1.5) | 0.4 (0.1) | |
| B–H, S | 8 | 0.3 (0.1–0.3) | 0.8 (0) | 0.5 (0.5) | 1.5 (0.5) | 43–44 (37.5–39) | 6 (2.5–3) | 0.7 (0.2–0.3) | |
| SI1 | |||||||||
| B, Hg, Hl, R | 4 | 0.6 (0.4) | 1.1–1.2 (0.5) | 0.6–0.7 (0.5) | 1.1 (0.8) | 8.2 (5.2) | 3.3–3.5 (2.1) | 0.9 (0.6) | |
| B–H, S | 4 | 0.6–0.9 (0.5–0.6) | 1.1–1.9 (0.5) | 0.6–1.9 (0.5–0.7) | 1.1–2.3 (0.8–1.1) | 8.2–10.1 (5.3–6.5) | 3.3–5.4 (2.1–2.2) | 0.9–1.8 (0.6–0.7) | |
| B, Hg, Hl, R | 8 | 0.9–1 (0) | 0.3–0.4 (0.3) | 0.5 (0.3) | 0.5 (0.3) | 49.5 (39) | 6.0–7.0 (2.0) | 0.5–0.6 (0.2) | |
| B–H, S | 8 | 1.6 (0.4–0.5) | 0.5–0.6 (0.3–0.4) | 0.8 (0.5) | 0.8–1 (0.3) | 51–52 (40.5–41) | 10–11 (3.5–4.5) | 1 (0.3–0.4) | |
| SI2 | |||||||||
| B, Hg, Hl, R | 4 | 11.2–11.5 (8.1–8.3) | 0.6–0.7 (0) | 1.2 (0.4) | 1.7 (0.8–1) | 5.5–5.7 (3.8–4) | 16.2–16.6 (11.8–12) | 3.3 (0.4–0.5) | 1.2 (1.1–1.2) |
| B–H, S | 4 | 12–15.9 (8.3–9.6) | 0.8–1.6 (0.3–0.5) | 1.4–2.7 (0.6–1.1) | 1.8–2.9 (1.1–1.6) | 6.3–8.9 (4–5.3) | 16.8–21.7 (11.8–13.6) | 3.6–6.1 (0.7–2.7) | 1.3–5.8 (1.2–3.2) |
| B, Hg, Hl, R | 8 | 10–10.6 (6.9–7.1) | 0.3 (0.1) | 0 (0) | 0.5 (0.3) | 23–23.5 (16) | 47.5–48.5 (36.0–36.5) | 2.0 (1.0) | 0.3 (0.1) |
| B–H, S | 8 | 13.6–16.4 (8.9–9.8) | 0.4 (0.3) | 0 (0) | 1.3–1.8 (0.5) | 26–29 (18.5–19) | 50–55.5 (37.5–38.5) | 3.5–4.5 (2.0) | 0.5–0.6 (0.3) |
| SI3 | |||||||||
| B, Hg, Hl, R | 4 | 4.9–5.5 (3.6) | 12–12.5 (8.5–8.6) | 9.3–9.9 (6.3–6.5) | 12.9–13.8 (8.7–8.8) | 1.7–1.8 (0.9) | 34.8–35.3 (24.5–24.6) | 1.7–1.8 (0.9) | 1.7–1.8 (0.9) |
| B–H, S | 4 | 6.8–10.8 (3.8–5.3) | 13.6–17.7 (9.5–11.2) | 12–17.1 (7.1–9.4) | 15.8–21.4 (9.4–11.7) | 2.3–3.9 (1.1–1.4) | 36.2–41.7 (25–28.6) | 2.3–3.9 (1.1–1.4) | 2.3–3.9 (1.1–1.4) |
NOTE.—p1, power to correctly detect at least one branch under positive selection. Values for branches under positive selection appear in bold. See legend to table 3.
Percentage (%) of Significant Replicates at the 5% Level Based on the Null Mixture Distribution or the Distribution (in parentheses) when Data are Simulated with Positive Selection
| Correction Procedure | s | B1 | B2 | B3 | B4 | B5 | p1 | FWER | FDR |
| SC | |||||||||
| B, Hg, Hl, R | 4 | 0.5–0.6 (0.2) | 0.7 (0.2) | 1 (0.4) | 0.6 (0.3) | 8.3–8.4 (6–6.2) | 2.6–2.7 (1.1) | 0.7 (0.3) | |
| B–H, S | 4 | 0.6–1.5 (0.2–0.5) | 0.9–2.1 (0.5–0.7) | 1.1–2.2 (0.4–0.7) | 0.8–1.5 (0.3–0.6) | 8.7–11.2 (6–7) | 3.2–5 (1.2–2) | 0.9–1.8 (0.4–0.6) | |
| B, Hg, Hl, R | 8 | 0.3 (0) | 0.3 (0) | 0.5 (0.3) | 0.8 (0.5) | 43–44 (37–37.5) | 4.5 (1.5) | 0.4 (0.1) | |
| B–H, S | 8 | 0.3 (0.1–0.3) | 0.8 (0) | 0.5 (0.5) | 1.5 (0.5) | 43–44 (37.5–39) | 6 (2.5–3) | 0.7 (0.2–0.3) | |
| SI1 | |||||||||
| B, Hg, Hl, R | 4 | 0.6 (0.4) | 1.1–1.2 (0.5) | 0.6–0.7 (0.5) | 1.1 (0.8) | 8.2 (5.2) | 3.3–3.5 (2.1) | 0.9 (0.6) | |
| B–H, S | 4 | 0.6–0.9 (0.5–0.6) | 1.1–1.9 (0.5) | 0.6–1.9 (0.5–0.7) | 1.1–2.3 (0.8–1.1) | 8.2–10.1 (5.3–6.5) | 3.3–5.4 (2.1–2.2) | 0.9–1.8 (0.6–0.7) | |
| B, Hg, Hl, R | 8 | 0.9–1 (0) | 0.3–0.4 (0.3) | 0.5 (0.3) | 0.5 (0.3) | 49.5 (39) | 6.0–7.0 (2.0) | 0.5–0.6 (0.2) | |
| B–H, S | 8 | 1.6 (0.4–0.5) | 0.5–0.6 (0.3–0.4) | 0.8 (0.5) | 0.8–1 (0.3) | 51–52 (40.5–41) | 10–11 (3.5–4.5) | 1 (0.3–0.4) | |
| SI2 | |||||||||
| B, Hg, Hl, R | 4 | 11.2–11.5 (8.1–8.3) | 0.6–0.7 (0) | 1.2 (0.4) | 1.7 (0.8–1) | 5.5–5.7 (3.8–4) | 16.2–16.6 (11.8–12) | 3.3 (0.4–0.5) | 1.2 (1.1–1.2) |
| B–H, S | 4 | 12–15.9 (8.3–9.6) | 0.8–1.6 (0.3–0.5) | 1.4–2.7 (0.6–1.1) | 1.8–2.9 (1.1–1.6) | 6.3–8.9 (4–5.3) | 16.8–21.7 (11.8–13.6) | 3.6–6.1 (0.7–2.7) | 1.3–5.8 (1.2–3.2) |
| B, Hg, Hl, R | 8 | 10–10.6 (6.9–7.1) | 0.3 (0.1) | 0 (0) | 0.5 (0.3) | 23–23.5 (16) | 47.5–48.5 (36.0–36.5) | 2.0 (1.0) | 0.3 (0.1) |
| B–H, S | 8 | 13.6–16.4 (8.9–9.8) | 0.4 (0.3) | 0 (0) | 1.3–1.8 (0.5) | 26–29 (18.5–19) | 50–55.5 (37.5–38.5) | 3.5–4.5 (2.0) | 0.5–0.6 (0.3) |
| SI3 | |||||||||
| B, Hg, Hl, R | 4 | 4.9–5.5 (3.6) | 12–12.5 (8.5–8.6) | 9.3–9.9 (6.3–6.5) | 12.9–13.8 (8.7–8.8) | 1.7–1.8 (0.9) | 34.8–35.3 (24.5–24.6) | 1.7–1.8 (0.9) | 1.7–1.8 (0.9) |
| B–H, S | 4 | 6.8–10.8 (3.8–5.3) | 13.6–17.7 (9.5–11.2) | 12–17.1 (7.1–9.4) | 15.8–21.4 (9.4–11.7) | 2.3–3.9 (1.1–1.4) | 36.2–41.7 (25–28.6) | 2.3–3.9 (1.1–1.4) | 2.3–3.9 (1.1–1.4) |
| Correction Procedure | s | B1 | B2 | B3 | B4 | B5 | p1 | FWER | FDR |
| SC | |||||||||
| B, Hg, Hl, R | 4 | 0.5–0.6 (0.2) | 0.7 (0.2) | 1 (0.4) | 0.6 (0.3) | 8.3–8.4 (6–6.2) | 2.6–2.7 (1.1) | 0.7 (0.3) | |
| B–H, S | 4 | 0.6–1.5 (0.2–0.5) | 0.9–2.1 (0.5–0.7) | 1.1–2.2 (0.4–0.7) | 0.8–1.5 (0.3–0.6) | 8.7–11.2 (6–7) | 3.2–5 (1.2–2) | 0.9–1.8 (0.4–0.6) | |
| B, Hg, Hl, R | 8 | 0.3 (0) | 0.3 (0) | 0.5 (0.3) | 0.8 (0.5) | 43–44 (37–37.5) | 4.5 (1.5) | 0.4 (0.1) | |
| B–H, S | 8 | 0.3 (0.1–0.3) | 0.8 (0) | 0.5 (0.5) | 1.5 (0.5) | 43–44 (37.5–39) | 6 (2.5–3) | 0.7 (0.2–0.3) | |
| SI1 | |||||||||
| B, Hg, Hl, R | 4 | 0.6 (0.4) | 1.1–1.2 (0.5) | 0.6–0.7 (0.5) | 1.1 (0.8) | 8.2 (5.2) | 3.3–3.5 (2.1) | 0.9 (0.6) | |
| B–H, S | 4 | 0.6–0.9 (0.5–0.6) | 1.1–1.9 (0.5) | 0.6–1.9 (0.5–0.7) | 1.1–2.3 (0.8–1.1) | 8.2–10.1 (5.3–6.5) | 3.3–5.4 (2.1–2.2) | 0.9–1.8 (0.6–0.7) | |
| B, Hg, Hl, R | 8 | 0.9–1 (0) | 0.3–0.4 (0.3) | 0.5 (0.3) | 0.5 (0.3) | 49.5 (39) | 6.0–7.0 (2.0) | 0.5–0.6 (0.2) | |
| B–H, S | 8 | 1.6 (0.4–0.5) | 0.5–0.6 (0.3–0.4) | 0.8 (0.5) | 0.8–1 (0.3) | 51–52 (40.5–41) | 10–11 (3.5–4.5) | 1 (0.3–0.4) | |
| SI2 | |||||||||
| B, Hg, Hl, R | 4 | 11.2–11.5 (8.1–8.3) | 0.6–0.7 (0) | 1.2 (0.4) | 1.7 (0.8–1) | 5.5–5.7 (3.8–4) | 16.2–16.6 (11.8–12) | 3.3 (0.4–0.5) | 1.2 (1.1–1.2) |
| B–H, S | 4 | 12–15.9 (8.3–9.6) | 0.8–1.6 (0.3–0.5) | 1.4–2.7 (0.6–1.1) | 1.8–2.9 (1.1–1.6) | 6.3–8.9 (4–5.3) | 16.8–21.7 (11.8–13.6) | 3.6–6.1 (0.7–2.7) | 1.3–5.8 (1.2–3.2) |
| B, Hg, Hl, R | 8 | 10–10.6 (6.9–7.1) | 0.3 (0.1) | 0 (0) | 0.5 (0.3) | 23–23.5 (16) | 47.5–48.5 (36.0–36.5) | 2.0 (1.0) | 0.3 (0.1) |
| B–H, S | 8 | 13.6–16.4 (8.9–9.8) | 0.4 (0.3) | 0 (0) | 1.3–1.8 (0.5) | 26–29 (18.5–19) | 50–55.5 (37.5–38.5) | 3.5–4.5 (2.0) | 0.5–0.6 (0.3) |
| SI3 | |||||||||
| B, Hg, Hl, R | 4 | 4.9–5.5 (3.6) | 12–12.5 (8.5–8.6) | 9.3–9.9 (6.3–6.5) | 12.9–13.8 (8.7–8.8) | 1.7–1.8 (0.9) | 34.8–35.3 (24.5–24.6) | 1.7–1.8 (0.9) | 1.7–1.8 (0.9) |
| B–H, S | 4 | 6.8–10.8 (3.8–5.3) | 13.6–17.7 (9.5–11.2) | 12–17.1 (7.1–9.4) | 15.8–21.4 (9.4–11.7) | 2.3–3.9 (1.1–1.4) | 36.2–41.7 (25–28.6) | 2.3–3.9 (1.1–1.4) | 2.3–3.9 (1.1–1.4) |
NOTE.—p1, power to correctly detect at least one branch under positive selection. Values for branches under positive selection appear in bold. See legend to table 3.
In scheme SC, only branches labeled B5 (fig. 1) have sites under positive selection. The FWER is then the proportion of replicates in which at least one of the branches labeled B1, B2, B3, and B4 is claimed to be under positive selection. When the mixture distribution was used, the FWER was about 3–5% for 4 taxa and 4.5–6% for 8 taxa, all close to the nominal 5%. When the distribution was used, the FWER was even lower (1–3%). The different correction procedures showed very similar performance. The power or proportion of replicates in which positive selection was detected on B5 was 8–11% for 4 taxa based on the mixture distribution and slightly lower (6–7%) based on the distribution. The power was much higher for the 8-taxa data, at 43–44% for the mixture distribution or 37–39% for the distribution. We suspect that the main reason for this large difference in power is that branch B5 in the 8-taxa tree is much longer than B5 in the 4-taxa tree, with 0.6 instead of 0.1 nucleotide substitutions per codon, and can harbor more substitutions, so that the 8-taxa data may be more informative. Furthermore, the 8-taxa tree has more background branches, which may provide more information about the selection pressures on the background branches.
Scheme SI1 is similar to SC, with only branch B5 under positive selection. In this scheme, branch–site model A is slightly violated. For 4 taxa, both the FWER and the power under this scheme were similar to the corresponding results under scheme SC. For 8-taxa data, the power under scheme SI1 was slightly higher than under SC (∼50% compared with ∼43% for the mixture distribution). The FWERs for the 4 FWER-controlling procedures were 6–7% based on the mixture distribution, slightly higher than but close to the nominal 5%. The FWERs for the 2 FDR-controlling procedures were 10–11% based on the mixture distribution, higher than 5%, whereas their FDR was 1%, far below 5%. Use of the distribution brought the FWER for all correction procedures down to below 5%.
In scheme SI2, 10% of sites were under positive selection along branches labeled B5 and another 10% of sites were under positive selection on branches labeled B1 (fig. 1 and table 2). Although the model used in data analysis was incorrect, the FWER based on the mixture distribution was close to or below the nominal 5% for all 6 multiple test correction procedures and for both the 4- and 8-taxa trees. Based on the mixture distribution, the power to detect positive selection on branch B5 was about 6–9% for the 4-taxa data and 23–29% for the 8-taxa data. The power to detect positive selection on B5 under this scheme was lower than under scheme SI1. This difference in power appears to be due to the fact that only 10% of sites evolved under positive selection on B5 under scheme SI2 compared with 20% under scheme SI1 (table 2). Based on the mixture distribution, the power to detect positive selection on branch B1 was about 11–12% for 4-taxa data and about 10–16% for the 8-taxa data. Positive selection was correctly detected on at least one of the branches in 16–22% and 48–56% of replicates for the 4- and 8-taxa trees, respectively. As under other schemes, use of the distribution made all tests more conservative, with reduced false-positive rates but also reduced power to detect positive selection.
Scheme SI3, suggested by a referee, may be considered a case of serious violation of the assumptions of the branch–site model. The same set of sites are under positive selection along branches B1, B2, B3, and B4 of the 4-taxa tree, whereas these sites are evolving nearly neutrally along branch B5. The FWER, which is also the type-I error rate of falsely detecting positive selection along the single branch B5, was very low, at 2–4% for the mixture distribution. The power to detect positive selection along at least one of the branches B1–B4 was reasonably high, at 35–42%. Use of the distribution reduced both the FWER and the power for all correction procedures.
The Effect of Sequence Divergence
To study the effect of sequence divergence, we simulated data sets using branch lengths that are ¼, ½, 2, and 5 times those in the 8-taxa tree of figure 1. The tree lengths, that is, the total number of nucleotide substitutions per codon along all branches on the tree, are 1.05, 2.1, 4.2, 8.4, 21 for the ¼×, ½×, 1×, 2×, and 5× data sets, respectively. Sequences in the 5× data sets are very divergent, and real sequences at such divergence levels are expected to be difficult to align reliably. We used simulation schemes NC1, NI, SC, and SI2. The results for the mixture distribution and the Benjamini and Hochberg correction are summarized in table 5. The results for the distribution and for other correction procedures are not shown.
Percentage of Significant Replicates of Branch–Site Test at the 5% Level at Different Sequence Divergences
| Simulation Scheme | Divergence | B1 | B2 | B3 | B4 | B5 | p1 | FWER | FDR |
| NC1 | ¼× | 0.4 | 0.1 | 0.5 | 0.3 | 0.5 | 3.0 | ||
| ½× | 0.5 | 0.1 | 0.0 | 0.5 | 1.0 | 4.5 | |||
| 1× | 0.5 | 0.5 | 0.0 | 0.5 | 0.0 | 5.0 | |||
| 2× | 0.3 | 0.3 | 0.5 | 0.0 | 1.5 | 4.5 | |||
| 5× | 0.1 | 0.1 | 0.5 | 0.5 | 0.5 | 3.5 | |||
| NI | ¼× | 0.8 | 0.4 | 0.3 | 0.0 | 1.5 | 6.0 | ||
| ½× | 0.5 | 0.3 | 0.3 | 0.0 | 0.5 | 3.5 | |||
| 1× | 1.9 | 0.0 | 0.5 | 0.5 | 1.5 | 9.0 | |||
| 2× | 1.1 | 2.3 | 0.3 | 0.5 | 0.8 | 11.5 | |||
| 5× | 3.9 | 4.5 | 6.0 | 1.5 | 11.5 | 25.0 | |||
| SC | ¼× | 0.5 | 0.4 | 0.3 | 0.3 | 6.5 | 4.0 | 0.4 | |
| ½× | 0.6 | 0.1 | 0.0 | 0.3 | 27.0 | 3.5 | 0.3 | ||
| 1× | 0.25 | 0.75 | 0.5 | 1.5 | 43.0 | 6.0 | 0.7 | ||
| 2× | 0.13 | 0.13 | 0.0 | 0.0 | 34.5 | 1.0 | 0.1 | ||
| 5× | 0.13 | 0.0 | 0.5 | 0.25 | 4.5 | 2.0 | 0.2 | ||
| SI2 | ¼× | 6.4 | 0.5 | 0.0 | 0.8 | 4.0 | 24.5 | 3.5 | 0.4 |
| ½× | 10.8 | 0.3 | 0.0 | 0.0 | 19.0 | 41.0 | 1.0 | 0.1 | |
| 1× | 13.6 | 0.4 | 0.0 | 1.3 | 26.0 | 50.0 | 3.5 | 0.5 | |
| 2× | 7.9 | 0.8 | 0.0 | 0.5 | 10.0 | 31.0 | 3.5 | 0.5 | |
| 5× | 2.8 | 1.4 | 0.5 | 0.0 | 0.0 | 9.0 | 6.5 | 0.8 |
| Simulation Scheme | Divergence | B1 | B2 | B3 | B4 | B5 | p1 | FWER | FDR |
| NC1 | ¼× | 0.4 | 0.1 | 0.5 | 0.3 | 0.5 | 3.0 | ||
| ½× | 0.5 | 0.1 | 0.0 | 0.5 | 1.0 | 4.5 | |||
| 1× | 0.5 | 0.5 | 0.0 | 0.5 | 0.0 | 5.0 | |||
| 2× | 0.3 | 0.3 | 0.5 | 0.0 | 1.5 | 4.5 | |||
| 5× | 0.1 | 0.1 | 0.5 | 0.5 | 0.5 | 3.5 | |||
| NI | ¼× | 0.8 | 0.4 | 0.3 | 0.0 | 1.5 | 6.0 | ||
| ½× | 0.5 | 0.3 | 0.3 | 0.0 | 0.5 | 3.5 | |||
| 1× | 1.9 | 0.0 | 0.5 | 0.5 | 1.5 | 9.0 | |||
| 2× | 1.1 | 2.3 | 0.3 | 0.5 | 0.8 | 11.5 | |||
| 5× | 3.9 | 4.5 | 6.0 | 1.5 | 11.5 | 25.0 | |||
| SC | ¼× | 0.5 | 0.4 | 0.3 | 0.3 | 6.5 | 4.0 | 0.4 | |
| ½× | 0.6 | 0.1 | 0.0 | 0.3 | 27.0 | 3.5 | 0.3 | ||
| 1× | 0.25 | 0.75 | 0.5 | 1.5 | 43.0 | 6.0 | 0.7 | ||
| 2× | 0.13 | 0.13 | 0.0 | 0.0 | 34.5 | 1.0 | 0.1 | ||
| 5× | 0.13 | 0.0 | 0.5 | 0.25 | 4.5 | 2.0 | 0.2 | ||
| SI2 | ¼× | 6.4 | 0.5 | 0.0 | 0.8 | 4.0 | 24.5 | 3.5 | 0.4 |
| ½× | 10.8 | 0.3 | 0.0 | 0.0 | 19.0 | 41.0 | 1.0 | 0.1 | |
| 1× | 13.6 | 0.4 | 0.0 | 1.3 | 26.0 | 50.0 | 3.5 | 0.5 | |
| 2× | 7.9 | 0.8 | 0.0 | 0.5 | 10.0 | 31.0 | 3.5 | 0.5 | |
| 5× | 2.8 | 1.4 | 0.5 | 0.0 | 0.0 | 9.0 | 6.5 | 0.8 |
NOTE.—Data were simulated on the 8-taxa tree, with branch lengths multiplied by ¼, ½, 1, 2, or 5. p values are calculated using the mixture distribution, with the Benjamini and Hochberg correction for multiple testing. Values for branches under positive selection are in bold. p1 is the proportion of replicates in which at least one of the truly selected branches is detected by the test; note that under scheme SI2, one branch labeled B5 and 4 branches labeled B1 (fig. 1b) are under positive selection.
Percentage of Significant Replicates of Branch–Site Test at the 5% Level at Different Sequence Divergences
| Simulation Scheme | Divergence | B1 | B2 | B3 | B4 | B5 | p1 | FWER | FDR |
| NC1 | ¼× | 0.4 | 0.1 | 0.5 | 0.3 | 0.5 | 3.0 | ||
| ½× | 0.5 | 0.1 | 0.0 | 0.5 | 1.0 | 4.5 | |||
| 1× | 0.5 | 0.5 | 0.0 | 0.5 | 0.0 | 5.0 | |||
| 2× | 0.3 | 0.3 | 0.5 | 0.0 | 1.5 | 4.5 | |||
| 5× | 0.1 | 0.1 | 0.5 | 0.5 | 0.5 | 3.5 | |||
| NI | ¼× | 0.8 | 0.4 | 0.3 | 0.0 | 1.5 | 6.0 | ||
| ½× | 0.5 | 0.3 | 0.3 | 0.0 | 0.5 | 3.5 | |||
| 1× | 1.9 | 0.0 | 0.5 | 0.5 | 1.5 | 9.0 | |||
| 2× | 1.1 | 2.3 | 0.3 | 0.5 | 0.8 | 11.5 | |||
| 5× | 3.9 | 4.5 | 6.0 | 1.5 | 11.5 | 25.0 | |||
| SC | ¼× | 0.5 | 0.4 | 0.3 | 0.3 | 6.5 | 4.0 | 0.4 | |
| ½× | 0.6 | 0.1 | 0.0 | 0.3 | 27.0 | 3.5 | 0.3 | ||
| 1× | 0.25 | 0.75 | 0.5 | 1.5 | 43.0 | 6.0 | 0.7 | ||
| 2× | 0.13 | 0.13 | 0.0 | 0.0 | 34.5 | 1.0 | 0.1 | ||
| 5× | 0.13 | 0.0 | 0.5 | 0.25 | 4.5 | 2.0 | 0.2 | ||
| SI2 | ¼× | 6.4 | 0.5 | 0.0 | 0.8 | 4.0 | 24.5 | 3.5 | 0.4 |
| ½× | 10.8 | 0.3 | 0.0 | 0.0 | 19.0 | 41.0 | 1.0 | 0.1 | |
| 1× | 13.6 | 0.4 | 0.0 | 1.3 | 26.0 | 50.0 | 3.5 | 0.5 | |
| 2× | 7.9 | 0.8 | 0.0 | 0.5 | 10.0 | 31.0 | 3.5 | 0.5 | |
| 5× | 2.8 | 1.4 | 0.5 | 0.0 | 0.0 | 9.0 | 6.5 | 0.8 |
| Simulation Scheme | Divergence | B1 | B2 | B3 | B4 | B5 | p1 | FWER | FDR |
| NC1 | ¼× | 0.4 | 0.1 | 0.5 | 0.3 | 0.5 | 3.0 | ||
| ½× | 0.5 | 0.1 | 0.0 | 0.5 | 1.0 | 4.5 | |||
| 1× | 0.5 | 0.5 | 0.0 | 0.5 | 0.0 | 5.0 | |||
| 2× | 0.3 | 0.3 | 0.5 | 0.0 | 1.5 | 4.5 | |||
| 5× | 0.1 | 0.1 | 0.5 | 0.5 | 0.5 | 3.5 | |||
| NI | ¼× | 0.8 | 0.4 | 0.3 | 0.0 | 1.5 | 6.0 | ||
| ½× | 0.5 | 0.3 | 0.3 | 0.0 | 0.5 | 3.5 | |||
| 1× | 1.9 | 0.0 | 0.5 | 0.5 | 1.5 | 9.0 | |||
| 2× | 1.1 | 2.3 | 0.3 | 0.5 | 0.8 | 11.5 | |||
| 5× | 3.9 | 4.5 | 6.0 | 1.5 | 11.5 | 25.0 | |||
| SC | ¼× | 0.5 | 0.4 | 0.3 | 0.3 | 6.5 | 4.0 | 0.4 | |
| ½× | 0.6 | 0.1 | 0.0 | 0.3 | 27.0 | 3.5 | 0.3 | ||
| 1× | 0.25 | 0.75 | 0.5 | 1.5 | 43.0 | 6.0 | 0.7 | ||
| 2× | 0.13 | 0.13 | 0.0 | 0.0 | 34.5 | 1.0 | 0.1 | ||
| 5× | 0.13 | 0.0 | 0.5 | 0.25 | 4.5 | 2.0 | 0.2 | ||
| SI2 | ¼× | 6.4 | 0.5 | 0.0 | 0.8 | 4.0 | 24.5 | 3.5 | 0.4 |
| ½× | 10.8 | 0.3 | 0.0 | 0.0 | 19.0 | 41.0 | 1.0 | 0.1 | |
| 1× | 13.6 | 0.4 | 0.0 | 1.3 | 26.0 | 50.0 | 3.5 | 0.5 | |
| 2× | 7.9 | 0.8 | 0.0 | 0.5 | 10.0 | 31.0 | 3.5 | 0.5 | |
| 5× | 2.8 | 1.4 | 0.5 | 0.0 | 0.0 | 9.0 | 6.5 | 0.8 |
NOTE.—Data were simulated on the 8-taxa tree, with branch lengths multiplied by ¼, ½, 1, 2, or 5. p values are calculated using the mixture distribution, with the Benjamini and Hochberg correction for multiple testing. Values for branches under positive selection are in bold. p1 is the proportion of replicates in which at least one of the truly selected branches is detected by the test; note that under scheme SI2, one branch labeled B5 and 4 branches labeled B1 (fig. 1b) are under positive selection.
Under scheme NC1, the FWER was 3–5% for the mixture distribution, at or below the nominal 5%. Under scheme NI, the FWER for the mixture distribution was close to 5% in the ¼× and ½× data sets but were too high in the 2× and 5× data sets, at 11.5% and 25%, respectively. Use of the distribution reduced the FWER to 5% for the 2× data sets but it remained too high at 23% for the 5× data sets. The Bonferroni correction using the mixture distribution had the FWER 3%, 3.5%, 8%, 9%, and 25% for the ¼×, ½×, 1×, 2×, and 5× data sets, respectively. Thus, extremely high sequence divergences combined with serious violation of model assumptions can lead to unacceptably high FWER.
Under scheme SC, the branch–site model was correct. The FWER was lower than or very close to 5% for all divergence levels. The power to detect positive selection on B5 was 6.5%, 27%, 43%, 34.5%, and 4.5% for the ¼×, ½×, 1×, 2×, and 5× data, respectively. As expected, the optimal power was achieved at intermediate divergence levels. A similar pattern concerning power was apparent under scheme SI2, when the branch–site model was violated. The FWER based on the mixture distribution under SI2 was either lower than or close to 5%.
Empirical Example
We analyzed gene sequences for the extracellular domain of the CD2 from 10 mammalian species. The data were previously analyzed by Lynn et al. (2005). Those authors used site models (Nielsen and Yang 1998; Yang et al. 2000) to detect amino acid residues under positive selection and found that positive selection affected sites mainly within the extracellular domain of CD2. Indeed, the CD2 enhances T-cell antigen recognition and lowers the T-cell activation threshold through interaction with its counterreceptor in antigen-presenting cells. The extracellular domain of CD2 is thus more likely to be under positive selection than the rest of the protein. To detect lineages affected by positive selection, Lynn et al. (2005) used the branch models (Yang 1998). These average the selective pressure across sites in the whole gene and often have less power than the branch–site test (Zhang et al. 2005). Here we apply the LRT based on the branch–site model to test every branch of the tree for evidence of positive selection.
The maximum likelihood tree was reconstructed using PHYML (Guindon and Gascuel 2003), and one poorly supported branch was collapsed, resulting in the topology of figure 2, which is also the tree used by Lynn et al. (2005). Table 6 summarizes maximum likelihood estimates and test statistics for 16 LRTs corresponding to the 16 branches of the tree. Three branches in the tree, that is, branches 2 (cow), 5 (cat), and 6 (ancestral to the clade including pig, cow, horse, and cat), were detected to be under positive selection at the 5% significance level based on the mixture distribution by all 6 multiple test correction procedures. By Storey's (2002) method, branch 3 (ancestral to pig and cow) was significant at the 5% level as well. When the more conservative distribution was used, branches 2 (cow) and 5 (cat) were significant at the 5% level by all correction procedures, but the procedure of Benjamini and Hochberg also detected branch 6, and Storey's method detected branches 6 and 3 (ancestral to pig and cow) as well. As many as 11 branches had estimates but for the majority of them the LRT was not significant (table 6). Note that branches showing the strongest evidence of positive selections (as indicated by the LRT statistic) may not have the largest estimate as the evidence is influenced not only by the ω ratio but also by the absolute numbers of synonymous and nonsynonymous substitutions.
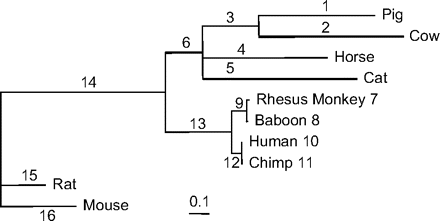
The maximum likelihood tree for mammalian CD2, with branches labeled. The branch lengths, measured as the expected number of nucleotide substitutions per codon, are estimated under the 1-ratio (M0) model.
Maximum Likelihood Estimates and LRT Statistics for the Extracellular Domain of CD2 Gene
| Foreground Branch | 2Δℓ | ||||||
| 1 | 1.75 | 0.093 | 0.186 | 0.24 | 0.459 | 0.15 | 2.79 |
| 2 | 15.45 | 0.000 | 0.000 | 0.22 | 0.41 | 0.15 | 11.12 |
| 3 | 4.41 | 0.018 | 0.036 | 0.28 | 0.52 | 0.16 | 24.14 |
| 4 | 0.87 | 0.176 | 0.352 | 0.31 | 0.61 | 0.17 | 5.69 |
| 5 | 8.88 | 0.001 | 0.003 | 0.29 | 0.51 | 0.18 | 6.64 |
| 6 | 7.69 | 0.003 | 0.006 | 0.30 | 0.61 | 0.17 | ∞ |
| 7 | 0.00 | 0.475 | 0.950 | 0.34 | 0.66 | 0.17 | 12.32 |
| 8 | 0.00 | 0.475 | 0.950 | 0.34 | 0.66 | 0.17 | 1.00 |
| 9 | 0.00 | 0.475 | 0.950 | 0.34 | 0.66 | 0.17 | 1.00 |
| 10 | 0.00 | 0.475 | 0.950 | 0.30 | 0.58 | 0.17 | 2.69 |
| 11 | 0.00 | 0.475 | 0.950 | 0.31 | 0.60 | 0.17 | 2.69 |
| 12 | 0.00 | 0.475 | 0.950 | 0.34 | 0.66 | 0.17 | 1.00 |
| 13 | 2.66 | 0.051 | 0.103 | 0.32 | 0.64 | 0.17 | 38.57 |
| 14 | 1.06 | 0.152 | 0.304 | 0.33 | 0.63 | 0.16 | 7.50 |
| 15 | 0.00 | 0.475 | 0.950 | 0.34 | 0.66 | 0.17 | 1.00 |
| 16 | 0.00 | 0.475 | 0.950 | 0.34 | 0.66 | 0.17 | 1.00 |
| Foreground Branch | 2Δℓ | ||||||
| 1 | 1.75 | 0.093 | 0.186 | 0.24 | 0.459 | 0.15 | 2.79 |
| 2 | 15.45 | 0.000 | 0.000 | 0.22 | 0.41 | 0.15 | 11.12 |
| 3 | 4.41 | 0.018 | 0.036 | 0.28 | 0.52 | 0.16 | 24.14 |
| 4 | 0.87 | 0.176 | 0.352 | 0.31 | 0.61 | 0.17 | 5.69 |
| 5 | 8.88 | 0.001 | 0.003 | 0.29 | 0.51 | 0.18 | 6.64 |
| 6 | 7.69 | 0.003 | 0.006 | 0.30 | 0.61 | 0.17 | ∞ |
| 7 | 0.00 | 0.475 | 0.950 | 0.34 | 0.66 | 0.17 | 12.32 |
| 8 | 0.00 | 0.475 | 0.950 | 0.34 | 0.66 | 0.17 | 1.00 |
| 9 | 0.00 | 0.475 | 0.950 | 0.34 | 0.66 | 0.17 | 1.00 |
| 10 | 0.00 | 0.475 | 0.950 | 0.30 | 0.58 | 0.17 | 2.69 |
| 11 | 0.00 | 0.475 | 0.950 | 0.31 | 0.60 | 0.17 | 2.69 |
| 12 | 0.00 | 0.475 | 0.950 | 0.34 | 0.66 | 0.17 | 1.00 |
| 13 | 2.66 | 0.051 | 0.103 | 0.32 | 0.64 | 0.17 | 38.57 |
| 14 | 1.06 | 0.152 | 0.304 | 0.33 | 0.63 | 0.16 | 7.50 |
| 15 | 0.00 | 0.475 | 0.950 | 0.34 | 0.66 | 0.17 | 1.00 |
| 16 | 0.00 | 0.475 | 0.950 | 0.34 | 0.66 | 0.17 | 1.00 |
NOTE.—See figure 2 for designation of foreground branches. Branches 2, 5, and 6 are detected to be under positive selection by all test procedures.
Maximum Likelihood Estimates and LRT Statistics for the Extracellular Domain of CD2 Gene
| Foreground Branch | 2Δℓ | ||||||
| 1 | 1.75 | 0.093 | 0.186 | 0.24 | 0.459 | 0.15 | 2.79 |
| 2 | 15.45 | 0.000 | 0.000 | 0.22 | 0.41 | 0.15 | 11.12 |
| 3 | 4.41 | 0.018 | 0.036 | 0.28 | 0.52 | 0.16 | 24.14 |
| 4 | 0.87 | 0.176 | 0.352 | 0.31 | 0.61 | 0.17 | 5.69 |
| 5 | 8.88 | 0.001 | 0.003 | 0.29 | 0.51 | 0.18 | 6.64 |
| 6 | 7.69 | 0.003 | 0.006 | 0.30 | 0.61 | 0.17 | ∞ |
| 7 | 0.00 | 0.475 | 0.950 | 0.34 | 0.66 | 0.17 | 12.32 |
| 8 | 0.00 | 0.475 | 0.950 | 0.34 | 0.66 | 0.17 | 1.00 |
| 9 | 0.00 | 0.475 | 0.950 | 0.34 | 0.66 | 0.17 | 1.00 |
| 10 | 0.00 | 0.475 | 0.950 | 0.30 | 0.58 | 0.17 | 2.69 |
| 11 | 0.00 | 0.475 | 0.950 | 0.31 | 0.60 | 0.17 | 2.69 |
| 12 | 0.00 | 0.475 | 0.950 | 0.34 | 0.66 | 0.17 | 1.00 |
| 13 | 2.66 | 0.051 | 0.103 | 0.32 | 0.64 | 0.17 | 38.57 |
| 14 | 1.06 | 0.152 | 0.304 | 0.33 | 0.63 | 0.16 | 7.50 |
| 15 | 0.00 | 0.475 | 0.950 | 0.34 | 0.66 | 0.17 | 1.00 |
| 16 | 0.00 | 0.475 | 0.950 | 0.34 | 0.66 | 0.17 | 1.00 |
| Foreground Branch | 2Δℓ | ||||||
| 1 | 1.75 | 0.093 | 0.186 | 0.24 | 0.459 | 0.15 | 2.79 |
| 2 | 15.45 | 0.000 | 0.000 | 0.22 | 0.41 | 0.15 | 11.12 |
| 3 | 4.41 | 0.018 | 0.036 | 0.28 | 0.52 | 0.16 | 24.14 |
| 4 | 0.87 | 0.176 | 0.352 | 0.31 | 0.61 | 0.17 | 5.69 |
| 5 | 8.88 | 0.001 | 0.003 | 0.29 | 0.51 | 0.18 | 6.64 |
| 6 | 7.69 | 0.003 | 0.006 | 0.30 | 0.61 | 0.17 | ∞ |
| 7 | 0.00 | 0.475 | 0.950 | 0.34 | 0.66 | 0.17 | 12.32 |
| 8 | 0.00 | 0.475 | 0.950 | 0.34 | 0.66 | 0.17 | 1.00 |
| 9 | 0.00 | 0.475 | 0.950 | 0.34 | 0.66 | 0.17 | 1.00 |
| 10 | 0.00 | 0.475 | 0.950 | 0.30 | 0.58 | 0.17 | 2.69 |
| 11 | 0.00 | 0.475 | 0.950 | 0.31 | 0.60 | 0.17 | 2.69 |
| 12 | 0.00 | 0.475 | 0.950 | 0.34 | 0.66 | 0.17 | 1.00 |
| 13 | 2.66 | 0.051 | 0.103 | 0.32 | 0.64 | 0.17 | 38.57 |
| 14 | 1.06 | 0.152 | 0.304 | 0.33 | 0.63 | 0.16 | 7.50 |
| 15 | 0.00 | 0.475 | 0.950 | 0.34 | 0.66 | 0.17 | 1.00 |
| 16 | 0.00 | 0.475 | 0.950 | 0.34 | 0.66 | 0.17 | 1.00 |
NOTE.—See figure 2 for designation of foreground branches. Branches 2, 5, and 6 are detected to be under positive selection by all test procedures.
Lynn et al. (2005) used the branch models to identify lineages potentially under positive selection. The 1-ratio model M0 is compared with the free-ratios model, which assumes that every branch on the tree has a free ω ratio and averages the ω ratio across all codons in the gene for every branch. The test was significant, indicating that the ω ratio is variable among branches. Maximum likelihood estimates of the ω ratio were greater than one for branches 1, 2, 3, 4, 5, and 15. Nevertheless, this branch-based test does not directly examine whether any ω ratio is significantly greater than one. The branch–site test explicitly tests whether some codons in the gene have ω ratio significantly greater than one. Nevertheless, the results of the 2 analyses are quite similar. Branches 2 (cow) and 5 (cat) showed the strongest evidence for positive selection in table 6 and also had the highest estimates of the average ω ratio (Lynn et al. 2005). Branch 6 is detected to be under positive selection in table 6 with an average ω ratio at 1.01. Branch 3 (ancestral to pig and cow) also showed marginal evidence for positive selection, as discussed above, and its average ω estimate was 1.25.
The factors potentially driving such lineage-specific positive selection in CD2 are not well understood. As discussed by Lynn et al. (2005), CD2 has different counterreceptors in different species (CD58 in humans, pigs, and cats but CD48 in rodents). As a result, there may be selective pressure to optimize the interaction of CD2 with its counterreceptor. Interactions with viral proteins could also be responsible for species-specific positive selection driving adaptive evolution in CD2, as different mammals act as hosts for different viruses.
Discussion
As mentioned in the Methods section, some of the conditions required for the multiple test correction procedures are not met when they are applied to test multiple branches on a phylogeny for positive selection. Nevertheless, our simulation results suggest that these procedures, when combined with the branch–site test of positive selection, were reliable and also had reasonable power. We examined the correlations between test statistics for the true null hypotheses in our simulation and found them to be in general very low (around or below 0.1), so that the independence assumption made by those procedures were almost right. Another reason for the low error rates of the procedures appears to be that the modified branch–site test was designed to guide against false positives due to model misspecification and that as a result the test tends to be conservative with the p values smaller than the significance level.
Corrections for multiple tests are clearly necessary in such tests of multiple hypotheses, as otherwise the FWER may be unacceptably high. Both theory and our simulations confirm that Bonferroni's correction is the most conservative, followed by Hochberg's (1988) method, and then by Hommel's (1989) and Rom's (1990) methods. Nevertheless, the difference in either FWER or power among those 4 FWER-controlling procedures was very small in our simulations. In particular, the simple Bonferroni correction appeared almost as good as the other less-conservative corrections. The 2 methods that control the FDR, by Benjamini and Hochberg (1995) and by Storey (2002), had slightly higher power but also elevated FWER in some simulation schemes, making them not very attractive.
We observed that extremely high sequence divergences combined with serious violations of model assumptions may cause the test to generate excessive false positives, with the FWER above the significance level. The reasons for this result are not well understood. We note also that highly divergent sequences are often accompanied by other problems as well, such as difficulty in constructing a reliable alignment, and different base compositions and codon frequencies in different sequences, which indicate a clear violation of the homogeneity and stationarity assumption of the codon substitution model (Goldman and Yang 1994). It may be noted that detection of positive selection through the ω ratio requires information on both synonymous and nonsynonymous changes, so that neither too similar nor too divergent sequences are suitable for such analysis. Highly similar sequences have little variation and little information content. Extremely divergent sequences on the other hand involve too many substitutions; in particular, the synonymous sites may well be saturated. We thus advise that caution should be exercised when the branch–site test is applied to highly divergent sequence data.
Furthermore, the branch–site model makes a number of restrictive assumptions about the evolutionary process of the gene. In particular, the assumptions about the ω values on branches and across sites are rather rigid, unlikely to be satisfied by real data. It is not always clear which of the simplifying assumptions have the greatest impact on the reliability (or type-I error rate) of the test. In this paper, we constructed simulation schemes to examine the performance of the test when the selection regime, as indicated by the distribution of the ω ratio over sites, is more complex than assumed in the model. For example, the null and alternative hypotheses used in the branch–site test assume only a few site classes and only 2 types of branches (foreground and background). In our simulation, many more site classes and branch types were used, and under some schemes, 2 or 4 branches were simultaneously under positive selection. The results suggest that the test was robust to these violations of assumptions. Nevertheless, our results may not apply to other situations not evaluated in this study, and caution should be exercised against overgeneralization. We welcome suggestions of simulation schemes under which the test may be expected to fail, as understanding such situations may help improve the selection-detection methods.
Recently, Kosakovsky Pond and Frost (2005) suggested a genetic algorithm to assign branches on the tree to several classes of ω ratios, searching for the best-fitting model using a genetic algorithm, with the fit of the model evaluated using Akaike's Information Criterion (AIC, Akaike 1974; Sugiura 1978). This approach does not require a priori specification of the lineages to be tested but does not appear to be a valid statistical test of positive selection. First, the AIC may not provide sufficient control for multiple testing, especially given that even the number of models explored in the genetic algorithm is unknown. Second, the procedure is not constructed to test the null hypothesis of no positive selection and may thus generate excessive false positives; the genetic algorithm may identify a best-fitting model with estimates of ω > 1 for some branches, but it does not test or reject the null hypothesis of no positive selection (ω = 1). Third, searching for the best set of foreground branches in a genetic algorithm may be less appropriate than testing one branch at a time because the branch–site model assumes that the same set of amino acid sites are under positive selection along all foreground branches, an assumption that may be hard to justify when our knowledge of the selective pressure on the protein is limited. The branch model does not have this problem, but it has too little power to be effective in this kind of test.
Another recent study (Guindon et al. 2006) discussed multiple test correction and calculation of the FDR in tests of positive selection affecting amino acid sites using the site-based codon models (Nielsen and Yang 1998; Yang et al. 2000). The authors discussed 2 approaches: the direct posterior probability approach of Newton et al. (2004) and a parametric bootstrap method devised by the authors. The former is a straightforward use of posterior probabilities that each site is from the class of positive selection as calculated by the CODEML program (Yang 1997; Nielsen and Yang 1998), whereas the latter appears to blur the distinction between Bayesian and Frequentist concepts. Nevertheless, all those studies serve to highlight the importance of multiple test corrections in large-scale analysis of genomic data.
We thank David Lynn for kindly providing the alignment of CD2. We are grateful to 2 anonymous reviewers for many critical comments on earlier versions of this manuscript. This study was supported by a grant from the Biotechnological and Biological Sciences Research Council and an award from GlaxoSmithKline, both to Z.Y.
References
Author notes
Adriana Briscoe, Associate Editor



