-
PDF
- Split View
-
Views
-
Cite
Cite
Meera Venkatesan, Catherine J. Westbrook, M. Claire Hauer, Jason L. Rasgon, Evidence for a Population Expansion in the West Nile Virus Vector Culex tarsalis, Molecular Biology and Evolution, Volume 24, Issue 5, May 2007, Pages 1208–1218, https://doi.org/10.1093/molbev/msm040
Close - Share Icon Share
Abstract
Population genetic structure of the West Nile Virus vector Culex tarsalis was investigated in 5 states in the western United States using 5 microsatellite loci and a fragment of the mitochondrial reduced form of nicotinamide adenine dinucleotide dehydrogenase 4 (ND4) gene. ND4 sequence analysis revealed a lack of isolation by distance, panmixia across all populations, an excess of rare haplotypes, and a star-like phylogeny. Microsatellites revealed moderate genetic differentiation and isolation by distance, with the largest genetic distance occurring between populations in southern California and New Mexico (FST = 0.146). Clustering analysis and analysis of molecular variance on microsatellite data indicated the presence of 3 broad population clusters. Mismatch distributions and site-frequency spectra derived from mitochondrial ND4 sequences displayed pattern's characteristic of population expansion. Fu and Li's D* and F*, Fu's FS, and Tajima's D statistics performed on ND4 sequences all revealed significant, negative deviations from mutation-drift equilibrium. Microsatellite-based multilocus heterozygosity tests showed evidence of range expansion in the majority of populations. Our results suggest that C. tarsalis underwent a range expansion across the western United States within the last 375,000–560,000 years, which may have been associated with Pleistocene glaciation events that occurred in the midwestern and western United States between 350,000 and 1 MYA.
Introduction
Culex tarsalis is implicated as a major mosquito vector of West Nile Virus (WNV) in the western United States (Goddard et al. 2002, Reisen et al. 2004, Bell et al. 2005, Turrell et al. 2005, DiMenna et al. 2006). The geographic range of C. tarsalis spans from the west coast to the Mississippi River and from northern Mexico to Canada (Darsie and Ward 1981). Larvae can develop in various freshwater habitats (Reisen and Reeves 1987) and adult populations commonly reach very high density, becoming important biting nuisance pests. Historically, C. tarsalis has played a prominent role in the maintenance and transmission of arboviruses including St. Louis Encephalitis Virus and Western Equine Encephalitis Virus. Laboratory studies have revealed that C. tarsalis is among the most efficient vectors of WNV known, with high rates of both oral and vertical transmission (Goddard et al. 2002, 2003). Culex tarsalis not only feeds primarily on birds (Reisen and Reeves 1987) and is hypothesized to play an important role in WNV amplification, but also feeds opportunistically on mammals (Reisen and Reeves 1987) and is abundant in peridomestic habitats, possibly serving as a bridge vector to humans and domestic animals. Given its broad range, large population sizes, and high capacity for WNV transmission, C. tarsalis is likely in part responsible for recent epidemics in western United States including outbreaks in Nebraska, Colorado, Arizona, New Mexico, and California (Hayes et al. 2005).
Studies of field-caught individuals indicate that there is significant spatial and temporal heterogeneity in the ability of C. tarsalis to transmit WNV. Northern California populations exhibited higher transovarial and oral transmission than populations in southern California (Goddard et al. 2002, 2003). WNV infection rates also appear to vary at different times of year (Reisen et al. 2006). The extent to which these observed temporal and spatial differences in WNV transmission are rooted in genetic variation and/or environmental influences is currently unknown. It is possible that part of the variation that C. tarsalis exhibits in viral transmissibility is due to genetic differences among populations. However, except for a single allozyme study (Gimnig et al. 1999), little is known about the genetic structure of C. tarsalis populations. This study was undertaken to begin characterizing population structure of C. tarsalis in the western United States.
We have characterized the genetic structure of C. tarsalis populations across a broad geographical range using both mitochondrial and nuclear markers. We conducted a genetic analysis of 12 C. tarsalis populations from California, Washington, Colorado, New Mexico, and Nebraska using 5 microsatellite markers and mitochondrial sequence data. Microsatellites revealed moderate genetic structure and isolation by distance, whereas mitochondrial sequences indicated panmixia across the study region. Both types of markers exhibit signatures indicative of a range expansion. Our findings have important implications for future studies on C. tarsalis population dynamics, the potential role of genetic structure in explaining variation in viral transmission, and the effect of past evolutionary events on current estimates of gene flow.
Materials and Methods
Mosquito Collections and Extractions of DNA
Adult mosquitoes were collected in California, Washington, New Mexico, Colorado, and Nebraska between June and August 2005 using Centers for Disease Control light traps (fig. 1). Specimens were either transported from the collection localities to the Johns Hopkins Bloomberg School of Public Health on dry ice or preserved in 100% ethanol and stored at −80° C until processed for DNA extraction. Specimens were identified as C. tarsalis according to Darsie and Ward (1981). DNA was extracted from individual mosquitoes using the DNeasy Tissue Kit (Qiagen, Valencia, CA) according to Appendix G of the manufacturer's protocol for insects or by salt extraction/ethanol precipitation as previously described (Black and DuTeau 1997). Extracted DNA was suspended in nuclease-free water and DNA concentration was quantified using a NanoDrop spectrophotometer (NanoDrop Technologies, Wilmington, DE), adjusted to 25–50 ng/μL, and stored at −20° C until used for Polymerase Chain Reaction (PCR).
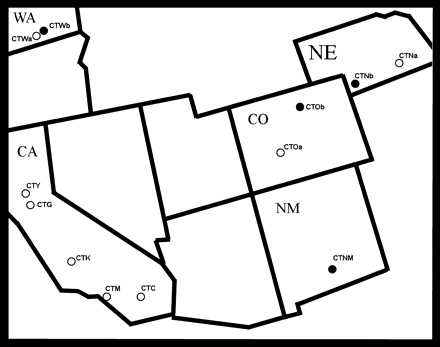
Summer 2005 Culex tarsalis collection sites. A total of 12 populations were sampled, including 5 in California, 2 each in Colorado, Washington and Nebraska, and 1 in New Mexico. Open circles denote sites where both microsatellite and mitochondrial sequence data were obtained and filled circles denote sites where only microsatellite data were obtained.
ND4 Mitochondrial DNA Amplification and Sequencing
A 389 bp fragment of the reduced form of nicotinamide adenine dinucleotide dehydrogenase gene subunit 4 was amplified using primers ND4+ and ND4− as previously described (Gorrochotegui-Escalante et al. 2000). Amplifications were carried out using DNA from 25 to 32 individuals from each California population and 16 individuals from 1 population each in Washington, Colorado, and Nebraska, for a total of 8 populations (N = 170). PCR conditions were as previously described (Gorrochotegui-Escalante et al. 2000). Amplicons were separated by 1% agarose gel electrophoresis, purified from the gel using Qiaquick columns (Qiagen), and sequenced in both directions at the Johns Hopkins Medical Institutes Core Sequencing Facility (Baltimore, MD). Because primer sequences contain degenerate sites, these portions were excluded from sequence analysis.
Microsatellite Amplification and Fragment Size Determination
Five trinucleotide repeat microsatellite loci were selected from 12 previously identified markers for analysis (CUTC6, CUTC12, CUTD107, CUTD113, and CUTD120) (Rasgon, Venkatesan et al. 2006). Primer sequences and PCR conditions were as previously described (Rasgon et al. 2006). Amplifications were carried out using DNA from 24 to 38 individuals from each of 12 populations (N = 356). Forward primers were 5′ labeled with either HEX or 6FAM for marker multiplexing. Labeled amplicons were resolved on an ABI Prism Genetic Analyzer 3100 Avant (Applied Biosystems, Foster City, CA). Allele sizes were automatically estimated with an internal ROX-500 size standard (Applied Biosystems) using GeneScan v. 3.1 and Genotyper software (Applied Biosystems).
Diversity and Population Structure Analyses
ND4 haplotype polymorphism and nucleotide diversity, estimated by π (the average number of nucleotide differences per site between 2 sequences, calculated according to Nei (1987), were determined using DnaSP 4.0 (Rozas et al. 2003). Microsatellite allele frequencies were analyzed for deviation from Hardy–Weinberg equilibrium and linkage disequilibrium using Arlequin 2.0 (Schneider et al. 2000) and GenePop software (Raymond and Rousset 1995). Genetic diversity values were not normally distributed, so diversity among populations was compared using the Wilcoxon matched-pairs sign-rank test for microsatellite loci and a Chi-square goodness of fit test for ND4 sequences.
Arlequin 2.0 was used to compute FST values (Wright 1951, Weir and Cockerham 1984) and significance determined by permutation tests (1,000 permutations). An unweighted pair group method with arithmatic mean (UPGMA) phylogenetic tree inferred from microsatellite-derived multilocus FST values was constructed using MEGA v. 3.1 (Kumar et al. 2004). Branch lengths were determined using the program PHYLIP (Felsenstein 1989). A statistical parsimony (Templeton et al. 1992) haplotype network of unique ND4 sequences was constructed using the program TCS 1.21 (Clement et al. 2000) with a 95% cutoff.
Structure 2.0 (Pritchard et al. 2000) was used to assign individuals from all populations to a predetermined number of clusters (K) based on multilocus microsatellite data. For each run, a burn-in period of 30,000 steps was followed by 1,000,000 iterations under the admixture model and the assumption of correlated allele frequencies among populations (gamma = 0.3468, calculated in 5 runs at K = 1). For each K of 1–6, 10 runs were performed. Log-likelihood scores were averaged across runs and compared to determine the posterior probability of each K. Arlequin 2.0 was used to partition genetic variation among regions of restricted gene flow (based on microsatellite-derived clustering results and FST values) using analysis of molecular variance (AMOVA). Regressions of linearized FST values on ln-transformed geographic distances among populations (Rousset 1997) were performed for microsatellite and ND4-derived data using STATA 8.0. Mantel probabilities were calculated using IBD 1.52 (Bohonak 2002).
Methods to Infer Population Expansion
Several test statistics have been developed to determine whether microsatellite and mitochondrial haplotype frequencies deviate from evolutionary neutrality. These statistics are based on a comparison of observed variability (measured by heterozygosity, haplotype or nucleotide diversity, and number of pairwise differences or segregating sites) to what would be expected under mutation-drift equilibrium or population growth. H and K tests (Depaulis and Veuille 1999) were performed on ND4 sequence data using the program Allelix (provided by S. Mousset). These tests compare observed haplotype diversity and number with an expected distribution of values under equilibrium conditions. Strobeck's S statistic (Strobeck 1987), the probability of having an equal number or fewer haplotypes than observed based on the gene frequency distribution derived from the inferred mutation rate θ, was computed for each population using the program DnaSP v. 4.0. Mismatch distributions (Rogers and Harpending 1992, Rogers 1995) and site-frequency spectra (Donnelly et al. 2001) produce characteristic patterns believed to reflect population expansion. Distributions and frequency spectra were plotted across all samples and for each population using DnaSP v. 4.0 along with the corresponding raggedness statistic (Harpending 1994) to quantify the smoothness of mismatch distributions.
Fu and Li's D* and F * (Fu and Li 1993), and Fu's Fs statistics test for deviation of sequence variation from evolutionary neutrality. Fu's Fs is based on the probability of the observed number of haplotypes or greater occurring under conditions of neutrality, whereas Fu and Li's D* and F* compare estimates of theta based on mutations in internal (older) and external (younger) branches of a genealogy. Negative values of these statistics are most often attributed to positive selective sweeps (such as genetic hitchhiking), recent population growth, or background selection. These events may all result in similar sequence patterns such as an excess of rare haplotypes, but different tests exhibit varying levels of sensitivity in detecting potential causes. Used in combination, these tests can provide evidence for or against particular evolutionary mechanisms. Fu and Li's D* and F* and Fu's Fs tests and confidence intervals (CI) calculated from coalescent simulations were conducted using DnaSP v. 4.0.
A multilocus test of expected homozygosity (and conversely heterozygosity) has been developed for microsatellite evolution under a variety of mutation models (Cornuet and Luikart 1996). Expected heterozygosity under Hardy–Weinberg allele frequencies (He) is compared with expected heterozygosity calculated from the expected number of alleles and sample size (Heq). Under conditions of rapid population growth, high mutation rates and low loss of variation from drift would cause both heterozygosity and allele number to increase, though allele number would increase at a more rapid rate. As a result, Heq would be greater than He (Cornuet and Luikart 1996), providing a signature of population expansion. Microsatellites generally follow the stepwise mutation model (SMM) or have a small percentage of multistep mutations (2-phase model or TPM) (Weber and Wong 1993, Di Rienzo et al. 1994, Primmer et al. 1998). Tests under strict SMM and TPM with 5%, 10%, and 15% multistep mutations were performed using the program Bottleneck (Cornuet and Luikart 1996).
Results
ND4 Haplotype and Nucleotide Polymorphism
Sixty-four ND4 haplotypes were detected in 170 C. tarsalis individuals across 8 populations. Forty-nine of 349 nucleotide positions were variable and only 5 substitutions were nonsynonymous. The number of haplotypes per population ranged from 9 to 17, with a mean of 12.75 (table 1). Once haplotype richness was weighted by sample size, no significant differences in haplotype number were observed. Haplotype diversity (Hd) ranged from 0.78 to 0.96 among populations and nucleotide diversity (π) ranged from 0.0050 to 0.0079. Haplotype diversity (Hd) and nucleotide diversity (π) did not vary significantly among populations.
Summary Statistics of ND4 Sequence Variation in 8 Culex tarsalis Populations from the Western United States
| Population | Location | N | H | S | Hd | π | K | D | r | Fs | S | D* | F* |
| CTC | Coachella, CA | 29 | 15 | 18 | 0.852 | 0.0066 | 2.32 | −1.81* | 0.041 | −9.07** | 1.00** | −2.25 | −2.48 |
| CTM | Los Angeles, CA | 26 | 16 | 17 | 0.948 | 0.0079 | 2.76 | −1.79 | 0.067 | −10.19** | 1.00** | −2.06 | −2.32 |
| CTK | Kern, CA | 23 | 11 | 15 | 0.775 | 0.0066 | 2.29 | −1.56 | 0.049 | −4.60** | 0.997** | −1.71 | −1.94 |
| CTG | Yolo, CA | 30 | 17 | 18 | 0.913 | 0.0063 | 2.21 | −1.77 | 0.047 | −12.85** | 1.00** | −2.82* | −2.92* |
| CTY | Yuba, CA | 16 | 9 | 9 | 0.858 | 0.0061 | 2.14 | −0.77 | 0.047 | −3.89* | 0.995* | −1.01 | −1.09 |
| CTWa | Benton, WA | 16 | 12 | 13 | 0.926 | 0.0069 | 2.40 | −1.43 | 0.052 | −9.94** | 1.00** | −1.05 | −1.34 |
| CTOa | Gunnison, CO | 16 | 10 | 10 | 0.867 | 0.0050 | 1.74 | −1.57 | 0.070 | −6.50** | 1.00** | −1.67 | −1.89 |
| CTNa | Adams, NE | 14 | 12 | 14 | 0.962 | 0.0076 | 2.64 | −1.72 | 0.051 | −7.87** | 1.00** | −2.17 | −2.35 |
| Overall | 170 | 64 | 49 | 0.887 | 0.0068 | 2.36 | −2.29** | 0.034 | −92.82** | 1.00** | −4.67* | −4.37* |
| Population | Location | N | H | S | Hd | π | K | D | r | Fs | S | D* | F* |
| CTC | Coachella, CA | 29 | 15 | 18 | 0.852 | 0.0066 | 2.32 | −1.81* | 0.041 | −9.07** | 1.00** | −2.25 | −2.48 |
| CTM | Los Angeles, CA | 26 | 16 | 17 | 0.948 | 0.0079 | 2.76 | −1.79 | 0.067 | −10.19** | 1.00** | −2.06 | −2.32 |
| CTK | Kern, CA | 23 | 11 | 15 | 0.775 | 0.0066 | 2.29 | −1.56 | 0.049 | −4.60** | 0.997** | −1.71 | −1.94 |
| CTG | Yolo, CA | 30 | 17 | 18 | 0.913 | 0.0063 | 2.21 | −1.77 | 0.047 | −12.85** | 1.00** | −2.82* | −2.92* |
| CTY | Yuba, CA | 16 | 9 | 9 | 0.858 | 0.0061 | 2.14 | −0.77 | 0.047 | −3.89* | 0.995* | −1.01 | −1.09 |
| CTWa | Benton, WA | 16 | 12 | 13 | 0.926 | 0.0069 | 2.40 | −1.43 | 0.052 | −9.94** | 1.00** | −1.05 | −1.34 |
| CTOa | Gunnison, CO | 16 | 10 | 10 | 0.867 | 0.0050 | 1.74 | −1.57 | 0.070 | −6.50** | 1.00** | −1.67 | −1.89 |
| CTNa | Adams, NE | 14 | 12 | 14 | 0.962 | 0.0076 | 2.64 | −1.72 | 0.051 | −7.87** | 1.00** | −2.17 | −2.35 |
| Overall | 170 | 64 | 49 | 0.887 | 0.0068 | 2.36 | −2.29** | 0.034 | −92.82** | 1.00** | −4.67* | −4.37* |
NOTE.—N, number of sequences analyzed; H, number of haplotypes; S, number of segregating sites; Hd, haplotype diversity; π, nucleotide diversity; K, average number of nucleotide differences; D, Tajima's statistic (Tajima 1989); r, raggedness statistic (Harpending 1994); FS, Fu's statistic (Fu 1997); S, Strobeck's statistic (Strobeck 1987); D* and F*, Fu and Li's statistics (Fu and Li 1993).
* P < 0.05; ** P < 0.01. Significance was determined using coalescent simulations in DnaSP v. 4.0.
Summary Statistics of ND4 Sequence Variation in 8 Culex tarsalis Populations from the Western United States
| Population | Location | N | H | S | Hd | π | K | D | r | Fs | S | D* | F* |
| CTC | Coachella, CA | 29 | 15 | 18 | 0.852 | 0.0066 | 2.32 | −1.81* | 0.041 | −9.07** | 1.00** | −2.25 | −2.48 |
| CTM | Los Angeles, CA | 26 | 16 | 17 | 0.948 | 0.0079 | 2.76 | −1.79 | 0.067 | −10.19** | 1.00** | −2.06 | −2.32 |
| CTK | Kern, CA | 23 | 11 | 15 | 0.775 | 0.0066 | 2.29 | −1.56 | 0.049 | −4.60** | 0.997** | −1.71 | −1.94 |
| CTG | Yolo, CA | 30 | 17 | 18 | 0.913 | 0.0063 | 2.21 | −1.77 | 0.047 | −12.85** | 1.00** | −2.82* | −2.92* |
| CTY | Yuba, CA | 16 | 9 | 9 | 0.858 | 0.0061 | 2.14 | −0.77 | 0.047 | −3.89* | 0.995* | −1.01 | −1.09 |
| CTWa | Benton, WA | 16 | 12 | 13 | 0.926 | 0.0069 | 2.40 | −1.43 | 0.052 | −9.94** | 1.00** | −1.05 | −1.34 |
| CTOa | Gunnison, CO | 16 | 10 | 10 | 0.867 | 0.0050 | 1.74 | −1.57 | 0.070 | −6.50** | 1.00** | −1.67 | −1.89 |
| CTNa | Adams, NE | 14 | 12 | 14 | 0.962 | 0.0076 | 2.64 | −1.72 | 0.051 | −7.87** | 1.00** | −2.17 | −2.35 |
| Overall | 170 | 64 | 49 | 0.887 | 0.0068 | 2.36 | −2.29** | 0.034 | −92.82** | 1.00** | −4.67* | −4.37* |
| Population | Location | N | H | S | Hd | π | K | D | r | Fs | S | D* | F* |
| CTC | Coachella, CA | 29 | 15 | 18 | 0.852 | 0.0066 | 2.32 | −1.81* | 0.041 | −9.07** | 1.00** | −2.25 | −2.48 |
| CTM | Los Angeles, CA | 26 | 16 | 17 | 0.948 | 0.0079 | 2.76 | −1.79 | 0.067 | −10.19** | 1.00** | −2.06 | −2.32 |
| CTK | Kern, CA | 23 | 11 | 15 | 0.775 | 0.0066 | 2.29 | −1.56 | 0.049 | −4.60** | 0.997** | −1.71 | −1.94 |
| CTG | Yolo, CA | 30 | 17 | 18 | 0.913 | 0.0063 | 2.21 | −1.77 | 0.047 | −12.85** | 1.00** | −2.82* | −2.92* |
| CTY | Yuba, CA | 16 | 9 | 9 | 0.858 | 0.0061 | 2.14 | −0.77 | 0.047 | −3.89* | 0.995* | −1.01 | −1.09 |
| CTWa | Benton, WA | 16 | 12 | 13 | 0.926 | 0.0069 | 2.40 | −1.43 | 0.052 | −9.94** | 1.00** | −1.05 | −1.34 |
| CTOa | Gunnison, CO | 16 | 10 | 10 | 0.867 | 0.0050 | 1.74 | −1.57 | 0.070 | −6.50** | 1.00** | −1.67 | −1.89 |
| CTNa | Adams, NE | 14 | 12 | 14 | 0.962 | 0.0076 | 2.64 | −1.72 | 0.051 | −7.87** | 1.00** | −2.17 | −2.35 |
| Overall | 170 | 64 | 49 | 0.887 | 0.0068 | 2.36 | −2.29** | 0.034 | −92.82** | 1.00** | −4.67* | −4.37* |
NOTE.—N, number of sequences analyzed; H, number of haplotypes; S, number of segregating sites; Hd, haplotype diversity; π, nucleotide diversity; K, average number of nucleotide differences; D, Tajima's statistic (Tajima 1989); r, raggedness statistic (Harpending 1994); FS, Fu's statistic (Fu 1997); S, Strobeck's statistic (Strobeck 1987); D* and F*, Fu and Li's statistics (Fu and Li 1993).
* P < 0.05; ** P < 0.01. Significance was determined using coalescent simulations in DnaSP v. 4.0.
H and K tests indicated that although overall ND4 haplotype diversity did not deviate from the expected distribution (observed Hd = 0.88; 95% CI of expected Hd = 0.81–0.94; P = 0.37), the number of observed haplotypes, at 64, is much greater than what would be expected under the neutral model (95% CI of expected number of haplotypes = 16–35; P < 0.0001).
Hardy–Weinberg Equilibrium, Linkage Disequilibrium, and Microsatellite Polymorphism
Significant deviation from Hardy–Weinberg equilibrium was found in 8 of 60 possible tests (Bonferroni adjusted α = 0.0008; table 2). All deviations were due to heterozygosity deficiency. None of the pairs of loci exhibited significant linkage disequilibrium (Bonferroni corrected α = 0.0004) in single pairwise tests. Fisher's global test for each pair of loci across all 12 populations also did not reveal significant linkage disequilibrium.
Sample Size (N), Number of Alleles, and Expected and Observed Heterozygosities (He and Ho) of 5 Microsatellite Loci in 12 C. tarsalis Populations from the Western United States
| Population | Location | N | Microsatellite Loci | |||||||||||||||||
| CUTC6 | CUTC12 | CUTD113 | CUTD107 | CUTD120 | Mean | |||||||||||||||
| Number of alleles | He | Ho | Number of alleles | He | Ho | Number of alleles | He | Ho | Number of alleles | He | Ho | Number of alleles | He | Ho | Number of alleles | He | Ho | |||
| CTC | Coachella, CA | 27 | 3 | 0.210 | 0.111 | 8 | 0.794 | 0.778 | 4 | 0.488 | 0.444 | 5 | 0.262 | 0.260 | 4 | 0.510 | 0.556 | 4.8 | 0.453 | 0.430 |
| CTM | Los Angeles, CA | 25 | 4 | 0.384 | 0.240 | 10 | 0.824 | 0.680 | 4 | 0.575 | 0.600 | 3 | 0.384 | 0.333 | 4 | 0.744 | 0.480 | 5.0 | 0.582 | 0.467 |
| CTK | Kern, CA | 24 | 4 | 0.354 | 0.000 | 10 | 0.834 | 0.792 | 4 | 0.404 | 0.167* | 3 | 0.541 | 0.400 | 5 | 0.664 | 0.333 | 5.2 | 0.559 | 0.338 |
| CTG | Yolo, CA | 29 | 4 | 0.481 | 0.103* | 7 | 0.822 | 0.552 | 5 | 0.460 | 0.345 | 3 | 0.425 | 0.143* | 5 | 0.629 | 0.517 | 4.8 | 0.563 | 0.332 |
| CTY | Yuba, CA | 32 | 5 | 0.262 | 0.094* | 7 | 0.732 | 0.563 | 6 | 0.633 | 0.656 | 3 | 0.479 | 0.344 | 5 | 0.643 | 0.469 | 5.2 | 0.550 | 0.425 |
| CTWA | Benton, WA | 30 | 4 | 0.394 | 0.200 | 8 | 0.802 | 0.767 | 6 | 0.565 | 0.500 | 3 | 0.129 | 0.100 | 6 | 0.623 | 0.200* | 5.4 | 0.503 | 0.353 |
| CTWB | Benton, WA | 38 | 3 | 0.092 | 0.063 | 10 | 0.787 | 0.688* | 6 | 0.384 | 0.344 | 4 | 0.207 | 0.125 | 6 | 0.694 | 0.313* | 5.8 | 0.433 | 0.306 |
| CTNM | Otero, NM | 30 | 4 | 0.245 | 0.167 | 8 | 0.536 | 0.467 | 7 | 0.736 | 0.714 | 4 | 0.421 | 0.333 | 6 | 0.660 | 0.567 | 5.8 | 0.520 | 0.450 |
| CTOA | Gunnison, CO | 32 | 3 | 0.185 | 0.097 | 10 | 0.840 | 0.688* | 7 | 0.577 | 0.531 | 4 | 0.403 | 0.452 | 5 | 0.695 | 0.258* | 5.8 | 0.540 | 0.405 |
| CTOB | Boulder, CO | 27 | 4 | 0.242 | 0.185 | 6 | 0.795 | 0.593 | 7 | 0.626 | 0.482 | 4 | 0.184 | 0.154 | 5 | 0.720 | 0.385 | 5.2 | 0.514 | 0.360 |
| CTNA | Adams, NE | 32 | 3 | 0.122 | 0.094 | 8 | 0.713 | 0.594 | 6 | 0.694 | 0.625 | 5 | 0.285 | 0.188 | 6 | 0.673 | 0.563 | 5.6 | 0.497 | 0.413 |
| CTNB | Chase, NE | 32 | 3 | 0.122 | 0.094 | 7 | 0.704 | 0.656 | 7 | 0.652 | 0.625 | 3 | 0.286 | 0.219 | 7 | 0.683 | 0.563 | 5.4 | 0.489 | 0.431 |
| Population | Location | N | Microsatellite Loci | |||||||||||||||||
| CUTC6 | CUTC12 | CUTD113 | CUTD107 | CUTD120 | Mean | |||||||||||||||
| Number of alleles | He | Ho | Number of alleles | He | Ho | Number of alleles | He | Ho | Number of alleles | He | Ho | Number of alleles | He | Ho | Number of alleles | He | Ho | |||
| CTC | Coachella, CA | 27 | 3 | 0.210 | 0.111 | 8 | 0.794 | 0.778 | 4 | 0.488 | 0.444 | 5 | 0.262 | 0.260 | 4 | 0.510 | 0.556 | 4.8 | 0.453 | 0.430 |
| CTM | Los Angeles, CA | 25 | 4 | 0.384 | 0.240 | 10 | 0.824 | 0.680 | 4 | 0.575 | 0.600 | 3 | 0.384 | 0.333 | 4 | 0.744 | 0.480 | 5.0 | 0.582 | 0.467 |
| CTK | Kern, CA | 24 | 4 | 0.354 | 0.000 | 10 | 0.834 | 0.792 | 4 | 0.404 | 0.167* | 3 | 0.541 | 0.400 | 5 | 0.664 | 0.333 | 5.2 | 0.559 | 0.338 |
| CTG | Yolo, CA | 29 | 4 | 0.481 | 0.103* | 7 | 0.822 | 0.552 | 5 | 0.460 | 0.345 | 3 | 0.425 | 0.143* | 5 | 0.629 | 0.517 | 4.8 | 0.563 | 0.332 |
| CTY | Yuba, CA | 32 | 5 | 0.262 | 0.094* | 7 | 0.732 | 0.563 | 6 | 0.633 | 0.656 | 3 | 0.479 | 0.344 | 5 | 0.643 | 0.469 | 5.2 | 0.550 | 0.425 |
| CTWA | Benton, WA | 30 | 4 | 0.394 | 0.200 | 8 | 0.802 | 0.767 | 6 | 0.565 | 0.500 | 3 | 0.129 | 0.100 | 6 | 0.623 | 0.200* | 5.4 | 0.503 | 0.353 |
| CTWB | Benton, WA | 38 | 3 | 0.092 | 0.063 | 10 | 0.787 | 0.688* | 6 | 0.384 | 0.344 | 4 | 0.207 | 0.125 | 6 | 0.694 | 0.313* | 5.8 | 0.433 | 0.306 |
| CTNM | Otero, NM | 30 | 4 | 0.245 | 0.167 | 8 | 0.536 | 0.467 | 7 | 0.736 | 0.714 | 4 | 0.421 | 0.333 | 6 | 0.660 | 0.567 | 5.8 | 0.520 | 0.450 |
| CTOA | Gunnison, CO | 32 | 3 | 0.185 | 0.097 | 10 | 0.840 | 0.688* | 7 | 0.577 | 0.531 | 4 | 0.403 | 0.452 | 5 | 0.695 | 0.258* | 5.8 | 0.540 | 0.405 |
| CTOB | Boulder, CO | 27 | 4 | 0.242 | 0.185 | 6 | 0.795 | 0.593 | 7 | 0.626 | 0.482 | 4 | 0.184 | 0.154 | 5 | 0.720 | 0.385 | 5.2 | 0.514 | 0.360 |
| CTNA | Adams, NE | 32 | 3 | 0.122 | 0.094 | 8 | 0.713 | 0.594 | 6 | 0.694 | 0.625 | 5 | 0.285 | 0.188 | 6 | 0.673 | 0.563 | 5.6 | 0.497 | 0.413 |
| CTNB | Chase, NE | 32 | 3 | 0.122 | 0.094 | 7 | 0.704 | 0.656 | 7 | 0.652 | 0.625 | 3 | 0.286 | 0.219 | 7 | 0.683 | 0.563 | 5.4 | 0.489 | 0.431 |
*P < 0.05 (Bonferroni corrected α).
Sample Size (N), Number of Alleles, and Expected and Observed Heterozygosities (He and Ho) of 5 Microsatellite Loci in 12 C. tarsalis Populations from the Western United States
| Population | Location | N | Microsatellite Loci | |||||||||||||||||
| CUTC6 | CUTC12 | CUTD113 | CUTD107 | CUTD120 | Mean | |||||||||||||||
| Number of alleles | He | Ho | Number of alleles | He | Ho | Number of alleles | He | Ho | Number of alleles | He | Ho | Number of alleles | He | Ho | Number of alleles | He | Ho | |||
| CTC | Coachella, CA | 27 | 3 | 0.210 | 0.111 | 8 | 0.794 | 0.778 | 4 | 0.488 | 0.444 | 5 | 0.262 | 0.260 | 4 | 0.510 | 0.556 | 4.8 | 0.453 | 0.430 |
| CTM | Los Angeles, CA | 25 | 4 | 0.384 | 0.240 | 10 | 0.824 | 0.680 | 4 | 0.575 | 0.600 | 3 | 0.384 | 0.333 | 4 | 0.744 | 0.480 | 5.0 | 0.582 | 0.467 |
| CTK | Kern, CA | 24 | 4 | 0.354 | 0.000 | 10 | 0.834 | 0.792 | 4 | 0.404 | 0.167* | 3 | 0.541 | 0.400 | 5 | 0.664 | 0.333 | 5.2 | 0.559 | 0.338 |
| CTG | Yolo, CA | 29 | 4 | 0.481 | 0.103* | 7 | 0.822 | 0.552 | 5 | 0.460 | 0.345 | 3 | 0.425 | 0.143* | 5 | 0.629 | 0.517 | 4.8 | 0.563 | 0.332 |
| CTY | Yuba, CA | 32 | 5 | 0.262 | 0.094* | 7 | 0.732 | 0.563 | 6 | 0.633 | 0.656 | 3 | 0.479 | 0.344 | 5 | 0.643 | 0.469 | 5.2 | 0.550 | 0.425 |
| CTWA | Benton, WA | 30 | 4 | 0.394 | 0.200 | 8 | 0.802 | 0.767 | 6 | 0.565 | 0.500 | 3 | 0.129 | 0.100 | 6 | 0.623 | 0.200* | 5.4 | 0.503 | 0.353 |
| CTWB | Benton, WA | 38 | 3 | 0.092 | 0.063 | 10 | 0.787 | 0.688* | 6 | 0.384 | 0.344 | 4 | 0.207 | 0.125 | 6 | 0.694 | 0.313* | 5.8 | 0.433 | 0.306 |
| CTNM | Otero, NM | 30 | 4 | 0.245 | 0.167 | 8 | 0.536 | 0.467 | 7 | 0.736 | 0.714 | 4 | 0.421 | 0.333 | 6 | 0.660 | 0.567 | 5.8 | 0.520 | 0.450 |
| CTOA | Gunnison, CO | 32 | 3 | 0.185 | 0.097 | 10 | 0.840 | 0.688* | 7 | 0.577 | 0.531 | 4 | 0.403 | 0.452 | 5 | 0.695 | 0.258* | 5.8 | 0.540 | 0.405 |
| CTOB | Boulder, CO | 27 | 4 | 0.242 | 0.185 | 6 | 0.795 | 0.593 | 7 | 0.626 | 0.482 | 4 | 0.184 | 0.154 | 5 | 0.720 | 0.385 | 5.2 | 0.514 | 0.360 |
| CTNA | Adams, NE | 32 | 3 | 0.122 | 0.094 | 8 | 0.713 | 0.594 | 6 | 0.694 | 0.625 | 5 | 0.285 | 0.188 | 6 | 0.673 | 0.563 | 5.6 | 0.497 | 0.413 |
| CTNB | Chase, NE | 32 | 3 | 0.122 | 0.094 | 7 | 0.704 | 0.656 | 7 | 0.652 | 0.625 | 3 | 0.286 | 0.219 | 7 | 0.683 | 0.563 | 5.4 | 0.489 | 0.431 |
| Population | Location | N | Microsatellite Loci | |||||||||||||||||
| CUTC6 | CUTC12 | CUTD113 | CUTD107 | CUTD120 | Mean | |||||||||||||||
| Number of alleles | He | Ho | Number of alleles | He | Ho | Number of alleles | He | Ho | Number of alleles | He | Ho | Number of alleles | He | Ho | Number of alleles | He | Ho | |||
| CTC | Coachella, CA | 27 | 3 | 0.210 | 0.111 | 8 | 0.794 | 0.778 | 4 | 0.488 | 0.444 | 5 | 0.262 | 0.260 | 4 | 0.510 | 0.556 | 4.8 | 0.453 | 0.430 |
| CTM | Los Angeles, CA | 25 | 4 | 0.384 | 0.240 | 10 | 0.824 | 0.680 | 4 | 0.575 | 0.600 | 3 | 0.384 | 0.333 | 4 | 0.744 | 0.480 | 5.0 | 0.582 | 0.467 |
| CTK | Kern, CA | 24 | 4 | 0.354 | 0.000 | 10 | 0.834 | 0.792 | 4 | 0.404 | 0.167* | 3 | 0.541 | 0.400 | 5 | 0.664 | 0.333 | 5.2 | 0.559 | 0.338 |
| CTG | Yolo, CA | 29 | 4 | 0.481 | 0.103* | 7 | 0.822 | 0.552 | 5 | 0.460 | 0.345 | 3 | 0.425 | 0.143* | 5 | 0.629 | 0.517 | 4.8 | 0.563 | 0.332 |
| CTY | Yuba, CA | 32 | 5 | 0.262 | 0.094* | 7 | 0.732 | 0.563 | 6 | 0.633 | 0.656 | 3 | 0.479 | 0.344 | 5 | 0.643 | 0.469 | 5.2 | 0.550 | 0.425 |
| CTWA | Benton, WA | 30 | 4 | 0.394 | 0.200 | 8 | 0.802 | 0.767 | 6 | 0.565 | 0.500 | 3 | 0.129 | 0.100 | 6 | 0.623 | 0.200* | 5.4 | 0.503 | 0.353 |
| CTWB | Benton, WA | 38 | 3 | 0.092 | 0.063 | 10 | 0.787 | 0.688* | 6 | 0.384 | 0.344 | 4 | 0.207 | 0.125 | 6 | 0.694 | 0.313* | 5.8 | 0.433 | 0.306 |
| CTNM | Otero, NM | 30 | 4 | 0.245 | 0.167 | 8 | 0.536 | 0.467 | 7 | 0.736 | 0.714 | 4 | 0.421 | 0.333 | 6 | 0.660 | 0.567 | 5.8 | 0.520 | 0.450 |
| CTOA | Gunnison, CO | 32 | 3 | 0.185 | 0.097 | 10 | 0.840 | 0.688* | 7 | 0.577 | 0.531 | 4 | 0.403 | 0.452 | 5 | 0.695 | 0.258* | 5.8 | 0.540 | 0.405 |
| CTOB | Boulder, CO | 27 | 4 | 0.242 | 0.185 | 6 | 0.795 | 0.593 | 7 | 0.626 | 0.482 | 4 | 0.184 | 0.154 | 5 | 0.720 | 0.385 | 5.2 | 0.514 | 0.360 |
| CTNA | Adams, NE | 32 | 3 | 0.122 | 0.094 | 8 | 0.713 | 0.594 | 6 | 0.694 | 0.625 | 5 | 0.285 | 0.188 | 6 | 0.673 | 0.563 | 5.6 | 0.497 | 0.413 |
| CTNB | Chase, NE | 32 | 3 | 0.122 | 0.094 | 7 | 0.704 | 0.656 | 7 | 0.652 | 0.625 | 3 | 0.286 | 0.219 | 7 | 0.683 | 0.563 | 5.4 | 0.489 | 0.431 |
*P < 0.05 (Bonferroni corrected α).
The 5 microsatellite loci had an average of 5.3 alleles per locus per population and ranged between 3 and 10 alleles in each population. Average heterozygosity per locus ranged between 0.12 and 0.71. No significant differences in allele number or heterozygosity were detected among populations.
Phylogenetic Analyses
An ND4 haplotype network was constructed using statistical parsimony with a 95% connection limit (parsimony cutoff = 7 mutational steps) (fig. 2). Approximately 1/3 of the individuals in each population shared haplotype X, which is inferred to be the ancestral haplotype (fig. 2). A star-like pattern of closely related haplotypes appeared to radiate from haplotype X. Of the remaining 63 haplotypes, 47 were unique, occurring in only one individual from the entire sample. Geographic clustering of haplotypes was not observed.
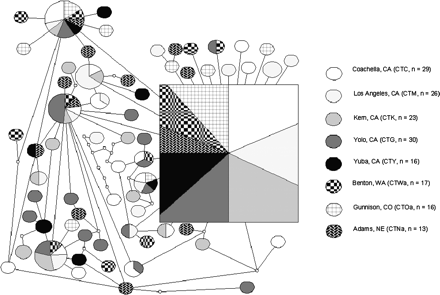
Statistical-parsimony haplotype network with 95% cutoff, inferred from ND4 sequence variation in 8 populations. Each node represents one nucleotide difference. Empty circles indicate inferred haplotypes. Oval or square size is proportional to haplotype frequency.
Population pairwise FST values based on microsatellite allele frequencies were used to generate a UPGMA population phylogeny, in which a constant rate of evolution across populations is assumed and genetic distances between populations are relative. Based on an FST cutoff of 0.05, considered to represent moderate genetic isolation (Wright 1978), 3 population clusters are present. These include 1) 4 California populations (CTM, CTG, CTY, and CTK) along with Colorado and Washington (CTOa, CTOb, CTWa, and CTWb), 2) New Mexico (CTNM) and Nebraska (CTNa and CTNb), and 3) population CTC in California (fig. 3). Population pairwise FST values based on ND4 haplotype frequencies ranged from 0.00 to 0.008. Because pairwise ND4 FST values were very low and nonsignificant, a phylogenetic tree constructed from these data is not presented here.
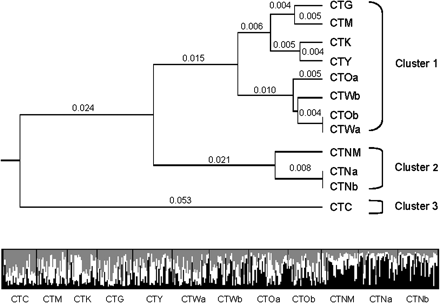
Microsatellite-based clustering analyses. Top panel: UPGMA tree inferred from multilocus microsatellite-derived pairwise FSTvalues. Brackets indicate possible genetic clustering of 3 groups based on cutoff of FST= 0.05. Genetic distance between Cluster 1 and Cluster 2, FST= 0.060; between Cluster 2 and Cluster 3, FST= 0.098; between Cluster 1 and Cluster 3, FST= 0.092. Bottom panel: Plot from microsatellite-based structure analysis at K= 3. Each individual is represented by a vertical bar displaying membership coefficients to each of 3 clusters, depicted as white, gray, and black. Individuals are grouped by collection site.
Population Genetic Structure
The posterior probability for K = 3 clusters in the microsatellite-based multilocus clustering analysis was 0.95. Posterior probabilities for K = 1, 2, and 4–6 were nearly 0. At K = 3, population CTC (Coachella, CA) appeared to be distinct, as did the cluster of CTNM, CTNa, and CTNb (fig. 3), corroborating results from the FST-based UPGMA tree. The remaining populations appear to share similar proportions of ancestry from each of the other 2 groups as well as from a 3rd group. In all cases, high levels of admixture were present within groups and individuals.
Microsatellite-based phylogenetic and cluster analyses were used to designate 3 genetically distinct groups of populations (fig. 3). An AMOVA conducted by partitioning variation among and within groups and populations revealed that ND4 haplotype variation was attributed solely to within-population differences (100%) and not to differences among populations or the 3 geographic regions delineated by microsatellite-derived genetic distances (FCT = −0.002, P = 0.45). In contrast, the microsatellite-based AMOVA indicated that 93% of observed variation in microsatellites was attributed to within-population differences. Approximately 6% of the variation in microsatellite allele frequencies was associated with differences among the 3 regions (FCT = 0.055, P < 0.001), whereas the remaining variation (<2%) was attributed to among-population differences (FST = 0.073, P < 0.001).
Gene Flow among Populations
The Mantel regression for ND4 sequence data (fig. 4) did not yield a significant relationship between genetic and geographic distance (Mantel probability P = 0.823). The Mantel regression of linearized microsatellite FST values on the natural logarithm of pairwise distances among collection sites (fig. 4) revealed isolation by distance. The relationship was positive (slope = 0.054; R2 = 0.084) and statistically significant (Mantel probability P < 0.004).
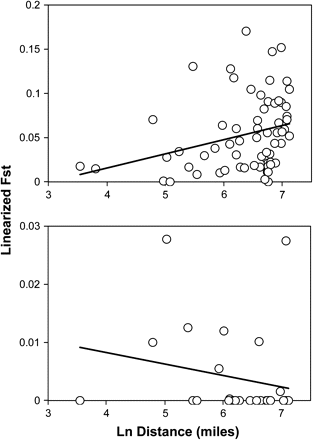
Mantel tests for isolation by distance. Top panel: Regression based on microsatellite-derived FSTvalues among 12 populations. Regression slope = 0.054 ±0.007. R2= 0.084. Mantel probability P<0.004. Bottom panel: Regression based on ND4-derived FSTvalues among 8 populations. Regression slope = −0.002 + 0.002. R2= 0.043. Mantel probability P= 0.81.
Pairwise FST values for ND4 haploytpe data ranged from 0.000 to 0.027, yielding estimated Nm's of 17.73 to infinity. Pairwise ND4 FST values were not significantly different among any of the populations. Mean pairwise FST values for microsatellite allele frequencies ranged from 0.000 to 0.146 resulting in Nm (estimated number of migrants between populations per generation) values between 1.5 and infinity among populations (table 3). Markov chain pairwise exact tests (Goudet et al. 1996) revealed significant differences between population CTC (Coachella, CA) and all other populations including neighboring population CTM (Los Angeles, CA). Both Nebraska populations (CTNa and CTNb) were genetically distinct from populations in all other states except for CTNM in Otero City, New Mexico. Patterns in pairwise FST values were consistent with population structure based on AMOVA and multilocus clustering analyses.
Microsatellite-Derived Pairwise Genetic Differentiation (FST) and Net Number of Migrants (NM) among 12 C. tarsalis Populations in California, Washington, Colorado, New Mexico, and Nebraska
| Coachella, CA | Los Angeles, CA | Kern, CA | Yolo, CA | Yuba, CA | Benton, WA | Benton, WA | Alamogordo, NM | Gunnison, CO | Boulder, CO | Adams, NE | Chase, NE | ||
| CTC | CTM | CTG | CTK | CTY | CTWa | CTWb | CTNM | CTOa | CTOb | CTNa | CTNb | ||
| Coachella, CA | CTC | — | 3.6a | 2.0 | 1.9 | 2.1 | 2.2 | 2.8 | 1.5 | 2.4 | 2.5 | 1.6 | 1.7 |
| Los Angeles, CA | CTM | 0.066b | — | 24.9 | 8.9 | 19.0 | 11.8 | 7.4 | 3.6 | 14.7 | 23.5 | 3.4 | 3.7 |
| Kern, CA | CTG | 0.113* | 0.010 | — | 14.9 | 14.4 | 14.8 | 5.4 | 2.8 | 9.8 | 8.0 | 2.4 | 2.8 |
| Yolo, CA | CTK | 0.115* | 0.027 | 0.016 | — | 30.5 | 4.2 | 5.0 | 3.0 | 8.6 | 4.5 | 2.2 | 2.7 |
| Yuba, CA | CTY | 0.105* | 0.013 | 0.017 | 0.008 | — | 8.3 | 8.1 | 11.6 | 14.0 | 11.3 | 4.8 | 5.7 |
| Benton, WA | CTWa | 0.103* | 0.021 | 0.017 | 0.056* | 0.029 | — | 16.5 | 3.5 | 12.7 | ∞ | 4.2 | 4.5 |
| Benton, WA | CTWb | 0.083* | 0.033 | 0.044* | 0.048* | 0.030* | 0.015 | — | 2.9 | 23.1 | 93.7 | 4.4 | 5.7 |
| Otero, NM | CTNM | 0.146* | 0.065* | 0.082* | 0.076* | 0.021 | 0.066* | 0.078* | — | 3.9 | 4.1 | 16.2 | 13.3 |
| Gunnison, CO | CTOa | 0.095* | 0.017 | 0.025 | 0.028 | 0.018 | 0.019 | 0.011 | 0.06* | — | 213.4 | 5.9 | 8.5 |
| Boulder, CO | CTOb | 0.089* | 0.011 | 0.030 | 0.053* | 0.022 | 0.000 | 0.003 | 0.057* | 0.001 | — | 6.5 | 7.3 |
| Adams, NE | CTNa | 0.132* | 0.069* | 0.095* | 0.102* | 0.049* | 0.056* | 0.053* | 0.015 | 0.041* | 0.037* | — | ∞ |
| Chase, NE | CTNb | 0.128* | 0.063* | 0.083* | 0.084* | 0.042* | 0.052* | 0.042* | 0.018 | 0.029 | 0.033 | 0.000 | — |
| Coachella, CA | Los Angeles, CA | Kern, CA | Yolo, CA | Yuba, CA | Benton, WA | Benton, WA | Alamogordo, NM | Gunnison, CO | Boulder, CO | Adams, NE | Chase, NE | ||
| CTC | CTM | CTG | CTK | CTY | CTWa | CTWb | CTNM | CTOa | CTOb | CTNa | CTNb | ||
| Coachella, CA | CTC | — | 3.6a | 2.0 | 1.9 | 2.1 | 2.2 | 2.8 | 1.5 | 2.4 | 2.5 | 1.6 | 1.7 |
| Los Angeles, CA | CTM | 0.066b | — | 24.9 | 8.9 | 19.0 | 11.8 | 7.4 | 3.6 | 14.7 | 23.5 | 3.4 | 3.7 |
| Kern, CA | CTG | 0.113* | 0.010 | — | 14.9 | 14.4 | 14.8 | 5.4 | 2.8 | 9.8 | 8.0 | 2.4 | 2.8 |
| Yolo, CA | CTK | 0.115* | 0.027 | 0.016 | — | 30.5 | 4.2 | 5.0 | 3.0 | 8.6 | 4.5 | 2.2 | 2.7 |
| Yuba, CA | CTY | 0.105* | 0.013 | 0.017 | 0.008 | — | 8.3 | 8.1 | 11.6 | 14.0 | 11.3 | 4.8 | 5.7 |
| Benton, WA | CTWa | 0.103* | 0.021 | 0.017 | 0.056* | 0.029 | — | 16.5 | 3.5 | 12.7 | ∞ | 4.2 | 4.5 |
| Benton, WA | CTWb | 0.083* | 0.033 | 0.044* | 0.048* | 0.030* | 0.015 | — | 2.9 | 23.1 | 93.7 | 4.4 | 5.7 |
| Otero, NM | CTNM | 0.146* | 0.065* | 0.082* | 0.076* | 0.021 | 0.066* | 0.078* | — | 3.9 | 4.1 | 16.2 | 13.3 |
| Gunnison, CO | CTOa | 0.095* | 0.017 | 0.025 | 0.028 | 0.018 | 0.019 | 0.011 | 0.06* | — | 213.4 | 5.9 | 8.5 |
| Boulder, CO | CTOb | 0.089* | 0.011 | 0.030 | 0.053* | 0.022 | 0.000 | 0.003 | 0.057* | 0.001 | — | 6.5 | 7.3 |
| Adams, NE | CTNa | 0.132* | 0.069* | 0.095* | 0.102* | 0.049* | 0.056* | 0.053* | 0.015 | 0.041* | 0.037* | — | ∞ |
| Chase, NE | CTNb | 0.128* | 0.063* | 0.083* | 0.084* | 0.042* | 0.052* | 0.042* | 0.018 | 0.029 | 0.033 | 0.000 | — |
Upper corner: NM (number of migrants per generation) estimated from FST values.
Lower corner: Pairwise FST values.
P < 0.001 using Bonferroni adjusted α. Significance was determined by permutation testing (1,000 permutations; Arlequin v. 2.0).
Microsatellite-Derived Pairwise Genetic Differentiation (FST) and Net Number of Migrants (NM) among 12 C. tarsalis Populations in California, Washington, Colorado, New Mexico, and Nebraska
| Coachella, CA | Los Angeles, CA | Kern, CA | Yolo, CA | Yuba, CA | Benton, WA | Benton, WA | Alamogordo, NM | Gunnison, CO | Boulder, CO | Adams, NE | Chase, NE | ||
| CTC | CTM | CTG | CTK | CTY | CTWa | CTWb | CTNM | CTOa | CTOb | CTNa | CTNb | ||
| Coachella, CA | CTC | — | 3.6a | 2.0 | 1.9 | 2.1 | 2.2 | 2.8 | 1.5 | 2.4 | 2.5 | 1.6 | 1.7 |
| Los Angeles, CA | CTM | 0.066b | — | 24.9 | 8.9 | 19.0 | 11.8 | 7.4 | 3.6 | 14.7 | 23.5 | 3.4 | 3.7 |
| Kern, CA | CTG | 0.113* | 0.010 | — | 14.9 | 14.4 | 14.8 | 5.4 | 2.8 | 9.8 | 8.0 | 2.4 | 2.8 |
| Yolo, CA | CTK | 0.115* | 0.027 | 0.016 | — | 30.5 | 4.2 | 5.0 | 3.0 | 8.6 | 4.5 | 2.2 | 2.7 |
| Yuba, CA | CTY | 0.105* | 0.013 | 0.017 | 0.008 | — | 8.3 | 8.1 | 11.6 | 14.0 | 11.3 | 4.8 | 5.7 |
| Benton, WA | CTWa | 0.103* | 0.021 | 0.017 | 0.056* | 0.029 | — | 16.5 | 3.5 | 12.7 | ∞ | 4.2 | 4.5 |
| Benton, WA | CTWb | 0.083* | 0.033 | 0.044* | 0.048* | 0.030* | 0.015 | — | 2.9 | 23.1 | 93.7 | 4.4 | 5.7 |
| Otero, NM | CTNM | 0.146* | 0.065* | 0.082* | 0.076* | 0.021 | 0.066* | 0.078* | — | 3.9 | 4.1 | 16.2 | 13.3 |
| Gunnison, CO | CTOa | 0.095* | 0.017 | 0.025 | 0.028 | 0.018 | 0.019 | 0.011 | 0.06* | — | 213.4 | 5.9 | 8.5 |
| Boulder, CO | CTOb | 0.089* | 0.011 | 0.030 | 0.053* | 0.022 | 0.000 | 0.003 | 0.057* | 0.001 | — | 6.5 | 7.3 |
| Adams, NE | CTNa | 0.132* | 0.069* | 0.095* | 0.102* | 0.049* | 0.056* | 0.053* | 0.015 | 0.041* | 0.037* | — | ∞ |
| Chase, NE | CTNb | 0.128* | 0.063* | 0.083* | 0.084* | 0.042* | 0.052* | 0.042* | 0.018 | 0.029 | 0.033 | 0.000 | — |
| Coachella, CA | Los Angeles, CA | Kern, CA | Yolo, CA | Yuba, CA | Benton, WA | Benton, WA | Alamogordo, NM | Gunnison, CO | Boulder, CO | Adams, NE | Chase, NE | ||
| CTC | CTM | CTG | CTK | CTY | CTWa | CTWb | CTNM | CTOa | CTOb | CTNa | CTNb | ||
| Coachella, CA | CTC | — | 3.6a | 2.0 | 1.9 | 2.1 | 2.2 | 2.8 | 1.5 | 2.4 | 2.5 | 1.6 | 1.7 |
| Los Angeles, CA | CTM | 0.066b | — | 24.9 | 8.9 | 19.0 | 11.8 | 7.4 | 3.6 | 14.7 | 23.5 | 3.4 | 3.7 |
| Kern, CA | CTG | 0.113* | 0.010 | — | 14.9 | 14.4 | 14.8 | 5.4 | 2.8 | 9.8 | 8.0 | 2.4 | 2.8 |
| Yolo, CA | CTK | 0.115* | 0.027 | 0.016 | — | 30.5 | 4.2 | 5.0 | 3.0 | 8.6 | 4.5 | 2.2 | 2.7 |
| Yuba, CA | CTY | 0.105* | 0.013 | 0.017 | 0.008 | — | 8.3 | 8.1 | 11.6 | 14.0 | 11.3 | 4.8 | 5.7 |
| Benton, WA | CTWa | 0.103* | 0.021 | 0.017 | 0.056* | 0.029 | — | 16.5 | 3.5 | 12.7 | ∞ | 4.2 | 4.5 |
| Benton, WA | CTWb | 0.083* | 0.033 | 0.044* | 0.048* | 0.030* | 0.015 | — | 2.9 | 23.1 | 93.7 | 4.4 | 5.7 |
| Otero, NM | CTNM | 0.146* | 0.065* | 0.082* | 0.076* | 0.021 | 0.066* | 0.078* | — | 3.9 | 4.1 | 16.2 | 13.3 |
| Gunnison, CO | CTOa | 0.095* | 0.017 | 0.025 | 0.028 | 0.018 | 0.019 | 0.011 | 0.06* | — | 213.4 | 5.9 | 8.5 |
| Boulder, CO | CTOb | 0.089* | 0.011 | 0.030 | 0.053* | 0.022 | 0.000 | 0.003 | 0.057* | 0.001 | — | 6.5 | 7.3 |
| Adams, NE | CTNa | 0.132* | 0.069* | 0.095* | 0.102* | 0.049* | 0.056* | 0.053* | 0.015 | 0.041* | 0.037* | — | ∞ |
| Chase, NE | CTNb | 0.128* | 0.063* | 0.083* | 0.084* | 0.042* | 0.052* | 0.042* | 0.018 | 0.029 | 0.033 | 0.000 | — |
Upper corner: NM (number of migrants per generation) estimated from FST values.
Lower corner: Pairwise FST values.
P < 0.001 using Bonferroni adjusted α. Significance was determined by permutation testing (1,000 permutations; Arlequin v. 2.0).
Evolutionary Neutrality and Population Expansion
The mismatch distribution of pairwise nucleotide differences among ND4 sequences among all populations exhibited a smooth unimodal distribution characteristic of a large population expansion (Slatkin and Hudson 1991, Rogers and Harpending 1992) (fig. 5). Similar patterns were observed in the individual distributions for each population except for CTK, which exhibited a more ragged distribution (data not shown). The raggedness statistic r (Harpending 1994) was lower than expected under conditions of constant growth (P (r < 0.0336) = 0.088). Study-wide site-frequency spectra reveal an excess of singleton mutations when compared with expected frequencies under neutrality and stable population size (fig. 5). Population-specific spectra produced similar patterns (data not shown).
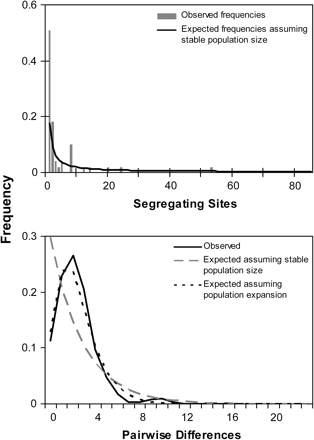
Population expansion signatures in mitochondrial ND4 sequence data. Top panel: Mismatch distribution of observed frequencies of pairwise differences among ND4 sequences and expected frequencies under the neutral model of evolution given the null hypothesis of 1) no population change and 2) population expansion. Bottom panel: Site-frequency spectrum indicating excess of singleton mutations in ND4 sequence. Spectrum compares observed frequencies of segregating sites to expected distribution under the null hypothesis of no population change.
Fu's Fs was negative (Fs = −92.81; P < 0.0001) which occurs when an excess of rare haplotypes is present and suggests that either population expansion or genetic hitchhiking has taken place (Fu 1997). Fu and Li's D* and F* were negative as well (D* = −4.68; P < 0.02; F* = −4.38; P < 0.02), indicating an excess of recently derived haplotypes and suggesting that either population expansion or background selection has occurred (Fu and Li 1993). Strobeck's S, the probability of obtaining equal or fewer haplotypes based on gene frequency and mutation rate was very high in all populations, ranging from 0.995 to 1.000. These results are consistent with deviation from neutrality due to either selection or population expansion.
We tested for signatures of population expansion in microsatellites using the heterozygosity test assuming 2 alternative models of microsatellite evolution. Both models gave results with qualitatively similar trends. Under the SMM, assuming that only single-repeat mutations occur, expected heterozygosity based on the number of alleles and sample size (Heq) was significantly higher than expected heterozygosity based on allele frequencies (He) in 10 of the 12 populations (table 4) Under the TPM, assuming that most mutations are single repeats but multistep mutations occur at a frequency of 5%, 10%, or 15%, the number of populations with significant excesses in Heq fell to 9, 8 and 6 of 12 populations, respectively. All populations with significant Heq > He exhibited this excess for at least 4 of the 5 loci.
Heterozygosity Test for Signatures of Population Expansion in 5 Microsatellite Loci in 12 C. tarsalis Populations in California, Washington, Colorado, New Mexico, and Nebraska
| California | Washington | New Mexico | Colorado | Nebraska | |||||||||
| CTC | CTM | CTG | CTK | CTY | CTWa | CTWb | CTNM | CTOa | CTOb | CTNa | CTNb | ||
| SMM | Heq > He | 5/5* | 4/5 | 4/5* | 4/5* | 5/5* | 5/5* | 4/5* | 5/5* | 5/5* | 3/5 | 5/5* | 5/5* |
| Mean SD | −2.30 | −1.06 | −1.09 | −1.77 | −1.79 | −2.14 | −2.99 | −2.18 | −2.13 | −2.59 | −2.62 | −2.85 | |
| S.E. | (2.26) | (1.55) | (1.35) | (1.80) | (2.35) | (1.13) | (2.09) | (1.74) | (1.82) | (2.84) | (1.79) | (1.41) | |
| TPM, 95% | Heq > He | 5/5* | 4/5 | 4/5 | 4/5* | 5/5* | 4/5* | 4/5* | 5/5* | 4/5* | 3/5 | 5/5* | 5/5* |
| Mean SD | −1.85 | −0.76 | −0.85 | −1.39 | −1.32 | −1.69 | −2.51 | −1.75 | −1.74 | −2.04 | −1.93 | −2.38 | |
| SE | (1.87) | (1.32) | (1.26) | (1.58) | (1.84) | (1.07) | (1.92) | (1.43) | (1.63) | (2.49) | (1.51) | (1.37) | |
| TPM, 90% | Heq > He | 4/5* | 3/5 | 4/5 | 4/5* | 4/5* | 4/5* | 4/5* | 5/5* | 3/5 | 3/5 | 5/5* | 5/5* |
| Mean SD | −1.64 | −0.63 | −0.65 | −1.26 | −1.10 | −1.50 | −2.23 | −1.41 | −1.43 | −1.79 | −1.80 | −1.98 | |
| SE | (1.91) | (1.27) | (1.17) | (1.59) | (1.86) | (1.03) | (1.85) | (1.20) | (1.47) | (2.36) | (1.53) | (1.30) | |
| TPM, 85% | Heq > He | 4/5* | 3/5 | 4/5 | 4/5 | 3/5 | 4/5* | 4/5* | 5/5* | 3/5 | 3/5 | 5/5* | 5/5* |
| Mean SD | −1.43 | −0.49 | −0.50 | −1.03 | −1.00 | −1.27 | −2.01 | −1.23 | −1.25 | −1.55 | −1.57 | −1.77 | |
| SE | (1.71) | (1.15) | (1.06) | (1.44) | (1.82) | (1.98) | (1.75) | (1.10) | (1.43) | (1.24) | (1.46) | (1.25) | |
| California | Washington | New Mexico | Colorado | Nebraska | |||||||||
| CTC | CTM | CTG | CTK | CTY | CTWa | CTWb | CTNM | CTOa | CTOb | CTNa | CTNb | ||
| SMM | Heq > He | 5/5* | 4/5 | 4/5* | 4/5* | 5/5* | 5/5* | 4/5* | 5/5* | 5/5* | 3/5 | 5/5* | 5/5* |
| Mean SD | −2.30 | −1.06 | −1.09 | −1.77 | −1.79 | −2.14 | −2.99 | −2.18 | −2.13 | −2.59 | −2.62 | −2.85 | |
| S.E. | (2.26) | (1.55) | (1.35) | (1.80) | (2.35) | (1.13) | (2.09) | (1.74) | (1.82) | (2.84) | (1.79) | (1.41) | |
| TPM, 95% | Heq > He | 5/5* | 4/5 | 4/5 | 4/5* | 5/5* | 4/5* | 4/5* | 5/5* | 4/5* | 3/5 | 5/5* | 5/5* |
| Mean SD | −1.85 | −0.76 | −0.85 | −1.39 | −1.32 | −1.69 | −2.51 | −1.75 | −1.74 | −2.04 | −1.93 | −2.38 | |
| SE | (1.87) | (1.32) | (1.26) | (1.58) | (1.84) | (1.07) | (1.92) | (1.43) | (1.63) | (2.49) | (1.51) | (1.37) | |
| TPM, 90% | Heq > He | 4/5* | 3/5 | 4/5 | 4/5* | 4/5* | 4/5* | 4/5* | 5/5* | 3/5 | 3/5 | 5/5* | 5/5* |
| Mean SD | −1.64 | −0.63 | −0.65 | −1.26 | −1.10 | −1.50 | −2.23 | −1.41 | −1.43 | −1.79 | −1.80 | −1.98 | |
| SE | (1.91) | (1.27) | (1.17) | (1.59) | (1.86) | (1.03) | (1.85) | (1.20) | (1.47) | (2.36) | (1.53) | (1.30) | |
| TPM, 85% | Heq > He | 4/5* | 3/5 | 4/5 | 4/5 | 3/5 | 4/5* | 4/5* | 5/5* | 3/5 | 3/5 | 5/5* | 5/5* |
| Mean SD | −1.43 | −0.49 | −0.50 | −1.03 | −1.00 | −1.27 | −2.01 | −1.23 | −1.25 | −1.55 | −1.57 | −1.77 | |
| SE | (1.71) | (1.15) | (1.06) | (1.44) | (1.82) | (1.98) | (1.75) | (1.10) | (1.43) | (1.24) | (1.46) | (1.25) | |
NOTE.—Fractions indicate number of loci (out of 5) with Heq > He. Mean SD and SE are mean standardized deviations from equilibrium heterozygosity along with associated standard error. s2 = 30 for all TPMs.
* Statistically significant Heq excess (1-tailed Wilcoxon rank-sum test; P < 0.05).
Heterozygosity Test for Signatures of Population Expansion in 5 Microsatellite Loci in 12 C. tarsalis Populations in California, Washington, Colorado, New Mexico, and Nebraska
| California | Washington | New Mexico | Colorado | Nebraska | |||||||||
| CTC | CTM | CTG | CTK | CTY | CTWa | CTWb | CTNM | CTOa | CTOb | CTNa | CTNb | ||
| SMM | Heq > He | 5/5* | 4/5 | 4/5* | 4/5* | 5/5* | 5/5* | 4/5* | 5/5* | 5/5* | 3/5 | 5/5* | 5/5* |
| Mean SD | −2.30 | −1.06 | −1.09 | −1.77 | −1.79 | −2.14 | −2.99 | −2.18 | −2.13 | −2.59 | −2.62 | −2.85 | |
| S.E. | (2.26) | (1.55) | (1.35) | (1.80) | (2.35) | (1.13) | (2.09) | (1.74) | (1.82) | (2.84) | (1.79) | (1.41) | |
| TPM, 95% | Heq > He | 5/5* | 4/5 | 4/5 | 4/5* | 5/5* | 4/5* | 4/5* | 5/5* | 4/5* | 3/5 | 5/5* | 5/5* |
| Mean SD | −1.85 | −0.76 | −0.85 | −1.39 | −1.32 | −1.69 | −2.51 | −1.75 | −1.74 | −2.04 | −1.93 | −2.38 | |
| SE | (1.87) | (1.32) | (1.26) | (1.58) | (1.84) | (1.07) | (1.92) | (1.43) | (1.63) | (2.49) | (1.51) | (1.37) | |
| TPM, 90% | Heq > He | 4/5* | 3/5 | 4/5 | 4/5* | 4/5* | 4/5* | 4/5* | 5/5* | 3/5 | 3/5 | 5/5* | 5/5* |
| Mean SD | −1.64 | −0.63 | −0.65 | −1.26 | −1.10 | −1.50 | −2.23 | −1.41 | −1.43 | −1.79 | −1.80 | −1.98 | |
| SE | (1.91) | (1.27) | (1.17) | (1.59) | (1.86) | (1.03) | (1.85) | (1.20) | (1.47) | (2.36) | (1.53) | (1.30) | |
| TPM, 85% | Heq > He | 4/5* | 3/5 | 4/5 | 4/5 | 3/5 | 4/5* | 4/5* | 5/5* | 3/5 | 3/5 | 5/5* | 5/5* |
| Mean SD | −1.43 | −0.49 | −0.50 | −1.03 | −1.00 | −1.27 | −2.01 | −1.23 | −1.25 | −1.55 | −1.57 | −1.77 | |
| SE | (1.71) | (1.15) | (1.06) | (1.44) | (1.82) | (1.98) | (1.75) | (1.10) | (1.43) | (1.24) | (1.46) | (1.25) | |
| California | Washington | New Mexico | Colorado | Nebraska | |||||||||
| CTC | CTM | CTG | CTK | CTY | CTWa | CTWb | CTNM | CTOa | CTOb | CTNa | CTNb | ||
| SMM | Heq > He | 5/5* | 4/5 | 4/5* | 4/5* | 5/5* | 5/5* | 4/5* | 5/5* | 5/5* | 3/5 | 5/5* | 5/5* |
| Mean SD | −2.30 | −1.06 | −1.09 | −1.77 | −1.79 | −2.14 | −2.99 | −2.18 | −2.13 | −2.59 | −2.62 | −2.85 | |
| S.E. | (2.26) | (1.55) | (1.35) | (1.80) | (2.35) | (1.13) | (2.09) | (1.74) | (1.82) | (2.84) | (1.79) | (1.41) | |
| TPM, 95% | Heq > He | 5/5* | 4/5 | 4/5 | 4/5* | 5/5* | 4/5* | 4/5* | 5/5* | 4/5* | 3/5 | 5/5* | 5/5* |
| Mean SD | −1.85 | −0.76 | −0.85 | −1.39 | −1.32 | −1.69 | −2.51 | −1.75 | −1.74 | −2.04 | −1.93 | −2.38 | |
| SE | (1.87) | (1.32) | (1.26) | (1.58) | (1.84) | (1.07) | (1.92) | (1.43) | (1.63) | (2.49) | (1.51) | (1.37) | |
| TPM, 90% | Heq > He | 4/5* | 3/5 | 4/5 | 4/5* | 4/5* | 4/5* | 4/5* | 5/5* | 3/5 | 3/5 | 5/5* | 5/5* |
| Mean SD | −1.64 | −0.63 | −0.65 | −1.26 | −1.10 | −1.50 | −2.23 | −1.41 | −1.43 | −1.79 | −1.80 | −1.98 | |
| SE | (1.91) | (1.27) | (1.17) | (1.59) | (1.86) | (1.03) | (1.85) | (1.20) | (1.47) | (2.36) | (1.53) | (1.30) | |
| TPM, 85% | Heq > He | 4/5* | 3/5 | 4/5 | 4/5 | 3/5 | 4/5* | 4/5* | 5/5* | 3/5 | 3/5 | 5/5* | 5/5* |
| Mean SD | −1.43 | −0.49 | −0.50 | −1.03 | −1.00 | −1.27 | −2.01 | −1.23 | −1.25 | −1.55 | −1.57 | −1.77 | |
| SE | (1.71) | (1.15) | (1.06) | (1.44) | (1.82) | (1.98) | (1.75) | (1.10) | (1.43) | (1.24) | (1.46) | (1.25) | |
NOTE.—Fractions indicate number of loci (out of 5) with Heq > He. Mean SD and SE are mean standardized deviations from equilibrium heterozygosity along with associated standard error. s2 = 30 for all TPMs.
* Statistically significant Heq excess (1-tailed Wilcoxon rank-sum test; P < 0.05).
The date of the population growth event in mutational time, or τ, was calculated to be 1.285 μ generations, where μ is the sequence's mutation rate per generation. Calculation of τ was based on the average number of pairwise differences among ND4 sequences (DnaSP v. 4.0). We used this value to estimate the approximate timing of the population expansion by the equation τ = 2μt (Slatkin and Hudson 1991), where μ was conservatively estimated as 5.7 × 10−8 substitutions/site/year (Tamura 1992) and t is time in generations. Solving for t, t = τ/2μ = 1.285/(2 × 5.7 × 10−8) = 11,271,930 generations. Assuming an average of 20–30 generations per year, we estimate that the population expansion occurred approximately 375,000–560,000 years ago. This date range should be regarded as preliminary due to the small size of the analyzed sequence and rough estimation of the gene's mutation rate.
Discussion
Sequence analysis of the ND4 mitochondrial DNA fragment from C. tarsalis populations across 4 states revealed a lack of isolation by distance, genetic structuring, and clustering of haplotypes by population or geographic region. Taken alone, ND4 results suggest that either: 1) current gene flow is very high across a large geographic range, 2) C. tarsalis experienced a selective mitochondrial sweep, or 3) C. tarsalis underwent an expansion that genetically homogenized populations after which there has been insufficient time for signatures of mitochondrial population structure to be detected. Previous allozyme data (Gimnig et al. 1999) and our microsatellite results suggest that populations are not panmictic across the collection range, refuting the 1st hypothesis. Evidence for selective mitochondrial sweeps in conjunction with invasion of maternally inherited Wolbachia endosymbionts have been observed in the congeneric Culex pipiens species complex (Rasgon, Cornel, Scott 2006), but because C. tarsalis is not infected with Wolbachia (Rasgon and Scott 2004) hypothesis 2 is not a likely explanation of our results.
The most likely explanation for our observations is that C. tarsalis underwent a population expansion some time in the relatively recent past. Statistical signatures of population expansion are detectable in both ND4 and microsatellite data. ND4 statistical parsimony analysis shows a star-shaped phylogeny (Slatkin and Hudson 1991) and a large number of rare haplotypes separated by single-nucleotide differences. H and K tests, Strobeck's S statistics, and site-frequency spectra were consistent with the presence of a rapidly growing population, whereas mismatch distributions indicated that a single or few haplotypes spread and mutated to generate several closely related haplotypes, as is often observed during population expansion (Rogers and Harpending 1992). Fu's Fs and Fu and Li's D* and F* all indicated a significant negative deviation from evolutionary neutrality. Though it is impossible to distinguish between selection and expansion as the cause of negative Fs, D*, and F* values, these statistics in combination with our microsatellite data are indicative of a deviation from equilibrium which was likely caused by population expansion.
Several populations demonstrated an excess in expected microsatellite heterozygosity based on microsatellite allele number (Heq) when compared with expected heterozygosity based on allele frequencies (He), which occurs under conditions of rapid population growth (Cornuet and Luikart 1996). Heterozygote excess based on allele number was most pronounced under the SMM, though populations exhibited moderate to widespread Heq excess and no significant deficiencies across all models tested, providing corroborative evidence of population expansion. An alternate explanation for Heq > He is the influx of rare alleles from genetically distinct populations (Cornuet and Luikart 1996). This phenomenon is unlikely because multiple populations over a large geographic range demonstrated the same pattern.
Our results represent an example of how current estimates of gene flow, particularly those based on mitochondrial sequences, may be exaggerated due to past events such as range expansion. Evidence of population expansion has recently been found in many disease vectors including Triatoma infestans, Amblyomma americanum, Anopheles funestus, Anopheles darlingi, Simulium tani, Anopheles gambiae, and A. dirus (Walton et al. 2000, Donnelly et al. 2001, Pramual et al. 2005, Bargues et al. 2006, Michel et al. 2006, Mirabello and Conn 2006, Mixson et al. 2006), suggesting that it may not be an uncommon phenomenon in arthropods. Because both extensive gene flow and range expansion can produce similar patterns in mitochondrial sequence data, lack of isolation by distance and significant partitioning of variance among groups or populations may not necessarily be indicative of current panmixia. Instead, they may reflect historical events and should be interpreted carefully.
ND4 sequences suggest that the expansion of C. tarsalis in the western United States occurred between 375,000 and 560,000 years ago. Other studies of Anopheles population dynamics have suggested that range expansions in Africa and Asia may be associated with changes in agricultural practices (Walton et al. 2000, Donnelly et al. 2001). Our estimate predates human civilization and the development of agriculture in North America by well over 300,000 years, suggesting that the expansion was likely not influenced by anthropogenic forces. Instead, it is more likely to have been associated with climatic changes such as the Nebraskan or Kansan stages of Pleistocene glaciation (Dreeszen 1970) that occurred in the midwestern and western United States between 350,000 and 1 MYA.
Microsatellites in our study reflected both signatures of population expansion (nonequilibrium conditions) and isolation by distance (consistent with evolutionary equilibrium). Microsatellites have been shown to have higher rates of mutation than mitochondrial genes, ranging in insects and mammals from 10−3 to 10−6 mutations per locus per generation (Dietrich et al. 1992; Edwards et al. 1992; Weber and Wong 1993; Schug et al. 1997, 1998), whereas mitochondrial gene mutation rates have been estimated at 9.4 × 10−8 substitutions per 4-fold degenerate site in mammals (Brown et al. 1982) and at 5.7 × 10−8 substitutions in Drosophila species (Tamura 1992). The discrepancy between microsatellite and mitochondrial-derived genetic structure may be attributed to the fact that after range expansion rapidly mutating microsatellites have begun to differentiate among populations, whereas the more slowly mutating mitochondrial gene does not reflect the presence of genetically isolated populations.
Microsatellite-based population structure did not appear to be associated with major geographic features such as the Cascade, Sierra Nevada, or Rocky Mountain ranges. The Tehachapi Mountain range has previously been associated with genetic structure among southern California C. tarsalis populations (Gimnig et al. 1999). Although we observed that populations south of the Tehachapis (CTC and CTM) were genetically distinct from each other, the divergence did not seem to be associated with this mountain range. Interestingly, although the 2 Nebraska populations appeared to be panmictic and cluster with New Mexico, they were genetically distinct from both Colorado populations, which fall on either side of the Rocky Mountains. These results suggest that there may be a barrier to gene flow between the 2 neighboring states that is not associated with the Rockies. The arid Great Plains, which ranges across eastern Colorado and New Mexico to Iowa, may limit migration between populations in Colorado and Nebraska.
Generally, patterns of gene flow inferred from microsatellite data exhibit isolation by distance and geographical clustering but are not sufficiently explained by topographical barriers or geographic distance alone. This phenomenon may result from an insufficient number of loci, movement of mosquitoes based on agricultural practices or other environmental features beyond distance and elevation, or residual effects of range expansion. The inclusion of more loci and populations from as yet unsampled regions will likely address the first 2 possibilities. Regardless, it is still likely that microsatellites reflect only a partial return to evolutionary equilibrium after the expansion event because they exhibit signatures of both equilibrium and nonequilibrium conditions. The fact that microsatellites may underestimate current levels of genetic isolation among populations in the western United States should be taken into account when gathering and interpreting further information on the genetic structure of C. tarsalis.
Culex tarsalis is known to exhibit significant spatial and temporal heterogeneity in a variety of phenotypic traits including autogeny, feeding behavior, and vertical and horizontal arboviral transmission. Thus far, genetic and environmental determinants of such phenotypic variation, including WNV transmission, are largely unknown. Although our findings of microsatellite-based genetic structure may not reflect the full extent of reproductive isolation across the western United States, they are indicative of significant genetic differentiation among mosquito populations and thus allow for the possibility of a relationship between genetic and spatial variation in WNV vector competence. Genetic determinants of vector–pathogen interactions have been identified in several other systems by quantitative trait locus (QTL) analysis, including transovarial transmission of LaCrosse virus in Ochlerotatus triseriatus, midgut infection and escape of dengue virus in Aedes aegypti, and Plasmodium resistance in A. gambiae (Bosio et al. 2000, Graham et al. 2003, Zheng et al. 2003, Gomez-Machorro et al. 2004). Recently, Plasmodium resistance was mapped in naturally occurring populations of A. gambiae in Kenya (Menge et al. 2006) and Mali (Riehle et al. 2006). QTL analyses such as these may lay the foundation for developing biomarkers of vector susceptibility and novel targets for genetic manipulation and disease control. Future studies on genetic and phenotypic spatial variation of C. tarsalis will provide the foundation for understanding genetic determinants of viral susceptibility and disease transmission in this important arboviral vector.
Supplementary Material
The sequence data for this paper appear in GenBank under accession numbers EF125799–EF125862.
We thank W. K. Reisen for kindly providing colony and field specimens. We thank H. Lothrop, D. Lemenager, A. Moser, M. Weissman, M. DiMenna, W. L. Kramer, and M. Stromer for providing field collections. This work was funded by National Institute of Environmental Health Sciences Training Grant T32 ES07141, National Institutes of Health Grant R01AI067371 and the Johns Hopkins Malaria Research Institute. Research conducted at The W. Harry Feinstone Department of Molecular Microbiology and Immunology, Bloomberg School of Public Health, Johns Hopkins University, Baltimore, MD.
References
Author notes
Marcy Uyenoyama, Associate Editor



