A decision support tool for the first stage of the tempering process of organic wheat grains in a mill

decision support tool, industry 4.0, multiple regression, wheat tempering

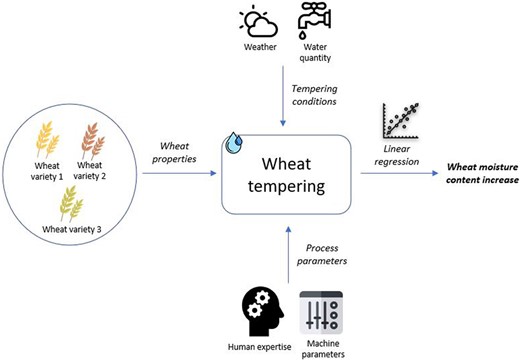
Highlights

The decision support tool is based on a multiple linear regression model
The LASSO model was found to outperform the other regression model with an average prediction error of 0.428%
The accuracy of predicting the increase in moisture content of organic wheat has been improved by considering weather conditions.
The flow of water and wheat were found to be the most influential parameters for an increase in wheat moisture content.

Introduction

Wheat is one of the most cultivated cereals in the world (FAO, 2021). Millers are responsible for transforming grains of wheat into types of flour that have different quality requirements (Posner & Hibbs, 2005). Quality requirements vary depending on the intended uses of the flour, the market and whether it is conventional or organic flour. Organic flour is produced from organic wheat without any synthetic preservatives (Rana & Paul, 2017) and with strictly limited, pre-authorised ingredients (Government of Canada, 2022). The global organic food and beverage market is rapidly growing. Recent data have shown that the sales of organic food continue to grow and reached a value of over 120 billion Euros in 2020 (Willer et al., 2022). This growing demand is driven by consumer expectations (Rana & Paul, 2017; Willer et al., 2022).

At a mill, grains of wheat are cleaned, eventually blended, tempered and finally, milled (Parrenin et al., 2023). Cleaning and tempering grains of wheat conditions it for milling operations (IAOM, 2018). By cleaning the grains of wheat, all impurities and foreign materials that could damage machines and impact flour quality are removed. Then, tempering is done by adding water to the grains to increase their moisture content. This operation improves the efficiency of milling (Rana & Paul, 2017).

Many studies have shown the importance and impact of the tempering process on milling performance, flour quality and energy grinding (Fang & Campbell, 2003; Kweon et al., 2009; Cappelli et al., 2020). Depending on the quality of the wheat grains and the desired quality of the flour, the miller must adjust the process. Complexity increases when wheat blends are involved (Hook et al., 1984). As wheat water absorption is different for each batch of wheat, the miller relies on his knowledge and experience to correctly adjust the tempering parameters. Better knowledge of the different factors and parameters that influence the water absorption of wheat in a mill would allow for effective decisions on tempering adjustments, under specific manufacturing conditions.

The objective of this paper is to develop a decision support tool to predict an increase in wheat moisture content at the end of the first stage of tempering, based on wheat properties, operating conditions and process parameters. From the model that is built, it would then be possible to acquire knowledge about the impact variables and their influence on the process.

A literature review is presented in Section 2. Section 3 presents the proposed decision support tool. Section 4 presents the results obtained. The results are analysed and assessed in Section 5.

Literature review

Tempering process in a wheat mill plant

The tempering process conditions the wheat before milling. An optimal wheat moisture level for the milling process is necessary. If the grains of wheat are over-dampened, the milling operation becomes difficult, and the flour yield of the mill is immediately reduced. Too little tempering moisture makes the grain crumbly and leads to bran contamination of the flour. Although Gwirtz (1998) shows the importance of the tempering process, this process remains difficult to control (Willm, 2009).

Figure 1 shows a diagram of the tempering process of the grains of wheat. The cleaned grain is stored in silos. Flow controllers on each silo control the flow of grains sent to the dampening machine. In the dampening machine, a constant flow of water is injected into the grains of wheat. The tempering screw in the dampening machine allows the movement of the wheat and efficiently mixes the wheat (Willm, 2009). Finally, the grains of tempered wheat are stored again in silos so that they can rest and absorb the water particles on their surface.

Figure 1

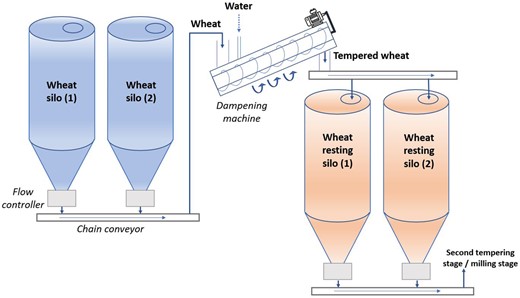
Diagram of the wheat grains' tempering process.

The tempering process acts in several stages. In each stage, a flow of water is sent to a moistening screw, through which the wheat grains pass. A rest period is then necessary for the grains in a silo to allow the water particles present on the surface to penetrate the grain. The number of stages depends on several factors, such as the quality of the wheat grains and environmental conditions. The tempering aims to moisten the wheat to facilitate the separation of the endosperm from the rest of the grain component in the milling process. This phenomenon is explained by the fact that the water absorption of the grains will increase the wheat bran's flexibility and soften the endosperm (Willm, 2009).

Although this mechanism is the one that is the most frequently used in a wheat mill, it is worth mentioning that different tempering techniques and dampening machines exist. Bühler developed a vortex dampener to dampen the grains of wheat in a less brutal way (Willm, 2009). Other than tempering grains of wheat by a flow of water, steam tempering is possible.

In a mill, the miller learns to master the tempering process from their own knowledge and experience. To reach a certain level of wheat moisture at the end of the tempering stage, the miller fixes a target moisture content. This target changes depending on the type of flour desired. The type of flour varies based on its final purpose and its quality attributes that include protein content (%), moisture content (%), ash content (%) and falling number (FN).

Considering the target moisture content (Ht), the flow of the wheat grains (Fwg) and the initial moisture content of the wheat grains (Hi), the miller calculates the flow of water required during the tempering process (Fw), as follows (Willm, 2009; IAOM, 2018):

Fw (L / h) = \frac{(Ht - Hi) * Fwg}{100 - Ht}

(1)

Analysis of experiments on tempering wheat grains

In the literature, there are various experiments that have been conducted to better understand wheat tempering in a controlled environment. These experiments could be grouped into two approaches: an analysis of the rate of water uptake into the grain, and an analysis of the influence of grain moisture content on milling operations.

The first approach analyses and models the rate of moisture uptake in wheat grains when they are immersed in water for several hours. The objective is to better understand the biological characteristics of grains and the process variables that could influence the rate of moisture uptake by conducting experiments. Different techniques are developed using deep learning algorithms and diffusion equations. Kang (1999) showed that the water uptake is faster in the endosperm than in the bran layer, suggesting that the bran layer of the wheat acts as a barrier to water absorption. When analysing the endosperm composition, Moss (1977) showed that the protein content and initial moisture content greatly influence water penetration into the wheat grain. Tagawa et al. (2003) determined different diffusion coefficients of water in a wheat grain for different water temperature levels, ranging from 10 to 50 degrees. They showed that the soaking temperature influences the water uptake of grains of wheat and that higher temperature increases the rate of water uptake. Kashaninejad et al. (2009) confirmed this result and showed the relevance of an artificial neural network (ANN) for simulating the soaking behaviour and the effect of temperature and time on the hydration in wheat grain. In this context, temperature and soaking time were used in the ANN model as input parameters, while water content was used as the output parameter that needed to be predicted. The application of higher temperatures during the tempering stage could reduce the necessary resting time for the grains of wheat.

The second approach is to study the different levels of grain moisture content and measure its effect on milling operations. Fang & Campbell (2003) predict flour particle size distribution from an extended breakage function based on different roll gaps and moisture content. A mathematical equation estimates the milling performance according to an operative milling setup (roller gaps and disposition) and the grain quality (grain moisture and grain size). Kweon et al. (2009) analysed the effect of tempering conditions for soft red winter wheat on milling performance and flour quality. A full factorial design of experience including initial wheat moisture, tempered wheat moisture, tempering temperature and tempering time at two levels for each factor was conducted. They found that the tempered wheat moisture had the largest effect on milling performance and flour quality. As the wheat tempering increases, flour yield decreases and flour quality increases. Similarly, Cappelli et al. (2020) evaluated the effect of milling speed and wheat tempering on milling performance, energy consumption, dough quality and bread quality. They confirmed previous results, indicating that the moisture content had a significant influence on mill performance and flour quality related to the rheology of the dough and the quality of the bread. From the four tempering moisture levels studied, they found that 13% moisture was the best compromise between milling and bread-making performance.

Both approaches are based on experimental measurements in a controlled environment. However, there is still a need to focus on the tempering of wheat grains in the manufacturing process. Indeed, wheat grains in a mill plant are subjected to environmental factors and often include grain mixtures. In this context, the development of a decision support tool that can take these factors into account seems of interest. It would help overcome actual manufacturing challenges that are not present in a controlled environment. The following section explains the materials and methods used in the development of this tool.

Materials and methods

The objective of the proposed decision support tool is to help operators adjust the tempering parameters in their environment to condition the grains of wheat as desired. The aim of this tool is to predict the wheat moisture level that would be reached at the end of the tempering process, based on the factors and process parameter inputs. The tool is developed and tested in a case study at an organic wheat mill plant. First, the characteristics of the organic wheat mill are presented. Then, the materials used at the mill to analyse the wheat samples and to perform the tempering operation are described. The predictive models used to build the decision support tools are explained. Finally, the method followed in the development of the decision support tool for the wheat grain tempering process is detailed.

Characteristics of the organic wheat mill plant

The organic wheat mill is located in Saint-Jean-Sur-Richelieu, Quebec, Canada, and is operated by the company La Milanaise. La Milanaise specialises in the transformation of organic cereals into organic flour in Canada. At the mill, up to three tempering stages can be performed to condition the grains of wheat. Four wheat resting silos, each with a capacity of approximately 80 metric tonnes are available for the first and second tempering stages. The third stage is achieved by recirculating the wheat at the beginning of the second stage. A second and third tempering stage is sometimes necessary when the desired moisture level of the wheat grains is not reached at the end of the first stage. This can be due to an excessive difference between the initial and the desired moisture level or to a relatively slow absorption rate of the wheat. This study focuses on the first stage, which is usually carried out, except when the moisture content of the grains is already sufficiently high (16% or above). The mill is located in a climate that is characterised by extremes of heat and cold throughout the year that tends to worsen with the effects of climate change (Almaraz et al., 2008). In Saint-Jean-Sur-Richelieu, wheat grains are subject to large temperature variations, from −32 °C on the coldest days to 36 °C on the warmest days of the year (Government of Canada, 2021). Based on historical weather data for the year 2021, large variations in relative humidity with a range extending from 36.5% to 95.5% are noted as well (Government of Canada, 2021). These conditions place this mill within a specific context that is different from other mills located in other regions of the world (e.g. Europe, North Africa or the United States). The production parameters of the tempering process must therefore be closely monitored throughout the year.

Materials

Raw materials and wheat tempering

Production data from the company, collected over an 18-month period from March 2020 to September 2021, were used to develop and analyse the prediction models. The data are separated into two sets: training and prediction.

The wheat that is studied was grown on organic farms in Canada. The wheat underwent a tempering stage before being milled. Upon arrival, organic wheat grains were pre-cleaned and stored in certain silos according to their quality, measured by the BEM (Brabender Energy Max) indicator (Rakita et al., 2018). Selected wheat grains are then cleaned and blended to be ready for the tempering process. At this stage, a sample of about 300 g of wheat grains is taken at the beginning and the end of the tempering process. An infrared thermometer is used to control the temperature of the grains of wheat. A near-infrared spectrometry (Perten IM9500 NIR) is used to analyse the protein and moisture content of the grains of wheat. The NIR technique has proven to be a reference in the grain milling industry to rapidly analyse the intrinsic properties of wheat grains. Miralbés (2003) showed that the NIR transmittance can be used to predict protein and moisture content of whole wheat grains with high levels of accuracy. The prediction of protein and moisture content reached an R² of 0.99 when compared to the reference method. These predictions can be used for wheat from different origins. The tempering process at this mill is realised with an intensive dampening machine. This machine sends a constant flow of water to the wheat grains, which is set up by the miller. The action of the tempering screw ensures that the wheat grains advance and are mixed well.

Predictive models

Despite the advances in deep learning models in terms of performance (Goodfellow et al., 2016) and their use in the field of wheat processing (Sabanci et al., 2020; Assadzadeh et al., 2022), models such as artificial neural network (ANN) are still difficult to interpret and require large amounts of data to be trained and to achieve good performance.

As a result of (i) the limited amount of data available in this study, (ii) the need to explain the model for the decision support tool and (iii) the prediction of a continuous output variable, regression models have been preferred. Several different regression models can be used in this specific case, such as linear regression, polynomial regression, RIDGE regression, LASSO regression, ElasticNet regression and regression trees. The goal is to produce a regression model that more accurately predicts the output variable, without overfitting the data. A multi-linear regression equation is mathematically represented as follows:

y = β_{0} + β_{1} X_{1} + \dots + β_{p} X_{p} + ϵ .

(2)

The output variable y will represent the percentage increase in the moisture content of the wheat that is achieved at the end of the first stage of tempering. Each independent variable (X_i) is associated with a coefficient (β_i) that indicates the importance and impact of the variable on the output variable. Residual sum of squares (RSS) is used to fit the regression model (see eqn 3). The β_i coefficients are adjusted to minimise this loss function. Ordinary least squares (OLS) is a statistical technique that best fits the coefficient of a linear regression model based on the RSS loss function (James et al., 2013).

RSS = \sum_{i = 1}^{n} {(y_{i} - β_{0} - \sum_{j = 1}^{p} β_{j} x_{ij})}^{2} .

(3)

If several independent variables are correlated, there is a risk of multicollinearity, which adds noise to the model. This implies that the estimated coefficient will not be able to generalise future data well, and the model will result in poor prediction performance. Regularisation models such as LASSO, RIDGE and Elastic Net are used to reduce the risk of multicollinearity. The adjustment of the hyperparameters in these models penalises specific correlated independent variables. The penalty terms added to the loss function aim to reduce or eliminate the influence of independent variables on the model depending on the regularisation model used. The difference between regularisation models is the penalty added to RSS:

L_{LASSO} = RSS + λ \sum_{j = 1}^{p} ∣ β_{j} ∣,

(4)

L_{Ridge} = RSS + λ \sum_{j = 1}^{p} β_{j}^{2},

(5)

L_{ElasticNet} = \frac{RSS}{2} + λ (\frac{1 - α}{2} \sum_{j = 1}^{p} β_{j}^{2} + α \sum_{j = 1}^{p} |β_{j}|) .

(6)

Linear regression is one of many algorithms that may be used to solve regression problems. Another method, among the supervised learning algorithms, that can be used as a regularisation technique for a regression problem is XGBoost. XGBoost is a gradient-boosted tree algorithm. Gradient-boosted models are trees built sequentially. Each new model uses a gradient descent optimisation to update the weights that are to be learned by the model to reach a local minima of the loss function. A new function is added in each step to predict the output. To fit the data, XGBoost uses a loss function and a regularisation term that can be expressed mathematically as follows (Chen & Guestrin, 2016):

L_{XGBoost} = \sum_{i = 1}^{n} l (y_{i}, {\hat{y}}_{i}^{(t - 1)} + f_{t} (x_{i})) + Ω (f_{t}) .

(7)

where Ω (f_{t}) = γT + \frac{1}{2} λ \sum_{j = 1}^{T} w_{j}^{2}

(1)

l measures the difference between the prediction ${\hat{y}}_{i}$ of the tth trees and the target $y_{i}$ ⁠. $f_{t} (x_{i})$ is the new function that is added to the previous prediction to minimise the loss function. The second term $Ω (f_{t})$ is the regularisation function that penalises the complexity of the model. In the regularisation function, $T$ represents the number of leaves and $w_{j}$ the weight of the leaf j. The terms $γ$ and $λ$ are two hyperparameters that act as penalty terms to reduce overfitting. The inclusion of a regularisation function in the loss function distinguishes XGBoost from most tree sets.

Method followed to develop a decision support tool in the wheat grain tempering process

The general method used to develop the proposed support decision tool comprises the following four steps: (i) collect relevant data, (ii) prepare the data, (iii) create the regression models and (iv) validate the model.

Collection of relevant data

First, different variables that influence the tempering process according to the literature review are included. They are as follows: wheat properties, tempering resting time and tempering bin space available. Then, based on interviews and observations at the mill, the different adjustments and decisions that are taken during the tempering process are added. These include the flow of water, the flow of the grains of wheat, the quantity of wheat, the duration of the resting time and the number of tempering stages. The flow of water used in the tempering process is calculated from Formula 1. Finally, millers and experts add that environmental conditions and wheat mixes are additional factors to consider to achieve a good amount of control in the process.

A mapping of the flow process on the production line was performed (Parrenin et al., 2020). The mapping identifies available data sources and the type of data recorded.

In the production process, most equipment at the mill is controlled by the Supervisory Control and Data Acquisition (SCADA) system. The SCADA system is linked to a relational database in which data are recorded at regular intervals every 10 min. The data that are stored include information about the quantity of grains of wheat transferred from one silo to another and the quantity of water used. This provides the quantity of grains of wheat used at the beginning of each tempering stage and the resting time of the grains of wheat that are tempered.

All of the production runs at the mill are saved in Excel files. An Excel file is created for each new production run that starts referenced by a production run number. The file lists the quantity of wheat used, the quality of the grains and the different tempering conditions, such as the flow of water, the date and time of the beginning and end of the process and the temperature of the grains. As each Excel file has the same structure, a Python program has been developed to efficiently collect the data.

Although the miller and experts take into account environmental conditions in their decision on the adjustment of the tempering parameters, no information regarding these attributes was stored in any of the various data sources. To obtain this information, a collection of meteorological data from a weather observation station closest to the mill was carried out.

If critical data are missing, dedicated sensor installation is considered. Different methods and protocols are used to collect the data, depending on the IT infrastructure and equipment present on the shop floor (Vermesan et al., 2014).

Finally, adjustable variables for the tempering process and non-adjustable variables are identified. Adjustable variables include target wheat moisture content, wheat flow rate, water flow rate, wheat quantity and resting time period for grains of wheat. Non-adjustable variables include initial wheat moisture content, wheat protein content, wheat temperature, daily mean relative humidity, daily mean temperature and water quantity. Among the given variables, water quantity is considered to be a non-adjustable variable because the quantity is theoretically defined by the flow of water, the flow of wheat and the quantity of wheat used. This variable is nevertheless considered in the model because the water supply is cut off manually by operators and is not always proportionate to the three controllable variables.

Preparation of the data

Fourteen different wheat categories are available with our partner and all wheat categories can be blended together depending on the objective. Of all of the different wheat blend categories, we select the most popular blend, which is a mix of wheat called ‘Meunier’ and ‘Force’. This selection restricts our data to 266 examples of the 873 available. The selection of only one specific wheat blend category aims at narrowing our field of study and investigating the increase in moisture content of wheat grains during the tempering process independently of grain hardness.

Regarding the SCADA database, the tables store many null values due to non-movement of wheat grains on the production line. These rows are deleted. Regarding Excel files, information is sometimes missing or incoherent due to manually completed information. Missing information such as wheat properties are in some cases completed by collecting additional information from other sources of data. In other cases, statistical averages are performed. For example, the average grain temperature over the week is used to fill in the missing data on this attribute. Sometimes, the attributes contain too much missing information that has been left blank by the user. Attributes like specific grain weight and waste quantity have been removed for this purpose.

Visualisation techniques such as pair plots and DBSCAN (Density-Based Spatial Clustering of Applications with Noise) plots are used to detect outliers in the data. DBSCAN is a clustering algorithm (Burkov, 2019) based on density that is effective at detecting outliers in a dataset (Ester et al., 1996). Outliers are, most of the time, sources of inconsistent values or errors. To apply the DBSCAN algorithm and visualise outliers, the data are first scaled by standardising the feature variables. Two hyperparameters are defined, $ε$ and n. $ε$ represents the maximal neighbourhood distance around one point, and n represents the minimum number of data points that are present in a neighbourhood to form a cluster. Isolated points are then considered outliers. Figure 2 shows a 3D graph in which the target wheat moisture increase (%), the real increase in wheat moisture (%) and the resting time period (hour) are plotted on the x, y and z axes respectively. Summer and winter seasons are represented by squares and circles.

Figure 2

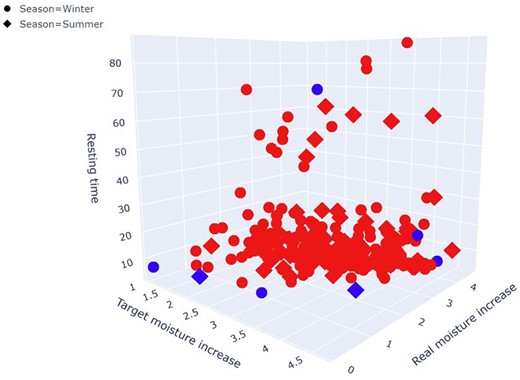
DBSCAN plot to detect potential outliers.

On Fig. 2, the potential outliers are identified in blue. Each potential outlier is specifically examined. In case of breakage or production shutdown, the example is removed. If errors or changes in operations are written down, the values are corrected based on the comments and notes of the operators written in the Excel file. In other cases, the values are left as they are. This cleaning method led to the removal of 9 examples from the 266 examples available. Finally, the data frame is divided such that 85% of the data are used for training and 15% are used for testing.

Creation of the predictive models

The different models are learned (LASSO, RIDGE, ElasticNet and a regression tree), such that the output variable is the increase in the moisture content of the grains of wheat after the first tempering stage. A resampling method is used, such as k-fold cross-validation with k = 5, and the average performance is evaluated. The hyperparameters are obtained using the GridSearchCV module available in the Scikit-Learn python library.

Validation of the models

Each model is evaluated on the test set using R² and root mean square error (RMSE). R² (eqn 8) represents the degree of variation explained by the model (James et al., 2013). R² fluctuates between 0 and 1. A high value of R² shows a good fit of the model to the data, making it accurate for future predictions. A threshold, scaled to the output variable and applied to RMSE (eqn 9), can indicate whether a model is accurate enough to make correct predictions, depending on a user's needs. The RMSE explains the average deviation between the predicted values and the actual values. These two performance indicators are used to evaluate and compare the performance of the regression models.

R^{2} = 1 - \frac{\sum_{i = 0}^{N} {(y_{i} - {\hat{y}}_{i})}^{2}}{\sum_{i = 0}^{N} {(y_{i} - {\bar{y}}_{i})}^{2}} .

(8)

RMSE = \sqrt{\frac{1}{N} \sum_{i = 0}^{N} {(y_{i} - {\hat{y}}_{i})}^{2}} .

(9)

N is the total number of examples (tempering production runs), $y_{i}$ is the real output for a tempering production run (i), ${\hat{y}}_{i}$ is the corresponding predicted value and ${\bar{y}}_{i}$ is the average output across N examples. Each example represents a tempering production run using a different batch of wheat and different tempering conditions.

Results

Table 1 illustrates the performance of the different models. R² and RMSE are used to rank the models. The models were evaluated in a first approach without weather data and then evaluated with them.

Table 1

Open in new tab

Performances of predictive models

Model	With weather data		Without weather data
Model	R²	RMSE	R²	RMSE
LASSO	0.647	0.428	0.600	0.456
RIDGE	0.639	0.433	0.601	0.455
Elastic Net	0.620	0.444	0.606	0.452
Regression tree (XGBoost)	0.578	0.469	0.574	0.471
OLS	0.585	0.571	0.567	0.586

Model	With weather data		Without weather data
Model	R²	RMSE	R²	RMSE
LASSO	0.647	0.428	0.600	0.456
RIDGE	0.639	0.433	0.601	0.455
Elastic Net	0.620	0.444	0.606	0.452
Regression tree (XGBoost)	0.578	0.469	0.574	0.471
OLS	0.585	0.571	0.567	0.586

Table 1

Open in new tab

Performances of predictive models

Model	With weather data		Without weather data
Model	R²	RMSE	R²	RMSE
LASSO	0.647	0.428	0.600	0.456
RIDGE	0.639	0.433	0.601	0.455
Elastic Net	0.620	0.444	0.606	0.452
Regression tree (XGBoost)	0.578	0.469	0.574	0.471
OLS	0.585	0.571	0.567	0.586

Model	With weather data		Without weather data
Model	R²	RMSE	R²	RMSE
LASSO	0.647	0.428	0.600	0.456
RIDGE	0.639	0.433	0.601	0.455
Elastic Net	0.620	0.444	0.606	0.452
Regression tree (XGBoost)	0.578	0.469	0.574	0.471
OLS	0.585	0.571	0.567	0.586

Table 1 shows that the model that performs the best for this problem is LASSO when weather data are included. It gets the highest R² score and the smallest RMSE value. We note that weather data improve the accuracy of predictions. Weather data, in our case, include the average relative humidity and the average temperature of the day when the tempering process occurs. This validates the information given by the miller in previous interviews to know the relevant variables.

Table 2

Open in new tab

Variables used in the models (controllable parameters in red)

In the LASSO model, 9 variables remained from the 11 variables available. The two variables that have been left out by the regression model are the target wheat moisture content and the initial wheat moisture content. The LASSO regression equation that predicts the increase in the moisture content of wheat grains (⁠ $y$ ⁠) is expressed as follows:

y = \begin{array}{l} 2.64 + 0.57 (X_{5}) - 0.27 (X_{3}) + 0.23 (X_{1}) - 0.21 (X_{6}) \\ + 0.19 (X_{4}) - 0.11 (X_{8}) + 0.09 (X_{9}) + 0.04 (X_{7}) - 0.01 (X_{2}) \end{array}

(10)

with _Xi defined in Table 2.

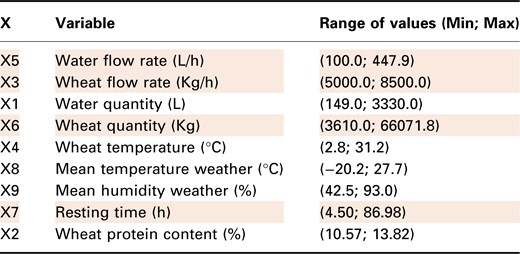
Table 2 presents the various variables used in the LASSO model by order of importance to explain the percentage increase in wheat moisture content. The lines highlighted in red are parameters that can be controlled by the miller during the tempering process. For each variable in Table 2, the range of values is mentioned. Based on the data collected at the mill and used in this study, the resting times range from 4.5 to 86.98 h. A high resting time often corresponds to a wheat resting time covering the entire weekend and extends several hours before or after.

The coefficients in the eqn 10 show the degree of influence of each feature variable on the increase in moisture content in the wheat. We note that among the four controllable parameters that the miller can adjust during the tempering stage, three have a significant impact: the flow of water and wheat that is sent to the dampening machine and the quantity of the wheat.

The flow of water and wheat could be adjusted based on the linear regression equation for a steep increase in the wheat moisture content of the grains of wheat. According to the standardisation made, an increase of 14 L of water per hour results in an increase of 0.1% in wheat moisture content at the end of the tempering stage. The quantity of wheat is mainly dependent on the wheat recipe, decided upon by the miller at the beginning of the production run and the number of resting silo available for the tempering stage. We observe that the weather features that include temperature and relative humidity have a significant role in the tempering process of the grains of wheat. Although the miller may be aware of these characteristics, the LASSO regression equation offers a way to estimate their degree of influence on the process.

Based on the OLS model, three variables were not found to be statistically significant. These include wheat protein content, resting time and mean weather temperature. However, these variables were nevertheless retained in the model mainly for two reasons. Firstly, based on the miller's expertise, protein content and the average weather temperature are two variables that influence the resting time required for wheat grains. Resting time is a key controllable parameter that would be interesting to optimise. Secondly, although they are not significant, they improve the performance of the model in this study. They reduce the average prediction error by 2.6%.

To get an overview of the performance of the LASSO model prediction, a graph representing the actual values versus the predicted values is presented in Fig. 3.

Figure 3

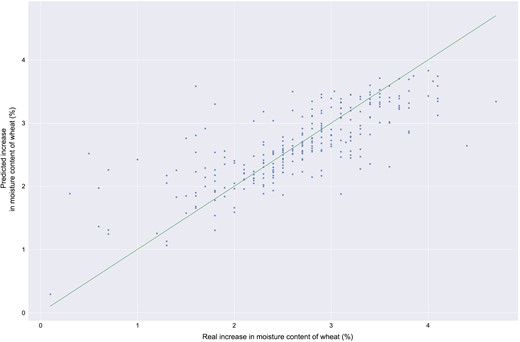
Scatter plot of predicted value from a LASSO model against real.

Although a linear trend can be observed, and most of the points are grouped around the green line, we notice that the model tends to predict values that are far from those expected. These values correspond to relatively low (between 0.5% and 1.5%) and very high (between 3.5% and 5%) moisture increases in the wheat grains.

Discussion

According to Table 1, the LASSO model offers the best performance, reaching an R² of 0.647 and an RMSE of around 0.428. This result is accurate enough to provide information about the tempering process and the adjustments that could be initiated by operators. With an RMSE of around 0.428, we obtained an average deviation error of 0.428% for the prediction of the increase in moisture content of the grains of wheat. Since most moisture content increase values fluctuate between 0% and 5%, the decision support tool based on this model provides some level of control to the operator in the tempering process.

From Table 2, among the input variables selected to build the model, we see that the LASSO regression model does not rely on the variable specifying the initial moisture content of the wheat kernels, or on the target moisture content. Yet, Almaraz et al. (2008) and Moss (1977) explain that the initial wheat moisture content is important in the speed and quantity of water particle absorption in the grain of wheat. A dry grain, like dry soil, will tend to absorb water slower than a humid grain or soil. The absence of these two input variables could be explained by information that was already entered when determining the water flow in eqn 1, which does take them into account. By removing these two variables, collinear variables are eliminated and the presence of noise in the data is reduced.

This decision support tool is based on a linear model that seeks to predict the rate with which moisture increases in wheat grains. However, a grain of wheat obviously cannot absorb an infinite amount of water and reacts differently depending on the moisture threshold reached. It is therefore important to remember that the tool is most useful in wheat grain tempering to condition it for milling. This conditioning aims to temper grains up to a maximum threshold of 17%–18% depending on the type of flour that will be produced.

In Fig. 3, we note that the model performs poorly for some ranges that predict an increase in wheat moisture, such as from 0.5% to 1.5% and 3.5% to 5%. This poor performance could be explained by the fact that few examples are available for these two ranges of increases in wheat moisture. Another reason for this low performance could be a lack of feature variables in the set of input variables. Additional key feature variables such as wheat hardness, wheat vitreosity or water temperature would provide information that could explain the reasons for a small or large increase at the end of the process that happens in specific cases. Even though Posner & Hibbs (2005) explain that wheat grain hardness affects the amount and rate of water uptake by a wheat grain, Butcher & Stenvert (1973) showed through a study of different Australian wheat varieties that hardness has no influence on the rate of water absorption in a grain. These contradictory results underscore the interest in analysing the importance of hardness in Canadian wheat varieties and their influence on the tempering process. In addition to wheat hardness, the vitreosity of the grain may also play an important role in water absorption. Vitreosity provides information about the appearance of a grain of wheat. Vitreous wheat grains have a dark, translucent and glassy appearance in contrast to mealy (non-vitreous) wheat grains (Dziki & Laskowski, 2005). According to Dobraszczyk et al. (2002), the vitreousness of the grains is correlated with the density of wheat grains. A denser grain with less porosity tends to be vitreous. High vitreosity makes the grain much more resistant to water penetration during tempering. This additional information would be useful in adjusting the controllable parameters of the tempering process to achieve the desired moisture content.

In this study, this decision support tool is limited to one category of wheat mixtures, which concerns hard wheat varieties suitable for all-purpose flour. To generalise the model for all types of wheat, the other categories will have to be taken into account. For this, a rigorous approach would be to measure the hardness and vitreousness of wheat to distinguish soft wheat from hard wheat.

Based on the literature review, the wheat hardness, the wheat vitreosity and water temperature are avenue that could explain better the water absorption of wheat grains in the tempering stage (Moss, 1977; IAOM, 2018). According to Moss (1977), the gradient of water migration in wheat grain is influenced by the bran morphology, endosperm structure, protein content and initial moisture content. In each variety of wheat, different bran morphologies and endosperm structures are found. Bran morphology is influenced by the vitreosity of the wheat grain (Moss, 1977). While the endosperm structure is influenced by the density and hardness of the wheat grain (Dobraszczyk et al., 2002). The wheat density and hardness are primarily determined by the wheat variety but are also strongly influenced by environmental factors during growth and development (Dobraszczyk et al., 2002). Collecting and adding variables that characterise wheat hardness, density and vitreosity, in addition to the protein content and initial moisture content of the wheat grain that we already have, would provide relevant information to the regression model about the water migration gradient for a wheat batch. This could improve the performance of the model in predicting the percentage increase in moisture content in a batch of wheat during the tempering process. Although these variables are not included in the regression model, the framework of the model presented in this paper is still applicable to other milling industries. For this, the LASSO regression model should be trained with the data collected at the mill to find the relevant coefficients for each variable considered. This approach makes it possible to measure the degree of influence of each variable on the increase in wheat moisture content at the end of the tempering process in a specific mill. It provides millers with relevant information on how to adjust the various controllable tempering parameters. Based on the regression model developed from the data collected at the mill, the coefficients explain the sensitivity of a variable on the increase in wheat moisture content.

In future work, one aspect that needs to be further investigated is the influence of the size and shape of water droplets used during the tempering process on wheat moisture increase. According to Chen et al. (2020), the use of steam water for wheat grain tempering accelerates the penetration of water particles into the grain compared to the use of water stream. Analysis of the size and shape of water droplets would be relevant to determine their influence on the increase in wheat moisture content and could further help predict this increase.

Conclusion

In this study, a decision support tool was built from data collected along the value chain in wheat milling. The goal is to offer better control of the tempering process that conditions the wheat grains before the milling process. The proper conditioning of the grain improves milling efficiency, which influences the mill's performance and the quality of the flour produced. This decision support tool will help new operators adjust the tempering parameters according to environmental factors, the properties of the grains of wheat and the desired type of flour.

The proposed tool is based on a multiple regression model. Several regression models have been built and compared to determine the wheat moisture at the end of the first tempering stage. The models have been trained on one specific wheat blend category to limit our field of study. Among the different models, the LASSO regression model offers the best accuracy, with an average prediction error of 0.428% and an R² of 0.647. This model shows the relevance of using meteorological data such as average temperature and average relative humidity. Moreover, the mathematical equation of the LASSO model enables an understanding of the influence of each input variable used in the final increase in the moisture content of the grains of wheat.

Although the LASSO model shows good results, more in-depth research is needed to improve the reliability of the model by trying to reduce the average prediction error. In this regard, further studies will be conducted to include wheat hardness, wheat vitreosity and water temperature. In addition, the analysis of the different categories of wheat mixtures will have to be taken into account in order to extend and generalise the model according to the type of wheat mixture made by the miller. Other than the properties of wheat grains, the shape and size of water droplets will also need to be explored in future work. Finally, to effectively control the entire tempering process, the second and third tempering stages will need to be studied.

Acknowledgments

We would like to thank our industrial partner, La Milanaise, for their support and collaboration in this project, as well as MAPAQ (project IA119053) for their financial support. All authors declare that they have no conflicts of interest.

Author contributions

Loic Parrenin: Formal analysis (lead); investigation (lead); methodology (lead); writing – original draft (lead); writing – review and editing (equal). Christophe Danjou: Supervision (lead); writing – original draft (supporting); writing – review and editing (equal). Bruno Agard: Supervision (lead); writing – original draft (supporting); writing – review and editing (equal). Robert Beauchemin: Resources (supporting); supervision (supporting).

Ethical approval

Ethics approval was not required for this research.

Peer review

The peer review history for this article is available at https://www.webofscience.com/api/gateway/wos/peer-review/10.1111/ijfs.16406.

Data availability statement

The author elects to not share data. The data used is confidential.

References

Almaraz

J.J.

Mabood

Zhou

Gregorich

E.G.

Smith

D.L.

(

2008

Climate change, weather variability and corn yield at a higher latitude locale: Southwestern Quebec

Climatic Change

187

–

197

Assadzadeh

Walker

C.K.

McDonald

L.S.

Panozzo

J.F.

(

2022

Prediction of milling yield in wheat with the use of spectral, colour, shape, and morphological features

Biosystems Engineering

214

–

Burkov

(

2019

The Hundred-Page Machine Learning Book

Quebec City

Burkov, A

Butcher

Stenvert

N.L.

(

1973

Conditioning studies on Australian wheat. III. The role of the rate of water penetration into the wheat grain

Journal of the Science of Food and Agriculture

1077

–

1084

Cappelli

Guerrini

Parenti

Palladino

Cini

(

2020

Effects of wheat tempering and stone rotational speed on particle size, dough rheology and bread characteristics for a stone-milled weak flour

Journal of Cereal Science

, 102879.

Chen

T. Q.

, &

Guestrin

(

2016

). XGBoost: A Scalable Tree Boosting System. Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining,

785

–

794

Chen

Y.-X.

Guo

X.-N.

Xing

J.-J.

Zhu

K.-X.

(

2020

Effects of tempering with steam on the water distribution of wheat grains and quality properties of wheat flour

Food Chemistry

323

, 126842.

Dobraszczyk

B.J.

Whitworth

M.B.

Vincent

J.F.V.

Khan

A.A.

(

2002

Single kernel wheat hardness and fracture properties in relation to density and the modelling of fracture in wheat endosperm

Journal of Cereal Science

245

–

263

Dziki

Laskowski

(

2005

Wheat kernel physical properties and milling process

Acta Agrophysica

–

Ester

Kriegel

Sander

(

1996

). A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise.

Fang

Campbell

G.M.

(

2003

On predicting roller milling performance V: effect of moisture content on the particle size distribution from first break milling of wheat

Journal of Cereal Science

–

FAO

(

2021

World Food and Agriculture – Statistical Yearbook 2021

Rome

R FAO

Goodfellow

Bengio

Courville

(

2016

Deep Learning

Cambridge

MIT Press

Government of Canada

. (

2021

). Data retrieved from Historical Climate data. https://climate.weather.gc.ca/historical_data/search_historic_data_e.html

Government of Canada

. (

2022

). Organic claims on food labels. https://inspection.canada.ca/food-labels/labelling/industry/organic-claims/eng/1623967517085/1623967517522#s9c9

Gwirtz

J.A.

(

1998

). Effects of Tempering Time, Moisture and Wheat Protein Level on Milling and Single Kernel Characterization System Measurements. PhD thesis, Kansas State University.

Hook

S.C.W.

Bone

G.T.

Fearn

(

1984

The conditioning of wheat. Moisture migration between the components of a mixed grist, and its effect on milling performance

Journal of the Science of Food and Agriculture

584

–

590

IAOM

(

2018

Wheat tempering (Conditioning), Fundamentals of Flour Milling

. Pp.

105

–

122

Lenexa

International Association of Operative Millers

James

Witten

Hastie

Tibshirani

(

2013

An Introduction to Statistical Learning: With Applications in R

New York

Springer

Kang

Delwiche

S.R.

(

1999

Moisture diffusion modeling of wheat kernels during soaking

Transactions of ASAE

1359

–

1366

Kashaninejad

Dehghani

A.A.

Kashiri

(

2009

Modeling of wheat soaking using two artificial neural networks (MLP and RBF)

Journal of Food Engineering

602

–

607

Kweon

Martin

Souza

(

2009

Effect of tempering conditions on milling performance and flour functionality

Cereal Chemistry

–

Miralbés

(

2003

Prediction chemical composition and Alveograph parameters on wheat by near-infrared transmittance spectroscopy

Journal of Agricultural and Food Chemistry

6335

–

6339

Moss

(

1977

The influence of endosperm structure, protein content and grain moisture on the rate of water penetration into wheat during conditioning [journal article]

International Journal of Food Science & Technology

275

–

283

Parrenin

Danjou

Agard

(

2020

). Développement d'un outil de suivi des mouvements des grains de blé biologique au niveau de la chaine d'approvisionnement. 13ème Conférence internationale de modelisation, optimisation et simulation (MOSIM2020), 12–14 Nov 2020, Agadir, Maroc.

Parrenin

Danjou

Agard

Beauchemin

(

2023

Future trends in organic flour milling: the role of AI

AIMS Agriculture and Food

–

Posner

E.S.

Hibbs

A.N.

(

2005

Wheat Flour Milling

St Paul

American Association of Cereal Chemists, Inc

Rakita

Dokić

Dapčević Hadnađev

Hadnađev

Torbica

(

2018

Predicting rheological behavior and baking quality of wheat flour using a GlutoPeak test

Journal of Texture Studies

339

–

347

Rana

Paul

(

2017

Consumer behavior and purchase intention for organic food: a review and research agenda

Journal of Retailing and Consumer Services

157

–

165

Sabanci

Aydin

Sayaslan

et al. (

2020

Wheat flour milling yield estimation based on wheat kernel physical properties using artificial neural networks

International Journal of Intelligent Systems and Applications in Engineering

–

Tagawa

Muramatsu

Nagasuna

Yano

Iimoto

Murata

(

2003

Water absorption characteristics of wheat and barley during soaking

Transactions of ASAE

, 361.

Vermesan

Friess

Guillemin

et al. (

2014

). Internet of things strategic research and innovation agenda. In:

Internet of Things from Research and Innovation to Market Deployment

(edited by

Vermesan

Friess

). Pp.

–

142

Aalborg

River Publisher

Willer

Trávníček

Meier

Schlatter

(

2022

The World of Organic Agriculture Statistics and Emerging Trends 2022

Bonn

Research Institute of Organic Agriculture FiBL, Frick, and IFOAM – Organics International

Willm

(

2009

La mouture du blé

Buenos Aires

Editions CEMP