ABSTRACT
The Nearest Neighbor Database (NNDB, http://rna.urmc.rochester.edu/NNDB) is a web-based resource for disseminating parameter sets for predicting nucleic acid secondary structure stabilities. For each set of parameters, the database includes the set of rules with descriptive text, sequence-dependent parameters in plain text and html, literature references to experiments and usage tutorials. The initial release covers parameters for predicting RNA folding free energy and enthalpy changes.
INTRODUCTION
Nearest neighbor approaches were developed to predict the folding stabilities of nucleic acid secondary structures (1). These parameter sets utilize empirical rules, generally derived from optical melting experimental data, as the basis of the predictions. For RNA, rules exist for predicting both free energy and enthalpy change of Watson–Crick helices, GU pairs and loops (2–5). Parameters for DNA have also been assembled for predicting Watson–Crick pair free energy and enthalpy change and free energy changes of loops (6,7). These parameter sets are the basis of computer programs that predict low free energy secondary structures. Such programs include Mfold/UnaFold (8,9), the Vienna RNA package (10), RNA structure (2), RNAsoft (11) and Sfold (12). Additional approaches that use statistical learning of parameters for RNA folding have also used the rules from the nearest neighbor methods and derived new parameter values (13,14).
Nearest neighbor parameter sets include both a set of rules, called either equations or features, for predicting stability and a set of parameter values used by the equations (14). For RNA, separate rules exist for predicting stabilities of helices, hairpin loops, small internal loops, large internal loops, bulge loops, multibranch loops, exterior loops and pseudoknots. Given the number of rules and constraints on the length of journal publications, it is difficult to assemble all the parameters in one publication and provide meaningful tutorials for using the parameters. This is a barrier to software development for novel algorithms that could take advantage of the parameters. For example, many software packages that use RNA parameters still implement the set of parameters assembled in 1999 (4), in spite of the fact the RNA parameters were updated in 2004 (2) based on experimental results.
The Nearest Neighbor Database (NNDB) is a web-based tool for assembling and archiving complete nearest neighbor sets, including rules and values. It is available online at http://rna.urmc.rochester.edu/NNDB. It provides documentation of parameter sets and tutorials on how to apply the parameters. Currently, the 1999 and 2004 sets of RNA folding parameters are provided (2–5).
WEBSITE ORGANIZATION
The NNDB is built using a set of static html, specifically XHTML 1.0 transitional pages with a page hierarchy shown in Figure 1. Text is encoded in Unicode (utf-8) to facilitate display of equations in pages with diverse browsers running on diverse operating systems. The top-level page provides access to a help page, available parameter sets and a page of references to RNA optical melting experiments. Additionally, links provide downloading of the whole database in either zip or gzipped tar format. The help page introduces the purpose of the database and defines basic terms, including the set of structural features defined by secondary structures. For example, Figure 2, from the help page, shows an RNA secondary structure that illustrates the loop features covered by nearest neighbor parameter sets. The basic equations for utilizing the parameters to extrapolate folding free energy changes to temperatures other than 37°C and to predict melting temperatures are also provided.
The webpage hierarchy of the NNDB. This figure illustrates the page hierarchy by following the linked pages down through the 1999 parameters and down to the hairpin loop pages. Note that there are five example calculations for hairpin loops to illustrate the separate sequence-dependent rules that are used depending on the specific loop.
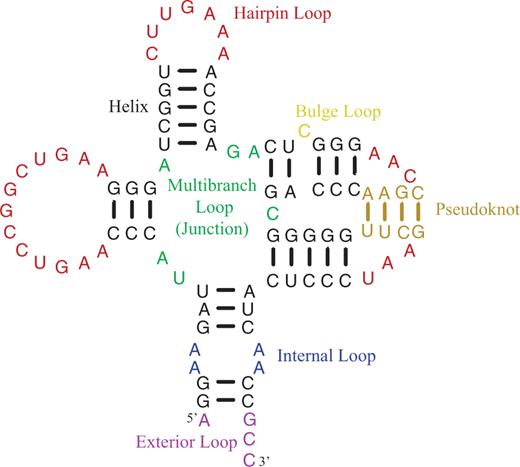
An RNA secondary structure illustrating the types of features included in nearest neighbor parameter sets. This figure appears on the help page of the website. Loops are composed of nucleotides not in canonical pairs. Hairpin loops have one exiting helix. Internal and bulge loops have two exiting helices. Internal loops have nucleotides not in canonical pairs on each of two strands, but bulge loops have nucleotides not in canonical pairs on only one strand. Multibranch loops, also called helical junctions, have three or more exiting helices. Exterior loops contain the ends of sequences and one or more exiting helices. Pseudoknots are canonical pairs connecting loop regions closed by other helices. Formally, a pseudoknot occurs when there are at least two pairs, with indices i paired to j and i′ paired to j′, that satisfy the condition i < i′ < j < j′. The pseudoknot helix is often considered to be composed of the fewest pairs that need to be removed to relieve the pseudoknot (19). In this structure, the tan nucleotides are in pairs that could be removed to relieve the pseudoknot.
For each set of parameters, a first page introduces the available parameters, which vary from set to set. For example, the 1999 RNA rules predict only folding free energy changes (4), but the 2004 rules can be used to predict both folding free energy and enthalpy changes (2,5). For each structural feature, a page defines the basic equations and provides links to parameter values (in plain text and html), references and tutorial pages (e.g. Figure 3). The number of tutorials varies from feature to feature; the set of tutorials is designed to cover each type of rule that can be encountered in practice. For example, the Watson–Crick helix parameters are covered with two tutorials, one for self-complementary and one for non-self-complementary strands. These two tutorials also demonstrate the difference in the calculation when there are terminal AU base pairs, which receive a free energy and enthalpy change penalty (3), because the self-complementary duplex example has two terminal AU pairs and the non-self-complementary case has no terminal AU pairs.
The individual pages are designed for ease of navigation and clarity. Individual pages above the level of value tables have top banner, a left navigation bar that allows the user to navigate back up the hierarchy to any level above and a bottom bar with the date of last editing. For pages edited after the database has gone online, previous versions of the page are available using this bottom content bar. To facilitate indexing by search engines, all pages have a descriptive title, including the set of parameters to which it belongs (if applicable).
WEBSITE CONTENT
The first release of the NNDB contains the RNA folding rules assembled in 1999 and 2004 (2–5). These rules represent the most recent set of parameters and a prior set that is widely used in software packages. Because folding rules are derived to work as a set, the two versions of rules and values should not be mixed and the website hierarchy reinforces this.
The website is designed to be expandable to additional sets of parameters. It is anticipated, for example, that additional pages will be written to include nearest neighbors for DNA folding (6,7) and for predicting RNA pseudoknot stabilities (15–18). Additionally, the values derived from the re-estimation of the values of the 1999 parameter set using the set of known RNA secondary structures will also be included (14).
DISCUSSION
The NNDB is designed to provide a convenient location for assembling parameter sets for predicting the stability of nucleic acid secondary structures. It is modular in design, which facilitates its future expansion to contain additional parameter sets. Furthermore, the web format makes it feasible to provide extensive tutorials for utilizing the parameters, which is generally not possible in print.
FUNDING
The creation of the NNDB was supported by United States National Institutes of Health grants GM076485 to D.H.M. and GM22939 to D.H.T. Funding for open access charge: United States National Institutes of Health.
Comments