Accuracy and Power of the Likelihood Ratio Test in Detecting Adaptive Molecular Evolution Free

Abstract

Introduction

Detecting positive Darwinian selection is a critical aspect of understanding the mechanisms of molecular evolution. Existing tests proposed in population genetics (see Wayne and Simonsen [1998] for a review) are powerful enough to reject the strictly neutral model. However, such tests are often not sufficient to distinguish different forms of natural selection or to detect adaptive molecular evolution (Yang and Bielawski2000) . A powerful method for detecting positive selection is through comparison of synonymous and nonsynonymous substitution rates. Selective pressure at the protein level is measured by ω = d_N/d_S, where d_N and d_S are nonsynonymous and synonymous substitution rates, respectively. If amino acid changes are advantageous, they will be fixed at a higher rate than synonymous changes, with d_N > d_S. Thus, a significantly higher nonsynonymous substitution rate (ω > 1) is evidence of adaptive molecular evolution. If amino acid changes are deleterious, purifying selection will reduce their fixation rate, such that d_N < d_S and ω < 1. Neutral mutations result in ω = 1, as selection on the protein has no effect on fitness.

Until recently, cases of positive selection have been difficult to demonstrate. A large-scale database search performed by Endo, Ikeo, and Gojobori (1996) identified only 17 out of 3,595 genes that might have undergone adaptive evolution. Endo, Ikeo, and Gojobori (1996) considered a gene to be under positive selection if the average d_N was greater than d_S in more than half of the pairwise sequence comparisons. This approach computes the ω ratio as an average over both amino acid sites and time; although popular, it has little power. For example, Crandall et al. (1999) found that the approach of pairwise comparison failed to detect positive selection in the protease gene of HIV-1 despite clear evidence of parallel evolution. Crandall et al. (1999) suggested that the ω ratio averaged over sites was a poor indicator of positive selection. Indeed, the assumption that all sites in a sequence are under equal selective pressure is unrealistic. Typically, adaptive evolution occurs at only a few sites, as most amino acids in a protein are under structural and functional constraints with d_N, and hence ω, close to 0 (e.g., Li 1997 ). Thus, calculating ω as an average over all amino acid sites substantially reduces the power to detect positive selection.

Codon-based models recently developed by Nielsen and Yang (1998) and Yang et al. (2000) account for variation of the ω ratio among sites. They are implemented in the maximum-likelihood (ML) framework and can be used (1) to test for the presence of codon sites affected by positive selection and (2) to identify such sites when they exist. The idea is to allow the ω ratio to take values from a number of discrete site classes or from a continuous distribution. The application of such models has led to detection of positive selection in many genes for which it has not previously been suggested. For example, using the ML model of Nielsen and Yang (1998) , Zanotto et al. (1999) detected positive selection in the nef gene of HIV-1, whereas in earlier studies of the same gene, the average ω ratio over sites provided no evidence for adaptive evolution (Plikat, Nieselt-Struwe, and Meyerhans 1997 ; da Silva and Huges 1998 ). Yang et al. (2000) detected diversifying positive selection in six out of ten genes from nuclear, mitochondrial, and viral genomes, while the ω ratio averaged over sites was less than one in all of those genes. Similarly, in an analysis of the fertility gene DAZ,Agulnik et al. (1998) found similar average synonymous and nonsynonymous rates and similar rates at the three codon positions and thus concluded that the DAZ gene family was not under any selective constraint. However, using models of variable ω ratios, Bielawski and Yang (2001) found that most amino acids in the DAZ gene were under strong functional constraints, while a few sites were under diversifying selection.

While the new models have been successfully applied to real data, the accuracy and power of the likelihood ratio test (LRT) have not been examined. Here, we use computer simulation to investigate the accuracy and power of the LRT in detecting positive selection. In cases considered here, the LRT statistic does not follow the χ² distribution due to the so-called boundary problem. This problem arises because the null hypothesis is equivalent to the alternative hypothesis with some parameters fixed at the boundary of the parameter space. The sample size (i.e., the sequence length) also affects the distribution of the LRT statistic; the χ² approximation is asymptotic and reliable for large samples only (e.g., Silvey 1970 , pp. 112−114). We attempted to characterize the minimum sample size required for the χ² approximation to be acceptable. Furthermore, we examined how the power of the LRT depends on the sequence divergence, the sequence length, the number of taxa, and the strength of positive selection. Finally, we tested the sensitivity of the LRT to misspecification of the ω distribution among sites.

Theory and Methods

Codon Substitution Models for Detecting Positive Selection at Sites

The Markov model of codon substitution proposed by Goldman and Yang (1994 ; see also Muse and Gaut 1994 ) was modified recently to account for heterogeneous ω ratios among sites (Nielsen and Yang 1998 ; Yang et al. 2000 ). Here, we present an overview of these models. Let h denote a site in the sequence and N denote the number of codons in the sequence (h = 1, 2, … , N). The relative instantaneous substitution rate from codon i to codon j (i ≠ j) at site h is given by

where π_j is the equilibrium frequency of codon j, κ is the transition/transversion rate ratio, and ω^(h) is the d_N/d_S ratio at site h. The transition probability matrix over time t is given by P(t) = e^Qt, where Q = {q^(h)_ij} (e.g., Lio and Goldman 1998 ).

Following the recommendations of Yang et al. (2000) , we consider the following models of ω ratio distribution among sites: M0 (one-ratio), M3 (discrete), M7 (beta), and M8 (beta&ω) (see table 1 ). M0 (one-ratio) assumes one ω ratio for all sites, so ω^(h) = ω for any h. Model M3 (discrete) classifies sites in the sequence into K discrete classes, with both the ω ratios ω₀, ω₁, … , ω_K−1 and the proportions p₀, p₁, … , p_K−1 estimated from the data. Three classes (K = 3) were used in this paper. Under model M7 (beta), the ω ratio varies according to the beta distribution B(p, q) with parameters p and q. The beta distribution is bounded within the interval (0, 1) and thus does not allow for positively selected sites. Model M8 (beta&ω) adds a discrete ω class to the beta model to account for sites under positive selection with ω > 1. A proportion p₀ of sites have ω drawn at random from the beta distribution B(p, q), while the rest (with proportion p₁ = 1 − p₀) have the same ratio ω. M0 (one-ratio) and M3 (discrete) are nested models and can be compared using an LRT. Similarly, models M7 (beta) and M8 (beta&ω) are nested and can be compared using an LRT.

Accuracy of the LRT

The type I error occurs if the null hypothesis H₀ is rejected when it is true. A test is accurate if the type I error rate is not greater than the chosen significance level α. If H₀ holds, the LRT statistic 2Δℓ (twice the log likelihood difference) can be approximated by the χ² distribution with the degree of freedom ν equal to the difference in the number of free parameters in the two nested models (e.g., Stuart, Ord, and Arnold 1999 , p. 241). This, however, is only true for large samples and under certain regularity conditions. For example, if the null model H₀ is equivalent to an alternative model H₁ with some parameters fixed at the boundary of the parameter space, the regularity conditions are not satisfied and the χ² approximation is not expected to apply. Such is the case with the LRTs considered here. For example, M0 (one-ratio) is a special case of M3 (discrete) by constraining two of the five free parameters in M3 (p₀ and p₁) to 0. This breaches the regularity conditions, as p₀ = 0 and p₁ = 0 lie on the boundary of the parameter space. Moreover, parameters ω₀ and ω₁ become undefined when p₀ = p₁ = 0. Comparison between M7 and M8 poses a similar problem. The transformation from M8 to M7 forces the parameter ω to become inestimable by fixing p₁ at 0, which is on the boundary of the parameter space. Therefore, in neither of our cases is the LTR statistic expected to follow the χ² distribution.

We assessed the accuracy of the test by simulating replicate data sets under the null hypothesis and analyzing them using both the null and the alternative hypotheses. The distribution of the test statistic 2Δℓ among replicates was then compared with the χ²_ν distribution, with ν = 4 for the M0-M3 comparison and ν = 2 for the M7-M8 comparison (table 1 ). The settings of the simulation experiments are summarized in table 2 . Trees used to simulate the data are shown in figure 1 . We do not assume the molecular clock (rate constancy over time), and all trees are unrooted. While the d_N/d_S rate ratio ω is the same among branches, the total rate, measured by the expected number of nucleotide substitutions per codon, varies among branches. We used codon frequencies empirically estimated from 17 vertebrate β-globin genes and from 23 HIV-1 pol genes (see table 2 ). The vertebrate β-globin gene is biased against adenine at third codon positions, whereas the HIV-1 pol gene is G-C rich at third positions. Simulation parameters were taken to represent the range of estimates from real data (Yang et al.2000) . We simulated sequences of N = 100 and 500 codons using trees of T = 5, 6, or 17 taxa. Sequence divergence was measured by the tree length S, the expected number of nucleotide substitutions per codon along the tree, and three values (“low,” “medium,” and “high”) were used for each tree (table 2 ).

Power of the LRT

The type II error of a test occurs if the test fails to reject H₀ when it is false. The power of a test is defined as 1 − type II error rate and is equal to the probability of rejecting H₀ given that H₀ is wrong and that the alternative hypothesis H₁ is correct. To examine the power of the LRT, we simulated replicate data sets under H₁ and analyzed them using both H₀ and H₁ to see whether H₀ was rejected by the LRT. We considered two measures. First, we counted the replicates for which positive selection was indicated by the parameter estimates in the alternative model, and we denote the proportion of such replicates by P₊. Formally, P₊ = Pr(there exists an ω̂ > 1 | H₁ is true), where ω̂ is the ML estimate of any of the parameters ω_i (i = 0, 1, 2) under M3 (discrete) or of the single ω parameter in model M8 (beta&ω) (see table 1 ). The second measure is more stringent and requires that positive selection is indicated by the parameter estimates in the alternative model and that the LRT is significant. We denote the proportion of such replicates by P_+s and refer to it as the power of the LRT. As P_+s depends on the significance level α, we also use the notation P_+s,α. In other words, P_+s,α = Pr(there exists ω̂ > 1 and 2Δℓ > χ²_ν,α | H₁ is true). Note that P₊ ≥ P_+s.

We also investigated the sensitivity of LRTs to misspecification of the distribution of the ω ratio among sites. We simulated data sets under M3 (discrete) and analyzed them using M7 (beta) and M8 (beta&ω). Similarly, we simulated data sets under M8 (beta&ω) and analyzed them using M0 (one-ratio) and M3 (discrete). Parameter settings used are listed in table 3 . As before, we used a number of parameter combinations to represent a variety of real data situations.

All sequence data sets were generated using the evolver program. Log likelihood values were calculated with the codeml program. Both programs are from the PAML package (Yang2000) .

Results

Accuracy

Results obtained from simulations examining the accuracy of the LRTs are presented in table 2 . In experiments A–C, data were simulated under M0 (one-ratio) and analyzed using M0 (one-ratio) and M3 (discrete), with χ²₄ used to test significance. If χ²₄ were the correct null distribution, H₀ would be rejected (type I error) in 5% of the replicates at the α = 0.05 significance level and in 1% of the replicates at α = 0.01. However, the regularity conditions for the χ² approximation are not satisfied. Results of table 2 (experiments A–C) suggest that the null hypothesis was rejected less often than allowed by the significance level. In most cases, the estimated type I error rate was 0 for α = 0.05 (table 2 ). Even at α = 0.1, the estimated probability of rejecting the null hypothesis never exceeded 6% and was often much lower than the expected 10% (results not shown). Thus, use of χ²₄ to compare M0 and M3 makes the LRT conservative.

The shapes of the 2Δℓ distribution were similar for all parameter combinations in experiments A–C, in which the LRT compared M0 (one-rate) against M3 (discrete). One example is shown in figure 2A for the combination N = 500 and S = 1.1 in experiment A. The simulated distribution has a skewed L-shape, while χ²₄ has a peak in the middle with a long tail to the right. The two distributions are very different. At very low sequence divergence (S = 0.11 in experiment A), there was a substantially higher peak near 2Δℓ = 0, such that M0 was rejected even less often and the LRT was even more conservative. Short sequences had an effect similar to that of low divergence, and the LRT was more conservative in data sets of 100 codons than in data sets of 500 codons (results not shown). The number of taxa did not appear to affect the shape of the distribution.

We simulated data sets under M7 (beta) in order to check whether the χ²₂ approximation was reliable for comparing M7 (beta) and M8 (beta&ω). ML estimation under M7 and M8 is time-consuming; hence, only three parameter combinations were used (experiment D in table 2 ). For S = 0.11, M7 was never rejected at α = 0.05, whereas for S = 1.1 and S = 11, M7 was rejected approximately as often as expected from the significance level α when α = 0.01, 0.05, and 0.1. Figure 2B compares the distribution of the 2Δℓ statistic with χ²₂ for the combination N = 500 and S = 1.1. The match is not good, and the simulated distribution is left-skewed. Therefore, use of the χ²₂ makes the LRT conservative. Furthermore, the LRT was even more conservative for data sets of highly similar sequences (S = 0.11), as in the comparison of M0 (one-ratio) and M3 (discrete).

The reliability of the χ² approximation could have been affected by both the boundary problem and a small sample size. To distinguish between these two factors, we conducted a simple experiment free from the boundary problem. One ω ratio was assumed for all sites (M0), and the hypothesis H₀: ω = 1 was tested against the alternative H₁: ω ≠ 1. The LRT statistic 2Δℓ was compared with χ²₁. The tree in figure 1A was used, and the parameters (with the exception of ω) were the same as in experiment A (table 2 ). The distribution of 2Δℓ fitted the expected χ²₁ distribution for all values of S and N.Figure 3A shows one case where the tree length S = 1.1 and the sequence length was only N = 50 codons. It is remarkable that the χ² distribution appears reliable for such short sequences. An equally good fit was observed for N = 100. Data sets of 50 codons with S = 0.11 were not analyzed, as such data carry little information and cause convergence problems. These results are compatible with those of Zhang (1999) , who found in nucleotide-based simulations that the χ² approximation is reliable in fairly small data sets. Besides the χ² approximation to the LRT statistic, asymptotic theory also predicts that ML estimates of parameters are normally distributed (e.g., Stuart, Ord, and Arnold 1999 , pp. 57–59). For N = 50, the distribution of ω̂ was left-skewed (fig. 3B ), and in 47% of the replicates, ω̂ was greater than 1. The mean of the distribution was 1.09, indicating that the ML estimate involves a positive bias in small samples (Yang and Nielsen2000) . This pattern was found to be typical for small samples. With an increase of N, the distribution looked much more concentrated and symmetrical. Compared with the χ² approximation to the LRT statistic, the normal approximation to ML parameter estimates appeared to require larger samples to be reliable.

To examine the performance of the LRT on a neutral gene, we also applied the LRT comparing M0 and M3 to data sets simulated under M0 (one-rate) with ω = 1. The parameter settings were the same as in figure 3 except that the sequence length was N = 500. In 72% of the replicates, estimates of at least one of the ω ratios under M3 were greater than 1, indicating positive selection. However, in most of them, the LRT was insignificant, and the type I error rate was only 0.004 at α = 0.05. Thus, the LRT was reliable.

Power Analysis

Results obtained from simulations examining the power of the LRT are summarized in table 3 . In experiment 1, we simulated data under M3 (discrete) using a six-taxon tree and analyzed them using M0 (one-ratio) and M3 (discrete). Both P₊ (probability of parameter estimates indicating positive selection) and P_+s (power of the LRT) were consistently higher when N = 500 than when N = 100. This effect of the sequence length was expected. The level of sequence divergence had a significant effect on the power of the test. At low sequence divergence (S = 0.11), ML parameter estimates under M3 suggested positive selection (P₊) in 33 data sets for N = 100 and in 48 data sets for N = 500 (table 3 ). However, in only a few of these cases was the evidence statistically significant (P_+s). For example, at α = 0.05, the LRT was significant in only one case for N = 100 and in only eight cases for N = 500 (table 3 ). Note that S = 0.11 means that the sequences are highly similar, with 2.4% of total divergence along the tree at a nonsynonymous site (d_N = 0.024) and 7.8% of divergence at a synonymous site (d_S = 0.078). The transformation from tree length S to d_N and d_S can be made using the relationships S = 3d_Sp_S + 3d_N(1 − p_S), and d_N/d_S = ω̄ (e.g., Yang and Nielsen2000) . Here, the average ω ratio ω̄ = 0.018 × 0.386 + 0.304 × 0.535 + 1.691 × 0.079 = 0.303 (see table 3 ), and the proportion of synonymous sites is p_S = 23.84% for the vertebrate β-globin gene (Yang et al.2000) . Increasing sequence divergence to the intermediate level (S = 1.1) yielded a substantial increase in both P₊ and P_+s. For example, with N = 500, parameter estimates in P₊ = 95% of replicates suggested positive selection, and in all of them, the LRT was significant at the 1% level (P_+s,0.05 = P_+s,0.01 = 95%) (table 3 ). The power decreased when S was increased to 11 (e.g., for N = 500, P₊ = 80% and P_+s,0.05 = 80%). At S = 55 nucleotide substitutions per codon, both P₊ and P_+s decreased dramatically (e.g., for N = 500, P₊ = 11% and P_+s,0.05 = 11%). Note that S = 55 represents unrealistically high sequence divergence, with d_N = 11.8 substitutions per nonsynonymous site and d_S = 39.1 substitutions per synonymous site along the tree. In summary, the power increased with increasing S, peaked at a medium level of S, and fell when sequences became highly divergent.

In experiment 2, we examined the effect of increasing the number of taxa to 17 (table 3 ). Here, P_+s was very high for most values of S and N. For example, even for the short sequences (N = 100) of rather low divergence (S = 2.11), ML estimates suggested positive selection in 93 data sets, with most of these cases being statistically significant (P_+s,0.01 = 91%). The LRT reached full power (P_+s = 100%) for long sequences and realistic S in the range 2.11–8.44. As in experiment 1, the power increased with the initial increase of S, peaked at a medium level of S, and thereafter decreased with a further increase of S. For example, increasing S to an unrealistically high value (S = 105.5) for the short sequences (N = 100) resulted in P₊ = 31% and P_+s,0.05 = 31%.

Experiment 3 examined the influence of the strength of positive selection; ω₂ was increased from 1.69 in experiment 1 to 4.74 (table 3 ). As expected, there was a rise in the power of the LRT as compared with experiment 1. For every combination of S and N, the power in experiment 3 was higher than the corresponding result in experiment 1. Once again the power was low for either very similar or highly divergent sequences and was highest at intermediate levels of sequence divergence (around S = 1.1). As before, increasing sequence length from 100 to 500 yielded an increase in the power.

Experiment 4 examined the power of the LRT using the tree topology, simulation parameters, and codon frequencies derived from the HIV-1 pol gene (Yang et al.2000) (table 3 ). As before, the power of the LRT was higher for longer sequences. Moreover, the power increased with the increase of S, peaked, and then decreased with a further increase in S. However, the level of sequence divergence at which the power began to fall differed from previous experiments. To enable a qualitative comparison, we used the average number of nucleotide changes per codon per branch as a relative measure of sequence divergence. This is S/(2T − 3), where 2T − 3 is the number of branches of an unrooted tree of T taxa. Unlike experiment 1, in which the highest power was observed at the medium level of sequence divergence (S = 1.1 and T = 6, or S/(2T − 3) = 0.12), here the highest power was obtained for relatively divergent data sets (S = 9.1 and T = 5, or S/(2T − 3) = 1.3). Hence, the optimal sequence divergence depends on the properties of the data and appears to be within the medium-to-high range.

In experiment 5, we simulated data under M8 (beta&ω) and analyzed them with M7 (beta) and M8 (beta&ω) (table 3 ). Although ω̂ derived from M8 often suggested positive selection, the power of the LRT was substantially lower than in experiment 1. For example, when N = 500 and S = 1.1, the power was P_+s,0.05 = 95% in experiment 1 but only 77% in experiment 5. This difference is due to the fact that M0 is less realistic than M7 and easier to reject (see below).

In experiment 6, we examined whether the LRT was sensitive to the true distribution of ω by simulating data under M3 (discrete) and analyzing them with M7 (beta) and M8 (beta&ω) (table 3 ). The results were compared with those of experiment 1, where the data were analyzed with M0 and M3. The null model M0 was rejected much more frequently than the null model M7. For example, for the combination N = 500 and S = 1.1, the power was P_+s,0.01 = 100% in experiment 1 and 48% in experiment 6. Comparison between M7 and M8 is clearly a more stringent test of positive selection than comparison between M0 and M3. In contrast to P_+s, P₊ was often higher in experiment 6 than in experiment 1 except for the combination N = 500 and S = 11 (table 3 ). In sum, parameter estimates under M8 tend to suggest positive selection more often than M3, but the LRT based on M8 is significant less often than the LRT based on M3.

In experiment 7, we simulated data under M8 (beta&ω) and analyzed them using M0 (one-ratio) and M3 (discrete) (table 3 ). The results were compared with those of experiment 5, in which the data were analyzed using models M7 (beta) and M8 (beta&ω). We observed the same pattern as in the comparison between experiments 1 and 6. First, the null model M0 (one-ratio) was rejected more frequently than the null model M7 such that the power P_+s was always higher for the LRT comparing M0 and M3 than for the LRT comparing M7 and M8. For example, for N = 500 and S = 1.1, the power was P_+s,0.01 = 100% in experiment 7 and 65% in experiment 5 (table 3 ). Second, the proportion of replicates in which positive selection was indicated by parameter estimates (P₊) was generally higher under M8 than under M3 (table 3 ).

Discussion

Accuracy of the χ² Approximation

If the type I error rate of a test is greater than α, the test is liberal and unreliable. If the type I error rate is less than α, the test is conservative and might lack power. It would be best to use the correct distribution of the LRT statistic 2Δℓ under the null hypothesis, or its close approximation, as then the type I error rate would match the significance level α. However, finding such a distribution for the two LRTs considered in this paper is problematic, mainly because of the boundary problem.

A number of special cases of LRTs under nonstandard conditions are discussed in Self and Liang (1987) , which remains the latest reference on this issue. If only one parameter is on the boundary of the parameter space, the LRT statistic is approximately distributed as a mixture ½χ²₀ + ½χ²₁ if no other parameter is tested (case 5 of Self and Liang 1987 ). Here, χ²₀ is the distribution that takes the value 0 with probability 1. An example is the comparison of the one-rate and gamma-rates models of among-sites rate variation. In this case, the null model (one-rate) is equivalent to fixing the shape parameter α of the gamma distribution at infinity (Yang 1996 ). Recent simulations (Goldman and Whelan 2000 ; Ota et al.2000) showed that the LRT statistic fits the above mixture distribution very well even when the sample size is not very large. However, increasing the number of boundary parameters complicates the case and, in some situations, might cause the LRT statistic not to be expressible as a mixture of χ² distributions (e.g., case 8 of Self and Liang 1987 ). Moreover, the existence of a consistent ML estimator is one of the main assumptions for the LRT statistic to asymptotically converge to the χ² or its mixture distributions (Self and Liang 1987 ). In the LRTs considered in this paper, some parameters are not estimable, so none of the known distributions or their mixtures are expected to apply.

Consequently, we used χ²₄ to compare M0 (one-ratio) and M3 (discrete), and we used χ²₂ to compare M7 (beta) and M8 (beta&ω), as suggested by Yang et al. (2000) . This approach makes the LRT conservative and leads to loss of power. This might be particularly important for data sets of highly similar sequences, as failure to detect positive selection might be due to the lack of power of the LRT. Note that when we examined the accuracy of the LRT (table 2 ), we considered the statistic 2Δℓ only, but when we examined the power of the test P_+s (table 3 ), we further required that parameter estimates in the alternative model (M3 or M8) suggested positive selection. Thus, the LRTs used in detecting positive selection as examined in table 3 are even more conservative than the results of table 2 suggest.

Besides the boundary problem, the χ² approximation can also be affected by insufficient sample sizes. However, our simulation with no boundary problem, as well as previous studies (e.g., Whelan and Goldman 1999 ; Zhang 1999 ), suggests that even with relatively short sequences (e.g., with 50 codons), the distribution of 2Δℓ fits the χ² quite well. Hence, analysis of short sequences appears feasible, although it might be difficult to get significant results. We should note that when the χ² approximation is unreliable, Monte Carlo simulation can be used to obtain the correct null distribution (Goldman 1993 ).

Power of LRT

Our simulations show several patterns of the power function, all of which are intuitively justified. Longer sequences exhibit an increased probability of detecting adaptive evolution, while for short sequences the power can be almost 0%. Very similar sequences carry little information, causing low power of the LRT. The power increases with sequence divergence until it reaches its maximal value, after which further increases of sequence divergence lead to reduced power. With multiple substitutions at the same site, the most recent changes might overwrite previous substitutions, causing loss of information. Thus, very divergent sequences do not contain much information.

The most efficient way of obtaining high power appears to be to use many sequences. Adding more sequences causes a spectacular rise in power, even when the sequence divergence is low. Increasing the strength of positive selection also leads to improved power. Increasing the proportion of positively selected sites should have a similar effect, although no simulations were performed to examine it.

Differences Between the Two LRTs

We obtained significant results much more often with the LRT that compares M0 (one-ratio) and M3 (discrete) than with the LRT that compares M7 (beta) and M8 (beta&ω). We note that M7 is a very flexible null model and accounts for both neutral and deleterious mutations with 0 < ω < 1. As a result, the M7-M8 comparison is a very stringent test of positive selection. The M0-M3 comparison, however, is more a test of variable selective pressure among sites (indicated by the ω ratio) than a test of positive selection. Since the selective pressure seems to be variable among sites in every functional protein, M0 is a very unrealistic model. For example, in all 10 data sets analyzed by Yang et al. (2000) , M0 was easily rejected when compared with M3, although in four of them positive selection was not detected. Thus, if by chance parameter estimates under M3 indicate positive selection, we might falsely claim positive selection using the LRT comparing M0 and M3. We performed one such simulation experiment where the assumption of M0 was violated. We simulated 500 replicate data sets, each with N = 500 codons, using parameter settings of experiment A in table 2 except that we used the neutral model (M1) for the ω distribution. M1 (neutral) assumes two site classes with the ω ratios ω₀ = 0 and ω₁ = 1. We set the proportions for the two site classes at p₀ = 0.5 and p₁ = 0.5. The simulated data were then analyzed using M0 and M3. In 75% of replicates, at least one of the three ω parameters in M3 was estimated to be greater than 1, and the LRT was also significant, leading to false detection of positive selection. The LRT comparing M7 and M8 applied to the same data sets were found to be robust to violation of assumptions and falsely detected positive selection in only 5% of the replicates at α = 0.05. Furthermore, if the data were analyzed using M1 (neutral) and M3 (discrete), the false-positive rate was 0.02 at α = 0.05. Following Yang et al. (2000) , we thus recommend that multiple models and tests be used in real data analysis and that caution be exercised when only the M0-M3 comparison suggests positive selection.

Open in new tab

Table 1 Models of Variable {ω} Ratios Among Sites Used to Investigate the Accuracy and Power of the Likelihood Ratio Test

Open in new tab

Table 1 Models of Variable {ω} Ratios Among Sites Used to Investigate the Accuracy and Power of the Likelihood Ratio Test

Open in new tab

Table 2 Type I Error Rate: Numbers of Cases out of 100 for Which the Null Hypothesis Was Rejected at the {α} = 1% (5%) Significance Levels

Open in new tab

Table 2 Type I Error Rate: Numbers of Cases out of 100 for Which the Null Hypothesis Was Rejected at the {α} = 1% (5%) Significance Levels

Open in new tab

Table 3 Power of the Likelihood Ratio Test (LRT): Numbers of Replicates out of 100 in Which Positive Selection Was Indicated by Parameter Estimates (P₊) or Detected by the LRT at the 1% (P_+s,0.01) and 5% (P_+s,0.05, in parentheses) Significance Levels

Open in new tab

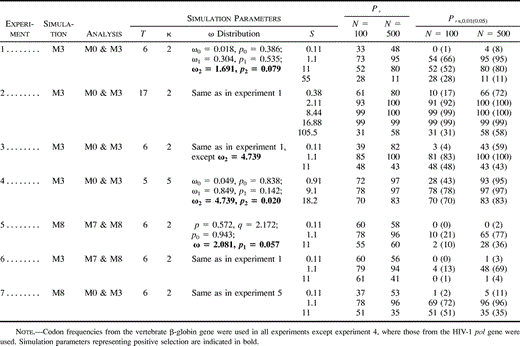
Table 3 Power of the Likelihood Ratio Test (LRT): Numbers of Replicates out of 100 in Which Positive Selection Was Indicated by Parameter Estimates (P₊) or Detected by the LRT at the 1% (P_+s,0.01) and 5% (P_+s,0.05, in parentheses) Significance Levels

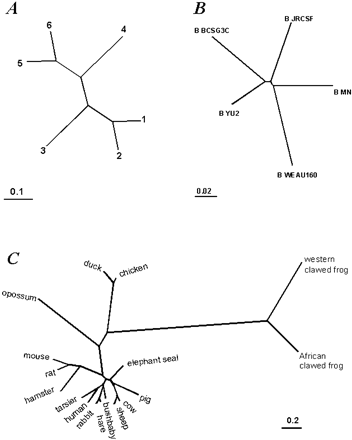
Fig. 1.—Tree topologies used in the simulations. A, Artificial six-taxon tree. B, Five-taxon subtree from a tree constructed for 23 HIV-1 pol gene sequences (Yang et al.2000) . C, A β-globin tree for 17 vertebrate species from Yang et al. (2000)

Open in new tabDownload slide

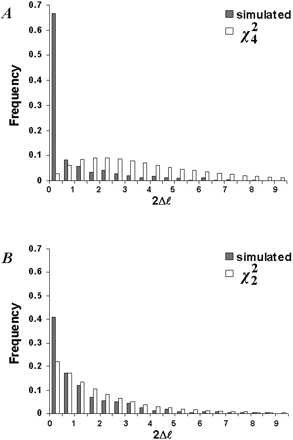
Fig. 2.—Comparison of the χ² distribution with the distribution of the likelihood ratio test (LRT) statistic 2Δℓ in 500 simulated replicates. A, The LRT compares M0 (one-ratio) and M3 (discrete) for N = 500 and S = 1.1 (table 2 , experiment A). B, The LRT compares M7 (beta) and M8 (beta&ω) for N = 500 and S = 1.1 (table 2 , experiment D)

Open in new tabDownload slide

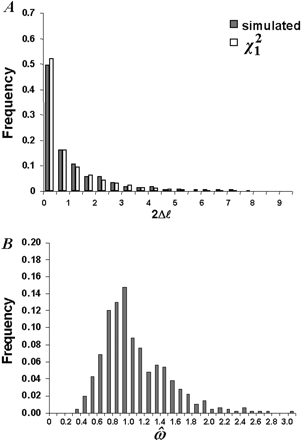
Fig. 3.—Accuracy of the asymptotic theory for the likelihood ratio test of H₀: ω = 1 against H₁: ω ≠ 1. One ω ratio (model M0) is assumed for all sites in both H₀ and H₁. Five hundred data sets were simulated using parameters taken from experiment A of table 2 , except that ω = 1. The six-taxon tree of figure 1A and the codon frequencies from the vertebrate β-globin gene were used. The tree length is S = 1.1 substitutions per codon along the tree. The sequence length is N = 50 codons. A, Comparison of χ²₁ with the simulated distribution of 2Δℓ. The two distributions are not significantly different from each other. B, The distribution of maximum-likelihood estimates of ω under H₁

Open in new tabDownload slide

We thank Willie Swanson and two anonymous referees for constructive comments. This study was supported by a Biotechnology and Biological Sciences Research Council grant to Z.Y. M.A. was supported by a Medical Research Council studentship.

References