-
PDF
- Split View
-
Views
-
Cite
Cite
Yun Jin, Chao Feng Chen, Xian-Rong Zhou, Yi-Yuan Cheng, H-J Schulze, Deformed K− nuclei in the Skyrme–Hartree–Fock approach, Progress of Theoretical and Experimental Physics, Volume 2019, Issue 12, December 2019, 123D03, https://doi.org/10.1093/ptep/ptz141
Close - Share Icon Share
Abstract
The properties of kaonic nuclei are studied using a two-dimensional Skyrme–Hartree–Fock model with a |$KN$| Skyrme force. We focus in particular on the instability of the solutions for a too strong |$KN$| interaction, which determines a maximum value of the kaon binding in this approach. We then analyze the change of the deformation properties of several core-deformed nuclei caused by the added kaon, and find a shrinking of the core and in some cases a complete loss of deformation.
1. Introduction
Kaonic nuclei are an important problem in the study of strangeness physics [1–4]. Experimental searches for |$K^-$|–nuclear bound states using stopped kaon reactions with neutrons or protons were conducted early at KEK and at DA|$\Phi$|NE [5–7]. In recent years, they were microscopically investigated using meson beams with new and upgraded experimental facilities at J-PARC, where the broad |$K^-pp$| bound-state structure is examined by current experiments [8,9]. Future experiments are foreseen at FAIR and HIAF [10].
One expects that theoretical calculations of kaonic nuclei to fit these experimental results may help us further explore the |$K^-N$| interaction (KNI). Kaonic nuclei have been theoretically investigated by different models, e.g. the relativistic mean field model [11–20], |$G$|-matrix model [21–23], chiral condensate model [24,25], self-consistent meson–baryon coupled-channel interaction model [26–43], Skyrme model [44,45], etc. Further constraints have been obtained by the study of electromagnetically bound kaonic atoms within the phenomenological density-dependent optical potential model [46].
In the relativistic mean field model, several |$K^-$| nuclei from |$^{12}_{\ K}$|C to |$^{208}_{\hspace{.7em}K}$|Pb were studied and the kaon binding energies of the |$1s$| state were obtained in the range |$49\sim76$| MeV [11]. Within the framework of antisymmetrized molecular dynamics, kaonic nuclei were calculated by a |$G$|-matrix approach [21], and |$^6_K$|Be, |$^8_K$|Be, and |$^9_K$|B were predicted as deeply bound kaonic nuclei. Within the relativistic mean field theory combined with a chiral model, the proton, neutron, and kaon density distributions of |$^{15}_{8K}$|O and its binding energy per kaon were calculated at two values of the |$K^-$| potential depth, |$V_K=-80$| MeV and |$V_K=-120$| MeV [25]. The results indicated that the nuclear density in the central region of multi-|$K^-$| nuclei is saturated for strangeness |$|S|\geqslant8$|. In the self-consistent meson–baryon coupled-channel interaction model, the |$K^-pp$| structure was found as a shallowly bound system, and the binding energy of the |$K^-pp$| cluster was obtained in the range |$14\sim50$| MeV [26]. The phenomenological density-dependent optical potential model predicts the deepest values of |$150\sim200$| MeV for the |$K^-$| potential depth [46–50].
However, there is still much controversy on the |$K^-$|–nucleus bound state and the depth of the kaon nuclear optical potential. Theoretical coupled-channel calculations employing only (chiral) two-body forces yield widely varying results for the real and imaginary parts of the optical potential [37,38]. The recent |$K^-$|–nuclear experiments investigate the possible existence of a deeply bound |$K^-pp$| state [8,9] in order to obtain experimental constraints on this problem, but currently the issue is still unsolved.
In 2005, the first evidence of a kaon bound state |$K^-pp$| was observed through its decay into a proton and |$\Lambda$| at DA|$\Phi$|NE by the FINUDA Collaboration [6]. They deduced a binding energy of |$115^{+6}_{-5}$|(stat.)|$^{+3}_{-4}$|(sys.) MeV, as well as a decay width of |$67^{+14}_{-11}$|(stat.)|$^{+2}_{-3}$|(sys.) MeV. In 2010, a deeply bound |$K^-pp$| state was indicated by the analysis of the DISTO experiment, which studied the intermediate |$K^-pp$| state in the |$p+p \rightarrow K^-pp + K^+ \rightarrow p + \Lambda + K^+$| reaction [51]. This was later questioned by the HADES Collaboration’s re-analysis of the |$p+p$| reaction data [52]. Recent experiments at J-PARC by the E15 and E27 Collaborations presented the latest results. E27 claimed that they had observed a deeply bound state |$K^-pp$|, which was produced in the |$\pi^+ + n+p \rightarrow K^-pp + K^+ \rightarrow \Sigma^0 + p + K^+$| reaction. And the E15 Collaboration observed a bound state |$K^-pp$| with a binding energy of |$47\pm3(\text{stat.})^{+3}_{-6}(\text{sys.})\,$|MeV [8].
In Refs. [44,45] we introduced the Skyrme–Hartree–Fock (SHF) approach for the study of kaonic nuclei; namely, we combined a standard |$NN$| Skyrme force with an effective KNI obtained within the chiral model of Ref. [24]. The purpose of our present paper is to continue this study by replacing the chiral KNI with a simpler but more general phenomenological |$KN$| Skyrme force, and in particular to investigate deformed nuclei within a two-dimensional (2D) Skyrme calculation. The motivation is that a rather strong KNI might cause profound changes of the nuclear core structure in some cases, which can be studied and understood in detail in our approach. In particular, we will consider the |$K^-$| nuclei with spherical core |$^{16}_{\ K}$|O (|$^{16}$|O+|$K^-$|), |$^{40}_{\ K}$|Ca (|$^{40}$|Ca+|$K^-$|), |$^{208}_{\hspace{.7em}K}$|Pb (|$^{208}$|Pb+|$K^-$|), and the deformed-core nuclei |$^{\,8}_{K}$|Be (|$^{8}$|Be+|$K^-$|), |$^{20}_{\ K}$|Ne (|$^{20}$|Ne+|$K^-$|), |$^{36}_{\ K}$|Ar (|$^{36}$|Ar+|$K^-$|).
The paper is organized as follows. In Sect. 2 the self-consistent SHF approach with a simple Skyrme force for the KNI is presented. Section 3 shows the obtained results and discusses the neutron, proton, and kaon mean fields and density distributions for the spherical |$K^-$| nuclei |$^{16}_{\ K}$|O, |$^{40}_{\ K}$|Ca, |$^{208}_{\hspace{.7em}K}$|Pb. In Sect. 4 the deformation and potential energy surfaces of |$^{\,8}_{K}$|Be, |$^{20}_{\ K}$|Ne, |$^{36}_{\ K}$|Ar are analyzed and compared with their core nuclei. Finally, we present a summary in Sect. 6.
2. Formalism
Our calculation is performed in the SHF approach with a density-dependent Skyrme force for the KNI. In this approach, the total energy of a nucleus is written as usual [53–60] as
where |$\varepsilon_{NN}$| is the nucleon–nucleon part of the energy-density functional, |$\varepsilon_{KN}$| is the kaon–nucleon part, and |$\varepsilon_{\rm C}$| is the electromagnetic part due to the Coulomb interaction of protons and kaons. These energy-density functionals depend in general on the one-body density |$\rho_q$|, kinetic density |$\tau_q$|, and spin-orbit current |$\boldsymbol{J}_q$| (only for nucleons),
where |$\phi^i_q$| (|$i=1,N_q$|) are the self-consistently calculated single-particle (s.p.) wave functions of the |$N_q$| occupied states for the different particles |$q=n,p,K^-$| in a nucleus.
The minimization of the total energy implies the SHF Schrödinger equation for each single-particle state,
with the mean fields (including the Coulomb interaction)
The spin-orbit mean field |$\boldsymbol W_{n,p}$| is that of the |$NN$| Skyrme force used here, and we put |$\boldsymbol W_K=0$| in this study.
For |$\varepsilon_{NN}$| we use a standard nucleonic Skyrme energy density functional [57–59] (in this paper the SLy4 parametrization [61–63]), depending on the densities |$\rho_{n,p}$|, |$\tau_{n,p}$|, |$\boldsymbol{J}_{n,p}$|, and for the kaonic contribution we make the simple ansatz
in view of the fact that currently not even the magnitude of the KNI is well known. With this definition in nearly symmetric systems, |$\rho_p\approx\rho_n$|, the results depend primarily on |$a_0$| and much less on |$x_0$|. For a rather strong asymmetric KNI, the |$n$| and |$p$| density distributions will be affected differently, and the dependence on |$x_0$| will become apparent. These features will be seen later.
We take into account pairing forces (between nucleons only) within BCS approximation, employing a density-dependent |$\delta$| force [64],
with |$V'_n=V'_p=410$||$\,\text{MeV}\,\text{fm}^{-3}$| as the pairing strength in light nuclei [65–67] and |$V'_p=1146$||$\,\text{MeV}\,\text{fm}^{-3}$|, |$V'_n=999$||$\,\text{MeV}\,\text{fm}^{-3}$| for medium-mass and heavy nuclei. A smooth energy cutoff is included in the BCS calculation [68].
In the following we will study the dependence of the main observables, such as kaon mean field |$V_K$|, kaon removal energy
(in this notation |$A$| is the nucleon number and |$Z$| is the proton number, not the charge number), and also deformation properties of some nuclei, on the KNI strength parameter |$a_0$|.
In microscopic approaches for the KNI [24,37,38], the |$K^-p$| interaction is usually much more important (attractive) than the |$K^-n$| interaction, and we take account of this fact by comparing in the following the two extreme choices |$x_0=0$| and |$x_0=1$|, respectively modeling a (|$p$|,|$n$|)-symmetric KNI and the case of neglecting the |$K^-n$| interaction completely, while doubling the |$K^-p$| interaction. We will study whether the two choices lead to significantly different predictions for some observables.
The choice of the KNI functional in Eq. (6) amounts to a simple linear density dependence of the kaon mean field,
In the future, once enough reliable data become available, the functional can of course be extended by adding nonlinear density dependence, surface terms, etc., as in the case of the SHF approach for |$\Lambda$| hypernuclei [55,60]. At the moment, it is clearly premature to determine all the KNI parameters of these terms.
A similar remark concerns the imaginary part of the KNI, due to the decay channels |$KN \rightarrow \pi Y$|, |$KNN \rightarrow YN$| (|$Y=\Lambda,\Sigma$|) [37,38,43]. While we study here the effect of the KNI strength parameters |$a_0$| and |$x_0$| of the real part |$\text{Re}\, V_K$| on the instability and properties of kaonic nuclei, we currently neglect the imaginary part in attendance of reliable data. It has been found that the effect of a moderate |$\text{Im}\,V_K\lesssim 20$| MeV (neglecting the kaon multinucleon absorption) on the real part is nearly negligible, whereas too large widths might make kaon bound states unobservable [37,38]. We consider this feature an open problem that can only be solved by future confrontation with accurate data. We give a brief estimate of the qualitative effect in our formalism in the next section, though.
Assuming axial symmetry of the mean field, the deformed SHF Schrödinger equation is solved in cylindrical coordinates |$(r,z)$| within the axially deformed harmonic oscillator basis [54,57–59]. This allows us to model axially deformed nuclei, which will be discussed in the following.
3. Results
We now study the properties of kaonic nuclei with spherical cores, |$^{16}_{\ K}$|O, |$^{40}_{\ K}$|Ca, |$^{208}_{\hspace{.7em}K}$|Pb, and deformed cores, |$^{\,8}_{K}$|Be, |$^{20}_{\ K}$|Ne, |$^{36}_{\ K}$|Ar. We first consider |$a_0$| as a free parameter (for both choices |$x_0=0,1$|) and study the strength of the binding as a function of its value. Then we illustrate the changes of nuclear structure in more detail for two reasonable choices of |$a_0$|.
3.1. Kaonic nuclei with spherical core: |$^{16}_{\ K}$|O, |$^{40}_{\ K}$|Ca, |$^{208}_{\hspace{.7em}K}$|Pb
Figure 1 shows the central kaon potential |$-V_K(r=0,z=0)$| and the kaon removal energy |$B_K$| as a function of the KNI parameter |$a_0$| for the three spherical kaonic nuclei |$^{16}_{\ K}$|O, |$^{40}_{\ K}$|Ca, |$^{208}_{\hspace{.7em}K}$|Pb. One observes that both quantities increase first linearly and then more rapidly with the KNI strength, until meeting instability points at |$a_0=845$|, 867, 902|$\,\text{MeV}\,\text{fm}^{-3}$| (|$B_K=123$|, 146, 165 MeV) for |$x_0=0$| and the three nuclei, respectively. For the asymmetric KNI, |$x_0=1$|, the instability occurs much earlier at |$a_0=359$|, 403, 559|$\,\text{MeV}\,\text{fm}^{-3}$| (|$B_K=32$|, 55, 88 MeV). We had encountered this phenomenon already in Refs. [44,45]: For a too strong attractive KNI, the central densities of nucleons and kaon may increase without limit, and at a certain point the nuclear core is no longer stable against collapse. This feature has been observed in Refs. [44,45] for different nucleonic Skyrme forces, which all yielded similar collapse points. It might be cured by introducing suitable repulsive |$NN$| and |$KN$| forces active at high density, and the maximum of |$a_0$| might then be enlarged. But until that can be reliably done, we consider the above limits on |$a_0$| as the possible reasonable range of our theoretical investigation.
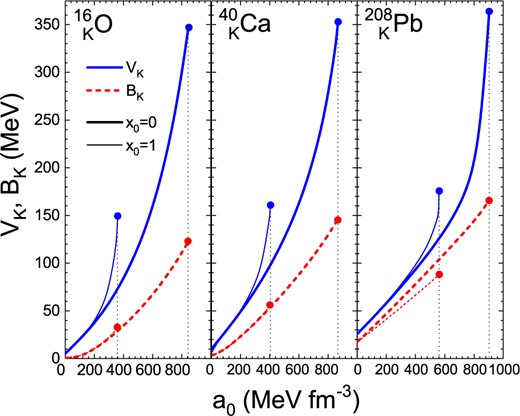
The central kaon potential |$-V_K(\boldsymbol{r}=\boldsymbol{0})$| (solid blue curves) and the kaon removal energy |$B_K$| (dashed red curves) of |$^{16}_{\ K}$|O, |$^{40}_{\ K}$|Ca, |$^{208}_{\hspace{.7em}K}$|Pb, calculated with the SLy4 |$NN$| force and the |$KN$| Skyrme force for different interaction parameters |$a_0$| and the two choices |$x_0=0$| (thick curves), 1 (thin curves). The markers indicate the onset of instability of the SHF solutions.
The difference between the |$x_0=0$| and |$x_0=1$| interactions is large, because in the latter case the proton component of the nucleonic core is much more distorted for a given |$a_0$| than in the former case, and therefore instability sets in earlier. Consequently, the maximum potential |$V_K^\text{max}$| and kaon removal energy |$B_K^\text{max}$| are much smaller than those for |$x_0=0$|. Note that in particular for the light nuclei, the possible value of the removal energy |$B_K$| is severely limited in this case. However, for a given value of |$a_0$|, |$B_K$| is nearly independent of the asymmetry parameter |$x_0$|.
In the following we fix the KNI parameter to two typical “weak” and “strong” values, |$a_0=300$| or 700|$\,\text{MeV}\,\text{fm}^{-3}$|, in order to investigate in more detail the changes of nuclear structure. The corresponding values of |$V_K$| and |$B_K$| for the different nuclei (and also for |$^{\,8}_{K}$|Be, |$^{20}_{\ K}$|Ne, |$^{36}_{\ K}$|Ar in spherical approximation) are listed in Table 1. For example, in |$^{40}_{\ K}$|Ca the two choices correspond to |$V_K\approx 70$| and 200 MeV, compared to a range |$V_K\approx\;$|(30–110) MeV currently obtained with more microscopic chiral forces [37].
The central kaon potential |$V_K \equiv -V_K(\boldsymbol{r}=\boldsymbol{0})$| and the kaon separation energy |$B_K$| for the (spherical) ground states of several nuclei in the case of |$a_0=300$|, 700|$\,\text{MeV}\,\text{fm}^{-3}$| and |$x_0=0,1$|. The maximum values of |$a_0$| for stable calculations and the corresponding |$V_K$| and |$B_K$| are also listed. Energies are given in MeV and |$a_0$| in |$\,\text{MeV}\,\text{fm}^{-3}$|.
| . | . | . | . | . | |$a_0=300$| . | . | |$a_0=700$| . | ||
|---|---|---|---|---|---|---|---|---|---|
| . | |$x_0$| . | |$a_0^\text{max}$| . | |$V_{\!K}^\text{max}$| . | |$B_{\!K}^\text{max}$| . | |$V_K$| . | |$B_K$| . | . | |$V_K$| . | |$B_K$| . |
| |$^{\,8}_{K}$|Be | 0 | 740 | 291.9 | 77.9 | 61.6 | 9.2 | 257.1 | 68.7 | |
| 1 | 330 | 169.4 | 14.4 | 88.5 | 10.3 | ||||
| |$^{16}_{\ K}$|O | 0 | 845 | 345.6 | 122.6 | 58.1 | 21.1 | 217.0 | 87.3 | |
| 1 | 359 | 150.1 | 31.6 | 73.0 | 22.1 | ||||
| |$^{20}_{\ K}$|Ne | 0 | 807 | 289.6 | 116.8 | 57.4 | 25.0 | 204.9 | 92.3 | |
| 1 | 351 | 122.7 | 33.8 | 69.3 | 25.8 | ||||
| |$^{36}_{\ K}$|Ar | 0 | 837 | 343.8 | 144.4 | 74.9 | 36.9 | 225.1 | 111.1 | |
| 1 | 376 | 170.6 | 50.9 | 86.5 | 37.2 | ||||
| |$^{40}_{\ K}$|Ca | 0 | 867 | 352.0 | 146.1 | 71.5 | 37.4 | 208.9 | 107.5 | |
| 1 | 403 | 162.1 | 55.1 | 79.0 | 37.6 | ||||
| |$^{208}_{\ \ K}$|Pb | 0 | 902 | 362.2 | 165.4 | 75.2 | 62.2 | 160.8 | 126.8 | |
| 1 | 559 | 173.7 | 87.7 | 77.3 | 53.7 | ||||
| . | . | . | . | . | |$a_0=300$| . | . | |$a_0=700$| . | ||
|---|---|---|---|---|---|---|---|---|---|
| . | |$x_0$| . | |$a_0^\text{max}$| . | |$V_{\!K}^\text{max}$| . | |$B_{\!K}^\text{max}$| . | |$V_K$| . | |$B_K$| . | . | |$V_K$| . | |$B_K$| . |
| |$^{\,8}_{K}$|Be | 0 | 740 | 291.9 | 77.9 | 61.6 | 9.2 | 257.1 | 68.7 | |
| 1 | 330 | 169.4 | 14.4 | 88.5 | 10.3 | ||||
| |$^{16}_{\ K}$|O | 0 | 845 | 345.6 | 122.6 | 58.1 | 21.1 | 217.0 | 87.3 | |
| 1 | 359 | 150.1 | 31.6 | 73.0 | 22.1 | ||||
| |$^{20}_{\ K}$|Ne | 0 | 807 | 289.6 | 116.8 | 57.4 | 25.0 | 204.9 | 92.3 | |
| 1 | 351 | 122.7 | 33.8 | 69.3 | 25.8 | ||||
| |$^{36}_{\ K}$|Ar | 0 | 837 | 343.8 | 144.4 | 74.9 | 36.9 | 225.1 | 111.1 | |
| 1 | 376 | 170.6 | 50.9 | 86.5 | 37.2 | ||||
| |$^{40}_{\ K}$|Ca | 0 | 867 | 352.0 | 146.1 | 71.5 | 37.4 | 208.9 | 107.5 | |
| 1 | 403 | 162.1 | 55.1 | 79.0 | 37.6 | ||||
| |$^{208}_{\ \ K}$|Pb | 0 | 902 | 362.2 | 165.4 | 75.2 | 62.2 | 160.8 | 126.8 | |
| 1 | 559 | 173.7 | 87.7 | 77.3 | 53.7 | ||||
The central kaon potential |$V_K \equiv -V_K(\boldsymbol{r}=\boldsymbol{0})$| and the kaon separation energy |$B_K$| for the (spherical) ground states of several nuclei in the case of |$a_0=300$|, 700|$\,\text{MeV}\,\text{fm}^{-3}$| and |$x_0=0,1$|. The maximum values of |$a_0$| for stable calculations and the corresponding |$V_K$| and |$B_K$| are also listed. Energies are given in MeV and |$a_0$| in |$\,\text{MeV}\,\text{fm}^{-3}$|.
| . | . | . | . | . | |$a_0=300$| . | . | |$a_0=700$| . | ||
|---|---|---|---|---|---|---|---|---|---|
| . | |$x_0$| . | |$a_0^\text{max}$| . | |$V_{\!K}^\text{max}$| . | |$B_{\!K}^\text{max}$| . | |$V_K$| . | |$B_K$| . | . | |$V_K$| . | |$B_K$| . |
| |$^{\,8}_{K}$|Be | 0 | 740 | 291.9 | 77.9 | 61.6 | 9.2 | 257.1 | 68.7 | |
| 1 | 330 | 169.4 | 14.4 | 88.5 | 10.3 | ||||
| |$^{16}_{\ K}$|O | 0 | 845 | 345.6 | 122.6 | 58.1 | 21.1 | 217.0 | 87.3 | |
| 1 | 359 | 150.1 | 31.6 | 73.0 | 22.1 | ||||
| |$^{20}_{\ K}$|Ne | 0 | 807 | 289.6 | 116.8 | 57.4 | 25.0 | 204.9 | 92.3 | |
| 1 | 351 | 122.7 | 33.8 | 69.3 | 25.8 | ||||
| |$^{36}_{\ K}$|Ar | 0 | 837 | 343.8 | 144.4 | 74.9 | 36.9 | 225.1 | 111.1 | |
| 1 | 376 | 170.6 | 50.9 | 86.5 | 37.2 | ||||
| |$^{40}_{\ K}$|Ca | 0 | 867 | 352.0 | 146.1 | 71.5 | 37.4 | 208.9 | 107.5 | |
| 1 | 403 | 162.1 | 55.1 | 79.0 | 37.6 | ||||
| |$^{208}_{\ \ K}$|Pb | 0 | 902 | 362.2 | 165.4 | 75.2 | 62.2 | 160.8 | 126.8 | |
| 1 | 559 | 173.7 | 87.7 | 77.3 | 53.7 | ||||
| . | . | . | . | . | |$a_0=300$| . | . | |$a_0=700$| . | ||
|---|---|---|---|---|---|---|---|---|---|
| . | |$x_0$| . | |$a_0^\text{max}$| . | |$V_{\!K}^\text{max}$| . | |$B_{\!K}^\text{max}$| . | |$V_K$| . | |$B_K$| . | . | |$V_K$| . | |$B_K$| . |
| |$^{\,8}_{K}$|Be | 0 | 740 | 291.9 | 77.9 | 61.6 | 9.2 | 257.1 | 68.7 | |
| 1 | 330 | 169.4 | 14.4 | 88.5 | 10.3 | ||||
| |$^{16}_{\ K}$|O | 0 | 845 | 345.6 | 122.6 | 58.1 | 21.1 | 217.0 | 87.3 | |
| 1 | 359 | 150.1 | 31.6 | 73.0 | 22.1 | ||||
| |$^{20}_{\ K}$|Ne | 0 | 807 | 289.6 | 116.8 | 57.4 | 25.0 | 204.9 | 92.3 | |
| 1 | 351 | 122.7 | 33.8 | 69.3 | 25.8 | ||||
| |$^{36}_{\ K}$|Ar | 0 | 837 | 343.8 | 144.4 | 74.9 | 36.9 | 225.1 | 111.1 | |
| 1 | 376 | 170.6 | 50.9 | 86.5 | 37.2 | ||||
| |$^{40}_{\ K}$|Ca | 0 | 867 | 352.0 | 146.1 | 71.5 | 37.4 | 208.9 | 107.5 | |
| 1 | 403 | 162.1 | 55.1 | 79.0 | 37.6 | ||||
| |$^{208}_{\ \ K}$|Pb | 0 | 902 | 362.2 | 165.4 | 75.2 | 62.2 | 160.8 | 126.8 | |
| 1 | 559 | 173.7 | 87.7 | 77.3 | 53.7 | ||||
For these parameter choices, Fig. 2 shows the density distributions in the three nuclei. Obviously the effect of the inserted kaon is larger in light nuclei, where the central proton and neutron distributions are substantially enhanced due to its presence. One can also see clearly the difference between neutron and proton core distortions for the |$x_0=1$| case, mentioned before. We can therefore anticipate a substantial reduction of the nuclear rms radius |$R_N$|, i.e. a shrinking of the nucleus. This will be studied in more detail in the following.
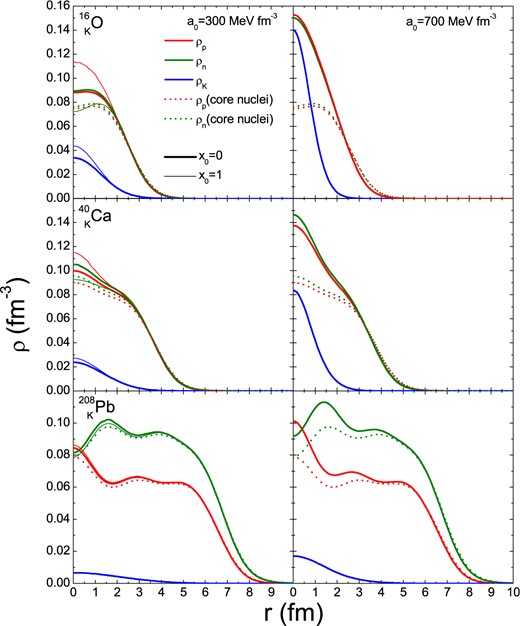
Proton, neutron, and kaon number density distributions of |$^{16}_{\ K}$|O, |$^{40}_{\ K}$|Ca, |$^{208}_{\hspace{.7em}K}$|Pb (solid curves) and their corresponding core nuclei (dotted curves) in the case of |$a_0=300$||$\,\text{MeV}\,\text{fm}^{-3}$| (left panels), 700|$\,\text{MeV}\,\text{fm}^{-3}$| (right panels) and for |$x_0=0$| (thick curves), 1 (thin curves in left panels).
Before that, we return to the problem of the imaginary part of the kaon optical potential, which we model by solving the SHF Schrödinger equation in Eq. (3) incorporating a complex kaon potential,
For simplicity we assume here a proportionality between both components,
in order to study the importance of the effect qualitatively. The imaginary part modifies the kaon wave function, single-particle energy, density distribution, and therefore the kaon removal energy. In Fig. 3 we display the (real part of the) kaon removal energy as a function of the absorption parameter |$\alpha$| for |$a_0=300$||$\,\text{MeV}\,\text{fm}^{-3}$|, |$x_0=0$|, and the three nuclei |$^{16}_{\ K}$|O, |$^{40}_{\ K}$|Ca, |$^{208}_{\hspace{.7em}K}$|Pb. One notes that the change of |$B_K$| is small, even up to a fairly large value |$\alpha=1$|. Furthermore, a given value of |$B_K$| could always be restored by slighty adjusting the value of |$a_0$| in this model. This demonstrates that the imaginary part of the kaon mean field does not play an important role in the SHF model, at least regarding its effect on the real part and the kaon removal energy. Treatment of real and imaginary part can be fairly well separated. Of course, more experimental information is required for a final parameter fitting beyond the simple proportionality assumption made here.
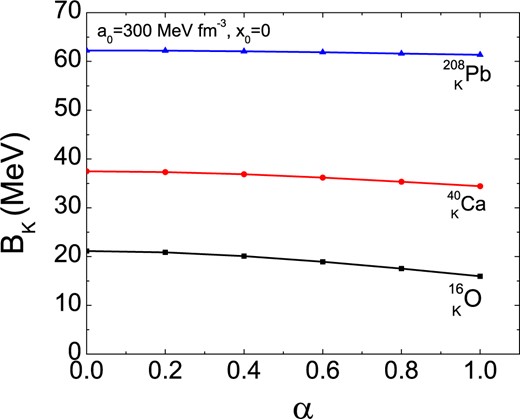
Kaon removal energy as a function of the absorption parameter |$\alpha$|, Eq. (12), for |$a_0=300$||$\,\text{MeV}\,\text{fm}^{-3}$|, |$x_0=0$|, and the nuclei |$^{16}_{\ K}$|O, |$^{40}_{\ K}$|Ca, |$^{208}_{\hspace{.7em}K}$|Pb.
3.2. Kaonic nuclei with deformed core |$^{\,8}_{K}$|Be, |$^{20}_{\ K}$|Ne, |$^{36}_{\ K}$|Ar
The strong contraction of the nuclear core observed in Fig. 2 motivates the extension of our model to deformed nuclei. In the case of |$\Lambda$| hypernuclei (with a substantially smaller |$\Lambda N$| interaction strength |$a_0^{(\Lambda N)}\approx 300$||$\,\text{MeV}\,\text{fm}^{-3}$| [60] compared to the |$KN$| one), the modification of the nuclear core by the inserted |$\Lambda$| is a well-known theoretical phenomenon [69–72], namely, both the nuclear core radius
and the nuclear quadrupole deformation
might be strongly affected by the added hyperon: shrinking and reduction of core deformation, respectively. We therefore carry out an equivalent analysis for kaonic nuclei now. At variance with |$\Lambda$| hypernuclei, however, the kaon decays on the same timescale as the eventual rearrangement of the nuclear structure, and this effect is neglected together with the imaginary part of the KNI in our present theoretical approach. Only a future dynamical simulation of the nuclear rearrangement could provide a more realistic picture.
Figure 4 shows the modification of the ground-state potential energy surfaces (PESs) of |$^{\,8}_{K}$|Be, |$^{20}_{\ K}$|Ne, |$^{36}_{\ K}$|Ar with increasing values of the parameter |$a_0$|. (The collapse points are |$a_0=740$|, 807, 837|$\,\text{MeV}\,\text{fm}^{-3}$| for |$x_0=0$| and |$a_0=330$|, 351, 376|$\,\text{MeV}\,\text{fm}^{-3}$| for |$x_0=1$|, respectively). In general, the PESs become increasingly flatter around the local minimum compared to the corresponding core nuclei. The deformation of the light nuclei |$^{\,8}_K$|Be and |$^{20}_{\ K}$|Ne might even completely vanish due to the added kaon for a sufficiently strong KNI, |$a_0>253 (243)$||$\,\text{MeV}\,\text{fm}^{-3}$| and |$a_0>768 (333)$||$\,\text{MeV}\,\text{fm}^{-3}$|, respectively, whereas for the heavier extended |$^{36}_{\ K}$|Ar nucleus the presence of a single kaon concentrated in the center is not enough to eliminate the deformation up to the highest possible values of |$a_0$|. As a word of caution, we remark that in general the predicted deformation properties of the core nuclei depend on the |$NN$| Skyrme force that is employed [72]; however, for the strongly deformed |$^8$|Be most Skyrme forces agree on a |$\beta_2\approx0.63$| [70]. A further comment regards the mean-field approximation employed here, which might be inadequate, in particular for weak PES minima, due to the neglect of configuration mixing. A beyond-mean-field treatment [73–76] might be required for a more realistic model.

Potential energy surfaces of |$^{\,8}_{K}$|Be, |$^{20}_{\ K}$|Ne, |$^{36}_{\ K}$|Ar for different KNI strengths |$a_0$| (in |$\,\text{MeV}\,\text{fm}^{-3}$|, numbers near the curves) and for |$x_0=0$| (left panels), 1 (right panels). The dotted red curves are those of the core nuclei. The minima are indicated by markers and connected by a green line.
Figure 5 summarizes the dependence on |$a_0$| of the nuclear and kaonic radii |$R_n$|, |$R_p$|, |$R_N$|, |$R_K$| (upper panels) and the deformation parameter |$\beta_2$| (central panels) at the minimum of the PES for the three kaonic nuclei. The shrinking of the nuclear cores, and in particular of the trapped kaon wave function, is clearly evident, with an associated reduction of |$\beta_2$|. The effect is more dramatic for the lightest nuclei, where the deformation vanishes completely for large enough |$a_0$|, as seen in Fig. 4. In the insets we emphasize the different behavior of |$R_n$| and |$R_p$| in the case of the asymmetric KNI |$x_0=1$|.
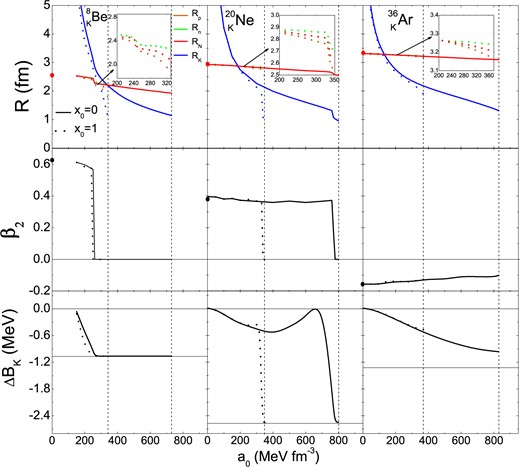
Root mean square radii |$R_p$|, |$R_n$|, |$R_N$|, |$R_K$| (upper panels), deformation parameter |$\beta_2$| (central panels), and change of kaon removal energy due to deformation, Eq. (15), (lower panels) at the minimum of the BES vs. |$a_0$| for |$^{\,8}_{K}$|Be, |$^{20}_{\ K}$|Ne, |$^{36}_{\ K}$|Ar and |$x_0=0$|, 1.
Finally, an interesting question related to the deformation phenomenon is the modification of the kaon removal energy due to this effect, i.e the quantity
obtained from comparing the results of 2D and 1D calculations. Figure 5 (lower panels) shows the dependence of this quantity on |$a_0$| for the three nuclei. Without any deformation of the kaonic nucleus, one would have a constant |$\Delta B_K = \Delta E(^AZ) < 0$| due to the deformation of the core nucleus only, which is indicated by horizontal lines in the figure. The fact that the kaonic nucleus is deformed increases the removal energy relative to this value, but the total result remains negative. The overall result is small, of the order of the depths of the deformation minima.
4. Conclusions
We studied the density dependence of the |$K^-$| nuclear potential and properties of kaonic nuclei using a 2D SHF model with a simple |$KN$| Skyrme force, which self-consistently accounts for the modification of the nuclear core due to the inserted kaon. We confirmed the existence of instabilities related to the unrestrained increase of central nucleon and kaon densities, which currently limits the maximum kaon binding in this approach to not much more than 150 MeV for heavy nuclei with the symmetric KNI (|$x_0=0$|) and much less for light nuclei and/or the asymmetric KNI (|$x_0=1$|). This demonstrates that it is premature to discuss the structure of very strongly bound kaonic nuclei, before the properties of the |$NN$| and |$KN$| interactions at high density are reliably known and theoretically under control.
We also studied the shape of |$K^-$| nuclei with a deformed nuclear core in the ground state and demonstrated a shrinking of the overall size of the nucleus, together with a slight reduction of the quadrupole deformation that might even vanish completely for light nuclei and a very strong KNI.
In the future, completing the construction of the |$KN$| Skyrme force and including the imaginary part of the kaon optical potential will render the approach more reliable and predictive. Hopefully, accurate experimental data on the kaon binding will become available and allow fitting of the parameters of the KNI for this purpose.
Acknowledgements
We thank Ji-Wei Cui for suggestive discussions. This work was supported by the National Science Foundation of China under contract Nos. 11775081 and 11875134, and the Natural Science Foundation of Shanghai under contract No. 17ZR1408900.



