Microscopic optical potentials including breakup effects for elastic scattering

Abstract

We construct a microscopic optical potential including breakup effects for the elastic scattering of weakly binding projectiles within the Glauber model, in which a nucleon–nucleus potential is derived using the |$g$|-matrix folding model. The derived microscopic optical potential is referred to as the eikonal potential. For |$d$| scattering, calculation with the eikonal potential, i.e., the EP model, reasonably reproduces the result of the exact calculation with the continuum-discretized coupled-channels method at intermediate energies. From the properties of the EP model, the inaccuracy of the eikonal approximation used in the Glauber model is partially excluded. Also analyzed with the eikonal potential is the scattering of |$^6$|He from |$^{12}$|C, and its applicability to scattering with many-body projectiles is shown.

1. Introduction

A microscopic understanding of the nucleon–nucleus (⁠|$NA$|⁠) and nucleus–nucleus (⁠|$AA$|⁠) optical potentials is one of the most important issues in the theory of nuclear reactions. Optical potentials are necessary for describing not only elastic scattering but also reactions including higher-order processes. For example, the distorted-wave Born approximation and the continuum-discretized coupled-channels method (CDCC) [1–3] require the optical potentials between constructs of a projectile (P) and a target (T) to describe inelastic scattering, breakup, and transfer reactions.

The |$g$|-matrix folding model has been widely used as a reliable method for describing optical potentials [4–10]. The |$g$| matrix is an effective nucleon–nucleon interaction [11–28] in nuclear matter and depends on the density |$\rho_{\rm m}$| of the nuclear matter. In the |$g$|-matrix folding model, optical potentials are derived by folding the |$g$| matrix with the target density |$\rho_{\rm T}$| for |$NA$| scattering and with |$\rho_{\rm T}$| and the projectile one |$\rho_{\rm P}$| for |$AA$| scattering. The procedures are referred to as the single-folding (SF) model for |$NA$| scattering and the double-folding (DF) model for |$AA$| scattering.

In the SF model, |$\rho_{\rm T}$| is regarded as being |$\rho_{\rm m}$| in the |$g$| matrix via the local density approximation. The |$NA$| optical potential thus obtained becomes nonlocal by taking into account knock-on exchange processes. The nonlocal potential is impractical in many applications but can be localized with good accuracy by using the Brieva–Rook approximation [14–16]. The localized potential is quite successful in reproducing experimental data systematically when reliable |$g$| matrices such as the Melbourne [23], complex effective Gaussian [19,20,25–27], and chiral effective field theory [28] ones are used.

On the other hand, it is more difficult to calculate the optical potential with the DF model for |$AA$| scattering than it is with the SF model for |$NA$| scattering. The main problem with the DF model is how to treat |$\rho_{\rm m}$| in the |$g$| matrix for |$AA$| scattering. In general, the sum of |$\rho_{\rm P}$| and |$\rho_{\rm T}$| is taken as |$\rho_{\rm m}$| in the |$g$| matrix, a procedure known as the frozen-density approximation (FDA). To reproduce experimental data, the optical potential derived using the DF model with the FDA often requires a normalization factor for its real and imaginary parts. Thus, the choice of |$\rho_{\rm m}$| in the |$g$| matrix for the DF model is a longstanding open problem.

In previous work on the scattering of |$^{3,4}$|He from various targets [29,30], we proposed the target-density approximation (TDA) in the DF model, where |$\rho_{\rm m}$| is estimated using only |$\rho_{\rm T}$|⁠. The DF model with the TDA (the DF-TDA model) does well at reproducing experimental data for |$^{3,4}$|He scattering at intermediate energies with no adjustable parameter, and it has been validated theoretically by using multiple-scattering theory [31–33]. Furthermore, as a practical version of the DF-TDA model, we also proposed the double–single folding (DSF) model for |$^{3,4}$|He scattering, in which the optical potential between |$^{3,4}$|He and the target is derived by folding the localized |$NA$| optical potential of the SF model with the |$^{3,4}$|He densities.

However, the optical potential calculated by the DSF model does not account for breakup effects in elastic scattering. In fact, as shown in Fig. 3(a) in Ref. [30], results with the DSF model differ slightly from experimental data for |$^3$|He scattering at low energies. This discrepancy is due to the breakup effects of |$^3$|He and can be corrected by applying a CDCC calculation, which can describe breakup effects accurately. The CDCC has been used successfully to analyze the scattering of weakly binding two- and three-body projectiles. However, although the CDCC is reliable for analyzing breakup reactions, it is difficult to apply it to the scattering of projectiles with more than five bodies (e.g., |$^{8}$|He) because of the high computational cost.

The Glauber model [34] has been proposed as a means of treating P and T excitation effects for many-body systems. In the Glauber model, the excitation effects are described under the adiabatic and eikonal approximations, which work well for scattering at high incident energies. An advantage of the Glauber model is that it allows an optical potential to be constructed that includes excitation effects. The obtained optical potential is referred to as the eikonal potential (EP) [34–36]. Because the eikonal potential is based on the adiabatic and eikonal approximations, it is expected to be highly valid for scattering at high incident energies. However, the validity of the eikonal potential for scattering at low incident energies is yet to be investigated, and the corresponding validity of the adiabatic and eikonal approximations has hardly been discussed to date.

In this paper, we investigate the validity of the eikonal potential by comparing with CDCC results for |$d$| scattering at 20–200 MeV/nucleon, which is described by a |$p$| + |$n$| + T three-body model. How the adiabatic and eikonal approximations affect the elastic scattering is also discussed. The optical potentials for |$p$|–T and |$n$|–T systems are derived using the SF model with the Melbourne |$g$| matrix. In the analysis, we also discuss the validity of the adiabatic and eikonal approximations for low-energy scattering. Furthermore, to show the applicability of the eikonal potential to many-body systems, we use it to analyze |$^6$|He scattering that is described by a |$^4$|He + |$n$| + |$n$| + T four-body model. Herein, we compare the EP model and the four-body CDCC for the first time.

The paper is organized as follows. In Sect. 2, we describe the theoretical framework for deriving the eikonal potential for |$d$| scattering. In Sect. 3, we present numerical results and discuss the properties of the eikonal potential. Finally, we summarize the paper in Sect. 4.

2. Theoretical framework

2.1. Glauber model

We consider |$d$| scattering on T using a |$p$| + |$n$| + T three-body model. The scattering is described by the three-body Schrödinger equation

$$\begin{eqnarray} \left[ -\frac{\hbar^2}{2\mu}\boldsymbol{\nabla}_{\boldsymbol{R}}^2 +U(\boldsymbol{r},\boldsymbol{R})+h_d-E \right]\Psi(\boldsymbol{r},\boldsymbol{R})=0, \label{eq:Sch-many} \end{eqnarray}$$

(1)

where |$\boldsymbol{R}$| and |$\mu$| are the relative coordinate and the reduced mass of the |$d$|–T system, respectively. The potential |$U$| between |$d$| and T is represented by

$$\begin{eqnarray} U(\boldsymbol{r},\boldsymbol{R})=U_{n}(\boldsymbol{r},\boldsymbol{R})+U_{p}(\boldsymbol{r},\boldsymbol{R})+V_{\rm C}(R), \end{eqnarray}$$

(2)

where |$U_{n}$| (⁠|$U_{p}$|⁠) is the optical potential between |$n$| (⁠|$p$|⁠) and T. In the present analysis, we neglect Coulomb breakup processes, and the Coulomb potential |$V_{\rm C}$| therefore depends only on |$R$|⁠. As the internal Hamiltonian |$h_d$| for |$d$|⁠, we adopt a simple form with the Ohmura potential between |$p$| and |$n$| [37].

Initially, |$d$| is the ground state and has |$\hbar\boldsymbol{K}$| as its relative momentum according to |$R$| at |$Z=-\infty$|⁠, where |$Z$| is the |$z$|-axis component of |$\boldsymbol{R}$| and |$\boldsymbol{K}$| is set to be parallel to |$Z$|⁠. Under this initial condition, |$\Psi$| is described as

$$\begin{eqnarray} \Psi(\boldsymbol{r},\boldsymbol{R}) \xrightarrow[Z\to-\infty]{} e^{iKZ+\cdots}\Phi_0(\boldsymbol{r}), \end{eqnarray}$$

(3)

where the ellipsis “|$\cdots$|” represents the effects of the Coulomb distortion. The ground-state wave function |$\Phi_0$| of |$d$| satisfies

$$\begin{eqnarray} h_d\Phi_0(\boldsymbol{r})&=&\epsilon_0\Phi_0(\boldsymbol{r}), \end{eqnarray}$$

(4)

and the total energy conservation is defined as

$$\begin{eqnarray} \frac{\hbar^2K^2}{2\mu}=E-\epsilon_0\equiv E_0. \end{eqnarray}$$

(5)

The Glauber model is based on the adiabatic and eikonal approximations. In the adiabatic approximation, |$h_d$| in Eq. (1) is replaced by |$\epsilon_0$|⁠. In the eikonal approximation, |$\Psi$| is described as the product of a plane wave and a new function |$\hat{\Psi}$|⁠,

$$\begin{eqnarray} \Psi(\boldsymbol{r},\boldsymbol{R})&=&e^{iKZ}\hat{\Psi}(\boldsymbol{r},\boldsymbol{R}). \label{eq:Eik-wf} \end{eqnarray}$$

(6)

Substituting Eq. (6) into Eq. (1) with the adiabatic approximation leads to the equation for |$\hat{\Psi}$|⁠, namely,

$$\begin{eqnarray} \left[ -\frac{\hbar^2}{2\mu}\boldsymbol{\nabla}_{\boldsymbol{R}}^2 -i\hbar v\frac{\partial}{\partial Z} +U(\boldsymbol{r},\boldsymbol{R}) \right]\hat{\Psi}(\boldsymbol{r},\boldsymbol{R})=0, \end{eqnarray}$$

(7)

where |$v=\hbar K/\mu$|⁠. For scattering at high energy, |$\hat{\Psi}$| is expected to vary smoothly in |$\boldsymbol{R}$|⁠. We then assume that the second-order derivative of |$\hat{\Psi}$| for |$\boldsymbol{R}$| is negligible with respect to the first-order derivative of |$\hat{\Psi}$| for |$Z$|⁠. This assumption is an essential part of the eikonal approximation. Accordingly, Eq. (7) is rewritten as

$$\begin{eqnarray} i\hbar v\frac{\partial}{\partial Z}\hat{\Psi}(\boldsymbol{r},\boldsymbol{R}) &=&U(\boldsymbol{r},\boldsymbol{R})\hat{\Psi}(\boldsymbol{r},\boldsymbol{R}).\label{eq:Eik-eq2} \end{eqnarray}$$

(8)

The conditions for the accuracy of the eikonal approximation are well known as

$$\begin{eqnarray} \frac{\left|U\right|}{E_0}<<1,\quad a_UK>>1, \label{eq:Eik-cond} \end{eqnarray}$$

(9)

where |$a_U$| is the radius of |$U$|⁠.

If |$V_{\rm C}$| is omitted in |$U$|⁠, then Eq. (8) can be solved analytically under the initial condition as

$$\begin{eqnarray} \hat{\Psi}(\boldsymbol{r},\boldsymbol{R})= \exp\left[ -\frac{i}{\hbar v}\int_{-\infty}^Z U(\boldsymbol{r},\boldsymbol{b},Z')dZ' \right]\Phi_0(\boldsymbol{r}), \end{eqnarray}$$

(10)

where |$\boldsymbol{b}$| is the projection of |$\boldsymbol{R}$| on the |$x$|–|$y$| plane. In the eikonal approximation, the elastic scattering amplitude is given by

$$\begin{eqnarray} f_{\rm el}(\boldsymbol{q})= \frac{iK}{2\pi} \int d\boldsymbol{b}e^{-i\boldsymbol{q}\cdot\boldsymbol{b}} \left[ 1-{\cal S}(\boldsymbol{b}) \right], \end{eqnarray}$$

(11)

where the forward-scattering approximation is adopted and |$\boldsymbol{q}$| is the transfer momentum. The eikonal |$S$| matrix, |${\cal S}_{\rm N}$|⁠, is defined as

$$\begin{eqnarray} {\cal S}_{\rm N}(b)= \langle\Phi_0|e^{i\chi_{\rm N}(\boldsymbol{r},b)}|\Phi_0\rangle \label{eq:SN} \end{eqnarray}$$

(12)

with the phase-shift function

$$\begin{eqnarray} \chi_{\rm N}(\boldsymbol{r},b)= -\frac{1}{\hbar v} \int_{-\infty}^\infty \left[U_n(\boldsymbol{r},\boldsymbol{R}) +U_p(\boldsymbol{r},\boldsymbol{R}) \right] dZ, \label{eq:chiN} \end{eqnarray}$$

(13)

where |${\cal S}_{\rm N}$| depends on only |$b=|\boldsymbol{b}|$| because |$U_n$| and |$U_p$| are only the central parts, as mentioned later. In the Glauber model, the breakup effects of |$d$| are included in |${\cal S}_{\rm N}$| within the adiabatic and eikonal approximations. The details of the Glauber model are given in Ref. [34].

If |$U$| includes |$V_{\rm C}$|⁠, then a special treatment is required because of the well-known logarithmic divergence of |$\chi_{\rm N}$|⁠. To date, various approaches have been proposed to describe scattering with the Coulomb interaction in the Glauber model. In this study, we use the relatively simple means of a sharply cut screened Coulomb potential with cut-off radius |$a_{\rm C}$|⁠, and thus the elastic scattering amplitude is rewritten as

$$\begin{eqnarray} f_{\rm el}^{\rm G}(\boldsymbol {q})&=& \left[ f_{\rm Ruth}(\boldsymbol {q}) +f_{\rm N}(\boldsymbol {q}) \right]e^{-2i\eta \ln (2ka_{\rm C})}. \label{eq:fq2} \end{eqnarray}$$

(14)

Here, |$f_{\rm Ruth}$| is the Rutherford amplitude with the Zommerfeld parameter |$\eta$|⁠, and the nuclear part of the scattering amplitude |$f_{\rm N}$| is defined as

$$\begin{eqnarray} f_{\rm N}(\boldsymbol {q})= \frac{iK}{2\pi}\int d\boldsymbol{b}\;e^{-i\boldsymbol{q}\cdot\boldsymbol{b}+2i\eta \ln (kb)} \left[ 1-{\cal S}_{\rm N}(\boldsymbol{b}) \right]. \end{eqnarray}$$

(15)

Note here that although |$f_{\rm el}$| of Eq. (14) depends on |$a_{\rm C}$|⁠, the differential cross section defined as |$|f_{\rm el}^{\rm G}(\boldsymbol{q})|^2$| does not. In this paper, we refer to the calculation with |$f_{\rm el}^{\rm G}(\boldsymbol {q})$| as the Glauber model.

2.2. Eikonal potential model

According to the approach proposed by Glauber [34], we can derive the local optical potential |$U_{\rm E}$| including breakup effects. The |$d$|–T scattering with |$U_{\rm E}$| is described by the two-body Schrödinger equation as

$$\begin{eqnarray} \left[ -\frac{\hbar^2}{2\mu}\boldsymbol{\nabla}_{\boldsymbol{R}}^2 +U_{\rm E}(R)+V_{\rm C}(R)-E_0 \right]\Psi_{\rm EP}(\boldsymbol{R})=0. \label{eq:Eik-model} \end{eqnarray}$$

(16)

If |$U_{\rm E}$| includes breakup effects perfectly, then we can obtain the exact scattering amplitude of the |$d$|–T scattering by solving Eq. (16) with no approximations. Following the approach of Ref. [34], we consider the eikonal |$S$| matrix of Eq. (16) defined as

$$\begin{eqnarray} \label{eq:Seik} {\cal S}_{\rm eik}(b) = \exp{ \left[ -\frac{i}{\hbar v} \int_{-\infty}^\infty U_{\rm E}(R)dZ \right] }, \end{eqnarray}$$

(17)

which can be obtained by solving Eq. (16) with the eikonal approximation. To incorporate breakup effects into |$U_{\rm E}$|⁠, |${\cal S}_{\rm eik}$| is replaced by |${\cal S}_{\rm N}$| in the Glauber model, and solving Eq. (17) for |$U_{\rm E}$| with |$U_{\rm E}(\infty)=0$| leads to

$$\begin{eqnarray} \label{eq:eik-pot} U_{\rm E}(R)&=&\frac{\hbar v}{i\pi}\frac{1}{R}\frac{d}{dR}\int_{R}^{\infty} bdb \frac{\ln{{\cal S}_{\rm N}(b)}}{\sqrt{b^2-R^2}}. \end{eqnarray}$$

(18)

Note here that |$U_{\rm E}$| takes into account breakup effects within the adiabatic and eikonal approximations because |${\cal S}_{\rm N}$| includes those effects as mentioned in Sect. 2.1. In Ref. [35], the difference between |$U_{\rm E}$| and the DSF potential was discussed by using the cumulant expansion of |$U_{\rm E}$|⁠, and the first term of the expansion corresponds to the DSF potential defined as

$$\begin{eqnarray} U_{\rm DSF}(R)&=&\langle\Phi_0|U_{n}(\boldsymbol{r},\boldsymbol{R}) +U_{p}(\boldsymbol{r},\boldsymbol{R})|\Phi_0\rangle, \end{eqnarray}$$

(19)

in which breakup effects are not taken into account. On the other hand, the higher-order terms of the expansion represent breakup effects and give the dynamical polarization (DP) potential defined as

$$\begin{eqnarray} \label{eq:dpp} U_{\rm DP}(R)&=&U_{\rm E}(R)-U_{\rm DSF}(R). \end{eqnarray}$$

(20)

The details of |$U_{\rm E}$| are given in Refs. [34–36], and |$U_{\rm E}$| thus obtained is referred to as the “eikonal potential”.

In the eikonal potential model (EP model), we solve Eq. (16) without the eikonal approximation, namely, with a fully quantum-mechanical approach. Meanwhile, solving Eq. (16) with the eikonal approximation leads to the same result as that of the Glauber model by definition. Therefore, the difference between the Glauber model and the EP model is whether the eikonal approximation is used, and we expect that the inaccuracy of the eikonal approximation in the EP model may be absent from the Glauber model even though |$U_{\rm E}$| is based on the adiabatic and eikonal approximations. The validity of the conjecture for the EP model will be investigated by analyzing |$d$|–T scattering.

2.3. |$NA$| optical potential

In the present analysis, we derive |$U_n$| and |$U_p$| by using the |$g$|-matrix folding model, in which the optical potential is calculated by folding the |$g$| matrix with the target density, and the knock-on exchange processes between the two interacting nucleons are considered as the dominant component of the antisymmetrization [38,39]. The folding potential is generally nonlocal because of the knock-on exchange process, but the nonlocality is localized well by using the Brieva–Rook method [14–16]. The localized folding potential is composed of the direct (DR) and exchange (EX) terms, namely

$$\begin{eqnarray} U_{j}(R_j) = U^{\rm DR}_{j}(R_j)+U^{\rm EX}_{j}(R_j), \end{eqnarray}$$

(21)

where |$j=n$| or |$p$| and |$R_{j}$| is the relative coordinate between particle |$j$| and T. Each term is written with the one-body and mixed densities |$\rho_{\rm T}$| and |$\tilde{\rho}_{\rm T}$|⁠, respectively, as

$$\begin{eqnarray} U^{\rm DR}_{j} (R_j)&=& \sum_{\nu} \int d\boldsymbol{r}_{\rm T} g^{\rm DR}_{j\nu}(s,\rho)\rho_{\rm T}^{(\nu)}(r_{\rm T}), \\ \end{eqnarray}$$

(22)

$$\begin{eqnarray} U^{\rm EX}_{j} (R_j)&=& \sum_{\nu} \int d\boldsymbol{r}_{\rm T} g^{\rm EX}_{j\nu}(s,\rho)\tilde{\rho}_{\rm T}^{(\nu)}(\boldsymbol{r}_{\rm T},\boldsymbol{R}_j) j_{0}(K(R_j)s). \end{eqnarray}$$

(23)

Here, the index |$\nu$| represents the |$z$|-component of isospin of the nucleons in T, |$\boldsymbol{r}_{\rm T}$| is the internal coordinate of T, and |$\boldsymbol{s}=\boldsymbol{r}_{\rm T}-\boldsymbol{R}_j$|⁠. The |$g$| matrix |$g^{\rm DR(EX)}$| is the direct (exchange) term of the |$g$| matrix among the considered nucleons. The |$g$| matrix is written as

$$\begin{eqnarray} &&g^{\rm DR}_{pp}=g^{\rm DR}_{nn}= \frac{1}{4}(g^{01}+3g^{11}) ,\\ \end{eqnarray}$$

(24)

$$\begin{eqnarray} &&g^{\rm EX}_{pp}=g^{\rm EX}_{nn}= \frac{1}{4}(g^{01}-3g^{11}) ,\\ \end{eqnarray}$$

(25)

$$\begin{eqnarray} &&g^{\rm DR}_{pn}=g^{\rm DR}_{np}= \frac{1}{8}(3g^{10}+g^{01}+g^{00}+3g^{11}) ,\\ \end{eqnarray}$$

(26)

$$\begin{eqnarray} &&g^{\rm EX}_{pn}=g^{\rm EX}_{np}= \frac{1}{8}(3g^{10}+g^{01}-g^{00}-3g^{11}) , \end{eqnarray}$$

(27)

in terms of |$g^{ST}$|⁠, the spin–isospin component (⁠|$S$| = 0 or 1 and |$T$| = 0 or 1) of the |$g$| matrix. The mixed density can be described by using the one-body density with the local Fermi gas approximation [40] as

$$\begin{eqnarray} \tilde{\rho}_{\rm T}(\boldsymbol{r}_{\rm T},\boldsymbol{R}_j) =\rho_{\rm T}(|\boldsymbol{r}_{\rm T}-\boldsymbol{s}/2|)\frac{3j_{1} (k_{\rm F}^{\rm T}s)}{k_{\rm F}^{\rm T}s}. \end{eqnarray}$$

(28)

In the present study, we use the Melbourne |$g$| matrix [23] constructed from Bonn-B nucleon–nucleon interaction [41]. The Melbourne |$g$| matrix reproduces well the nucleon elastic scattering either with or without localization of the exchange term [23,42]. For |$^{208}$|Pb, the matter density is calculated using the spherical Hartree–Fock method with the Gogny-D1S interaction [43], and the spurious center-of-mass motion is removed using the standard procedure [10]. For |$^{12}$|C, we take the phenomenological proton density determined from electron scattering [44]; here, the finite-size effect of the proton charge is unfolded using the standard procedure [45], and the neutron density is assumed to have the same geometry as the proton one.

3. Results and discussion

3.1. Differential cross section for |$d$| scattering

We consider the scattering of |$d$| from |$^{12}$|C and |$^{208}$|Pb at |$E_{\rm in}/A_{\rm P}=$|20–200 MeV. In the present analysis, the CDCC results are regarded as the exact solution. The CDCC has been used to analyze the scattering of |$d$|⁠, and it reproduced the experimental data well. Figure 1 shows the differential cross section as the ratio to Rutherford cross section for |$d$| scattering calculated using the CDCC and the DSF model, where the latter neglects the breakup effects of |$d$|⁠. The solid and dashed lines are the CDCC and DSF results, respectively. Clearly, the present CDCC calculations reproduce the experimental data well. The minor differences between the data and the calculation around the dips are due to neglecting the spin–orbit interaction between |$d$| and the target.

$Differential cross section as the ratio to Rutherford cross section depending on transfer momentum $q$ for $d$ scattering from $^{12}$C targets at $E_{\rm in}/A_{\rm P} = 20$–$80$ MeV and $^{208}$Pb targets at $E_{\rm in}/A_{\rm P} = 40$ MeV. The solid line is the result of the CDCC and the dashed line is that of the DSF model. The experimental data are from Refs. [46–48]. Each cross section is multiplied by the factor shown in the figure, as are the corresponding experimental data.$

Fig. 1.

Differential cross section as the ratio to Rutherford cross section depending on transfer momentum |$q$| for |$d$| scattering from |$^{12}$|C targets at |$E_{\rm in}/A_{\rm P} = 20$|–|$80$| MeV and |$^{208}$|Pb targets at |$E_{\rm in}/A_{\rm P} = 40$| MeV. The solid line is the result of the CDCC and the dashed line is that of the DSF model. The experimental data are from Refs. [46–48]. Each cross section is multiplied by the factor shown in the figure, as are the corresponding experimental data.

Open in new tab Download slide

In Fig. 2, we compare the results of the CDCC with those of the EP model. The solid, dashed, and dot-dashed lines are the results of the EP model, DSF, and CDCC, respectively. The EP model reproduces the CDCC results well at high incident energies, thereby showing that the EP model can treat the breakup effects of |$d$| reasonably. At low incident energies, there are some deviations between the results of the CDCC and EP model due to the inaccuracies of the adiabatic and eikonal approximations used in the EP model. We will discuss the validity of the adiabatic and eikonal approximations for |$d$| scattering.

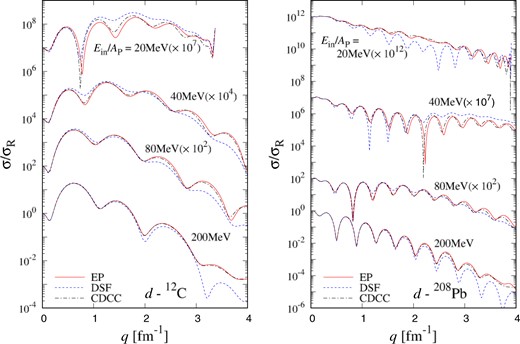
$Differential cross section as the ratio to Rutherford cross section depending on transfer momentum $q$ for $d$ scattering from (left) $^{12}$C and (right) $^{208}$Pb targets at $E_{\rm in}/A_{\rm P} = 20$–$200$ MeV. The solid line is the result of the EP model, the dashed line is that of the DSF model, and the dot-dashed line is that of the CDCC. Each cross section is multiplied by the factor shown in the figure.$

Fig. 2.

Differential cross section as the ratio to Rutherford cross section depending on transfer momentum |$q$| for |$d$| scattering from (left) |$^{12}$|C and (right) |$^{208}$|Pb targets at |$E_{\rm in}/A_{\rm P} = 20$|–|$200$| MeV. The solid line is the result of the EP model, the dashed line is that of the DSF model, and the dot-dashed line is that of the CDCC. Each cross section is multiplied by the factor shown in the figure.

Open in new tab Download slide

Figure 3 shows the results of the Glauber model, adiabatic-CDCC, and CDCC for |$d$| scattering. For the adiabatic-CDCC, we solve the CDCC equation with the adiabatic approximation, where the excited energy of each state is replaced by the ground-state energy. The solid, dashed, and dot-dashed lines are the results of the CDCC, adiabatic-CDCC, and Glauber model, respectively. The difference between the CDCC and adiabatic-CDCC results is due to the inaccuracy of the adiabatic approximation, and that between the Glauber model and adiabatic-CDCC results is due to the inaccuracy of the eikonal approximation. Clearly, the three calculations are consistent at high incident energies, where both the adiabatic and eikonal approximations work well. For the scattering at low incident energies, the results of the Glauber model are distinct from those of the adiabatic-CDCC and CDCC while the latter two are almost the same. This shows that the eikonal approximation worsens quickly as the incident energy decreases, whereas the adiabatic approximation still holds even at |$E_{\rm in}/A_{\rm P}=$|20 MeV. Furthermore, it is difficult to apply the eikonal approximation to the scattering of a heavy target. In fact, the results of the Glauber model for the scattering of |$d$| from |$^{208}$|Pb are inconsistent with the CDCC results even at forward angles. This is because the eikonal approximation cannot describe exactly the scattering with the Coulomb interaction, as shown in Sect. 2.1.

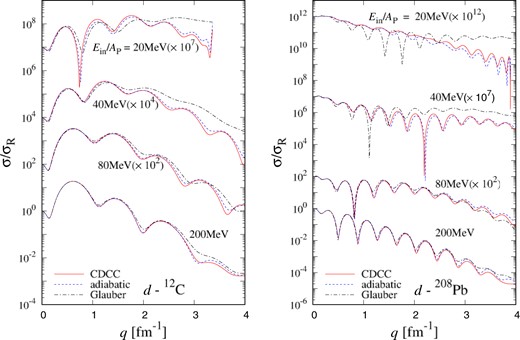
$Differential cross section as the ratio to Rutherford cross section depending on transfer momentum $q$ for $d$ scattering from (left) $^{12}$C and (right) $^{208}$Pb targets at $E_{\rm in}/A_{\rm P} = 20$–$200$ MeV. The solid line is the result of the CDCC, the dashed line is that of the adiabatic-CDCC, and the dot-dashed line is that of the Glauber model. Each cross section is multiplied by the factor shown in the figure.$

Fig. 3.

Differential cross section as the ratio to Rutherford cross section depending on transfer momentum |$q$| for |$d$| scattering from (left) |$^{12}$|C and (right) |$^{208}$|Pb targets at |$E_{\rm in}/A_{\rm P} = 20$|–|$200$| MeV. The solid line is the result of the CDCC, the dashed line is that of the adiabatic-CDCC, and the dot-dashed line is that of the Glauber model. Each cross section is multiplied by the factor shown in the figure.

Open in new tab Download slide

In Fig. 4, we compare the results of the EP model with those of the Glauber model and adiabatic-CDCC for |$d$| scattering at 20–40 MeV. Clearly, the results of the EP model reproduce those of the adiabatic-CDCC well. In particular, the EP model is more consistent with the adiabatic-CDCC around |$q=2$| fm|$^{-1}$| than with the CDCC. This shows that the deviations between the results of the CDCC and EP model at low energies as shown in Fig. 2 come mainly from the inaccuracy of the adiabatic approximation. On the other hand, the inaccuracy of the eikonal approximation in the EP model is partially excluded. Thus we conclude that the eikonal potential can be regarded as an optical potential that includes breakup effects within the adiabatic approximation only, even though the eikonal potential is based on both the eikonal and adiabatic approximations.

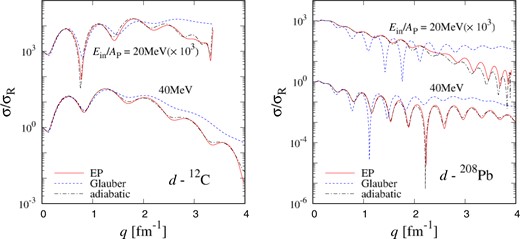
$Differential cross section as the ratio to Rutherford cross section depending on transfer momentum $q$ for $d$ scattering from (left) $^{12}$C and (right) $^{208}$Pb targets at $E_{\rm in}/A_{\rm P} = 20$–$40$ MeV. The solid line is the result of the EP model, the dashed line is that of the Glauber model, and the dot-dashed line is that of the adiabatic-CDCC. Each cross section is multiplied by the factor shown in the figure.$

Fig. 4.

Differential cross section as the ratio to Rutherford cross section depending on transfer momentum |$q$| for |$d$| scattering from (left) |$^{12}$|C and (right) |$^{208}$|Pb targets at |$E_{\rm in}/A_{\rm P} = 20$|–|$40$| MeV. The solid line is the result of the EP model, the dashed line is that of the Glauber model, and the dot-dashed line is that of the adiabatic-CDCC. Each cross section is multiplied by the factor shown in the figure.

Open in new tab Download slide

3.2. Differential cross section of |$^6$|He scattering

Next, we use the EP model to analyze |$^6$|He + |$^{12}$|C scattering, which is described as a |$^4$|He + |$n$| + |$n$| + T four-body model. As the exact calculation for the four-body scattering system, we adopt the four-body CDCC that has been successful in analyzing the breakup reaction of |$^6$|He [49–51]. In the EP model for the four-body system, the eikonal |$S$| matrix defined in Eq. (12) is rewritten as

$$\begin{eqnarray} {\cal S}_{\rm N}(\boldsymbol{b})= \langle\Phi_0|e^{i\chi_{\rm N}(\boldsymbol {\xi},\boldsymbol{b})}|\Phi_0\rangle, \label{eq:SN4} \end{eqnarray}$$

(29)

and the phase-shift function is defined as

$$\begin{eqnarray} \chi_{\rm N}(\boldsymbol {\xi},\boldsymbol{b}) &=&-\frac{1}{\hbar v} \int_{-\infty}^{\infty}U(\boldsymbol {\xi},\boldsymbol {R})dZ \label{eq:chiN4} \end{eqnarray}$$

(30)

with

$$\begin{eqnarray} U(\boldsymbol {\xi},\boldsymbol {R})&=&U_{n}(\boldsymbol {\xi},\boldsymbol {R}) +U_{n}(\boldsymbol {\xi},\boldsymbol {R})+U_\alpha(\boldsymbol {\xi},\boldsymbol {R}). \end{eqnarray}$$

(31)

Here, |$\boldsymbol {\xi}$| is the internal coordinate of |$^6$|He and |$U_n$| (⁠|$U_\alpha$|⁠) is the optical potential between |$n$| (⁠|$^4$|He) and T. For |$U_n$|⁠, we use the same potential as that used in the analysis of |$d$| scattering, and |$U_\alpha$| is obtained by folding |$U_n$| and |$U_p$| with the |$^4$|He density. The ground-state wave function |$\Phi_0$| of |$^6$|He is calculated using the Gaussian expansion method (GEM) with a |$^4$|He + |$n$| + |$n$| three-body model. In the GEM, the model Hamiltonian of |$^6$|He and the parameter set of the Gaussian basis functions are the same ones used in Ref. [52].

Figure 5 shows the results of the EP model (solid line), DSF model (dotted line), and CDCC (dot-dashed line) for |$^6$|He scattering from |$^{12}$|C at |$E_{\rm in}/A_{\rm P}=20$|–200 MeV. The dots are the experimental data [53]. Clearly, the breakup effects of |$^6$|He as represented by the differences between the results of the DSF model and CDCC are stronger than those for |$d$| scattering. Furthermore, the EP model reproduces the CDCC results well, even at |$E_{\rm in}/A_{\rm P}\leq40$| MeV. One reason for this is that the condition represented by Eq. (9) is satisfied well because |$K$| of the |$^6$|He scattering is larger than that of the |$d$| scattering for the same |$E_{\rm in}/A_{\rm P}$|⁠. Thus we expect the EP model to work well for scattering with heavier projectiles.

$As Fig. 1 but for $^6$He scattering from $^{12}$C at $E_{\rm in}/A_{\rm P} = 20$–$200$ MeV. The experimental data are from Ref. [53].$

Fig. 5.

As Fig. 1 but for |$^6$|He scattering from |$^{12}$|C at |$E_{\rm in}/A_{\rm P} = 20$|–|$200$| MeV. The experimental data are from Ref. [53].

Open in new tab Download slide

3.3. Dynamical polarization potential

Finally, we discuss the breakup effects of the optical potential for |$^6$|He scattering. Figure 6 shows the optical potentials derived using the EP and DSF models for |$^6$|He scattering from |$^{12}$|C at |$E_{\rm in}/A_{\rm P} = 40$| MeV. The solid line corresponds to the eikonal potential and the dashed line corresponds to the DSF potential, the latter excluding as it does the breakup effects of |$^6$|He. The dot-dashed line corresponds to the DP potential |$U_{\rm DP}$| defined as Eq. (20), which represents the breakup effects of |$^6$|He on the optical potential between |$^6$|He and |$^{12}$|C. In Fig. 6, the strength of the DP potential is multiplied by four. In the EP model, the DP potential is independent of the orbital angular momentum |$L$|⁠, although the DP potential calculated using the CDCC with the equivalent approach [1,49] depends on |$L$| and has singularities at the nodes of the total wave function. As another approach to obtain the |$L$|-independent DP potential from the coupled-channels calculation, the weight mean approach has been proposed [54]. It will be interesting to compare the DP potentials in future work.

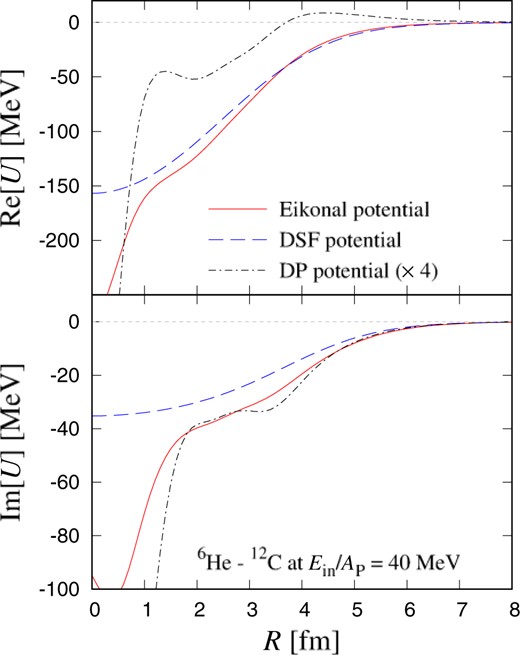
$$R$ dependence of potentials for $^6$He scattering from $^{12}$C at $E_{\rm in}/A_{\rm P}=40$ MeV. The solid and dashed lines represent the eikonal potential and the DSF potential, respectively. The dot-dashed line represents the DP potential and is multiplied by four.$

Fig. 6.

|$R$| dependence of potentials for |$^6$|He scattering from |$^{12}$|C at |$E_{\rm in}/A_{\rm P}=40$| MeV. The solid and dashed lines represent the eikonal potential and the DSF potential, respectively. The dot-dashed line represents the DP potential and is multiplied by four.

Open in new tab Download slide

In Fig. 6, the real part of the DP potential is repulsive in the peripheral region and the imaginary part is absorptive in the whole region. The behavior of the DP potential is almost the same as the previous result of the |$L$|-dependent DP potential in Ref. [49]. To understand the behavior, we calculate the |$S$| matrices for the scattering. In the eikonal approximation as shown in Eqs. (29) and (30), the real part of the optical potential is related to the argument of the |$S$| matrix, and the imaginary part of the optical potential is the absolute value of the |$S$| matrix. Figure 7 shows the |$S$| matrices for the scattering. The crosses, circles, and squares are the results of the EP, DSF models, and the CDCC, respectively. The |$S$| matrices are plotted from the grazing angular momentum |$L=25$|⁠. Here, this momentum is defined as the position of the peak in the partial breakup cross section. The differences between the results of the DSF model and the CDCC represent the breakup effects on the |$S$| matrix, and the results of the EP model agree well with those of the CDCC. Clearly, the absolute value of the |$S$| matrix for the CDCC is smaller than that for the DSF model, and the argument of the |$S$| matrix for the CDCC is also smaller than that for the DSF model. This shows that the breakup effects make the real part of the optical potential shallow and the imaginary one deep.

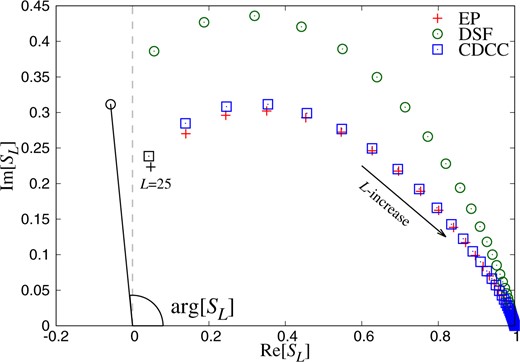
$$S$ matrices for $^6$He scattering from $^{12}$C at $E_{\rm in}/A_{\rm P}=40$ MeV plotted from the grazing angular momentum. The crosses, circles, and squares are the results of the EP, DSF models, and the CDCC, respectively. $L$ is the orbital angular momentum and increases toward $S=(1,0)$.$

Fig. 7.

|$S$| matrices for |$^6$|He scattering from |$^{12}$|C at |$E_{\rm in}/A_{\rm P}=40$| MeV plotted from the grazing angular momentum. The crosses, circles, and squares are the results of the EP, DSF models, and the CDCC, respectively. |$L$| is the orbital angular momentum and increases toward |$S=(1,0)$|⁠.

Open in new tab Download slide

4. Summary

We constructed a microscopic optical potential including the excitation effects of P and T based on the Glauber model, namely, the eikonal potential. To investigate the validity of the eikonal potential, we analyzed deuteron scattering from |$^{12}$|C and |$^{208}$|Pb at 20–200 MeV and compared the results of the EP model with those of the CDCC. The EP model reproduced the CDCC results well with increasing incident energy, from which we found the eikonal potential to be a reliable potential including the breakup effects of |$d$| at intermediate energies. Meanwhile, for low-energy scattering, there were some deviations between the results of the EP model and those of the CDCC. Those deviations came from the inaccuracy of the adiabatic approximation in the EP model. On the other hand, the eikonal approximation could be partially excluded from the EP model. Thus, the EP model provides results similar to those of the adiabatic approximation, and the eikonal potential is regarded as an optical potential that includes breakup effects within the adiabatic approximation.

We also used the EP model to analyze |$^6$|He+|$^{12}$|C scattering at 20–200 MeV, which was described by a |$^4$|He + |$n$| + |$n$| + |$^{12}$|C four-body model. In the analyses, the EP model also reproduced well the results of the four-body CDCC, which has been successful in analyzing the breakup reactions of |$^6$|He. This shows the applicability of the EP model to many-body systems. In future work, we will use the EP model to analyze |$^8$|He scattering, which is described by a |$^4$|He + |$n$| + |$n$| + |$n$| + |$n$| + T six-body model.

On the other hand, the EP model has some problems, such as the inaccuracy of the adiabatic approximation and the treatment of the Coulomb interaction, which are important for various breakup reactions. Some approaches have been proposed to solve these problems [55,56]. For example, an eikonal-CDCC could reduce the eikonal potential without the inaccuracy of the adiabatic approximation.

Acknowledgements

This work was supported in part by a Grant-in-Aid for Scientific Research (No. JP18K03650) from the Japan Society for the Promotion of Science (JSPS).

References

[1]

Kamimura

Yahiro

Iseri

Sakuragi

Kameyama

, and

Kawai

Prog. Theor. Phys. Suppl.

(

1986

). (

https://doi.org/10.1143/PTPS.89.1

)

Crossref

Search ADS

[2]

Austern

Iseri

Kamimura

Kawai

Rawitscher

, and

Yahiro

Phys. Rep.

154

125

(

1987

). (

https://doi.org/10.1016/0370-1573(87)90094-9

)

Crossref

Search ADS

[3]

Yahiro

Ogata

Matsumoto

, and

Minomo

Prog. Theor. Exp. Phys.

2012

01A206

(

2012

). (

https://doi.org/10.1093/ptep/pts008

)

Crossref

Search ADS

[4]

Arellano

H. F.

Brieva

F. A.

, and

Love

W. G.

Phys. Rev. C

301

(

1995

). (

https://doi.org/10.1103/PhysRevC.52.301

)

Crossref

Search ADS

[5]

Minomo

Ogata

Kohno

Shimizu

Y. R.

, and

Yahiro

J. Phys. G: Nucl. Part. Phys.

085011

(

2010

). (

https://doi.org/10.1088/0954-3899/37/8/085011

)

Crossref

Search ADS

[6]

Sinha

Phys. Rep.

(

1975

). (

https://doi.org/10.1016/0370-1573(75)90011-3

)

Crossref

Search ADS

[7]

Sinha

and

Moszkowski

S. A.

Phys. Lett. B

289

(

1979

). (

https://doi.org/10.1016/0370-2693(79)90337-X

)

Crossref

Search ADS

[8]

Khoa

D. T.

von Oertzen

Bohlen

H. G.

, and

Ohkubo

J. Phys. G: Nucl. Part. Phys.

R111

(

2007

). (

https://doi.org/10.1088/0954-3899/34/3/R01

)

Crossref

Search ADS

[9]

Furumoto

Sakuragi

, and

Yamamoto

Phys. Rev. C

044612

(

2010

). (

https://doi.org/10.1103/PhysRevC.82.044612

)

Crossref

Search ADS

[10]

Sumi

Minomo

Tagami

Kimura

Matsumoto

Ogata

Shimizu

Y. R.

, and

Yahiro

Phys. Rev. C

064613

(

2012

). (

https://doi.org/10.1103/PhysRevC.85.064613

)

Crossref

Search ADS

[11]

Bertsch

Borysowicz

McManus

, and

Love

W. G.

Nucl. Phys. A

284

399

(

1977

). (

https://doi.org/10.1016/0375-9474(77)90392-X

)

Crossref

Search ADS

[12]

Jeukenne

J.-P.

Lejeune

, and

Mahaux

Phys. Rev. C

(

1977

). (

https://doi.org/10.1103/PhysRevC.16.80

)

Crossref

Search ADS

[13]

Jeukenne

J.P.

Lejeune

, and

Mahaux

Phys. Rep.

(

1976

). (

https://doi.org/10.1016/0370-1573(76)90017-X

)

Crossref

Search ADS

[14]

Brieva

F. A.

and

Rook

J. R.

Nucl. Phys. A

291

299

(

1977

). (

https://doi.org/10.1016/0375-9474(77)90322-0

)

Crossref

Search ADS

[15]

Brieva

F. A.

and

Rook

J. R.

Nucl. Phys. A

291

317

(

1977

). (

https://doi.org/10.1016/0375-9474(77)90323-2

)

Crossref

Search ADS

[16]

Brieva

F. A.

and

Rook

J. R.

Nucl. Phys. A

297

206

(

1978

). (

https://doi.org/10.1016/0375-9474(78)90272-5

)

Crossref

Search ADS

[17]

Satchler

G. R.

and

Love

W. G.

Phys. Rep.

183

(

1979

). (

https://doi.org/10.1016/0370-1573(79)90081-4

)

Crossref

Search ADS

[18]

Satchler

G. R.

Direct Nuclear Reactions

(

Oxford University Press

Oxford, UK

1983

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

[19]

Yamaguchi

Nagata

, and

Matsuda

Prog. Theor. Phys.

459

(

1983

). (

https://doi.org/10.1143/PTP.70.459

)

Crossref

Search ADS

[20]

Yamaguchi

Nagata

, and

Michiyama

Prog. Theor. Phys.

1289

(

1986

). (

https://doi.org/10.1143/PTP.76.1289

)

Crossref

Search ADS

[21]

Rikus

Nakano

, and

Von Geramb

H. V.

Nucl. Phys. A

414

413

(

1984

). (

https://doi.org/10.1016/0375-9474(84)90611-0

)

Crossref

Search ADS

[22]

Rikus

and

Von Geramb

H. V.

Nucl. Phys. A

426

496

(

1984

). (

https://doi.org/10.1016/0375-9474(84)90160-X

)

Crossref

Search ADS

[23]

Amos

Dortmans

P. J.

Von Geramb

H. V.

Karataglidis

, and

Raynal

, in

Advances in Nuclear Physics

, eds.

Negele

J. W.

and

Vogt

(

Plenum

New York

2000

), Vol. 2

, p.

275

[24]

Saliem

S. M.

and

Haider

J. Phys. G: Nucl. Part. Phys.

1313

(

2002

). (

https://doi.org/10.1088/0954-3899/28/6/313

)

Crossref

Search ADS

[25]

Furumoto

Sakuragi

, and

Yamamoto

Phys. Rev. C

044610

(

2008

). (

https://doi.org/10.1103/PhysRevC.78.044610

)

Crossref

Search ADS

[26]

Furumoto

Sakuragi

, and

Yamamoto

Phys. Rev. C

011601(R)

(

2009

). (

https://doi.org/10.1103/PhysRevC.79.011601

)

Crossref

Search ADS

[27]

Furumoto

Sakuragi

, and

Yamamoto

Phys. Rev. C

044614

(

2009

);

029908

(

2010

) [erratum]. (

https://doi.org/10.1103/PhysRevC.80.044614; https://doi.org/10.1103/PhysRevC.82.029908

)

Crossref

Search ADS

[28]

Toyokawa

Yahiro

Matsumoto

Minomo

Ogata

, and

Kohno

Phys. Rev. C

024618

(

2015

);

059905

(

2017

) [erratum]. (

https://doi.org/10.1103/PhysRevC.92.024618; https://doi.org/10.1103/PhysRevC.96.059905

)

Crossref

Search ADS

[29]

Egashira

Minomo

Toyokawa

Matsumoto

, and

Yahiro

Phys. Rev. C

064611

(

2014

). (

https://doi.org/10.1103/PhysRevC.89.064611

)

Crossref

Search ADS

[30]

Toyokawa

Matsumoto

Minomo

, and

Yahiro

Phys. Rev. C

064610

(

2015

). (

https://doi.org/10.1103/PhysRevC.91.064610

)

Crossref

Search ADS

[31]

Watson

K. M.

Phys. Rev.

575

(

1953

). (

https://doi.org/10.1103/PhysRev.89.575

)

Crossref

Search ADS

[32]

Kerman

A. K.

McManus

, and

Thaler

R. M.

Ann. Phys.

551

(

1959

). (

https://doi.org/10.1016/0003-4916(59)90076-4

)

Crossref

Search ADS

[33]

Yahiro

Minomo

Ogata

, and

Kawai

Prog. Theor. Phys.

120

767

(

2008

). (

https://doi.org/10.1143/PTP.120.767

)

Crossref

Search ADS

[34]

Glauber

R. J.

, in

Lectures in Theoretical Physics

, ed.

Brittin

W. E.

(

Interscience

New York

1959

), Vol.

, p.

315

[35]

Yabana

Ogawa

, and

Suzuki

Phys. Rev. C

2909

(

1992

). (

https://doi.org/10.1103/PhysRevC.45.2909

)

Crossref

Search ADS

[36]

Abu-Ibrahim

and

Suzuki

Phys. Rev. C

034608

(

2000

). (

https://doi.org/10.1103/PhysRevC.62.034608

)

Crossref

Search ADS

[37]

Ohmura

Imanishi

Ichimura

, and

Kawai

Prog. Theor. Phys.

347

(

1970

). (

https://doi.org/10.1143/PTP.43.347

)

Crossref

Search ADS

[38]

Tang

Y. C.

LeMere

, and

Thompsom

D. R.

Phys. Rep.

167

(

1978

). (

https://doi.org/10.1016/0370-1573(78)90175-8

)

Crossref

Search ADS

[39]

Aoki

and

Horiuchi

Prog. Theor. Phys.

857

(

1983

) (

https://doi.org/10.1143/PTP.69.857

), and references therein.

Crossref

Search ADS

[40]

Negele

J. W.

and

Vautherin

Phys. Rev. C

1472

(

1972

). (

https://doi.org/10.1103/PhysRevC.5.1472

)

Crossref

Search ADS

[41]

Machleidt

Holinde

, and

Elster

Ch.

Phys. Rep.

149

(

1987

). (

https://doi.org/10.1016/S0370-1573(87)80002-9

)

Crossref

Search ADS

[42]

Toyokawa

Minomo

, and

Yahiro

Phys. Rev. C

054602

(

2013

). (

https://doi.org/10.1103/PhysRevC.88.054602

)

Crossref

Search ADS

[43]

Berger

J. F.

Girod

, and

Gogny

Comput. Phys. Commun.

365

(

1991

). (

https://doi.org/10.1016/0010-4655(91)90263-K

)

Crossref

Search ADS

[44]

de Vries

de Jager

C. W.

, and

De Vries

At. Data Nucl. Data Tables

495

(

1987

). (

https://doi.org/10.1016/0092-640X(87)90013-1

)

Crossref

Search ADS

[45]

Singhal

R. P.

Macauley

M. W. S.

, and

De Witt Huberts

P. K. A.

Nucl. Instrum. Meth.

148

113

(

1978

). (

https://doi.org/10.1016/0029-554X(78)90342-7

)

Crossref

Search ADS

[46]

Kato

Matsuoka

Noro

Saito

Sakai

Nakamura

Yosoi

Ichihara

Hatanaka

, and

Ogawa

Nucl. Instrum. Meth. A

238

453

(

1985

). (

https://doi.org/10.1016/0168-9002(85)90484-X

)

Crossref

Search ADS

[47]

Duhamel

Marcus

Langevin-Joliot

Didelez

J. P.

Narboni

, and

Stephan

Nucl. Phys. A

174

485

(

1971

). (

https://doi.org/10.1016/0375-9474(71)90398-8

)

Crossref

Search ADS

[48]

Bäumer

, et al. ,

Phys. Rev. C

037601

(

2001

). (

https://doi.org/10.1103/PhysRevC.63.037601

)

Crossref

Search ADS

[49]

Matsumoto

Hiyama

Ogata

Iseri

Kamimura

Chiba

, and

Yahiro

Phys. Rev. C

061601(R)

(

2004

). (

https://doi.org/10.1103/PhysRevC.70.061601

)

Crossref

Search ADS

[50]

Matsumoto

Egami

Ogata

Iseri

Kamimura

, and

Yahiro

Phys. Rev. C

051602(R)

(

2006

). (

https://doi.org/10.1103/PhysRevC.73.051602

)

Crossref

Search ADS

[51]

Rodríguez-Gallardo

Arias

J. M.

Gómez-Camacho

Johnson

R. C.

Moro

A. M.

Thompson,

I. J.

and

Tostevin

J. A.

Phys. Rev. C

064609

(

2008

). (

https://doi.org/10.1103/PhysRevC.77.064609

)

Crossref

Search ADS

[52]

Kikuchi

Matsumoto

Minomo

, and

Ogata

Phys. Rev. C

021602(R)

(

2013

). (

https://doi.org/10.1103/PhysRevC.88.021602

)

Crossref

Search ADS

[53]

Al-Khalili

J. S.

, et al. ,

Phys. Lett. B

378

(

1996

). (

https://doi.org/10.1016/0370-2693(96)00336-X

)

Crossref

Search ADS

[54]

Thompson

I. J.

Nagarajan

M. A.

Lilley

J. S.

, and

Smithson

M. J.

Nucl. Phys. A

505

(

1989

). (

https://doi.org/10.1016/0375-9474(89)90417-X

)

Crossref

Search ADS

[55]

Ogata

Yahiro

Iseri

Matsumoto

, and

Kamimura

Phys. Rev. C

064609

(

2003

). (

https://doi.org/10.1103/PhysRevC.68.064609

)

Crossref

Search ADS

[56]

Capel

Baye

, and

Suzuki

Phys. Rev. C

054602

(

2008

). (

https://doi.org/10.1103/PhysRevC.78.054602

)

Crossref

Search ADS

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted reuse, distribution, and reproduction in any medium, provided the original work is properly cited.

Download all slides

Month:	Total Views:
December 2019	64
January 2020	75
February 2020	34
March 2020	29
April 2020	9
May 2020	15
June 2020	12
July 2020	12
August 2020	14
September 2020	14
October 2020	15
November 2020	16
December 2020	6
January 2021	5
February 2021	21
March 2021	15
April 2021	28
May 2021	13
June 2021	16
July 2021	13
August 2021	17
September 2021	16
October 2021	29
November 2021	9
December 2021	10
January 2022	14
February 2022	12
March 2022	11
April 2022	24
May 2022	8
June 2022	9
July 2022	10
August 2022	22
September 2022	19
October 2022	25
November 2022	9
December 2022	13
January 2023	17
February 2023	17
March 2023	13
April 2023	9
May 2023	8
June 2023	3
July 2023	8
August 2023	8
September 2023	6
October 2023	3
November 2023	18
December 2023	10
January 2024	8
February 2024	4
March 2024	3
April 2024	12
May 2024	6
June 2024	9
July 2024	4
August 2024	2
September 2024	12
October 2024	3
November 2024	2
December 2024	9
January 2025	6
February 2025	5
March 2025	23
April 2025	5

Article Contents

Microscopic optical potentials including breakup effects for elastic scattering

Abstract

1. Introduction

2. Theoretical framework

2.1. Glauber model

2.2. Eikonal potential model

2.3. |$NA$| optical potential

3. Results and discussion

3.1. Differential cross section for |$d$| scattering

3.2. Differential cross section of |$^6$|He scattering

3.3. Dynamical polarization potential

4. Summary

Acknowledgements

References

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Microscopic optical potentials including breakup effects for elastic scattering Open Access

Abstract

1. Introduction

2. Theoretical framework

2.1. Glauber model

2.2. Eikonal potential model

2.3. |$NA$| optical potential

3. Results and discussion

3.1. Differential cross section for |$d$| scattering

3.2. Differential cross section of |$^6$|He scattering

3.3. Dynamical polarization potential

4. Summary

Acknowledgements

References

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Microscopic optical potentials including breakup effects for elastic scattering