Abstract
A dipole resonance of |$^{11}$|Li is found by a |$^9$|Li + |$n$| + |$n$| three-body model analysis with the complex-scaling method. The resonance can be interpreted as a bound state in the |$^{10}$|Li + |$n$| system, i.e., a Feshbach resonance in the |$^9$|Li + |$n$| + |$n$| system. As a characteristic feature of the Feshbach resonance of |$^{11}$|Li, the |$^{10}$|Li + |$n$| threshold is open above the |$^{9}$|Li + |$n$| + |$n$| one, which reflects a distinctive property of the Borromean system. A microscopic four-body reaction calculation for the |$^{11}$|Li(|$p$|,|$p'$|) reaction at 6 MeV/nucleon is performed by taking into account the resonant and nonresonant continuum states of the three-body system. The calculation of angular distributions of the elastic and inelastic scattering as well as the energy spectrum reproduced a recent experimental result. Furthermore, the |$E1$| strength distribution from a Coulomb dissociation experiment was also reproduced in this framework. This means that the existence of the Borromean Feshbach resonance may consistently answer a long-standing open question of an excited state of |$^{11}$|Li.
1. Introduction
Elucidation of resonances, which are omnipresent in different hierarchies in nature, is one of the most important subjects in physics. For example, the tetraquark and pentaquark baryons in hadron physics [1] as well as the so-called Efimov resonance [2,3] of ultracold atoms in atomic physics have attracted the attention of many experimentalists and theorists. In nuclear physics, various resonances have been discovered and investigated in detail. Studies of resonances in nuclear physics will be characterized by diversity. Nuclei, self-organized strongly interacting systems, show a wide variety of structures as the atomic number, the mass number, and the excitation energy change. From a different point of view, we have better knowledge on the basic interaction that forms many-nucleon systems than on hadron physics. Various types of resonances, e.g., single-particle resonances, gas-like |$\alpha$| cluster states, and giant resonances have therefore been investigated on a solid basis. Nowadays, resonant structures for nuclei near and even beyond the neutron dripline have been intensively pursued. Furthermore, a recent experiment suggested that four neutrons form a resonance, i.e., the so-called tetraneutron [4].
Some nuclei near the dripline such as |$^6$|He, |$^{11}$|Li, |$^{14}$|Be, and |$^{22}$|C are known as two-neutron halo nuclei [5–9], consisting of a core nucleus and two loosely bound neutrons. These nuclei have a Borromean structure, meaning that there is no bound state for each pair of the three constituents. Except for |$^6$|He, experimental information on resonances of such Borromean nuclei is very scarce. The existence of a resonance of |$^{11}$|Li, the first-discovered Borromean nucleus, is a long-standing open question in particular [10–24]. Hadronic scattering and the Coulomb dissociation experiments provided especially contradictory results. While the peak structures were observed with several hadronic scatterings, the low-lying peak of the recent Coulomb dissociation experiments can be explained by only the |$E1$| direct breakup component without resonances; the other apparent resonant state was not observed [14]. Because of their experimental difficulties, the hadronic scattering experiments had fewer statistics or poor resolutions compared to the Coulomb dissociation experiments.
Very recently, a measurement of the |$^{11}$|Li(|$p,p'$|) reaction at 6 MeV/nucleon with high statistics and high resolution has been performed [25] to clarify this situation, and a low-lying excited state of |$^{11}$|Li has clearly been identified. In the analysis, the authors adopted a macroscopic model for the transition of |$^{11}$|Li combined with the distorted-wave Born approximation (DWBA); a form factor of the isoscalar electric dipole (|$E1$|) excitation is assumed. The macroscopic model, however, does not describe the Borromean nature of |$^{11}$|Li and the energy spectrum of the breakup cross section. On the reaction side, the applicability of DWBA in the energy region of interest is quite questionable. In other words, if the reaction observable suffers from higher-order processes, it is not trivial at all to relate the observable and the response of a nucleus to a specific transition operator. Furthermore, there is no guarantee that a single operator is responsible for the proton inelastic scattering measured at backward angles. In order to elucidate the structure of the low-lying continuum states of |$^{11}$|Li, an analysis with microscopic structure and reaction models is eagerly desired.
The purpose of this paper is to analyze the |$^{11}$|Li(|$p,p'$|) cross sections at 6 MeV/nucleon with a sophisticated reaction model, i.e., the microscopic four-body continuum-discretized coupled-channel method (CDCC) [26–30]. The advantages of the present analysis are that the angular distribution and energy spectrum of the breakup cross section can be calculated and the contributions of resonant and nonresonant states in |$^{11}$|Li to the cross sections can be investigated. A complete set of the |$^9$|Li + |$n$| + |$n$| three-body wave functions in a space relevant to the |$^{11}$|Li(|$p,p'$|) reaction is implemented in CDCC and thereby the validity of the continuum structure of |$^{11}$|Li is examined. Classification of the three-body wave functions with the complex-scaling method (CSM) [31–33] suggests a low-lying three-body Feshbach resonance [34,35] of |$^{11}$|Li, which is the principal finding of the present study. We also discuss the electric dipole distribution calculated with the three-body model of |$^{11}$|Li.
This paper is organized as follows: in Sect. 2, we describe the theoretical framework for the present analysis of the |$^{11}$|Li(|$p,p'$|) reaction. In Sect. 3, we investigate the resonance of |$^{11}$|Li by comparing the theoretical results with the experimental data. Finally, we give a conclusion in Sect. 4.
2. Theoretical framework
Here, |$K_{r}$| and |$K_y$| are the kinetic energy operators for the Jacobi coordinates |$\boldsymbol{r}$| and |$\boldsymbol{y}$| shown in Fig. 1, respectively. In the text, we omit the subscript of each coordinate representing the channel of Jacobi coordinates. |$V_{nn}$| (|$V_{cn}$|) is a two-body interaction between the two neutrons (|$^{9}$|Li and a neutron), and |$V_{cnn}$| is a phenomenological three-body force (3BF). |$\Phi_{I^\pi \nu}$| is explicitly antisymmetrized for the exchange between the two valence neutrons, whereas the exchange between each valence neutron and a nucleon in |$^9$|Li is approximately treated by the orthogonality condition model [36].
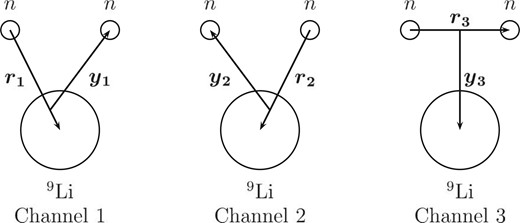
Jacobi coordinates of three rearrangement channels adopted for the |$^9$|Li + |$n$| + |$n$| model of |$^{11}$|Li structure.
Here |$\boldsymbol{s}_j$| is the coordinate of the |$j$|th nucleon in |$^{11}$|Li relative to the center-of-mass of |$^{11}$|Li.
3. Results and discussion
3.1. Numerical inputs
We take the Minnesota force [37] for |$V_{nn}$| and the interaction used in Ref. [38] is adopted as |$V_{cn}$|. The |$V_{cn}$| generates a resonance of |$^{10}$|Li in the |$0p_{1/2}$| state with a resonant energy (decay width) of |$0.46$| MeV (|$0.36$| MeV). This resonance is denoted by |$^{10}$|Li below for simplicity. This value of the resonant energy is in good agreement with the latest experimental data [39]. For |$V_{cnn}$|, we adopt the volume-type 3BF [40] given by a product of Gaussian functions for the two Jacobi coordinates; the range parameter for each coordinate is set to 2.64 fm and the strength |$V_3$| is determined to optimize the ground-state energy |$\varepsilon_0=-0.369$| MeV [41] of |$^{11}$|Li. We employ the Jeukenne–Lejeune–Mahaux (JLM) effective nucleon–nucleon interaction [42] as |$v_{0i}$|. As in the preceding works [43–45], a normalization factor |$N_I$| for the imaginary part of the JLM interaction is introduced; |$N_I$| is determined to be 0.55 so as to reproduce both the elastic and breakup cross section data around 100|$^\circ$|, where the breakup cross section data exist. Eigenstates of |$h$| and |$h^{\theta_c}$| are obtained by the Gaussian expansion method [46], where we adopt the parameter set II for |$h$| and set III for |$h^\theta_c$|, shown in Table I in Ref. [30]. In CSM, the scaling angle |$\theta_c$| is set to |$20^\circ$|. In the CDCC calculation, we select the |$\Phi_{I^\pi\nu}$| with |$\varepsilon<5$| MeV and the resulting number of states is 93, 111, and 131 for |$I^\pi=0^+$|, |$1^-$|, and |$2^+$|, respectively. The model space gives good convergence of the elastic and breakup cross sections.
3.2. Structure of the |$1^-$| continuum
In Fig. 2 we plot the eigenenergies of |$h^{\theta_c}$| with |$I^\pi=1^{-}$| on the complex-energy plane. The solid square shows the three-body resonance of |$^{11}$|Li having |$\varepsilon_{\rm R}=0.42$| MeV and |$\Gamma/2=0.14$| MeV. The open circles represent three-body nonresonant continuum states of the |$^9$|Li + |$n$| + |$n$| system, whereas the closed circles indicate two-body continuum states between the valence neutron and |$^{10}$|Li. One finds that the three-body resonance is located near the |$^{10}$|Li–|$n$| threshold and the energy of the valence neutron is negative with respect to |$^{10}$|Li. This indicates that the dipole resonance of |$^{11}$|Li is a Feshbach resonance [34,35] in a three-body system as discussed below. For the |$I^\pi=0^+$| and |$2^+$| states, there is no resonance in the present calculation.
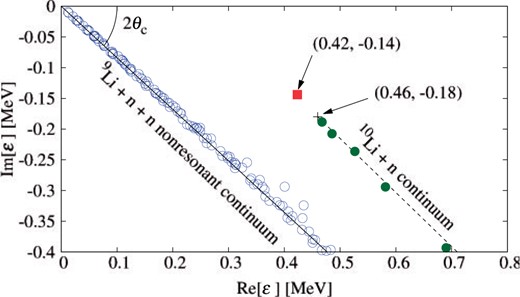
Eigenenergies for |$1^-$| states calculated with CSM on the complex-energy plane measured from the |$^9$|Li + |$n$| + |$n$| threshold. The scaling angle |$\theta_{c}$| is taken to be 20|$^\circ$|, and the cross mark shows the |$^{10}$|Li–|$n$| threshold on the complex plane.
In Fig. 3, we summarize the properties of the complex-scaled states shown in Fig. 2. In the three-body Feshbach resonance, the |$^9$|Li + |$n$| + |$n$| threshold energy is lower than the |$^{10}$|Li–|$n$| threshold, which is a distinctive character of the Borromean system. We thus refer to this resonance as a Borromean Feshbach resonance. It should be noted that some indications of a dipole resonance in |$^{11}$|Li have been discussed in preceding studies [19,20]. It will be interesting to see the correspondence between these findings and the result in the current study. In the following subsections, we discuss how the |$1^-$| resonance appears in reaction observables.
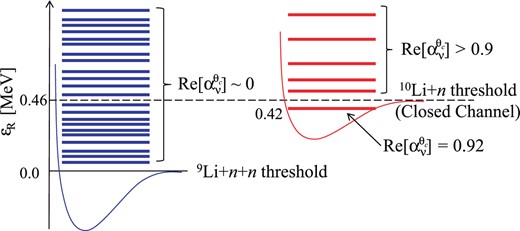
A schematic representation of complex-scaled states of |$^{11}$|Li for |$I^\pi=1^-$|.
3.3. |$^{11}$|Li resonance in proton inelastic scattering
First, we discuss the proton elastic scattering on |$^{11}$|Li that is used as a primary constraint for the adjustable parameter |$N_I$| contained in the present reaction model. Figure 4 shows the angular distribution of the elastic cross section at 6 MeV/nucleon. The solid line is the result of the microscopic four-body CDCC calculation; |$N_I=0.55$| is chosen so as to reproduce the data around 100|$^\circ$|, in which the proton inelastic scattering data are measured. We remark here that because the |$N_I$| dependence of the elastic cross section is not very strong, for the fine tuning of |$N_I$|, we have also used the data for inelastic scattering shown below. The solid line also agrees well with the data from 40|$^\circ$| to 60|$^\circ$|. One may notice a deviation in the result from the data around the dip of the cross section. It is known that in this region a spin–orbit part of the distorting potential, which is disregarded in the present study, plays an important role. It should also be noted that, to be strict, the JLM is applicable to nucleon scattering above 10 MeV [42]. This point is one of the reasons for the disagreement with the data at forward angles. Considering these things, we conclude that the agreement between the solid line and the experimental data is satisfactory. The dotted line is the result with neglecting the breakup channels of |$^{11}$|Li. One sees that the breakup effect represented by the difference between the dotted and solid lines is significant for the elastic scattering.
![Angular distribution of the differential elastic cross section for the $^{11}$Li + $p$ scattering at 6 MeV/nucleon [25]. The solid and dotted lines represent results of the microscopic four-body CDCC and without breakup channels, respectively.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/ptep/2019/12/10.1093_ptep_ptz126/2/m_ptz126f4.jpeg?Expires=1750211641&Signature=JrSTjny~452sldaTH-PxUf7-7uIQbNMTllHjijj4fVUf4RASeOqnGnHineRSPYvqeP-WcrhQxQ2ySX5bhkFTwYjiwShozOyCJ7O7BI7I9EKifqlOTziQP8EOG2EJhjIH2INkjY8F9eeE-jDV4vVzSg~TPTvHlzJgPoDcK5cQArgVRwmhGKqQO~7U5EqXOjV14pkmXT2~1bStbA53S8rdW7mgRw9YW~mNDyT3CuU~MNNQioH8yV1aGmBPXLm78Q3xbDW0j-nfwdWeCTG7CRokTIe14Wma2OTtvEP4b8~VQ~zzmDUvO9tjHPZGqm72lX1UxfnqEgq-NZhtRL62Ylv~gw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Angular distribution of the differential elastic cross section for the |$^{11}$|Li + |$p$| scattering at 6 MeV/nucleon [25]. The solid and dotted lines represent results of the microscopic four-body CDCC and without breakup channels, respectively.
In Fig. 5(a) we show the angular distribution of the breakup cross section; |$d^2\sigma/(d\varepsilon d\Omega)$| is integrated over |$\varepsilon$| from 0 MeV to 1.13 MeV so as to cover well the peak structure of the cross section in Fig. 5(b). It should be noted that the experimental data in Fig. 5(a) are different from those in Fig. 5 of Ref. [25]. The former are evaluated from the black line in Fig. 3 of Ref. [25] with the cut energy mentioned above, the latter from the red line within the all-energy region. The thick solid line represents the result of the microscopic four-body CDCC; it reproduces the experimental data around 100|$^\circ$|, as |$N_I$| is chosen so. The slight deviation of the solid line from the data around 80|$^\circ$| will come from the same reason as for the elastic cross section. The dotted, dashed, and dot-dashed lines represent the breakup cross sections to the |$0^+$|, |$1^-$|, and |$2^+$| states, respectively. One sees that the breakup cross section to the |$1^-$| state is dominant but the |$0^+$| and |$2^+$| components are not negligible in the region where experimental data exist. In other words, a model that assumes a pure dipole transition of |$^{11}$|Li will not explain the measured cross sections unless an unrealistic structural model of |$^{11}$|Li is adopted. Furthermore, since the transition potential adopted in the present calculation cannot be written as a simple functional form, the use of a single transition operator cannot be justified. Our final remark on Fig. 5(a) is the importance of the coupled-channel effects. The thin solid line shows the result of a one-step calculation that severely overestimates the thick solid line by about one order at middle angles. We therefore conclude that DWBA is not applicable to the |$^{11}$|Li(|$p,p'$|) at 6 MeV/nucleon.
![(a) Angular distribution of the differential breakup cross section and (b) the breakup cross section as a function of the three-body breakup energy $\varepsilon$ of $^{11}$Li in the $^{11}$Li($p,p'$) reaction [25]. The cross section in (a) is obtained by integrating $d^2\sigma/(d\varepsilon d\Omega)$ over $\epsilon$ from 0 MeV to 1.13 MeV, and that in (b) over $\theta_{\rm c.m.}$ from 115$^\circ$ to 124$^{\circ}$. The dotted, dashed, and dot-dashed lines represent calculated cross sections to the $0^+$, $1^-$, and $2^+$ breakup states, respectively, and the sum of them is shown by the thick solid line. The thin solid line shows the total cross section calculated with a one-step approximation in panel (a) and the contribution of the three-body resonance of $^{11}$Li in panel (b).](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/ptep/2019/12/10.1093_ptep_ptz126/2/m_ptz126f5.jpeg?Expires=1750211641&Signature=K200XlAgWkLFgv0Dru6ffa-SLNKXV9mI2UMKHS2kiyM5ythsZP-fhSlY212--d1SBY4JVc~EE370ZokceOGPaGBph3qV08dQVGZVV5DwsBlY78cQ2Ca1KQjdkjBtCwXmu7yLcEE9syYPvC2taFaaafI7rTOZwUunq7eO7NZ38KDO7NRTEQbDEl-l-qY2saZMiCt2--GjWV98Fn1J9sVsVyrcTu2Ijma4aIfo2L-475crvs5eYoSk3xsux0iD8E1e1JHi7Noen6~TqqGNJFLg2p4PElOXkcfvls1kBpnRnHBjXGxnwlLpQT29lXDYjqn1nZDkvzz3mLaNAPSOgbtXLg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
(a) Angular distribution of the differential breakup cross section and (b) the breakup cross section as a function of the three-body breakup energy |$\varepsilon$| of |$^{11}$|Li in the |$^{11}$|Li(|$p,p'$|) reaction [25]. The cross section in (a) is obtained by integrating |$d^2\sigma/(d\varepsilon d\Omega)$| over |$\epsilon$| from 0 MeV to 1.13 MeV, and that in (b) over |$\theta_{\rm c.m.}$| from 115|$^\circ$| to 124|$^{\circ}$|. The dotted, dashed, and dot-dashed lines represent calculated cross sections to the |$0^+$|, |$1^-$|, and |$2^+$| breakup states, respectively, and the sum of them is shown by the thick solid line. The thin solid line shows the total cross section calculated with a one-step approximation in panel (a) and the contribution of the three-body resonance of |$^{11}$|Li in panel (b).
In Fig. 5(b), we show the breakup cross section with respect to the three-body energy |$\varepsilon$| after breakup, which is obtained by integrating |$d^2 \sigma/(d\varepsilon d\Omega)$| over |$\theta_{\rm c.m.}$| from 115|$^\circ$| to 124|$^\circ$|. Here, we have taken into account the energy resolution of the experimental data. The total breakup cross section represented by the thick solid line reproduces the experimental data up to |$\varepsilon\sim1.0$| MeV including a low-lying peak. One sees that the contribution from the dipole resonance of |$^{11}$|Li shown by the thin solid line dominates the low-lying peak. It should be noted that the peak position (energy) of the experimental data as well as the thin solid line is somewhat higher than the resonant energy, |$\varepsilon_{\rm R}=0.42$| MeV, which is mainly due to the energy resolution. Furthermore, the calculated resonant width |$\Gamma=0.28$| MeV is narrow compared with the evaluation |$\Gamma=1.15\pm0.06$| MeV in Ref. [25]. This is because of the contributions from the |$0^+$| and |$2^+$| nonresonant components. Therefore, in order to extract reliable information on the width of the resonance, the nonresonant components should be properly evaluated and subtracted from the measured spectrum. For |$\epsilon\lesssim$|1.0 MeV, it can be concluded that the low-lying continuum structure of |$^{11}$|Li including the dipole resonance shown in Fig. 2 is consistent with the measured cross sections. On the other hand, the calculated cross section undershoots the data for |$\varepsilon\gtrsim$|1.0 MeV, which will be due to some other degrees of freedom that are not taken into account in the present calculation, e.g., a transition to higher spin states and a core excitation in |$^9$|Li. In order to clarify properties of the continuum structure of |$^{11}$|Li including the higher excited states, we require more reliable calculations of |$^{11}$|Li with the core excitation in |$^9$|Li.
Next, we investigate the behavior of the breakup energy spectrum of |$^{11}$|Li with varying the strength |$V_3$| of the 3BF for the |$1^-$| states. For the |$0^+$| and |$2^+$| states, |$V_3$| is kept at |$-11$| MeV, which has been determined to reproduce the ground-state energy of |$^{11}$|Li. In Ref. [20], a certain correspondence between the |$^{11}$|Li resonance and the |$^{10}$|Li resonance has been investigated by changing the |$^9$|Li–|$n$| interaction. We do not change the |$^{9}$|Li–|$n$| interaction, however, in this work to keep the physical resonant energy of |$^{10}$|Li and the binding energy of |$^{11}$|Li. Figure 6(a) shows the breakup energy spectrum of |$^{11}$|Li. The solid line is the same as in Fig. 5(b). The dashed, dotted, dash-dotted, and dash-dot-dotted lines show the results with |$V_3=0$|, 11, 20, and 50 MeV, respectively. It is found that, for |$V_3 \ge 11$| MeV, the dipole resonance disappears because an attractive interaction between |$^{10}$|Li and |$n$| is not enough to make a bound state. This behavior of the dipole resonance for |$V_3$| is evidence that it is a Feshbach resonance. If the dipole resonance was not a Feshbach resonance, the pole on the complex-energy plane could exist even when |$\varepsilon_{\rm R}$| is over 0.46 MeV. The contribution of the dipole resonance for |$V_3\ge 11$| MeV to the cross section is dispersed into those from other |$^{10}$|Li–|$n$| nonresonant states. Consequently, even when the dipole resonance does not exist, the breakup cross section has a peak at a certain |$\varepsilon$| depending on |$V_3$|. In the present analysis, the calculated cross section with |$V_3=-11$| MeV, i.e., with the dipole resonance shown in Fig. 2, most closely matches the experimental data.
The same as Fig. 5(b) but for the dependence of the strength |$V_3$| of the 3BF for the |$1^-$| states. Panels (a) and (b) correspond to the result with CDCC and the one-step calculation, respectively. The solid, dashed, dotted, dash-dotted, and dash-dot-dotted lines show the results with |$V_3=-11$|, 0, 11, 20, and 50 MeV, respectively.
It will be interesting to do this analysis with the one-step calculation. As shown in Fig. 6(b), the dependence of the cross section on |$V_3$| is somewhat weakened. One may conclude, therefore, that the higher-order coupling emphasizes the |$V_3$| dependence. This can be an advantage for the low-energy proton inelastic scattering to clarify the existence of the dipole resonance in |$^{11}$|Li.
3.4. Electric dipole transition
The dipole resonance has been discussed through the observation of the electric dipole distribution, |$dB(E1)/d\varepsilon$|. In Fig. 7, we show |$dB(E1)/d\varepsilon$| calculated with the present three-body model of |$^{11}$|Li and the experimental data [14]. The correspondence between each line and |$V_3$| is the same as in Fig. 6. For the theoretical calculation, the continuous energy spectrum of the |$E1$| strength can be obtained by using the same procedure described in Eqs. (9)–(11), in which |$T_\gamma$| is replaced by the |$E1$| transition matrix element. We have taken into account the energy resolution of the experimental data.
![$E1$ strength distribution as a function of the internal energy of $^{11}$Li. The calculated results take into account the experimental energy resolution, and the correspondence between each line and $V_3$ is the same as in Fig. 6. The experimental data are taken from Ref. [14].](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/ptep/2019/12/10.1093_ptep_ptz126/2/m_ptz126f7.jpeg?Expires=1750211641&Signature=lYXesb3Dh~oHQv4lMwO9ymcP7i0ZWW-MQh76Lt0gDaqoXLB2lrIxR14kBx-~~kvOaeu1y7aFRmqD~aIUZJhaiHIaDFckl-nW1mDxXl58T92r71ypuOJt70tVbloC0-GXEZ0-PZFhqBdWhF-BPNOw9411ZK34DBea6C3UwGyboYUmg3GYB6YXTmN~FWndXhfPPlNbYOMI~H4xJnfPNQd4pfP0WxfTehgmM7TOPvfAu0AZTt7~2SF8N~dq0DAJLTxv5C1TvOKOpZhvcuzefwxtkTEAvs0gl2grmswLyaJsTiLNnwFT3bOM8T1Z5RGyn0f~A6NrsM~pejQ~2X6LR2Cw0Q__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The peaks of the solid and dashed lines are at 0.42 MeV and 0.44 MeV, respectively, reflecting the eigenenergy of the dipole resonance corresponding to |$V_3$|. Once the dipole resonance disappears, the peak position has no dependence on |$V_3$| and is fixed at 0.46 MeV, the threshold energy of the |$^{10}$|Li–|$n$| channel. Because the resonant energy is very close to the |$^{10}$|Li–|$n$| threshold, it will be difficult to draw a conclusion from Fig. 7 on the existence of the dipole resonance. Another remark is that the experimental data for |$dB(E1)/d\varepsilon$| are extracted from the breakup cross section of |$^{11}$|Li by a |$^{208}$|Pb target at 70 MeV/nucleon. Even though the events corresponding to forward scattering are selected, the nuclear breakup components and higher-order effects may still play a role. Furthermore, at larger |$\varepsilon$|, contributions from target excitation can be expected, as indicated by a recent analysis of |$^6$|He breakup by |$^{208}$|Pb at 70 MeV/nucleon (Y. Sun et al., manuscript in preparation). Taking these into account, the calculated results describe the experimental data semi-quantitatively. Although the behavior of the data at small |$\varepsilon$| seems to be reproduced best by the solid line, it will be not so conclusive in the current situation.
4. Conclusion
In conclusion, we have found a dipole resonance in |$^{11}$|Li at |$\varepsilon_{\rm R}=0.42$| MeV with a width |$\Gamma$| of 0.28 MeV in a |$^9$|Li + |$n$| + |$n$| three-body model calculation with CSM. The validity of the low-lying continuum structure of the three-body system including the resonance has been shown by the good agreement between the results of the microscopic four-body CDCC calculation and the recently measured |$^{11}$|Li(|$p,p'$|) data at 6 MeV/nucleon for both the angular distribution and the breakup energy spectrum, although ambiguities in the higher excited states remain. Important remarks on the comparison with the experimental data are i) the contribution of not only the resonance but also the nonresonant continuum states is important, ii) a one-step calculation (DWBA) does not work at all, and iii) the transition operator cannot be written in a simple form, as assumed in preceding studies. It is also found that the present three-body model of |$^{11}$|Li can reproduce qualitatively the |$E1$| strength distribution. The peak of the breakup energy distribution of the |$(p,p')$| process turns out to reflect the behavior of the dipole resonance, and the data are explained well when a resonance with |$\varepsilon_{\rm R}=0.42$| and |$\Gamma=0.28$| MeV exists. On the other hand, the correspondence between the |$E1$| strength distribution and the dipole resonance is found to be less clear.
The structure–reaction combined analysis carried out in this work will bring non-contradictory understanding of hadronic scattering and the Coulomb dissociation experiments. The |$^{11}$|Li resonance is interpreted as a bound state of the valence neutron with respect to |$^{10}$|Li, i.e., a Borromean Feshbach resonance. It should be noted that the |$^{10}$|Li–|$n$| threshold is above the |$^{9}$|Li + |$n$| + |$n$| three-body threshold, which is a distinctive characteristic of a Borromean system. The ordinary Feshbach resonance has been intensively discussed, mainly in atomic physics. The finding of the Borromean Feshbach resonance in the present study will be characterized by its appearance in a Borromean system that is unique in the nucleonic system. Another important feature is that we have some information on the interactions between the constituents of |$^{11}$|Li. This allows one to carry out realistic studies on the |$^{11}$|Li resonance. Nevertheless, more information on the |$^9$|Li–|$n$| interaction is desirable, to make our understanding of the continuum structure of |$^{11}$|Li more profound and complete. Inclusion of the intrinsic spin of |$^{9}$|Li as well as the excitation of the |$^{9}$|Li core will also be very important and will have an effect on the resonance energy and width. As one of the experiments for the |$^9$|Li–|$n$| interaction, the |$^{11}$|Li(|$p$|,|$d$|)|$^{10}$|Li reaction has been measured in Ref. [48], and inclusion of the transfer channel will be an interesting challenge for future work.
Acknowledgements
The authors are grateful to Prof. I. Tanihata and Prof. N. Aoi for fruitful discussions. J.T. gratefully acknowledges the support by the Hirao Taro Foundation of the Konan University Association for Academic Research. This work has been supported in part by Grants-in-Aid of the Japan Society for the Promotion of Science (Grants Nos. JP16K05352 and JP18K03650).
