-
PDF
- Split View
-
Views
-
Cite
Cite
Rama Reddy Goluguri, Catherine Ghosh, Joshua Quintong, Mourad Sadqi, Victor Muñoz, How to scan naked DNA using promiscuous recognition and no clamping: a model for pioneer transcription factors, Nucleic Acids Research, Volume 52, Issue 18, 14 October 2024, Pages 11098–11114, https://doi.org/10.1093/nar/gkae790
Close - Share Icon Share
Abstract
Most DNA scanning proteins uniquely recognize their cognate sequence motif and slide on DNA assisted by some sort of clamping interface. The pioneer transcription factors that control cell fate in eukaryotes must forgo both elements to gain access to DNA in naked and chromatin forms; thus, whether or how these factors scan naked DNA is unknown. Here, we use single-molecule techniques to investigate naked DNA scanning by the Engrailed homeodomain (enHD) as paradigm of highly promiscuous recognition and open DNA binding interface. We find that enHD scans naked DNA quite effectively, and about 200000-fold faster than expected for a continuous promiscuous slide. To do so, enHD scans about 675 bp of DNA in 100 ms and then redeploys stochastically to another location 530 bp afar in just 10 ms. During the scanning phase enHD alternates between slow- and medium-paced modes every 3 and 40 ms, respectively. We also find that enHD binds nucleosomes and does so with enhanced affinity relative to naked DNA. Our results demonstrate that pioneer-like transcription factors can in principle do both, target nucleosomes and scan active DNA efficiently. The hybrid scanning mechanism used by enHD appears particularly well suited for the highly complex genomic signals of eukaryotic cells.
Introduction
The ability to efficiently scan genomic DNA is an essential feature for all proteins with biological functions that rely on binding to target DNA sites (1). This requirement applies to most members of the large class of DNA binding proteins (DBP) (2), including enzymes involved in DNA repair, synthesis, degradation, editing, and scaffolding. Another important group of DNA scanners is made of transcription factors (TF), which activate/repress the expression of target genes by locating and binding to cognate sequence motifs present in the relevant control elements (3). It is widely accepted that TFs must recognize their cognate motifs specifically to perform their function. The specificity in recognition is supported by a variety of high-throughput selection assays, which have consistently produced well defined sequence binding logos for TFs (4). Structurally, specific cognate binding is achieved via detailed interactions formed between the TF and nitrogenous bases from the cognate motif, which stabilize the complex in combination with a generic electrostatic attraction to the DNA backbone (5). Cognate binding typically results in affinities in the low nM range, coinciding with the concentrations at which TFs are present in living cells (6).
Once endowed with specific recognition, DBPs must also effectively find their target site(s) among hundreds of millions of alternatives that are present in a genome, a challenge that involves thermodynamic and kinetic considerations (7–9). The accepted mechanism for facilitating this search involves an additional non-specific binding mode that recognizes all other DNA sequences uniformly (10,11). Non-specific binding must be weak to avoid outcompeting cognate recognition by sheer numbers (12), and enables a diffusive motion along the DNA that simplifies the stochastic search relative to conventional 3D diffusion-collision kinetics (11). A DBP can thus scan the DNA sequence following a spiralling sliding motion around the DNA contour length with diffusion coefficient (Dsliding) defined by Schurr's equation (13),
where η is the solvent viscosity, a is the radius of the DBP, and b is the displacement of a full rotation of the protein around the DNA helix (|$b = 3.4 \times {10^{ - 7}}\;{\rm cm}$|). Sliding results on full sequence scans, but this motion is significantly slower than linear diffusion due to its rotational component. In addition, equation 1 defines the sliding speed limit, but the actual sliding dynamics will be further slowed by friction. This is so because moving to the next position along the DNA requires breaking, even if transiently, the non-specific interactions that keep the protein bound to the DNA, as well as displacing loosely associated counterions (13,14). Friction could even be higher in vivo due to the abundance of other DNA associated proteins that can interfere with the sliding motion (15). Hence, it has been noted that optimal DNA scanning should occur when 1D and bulk 3D diffusion are equally mixed (16,17). Mechanistically, maximizing DNA scanning involves balancing the extension of the sliding runs against the friction that ensues from a stronger non-specific DNA association.
1D diffusion on DNA is usually studied using single-molecule fluorescence microscopy (18). Such experiments have demonstrated 1D diffusion on a variety of DBPs, most of them enzymes (19–27). Interestingly, despite the large variety in biological functions, 3D structures, DNA interfaces, protein sizes, and even experimental conditions, the existing data reveal a remarkably consistent scanning behaviour. For instance, the DBP remains associated to DNA for relatively long times (0.2–10 seconds) and moves along the DNA with D values ranging between 3 × 10−11 and 10−8 cm2 s−1. Perhaps more significantly, the measured D values are just 1–2 orders of magnitude slower than the corresponding sliding speed limits set forth by equation 1, which implies that facilitated diffusion generally incurs little friction, i.e. ≲2.5 kBT (22,26,28). Such consistency in DNA scanning suggests two major driving factors. One factor involves ensuring that the DNA recognition process is binary, that is, that non-specific binding is uniformly sequence independent. Binary recognition makes the DNA landscape energetically flat for easy sliding. In structural terms, DNA binding becomes sequence independent when it relies exclusively on electrostatic interactions with the phosphate backbone (29). The second factor is an interaction interface that encircles the DNA axis to mechanically sustain the sliding motion without engaging in strong non-specific interactions. A closed circle interface results in a sliding clamp (30), which often requires active loading onto the DNA (31). But when formed, the sliding clamp enables an extended and fast scanning motion (32). Importantly, all the DBPs that have been shown to diffuse on DNA thus far use DNA interfaces that provide some degree of clamping support, whether by fully or partially encircling the DNA via tandem arrays of DNA binding motifs or by oligomerization. An interesting mechanical alternative is a monkey-bar motion that can be performed by proteins that use separate domains for cognate and non-specific recognition connected with a flexible linker (33).
On the other hand, there is a fundamental group of eukaryotic TFs that control cell fate during embryonic development, morphogenesis, and cell reprogramming (34), including homeodomain proteins (35), which cannot possibly abide by those rules for scanning naked DNA. These TFs recognize cognate motifs in DNA that is both naked and wrapped into nucleosomes, which allows them to act on active and silent chromatin as pioneers in starting global transcription programs (36). It has been shown that to access DNA on nucleosomes the TF must recognize cognate motifs that are short enough to be displayable on the nucleosome surface (≤8 bp) and interact with the DNA via an open interface that avoids clashes with the histone proteins comprising the nucleosome core (37). These requirements appear in stark conflict with what we understand makes for efficient scanning of naked DNA by facilitated diffusion. A short sequence motif has fewer cognate interacting partners, being less conducive to binary DNA recognition. In that regard, we recently discovered that the Engrailed homeodomain is highly promiscuous, binding DNA with a ladder of affinities that runs proportionally to the similarity of the sequence with its cognate logo (38). New high-throughput selection methods designed to sample broad affinity ranges are now reporting similarly promiscuous profiles for other eukaryotic TFs (39). A ladder of affinities results on DNA binding landscapes that are energetically rugged, and thus likely to elicit high friction during sliding. Furthermore, the need for an open interaction interface to access DNA on nucleosomes eliminates the clamping support for sliding. Accordingly, this group of pioneer TFs must rely exclusively on direct interactions with the DNA to sustain a 1D diffusive motion.
The special DNA binding properties of pioneer TFs pose a major puzzle since their biological functions still require them to effectively scan active naked DNA as well as DNA packed in chromatin. As master regulators of cell fate, pioneer TFs control the expression of hundreds of genes (40,41), and operate on DNA regulatory elements consisting of kb long regions that are localized to nearby a gene (cis, intergenic regions) or longer distance along or between chromosome territories (trans, enhancers) (42). Intriguingly, such long DNA regions contain large clusters of imperfect versions of cognate motifs for key TFs (12,43). These imperfect motif clusters are known to increase local TF occupancy in vivo (44), and their removal from enhancers impairs cell fate stability during embryonic development (45,46). However, the functional roles that these motif clusters may play in how the TF searches for its targets remain undefined (47–49). A particularly compelling role has emerged in the context of promiscuous DNA recognition, which turns the clusters of imperfect motifs onto a tracking device or transcription antenna that can attract multiple copies of the relevant TFs to dynamically co-localize with the region of interest (38). Whatever is the role(s) of imperfect-motif clusters in global localization, it is undeniable that such clusters make the DNA landscapes energetically rugged, and hence potentially much harder to scan using conventional facilitated diffusion. But there currently is no experimental data available on the facilitated diffusion of naked DNA by pioneer TFs, or by any other protein with equivalent DNA binding properties. Whether or how members of this important group of eukaryotic TFs scan active DNA remains unknown.
Here, we address this fundamental question by investigating the DNA scanning of the Engrailed homeodomain (enHD) at the single-molecule level. Engrailed is an evolutionary conserved (50) master regulator that in Drosophila controls cell identity and patterning (51). Engrailed controls the expression of over 200 genes, playing both activator and repressor roles (52). In humans, Engrailed-1 is linked to brain and eye defects (53,54) and its misexpression has been linked to cancer (55). From a nucleosome targeting standpoint, homeodomains often target DNA all around the nucleosome perimeter (37). EnHD is solely responsible for DNA binding in Engrailed and epitomizes the two DNA binding properties of pioneer TFs. The enHD cognate motif is just 6 bp and palindromic (56), offering two laterally symmetric target sites. X-ray structures of enHD in complex with cognate DNA demonstrate a widely open interaction interface that lacks clamping support (Figure 1A). The interface is formed by the lateral insertion of enHD’s C-terminal α-helix (H3) into the DNA major groove together with interactions of two N-terminal arginine sidechains with the adjacent minor groove. This interface allows for interactions with cognate bases that are indirect, occurring through interstitial water molecules (57). Furthermore, enHD binds DNA promiscuously both in vitro and in vivo with sequence preferences that have been integrated onto a statistical mechanical model for predicting the enHD binding free energy landscape of any DNA sequence (38). Here, we capitalize on such capability to directly compare the 1D diffusion along naked DNA of enHD, as measured by single-molecule fluorescence tracking, with the existing map of its DNA binding energetics. From such vis-à-vis comparison we can uniquely estimate what fraction of the energetic cost of breaking the interactions formed at any given DNA location is converted to effective friction during DNA scanning. This information is important to interpret 1D diffusion on DNA in mechanistic terms but has not been usually available for other DBPs. To examine DNA scanning by enHD we use a variant labelled with the fluorophore Alexa-488 at the C-terminal end, which minimizes any interference with DNA binding (Figure 1B), as showed previously (38).
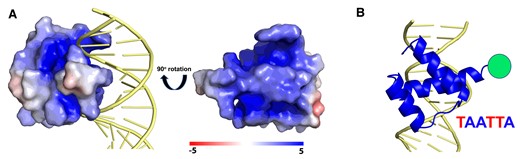
The DNA Interaction Interface of the Engrailed Homeodomain. (A) The structure of enHD in complex with DNA (PDB: 1HDD) representing the electrostatic surface of enHD with the DNA in cartoon. The complex shows that the interaction interface is wide open and lacks clamping. The rotated structure of enHD (right) shows the face that interacts with DNA, highlighting the strongly positive electrostatic potential of the two depressions that flank α-helix 3 and which interact directly with the DNA phosphate backbone. (B) Cartoon representation showing the insertion of α-helix 3 in the DNA major groove parallel to the phosphate backbone and the minor groove interactions of the N-terminus. The figure also shows the position of the Alexa 488 fluorophore used for tracking on the DNA and the cognate motif of enHD.
Materials and methods
Protein expression, purification and labelling
The enHD protein used in this study is identical to the one we used to characterize binding promiscuity, and was produced as described previously (38). We also studied the binding properties of the Q50K mutant of enHD (58). This variant was produced by site-directed mutagenesis of the gene encoding for the wild-type sequence. The protein was purified and labelled with fluorophores following the same procedures used for the wild type.
Tracking alexa 488-labeled EnHD on the lambda-based DNA
All the experiments of enHD binding to the lambda-based DNA were performed on a commercially available dual beam optical trap coupled to confocal microscope (C-Trap, Lumicks) in 20 mM Tris buffer at pH 7.5 with NaCl concentrations ranging from 25 to 100 mM. The buffer also contained a photo-protection cocktail comprising of 100 μg/ml glucose oxidase, 20 μg/ml catalase, 5 mg/ml glucose and 1mM Trolox. 0.05% v/v tween 20 was added to all buffers to prevent the labelled protein from sticking to surfaces of the tubes and flow cell. Biotinylated double stranded lambda DNA was tethered in between two streptavidin coated polystyrene beads of 3.1 μm diameter. The binding of Alexa 488 labelled enHD to the lambda DNA was probed by performing fluorescence line scans along the DNA using the correlative confocal microscope. The scans were performed with 200 nm spacing and imaging each pixel for 100 μs. Fluorescence line scans completed every 20 ms were aligned in series to produce a kymograph whose x-axis represents time and y-axis represents position along the lambda phage DNA.
1D Diffusive trajectory data analysis
The kymographs obtained from the C-trap instrument were analysed using a custom algorithm written in Python (59). The position and time information of each binding trajectory derived from the Python script were further analysed in MATLAB to determine the dwell time on the DNA molecule, total distance travelled along the DNA, and the diffusion coefficient of each trajectory using custom-built code. The average dwell time was calculated from the distribution of dwell times obtained from the individual 1D trajectories. The total distance travelled per 1D diffusive event is obtained by summing the distance displacements between time points over the entire trajectory. We calculated the diffusion coefficient for each trajectory in two different ways. In the first method we calculated D from the total sum of squared distance displacements using the formula:
where n is the total number of time points along the trajectory, |${d_{i,i - 1}}$| is the displacement of the protein between times points i-1 and i, and |${\tau _{dwell}}$|is the duration of the 1D trajectory. In the second method, we obtained the diffusion coefficient from half the slope of the linear regression of the squared displacement versus time. Both methods rendered very similar values. The diffusion coefficient in cm2s−1 is converted to stepping rate using the formula:
Naked and nucleosome-wrapped DNA for binding studies
The naked and nucleosome-wrapped DNA binding experiments were performed with a 146 bp DNA purchased from Integrated DNA Technologies (IDT). The DNA molecule was designed to contain 14 cognate motif (TAATTA) sites interspersed at regular intervals, giving the sequence:
ACTCGTAATTAGTGCTAATTACTACTAATTAGTGCTAATTAGGACTAATTACTACTAATTAGCACTAATTAAGGATAATTACTGATAATTAGGACTAATTACTCGTAATTAGTGCTAATTACAGCTAATTACTCGTAATTAGTGCA
Nucleosomes were prepared using the Chromatin Assembly Kit (product number: 53500) from Active Motif (Carlsbad, CA). The kit is based on an ATP-dependent assembly method that uses purified components to generate high-quality chromatin from supercoiled and linear DNA without the need for a nucleosome positioning sequence. The kit utilizes the purified recombinant Drosophila chromatin assembly complex ACF and human histone chaperone NAP-1 (h-NAP-1) with purified HeLa core histones for in vitro assembly of nucleosomes.
DNA binding by fluorescence correlation spectroscopy
Fluorescence Correlation Spectroscopy (FCS) experiments were performed at room temperature with 150 μl samples in 10mM Tris–HCl pH 7.5, 0.1 mM EDTA, 50 mM NaCl, prepared with enHD at 200 pM. Series of experiments at various naked DNA and nucleosomal DNA concentrations were performed to ensure coverage of the entire binding curve (from the pM to nM range). The samples also contained 1 mM Trolox and 10 mM Cysteamine as photo-protection cocktail (60). 0.05% v/v Tween 20 was added to prevent the labelled protein from sticking to the glass coverslips. PEG functionalized glass coverslips were prepared following a protocol previously outlined (38). All binding measurements were carried out on a custom built confocal fluorescence microscope. The KD for the enHD binding to the naked and nucleosome wrapped DNA were determined by globally fitting the autocorrelation function decays for a series of FCS experiments at varying concentrations of naked or nucleosomal DNA, respectively.
More methodological details are provided in the Extended Methods section of Supplementary Information.
Results
The genome of phage λ as proxy of an engrailed control element
As DNA scanning substrate we chose a 48.5 kb long DNA molecule corresponding to the genome of bacteriophage λ. We examined the binding profile of the λ-phage genome with the existing statistical mechanical model of enHD promiscuous recognition (38). Using this model, we calculated the free energy landscape for enHD binding of the λ-DNA sequence (total of 96994 possible binding sites) at the same conditions of the scanning experiments to enable direct comparisons. Figure 2 shows in teal the λ-DNA binding free energy landscape converted onto dissociation equilibrium constants integrated over a 45 bp window to reduce site-to-site fluctuations and facilitate visual inspection. The calculation renders a < KD> 45-bp ∼ 4 × 10−8 M at 25 mM salt, which confirms that enHD binds much more tightly to the λ-DNA than expected for typical non-specific binding. At this resolution the binding profile still shows large local fluctuations in affinity. The profile shows a few high affinity spikes (∼10−9 M) that correspond to 45 bp segments containing two enHD cognate binding sites (forward and reverse palindromes) and a central ∼8 kb region containing clusters of imperfect cognate motifs. Interestingly, the enHD binding pattern of the λ-DNA is similar to the profiles we previously reported for the non-coding regions of genes known to be under Engrailed control (38), indicating that this DNA molecule is a reasonable proxy for an Engrailed control element.
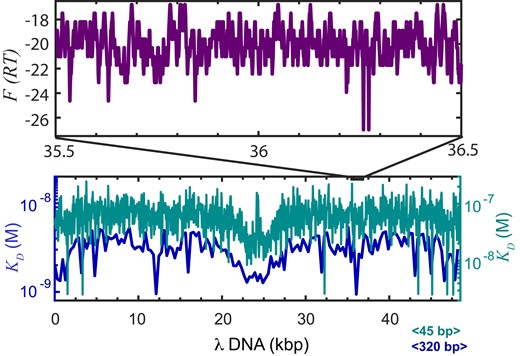
The DNA binding landscape for EnHD of the λ-phage genome. The enHD binding profile of the 48.5 kb λ-phage sequence calculated with the statistical mechanical model derived from the analysis of enHD promiscuous recognition (38). The equilibrium dissociation constant for enHD integrated over windows of 45 bp (teal) or 320 bp (navy blue) is shown on the bottom. The top box shows in purple a 1 kb detail of the binding free energy landscape (RT units) at single-site resolution corresponding to the 35500–36500 bp segment of the λ-phage genome in the 5′ to 3′direction (binding is bidirectional).
The central region of λ-DNA can thus be considered equivalent to a transcription antenna. The navy-blue profile shows the same equilibrium binding profile integrated over a 320 bp window that is comparable to the position accuracy of our fluorescence tracking experiments (see Sup. Inf. and Supplementary Figure S1). At this resolution, the fluctuations in binding affinity are largely averaged out but the profile still highlights up to 4-fold affinity differences along the sequence. From a mechanistic standpoint it is more informative to look at the binding free energy landscape at single-site resolution (6 bp). Figure 2 also shows in purple a 1 kb segment (35.5–36.5 kb) as an example, which illustrates the inherent roughness for binding. This zoomed region shows that the fluctuations in binding free energy between neighbouring sites can be as high as 10 RT, resulting in ∼22 000-fold differences in binding occupancy between adjacent sites. The high magnitude and frequency of these free energy fluctuations suggest that enHD should experience an extremely sluggish sliding motion along the λ-DNA.
Optical tweezers with correlative confocal fluorescence microscopy to measure EnHD diffusion along the λ-DNA
We use two independent optical traps to mechanically control the position and extension of a single λ-DNA molecule tethered to two beads, and correlative confocal fluorescence microscopy to scan the DNA molecule and track the position of fluorescently labelled protein molecules as they move on the DNA (Figure 3A). This technique has been recently applied to measure 1D diffusion of Cas12a (25). We used λ-DNA biotinylated at both ends to form tethers to streptavidin coated polystyrene beads. The optical traps are used to capture the two beads and control the tethered DNA mechanically, and a multichannel microfluidics chip is used to deliver the different components of the assay in sequence (Figure 3B). Figure 3C shows a 2D image of one molecule of λ-DNA tethered to ∼3.1 μm beads and stretched to its maximally extended relaxed configuration resulting in a separation of 16.5 μm (48502 × 0.34 nm per base pair). The image also shows several A488-labelled enHD molecules associated to different locations of the λ-DNA. Figure 3D corresponds to a kymograph constructed from fluorescence confocal line scans along the DNA length, each taking ∼20 ms. From the kymographs we obtain the dwell times and diffusive motions of individual A488-enHD molecules as they travel along the λ-DNA
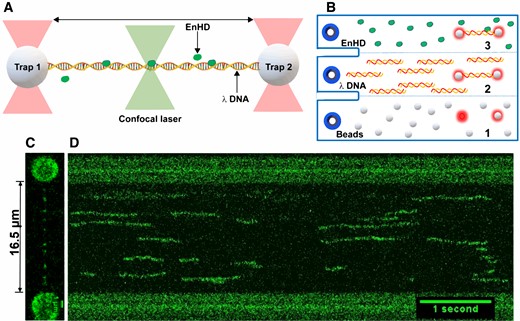
Single-molecule imaging of DNA scanning by EnHD. (A) Illustration of the experimental setup for imaging 1D diffusion on DNA using a dual trap correlative fluorescence confocal microscope. The two optical traps mechanically control a single copy of biotinylated 48.5 kb λ-DNA tethered to streptavidin-coated beads. The confocal microscope is scanned along the DNA length to image binding and diffusion of enHD molecules labelled with Alexa 488 at the C-terminus. (B) Microfluidics laminar-flow cell of the instrument showing the workflow for DNA trapping and single-molecule imaging: (1) streptavidin coated beads are flowed on the bottom channel and the two traps are positioned to trap one bead each; (2) the trapped beads are moved to the middle channel containing the biotinylated λ-DNA at a close distance from one another until the tethered to both beads of one DNA molecule is detected in the force extension profile; (3) the traps with one tethered DNA copy are moved to channel 3 containing the A488-labelled enHD to perform the scanning studies. (C) Image of one molecule of λ-DNA tethered to 3.1 μm beads and mechanically stretched to its maximal relaxed extension of 16.5 μm showing several Alexa-488-enHD molecules bound. (D) Kymograph with 20 ms line scans along the λ-DNA (y-axis) taken as a function of time (x-axis).
EnHD is an extensive and fast scanner of naked DNA
We performed experiments such as shown in Figure 3 for enHD wild-type and the Q50K mutant, which enhances DNA affinity (58). The experiments were performed at various ionic strengths to investigate the effect of modulating DNA binding through the shielding of electrostatic interactions. We used 25 and 50 mM NaCl for the wild-type, and added 75 and 100 mM for the Q50K, taking advantage of its higher affinity for DNA. This ionic strength range facilitates the comparison with previous data since it is equivalent to the ranges used for most 1D diffusion experiments on other DBPs (19–27), and also to the range explored in the characterization of enHD’s promiscuous DNA binding (38). The somewhat lower than physiological ionic strength is useful to enhance the dwell times on the DNA, and thus increase the resolution attainable by single-molecule detection. In our experiments with enHD we typically obtained several hundreds of trajectories of individual molecules diffusing along one λ-DNA molecule. The trajectories were analysed to determine the dwell time on the DNA, mean squared displacement, net distance travelled, and average diffusion coefficient for each trajectory (see Methods and Supplementary Information). Figure 4 summarizes the results for the wild type at 25 mM NaCl (521 trajectories). The data for all tested conditions on the wild type and Q50K mutant are given as supplementary information (Supplementary Figures S2, S3). Figure 4A shows a distribution of dwell times that is roughly exponential with a characteristic time on λ-DNA of ∼0.6 s. The distribution of travelled distances has a median of ∼1540 bp (or ∼0.51 μm) (Figure 4B). Therefore, at an intermediate ionic strength relative to previous facilitated diffusion studies, enHD diffuses along DNA as extensively as do DBPs endowed with DNA interfaces that provide clamping support. Figure 4C shows a broad distribution of D values with an average D of ∼3.7 × 10−9 cm2s−1. We performed an error analysis of the contributions to the observed D values of our experimental position accuracy (see Supplementary Information). This analysis indicated that a position accuracy of ±50 nm (see Supplementary Figure S1) overestimates the average D by 0.14 log10 units, indicating that the ‘true’ <D> is about 3 × 10−9 cm2s−1. This corrected < D> coincides with the median diffusion coefficient |$\tilde D$|, also 3 × 10−9 cm2s−1 (black line in Figure 5C).
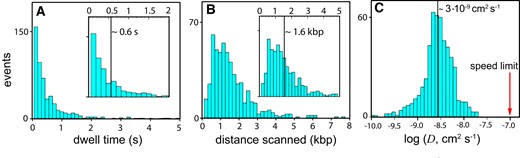
DNA Scanning Properties of EnHD. (A) Histogram of dwell times of the wild-type enHD on the λ-DNA. The inset shows the median dwell time as a vertical line on the section of the histogram up to 2 s. (B) Histogram of the distances scanned along the λ-DNA on single trajectories. The inset shows the median distance scanned as a vertical line on the histogram section up to 5 kb. (C) Histogram of the 1D diffusion coefficients (D) with median indicated as a thick vertical black line. The red arrow signals the sliding speed limit for enHD calculated with equation (1) and a = 1.7 nm and b = 3.4 nm.
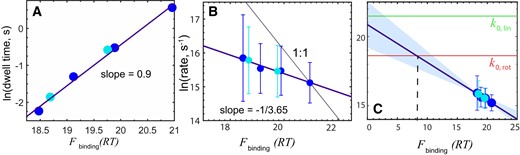
DNA scanning speed versus free energy of binding. Data obtained at different NaCl concentrations for the wild-type enHD (cyan) and Q50K mutant (blue) compared to binding strength to the λ-DNA in RT, calculated from the statistical mechanical model (38). (A) Experimental dwell times. (B) Natural logarithm of the experimental stepping rate in bp s−1 (converted from D with equation 3). The circles indicate the mean and the bars the standard deviation of all the trajectories measured at each experimental condition. The thick purple line is the linear fit with slope of -1/3.65. The thin black line shows the expectation for a 1 to 1 correspondence. (C) As in B but showing the extrapolation of the correlation all the way to zero binding free energy. The red horizontal line indicates the rotational sliding speed limit (as in Figure 4C) and the green horizontal line the limit for a linear 1D diffusion motion along the DNA with no friction. Both limits were calculated using a 1.7 nm hydrodynamic radius for enHD.
The Q50K mutant exhibits comparable behaviour (Supplementary Figure S3), but one that is shifted in terms of ionic strength relative to wild type (Supplementary Figure S4). The shift is consistent with the stronger DNA binding of this mutant, which has slightly lower affinity for the cognate TAATTA but significantly stronger binding to the alternate sequence TAATCC (58). To properly compare the wild-type and Q50K mutant we thus need to correct for their different overall affinity. The λ-DNA contains 16 TAATTA and 19 TAATCC sites and thus offers comparable scanning landscapes for both variants. We then estimated the overall correction factor empirically from the ratio between the protein concentrations that we had to use in the optical traps-confocal experiments to attain roughly equal binding occupancies on the λ-DNA for both variants. The ratio we determined this way is equivalent to ∼1.2 RT stronger overall affinity for Q50K. Once this empirical correction is applied, the dwell times and diffusion coefficients for both variants exhibit the same trends (Figure 5).
Our data demonstrates that enHD scans DNA in the fast-intermediate range compared to other studied DBPs. As a small monomeric protein, enHD has a comparatively fast translational diffusion coefficient. Nevertheless, we note that |$\tilde D$| is only ∼30-fold slower than the sliding speed calculated for enHD with equation 1 (red arrow in Figure 4C), and therefore, enHD does scan fast also in relative terms. The slowdown in enHD is comparable to those reported on DBPs that enjoy some degree of DNA clamping support. The distinction is that the DNA binding landscape for enHD is highly rugged, as illustrated in Figure 2 for the 48.5 kb λ-phage genome. Landscape ruggedness should increase the friction during sliding thus slowing down its scanning rate. The key question is how much of an acceleration the D experimentally observed for enHD really implies relative to a continuous sliding motion. At the microscopic level, sliding can be described as a series of discrete steps in which the protein breaks off the interactions at the currently occupied DNA site, moves to the adjacent site, and forms new interactions. A sustained sliding motion requires a force that keeps the protein associated to the DNA while in motion. For enHD such force can only be electrostatics given that its binding interface lacks DNA clamping altogether (Figure 1A). We indeed find that the dwell time on DNA of both enHD variants is directly proportional to the average free energy of binding to the λ-phage genome, as calculated with the statistical mechanical model for enHD DNA binding (38) (Figure 5A). The linear correlation is very strong (r = 0.996 and slope close to 1), confirming that what keeps enHD associated to the DNA during 1D diffusion are the same interactions involved in its promiscuous binding. The main contributor to the attraction during diffusion appears to be electrostatics given that the changes in average binding free energy plotted in Figure 5 were induced by either salt concentration and/or the Q50K mutation, which adds one extra positive charge to the DNA binding interface.
DNA scanning by EnHD versus a continuous sliding motion
A critical issue is how enHD’s scanning of naked DNA compares to a continuous sliding motion. We investigate that issue by estimating what fraction of enHD’s DNA binding free energy corresponds to the minimal electrostatic attraction required for a sustained sliding motion. The diffusive stepping rate in ln(bp/s) units scales with the binding free energy in inversely proportional fashion, resulting on a linear correlation (r = 0.976; Figure 5B). Figure 5C presents these same data extended to zero binding free energy. Significantly, enHD’s extrapolated stepping rate intersects with the theoretical rotational sliding speed limit, k0,rot, at ∼8 RT (Figure 5C). We use this intersect as empirical estimate of the minimal interaction energy to sustain enHD’s sliding motion. 8 RT is roughly 55% of the total electrostatic attraction between enHD and DNA at 25 mM NaCl (38). From these elements we can build a simple microscopic model of the transition state for a sliding step. In this transition state, enHD is halfway between two adjacent sites along the DNA, and sufficiently afar from the DNA axis as to reduce the overall electrostatic attraction by about 45% (Figure 6), which is long enough to dislodge the interactions with the bases. The effective D for such promiscuous sliding motion can be evaluated with the expression:
where the first term is the sliding speed limit (equation 1); the second term accounts for the electrostatic penalty of separating enHD from the DNA axis to enable the sliding motion, as per Figure 6; and the third term is the friction from the roughness of the DNA scanning landscape (61), which accounts for the sequence-specific differences in binding free energy between adjacent sites. To calculate the diffusion coefficient for enHD’s promiscuous sliding we use 17 and 8 RT for Ub and Us, respectively, and 1.35 RT for ϵ, corresponding to the standard deviation in binding free energy along the λ-phage genome (Figure 2). This calculation indicates that enHD’s 1D diffusion on the λ-DNA is about 200000 times faster than expected for a continuous promiscuous sliding motion.
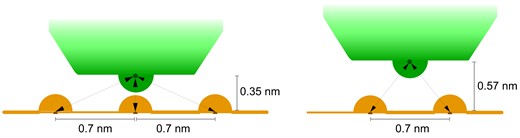
Microscopic model for promiscuous rotational sliding for EnHD. The left scheme represents the bound state with enHD shown in green and the DNA phosphate backbone in orange. The arrows represent the electrostatic interactions formed between one positively charged residue of enHD and the DNA phosphate groups. Because electrostatic interactions are long range, when the positive residue is perfectly aligned with one phosphate, it still has weak interactions with the flanking phosphate groups. This pattern should be roughly conserved for other positively charged residues at the interface. The right scheme represents a microscopic ‘transition state’ model for a sliding motion between two adjacent sites. In this ‘transition state’ model enHD is placed halfway between two phosphate groups and slightly detached from the DNA (by 0.23 nm) to break the promiscuous interactions with the bases and facilitate the motion. EnHD is still loosely associated to the DNA via a fraction of the electrostatic energy that stabilizes the DNA bound form. The distances and specific electrostatic interactions depicted here would result on an electrostatic attraction |${E_{sliding}} \propto ( {\frac{2}{{{r_s}}}} )\exp ( { - k{r_s}} )$|, where |${r_s} = \sqrt {2 \cdot {{0.57}^2}}$|, compared to the DNA bound electrostatic attraction |${E_{bound}} \propto ( {\frac{1}{{{r_1}}}} )\exp ( { - k{r_1}} ) + ( {\frac{2}{{{r_2}}}} )\exp ( { - k{r_2}} )$|, where r1 is 0.35 and |${r_2} = \sqrt {{{0.35}^2} + {{0.7}^2}}$|. For a Debye length of 1 nm, Esliding≈ 0.47 Ebound.
In an alternative model of a continuous 1D diffusive motion enHD fully detaches from a DNA site and nano hops to another site in close vicinity, e.g. within 1 nm. In this case enHD moves via its much faster free diffusion coefficient (green line in Figure 5C) and without experiencing DNA friction but pays the penalty of breaking all the interactions with DNA at every step. For enHD wild type at 25 mM NaCl such penalty is 20 RT on average (Figure 5B), giving an estimate about 5 times slower than the promiscuous sliding from equation (4), or 1000000 times slower than the experimental |$\tilde D$|. Interestingly, both motions would have the same estimated D if the nano-hops happen to retain 15–20% of the DNA-bound electrostatic attraction.
These calculations highlight that the clamp-less diffusion on DNA of enHD is supercharged relative to the expectation for a continuous scanning motion, whether the motion is via the sliding or the nano-hopping mechanisms. EnHD’s scanning also appears impervious to the local fluctuations in binding strength that it encounters along the DNA sequence landscape. Such imperviousness is further evidenced by the Q50K mutant, which is even more promiscuous than the wild-type but scans with essentially the same |$\tilde D$| at experimental conditions matching the overall affinity for the λ-DNA (Figure 5B, C). Summarizing, enHD scans DNA extensively without clamping support, at a highly accelerated rate relative to a microscopically continuous 1D diffusive motion, and largely unaffected by the ruggedness of the DNA landscape.
EnHD’s scanning rate is fractionally sensitive to DNA binding strength
The stepping rate (or D) increases by roughly one fourth of the respective decrease in binding free energy (Figure 5B). Practically this means that enHD’s scanning speed is only fractionally affected by the strength of the interactions that it makes to bind to DNA (38) or to stay diffusing along it (Figure 5A). There are two scenarios that could explain this result. In one such scenario enHD uses a uniform 1D diffusive motion in which the interactions with DNA are significantly weaker than dictated by its equilibrium binding thermodynamics. The second scenario involves a hybrid motion in which enHD alternates between binding-mediated and unbound 1D diffusive modes. We further note that the extrapolation to zero binding free energy reaches an intermediate value between the two speed limits shown in red and green in Figure 5C. This comparison suggests that enHD’s scanning at conditions of ‘zero binding’ is consistent with a mix of rotational sliding and linear 1D diffusion. The extrapolated rate is also consistent with roughly 1/4 of the slowdown expected for a pure rotational sliding motion relative to linear 1D diffusion. Therefore, there is a quantitative relationship between the scanning motion dynamics, as estimated from the stepping rate extrapolation, and its dependence with binding strength, which reflects the energetics of diffusion. This correspondence further supports a hybrid motion in which one mode does not interact with the DNA. However, the confidence interval for the ‘zero binding’ rate is broad due to the long extrapolation and thus the extrapolated rate is still statistically compatible with any value in between the two limits (swath in Figure 5C).
Additionally, we must consider that the fractional slope (energetics) and intercept (dynamics) shown in Figure 5B and C are still consistent with a single scanning mode that is fractionally affected by the binding strength. This is so because, whereas binding is local and site specific, D is measured over trajectories that cover long distances (i.e. ∼1.5 kb on average, Figure 4B) and thus reflects averages over hundreds of binding-release events. These comparisons are also indirect because they rely on calculations and extrapolations. Figure 5A provides an alternative that compares two properties determined experimentally from the same diffusive trajectories: the stepping rate and the dwell time. This comparison can be more distinctive of the two scenarios. For instance, if 1D diffusion follows a uniform motion with fractional dependence on DNA binding, electrostatic weakening by ionic screening should affect the stepping rate and dwell time in opposite directions but in the same proportion. A hybrid motion that alternates between DNA-bound and DNA-free modes will produce a different behaviour. The interactions in the DNA-bound mode will determine both the stepping rate for that mode and the recapture probability after each microscopic dissociation-displacement step. Since enHD does not clamp the DNA, the recapture probability is solely responsible for determining how long enHD remains associated to the DNA, that is, the dwell time. The stepping rate of the non-bound mode should instead be insensitive to the binding strength. Accordingly, the ionic strength will impact the average stepping rate only through the trajectory segments during which the protein is DNA bound, producing a fractional sensitivity on average. The hybrid scenario thus appears more consistent with the data, as it naturally explains the 1:1 dependence of the dwell time and fractional dependence of the stepping rate shown in Figure 5B-C.
But the observations of Figure 5 could still be consistent with a uniform scanning mechanism in the special case by which the ionic strength has two counterbalancing effects on 1D diffusion: (i) weakening the enHD–DNA interactions, which would reduce the dwell time and increase the stepping rate proportionally and (ii) reducing the stepping rate by added friction arising from the need to displace more counterions (13). We rule out this possibility by noting that, when looked at the same ionic strength, the stepping rate of Q50K relative to the wild type decreases by 1/4 of the 1.2 RT enhancement in binding affinity induced by the mutation. That is, only a small fraction of enHD’s DNA binding free energy affects its scanning speed, whether binding strength is tuned by ionic strength or mutation. Overall, all the evidence favours a hybrid mechanism for DNA scanning in which enHD alternates between DNA-bound and DNA-unbound modes.
Large heterogeneity in 1D diffusive behaviour
Another significant feature is the high variability in D values for different trajectories, which spans 2.5 orders of magnitude for both variants (Figure 4C, Supplementary Figures S2 and S3). Error analysis indicates that, given the position accuracy of our measurements (Supplementary Figure S1) and the stochastic fluctuations of Brownian motion, the D for individual trajectories should fluctuate by ±0.06 to ±0.2 log10 units (±15% to ±59%) for trajectories of 1 s or 0.24 s duration, respectively (see Supplementary Tables S1-S2). The experimental D values vary by nearly 1000-fold, regardless of whether we determined D directly from the summed mean squared displacements (MSD), or from the MSD versus time linearized slope (see Materials and Methods). Therefore, enHD appears to scan naked DNA using an inherently heterogeneous mechanism, consistently with the results presented in the previous section.
To look closer into such heterogeneity, we determined D over short time intervals along each trajectory to obtain a distribution of ‘quasi-instantaneous’ D values (Dqi), which reflects diffusion at the local level (62). We calculated D for every 60 ms segment of trajectory. Exemplary Dqi distributions for the wild type and Q50K are shown in Figure 7A and B, respectively. These datasets are equivalent in terms of dwell time and average diffusion coefficient (cyan and blue points closest to 20 RT in Figure 5B, C), and they give similar Dqi distributions as well. These distributions are very broad in log10 scale, showing differences over 3-orders of magnitude. There are, however, several sources for the variability in Dqi that we must consider. An obvious factor is the increased uncertainty from using only three datapoints to determine each Dqi value. We explored the contributions from this factor using error analysis (see Sup. Inf.), which indicated that a ±50 nm position uncertainty results on standard deviations of about 0.57 log10 units, or 3.7-fold, in Dqi (Supplementary Table S2). The empirical uncertainty in Dqi is thus quite large, as expected, but is still insufficient to account for the full width of the experimental Dqi distributions of Figure 7A and B.
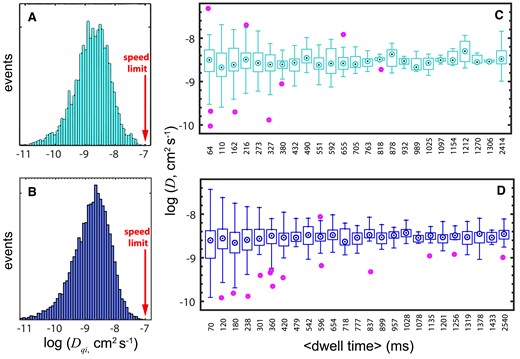
Heterogeneous DNA Scanning by EnHD. 1D diffusive properties of enHD wild type (cyan, panels A, C) and Q50K (blue, panels B, D) on the λ-DNA. The wild type data is at 25 mM salt and the Q50K data is at 50 mM salt. (A, B) Histograms of ‘quasi-instantaneous’ D (Dqi) obtained by binning all the 1D diffusive trajectories in 60 ms intervals. The sliding speed limit is shown with a red arrow. (B, D) Whisker plots showing the variation in trajectory-averaged D as a function of the trajectory duration. Whiskers show the end points, box edges the lower-upper quartiles, and dotted circles the bin medians. Purple circles are outliers.
In fact, the experimental data exhibit at least ±2.1-fold of additional diffusive heterogeneity that is likely inherent to the process. One logical source comes from the topography of the rugged binding landscape. The binding profile of the λ-DNA calculated with a rolling average of 320 bp (Figure 2, navy blue), which is comparable to a ±50 nm uncertainty in DNA position, indicates that the mean binding affinity between neighbouring 300 bp segments of the λ-DNA fluctuates by 0.27 log10 units or ±1.9 fold. These fluctuations in binding strength should affect enHD’s local diffusion coefficient by ±0.5 fold according to the slope from Figure 5B. Another potential source of heterogeneity in local diffusion is the hybrid scanning motion that we advanced in previous sections.
A puzzle is that, while extremely broad, the Dqi distributions are still distinctly unimodal, suggesting uniform scanning. We do note that a hybrid motion might still produce broad unimodal distributions if the slow and fast modes interconvert at a timescale comparable to the 60 ms used in determining Dqi,, which would result in partial dynamic averaging. We explored this scenario by performing stochastic kinetic simulations with an elementary model in which enHD interconverts between two scanning modes with vastly different D (see Supplementary Information). The stochastic simulations confirmed that a hybrid slow-fast scanning process results in unimodal D distributions (in log10 scale) when mode switching occurs in timescales comparable to, or slightly faster than the time interval for determining D (Supplementary Figure S5A). For instance, we found that the D distribution for trajectories that are slightly shorter than one switching cycle spans the full range defined by the characteristic diffusion coefficients of the slow and fast modes. The distribution narrows down appreciably for trajectories that contain two cycles, and progressively more for increasing numbers of cycles, reflecting more dynamic averaging (Supplementary Figure S5B).
The simulations also indicated that such behaviour should be evident in our experimental data. We thus classified all the experimental trajectories from each dataset into bins according to their dwell time and performed a simple statistical analysis for each bin. Figure 7C-D show box plots that summarize such analysis for the wild-type at 25 mM and Q50K at 50 mM, respectively. The plots demonstrate that the full spread in D, as indicated by the whisker ends, is inversely proportional to the dwell time. The spread is largest for the bin containing the shortest trajectories (∼70 ms), where it spans ∼2.5 orders of magnitude, and decreases progressively with fluctuations for longer trajectories. The median D per bin is essentially constant, e.g. (2 ± 0.36) × 10−9 cm2 s−1 for Q50K at 50 mM salt, indicating that the data contained within each bin provides reasonable sampling of the underlying distribution. Significantly, the experimental trends in Figure 7C and D are markedly consistent with the predictions from the stochastic kinetic simulations. Such close agreement provides further support to the hypothesis that enHD scans naked DNA using a hybrid motion that alternates between scanning modes with vastly different D. Furthermore, the experimental data recapitulates the decrease in log10(D) variance as a function of trajectory duration of the simulations (Supplementary Figure S5C).
Resolving the hybrid DNA scanning mechanism of EnHD
With the simulations as reference, the decay in experimental D variance with time would suggest that enHD switches between slow and fast modes roughly every 100 ms. Such a timescale should produce distinct, detectable, signatures in the experimental diffusive trajectories. One such signature would be gaps in fluorescence of about 1–2 pixels on the kymographs every time a jump to the fast mode occurs. Gaps in fluorescence like that are readily apparent in the experimental 1D diffusive trajectories of enHD (e.g. see Figure 3C). We further analysed these signatures by inspecting the trajectories expressed in terms of mean square displacement as a function of time. Supplementary Figure S6 shows eight such trajectories for the wild type at 25 mM NaCl as representative examples of the major patterns present in the dataset. The examples do reveal high heterogeneity in DNA scanning behaviour. Some of the trajectories are consistent with uniform scanning with D = 3 × 10−9 cm2 s−1 (cyan in Supplementary Figure S6A-B). Others display a much faster diffusivity composed of long slower segments alternating with short segments in which diffusion is drastically accelerated (teal in Supplementary Figure S6A, B). The data also contain trajectories with much slower than average diffusion (cyan in Supplementary Figure S6C, D) and others in which very slow diffusion segments alternate with long jumps (teal in Supplementary Figure S6C, D).
To further investigate these complex stochastic patterns, we analysed the data with a Hidden Markov Model (HMM) composed of three stochastically alternating diffusive modes: slow, medium, and fast (see Extended Methods in Sup. Inf.). The fundamental scheme of the three-mode HMM and the results obtained for enHD wild-type at 25 mM salt are summarized in Figure 8. The HMM results for all datasets are given in Supplementary Tables S2 and S3. In this analysis we fixed the diffusion coefficient of the slow mode to 6.25 × 10−10 cm2 s−1 to match the resolution limit set by our ±50 nm experimental position accuracy. This mode then aggregates all diffusive motions that are slower than the resolution limit. The HMM assumes that the slow and fast modes are only connected via the medium mode, which acts as gateway between them. In addition, we analysed the data with two-mode and single mode (uniform scanning) HMMs to ascertain whether there is indeed sufficient information in the data to extract the three modes. The likelihood ratios for 2-mode versus 1-mode and 3-mode versus 2-mode HMMs are also given in Figure 8 and Supplementary Tables S3 and S4. Overall, we observed a huge increase in likelihood between the 1-mode and the 2-mode HMM for both variants at all conditions. Therefore, the HMM analysis demonstrates that enHD uses a hybrid-mode mechanism to scan DNA. The likelihood increases of the 3-mode relative to the 2-mode HMM are comparatively much smaller (Supplementary Tables S2-S3), but robust in statistical terms with the 3-mode being better at >99% confidence for all cases. The implication is that there is enough information in the data to resolve the stochastic exchange between three diffusive modes. The only exception was the Q50K data at 100 mM salt for which the interconversions between the medium and slow modes become too fast relative to the 20 ms time steps, and hence are not well resolved. For this dataset we provide the results from the 2-mode (medium-fast) HMM in Supplementary Table S4.
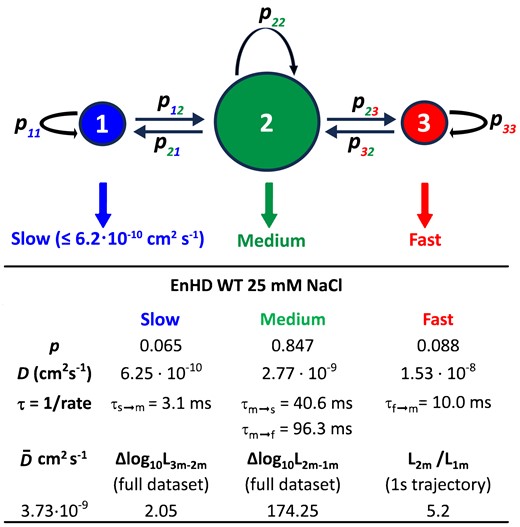
Hidden Markov modelling of 1D diffusion of EnHD. The fundamental structure of the 3-mode HMM model used to analyse the 1D diffusive trajectories of enHD variants is shown at the top. The diameter of the circles represents the approximate probabilities for the three modes. The slow mode has a fixed D = 6.25 × 10−10 cm2 s−1 corresponding to an experimental position accuracy of ±50 nm. The HMM parameters obtained by maximizing the likelihood of the wild type enHD at 25 mM salt are also shown as reference.
The HMM analysis provides a wealth of information about how enHD scans naked DNA. For instance, it reveals that, at 25 mM salt, the wild type spends about 85% of the time in the medium mode, alternating with slow and fast modes that are relatively rare, with populations of 6.5% and 8.8%, respectively (Figure 8). The medium mode recapitulates the overall |$\tilde D$|, and hence is comparable to the global diffusive behaviour. The fast mode represents a 5.5-fold accelerated diffusion and lasts for 10 ms on average, during which time enHD travels about ∼175 nm, or ∼530 bp, on the DNA. This fast mode occurs every 96 ms, resulting in (slow↔medium)-fast cycles of ∼106 ms. On the other hand, the (slow↔□medium) segments consist of quick exchanges in which enHD visits the slow mode 2.4 times on average, with each visit lasting just 3 ms (Figure 8). This short dwell time arises from an HMM transition probability of 0.93 that still permits to be well resolved. The total distance covered via the (slow↔medium) segment is about 222 nm, or 675 bp. Significantly, out of this distance, the slow mode accounts for less than 29 nm. Therefore, wild type enHD scans about 400–425 nm (1200–1290 bp) of DNA per full (slow↔medium)-fast cycle at 25 mM salt.
The Q50K mutant and the effect of salt concentration add further details. The Q50K mutant at 50 mM salt matches the overall scanning performance of the wild-type at 25 mM (Figure 5B, C). However, Q50K achieves that performance with a different balance of the hybrid mechanism. In this case the slow mode lasts longer and is visited more often from the medium mode (every 26 ms), which has a somewhat slower D (Supplementary Table S4). These changes result on slower overall diffusion during the (slow↔medium) segment of the cycle. But Q50K also stays longer on the fast mode, which lasts 21 ms and converts from the medium mode each 189 ms, giving twice longer full cycles. Q50K thus covers 243 nm, or 735 bp, of DNA in 21 ms in each fast mode excursion. This means that Q50K at 50 mM travels the same overall distance on the DNA per unit of time than the wild type at 25 mM, but a larger fraction of that distance is travelled using the fast mode.
In general, strengthening the electrostatic attraction to the DNA by lowering the ionic strength should increase the DNA recapture probability. We have seen that this effect results on a longer dwell time on the DNA, e.g. 3-fold longer for Q50K in going from 50 to 25 mM salt (Figure 5A). Significantly, the HMM analysis reveals that the 50 to 25 mM drop in salt stabilizes the interconversions between the slow and medium modes, both becoming 4-fold longer lived, and slows down the medium mode D by 25% (Supplementary Table S4). In contrast, the fast mode is essentially unaffected (Supplementary Table S4). In combination, these observations point to the slow mode being the truly DNA-bound motion, whereas the medium mode might be composed of DNA-bound and unbound motions that interconvert too quickly to be resolved with the current experimental resolution. In other words, the slow and fast modes probably are the fundamental motions of the hybrid DNA scanning mechanism of enHD, whereas the medium mode likely represents their mix. This idea is consistent with a D that recapitulates the global scanning behaviour in terms of the median |$\tilde D$| (Figure 4C) and has a 25% fractional dependence on ionic strength (Figure 5B). The effects of further increasing ionic strength are somewhat less obvious (Supplementary Tables S3 and S4). This is likely because at those conditions there are fewer and shorter trajectories and the mode interconversions are faster. Nevertheless, the results at higher ionic strengths are generally consistent with the trends outlined.
EnHD recognizes nucleosomal DNA with enhanced affinity
In the previous sections we demonstrated that enHD scans naked DNA fast and efficiently despite its promiscuous DNA recognition and lack of clamping interface. To consider enHD’s mechanism as a possible model for how pioneer transcription factors scan naked DNA, the question that remains is whether enHD can also recognize and bind to DNA wrapped in nucleosomes. Other homeodomains have been shown to bind to cognate DNA sites that are displayed around the nucleosome perimeter (37), but such ability has not been established for enHD yet. We thus investigated the targeting of DNA on nucleosomes by enHD using fluorescence correlation spectroscopy (FCS). We used for that purpose a 146 bp model DNA containing 14 TAATTA cognate sites per strand that we assembled onto single nucleosomes using an enzymatic method, which does not require nucleosome positioning sequence (see Materials and Methods). The nucleosome reaction was analysed using a DNA electrophoretic mobility shift assay, which indicated a nucleosome assembly efficiency of nearly 100%, as judged by the lack of naked 146 DNA after the reaction and the strong protein staining of a band migrating with a mobility equivalent to that of a 1 kbp naked DNA (Supplementary Figure S7).
We monitored binding of A488-labelled enHD to either the naked or nucleosome-wrapped DNA via the FCS autocorrelation function. In these experiments the degree of binding is determined from the slowdown in the average diffusion induced by the formation of the much larger, slower moving complex as the DNA concentration increases. The main results of these experiments are summarized in Figure 9, with the full datasets and global fits to a simple binding model given in Supplementary Figures S8-S9. We find that enHD binds to the naked DNA with high affinity, as expected given the 14 palindromic cognate sites that it bears (Figure 9A). The KD = 316 pM obtained from the global fit (Figure 9C) is about 13 times lower than previous FCS determinations for DNA that only carried one cognate site (38), indicating that the increment in target sites has a cumulative effect in overall binding. The experiments with the nucleosome-wrapped DNA reveal that enHD also binds to nucleosomes, and it does so with enhanced affinity (Figure 9B). The affinity enhancement for the nucleosomal DNA is considerable. The global fit produces a KD = 55 pM, which is nearly 6-fold lower than for the naked form (Figure 9C). Furthermore, this 6-fold affinity enhancement does not take into account the limitations in sequence accessibility imposed by the nucleosome. The wrapping around the histones should directly hide half of the possible binding sites because one of the palindromic orientations of each motif will inevitably face inwards. Besides, some of the sites pointing outwards might be only displayed partially, which should not impede binding of a promiscuous binder such as enHD but will impact the affinity. These structural considerations reduce the number of nucleosome accessible targets possibly by >3-fold, from which we estimate a 20-fold affinity enhancement for enHD’s binding to a cognate site displayed on the nucleosome versus being naked. This binding enhancement corresponds to a change in free energy of 3 RT, which could be employed by enHD for selective targeting of chromatin-packed regions, or to impinge mechanical effects on the DNA upon binding.
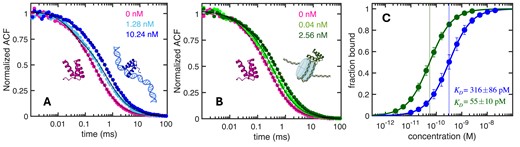
Binding of EnHD to Naked and Nucleosomal DNA by FCS. (A) Normalized FSC autocorrelation decays of enHD alone (pink) and in the presence of naked 146 bp DNA at two exemplary concentrations (shades of blue). (B) As A but for enHD in the presence of exemplary concentrations of nucleosome-wrapped 146 bp DNA (shades of green). The thin black curves show the results from the global fits to the data at all DNA concentrations (shown in Supplementary Figures S7 and S8). (C) Binding isotherms of enHD to nucleosome-wrapped (green) and naked (blue) 146 bp DNA calculated from the global fits. The error bars on the data and the uncertainty of the KD values are given at a 95% confidence.
Discussion
Physical determinants for DNA scanning without clamping
Here, we show that enHD carries out 1D diffusion on DNA that is extensive and fast relative to its theoretical speed limit (Figure 4), and on par with oligomeric multidomain TFs such as p53 (63). A key difference is that, whereas previously studied DBPs use interfaces that provide clamping by either fully or partially engulfing the DNA, enHD uses an open interaction interface that engages the DNA laterally (Figure 1A). With such an interface enHD can only maintain its association with the DNA by directly interacting with it. Our results on enHD thus demonstrate that DNA clamping is not a necessary requirement for achieving extensive and fast DNA scanning. The unexpected 1D diffusive properties of enHD shed new light on the structural and energetic factors of facilitated diffusion by DBPs in general, and especially by those that also use an open binding interface. The structure of enHD in complex with DNA points to the electrostatic attraction as the one factor that can hold them together during 1D diffusion. EnHD’s electrostatic potential is indeed strongly positive due to an accumulation of positive charge on the face that interacts with DNA (Figure 1A). This positive charge is known to be highly destabilizing of the enHD native structure (64). Recent work has shown that such charge distribution makes for an electrostatic spring-loaded latch mechanism that enHD uses for the conformational control of cognate DNA recognition (65). From a DNA scanning viewpoint, a strong electrostatic attraction could enable 1D diffusion by acting at long distances. The distance range for electrostatic interactions in aqueous solution is determined by the Debye length, which is estimated to be about 1 nm (9). The question is whether such conditions could be sufficient to maintain a loose but continuous electrostatic association between TF and DNA over long 1D diffusive trajectories.
In general, our experimental results provide strong support for electrostatics being responsible for the extensive 1D diffusion on DNA of enHD. We find that moderate increases in electrostatic screening by ionic strength reduce the dwell time on DNA drastically. For example, raising the salt concentration from 25 to 100 mM decreases the dwell time of Q50K by 20-fold (3 natural log units, Supplementary Figure S4). Ionic strength thus affects the dwell time on DNA in the same proportion than it does its thermodynamic binding affinity (Figure 5A). The implication is that the time that enHD spends diffusing on DNA is controlled by the same interactions that determine its DNA binding affinity. The Q50K mutant's behaviour provides further evidence. Q50K has one extra positive charge located right at the interface with DNA and which enhances its overall affinity for DNA (58). At the same ionic strength, Q50K dwells on the DNA longer than the wild type in the exact same proportion than its binding affinity increases (Figure 5A, Supplementary Figure S4). Taken together, these results confirm that what makes enHD hold onto DNA during 1D diffusion is the effective range of the attractive electrostatic potential between them.
Hybrid DNA scanning for navigating rugged landscapes
The mechanism of facilitated diffusion typically assumes a binary interplay between cognate binding, used for recognition, and weaker non-specific binding for DNA scanning (11). These elements make for a search landscape that is one-dimensionally flat and smooth, with a single minimum at the target site. The promiscuous recognition of enHD drastically changes the scenario by making the DNA binding landscapes highly rugged (e.g. Figure 2). Such landscapes should make the sliding motion sluggish. Yet, our results show that enHD diffuses along DNA extensively and with |$\tilde D$| that is close to the fastest previously characterized DBPs and only ∼30-fold below its theoretical speed limit (Figure 4C). We estimate that enHD’s 1D diffusion on DNA is about 200000 times faster than expected from a continuous canonical sliding motion on the highly promiscuous binding landscape presented by the λ-DNA. Therefore, DNA scanning by enHD appears impervious to the ruggedness of the binding landscape, resulting in what appears as supercharged 1D diffusion. At the core of such scanning behaviour there is a hybrid 1D diffusive motion composed of stochastic alternants among slow, medium, and fast modes. The stochastic mode-switching of enHD occurs in timescales comparable to the 20 ms time-resolution of our experiments, resulting in long jumps that are clearly apparent in the diffusive trajectories of enHD (Supplementary Figure S6). We find that the fast mode is relatively rare, with populations generally below 10%. The fast mode is also short-lived, converting from the medium mode every 100 ms and lasting for about 10 ms for wild type enHD (Figure 8). The fast mode allows enHD to quickly deploy to a new DNA location that is about 175 nm away for the wild type. The diffusive trajectories also contain transient segments during which enHD diffuses at rates below our experimental resolution limit. This slow mode is also minimally populated and interconverts with the medium mode at even faster rates (Supplementary Tables S3-S4). Importantly, the DNA sequence scanned via the slow mode is less than 75 bp, or 25 nm, per cycle. In contrast, the medium mode accounts for 80% of the scanning time and its diffusion coefficient is like the global |$\tilde D$|. Practically, this means that wild type enHD scans DNA in sweeps of 660–720 bp at medium-low speed followed by fast deployments to neighbouring regions about 530 bp away, where it starts the next sequence sweep. Interestingly, this scanning mechanism mimics the search strategy of a stochastic gradient descent algorithm (66); where the slow-medium mode segments act as local gradient descent optimization steps, and the fast mode enhances stochastic sampling by enabling the escape and deployment to another nearby region. The stochastic mode-switching of enHD thus emerges as an elegant solution to solving the speed vs. stability paradox (8,14,67,68) for cases in which the DNA binding landscapes are energetically rugged due to promiscuous recognition, like it possibly occurs for a majority of eukaryotic TFs.
A closer look at the slow-medium diffusion: sliding, hopping and gliding?
Each slow-medium scanning segment involves a few brief transitions to the slow mode, which is when the deeper sequence sweeps are most likely performed. Unfortunately, we do not have the experimental resolution to directly determine the slow mode's diffusion coefficient. But we can conclude that it differs drastically from the canonical lock into target of DBPs endowed with highly specific recognition, such as the Lac repressor which takes minutes to dissociate from one operator site (69). In contrast, enHD visits the slow mode every 40 ms, regardless of its location on the DNA, and dwells only 3–8 ms on it. This scanning pattern is in fact consistent with the uniformly rugged binding landscape of the λ-DNA (Figure 2), as opposed to a flat landscape with a single high-affinity target. We thus argue that enHD does not stall in the slow mode but actively scans the DNA. In this regard, for the wild type at 25 mM salt, we found that the highest HMM likelihood is obtained when the D for the slow mode is set to 8.1 × 10−10 cm2 s−1, or 30% higher than our resolution limit. The likelihood increases by two-fold for the entire dataset, and hence it might not be statistically significant given that an additional parameter is used. Nevertheless, taking this result by face value provides an estimate for the actual slow-mode diffusion coefficient of 1.9 × 10−10 cm2 s−1 once we correct for the contribution from position accuracy to the experimental |$\tilde D$|. This value provides an upper bound of 17.5 nm, or 53 bp, for the DNA sequence scanned by enHD via the slow mode per cycle.
The medium mode is at least 10-fold faster. The medium mode D is in fact just halfway between those of the slow and fast modes (Figure 8, Supplementary Tables S3 and S4). This result together with other evidence, including the fractional dependence of D with binding free energy (Figure 5B), suggests that the medium mode might itself be a hybrid motion. For instance, it could be composed of the same slow and fast modes but alternating at higher frequency. In that regard, we note that a switching rate that is just 3-fold faster than the slow to medium transitions we detected with the HMM would already appear as uniform diffusion with the current resolution. The data for Q50K at the highest salt exemplifies this phenomenon since the slow mode becomes too short-lived to be effectively separated it from the medium mode at these conditions (Supplementary Table S4). These observations suggest that the slow-medium mode segments represent a mix of short sliding runs connected by local hops and/or glides. Hopping implies the brief detachment from the DNA to hop and land in a nearby location (10,11). Gliding consists of series of ‘kiss and ride’ local contacts with the phosphate backbone by which the protein moves along the DNA length fast with no rotation (70). Both microscopic motions have proven very difficult to resolve in single molecule tracking experiments, likely due to limitations in the resolution of current imaging methods. However, there is mounting evidence that the apparently continuous 1D diffusion of other DBPs is likely a mix of sliding, hopping, and possibly gliding motions. For instance, bulk kinetic DNA translocation experiments on DNA repair proteins indicated that continuous sliding covers less than 10 bp (71). A recent high-resolution single-molecule study identified that Lac repressor performs a full DNA rotation every ∼40 bp during scanning, alternating between hops and sliding runs of ∼20 bp every 0.5 ms (72). In this regard, we note that the extrapolation of enHD’s stepping rate (or D) to ‘zero binding’ is significantly faster than the speed limit for pure rotational sliding (Figure 5C). Propagation errors notwithstanding, this extrapolation is consistent with enHD covering about 4 DNA helical turns, or 44 bp, per full rotation. Hence, the slow-medium diffusive segments of enHD appear to be composed of a similar combination of sliding, hopping, and gliding motions.
The fast-scanning mode: 3D diffusion or long jumping?
The fast mode we find in enHD deserves further attention. A direct interpretation is that it represents a complete detachment from the DNA followed by a brief 3D diffusion-collision search for a new location. However, the distances that enHD travels along the DNA via the fast mode appear too long and transient to occur via random 3D diffusion. For instance, our results indicate that enHD travels in the fast mode an average of ∼175 nm in 10 ms (Figure 8). A freely diffusing enHD molecule with D ∼10−6cm2⋅s−1 would only need about 40 μs to diffuse 175 nm away from its starting position. But in the absence of directional bias, such distance would be travelled in any 3D direction, which highly reduces the probability for landing on a ∼300 bp DNA target (±50 nm as per our position accuracy) located about 175 nm on either side of the take off point. We can estimate this probability from the ratio between twice the cylindrical capture volume of a 300 bp section of DNA and the volume of a sphere with 175 nm radius. Even assuming a generous 3 nm radius for the capture cross-section of DNA (i.e. 2 nm beyond the DNA perimeter) we still obtain a very small landing probability of ∼10−4, which translates onto 400 ms of search time. Therefore, our experimental results strongly suggest that enHD does not perform unbiased 3D diffusion during the fast mode but remains spatially correlated with the DNA moving along its length. In other words, the fast mode is more like long jumps that occur in between (slow-medium) scanning segments following a stochastic series that continues until the protein eventually escapes to bulk, thus ending the 1D diffusion trajectory. To sustain a contactless correlated motion over 175 nm displacements on the DNA, the electrostatic field induced by the DNA must be strong and far reaching, consistently with previous arguments by others (71).
Functional implications for the control of gene expression programs in eukaryotes
Our results on enHD provide useful insights about the molecular mechanisms that control transcription in eukaryotes. In general, the DNA scanning requirements of eukaryotic TFs are far more demanding than the search for one target site in one operon. Eukaryotic TFs often act on multiple, even hundreds, of genes that can be distributed among multiple chromosome territories. This is particularly true for master regulators or pioneer TFs, which control global gene expression programs. Individual eukaryotic genes can also depend on multiple regulatory elements, some of which are nearby, acting in cis (73), while others operate in trans as enhancers (42). It appears evident that simultaneous operation in a multitude of chromosome territories may require a specialized mechanism for tracking target genes and regulatory elements. One recently proposed tracking mechanism combines the discovery of promiscuous DNA recognition with the repetitive clusters of imperfect cognate motifs that are found in eukaryotic regulatory regions (38). In this mechanism, the clusters of imperfect motifs operate as a transcription antenna that draws molecules of a promiscuous TF by engaging them in myriads of local, mid-affinity binding events. Our binding studies to a 146 naked DNA carrying 14 enHD-cognate sites shows that the presentation of multiple target sites to enHD results in stronger binding and cumulative occupancy, thereby practically demonstrating the attractor effect proposed for transcription antennas.
On the other hand, once a TF is circumscribed to a given genomic location by the transcription antenna effect, it must still scan large segments of DNA to perform its function. This regional scanning process requires dealing with DNA that is dynamically unpacked (active) and packed (silenced), as well as with recruiting cofactors, chromatin remodellers and additional copies of the same TF to the region of interest. One issue here is that the same rugged DNA binding landscapes that serve as attractors for promiscuous TFs could seriously impair their ability to scan through the DNA region of interest. Our 1D diffusion experiments on enHD demonstrate that a promiscuous TF that binds DNA with an open interface, and hence without clamping assistance, can effectively scan naked DNA that presents a binding landscape as rugged as those of active regulatory regions. We find that such scanning is fast and extensive, with enHD moving about 200000-fold faster than it would using a continuous promiscuous sliding motion. The key behind this ability is a hybrid mechanism that alternates stochastically between slow-medium paced local sequence sweeps and quick redeployments to alternative regions for further scanning. Interestingly, this hybrid mechanism is consistent and can further explain the highly dynamic chromatin scanning patterns in living cells that have been reported for other TFs with pioneer functions (74,75).
We also find that enHD effectively targets nucleosomes containing clusters of cognate motifs. Importantly, enHD’s binding to nucleosomes occurs with much enhanced affinity relative to the same DNA sequence in naked form, revealing that enHD preferentially targets packed DNA. EnHD’s functional behaviour is thus different from that reported for the yeast TFs Reb1 and Cbf1, which bind nucleosomes and naked DNA with equal affinity (76). Furthermore, our experiments indicate that several enHD molecules bind simultaneously to one nucleosome (e.g. a minimum of two molecules per nucleosome at the KD of 55 pM). This observation is consistent with enHD binding the nucleosome around its perimeter, as previously found for other homeodomains (37). Based on these properties we infer that a cluster of partial cognate motifs mounted on a nucleosome can work as a superstrong attractor, making enHD molecules to stay there long enough to facilitate the recruitment of partners and/or promote swarming of more enHD molecules to act collectively on DNA packing. The preferential targeting of nucleosomes by enHD suggests that its binding stabilizes the DNA in the packed configuration, which would accordingly help silencing it. Based on our data, a local swarm of N enHD molecules bound to one nucleosome should stabilize it versus the naked form by 3×N RT, or 22.5 kJ/mol for just three copies of enHD simultaneously bound to one nucleosome. This stabilization effect amounts to about half of the 4 pN required to mechanically unwrap the first 20 nm of DNA from one nucleosome (77). We also note that, in the biological context of dynamically remodeled chromatin, the long jumps via the fast mode that enHD undertakes in naked DNA could provide a well-suited escape mechanism for leaping from one motif clustered region to the next one within a regulatory locus of interest in either active or silent forms. Such an escape mechanism can be particularly useful to navigate the regulatory regions of higher-order organisms, which contain large clusters of cognate motifs organized as islands within archipelagos (78).
Finally, given the paradigmatic DNA binding and functional properties of Engrailed, it is not unreasonable to expect that the DNA scanning mechanism we hereby outline for enHD might be used by other eukaryotic factors that function as pioneer TFs.
Data availability
The data underlying this article will be shared on reasonable request to the corresponding author.
Supplementary data
Supplementary Data are available at NAR Online.
Acknowledgements
We thank Suhani Nagpal for technical assistance in processing the kymograph data to be prepared for further analysis.
Author contributions: Rama Reddy Goluguri: Methodology, Investigation, Formal Analysis, Writing—original draft. Catherine Ghosh: Methodology, Investigation, Formal Analysis. Joshua Quintong: Methodology, Investigation. Mourad Sadqi: Methodology, Investigation. Victor Muñoz: Conceptualization, Methodology, Formal Analysis, Supervision, Writing—review & editing.
Funding
National Institutes of Health [R01-GM152623 to V.M.]; National Science Foundation [MCB-2112710 to V.M., HRD-2112675 to V.M., MCB-1616759 to V.M., HRD-1547848 to V.M.]; W.M. Keck Foundation Biomedical Research Program. Funding for open access charge: NIH [R01-GM152623].
Conflict of interest statement. None declared.
Notes
Present address: Rama Reddy Goluguri, Department of Biochemistry, Stanford University, Palo Alto, CA 94305, USA.




Comments