-
PDF
- Split View
-
Views
-
Cite
Cite
Rebecca Briffa, Celia Escamilla-Rivera, Jackson Levi Said, Jurgen Mifsud, Growth of structures using redshift space distortion in f(T) cosmology, Monthly Notices of the Royal Astronomical Society, Volume 528, Issue 2, February 2024, Pages 2711–2727, https://doi.org/10.1093/mnras/stae103
Close - Share Icon Share
ABSTRACT
Cosmology faces a pressing challenge with the Hubble constant (H0) tension, where the locally measured rate of the Universe’s expansion does not align with predictions from the cosmic microwave background calibrated with lambda-cold dark matter model. Simultaneously, there is a growing tension involving the weighted amplitude of matter fluctuations, known as S8,0 tension. Resolving both tensions within one framework would boost confidence in any one particular model. In this work, we analyse constraints in f(T) gravity, a framework that shows promise in shedding light on cosmic evolution. We thoroughly examine prominent f(T) gravity models using a combination of data sources, including pantheon+ (SN), cosmic chronometers, baryonic acoustic oscillations, and redshift space distortion data. We use these models to derive a spectrum of H0 and S8,0 values, aiming to gauge their ability to provide insights into, and potentially address, the challenges posed by the H0 and S8,0 tensions.
1 INTRODUCTION
Measurements of the accelerating expansion of the Universe (Riess et al. 1998; Perlmutter et al. 1999) have led to the prospect that it may be expanding faster than predicted by the lambda-cold dark matter (ΛCDM) model (Di Valentino et al. 2021a). This may open the possibility that the concordance model description of gravitation through general relativity (GR), the as yet unobserved CDM (Gaitskell 2004; Bertone, Hooper & Silk 2005; Baudis 2016), and the theoretically problematic cosmological constant (Peebles & Ratra 2003; Copeland, Sami & Tsujikawa 2006) may require additions or corrections to its explanation of some kind. Over the last few years this has been expressed primarily through the value of the Hubble constant (Di Valentino et al. 2021c) and fσ8,0 (Di Valentino et al. 2021b). The appearance of cosmic tensions has shaped into a tension between observations based on direct measurements of the late Universe such as those based on Type Ia supernovae (SNIa), the tip of the red giant branch measurements, strong lensing measurements (Freedman et al. 2020; Wong et al. 2020; Riess et al. 2022; Anderson, Koblischke & Eyer 2023), and indirect measurements coming from analyses of early time data from the cosmic microwave background (CMB) radiation as well as big bang nucleosynthesis (BBN) data (Cooke, Pettini & Steidel 2018; Alam et al. 2021; Abbott et al. 2022; Zhang et al. 2022) and others (Benisty, Davis & Evans 2023). Furthermore, recent data forecasting from new missions that include structure formation have increased this tension at local level (Atek et al. 2022; Lu et al. 2022), however, considering new systematic techniques on the measurements these tensions can be treated (Maldonado Alonso, Escamilla-Rivera & Sandoval-Orozco 2023). The growth in both these tensions has led to a reinvigorated exploration of possible modifications of the concordance model that have been developed in the literature over the last few decades.
The literature features a myriad of novel approaches in which to confront the growing issue of cosmic tensions. There have been proposals involving a re-evaluation of the cosmological principle (Krishnan et al. 2021, 2022), possible impacts of early Universe dark energy (Poulin, Smith & Karwal 2023), the appearance of extra degrees of freedom in the form of additional neutrino species in the early Universe (Di Valentino & Melchiorri 2022; Di Valentino et al. 2022), as well as modifications to gravity (Barack et al. 2019; Alves Batista et al. 2021; Saridakis et al. 2021; Abdalla et al. 2022) and others (Addazi et al. 2022). Many of these approaches modify a small part of the evolution of the Universe using new physics. On the other hand, modified gravity has the potential to make smaller changes that infiltrate the larger range of redshifts. Moreover, modifications to GR will also provide changes both at background and perturbative levels. In the space of possible modifications to GR, one approach that has become popular in recent years and which natively builds a competitive way in which to consider new physics is metric-affine gravity which is based on the exchange of the underlying connection with other possible geometries (Hehl et al. 1995; Beltrán Jiménez, Heisenberg & Koivisto 2019). In teleparallel gravity (TG), the geometric curvature of the Levi–Civita connection |$\overset{\circ }{{\Gamma }}^{\sigma }{}_{\mu \nu }$| (overcircles denote quantities based on the curvature of the Levi–Civita connection in this work) is interchanged with the torsion of the teleparallel connection Γσμν. This may provide a more intuitive approach in which to consider new physics in gravitational theory.
The connection of TG is curvature-free (Cai et al. 2016; Krssak et al. 2019; Bahamonde et al. 2021) and produces an altogether novel formulation of gravity. There exists a particular combination of scalars in the theory that can produce a teleparallel equivalent of general relativity (TEGR), which is dynamically equivalent to GR but may have different IR completions (Mylova, Said & Saridakis 2023). A natural consequence of this is that both GR and TEGR are identical at the level of phenomenological predictions. Taking the same rationale as in |$f(\overset{\circ }{{R}})$| gravity (De Felice & Tsujikawa 2010; Sotiriou & Faraoni 2010; Capozziello & De Laurentis 2011), TEGR can be generalized to an f(T) general class of models (Ferraro & Fiorini 2007, 2008; Bengochea & Ferraro 2009; Linder 2010; Chen et al. 2011; Farrugia & Levi Said 2016; Finch & Said 2018; Paliathanasis, Levi Said & Barrow 2018; Bahamonde, Flathmann & Pfeifer 2019; Bahamonde, Levi Said & Zubair 2020; Farrugia, Levi Said & Finch 2020; Bahamonde et al. 2022) where the TEGR Lagrangian is simple the torsion scalar T. This is an interesting model since it produces organically second-order equations of motion and agrees with the polarization modes of GR despite being fundamentally different.
f(T) cosmology has been probed in various scenarios. At background level, f(T) models have probed against several different types of data showing consistent results with the relatively high value of the Hubble constant (Briffa et al. 2022). Most recently this has been in work that incorporates the latest pantheon+ data set (Briffa et al. 2020; Cai, Khurshudyan & Saridakis 2020; Ren et al. 2022; Briffa et al. 2023). There has also been working that probes the early Universe using either BBN (Benetti, Capozziello & Lambiase 2020), or constraints from the CMB (Nunes 2018; Nunes, Pan & Saridakis 2018; Kumar, Nunes & Yadav 2023) with interesting results related to the best-fit values of the model parameters compared with both early and late time constraints. Also, constraints from primordial black holes seem to be consistent with a wide range of observations (Papanikolaou et al. 2023) giving more freedom to the possible cosmological models. From foundational physics recent work has also been done on non-flat cosmologies (Bahamonde et al. 2023) which may open a way to compare recent proposals in the literature (Di Valentino, Melchiorri & Silk 2019) on the topic in ΛCDM cosmology. Other works in the literature have explored possible effects on the fine structure constant (Levi Said et al. 2020) which are consistent with there being no variation.
In the current work, we are interested in determining constraints on models of f(T) cosmology using fσ8(z) data. This window into the large-scale structure of the Universe will be a key tool in understanding the viability of new proposals for cosmology. The topic has been explored for previous data sets in Nesseris et al. (2013) where it was shown that f(T) cosmological models are largely consistent with this probe of large-scale structure. Later in Anagnostopoulos, Basilakos & Saridakis (2019), these analyses were combined with background data sets which gave stricter constraints on model parameters. Recently, the fσ8(z) data have also been used to check for consistency with background data in the context of model-independent approaches to reconstructing modified cosmological models (Levi Said et al. 2021). We start by briefly introducing the background of TG and its predictions for fσ8 in Section 2. We then discuss our observational data sets under consideration in Section 3. This is then followed by a presentation of our model constraints in Section 4, and a comparative analysis in Section 5. The results are summarized and discussed in our conclusion in Section 6.
2 f(T) GRAVITY AND SCALAR PERTURBATIONS
TG is based on the exchange of curvature with torsion through the geometric connection, which is realized through the teleparallel connection |$\Gamma ^{\sigma }_{\mu \nu }$|. This renders all measures of curvature identically zero, since |${\overset{\circ }{{\Gamma}^{\sigma }}}_{\mu \nu }$| is curvature-less and satisfies metricity. While the regular Levi–Civita objects remain non-vanishing, such as the regular Riemann tensor |${\overset{\circ }{{R}^{\sigma }}}_{\mu \nu \rho} \ne 0$|, its torsional analogue will vanish |${R}^{\sigma }_{\mu \nu \rho} = 0$|. This means that a different class of torsional objects must be utilized to express the geometric deformation that embodies gravitation effects from the energy-momentum tensor (see reviews in Aldrovandi & Pereira 2013; Cai et al. 2016; Krssak et al. 2019; Bahamonde et al. 2021).
Another important aspect of TG is that it can be expressed in terms of a tetrad field that embodies the gravitational effect of the metric tensor through
where |${E}_{A}^{\mu }$| is the tetrad inverse, and where Latin indices represent local inertial coordinates, while Greek ones denote general space–time coordinates. For internal consistency, these tetrads must also satisfy orthogonality conditions
The tetrad encompasses the gravitational freedom of the metric, while the Lorentz invariance freedom can be assigned to the spin connection |${\omega }^{a}_{b\mu }$|. The teleparallel connection can then be defined as Cai et al. (2016) and Krssak et al. (2019)
Given a metric, the infinite possible tetrad solutions in equation (1) are balanced by the spin connection components to retain general diffeomorphism invariance of the underlying theory. Together, the tetrad–spin connection pair defines a space–time.
The tensor structure of TG can be written in terms of the torsion tensor which is defined as
where square brackets denote an antisymmetric operator which represents the translation field strength of TG (Aldrovandi & Pereira 2013). Taking a suitable choice of contractions of the torsion tensor, we can write the torsion scalar as Hayashi & Shirafuji (1979) and Bahamonde, Böhmer & Krššák (2017)
which is dependent only on the teleparallel connection in an analogous way to the dependence of the Riemann tensor on the Levi–Civita connection.
Naturally, the teleparallel Ricci scalar will vanish, namely R = 0, while the teleparallel-based Ricci scalar turns out to be equal to the torsion scalar (up to a total divergence term), that is
where |$B = (2/e)\partial _\mu (eT^\mu)$| is a boundary term and |$e=\det \left({e}^{a}_{\mu }\right)=\sqrt{-g}$| is the tetrad determinant. This relation ensures that the equations of motion of the Einstein–Hilbert action will be the same as those from the so-called TEGR which is based on the linear form of the torsion scalar. TEGR is dynamically equivalent to GR, but may differ in its UV completion. The TEGR Lagrangian can readily be generalized using the same reasoning as |$f(\overset{\circ }{{R}})$| gravity (De Felice & Tsujikawa 2010; Capozziello & De Laurentis 2011), except that we now consider an arbitrary function of the torsion scalar through (Ferraro & Fiorini 2007, 2008; Bengochea & Ferraro 2009; Linder 2010; Chen et al. 2011; Capozziello, De Falco & Ferrara 2022; Calzá & Sebastiani 2023)
where κ2 = 8πG, |$\mathcal {L}_{\text{m}}$| is the matter Lagrangian, and |$e=\det \left({e}^{a}_{\mu }\right)=\sqrt{-g}$| is the tetrad determinant.
The most impactful practical difference between |$f(\overset{\circ }{{R}})$| and |$\mathcal {F}(T)$| gravity theories is that the boundary term is no longer a total divergence term for |$f(\overset{\circ }{{R}})$| gravity and so leads to fourth order equations of motion, while |$\mathcal {F}(T)$| gravity retains generally second-order equations of motion. This may be advantageous both for numerical reasons as well as theoretical motivations when considering certain types of ghosts in the theory. By taking a variation with respect to the tetrad field, the field equations follow
where subscripts denote derivatives (|$\mathcal {F}_T=\partial \mathcal {F}/\partial T$| and |$\mathcal {F}_{TT}=\partial ^2 \mathcal {F}/\partial T^2$|), and |${\Theta }_{\rho }^{\nu } = \delta \mathcal {L}_{\text{m}}/ \delta {e}^{a}_{\mu }$| is the regular energy-momentum tensor. This limits to TEGR as |$\mathcal {F}(T) \rightarrow 0$|. TG contains two dynamical variables, namely, the tetrad and spin connection which both have associated variations of the |$\mathcal {F}(T)$| action. It turns out that they can both be expressed in terms of the above tetrad variation as
where the tetrad and spin connection field equations are, respectively, the symmetric and antisymmetric operators acted upon Wμν (Bahamonde et al. 2021). Indeed, a particular choice of tetrad components exists in which the spin connection components vanish, called the Weitzenböck gauge. Here, the spin connection equations on motion are identically satisfied. More generally, the six spin connection field equations express the Lorentz invariance freedom (three translations and three rotations), while the 10 tetrad field equations manifest the gravitational equations of motion.
We can now consider a flat homogeneous and isotropic cosmology through the regular flat Friedmann–Lemaître–Robertson–Walker (FLRW) metric
from which we can identify the Hubble parameter as |$H=\dot{a}/a$|, and where overdots refer to derivatives with respect to cosmic time. It can be shown that the tetrad (Tamanini & Boehmer 2012; Krššák & Saridakis 2016)
is compatible with the Weitzenböck gauge and so the spin connection components can be set to zero (Hohmann et al. 2019). By considering the tetrad field equations (9), the modified Friedmann equations can be written as
where ρ and p denote the energy density and pressure of the matter components, respectively.
TG can be used to interpret large-scale structure data by considering scalar perturbations of the flat FLRW metric. We probe this data through the growth rate measurements of |$f\sigma _8^{}(z)$| from RSD. This is expressed by the logarithm derivative of the matter perturbation δ(z) with respect to the logarithm of the cosmic scale factor, namely
where a prime denotes a derivative with respect to redshift z = a−1 − 1. On the other hand, the linear theory root-mean-square mass fluctuation within a sphere of radius 8 h−1 Mpc can be expressed as
where a 0 – subscript denotes the respective value at z = 0. Thus, the growth rate can be generally written as
which directly leads to the normalized form of δ′(z) through
By integrating this expression, the normalized redshift evolution of the matter perturbation can be written as
while equation (17) also gives the second-order derivative
The result is the redshift evolution of f can now be determined
In the subhorizon limit, the linear matter perturbations equation can then be written as
where Geff is the effective Newton’s constant which is in general a function of z and cosmic wave vector k (Amendola & Tsujikawa 2010; Hernández 2017). However for this limit and the data sets under consideration, the Geff can be taken to be independent of k. In this setting, equation (22) takes the form
where |$\Omega _{m,0}^{}$| denotes the current matter fractional density, |$H_0^{}$| is Hubble’s constant, and |$G_N^{}$| is Newton’s gravitational constant. We can also express this relation in terms of the growth rate f, giving
In the case of |$\mathcal {F}(T)$| gravity, the linear matter perturbation evolution equation (18) is expressed through Golovnev & Koivisto (2018), Nunes (2018), Levi Said et al. (2020), and Sahlu et al. (2020)
Hence, the linear matter perturbation equation is sensitive to |$\mathcal {F}(T)$| gravity and so large-scale structure data sets can be used to probe observational constraints on potential models.
In order to utilize equations like equations (22) and (23), we need to determine the value of H′(z), obtained from the second Friedmann equation (13), via
3 OBSERVATIONAL DATA
In this section, we will provide an overview of how we utilized observational data in our research to evaluate the most favourable f(T) models from the literature. We include a variety of observational data, such as the pantheon+ sample of SNIa data, baryon acoustic oscillations (BAO) data, cosmic chronometers (CC) data, and growth rate (redshift space distortion, RSD) data. To analyse the data, we implemented an MCMC (Monte Carlo Markov Chain) approach using the emcee package publicly available at Foreman-Mackey et al. (2013). This enabled us to constrain the model and cosmological parameters and thus, investigate the posterior of the parameter space. This yielded one-dimensional distributions that illustrate the parameter’s posterior distribution, and two-dimensional distributions that demonstrate the covariance between two different parameters. These distributions were complemented by the 1σ and 2σ confidence levels as will be shown in Section 4.
3.1 Cosmic chronometers
CC offer a useful tool to directly constrain the Hubble rate H(z) at different redshifts. To this end, we adopt 31 data points as compiled from Jimenez et al. (2003), Simon, Verde & Jimenez (2005), Stern et al. (2010), Moresco et al. (2012, 2016), Zhang et al. (2014), and Moresco (2015). The CC method involves using spectroscopic dating techniques on passively evolving galaxies to estimate the age difference between two galaxies at different redshifts. By measuring this age difference, Δz/Δt can be inferred from observations, allowing for the computation of H(z) = −(1 + z)−1Δz/Δt. Thus, CC data were found to be particularly reliable because they are independent of any cosmological model, avoid any complex integration, and rely on the absolute age determination of galaxies (Jimenez & Loeb 2002).
In our MCMC analysis, we used |$\chi ^2_\mathrm{CC}$| to evaluate the agreement between the theoretical Hubble parameter values H(zi, Θ), with model parameters Θ, and the observational Hubble data values Hobs(zi), with an observational error of σH(zi). The |$\chi ^2_\mathrm{CC}$| was calculated using
3.2 Type Ia supernovae–pantheon+ data set
The SNIa data set used in this study is the pantheon+ (PN+ & SH0ES) sample (Scolnic et al. 2022), which is one of the largest compilations of SNIa data and contains 1701 SNIa measurements spanning a redshift range of 0.0–2.26. The pantheon+ analysis (Brout et al. 2022), incorporates SH0ES Cepheid host distance anchors, Riess et al. (2019) in the likelihood, effectively addressing the degeneracy between parameters M and H0 in SNIa analysis. Following this approach, we also adopt the label ‘PN+ & SH0ES’ to signify our incorporation of the same methodology.
SNIa can be used to determine the expansion rate of the Universe, H(z), by measuring the observed apparent magnitude, m, and the absolute magnitude, M, through the equation:
where Θ represents the set of cosmological parameters that describe the Universe, zi is the redshift of the SNIa measurement, and DL(zi, Θ) is the luminosity distance given by
where c is the speed of light. To calibrate the observed apparent magnitude of each SNIa, a fiducial absolute magnitude M is used, as shown in equation (27). In our MCMC analyses, we treat M as a nuisance parameter.
To constrain the cosmological parameters, the minimum χ2 is calculated through Conley et al. (2011),
where (Δμ(zi), Θ)) = (μ(zi), Θ) − μ(zi)obs and CSN is the corresponding covariance matrix which accounts for the statistical and systematic uncertainties.
3.3 Baryon acoustic oscillations
In this study, we use a variety of observational missions to constrain cosmological parameters. These data sets include measurements from the 6dF Galaxy Survey at an effective redshift of zeff = 0.106 (Beutler et al. 2011), the Baryon Oscillation Spectroscopic Survey (BOSS) Data Release 11 (DR11) quasar Lyman-alpha measurements at an effective redshift of zeff = 2.4 (du Mas des Bourboux et al. 2017), and the Sloan Digital Sky Survey (SDSS) Main Galaxy sample at an effective redshift of zeff = 0.15 (Ross et al. 2015). Additionally, measurements of the Hubble parameter and the corresponding comoving angular diameter at zeff = 0.38, 0.51 were obtained from the third generation of the SDSS mission (SDSS BOSS DR12, Alam et al. 2021). We also include H(z) measurements and angular diameter distances at zeff = 0.98, 1.23, 1.52, and 1.94 from the fourth generation of the SDSS mission (SDSS-IV BOSS DR12, Zhao et al. 2019).
As has been mentioned these different data sets report different observational quantities that are related to one another. For the BAO data sets under consideration, we compute the Hubble distance DH(z) given by |$D_H(z) = \frac{c}{H(z)}$|. We also consider the angular diameter distance DA(z) defined as
from which two other quantities can be derived. The first is the comoving angular diameter distance DM given trough DM = (1 + z)DA(z) whilst the second one is the volume average distance given by
Using the BAO results, we calculate the corresponding combination of results |$\mathcal {G}(z_i)=D_V(z_i)/r_s(z_d),\, r_s(z_d)/D_V(z_i),\, D_H(z_i),\, D_M(z_i)(r_{s,\mathrm{fid}}(z_d)/r_s(z_d)),\\\, H(z_i)(r_s(z_d)/r_{s,\mathrm{fid}}(z_d)),\, D_A(z_i)(r_{s,\mathrm{fid}}(z_d)/r_s(z_d))$|. In this case, we require the comoving sound horizon at the end of the baryon drag epoch at zd ∼ 1059.94 (Aghanim et al. 2020) which can be calculated using
where we have adopted a fiducial value of rs, fid(zd) = 147.78 Mpc (Aghanim et al. 2020) with an assumption of Ωb, 0 = 0.02242 (Aghanim et al. 2020) and T0 = 2.7255 K (Fixsen 2009) Therefore, the corresponding χ2 is calculated through
where ΔG(zi, Θ) = G(zi, Θ) − Gobs(zi)and CBAO is the corresponding covariance matrix for the BAO observations. The total |$\chi ^2_{\mathrm{BAO}}$| is therefore the sum of all the individual χ2 corresponding to each data set.
3.4 Growth rate data (RSD)
The final data compilation we used in this work is the growth rate data compilation presented in table II of appendix A in Alestas, Kazantzidis & Nesseris 2022). This data set consists of measurements of the growth of cosmic structure and is commonly referred to as RSD data, due to a phenomenon that occurs during observations at both large and small scales. The peculiar velocity of galaxies causes high-density regions of the Universe to appear elongated in the line-of-sight direction at small scales and flattened at large scales. As a result, maps of galaxies where distances are measured from spectroscopic redshifts exhibit anisotropic deviations from the true galaxy distribution. Therefore, RSD measurements can provide valuable insights into the large-scale structure of the Universe, which is shaped by the underlying theory of gravity governing the evolution and formation of cosmic structure. Consequently, RSD presents a promising approach to testing modified theories of gravity.
The growth rate f(z), can be estimated using RSD cosmological probes as a way to constrain cosmological models (Gupta, Sen & Sen 2012; Gonzalez, Alcaniz & Carvalho 2016; Lambiase et al. 2019). However, instead of reporting the growth rate directly, Large Scale Structure (LSS) surveys typically report the density-weighted growth rate, fσ8 ≡ f(z)σ8(z) which is bias-independent (Kazantzidis & Perivolaropoulos 2018). Furthermore, we should acknowledge the Alcock–Paczynski effect, which emerges from the requirement of assuming a cosmological model for the conversion of redshifts into distances. However, recent studies, including those outlined in Levi Said et al. (2021), have indicated that the influence of this effect is minimal and thus has been disregarded in our analysis.
Therefore, while the theoretical prediction can be made from equation (16), the aforementioned RSD data can be used to constrain cosmological parameters, in particular σ8,0 such the corresponding |$\chi ^2_{\mathrm{min}}$| can be given as
where Q(zi, Θ) = (fσ8(zi, Θ)theo − fσ8obs(zi)) and |$C_{\text{RSD}}^{-1}$| is the inverse covariance matrix which is assumed to be a diagonal matrix except for the WiggleZ subset data which can be found in Blake et al. (2012). Therefore, the total covariance matrix can be written as
To compute Q(zi, Θ), we start by obtaining the theoretical values of fσ8(zi, Θ)theo using equation (22) along with equation (16). On the other hand, fσ8(zi, Θ)obs is extracted from the compiled observational data as described earlier.
4 RESULTS
In this section, we delve into the outcomes yielded by various combinations of data sets. Each subsection is dedicated to distinct f(T) models, selected based on their potential to accurately reflect our cosmological history, as demonstrated in previous studies (Nunes et al. 2016; Briffa et al. 2022, 2023; dos Santos, Gonzalez & Silva 2022; Sandoval-Orozco et al. 2023). For every model, we showcase the 1σ and 2σ uncertainty ranges. These results are accompanied by a table showing the final results that include the Hubble constant (H0) expressed in kms−1Mpc−1, the matter density parameter Ωm,0 and σ8,0 along with other model parameters. This will give us an insight into how the different models and data set combinations affect the H0 tension and S8,0 cosmological tensions.
4.1 Power-law model
The power-law model, initially proposed by Bengochea and Ferraro in their work (Bengochea & Ferraro 2009), was adopted due to its capability to replicate the observed late-universe acceleration without the need for dark energy. Henceforth, this model will be referred to as f1CDM and is specified by
This power-law form is characterized by two constants, namely α1 and p1 which is introduced as a modification to |$\mathcal {F}(T)$| function. Being a constant α1 can be evaluated at any time and therefore, it can be calculated at the current time by using the Friedmann equation (12), which results in
where the density parameter for matter and radiation is represented by Ωm,0 and Ωr,0 respectively. Consequently, by utilizing equation (37), the f1CDM model introduces only one new parameter, namely p1, thereby enhancing its elegance and simplicity. In combination with the parameters H0, Ωm,0, and σ8,0, we determine the model parameter p1 through MCMC analyses performed on observational data.
By substituting the above equation into the Friedmann equation (12), we derive the resulting Friedmann equation for this model
where |$E(z):= \frac{H(z)}{H_0}$|. It is worth noting that this equation cannot be solved analytically, so we employ numerical methods to calculate E(z) at each redshift point. Consequently, using MCMC analysis, we solve for each redshift point where observational data exists to obtain parameter values. Specifically, we extract values for H0, Ωm,0, and p1. Additionally, when RSD data are included, we can obtain values for σ8,0 allowing us to assess the model’s compatibility with observational data and refine our understanding of the Universe’s properties. When examining equation (36), it becomes apparent that the ΛCDM limit can be attained when p1 = 0. On the other hand, when p1 = 1, the model converges to the GR limit. In this scenario, an additional component in the Friedmann equation emerges, introducing a re-scaled gravitational constant term within the density parameters.
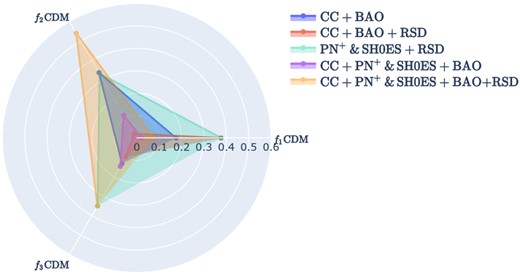
The contour plots together with their posteriors for the f1CDM model are shown in Fig. 1. In this and subsequent models, the blue and green contours represent the CC+BAO and CC+PN+ +BAO data sets, respectively. The remaining colours correspond to various data sets that incorporate the RSD data. On the other hand, the precise values for the parameters are tabulated in Table 1. Notably, this table highlights that the highest H0 value is obtained when combining the PN+ & SH0ES data with the RSD data is used. This result aligns with expectations, as the PN+& SH0ES data converges with values reported by the SH0ES team, which reports a value of |$H_0 = 73.30 \pm 1.04 {\rm \, km \, s}^{-1} {\rm Mpc}^{-1}$| (Scolnic et al. 2022). Conversely, the lowest value for the H0 parameter is derived from the CC+BAO data sets, primarily influenced by the BAO data, which relates to conditions in the early Universe.
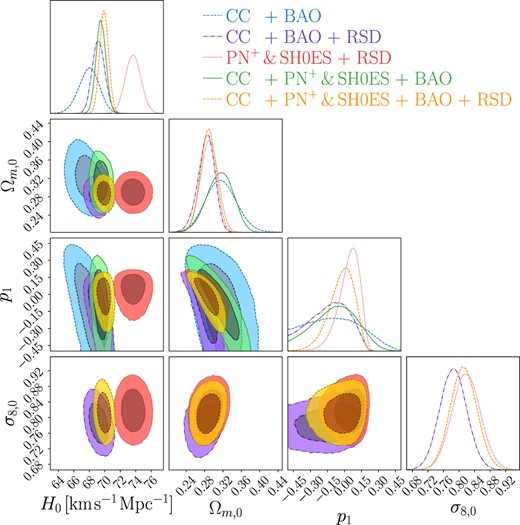
Confidence contours and posterior distributions for the f1CDM model (power-law model) parameters, including H0, Ωm,0, and p1. In cases where the RSD data are incorporated (purple, red, and yellow contours), the σ8,0 parameter is also displayed.
Exact results for f1 model that include the parameters H0, Ωm,0, and p1. The σ8,0 parameter and the nuisance parameter M, are provided for data sets that include RSD or PN+ & SH0ES, respectively otherwise, they are left empty.
| Data sets . | |$H_0 \mathrm{[km s^{-1} Mpc ^{-1}]}$| . | Ωm,0 . | p1 . | σ8,0 . | M . |
|---|---|---|---|---|---|
| CC + BAO | |$68.1^{+1.2}_{-1.4}$| | |$0.314^{+0.034}_{-0.033}$| | |$-0.09^{+0.24}_{-0.30}$| | – | – |
| CC + BAO + RSD | 69.17 ± 0.81 | |$0.287^{+0.016}_{-0.020}$| | |$-0.09^{+0.17}_{-0.20}$| | 0.785 ± 0.035 | – |
| PN+ & SH0ES + RSD | 73.7 ± 1.0 | |$0.290^{+0.019}_{-0.018}$| | |$0.076^{+0.075}_{-0.102}$| | |$0.817^{+0.037}_{-0.035}$| | |$-19.252^{+0.029}_{-0.030}$| |
| CC + PN+ & SH0ES + BAO | |$69.45^{+0.69}_{-0.58}$| | |$0.316^{+0.028}_{-0.029}$| | |$-0.06^{+0.19}_{-0.22}$| | – | −19.375 ± 0.017 |
| CC + PN+ & SH0ES + BAO + RSD | 69.90 ± 0.58 | |$0.289^{+0.016}_{-0.018}$| | |$0.014^{+0.091}_{-0.125}$| | |$0.810^{+0.036}_{-0.033}$| | |$-19.367^{+0.016}_{-0.017}$| |
| Data sets . | |$H_0 \mathrm{[km s^{-1} Mpc ^{-1}]}$| . | Ωm,0 . | p1 . | σ8,0 . | M . |
|---|---|---|---|---|---|
| CC + BAO | |$68.1^{+1.2}_{-1.4}$| | |$0.314^{+0.034}_{-0.033}$| | |$-0.09^{+0.24}_{-0.30}$| | – | – |
| CC + BAO + RSD | 69.17 ± 0.81 | |$0.287^{+0.016}_{-0.020}$| | |$-0.09^{+0.17}_{-0.20}$| | 0.785 ± 0.035 | – |
| PN+ & SH0ES + RSD | 73.7 ± 1.0 | |$0.290^{+0.019}_{-0.018}$| | |$0.076^{+0.075}_{-0.102}$| | |$0.817^{+0.037}_{-0.035}$| | |$-19.252^{+0.029}_{-0.030}$| |
| CC + PN+ & SH0ES + BAO | |$69.45^{+0.69}_{-0.58}$| | |$0.316^{+0.028}_{-0.029}$| | |$-0.06^{+0.19}_{-0.22}$| | – | −19.375 ± 0.017 |
| CC + PN+ & SH0ES + BAO + RSD | 69.90 ± 0.58 | |$0.289^{+0.016}_{-0.018}$| | |$0.014^{+0.091}_{-0.125}$| | |$0.810^{+0.036}_{-0.033}$| | |$-19.367^{+0.016}_{-0.017}$| |
Exact results for f1 model that include the parameters H0, Ωm,0, and p1. The σ8,0 parameter and the nuisance parameter M, are provided for data sets that include RSD or PN+ & SH0ES, respectively otherwise, they are left empty.
| Data sets . | |$H_0 \mathrm{[km s^{-1} Mpc ^{-1}]}$| . | Ωm,0 . | p1 . | σ8,0 . | M . |
|---|---|---|---|---|---|
| CC + BAO | |$68.1^{+1.2}_{-1.4}$| | |$0.314^{+0.034}_{-0.033}$| | |$-0.09^{+0.24}_{-0.30}$| | – | – |
| CC + BAO + RSD | 69.17 ± 0.81 | |$0.287^{+0.016}_{-0.020}$| | |$-0.09^{+0.17}_{-0.20}$| | 0.785 ± 0.035 | – |
| PN+ & SH0ES + RSD | 73.7 ± 1.0 | |$0.290^{+0.019}_{-0.018}$| | |$0.076^{+0.075}_{-0.102}$| | |$0.817^{+0.037}_{-0.035}$| | |$-19.252^{+0.029}_{-0.030}$| |
| CC + PN+ & SH0ES + BAO | |$69.45^{+0.69}_{-0.58}$| | |$0.316^{+0.028}_{-0.029}$| | |$-0.06^{+0.19}_{-0.22}$| | – | −19.375 ± 0.017 |
| CC + PN+ & SH0ES + BAO + RSD | 69.90 ± 0.58 | |$0.289^{+0.016}_{-0.018}$| | |$0.014^{+0.091}_{-0.125}$| | |$0.810^{+0.036}_{-0.033}$| | |$-19.367^{+0.016}_{-0.017}$| |
| Data sets . | |$H_0 \mathrm{[km s^{-1} Mpc ^{-1}]}$| . | Ωm,0 . | p1 . | σ8,0 . | M . |
|---|---|---|---|---|---|
| CC + BAO | |$68.1^{+1.2}_{-1.4}$| | |$0.314^{+0.034}_{-0.033}$| | |$-0.09^{+0.24}_{-0.30}$| | – | – |
| CC + BAO + RSD | 69.17 ± 0.81 | |$0.287^{+0.016}_{-0.020}$| | |$-0.09^{+0.17}_{-0.20}$| | 0.785 ± 0.035 | – |
| PN+ & SH0ES + RSD | 73.7 ± 1.0 | |$0.290^{+0.019}_{-0.018}$| | |$0.076^{+0.075}_{-0.102}$| | |$0.817^{+0.037}_{-0.035}$| | |$-19.252^{+0.029}_{-0.030}$| |
| CC + PN+ & SH0ES + BAO | |$69.45^{+0.69}_{-0.58}$| | |$0.316^{+0.028}_{-0.029}$| | |$-0.06^{+0.19}_{-0.22}$| | – | −19.375 ± 0.017 |
| CC + PN+ & SH0ES + BAO + RSD | 69.90 ± 0.58 | |$0.289^{+0.016}_{-0.018}$| | |$0.014^{+0.091}_{-0.125}$| | |$0.810^{+0.036}_{-0.033}$| | |$-19.367^{+0.016}_{-0.017}$| |
It is noteworthy to notice the relationship between the Hubble parameter (H0) and the matter density parameter (Ωm,0). As H0 increases, indicating a faster expansion rate of the Universe, the matter density decreases. This effect is particularly pronounced in the PN+ & SH0ES+RSD combination, where the Universe’s energy predominantly manifests as an effective form of dark energy, driven by the elevated H0 parameter. The presence of this phenomenon is further confirmed by the apparent anticorrelation depicted in Fig. 1.
As noted, the ΛCDM limit is reached for when p1 = 0. Indeed, the resultant values for p1 are in proximity of 0, and this limit falls within the 1σ range. Furthermore, it can be observed that the inclusion of the RSD data leads to tighter constraints on the p1 parameter. However, this effect is not exclusive to the p1 parameter alone; it also extends to other parameters, as evident from the contour plots in Fig. 1.
Incorporating the RSD data has been instrumental in constraining the amplitude of mass fluctuations, σ8,0. Upon initial examination of Table 1, it appears that there is a correlation between the H0 parameter and σ8,0, where a higher H0 tends to correspond to a slightly higher σ8,0. However, the contour plots suggest a more complex and degenerate relationship between these parameters. It is worth noting that the RSD data appears to have more Gaussian errors when compared to the other data sets. The influence of these growth structure data is encapsulated by the parameter Geff, which, in this model, is expressed as
where the specific values for the parameters are extracted from the relevant table, and as a result, we observe that Geff approximates GN under these conditions.
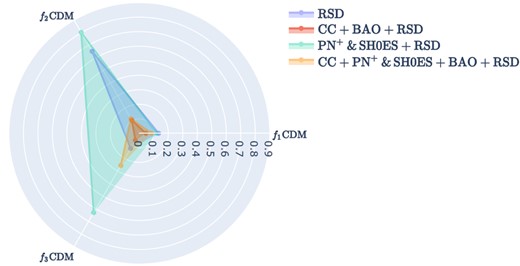
Additionally, the constraint on these parameters has enabled us to explore a tension quantified in terms of |$S_{8,0} \equiv \sigma _{8,0}\sqrt{\Omega _{m,0}/0.3}$| (Anchordoqui et al. 2021; Beltrán Jiménez et al. 2021; Benisty 2021; Brieden, Gil-Marín & Verde2023; Clark et al. 2023; Preston, Amon & Efstathiou 2023; Rubira, Mazoun & Garny 2023). The results and the posteriors of these parameters can be found in Table 2 and Fig. 2, respectively. Reflecting the values obtained for σ8,0, the highest value observed for S8,0 was attained for the PN+ & SH0ES+RSD combination, measuring at |$S_{8,0} = 0.801^{+0.052}_{-0.046}$|. However, it is worth noting that we also provide values for the RSD data set alone to isolate the impact of RSD data on this parameter, where in this case, the value for the RSD data set reaches a minimum. Furthermore, it is evident that across all data sets, the constraints for such parameters are notably tight. We also examine the relationship between the S8,0 parameter and the model parameter p1, which is depicted in Fig. A1 found in Appendix A. A significant anticorrelation exists between these two parameters. In return, this might suggest that changes in the power-law exponent (p1) might have a direct impact on the amplitude of mass fluctuations (S8,0).
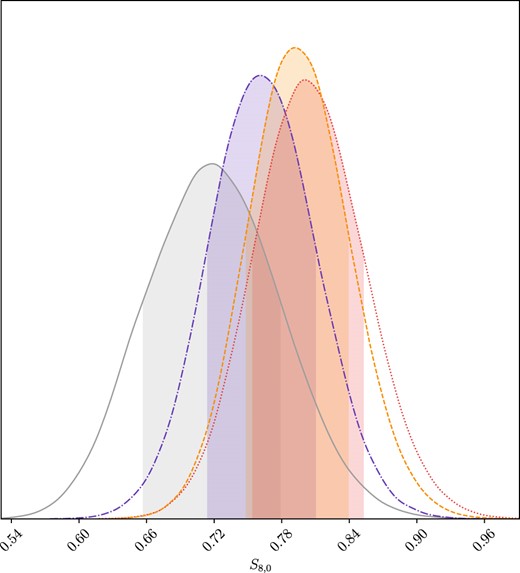
Posterior distribution for the S8,0 parameter in the f1CDM model. Legend: grey denotes the RSD data, purple corresponds to CC+BAO+RSD data, red represents the PN+ & SH0ES + RSD data set, while orange indicates CC + PN+ & SH0ES + BAO + RSD data.
| Data sets . | S8,0 . |
|---|---|
 | |
| Data sets . | S8,0 . |
|---|---|
 | |
| Data sets . | S8,0 . |
|---|---|
 | |
| Data sets . | S8,0 . |
|---|---|
 | |
4.2 Linder model
The second model under consideration is the Linder (2009) model, explicitly developed to explain the Universe’s late-time acceleration without invoking the presence of dark energy. This model introduces an exponential component that incorporates the torsion scalar, denoted as T, and is expressed as follows
where both α2 and p2 are constants, while |$T_0 = T|_{t=t_0}= -6H_0^2$| represents the torsion scalar at the current epoch. Similar to the previous model, if α2 is a constant, it can be immediately determined from the Friedman equation at the present time, yielding
Therefore, in the Linder model, hereafter referred to as f2CDM, the only new model parameter is denoted as p2, and it will be constrained through the MCMC analysis. Consequently, equation (41) allows us to express the Friedmann equation in terms of H0, Ωm,0, and p2, resulting in the following form
Contrary to the f1CDM model, this model can be reduced to the ΛCDM when p2 → ∞. However, for numerical stability, the analysis is conducted with the reciprocal of p2, in such a way that the limit effectively becomes 1/p2 → 0+.
The posterior distributions and confidence levels of the constrained parameters are depicted in Fig. 3. Similar to the f1CDM model, the highest value for the H0 parameter is obtained when combining PN+ +RSD data as indicated by the precise values in Table 3. However, in this case, the lowest H0 value, specifically |$H_0=66.5^{+2.2}_{-1.3} {\rm \, km \, s}^{-1} {\rm Mpc}^{-1}$|, is obtained for the CC+BAO+RSD combination. Overall, in this scenario, the parameter values trend slightly lower compared to the f1CDM model.
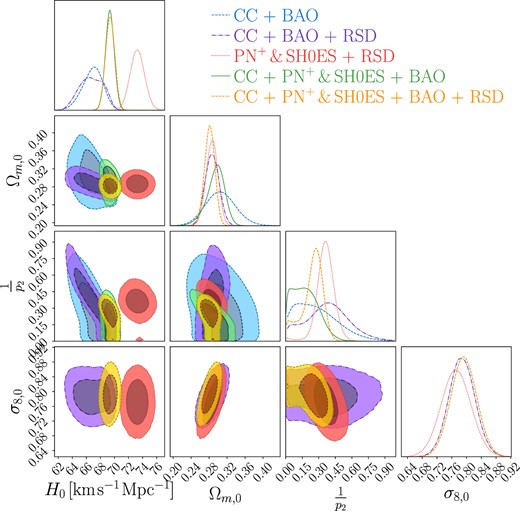
Confidence contours and posterior distributions for the f2CDM model (Linder model) parameters, including H0, Ωm,0, and |$\frac{1}{p_2}$|. In cases where the RSD data are incorporated (purple, red, and yellow contours), the σ8,0 parameter is also displayed.
Exact results for f2 model that include the parameters H0, Ωm,0, and |$\frac{1}{p_2}$|. The σ8,0 parameter and the nuisance parameter M, are provided for data sets that include RSD or PN+ & SH0ES, respectively otherwise, they are left empty.
| Data Sets . | |$H_0 \mathrm{[km s^{-1} Mpc ^{-1}]}$| . | Ωm,0 . | |$\frac{1}{p_2}$| . | σ8,0 . | M . |
|---|---|---|---|---|---|
| CC + BAO | |$67.2^{+1.2}_{-1.6}$| | |$0.302^{+0.035}_{-0.030}$| | |$0.00^{+0.37}_{-0.00}$| | – | – |
| CC + BAO + RSD | |$66.5^{+2.2}_{-1.3}$| | |$0.286^{+0.016}_{-0.015}$| | |$0.39^{+0.21}_{-0.22}$| | |$0.784^{+0.038}_{-0.032}$| | – |
| PN+ & SH0ES + RSD | 73.2 ± 1.0 | 0.287 ± 0.013 | |$0.359^{+0.077}_{-0.071}$| | |$0.770^{+0.042}_{-0.039}$| | |$-19.26^{+0.33}_{-0.31}$| |
| CC + PN+ & SH0ES + BAO | |$69.35^{+0.61}_{-0.63}$| | |$0.299^{+0.017}_{-0.021}$| | |$0.167^{+0.080}_{-0.154}$| | – | |$-19.40^{+0.21}_{-0.16}$| |
| CC + PN+ & SH0ES + BAO + RSD | |$69.38^{+0.67}_{-0.68}$| | 0.282 ± 0.011 | |$0.275^{+0.083}_{-0.096}$| | 0.793 ± 0.035 | |$-19.37^{+0.31}_{-0.30}$| |
| Data Sets . | |$H_0 \mathrm{[km s^{-1} Mpc ^{-1}]}$| . | Ωm,0 . | |$\frac{1}{p_2}$| . | σ8,0 . | M . |
|---|---|---|---|---|---|
| CC + BAO | |$67.2^{+1.2}_{-1.6}$| | |$0.302^{+0.035}_{-0.030}$| | |$0.00^{+0.37}_{-0.00}$| | – | – |
| CC + BAO + RSD | |$66.5^{+2.2}_{-1.3}$| | |$0.286^{+0.016}_{-0.015}$| | |$0.39^{+0.21}_{-0.22}$| | |$0.784^{+0.038}_{-0.032}$| | – |
| PN+ & SH0ES + RSD | 73.2 ± 1.0 | 0.287 ± 0.013 | |$0.359^{+0.077}_{-0.071}$| | |$0.770^{+0.042}_{-0.039}$| | |$-19.26^{+0.33}_{-0.31}$| |
| CC + PN+ & SH0ES + BAO | |$69.35^{+0.61}_{-0.63}$| | |$0.299^{+0.017}_{-0.021}$| | |$0.167^{+0.080}_{-0.154}$| | – | |$-19.40^{+0.21}_{-0.16}$| |
| CC + PN+ & SH0ES + BAO + RSD | |$69.38^{+0.67}_{-0.68}$| | 0.282 ± 0.011 | |$0.275^{+0.083}_{-0.096}$| | 0.793 ± 0.035 | |$-19.37^{+0.31}_{-0.30}$| |
Exact results for f2 model that include the parameters H0, Ωm,0, and |$\frac{1}{p_2}$|. The σ8,0 parameter and the nuisance parameter M, are provided for data sets that include RSD or PN+ & SH0ES, respectively otherwise, they are left empty.
| Data Sets . | |$H_0 \mathrm{[km s^{-1} Mpc ^{-1}]}$| . | Ωm,0 . | |$\frac{1}{p_2}$| . | σ8,0 . | M . |
|---|---|---|---|---|---|
| CC + BAO | |$67.2^{+1.2}_{-1.6}$| | |$0.302^{+0.035}_{-0.030}$| | |$0.00^{+0.37}_{-0.00}$| | – | – |
| CC + BAO + RSD | |$66.5^{+2.2}_{-1.3}$| | |$0.286^{+0.016}_{-0.015}$| | |$0.39^{+0.21}_{-0.22}$| | |$0.784^{+0.038}_{-0.032}$| | – |
| PN+ & SH0ES + RSD | 73.2 ± 1.0 | 0.287 ± 0.013 | |$0.359^{+0.077}_{-0.071}$| | |$0.770^{+0.042}_{-0.039}$| | |$-19.26^{+0.33}_{-0.31}$| |
| CC + PN+ & SH0ES + BAO | |$69.35^{+0.61}_{-0.63}$| | |$0.299^{+0.017}_{-0.021}$| | |$0.167^{+0.080}_{-0.154}$| | – | |$-19.40^{+0.21}_{-0.16}$| |
| CC + PN+ & SH0ES + BAO + RSD | |$69.38^{+0.67}_{-0.68}$| | 0.282 ± 0.011 | |$0.275^{+0.083}_{-0.096}$| | 0.793 ± 0.035 | |$-19.37^{+0.31}_{-0.30}$| |
| Data Sets . | |$H_0 \mathrm{[km s^{-1} Mpc ^{-1}]}$| . | Ωm,0 . | |$\frac{1}{p_2}$| . | σ8,0 . | M . |
|---|---|---|---|---|---|
| CC + BAO | |$67.2^{+1.2}_{-1.6}$| | |$0.302^{+0.035}_{-0.030}$| | |$0.00^{+0.37}_{-0.00}$| | – | – |
| CC + BAO + RSD | |$66.5^{+2.2}_{-1.3}$| | |$0.286^{+0.016}_{-0.015}$| | |$0.39^{+0.21}_{-0.22}$| | |$0.784^{+0.038}_{-0.032}$| | – |
| PN+ & SH0ES + RSD | 73.2 ± 1.0 | 0.287 ± 0.013 | |$0.359^{+0.077}_{-0.071}$| | |$0.770^{+0.042}_{-0.039}$| | |$-19.26^{+0.33}_{-0.31}$| |
| CC + PN+ & SH0ES + BAO | |$69.35^{+0.61}_{-0.63}$| | |$0.299^{+0.017}_{-0.021}$| | |$0.167^{+0.080}_{-0.154}$| | – | |$-19.40^{+0.21}_{-0.16}$| |
| CC + PN+ & SH0ES + BAO + RSD | |$69.38^{+0.67}_{-0.68}$| | 0.282 ± 0.011 | |$0.275^{+0.083}_{-0.096}$| | 0.793 ± 0.035 | |$-19.37^{+0.31}_{-0.30}$| |
Regarding the Ωm,0 parameter, we observe a similar trend to that of the H0 parameter, with lower values being reported. However, the consistent pattern persists, where data sets that include RSD values yield lower values for Ωm,0 compared to their counterparts that do not incorporate RSD data. The anticorrelation between the H0 parameter and the Ωm,0 parameter is still visible. However, in comparison to the f1CDM model, the anticorrelation between Ωm,0 and the model parameter is not as pronounced, resulting in a higher degree of degeneracy between these two parameters.
The 1/p2 parameter values obtained are slightly higher than those in the f1CDM model. Additionally, in contrast to the previous model, the ΛCDM limit does not fall within the 1σ region of the ΛCDM, indicating a slight deviation from the ΛCDM model.
Furthermore, the parameter σ8,0 continues to exhibit the same trend observed previously, with lower values consistently reported. Notably, we observe a correlation between this parameter and Ωm,0 across all data sets. However, the degeneracy between σ8,0 and H0 remains valid in this model. Similar trend to previous model is also seen with regards Geff, where Geff ≈ GN where
In the cases where RSD is included, we once again calculate the quantity S8,0, and we obtain slightly different results compared to the previous model as shown in Table 4 and Fig. 4. Similar results are obtained for the CC+BAO+RSD data sets, but we observe a lower value for the PN+ & SH0ES+RSD combination. Conversely, we obtain higher values for the RSD data set on its own and for CC + PN+ & SH0ES + BAO + RSD, with the maximum value being achieved for the former data set, whereas previously it had exhibited the minimum value. Lastly, we again check the correlation between the parameters p and S8,0 where the degeneracy in the RSD data persists, however, when the PN+ & SH0ES data are combined with the RSD data, we now notice an anticorrelation that was not previously evident. A visual representation of these findings can be found in Appendix A, specifically in Fig. A1.
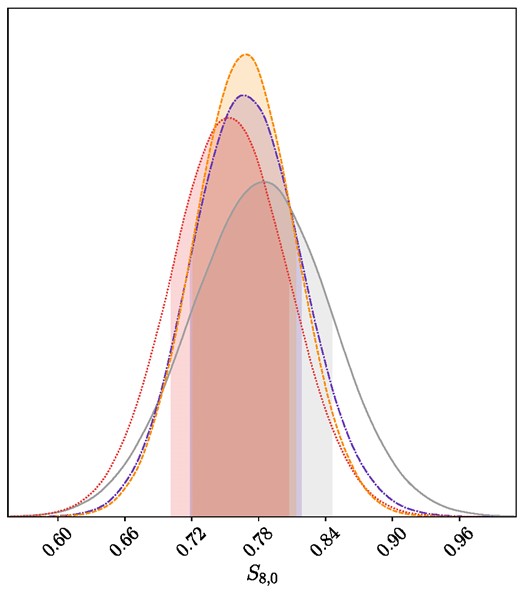
Posterior distribution for the S8,0 parameter in the f2CDM model. Legend: grey denotes the RSD data, purple corresponds to CC+BAO+RSD data, red represents the PN+ & SH0ES + RSD data set, while orange indicates CC + PN+ & SH0ES + BAO + RSD data.
| Data sets . | S8,0 . |
|---|---|
 | |
| Data sets . | S8,0 . |
|---|---|
 | |
| Data sets . | S8,0 . |
|---|---|
 | |
| Data sets . | S8,0 . |
|---|---|
 | |
4.3 Exponential model
The next model under consideration in this analysis is the exponential model, hereafter f3CDM, which draws inspiration from previous works on |$f(\overset{\circ }{{R}})$| (Linder 2009). In fact, a variant of the Linder model is proposed in Nesseris et al. (2013), where the square root in the exponential form is no longer present. In this case, |$\mathcal {F}_3$| is expressed as an exponential function with two model constants, α3 and p3, along with the current torsion scalar T0 and the variable T, such that
By evaluating the Friedmann equation at the present time, we can determine the value of the constant α3, which is calculated as
Therefore, by substituting equation (45) into the modified Friedmann equation (12), we can derive the Friedmann equation for this model, which can be solved numerically
This model exhibits behaviour similar to the Linder model, where the ΛCDM limit is approached as p3 → ∞. Therefore, as previously discussed, we perform the analyses using 1/p3 to ensure numerical stability, as this approach aligns with the previous model. In this case the Geff is defined as
where this model exhibits a similar trend to the previous ones.
The confidence levels and the posteriors are found in Fig. 5, whilst the constrained values are found in Table 5. Removing the square root component has notably influenced the constraints, particularly on σ8,0. The σ8,0 values are considerably higher in this model compared to those reported in f2CDM.
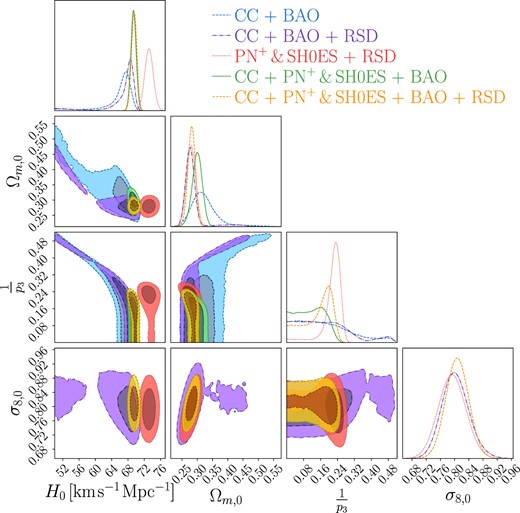
Confidence contours and posterior distributions for the f3CDM model (exponential model) parameters, including H0, Ωm,0, and |$\frac{1}{p_3}$|. In cases where the RSD data are incorporated (purple, red, and yellow contours), the σ8,0 parameter is also displayed.
Exact results for f3 model that include the parameters H0, Ωm,0, and |$\frac{1}{p_3}$|. The σ8,0 parameter and the nuisance parameter M, are provided for data sets that include RSD or PN+ & SH0ES, respectively otherwise, they are left empty.
| Data Sets . | |$H_0 \mathrm{[km s^{-1} Mpc ^{-1}]}$| . | Ωm,0 . | |$\frac{1}{p_3}$| . | σ8,0 . | M . |
|---|---|---|---|---|---|
| CC + BAO | |$67.5^{+1.7}_{-2.3}$| | |$0.311^{+0.039}_{-0.034}$| | |$0.058^{+0.182}_{-0.056}$| | – | – |
| CC + BAO + RSD | |$68.6^{+1.3}_{-1.9}$| | |$0.276^{+0.016}_{-0.015}$| | |$0.026^{+0.214}_{-0.025}$| | |$0.798^{+0.040}_{-0.036}$| | – |
| |$\mathrm{PN}^+\, \&\,$|SH0ES + RSD | |$73.2^{+1.0}_{-1.1}$| | |$0.280^{+0.014}_{-0.015}$| | |$0.232^{+0.027}_{-0.031}$| | |$0.793^{+0.038}_{-0.039}$| | −19.25 ± 0.11 |
| CC + |$\mathrm{PN}^+\, \&\,$|SH0ES + BAO | |$69.34^{+0.65}_{-0.64}$| | |$0.300^{+0.017}_{-0.016}$| | |$0.160^{+0.029}_{-0.126}$| | – | |$-19.34^{+0.24}_{-0.31}$| |
| CC + |$\mathrm{PN}^+\, \&\,$|SH0ES + BAO + RSD | |$69.54^{+0.64}_{-0.66}$| | 0.282 ± 0.012 | |$0.197^{+0.038}_{-0.092}$| | 0.807 ± 0.032 | |$-19.38^{+0.20}_{-0.19}$| |
| Data Sets . | |$H_0 \mathrm{[km s^{-1} Mpc ^{-1}]}$| . | Ωm,0 . | |$\frac{1}{p_3}$| . | σ8,0 . | M . |
|---|---|---|---|---|---|
| CC + BAO | |$67.5^{+1.7}_{-2.3}$| | |$0.311^{+0.039}_{-0.034}$| | |$0.058^{+0.182}_{-0.056}$| | – | – |
| CC + BAO + RSD | |$68.6^{+1.3}_{-1.9}$| | |$0.276^{+0.016}_{-0.015}$| | |$0.026^{+0.214}_{-0.025}$| | |$0.798^{+0.040}_{-0.036}$| | – |
| |$\mathrm{PN}^+\, \&\,$|SH0ES + RSD | |$73.2^{+1.0}_{-1.1}$| | |$0.280^{+0.014}_{-0.015}$| | |$0.232^{+0.027}_{-0.031}$| | |$0.793^{+0.038}_{-0.039}$| | −19.25 ± 0.11 |
| CC + |$\mathrm{PN}^+\, \&\,$|SH0ES + BAO | |$69.34^{+0.65}_{-0.64}$| | |$0.300^{+0.017}_{-0.016}$| | |$0.160^{+0.029}_{-0.126}$| | – | |$-19.34^{+0.24}_{-0.31}$| |
| CC + |$\mathrm{PN}^+\, \&\,$|SH0ES + BAO + RSD | |$69.54^{+0.64}_{-0.66}$| | 0.282 ± 0.012 | |$0.197^{+0.038}_{-0.092}$| | 0.807 ± 0.032 | |$-19.38^{+0.20}_{-0.19}$| |
Exact results for f3 model that include the parameters H0, Ωm,0, and |$\frac{1}{p_3}$|. The σ8,0 parameter and the nuisance parameter M, are provided for data sets that include RSD or PN+ & SH0ES, respectively otherwise, they are left empty.
| Data Sets . | |$H_0 \mathrm{[km s^{-1} Mpc ^{-1}]}$| . | Ωm,0 . | |$\frac{1}{p_3}$| . | σ8,0 . | M . |
|---|---|---|---|---|---|
| CC + BAO | |$67.5^{+1.7}_{-2.3}$| | |$0.311^{+0.039}_{-0.034}$| | |$0.058^{+0.182}_{-0.056}$| | – | – |
| CC + BAO + RSD | |$68.6^{+1.3}_{-1.9}$| | |$0.276^{+0.016}_{-0.015}$| | |$0.026^{+0.214}_{-0.025}$| | |$0.798^{+0.040}_{-0.036}$| | – |
| |$\mathrm{PN}^+\, \&\,$|SH0ES + RSD | |$73.2^{+1.0}_{-1.1}$| | |$0.280^{+0.014}_{-0.015}$| | |$0.232^{+0.027}_{-0.031}$| | |$0.793^{+0.038}_{-0.039}$| | −19.25 ± 0.11 |
| CC + |$\mathrm{PN}^+\, \&\,$|SH0ES + BAO | |$69.34^{+0.65}_{-0.64}$| | |$0.300^{+0.017}_{-0.016}$| | |$0.160^{+0.029}_{-0.126}$| | – | |$-19.34^{+0.24}_{-0.31}$| |
| CC + |$\mathrm{PN}^+\, \&\,$|SH0ES + BAO + RSD | |$69.54^{+0.64}_{-0.66}$| | 0.282 ± 0.012 | |$0.197^{+0.038}_{-0.092}$| | 0.807 ± 0.032 | |$-19.38^{+0.20}_{-0.19}$| |
| Data Sets . | |$H_0 \mathrm{[km s^{-1} Mpc ^{-1}]}$| . | Ωm,0 . | |$\frac{1}{p_3}$| . | σ8,0 . | M . |
|---|---|---|---|---|---|
| CC + BAO | |$67.5^{+1.7}_{-2.3}$| | |$0.311^{+0.039}_{-0.034}$| | |$0.058^{+0.182}_{-0.056}$| | – | – |
| CC + BAO + RSD | |$68.6^{+1.3}_{-1.9}$| | |$0.276^{+0.016}_{-0.015}$| | |$0.026^{+0.214}_{-0.025}$| | |$0.798^{+0.040}_{-0.036}$| | – |
| |$\mathrm{PN}^+\, \&\,$|SH0ES + RSD | |$73.2^{+1.0}_{-1.1}$| | |$0.280^{+0.014}_{-0.015}$| | |$0.232^{+0.027}_{-0.031}$| | |$0.793^{+0.038}_{-0.039}$| | −19.25 ± 0.11 |
| CC + |$\mathrm{PN}^+\, \&\,$|SH0ES + BAO | |$69.34^{+0.65}_{-0.64}$| | |$0.300^{+0.017}_{-0.016}$| | |$0.160^{+0.029}_{-0.126}$| | – | |$-19.34^{+0.24}_{-0.31}$| |
| CC + |$\mathrm{PN}^+\, \&\,$|SH0ES + BAO + RSD | |$69.54^{+0.64}_{-0.66}$| | 0.282 ± 0.012 | |$0.197^{+0.038}_{-0.092}$| | 0.807 ± 0.032 | |$-19.38^{+0.20}_{-0.19}$| |
As with f1CDM, the model f3CDM exhibits the highest constrained value for H0 when considering the PN+ & SH0ES+RSD data (|$H_0 = 73.2^{+1.1}_{-1.14} {\rm \, km \, s}^{-1} {\rm Mpc}^{-1}$|) combination, while the lowest value is obtained for CC+BAO data (|$H_0 = 67.5^{+1.7}_{-2.3} {\rm \, km \, s}^{-1} {\rm Mpc}^{-1}$|). Similarly, the density parameter Ωm,0 also shows the highest value for CC+BAO (|$\Omega _{m,0} = 0.311^{+0.039}_{-0.034}$|) and the lowest for CC+PN+ & SH0ES+BAO (Ωm,0 = 0.211 ± 0.012). In addition, the RSD data appear to impose more stringent constraints on these parameters, particularly on the density parameter.
Regarding the model parameter, unlike in the case of f2CDM, we observe that its range within the 1σ and 2σ confidence intervals is narrower. In this instance, the 2σ interval spans from 0 to a maximum of 0.5, but akin in f2CDM still lie within 2σ of the ΛCDM limit.
However, the most significant difference in this model becomes evident in the σ8,0 parameter. This model reports a higher value for this parameter. Furthermore, a correlation between the parameters Ω8, 0 and σ8,0 is now evident, which was not observed in the f1CDM model but is apparent in the f2CDM model. The degeneracy between the H0 and σ8,0 parameters, however, remains apparent, as observed in the other cases.
The highest value for σ8,0 is obtained for the CC + PN+ & SH0ES + BAO + RSD combination, yielding a value of σ8,0 = 0.793 ± 0.035, as detailed in Table 6 and illustrated in Fig. 6. Conversely, the lowest value for S8,0 is achieved when using the PN+ & SH0ES+RSD data, as indicated in both tables presenting the σ8,0 and S8,0 values respectively. Additionally, consistent with previous models, the value for S8,0 obtained using the RSD data alone is relatively low, akin to the f1CDM model.
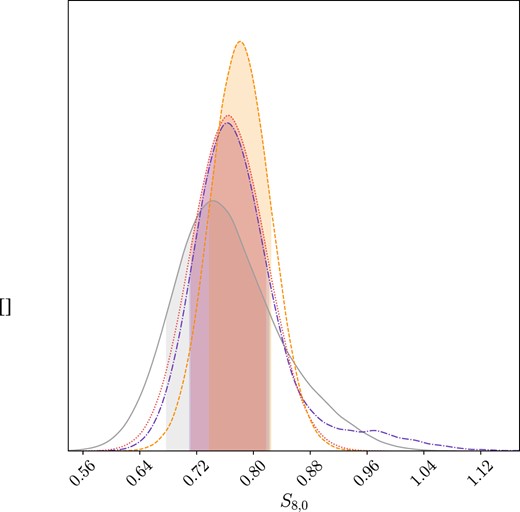
Posterior distribution for the S8,0 parameter in the f3CDM model. Legend: grey denotes the RSD data, purple corresponds to CC+BAO+RSD data, red represents the PN+ & SH0ES + RSD data set, while orange indicates CC + PN+ & SH0ES + BAO + RSD data.
| Data sets . | S8,0 . |
|---|---|
 | |
| Data sets . | S8,0 . |
|---|---|
 | |
| Data sets . | S8,0 . |
|---|---|
 | |
| Data sets . | S8,0 . |
|---|---|
 | |
The final piece of analysis for the f3CDM model is depicted in Fig. A1 in Appendix A. Here, we observe a degenerate relationship between the parameters p3 and S8,0, which transitions into an anticorrelation at higher values of p3. This effect is particularly noticeable for the data sets that incorporate BAO measurements.
4.4 Logarithmic model
The last model, hereafter referred to as f4CDM, which was proposed by Bamba et al. (2011), is known as the logarithmic model. This model is characterized by the following expression
where α4 and p4 are the two model constants. To determine the constant α4, we follow the standard procedure of evaluating the Friedmann equation (13), at the current time, resulting in
This simplifies the Friedmann equation to a more straightforward form
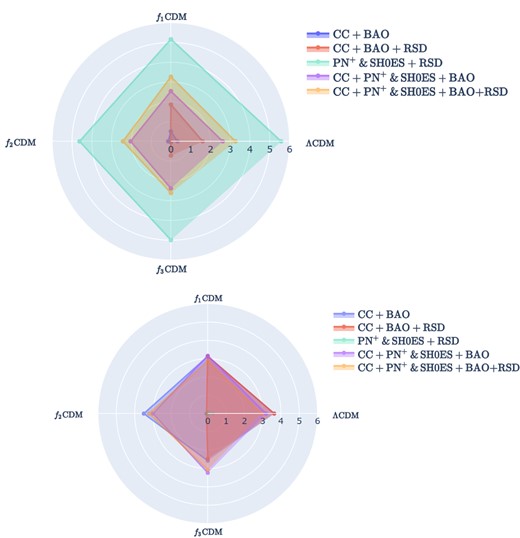
Interestingly, the additional model parameter p4 does not feature in equation (50), indicating that at background level this parameter cannot be constrained. None the less, it is noteworthy that this parameter does come into play at the perturbative level, particularly in the context of linear matter perturbations, as illustrated in equation (22), where p4 is featured in the Geff term, in particular in the |$\mathcal {F}_T$| term. Therefore, as can be seen in the contour plots in Fig. 7 and Table| 7, the p4 parameter does not feature in the CC+BAO (blue contours) and CC+PN+ & SH0ES+BAO (green contour), but is relevant for the rest of the data sets that include the RSD data.
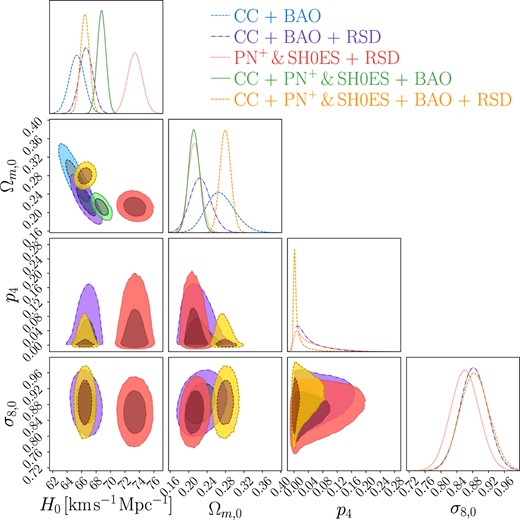
Confidence contours and posterior distributions for the f4CDM model (logarithmic model) parameters, including H0 and Ωm,0. In cases where the RSD data are incorporated (purple, red, and yellow contours), the σ8,0 and p4 parameter is also displayed.
Exact results for f4 model that include the parameters H0 and Ωm,0. The σ8,0 and p4 parameter together with the nuisance parameter M, are provided for data sets that include RSD or PN+ & SH0ES, respectively otherwise, they are left empty.
| Data Sets . | |$H_0 \mathrm{[km s^{-1} Mpc ^{-1}]}$| . | Ωm,0 . | p4 . | σ8,0 . | M . |
|---|---|---|---|---|---|
| CC + BAO | |$65.3^{+1.1}_{-1.0}$| | |$0.266^{+0.031}_{-0.030}$| | – | – | – |
| CC + BAO + RSD | |$66.62^{+0.87}_{-0.91}$| | |$0.224^{+0.022}_{-0.020}$| | |$0.005^{+0.031}_{-0.000}$| | 0.883 ± 0.033 | – |
| |$\mathrm{PN}^+\, \&\,$|SH0ES + RSD | |$73.40^{+0.97}_{-1.06}$| | |$0.213^{+0.013}_{-0.014}$| | |$0.007^{+0.057}_{-0.013}$| | |$0.860^{+0.036}_{-0.035}$| | |$-19.09^{+0.16}_{-0.23}$| |
| CC + |$\mathrm{PN}^+\, \&\,$|SH0ES + BAO | |$68.78^{+0.58}_{-0.63}$| | 0.211 ± 0.012 | – | – | −19.388 ± 0.017 |
| CC + |$\mathrm{PN}^+\, \&\,$|SH0ES + BAO + RSD | |$66.41^{+0.67}_{-0.56}$| | |$0.280^{+0.011}_{-0.012}$| | |$0.0015^{+0.009}_{-0.005}$| | |$0.883^{+0.038}_{-0.036}$| | |$-19.57^{+0.16}_{-0.15}$| |
| Data Sets . | |$H_0 \mathrm{[km s^{-1} Mpc ^{-1}]}$| . | Ωm,0 . | p4 . | σ8,0 . | M . |
|---|---|---|---|---|---|
| CC + BAO | |$65.3^{+1.1}_{-1.0}$| | |$0.266^{+0.031}_{-0.030}$| | – | – | – |
| CC + BAO + RSD | |$66.62^{+0.87}_{-0.91}$| | |$0.224^{+0.022}_{-0.020}$| | |$0.005^{+0.031}_{-0.000}$| | 0.883 ± 0.033 | – |
| |$\mathrm{PN}^+\, \&\,$|SH0ES + RSD | |$73.40^{+0.97}_{-1.06}$| | |$0.213^{+0.013}_{-0.014}$| | |$0.007^{+0.057}_{-0.013}$| | |$0.860^{+0.036}_{-0.035}$| | |$-19.09^{+0.16}_{-0.23}$| |
| CC + |$\mathrm{PN}^+\, \&\,$|SH0ES + BAO | |$68.78^{+0.58}_{-0.63}$| | 0.211 ± 0.012 | – | – | −19.388 ± 0.017 |
| CC + |$\mathrm{PN}^+\, \&\,$|SH0ES + BAO + RSD | |$66.41^{+0.67}_{-0.56}$| | |$0.280^{+0.011}_{-0.012}$| | |$0.0015^{+0.009}_{-0.005}$| | |$0.883^{+0.038}_{-0.036}$| | |$-19.57^{+0.16}_{-0.15}$| |
Exact results for f4 model that include the parameters H0 and Ωm,0. The σ8,0 and p4 parameter together with the nuisance parameter M, are provided for data sets that include RSD or PN+ & SH0ES, respectively otherwise, they are left empty.
| Data Sets . | |$H_0 \mathrm{[km s^{-1} Mpc ^{-1}]}$| . | Ωm,0 . | p4 . | σ8,0 . | M . |
|---|---|---|---|---|---|
| CC + BAO | |$65.3^{+1.1}_{-1.0}$| | |$0.266^{+0.031}_{-0.030}$| | – | – | – |
| CC + BAO + RSD | |$66.62^{+0.87}_{-0.91}$| | |$0.224^{+0.022}_{-0.020}$| | |$0.005^{+0.031}_{-0.000}$| | 0.883 ± 0.033 | – |
| |$\mathrm{PN}^+\, \&\,$|SH0ES + RSD | |$73.40^{+0.97}_{-1.06}$| | |$0.213^{+0.013}_{-0.014}$| | |$0.007^{+0.057}_{-0.013}$| | |$0.860^{+0.036}_{-0.035}$| | |$-19.09^{+0.16}_{-0.23}$| |
| CC + |$\mathrm{PN}^+\, \&\,$|SH0ES + BAO | |$68.78^{+0.58}_{-0.63}$| | 0.211 ± 0.012 | – | – | −19.388 ± 0.017 |
| CC + |$\mathrm{PN}^+\, \&\,$|SH0ES + BAO + RSD | |$66.41^{+0.67}_{-0.56}$| | |$0.280^{+0.011}_{-0.012}$| | |$0.0015^{+0.009}_{-0.005}$| | |$0.883^{+0.038}_{-0.036}$| | |$-19.57^{+0.16}_{-0.15}$| |
| Data Sets . | |$H_0 \mathrm{[km s^{-1} Mpc ^{-1}]}$| . | Ωm,0 . | p4 . | σ8,0 . | M . |
|---|---|---|---|---|---|
| CC + BAO | |$65.3^{+1.1}_{-1.0}$| | |$0.266^{+0.031}_{-0.030}$| | – | – | – |
| CC + BAO + RSD | |$66.62^{+0.87}_{-0.91}$| | |$0.224^{+0.022}_{-0.020}$| | |$0.005^{+0.031}_{-0.000}$| | 0.883 ± 0.033 | – |
| |$\mathrm{PN}^+\, \&\,$|SH0ES + RSD | |$73.40^{+0.97}_{-1.06}$| | |$0.213^{+0.013}_{-0.014}$| | |$0.007^{+0.057}_{-0.013}$| | |$0.860^{+0.036}_{-0.035}$| | |$-19.09^{+0.16}_{-0.23}$| |
| CC + |$\mathrm{PN}^+\, \&\,$|SH0ES + BAO | |$68.78^{+0.58}_{-0.63}$| | 0.211 ± 0.012 | – | – | −19.388 ± 0.017 |
| CC + |$\mathrm{PN}^+\, \&\,$|SH0ES + BAO + RSD | |$66.41^{+0.67}_{-0.56}$| | |$0.280^{+0.011}_{-0.012}$| | |$0.0015^{+0.009}_{-0.005}$| | |$0.883^{+0.038}_{-0.036}$| | |$-19.57^{+0.16}_{-0.15}$| |
The inclusion of the logarithmic function makes a noticeable difference in this model, particularly when examining the relationship between the H0 and Ωm,0 parameters. In this case, the relationship exhibits a distinct anticorrelation, which is more pronounced in this model compared to the previous ones. Interestingly, this results in more extreme values for the H0 parameter, with the highest value achieved being |$H_0 = 73.40^{+0.97}_{-1.06} {\rm \, km \, s}^{-1} {\rm Mpc}^{-1}$| for the PN+ & SH0ES data set. Conversely, the lowest value was obtained for the CC+BAO data set, with a value of |$H_0 = 65.3^{+1.1}_{-1.0} {\rm \, km \, s}^{-1} {\rm Mpc}^{-1}$|
The values of Ωm,0 also exhibit significant variations. In this case, the lowest value is achieved for the CC+PN+ & SH0ES+BAO data set, while the highest is for the same data set but with the inclusion of the RSD data (i.e CC+PN+ & SH0ES+BAO+RSD). It seems like when the RSD model is included in the data sets, either the H0 parameter or the Ωm,0 is driven to higher values when compared to its counterpart data set without the RSD data set. Therefore, in this model, it appears that the presence of RSD data influences the understanding of the Universe’s current acceleration and the role of baryonic and dark matter components within this model. This influence can be attributed to RSD data’s exceptional sensitivity to the distribution of matter, which in turn plays a crucial role in shaping the large-scale structure of the Universe through its gravitational interactions.
A particularly intriguing aspect of this model, which sets it apart from the f1 − f3CDM models, is the absence of a ΛCDM limit both at the background and perturbative levels. At the perturbative level, the parameter p4 appears in Geff, which is expressed as
In this scenario, no choice of the value of p4 can reproduce a ΛCDM model. Furthermore, given that it appears in the logarithmic function, the parameter p4 must be greater than zero, as illustrated in Fig. 7. However, Table 7, still shows that the value of p4 is very close to zero, which makes Geff, slightly higher than GN, throughout the redshift span.
The σ8,0 parameter in this model appears to be significantly higher when compared to the other models. Interestingly, the CC+BAO+RSD and CC+PN+ & SH0ES+BAO+RSD data sets both report the same value for σ8,0, suggesting that the inclusion of PN+ & SH0ES data has a minimal effect on this parameter in this particular model. The CC+PN+ & SH0ES + RSD data set reports a slightly lower value for σ8,0. This observation leads us to consider Fig. 8 and Table 8, where we can see the values obtained for this parameter. In this case, it’s evident that Ωm,0 has a notable impact on this parameter. While σ8,0 is the same for CC+BAO+RSD and CC+PN+ & SH0ES+BAO+RSD, S8,0 varies significantly between the two data sets. A higher value is obtained when PN+ & SH0ES data are included, making it the data set with the highest S8,0 value.
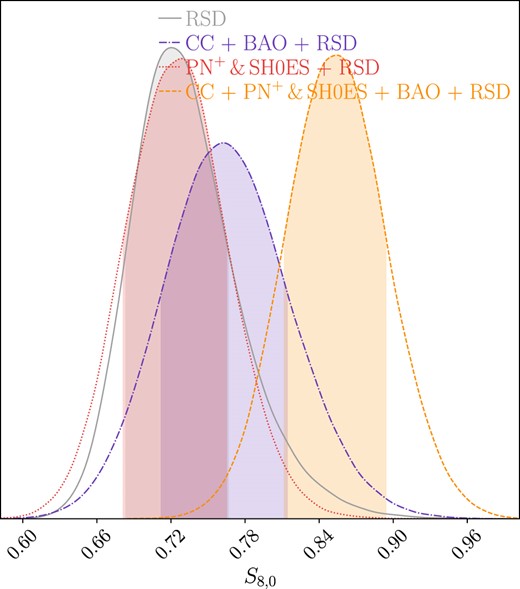
Posterior distribution for the S8,0 parameter in the f4CDM model. Legend: grey denotes the RSD data, purple corresponds to CC+BAO+RSD data, red represents the PN+ & SH0ES + RSD data set, while orange indicates CC + PN+ & SH0ES + BAO + RSD data.
| Data sets . | S8,0 . |
|---|---|
 | |
| Data sets . | S8,0 . |
|---|---|
 | |
| Data sets . | S8,0 . |
|---|---|
 | |
| Data sets . | S8,0 . |
|---|---|
 | |
The last Fig. A1 (Appendix A), shows the relationship between the S8,0 and p4. As expected based on previous models, we observe a degeneracy between these parameters, particularly concentrated within the 1σ region near p4 = 0.
5 ANALYSIS
To evaluate how well each fiCDM model performs with various data sets, we employ several statistical measures. First, we calculate the minimum |$\chi ^2_\mathrm{min}$| values for each model and data set. These values are derived from the maximum likelihood Lmax, with the relationship being |$\chi ^2_\mathrm{min} = -2 \ln L_\mathrm{max}$|. A lower |$\chi ^2_\mathrm{min}$| indicates a better fit of the model to the data.
In addition to |$\chi ^2_\mathrm{min}$|, we also compare the models to the standard ΛCDM model using two criteria: the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC). These criteria consider both the model’s goodness of fit, represented by |$\chi ^2_\mathrm{min}$|, and its complexity, which is determined by the number of parameters n. The AIC is calculated as
where a lower AIC value indicates a model that fits the data better while accounting for complexity. It penalizes models with more parameters, even if they exhibit a superior data fit. On the other hand, the BIC is given by
where m is the sample size of the observational data combination. Similar to the AIC, the BIC aims to balance data fit against model complexity. However, it imposes a heavier penalty on models with more parameters as the sample size increases. Therefore, by comparing the AIC and BIC values of different models, we can determine which model is better supported by the data. Generally, models with lower AIC and BIC values are preferred, provided the differences are significant.
To assess the performance of different models using various combinations of data sets, we calculate the differences in AIC and BIC between each model (fiCDM) and the reference model, which is the ΛCDM model. This comparison helps us understand how well each model aligns with the standard model of cosmology. The differences in AIC and BIC are denoted as ΔAIC |$= \Delta \chi ^2_\mathrm{min} + 2 \Delta n$|, and ΔBIC |$= \Delta \chi ^2_\mathrm{min} + \Delta n \ln m$|, respectively. These metrics quantify how each model deviates from the reference model (in this case, ΛCDM) in which, smaller values of ΔAIC and ΔBIC indicate that a model, along with its chosen data set, is more similar to the ΛCDM model, suggesting better performance. Table 9 provides a comparison of these metrics for two specific data set combinations: CC+BAO and CC+BAO+RSD. Similarly, Table 10 allows us to compare the AIC and BIC values for three different sets of data combinations: |$\mathrm{PN}^+ \&$|SH0ES+RSD, CC+|$\mathrm{PN}^+ \&$|SH0ES+BAO and CC+|$\mathrm{PN}^+ \&$|SH0ES+BAO+RSD.
Comparison of |$\chi ^2_\mathrm{min}$| and differences in AIC and BIC between the models and ΛCDM (i.e ΔAIC and ΔBIC). On the left-hand side, results are presented for CC+BAO, while the right-hand side includes RSD.
| . | CC+BAO . | CC+BAO+RSD . | ||||
|---|---|---|---|---|---|---|
| . | |$\chi ^2_\mathrm{min}$| . | ΔAIC . | ΔBIC . | |$\chi ^2_\mathrm{min}$| . | ΔAIC . | ΔBIC . |
| ΛCDM | 20.93 | 0 | 0 | 37.14 | 0 | 0 |
| f1CDM | 20.87 | 1.94 | 1.61 | 37.04 | 1.91 | 3.15 |
| f2CDM | 20.93 | 2.00 | 1.66 | 35.41 | 0.28 | 1.52 |
| f3CDM | 20.93 | 2.00 | 1.66 | 37.21 | 2.08 | 3.32 |
| f4CDM | 27.95 | 7.02 | 7.02 | 42.03 | 6.89 | 8.14 |
| . | CC+BAO . | CC+BAO+RSD . | ||||
|---|---|---|---|---|---|---|
| . | |$\chi ^2_\mathrm{min}$| . | ΔAIC . | ΔBIC . | |$\chi ^2_\mathrm{min}$| . | ΔAIC . | ΔBIC . |
| ΛCDM | 20.93 | 0 | 0 | 37.14 | 0 | 0 |
| f1CDM | 20.87 | 1.94 | 1.61 | 37.04 | 1.91 | 3.15 |
| f2CDM | 20.93 | 2.00 | 1.66 | 35.41 | 0.28 | 1.52 |
| f3CDM | 20.93 | 2.00 | 1.66 | 37.21 | 2.08 | 3.32 |
| f4CDM | 27.95 | 7.02 | 7.02 | 42.03 | 6.89 | 8.14 |
Comparison of |$\chi ^2_\mathrm{min}$| and differences in AIC and BIC between the models and ΛCDM (i.e ΔAIC and ΔBIC). On the left-hand side, results are presented for CC+BAO, while the right-hand side includes RSD.
| . | CC+BAO . | CC+BAO+RSD . | ||||
|---|---|---|---|---|---|---|
| . | |$\chi ^2_\mathrm{min}$| . | ΔAIC . | ΔBIC . | |$\chi ^2_\mathrm{min}$| . | ΔAIC . | ΔBIC . |
| ΛCDM | 20.93 | 0 | 0 | 37.14 | 0 | 0 |
| f1CDM | 20.87 | 1.94 | 1.61 | 37.04 | 1.91 | 3.15 |
| f2CDM | 20.93 | 2.00 | 1.66 | 35.41 | 0.28 | 1.52 |
| f3CDM | 20.93 | 2.00 | 1.66 | 37.21 | 2.08 | 3.32 |
| f4CDM | 27.95 | 7.02 | 7.02 | 42.03 | 6.89 | 8.14 |
| . | CC+BAO . | CC+BAO+RSD . | ||||
|---|---|---|---|---|---|---|
| . | |$\chi ^2_\mathrm{min}$| . | ΔAIC . | ΔBIC . | |$\chi ^2_\mathrm{min}$| . | ΔAIC . | ΔBIC . |
| ΛCDM | 20.93 | 0 | 0 | 37.14 | 0 | 0 |
| f1CDM | 20.87 | 1.94 | 1.61 | 37.04 | 1.91 | 3.15 |
| f2CDM | 20.93 | 2.00 | 1.66 | 35.41 | 0.28 | 1.52 |
| f3CDM | 20.93 | 2.00 | 1.66 | 37.21 | 2.08 | 3.32 |
| f4CDM | 27.95 | 7.02 | 7.02 | 42.03 | 6.89 | 8.14 |
Comparison of |$\chi ^2_\mathrm{min}$| and differences in AIC and BIC between the models and ΛCDM (i.e ΔAIC and ΔBIC). On the left-hand side, results are presented for PN+ & SH0ES+RSD, whilst in the middle CC+PN+ & SH0ES+BAO. On the right-hand side, the results for CC+PN+ & SH0ES+BAO+RSD are displayed.
| . | PN+ & SH0ES+RSD . | CC+PN+ & SH0ES+BAO . | CC+PN+ & SH0ES+BAO+RSD . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| . | |$\chi ^2_{\mathrm{min}}$| . | ΔAIC . | ΔBIC . | |$\chi ^2_{\mathrm{min}}$| . | ΔAIC . | ΔBIC . | |$\chi ^2_{\mathrm{min}}$| . | ΔAIC . | ΔBIC . |
| ΛCDM | 1550.20 | 0 | 0 | 1572.60 | 0 | 0 | 1590.71 | 0 | 0 |
| f1CDM | 1549.52 | 1.32 | 2.56 | 1572.56 | 1.96 | 1.78 | 1590.56 | 1.85 | 3.10 |
| f2CDM | 1541.46 | −6.74 | −5.50 | 1572.50 | 1.89 | 1.72 | 1587.49 | −1.21 | 0.04 |
| f3CDM | 1543.13 | −5.07 | −3.84 | 1572.31 | 1.71 | 1.53 | 1588.33 | −0.37 | 0.88 |
| f4CDM | 1539.71 | −8.48 | −7.25 | 1586.67 | 14.07 | 14.07 | 1663.50 | 74.80 | 76.04 |
| . | PN+ & SH0ES+RSD . | CC+PN+ & SH0ES+BAO . | CC+PN+ & SH0ES+BAO+RSD . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| . | |$\chi ^2_{\mathrm{min}}$| . | ΔAIC . | ΔBIC . | |$\chi ^2_{\mathrm{min}}$| . | ΔAIC . | ΔBIC . | |$\chi ^2_{\mathrm{min}}$| . | ΔAIC . | ΔBIC . |
| ΛCDM | 1550.20 | 0 | 0 | 1572.60 | 0 | 0 | 1590.71 | 0 | 0 |
| f1CDM | 1549.52 | 1.32 | 2.56 | 1572.56 | 1.96 | 1.78 | 1590.56 | 1.85 | 3.10 |
| f2CDM | 1541.46 | −6.74 | −5.50 | 1572.50 | 1.89 | 1.72 | 1587.49 | −1.21 | 0.04 |
| f3CDM | 1543.13 | −5.07 | −3.84 | 1572.31 | 1.71 | 1.53 | 1588.33 | −0.37 | 0.88 |
| f4CDM | 1539.71 | −8.48 | −7.25 | 1586.67 | 14.07 | 14.07 | 1663.50 | 74.80 | 76.04 |
Comparison of |$\chi ^2_\mathrm{min}$| and differences in AIC and BIC between the models and ΛCDM (i.e ΔAIC and ΔBIC). On the left-hand side, results are presented for PN+ & SH0ES+RSD, whilst in the middle CC+PN+ & SH0ES+BAO. On the right-hand side, the results for CC+PN+ & SH0ES+BAO+RSD are displayed.
| . | PN+ & SH0ES+RSD . | CC+PN+ & SH0ES+BAO . | CC+PN+ & SH0ES+BAO+RSD . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| . | |$\chi ^2_{\mathrm{min}}$| . | ΔAIC . | ΔBIC . | |$\chi ^2_{\mathrm{min}}$| . | ΔAIC . | ΔBIC . | |$\chi ^2_{\mathrm{min}}$| . | ΔAIC . | ΔBIC . |
| ΛCDM | 1550.20 | 0 | 0 | 1572.60 | 0 | 0 | 1590.71 | 0 | 0 |
| f1CDM | 1549.52 | 1.32 | 2.56 | 1572.56 | 1.96 | 1.78 | 1590.56 | 1.85 | 3.10 |
| f2CDM | 1541.46 | −6.74 | −5.50 | 1572.50 | 1.89 | 1.72 | 1587.49 | −1.21 | 0.04 |
| f3CDM | 1543.13 | −5.07 | −3.84 | 1572.31 | 1.71 | 1.53 | 1588.33 | −0.37 | 0.88 |
| f4CDM | 1539.71 | −8.48 | −7.25 | 1586.67 | 14.07 | 14.07 | 1663.50 | 74.80 | 76.04 |
| . | PN+ & SH0ES+RSD . | CC+PN+ & SH0ES+BAO . | CC+PN+ & SH0ES+BAO+RSD . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| . | |$\chi ^2_{\mathrm{min}}$| . | ΔAIC . | ΔBIC . | |$\chi ^2_{\mathrm{min}}$| . | ΔAIC . | ΔBIC . | |$\chi ^2_{\mathrm{min}}$| . | ΔAIC . | ΔBIC . |
| ΛCDM | 1550.20 | 0 | 0 | 1572.60 | 0 | 0 | 1590.71 | 0 | 0 |
| f1CDM | 1549.52 | 1.32 | 2.56 | 1572.56 | 1.96 | 1.78 | 1590.56 | 1.85 | 3.10 |
| f2CDM | 1541.46 | −6.74 | −5.50 | 1572.50 | 1.89 | 1.72 | 1587.49 | −1.21 | 0.04 |
| f3CDM | 1543.13 | −5.07 | −3.84 | 1572.31 | 1.71 | 1.53 | 1588.33 | −0.37 | 0.88 |
| f4CDM | 1539.71 | −8.48 | −7.25 | 1586.67 | 14.07 | 14.07 | 1663.50 | 74.80 | 76.04 |
Table 9 highlights that the CC+BAO data set generally exhibits a lower |$\chi ^2_\mathrm{min}$|, implying a better fit without RSD. However, closer inspection of the ΔAIC values for CC+BAO+RSD reveals a significant reduction, indicating the increased favourability of this data set in certain cases. It is noteworthy that the BIC values for CC+BAO+RSD are slightly higher due to more data points. Regarding model performance, the f2 model consistently presents the lowest ΔAIC and ΔBIC values, signifying its reliable performance. The f1 and f3 models also perform well, showing suitability for this data set. In contrast, the f4CDM model tends to lean towards the ΛCDM model, as suggested by higher ΔAIC and ΔBIC values, indicating weaker data support for f4CDM.
Table 10 reveals intriguing findings. Starting with the PN+ & SH0ES+RSD data set, the models are favoured over ΛCDM, as reflected in negative AIC and BIC values, indicating a preference for the models. While this preference is not consistent across all models for the CC+PN+ & SH0ES+BAO data set, it re-emerges for CC+PN+ & SH0ES+BAO+RSD, especially pronounced for the f2 and f3 models. This suggests that, for these two models within the CC+PN+ & SH0ES+BAO+RSD data sets, the data lean towards favouring these models over ΛCDM. However, it is important to note that the evidence is not strong enough to definitively favour these models over ΛCDM. The BIC values, although not negative, are nearly zero, indicating an inconclusive preference for either model. Conversely, the f4 model shows strong disfavour and preference for ΛCDM, prompting its exclusion from further analysis, shifting our focus to the first three models.
The previous analysis is further supported by Fig. 9. In this figure, we compare the values of H0 obtained from fi(T) (i = 1, 2, 3) models to the values of H0 obtained from the ΛCDM model for the same data sets, as shown in Appendix B. This visualization illustrates the variations in H0 across different data sets, expressed in terms of σ units, with each data set represented by a distinct colour. For each f(T) model, we observe that the H0 values fall within 1σ of the corresponding ΛCDM values. Therefore, the H0 values obtained for the different data sets are consistent with those of ΛCDM.
Distances measured in standard deviations (σ units) between the constrained H0 values obtained from the f1 − 3CDM models and their corresponding values in the ΛCDM model.
The discrepancy between the locally measured expansion rate of the Universe and the values inferred from observations of the CMB has prompted us to extend our previous analysis. We aim to investigate how these models perform with different values of H0, specifically considering the P18 value |$H^{\mathrm{P18}}_0 = 67.4 \pm 0.5 {\rm \, km \, s}^{-1} {\rm Mpc}^{-1}$| (Aghanim et al. 2020) and R22 value of |$H^{\mathrm{R22}}_0 = 73.30 \pm 1.4 {\rm \, km \, s}^{-1} {\rm Mpc}^{-1}$| (Riess et al. 2022), as shown in Fig. 10 (in both cases we include the ΛCDM values from Appendix B).
Distances measured in standard deviations (σ units) between the constrained H0 values obtained from the f1 − 3CDM models together with ΛCDM and the |$H_0^{\mathrm{P18}}$| value on the left-hand side and |$H_0^{\mathrm{R22}}$| on the right-hand side.
In Fig. 10, on the left-hand-side, we observe that the H0 values are within 3.5σ of the P18 value, except for the PN+ & SH0ES data set. However, in the figure, we also include values from RSD data only. This high σ value for the PN+ & SH0ES data is expected, as it dominates and is included within the R22 value itself. Similarly, in Fig. 10, on the right-hand side, we also see that the H0 values are within approximately 3.5σ of the R22 value. This suggests that the H0 values obtained from our analysis fall approximately midway between the two quoted values of P18 and R22.
Additionally, we present a comprehensive comparison of our S8,0 values with the Planck Collaboration’s |$S_{8,0}^{\mathrm{P18}} = 0.834 \pm 0.016$| (Aghanim et al. 2020) and Kilo-Degree Survey (KiDS-1000) value |$S_{8,0}^{\mathrm{KiDS}} = 0.766^{+0.020}{-0.014}$| (Asgari et al. 2021). The results are summarized in Fig. 11, highlighting the impact of different data sets on our models. a comparison between S8,0 values in our models and those in ΛCDM is presented in Fig. 12. Furthermore, Fig. 13 provides a comparison of |$S_{8,0}^{\mathrm{P18}}$| and |$S_{8,0}^{\mathrm{KiDS}}$| with values derived from f1 − 3CDM models in σ units. When compared to |$S_{8,0}^{\mathrm{P18}}$|, on the left-hand side of same figure, we find a maximum discrepancy of 2σ between the values derived from ΛCDM and the f(T) models, and this is primarily observed when considering the RSD data set in isolation. However, as more data sets are included, particularly CC+PN+ & SH0ES+BAO+RSD, which is the most comprehensive data set in our analysis, this discrepancy diminishes.
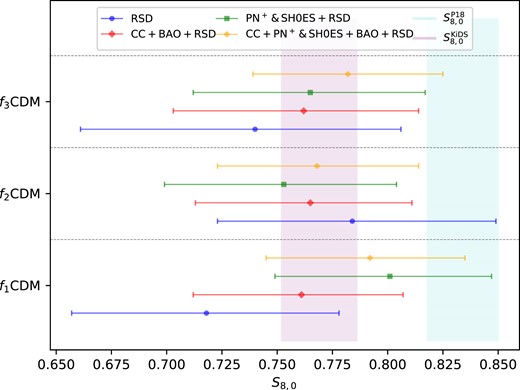
A whisker plot illustrating the constrained values of S8,0 as derived from the f1 − 3CDM models. The cyan and purple vertical bands depict the respective 1σ ranges of |$S_{8,0}^{\mathrm{P18}}$| and |$S_{8,0}^{\mathrm{KiDS}}$|, whilst the error bars illustrate the inferred model dependent 1σ constraints from each respective data set.
Distances measured in standard deviations (σ units) between the constrained S8,0 values obtained from the f1 − 3CDM models and their corresponding values in the ΛCDM model.
On the right-hand panel of Fig. 13, where we compare with |$S_{8,0}^{\mathrm{KiDS}}$|, the discrepancy is further reduced to 1σ, indicating that the values obtained from our analysis are closer to the KiDS-1000 measurements than the Planck values. Notably, CC+PN+ & SH0ES+BAO+RSD performs well in this regard, significantly reducing the σ values. Consequently, it appears that with the combination of the available data sets and the f1 − 3(T) models, the tensions between the CMB and locally determined values are reduced, especially for S8,0.
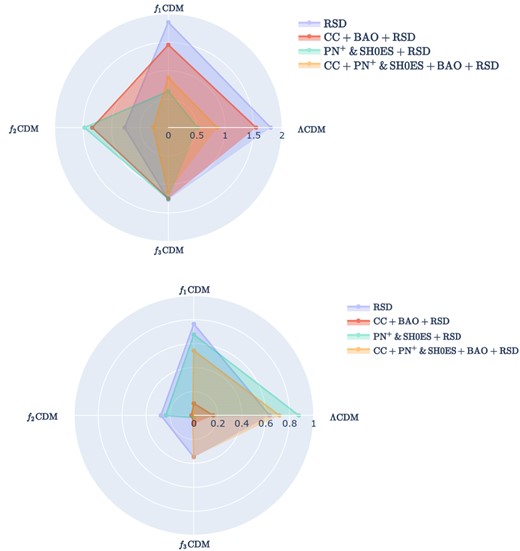
Distances measured in standard deviations (σ units) between the constrained S8,0 values obtained from the f1 − 3CDM models together with ΛCDM and the |$S_{8,0}^{\mathrm{P18}}$| value on the left-hand side and |$S_{8,0}^{\mathrm{R22}}$| on the right-hand side.
6 CONCLUSION
The most popular models in the literature of TG have been probed in this work against the latest expansion data as well as RSD measurements which has expanded the constraint profile of each of these models, as well as their impact on physically observable cosmological parameters. For the local data being used, we had a combination of CC, PN+ & SH0ES, and BAO data. Besides being the most populated data sets and highest precision, these data sets give a range of points across redshift space. In particular, the PN+ & SH0ES sample is the largest SNIa in the literature and the principal late-time indicator of the cosmic tensions problem in the Hubble constant. We use RSD data since it is sensitive to the growth of structure formation and so can be used to constrain the perturbative sector of the models under consideration. In each of these models and for each data set combination, we performed a full MCMC analysis obtaining constraints on all the cosmological parameters. Additionally, we compared the performance of each model for each data set combination against the standard ΛCDM model using the |$\chi ^2_\mathrm{min}$|, AIC, and BIC statistical indicators. Given the increasing tension being reported by various studies on the value of the Hubble constant, we study its constrained value, but also consider the effect of a changing Hubble constant will have on the parameters related to the growth of structure formation, namely, σ8,0 and S8,0.
For reference purposes, we provide the ΛCDM constraint values for each of the data set combinations we consider. This is done in Appendix B, which is important for estimating the statistical indicators in the model sections. Generally, our analysis shows consistency with ΛCDM but some differences do arise, which may show further distinction as the precision in measurements improves. As one might expect, the strongest data set in the analysis was the PN+ & SH0ES sample since it consistently drastically reduces the statistical error for any baseline data set. On the other hand, the statistical metrics show that expansion data CC+PN+ & SH0ES+BAO combination provides evidence for ΛCDM while when the RSD data set is included, there is marginal preference for the f(T) model under consideration. Moreover, they offer best fits on cosmic parameters that are more aligned with a higher Hubble constant. As for the S8,0 parameter, the models are largely consistent with the most recent reported values in the literature.
This analysis offers precision insights into the behaviour of these models, but also on TG more generally, when using combinations of this expansion profile and RSD data sets. The study suggests that these models may offer some promise as toy models for modified cosmological scenario model building. We intend to use these observations to extend this analysis to include CMB power spectra as well as other early Universe data sets to more fully assess the competitiveness of these models.
DATA AVAILABILITY
The data used in this study are described in detail in Section 3. For further information on the data underlying this article, contact the corresponding author who will provide any additional information.
References
APPENDIX A: MODEL PARAMETER pi VERSUS S8,0 PLOTS
In this section, we present the posteriors together with their confidence regions of the pi and S8,0 parameters to investigate the correlation between the two.
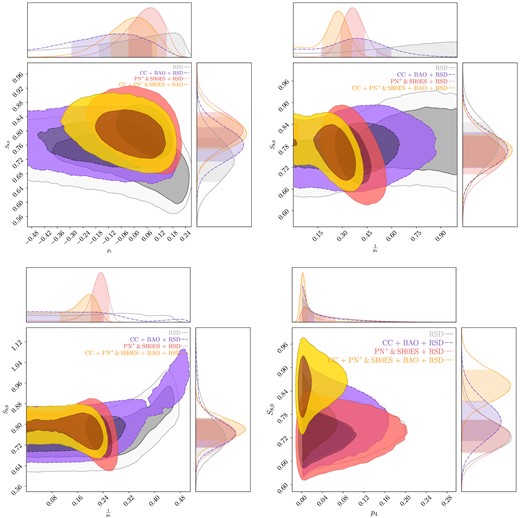
Top left: contour plots showing the relationship between the p1 parameter and the S8,0 parameter for the f1CDM model (power-law model). Top right: contour plots showing the relationship between the |$\frac{1}{p_2}$| parameter and the S8,0 parameter for the f2CDM model (Linder model). Left bottom: contour plots showing the relationship between the |$\frac{1}{p_3}$| parameter and the S8,0 parameter for the f1CDM model (exponential model). Right bottom: contour plots showing the relationship between the p4 parameter and the S8,0 parameter for the f1CDM model (logarithmic model).
APPENDIX B: ΛCDM MODEL
In Section 5, we provide comparisons between the models and their corresponding ΛCDM values. Here, we present the posterior distributions and confidence regions of the ΛCDM model in Fig. B1 and provide additional details and precise values in Table B1. In Fig. B2 the posetriors of the S8,0 parameter for the ΛCDM is shown, whilst in Table B2 the exact values for the corresponding data sets are presented.
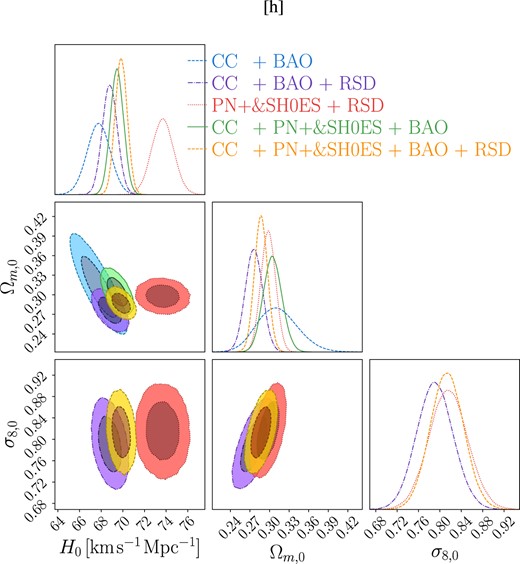
Confidence contours and posterior distributions for the ΛCDM model (logarithmic model) parameters, including H0 and Ωm,0. In cases where the RSD data are incorporated (purple, red, and yellow contours), the σ8,0 parameter is also displayed.
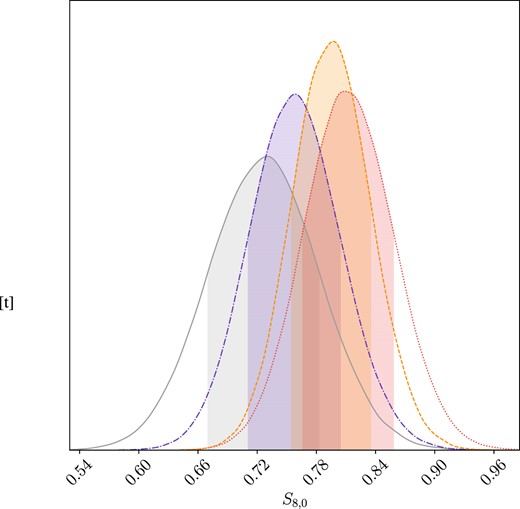
Posterior distribution for the S8,0 parameter in the ΛCDM model. Legend: grey denotes the RSD data, purple corresponds to CC+BAO+RSD data, red represents the PN+ & SH0ES + RSD data set, while orange indicates CC + PN+ & SH0ES + BAO + RSD data.
Exact results for ΛCDM model that include the parameters H0 and Ωm,0. The σ8,0 parameter and the nuisance parameter M, are provided for data sets that include RSD or PN+ & SH0ES, respectively otherwise, they are left empty.
| Data sets . | |$H_0 \mathrm{[km s^{-1} Mpc ^{-1}]}$| . | Ωm,0 . | σ8,0 . | M . |
|---|---|---|---|---|
| CC + BAO | 67.8 ± 1.1 | |$0.308^{+0.032}_{-0.029}$| | – | – |
| CC + BAO + RSD | |$68.77^{+0.71}_{-0.67}$| | |$0.276^{+0.013}_{-0.014}$| | |$0.789^{+0.035}_{-0.033}$| | – |
| PN+ & SH0ES + RSD | |$73.71^{+0.97}_{-1.06}$| | |$0.298^{+0.011}_{-0.012}$| | |$0.814^{+0.037}_{-0.034}$| | |$-19.249^{+0.027}_{-0.032}$| |
| CC + PN+ & SH0ES + BAO | |$69.47^{+0.59}_{-0.63}$| | |$0.304^{+0.015}_{-0.014}$| | – | −19.375 ± 0.017 |
| CC + PN+ & SH0ES + BAO + RSD | |$69.84^{+0.55}_{-0.56}$| | |$0.288^{+0.010}_{-0.010}$| | |$0.815^{+0.030}_{-0.033}$| | |$-19.369^{+0.016}_{-0.017}$| |
| Data sets . | |$H_0 \mathrm{[km s^{-1} Mpc ^{-1}]}$| . | Ωm,0 . | σ8,0 . | M . |
|---|---|---|---|---|
| CC + BAO | 67.8 ± 1.1 | |$0.308^{+0.032}_{-0.029}$| | – | – |
| CC + BAO + RSD | |$68.77^{+0.71}_{-0.67}$| | |$0.276^{+0.013}_{-0.014}$| | |$0.789^{+0.035}_{-0.033}$| | – |
| PN+ & SH0ES + RSD | |$73.71^{+0.97}_{-1.06}$| | |$0.298^{+0.011}_{-0.012}$| | |$0.814^{+0.037}_{-0.034}$| | |$-19.249^{+0.027}_{-0.032}$| |
| CC + PN+ & SH0ES + BAO | |$69.47^{+0.59}_{-0.63}$| | |$0.304^{+0.015}_{-0.014}$| | – | −19.375 ± 0.017 |
| CC + PN+ & SH0ES + BAO + RSD | |$69.84^{+0.55}_{-0.56}$| | |$0.288^{+0.010}_{-0.010}$| | |$0.815^{+0.030}_{-0.033}$| | |$-19.369^{+0.016}_{-0.017}$| |
Exact results for ΛCDM model that include the parameters H0 and Ωm,0. The σ8,0 parameter and the nuisance parameter M, are provided for data sets that include RSD or PN+ & SH0ES, respectively otherwise, they are left empty.
| Data sets . | |$H_0 \mathrm{[km s^{-1} Mpc ^{-1}]}$| . | Ωm,0 . | σ8,0 . | M . |
|---|---|---|---|---|
| CC + BAO | 67.8 ± 1.1 | |$0.308^{+0.032}_{-0.029}$| | – | – |
| CC + BAO + RSD | |$68.77^{+0.71}_{-0.67}$| | |$0.276^{+0.013}_{-0.014}$| | |$0.789^{+0.035}_{-0.033}$| | – |
| PN+ & SH0ES + RSD | |$73.71^{+0.97}_{-1.06}$| | |$0.298^{+0.011}_{-0.012}$| | |$0.814^{+0.037}_{-0.034}$| | |$-19.249^{+0.027}_{-0.032}$| |
| CC + PN+ & SH0ES + BAO | |$69.47^{+0.59}_{-0.63}$| | |$0.304^{+0.015}_{-0.014}$| | – | −19.375 ± 0.017 |
| CC + PN+ & SH0ES + BAO + RSD | |$69.84^{+0.55}_{-0.56}$| | |$0.288^{+0.010}_{-0.010}$| | |$0.815^{+0.030}_{-0.033}$| | |$-19.369^{+0.016}_{-0.017}$| |
| Data sets . | |$H_0 \mathrm{[km s^{-1} Mpc ^{-1}]}$| . | Ωm,0 . | σ8,0 . | M . |
|---|---|---|---|---|
| CC + BAO | 67.8 ± 1.1 | |$0.308^{+0.032}_{-0.029}$| | – | – |
| CC + BAO + RSD | |$68.77^{+0.71}_{-0.67}$| | |$0.276^{+0.013}_{-0.014}$| | |$0.789^{+0.035}_{-0.033}$| | – |
| PN+ & SH0ES + RSD | |$73.71^{+0.97}_{-1.06}$| | |$0.298^{+0.011}_{-0.012}$| | |$0.814^{+0.037}_{-0.034}$| | |$-19.249^{+0.027}_{-0.032}$| |
| CC + PN+ & SH0ES + BAO | |$69.47^{+0.59}_{-0.63}$| | |$0.304^{+0.015}_{-0.014}$| | – | −19.375 ± 0.017 |
| CC + PN+ & SH0ES + BAO + RSD | |$69.84^{+0.55}_{-0.56}$| | |$0.288^{+0.010}_{-0.010}$| | |$0.815^{+0.030}_{-0.033}$| | |$-19.369^{+0.016}_{-0.017}$| |
| Model . | S8,0 . |
|---|---|
 | |
| Model . | S8,0 . |
|---|---|
 | |
| Model . | S8,0 . |
|---|---|
 | |
| Model . | S8,0 . |
|---|---|
 | |



