-
PDF
- Split View
-
Views
-
Cite
Cite
Da-Ming Yang, Jan-Torge Schindler, Riccardo Nanni, Joseph F Hennawi, Eduardo Bañados, Xiaohui Fan, Anniek Gloudemans, Chiara Mazzucchelli, Huub Rottgering, Bram Venemans, Feige Wang, Jinyi Yang, High-z quasar candidate archive: a spectroscopic catalogue of quasars and contaminants in various quasar searches, Monthly Notices of the Royal Astronomical Society, Volume 528, Issue 2, February 2024, Pages 2679–2710, https://doi.org/10.1093/mnras/stae094
Close - Share Icon Share
ABSTRACT
We present the high-z quasar candidate archive (HzQCA), summarizing the spectroscopic observations of 207 z ≳ 5 quasar candidates using Keck/LRIS, Keck/MOSFIRE, and Keck/NIRES. We identify 14 candidates as z ∼ 6 quasars, with 10 of them newly reported here and 63 candidates as brown dwarfs. In the remaining sources, 79 candidates are unlikely to be quasars; 2 sources are inconclusive; the others could not be fully reduced or extracted. Based on the classifications, we investigate the distributions of quasars and contaminants in colour space with photometry measurements from DELS (z), VIKING/UKIDSS (YJHKs/YJHK), and unWISE (W1W2). We find that the identified brown dwarfs are consistent with the empirical brown dwarf model that is commonly used in quasar candidate selection methods. To refine spectroscopic confirmation strategies, we simulate synthetic spectroscopy of high-z quasars and contaminants for all three instruments. The simulations utilize the spectroscopic data in HzQCA. We predict the required exposure times for quasar confirmation and propose an optimal strategy for spectroscopic follow-up observations. For instance, we demonstrate that we can identify a mJ = 21.5 at z = 7.6 or a mJ = 23.0 at z = 7.0 within 15 min of exposure time with LRIS. With the publication of the HzQCA, we aim to provide guidance for future quasar surveys and candidate classification.
1 INTRODUCTION
Large samples of high-redshift (high-z) quasars can help us understand various fundamental questions in extragalactic astronomy. The existence of quasars with ∼109 M⊙ super massive black hole (SMBH) in their centres only ∼1 Gyr after the big bang already poses a stringent constrain on the classic SMBH formation theory (e.g. Volonteri 2010). Theories involving the formation of massive black hole seeds (M > 104 M⊙) via direct collapse (e.g. Begelman, Volonteri & Rees 2006; Dayal et al. 2019), or rapid growth through super-Eddington and hyper-Eddington accretion (e.g. Inayoshi, Haiman & Ostriker 2016; Davies, Hennawi & Eilers 2019) have been proposed to explain the observations (see Inayoshi, Visbal & Haiman 2020, for a review). Further estimation of the accretion time-scale of certain quasars, i.e. the quasar lifetime tQ, with the proximity zones in their spectra posts even more challenges to the accretion theory (e.g. Eilers et al. 2017; Eilers, Hennawi & Davies 2018b; Eilers et al. 2020). Moreover, high-z quasar is a powerful tool to study the evolution of the epoch of reionization (EoR). The damping wing feature (Miralda-Escudé 1998) in spectra of high-z quasars implies that the intergalactic medium (IGM) is significantly neutral at z ≳ 7 (Mortlock et al. 2011; Bañados et al. 2018; Davies et al. 2018; Yang et al. 2020a; Wang et al. 2021) but highly ionized at z ≲ 6 (e.g. Eilers, Davies & Hennawi 2018a; Yang et al. 2020b). Other observation based on the deep quasar spectroscopy, such as the mean optical depth of Lyman-α (e.g. Becker et al. 2021; Bosman et al. 2022) and some extreme Lyman-α trough, further provide diverse constraints on the reionization mechanism and neutral fraction evolution at z ≃ 5–6. These measurements provide an important way to probe the evolution of the neutral fraction during the EoR, complementing the results based on the cosmic microwave background polarization (Planck Collaboration 2020).
Since the discovery of the first quasar 3C273 at z = 0.158 (Schmidt 1963), astronomers have invested tremendous effort in finding quasars with increasingly higher redshifts. Because quasars are extremely rare objects (Wang et al. 2019; Matsuoka et al. 2023; Schindler et al. 2023), these searches are typically conducted using large imaging surveys. Optical surveys such as Sloan Digital Sky Survey (e.g. Fan et al. 2006; Jiang et al. 2008, 2016), Panoramic Survey Telescope & Rapid Response System 1 survey (PS1; e.g. Bañados et al. 2016; Banados et al. 2022), Dark Energy Spectroscopic Instrument Legacy Imaging Surveys (DELS; Wang et al. 2017, 2019), and Subaru High-z Exploration of Low-Luminosity Quasars (e.g. Matsuoka et al. 2022) have been extensively searched for quasars in the range 5.7 < z ≤ 7.0. To date, over 500 quasars with z > 5.3 have been found, with ∼70 of them have 6.5 < z < 7 (for a recent review article see Fan, Banados & Simcoe 2022). Several searches based on near-infrared (NIR) imaging surveys have also paved the way for the discovery of quasars with even higher redshifts, such as the United Kingdom Infrared Telescope (UKIRT) Infrared Deep Sky Survey (UKIDSS; e.g. Mortlock et al. 2011; Bañados et al. 2018), the Visible and Infrared Survey Telescope for Astronomy (VISTA) Kilo-degree Infrared Galaxy Survey (VIKING; e.g. Venemans et al. 2013), the UKIRT Hemisphere Survey (UHS; e.g. Yang et al. 2020a), and the VISTA Hemisphere Survey (VHS; e.g. Wang et al. 2021). With the IR surveys, three quasars with z > 7.5 (Bañados et al. 2018; Yang et al. 2020a; Wang et al. 2021) have been found in the past few years.
The study of high-z quasars is about to be revolutionized by the advent of the new wide survey like the ESA’s Euclid mission (Laureijs et al. 2011) and the Legacy Survey of Space and Time (LSST) by the Vera C. Rubin Observatory (Ivezić et al. 2019). With the deep optical bands of LSST.1, and the deep infrared YJH bands2 as well as the 15 000 deg2 sky coverage provided by Euclid, we expect to find over 100 quasars with 7.0 < z < 7.5, and ∼25 quasars beyond z = 7.5, including ∼8 beyond z = 8.0 (Euclid Collaboration: Barnett et al. 2019). However, quasar searches with these deeper surveys also introduce several new challenges. The first one is a requirement for a more efficient candidate selection algorithm. The expected number density of z ≳ 7 quasars is ∼10−3 deg−2 at JAB > 21 (Wang et al. 2019; Matsuoka et al. 2023), while the contaminants, mostly Galactic brown dwarfs, are far more numerous, ∼10 deg−2 at JAB = 21 (Euclid Collaboration: Barnett et al. 2019). Meanwhile, given the deep detection limit and larger survey area of Euclid, there will be a large number of faint candidates. However, the widely used colour selection methods will be less efficient when selecting candidates from faint sources owing to the low quality of the photometry measurements. More advanced probabilistic selection methods have been proposed to segregate quasars from the contaminants in an attempt to improve the success rate (e.g. Bovy, Hogg & Roweis 2011; Mortlock et al. 2012; Nanni et al. 2022). With the method in Mortlock et al. (2012), several successful quasar searches with optical survey have been conducted (e.g. Matsuoka et al. 2022), leading to an abundant discoveries of z < 7 quasars with very high success rate (|$\gtrsim 50~{{\ \rm per\ cent}}$|). Nanni et al. (2022) proposed the XDHZQSO, another Bayesian approach based on extreme deconvolution (XD; Bovy, Hogg & Roweis 2011). The model for contaminants is purely empirical and all the contaminants are considered as one class. These probabilistic methods need further refinement to prepare for future surveys, and the key to do so is a deeper understanding towards the contaminant population. Moreover, the regime of higher redshift and/or fainter luminosity is poorly explored. Quasars that can be found by Euclid will be as faint as JAB ≃ 24.0 (Euclid Collaboration: Barnett et al. 2019), whereas we have only found very few quasars with mJ > 22.0 due to the detection limits of previous surveys. In addition, only 9 quasars with z > 7 have be discovered (Mortlock et al. 2011; Bañados et al. 2018; Wang et al. 2018; Yang et al. 2019; Matsuoka et al. 2019a, b; Yang et al. 2020a; Wang et al. 2021), while with Euclid we expect to find over 100 of them. Before stepping into this unexplored regime, we have to answer the following questions: Can we still use ground-based telescopes to effectively confirm a considerable number of quasars with higher redshifts or fainter magnitudes? If so, what is the optimal observing strategy, i.e. for quasars with different redshifts, which instruments provide the fastest confirmation and what are the required exposure times?
To cope with these difficulties, in this paper we exploit the spectroscopic observations of hundreds of high-z quasar candidates with Keck in the past three years. We reduce all the spectra in a consistent manner and construct a catalogue of all of the observations, which we refer to as the High-z Quasar Candidate Archive (HzQCA). Using this archive, we explore both the contaminants in our candidate samples and the optimal observing strategies to provide insights for future quasar searches. First, we investigate the distribution of the contaminants in colour space and compare it with the brown dwarf model adopted in many quasar selection methods. Secondly, we use real archival data to simulate spectroscopic observations of mock quasars, allowing us to determine the exposure times required to identify Euclid quasars with Keck instruments. The results also aid us to establish an optimal spectroscopic confirmation strategy. In Section 2, we describe the construction of the archive, including the surveys involved, the instruments we use for confirmation, and the data reduction procedure. In Section 3, we present the final data products and analyse the contaminant population. In Section 4, we introduce the simulations used to estimate the required exposure times and discuss refinements to the observing strategy. Throughout the paper, we adopt a flat cosmological model with H0 = 68.5 km s−1 Mpc−1 (Betoule et al. 2014), ΩM = 0.3, ΩΛ = 0.7. All the magnitudes are given in the AB system, while the uncertainties of our reported measurements are at 1σ confidence level.
2 CONSTRUCTION OF THE ARCHIVE
The HzQCA includes all the high-z quasar candidates observed in two Keck programs. The first one, Searching for Quasars Deep Into the Epoch of Reionization (U170, PI: Hennawi), uses the Near-InfraRed Echellette Spectrometer (NIRES; Wilson et al. 2004) and the Multi-Object Spectrometer For Infra-Red Exploration (MOSFIRE; McLean et al. 2012) to hunt for z > 7 quasars from 2018 to 2021. The second one, Paving the Way for Euclid and JWST via Optimal Selection of High-z Quasars (U055, PI: Hennawi), uses the Low-Resolution Imaging Spectrometer (LRIS; Oke et al. 1995; Rockosi et al. 2010) and MOSFIRE to search for high-z quasars with the XDHZQSO algorithm. The latter program is designed to demonstrate, characterize, and improve the efficacy of the XDHZQSO in preparation for quasars selection with Euclid and JWST. These two programs comprise a total of 20 nights in 10 observing runs, as listed in Table 1. The targets in these runs were observed with a typical seeing of 0|${_{.}^{\prime\prime}}$|5–1|${_{.}^{\prime\prime}}$|2. During the observations, on-the-fly ‘quick-look’ reductions were performed with pypeit (see Section 2.3), allowing the observers to classify the candidates in real time. We usually terminated sequences if there was no sign of Lyman break in the quick-look results, which is part of our observing strategy.
Observation runs included in the archive. The ‘Surveys’ column indicates the quasar surveys involved in the given observing runs (see the description in Section 2). Several candidates from XDHZQSO selection were observed with other instruments, including Keck/DEIMOS, VLT/FORS2, and Magellan/FIRE. Six quasars were confirmed in these observations and are included in the last row (Observation Run = Other). The last two columns display the numbers of the total candidates and the non-FAIL candidates, i.e. the candidates that do not belong to ‘FAIL’ class (see Section 2.4).
| Observation run . | Dates . | Keck program ID . | Surveys . | Seeing . | Total candidates/non-FAIL . | |
|---|---|---|---|---|---|---|
| NIRES-1903 | 2019 March 03–04 | U170 | Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|7–1|${_{.}^{\prime\prime}}$|1 | 15 | 12 |
| NIRES-1905 | 2019 May 19, 2019 | U170 | Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|6–1|${_{.}^{\prime\prime}}$|0 | 6 | 4 |
| MOSFIRE-1911 | 2019 November 18–20 | U179 | Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|9–1|${_{.}^{\prime\prime}}$|2 | 15 | 5 |
| MOSFIRE-2005 | 2020 May 27–29 | U179 | Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|5–0|${_{.}^{\prime\prime}}$|7 | 13 | 3 |
| MOSFIRE-2010 | 2020 May 22–25 | U179 | Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|5–0|${_{.}^{\prime\prime}}$|7 | 34 | 25 |
| MOSFIRE-2201 | 2022 January 10–11 | U055 | XDHZQSO, Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|6–0|${_{.}^{\prime\prime}}$|7 | 7 | 4 |
| MOSFIRE-2204 | 2022 April 9 | U055 | XDHZQSO, Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|6–1|${_{.}^{\prime\prime}}$|2 | 9 | 8 |
| LRIS-2201 | 2022 January 27 | U055 | XDHZQSO, PS1COLOUR | 0|${_{.}^{\prime\prime}}$|8–1|${_{.}^{\prime\prime}}$|0 | 19 | 18 |
| LRIS-2203 | 2022 March 05–06 | U055 | XDHZQSO, PS1COLOUR | 0|${_{.}^{\prime\prime}}$|6–0|${_{.}^{\prime\prime}}$|8 | 31 | 30 |
| LRIS-2204 | 2022 April 23 | U055 | XDHZQSO, LOFAR, Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|8–1|${_{.}^{\prime\prime}}$|0 | 30 | 25 |
| LRIS-2209 | 2022 September 27 | U055 | XDHZQSO | 0|${_{.}^{\prime\prime}}$|5–0|${_{.}^{\prime\prime}}$|9 | 5 | 5 |
| LRIS-2210 | 2022 October 26–28 | U055 | XDHZQSO | 0|${_{.}^{\prime\prime}}$|7–1|${_{.}^{\prime\prime}}$|0 | 19 | 14 |
| Other | – | – | XDHZQSO | – | 6 | 6 |
| Total | 207 | 159 | ||||
| Observation run . | Dates . | Keck program ID . | Surveys . | Seeing . | Total candidates/non-FAIL . | |
|---|---|---|---|---|---|---|
| NIRES-1903 | 2019 March 03–04 | U170 | Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|7–1|${_{.}^{\prime\prime}}$|1 | 15 | 12 |
| NIRES-1905 | 2019 May 19, 2019 | U170 | Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|6–1|${_{.}^{\prime\prime}}$|0 | 6 | 4 |
| MOSFIRE-1911 | 2019 November 18–20 | U179 | Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|9–1|${_{.}^{\prime\prime}}$|2 | 15 | 5 |
| MOSFIRE-2005 | 2020 May 27–29 | U179 | Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|5–0|${_{.}^{\prime\prime}}$|7 | 13 | 3 |
| MOSFIRE-2010 | 2020 May 22–25 | U179 | Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|5–0|${_{.}^{\prime\prime}}$|7 | 34 | 25 |
| MOSFIRE-2201 | 2022 January 10–11 | U055 | XDHZQSO, Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|6–0|${_{.}^{\prime\prime}}$|7 | 7 | 4 |
| MOSFIRE-2204 | 2022 April 9 | U055 | XDHZQSO, Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|6–1|${_{.}^{\prime\prime}}$|2 | 9 | 8 |
| LRIS-2201 | 2022 January 27 | U055 | XDHZQSO, PS1COLOUR | 0|${_{.}^{\prime\prime}}$|8–1|${_{.}^{\prime\prime}}$|0 | 19 | 18 |
| LRIS-2203 | 2022 March 05–06 | U055 | XDHZQSO, PS1COLOUR | 0|${_{.}^{\prime\prime}}$|6–0|${_{.}^{\prime\prime}}$|8 | 31 | 30 |
| LRIS-2204 | 2022 April 23 | U055 | XDHZQSO, LOFAR, Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|8–1|${_{.}^{\prime\prime}}$|0 | 30 | 25 |
| LRIS-2209 | 2022 September 27 | U055 | XDHZQSO | 0|${_{.}^{\prime\prime}}$|5–0|${_{.}^{\prime\prime}}$|9 | 5 | 5 |
| LRIS-2210 | 2022 October 26–28 | U055 | XDHZQSO | 0|${_{.}^{\prime\prime}}$|7–1|${_{.}^{\prime\prime}}$|0 | 19 | 14 |
| Other | – | – | XDHZQSO | – | 6 | 6 |
| Total | 207 | 159 | ||||
Observation runs included in the archive. The ‘Surveys’ column indicates the quasar surveys involved in the given observing runs (see the description in Section 2). Several candidates from XDHZQSO selection were observed with other instruments, including Keck/DEIMOS, VLT/FORS2, and Magellan/FIRE. Six quasars were confirmed in these observations and are included in the last row (Observation Run = Other). The last two columns display the numbers of the total candidates and the non-FAIL candidates, i.e. the candidates that do not belong to ‘FAIL’ class (see Section 2.4).
| Observation run . | Dates . | Keck program ID . | Surveys . | Seeing . | Total candidates/non-FAIL . | |
|---|---|---|---|---|---|---|
| NIRES-1903 | 2019 March 03–04 | U170 | Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|7–1|${_{.}^{\prime\prime}}$|1 | 15 | 12 |
| NIRES-1905 | 2019 May 19, 2019 | U170 | Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|6–1|${_{.}^{\prime\prime}}$|0 | 6 | 4 |
| MOSFIRE-1911 | 2019 November 18–20 | U179 | Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|9–1|${_{.}^{\prime\prime}}$|2 | 15 | 5 |
| MOSFIRE-2005 | 2020 May 27–29 | U179 | Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|5–0|${_{.}^{\prime\prime}}$|7 | 13 | 3 |
| MOSFIRE-2010 | 2020 May 22–25 | U179 | Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|5–0|${_{.}^{\prime\prime}}$|7 | 34 | 25 |
| MOSFIRE-2201 | 2022 January 10–11 | U055 | XDHZQSO, Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|6–0|${_{.}^{\prime\prime}}$|7 | 7 | 4 |
| MOSFIRE-2204 | 2022 April 9 | U055 | XDHZQSO, Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|6–1|${_{.}^{\prime\prime}}$|2 | 9 | 8 |
| LRIS-2201 | 2022 January 27 | U055 | XDHZQSO, PS1COLOUR | 0|${_{.}^{\prime\prime}}$|8–1|${_{.}^{\prime\prime}}$|0 | 19 | 18 |
| LRIS-2203 | 2022 March 05–06 | U055 | XDHZQSO, PS1COLOUR | 0|${_{.}^{\prime\prime}}$|6–0|${_{.}^{\prime\prime}}$|8 | 31 | 30 |
| LRIS-2204 | 2022 April 23 | U055 | XDHZQSO, LOFAR, Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|8–1|${_{.}^{\prime\prime}}$|0 | 30 | 25 |
| LRIS-2209 | 2022 September 27 | U055 | XDHZQSO | 0|${_{.}^{\prime\prime}}$|5–0|${_{.}^{\prime\prime}}$|9 | 5 | 5 |
| LRIS-2210 | 2022 October 26–28 | U055 | XDHZQSO | 0|${_{.}^{\prime\prime}}$|7–1|${_{.}^{\prime\prime}}$|0 | 19 | 14 |
| Other | – | – | XDHZQSO | – | 6 | 6 |
| Total | 207 | 159 | ||||
| Observation run . | Dates . | Keck program ID . | Surveys . | Seeing . | Total candidates/non-FAIL . | |
|---|---|---|---|---|---|---|
| NIRES-1903 | 2019 March 03–04 | U170 | Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|7–1|${_{.}^{\prime\prime}}$|1 | 15 | 12 |
| NIRES-1905 | 2019 May 19, 2019 | U170 | Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|6–1|${_{.}^{\prime\prime}}$|0 | 6 | 4 |
| MOSFIRE-1911 | 2019 November 18–20 | U179 | Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|9–1|${_{.}^{\prime\prime}}$|2 | 15 | 5 |
| MOSFIRE-2005 | 2020 May 27–29 | U179 | Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|5–0|${_{.}^{\prime\prime}}$|7 | 13 | 3 |
| MOSFIRE-2010 | 2020 May 22–25 | U179 | Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|5–0|${_{.}^{\prime\prime}}$|7 | 34 | 25 |
| MOSFIRE-2201 | 2022 January 10–11 | U055 | XDHZQSO, Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|6–0|${_{.}^{\prime\prime}}$|7 | 7 | 4 |
| MOSFIRE-2204 | 2022 April 9 | U055 | XDHZQSO, Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|6–1|${_{.}^{\prime\prime}}$|2 | 9 | 8 |
| LRIS-2201 | 2022 January 27 | U055 | XDHZQSO, PS1COLOUR | 0|${_{.}^{\prime\prime}}$|8–1|${_{.}^{\prime\prime}}$|0 | 19 | 18 |
| LRIS-2203 | 2022 March 05–06 | U055 | XDHZQSO, PS1COLOUR | 0|${_{.}^{\prime\prime}}$|6–0|${_{.}^{\prime\prime}}$|8 | 31 | 30 |
| LRIS-2204 | 2022 April 23 | U055 | XDHZQSO, LOFAR, Z7DROPOUT | 0|${_{.}^{\prime\prime}}$|8–1|${_{.}^{\prime\prime}}$|0 | 30 | 25 |
| LRIS-2209 | 2022 September 27 | U055 | XDHZQSO | 0|${_{.}^{\prime\prime}}$|5–0|${_{.}^{\prime\prime}}$|9 | 5 | 5 |
| LRIS-2210 | 2022 October 26–28 | U055 | XDHZQSO | 0|${_{.}^{\prime\prime}}$|7–1|${_{.}^{\prime\prime}}$|0 | 19 | 14 |
| Other | – | – | XDHZQSO | – | 6 | 6 |
| Total | 207 | 159 | ||||
In Section 2.1, we summarize the different quasar searches that provide the candidates. In Section 2.2, we give a brief introduction of the spectrometers used in this work. In Section 2.3, we describe our data reduction procedures. In Section 2.4, we present our classification scheme to classify the candidates with their reduced spectra.
2.1 Quasar searches
The quasar candidates observed in the aforementioned observing runs comprise sources from various quasar searches. We briefly summarize them in this section. For brevity, we use short names of the selection methods to represent different searches. The imaging surveys involved are introduced in each subsection of the search.
2.1.1 XDHZQSO: VIKING/UKIDSS+WISE+DELS+PS1
Nanni et al. (2022) searched for high-z quasars in the ∼1000 deg2 overlapping area from the DELS (Dye et al. 2006), the VIKING Survey (Edge et al. 2013)3, and the unWISE imaging surveys (Meisner et al. 2019; Schlafly, Meisner & Green 2019) with the XDHZQSO method. They studied the distributions of both quasars and contaminants in the colour space constructed by z-band from DELS, YJHKs from VIKING, and W1W2 from unWISE. They performed forced photometry on VIKING images with a 1|${_{.}^{\prime\prime}}$|5 aperture. For sources with non-detection in DELS, they performed forced photometry with a 1|${_{.}^{\prime\prime}}$|5 aperture. They also performed forced photometry on the unWISE images with a 7 arcsec aperture. After obtaining the photometric data, they constructed the parent catalogue by applying several signal-to-noise cuts. They then trained the probability density of the contaminants on the entire parent catalogue and train the probability density of quasars on simulated sources with synthetic photometry generated from simqso (McGreer et al. 2013). With the trained densities, they predicted the probability of a given source being a quasar in certain redshift bin (PQSO) and sources with PQSO > 0.1 were selected as candidates. There were 138 and 43 candidates in the range 6 ≤ z ≤ 7, and 7 ≤ z ≤ 8, respectively. See Nanni et al. (2022) for more detailed descriptions of the methodology and the survey.
Following the approach from Nanni et al. (2022), we performed another search in the ∼4000 deg2 Large Area Survey (LAS) in the UKIDSS (Lawrence et al. 2007) footprint4 At NIR wavelengths, we used Y-, J-, H-, and K-bands from UKIDSS DR11. The UKIDSS data were obtained from the UKIRT Science Archive.5 We also used the W1- and W2-bands from the unWISE DR1. For optical bands, we used grz-bands data from the DELS DR8, and the grizy-bands data from Pan-STARRS 1 (PS1; Chambers et al. 2016) in our selection. The detailed procedures to construct the UKIDSS candidate list are as follows:
We selected all the sources with J-band signal-to-noise ratio S/N(J) ≥ 5 first, amounting for a total of 52 273 874 sources. We also removed bright sources (mJ < 17), as we found they were often artifacts or bright stars, after performing a visual inspection of a few hundreds of them.
Since the UKIDSS survey is affected by the presence of a large number of spurious sources resulting from detector cross-talk (Dye et al. 2006), we decided to split the UKIDSS J-band detected sample into two sub-catalogues: one used for 6 ≤ z ≤ 7 quasar selection and another for 7 ≤ z ≤ 8 quasar selection.
We constructed the 6 ≤ z ≤ 7 quasar search catalogue by cross-matching the UKIDSS J-band detected sources with DELS, using a radius of 2 arcsec. We only kept sources with S/N(z) ≥ 5. Since z ≥ 6 quasars drop out in the bluest optical filters, we further required our objects to have S/N(g, r) < 3.
On the other hand, we constructed the 7 ≤ z ≤ 8 quasar search catalogue by cross-matching the UKIDSS J-band detected sources with unWISE, using a radius 2 arcsec. We kept all the sources with S/N(W1) ≥ 5. For these sources we performed forced photometry on the Dark Energy Camera Legacy Survey (DECaLS; Dey et al. 2019) images with an aperture radius of 1|${_{.}^{\prime\prime}}$|5, and then further required them to have S/N(g, r) < 3.
Then, for both the 6 ≤ z ≤ 7 and 7 ≤ z ≤ 8 quasar search catalogues, we performed forced photometry on the PS1-grizy band images and removed objects with S/N(gPS1, rPS1) ≥ 3, and S/N(iPS1) ≥ 5. For the 6 ≤ z ≤ 7 search, we also remove objects with iPS1 − zPS1 < 2.
For the surviving sources, we performed forced photometry on the UKIDSS-YHK images, using an aperture radius of 1|${_{.}^{\prime\prime}}$|5.
Finally, we removed sources that have no coverage in all the requested filters (UKIDSS-YHK, DECaLS-z, PS1-izy, unWISE-W1W2). The final two parent catalogues contains 204 882, and 458 513 sources at 6 ≤ z ≤ 7 and 7 ≤ z ≤ 8, respectively.
We used these two UKIDSS parent catalogues, appropriate for selecting either 6 ≤ z ≤ 7 or 7 ≤ z ≤ 8 quasars, as the inputs to construct the contaminant models in the XDHZQSO Bayesian formalism. We adopt the same quasar probability threshold as Nanni et al. (2022), PQSO > 0.1. Combining with the candidates in Nanni et al. (2022), there are in total 48 (83) candidates at 6 ≤ z ≤ 7 (7 ≤ z ≤ 8). To date, 100 candidates have been observed. Among them, 59 are selected from VIKING and 52 are from UKIDSS. Eleven sources are selected by both searches.
2.1.2 Z7DROPOUT: UKIDSS/UHS/VHS+WISE+DELS+PS1
A series of searches following the selections of Bañados et al. (2018), Yang et al. (2020a), and Wang et al. (2021) was conducted by the same investigators. These searches aimed at finding quasars with z > 7.2 (z-band dropout) or even z > 7.5 (y-band dropout) among sources that dropped out in the optical bands. They primarily used the y-band from PS1 and z-band from DELS as dropout bands. They also utilized infrared bands from UKIDSS/UHS/VHS and WISE as detection bands. They further used the infrared colours to remove the contamination from galactic brown dwarfs. Additionally, they used forced aperture photometry and visual inspection to reject contaminants and bad photometry measurements. We observed 83 candidates from these searches in our Keck programs, but none of them were classified as quasars.
2.1.3 PS1COLOUR: PS1
Banados et al. (2022) reports the latest findings in the discoveries of z ∼ 6 quasars in the PS1 survey. They also includes results from a search in the VIKING survey, with an area of 1350 |$\rm deg^2$|. Both searches are based on colour cuts. The procedures of the PS1 search are described in detail in Bañados et al. (2016). Ten candidates were observed in our Keck programs, and two of them were confirmed as quasars.
2.1.4 LOFAR: DELS+WISE+LoTSS
In contrast to the previous quasar searches that only used optical/IR imaging, Gloudemans et al. (2022) used radio detection from the LOFAR Two-metre Sky Survey (LoTSS, 144MHz; Shimwell et al. 2017). The initial sample was built from DELS based on the photometric redshift estimates in Duncan (2022) and optical (DELS-grz, DR8) and NIR (WISE-W1) colours. They further required the sources in the initial sample to have a radio detection from LoTSS. The extra constraint on radio emission can remove a large fraction of stellar contaminants. Additionally, they performed SED fitting with both galaxy and quasar templates to narrow down the candidates with inferred redshift. A final sample of 142 candidates were selected for spectroscopic confirmation. Four of them were observed with Keck/LRIS in our programs, and two of them were confirmed as quasars.
2.2 Optical and near-infrared spectroscopy
In the two Keck programs, we utilize three different spectrometers to search for high-z quasars, namely LRIS, MOSFIRE and NIRES. Below we provide relevant information for the observation with each instrument.
LRIS is an optical spectrometer with a double spectrometer. For the purpose of high-z quasar confirmation we only use the red part with a pixel scale of 0|${_{.}^{\prime\prime}}$|123 per pixel. Owing to the upgraded red detector (Rockosi et al. 2010) and its working wavelength (optical), LRIS has significantly higher sensitivity for quasar confirmation than the other two spectrometers at the same wavelength. Specifically, we used the 1arcsec slit, the gold coated 600/10 000 grating, and the D680 dichroic in our observation. These result in a wavelength coverage from ∼7500 to ∼10 600 Å; and a spectral resolution of 214 km s−1 at 9700 Å;. For each candidate observed with LRIS, we generally take 2 × 300 s exposures to achieve S/N ∼ 3 per resolution element. Moreover, we did not dither between exposures during the LRIS observations. In ideal conditions, the upper bound of the wavelength coverage enables us to confirm quasars up to z ∼ 7.6. But in order to test whether we can reach such a high redshift in practice, we perform simulations on the observations with LRIS, as described in Section 4.
MOSFIRE is an infrared multi-object spectrometer. For MOSFIRE observations, we dithered along the slit to enable data reduction via image differencing as is customary in the NIR. We take MOSFIRE spectroscopy in the Y-band with a slit width of 1 arcsec. The wavelength coverage of the Y-band is from 9716 to 11 250 Å;. The spectral resolution with this setting is approximately 240 km s−1 at 9700 Å;. The exposure time for each frame is 150 s and each dithering sequence is usually consist of four frames in ABAB pattern. We take at least one sequence for each target, thus the minimal total exposure time is 600 s.
NIRES is an infrared echellette spectrometer. The wavelength coverage of NIRES is |$0.8-2.4\rm{\mu m}$| in echelle format, spanning five orders. The slit width of NIRES is fixed to 0|${_{.}^{\prime\prime}}$|55, leading to a resolution of 120 km s−1 at |$1\rm{\mu m}$| in the bluest orders. In NIRES observation, we dither along the slit following an ABBA pattern with an exposure time of 300 or 360 s per frame in the sequence. The typical total exposure time for a target is thus 1200 s.
In Fig. 1, we show the throughput curves of LRIS, MOSFIRE, and NIRES (1) under a condition of 0|${_{.}^{\prime\prime}}$|9 seeing and (2) corrected for the slit loss, assuming the standard stars are perfectly centred in the slit. The throughput of LRIS was originally measured with a 1 arcsec slit width in LRIS-2203 run, with a seeing of 0|${_{.}^{\prime\prime}}$|74. The MOSFIRE Y-band throughput was obtained with a 1 arcsec slit width and a 0|${_{.}^{\prime\prime}}$|76 seeing in MOSFIRE-2201 run. The NIRES throughput here was measured with a 0|${_{.}^{\prime\prime}}$|55 slit width in NIRES-1905 run with a seeing of 0|${_{.}^{\prime\prime}}$|9 in the bluest order. The throughput curves are then scaled to 0|${_{.}^{\prime\prime}}$|9 or corrected for the slit loss following the procedures described in Section 2.3.
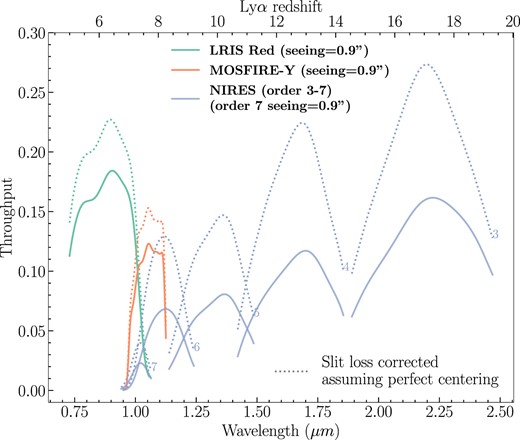
The solid lines are throughput curves of the three spectrometers, corresponding to an 0|${_{.}^{\prime\prime}}$|9 seeing for LRIS, MOSFIRE, and order 7 of NIRES. The throughput of LRIS was originally measured with an 1 arcsec slit width in LRIS-2203 run, with a seeing of 0|${_{.}^{\prime\prime}}$|74. The MOSFIRE Y-band throughput was obtained with a 1 arcsec slit width and a 0|${_{.}^{\prime\prime}}$|76 seeing in MOSFIRE-2201 run. The NIRES throughput here was measured with a 0|${_{.}^{\prime\prime}}$|55 slit width in NIRES-1905 run with a seeing of 0|${_{.}^{\prime\prime}}$|9 in the order 7. The LRIS and MOSFIRE throughput curves are then scaled to a seeing of 0|${_{.}^{\prime\prime}}$|9. The dotted lines are throughput curves corrected for the slit loss, assuming a perfect centring of the star on the slit. The upper axis shows the corresponding Lyα redshift of high-z quasars that they can reach. For all instruments, the throughput curves are determined from observation of the standard star GD153.
Several candidates from XDHZQSO selection (see Section 2.1.1) were observed with other instruments, including Keck/DEIMOS (Faber et al. 2003), VLT/FORS2 (Appenzeller & Rupprecht 1992), and Magellan/FIRE (Simcoe et al. 2008, 2013). We only include the confirmed quasars observed by these instruments in this work. However, for the instrument-related analysis in Section 4, we only confine to the three Keck spectrometers mentioned above.
2.3 Spectroscopic data reduction with pypeit
We use the Python Spectroscopic Data Reduction Pipeline (pypeit; Prochaska et al. 2020) to reduce all the data in a consistent manner. In the following, we will briefly describe the reduction procedures using pypeit. A more comprehensive description can be found in the pypeit documentation.6
First, we perform a standard automated pypeit reduction with the script run_pypeit on all the science frames. This includes the following steps:
Basic image processing including gain correction, bias subtraction, dark subtraction, and flat fielding.
Construction of the wavelength solutions and the wavelength tilt models based on either arc (mostly for LRIS) or science frames (i.e. using sky OH lines, mostly for NIR instruments).
Cosmic rays removal with the L. A. COSMIC algorithm (van Dokkum 2001).
Sky subtraction, which is split into multiple steps: The first global-sky subtraction is performed with a B-spline fitting procedure (e.g. Kelson 2003), following by the first object detection. Then the second global-sky subtraction is performed, masking the objects previously detected. The second object detection is then implemented. Finally, a local sky-subtraction is applied on all the objects.
After the general reduction, we calculate the sensitivity function using the observation on the standard stars with pypeit script pypeit_sensfunc. With the sensitivity function, we perform the following procedures to produce fully reduced spectra:
Flux calibration that converts the spectra in pixel counts into flux with the sensitivity function using pypeit script pypeit_flux_calib.
Co-addition of the multiple frames of the same targets together to achieve higher S/N. For bright objects, we combine the 1d spectra directly using pypeit script pypeit_coadd_1d. For faint objects, we combine their 2D spectra following the dithering pattern with pypeit script pypeit_coadd_2d and extract the 1D spectra afterward. All the 1D spectra are extracted with both boxcar and optimal extraction method (Horne 1986).
Telluric correction with pypeit script pypeit_tellfit. For confirmed quasars, we correct for telluric absorption with quasar model. For the other candidates, we use a polynomial model with an order of 7.
The throughput curves in Fig. 1 are intermediate products of the reduction. To derive the throughput curves with full transmission or a given seeing, we start with assuming that the standard stars are at the centre of the slits, and then use the fitted full width at half-maximum (FWHM) profiles7 of the targets and the slit width to correct for the slit losses. To scale to another seeing, we use the ratio between the desired seeing and the mean FWHM of the trace to scale the FWHM profile and repeat the previous calculation again.
All the pypeit files to reproduce the reduction are publicly available in a Github repository8
2.4 Classification of the candidates
After obtaining the fluxed and telluric-corrected spectrum for each candidate, the next step is to classify them. We first visually select out quasars and inconclusive ones, i.e. potential quasars but need re-observation to confirm. Then, we use stellar templates (late M types to T type) to fit the spectra of all the other targets. We visually inspect the fitting and identify the sources with a good fit as brown dwarfs. The others are then non-quasar objects with unknown classification. The detailed classification scheme and criteria are as follows:
QSO: A sharp continuum break in the spectrum which in most cases is accompanied by emission line (see Figs 2 and 3).
INCONCLUSIVE: A drop in the flux can been identified in the spectrum, however, the break is too close to the blue end of the spectrum (thus all of them are from NIR observation), and the spectrum is fainter than expected based on the corresponding J-band magnitude (see Section 4). We classify objects with these characteristics as inconclusive targets, which require re-observation to confirm their classification (see Fig. 4).
STAR: To select stellar objects from the sources that do not belong to QSO or INCONCLUSIVE class, we fit the spectra of them with existing brown dwarf spectra from Kirkpatrick, Henry & McCarthy (1991) and Kirkpatrick et al. (1999), with the spectral type ranging from late M types to early T types. We apply standard χ2 fitting to all the sources that do not belong to QSO type, and determine the best-fitting spectral type as the one with the minimal χ2. We visually inspect the best-fitting result and classify the sources with a good fit as STAR. The best-fitting spectral type is also appended to each STAR type target. See Figs 4 and 5 as examples.
UNQ: We classify the rest of the sources as UNQ, short for unknown non-quasar. Many of UNQ objects also show gradually declining shape towards the blue end or absorption features like brown dwarfs, but the S/N of their spectra are too low to support reliable STAR classification. See Figs 6, 4, and 5 as examples.
FAIL: Sources in this type do not have corresponding final 1d spectra due to several reasons. The major cause is the absence of the target trace in the 2D spectrum, most probably due to very bad observing conditions. Other possible reason is the contamination of moving objects (Bosman, Davies & Bañados 2023). Alternatively, the coordinates for these targets were incorrect or the acquisition procedure failed. Also, a few sources were close to the moon when they were observed, which might explain some of the failures.

Reduced 2D and 1D spectra of the new quasars confirmed with Keck/LRIS. Four of them belong to the XDHZQSO selection described in Section 2.1.1. The reduced 2D spectra are sky-subtracted but not flux-calibrated and telluric-corrected. The 1D spectra here are flux-calibrated and telluric-corrected. The blue curves are the noise. The grey curve in the bottom panel is the average telluric model. The spectra and noise are smoothed with a 5 pixel boxcar filter, using the inverse variance as relative weights.
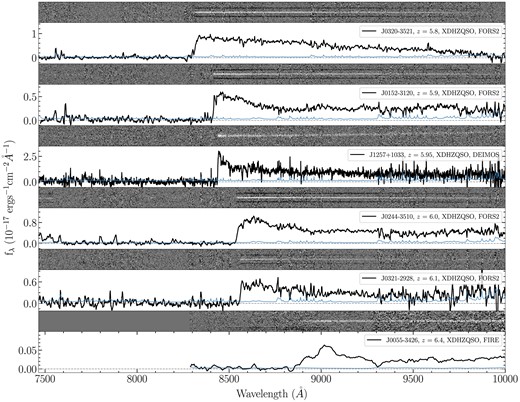
Reduced 2D and 1D spectra of the new quasars confirmed with VLT/FORS2, Keck/DEIMOS, and Magellan/FIRE. All of them are candidates from XDHZQSO selection (see Section 2.1.1). J0055-3426 was selected by Jinyi Yang as high-z quasar candidate independently. The reduced 2D spectra are sky-subtracted, but not flux-calibrated and telluric-corrected. The 1D spectra here are flux-calibrated and telluric-corrected. The blue curves are the noise. The grey curve in the bottom panel is the average telluric model. The spectra and noise are smoothed with a 5 pixel boxcar filter using the inverse variance as relative weights.
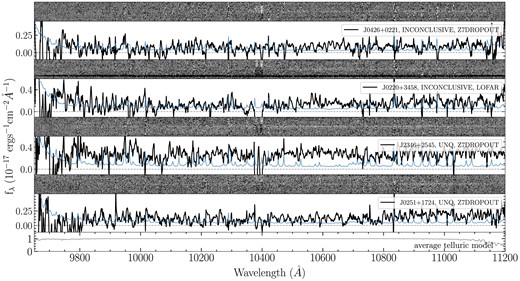
Reduced 2D and 1D spectra of two INCONCLUSIVE type and two UNQ type objects observed with MOSFIRE. The reduced 2D spectra are sky-subtracted but not flux-calibrated or telluric-corrected. The 1d spectra here are flux-calibrated and telluric-corrected. The blue curves are the noise. The grey curve in the bottom panel is the average telluric model. The spectra and noise are smoothed using the inverse variance with a smoothing window of 5.
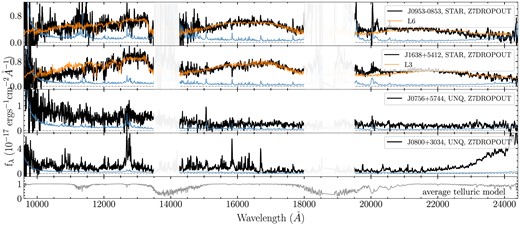
Reduced 2D and 1D spectra of two STAR type and two UNQ objects observed with NIRES. The 1D spectra here are flux-calibrated and telluric-corrected, and the orange curves are the brown dwarf spectra with the lowest reduced χ2 values. The blue curves are the noise. The grey curve in the bottom panel is the average telluric model. The spectra and noise are smoothed using the inverse variance with a smoothing window of 9 pixels. We do not show the 2D spectra here because NIRES has multiple orders. We note that the flux in the red end of J0800+3034 is not real, but a saturating issue.
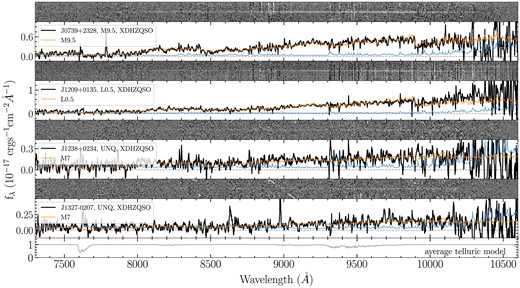
Reduced 2D and 1D spectra of several STAR and UNQ types objects observed with LRIS. The reduced 2D spectra are sky-subtracted but not flux-calibrated or telluric-corrected. The 1D spectra here are flux-calibrated and telluric-corrected. The blue curves are the noise, and the orange curves are the brown dwarf spectra with the lowest reduced χ2 values. The grey curve in the bottom panel is the average telluric model. The spectra and noise are smoothed using the inverse variance with a smoothing window of 5.
3 HIGH-z QUASAR CANDIDATE ARCHIVE
In this section, we present the content of the HzQCA and analyse the contaminant population with it. In Section 3.1, we display reduced 2d and 1d spectra of all the new quasars (QSO) and INCONCLUSIVE type objects, as well as several spectra of the STAR and UNQ types as examples. In Section 3.2, we describe the contents of the HzQCA catalogue. In Section 3.3, we analyse the distribution of our spectroscopically identified brown dwarfs in colour space and compare with empirical brown dwarf models that have been adopted in the quasar selection literature.
3.1 Reduced spectra
3.1.1 New QSOs
In this work, we discover 14 new z > 5.5 quasars, which are selected by the XDHZQSO, PS1COLOUR, and LOFAR searches. J1401+4542, J1523+2935 (J1458+1012, J1724+3718) are from LOFAR (PS1COLOUR) searches, and are previously reported in Gloudemans et al. (2022) and Banados et al. (2022), respectively. We present here eight new quasars selected with the XDHZQSO method (see Section 2.1.1). Out of the 14 quasars, eight of them were observed with Keck/LRIS, while the other were observed with Keck/DEIMOS, VLT/FORS2, and Magellan/FIRE. We display the reduced 2D and 1D spectra of quasars identified by Keck/LRIS in Fig. 2, and the spectra of the other quasars in Fig. 3. All of them are listed in Table 2. The reduced 2D spectra are sky-subtracted, but not flux-calibrated or telluric-corrected. The 1D spectra here are flux-calibrated and telluric-corrected. They are also smoothed with a 5 pixel boxcar filter, but using the inverse variance as relative weights. The new quasars from PS1COLOUR and LOFAR searches have also been reported in Banados et al. (2022) and Gloudemans et al. (2022). J1523+2935, J0320-3521, and J0055-3426 were also independently discovered by Wenzl et al. (2021), Ighina et al. (2023), and Yang et al. (in prep.), respectively. The redshifts reported here have been determined by visual inspection.
New QSOs discovered in this work. J1401+4542, J1523+2935 (J1458+1012, J1724+3718) are from LOFAR (PS1COLOUR) searches and are previously reported in Gloudemans et al. (2022) and Banados et al. (2022), respectively. J0055-3426, J0320-3521, and J1523+2935 were independently selected by Yang et al. (in prep.), Ighina et al. (2023), and Wenzl et al. (2021), respectively. The ‘Survey’ column refers to the surveys mentioned in Section 2.1. References for the acquisition of the photometry measurements are also described in Section 2.1. The instruments that were used to obtain the spectra are also listed here. The dates of the observations can be found in the electronic version of the full table.
| Name . | RA . | Dec. . | Redshift . | Survey . | z . | Y . | J . | H . | K . | W1 . | W2 . | Telescope/Instrument . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| J0055-3426 | 00:55:37.07 | −34:26:36.30 | 6.40 | XDHZQSO | 21.55 | 21.38 | 20.99 | 20.82 | 20.73 | 20.72 | 20.25 | Magellan/FIRE |
| J0126-3055 | 01:26:52.90 | −30:55:35.84 | 6.20 | XDHZQSO | 21.31 | 21.37 | 21.43 | 21.87 | 21.30 | 20.97 | 21.82 | Keck/LRIS |
| J0152-3120 | 01:52:37.93 | −31:20:23.99 | 5.90 | XDHZQSO | 21.36 | 21.48 | 21.18 | 21.28 | 21.06 | 21.07 | 20.85 | VLT/FORS2 |
| J0244-3510 | 02:44:26.25 | −35:10:33.21 | 6.00 | XDHZQSO | 20.71 | 20.94 | 20.70 | 20.44 | 20.32 | 20.40 | 20.69 | VLT/FORS2 |
| J0320-35219 | 03:20:21.44 | −35:21:04.19 | 5.80 | XDHZQSO | 20.51 | 20.56 | 20.23 | 20.30 | 20.21 | 20.09 | 20.37 | VLT/FORS2 |
| J0321-2928 | 03:21:23.05 | −29:28:57.19 | 6.10 | XDHZQSO | 21.32 | 21.77 | 21.26 | 20.96 | 21.30 | 20.84 | 21.10 | VLT/FORS2 |
| J0901+2906 | 09:01:38.13 | +29:06:55.54 | 6.10 | XDHZQSO | 20.86 | 20.51 | 20.59 | 21.43 | 20.05 | 20.11 | 20.01 | Keck/LRIS |
| J1111+0640 | 11:11:25.15 | +06:40:53.98 | 6.00 | XDHZQSO | 20.83 | 21.46 | 20.75 | 20.48 | 21.20 | 20.66 | 20.40 | Keck/LRIS |
| J1257+1033 | 12:57:14.14 | +10:33:30.35 | 5.95 | XDHZQSO | 21.04 | 20.91 | 20.54 | 20.35 | 20.73 | 20.29 | 19.78 | Keck/DEIMOS |
| J1319+0101 | 13:19:27.52 | +01:01:56.30 | 5.70 | XDHZQSO | 21.24 | 21.55 | 21.43 | 21.09 | 21.04 | 21.66 | 21.93 | Keck/LRIS |
| J1401+4542 | 14:01:20.86 | +45:42:53.46 | 5.50 | LOFAR | – | – | – | – | – | – | – | Keck/LRIS |
| J1458+1012 | 14:58:36.16 | +10:12:49.65 | 5.60 | PS1COLOUR | – | – | – | – | – | – | – | Keck/LRIS |
| J1523+2935 | 15:23:30.67 | +29:35:39.67 | 5.70 | LOFAR | – | – | – | – | – | – | – | Keck/LRIS |
| J1724+3718 | 17:24:29.93 | +37:18:21.78 | 5.74 | PS1COLOUR | – | – | – | – | – | – | – | Keck/LRIS |
| Name . | RA . | Dec. . | Redshift . | Survey . | z . | Y . | J . | H . | K . | W1 . | W2 . | Telescope/Instrument . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| J0055-3426 | 00:55:37.07 | −34:26:36.30 | 6.40 | XDHZQSO | 21.55 | 21.38 | 20.99 | 20.82 | 20.73 | 20.72 | 20.25 | Magellan/FIRE |
| J0126-3055 | 01:26:52.90 | −30:55:35.84 | 6.20 | XDHZQSO | 21.31 | 21.37 | 21.43 | 21.87 | 21.30 | 20.97 | 21.82 | Keck/LRIS |
| J0152-3120 | 01:52:37.93 | −31:20:23.99 | 5.90 | XDHZQSO | 21.36 | 21.48 | 21.18 | 21.28 | 21.06 | 21.07 | 20.85 | VLT/FORS2 |
| J0244-3510 | 02:44:26.25 | −35:10:33.21 | 6.00 | XDHZQSO | 20.71 | 20.94 | 20.70 | 20.44 | 20.32 | 20.40 | 20.69 | VLT/FORS2 |
| J0320-35219 | 03:20:21.44 | −35:21:04.19 | 5.80 | XDHZQSO | 20.51 | 20.56 | 20.23 | 20.30 | 20.21 | 20.09 | 20.37 | VLT/FORS2 |
| J0321-2928 | 03:21:23.05 | −29:28:57.19 | 6.10 | XDHZQSO | 21.32 | 21.77 | 21.26 | 20.96 | 21.30 | 20.84 | 21.10 | VLT/FORS2 |
| J0901+2906 | 09:01:38.13 | +29:06:55.54 | 6.10 | XDHZQSO | 20.86 | 20.51 | 20.59 | 21.43 | 20.05 | 20.11 | 20.01 | Keck/LRIS |
| J1111+0640 | 11:11:25.15 | +06:40:53.98 | 6.00 | XDHZQSO | 20.83 | 21.46 | 20.75 | 20.48 | 21.20 | 20.66 | 20.40 | Keck/LRIS |
| J1257+1033 | 12:57:14.14 | +10:33:30.35 | 5.95 | XDHZQSO | 21.04 | 20.91 | 20.54 | 20.35 | 20.73 | 20.29 | 19.78 | Keck/DEIMOS |
| J1319+0101 | 13:19:27.52 | +01:01:56.30 | 5.70 | XDHZQSO | 21.24 | 21.55 | 21.43 | 21.09 | 21.04 | 21.66 | 21.93 | Keck/LRIS |
| J1401+4542 | 14:01:20.86 | +45:42:53.46 | 5.50 | LOFAR | – | – | – | – | – | – | – | Keck/LRIS |
| J1458+1012 | 14:58:36.16 | +10:12:49.65 | 5.60 | PS1COLOUR | – | – | – | – | – | – | – | Keck/LRIS |
| J1523+2935 | 15:23:30.67 | +29:35:39.67 | 5.70 | LOFAR | – | – | – | – | – | – | – | Keck/LRIS |
| J1724+3718 | 17:24:29.93 | +37:18:21.78 | 5.74 | PS1COLOUR | – | – | – | – | – | – | – | Keck/LRIS |
New QSOs discovered in this work. J1401+4542, J1523+2935 (J1458+1012, J1724+3718) are from LOFAR (PS1COLOUR) searches and are previously reported in Gloudemans et al. (2022) and Banados et al. (2022), respectively. J0055-3426, J0320-3521, and J1523+2935 were independently selected by Yang et al. (in prep.), Ighina et al. (2023), and Wenzl et al. (2021), respectively. The ‘Survey’ column refers to the surveys mentioned in Section 2.1. References for the acquisition of the photometry measurements are also described in Section 2.1. The instruments that were used to obtain the spectra are also listed here. The dates of the observations can be found in the electronic version of the full table.
| Name . | RA . | Dec. . | Redshift . | Survey . | z . | Y . | J . | H . | K . | W1 . | W2 . | Telescope/Instrument . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| J0055-3426 | 00:55:37.07 | −34:26:36.30 | 6.40 | XDHZQSO | 21.55 | 21.38 | 20.99 | 20.82 | 20.73 | 20.72 | 20.25 | Magellan/FIRE |
| J0126-3055 | 01:26:52.90 | −30:55:35.84 | 6.20 | XDHZQSO | 21.31 | 21.37 | 21.43 | 21.87 | 21.30 | 20.97 | 21.82 | Keck/LRIS |
| J0152-3120 | 01:52:37.93 | −31:20:23.99 | 5.90 | XDHZQSO | 21.36 | 21.48 | 21.18 | 21.28 | 21.06 | 21.07 | 20.85 | VLT/FORS2 |
| J0244-3510 | 02:44:26.25 | −35:10:33.21 | 6.00 | XDHZQSO | 20.71 | 20.94 | 20.70 | 20.44 | 20.32 | 20.40 | 20.69 | VLT/FORS2 |
| J0320-35219 | 03:20:21.44 | −35:21:04.19 | 5.80 | XDHZQSO | 20.51 | 20.56 | 20.23 | 20.30 | 20.21 | 20.09 | 20.37 | VLT/FORS2 |
| J0321-2928 | 03:21:23.05 | −29:28:57.19 | 6.10 | XDHZQSO | 21.32 | 21.77 | 21.26 | 20.96 | 21.30 | 20.84 | 21.10 | VLT/FORS2 |
| J0901+2906 | 09:01:38.13 | +29:06:55.54 | 6.10 | XDHZQSO | 20.86 | 20.51 | 20.59 | 21.43 | 20.05 | 20.11 | 20.01 | Keck/LRIS |
| J1111+0640 | 11:11:25.15 | +06:40:53.98 | 6.00 | XDHZQSO | 20.83 | 21.46 | 20.75 | 20.48 | 21.20 | 20.66 | 20.40 | Keck/LRIS |
| J1257+1033 | 12:57:14.14 | +10:33:30.35 | 5.95 | XDHZQSO | 21.04 | 20.91 | 20.54 | 20.35 | 20.73 | 20.29 | 19.78 | Keck/DEIMOS |
| J1319+0101 | 13:19:27.52 | +01:01:56.30 | 5.70 | XDHZQSO | 21.24 | 21.55 | 21.43 | 21.09 | 21.04 | 21.66 | 21.93 | Keck/LRIS |
| J1401+4542 | 14:01:20.86 | +45:42:53.46 | 5.50 | LOFAR | – | – | – | – | – | – | – | Keck/LRIS |
| J1458+1012 | 14:58:36.16 | +10:12:49.65 | 5.60 | PS1COLOUR | – | – | – | – | – | – | – | Keck/LRIS |
| J1523+2935 | 15:23:30.67 | +29:35:39.67 | 5.70 | LOFAR | – | – | – | – | – | – | – | Keck/LRIS |
| J1724+3718 | 17:24:29.93 | +37:18:21.78 | 5.74 | PS1COLOUR | – | – | – | – | – | – | – | Keck/LRIS |
| Name . | RA . | Dec. . | Redshift . | Survey . | z . | Y . | J . | H . | K . | W1 . | W2 . | Telescope/Instrument . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| J0055-3426 | 00:55:37.07 | −34:26:36.30 | 6.40 | XDHZQSO | 21.55 | 21.38 | 20.99 | 20.82 | 20.73 | 20.72 | 20.25 | Magellan/FIRE |
| J0126-3055 | 01:26:52.90 | −30:55:35.84 | 6.20 | XDHZQSO | 21.31 | 21.37 | 21.43 | 21.87 | 21.30 | 20.97 | 21.82 | Keck/LRIS |
| J0152-3120 | 01:52:37.93 | −31:20:23.99 | 5.90 | XDHZQSO | 21.36 | 21.48 | 21.18 | 21.28 | 21.06 | 21.07 | 20.85 | VLT/FORS2 |
| J0244-3510 | 02:44:26.25 | −35:10:33.21 | 6.00 | XDHZQSO | 20.71 | 20.94 | 20.70 | 20.44 | 20.32 | 20.40 | 20.69 | VLT/FORS2 |
| J0320-35219 | 03:20:21.44 | −35:21:04.19 | 5.80 | XDHZQSO | 20.51 | 20.56 | 20.23 | 20.30 | 20.21 | 20.09 | 20.37 | VLT/FORS2 |
| J0321-2928 | 03:21:23.05 | −29:28:57.19 | 6.10 | XDHZQSO | 21.32 | 21.77 | 21.26 | 20.96 | 21.30 | 20.84 | 21.10 | VLT/FORS2 |
| J0901+2906 | 09:01:38.13 | +29:06:55.54 | 6.10 | XDHZQSO | 20.86 | 20.51 | 20.59 | 21.43 | 20.05 | 20.11 | 20.01 | Keck/LRIS |
| J1111+0640 | 11:11:25.15 | +06:40:53.98 | 6.00 | XDHZQSO | 20.83 | 21.46 | 20.75 | 20.48 | 21.20 | 20.66 | 20.40 | Keck/LRIS |
| J1257+1033 | 12:57:14.14 | +10:33:30.35 | 5.95 | XDHZQSO | 21.04 | 20.91 | 20.54 | 20.35 | 20.73 | 20.29 | 19.78 | Keck/DEIMOS |
| J1319+0101 | 13:19:27.52 | +01:01:56.30 | 5.70 | XDHZQSO | 21.24 | 21.55 | 21.43 | 21.09 | 21.04 | 21.66 | 21.93 | Keck/LRIS |
| J1401+4542 | 14:01:20.86 | +45:42:53.46 | 5.50 | LOFAR | – | – | – | – | – | – | – | Keck/LRIS |
| J1458+1012 | 14:58:36.16 | +10:12:49.65 | 5.60 | PS1COLOUR | – | – | – | – | – | – | – | Keck/LRIS |
| J1523+2935 | 15:23:30.67 | +29:35:39.67 | 5.70 | LOFAR | – | – | – | – | – | – | – | Keck/LRIS |
| J1724+3718 | 17:24:29.93 | +37:18:21.78 | 5.74 | PS1COLOUR | – | – | – | – | – | – | – | Keck/LRIS |
3.1.2 STAR, UNQ, and INCONCLUSIVE
In Fig. 6, we show four examples of STAR and UNQ types objects observed with LRIS. The best-fitting brown dwarf templates are also shown (orange lines). The first two objects that have a good fitting results are labelled as STAR and the other two are UNQ. Like many other UNQ type objects, J1238+0234 in this figure shows gradually declining continuum towards the blue end, similar with a brown dwarf. But the S/N of these spectra are not high enough to support a reliable brown dwarf classification.
In Fig. 4, we show the spectra of two INCONCLUSIVE type and two UNQ type objects observed with MOSFIRE. The spectra of the two INCONCLUSIVE type objects drop near the blue end. However, as the throughput curve of MOSFIRE drops steeply |$\lesssim 1\rm{\mu m}$| as well, we cannot confidently identify such drops in fluxes as continuum breaks. It is also possible that some of the UNQ type objects observed with MOSFIRE are actually quasars with lower redshift, or with a reddened spectrum. But we will need higher S/N optical spectra to make such classification.
Finally, two STAR type and two UNQ type objects observed with NIRES are displayed in Fig. 5. We can see that the STAR type objects are cooler brown dwarfs than those in LRIS runs (see Fig. 6). This is expected as all the candidates in NIRES observation runs are from the Z7DROPOUT searches (see Section 2.1.2), where most of the contaminants are late L type and T type brown dwarfs. We note that the flux in the red end of J0800+3034 is not real, but a saturating issue.
The spectra of other sources that belong to STAR and UNQ types (there are only two INCONCLUSIVE type objects, and are all displayed in Fig. 4) are provided in Appendix A.
3.2 The catalogue
In this section, we describe the contents of the HzQCA. The classification results, following Section 2.4, are summarized in Table 3. There are 14 quasars discovered in these observation and eight of them are newly reported in this paper (see Section 2). There are 51 sources classified as brown dwarfs, while 74 sources are UNQ objects. Two candidates in MOSFIRE runs fall into the INCONCLUSIVE class. Finally, 42 objects are labelled as FAIL. Most of the objects in the FAIL type were observed in the first two runs with MOSFIRE, when the observing strategy was under testing. The observing condition of the MOSFIRE-1911 run was also not good due to a bad seeing, leading to more objects with lower S/N.
Summary of the classification. See Section 2.4 for the details of different classes.
| Type . | Number . | Fraction . |
|---|---|---|
| QSO | 14 | 7 per cent |
| INCONCLUSIVE | 2 | 1 per cent |
| STAR | 63 | 30 per cent |
| uNQ | 79 | 38 per cent |
| FAIL | 49 | 24 per cent |
| Total | 207 | 100 per cent |
| Type . | Number . | Fraction . |
|---|---|---|
| QSO | 14 | 7 per cent |
| INCONCLUSIVE | 2 | 1 per cent |
| STAR | 63 | 30 per cent |
| uNQ | 79 | 38 per cent |
| FAIL | 49 | 24 per cent |
| Total | 207 | 100 per cent |
Summary of the classification. See Section 2.4 for the details of different classes.
| Type . | Number . | Fraction . |
|---|---|---|
| QSO | 14 | 7 per cent |
| INCONCLUSIVE | 2 | 1 per cent |
| STAR | 63 | 30 per cent |
| uNQ | 79 | 38 per cent |
| FAIL | 49 | 24 per cent |
| Total | 207 | 100 per cent |
| Type . | Number . | Fraction . |
|---|---|---|
| QSO | 14 | 7 per cent |
| INCONCLUSIVE | 2 | 1 per cent |
| STAR | 63 | 30 per cent |
| uNQ | 79 | 38 per cent |
| FAIL | 49 | 24 per cent |
| Total | 207 | 100 per cent |
The format of the full catalogue is presented in Table 4. The full archive is provided in the electronic version of the journal.
| Candidate . | RA . | Dec. . | mJ . | Label . | Spectral type . | Redshift . | Survey . |
|---|---|---|---|---|---|---|---|
| LRIS-2203 (Part) | |||||||
| J0810+2352 | 122°40′04|${_{.}^{\prime}}$|44 | 23°52′35|${_{.}^{\prime}}$|04 | 20.20 | STAR | M9 | – | XDHZQSO |
| J0850+0146 | 132°32′06|${_{.}^{\prime}}$|72 | 01°46′42|${_{.}^{\prime}}$|96 | 20.95 | STAR | L2 | – | XDHZQSO |
| J0901+2906 | 135°24′32|${_{.}^{\prime}}$|04 | 29°06′55|${_{.}^{\prime}}$|44 | 20.59 | QSO | – | 6.10 | XDHZQSO |
| J0911+0022 | 137°55′04|${_{.}^{\prime}}$|44 | 00°22′42|${_{.}^{\prime}}$|60 | 21.29 | STAR | M9 | – | XDHZQSO |
| J0947+0111 | 146°58′52|${_{.}^{\prime}}$|32 | 01°11′26|${_{.}^{\prime}}$|88 | 20.57 | STAR | M8 | – | XDHZQSO |
| J1100+0203 | 165°00′43|${_{.}^{\prime}}$|56 | 02°03′00|${_{.}^{\prime}}$|36 | 21.52 | UNQ | – | – | XDHZQSO |
| J1143-0248 | 175°59′01|${_{.}^{\prime}}$|68 | −02°48′29|${_{.}^{\prime}}$|52 | 21.76 | UNQ | – | – | XDHZQSO |
| J1153-2239 | 178°20′23|${_{.}^{\prime}}$|28 | −22°39′01|${_{.}^{\prime}}$|08 | – | STAR | M9 | – | PS1COLOUR |
| J1200+0112 | 180°00′47|${_{.}^{\prime}}$|52 | 01°12′14|${_{.}^{\prime}}$|40 | 21.67 | UNQ | – | – | XDHZQSO |
| Candidate . | RA . | Dec. . | mJ . | Label . | Spectral type . | Redshift . | Survey . |
|---|---|---|---|---|---|---|---|
| LRIS-2203 (Part) | |||||||
| J0810+2352 | 122°40′04|${_{.}^{\prime}}$|44 | 23°52′35|${_{.}^{\prime}}$|04 | 20.20 | STAR | M9 | – | XDHZQSO |
| J0850+0146 | 132°32′06|${_{.}^{\prime}}$|72 | 01°46′42|${_{.}^{\prime}}$|96 | 20.95 | STAR | L2 | – | XDHZQSO |
| J0901+2906 | 135°24′32|${_{.}^{\prime}}$|04 | 29°06′55|${_{.}^{\prime}}$|44 | 20.59 | QSO | – | 6.10 | XDHZQSO |
| J0911+0022 | 137°55′04|${_{.}^{\prime}}$|44 | 00°22′42|${_{.}^{\prime}}$|60 | 21.29 | STAR | M9 | – | XDHZQSO |
| J0947+0111 | 146°58′52|${_{.}^{\prime}}$|32 | 01°11′26|${_{.}^{\prime}}$|88 | 20.57 | STAR | M8 | – | XDHZQSO |
| J1100+0203 | 165°00′43|${_{.}^{\prime}}$|56 | 02°03′00|${_{.}^{\prime}}$|36 | 21.52 | UNQ | – | – | XDHZQSO |
| J1143-0248 | 175°59′01|${_{.}^{\prime}}$|68 | −02°48′29|${_{.}^{\prime}}$|52 | 21.76 | UNQ | – | – | XDHZQSO |
| J1153-2239 | 178°20′23|${_{.}^{\prime}}$|28 | −22°39′01|${_{.}^{\prime}}$|08 | – | STAR | M9 | – | PS1COLOUR |
| J1200+0112 | 180°00′47|${_{.}^{\prime}}$|52 | 01°12′14|${_{.}^{\prime}}$|40 | 21.67 | UNQ | – | – | XDHZQSO |
| Candidate . | RA . | Dec. . | mJ . | Label . | Spectral type . | Redshift . | Survey . |
|---|---|---|---|---|---|---|---|
| LRIS-2203 (Part) | |||||||
| J0810+2352 | 122°40′04|${_{.}^{\prime}}$|44 | 23°52′35|${_{.}^{\prime}}$|04 | 20.20 | STAR | M9 | – | XDHZQSO |
| J0850+0146 | 132°32′06|${_{.}^{\prime}}$|72 | 01°46′42|${_{.}^{\prime}}$|96 | 20.95 | STAR | L2 | – | XDHZQSO |
| J0901+2906 | 135°24′32|${_{.}^{\prime}}$|04 | 29°06′55|${_{.}^{\prime}}$|44 | 20.59 | QSO | – | 6.10 | XDHZQSO |
| J0911+0022 | 137°55′04|${_{.}^{\prime}}$|44 | 00°22′42|${_{.}^{\prime}}$|60 | 21.29 | STAR | M9 | – | XDHZQSO |
| J0947+0111 | 146°58′52|${_{.}^{\prime}}$|32 | 01°11′26|${_{.}^{\prime}}$|88 | 20.57 | STAR | M8 | – | XDHZQSO |
| J1100+0203 | 165°00′43|${_{.}^{\prime}}$|56 | 02°03′00|${_{.}^{\prime}}$|36 | 21.52 | UNQ | – | – | XDHZQSO |
| J1143-0248 | 175°59′01|${_{.}^{\prime}}$|68 | −02°48′29|${_{.}^{\prime}}$|52 | 21.76 | UNQ | – | – | XDHZQSO |
| J1153-2239 | 178°20′23|${_{.}^{\prime}}$|28 | −22°39′01|${_{.}^{\prime}}$|08 | – | STAR | M9 | – | PS1COLOUR |
| J1200+0112 | 180°00′47|${_{.}^{\prime}}$|52 | 01°12′14|${_{.}^{\prime}}$|40 | 21.67 | UNQ | – | – | XDHZQSO |
| Candidate . | RA . | Dec. . | mJ . | Label . | Spectral type . | Redshift . | Survey . |
|---|---|---|---|---|---|---|---|
| LRIS-2203 (Part) | |||||||
| J0810+2352 | 122°40′04|${_{.}^{\prime}}$|44 | 23°52′35|${_{.}^{\prime}}$|04 | 20.20 | STAR | M9 | – | XDHZQSO |
| J0850+0146 | 132°32′06|${_{.}^{\prime}}$|72 | 01°46′42|${_{.}^{\prime}}$|96 | 20.95 | STAR | L2 | – | XDHZQSO |
| J0901+2906 | 135°24′32|${_{.}^{\prime}}$|04 | 29°06′55|${_{.}^{\prime}}$|44 | 20.59 | QSO | – | 6.10 | XDHZQSO |
| J0911+0022 | 137°55′04|${_{.}^{\prime}}$|44 | 00°22′42|${_{.}^{\prime}}$|60 | 21.29 | STAR | M9 | – | XDHZQSO |
| J0947+0111 | 146°58′52|${_{.}^{\prime}}$|32 | 01°11′26|${_{.}^{\prime}}$|88 | 20.57 | STAR | M8 | – | XDHZQSO |
| J1100+0203 | 165°00′43|${_{.}^{\prime}}$|56 | 02°03′00|${_{.}^{\prime}}$|36 | 21.52 | UNQ | – | – | XDHZQSO |
| J1143-0248 | 175°59′01|${_{.}^{\prime}}$|68 | −02°48′29|${_{.}^{\prime}}$|52 | 21.76 | UNQ | – | – | XDHZQSO |
| J1153-2239 | 178°20′23|${_{.}^{\prime}}$|28 | −22°39′01|${_{.}^{\prime}}$|08 | – | STAR | M9 | – | PS1COLOUR |
| J1200+0112 | 180°00′47|${_{.}^{\prime}}$|52 | 01°12′14|${_{.}^{\prime}}$|40 | 21.67 | UNQ | – | – | XDHZQSO |
This archive mainly serves two purposes: first, future quasar searches will benefit from the archive as a reference for already observed targets; secondly, we provide a large sample of the contaminant population for systematic analysis. In the following section, we look into the distribution of both quasars and contaminants in the colour space.
3.3 Distributions of the quasars and contaminants in colour space
It is of significant interest for quasar selection to understand how quasars and their contaminants populate the colour space. We examine the colours of the spectroscopically classified targets in our archive with photometric measurements from DELS (z), VIKING/UKIDSS (YJHKs/YJHK), and unWISE (W1W2). In the following analysis, we only include sources covered in the VIKING/UKIDSS+DELS+unWISE footprints, which are generally the sources from the XDHZQSO search. We use the same photometric data as used in the XDHZQSO search candidate selection. We also compute relative fluxes in addition to colours because the distribution of observational uncertainties of relative fluxes resembles a Gaussian distribution, and magnitudes cannot represent negative flux measurements (see e.g. Bovy, Hogg & Roweis 2011; Nanni et al. 2022). We always use the J-band as the reference band to be consistent with Nanni et al. (2022), i.e. the relative fluxes are always fluxes in different bands divided by the J-band flux.
On the left-hand side of Fig. 7, we show the distributions of the sources in three different relative flux diagrams, i.e. fz/fJ versus fW1/fJ, fz/fJ versus fY/fJ, and fY/fJ versus fW1/fJ. The corresponding colour–colour diagrams are shown on the right-hand side of the figure. The filled symbols represent the QSO (pink), STAR (blue), and UNQ (brown) classes. The red contour is the distribution of 440 000 simulated quasars (6 ≤ z ≤ 8) generated with simqso. We also convolve the fluxes of all the simulated quasars with measurement uncertainties obtained from real data following the noise modeling procedures described in Nanni et al. (2022). The cyan contour represents the distribution of brown dwarf flux ratios (colours) based on the empirical brown dwarf colours. (Skrzypek et al. 2015) measured the colours of brown dwarfs with different spectral types, from M5 to T8. We then convolve the fluxes (assume mJ = 21) with errors following Nanni et al. (2022) to get 100 000 synthetic measurements, and built the contour based on these points. This cyan contour is essentially similar to the brown dwarf model adopted in several probabilistic candidate selection methods (e.g. Mortlock et al. 2012; Matsuoka et al. 2022). The grey contour is the distribution of all the contaminants used for implementing XDHZQSO in the VIKING/UKIDSS searches (see Section 2.1.1). For a reference, we display the colour selection boxes from Wang et al. (2017) in the fz/fJ versus fW1/fJ diagram and the corresponding colour–colour diagram. Finally, we show the average covariance matrices10 of the QSO (pink), STAR (blue), and UNQ (brown) classes as three ellipses in the lower right position of each panel. The complete relative flux diagrams which includes the zYHKW1W2 bands is shown in Fig. 8.
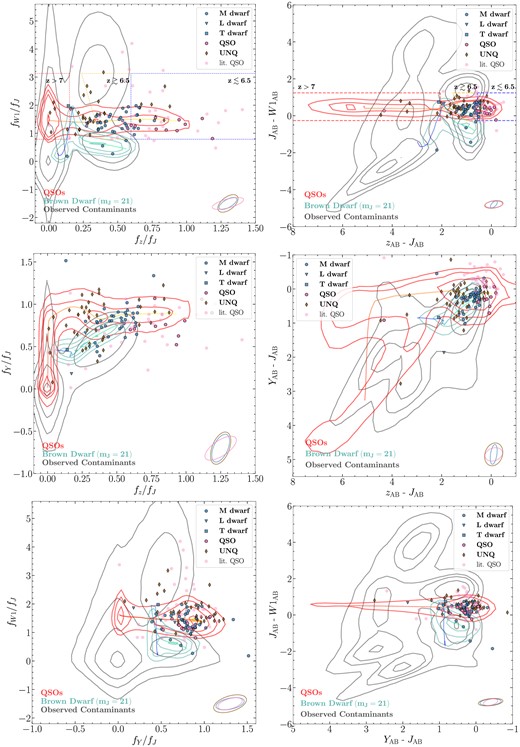
(Left-hand panels) The relative flux diagrams. The filled symbols are the sources in the HzQCA, including QSO (pink), STAR (blue), and UNQ (brown) types objects. Quasars from literature in the VIKING/UKIDSS footprints are overplotted in pale pink. The red contour is the density of 440 000 simulated 6 ≤ z ≤ 8 quasars generated with simqso. The cyan contour is the density of 100 000 synthetic brown dwarfs, generated from convolving the empirical brown dwarf colours in Skrzypek et al. (2015) and the measurement errors, following the noise modeling procedures described in Nanni et al. (2022). The cyan line in it indicates different spectral types. The green end of this track is M5 type, while the blue end is the T8 type. The grey contour is the density of the contaminants used to train the contaminant model in XDHZQSO searches (see Section 2.1.1). The dashed lines in the upper panels are the colour selection cuts from Wang et al. (2017). The ellipses are the mean uncertainties of QSO, STAR, UNQ type objects. (Right-hand panels) Corresponding colour-colour diagrams. The levels of the contours are 11.75 per cent, 39.35 per cent, 67.53 per cent, and 86.47 per cent.
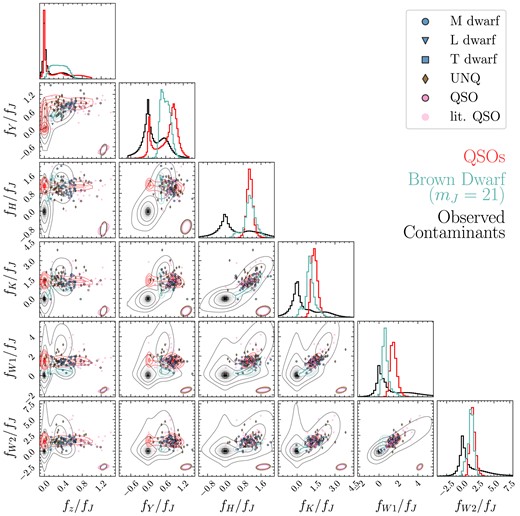
The complete relative flux diagrams. The filled symbols are the sources in the archive, including QSO (pink), STAR (blue), and UNQ (brown) types objects. Quasars from literature in the VIKING/UKIDSS footprints are overplotted in pale pink. The red contour is the density of 440 000 simulated 6 ≤ z ≤ 8 quasars generated with simqso. The cyan contour is the density of 100 000 synthetic brown dwarfs, generated from convolving the empirical brown dwarf colours in Skrzypek et al. (2015) and the measurement errors, following the noise modeling procedures described in Nanni et al. (2022). The grey contour is the density of the contaminants used to train the contaminant model in XDHZQSO searches (see Section 2.1.1). The levels of the contours are 11.75 per cent, 39.35 per cent, 67.53 per cent, and 86.47 per cent.
From Fig. 7, we can see that the contaminants in our samples mostly inhabit the quasar locus as is expected, as the Nanni et al. (2022) selection will primarily select quasars in this region. Consequently, the spectroscopically confirmed brown dwarfs in our sample deviate from the general brown dwarf locus indicated by the cyan contours. Given our large sample of spectroscopically confirmed brown dwarfs, we are in a good position to test if the brown dwarfs in our sample are consistent with the commonly presumed models (cyan contour). We note that the flux distribution of our identified brown dwarfs is biased as the sources were selected to be quasars and to lie within the red contours. Nevertheless, we test whether the distribution of classified brown dwarfs are consistent of being outliers of the brown dwarf locus (cyan contours) given our survey area and depth.
We first use the 1000 000 synthetic brown dwarfs to fit the brown dwarf density distribution in the 6D relative flux space (see e.g. Fig. 8). We then used a simple Gaussian Mixture Model (GMM) with 5 Gaussians components to fit the distribution. With the fitted GMM, we calculate the log probability density (probability in relative flux space) ln (p) of each synthetic object and obtain a cumulative distribution function (CDF) of ln (p). The surface density of brown dwarfs is measured to be ∼25/deg2 for 20 < mJ < 22 (Euclid Collaboration: Barnett et al. 2019), and the survey area of VIKING is ∼1000 deg2. Therefore, we expect to have ∼25 000 brown dwarfs in the VIKING footprints with 20 < mJ < 22. We scale the CDF of ln (p) to the expected total number. With the fitted GMM, we estimate ln (p) of all the spectroscopically identified brown dwarfs. Both the CDFs of identified brown dwarfs and synthetic brown dwarfs are shown in Fig. 9.
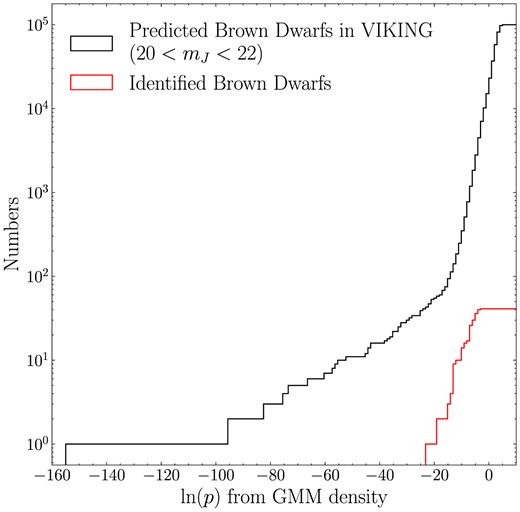
The cumulative distribution functions of the brown dwarf probability density (ln (p)) estimated with GMM. The black curve represents the CDF of the predicted brown dwarf samples in the VIKING footprint with 20 < mJ < 22, which is essentially based on the brown dwarf density aforementioned (the cyan contour in Figs 7 and 8). The red curve is the CDF of identified brown dwarfs in this work. Including the contribution of brown dwarfs from UKIDSS to the analysis will enlarge the difference. The red curve lies fully beneath the black curve, indicating that the spectroscopically identified brown dwarfs, though being scattered away from the general brown dwarf distribution (cyan contours in Figs 7 and 8), are consistent with the brown dwarf model described in Section 3.3 given the large number of total samples.
As indicated by Fig. 9, the detected brown dwarfs (denoted by blue points in Figs 7 and 8) seem to be in accordance with the empirical brown dwarf model (illustrated by cyan contours in the same figures). Rather than being extreme outliers, a more plausible interpretation is that these celestial objects deviate from the general population due to flux measurement uncertainties. We also note that the way we incorporate measurement uncertainties here is an approximation. To more rigorously assess this issue, one can incorporate the uncertainties by marginalizing over noiseless fluxes when calculating the likelihood, as demonstrated by Nanni et al. (2022).
Meanwhile, from Figs 7 and 8, we can also see that the UNQ type objects inhabit different regions from brown dwarfs. Despite the fact that a fraction of these objects may be brown dwarfs as well, a significant proportion is likely to be non-stellar in nature, evidenced by the absence of prominent stellar features in their spectra. Possible explanations for these non-stellar sources could include faint galaxies at intermediate redshifts exhibiting Balmer breaks, or high redshift Lyman break galaxies. Empirical models like XDHZQSO incorporate all candidates to model the distribution of contaminants, which enables these methods to effectively address these sources in future investigations.
4 IMPROVING THE OBSERVING EFFICIENCY WITH SIMULATED OBSERVATIONS
In the following, we assess our observing strategy for future high-z quasar searches with Euclid based on the spectroscopic data set we built in this work. Although LRIS has the best performance among the three instruments, the feasibility of using LRIS to observe fainter, more distant quasars that are common in future surveys remains unknown. Moreover, since LRIS is an optical spectrometer (see Fig. 1), above what redshift should we shift to IR instruments like MOSFIRE and NIRES, or even JWST? These questions arise from our limited experience confirming z > 7 quasars.
The key to address these issues is to precisely estimate the required exposure time to identify the quasars that we have barely seen, e.g. mJ ∼ 23, or z > 7. To accomplish this goal, we simulate a spectroscopic observation of a quasar, given its redshift and apparent magnitude, and then measure its S/N. We can then use the relation between S/N and exposure time to estimate the required exposure time for identification. We present our simulation procedures in the next section.
4.1 Synthetic observations
We start from a rest-frame quasar template (Selsing et al. 2016) and a real 2D and 1D spectrum (stored as Spec2DObj and SpecObjs objects with PypeIt) from the HzQCA. The inputs are the redshift (z) and apparent magnitude (mJ) of the desired quasar. We implement the following steps to simulate the quasar on the 2D spectrum with pyeit functions and routines:
We first shift the wavelength of the 1D template by a factor of (1 + z), where z is the given redshift. We let the fluxes blueward than the redshifted Ly-α wavelength ((1 + z) × 1216 Å;) to zero, mimicking the hydrogen absorption of the IGM at high redshifts.
We then measure the J-band apparent magnitude |$m^{\prime }_{\rm J}$| of the redshifted quasar template with UKIDSS-J transmission curve. We rescale the spectrum with a factor of |$10^{-(m_{\rm J}-m^{\prime }_{\rm J})/2.5}$| to match with the provided magnitude mJ.
- After rescaling, we convert the spectrum from flux units into photon counts per second per angstrom with the sensitivity function generated with the standard star observation in the same run as the real 2D spectrum:(1)$$\begin{eqnarray} N_\lambda = S_\lambda F_\lambda ~, \end{eqnarray}$$
where Sλ is the sensitivity function.
- Then, we convert Nλ into Npix (photon counts per pixel) following:(2)$$\begin{eqnarray} N_{\rm pix} = N_\lambda \times \frac{\mathrm{d}\lambda }{\mathrm{d}\rm pix} \times t_{\rm exp}~, \end{eqnarray}$$
where |$\frac{\mathrm{d}\lambda }{\mathrm{d}\rm pix}$| is the wavelength spacing per pixel which can be obtained from the real 2D spectrum, and texp is the exposure time of the 2D spectrum.
Next, we ‘duplicate’ one of the point sources extracted from the real 2D sky-subtracted frame by shifting its trace11to a ‘blank’ region of the spectrum free of sources. The variation of FWHM along the trace is estimated by pypeit for the real source and is also used for the synthetic duplicate source. We then generate a 2D spatial profile along the duplicated trace using the FWHM values, i.e. we put a Gaussian profile centred at each pixel along the trace, and determine the width of the Gaussian with the FWHM value at that pixel.
We interpolate the simulated quasar spectrum onto the wavelength grid corresponding to the duplicated trace in the 2D spectrum. Finally, we scale the Gaussian profiles individually to force the boxcar extracted value of the duplicated trace to be the same as the interpolated spectrum in counts per pixel.
After successfully injecting the simulated quasar into the 2D spectrum, we perform a boxcar extraction to obtain the final 1D spectrum.
The primary benefit of these procedures is that we can use the real empirical noise realization from the 2D spectrum as the noise for our synthetic observations. pyeit performs both global and local sky-subtraction, as described in Section 2.3. A fair comparison between real and simulated objects requires performing the local sky-subtraction on the simulated object as well. To do so, we re-ran the reduction on the 2D spectrum, and manually extract the location where we intend to put the simulated quasar as a workaround.
In Figs 10 and 11, we show simulated observations of a quasar and a brown dwarf using LRIS. The simulated sources have the same mJ and redshift (for the quasar) as the real sources in the same 2D spectra. We can see that the simulated and observed spectrum are highly consistent.
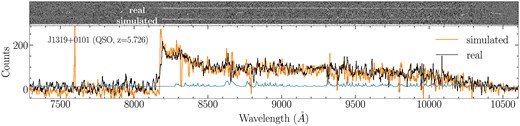
Simulated quasar J1319+0101 in LRIS. (Upper panel) 2D spectrum of the real and fake quasars. (Lower panel) 1D spectrum of them. The S/N of real and fake quasars are consistent.
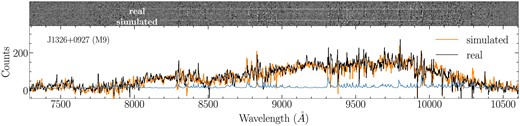
Simulated brown dwarf J1326+0927 in LRIS. (Upper panel) 2D spectrum of the real and fake dwarfs. (Lower panel) 1D spectrum of them. The S/N of real and fake dwarfs are consistent.
4.2 Estimating required exposure time for LRIS, MOSFIRE, and NIRES
With the simulated quasars, the next step is to define at what signal-to-noise level, we can identify a quasar. We use the mean S/N of a spectrum to investigate this:
where Ni represents the Npix from the source in the i-th pixel, and σi is the corresponding uncertainty. In practice, we use the rest-frame wavelength range 1217–1227 Å; to calculate the mean S/N of a quasar. For the brown dwarf we use the observed-frame wavelength range 9600–9700 Å; (for IR instruments, we use 10 500–10 600 Å;) to avoid the molecular absorption bands in brown dwarf spectra.
As the minimum S/N to successfully classify a candidate, we decide to set a threshold to S/N = 6 based on our observing experience. With this threshold and the measured S/N of the simulated source, we use the scaling relation between exposure time and S/N to estimate the required exposure time for an unanimous classification:
where N* is the count rate in photons (electrons) per second for the source of interest, Ns is the pixel count rate from the sky background, and texp is the exposure time. We assume the noise is background dominated here, i.e. Ns ≪ N*.
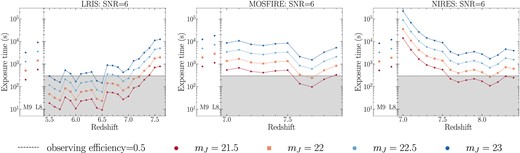
Now that we can simulate a quasar with arbitrary redshift z and apparent magnitude mJ, and have defined that we can identify it with S/N ≥ 6, we use equation (4) to estimate the required exposure time to identify this quasar with LRIS, MORSFIRE, or NIRES. We show the results in Fig. 12. As a comparison, we also show the required exposure times for brown dwarfs with different mJ in the same figure. The average overheads time is ∼300 s, thus an observing efficiency of 0.5 in the plot indicates exposing for 300 s as well. The shape of the z-texp curves for quasars is generally determined by the throughput of the spectrometer and the telluric absorption bands.
The exposure time to reach mean S/N = 6 for quasars with given redshift and mJ, as well as brown dwarfs with given spectral type and mJ, using (left) LRIS, (middle) MOSFIRE, (right) NIRES. An observing efficiency of 0.5 indicates an exposure time of 300 s, close to the average overheads time. When the exposure time gets lower, the CCD equation will deviate from equation (4) and at certain point the readout noise term is no longer negligible. The exposure time is therefore underestimated at the short exposure time regime.
For bright quasars, the exposure time can be surprisingly low, while stars with similar apparent magnitude require much longer exposure time. This is consistent with the fact that the observed quasars are generally much brighter than the contaminants. In Fig. 13, we show a quasar spectrum and a brown dwarf spectrum with the same mJ. They are similarly bright in the detection band (J-band) and drop-out band (z-band), but the quasar fluxes are concentrated in a much smaller wavelength range, and therefore produce a higher signal-to-noise detection in the LRIS spectrum. Provided with the required exposure time to confirm different quasars, we can enhance the confirmation efficiency by reducing the exposure time. Even though we do not know the nature of a candidate a priori, we can more efficiently exclude the possibility of it being a quasar if no sign of quasar is observed after exposing for the required time.
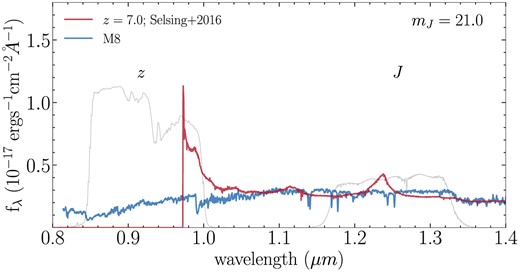
The spectrum of quasar and M8 dwarf with mJ = 21.0 and a similar z-band magnitudes. We can see that the quasar will look much brighter than the brown dwarf in LRIS working wavelength, explaining the relative short exposure times to identify a quasar.
With Fig. 12, we also confirm that we can identify quasars up to z ∼ 7.6 with LRIS. We can identify a z ∼ 7.5, mJ = 21.5 quasar with a ∼15 min exposure. It is also possible to identify faint quasars that are common in Euclid with LRIS. We can confirm a z ∼ 7.0, mJ = 23.0 quasar around 15 min, a z ∼ 7.5, mJ = 23.0 quasar within 3 h.
In Fig. 14, we combine the results of all three instruments. From these figures, we can have a clearer idea of the optimal observing strategy: for z < 7.5 quasar candidates, LRIS is the most suitable instrument; for candidates with higher estimated redshifts, IR instruments like MOSFIRE or NIRES are required. Alternatively, we can use LRIS for all the candidates first, and use the other two instruments to observe the candidates with no LRIS fluxes.
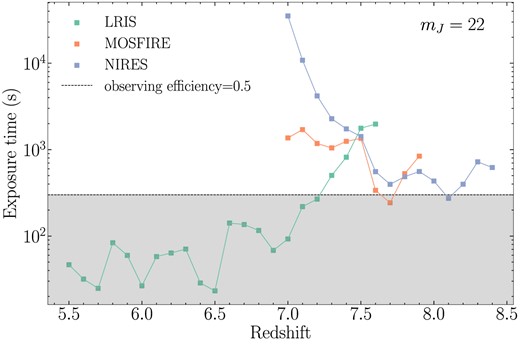
The exposure time to reach mean S/N = 6 for quasars with mJ = 22 and given redshift, observed with three different instruments.
The exposure time calculators provided by Keck12 are not well-tested for the purpose of quasar confirmation. Our simulation with noise maps from real observations should be more robust in practice. Furthermore, the visualization of the 2d spectrum is highly informative to support classifications for future quasar search campaigns. We also note that this simulation tool which is based on the PypeIt routine can be useful to simulate other kinds of sources. A future improvement is to enable changing different observing condition, e.g. the seeing. At present, the simulation’s observing condition is limited by the condition of the actual observation it uses.
5 SUMMARY
In this paper, we present the spectroscopic observations of 207 z ≳ 5 quasar candidates from various quasar searches. We reduce the spectra taken with Keck/LRIS, Keck/MOSFIRE, and Keck/NIRES using the pyeit package. Based on the resulting 2D and 1D spectra, we classify sources into quasars and brown dwarfs where possible. The main results based on these data are summarized below:
We identify 14 z ∼ 6 quasars, ten of which were selected with XDHZQSO (Nanni et al. 2022) using VIKING/UKIDSS and are newly reported in this paper. We also classify 63 candidates as dwarf stars with spectral types M, L, and T (STAR). The spectra of 79 candidates do not resemble quasars but cannot be further classified (UNQ) due to the low-signal-to-noise ratio of the spectra. Two candidates have low S/N spectra and/or too short wavelength coverage. As they could possibly be high-z quasars, we label them inconclusive (INCONCLUSIVE). For 49 sources, we could not fully reduce and/or extract the spectroscopy. These candidates have no classification and are labelled FAIL.
Based on the classifications, we show the distribution of all the sources in the colour space and relative flux space with photometry measurements from DELS (z), VIKING/UKIDSS (YJHKs/YJHK), and unWISE (W1W2) (Fig. 8). We estimate the probability that the confirmed brown dwarfs are consistent with the empirical brown dwarf model (Section 3.3). Our order-of-magnitude estimate suggests that the observed brown dwarf samples are consistent with the model.
We simulate the spectroscopic observations of high-z quasars. Based on the synthetic spectroscopy, we estimate the required exposure time to identify a quasar with a given redshift and J-band magnitude using Keck/LRIS, Keck/MOSFIRE, and Keck/NIRES. We prove the feasibility of using LRIS to identify z < 7.6 quasars and quasars as faint as mJ ∼ 23. We also find that the required exposure time to identify a quasar with LRIS is generally smaller than the time to identify a brown dwarf with the same apparent magnitude, which is due to the difference between their spectral shapes. We compare the required exposure time to reach a signal-to-noise ratio of 6 for a mJ = 22 quasars at different redshifts using LRIS, MOSFIRE, and NIRES (Fig. 14). We conclude that the optimal strategy is to use LRIS to identify z < 7.5 quasar candidates, and to utilize the other two IR instruments for candidates with higher estimated redshifts.
ACKNOWLEDGEMENTS
We thank Suk Sien Tie, Silvia Onorato, and Ben Wang who supported this project during observing runs. We also thank the ENIGMA group members at Leiden University and University of California, Santa Barbara for providing valuable comments on the manuscript.
JTS, RN, and JFH acknowledge funding from the European Research Council (ERC) Advanced Grant program under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 885301).
The data presented herein were obtained at the W. M. Keck Observatory, which is operated as a scientific partnership among the California Institute of Technology, the University of California and the National Aeronautics and Space Administration. The Observatory was made possible by the generous financial support of the W. M. Keck Foundation. This research has also made use of the Keck Observatory Archive (KOA), which is operated by the W. M. Keck Observatory and the NASA Exoplanet Science Institute (NExScI), under contract with the National Aeronautics and Space Administration.
This work is based on observations made with European Southern Observatory Telescopes at the La Silla Paranal Observatory under programs 106.20WQ.002, 106.20WQ.001, and 105.204A.002
This paper also includes data gathered with the 6.5 m Magellan Telescopes located at Las Campanas Observatory, Chile.
Software:astropy (The Astropy Collaboration 2018), pypeit (Prochaska et al. 2020), simqso (McGreer et al. 2013), scikit-learn (Pedregosa et al. 2011), numpy (Harris et al. 2020), and matplotlib (Hunter 2007).
DATA AVAILABILITY
The HzQCA catalogue is published in the electronic version of the journal. The scripts to reduce all the spectroscopic data and reproduce all the results in this paper are stored in the following Github repository: https://github.com/enigma-igm/highz_qso_arxiv. All the data are available from the corresponding author upon reasonable request. This work uses publicly available data from the UKIDSS DR11, VIKING DR4, the Pan-STARRS, and the DELS surveys.
Footnotes
The z and y band of LSST will reach 5σ depths of 25–26 mag with 5–10 yr’ co-added images (Ivezić et al. 2019).
The median 5σ depths of ZYJHKs are mAB = 23.1, 22.3, 22.1, 21.5, and 21.2, respectively (Edge et al. 2013).
The median 5σ depth of the LAS is JVega = 19.9 (Lawrence et al. 2007).
The fitting is done by PypeIt automatically.
test
The errors are covariant since both relative fluxes (colours) depend on fJ (mJ).
We refer to the positions of the centre of the source spectrum as a function of wavelength (spectral position) as the trace.
The calculator for LRIS is available at: http://etc.ucolick.org/web_s2n/lris, for MOSFIRE at: https://www2.keck.hawaii.edu/inst/mosfire/etc.html.
References
APPENDIX A: REDUCED SPECTRA
From Figure A1–A5, we display the reduced 1d spectra of all the sources in the catalogue.
Final 1D spectra of STAR targets in LRIS runs. The 1D spectra here are fluxed and telluric corrected, and the orange curves are the brown dwarf spectra with the lowest reduced χ2 values. The blue curves are the noise. The grey curve in the bottom panel is the average telluric model. The spectra and noise are smoothed using the inverse variance with a smoothing window of 5.
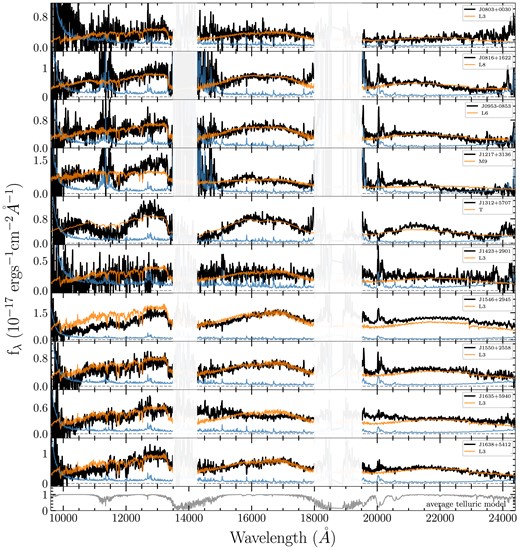
Final 1D spectra of STAR targets in NIRES runs. The 1d spectra here are fluxed and telluric corrected, and the orange curves are the brown dwarf spectra with the lowest reduced χ2 values. The blue curves are the noise. The grey curve in the bottom panel is the average telluric model. The spectra and noise are smoothed using the inverse variance with a smoothing window of 5.
Final 1D spectra of UNQ targets in LRIS runs. The 1d spectra here are fluxed and telluric corrected. The blue curves are the noise. The grey curve in the bottom panel is the average telluric model. The spectra and noise are smoothed using the inverse variance with a smoothing window of 5.
Final 1D spectra of UNQ targets in MOSFIRE runs. The 1d spectra here are fluxed and telluric corrected. The blue curves are the noise. The grey curve in the bottom panel is the average telluric model. The spectra and noise are smoothed using the inverse variance with a smoothing window of 5.
Final 1D spectra of UNQ targets in NIRES runs. The 1d spectra here are fluxed and telluric corrected. The blue curves are the noise. The grey curve in the bottom panel is the average telluric model. The spectra and noise are smoothed using the inverse variance with a smoothing window of 5.

















