-
PDF
- Split View
-
Views
-
Cite
Cite
Francesca Gerardi, Andrei Cuceu, Benjamin Joachimi, Seshadri Nadathur, Andreu Font-Ribera, Optimal data compression for Lyman-α forest cosmology, Monthly Notices of the Royal Astronomical Society, Volume 528, Issue 2, February 2024, Pages 2667–2678, https://doi.org/10.1093/mnras/stae092
Close - Share Icon Share
ABSTRACT
The Lyman-α three-dimensional correlation functions have been widely used to perform cosmological inference using the baryon acoustic oscillation scale. While the traditional inference approach employs a data vector with several thousand data points, we apply near-maximal score compression down to tens of compressed data elements. We show that carefully constructed additional data beyond those linked to each inferred model parameter are required to preserve meaningful goodness of fit tests that guard against unknown systematics, and to avoid information loss due to non-linear parameter dependences. We demonstrate, on suites of realistic mocks and Data Release 16 data from the Extended Baryon Oscillation Spectroscopic Survey, that our compression approach is lossless and unbiased, yielding a posterior that is indistinguishable from that of the traditional analysis. As an early application, we investigate the impact of a covariance matrix estimated from a limited number of mocks, which is only well conditioned in compressed space.
1 INTRODUCTION
In recent decades, the Lyman-α (Ly α) forest gained popularity as a probe of the distribution of matter at redshifts z > 2. The forest consists of a sequence of absorption lines in high-redshift quasar (QSO) spectra, caused by neutral hydrogen placed along the line of sight, and hence it is a tracer of the intergalactic medium. Therefore, it contains cosmological information, and in particular Ly α clustering shows the distinct baryon acoustic oscillations (BAOs) feature. This feature was first detected in the Ly α autocorrelation function using the Baryon Oscillation Spectroscopic Survey (BOSS) Data Release 9 (DR9) data (Busca et al. 2013; Kirkby et al. 2013; Slosar et al. 2013), and subsequently extracted from the Ly α cross-correlation with QSOs using DR11 data (Font-Ribera et al. 2014).
The Ly α forest autocorrelation and its cross-correlation with quasars have been widely used to place constraints on the cosmological model (e.g. Aubourg et al. 2015; Alam et al. 2017, 2021; Cuceu et al. 2019, 2023a). These two correlation functions are typically computed on a two-dimensional (2D) grid in comoving coordinates along and across the line of sight, resulting in high-dimensional data vectors, usually 2500 long for the autocorrelation and 5000 for the cross-correlation. However, standard BOSS and Extended Baryon Oscillation Spectroscopic Survey (eBOSS; du Mas des Bourboux et al. 2020, hereafter dMdB20) Ly α forest analyses have so far focused on extracting cosmological information from the BAO peak, which is well localized to a smaller subset of bins. This means that the vector can be reduced to a smaller dimensionality, encoding the information we wish to capture. Hence, in this context, applying a data compression scheme could be useful to optimize the inference. In addition, the accuracy of the parameter estimates is tightly linked to the covariance matrix of the data vector, under the assumption of a Gaussian likelihood. As the true covariance |$\boldsymbol{\mathsf{\Sigma}}$| of the correlation function is inaccessible, standard analyses usually estimate it either from large set of mocks or analytically from models of the covariance matrix (Kitaura et al. 2016; Wadekar, Ivanov & Scoccimarro 2020). In Ly α analyses, producing mocks can be a highly computationally expensive process, therefore only a limited number is available, 100 in the case of dMdB20. However, if the number of samples is significantly lower than the number of data points, the estimate of the covariance is singular and has no inverse (Hartlap, Simon & Schneider 2007; Dodelson & Schneider 2013; Taylor & Joachimi 2014; Sellentin & Heavens 2015; Percival et al. 2021).
In the eBOSS DR16 analysis, the covariance matrix |$\boldsymbol{\mathsf{C}}$| is computed via the subsampling method, which, given some data set, consists of computing the covariance of correlation functions obtained in individual subsamples of the sky. Despite being larger (∼800) than the number of mocks (100), the number of subsamples is still lower than the number of data points (2500–5000); hence, the covariance matrix must be tested. Alternatively, in the same analysis, the authors computed a Gaussian covariance matrix using the Wick approximation (Delubac et al. 2015) and used it to benchmark the covariance computed from the subsampling method. The accuracy of the covariance matrix would increase by alleviating the mismatch between the number of bins and the number of mocks. This can be done by applying a data compression algorithm and evaluating the (compressed) data covariance matrix in a new space characterized by a lower dimensionality. In particular, given the available set of a hundred mocks, we reduce each of them to a set of compressed data vectors and compute a newly defined mock sample covariance, which is a good estimator of the true covariance, given that the length of the compressed data vector is now much smaller than the number of mocks. Then, a comparison between the covariance matrix of the data, mapped into the compressed space, and the mock sample covariance, obtained from the compressed vector, can clarify whether there has been an underestimation or overestimation of the contours in the standard analyses. Moreover, we are interested in obtaining a more sensitive goodness of fit test. The length of Ly α correlation data vectors is of the order of |$\mathcal {O}(10^3)$|, which could easily hide any bad fit in a subset of the data. By reducing the dimensionality of the data vector through compression, we wish to obtain a test that would highlight when a few important points are off.
Driven by these optimization problems, we perform the inference analysis on realistic Ly α × Ly α autocorrelation and Ly α × QSO cross-correlation functions in a data compression framework. The compression algorithm we use is score compression (Alsing & Wandelt 2018), under the hypothesis of a Gaussian likelihood (and hence analogous to the Multiple Optimised Parameter Estimation and Data compression (MOPED) scheme; see Heavens, Jimenez & Lahav 2000). By construction, the dimensionality of the compressed data vector will be equal to the number of parameters we wish to keep information of, namely |$\mathcal {O}(10)$|.
The paper is structured as follows. We start in Section 2 by outlining the method, explaining the computation of the covariance matrix, and introducing the modelling and the basic idea behind score compression. We proceed in Section 3 by testing the compression algorithm against loss of information, comparing the inferred posterior distribution for our sampled parameters in the traditional and compressed frameworks. In Section 4, we compare the constraining power of the original estimated covariance matrix against the mock-to-mock covariance. We then perform goodness of fit tests in the compressed framework in Section 5. Throughout the analysis, a tight prior on the BAO parameters is imposed to overcome the problem of the non-linear relation between these and their corresponding summary statistics components. We relaxed the prior constraint, and hence made the analysis more generalizable, by extending the framework as described in Section 6. An application of our new framework to eBOSS DR16 data is presented in Section 7. Conclusions are drawn in Section 8.
Making sure that the analysis is both optimized and reliable is key to interpret the vast amount of Ly α forest data, which will become available from the Dark Energy Spectroscopic Instrument (DESI).
2 METHOD
Generically referring to the Ly α autocorrelation and cross-correlation as the data vectors, the goal of this work is to study data compression in the context of Ly α forest three-dimensional analyses. In particular, this means compressing the data down to a set of summary statistics t, which will encode into a shorter vector the information we are interested in. As we have just seen, this also benefits the computation of the covariance matrix. The new ‘compressed’ framework is tested against the traditional analysis while performing parameter inference. To evaluate posterior distributions, we use the nested sampler polychord (Handley, Hobson & Lasenby 2015a, b).
We start in Section 2.1 by introducing the mocks used in this analysis, with a focus on the computation of the covariance matrix. We then describe the modelling of the Ly α × Ly α and the cross- Ly α × QSO power spectra in Section 2.2, as implemented in vega1 (Cuceu et al. 2023b), and the set of randomly generated Monte Carlo realizations of the correlation function in Section 2.3. In Section 2.4, we finally outline the compression method used, namely score compression.
2.1 Synthetic data vector and covariance
In this work, we use a set of 100 realistic Ly α mocks, with and without contaminants, which were produced for the Ly α eBOSS DR16 analysis (dMdB20). The synthetic Ly α transmitted fluxes are produced using the colore (Ramírez-Pérez et al. 2022) and lyacolore (Farr et al. 2020) packages, from the same cosmology for all the mocks. Synthetic quasar spectra are then generated given some astrophysical and instrumental prescriptions, and contaminants are added if requested. Then, the mocks run through the same analysis pipeline (picca)2 as the real data, resulting in measured autocorrelation and cross-correlation functions (dMdB20). These are derived from computing the correlation function in each healpix3 (Górski et al. 2005) pixel – about 880 pixels (subsamples) for the eBOSS footprint (NSIDE = 16) – and evaluating the mean and covariance over the full set of pixels of the mock, to be then assigned to the entire survey. In this way, for every ith mock, there will be a measurement of both the correlation function and the covariance matrix |$\boldsymbol{\mathsf{C}}_i$|, which will be only an estimate of the true covariance |$\boldsymbol{\mathsf{\Sigma}}$| as mentioned above. In each subsample, the correlation has a size of either 2500 (ξauto) or 5000 (ξcross) bins; hence, the number of subsamples (880 pixels) is significantly lower than the number of data points (2500 or 5000). This means that the covariance should be singular; however, off-diagonal elements of the correlation matrix are smoothed to make it positive definite (dMdB20).
Finally, given the same 100 mocks, it is possible to define a stack of them. In particular, the correlation function for the stack of mocks is obtained by collecting all the subsamples (for all the 100 mocks), and computing the mean and covariance of the correlation functions computed in each of them, effectively reducing the noise. We will refer to the contaminated auto- and cross- mock correlations of the stack as stacked correlations.
In this analysis, we use the same scale cuts as in eBOSS DR16 (dMdB20), assuming |$r_{\rm {min}} = 10 \ h^{-1} \, \rm {Mpc}$|, up to |$r_{\rm {max}} = 180 \ h^{-1} \, \rm {Mpc}$|. The effective redshift of the correlation functions is zeff = 2.3.
2.2 Modelling and parameter space
To model the Ly α correlation functions, we follow equation (27) of dMdB20, while applying the same prescriptions as in Gerardi et al. (2022). Given a certain cosmological model and a corresponding isotropic linear matter power spectrum P(k, z), the Ly α auto- and Ly α-QSO cross- power spectra are computed as
where μk = k∥/k, with k and k∥ the wave vector modulus and its line-of-sight component, respectively. On one hand, the Ly α × Ly α power spectrum in equation (1) depends on the Ly α forest linear bias bLy α and redshift-space distortion (RSD) parameter |$\beta _{\rm {Ly}\, \alpha } = {b_{\rm {\eta,\, Ly\,}\alpha } f(z)}/{b_{\rm {Ly}\, \alpha }}$|, where bη, Ly α is an extra unknown bias, the velocity divergence bias, and f(z) the logarithmic growth rate. The |$F_{ \rm {nl,\,Ly\,}\alpha }$| term accounts for non-linear corrections (Arinyo-i-Prats et al. 2015). On the other hand, the quasar parameters that contribute to the Ly α × QSO power spectrum in equation (2) are the quasar linear bias bQSO and the RSD term βQSO = f(z)/bQSO. Finally, we model non-linear effects of quasars and redshift errors following dMdB20, using a Lorentzian function
where |$\sigma _{v}$| is the velocity dispersion.
The power spectra in equations (1) and (2) only account for Ly α flux and in reality this is also contaminated by absorption lines due to heavy elements, generally referred to as metals, and high column density (HCD) systems (Font-Ribera et al. 2012; Bautista et al. 2017). Let us first focus on the modelling of the HCDs. Font-Ribera et al. (2012) showed that their broadening effect along the line of sight can be modelled at the level of new effective Ly α bias and RSD parameters
with bHCD and βHCD being the linear bias and RSD parameters, respectively. FHCD(k∥) is a function of the line-of-sight wavenumber, and it is modelled following dMdB20. On the other hand, metals contribute to the final autocorrelation and cross-correlation functions as per
where m generically refers to a metal and the sums are performed over all possible metals considered. The modelling of the cross-correlation of a metal with other metals (|$\xi _{m_1 \times m_2}$|) and with Ly α (ξLy α × m) and QSO (ξQSO × m) follows the modelling of the autocorrelation and cross-correlation of the Ly α, and each metal line has a linear bias bm and RSD parameter βm = bη, mf(z)/bm. Following dMdB20, we fix all βm = 0.5, and sample the metal biases.
Based on this modelling, we use the code vega to compute the 2D correlation function |$\boldsymbol{\xi }$|. This same code computes both the BAO feature parameters {α∥, α⊥}, which shift the peak along and across the line of sight, and the Gaussian smoothing (Farr et al. 2020), which accounts for the low resolution of the mocks and is parametrized by {σ∥, σ⊥} smoothing parameters.
At the inference level, the set of sampled parameters is |${\boldsymbol{ p}_{\rm {s}}} = \lbrace \alpha _{\parallel }, \alpha _{\perp }, b_{\rm {Ly}\, \alpha }, \beta _{\rm {Ly}\, \alpha }, b_{\rm {QSO}}, \beta _{\rm {QSO}}, \sigma _{v}, \sigma _{\parallel }, \sigma _{\perp } \rbrace$|, which is extended to include also {bη, m, bHCD, βHCD} when also fitting for contaminants. In this notation, bη, m is the velocity divergence bias for the metal m – here, we consider Si ii(1260), Si ii(1193), Si iii(1207), and Si ii(1190).
For all these parameters, we choose uniform priors, which are listed in Table 1. The only exception is given by βHCD, for which, following the previous eBOSS DR16 analysis, we impose an informative Gaussian prior.
Full set of sampled parameters, alongside with the fiducial values used to compute the summary statistics (see equation 8), priors, and the 1D marginals (68 per cent CL). Uniform (|$\mathcal {U}$|) priors are adopted for the sampling procedure, while we assign a Gaussian prior on βHCD, where by notation the Gaussian distribution |$\mathcal {N}(\mu ,\sigma)$| has mean μ and standard deviation σ. Results are split into ‘Testing the framework (stacked)’ and ‘Testing the covariance (single mock)’, which, respectively, refer to the set-up in Sections 3 and 4. The former set of results shows the comparison between the traditional and the compressed inference pipelines using the stacked autocorrelation and cross-correlation mocks, while the latter shows the comparison between the compressed methods using either the original covariance |$\boldsymbol{\mathsf{C}}$| (which is mapped into the compressed space) or the mock-to-mock covariance |$\boldsymbol{\mathsf{C}}_{t}$|, for a single mock.
| . | . | . | Testing the framework (stacked) . | Testing the covariance (single mock) . | ||
|---|---|---|---|---|---|---|
| Parameter . | Fiducial . | Prior . | Traditional . | Compression . | Original covariance . | Mock-to-mock covariance . |
| α∥ | 1.00 | |$\mathcal {U}(0.88, 1.14)$| | 1.000 ± 0.002 | 1.000 ± 0.002 | 1.003 ± 0.019 | 1.003 ± 0.019 |
| α⊥ | 1.01 | |$\mathcal {U}(0.88, 1.14)$| | 1.004 ± 0.003 | 1.004 ± 0.003 | 1.002 ± 0.027 | |$1.004^{+0.029}_{-0.032}$| |
| bLy α | −0.14 | |$\mathcal {U}(-2,0)$| | −0.135 ± 0.001 | −0.135 ± 0.001 | −0.125 ± 0.004 | −0.124 ± 0.006 |
| βLy α | 1.41 | |$\mathcal {U}(0,5)$| | 1.47 ± 0.01 | 1.47 ± 0.01 | |$1.67^{+0.07}_{-0.08}$| | |$1.68^{+0.09}_{-0.10}$| |
| bQSO | 3.81 | |$\mathcal {U}(0,10)$| | 3.80 ± 0.01 | 3.80 ± 0.01 | 3.82 ± 0.08 | 3.81 ± 0.07 |
| βQSO | 0.25 | |$\mathcal {U}(0,5)$| | 0.25 ± 0.01 | 0.25 ± 0.01 | 0.27 ± 0.04 | |$0.27^{+0.03}_{-0.04}$| |
| |$\sigma_{v}$| (Mpc h−1) | 2.87 | |$\mathcal {U}(0,15)$| | 2.82 ± 0.04 | 2.82 ± 0.04 | |$3.22^{+0.32}_{-0.28}$| | 3.24 ± 0.26 |
| σ∥, sm | 2.05 | |$\mathcal {U}(0, 10)$| | 2.08 ± 0.01 | 2.08 ± 0.01 | 2.10 ± 0.09 | |$2.10^{+0.09}_{-0.08}$| |
| σ⊥, sm | 2.35 | |$\mathcal {U}(0, 10)$| | 2.33 ± 0.01 | 2.33 ± 0.01 | 2.23 ± 0.11 | 2.21 ± 0.11 |
| bHCD (×10−2) | −1.70 | |$\mathcal {U}(-20,0)$| | −2.12 ± 0.08 | −2.13 ± 0.07 | −2.98 ± 0.54 | −3.06 ± 0.68 |
| βHCD | 1.57 | |$\mathcal {N}(0.5, 0.09)$| | 0.86 ± 0.06 | 0.86 ± 0.06 | 0.50 ± 0.09 | 0.50 ± 0.09 |
| bη, Si ii(1260) (×10−3) | −0.58 | |$\mathcal {U}(-50, 50)$| | −0.59 ± 0.04 | −0.59 ± 0.04 | −0.83 ± 0.33 | −0.88 ± 0.37 |
| bη, Si ii(1193) (×10−3) | −1.12 | |$\mathcal {U}(-50, 50)$| | −1.09 ± 0.03 | −1.09 ± 0.03 | −0.83 ± 0.27 | −0.84 ± 0.28 |
| bη, Si iii(1207) (×10−3) | −1.75 | |$\mathcal {U}(-50, 50)$| | −1.64 ± 0.03 | −1.63 ± 0.03 | −1.54 ± 0.31 | −1.52 ± 0.30 |
| bη, Si ii(1190) (×10−3) | −1.00 | |$\mathcal {U}(-50, 50)$| | −1.00 ± 0.03 | −1.00 ± 0.03 | −0.75 ± 0.27 | −0.75 ± 0.29 |
| . | . | . | Testing the framework (stacked) . | Testing the covariance (single mock) . | ||
|---|---|---|---|---|---|---|
| Parameter . | Fiducial . | Prior . | Traditional . | Compression . | Original covariance . | Mock-to-mock covariance . |
| α∥ | 1.00 | |$\mathcal {U}(0.88, 1.14)$| | 1.000 ± 0.002 | 1.000 ± 0.002 | 1.003 ± 0.019 | 1.003 ± 0.019 |
| α⊥ | 1.01 | |$\mathcal {U}(0.88, 1.14)$| | 1.004 ± 0.003 | 1.004 ± 0.003 | 1.002 ± 0.027 | |$1.004^{+0.029}_{-0.032}$| |
| bLy α | −0.14 | |$\mathcal {U}(-2,0)$| | −0.135 ± 0.001 | −0.135 ± 0.001 | −0.125 ± 0.004 | −0.124 ± 0.006 |
| βLy α | 1.41 | |$\mathcal {U}(0,5)$| | 1.47 ± 0.01 | 1.47 ± 0.01 | |$1.67^{+0.07}_{-0.08}$| | |$1.68^{+0.09}_{-0.10}$| |
| bQSO | 3.81 | |$\mathcal {U}(0,10)$| | 3.80 ± 0.01 | 3.80 ± 0.01 | 3.82 ± 0.08 | 3.81 ± 0.07 |
| βQSO | 0.25 | |$\mathcal {U}(0,5)$| | 0.25 ± 0.01 | 0.25 ± 0.01 | 0.27 ± 0.04 | |$0.27^{+0.03}_{-0.04}$| |
| |$\sigma_{v}$| (Mpc h−1) | 2.87 | |$\mathcal {U}(0,15)$| | 2.82 ± 0.04 | 2.82 ± 0.04 | |$3.22^{+0.32}_{-0.28}$| | 3.24 ± 0.26 |
| σ∥, sm | 2.05 | |$\mathcal {U}(0, 10)$| | 2.08 ± 0.01 | 2.08 ± 0.01 | 2.10 ± 0.09 | |$2.10^{+0.09}_{-0.08}$| |
| σ⊥, sm | 2.35 | |$\mathcal {U}(0, 10)$| | 2.33 ± 0.01 | 2.33 ± 0.01 | 2.23 ± 0.11 | 2.21 ± 0.11 |
| bHCD (×10−2) | −1.70 | |$\mathcal {U}(-20,0)$| | −2.12 ± 0.08 | −2.13 ± 0.07 | −2.98 ± 0.54 | −3.06 ± 0.68 |
| βHCD | 1.57 | |$\mathcal {N}(0.5, 0.09)$| | 0.86 ± 0.06 | 0.86 ± 0.06 | 0.50 ± 0.09 | 0.50 ± 0.09 |
| bη, Si ii(1260) (×10−3) | −0.58 | |$\mathcal {U}(-50, 50)$| | −0.59 ± 0.04 | −0.59 ± 0.04 | −0.83 ± 0.33 | −0.88 ± 0.37 |
| bη, Si ii(1193) (×10−3) | −1.12 | |$\mathcal {U}(-50, 50)$| | −1.09 ± 0.03 | −1.09 ± 0.03 | −0.83 ± 0.27 | −0.84 ± 0.28 |
| bη, Si iii(1207) (×10−3) | −1.75 | |$\mathcal {U}(-50, 50)$| | −1.64 ± 0.03 | −1.63 ± 0.03 | −1.54 ± 0.31 | −1.52 ± 0.30 |
| bη, Si ii(1190) (×10−3) | −1.00 | |$\mathcal {U}(-50, 50)$| | −1.00 ± 0.03 | −1.00 ± 0.03 | −0.75 ± 0.27 | −0.75 ± 0.29 |
Full set of sampled parameters, alongside with the fiducial values used to compute the summary statistics (see equation 8), priors, and the 1D marginals (68 per cent CL). Uniform (|$\mathcal {U}$|) priors are adopted for the sampling procedure, while we assign a Gaussian prior on βHCD, where by notation the Gaussian distribution |$\mathcal {N}(\mu ,\sigma)$| has mean μ and standard deviation σ. Results are split into ‘Testing the framework (stacked)’ and ‘Testing the covariance (single mock)’, which, respectively, refer to the set-up in Sections 3 and 4. The former set of results shows the comparison between the traditional and the compressed inference pipelines using the stacked autocorrelation and cross-correlation mocks, while the latter shows the comparison between the compressed methods using either the original covariance |$\boldsymbol{\mathsf{C}}$| (which is mapped into the compressed space) or the mock-to-mock covariance |$\boldsymbol{\mathsf{C}}_{t}$|, for a single mock.
| . | . | . | Testing the framework (stacked) . | Testing the covariance (single mock) . | ||
|---|---|---|---|---|---|---|
| Parameter . | Fiducial . | Prior . | Traditional . | Compression . | Original covariance . | Mock-to-mock covariance . |
| α∥ | 1.00 | |$\mathcal {U}(0.88, 1.14)$| | 1.000 ± 0.002 | 1.000 ± 0.002 | 1.003 ± 0.019 | 1.003 ± 0.019 |
| α⊥ | 1.01 | |$\mathcal {U}(0.88, 1.14)$| | 1.004 ± 0.003 | 1.004 ± 0.003 | 1.002 ± 0.027 | |$1.004^{+0.029}_{-0.032}$| |
| bLy α | −0.14 | |$\mathcal {U}(-2,0)$| | −0.135 ± 0.001 | −0.135 ± 0.001 | −0.125 ± 0.004 | −0.124 ± 0.006 |
| βLy α | 1.41 | |$\mathcal {U}(0,5)$| | 1.47 ± 0.01 | 1.47 ± 0.01 | |$1.67^{+0.07}_{-0.08}$| | |$1.68^{+0.09}_{-0.10}$| |
| bQSO | 3.81 | |$\mathcal {U}(0,10)$| | 3.80 ± 0.01 | 3.80 ± 0.01 | 3.82 ± 0.08 | 3.81 ± 0.07 |
| βQSO | 0.25 | |$\mathcal {U}(0,5)$| | 0.25 ± 0.01 | 0.25 ± 0.01 | 0.27 ± 0.04 | |$0.27^{+0.03}_{-0.04}$| |
| |$\sigma_{v}$| (Mpc h−1) | 2.87 | |$\mathcal {U}(0,15)$| | 2.82 ± 0.04 | 2.82 ± 0.04 | |$3.22^{+0.32}_{-0.28}$| | 3.24 ± 0.26 |
| σ∥, sm | 2.05 | |$\mathcal {U}(0, 10)$| | 2.08 ± 0.01 | 2.08 ± 0.01 | 2.10 ± 0.09 | |$2.10^{+0.09}_{-0.08}$| |
| σ⊥, sm | 2.35 | |$\mathcal {U}(0, 10)$| | 2.33 ± 0.01 | 2.33 ± 0.01 | 2.23 ± 0.11 | 2.21 ± 0.11 |
| bHCD (×10−2) | −1.70 | |$\mathcal {U}(-20,0)$| | −2.12 ± 0.08 | −2.13 ± 0.07 | −2.98 ± 0.54 | −3.06 ± 0.68 |
| βHCD | 1.57 | |$\mathcal {N}(0.5, 0.09)$| | 0.86 ± 0.06 | 0.86 ± 0.06 | 0.50 ± 0.09 | 0.50 ± 0.09 |
| bη, Si ii(1260) (×10−3) | −0.58 | |$\mathcal {U}(-50, 50)$| | −0.59 ± 0.04 | −0.59 ± 0.04 | −0.83 ± 0.33 | −0.88 ± 0.37 |
| bη, Si ii(1193) (×10−3) | −1.12 | |$\mathcal {U}(-50, 50)$| | −1.09 ± 0.03 | −1.09 ± 0.03 | −0.83 ± 0.27 | −0.84 ± 0.28 |
| bη, Si iii(1207) (×10−3) | −1.75 | |$\mathcal {U}(-50, 50)$| | −1.64 ± 0.03 | −1.63 ± 0.03 | −1.54 ± 0.31 | −1.52 ± 0.30 |
| bη, Si ii(1190) (×10−3) | −1.00 | |$\mathcal {U}(-50, 50)$| | −1.00 ± 0.03 | −1.00 ± 0.03 | −0.75 ± 0.27 | −0.75 ± 0.29 |
| . | . | . | Testing the framework (stacked) . | Testing the covariance (single mock) . | ||
|---|---|---|---|---|---|---|
| Parameter . | Fiducial . | Prior . | Traditional . | Compression . | Original covariance . | Mock-to-mock covariance . |
| α∥ | 1.00 | |$\mathcal {U}(0.88, 1.14)$| | 1.000 ± 0.002 | 1.000 ± 0.002 | 1.003 ± 0.019 | 1.003 ± 0.019 |
| α⊥ | 1.01 | |$\mathcal {U}(0.88, 1.14)$| | 1.004 ± 0.003 | 1.004 ± 0.003 | 1.002 ± 0.027 | |$1.004^{+0.029}_{-0.032}$| |
| bLy α | −0.14 | |$\mathcal {U}(-2,0)$| | −0.135 ± 0.001 | −0.135 ± 0.001 | −0.125 ± 0.004 | −0.124 ± 0.006 |
| βLy α | 1.41 | |$\mathcal {U}(0,5)$| | 1.47 ± 0.01 | 1.47 ± 0.01 | |$1.67^{+0.07}_{-0.08}$| | |$1.68^{+0.09}_{-0.10}$| |
| bQSO | 3.81 | |$\mathcal {U}(0,10)$| | 3.80 ± 0.01 | 3.80 ± 0.01 | 3.82 ± 0.08 | 3.81 ± 0.07 |
| βQSO | 0.25 | |$\mathcal {U}(0,5)$| | 0.25 ± 0.01 | 0.25 ± 0.01 | 0.27 ± 0.04 | |$0.27^{+0.03}_{-0.04}$| |
| |$\sigma_{v}$| (Mpc h−1) | 2.87 | |$\mathcal {U}(0,15)$| | 2.82 ± 0.04 | 2.82 ± 0.04 | |$3.22^{+0.32}_{-0.28}$| | 3.24 ± 0.26 |
| σ∥, sm | 2.05 | |$\mathcal {U}(0, 10)$| | 2.08 ± 0.01 | 2.08 ± 0.01 | 2.10 ± 0.09 | |$2.10^{+0.09}_{-0.08}$| |
| σ⊥, sm | 2.35 | |$\mathcal {U}(0, 10)$| | 2.33 ± 0.01 | 2.33 ± 0.01 | 2.23 ± 0.11 | 2.21 ± 0.11 |
| bHCD (×10−2) | −1.70 | |$\mathcal {U}(-20,0)$| | −2.12 ± 0.08 | −2.13 ± 0.07 | −2.98 ± 0.54 | −3.06 ± 0.68 |
| βHCD | 1.57 | |$\mathcal {N}(0.5, 0.09)$| | 0.86 ± 0.06 | 0.86 ± 0.06 | 0.50 ± 0.09 | 0.50 ± 0.09 |
| bη, Si ii(1260) (×10−3) | −0.58 | |$\mathcal {U}(-50, 50)$| | −0.59 ± 0.04 | −0.59 ± 0.04 | −0.83 ± 0.33 | −0.88 ± 0.37 |
| bη, Si ii(1193) (×10−3) | −1.12 | |$\mathcal {U}(-50, 50)$| | −1.09 ± 0.03 | −1.09 ± 0.03 | −0.83 ± 0.27 | −0.84 ± 0.28 |
| bη, Si iii(1207) (×10−3) | −1.75 | |$\mathcal {U}(-50, 50)$| | −1.64 ± 0.03 | −1.63 ± 0.03 | −1.54 ± 0.31 | −1.52 ± 0.30 |
| bη, Si ii(1190) (×10−3) | −1.00 | |$\mathcal {U}(-50, 50)$| | −1.00 ± 0.03 | −1.00 ± 0.03 | −0.75 ± 0.27 | −0.75 ± 0.29 |
2.3 Monte Carlo realizations
We here introduce a different kind of simulated data, which we will later use, defined as Monte Carlo realizations. They are correlation functions obtained by adding noise on top of the model, as defined in Section 2.2. The noise is given by a covariance matrix from 1 of the 100 mock correlations that have been seen so far. What this means is that we can imagine every data point to be generated from a normal distribution |$\mathcal {N}(\boldsymbol{\xi }, \boldsymbol{\mathsf{C}})$|, where |$\boldsymbol{\xi }$| is the model correlation function and |$\boldsymbol{\mathsf{C}}$| is given by the covariance of the first realistic mock. Using Monte Carlo simulations comes with two advantages. First, it is possible to generate as many as needed to build any statistics. Secondly, we have control over the model and there will be clear knowledge of the underlying physics.
2.4 Score compression
To reduce the dimensionality of our data sets, we use score compression (Alsing & Wandelt 2018). Given a known form for the log-likelihood function |$\mathcal {L}$|, this method corresponds to linear transformations of the data, based on the idea of compressing them down to the score function |$\boldsymbol{s} = \nabla \boldsymbol{\mathcal {L}}_*$|. The components of the compressed vector are the derivatives of the log-likelihood function, evaluated at some fiducial set of parameters |$\boldsymbol{\theta }_*$|, with respect to the parameters of interest |$\boldsymbol{\theta }$|. Under the assumptions that the likelihood function is Gaussian and the covariance |$\boldsymbol{\mathsf{C}}$| does not depend on parameters, from the data |$\boldsymbol{d}$|, the compressed data vector is obtained as
where |$\boldsymbol{\mu }_*$| is the fiducial model. Under these assumptions, the compression is identical to the widely used MOPED scheme (Heavens et al. 2000) apart from a bijective linear transformation.
In our case, the model corresponds to the correlation function |$\boldsymbol{\xi }$|, described earlier in Section 2.2. The corresponding likelihood distribution in compressed space will be then given by
where n is the length of |$\boldsymbol{t}$|, |$\boldsymbol{\mu }_{\boldsymbol{t}}(\boldsymbol{\theta })$| is the compressed model |$\boldsymbol{\mu }$| evaluated at |$\boldsymbol{\theta }$|, namely |$\boldsymbol{\mu }_{\boldsymbol{t}}(\boldsymbol{\theta }) = \nabla \boldsymbol{\mu }_*^T \boldsymbol{\mathsf{C}}^{-1} [\boldsymbol{\mu }(\boldsymbol{\theta })-\boldsymbol{\mu }_*]$|, and
is the Fisher matrix.
When considering both the autocorrelation and cross-correlation, some parameters will be in common; for this reason, there is the need to build a joint summary statistic. If we define independently the Ly α auto- and cross- data vectors, characterized by the covariances Cauto and Ccross, respectively, and given they do not correlate with each other, in the joint analysis the full covariance matrix will be given by
Then, the resulting summary statistics vector and Fisher matrix will be, respectively, obtained as |$\boldsymbol{t} = \boldsymbol{t}_{\rm {auto}} + \boldsymbol{t}_{\rm {cross}}$| and |$\boldsymbol{\mathsf{F}} = \boldsymbol{\mathsf{F}}_{\rm {auto}} + \boldsymbol{\mathsf{F}}_{\rm {cross}}$|.
This compression method is dependent on the choice of the fiducial set of parameters |$\boldsymbol{\theta }_*$|, which might not be known a priori. However, Alsing & Wandelt (2018) suggest iterating over the Fisher scoring method for maximum-likelihood estimation
until convergence of the full set of parameters. How this is done in our particular case is described at the beginning of Section 3. An important note is that this iterative procedure does not take into account parameters’ priors, which means that it can potentially lead to unusual values for those parameters that are not well constrained by the data.
In computing the score compression components over the parameters {α∥, α⊥}, we realized that their relation with their corresponding summary statistics components, namely |$\lbrace \boldsymbol{t}_{\alpha _{\parallel }},\boldsymbol{t}_{\alpha _{\perp }} \rbrace$|, was not monotonic, as per Fig. 1. This is problematic as this means that the posterior can have more than one peak (Graff, Hobson & Lasenby 2011) if we sample over the full [0.01, 1.99] interval. We overcame this complexity by imposing a tighter prior on {α∥, α⊥} at the sampling step. This prior is designed to allow for α∥ values in between the minimum and maximum of |$\boldsymbol{t}_{\alpha _{\parallel }}(\alpha _{\parallel })$|. The same prior is imposed on α⊥. This tightening does not affect the inference when performed on the correlation function of the stacked mock, in which case posteriors are well within this prior, but it reveals to be quite important when evaluating the posteriors on the individual mocks. For this reason, we make sure that we provide example results for those mocks whose contours are within the prior range.
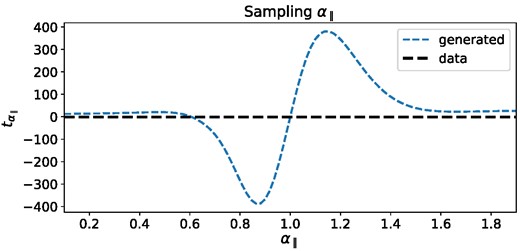
This plot shows the behaviour of the summary component |$t_{\alpha _{\parallel }}$| as a function of α∥, which is the parameter it is related to as per equation (8), against the value of |$t_{\alpha _{\parallel }}$| evaluated using α∥ = 1.00 (see Table 1), denoted as ‘data’. The remainder of the parameters are set to the fiducial values listed in Table 1. This figure highlights a non-monotonic relationship between the two parameters, which would lead to multiple peaks in the posterior if a tight prior is not imposed.
Later, in Section 6 we will see how we can remove the tight prior constraint by evaluating the summary statistics components associated with {α∥, α⊥} at multiple fiducial values of the BAO parameters, effectively enlarging the compressed vector.
3 COMPRESSION PERFORMANCE
In this section, we apply the score compression algorithm, outlined in Section 2.4, to Ly α autocorrelation and cross-correlation measured from contaminated mocks. The pipeline starts by choosing a fiducial set of parameters for computing the score compressed vector, as per equation (8). The fiducial is obtained by iterating over equation (12), with |$\boldsymbol{\theta }_0$| given by the best fit of the stacked correlation functions. Given this initial guess, we then iterated assigning to |$\boldsymbol{\theta }_{k+1}$| the median of the |$\boldsymbol{\theta }$| values over the 100 mocks at the kth step.
The likelihood is assumed to be Gaussian, which has a major impact on the final form of the compressed vector, given that the latter is computed as the gradient of the log-likelihood. Based on previous analyses, we assume that the data are normally distributed and this assumption of Gaussianity will also be inherited in the compressed space. In general, when mapping in a compressed space, this property might not be preserved, but given that score compression is a linear transformation, that is the case. We make a consistency check by running the Henze–Zirkler test (Henze & Zirkler 1990) for multivariate normality in the compressed space. Intuitively, this test measures the distance between the measured and target (multivariate) distributions, and it was shown to perform well in high-dimensional problems. We found that the summary statistics, computed for the 100 mocks at the end of the iterative process, follows a multivariate normal distribution.
Provided the fiducial model and the Gaussianity checks, we first test the compression method on the stack of the mocks, with results presented in this section, and later, in Section 4, we compute the covariance matrix for the summary statistics over the set of 100 mocks and compare it to the Fisher matrix as defined in equation (10). It is important to keep in mind that, when referring to the Fisher matrix, we are simply referring to the mapping of the data covariance matrix |$\boldsymbol{\mathrm{ C}}$| into the compressed space.
To test the score compression algorithm against the traditional approach, for simplicity, we employ both the contaminated auto- and cross- stacked correlations, which are almost noise-free. This choice is motivated by the fact that we imposed a tight prior on the {α∥, α⊥} parameters to overcome the challenges coming from the non-monotonic relationship between these parameters and their corresponding summary statistics components (see Fig. 1). Thus, experimenting over less noisy mock data facilitates running the test in a case where it is granted that posteriors will not hit the priors.
For both the traditional (uncompressed data) and the compressed frameworks, we run the polychord sampler for the auto- and cross- stacked correlations, while sampling the full set of 15 model parameters {α∥, α⊥, bLy α, βLy α, bQSO, βQSO, |$\sigma_{v}$|, σ∥, σ⊥, bη, Si ii(1260), bη, Si ii(1193), bη, Si iii(1207), bη, Si ii(1190), bHCD, βHCD} and results are presented in Fig. 2. The two methods agree well with each other, leading to almost identical results. The numerical values of the peaks and 1σ confidence intervals of the one-dimensional (1D) marginals are presented in Table 1 as part of the ‘Testing the framework (stacked)’ set of columns. From the table, it can be noticed that in some cases the fiducial parameters used to compute the compression are not within the 3σ confidence interval. Despite the fiducial being a first guess, and not necessarily accurate, the contours of the two methods agree well with each other.
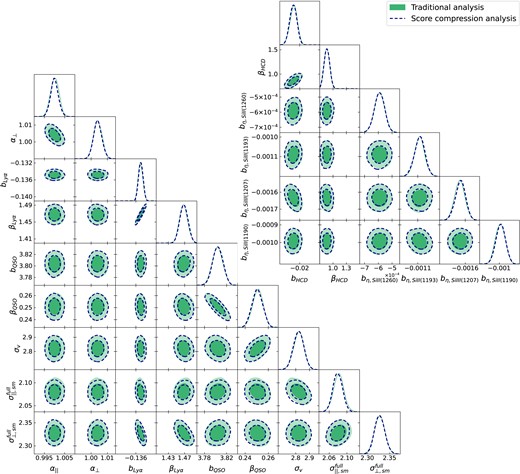
Triangle plots of the parameters of interest for the stack of correlation functions computed from a set of 100 mocks. Results are split, for presentation purposes only, into the set of standard parameters {α∥, α⊥, bLy α, βLy α, bQSO, βQSO, |$\sigma_{v}$|, σ∥, σ⊥} (lower left panel) and contaminant parameters {bη, Si ii(1260), bη, Si ii(1193), bη, Si iii(1207), bη, Si ii(1190), bHCD, βHCD} (upper right panel). The green filled contours refer to the results obtained performing the inference using the full uncompressed data vector, which we denote as ‘Traditional analysis’, while the blue dashed contours refer to the compressed analysis results, denoted as ‘Score compression analysis’.
We just demonstrated that the score compression inference pipeline leads to the same results as the standard approach. This shows the linearity of the parameters in the model to a good approximation. However, it is important to bear in mind that, in this case, this only holds locally around the fiducial, because of the non-linearity of the components that relate to α∥ and α⊥, on which we imposed a tight prior.
4 TESTING THE COVARIANCE MATRIX
An interesting application of the compression algorithm consists of evaluating the accuracy of the covariance matrix |$\boldsymbol{\mathsf{C}}$| by comparing it to the mock-to-mock covariance |$\boldsymbol{\mathsf{C}_{t}}$|, which is the covariance matrix of the summary statistics vectors of the set of 100 mocks. We now showcase this application using a single mock.
We recall that the computation of the standard data covariance happens in a set-up where the length of the data vector is larger than the number of samples, which is sub-optimal. The covariance should be singular; however, the off-diagonal elements of the correlation matrix are smoothed to make it positive definite (dMdB20). Reducing the dimensionality of the data vector via score compression allows us to compute a new covariance matrix |$\boldsymbol{\mathsf{C}_{t}}$|, which has a dimensionality significantly lower than the number of samples used to compute it, given that the new data vector will be |$\sim\!\! \mathcal {O}(10)$| long. The fact that now the number of mock samples is larger than the number of compressed data points means that we are now in a framework where the estimated |$\boldsymbol{\mathsf{C}_{t}}$| is in principle a better estimator of the true covariance |$\boldsymbol{\mathsf{\Sigma}}$| in compressed space than |$\boldsymbol{\mathsf{F}}$|, which is obtained by mapping the covariance |$\boldsymbol{\mathsf{C}}$| into this space.
We now repeat the same experiment as in Section 3 over a single mock and evaluate the posterior using polychord for the full set of parameters {α∥, α⊥, bLy α, βLy α, bQSO, βQSO, |$\sigma_{v}$|, σ∥, σ⊥, bη, Si ii(1260), bη, Si ii(1193), bη, Si iii(1207), bη, Si ii(1190), bHCD, βHCD}. This is either done using the original covariance |$\boldsymbol{\mathsf{C}}$| matrix (mapped into the compressed space, to the Fisher matrix) in the Gaussian likelihood in equation (9) or instead using the mock-to-mock covariance |$\boldsymbol{\mathsf{C}_t}$| adopting a t-distribution as a likelihood function, as proposed in Sellentin & Heavens (2015). The latter is of the form of
with
where ns is the number of mocks, nt is the length of the compressed data vector, and Γ is the Gamma function. Once again, the choice of the tight prior on both {α∥, α⊥} affected the choice of the set of mocks in order to run this second experiment. However, the goal of this second experiment is to provide an example case of testing the accuracy of the subsampling estimation of the covariance matrix. If the method is demonstrated to effectively work over some subset of mocks, it is expected that will also be the case for the others.
The results for the BAO parameters {α∥, α⊥} and the Ly α parameters {bLy α, βLy α} are shown in Fig. 3, while the full set is presented in Appendix A and listed in Table 1 (‘Testing the covariance (single mock)’ columns). In this test case, using the mock-to-mock covariance results in a small enlargement of the posterior for the α⊥ parameter: while using the original covariance matrix provides α⊥ = 1.002 ± 0.027, the mock-to-mock covariance results in |$\alpha _{\perp } = 1.004^{0.029}_{-0.032}$|. On the other hand, the Ly α linear bias and RSD parameter absolute errors increase by |$50$| and |$\sim\!\! 25{{\ \rm per\, cent}}$|, respectively, with final relative error of about |$5\!\!-\!\!6{{\ \rm per\, cent}}$|. The uncertainty of the vast majority of the other parameters agrees remarkably well.

Triangle plots of the BAO parameters of interest {α∥, α⊥} and the Ly α parameters {bLy α, βLy α} for one set of the Ly α auto- and cross- mock correlations. The blue filled contours refer to the results obtained performing the inference using the original covariance matrix |$\boldsymbol{\mathsf{C}}$| (mapped into the compressed space) in the likelihood function, and hence are denoted as ‘Original covariance’. On the other hand, the red dashed results, denoted as ‘Mock-to-mock covariance’, refer to the case in which the mock-to-mock covariance matrix is used instead, while adopting a t-distribution likelihood.
We end this discussion on covariance matrix estimation by noting that the test presented here is meant as a showcase of the usefulness of compressing Ly α forest correlation functions. However, proper testing of the Ly α forest covariance matrices would require a more comprehensive analysis using a larger sample of mocks,4 and comparison with other estimation methods (see e.g. dMdB20).
5 GOODNESS OF FIT TEST
In this section, we make a step forward with respect to the original aim of the work, by considering goodness of fit tests. For Ly α correlation functions, the length of the data vector can go from 2500, considering only the autocorrelation, to 7500 if considering also the cross-correlation. In a context where only |$\sim\!\! \mathcal {O}(10)$| parameters are sampled, any bad fit for noisy data can be hard to detect. Reducing the dimensionality of the data via score compression, we investigate whether it would be easier for any bad fit to be spotted. Hence, given the results presented in Section 3, we test the robustness of the method against unmodelled effects in the correlation functions, via the χ2 statistics.
To this end, we test the goodness of fit on contaminated data when metals are not modelled. For simplicity, here we restrict to the Ly α autocorrelation alone and without considering contamination from HCD. The sampled parameters will only be {α∥, α⊥, bLy α, βLy α, σ∥, σ⊥}. Tests are run by constructing the χ2 distributions over a set of 300 Monte Carlo realizations of the autocorrelation, introduced in Section 2.3: for each realization, we run a minimizer and evaluate the χ2 at the best fit.
We considered two main Monte Carlo populations: with and without metal contamination. The difference between the two is shown in the wedge plot of Fig. 4, which is built by averaging over the values of the correlation function in the ‘wedge’ of the space {r∥, r⊥} identified by values of |μ| = |r∥/r| between 0.95 and 1.0. To generate them, we used the best-fitting values of {α∥, α⊥, bLy α, βLy α, σ∥, σ⊥, bη, Si ii(1260), bη, Si ii(1193), bη, Si iii(1207), bη, Si ii(1190)} for the contaminated stacked Ly α mock autocorrelation, where depending on the population (contaminated or uncontaminated) the metals’ parameters were either included or not.
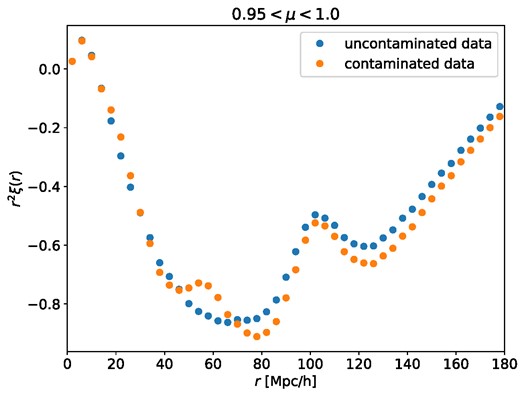
This wedge plot, for |μ| = |r∥/r| between 0.95 and 1.0, shows the effect of adding metals (in orange) to the correlation model |$\boldsymbol{\xi }$| without metals (in blue) along the line of sight. For simplicity in the χ2 analysis, we do not include contamination coming from HCD, so these features are only the effects of metal lines. Also, in this example, in order to better visualize the difference between the two, we have been generating noise from the covariance matrix of the stacked autocorrelation mock.
5.1 Maximal compression
For both the contaminated and uncontaminated mock data, we apply a compression down to the same number of sampled parameters without including contamination in the modelling, with the summary statistics thus given by |$\boldsymbol{t}_{\mathrm{max}} = \lbrace t_{\alpha _{\parallel }}, t_{\alpha _{\perp }}, t_{b_{\rm {Ly}\, \alpha }}, t_{\beta _{\rm {Ly}\, \alpha }}, t_{\sigma _{\parallel }}, t_{\sigma _{\perp }} \rbrace$|. This is defined as maximal compression. In what follows, we are interested in learning about the χ2 distribution for the two Monte Carlo populations.
We found that for both contaminated and uncontaminated data, the χ2 distributions are similar, with values of the order of |$\mathcal {O}(10^{-10} \ \mathrm{ to} \ 10^{-3})$| (left panel of Fig. 5). However, comparing the fits to the contaminated and uncontaminated data, the best-fitting parameter values are systematically shifted for some parameters. The distributions of the best-fitting values for bLy α and βLy α are shown in the right panels of Fig. 5: for the fits to contaminated data, 80 and 90 per cent of the best-fitting values, respectively, for each parameter are below the true value.
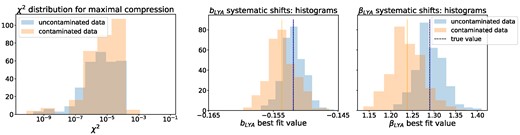
χ2 histograms (left panel) for the maximal compression and corresponding best-fitting values’ histograms for the Ly α parameters (right panels), where blue refers to the uncontaminated case and orange to contaminated. In the maximal compression set-up, |$\boldsymbol{t} = \boldsymbol{t}_{\mathrm{max}} = \lbrace t_{\alpha _{\parallel }}, t_{\alpha _{\perp }}, t_{b_{\mathrm{Ly}\, \alpha }}, t_{\beta _{\mathrm{Ly}\, \alpha }}, t_{\sigma _{\parallel }}, t_{\sigma _{\perp }} \rbrace$|. The black dashed lines in the two panels on the right correspond to the true values used to generate the Monte Carlo realizations.
The χ2 values remain very small for the fits to contaminated data, which indicates that in the compressed space, the model without contaminants still has enough flexibility to perfectly fit the data: the system has zero degrees of freedom, given that we are sampling six parameters, and the compressed data vector has six components. Instead of the mismatch between the model without contaminants and the contaminated data being visible in the form of large χ2 values, it is manifested through a systematic shift in the recovered parameter values from the truth, which in a realistic data fitting scenario could not be detected. This is linked to the fact that we are very close to a linear model scenario, meaning that in the compressed space the model still has enough flexibility to fit the data. This motivated a deeper testing of the framework, extending it to extra degrees of freedom as follows.
5.2 Non-maximal compression
Given the problem highlighted in the maximal framework, we tested the pipeline in a non-maximal compression case, where the extra degrees of freedom are given by the metals contaminating the data. Namely, the maximal summary statistics is now extended to include |$\boldsymbol{t}_{\mathrm{extra}}=\lbrace t_{b_{\eta ,\, \mathrm{Si\, \rm{\small II}(1260)}}}, t_{b_{\eta ,\, \mathrm{Si\, \rm{\small II}(1193)}}}, t_{b_{\eta ,\, \mathrm{Si\, \rm {\small III}(1207)}}}, t_{b_{\eta ,\, \rm{Si\, {\small II}(1190)}}} \rbrace$|. Still, metals will not be included in the likelihood modelling. This means that if the quantities of reference here are the compressed data vector
the compressed model
and they enter the χ2 as per
the fiducial model |$\boldsymbol{\mu }_*$| and its gradient will now include contaminants, whereas |$\boldsymbol{\mu (\theta)}$| will not and |$\boldsymbol{d}$| will be either contaminated or uncontaminated data depending on the population used to build the χ2 statistics. Now, |$\boldsymbol{t} = \lbrace \boldsymbol{t}_{\mathrm{max}},\boldsymbol{t}_{\mathrm{extra}} \rbrace$|. The length of the compressed data vector is 10, where the first 6 components refer to the sampled parameters, with a remainder of 4 components, which are fixed and constitute our extra degrees of freedom. Under the approximation that the mean of a χ2 distribution indicates the number of degrees of freedom of the problem, we would expect that mean to be at least equal to the number of extra degrees of freedom we added. In our case, we expect that for the uncontaminated case, for which we know the modelling is good, the mean will be close to 4 (four metals). We want to test whether in this case a bad fit to the contaminated data is apparent as a mean χ2 significantly larger than 4.
The χ2 histograms are shown in the left panel of Fig. 6: the mean values for the uncontaminated and contaminated cases are, respectively, 3.89 and 67.51. Considering a χ2 with number of degrees of freedom equal to 4, the p-values for the two means are, respectively, 0.4 and 10−14: the bad fit in the contaminated case has emerged.
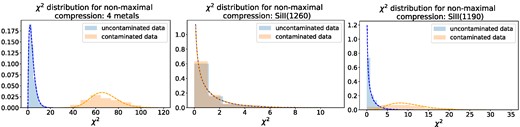
Normalized χ2 histograms for the three non-maximal compression cases presented in Section 5.2: starting from the left, all four metals, Si ii(1260), and Si ii(1190) were used to build extra degrees of freedom. In blue are the histograms and χ2 distributions for the uncontaminated data, and in orange for contaminated data. The corresponding χ2 distributions (dashed lines) are generated assuming as number of degrees of freedom the mean of the histogram distributions. The first set of histograms, which relates to all four extra degrees of freedom, presents a strong shift between the orange and the blue distributions: their corresponding means are 3.89 and 67.51, respectively. In the Si ii(1260) case, both distributions have a mean of ∼1.1, while in the Si ii(1190), the mean for the uncontaminated case is 1.01, against 10.04 in the contaminated case.
We further experimented over the addition of metals and we considered adding a single extra degree of freedom at a time, associated with either one of the following metals: the Si ii(1260) and the Si ii(1190). The resulting χ2 histograms are shown in the middle and right panels of Fig. 6, respectively. These two metal lines were chosen because of how differently they affect the data: while the Si ii(1260) contamination happens around the BAO scale along the line of sight, the Si ii(1190) contributes to the peak at ∼60 Mpc h−1. We run the same exact experiment and find that the addition of |$t_{b_{\eta ,\, \mathrm{Si\, \rm{\small II}(1190)}}}$| does bring out the bad fit, while the other does not. Specifically, the two χ2 distributions when the extra degree of freedom is given by bη, Si ii(1260) have a mean of ∼1, again equal to the number of degrees of freedom, but they cannot be distinguished. The p-values for both distributions, assuming 1 degree of freedom, are all above a threshold of 0.01. Both distributions are indicative of an acceptable fit. On the contrary, adding the extra compressed component related to Si ii(1190) results in having a mean χ2 of 1.01 in the uncontaminated case and 10.04 in the contaminated one, with corresponding p-values of 0.3 and 10−3, respectively, if we consider a target χ2 distribution of 1 degree of freedom. This perhaps is indicative about the fact that in order to capture a bad fit, adding extra degrees of freedom is not enough: these extra degrees of freedom must be informative about features not captured by the core set of parameters. The Si ii(1260) affects the model at scales of the correlation function that are on top of the BAO peak, which we model for, whereas Si ii(1190) effectively adds information on a feature that is completely unmodelled.
In light of this, a possible solution is to add some extra degrees of freedom to the maximal compression vector, which are designed to be orthogonal to the already known components in the compressed space. This would allow the extra flexibility, which is not captured in the model, to highlight for a bad fit in the compressed framework. This is an interesting problem that is left for future work. However, a similar solution has already been implemented in the context of MOPED (Heavens, Sellentin & Jaffe 2020), specifically to allow new physics to be discovered.
Not modelling the Si ii(1260) line in the uncompressed traditional framework does not result in any bad fit, which makes this an example of systematics hidden in the large original data vector. At the same time, the fact that the Si ii(1260) test in the compressed framework fails to show a bad fit at the level of the χ2 is quite problematic, given this metal line is one of the primary contaminants we have to be careful of in BAO measurement, affecting the peak’s scale. The worry is then that, despite constructing an extended framework, there is a chance that some systematics hiding in the signal could be missed. This effectively means that in order to apply data compression, the underlying physics must be already well known to a good extent. Because some systematics could be hard either to model or to detect, in this example, we deliberately assumed that we had no knowledge about known systematics, where in principle we could have also marginalized over them (Alsing & Wandelt 2019).
6 ROBUSTNESS TO PARAMETER NON-LINEARITIES
Each component of the score-compressed data vector relates to a specific model parameter, as per equation (8), via the gradient. Throughout the analysis, the BAO parameters proved to be a source of non-linearities in relation to their summary statistics components (see Fig. 1), sometimes resulting in a multipeaked posterior distribution. With the intent of mitigating this effect, we were forced to impose a tight prior on both {α∥, α⊥}, which reduces the generalizability of the approach.
Based on the work of Protopapas, Jimenez & Alcock (2005), we explore extensions to the algorithm by considering an ensemble of fiducial values of the BAO parameters to compute the score-compressed vector components related to {α∥, α⊥}. For any extra set of BAO parameters |$\lbrace \alpha ^{\mathrm{extra}}_{\parallel },\alpha ^{\mathrm{extra}}_{\perp } \rbrace$|, we introduce two extra summary statistics components:
where |$\boldsymbol{\mu }_{\mathrm{extra}}$| is the model evaluated at |$\lbrace \boldsymbol{\alpha }^{\mathrm{extra}}_{\parallel },\boldsymbol{\alpha }^{\mathrm{extra}}_{\perp } \rbrace$|, keeping the previously defined fiducial values for the other parameters. As these extra components effectively represent an extension of the compressed data set, the Fisher matrix in equation (10) will also be expanded to include |$[\nabla _{\alpha _{\parallel ,\perp }} \boldsymbol{\mu }_{\mathrm{extra}}]^T \boldsymbol{\mathsf{C}}^{-1}[\nabla _{\alpha _{\parallel ,\perp }}^{T} \boldsymbol{\mu }_{\mathrm{extra}}]$|. We test this extension on the same mock that was used to test the subsampling covariance matrix in Section 4, and results are presented in Fig. 7, imposing a physically motivated uniform prior [0.65, 1.35] for both α∥ and α⊥. The ensemble of extra fiducials is given by the set [{α∥ = 0.8, α⊥ = 1.2}, {α∥ = 1.2, α⊥ = 0.8}, {α∥ = 1.3, α⊥ = 0.7}, {α∥ = 0.9, α⊥ = 1.1}], in addition to the original {α∥ = 1.00, α⊥ = 1.01} (see Table 1). From Fig. 7, it can be seen that the constraining power on the BAO parameters between the traditional and compressed methods match. This same result is also true for the other parameters, not shown here.
![Triangle plots of the BAO parameters of interest {α∥, α⊥} for one set of the Ly α auto- and cross- mock correlations, with relaxed priors. The green filled contours refer to the results obtained performing the inference using the full uncompressed data vector, which we denote as ‘Traditional analysis’, while the blue dashed contours refer to the compressed analysis results, denoted as ‘Score compression analysis’. The framework of the latter is extended here to the assumption of multiple fiducial values for {α∥, α⊥} when performing the compression, namely [{α∥ = 1.00, α⊥ = 1.01}, {α∥ = 0.8, α⊥ = 1.2}, {α∥ = 1.2, α⊥ = 0.8}, {α∥ = 1.3, α⊥ = 0.7}, {α∥ = 0.9, α⊥ = 1.1}].](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/528/2/10.1093_mnras_stae092/1/m_stae092fig7.jpeg?Expires=1749908439&Signature=JXWBNhQfZ7ySe8Sc4Fqh128zXvf11fUsSSEykG5-NvsuENLRDzZ79YKXy9KkevSuyLhQ0sjjft0ntTo4ss44IJbqEo-1bHX99CP1jy-wWjoCsG3onH5zven4oPc-vbeb1z0zPHoMJFzhCjiS0iZBLoxVYWpjad5S9xcfZ96gBf4RCI8X~zOi41CysKU3EYixR1GnYz4-0ydJ9~koRRfev3oZ~OGH90y-jn2y4l~9JDJv7vdi0a4wDIFgz5S~kv5Tl8sT1pBOghsrW9oXce1wj9FCHWKYSIGvefIhPLfY3r7i68F6~3VWBEzWqelokSg8MpA3H4W3YDqIra239cNLZw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Triangle plots of the BAO parameters of interest {α∥, α⊥} for one set of the Ly α auto- and cross- mock correlations, with relaxed priors. The green filled contours refer to the results obtained performing the inference using the full uncompressed data vector, which we denote as ‘Traditional analysis’, while the blue dashed contours refer to the compressed analysis results, denoted as ‘Score compression analysis’. The framework of the latter is extended here to the assumption of multiple fiducial values for {α∥, α⊥} when performing the compression, namely [{α∥ = 1.00, α⊥ = 1.01}, {α∥ = 0.8, α⊥ = 1.2}, {α∥ = 1.2, α⊥ = 0.8}, {α∥ = 1.3, α⊥ = 0.7}, {α∥ = 0.9, α⊥ = 1.1}].
We tested the extension in terms of generalizability by progressively adding extra points to the ensemble, with reasonable spread, and found that with an ensemble of three to four extra fiducial sets of BAO parameters the algorithm is able to effectively get rid of the secondary posterior peaks and increase the accuracy of the measurement. Hence, the assumption of multiple fiducials for the BAO parameters, for which we had to impose a tight prior, enables us to relax the prior constraints.
7 APPLICATION TO REAL DATA
The score compression framework has so far been tested on realistic mocks; hence, it is straightforward to apply this same algorithm to real eBOSS DR16 Ly α data, for which we refer to dMdB20. The set of nuisance parameters is now extended to also include the contamination from carbon absorbers, the systematic quasar redshift error Δr∥, the quasar radiation strength |$\xi _0^{\mathrm{TP}}$|, and the sky-subtraction parameters Asky, Ly α and σsky, Ly α. The results presented in Section 6 motivate a direct test of the whole extended framework, which gets rid of the tight prior, to the real data. The ensemble of BAO parameter fiducial values is given by the set of {α∥ = 1.05, α⊥ = 0.96} – which are the best-fitting values obtained through the traditional analysis – and [{α∥ = 0.8, α⊥ = 1.2}, {α∥ = 1.2, α⊥ = 0.8}, {α∥ = 1.3, α⊥ = 0.7}, {α∥ = 0.9, α⊥ = 1.1}], which were found to be effective in Section 6. The fiducial values of the other parameters are set to the best fit found with the standard uncompressed analysis. In Fig. 8, we present the agreement of the extended framework against the traditional approach at the level of |$\lbrace \alpha _{\parallel }, \alpha _{\perp }, b_{\eta ,\, \rm {Ly}\, \alpha }, \beta _{\rm {Ly}\, \alpha }, \Delta r_{\parallel }, \beta _{\rm {QSO}}, \sigma _{v} \rbrace$|. The nuisance parameters are also found to be in excellent agreement.
![Triangle plot for fits to the real eBOSS DR16 data Ly α autocorrelation and cross-correlation, using the traditional approach (filled green) and the score compression framework (dashed blue) extended to include extra fiducial values of the BAO parameters at [{α∥ = 0.8, α⊥ = 1.2}, {α∥ = 1.2, α⊥ = 0.8}, {α∥ = 1.3, α⊥ = 0.7}, {α∥ = 0.9, α⊥ = 1.1}]. The results shown here are for the standard parameters $\lbrace \alpha _{\parallel }, \alpha _{\perp }, b_{\eta ,\, \rm {Ly}\, \alpha }, \beta _{\rm {Ly}\, \alpha }, \Delta r_{\parallel }, \beta _{\rm {QSO}}, \sigma _{v} \rbrace$.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/528/2/10.1093_mnras_stae092/1/m_stae092fig8.jpeg?Expires=1749908439&Signature=z67m4fP664bzGGMVd1ahXz3U4vDyC6NJxnViF3Y5WeE9WatmOQge3-8FMRk3PdF3Fvg3S823QuxOUD2F1hBrlMUc7OvpQQCb0XjbrJ4T8wDl5rQiw4VGVVW6Z-QPhajB504MFCq92sorvn3N0hTXDVXH0c6beXCj7ywQ2xc524nzZLmMrcRBUPQJmuFYChZQCoyoTCycW-Qyhuh7U3rnn7q3csjGERXiJ59RFCCOMDke~kC85CJKz9m~6H~uIG5SpjLkaYkzRPeKeJZU04Jfp1z~xeP0fulFCkyVMCVv0lohttWJ7oQjyj3rEHdsP-~psMD~EZolouXWxaj6ojKvgw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Triangle plot for fits to the real eBOSS DR16 data Ly α autocorrelation and cross-correlation, using the traditional approach (filled green) and the score compression framework (dashed blue) extended to include extra fiducial values of the BAO parameters at [{α∥ = 0.8, α⊥ = 1.2}, {α∥ = 1.2, α⊥ = 0.8}, {α∥ = 1.3, α⊥ = 0.7}, {α∥ = 0.9, α⊥ = 1.1}]. The results shown here are for the standard parameters |$\lbrace \alpha _{\parallel }, \alpha _{\perp }, b_{\eta ,\, \rm {Ly}\, \alpha }, \beta _{\rm {Ly}\, \alpha }, \Delta r_{\parallel }, \beta _{\rm {QSO}}, \sigma _{v} \rbrace$|.
8 CONCLUSIONS
Standard analyses of the Ly α forest correlation functions focus on a well-localized region, which corresponds to the BAO peak. However, these correlation functions usually have dimensions of 2500 or 5000, which means that the cosmological signal is extracted from a small subset of bins. This means that reducing the dimensionality of the data vector, while retaining the information we care about, could be a step forward in optimizing the analysis. At the same time, as extensively explained in Section 2, the covariance matrix C used for Ly α correlation analyses is estimated via subsampling. However, the dimensionality of the correlation functions is much larger than the number of data samples used to estimate the covariance. Reducing the dimensionality of the data vector to |$\mathcal {O}(10)$| allows for a reliable estimate of the covariance matrix. Given these premises, the goal of this work is to apply and explore a data compression algorithm for realistic Ly α autocorrelation and cross-correlation functions.
We reduced the dimensionality of the data vector to a set of summary statistics t using score compression. We assume a Gaussian likelihood, test for its validity, and show that this assumption is preserved in the compressed space as well, as the compression is a linear transformation. In the compressed space, the covariance can be given either by the mapped traditional covariance or by a covariance estimated directly in such a space.
We tested the compressed framework against the traditional approach at the posterior level, when using the original covariance C, and found that the two of them agree, and no bias is introduced. We then showcased a test example of covariance matrix evaluation in the compressed space, which is a key benefit of the approach, enabling a comparison to the covariance matrix obtained in the traditional sub-optimal framework. Because of non-linear relationship between the BAO parameters and their summary statistics components, throughout the analysis we adopted a tight prior on {α∥, α⊥}. Later in the analysis, with the aim of increasing the generalizability of the approach, while relaxing the prior constraint, we successfully tested extensions to the framework by assuming an ensemble of fiducial values for these problematic parameters.
We then further examined the compressed framework, by testing the inference against unmodelled effects and we find that if any information about the unmodelled features in the correlation function is not captured by the compressed data vector |$\boldsymbol{t}$|, this can potentially lead to biases, which do not emerge at the level of the χ2 goodness of fit test. Hence, we advise against performing goodness of fit tests in compressed space, unless the compressed vector is extended to include extra degrees of freedom, analogous to what is done in Heavens et al. (2020). Extending the framework in this sense is left for future work.
We applied our extended compression framework to DR16 data from the eBOSS and demonstrated that the posterior constraints are accurately recovered without loss of information. A step change in constraining power, and thus accuracy requirements, is expected for forthcoming Ly α cosmology analyses by the ongoing DESI experiment (see e.g. Gordon et al. 2023), which will observe up to 1 million high-redshift quasars with z > 2. Optimal data compression as proposed in this work will facilitate these analyses through inference that is complementary to the traditional approach and through additional consistency and validation tests.
ACKNOWLEDGEMENTS
We thank Alan Heavens, Niall Jeffrey, and Peter Taylor for helpful discussions. This work was partially enabled by funding from the UCL Cosmoparticle Initiative. AC acknowledges support provided by NASA through the NASA Hubble Fellowship grant HST-HF2-51526.001-A awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Incorporated, under NASA contract NAS5-26555. BJ acknowledges support by STFC Consolidated Grant ST/V000780/1. SN acknowledges support from an STFC Ernest Rutherford Fellowship, grant reference ST/T005009/2. AF-R acknowledges support by the programme Ramon y Cajal (RYC-2018-025210) of the Spanish Ministry of Science and Innovation and from the European Union’s Horizon Europe research and innovation programme (COSMO-LYA, grant agreement 101044612). IFAE is partially funded by the CERCA programme of the Generalitat de Catalunya. For the purpose of open access, the authors have applied a creative commons attribution (CC BY) licence to any author-accepted manuscript version arising.
DATA AVAILABILITY
The code is publicly available at the ‘compression’ branch of https://github.com/andreicuceu/vega.git. The data underlying this article will be shared on reasonable request to the corresponding author.
Footnotes
Note also that this kind of analysis heavily relies on mocks being consistent with each other (both in terms of mock production and in terms of analysis), in order to avoid introducing extra variance.
References
APPENDIX A: FULL RESULTS FOR THE MOCK-TO-MOCK COVARIANCE TEST
We here present in Fig. A1 the full set of results from the mock-to-mock covariance test, presented in Section 4, against the contours obtained using the original covariance in the compressed framework. Numerical values are reported in Table 1. The contours agree well with each other. The most striking enlargements of the posteriors are visible for the parameters {α⊥, bLy α, βLy α, bHCD}. Because the ‘Original covariance’ set-up has been shown to agree with the standard analysis in Section 3, this comparison automatically becomes a comparison to the standard approach.
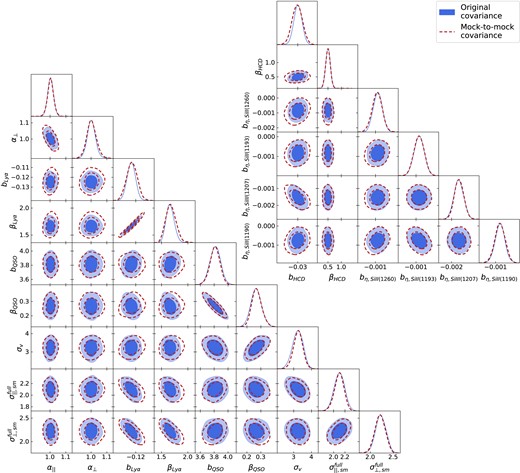
Triangle plots of the parameters of interest for one set of the Ly α autocorrelation and cross-correlation mocks. Results are split, for presentation purposes only, into the set of standard parameters {α∥, α⊥, bLy α, βLy α, bQSO, βQSO, |$\sigma_{v}$|, σ∥, σ⊥} (lower left panel) and contaminant parameters {bη, Si ii(1260), bη, Si ii(1193), bη, Si iii(1207), bη, Si ii(1190), bHCD, βHCD} (upper right panel). The blue filled contours refer to the results obtained performing the inference using the original covariance matrix |$\boldsymbol{\mathsf{C}}$| mapped into the compressed space (the Fisher matrix) in the likelihood function, and hence are denoted as ‘Original covariance’. On the other hand, the red dashed results, denoted as ‘Mock-to-mock covariance’, refer to the case in which the mock-to-mock covariance matrix is used instead, while adopting a t-distribution likelihood.
Author notes
NASA Einstein Fellow.



