-
PDF
- Split View
-
Views
-
Cite
Cite
Ying Ding, Yi Qi, Dong Qiao, Determination method of co-orbital objects in the solar system, Monthly Notices of the Royal Astronomical Society, Volume 526, Issue 1, November 2023, Pages 600–615, https://doi.org/10.1093/mnras/stad2697
Close - Share Icon Share
ABSTRACT
In this paper, based on two-dimensional maps from the semi-analytical Hamiltonian approach, we proposed an improved determination method to classify co-orbital objects in the solar system without numerical integration. Taking advantage of a simple pattern analysis, we present two certainty conditions to recognize co-orbital objects with uncertain orbital parameters. Then, our determination method is applied to classify potential co-orbital objects (PCOs) of Mars, Jupiter, Saturn, Uranus, and Neptune, and then their results are verified through numerical integration in the multiplanet model, respectively. Through our method, we identify 11 new co-orbital objects for the first time, including four Mars trojans i.e. tadpole (TP) objects, one short-term Mars quasi-satellite (QS), one Mars horseshoe (HS), one Jupiter QS, one short-term Uranus trojan, one Uranus PCO, and one Neptune PCO with short-term transitions between QS and HS, and one Neptune PCO with short-term transition between QS and TP. Numerical computation shows that except Saturn PCOs significantly perturbed by Jupiter, our determination method for co-orbital objects in the solar system is effective, but it cannot deal with the classification of PCOs near the boundary of different co-orbital regions. Since our method does not rely on time-consuming numerical integration, it is efficient and suitable for a large amount of screening for numerous co-orbital objects in the solar system.
1 INTRODUCTION
The 1:1 mean motion resonance (MMR), or co-orbital motion, is an important orbital type in both aerospace and astronomy. Taking the Sun–planet–asteroid restricted three-body problem as an example, the asteroid locked in the co-orbital motion with a planet is termed the co-orbital object. Based on the mean longitude difference between the co-orbital object and the planetary host, there are three classical co-orbital types: tadpole (TP) orbits are locked in a libration around L4 or L5 Lagrange point; horseshoe (HS) orbits are in a libration around L3 Lagrange point; quasi-satellite (QS) orbits librate around the planetary host. Except for the above three classical co-orbital motions, in the spatial case, due to the presence of eccentricity and inclination, compound co-orbital motions (or recurrent transitions) between different co-orbital behaviours are possible (Namouni 1999).
The co-orbital motion can be applied to deep space exploration. In the aerospace field, QS orbits usually are also called distant retrograde orbits (DROs). Particularly, lunar DROs have potential utilization in cislunar space due to their orbital stability and unique orbital dynamics (Peng et al. 2022). Recently, NASA’s Artemis I mission sent an uncrewed Orion vehicle to a lunar DRO (Batcha et al. 2020). In the Martian Moon eXploration (MMX) mission proposed by JAXA, the spacecraft is planned to observe polar regions of Phobos from a QS orbit moving out of the equatorial plane of Phobos (Nakamura et al. 2021). New opportunities for solar physics could be realized by future missions providing sustained observations from the far side of the Sun (e.g. the Sun–Earth L3 point), or from near-quadrature angles relative to the Earth (e.g. the Sun–Earth L4 and L5 points; Gibson et al. 2018). The Solar TErrestrial RElations Observatory B (STEREO-B) spacecraft has visited the Sun–Earth L5 point (Kaiser et al. 2008). The ESA Vigil mission will deploy a spacecraft on a TP orbit in the neighbourhood of Sun–Earth L5 point and is expected to continuously monitor rapidly changing solar activity and deliver early warning of possibly harmful space weather (Palomba & Luntama 2022).
Co-orbital asteroids are widely distributed in the solar system. For example, TP asteroids are termed trojans, and numerous trojan companions have been found co-orbiting with Jupiter (Marzari et al. 2002; Stacey & Connors 2008). Some Jupiter trojans are very primitive and might be the remnants of the physical and dynamical processes that molded the planetary host (Kortenkamp, Malhotra & Michtchenko 2004). Therefore, co-orbital objects are very important exploration targets in the research of the solar system. NASA’s Lucy Mission sent a highly capable and robust spacecraft to investigate seven primitive Jupiter trojans, which have been preserved since early in solar system history (Levison et al. 2021). Asteroid 469 219 Kamo‘oalewa (2016 HO3), an elongated asteroid (Li & Scheeres 2021; Li, Scheeres & Qiao 2023), switches repeatedly between the QS and HS motions (De la Fuente Marcos & De la Fuente Marcos 2016b) and is selected as a target for Chinese asteroid sample-return and comet exploration mission (Zhang et al. 2019). Mars trojans were identified by Scholl, Marzari & Tricarico (2005b) and Christou et al. (2020a, b). Venus possesses several unstable or transient trojans Brasser et al. (2004) and Scholl, Marzari & Tricarico (2005a). Neptune (Almeida, Peixinho & Correia 2009; Wu, Zhou & Zhou 2019) and Earth (Markwardt et al. 2020; Hui et al. 2021) also have TP companies. Saturn’s moons Epimetheus and Janus move on HS orbits with respect to each other, which is the first HS case observed in the solar system. The Earth has several HS companions (Brasser et al. 2004; Christou & Asher 2011; De la Fuente Marcos & De la Fuente Marcos 2016a; Kaplan & Cengiz 2020), but many of them are unstable and may get lost soon after being discovered due to the observational challenges (Fuente Marcos & De la Fuente Marcos 2016a). The first small body to be confirmed on a QS orbit was 2002 VE68, a companion to Venus (Mikkola et al. 2004). Jupiter appears to host several QS companions (Kinoshita & Nakai 2007; Qi & de Ruiter 2021), and the Earth also hosts some confirmed QS companions (Connors et al. 2004; Mikkola et al. 2006; Connors 2013; Fuente Marcos & De la Fuente Marcos 2016b; Rezky & Soegiartini 2020).
Fuente Marcos & De la Fuente Marcos (2016b) pointed out that having a particular set of orbital elements at present is not enough to claim a co-orbital relationship with a host, so it is necessary to implement numerical integration forward and backward in time for a representative set of statistically compatible orbits to check whether the dynamical evolution of the object over a reasonable amount of time is still consistent with being locked in a 1:1 MMR with the host. However, in the last decade, with the rapid improvement of the detection ability for asteroids, the number of newly discovered asteroids are rising. It is necessary to develop an efficient method to identify co-orbital objects. Di Ruzza, Pousse & Alessi (2023) proposed an integrable model obtained with averaging techniques to classify asteroids in quasi-coplanar co-orbital motion in a medium-term time-scale without numerical integration. Data from real observations fit very well with their theory. Qi & Qiao (2022) studied the dynamical stability of spatial Earth co-orbital objects through a two-dimensional map, which can also be used to classify co-orbital types preliminarily without numerical integration. However, the above determination methods for co-orbital objects still have some deflects as follows.
The traditional determination method by numerical integration forward and backward over a reasonable amount of time is inefficient and needs numerous calculation times.
The classification method for a quasi-coplanar co-orbital motion proposed by Di Ruzza et al. (2023) cannot be used for spatial co-orbital objects.
The stability analysis for Earth co-orbital objects in the two-dimensional map proposed by Qi & Qiao (2022) cannot provide the detailed determination criteria or address co-orbital objects with poor orbit determinations.
In this paper, based on the two-dimensional map in Qi & Qiao (2022), we present an improved determination method for co-orbital objects in the solar system. Taking advantage of simple pattern analysis, our method can treat data uncertainties of co-orbital objects. Since it does not rely on numerical integration, it is efficient and suitable for a large amount of screening for numerous co-orbital objects in the solar system.
Based on the above discussion, this paper is divided into four parts. In Section 2, we introduce the background of this paper. In Section 3, a determination method for potential co-orbital objects (PCOs) in the Sun–planet system is proposed. In Section 4, our determination method is applied to analyse the co-orbital objects in the solar system, and several interesting examples are presented. Finally, the conclusions of this paper are presented in Section 5.
2 BACKGROUND
2.1 Semi-analytical Hamiltonian form
In the Sun–planet–asteroid circular restricted three-body problem (CRTBP), we use a, e, i, ω, Ω, and M to denote the asteroid’s osculating semimajor axis, eccentricity, inclination, argument of perihelion, the longitude of node, and mean anomaly in the heliocentric coordinate system, respectively. The quantities with the subscript ‘p’ refer to the planetary host.
For the co-orbital motion in the Sun–planet–asteroid CRTBP, a constant N can be expressed as (Morbidelli 2002)
where im denotes the maximum of i when e = 0 for the given values of a and N. In some references (Fuente Marcos & De la Fuente Marcos 2016b), |$\cos i_ \mathrm{ m}=\sqrt{1-e^2}\cos i$| was called the Kozai–Lidov parameter.
For the given im, the Hamiltonian for the co-orbital motion can be simplified to (Qi & Qiao 2022)
where φ = λ − λp denotes the mean longitude difference between the asteroid and the planetary host (Murray & Dermott 1999). λ = M + ω + Ω is the mean longitude of the co-orbital object and λp = Mp + ωp + Ωp the same variable for the planetary host. μ is the mass ratio of the planet and is equal to mplanet/msun, where mplanet and msun are masses of the planet and the Sun, respectively. In addition, the unit of mass is set to the sum of masses of the Sun and the planetary host, the unit of length (LU) is set to ap, and the unit of time is equal to Tp/2π, where Tp is the period of the planetary host around the Sun. In the dimensionless heliocentric frame, the Keplerian term |$\mathcal {H}_{0}$| is expressed by
The perturbation term |$\mu \bar{\mathcal {H}}_{1}$| can be approximated using the following averaging method (Morbidelli 2002),
where vectors |$\boldsymbol r$| and |$\boldsymbol r_p$| are the positions of the asteroid and the planet in the dimensionless heliocentric frame, respectively. As we can see from the above equation, for the given im, the |$\bar{\mathcal {H}}_{1}$| value is determined by a, e, ω, and φ, independent of the mass ratio μ.
Since a librates around ap in the co-orbital motion, we fix the value of a and set it as a0, |$\mathcal {H}$| in equation (2) can be approximated by Qi & Qiao (2022)
|$\bar{\mathcal {H}}(a_0,e,\omega ,\varphi)$| is a pseudo-Hamiltonian and not a constant because the real a is time-varying in the CRTBP. However, since the variation of a is quite small for the co-orbital motions studied here, |$\bar{\mathcal {H}}$| defined in equation (5) is approximately equal to the real |$\mathcal {H}$|.
Based on equation (3), |$\mathcal {H}_{0}$| is fixed for the given a0. In equation (5), the value of |$\bar{\mathcal {H}}$| is determined by e, ω, and φ for the given a0 and im. Hence, if we go through the whole feasible domain of e, ω, and φ and calculate the corresponding |$\bar{\mathcal {H}}$| values, we can obtain the |$\bar{\mathcal {H}}$| structure in the (e, ω, φ) space. Apparently, in the calculation of |$\bar{\mathcal {H}}$| structure, the computation time is dominated by the averaging process of |$\bar{\mathcal {H}}_{1}$|. Fortunately, as we can see from equation (4), for the given im and a, the |$\bar{\mathcal {H}}_{1}$| value is independent of the mass ratio μ.
Based on the above analysis, if we have obtained |$\bar{\cal H}$| values for a given μ and im, we can calculate other |$\bar{\cal H}$| values with the same im but different μ. For example, in the CRTBP with μ*, its |$\bar{\cal H}^{*}$| can be obtained from
2.2 Hamiltonian isosurfaces and two-dimensional map
For the given im and a0, the co-orbital motion in the CRTBP can be approximately described in the (e, ω, φ) phase space. The ranges of ω and φ are both from 0° to 360°, and the range of e is from zero to emax , where emax is the maximum value allowed for the eccentricity in the phase space for the given im and can be obtained from |$e_{\max }=\sqrt {1-\cos ^2 i_ \mathrm{ m}}=\sin i_ \mathrm{ m}$| based on equation (1). As stated in Qi & de Ruiter (2020a), phase structures of different co-orbital behaviours can be shown in the torus space clearly. Fig. 1 shows the |$\bar{ \mathcal {H}}$| isosurface structure of the Sun–Jupiter CRTBP with im = 20° and a = ap = 1 LU in the torus space. In Fig. 1, the torus space is formed by sweeping a disc around a circle. The radius of this circle is set as e0 = 3emax , and the phase angle of the disc in this circle is φ. The maximum radius of the disc is set as emax . Different colours denote different |$\bar{ \mathcal {H}}$| values. Red closed isosurfaces around φ = ±60° correspond the TP motion of L4 and L5, respectively, or L4TP and L5TP for short. Green isosurfaces correspond to HS motion, and the grey cylinder isosurface around φ = 0° corresponds to the QS motion. According to Qi & de Ruiter (2020a), QS surfaces are topologically different from TP (or HS) surfaces, and with the decrease of |$\bar{ \mathcal {H}}$|, φ ranges of TP, HS, and QS isosurfaces all gradually expand. Therefore, the QS surface starts to contact the TP (or HS) surface as |$\bar{\mathcal {H}}$| decreases to a certain value. This case corresponds to the yellow surface in Fig. 1, which is defined as the critical compound surface, and according to Qi & de Ruiter (2020b), the four contact points (see red points in Fig. 1) correspond to L4 and L5 axial orbits and play roles of transport gateways among different co-orbital motions. The |$\bar{\mathcal {H}}$| value of the critical compound surface is denoted by |$\bar{\mathcal {H}}_a$|. If |$\bar{\mathcal {H}}$| continues to decrease, |$\bar{\mathcal {H}}$| isosurfaces gradually approach the collision curves, which are denoted by black lines in Fig. 1. Co-orbital motions near the collision curves are unstable and chaotic (Qi & Qiao 2022).
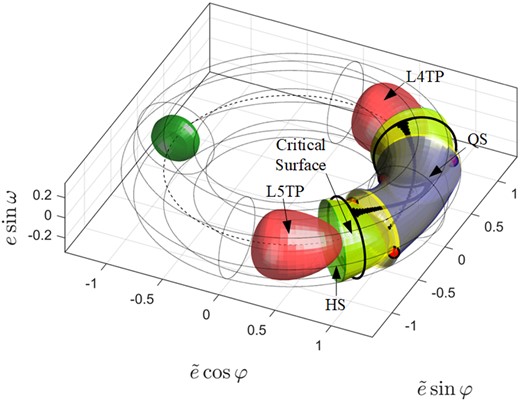
|$\bar{ \mathcal {H}}$| isosurface structure of the Sun–Jupiter CRTBP with im = 20° and a = ap = 1 LU in the torus space.
Qi & Qiao (2022) presented a method to approximately calculate the maximum |$\bar{\mathcal {H}}$| values of TP, HS, QS, critical compound surfaces, and collision curves in the (e, ω, φ) space. Then, different co-orbital types can be determined efficiently through a pattern in the |$(i_ \mathrm{ m}, \bar{\mathcal {H}})$| frame without long-term numerical integration. Fig. 2 displays distributions of co-orbital types in the |$(i_ \mathrm{ m}, \bar{\mathcal {H}})$| plot for the Sun–Jupiter CRTBP. In this figure, the sign ‘/’ denotes that two kinds of different co-orbital behaviours can coexist under the same |$(i_ \mathrm{ m}, \bar{\mathcal {H}})$|, while the sign ‘−’ denotes that two kinds of different co-orbital behaviours can transit and exchange (Qi & de Ruiter 2020a). In addition, based on Qi & de Ruiter (2020b), the Jacobi constant C ≈ 1 + 2cos im. If im is close to zero, C is approximately equal to 3 and the co-orbital object is close to the planet host. In this circumstance, our semi-analytical method based on the torus structure is not feasible, especially for smaller |$\bar{\mathcal {H}}$| values. In this paper, we require that the left boundary of the two-dimensional map in the |$(i_ \mathrm{ m}, \bar{\mathcal {H}})$| frame should be larger than im = 2°.
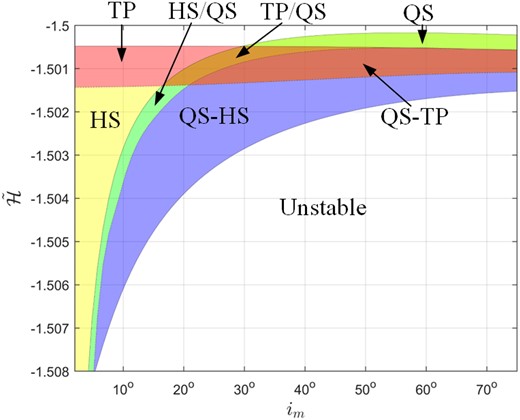
Distributions of co-orbital types in the |$(i_ \mathrm{ m}, \bar{\mathcal {H}})$| plot for the Sun–Jupiter CRTBP.
Based on the location of contact points of the critical compound surface in the torus space, we can obtain φ values of L4 and L5 axial orbits. Fig. 3 shows φ values of L4 and L5 axial orbits with different im in the Sun–Jupiter CRTBP, which can be roughly regarded as the separatrix between current TP (or HS) and QS stages: the green and red regions correspond to the TP (or HS) and QS stages, respectively. This criterion can differentiate the TP (or HS) and QS motions in the TP/QS (or HS/QS) region.
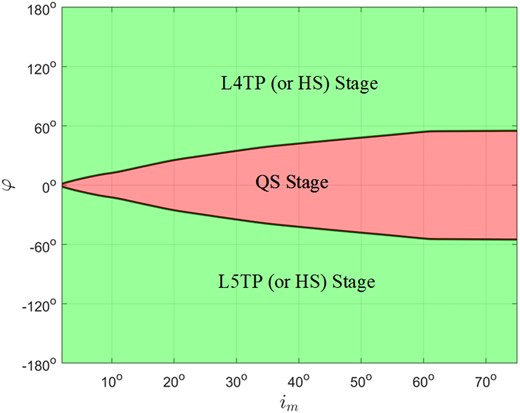
Distributions of co-orbital types in the (im, φ) plot, where the green and red regions correspond to the TP (or HS) and QS stages, respectively.
According to equation (6), under the given im and a0 = 1 LU, if |${\bar{\cal H}}({e_1},{\omega }_1,{\varphi }_1)={\bar{\cal H}}({e_2},{\omega }_2,{\varphi }_2)$| for a given μ, |${\bar{\cal H}^{*}}({e_1},{\omega }_1,{\varphi }_1)={\bar{\cal H}^{*}}({e_2},{\omega }_2,{\varphi }_2)$| for μ*. Then, we conclude that although |${\bar{\cal H}}$| values differ with μ, their isosurface structure are identical. For example, the φ curve of L4 and L5 axial orbits in Fig. 3 is available for different Sun–planet CRTBP. Furthermore, once |${\bar{\cal H}}$| values of a given Sun–planet CRTBP, equation (6) provides a fast method to calculate |${\bar{\cal H}}$| values for other Sun–planet systems. As we can see from equation (6), for the given a0, im, and (e, ω, φ) position in the torus space, the larger μ* the larger |${\bar{\cal H}^{*}}$| is. Compared to the method of Di Ruzza et al. (2023) for a quasi-coplanar co-orbital motion, the method stemming from the spatial torus space can be applied to analysing spatial co-orbital objects.
It should be noted that when we use the |$(i_ \mathrm{ m}, \bar{\mathcal {H}})$| and (im, φ) frames to determine the co-orbital state, there might be two kinds of misjudgment situations which fall on the boundaries of our classification scheme as follows.
The misjudgment is attributed to the boundary line between TP and HS motions in the |$(i_ \mathrm{ m}, \bar{\mathcal {H}})$| frame. Taking the Jupiter co-orbital motion with im = 15° as an example, Fig. 4(a) and (b) show isosurfaces of |$\bar{\mathcal {H}}= -1.5014028$| and −1.5014165 in the torus space, respectively. As we can see from Fig. 4(a), when |$\bar{\mathcal {H}}= -1.5014028$|, L4TP and L5TP surfaces begin to merge at φ = 180°. When |$\bar{\mathcal {H}}$| decreases to −1.5014165, L4TP and L5TP surfaces almost totally turn into the HS surfaces (Qi & de Ruiter 2020a). Therefore, this merging process from |$\bar{\mathcal {H}}= -1.5014028$| to −1.5014165 corresponds to the fuzzy area between TP and HS regions in the |$(i_ \mathrm{ m}, \bar{\mathcal {H}})$| frame, resulting in the misjudgment of our determination method.
The misjudgment is attributed to the boundary line between QS and TP (or HS) regions in the (im, φ) frame. Taken the Jupiter co-orbital motion with im = 30° and |$\bar{\mathcal {H}}= -1.500765$| as an example, Fig. 4(c) shows corresponding |$\bar{\mathcal {H}}$| isosurfaces in the torus space. As we can see from this figure, this case is located in the TP/QS region in the |$(i_ \mathrm{ m}, \bar{\mathcal {H}})$| frame. Hence, it is necessary to further determine its co-orbital motion through the (im, φ) frame. However, as we can see from Fig. 4(c), there are several overlap areas between QS and TP surfaces having the identical φ values (see blue regions). These overlap regions are close to the boundary line between QS and TP (or HS) regions in the (im, φ) frame. Apparently, if the co-orbital motion is located in overlap regions, it is infeasible to determine whether it is the TP or QS motion just through the (im, φ) frame.
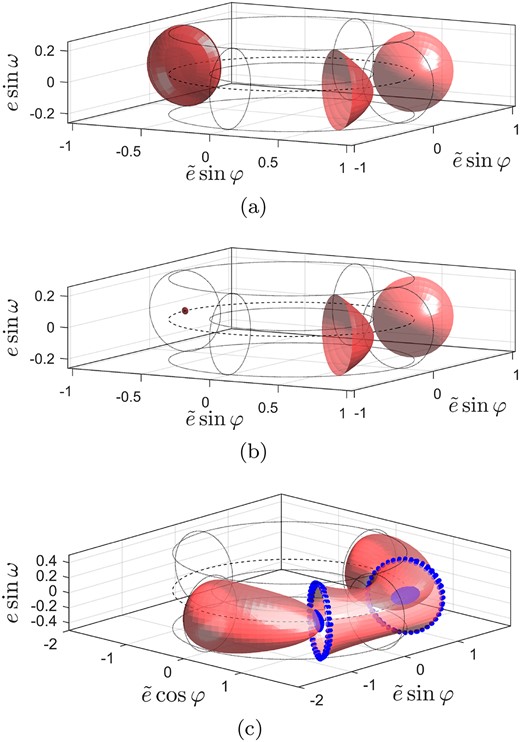
(a) |$\bar{\mathcal {H}}$| isosurfaces with im = 15° and |$\bar{\mathcal {H}}= -1.5014028$|, (b) |$\bar{\mathcal {H}}$| isosurfaces with im = 15° and |$\bar{\mathcal {H}}= -1.5014165$|, and (c) |$\bar{\mathcal {H}}$| isosurfaces with im = 30° and |$\bar{\mathcal {H}}= -1.500765$|, where blue regions denotes overlap areas between QS and TP surfaces having the identical φ values.
3 PCOS
In this section, we study PCOs in the Sun–planet system and use the above semi-analytical methods to determine their co-orbital state. This work focuses on co-orbitals of Mars, Jupiter, Saturn, Uranus, and Neptune. Since Earth’s co-orbitals had been investigated in Qi & Qiao (2022), they are excluded from this work. In addition, the existence of Venus’s co-orbital dust ring implies that there are a stable population of objects co-orbiting with Venus (Pokornỳ, Kuchner & Sheppard 2020). However, Venus PCOs are also not investigated herein for the sake of space.
3.1 Preliminary statistic analysis
In this paper, we think that the semimajor axis a of a PCO should satisfy 0.98ap ≤ a ± 3σa ≤ 1.02ap, where σa denotes the 1σ uncertainty of the semimajor axis. In addition, we also require that im values of PCOs must be larger than 2° to apply our semi-analytical two-dimensional maps in Section 2.2. We use the osculating orbital elements from JPL’s Small-Body Database Search Engine1to search PCOs that meet these requirements. Numerical computation shows that there are 1234 Mars PCOs, 11 211 Jupiter PCOs, 15 Saturn PCOs, 24 Uranus PCOs, and 42 Neptune PCOs satisfying the above requirements. In this subsection, the preliminary statistic analysis of those PCOs is implemented.
In Section 2.1, the equations to calculate the corresponding im, |$\bar{\cal H}$|, and the position in the torus space are all established in the CRTBP i.e. we assume the planet’s eccentricity ep = 0 and inclination ip = 0. However, real planets’ osculating eccentricity and inclination are non-zero in the heliocentric ecliptic J2000 frame. We can adopt the calculation method proposed by Qi & de Ruiter (2021) to obtain the relative eccentricity er, the relative inclination ir, and the relative argument of perihelion ωr instead of the osculating e, i, and ω. In addition, based on Qi & Qiao (2022), in the calculation of |$\bar{\mathcal {H} }$| of PCOs, a0 should be set as the current osculating value.
Fig. 5(a) displays the frequency distribution histograms of the number of Mars PCOs, where the 5th, 50th, and 95th percentiles of im are indicated as blue dashed lines. As we can see from the figure, most of im values of Mars PCOs concentrate between 15° and 47°, and the number with im < 10° or im > 60° is very small. Numerical computation shows that the 5th, 50th, and 95th percentiles of im are 15.0601°, 25.9793°, and 47.2034°, respectively. Fig. 5(b) displays the statistic results of Jupiter PCOs. By looking at Fig. 5(b), we find that the population of Jupiter PCOs is mostly distributed from 6° to 31°, and their average im is significantly smaller than that of Mars PCOs. Numerical computation shows that the 5th, 50th, and 95th percentiles of im are 5.1344°, 12.8925°, and 30.4134°, respectively.
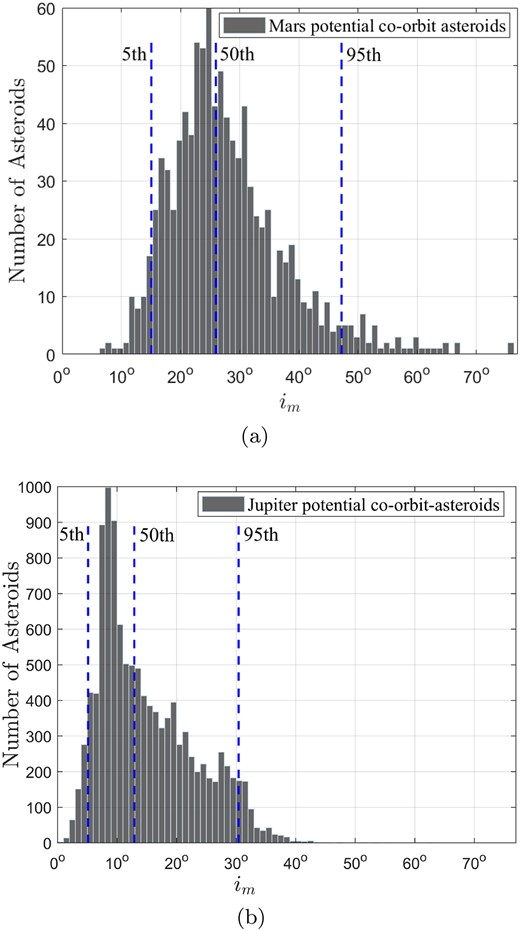
(a) Frequency distribution histograms of the number of Mars PCOs, and (b) frequency distribution histograms of the number of Jupiter PCOs, where the 5th, 50th, and 95th percentiles of im are indicated as blue dashed lines.
Since the number of Saturn PCOs, Uranus PCOs, and Neptune PCOs are quite small compared to those of Mars and Jupiter, frequency distribution histograms of them are not shown herein.
3.2 Determination of the co-orbital state
In this subsection, the co-orbital state of PCOs is determined through the patterns in the |$(i_ \mathrm{ m}, \bar{\mathcal {H}})$| and (im, φ) frames.
First, we analyse the influence of orbital uncertainties of PCOs on their co-orbital motions. Due to the observational uncertainty, the osculating orbital elements of each PCO obtained from JPL’s Small-Body Database Search Engine have a certain degree of uncertainty. Some PCOs with large uncertainties will significantly influence the determination of the co-orbital state. Therefore, the uncertainties of osculating orbital elements of PCOs should be taken into consideration. Based on Qi & Qiao (2022), the uncertainty parameter U obtained from the JPL Small-Body Database Search Engine can be regarded as the index to evaluate the uncertainty: objects having U ≤ 2 are well-determined, while those with U > 2 have poor orbit determinations.
From the JPL Small-Body Database Search Engine, the 1σ uncertainties of orbital elements can be retrieved. We implement Monte Carlo simulations to investigate the influence of orbital uncertainties with U > 2 on the determination of the co-orbital state. According to the assumption of standard normal distributions, Monte Carlo samples for each PCO with U > 2 are obtained, and then we can calculate their corresponding im, |$\bar{\mathcal {H} }$|, and φ values. Based on the analysis in Section 2.2, the allowable |$(i_ \mathrm{ m},\bar{\cal H})$| and (im, φ) regions for given co-orbital types is proposed and listed in Table 1, where ‘|$\Longleftrightarrow$|’ denotes the allowable dispersion between different regions.
| Type . | |$(i_ \mathrm{ m},\bar{\cal H})$| regions . | (im, φ) regions . |
|---|---|---|
| QS | QS |$\Longleftrightarrow$| QS/TP |$\Longleftrightarrow$| QS/HS | QS |
| L4TP | TP |$\Longleftrightarrow$| QS/TP | L4TP (or HS) |
| L5TP | TP |$\Longleftrightarrow$| QS/TP | L5TP (or HS) |
| HS | HS |$\Longleftrightarrow$| QS/HS | TP (or HS) |
| QS-TP | QS-TP | No limit |
| QS-HS | QS-HS | No limit |
| Type . | |$(i_ \mathrm{ m},\bar{\cal H})$| regions . | (im, φ) regions . |
|---|---|---|
| QS | QS |$\Longleftrightarrow$| QS/TP |$\Longleftrightarrow$| QS/HS | QS |
| L4TP | TP |$\Longleftrightarrow$| QS/TP | L4TP (or HS) |
| L5TP | TP |$\Longleftrightarrow$| QS/TP | L5TP (or HS) |
| HS | HS |$\Longleftrightarrow$| QS/HS | TP (or HS) |
| QS-TP | QS-TP | No limit |
| QS-HS | QS-HS | No limit |
| Type . | |$(i_ \mathrm{ m},\bar{\cal H})$| regions . | (im, φ) regions . |
|---|---|---|
| QS | QS |$\Longleftrightarrow$| QS/TP |$\Longleftrightarrow$| QS/HS | QS |
| L4TP | TP |$\Longleftrightarrow$| QS/TP | L4TP (or HS) |
| L5TP | TP |$\Longleftrightarrow$| QS/TP | L5TP (or HS) |
| HS | HS |$\Longleftrightarrow$| QS/HS | TP (or HS) |
| QS-TP | QS-TP | No limit |
| QS-HS | QS-HS | No limit |
| Type . | |$(i_ \mathrm{ m},\bar{\cal H})$| regions . | (im, φ) regions . |
|---|---|---|
| QS | QS |$\Longleftrightarrow$| QS/TP |$\Longleftrightarrow$| QS/HS | QS |
| L4TP | TP |$\Longleftrightarrow$| QS/TP | L4TP (or HS) |
| L5TP | TP |$\Longleftrightarrow$| QS/TP | L5TP (or HS) |
| HS | HS |$\Longleftrightarrow$| QS/HS | TP (or HS) |
| QS-TP | QS-TP | No limit |
| QS-HS | QS-HS | No limit |
We postulate that the co-orbital state is determinate if the distribution of Monte Carlo results should satisfy the following two conditions:
Monte Carlo points for a given co-orbital state should be all distributed in the allowable regions in the |$(i_ \mathrm{ m},\bar{\cal H})$| frame (see Table 1).
Monte Carlo points for a given co-orbital state should be all distributed in the allowable regions in the (im, φ) frame (see Table 1).
Taking Jupiter PCOs as examples, we find that there are 737 PCOs with U > 2 from JPL’s Small-Body Database Search Engine. Based on the above certainty conditions, Monte Carlo simulations with 1000 samples for each Jupiter PCO are implemented to testify their co-orbital certainties. Numerical computation indicates that 17 out of those 737 PCOs cannot satisfy the above two conditions, and all of them have U > 4. Fig. 6 displays their distributions in the (a) |$(i_ \mathrm{ m},\bar{\cal H})$| frame and (b) (im, φ) frame, respectively, where different colours correspond to different PCOs. As we can see from these figures, Monte Carlo points of those uncertain co-orbital objects widely spread, and some even intrude into the unstable region. Hence, we think that it is difficult to determine their co-orbital motions, which will be excluded from the following analysis. Compared to the method of Qi & Qiao (2022), certainty conditions of the co-orbital state in Table 1 can help us address co-orbital objects with poor orbit determinations, which are infeasible for the previous method.
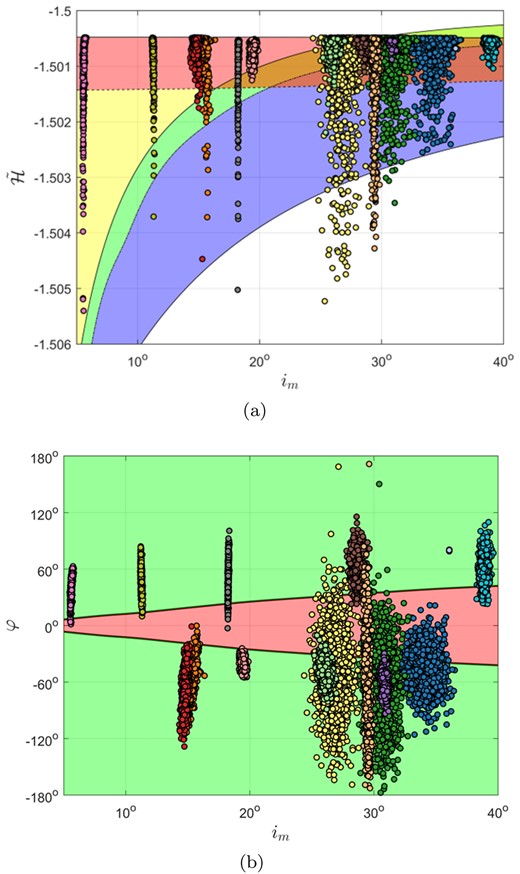
Distributions of Jupiter PCOs with uncertain co-orbital state in the (a) |$(i_ \mathrm{ m},\bar{\cal H})$| frame and (b) (im, φ) frame, where different colours correspond to different PCOs.
After the above screening method, 11 192 Jupiter PCOs with certain co-orbital state are obtained and displayed in Fig. 7. From Fig. 7, we can observe that numerous Jupiter PCOs are distributed in the TP and TP/QS regions. There is no PCO in the HS region. The numerical calculation indicates that about 64.72 per cent of them are L4 trojans, and about 34.98 per cent are L5 trojans. In addition, five QS, 22 QS-TP, and seven QS-HS objects of Jupiter are also identified based on their current osculating orbital elements.
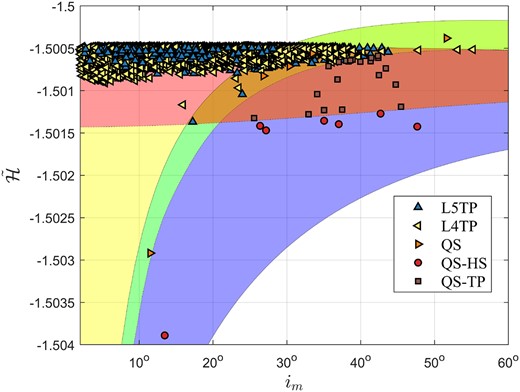
Jupiter PCOs with certain co-orbital states in the |$(i_ \mathrm{ m},\bar{\cal H})$| frame.
In the same way, Mars PCOs, Saturn PCOs, Uranus PCOs, and Neptune PCOs with certain co-orbital states can be determined. For example, numerical computation shows that about 96.27 per cent of 1234 Mars PCOs are unstable or uncertain objects. Fig. 8(a) shows 46 Mars PCOs with certain co-orbital states in the |$(i_ \mathrm{ m},\bar{\cal H})$| frame of Mars. As we can see from this figure, most of them are distributed in the QS-HS region, and several stable L5TP objects with larger |$\bar{\cal H}$| values gather in the TP region. Detailed analysis indicates that they include three L5TP, 15 L4TP, one QS, three HS, 23 QS-HS, and one QS-TP object of Mars.
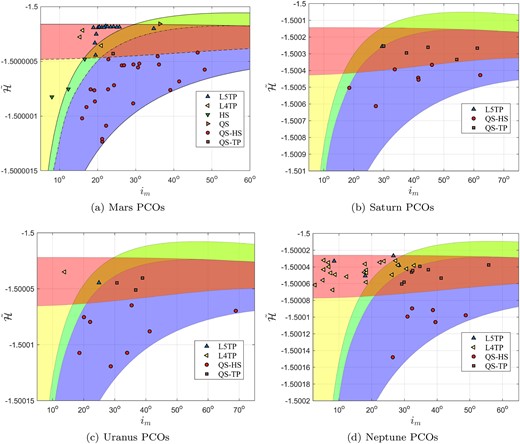
Distributions of PCOs with certain co-orbital state in the |$(i_ \mathrm{ m},\bar{\cal H})$| frame.
Saturn’s and Uranus’s PCOs with certain co-orbital states are displayed in Fig. 8(b) and (c), respectively. Compared to Jupiter and Mars, numbers of Saturn’s and Uranus’s PCOs are both few, and they mostly belong to QS-HS and QS-TP types. Numerical computation shows that Saturn has one L5TP, seven QS-HS, and five QS-TP objects; and Uranus has one L4TP, one L5TP, eight QS-HS, and three QS-TP objects. Fig. 8(d) shows the distribution of |$(i_ \mathrm{ m},\bar{\cal H})$| of Neptune’s PCOs. Apparently, Neptune possesses more co-orbital objects than Saturn and Uranus. The numerical calculation indicates that four L5TP, 22 L4TP, six QS-HS, and eight QS-TP objects of Neptune are identified.
4 DYNAMICAL EVOLUTION OF CO-ORBITAL OBJECTS
Based on Qi & Qiao (2022), the orbital analysis for Earth co-orbital objects based on the distribution of (|$i_ \mathrm{ m}, \bar{\mathcal {H} }$|) is applicable for the multiplanet model. In this section, the determination results for Mars PCOs, Jupiter PCOs, Saturn PCOs, Uranus PCOs, and Neptune PCOs in Section 3.2 will be verified through numerical integration, respectively. In the numerical integration, we use the mercury (Chambers 1999) package2 with an accuracy parameter 10−12. The hybrid Bulirsch–Stoer integrator exhibits no long-term accumulation of energy error, even in the close encounter term (Chambers 1999), and is employed while considering the gravitational forces of the eight major planets of the Solar system, the Moon, and the dwarf planet Pluto throughout the forward and backward integration. The initial states of the eight major planets, the Moon and the dwarf planet Pluto are obtained from the JPL HORIZONS System3 (Park et al. 2021). The epoch t = 0 of the numerical integration is set as JD 2459600.5 (Gregorian calendar 2022 January 21). In this paper, integration times are determined by orbital periods of different planetary hosts. Forward and backward integration times of Mars, Jupiter, Saturn, Uranus, and Neptune are set as 0.2, 0.3, 0.4, 0.8, and 1.2 Myr, respectively.
Taking 100 Jupiter PCOs as examples, we implement numerical simulations in a desktop with an AMD Ryzen 9 5000 @3.7 GHz to compare the calculation time of our method and numerical integration. Numerical computation shows that we need 0.2 s via MATLAB to obtain their im and |$\bar{\cal H}$| values for our determination method, while numerical integration of these PCOs from −0.3 to 0.3 Myr needs about 165 min via mercury package in Ubuntu. Apparently, our method can efficiently save the computation time compared to numerical integration.
4.1 Mars co-orbital objects
As mentioned in Section 3.2, we recognized three L4TP, 15 L5TP, one QS, three HS, 23 QS-HS, and one QS-TP objects of Mars. For the sake of space, in this section, we focus on three typical co-orbital states i.e. Mars TP, HS, and QS objects of them.
At present, the co-orbital objects known on Mars are Mars trojans. There are 15 long-term stable TP objects reported, including one L4TP and 14 L5TP objects. Nine of them had been recognized by the Minor Planet Center (MPC; retrieved in 2023 April). Based on the determination method proposed in the last section, 18 potential TP objects are identified. Table 2 listed reported Mars trojans and our determination results.
| Name . | Epoch . | a(au) . | im(deg) . | |$\bar{\cal H}$| . | φ(deg) . | Reported type . | Our determination . | U . |
|---|---|---|---|---|---|---|---|---|
| 121 514 (1999 UJ7) | 2460000.5 | 1.524549 | 16.613365 | −1.50000048 | 80.6714042 | L4TP | HS | 0 |
| 5261 Eureka (1990 MB) | 2460000.5 | 1.523563 | 22.126149 | −1.50000018 | 302.061404 | L5TP | L5TP | 0 |
| 311999 (2007 NS2) | 2460000.5 | 1.523791 | 21.116922 | −1.50000019 | 304.901404 | L5TP | L5TP | 0 |
| 385250 (2001 DH47) | 2460000.5 | 1.523851 | 25.718096 | −1.50000019 | 303.251404 | L5TP | L5TP | 0 |
| 2011 SL25 | 2460000.5 | 1.523912 | 21.678550 | −1.50000019 | 294.221404 | L5TP | L5TP | 1 |
| 2011 SP189 | 2460000.5 | 1.523859 | 20.099993 | −1.50000019 | 291.081404 | L5TP | L5TP | 2 |
| 2011 SC191 | 2460000.5 | 1.523905 | 18.899545 | −1.50000019 | 291.271404 | L5TP | L5TP | 0 |
| 2011 UN63 | 2460000.5 | 1.523784 | 22.588311 | −1.50000018 | 306.101404 | L5TP | L5TP | 0 |
| 2011 UB256 | 2460000.5 | 1.523699 | 23.419405 | −1.50000019 | 304.591404 | L5TP | L5TP | 0 |
| 2016 CP31 | 2460000.5 | 1.523645 | 25.042843 | −1.50000019 | 303.411404 | L5TP | L5TP | 1 |
| 2018 EC4 | 2460000.5 | 1.523649 | 20.458952 | −1.50000019 | 292.701404 | L5TP | L5TP | 1 |
| 2018 FC4 | 2460000.5 | 1.523882 | 24.165318 | −1.50000018 | 301.751404 | L5TP | L5TP | 3 |
| 101429 (1998 VF31) | 2460000.5 | 1.524285 | 34.726080 | −1.50000020 | 288.711404 | L5TP | L5TP | 0 |
| 2009 SE | 2460000.5 | 1.524509 | 19.467351 | −1.50000044 | 299.101404 | L5TP | L5TP | 3 |
| 2016 AA165 | 2460000.5 | 1.522985 | 19.633292 | −1.50000025 | 288.711404 | L5TP | L5TP | 0 |
| 36017 (1999 ND43) | 2460000.5 | 1.523564 | 16.076545 | −1.50000022 | 73.9814042 | None | L4TP | 0 |
| 2015 TL144 | 2460000.5 | 1.523931 | 19.281411 | −1.50000033 | 247.191404 | None | L5TP | 3 |
| 2021 GM4 | 2460000.5 | 1.523592 | 20.952928 | −1.50000036 | 118.731404 | None | L4TP | 0 |
| 2016 QY10 | 2460000.5 | 1.522668 | 15.338089 | −1.50000028 | 51.5614042 | None | L4TP | 5 |
| 2020 LE1 | 2460000.5 | 1.523847 | 36.342579 | −1.50000015 | 18.8614042 | None | QS | 1 |
| 391595 (2007 UR2) | 2460000.5 | 1.525426 | 8.0020533 | −1.50000083 | 336.761404 | None | HS | 0 |
| Name . | Epoch . | a(au) . | im(deg) . | |$\bar{\cal H}$| . | φ(deg) . | Reported type . | Our determination . | U . |
|---|---|---|---|---|---|---|---|---|
| 121 514 (1999 UJ7) | 2460000.5 | 1.524549 | 16.613365 | −1.50000048 | 80.6714042 | L4TP | HS | 0 |
| 5261 Eureka (1990 MB) | 2460000.5 | 1.523563 | 22.126149 | −1.50000018 | 302.061404 | L5TP | L5TP | 0 |
| 311999 (2007 NS2) | 2460000.5 | 1.523791 | 21.116922 | −1.50000019 | 304.901404 | L5TP | L5TP | 0 |
| 385250 (2001 DH47) | 2460000.5 | 1.523851 | 25.718096 | −1.50000019 | 303.251404 | L5TP | L5TP | 0 |
| 2011 SL25 | 2460000.5 | 1.523912 | 21.678550 | −1.50000019 | 294.221404 | L5TP | L5TP | 1 |
| 2011 SP189 | 2460000.5 | 1.523859 | 20.099993 | −1.50000019 | 291.081404 | L5TP | L5TP | 2 |
| 2011 SC191 | 2460000.5 | 1.523905 | 18.899545 | −1.50000019 | 291.271404 | L5TP | L5TP | 0 |
| 2011 UN63 | 2460000.5 | 1.523784 | 22.588311 | −1.50000018 | 306.101404 | L5TP | L5TP | 0 |
| 2011 UB256 | 2460000.5 | 1.523699 | 23.419405 | −1.50000019 | 304.591404 | L5TP | L5TP | 0 |
| 2016 CP31 | 2460000.5 | 1.523645 | 25.042843 | −1.50000019 | 303.411404 | L5TP | L5TP | 1 |
| 2018 EC4 | 2460000.5 | 1.523649 | 20.458952 | −1.50000019 | 292.701404 | L5TP | L5TP | 1 |
| 2018 FC4 | 2460000.5 | 1.523882 | 24.165318 | −1.50000018 | 301.751404 | L5TP | L5TP | 3 |
| 101429 (1998 VF31) | 2460000.5 | 1.524285 | 34.726080 | −1.50000020 | 288.711404 | L5TP | L5TP | 0 |
| 2009 SE | 2460000.5 | 1.524509 | 19.467351 | −1.50000044 | 299.101404 | L5TP | L5TP | 3 |
| 2016 AA165 | 2460000.5 | 1.522985 | 19.633292 | −1.50000025 | 288.711404 | L5TP | L5TP | 0 |
| 36017 (1999 ND43) | 2460000.5 | 1.523564 | 16.076545 | −1.50000022 | 73.9814042 | None | L4TP | 0 |
| 2015 TL144 | 2460000.5 | 1.523931 | 19.281411 | −1.50000033 | 247.191404 | None | L5TP | 3 |
| 2021 GM4 | 2460000.5 | 1.523592 | 20.952928 | −1.50000036 | 118.731404 | None | L4TP | 0 |
| 2016 QY10 | 2460000.5 | 1.522668 | 15.338089 | −1.50000028 | 51.5614042 | None | L4TP | 5 |
| 2020 LE1 | 2460000.5 | 1.523847 | 36.342579 | −1.50000015 | 18.8614042 | None | QS | 1 |
| 391595 (2007 UR2) | 2460000.5 | 1.525426 | 8.0020533 | −1.50000083 | 336.761404 | None | HS | 0 |
| Name . | Epoch . | a(au) . | im(deg) . | |$\bar{\cal H}$| . | φ(deg) . | Reported type . | Our determination . | U . |
|---|---|---|---|---|---|---|---|---|
| 121 514 (1999 UJ7) | 2460000.5 | 1.524549 | 16.613365 | −1.50000048 | 80.6714042 | L4TP | HS | 0 |
| 5261 Eureka (1990 MB) | 2460000.5 | 1.523563 | 22.126149 | −1.50000018 | 302.061404 | L5TP | L5TP | 0 |
| 311999 (2007 NS2) | 2460000.5 | 1.523791 | 21.116922 | −1.50000019 | 304.901404 | L5TP | L5TP | 0 |
| 385250 (2001 DH47) | 2460000.5 | 1.523851 | 25.718096 | −1.50000019 | 303.251404 | L5TP | L5TP | 0 |
| 2011 SL25 | 2460000.5 | 1.523912 | 21.678550 | −1.50000019 | 294.221404 | L5TP | L5TP | 1 |
| 2011 SP189 | 2460000.5 | 1.523859 | 20.099993 | −1.50000019 | 291.081404 | L5TP | L5TP | 2 |
| 2011 SC191 | 2460000.5 | 1.523905 | 18.899545 | −1.50000019 | 291.271404 | L5TP | L5TP | 0 |
| 2011 UN63 | 2460000.5 | 1.523784 | 22.588311 | −1.50000018 | 306.101404 | L5TP | L5TP | 0 |
| 2011 UB256 | 2460000.5 | 1.523699 | 23.419405 | −1.50000019 | 304.591404 | L5TP | L5TP | 0 |
| 2016 CP31 | 2460000.5 | 1.523645 | 25.042843 | −1.50000019 | 303.411404 | L5TP | L5TP | 1 |
| 2018 EC4 | 2460000.5 | 1.523649 | 20.458952 | −1.50000019 | 292.701404 | L5TP | L5TP | 1 |
| 2018 FC4 | 2460000.5 | 1.523882 | 24.165318 | −1.50000018 | 301.751404 | L5TP | L5TP | 3 |
| 101429 (1998 VF31) | 2460000.5 | 1.524285 | 34.726080 | −1.50000020 | 288.711404 | L5TP | L5TP | 0 |
| 2009 SE | 2460000.5 | 1.524509 | 19.467351 | −1.50000044 | 299.101404 | L5TP | L5TP | 3 |
| 2016 AA165 | 2460000.5 | 1.522985 | 19.633292 | −1.50000025 | 288.711404 | L5TP | L5TP | 0 |
| 36017 (1999 ND43) | 2460000.5 | 1.523564 | 16.076545 | −1.50000022 | 73.9814042 | None | L4TP | 0 |
| 2015 TL144 | 2460000.5 | 1.523931 | 19.281411 | −1.50000033 | 247.191404 | None | L5TP | 3 |
| 2021 GM4 | 2460000.5 | 1.523592 | 20.952928 | −1.50000036 | 118.731404 | None | L4TP | 0 |
| 2016 QY10 | 2460000.5 | 1.522668 | 15.338089 | −1.50000028 | 51.5614042 | None | L4TP | 5 |
| 2020 LE1 | 2460000.5 | 1.523847 | 36.342579 | −1.50000015 | 18.8614042 | None | QS | 1 |
| 391595 (2007 UR2) | 2460000.5 | 1.525426 | 8.0020533 | −1.50000083 | 336.761404 | None | HS | 0 |
| Name . | Epoch . | a(au) . | im(deg) . | |$\bar{\cal H}$| . | φ(deg) . | Reported type . | Our determination . | U . |
|---|---|---|---|---|---|---|---|---|
| 121 514 (1999 UJ7) | 2460000.5 | 1.524549 | 16.613365 | −1.50000048 | 80.6714042 | L4TP | HS | 0 |
| 5261 Eureka (1990 MB) | 2460000.5 | 1.523563 | 22.126149 | −1.50000018 | 302.061404 | L5TP | L5TP | 0 |
| 311999 (2007 NS2) | 2460000.5 | 1.523791 | 21.116922 | −1.50000019 | 304.901404 | L5TP | L5TP | 0 |
| 385250 (2001 DH47) | 2460000.5 | 1.523851 | 25.718096 | −1.50000019 | 303.251404 | L5TP | L5TP | 0 |
| 2011 SL25 | 2460000.5 | 1.523912 | 21.678550 | −1.50000019 | 294.221404 | L5TP | L5TP | 1 |
| 2011 SP189 | 2460000.5 | 1.523859 | 20.099993 | −1.50000019 | 291.081404 | L5TP | L5TP | 2 |
| 2011 SC191 | 2460000.5 | 1.523905 | 18.899545 | −1.50000019 | 291.271404 | L5TP | L5TP | 0 |
| 2011 UN63 | 2460000.5 | 1.523784 | 22.588311 | −1.50000018 | 306.101404 | L5TP | L5TP | 0 |
| 2011 UB256 | 2460000.5 | 1.523699 | 23.419405 | −1.50000019 | 304.591404 | L5TP | L5TP | 0 |
| 2016 CP31 | 2460000.5 | 1.523645 | 25.042843 | −1.50000019 | 303.411404 | L5TP | L5TP | 1 |
| 2018 EC4 | 2460000.5 | 1.523649 | 20.458952 | −1.50000019 | 292.701404 | L5TP | L5TP | 1 |
| 2018 FC4 | 2460000.5 | 1.523882 | 24.165318 | −1.50000018 | 301.751404 | L5TP | L5TP | 3 |
| 101429 (1998 VF31) | 2460000.5 | 1.524285 | 34.726080 | −1.50000020 | 288.711404 | L5TP | L5TP | 0 |
| 2009 SE | 2460000.5 | 1.524509 | 19.467351 | −1.50000044 | 299.101404 | L5TP | L5TP | 3 |
| 2016 AA165 | 2460000.5 | 1.522985 | 19.633292 | −1.50000025 | 288.711404 | L5TP | L5TP | 0 |
| 36017 (1999 ND43) | 2460000.5 | 1.523564 | 16.076545 | −1.50000022 | 73.9814042 | None | L4TP | 0 |
| 2015 TL144 | 2460000.5 | 1.523931 | 19.281411 | −1.50000033 | 247.191404 | None | L5TP | 3 |
| 2021 GM4 | 2460000.5 | 1.523592 | 20.952928 | −1.50000036 | 118.731404 | None | L4TP | 0 |
| 2016 QY10 | 2460000.5 | 1.522668 | 15.338089 | −1.50000028 | 51.5614042 | None | L4TP | 5 |
| 2020 LE1 | 2460000.5 | 1.523847 | 36.342579 | −1.50000015 | 18.8614042 | None | QS | 1 |
| 391595 (2007 UR2) | 2460000.5 | 1.525426 | 8.0020533 | −1.50000083 | 336.761404 | None | HS | 0 |
As we can see from this table, four Mars trojans, including 36 017 (1999 ND43), 2015 TL144, 2021 GM4, and 2016 QY10, are identified for the first time by our determination method. Fig. 9 illustrates their position in the |$(i_ \mathrm{ m},\bar{\cal H})$| frame. From Table 2, we find that uncertainty parameters U of 36 017 (1999 ND43) and 2021 GM4 are both equal to zeros, so their orbits are certain. Fig. 10 shows the time evolution of orbital elements of these two newly identified Mars trojans, where blue dashed lines denote the semimajor axis of Mars. By looking at these figures, we can observe that the osculating semimajor axes of these two asteroids both currently librate around that of Mars, so they are temporarily locked in co-orbital motions. According to their φ curves, we find that 36 017 (1999 ND43) can maintain its L4TP stage from t = −2500 yr to 500 yr, while 2021 GM4’s L4TP stage is much shorter, from −50 yr to about 100 yr. These results both are in agreement with our determination results, although their TP behaviours are not long-term stable and can only be maintained for a medium-term time-scale defined by Di Ruzza et al. (2023).
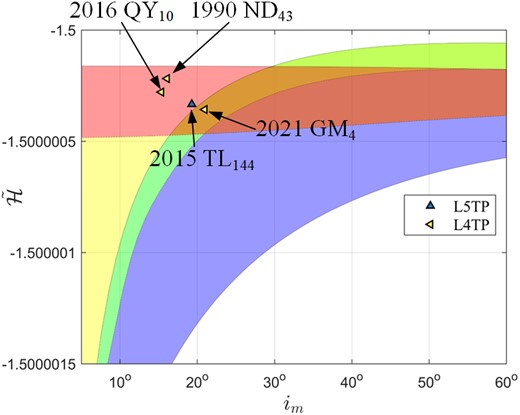
Distributions of the four newly identified Mars trojans in the |$(i_ \mathrm{ m},\bar{\cal H})$| frame.
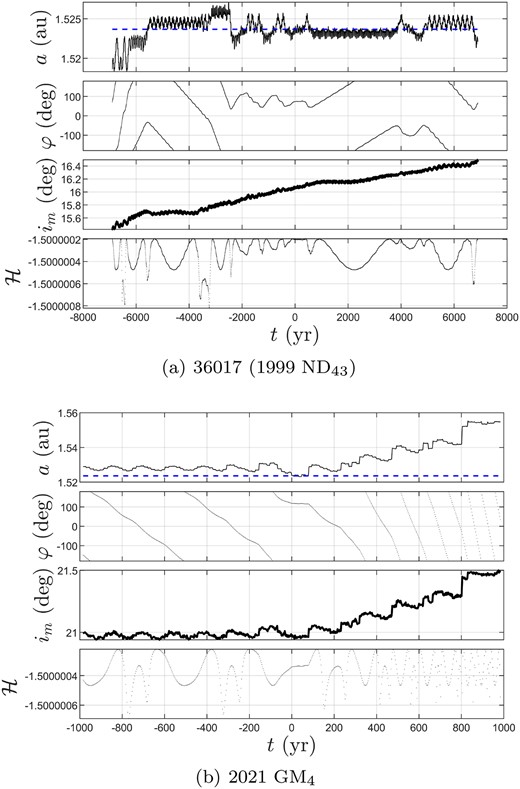
Time evolution of orbital elements of 36 017 (1999 ND43) and 2021 |$\rm {GM_4}$|, where blue dashed lines denote the semimajor axis of Mars.
From Table 2, uncertainty parameters U of 2015 |$\rm {TL_{144}}$| and 2016 |$\rm {QY_{10}}$| are larger than 2. Therefore, we need to implement Monte Carlo simulations to verify our determination for them. We assume that initial orbital elements for numerical integration have standard normal distributions, and their 1σ uncertainties can be retrieved from the JPL Small-Body Database Search Engine. Then, Monte Carlo orbits for a given PCO can be obtained through forward and backward numerical integration.
Taking 2016 |$\rm {QY_{10}}$| with U = 5 as an example, Fig. 11 shows the time evolution of φ of 100 Monte Carlo simulations, where different colours denote different Monte Carlo orbits. As we can see from this figure, although φ curves of 500 Monte Carlo simulations all gradually deviated from L4TP with time, they can all remain their L4TP behaviours from t = −1000 to 5000 yr at least, in agreement with our prediction. Let Dtp denote the duration of the TP stage for each Monte Carlo result. Apparently, the larger Dtp the more accurate our determination method is. Fig. 12 displays the histogram of Dtp of 500 Monte Carlo points, where Dtp is described by a base-10 logarithmic scale on the x-axis and MC denotes Monte Carlo results for short. As we can see from this figure, their L4TP state can mostly remain above 1 × 104 yr. Therefore, we confirm that 2016 |$\rm {QY_{10}}$| is a Mars L4 trojan although its orbital uncertainty U is quite high.
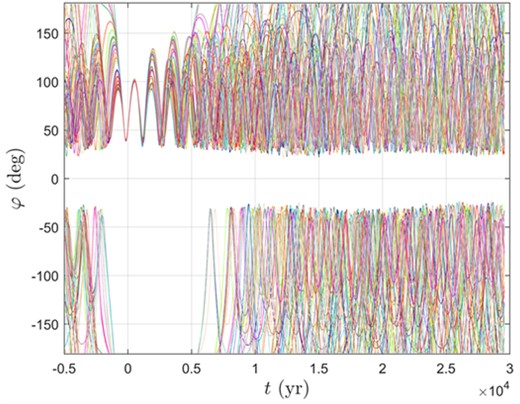
Time evolution of φ of 100 Monte Carlo simulations of 2016 |$\rm {QY_{10}}$|, where different colours denote different Monte Carlo orbits.
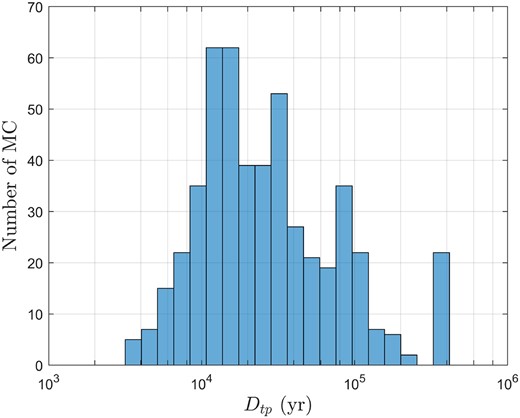
Histogram of Dtp of 500 Monte Carlo samples of 2016 |$\rm {QY_{10}}$|.
Based on orbital elements of 2015 |$\rm {TL_{144}}$| without orbital uncertainty, we plot the corresponding orbit over the whole integration time in the Sun–Mars dimensionless rotating frame in Fig. 13. Obviously, in this situation, 2015 |$\rm {TL_{144}}$| is a long-term stable Mars L5 trojan for over 0.4 Myr. On the other hand, the uncertainty parameter U of 2015 |$\rm {TL_{144}}$| is equal to 3, so it is necessary to testify its Monte Carlo results. However, the Monte Carlo simulation of 2015 |$\rm {TL_{144}}$| indicates that their L5TP motions all can remain for over 0.4 Myr, similar to that in Fig. 13. Therefore, we are sure that 2015 |$\rm {TL_{144}}$| is a long-term stable Mars L5 trojan unreported.
2015 |$\rm {TL_{144}}$|’s orbit in the Sun–Mars dimensionless rotating frame.
Based on Fig. 8(a), one QS and two HS Mars PCOs have been screened through our determination method. Fig. 14 shows their locations in the |$(i_ \mathrm{ m},\bar{\cal H})$| frame, and Table 2 lists their orbital data. According to these figures and table, their orbital elements are all vary certain: 2020 |$\rm {LE_1}$| is classified as the Mars QS object, and 121 514 (1999 UJ7) and 391 595 (2007 UR2) are classified as Mars HS objects. However, 121 514 (1999 UJ7) has been reported and known as a long-term stable Mars trojan. Numerical integration confirms that it is really a Mars L4 trojan. We think that the misjudgment of our determination method is attributed to the ambiguous location of 121 514 (1999 UJ7) on the boundary line between TP and HS (see Fig. 14).
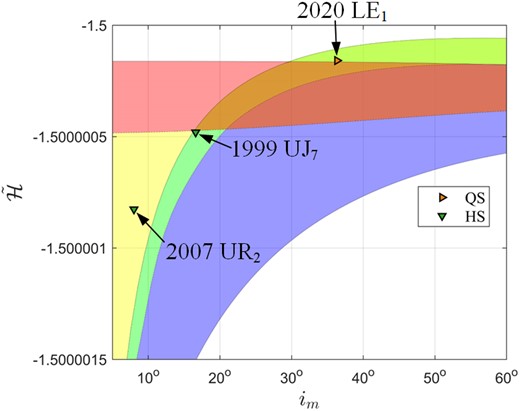
Distributions of 2020 |$\rm {LE_1}$|, 121 514 (1999 UJ7) and 391 595 (2007 UR2) in the |$(i_ \mathrm{ m},\bar{\cal H})$| frame.
Fig. 15 displays time evolution of orbital elements of 2020 |$\rm {LE_1}$| through numerical integration, where the blue dashed line denotes the semimajor axis of Mars. As we can see from this figure, 2020 |$\rm {LE_1}$| is in a short-term QS co-orbital state from about t = −4000 to 5000 yr, in agreement with our determination. Therefore, we confirm that 2020 |$\rm {LE_1}$| is a new Mars QS object unreported before.
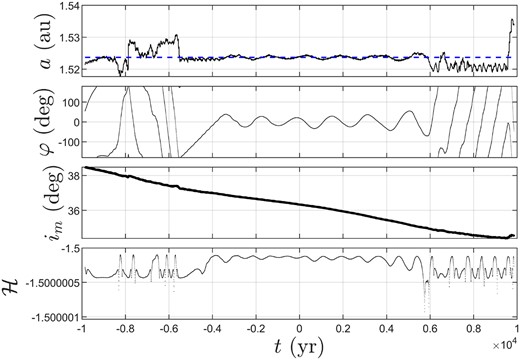
Time evolution of orbital elements of 2020 |$\rm {LE_1}$|, where the blue dashed line denotes the semimajor axis of Mars.
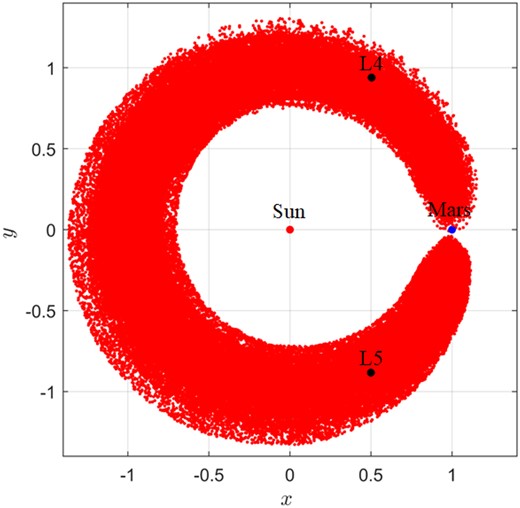
Fig. 16 shows that 391 595 (2007 UR2)’s orbit around L5 point for 0.4 Myr in the Sun–Mars dimensionless rotating frame. Apparently, 391 595 (2007 UR2) is trapped in a long-term stable HS stage for over 0.4 Myr, in agreement with our prediction. We confirm that it is a new Mars HS object unreported before.
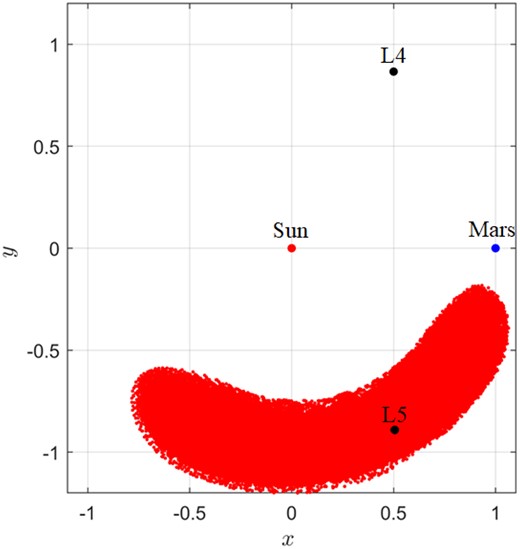
391595 (2007 UR2)’s orbit in the Sun–Mars dimensionless rotating frame.
4.2 Jupiter co-orbital objects
Most of co-orbital objects known on Jupiter are Jupiter trojans, which have been widely investigated. However, there are few researches on other Jupiter co-orbital types. In this subsection, we focus on Jupiter QS objects obtained from our determination method except for Jupiter trojans. As mentioned in Section 3.2, there are five Jupiter QS objects recognized by our determination method. Table 3 lists data of the five Jupiter QS results. From the table, we can observe that 2000 |$\rm {CN_3}$| and 2000 |$\rm {SL_{174}}$| are known as Jupiter trojans, different from our determination, and 2020 |$\rm {MM_5}$| and 404P/Bressi are first reported.
| Name . | Epoch . | a(au) . | im(deg) . | |$\bar{\cal H}$| . | φ(deg) . | Reported type . | Our determination . | U . |
|---|---|---|---|---|---|---|---|---|
| P/2012 US27 (Siding Spring) | 2456294.5 | 5.181389 | 51.613107 | −1.50038066 | 338.336814 | QS | QS | 4 |
| 15539 (2000 CN3) | 2460000.5 | 5.262085 | 26.820286 | −1.50082537 | 31.6822564 | L4TP | QS | 0 |
| 32467 (2000 SL174) | 2460000.5 | 5.236618 | 30.355216 | −1.50071136 | 326.092256 | L5TP | QS | 0 |
| 2020 MM5 | 2460000.5 | 5.249806 | 33.451511 | −1.50056212 | 28.3322564 | None | QS | 3 |
| 404P/Bressi | 2457955.5 | 5.139585 | 11.499543 | −1.50291844 | 13.6044237 | None | QS | 0 |
| Name . | Epoch . | a(au) . | im(deg) . | |$\bar{\cal H}$| . | φ(deg) . | Reported type . | Our determination . | U . |
|---|---|---|---|---|---|---|---|---|
| P/2012 US27 (Siding Spring) | 2456294.5 | 5.181389 | 51.613107 | −1.50038066 | 338.336814 | QS | QS | 4 |
| 15539 (2000 CN3) | 2460000.5 | 5.262085 | 26.820286 | −1.50082537 | 31.6822564 | L4TP | QS | 0 |
| 32467 (2000 SL174) | 2460000.5 | 5.236618 | 30.355216 | −1.50071136 | 326.092256 | L5TP | QS | 0 |
| 2020 MM5 | 2460000.5 | 5.249806 | 33.451511 | −1.50056212 | 28.3322564 | None | QS | 3 |
| 404P/Bressi | 2457955.5 | 5.139585 | 11.499543 | −1.50291844 | 13.6044237 | None | QS | 0 |
| Name . | Epoch . | a(au) . | im(deg) . | |$\bar{\cal H}$| . | φ(deg) . | Reported type . | Our determination . | U . |
|---|---|---|---|---|---|---|---|---|
| P/2012 US27 (Siding Spring) | 2456294.5 | 5.181389 | 51.613107 | −1.50038066 | 338.336814 | QS | QS | 4 |
| 15539 (2000 CN3) | 2460000.5 | 5.262085 | 26.820286 | −1.50082537 | 31.6822564 | L4TP | QS | 0 |
| 32467 (2000 SL174) | 2460000.5 | 5.236618 | 30.355216 | −1.50071136 | 326.092256 | L5TP | QS | 0 |
| 2020 MM5 | 2460000.5 | 5.249806 | 33.451511 | −1.50056212 | 28.3322564 | None | QS | 3 |
| 404P/Bressi | 2457955.5 | 5.139585 | 11.499543 | −1.50291844 | 13.6044237 | None | QS | 0 |
| Name . | Epoch . | a(au) . | im(deg) . | |$\bar{\cal H}$| . | φ(deg) . | Reported type . | Our determination . | U . |
|---|---|---|---|---|---|---|---|---|
| P/2012 US27 (Siding Spring) | 2456294.5 | 5.181389 | 51.613107 | −1.50038066 | 338.336814 | QS | QS | 4 |
| 15539 (2000 CN3) | 2460000.5 | 5.262085 | 26.820286 | −1.50082537 | 31.6822564 | L4TP | QS | 0 |
| 32467 (2000 SL174) | 2460000.5 | 5.236618 | 30.355216 | −1.50071136 | 326.092256 | L5TP | QS | 0 |
| 2020 MM5 | 2460000.5 | 5.249806 | 33.451511 | −1.50056212 | 28.3322564 | None | QS | 3 |
| 404P/Bressi | 2457955.5 | 5.139585 | 11.499543 | −1.50291844 | 13.6044237 | None | QS | 0 |
To explain the difference between our results and reported types, Fig. 17 illustrates locations of the five objects in the (a) |$(i_ \mathrm{ m},\bar{\cal H})$| and (b) (im, φ) frames, respectively. As we can see from Fig. 17(a), 15 539 (2000 CN3) and 32 467 (2000 SL174) are both located in the QS/TP region, so in the view of |$\bar{\cal H}$| isosurface, they might be QS or TP types. Their further classification of co-orbital types depends on their (im, φ) locations. From Fig. 17(b), we can observe that 15 539 (2000 CN3) and 32 467 (2000 SL174) are located on the boundary of QS and TP (or HS) regions. Similar to the conclusion for 121 514 (1999 UJ7) in Fig. 14, it is possible to misjudge the co-orbital type of PCO on the boundary of different co-orbital regions in the |$(i_ \mathrm{ m},\bar{\cal H})$| or (im, φ) frames. Therefore, we postulate that our determination method cannot deal with the classification of the boundary of different co-orbital regions. In addition, we find that 404P/Bressi is located at the QS/HS region (Fig. 17a) and also located on the boundary of QS and TP (or HS) regions (Fig. 17b). Hence, we think that it is difficult to distinguish whether it is a Jupiter QS or HS object. Fig. 18 shows time evolution of orbital elements of 404P/Bressi, where the blue dashed line denotes the semimajor axis of Jupiter. Obviously, it is a short-term Jupiter HS object for about 300 yr.
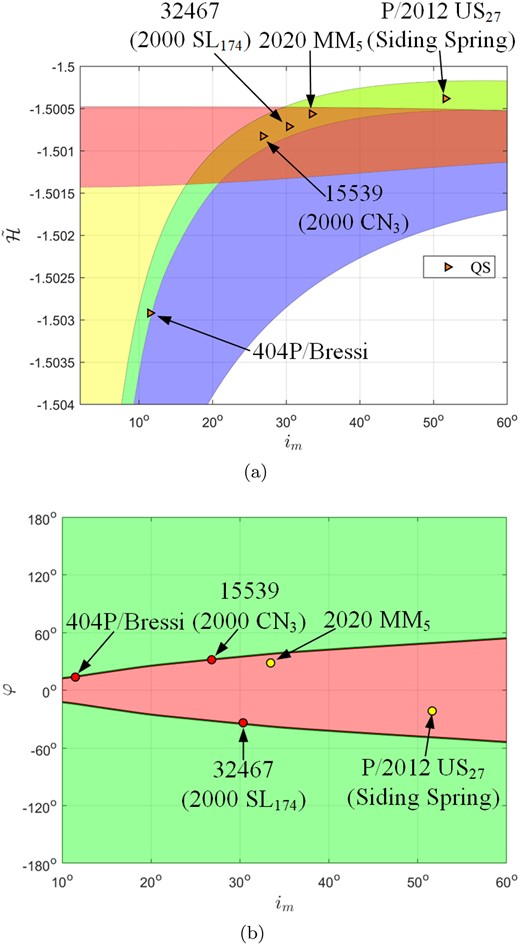
Locations of 404P/Bressi, 15 539 (2000 CN3), 32 467 (2000 SL174), 2020 MM5, and P/2012 US27 (Siding Spring) in the (a) |$(i_ \mathrm{ m},\bar{\cal H})$| and (b) (im, φ) frames.

Time evolution of orbital elements of 404P/Bressi, where the blue dashed line denotes the semimajor axis of Jupiter.
P/2012 US27 (Siding Spring) is known as a Jupiter QS (Qi & de Ruiter 2021), but its uncertainty parameter U = 4. Therefore, similar to the analysis in the last subsection, we implement Monte Carlo simulations to further testify to the certainty of its QS state. Fig. 19 shows the histogram of Dqs of 500 Monte Carlo samples of P/2012 US27 (Siding Spring), where Dqs denotes the duration of QS stage for each Monte Carlo result. As we can see from this figure, their QS stages can remain mostly above 1 × 104 yr. Therefore, we confirm that P/2012 US27 (Siding Spring) is a Jupiter QS object, and our determination method is feasible for PCOs with uncertainty parameters.
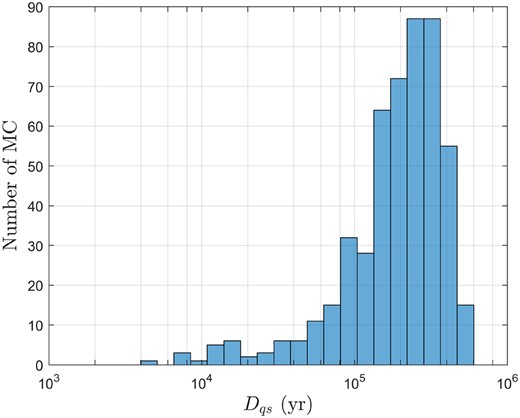
Histogram of Dqs of 500 Monte Carlo samples of P/2012 US27 (Siding Spring).
Fig. 20(a) displays the time evolution of orbital elements of 2020 MM5 based on its orbital elements without orbital uncertainty. From this figure, we can observe that in this situation, 2020 MM5 can remain this QS behaviour from t = −2.85 × 105 yr to 8.2 × 104 yr. Since its U = 3, we also implement Monte Carlo simulations to testify the certainty of its QS state. Fig. 20(b) shows the histogram of Dqs of 500 Monte Carlo samples of 2020 MM5. As we can see from this figure, their QS lifetimes can mostly remain above 6 × 104 yr, whose durations are similar to P/2012 US27 (Siding Spring). Therefore, we confirm that 2020 MM5 is a new long-term stable Jupiter QS object, which has not been reported yet.
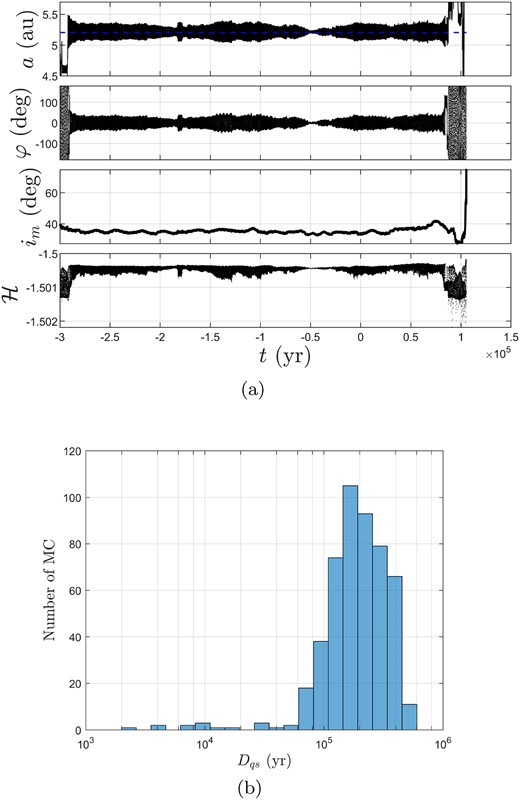
(a) Time evolution of orbital elements of 2020 MM5 without orbital uncertainty, and (b) its histogram of Dqs of Monte Carlo samples.
4.3 Saturn co-orbital objects
As stated in Section 3.2, Saturn has one L5TP, seven QS-HS, and five QS-TP objects. Almost all of them are Centaurs. Numerical integration shows that they are unstable and can only be captured by Saturn for a very short time. Therefore, our determination method seems infeasible for those Saturn PCOs. For the sake of space, we pick an example, 2016 BJ81, herein to demonstrate their orbital behaviours.
According to our semi-analytic analysis method, 2016 BJ81 is a L5TP object in Fig. 8(b), and its U = 2 based on JPL Small-Body Database. Therefore, we think that its orbital parameter is certain. Fig. 21 a shows that 2016 BJ81 is a L5TP co-orbital object at present, but soon its semimajor axis begins to change drastically. As shown in the picture, the φ curve is chaotic and its im generally increases with time. Therefore, 2016 BJ81 is an unstable co-orbital object. However, if the perturbation of Jupiter is deducted from the multiplanet model, Saturn PCOs can be stable. Fig. 21(b) displays the time evolution of orbital elements of 2016 BJ81 without the influence of Jupiter. Apparently, in this case, 2016 BJ81 is a long-term stable L5TP object for over 8 × 105 yr.
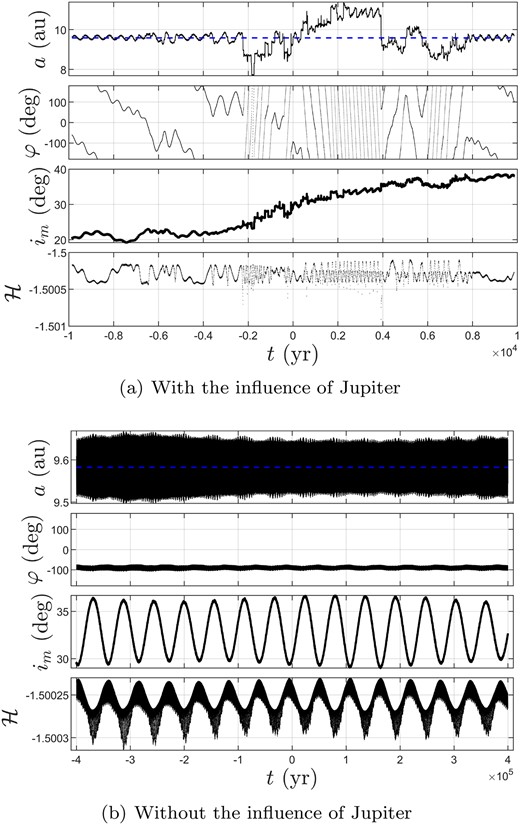
Time evolution of orbital elements of 2016 BJ81 with and without the influence of Jupiter.
Consequently, through numerical integration, we postulate that Saturn PCOs are very unstable due to the perturbation of Jupiter. As stated in Michtchenko & Ferraz-Mello (2001), there is an approximate resonance between Jupiter and Saturn, so Saturn’s PCOs are significantly influenced by Jupiter and there are no Saturn trojans (Dvorak, Bazsó & Zhou 2010). Although our determination method based on the two-dimensional maps through the semi-analytical Hamiltonian approach in the Sun–planet CRTBP can be extended to the multiplanet model, the significant perturbation from Jupiter in the Sun–Saturn system apparently is beyond the validity of our method. In this situation, numerical integration is still necessary to confirm that Saturn PCOs are actually short lived.
4.4 Uranus co-orbital objects
As stated in Section 3.2, Uranus has four kinds of co-orbital objects, including L4TP, L5TP, QS-HS, and QS-TP types. Like Saturn, numerical integration shows that Uranus has no long-term stable co-orbital objects.
In this subsection, for the sake of space, we pick one object from each of the four types as examples. Table 4 lists their data, and Fig. 22 illustrated their locations in the |$(i_ \mathrm{ m},\bar{\cal H})$| frame. As we can see from Table 4, uncertainty parameter U values of the four asteroids are all smaller or equal to 2, so we think that their orbital elements are certain.
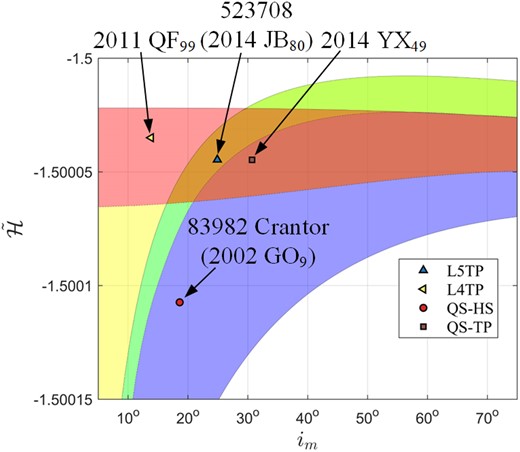
Locations of 2011 QF99, 2014 YX49, 523 708 (2014 JB80) and 83 982 Crantor (2002 GO9) in the |$(i_ \mathrm{ m},\bar{\cal H})$| frame.
| Name . | Epoch . | a(au) . | im(deg) . | |$\bar{\cal H}$| . | φ(deg) . | Reported type . | Our determination . | U . |
|---|---|---|---|---|---|---|---|---|
| 2011 QF99 | 2460000.5 | 19.14497 | 13.827605 | −1.50003492 | 45.6894809 | L4TP | L4TP | 2 |
| 2014 YX49 | 2460000.5 | 19.09632 | 30.689897 | −1.50004468 | 60.8594808 | L4TP | QS-TP | 1 |
| 523708 (2014 JB80) | 2460000.5 | 19.29494 | 24.902611 | −1.50004461 | 255.309481 | None | L5TP | 2 |
| 83982 Crantor (2002 GO9) | 2460000.5 | 19.46948 | 18.613477 | −1.50010731 | 245.689481 | None | QS-HS | 1 |
| Name . | Epoch . | a(au) . | im(deg) . | |$\bar{\cal H}$| . | φ(deg) . | Reported type . | Our determination . | U . |
|---|---|---|---|---|---|---|---|---|
| 2011 QF99 | 2460000.5 | 19.14497 | 13.827605 | −1.50003492 | 45.6894809 | L4TP | L4TP | 2 |
| 2014 YX49 | 2460000.5 | 19.09632 | 30.689897 | −1.50004468 | 60.8594808 | L4TP | QS-TP | 1 |
| 523708 (2014 JB80) | 2460000.5 | 19.29494 | 24.902611 | −1.50004461 | 255.309481 | None | L5TP | 2 |
| 83982 Crantor (2002 GO9) | 2460000.5 | 19.46948 | 18.613477 | −1.50010731 | 245.689481 | None | QS-HS | 1 |
| Name . | Epoch . | a(au) . | im(deg) . | |$\bar{\cal H}$| . | φ(deg) . | Reported type . | Our determination . | U . |
|---|---|---|---|---|---|---|---|---|
| 2011 QF99 | 2460000.5 | 19.14497 | 13.827605 | −1.50003492 | 45.6894809 | L4TP | L4TP | 2 |
| 2014 YX49 | 2460000.5 | 19.09632 | 30.689897 | −1.50004468 | 60.8594808 | L4TP | QS-TP | 1 |
| 523708 (2014 JB80) | 2460000.5 | 19.29494 | 24.902611 | −1.50004461 | 255.309481 | None | L5TP | 2 |
| 83982 Crantor (2002 GO9) | 2460000.5 | 19.46948 | 18.613477 | −1.50010731 | 245.689481 | None | QS-HS | 1 |
| Name . | Epoch . | a(au) . | im(deg) . | |$\bar{\cal H}$| . | φ(deg) . | Reported type . | Our determination . | U . |
|---|---|---|---|---|---|---|---|---|
| 2011 QF99 | 2460000.5 | 19.14497 | 13.827605 | −1.50003492 | 45.6894809 | L4TP | L4TP | 2 |
| 2014 YX49 | 2460000.5 | 19.09632 | 30.689897 | −1.50004468 | 60.8594808 | L4TP | QS-TP | 1 |
| 523708 (2014 JB80) | 2460000.5 | 19.29494 | 24.902611 | −1.50004461 | 255.309481 | None | L5TP | 2 |
| 83982 Crantor (2002 GO9) | 2460000.5 | 19.46948 | 18.613477 | −1.50010731 | 245.689481 | None | QS-HS | 1 |
2011 QF99 and 2014 YX49 have been reported, and both of them were believed to be unstable trojans (Dvorak et al. 2010). Fig. 23 shows time evolution of orbital elements of 2011 QF99 and 2014 YX49, where blue dashed lines denote the semimajor axis of Uranus. By looking at Fig. 23(a), we can observe that 2011 QF99 can maintain its L4TP state from t = −5 × 105 yr to about 1 × 105 yr, in agreement with our determination. Before and after this period, it seems to be locked in the QS-HS stages. In Fig. 23(b), we find that the L4TP state of 2014 YX49 is very short (about 1.7 × 105 yr), and then it will experience co-orbital transitions between the L4TP and QS phases with respect to Uranus, in the agreement of our conclusion for its co-orbital type, QS-TP.
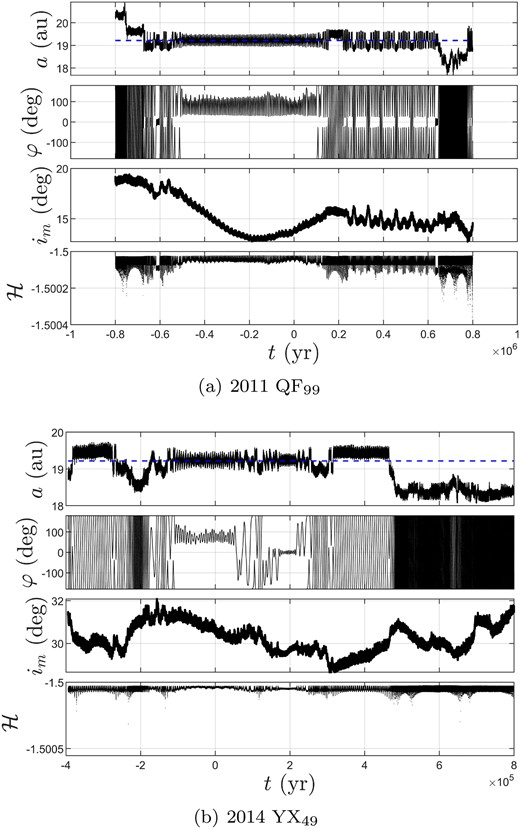
Time evolution of orbital elements of 2011 QF99 and 2014 YX49, where blue dashed lines denote the semimajor axis of Uranus.
Fig. 24 shows time evolution of orbital elements of a newly identified Uranus L5 trojan, 523 708 (2014 JB80), where the blue dashed line denotes the semimajor axis of Uranus. As we can see from this figure, the L5TP behaviour of 523 708 (2014 JB80) was maintained from about t = −1.2 × 104 yr to about 0.1 × 104 yr. Therefore, it is a short-term L5 trojan, in accordance with our prediction.
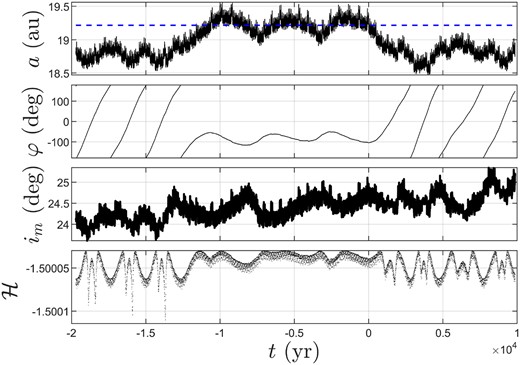
Time evolution of orbital elements of 523 708 (2014 JB80), where the blue dashed line denotes the semimajor axis of Uranus.
Fig. 25 displays time evolution of orbital elements of 83 982 Crantor (2002 GO9). As we can see from this figure, it experiences a transition between HS and QS state for about 4 × 104 yr, although its QS stages are short and transient. This result is in agreement with our prediction based on Fig. 22.
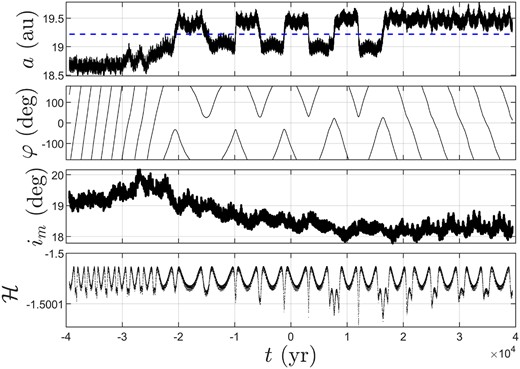
Time evolution of orbital elements of 83 982 Crantor (2002 GO9), where the blue dashed line denotes the semimajor axis of Uranus.
4.5 Neptune co-orbital objects
At present, the co-orbital objects known on Neptune are basically Neptune trojans. There are 31 long-term stable TP objects announced by MPC (retrieved in April 2023), including 27 L4TP and 4 L5TP. Based on the determination method we proposed, 26 potential TP objects are identified. Table 5 listed reported Neptune trojans and our TP results. Our results are mostly consistent with the MPC results, but there are five reported L4 trojans wrongly classified to QS-TP types by our method.
| Name . | Epoch . | a(au) . | im(deg) . | |$\bar{\cal H}$| . | φ(deg) . | Reported type . | Our determination . | U . |
|---|---|---|---|---|---|---|---|---|
| 2013 KY18 | 2460000.5 | 30.17090 | 8.4945849 | −1.50003319 | 288.956830 | L5TP | L5TP | 2 |
| 2011 HM102 | 2460000.5 | 30.22914 | 28.309835 | −1.50003789 | 302.856830 | L5TP | L5TP | 3 |
| 2004 KV18 | 2460000.5 | 30.18669 | 18.004097 | −1.50005041 | 258.376830 | L5TP | L5TP | 4 |
| 2008 LC18 | 2460000.5 | 30.02992 | 26.629041 | −1.50002688 | 297.506830 | L5TP | L5TP | 4 |
| 2010 TS191 | 2460000.5 | 30.16727 | 5.3397517 | −1.50003187 | 69.5568301 | L4TP | L4TP | 2 |
| 2010 TT191 | 2460000.5 | 30.20027 | 6.8786907 | −1.50003998 | 81.4068301 | L4TP | L4TP | 4 |
| 2012 UV177 | 2460000.5 | 30.19977 | 22.461784 | −1.50003455 | 65.2468301 | L4TP | L4TP | 3 |
| 2013 RC158 | 2460000.5 | 30.25599 | 7.4155135 | −1.50004652 | 45.4868301 | L4TP | L4TP | 4 |
| 2013 RL124 | 2460000.5 | 30.27629 | 8.7858339 | −1.50004858 | 46.2168301 | L4TP | L4TP | 4 |
| 2013 TK227 | 2460000.5 | 30.28748 | 18.243401 | −1.50005789 | 38.5068301 | L4TP | L4TP | 4 |
| 2013 TZ187 | 2460000.5 | 30.31406 | 12.317593 | −1.50005263 | 55.9968301 | L4TP | L4TP | 3 |
| 2014 QO441 | 2460000.5 | 30.27395 | 18.390957 | −1.50004766 | 49.9968301 | L4TP | L4TP | 4 |
| 2014 QP441 | 2460000.5 | 30.26672 | 18.354468 | −1.50004334 | 59.8068301 | L4TP | L4TP | 4 |
| 2015 VV165 | 2460000.5 | 30.26445 | 17.714858 | −1.50004721 | 77.0768301 | L4TP | L4TP | 3 |
| 2015 VW165 | 2460000.5 | 30.24844 | 5.3169036 | −1.50004302 | 73.6168301 | L4TP | L4TP | 3 |
| 2015 VX165 | 2460000.5 | 30.19652 | 17.970819 | −1.50003618 | 72.8868301 | L4TP | L4TP | 4 |
| 385571 Otrera (2004 UP10) | 2460000.5 | 30.34777 | 2.6440677 | −1.50006124 | 50.0268301 | L4TP | L4TP | 4 |
| 385695 Clete (2005 TO74) | 2460000.5 | 30.33115 | 5.0569488 | −1.50005614 | 55.4368301 | L4TP | L4TP | 4 |
| 530664 (2011 SO277) | 2460000.5 | 30.36368 | 8.0553776 | −1.50006846 | 44.2068301 | L4TP | L4TP | 3 |
| 530930 (2011 WG157) | 2460000.5 | 30.16025 | 23.750524 | −1.50003314 | 74.4768301 | L4TP | L4TP | 3 |
| 613490 (2006 RJ103) | 2460000.5 | 30.20993 | 6.7658338 | −1.50003497 | 62.1668301 | L4TP | L4TP | 2 |
| 2005 TN53 | 2460000.5 | 30.30348 | 26.188059 | −1.50005015 | 57.5468301 | L4TP | L4TP | 4 |
| 2013 VX30 | 2460000.5 | 30.25547 | 30.646881 | −1.50004173 | 60.6668301 | L4TP | L4TP | 3 |
| 2014 RO74 | 2460000.5 | 30.21569 | 28.034461 | −1.50003719 | 49.7368301 | L4TP | L4TP | 4 |
| 2014 SC374 | 2460000.5 | 30.22946 | 32.950241 | −1.50003814 | 56.9168301 | L4TP | L4TP | 4 |
| 527604 (2007 VL305) | 2460000.5 | 30.16479 | 27.310887 | −1.50003289 | 72.2768301 | L4TP | L4TP | 2 |
| 2012 UD185 | 2460000.5 | 30.34578 | 29.161299 | −1.50005958 | 63.7368301 | L4TP | QS-TP | 4 |
| 2014 UU240 | 2460000.5 | 30.23537 | 34.725041 | −1.50003870 | 54.9968301 | L4TP | QS-TP | 4 |
| 2014 YB92 | 2460000.5 | 30.34005 | 29.869351 | −1.50005827 | 57.9268301 | L4TP | QS-TP | 3 |
| 2015 RW277 | 2460000.5 | 30.20915 | 32.213168 | −1.50004618 | 35.5168301 | L4TP | QS-TP | 2 |
| 2015 VU207 | 2460000.5 | 30.24807 | 37.304499 | −1.50004309 | 44.2068301 | L4TP | QS-TP | 4 |
| 2012 UW177 | 2460000.5 | 30.19023 | 55.795582 | −1.50003775 | 73.2068301 | None | QS-TP | 4 |
| 309239 (2007 RW10) | 2460000.5 | 30.41770 | 38.706573 | −1.50009104 | 9.42683013 | None | QS-HS | 2 |
| Name . | Epoch . | a(au) . | im(deg) . | |$\bar{\cal H}$| . | φ(deg) . | Reported type . | Our determination . | U . |
|---|---|---|---|---|---|---|---|---|
| 2013 KY18 | 2460000.5 | 30.17090 | 8.4945849 | −1.50003319 | 288.956830 | L5TP | L5TP | 2 |
| 2011 HM102 | 2460000.5 | 30.22914 | 28.309835 | −1.50003789 | 302.856830 | L5TP | L5TP | 3 |
| 2004 KV18 | 2460000.5 | 30.18669 | 18.004097 | −1.50005041 | 258.376830 | L5TP | L5TP | 4 |
| 2008 LC18 | 2460000.5 | 30.02992 | 26.629041 | −1.50002688 | 297.506830 | L5TP | L5TP | 4 |
| 2010 TS191 | 2460000.5 | 30.16727 | 5.3397517 | −1.50003187 | 69.5568301 | L4TP | L4TP | 2 |
| 2010 TT191 | 2460000.5 | 30.20027 | 6.8786907 | −1.50003998 | 81.4068301 | L4TP | L4TP | 4 |
| 2012 UV177 | 2460000.5 | 30.19977 | 22.461784 | −1.50003455 | 65.2468301 | L4TP | L4TP | 3 |
| 2013 RC158 | 2460000.5 | 30.25599 | 7.4155135 | −1.50004652 | 45.4868301 | L4TP | L4TP | 4 |
| 2013 RL124 | 2460000.5 | 30.27629 | 8.7858339 | −1.50004858 | 46.2168301 | L4TP | L4TP | 4 |
| 2013 TK227 | 2460000.5 | 30.28748 | 18.243401 | −1.50005789 | 38.5068301 | L4TP | L4TP | 4 |
| 2013 TZ187 | 2460000.5 | 30.31406 | 12.317593 | −1.50005263 | 55.9968301 | L4TP | L4TP | 3 |
| 2014 QO441 | 2460000.5 | 30.27395 | 18.390957 | −1.50004766 | 49.9968301 | L4TP | L4TP | 4 |
| 2014 QP441 | 2460000.5 | 30.26672 | 18.354468 | −1.50004334 | 59.8068301 | L4TP | L4TP | 4 |
| 2015 VV165 | 2460000.5 | 30.26445 | 17.714858 | −1.50004721 | 77.0768301 | L4TP | L4TP | 3 |
| 2015 VW165 | 2460000.5 | 30.24844 | 5.3169036 | −1.50004302 | 73.6168301 | L4TP | L4TP | 3 |
| 2015 VX165 | 2460000.5 | 30.19652 | 17.970819 | −1.50003618 | 72.8868301 | L4TP | L4TP | 4 |
| 385571 Otrera (2004 UP10) | 2460000.5 | 30.34777 | 2.6440677 | −1.50006124 | 50.0268301 | L4TP | L4TP | 4 |
| 385695 Clete (2005 TO74) | 2460000.5 | 30.33115 | 5.0569488 | −1.50005614 | 55.4368301 | L4TP | L4TP | 4 |
| 530664 (2011 SO277) | 2460000.5 | 30.36368 | 8.0553776 | −1.50006846 | 44.2068301 | L4TP | L4TP | 3 |
| 530930 (2011 WG157) | 2460000.5 | 30.16025 | 23.750524 | −1.50003314 | 74.4768301 | L4TP | L4TP | 3 |
| 613490 (2006 RJ103) | 2460000.5 | 30.20993 | 6.7658338 | −1.50003497 | 62.1668301 | L4TP | L4TP | 2 |
| 2005 TN53 | 2460000.5 | 30.30348 | 26.188059 | −1.50005015 | 57.5468301 | L4TP | L4TP | 4 |
| 2013 VX30 | 2460000.5 | 30.25547 | 30.646881 | −1.50004173 | 60.6668301 | L4TP | L4TP | 3 |
| 2014 RO74 | 2460000.5 | 30.21569 | 28.034461 | −1.50003719 | 49.7368301 | L4TP | L4TP | 4 |
| 2014 SC374 | 2460000.5 | 30.22946 | 32.950241 | −1.50003814 | 56.9168301 | L4TP | L4TP | 4 |
| 527604 (2007 VL305) | 2460000.5 | 30.16479 | 27.310887 | −1.50003289 | 72.2768301 | L4TP | L4TP | 2 |
| 2012 UD185 | 2460000.5 | 30.34578 | 29.161299 | −1.50005958 | 63.7368301 | L4TP | QS-TP | 4 |
| 2014 UU240 | 2460000.5 | 30.23537 | 34.725041 | −1.50003870 | 54.9968301 | L4TP | QS-TP | 4 |
| 2014 YB92 | 2460000.5 | 30.34005 | 29.869351 | −1.50005827 | 57.9268301 | L4TP | QS-TP | 3 |
| 2015 RW277 | 2460000.5 | 30.20915 | 32.213168 | −1.50004618 | 35.5168301 | L4TP | QS-TP | 2 |
| 2015 VU207 | 2460000.5 | 30.24807 | 37.304499 | −1.50004309 | 44.2068301 | L4TP | QS-TP | 4 |
| 2012 UW177 | 2460000.5 | 30.19023 | 55.795582 | −1.50003775 | 73.2068301 | None | QS-TP | 4 |
| 309239 (2007 RW10) | 2460000.5 | 30.41770 | 38.706573 | −1.50009104 | 9.42683013 | None | QS-HS | 2 |
| Name . | Epoch . | a(au) . | im(deg) . | |$\bar{\cal H}$| . | φ(deg) . | Reported type . | Our determination . | U . |
|---|---|---|---|---|---|---|---|---|
| 2013 KY18 | 2460000.5 | 30.17090 | 8.4945849 | −1.50003319 | 288.956830 | L5TP | L5TP | 2 |
| 2011 HM102 | 2460000.5 | 30.22914 | 28.309835 | −1.50003789 | 302.856830 | L5TP | L5TP | 3 |
| 2004 KV18 | 2460000.5 | 30.18669 | 18.004097 | −1.50005041 | 258.376830 | L5TP | L5TP | 4 |
| 2008 LC18 | 2460000.5 | 30.02992 | 26.629041 | −1.50002688 | 297.506830 | L5TP | L5TP | 4 |
| 2010 TS191 | 2460000.5 | 30.16727 | 5.3397517 | −1.50003187 | 69.5568301 | L4TP | L4TP | 2 |
| 2010 TT191 | 2460000.5 | 30.20027 | 6.8786907 | −1.50003998 | 81.4068301 | L4TP | L4TP | 4 |
| 2012 UV177 | 2460000.5 | 30.19977 | 22.461784 | −1.50003455 | 65.2468301 | L4TP | L4TP | 3 |
| 2013 RC158 | 2460000.5 | 30.25599 | 7.4155135 | −1.50004652 | 45.4868301 | L4TP | L4TP | 4 |
| 2013 RL124 | 2460000.5 | 30.27629 | 8.7858339 | −1.50004858 | 46.2168301 | L4TP | L4TP | 4 |
| 2013 TK227 | 2460000.5 | 30.28748 | 18.243401 | −1.50005789 | 38.5068301 | L4TP | L4TP | 4 |
| 2013 TZ187 | 2460000.5 | 30.31406 | 12.317593 | −1.50005263 | 55.9968301 | L4TP | L4TP | 3 |
| 2014 QO441 | 2460000.5 | 30.27395 | 18.390957 | −1.50004766 | 49.9968301 | L4TP | L4TP | 4 |
| 2014 QP441 | 2460000.5 | 30.26672 | 18.354468 | −1.50004334 | 59.8068301 | L4TP | L4TP | 4 |
| 2015 VV165 | 2460000.5 | 30.26445 | 17.714858 | −1.50004721 | 77.0768301 | L4TP | L4TP | 3 |
| 2015 VW165 | 2460000.5 | 30.24844 | 5.3169036 | −1.50004302 | 73.6168301 | L4TP | L4TP | 3 |
| 2015 VX165 | 2460000.5 | 30.19652 | 17.970819 | −1.50003618 | 72.8868301 | L4TP | L4TP | 4 |
| 385571 Otrera (2004 UP10) | 2460000.5 | 30.34777 | 2.6440677 | −1.50006124 | 50.0268301 | L4TP | L4TP | 4 |
| 385695 Clete (2005 TO74) | 2460000.5 | 30.33115 | 5.0569488 | −1.50005614 | 55.4368301 | L4TP | L4TP | 4 |
| 530664 (2011 SO277) | 2460000.5 | 30.36368 | 8.0553776 | −1.50006846 | 44.2068301 | L4TP | L4TP | 3 |
| 530930 (2011 WG157) | 2460000.5 | 30.16025 | 23.750524 | −1.50003314 | 74.4768301 | L4TP | L4TP | 3 |
| 613490 (2006 RJ103) | 2460000.5 | 30.20993 | 6.7658338 | −1.50003497 | 62.1668301 | L4TP | L4TP | 2 |
| 2005 TN53 | 2460000.5 | 30.30348 | 26.188059 | −1.50005015 | 57.5468301 | L4TP | L4TP | 4 |
| 2013 VX30 | 2460000.5 | 30.25547 | 30.646881 | −1.50004173 | 60.6668301 | L4TP | L4TP | 3 |
| 2014 RO74 | 2460000.5 | 30.21569 | 28.034461 | −1.50003719 | 49.7368301 | L4TP | L4TP | 4 |
| 2014 SC374 | 2460000.5 | 30.22946 | 32.950241 | −1.50003814 | 56.9168301 | L4TP | L4TP | 4 |
| 527604 (2007 VL305) | 2460000.5 | 30.16479 | 27.310887 | −1.50003289 | 72.2768301 | L4TP | L4TP | 2 |
| 2012 UD185 | 2460000.5 | 30.34578 | 29.161299 | −1.50005958 | 63.7368301 | L4TP | QS-TP | 4 |
| 2014 UU240 | 2460000.5 | 30.23537 | 34.725041 | −1.50003870 | 54.9968301 | L4TP | QS-TP | 4 |
| 2014 YB92 | 2460000.5 | 30.34005 | 29.869351 | −1.50005827 | 57.9268301 | L4TP | QS-TP | 3 |
| 2015 RW277 | 2460000.5 | 30.20915 | 32.213168 | −1.50004618 | 35.5168301 | L4TP | QS-TP | 2 |
| 2015 VU207 | 2460000.5 | 30.24807 | 37.304499 | −1.50004309 | 44.2068301 | L4TP | QS-TP | 4 |
| 2012 UW177 | 2460000.5 | 30.19023 | 55.795582 | −1.50003775 | 73.2068301 | None | QS-TP | 4 |
| 309239 (2007 RW10) | 2460000.5 | 30.41770 | 38.706573 | −1.50009104 | 9.42683013 | None | QS-HS | 2 |
| Name . | Epoch . | a(au) . | im(deg) . | |$\bar{\cal H}$| . | φ(deg) . | Reported type . | Our determination . | U . |
|---|---|---|---|---|---|---|---|---|
| 2013 KY18 | 2460000.5 | 30.17090 | 8.4945849 | −1.50003319 | 288.956830 | L5TP | L5TP | 2 |
| 2011 HM102 | 2460000.5 | 30.22914 | 28.309835 | −1.50003789 | 302.856830 | L5TP | L5TP | 3 |
| 2004 KV18 | 2460000.5 | 30.18669 | 18.004097 | −1.50005041 | 258.376830 | L5TP | L5TP | 4 |
| 2008 LC18 | 2460000.5 | 30.02992 | 26.629041 | −1.50002688 | 297.506830 | L5TP | L5TP | 4 |
| 2010 TS191 | 2460000.5 | 30.16727 | 5.3397517 | −1.50003187 | 69.5568301 | L4TP | L4TP | 2 |
| 2010 TT191 | 2460000.5 | 30.20027 | 6.8786907 | −1.50003998 | 81.4068301 | L4TP | L4TP | 4 |
| 2012 UV177 | 2460000.5 | 30.19977 | 22.461784 | −1.50003455 | 65.2468301 | L4TP | L4TP | 3 |
| 2013 RC158 | 2460000.5 | 30.25599 | 7.4155135 | −1.50004652 | 45.4868301 | L4TP | L4TP | 4 |
| 2013 RL124 | 2460000.5 | 30.27629 | 8.7858339 | −1.50004858 | 46.2168301 | L4TP | L4TP | 4 |
| 2013 TK227 | 2460000.5 | 30.28748 | 18.243401 | −1.50005789 | 38.5068301 | L4TP | L4TP | 4 |
| 2013 TZ187 | 2460000.5 | 30.31406 | 12.317593 | −1.50005263 | 55.9968301 | L4TP | L4TP | 3 |
| 2014 QO441 | 2460000.5 | 30.27395 | 18.390957 | −1.50004766 | 49.9968301 | L4TP | L4TP | 4 |
| 2014 QP441 | 2460000.5 | 30.26672 | 18.354468 | −1.50004334 | 59.8068301 | L4TP | L4TP | 4 |
| 2015 VV165 | 2460000.5 | 30.26445 | 17.714858 | −1.50004721 | 77.0768301 | L4TP | L4TP | 3 |
| 2015 VW165 | 2460000.5 | 30.24844 | 5.3169036 | −1.50004302 | 73.6168301 | L4TP | L4TP | 3 |
| 2015 VX165 | 2460000.5 | 30.19652 | 17.970819 | −1.50003618 | 72.8868301 | L4TP | L4TP | 4 |
| 385571 Otrera (2004 UP10) | 2460000.5 | 30.34777 | 2.6440677 | −1.50006124 | 50.0268301 | L4TP | L4TP | 4 |
| 385695 Clete (2005 TO74) | 2460000.5 | 30.33115 | 5.0569488 | −1.50005614 | 55.4368301 | L4TP | L4TP | 4 |
| 530664 (2011 SO277) | 2460000.5 | 30.36368 | 8.0553776 | −1.50006846 | 44.2068301 | L4TP | L4TP | 3 |
| 530930 (2011 WG157) | 2460000.5 | 30.16025 | 23.750524 | −1.50003314 | 74.4768301 | L4TP | L4TP | 3 |
| 613490 (2006 RJ103) | 2460000.5 | 30.20993 | 6.7658338 | −1.50003497 | 62.1668301 | L4TP | L4TP | 2 |
| 2005 TN53 | 2460000.5 | 30.30348 | 26.188059 | −1.50005015 | 57.5468301 | L4TP | L4TP | 4 |
| 2013 VX30 | 2460000.5 | 30.25547 | 30.646881 | −1.50004173 | 60.6668301 | L4TP | L4TP | 3 |
| 2014 RO74 | 2460000.5 | 30.21569 | 28.034461 | −1.50003719 | 49.7368301 | L4TP | L4TP | 4 |
| 2014 SC374 | 2460000.5 | 30.22946 | 32.950241 | −1.50003814 | 56.9168301 | L4TP | L4TP | 4 |
| 527604 (2007 VL305) | 2460000.5 | 30.16479 | 27.310887 | −1.50003289 | 72.2768301 | L4TP | L4TP | 2 |
| 2012 UD185 | 2460000.5 | 30.34578 | 29.161299 | −1.50005958 | 63.7368301 | L4TP | QS-TP | 4 |
| 2014 UU240 | 2460000.5 | 30.23537 | 34.725041 | −1.50003870 | 54.9968301 | L4TP | QS-TP | 4 |
| 2014 YB92 | 2460000.5 | 30.34005 | 29.869351 | −1.50005827 | 57.9268301 | L4TP | QS-TP | 3 |
| 2015 RW277 | 2460000.5 | 30.20915 | 32.213168 | −1.50004618 | 35.5168301 | L4TP | QS-TP | 2 |
| 2015 VU207 | 2460000.5 | 30.24807 | 37.304499 | −1.50004309 | 44.2068301 | L4TP | QS-TP | 4 |
| 2012 UW177 | 2460000.5 | 30.19023 | 55.795582 | −1.50003775 | 73.2068301 | None | QS-TP | 4 |
| 309239 (2007 RW10) | 2460000.5 | 30.41770 | 38.706573 | −1.50009104 | 9.42683013 | None | QS-HS | 2 |
Locations of the five misjudged Neptune trojans are shown in Fig. 26. As we can see from this figure, they are all located in the QS-TP region, near the boundary between QS-TP and QS/TP regions. Based on the analysis in Qi & Qiao (2022), the stability estimation method in the |$(i_ \mathrm{ m},\bar{\cal H})$| frame is conservative, so its corresponding |$\bar{\cal H}$| value might be smaller than the real one. In this situation, as we can see from Fig. 26, some TP objects may be wrongly determined as QS-TP objects.
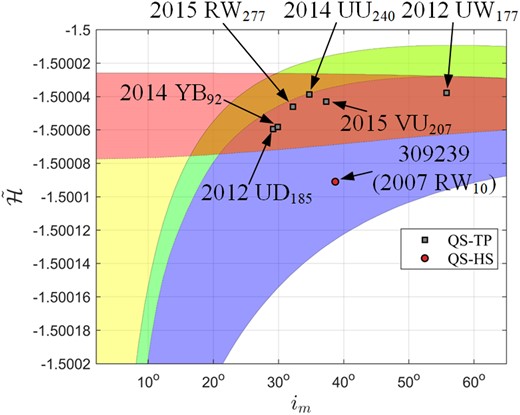
Locations of the five misjudged Neptune trojans in the |$(i_ \mathrm{ m},\bar{\cal H})$| frame.
In addition, we found one Neptune QS-TP and one QS-HS objects unreported before, which are 2012 UW177 and 309 239 (2007 RW10) in Fig. 26, respectively. Fig. 27(a) displays the time evolution of orbital elements of 2012 UW177 based on its orbital elements without orbital uncertainty. From this figure, we can observe that in this situation, 2012 UW177 can remain this QS-TP behaviour for over 2.4 Myr. Since its U = 4, we also implement Monte Carlo simulations to further testify the certainty of its QS-TP state. Fig. 27(b) shows the histogram of Dqstp of 500 Monte Carlo samples of 2012 UW177, where Dqstp denotes the duration of the QS-TP behaviour. As we can see from this figure, their QS-TP lifetimes can remain above 1.4 Myr. Therefore, we confirm that 2012 UW177 is a new long-term stable Neptune QS-TP object, which has not been reported yet.
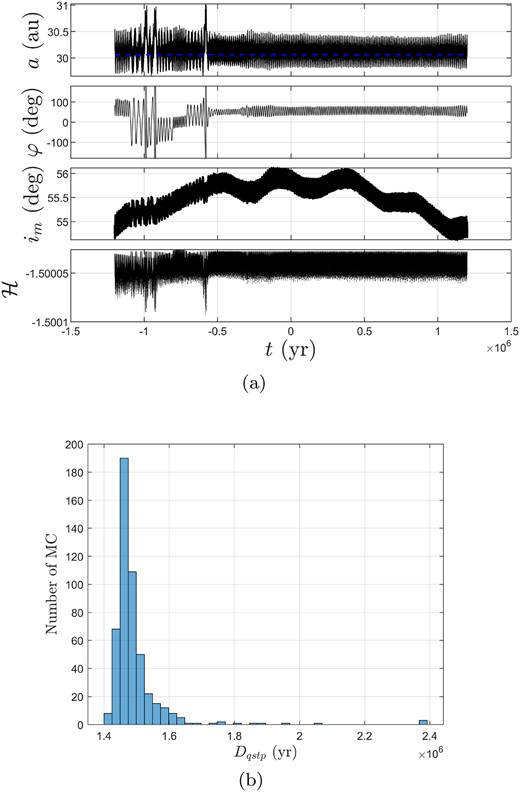
(a) Time evolution of orbital elements of 2012 UW177 without orbital uncertainty, and (b) its histogram of Monte Carlo results.
Fig. 28 shows the time evolution of orbital elements of 309 239 (2007 RW10), where the blue dashed line denotes the semimajor axis of Neptune. From this figure, we observe that it is a trapper in a QS-HS state as we predicted, and it is currently in a QS phase for about 2.5 × 104 yr. Therefore, we confirm that 309 239 (2007 RW10) is a newly Neptune QS-HS object never reported yet, but it is not a long-term stable QS-HS, whose lifetime is shorter than 2 × 105 yr.
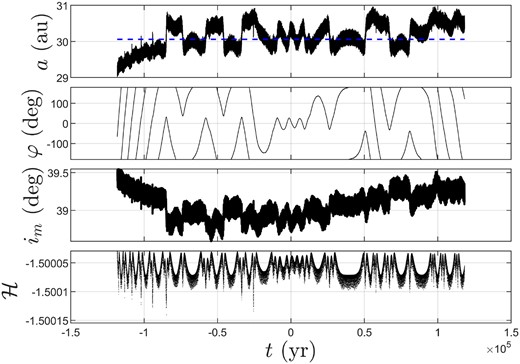
Time evolution of orbital elements of 309 239 (2007 RW10), where the blue dashed line denotes the semimajor axis of Neptune.
5 CONCLUSIONS
In this paper, based on two-dimensional maps from the semi-analytical Hamiltonian approach, we proposed an improved determination method to classify co-orbital objects in the solar system. Different from our previous paper (Qi & Qiao 2022) just focusing on the stability analysis for Earth co-orbital objects, the method of this paper developed a general and effective approach to determine co-orbital objects for other planets.
Based on the topological structure of Hamiltonian isosurface in the torus space, distributions of different co-orbital types are divided in the |$(i_ \mathrm{ m}, \bar{\mathcal {H}})$| and (im, φ) frames for the Sun–planet system. Then, according to the location of a PCO in those frames, its co-orbital type can be classified efficiently without numerical integration. In addition, taking advantage of a simple pattern analysis, we presented certainty conditions to determine orbital state of some co-orbital objects with poor orbit determinations, which are infeasible for the previous method in Qi & Qiao (2022). Then, our determination method was implemented to analyse PCOs of Mars, Jupiter, Saturn, Uranus, and Neptune. Based on our determination method, detailed numbers of PCOs with certain co-orbital states were identified. Then, our determination results for those PCOs were verified through numerical integration in the multiplanet model.
Comparing the reported Mars trojans, we identified four Mars trojans for the first time by our determination method, including 36 017 (1999 ND43), 2015 TL144, 2021 GM4, and 2016 QY10. Numerical integration showed that 36 017 (1999 ND43) and 2021 GM4 with certain orbital elements are temporarily locked in TP behaviours. Monte Carlo simulations of 2015 TL144 and 2016 QY10 with high uncertainty parameters indicated that 2016 QY10 can remain its L4TP state over 2000 yr at least, and 2015 TL144 is a long-term stable Mars L5 trojan. In addition, we confirmed a new short-term Mars QS, 2020 LE1, and a new Mars HS object, 2007 UR2, obtained from our determination method. It should be noted that 1999 UJ7 was classified as a Mars HS object, but it has been reported and known as a long-term stable Mars trojan. We thought that the misjudgment of our determination method is attributed to its ambiguous location on the boundary between the TP and HS regions. Therefore, we postulated that our determination method for co-orbital objects is effective but it cannot deal with the classification of the boundary of different co-orbital regions.
Five Jupiter QS objects recognized by our determination method, including P/2012 US27 (Siding Spring), 2000 CN3, 32 467 (2000 SL174), 2020 MM5, and 404P/Bressi, were analysed in detail. 2000 CN3 and 32 467 (2000 SL174) are known as Jupiter trojans, different from our determination, and 2020 MM5 and 404P/Bressi are first reported. In the (im, φ) frame, 2000 CN3 and 32 467 (2000 SL174) are located on the boundary of QS and TP (or HS) regions, so it is possible to misjudge their co-orbital type. 404P/Bressi is located on the boundary of the QS and TP (or HS) regions. Hence, it is also difficult to distinguish whether it is a Jupiter QS or HS object. Numerical integration showed that 404P/Bressi is a short-term Jupiter HS object for about 300 yr. P/2012 US27 (Siding Spring) was known as a Jupiter QS, but its uncertainty parameter U = 4. Therefore, we implemented Monte Carlo simulations to further testify to the certainty of its QS state. Monte Carlo simulations confirmed that P/2012 US27 (Siding Spring) is a Jupiter QS object, and our determination method is feasible for PCOs with uncertainty parameters. Monte Carlo simulations also verified that 2020 MM5 is a new long-term stable Jupiter QS object, which has not been reported yet.
Numerical integration showed that Saturn’s co-orbital objects are unstable and can only be captured by Saturn for a very short time. Therefore, our determination method seems infeasible for those Saturn PCOs. Taking 2016 BJ81 as an example, we found that 2016 BJ81 is a TP co-orbital object at present, but soon its semimajor axis begins to change drastically. However, if the influence of Jupiter is deducted, 2016 BJ81 can be a long-term stable TP co-orbital object. Although our determination method based on the two-dimensional maps through the semi-analytical Hamiltonian approach in the Sun–planet CRTBP can be extended to the multiplanet model, the significant perturbation from Jupiter in the Sun–Saturn system apparently is beyond the validity of our method.
Numerical integration showed that 2014 YX49, a reported Uranus trojan, experiences co-orbital transitions between the L4TP and QS phases with respect to Uranus, in agreement with our conclusion for its co-orbital type, QS-TP. 523 708 (2014 JB80), a newly identified Uranus L5 trojan by our method was maintained for about 1.3 × 104 yr, in accord with our prediction. In addition, we found a Uranus QS-HS object, 2002 GO9, and numerical integration indicated that it experiences transition between HS and QS state for about 4 × 104 yr, although its QS stages are short and transient. Neptune trojans we recognized through our method are mostly consistent with the MPC results, but there are five reported L5 trojans wrongly classified as QS-TP types by our method. Numerical computation indicated that these misjudgments are attributed to the conservative stability estimation of our method in the |$(i_ \mathrm{ m},\bar{\cal H})$| frame. In addition, we found one Neptune QS-TP and one QS-HS objects unreported before, which are 2012 UW177 and 309 239 (2007 RW10), respectively. Numerical integration showed that they are both short-term co-orbital objects, in accord with our prediction.
Based on the above co-orbital examples in the solar system, we concluded that except Saturn PCOs, our determination method for co-orbital objects is generally feasible in the solar system. Since our method does not rely on time-consuming numerical integration, it is efficient and suitable for a large amount of screening for numerous co-orbital objects in the solar system.
Last but not least, limitations of our semi-analytical method are summarized as follows:
Our method cannot address the determination of PCOs with im < 2°, because those PCOs are close to the planet and their orbital behaviours are unstable.
There are two kinds of misjudgment situations which fall on the boundaries of our determination method in the |$(i_ \mathrm{ m}, \bar{\mathcal {H}})$| and (im, φ) frames.
The significant perturbation from Jupiter in the Sun–Saturn system is beyond the validity of our method. In this situation, numerical integration is still necessary to confirm that Saturn PCOs are actually short lived.
PCOs with a large uncertainty parameter U cannot meet the certainty condition proposed in Section 3.2. Hence, it is difficult to determine their co-orbital motions through our method.
ACKNOWLEDGEMENTS
This work is supported by the National Natural Science Foundation of China under Grant 12202047, and Beijing Institute of Technology Research Fund Program for Young Scholars.
DATA AVAILABILITY
The data underlying this article are available in the article and in its online supplementary material.
Footnotes
https://ssd.jpl.nasa.gov/sbdb_query.cgi, retrieved in December 2019, managed by Ryan S. Park (Chamberlin et al. 1997; Giorgini 2020).
https://ssd.jpl.nasa.gov/announcements/an20210412a.html, retrieved in 2022 February.



