-
PDF
- Split View
-
Views
-
Cite
Cite
Ethan D Jahn, Laura V Sales, Federico Marinacci, Mark Vogelsberger, Paul Torrey, Jia Qi, Aaron Smith, Hui Li, Rahul Kannan, Jan D Burger, Jesús Zavala, Real and counterfeit cores: how feedback expands haloes and disrupts tracers of inner gravitational potential in dwarf galaxies, Monthly Notices of the Royal Astronomical Society, Volume 520, Issue 1, March 2023, Pages 461–479, https://doi.org/10.1093/mnras/stad109
Close - Share Icon Share
ABSTRACT
The tension between the diverging density profiles in Lambda cold dark matter simulations and the constant-density inner regions of observed galaxies is a long-standing challenge known as the ‘core–cusp’ problem. We demonstrate that the SMUGGLE galaxy formation model implemented in the arepo moving mesh code forms constant-density cores in idealized dwarf galaxies of M⋆ ≈ 8 × 107 Msun with initially cuspy dark matter (DM) haloes of M200 ≈ 1010 Msun. Identical initial conditions run with an effective equation of state interstellar medium model preserve cuspiness. Literature on the subject has pointed to the low density threshold for star formation, ρth, in such effective models as an obstacle to baryon-induced core formation. Using a SMUGGLE run with equal ρth, we demonstrate that core formation can proceed at low density thresholds, indicating that ρth is insufficient on its own to determine whether a galaxy develops a core. We reaffirm that the ability to resolve a multiphase interstellar medium at sufficiently high densities is a more reliable indicator of core formation than any individual model parameter. In SMUGGLE, core formation is accompanied by large degrees of non-circular motion, with gas rotational velocity profiles that consistently fall below the circular velocity |$v_\text{circ} = \sqrt{GM/R}$| out to ∼2 kpc. Asymmetric drift corrections help recover the average underlying DM potential for some of our less efficient feedback runs, but time-variations in the instantaneous azimuthal gas velocity component are substantial, highlighting the need for careful modelling in the inner regions of dwarfs to infer the true distribution of DM.
1 INTRODUCTION
The difference between the structure of dark matter (DM) haloes as predicted by the Lambda cold dark matter cosmological model (ΛCDM) and that which is inferred by observations of gas rotational profiles in galaxies is a long-standing problem in modern cosmology (Flores & Primack 1994; Moore 1994) with a wide range of postulated solutions. The structure of DM haloes as predicted by DM-only simulations (e.g. White & Rees 1978; Springel et al. 2008) is characterized by steeply rising density profiles (‘cusps’) in the inner regions of haloes, parametrized by the NFW profile (Navarro, Frenk & White 1996b) which gives a power-law slope of α = −1 in this inner region. Early measurements of rotation curves in dwarf galaxies have shown regions of constant density known as ‘cores’ with power-law slopes of α ∼ 0 (e.g. Burkert 1995; de Blok et al. 2001, 2008; Kuzio de Naray, McGaugh & de Blok 2008). While there is substantial evidence for the existence of cores in dwarf galaxies (e.g. Gilmore et al. 2007; Kormendy et al. 2009; Oh et al. 2011, 2015; Lelli, McGaugh & Schombert 2016), there is debate over the reliability of certain techniques for the inference of the true DM potential (Genina et al. 2018; Oman et al. 2019).
Another complication to this dilemma is that observed rotation curves in dwarf galaxies exhibit a wide variety of behaviour, including rotation curves that rise more rapidly than the NFW profile, consistent with a contraction of the halo, and those that rise significantly more slowly, consistent with expansion. Despite their success in reproducing many observed properties of galaxies, both local and statistical (Vogelsberger et al. 2020), hydrodynamical simulations of galaxy formation have consistently predicted a uniform shape for rotation curves, posing a problem in replicating the observed diversity (Oman et al. 2015, 2019; Read et al. 2016; Santos-Santos et al. 2018, 2020).
A theoretically appealing solution to these discrepancies is that the nature of DM is more complex than proposed in ΛCDM. Proposed models include warm DM (Dodelson & Widrow 1994; Bode, Ostriker & Turok 2001) and self-interacting DM (SIDM, Yoshida et al. 2000; Spergel & Steinhardt 2000; Vogelsberger, Zavala & Loeb 2012; Rocha et al. 2013; Tulin & Yu 2018; Vogelsberger et al. 2019). SIDM has been fairly successful in reproducing diverse rotation curves (e.g. Creasey et al. 2017; Ren et al. 2019; Kaplinghat, Ren & Yu 2020) and explaining the diversity of MW satellites (Zavala et al. 2019). It is worth noting, however, that results for SIDM can depend strongly on the adopted cross-section. Another interesting proposal includes a new hypothetical ultralight scalar particle with a de Broglie wavelength on astrophysical scales, forming a Bose–Einstein condensate the size of the DM halo, known as fuzzy DM (Hu, Barkana & Gruzinov 2000; Mocz et al. 2017; Burkert 2020; Lancaster et al. 2020). While these models prove viable alternatives to ΛCDM with testable predictions (Robles et al. 2017; Bozek et al. 2019), they may remain difficult to distinguish from CDM on small scales, especially when the effects of galaxy formation are taken into account (Elbert et al. 2018; Fitts et al. 2019).
It has also been proposed that the feedback-driven motion of baryons within the halo can gravitationally perturb the DM potential, leading to expansion (Navarro, Eke & Frenk 1996a). The repeated outflow of gas following bursts of star formation (SF) has been demonstrated to be a more realistic mechanism for core formation than single, highly violent outbursts (Read & Gilmore 2005; Governato et al. 2010). This framework was theoretically quantified by Pontzen & Governato (2012) who introduced an analytical model for core formation in which DM particles acquire energy and migrate to more distant orbits via repeated oscillations in the central gravitational potential, driven by supernova (SN) feedback.
Since the physics of star formation and feedback have not been fully constrained, different effective models of interstellar medium (ISM) physics implemented across the literature have produced different outcomes. For example, the Illustris simulations have been successful in reproducing many properties of galaxies (Genel et al. 2014; Vogelsberger et al. 2014a, c), but have not been able to produce DM cores (Chua et al. 2019). The EAGLE simulations (Schaye et al. 2015) have also been shown to not produce DM cores under their fiducial model (Schaller et al. 2015; Benítez-Llambay et al. 2019). Zoom-in simulations using the same prescriptions as EAGLE and Illustris have been performed and similarly demonstrate an inability to induce expansion in the DM halo (e.g. Bose et al. 2019), indicating that resolution is not responsible for this effect in these models. Meanwhile, other simulations, including Zolotov et al. (2012), the FIRE project (Hopkins et al. 2014, 2018; Chan et al. 2015; Wetzel et al. 2016; Fitts et al. 2017), and NIHAO (Wang et al. 2015; Dutton et al. 2016; Tollet et al. 2016), have been able to produce cores in dwarf galaxies that more closely match observations, indicating that the prediction of DM cores is model-dependent to some degree.
Differences in the modelling of baryonic physics have long been quantified by the SF density threshold, which is the minimum gas density required to form a star particle. Pontzen & Governato (2012) showed that cosmological zoom-in simulations run with the gasoline code were unable to induce core formation when using a value of ρth = 0.1 cm−3, but cores did indeed form when increased to ρth = 100 cm−3, a value consistent with the observed densities of molecular clouds (Ferrière 2001). They were clear to point out that the physical motions of baryons within the simulation were the driving factor of core formation and not the particular value of ρth assumed. The authors discuss that the density threshold should be set as high as physically consistent with the numerical resolution and cooling temperatures in the model.
Recent work has focused heavily on the role of the density threshold for star formation, arriving at similar conclusions between the EAGLE (Benítez-Llambay et al. 2019), and NIHAO (Dutton et al. 2019) simulations. It is generally claimed that ‘bursty’ SF drives repeated outflows, thereby expanding the DM halo by driving mass to the outer regions (Brooks & Zolotov 2014). Benítez-Llambay et al. (2019) conclude from their numerical tests on the density threshold that rapid fluctuations in gas content resulting from bursty SF are insufficient to alter the inner DM halo, but that gas must accrete to high levels of density, dominating the inner gravitational potential before being blown away in order to induce core formation. They also make note that there is no simple relation between SF history and core formation. Dutton et al. (2019) also find that a higher value of ρth induces cores in the NIHAO simulations, but their analysis suggests that fluctuations in SF feedback (and therefore gas content) must occur on sub-dynamical time-scales in order to induce core formation. Both authors agree that SF burstiness is insufficient to fully explain halo expansion, and that the density threshold is strongly indicative of a resulting flattened inner DM distribution.
The energetics of core formation discussed in Pontzen & Governato (2012) require rapid motion of sufficiently dense gas clouds in the inner regions of galaxies in order to perturb the gravitational potential and transfer DM to larger orbits. High-resolution simulations that lack detailed physical modelling are unable to capture the small-scale effects of energetic coupling between SF and the ISM due to the use of low star formation threshold, often with ρth = 0.1cm−3, as well as effective equations of state rather than explicitly implemented cooling physics. Meanwhile, detailed ISM models that self-consistently treat a multiphase, structured ISM are relatively new and have not been directly applied to the problem of core formation. In short, the majority of models that have been used to study this problem are empirically calibrated to reproduce scaling relations of populations of galaxies and implemented in large-volume simulations. These models have been adapted to high resolution zoom-in simulations, with mixed results (Benítez-Llambay et al. 2019; Bose et al. 2019). Fewer studies have focused on studying core formation as a thoroughly small-scale problem, requiring both high resolution zoom-in simulations and models that capture the local details of physical processes relevant to the state of the ISM. More details of the varying approaches to galaxy modelling are given in a recent review of cosmological simulations (Vogelsberger et al. 2020).
While there is broad agreement in the literature that high thresholds induce cores (e.g. Governato et al. 2010; Macciò et al. 2012; Teyssier et al. 2013; Di Cintio et al. 2014, among the previously listed) and low thresholds do not (Oman et al. 2015; Schaller et al. 2015; Bose et al. 2019), there have been limited systematic investigations of the physical outcomes of modelling choices, including comparative analyses of parameters within the same overall modelling scheme. The consistency of models with similar ρth does not rule out the possibility that other modelling choices contribute to halo expansion, including ones that cannot be neatly quantified by a single parameter.
Beyond the physical effects of baryons, difficulties in observing and modelling gas rotation curves in galaxies have led to speculation that large uncertainties might be partially responsible for the observed diversity of galactic rotation curves. While extensive work has been done to improve observational techniques for estimating velocity profiles (Kuzio de Naray et al. 2006; Kuzio de Naray et al. 2008; Adams et al. 2014), techniques based on alignment of metallicity populations (e.g. Walker & Peñarrubia 2011) and tilted-ring modelling (e.g. Rogstad, Lockhart & Wright 1974; Iorio et al. 2017) have been recently been demonstrated via application to the APOSTLE simulations to predict DM cores when none actually exist (Genina et al. 2018; Oman et al. 2019). This, combined with the large degeneracies in modelling rotational velocities in the presence of non-circular motions (Marasco et al. 2018; Santos-Santos et al. 2020) suggest that the observed diversity of rotation curves might not be solely a result of physical processes within galaxies, be they baryonic or dark.
In this study, we compare the novel Stars and MUltiphase Gas in GaLaxiEs (SMUGGLE) feedback model (Marinacci et al. 2019) to the classic Springel & Hernquist Springel & Hernquist (2003; SH03 hereafter) model, as they represent two paradigms of galaxy formation modelling (i.e. top-down – SH03, and bottom-up – SMUGGLE) while implementing the same method of solving gravity + hydrodynamics (arepo; Springel 2010). We aim to investigate the differences in and relationship between galaxy formation and DM distribution within these two modelling paradigms in a controlled environment through the use of idealized simulations of a single dwarf galaxy. We also implement variations in model parameters (density threshold and local SH efficiency) within SMUGGLE to shed light on their relevance to core formation within this model, and how their differential effects within this model compare to previous numerical experiments.
The paper is organized as follows: in Section 2, we discuss the set up of our isolated dwarf galaxy simulations; in Section 3, we compare the phenomenological differences between an isolated dwarf galaxy (M⋆ ∼ 108 Msun, M200 ∼ 1010 Msun) run with each model, and then introduce variations in the SMUGGLE model to investigate the physical nature of core formation in Section 4. We conclude in Section 5 by examining the morphology of each run, including an investigation of the variation of rotational velocity curves of gas. We summarize our findings in Section 6.
2 METHODS
We analyse a set of high-resolution, idealized simulations of isolated dwarf galaxies of M⋆ ≈ 108 Msun in haloes of mass M200 ≈ 1010 Msun run with the moving mesh code arepo (Springel 2010; Weinberger, Springel & Pakmor 2020). This scale of stellar mass to halo mass has been demonstrated to form feedback-driven cores in other simulation codes (e.g. Di Cintio et al. 2014; Tollet et al. 2016).
Initial conditions were generated via the method described in Springel, Di Matteo & Hernquist (2005), while star formation and feedback were subsequently enabled via the SMUGGLE model (Marinacci et al. 2019). SMUGGLE implements a wide variety of sub-resolution processes, including gas heating and cooling from which a detailed, multiphase interstellar medium (ISM) emerges, a stochastic formation process for stars, and feedback via supernovae (SNe), radiation, and stellar winds.
Previous work with SMUGGLE includes Li et al. (2020), who study the formation of giant molecular clouds (GMCs) in Milky Way-mass galaxies, in particular the response of GMCs to various choices of the local star formation efficiency – a parameter we study here as well. They find that SMUGGLE is able to regulate star formation through feedback, with a 3-fold increase in star formation rate (SFR) in runs with no feedback processes enabled. This result is encouraging as it enables self-consistent prediction of kpc-scale galaxy properties. Further, they demonstrate that SN feedback disrupts the spatial correlation of GMCs on scales >0.2 kpc, which is relevant to our discussion on core formation later on. In addition, the SMUGGLE has been further refined with the development of a state-of-the-art model for the treatment of radiation fields, dust physics, molecular chemistry, and metal cooling by Kannan et al. (2020). This model is able to produce a more complex picture of the ISM of galaxies while maintaining consistent global properties, such as SFR.
2.1 The SMUGGLE ISM model
In this work, we implement the standard SMUGGLE model as described in Marinacci et al. (2019). Here, we summarize the main physical modelling choices. The primary processes include gravitational hydrodynamics, which is solved by arepo (Springel 2010), gas heating, and cooling which produce an emergent multiphase ISM, the stochastic formation of star particles, and feedback from stars and SNe.
2.1.1 Heating and cooling
One of the biggest differences in SMUGGLE compared to previously implemented ISM models in arepo (e.g. SH03, Vogelsberger et al. 2014a; Pillepich et al. 2018) is its ability to explicitly model a cold gas phase with temperatures falling below Tgas ∼ 104 K. First, a primordial mix of hydrogen and helium is modelled by a network of two-body processes including collisions, recombination, Compton cooling via CMB photons (Ikeuchi & Ostriker 1986), and UV-background photoionization (Faucher-Giguère et al. 2009).
Cooling has two main regimes, metal-line cooling driving the gas temperature down to the warm phase (Tgas ∼ 104 K) – which was included in previous ISM models – while fine structure and molecular cooling implemented in SMUGGLE allows the gas to further cool to T ∼ 10 K. Cooling rates are calculated in a UV background with the Hopkins et al. (2018) fit as a function of temperature, metallicity, gas density, and redshift, with self-shielding taken into account at z ≤ 6 as in Rahmati et al. (2013). The calculated rates are then scaled to the metallicity of the gas cell. By default, metallicities are updated self-consistently as the simulation evolves in arepo. However, for idealized set-ups metallicity can be fixed to offset the lack of replenishment of pristine gas from cosmological infall. For simplicity, in this paper we fix the metallicity of our idealized runs to the solar value.
2.1.2 Star formation
Star particles representing single stellar populations with a Chabrier (2001) initial mass function are formed probabilistically in cold, dense gas. Gas is determined to be eligible for star formation based on several criteria. The first is the gas density threshold, below which no gas can be converted into a star particle. SMUGGLE adopts a value of 100 cm−3, in line with observations of giant molecular clouds (Ferrière 2001). Star formation is also restricted to gravitationally self-bound regions (see Hopkins et al. 2018). Additionally, star formation rates may be computed according to the H2 fraction, though it is usually ∼1 in sufficiently dense gas. We find that SMUGGLE forms stars in gas with an average temperature of 37 K in our fiducial high-resolution run.
The probability of an eligible gas cell to be turned into stars is determined via |$\dot{M}_\star =$| εsf Mgas/tdyn, where tdyn is the gravitational dynamical time of the gas and |$\dot{M}_\star$| its star formation rate. In its default mode, the local SF efficiency parameter εsf is assigned a value of 0.01 to match the low efficiencies measured in observations (Smith, Sijacki & Shen 2018), although Hopkins et al. (2018) showed that the exact level of feedback-regulated star formation is independent of εsf. We explore in Section 4 the effect of εsf on our SMUGGLE simulations.
2.1.3 Feedback
Stellar feedback is modelled locally according to several sources including stellar winds, radiation from young stars and supernovae (SNe). Stellar winds due to massive OB and AGB stars contribute to the mass return to the ISM and are taken into account during the pre-processing of the gas. Cumulative mass-loss from OB stars, as well as energy and momentum returned from both OB and AGB stars are determined via the parametrizations presented in Hopkins et al. (2018), while AGB wind mass transfer is given by Vogelsberger et al. (2013). All the properties determined from the different feedback channels are then injected with corresponding metallicity to the surrounding gas in the rest frame of the star. Stellar winds are a continuous process, and are thus treated continuously across each time-step for each star particle.
Radiative feedback from young stars change the ionization, thermal, and dynamical state of the ISM, pre-processing the media where later SNe will go off. SMUGGLE includes a treatment of photoionization aimed at capturing the formation of H ii regions by young, massive stars. Ionizing photon rates from young stellar particles are calculated by choosing a mass-to-light ratio and average ionizing photon (>13.6 eV) energy to correspond with a T = 4 × 104 K blackbody spectrum, consistent with OB-type stars. The number of available photons in a given time-step is used to stochastically photoionize neighboring gas cells after accounting for the expected number of recombinations. Photoionized cells are then updated to be fully ionized and placed at a temperature T = 1.7 × 104 K. In addition to photoionization, young stars exert radiation pressure on neighboring gas cells, which is calculated according to their optical depth and position within the kernel. Multiple IR scattering is included, by assuming an average opacity |$\tau = 10\, Z/Z_\odot$| cm2 g−1 (Hopkins et al. 2018). In the regime of small-mass galaxies explored here, photoionization is expected to dominate among the radiation effects on the ISM, lowering the density of gas in the neighbourhood of massive stars (Sales et al. 2014; Hopkins et al. 2018).
Lastly, we stochastically model the injection of energy and momentum by discrete SN events on to neighbouring gas cells. It is important to note that SMUGGLE resolves individual SN explosions, and as such, the injected rates of energy and momentum are not continuous. The temporal distribution of individual Type Ia events is found by integrating the delay time distribution, which accounts for the approximate lifespan of an 8 Msun main-sequence star, with rates and energetics consistent with observations (Greggio 2005) as well as previous implementations in arepo (Vogelsberger et al. 2013), with each event releasing the same mass of ejecta (Thielemann et al. 2003). The total number of Type II SNe is found by integrating the Chabrier IMF of each stellar particle. If necessary, we account for PdV work in the (unresolved) Sedov–Taylor phase by applying a momentum boost to match the terminal momentum per SN, which depends primarily on local density and metallicity (e.g. Cioffi, McKee & Bertschinger 1988). Energy and momentum are distributed to surrounding gas cells following a kernel weighting and a maximum coupling radius, as described in detail in Marinacci et al. (2019).
2.1.4 Variations on the fiducial SMUGGLE model
We will explore in Section 4, the effect of changing some of the default choices in SMUGGLE and how this affects the formation of DM cores and the properties of our simulated dwarfs. The changes will be inspired by results presented previously in the literature, including Read et al. (2016), Benítez-Llambay et al. (2019), and Bose et al. (2019). More specifically, we choose to vary the star formation gas density threshold ρth and the local star formation efficiency εsf.
Table 1 summarizes our runs, which include the fiducial SMUGGLE run, SH03, and three variations on SMUGGLE as discussed in Section 4.1: (i) rho0.1, using a reduced star formation density threshold of ρth = 0.1 cm−3; (ii) eSF100, which maximizes the local star formation efficiency to 100 per cent, εsf = 1; and (iii) vareff, a variable efficiency model that chooses a value between εsf = 0.01 and εsf = 1 depending on the density of the surrounding ISM. The fiducial SMUGGLE model implements these parameters with values of ρth = 100 cm−3 and εsf = 0.01.
List of simulations used in this study. All initial conditions were generated according to Springel et al. (2005) and run for 2 Gyr h−1, where we take h = 0.7. Our standard resolution initializes a 2.17 × 1010 Msun halo with 3 × 107 DM particles, and 106 gas particles, corresponding to a baryonic mass per cell of ∼850 Msun and DM mass per cell of ∼7200 Msun. We adopt a gravitational force softening of ϵ = 16 pc for all particle types. Also listed are the core radius (measured as described in Section 3.1), inner DM power-law slope α, and stellar mass formed (i.e. not including the disc and bulge from initial conditions), all taken at final time.
| Name . | rcore (pc) . | α . | M⋆ (Msun) . | Model description . |
|---|---|---|---|---|
| SMUGGLE / fiducial | 431.3 | −0.13 | 7.76 × 107 M⊙ | Default SMUGGLE model |
| SH03 | 160.2 | −0.52 | 4.29 × 107 M⊙ | Springel & Hernquist (2003) model |
| rho0.1 | 324.2 | −0.05 | 9.69 × 107 M⊙ | SMUGGLE with reduced gas density threshold, ρth = 0.1 cm−3 |
| eSF100 | 490.7 | −0.03 | 8.39 × 107 M⊙ | SMUGGLE with maximized local SF efficiency, εsf = 1 |
| vareff | 528.3 | −0.03 | 9.12 × 107 M⊙ | SMUGGLE with the variable efficiency model, see Section 2.1.2 |
| Name . | rcore (pc) . | α . | M⋆ (Msun) . | Model description . |
|---|---|---|---|---|
| SMUGGLE / fiducial | 431.3 | −0.13 | 7.76 × 107 M⊙ | Default SMUGGLE model |
| SH03 | 160.2 | −0.52 | 4.29 × 107 M⊙ | Springel & Hernquist (2003) model |
| rho0.1 | 324.2 | −0.05 | 9.69 × 107 M⊙ | SMUGGLE with reduced gas density threshold, ρth = 0.1 cm−3 |
| eSF100 | 490.7 | −0.03 | 8.39 × 107 M⊙ | SMUGGLE with maximized local SF efficiency, εsf = 1 |
| vareff | 528.3 | −0.03 | 9.12 × 107 M⊙ | SMUGGLE with the variable efficiency model, see Section 2.1.2 |
List of simulations used in this study. All initial conditions were generated according to Springel et al. (2005) and run for 2 Gyr h−1, where we take h = 0.7. Our standard resolution initializes a 2.17 × 1010 Msun halo with 3 × 107 DM particles, and 106 gas particles, corresponding to a baryonic mass per cell of ∼850 Msun and DM mass per cell of ∼7200 Msun. We adopt a gravitational force softening of ϵ = 16 pc for all particle types. Also listed are the core radius (measured as described in Section 3.1), inner DM power-law slope α, and stellar mass formed (i.e. not including the disc and bulge from initial conditions), all taken at final time.
| Name . | rcore (pc) . | α . | M⋆ (Msun) . | Model description . |
|---|---|---|---|---|
| SMUGGLE / fiducial | 431.3 | −0.13 | 7.76 × 107 M⊙ | Default SMUGGLE model |
| SH03 | 160.2 | −0.52 | 4.29 × 107 M⊙ | Springel & Hernquist (2003) model |
| rho0.1 | 324.2 | −0.05 | 9.69 × 107 M⊙ | SMUGGLE with reduced gas density threshold, ρth = 0.1 cm−3 |
| eSF100 | 490.7 | −0.03 | 8.39 × 107 M⊙ | SMUGGLE with maximized local SF efficiency, εsf = 1 |
| vareff | 528.3 | −0.03 | 9.12 × 107 M⊙ | SMUGGLE with the variable efficiency model, see Section 2.1.2 |
| Name . | rcore (pc) . | α . | M⋆ (Msun) . | Model description . |
|---|---|---|---|---|
| SMUGGLE / fiducial | 431.3 | −0.13 | 7.76 × 107 M⊙ | Default SMUGGLE model |
| SH03 | 160.2 | −0.52 | 4.29 × 107 M⊙ | Springel & Hernquist (2003) model |
| rho0.1 | 324.2 | −0.05 | 9.69 × 107 M⊙ | SMUGGLE with reduced gas density threshold, ρth = 0.1 cm−3 |
| eSF100 | 490.7 | −0.03 | 8.39 × 107 M⊙ | SMUGGLE with maximized local SF efficiency, εsf = 1 |
| vareff | 528.3 | −0.03 | 9.12 × 107 M⊙ | SMUGGLE with the variable efficiency model, see Section 2.1.2 |
2.2 The Springel and Hernquist model
In addition to the fiducial SMUGGLE model, we run a simulation with the SH03 model (Springel & Hernquist 2003), which forms the basis for the ISM treatments in Illustris (Vogelsberger et al. 2014a, c), Auriga (Grand et al. 2017) simulations, EAGLE (Schaye et al. 2015), APOSTLE (Sawala et al. 2016), HorizonAGN (Dubois et al. 2014), SIMBA (Davé et al. 2019), and others. The SH03 model, also run with the arepo gravity and hydrodynamics solver, uses an equation of state treatment of cold gas modelled with a two-fluid approach (cold clouds embedded in a lower density hot gas bath) to describe the interstellar medium. This approach, which has been demonstrated to be successful at modelling the kpc-scale properties of galaxies, has been found to not form DM cores (Vogelsberger et al. 2014b; Bose et al. 2019).
We explicitly include stellar winds in the SH03 run with the wind velocity calculated directly from the energy and momentum summation of all SN in a given time-scale and independent of halo properties. This is different from, for instance, the Illustris or Auriga projects, where the wind velocity is scaled to the DM velocity dispersion of the subhalo. Although such scheme is de-facto closer to the scalings expected for momentum-driven winds (Murray, Quataert & Thompson 2005) and shown to more accurately reproduce some galaxy and CGM observables (e.g. Davé, Oppenheimer & Finlator 2011), we choose a simpler wind model where no pre-assumptions are made with respect to the properties of the host halo, in an attempt to establish a fairer comparison with the SMUGGLE runs where no input information is required about the galaxy host. Ultimately, the impact of the exact modelling of the winds in our SH03 run is subdominant to the differences imprinted by the modelling of the ISM itself. As is the case in Illustris, Auriga, and other projects mentioned above, the wind particles in the SH03 model are artificially decoupled from the hydrodynamics for a short period of time, while such a treatment is not necessary in our new SMUGGLE prescription where outflows naturally arise from the kinematics and thermodynamics of stellar winds and SN explosions.
2.3 Isolated Galaxy setup
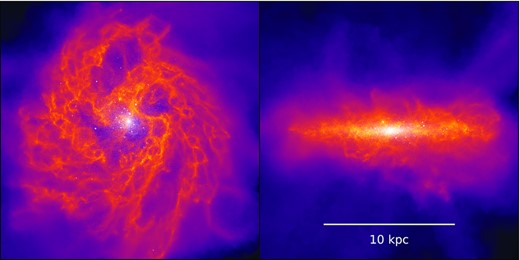
Face-on and edge-on surface density projections of the isolated dwarf galaxy on the fiducial SMUGGLE model generated with the Cosmic Ly α Transfer code (Smith et al. 2015; Smith, Bromm & Loeb 2017). Stars formed during the duration of the simulation are shown in white, with gas colour-weighted according to surface mass density. The width of each frame is 20 kpc. The richly structured ISM is a result of the detailed ISM physics included in the SMUGGLE model.
The galaxy itself is initialized with an exponential disc of scale-length h for both stars and gas, in addition to a spherical stellar bulge modeled by the Hernquist profile. See section 2 of Springel et al. (2005) for more details on the model galaxy setup. We choose parameters for our model galaxy consistent with the ‘Dwarf/SMC’ setup described in Hopkins, Quataert & Murray (2011), which gives a DM-dominated dwarf galaxy similar to the pre-infall Small Magellanic Cloud with total baryonic mass Mbary = 8.9 × 108 Msun, gaseous disc with Mgas = 7.5 × 108 Msun, and DM halo with M200 = 2 × 1010 Msun and concentration parameter c = 15.
The partitioning of cells in the initial conditions is done by setting the number of gas particles, Ngas, with NDM = 30Ngas, Ndisc = 0.2Ngas, and Nbulge = 0.02Ngas. For the runs analysed herein, we choose Ngas = 106, resulting in a particle mass of mbary ≈ 850 Msun. We choose the same value of gravitational softening for all particle types, with ϵ = 16 pc. We have also run a set of simulations with an order of magnitude lower resolution (Ngas = 105, ϵ = 32 pc) for convergence testing. We find excellent agreement between the two resolution levels tested, as shown in Fig. A1.
We note that the stellar masses of our idealized galaxies presented in Table 1 may be at the high-end of expectations from observations of nearby isolated dwarfs (Katz et al. 2017; Read et al. 2017; Posti, Fraternali & Marasco 2019). We note that this is a direct consequence of our initial set-up and arbitrary duration of the simulation. Changes in the halo concentration, old-stars distribution and gas profile may all impact the final stellar masses in our runs and, through it, the expected sizes of the formed DM cores. We emphasize that the main aim of our work is therefore to compare between the DM and baryonic properties of galaxies formed in different variations of SMUGGLE. We also wish to gain insight as to potential challenges in modelling realistic dwarf galaxies in a universe where feedback couples with different efficiency levels to the surrounding ISM. An evaluation of core properties and whether they are in good agreement (or not) with observed galaxies will be addressed in forthcoming work using cosmological runs.
3 FORMING DARK MATTER CORES IN SMUGGLE
We explore the evolution of the DM density profile in our simulated dwarf galaxy in Fig. 2, where each panel corresponds to different times, as labeled. The results of the default SMUGGLE model are shown in the solid black line, which demonstrates a clear flattening in the inner regions corresponding to the formation of a DM core in our initially cuspy halo. For reference, we include the initial DM distribution in each panel with a solid grey line.
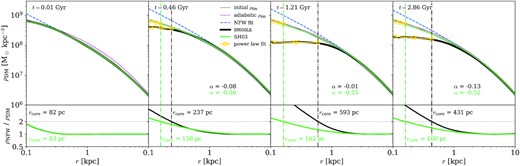
DM density profiles of the isolated dwarf galaxy run with the fiducial SMUGGLE feedback model (black) and the SH03 feedback model (green) at selected times. The top row shows the DM density at each labelled time. Light grey lines represent the DM density profiles at t = 0, and the blue dashed line is the NFW profile fit to r > 3 kpc to account for variations in the inner region. The core radius rcore is defined as the radius where ρNFW/ρDM = 2, and which can be seen in the bottom panels, including the horizontal line at 2. The vertical dashed–dotted lines in each panel represented our measured rcore, which consistently capture the changes in DM density. In addition, power-law slopes (ρ ∝ rα) are shown in yellow, and are fit for |$r_\text{DM}^\text{conv} \lt r \lt r_\text{core}$|. Values for the convergence radius |$r_\text{DM}^\text{conv}$| are typically around 50 pc.
3.1 A consistent method for core size measurements
3.1.1 Caveats and numerical effects
Fig. 2 shows density profiles for various runs implementing the same ICs. We find the best-fitting NFW profile to the outer (r > rfit = 3 kpc) DM distribution. The bottom panels in Fig. 2 show the ratio between the analytic NFW fit and the measured DM density in the fiducial SMUGGLE simulations (solid black lines). Although in the outskirts the simulated profiles are very well described by the NFW fits (ρNFW/ρdm ∼ 1), in the inner regions the analytic profile clearly overestimates the DM density in all cases. This is partially due to adiabatic contraction, demonstrated by the magenta line. In the case of SH03, feedback is not capable of producing further changes in the DM distribution, resulting in a profile almost identical to the adiabatic run, while the SMUGGLE model is able to produce an extended region of constant density by later times. Additionally, the shape of the galaxy can affect the resultant DM distribution. In the case of discs, this can lead to shallower central profiles (Burger & Zavala 2021).
We note that numerical effects can spuriously transfer kinetic energy between particles of different masses, such as our gas and DM particles (Ludlow et al. 2019a). A thorough investigation of the effects of gravitational softening and ‘numerical feedback’ have been presented in Ludlow, Schaye & Bower (2019b) and Ludlow et al. (2020). While we adopt softening on the order suggested by Van den Bosch & Ogiya (2018) – approximately three times lower than the convergence radius |$r_{\rm dm}^{\rm conv}$| – it is possible that spurious energy transfer between DM and baryonic particles via 2-body interactions contributes to the observed halo expansion. However, our tests are designed to isolate the effects of feedback. Numerical effects will be present in all our simulations, including the adiabatic and SH03 runs, but the methods of feedback coupling to the ISM vary. As such, our claims are about the differential effects between feedback implementations, not predictions of the absolute core sizes expected within dwarf galaxies in a cosmological context.
3.1.2 Core size measurement
Following Benítez-Llambay et al. (2019), we define rcore as the location where the simulated DM density is a factor of 2 lower than the extrapolated best-fitting NFW profile, ρNFW/ρdm = 2. However, we note that the authors compare against a low-threshold run rather than an NFW. Hydrodynamic relaxation may lead to a difference in predicted core radius. The measured rcore is indicated with a vertical dashed line and listed in the lower panels.
This definition is robust to variations on rfit in the range 1–10 kpc (see Fig. A2 in the Appendix). Fig. 2 shows that the density profile within rcore for the fiducial SMUGGLE run is nearly flat at later times. We quantify this by finding the slope α of a power-law fit to the DM density between the convergence radius |$r_{\rm dm}^{\rm conv}$| and rcore, where |$r_{\rm dm}^{\rm conv}$| is defined as the radius containing 200 DM particles (as in Klypin et al. 2001; Hopkins et al. 2018), and is typically around 50 pc in size. For reference, the measured slopes α are quoted in each panel.
While the initial DM distributions of our simulations follow a Hernquist profile, we find no difference in measured core radius when using Hernquist or NFW parametrizations, consistent with the intended similarity between the fits for r ≪ r200. While some choices of our methodology are arbitrary, we find that it consistently produces an accurate characterization of the physical extent and slope of the constant density inner regions. We show in the Appendix that core formation is well converged and robust to numerical choices, such as resolution and rfit (see Figs A1 and A2).
Other methods for measuring DM core sizes include the isothermal sphere model (PITS) which has proven successful in the fitting of rotation curves of dwarf galaxies (Begeman, Broeils & Sanders 1991; Kuzio de Naray et al. 2006; Kuzio de Naray et al. 2008; Teyssier et al. 2013). However, choosing a particular exponential fit for the DM profile introduces potential bias into the measurement, and may produce core sizes that do not reflect the actual size of the region where the DM density profile appears flat. Instead, our model assumes no particular parametric form of the DM profile, and is designed to consistently represent the region of constant DM density.
We find that the core radius produced by the PITS model does not accurately reflect the physical extent of the portion of the DM profile where ρ ∝ r0 (see Fig. A6). While the overall fit provided by the model is quite accurate, the numerical value of the core radius parameter does not correspond to a particular physical property of the underlying DM distribution. This is because the core radius parameter is a feature of a particular numerical model rather than a direct calculation using the DM profile. We show that the overall trend followed by the measured core radius is the same in our model as compared to the PITS model, but that we find difficulty in measuring the core slope with PITS. Further, we have explicitly checked that our procedure to measure core radius results in cores about 2–3 times smaller than that of PITS for our fiducial run (Fig. A6). When comparing measured core radii in the literature, it is important to take into account that a variety of different methodologies exist. We are interested in measuring the physical extent of the flattened DM profile, so we adopt a methodology designed for such a purpose. As such, our reported numerical core radii may be smaller than those reported using parametric fitting methods.
3.2 Halo response to SMUGGLE versus SH03 models
Interestingly, and in contrast to previous results of model implementations within arepo (e.g. Marinacci, Pakmor & Springel 2014; Bose et al. 2019; Chua et al. 2019), we find that the new SMUGGLE model develops a well-defined constant-density core with radius 200–600 pc in our idealized M200 ∼ 1010 Msun dwarf halo. In comparison, the same initial setup run with the SH03 model does not robustly form a core.
In practice, our method suggests rcore ≈175 pc (see bottom panels) for the SH03 run, although this is more consistent with a relaxation effect than a true DM core achieved by repeated perturbation of the potential. This is further supported by the inner slope α, which is far from being a flat constant density distribution (α ∼ 0) as found for our fiducial SMUGGLE run and instead remains steep (α ∼ −0.55), consistent with that of the initial condition over a similar distance range. In addition, we have run an adiabatic (i.e. no star formation or feedback) version of the same initial setup for t ∼ 0.7 Gyr. By our methods, we calculate time-averaged values of rcore = 150 pc and α = −0.57 for the adiabatic run, indicating that the behaviour seen in SH03 is consistent with relaxation and is not representative of a feedback-induced core. Note the similarity between the green SH03 and magenta adiabatic curves in Fig. 2.
We therefore find that the SH03 ISM treatment does not create a core, in agreement with previous studies implementing similar models (e.g. Marinacci et al. 2014; Bose et al. 2019) while the new ISM treatment SMUGGLE results in clear halo expansion. The measured core extends over several hundred pc, which is well beyond the gravitational softening for the DM ϵ = 16 pc or the convergence radius |$r_{\rm DM}^{\rm conv} \approx 50$| pc.
A more detailed description of the time evolution for the core is shown in the panels (a) and (b) of Fig. 3, showing the core radius rcore and the power-law slope α of the inner region |$r^{\rm DM}_{\rm conv} \lt r \lt r_\text{core}$| of the DM density profile. In SMUGGLE, the core radius grows during the first Gyr, after which it settles on an average rcore ∼400 pc with fluctuations. The slope flattens from α = −0.55 to −0.09 in the first half Gyr, where it remains for the rest of the simulation. In contrast, SH03 relaxes into a stable density distribution with rcore ∼ 160 pc and no significant change in slope, resulting in a cusp rather than a core.
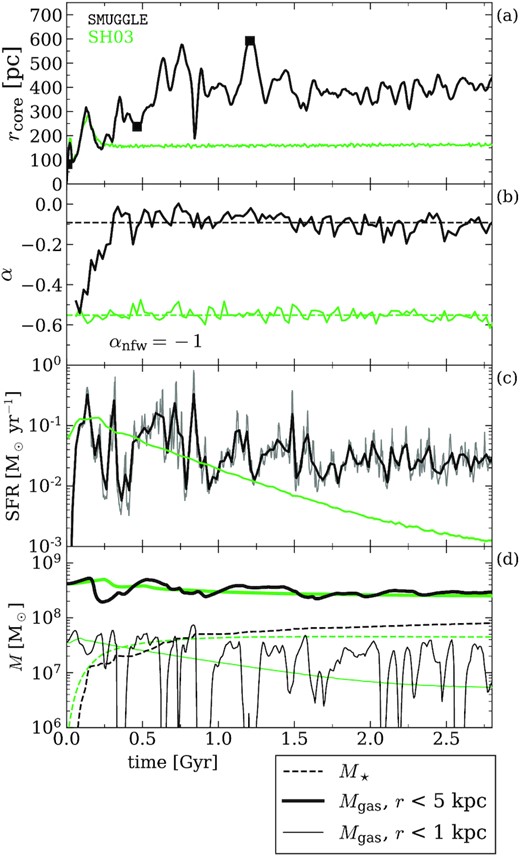
Time-evolving properties of the simulated isolated dwarf galaxy run with the fiducial SMUGGLE model in black and the SH03 feedback model in green. (a) Measured core radius rcore versus time. Black squares indicate timestamps of density profiles shown in Fig. 2. See text for definition of rcore. (b) Power-law slopes α fitted to |$r_\text{DM}^\text{conv} \lt r \lt r_\text{core}$|, binned with Δt = 25 Myr. Dashed lines indicate the average slope for t > 0.5 Gyr to account for initial relaxation effects. The SMUGGLE model results in a very flat inner profile (α ∼ −0.1) which extends over a larger portion of the galaxy with rcore∼ 400 pc, in contrast to the steeper (α ∼ −0.6), more concentrated (rcore∼ 150 pc) profile formed by SH03. (c) Star formation rate (SFR) versus time. The SFR is smoothed over Δt = 25 Myr bins. We find that fiducial produces a substantially burstier star formation history (SFH) than SH03, and that the average magnitude of SFR for SH03 agrees with that of fiducial in early times, but declines to much smaller levels after t ≈ 1.5 Gyr. (d) Stellar mass (M⋆, dashed), gas mass within r < 5 kpc (solid, thick), and gas mass within r < 1 kpc (solid, thin). SMUGGLE results in frequent and significant changes in gas mass in the inner regions, while the gas mass < 1 kpc in SH03 smoothly decreases.
Panel (c) of Fig. 3 compares the star formation histories in the SMUGGLE and SH03 runs. The rapid fluctuations in the SMUGGLE run are sustained throughout the ∼3 Gyr of run time, though with decreased burstiness after t ∼ 1 Gyr. This contrasts the smoother SFR from the SH03 ISM model. In fact, SH03 shows a declining SFR, likely due to the lack of cold inflows and depletion of all eligible star-forming gas. The cooling implementation of SH03 results in an effective temperature floor of ∼104 K, such that, with the lack of cold inflows, no new gas is able to condense to sufficiently high densities to fuel star formation. As a result, the final stellar mass formed in SMUGGLE is |$\sim 50{{\ \rm per\ cent}}$| larger compared to SH03.
Note that this burstiness in the star formation of SMUGGLE is associated with fluctuations on the gas mass in the inner 1 kpc (Fig. 3, panel d), while SH03 simply depletes the gas content in this region. As discussed in Pontzen & Governato (2012), such mass fluctuations in short time-scales can cause the local gravitational potential to non-adiabatically change resulting in the expansion of DM orbits and, consequently, on the formation of a lower density core. In the case of SMUGGLE, although the gas content is changing very abruptly in the very inner regions (thin) and less so outwards, the mass fluctuation can be discerned quite far out into the main body of the galaxy, r ∼ 5 kpc.
What is driving these differences between the ISM models? Discussions in the literature have cited rapid fluctuations of the potential in the inner regions (Navarro et al. 1996a; Pontzen & Governato 2012), burstiness of star formation rates (Madau, Shen & Governato 2014; Chan et al. 2015; Tollet et al. 2016; Dutton et al. 2019), and high gas densities such that it dominates the central potential (Benítez-Llambay et al. 2019). These features are all present in the SMUGGLE treatment but not in the SH03-like models, explaining why core formation is achieved in SMUGGLE but not in previous ISM treatments in arepo.
Fig. 4 shows the time-averaged gas density distribution within 1 kpc for each run. This distribution is calculated with equal logarithmically spaced bins between |$\rho _\text{gas}=10^{-6}\, \text{cm}^{-3}$| and |$\rho _\text{gas}=10^{6}\, \text{cm}^{-3}$| at each snapshot. The median gas density is then calculated for each bin to construct the final gas density distribution, with standard deviation about the median shown as shaded regions.
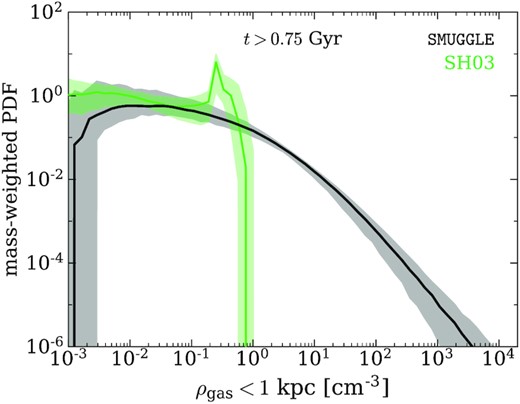
Median mass-weighted probability density function of gas density for t > 0.75 Gyr for the inner 1 kpc, with shaded regions representing the 68 per cent confidence interval in each ρ bin. The fiducial SMUGGLE run is able to achieve gas densities of >103 cm−3, while SH03 is unable to obtain densities >1 cm−3. The higher densities achieved by SMUGGLE allow its gas to gravitationally influence the DM to a stronger degree than in SH03.
As a result of the molecular cooling and other physics modeled in SMUGGLE, the typical gas densities achieved in SMUGGLE can be several orders of magnitude higher than in SH03. This run results in very few gas particles denser than ρ = 1 cm−3 (green curve) while about half of the gas in the SMUGGLE run is above that threshold and up to ∼104 cm−3. The high gas densities achieved by SMUGGLE are instrumental in gravitationally perturbing the DM to create cores, while the wide range of densities reached in the inner 1 kpc indicates repeated disruption of dense gas from feedback in central star forming regions, maintaining a multiphase nature that compares well with observations of real galaxies. While models based on an equation-of-state ISM treatment might be able to reproduce and predict statistical properties of galaxy populations as well as large-scale structure with remarkable success (e.g. Marinacci et al. 2014; Vogelsberger et al. 2014a; Schaye et al. 2015; Sawala et al. 2016; Grand et al. 2017; Pillepich et al. 2018), they cannot capture the interplay between DM and baryons on small scales, where the contribution of baryons to the gravitational potential is significant.
4 THE EFFECT OF THE ISM MODEL PARAMETERS
4.1 Variations on SMUGGLE
In addition to the fiducial SMUGGLE model and SH03, we have run three simulations using the same initial conditions with variations on key parameters in the SMUGGLE ISM model: (i) rho0.1 reduces the star formation gas density threshold1 from the fiducial value of ρth = 100 cm−3 to ρth = 0.1 cm−3 to mimic the value used in simulations such as SH03 and EAGLE (Vogelsberger et al. 2013; Crain et al. 2015, respectively); (ii) eSF100 increases the star formation efficiency from the fiducial value of εsf = 0.01 to εsf = 1 to compare with FIRE (Hopkins et al. 2018); and (iii) vareff, which parametrizes εsf (see Section 2.1.4, equation 1) to maximize star formation in dense, self-gravitating gas clouds. Table 1 summarizes these runs and their key features.
Fig. 5 shows time-dependent properties of the variations on SMUGGLE, with the original two runs shown in faded, thin lines. The core radius and slope are shown in Panels (a) and (b). We find that all SMUGGLE runs form clearly defined cores, with shallow slopes and core sizes larger than demonstrated in SH03. We find that time-averaged (t > 0.75 Gyr) values of rcore vary from 275 to 400 pc in extent, with slopes of α = −0.07 ± 0.06. This is within the range of core sizes observed for dwarf galaxies in the literature, with typical values of α = −0.2 ± 0.2 (de Blok et al. 2001; Oh et al. 2011, 2015).
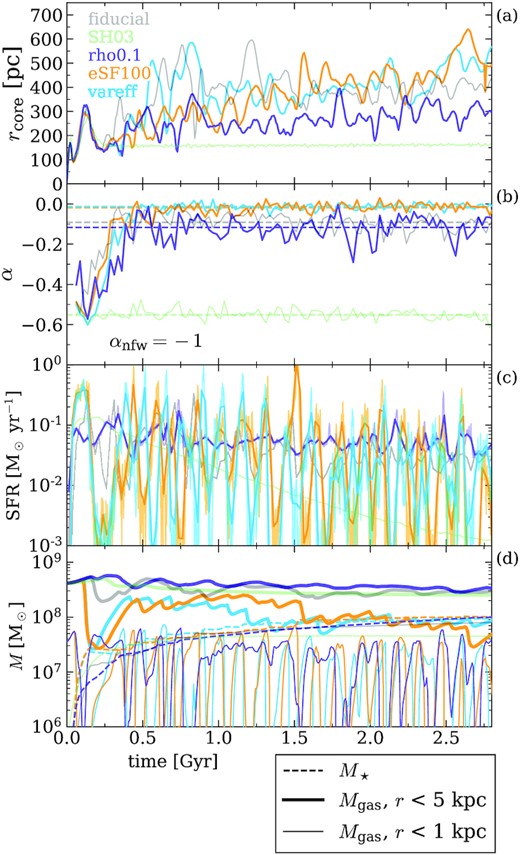
Selected properties for rho0.1 (purple), eSF100 (orange), and vareff (blue), as in Fig. 3, including faint lines for fiducial and SH03. All variations on the SMUGGLE model are able to form flattened DM cores between approximately 250–400 pc in extent and with α ∼ −0.1–0. rho0.1 shows the least bursty SFR of the SMUGGLE runs, while both eSF100 and vareff have SFRs that are significantly burstier than the fiducial SMUGGLE model. Remarkably, all SMUGGLE runs converge in M⋆ within ∼20 per cent, despite differences in SFR and gas content. The effect of different SFRs can be seen in the bottom panel as sharp jumps in M⋆ and decreases in Mgas (outflows), or the lack thereof. We see that the high efficiency runs undergo repeated outflows, slowly depleting their gas reserves, while fiducial, rho0.1, and SH03 retain a majority of their original gas content.
We find variation between the different SMUGGLE runs. The low threshold rho0.1 forms the smallest rcore, as expected, though much more of a robust core than the mild expansion seen in SH03. Interestingly, the high efficiency run eSF100 appears to form its core slower than fiducial, but ends up with a larger core by the final time. The variable efficiency run vareff forms its core early on – similar to fiducial – but continues to grow at later times. These variations, however, are relatively minor. The primary distinction between the fiducial SMUGGLE model and its two increased efficiency variations appears to the continued growth of the core over time as a result of the sustained burstiness of their star formation. This is likely due to the increased energy injection into the ISM via the efficient star formation and SN feedback. That is, a much higher fraction of gas that is eligible to turn into star particles is converted. For contrast, the fiducial SMUGGLE model only turns ∼1 per cent of the eligible gas into stars (on an average, not per-particle basis), in accordance with observations of GMCs (Smith et al. 2018). These strong blow-outs represent a somewhat different, more violent mode of core formation than exhibited in the fiducial run, which experiences smaller, more frequent outbursts. Convergence among runs to universally shallow slopes is notable. However, we do still observe that the higher efficiency runs eSF100 and vareff form slightly shallower cores with α ∼ −0.03, while rho0.1 and fiducial form cores with α ∼ −0.1.
Panels (c) and (d) of Fig. 5 show the SFR, stellar mass, and gas mass versus time for all runs. The SFRs we observe in the new SMUGGLE models are within expectation. The rho0.1 run maintains a higher average SFR due to a lower ρth, which effectively increases the amount of gas that is eligible for SF at any given time-step. Meanwhile, the higher efficiency runs see extremely bursty star formation histories due to a cycle of intense star formation, feedback that blows gas out of the inner regions, and re-accretion of gas to eligible SF densities. Despite these differences in star formation, we find excellent convergence in M⋆ for all SMUGGLE runs, with all runs reaching a final value within ∼20 per cent of one another.
However, we do find differences in gas content and nature of outflows between these runs. We see that rho0.1 retains more of its gas within 5 kpc than fiducial while also undergoing fewer and shallower outflows (seen as dips in the gas mass). In stark contrast, the highly efficient runs lose a majority of their initial gas content by the end of the simulation, undergoing frequent and larger outflows than either rho0.1 or fiducial, retaining only ∼20 per cent of their original gas mass by t = 2.0 Gyr h−1.
Fig. 6 shows the DM velocity dispersion for all runs, averaged over the final 0.5 Gyr of the simulations. We find results roughly as expected: the velocity dispersion of SH03 is consistent with a cuspy NFW profile, while the SMUGGLE runs form ever-flatter inner profiles, approaching the constant-σ signature of an isothermal profile with the higher efficiency runs, as expected from self-interacting DM models (Vogelsberger et al. 2012; Rocha et al. 2013; Tulin & Yu 2018; Burger & Zavala 2019).
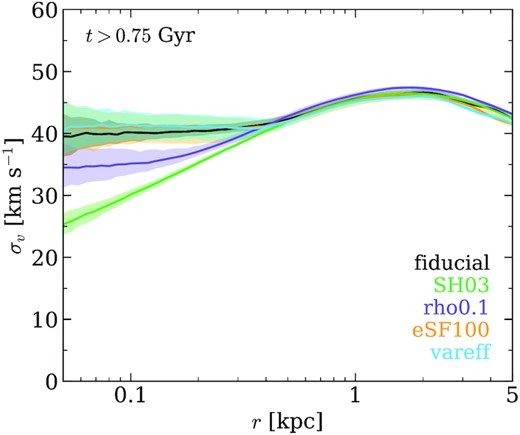
Time-averaged DM velocity dispersion profiles for each run. We find that the high efficiency variations on SMUGGLE approximately reproduce an isothermal (constant σv) core in the inner regions, while the SH03 run produces a decreasing profile similar to an NFW.
While it is interesting to see isothermal velocity dispersion profiles generated as a result of baryonic feedback, these results are not identical with expectation from SIDM. For example, profiles in SIDM are isothermal to much larger radii, then immediately decline, whereas the contribution from baryons results in a sizable bump at intermediate radii with a smoother tail. This may a possible avenue to distinguish SIDM from baryonic feedback (Fitts et al. 2019). Additionally, the isothermal profiles seen in the SMUGGLE runs demonstrate that they are not in dynamical equilibrium, an effect we discuss in Section 5.2.
As discussed previously, examining average gas densities can be a useful exercise to understand the behaviour of both the DM and the baryons. Fig. 7 shows the same time-averaged gas density calculation as Fig. 4, but for all runs, including shaded regions for standard deviations.
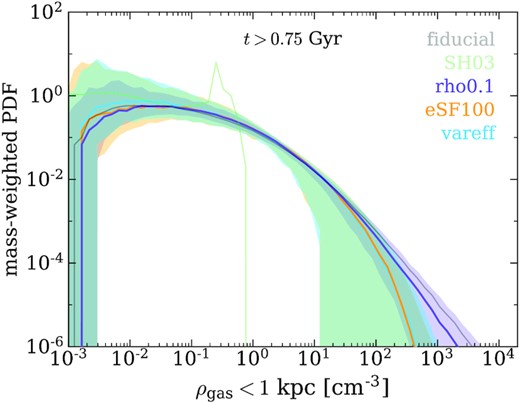
Median gas density distribution for each run over the run time of the simulation after t = 0.75 Gyr, with shaded regions representing the 68 per cent confidence interval in each ρ bin. Both fiducial and rho0.1 are able to produce an ISM with a substantial fraction of the gas above their star formation thresholds, while the median gas densities achieved by eSF100 and vareff demonstrate a more rapidly decreasing high density tail. This is a result of different star formation efficiencies: in the high efficiency runs, gas that reaches ρth is quickly turned into stars, while low efficiency preserves a component of highly dense gas.
Interestingly, we find that rho0.1 is able to produce gas densities well above its star formation threshold of ρth = 0.1 cm−3, with an almost identical distribution to fiducial, though slightly favoring lower densities. In contrast, the runs with higher efficiencies (eSF100 and vareff) are limited to gas densities at or near the standard value of ρth = 100 cm−3, with slightly lower values in the fully efficient eSF100 than in the selectively efficient vareff. The changes in the high-density tail between fiducial SMUGGLE model and eSF100 are consistent with results from Li et al. (2020), who investigated the effects of this parameter on GMCs in MW-mass galaxies.
4.2 The role of modelling parameters
As discussed in Section 3, we find that the same isolated galaxy setup run with the SH03 feedback model does not form cores due to its relatively low density gas and its lack of bursty star formation. It is generally claimed that these features are governed by the choice of ρth in the model. The clear differences between SH03 and rho0.1, both of which implement a low density threshold of ρth = 0.1 cm−3, demonstrate that the physics of core formation is dependent on factors beyond this parameter. This is consistent with the framework of Pontzen & Governato (2012), who suggested that rapid and repeated fluctuations of baryonic matter content in the inner regions of galaxies can gravitationally expand the DM core.
The physical differences between these runs is clear: rho0.1 has somewhat bursty star formation, dense gas, and SN-driven outflows of gas from the central regions, while SH03 has monotonically decreasing SFR, sparse gas, and no discernible feedback-driven outflows. If both runs implement ρth = 0.1 cm−3 yet achieve such different outcomes, other differences in subgrid physics must be to blame. The unstructured ISM of the SH03 feedback model is a result of its conception as a model for large-scale structure simulations, and is not particularly well suited for studying small-scale structures of galaxies and their haloes, such as DM cores. The detailed ISM model implemented in SMUGGLE is able to achieve much higher gas densities, resolving multiple physical gas phases at smaller scales, as well as achieving the bursty star formation necessary to form cores.
The difference in density achieved by these two runs (Fig. 7) therefore points to two facts: (1) the physical gas density achieved by a simulation is not solely governed by ρth, especially when using local star formation efficiencies lower than 100 per cent and (2) gas density and star formation burstiness (which drive outflows and subsequently core formation) are a product of the subgrid physics model as a holistic enterprise, including processes such as cooling physics and self-shielding, as well as resolution to the extent that such processes are resolution-dependent, rather than any individual parameter. However, changes in relevant parameters, as demonstrated here and in many other works, (e.g. Pontzen & Governato 2012; Benítez-Llambay et al. 2019; Burger et al. in preparation) do indeed produce observable differences within the same overall modelling scheme.
In their seminal work, Pontzen & Governato (2012) compare cosmological zoom simulations run with the SPH gasoline code (Wadsley, Stadel & Quinn 2004; Stinson et al. 2006) run with two different value of ρth, corresponding to our fiducial value of ρth = 100 cm−3 and a low threshold run with ρth = 0.1 cm−3, as in our rho0.1 run. They find that the low threshold run does not form a core, yet the high threshold run does, comparing the same overall ISM model in both cases. They point out that fluctuations in potential result in the expansion of the orbits of DM particles in the inner halo. We emphasize in this discussion that it is the ability of a model to create these physical density fluctuations that matters in producing DM cores.
As noted by Benítez-Llambay et al. (2019), it is indeed surprising that few systematic tests of the star formation density threshold have been conducted by this time. The authors investigate the effect of a variety of values for ρth spanning 0.1 cm−3 up to 640 cm−3 for cosmological haloes in the EAGLE simulations (Crain et al. 2015). They find that core formation is maximized for values between 1 and 160 cm−3, but find smaller cores for smaller values of ρth due to the lack of gravitationally dominant gas, and also for larger values due to the inefficiency of EAGLE’s feedback model in this regime. They identify that core formation in dwarf galaxies is not sufficiently explained by either burstiness of star formation or strong outflows of gas within the EAGLE model. Instead, they point to features in the SFH of different haloes that produce differences in outcomes of core sizes.
A similar investigation, though over a smaller range of threshold values, was conducted by Dutton et al. (2019, 2020) for the NIHAO simulation project (Wang et al. 2015). They find that, of their haloes run with ρth = 0.1, 1, and 10 cm−3, only those with ρth = 10 cm−3 and stellar mass to halo-mass ratio of 0.1–1 per cent underwent strong expansion, in agreement with the trend pointed out in Di Cintio et al. (2014). Further, they identify that variability in star formation feedback must occur at sub-dynamical time-scales to produce expansion of the DM halo.
In the case of gasoline, a change in density threshold was able to predictably alter the outcome of core formation. The picture is somewhat more complex for EAGLE and NIHAO, which find that core formation, while increasing with ρth, is further dependent on SFH, time-scale of burstiness, and halo mass, among other things. All these studies examined cosmological simulations. Our idealized numerical experiments seek to eliminate the complexities of cosmological runs, which produce substantial halo-to-halo variations in M⋆/M200, SFH, merger histories, gas fractions, etc. These are all important factors in understanding the diversity of observed galaxies, but can serve to obscure the impact of modelling choices.
Our idealized SMUGGLE runs produced cores for both the fiducial threshold of ρth = 100 cm−3 and the lowered threshold of ρth = 0.1 cm−3, though rho0.1 did produce a somewhat smaller core radius (∼300 pc, versus ∼400 pc for the fiducial run). When compared to the cuspy profiles of SH03, the core size within these two variations of SMUGGLE can be considered quite similar. This similarity in core size and shape between the two SMUGGLE variations makes sense in light of their achieved physical gas density distributions (Fig. 7) versus the highly truncated distribution of SH03, which is incapable of producing ρgas ≳ 1cm−3. With an initial mean DM density of ∼ 4 mp cm−3 within 1 kpc, it is clear that, even if SH03 produced fluctuations in gas mass within this region, it would be insufficient to perturb the DM potential.
Another factor that impacts the physics of core formation is the ability of the gravity solver to resolve the free-fall time-scale of gas in the centermost star-forming regions of the galaxy. When larger softening lengths are used, the collapse of gas into dense clouds is delayed, and the resulting star formation process will be smoothed out. This leads to fewer discrete star formation events, and a reduction in both the burstiness of star formation and maximum gas density achieved in star forming regions, limiting the growth of cores.
We emphasize that it is the ability of a model to produce both sufficiently dense gas and sufficient variation in baryonic mass in the inner regions of a halo that will allow it to form cores. The ability of ρth to affect these physical phenomena depends (i) on how the chosen modelling prescriptions modulate the effect of that parameter on star formation, (ii) on how energy injection and dissipation distribute energy throughout the ISM, and (iii) on the interplay between resolution and all of the above. In short, the precise role of ρth in core formation is model-dependent. For example, SMUGGLE produces similar inner gas density distributions regardless of the adopted value of ρth, and forms a feedback-induced core in all our explored variations. While the density threshold parameter is a commonly used parameter in ISM models, making it an appealing avenue for study, more attention must be given to the differences between modelling prescriptions with respect to their resulting physical properties (such as the gas density distribution and fluctuations in baryonic mass) before the effects of individual parameters can be understood in proper context.
For example, most treatments of star formation use relatively low values when implementing fixed local star formation efficiencies: εsf = 0.01–0.1 (Stinson et al. 2006; Wang et al. 2015). As in our rho0.1, the density threshold is therefore not necessarily an accurate tracer of the actual density achieved by the gas. The actual distribution of gas density will depend more complexly on modelling prescriptions (i.e. realistic versus effective cooling treatments) when using εsf ≪1. For this reason, comparing simulations run with distinct modelling treatments but similar ρth does not make sense when considering the dependence of core formation on ρth, as the resulting distribution of gas density and its sensitivity to feedback can vary substantially between models.
5 GALAXY STRUCTURE
Fig. 8 shows face-on and edge-on projections of the four alterations of the SMUGGLE model we consider, with the stellar half-mass radius (rh⋆) shown in green and rcore shown in magenta. The SH03 model shows a uniform disc with an unstructured ISM, along with large rh⋆ and small rcore, while fiducial and rho0.1 show a much more structured ISM, with clear fragmentation containing regions of both dense and rarefied gas. In addition, small pockets representing SN shock fronts can be seen in the face-on image. The disc remains well-behaved, with clear rotation and a roughly even distribution of gas throughout the disc. The ISM of fiducial is somewhat less evenly distributed than rho0.1, resulting in larger pockets of dense and rarefied gas, with an overall more centrally concentrated ISM (as seen in the edge-on projections), though it does maintain a disc morphology with clear cohesive rotation. Conversely, both eSF100 and vareff have highly disturbed gaseous components with no clear rotation and strong radial outflows from more energetic SN feedback. Even the edge-on projections show little traditional disc structure, with the galaxies appearing irregular in structure. In addition, they are much more compact, with rh⋆ roughly half the size of those of SH03 or rho0.1. The core radii of the three SMUGGLE models are larger than that of the SH03 model (as shown previously).
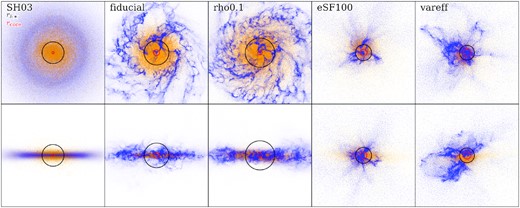
Face-on (top row) and edge-on (bottom row) projections of stars (orange) and gas (blue) for all runs. We only include star particles that were formed after the simulation began, not the old disc and bulge components from the initial condition. Each panel edge is 15 kpc in length, with the half stellar mass radius rh⋆shown in black (again, only new stars), and the core radius rcore shown in red. Both the fiducial run and rho0.1 maintain fairly well behaved discs, though with somewhat more disturbance and fragmentation in fiducial as well as a more compact distribution of stars, while rho0.1 has a more extended stellar distribution with a smaller core radius. Both eSF100 and vareff show a highly disturbed ISM, with gas extending much further in the z-direction (perpendicular to the disc). Both galaxies have more compact stellar distributions than the fiducial run.
5.1 Morphology and cores
Fig. 9 shows the core radius versus the half stellar mass radius for each run at t > 0.75 Gyr. We find a fair degree of stratification of the runs with rh⋆, indicating the effects of different modelling choices on galaxy structure. The variable efficiency run demonstrates the most compact galaxy size overall, mostly hovering aroung rh⋆ = 1 kpc. This concentrated morphology is a result of the maximized star formation efficiency in dense regions (which tend to be near the centre of the galaxy) used in this model. The globally maximized star formation efficiency in eSF100 produces a more concentrated galaxy than the fiducial SMUGGLE model, though it also has more variation. This run experienced a large burst of star formation at early times, expanding the initial galaxy, only contracting at later times. This expansion and contraction are seen in the orange dots that extend to the right of rh⋆ = 1.5 kpc, overlapping somewhat with our largest galaxy, rho0.1.
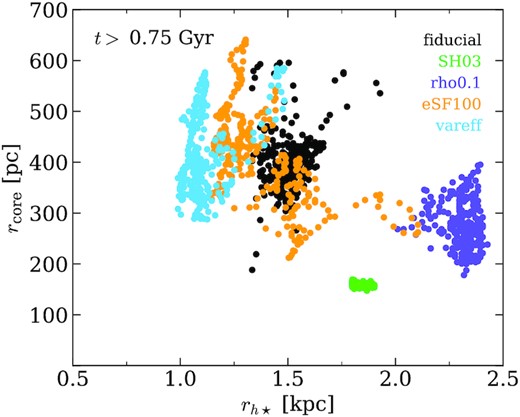
Core radius versus stellar half-mass radius for each run, with each point indicating a different snapshot after t = 0.75 Gyr. As in Fig. 8, rh⋆ only includes star particles that were formed after the simulation began. Naturally, SH03 forms the tightest grouping, while the SMUGGLE runs are stratified according to galaxy size. It is a clear consequence of vareff’s prioritization of star formation in dense gas that it forms the most compact galaxy, while the global high efficiency of eSF100 produces large fluctuations in galaxy size (and core radius). The low threshold of rho0.1 allows for less dense gas in the outer regions to form stars, resulting in a more extended galaxy.
Interestingly, the large core sizes and compact galaxies seen in eSF100 and vareff are contrary to the observed trend in which large cores are expected in low surface-brightness galaxies (Santos-Santos et al. 2020). This may indicate that cores can form in high surface brightness galaxies, but have not yet been detected (either due to incompleteness or the disruption of gas kinematics in systems that may mimic these runs), or it may indicate that high star formation efficiency is not an empirically consistent modelling choice. The latter may be more likely, since most ISM treatments that calibrate this parameter to observed data choose values in the range 0.01–0.1 (Stinson et al. 2006; Wang et al. 2015), while models that implement such high efficiencies have other strict criteria on star formation (Hopkins et al. 2014). Again, the effect of this parameter is indeed model-dependent. At least within SMUGGLE, an increased local SF efficiency parameter produces a trend counter to what is currently expected from observational data.
The large extent of rho0.1 is a result of the reduced density threshold, which allows more rarefied gas in the outskirts of the galaxy to form stars, rather than concentrating star formation to the dense gas which collects near the centre. The fiducial SMUGGLE model balances each of these effects, producing an intermediate-size galaxy, with rh⋆ ≈ 1.5 kpc throughout its evolution. Each SMUGGLE model produces variation in both the core size and stellar half-mass radius. The SH03 model on the other hand maintains the same core radius and galaxy size throughout its evolution, forming a tight cluster of points. We note again that SH03 did not form a robust feedback-induced core. We include the data here only for contrast with our SMUGGLE runs which did form robust cores.
The variation in both core size and half stellar mass radius is worth noting. Observed galaxies can effectively only be measured at one point in their evolution. While a large sample of observed galaxies helps to sample the variation, it is still impossible to take into account the variation in these properties over a given galaxy’s lifetime. It is certainly possible that extreme values of inner DM density from highly overdense cusps to underdense cores represent local maxima or minima in their fluctuations. We emphasize that a given observation is not necessarily representative of the property’s expectation value. Numerically constraining the predicted fluctuation in such properties like DM core sizes may be a worthwhile addition to the discussion on diversity of rotation curves.
To quantify differences in the kinematic structure between our runs, Fig. 10 shows time-averaged (for t > 0.75 Gyr) stellar velocity dispersion profiles in cylindrical coordinates, with σR (radial direction) on the top panel, σϕ (direction of disc rotation) in the centre, and σz (direction perpendicular to the disc plane) on the bottom panel. We see that all four SMUGGLE runs have higher σR than SH03. The grouping of models echos that of their density distributions in Fig. 7: fiducial and rho0.1 have similar σR profiles, and smaller than both eSF100 and vareff, which are also similar to each other. This is a natural result of their higher star formation efficiencies, which results in stronger feedback, disturbing the ISM and causing increased radial motion into the gas due to increase SN activity.
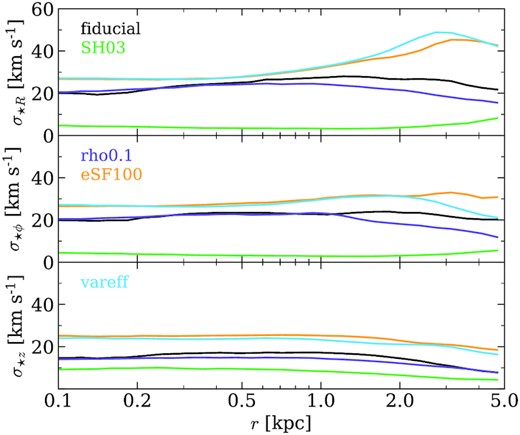
Time-averaged (t > 0.75 Gyr) stellar velocity dispersion σ⋆ in cylindrical coordinates. Standard errors are shown but appear smaller than the width of the lines. We find that SH03 preserves disc coherence better than the SMUGGLE models, which all produce stronger feedback that disrupts the rotational structure of the galaxy. The high efficiency variations distribute stellar motion more evenly between all three cylindrical components, indicating a dispersion-dominated galactic structure.
The centre panel shows σϕ, representing the rotation of the disc. We find a similar grouping of models as in σR, though decreased radial dependence as the values for σϕ remain roughly constant with radius. Rho0.1 and vareff show minor decreases in σϕ towards their outskirts, while the remaining models are more consistently flat. The increased σϕ in the high efficiency models indicates that circular motions in these models have been more disrupted than in the others, for example with SH03 showing near unity σϕ, indicating orderly rotation. The bottom panel shows σz, the velocity dispersion of stars in the azimuthal direction. While there is a minor decrease in σz towards outer radii, there is no significant radial dependence of this component. We observe the same model grouping as the other two components, indicating increased random motions in all directions for the high efficiency runs, and highly uniform motion in SH03.
5.2 Diversity of rotation curves
Fig. 11 shows the rotational velocity vϕ of the gas (thin dotted lines) as well as vcirc = |$\sqrt{\text{GM}(\lt r)/r}$| for each run, averaged over t > 0.75 Gyr for each run.
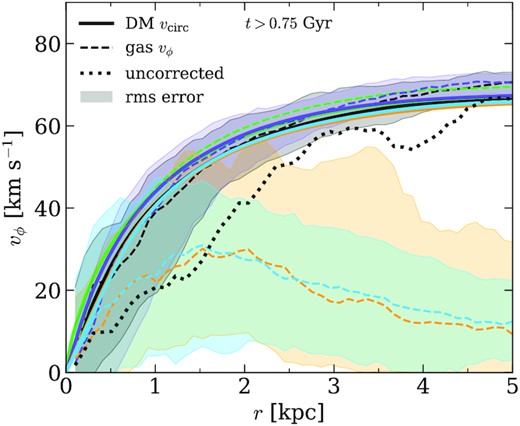
Median rotational velocity (vϕ) profile of gas (dashed line) and total circular velocity vcirc = |$\sqrt{\text{GM}(\lt r)/r}$| (solid line). We have corrected our baryonic velocities using the asymmetric drift correction as in Leaman et al. (2012). The uncorrected median vϕ profile is included for comparison and is shown as the black dotted line. Shaded regions represent the 1σ deviation from median (inner 68 per cent confidence interval) within each r bin across time. We see that the (relatively) well-behaved ISM of fiducial and rho0.1 trace the gravitational potential of the galaxy much better than the disturbed ISMs of eSF100 and vareff. The large shaded errors indicate substantial variations in rotational velocity profiles over the course of the simulation.
We find that the ISM of SH03 traces the potential of the galaxy remarkably well. In contrast, the high efficiency SMUGGLE runs eSF100 and vareff are so kinematically disrupted that there is little to no measurable rotation. El-Badry et al. (2018) found similarly dispersion-supported gas in dwarf galaxies within the FIRE simulations (Hopkins et al. 2018), and that rotational support increases with increasing mass. Further, they find that the majority of FIRE galaxies across 6.3 < log10(M⋆/M⊙) < 11.1 have little rotational support, and while the higher mass galaxies have morphological gas discs, only a fraction of the dwarf galaxies (M⋆ ≲ 109 Msun) host this feature.
It is notable that even within the ‘well-behaved’ variations on SMUGGLE, we find that the rotational velocity of the gas does not accurately trace the vcirc implied by the gravitational potential. A naive reading of the gas vϕ distribution in Fig. 11 could suggest a core radius of ≳2 kpc for the fiducial SMUGGLE model and rho0.1, while our method of core size measurement relying only on DM density profiles (see Section 3) results in values of a few hundred parsecs.
Corrected gas rotation velocity curves are now closer to the DM circular velocity profiles, but are systematically biased low in the inner regions supporting the presence of cores that are more pronounced and extended than those measured in the density profile of these systems. These results are in agreement with previous findings in the literature (e.g. Teyssier et al. 2013; Oman et al. 2019), and highlight the overall importance of a careful modelling of non-circular orbits and the need for higher order corrections of the gas motions in the inner regions of dwarf galaxies to recover their true mass distribution. Asymmetric drift corrections in eSF100 and vareff are insufficient to recover the true mass content in the inner regions of these galaxies.
The variability in the vϕ distribution indicates another problem of time sampling bias. The measured gas rotational velocity is subject to frequent and substantial variation as a result of energy injection via feedback, as depicted by the shaded regions on Fig. 11 representing the variation due to time-averaging. Measurements of the vϕ distribution taken at times which fall towards the extrema of this range could either produce rapidly rising rotation curves implying a mass distribution consistent with ΛCDM, or a slowly rising rotation curve implying an inner mass deficit and substantial core.
Fig. A5 plots the individual vϕ profiles for each snapshot of the fiducial SMUGGLE run over the final 0.5 Gyr. Here, we see that, while the majority of rotation curves are below the actual DM vcirc, there are a handful of profiles that demonstrate rotation speeds faster than the DM in the inner regions, i.e. profiles that would be interpreted as cuspy. Based on the number of snapshots with rotation curves that rise faster than an NFW, we place an upper limit on the presence of highly cuspy rotation curves at approximately 10 per cent. While this is an unlikely result, it indicates that cuspy profiles as a result of gas kinematics are indeed possible.
The discrepancy between the rotational velocity vϕ profile and the circular velocity profile vcirc indicates that the rotation of gas is not always a reliable tracer of the DM potential in dwarf galaxies due to its sensitivity to energy injection via feedback. Our simulations predict that a diversity of rotation curves should be expected within the same dwarf galaxy across time. The variability of gas content and velocity in the inner regions of the galaxy on time-scales ≲100 Myr poses a challenge to the assumption of virial equilibrium (i.e. ‘steady-state’) that underlies the inference of DM distributions from gas velocity profiles. As suggested by Read et al. (2016), expanding bubbles of H i can be used to identify post-starburst galaxies which are likely out of equilibrium. Collisionless stars may be a better tracer of the inner gravitational potential than gas.
While the fiducial and low-threshold SMUGGLE models produce rotational profiles that coincide on average with the DM circular velocity, the large degree of time-variability, including frequent under-estimation within inner regions, as well as the lack of consistency between gas kinematics and DM circular velocities in our high-efficiency runs are consistent with previous attempts to reconcile the observed diversity of rotation curves with baryonic physics (Oman et al. 2015, 2019; Read et al. 2016; Tollet et al. 2016; Santos-Santos et al. 2018, 2020). This indicates either that our understanding of small-scale ISM physics within galaxies is incomplete, or that another mechanism is responsible for creating rapidly rising rotation curves. It is possible that higher mass systems with stronger potentials are less susceptible to this effect, but we emphasize that this must be demonstrated explicitly rather than taken as an assumption.
The above considerations are only a result of ISM kinematics within an idealized, non-cosmological simulation and do not take into account additional bias introduced by observational measurement techniques, such as tilted-ring modelling and Jeans modelling, nor do they take into account evolutionary histories consistent with real galaxies or effects of cosmological environments such as mergers and infall of cold gas from filaments. Rather, these idealized tests isolate the effects of ISM modelling from other complex phenomena, allowing us to directly test the effects of baryonic feedback on the DM distribution of dwarf galaxies.
6 SUMMARY AND CONCLUSIONS
We study the behaviour of the SMUGGLE (Marinacci et al. 2019) feedback and ISM model for the arepo (Springel 2010) moving mesh simulation code. In particular, we investigate the formation of DM ‘cores’ in idealized (non-cosmological) dwarf galaxies with M⋆ ≈ 8 × 107 Msun and M200 ≈ 2 × 1010 Msun by comparing runs with identical initial conditions under both SMUGGLE and the SH03 model (Springel & Hernquist 2003), a precursor to the model used in Illustris and Auriga (Vogelsberger et al. 2014a; Grand et al. 2017) simulations, among others. We develop a self-consistent method of measuring the core radius to track its evolution over time. We define the core radius to be the location where the actual DM density falls below the predicted DM density of an NFW profile fit to the outer regions of the halo (r > 3 kpc) by a factor or 2 (Fig. 2). We then measure the slope of a power-law fit to the resolved region within the measured core radius. Tracing these metrics over time, we find that SH03 does not produce a constant-density DM core, while the fiducial SMUGGLE model creates a flattened core of radius ∼350 pc within the first 0.75 Gyr. We show that the origin of these cores is linked to the successful self-regulation of the star formation history in SMUGGLE which establishes a bursty star formation mode. These bursty cycles then create significant variations in the enclosed gas mass within 1 kpc, resulting in non-adiabatic expansion of the inner DM distribution. Contrary to the self-regulation seen in SMUGGLE, SH03 produces a steadily declining SFH, with a constant mass of gas reached after most of the originally eligible gas for star formation has been transformed into stars. This equilibrium state then preserves the steep inner density profiles that have been reported previously in the literature (Fig. 3). In addition, we run three simulations of identical initial set up including alterations to key feedback parameters: (i) rho0.1 changes the star formation density threshold from the fiducial value of ρth =100 cm−3 to a reduced value of ρth = 0.1 cm−3; (ii) eSF100 changes the local star formation efficiency (the mass fraction of eligible star-forming gas that is converted into stars) from the fiducial value of εsf = 0.01 to an increased value of εsf = 1; and (iii) vareff, which implements a parametrization of the star formation efficiency based on the virial parameter (a measure of local self-gravitation; see Section 2.1.4). We find that the formation of a core is robust to these changes in SMUGGLE (though rho0.1 does form an ∼25 per cent smaller core, and the high efficiency models exhibit stronger growth over time).
It is significant that rho0.1 forms a feedback-induced core while SH03 does not. Since both implementations use the same star formation density threshold ρth = 0.1 cm−3, this is an indication that the density threshold alone is not a good predictor of core formation for detailed ISM models such as SMUGGLE. It is important to note that while SH03 does not generate a core through feedback, it does experience a halo expansion due to relaxation effects and the influence of the baryonic component (Burger & Zavala 2021). Its expansion was smaller than in all SMUGGLE runs and was shown to be consistent with an adiabatic run, indicating that feedback was not a relevant factor. In contrast, rho0.1 demonstrates large fluctuations of baryonic matter in the inner regions of the halo, linking feedback to core formation. The density threshold for star formation is therefore not a sole indicator of whether cores can or not form in a simulation. While ρth might, in practice, be set as a free parameter in some codes, it is defined by the combination of numerical resolution and physics included in the run and should be set close to the highest possible value given the requirement of a resolved Jeans mass collapse (Governato et al. 2010; Pontzen & Governato 2012). We are able to drive outflows and core formation in SMUGGLE even using a density threshold as low as ρth = 0.1 cm−3.
Instead, we find that the ability to resolve dense gas (ρgas ≳ 102 cm−3; see Fig. 7) and its repeated gas inflow/outflow are more predictive of core formation, in agreement with findings from previous works (e.g. Teyssier et al. 2013; Chan et al. 2015; Read et al. 2016). For example, rho0.1 resolves gas up to ρ ∼ 104 cm−3 while SH03 only resolves gas up to ρ ∼ 1 cm−3. This indicates that the SF density threshold is not a good proxy for actual gas density when using low local star formation efficiencies εsf ≪1. This then allows the dense gas to linger around and affect locally the gravitational potential even if the density threshold for star formation is nominally low. Note that this is different from predictions in other ISM implementations, such as NIHAO (Dutton et al. 2019, 2020).
Our high efficiency runs eSF100 and vareff have more bursty star formation than fiducial or rho0.1, yet they do not form substantially larger cores (Fig. 5). This indicates that core size and burstiness are not tightly correlated, but that sufficiently bursty star formation, like sufficiently high gas density, are necessary conditions for core formation, as predicted previously (Pontzen & Governato 2012; Benítez-Llambay et al. 2019; Dutton et al. 2019). All SMUGGLE variations also demonstrate mild time-dependence over the course of our runs, indicating that core expansion should continue over cosmological time-scales. We hypothesize that the source of this continued expansion is the continued bursty star formation in these runs. The core evolution in the fiducial SMUGGLE run is inconclusive in its time-dependence due to the short runtime of these simulations. Density profiles of the SMUGGLE variations can be found in Fig. A3.
While there is broad agreement in core formation between the SMUGGLE variations, there are still differences between the models: rho0.1 forms the smallest core of the SMUGGLE models, with rcore ∼ 300 pc by final time, while vareff and eSF100 reach final core radii of ∼500 pc. Despite this difference, we maintain that rho0.1 does indeed form a comparable core due to its highly flattened inner slope consistent with the fiducial SMUGGLE model. Interestingly, the fluctuations in gas mass within 1 kpc for all SMUGGLE runs are comparable (though with rho0.1 having less frequent outflows). This is likely the source of the similarity in core sizes and shapes between the runs.
This similarity between variations of SMUGGLE indicates that the physical consequences of changing parameters such as the SF density threshold ρth are highly model dependent. As mentioned, ρth is not an accurate tracer of physical gas densities achieved by simulations when using empirically calibrated models that limit the local SF efficiency εsf to values ≪1. Local gas densities will be highly dependent on implementations of subgrid physics. In particular, molecular and fine-structure cooling allows gas to naturally reach temperatures far lower than 104 K and achieve densities comparable to or higher than the average density of DM in the inner regions. The implemented modes of feedback-driven energy injection into the ISM allow this dense gas to be disrupted and flow to outer regions of the halo, repeatedly perturbing the DM potential as suggested by Pontzen & Governato (2012). That is to say, changes in model parameters must result in the required physical changes within the simulation to accurately capture the details of baryon-induced core formation. Simulations that do not produce sufficiently dense gas (due either to modelling choices or resolution) are simply unable to follow the physics expected to lead to core formation.
We also investigate the implications various modelling choices have on morphology. The fiducial SMUGGLE model and rho0.1 both form rotationally supported discs with structured ISMs, while SH03 naturally produces a stable galaxy with featureless ISM (see Figs 8 and 10). On the other hand, the high efficiency models produce dispersion-dominated spheroid galaxies with lower gas fractions. This is a natural result of the increased burstiness and feedback of these models, and is in agreement with the FIRE simulations (Hopkins et al. 2018), which implement εsf = 1 and also observe dwarf galaxies with spheroid morphology and dispersion supported ISM (El-Badry et al. 2018). Interestingly, we find that the most compact galaxies (eSF100 and vareff) form the largest cores, while the most diffuse galaxies (rho0.1) form the smallest cores (Fig. 9), in agreement with Burger & Zavala (2021).
Our examination of the rotational velocity (vϕ) profiles of the gas content (Fig. 11) indicates that a careful modelling of the ISM kinematics is essential to recover the DM potential in the inner regions. Even when corrections such as asymmetric drift are applied the ability to trace the DM profile are ultimately susceptible to frequent disturbances induced by feedback induced time-variations indicating that measurements taken after recent starburst events may possess altered ISM kinematics that underestimate the DM potential.
This is true for all SMUGGLE variations, though the fiducial model and rho0.1 are better able to trace the DM vcirc on average, while eSF100 and vareff demonstrate almost no consistent rotational velocity at any radius. The significant variation in the vϕ profiles across time suggest that a diverse morphology of rotation curves can be observed at different times within the same galaxy. We find that individual vϕ profiles can vary between exceeding the expected DM circular velocity and drastically underestimating it (Fig. A5). The lack of consistent tracing of the DM profile by gas kinematics in our SMUGGLE galaxies is in agreement with previous work (Oman et al. 2019; Santos-Santos et al. 2020), further indicating that the baryon-induced core formation scheme struggles to reproduce the steep end of the diversity of rotation curves problem.
Our analysis indicates that feedback-induced core formation is fundamentally a small-scale problem. Its effects may be observed on the scale of a few kpc, but the physics which generates these observables occur on the scales of star formation and feedback, i.e. 10–100 pc, as well as sub-pc processes that are yet unresolved and only implemented through sub-grid modelling. Lack of cores in models which are not able (and do not attempt) to produce this microphysics is not evidence against the validity of baryon-induced core formation, but evidence against the suitability of such models to study this process.
Finally, our results suggest that even if perfect observations of gas rotation curves are obtained, these do not necessarily trace the DM potential in non-equilibrium systems such as dispersion-dominated dwarf galaxies. Caution is needed when attempting to infer DM distributions from gas rotation. It is important to investigate the assumption of equilibrium for dwarf galaxies, whose small sizes make them susceptible to large fluctuations in gas content and kinematics.
ACKNOWLEDGEMENTS
The authors would like to thank the referee of this article for insightful and constructive comments that helped improve the first version of this draft. EDJ and LVS acknowledge support from the NASA ATP 80NSSC20K0566, NSF AST 1817233, and NSF CAREER 1945310 grants. FM acknowledges support through the program ’Rita Levi Montalcini’ of the Italian MIUR. MV acknowledges support through NASA ATP grants 16-ATP16-0167, 19-ATP19-0019, 19-ATP19-0020, 19-ATP19-0167, and NSF grants AST-1814053, AST-1814259, AST-1909831, AST-2007355, and AST-2107724. PT and JQ acknowledge support from NSF grants AST-200849. PT acknowledges support from NASA ATP grant 80NSSC20K0502. AS and HL acknowledge support for Program numbers HST-HF2-51421.001-A and HST-HF2-51438.001-A provided by NASA through a grant from the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Incorporated, under NASA contract NAS5-26555. JB acknowledges support by a Grant of Excellence from the Icelandic Center for Research (Rannís; grant number 173929) JZ acknowledges support by a Grant of Excellence from the Icelandic Research fund (grant number 206930).
DATA AVAILABILITY
The data that support the findings of this study are available from the corresponding author, upon reasonable request.
Footnotes
The H2 star formation requirement discussed in Section 2.1 was lifted to allow the density threshold to take full effect.
REFERENCES
APPENDIX A: ADDITIONAL MATERIAL
To demonstrate the resolution convergence of the SMUGGLE model, Fig. A1 shows our standard high resolution run with mbary = 850 Msun compared to a run at 10 times lower resolution (mbary = 8500 Msun). We find good agreement in all measured quantities. The lower resolution run demonstrates marginally less bursty star formation rates. We also find stronger time dependence in the measured core radius and power-law slope in the lower resolution run, but good agreement in values for these quantities across the run time. A notable similarity between the runs is their rapid fluctuations in gas mass within 1 kpc.
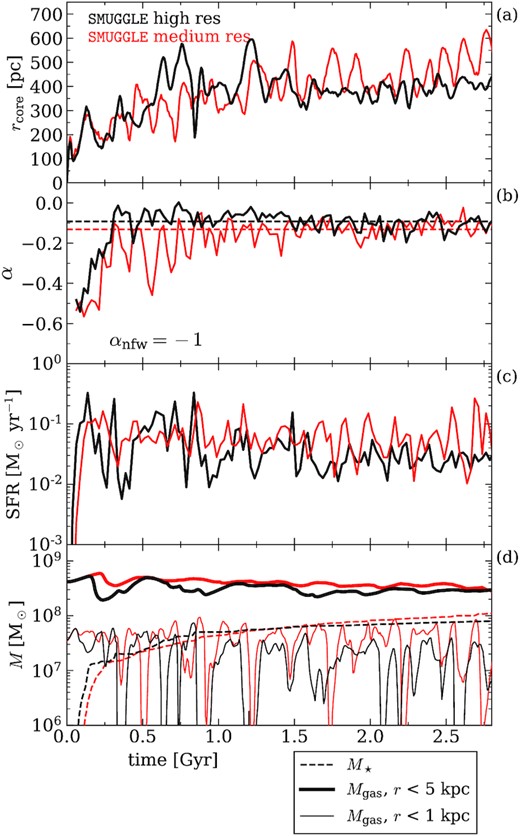
Comparison between the fiducial SMUGGLE model ran at our presented resolution of mbary = 850 Msun (high res), and at a 10 × lower resolution of mbary = 8500 Msun (medium res).
Fig. A2 shows the measured values of core radius and inner power-law slope for the fiducial SMUGGLE model with different values of radial cutoff for the fitted NFW profile (see Section 3.1). We find that the measured values of rcore and inner slope α are robust to choice of NFW radial fitting cutoff in the range 1–10 kpc.
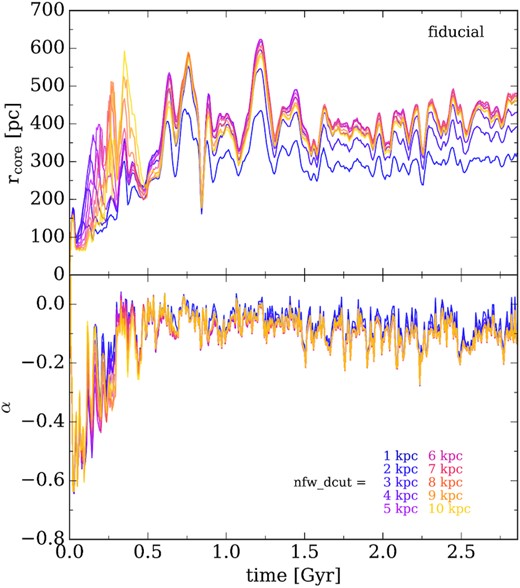
Comparison of the core radius and slope measured using NFW reference profiles fit to r > nfw_dcut, as listed on the figure. We find that our measurements are robust to choice of this parameter.
Fig. A3 depicts density profiles for the three SMUGGLE variations we explore in Section 4.1, similar to Fig. 2. Each panel shows a different timestamp of the simulation, including the final snapshot in the rightmost panel. The bottom panels, as in Fig. 2, show the ratio of densities of the fitted NFW profile to the physical DM density achieved in the simulation. The NFW profile is fitted to r > 3 kpc, and the core radius is chosen as the radial distance where ρNFW = 2ρdm. The core radius is depicted as a vertical dashed–dotted line, and its value at each timestamp is listed on the bottom panels. We find that eSF100 and vareff, models with increased local star formation efficiency, demonstrate large, flattened core. Our run with density threshold of ρ = 0.1 cm−3 (rho0.1), forms a core that is somewhat smaller than those of the high efficiency runs, though it is still consistent with the fiducial SMUGGLE model, and clearly distinct from the lack of core found in SH03, as discussed in Section 4.1.
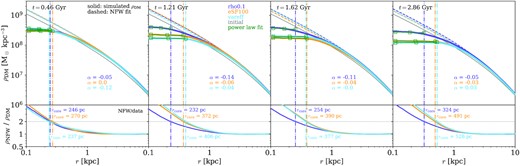
DM density profiles at select times for the runs with variations in the ISM model of SMUGGLE. Dashed lines indicate NFW profiles fit to the run of the corresponding colour. Power-law fits are shown as dark green square, and the core radius is indicated with a vertical line.
Fig. A4 plots the same density profiles as shown in Fig. 2, but instead we fit a pseudo-isothermal sphere model. We note that this model performs well in fitting cored DM profiles as in the third and fourth panels, but reports a core radius that is numerically larger than the physical extent of the region where the DM density remains constant.
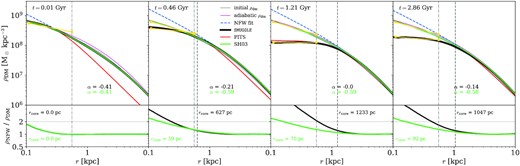
DM density profiles at the same select times as reported in Section 3. Here, we fit a pseudo-isothermal sphere model and core radius rather than the measuring the core radius using the method described earlier. We find that, despite matching the physical DM density profile when a core is present (e.g. panels 3 and 4), the numerical core radius parameter produced by this model does not match the characteristic ’flattened’ region of DM density.
We plot the rotational velocity profiles of gas for both the fiducial SMUGGLE model and SH03 (Springel & Hernquist 2003) for each snapshot of the final 0.5 Gyr of run time in Fig. A5, corrected by asymmetric drift following equation (3). The median gas vϕ profile for all models is shown in Fig. 11. We plot these individual profiles to explicitly show the variety of shapes that can be produced through feedback effects on the gas in SMUGGLE, and the uniformity of profiles achieved in SH03. We find that a handful of profiles (no more than 10 per cent) demonstrate steeply rising inner velocity profiles, suggesting that baryonic feedback can account for some of the observed diversity of rotation curves. Overall, we find rotational velocity profiles that tend to underestimate the circular velocity (thicker lines). These rotational profiles can also demonstrate strong fluctuations with radius, as well as time, indicating a gaseous component that is in a constant state of flux.
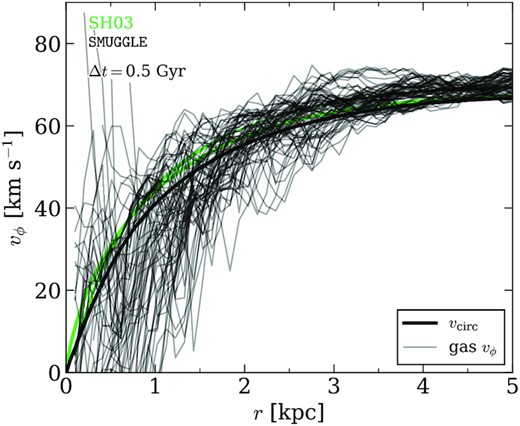
Gas rotational velocity profiles of the fiducial SMUGGLE model for each snapshot in the last 0.5 Gyr of its run time. Realistic modelling of ISM physics produces large variation in the rotational component of gas within the galaxy, leading to a large diversity of rotation curves.
Fig. A6 reports the core radius and power-law slope as determined by the pseudo-isothermal sphere model. As seen in Fig. A4, the value of core radii fit by this model is larger than that produced by our method as discussed in the main text, though the overall trend remains the same. We also find that the power-law slope appears slightly lower due to being fit to a higher radius. Due to the lower reported values of the core radius in the SH03 model, the fitted power-law slope appears more highly variable as it is being fit within a more narrow window.
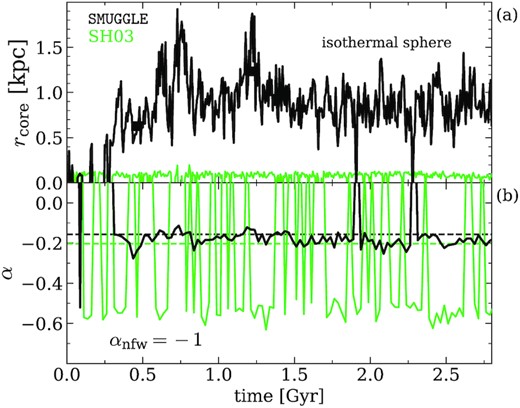
The core radius and power-law slope produced by fitting a pseudo-isothermal sphere model at each snapshot. We recover the same general trend as reported in Section 3, though with an increased value of reported core radii, and slightly decreased values of the power-law slope (likely due to being fit to a larger radius).
Author notes
NHFP Einstein Fellow.
NHFP Hubble Fellow.



