-
PDF
- Split View
-
Views
-
Cite
Cite
Gwenaëlle Dufour, Steven B Charnley, Johan E Lindberg, Oscillations in gas-grain astrochemical kinetics, Monthly Notices of the Royal Astronomical Society, Volume 520, Issue 1, March 2023, Pages 480–488, https://doi.org/10.1093/mnras/stad110
Close - Share Icon Share
ABSTRACT
We have studied gas-grain chemical models of interstellar clouds to search for non-linear dynamical evolution. A prescription is given for producing oscillatory solutions when a bistable solution exists in the gas-phase chemistry and we demonstrate the existence of limit cycle and relaxation oscillation solutions. As the autocatalytic chemical processes underlying these solutions are common to all models of interstellar chemistry, the occurrence of these solutions should be widespread. We briefly discuss the implications for interpreting molecular cloud composition with time-dependent models and some future directions for this approach.
1 INTRODUCTION
The systems of differential equations governing the kinetics of chemical reaction networks can exhibit a wide range of non-linear dynamical phenomena: limit cycles, complex oscillations and chaos can all emerge from stable stationary solutions, subject to variation of externally-controlled bifurcation parameters (Scott 1991; Gray & Scott 1996). One signpost of possible non-linear chemical kinetics is the presence of bistability in the stationary, steady-state, solutions (i.e. the fixed points) of the associated system of differential equations. In chemical systems, multistability can arise when autocatalysis is present, i.e. when one species, the autocatalyst, can take part in reaction sequences which promote its formation. When the stationary solutions become unstable a Hopf bifurcation emerges and limit cycle oscillations can occur.
In the simplest, purely gas-phase, chemical models of dense interstellar clouds, the chemistry is driven by cosmic-ray ionization of H2 and evolves to approach a steady-state on time-scales of typically |$\sim \rm few \times 10^6$| yr. In all cases the chemistry tends to follow well-defined evolutionary pathways and, when making comparisons with observed molecular abundances, it has become common to label this as ‘late-time’ chemistry. By contrast, ‘early-time’ chemistry occurs around |$\sim \rm few \times 10^5$| yr (Leung, Herbst & Huebner 1984a) and is strongly dependent on the initial conditions. The accretion and desorption of atomic and molecular material onto and from dust grains leads to the formation of molecular ice mantles. When desorption is inefficient, species can be completely lost from the gas (e.g. Leung, Herbst & Huebner 1984b); when desorption mechanisms can compete with accretion a quasi-steady-state can persist (e.g. Willacy & Williams 1993; Willacy & Millar 1998; Charnley, Rodgers & Ehrenfreund 2001). This occurs at a time-scale determined by the physical conditions such as the gas density, the grain-size distribution and the dust physics, but the quasi-steady-state is typically comparable to, or longer than, ‘early-time’ chemistry and shorter than ‘late-time’ chemistry. Hence, the possibility of oscillatory and chaotic solutions manifesting themselves would have major implications for modeling, interstellar clouds and astrochemistry in general.
The existence of bistable solutions in interstellar gas-phase chemistry has been recognized for some time (Pineau des Forets, Roueff & Flower 1992; Le Bourlot et al. 1993) and has been the subject of several studies (e.g. Le Bourlot, Pineau des Forets & Roueff 1995a; Le Bourlot et al. 1995b; Lee et al. 1998; Pineau Des Forêts & Roueff 2000; Viti et al. 2001; Charnley & Markwick 2003; Wakelam et al. 2006). This raises the prospect that oscillations and chaos could be common but heretofore unrealized solutions to well-studied chemical models. However, it is only recently that limit cycle oscillations have been reported.1 Roueff & Le Bourlot (2020) showed that sustained chemical oscillations, could occur in purely gas-phase models of dense molecular clouds. They found that the oscillations originated in the nitrogen chemistry for temperatures in the range T ≈ 7–15 K and was controlled by the H2 ortho/para ratio. Roueff & Le Bourlot presented an overview of the important chemical reactions in their model, identifying deuterium chemistry as an important component, but no underlying mechanism, such as emergence from a bistable state, was identified.
Dufour & Charnley (2019; Paper I) demonstrated that the known astrochemical bistable solutions have an autocatalytic origin in oxygen chemistry. Dufour & Charnley (2021; Paper II) further showed that autocatalysis and bistability can also occur in the nitrogen and carbon chemistry of dense molecular clouds. In each case, autocatalysis involves dimer-autocatalyst pairs: O2–O, N2–N, H–C2H2, with other autocatalytic cycles also being possible in carbon chemistry (e.g. C2–C). It is known that limit cycle oscillations can be induced in a bistable chemical system in which species crucial to autocatalysis are removed and re-introduced by an additional feedback process which occurs on a time-scale longer or comparable to that of the chemical reactions, i.e. the feedback renders the stationary solutions unstable (e.g. Sagués & Epstein 2003). In interstellar clouds, the exchange of atoms and molecules between gas and dust grains naturally provides this process.
The plan of this article is as follows. In Section 2 we summarize the mathematical structure of the model with respect to bistable gas-phase solutions and the gas-grain interaction. The parameters adopted in a reference chemical model are presented in Section 3. In Section 4 we show that introducing accretion and desorption of atomic and molecular oxygen into a simple reduced model of interstellar chemistry, with known autocatalytic pathways and bistable solutions, leads to chemical oscillations. We then show that oscillatory solutions are also present in more realistic models of dense cloud chemical evolution (Section 5). Extension of the modeling are briefly discussed in Section 6 and conclusions are given in Section 7.
2 THEORY
2.1 Bistable Solutions in gas-phase chemistry
The appearance/disappearance of bistable solutions is principally controlled by variation of the bifurcation parameters: the cosmic-ray ionization of H2 and He, through the ratios ζ/nH and ζHe/nH, the presence of cosmic ray-induced photons βcrp, the relative elemental depletions |$Y^{\rm T}_j$|, and the H|$_3^+$| electron recombination rate, |$\rm \alpha _3$| (Le Bourlot et al. 1993, 1995a; Lee et al. 1998; Pineau Des Forêts & Roueff 2000; Wakelam et al. 2006; Dufour & Charnley 2019, 2021).
2.2 Gas-grain interaction in cold interstellar clouds
2.2.1 Accretion
In dense clouds, electron sticking leads to negatively-charged grains dominating the dust distribution (Umebayashi & Nakano 1990). We assume that when atomic ions collide with grains they are neutralized and released into the gas. Molecular ions will not be affected by grain interaction as electron recombination is more efficient at the densities of interest. As shown in Paper I, only grain neutralization of |$\rm H^+$| and |$\rm S^+$| can affect bistable solutions. However, this requires both the total grain-surface cross-section and elemental S abundance both to have values that are far larger than those inferred for dense molecular clouds (see Table 1). The values adopted here exclude the possibility of ion-grain neutralization affecting the occurrence of bistable solutions.
| Hydrogen number density |$(\rm cm^{-3})$| | nH | 1.0 × 104; 1.0 × 105 |
| Cosmic ray ionization rate (|$\rm s^{-1}$|) | |$\zeta _{_ {\rm 0}}$| | 1.3 × 10−17 |
| Dust temperature (K) | Tgr | |$\rm see ~ text$| |
| Visual extinction (mag.) | AV | 10 |
| H|$_3^+$| electron recombination rate (|$\rm cm^{3}~s^{-1})\, ^\dagger$| | |$\alpha _{_{\rm 3}}$| | |$6.7\times 10^{-8} T_3^{-0.52}$| |
| Total dust cross-section (|$\rm cm^{2}$|) | |$D^{^{\rm 0}} _{\rm gr}$| | 10−22π |
| Gas temperature (K) | T | Tgr |
| Total elemental abundances: | |$Y^{\rm T}_{_ {\rm He }}$| | 0.14 |
| |$Y^{\rm T}_{_ {\rm O}}$| | 1.6 × 10−4 | |
| |$Y^{\rm T}_{_ {\rm C }}$| | 6.0 × 10−5 | |
| |$Y^{\rm T}_{_ {\rm N }}$| | 2.0 × 10−5 | |
| |$Y^{\rm T}_{_ {\rm S }}$| | 2.0 × 10−8 | |
| |$Y^{\rm T}_{_ {\rm Si }}$| | 0 | |
| |$Y^{\rm T}_{_ {\rm Na }}$| | 2.0 × 10−9 | |
| Surface binding energies (K)‡: | ||
| |$E_{_ {\rm O}}$| | 800 K | |
| |$E_{_ {\rm N}}$| | 800 K | |
| |$E_{_ {\rm C}}$| | 800 K | |
| |$E_{_ {\rm S}}$| | 1100 K | |
| |$E_{_ {\rm O_2}}$| | 1000 K | |
| |$E_{_ {\rm N_2}}$| | 790 K | |
| |$E_{_ {\rm CO}}$| | 1150 K |
| Hydrogen number density |$(\rm cm^{-3})$| | nH | 1.0 × 104; 1.0 × 105 |
| Cosmic ray ionization rate (|$\rm s^{-1}$|) | |$\zeta _{_ {\rm 0}}$| | 1.3 × 10−17 |
| Dust temperature (K) | Tgr | |$\rm see ~ text$| |
| Visual extinction (mag.) | AV | 10 |
| H|$_3^+$| electron recombination rate (|$\rm cm^{3}~s^{-1})\, ^\dagger$| | |$\alpha _{_{\rm 3}}$| | |$6.7\times 10^{-8} T_3^{-0.52}$| |
| Total dust cross-section (|$\rm cm^{2}$|) | |$D^{^{\rm 0}} _{\rm gr}$| | 10−22π |
| Gas temperature (K) | T | Tgr |
| Total elemental abundances: | |$Y^{\rm T}_{_ {\rm He }}$| | 0.14 |
| |$Y^{\rm T}_{_ {\rm O}}$| | 1.6 × 10−4 | |
| |$Y^{\rm T}_{_ {\rm C }}$| | 6.0 × 10−5 | |
| |$Y^{\rm T}_{_ {\rm N }}$| | 2.0 × 10−5 | |
| |$Y^{\rm T}_{_ {\rm S }}$| | 2.0 × 10−8 | |
| |$Y^{\rm T}_{_ {\rm Si }}$| | 0 | |
| |$Y^{\rm T}_{_ {\rm Na }}$| | 2.0 × 10−9 | |
| Surface binding energies (K)‡: | ||
| |$E_{_ {\rm O}}$| | 800 K | |
| |$E_{_ {\rm N}}$| | 800 K | |
| |$E_{_ {\rm C}}$| | 800 K | |
| |$E_{_ {\rm S}}$| | 1100 K | |
| |$E_{_ {\rm O_2}}$| | 1000 K | |
| |$E_{_ {\rm N_2}}$| | 790 K | |
| |$E_{_ {\rm CO}}$| | 1150 K |
†T3 = T/300 K
‡ For the most volatile species; McElroy et al. (2013).
| Hydrogen number density |$(\rm cm^{-3})$| | nH | 1.0 × 104; 1.0 × 105 |
| Cosmic ray ionization rate (|$\rm s^{-1}$|) | |$\zeta _{_ {\rm 0}}$| | 1.3 × 10−17 |
| Dust temperature (K) | Tgr | |$\rm see ~ text$| |
| Visual extinction (mag.) | AV | 10 |
| H|$_3^+$| electron recombination rate (|$\rm cm^{3}~s^{-1})\, ^\dagger$| | |$\alpha _{_{\rm 3}}$| | |$6.7\times 10^{-8} T_3^{-0.52}$| |
| Total dust cross-section (|$\rm cm^{2}$|) | |$D^{^{\rm 0}} _{\rm gr}$| | 10−22π |
| Gas temperature (K) | T | Tgr |
| Total elemental abundances: | |$Y^{\rm T}_{_ {\rm He }}$| | 0.14 |
| |$Y^{\rm T}_{_ {\rm O}}$| | 1.6 × 10−4 | |
| |$Y^{\rm T}_{_ {\rm C }}$| | 6.0 × 10−5 | |
| |$Y^{\rm T}_{_ {\rm N }}$| | 2.0 × 10−5 | |
| |$Y^{\rm T}_{_ {\rm S }}$| | 2.0 × 10−8 | |
| |$Y^{\rm T}_{_ {\rm Si }}$| | 0 | |
| |$Y^{\rm T}_{_ {\rm Na }}$| | 2.0 × 10−9 | |
| Surface binding energies (K)‡: | ||
| |$E_{_ {\rm O}}$| | 800 K | |
| |$E_{_ {\rm N}}$| | 800 K | |
| |$E_{_ {\rm C}}$| | 800 K | |
| |$E_{_ {\rm S}}$| | 1100 K | |
| |$E_{_ {\rm O_2}}$| | 1000 K | |
| |$E_{_ {\rm N_2}}$| | 790 K | |
| |$E_{_ {\rm CO}}$| | 1150 K |
| Hydrogen number density |$(\rm cm^{-3})$| | nH | 1.0 × 104; 1.0 × 105 |
| Cosmic ray ionization rate (|$\rm s^{-1}$|) | |$\zeta _{_ {\rm 0}}$| | 1.3 × 10−17 |
| Dust temperature (K) | Tgr | |$\rm see ~ text$| |
| Visual extinction (mag.) | AV | 10 |
| H|$_3^+$| electron recombination rate (|$\rm cm^{3}~s^{-1})\, ^\dagger$| | |$\alpha _{_{\rm 3}}$| | |$6.7\times 10^{-8} T_3^{-0.52}$| |
| Total dust cross-section (|$\rm cm^{2}$|) | |$D^{^{\rm 0}} _{\rm gr}$| | 10−22π |
| Gas temperature (K) | T | Tgr |
| Total elemental abundances: | |$Y^{\rm T}_{_ {\rm He }}$| | 0.14 |
| |$Y^{\rm T}_{_ {\rm O}}$| | 1.6 × 10−4 | |
| |$Y^{\rm T}_{_ {\rm C }}$| | 6.0 × 10−5 | |
| |$Y^{\rm T}_{_ {\rm N }}$| | 2.0 × 10−5 | |
| |$Y^{\rm T}_{_ {\rm S }}$| | 2.0 × 10−8 | |
| |$Y^{\rm T}_{_ {\rm Si }}$| | 0 | |
| |$Y^{\rm T}_{_ {\rm Na }}$| | 2.0 × 10−9 | |
| Surface binding energies (K)‡: | ||
| |$E_{_ {\rm O}}$| | 800 K | |
| |$E_{_ {\rm N}}$| | 800 K | |
| |$E_{_ {\rm C}}$| | 800 K | |
| |$E_{_ {\rm S}}$| | 1100 K | |
| |$E_{_ {\rm O_2}}$| | 1000 K | |
| |$E_{_ {\rm N_2}}$| | 790 K | |
| |$E_{_ {\rm CO}}$| | 1150 K |
†T3 = T/300 K
‡ For the most volatile species; McElroy et al. (2013).
2.2.2 Desorption
Thermal desorption is actually the most restrictive choice for this mechanism. ISM thermal physics in dark clouds predicts T ≈ Tgr, thus affecting λi through the T1/2 dependence, non-linearly coupling the desorption and accretion rates, and the bifurcations. This coupling does not occur for non-thermal desorption rates, |$\xi _{_{\rm NT}}$|. We briefly discuss other possible desorption mechanisms in Section 6.
2.2.3 Grain-surface reactions
Assuming that all accreted reactive species are instantaneously hydrogenated (e.g. C, CH, CH2, and CH3 become CH4; N, NH, and NH2 become NH3; O and OH become H2O; S and HS become H2S, (e.g. Brown & Charnley 1990) means that no desorption can occur and that there will be no non-linear feedback. As the gas-dust exchange of particles is accounted for by equations (3) and (4), the simplest approach is to neglect surface reactions. Our neglect of surface hydrogenation in particular will be justified a posteriori as we find that non-linear kinetic effects become important when Tgr ≈ 15 K and so H atom thermal desorption can be expected to suppress surface hydrogenation reactions (E|$_{ H}\, \approx$| 600 K). We return to this issue in Section 6.
3 CHEMICAL MODEL
Table 1 lists the physical parameters of the reference dense cloud model. We employ the same gas-phase chemical reaction network as in Paper II. The reactions are taken from the UMIST 2012 database (McElroy et al. 2013) and consists for 2001 reactions involving 136 chemical species containing H, He, C, O, N, S, Na, and Si atoms. Only photoprocesses resulting from cosmic-ray-induced photons are considered (Prasad & Tarafdar 1983). We only consider a single value for the H|$_3^+$| recombination rate |$\rm \alpha _3$| (cf. Paper I). The chemical evolution is solved by integrating the system of differential equations in Section 2.1 with all species initially present as atoms, except for H2.
3.1 Surface binding energies
For consistency, we have adopted the binding energies, |$E_{_ {\rm i}}$|, listed in the UMIST database (McElroy et al. 2013) for this initial study. Alternative compilations exist (e.g. Penteado, Walsh & Cuppen 2017) but we take the UMIST values as a reference for comparison with future studies. The binding energies of helium atoms and H2 molecules are so small that they do not stick to grains even at at the low temperatures of our models. For atomic C, O, and N we have taken the single value |$E_{_ {\rm i}} =800$| K, based on simple polarizability arguments (Tielens & Allamandola 1987), and so there is no difference in the desorption rates of these species that could complicate the analysis.
The UMIST |$E_{_ {\rm i}}$| values are consistent with recent calculations and experiments for O2, CO, N, and N2 (Penteado et al. 2017; Wakelam et al. 2017; Ferrero et al. 2020; Molpeceres, Zaverkin & Kästner 2020) but recent work indicates differences in the binding energies of C and O atoms. The influence of O atom binding energies on the models are discussed in Section 6. For C atoms, calculations by Shimonishi et al. (2018) indicate that they bind to water by chemisorption with |$E_{_ {\rm C}} \sim 16 \, 000$| K. Our results should not be particularly sensitive to the atomic C thermal desorption rate since the chemical evolution of interest in our models only begins at around the gas-grain accretion time-scale, at which point most of the initially abundant atomic C has already been incorporated into CO (after |$\sim \rm few \times 10^5$| yr).
4 BIFURCATIONS AND OSCILLATIONS IN INTERSTELLAR OXYGEN CHEMISTRY
We first consider a simple reduced model, containing only hydrogen, helium and oxygen, that was previously studied in Paper I and Paper II. This model has two possible autocatalytic pathways in the O–O2 chemistry and is useful for understanding the network kinetics before considering larger, more realistic, chemical models. In the first instance, for this model and those considered later, we are primarily interested in the non-linear dynamical evolution of the system of ODEs. We therefore integrate over time-scales (∼107–108 yrs) longer than the estimated lifetime of molecular clouds (Kennicutt & Evans 2012) or the time-scale to reach a gas-phase chemical steady-state (in the absence of accretion onto dust) so that the evolution of any instabilities can be followed in the long term.
For the model parameters of Table 1, we compute the bifurcation diagram as a function of nH for different values of Tgr. We find that that oscillating solutions can exist in a limited range Tgr ≈ 14.5–15 K. Fig. 1(a) shows the bifurcation diagram for the case of Tgr = 14.70 K. The bistable stationary states at low nH involve a fold bifurcation as found in earlier studies. It is due entirely to gas-phase chemistry and is set by ζ/nH (Lee et al. 1998) and |$Y^{\rm T}_{_ {\rm O}}$|; depletion of species onto dust is negligible and so the abundance of O nuclei in the gas, |$Y_{_ {\rm O}}$|, approximately equals |$Y^{\rm T}_{_ {\rm O}}$|. From Paper II, neglecting dust, as |$Y^{\rm T}_{_ {\rm O}}$| is reduced this bifurcation moves to higher densities. Inclusion of the gas-dust exchange of species leads to |$Y_{_ {\rm O}}$| being set by accretion-desorption of oxygen atoms and molecules and the emergence of two Hopf bifurcations, where the system transitions from stationary to periodic solutions. The Hopf points H1 and H2, cover the interval |$7\times 10^{2} \lesssim n_ {\rm H} \lesssim 2\times 10^{4}\, \rm cm^{-3}$|, and |$Y_{_ {\rm O}} \ll Y^{\rm T}_{_ {\rm O}}$|.
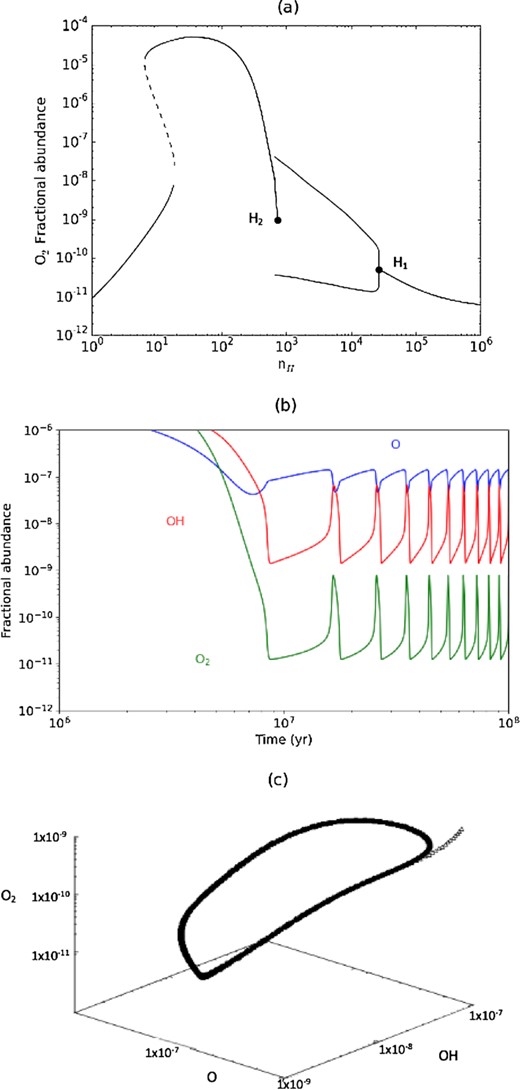
(a) Bifurcation diagram for the O2 abundance in the reduced model for Tgr = 14.70 K; H1 and H2 denote the Hopf bifurcation points; (b) Time series for |$y_{_ {\rm O}}(t)$|, |$y_{_ {\rm OH}}(t)$| and |$y_{_ {\rm O_2}}(t)$| at |$n_ {\rm H} = 1\times 10^{4}\, \rm cm^{-3}$| in the bifurcation diagram; (c) Phase space evolution of the time series of (b).
We were unable to fully characterize the Hopf bifurcations using Newton–Raphson iteration due to problems with branching and continuation to obtain the unstable solutions. The periodic solutions shown are those obtained with the ODE solver when carried out to 108 yr. This approach was based on the premise that if stable periodic (limit cycle) oscillations emerge they will still be present on this time-scale and the amplitude maxima and minima for each species, |$y_{_ {\rm max}}$| and |$y_{_ {\rm min}}$|, should be constant; the solutions presented thus plot these (|$y_{_ {\rm max}}, y_{_ {\rm min}}$|) pairs at each nH.
The Hopf bifurcations in Fig. 1(a) can be classified as follows (Seydel 2009). H1 is a supercritical Hopf bifurcation. Periodic solutions are present in the immediate vicinity of H1 where there is a soft transition from the stationary state. H1 has a pitchfork structure with an unstable stationary state connecting it to H2 (not shown). H2 is a subcritical Hopf bifurcation where, in this case, the periodic solutions occur after a jump from the stationary state, i.e. a hard transition. H2 is connected to the two adjacent stable periodic solutions by two unstable periodic solutions (not shown).
Fig. 1(b) shows the time series for the oscillatory solutions for |$y_{_ {\rm O}}(t)$|, |$y_{_ {\rm OH}}(t)$| and |$y_{_ {\rm O_2}}(t)$| at |$n_ {\rm H} = 1\times 10^{4}\, \rm cm^{-3}$|. These are limit cycle oscillations, as confirmed in the phase plane evolution shown in Fig. 1(c).
5 RELAXATION OSCILLATIONS IN MOLECULAR CLOUDS
In Paper I and Paper II we demonstrated that the simple model of the preceding section is bistable for all values of |$Y^{\rm T}_{_ {\rm O}}$| and that these solutions can persist in more realistic molecular cloud chemical models. We now show that this is also the case for chemical oscillations. Fig. 2 shows the chemical evolution for the reference dense cloud model at |$n_ {\rm H} = 1\times 10^{4}\, \rm cm^{-3}$| and two values of Dgr. We find that slightly higher values of Tgr are required for oscillations to appear than in the pure oxygen chemistry because the presence of other elements (C,N,S) can shift the range of ζ/nH for bistability to higher nH (Paper I).
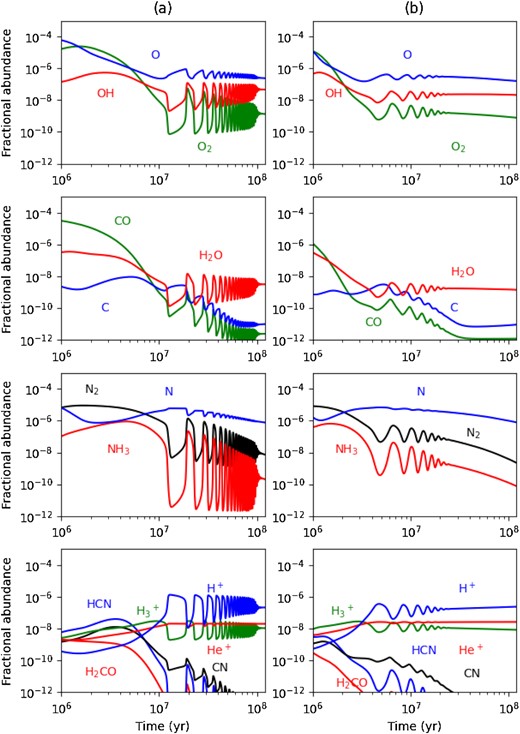
Gas-grain chemical evolution in a dense molecular cloud for |$\zeta = \zeta _{_ {\rm 0}}$| and |$n_ {\rm H} = 1\times 10^{4}\, \rm cm^{-3}$|: (a) Left-hand panels, |$D_{\rm gr}=D^{^{\rm 0}}_{\rm gr}$|, Tgr = 15.26 K; (b) Right-hand panels |$D_{\rm gr}=5D^{^{\rm 0}}_{\rm gr}$|, Tgr = 15.46 K.
5.1 Relaxation oscillations at nH = 1 × 104 cm−3
Our conservative choice of dust parameters (Table 1) and the gas density leads to the non-linear oscillations appearing, as in the H–He–O model, on time-scales (|$\gtrsim \, 10^7$| yr) that exceed estimated molecular cloud lifetimes. We note that some estimates of Milky Way GMC lifetimes (∼1.5–4 × 107 yr) are in range where chemical oscillations could arise (Murray 2011). Fig. 2(b) shows the chemical evolution in a model with |$D_{\rm gr}=5D^{^{\rm 0}}_{\rm gr}$| and Tgr = 15.46 K. With a slight increase of Tgr and a larger dust cross-section, the oscillations can be made to begin at earlier times (≳4 × 106 yr), but with a lower maximum amplitude than in Fig.2(a). Solutions with larger amplitude oscillations should also exist but are difficult to find without a bifurcation diagram for the system; we return to this point in Section 6.
The presence of the relaxation oscillations is a characteristic of a non-linear dynamical system that has undergone Hopf bifurcation but in which some of the bifurcation parameters vary slowly in time (e.g. Seydel 2009). In this model the combination of bifurcation parameters [|$\zeta /n_ {\rm H} ; \lambda _k / \xi _k, k=\rm O, O_2$|] are fixed (at given Tgr) and, to first order, determine the appearance of the Hopf bifurcation (recall that these also initially fix |$Y_{_ {\rm O}}$|). However, chemical reactions convert O, N, and C nuclei in the gas into molecules that can be permanently removed by accretion, depending on Tgr. This means that the gaseous elemental abundances |$Y_{_ {\rm O}}(t)$|, |$Y_{_ {\rm N}}(t)$|, and |$Y_{_ {\rm C}}(t)$| undergo a slow quasi-stationary drift in time; even very small changes can have dramatic effects on the evolution. Specifically, |$Y_{_ {\rm N}}(t)$| declines due to loss of N nuclei in NH3, NH2, NH, and NO; this affects the oxygen chemistry though the sequence (9) and by the direct removal of O nuclei by NO accretion. The slow conversion of the trace amounts of atomic C to CO in reactions (11) and (12), followed by CO accretion, also influences |$Y_{_ {\rm O}}(t)$| and |$Y_{_ {\rm C}}(t)$|.
5.2 Relaxation oscillations at nH = 1 × 105 cm−3
These chemical models are similar in composition to observed cloud cores in which gaseous CO has a low abundance, disappearing at the highest densities while those of N2 (|$\rm N_2H^+$|) and NH3 can still be present (e.g. Bergin & Tafalla 2007; Wirström et al. 2012; Sipilä et al. 2019). Such CO-depleted cores typically have ∼10–100 times greater densities and so we next consider a higher density model.
Adopting |$n_ {\rm H} = 1\times 10^{5}\, \rm cm^{-3}$|, we also set |$\zeta = 10\zeta _{_ {\rm 0}}$| to maintain the same ζ/nH ratio so that a gas-phase bistable solution can approximately be recovered. As before, slightly higher Tgr values are required for oscillations to occur. Fig. 3 shows the time series for the long-term evolution of selected species as a function of Tgr and that relaxation oscillations now begin after one accretion time (≳ 106 yr), a time-scale that is relevant for comparison with molecular cloud chemistry.
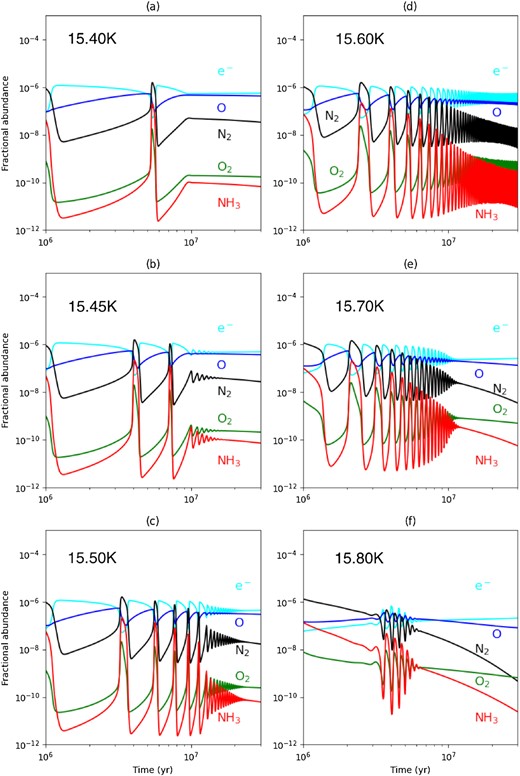
Gas-grain chemical evolution of selected species as a function of the bifurcation parameter Tgr. This model has |$\zeta = 10\zeta _{_ {\rm 0}}$|, |$n_ {\rm H} = 1\times 10^{5}\, \rm cm^{-3}$|, |$D_{\rm gr}=D^{^{\rm 0}}_{\rm gr}$|, and the Tgr are given in the upper left-hand corner of each panel.
5.3 Initial conditions
The assumption of completely atomic initial conditions for elemental C, O, N, S neglects the fact that dense cloud gas is presented by a diffuse/translucent cloud phase and so initial molecular abundances should realistically be non-zero (cf. Snow & McCall 2006). Roueff & Le Bourlot (2020) have demonstrated that the choice of initial conditions, specifically the CO/C+ or CO/C ratios, can lead to different ’early-time’ chemistry which affects the subsequent evolution of the purely gas-phase oscillations.
As the oscillations reported here are controlled by the gas-dust exchange of material; they occur on time-scales much longer than that of ’early-time’ chemistry, and so are likely less sensitive to the adopted initial conditions. We computed dense cloud models in which initial conditions were modified such that almost all carbon is present as C and CO; such that CO/C = 10 (Burgh, France & Jenkins 2010), with the remaining traced molecules having abundances appropriate for the diffuse ISM (Snow & McCall 2006; fig. 2). We find that these initial conditions do not affect the onset or characteristics of the gas-grain oscillations found here.
6 DISCUSSION
The gas-grain models considered here, evolve to produce the conditions of CO-depleted dense cores (e.g. Bergin & Tafalla 2007). When the mechanism mediating the gas-grain exchange of molecules is thermal desorption, grain temperatures of Tgr ≳ 20 K would be required for the models to maintain significant CO abundances at later times. The C and C+ released from CO could then influence the O2–O autocatalysis and the non-linear solutions found here (Section 5, Paper I). Furthermore, alternatives to the UMIST |$E_{_ {\rm i}}$| values of Table 1 exist2 experimental measurements of |$E_{_ {\rm i}}$| for O atom binding on water ice lie in the range 1440–1660 K (He et al. 2015; Minissale et al. 2022). Thus, to produce oscillations in these models via O2–O desorption requires higher dust temperatures to match the desorption rates considered here; ξO(Tgr) and |$\xi {_ {\rm O_2}}(T_{\rm gr})$| at 15 K requires Tgr ≈ 27–31 K. However, while Tgr in this range will also desorb CO and other molecules, making the chemistry similar to that of dense clouds, the ζ/nH range for bistability in the gas will be different due to the presence of the additional elements, particularly C and S (Paper I) and so a search of the parameter space for Hopf bifurcations would be required.
In fact, other autocatalytic cycles and bistable solutions are present in interstellar chemistry (Paper II) and these could also be made to undergo Hopf bifurcation. Atomic nitrogen can act as an autocatalyst and bistable states appear at densities of |$\rm \sim 10^5$| cm−3 and higher, for all values of |$Y^{\rm T}_{_ {\rm N}}$|. Although we did not consider grain-surface chemistry explicitly, we note that estimates of the binding energies of CHn with n = 1, 3; species are low enough (Penteado et al. 2017; Wakelam et al. 2017) that they could be desorbed, along with CH4, either thermally or by reactive desorption (e.g. Brown & Charnley 1990). As gas-phase carbon chemistry has an autocatalytic cycle, non-linear oscillations could then be generated by gas-dust exchange of the methylidyne radical autocatalyst (CH).
Other desorption mechanisms are possible, including non-thermal desorption and reactive desorption (e.g. Leger, Jura & Omont 1985; Minissale et al. 2016; Chuang et al. 2018; Sipilä, Silsbee & Caselli 2021; Wakelam et al. 2021). As long as the rates of any alternative desorption mechanism returns O and O2 at the same rates as those considered here oscillations should still occur, i.e. for non-thermal desorption |$\xi _{_ {\rm NT}} \sim \xi {_ {\rm O}} ~ (T_{\rm gr}) \approx 15$| K). Our assumption that T = Tgr is consistent with thermal balance in dense clouds but is not necessarily applicable when non-thermal desorption is considered. However, we find that models in which this condition is relaxed (T ≠ Tgr) produce similar dynamical solutions. Reactive desorption of grain-surface reaction products could, in principle, still produce oscillations if the sum of the their desorption rates, and the rate of their subsequent breakdown in gas-phase reactions to an X2-X pair, matches the thermal desorption rates found here.
In fact, in a parameter-space (grid model) study of dark cloud chemistry, in which reactive desorption was employed as the sole desorption mechanism, Maffucci et al. (2018) claimed to have found oscillatory solutions for some species, specifically for the abundances of long carbon-chain molecules. However, we can discount the presence of limit cycles or relaxation oscillations in the model of Maffucci et al. since, if present, all species should oscillate in abundance (cf. Roueff & Le Bourlot 2020).
In a recent grid model study, Entekhabi et al. (2022) found one model in which that oscillations could develop. This model had very large cosmic ray ionization rate (|$\zeta = 10^{-13} \rm s^{-1}$|) with molecules desorbed through photodesorption by cosmic ray-induced photons. These oscillations began at ∼103 yr and ended at ∼103 yr once molecules had been significantly destroyed. This early onset time-scale indicates that the gas-grain interaction was not involved. Nevertheless, this points to another astrophysical environment where exotic kinetics could occur.
Finally, the above brings us to the important point that searching for oscillations without bifurcation diagrams (i.e. employing ODEs or scaling from known solutions) is risky. Their appearance depends sensitively on the bifurcation parameters, ζ/nH and λk/ξk, which are are coupled through nH and T (when T = Tgr is assumed), and the relative elemental abundances.
To find Hopf bifurcations and oscillations would first require a bifurcation analysis of the full CHONS gas-phase chemistry to locate the range of ζ/nH and elemental abundances to produce bistable solutions (Dufour & Charnley, in preparation). This can then be followed by mathematical analysis of the stability of the solutions for the gas-grain chemistry (Gray & Scott 1996). Analysis of this model from the perspective of the non-linear dynamics is beyond the scope of this article and will be considered elsewhere.
7 CONCLUSIONS
Autocatalysis in interstellar gas-phase chemistry can lead to bistability which, when coupled with the gas-grain exchange of key species, can undergo Hopf bifurcation and lead to the appearance of limit cycles and chemical relaxation oscillations. The non-linear oscillations in these models occur on time-scales relevant for comparison with molecular cloud composition, particularly the first few periods.
These results complement the oscillations recently presented by Roueff & Le Bourlot (2020), except that, in realistic molecular clouds, gas-grain oscillations are not permanent limit cycles (see Section 2, Fig. 1). Both these studies indicate the early-time/late-time dichotomy of molecular cloud modeling can be broken, and predict dramatically different chemical evolution from that found heretofore. The chemical processes that determine the oscillatory solutions are central to almost all chemical models of astrophysical sources, including interstellar clouds and protoplanetary disks. Oscillations are therefore fundamental outcomes in astrochemical kinetics, indicating that a wealth of non-linear dynamical phenomena can be present in cold molecular clouds.
ACKNOWLEDGEMENTS
This research was supported by the NASA Planetary Science Division Internal Scientist Funding Program through the Fundamental Laboratory Research work package (FLaRe) and by the NASA Goddard Science Innovation Fund. JEL is a NASA Postdoctoral Program Fellow at NASA Goddard Space Flight Center, administered by Universities Space Research Association through a contract with NASA.
8 DATA AVAILABILITY
The data underlying this article are available in the article and in its online supplementary material.
Footnotes
Le Bourlot et al. (1993) did previously report one case of limit cycle oscillations in a gas-phase dense cloud model.
See Minissale et al. (2022) for a recent review of the physics of thermal desorption relevant to interstellar dust.



