Search
Close
Search
Advanced Search
Search Menu
AI Discovery Assistant

ABSTRACT

We study the effect of dynamical friction on globular clusters (GCs) and on the stars evaporated from the GCs (stellar streams) moving in the Galactic halo. Due to dynamical friction, the position of a GC as a stream progenitor starts to shift with respect to its original position in the reference frame of initial GC orbit. Therefore the stars that have evaporated at different times have different mean position with respect to the GC position. This shifting results in a certain asymmetry in stellar density distribution between the leading and trailing arms of the stream. The degree of the asymmetry depends on the characteristics of the environment in which the GC and the stream stars move. As GCs are located mainly in outer parts of a galaxy, this makes dynamical friction a unique probe to constrain the underlying dark matter spatial density and velocity distributions. For a GC NGC 3201 we compared our theoretical shift estimates with available observations. Due to large uncertainties in current observation data, we can only conclude that the derived estimates have the same order of magnitude.

globular clusters: general, Galaxy: kinematics and dynamics, dark matter

1 INTRODUCTION

Stellar streams that form from the evaporating globular clusters (GCs) allow to constrain the mass distribution models of the Milky Way (MW) galaxy. For example, by using the general shape of the stream orbits Bovy et al. (2016) has determined the flatness of the mass distribution of the inner 20 kpc of the MW. Since the stars that evaporate from GCs have no preferred direction (in cluster’s reference frame), initially the streams formed at Lagrangian points L1 and L2 should be symmetrical.

The stellar linear density along a stream is not uniform, because epicyclic motion of evaporated stars define fluctuations in density, but these fluctuations can be estimated (see e.g. Capuzzo Dolcetta, Di Matteo & Miocchi 2005; Küpper, MacLeod & Heggie 2008; Küpper, Lane & Heggie 2012). In addition, density gaps may occur, as streams may interact with massive molecular clouds when passing through the galactic disc (Dehnen et al. 2004; Amorisco et al. 2016). An especially interesting topic is the possible interaction of streams with the dark matter (DM) subhaloes and the study of resulting gaps in density distribution of the streams and corresponding perturbations in velocities of stream stars (Ibata et al. 2002; Carlberg 2012; Erkal & Belokurov 2015; Erkal et al. 2016b; Bovy, Erkal & Sanders 2017; Erkal, Koposov & Belokurov 2017)

According to the Λ cold dark matter (CDM) model, at present epoch, the DM subhaloes provide up to |${\sim } 10{{\ \rm per\ cent}}$| of the overall DM halo mass for an MW size galaxy with a specific (approximate power-law) mass spectrum (Diemand et al. 2008; Springel et al. 2008). Power spectrum of density distribution fluctuations may make it possible to constrain the mass distribution of DM subhaloes (Bovy et al. 2017), which in turn may constrain possible warm DM (WDM) particle masses (Viel et al. 2013; Pullen, Benson & Moustakas 2014; Richings et al. 2018) or charged DM particle masses (Kamada et al. 2013).

The asymmetry of the mass distribution of the MW (a rotating bar) and corresponding non-stationarity creates short streams (Hattori, Erkal & Sanders 2016; Price-Whelan et al. 2016) and an asymmetry between the two branches of the stream (Pearson, Price-Whelan & Johnston 2017). Simulating Palomar 5 stream asymmetry Pearson et al. (2017) found that for a certain bar pattern speed the observed asymmetry can be produced.

In this work we study how the dynamical friction due to stellar and DM halo environment creates asymmetry in stellar streams. Dynamical friction effect (deceleration) is proportional to the mass of the body and to the density of the environment. Thus deceleration is different for the GCs and for the stars in corresponding stellar streams. Position of a progenitor GC in a stream changes with respect to its initial position. This in turn creates a certain asymmetry in the stellar density distribution between the leading and trailing parts of the stream. The deceleration of the GC can be calculated by measuring this asymmetry.

When the deceleration is known it is possible to calculate the density of the environment. If the environment consists of different ingredients (gas particles, stars, diffuse DM particles, DM subhaloes), and if the gas and stellar densities are known from independent measurements, it is possible to estimate the DM density and potentially discriminate the smooth DM component from the more dense DM subhaloes.

Outline of the paper is as follows. In Section 2 we discuss the formation of a stellar stream and present a model to calculate the shift of a GC with respect to its original position within previously evaporated stars due to dynamical friction. In Section 3 we give the details of the MW model used in subsequent calculations. Section 4 presents our main results. Results are given for a large sample of GCs and thereafter we compare them with available stream data. Section 5 is left for discussion and conclusions.

2 STELLAR STREAMS OF GLOBULAR CLUSTERS

2.1 Formation of a stream

In an axisymmetric galaxy, all the test particles (stars, GCs, etc.) move in orbits that conserve integrals of motion, such as the energy and the z-directional angular momentum Lz. Interactions between the galactic objects can change their integrals of motion, which also changes their orbits [see e.g. Sellwood (2013)].

In case of the dynamical evolution of a GC interactions between the stars within the GC cause their evaporation from the GC and subsequent formation of stellar streams (Fall & Rees 1977; Gnedin & Ostriker 1997; Odenkirchen et al. 2001). At the moment stars evaporate from the GC [primarily through the Lagrangian points L1 and L2, see Küpper et al. (2008, 2012) and Bowden, Belokurov & Evans (2015)] they have a shift in positions and velocities with respect to the centre-of-mass values of the GC. Thus, the integrals of motion for the GC and corresponding evaporated stars are slightly different, causing GC and its stream stars to move along slightly different orbits (Eyre & Binney 2011; Bovy 2014; Carlberg 2017). Small differences in velocities between individual stream stars at Lagrangian points result in slightly different orbits for them, hence, the stream has also some thickness.

The evaporation through two Lagrangian points results in two stream arms – the leading and the trailing arm. As GCs can be assumed to be symmetrical, with their physical sizes very small in comparison to the parent galaxy, the gravitational potential of the galaxy close to the GC can be approximated with a linear function. In this case, both Lagrangian points are at the same distance from the centre of the GC and intrinsically the stellar stream is symmetric – leading and trailing arms have statistically the same distribution of stars with respect to the GC centre. Erkal, Sanders & Belokurov (2016a) showed that precession and nutation that cause non-uniformity of the stream come forth for longer streams.

In a non-stationary galaxy stream arms are not symmetrical. Non-stationarity may be caused by large-scale interactions or by a rotating bar (e.g. Pearson et al. 2017). However, small non-stationarities may also be caused by, e.g. dynamical friction effects, leading to slight incremental changes in GC orbits over time.

In this paper we analyse the asymmetry of stellar streams caused by small changes of GC orbit (or corresponding integrals of motion) between different evaporation events. Changes in a GC orbit are primarily caused by the dynamical friction in a host galaxy.

In case of a stationary galaxy and a symmetric stream, the position of the progenitor GC and the overall centre of the symmetry of stream stars are the same and remain the same in time. However, if the GC orbit changes between ejections of stars compared to the initial orbit, subsequent stream stars will be ejected symmetrically with respect to the new orbital position of the progenitor GC. As a result, the mean position of all stream stars does not coincide now with the GC. The shift between the centre of the GC and the centre of stream stars changes in time. Evolution of the shift for a simple model including the dynamical friction effect (a constant deceleration) is illustrated in Fig. 1. Deceleration value for this illustration was not calculated from friction model but was taken simply to be 0.03 km s−1 Gyr−1. Velocities of evaporated stars were taken from a Gaussian distribution with the same mean value and dispersion as the GCs orbital velocity and a typical GC velocity dispersion. Since dynamical friction affects only GC orbit and keeps the orbits of the evaporated stars intact,1 time-evolving shift between the mean position of evaporated stars and GC location appears (left-hand panel in Fig. 1). As a result, the averaged number densities of stream stars are not symmetrical between the two arms of the stream (right-hand panel in Fig. 1).

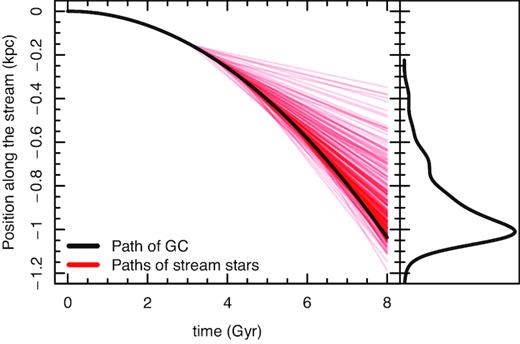
An illustration about the shift of GC position due to dynamical friction along a stream with respect to its initial position as a function of time. In the left-hand panel the black solid line depicts GC position shift, thin red lines denote individual evaporated stars. It is seen that at every moment the projected positions of stream stars are not symmetrical with respect to the GC position. Asymmetry increases in time. In the right-hand panel the resulting number density distribution of evaporated stars along the stream at t = 8 Gyr is given. Density distribution asymmetry with respect to the GC position at t = 8 Gyr is clearly visible.
Figure 1.

An illustration about the shift of GC position due to dynamical friction along a stream with respect to its initial position as a function of time. In the left-hand panel the black solid line depicts GC position shift, thin red lines denote individual evaporated stars. It is seen that at every moment the projected positions of stream stars are not symmetrical with respect to the GC position. Asymmetry increases in time. In the right-hand panel the resulting number density distribution of evaporated stars along the stream at t = 8 Gyr is given. Density distribution asymmetry with respect to the GC position at t = 8 Gyr is clearly visible.

Open in new tabDownload slide

Dynamical friction has small effect on a GC orbit. For this reason, we characterize the changes of a GC orbit and positions of objects along the orbit simply as shifts projected to the initial GC orbit – shifts along the orbit. These shifts along and with respect to the initial GC orbit are denoted as Δx.

2.2 Dynamical friction

Dynamical friction is a drag force on a massive object moving through the field of lighter objects and collecting a temporary mass wake behind it (Chandrasekhar 1943). The wake applies force to the massive object and decelerates it.

A general formula for the force per unit mass caused by the dynamical friction is given as (see e.g. Binney & Tremaine 2008)
(1)
where vGC and M are the velocity and the mass of the massive object (e.g. GC), respectively, ρ is the spatial density of field objects and f is their phase space density normalized to one, ln Λ is the Coulomb logarithm and G is the gravitational constant. The matter contributing to the dynamical friction consists mainly of stars and the DM halo particles. In case of the isotropic velocity distribution of field objects, this equation simplifies considerably, and is called Chandrasekhar’s formula (see Chandrasekhar 1943).

From equation (1) we see that the effect of dynamical friction is stronger for more massive GC and for the ones that move with similar velocities as the field objects [denominator under the integral in equation (1) is small].

2.3 Combined measurable quantities

The orbital segments of stream stars and of the parent GC are approximately parallel to each other. For simplicity, we measure distances only along the GC orbit and positions of stars along the stream orbit are projected to the GC orbit. Let Δx be a shift of a GC and evaporated stars with respect to the initial GC position projected to the initial GC orbit. Hence, the shift Δx results mainly from velocity differences between different orbits and in calculations we approximate the shift Δx based on velocities along the GC initial orbit.

Thus, the shift Δx at time t can be calculated as
(2)
(3)
where Δv(t) is the velocity difference at time t and a is the acceleration. Quantities Δx, Δv, and a are measured along the orbit of GC and can be calculated from the total force per unit mass |$\bf \boldsymbol{ F}$|⁠. The forces were calculated based on orbit after its integration, hence the friction was not included in orbit integration. This is justified since the first-hand estimation of dynamical friction does not change the orbit noticeably.
To estimate the acceleration a from |$\bf \boldsymbol{ F}$| we have to take into account the response of velocity to the torque via changes of angular momentum Lz. The origin of the torque is the dynamical friction. This can be approximated by the so-called ‘donkey effect’ (see Binney & Tremaine 2008)
(4)
(5)
where φ, θ, r are spherical coordinates and r measures the distance from the centre of host galaxy. In the last equation we have assumed the usual Oort constants and circular velocity (vc) denotations
(6)
(7)
(8)
Here R is the distance from the centre of a galaxy in the Galactic plane and Φ denotes gravitational potential. In case of flat rotation curve A/B reduces to −1, in case of adopted Galactic potential (see Section 3), A/B varies between −0.2...−1.5.

The acceleration a used in equation (2) is the projection of |$\bf \boldsymbol{ a}$| to the GC orbit at a given point.

3 DESCRIPTION OF THE MILKY WAY MODEL

To calculate the asymmetry in a stellar stream density distribution, described in the previous section, we need to know the mass density distribution ρ and the phase space density distribution (in fact, the velocity distribution) f for a region of the Galaxy where the stream is located.

3.1 Spatial densities and velocity distributions of Galactic components

To calculate the orbits of progenitor GCs we used galpypython package developed by Bovy (2015) with MWPotential2014. To calculate the dynamical friction effect from equation (1) we need density and velocity distributions of corresponding individual components. Although the components in MWPotential2014 included a bulge, a Miyamoto–Nagai disc and an NFW dark halo, the first two components do not contribute in outer regions of the MW, where the dynamical friction effects are calculated. However, a stellar halo may contribute to the dynamical friction. Thus, we added a stellar halo from a model by Jurić et al. (2008).

We also need to know the velocity distribution function at the orbital points of GCs. Dynamical friction results from the stars of stellar halo and from the DM particles. For the stellar halo all three velocity dispersion components were taken from Bird et al. (2019). Unfortunately, this kind of data is not available for the DM halo. To derive velocity dispersions for the DM halo we solved Jeans equations. Two forms for the corresponding velocity ellipsoids were assumed: (i) an isotropic velocity distribution, and (ii) a distribution with constant anisotropy. The solutions for the Jeans equations for these two cases are
(9)
for constant anisotropy case, where |$\gamma =2-2\sigma ^2_{\theta ,\phi }/\sigma ^2_r$| is an anisotropy parameter, and
(10)
for the isotropic case. The anisotropy parameter in equation (9) was assumed to be the same as the mean anisotropy of the stellar halo, σθ,ϕ/σr = 0.62, taken as the average from the halo profile of Bird et al. (2019).

A typical GC orbit is mostly located in the outer regions of the galaxy, where the DM halo dominates the density distribution. The contributions of stellar disc and stellar halo to the dynamical friction are rather small. We tested this by selecting their average velocity distribution parameters according to Bland-Hawthorn & Gerhard (2016). The result is presented in Fig. 2 for a typical GC with mean distance of r = 35 kpc from the Galactic centre. The stellar halo and disc provide about an order of magnitude smaller contribution integrated over time than the DM. Hence, in subsequent dynamical friction calculations we ignore the contributions of both stellar components.

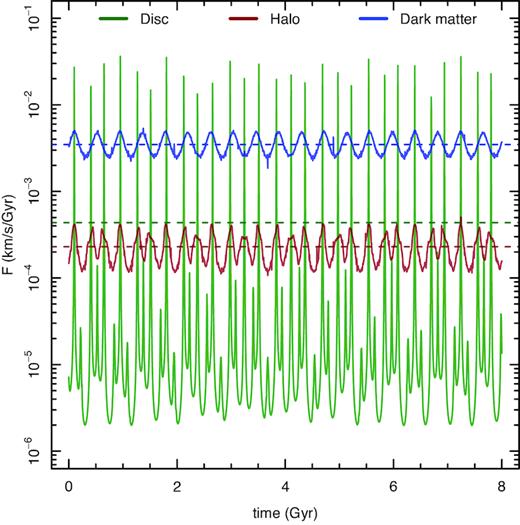
Contribution of different galaxy components to the overall dynamical friction for a GC NGC 5024. The mean contribution from stellar components (green and red lines) are about an order of magnitude smaller than from the dark matter component (blue line). Horizontal dashed lines show average contribution of the corresponding component.
Figure 2.

Contribution of different galaxy components to the overall dynamical friction for a GC NGC 5024. The mean contribution from stellar components (green and red lines) are about an order of magnitude smaller than from the dark matter component (blue line). Horizontal dashed lines show average contribution of the corresponding component.

Open in new tabDownload slide

3.2 Globular clusters in the Milky Way

GCs analysed in this paper and their parameters were taken from a compilation by Baumgardt et al. (2019).2 For each GC we calculated their orbits and shift Δx.

The Coulomb logarithm in equation (1) determines the region along the GC path that is contributing to the dynamical friction. We used the value ln Λ = 5.8 by assuming a maximum impact parameter of |$1\, {\rm kpc}$|⁠, and a minimum impact parameter |$3\, {\rm pc}$| corresponding to the typical half-light radius of GCs.

4 RESULTS

We calculated the effect of dynamical friction for the GCs in Baumgardt et al. (2019) selection. In Section 4.1 we describe the effect of dynamical friction in detail by using one GC as an example. In Section 4.2 we present the results for all GCs and in Section 4.3 we discuss some GCs in more detail.

4.1 Dynamical friction effect for a typical GC

We selected a well-observed GC NGC 3201 as an example for which we present possible stellar stream asymmetry sources in detail. Fig. 3 shows the calculated decelerations, resulting velocity, and position shifts along the original GC orbit over the last 8 Gyr. Both the total deceleration (black lines) and the contribution from individual deceleration components (green for radial component, red and blue for tangential ones) are given. Periodicity seen in deceleration values corresponds to different locations of the GC in the Galaxy. During the pericentre passages, the deceleration has prominent peaks due to increased DM densities. During the apocentre passages, there are secondary peaks caused by the slower motion of the GC (or even nearly standing still along the radial direction). This effect results from the integral part of equation (1). It means also that the radial acceleration contribution to the dynamical friction (projected to the GC orbit) is zero during the apocentric passages.

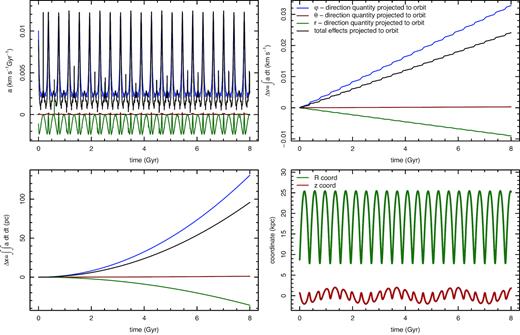
Evolution of calculated acceleration values (top left), velocity shift components (top right, see equation 3) and position shift along the orbit (bottom left, see equation 2) for a sample GC NGC 3201. Colour coding for these three panels is the same. Bottom right panel shows the shape of the orbit (radius and height from the Galactic plane). Calculations were made assuming an isotropic velocity distribution. GC orbit is calculated over 8 Gyr assuming that MW potential does not change during this time.
Figure 3.

Evolution of calculated acceleration values (top left), velocity shift components (top right, see equation 3) and position shift along the orbit (bottom left, see equation 2) for a sample GC NGC 3201. Colour coding for these three panels is the same. Bottom right panel shows the shape of the orbit (radius and height from the Galactic plane). Calculations were made assuming an isotropic velocity distribution. GC orbit is calculated over 8 Gyr assuming that MW potential does not change during this time.

Open in new tabDownload slide

It is also seen that acceleration directions (positive or negative) and shift values along the orbit are different for different acceleration vector components. This is caused by the donkey effect (see Section 2.3). Depending on the nature of GC orbit (radial or circular orbits), the shifts can be positive or negative with respect to the orbital motion since the orbit determines how strongly the donkey effect affects the shift. Hence, it depends on the nature of a GC orbit whether the leading or the trailing arm of a stellar stream is longer. For NGC 3201, the trailing arm is longer than the leading arm. Fig. 3 shows that θ-component (red line) accelerations are very small and thus have nearly negligible contribution to the coordinate and velocity shifts. This is not surprising since NGC 3201 orbit is quite close to the Galactic plane and oscillates slowly in vertical direction (see the bottom right panel on Fig. 3).

An additional point of interest is that the cumulative effect of the dynamical friction (shift Δx along the orbit) depends quite strongly on time. Hence, the asymmetry between leading and trailing arms is strongest for stars that are evaporated during earlier times in cluster’s dynamical evolution. Due to mass segregation, stars evaporated earlier tend to be less massive and are, unfortunately, relatively faint and are difficult to observe.

4.2 Dynamical friction effect for the total sample of GCs

The effect of dynamical friction (shifts along the orbit) as a function of GC pericentre distance is presented in Fig. 4. The shifts are calculated for a |$5\,$| Gyr time span for all GCs from Baumgardt catalogue (Baumgardt et al. 2019) with known phase space coordinates. The figure shows that calculations assuming isotropic or anisotropic velocity distribution give similar results. Shifts calculated by assuming a constant anisotropy fixed to stellar halo value are smaller when compared to the isotropic case. GCs with small pericentric distances might be influenced by the MW bar. Hence, at present (when the bar effects cannot be modelled reliably) the shift estimates for these GCs are not reliable.

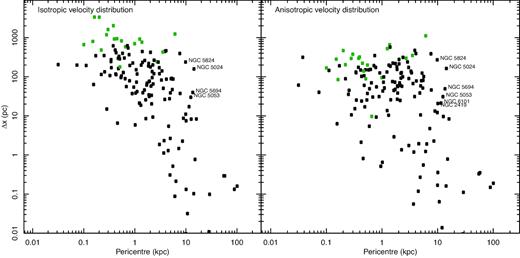
Calculated dynamical friction shift along the orbit for all GCs with known phase space coordinates. To characterize the strength of influence of the Galactic bar on the stream asymmetry, the x-axis shows the pericentric distance to the GC orbit. The calculations assume isotropic velocity distribution for left-hand panel, and anisotropic one for right-hand panel. Some of the most interesting GCs are indicated with labels.
Figure 4.

Calculated dynamical friction shift along the orbit for all GCs with known phase space coordinates. To characterize the strength of influence of the Galactic bar on the stream asymmetry, the x-axis shows the pericentric distance to the GC orbit. The calculations assume isotropic velocity distribution for left-hand panel, and anisotropic one for right-hand panel. Some of the most interesting GCs are indicated with labels.

Open in new tabDownload slide

Labelled GCs at the upper right part of Fig. 4 are the best candidates to detect the dynamical friction effect from dark matter halo. These GCs are in orbits with large pericentre values and the effect of dynamical friction for these GCs is the largest. In the next subsection we will discuss some of these GCs in more detail. Large shift is not the only criterion for observational detection of dynamical friction effects, because GC location at a low Galactic latitude or at a large distance from us makes observing streams challenging.

Another subset of GCs in Fig. 4 is marked with green symbols and they denote the GCs that have shifts which translate to largest angular distance in the sky. These GCs are mostly located close to the Sun. Although from observational aspect their stream asymmetries are easier to detect than ones having large shift, their position is too close to the bar and possible asymmetry detection does not allow us to conclude that the dominant cause of the shifts is dynamical friction.

The |$5\,$| Gyr shifts along the orbit for all analysed GCs are listed in Table A1. There we also present angular shifts, i.e. shifts projected from orbital arc to the sky plane. The angular distance estimate includes the projection of orbital arc perpendicular to line of sight, but does not include orbital velocity inhomogeneities.

4.3 Specific GCs

In this section we discuss GCs that are most promising for pure dynamical friction analysis. We included only GCs for which we found relevant references in literature.

4.3.1 NGC 3201

Based on 13 RR Lyra stars compiled by Kundu, Minniti & Singh (2019) there is a shift between the GC and GC stream centre to be |$18\pm 23\, {\rm pc}$| (this error includes only statistical one, and does not include any of the selectional sources). Our dynamical friction model estimate (see Fig. 3) is |$25\dots 43 \, {\rm pc}$| (for 5 Gyr), which is in good accordance with the measured value. In principle, the observed value is within the errors consistent also with no shift.

4.3.2 Palomar 5

GC Palomar 5 has long and prominent leading and trailing streams. Palomar 5 might be in resonance with the MW bar (Pearson et al. 2017), thus unfortunately not eligible for the friction-only analysis. In addition, Palomar 5 has too small mass for a noticeable dynamical friction effect from dark matter halo.

4.3.3 NGC 5824, NGC 5024, NGC 5694, NGC 2419, NGC 3201, NGC 6101

GCs NGC 5824, NGC 5024, NGC 5694, NGC 2419, NGC 201, and NGC 6101 have strong potential to exhibit detectable effects from pure dark matter dynamical friction. We searched for stellar streams in the neighbourhoods of these GCs, using data from the Gaia DR2 catalogue (Gaia Collaboration 2016, 2018). The search process in the case of NGC 5824 is illustrated in Fig. 5. First, we selected stars that had proper motions similar to the respective GC. Next, we plotted the colour–magnitude (GBP − GRP versus G) diagram (CMD) for each GC, and narrowed the star selection in the GC neighbourhood with stars that followed the GC isochrone on CMD. The resulting selections were visually inspected. No streams were apparent around the above-mentioned GCs.

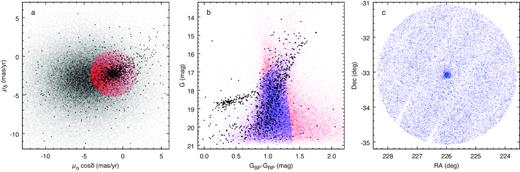
Search for a stream within two-degree radius from the GC NGC 5824. Panel a shows proper motions of all stars in the area (grey dots). Selected stars with proper motions similar to the GC are plotted with red dots and overlaid with GC stars (black dots), taken from an area with 3 arcmin radius from the cluster centre. The colour–magnitude diagram is shown in panel b: red dots denote all stars from the proper-motion cut, blue dots denote selected stars. The selection was based on the location of GC stars, overlaid with black dots. The sky plot of the final selection is shown in panel c.
Figure 5.

Search for a stream within two-degree radius from the GC NGC 5824. Panel a shows proper motions of all stars in the area (grey dots). Selected stars with proper motions similar to the GC are plotted with red dots and overlaid with GC stars (black dots), taken from an area with 3 arcmin radius from the cluster centre. The colour–magnitude diagram is shown in panel b: red dots denote all stars from the proper-motion cut, blue dots denote selected stars. The selection was based on the location of GC stars, overlaid with black dots. The sky plot of the final selection is shown in panel c.

Open in new tabDownload slide

5 DISCUSSION AND CONCLUSIONS

5.1 Observational aspects

We estimated how much the effect of dynamical friction influences the asymmetry of GC stellar streams. The constant lagging of a GC behind on its orbit when compared with the stream stars produces a shift of the GC with respect to the previously evaporated stars and thus an asymmetry between the leading and trailing parts of the stream. Thus, the distribution of recently evaporated stars is preferably more lopsided compared to the earlier evaporated stars. From the observational perspective, it is seen as an asymmetry in surface density distributions between the two branches of the stellar stream.

We calculated shifts (Δx) of the progenitor GC and its evaporated stream stars with respect to the initial position of the progenitor GC or the centre of the symmetry of the oldest parts of the stream. In most cases, either calculated shifts are too small to be detected within current observational data, or pericentres of GC orbits are too near the MW central bar, which can be another source of asymmetry in observed stellar streams. Although there are numerous hindrances, it should still be possible to study the dark matter by taking these effects into account and provided deep photometric observations of the stream. The diversity of the distances, evaporation histories, and densities of the streams do not allow us to deduce a certain brightness limit for needed observations.

On the other hand, calculated shifts, depending on the GC orbit and evaporation process details, may be quite large compared to the width of the stream. In case of short stellar streams (recently evaporated stars) the shift Δx is more easily measurable. In principle, there exists a possibility that for some GC there might be even only one stream arm, if the radial derivative of the angular velocity in the orbit is small and dynamical friction is large. In a similar case, when the GC has moved backwards and inward with respect to one arm of the stream and still evaporates stars, it might be possible to have two parallel streams. As an example, a short double stream structure near GD-1 has been found by Malhan et al. (2018; not the longer one found by Grillmair & Dionatos 2006), but another possible explanation of this double structure is simply a massive perturber (Bonaca et al. 2018; Price-Whelan & Bonaca 2018).

Dynamical friction and resulting inward migration of a GC orbit is an aspect which should be taken into account also when streams are used to constrain overall properties of the gravitational potential of a parent galaxy. This is especially important when a GC and corresponding stream is moving in an elongated high-energy orbit which allows to probe the friction it had near the apocentre, i.e. further away than the current position.

In this paper we assumed a simple virialized halo. A first-order estimate how much results can vary when loosening this assumption can be seen by comparing panels of Fig. 4. Incorporating of more complicated haloes to our model [e.g. by using the halo from Helmi et al. (2018)] can be done by including halo substructures to the phase space function f and include their orbital evolution.

5.2 DM implications

Assuming that with future detailed measurements of GCs it is feasible to determine the strength of dynamical friction in several locations over the Galactic halo, one would certainly hope to learn valuable information about the properties of DM – the dominant form of material filling the halo.

On the one hand, the assumption used for deriving equation (1) is that an elementary unit of DM is much lighter than the mass of the target object moving in that medium, and thus, it does not important if the medium consists of particle DM (e.g. axions, WIMPs, etc.) or even of primordial black holes with masses up to and exceeding the Solar mass-scale – the instantaneous dynamical friction is determined simply by the density of the medium. On the other hand, the realistic density and velocity-space structure of the DM halo – DM streams, subhaloes, etc. – is far from uniform and depends crucially on (i) halo assembly history (i.e. on particular small-scale realization of initial fluctuations) and (ii) on DM microphysics [e.g. WDM, fuzzy DM, self-interacting DM – popular alternatives to the standard CDM]. For example, in the standard CDM scenario one expects |${\cal O}(10){{\ \rm per\ cent}}$| of the DM halo to be in the form of substructures (e.g. Gao et al. 2004), while for the cases of WDM and fuzzy DM the amount of small-scale substructures is significantly reduced (e.g. Schneider et al. 2012; Du, Behrens & Niemeyer 2017).

In order to have a measurable orbital lag of the GC with respect to the ejected stars one has to use long enough sections of the tidal tails, and thus effectively probe the density of the DM medium averaged over the corresponding section of the cluster’s orbit. In cases with large amount of substructures the chances of passing through denser DM clumps is enhanced, leading to a boost in dynamical friction, and thus, in principle giving us sensitivity to differentiate between alternative DM models. Of course, this can be done only statistically once one has several detailed GC measurements available over the MW’s DM halo.

The power to discriminate between various DM models is further complicated by the fact that a substantial fraction of GCs in Galactic halo, in particular the metal-poor blue population, is not expected to be formed in situ, rather being accreted as member systems of the MW’s satellite galaxies (e.g. Searle & Zinn 1978; Renaud, Agertz & Gieles 2017). Thus, one would expect the orbits of these GCs for quite some time to be correlated with the tidal DM debris left over from the disruption of their parent haloes, this way enhancing the level of dynamical friction. Also, more recently accreted GCs are expected to have significant velocities with respect to the DM halo, such that the effective velocity distribution function entering in dynamical friction calculations can be significantly anisotropic in GC’s frame of reference.

The main goal of this paper was to estimate the size of the GC displacement due to dynamical friction and to further provide initial investigation under what conditions can the effect be realistically measurable. A more detailed investigation regarding the possibility to distinguish between the alternative DM models is beyond the scope of this paper and is left for the future study.

ACKNOWLEDGEMENTS

We thank the referee for useful suggestions and comments. This work was supported by institutional research funding IUT26-2 and IUT40-2 of the Estonian Ministry of Education and Research. We acknowledge the support by the Centre of Excellence ‘Dark side of the Universe’ (TK133) and by the grant MOBTP86 financed by the European Union through the European Regional Development Fund. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement.

Footnotes

1

The dynamical friction on stream stars is completely negligible, 4−5 orders of magnitude smaller.

2

Data available from web page https://people.smp.uq.edu.au/HolgerBaumgardt/globular/.

REFERENCES

Amorisco
N. C.
,
Gómez
F. A.
,
Vegetti
S.
,
White
S. D. M.
,
2016
,
MNRAS
,
463
,
L17
10.1093/mnrasl/slw148

Crossref
Search ADS
 

Baumgardt
H.
,
Hilker
M.
,
Sollima
A.
,
Bellini
A.
,
2019
,
MNRAS
,
482
,
5138
10.1093/mnras/sty2997

Crossref
Search ADS
 

Binney
J.
,
Tremaine
S.
,
2008
,
Galactic Dynamics
, 2nd edn.
Princeton Univ. Press
,
Princeton, NJ

Google Scholar

OpenURL Placeholder Text

 

Bird
S. A.
,
Xue
X.-X.
,
Liu
C.
,
Shen
J.
,
Flynn
C.
,
Yang
C.
,
2019
,
AJ
,
157
,
104
10.3847/1538-3881/aafd2e

Crossref
Search ADS
 

Bland-Hawthorn
J.
,
Gerhard
O.
,
2016
,
ARA&A
,
54
,
529
10.1146/annurev-astro-081915-023441

Crossref
Search ADS
 

Bonaca
A.
,
Hogg
D. W.
,
Price-Whelan
A. M.
,
Conroy
C.
,
2018
,
preprint (arXiv:e-prints)

Bovy
J.
,
2014
,
ApJ
,
795
,
95
10.1088/0004-637X/795/1/95

Crossref
Search ADS
 

Bovy
J.
,
2015
,
ApJS
,
216
,
29
10.1088/0067-0049/216/2/29

Crossref
Search ADS
 

Bovy
J.
,
Bahmanyar
A.
,
Fritz
T. K.
,
Kallivayalil
N.
,
2016
,
ApJ
,
833
,
31
10.3847/1538-4357/833/1/31

Crossref
Search ADS
 

Bovy
J.
,
Erkal
D.
,
Sanders
J. L.
,
2017
,
MNRAS
,
466
,
628
10.1093/mnras/stw3067

Crossref
Search ADS
 

Bowden
A.
,
Belokurov
V.
,
Evans
N. W.
,
2015
,
MNRAS
,
449
,
1391
10.1093/mnras/stv285

Crossref
Search ADS
 

Capuzzo Dolcetta
R.
,
Di Matteo
P.
,
Miocchi
P.
,
2005
,
AJ
,
129
,
1906
10.1086/426006

Crossref
Search ADS
 

Carlberg
R. G.
,
2012
,
ApJ
,
748
,
20
10.1088/0004-637X/748/1/20

Crossref
Search ADS
 

Carlberg
R. G.
,
2017
,
ApJ
,
838
,
39
10.3847/1538-4357/aa6479

Crossref
Search ADS
 

Chandrasekhar
S.
,
1943
,
ApJ
,
97
,
255
10.1086/144517

Crossref
Search ADS
 

Dehnen
W.
,
Odenkirchen
M.
,
Grebel
E. K.
,
Rix
H.-W.
,
2004
,
AJ
,
127
,
2753
10.1086/383214

Crossref
Search ADS
 

Diemand
J.
,
Kuhlen
M.
,
Madau
P.
,
Zemp
M.
,
Moore
B.
,
Potter
D.
,
Stadel
J.
,
2008
,
Nature
,
454
,
735
10.1038/nature07153

Crossref
Search ADS
PubMed
 

Du
X.
,
Behrens
C.
,
Niemeyer
J. C.
,
2017
,
MNRAS
,
465
,
941
10.1093/mnras/stw2724

Crossref
Search ADS
 

Erkal
D.
,
Belokurov
V.
,
2015
,
MNRAS
,
454
,
3542
10.1093/mnras/stv2122

Crossref
Search ADS
 

Erkal
D.
,
Sanders
J. L.
,
Belokurov
V.
,
2016a
,
MNRAS
,
461
,
1590
10.1093/mnras/stw1400

Crossref
Search ADS
 

Erkal
D.
,
Belokurov
V.
,
Bovy
J.
,
Sanders
J. L.
,
2016b
,
MNRAS
,
463
,
102
10.1093/mnras/stw1957

Crossref
Search ADS
 

Erkal
D.
,
Koposov
S. E.
,
Belokurov
V.
,
2017
,
MNRAS
,
470
,
60
10.1093/mnras/stx1208

Crossref
Search ADS
 

Eyre
A.
,
Binney
J.
,
2011
,
MNRAS
,
413
,
1852
10.1111/j.1365-2966.2011.18270.x

Crossref
Search ADS
 

Fall
S. M.
,
Rees
M. J.
,
1977
,
MNRAS
,
181
,
37P
10.1093/mnras/181.1.37P

Crossref
Search ADS
 

Gaia Collaboration
,
2016
,
A&A
,
595
,
A1
10.1051/0004-6361/201629272

Crossref
Search ADS
 

Gaia Collaboration
2018
,
A&A
,
616
,
A1
10.1051/0004-6361/201833051

Crossref
Search ADS
 

Gao
L.
,
White
S. D. M.
,
Jenkins
A.
,
Stoehr
F.
,
Springel
V.
,
2004
,
MNRAS
,
355
,
819
10.1111/j.1365-2966.2004.08360.x

Crossref
Search ADS
 

Gnedin
O. Y.
,
Ostriker
J. P.
,
1997
,
ApJ
,
474
,
223
10.1086/303441

Crossref
Search ADS
 

Grillmair
C. J.
,
Dionatos
O.
,
2006
,
ApJ
,
643
,
L17
10.1086/505111

Crossref
Search ADS
 

Hattori
K.
,
Erkal
D.
,
Sanders
J. L.
,
2016
,
MNRAS
,
460
,
497
10.1093/mnras/stw1006

Crossref
Search ADS
 

Helmi
A.
,
Babusiaux
C.
,
Koppelman
H. H.
,
Massari
D.
,
Veljanoski
J.
,
Brown
A. G. A.
,
2018
,
Nature
,
563
,
85
10.1038/s41586-018-0625-x

Crossref
Search ADS
PubMed
 

Ibata
R. A.
,
Lewis
G. F.
,
Irwin
M. J.
,
Quinn
T.
,
2002
,
MNRAS
,
332
,
915
10.1046/j.1365-8711.2002.05358.x

Crossref
Search ADS
 

Jurić
M.
et al. .,
2008
,
ApJ
,
673
,
864
10.1086/523619

Crossref
Search ADS
 

Kamada
A.
,
Yoshida
N.
,
Kohri
K.
,
Takahashi
T.
,
2013
,
J. Cosmol. Astropart. Phys.
,
3
,
008
10.1088/1475-7516/2013/03/008

Crossref
Search ADS
 

Kundu
R.
,
Minniti
D.
,
Singh
H. P.
,
2019
,
MNRAS
,
483
,
1737
10.1093/mnras/sty3239

Crossref
Search ADS
 

Küpper
A. H. W.
,
MacLeod
A.
,
Heggie
D. C.
,
2008
,
MNRAS
,
387
,
1248
10.1111/j.1365-2966.2008.13323.x

Crossref
Search ADS
 

Küpper
A. H. W.
,
Lane
R. R.
,
Heggie
D. C.
,
2012
,
MNRAS
,
420
,
2700
10.1111/j.1365-2966.2011.20242.x

Crossref
Search ADS
 

Malhan
K.
,
Ibata
R. A.
,
Goldman
B.
,
Martin
N. F.
,
Magnier
E.
,
Chambers
K.
,
2018
,
MNRAS
,
478
,
3862
10.1093/mnras/sty1338

Crossref
Search ADS
 

Odenkirchen
M.
et al. .,
2001
,
ApJ
,
548
,
L165
10.1086/319095

Crossref
Search ADS
 

Pearson
S.
,
Price-Whelan
A. M.
,
Johnston
K. V.
,
2017
,
Nat. Astron.
,
1
,
633
10.1038/s41550-017-0220-3

Crossref
Search ADS
 

Price-Whelan
A. M.
,
Bonaca
A.
,
2018
,
ApJ
,
863
,
L20
10.3847/2041-8213/aad7b5

Crossref
Search ADS
 

Price-Whelan
A. M.
,
Johnston
K. V.
,
Valluri
M.
,
Pearson
S.
,
Küpper
A. H. W.
,
Hogg
D. W.
,
2016
,
MNRAS
,
455
,
1079
10.1093/mnras/stv2383

Crossref
Search ADS
 

Pullen
A. R.
,
Benson
A. J.
,
Moustakas
L. A.
,
2014
,
ApJ
,
792
,
24
10.1088/0004-637X/792/1/24

Crossref
Search ADS
 

Renaud
F.
,
Agertz
O.
,
Gieles
M.
,
2017
,
MNRAS
,
465
,
3622
10.1093/mnras/stw2969

Crossref
Search ADS
 

Richings
J.
,
Frenk
C.
,
Jenkins
A.
,
Robertson
A.
,
2018
,
preprint (arXiv:e-prints)

Schneider
A.
,
Smith
R. E.
,
Macciò
A. V.
,
Moore
B.
,
2012
,
MNRAS
,
424
,
684
10.1111/j.1365-2966.2012.21252.x

Crossref
Search ADS
 

Searle
L.
,
Zinn
R.
,
1978
,
ApJ
,
225
,
357
10.1086/156499

Crossref
Search ADS
 

Sellwood
J. A.
,
2013
,
ApJ
,
769
,
L24
10.1088/2041-8205/769/2/L24

Crossref
Search ADS
 

Springel
V.
et al. .,
2008
,
MNRAS
,
391
,
1685
10.1111/j.1365-2966.2008.14066.x

Crossref
Search ADS
 

Viel
M.
,
Becker
G. D.
,
Bolton
J. S.
,
Haehnelt
M. G.
,
2013
,
Phys. Rev. D
,
88
,
043502
10.1103/PhysRevD.88.043502

Crossref
Search ADS
 

APPENDIX: COMPLETE TABLE OF DYNAMICAL FRICTION ESTIMATES

Table A1.
Open in new tab

The estimation of shift along the orbit (Δx) produced by dynamical friction from only dark matter over the 5 Gyr time span. Angular shift (Δϕ) shows the angular distance between the GC and stream centre along the orbit as viewed from the Sun. D⊙ denotes the distance of the GC from the Sun. l and b denote the Galactic longitude and latitude of the GC. The calculations are made by assuming either isotropic or constant anisotropic dark matter particle velocity dispersion tensor with the anisotropy value adopted from stellar halo.

GClbD⊙Δx (isotropic)Δϕ (isotropic)ΔxΔϕPericentre
(deg)(deg)(kpc)(pc)(deg)(pc)(deg)(kpc)
NGC 65221.02−3.928.0335222.73850.610.2
NGC 64407.733.808.2333121.474673.160.2
Ter 1357.560.996.7202313.522972.040.4
NGC 104305.89−44.894.412388.5311147.716.2
NGC 6380350.18−3.429.816118.313761.960.3
NGC 66267.80−5.585.48277.511991.820.6
NGC 5139309.1014.975.27667.486586.441.4
NGC 6273356.879.388.311867.222931.800.3
NGC 64013.453.987.79416.722211.590.5
NGC 6266353.577.326.49196.485233.711.3
NGC 65445.84−2.202.62936.431403.080.5
Pal 62.091.785.88014.682811.650.2
NGC 6752336.49−25.634.24274.633513.813.6
NGC 6093352.6719.468.96634.251681.080.1
NGC 66569.89−7.553.22424.042984.982.8
NGC 671225.35−4.327.04813.962041.680.2
NGC 6453355.72−3.8711.69233.893201.350.4
NGC 6121350.9715.972.01793.56891.770.5
NGC 6441353.53−5.0111.87003.39950.461.0
NGC 640221.3214.809.35862.64100.040.7
NGC 4833303.60−8.026.22862.621511.380.5
NGC 5986337.0213.2710.64812.541490.790.4
NGC 6388345.56−6.7410.74422.255712.901.4
NGC 65690.48−6.6810.64222.232771.462.1
NGC 66387.90−7.1510.36192.041740.570.4
NGC 620559.0140.916.83972.031500.770.6
NGC 651719.236.7610.66192.021930.630.7
NGC 527242.2278.719.63932.013861.977.7
NGC 6355359.585.438.74131.991020.490.4
NGC 6304355.835.385.82181.841541.301.9
NGC 2808282.19−11.2510.25431.693471.080.8
NGC 65535.25−3.036.81981.661981.661.4
NGC 634168.3434.868.43451.631900.900.2
NGC 6293357.627.839.23321.62170.080.5
NGC 5946327.584.1910.62721.461260.680.3
Ter 53.841.695.51511.45730.701.1
NGC 621815.7126.314.71201.441001.202.4
NGC 66429.81−6.448.11981.40400.280.1
NGC 707865.01−27.3110.24451.394721.474.0
NGC 362301.53−46.259.22441.371320.740.3
NGC 6256347.793.316.42001.341270.852.3
NGC 6284358.359.9415.13661.321730.630.8
NGC 653920.806.787.82331.291861.031.4
NGC 6397338.17−11.962.4581.26701.532.1
NGC 63250.978.007.81711.23250.180.4
NGC 708953.37−35.7710.53011.201540.610.6
NGC 6541349.29−11.198.02611.202221.021.6
Ter 2356.322.307.53481.09350.110.3
Ter 4356.021.316.71281.0250.040.6
NGC 5286311.6110.5711.42240.961250.540.9
NGC 4372300.99−9.885.82360.952390.962.9
NGC 63566.7210.2215.12650.873131.032.4
NGC 677962.668.349.71620.841060.550.5
NGC 66242.79−7.917.21180.7720.010.4
Ter 104.42−1.875.8790.7690.090.8
NGC 65403.29−3.315.2680.75470.521.8
NGC 625415.1423.085.01890.751780.701.9
NGC 5897342.9530.2912.61700.741730.753.1
NGC 66812.85−12.519.32040.69610.210.0
NGC 59043.8646.807.6910.671240.915.4
NGC 6139342.376.949.81170.66520.291.1
NGC 6352341.42−7.175.91190.58900.433.1
FSR 1735339.19−1.859.81280.57490.220.6
IC 127621.835.675.41410.561260.503.5
UKS 15.120.767.81040.56370.200.6
NGC 66521.53−11.3810.01080.55150.080.3
NGC 683856.75−4.564.0890.50790.455.2
NGC 65281.14−4.177.53020.49600.100.5
NGC 636618.4116.043.7310.48380.591.9
NGC 676036.11−3.928.01780.472140.562.1
NGC 5024332.9679.7617.91580.461630.4814.6
NGC 67230.07−17.308.3730.46990.621.1
NGC 65580.20−6.027.21130.43240.090.4
Pal 814.11−6.8012.8950.41920.402.2
Djor 22.76−2.516.3540.4110.001.0
NGC 6362325.56−17.577.41360.411230.372.2
NGC 5927326.604.868.24630.403920.344.2
NGC 61713.3723.016.0420.39510.481.1
NGC 1851244.51−35.0411.31940.391450.290.1
2MASS-GC02 09.78−0.627.1960.38260.100.5
NGC 62870.1311.029.41340.37450.130.3
NGC 5824332.5622.0731.82380.352710.4010.0
NGC 63335.5410.718.41940.35550.100.8
FSR 1716329.78−1.597.5650.35570.312.3
Pal 1052.442.735.9870.35780.314.2
NGC 1904227.23−29.3513.31140.35890.270.2
Ter 93.60−1.997.1630.3460.030.2
BH 2613.36−5.276.5390.34260.231.5
Lynga 7328.77−2.808.0610.33730.391.7
Ter 3345.089.198.1770.32560.242.0
NGC 66371.72−10.278.8560.32300.170.7
NGC 3201277.238.644.5370.32460.397.8
Pal 1131.80−15.5814.3870.32810.295.6
NGC 6144351.9315.708.9750.27580.211.9
NGC 288151.28−89.3810.0510.25670.333.7
Ton 2350.80−3.426.4340.21270.161.9
NGC 1261270.54−52.1215.5880.211010.255.7
NGC 709927.18−46.848.0460.19750.311.6
NGC 63424.909.728.4370.11310.090.9
NGC 6496348.03−10.0111.3260.11310.133.9
NGC 6235358.9213.5213.5270.11380.154.9
NGC 686420.30−25.7521.6820.101390.173.4
NGC 5053335.7078.9517.2300.10310.1012.7
NGC 671712.88−10.907.1210.09140.061.3
NGC 6316357.185.7611.6210.091320.531.2
NGC 674936.19−2.217.8260.08450.141.7
NGC 698135.16−32.6817.0470.08510.095.5
NGC 2298245.63−16.0110.8190.08100.041.3
NGC 6584342.14−16.4113.2200.07600.212.2
NGC 622973.6440.3130.6890.06700.050.7
ESO 452-SC11351.9112.106.570.0610.010.5
NGC 68098.79−23.275.3380.06430.061.1
NGC 5634342.2149.2627.2390.05580.085.1
NGC 6101317.75−15.8216.1170.05210.0611.7
NGC 653527.1810.446.560.0410.001.0
NGC 4590299.6336.0510.190.03130.059.1
Ter 128.36−2.103.420.0220.023.1
NGC 546642.1573.5916.980.02100.0312.9
NGC 5694331.0630.3637.3400.02490.0313.9
Pal 50.8545.8623.280.0280.0216.3
ESO 280-SC06346.90−12.5722.990.0230.011.7
Pal 2170.53−9.0727.2340.02250.012.2
NGC 693452.10−18.8915.450.0220.014.7
NGC 749253.39−63.4826.6110.01120.0210.1
NGC 4147252.8577.1918.2150.01110.010.3
IC 125716.5315.1425.090.0110.002.3
E 3292.27−19.028.120.0120.018.7
IC 4499307.35−20.4718.230.01110.035.0
NGC 2419180.3725.2483.270.00210.0110.3
Pal 1130.0619.0311.010.0010.0015.4
Ter 73.39−20.0722.810.0000.003.8
Djor 1356.68−2.4813.710.0010.005.6
Rup 106300.8911.6721.210.0000.004.6
Ter 85.76−24.5626.700.0020.006.5
Pyxis 0261.327.0039.400.0000.005.0
Pal 1518.8524.3445.120.0010.003.8
Pal 1230.51−47.6819.000.0000.0014.5
NGC 700663.77−19.4142.810.0050.007.4
Pal 3240.1441.8792.500.0000.0058.7
Whiting 1161.62−60.6431.300.0000.0029.6
Arp 28.54−20.7928.600.0010.006.2
Eridanus 0218.11−41.3390.100.0000.0056.1
AM 1258.36−48.47123.300.0000.00102.3
Pal 1387.10−42.7024.800.0000.0010.9
Crater 0274.8147.85145.000.0000.0090.4
NGC 642628.0916.2335.300.0000.0028.8
AM 4320.2833.5132.200.0000.0012.3
Pal 1428.7542.1971.000.0000.0010.3
Pal 4202.3171.80103.000.0000.0010.2
GClbD⊙Δx (isotropic)Δϕ (isotropic)ΔxΔϕPericentre
(deg)(deg)(kpc)(pc)(deg)(pc)(deg)(kpc)
NGC 65221.02−3.928.0335222.73850.610.2
NGC 64407.733.808.2333121.474673.160.2
Ter 1357.560.996.7202313.522972.040.4
NGC 104305.89−44.894.412388.5311147.716.2
NGC 6380350.18−3.429.816118.313761.960.3
NGC 66267.80−5.585.48277.511991.820.6
NGC 5139309.1014.975.27667.486586.441.4
NGC 6273356.879.388.311867.222931.800.3
NGC 64013.453.987.79416.722211.590.5
NGC 6266353.577.326.49196.485233.711.3
NGC 65445.84−2.202.62936.431403.080.5
Pal 62.091.785.88014.682811.650.2
NGC 6752336.49−25.634.24274.633513.813.6
NGC 6093352.6719.468.96634.251681.080.1
NGC 66569.89−7.553.22424.042984.982.8
NGC 671225.35−4.327.04813.962041.680.2
NGC 6453355.72−3.8711.69233.893201.350.4
NGC 6121350.9715.972.01793.56891.770.5
NGC 6441353.53−5.0111.87003.39950.461.0
NGC 640221.3214.809.35862.64100.040.7
NGC 4833303.60−8.026.22862.621511.380.5
NGC 5986337.0213.2710.64812.541490.790.4
NGC 6388345.56−6.7410.74422.255712.901.4
NGC 65690.48−6.6810.64222.232771.462.1
NGC 66387.90−7.1510.36192.041740.570.4
NGC 620559.0140.916.83972.031500.770.6
NGC 651719.236.7610.66192.021930.630.7
NGC 527242.2278.719.63932.013861.977.7
NGC 6355359.585.438.74131.991020.490.4
NGC 6304355.835.385.82181.841541.301.9
NGC 2808282.19−11.2510.25431.693471.080.8
NGC 65535.25−3.036.81981.661981.661.4
NGC 634168.3434.868.43451.631900.900.2
NGC 6293357.627.839.23321.62170.080.5
NGC 5946327.584.1910.62721.461260.680.3
Ter 53.841.695.51511.45730.701.1
NGC 621815.7126.314.71201.441001.202.4
NGC 66429.81−6.448.11981.40400.280.1
NGC 707865.01−27.3110.24451.394721.474.0
NGC 362301.53−46.259.22441.371320.740.3
NGC 6256347.793.316.42001.341270.852.3
NGC 6284358.359.9415.13661.321730.630.8
NGC 653920.806.787.82331.291861.031.4
NGC 6397338.17−11.962.4581.26701.532.1
NGC 63250.978.007.81711.23250.180.4
NGC 708953.37−35.7710.53011.201540.610.6
NGC 6541349.29−11.198.02611.202221.021.6
Ter 2356.322.307.53481.09350.110.3
Ter 4356.021.316.71281.0250.040.6
NGC 5286311.6110.5711.42240.961250.540.9
NGC 4372300.99−9.885.82360.952390.962.9
NGC 63566.7210.2215.12650.873131.032.4
NGC 677962.668.349.71620.841060.550.5
NGC 66242.79−7.917.21180.7720.010.4
Ter 104.42−1.875.8790.7690.090.8
NGC 65403.29−3.315.2680.75470.521.8
NGC 625415.1423.085.01890.751780.701.9
NGC 5897342.9530.2912.61700.741730.753.1
NGC 66812.85−12.519.32040.69610.210.0
NGC 59043.8646.807.6910.671240.915.4
NGC 6139342.376.949.81170.66520.291.1
NGC 6352341.42−7.175.91190.58900.433.1
FSR 1735339.19−1.859.81280.57490.220.6
IC 127621.835.675.41410.561260.503.5
UKS 15.120.767.81040.56370.200.6
NGC 66521.53−11.3810.01080.55150.080.3
NGC 683856.75−4.564.0890.50790.455.2
NGC 65281.14−4.177.53020.49600.100.5
NGC 636618.4116.043.7310.48380.591.9
NGC 676036.11−3.928.01780.472140.562.1
NGC 5024332.9679.7617.91580.461630.4814.6
NGC 67230.07−17.308.3730.46990.621.1
NGC 65580.20−6.027.21130.43240.090.4
Pal 814.11−6.8012.8950.41920.402.2
Djor 22.76−2.516.3540.4110.001.0
NGC 6362325.56−17.577.41360.411230.372.2
NGC 5927326.604.868.24630.403920.344.2
NGC 61713.3723.016.0420.39510.481.1
NGC 1851244.51−35.0411.31940.391450.290.1
2MASS-GC02 09.78−0.627.1960.38260.100.5
NGC 62870.1311.029.41340.37450.130.3
NGC 5824332.5622.0731.82380.352710.4010.0
NGC 63335.5410.718.41940.35550.100.8
FSR 1716329.78−1.597.5650.35570.312.3
Pal 1052.442.735.9870.35780.314.2
NGC 1904227.23−29.3513.31140.35890.270.2
Ter 93.60−1.997.1630.3460.030.2
BH 2613.36−5.276.5390.34260.231.5
Lynga 7328.77−2.808.0610.33730.391.7
Ter 3345.089.198.1770.32560.242.0
NGC 66371.72−10.278.8560.32300.170.7
NGC 3201277.238.644.5370.32460.397.8
Pal 1131.80−15.5814.3870.32810.295.6
NGC 6144351.9315.708.9750.27580.211.9
NGC 288151.28−89.3810.0510.25670.333.7
Ton 2350.80−3.426.4340.21270.161.9
NGC 1261270.54−52.1215.5880.211010.255.7
NGC 709927.18−46.848.0460.19750.311.6
NGC 63424.909.728.4370.11310.090.9
NGC 6496348.03−10.0111.3260.11310.133.9
NGC 6235358.9213.5213.5270.11380.154.9
NGC 686420.30−25.7521.6820.101390.173.4
NGC 5053335.7078.9517.2300.10310.1012.7
NGC 671712.88−10.907.1210.09140.061.3
NGC 6316357.185.7611.6210.091320.531.2
NGC 674936.19−2.217.8260.08450.141.7
NGC 698135.16−32.6817.0470.08510.095.5
NGC 2298245.63−16.0110.8190.08100.041.3
NGC 6584342.14−16.4113.2200.07600.212.2
NGC 622973.6440.3130.6890.06700.050.7
ESO 452-SC11351.9112.106.570.0610.010.5
NGC 68098.79−23.275.3380.06430.061.1
NGC 5634342.2149.2627.2390.05580.085.1
NGC 6101317.75−15.8216.1170.05210.0611.7
NGC 653527.1810.446.560.0410.001.0
NGC 4590299.6336.0510.190.03130.059.1
Ter 128.36−2.103.420.0220.023.1
NGC 546642.1573.5916.980.02100.0312.9
NGC 5694331.0630.3637.3400.02490.0313.9
Pal 50.8545.8623.280.0280.0216.3
ESO 280-SC06346.90−12.5722.990.0230.011.7
Pal 2170.53−9.0727.2340.02250.012.2
NGC 693452.10−18.8915.450.0220.014.7
NGC 749253.39−63.4826.6110.01120.0210.1
NGC 4147252.8577.1918.2150.01110.010.3
IC 125716.5315.1425.090.0110.002.3
E 3292.27−19.028.120.0120.018.7
IC 4499307.35−20.4718.230.01110.035.0
NGC 2419180.3725.2483.270.00210.0110.3
Pal 1130.0619.0311.010.0010.0015.4
Ter 73.39−20.0722.810.0000.003.8
Djor 1356.68−2.4813.710.0010.005.6
Rup 106300.8911.6721.210.0000.004.6
Ter 85.76−24.5626.700.0020.006.5
Pyxis 0261.327.0039.400.0000.005.0
Pal 1518.8524.3445.120.0010.003.8
Pal 1230.51−47.6819.000.0000.0014.5
NGC 700663.77−19.4142.810.0050.007.4
Pal 3240.1441.8792.500.0000.0058.7
Whiting 1161.62−60.6431.300.0000.0029.6
Arp 28.54−20.7928.600.0010.006.2
Eridanus 0218.11−41.3390.100.0000.0056.1
AM 1258.36−48.47123.300.0000.00102.3
Pal 1387.10−42.7024.800.0000.0010.9
Crater 0274.8147.85145.000.0000.0090.4
NGC 642628.0916.2335.300.0000.0028.8
AM 4320.2833.5132.200.0000.0012.3
Pal 1428.7542.1971.000.0000.0010.3
Pal 4202.3171.80103.000.0000.0010.2
Table A1.
Open in new tab

The estimation of shift along the orbit (Δx) produced by dynamical friction from only dark matter over the 5 Gyr time span. Angular shift (Δϕ) shows the angular distance between the GC and stream centre along the orbit as viewed from the Sun. D⊙ denotes the distance of the GC from the Sun. l and b denote the Galactic longitude and latitude of the GC. The calculations are made by assuming either isotropic or constant anisotropic dark matter particle velocity dispersion tensor with the anisotropy value adopted from stellar halo.

GClbD⊙Δx (isotropic)Δϕ (isotropic)ΔxΔϕPericentre
(deg)(deg)(kpc)(pc)(deg)(pc)(deg)(kpc)
NGC 65221.02−3.928.0335222.73850.610.2
NGC 64407.733.808.2333121.474673.160.2
Ter 1357.560.996.7202313.522972.040.4
NGC 104305.89−44.894.412388.5311147.716.2
NGC 6380350.18−3.429.816118.313761.960.3
NGC 66267.80−5.585.48277.511991.820.6
NGC 5139309.1014.975.27667.486586.441.4
NGC 6273356.879.388.311867.222931.800.3
NGC 64013.453.987.79416.722211.590.5
NGC 6266353.577.326.49196.485233.711.3
NGC 65445.84−2.202.62936.431403.080.5
Pal 62.091.785.88014.682811.650.2
NGC 6752336.49−25.634.24274.633513.813.6
NGC 6093352.6719.468.96634.251681.080.1
NGC 66569.89−7.553.22424.042984.982.8
NGC 671225.35−4.327.04813.962041.680.2
NGC 6453355.72−3.8711.69233.893201.350.4
NGC 6121350.9715.972.01793.56891.770.5
NGC 6441353.53−5.0111.87003.39950.461.0
NGC 640221.3214.809.35862.64100.040.7
NGC 4833303.60−8.026.22862.621511.380.5
NGC 5986337.0213.2710.64812.541490.790.4
NGC 6388345.56−6.7410.74422.255712.901.4
NGC 65690.48−6.6810.64222.232771.462.1
NGC 66387.90−7.1510.36192.041740.570.4
NGC 620559.0140.916.83972.031500.770.6
NGC 651719.236.7610.66192.021930.630.7
NGC 527242.2278.719.63932.013861.977.7
NGC 6355359.585.438.74131.991020.490.4
NGC 6304355.835.385.82181.841541.301.9
NGC 2808282.19−11.2510.25431.693471.080.8
NGC 65535.25−3.036.81981.661981.661.4
NGC 634168.3434.868.43451.631900.900.2
NGC 6293357.627.839.23321.62170.080.5
NGC 5946327.584.1910.62721.461260.680.3
Ter 53.841.695.51511.45730.701.1
NGC 621815.7126.314.71201.441001.202.4
NGC 66429.81−6.448.11981.40400.280.1
NGC 707865.01−27.3110.24451.394721.474.0
NGC 362301.53−46.259.22441.371320.740.3
NGC 6256347.793.316.42001.341270.852.3
NGC 6284358.359.9415.13661.321730.630.8
NGC 653920.806.787.82331.291861.031.4
NGC 6397338.17−11.962.4581.26701.532.1
NGC 63250.978.007.81711.23250.180.4
NGC 708953.37−35.7710.53011.201540.610.6
NGC 6541349.29−11.198.02611.202221.021.6
Ter 2356.322.307.53481.09350.110.3
Ter 4356.021.316.71281.0250.040.6
NGC 5286311.6110.5711.42240.961250.540.9
NGC 4372300.99−9.885.82360.952390.962.9
NGC 63566.7210.2215.12650.873131.032.4
NGC 677962.668.349.71620.841060.550.5
NGC 66242.79−7.917.21180.7720.010.4
Ter 104.42−1.875.8790.7690.090.8
NGC 65403.29−3.315.2680.75470.521.8
NGC 625415.1423.085.01890.751780.701.9
NGC 5897342.9530.2912.61700.741730.753.1
NGC 66812.85−12.519.32040.69610.210.0
NGC 59043.8646.807.6910.671240.915.4
NGC 6139342.376.949.81170.66520.291.1
NGC 6352341.42−7.175.91190.58900.433.1
FSR 1735339.19−1.859.81280.57490.220.6
IC 127621.835.675.41410.561260.503.5
UKS 15.120.767.81040.56370.200.6
NGC 66521.53−11.3810.01080.55150.080.3
NGC 683856.75−4.564.0890.50790.455.2
NGC 65281.14−4.177.53020.49600.100.5
NGC 636618.4116.043.7310.48380.591.9
NGC 676036.11−3.928.01780.472140.562.1
NGC 5024332.9679.7617.91580.461630.4814.6
NGC 67230.07−17.308.3730.46990.621.1
NGC 65580.20−6.027.21130.43240.090.4
Pal 814.11−6.8012.8950.41920.402.2
Djor 22.76−2.516.3540.4110.001.0
NGC 6362325.56−17.577.41360.411230.372.2
NGC 5927326.604.868.24630.403920.344.2
NGC 61713.3723.016.0420.39510.481.1
NGC 1851244.51−35.0411.31940.391450.290.1
2MASS-GC02 09.78−0.627.1960.38260.100.5
NGC 62870.1311.029.41340.37450.130.3
NGC 5824332.5622.0731.82380.352710.4010.0
NGC 63335.5410.718.41940.35550.100.8
FSR 1716329.78−1.597.5650.35570.312.3
Pal 1052.442.735.9870.35780.314.2
NGC 1904227.23−29.3513.31140.35890.270.2
Ter 93.60−1.997.1630.3460.030.2
BH 2613.36−5.276.5390.34260.231.5
Lynga 7328.77−2.808.0610.33730.391.7
Ter 3345.089.198.1770.32560.242.0
NGC 66371.72−10.278.8560.32300.170.7
NGC 3201277.238.644.5370.32460.397.8
Pal 1131.80−15.5814.3870.32810.295.6
NGC 6144351.9315.708.9750.27580.211.9
NGC 288151.28−89.3810.0510.25670.333.7
Ton 2350.80−3.426.4340.21270.161.9
NGC 1261270.54−52.1215.5880.211010.255.7
NGC 709927.18−46.848.0460.19750.311.6
NGC 63424.909.728.4370.11310.090.9
NGC 6496348.03−10.0111.3260.11310.133.9
NGC 6235358.9213.5213.5270.11380.154.9
NGC 686420.30−25.7521.6820.101390.173.4
NGC 5053335.7078.9517.2300.10310.1012.7
NGC 671712.88−10.907.1210.09140.061.3
NGC 6316357.185.7611.6210.091320.531.2
NGC 674936.19−2.217.8260.08450.141.7
NGC 698135.16−32.6817.0470.08510.095.5
NGC 2298245.63−16.0110.8190.08100.041.3
NGC 6584342.14−16.4113.2200.07600.212.2
NGC 622973.6440.3130.6890.06700.050.7
ESO 452-SC11351.9112.106.570.0610.010.5
NGC 68098.79−23.275.3380.06430.061.1
NGC 5634342.2149.2627.2390.05580.085.1
NGC 6101317.75−15.8216.1170.05210.0611.7
NGC 653527.1810.446.560.0410.001.0
NGC 4590299.6336.0510.190.03130.059.1
Ter 128.36−2.103.420.0220.023.1
NGC 546642.1573.5916.980.02100.0312.9
NGC 5694331.0630.3637.3400.02490.0313.9
Pal 50.8545.8623.280.0280.0216.3
ESO 280-SC06346.90−12.5722.990.0230.011.7
Pal 2170.53−9.0727.2340.02250.012.2
NGC 693452.10−18.8915.450.0220.014.7
NGC 749253.39−63.4826.6110.01120.0210.1
NGC 4147252.8577.1918.2150.01110.010.3
IC 125716.5315.1425.090.0110.002.3
E 3292.27−19.028.120.0120.018.7
IC 4499307.35−20.4718.230.01110.035.0
NGC 2419180.3725.2483.270.00210.0110.3
Pal 1130.0619.0311.010.0010.0015.4
Ter 73.39−20.0722.810.0000.003.8
Djor 1356.68−2.4813.710.0010.005.6
Rup 106300.8911.6721.210.0000.004.6
Ter 85.76−24.5626.700.0020.006.5
Pyxis 0261.327.0039.400.0000.005.0
Pal 1518.8524.3445.120.0010.003.8
Pal 1230.51−47.6819.000.0000.0014.5
NGC 700663.77−19.4142.810.0050.007.4
Pal 3240.1441.8792.500.0000.0058.7
Whiting 1161.62−60.6431.300.0000.0029.6
Arp 28.54−20.7928.600.0010.006.2
Eridanus 0218.11−41.3390.100.0000.0056.1
AM 1258.36−48.47123.300.0000.00102.3
Pal 1387.10−42.7024.800.0000.0010.9
Crater 0274.8147.85145.000.0000.0090.4
NGC 642628.0916.2335.300.0000.0028.8
AM 4320.2833.5132.200.0000.0012.3
Pal 1428.7542.1971.000.0000.0010.3
Pal 4202.3171.80103.000.0000.0010.2
GClbD⊙Δx (isotropic)Δϕ (isotropic)ΔxΔϕPericentre
(deg)(deg)(kpc)(pc)(deg)(pc)(deg)(kpc)
NGC 65221.02−3.928.0335222.73850.610.2
NGC 64407.733.808.2333121.474673.160.2
Ter 1357.560.996.7202313.522972.040.4
NGC 104305.89−44.894.412388.5311147.716.2
NGC 6380350.18−3.429.816118.313761.960.3
NGC 66267.80−5.585.48277.511991.820.6
NGC 5139309.1014.975.27667.486586.441.4
NGC 6273356.879.388.311867.222931.800.3
NGC 64013.453.987.79416.722211.590.5
NGC 6266353.577.326.49196.485233.711.3
NGC 65445.84−2.202.62936.431403.080.5
Pal 62.091.785.88014.682811.650.2
NGC 6752336.49−25.634.24274.633513.813.6
NGC 6093352.6719.468.96634.251681.080.1
NGC 66569.89−7.553.22424.042984.982.8
NGC 671225.35−4.327.04813.962041.680.2
NGC 6453355.72−3.8711.69233.893201.350.4
NGC 6121350.9715.972.01793.56891.770.5
NGC 6441353.53−5.0111.87003.39950.461.0
NGC 640221.3214.809.35862.64100.040.7
NGC 4833303.60−8.026.22862.621511.380.5
NGC 5986337.0213.2710.64812.541490.790.4
NGC 6388345.56−6.7410.74422.255712.901.4
NGC 65690.48−6.6810.64222.232771.462.1
NGC 66387.90−7.1510.36192.041740.570.4
NGC 620559.0140.916.83972.031500.770.6
NGC 651719.236.7610.66192.021930.630.7
NGC 527242.2278.719.63932.013861.977.7
NGC 6355359.585.438.74131.991020.490.4
NGC 6304355.835.385.82181.841541.301.9
NGC 2808282.19−11.2510.25431.693471.080.8
NGC 65535.25−3.036.81981.661981.661.4
NGC 634168.3434.868.43451.631900.900.2
NGC 6293357.627.839.23321.62170.080.5
NGC 5946327.584.1910.62721.461260.680.3
Ter 53.841.695.51511.45730.701.1
NGC 621815.7126.314.71201.441001.202.4
NGC 66429.81−6.448.11981.40400.280.1
NGC 707865.01−27.3110.24451.394721.474.0
NGC 362301.53−46.259.22441.371320.740.3
NGC 6256347.793.316.42001.341270.852.3
NGC 6284358.359.9415.13661.321730.630.8
NGC 653920.806.787.82331.291861.031.4
NGC 6397338.17−11.962.4581.26701.532.1
NGC 63250.978.007.81711.23250.180.4
NGC 708953.37−35.7710.53011.201540.610.6
NGC 6541349.29−11.198.02611.202221.021.6
Ter 2356.322.307.53481.09350.110.3
Ter 4356.021.316.71281.0250.040.6
NGC 5286311.6110.5711.42240.961250.540.9
NGC 4372300.99−9.885.82360.952390.962.9
NGC 63566.7210.2215.12650.873131.032.4
NGC 677962.668.349.71620.841060.550.5
NGC 66242.79−7.917.21180.7720.010.4
Ter 104.42−1.875.8790.7690.090.8
NGC 65403.29−3.315.2680.75470.521.8
NGC 625415.1423.085.01890.751780.701.9
NGC 5897342.9530.2912.61700.741730.753.1
NGC 66812.85−12.519.32040.69610.210.0
NGC 59043.8646.807.6910.671240.915.4
NGC 6139342.376.949.81170.66520.291.1
NGC 6352341.42−7.175.91190.58900.433.1
FSR 1735339.19−1.859.81280.57490.220.6
IC 127621.835.675.41410.561260.503.5
UKS 15.120.767.81040.56370.200.6
NGC 66521.53−11.3810.01080.55150.080.3
NGC 683856.75−4.564.0890.50790.455.2
NGC 65281.14−4.177.53020.49600.100.5
NGC 636618.4116.043.7310.48380.591.9
NGC 676036.11−3.928.01780.472140.562.1
NGC 5024332.9679.7617.91580.461630.4814.6
NGC 67230.07−17.308.3730.46990.621.1
NGC 65580.20−6.027.21130.43240.090.4
Pal 814.11−6.8012.8950.41920.402.2
Djor 22.76−2.516.3540.4110.001.0
NGC 6362325.56−17.577.41360.411230.372.2
NGC 5927326.604.868.24630.403920.344.2
NGC 61713.3723.016.0420.39510.481.1
NGC 1851244.51−35.0411.31940.391450.290.1
2MASS-GC02 09.78−0.627.1960.38260.100.5
NGC 62870.1311.029.41340.37450.130.3
NGC 5824332.5622.0731.82380.352710.4010.0
NGC 63335.5410.718.41940.35550.100.8
FSR 1716329.78−1.597.5650.35570.312.3
Pal 1052.442.735.9870.35780.314.2
NGC 1904227.23−29.3513.31140.35890.270.2
Ter 93.60−1.997.1630.3460.030.2
BH 2613.36−5.276.5390.34260.231.5
Lynga 7328.77−2.808.0610.33730.391.7
Ter 3345.089.198.1770.32560.242.0
NGC 66371.72−10.278.8560.32300.170.7
NGC 3201277.238.644.5370.32460.397.8
Pal 1131.80−15.5814.3870.32810.295.6
NGC 6144351.9315.708.9750.27580.211.9
NGC 288151.28−89.3810.0510.25670.333.7
Ton 2350.80−3.426.4340.21270.161.9
NGC 1261270.54−52.1215.5880.211010.255.7
NGC 709927.18−46.848.0460.19750.311.6
NGC 63424.909.728.4370.11310.090.9
NGC 6496348.03−10.0111.3260.11310.133.9
NGC 6235358.9213.5213.5270.11380.154.9
NGC 686420.30−25.7521.6820.101390.173.4
NGC 5053335.7078.9517.2300.10310.1012.7
NGC 671712.88−10.907.1210.09140.061.3
NGC 6316357.185.7611.6210.091320.531.2
NGC 674936.19−2.217.8260.08450.141.7
NGC 698135.16−32.6817.0470.08510.095.5
NGC 2298245.63−16.0110.8190.08100.041.3
NGC 6584342.14−16.4113.2200.07600.212.2
NGC 622973.6440.3130.6890.06700.050.7
ESO 452-SC11351.9112.106.570.0610.010.5
NGC 68098.79−23.275.3380.06430.061.1
NGC 5634342.2149.2627.2390.05580.085.1
NGC 6101317.75−15.8216.1170.05210.0611.7
NGC 653527.1810.446.560.0410.001.0
NGC 4590299.6336.0510.190.03130.059.1
Ter 128.36−2.103.420.0220.023.1
NGC 546642.1573.5916.980.02100.0312.9
NGC 5694331.0630.3637.3400.02490.0313.9
Pal 50.8545.8623.280.0280.0216.3
ESO 280-SC06346.90−12.5722.990.0230.011.7
Pal 2170.53−9.0727.2340.02250.012.2
NGC 693452.10−18.8915.450.0220.014.7
NGC 749253.39−63.4826.6110.01120.0210.1
NGC 4147252.8577.1918.2150.01110.010.3
IC 125716.5315.1425.090.0110.002.3
E 3292.27−19.028.120.0120.018.7
IC 4499307.35−20.4718.230.01110.035.0
NGC 2419180.3725.2483.270.00210.0110.3
Pal 1130.0619.0311.010.0010.0015.4
Ter 73.39−20.0722.810.0000.003.8
Djor 1356.68−2.4813.710.0010.005.6
Rup 106300.8911.6721.210.0000.004.6
Ter 85.76−24.5626.700.0020.006.5
Pyxis 0261.327.0039.400.0000.005.0
Pal 1518.8524.3445.120.0010.003.8
Pal 1230.51−47.6819.000.0000.0014.5
NGC 700663.77−19.4142.810.0050.007.4
Pal 3240.1441.8792.500.0000.0058.7
Whiting 1161.62−60.6431.300.0000.0029.6
Arp 28.54−20.7928.600.0010.006.2
Eridanus 0218.11−41.3390.100.0000.0056.1
AM 1258.36−48.47123.300.0000.00102.3
Pal 1387.10−42.7024.800.0000.0010.9
Crater 0274.8147.85145.000.0000.0090.4
NGC 642628.0916.2335.300.0000.0028.8
AM 4320.2833.5132.200.0000.0012.3
Pal 1428.7542.1971.000.0000.0010.3
Pal 4202.3171.80103.000.0000.0010.2
© 2019 The Author(s) Published by Oxford University Press on behalf of the Royal Astronomical Society
This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)
Issue Section:
Article
Download all slides