-
PDF
- Split View
-
Views
-
Cite
Cite
Takanobu Kirihara, Ataru Tanikawa, Tomoaki Ishiyama, Effect of interstellar objects on metallicity of low-mass first stars formed in a cosmological model, Monthly Notices of the Royal Astronomical Society, Volume 486, Issue 4, July 2019, Pages 5917–5923, https://doi.org/10.1093/mnras/stz1277
Close - Share Icon Share
ABSTRACT
We investigate metal pollution on to the surface of low-mass population III stars (Pop. III survivors) via interstellar objects (ISOs) floating in the Galactic interstellar medium. Only recently, Tanikawa et al. analytically estimated how much metal should collide to an orbiting Pop. III survivor encouraged by the recent discovery of 'Oumuamua and suggested that ISOs are the most dominant contributor of metal enrichment of Pop. III survivors. When we consider a distribution of ISOs in the Galactic disc, Pop. III survivors’ orbits are significant properties to estimate the accretion rate of them though Tanikawa et al. assumed one modelled orbit. To take more realistic orbits into calculating the accretion rate, we use a high-resolution cosmological N-body simulation that resolves dark matter minihaloes. Pop. III survivors located at solar neighbourhood have a number of chances of ISO (>100 m) collisions, typically 5 × 106 times in the last 5 Gyr, which is one order of magnitude greater than estimated in the previous study. When we assume a power-law parameter α of the ISO cumulative number density with size greater than D as n ∝ D−α, |$0.80 \, \mathrm{M}_\odot$| stars should be typically polluted [Fe/H] ∼ −2 for the case of α = 2.0. Even in the cases of 0.70 and |$0.75 \, \mathrm{M}_\odot$| stars, the typical surface metallicity are around [Fe/H] = −6 ∼ −5. From the presence of stars with their [Fe/H], we can constrain on the lower limit of the power α, as α ≳ 2.0, which is consistent with α of km-size asteroids and comets in the Solar system. Furthermore, we provide six candidates as the ISO-polluted Pop. III stars in the case of α ∼ 2.5. Metal-poor stars so far discovered are possible to be metal-free Pop. III stars on birth.
1 INTRODUCTION
Formation of the first stars, so-called Population III (Pop. III) stars, is expected to play an essential role in cosmic history. Pop. III stars were formed in pristine gas and marked the end of ‘Dark Age’ of the universe. They produced first heavy elements in the universe, and the metals derive the next-generation stars. To investigate the nature of the first objects, a number of studies have simulated the formation of primordial clouds considering H2 cooling (e.g. Tegmark et al. 1997; Omukai & Nishi 1998; Nakamura & Umemura 2001; Omukai & Palla 2001, 2003; Abel, Bryan & Norman 2002; Bromm, Coppi & Larson 2002; Schneider et al. 2002; Yoshida et al. 2006; Yoshida, Omukai & Hernquist 2008; Bromm et al. 2009; Hosokawa et al. 2011; Stacy, Greif & Bromm 2012). In the Lambda cold dark matter universe, the formation of Pop. III stars began at z ∼ 20 in dark matter minihaloes with their mass of |$10^5{-}10^6 \, \mathrm{M}_\odot$| (Abel et al. 2002; Bromm et al. 2002, 2009). Cosmological radiation hydrodynamical simulations have suggested that typical Pop. III stars are very massive |$10{\rm {-}}1000 \, \mathrm{M}_\odot$| (Susa, Hasegawa & Tominaga 2014; Hirano et al. 2014, 2015). Pop. III star formation in minihaloes lasts in reionization epoch (z ∼ 10) due to the photodissociation of H2 molecule. Since lifetimes of such massive stars are short ∼10 Myr, in situ Pop. III stars should be explored in the high-redshift universe. Therefore, direct observation of the signal is still quite difficult (Barkana 2018).
Alternatively, we have a chance to directly explore Pop. III stars in the Milky Way (MW). If Pop. III stars are born as low-mass stars and their mass is |${\lesssim } 0.8 \, \mathrm{M}_\odot$|, they have much longer lifetimes and could survive in the present-day universe (hereafter, Pop. III survivors). As recent cosmological hydrodynamic simulations show, circumstellar discs around first protostars are unstable and gravitational fragmentation is induced (e.g. Machida et al. 2008; Clark et al. 2011a,b; Greif et al. 2011, 2012; Susa et al. 2014). Low-mass Pop. III stars are expected to be born in the discs via such fragmentation (e.g. Greif et al. 2012; Susa 2019). However, no metal-free star has been discovered so far although there have been great efforts for finding Pop. III survivors with large surveys of more than 105 field stars in the MW (Frebel & Norris 2015, and the references therein).
One possible interpretation of the lack of metal-free stars in the MW is that metals in the interstellar medium might pollute their surface (Yoshii 1981; Komiya et al. 2009; Komiya, Suda & Fujimoto 2015; Shen et al. 2017). It means that Pop. III survivors might not be able to keep metal-free in the MW. Komiya et al. (2015) showed the surface of Pop. III stars can be polluted up to [Fe/H] ∼ −5. Shen et al. (2017) investigated such metal pollution using a cosmological simulation and showed the typical metallicity of Pop. III stars with |$0.8 \, \mathrm{M}_\odot$| is [Fe/H] = −6 ∼ −5. In the context, metal enrichment occurs in the shallow convection layer; therefore, a relatively small amount of accreted heavy elements affects the observed metal abundance of stars. When calculating gas accretion, however, Bondi–Hoyle accretion model was always adopted (Komiya et al. 2009; Komiya et al. 2015; Shen et al. 2017). Tanaka et al. (2017) and Suzuki (2018) evaluated the effects of stellar wind to such accreting gas and concluded that stellar wind prevents accretion of heavy elements. Then, the resultant metallicity becomes only up to [Fe/H] ∼ −14 (Tanaka et al. 2017). Interstellar dust should not pollute Pop. III survivors, either. It is sublimated to gas by stellar radiation before it reaches to stellar surface, and is blown away by stellar wind.
Only recently, Tanikawa, Suzuki & Doi (2018) first pointed out the importance of the metal pollution of colliding interstellar objects (ISOs) or interstellar asteroids like 'Oumuamua, which is the first ISO observed passing through the Solar system using the Pan-STARRS1 telescope (Meech et al. 2017). Tanikawa et al. (2018) analytically estimated how much metal should collide to an orbiting Pop. III survivor. In their study, they focused on how ISOs provided their metal varying the size distribution of ISOs and suggested that ISOs are the most dominant contributor of metal enrichment of Pop. III survivors.
After the discovery of 'Oumuamua, the origin and the number density of similar objects have been actively discussed. Do, Tucker & Tonry (2018) estimated the number density of ISOs as 0.2 au−3 considering the detection of 'Oumuamua with the survey volume and time of Pan-STARRS. They considered the origin as the released object of exoplanetary Oort cloud at the end of a star’s main-sequence lifetime and the progenitor might be a white dwarf. Similar objects could be produced in tidal disruption events of asteroids or planets by white dwarfs (Rafikov 2018), and in a fragment of a comet-like planetesimal born in a planet-forming disc (Raymond, Armitage & Veras 2018). The high number density can be explained by the amount of debris ejected during the formation process of planets (Portegies Zwart et al. 2018). However, the situation that non-gravitational acceleration was observed despite no sign of a cometary tail (Meech et al. 2017; Fitzsimmons et al. 2018) is still puzzling (Bialy & Loeb 2018).
In this paper, we revisit investigating metal pollution on to Pop. III survivors via ISOs floating in the Galactic interstellar medium. One key parameter is the accretion rate of ISOs that would be significantly affected by the orbit of Pop. III survivors because how long the survivors spend their lives in ISO-rich region decides it. However, the estimation of the accretion rate in Tanikawa et al. (2018) was derived by assuming one modelled survivor’s orbit. To take more realistic orbits into calculating the accretion rate, we use a high-resolution cosmological simulation and a Pop. III formation model carried out by Ishiyama et al. (2016). The cosmological N-body simulation resolves dark matter minihaloes to predict where low-mass Pop. III survivors are distributed in the halo of the MW.
This paper is organized as follows. In Section 2, we describe our numerical modelling for the estimation of metal pollution of Pop. III survivors using the cosmological N-body simulation. The accretion rate of ISOs to Pop. III stars and the resultant surface metallicity of Pop. III stars are described in Section 3. In Section 4, we state discussions for recent observations of metal-poor stars. In Section 5, we present a brief summary.
2 NUMERICAL MODELLING
2.1 Cosmological N-body simulation
We focus on orbits of surviving low-mass Pop. III stars in the MW via hierarchical structure formation based on the Lambda cold dark matter model. For this purpose, we adopt a high-resolution cosmological N-body simulation conducted by Ishiyama et al. (2016) using a massively parallel TreePM code GreeM (Ishiyama, Fukushige & Makino 2009; Ishiyama, Nitadori & Makino 2012). The simulation adopts the cosmological parameter set of Ω0 = 0.31, Ωb = 0.048, λ0 = 0.69, h = 0.68, ns = 0.96 and σ8 = 0.83 (Planck Collaboration XVI 2014), and is run with 20483 dark matter particles in a comoving box of 8 |$\, h^{-1}\, \rm Mpc$|. A particle mass is |$5.13\times 10^3\, h^{-1}\, \mathrm{M}_{\odot }$| and the gravitational softening is 120 |$\, h^{-1}\, \rm pc$|.
It is widely believed that Pop. III stars are born in H2 molecule cooling minihaloes without metals. Ishiyama et al. (2016) combined the cosmological N-body simulation and the Pop. III star formation modelling the Pop. III formation under cosmic UV radiation. They imposed the upper and lower criteria of the virial temperature of the minihaloes for the Pop. III formation. Dark matter haloes are identified by Friends-of-Friends (FoF) algorithm (Davis et al. 1985) adopting a linking parameter of b = 0.2. The details of constructing merger trees are described in Ishiyama et al. (2015). The smallest haloes consist of 32 particles that resolve dark matter minihaloes where Pop. III stars are expected to be formed. In this study, we assume that one low-mass (|$0.7{-}0.8 \, \mathrm{M}_\odot$|) Pop. III survivor exists in each minihalo, and the star is represented by the particle which is gravitationally most bound at the formation redshift of the Pop. III star.
The cosmological simulation contains nine MW-sized haloes at z = 0. Only to obtain time evolution of MW-sized haloes, we use catalogues generated by ROCKSTAR (Robust Overdensity Calculation using K-Space Topologically Adaptive Refinement) halo finder (Behroozi, Wechsler & Wu 2013a) and a consistent trees code (Behroozi et al. 2013b). In post-process, we track Pop. III survivors’ orbits and calculate how long and where they are in the disc. We track Pop. III survivors’ orbits adopting a linear interpolate between snapshots of the cosmological N-body simulation spaced by 0.01 in Δlog10(1 + z), and the number of interpolation is set to 100. For the purpose, we embed a stable Galactic disc to the central region of the host halo taken from the cosmological N-body simulation. As a working hypothesis, the angular momentum of the disc is always set to point the same direction as that of the host halo. For a safety selection, we select a halo which does not experience a major merger since 5 Gyr ago and whose angular momentum changes little since then. Sales et al. (2012) suggested that disc galaxies tend to have roughly aligned angular momentum from inner region to outer region. The selected halo is the third most massive halo, which has the virial mass and virial radius of |$2.27\times 10^{12} \, \mathrm{M}_\odot$| and 345 kpc, respectively. We rotate all the halo particles as the pole of the disc points z-axis in Cartesian coordinate.
2.2 ISO number density and size distribution
ISOs are made from heavy elements. The spatial distribution of ISOs is still under debate, however, one possibility of their origin is that planet-forming discs around Pop. I stars produce them. Therefore, ISOs are thought to be distributed in the Galactic disc, which consists of metal-rich Pop. I stars (Seligman & Laughlin 2018). To calculate the ISO accretion rate, we assume that the spatial distribution of ISOs is proportional to the stellar density of the Galactic thin disc.
2.3 ISO accretion rate
Tanikawa et al. (2018) adopted a constant relative velocity of 310 km s−1, which is multiplied by |$\sqrt{2}$| to the circular velocity of the Galactic disc. The value f was also a constant parameter of 0.032 that was calculated by the assuming orbit. Then, Tanikawa et al. (2018) obtained the accretion rate of |$1.4\times 10^{-4}\, {\rm yr^{-1}}$|. It means the number of chances that an ISO accretes to a Pop. III survivor is 1.4 × 105 times per 1 Gyr.
Dmin is the minimum radius of an ISO, which can collide to the surface of Pop. III survivors. When a smaller ISO approaches a Pop. III survivor, it would be radiated and sublimated by the Pop. III survivor. Once the ISO is sublimated, the debris would be blown away by stellar wind and would not accrete to the Pop. III survivor. According to Tanikawa et al. (2018), Dmin is estimated to be 3 km considering the sublimation effect. Dmax is the maximum radius of ISOs, which can collide with a Pop. III survivor once at least. It depends on the accretion rate of ISOs, which we obtain for each Pop. III survivor from our cosmological simulation.
2.4 Metal enrichment of Pop. III survivors
We estimate the metallicity of the surface of Pop. III survivors for three stellar masses (|$0.7$|, |$0.75$|, and |$0.8 \, \mathrm{M}_\odot$|) varying the power-law parameter α. Calculation of the amount of metal supplied by an ISO accretion is completely following Tanikawa et al. (2018). We here put a brief description of the method, and Tanikawa et al. (2018) give further details.
We consider surface pollution of Pop. III survivors. Accreting metals are mixed only within their convection zone under their surface. Pop. III stars are thought to be born after <1 Gyr of the big bang. Their ages are therefore >12 Gyr if such stars are observed in the MW. According to Richard, Michaud & Richer (2002), metal-poor stars with the stellar masses of |$0.8 \, \mathrm{M}_\odot$| survive for >12 Gyr.
Richard et al. (2002) calculated stellar evolution and obtained the mass above the base of the surface convection zone in each stellar mass. We here adopt their calculation for cases of |$0.7$|, |$0.75$|, and |$0.8 \, \mathrm{M}_\odot$|. In the case of |$0.7$| and |$0.75 \, \mathrm{M}_\odot$| stars, the mass fraction of convection zones are respectively approximately 10−2 and 10−2.5 at 5 Gyr ago, and these values are slightly decreasing with time. In the case of |$0.8 \, \mathrm{M}_\odot$| stars, the fraction rapidly decreases with time from 10−3.5 at ∼5 Gyr to 10−6 at the last ∼1 Gyr. It means that the efficiency of metal pollution is boosted at the end of their lifetimes.
3 NUMERICAL RESULTS
3.1 ISO accretion rate
Fig. 1 shows the distribution of the ISO accretion rate |$\dot{N}_{{\rm acc}, 0}$| on to Pop. III survivors in the last 5 Gyr (≡ ΔtISO). We select the Pop. III survivors distributed in the Galactocentric distance of |$7\, {\rm kpc} \lt R\lt 9\, {\rm kpc}$| and in the Galactic plane (|Z| < 400 pc) at z = 0 The median and average accretion rates are showed with higher and lower bars, respectively. The typical value of |$\dot{N}_{{\rm acc}, 0}$| is around 10−3, which is approximately one order of magnitude greater than the analytical estimation by Tanikawa et al. (2018) as shown with the blue dashed line. Even in the case of the flat disc model, which is mimicking Tanikawa et al. (2018), is higher by a factor of five than the analytical estimation. Such a high accretion rate of ISOs on to Pop. III survivors is first revealed by the use of cosmological simulation. Orbiting within the Galactic disc and/or similar trail of a Pop. III survivor to the galactic rotation seem to be the causes of greater |$\dot{N}_{{\rm acc}, 0}$|. The accretion rate in the case of the exponential disc is roughly higher by a factor of 2 than that of the flat disc model. Since orbiting time in the Galactic disc in each model is the same, it means that most Pop. III survivors have more chance to pass through inner |$8\, {\rm kpc}$| than |$8\, {\rm kpc}\lt R\lt 10\, {\rm kpc}$|. In fact, some Pop. III survivors with higher accretion rate approach Galactic centre in their orbital motion. We hereafter consider only the case of the exponential disc model. Most noticeably, the survivors have more chances to get metal polluted by ISOs estimated so far. If |$\dot{N}_{{\rm acc}, 0}$| is |$10^{-3}\, {\rm yr}^{-1}$|, the number of collisions is estimated to 5 × 106 times in 5 Gyr.
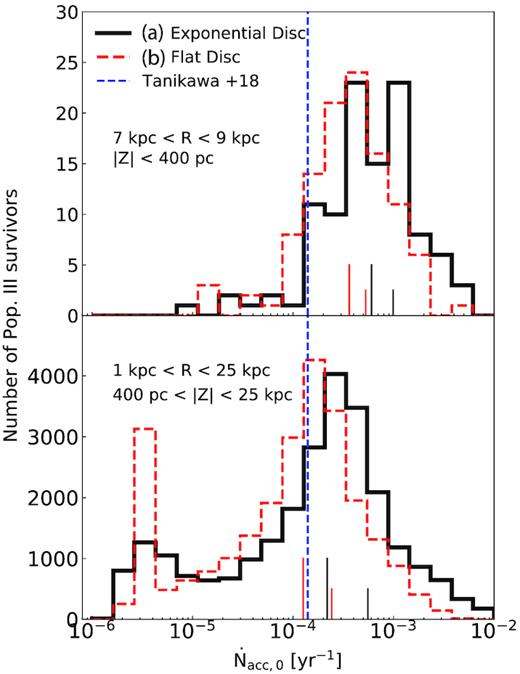
Top panel: ISO accretion rate on to Pop. III survivors, which are distributed in the Galactocentric distance of |$7\, {\rm kpc}\lt R\lt 9\, {\rm kpc}$| and in the Galactic plane |$|Z|\lt 400\, {\rm pc}$| at z = 0. Black solid and red dashed lines show the cases of (a) the exponential disc model and (b) the flat disc model, respectively. The blue dashed line indicates the analytical estimation by Tanikawa et al. (2018). Higher and lower bars show the median and average accretion rate, respectively. Bottom panel: ISO accretion rate on to Pop. III survivors, which are distributed in the inner galactic halo and outside of the disc (|$1\, {\rm kpc}\lt R\lt 25\, {\rm kpc}$| and |$400\, {\rm pc}\lt |Z|\lt 25\, {\rm kpc}$|) at z = 0. Higher and lower bars, respectively, show the median and average accretion rate except for metal-free samples.
The bottom panel of Fig. 1 shows the ISO accretion rates on to Pop. III survivors, which are distributed in the galactic inner halo (|$1\, {\rm kpc}\lt R\lt 25\, {\rm kpc}$| and |$400\, {\rm pc}\lt |Z|\lt 25\, {\rm kpc}$|) at z = 0. The samples are less polluted by ISOs floating in the Galactic disc compared with those of the solar neighbourhood. Under the condition of the ISO distribution, ∼80 per cent of Pop. III survivors experienced disc-crossing at least once in the last 5 Gyr. The median value of the ISO accretion rate for the surface-polluted samples is the same degree estimated by Tanikawa et al. (2018). The median surface metallicity of Pop. III survivors is smaller than that of the solar neighbourhood samples by ∼0.5−1 dex in Fig. 2. Well-measured metal-poor stars tend to be located in the solar neighbourhood (e.g. Sestito et al. 2019); therefore, we mainly focus on the samples that are located in the solar neighbourhood.
![Number distribution of Pop. III survivors as a function of the surface metallicity [Fe/H] with (a) α = 3.0, (b) α = 2.5, and (c) α = 2.0. The difference of each line is the adopted stellar mass of Pop. III survivors of $M_*=0.80 \, \mathrm{M}_\odot$ (black line), $M_*=0.75 \, \mathrm{M}_\odot$ (red line), and $M_*=0.70 \, \mathrm{M}_\odot$ (blue line). In panel (a), we additionally plot the case of $(M_*, \alpha)=(0.80 \, \mathrm{M}_\odot , 3.5)$ with magenta line. We select the survivors whose current loci are in the Galactocentric distance of $7\, {\rm kpc}\lt R\lt 9\, {\rm kpc}$ and in the Galactic disc (|Z| < 400 pc).](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/486/4/10.1093_mnras_stz1277/1/m_stz1277fig2.jpeg?Expires=1750504652&Signature=LJTuTJYcj~VyYnIZ7STR00uZ28e8F9yDcqR2Q9k5iGcJ5hHYjpQpi2gYgMN3SyGEtESeW5wXWQcedS-V12szWKEeu7G-QWuOaU4F7EDNmZLc2vlgjsifTVU1XubWP7jb0Mkfcw8KLhiSXl7kXG5z26p~ZeHBPvyIUXrkZETZe6062HpnKdIeA5BqePA3YDas-2WmQndVno6ZXXX1eY3Io4MmhQ7rquY~Fy39tiIqivosos86Bj~rV0F0B7K35KAVmhdAkldMMOGWIlrQs6x-E11aWE7PfgBJCEwW250qjg~AQIunNQjwL1EXHjhRHQjhD1Xgh4t0FF0srIZNm8doAQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Number distribution of Pop. III survivors as a function of the surface metallicity [Fe/H] with (a) α = 3.0, (b) α = 2.5, and (c) α = 2.0. The difference of each line is the adopted stellar mass of Pop. III survivors of |$M_*=0.80 \, \mathrm{M}_\odot$| (black line), |$M_*=0.75 \, \mathrm{M}_\odot$| (red line), and |$M_*=0.70 \, \mathrm{M}_\odot$| (blue line). In panel (a), we additionally plot the case of |$(M_*, \alpha)=(0.80 \, \mathrm{M}_\odot , 3.5)$| with magenta line. We select the survivors whose current loci are in the Galactocentric distance of |$7\, {\rm kpc}\lt R\lt 9\, {\rm kpc}$| and in the Galactic disc (|Z| < 400 pc).
3.2 Metal enrichment of Pop. III survivors
In Fig. 2, we plot the number distribution of Pop. III survivors in solar neighbourhood as a function of [Fe/H]. ISO pollution strongly depends on power-law α. Typical surface metallicity in all stellar mass models decreases with increasing α.
Surprisingly, in the case of |$0.8 \, \mathrm{M}_\odot$| stars and α = 2.0, the typical Pop. III survivors are much more metal rich than the so far observed most metal-poor stars. Even in the cases of 0.7 and |$0.75 \, \mathrm{M}_\odot$| stars, the typical surface metallicity are around [Fe/H] = −6 ∼ −5. The metallicity profile is highly depending on the power-law parameter α. It should be noted that the metal pollution is caused by cumulative ISO accretion.
One possibility to distinguish between originally metal-poor stars and metal-polluted Pop. III stars is to see the metal abundance pattern. That is because the metal abundance pattern of metal-enriched Pop. III stars is originated in ISOs. We expect that the metal abundance pattern is similar to the solar metal abundance pattern.
Fig. 3 shows the average [Fe/H] distribution of Pop. III survivors as a function of the Galactocentric radius R. To plot this figure, we select the survivors whose current loci are in the Galactic disc (|Z| < 400 pc). From the plot, we obtain a metallicity gradient for typical metallicity of surface metal-polluted Pop. III survivors. The average metallicity decreases in all models with increasing the Galactocentric radius. When we look at Pop. III survivors near the Galactic centre, they would be polluted typically [Fe/H] ≳ −2 if α ≲ 2.5. We may not be able to distinguish between such highly polluted Pop. III survivors and originally metal-poor stars. In each line, there is a break at R = 10 kpc due to the assuming ISO distribution. The Pop. III survivors are located at outer the edge of the Galactic disc at z = 0. This situation causes the break in the profile around the edge.
![Average [Fe/H] distribution of Pop. III survivors as a function of the Galactocentric radius R with (a) α = 3.0, (b) α = 2.5, and (c) α = 2.0. The difference of each line is the adopted stellar mass of Pop. III survivors of $M_*=0.80 \, \mathrm{M}_\odot$ (black line), $M_*=0.75 \, \mathrm{M}_\odot$ (red line), and $M_*=0.70 \, \mathrm{M}_\odot$ (blue line). The magenta line in panel (a) shows the case of $(M_*, \alpha)=(0.80 \, \mathrm{M}_\odot , 3.5)$. We select the survivors whose current loci are in the Galactic disc (|Z| < 400 pc). The vertical dashed line corresponds to the Galactocentric solar distance.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/486/4/10.1093_mnras_stz1277/1/m_stz1277fig3.jpeg?Expires=1750504652&Signature=N0mmtJqN-m~4lUgQ8KWvlmeAz9dpU52gGjTEpl57mohaY9JSVMcj5bKbRtT57GKww3EjhhuOg1hIZmkFMn1oHBxM9KhDxnEljo7ajHvVkbtU1SV8RvixSGN8UFVk8wZJ7wLB5ks-va-E4mMK-r9qXz2LeoY-yh1OoAtYe4kgQHrQN5Uh~JHxlKYXgiNG1eyqMxvilMR82dVdj98OBnooiBCOlA~Al5D3FVBhaRKA1lcxcFO4OJOEKZmqujqShrXrHEy9aTWQ0o7g2yxSVT8a-neu7pbvazVDnAaYlH74eo41IG3KVR2McGZYTcg2JqGI0Mrk68wn3w1bXaQMXYUZhQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Average [Fe/H] distribution of Pop. III survivors as a function of the Galactocentric radius R with (a) α = 3.0, (b) α = 2.5, and (c) α = 2.0. The difference of each line is the adopted stellar mass of Pop. III survivors of |$M_*=0.80 \, \mathrm{M}_\odot$| (black line), |$M_*=0.75 \, \mathrm{M}_\odot$| (red line), and |$M_*=0.70 \, \mathrm{M}_\odot$| (blue line). The magenta line in panel (a) shows the case of |$(M_*, \alpha)=(0.80 \, \mathrm{M}_\odot , 3.5)$|. We select the survivors whose current loci are in the Galactic disc (|Z| < 400 pc). The vertical dashed line corresponds to the Galactocentric solar distance.
4 DISCUSSION
4.1 Constraint on ISO pollution
ISOs should pollute not only Pop. III survivors but also originally metal-poor stars, which are born from metal-enriched gas. In other words, ISO pollution prohibits the presence of stars with [Fe/H] less than a certain value dependent on α. Thus, we can constrain on the lower limit of the power α (or the upper limit of ISO pollution) from the presence of metal-poor stars discovered so far.
For this purpose, we pick up metal-poor stars from the SAGA data base (Suda et al. 2008). We confine metal-poor stars to those in the MW. We can use only main-sequence metal-poor stars. Since post main-sequence stars, such as red giant stars, have massive convection zones, ISO pollution should be diluted by several orders of magnitude and should be erased. We adopt the definition of main-sequence stars in the SAGA data base. We have to estimate the mass and convection zones of metal-poor stars, on which ISO pollution strongly depends (see Fig. 2). For this estimate, we refer to effective temperature (Teff) of metal-poor stars. We assume stars with Teff ≲ 6000 K, 6000 K ≲ Teff ≲ 6400 K, and Teff ≳ 6400 K have 0.7, 0.75, and |$0.8 \, \mathrm{M}_\odot$|, respectively, based on Richard et al. (2002). Note that this can be applied for stars with [Fe/H] ≲ − 3.31. Stars with Teff ≲ 6400 K can have |$0.8 \, \mathrm{M}_\odot$|, when they are young, several Gyr old. We can regard such stars ISO-polluted to the same extent as stars with 0.7–|$0.75 \, \mathrm{M}_\odot$|, since such stars have as thick a convection zone as stars with 0.7 and |$0.75 \, \mathrm{M}_\odot$| do. Thus, our assumption on the relation between stellar mass and Teff is valid.
First, we search for the most metal-poor stars with |$0.8 \, \mathrm{M}_\odot$|, since they should be drastically polluted by ISOs (see Fig. 2). We find one star with [Fe/H] < −3.8 (SDSS J2209−0028), and six stars with −3.8 < [Fe/H] < −3.6 (HE 0228−4047, HE 0049−3948, BPS CS22876−032A, SDSS J214633−003910, HE 2032−5633, and SDSS J0825+0403), where BPS CS22876−032A indicates binarity. We remark that all the above stars have 6400 K ≲ Teff ≲ 6600 K. They can never be present typically if α ≲ 2.5. This is because Fig. 2 shows half of Pop. III survivors with |$0.8 \, \mathrm{M}_\odot$| are polluted to [Fe/H] ≳ − 4 in the case of α = 2.5. Thus, the lower limit of α can be 2.5. Nevertheless, the lower limit of α might be 2.0. A slight fraction of Pop. III survivors can remain [Fe/H] ≲ − 4, even if α = 2.0. To assess whether they are the least polluted end, we need the orbits of the seven stars. However, their orbits have not been investigated so far.
Secondly, we search for metal-poor stars with 0.7 and |$0.75 \, \mathrm{M}_\odot$|. HE 1327−2326 can put the strictest constraint on α among these stars. Its Teff and [Fe/H] are 6180 K and −5.71, respectively. We estimate from its Teff that its mass is |$0.75 \, \mathrm{M}_\odot$|, and so its [Fe/H] is the lowest among main-sequence stars with |${\lesssim } 0.75 \, \mathrm{M}_\odot$|. It can never be present typically in the case of α ≲ 2.0, since half of Pop. III survivors with |$0.75 \, \mathrm{M}_\odot$| are polluted to [Fe/H] ≳ − 5.5. Thus, the lower limit of α should be 2.0. This constraint is weaker than metal-poor stars with |$0.8 \, \mathrm{M}_\odot$| put, however.
In summary, we constrain the lower limit of α as α ≳ 2.0 conservatively. This is consistent with α of km-size asteroids and comets in the Solar system (Kenyon & Bromley 2004; Gladman et al. 2009; Fernández & Sosa 2012).
4.2 Candidates of Pop. III survivors
We assess whether metal-poor stars so far discovered can be Pop. III survivors polluted by ISOs. We choose non-carbon-enhanced metal-poor (non-CEMP) and main-sequence stars in the MW galaxy as candidates of polluted Pop. III survivors. We exclude CEMP stars from these candidates since we conservatively assume ISO compositions are similar to solar abundance pattern. Assuming the solar abundance pattern as the abundance of ISOs might lead non-realistic metal pollution of Pop. III stars. A part of asteroids exhibits Fe-rich abundant based on the near-infrared absorption features in the reflected light spectra (Ockert-Bell et al. 2010). On the other hand, an elemental abundance of directly collected cometary dust of the comet 67P/Churyumov–Gerasimenko was measured (Bardyn et al. 2017), and it showed C/Fe in number as ∼19. Considering C/Fe of the Sun (Lodders 2010), [C/Fe] of the comet |${\sim } \, {\rm log}(19/8.5)\sim 0.35$|. Although observations of the surface elemental abundance of them show different patterns with solar abundance, the inner elemental abundances of comets and asteroids are still less knowledgeable. Even if individual ISOs have peculiar abundance pattern, their peculiarities should be smoothed out by collisions million times during several Gyr (see Fig. 1). We, therefore, assume the solar abundance for ISOs as a safer working hypothesis. We focus on only main-sequence stars. Post main-sequence stars have thick convection zone. We pick up these candidates from the SAGA data base (Suda et al. 2008) again. We adopt the definition of non-CEMP and main-sequence stars in the SAGA data base.
Whether a metal-poor star is a Pop. III candidate strongly depends on the power α. Thus, we show Pop. III candidates in each α. In the case of α ≳ 3.0, there is no Pop. III candidate. In the case of α ∼ 2.5, |$0.80 \, \mathrm{M}_\odot$| stars shown in Section 4.1 (HE 0228−4047, HE 0049−3948, BPS CS22876−032A, SDSS J214633−003910, HE 2032−5633, and SDSS J0825+0403) are the most promising candidates of Pop. III survivors. Note that SDSS J2209−0028 is a CEMP-s star.
In the case of α ∼ 2.0, non-CEMP and main-sequence stars with Teff ∼ 6500 K (|$0.80 \, \mathrm{M}_\odot$|) and [Fe/H] ≲ − 3 are candidates of Pop. III survivors, which include the six stars. Moreover, there is a Pop. III candidate with |${\lesssim } 0.75 \, \mathrm{M}_\odot$|: SDSS J164234+443004 (Teff = 6280 K and [Fe I/H] = −4.05). From its Teff, it should have |$0.75 \, \mathrm{M}_\odot$|. Thus, it has to be the most polluted end as seen in Fig. 2. Nevertheless, it should be a Pop. III candidate in the following reason. From our analysis, we find the most polluted end has low altitude from the Galactic disc (≲ 4 kpc), and small perigalacticon (∼2 kpc). SDSS J164234+443004 has such an orbit (Sestito et al. 2019).
There are several candidates with [Fe/H] ≲ − 4: SDSS J102915+172927 (Teff = 5811 K and [Fe I/H] = −4.71), HE 2239−5019 (Teff = 6100 K and [Fe I/H] = −4.15), and SDSS J144256−001542 (Teff = 5850 K and [Fe I/H] = −4.09). However, they must not be the most polluted end from their orbits obtained from Sestito et al. (2019), and so must not be ISO-polluted Pop. III survivors. Although SDSS J102915+172927 has low altitude from the Galactic disc (∼2 kpc), its perigalacticon is ∼8 kpc. HE 2239−5019 and SDSS J144256−001542 have high altitudes from the Galactic disc to several 10 kpc. Although metal-poor stars with −4 ≲ [Fe/H] ≲ − 3.5 should be assessed, their orbits have not been in the literature.
In summary, there are six candidates in the case of α ∼ 2.5: HE 0228−4047, HE 0049−3948, BPS CS22876−032A, SDSS J214633−003910, HE 2032−5633, and SDSS J0825+0403. In the case of α ∼ 2.0, there are many candidates with |$0.80 \, \mathrm{M}_\odot$| including the above six stars, and moreover there is one candidate with |${\lesssim } 0.75 \, \mathrm{M}_\odot$|: SDSS J164234+443004. Note that we exclude a CEMP star SDSS J1035+0641 from these candidates, although Tanikawa et al. (2018) have said it can be a Pop. III candidate.
4.3 Strategy to discover Pop. III survivors
We cannot distinguish between polluted Pop. III survivors and originally metal-poor stars since the abundance pattern of ISOs has been unknown. Thus, we should consider a method to search for unpolluted Pop. III survivors in order to discover them.
We should avoid the following two types of stars. The first type is stars with |$0.8\, \mathrm{M}_\odot$| (or Teff ∼ 6500 K). We can see from Fig. 3 that these stars are typically polluted to [Fe/H] ∼− 4 over the MW if α ≲ 2.5. The second type is stars with |${\lesssim } 0.75\, \mathrm{M}_\odot$| (or Teff ≲ 6400 K) in the Galactic disc, and at the Galactic centre. They can be polluted to [Fe/H] ∼− 4 in the case of α ∼ 2.0 (see Figs 2 and 3).
In short, we may possibly discover unpolluted Pop. III survivors, surveying stars with Teff ≲ 6400 K at the Galactocentric radii of ≳15 kpc. At those radii, these stars should be typically polluted only to [Fe/H] ∼− 6 even if α ∼ 2.0 (see Fig. 3).
The number estimation of low-mass Pop. III stars in the MW is another important information to find low-mass Pop. III stars (Hartwig et al. 2015; Ishiyama et al. 2016; Griffen et al. 2018; Magg et al. 2018, 2019). However, the number highly depends on the assumption of the low-mass cut-off of the initial mass function of Pop. III stars. Moreover, low-mass Pop. III stars are assumed to be still metal-free stars in the MW in previous studies. Considering the observational bias of metal-poor stars, Magg et al. (2019) concluded that a more significant number of metal-free stars should be observed unless reducing the star formation of low-mass Pop. III stars or external pollution of metal-free stars. Our results suggest that the apparent number of metal-free stars get smaller due to the surface ISO metal pollution in the solar neighbourhood.
5 SUMMARY
In this work, we investigated metal pollution of Pop. III survivors via ISOs floating in the Galactic interstellar medium. Using a high-resolution cosmological N-body simulation, we calculated the accretion rate in each time-step monitoring the position of the Pop. III survivor whether or not in the Galactic disc. To take realistic orbits of Pop. III survivors based on the cosmological framework into calculating the accretion rate, we obtained that the typical accretion rate is one order of magnitude greater than estimated by the previous analytical study (Tanikawa et al. 2018). When we give a cumulative number density of ISOs as described in Section 2.2, we can obtain that the number of chances of ISO (>100 m) collisions is typically 5 × 106 times in the last 5 Gyr for Pop. III survivors near solar neighbourhood.
When we adopt the ISO cumulative number distribution expressed with a power-law parameter α, |$0.80 \, \mathrm{M}_\odot$| stars should be typically polluted [Fe/H] ∼ −2, −4, and −5.5 for the case of α = 2.0, 2.5, and 3.0, respectively. We can constrain on the lower limit of the power α as α ≳ 2.0 from the presence of so far observed metal-poor stars. The constraint is consistent with α of km-size asteroids and comets in the Solar system. Furthermore, we provide six candidates as the ISO metal-enriched Pop. III stars in the case of α ∼ 2.5. Owing to the Gaia photometric and astrometric observation, highly accurate orbital information of each star is getting available (Gaia Collaboration 2018). Most earlier studies have considered that the observed metallicity of stars is unchanged from their birth. We again note that metal-poor stars so far discovered are possible to be metal-free Pop. III stars on birth and are later metal polluted by ISOs.
ACKNOWLEDGEMENTS
TK is grateful to Yu Morinaga for providing fruitful suggestions about the treatment of the merger tree. We thank an anonymous referee for the constructive comments. Numerical calculations were partially carried out on Aterui supercomputer at Center for Computational Astrophysics, CfCA, of National Astronomical Observatory of Japan and the K computer at the Riken Institute for Computational Science (Proposal numbers hp150226 and hp160212). This research has been supported in part by MEXT program for the Development and Improvement for the Next Generation Ultra High-Speed Computer System under its Subsidies for Operating the Specific Advanced Large Research Facilities, and by Grants-in-Aid for Scientific Research (16K17656, 17H01101, 17H04828, 17H06360, 18H04337 and 19K03907) from the Japan Society for the Promotion of Science. We thank the SAGA developers for making up such a useful data base.
REFERENCES



