-
PDF
- Split View
-
Views
-
Cite
Cite
Nicola Giacobbo, Michela Mapelli, The impact of electron-capture supernovae on merging double neutron stars, Monthly Notices of the Royal Astronomical Society, Volume 482, Issue 2, January 2019, Pages 2234–2243, https://doi.org/10.1093/mnras/sty2848
Close - Share Icon Share
ABSTRACT
Natal kicks are one of the most debated issues about double neutron star (DNS) formation. Several observational and theoretical results suggest that some DNSs have formed with low natal kicks (≲ 50 km s−1), which might be attributed to electron-capture supernovae (ECSNe). We investigate the impact of ECSNe on the formation of DNSs by means of population synthesis simulations. In particular, we assume a Maxwellian velocity distribution for the natal kick induced by ECSNe with one-dimensional root mean square σECSN = 0, 7, 15, 26, 265 km s−1. The total number of DNSs scales inversely with σECSN and the number of DNS mergers is higher for relatively low kicks. This effect is particularly strong if we assume low efficiency of common-envelope ejection (described by the parameter α = 1), while it is only mild for high efficiency of common-envelope ejection (α = 5). In most simulations, more than 50 per cent of the progenitors of merging DNSs undergo at least one ECSN and the ECSN is almost always the first SN occurring in the binary system. Finally, we have considered the extreme case in which all neutron stars receive a low natal kick (≲ 50 km s−1). In this case, the number of DNSs increases by a factor of 10 and the percentage of merging DNSs that went through an ECSN is significantly suppressed (<40 per cent).
1 INTRODUCTION
GW170817, the first detection of a merger between two neutron stars (NSs; Abbott et al. 2017a), marked the beginning of multimessenger astronomy. For the first time, electromagnetic emission accompanying the gravitational wave (GW) event was observed (Abbott et al. 2017b), ranging from gamma-rays (e.g. Abbott et al. 2017b; Goldstein et al. 2017; Savchenko et al. 2017) to X-rays (e.g. Margutti et al. 2017), to optical, near-infrared (e.g. Chornock et al. 2017; Coulter et al. 2017; Cowperthwaite et al. 2017; Nicholl et al. 2017; Pian et al. 2017; Soares-Santos et al. 2017), and radio wavelengths (e.g. Alexander et al. 2017).
The formation of merging double NSs (DNSs) like GW170817 is still matter of debate: understanding this process would provide crucial insights for both stellar evolution and GW astrophysics. Merging DNSs are expected to form either from the evolution of isolated close binaries (e.g. Flannery & van den Heuvel 1975; Bethe & Brown 1998; Belczynski, Kalogera & Bulik 2002; Dewi & Pols 2003; Voss & Tauris 2003; Podsiadlowski et al. 2004; Dewi, Podsiadlowski & Pols 2005; Andrews et al. 2015; Chruslinska et al. 2017; Tauris et al. 2017; Giacobbo & Mapelli 2018; Kruckow et al. 2018; Mapelli & Giacobbo 2018; Mapelli et al. 2018; Vigna-Gómez et al. 2018) or through dynamical interactions in star clusters (e.g. Grindlay, Portegies Zwart & McMillan 2006; Lee, Ramirez-Ruiz & van de Ven 2010; East & Pretorius 2012; Ziosi et al. 2014).
Many uncertainties still affect both formation channels. In particular, one of the most debated and also one of the most important physical ingredients for the formation of DNSs is the magnitude of the natal kick imparted by the supernova (SN) explosion to the newborn NS (Janka 2012).
From a study on the proper motion of 233 young isolated pulsars, Hobbs et al. (2005) estimated that their velocity distribution follows a Maxwellian curve with a one-dimensional root-mean-square (1D rms) velocity σ = 265 km s−1 and an average natal kick speed of ∼420 km s−1. On the other hand, there is increasing evidence that some NSs form with a significantly smaller natal kick.
Several studies (Cordes & Chernoff 1998; Arzoumanian, Chernoff & Cordes 2002; Brisken et al. 2003; Schwab, Podsiadlowski & Rappaport 2010; Verbunt, Igoshev & Cator 2017) claim that the velocity distribution proposed by Hobbs et al. (2005) underestimates the number of pulsars with a low velocity and suggest that the natal kick distribution of NSs is better represented by a bimodal velocity distribution. This bimodal distribution might result from two different mechanisms of NS formation. For instance, two out of nine accurate pulsar velocities computed by Brisken et al. (2002) are smaller than 40 km s−1. Moreover, Pfahl et al. (2002) study a new class of high-mass X-ray binaries with small eccentricities and long orbital periods, which imply a low natal kick velocity (≲ 50 km s−1) for the newborn NSs. Similarly, Knigge, Coe & Podsiadlowski (2011) show that Be X-ray binaries could be divided in two subpopulations: one with short (∼10 s) and one with long (∼200 s) spin period. The two populations are characterized also by different orbital period and eccentricity distributions, indicative of two natal kick distributions. Even considerations about the orbital elements of some Galactic DNSs suggest that a low natal kick is required (van den Heuvel 2007; Beniamini & Piran 2016).
It has been proposed that NSs with a low natal kick come from electron-capture SNe (ECSNe; Miyaji et al. 1980; Nomoto 1984, 1987; van den Heuvel 2007), a more rapid and less energetic process with respect to iron core-collapse SNe (CCSNe; Dessart et al. 2006; Kitaura, Janka & Hillebrandt 2006). In ECSN explosions, the asymmetries are more difficult to develop and the newborn NS receives a lower kick (Dessart et al. 2006; Jones et al. 2013; Schwab, Quataert & Bildsten 2015; Gessner & Janka 2018).
Low natal kicks might occur not only in ECSNe, but in all low-mass progenitors (≲ 10 M⊙), because of their steep density profile at the edge of the core, which allows for rapid acceleration of the SN shock wave. The shock is revived on a shorter time scale than in more massive progenitors, and therefore there is less time for large-scale asymmetries (which would result in a larger kick) to develop (see e.g. Müller 2016).
Alternatively, the low kick of some DNSs could be explained also by the fact that they come from ultrastripped SNe, i.e. from the SN explosion of a naked helium star that was stripped by its compact companion (Tauris et al. 2013, 2017; Tauris, Langer & Podsiadlowski 2015). In this case, the natal kick is thought to be lower because of the low mass of the ejecta.
In this paper, we use our new population-synthesis code mobse (Giacobbo, Mapelli & Spera 2018) to investigate the impact of ECSNe and low natal kicks on the formation of merging DNSs. We show that ECSNe are an important channel for the formation of DNSs, if they are associated to low natal kicks. Moreover, we discuss the extreme case in which all NSs receive a small kick, regardless of the SN process.
2 METHODS
mobse is an updated version of the bse code (Hurley, Pols & Tout 2000; Hurley, Tout & Pols 2002). Here, we summarize the main characteristics of mobse and we describe the new features we have added to it for this work. A more detailed discussion of mobse can be found in Giacobbo et al. (2018) and in Mapelli et al. (2017). In this paper, we adopt the version of mobse described as mobse1 in Giacobbo et al. (2018).
where fLBV = 1.5 (Belczynski et al. 2010) and Z is the metallicity.
The new prescriptions for core-collapse SNe (CCSNe) in mobse include the rapid and the delayed SN model described by Fryer et al. (2012, see also Spera, Mapelli & Bressan 2015). The rapid SN model is adopted for the simulations presented in this paper, because it allows us to reproduce the remnant mass gap between ∼2 and ∼5 M⊙ (Özel et al. 2010; Farr et al. 2011). Pair-instability and pulsational pair-instability SNe are also implemented in mobse using the fitting formulas by Spera & Mapelli (2017).
Finally, we have also updated the prescriptions for core radii following Hall & Tout (2014), we have extended the mass range up to 150 M⊙ (Mapelli 2016), and we have revised the treatment of Hertzsprung-gap (HG) donors in common envelope (CE): HG donors are assumed to always merge with their companions if they enter a CE phase.
For this work, we have added several updates to the description of ECSNe and natal kicks in mobse, as we describe in the following sections.
2.1 Electron-capture SNe
NSs can form via CCSN, via ECSN or through the accretion-induced collapse of a white dwarf (WD). In mobse, the outcome of a CCSN is considered an NS if its mass is less than 3.0 |$\, \textrm{M}_{\odot }$| and a black hole (BH) otherwise. This approach is overly simplified, but more constraints on the equation of state of an NS are required for a better choice of the transition between NS and BH.
In the case of both an ECSN and an accretion-induced WD collapse, the NS forms when the degenerate oxygen-neon (ONe) core collapses as a consequence of electron-capture reactions, inducing a thermonuclear runaway (Miyaji et al. 1980; Nomoto 1984, 1987; Nomoto & Kondo 1991; Kitaura et al. 2006; Fisher et al. 2010; Jones et al. 2013; Takahashi, Yoshida & Umeda 2013; Schwab et al. 2015; Jones et al. 2016).
In mobse, we decide whether a star will undergo an ECSN by following the procedure described by Hurley et al. (2000) and Fryer et al. (2012). First, we look at the helium core mass at the base of the asymptotic giant branch1 (MBABG). If 1.6 |$\, \textrm{M}_{\odot }$| ≤MBABG < 2.25 |$\, \textrm{M}_{\odot }$|, the star forms a partially degenerate carbon-oxygen (CO) core. If the CO core grows larger than ∼1.08 M⊙, it can form a degenerate ONe core. If this degenerate ONe core reaches the mass MECSN = 1.38 |$\, \textrm{M}_{\odot }$|, it collapses due to the electron-capture on 24Mg and on 20Ne (Miyaji et al. 1980; Nomoto 1984, 1987), otherwise it forms an ONe WD, which can still collapse to an NS if it will accrete sufficient mass.
Even if only a few per cent of all SN events should be produced by electron-capture reactions in single stars (Poelarends 2007; Doherty et al. 2015), this fraction could drastically raise if we consider binary systems (Podsiadlowski et al. 2004). In binary systems, the possibility of accreting material by a companion broadens the mass range of progenitor stars in which the electron-capture collapse may occur, because mass transfer can significantly change the evolution of the core (Sana et al. 2012; Dunstall et al. 2015; Poelarends et al. 2017). In Appendix A, we show that the mass range of ECSNe is crucially affected by binary evolution. In particular, we find that mass transfer tends to widen the mass range of ECSNe.
Recently, Jones et al. (2016) have shown that an ECSN might lead to the ejection of a portion of the degenerate core, rather than to the collapse into an NS. The collapse and the formation of an NS takes place only if the ignition density is ≳ 2 × 1010 g cm−3. This finding must be taken into account when interpreting the outcomes of our simulations; our results should be regarded as upper limits to the impact of ECSNe on the statistics of DNSs.
2.2 Natal kicks
Given the uncertainties on the natal kick distribution, we have implemented in mobse the possibility to draw the natal kick from two Maxwellian curves with a different value of the 1D rms: σCCSN and σECSN, for iron CCSNe and ECSNe, respectively.
σ = 265 km s−1 is adopted as a default value for CCSNe in mobse. This value was derived by Hobbs et al. (2005), studying the proper motion of 233 young isolated Galactic pulsars and corresponds to an average natal kick speed of ∼420 km s−1.
In this paper, we consider different values of σECSN, ranging from 0 to 265 km s−1, to investigate the impact of ECSNe on the statistics of DNSs.
Because low natal kicks might originate not only from ECSNe, but also from iron CCSNe involving low-mass progenitors and from ultrastripped SNe, we have run also an extreme case (σCCSN = σECSN = 15 km s−1), in which all NSs receive a low natal kick independently on the SN type (see Table 1). We will discuss this extreme case in Section 3.4.
| ID . | σECSN . | σCCSN . | α . |
|---|---|---|---|
| . | (km s−1) . | (km s−1) . | . |
| EC0α1 | 0.0 | 265.0 | 1 |
| EC7α1 | 7.0 | 265.0 | 1 |
| EC15α1 | 15.0 | 265.0 | 1 |
| EC26α1 | 26.0 | 265.0 | 1 |
| EC265α1 | 265.0 | 265.0 | 1 |
| EC0α5 | 0.0 | 265.0 | 5 |
| EC7α5 | 7.0 | 265.0 | 5 |
| EC15α5 | 15.0 | 265.0 | 5 |
| EC26α5 | 26.0 | 265.0 | 5 |
| EC265α5 | 265.0 | 265.0 | 5 |
| CC15α1 | 15.0 | 15.0 | 1 |
| CC15α5 | 15.0 | 15.0 | 5 |
| ID . | σECSN . | σCCSN . | α . |
|---|---|---|---|
| . | (km s−1) . | (km s−1) . | . |
| EC0α1 | 0.0 | 265.0 | 1 |
| EC7α1 | 7.0 | 265.0 | 1 |
| EC15α1 | 15.0 | 265.0 | 1 |
| EC26α1 | 26.0 | 265.0 | 1 |
| EC265α1 | 265.0 | 265.0 | 1 |
| EC0α5 | 0.0 | 265.0 | 5 |
| EC7α5 | 7.0 | 265.0 | 5 |
| EC15α5 | 15.0 | 265.0 | 5 |
| EC26α5 | 26.0 | 265.0 | 5 |
| EC265α5 | 265.0 | 265.0 | 5 |
| CC15α1 | 15.0 | 15.0 | 1 |
| CC15α5 | 15.0 | 15.0 | 5 |
Note. Column 1: simulation name; columns 2–3: 1D rms of the Maxwellian natal kick distribution for ECSNe and CCSNe, respectively (see Section 2.2); column 4: values of α in the CE formalism (see Section 2.3). Simulations CC15α1 and CC15α5 are the same as we already presented in Giacobbo & Mapelli (2018).
| ID . | σECSN . | σCCSN . | α . |
|---|---|---|---|
| . | (km s−1) . | (km s−1) . | . |
| EC0α1 | 0.0 | 265.0 | 1 |
| EC7α1 | 7.0 | 265.0 | 1 |
| EC15α1 | 15.0 | 265.0 | 1 |
| EC26α1 | 26.0 | 265.0 | 1 |
| EC265α1 | 265.0 | 265.0 | 1 |
| EC0α5 | 0.0 | 265.0 | 5 |
| EC7α5 | 7.0 | 265.0 | 5 |
| EC15α5 | 15.0 | 265.0 | 5 |
| EC26α5 | 26.0 | 265.0 | 5 |
| EC265α5 | 265.0 | 265.0 | 5 |
| CC15α1 | 15.0 | 15.0 | 1 |
| CC15α5 | 15.0 | 15.0 | 5 |
| ID . | σECSN . | σCCSN . | α . |
|---|---|---|---|
| . | (km s−1) . | (km s−1) . | . |
| EC0α1 | 0.0 | 265.0 | 1 |
| EC7α1 | 7.0 | 265.0 | 1 |
| EC15α1 | 15.0 | 265.0 | 1 |
| EC26α1 | 26.0 | 265.0 | 1 |
| EC265α1 | 265.0 | 265.0 | 1 |
| EC0α5 | 0.0 | 265.0 | 5 |
| EC7α5 | 7.0 | 265.0 | 5 |
| EC15α5 | 15.0 | 265.0 | 5 |
| EC26α5 | 26.0 | 265.0 | 5 |
| EC265α5 | 265.0 | 265.0 | 5 |
| CC15α1 | 15.0 | 15.0 | 1 |
| CC15α5 | 15.0 | 15.0 | 5 |
Note. Column 1: simulation name; columns 2–3: 1D rms of the Maxwellian natal kick distribution for ECSNe and CCSNe, respectively (see Section 2.2); column 4: values of α in the CE formalism (see Section 2.3). Simulations CC15α1 and CC15α5 are the same as we already presented in Giacobbo & Mapelli (2018).
2.3 Simulations and initial distributions
For the CE phase, we have adopted the αλ formalism (see Webbink 1984; Ivanova et al. 2013). This formalism relies on two parameters, λ (which measures the concentration of the envelope) and α (which quantifies the energy available to unbind the envelope). To compute λ, we used the prescriptions derived by Claeys et al. (2014, see their Appendix A for more details) that are based on Dewi & Tauris (2000).
We have run 12 sets of simulations, by changing the value of α and that of both σECSN and σCCSN (see Table 1).
In the first 10 simulations reported in Table 1, we have fixed σCCSN = 265 km s−1 and we have varied |$\alpha {}=1,\, {}5$| and σECSN = 0, 7, 15, 26, 265 km s−1 (corresponding to an average natal kick of about 0,11,23,41,420 km s−1, respectively).
In the last two simulations reported in Table 1 (CC15α1 and CC15α5), we have set σCCSN = σECSN = 15 km s−1 for both α = 1, 5. We will discuss simulations CC15α1 and CC15α5 in Section 3.4, while in the following sections we will focus on the other 10 simulations (i.e. on the effect of σECSN on the statistics of DNSs).
Finally, for each set of simulations we considered 12 subsets with different metallicities Z = 0.0002, 0.0004, 0.0008, 0.0012, 0.0016, 0.002, 0.004, 0.006, 0.008, 0.012, 0.016, and 0.02. In each subset, we simulated 107 binary systems. Thus, each set of simulations is composed of 1.2 × 108 massive binaries.
3 RESULTS
3.1 Impact of σECSN on DNSs
The left-hand panel of Fig. 1 shows all DNSs formed in our simulations as a function of metallicity. It is apparent that the lower σECSN is, the higher the total number of DNSs. This is not surprising, because a lower σECSN implies a lower probability to unbind the system.
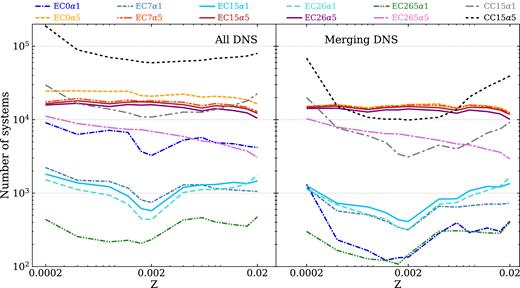
Impact of different kick velocities for ECSNe on the number of DNSs. Left: number of DNSs in each set of simulations (see Table 1) as a function of progenitor’s metallicity. Right: number of DNSs merging in less than a Hubble time (hereafter: merging DNSs) as a function of progenitor’s metallicity. Different runs are indicated by different lines, as explained in the legend and in Table 1.
This effect is particularly strong for the simulations with α = 1, in which the number of DNSs is ∼10–25 times higher if σECSN = 0 than if σECSN = 265 km s−1. In the simulations with α = 5, the number of DNSs is three to six times higher if σECSN = 0 than if σECSN = 265 km s−1. We also note that DNSs form more efficiently if α = 5 than if α = 1.
In our simulations, the number of DNSs depends on metallicity, especially if α = 1. In particular, the number of DNSs is minimum for Z ∼ 0.002. This trend originates from the evolution of stellar radii of ∼8–20 M⊙ stellar progenitors, which are significantly larger for Z ∼ 0.002, than for the other metallicities (especially in the terminal main sequence and in the HG phases). The trend is stronger for α = 1 than for α = 5, because a low value of α corresponds to a more efficient shrinkage of the orbit during CE: two main-sequence or HG stars are more likely to merge during CE if α is low.
The right-hand panel of Fig. 1 shows only the DNSs that merge in less than a Hubble time (hereafter: merging DNSs). In the simulations with α = 5, we find again a monotonic trend with σECSN, but the differences are much less significant.
In the simulations with α = 1, the number of merging DNSs does not show a monotonic trend with σECSN: runs with σECSN = 7–26 km s−1 produce a factor of ∼5 more merging DNSs than simulations with σECSN = 0 and 265 km s−1. The only exception is represented by very metal-poor stars (Z = 0.0002), for which the number of merging DNSs with σECSN = 0 is similar to the one of systems with σECSN = 7–26 km s−1.
Equation (10) implies that more eccentric binaries have a shorter merging time. Moderate natal kicks do not unbind a binary, but increase its eccentricity, shortening its merging time. Since most binaries evolve through processes that tend to circularize their orbits (e.g. tidal torques, mass transfer, and CE phase), the natal kicks are a fundamental ingredient to obtain highly eccentric orbits.
This behaviour is shown in the left-hand column of Fig. 2, where the initial eccentricity distribution of all DNSs is compared with that of the merging DNSs (here ‘initial’ refers to the time when the second NS is formed). A large number of DNSs have initial eccentricity close to zero in run EC0α1 (corresponding to σECSN = 0 and α = 1), but only very few of them merge within a Hubble time.
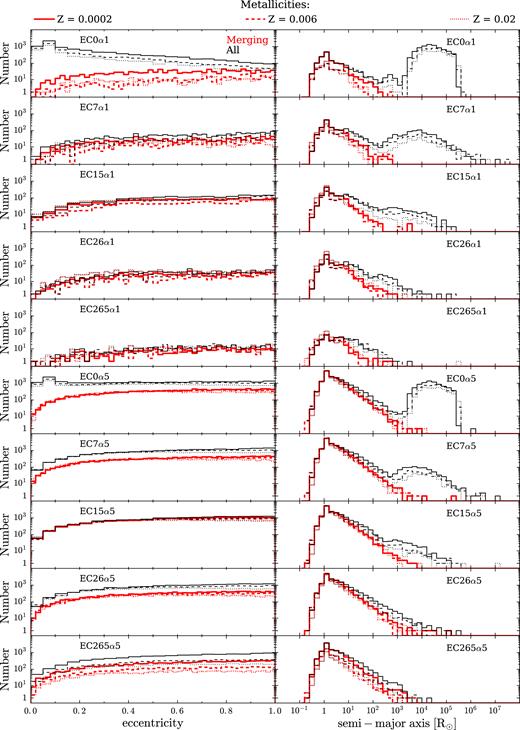
Distribution of eccentricity (left-hand column) and semimajor axis (right-hand column) for all DNSs (black thin lines) and only for merging DNSs (red thick lines). For each simulation, we show the distributions obtained at three different metallicities: Z = 0.02 (dotted lines), 0.006 (dashed lines), and 0.0002 (solid lines). Simulations CC15α1 and CC15α5 are not shown in this figure, because they have already been discussed in Giacobbo & Mapelli (2018).
Many DNSs have initial eccentricity close to zero and most of them do not merge within a Hubble time also in run EC0α5 (corresponding to σECSN = 0 and α = 5). However, run EC0α5 is also efficient in producing DNSs with non-zero eccentricity, which are able to merge within a Hubble time. In contrast, only few DNSs with eccentricity close to zero form in the other runs, because of the SN kicks. We note that the second NS originates from an ECSN in the vast majority of DNSs with eccentricity e ∼ 0.
The right-hand column of Fig. 2 compares the distribution of the initial semimajor axis of all DNSs with that of the merging systems. We see that increasing σECSN the widest systems tend to disappear, because they can be disrupted more easily by the natal kicks.
3.2 DNS formation channels
From our simulations, we find that the most likely formation channel for merging DNSs is consistent with the standard scenario described in Tauris et al. (2017, see their fig. 1): first the primary star expands and fills its Roche lobe, transferring mass to the companion; then the primary explodes leaving an NS; when the secondary expands, the system enters CE; after CE ejection, the system is composed of an NS and a naked helium star and the NS starts stripping its companion; the stripped helium star undergoes an SN explosion, which is most likely an ultrastripped SN (Tauris et al. 2013; Tauris et al. 2015, 2017); the final system is a close DNS that will merge within a Hubble time.
Fig. 3 shows the fraction of merging DNSs that follow the standard scenario we have just described (fstd). For α = 5, fstd is nearly independent of the metallicity of the progenitor, while it depends on the natal kicks. At low kicks (σECSN ≤ 26 km s−1), >>80 per cent of merging DNSs form via the standard scenario, while if σECSN = 265 km s−1 the percentage lowers to ∼60–70 per cent.
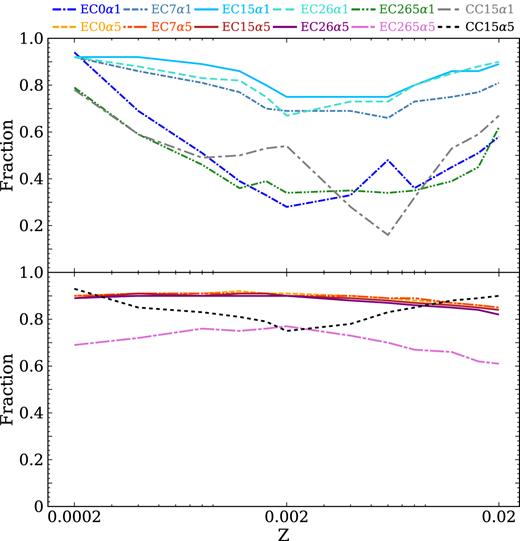
The percentage of merging DNSs that follow the standard scenario (see Section 3.2) as a function of progenitor’s metallicity. Top: simulations with α = 1. Bottom: simulations with α = 5.
For α = 1, fstd depends on both the metallicity and the natal kicks. For a given kick distribution, fstd is minimum at metallicity Z ∼ 0.0016–0.006 (especially in run EC0α1 and EC265α1), while for a fixed metallicity fstd is maximum (∼80–90 per cent) for σECSN = 7–26 km s−1.
This behaviour confirms that ECSNe are a fundamental process for the formation of DNSs, but what is the fraction of systems undergoing an ECSN? Is ECSN more frequently the first or the second SN of a merging system?
Fig. 4 shows the fraction of merging DNSs in which at least one of the two SN explosions is an ECSN. Most merging DNSs (∼50–90 per cent) undergo at least one ECSN in the vast majority of simulations (EC7α1, EC15α1, EC26α1, EC0α5, EC7α5, EC15α5, and EC26α5). In the simulation EC0α1 (σECSN = 0 and α = 1), ECSNe are important at low metallicity (Z = 0.0002) and negligible for intermediate and high metallicity. Only in the simulations with large ECSN kicks (runs EC265α1 and EC265α5), the fraction of DNSs undergoing at least one ECSN is always less than 50 per cent.
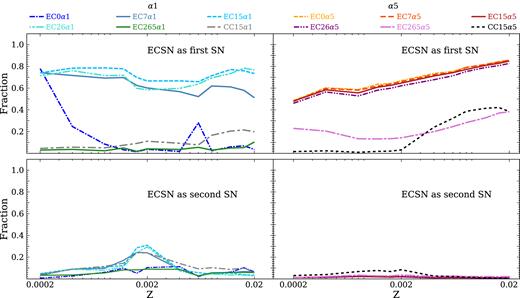
Top (bottom) panels: fraction of merging DNSs in which the first (second) SN is an ECSN as a function of progenitor’s metallicity. Left-hand (right-hand) panels: simulations with α = 1 (α = 5).
Moreover, in simulations with α = 5 the percentage of DNSs that undergo at least one ECSN increases with the progenitor’s metallicity.
Overall, we find that the ECSN is the first SN in the vast majority of merging DNSs. Less than ∼10 per cent of merging DNSs go through an ECSN as second SN, independently of the assumptions about natal kicks and CE efficiency. This result is in agreement with Chruslinska et al. (2017) and (Kruckow et al. 2018, but see Tauris et al. 2017 for a different argument).
This is likely due to the fact that the first SN explosion occurs before that other processes (e.g. a CE phase) are able to shrink the binary; therefore, the system is less bound and it can be more easily disrupted if the natal kick of the newborn NS is too strong. In contrast, the second SN explosion tends to occur after a CE, when the system is usually on a very close and less eccentric orbit, hence it can survive even stronger kicks. Moreover, the fact that the second SN explosion induces a high kick velocity facilitates the formation of highly eccentric orbits, which are more likely to merge via GW emission.
The fact that the ECSN is often the first SN occurring in a merging DNS might seem awkward, because ECSN progenitors are usually less massive than iron CCSN progenitors. Indeed, this happens because most merging DNSs originate from very close binary systems, in which the primary has lost a significant fraction of its mass by mass transfer during Roche lobe overflow. Because of mass-loss, the primary enters the regime of ECSNe. In contrast, the secondary accretes part of the mass lost by the primary and enters the regime of iron CCSNe. This explains why the first SN is more often an ECSN in the progenitors of merging DNSs.
3.3 GW170817-like systems
Fig. 5 shows the number of GW170817-like systems that form in our simulations. We define as GW170817-like systems those merging DNSs with |$M_{\rm rem,1} \in [1.36, 1.60] \, \textrm{M}_{\odot }$| and |$M_{\rm rem,2} \in [1.17, 1.36] \, \textrm{M}_{\odot }$| (Mrem, 1 and Mrem, 2 being the mass of the primary and of the secondary NS, assuming effective spin ≤0.05; Abbott et al. 2017a). Because of its large mass (|$1.36\text{--}1.60\ \, \textrm{M}_{\odot }$|), the most massive component of GW170817-like systems cannot have formed via ECSN. In other words, at least one of the two SNe must be a CCSN, in order to form a GW170817-like system.
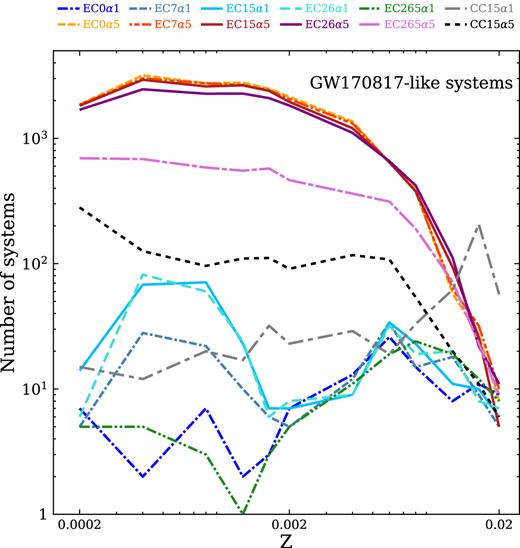
Number of GW170817-like simulated merging DNSs as a function of progenitor’s metallicity.
Fig. 5 shows that at high metallicity (Z ≳ 0.002 for α = 1 and Z ≳ 0.012 for α = 5), all simulations follow a similar trend independently of the value of σECSN, while for lower metallicities the number of GW170817-like systems becomes sensitive to the value of σECSN. In particular, the higher σECSN is, the lower the number of GW170817-like systems. Furthermore, in the simulations with α = 5 the number of GW170817-like systems increases with decreasing metallicity.
The reason is that at high metallicity the majority of GW170817-like systems form from binaries that undergo two iron CCSNe (see Fig. 6), while at low metallicity most of the progenitors pass through at least one ECSN. Fig. 6 shows that the effect of increasing the value of α is to increase the maximum metallicity at which the majority of GW170817-like systems form through at least one ECSN from Z ∼ 0.002 (α = 1) to Z ∼ 0.012 (α = 5).
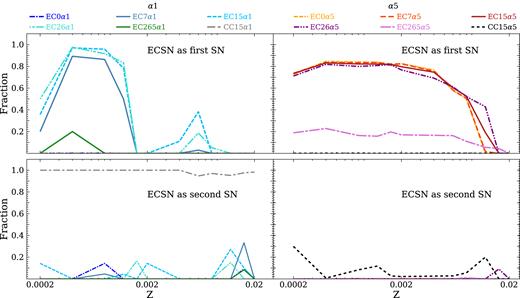
Top (bottom) panels: fraction of GW170817-like systems in which the first (second) SN is an ECSN as a function of progenitor’s metallicity. The left-hand (right-hand) panels are for the simulation with α = 1 (α = 5).
3.4 Low kicks in iron CCSNe
Low natal kicks might occur not only in ECSNe but also in iron CCSNe, especially in the case of low-mass progenitors (Müller 2016) and ultrastripped SNe (Tauris et al. 2017). Moreover, Giacobbo & Mapelli (2018) and Mapelli & Giacobbo (2018) have shown that population-synthesis simulations can reproduce the local merger rate of DNSs inferred from GW170817 (Abbott et al. 2017a) only if low natal kicks (≲ 50 km s−1) are assumed for all DNSs.
Thus, in this section we discuss how much the main results of this paper change if we make the extreme assumption that all NSs receive a low natal kick, i.e. σECSN = σCCSN = 15 km s−1. To this purpose, we have considered two additional runs: CC15α1 and CC15α5, which have been already presented in Giacobbo & Mapelli (2018) and Mapelli & Giacobbo (2018). Simulation CC15α1 (CC15α5) differs from simulation EC15α1 (EC15α5) only for the choice of σCCSN (see Table 1).
From Fig. 1, it is apparent that the number of DNSs is about one order of magnitude larger in simulation CC15α1 (CC15α5) than in simulation EC15α1 (EC15α5). This is not surprising, because a lower CCSN kick implies a lower probability to unbind the system.
On the other hand, if we consider only the DNSs merging within a Hubble time, we find an interesting difference. The number of merging DNSs is a factor of 10 larger in simulation CC15α1 than in simulation EC15α1, whereas the number of merging DNSs in simulations CC15α5 and EC15α5 are comparable. Moreover, simulations CC15α5 and EC15α5 show a significantly different trend with metallicity. As already discussed in Giacobbo & Mapelli (2018), there is a strong interplay between the effects of natal kicks and those of CE efficiency.
Fig. 4 shows that the percentage of merging DNSs that underwent at least one ECSN is dramatically affected by the choice of σCCSN: less than ∼40 per cent of all merging DNSs underwent at least one ECSN if σCCSN = 15 km s−1. This difference is particularly strong for the first SN. In fact, the binary system is still quite large at the time of the first SN explosion and can be easily broken by the SN kick.
This result has relevant implications for the GW170817-like systems. As shown in Fig. 6, no GW170817-like systems underwent an ECSN as first SN in simulations CC15α1 and CC15α5. This comes from the trend we described above, plus the fact that the first SN usually produces the most massive NS of the system in runs CC15α1 and CC15α5. In our models, the mass of an NS born from ECSN is assumed to be 1.26 M⊙, insufficient to match the mass of the primary member of GW170817 (under the assumption of low spins). In contrast, the second SN is always an ECSN in the GW170817-like systems formed in simulation CC15α1. We stress, however, that this result critically depends on the assumption about the mass of an NS formed via ECSN (Hurley et al. 2000; Fryer et al. 2012).
4 SUMMARY
We have investigated the importance of ECSNe on the formation of DNSs. ECSNe are thought to occur frequently in interacting binaries (Podsiadlowski et al. 2004; Tauris et al. 2017) and to produce relatively small natal kicks (Dessart et al. 2006; Jones et al. 2013; Schwab et al. 2015). We assumed that natal kicks generated by ECSNe (iron CCSNe) are distributed according to a Maxwellian function with 1D rms σECSN (σCCSN). First, we have assumed σCCSN = 265 km s−1 (according to Hobbs et al. 2005) and we have explored five different values of σECSN = 0, 7, 15, 26, and 265 km s−1. Moreover, we have also investigated the impact of CE, by considering α = 1 and 5.
We find that the number of simulated DNSs scales inversely with σECSN. In particular, the largest (smallest) number of DNSs form if σECSN = 0 (σECSN = 265 km s−1). This effect is maximum for α = 1, while it is only mild for α = 5. The number of DNSs merging within a Hubble time also depends on σECSN, but with a rather different trend depending on the assumed value for α. For α = 5, the number of merging systems follows the same trend as the total number of DNSs. For α = 1, the number of DNS mergers is maximum for σECSN = 7–26 km s−1, while it drops by a factor of ∼3–10 if σECSN = 0 and if σECSN = 265 km s−1.
The reason is that very large kicks (σECSN = 265 km s−1) completely break the binary, while moderate kicks (σECSN = 7–26 km s−1) leave the binary bound but increase its eccentricity. A larger eccentricity implies a shorter timescale for merger by GW emission, as shown by Peters (1964). In contrast, null natal kicks produce a large number of systems with zero initial eccentricity, which have longer merger times.
A large percentage (∼50–90 per cent) of merging DNSs undergo at least one ECSN explosion in most of our simulations. This percentage drops below 40 per cent only if σECSN = 265 km s−1, or if σCCSN = 15 km s−1, or if σECSN = 0 km s−1, α = 1 and Z > 0.0002.
In the majority of merging DNSs, the ECSN is the first SN occurring in the binary. This happens because, in most cases, the first SN occurs before the binary has shrunk significantly (e.g. by CE) and is easily broken if the kick is too strong.
Moreover, we have selected the simulated DNSs whose mass matches that of GW170817. We call these systems GW170817-like systems. At high metallicity (Z ≳ 0.002 for α = 1 and Z ≳ 0.012 for α = 5), the formation of GW170817-like systems is independent of σECSN, because most GW170817-like systems form through iron CCSNe, while for lower metallicity most GW170817-like systems undergo at least one ECSN and their statistics depends on σECSN.
Finally, we have considered an extreme case in which not only ECSNe but also CCSNe are associated to low kicks, by imposing σCCSN = σECSN = 15 km s−1. Mapelli & Giacobbo (2018) and Giacobbo & Mapelli (2018) suggest that this extreme assumption is necessary to match the local DNS merger rate density inferred from GW170817 (Abbott et al. 2017a).
The number of simulated DNSs increases by a factor of 10 if we assume σCCSN = 15 km s−1, because less binary systems are disrupted by the first SN explosion. Moreover, this assumption strongly suppresses the percentage of merging DNSs (especially GW170817-like systems) that evolved through an ECSN as first SN. These results confirm the importance of natal kicks to understand the properties of merging DNSs.
ACKNOWLEDGEMENTS
We thank the referee, Samuel Jones, for his critical reading which significantly improved this work. The authors are grateful to Alessandro Bressan, Mario Spera, and Chris Pankow for useful discussions. Numerical calculations have been performed through a CINECA-INFN agreement and through a CINECA-INAF agreement, providing access to resources on GALILEO and MARCONI at CINECA. NG acknowledges financial support from Fondazione Ing. Aldo Gini and thanks the Institute for Astrophysics and Particle Physics of the University of Innsbruck for hosting him during the preparation of this paper. MM acknowledges financial support from the MERAC Foundation through grant ‘The physics of gas and protoplanetary discs in the Galactic Centre’, from INAF through PRIN-SKA ‘Opening a new era in pulsars and compact objects science with MeerKat’, from MIUR through Progetto Premiale ‘FIGARO’ (Fostering Italian Leadership in the Field of Gravitational Wave Astrophysics) and ‘MITiC’ (MIning The Cosmos: Big Data and Innovative Italian Technology for Frontier Astrophysics and Cosmology), and from the Austrian National Science Foundation through FWF stand-alone grant P31154-N27 ‘Unravelling merging neutron stars and black hole–neutron star binaries with population-synthesis simulations’. This work benefited from support by the International Space Science Institute (ISSI), Bern, Switzerland, through its International Team programme ref. no. 393 The Evolution of Rich Stellar Populations & BH Binaries (2017–18).
Footnotes
Mass-loss during the asymptotic giant branch and dredge-up efficiency are assumed to be the same as in Hurley et al. (2000).
REFERENCES
APPENDIX A: ECSN IN BINARY EVOLUTION
We describe the impact of binary evolution on the mass range of stars that undergo an ECSN. We consider only the case with σECSN = 15 km s−1 and σCCSN = 265 km s−1, because different assumptions on natal kicks do not affect the mass range. Thus, we analyse a subsample of runs EC15α1 and EC15α5 with metallicity Z = 0.02, 0.002, 0.0002 (we randomly select 105 binaries for each metallicity).
In Fig. A1, we compare the zero-age main-sequence (ZAMS) mass range of single stars that undergo an ECSN (gray regions) with the ZAMS mass distribution of stars that undergo an ECSN as a consequence of binary evolution (green histograms). In agreement with previous studies (e.g. Podsiadlowski et al. 2004; Sana et al. 2012; Dunstall et al. 2015; Poelarends et al. 2017), we find that binary evolution broadens the mass range of stars undergoing an ECSN.
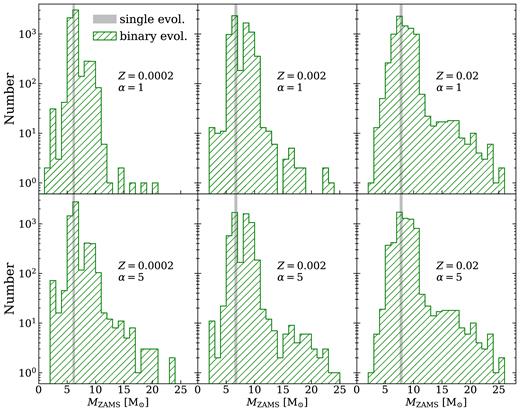
Green hatched histograms: distribution of the ZAMS mass (MZAMS) of binary stars undergoing an ECSN. From left to right: Z = 0.0002, 0.002, and 0.02, respectively. For each metallicity, we consider 105 binary systems randomly selected from runs EC15α1 (top) and EC15α5 (bottom). Grey shadowed regions (with arbitrary normalization): mass range of single stars undergoing an ECSN.
This happens because non-conservative mass transfer changes the mass of close binary members significantly. For instance, it can happen that a primary star with MZAMS up to ∼25 |$\, \textrm{M}_{\odot }$| loses most of its mass and enters the ECSN regime. On the other hand, if a secondary star with MZAMS ≳ 2.5 |$\, \textrm{M}_{\odot }$| accretes enough matter from the companion it can even undergo an ECSN.
The ZAMS mass range of stars undergoing ECSNe seems to be almost insensitive on the efficiency of CE, especially at high metallicity. Furthermore, the mass range mildly depends on metallicity: the lower the metallicity is, the lower the maximum mass for a star to undergo an ECSN as a consequence of mass transfer (this is likely an effect of stellar winds).
Finally, we estimate that ∼16 per cent of NSs undergo an ECSN if α = 1 and Z = 0.02, when we account for binary evolution. This percentage increases with decreasing metallicity. In particular, we find that ∼13 per cent of SNe are ECSNe if α = 1 and Z = 0.002, and ∼8 per cent if α = 1 and Z = 0.0002. If α = 5, we find a slightly lower number of ECSNe: ∼13, 10, 7 per cent at Z = 0.02, 0.002, 0.0002, respectively.



