-
PDF
- Split View
-
Views
-
Cite
Cite
M. Hernández Vera, F. Lique, J. Kłos, F. Dumouchel, J. Rubayo Soneira, Cyanides/isocyanides abundances in the interstellar medium – IV. Temperature dependence of SiCN/SiNC rate coefficients and astrophysical applications, Monthly Notices of the Royal Astronomical Society, Volume 451, Issue 2, 01 August 2015, Pages 1199–1211, https://doi.org/10.1093/mnras/stv1018
Close - Share Icon Share
Abstract
Accurate determination of collisional rate coefficients is an essential step in the estimation of the SiCN and SiNC abundances in the interstellar and circumstellar media. In this paper, we carry out calculations of rate coefficients for the rotational (de-)excitation of SiCN and SiNC molecules in collision with He. The calculations are based on new two-dimensional potential energy surfaces obtained from highly correlated ab initio calculations. Coupled-States quantum approximation was used in the scattering calculations to obtain collisional (de-)excitation cross-sections of SiCN and SiNC by He. The spin–orbit coupling and Λ-doublet splitting of SiCN and SiNC levels were taken into account explicitly. Rate coefficients for transitions among the first 92 rotational levels of SiCN and SiNC were calculated for temperatures ranging from 5 to 100 K. Moderate differences exist between the rate coefficients of both isomers. Subsequently, the new collisional data are used to simulate the excitation of SiCN and SiNC in the circumstellar gas. We obtain the brightness and excitation temperatures of selected lines frequently observed towards the circumstellar envelopes and we find that local thermodynamic equilibrium conditions are not fulfilled for these species. Radiative transfer calculations are then needed in order to accurately determine their abundances. Our results also show that previous estimations of the cyanides/isocyanides abundance ratios were incorrect and the present calculations show that SiCN, the most stable isomer, is more abundant than SiNC. This shows again the evidence of selective cyanide chemistry.
1 INTRODUCTION
Cyanide molecules are ubiquitous in the interstellar and circumstellar media (Snyder & Buhl 1971; Guelin et al. 1986; Ziurys et al. 1995, 2002; Guélin et al. 2000, 2004; Pulliam et al. 2010; Zack, Halfen & Ziurys 2011). Cyanide species are the most common metal-bearing molecules in the circumstellar gas (Dunbar & Petrie 2002) and the hydrogen cyanide (HCN) is one of the most abundant interstellar molecules that is frequently used as tracer of interstellar regions such as dark cold clouds (e.g. Irvine & Schloerb 1984), circumstellar envelopes, (e.g. Cernicharo et al. 1996), cool carbon stars (Harris et al. 2003) or comets (e.g. Lis et al. 1997).
Usually, cyanide compounds display structural isomerism. Frequently, large abundances correspond to the most stable isomers as found for MgNC. MgCN is less stable than MgNC by about 650 cm−1 (1 cm−1 ≡ 1.438 K) and the MgNC/MgCN abundance ratio has been estimated to be ≃20 by Ziurys et al. (1995). Nevertheless, the ratio is not systematically governed by the relative stabilities of the two isomers. Thus, in contrast to purely thermochemical considerations (HNC is less stable than HCN by about ≃ 5000 cm−1 Bowman et al. 1993), the abundance of HNC in space is large: the HNC/HCN abundance ratio is estimated to be around unity in dark cold clouds (Sarrasin et al. 2010). Another pair of isomers that seems to deviate from this trend are the SiCN and SiNC molecules. Their abundance has been determined to be similar (Guélin et al. 2004) even though, energetically, SiNC is less stable than SiCN by about 550 cm−1 (Senent, Dumouchel & Lique 2012, hereafter Paper I).
Molecular abundances in the interstellar medium (ISM) have to be understood in terms of molecular stabilities, reaction probabilities and radiative and collisional excitations. In order to have a new insight in the cyanides/isocyanides abundance in the ISM, we have initiated a series of papers in order to provide the molecular data needed for cyanides/isocyanides abundance determination. In Paper I, we have determined theoretical spectroscopic and structural properties of species containing third-period metals Na, Mg, Al and Si that were in very good agreement with available experimental data and that gathered complete information on these species.
In Hernández Vera et al. (2013, hereafter Paper II), we have presented the calculation of collisional excitation rate coefficients of AlCN, AlNC, MgCN and MgNC molecules by He (as a model of H2) for temperatures ranging from 5 to 100 K. In Hernández Vera & Lique (2015, hereafter Paper III), we have used these new data to simulate the excitation of these species by performing radiative transfer calculations for typical physical conditions encountered in the circumstellar gas. The calculations have shown that the estimation of the cyanides/isocyanides abundance ratio deduced from lines intensity ratio leads to large differences compared to exact radiative transfer calculations. We have also confirmed that AlCN and MgCN are significantly less abundant than AlNC and MgNC, respectively. It confirms the evidence of selective cyanides chemistry.
In this fourth paper, we focus on the excitation of the SiCN and SiNC isomers. SiCN and SiNC were observed for the first time in the circumstellar gas more than 10 years ago. SiCN was detected in the expanding shell of the evolved carbon star IRC+10216 by Guélin et al. (2000). SiNC was discovered four years later in the same source (Guélin et al. 2004). SiNC and SiCN have been found to have similar abundance in IRC+10216 (∼4 × 10−9 with respect to H2, Guélin et al. 2004). Such findings could be surprising because of the different stabilities of the two isomers but SiCN and SiNC molecule have been later observed in spectral survey of IRC+10216 (Cernicharo, Agúndez & Guélin 2011) and of Orion-KL (Tercero et al. 2011). The analysis of these new observations confirms that SiCN and SiNC might be in similar abundances. Note that the observations interpretations were performed assuming local thermodynamic equilibrium (LTE) conditions that are not necessary fulfilled in these media.
In the circumstellar gas, in addition to these two species, a surprisingly rich silicon chemistry has been discovered, even in regions where the temperature is fairly low (Takano, Saito & Tsuji 1992). Silicon is known to be strongly depleted from the gas phase due to its incorporation into silicate grains. However, it is unclear what fraction of silicon remains in the gas phase. Accurate abundance determination of silicon-bearing molecules (including SiCN and SiNC) in the ISM will enable a better understanding of the interstellar and circumstellar silicon chemistry.
In astrophysical media, collisions compete with radiative processes in altering populations in molecular ro-vibrational levels. The estimation of molecular abundances from spectral line data requires collisional rate coefficients with most abundant interstellar species such as He or H2. He is often assumed to be a model for H2 (Lique et al. 2008; Roueff & Lique 2013). The use of He as a substitute for H2 could lead to significant uncertainty in case of collisions with light hydrides but is expected to be reasonable for heavy molecules (Roueff & Lique 2013) such as SiCN and SiNC that are presently studied. Without these rates, only approximate estimates of the molecular abundance are possible assuming LTE, which is generally not a good approximation even for these cyanide/isocyanide species (Paper III). Rate coefficients are also crucial to determine accurately the SiCN/SiNC abundance ratios.
In this paper, we extend the work of our previous publications (Paper I, II and III) to the excitation of the SiCN and SiNC molecules. Here, we present new rotational rate coefficients for SiCN and SiNC based on highly accurate SiCN–He and SiNC–He potential energy surfaces (PES). The paper is organized as follows. Section 2 describes the PES used in this work. Section 3 then contains a brief description of the scattering calculations. In Section 4, we present and discuss our results. Finally, we analyse in Section 5 the effect of these new rate coefficients on the excitation of SiCN and SiNC by their modelling through a large velocity gradient (LVG) radiative transfer code.
2 POTENTIAL ENERGY SURFACES
2.1 ab initio calculations
When the SiCN(X2Π) and SiNC(X2Π) radicals interact with a spherical structureless target, the doubly-degenerate Π electronic state is split into two states, one of A′ symmetry and one of A′′ symmetry. These two states correspond to the singly occupied π orbital lying in, or perpendicular to, the tetratomic plane, respectively.
Within their ground electronic state, SiCN and SiNC molecules have linear geometries (Paper I). Therefore, SiCN and SiNC can be considered as a linear rigid rotor. The SiCN–He and SiNC–He ‘rigid rotor’ PESs are described by the two Jacobi coordinates R, the distance from the centre of mass of SiCN/SiNC molecules to the He atom, and θ, the angle between |$\boldsymbol R$| and the SiCN/SiNC bond axis |$\boldsymbol R$|, with θ = 0 degree corresponding to collinear He–CN/NC–Si.
The intermolecular bond distances of the SiCN and SiNC were frozen at their experimental equilibrium values [rSiC = 3.50 bohr and rCN = 2.21 bohr for SiCN–He; rSiN = 3.28 bohr and rNC = 2.25 bohr for SiNC–He] (Paper I and references therein). As demonstrated by Lique & Spielfiedel (2007) for the CS–He system and by Denis-Alpizar et al. (2013) for the HCN–He system, for non-hydride molecules, two-dimensional PESs calculated for a frozen bond distance or obtained from full dimensional PESs by averaging over the intermolecular ground state vibrational wavefunction are very similar. Consequently, in the present case, we anticipate that restricting intermolecular distances to their equilibrium value will introduce little error into the calculated inelastic rate coefficients.
For all four atoms, we used the standard correlation-consistent polarized valence-triple-zeta basis sets of Dunning (Dunning 1989) (cc-pVTZ) augmented with the diffuse functions of s, p, d, f and g symmetries (aug-cc-pVTZ) (Kendall, Dunning & Harrison 1992). This basis set was further augmented by the [3s3p2d2f1g] bond functions optimized by Cybulski & Toczyłowski (1999) and placed at mid-distance between the He atom and the SiCN/SiNC centre of mass.
The calculations were carried out for θ angle values from 0° to 180° in steps of 10°. R-distances were varied from 4.0 to 20.0 a0, yielding 31 points for each angular orientation.
2.2 Analytical representations
For all the potentials in this work, we set lmax = 16. This ensures that the relatively high anisotropy of these potentials is well represented. We determine the Vlμ(R) (μ = 0, 2) radial coefficients by linear list square fitting of the angular expansion at each discrete radial point to a set of angular ab initio points. The highly repulsive energies were weighted in the fit with a weight of 1/E6 to influence better description of the potential in the energies that will be sampled during the scattering process. The worst relative errors of the analytical representations are 10 to 30 per cent for the distance R = 4 a0 for the collinear geometries where the energies are already very repulsive, of the order of 106 cm−1. For the remaining angles, the relative error is around 1 per cent for this distance. The relative errors of the fits for larger distances are very small for both complexes, from 0.1 to 10−3 per cent. The absolute error in the region of the attractive long-range interaction is usually of the order of 10−1–10−3 cm−1 or better. The radial expansion coefficients Vlμ(R) obtained in this way are then represented by the one-dimensional Reproducing Kernel Hilbert Space interpolation fits Ho & Rabitz (1996) with the smoothness parameter m = 2 and with the fixed long range R−6 radial kernel for the extrapolation beyond the last ab initio radial point at 20 a0. The Fortran routines for the PES are given as supplementary data to this paper.
We will now describe features of the SiCN–He and SiNC–He PESs. Both systems reveal qualitatively similar shape, with the T-shape minima located around 3–4 a0 closer than minima for the collinear approaches, due to the length of the SiCN or SiNC molecule. Also for both complexes, the global minimum is located on the A′′ adiabatic potential.
The global minimum for the SiCN–He interaction is located on the A′′ adiabatic potential, shown in the bottom panel of Fig. 1, for the T-shape geometry. The global minimum of −52.85 cm−1 is located at Re = 6.1 a0 and θe = 98°. The SiCN–He A′ adiabatic potential shown in the upper panel of Fig. 1 is characterized by a skewed minimum of −30.8 cm−1 located at R = 7.1 a0 and θ = 68°. There is another local minimum of −14.06 cm−1 located at R = 10.0 a0 and θ = 180°, which corresponds to the He–Si-C-N arrangement. The He–N-C-Si collinear arrangement (θ = 0°) has a saddle of −20.14 cm−1 at R = 10.0 a0. The Vsum diabatic potential shown in top panel of Fig. 2 has a minimum of −29.61 cm−1 for θ = 72° at R = 7.1 a0.
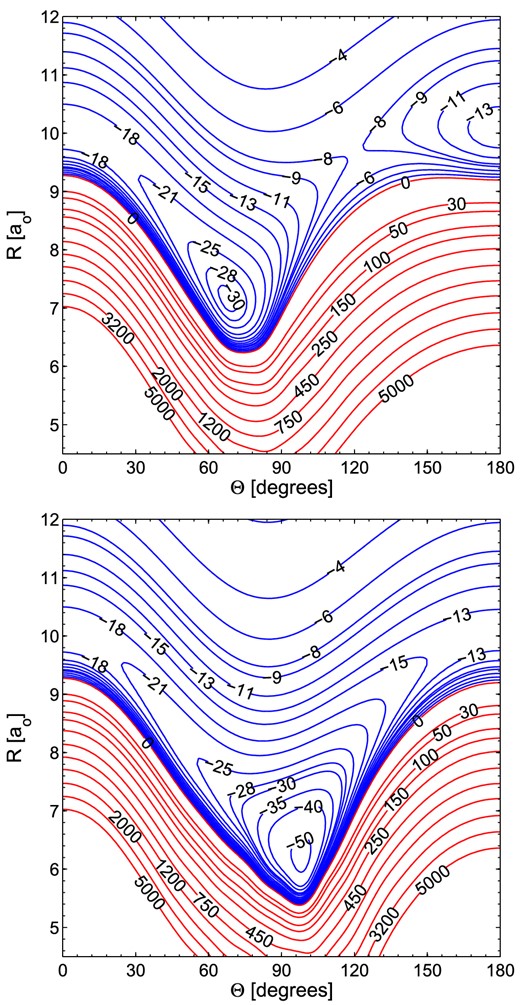
Contour plots of the SiCN–He A′ (upper panel) and A′′ (lower panel) PES. Energy is in cm−1. Red contour lines represent repulsive interaction energies.
Similarly, the SiNC–He interaction has a global minimum of −41.83 cm−1 on the A′′ adiabatic potential shown in the bottom panel of Fig. 3 at Re = 6.5 a0 at θe = 96°. The SiNC–He A′ potential has a skewed minimum of −33.80 cm−1 at R = 7.0 a0 and θ = 71°. The Vsum diabatic potential shown in the top panel of Fig. 4 has a minimum of −31.65 cm−1 for θ = 74° at R = 6.9 a0. The local collinear minimum at θ = 180° corresponding to the He–Si-N-C arrangement is −15.76 cm−1 at R = 9.7 a0. The other collinear minimum, for the He–C-N-Si arrangement, is −14.41 cm−1 at R = 10.7 a0. One can notice in this case, that the collinear minima are much similar in energy than for the SiCN–He case, which are around 6 cm−1 apart. Also the difference in minima between the A′′ and A′ potentials in the T-shape geometry is much smaller than for SiCN–He complex.
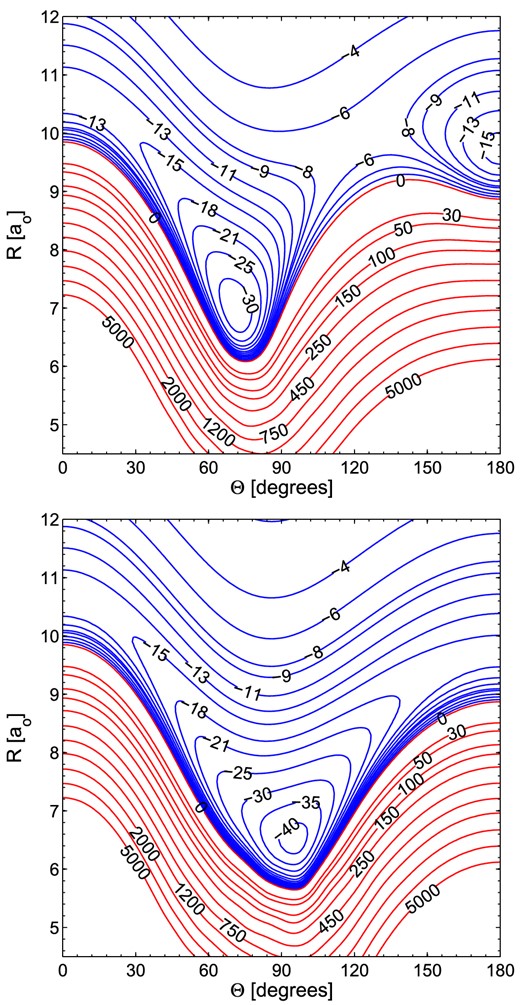
Contour plots of the SiNC–He A′ (upper panel) and A′′ (lower panel) PES. Energy is in cm−1. Red contour lines represent repulsive interaction energies.
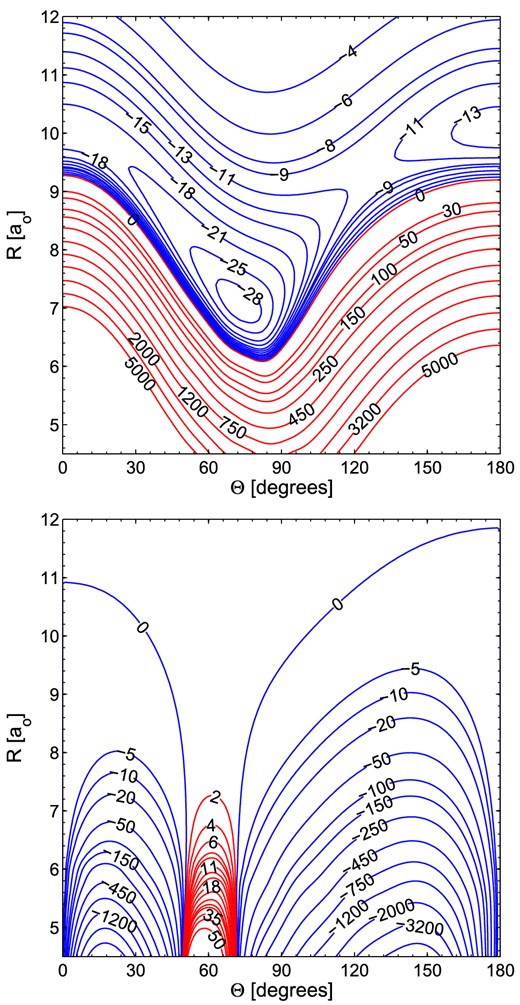
Contour plots of SiCN–He Vsum (upper panel), and Vdiff (lower panel) potentials from this work. Energy is in cm−1. Red contour lines represent repulsive interaction energies.
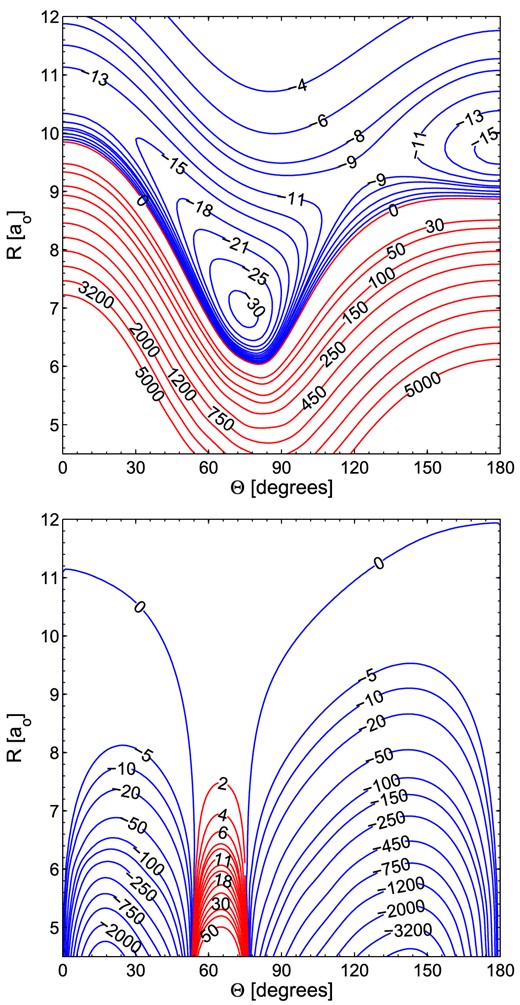
Contour plots of SiNC–He Vsum (upper panel), and Vdiff (lower panel) potentials from this work. Energy is in cm−1. Red contour lines represent repulsive interaction energies.
3 SCATTERING CALCULATIONS
As we mentioned in previous section, the open-shell SiCN and SiNC molecules have 2Π electronic ground states. For both molecules, the electronic orbital angular momentum and the electron spin have well-defined projections of Λ = ±1 and Σ = ±1/2, on to the internuclear axis. Because of this, there are two spin–orbit manifolds; the lower energy 2Π1/2 with |Ω| = |Λ + Σ| = 1/2 (labelled F1), and the higher energy 2Π3/2 with |Ω| = 3/2 (labelled F2). Each rotational level j is split into two close lying Λ-doublet levels labelled e (total parity +(−1)j − 1/2) and f (total parity −(−1)j − 1/2) Brown et al. (1975).
Despite the theoretical rotational and spin–orbit constants of Paper I agree relatively well with the experimental values, we have chosen to compute the SiCN and SiNC rotational levels from the experimental constants for our calculations. Such procedure is expected to improve the accuracy of the collisional data. Table 1 gives the energy of the first rotational levels of both SiCN and SiNC molecules computed from experimental molecular constants of Apponi et al. (2000).
| j . | ϵ . | Ω . | ESiNC . | ESiCN . |
|---|---|---|---|---|
| 0.5 | e | 0.5 | 0.000 | 0.000 |
| 0.5 | f | 0.5 | 0.000 | 0.001 |
| 1.5 | e | 0.5 | 0.638 | 0.553 |
| 1.5 | f | 0.5 | 0.638 | 0.555 |
| 2.5 | e | 0.5 | 1.700 | 1.475 |
| 2.5 | f | 0.5 | 1.702 | 1.477 |
| 3.5 | e | 0.5 | 3.189 | 2.765 |
| 3.5 | f | 0.5 | 3.190 | 2.769 |
| 4.5 | e | 0.5 | 5.102 | 4.425 |
| 4.5 | f | 0.5 | 5.104 | 4.429 |
| 5.5 | e | 0.5 | 7.440 | 6.453 |
| 5.5 | f | 0.5 | 7.443 | 6.458 |
| 6.5 | e | 0.5 | 10.204 | 8.850 |
| 6.5 | f | 0.5 | 10.207 | 8.857 |
| 7.5 | e | 0.5 | 13.393 | 11.616 |
| 7.5 | f | 0.5 | 13.396 | 11.624 |
| 8.5 | e | 0.5 | 17.008 | 14.751 |
| 8.5 | f | 0.5 | 17.011 | 14.760 |
| ... | ... | ... | ... | ... |
| 1.5 | e | 1.5 | 59.023 | 71.036 |
| 1.5 | f | 1.5 | 59.023 | 71.036 |
| 2.5 | e | 1.5 | 60.094 | 71.963 |
| 2.5 | f | 1.5 | 60.094 | 71.963 |
| 3.5 | e | 1.5 | 61.593 | 73.261 |
| 3.5 | f | 1.5 | 61.593 | 73.261 |
| 4.5 | e | 1.5 | 63.521 | 74.929 |
| 4.5 | f | 1.5 | 63.521 | 74.929 |
| 5.5 | e | 1.5 | 65.877 | 76.969 |
| 5.5 | f | 1.5 | 65.877 | 76.969 |
| 6.5 | e | 1.5 | 68.661 | 79.379 |
| 6.5 | f | 1.5 | 68.661 | 79.379 |
| 7.5 | e | 1.5 | 71.873 | 82.160 |
| 7.5 | f | 1.5 | 71.874 | 82.160 |
| 8.5 | e | 1.5 | 75.514 | 85.312 |
| 8.5 | f | 1.5 | 75.515 | 85.312 |
| j . | ϵ . | Ω . | ESiNC . | ESiCN . |
|---|---|---|---|---|
| 0.5 | e | 0.5 | 0.000 | 0.000 |
| 0.5 | f | 0.5 | 0.000 | 0.001 |
| 1.5 | e | 0.5 | 0.638 | 0.553 |
| 1.5 | f | 0.5 | 0.638 | 0.555 |
| 2.5 | e | 0.5 | 1.700 | 1.475 |
| 2.5 | f | 0.5 | 1.702 | 1.477 |
| 3.5 | e | 0.5 | 3.189 | 2.765 |
| 3.5 | f | 0.5 | 3.190 | 2.769 |
| 4.5 | e | 0.5 | 5.102 | 4.425 |
| 4.5 | f | 0.5 | 5.104 | 4.429 |
| 5.5 | e | 0.5 | 7.440 | 6.453 |
| 5.5 | f | 0.5 | 7.443 | 6.458 |
| 6.5 | e | 0.5 | 10.204 | 8.850 |
| 6.5 | f | 0.5 | 10.207 | 8.857 |
| 7.5 | e | 0.5 | 13.393 | 11.616 |
| 7.5 | f | 0.5 | 13.396 | 11.624 |
| 8.5 | e | 0.5 | 17.008 | 14.751 |
| 8.5 | f | 0.5 | 17.011 | 14.760 |
| ... | ... | ... | ... | ... |
| 1.5 | e | 1.5 | 59.023 | 71.036 |
| 1.5 | f | 1.5 | 59.023 | 71.036 |
| 2.5 | e | 1.5 | 60.094 | 71.963 |
| 2.5 | f | 1.5 | 60.094 | 71.963 |
| 3.5 | e | 1.5 | 61.593 | 73.261 |
| 3.5 | f | 1.5 | 61.593 | 73.261 |
| 4.5 | e | 1.5 | 63.521 | 74.929 |
| 4.5 | f | 1.5 | 63.521 | 74.929 |
| 5.5 | e | 1.5 | 65.877 | 76.969 |
| 5.5 | f | 1.5 | 65.877 | 76.969 |
| 6.5 | e | 1.5 | 68.661 | 79.379 |
| 6.5 | f | 1.5 | 68.661 | 79.379 |
| 7.5 | e | 1.5 | 71.873 | 82.160 |
| 7.5 | f | 1.5 | 71.874 | 82.160 |
| 8.5 | e | 1.5 | 75.514 | 85.312 |
| 8.5 | f | 1.5 | 75.515 | 85.312 |
| j . | ϵ . | Ω . | ESiNC . | ESiCN . |
|---|---|---|---|---|
| 0.5 | e | 0.5 | 0.000 | 0.000 |
| 0.5 | f | 0.5 | 0.000 | 0.001 |
| 1.5 | e | 0.5 | 0.638 | 0.553 |
| 1.5 | f | 0.5 | 0.638 | 0.555 |
| 2.5 | e | 0.5 | 1.700 | 1.475 |
| 2.5 | f | 0.5 | 1.702 | 1.477 |
| 3.5 | e | 0.5 | 3.189 | 2.765 |
| 3.5 | f | 0.5 | 3.190 | 2.769 |
| 4.5 | e | 0.5 | 5.102 | 4.425 |
| 4.5 | f | 0.5 | 5.104 | 4.429 |
| 5.5 | e | 0.5 | 7.440 | 6.453 |
| 5.5 | f | 0.5 | 7.443 | 6.458 |
| 6.5 | e | 0.5 | 10.204 | 8.850 |
| 6.5 | f | 0.5 | 10.207 | 8.857 |
| 7.5 | e | 0.5 | 13.393 | 11.616 |
| 7.5 | f | 0.5 | 13.396 | 11.624 |
| 8.5 | e | 0.5 | 17.008 | 14.751 |
| 8.5 | f | 0.5 | 17.011 | 14.760 |
| ... | ... | ... | ... | ... |
| 1.5 | e | 1.5 | 59.023 | 71.036 |
| 1.5 | f | 1.5 | 59.023 | 71.036 |
| 2.5 | e | 1.5 | 60.094 | 71.963 |
| 2.5 | f | 1.5 | 60.094 | 71.963 |
| 3.5 | e | 1.5 | 61.593 | 73.261 |
| 3.5 | f | 1.5 | 61.593 | 73.261 |
| 4.5 | e | 1.5 | 63.521 | 74.929 |
| 4.5 | f | 1.5 | 63.521 | 74.929 |
| 5.5 | e | 1.5 | 65.877 | 76.969 |
| 5.5 | f | 1.5 | 65.877 | 76.969 |
| 6.5 | e | 1.5 | 68.661 | 79.379 |
| 6.5 | f | 1.5 | 68.661 | 79.379 |
| 7.5 | e | 1.5 | 71.873 | 82.160 |
| 7.5 | f | 1.5 | 71.874 | 82.160 |
| 8.5 | e | 1.5 | 75.514 | 85.312 |
| 8.5 | f | 1.5 | 75.515 | 85.312 |
| j . | ϵ . | Ω . | ESiNC . | ESiCN . |
|---|---|---|---|---|
| 0.5 | e | 0.5 | 0.000 | 0.000 |
| 0.5 | f | 0.5 | 0.000 | 0.001 |
| 1.5 | e | 0.5 | 0.638 | 0.553 |
| 1.5 | f | 0.5 | 0.638 | 0.555 |
| 2.5 | e | 0.5 | 1.700 | 1.475 |
| 2.5 | f | 0.5 | 1.702 | 1.477 |
| 3.5 | e | 0.5 | 3.189 | 2.765 |
| 3.5 | f | 0.5 | 3.190 | 2.769 |
| 4.5 | e | 0.5 | 5.102 | 4.425 |
| 4.5 | f | 0.5 | 5.104 | 4.429 |
| 5.5 | e | 0.5 | 7.440 | 6.453 |
| 5.5 | f | 0.5 | 7.443 | 6.458 |
| 6.5 | e | 0.5 | 10.204 | 8.850 |
| 6.5 | f | 0.5 | 10.207 | 8.857 |
| 7.5 | e | 0.5 | 13.393 | 11.616 |
| 7.5 | f | 0.5 | 13.396 | 11.624 |
| 8.5 | e | 0.5 | 17.008 | 14.751 |
| 8.5 | f | 0.5 | 17.011 | 14.760 |
| ... | ... | ... | ... | ... |
| 1.5 | e | 1.5 | 59.023 | 71.036 |
| 1.5 | f | 1.5 | 59.023 | 71.036 |
| 2.5 | e | 1.5 | 60.094 | 71.963 |
| 2.5 | f | 1.5 | 60.094 | 71.963 |
| 3.5 | e | 1.5 | 61.593 | 73.261 |
| 3.5 | f | 1.5 | 61.593 | 73.261 |
| 4.5 | e | 1.5 | 63.521 | 74.929 |
| 4.5 | f | 1.5 | 63.521 | 74.929 |
| 5.5 | e | 1.5 | 65.877 | 76.969 |
| 5.5 | f | 1.5 | 65.877 | 76.969 |
| 6.5 | e | 1.5 | 68.661 | 79.379 |
| 6.5 | f | 1.5 | 68.661 | 79.379 |
| 7.5 | e | 1.5 | 71.873 | 82.160 |
| 7.5 | f | 1.5 | 71.874 | 82.160 |
| 8.5 | e | 1.5 | 75.514 | 85.312 |
| 8.5 | f | 1.5 | 75.515 | 85.312 |
The rotational constant of SiCN is slightly lower than the one of SiNC. This leads to a more compact structure for the SiCN isomer. Nevertheless, we did not expect significant differences in the collisional excitation cross-sections arising from the different rotational energy levels.
In the pure Hund's case (a) limit, it is Vsum potential that governs the inelastic collisions within a given spin–orbit manifold, and Vdiff which governs the inelastic collisions between the two (Ω = 1/2) and (Ω = 3/2) spin–orbit manifold Alexander (1985).
For both the SiCN/SiNC–He systems, as the A′ and A′′ PESs are quite similar so that we do not anticipate any sizeable cross-sections/rate coefficients for spin–orbit changing transitions. We then expect that most of the transitions occur within a spin–orbit manifold.
The accuracy of the CS approximation compared to the almost exact close coupling (CC) approach has been evaluated for a small number of energies. Tables 2 and 3 present the comparison for SiCN and SiNC isomers, respectively.
Comparison between CC and CS SiCN–He cross-sections (in Å2) at selected total energies (E). Transitions were chosen among levels in the F1 spin–orbit manifold.
| . | E = 20 cm−1 . | E = 50 cm−1 . | E = 100 cm−1 . | E = 300 cm−1 . | ||||
|---|---|---|---|---|---|---|---|---|
| Transitions . | CC . | CS . | CC . | CS . | CC . | CS . | CC . | CS . |
| j = 1.5, f → j = 0.5, f | 6.607 | 9.068 | 2.762 | 3.523 | 1.482 | 1.854 | 0.617 | 0.765 |
| j = 2.5, f → j = 0.5, f | 6.262 | 7.517 | 4.490 | 5.421 | 3.021 | 3.663 | 1.440 | 2.082 |
| j = 2.5, f → j = 1.5, f | 10.70 | 13.33 | 4.279 | 5.259 | 2.321 | 2.807 | 0.959 | 1.158 |
| j = 3.5, f → j = 1.5, f | 1.051 | 1.123 | 6.527 | 7.618 | 4.463 | 5.246 | 2.170 | 3.015 |
| j = 5.5, f → j = 0.5, f | 1.731 | 1.812 | 0.843 | 0.837 | 0.409 | 0.410 | 0.166 | 0.167 |
| j = 6.5, f → j = 1.5, f | 3.318 | 3.542 | 1.559 | 1.522 | 0.753 | 0.741 | 0.290 | 0.279 |
| j = 6.5, f → j = 5.5, f | 20.87 | 30.01 | 7.744 | 8.990 | 4.033 | 4.629 | 1.498 | 1.806 |
| j = 7.5, f → j = 5.5, f | 19.00 | 16.30 | 10.56 | 10.56 | 6.819 | 7.373 | 3.345 | 4.305 |
| j = 10.5, f → j = 0.5, f | – | – | 0.126 | 0.125 | 0.204 | 0.146 | 0.141 | 0.115 |
| j = 10.5, f → j = 1.5, f | – | – | 0.126 | 0.125 | 0.406 | 0.403 | 0.138 | 0.129 |
| j = 10.5, f → j = 5.5, f | – | – | 3.385 | 3.665 | 1.747 | 1.785 | 0.602 | 0.619 |
| j = 11.5, f → j = 10.5, f | – | – | 13.13 | 14.29 | 5.391 | 6.067 | 1.722 | 2.227 |
| j = 12.5, f → j = 10.5, f | – | – | 15.15 | 11.23 | 8.351 | 8.167 | 3.608 | 4.883 |
| j = 15.5, f → j = 10.5, f | – | – | – | – | 2.721 | 2.928 | 0.843 | 0.925 |
| . | E = 20 cm−1 . | E = 50 cm−1 . | E = 100 cm−1 . | E = 300 cm−1 . | ||||
|---|---|---|---|---|---|---|---|---|
| Transitions . | CC . | CS . | CC . | CS . | CC . | CS . | CC . | CS . |
| j = 1.5, f → j = 0.5, f | 6.607 | 9.068 | 2.762 | 3.523 | 1.482 | 1.854 | 0.617 | 0.765 |
| j = 2.5, f → j = 0.5, f | 6.262 | 7.517 | 4.490 | 5.421 | 3.021 | 3.663 | 1.440 | 2.082 |
| j = 2.5, f → j = 1.5, f | 10.70 | 13.33 | 4.279 | 5.259 | 2.321 | 2.807 | 0.959 | 1.158 |
| j = 3.5, f → j = 1.5, f | 1.051 | 1.123 | 6.527 | 7.618 | 4.463 | 5.246 | 2.170 | 3.015 |
| j = 5.5, f → j = 0.5, f | 1.731 | 1.812 | 0.843 | 0.837 | 0.409 | 0.410 | 0.166 | 0.167 |
| j = 6.5, f → j = 1.5, f | 3.318 | 3.542 | 1.559 | 1.522 | 0.753 | 0.741 | 0.290 | 0.279 |
| j = 6.5, f → j = 5.5, f | 20.87 | 30.01 | 7.744 | 8.990 | 4.033 | 4.629 | 1.498 | 1.806 |
| j = 7.5, f → j = 5.5, f | 19.00 | 16.30 | 10.56 | 10.56 | 6.819 | 7.373 | 3.345 | 4.305 |
| j = 10.5, f → j = 0.5, f | – | – | 0.126 | 0.125 | 0.204 | 0.146 | 0.141 | 0.115 |
| j = 10.5, f → j = 1.5, f | – | – | 0.126 | 0.125 | 0.406 | 0.403 | 0.138 | 0.129 |
| j = 10.5, f → j = 5.5, f | – | – | 3.385 | 3.665 | 1.747 | 1.785 | 0.602 | 0.619 |
| j = 11.5, f → j = 10.5, f | – | – | 13.13 | 14.29 | 5.391 | 6.067 | 1.722 | 2.227 |
| j = 12.5, f → j = 10.5, f | – | – | 15.15 | 11.23 | 8.351 | 8.167 | 3.608 | 4.883 |
| j = 15.5, f → j = 10.5, f | – | – | – | – | 2.721 | 2.928 | 0.843 | 0.925 |
Comparison between CC and CS SiCN–He cross-sections (in Å2) at selected total energies (E). Transitions were chosen among levels in the F1 spin–orbit manifold.
| . | E = 20 cm−1 . | E = 50 cm−1 . | E = 100 cm−1 . | E = 300 cm−1 . | ||||
|---|---|---|---|---|---|---|---|---|
| Transitions . | CC . | CS . | CC . | CS . | CC . | CS . | CC . | CS . |
| j = 1.5, f → j = 0.5, f | 6.607 | 9.068 | 2.762 | 3.523 | 1.482 | 1.854 | 0.617 | 0.765 |
| j = 2.5, f → j = 0.5, f | 6.262 | 7.517 | 4.490 | 5.421 | 3.021 | 3.663 | 1.440 | 2.082 |
| j = 2.5, f → j = 1.5, f | 10.70 | 13.33 | 4.279 | 5.259 | 2.321 | 2.807 | 0.959 | 1.158 |
| j = 3.5, f → j = 1.5, f | 1.051 | 1.123 | 6.527 | 7.618 | 4.463 | 5.246 | 2.170 | 3.015 |
| j = 5.5, f → j = 0.5, f | 1.731 | 1.812 | 0.843 | 0.837 | 0.409 | 0.410 | 0.166 | 0.167 |
| j = 6.5, f → j = 1.5, f | 3.318 | 3.542 | 1.559 | 1.522 | 0.753 | 0.741 | 0.290 | 0.279 |
| j = 6.5, f → j = 5.5, f | 20.87 | 30.01 | 7.744 | 8.990 | 4.033 | 4.629 | 1.498 | 1.806 |
| j = 7.5, f → j = 5.5, f | 19.00 | 16.30 | 10.56 | 10.56 | 6.819 | 7.373 | 3.345 | 4.305 |
| j = 10.5, f → j = 0.5, f | – | – | 0.126 | 0.125 | 0.204 | 0.146 | 0.141 | 0.115 |
| j = 10.5, f → j = 1.5, f | – | – | 0.126 | 0.125 | 0.406 | 0.403 | 0.138 | 0.129 |
| j = 10.5, f → j = 5.5, f | – | – | 3.385 | 3.665 | 1.747 | 1.785 | 0.602 | 0.619 |
| j = 11.5, f → j = 10.5, f | – | – | 13.13 | 14.29 | 5.391 | 6.067 | 1.722 | 2.227 |
| j = 12.5, f → j = 10.5, f | – | – | 15.15 | 11.23 | 8.351 | 8.167 | 3.608 | 4.883 |
| j = 15.5, f → j = 10.5, f | – | – | – | – | 2.721 | 2.928 | 0.843 | 0.925 |
| . | E = 20 cm−1 . | E = 50 cm−1 . | E = 100 cm−1 . | E = 300 cm−1 . | ||||
|---|---|---|---|---|---|---|---|---|
| Transitions . | CC . | CS . | CC . | CS . | CC . | CS . | CC . | CS . |
| j = 1.5, f → j = 0.5, f | 6.607 | 9.068 | 2.762 | 3.523 | 1.482 | 1.854 | 0.617 | 0.765 |
| j = 2.5, f → j = 0.5, f | 6.262 | 7.517 | 4.490 | 5.421 | 3.021 | 3.663 | 1.440 | 2.082 |
| j = 2.5, f → j = 1.5, f | 10.70 | 13.33 | 4.279 | 5.259 | 2.321 | 2.807 | 0.959 | 1.158 |
| j = 3.5, f → j = 1.5, f | 1.051 | 1.123 | 6.527 | 7.618 | 4.463 | 5.246 | 2.170 | 3.015 |
| j = 5.5, f → j = 0.5, f | 1.731 | 1.812 | 0.843 | 0.837 | 0.409 | 0.410 | 0.166 | 0.167 |
| j = 6.5, f → j = 1.5, f | 3.318 | 3.542 | 1.559 | 1.522 | 0.753 | 0.741 | 0.290 | 0.279 |
| j = 6.5, f → j = 5.5, f | 20.87 | 30.01 | 7.744 | 8.990 | 4.033 | 4.629 | 1.498 | 1.806 |
| j = 7.5, f → j = 5.5, f | 19.00 | 16.30 | 10.56 | 10.56 | 6.819 | 7.373 | 3.345 | 4.305 |
| j = 10.5, f → j = 0.5, f | – | – | 0.126 | 0.125 | 0.204 | 0.146 | 0.141 | 0.115 |
| j = 10.5, f → j = 1.5, f | – | – | 0.126 | 0.125 | 0.406 | 0.403 | 0.138 | 0.129 |
| j = 10.5, f → j = 5.5, f | – | – | 3.385 | 3.665 | 1.747 | 1.785 | 0.602 | 0.619 |
| j = 11.5, f → j = 10.5, f | – | – | 13.13 | 14.29 | 5.391 | 6.067 | 1.722 | 2.227 |
| j = 12.5, f → j = 10.5, f | – | – | 15.15 | 11.23 | 8.351 | 8.167 | 3.608 | 4.883 |
| j = 15.5, f → j = 10.5, f | – | – | – | – | 2.721 | 2.928 | 0.843 | 0.925 |
Comparison between CC and CS SiNC–He cross-sections (in Å2) at selected total energies (E). Transitions were chosen among levels in the F1 spin–orbit manifold.
| . | E = 20 cm−1 . | E = 50 cm−1 . | E = 100 cm−1 . | E = 300 cm−1 . | ||||
|---|---|---|---|---|---|---|---|---|
| Transitions . | CC . | CS . | CC . | CS . | CC . | CS . | CC . | CS . |
| j = 1.5, f → j = 0.5, f | 3.080 | 4.342 | 1.753 | 2.282 | 1.041 | 1.400 | 0.427 | 0.544 |
| j = 2.5, f → j = 0.5, f | 6.704 | 7.533 | 4.207 | 4.777 | 2.785 | 3.241 | 1.415 | 1.961 |
| j = 2.5, f → j = 1.5, f | 4.992 | 7.569 | 2.837 | 3.670 | 1.718 | 2.295 | 0.715 | 0.875 |
| j = 3.5, f → j = 1.5, f | 1.051 | 1.123 | 6.272 | 6.768 | 4.166 | 4.658 | 2.106 | 2.829 |
| j = 5.5, f → j = 0.5, f | 1.533 | 2.001 | 5.673 | 7.210 | 3.213 | 4.115 | 0.135 | 0.141 |
| j = 6.5, f → j = 1.5, f | 3.226 | 4.026 | 1.005 | 1.297 | 0.577 | 0.727 | 0.239 | 0.239 |
| j = 6.5, f → j = 5.5, f | 16.44 | 17.29 | 5.209 | 6.490 | 2.977 | 3.870 | 1.175 | 1.439 |
| j = 7.5, f → j = 5.5, f | 28.66 | 28.32 | 10.68 | 9.901 | 6.727 | 6.783 | 3.242 | 4.071 |
| j = 10.5, f → j = 0.5, f | – | – | 0.537 | 0.608 | 0.185 | 0.237 | 0.112 | 0.105 |
| j = 10.5, f → j = 1.5, f | – | – | 0.336 | 0.273 | 0.311 | 0.238 | 0.165 | 0.139 |
| j = 10.5, f → j = 5.5, f | – | – | 2.594 | 3.326 | 1.214 | 1.554 | 0.475 | 0.521 |
| j = 11.5, f → j = 10.5, f | – | – | 10.58 | 10.92 | 4.054 | 5.107 | 1.365 | 1.807 |
| j = 12.5, f → j = 10.5, f | – | – | 19.54 | 17.97 | 8.820 | 7.834 | 3.609 | 4.646 |
| j = 15.5, f → j = 10.5, f | – | – | – | – | 1.967 | 2.569 | 0.659 | 0.767 |
| . | E = 20 cm−1 . | E = 50 cm−1 . | E = 100 cm−1 . | E = 300 cm−1 . | ||||
|---|---|---|---|---|---|---|---|---|
| Transitions . | CC . | CS . | CC . | CS . | CC . | CS . | CC . | CS . |
| j = 1.5, f → j = 0.5, f | 3.080 | 4.342 | 1.753 | 2.282 | 1.041 | 1.400 | 0.427 | 0.544 |
| j = 2.5, f → j = 0.5, f | 6.704 | 7.533 | 4.207 | 4.777 | 2.785 | 3.241 | 1.415 | 1.961 |
| j = 2.5, f → j = 1.5, f | 4.992 | 7.569 | 2.837 | 3.670 | 1.718 | 2.295 | 0.715 | 0.875 |
| j = 3.5, f → j = 1.5, f | 1.051 | 1.123 | 6.272 | 6.768 | 4.166 | 4.658 | 2.106 | 2.829 |
| j = 5.5, f → j = 0.5, f | 1.533 | 2.001 | 5.673 | 7.210 | 3.213 | 4.115 | 0.135 | 0.141 |
| j = 6.5, f → j = 1.5, f | 3.226 | 4.026 | 1.005 | 1.297 | 0.577 | 0.727 | 0.239 | 0.239 |
| j = 6.5, f → j = 5.5, f | 16.44 | 17.29 | 5.209 | 6.490 | 2.977 | 3.870 | 1.175 | 1.439 |
| j = 7.5, f → j = 5.5, f | 28.66 | 28.32 | 10.68 | 9.901 | 6.727 | 6.783 | 3.242 | 4.071 |
| j = 10.5, f → j = 0.5, f | – | – | 0.537 | 0.608 | 0.185 | 0.237 | 0.112 | 0.105 |
| j = 10.5, f → j = 1.5, f | – | – | 0.336 | 0.273 | 0.311 | 0.238 | 0.165 | 0.139 |
| j = 10.5, f → j = 5.5, f | – | – | 2.594 | 3.326 | 1.214 | 1.554 | 0.475 | 0.521 |
| j = 11.5, f → j = 10.5, f | – | – | 10.58 | 10.92 | 4.054 | 5.107 | 1.365 | 1.807 |
| j = 12.5, f → j = 10.5, f | – | – | 19.54 | 17.97 | 8.820 | 7.834 | 3.609 | 4.646 |
| j = 15.5, f → j = 10.5, f | – | – | – | – | 1.967 | 2.569 | 0.659 | 0.767 |
Comparison between CC and CS SiNC–He cross-sections (in Å2) at selected total energies (E). Transitions were chosen among levels in the F1 spin–orbit manifold.
| . | E = 20 cm−1 . | E = 50 cm−1 . | E = 100 cm−1 . | E = 300 cm−1 . | ||||
|---|---|---|---|---|---|---|---|---|
| Transitions . | CC . | CS . | CC . | CS . | CC . | CS . | CC . | CS . |
| j = 1.5, f → j = 0.5, f | 3.080 | 4.342 | 1.753 | 2.282 | 1.041 | 1.400 | 0.427 | 0.544 |
| j = 2.5, f → j = 0.5, f | 6.704 | 7.533 | 4.207 | 4.777 | 2.785 | 3.241 | 1.415 | 1.961 |
| j = 2.5, f → j = 1.5, f | 4.992 | 7.569 | 2.837 | 3.670 | 1.718 | 2.295 | 0.715 | 0.875 |
| j = 3.5, f → j = 1.5, f | 1.051 | 1.123 | 6.272 | 6.768 | 4.166 | 4.658 | 2.106 | 2.829 |
| j = 5.5, f → j = 0.5, f | 1.533 | 2.001 | 5.673 | 7.210 | 3.213 | 4.115 | 0.135 | 0.141 |
| j = 6.5, f → j = 1.5, f | 3.226 | 4.026 | 1.005 | 1.297 | 0.577 | 0.727 | 0.239 | 0.239 |
| j = 6.5, f → j = 5.5, f | 16.44 | 17.29 | 5.209 | 6.490 | 2.977 | 3.870 | 1.175 | 1.439 |
| j = 7.5, f → j = 5.5, f | 28.66 | 28.32 | 10.68 | 9.901 | 6.727 | 6.783 | 3.242 | 4.071 |
| j = 10.5, f → j = 0.5, f | – | – | 0.537 | 0.608 | 0.185 | 0.237 | 0.112 | 0.105 |
| j = 10.5, f → j = 1.5, f | – | – | 0.336 | 0.273 | 0.311 | 0.238 | 0.165 | 0.139 |
| j = 10.5, f → j = 5.5, f | – | – | 2.594 | 3.326 | 1.214 | 1.554 | 0.475 | 0.521 |
| j = 11.5, f → j = 10.5, f | – | – | 10.58 | 10.92 | 4.054 | 5.107 | 1.365 | 1.807 |
| j = 12.5, f → j = 10.5, f | – | – | 19.54 | 17.97 | 8.820 | 7.834 | 3.609 | 4.646 |
| j = 15.5, f → j = 10.5, f | – | – | – | – | 1.967 | 2.569 | 0.659 | 0.767 |
| . | E = 20 cm−1 . | E = 50 cm−1 . | E = 100 cm−1 . | E = 300 cm−1 . | ||||
|---|---|---|---|---|---|---|---|---|
| Transitions . | CC . | CS . | CC . | CS . | CC . | CS . | CC . | CS . |
| j = 1.5, f → j = 0.5, f | 3.080 | 4.342 | 1.753 | 2.282 | 1.041 | 1.400 | 0.427 | 0.544 |
| j = 2.5, f → j = 0.5, f | 6.704 | 7.533 | 4.207 | 4.777 | 2.785 | 3.241 | 1.415 | 1.961 |
| j = 2.5, f → j = 1.5, f | 4.992 | 7.569 | 2.837 | 3.670 | 1.718 | 2.295 | 0.715 | 0.875 |
| j = 3.5, f → j = 1.5, f | 1.051 | 1.123 | 6.272 | 6.768 | 4.166 | 4.658 | 2.106 | 2.829 |
| j = 5.5, f → j = 0.5, f | 1.533 | 2.001 | 5.673 | 7.210 | 3.213 | 4.115 | 0.135 | 0.141 |
| j = 6.5, f → j = 1.5, f | 3.226 | 4.026 | 1.005 | 1.297 | 0.577 | 0.727 | 0.239 | 0.239 |
| j = 6.5, f → j = 5.5, f | 16.44 | 17.29 | 5.209 | 6.490 | 2.977 | 3.870 | 1.175 | 1.439 |
| j = 7.5, f → j = 5.5, f | 28.66 | 28.32 | 10.68 | 9.901 | 6.727 | 6.783 | 3.242 | 4.071 |
| j = 10.5, f → j = 0.5, f | – | – | 0.537 | 0.608 | 0.185 | 0.237 | 0.112 | 0.105 |
| j = 10.5, f → j = 1.5, f | – | – | 0.336 | 0.273 | 0.311 | 0.238 | 0.165 | 0.139 |
| j = 10.5, f → j = 5.5, f | – | – | 2.594 | 3.326 | 1.214 | 1.554 | 0.475 | 0.521 |
| j = 11.5, f → j = 10.5, f | – | – | 10.58 | 10.92 | 4.054 | 5.107 | 1.365 | 1.807 |
| j = 12.5, f → j = 10.5, f | – | – | 19.54 | 17.97 | 8.820 | 7.834 | 3.609 | 4.646 |
| j = 15.5, f → j = 10.5, f | – | – | – | – | 1.967 | 2.569 | 0.659 | 0.767 |
It is found that the CS approach can lead to inaccuracies of 20–30 per cent for very low total energy cross-sections (<50 cm−1) but agreement improves between CC and CS cross-sections when the total energy is greater than 50 cm−1 and we expect that the corresponding rate coefficients will be accurate since they are not as sensitive to the accuracy of description of the resonances that occurs at low collisional energies. The relative accuracy of the CS approximation compared to full CC approach can be explained by the relatively small energy spacing between SiCN and SiNC rotational levels.
4 RESULTS
Using the new ab initio PESs and the computational scheme described above, we have obtained the energy dependence of the SiCN–He and SiNC–He cross-sections and the corresponding temperature dependence of the rate coefficients. The complete set of (de-)excitation rate coefficients will be made available through the LAMDA (Schöier et al. 2005) and BASECOL (Dubernet et al. 2013) data bases.
Fig. 5 shows the temperature dependence of the SiCN–He collisional de-excitation rate coefficients for transitions out of the j = 8.5, e/f levels in both the ground (F1) and excited (F2) spin–orbit manifolds.
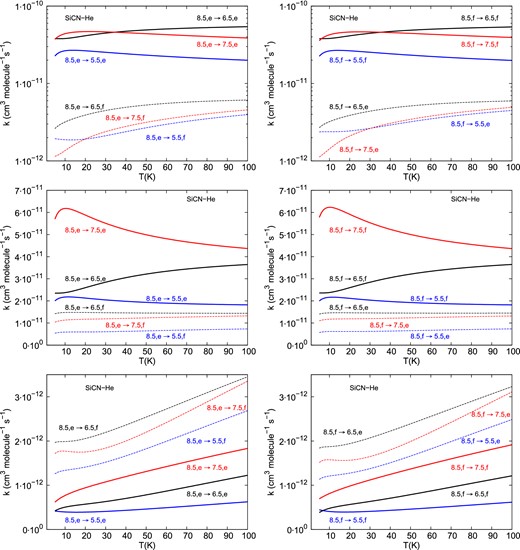
Temperature dependence of the SiCN–He collisional de-excitation rate coefficients for transitions out of the j = 8.5, e/f, F1/F2. The upper panels correspond to transitions within the F1 spin–orbit manifold. The middle panels correspond to transitions within the F2 spin–orbit manifold. The lower panels correspond to spin–orbit changing (F2 → F1) transitions.
First of all, for spin–orbit conserving transitions, one can see a strong propensity in favour of Λ-doublet conserving transitions (e → e or f → f). The propensity is slightly more pronounced for high rotational states than for low ones and for transitions within the F1 spin–orbit manifold than within the F2 spin–orbit manifold.
As expected, the spin–orbit changing transitions are lower than the spin–orbit conserving transitions. For spin–orbit changing transitions, the rate coefficients show a propensity to populate e final levels when starting from initial f levels or to populate f final levels when starting from initial e levels. Such behaviour has been already observed for NO–He collisions (Kłos, Lique & Alexander 2008). The magnitude of the spin–orbit changing transition increase with increasing temperature and one could anticipate that at higher temperatures, there may be a clear competition between spin–orbit changing and spin–orbit conserving transitions.
Fig. 6 shows the temperature dependence of the SiNC–He collisional de-excitation rate coefficients for transitions out of the j = 8.5, e/f levels in both the ground (F1) and excited (F2) spin–orbit manifolds.
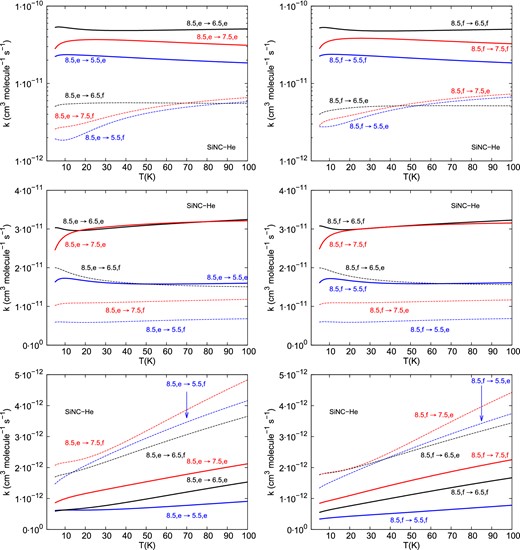
Temperature dependence of the SiNC–He collisional de-excitation rate coefficients for transitions out of the j = 8.5, e/f, F1/F2. The upper panels correspond to transitions within the F1 spin–orbit manifold. The middle panels correspond to transitions within the F2 spin–orbit manifold. The lower panels correspond to spin–orbit manifold changing (F2 → F1) transitions.
The propensity rules are exactly the same as for the SiCN–He collisional system. Such similarity could have been anticipated after inspecting the PESs and the rotational structure.
However, it is interesting to compare state-to-state SiCN–He and SiNC–He rate coefficients. Fig. 7 shows the SiCN–He and SiNC–He de-excitation rate coefficients from the j = 8.5, f, F1/F2 level at 25 K.
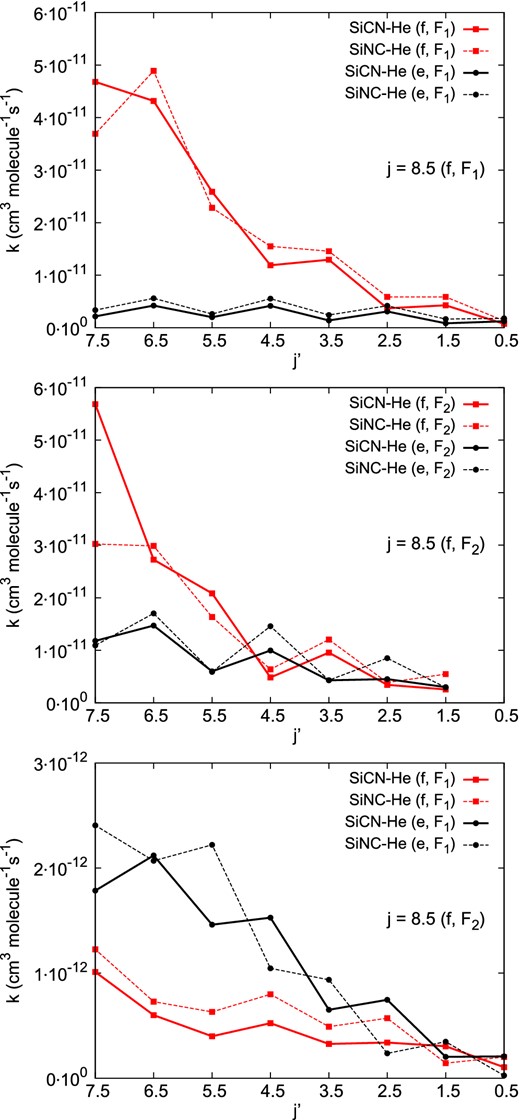
Comparison between the SiCN-He and SiNC-He rate coefficients at 25 K for spin–orbit-conserving F1 → F1 (upper panel), F2 → F2 (middle panel) and spin–orbit-changing F2 → F1 transitions out of the j = 8.5, f, F1/F2 level.
We note that the two sets of data are in general rather similar. However, there are interesting differences that may impact the radiative transfer calculations. For some transitions, the propensity rules in the two sets of rate coefficients differ. For both spin–orbit-conserving F1 → F1 and F2 → F2, the SiCN-He rate coefficients present a propensity in favour of transitions with Δj = 1 whereas the SiNC-He rate coefficients present a slight propensity in favour of transitions with Δj = 2. The differences are more pronounced for transitions within the F2 spin–orbit manifold than for transitions within the F1 spin–orbit manifold. These propensities are due to the shape of the different PESs. Even if they seem to be similar, the anisotropy of the SiCN PES is larger than the one of the SiNC, so that the propensity rules with respect to odd or even Δj transitions are not the same (McCurdy & Miller 1977). Such effect has been already observed by Sarrasin et al. (2010) and Dumouchel, Faure & Lique (2010) for the HCN/HNC isomers and in Paper II for the MgCN/MgNC isomers.
5 ASTROPHYSICAL APPLICATIONS
In this section, we employ the new thermal SiCN–He and SiNC–He rate coefficients to simulate the excitation of SiCN and SiNC molecules for typical physical conditions of the circumstellar gas. This will allow us to understand and accurately analyse the emission of these molecules from the circumstellar gas.
5.1 Critical density
We consider in the above expression collisional rate coefficients among both the F1 and F2 spin–orbit manifolds. We apply a scaling factor of 1.38 to the He rate coefficients in order to estimate H2 rate coefficients. As discussed in Paper III, such approximation appears to be reasonably accurate for heavy molecules (Roueff & Lique 2013) so that we can expect that the estimation of SiCN–H2 and SiNC–H2 rate coefficients will be accurate within a factor of 2.
Einstein coefficients were computed from the experimental frequencies of the rotational transitions and from the dipole moments of Paper I. We recall here that the computed dipole moments of SiCN and SiNC molecules are 2.82 and 2.73 D, respectively. Analysis of SiCN and SiNC emissions were previously performed using dipole moments computed by Largo-Cabrerizo (1988) (2.9 D for SiCN and 2.0 D for SiNC). Whereas the value of Paper I is in good agreement with that of Largo-Cabrerizo (1988) for SiCN, the value of Paper I significantly differ for SiNC compared to that Largo-Cabrerizo (1988). Such difference were already noted by Richardson, Yamaguchi & Schaefer (2003) that found a dipole moment of 2.65 D. Such difference between previous and new SiNC dipole moment will induce important consequences on the astrophysical modelling as we will see below and we strongly recommend to update molecular data base with the new data.
Table 4 shows the critical densities |$n^{\star}_i$| for SiCN/SiNC collisions (in cm−3) at 20, 50 and 100 K for a selection of observed transitions. For densities above the critical density, emissions are thermal in origin, and we can assume LTE in order to describe the molecular emission process. However, below this density, our collisional rate coefficients are essential for a proper simulation of the SiNC and SiCN emissions.
Critical densities |$n^{\star}_i$| for SiCN/SiNC collisions (in cm−3) at 20, 50 and 100 K. All transitions correspond to the F1 spin–orbit manifold. j denotes the initial state of the radiative transition.
| . | . | 20 K . | 50 K . | 100 K . | |||
|---|---|---|---|---|---|---|---|
| j . | ϵ . | |$n^{\star}_i$| (SiCN) . | |$n^{\star}_i$| (SiNC) . | |$n^{\star}_i$| (SiCN) . | |$n^{\star}_i$| (SiNC) . | |$n^{\star}_i$| (SiCN) . | |$n^{\star}_i$| (SiNC) . |
| 1.5 | e | 2.011(2) | 1.836(2) | 2.285(2) | 2.081(2) | 2.531(2) | 2.250(2) |
| 1.5 | f | 1.218(3) | 1.041(3) | 1.468(3) | 1.295(3) | 1.695(3) | 1.474(3) |
| 2.5 | e | 3.923(3) | 6.881(3) | 4.308(3) | 7.442(3) | 4.696(3) | 7.898(3) |
| 2.5 | f | 3.173(3) | 5.195(3) | 3.591(3) | 6.017(3) | 4.009(3) | 6.632(3) |
| 3.5 | e | 1.095(4) | 1.898(4) | 1.202(4) | 2.026(4) | 1.302(4) | 2.143(4) |
| 3.5 | f | 9.607(3) | 1.554(4) | 1.071(4) | 1.766(4) | 1.175(4) | 1.925(4) |
| 4.5 | e | 2.217(4) | 3.712(4) | 2.408(4) | 3.958(4) | 2.581(4) | 4.179(4) |
| 4.5 | f | 2.056(4) | 3.284(4) | 2.241(4) | 3.630(4) | 2.414(4) | 3.903(4) |
| 5.5 | e | 3.983(4) | 6.341(4) | 4.198(4) | 6.661(4) | 4.417(4) | 6.973(4) |
| 5.5 | f | 3.759(4) | 5.824(4) | 3.977(4) | 6.284(4) | 4.193(4) | 6.656(4) |
| 6.5 | e | 6.419(4) | 9.854(4) | 6.641(4) | 1.027(4) | 6.875(4) | 1.064(5) |
| 6.5 | f | 6.223(4) | 9.449(4) | 6.403(4) | 9.944(4) | 6.606(4) | 1.035(5) |
| 7.5 | e | 1.016(5) | 1.461(5) | 1.004(5) | 1.500(5) | 1.011(5) | 1.533(5) |
| 7.5 | f | 9.968(4) | 1.413(5) | 9.779(4) | 1.462(5) | 9.800(4) | 1.500(5) |
| 8.5 | e | 1.540(5) | 2.008(5) | 1.447(5) | 2.070(5) | 1.420(5) | 2.104(5) |
| 8.5 | f | 1.523(5) | 1.948(5) | 1.422(5) | 2.032(5) | 1.388(5) | 2.073(5) |
| 9.5 | e | 2.179(5) | 2.649(5) | 1.982(5) | 2.758(5) | 1.913(5) | 2.793(5) |
| 9.5 | f | 2.166(5) | 2.623(5) | 1.963(5) | 2.746(5) | 1.883(5) | 2.784(5) |
| 10.5 | e | 2.874(5) | 3.562(5) | 2.603(5) | 3.641(5) | 2.496(5) | 3.644(5) |
| 10.5 | f | 2.864(5) | 3.538(5) | 2.590(5) | 3.639(5) | 2.471(5) | 3.648(5) |
| . | . | 20 K . | 50 K . | 100 K . | |||
|---|---|---|---|---|---|---|---|
| j . | ϵ . | |$n^{\star}_i$| (SiCN) . | |$n^{\star}_i$| (SiNC) . | |$n^{\star}_i$| (SiCN) . | |$n^{\star}_i$| (SiNC) . | |$n^{\star}_i$| (SiCN) . | |$n^{\star}_i$| (SiNC) . |
| 1.5 | e | 2.011(2) | 1.836(2) | 2.285(2) | 2.081(2) | 2.531(2) | 2.250(2) |
| 1.5 | f | 1.218(3) | 1.041(3) | 1.468(3) | 1.295(3) | 1.695(3) | 1.474(3) |
| 2.5 | e | 3.923(3) | 6.881(3) | 4.308(3) | 7.442(3) | 4.696(3) | 7.898(3) |
| 2.5 | f | 3.173(3) | 5.195(3) | 3.591(3) | 6.017(3) | 4.009(3) | 6.632(3) |
| 3.5 | e | 1.095(4) | 1.898(4) | 1.202(4) | 2.026(4) | 1.302(4) | 2.143(4) |
| 3.5 | f | 9.607(3) | 1.554(4) | 1.071(4) | 1.766(4) | 1.175(4) | 1.925(4) |
| 4.5 | e | 2.217(4) | 3.712(4) | 2.408(4) | 3.958(4) | 2.581(4) | 4.179(4) |
| 4.5 | f | 2.056(4) | 3.284(4) | 2.241(4) | 3.630(4) | 2.414(4) | 3.903(4) |
| 5.5 | e | 3.983(4) | 6.341(4) | 4.198(4) | 6.661(4) | 4.417(4) | 6.973(4) |
| 5.5 | f | 3.759(4) | 5.824(4) | 3.977(4) | 6.284(4) | 4.193(4) | 6.656(4) |
| 6.5 | e | 6.419(4) | 9.854(4) | 6.641(4) | 1.027(4) | 6.875(4) | 1.064(5) |
| 6.5 | f | 6.223(4) | 9.449(4) | 6.403(4) | 9.944(4) | 6.606(4) | 1.035(5) |
| 7.5 | e | 1.016(5) | 1.461(5) | 1.004(5) | 1.500(5) | 1.011(5) | 1.533(5) |
| 7.5 | f | 9.968(4) | 1.413(5) | 9.779(4) | 1.462(5) | 9.800(4) | 1.500(5) |
| 8.5 | e | 1.540(5) | 2.008(5) | 1.447(5) | 2.070(5) | 1.420(5) | 2.104(5) |
| 8.5 | f | 1.523(5) | 1.948(5) | 1.422(5) | 2.032(5) | 1.388(5) | 2.073(5) |
| 9.5 | e | 2.179(5) | 2.649(5) | 1.982(5) | 2.758(5) | 1.913(5) | 2.793(5) |
| 9.5 | f | 2.166(5) | 2.623(5) | 1.963(5) | 2.746(5) | 1.883(5) | 2.784(5) |
| 10.5 | e | 2.874(5) | 3.562(5) | 2.603(5) | 3.641(5) | 2.496(5) | 3.644(5) |
| 10.5 | f | 2.864(5) | 3.538(5) | 2.590(5) | 3.639(5) | 2.471(5) | 3.648(5) |
Critical densities |$n^{\star}_i$| for SiCN/SiNC collisions (in cm−3) at 20, 50 and 100 K. All transitions correspond to the F1 spin–orbit manifold. j denotes the initial state of the radiative transition.
| . | . | 20 K . | 50 K . | 100 K . | |||
|---|---|---|---|---|---|---|---|
| j . | ϵ . | |$n^{\star}_i$| (SiCN) . | |$n^{\star}_i$| (SiNC) . | |$n^{\star}_i$| (SiCN) . | |$n^{\star}_i$| (SiNC) . | |$n^{\star}_i$| (SiCN) . | |$n^{\star}_i$| (SiNC) . |
| 1.5 | e | 2.011(2) | 1.836(2) | 2.285(2) | 2.081(2) | 2.531(2) | 2.250(2) |
| 1.5 | f | 1.218(3) | 1.041(3) | 1.468(3) | 1.295(3) | 1.695(3) | 1.474(3) |
| 2.5 | e | 3.923(3) | 6.881(3) | 4.308(3) | 7.442(3) | 4.696(3) | 7.898(3) |
| 2.5 | f | 3.173(3) | 5.195(3) | 3.591(3) | 6.017(3) | 4.009(3) | 6.632(3) |
| 3.5 | e | 1.095(4) | 1.898(4) | 1.202(4) | 2.026(4) | 1.302(4) | 2.143(4) |
| 3.5 | f | 9.607(3) | 1.554(4) | 1.071(4) | 1.766(4) | 1.175(4) | 1.925(4) |
| 4.5 | e | 2.217(4) | 3.712(4) | 2.408(4) | 3.958(4) | 2.581(4) | 4.179(4) |
| 4.5 | f | 2.056(4) | 3.284(4) | 2.241(4) | 3.630(4) | 2.414(4) | 3.903(4) |
| 5.5 | e | 3.983(4) | 6.341(4) | 4.198(4) | 6.661(4) | 4.417(4) | 6.973(4) |
| 5.5 | f | 3.759(4) | 5.824(4) | 3.977(4) | 6.284(4) | 4.193(4) | 6.656(4) |
| 6.5 | e | 6.419(4) | 9.854(4) | 6.641(4) | 1.027(4) | 6.875(4) | 1.064(5) |
| 6.5 | f | 6.223(4) | 9.449(4) | 6.403(4) | 9.944(4) | 6.606(4) | 1.035(5) |
| 7.5 | e | 1.016(5) | 1.461(5) | 1.004(5) | 1.500(5) | 1.011(5) | 1.533(5) |
| 7.5 | f | 9.968(4) | 1.413(5) | 9.779(4) | 1.462(5) | 9.800(4) | 1.500(5) |
| 8.5 | e | 1.540(5) | 2.008(5) | 1.447(5) | 2.070(5) | 1.420(5) | 2.104(5) |
| 8.5 | f | 1.523(5) | 1.948(5) | 1.422(5) | 2.032(5) | 1.388(5) | 2.073(5) |
| 9.5 | e | 2.179(5) | 2.649(5) | 1.982(5) | 2.758(5) | 1.913(5) | 2.793(5) |
| 9.5 | f | 2.166(5) | 2.623(5) | 1.963(5) | 2.746(5) | 1.883(5) | 2.784(5) |
| 10.5 | e | 2.874(5) | 3.562(5) | 2.603(5) | 3.641(5) | 2.496(5) | 3.644(5) |
| 10.5 | f | 2.864(5) | 3.538(5) | 2.590(5) | 3.639(5) | 2.471(5) | 3.648(5) |
| . | . | 20 K . | 50 K . | 100 K . | |||
|---|---|---|---|---|---|---|---|
| j . | ϵ . | |$n^{\star}_i$| (SiCN) . | |$n^{\star}_i$| (SiNC) . | |$n^{\star}_i$| (SiCN) . | |$n^{\star}_i$| (SiNC) . | |$n^{\star}_i$| (SiCN) . | |$n^{\star}_i$| (SiNC) . |
| 1.5 | e | 2.011(2) | 1.836(2) | 2.285(2) | 2.081(2) | 2.531(2) | 2.250(2) |
| 1.5 | f | 1.218(3) | 1.041(3) | 1.468(3) | 1.295(3) | 1.695(3) | 1.474(3) |
| 2.5 | e | 3.923(3) | 6.881(3) | 4.308(3) | 7.442(3) | 4.696(3) | 7.898(3) |
| 2.5 | f | 3.173(3) | 5.195(3) | 3.591(3) | 6.017(3) | 4.009(3) | 6.632(3) |
| 3.5 | e | 1.095(4) | 1.898(4) | 1.202(4) | 2.026(4) | 1.302(4) | 2.143(4) |
| 3.5 | f | 9.607(3) | 1.554(4) | 1.071(4) | 1.766(4) | 1.175(4) | 1.925(4) |
| 4.5 | e | 2.217(4) | 3.712(4) | 2.408(4) | 3.958(4) | 2.581(4) | 4.179(4) |
| 4.5 | f | 2.056(4) | 3.284(4) | 2.241(4) | 3.630(4) | 2.414(4) | 3.903(4) |
| 5.5 | e | 3.983(4) | 6.341(4) | 4.198(4) | 6.661(4) | 4.417(4) | 6.973(4) |
| 5.5 | f | 3.759(4) | 5.824(4) | 3.977(4) | 6.284(4) | 4.193(4) | 6.656(4) |
| 6.5 | e | 6.419(4) | 9.854(4) | 6.641(4) | 1.027(4) | 6.875(4) | 1.064(5) |
| 6.5 | f | 6.223(4) | 9.449(4) | 6.403(4) | 9.944(4) | 6.606(4) | 1.035(5) |
| 7.5 | e | 1.016(5) | 1.461(5) | 1.004(5) | 1.500(5) | 1.011(5) | 1.533(5) |
| 7.5 | f | 9.968(4) | 1.413(5) | 9.779(4) | 1.462(5) | 9.800(4) | 1.500(5) |
| 8.5 | e | 1.540(5) | 2.008(5) | 1.447(5) | 2.070(5) | 1.420(5) | 2.104(5) |
| 8.5 | f | 1.523(5) | 1.948(5) | 1.422(5) | 2.032(5) | 1.388(5) | 2.073(5) |
| 9.5 | e | 2.179(5) | 2.649(5) | 1.982(5) | 2.758(5) | 1.913(5) | 2.793(5) |
| 9.5 | f | 2.166(5) | 2.623(5) | 1.963(5) | 2.746(5) | 1.883(5) | 2.784(5) |
| 10.5 | e | 2.874(5) | 3.562(5) | 2.603(5) | 3.641(5) | 2.496(5) | 3.644(5) |
| 10.5 | f | 2.864(5) | 3.538(5) | 2.590(5) | 3.639(5) | 2.471(5) | 3.648(5) |
The critical densities of the first radiative transitions are of the order of 102–103 cm−3, whatever the temperature is. The values are weakly dependent on the temperature because of the weak temperature dependence of the SiCN/SiNC rate coefficients. For both isomers, the computed critical densities increase with the excited rotational levels. This can be explained by the fact that the Einstein emission coefficients increase approximately as j3, whereas, in most of the cases, the collisional rate coefficients stay within the same order of magnitude. Indeed, for the most frequently observed lines of SiCN and SiNC (those from initial energy levels with j between 6.5 and 10.5), the calculations show that the critical densities are of the order of 1–5 × 105 cm−3.
Taking into account that the typical hydrogen density in the outer envelope of the circumstellar gas have been estimated to be 104–106 cm−3, we can anticipate that the LTE condition will not be fully met in the outer envelope of the circumstellar gas. Hence, non-LTE radiative transfer calculations will have to be performed in order to determine the SiCN/SiNC abundance in these regions.
We also note that the critical densities of the SiNC lines are slightly larger than the ones of SiCN because of their slightly larger Einstein coefficients.
5.2 Radiative transfer calculations
Using the newly computed rate coefficients, we perform non-LTE radiative transfer calculations using the LVG approximation for an expanding sphere and the radex code (van der Tak et al. 2007) The LVG approach, first proposed by Sobolev (1960), provides a local expression for the angle-averaged mean intensity that thoroughly simplifies the resolution of the statistical equilibrium equations. This approximation implies that the velocity gradient is large enough to decouple radiatively the different points of the cloud. For each point of the cloud, the excitation conditions depend only on the local density, the kinetic temperature and the escape probability.
Collisional excitation of SiCN and SiNC is induced by collisions with H2 and by absorption of photons. The cosmic microwave background radiation was fixed at 2.73 K. In all calculations, a linewidth of 29 km s−1 was taken into account, in agreement with the observations (Guélin et al. 2004). Such a broad linewidth corresponds to the typical width of the emission lines coming from the outer envelope of the IRC+10216 (i.e. from where SiCN/SiNC have been detected for the first time).
As mentioned in the Introduction, SiCN and SiNC have been mainly observed in the circumstellar gas. The detection of the SiCN was first reported by Guélin et al. (2000) in the outer envelope of the IRC+10216, using the IRAM 30-m telescope. Six emission lines were observed, corresponding to the j = 7.5 → 6.5 (e) and (f), 8.5 → 7.5 (e) and (f) and 9.5 → 8.5 (e) and (f) rotational transitions. Guélin et al. (2000) derived for SiCN a column density along the line of sight of 2 × 1012 cm−2. A little later, Guélin et al. (2004) reported the detection of the SiNC in the same source. Five lines were detected at the frequencies of the j = 6.5 → 5.5 (e), 7.5 → 6.5 (f), 8.5 → 7.5 (f) and 10.5 → 9.5 (e) and (f) rotational transitions. These authors derived a column density of 2 × 1012 cm−2, similar to that of SiCN.
The IRC+10216 outer envelope, where SiCN and SiNC were detected, is usually assumed to be the region located between 1016 and 1017 cm from the star (Cordiner & Millar 2009). The physical conditions used in our calculations are the same conditions observed in this region. The kinetic temperature have been estimated within the range 10–100K, while molecular hydrogen is constrained in the interval 104–106 cm−3. Thus, in our calculations, we have chosen two different kinetic temperatures: 20 and 50 K. The column densities were set at three different values: 1011, 1012 and 1013 cm−2. We also considered molecular hydrogen densities in a range from 102 to 108 cm−3.
In the calculations, we included all the energy levels for which both radiative and collisional data are available. We take into account the first 52 rotational levels of F1 spin–orbit manifold and the first 46 levels of the F2 spin–orbit manifold. By testing the sensitivity of the radiative transfer calculations with respect to the number of considered rotational levels, we found that the calculations are fully converged for temperatures up to 50 K.
In this section, we only show results for the observed 7.5 → 6.5 (f) and 8.5 → 7.5 (f) transitions of the SiCN and SiNC molecules. These transitions are within the F1 spin–orbit manifold.
Figs 8 and 9 show the excitation temperature (TEx) of the SiCN and SiNC lines as a function of molecular hydrogen density for temperatures of 20 and 50 K. We vary the column density of SiCN/SiNC from 1011 to 1013 cm−2, but we found that in this range, the variation of the column density has almost no impact on the magnitude of the excitation temperature. Actually, the three curves cannot be distinguished in the plots. This can be explained by the fact that SiCN/SiNC lines are optically thin for the physical conditions considered in this work.
![Excitation temperature (TEx, dashed lines), brightness temperature (TB, solid lines) and brightness temperature ratios (TB[SiCN]/TB[SiNC], right-hand panels) for the j = 8.5 → 7.5 (f) and N = 7.5 → 6.5 (f) lines of SiCN and SiNC. The H2 volume density varies between 100 and 108 cm−3 and the SiCN and SiNC column density from 1011 to 1013 cm−2 by a step factor of 10. The kinetic temperature is 20 K. The line width is 29 km s−1](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/451/2/10.1093_mnras_stv1018/2/m_stv1018fig8.jpeg?Expires=1749937214&Signature=MMgpFK-nj860VWHR8znDXbWe6kXEutRbO4YfNjhLQzI5~SZExuhT1DDAgbmDMRZot4HqyTvXrZSMDlwYAtFP2rzdYWPbYMGPUdytC3o0RnlVa1jcCUac7W24PWDuYFRSdPNVwit-A6wQhvlpAITPZ86QQE09sa3nUtFw56UHPpUSpeDPi3vaCGz-xyDPV25MXDtFs1~rnYycNQG9JI2~o--ufqzW8ZiUGM-P5jDEaqj~~-UGInFvxMTM6hRzhegzic5PqJNNADCeZeCWNL-X~nJnbJVXgBgP5aEEyRPUOXYqPodSMyHmkXMkE6fJ~XwwBrvGDCiXJP-U1x5wLr5ynA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Excitation temperature (TEx, dashed lines), brightness temperature (TB, solid lines) and brightness temperature ratios (TB[SiCN]/TB[SiNC], right-hand panels) for the j = 8.5 → 7.5 (f) and N = 7.5 → 6.5 (f) lines of SiCN and SiNC. The H2 volume density varies between 100 and 108 cm−3 and the SiCN and SiNC column density from 1011 to 1013 cm−2 by a step factor of 10. The kinetic temperature is 20 K. The line width is 29 km s−1

At very low densities of molecular hydrogen, the excitation temperatures tend, for both isomers, to be equal to the adopted value of the background radiation field (2.7 K). The excitation temperatures rise to higher values as collisional excitation becomes more important. At densities above a critical value, the excitation temperature reaches the kinetic temperature, at which point the LTE conditions are available.
At low temperatures (≃20 K), the critical density lies in the interval 105–106 cm−3, while for higher temperatures, the critical density is slightly lower but stays above 105 cm−3 as already noticed in the critical densities evaluation.
By matching the critical densities presented in Table 4 and the informations of Figs 8 and 9, we can conclude that at typical physical conditions of the outer shell of the circumstellar gas (104 cm−3 < n(H2) < 106 cm−3), SiCN and SiNC lines are not thermalized and non-LTE analysis is required.
Figs 8 and 9 also show the brightness temperatures of the SiCN and SiNC lines as a function of molecular hydrogen density. As the optical depth is small for these lines (τ ≪1), TB is proportional to the column densities. TB increase gradually with the density before being constant at around n(H2) = 105–106 cm−3 when LTE conditions are reached.
To compare SiCN and SiNC emissions, we show in Figs 8 and 9 the brightness temperature ratios TB[SiCN]/TB[SiNC]. From this plot, one can see that SiCN isomer presents a slightly stronger emission than the SiNC one for low densities of molecular hydrogen. At the opposite, it can be seen that SiCN emission is weaker than that of SiNC at larger densities of molecular hydrogen. This behaviour remains when the temperature increases from 20 to 50 K.
When LTE conditions are reached, populations of the energy levels are determined by a Boltzmann distribution. The fact that in these conditions, SiCN lines are weaker than the SiNC ones can be explained by the weaker Einstein coefficients of the SiCN lines.
However, on can note that the excitation of SiCN and SiNC in the circumstellar gas is similar. The differences in the brightness temperature are generally less than 10 per cent so that considering that the excitation of both isomers is the same is certainly valid. This contrast with others cyanides and isocyanides like AlCN/AlNC, MgCN/MgNC (Paper III) or HCN/HNC (Sarrasin et al. 2010). For SiCN and SiNC molecules, the moderate differences seen in the excitation can certainly be explained by the weak differences in the collisional rate coefficients.
Finally, Fig. 10 shows the dependence of the SiCN/SiNC brightness temperatures with the column density, at 20 K and for the j = 8.5 → 7.5 (f) and j = 7.5 → 6.5 (f) transitions. In these calculations, the hydrogen density n(H2) was fixed at 3 × 104 cm−3.
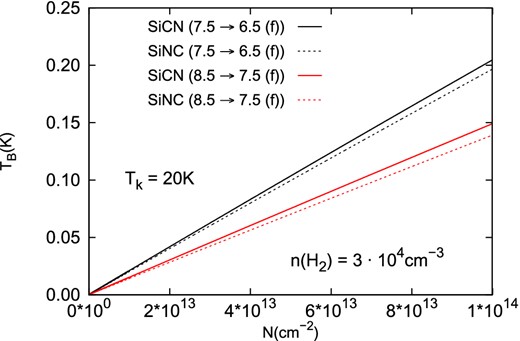
Column density dependence of the brightness temperature for j = 8.5 → 7.5 (f) and j = 7.5 → 6.5 (f) transition of SiCN and SiNC at 20 K. The line width is 29 km s−1.
Contrarily to others metal cyanides and isocyanides (Paper III), the excitation of SiCN and SiNC is very similar. Nevertheless, equation (7) have to be preferentially used to estimate the [SiNC]/[SiCN] abundance ratio.
Hence, we have determined the [SiCN]/[SiNC] abundance ratio in IRC+10216 from the observations of Guélin et al. (2000, 2004). Using the same physical parameters (n(H2) = 3 × 104 cm−3, T = 20 K) and the same brightness temperature ratio as Guélin et al. (2004), we obtained a new [SiCN]/[SiNC] abundance ratio of ∼ 2.
This result is in significant contradiction with that of Guélin et al. (2004) that concluded that the abundance of SICN and SiNC was similar. The difference can be explained mainly by the use of a wrong dipole moment by Guélin et al. (2004) to analyse SiNC observations. Indeed, these authors consider that the dipole moment of SiNC was 40 per cent lower than that of SiCN so that they overestimate the abundance of SiNC by a factor of ≃2. This clearly shows the need for accurate molecular data in order to precisely determine molecular abundance in astrophysical media.
6 DISCUSSION AND CONCLUSION
We have used quantum scattering calculations to investigate rotational energy transfer in collisions of SiCN and SiNC molecules with He atoms. The calculations are based on highly accurate 2-D PESs obtained using highly accurate electronic structure methods. Rate coefficients for transitions involving the lowest 92 levels of both SiCN and SiNC were determined for temperatures ranging from 5 to 100 K.
The rate coefficients for spin–orbit conserving transitions were found to be significantly larger than the one corresponding to spin–orbit changing transitions. For these transitions, a clear propensity was found for Λ-doubling conserving transitions.
In addition, for these dominant transitions, a propensity for Δj = 1 transitions was found for the SiCN–He system whereas a propensity for Δj = 2 transitions was found for SiNC–He system. However, the difference between the two sets of data are moderate and we cannot anticipate very different excitation of SiNC and SiNC in astrophysical media.
As an application of our new rate coefficients, we have simulated the excitation of the two isomers in the circumstellar gas. We have found that, at typical physical conditions of the outer shells of the circumstellar gas, the observed lines of SiCN and SiNC are not thermalized and non-LTE analysis is required. In contrast to others cyanides and isocyanides, the excitation of the two isomers is similar.
Previous observations have shown that SiCN emission lines were larger the SiNC ones. As a consequence, the abundance of SiCN is larger than the one of SiNC showing evidence of selective cyanides chemistry. The present conclusion is in better agreement with thermodynamical considerations since SiCN is more stable than SiNC (Paper I). Further investigations have nevertheless to be performed to accurately estimate SiCN and SiNC abundances.
This research was supported by the CNRS national program ‘Physique et Chimie du Milieu Interstellaire’. MHV and FL acknowledge the french embassy of Cuba and Campus France for financial support. We also thank the CPER Haute-Normandie/CNRT/Energie, Electronique, Matériaux. JK is grateful for support from the US National Science Foundation (Grant No. CHE-1213332 to professor M. H. Alexander). JK acknowledges financial support from the CNRS for the visiting position at University of Le Havre.
The hibridon package was written by M. H. Alexander, D. E. Manolopoulos, H.-J. Werner, and B. Follmeg, with contributions by P. F. Vohralik, D. Lemoine, G. Corey, R. Gordon, B. Johnson, T. Orlikowski, A. Berning, A. Degli-Esposti, C. Rist, P. Dagdigian, B. Pouilly, G. van der Sanden, M. Yang, F. de Weerd, S. Gregurick, J. Kłos and F. Lique, http://www2.chem.umd.edu/groups/alexander/.
REFERENCES
SUPPORTING INFORMATION
Additional Supporting Information may be found in the online version of this paper.
sinc_he_pes.f
sicn_he_pes.f
Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the paper.



