X-ray haloes and star formation in early-type galaxies Free

Main properties of the galaxy models.

Name	L_B	R_e	M_*	M_h	σ_e8	f_DM	c
	(10¹¹L_⊙)	(kpc)	(10¹¹ M_⊙)	(10¹¹ M_⊙)	(km s⁻¹)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
EO4\|$^{200}_{\rm {IS}}$\|	0.26	4.09	1.25	25	166	0.63	37
EO7\|$^{200}_{\rm {IS}}$\|	0.26	4.09	1.25	25	124	0.66	37
FO4\|$^{200}_{\rm {IS}}$\|	0.26	4.09	1.25	25	178	0.59	37
FO7\|$^{200}_{\rm {IS}}$\|	0.26	4.09	1.25	25	150	0.57	37
EO4\|$^{250}_{\rm {IS}}$\|	0.62	7.04	3.35	67	207	0.62	28
EO7\|$^{250}_{\rm {IS}}$\|	0.62	7.04	3.35	67	154	0.66	28
EO4\|$^{300}_{\rm {IS}}$\|	1.32	11.79	7.80	160	248	0.64	22
EO7\|$^{300}_{\rm {IS}}$\|	1.32	11.79	7.80	160	185	0.68	22
FO4\|$^{300}_{\rm {IS}}$\|	1.32	11.79	7.80	160	266	0.60	22
FO7\|$^{300}_{\rm {IS}}$\|	1.32	11.79	7.80	160	224	0.59	22

Name	L_B	R_e	M_*	M_h	σ_e8	f_DM	c
	(10¹¹L_⊙)	(kpc)	(10¹¹ M_⊙)	(10¹¹ M_⊙)	(km s⁻¹)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
EO4\|$^{200}_{\rm {IS}}$\|	0.26	4.09	1.25	25	166	0.63	37
EO7\|$^{200}_{\rm {IS}}$\|	0.26	4.09	1.25	25	124	0.66	37
FO4\|$^{200}_{\rm {IS}}$\|	0.26	4.09	1.25	25	178	0.59	37
FO7\|$^{200}_{\rm {IS}}$\|	0.26	4.09	1.25	25	150	0.57	37
EO4\|$^{250}_{\rm {IS}}$\|	0.62	7.04	3.35	67	207	0.62	28
EO7\|$^{250}_{\rm {IS}}$\|	0.62	7.04	3.35	67	154	0.66	28
EO4\|$^{300}_{\rm {IS}}$\|	1.32	11.79	7.80	160	248	0.64	22
EO7\|$^{300}_{\rm {IS}}$\|	1.32	11.79	7.80	160	185	0.68	22
FO4\|$^{300}_{\rm {IS}}$\|	1.32	11.79	7.80	160	266	0.60	22
FO7\|$^{300}_{\rm {IS}}$\|	1.32	11.79	7.80	160	224	0.59	22

Notes. (1) Model name: ‘EO’ or ‘FO’ indicate the procedure (EO-building or FO-building) applied to the spherical (E0) model to obtain the shape indicated by the number (E4 or E7 shapes); the superscript indicates σ_e8 of the corresponding E0 model; the subscript ‘IS’ indicates the kinematical configuration of the isotropic rotator (for example, FO4|$^{200}_{\rm {IS}}$| is an E4 isotropic rotator, FO-built from a spherical model with σ_e8 = 200 km s⁻¹). (2) Luminosities in the B band. (3) Effective radius (for an FO view for FO-built models, and an EO view for EO-built models). (4) Total stellar mass of the original (old) stellar population. The first four models are LM models, the next two are intermediate mass models, and the last four are HM models. (5) Total dark matter mass. (6) Luminosity-weighted average of the stellar velocity dispersion within a circular aperture of radius R_e/8; for non-spherical models, σ_e8 is the edge-on viewed value. (7) Dark matter fraction enclosed within a sphere of radius R_e. (8) Concentration parameter of the dark matter profile.

The properties listed above, for the EO4²⁵⁰ and EO7²⁵⁰ models with k = 0.1, are not reported, since they are equal to those of the EO4|$^{250}_{\rm {IS}}$| and EO7|$^{250}_{\rm {IS}}$| ones, except for σ_e8, which is, respectively, 223 km s⁻¹ for the EO4|$^{250}_{k\rm {=0.1}}$| model, and 184 km s⁻¹ for the EO7|$^{250}_{k\rm {=0.1}}$| model.

Table 1.

Main properties of the galaxy models.

Name	L_B	R_e	M_*	M_h	σ_e8	f_DM	c
	(10¹¹L_⊙)	(kpc)	(10¹¹ M_⊙)	(10¹¹ M_⊙)	(km s⁻¹)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
EO4\|$^{200}_{\rm {IS}}$\|	0.26	4.09	1.25	25	166	0.63	37
EO7\|$^{200}_{\rm {IS}}$\|	0.26	4.09	1.25	25	124	0.66	37
FO4\|$^{200}_{\rm {IS}}$\|	0.26	4.09	1.25	25	178	0.59	37
FO7\|$^{200}_{\rm {IS}}$\|	0.26	4.09	1.25	25	150	0.57	37
EO4\|$^{250}_{\rm {IS}}$\|	0.62	7.04	3.35	67	207	0.62	28
EO7\|$^{250}_{\rm {IS}}$\|	0.62	7.04	3.35	67	154	0.66	28
EO4\|$^{300}_{\rm {IS}}$\|	1.32	11.79	7.80	160	248	0.64	22
EO7\|$^{300}_{\rm {IS}}$\|	1.32	11.79	7.80	160	185	0.68	22
FO4\|$^{300}_{\rm {IS}}$\|	1.32	11.79	7.80	160	266	0.60	22
FO7\|$^{300}_{\rm {IS}}$\|	1.32	11.79	7.80	160	224	0.59	22

Name	L_B	R_e	M_*	M_h	σ_e8	f_DM	c
	(10¹¹L_⊙)	(kpc)	(10¹¹ M_⊙)	(10¹¹ M_⊙)	(km s⁻¹)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
EO4\|$^{200}_{\rm {IS}}$\|	0.26	4.09	1.25	25	166	0.63	37
EO7\|$^{200}_{\rm {IS}}$\|	0.26	4.09	1.25	25	124	0.66	37
FO4\|$^{200}_{\rm {IS}}$\|	0.26	4.09	1.25	25	178	0.59	37
FO7\|$^{200}_{\rm {IS}}$\|	0.26	4.09	1.25	25	150	0.57	37
EO4\|$^{250}_{\rm {IS}}$\|	0.62	7.04	3.35	67	207	0.62	28
EO7\|$^{250}_{\rm {IS}}$\|	0.62	7.04	3.35	67	154	0.66	28
EO4\|$^{300}_{\rm {IS}}$\|	1.32	11.79	7.80	160	248	0.64	22
EO7\|$^{300}_{\rm {IS}}$\|	1.32	11.79	7.80	160	185	0.68	22
FO4\|$^{300}_{\rm {IS}}$\|	1.32	11.79	7.80	160	266	0.60	22
FO7\|$^{300}_{\rm {IS}}$\|	1.32	11.79	7.80	160	224	0.59	22

Notes. (1) Model name: ‘EO’ or ‘FO’ indicate the procedure (EO-building or FO-building) applied to the spherical (E0) model to obtain the shape indicated by the number (E4 or E7 shapes); the superscript indicates σ_e8 of the corresponding E0 model; the subscript ‘IS’ indicates the kinematical configuration of the isotropic rotator (for example, FO4|$^{200}_{\rm {IS}}$| is an E4 isotropic rotator, FO-built from a spherical model with σ_e8 = 200 km s⁻¹). (2) Luminosities in the B band. (3) Effective radius (for an FO view for FO-built models, and an EO view for EO-built models). (4) Total stellar mass of the original (old) stellar population. The first four models are LM models, the next two are intermediate mass models, and the last four are HM models. (5) Total dark matter mass. (6) Luminosity-weighted average of the stellar velocity dispersion within a circular aperture of radius R_e/8; for non-spherical models, σ_e8 is the edge-on viewed value. (7) Dark matter fraction enclosed within a sphere of radius R_e. (8) Concentration parameter of the dark matter profile.

The properties listed above, for the EO4²⁵⁰ and EO7²⁵⁰ models with k = 0.1, are not reported, since they are equal to those of the EO4|$^{250}_{\rm {IS}}$| and EO7|$^{250}_{\rm {IS}}$| ones, except for σ_e8, which is, respectively, 223 km s⁻¹ for the EO4|$^{250}_{k\rm {=0.1}}$| model, and 184 km s⁻¹ for the EO7|$^{250}_{k\rm {=0.1}}$| model.

2.2 Star formation in the code

We employed two different schemes for SF, a passive (pSF) one and an active (aSF) one. In the pSF, only cold gas removal from the numerical mesh is allowed; in the aSF, we also consider the injection of mass, momentum and energy from the newly forming stellar population, for simplicity limiting in this work to the evolution of stars more massive than 8 M_⊙ (ending with SNII explosions); note however that for reasonable stellar initial mass functions (IMF) these massive stars are major contributors to the total mass return rate. We describe below the main inputs and sinks of mass and energy for the gas flow, due to both the original stellar population (of total mass M_*) and the newly forming stars, and the corresponding equations of hydrodynamics solved by the code.

2.2.1 The mass injection and sink terms

The mass inputs are stellar winds and SNIa's ejecta produced during the passive evolution of the original stellar population of the galaxy (at a rate per unit volume, respectively, of |$\dot{\rho }_*$| and |$\dot{\rho }_{\rm Ia}$|⁠, for which we adopt the standard recipes coming from the stellar evolution theory; e.g. N14), and the Type II supernovae ejecta produced by the newly born stellar population (at a rate of |$\dot{\rho }_{\rm II}$|⁠, calculated as detailed below).

The mass sink is due to SF subtracting gas from the grid, at an adopted rate per unit volume of:

\begin{equation} \dot{\rho }_{\rm SF} = \frac{\eta _{\rm SF} \rho }{t_{\rm SF}},\qquad t_{\rm SF}=\mathrm{max}(t_\mathrm{cool},t_\mathrm{dyn}), \end{equation}

(1)

where ρ is the gas density, and η_SF is the SF efficiency, for which we adopt two values of η_SF = 0.01 and 0.1. The rate |$\dot{\rho }_{\rm SF}$| depends on the maximum between the cooling time-scale |$t_\mathrm{cool}\equiv E/\cal {L}$| (where E is the ISM internal energy density, and |$\cal {L}$| is the ISM bolometric luminosity per unit volume), and the dynamical time-scale |$t_\mathrm{dyn} \equiv \sqrt{ 3\pi /32 G\rho }$| (see also Ciotti & Ostriker 2007).

When SF takes place in a computational cell, the ISM is removed and an equal mass in stars ΔM_* appears at the same place. These new stars are assumed to form with a Salpeter IMF, thus for a given ΔM_*, the number of stars having a mass greater than 8 M_⊙, that will explode as SNII, is N_II ≃ 7 × 10⁻³ΔM_*( M_⊙). These new stars in turn inject mass into the ISM. By integration of the mass difference between the mass of the progenitor and that of the remnant, for the Salpeter IMF, one finds that the mass injected by SNII's is ≃ 0.2ΔM_*. The final SNII mass source term |$\dot{\rho }_{\rm II}$| comes from considering that a given SF episode generates SNII's that inject mass at a rate exponentially declining on a time-scale τ_II = 2 × 10⁷ yr, and that at a certain time during the evolution of an SF episode, another episode may take place, forming younger SNII's that in turn eject mass into the ISM. The whole process can be formalized as

\begin{equation} \frac{\mathop {}\!\mathrm{d}\dot{\rho }_{\rm II}}{\mathop {}\!\mathrm{d}t} = -\frac{\dot{\rho }_{\rm II}}{\tau _{\rm II} } + \frac{0.2 \dot{\rho }_{\rm SF}}{\tau _{\rm II}}, \end{equation}

(2)

(Ciotti & Ostriker 2007). The equation above is very useful in numerical works, as it allows us to compute the mass return of the new stars formed at each timestep without storing the whole SF history at each gridpoint, but only the current value and the value of the mass return at the previous timestep. For more complex recipes, built on the scheme above, see Calura, Ciotti & Nipoti (2014).

2.2.2 The energy injection and sink terms

Energy is injected into the ISM by the thermalization of the kinetic energy of SNIa and SNII explosions, and by the thermalization of random and streaming stellar motions for the stellar winds. The rate of SNIa's explosions is the same entering |$\dot{\rho }_\mathrm{Ia}$| defined in Section 2.2.1. The energy input rate per unit volume from the original (old) stellar population is then:

\begin{equation} {\dot{E}}_{\mathrm{old}} = {\dot{E}}_{\mathrm{Ia}} + \frac{\dot{\rho }_{\rm Ia}+\dot{\rho }_*}{2} \left[ \left\Vert v_{\varphi }{{\hat{{\boldsymbol {e}}}}_{\varphi }} -{\boldsymbol {u}} \right\Vert ^2 + \mathrm{Tr}({\boldsymbol {\sigma }}^2) \right], \end{equation}

(3)

where |${\dot{E}}_{\mathrm{Ia}} = \dot{\rho }_\mathrm{Ia}\vartheta _\mathrm{SNIa} E_\mathrm{SN}/{\rm 1.4\,M_{\odot }}$|⁠, ϑ_SNIa is the thermalization efficiency (for which we adopt the value of 0.85, see Thornton et al. 1998; Tang & Wang 2005), E_SN = 10⁵¹ erg, and 1.4 M_⊙ is the mass that is ejected by one SNIa event; v_φ is the stellar streaming velocity field, |${\boldsymbol {u}}$| is the velocity of the ambient gas, |$\boldsymbol {\sigma }^2$| is the stellar velocity dispersion tensor of the stars.

The energy input rate |${\dot{E}}_\mathrm{new}$| from the newly born stellar population is derived as follows. A mass of newly formed stars ΔM_* injects energy through SNII with an efficiency

\begin{equation} \varepsilon _\mathrm{II} = \frac{N_\mathrm{II} E_\mathrm{SN}}{\Delta M_* c^2} \simeq 3.9\times 10^{-6}. \end{equation}

(4)

Consistently with equation (2), the SNII energy injection rate |${\dot{E}}_{\rm II}$| due to the thermalization of the ejecta is given by

\begin{equation} \frac{{\rm d} {\dot{E}}_{\rm II}}{{\rm d}t} = -\frac{\dot{E}_{\rm II}}{\tau _{\rm II} } + \frac{\varepsilon _\mathrm{II} c^2 \dot{\rho }_{\rm SF} \vartheta _\mathrm{SNII}}{\tau _{\rm II}}, \end{equation}

(5)

where we take the fiducial value of ϑ_SNII = ϑ_SNIa/5 = 0.17 to account for the lower thermalization efficiency of SNII exploding in a cold and dense medium. We assume that the new stars inherit the kinematical configuration of the original stellar component in the place where they are born (i.e. the velocity dispersion and rotation of the new stars are the same as those of the original stellar distribution in the same place). This allows us to treat the heating terms described in equation (7) below by using the same properties of the old stars. Note however that this choice is not unreasonable, because the bulk of SF takes place in the cold and rotationally supported disc, whose rotational properties are very similar to those of the stars. Thus, the total heating rate per unit volume due to Type II SNe is

\begin{equation} \dot{E}_\mathrm{new} = {\dot{E}}_{\rm II} + \frac{\dot{\rho }_{\rm II}}{2} \left[ \left\Vert v_{\varphi }{\hat{{\boldsymbol {e}}}}_{\varphi }-{\boldsymbol {u}} \right\Vert ^2 + \mathrm{Tr}({\boldsymbol {\sigma }}^2) \right]. \end{equation}

(6)

The total energy injection due to the old and new stellar populations is then |$\dot{E} = \dot{E}_\mathrm{old} + \dot{E}_\mathrm{new}$|⁠, that is:

\begin{equation} \dot{E} = {\dot{E}}_{\mathrm{Ia}} + {\dot{E}}_{\mathrm{II}} + \frac{\dot{\rho }_{\mathrm{Ia}}+\dot{\rho }_* + \dot{\rho }_{\mathrm{II}}}{2} \left[ \left\Vert v_{\varphi }{{\hat{{\boldsymbol {e}}}}_{\varphi }} -{\boldsymbol {u}} \right\Vert ^2 + \mathrm{Tr}({\boldsymbol {\sigma }}^2) \right]. \end{equation}

(7)

Finally, an energy and momentum sink associated with SF are present; they are, respectively, written as

\begin{equation} {\dot{E}}_{\rm SF} = \frac{\eta _{\rm SF} E}{t_{\rm SF} }, \quad \quad \quad {\dot{{\boldsymbol {m}}}_\mathrm{SF}} = \frac{\eta _{\rm SF} {\boldsymbol {m}}}{t_{\rm SF} }, \end{equation}

(8)

where E and |$\boldsymbol {m}$| are the internal energy and momentum density of the ISM.

2.2.3 The hydrodynamical equations

The hydrodynamical equations are the same as in N14, with the addition of all the source and sink terms related with the SF process described above:

\begin{eqnarray*} &&{\frac{\mathrm{\partial} \rho }{\mathrm{\partial} t}\,+\,\nabla \cdot (\rho {\boldsymbol {u}})\,=\,\dot{\rho }_\mathrm{Ia}\,+\dot{\rho }_{\ast}\,+\,\dot{\rho }_{\rm II} - \dot{\rho }_{\rm SF},} \nonumber\\ &&{\rho \frac{\mathrm{\partial} \boldsymbol {u}}{\mathrm{\partial} t}\,+\,\rho \left(\boldsymbol {u} \cdot \nabla \right){\boldsymbol {u}}=-\nabla p -\rho \nabla \Phi _\mathrm{tot} +}\nonumber\\ &&{\qquad\;\;+\; (\dot{\rho }_\mathrm{Ia}\,+\,\dot{\rho }_* +\dot{\rho }_{\rm II}) (v_{\varphi }{\hat{{\boldsymbol {e}}}}_{\varphi }- {\boldsymbol {u}}),} \nonumber\\ &&{\frac{\mathrm{\partial} E}{\mathrm{\partial} t}\,+\,\nabla \cdot (E{\boldsymbol {u}})\,=\,-p \nabla \cdot {\boldsymbol {u}} - {\mathcal {L}}\,+\,\dot{E} -\dot{E}_\mathrm{SF},} \end{eqnarray*}

where ρ, |${\boldsymbol {u}}$|⁠, E, p, Φ_tot, and |${\cal L}$| are, respectively, the ISM mass density, velocity, internal energy density, pressure, total gravitational potential, and bolometric luminosity per unit volume. The gas is assumed to be an ideal monoatomic fully ionized plasma, so that p = (γ − 1)E, where γ = 5/3 is the adiabatic index. The chemical composition is fixed to solar (μ ≃ 0.62), and the gas self-gravity is neglected.

In the pSF scheme, the source terms |$\dot{\rho }_{\rm II}$| and |${\dot{E}}_{\mathrm{II}}$| are zero, thus they either do not enter the hydrodynamical equations above and they do not contribute to |$\dot{E}$|⁠. In the more realistic aSF, |$\dot{\rho }_{\rm II}$| and |${\dot{E}}_{\mathrm{II}}$| are non-zero. Most galaxy models are simulated with pSF and aSF; for each of the two schemes, we adopted two values of the SF efficiency in equations (1) and (8), η_SF = 10⁻¹ and η_SF = 10⁻² (see Section 3 below).

We tested that the code conserves the total mass and energy; the total mass at any time t is |$M_\mathrm{gas} +M_\mathrm{esc} = M_\mathrm{inj} +M_\mathrm{inj}^{\rm II}-M_*^{\rm new}$|⁠, where M_gas is the gas mass within the simulation box, M_esc is the cumulative escaped mass out of the simulation box, until that time; M_inj, |$M_\mathrm{inj}^{\rm II}$|⁠, and |$M_*^{\rm new}$| are the cumulative masses, respectively, injected by the passively evolving stellar population, injected by SNII events due to the newly born stellar population, and of the new stars. The values of these masses at the end of the simulations are given in Tables 2–5. Finally, the radiative cooling is implemented by adopting a modified version of the cooling law of Sazonov et al. (2005), with a lower limit for the ISM temperature of T = 10⁴ K. The total X-ray emission in the 0.3–8 keV band (L_X), and the emission weighted temperature in the same band (T_X), are calculated as volume integrals over the whole computational grid, using as weight the emissivity in the 0.3–8 keV band of a hot, collisionally ionized plasma (see N14 for more details).

Table 2.

Relevant quantities at t = 13 Gyr for the rotating models (k = 1) with σ_e8=300 km s⁻¹.

Name	SF	η_SF	M_inj	M_esc	M_gas	M_hot	M_c	\|$M_*^{\rm new}$\|	\|$M_\mathrm{inj}^{\rm II}$\|	\|$\langle t\rangle _*^{\rm new}$\|	\|$M_^{\rm ew}/\langle t\rangle _^{\rm new}$\|	SFR	L_X	L_SNIa	L_SNII	T_X
			(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(Gyr)	(M_⊙ yr⁻¹)	(M_⊙ yr⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(keV)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(15)	(16)	(17)
EO4\|$^{300}_{\rm {IS}}$\|	×	–	69.38	14.10	56.04	6.52	49.8	–	–	–	–	–	1.34	47.7	–	0.68
EO7\|$^{300}_{\rm {IS}}$\|	×	–	65.46	15.87	50.24	6.13	44.5	–	–	–	–	–	1.04	45.0	–	0.56
FO4\|$^{300}_{\rm {IS}}$\|	×	–	71.81	11.93	60.92	6.11	54.7	–	–	–	–	–	1.35	49.4	–	0.68
FO7\|$^{300}_{\rm {IS}}$\|	×	–	71.93	11.14	61.82	5.07	56.7	–	–	–	–	–	0.90	49.5	–	0.59
EO4\|$^{300}_{\rm {IS}}$\|	P	0.01	70.53	13.85	14.87	6.86	7.93	41.81	–	5.02	8.33	2.24	1.47	48.5	–	0.69
EO7\|$^{300}_{\rm {IS}}$\|	P	0.01	66.56	15.68	17.02	6.50	10.4	33.86	–	5.34	6.34	2.10	1.07	45.8	–	0.58
FO4\|$^{300}_{\rm {IS}}$\|	P	0.01	72.94	11.75	14.15	6.23	7.85	47.04	–	4.90	9.6	2.47	1.38	50.2	–	0.68
FO7\|$^{300}_{\rm {IS}}$\|	P	0.01	73.01	10.83	16.13	5.07	10.9	46.06	–	4.98	9.25	2.54	0.89	50.2	–	0.55
EO4\|$^{300}_{\rm {IS}}$\|	P	0.1	70.53	13.89	8.23	6.90	1.24	48.41	–	4.36	11.10	1.99	1.54	48.5	–	0.68
EO7\|$^{300}_{\rm {IS}}$\|	P	0.1	66.56	15.77	7.82	6.45	1.31	42.96	–	4.42	9.72	1.66	1.04	45.8	–	0.59
FO4\|$^{300}_{\rm {IS}}$\|	P	0.1	72.94	11.71	7.73	6.40	1.22	53.50	–	4.25	12.59	2.12	1.50	50.2	–	0.68
FO7\|$^{300}_{\rm {IS}}$\|	P	0.1	73.01	10.87	6.86	5.30	1.47	55.29	–	4.19	13.2	2.03	0.92	50.2	–	0.58
EO4\|$^{300}_{\rm {IS}}$\|	A	0.01	70.53	13.83	15.98	6.95	8.97	50.89	10.17	5.12	9.94	3.08	1.56	48.5	11.5	0.69
EO7\|$^{300}_{\rm {IS}}$\|	A	0.01	66.56	15.71	18.53	6.22	12.3	40.38	8.07	5.47	7.38	2.67	0.99	45.8	10.2	0.58
FO4\|$^{300}_{\rm {IS}}$\|	A	0.01	72.94	11.79	15.06	6.27	8.73	57.60	11.51	4.94	11.66	3.21	1.44	50.2	11.9	0.68
FO7\|$^{300}_{\rm {IS}}$\|	A	0.01	73.01	10.86	17.79	5.36	12.4	55.45	11.08	5.07	10.94	3.09	0.94	50.2	11.8	0.57
EO4\|$^{300}_{\rm {IS}}$\|	A	0.1	70.53	13.95	8.55	7.05	1.42	60.03	12.00	4.43	13.55	2.51	1.65	48.5	9.83	0.69
EO7\|$^{300}_{\rm {IS}}$\|	A	0.1	66.56	15.89	8.23	6.58	1.58	53.03	10.60	4.50	11.78	2.07	1.13	45.8	7.76	0.58
FO4\|$^{300}_{\rm {IS}}$\|	A	0.1	72.94	11.89	8.04	6.61	1.36	66.25	13.24	4.29	15.44	2.65	1.65	50.2	10.1	0.70
FO7\|$^{300}_{\rm {IS}}$\|	A	0.1	73.01	11.04	7.40	5.72	1.59	68.21	13.63	4.23	16.13	2.49	1.09	50.2	9.42	0.57

Name	SF	η_SF	M_inj	M_esc	M_gas	M_hot	M_c	\|$M_*^{\rm new}$\|	\|$M_\mathrm{inj}^{\rm II}$\|	\|$\langle t\rangle _*^{\rm new}$\|	\|$M_^{\rm ew}/\langle t\rangle _^{\rm new}$\|	SFR	L_X	L_SNIa	L_SNII	T_X
			(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(Gyr)	(M_⊙ yr⁻¹)	(M_⊙ yr⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(keV)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(15)	(16)	(17)
EO4\|$^{300}_{\rm {IS}}$\|	×	–	69.38	14.10	56.04	6.52	49.8	–	–	–	–	–	1.34	47.7	–	0.68
EO7\|$^{300}_{\rm {IS}}$\|	×	–	65.46	15.87	50.24	6.13	44.5	–	–	–	–	–	1.04	45.0	–	0.56
FO4\|$^{300}_{\rm {IS}}$\|	×	–	71.81	11.93	60.92	6.11	54.7	–	–	–	–	–	1.35	49.4	–	0.68
FO7\|$^{300}_{\rm {IS}}$\|	×	–	71.93	11.14	61.82	5.07	56.7	–	–	–	–	–	0.90	49.5	–	0.59
EO4\|$^{300}_{\rm {IS}}$\|	P	0.01	70.53	13.85	14.87	6.86	7.93	41.81	–	5.02	8.33	2.24	1.47	48.5	–	0.69
EO7\|$^{300}_{\rm {IS}}$\|	P	0.01	66.56	15.68	17.02	6.50	10.4	33.86	–	5.34	6.34	2.10	1.07	45.8	–	0.58
FO4\|$^{300}_{\rm {IS}}$\|	P	0.01	72.94	11.75	14.15	6.23	7.85	47.04	–	4.90	9.6	2.47	1.38	50.2	–	0.68
FO7\|$^{300}_{\rm {IS}}$\|	P	0.01	73.01	10.83	16.13	5.07	10.9	46.06	–	4.98	9.25	2.54	0.89	50.2	–	0.55
EO4\|$^{300}_{\rm {IS}}$\|	P	0.1	70.53	13.89	8.23	6.90	1.24	48.41	–	4.36	11.10	1.99	1.54	48.5	–	0.68
EO7\|$^{300}_{\rm {IS}}$\|	P	0.1	66.56	15.77	7.82	6.45	1.31	42.96	–	4.42	9.72	1.66	1.04	45.8	–	0.59
FO4\|$^{300}_{\rm {IS}}$\|	P	0.1	72.94	11.71	7.73	6.40	1.22	53.50	–	4.25	12.59	2.12	1.50	50.2	–	0.68
FO7\|$^{300}_{\rm {IS}}$\|	P	0.1	73.01	10.87	6.86	5.30	1.47	55.29	–	4.19	13.2	2.03	0.92	50.2	–	0.58
EO4\|$^{300}_{\rm {IS}}$\|	A	0.01	70.53	13.83	15.98	6.95	8.97	50.89	10.17	5.12	9.94	3.08	1.56	48.5	11.5	0.69
EO7\|$^{300}_{\rm {IS}}$\|	A	0.01	66.56	15.71	18.53	6.22	12.3	40.38	8.07	5.47	7.38	2.67	0.99	45.8	10.2	0.58
FO4\|$^{300}_{\rm {IS}}$\|	A	0.01	72.94	11.79	15.06	6.27	8.73	57.60	11.51	4.94	11.66	3.21	1.44	50.2	11.9	0.68
FO7\|$^{300}_{\rm {IS}}$\|	A	0.01	73.01	10.86	17.79	5.36	12.4	55.45	11.08	5.07	10.94	3.09	0.94	50.2	11.8	0.57
EO4\|$^{300}_{\rm {IS}}$\|	A	0.1	70.53	13.95	8.55	7.05	1.42	60.03	12.00	4.43	13.55	2.51	1.65	48.5	9.83	0.69
EO7\|$^{300}_{\rm {IS}}$\|	A	0.1	66.56	15.89	8.23	6.58	1.58	53.03	10.60	4.50	11.78	2.07	1.13	45.8	7.76	0.58
FO4\|$^{300}_{\rm {IS}}$\|	A	0.1	72.94	11.89	8.04	6.61	1.36	66.25	13.24	4.29	15.44	2.65	1.65	50.2	10.1	0.70
FO7\|$^{300}_{\rm {IS}}$\|	A	0.1	73.01	11.04	7.40	5.72	1.59	68.21	13.63	4.23	16.13	2.49	1.09	50.2	9.42	0.57

Notes. (1) Model name. (2) SF scheme adopted (×= noSF, P = pSF, A = aSF). (3) SF efficiency. (4)–(5) Cumulative mass injected by the evolution of the original stellar population, and mass escaped from the numerical grid, respectively. Differences in M_inj for models of same L_B are accounted for by different sampling of the stellar density profile over the numerical grid. (6) Total ISM mass retained within the galaxy. (7)–(8) ISM mass with T > 10⁶ K, and T < 2 × 10⁴ K, respectively. (9) Mass of the new stars. (10) Cumulative mass ejected by type II SNe. (11)–(13) Mean formation time of the new stars, mean SFR, and SFR at the end of the simulations. (14) ISM X-ray luminosity in the 0.3–8 keV band. (15)–(16): SNIa and SNII kinetic energy input per unit time (Section 2.2.2). (17) ISM X-ray emission weighted temperature in the 0.3–8 keV band.

Table 2.

Relevant quantities at t = 13 Gyr for the rotating models (k = 1) with σ_e8=300 km s⁻¹.

Name	SF	η_SF	M_inj	M_esc	M_gas	M_hot	M_c	\|$M_*^{\rm new}$\|	\|$M_\mathrm{inj}^{\rm II}$\|	\|$\langle t\rangle _*^{\rm new}$\|	\|$M_^{\rm ew}/\langle t\rangle _^{\rm new}$\|	SFR	L_X	L_SNIa	L_SNII	T_X
			(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(Gyr)	(M_⊙ yr⁻¹)	(M_⊙ yr⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(keV)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(15)	(16)	(17)
EO4\|$^{300}_{\rm {IS}}$\|	×	–	69.38	14.10	56.04	6.52	49.8	–	–	–	–	–	1.34	47.7	–	0.68
EO7\|$^{300}_{\rm {IS}}$\|	×	–	65.46	15.87	50.24	6.13	44.5	–	–	–	–	–	1.04	45.0	–	0.56
FO4\|$^{300}_{\rm {IS}}$\|	×	–	71.81	11.93	60.92	6.11	54.7	–	–	–	–	–	1.35	49.4	–	0.68
FO7\|$^{300}_{\rm {IS}}$\|	×	–	71.93	11.14	61.82	5.07	56.7	–	–	–	–	–	0.90	49.5	–	0.59
EO4\|$^{300}_{\rm {IS}}$\|	P	0.01	70.53	13.85	14.87	6.86	7.93	41.81	–	5.02	8.33	2.24	1.47	48.5	–	0.69
EO7\|$^{300}_{\rm {IS}}$\|	P	0.01	66.56	15.68	17.02	6.50	10.4	33.86	–	5.34	6.34	2.10	1.07	45.8	–	0.58
FO4\|$^{300}_{\rm {IS}}$\|	P	0.01	72.94	11.75	14.15	6.23	7.85	47.04	–	4.90	9.6	2.47	1.38	50.2	–	0.68
FO7\|$^{300}_{\rm {IS}}$\|	P	0.01	73.01	10.83	16.13	5.07	10.9	46.06	–	4.98	9.25	2.54	0.89	50.2	–	0.55
EO4\|$^{300}_{\rm {IS}}$\|	P	0.1	70.53	13.89	8.23	6.90	1.24	48.41	–	4.36	11.10	1.99	1.54	48.5	–	0.68
EO7\|$^{300}_{\rm {IS}}$\|	P	0.1	66.56	15.77	7.82	6.45	1.31	42.96	–	4.42	9.72	1.66	1.04	45.8	–	0.59
FO4\|$^{300}_{\rm {IS}}$\|	P	0.1	72.94	11.71	7.73	6.40	1.22	53.50	–	4.25	12.59	2.12	1.50	50.2	–	0.68
FO7\|$^{300}_{\rm {IS}}$\|	P	0.1	73.01	10.87	6.86	5.30	1.47	55.29	–	4.19	13.2	2.03	0.92	50.2	–	0.58
EO4\|$^{300}_{\rm {IS}}$\|	A	0.01	70.53	13.83	15.98	6.95	8.97	50.89	10.17	5.12	9.94	3.08	1.56	48.5	11.5	0.69
EO7\|$^{300}_{\rm {IS}}$\|	A	0.01	66.56	15.71	18.53	6.22	12.3	40.38	8.07	5.47	7.38	2.67	0.99	45.8	10.2	0.58
FO4\|$^{300}_{\rm {IS}}$\|	A	0.01	72.94	11.79	15.06	6.27	8.73	57.60	11.51	4.94	11.66	3.21	1.44	50.2	11.9	0.68
FO7\|$^{300}_{\rm {IS}}$\|	A	0.01	73.01	10.86	17.79	5.36	12.4	55.45	11.08	5.07	10.94	3.09	0.94	50.2	11.8	0.57
EO4\|$^{300}_{\rm {IS}}$\|	A	0.1	70.53	13.95	8.55	7.05	1.42	60.03	12.00	4.43	13.55	2.51	1.65	48.5	9.83	0.69
EO7\|$^{300}_{\rm {IS}}$\|	A	0.1	66.56	15.89	8.23	6.58	1.58	53.03	10.60	4.50	11.78	2.07	1.13	45.8	7.76	0.58
FO4\|$^{300}_{\rm {IS}}$\|	A	0.1	72.94	11.89	8.04	6.61	1.36	66.25	13.24	4.29	15.44	2.65	1.65	50.2	10.1	0.70
FO7\|$^{300}_{\rm {IS}}$\|	A	0.1	73.01	11.04	7.40	5.72	1.59	68.21	13.63	4.23	16.13	2.49	1.09	50.2	9.42	0.57

Name	SF	η_SF	M_inj	M_esc	M_gas	M_hot	M_c	\|$M_*^{\rm new}$\|	\|$M_\mathrm{inj}^{\rm II}$\|	\|$\langle t\rangle _*^{\rm new}$\|	\|$M_^{\rm ew}/\langle t\rangle _^{\rm new}$\|	SFR	L_X	L_SNIa	L_SNII	T_X
			(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(Gyr)	(M_⊙ yr⁻¹)	(M_⊙ yr⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(keV)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(15)	(16)	(17)
EO4\|$^{300}_{\rm {IS}}$\|	×	–	69.38	14.10	56.04	6.52	49.8	–	–	–	–	–	1.34	47.7	–	0.68
EO7\|$^{300}_{\rm {IS}}$\|	×	–	65.46	15.87	50.24	6.13	44.5	–	–	–	–	–	1.04	45.0	–	0.56
FO4\|$^{300}_{\rm {IS}}$\|	×	–	71.81	11.93	60.92	6.11	54.7	–	–	–	–	–	1.35	49.4	–	0.68
FO7\|$^{300}_{\rm {IS}}$\|	×	–	71.93	11.14	61.82	5.07	56.7	–	–	–	–	–	0.90	49.5	–	0.59
EO4\|$^{300}_{\rm {IS}}$\|	P	0.01	70.53	13.85	14.87	6.86	7.93	41.81	–	5.02	8.33	2.24	1.47	48.5	–	0.69
EO7\|$^{300}_{\rm {IS}}$\|	P	0.01	66.56	15.68	17.02	6.50	10.4	33.86	–	5.34	6.34	2.10	1.07	45.8	–	0.58
FO4\|$^{300}_{\rm {IS}}$\|	P	0.01	72.94	11.75	14.15	6.23	7.85	47.04	–	4.90	9.6	2.47	1.38	50.2	–	0.68
FO7\|$^{300}_{\rm {IS}}$\|	P	0.01	73.01	10.83	16.13	5.07	10.9	46.06	–	4.98	9.25	2.54	0.89	50.2	–	0.55
EO4\|$^{300}_{\rm {IS}}$\|	P	0.1	70.53	13.89	8.23	6.90	1.24	48.41	–	4.36	11.10	1.99	1.54	48.5	–	0.68
EO7\|$^{300}_{\rm {IS}}$\|	P	0.1	66.56	15.77	7.82	6.45	1.31	42.96	–	4.42	9.72	1.66	1.04	45.8	–	0.59
FO4\|$^{300}_{\rm {IS}}$\|	P	0.1	72.94	11.71	7.73	6.40	1.22	53.50	–	4.25	12.59	2.12	1.50	50.2	–	0.68
FO7\|$^{300}_{\rm {IS}}$\|	P	0.1	73.01	10.87	6.86	5.30	1.47	55.29	–	4.19	13.2	2.03	0.92	50.2	–	0.58
EO4\|$^{300}_{\rm {IS}}$\|	A	0.01	70.53	13.83	15.98	6.95	8.97	50.89	10.17	5.12	9.94	3.08	1.56	48.5	11.5	0.69
EO7\|$^{300}_{\rm {IS}}$\|	A	0.01	66.56	15.71	18.53	6.22	12.3	40.38	8.07	5.47	7.38	2.67	0.99	45.8	10.2	0.58
FO4\|$^{300}_{\rm {IS}}$\|	A	0.01	72.94	11.79	15.06	6.27	8.73	57.60	11.51	4.94	11.66	3.21	1.44	50.2	11.9	0.68
FO7\|$^{300}_{\rm {IS}}$\|	A	0.01	73.01	10.86	17.79	5.36	12.4	55.45	11.08	5.07	10.94	3.09	0.94	50.2	11.8	0.57
EO4\|$^{300}_{\rm {IS}}$\|	A	0.1	70.53	13.95	8.55	7.05	1.42	60.03	12.00	4.43	13.55	2.51	1.65	48.5	9.83	0.69
EO7\|$^{300}_{\rm {IS}}$\|	A	0.1	66.56	15.89	8.23	6.58	1.58	53.03	10.60	4.50	11.78	2.07	1.13	45.8	7.76	0.58
FO4\|$^{300}_{\rm {IS}}$\|	A	0.1	72.94	11.89	8.04	6.61	1.36	66.25	13.24	4.29	15.44	2.65	1.65	50.2	10.1	0.70
FO7\|$^{300}_{\rm {IS}}$\|	A	0.1	73.01	11.04	7.40	5.72	1.59	68.21	13.63	4.23	16.13	2.49	1.09	50.2	9.42	0.57

Notes. (1) Model name. (2) SF scheme adopted (×= noSF, P = pSF, A = aSF). (3) SF efficiency. (4)–(5) Cumulative mass injected by the evolution of the original stellar population, and mass escaped from the numerical grid, respectively. Differences in M_inj for models of same L_B are accounted for by different sampling of the stellar density profile over the numerical grid. (6) Total ISM mass retained within the galaxy. (7)–(8) ISM mass with T > 10⁶ K, and T < 2 × 10⁴ K, respectively. (9) Mass of the new stars. (10) Cumulative mass ejected by type II SNe. (11)–(13) Mean formation time of the new stars, mean SFR, and SFR at the end of the simulations. (14) ISM X-ray luminosity in the 0.3–8 keV band. (15)–(16): SNIa and SNII kinetic energy input per unit time (Section 2.2.2). (17) ISM X-ray emission weighted temperature in the 0.3–8 keV band.

Table 3.

Relevant quantities at t = 13 Gyr for the rotating models (k = 1) with σ_e8=200 km s⁻¹.

Name	SF	η_SF	M_inj	M_esc	M_gas	M_hot	M_c	\|$M_*^{\rm new}$\|	\|$M_\mathrm{inj}^{\rm II}$\|	\|$\langle t\rangle _*^{\rm new}$\|	\|$M_^{\rm new}/\langle t\rangle _^{\rm new}$\|	SFR	L_X	L_SNIa	L_SNII	T_X
			(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(Gyr)	(M_⊙ yr⁻¹)	(M_⊙ yr⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(keV)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(15)	(16)	(17)
EO4\|$^{200}_{\rm {IS}}$\|	×	–	11.92	9.76	2.39	0.15	2.24	–	–	–	–	–	0.0007	10.2	–	0.50
EO7\|$^{200}_{\rm {IS}}$\|	×	–	11.93	10.34	1.84	0.24	1.57	–	–	–	–	–	0.002	10.2	–	0.49
FO4\|$^{200}_{\rm {IS}}$\|	×	–	12.00	3.32	8.80	1.73	6.97	–	–	–	–	–	0.449	10.3	–	0.37
FO7\|$^{200}_{\rm {IS}}$\|	×	–	11.96	3.41	8.69	1.36	7.16	–	–	–	–	–	0.248	10.2	–	0.32
EO4\|$^{200}_{\rm {IS}}$\|	P	0.01	12.07	4.32	3.28	1.63	1.57	4.47	–	6.61	0.68	0.45	0.110	10.3	–	0.39
EO7\|$^{200}_{\rm {IS}}$\|	P	0.01	12.09	10.43	0.34	0.27	3.99E-2	1.32	–	3.84	0.34	0.02	0.003	10.3	–	0.50
FO4\|$^{200}_{\rm {IS}}$\|	P	0.01	12.14	6.65	0.68	0.43	2.19E-1	4.80	–	4.20	1.14	0.08	0.006	10.4	–	0.40
FO7\|$^{200}_{\rm {IS}}$\|	P	0.01	12.08	2.98	3.12	1.57	1.40	5.99	–	5.39	1.11	0.37	0.163	10.3	–	0.36
EO4\|$^{200}_{\rm {IS}}$\|	P	0.1	12.07	4.65	2.00	1.77	7.31E-2	5.42	–	5.74	0.94	0.12	0.086	10.3	–	0.40
EO7\|$^{200}_{\rm {IS}}$\|	P	0.1	12.09	10.07	0.32	0.29	0.00	1.71	–	2.37	0.72	0.00	0.003	10.3	–	0.51
FO4\|$^{200}_{\rm {IS}}$\|	P	0.1	12.14	3.75	3.64	2.88	8.98E-4	4.74	–	3.28	1.45	0.08	0.587	10.4	–	0.43
FO7\|$^{200}_{\rm {IS}}$\|	P	0.1	12.08	5.79	0.49	0.40	1.98E-2	5.81	–	3.43	1.69	0.04	0.010	10.3	–	0.50
EO4\|$^{200}_{\rm {IS}}$\|	A	0.01	12.07	9.40	0.27	0.17	9.92E-2	3.00	0.60	3.90	0.77	0.05	0.001	10.3	0.18	0.54
EO7\|$^{200}_{\rm {IS}}$\|	A	0.01	12.09	9.70	0.47	0.24	2.09E-1	2.40	0.48	4.39	0.55	0.06	0.002	10.32	0.24	0.49
FO4\|$^{200}_{\rm {IS}}$\|	A	0.01	12.14	6.77	0.98	0.72	1.86E-1	5.47	1.09	4.11	1.33	0.09	0.011	10.4	0.36	0.43
FO7\|$^{200}_{\rm {IS}}$\|	A	0.01	12.08	3.09	3.77	1.42	2.19	6.53	1.30	5.27	1.24	0.69	0.460	10.3	2.58	0.29
EO4\|$^{200}_{\rm {IS}}$\|	A	0.1	12.07	7.77	0.29	0.28	7.34E-4	5.02	1.00	3.72	1.35	0.00	0.002	10.3	0.01	0.53
EO7\|$^{200}_{\rm {IS}}$\|	A	0.1	12.09	8.27	0.80	0.62	5.66E-2	3.78	0.76	5.34	0.71	0.06	0.012	10.3	0.24	0.44
FO4\|$^{200}_{\rm {IS}}$\|	A	0.1	12.14	6.00	1.48	1.19	8.70E-4	5.81	1.16	3.10	1.88	0.01	0.041	10.4	0.05	0.44
FO7\|$^{200}_{\rm {IS}}$\|	A	0.1	12.08	3.82	3.82	3.28	2.55E-3	5.57	1.11	2.92	1.91	0.11	0.982	10.3	0.40	0.41

Name	SF	η_SF	M_inj	M_esc	M_gas	M_hot	M_c	\|$M_*^{\rm new}$\|	\|$M_\mathrm{inj}^{\rm II}$\|	\|$\langle t\rangle _*^{\rm new}$\|	\|$M_^{\rm new}/\langle t\rangle _^{\rm new}$\|	SFR	L_X	L_SNIa	L_SNII	T_X
			(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(Gyr)	(M_⊙ yr⁻¹)	(M_⊙ yr⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(keV)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(15)	(16)	(17)
EO4\|$^{200}_{\rm {IS}}$\|	×	–	11.92	9.76	2.39	0.15	2.24	–	–	–	–	–	0.0007	10.2	–	0.50
EO7\|$^{200}_{\rm {IS}}$\|	×	–	11.93	10.34	1.84	0.24	1.57	–	–	–	–	–	0.002	10.2	–	0.49
FO4\|$^{200}_{\rm {IS}}$\|	×	–	12.00	3.32	8.80	1.73	6.97	–	–	–	–	–	0.449	10.3	–	0.37
FO7\|$^{200}_{\rm {IS}}$\|	×	–	11.96	3.41	8.69	1.36	7.16	–	–	–	–	–	0.248	10.2	–	0.32
EO4\|$^{200}_{\rm {IS}}$\|	P	0.01	12.07	4.32	3.28	1.63	1.57	4.47	–	6.61	0.68	0.45	0.110	10.3	–	0.39
EO7\|$^{200}_{\rm {IS}}$\|	P	0.01	12.09	10.43	0.34	0.27	3.99E-2	1.32	–	3.84	0.34	0.02	0.003	10.3	–	0.50
FO4\|$^{200}_{\rm {IS}}$\|	P	0.01	12.14	6.65	0.68	0.43	2.19E-1	4.80	–	4.20	1.14	0.08	0.006	10.4	–	0.40
FO7\|$^{200}_{\rm {IS}}$\|	P	0.01	12.08	2.98	3.12	1.57	1.40	5.99	–	5.39	1.11	0.37	0.163	10.3	–	0.36
EO4\|$^{200}_{\rm {IS}}$\|	P	0.1	12.07	4.65	2.00	1.77	7.31E-2	5.42	–	5.74	0.94	0.12	0.086	10.3	–	0.40
EO7\|$^{200}_{\rm {IS}}$\|	P	0.1	12.09	10.07	0.32	0.29	0.00	1.71	–	2.37	0.72	0.00	0.003	10.3	–	0.51
FO4\|$^{200}_{\rm {IS}}$\|	P	0.1	12.14	3.75	3.64	2.88	8.98E-4	4.74	–	3.28	1.45	0.08	0.587	10.4	–	0.43
FO7\|$^{200}_{\rm {IS}}$\|	P	0.1	12.08	5.79	0.49	0.40	1.98E-2	5.81	–	3.43	1.69	0.04	0.010	10.3	–	0.50
EO4\|$^{200}_{\rm {IS}}$\|	A	0.01	12.07	9.40	0.27	0.17	9.92E-2	3.00	0.60	3.90	0.77	0.05	0.001	10.3	0.18	0.54
EO7\|$^{200}_{\rm {IS}}$\|	A	0.01	12.09	9.70	0.47	0.24	2.09E-1	2.40	0.48	4.39	0.55	0.06	0.002	10.32	0.24	0.49
FO4\|$^{200}_{\rm {IS}}$\|	A	0.01	12.14	6.77	0.98	0.72	1.86E-1	5.47	1.09	4.11	1.33	0.09	0.011	10.4	0.36	0.43
FO7\|$^{200}_{\rm {IS}}$\|	A	0.01	12.08	3.09	3.77	1.42	2.19	6.53	1.30	5.27	1.24	0.69	0.460	10.3	2.58	0.29
EO4\|$^{200}_{\rm {IS}}$\|	A	0.1	12.07	7.77	0.29	0.28	7.34E-4	5.02	1.00	3.72	1.35	0.00	0.002	10.3	0.01	0.53
EO7\|$^{200}_{\rm {IS}}$\|	A	0.1	12.09	8.27	0.80	0.62	5.66E-2	3.78	0.76	5.34	0.71	0.06	0.012	10.3	0.24	0.44
FO4\|$^{200}_{\rm {IS}}$\|	A	0.1	12.14	6.00	1.48	1.19	8.70E-4	5.81	1.16	3.10	1.88	0.01	0.041	10.4	0.05	0.44
FO7\|$^{200}_{\rm {IS}}$\|	A	0.1	12.08	3.82	3.82	3.28	2.55E-3	5.57	1.11	2.92	1.91	0.11	0.982	10.3	0.40	0.41

Note. All quantities as in Table 2.

Table 3.

Relevant quantities at t = 13 Gyr for the rotating models (k = 1) with σ_e8=200 km s⁻¹.

Name	SF	η_SF	M_inj	M_esc	M_gas	M_hot	M_c	\|$M_*^{\rm new}$\|	\|$M_\mathrm{inj}^{\rm II}$\|	\|$\langle t\rangle _*^{\rm new}$\|	\|$M_^{\rm new}/\langle t\rangle _^{\rm new}$\|	SFR	L_X	L_SNIa	L_SNII	T_X
			(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(Gyr)	(M_⊙ yr⁻¹)	(M_⊙ yr⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(keV)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(15)	(16)	(17)
EO4\|$^{200}_{\rm {IS}}$\|	×	–	11.92	9.76	2.39	0.15	2.24	–	–	–	–	–	0.0007	10.2	–	0.50
EO7\|$^{200}_{\rm {IS}}$\|	×	–	11.93	10.34	1.84	0.24	1.57	–	–	–	–	–	0.002	10.2	–	0.49
FO4\|$^{200}_{\rm {IS}}$\|	×	–	12.00	3.32	8.80	1.73	6.97	–	–	–	–	–	0.449	10.3	–	0.37
FO7\|$^{200}_{\rm {IS}}$\|	×	–	11.96	3.41	8.69	1.36	7.16	–	–	–	–	–	0.248	10.2	–	0.32
EO4\|$^{200}_{\rm {IS}}$\|	P	0.01	12.07	4.32	3.28	1.63	1.57	4.47	–	6.61	0.68	0.45	0.110	10.3	–	0.39
EO7\|$^{200}_{\rm {IS}}$\|	P	0.01	12.09	10.43	0.34	0.27	3.99E-2	1.32	–	3.84	0.34	0.02	0.003	10.3	–	0.50
FO4\|$^{200}_{\rm {IS}}$\|	P	0.01	12.14	6.65	0.68	0.43	2.19E-1	4.80	–	4.20	1.14	0.08	0.006	10.4	–	0.40
FO7\|$^{200}_{\rm {IS}}$\|	P	0.01	12.08	2.98	3.12	1.57	1.40	5.99	–	5.39	1.11	0.37	0.163	10.3	–	0.36
EO4\|$^{200}_{\rm {IS}}$\|	P	0.1	12.07	4.65	2.00	1.77	7.31E-2	5.42	–	5.74	0.94	0.12	0.086	10.3	–	0.40
EO7\|$^{200}_{\rm {IS}}$\|	P	0.1	12.09	10.07	0.32	0.29	0.00	1.71	–	2.37	0.72	0.00	0.003	10.3	–	0.51
FO4\|$^{200}_{\rm {IS}}$\|	P	0.1	12.14	3.75	3.64	2.88	8.98E-4	4.74	–	3.28	1.45	0.08	0.587	10.4	–	0.43
FO7\|$^{200}_{\rm {IS}}$\|	P	0.1	12.08	5.79	0.49	0.40	1.98E-2	5.81	–	3.43	1.69	0.04	0.010	10.3	–	0.50
EO4\|$^{200}_{\rm {IS}}$\|	A	0.01	12.07	9.40	0.27	0.17	9.92E-2	3.00	0.60	3.90	0.77	0.05	0.001	10.3	0.18	0.54
EO7\|$^{200}_{\rm {IS}}$\|	A	0.01	12.09	9.70	0.47	0.24	2.09E-1	2.40	0.48	4.39	0.55	0.06	0.002	10.32	0.24	0.49
FO4\|$^{200}_{\rm {IS}}$\|	A	0.01	12.14	6.77	0.98	0.72	1.86E-1	5.47	1.09	4.11	1.33	0.09	0.011	10.4	0.36	0.43
FO7\|$^{200}_{\rm {IS}}$\|	A	0.01	12.08	3.09	3.77	1.42	2.19	6.53	1.30	5.27	1.24	0.69	0.460	10.3	2.58	0.29
EO4\|$^{200}_{\rm {IS}}$\|	A	0.1	12.07	7.77	0.29	0.28	7.34E-4	5.02	1.00	3.72	1.35	0.00	0.002	10.3	0.01	0.53
EO7\|$^{200}_{\rm {IS}}$\|	A	0.1	12.09	8.27	0.80	0.62	5.66E-2	3.78	0.76	5.34	0.71	0.06	0.012	10.3	0.24	0.44
FO4\|$^{200}_{\rm {IS}}$\|	A	0.1	12.14	6.00	1.48	1.19	8.70E-4	5.81	1.16	3.10	1.88	0.01	0.041	10.4	0.05	0.44
FO7\|$^{200}_{\rm {IS}}$\|	A	0.1	12.08	3.82	3.82	3.28	2.55E-3	5.57	1.11	2.92	1.91	0.11	0.982	10.3	0.40	0.41

Name	SF	η_SF	M_inj	M_esc	M_gas	M_hot	M_c	\|$M_*^{\rm new}$\|	\|$M_\mathrm{inj}^{\rm II}$\|	\|$\langle t\rangle _*^{\rm new}$\|	\|$M_^{\rm new}/\langle t\rangle _^{\rm new}$\|	SFR	L_X	L_SNIa	L_SNII	T_X
			(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(Gyr)	(M_⊙ yr⁻¹)	(M_⊙ yr⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(keV)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(15)	(16)	(17)
EO4\|$^{200}_{\rm {IS}}$\|	×	–	11.92	9.76	2.39	0.15	2.24	–	–	–	–	–	0.0007	10.2	–	0.50
EO7\|$^{200}_{\rm {IS}}$\|	×	–	11.93	10.34	1.84	0.24	1.57	–	–	–	–	–	0.002	10.2	–	0.49
FO4\|$^{200}_{\rm {IS}}$\|	×	–	12.00	3.32	8.80	1.73	6.97	–	–	–	–	–	0.449	10.3	–	0.37
FO7\|$^{200}_{\rm {IS}}$\|	×	–	11.96	3.41	8.69	1.36	7.16	–	–	–	–	–	0.248	10.2	–	0.32
EO4\|$^{200}_{\rm {IS}}$\|	P	0.01	12.07	4.32	3.28	1.63	1.57	4.47	–	6.61	0.68	0.45	0.110	10.3	–	0.39
EO7\|$^{200}_{\rm {IS}}$\|	P	0.01	12.09	10.43	0.34	0.27	3.99E-2	1.32	–	3.84	0.34	0.02	0.003	10.3	–	0.50
FO4\|$^{200}_{\rm {IS}}$\|	P	0.01	12.14	6.65	0.68	0.43	2.19E-1	4.80	–	4.20	1.14	0.08	0.006	10.4	–	0.40
FO7\|$^{200}_{\rm {IS}}$\|	P	0.01	12.08	2.98	3.12	1.57	1.40	5.99	–	5.39	1.11	0.37	0.163	10.3	–	0.36
EO4\|$^{200}_{\rm {IS}}$\|	P	0.1	12.07	4.65	2.00	1.77	7.31E-2	5.42	–	5.74	0.94	0.12	0.086	10.3	–	0.40
EO7\|$^{200}_{\rm {IS}}$\|	P	0.1	12.09	10.07	0.32	0.29	0.00	1.71	–	2.37	0.72	0.00	0.003	10.3	–	0.51
FO4\|$^{200}_{\rm {IS}}$\|	P	0.1	12.14	3.75	3.64	2.88	8.98E-4	4.74	–	3.28	1.45	0.08	0.587	10.4	–	0.43
FO7\|$^{200}_{\rm {IS}}$\|	P	0.1	12.08	5.79	0.49	0.40	1.98E-2	5.81	–	3.43	1.69	0.04	0.010	10.3	–	0.50
EO4\|$^{200}_{\rm {IS}}$\|	A	0.01	12.07	9.40	0.27	0.17	9.92E-2	3.00	0.60	3.90	0.77	0.05	0.001	10.3	0.18	0.54
EO7\|$^{200}_{\rm {IS}}$\|	A	0.01	12.09	9.70	0.47	0.24	2.09E-1	2.40	0.48	4.39	0.55	0.06	0.002	10.32	0.24	0.49
FO4\|$^{200}_{\rm {IS}}$\|	A	0.01	12.14	6.77	0.98	0.72	1.86E-1	5.47	1.09	4.11	1.33	0.09	0.011	10.4	0.36	0.43
FO7\|$^{200}_{\rm {IS}}$\|	A	0.01	12.08	3.09	3.77	1.42	2.19	6.53	1.30	5.27	1.24	0.69	0.460	10.3	2.58	0.29
EO4\|$^{200}_{\rm {IS}}$\|	A	0.1	12.07	7.77	0.29	0.28	7.34E-4	5.02	1.00	3.72	1.35	0.00	0.002	10.3	0.01	0.53
EO7\|$^{200}_{\rm {IS}}$\|	A	0.1	12.09	8.27	0.80	0.62	5.66E-2	3.78	0.76	5.34	0.71	0.06	0.012	10.3	0.24	0.44
FO4\|$^{200}_{\rm {IS}}$\|	A	0.1	12.14	6.00	1.48	1.19	8.70E-4	5.81	1.16	3.10	1.88	0.01	0.041	10.4	0.05	0.44
FO7\|$^{200}_{\rm {IS}}$\|	A	0.1	12.08	3.82	3.82	3.28	2.55E-3	5.57	1.11	2.92	1.91	0.11	0.982	10.3	0.40	0.41

Note. All quantities as in Table 2.

Table 4.

Relevant quantities at t = 13 Gyr for the rotating models (k = 1) with σ_e8=250 km s⁻¹ (aSF only).

Name	SF	η_SF	M_inj	M_esc	M_gas	M_hot	M_c	\|$M_*^{\rm new}$\|	\|$M_\mathrm{inj}^{\rm II}$\|	\|$\langle t\rangle _*^{\rm new}$\|	\|$M_^{\rm new}/\langle t\rangle _^{\rm new}$\|	SFR	L_X	L_SNIa	L_SNII	T_X
			(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(Gyr)	(M_⊙ yr⁻¹)	(M_⊙ yr⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(keV)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(15)	(16)	(17)
EO4\|$^{250}_{\rm {IS}}$\|	×	–	31.68	8.28	23.84	4.02	19.8	–	–	–	–	–	0.76	23.9	–	0.55
EO7\|$^{250}_{\rm {IS}}$\|	×	–	30.63	11.42	19.71	3.42	16.3	–	–	–	–	–	0.33	23.1	–	0.55
EO4\|$^{250}_{\rm {IS}}$\|	A	0.1	32.14	8.39	4.84	4.41	0.40	23.64	4.72	4.35	5.43	0.86	1.01	24.2	3.25	0.57
EO7\|$^{250}_{\rm {IS}}$\|	A	0.1	31.10	11.42	4.47	4.31	0.16	19.01	3.80	4.13	4.60	0.42	0.66	23.4	1.57	0.58
EO4\|$^{250}_{\rm {IS}}$\|	A	0.01	32.14	8.28	7.17	4.06	3.08	20.87	4.17	5.06	4.12	1.14	0.82	24.2	4.31	0.56
EO7\|$^{250}_{\rm {IS}}$\|	A	0.01	31.10	11.18	6.92	4.00	2.90	16.24	3.24	5.32	3.05	0.93	0.51	23.4	3.55	0.52

Name	SF	η_SF	M_inj	M_esc	M_gas	M_hot	M_c	\|$M_*^{\rm new}$\|	\|$M_\mathrm{inj}^{\rm II}$\|	\|$\langle t\rangle _*^{\rm new}$\|	\|$M_^{\rm new}/\langle t\rangle _^{\rm new}$\|	SFR	L_X	L_SNIa	L_SNII	T_X
			(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(Gyr)	(M_⊙ yr⁻¹)	(M_⊙ yr⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(keV)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(15)	(16)	(17)
EO4\|$^{250}_{\rm {IS}}$\|	×	–	31.68	8.28	23.84	4.02	19.8	–	–	–	–	–	0.76	23.9	–	0.55
EO7\|$^{250}_{\rm {IS}}$\|	×	–	30.63	11.42	19.71	3.42	16.3	–	–	–	–	–	0.33	23.1	–	0.55
EO4\|$^{250}_{\rm {IS}}$\|	A	0.1	32.14	8.39	4.84	4.41	0.40	23.64	4.72	4.35	5.43	0.86	1.01	24.2	3.25	0.57
EO7\|$^{250}_{\rm {IS}}$\|	A	0.1	31.10	11.42	4.47	4.31	0.16	19.01	3.80	4.13	4.60	0.42	0.66	23.4	1.57	0.58
EO4\|$^{250}_{\rm {IS}}$\|	A	0.01	32.14	8.28	7.17	4.06	3.08	20.87	4.17	5.06	4.12	1.14	0.82	24.2	4.31	0.56
EO7\|$^{250}_{\rm {IS}}$\|	A	0.01	31.10	11.18	6.92	4.00	2.90	16.24	3.24	5.32	3.05	0.93	0.51	23.4	3.55	0.52

Note. All quantities are as in Table 2.

Table 4.

Relevant quantities at t = 13 Gyr for the rotating models (k = 1) with σ_e8=250 km s⁻¹ (aSF only).

Name	SF	η_SF	M_inj	M_esc	M_gas	M_hot	M_c	\|$M_*^{\rm new}$\|	\|$M_\mathrm{inj}^{\rm II}$\|	\|$\langle t\rangle _*^{\rm new}$\|	\|$M_^{\rm new}/\langle t\rangle _^{\rm new}$\|	SFR	L_X	L_SNIa	L_SNII	T_X
			(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(Gyr)	(M_⊙ yr⁻¹)	(M_⊙ yr⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(keV)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(15)	(16)	(17)
EO4\|$^{250}_{\rm {IS}}$\|	×	–	31.68	8.28	23.84	4.02	19.8	–	–	–	–	–	0.76	23.9	–	0.55
EO7\|$^{250}_{\rm {IS}}$\|	×	–	30.63	11.42	19.71	3.42	16.3	–	–	–	–	–	0.33	23.1	–	0.55
EO4\|$^{250}_{\rm {IS}}$\|	A	0.1	32.14	8.39	4.84	4.41	0.40	23.64	4.72	4.35	5.43	0.86	1.01	24.2	3.25	0.57
EO7\|$^{250}_{\rm {IS}}$\|	A	0.1	31.10	11.42	4.47	4.31	0.16	19.01	3.80	4.13	4.60	0.42	0.66	23.4	1.57	0.58
EO4\|$^{250}_{\rm {IS}}$\|	A	0.01	32.14	8.28	7.17	4.06	3.08	20.87	4.17	5.06	4.12	1.14	0.82	24.2	4.31	0.56
EO7\|$^{250}_{\rm {IS}}$\|	A	0.01	31.10	11.18	6.92	4.00	2.90	16.24	3.24	5.32	3.05	0.93	0.51	23.4	3.55	0.52

Name	SF	η_SF	M_inj	M_esc	M_gas	M_hot	M_c	\|$M_*^{\rm new}$\|	\|$M_\mathrm{inj}^{\rm II}$\|	\|$\langle t\rangle _*^{\rm new}$\|	\|$M_^{\rm new}/\langle t\rangle _^{\rm new}$\|	SFR	L_X	L_SNIa	L_SNII	T_X
			(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(Gyr)	(M_⊙ yr⁻¹)	(M_⊙ yr⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(keV)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(15)	(16)	(17)
EO4\|$^{250}_{\rm {IS}}$\|	×	–	31.68	8.28	23.84	4.02	19.8	–	–	–	–	–	0.76	23.9	–	0.55
EO7\|$^{250}_{\rm {IS}}$\|	×	–	30.63	11.42	19.71	3.42	16.3	–	–	–	–	–	0.33	23.1	–	0.55
EO4\|$^{250}_{\rm {IS}}$\|	A	0.1	32.14	8.39	4.84	4.41	0.40	23.64	4.72	4.35	5.43	0.86	1.01	24.2	3.25	0.57
EO7\|$^{250}_{\rm {IS}}$\|	A	0.1	31.10	11.42	4.47	4.31	0.16	19.01	3.80	4.13	4.60	0.42	0.66	23.4	1.57	0.58
EO4\|$^{250}_{\rm {IS}}$\|	A	0.01	32.14	8.28	7.17	4.06	3.08	20.87	4.17	5.06	4.12	1.14	0.82	24.2	4.31	0.56
EO7\|$^{250}_{\rm {IS}}$\|	A	0.01	31.10	11.18	6.92	4.00	2.90	16.24	3.24	5.32	3.05	0.93	0.51	23.4	3.55	0.52

Note. All quantities are as in Table 2.

Table 5.

Relevant quantities at t = 13 Gyr for the mildly rotating models (k = 0.1) with σ_e8=250 km s⁻¹ (aSF only).

Name	SF	η_SF	M_inj	M_esc	M_gas	M_hot	M_c	\|$M_*^{\rm new}$\|	\|$M_\mathrm{inj}^{\rm II}$\|	\|$\langle t\rangle _*^{\rm new}$\|	\|$M_^{\rm new}/\langle t\rangle _^{\rm new}$\|	SFR	L_X	L_SNIa	L_SNII	T_X
			(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(Gyr)	(M_⊙ yr⁻¹)	(M_⊙ yr⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(keV)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(15)	(16)	(17)
EO4\|$^{250}_{k=0.1 }$\|	×	–	32.14	8.63	23.51	4.78	18.7	–	–	–	–	–	5.82	24.2	–	0.69
EO7\|$^{250}_{k=0.1 }$\|	×	–	31.10	12.94	18.17	3.44	14.7	–	–	–	–	–	2.20	23.4	–	0.69
EO4\|$^{250}_{k\rm {=0.1}}$\|	A	0.1	32.14	8.46	5.13	5.04	0.086	23.20	4.64	4.28	5.42	1.01	6.33	24.2	3.76	0.67
EO7\|$^{250}_{k\rm {=0.1}}$\|	A	0.1	31.10	13.06	3.63	3.56	0.065	18.01	3.60	4.03	4.47	0.45	2.78	23.4	1.76	0.68
EO4\|$^{250}_{k\rm {=0.1}}$\|	A	0.01	32.14	8.58	5.28	4.84	0.442	22.84	4.56	4.46	5.12	0.91	6.39	24.2	3.69	0.66
EO7\|$^{250}_{k\rm {=0.1}}$\|	A	0.01	31.10	12.96	4.14	3.48	0.656	17.50	3.50	4.22	4.14	0.63	2.51	23.4	2.32	0.68

Name	SF	η_SF	M_inj	M_esc	M_gas	M_hot	M_c	\|$M_*^{\rm new}$\|	\|$M_\mathrm{inj}^{\rm II}$\|	\|$\langle t\rangle _*^{\rm new}$\|	\|$M_^{\rm new}/\langle t\rangle _^{\rm new}$\|	SFR	L_X	L_SNIa	L_SNII	T_X
			(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(Gyr)	(M_⊙ yr⁻¹)	(M_⊙ yr⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(keV)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(15)	(16)	(17)
EO4\|$^{250}_{k=0.1 }$\|	×	–	32.14	8.63	23.51	4.78	18.7	–	–	–	–	–	5.82	24.2	–	0.69
EO7\|$^{250}_{k=0.1 }$\|	×	–	31.10	12.94	18.17	3.44	14.7	–	–	–	–	–	2.20	23.4	–	0.69
EO4\|$^{250}_{k\rm {=0.1}}$\|	A	0.1	32.14	8.46	5.13	5.04	0.086	23.20	4.64	4.28	5.42	1.01	6.33	24.2	3.76	0.67
EO7\|$^{250}_{k\rm {=0.1}}$\|	A	0.1	31.10	13.06	3.63	3.56	0.065	18.01	3.60	4.03	4.47	0.45	2.78	23.4	1.76	0.68
EO4\|$^{250}_{k\rm {=0.1}}$\|	A	0.01	32.14	8.58	5.28	4.84	0.442	22.84	4.56	4.46	5.12	0.91	6.39	24.2	3.69	0.66
EO7\|$^{250}_{k\rm {=0.1}}$\|	A	0.01	31.10	12.96	4.14	3.48	0.656	17.50	3.50	4.22	4.14	0.63	2.51	23.4	2.32	0.68

Note. All quantities are as in Table 2.

Table 5.

Relevant quantities at t = 13 Gyr for the mildly rotating models (k = 0.1) with σ_e8=250 km s⁻¹ (aSF only).

Name	SF	η_SF	M_inj	M_esc	M_gas	M_hot	M_c	\|$M_*^{\rm new}$\|	\|$M_\mathrm{inj}^{\rm II}$\|	\|$\langle t\rangle _*^{\rm new}$\|	\|$M_^{\rm new}/\langle t\rangle _^{\rm new}$\|	SFR	L_X	L_SNIa	L_SNII	T_X
			(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(Gyr)	(M_⊙ yr⁻¹)	(M_⊙ yr⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(keV)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(15)	(16)	(17)
EO4\|$^{250}_{k=0.1 }$\|	×	–	32.14	8.63	23.51	4.78	18.7	–	–	–	–	–	5.82	24.2	–	0.69
EO7\|$^{250}_{k=0.1 }$\|	×	–	31.10	12.94	18.17	3.44	14.7	–	–	–	–	–	2.20	23.4	–	0.69
EO4\|$^{250}_{k\rm {=0.1}}$\|	A	0.1	32.14	8.46	5.13	5.04	0.086	23.20	4.64	4.28	5.42	1.01	6.33	24.2	3.76	0.67
EO7\|$^{250}_{k\rm {=0.1}}$\|	A	0.1	31.10	13.06	3.63	3.56	0.065	18.01	3.60	4.03	4.47	0.45	2.78	23.4	1.76	0.68
EO4\|$^{250}_{k\rm {=0.1}}$\|	A	0.01	32.14	8.58	5.28	4.84	0.442	22.84	4.56	4.46	5.12	0.91	6.39	24.2	3.69	0.66
EO7\|$^{250}_{k\rm {=0.1}}$\|	A	0.01	31.10	12.96	4.14	3.48	0.656	17.50	3.50	4.22	4.14	0.63	2.51	23.4	2.32	0.68

Name	SF	η_SF	M_inj	M_esc	M_gas	M_hot	M_c	\|$M_*^{\rm new}$\|	\|$M_\mathrm{inj}^{\rm II}$\|	\|$\langle t\rangle _*^{\rm new}$\|	\|$M_^{\rm new}/\langle t\rangle _^{\rm new}$\|	SFR	L_X	L_SNIa	L_SNII	T_X
			(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(10⁹ M_⊙)	(Gyr)	(M_⊙ yr⁻¹)	(M_⊙ yr⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(10⁴⁰ erg s⁻¹)	(keV)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(15)	(16)	(17)
EO4\|$^{250}_{k=0.1 }$\|	×	–	32.14	8.63	23.51	4.78	18.7	–	–	–	–	–	5.82	24.2	–	0.69
EO7\|$^{250}_{k=0.1 }$\|	×	–	31.10	12.94	18.17	3.44	14.7	–	–	–	–	–	2.20	23.4	–	0.69
EO4\|$^{250}_{k\rm {=0.1}}$\|	A	0.1	32.14	8.46	5.13	5.04	0.086	23.20	4.64	4.28	5.42	1.01	6.33	24.2	3.76	0.67
EO7\|$^{250}_{k\rm {=0.1}}$\|	A	0.1	31.10	13.06	3.63	3.56	0.065	18.01	3.60	4.03	4.47	0.45	2.78	23.4	1.76	0.68
EO4\|$^{250}_{k\rm {=0.1}}$\|	A	0.01	32.14	8.58	5.28	4.84	0.442	22.84	4.56	4.46	5.12	0.91	6.39	24.2	3.69	0.66
EO7\|$^{250}_{k\rm {=0.1}}$\|	A	0.01	31.10	12.96	4.14	3.48	0.656	17.50	3.50	4.22	4.14	0.63	2.51	23.4	2.32	0.68

Note. All quantities are as in Table 2.

3 RESULTS

Each simulation starts with the galaxy empty of gas, when the age of the original stellar population is 2 Gyr, and the ISM evolution is followed for the next 11 Gyr. Tables 2–5 list for all models the main quantities of interest at the end of the simulations; the tables also list the same quantities for the corresponding models without SF taken from N14 (hereafter ‘noSF’ models). First (Section 3.1), we present the main results focusing on the two sets of re-simulated models with largely differing values for the galaxy mass (i.e. the two sets with E0 counterpart of σ_e8 = 200 and 300 km s⁻¹, the LM and HM models). In Section 3.2, we concentrate on the intermediate mass models (run only for the aSF), where this time k is equal to 1 or lower (k = 0.1). In Sections 3.3 and 3.4, we discuss the consumption of cold gas mass and the formation of new stars. Finally, we investigate the relationship between the adopted recipe for SF (equation 1) and the Kennicutt–Schmidt relation (Section 3.5).

3.1 Comparison between noSF and SF models

In a short summary, for noSF models, N14 found that rotation in LM galaxies favours the establishment of global winds, with the consequent reduction of L_X; in medium-to-high mass galaxies the conservation of angular momentum lowers the hot gas density in the central galactic region, leading again to a reduction of L_X, and also of T_X (because the external and colder regions weight more in the computation of T_X). In LM galaxies, instead, T_X can become higher if rotation triggers a wind, due to the decrease of the ISM density, and the additional heating due to the high meridional velocities of the escaping material (see equation 7).

The first important result here is that when SF is added (both in the pSF and aSF modalities), the hot ISM evolution remains substantially similar to that found by N14 without SF, for models of the same mass. As a consequence of the insensitivity of the general behaviour to the addition of SF, the values of L_X and T_X for the models with SF, and their trends with the main galactic structural properties, are on average very similar to those found by N14. Therefore, the conclusions of N14 about the importance of shape and rotation in determining L_X and T_X, also as a function of galaxy mass, are confirmed. Fig. 1 demonstrates this result by plotting the final L_X and T_X values for the same rotating galaxy models evolved with noSF and with SF (with η_SF = 0.01): the distribution of the points in the noSF and SF panels is very similar (and the analogous figure with the η_SF = 0.1 models produces the same conclusions). In particular, L_X of HM models is only marginally sensitive to the presence of SF, while in LM models SF can introduce variations of L_X; however, these keep within the (large) range of L_X values already found in N14 without SF. Thus, SF adds another cause of spread for L_X, at lower galaxy masses. Fig. 2 shows the resulting L_X versus T_X for the aSF models, compared with the same quantities derived recently from Chandra data for the hot gas of ETGs (Boroson et al. 2011; Kim & Fabbiano 2015). From the latter two samples, we have selected only ETGs of morphological type later than E3, for a proper comparison with our models. Overall, the simulation results agree well with the observed X-ray properties of real ETGs (except perhaps for the most X-ray luminous models that may be slightly hotter than observed).

Figure 1.

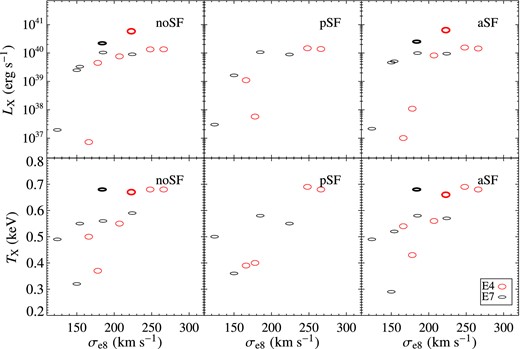
Top panels: ISM X-ray luminosity L_X in the 0.3–8 keV band at 13 Gyr as a function of σ_e8, for the selection of 10 models from N14 re-simulated here (Table 1), plus two models with σ_e8 = 250 km s⁻¹ for the E0 counterpart, and k = 0.1 (shown with thicker ellipses). The three panels (from left to right) refer to the same models without SF (from N14), with passive SF, and with active SF (with η_SF = 0.01). Bottom panels: the same for the X-ray emission weighted temperature T_X in the 0.3–8 keV band at 13 Gyr. All L_X and T_X values are given in Tables 2–5. See Section 3.1 for more details.

Figure 2.

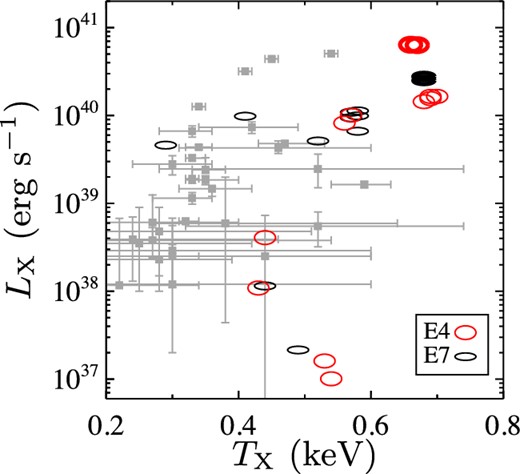
L_X as a function of T_X for aSF models listed in Tables 1–5 (open ellipses, as in Fig. 1), compared with Chandra data for the hot gas of ETGs taken from Boroson, Kim & Fabbiano (2011) and Kim & Fabbiano (2015, grey squares with error bars). From the latter two samples, we selected only ETGs of morphological type later than E3, for a proper comparison with our models.

The reason for variations in L_X linked with SF in LM models is given by anticipations or delays in the most conspicuous features of their typical flow behaviour: N14 found (and the present simulations confirm) that the ISM in rotating models experiences periodic cooling episodes, where the gas injected by the stellar population accumulates until the radiative losses become catastrophic. In these episodes, the ISM quickly cools, emitting a large part of its internal energy as radiation; peaks in L_X and throats in T_X are then produced, as apparent in Fig. 5. The tenuous hot atmosphere left after a major cooling is then replenished by the new mass injection from the stellar population. In correspondence of the formation of these significant amounts of cold material (with short cooling times) SF is enhanced, and peaks in pace with L_X, as discussed in Section 3.4. On the contrary, very little variations of the flow due to SF are seen in HM galaxies. Figs 3 –5 give particular examples of the general similarity in the hydrodynamical evolution of noSF and SF models, by plotting in parallel the ISM evolution for the noSF, pSF, and aSF cases; at the same time, the figures point out how this similarity is very close for HM models (see Fig. 4, for the HM model EO7|$^{300}_{\rm IS}$|⁠), while some differences can be present in LM ones (see Fig. 3, for the LM model EO7|$^{200}_{\rm IS}$|⁠). Notably, the hot ISM evolution in the HM models is practically identical with and without SF (see also Fig. 5): a massive cold disc forms early, and afterwards, even when it is mostly consumed by SF (see Section 3.3 below), around the disc the hot ISM evolution proceeds almost unaltered by the energy and mass injection from SNII's. Less massive models, instead, are sensitive to the inclusion of SF, similarly to what found in previous studies where they showed to be very sensitive to any change in the galaxy properties (e.g. the mass distribution, the stellar population inputs, the stellar kinematics; Ciotti et al. 1991, N14). As shown by Figs 3 and 5, for the EO7|$^{200}_{\rm IS}$| galaxy, at around 4 Gyr the noSF and the pSF models have already past their major cooling episode (see the peak in L_X in Fig. 5) followed by the onset of a wind, and the equatorial outflow becomes stronger and stronger thereafter (see how the purple regions become more and more extended in Fig. 3, starting from 4.6 Gyr, and the sharp and steady decline in L_X in Fig. 5). The aSF model, instead, has its major cooling catastrophe much later, as shown by the prominent dark green region in Fig. 3 at ≃8 Gyr, which emits a conspicuous amount of radiation in the X-ray band, thus prompting the corresponding peak in L_X in Fig. 5. This delay in the major cooling episode, preceding the onset of a wind, is due to the newly formed stars that inject mass, and most importantly heat, in the ISM; thanks to this heat the galaxy can remain hot gas rich until ≃8 Gyr, when finally the major cooling takes place. pSF, where mass is not injected instead, corresponds to an evolution very similar to that without SF.

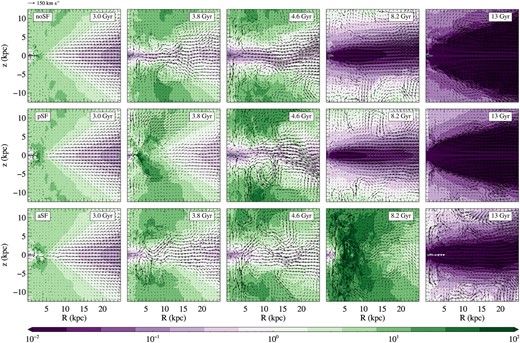
$Meridional sections of the heating over cooling time ratio for the LM EO7$^{200}_\mathrm{IS}$ model, at a selection of representative times (indicated as galaxy ages in the top right of each panel). The heating time is $t_\mathrm{heat}=E/\dot{E}$ (where $\dot{E}$ is the source term given in equation 7); the cooling time is defined in Section 2.2.1. From left to right, each column refers to the noSF, pSF, and aSF (with ηSF = 0.1) models, respectively. Arrows describe the meridional velocity field; their length is proportional to the modulus of the gas velocity in the (z, R) plane, according to a scale shown in the bottom-left corner. See Section 3.1 for more details.$

Figure 3.

Meridional sections of the heating over cooling time ratio for the LM EO7|$^{200}_\mathrm{IS}$| model, at a selection of representative times (indicated as galaxy ages in the top right of each panel). The heating time is |$t_\mathrm{heat}=E/\dot{E}$| (where |$\dot{E}$| is the source term given in equation 7); the cooling time is defined in Section 2.2.1. From left to right, each column refers to the noSF, pSF, and aSF (with η_SF = 0.1) models, respectively. Arrows describe the meridional velocity field; their length is proportional to the modulus of the gas velocity in the (z, R) plane, according to a scale shown in the bottom-left corner. See Section 3.1 for more details.

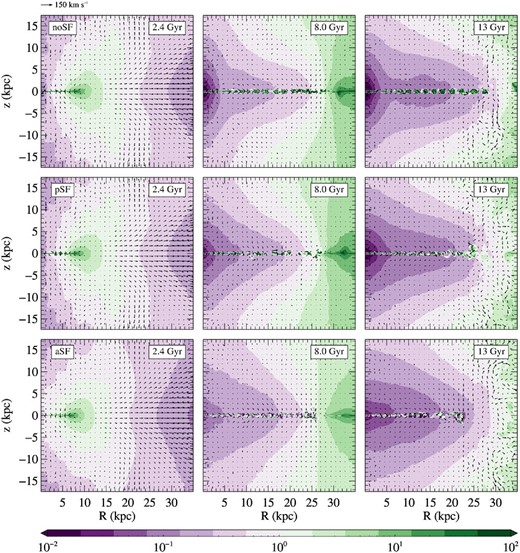
$Meridional sections of the heating over cooling time ratio for the HM EO7$^{300}_\mathrm{IS}$ model. From top to bottom, each row refers to the noSF, pSF, and aSF (with ηSF = 0.1) models, respectively. Arrows describe the velocity field, as in Fig. 3. Note the large cold disc, that does not completely disappear with SF. See Section 3.1 for more details.$

Figure 4.

Meridional sections of the heating over cooling time ratio for the HM EO7|$^{300}_\mathrm{IS}$| model. From top to bottom, each row refers to the noSF, pSF, and aSF (with η_SF = 0.1) models, respectively. Arrows describe the velocity field, as in Fig. 3. Note the large cold disc, that does not completely disappear with SF. See Section 3.1 for more details.

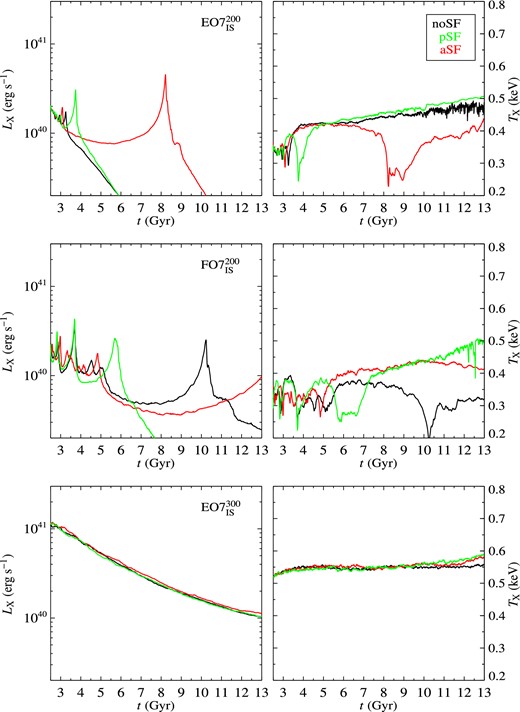
$Time evolution of the X-ray luminosity LX and X-ray emission weighted temperature TX for the EO7$^{200}_\mathrm{IS}$ (top panels), FO7$^{200}_\mathrm{IS}$ (middle panels), EO7$^{300}_\mathrm{IS}$ (bottom panels) models. The black, green, and red lines refer to the noSF model, and to the passive and active SF schemes, respectively, with ηSF = 0.1. The FO7$^{300}_\mathrm{IS}$ model has an evolution almost identical to that of EO7$^{300}_\mathrm{IS}$ shown here. See Section 3.1 for more details.$

Figure 5.

Time evolution of the X-ray luminosity L_X and X-ray emission weighted temperature T_X for the EO7|$^{200}_\mathrm{IS}$| (top panels), FO7|$^{200}_\mathrm{IS}$| (middle panels), EO7|$^{300}_\mathrm{IS}$| (bottom panels) models. The black, green, and red lines refer to the noSF model, and to the passive and active SF schemes, respectively, with η_SF = 0.1. The FO7|$^{300}_\mathrm{IS}$| model has an evolution almost identical to that of EO7|$^{300}_\mathrm{IS}$| shown here. See Section 3.1 for more details.

A complementary illustration of the different behaviour between the HM and the LM galaxies is given by Fig. 5, that shows the L_X and T_X evolution for the same models of Figs 3 and 4, plus another set of three models representative of the LM class, the FO7|$^{200}_{\rm IS}$| ones. In LM models, a number of cooling episodes (peaks in L_X) typically take place, possibly terminated by a major one that is followed by the onset of a wind and the clearing of the ISM from the galaxy (as in N14). The galaxy mass distribution in the FO7|$_{\rm IS}^{\rm 200}$| models (middle panels of Fig. 5), is more concentrated than in the EO7|$^{200}_{\rm IS}$| ones, thus the last major peak in L_X is delayed with respect to what happens for the EO7|$^{200}_{\rm IS}$| models. Thus, in the FO7|$_{\rm IS}^{\rm 200}$| galaxy, aSF produces a delay in the major cooling episode that is even longer than for the EO7|$_{\rm IS}^{\rm 200}$| aSF model, to the point that it does not take place within the present epoch. pSF instead produces its anticipation with respect to what shown in the noSF case (Fig. 5), due to pSF subtracting gas and leaving a lower density region, radiating less and more easy to push out of the galaxy.

A final, general result is also that the evolution of a model with SF is more and more different from that of its corresponding noSF model, when increasing η_SF.

For illustration purposes, Fig. 6 shows a meridional section of the density distribution of the newly formed stars at the end of the simulations, for the models in Fig. 5. One can notice the more extended and massive disc in HM models, where it is also quite independent of the pSF or aSF scheme. On the contrary, in LM models, the disc is much less extended, and it can become larger (for the EO7|$^{200}_\mathrm{IS}$| model) or smaller (for the FO7|$^{300}_\mathrm{IS}$| model) when switching from the pSF to the aSF scheme; this is another evidence of the high sensitivity of the flow evolution to any change in the input parameters, at low galaxy masses.

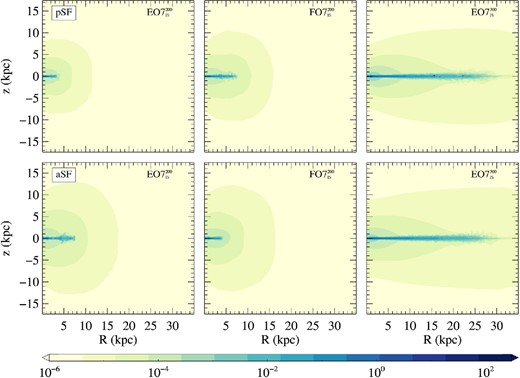
$Meridional sections of the density distribution of the new stars formed up to 13 Gyr (in units of M⊙ pc−3), for the same models of Figs 5 and 8: EO7$^{200}_\mathrm{IS}$ (left-hand panels), FO7$^{200}_\mathrm{IS}$ (middle panels), and EO7$^{300}_\mathrm{IS}$ models (right-hand panels). Top and bottom panels refer, respectively, to pSF and aSF simulations, with ηSF = 0.1.$

Figure 6.

Meridional sections of the density distribution of the new stars formed up to 13 Gyr (in units of M_⊙ pc⁻³), for the same models of Figs 5 and 8: EO7|$^{200}_\mathrm{IS}$| (left-hand panels), FO7|$^{200}_\mathrm{IS}$| (middle panels), and EO7|$^{300}_\mathrm{IS}$| models (right-hand panels). Top and bottom panels refer, respectively, to pSF and aSF simulations, with η_SF = 0.1.

3.2 Intermediate mass ETGs

Here, we present the results for two representative models, of E4 and E7 shapes, with intermediate galaxy mass (σ_e8 = 250 km s⁻¹ for the E0 counterpart, see Table 1), that have been run with the same kinematic configuration of the LM and HM models presented previously (k = 1, isotropic rotator), and also with a lower rotation (k = 0.1). For these, only aSF has been considered, with η_SF = 0.01 and η_SF = 0.1. The final values for the most relevant quantities of these eight models are presented in Tables 4 and 5.

The E4 models with k = 1 show the same smooth evolution of the HM models, i.e. no or very small oscillations in L_X and T_X (see the dashed lines in Fig. 7, similar to those in Fig. 5); in fact, the evolution of the hot gas is similarly not affected by SF. The E7 models with k = 1, instead, show oscillations in L_X and T_X, similar to those of the EO7|$^{200}_{\rm IS}$| and FO7|$^{200}_{\rm IS}$| models, but fewer and less pronounced (see the solid lines in Fig. 7, to be compared with those in Fig. 5). In the aSF model the final L_X is larger than for the noSF case, as found for the FO7|$^{200}_{\rm IS}$| models (Section 3.1).

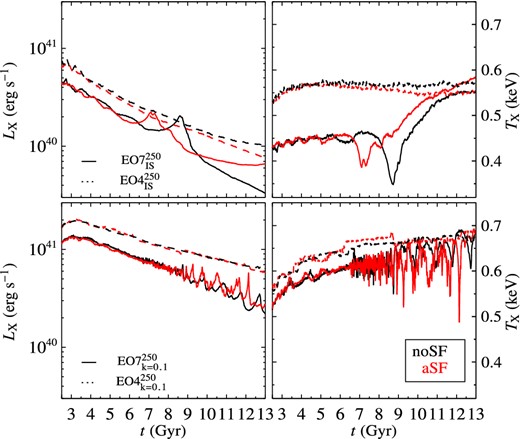
$Time evolution of the X-ray luminosity LX and X-ray emission weighted temperature TX for the EO4$^{250}_\mathrm{IS}$ and EO7$^{250}_\mathrm{IS}$ models (top panels), and for the EO4$^{250}_{k=0.1}$ and EO7$^{250}_{k=0.1}$ models (bottom panels). For the aSF models, ηSF = 0.1. See Section 3.2 for more details.$

Figure 7.

Time evolution of the X-ray luminosity L_X and X-ray emission weighted temperature T_X for the EO4|$^{250}_\mathrm{IS}$| and EO7|$^{250}_\mathrm{IS}$| models (top panels), and for the EO4|$^{250}_{k=0.1}$| and EO7|$^{250}_{k=0.1}$| models (bottom panels). For the aSF models, η_SF = 0.1. See Section 3.2 for more details.

In models with rotational velocities reduced by a factor of 10 (k = 0.1), L_X and T_X increase largely, as expected from the results of N14 showing a larger L_X and T_X in non-rotating galaxies (k = 0). Again the E4 models show no oscillations in L_X and T_X, while the E7 models show numerous small oscillations in L_X and T_X, that increase in amplitude with time increasing (Fig. 7). The cold gas disc is much less extended: its radius is ≲ 1 kpc for k = 0.1, and ≲ 10 kpc for k = 1 (slightly larger for flatter shape, and for lower η_SF).

3.3 Mass exchange between the cold disc and the new stars

The second main result of the new simulations is that most of the cold gas disc is consumed by SF, both for pSF and aSF. This result, of general validity, is shown for the particular models of Fig. 5 in Fig. 8, where the cold gas mass M_c of the noSF models (black solid line) is at the end very close to that of the new stars |$M_*^{\rm new}$| (dashed lines). For example, the EO7|$_\mathrm{IS}^{\rm 200}$| model in the noSF case has a cold disc extending out to a 2.5 kpc radius, of M_c = 1.6 × 10⁹ M_⊙, while the corresponding pSF model at the end has no cold disc, and a mass in new stars of |$M_*^{\rm new}\simeq 1.7\times 10^9$| M_⊙ (a bit more gas has cooled in the pSF case than in the noSF case). Similarly, this same galaxy model, with aSF and η_SF = 0.1, at the end has a cold disc of just M_c ≃ 5.7 × 10⁷ M_⊙, and |$M_*^{\rm new}\simeq 3.8\times 10^9$| M_⊙. This |$M_*^{\rm new}$| is larger (approximately double) than for the pSF case, a fact that is partly accounted for by the injected mass from the new stars in the aSF model,² and mostly by the delay in the final cooling episode after which a galactic wind is established (Fig. 5); this delay keeps the galaxy gas-rich and star forming for a longer time (which is proved also by the lower escaped mass M_esc in the aSF than in the pSF case, see Table 3).

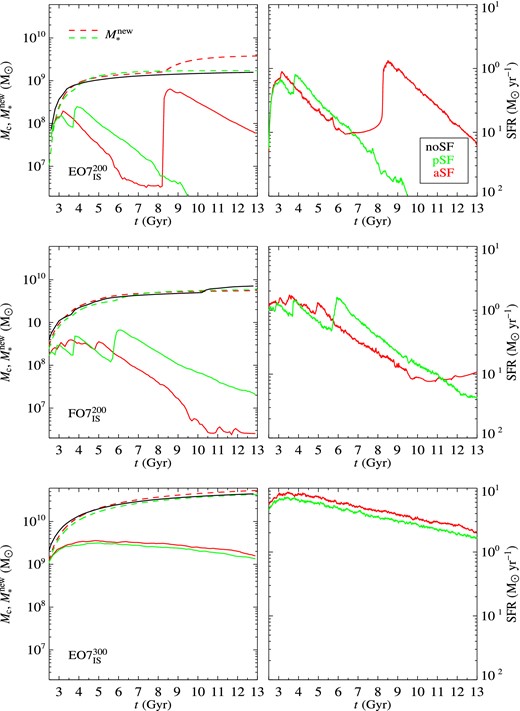
$Left-hand panels: time evolution of the cold gas mass Mc (solid lines), and of the cumulative mass in newly formed stars $M_*^{\rm new}$ (dashed lines). Right-hand panels: time evolution of the SFR rates. The models are the same of Fig. 5. The black line refers to the noSF model, green, and red lines refer to pSF and aSF, respectively, with ηSF = 0.1. Note how Mc is much reduced in the SF models (green and red solid lines) with respect to the noSF models (black lines), and how at the same time $M_*^{\rm new}$ (dashed lines) reaches close to the noSF Mc values. See Section 3.3 for more details.$

Figure 8.

Left-hand panels: time evolution of the cold gas mass M_c (solid lines), and of the cumulative mass in newly formed stars |$M_*^{\rm new}$| (dashed lines). Right-hand panels: time evolution of the SFR rates. The models are the same of Fig. 5. The black line refers to the noSF model, green, and red lines refer to pSF and aSF, respectively, with η_SF = 0.1. Note how M_c is much reduced in the SF models (green and red solid lines) with respect to the noSF models (black lines), and how at the same time |$M_*^{\rm new}$| (dashed lines) reaches close to the noSF M_c values. See Section 3.3 for more details.

In general, the LM models with SF show a final M_c that can range from 0 to 10⁹ M_⊙, but is typically ≲ 10⁸ M_⊙ (Fig. 9 and Table 3). The final mass in the newly formed stellar disc is of the order of |$M_*^{\rm new}\simeq$|a few ×10⁹ M_⊙; thus, the |$M_*^{\rm new}$| values reach almost those of the M_c of the corresponding noSF models (Table 3; Fig. 9). temperature below 2× 10⁴K.

$Top panels: final values of the cold gas mass, for the models in Tables 2–5 without SF (left-hand panel), and with aSF, for the two different ηSF values adopted here. Middle and bottom panels: final values of the stellar mass in newly formed stars $M_*^{\rm new}$, of the SFR normalized to the original M*, and of the mean formation time of the new stars $\langle t\rangle _*^{\rm new}$, calculated from the beginning of the simulation, for the same models with aSF in the top panels. All values are given in Tables 2–5. See Sections 3.3 and 3.4 for more details.$

Figure 9.

Top panels: final values of the cold gas mass, for the models in Tables 2–5 without SF (left-hand panel), and with aSF, for the two different η_SF values adopted here. Middle and bottom panels: final values of the stellar mass in newly formed stars |$M_*^{\rm new}$|⁠, of the SFR normalized to the original M_*, and of the mean formation time of the new stars |$\langle t\rangle _*^{\rm new}$|⁠, calculated from the beginning of the simulation, for the same models with aSF in the top panels. All values are given in Tables 2–5. See Sections 3.3 and 3.4 for more details.

Also in the HM models, similarly to what found for the LM models, |$M_*^{\rm new}$| at the end of the simulations is of the order of the M_c values of the noSF models. A larger massive disc remains in the HM models, though, even when including SF (e.g. Figs 8 and 9). Their final M_c is ≃10⁹ M_⊙, for η_SF = 0.1 (≃1/50 of M_c without SF), and (8–12) × 10⁹ M_⊙, if η_SF = 0.01 (M_c ≃ 1/5 of M_c without SF), independently of pSF or aSF. As found for the LM galaxies, in the aSF models |$M_*^{\rm new}$| is larger than in the pSF ones, and can be even larger than M_c of the noSF models (Figs 8 and 9). This time, though, the difference is lower, of ≃20 per cent, and corresponds to secondary SF sustained by the material injected by the new stars. The final mass in the newly formed stellar disc is of the order of |$M_*^{\rm new}\simeq$|a few× 10¹⁰ M_⊙ (Table 2). However, it must be noted that the structural properties of the HM models may not be very realistic: ETGs of this mass with the isotropic rotator kinematics are quite unlikely, since they are not observed to rotate this much (Emsellem et al. 2011). Real massive galaxies will have less rotation than adopted here with k = 1, and then they will have less cold gas and less new stars.

More realistic massive and rotating ETGs are those of Section 3.2, with aSF. For these, if k = 1, the final cold gas mass is again largely reduced when introducing SF, by a factor of ≃ 50 (E4) and ≃ 100 (E7), when η_SF = 0.1. At 13 Gyr, M_c is few× 10⁹ M_⊙ for η_SF = 0.01, and few× 10⁸ M_⊙ for η_SF = 0.1; |$M_*^{\rm new}$| is ≃2 × 10¹⁰ M_⊙, for both η_SF values. If k = 0.1, the final M_c is reduced even more than for the k = 1 models (Fig. 9), for both the E4 and E7 shapes: M_c is a few ×10⁸ M_⊙ (η_SF = 0.01), and ≲ 10⁸ M_⊙ (η_SF = 0.1). Note that the final cold mass M_c, without SF, is similarly large for the k = 1 and 0.1 models (Tables 4 and 5; Fig. 9), but it is instead lower for the k = 0.1 models than for the k = 1 ones, when adding SF; one could conclude that in the k = 0.1 models SF is more efficient, because it takes place in a cold disc which is smaller and denser, or that the evolution is different, if less gas overall cooled (the heating was more efficient). The second hypothesis is supported by the finding that, at the end of the simulations, |$M_*^{\rm new}$| is similar for k = 1 and 0.1 (e.g. 2.4 and 2.3 × 10¹⁰ M_⊙ for the E4 models, respectively, with k = 1 and 0.1, for η_SF = 0.1), and similarly larger than M_c of the corresponding noSF models (e.g. 2.0 and 1.9 × 10¹⁰ M_⊙, for the E4 models, respectively, with k = 1 and 0.1).

In conclusion, SF seems to be an important mechanism to solve the worrisome feature of massive cold gas discs in rotating ETGs without SF. In addition, we found the following trends, at the end of the simulations (see also the top two rows of panels of Fig. 9): M_c increases with M_*, and has a large spread for LM models, that increases for larger η_SF; M_c/M_* is roughly constant with M_*, with a spread reaching down to values much lower than this constant for LM models; at any M_*, M_c decreases when η_SF increases. |$M_*^{\rm new}$| and |$M_*^{\rm new}/M_*$| increase with M_*, with a spread for LM models, and are roughly independent of η_SF. This latter result means that more massive ETGs have been overall more efficient in forming stars from recycled material, considering their past ≃11 Gyr.

3.4 The SF history

SF is not only responsible for the final mass budget of M_c and |$M_*^{\rm new}$|⁠, but also for the rate of SF (SFR), its evolution, and the (fiducial) age of |$M_*^{\rm new}$|⁠; that is, for the SF history that we discuss here. SF shows a different evolution in LM and HM galaxies, in pace with their different ISM evolution (see Fig. 8). In LM galaxies, where major cooling episodes take place recursively, the SFR peaks suddenly in correspondence of these cooling events due to the increased density of cold gas, and declines right after, going eventually to practically zero either if the cold gas reservoir is completely consumed or the cooling episode is followed by a global wind (Section 3.1). Thus, in general LM galaxies have a larger and peaked SFR in their past (reaching 1–2 M_⊙ yr⁻¹), when the rate of stellar mass losses due to the original stellar population was much larger, and a low SFR ( ≲ 0.1 M_⊙ yr⁻¹) at the present epoch. Typical values at 13 Gyr can be as low as zero, and at most as high as 0.45 M_⊙ yr⁻¹ (Table 3). These values compare well with the current rates estimated for the ATLAS^3D sample, that range from ≈0.01 and 3 M_⊙ yr⁻¹, with a median value of 0.15 M_⊙ yr⁻¹ for ETGs of σ_e8 comparable to those of the LM models run here (Davis et al. 2014). HM galaxies, instead, show a more regular and steady production of cold gas, and so is their SFR (Fig. 8); at 13 Gyr, their SFR is 2–3 M_⊙ yr⁻¹ (Table 2; but we recall these models are not realistic). In the intermediate mass models (Section 3.2), the SFR is larger for the E4 models without oscillations in L_X than for the E7 ones. Overall, the SFR at 13 Gyr is similar for k = 1 and 0.1: for k = 1, the SFR ranges from 0.42 to 1.1 M_⊙ yr⁻¹ (i.e. it is larger than for the LM models of same k = 1); when k = 0.1, the SFR ranges from 0.45 to 1.0 M_⊙ yr⁻¹. Fig. 9 summarizes the present epoch SFR behaviour, as a function of M_*, for the aSF models. To compare models of different mass, the plotted quantity is the SFR normalized to M_*. This quantity is ∼(1–4) × 10⁻³ Gyr⁻¹, quite independent of η_SF, for the intermediate mass and HM models; it can be largely varying for the LM models (from 4 × 10⁻⁴ to 6 × 10⁻³ Gyr⁻¹, for η_SF = 0.1, and from 8 × 10⁻⁵ to ∼10⁻³ Gyr⁻¹, for η_SF = 0.01). On average, the present epoch SFR/M_* increases with M_*, a result similar to that of the previous Section 3.3, where we found that the integration over time of the SFR, that is |$M_*^{\rm new}$|⁠, and |$M_*^{\rm new}/M_*$|⁠, increase with M_*.

Tables 2 and 3 also list the mean formation time |$\langle t\rangle _*^{\rm new}$| of the new stars since the beginning of the simulation (t₀ = 2 Gyr), and the mean SFR (defined as |$M_*^{\rm new}/\langle t \rangle _*^{\rm new}$|⁠), both at 13 Gyr. |$\langle t\rangle _*^{\rm new}$| as a function of time is defined as

\begin{equation} \langle t\rangle _*^{\rm new} (t)=\frac{1}{M_*^{\rm new}(t)} \int _{t_0} ^t (t^{\prime }-t_0) \, {\rm SFR}(t^{\prime }) \mathop {}\!\mathrm{d}t^{\prime }, \end{equation}

(9)

where the SFR(t) is the volume integrated, instantaneous SFR. The values of |$\langle t\rangle _*^{\rm new}$| at the present epoch are shown in Fig. 9 for the aSF cases. They range from 2.4 to 6.6 Gyr, for the LM models, with a tendency to be lower for the aSF than for the pSF, and for the larger η_SF. The HM and intermediate mass models have |$\langle t\rangle _*^{\rm new}$| in a narrower range (from 4.2 to 5.5 Gyr), independent of the aSF or pSF, and are again lower for the larger η_SF (Fig. 9). Therefore, the new stars in LM models have a larger spread of formation times, and correspondingly a larger range of ages at the current epoch, than in larger mass models.

For the aSF, for η_SF = 0.01, the upper envelope of the more recent formation times (largest |$\langle t\rangle _*^{\rm new}$| values) is ≃ 5.5 Gyr, roughly independent of M_*, while the lower envelope (lowest |$\langle t\rangle _*^{\rm new}$| values) increases with M_*. A similar trend is shown by the HM and intermediate mass models, for η_SF = 0.1, but shifted towards lower |$\langle t\rangle _*^{\rm new}$| values ( ≲ 4.5 Gyr); the spread of |$\langle t\rangle _*^{\rm new}$| for LM models keeps instead large, extending to even lower |$\langle t\rangle _*^{\rm new}$| values of ≃ 3 Gyr. The decrease of |$\langle t\rangle _*^{\rm new}$| for larger η_SF, i.e. for a more efficient SF, obtained here from hydrodynamical simulations provides support to the similar conclusion drawn in galaxy formation models focused on chemical evolution: these assume that the efficiency of SF is an increasing function of mass, which for them has – among others – the consequence that smaller galaxies continue to form stars for longer periods, while more massive galaxies host an older stellar population (e.g. Matteucci 1994).

It is interesting that |$\langle t\rangle _*^{\rm new}$| decreases slightly, or remains similar, when switching from pSF to aSF; in fact, one could expect a more extended SF, due to the injection of material from the new stars, for the aSF. Evidently, the net results of the injection of both mass and energy is to produce the bulk of SF at roughly the same time, for the pSF and aSF schemes; only, the final mass in new stars is larger for aSF.

The mean age of the newly formed stars in Gyr is 13|$-t_0-\langle t\rangle _*^{\rm new}$|⁠. This age is in any case larger than ∼5.5 Gyr, for the aSF.

3.5 The SF recipe and the Kennicutt–Schmidt relation

From equation (1) it follows that SF is favoured in regions of high density, and relatively short t_SF. These conditions are naturally present in low-temperature regions; accordingly, the simulations show that most of the SF takes place where the gas temperature is ≲ 2 × 10⁴K, i.e. in the cold rotating disc.

Quite obviously, our results depend somehow on the adopted prescription for the SF, while a realistic, physically consistent, description of SF is not available. Yet, it is interesting to ask at what level our implementation of SF recovers some basic observational features of SF. More than half a century ago Schmidt (1959) conjectured that the rate of SF should vary as a power law of the gas density, and later Kennicutt (1998) suggested the parametrization in terms of mass surface densities |$\Sigma _{\rm SFR} = A\Sigma _\mathrm{cold\, gas}^N$|⁠, valid for star-forming galaxies, with N ≃ 1.4–1.5 (Kennicutt & Evans 2012). We investigate here what scaling (if any) the adopted SF recipe of equation (1) produces in terms of Σ_SFR versus Σ_gas, when implemented in the simulations.

Fig. 10 shows for a few representative models at the end of the simulation the relationship between Σ_SFR and Σ_gas, calculated separately for the hotter (T > 2 × 10⁴K) and colder (T ≤ 2 × 10⁴K) phases of the gas; Σ_SFR is the face-on projection of |$\dot{\rho }_\mathrm{SF}$|⁠. The figure shows for comparison a recent scaling for the Kennicutt–Schmidt relation, derived by Davis et al. (2014) for the ATLAS^3D sample of molecular gas-rich ETGs (this has a slope of N = 1.4). Fig. 10 tells that SF in the gas takes place basically in two regimes, and by far most of it is due to cold gas. The behaviour of the cold gas shows two remarkable features: the first is that a scaling similar to that of the Kennicutt–Schmidt relation is followed quite closely by the blue (cold gas) points; the second is that even the normalization is reasonably well reproduced by our scheme of ‘active SF’, when η_SF = 0.01 (models with η_SF = 0.1 correspond instead to a normalization that is too large). In particular, the cold gas in the logΣ_SFR–logΣ_gas plane follows a trend best fitted by a line of slope of ≃ 1.4–1.5, a fact that can be explained as follows. SF in the cold gas is most likely regulated by the dynamical time-scale t_dyn, being t_cool very short at such temperatures and densities; thus, one roughly expects that |$\dot{\rho }_{\rm SF} \propto \rho ^{1.5}$|⁠. A slope for the Σ_SFR–Σ_gas relation close to the empirical one then follows when neglecting the difference between volume and surface density, which is not unreasonable considering that the cold disc resides mainly in a thin region above and below the equatorial plane, extending vertically for just a couple of gridpoints (<200 pc; see also Kennicutt & Evans 2012). For the hotter gas, the red points in Fig. 10 are invariably fitted by a steeper line, with slope ≃ 2; this is explained by a longer cooling time than the dynamical time, and then by |$\dot{\rho }_{\rm SF} \propto \rho ^{2}$|⁠.

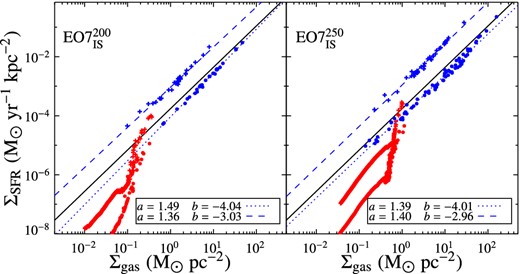
$Projected SFR versus mass surface density of the gas (at T < 2 × 104K, for the blue symbols, and at T > 2 × 104K, for the red ones), for two aSF models: EO7$^{200}_{\rm IS}$ on the left, and EO7$^{250}_{\rm IS}$ on the right. Full circles refer to ηSF = 0.01 and crosses to ηSF = 0.1. The lower ηSF = 0.01 coefficient for the SF recipe (equation 1) reproduces better the empirical Kennicutt–Schmidt scaling, that is shown by the solid line (with a slope of N = 1.4, and normalized as in Davis et al. (2014) for their ATLAS3D sample of molecular gas-rich ETGs). The blue dotted and dashed lines show the best fits for the cold gas only (coefficients in the frames in the lower right corners). See Section 3.5 for more details.$

Figure 10.

Projected SFR versus mass surface density of the gas (at T < 2 × 10⁴K, for the blue symbols, and at T > 2 × 10⁴K, for the red ones), for two aSF models: EO7|$^{200}_{\rm IS}$| on the left, and EO7|$^{250}_{\rm IS}$| on the right. Full circles refer to η_SF = 0.01 and crosses to η_SF = 0.1. The lower η_SF = 0.01 coefficient for the SF recipe (equation 1) reproduces better the empirical Kennicutt–Schmidt scaling, that is shown by the solid line (with a slope of N = 1.4, and normalized as in Davis et al. (2014) for their ATLAS^3D sample of molecular gas-rich ETGs). The blue dotted and dashed lines show the best fits for the cold gas only (coefficients in the frames in the lower right corners). See Section 3.5 for more details.

Overall, Fig. 10 proves that the recipe of equation (1) is very reasonable for SF, and, together with the chosen range of normalization for η_SF, it provides a scaling close to that observed for normal to starburst galaxies. These considerations add strength to the overall results obtained in this study.

4 CONCLUSIONS

In this work, we have explored the effects of SF on the evolution of rotating hot gas flows in ETGs; our previous (N14) high-resolution 2D hydrodynamical simulations of such flows, run for axisymmetric two-component models, were successful in producing the observed L_X and T_X of flat and rotating ETGs, but also revealed the formation of very massive cooled gas discs. To study the SF effects, we performed hydrodynamical simulations using the same numerical code of N14, where SF with a Salpeter IMF is inserted, following a simple recipe depending on the gas density, and the cooling and dynamical time-scales of the ISM (equation 1), with two possible values for the efficiency of SF (η_SF = 0.01 and 0.1). We considered the new stellar generations to be passive (a pure sink of gas), or active (the new stars contribute mass and energy to the gas flow, via stellar winds and SNIIs). The new simulations have been run for a subsample of the N14 models, of high, intermediate and low galaxy masses, of E4 and E7 shapes, with the ordered stellar rotation described by the isotropic rotator, or with the rotational velocities reduced by a factor of 10.

It is found that subsequent generations of stars are formed from the cold gas that accumulates in the equatorial plane, and that most of the extended and massive cold disc found by N14 is consumed by this process. In particular, the main conclusions are summarized as follows.

Remarkably, both for the passive and the active SF implementation, we confirm the results of the previous investigation without SF, concerning the trends of L_X and T_X of the hot ISM with galactic rotation. As found by N14, L_X is lowered by rotation: in low-mass ETGs this happens because rotation favours the establishment of global winds, and in medium-to-high mass ETGs because rotation lowers the hot gas density in the central galactic region. The average temperature T_X is also lower in intermediate/high mass ETGs, when rotation is important, due to the lower contribution of the central regions (usually hotter and denser in non-rotating systems), while it can be higher in low-mass ETGs, if rotation triggers a wind, due to the thermalization of meridional winds.
The robustness of the N14 results even after the addition of SF is explained differently for HM and LM galaxies. In HM galaxies, the evolution of the hot ISM is only marginally sensitive to the presence of SF, and L_X and T_X evolve smoothly as without SF: a massive cold disc forms early, it is mostly consumed by SF, and around it the hot ISM evolution proceeds almost unaltered by SF (even in presence of energy and mass injection by SNII's). In less massive models, instead, the evolution of L_X is not smooth, but shows many peaks corresponding to major cooling episodes, as in N14. The time-occurrence of the peaks depends on SF, thus SF can induce variations of L_X at a certain chosen epoch; however, these keep within the already large range of L_X values typical of these masses, even without SF, being the gas flow very sensitive to many factors (as already found previously, e.g. Ciotti et al. 1991, N14).
For what concerns the global gas mass budget, at the end of the simulations the cold gas mass left in the equatorial disc M_c on average increases with M_*, with a larger spread for LM models; at fixed M_*, M_c is lower for lower stellar ordered rotation, and for larger η_SF. In addition, the ratio M_c/M_* is roughly constant with M_*, with a spread reaching down to values much lower than this constant for LM models. In any case, |$M_\mathrm{c}\lesssim 2\times 10^9$| M_⊙ for galaxies with M_* ≤ 4 × 10¹¹ M_⊙. Typical values for M_c are ≲ a few × 10⁷ M_⊙ for LM galaxies (with the maximum rotational level of k = 1), with exceptions of M_c ≃ 10⁹ M_⊙; and a few × 10⁷ M_⊙ (if k = 0.1) to 3 × 10⁹ M_⊙ (if k = 1) for ETGs of intermediate mass. These values compare well with those recently observed (Serra et al. 2012, 2014; Young et al. 2014). In particular, they can explain the observation that massive, fast-rotating ETGs often have kinematically aligned gas, independent of environment (Davis et al. 2011, 2013).
The mass in newly formed stars |$M_*^{\rm new}$|⁠, and the ratio |$M_*^{\rm new}/M_*$|⁠, increase with M_*, again with a large spread for LM models, and are roughly independent of η_SF. This result means that more massive (rotating) ETGs have been overall more efficient in forming stars via recycling of their stellar mass losses, during the past ≃ 10 Gyr. The mass in secondary generations of stars is (1 − 6) × 10⁹ M_⊙ (if k = 1) for LM models, and ≃2 × 10¹⁰ M_⊙ (for both k = 1 and 0.1) for intermediate mass models. These should reside mostly in a disc, as most fast rotator ETGs possess, and be related to the birth of a younger, more metal-rich discy stellar component that is indeed observed (Krajnović et al. 2008; Cappellari et al. 2013). They should not be recognized as a ‘young’ stellar population in an absolute sense, though, since most of |$M_*^{\rm new}$| formed a few Gyr ago, as can be evaluated from the evolution of their SFR.
The time evolution of the SFR depends on the mass of the galaxy. LM galaxies (M_* = 1.25 × 10¹¹ M_⊙) have a larger and peaked SFR in their far past (reaching 1–2 M_⊙ yr⁻¹), when the rate of stellar mass losses due to the original stellar population was much larger, and when major cooling episodes were frequent. In fact, the average age of the new stars of LM models ranges from 5 to 8 Gyr (for the aSF scheme). At the present epoch, their SFR is low ( ≲ 0.1 M_⊙ yr⁻¹ typically), with the full range of values going from zero to ≃ 0.7 M_⊙ yr⁻¹. These results agree nicely with the low degree of SF and young stellar populations that is detected only in fast rotators, in the ATLAS^3D sample (Kuntschner et al. 2010; Sarzi et al. 2013); also, they compare well with the current estimated rates, whose median value is ≈0.15 M_⊙ yr⁻¹ (Davis et al. 2014). More massive galaxies, instead, show a more regular and steady production of cold gas, and so is their SFR; the average age of their new stars ranges from 5.5 to 7.0 Gyr (in the aSF scheme). At 13 Gyr the SFR is ≃ (0.4–1) M_⊙ yr⁻¹, larger than for LM models, and somewhat larger than observed (e.g. McDermid et al. 2015); this could be fixed by assuming a lower η_SF, or a lower ordered stellar rotation, at larger galaxy masses (Fig. 9). Thus, our models may still be rotating too much and producing too much cold gas, at galaxy masses >2 × 10¹¹ M_⊙. The current SFR/M_*, instead, remains quite constant from LM to intermediate mass models, with a larger spread for LM models (as already found for other properties).

Finally, the SF recipe adopted for this work proved to be a reasonable one, given that it reproduces the slope of the Kennicutt–Schmidt relation, and even the normalization if η_SF ≃ 0.01.

Overall, we can suggest an origin (mostly) in the SF from cooling hot gas, for the presence of cold gas phases kinematically aligned with the stars, and for the low-level degree of SF, all features detected only in fast rotators in the ATLAS^3D sample.

In the perspective of the galaxy evolution, we finally recall that the precise knowledge of the amount of gas flowing towards the galactic centre is of great importance for a proper study of feedback effects from the central black hole in rotating galaxies (e.g. Novak, Ostriker & Ciotti 2011; Gan et al. 2014). A major implication of this work is the fact that, if the gas produced by stellar evolution forms new stars, the amount of gas in principle available for fuelling the central supermassive black hole is much lowered. Of course, such fuelling would be impossible in presence of rotation and absence of viscosity. Disc instabilities, though, could break axial symmetry, and allow for the gas infall on to the black hole, possibly escaping SF. Phenomenologically, the effect of gravitational instabilities in the disc can be modelled as an effective gravitational viscosity (e.g. Bertin & Lodato 2001; Hopkins & Quataert 2011; Rafikov 2015), that favours accretion of cold gas towards the centre. Indeed, viscosity (that could be due for example to magnetorotational instability) is another ingredient not present in the current simulations, but that could affect the disc evolution. As the code is axisymmetric, we cannot follow the complex physics of (non-axisymmetric) disc instabilities that could be present. Although self-gravity of the gas is not considered in our simulations, yet for some models at a selection of times we computed the fiducial value of the radial profile of the stability parameter |$Q(R)= c_\mathrm{s} k_R/\pi G\Sigma _\mathrm{c}$|⁠, where k_R is the local epicyclic frequency of the galaxy, and c_s and Σ_c are, respectively, the vertically mass-averaged values of the ISM sound velocity, and the surface density of the cold rotating gas. The Q values were computed for a layer Δz ≃ 200 pc thick above and below the galaxy equatorial plane; these Q turned out to be quite independent of the adopted thickness value Δz, being dominated by the cold disc. These fiducial Q values maintained invariably larger than unity (indicating stability) when SF is allowed, while Q < 1 on a central ≃kpc-size region, in absence of SF. From this preliminary and qualitative analysis, it follows that SF andQ-instability are both present in the gaseous rotating discs. The relevant question is then if and what of the two processes is dominant in the disc. In a future work, we plan to extend further the present investigation by implementing in the code the cooperating effects of SF and mass discharge from the disc to the centre. In this new study, we will also consider the neglected late-time mass return from the newly born stellar population, that is the mass injected by stars of mass <8 M_⊙; this input could be modelled with the method described in Calura et al. (2014).

We acknowledge Giuseppe Lodato and Jerry Ostriker for useful discussions, and Silvia Posacki for providing the galaxy models of N14. LC and SP were supported by the MIUR grant PRIN 2010-2011, project ‘The Chemical and Dynamical Evolution of the Milky Way and Local Group Galaxies’, prot. 2010LY5N2T.

1

In fact the phase of the gas flow (that can range from a wind to an inflow) is basically determined by the different relative importance of SN heating in galaxies of different mass, as already thoroughly discussed in Ciotti et al. 1991.

2

We recall that, in the aSF scheme, the mass injected back into the ISM by the new stars can itself condense and produce new stars, that in turn contribute to the computation of |$M_*^{\rm new}$|⁠.

REFERENCES

Bertin

G.

Lodato

G.

,

A&A

,

2001

, vol.

370

pg.

342

Boroson

B.

Kim

D.-W.

Fabbiano

G.

,

ApJ

,

2011

, vol.

729

pg.

12

Calura

F.

Ciotti

L.

Nipoti

C.

,

MNRAS

,

2014

, vol.

440

pg.

3341

Cappellari

M.

et al. ,

MNRAS

,

2011

, vol.

413

pg.

813

Cappellari

M.

et al. ,

MNRAS

,

2013

, vol.

432

pg.

1862

Ciotti

L.

Ostriker

J. P.

,

ApJ

,

2007

, vol.

665

pg.

1038

Ciotti

L.

D'Ercole

A.

Pellegrini

S.

Renzini

A.

,

ApJ

,

1991

, vol.

376

pg.

380

Combes

F.

Young

L. M.

Bureau

M.

,

MNRAS

,

2007

, vol.

377

pg.

1795

David

L. P.

Forman

W.

Jones

C.

,

ApJ

,

1991

, vol.

380

pg.

39

Davis

T. A.

et al. ,

MNRAS

,

2011

, vol.

417

pg.

882

Davis

T. A.

et al. ,

MNRAS

,

2013

, vol.

429

pg.

534

Davis

T. A.

et al. ,

MNRAS

,

2014

, vol.

444

pg.

3427

de Vaucouleurs

G.

,

Ann. Astrophys.

,

1948

, vol.

11

pg.

247

di Serego Alighieri

S.

et al. ,

A&A

,

2007

, vol.

474

pg.

851

Dubois

Y.

Gavazzi

R.

Peirani

S.

Silk

J.

,

MNRAS

,

2013

, vol.

433

pg.

3297

Edge

A. C.

et al. ,

A&A

,

2010

, vol.

518

pg.

L47

Emsellem

E.

et al. ,

MNRAS

,

2011

, vol.

414

pg.

888

Eskridge

P. B.

Fabbiano

G.

Kim

D.-W.

,

ApJS

,

1995

, vol.

97

pg.

141

Fabbiano

G.

,

ARA&A

,

1989

, vol.

27

pg.

87

Gan

Z.

Yuan

F.

Ostriker

J. P.

Ciotti

L.

Novak

G. S.

,

ApJ

,

2014

, vol.

789

pg.

150

Grossi

M.

et al. ,

A&A

,

2009

, vol.

498

pg.

407

Hopkins

P. F.

Quataert

E.

,

MNRAS

,

2011

, vol.

415

pg.

1027

Kennicutt

R. C.

Evans

N. J.

,

ARA&A

,

2012

, vol.

50

pg.

531

Kennicutt

R. C.

Jr

,

ApJ

,

1998

, vol.

498

pg.

541

Khochfar

S.

et al. ,

MNRAS

,

2011

, vol.

417

pg.

845

Kim

D.-W.

Fabbiano

G.

,

2015

preprint (arXiv:1504.00899)

Ko

J.

Hwang

H. S.

Im

M.

Le Borgne

D.

Lee

J. C.

Elbaz

D.

,

ApJ

,

2014

, vol.

791

pg.

134

Krajnović

D.

et al. ,

MNRAS

,

2008

, vol.

390

pg.

93

Kuntschner

H.

et al. ,

MNRAS

,

2010

, vol.

408

pg.

97

Lagos

C. d. P.

Davis

T. A.

Lacey

C. G.

Zwaan

M. A.

Baugh

C. M.

Gonzalez-Perez

V.

Padilla

N. D.

,

MNRAS

,

2014

, vol.

443

pg.

1002

Li

J.-T.

Wang

Q. D.

Li

Z.

Chen

Y.

,

ApJ

,

2011

, vol.

737

pg.

41

McDermid

R. M.

et al. ,

MNRAS

,

2015

, vol.

448

pg.

3484

McDonald

M.

Veilleux

S.

Rupke

D. S. N.

Mushotzky

R.

Reynolds

C.

,

ApJ

,

2011

, vol.

734

pg.

95

Martig

M.

et al. ,

MNRAS

,

2013

, vol.

432

pg.

1914

Mathews

W. G.

,

AJ

,

1989

, vol.

97

pg.

42

Mathews

W. G.

Baker

J. C.

,

ApJ

,

1971

, vol.

170

pg.

241

Matteucci

F.

,

A&A

,

1994

, vol.

288

pg.

57

Mellier

Y.

Mathez

G.

,

A&A

,

1987

, vol.

175

pg.

1

Morganti

R.

et al. ,

MNRAS

,

2006

, vol.

371

pg.

157

Naab

T.

et al. ,

MNRAS

,

2014

, vol.

444

pg.

3357

Navarro

J. F.

Frenk

C. S.

White

S. D. M.

,

ApJ

,

1997

, vol.

490

pg.

493

Negri

A.

Ciotti

L.

Pellegrini

S.

,

MNRAS

,

2014a

, vol.

439

pg.

823

Negri

A.

Posacki

S.

Pellegrini

S.

Ciotti

L.

,

MNRAS

,

2014b

, vol.

445

pg.

1351

(N14)

Novak

G. S.

Ostriker

J. P.

Ciotti

L.

,

ApJ

,

2011

, vol.

737

pg.

26

O'Sullivan

E.

Forbes

D. A.

Ponman

T. J.

,

MNRAS

,

2001

, vol.

324

pg.

420

Oser

L.

Ostriker

J. P.

Naab

T.

Johansson

P. H.

Burkert

A.

,

ApJ

,

2010

, vol.

725

pg.

2312

Parriott

J. R.

Bregman

J. N.

,

ApJ

,

2008

, vol.

681

pg.

1215

Pellegrini

S.

,

ApJ

,

2011

, vol.

738

pg.

57

Pellegrini

S.

Kim

D.-W.

Pellegrini

S.

,

Astrophysics and Space Science Library, Vol. 378, Hot Interstellar Matter in Elliptical Galaxies

,

2012

Berlin

Springer-Verlag

pg.

21

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Pellegrini

S.

Held

E. V.

Ciotti

L.

,

MNRAS

,

1997

, vol.

288

pg.

1

Posacki

S.

Pellegrini

S.

Ciotti

L.

,

MNRAS

,

2013

, vol.

433

pg.

2259

Rafikov

R. R.

,

ApJ

,

2015

, vol.

804

pg.

62

Sarzi

M.

et al. ,

MNRAS

,

2006

, vol.

366

pg.

1151

Sarzi

M.

et al. ,

MNRAS

,

2010

, vol.

402

pg.

2187

Sarzi

M.

et al. ,

MNRAS

,

2013

, vol.

432

pg.

1845

Sazonov

S. Y.

Ostriker

J. P.

Ciotti

L.

Sunyaev

R. A.

,

MNRAS

,

2005

, vol.

358

pg.

168

Schmidt

M.

,

ApJ

,

1959

, vol.

129

pg.

243

Serra

P.

et al. ,

MNRAS

,

2012

, vol.

422

pg.

1835

Serra

P.

et al. ,

MNRAS

,

2014

, vol.

444

pg.

3388

Suh

H.

Jeong

H.

Oh

K.

Yi

S. K.

Ferreras

I.

Schawinski

K.

,

ApJS

,

2010

, vol.

187

pg.

374

Tang

S.

Wang

Q. D.

,

ApJ

,

2005

, vol.

628

pg.

205

Thornton

K.

Gaudlitz

M.

Janka

H.-T.

Steinmetz

M.

,

ApJ

,

1998

, vol.

500

pg.

95

Yi

S. K.

et al. ,

ApJ

,

2005

, vol.

619

pg.

L111

Young

L. M.

et al. ,

MNRAS

,

2011

, vol.

414

pg.

940

Young

L. M.

et al. ,

MNRAS

,

2014

, vol.

444

pg.

3408