-
PDF
- Split View
-
Views
-
Cite
Cite
Jeremy S. Ritter, Alan Sluder, Chalence Safranek-Shrader, Miloš Milosavljević, Volker Bromm, Metal transport and chemical heterogeneity in early star forming systems, Monthly Notices of the Royal Astronomical Society, Volume 451, Issue 2, 01 August 2015, Pages 1190–1198, https://doi.org/10.1093/mnras/stv982
Close - Share Icon Share
Abstract
To constrain the properties of the first stars with the chemical abundance patterns observed in metal-poor stars, one must identify any non-trivial effects that the hydrodynamics of metal dispersal can imprint on the abundances. We use realistic cosmological hydrodynamic simulations to quantify the distribution of metals resulting from one Population III supernova and from a small number of such supernovae exploding in close succession. Overall, supernova ejecta are highly inhomogeneously dispersed throughout the simulations. When the supernova bubbles collapse, quasi-virialized metal-enriched clouds, fed by fallback from the bubbles and by streaming of metal-free gas from the cosmic web, grow in the centres of the dark matter haloes. Partial turbulent homogenization on scales resolved in the simulation is observed only in the densest clouds where the vortical time-scales are short enough to ensure true homogenization on subgrid scales. However, the abundances in the clouds differ from the gross yields of the supernovae. Continuing the simulations until the cloud have gone into gravitational collapse, we predict that the abundances in second-generation stars will be deficient in the innermost mass shells of the supernova (if only one has exploded) or in the ejecta of the latest supernovae (when multiple have exploded). This indicates that hydrodynamics gives rise to biases complicating the identification of nucleosynthetic sources in the chemical abundance spaces of the surviving stars.
1 INTRODUCTION
The chemical abundance patterns of metal-poor and ancient stellar populations and intergalactic absorption systems provide information about the earliest stages of chemical enrichment (for reviews, see Beers & Christlieb 2005; Frebel & Norris 2013; Karlsson, Bromm & Bland-Hawthorn 2013; Frebel & Norris 2015). Because the first stellar systems were likely enriched by only a few discrete sources, one must interpret the inherent complexity of enrichment in relating the abundance patterns measured in metal-poor stars to theoretical models (Audouze & Silk 1995; Shigeyama & Tsujimoto 1998). Cosmic star formation, the driver of enrichment, is already stochastic thanks to the randomness of cosmic primordial density fluctuations. Significant additional complexity enters chemical enrichment through the turbulent hydrodynamics of the intergalactic, circumgalactic, and interstellar medium, the stochasticity of the star formation process, and the mechanics of the dispersal of nucleosynthetic products from their sources – supernovae and stellar mass-loss. The effects of complexity are partially, though perhaps not completely erased through the stirring and mixing in mature star-forming systems like the Milky Way's disc. But in ancient stellar populations, we expect vestiges of the complexity to persist, requiring us to model it as much as possible from first principles.
The recent years have seen a class of high-resolution simulations of small numbers of primordial star-forming systems (e.g. Wise & Abel 2008; Greif et al. 2010; Ritter et al. 2012; Wise et al. 2012, 2014; Jeon et al. 2014) as well as of moderate-resolution simulations (somewhat farther removed from the first-principles philosophy) that allow the authors to track large samples of such systems (e.g. Ricotti, Gnedin & Shull 2008; Bovill & Ricotti 2009; Tassis, Gnedin & Kravtsov 2012; Muratov et al. 2013; O'Shea et al. 2015). Without exception, these works study the local enrichment amplitude as quantified by the metallicity but do not attempt to investigate potential complex effects that could influence differential chemical abundance patterns.
A critical source of uncertainty entering chemical evolution models is the chemical yields of supernovae. The yields could vary drastically with the progenitor mass, rotation rate, the presence of a binary companion, and initial metal content (e.g. Heger & Woosley 2002, 2010). In the case of core-collapse supernovae, first-principles theoretical modelling is still not sufficiently predictive to permit direct synthesis of the observed stellar chemical abundance patterns. What is worse, the yields may not be deterministic and could be sensitive to instabilities taking place immediately prior to and in the course of the explosion (e.g. Arnett & Meakin 2011; Ellinger et al. 2012; Wongwathanarat, Janka & Müller 2013; Smith & Arnett 2014; Couch et al. 2015). It has therefore been a longstanding hope that the process of nucleosynthesis will be reverse engineered from the abundance patterns (e.g. Talbot & Arnett 1973; Nomoto, Kobayashi & Tominaga 2013). Principal component analysis (PCA) can be applied in the stellar chemical abundance space to discern the contributing classes of nucleosynthetic sources, be they individual stars or star clusters (e.g. Ting et al. 2012), if one posits that abundance patterns of the sources define monolithic basis vectors of the resulting stellar chemical abundance space. This is becoming a particularly promising direction with the arrival of large spectroscopic surveys such as HERMES-GALAH (Zucker et al. 2012; De Silva et al. 2015) and Gaia-ESO (Gilmore et al. 2012) surveys. However, the applicability of PCA becomes less clear if the hydrodynamics of metal dispersal skews the patterns, introducing biases deviating the patterns from linear superpositions of the patterns of well-defined nucleosynthetic source classes. Properly characterizing such biases would place the recovery of the properties of nucleosynthetic sources from stellar abundance data on much firmer footing.
The most primitive and metal-poor stellar populations known are the ultrafaint dwarf spheroidal satellites of the Milky Way (UFDs; Brown et al. 2012; Frebel & Bromm 2012; Vargas et al. 2013; Frebel, Simon & Kirby 2014), the Milky Way's stellar halo which is thought to have formed (at least in part) through the disruption of dwarf satellite galaxies (Kirby et al. 2008; Norris et al. 2010b; Lai et al. 2011, but see, e.g. Lee et al. 2013) and possibly an old, metal-poor sub-population within the Milky Way bulge.1 The prominent chemical heterogeneity in UFDs is often invoked as a potential indicator of poor mixing of supernova ejecta or an enrichment by a small number of contributing supernovae (e.g. Norris et al. 2010a; Simon et al. 2015). The primitive populations could be particularly sensitive to hydrodynamical biases, given the low masses and gravitational potential well depths of the progenitor star-forming systems and the low numbers of contributing supernovae and asymptotic giant branch (AGB) stars.
Here, we make an initial attempt to identify these biases with ultrahigh-resolution cosmological hydrodynamic simulations. We track the degree of chemical heterogeneity in the enrichment by a single supernova, and by a cluster of seven consecutive supernovae. The supernovae explode in a previously metal-free cosmic minihalo, a plausible UFD progenitor (Ricotti et al. 2008; Salvadori & Ferrara 2009). The two simulations are initialized from Gaussian cosmological fluctuations, ensuring that the cosmic environment being enriched is realistic.
The finite resolution of the simulations implies that we are able to directly place only a lower limit on the degree of coarse-grained chemical heterogeneity. Perfect chemical homogeneity, down to molecular scales, is expected only if the gas has been stirred by such processes as gravitational infall, the mechanical feedback from star formation, and thermal instability, to the extent that would facilitate microscopic diffusion across chemically heterogeneous sheets produced by turbulent folding. Efficient stirring generally requires that the vortical time |$\sim |{\rm \nabla }\times {\boldsymbol v}|^{-1}$| be much shorter than the lifetime of a cloud before it collapses to form new stars (see e.g. Pan & Scannapieco 2010, and references therein). This condition can be fulfilled in specific sites, but certainly not in general.2
We study the transport of supernova ejecta resolved by the mass coordinate inside the progenitor star (in the simulation with one supernova) and by the temporal order of the explosion (in the simulation with multiple supernovae). We follow the transport until gas clouds have assembled in which second-generation stars can be expected to form. This allows us to determine if these nucleosynthetic sources contribute monolithically, defining invariant basis vectors of the chemical abundance space, or if, perhaps, the hydrodynamics of supernova remnant evolution favours the reprocessing into new stars of only a biased sub-sample of the gross nucleosynthetic yields, skewing towards the reprocessing of some elements but not others.
2 NUMERICAL METHODOLOGY
The simulations were initialized from the same realization of cosmological initial conditions as in Safranek-Shrader et al. (2012) and Ritter et al. (2012). We simulated the gravitational collapse of collisionless dark matter and baryonic fluid in a box of size 1 Mpc (comoving) starting at redshift z = 146. The initial density and velocity perturbations were generated with the multiscale cosmological initial conditions package grafic2 (Bertschinger 2001) with Wilkinson Microwave Anisotropy Probe 7-yr cosmological parameters (Komatsu et al. 2011). We utilized two levels of nested refinement to achieve an effective resolution of 5123, corresponding to 230 M⊙ per dark matter particle, in a patch encompassing the density maximum on mass scales 108 M⊙. Time integration was carried out with the adaptive mesh refinement (AMR) code flash (Fryxell et al. 2000) as described in Safranek-Shrader et al. (2012). In what follows, we use physical units as opposed to comoving units. Metallicities are quoted in absolute metal mass fractions unless specified otherwise.
Gas cooled by H2 rovibrational emission collapsed to form a ≈106 M⊙ minihalo at redshift z ∼ 19.6. We inserted a single collisionless particle at the location of the gas density maximum within the minihalo to represent a Population III star (simulation 1sn) or a small cluster of such stars (simulation 7sn). The equivalent gas mass was removed by reducing the nearby gas density to a constant maximum level. In view of the recent realization that protostellar disc fragmentation (Stacy, Greif & Bromm 2010; Clark et al. 2011a,b; Greif et al. 2011, 2012) and evaporation by protostellar radiation (Hosokawa et al. 2011; Stacy, Greif & Bromm 2012) can limit the masses of Population III stars in the few tens of solar masses, we picked their masses to be in the range 20–80 M⊙ with typical values ∼40 M⊙ and assumed for simplicity that they all exploded with energies 1051 erg. Preceding the first explosion, we let the collisionless particle emit ionizing radiation for 3 Myr with an ionizing luminosity Qion and create an H ii region. Hydrodynamic expansion of the ionized gas reduced the central gas density to n ∼ 0.3 cm−3. After 3 Myr, we either inserted a single supernova remnant (1sn; Qion = 6 × 1049 photons s−1) or initiated a sequence of seven consecutive supernovae (7sn; Qion = 2.2 × 1050 photons s−1), all centred on the location of the collisionless particle.
In 1sn, we excised from the cosmological simulation a 1 kpc region centred on the collisionless particle, replacing the dark matter particles with a simple, parametric, spherically symmetric, time-dependent analytical dark matter density profile. The analytical profile was centred in the initial, instantaneous local rest frame of the host dark matter halo. The baryonic density and velocity field from the cosmological box was mapped directly on to the excised region, allowing us to continue the simulation in the interior of the excised region at high spatial resolution. The supernova ejecta mass was set to 40 M⊙. In 7sn, the seven supernova delay times 3.1–7.7 Myr (measured after collisionless particle insertion) were selected to represent the lifetimes of stars with masses decreasing from 80 to 20 M⊙, following a stellar initial mass function (IMF) with a flat dN/d ln M. Each of the supernovae was inserted in the free expansion phase, with ESN = 1051 erg in kinetic energy and an initial radius smaller than one-tenth of the radius containing gas mass equal to that of the ejecta. The ejecta masses were in the range 25–18.5 M⊙, decreasing with the order of the explosion.
We terminated each simulation when sufficient gas returned to the halo centre to form a self-gravitating cloud with density >103 cm−3, which happened 56 and 198 Myr after collisionless particle insertion in simulations 1sn and 7sn, respectively.
2.1 Thermodynamic evolution
Preceding the insertion of the collisionless star particle, we integrated the full set of coupled rate equations of the non-equilibrium chemical network for the primordial chemical species H, He, and D, their common ions, and the molecules H2 and HD (Safranek-Shrader et al. 2012). After insertion of the star particle we turned on an ionizing point source. We mapped the gas density on to a source-centred spherical grid partitioned using the healpix (Górski et al. 2005) algorithm in the angular coordinate (3000 pixels) and logarithmically in the radial coordinate (100 radial bins). The flux in any spherical cell was diminished by the cumulative extinction in the cells at smaller radii. We then mapped the flux from the spherical grid back on to the Cartesian simulation grid. On the basis of the mapped flux, we determined if a cell was expected to be ionized. We assumed photoionization equilibrium in ionized cells and interpolated the local thermodynamic state of the gas from data tabulated with the code cloudy (Ferland et al. 2013) as a function of the ionization parameter proportional to the local hydrogen-ionizing flux divided by the total hydrogen number density.3
When the first supernova remnant was inserted, we switched off the photoionizing source and began computing the cooling rates assuming that the species’ abundances were in collisional ionization equilibrium. Here, the cooling rate and the ionization state were again interpolated from tables pre-computed with cloudy, now as a function of density, temperature, and metallicity. For the interpolation we used the metallicity as defined by the passive mass scalar metallicity on the Cartesian grid. Artificial diffusion (or, better, ‘numerical teleportation’) of the passive scalar metallicity is a problem hitherto unsolved in Eulerian codes (see e.g. footnote 6 in Ritter et al. 2012). It produces pseudo-exponential low-metallicity tails ahead of advancing metallicity fronts. In the hot, shocked shell preceding the supernova ejecta, the teleportation tail is present, but the metallicity in the tail is too low to contribute to gas cooling. In gas with temperature ≫104 K, metal cooling begins to dominate only at metallicities ≳0.1 Z⊙, higher than in the artificial tail. On the other hand, at low temperatures ≪104 K, metallicities even as low as ≲10−3 Z⊙ (and ∼10−6 Z⊙ in the presence of dust) can define the cooling rate.
Similar to the numerical teleportation of chemical abundance scalar tracers, there is the potential of insidious mass teleportation at the contact discontinuity separating the hot, shock-heated gas of the supernova bubble from the much colder gas inside the enveloping dense cooling shell. Our calculations do not include the conduction of heat from the hot to the cold side of the interface. The net effect of thermal conduction should either be a cooling flow condensing the hot into the cold phase, or a reverse, evaporation flow, depending on the structure of the interface. For the specific temperature gradients and densities in our simulations, one would expect the heat conduction to produce an evaporation rather than a cooling flow (e.g. Cowie & McKee 1977; Draine 2011). The simulations exhibit a pressure dip at the interface, implying a narrow cooling layer. This arises from the artificial numerical smearing of the contact discontinuity. Dense gas from the cold side smears over on to the hot side thus artificially lowering the cooling time in a layer one cell thick. The cell-thick pressure dip is an under-resolved hydrodynamic feature. The numerical artefacts that it may produce should be sensitive to the particulars of the numerical scheme such as the choice of slope limiter and approximate Riemann solver. We will perform a systematic study of numerical behaviour at contact discontinuities in radiating flows in a separate, technical paper.
Since accurate tracking of molecular processes requires integration of stiff and computationally expensive chemical rate equations, to accelerate the computation, we did not track the H2 abundance and did not include molecular cooling after the first supernova remnant insertion. This is a potential oversimplification as H2 should form as the photo- and supernova-ionized gas recombines. Absent a high dust abundance that would drive molecule formation on grains (we do not track dust but its abundance is limited from above by the metallicity that remains low), H2 abundance in the recombined gas should be |$n_{{\rm H}_2} / n_{\rm H} \sim 10^{-3}{\rm -}10^{-2}$| (e.g. Mac Low & Shull 1986; Shapiro & Kang 1987; Kang & Shapiro 1992). Molecule abundance reaches maximum within about a million years after gas cools below 104 K. In our simulation, this gas has metallicity ≪10−2 Z⊙ and cooling by H2 should dominate (Glover & Clark 2014), at least in a relatively narrow density range nH ∼ 10–100 cm−3 (see e.g. fig. 6 in Safranek-Shrader, Milosavljević & Bromm 2014). Again barring a full atomic-to-molecular transition that would require abundant dust, at still higher densities ≳100 cm−3, metal line cooling dominates even before molecular transitions thermalize at ∼104 cm−3.
The artefact of our neglecting molecular cooling at densities ∼10–100 cm−3 is that the supernova-enriched, recollapsed gas will linger longer under quasi-hydrostatic conditions; a longer interval will pass before gravitational potential well becomes deep enough to compress the quasi-isothermal gas to the threshold of runaway gravitational collapse. The results that follow should be interpreted as placing an upper limit on the cooling and recollapse time in a supernova-enriched dark matter minihalo following a single supernova or a cluster of supernovae. The limit is strictly valid only in the fine-tuned regime in which molecule formation is completely suppressed by a dissociating UV background. The true recollapse time could be factor of a few shorter than in our simulations if the molecular abundance is significant. We will specifically address molecular cooling in our next work on this topic.
2.2 AMR control
Throughout the simulation, the AMR resolution was dynamically and adaptively adjusted to resolve the structures of interest. The refinement level ℓ of AMR blocks relates the size of the computational box L to size of an individual AMR grid cell by Δx = 2−ℓ + 1 − 3L, where the factor of 2−3 arises from the sub-division of AMR blocks into eight cells along each axis (83 = 512 cells per block). During the initial gravitational collapse of dark matter and gas leading to the formation of a minihalo we refined based on the gas density ρ. Specifically we raised the refinement to level ℓ to satisfy the condition |$\rho < 3\bar{\rho }\, 2^{3(1+\phi )(\ell -\ell _{\rm base})}$|, where ℓbase = 5 is the initial refinement level at the start of the simulation, |$\bar{\rho }$| is the mean density in the box, and ϕ = −0.3 (see e.g. Safranek-Shrader et al. 2012, and references therein). After the insertion of a star particle, which takes place in the most massive dark matter minihalo in the box, we discontinued enforcing density-based refinement in other haloes. At the evolving location of the star particle we maintained the maximum refinement level attained when refining based on gas density even after the H ii region broke out and gas density dropped.
In order the resolve the free expansion phase of a supernova remnant, it is necessary to resolve scales much smaller than the radius at which the expanding blastwave sweeps up a gas mass similar to the ejecta mass. The grid resolution at each supernova insertion was forced to be ≤0.03 pc and somewhat coarser for the later supernovae in 7sn that explode in the bubble containing gas shocked by early supernovae. We additionally refined the grid up to the maximum resolution anywhere in the box using the standard second-derivative refinement criterion in flash tuned to aggressively refine ahead of compositional discontinuities where metallicity jumps. This ensured that the forward shock wave, contact discontinuity, and reverse shock were maintained at the highest available grid refinement level. As each remnant expanded, we degraded the resolution while ensuring that the diameter of the remnant (or superbubble) was resolved by at least 256 cells. In the late stages of the simulations focused on the recollapse in the halo, we degraded the resolution in regions causally disconnected from the halo centre, outside the virial radius of the halo.
In all supernovae, we assumed that 10 per cent of the ejecta mass was in metals, with α-enhanced solar abundances ([α/Fe] = 0.5). In the thermodynamic calculations (but not in tracking metal dispersal in 1sn), we assumed that the metal abundances were homogeneous within each supernova's ejecta. The tracking of ejecta was carried out with Lagrangian passive tracer particles, Ntrace = 107 in 1sn and (2–3) × 106 per supernova or a total of Ntrace ≈ 2 × 107 in 7sn. The tracers allowed us to connect ejecta fluid elements to their origin in the explosions. In 1sn they allowed us to distinguish between the ejecta originating in distinct mass shells within the explosion, and in 7sn between the ejecta originating in different supernovae. It is worth noting that the numerical limitations affecting tracers, e.g. associated with the finiteness of the order of the velocity field representation on the computational mesh, are distinct from the numerical teleportation problem mentioned in Section 2.1. Thus, the simulated metallicity is generally to be trusted in cells in which the Eulerian and Lagrangian tracers indicate consistent values of the metallicity.
3 HYDRODYNAMIC EVOLUTION
The supernova remnants evolved through the free expansion, Sedov–Taylor, pressure-driven and momentum-conserving snowplow phases, and eventually, underwent partial collapse along the direction of the cosmic gas inflow, parallel to the filaments of the cosmic web. In 7sn, the later exploding supernovae expanded in the hot, low-density bubble evacuated by earlier ones, with blastwaves colliding with the dense radiative shell before the reverse shocks have completed traversal of the ejecta.
For the hydrodynamic and chemical evolution of the entire remnant or bubble, it is important that the photoionization by the supernova progenitor stars did not completely photoevaporate the densest primordial clouds inside the halo (Abel, Wise & Bryan 2007; Bland-Hawthorn, Sutherland & Karlsson 2011; Ritter et al. 2012). While the photoevaporation flows are difficult to adequately resolve in cosmological simulations, survival of neutral clouds inside the primordial H ii region is expected from the analytical evaporation solutions of Bertoldi & McKee (1990). The densest clouds with central densities n ≲ 10 cm−3 and distances ∼50–100 pc from the centre of the halo are associated with the filamentary inflow from the cosmic web. Supernova blastwaves swept past these clouds, partially ablating them and depositing some ejecta material at the perimeters of the clouds. The blastwave–cloud interaction drove turbulence inside the bubble. The ablated primordial gas found itself inside the hot, turbulent interior, where it appeared to be susceptible to turbulent-stirring-aided mixing, especially in the multisupernova simulation. This intrabubble mixing resulted in a modest, factor of ≲10 dilution of the ejecta by the primordial gas.
After ∼0.13 and ∼1 Myr from the (first) explosion in simulation 1sn and 7sn, respectively, the ejecta material started to accumulate in the pressure-driven snowplow shell. The shell was thin <10 pc and not adequately resolved at grid resolution ∼0.5–1 pc. The insufficient resolution blurred the contact discontinuity and its associated compositional gradient. As a result, the metallicity derived from the passive mass scalar was diluted to Z ∼ 10−4–10−3 in the thin shell. Rayleigh–Taylor (RT) fingers first became prominent in the shell after ∼3 Myr and then became extended, with length-scales comparable to the radius of the bubble, at ∼20 Myr. The long-term hydrodynamical evolution of the supernova bubble was highly anisotropic, with a fraction of the ejecta and swept-up primordial medium travelling many halo virial radii perpendicular to the cosmic web filaments, and another ∼50 per cent of the ejecta remaining within the virial radius.4
After the supernova bubbles started to collapse, the bubble interiors cooled to ∼104 K and began intermixing with the ambient unshocked gas. Dual inflows fed towards the halo centre: from the infall of unenriched, primordial clouds (including from merging haloes in 7sn), and from the fragments of the buckling thin shell. The terminus of the inflows was a turbulent quasi-virialized (or quasi-hydrostatic) cloud in which turbulence was stirred by gravitational infall. Fig. 1 illustrates the overall geometry of the metal distribution at this stage. It shows a homogenized low-metallicity interior surrounded by more metal rich, inhomogeneous clouds.
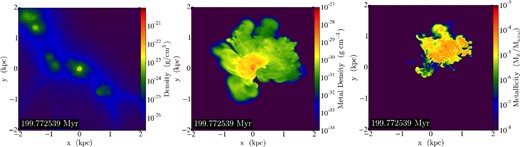
Simulation 7sn 200 Myr after the first supernova explosion: density-weighted density projection (∫ρ2dz/∫ρdz, left), metal-density-weighted metal density projection (|$\int \rho _{Z}^2\mathrm{d}z/\int \rho _Z \mathrm{d}z$|, middle), and metallicity slice through the cell with maximum density (right). The metal density is derived from the advected passive scalar tracing supernova ejecta. The cosmic web filament extends diagonally from top left. Note the relatively low metallicity near the centre, resulting from a dilution of supernova ejecta with metal-free gas streaming down the cosmic web filament.
Fig. 2, plotting the amplitude of the fluid vorticity, shows that vortical time-scales in the quasi-virialized cloud are |$|\nabla \times {\boldsymbol v}|^{-1} \sim 0.1{\rm -}1\,\textrm {Myr}$|, short enough to facilitate turbulent-cascade-aided fluid mixing in ∼10 Myr. Vorticity is the highest near the centre of each plot, where the metal-enriched gas has gone into runaway gravitational collapse. We expect the collapse to ultimately lead to the formation of second-generation stars. Outside the quasi-virialized cloud, the vortical time-scales are longer, 10–100 Myr, precluding mixing. Fig. 3 shows the joint distribution of gas density and metallicity in the two simulations. Metallicity spread in low-density gas is high, indicating a high degree of inhomogeneity. The spread decreases with increasing density, becoming narrow for n ≳ 10–100 cm−3. The narrowing of the metallicity spread is a consequence of rapid turbulent homogenization. The densest gas has negligible metallicity spread with Z ≈ 5 × 10−6 in 1sn and 5 × 10−7 in 7sn. We can conclude that the very first generation of metal-enriched stars will be chemically homogeneous on the scale of a stellar group or cluster. Recently, Feng & Krumholz (2014) observed the same in simulations of star clusters forming in a very different environment, the Milky Way disc (see, also, Bland-Hawthorn et al. 2010). We shall see in the following section, however, that stellar abundance patterns in the first metal-enriched star-forming systems will not be simple superpositions of the yield patterns of the contributing supernovae.
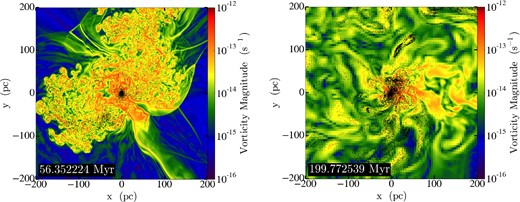
A slice of vorticity magnitude |$|\nabla \times \boldsymbol {v}|$| in the centre of 1sn (left) and 7sn (right) overplotting ejecta tracer particles in a 5 pc thick slab containing the slice (black dots). Note that metal ejecta are unmixed outside the central high-vorticity core, tens of parsecs in radius.
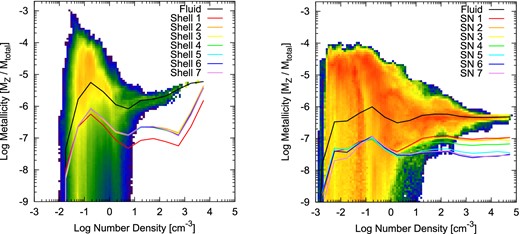
Metallicity as a function of gas density at the end of the simulation 1sn at 56 Myr after the first explosion (left-hand plot) and 7sn at 200 Myr after the first explosion (right-hand plot). From red to blue, the colour scales with the logarithm of the fluid mass in the density and metallicity bin. Solid curve is the mean metallicity and coloured curves are the fractional contributions from the seven radial mass bins (1sn) and seven supernovae (7sn).
4 MONOLITHIC AND BIASED ENRICHMENT
We procede to analyse how hydrodynamic dispersal depends on the nucleosynthetic site. In analysing simulation 1sn, we split the ejecta at supernova insertion into Nbin = 7 radial bins containing equal ejecta masses and treat the bin index i = 1, …, Nbin as a crude proxy for the isotopic group synthesized in the corresponding bin. For example, the innermost bins could contain the explosively synthesized Fe peak and α elements, the intermediate bins could be rich in light hydrostatic elements (C and O), and the outermost bins would contain H and He. This idealizes the explosion as preserving spherical symmetry, which is certainly not the case, as symmetry is strongly broken by convection preceding and during the collapse and by RT fingering during the explosion (our simulations can capture the RT instability in the remnant but not in the explosion). However, we expect that the radial ‘dredging’ of elements by instabilities (and rotation-driven mixing, see e.g. Maeder & Meynet 2012) is incomplete and that some radial stratification is preserved until the ejecta enter free expansion. In analysing simulation 7sn, we ignore the stratification inside each explosion and take the bin index i = 1, …, Nbin to range over the Nbin = NSN = 7 supernovae.
We first examine the degree to which the ejecta in different bins are stirred with each other (to be further discussed in a forthcoming follow-up paper). In 1sn, the outer, high-velocity mass shells of the ejecta are well-stirred between themselves, but inner mass shells remain highly inhomogeneous. In 7sn, the ejecta from supernovae separated by short time intervals are well-stirred with each other. The ejecta from later supernovae, separated from the earlier supernovae by the longest time intervals, remain inhomogeneous.
The metallicities resulting from individual events |$Z^{(\mathcal {E})}(\boldsymbol {x},t)$| are random variables determined by the hydrodynamics of metal dispersal. They endow stellar metallicities with scatter. If a sufficient number of events contributes and the events are statistically independent, the central limit theorem implies that the scatter is Gaussian, justifying the PCA approach.
If source contributions are monolithic then wi ≡ 1/Nbin, but in general, the enrichment at a specific location could be biased towards some bins, giving them higher weights. The dimensionality of the chemical abundance space can now be much larger than the number of nucleosynthetic source classes. The weights encapsulate the biases that hydrodynamics introduces into abundance patterns. If the weights are completely random and possess unknown statistics, this introduces uncontrolled biases frustrating the recovery of nucleosynthetic source classes from stellar abundance data. Here, we make the first step towards characterizing the nature of the biases, aspiring to detect regularities that can be factored into chemical abundance analysis. Fig. 3 shows bin-specific metallicities Zi spherically averaged around the centre of gravitational collapse. In both simulations, in dense gas n ≳ 1 cm−3, departures from monolithic enrichment are evident. In 1sn, the innermost radial bin, which is expected to carry explosive elements, is deficient by a factor of ∼3 relative to the other bins, |$\langle w_1\rangle \sim \frac{1}{3}\langle w_2\rangle$| and 〈w2〉 ∼, …, ∼〈w7〉, where the averages refer to gas-mass-weighted averages of wi in the dense gas. In 7sn, ejecta from the first two supernovae are ∼3 times as abundant as the ejecta from the last two supernovae, 〈w1〉 ∼ 〈w2〉 ∼ 3〈w6〉 ∼ 3〈w7〉.
We propose the following physical interpretation. In the case of the solitary supernova, the reverse shock raises the inner ejecta shells, which it sweeps later and at lower densities, to a higher entropy than the outer shells, which it sweeps earlier and at higher densities. This can be seen by considering the Sedov–Taylor point explosion, in which the pressure asymptotes to a constant value near the centre, but density decreases towards the centre as ρ ∝ r3/(γ − 1). Therefore, with γ = 5/3, the entropy s = ln (P/ργ) + const rises towards the centre of the ejecta as |$s\sim -\frac{15}{2}\ln r+\textrm {const}$|. This is significant because as the ejecta become quasi-isobaric inside the remnant, the radiative cooling time is a steeply increasing function of entropy. The outer ejecta shells cool first and are incorporated into the snowplow shell, while the innermost ejecta avoid cooling. As the remnant stalls and collapses, the innermost ejecta, having higher entropy, are outward buoyant and rise to larger radii, thus avoiding collapse and allowing low-entropy outer ejecta mass shells to fall in to enrich the quasi-virialized cloud. In 1sn, the ejecta tracer particle radii containing 25 per cent of the ejecta in bins 1 (the innermost bin) and 2 cross at ∼0.2 Myr after the explosion and then bin 1 interchanges with bins ≥3 at ∼0.3 Myr.
In the case of clustered supernovae, the situation is similar, but now since the density inside the supernova bubble keeps dropping as the bubble expands, the ejecta from later supernovae are on average raised to higher entropies than those of earlier ones and are less susceptible to cooling. Since the ejecta of the latest supernovae remain hot, they are outward buoyant. Upon the collapse of the bubble, the hot ejecta of the later supernovae interchange with the cooled ejecta of the earlier supernovae. The latter fall in to enrich the central cloud.
5 CONFRONTING THE EMPIRICAL RECORD
Our results have important implications for understanding the early stages of cosmic chemical evolution. More precisely, the hydrodynamic biases in the transport of individual elements, introduced by the post-explosion evolution, need to be taken into account when confronting the empirical abundance trends. The ultimate goal here is to achieve a robust mapping from the observed abundance pattern in metal-poor stars or systems thereof to the individual sources of those metals. In the absence of any monolithic mapping between sources and fossil record (see Section 4), the hydrodynamic transport process constitutes the missing link in our current understanding. Simulations along the lines of our exploratory work here promise to bridge this crucial gap. However, we can already now address a long-standing problem in Galactic chemical evolution in a new light. This concerns the prevalence of peculiar abundance ratios in low-metallicity stars and systems.
To briefly summarize the main phenomenology, observations of metal-poor stars in the Galactic halo, assembled over more than two decades, have provided intriguing constraints on the nature of early chemical evolution (reviewed in Beers & Christlieb 2005; Frebel & Norris 2013; Karlsson et al. 2013). The current state of the art is defined by a large sample of halo red giant stars, where key lines are sufficiently strong to enable high signal-to-noise spectroscopy (Cayrel et al. 2004; François et al. 2007). The main lessons are two-fold: both α-elements (Mg, Ca, Si, Ti), and iron-peak elements (V to Zn) exhibit extremely small scatter, down to [Fe/H] ∼ −3.5. The neutron-capture elements, comprising elements beyond Zn, on the other hand, exhibit equally small scatter down to [Fe/H] ∼ −3, but show extremely large scatter, up to 5 dex, below this (Qian & Wasserburg 2002; Truran et al. 2002; Sneden, Cowan & Gallino 2008). Finally, the lighter elements (C, N, O) again show large abundance variations at [Fe/H] < −4, and approach well-defined trends for less metal-poor stars.6 The most dramatic manifestation of this transition to well-behaved abundance trends, once a threshold metallicity is reached, is provided by the huge scatter in r-process abundances, seen in Galactic halo stars with [Fe/H] ≲ −3 (reviewed in Sneden et al. 2008). The origin of r-process nucleosynthesis, such as the mass and properties of the supernova progenitor star, is still highly uncertain. There is, however, tentative evidence that the r-process might operate in progenitor stars with a very narrow mass range, possibly close to the lower mass limit for core-collapse supernovae (e.g. Qian & Wasserburg 2008).
It has been challenging to explain all of these trends within one comprehensive framework, but our work suggests a promising ansatz to do so. Basically, our results show that early enrichment is differential, non-monolithic in nature. This specifically implies that second-generation star formation does not sample the enrichment from the full IMF, and possibly not even that from a single explosion (see Fig. 3). Our simulations build on earlier analytical work that had postulated a minimum number of supernovae, NSN ≳ 20, needed to average out any yield inhomogeneity from individual explosion sites (see e.g. Tsujimoto & Shigeyama 1998; Tsujimoto, Shigeyama & Yoshii 1999). This absence of effective source-averaging, then, such that only a small number of explosion sites contribute, is the key requirement to preserve peculiar abundance ratios. Next to the classical r-process elements, a similar explanation may pertain to the strong odd–even pattern that is predicted for pair-instability supernova enrichment, but has not been detected so far (Heger & Woosley 2002; Karlsson, Johnson & Bromm 2008). We note that our explanation of the r-process record, understanding huge scatter as a result of sparse IMF-sampling, where only a very narrow progenitor mass range gives rise to the r-process, does not require any stochastic contribution from neutron star mergers, as has recently been suggested (Shen et al. 2014; van de Voort et al. 2015).
Once cosmological structure formation advances to more massive systems, with deeper potential wells to facilitate the near-uniform mixing of the ejecta from a large number of supernovae, convergence towards well-defined, smooth abundance trends will set in. Extragalactic observations targeting systems of greatly different virial mass are in agreement with this overall picture. Specifically, recent medium- and high-resolution spectroscopy of red giant stars in Milky Way dwarf satellites has established that their abundance properties, including the degree of scatter, are indistinguishable from the metal-poor tail of the Galactic halo stars (Frebel et al. 2010, 2014). A complementary view into early metal enrichment is provided by the abundances measured in damped Lyman α (DLA) systems. Here, the evidence points towards extremely low scatter, at least for the prominent α-elements (Cooke et al. 2011; Becker et al. 2012). This may be indicative of the onset of efficient gas-phase mixing in the deep potential wells of the DLA dark matter host haloes. An intriguing question for future simulation work is to test whether the empirical threshold metallicity, roughly measured by [Fe/H], for the disappearance of such anomalous abundance signatures can be reproduced.
Of special interest is the observed dichotomy of carbon-enhanced and carbon-normal metal-poor stars (e.g. Beers & Christlieb 2005; Gilmore et al. 2013). Cooke & Madau (2014, hereafter CM14) have recently suggested that the strength of supernova driven outflows may be responsible for this bimodality. These authors invoke two classes of supernovae with greatly different times for recovery from the supernova explosions with different explosion energies. More energetic explosions ESN ≫ 1051 erg imply longer recovery times (Jeon et al. 2014). According to CM14, rapid recovery is connected to weak explosions with large carbon overabundances, and slow recovery with strong explosions with normal carbon yields. Our simulation 1sn, where we find the return of supernova ejecta into the halo centre deficient in the ejecta originating from the innermost 10 per cent of the ejecta, suggests another mechanism for carbon-enhanced metal-poor stars. A core-collapse explosion ejects a normal carbon-to-iron ratio [C/Fe] < 1, but the iron-bearing ejecta are raised to a higher entropy upon reverse shock traversal than the carbon-bearing ejecta, and subsequently do not cool and settle into the halo centre to form second-generation stars.
6 SUMMARY AND CONCLUSIONS
We have carried out two complementary very high resolution cosmological simulations of how the metals produced in the first supernova explosions are transported into the cold, dense gas out of which the second generation of (Population II) stars is formed. The first simulation followed the ejecta from a single explosion, whereas the second traced the metal dispersal from seven sources. We arrived at two main conclusions. The re-condensed Population II star forming material exhibits strong turbulent vorticity, implying a likely fine-grained turbulent mixing of gas down to very small, unresolved, scales. Stellar clusters or groups forming out of this material are thus predicted to be chemically uniform, unless any self-enrichment process may operate during the later stages of stellar evolution. Our results also indicate that the hydrodynamic metal transport proceeds differentially, such that the monolithic mapping of source abundances into the fossil record is broken.
The hydrodynamically biased nature of early metal enrichment, as demonstrated in our pathfinder simulations, has multiple implications, requiring that we rethink a number of our traditional assumptions and methodologies. On the theory side, a common approach to chemical enrichment is to assume that homogenization of the chemical composition is instantaneous and complete in certain ‘mixing volumes’, normally centred on nucleosynthetic sources, but that the volumes themselves occur stochastically and intermittently, tracing star formation. This approach provides a rudimentary model of inhomogeneous chemical evolution, but since the choice of mixing volumes is ad hoc, its predictive power is limited. It is standard to motivate the choice of mixing volumes by considering the spatial extent of supernova remnants and galactic superbubbles, assuming that the medium is chemically homogeneous within these structures (Argast et al. 2000; Oey 2000, 2003; Karlsson 2005; Karlsson & Gustafsson 2005; Karlsson et al. 2008; Bland-Hawthorn et al. 2010; Corlies et al. 2013). In the absence of monolithic source mapping, it is not obvious how to adjust this technique.
Our results also present a challenge to the standard interpretational framework of near-field cosmology. The hydrodynamic biases need to be quantified as a function of the star-forming environment by carrying out a dedicated programme of simulations. Once these chemical transport ‘maps’ are in hand, the full power of stellar archaeology can be unleashed. Such a programme is very timely, given the advent of large survey projects, including the dedicated efforts connected to Gaia-ESO, which promise a record of early chemical evolution in unprecedented detail.
ACKNOWLEDGEMENTS
We acknowledge helpful conversations with Anna Frebel, John Scalo, and Craig Wheeler. The flash code was in part developed by the DOE-supported Flash Center for Computational Science at the University of Chicago. The authors acknowledge the Texas Advanced Computing Center at The University of Texas at Austin for providing HPC resources under XSEDE allocation TG-AST120024. CSS is grateful for support provided by the NASA Earth and Space Science Fellowship (NESSF) programme. This study was supported by the NSF grant AST-1009928 and by the NASA grant NNX09AJ33G. Many of the visualizations were made with the yt package (Turk et al. 2011).
We can define a stellar population as ‘primitive’ if the number of times the nucleosynthetic output of individual supernovae and AGB stars has been recycled is small.
Microscopic chemical mixing is a sufficient, but not a necessary condition for chemical homogeneity, since any residual heterogeneity on sub-stellar mass scales is erased in the stars themselves.
While not photon-conserving, this method is sufficient to simulate the anisotropic H ii region expansion in the relatively dense gas of our minihalo.
The morphological evolution of the metal-enriched volume bears similarities to both the centred and off-centre idealized non-cosmological simulations of Webster, Sutherland & Bland-Hawthorn (2014).
Here and in what follows, coarse graining of ρA on the spatial scales of star-forming clumps is implied.



