Corotating light cylinders and Alfvén waves

Abstract

1 INTRODUCTION

Despite the pioneering work of Goldreich & Julian (1969) on pulsar magnetospheres created by a rotating aligned dipole and of Michel (1973) on relativistic winds, both of which have been further explored in Mestel (1999), there are few exact analytic solutions in relativistic magnetohydrodynamics (MHD). Prendergast's (2005) solution for a point explosion of force-free magnetic energy was the foundation of our recent work on that theme (Gourgouliatos & Lynden-Bell 2008; Gourgouliatos 2009; Gourgouliatos & Vlahakis 2010), but recent advances have been mainly computational. The early axisymmetric static solution by Scharlemann & Wagoner (1973) has been followed by accurate computations of Komissarov (2006) and Goodwin et al. (2004) which give solutions for the steady aligned pulsar, while Kalapotharakos & Contopoulos (2009) considered both time-dependent instabilities at the edge of the corotating zone and the non-aligned case. Spitkovsky (2006) studied the time-dependent relativistic problem of both the aligned and the oblique rotator; in the case of the aligned rotator he confirmed the results of Contopoulos, Kazanas & Fendt (1999) who have studied the time-independent problem, whereas for the oblique rotator he presented the three-dimensional structure of the magnetosphere. Recent evidence that the pulses are generated near the light cylinder reinforce ideas put forward by da Costa & Kahn (1982, 1985) who considered the orthogonally aligned cylindrical pulsar. Numerical solutions more relevant to active galactic nuclei have been developed by Gammie, McKinney & Tóth (2003) and McKinney & Narayan (2007). More recently Tchekhovskoy, McKinney & Narayan (2009) have studied the problem of a spinning monopole, and they found that the combined effect of rotation and the magnetic field provide sufficient conversion of magnetic energy to kinetic, with profound applications to gamma-ray bursts but also to pulsar systems.

Force-free fields have been used as an approximation for pulsar magnetospheres. Leaving a magnetic field configuration to relax, we take a final state of a force-free magnetic field. Taking into account that the pulsar magnetosphere is dominated by the electromagnetic fields and considering that the effects of inertia are weaker makes the force-free assumption a valid starting point. The non-relativistic force-free approximation requires that the electric current flows along the magnetic field lines but neglects any effect of the electric field on the charges. In relativistic MHD the electric field is no more negligible as the electric field, in non-resistive MHD, is given by the cross product of the magnetic field with the velocity scaled to the speed of light. Thus the relativistic force-free approximation requires that the force of the magnetic field on the currents and that of the induced electric field on the charges add to zero.

Here we explore the simplest exact relativistic force-free fields, those with cylindrical symmetry, and their coupling to rotating magnetospheres which corotate out to the light cylinder. While these solutions are very limited they allow us to answer questions such as the following. When one end of a cylinder of force-free field is rotated at relativistic speed, is its flux per unit area greater than or less than the static field that surrounds it in pressure equilibrium, i.e. if we start rotating one end of a tube of flux, does the twist generated in it lead to its expansion or does its cross-section remain the same or even contract? What if anything happens as the rotation velocity of the tube approaches the speed of light? How rapidly does the rotation advance along the tube? For non-relativistic MHD, this problem was treated in detail in Sturrock (1994) but inevitably that has little bearing on light cylinders. We are studying idealized MHD in which the effects of resistivity are absent, therefore field lines that join the source of twist rotate while those that do not are left static. Thus a discontinuity is no surprise. In Section 2 we give the basic equations and solve them to find the general steady cylindrical force-free fields. Section 3 explores some simple special cases in greater detail, while Section 4 gives the time-dependent exact solution for rotationally generated Alfvén waves travelling down a uniform field. Section 5 considers how a rotating star or a pulsar might generate such waves in the interstellar magnetic field. It also presents the conundrum of how a pulsar's field that extends beyond the light cylinder can connect to an anti-aligned interstellar field and suggests a possible resolution.

2 BASIC EQUATIONS

We take the magnetic field and the velocity of the fluid to lie on cylinders and in cylindrical polars (R, φ, z) so ∇·B = 0 and

1

2

The fluid is perfectly conducting, so

3

Since E_R is independent of φ and z it follows that ∇×E = 0, so B is time independent. The charge density, ρ, is given by

4

Provided V is independent of time the current density, j, is given by

5

The force-free condition is

6

Using the expressions for ρ and j above, this becomes

7

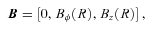
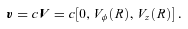
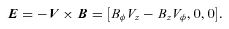
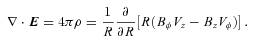
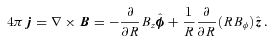
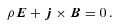
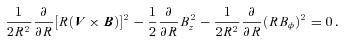
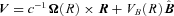We note that only the component of V perpendicular to B plays any role in equation (7). It is then convenient to write V in the form ⁠, where 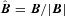is the unit vector along B. We note that V_B is not the component of V along B which contains also (Ω×R) ·B/|cB|. Thus any of our velocity fields may be considered as a (differential) rotation with flow along B superposed. Since the flow along B does not contribute to the (V×B)² term in (7) that equation becomes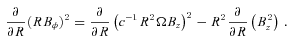

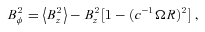
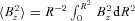8

Integrating the last term by parts and then dividing by R² we find

9

where is the area average of B²_z up to R. Evidently if Ω(R) and B_z(R) are specified such that the right-hand side of (9) is non-negative, then (9) determines B_φ (up to a sign). With B and V×B then known, E follows from (3), ρ from (4) and j from (5). Thus the whole electromagnetic configuration is determined, but to find the flow we must also specify the velocity V_B(R) along B. This is subject to the restriction that V²≤ 1 which gives (RΩ/c +V_BB_φ/B)²+V²_BB²_z/B²≤ 1 that is V²_B+ 2V_B(RΩ/c)(B_φ/B) ≤ 1 −R²Ω²/c², which can be satisfied by a real V_B, for example V_B =−2(RΩ/c)(B_φ/B) provided 1 − (RΩ/c)² (B_z/B)²≥ 0 which is always satisfied since from (9) the expression on the left-hand side is 〈B²_z〉/B². Note that there is no restriction that RΩ/c ≤ 1 because the fluid can move along the lines of the force to counteract such a ‘superluminal’ rotation leaving its total V < 1. This is true however large RΩ/c becomes!

3 SIMPLE SPECIAL CASES

Looking at equation (9) there are several special cases that are worth noting because they illustrate situations of particular simplicity. All the fields so far discussed are helical, so it is useful here to define the pitch κ(R) of a helical field line. The equation of such a field line is given by R d φ/B_φ = d z/B_z with R constant. The pitch is defined as κ(R) = d φ/d z so κR =B_φ/B_z.

• If B_z is independent of R, then 〈B²_z〉=B²_z, so from equation (9)B²_φ = (ΩR²/c²)B²_z. When ΩR =c, B_φ=±B_z, but as pointed out above there is no restriction that ΩR < c so we can have situations with |B_φ| > |B_z| at large R. There is however a tendency for such solutions to be unstable. In all cases the lines of force are given by R = constant and R d φ/B_φ = d z/B_z. The pitch of the resultant helix is κ = d φ/d z, so κR =B_φ/B_z.

• Writing equation (9) in terms of the pitch κ(R) we find

  

  10

  A remarkable special case occurs when κ²−Ω²/c² is independent of R. This occurs when for example both the pitch and the angular velocity are constant. Then we may multiply equation (10) by R² and differentiate the result with respect to R²; this gives us B²_z on the right-hand side which cancels against a term on the left-hand side. Dividing the resultant equation by R² yields

  

  11

  This integrates to give, on taking the square root,

  

  12

  Note that the field is uniform if κ²=Ω²/c². If now a rotating tube of force is surrounded by a static uniform field B₀ at equilibrium with it at R =a,

  

  13

  where σ is the surface charge on the rotating cylinder and E_R is the electric field component inside the boundary R =a. By Gauss's theorem 4πσ=−E_R(a), and from equation (3)E²_R = (c⁻¹ΩaB_z)². Hence |B_z(a)| =B₀/F^1/2, where F = 1 + (κ²−Ω²/c²)a². Thus when κ=Ω/c, the rotating uniform field has the same |B_z | as the non-rotating field outside. More generally the flux along the cylinder of radius a is

  

  14

  This function of F maximizes at πa²B₀ when F = 1, that is when Ω=cκ. In all other cases, the equilibrium twisted field configuration carries less flux over the circle R < a than the straight bounding field B₀. Thus although some feel that the twisting of the field should cause it to contract under the influence of the hoop stresses so generated, nevertheless this is more than offset by the increase in field strength per unit longitudinal flux which is also caused by the twisting of the field. Note however we have only proved this when κ²−Ω²/c² is independent of R within the twisted region. However, for (κ²−Ω²/c²)a² between −0.5 and +1.0, the flux decrease is less than 2 per cent so there is only a <1 per cent increase in the radius of the twisted rotating cylinder in such circumstances. An untwisted B field spinning about the axis of a cylinder whose top speed is of the velocity of light only increases its radius by about 1 per cent.
• Now suppose that the rotation is uniform out to R =b, but thereafter takes the Keplerian profile Ω=Ω₀(b/R)^3/2. We substitute this velocity profile in equation (9),

  

  15

Now the Alfvén waves generated by such a rotation will travel at the speed of light in a force-free field (see Section 4). The pitch generated is given by κ = d φ/d z =−Ω(R) d t/(c d t), so B_φ=B_zΩ(R)R/c. The first and last terms of equation (15) cancel and we are left with 〈B²_z〉=B²_z. Thus the z-component of the field is uniform despite its differential rotation, i.e. we are back to (i).

4 TIME-DEPENDENT SOLUTIONS

Since the solutions that leave the flux through the cylinder unchanged have a uniform B_z, we now look for time-dependent solutions of the form B=[0, B_φ(R, z, t), B₀] so ∇·B = 0,

16

then,

17

18

19

20

21

22

From the force-free condition (6) we have

23

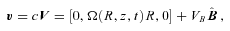
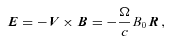
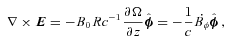
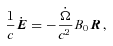
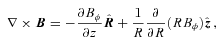
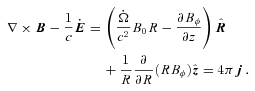
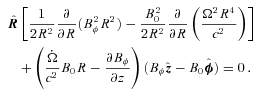
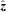The and 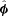components of this equation are satisfied provided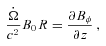

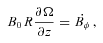
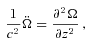
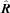24

but by equation (18)

25

hence

26

which is satisfied by Ω=Ω[R, (t −z/c)]. Then B_φ=−B₀RΩ/c and putting this back into equation (23) the component is satisfied identically, so we have an exact solution for any waveform Ω(t −z/c). Of course we could superpose any Ω(t +z/c), but to solve the problem of a perfectly conducting disc at z = 0 forced to rotate at a given time-dependent rate Ω(t) we need the wave that travels out from the origin. Then the magnetic field at z > 0, R < a rotates at Ω(t −z/c) and that at z < 0, R < a rotates at Ω(t +z/c), see Fig. 1. Thus we have Alfvén waves generated by a rotating disc. At R =a there is a surface density of charge 4πσ = (1/c)Ωa B₀; Ωa < c, which accounts for the electric field outside R =a. The c hanging surface density of charge involves a sheet current along the cylinder given by integrating (23) across the discontinuity in B_φ at R =a, thus 4πJ_z=B₀aΩ/c and 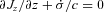as required by charge conservation. Note that the net charge of the rotating cylinder is zero as the volume charge density given by (4) and the surface charge density when integrated over the cylindrical volume and the discontinuity surface, respectively, add up to zero, so the electric field outside the cylinder is zero. Komissarov (2002) in the context of Blandford–Znajek mechanism has investigated similar solutions.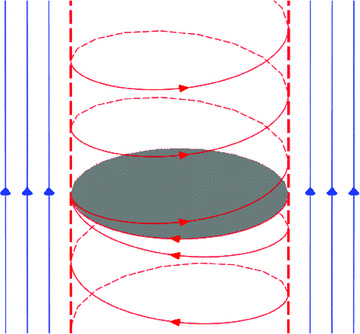

Figure 1

The magnetic field lines attached to a disc which is rotating rigidly. The twisted field is confined by a uniform external field. The heavy dashed line is the separatrix which carries a surface charge. When the tip speed of the disc is c, this is also the light cylinder.

Open in new tabDownload slide

5 ROTATING MAGNETIC FIELDS IN THE INTERSTELLAR GAS

So far our solutions have been exact but abstract. We now take a step nearer to the real world but the application is somewhat forced and the solution inexact.

Consider a star with a dipolar magnetic field with axis along Oz. Let it be embedded in an interstellar magnetic field oriented in the same direction. The field is as shown in Fig. 2 where the separatrix has been emphasized. The closed field lines near the star will lie in meridional planes and rotate with the star. The outermost field lines outside any separatrix will not rotate at all just like the outer field lines in Fig. 1. The remaining field lines that join the star to the interstellar gas will carry the torque that generates the Alfvén wave that propagates along the interstellar field to great distances from the star. In our force-free approximation these Alfvén waves travel at the velocity of light, but in reality the fields will probably be too weak well away from the star, so there the rotational disturbance will travel at the Alfvén speed given by c²_A=c²B²₀/(B²₀+ 4πρ₀c²), where ρ₀ is the gas density. In Fig. 2 we have assumed that the light cylinder lies beyond the asymptotic radius of the separatrix. For a strong stellar dipole or a weaker interstellar field this will not be true. We shall consider that situation afterwards. We write the field in the form

27

Then for a dipole M in a straight external field we find

28

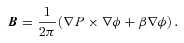
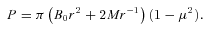
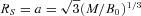The separatrix P =P_S = 3πB^1/3₀M^2/3 which for large z gives ⁠. Thus all the flux with P < P_S links the star to the interstellar magnetic field. At large z we have from point (i) in Section 3 and under equation (27) β=−2πR²B₀Ω/c =−2ΩP/c. Since near the star we need β to carry the torque away from the star, we set β=−2Ω(t) P/c for z ≈ 0, P < P_S and β=−2Ω(t −z/c)P/c for large z as that gives the field found in Section 4. We therefore choose as our approximation β=−2Ω(t −z/c)P/c whenever z > 0 and P < P_S. For P > P_S, β = 0 (see Fig. 3). Since we have used the P of the non-rotating configuration which will in practice be modified by the rotating charges this is only approximate; however, we note that in our rotating cylinder the B_z remained at B₀ even in the presence of the rotation, so at large z the proposed solution is exact.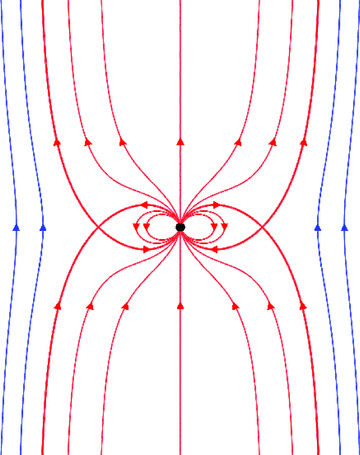

Figure 2

The magnetic field of a dipole embedded inside a uniform external magnetic field of the same polarity. The thick red line is the separatrix of the field lines that are attached to the dipole field and those detached. Note that amongst the attached field lines the ones emerging near the poles reach infinity, whereas the ones emerging from the area near the equator close in the other hemisphere of the dipole.

Open in new tabDownload slide

Figure 3

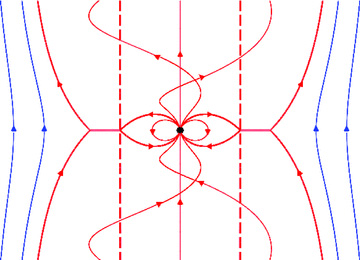
The magnetic field of a rotating dipole embedded inside a uniform external magnetic field of the same polarity. The discontinuity of the toroidal component of the magnetic field on the separatrix leads to the formation of a current sheet. We have assumed that the combination of the pulsar magnetic field, interstellar magnetic field and rotation velocity is such that the light cylinder occurs outside the corotating loops. It is possible that the light cylinder while being outside the corotating loop intersects with the separatrix, in which case some of the pulsar's twisted field lines will pass through the light cylinder.

Open in new tabDownload slide

Now we consider the case in which the light cylinder is of smaller radius than the asymptotic radius, a, of the separatrix of the static field. Close to the light cylinder the interstellar magnetic field is far too weak to have any effect, so for the aligned pulsar the work of Goldreich & Julian (1969) as modified by Scharlemann & Wagoner (1973) and most recently treated by Goodwin et al. (2004) is appropriate. However, in those treatments the far field has a weak poloidal component and spirals off to infinity with that component not far from radial. There the field will be radically modified if the pulsar resides in an asymptotic field from the interstellar medium because asymptotically the field from the pulsar must align along the cylinders and produce Alfvén waves propagating along them. ΩR will be much greater than c. Fig. 4 illustrates the type of the field configuration that we envisage. All the pulsar field lines that do not close within the light cylinder end up winding around the interstellar field and their Ω is still that of the pulsar.

Figure 4

The magnetic field of a rotating dipole embedded inside a uniform external magnetic field of the same polarity. The discontinuity of the toroidal component of the magnetic field on the separatrix leads to the formation of a current sheet. Unlike Fig. 3 the combination of the fields and rotation velocity is such that the light cylinder occurs near the star. In this case a sheet current forms on the equator.

Open in new tabDownload slide

The flux function for the pure dipolar field is P = 2πM (1 −μ²)/r, so the flux that fails to reach the equator within the light cylinder in such a field would be P_c = 2πMΩ/c. In reality the field is distorted by the rotation to be more like P = 2πM/r[1 + (1/2)(r/r_c)³](1 −μ²) for r < r_c =c/Ω which gives P_c = 3πMΩ/c. A very rough model that gets the fluxes right (but is not force-free) is given by the P above for r < r_c, P =P_c(1 −μ²) for r_c < r < r_s where r²_s=P_c/(3πB₀) and P =πB₀r²[1 + 2(r_s/r)³] for r > r_s. As before the toroidal field is given as in equation (28) with β(P) =−2Ω(t − |z|/c)P/c for P < P_c and zero elsewhere.

To see the orders of magnitude consider a pulsar whose polar field is B_p and suppose the radius of the polar cap whose field does not close within the light cylinder is R_p, and the interstellar field is B₀. Then the asymptotic radius of the field attached to the pulsar will be ⁠; suitable values might be B_p = 3 × 10¹² G, B₀ = 3 × 10⁻⁶ G and R_p = 1 km giving a = 10¹⁴ cm. The value of R_p is linked to the pulsars' rotation rate Ω and radius r_s by which gives R_p = 1 km for r_s = 11 km for a pulsar with a period of 28 ms. More generally ⁠, where T is the pulsar period. For the numbers above but general T, we find that Ωa = 3.5 × 10³c (T/s)^−3/2 which can be many times the speed of light. If the Alfvén wave advances at c, then in the interstellar gas B_φ/B₀ = 3.5 × 10³ (T/s)^−3/2 in the idealized model, and this is increased by the factor c/c_A if the Alfvén speed is c_A. However, such highly wound magnetic fields are likely to be highly unstable. In the ideal case the plasma has to move along the field so that v_z = (B₀/B_φ)c_A. The field winds through the plasma like an Archimidean screw winds up the water. While these estimates will be complicated by instabilities, they do indicate that pulsars generate much enhanced fields in the interstellar medium albeit over tubes of force with diameters similar to that of the Solar system.

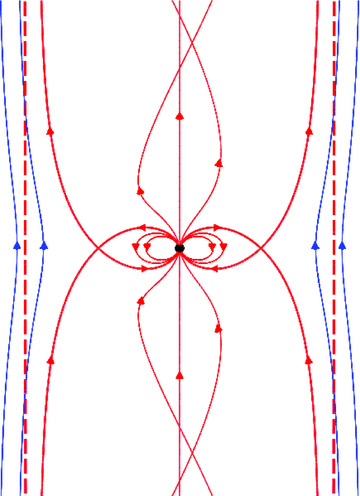
A different but interesting situation occurs when the interstellar field is aligned oppositely to magnetic moment of the pulsar. The total flux of the pulsar outside its light cylinder, P_c, will be unable to counteract the flux of the interstellar field equatorially all the way to infinity since the latter grows like R². Furthermore the pulsar's flux cannot cross its equatorial plane outside the light cylinder as by symmetry it would have to cross perpendicularly and the plasma attached would then move faster than light. However, the flux from the pulsar has to reach infinity since it carries the flow of plasma pushed by the Archimedian screw of the whirling field. The only place where the flux from the pulsar can deform the field over large distances is close to the axis; indeed in the non-rotating case there would be a neutral point on axis (Dungey 1958; see Fig. 5). As the pulsar rotates, the equatorial diameter of the field structure around it grows, and this neutral point is sent to infinity along the axis. An oppositely directed poloidal field is generated near the axis and is accompanied by the B_φ and the plasma flow due to the pulsar's rotation. We illustrate both the weak-spin case when all the star's field lies within the light cylinder and rotates with the star (Fig. 5) and the pulsar case just described in Fig. 6. Corresponding to any solution such as that shown in Fig. 4, there is another solution with the field reversed outside the separatrix. If the longitudinal field inside the separatrix is small compared to the toroidal field there, the field pressures and tension still balance along the separatrix. The argument given above leads us to believe that this is the field configuration of the steady anti-aligned pulsar.

Figure 5

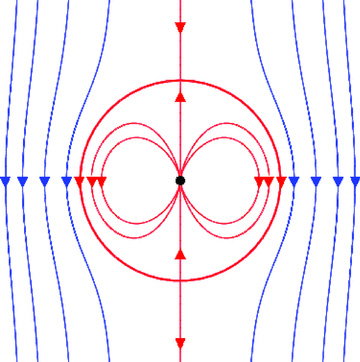
The magnetic field of a dipole embedded inside a uniform external magnetic field of the opposite polarity. The attached field lines to the dipole are enclosed within a spherical surface. The external field lines are deformed from being uniform close to the equator.

Open in new tabDownload slide

Figure 6

The magnetic field of a rotating dipole embedded inside a uniform magnetic field of the opposite polarity. The field's configuration is similar to that of Fig. 4; however, the direction of the field lines is different. There is a discontinuity on the separatrix of the poloidal component of the magnetic field enhancing the current sheet that already exists because of the discontinuity on the toroidal component of the field.

Open in new tabDownload slide

6 CONCLUSIONS

In this paper we have studied analytical solutions of rotating magnetic fields emerging from dipoles or discs embedded in uniform magnetic fields. This study is based on the assumption that the dipole field is either aligned or counteraligned to the external field. Fields at an angle i to the dipole may be considered by taking the solutions above with B₀ replaced by B₀ cos i and superposing a lateral field parallel to the plane of the disc of magnitude B₀ sin i, but this gives only orders of magnitude and is no substitute for a full non-axially symmetric treatment.

We find that the spinning field will form Alfvén waves in the interstellar gas. There is no need to confine these Alfvén waves inside the light cylinder, as the plasma can have a velocity component parallel to the magnetic field and not exceed the speed of light, and we find that for typical pulsar values they will occupy cylinders whose cross-sectional areas are of the size of the Solar system. These field configurations with tightly wound fields outside the light cylinder are probably very unstable, in particular the pressure of the whole tube along the axis is very large, so any departure from axial symmetry will be enhanced by an instability analogous to the fire-hose instability. However, there remains the interesting possibility that the magnetic fields generated over small regions by the thrashing field lines might be surprisingly large although smaller than the maxima estimated via these axially symmetric models.

REFERENCES