-
PDF
- Split View
-
Views
-
Cite
Cite
Ziheng Yang, Mario dos Reis, Statistical Properties of the Branch-Site Test of Positive Selection, Molecular Biology and Evolution, Volume 28, Issue 3, March 2011, Pages 1217–1228, https://doi.org/10.1093/molbev/msq303
Close - Share Icon Share
Abstract
The branch-site test is a likelihood ratio test to detect positive selection along prespecified lineages on a phylogeny that affects only a subset of codons in a protein-coding gene, with positive selection indicated by accelerated nonsynonymous substitutions (with ω = dN/dS > 1). This test may have more power than earlier methods, which average nucleotide substitution rates over sites in the protein and/or over branches on the tree. However, a few recent studies questioned the statistical basis of the test and claimed that the test generated too many false positives. In this paper, we examine the null distribution of the test and conduct a computer simulation to examine the false-positive rate and the power of the test. The results suggest that the asymptotic theory is reliable for typical data sets, and indeed in our simulations, the large-sample null distribution was reliable with as few as 20–50 codons in the alignment. We examined the impact of sequence length, the strength of positive selection, and the proportion of sites under positive selection on the power of the branch-site test. We found that the test was far more powerful in detecting episodic positive selection than branch-based tests, which average substitution rates over all codons in the gene and thus miss the signal when most codons are under strong selective constraint. Recent claims of statistical problems with the branch-site test are due to misinterpretations of simulation results. Our results, as well as previous simulation studies that have demonstrated the robustness of the test, suggest that the branch-site test may be a useful tool for detecting episodic positive selection and for generating biological hypotheses for mutation studies and functional analyses. The test is sensitive to sequence and alignment errors and caution should be exercised concerning its use when data quality is in doubt.
Introduction
The branch-site test aims to detect episodic Darwinian selection along prespecified branches on a tree that affects only a few codons in a protein-coding gene, with selection measured by the nonsynonymous/synonymous rate ratio (ω = dN/dS) and positive selection indicated by ω > 1 (Yang and Nielsen 2002; Yang et al. 2005; Zhang et al. 2005). By focusing on individual amino acid residues and particular lineages, the test is expected to be more powerful than previous branch-based tests, which average over all sites in the protein (Messier and Stewart 1997; Zhang et al. 1997; Yang 1998), or the site-based tests, which average over all branches on the phylogeny (Nielsen and Yang 1998; Suzuki and Gojobori 1999; Yang et al. 2000). The original branch-site test formulated by Yang and Nielsen (2002) was found to generate excessive false positives when its assumptions are violated (Zhang 2004). A slight modification introduced later appears to have made the test far more robust (Yang et al. 2005; Zhang et al. 2005). This modified test is now commonly used.
In a recent simulation study, Nozawa et al. (2009a; see also Suzuki 2008) claimed that the branch-site test produced excessive false positives. However, the false-positive rate found by those authors was only 0.23%, much lower than the significance level (5%) (Yang et al. 2009). In another simulation, Nozawa et al. (2009b) discovered that the P value for the branch-site test generated under the null hypothesis showed a U-shaped distribution, with a slight peak (7.3%) in the interval (0, 0.05) and a very high peak in (0.95, 1.00), very different from the uniform distribution they expected. The authors considered the result to indicate an “abnormal behavior” of the likelihood ratio test and attributed it to small sample sizes in their simulation.
However, the expectation of a uniform distribution for the P value is incorrect, as discussed by Zhang et al. (2005, p. 2473). The null and alternative hypotheses of the branch-site test are described in table 1. In the null hypothesis, ω2 is fixed at 1, a value at the boundary of the parameter space for the alternative hypothesis (which constrains ω2 ≥ 1). Thus, the test statistic (2Δℓ) does not have an asymptotic distribution. Instead, the correct null distribution is a 1:1 mixture of point mass 0 and (Chernoff 1954; see also Self and Liang 1987, case 5), with the critical values to be 2.71 at 5% and 5.41 at 1%, rather than 3.84 at 5% and 6.63 at 1% according to . The asymptotic behavior of the likelihood ratio test in such nonstandard conditions is well studied and is not “abnormal.” In phylogenetics, the same situation arises in the test of the internal branch length (with H0: b = 0 and H1: b ≥ 0) and in the test of rate variation among sites (with H0: α = ∞ and H1: 0 < α < ∞) (Yang 1996; Ota et al. 2000; Whelan and Goldman 2000). Intuitively, if the true parameter value is inside the space, its estimate will approximately have a normal distribution around the true value and will be greater or less than the true value, each half of the times. If the true value is at the boundary, half of the times the estimate would be outside the space if there were no constraint; in such cases, the estimate will be forced to the true value and the likelihood ratio statistic will be 0. In the other half of data sets, the likelihood ratio statistic will follow . (We note that the mixture distribution may not apply under certain complex scenarios of the branch-site model: e.g., when p0 + p1 = 1, parameter p2 will be at the boundary of the parameter space for the alternative model and ω2 will be unidentifiable.) Zhang et al. (2005) recommended the use of to make the branch-site test conservative to guide against violations of model assumptions. The use of by Nozawa et al. (2009b) appears to be largely responsible for the high peak for large P values (i.e., P = 1 when 2Δℓ = 0). In real data analysis, large P values (or small 2Δℓ) all lead to acceptance of the null, so that their precise distribution is unimportant. What matter more are the small P values and in particular the false-positive rate.
| Site Class | Proportion | Background | Foreground |
| 0 | p0 | 0 < ω0 < 1 | 0 < ω0 < 1 |
| 1 | p1 | ω1 = 1 | ω1 = 1 |
| 2a | (1 − p0 − p1) p0/(p0 + p1) | 0 < ω0 < 1 | ω2 ≥ 1 |
| 2b | (1 − p0 − p1) p1/(p0 + p1) | ω1 = 1 | ω2 ≥ 1 |
| Site Class | Proportion | Background | Foreground |
| 0 | p0 | 0 < ω0 < 1 | 0 < ω0 < 1 |
| 1 | p1 | ω1 = 1 | ω1 = 1 |
| 2a | (1 − p0 − p1) p0/(p0 + p1) | 0 < ω0 < 1 | ω2 ≥ 1 |
| 2b | (1 − p0 − p1) p1/(p0 + p1) | ω1 = 1 | ω2 ≥ 1 |
NOTE.—This model is the alternative hypothesis for the branch-site test of positive selection. The null hypothesis is the same model but with ω2 = 1 fixed.
| Site Class | Proportion | Background | Foreground |
| 0 | p0 | 0 < ω0 < 1 | 0 < ω0 < 1 |
| 1 | p1 | ω1 = 1 | ω1 = 1 |
| 2a | (1 − p0 − p1) p0/(p0 + p1) | 0 < ω0 < 1 | ω2 ≥ 1 |
| 2b | (1 − p0 − p1) p1/(p0 + p1) | ω1 = 1 | ω2 ≥ 1 |
| Site Class | Proportion | Background | Foreground |
| 0 | p0 | 0 < ω0 < 1 | 0 < ω0 < 1 |
| 1 | p1 | ω1 = 1 | ω1 = 1 |
| 2a | (1 − p0 − p1) p0/(p0 + p1) | 0 < ω0 < 1 | ω2 ≥ 1 |
| 2b | (1 − p0 − p1) p1/(p0 + p1) | ω1 = 1 | ω2 ≥ 1 |
NOTE.—This model is the alternative hypothesis for the branch-site test of positive selection. The null hypothesis is the same model but with ω2 = 1 fixed.
To biologists using the branch-site test in analysis of real data, an important question is whether typical data sets are large enough for the asymptotic approximation to be reliable. This problem has not been directly examined in previous simulation studies (Zhang et al. 2005; Bakewell et al. 2007; Nozawa et al. 2009a), which considered the robustness of the test when the model assumptions are violated.
In this paper, we conduct computer simulations to examine the false-positive rate of the branch-site test when the data are simulated under the null model. We are interested in how large the sample size has to be for the asymptotic theory to be reliable. We also examine the power of the test when positive selection operates on the foreground branch but affects only a small proportion of the sites. We compare the branch-site test with a few alternative tests, including branch-based tests, which average the ω ratio over all sites in the protein. We also discuss potential problems with the application of the branch-site test, especially its sensitivity to sequence and alignment errors.
Materials and Methods
Simulation
The EVOLVER program in the PAML package (Yang 2007) is used to generate alignments of codon sequences. Two trees are used, with 8 and 16 species, respectively (fig. 1). On each tree, either an internal or an external branch is used as the foreground branch for the branch-site model (fig. 1). The transition/transversion rate ratio is fixed at κ = 2, and the 61 sense codons have the same frequency (1/61). The number of simulated replicates is R = 1,000.
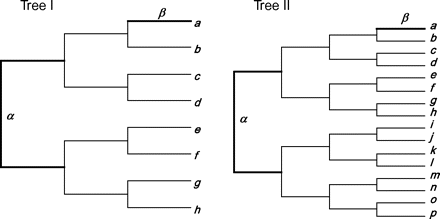
Two trees used to simulate sequence alignments under the branch-site model, with one of branches α and β used as the foreground branch. All branch lengths are 0.3 nt substitutions per codon. The total tree length is thus 4.2 and 9.0 nt substitutions per codon for trees I and II, respectively. Although the branch lengths on both trees conform to the molecular clock, the codeml analysis used the unrooted trees without the clock assumption, with the length of the single branch around the root estimated from the data.
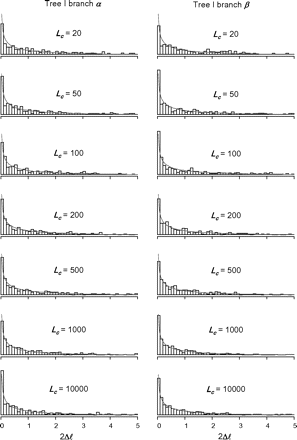
Histograms of the likelihood ratio test statistic (2Δℓ) for the branch-site test with data of different sequence lengths (Lc) simulated under the null hypothesis, using branches α or β on tree I as the foreground branch. Only those replicate data sets in which 2Δℓ > 0 are used in the plots. The curve is the density.
The data are simulated under either the null or the alternative hypotheses of the branch-site test. For the null hypothesis, we used the parameter values p0 = 0.6, p1 = 0.3, ω0 = 0.2, and ω2 = 1 (see table 1). The average ω over the whole gene is thus 0.47 and 0.52 for the background and foreground branches, respectively. We used a variety of sequence lengths, with Lc = 20, 50, 100, 200, 500, 1,000, and 10,000 codons.
For simulation under the alternative hypothesis to examine power, the parameter values are as above except that ω2 = 4. The sequence length is fixed at Lc = 500 codons, which is close to the mean value (469) among proteins in the human genome (Lander et al. 2001). The average ω across the site classes is 0.47 and 0.82 for the background and foreground branches, respectively. In addition, we varied the sequence length Lc, the strength of positive selection indicated by ω2, and the proportion of sites under positive selection p2 to examine the impact of those factors on the power of the branch-site test.
Analysis
All analyses are conducted using the CODEML program from the PAML package. First, each replicate data set is analyzed under the null and alternative models of the branch-site test. The correct tree topology and foreground branch are used, whereas the branch lengths and other parameters are estimated by maximum likelihood under each model. We note that the correct identification of foreground and background branches in our analysis should lead to higher power for the test compared with testing every branch on the tree and applying a multiple-test correction (Anisimova and Yang 2007). As the branch-site model is known to cause computational difficulties for the numerical optimization algorithm in PAML, each analysis is conducted three times with different starting values to ensure that the global peak is found. In 97% of all analyses, the three runs produced identical results, whereas in other cases, the results corresponding to the highest log likelihoods are used. The mixture distribution is used to calculate the P value for the branch-site test, and the test is considered significant if P < 5%.
For comparison, we examined the power of four alternative tests, referred to as the branch test (Yang 1998), Pair Heuristic, Pair M0, and Pair M1a–M2a. These are expected to have low false–positive rates in our simulation conditions (<5%). Here, we examine their power only, by applying them to the data generated under the alternative hypothesis with positive selection. The branch test (Yang 1998) assigns two different ω parameters (ωF and ωB) to the foreground and background branches on the tree. The null hypothesis of the test is H0: ωF = 1, whereas the alternative is H1: ωF ≥ 1, with ωB to be a free parameter under both hypotheses. We use the 1:1 mixture of 0 and to conduct the likelihood ratio test. This may be considered a statistically more rigorous implementation of the heuristic tests of Messier and Stewart (1997) and Zhang et al. (1997).
The next three tests, Pair Heuristic, Pair M0, and Pair M1a–M2a, are applied to the two sequences at the ends of the foreground branch, with the true ancestral sequences generated during the simulation used. This analysis allows us to examine the performance of the branch-based tests under the ideal situation where the true ancestral sequences were known. Pair Heuristic is our implementation of the heuristic test of Zhang et al. (1997) in idealized conditions. While Messier and Stewart (1997) used the (reconstructed) ancestral sequences to calculate dS and dN and to test whether dN is significantly greater than dS, Zhang et al. (1997) counted the numbers of synonymous and nonsynonymous differences (cS and cN) and tested whether the number of nonsynonymous differences significantly exceeds the neutral expectation. We use the true sequences at the ends of the foreground branch to count the numbers of synonymous and nonsynonymous sites (S and N) assuming the true value of κ = 2. The “probability” pN = N/(S + N) thus reflects the neutral expectation. The numbers of synonymous and nonsynonymous differences (cS and cN) between the two sequences are counted using the method of Nei and Gojobori (1986). We then test whether the observed proportion cN/(cS + cN) is significantly greater than the expected pN. The P value is then calculated as the tail probability from the binomial distribution: (Zhang et al. 1997).
Note that this test is heuristic. First, pN is not a known probability and cS + cN is not a fixed number of binomial trials so the binomial distribution does not strictly apply. Second, the differences are treated as substitutions, and there is no correction for multiple hits (Yang 2002). The test of Messier and Stewart (1997) does not have those two problems and may be slightly better for sequences that are not highly similar. Lastly, both the tests of Messier and Stewart (1997) and of Zhang et al. (1997) use inferred ancestral sequences as if they were observed data. For those reasons, we expect the likelihood ratio test (Yang 1998) to have more power than both heuristic tests of Messier and Stewart (1997) and of Zhang et al. (1997). The likelihood ratio test also has more flexibility in accommodating such features of sequence evolution as transition–transversion rate difference and unequal codon usage. Nevertheless, our main concern here is the common problem of all those branch-based tests: They average synonymous and nonsynonymous rates over the whole gene and may thus have little power when the majority of codons are under strong selective constraint.
Pair M0 compares the two sequences under the one-ratio (M0) model, which assumes the same ω for all codons in the gene. The hypotheses H0: ω = 1 and H1: ω ≥ 1 are compared using a likelihood ratio test, with 2Δℓ compared against the 1:1 mixture of 0 and . Pair M1a–M2a fits the site models M1a (neutral) and M2a (selection) to the two sequences (Nielsen and Yang 1998; Yang et al. 2000, 2005). The null hypothesis M1a assumes two site classes in proportions p0 and p1, with ω0 < 1 and ω1 = 1, whereas the alternative hypothesis M2a adds another site class in proportion p2 with ω2 ≥ 1. The null distribution of this likelihood ratio test is unknown as there are two nonstandard features with the test: When p2 = 0 (i.e., when M2a reduces to M1a), first the value 0 is a boundary point and second parameter ω2 becomes unidentifiable. We use to conduct the test but suspect that this makes the test too conservative.
Results
False Positives
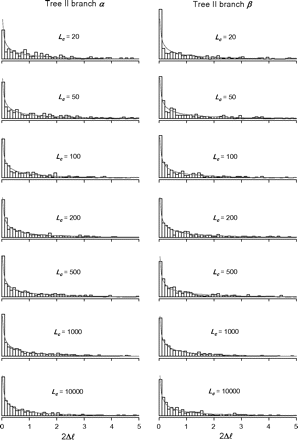
The false-positive rates of the branch-site test calculated from data simulated under the null hypothesis are shown in table 2. They range from 4.0% to 6.4% and are close to 5%. These are all within twice the standard deviation of the expected 5%, with the standard deviation given by the binomial sampling model as (0.05 × 0.95/1000)½ = 0.0067. The proportions of replicates in which 2Δℓ = 0 are also shown in table 2. They range from 49% to 68% for tree I and from 48% to 72% for tree II. The proportion is greater than 50% for small data sets with Lc < 100 but is close to 50% for Lc > 100. The histogram of 2Δl for datasets with 2Δl > 0 are shown in figures 2 and 3 for trees I and II, respectively. They appear to be closely matched by the χ12 distribution.
False-Positive Rates for the Branch-Site Test in Simulations under the Null Model.
| Sequence Length | Internal Branch α | External Branch β |
| Tree I | ||
| 20 | 0.051 (0.68) | 0.043 (0.67) |
| 50 | 0.049 (0.64) | 0.041 (0.68) |
| 100 | 0.051 (0.62) | 0.048 (0.67) |
| 200 | 0.049 (0.62) | 0.042 (0.65) |
| 500 | 0.063 (0.55) | 0.040 (0.60) |
| 1,000 | 0.064 (0.50) | 0.049 (0.53) |
| 10,000 | 0.057 (0.49) | 0.056 (0.50) |
| Tree II | ||
| 20 | 0.046 (0.68) | 0.041 (0.72) |
| 50 | 0.045 (0.65) | 0.039 (0.70) |
| 100 | 0.043 (0.63) | 0.044 (0.68) |
| 200 | 0.050 (0.55) | 0.051 (0.62) |
| 500 | 0.052 (0.48) | 0.049 (0.57) |
| 1,000 | 0.056 (0.50) | 0.046 (0.51) |
| 10,000 | 0.053 (0.51) | 0.056 (0.51) |
| Sequence Length | Internal Branch α | External Branch β |
| Tree I | ||
| 20 | 0.051 (0.68) | 0.043 (0.67) |
| 50 | 0.049 (0.64) | 0.041 (0.68) |
| 100 | 0.051 (0.62) | 0.048 (0.67) |
| 200 | 0.049 (0.62) | 0.042 (0.65) |
| 500 | 0.063 (0.55) | 0.040 (0.60) |
| 1,000 | 0.064 (0.50) | 0.049 (0.53) |
| 10,000 | 0.057 (0.49) | 0.056 (0.50) |
| Tree II | ||
| 20 | 0.046 (0.68) | 0.041 (0.72) |
| 50 | 0.045 (0.65) | 0.039 (0.70) |
| 100 | 0.043 (0.63) | 0.044 (0.68) |
| 200 | 0.050 (0.55) | 0.051 (0.62) |
| 500 | 0.052 (0.48) | 0.049 (0.57) |
| 1,000 | 0.056 (0.50) | 0.046 (0.51) |
| 10,000 | 0.053 (0.51) | 0.056 (0.51) |
NOTE.—The test is conducted using the mixture of 0 and with critical value 2.71 at the 5% significant level. The proportion of data sets in which 2Δℓ = 0 is shown in parentheses.
False-Positive Rates for the Branch-Site Test in Simulations under the Null Model.
| Sequence Length | Internal Branch α | External Branch β |
| Tree I | ||
| 20 | 0.051 (0.68) | 0.043 (0.67) |
| 50 | 0.049 (0.64) | 0.041 (0.68) |
| 100 | 0.051 (0.62) | 0.048 (0.67) |
| 200 | 0.049 (0.62) | 0.042 (0.65) |
| 500 | 0.063 (0.55) | 0.040 (0.60) |
| 1,000 | 0.064 (0.50) | 0.049 (0.53) |
| 10,000 | 0.057 (0.49) | 0.056 (0.50) |
| Tree II | ||
| 20 | 0.046 (0.68) | 0.041 (0.72) |
| 50 | 0.045 (0.65) | 0.039 (0.70) |
| 100 | 0.043 (0.63) | 0.044 (0.68) |
| 200 | 0.050 (0.55) | 0.051 (0.62) |
| 500 | 0.052 (0.48) | 0.049 (0.57) |
| 1,000 | 0.056 (0.50) | 0.046 (0.51) |
| 10,000 | 0.053 (0.51) | 0.056 (0.51) |
| Sequence Length | Internal Branch α | External Branch β |
| Tree I | ||
| 20 | 0.051 (0.68) | 0.043 (0.67) |
| 50 | 0.049 (0.64) | 0.041 (0.68) |
| 100 | 0.051 (0.62) | 0.048 (0.67) |
| 200 | 0.049 (0.62) | 0.042 (0.65) |
| 500 | 0.063 (0.55) | 0.040 (0.60) |
| 1,000 | 0.064 (0.50) | 0.049 (0.53) |
| 10,000 | 0.057 (0.49) | 0.056 (0.50) |
| Tree II | ||
| 20 | 0.046 (0.68) | 0.041 (0.72) |
| 50 | 0.045 (0.65) | 0.039 (0.70) |
| 100 | 0.043 (0.63) | 0.044 (0.68) |
| 200 | 0.050 (0.55) | 0.051 (0.62) |
| 500 | 0.052 (0.48) | 0.049 (0.57) |
| 1,000 | 0.056 (0.50) | 0.046 (0.51) |
| 10,000 | 0.053 (0.51) | 0.056 (0.51) |
NOTE.—The test is conducted using the mixture of 0 and with critical value 2.71 at the 5% significant level. The proportion of data sets in which 2Δℓ = 0 is shown in parentheses.
We thus conclude that the histogram of P values in figure 1b of Nozawa et al. (2009b) is consistent with the asymptotic theory concerning the likelihood ratio test statistic. Nozawa et al. (2009b) simulated alignments of 450 codons in length under the branch model on a three-species tree, with ωF = 1 and ωB = 0.25 for the foreground and background branches, respectively, and used the distribution to conduct the test. They observed that the P value had a slight peak (7.3%) in the interval (0, 0.05) and a very high peak in (0.95, 1.00). The high peak for large P values is mainly due to data sets in which 2Δℓ = 0. The lower peak for small values indicates a false-positive rate of 7.3%, slightly higher than 5%. Our repetition of the same simulation (using as did Nozawa et al.) produced a false-positive rate of 4.8%. The precise reason for this difference is uncertain but we suspect that Nozawa et al. (2009b) used a wrong model concerning codon frequencies. The results do not indicate “an abnormal behavior” of the test, as Nozawa et al. (2009b) suggested. The authors were incorrect to attribute the pattern to small sample sizes, an interpretation contradicted by their own results, as they observed no difference when the data size was doubled.
Power
We simulated data sets of Lc = 500 codons under the alternative model of the branch-site test, with ω2 = 4, to examine the power of the branch-site test in comparison with a few other tests. The results are summarized in table 3.
Power of the Branch-Site and a Few Other Tests When the Data Are Simulated Under the Alternative Model with Positive Selection.
| Branch-Site | Branch | Pair Heuristic | Pair M0 | Pair M1a–M2a | |
| Tree I branch α | 0.774 | 0.000 | 0.000 | 0.001 | 0.400 |
| Tree I branch β | 0.643 | 0.003 | 0.000 | 0.012 | 0.305 |
| Tree II branch α | 0.806 | 0.000 | 0.000 | 0.001 | 0.386 |
| Tree II branch β | 0.620 | 0.001 | 0.000 | 0.008 | 0.270 |
| Branch-Site | Branch | Pair Heuristic | Pair M0 | Pair M1a–M2a | |
| Tree I branch α | 0.774 | 0.000 | 0.000 | 0.001 | 0.400 |
| Tree I branch β | 0.643 | 0.003 | 0.000 | 0.012 | 0.305 |
| Tree II branch α | 0.806 | 0.000 | 0.000 | 0.001 | 0.386 |
| Tree II branch β | 0.620 | 0.001 | 0.000 | 0.008 | 0.270 |
NOTE.—The sequence length is 500 codons. The branch-site test and Pair M0 are conducted using the mixture of 0 and with critical value 2.71. Pair M1a–M2a is conducted using with critical value 5.99. Pair Heuristic is conducted using Fisher’s exact test.
Power of the Branch-Site and a Few Other Tests When the Data Are Simulated Under the Alternative Model with Positive Selection.
| Branch-Site | Branch | Pair Heuristic | Pair M0 | Pair M1a–M2a | |
| Tree I branch α | 0.774 | 0.000 | 0.000 | 0.001 | 0.400 |
| Tree I branch β | 0.643 | 0.003 | 0.000 | 0.012 | 0.305 |
| Tree II branch α | 0.806 | 0.000 | 0.000 | 0.001 | 0.386 |
| Tree II branch β | 0.620 | 0.001 | 0.000 | 0.008 | 0.270 |
| Branch-Site | Branch | Pair Heuristic | Pair M0 | Pair M1a–M2a | |
| Tree I branch α | 0.774 | 0.000 | 0.000 | 0.001 | 0.400 |
| Tree I branch β | 0.643 | 0.003 | 0.000 | 0.012 | 0.305 |
| Tree II branch α | 0.806 | 0.000 | 0.000 | 0.001 | 0.386 |
| Tree II branch β | 0.620 | 0.001 | 0.000 | 0.008 | 0.270 |
NOTE.—The sequence length is 500 codons. The branch-site test and Pair M0 are conducted using the mixture of 0 and with critical value 2.71. Pair M1a–M2a is conducted using with critical value 5.99. Pair Heuristic is conducted using Fisher’s exact test.
When the branch-site test is conducted at the 5% level using the mixture distribution, the null hypothesis is rejected correctly in 62–81% of the simulated data sets (table 3). The power is quite high, partly because the positive selection pressure assumed in the simulation model is fairly strong, with on average 10% of codons (50 codons) under positive selection with ω2 = 4. On both trees I and II, the power is higher when branch α instead of branch β is used as the foreground branch. This is clearly due to the fact that branch α is twice as long as branch β. The differences between the two trees are small. Because the branch-site test focuses on one branch on the tree, adding sequences to other parts of the tree does not appear to add much more information.
We then analyzed the same data using the branch test (Yang 1998). This test assumes that the same ω applies to all codons in the gene and tests whether ωF for the foreground branch is greater than 1. The power of the test is ∼0%, in sharp contrast to the high power of the branch-site test in those data sets (table 3).
We also applied three tests to the two sequences at the ends of the foreground branch, with the true ancestral sequences used when needed. The results are shown in table 3 in the columns headed Pair Heuristic, Pair M0, and Pair M1a–M2a. Pair Heuristic mimics the test of Zhang et al. (1997) but uses the true ancestral sequences and the true value for κ. It has 0% power in those data sets. Pair M0 is a likelihood ratio test under the assumption of the same ω for all codons (the M0 model) and tests whether ω > 1. This has power 0–1%, similar to the branch test discussed above but appears to have more power than Pair Heuristic. Pair M1a–M2a compares the site models M1a (neutral) with M2a (selection). Those models account for variable selective pressures among codons. The power for this test is 27–40%, which is much higher than for the branch-based test but much lower than for the branch-site test. The difference between Pair M1a–M2a and the branch-site test is somewhat surprising because Pair M1a–M2a uses the true ancestral sequences, whereas this information is not used in the branch-site test and because one may expect that additional sequences may not contain much useful information for testing positive selection along the foreground branch given that the sequences at the two sides of that branch are already available. The reasons for this performance difference are not well understood, but two factors seem important. First, our use of in Pair M1a–M2a may have made the test too conservative, as mentioned above. Second, the use of many sequences may have allowed the branch-site model to estimate some parameters (such as κ, p0, p1, and ω0) more reliably, which may in turn help the estimation and test concerning ω2. This explanation, if correct, highlights an advantage of joint likelihood analysis of multiple species when the genes have the same function and are under similar selective pressures along the background lineages: The joint analysis allows the model to estimate the proportion of conserved and neutral codons reliably, which may then help to improve the power of detecting positive selection on the foreground branch.
The power of the branch-site test is expected to depend on a number of factors. Here, we examine the impact of the sequence length (Lc), the strength of positive selection (measured by ω2), and the proportion of sites under positive selection on the foreground branch (p2), using branches α and β in tree I as the foreground branch. In each case, one of those three factors is varied, whereas other parameter settings are kept the same as in table 3. The results are summarized in figure 4. As expected, this simulation generated a wide range of power results. When the sequences are short, selection is weak or very few sites are under positive selection, the power of the test can be very low but it increases quickly with the increase in sequence length, the strength of positive selection, and the proportion of sites under positive selection. Similarly, the power of the branch-site test is seen to vary considerably among previous simulation studies, as a result of differences in the level of sequence divergence, sequence length, selective scheme, etc. (table 4).
| Test | False Positive Under Correct Null (%) | False Positive with Model Violation (%) | Power with Variable Selective Pressures among Codons (%) |
| Branch-site test | ∼5 | 0–8 | 3–44 (Zhang et al. 2005) |
| 21–33 (Bakewell et al. 2007) | |||
| 62–81 (this study) | |||
| Heuristic test | ∼5 | <5 | ∼0 |
| Random guess | 5 | 5 | 5 |
| Test D1 | 0 | 0 | 0 |
| Test D2 | 100 | 100 | 100 |
| Test | False Positive Under Correct Null (%) | False Positive with Model Violation (%) | Power with Variable Selective Pressures among Codons (%) |
| Branch-site test | ∼5 | 0–8 | 3–44 (Zhang et al. 2005) |
| 21–33 (Bakewell et al. 2007) | |||
| 62–81 (this study) | |||
| Heuristic test | ∼5 | <5 | ∼0 |
| Random guess | 5 | 5 | 5 |
| Test D1 | 0 | 0 | 0 |
| Test D2 | 100 | 100 | 100 |
NOTE.—Random guess declares positive selection in 5% of data sets chosen at random. Test D1 always accepts the null and test D2 always rejects the null.
| Test | False Positive Under Correct Null (%) | False Positive with Model Violation (%) | Power with Variable Selective Pressures among Codons (%) |
| Branch-site test | ∼5 | 0–8 | 3–44 (Zhang et al. 2005) |
| 21–33 (Bakewell et al. 2007) | |||
| 62–81 (this study) | |||
| Heuristic test | ∼5 | <5 | ∼0 |
| Random guess | 5 | 5 | 5 |
| Test D1 | 0 | 0 | 0 |
| Test D2 | 100 | 100 | 100 |
| Test | False Positive Under Correct Null (%) | False Positive with Model Violation (%) | Power with Variable Selective Pressures among Codons (%) |
| Branch-site test | ∼5 | 0–8 | 3–44 (Zhang et al. 2005) |
| 21–33 (Bakewell et al. 2007) | |||
| 62–81 (this study) | |||
| Heuristic test | ∼5 | <5 | ∼0 |
| Random guess | 5 | 5 | 5 |
| Test D1 | 0 | 0 | 0 |
| Test D2 | 100 | 100 | 100 |
NOTE.—Random guess declares positive selection in 5% of data sets chosen at random. Test D1 always accepts the null and test D2 always rejects the null.
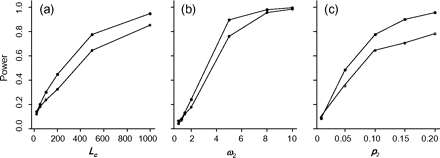
Power of the branch-site test plotted against (a) the sequence length Lc, (b) the strength of positive selection measured by ω2, and (c) the proportion of sites under positive selection p2. The foreground branches are branch α (filled circles) and β (empty circles) in tree I. For Lc = 10,000, the power was ∼100% for both branches and is not shown in (a).
Discussion
Minimum Number of Nonsynonymous Substitutions and Suzuki Effect
Nozawa et al. (2009a) suggested an intuitive rule, that is, that there must be at least nine (or four according to Suzuki 2008) nonsynonymous substitutions along the foreground branch for positive selection to be detected. They then used this rule to criticize the branch-site test because that test often detected positive selection even when there were far fewer nonsynonymous substitutions. However, the test that those authors considered is the heuristic test of Zhang et al. (1997), referred to by the authors as the “small-sample method,” which averages ω over the whole gene and detects positive selection only if this average is significantly greater than 1. This test is at best as good as the Pair Heuristic test examined in this paper. It has little power because in a typical protein, most amino acid residues are highly conserved due to structural and functional requirements of the protein, and when positive selection operates, it most likely affects only a small subset of sites. Estimates from real data suggest that the average ω is less than 1 in almost all genes, including the best-known examples of positive selection, such as human leukocyte antigen gene (Yang and Swanson 2002) or the HIV envelop gene (Yang et al. 2003). In our simulation, averaging the rates over the whole gene led to total loss of power in the branch-based tests even when the branch-site test had high power (table 3). Calculation by Nozawa et al. (2009a), based on the heuristic test of Zhang et al. (1997), does not apply to the branch-site test. Indeed, it does not even apply to the branch-based likelihood ratio test (Yang 1998), which uses the information in the data more efficiently than the heuristic test (see below).
Nozawa et al. (2009a) further discovered a so-called Suzuki effect, which states that at low sequence divergence, the presence of a codon with two or three position differences along the foreground branch is almost guaranteed to cause the branch-site test to detect positive selection. We suggest that this behavior is reasonable. At low sequence divergence, when there are only two (say) nonsynonymous substitutions in the whole gene over the foreground branch, it should be very surprising for both substitutions to occur in the same codon if there is no positive selection, but it is less surprising if a few critical codons are under strong positive selection on the lineage. Two nonsynonymous substitutions that occur in the same codon are thus stronger evidence for positive selection than if they occur in different codons. The evidence is even stronger if both nonsynonymous substitutions are transversions instead of transitions. Weighing the strength of such evidence appropriately requires consideration of the transition/transversion rate ratio, the sequence divergence level (branch length), etc. and is hard if one relies on intuition and simple counting. The branch-site test, through its use of the likelihood function under the codon model, relies on the probability calculus to do this difficult job. Of course, two nonsynonymous substitutions may occur in the same codon just by chance, in which case the test will generate a false-positive error, but the test is acceptable if the error rate is <5%. In the case analyzed in Suzuki (2008), this error occurred in ∼99 of 14,000 replicates, with an error rate of 0.7%.
In contrast, the heuristic test of Zhang et al. (1997), which Nozawa et al. (2009a) favored, summarizes the sequence data into (inferred) counts of synonymous and nonsynonymous substitutions on the foreground branch (cS and cN) and ignores important information in the data, such as whether the substitutions are transitions or transversions and whether they occur in the same codon. Thus, the Suzuki effect highlights a deficiency in the heuristic test, which may cause it to have very little power. Of course, another (probably more important) reason for its lack of power is that it averages rates over all codons in the gene.
In this regard, it may be worth noting that sometimes a codon site with “synonymous differences” is identified by codon-based analysis to be under positive selection. This occurs at sites occupied by codons encoding serine, for example, TCT and AGT. The codon model assumes that mutations occur independently at the three codon positions and the chance of two or three instantaneous substitutions is infinitely small. Two explanations of this result appear reasonable. The first is that one mutation event changed both codon positions, so that the mutation is synonymous and neutral, and the codon-based analysis generated a false positive. The second is that one codon position changed first, with the mutation being deleterious, whereas the second mutation is compensatory, driven to fixation by natural selection. In this case, the codon-based analysis does not appear to be wrong in suggesting positive selection, even though this may not be the kind of positive selection driving functional divergences that we are interested in. It is unclear which scenario is more common in reality. Note that empirical codon models that allow substitutions at two or three positions have been developed (Kosiol et al. 2007), even though they do not have the power to distinguish between the two scenarios.
Performance of the Branch-Site Test in Simulations
A statistical test is evaluated by considering two types of errors (Lehmann 1997). The type I error or false-positive error refers to incorrect rejection of the null hypothesis when the null is true, whereas the type II error refers to failure to reject the null when the null is false. The type I error is usually considered to be more serious than the type II error. The convention for developing a statistical test is to have the false-positive rate under control (i.e., to be ≤α, the significance level) and then to maximize the power of the test (i.e., minimize the type II error). Evaluation of a test almost invariably involves examination of both types of errors. The simulations of Nozawa et al. (2009a; see also Suzuki 2008) appear to be unique in that they considered the type I error only while ignoring the type II error (or power) completely. By such a criterion, a test that never rejects the null (test D1 in table 4) will have perfect performance.
The null distribution for the branch-site test is based on an asymptotic approximation of the likelihood ratio test statistic. The sample size required for the asymptotic theory to be reliable depends on the particular problem. Our simulation in this study suggests that data sets with as few as 20–50 codons are large enough for the theory to be trustable. This result is consistent with previous simulations examining likelihood ratio tests under nucleotide and codon models, which suggest that about 50 sites are enough for the theory to be applicable (e.g., Whelan and Goldman 1999; Zhang 1999; Anisimova et al. 2001). Nozawa et al.’s (2009a) claim that “the numbers of synonymous (cS) and nonsynonymous (cN) substitutions per gene per branch were so small that the applicability of the large-sample theory of LRT is questionable” does not appear to be based on any evidence and confused the inferred number of changes with the sample size. Here, the sample size is the number of codons in the alignment: In very short but highly divergent sequences, the asymptotic theory may be unreliable even if there are many changes.
The asymptotic theory is valid only if the model is correct. In this regard, previous simulation studies have examined the robustness of the branch-site test and found it to be fairly robust to violations of model assumptions. Zhang et al. (2005) and Bakewell et al. (2007) simulated data using complex selection schemes, with many more site classes than assumed by the branch-site model, and found the false-positive rate to be 0–5% in most cases, with the highest at ∼8%. Suzuki (2008) and Nozawa et al. (2009a) simulated data under the branch model, with ωF and ωB for the foreground and background branches, respectively, on a tree of three species. In the simulation of Nozawa et al. (2009a), the false-positive rate was 0–5% in most cases, with the highest at 7%. Suzuki (2008) observed false-positive rates as high as ∼12% or 20% when ωF = 1 and ωB = 0 or 5. The assumption that ωB = 0 or 5 for all codons in the gene appears highly unrealistic, as acknowledged by Suzuki (2008), and the performance of the test in such extreme conditions may not be relevant to practical data analysis. For other parameter combinations considered by Suzuki (2008, table 1), the false-positive rate was mostly at 0–5%, with the highest at ∼8%. While false-positive rates of 7–8% are above the required 5% and while there is a need to improve the branch-site test to make it even more robust, we suggest that those error rates are not excessively high given the serious model violations in those simulations.
Nozawa et al. (2009a) cited the outdated studies of Suzuki and Nei (2001, 2002) as evidence that the likelihood ratio test based on codon models often gave false positives. However, those results have already been shown by Wong et al. (2004) to be either incorrect (Suzuki and Nei 2001) or most likely caused by numerical optimization problems or simulation errors (Suzuki and Nei 2002).
Nozawa et al. (2009a, 2009b) criticized the practice of running the branch-site test on thousands of genes and then speculating on biological meanings of selection for each gene detected to be under positive selection, suggesting that “the frequency of occurrence of P < 0.05 (the false-positive rate) is irrelevant for biologists because they believe each gene evolves differently.” We agree that biologists should ideally have a prior hypothesis about which genes are likely to be under positive selection and which lineage should be affected and thus designated the foreground branch. However, it is not fair to attribute inappropriate uses of a test as poor performance of the test. Furthermore, it should be noted that genome scans for genes under positive selection have their value, in generating biological hypotheses for experimental verification.
In contrast, the lack of power of tests of positive selection based on synonymous–nonsynonymous rate comparison is a major concern. A test with false-positive rate ≤α and power ≥α is said to be unbiased (Lehmann 1997, p. 134). This unbiasedness is a weak requirement because a test that does not meet this requirement is worse than a random guess which simply rejects the null in 5% of the data sets: such a random guess has the false-positive rate under control and also has more power than a biased test. It seems that in most realistic conditions, where the selective pressure varies over codons in the gene, the branch-based tests (Messier and Stewart 1997; Zhang et al. 1997; Yang 1998) are worse than a random guess (table 4).
The test of Zhang et al. (1997) is a modification of the test of Messier and Stewart (1997). The latter used the likelihood method (Yang et al. 1995) to reconstruct ancestral sequences and then used the method of Li (1993) to estimate dN and dS for each branch. Zhang et al. (1997) used parsimony to reconstruct ancestral sequences and then used them to count synonymous and nonsynonymous changes on each branch (cS and cN) to test whether there is an excess of nonsynonymous substitutions. Note that Nozawa et al.’s (2009a) description that “positive selection is suggested only when cN is significantly greater than cS” is incorrect: The null hypothesis of the test is not that the ratio of the numbers of nonsynonymous and synonymous substitutions equals 1, as the authors stated, but that the ratio equals the neutral expectation (N/S ≈ 3) (see Materials and Methods). Both heuristic approaches suffer from treating inferred pseudodata as real observed data. Even with the extremely similar sequences simulated by Suzuki (2008) and Nozawa et al. (2009a), errors in ancestral reconstruction can be considerable. For example, Suzuki (2008, table 2) listed 99 cases, of which 13 (13%) showed differences of one or more in the counts cN and cS, even though the counts are very low, mostly at 2–5. In more divergent sequences, the systematic and random errors in ancestral reconstruction can be substantial. Unlike the test of Messier and Stewart (1997), the test of Zhang et al. (1997) does not correct for multiple hits and can overcount as well as undercount substitutions (Yang 2002). Furthermore, counts of sites (N and S) are affected by the transition–transversion rate difference and uneven codon usage. In summary, Fisher’s exact test is not exact because it is applied to inferred pseudocounts rather than observed data.
Performance of the Branch-Site Test in Real Data Analysis
The branch-site test has been used to analyze a number of real data sets. As the truth is typically unknown in real data, it is hard to assess what percentage of the detected positives are true positives and what percentage of the detected negatives are true negatives. Here, we discuss a few recent cases where the gene function is thought to be well understood or where the experimental evidence appears convincing, as well as two examples that are supposed to demonstrate problems with the branch-site test. We make no attempt to be exhaustive or even representative.
First, we note that in large-scale analysis, genes involved in host–pathogen antagonism are most often detected to be under positive selection (see, e.g., Nielsen 2005; Yang 2006, chapter 8; Kosiol et al. 2008 for reviews). Similarly, genes involved in male and female reproduction are often detected to be under positive selection (see Swanson and Vacquier 2002 for a review). Those genes appear to be involved in a genetic arms race (either between the host and pathogen or between the male and the female), evolving fast under continual positive (diversifying) selective pressure. Another category of genes commonly detected to be under positive selection consists of gene copies (paralogues) that have acquired new functions after gene duplication. Those cases are biologically sensible and may serve as “positive controls” for the test.
Adaptation of Mitochondrial Respiratory Chain Proteins during the Origin of Flight in Bats
Shen et al. (2010) used the branch-site test to identify genes under positive selection when bats acquired the ability of flight. Positive selection was detected on the branch ancestral to bats in 3 (23%) of 13 mitochondrial-encoded and in 5 (4.9%) of 102 nuclear-encoded oxidative phosphorylation genes, whereas the same test on the branch ancestral to rodents (which do not fly) detected 0 (0%) and 2 (2.0%) genes, respectively. The results support the hypothesis that drastic increase in energy metabolism in bats has driven adaptive amino acid changes in proteins involved in the mitochondrial respiratory chain. The analysis appears to have opened up opportunities for studying critical amino acid changes that have shaped the origin and evolution of flight in mammals.
Functional Specialization of AGPase, an Enzyme Involved in Starch Synthesis
Georgelis et al. (2009) analyzed the evolution of ADP-glucose pyrophosphorylase (AGPase), which catalyzes a rate-limiting step in glycogen synthesis in bacteria and starch synthesis in plants. The large subunit of AGPase has duplicated extensively giving rise to groups with different kinetic and allosteric properties. The branch-site test is used to detect positive selection along lineages that led to those groups. Site-directed mutagenesis confirmed the importance of a number of positive-selected amino acid residues to the kinetic and allosteric properties of the enzyme. The authors suggest that the evolutionary comparison greatly facilitated enzyme structure–function analyses.
Adaptive Evolution of Rhodopsins in Vertebrates and Butterflies
Yokoyama et al. (2008) analyzed the evolution of dim-light vision proteins, the rhodopsins, in vertebrates. Modern species have highly variable niches, and their rhodopsins are adapted to light of different wavelengths, characterized by λmax, the wavelength of maximal absorption. The authors found that the site-based tests (Nielsen and Yang 1998; Yang et al. 2000) failed to detect positive selection in a large data set of 38 vertebrate species. This result appears to be a false negative, as suggested by Yokoyama et al. The site models average the substitution rates over all lineages on the phylogeny. One may expect positive selection to operate only around the time a species moved into a new habitat, whereas over the majority of the evolutionary time, the gene should be dominated by selective constraint. The lack of power of those tests in detecting episodic positive selection is well known.
Yokoyama et al. (2008) also found that the site-based tests detected some positive selection sites in a smaller data set of 11 squirrelfish species, but those sites had no impact on λmax. This result may have two explanations. The first is that the detected sites are false positives, as suggested by Yokoyama et al. Even so, the failure of a statistical test in one single data set does not say much about its statistical properties, and the test will still be acceptable if it does not generate false positives in more than 5% of data sets. An alternative explanation is that the detected sites may affect fitness, but the effect was too small or was otherwise not detected in experiment by Yokoyama et al. First, λmax may not be equivalent to fitness. Second, small fitness differences that are extremely difficult to measure experimentally can be significant on the evolutionary timescale. Third, the authors did not mutate all the detected amino acids to examine their impact on λmax, which does not appear feasible given the complex interactions among amino acid residues and the great number of combinations of mutations at many amino acid sites. Yokoyama et al. (2008, table 4) used the observation that two rhodopsins different at, say, 50 sites (of 191) have the same λmax as evidence that all those sites have no effect on λmax. This reasoning may not be sound. There appears to be stabilizing selection on λmax when the rhodopsin is fine-tuned to the habitat of the fish species, so that mutations at some sites which change λmax may be compensated by mutations at other sites, with the net effect of little change in λmax. A decade ago, three or five critical sites were believed to fully determine λmax in vertebrates, hence the so-called three-sites rule and five-sites rule (Yokoyama and Radlwimmer 2001). The list has since expanded to include 12 sites (Yokoyama et al. 2008). It is imaginable that future research by Yokoyama and colleagues may undercover more functional sites.
In contrast, the branch-site test appeared to have been more successful in another analysis of rhodopsin evolution. Briscoe et al. (2010a) discovered that Heliconius butterflies have two ultraviolet (UV)-sensitive rhodopsins (UVRh1 and UVRh2). They used the branch-site test to detect positive selection in UVRh2 immediately following the gene duplication. Some of the inferred positive selection sites are important to spectral tuning in vertebrates, and indeed, the two duplicate copies of the visual pigments in Heliconius are functionally distinct. The functional diversification of UV-sensitive visual pigments in Heliconius coincides with the expansion of UV-yellow colors on the wings of the butterflies, implicating a role of UV-sensitive rhodopsins in species recognition during the adaptive radiation of this species group. The authors emphasized the advantages of an integrated approach of statistical analysis, structural modeling, and physiological characterization in discovering new gene functions (Briscoe et al. 2010b).
Positive Selection in Hominoids
Bakewell et al. (2007) used the branch-site test to analyze ∼14,000 genes from the human, chimpanzee, and macaque and detected more genes to be under positive selection on the chimpanzee lineage than on the human lineage (233 vs. 154). The same pattern was also observed by Arbiza et al. (2006), Gibbs et al. (2007), and Vamathevan et al. (2008).
Mallick et al. (2010) reexamined 59 genes detected to be under positive selection on the chimpanzee lineage by Bakewell et al. (2007), using more stringent filters to remove less reliable nucleotides and using synteny information to remove misassembled and misaligned regions. They found that with improved data quality, the signal of positive selection disappeared in most of the cases when the branch-site test was applied. It now appears that, as suggested by Mallick et al. (2010), the earlier discovery of more frequent positive selection on the chimpanzee lineage than on the human lineage is an artifact of the poorer quality of the chimpanzee genomic sequence. This interpretation is also consistent with a few recent studies analyzing both real and simulated data, which suggest that sequence and alignment errors may cause excessive false positives by the branch-site test (Schneider et al. 2009; Fletcher and Yang 2010). For example, most commonly used alignment programs tend to place nonhomologous codons or amino acids into the same column (Löytynoja and Goldman 2005, 2008), generating the wrong impression that multiple nonsynonymous substitutions occurred at the same site and misleading the codon models into detecting positive selection (Fletcher and Yang 2010).
It appears very challenging to develop a test of positive selection that is robust to errors in the sequences or alignments. Instead we advise caution concerning the use of the branch-site test when the data quality is in doubt. Nevertheless, we suggest that the impact of sequence and alignment errors should not be confused with the poor performance of the test (cf. Nozawa et al. 2009a).
Potential Problems with the Branch-Site Test
As the branch-site test is increasingly used in comparative analysis of genes and genomes, we note here a few of its major limitations. First, sequence divergence is often a major issue. Codon-based analysis requires information concerning both synonymous and nonsynonymous substitutions, so that the sequences should not be either too similar or too divergent. Highly similar sequences contain little information so that the test will have little power. For example, simulations suggest that for site-based analysis to have any power in analysis of population data, more than 1,000 sequences are needed (Anisimova 2003, p. 106–108). Indeed, the results of Bakewell et al. (2007) and Mallick et al. (2010) suggest that the sequences from the human and the chimpanzee are so similar that the branch-site test has very little power in detecting positive selection along those lineages. In contrast, divergent sequences contain too much noise, with synonymous substitutions reaching saturation. High sequence divergence alone does not appear to be a serious problem for the likelihood method, but high sequence divergence is often accompanied by other problems, such as alignment difficulties and differences in codon usage patterns between species, which may cause the branch-site test to generate false positives (Schneider et al. 2009; Fletcher and Yang 2010; Mallick et al. 2010).
It is sometimes attempted to use the estimate of ω2 as a measure of the strength of selection in the gene on the foreground branch. As discussed by Bakewell et al. (2007) and Nozawa et al. (2009a), point estimates of ω2 produced by the codeml program are often infinite and unreliable. Note that the test may be able to decide whether ω2 > 1, even if it cannot estimate ω2 reliably, and the occurrence of in a data set does not invalidate the test. Furthermore,
does not necessarily mean rejection of the null hypothesis. For the branch model, the estimate of ω for a branch will be ∞ if at least one nonsynonymous substitution occurred but no synonymous substitution occurred on the branch. For the branch-site model, infinite estimates will occur more often, if there are no synonymous substitutions at the few codons that appear to have come from site classes 2a and 2b. If one is interested in estimating ω2, a useful approach may be to assign a prior on ω2 and to produce a posterior estimate. One could in theory use the Bayes empirical Bayes estimate if many categories are used to discretize the ω distribution (Yang et al. 2005). However, a difficulty is that estimates of p2 and ω2 are strongly negatively correlated, as it is difficult to distinguish a smaller number of codons under stronger selection from a larger number of codons under weaker selection. It is unclear whether the product p2ω2 or p2(ω2 − 1) may provide a better measure of the strength of positive selection than ω2 alone.
Codon-based analyses or comparison between synonymous and nonsynonymous substitution rates are able to detect persistent diversifying selection, which generates many nonsynonymous substitutions. They tend to lack power in detecting one-off directional selection in which one or a few advantageous nonsynonymous mutations reach fixation quickly, followed by purifying selection. The branch-site model, by focusing on a narrow time window and by allowing variable selective pressures among codons, appears to have some power in detecting such episodic positive selection. Future applications of the test to real data sets may help us understand its strengths and weaknesses.
We thank Rasmus Nielsen for discussions, and Rasmus Nielsen, Jeff Thorne, and two anonymous referees for comments. This study was conducted using the high-performance computing cluster LEGION of University College London. Z.Y. is a Royal Society/Wolfson Merit Award Holder. Z.Y. gratefully acknowledges the support of K.C. Wong Education Foundation, Hong Kong.
References
Author notes
Associate editor: Alexei Drummond



