-
PDF
- Split View
-
Views
-
Cite
Cite
Tobias Warnecke, Laurence D. Hurst, Evidence for a Trade-Off between Translational Efficiency and Splicing Regulation in Determining Synonymous Codon Usage in Drosophila melanogaster, Molecular Biology and Evolution, Volume 24, Issue 12, December 2007, Pages 2755–2762, https://doi.org/10.1093/molbev/msm210
Close - Share Icon Share
Abstract
In Drosophila melanogaster, synonymous codons corresponding to the most abundant cognate tRNAs are used more frequently, especially in highly expressed genes. Increased use of such “optimal” codons is considered an adaptation for translational efficiency. Need it always be the case that selection should favor the use of a translationally optimal codon? Here, we investigate one possible confounding factor, namely, the need to specify information in exons necessary to enable correct splicing. As expected from such a model, in Drosophila many codons show different usage near intron–exon boundaries versus exon core regions. However, this finding is in principle also consistent with Hill–Robertson effects modulating usage of translationally optimal codons. However, several results support the splice model over the translational selection model: 1) the trends in codon usage are strikingly similar to those in mammals in which codon usage near boundaries correlates with abundance in exonic splice enhancers (ESEs), 2) codons preferred near boundaries tend to be enriched for A and avoid C (conversely those avoided near boundaries prefer C rather than A), as expected were ESEs involved, and 3) codons preferred near boundaries are typically not translationally optimal. We conclude that usage of translationally optimal codons usage is compromised in the vicinity of splice junctions in intron-containing genes, to the effect that we observe higher levels of usage of translationally optimal codons at the center of exons. On the gene level, however, controlling for known correlates of codon bias, the impact on codon usage patterns is quantitatively small. These results have implications for inferring aspects of the mechanism of splicing given nothing more than a well-annotated genome.
Introduction
In a wide range of genomes analyzed to date, synonymous codons are not used with equal frequency despite coding for the same amino acid. Rather, codon usage is typically biased towards certain codons, reflecting a balance between mutational biases, drift, and selective forces (Ikemura 1985; Duret 2002; Bierne and Eyre-Walker 2006). This balance varies not only between species but also between genes within the same organism. Notably, in a variety of species, including Drosophila, some synonymous codons are used more frequently in highly expressed genes (Duret and Mouchiroud 1999). These preferred codons have been termed “optimal” because their use is thought to minimize the time of ribosomal occupancy and/or the rate of amino acid misincorporation relative to alternative synonymous codons (Akashi 1994; Duret 2002). Selection for rate or accuracy of translation, we refer to generically as selection on translational “efficiency.” The translational efficiency hypothesis is supported by the observation that in many, often distantly related species optimal codons correspond to the most abundant cognate tRNAs (Ikemura 1985; Kanaya et al. 2001).
The genomic signature of this relationship is less pronounced in fruitfly than in some other eukaryotes (Kanaya et al. 2001). However, this is likely owing to weakened selection following a recent reduction in population size (Akashi 1995; McVean and Vieira 2001) rather than to qualitatively different selective forces operating on codon usage in Drosophila. Additional factors contributing to skewed codon usage are usually analyzed within this translational efficiency framework. For example, the degree of selective constraint on the encoded protein (Bierne and Eyre-Walker 2006), mutational biases (e.g., biased gene conversion) (Kliman and Hey 1994; Duret 2002; Bierne and Eyre-Walker 2006), recombination rate (Hey and Kliman 2002), Hill–Robertson interference (Hey and Kliman 2002; Bierne and Eyre-Walker 2006), and protein length (Duret and Mouchiroud 1999) are considered to correlate with or modulate selection for translationally optimal codon usage.
Need it always be the case that selection, if unrestricted, should favor the use of a translationally optimal codon? Here, we investigate one possible confounding factor, namely, the need to specify information in exons necessary to enable correct splicing. This can include binding sites in exons for serine-arginine–rich (SR) type proteins (Blencowe 2000). These binding sites, known as exonic splice enhancers (ESEs), are critical for the faithful removal of introns from pre-mRNA transcripts, especially in species with a complex intron–exon structure where regulated splicing may require weak splice sites (Ast 2004; Dewey et al. 2006; Garg and Green 2007; Ram and Ast 2007).
Efforts to characterize ESEs on a genome-wide scale have been made for human and mouse (Fairbrother et al. 2002; Fairbrother, Yeo, et al. 2004), zebrafish (Yeo et al. 2004), Caenorhabditis elegans (Robinson 2005), and recently Arabidopsis thaliana (Pertea et al. 2007). To our knowledge, a comprehensive, genome-wide survey of ESE motifs in Drosophila has yet to be undertaken. However, the available evidence suggests that they are important in Drosophila and function like those characterized in mammals. Firstly, in genes where exonic splicing regulation has been examined in some detail, notably ‘doublesex’ and ‘fruitless,’ purine-rich elements have been attributed key roles (Lynch and Maniatis 1996; Heinrichs et al. 1998; Labourier et al. 1999), just as they have in mammals (Blencowe 2000). Secondly, Drosophila ESEs interact with members of the SR protein family (Labourier et al. 1999; Kim et al. 2003), which is strongly associated with ESEs in vertebrates (Blencowe 2000).
With a genome-wide characterization of ESEs currently lacking in Drosophila, we use the enrichment of codons near intron–exon boundaries as a possible surrogate for the involvement of codons in splice-regulatory elements. Although patterns of enrichment may be caused by splice-related factors other than ESEs, for example, the avoidance of cryptic splice sites (Eskesen et al. 2004), prior evidence suggests that ESE involvement is the best predictor (Chamary and Hurst 2005a; Parmley et al. 2007).
We find that, in Drosophila, certain codons are indeed significantly enriched or avoided near intron–exon boundaries. Aside from splice-related constraints, there is, however, a qualitatively different explanation for such deviations, namely, that they reflect stronger selection for translational efficiency owing to reduced Hill–Robertson interference (for a recent explanation of the Hill–Robertson effect, see Comeron et al. 2007). The finding that in intronless Drosophila genes usage of translationally optimal codons is reduced in the center of the gene is consistent with such a force (Comeron and Kreitman 2002). As applied to patterns within exons, this model rests on the presumption that selection is weaker in introns than in exons, hence codons near intron–exon boundaries have strong selection on only one side of them, whereas those in exon cores are flanked by sites under selection in both 5′ and 3′ directions. In this paper, in part, we ask whether the trends we observe are better explained by selection for splicing than by Hill–Robertson effects modulating the use of translationally optimal codons.
To this end, we ask whether the trends in codon usage near intron–exon boundaries concord with those seen in species (notably mouse) in which ESEs have been described and in which ESE involvement accounts for much of the pattern of codon usage near intron–exon boundaries (Parmley and Hurst 2007). In addition, as codons participating in ESE motifs, characterized in some details in a number of vertebrates, were found to be A-rich and C-poor (Blencowe 2000; Fairbrother, Yeo, et al. 2004; Parmley et al. 2007), we ask whether preferred codons tend to be rich in A and avoid C (and conversely whether those codons avoided near boundaries are more commonly rich in C rather than A). Thirdly, we ask whether there is an incongruity between synonymous codons preferred near boundaries and those identified as translationally optimal. We report that in all 3 tests, splice control is a better explanation for the trends than Hill–Robertson effects. Finally then, we attempt to quantify to what extent, in intron-containing genes, the need to accommodate splicing-related sequence compromises optimal codon usage. To this end, we quantify the deviation from translational optimality introduced by the presence of introns and ask whether it is greater for genes with a higher proportion of sequence in the vicinity of splice sites and how it compares to known correlates of codon usage bias.
Material and Methods
Expression Data
Organism-wide gene expression data for adult Drosophila melanogaster were obtained from Flyatlas (www.flyatlas.org) using the FlyMean track. Unspecific hybridization and other factors can lead to transcripts being incorrectly identified as expressed when, in fact, they are not. In order to reduce the number of such false positives, especially among the set of genes expressed at low levels, only transcripts that show significant expression in at least 3 out of 4 replicates, as computed by Affymetrix software (FlyCall ≥ 3), were retained. In addition, we excluded all transcripts of genes present in the codon usage training set of Carbone et al. (2003) (141 genes, available at http://www.ihes.fr/∼materials/genomes/Dmelanogaster/refset.txt) as well as all transcripts annotated as ribosomal by the Gene Ontology Consortium (GO:0005840), of which many show high homology and/or coexpression and may as a result have biased regression analyses by forming a cluster of high leverage at the upper end of the expression range.
Sequence Data
For all transcripts in the reduced Flyatlas data set, sequences with annotated intron–exon structure were downloaded from the University of California Santa Cruz genome browser (http://genome.ucsc.edu/cgi-bin/hgTables) using the Flybase gene track (April 2004 assembly). Genes were discarded in either of the following cases: 1) transcripts had no conventional start (ATG) or termination codon (TAA, TAG, TGA), 2) transcripts had an internal in-frame stop codon, 3) exonic sequence was not a multiple of 3 nt and hence unlikely to be coding for a protein product, and 4) one or more introns in the gene had other than canonical splice sites (GT–AG). Furthermore, given the analytical importance of distinguishing whether or not exonic sequence is proximal to intronic sequence and therefore possibly involved in splicing regulation, we excluded all apparently intronless transcripts (1,873) for which alternative intron-containing splice products were annotated in Flybase (119) or which had more than one exon annotated in matching RefSeq entries (11).
The final data set for which adequate and reliable information was available for both expression and sequence characteristics comprises 9,745 transcripts, including 1,703 intronless transcripts. Supplementary table 3 (Supplementary Material online) contains by-gene information about relevant sequence characteristics and codon usage biases.
Codon Abundance
Exons were trimmed to contain only full codons. First and last full codons were discarded given their known involvement in splice site consensus. For each codon separately, relative abundance near the intron–exon boundary was determined for the first 34 codon positions across all trimmed exons, separately for the 5′ and 3′ ends of exons (for details, see Parmley et al. 2007).
Codon Adaptation Index
The codon adaptation index (CAI) measures the extent to which a gene uses synonymous codons thought to be translationally favorable because they are more abundant in very highly expressed genes. Values range from 0 to 1, with 1 indicating perfect adaptation. CAI is highly correlated to some other commonly used measures of codon bias (Hey and Kliman 2002) and provides an accurate description of codon bias even for relatively short sequences (Comeron and Aguade 1998). CAI for full and partial coding sequences was computed using the codonW program (J. Peden) supplying D. melanogaster–specific CAI adaptiveness values as determined by Carbone et al. (2003) (http://www.ihes.fr/∼materials/genomes/Dmelanogaster/wv.txt).
Conflict Resolution Index
Conflict resolution index (CRI) was computed as follows. Codons were assigned to 1 of 3 classes, “favoring translation efficiency” (coded c = 1; 19 codons, black background in fig. 2), “favoring splicing regulation” (coded c = 2; 18 codons, white background), or “uninformative” (ignored; 22 codons, gray background). Each informative codon was assigned a weight representing the conflict-relevant degeneracy of the associated amino acid. For example, the 4-fold degenerate (d = 4) amino acid proline (P) has 1 codon that resolves the conflict in favor of translation efficiency (CCC, s = 1) and 2 codons preferred near the boundary and hence assumed to resolve the conflict in favor of ESEs (CCA, CCT, s = 2); the weight for CCC is then simply taken as the ratio of degeneracy over the number of solutions in favor of the demand under consideration, that is, for CCC: 4/1 = 4 and for CCA or CCT: 4/2 = 2. CRI is then computed as the sum of weighted codes divided by the sum of weights over all informative codons.
![Relationship between slope coefficients (ß) of linear regression models fitted to codon abundance patterns across (A) the 5′ ends and (B) the 3′ ends of mouse and Drosophila internal exons, respectively. Each data point represents one degenerate codon. Negative values indicate that the respective codon is relatively more frequent near the intron–exon boundary. The steeper the negative/positive slope the more dramatic the preference/avoidance trend (for details on particular codons, see supplementary table 1 [Supplementary Material online]). Slope coefficients, taken to indicate similar preference or avoidance patterns, are highly correlated (ßDrosophila ∼ ßhuman 5′: Spearman's r = 0.74, 3′: r = 0.77; ßDrosophila ∼ ßmouse 5′: r = 0.74, 3′: r = 0.71; all: P < 2.2E−16, N = 59), that is, similar codons are preferred or avoided in mouse and Drosophila at exon termini, respectively.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mbe/24/12/10.1093_molbev_msm210/2/m_molbiolevolmsm210f01_lw.jpeg?Expires=1750268354&Signature=FbJz9XRuDRr4jPF7TMJOQT5DJSquS1LJFgdiv81JqYWfzcbtoMf~lykv~bsZP484CtEKADmKEuD3Pkc3CfujN34lYJ~TIcLz7acodAVp1RMWG0Hu6Pr40QfViqfpuy5sQW0SQz1D2tLcixh~oPDPSq5vrtgld-1ZiqkksmwVilEk3Yu6R0tBW0G-~LcYQRJnckomQD2hVna6U6~PCE1aRV7xe0NBBk-IAEYbrX0bSFx~KxkVSEtUbioi9AmjrxuIfl8dr4CLZWWj88UDxryV7b~BTnY0vQx9aa6vwdnQadTcqHtHc~loUZSpdgD6NJo47znxwSoNDD~2RfHyHNNuTQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Relationship between slope coefficients (ß) of linear regression models fitted to codon abundance patterns across (A) the 5′ ends and (B) the 3′ ends of mouse and Drosophila internal exons, respectively. Each data point represents one degenerate codon. Negative values indicate that the respective codon is relatively more frequent near the intron–exon boundary. The steeper the negative/positive slope the more dramatic the preference/avoidance trend (for details on particular codons, see supplementary table 1 [Supplementary Material online]). Slope coefficients, taken to indicate similar preference or avoidance patterns, are highly correlated (ßDrosophila ∼ ßhuman 5′: Spearman's r = 0.74, 3′: r = 0.77; ßDrosophila ∼ ßmouse 5′: r = 0.74, 3′: r = 0.71; all: P < 2.2E−16, N = 59), that is, similar codons are preferred or avoided in mouse and Drosophila at exon termini, respectively.
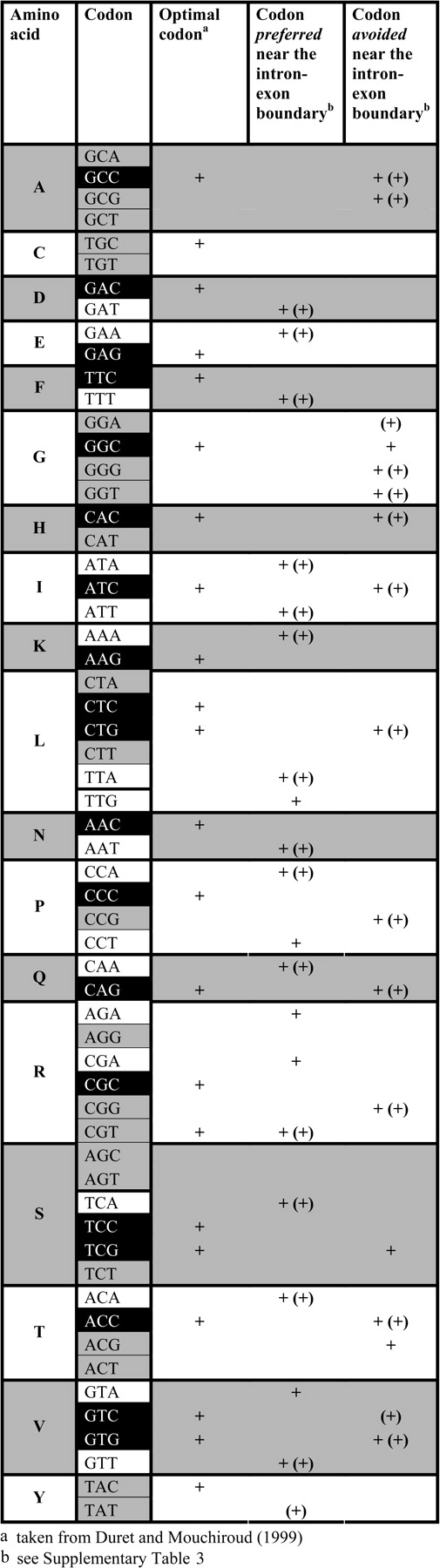
Information on optimal codons and relative codon abundance near intron–exon boundaries for all degenerately coded amino acids in Drosophila melanogaster. A codon is marked as preferred or avoided near the intron–exon boundary when there is a significant correlation between distance from the boundary and relative codon abundance after correction for multiple testing (see supplementary table 3, Supplementary Material online). Significant correlations obtained using a random 50% sample of the original set of genes are marked (+). Note that ‘preferred’ codons and optimal codons form almost perfectly exclusive groups and that, moreover, optimal codons are frequently classified as ‘avoided.’ See Material and Methods for the relevance of differential codon shading.
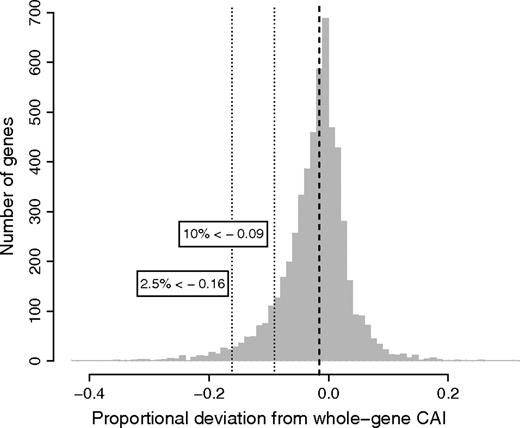
Distribution of proportional deviations of CAIcore from CAIwhole-gene for Drosophila genes with a minimum of 192 nt in concatenated flank as well as core regions (N = 5,529). The dashed line indicates the median (median deviation = −0.0151, P = 0, Wilcoxon signed-rank test). Dotted lines and associated labels indicate that CAIcore values for 10% (2.5%) of genes are at least 9% (16%) larger than CAI values derived under inclusion of sequence flanking intron–exon boundaries.
Supplementary table 4 (Supplementary Material online) contains a full list of codes and weights for all informative codons.
Results
Trends in Codon Usage near Intron–Exon Boundaries Are Well Conserved and Reflect ESE Nucleotide Content
In human and mouse, relative amino acid abundances change as one approaches the intron–exon boundary, and these changes are well predicted by the involvement of the underlying codons in ESEs (Parmley et al. 2007). A subsequent analysis revealed that equivalent patterns exist in Drosophila exons and that amino acids preferred or avoided near intron–exon junctions correspond almost perfectly to those observed in vertebrates (Warnecke T, Parmley JL, Hurst LD, unpublished data). We now confirm that this correspondence extends to the codon level, just as it does in mammals (Parmley and Hurst 2007).
We fitted linear regression models to describe each trend in codon abundance (relative codon usage vs. distance from intron–exon boundary). A negative slope indicates a codon preferred near boundaries. We then compared the slope coefficients (ß), as a measure of both the direction and strength of preference trends, for all degenerate codons between Drosophila and vertebrates. We found them to be very highly correlated (fig. 1). This indicates a striking level of conservation of patterns of codon usage across metazoa in the vicinity of exon–intron boundaries. Moreover, given that vertebrate patterns can be accounted for in large part by the need to specify SR-binding motifs (i.e., ESEs) (Parmley and Hurst 2007; Parmley et al. 2007), this strongly suggests that ESE coding might also explain abundance trends in the vicinity of intron–exon boundaries in Drosophila.
Are the codons preferred near boundaries rich in A and depleted for C as expected if owing to selection on ESEs? We find this to be so: codons significantly enriched near the boundary are uncommonly rich in A (43% of nucleotides) but depleted in C (10%), whereas the reverse is observed in codons that are avoided (A: 8%, C: 27%; chi-square test statistic = 7.6, P < 0.006), a pattern also characteristic of ESEs in vertebrates (Parmley et al. 2007).
Translationally Optimal Codons Are Not Splice Optimal Codons
Were the translational selection model correct, we should expect that those codons preferred near splice sites should, owing to weaker Hill–Robertson interference, be the translationally optimal ones, just as such codons are enriched at the periphery of intronless genes. Are then codons favored near boundaries translationally optimal? Figure 2 shows significant codon abundance trends near the boundary across internal exons in Drosophila (applying Bonferroni-corrected significance thresholds; see supplementary table 1 (Supplementary Material online) for statistics for boundary-proximal trends for all codons) alongside information on which codon is translationally optimal for any one degenerately coded amino acid. We find that, with the exception of CGT, codons putatively involved in ESEs (preferred near the boundary) are never translationally optimal codons. Furthermore, translationally optimal codons are frequently avoided near the boundary. It follows that a majority of synonymous codons (37/59 = 62.71%) can be reconciled with either exonic splicing regulation or translation efficiency but not both, whereas only a single codon caters for both needs (CGT: 1/59 = 1.69%), with the remaining codons not attributable to either group (21/59 = 35.59%).
Adaptation for Translation Efficiency Is Lower in Exonic Sequence Flanking Introns
Given the above results, we should expect that exon cores should be enriched in translationally optimal codons compared with exon flanks. Moreover, we should expect that the difference between cores and flanks should be more marked for highly expressed genes. To address these issues, we compiled a set of 9,745 nuclear Drosophila genes for which reliable expression and sequence information were available (see Material and Methods). The majority of primary transcripts (8,042/9,745 = 83%) are interrupted by at least one intron. In the absence of comprehensive protein abundance data for Drosophila, we approximated translation levels by transcription levels in adult fruitfly as determined by microarray analysis. We use the CAI (Sharp and Li 1987) as a measure of adaptation for translational efficiency (see Material and Methods).
As previously reported (Duret and Mouchiroud 1999; Bierne and Eyre-Walker 2006), quantitative differences in expression correlates with CAI, explaining approximately 9% of the variance in CAI (supplementary fig. 1, Supplementary Material online). To test the splice constraint model, we examined the difference in CAI between sequence in the center of exons (cores) and sequence proximal to introns (flanks) for individual genes (ΔCAI = (CAIcore − CAIflank)/((CAIcore + CAIflank)/2)). Flanks were defined as sequence within 48 nt of an intron–exon boundary. This figure was chosen as the vast majority of functional ESEs can be assumed to fall within this region, especially because we know that ESEs function in a position-dependent manner and catalyze splicing less efficiently with increasing distance from the splice site (Graveley et al. 1998).
For each gene, we concatenated all flanks and all cores, respectively, trimmed so that they only contained complete codons. Only genes with a minimum of 192 nt in each category were considered in analyses relating to flank/core differences. This effectively excludes genes with less than 2 introns (48 × 2 × [N = 2] = 192, N being the number of introns) but was considered prudent to avoid misleading CAI values for short sequences. We find that, as expected, for the average gene, adaptation towards translation efficiency is higher in exon cores (median [ΔCAI] = 0.06993, P = 0, Wilcoxon signed-rank test; N = 5,529). The deviation is even stronger considering individual internal exons (≥192 nt), regardless of whether we define cores to be the total exonic sequence minus flanks (≥96 nt; median [ΔCAI] = 0.073, P = 0, Wilcoxon signed-rank test; N = 12,026) or the center-most portion of an exon of equal length to the flanks (=96 nt; median [ΔCAI] = 0.086, P = 0, Wilcoxon signed-rank test; N = 12,026).
Also as predicted, the difference between cores and flanks is more pronounced in highly expressed genes (Spearman's r = 0.04986, P = 0.0002, N = 5,529), albeit marginally so, suggesting that the leverage of selection to produce translationally well-adapted sequence is somewhat lower in regions flanking intron–exon boundaries.
The above results, although certainly supportive of the role of selection for splice efficiency near intron–exon boundaries, fail to explicitly consider the dual demands on selection for translationally optimal codons and for splice optimal codons. To examine this, we developed the CRI to measure to what extent degenerate amino acids in a given sequence are specified by either splice optimal or translationally optimal codons (see Material and Methods). CRI values closer to 1 indicate that there is a greater tendency to encode amino acids with translationally optimal codons. In the current analysis, we examined intragenic differences so that controlling for regional nucleotide background was not considered imperative.
When we computed gene-specific differences in conflict resolution between exon cores and flanks (ΔCRI) for the same set of genes (N = 5,529), we found that, on average, exon cores have lower CRI values (median [ΔCRI] = −0.0285, P = 0, Wilcoxon signed-rank test; N = 5,529) indicating, as expected, that the conflict is resolved in favor of translation efficiency more frequently than in exon flanks. We obtained qualitatively equivalent results when we determined codon abundance trends from a random 50% sample of genes (indicated in parentheses in fig. 2) and use those trends to calculate CRI in the remaining 50% of genes.
Like ΔCAI, ΔCRI shows a weak association with expression in the expected direction (Spearman's r = −0.0385, P = 0.004, N = 5,592). These results support the conclusions made on the basis of ΔCAI values but tie them more cogently to both conflicting coding demands. Redefining flanks to be shorter only strengthens the results (flank: 21 nt, minimum concatenated flank 84 nt: ΔCAI = 0.109, ΔCRI = −0.0452, N = 5,498; flank: 30 nt, minimum concatenated flank 120 nt: ΔCAI = 0.091, ΔCRI = −0.038; N = 5,809; all P << 0.0001), presumably because shorter flanks can be expected to have higher average ESE density (Fairbrother, Holste, et al. 2004).
Genes with a Higher Proportion of Coding Sequence near the Boundary Exhibit Lower CAI, but the Effect Is Weak
The above results all strongly argue against the translational selection/Hill–Robertson model and for the splice constraint model as an explanation for altered codon usage near exon–intron boundaries in Drosophila. Assuming this, we can then ask how much selection for translationally optimal codons is underestimated if a gene has introns. Making the assumption that CAI in core regions more adequately reflects the degree to which codon usage has been optimized for translation efficiency, we can estimate the error introduced when looking at the entire coding sequence of a gene. Figure 3 plots the proportional deviation of core CAI from whole-gene CAI. The median of the distribution is shifted to the left (median = −0.0151, P = 0, Wilcoxon signed-rank test; N = 5,529) suggesting that whole-gene estimates of CAI will on average underestimate true adaptation by 1.5% in comparison to intronless genes where CAIcore = CAIwhole-gene. Thus, the average effect of eliminating exon flanks when calculating CAI is very modest in quantitative terms. However, for an appreciable proportion of genes, CAI is underestimated rather more substantially (see fig. 3).
The above results suggest that genes with a high proportion of coding sequence near (e.g., within 50 nt) intron–exon boundaries should, other things being equal, show less optimal adaptation for translational efficiency. But, on the gene level, how strong is any such effect compared with other predictors of CAI? Given that the proportion of sequence near the boundary (proportion of sequence within 50 nt of an intron–exon boundary [Prop50]) is correlated to known predictors of codon usage bias, notably protein length (Spearman's r = −0.5609, P = 0, N = 5,529), often in a nonlinear fashion, we employed an ordinal logistic regression model to tease out any independent contribution of Prop50.
CAIwhole-gene values were partitioned into bins containing an equal number of genes and used as the dependent variable. Prop50 was entered alongside other variables (table 1) as a potential predictor. The variance explained by such a model is necessarily small because we lose prodigious amounts of information by considering ordinal bins. However, we can nonetheless gain an insight into whether Prop50 makes an independent contribution, its relative size and direction. We recover (in order of relative contribution) expression level, protein length, total length of intronic sequence (compare Comeron and Kreitman 2002), and also Prop50 as independent predictors of CAI. Table 1 contains the results of a mixed stepwise ordinal logistic regression model using 10 bins, but the results are robust for a range of bin sizes (supplementary table 2, Supplementary Material online).
Results from an Ordinal Logistic Regression (10 Bins, Stepwise Mixed Parameter Selection)
| Parameter | Wald/Score Chi-Squarea | P | R2 | Step Entered |
| Expression level | 585.1109 | 0* | 0.0306 | 1 |
| Protein length | 127.3125 | 0* | 0.0371 | 2 |
| Length of intronic sequence | 29.64017 | 0* | 0.0385 | 3 |
| Prop50 | 7.848092 | 0.0051* | 0.0389 | 4 |
| Number of introns | 0.39133 | 0.5316 | Not applicable | Not entered |
| Parameter | Wald/Score Chi-Squarea | P | R2 | Step Entered |
| Expression level | 585.1109 | 0* | 0.0306 | 1 |
| Protein length | 127.3125 | 0* | 0.0371 | 2 |
| Length of intronic sequence | 29.64017 | 0* | 0.0385 | 3 |
| Prop50 | 7.848092 | 0.0051* | 0.0389 | 4 |
| Number of introns | 0.39133 | 0.5316 | Not applicable | Not entered |
Derived from 5,529 genes.
P<0.01.
Results from an Ordinal Logistic Regression (10 Bins, Stepwise Mixed Parameter Selection)
| Parameter | Wald/Score Chi-Squarea | P | R2 | Step Entered |
| Expression level | 585.1109 | 0* | 0.0306 | 1 |
| Protein length | 127.3125 | 0* | 0.0371 | 2 |
| Length of intronic sequence | 29.64017 | 0* | 0.0385 | 3 |
| Prop50 | 7.848092 | 0.0051* | 0.0389 | 4 |
| Number of introns | 0.39133 | 0.5316 | Not applicable | Not entered |
| Parameter | Wald/Score Chi-Squarea | P | R2 | Step Entered |
| Expression level | 585.1109 | 0* | 0.0306 | 1 |
| Protein length | 127.3125 | 0* | 0.0371 | 2 |
| Length of intronic sequence | 29.64017 | 0* | 0.0385 | 3 |
| Prop50 | 7.848092 | 0.0051* | 0.0389 | 4 |
| Number of introns | 0.39133 | 0.5316 | Not applicable | Not entered |
Derived from 5,529 genes.
P<0.01.
The relative contribution of Prop50 is small, consistently less than 5% of the variance explained by expression level, but significant and in the expected direction, that is, genes with higher proportion of sequence near the boundary show lower CAI. The number of introns makes no independent contribution when Prop50 is included but features among the significant predictors when Prop50 is not considered (data not shown). We also find a positive correlation between CAI and the total length of intronic sequence, which might be explained by Hill–Robertson effects, with long interspersed introns reducing selection interference between loci within the same gene (Comeron and Kreitman 2002).
Might Stronger Hill–Robertson Effects near Intron–Exon Junctions Explain Observed Trends?
In drawing conclusions about the relative importance of splice-related selection over selection on translational efficiency in determining codon usage near intron–exon boundaries, we make the assumption that interference is weaker in coding regions flanking introns than in exon cores. The inverse scenario, namely, that Hill–Robertson interference is stronger in sites flanking introns, would provide an alternative explanation of reduced codon bias at intron–exon junctions but appears unparsimonious for 3 reasons.
First, although there is evidence for Drosophila intronic sequence to be frequently under greater selective constraint than synonymous sites (Andolfatto 2005), we would still expect coding sequence, composed to two-thirds of typically much more highly constrained nonsynonymous sites (Andolfatto 2005), to exhibit higher levels of interference. This expectation is confirmed by empirical evidence from Drosophila that the presence of intronic sequence does in fact ameliorate rather then intensify Hill–Robertson interference (Comeron and Kreitman 2002).
Second, such a model fails, for example, to explain why the observed trends should both match those observed in mice and accord with the predicted overrepresentation of A and underrepresentation of C. Finally, the model is inconsistent with data from long exons. If introns impose greater Hill–Robertson interference than exons, then we expect the core regions of very large exons to show the greatest difference in CAI compared with exon flanks, as they would be most distant from the strongly interfering sites. By contrast, if coding sequence imposes stronger interference, we expect core parts of long exons to show lower CAI and less difference between center and flanks. Analysis of long individual exons (upper 5% of exon length distribution equivalent to exons longer than 1,218 nt) supports the second possibility: exon cores show only very weakly higher codon adaptation (median [ΔCAI] = 0.01, P = 0.028, Wilcoxon signed-rank test; N = 1,070) and the difference disappears when defining cores as centrally located sequence of the same length as the flanking regions (=96 nt, median [ΔCAI] = −0.003, P = 0.683, Wilcoxon signed-rank test; N = 1,070). We conclude that our assumption of weaker Hill–Robertson interference in exon flanks is robust.
Discussion
Selection to use translationally optimal codons is phylogenetically widespread but heterogeneous within genomes and even within individual genes, reflecting a complex interplay of neutral and selective forces. In addition, it has become increasingly apparent that selection on synonymous sites is as mechanistically diverse as it is frequent (Chamary and Hurst 2005a, 2005b; Chamary et al. 2006; Resch et al. 2007). Indeed, we are not the first to point out that the presence of multiple selection pressures can lead to conflicts about which synonymous codon to use. For example, the need to encode ribosome-binding motifs has been shown to bring about translationally suboptimal codon choice in Escherichia coli (Smith and Eyre-Walker 2001). Likewise, Carlini et al. (2001) showed for some highly transcribed Drosophila genes that optimal codons are avoided because they would generate adverse mRNA secondary structures (Carlini et al. 2001). Furthermore, 5′ and 3′ regions of genes can show markedly reduced frequencies of optimal codons, likely owing to the presence of regulatory elements (Qin et al. 2004).
Similarly, aside from splice-related selection that we have described here, several other forces may contribute to intragenic variation in codon usage. Qin et al. (2004) showed for some prokaryotes and budding yeast that codon usage bias has a tendency to increase towards the 3′ end of a gene. This is consistent with purifying selection against nonsense errors, which are more costly the more partial protein has already been produced (Bulmer 1988; Eyre-Walker and Bulmer 1993). Systematic intragenic variation is also associated with differences in domain-specific functional importance of amino acid residues (Lin et al. 2003), trinucleotide repeats (Desai et al. 2004), and the origin and differential expression history of gene parts (chimeric jingwei gene in Drosophila) (Zhang et al. 2005). That participation of sequence in alternative or constitutive exons (Iida and Akashi 2000) also correlates with codon usage may reflect expression-related selection or splice-related selection.
These findings and the current study highlight that, to understand both intra- and interlocus variation in codon usage, we need to be aware that competing demands on synonymous sites exist and that selection can modify codon usage on a very fine spatial scale. Codon bias in a larger sequence is unlikely to be the result of forces acting homogeneously across the sequence range but rather constitutes the combined effect of regional sequence characteristics and locally resolved conflicting selection pressures.
A further important corollary of our work is that one should not extrapolate findings from single-exon genes to single exons within genes. Although for single-exon genes, codon usage bias in Drosophila follows a U-shaped trajectory, considered to be owing to Hill–Robertson interference (Comeron and Kreitman 2002; Qin et al. 2004; Comeron and Guthrie 2005), the opposite is true in individual exons. Although Hill–Robertson forces might still be present (they may indeed make selection on splice efficiency less subject to interference), they do not leave their mark as an enrichment in translationally optimal codons in the vicinity of intron–exon boundaries.
That splice-related selection dominates over translational selection at the flanks of exons has at least 2 further important implications. First, attempts to ascertain what sequence functions as ESEs are typically labor intensive and require a considerable amount of experimentation. If we assume that the patterns in codon usage in the vicinity of intron–exon boundaries reflect selection for preservation of ESEs, rather than selection for translationally optimal codons, this opens up the possibility of inferring the sequences that have a high probability of functioning as ESE, given nothing more than a well-annotated genome. Those codons with negative slopes are more likely to be involved, those with positive slopes less likely. Translating this possibility into a robust method is beyond the scope of this paper and is left to future work.
Second, given that Drosophila's patterns of codon usage near intron–exon boundaries correlates so well with that in mammals, inference from sequence alone can be drawn as to whether a species uses SR proteins bound to ESEs in the splicing process. If we find the same A-rich and C-poor codons preferred near boundaries, we may, with no more information, conclude that the species in question employs SR protein–based mechanisms for intron removal.
T.W. is funded by the Medical Research Council, United Kingdom.
References
Author notes
Dan Graur, Associate Editor



