-
PDF
- Split View
-
Views
-
Cite
Cite
Keyue Ding, Kaixin Zhou, Jing Zhang, Joanne Knight, Xuegong Zhang, Yan Shen, The Effect of Haplotype-Block Definitions on Inference of Haplotype-Block Structure and htSNPs Selection, Molecular Biology and Evolution, Volume 22, Issue 1, January 2005, Pages 148–159, https://doi.org/10.1093/molbev/msh266
Close - Share Icon Share
Abstract
It has been recently suggested that the human genome is organized as a series of haplotype blocks, and efforts to create a genome-wide haplotype map are already underway. Several computational algorithms have been proposed to partition the genome. However, little is known about their behaviors in relation to the haplotype-block partitioning and haplotype-tagging SNPs selection. Here, we present a systematic comparison of three classes of haplotype-block partition definitions, a diversity-based method, a linkage-disequilibrium (LD)–based method, and a recombination-based method. The data used were derived from a coalescent simulation under both a uniform recombination model and one that assumes recombination hotspots. There were considerable differences in haplotype information loss in the measure of entropy when the partition methods were compared under different population-genetics scenarios. Under both recombination models, the results from the LD-based definition and the recombination-based definition were more similar to each other than were the results from the diversity-based definition. This work demonstrates that when undertaking haplotype-based association mapping, the choice of haplotype-block definition and SNP selection requires careful consideration.
Introduction
There is currently great interest in the prospect of statistically powerful genetic association studies to identify the genetic variants that increase susceptibility to human complex diseases. The haplotype-based approaches to the analysis of candidate genes and genome-wide linkage-disequilibrium (LD) mapping have gained central stage (Hoehe 2003). To design these studies appropriately, it is important to understand the pattern of LD in candidate genes or genomic regions of interests (Kruglyak 1999). It has been suggested that the pattern of LD in the human genome cannot be reconciled with a uniform distribution of recombination events, but crossovers appear to be localized in short hotspots that separate longer stretches of DNA (i.e., haplotype blocks) (Daly et al. 2001; Jeffreys, Kauppi, and Neumann 2001; Goldstein et al. 2001; Patil et al. 2001; Stumpf 2002). Each haplotype block, in which the genome is largely made up of regions of low diversity, can be characterized by a small number of SNPs, which are referred to as haplotype-tagging SNPs (htSNPs) (Johnson et al. 2001). The haplotype-block model has important implications for LD mapping, because it implies that, by identifying haplotype blocks, it is possible to predict the likely configurations of alleles at unobserved sites (Wall and Pritchard 2003). The construction of haplotype block and selection of htSNPs presents a possible way to reduce the complexity of the problem of association mapping of complex diseases.
Thus far, a consensus definition for haplotype blocks based on the LD structure has not been established. However, a range of operational definitions has been used to identify haplotype-block structures (Patil et al. 2001; Gabriel et al. 2002; Wang et al. 2002; Zhang et al. 2002), which can be roughly classed into three groups. First, there are methods based on diversity in the sequence, such as that of Patil et al. (2001) and Zhang, et al. (2002), which define blocks so as to enforce low sequence diversity by some diversity measure within each block. The second group consists of LD methods, such as that of Gabriel et al. (2002), which define blocks so as to enforce generally high pairwise LD within blocks and generally low pairwise LD between blocks. Finally, there are methods that look for direct evidence of recombination, such as that of Wang et al. (2002), using the four-gamete test developed by Hudson and Kaplan (1985) and defining blocks as apparently recombination-free regions. Recently, Schwartz et al. (2003) examined the validity of the haplotype-block concept by comparing block decompositions derived from two public empirical data sets by several leading methods of block detection. They concluded that the different block-finding algorithms identify similar structure to an extent that cannot be explained by chance, and the absolute correspondence between block assignments can differ markedly in response to changes in both block definition and optimization criterion. However, there is still a lack of studies that systematically compare identification of haplotype blocks and selection of htSNPs under these various definitions. Whether these different haplotype-block definitions show similar behaviors on the haplotype-block partition and htSNPs selection is still unclear.
Using simulation studies, we explored three popular methods for defining haplotype blocks and their behaviors under different population-genetics scenarios and two distinct recombination models. Furthermore, we compared average haplotype-block size, average htSNPs number, and average information loss identified by each method, because these variables are critical in association mapping. We also compared the proportion of the genome covered by blocks. Our article aims to address three issues: (1) How are the properties of different haplotype-block definitions affected by population-genetics parameters? (2) Are different haplotype-block definitions affected by different recombination models? (3) What is the impact of haplotype-block definitions on htSNPs selection?
Materials and Methods
Haplotype-Block Definitions
We compared the effect of three major methods to define haplotype blocks on htSNPs selection: diversity-based (Patil et al. 2001; Zhang et al. 2002), LD-based (Gabriel et al. 2002), and recombination-based (Wang et al. 2002). The different methods are described in detail in the original papers and briefly summarized below.
For a diversity-based test, Patil et al. (2001) defined a haplotype block as a region in which a fraction of α percent or more of all the observed haplotypes are represented at least n times or at a given threshold in the sample. The particular case implemented in our study required that in haplotype blocks, at least 80% of the observed haplotypes should be observed in at least 5% of the sample. To implement this method, we applied the optimization criteria outlined by Zhang et al. (2002). Their paper describes a general algorithm that defines block boundaries in a way that minimizes the number of SNPs that are required to identify all the haplotype in a region. We solved it optimally using the dynamic programming algorithm of Zhang et al. (2002). Secondly, for a LD-based test, we used the method of Gabriel et al. (2002) that defined blocks to be a region in which a small proportion of marker pairs show evidence for historical recombination. We modified the criteria suggested by Wall and Pritchard (2003) for handling haplotype data instead of unphased genotype data. Blocks are partitioned according to whether the upper and lower confidence limits on estimates of pairwise D′ measure fall within certain threshold values. Finally, we use the four-gamete test of Hudson and Kaplan (1985) as the example of a recombination-based test (Wang et al. 2002), which defined blocks as apparently recombination-free regions under the infinite-sites assumption.
Statistic for Comparing Block Partitions
htSNPs Selection Algorithm
There is currently no consensus on the best criterion to use to select a set of htSNPs that will capture most information in the haplotype block (Goldstein et al. 2003). We used the criteria that at least 80% of haplotypes that occur in at least 5% of the sample could be explained by the htSNPs (Zhang et al. 2002; Patil et al. 2001). To decrease the running time and guarantee the optimal selection of htSNPs in simulated data set, which has been proved to be an NP-complete problem (Garey and Johnson 1979), we used the branch-and-bound algorithm (De Bontridder et al. 2002) to select htSNPs in each haplotype block.
Evaluation of htSNPs Selection in the Simulated Haplotype
Simulation Data Sets
The coalescent process is a powerful tool for population genetics, which is used to model a wide variety of biological phenomena (Hudson 1983; Fu and Li 1999). A helpful simulation tool (e.g., mksamples [Hudson 2002]) was provided to generate realistic data under various population scenarios about underlying biology and demography. We used this tool to simulate the genetic data under the uniform recombination rate. To simulate the genetic data under the simple single-hotspot model for recombination variation, we used the algorithm in Li and Stephens (2003) to postprocess the output from mksamples.
Coalescent Model with Uniform-Recombination Rate
We followed the methods suggested in Wang et al. (2002) to simulate the data set under the uniform recombination rate. The simulations had a sample size of n = 50 (n is the number of chromosomes) under the variable population-mutation rate (θ = 4Neμ, where Ne is the effective population size and μ is the mutation rate per locus per generation) and population-recombination rate (ρ = 4Ner, where r is the recombination rate per locus per generation). To examine the effects of population parameters on haplotype-block pattern and htSNPs selection under the different haplotype-block definitions, we simulated a data set using three values of θ (5, 10, and 25) and varying ρ from 0.1θ to 5.0θ. The three values of θ corresponds to Ne of 2,000, 4,000, 10,000, respectively, μ, the mutation rate is fixed at 10−9 per site per year.
Furthermore, we examined the contribution of θ to haplotype-block characteristics by allowing θ to vary for fixed values of ρ (ρ = 0.4, 2, 6, and 10, respectively). We set θ = 1, 2, 3, 4, 5, 6, 7, 8, 10, 15, 20, and 25.
Coalescent Model with Recombination Hotspot
For simulating the genetic data under recombination hotspot, we assumed that haplotype blocks with a low recombination rates are separated by short recombination hotspot. We used the algorithm in Li and Stephens (2003) to postprocess the output from mksamples (Hudson 2002) to simulate data under the single-hotspot model for recombination variation. We illustrated this algorithm as follows:
Suppose a sample was simulated with approximately S segregating sites. The background recombination rate is ρ. A hotspot of width w = (b − a) lies between positions a and b, with recombination rate λρ where λ > 1, which quantifies the magnitude of the recombination hotspot. We followed these steps:
Simulate samples with S′ = (1 + w(λ − 1))S segregating sites and constant recombination rate ρ′ = (1 + w(λ − 1))ρ by mksamples program.
Multiply the position of each site by a factor of 1 + w(λ − 1).
Randomly delete sites within a and a + wλ with a probability of 1 − 1/λ.
For the remaining sites within a and a + wλ, shrink the distance of adjacent sites by a factor of λ.
Shift the positions of the sites to the right of the hotspot (subtract w(λ − 1)).
Each data set was simulated to have about 120 segregating sites and n = 50, with variable ρ (from 1 to 25), and variable λ (20, 50, and 100). The recombination hotspot was located in the center of the region, where a = 0.48 and b = 0.52 (i.e., the recombination hotspot has a width of 1 kb).
We ran 1,000 replicates for all of the simulations. Programs for the analyses were written in C++ or Perl and are available from the authors on request.
Empirical Data Sets
Polymorphism data (both SNPs and indels) were downloaded from the SeattleSNPs on August 23, 2003. A total of 130 loci were available on that date. The data were obtained by DNA resequencing of 24 unrelated African Americans and 23 unrelated European Americans from the Coriell Cell Repository. We reconstructed the haplotype from these unphased genotypic data by using PHASE (Stephens, Smith, and Donnelly 2001).
Results
Coalescent Model with Uniform Recombination
First, we demonstrated the behaviors (i.e., haplotype-block partition, htSNP selection, and haplotype information loss) of different haplotype definitions in a simple way. Under the coalescent model with a uniform recombination framework, the properties of different haplotype-block definitions were affected by the population parameters (e.g., the effective population size and recombination rate). The relationships between the average haplotype-block size, the average htSNPs number, and the average information loss with population parameters were shown in figure 1. In this figure, ρ varied from 0.1θ to 5.0θ, which corresponded to a change in r from 0.25 × 10−8 to 12.5 × 10−8 per generation for the mutation rate μ = 10−9 per site per year (Satta et al. 1993). With increasing ρ, the average haplotype-block sizes decreased, and the average htSNPs number increased for a fixed θ. It is obvious that when population parameters are fixed, the average information loss decreases with increasing average htSNPs numbers. For a fixed ρ, as θ increases, the average haplotype-block size decreases and the average information loss decreases.
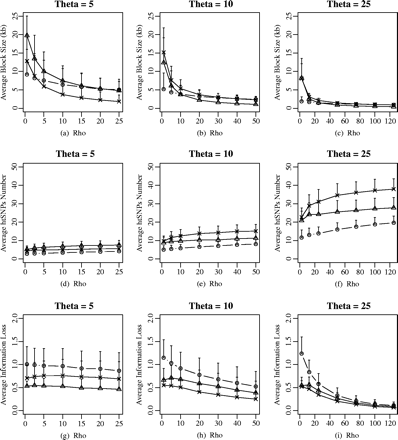
The effect of population parameters on haplotype-block characteristics and htSNPs selection under different haplotype-block definitions: average haplotype-block size ±SD, average htSNPs number ±SD, and average information loss ±SD versus recombination level (in units of θ) for a sample size of 50. The effective population size (Ne) was adjusted by fixing the ratio of ρ/θ. The value of θ considered is 5, 10, and 25, which corresponds to Ne of 2,000, 4,000, and 10,000, respectively. The different labels in the figure represent different haplotype block definitions: circle, diversity-based method; triangle, LD-based method; star, recombination-based method.
The different haplotype-block definitions also affected these descriptive statistics (fig. 1). In terms of haplotype information loss, when θ is similar to ρ, the recombination-based method appears much closer to the LD-based method than either of those to the diversity-based method. When ρ was small (less than 1θ), the average haplotype-block sizes were larger in LD-based method and recombination-based method than that in diversity-based method. For a fixed θ and ρ, the average htSNPs number was larger in the LD-based and recombination-based method than in the diversity-based method. The diversity-based method had less htSNPs on average than the other two methods, which would reduce the genotyping cost of htSNPs-based association study. However, there was more loss of haplotype information because of reduced number of htSNPs. When θ was small, there was not much difference in the average htSNPs number under the different haplotype-block definitions (fig. 1d), whereas with increasing θ, the difference increased. For large ρ and θ, the average information loss under the diversity-based method was the same as that under the other two methods. The properties of different haplotype-block definitions demonstrated that the htSNPs-based association mapping was highly variable.
To further characterize the haplotype-block pattern in the simulated data set, that is, to illustrate whether the haplotype-block model can explain the whole LD structure, we prepared plots that showed the parts of each region that were contained in haplotype blocks of various sizes (fig. 2). These plots indicated that the population-genetics parameters, as well as the different haplotype-block definitions affected the distribution of haplotype-block sizes. As might be expected, there was an inverse correlation between the proportion of sequence that was contained in haplotype blocks and the recombination rate. Relatively smaller blocks were identified with the higher population effective size. In this figure, the different haplotype-block definitions also demonstrated the block size distribution. For the diversity-based method (fig. 2a–c), approximately 20% of the chromosome regions could not be covered by haplotype block under the different ratio of ρ/θ for a fixed θ; even with the effective population size (Ne) increasing from 2,000 or 4,000 to 10,000, approximately 20% of the chromosome regions could not be covered and the proportions of relatively small blocks (0–5 kb) increases from approxiamtely 20% to approximately 60%. It should be noticed that there is more variance in the proportions that cannot be covered by haplotype block for LD-based methods (fig. 2d–f), increasing from approximately 20% to approximately 80% when ρ/θ increased from 0.1 to 5 under different population effective size (Ne). It also showed that the haplotype block with larger size (>10 kb) could be observed when and only when ρ/θ was small. For the recombination-based method (fig. 2g–i), approximately 10% to approximately 30% of the chromosome regions could not be covered with haplotype blocks. When ρ/θ ≤ 2, there was much variance in the haplotype-block distribution; whereas when ρ/θ > 2, the distribution was not affected by recombination rate ρ.
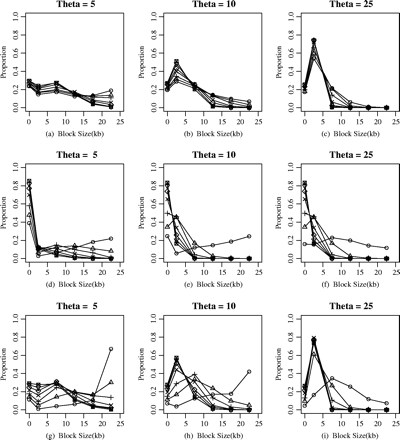
The effect of population parameters on the proportion of sequences contained in haplotype blocks of various sizes under different haplotype-block definitions; the proportion versus the block size. The different lines in the plot panel represent the different ratios of ρ/θ, from 0.1 to 5.0, and each point demonstrates the proportion of sequence contained in haplotype blocks with the size between the adjacent intervals in the abscissa. The haplotype-block definition in the plot panel: (a–c) diversity-based method, (d–f) LD-based method, and (g–i) recombination-base method. The different labels in the figure represent the different ratios of ρ/θ: circle, ρ/θ = 0.1; triangle, ρ/θ = 0.5; plus sign, ρ/θ = 1; star, ρ/θ = 2; diamond, ρ/θ = 3; reverse triangle, ρ/θ = 4; square, ρ/θ = 5.
Furthermore, we studied the behaviors of the different haplotype-block definitions when θ was allowed to vary for fixed values of ρ (fig. 3). For each ρ in figure 3, the average haplotype-block size increased slightly when θ was very small and then decreased until an equilibrium value of θ was reached for each of the haplotype-block definitions. A low θ value would lead to a small number of markers in the populations and samples, regardless of whether this is caused by either a low mutation rate or low SNP density (Wang et al. 2002). When θ was small, the size of block covered by SNP markers was comparatively small. When θ increased, the covered region became larger, whereas the block number remained the same. With θ increased further, the increasing block number led to the average block size decreasing. However, there was more variance between the different haplotype-block definitions when ρ was very small, even when θ was also small. The plot in figure 4 showed the effect of different haplotype-block definitions under the different parameters. For the diversity-based method, the average haplotype-block size decreased more dramatically when θ > 4, and decreases with increasing θ in a similar trend for the four different values of ρ (fig. 4a). The average block size almost remained the same for a given θ under the four different values of ρ. For the LD-based and recombination-based methods, the population-recombination rate ρ affected the average haplotype-block size to a great extent (fig. 4b–c). With the ρ increased to 10, the average haplotype-block size was similar for different haplotype-block definitions. There was a positive correlation between the average htSNP number and θ for a fixed ρ (fig. 3e–h). Although less average htSNPs were selected for the diversity-based method, there was more information loss in comparison with the LD-based and recombination-based methods (fig. 3i–l).
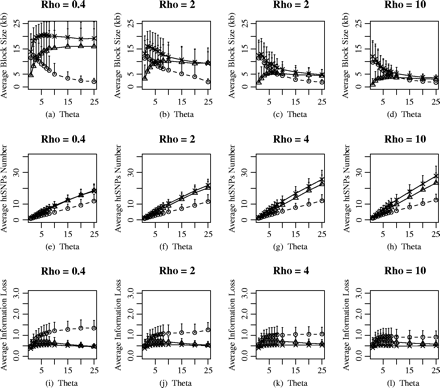
The effects of mutation rate or SNPs marker density of haplotype-block characteristics and htSNPs selection. The population-recombination rate ρ considered is 0.4, 2, 6, and 10 and the population mutation rate θ is set as 1 to 25.The plot (a–d) demonstrate the average block size versus θ; (e–h) the average htSNPs number versus θ; (i–l) the average information loss versus θ. The different labels in the figure represent the different haplotype-block definitions: circle, diversity-based method; triangle, LD-based method; star, recombination-based method.
The effects of θ on average block size for a given fixed ρ under the diversity-based, the recombination-based, and the LD-based haplotype-block definition, respectively. The different labels in the figure represent the different population-recombination rate ρ: circle, ρ = 0.4; triangle, ρ = 2; star, ρ = 4; reverse triangle, ρ = 10.
Coalescent Model with Recombination Hotspot
Recent experimental findings suggest that the assumption of a homogeneous recombination rate along the human genome is too naïve (Daly et al. 2001; Jeffreys, Kauppi, and Neumann 2001; Johnson et al. 2001). These findings point to block-structured and certain regions (i.e., hotspots) that are more prone than others to recombination. To further study the behaviors of the different block definitions on block partitioning and htSNPs selection, we simulated the data under the coalescent model with recombination hotspots. Several recent studies have modeled the recombination hotspots based on the coalescent process (Wiuf and Posada 2003; Li and Stephens 2003). We simulated data sets under the simple single-hotspot model in which the data sets were simulated to have about 120 segregating sites and 50 chromosomes, the value of ρ varied from 1 to 25, and λ = 20, 50, 100, respectively. The recombination hotspot was assumed to be located in the middle of the simulated region with width of 1 kb. Figure 5 illustrates the different results from the different haplotype-block definitions on haplotype-block partition under this model. In this figure, the recombination hotspot could not be recognized by the diversity-based method under various scenarios. For recombination-based and LD-based methods, the average haplotype-block sizes of 10 to 15 kb could be observed when the background recombination is low (ρ = 1, corresponding to the recombination rate of 0.1 CM/MB, given Ne = 10,000). The average block size decreased with the increase of background recombination rate until an equilibrium value was reached (ρ > 10), where the three haplotype-block methods showed similar values of average block size. It is surprising to find that LD-based methods and recombination-based methods showed the consistent behaviors in average haplotype-block size (fig. 5a–c). To observe the haplotype-block size distribution, we prepared the plots that indicated the parts of each region that were contained in haplotype blocks of various sizes for the simulated data sets (fig. 6). For the diversity-based method, relatively small haplotype-block sizes (0–5 kb) accounted for approximatrly 60% of the chromosome regions under the different background recombination rates and the different recombination intensity (fig. 6a–c). The proportion of haplotype-block sizes of 10 to 15 kb is 30% to 40% when the background recombination rate is low (ρ = 1 or 2) for the LD-based method (fig. 6d–f) and the recombination-based method (fig. 6g–i). When ρ increased to 3, the proportion drops to approximately 10%. The average htSNPs number increased slightly with the background recombination rate. In comparison with the LD-based and the recombination-based methods, the average htSNPs number was much less under the diversity-based method (fig. 5d–f), which led to much more loss of haplotype information (fig. 5g–i).
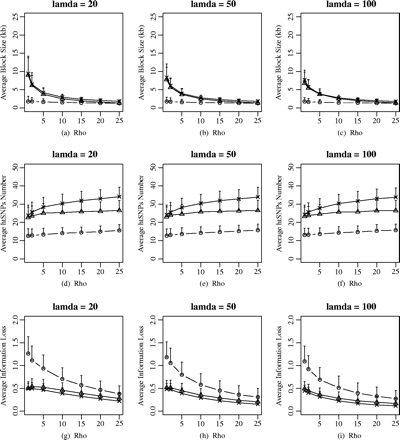
The effects of background recombination rate (ρ) and the magnitude of recombination hotspot (λ) on haplotype-block characteristic and htSNPs selection. In the coalescent with recombination model, we assume the genome region with approximately 120 segregating site, and the value of background recombination rates are 1, 2, 5, 10, 15, 20, and 25. The different labels in the figure represent the different haplotype-block definitions: circle, diversity-based method; triangle, LD-based method; star, recombination-based method.

The effect of background recombination rate (ρ) and the magnitude of recombination hotspot (λ) on the proportion of sequence contained in haplotype blocks of various sizes under different haplotype-block definitions; the proportion versus the block size. The different lines in the plot panel represent the different background recombination rates, from 1 to 25, and each point demonstrates the proportion of sequence contained in haplotype blocks, with the size between the adjacent intervals in the abscissa. The haplotype-block definition in the plot panel: (a–c) diversity-based method; (d–f) LD-based method, and (g–i) recombination-base method. The different labels in the figure represent the different background recombination rate (ρ): circle, ρ = 1; triangle, ρ = 2; plus sign, ρ = 5; star, ρ = 10; diamond, ρ = 15; reverse triangle, ρ = 20; square, ρ = 25.
We also studied the effect of the magnitude of recombination at the hotspot, measured by the ratio of the hotspot-recombination rate and the background recombination rate, on the haplotype- block partitioning and htSNPs selection. The average haplotype-block sizes decreased slightly when ρ was low (fig. 5), with the magnitude of recombination hotspot increasing (i.e. λ = 20, 50 and 100). The recombination intensity had little effect on the distribution of different haplotype-block sizes (fig. 6). There was no obvious effect of the magnitude of recombination hotspot on the htSNPs selection and haplotype information loss.
The Block Comparison
The measure derived by Bafna et al. (2003) and Schwartz et al. (2003) was used to determine whether the block boundaries derived from the different methods were comparable. For each data sample in the simulated data set, we calculated the P value for the intersection of the two partitions being random. If the P value is less than a threshold (0.05), the null hypothesis that two partitions are independent could be rejected. We calculated the proportion of samples that had a significant P value from the 1,000 simulated data sets. Table 1 and table 2 show the pairwise comparison of the different methods applied to the simulated data. Under the uniform recombination model, less than half of the 1,000 simulated sample showed that two partitions were related, ranging from 0.005 to 0.498. In comparison, more samples demonstrated dependence under the recombination-hotspot model. The results from both models show some degree of similarity between the LD-based method and the diversity-based method. However, there appears to be no relationship between the diversity-based and the recombination-based methods. This is consistent with the result obtained by analyzing the chromosome 21 haplotype data set and human lipoprotein lipase (LPL) data set (Schwartz et al. 2003). The observation on the average block size in figures 1 and 5 also provided the evidence that recombination-based method and LD-based method showed more similar behavior on the haplotype-block partition than any other pairwise comparison.
The Proportions That Pairwise Comparisons of Haplotype-Block Definitions Showed the Significant P Value in the 1,000 Simulated Data Under Uniform-Recombination Model
. | θ = 5 . | . | . | θ = 10 . | . | . | θ = 25 . | . | . | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ρ/θa . | Ab − Bc . | A − Cd . | B − C . | A − B . | A − C . | B − C . | A − B . | A − C . | B − C . | ||||||
| 0.1 | 0.089 | 0.275 | 0.108 | 0.123 | 0.248 | 0.190 | 0.131 | 0.191 | 0.351 | ||||||
| 0.5 | 0.055 | 0.173 | 0.102 | 0.068 | 0.133 | 0.189 | 0.078 | 0.155 | 0.435 | ||||||
| 1 | 0.034 | 0.115 | 0.081 | 0.047 | 0.128 | 0.167 | 0.067 | 0.128 | 0.426 | ||||||
| 2 | 0.022 | 0.092 | 0.054 | 0.022 | 0.108 | 0.139 | 0.035 | 0.102 | 0.299 | ||||||
| 3 | 0.013 | 0.091 | 0.025 | 0.012 | 0.080 | 0.084 | 0.019 | 0.091 | 0.214 | ||||||
| 4 | 0.005 | 0.082 | 0.021 | 0.016 | 0.063 | 0.050 | 0.014 | 0.088 | 0.159 | ||||||
| 5 | 0.010 | 0.079 | 0.021 | 0.005 | 0.089 | 0.046 | 0.009 | 0.071 | 0.106 | ||||||
. | θ = 5 . | . | . | θ = 10 . | . | . | θ = 25 . | . | . | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ρ/θa . | Ab − Bc . | A − Cd . | B − C . | A − B . | A − C . | B − C . | A − B . | A − C . | B − C . | ||||||
| 0.1 | 0.089 | 0.275 | 0.108 | 0.123 | 0.248 | 0.190 | 0.131 | 0.191 | 0.351 | ||||||
| 0.5 | 0.055 | 0.173 | 0.102 | 0.068 | 0.133 | 0.189 | 0.078 | 0.155 | 0.435 | ||||||
| 1 | 0.034 | 0.115 | 0.081 | 0.047 | 0.128 | 0.167 | 0.067 | 0.128 | 0.426 | ||||||
| 2 | 0.022 | 0.092 | 0.054 | 0.022 | 0.108 | 0.139 | 0.035 | 0.102 | 0.299 | ||||||
| 3 | 0.013 | 0.091 | 0.025 | 0.012 | 0.080 | 0.084 | 0.019 | 0.091 | 0.214 | ||||||
| 4 | 0.005 | 0.082 | 0.021 | 0.016 | 0.063 | 0.050 | 0.014 | 0.088 | 0.159 | ||||||
| 5 | 0.010 | 0.079 | 0.021 | 0.005 | 0.089 | 0.046 | 0.009 | 0.071 | 0.106 | ||||||
The ratio of population-recombination rate and population mutation rate.
Diversity-based definition.
LD-based definition.
Recombination-based definition.
The Proportions That Pairwise Comparisons of Haplotype-Block Definitions Showed the Significant P Value in the 1,000 Simulated Data Under Uniform-Recombination Model
. | θ = 5 . | . | . | θ = 10 . | . | . | θ = 25 . | . | . | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ρ/θa . | Ab − Bc . | A − Cd . | B − C . | A − B . | A − C . | B − C . | A − B . | A − C . | B − C . | ||||||
| 0.1 | 0.089 | 0.275 | 0.108 | 0.123 | 0.248 | 0.190 | 0.131 | 0.191 | 0.351 | ||||||
| 0.5 | 0.055 | 0.173 | 0.102 | 0.068 | 0.133 | 0.189 | 0.078 | 0.155 | 0.435 | ||||||
| 1 | 0.034 | 0.115 | 0.081 | 0.047 | 0.128 | 0.167 | 0.067 | 0.128 | 0.426 | ||||||
| 2 | 0.022 | 0.092 | 0.054 | 0.022 | 0.108 | 0.139 | 0.035 | 0.102 | 0.299 | ||||||
| 3 | 0.013 | 0.091 | 0.025 | 0.012 | 0.080 | 0.084 | 0.019 | 0.091 | 0.214 | ||||||
| 4 | 0.005 | 0.082 | 0.021 | 0.016 | 0.063 | 0.050 | 0.014 | 0.088 | 0.159 | ||||||
| 5 | 0.010 | 0.079 | 0.021 | 0.005 | 0.089 | 0.046 | 0.009 | 0.071 | 0.106 | ||||||
. | θ = 5 . | . | . | θ = 10 . | . | . | θ = 25 . | . | . | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ρ/θa . | Ab − Bc . | A − Cd . | B − C . | A − B . | A − C . | B − C . | A − B . | A − C . | B − C . | ||||||
| 0.1 | 0.089 | 0.275 | 0.108 | 0.123 | 0.248 | 0.190 | 0.131 | 0.191 | 0.351 | ||||||
| 0.5 | 0.055 | 0.173 | 0.102 | 0.068 | 0.133 | 0.189 | 0.078 | 0.155 | 0.435 | ||||||
| 1 | 0.034 | 0.115 | 0.081 | 0.047 | 0.128 | 0.167 | 0.067 | 0.128 | 0.426 | ||||||
| 2 | 0.022 | 0.092 | 0.054 | 0.022 | 0.108 | 0.139 | 0.035 | 0.102 | 0.299 | ||||||
| 3 | 0.013 | 0.091 | 0.025 | 0.012 | 0.080 | 0.084 | 0.019 | 0.091 | 0.214 | ||||||
| 4 | 0.005 | 0.082 | 0.021 | 0.016 | 0.063 | 0.050 | 0.014 | 0.088 | 0.159 | ||||||
| 5 | 0.010 | 0.079 | 0.021 | 0.005 | 0.089 | 0.046 | 0.009 | 0.071 | 0.106 | ||||||
The ratio of population-recombination rate and population mutation rate.
Diversity-based definition.
LD-based definition.
Recombination-based definition.
The Proportions That Pairwise Comparisons of Haplotype-Block Definitions Showed the Significant P Value in the 1,000 Simulated Data Under Recombination-Hotspot Model
. | λa = 20 . | . | . | λ = 50 . | . | . | λ = 100 . | . | . | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pb . | Ac − Bd . | A − Ce . | B − C . | A − B . | A − C . | B − C . | A − B . | A − C . | B − C . | ||||||
| 1 | 0.124 | 0.200 | 0.352 | 0.130 | 0.221 | 0.398 | 0.152 | 0.258 | 0.458 | ||||||
| 2 | 0.112 | 0.198 | 0.415 | 0.126 | 0.235 | 0.467 | 0.144 | 0.263 | 0.498 | ||||||
| 5 | 0.113 | 0.195 | 0.457 | 0.096 | 0.218 | 0.454 | 0.118 | 0.245 | 0.453 | ||||||
| 10 | 0.088 | 0.175 | 0.430 | 0.087 | 0.223 | 0.432 | 0.102 | 0.235 | 0.412 | ||||||
| 15 | 0.081 | 0.171 | 0.425 | 0.080 | 0.217 | 0.417 | 0.090 | 0.214 | 0.400 | ||||||
| 20 | 0.065 | 0.161 | 0.431 | 0.060 | 0.189 | 0.403 | 0.062 | 0.188 | 0.355 | ||||||
| 25 | 0.054 | 0.155 | 0.379 | 0.053 | 0.185 | 0.360 | 0.051 | 0.164 | 0.341 | ||||||
. | λa = 20 . | . | . | λ = 50 . | . | . | λ = 100 . | . | . | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pb . | Ac − Bd . | A − Ce . | B − C . | A − B . | A − C . | B − C . | A − B . | A − C . | B − C . | ||||||
| 1 | 0.124 | 0.200 | 0.352 | 0.130 | 0.221 | 0.398 | 0.152 | 0.258 | 0.458 | ||||||
| 2 | 0.112 | 0.198 | 0.415 | 0.126 | 0.235 | 0.467 | 0.144 | 0.263 | 0.498 | ||||||
| 5 | 0.113 | 0.195 | 0.457 | 0.096 | 0.218 | 0.454 | 0.118 | 0.245 | 0.453 | ||||||
| 10 | 0.088 | 0.175 | 0.430 | 0.087 | 0.223 | 0.432 | 0.102 | 0.235 | 0.412 | ||||||
| 15 | 0.081 | 0.171 | 0.425 | 0.080 | 0.217 | 0.417 | 0.090 | 0.214 | 0.400 | ||||||
| 20 | 0.065 | 0.161 | 0.431 | 0.060 | 0.189 | 0.403 | 0.062 | 0.188 | 0.355 | ||||||
| 25 | 0.054 | 0.155 | 0.379 | 0.053 | 0.185 | 0.360 | 0.051 | 0.164 | 0.341 | ||||||
The magnitude of recombination hotspot.
Background recombination rate.
Diversity-based definition.
LD-based definition.
Recombination-based definition.
The Proportions That Pairwise Comparisons of Haplotype-Block Definitions Showed the Significant P Value in the 1,000 Simulated Data Under Recombination-Hotspot Model
. | λa = 20 . | . | . | λ = 50 . | . | . | λ = 100 . | . | . | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pb . | Ac − Bd . | A − Ce . | B − C . | A − B . | A − C . | B − C . | A − B . | A − C . | B − C . | ||||||
| 1 | 0.124 | 0.200 | 0.352 | 0.130 | 0.221 | 0.398 | 0.152 | 0.258 | 0.458 | ||||||
| 2 | 0.112 | 0.198 | 0.415 | 0.126 | 0.235 | 0.467 | 0.144 | 0.263 | 0.498 | ||||||
| 5 | 0.113 | 0.195 | 0.457 | 0.096 | 0.218 | 0.454 | 0.118 | 0.245 | 0.453 | ||||||
| 10 | 0.088 | 0.175 | 0.430 | 0.087 | 0.223 | 0.432 | 0.102 | 0.235 | 0.412 | ||||||
| 15 | 0.081 | 0.171 | 0.425 | 0.080 | 0.217 | 0.417 | 0.090 | 0.214 | 0.400 | ||||||
| 20 | 0.065 | 0.161 | 0.431 | 0.060 | 0.189 | 0.403 | 0.062 | 0.188 | 0.355 | ||||||
| 25 | 0.054 | 0.155 | 0.379 | 0.053 | 0.185 | 0.360 | 0.051 | 0.164 | 0.341 | ||||||
. | λa = 20 . | . | . | λ = 50 . | . | . | λ = 100 . | . | . | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pb . | Ac − Bd . | A − Ce . | B − C . | A − B . | A − C . | B − C . | A − B . | A − C . | B − C . | ||||||
| 1 | 0.124 | 0.200 | 0.352 | 0.130 | 0.221 | 0.398 | 0.152 | 0.258 | 0.458 | ||||||
| 2 | 0.112 | 0.198 | 0.415 | 0.126 | 0.235 | 0.467 | 0.144 | 0.263 | 0.498 | ||||||
| 5 | 0.113 | 0.195 | 0.457 | 0.096 | 0.218 | 0.454 | 0.118 | 0.245 | 0.453 | ||||||
| 10 | 0.088 | 0.175 | 0.430 | 0.087 | 0.223 | 0.432 | 0.102 | 0.235 | 0.412 | ||||||
| 15 | 0.081 | 0.171 | 0.425 | 0.080 | 0.217 | 0.417 | 0.090 | 0.214 | 0.400 | ||||||
| 20 | 0.065 | 0.161 | 0.431 | 0.060 | 0.189 | 0.403 | 0.062 | 0.188 | 0.355 | ||||||
| 25 | 0.054 | 0.155 | 0.379 | 0.053 | 0.185 | 0.360 | 0.051 | 0.164 | 0.341 | ||||||
The magnitude of recombination hotspot.
Background recombination rate.
Diversity-based definition.
LD-based definition.
Recombination-based definition.
We also used the empirical data set from SeattleSNPs to perform pairwise comparison of the different haplotype-block definitions. Relatively small proportions showed that two partitions are related, ranging from 11 to 39 for 130 loci in American descents and European descents, respectively (data not shown).
Discussion
Because of different haplotype-block definitions and reconstruction algorithms, or different subjectively determined thresholds, the haplotype-block pattern varied. Given the importance that haplotype block and htSNPs are believed to have for genome-wide association mapping, we wanted to address several important questions about the nature of different haplotype-block definitions. How do different haplotype-block definitions compare in terms of not only the identification of haplotype blocks but also the proportions of a genome that can be covered by haplotype blocks? How do different haplotype-block definitions compare in terms of htSNPs selection and haplotype information loss? How do these properties affected by population-genetics parameters and different recombination models? From our simulated data, one can see that different haplotype definitions give very different results both on haplotype-block partition and on htSNPs selection.
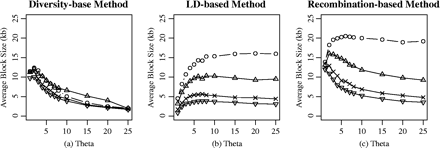
We have observed the varying haplotype-block patterns under different population-genetics scenarios and two coalescent models; that is, with a uniform recombination rate versus recombination hotspots. For the uniform recombination model, the diversity-based method is less sensitive to the population-recombination rate (fig. 1a–c) and population history (figs. 3a–d and 4a–c) than both the LD-based and the recombination-based method. In the recombination-hotspot model, the diversity-based method is unable to recognize the haplotype-block structure in the simulated data set (fig. 5a–c).
The block partition and htSNPs selection results should provide information about the genotyping effort needed to cover a region or the whole genome sufficiently. Results relating to the proportion of the genome covered by blocks varies considerably with population-genetics parameters, when either the LD-based method (figs. 2d–f and 6a–c) or the recombination-based method (figs. 2g–i and 6d–f) are used. The proportion covered by the diversity-based method (figs. 2a–c and 6g–i) is even less variable.
Based on the descriptive statistics and the P value for testing whether the two haplotype-block methods are related, we conclude that the recombination-based method appears to be much closer to the LD-based method than either of those is to the diversity-based method under these two recombination models. This conclusion is consistent with the empirical data analysis on the Patil et al. (2001) 21-chromosome haplotype data and the Nickerson et al. (2000) LPL data by Schwartz el al. (2003). These results should be tested on more empirical data because only less than half of the P value showed the two methods are related in our simulations and empirical data analysis.
How can these differences across the different haplotype-block definitions be explained? In our simulation study, under both the recombination-uniform model and the recombination-hotspot model, our results indicate that population-recombination rate and population history have critical effects on the haplotype-block partitioning under different haplotype-block definitions. In the recombination-hotspot model, the haplotype-block structure cannot be recognized when the background recombination rate is high. The imperfect nature of the haplotype-block concept has been considered as the cause of the differences across the different definitions (Schwartz et al. 2003). Several studies have suggested that haplotype blocks can arise not only by recombination (Daly et al. 2001; Gabriel et al. 2002; Goldstein et al. 2001) but also by factors such as natural selection, population bottlenecks, population admixture, choices of marker spacing, and allele frequencies (Phillips et al. 2003; Stumpf and Goldstein 2003).
There is currently no consensus on the criterion that best measures the performance of a set of htSNPs in capturing information on haplotype structure within a genome region of interest. The criteria used by Johnson et al. (2001) and Weale et al. (2003) can be split into two classes: those based on capturing as much as possible of the original haplotype diversity present in the set of known SNPs when they are reduced to the smaller set of htSNPs (Patil et al. 2001; Zhang et al. 2002; Johnson et al. 2001; Clayton 2002) and those based on establishing as high an association as possible between the reduced htSNPs set and the larger set (Weale et al. 2003). The different criteria for htSNPs selection in each haplotype block would lead to different performance of the htSNPs or tagging-SNPs selection (Weale et al. 2003). We only used one of the diversity-based criteria (Patil et al. 2001; Zhang et al. 2002) to perform an initial study of the comparison of the htSNPs selection under different haplotype-block definitions. The different haplotype-block definitions lead to different numbers of SNPs, which results in different haplotype information loss in the measure of entropy. The alternative selections of htSNPs under different haplotype- block definitions will probably make the haplotype-block–based association mapping for complex disease quite variable. On the haplotype-block–based study, whether the haplotype-block definitions have a different effect on the statistical power either on the candidate-gene association study or on the whole-genome association study is still an important issue to be solved in the future. However, both diversity-based and association-based criteria for selecting htSNPs could, in fact, be applied without regard to the underlying block structure, as was, in fact, advocated by several previous papers (Weale et al. 2003; Goldstein et al. 2003).
In conclusion, we performed an initial systematic simulation study to compare haplotype-block definitions both under various population-genetics parameters and under two different recombination models. Based on our study, we conclude the following: (1) The behaviors of haplotype block under different haplotype definitions are affected by population-genetics parameters, especially by population-mutation rate and population-recombination rate for the coalescent with uniform recombination framework. (2) The recombination intensity has no effect on the haplotype-block partition and htSNPs selection for the coalescent with recombination-hotspot framework. (3) Under both recombination models, the LD-based definitions is more similar or related to the recombination-based definitions. (4) Under both recombination models, there is more variance in illustrating the LD structure under the LD-based and recombination-based definitions because they appear to be affected by the population-recombination rate, whereas the diversity-based definition is not as sensitive to population-recombination rate.(5) Different haplotype-block definitions lead to the different selection of average htSNPs number; under the diversity-based definition, the reduced number of htSNPs selected leads to an increase in the haplotype information loss. To perform haplotype-block–based association mapping, consideration is needed when choosing the haplotype-block definitions and htSNPs.
David Goldstein, Associate Editor
We thank the editor and two anonymous reviewers, for helpful comments, and Mr. B. Hao, Dr. H. Wang, Dr. X. Chen and Mr. B. Neale for helpful discussion. This work is supported in part by Chinese National Key program on Basic Research (Grant G1998051003), Chinese National High-Tech R&D Program (Grant 863-102-10-03-05), and National Natural Science Foundation of China (Grant 39625007 and 39993420).
References
Avi-Itzhak, H. I., X. Su, and F. M. De La Vega.
Bafna, V., B. V. Halldórsson, R. Schwartz, A. G. Clark, and S. Istrail.
Clayton, D.
Daly, M. J., J. D. Rioux, S. F. Schaffner, T. J. Hudson, and E. S. Lander.
De Bontridder, K. M. J., B. J. Lageweg, J. K. Lenstra et al.
Fu, Y. X., and W. H. Li.
Gabriel, S. B., S. F. Schaffner, H. Nguyen et al. (18 co-authors).
Garey, M. R., and D. S. Johnson.
Goldstein, D. B., K. R. Ahmadi, M. E. Weale, and N. W. Wood.
Hoehe, M. R.
Hudson, R. R.
———.
Hudson, R. R., and N. Kaplan.
Jeffreys, A. J., L. Kauppi, and R. Neumann.
Johnson, G. C., L. Esposito, B. J. Barratt et al. (21 co-authors).
Judson, R., B. Salisbury, J. Schneider, A. Windemuth, and J. C. Stephens.
Kruglyak, L.
Li, N., and M. Stephens.
Nickerson, D. A., S. L. Taylor, S. M. Fullerton, K. M. Weiss, A. G. Clark, J. H. Stengaard, V. Salomaa, E. Boerwinkle, and C. F. Sing.
Patil, N., A. J. Berno, D. A. Hinds et al. (22 co-authors).
Phillips, M. S., R. Lawrence, R. Sachidanandam et al. (35 co-authors).
Satta, Y., C. Ohuigin, N. Takahata, and J. Klein.
Schwartz, R., B. V. Halldósson, V. Bafna, A. G. Clark, and S. Istrail.
SeattleSNPs.NHLBI program for genomic applications. UW-FHCRC, Seattle, Wash. (http://pga.gs.Washington.edu) August, 2003 accessed.
Stephens, M., N. J. Smith, and P. Donnelly.
Stumpf, M.P.H.
Stumpf, M. P. H., and D. B. Goldstein.
Wall, J. D., and J. K. Pritchard.
Wang, N., J. M. Akey, K. Zhang, R. Chakraborty, and J. Li.
Weale, M. E., D. Chantal, S. J. Macdonald, A. Smith, P. S. Lai, S. D. Shorvon, N. W. Wood, and D. B. Goldstein.
Author notes
*National Laboratory of Medical Molecular Biology, Institute of Basic Medical Sciences, Chinese Academy of Medical Sciences (CAMS) and Peking Union Medical College (PUMC), Beijing, People's Republic of China; †Chinese National Human Genome Center, Beijing, People's Republic of China; ‡MOE Key Laboratory of Bioinformatics, Department of Automation, Tsinghua University, Beijing, People's Republic of China; and §SGDP, Institute of Psychiatry, Kings College, London, United Kingdom



