-
PDF
- Split View
-
Views
-
Cite
Cite
Sonja Meyer, Arndt von Haeseler, Identifying Site-Specific Substitution Rates, Molecular Biology and Evolution, Volume 20, Issue 2, February 2003, Pages 182–189, https://doi.org/10.1093/molbev/msg019
Close - Share Icon Share
Abstract
A maximum likelihood framework for estimating site-specific substitution rates is presented that does not require any prior assumptions about the rate distribution. We show that, when the branching pattern of the underlying tree is known, the analysis of pairs of positions is sufficient to estimate site-specific rates. In the abscense of a known topology, we introduce an iterative procedure to estimate simultaneously the branching pattern, the branch lengths, and site-specific substitution rates. Simulations show that the evolutionary rate of fast-evolving sites can be reliably inferred and that the accuracy of rate estimates depends mainly on the number of sequences in the data set. Thus, large sets of aligned sequences are necessary for reliable site-specific rate estimates. The method is applied to the complete mitochondrial DNA sequence of 53 humans, providing a complete picture of the site-specific substitution rates in human mitochondrial DNA.
Introduction
In a nucleotide or amino acid sequence not all sites evolve with the same speed. Some sites experience more changes than others, mainly because different selective constraints act on the different sites of the sequence. Examples for sequences with heterogeneous substitution rates among sites are coding regions of the genome where the three codon positions evolve with different rates; noncoding regions where some but not all sites have regulatory and control functions, like the hypervariable regions of mitochondrial DNA (Clayton 2000); or regions of the genome that are involved in the formation of secondary structure, like the large and small subunit ribosomal RNAs (Van de Peer et al. 1993; De Rijk et al. 1995). Because of the relationship between substitution rate and selective constraint, we can gain valuable insight into the structural and functional constraints that act on a sequence by quantifying the rate of substitution at each sequence position. In addition, various sequence analyses can, in principle, benefit from the consideration of site-specific substitution rates. Substitution models or distance estimates, and thus tree reconstruction, can become more accurate, and population genetic inference can be influenced. The bias introduced in sequence analysis by ignoring heterogeneous rates among sites has been studied in population genetics (cf. Aris-Brosou and Excoffier 1996) and phylogenetic reconstruction (cf. Yang 1996).
To assess site-specific rate heterogeneity, several approaches were developed. They can be separated into three categories: Parsimonious attempts (Hasegawa et al. 1993; Wakeley 1993), maximum likelihood–based methods (Felsentein 1981; Olsen, Pracht, and Overbeek, personal communication; Yang 1993; Nielsen 1997; Excoffier and Yang 1999; Meyer, Weiss, and von Haeseler 1999), and empirical “pairwise” methods (Van de Peer et al. 1993, 2000; Pesole and Saccone 2001).
In the parsimonious approach the number of substitutions each site requires in a most parsimonious tree is counted, and those sites that exceed a cut-off value—i.e., if a site falls in the upper 10% quantile of the distribution of substitutions (Wakeley 1993)—are coined “fast sites.” However, as the assumptions of parsimony are not always valid, this method tends to underestimate the amount of rate variation. Likewise, skewed base composition and biased substitutions among nucleotides (or amino acids), which both are known to mimic effects of rate variation among sites, cannot be taken fully into account. Thus, only approximate estimates of site-specific variability are inferred.
Maximum likelihood methods in contrast have a statistically well-defined basis and can cope with recurrent mutations, skewed base composition, and biased variation in rate by specifying a model of sequence evolution (Yang 1993). However, the drawback of such methods is that they are computationally intensive, such that the estimation of site-specific rates is not possible without assuming either a tree topology including branch lengths (Olsen, Pracht, and Overbeek, personal communication; Kelly and Rice 1996; Nielsen 1997) or a specific distribution of rates a priori (Felsenstein 1981; Yang 1995; Kelly and Rice 1996; Excoffier and Yang 1999; Meyer, Weiss, and von Haeseler 1999). Typically one assumes that rates are distributed according to the Gamma distribution. Yang (1994) suggested the discrete Gamma distribution, which has been used to obtain site-specific rate estimates (Excoffier and Yang 1999; Meyer, Weiss, and von Haeseler 1999). From a biological point of view, there is no reason to assume that sites evolve with “discrete” rates. Moreover, the discrete approach has the tendency to underestimate the rate of fast-evolving sites. Thus, the use of a continuous distribution would, in principle, be favorable (Meyer, Weiss, and von Haeseler 1999). Unfortunately, this is at present computationally infeasible.
Empirical “pairwise” methods circumvent the construction of a tree by focusing on pairs of sequences (Van de Peer et al. 1993, 2000; Pesole and Saccone 2001). In each sequence pair, a position contains either a pair of different nucleotides or the identical nucleotides, where the probability to observe the events depends on the site-specific substitution rate and the evolutionary distance separating the sequences. Van de Peer et al. (1993) used this relation to infer site-specific rates of alignment positions. Although their approach yields sensible results, their statistical basis is not well understood. Thus, we introduce a maximum likelihood framework for estimating site-specific substitution rates from pairs of sequences based on the ideas of Van de Peer et al. (1993). Moreover, we suggest an iterative maximum likelihood procedure to compute site-specific rates and the phylogenetic tree simultaneously. The performance of the method is evaluated by simulations. As an illustrative example, we applied the estimation procedure to the dataset of 53 complete mitochondrial DNA (mtDNA) sequences of humans (Ingman et al. 2000) and obtained the full rate spectrum.
Modeling Substitutions
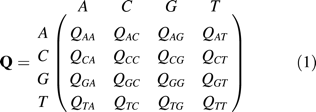


We will use d = r · t for the expected number of substitutions between two sequences.
Rate Heterogeneity


Inferring the Evolutionary Distance
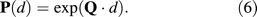

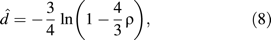
Inferring Site-Specific Rates
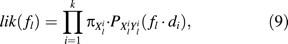
Analyzing Real Data
To estimate f = ( f1, …, fℓ), equation 9 requires the knowledge of the d1, d2, …, dk. Several approaches are possible: One can compute the pairwise distances for each pair separately and then estimate the site-specific rates. Another option is to use the known phylogeny of the 2k sequences to identify independent sequence pairs in the tree and to deduce their distances from the branch lengths in the tree. Here, independence means that the path i, (i = 1, …, k) that connects the sequence pair (Xi, Yi) in the tree is disjoint from the remaining k − 1 paths in the tree. This approach will be abbreviated IP-method (independent pairs). A second approach is simply taking all possible distance pairs from a known phylogeny, ignoring the fact that the pairs are not independent. We will call this the AP-method (all pairs). Both methods require the knowledge of the phylogeny and the evolutionary model Q. Note also that the AP-method is a generalization of the method suggested by Van de Peer et al. (1993).
If, however, no information on the phylogenetic relationship of the sequences is available, we suggest an iterative procedure, which includes the estimation of the model of sequence evolution, the phylogeny, and heterogeneous rates among sites. To compute the maximum likelihood estimates of the tree, either PUZZLE (Strimmer and von Haeseler 1996) or DNAML from PHYLIP is used (Felsenstein 1981).
Algorithm 1: Iterative Procedure
Compute the maximum likelihood tree
\(\mathcal{T}\)0 and the parameters of the model Q assuming no rate heterogeneity. Call the likelihood lik(\(\mathcal{T}\)0).Apply IP or AP to compute d(
\(\mathcal{T}\)0) derived from the tree\(\mathcal{T}\)0 and use equation 9 to estimate the site rate vector f.Rescale f̂ such that (1/ℓ)
\({\sum}^{{\ell}}_{\mathit{l}{=}1}\)f̂l = 1.Use f̂ to compute lik(
\(\mathcal{T}\)1), the corresponding maximum likelihood tree.If lik(
\(\mathcal{T}\)1) > lik(\(\mathcal{T}\)0) then(a) replace
\(\mathcal{T}\)0 by\(\mathcal{T}\)1.(b) goto 2.
Otherwise goto 6.
Output
\(\mathcal{T}\)0 and f.
Step 3 of the iterative procedure puts constraints on the rates and ensures that we are analyzing relative rates with respect to the average evolutionary rate.
Efficiency
If we had a collection of independent pairs of sequences together with a distance estimate di for each pair (i = 1, …, k), then equation 9 would estimate fl (l = 1, …, ℓ) if k is large (data not shown).
In real applications of the method, sequences are related by a tree, and estimates are therefore dependent. To test the performance of equation 9 to estimate f for a collection of aligned sequences, we employed computer simulations, in which we compared the estimated site-specific rates with the rates modeled (“true” rates).
To this end, random tree topologies based on the coalescence (Hudson 1991) were generated. Sequences were evolved according to the Jukes-Cantor model (Jukes and Cantor 1969) with Gamma-distributed rates using Seq-Gen (Rambaut and Grassly 1997), where the shape parameter α is an indicator of the amount of rate heterogeneity. A small value of α implies a pronounced rate heterogeneity.
To test the influence of the number of sequence pairs on the reliability of the estimates, data sets with n = 25, 50, 100, 250 sequences were generated. Because of the complexity of the problem, we confine ourselves to three types of simulations. The simulation conditions are summarized in table 1.
The performance of simulations 1 to 3 was analyzed by plotting the “true” rates against the respective rate estimate. Moreover, we calculated the correlation coefficient (Yang and Wang 1995) to measure the degree of linear dependency between true rates and their estimates. The slope of the regression line between true and estimated rates is used to check for a possible bias. A slope close to 1 is an indication of an unbiased procedure.
Simulation 1—IP versus AP
Here we wanted to elucidate the influence of the usage of all possible n(n − 1)/2 pairs of sequences and their respective distances on the estimation of f as compared to the usage of only n/2 pairs of sequences, if independent pairs were used.
Figure 1 shows the scatter plots for a sample of n = 25 and n = 100 sequences. For both approaches the accuracy of the estimates increases if the number of sequences is increased, as can be seen from the reduced variation of the dot plot. For n = 25 it sometimes happened that the maximization of equation 9 did not converge. In those instances an arbitrary large rate of 75 was assigned. For n = 100 the maximization always worked. Moreover, for large data sets the effect of observing horizontal lines of rate estimates (see fig. 1a) disappears. Thus a much finer resolution of rate estimates seems possible.
Calculation of correlation coefficients and the slope of the regression lines corroborates the observation (table 2) that larger data sets lead to an increased precision of rate estimates. If 250 sequences are analyzed, the correlation coefficient equals 0.9391 for the IP-method and 0.9714 for the AP-method; the slope equals 1.0109 and 1.0110, respectively. Thus, a bias in the estimates is not observed. Surprisingly, the AP-method yields consistently better estimates of correlation coefficient and slope. It appears that the larger sample size of AP outbalances possible biases introduced by the nonindependence of pairs of sequences. Therefore, the AP-method is the method of choice and will be used in the following simulations.
Simulation 2—Influence of α
We investigated the performance of the AP-method when the shape parameter α of the Γ-distribution is changed from extreme rate heterogeneity (α = 0.1) to weak heterogeneity (α = 5) and when the phylogenetic tree is also varied. To accomplish this investigation, the AP-method was applied to 100 random trees.
Figure 2 summarizes the results. The overall performance of the estimates increases as the number of sequences is increased, but the AP-method performs best if strong rate heterogeneity is present. If α = 5.0 then an average correlation coefficient of 0.5212 is observed for n = 250 sequences, which increases to 0.9531 if α = 0.1 (see fig. 2). In the latter case the correlation coefficients range between 0.85 and 0.95, indicating a high degree of correlation between estimated rates and true rates. Moreover, the range of the distribution of the correlation coefficients is narrower if rate heterogeneity is strong. Also, the variance of the empirical distribution of correlation coefficients is reduced as n is increased.
As already observed in Simulation 1, IP versus AP, the estimations appear unbiased, as the slope of the regression line ranges between 0.9734 and 1.2996, irrespective of the choice of α or the number n of sequences.
Because the results are averaged over 100 random trees, our conclusions are independent of the underlying tree. Thus, the method seems to work with good accuracy as long as the data set is sufficiently large and rate heterogeneity is present.
Simulation 3—The Iterative Procedure
Finally, we investigated the performance of the iterative procedure (algorithm 1). As maximum likelihood tree reconstruction is the time-limiting factor (step 3 of the algorithm), we employed the subsampling strategy for the simulated data with n = 100 and 250 sequences (Meyer, Weiss, and von Haeseler 1999). Here, 10 random subsamples of 50 sequences were drawn. For each subsample, site-specific rates were estimated using the iterative procedure, and the estimates at each site were averaged.
The iterative procedure stopped in all instances (see table 1 Sim3) after seven iterations. The analysis that follows is for the resulting tree and the corresponding rate vector. The crosses in figure 2 display the results of the iterative method. If we can compute the overall maximum likelihood tree (n ≤ 50), then the correlation coefficients of the iterative method fall within the range of the coefficients obtained when the tree is given (Sim 2). However, if n = 100 or 250, then we observe a reduced correlation compared to Sim 2. The correlation coefficients overlap with the coefficients one would obtain if 50 sequences were analyzed. Thus the reduction in correlation between true and estimated rates may be attributed to the fact that we have employed the subsampling strategy. If we were able to compute maximum likelihood trees for large data sets in reasonable time, this reduction in correlation would disappear.
Simulation 2 and Simulation 3 both show the phenomenon of a high correlation coefficient when strong rate heterogeneity is present and a reduced correlation coefficient when the sequence positions evolve with weak heterogeneity. Figure 3 shows the scatter plots of one simulation of the rate estimates after convergence of algorithm 1 for 50 sequences, assuming α = 5.0 (fig. 3a), α = 0.8 (fig. 3b), and α = 0.1 (fig. 3c). Whereas the slope equals 1.0147 (α = 5.0), 1.0868 (α = 0.8), and 1.0195 (α = 0.1), the correlation coefficients vary from 0.4844, 0.7746, to 0.9164. Thus, while the slope is for all examples close to 1, we observe a reduced correlation for the weak rate heterogeneity case. An explanation may be the lack of fast-evolving positions, which are present for α = 0.1, say (see fig. 3c); these fast-evolving positions (true rates larger than 30), can be reliably estimated and cause the high correlation. In summary, our simulations show that we are able to estimate site-specific rates in reasonable computation time. Moreover, they show that knowledge of the phylogeny is not necessary to infer the rates.
Site-Specific Rates of Human Mitochondrial DNA
To apply the iterative procedure, we analyzed the 53 complete human mtDNA sequences (Ingman et al. 2000). The sequences were aligned by eye, resulting in an alignment of length 16,591. According to the Anderson reference sequence (Anderson et al. 1981), we identified 23 gapped positions (44.1, 309.1–309.2, 317.1–317.3, 523.1–523.4, 573.1–573.6, 2161.1, 2232.1, 5909.1, 16193.1–16193.4), which were excluded from the analysis. Position 3107 was also excluded because it is missing in all 53 sequences. Thus, we analyzed 16,567 positions with the iterative procedure. The initial tree of the algorithm was estimated using the PUZZLE program (Strimmer and von Haeseler 1996) with the Tamura Nei model (Tamura and Nei 1993), where the model parameters were estimated from the data. Based on this tree, the iterative procedure was begun. After three iterations the algorithm stopped. The resulting site-specific rate estimates are shown in figure 4. In total, 660 varied positions are observed scattered along the entire mitochondrial genome. The majority (474/660) of these varied position evolves with relative rates less than 20, and only a small fraction (39 positions) evolves with rates larger than 100. Using the PUZZLE-program (Strimmer and von Haeseler 1996), we estimated a shape parameter α = 0.002, which indicates extreme rate heterogeneity. If we were to take this value as face value, then we would expect about 40 positions among the total of 16,567 positions with a relative rate above 100. This rough estimate agrees fairly well with our calculations, yet the distribution of the fast-evolving sites along the genome is far from a uniform distribution along the sequence. Of the varied sites, 124 are located in the hypervariable regions (H1 and H2), which comprise only (359 + 320)/16,567 = 4% of the complete genome. More precisely, in H1 23.39% of the sites are variable, and in H2 12.5% of the positions show variation, whereas the rest of the genome shows 3.37% variable sites. In contrast, regions which seem to be particularly conserved are regions of known functions in the D-Loop (subsections 1, 2, and 3) as well as the central region separating H1 and H2, all tRNA genes, the 12S rRNA, and the 16S rRNA. It is interesting to note, however, that single sites with very high relative rates (>150) are interspersed throughout the genome and are found in ND1, ATP6, COIII, ND3, ND4, ND5, Cytb, and in one tRNA (Serine).
Thus, our method is able to pinpoint well-known regions of high evolutionary rates and to detect other positions of high substitution rates. We should keep in mind, however, that we can only generate hypotheses about the mode of evolution of single positions; the precise nature of the substitution process and its dependency from the sequence environment still remains unclear.
Discussion
We have presented a maximum likelihood framework for the estimation of site-specific rates from pairs of sequences. This approach comprises a generalization of the method by Van de Peer et al. (1993). Based on simulation studies, we show that the method is able to estimate site-specific rates, even if we need to estimate the tree and the model. To obtain reliable estimates, however, large data sets are necessary. Our approach is based on the analyses of pairs of sequences. Whether this method is advantageous compared to the optimization of the likelihood of a given site pattern (Olsen et al. 1994; Kelly and Rice 1996; Nielsen 1997), is at present unclear. It will be interesting to compare these two approaches in further detail.
With the proposed method, continuous rate estimates are obtained. This is a major advantage when pronounced rate heterogeneity is present, and thus the suggested method seems superior to other approaches, where evolutionary rates are more or less arbitrarily pooled in discrete categories (Excoffier and Yang 1999; Meyer, Weiss, and von Haeseler 1999).
If rate heterogeneity is low (α = 5.0), the correlation of true and estimated rates is small. This finding is explained by the fact that the absolute differences between rates are small. In fact, if α = 5.0, approximately 90% of the sites evolve with relative rates between 0.25 and 1.75. In contrast, for α = 0.1, only 14% of the sites are in that range, and the absolute differences in rates between sites are larger. Thus, we find sites evolving with relative rates between 0 and 50 (see fig. 3c). Our results show that the method is able to distinguish between fast- and slow-evolving sites with high reliability. This is true even when we have to estimate the tree with the iterative procedure. Here our method faces a bottleneck, which can be overcome only by faster maximum likelihood tree reconstruction programs (e.g., Schmidt et al. 2002). To estimate site-specific rates reliably, we need large data sets; however, at present it is impossible to estimate maximum likelihood trees for more than 50 sequences. More work is necessary to develop further approximation procedures.
Further extensions of our approach are straightforward: we need to incorporate more complex models of sequence evolution and to introduce a statistical framework to estimate the significance of estimates obtained. Moreover, the method makes the assumption that the distribution of variable sites is the same in all sequences. We do not expect that this is a problem for the population sequence data we have studied. However, if very distantly related sequences are studied, it is possible that the distribution of sites free to vary does change across the phylogeny (e.g., Fitch 1971; Miyamoto and Fitch 1995; Lockhart et al. 2000; Galtier 2001; Lopez, Casane, and Philippe 2002; Huelsenbeck 2002). At present it is not clear how to include rate changes at a single position in our analyses.
Appendix
A computer program to determine site-specific rates is available. It is written in ANSI C and should run on most popular platforms after proper compilation. The current version of the program, together with a detailed analysis of our example, is available on request. Parts of the source code have been taken from the free software Puzzle (Strimmer and von Haeseler 1996).
E-mail: [email protected].
William Martin, Associate Editor
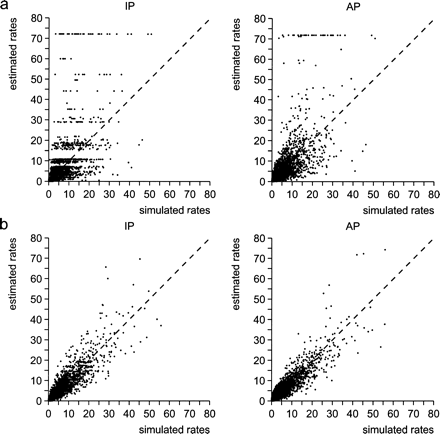
Scatter plot of the “true” rate versus the respective rate estimate for that position. a, Results for the data set of 25 sequences. b, Results for the data set of 100 sequence. For exact simulation conditions see table 1. For values of correlation coefficients and slope of regression line, see table 2. For each of the two data sets, two variants of the estimation method are shown (AP and IP)

Correlation coefficients between the “true” and the estimated rates as a function of the number of sequences and the amount of rate heterogeneity (α). The squares represent the average correlation coefficients computed from the rate estimates obtained from 100 random trees (see table 1, Sim2). The bars show the range of correlation coefficients. The crosses represent correlation coefficients obtained from the iterative procedure, where the tree is unknown and needs to be estimated jointly with the site-specific rates (see table 1, Sim3)

Scatter plots of the “true” rates versus estimated rates for 50 sequences calculated using the iterative procedure, assuming various degrees of rate heterogeneity. a, For low rate heterogeneity (α = 5.0); b, for moderate heterogeneity (α = 0.8); c, for strong rate heterogeneity (α = 0.1)
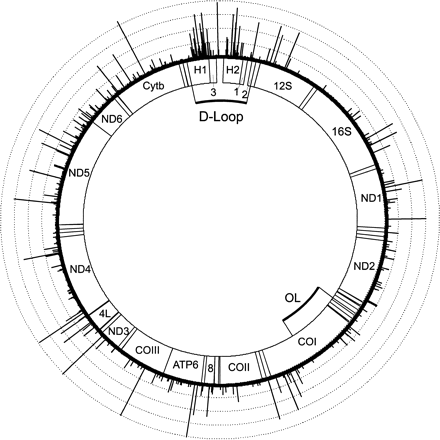
Site-specific rate estimates for the human mitochondrial DNA. The lengths of the bars reflect the relative rate at each site, where the average substitution rate is normalized to 1. The dotted circles are spaced at intervals of 50 relative rate units. The three small subsections (1, 2, and 3) within the D-Loop summarize several control elements. The labeled sections indicate the locations of the genes for the 12S and 16S rRNAs (12S,16S), NADH dehydrogenase subunits 1, 2, 3, 4L, 4, 5, and 6 (ND1 to ND6), cytochrome c oxidase subunits I, II, and III (COI to III), ATPase subunit 6 and 8 (ATP6 and 8) and cytochrome b (Cytb). The small, not labeled sections outside the D-Loop show the locations of the 22 different tRNA genes. OL denotes the origin of L-strand replication. The exact positions of the gene products and their original references are compiled in MITOMAP (Kogelnik et al. 1998)
| . | Sim1: IP versus AP . | Sim2: Influence of α . | Sim3: Iterative Procedure . |
|---|---|---|---|
| Number n of sequences: | ·········25, 50, 100, 250········· | ||
| Sequence length (bp): | 20,000 | 1,000 | 1,000 |
| Number of random trees: | 1 | 100 | 5 |
| Phylogenetic tree(s): | Known | Known | Estimated |
| Shape parameter α: | 0.1 | ·········0.1, 0.8, 5.0········· |
| . | Sim1: IP versus AP . | Sim2: Influence of α . | Sim3: Iterative Procedure . |
|---|---|---|---|
| Number n of sequences: | ·········25, 50, 100, 250········· | ||
| Sequence length (bp): | 20,000 | 1,000 | 1,000 |
| Number of random trees: | 1 | 100 | 5 |
| Phylogenetic tree(s): | Known | Known | Estimated |
| Shape parameter α: | 0.1 | ·········0.1, 0.8, 5.0········· |
Note:—Summary of the simulation conditions used to study the performance of the rate-estimation procedure. The vector f of site-specific rate heterogeneity was estimated for each parameter combination and compared to the simulated rates.
| . | Sim1: IP versus AP . | Sim2: Influence of α . | Sim3: Iterative Procedure . |
|---|---|---|---|
| Number n of sequences: | ·········25, 50, 100, 250········· | ||
| Sequence length (bp): | 20,000 | 1,000 | 1,000 |
| Number of random trees: | 1 | 100 | 5 |
| Phylogenetic tree(s): | Known | Known | Estimated |
| Shape parameter α: | 0.1 | ·········0.1, 0.8, 5.0········· |
| . | Sim1: IP versus AP . | Sim2: Influence of α . | Sim3: Iterative Procedure . |
|---|---|---|---|
| Number n of sequences: | ·········25, 50, 100, 250········· | ||
| Sequence length (bp): | 20,000 | 1,000 | 1,000 |
| Number of random trees: | 1 | 100 | 5 |
| Phylogenetic tree(s): | Known | Known | Estimated |
| Shape parameter α: | 0.1 | ·········0.1, 0.8, 5.0········· |
Note:—Summary of the simulation conditions used to study the performance of the rate-estimation procedure. The vector f of site-specific rate heterogeneity was estimated for each parameter combination and compared to the simulated rates.
Correlation Coefficients and Slope of the Regression Line as a Function of the Number of Sequences.
| Number of Sequences . | Correlation Coefficient . | Slope . | ||
|---|---|---|---|---|
| . | IP . | AP . | IP . | AP . |
| 25 | 0.6784 | 0.7422 | 0.9634 | 0.9635 |
| 50 | 0.8508 | 0.8665 | 1.0148 | 1.0148 |
| 100 | 0.9235 | 0.9318 | 1.0363 | 1.0363 |
| 250 | 0.9391 | 0.9714 | 1.0109 | 1.0110 |
| Number of Sequences . | Correlation Coefficient . | Slope . | ||
|---|---|---|---|---|
| . | IP . | AP . | IP . | AP . |
| 25 | 0.6784 | 0.7422 | 0.9634 | 0.9635 |
| 50 | 0.8508 | 0.8665 | 1.0148 | 1.0148 |
| 100 | 0.9235 | 0.9318 | 1.0363 | 1.0363 |
| 250 | 0.9391 | 0.9714 | 1.0109 | 1.0110 |
Note:—Simulation conditions are explained in table 1.
Correlation Coefficients and Slope of the Regression Line as a Function of the Number of Sequences.
| Number of Sequences . | Correlation Coefficient . | Slope . | ||
|---|---|---|---|---|
| . | IP . | AP . | IP . | AP . |
| 25 | 0.6784 | 0.7422 | 0.9634 | 0.9635 |
| 50 | 0.8508 | 0.8665 | 1.0148 | 1.0148 |
| 100 | 0.9235 | 0.9318 | 1.0363 | 1.0363 |
| 250 | 0.9391 | 0.9714 | 1.0109 | 1.0110 |
| Number of Sequences . | Correlation Coefficient . | Slope . | ||
|---|---|---|---|---|
| . | IP . | AP . | IP . | AP . |
| 25 | 0.6784 | 0.7422 | 0.9634 | 0.9635 |
| 50 | 0.8508 | 0.8665 | 1.0148 | 1.0148 |
| 100 | 0.9235 | 0.9318 | 1.0363 | 1.0363 |
| 250 | 0.9391 | 0.9714 | 1.0109 | 1.0110 |
Note:—Simulation conditions are explained in table 1.
We express special thanks to Matthias Deliano, Roland Fleißner, Dirk Metzler, and Heiko Schmidt for stimulating discussions. Financial support from the DFG and MPG is greatly appreciated.
Literature Cited
Anderson, S., A. T. Bankier, B. G. Barrell, et al. (14 co-authors).
Aris-Brosou, S., and L. Excoffier.
De Rijk, P., Y. Van de Peer, I. Van den Broeck, and R. De Wachter.
Excoffier, L., and Z. Yang.
Felsenstein, J.
Fitch, W. M.
Galtier, N.
Gu, X., Y.-X. Fu, and W.-H. Li.
Hasegawa, M., A. D. Rienzo, T. D. Kocher, and A. C. Wilson.
Huelsenbeck, J. P.
Ingman, M., H. Kaessmann, S. Pääbo, and U. Gyllensten.
Jukes, T. H., and C. R. Cantor.
Kelly, C., and J. Rice.
Kogelnik, A. M., M. T. Lott, M. D. Brown, S. B. Navathe, and D. C. Wallace.
Lockhart, P. J., D. Huson, U. Maier, M. J. Fraunholz, Y. V. D. Peer, A. C. Barbrook, C. J. Howe, and M. A. Steel.
Lopez, P., D. Casane, and H. Philippe.
Meyer, S., G. Weiss, and A. von Haeseler.
Miyamoto, M. M., and W. M. Fitch.
Nielsen, R.
Pesole, G., and C. Saccone.
Rambaut, A., and N. C. Grassly.
Schmidt, H. A., K. Strimmer, M. Vingron, and A. von Haeseler.
Strimmer, K., and A. von Haeseler.
Swofford, D. L., G. J. Olsen, P. J. Waddell, and D. M. Hillis.
Tamura, K., and M. Nei.
Tavaré, S.
Van de Peer, Y., S. L. Baldauf, W. F. Doolittle, and A. Meyer.
Van de Peer, Y., J. M. Neefs, P. D. Rijk, and R. D. Wachter.
Wakeley, J.
Yang, Z.
Yang, Z.
Yang, Z.
Yang, Z.



