-
PDF
- Split View
-
Views
-
Cite
Cite
Michael Worobey, A Novel Approach to Detecting and Measuring Recombination: New Insights into Evolution in Viruses, Bacteria, and Mitochondria, Molecular Biology and Evolution, Volume 18, Issue 8, August 2001, Pages 1425–1434, https://doi.org/10.1093/oxfordjournals.molbev.a003928
Close - Share Icon Share
Abstract
An accurate estimate of the extent of recombination is important whenever phylogenetic methods are applied to potentially recombining nucleotide sequences. Here, data sets from viruses, bacteria, and mitochondria were examined for deviations from clonality using a new approach for detecting and measuring recombination. The apparent rate heterogeneity (ARH) among sites in a sequence alignment can be inflated as an artifact of recombination. However, the composition of polymorphic sites will differ in a data set with recombination-generated ARH versus a clonal data set that exhibits the equivalent degree of rate heterogeneity. This is because recombinant data sets, encompassing regions of conflicting phylogenetic history, tend to yield “starlike” trees that are superficially similar to those inferred from clonal data sets with weak phylogenetic signal throughout. Specifically, a recombinant data set will be unexpectedly rich in conflicting phylogenetic information compared with clonally generated data sets supporting the same tree shape. Its value of q—defined as the proportion of two-state parsimony-informative sites to all polymorphic sites—will be greater than that expected for nonrecombinant data. The method proposed here, the informative-sites test, compares the value of q against a null distribution of values found using Monte Carlo–simulated data evolved under the null hypothesis of clonality. A significant excess of q indicates that the assumption of clonality is not valid and hence that the ARH in the data is at least partly an artifact of recombination. Investigations of the procedure using simulated sequences indicated that it can successfully detect and measure recombination and that it is unlikely to produce “false positives.” Simulations also showed that for recombinant data, naïve use of maximum-likelihood models incorporating rate heterogeneity can lead to overestimation of the time to the most recent common ancestor. Application of the test to real data revealed for the first time that populations of viruses, like those of bacteria, can be brought close to complete linkage equilibrium by pervasive recombination. On the other hand, the test did not reject the hypothesis of clonality when applied to a data set from the coding region of human mitochondrial DNA, despite its high level of ARH and homoplasy.
Introduction
Evolutionary models that incorporate estimates of site-specific rate heterogeneity are now routinely used for reconstructing phylogenetic trees (Yang 1996a ). Recently, it has become clear that variation in rates among sites can be expected in many nucleotide sequence data sets and that ignoring this variation can lead to serious errors in phylogenetic inference (Yang 1996a ). For instance, assuming rate homogeneity when rates are in fact variable among sites tends to lead to the underestimation of genetic distances and divergence dates, since some substitutions at fast-changing sites are overlooked (Yang 1996b ). Crucially, the effects of rate heterogeneity can also mistakenly be interpreted as evidence of recombination, since both processes generate conflicting phylogenetic signal.
The most common approach to accounting for site-specific rate heterogeneity is to apply a maximum-likelihood (ML) method to the original sequence data, with rate variation modeled by the gamma distribution (reviewed in Yang 1996a ). Likelihood modeling is appealing because it can simultaneously account not only for site-specific rate variation, but also for transition/transversion rate bias and unequal base frequencies, by using an explicit model of nucleotide substitution. The gamma distribution accommodates different degrees of rate heterogeneity by varying a single parameter, α. When the α parameter is small, the distribution conforms to cases in which most changes have occurred at a minority of sites (high rate heterogeneity); as α approaches infinity, the gamma model reduces to the special case of equal rates for all sites (rate homogeneity).
It is worth noting that this method for estimating α depends on a phylogenetic tree, which is itself an assumption about the evolutionary history of the sequences in question. Often, this tree assumption will be of little consequence when measuring rate heterogeneity. Many sets of gene sequences (e.g., interspecies data sets) have treelike histories that are uncomplicated by recombination, and simulation studies have shown that estimates of α are robust to uncertainty in the inference of the phylogenetic tree (Sullivan, Holsinger, and Simon 1996 ). In such cases, the standard interpretation for observed site-specific rate heterogeneity holds: point substitutions occur more readily at some sites than at others due to mutation rate bias or, perhaps more commonly, different selective constraints among sites.
However, if recombination has contributed to the genetic diversity among the sequences under scrutiny—and there is an impressive body of evidence for this, notably within populations of viruses (Sharp, Robertson, and Hahn 1995 ; Worobey and Holmes 1999 ) and bacteria (Maynard Smith et al. 1993 )—then a single tree cannot accurately model their history. This leads to an often overlooked bias when estimating site-specific rate heterogeneity (but see Schierup and Hein2000) . If no single tree can accurately depict the evolutionary history of all the sites in a recombinogenic data set, even the best “compromise” tree will require extra changes at some sites to account for the homoplasies introduced by recombination. Such sites will appear to exhibit inflated substitution rates when shoehorned onto this inaccurate tree. Thus, even if all sites have actually shared an identical underlying rate of point substitutions, recombination will create the appearance of site-specific rate heterogeneity. Higher levels of recombination will tend to generate greater apparent rate heterogeneity (ARH). Note that ARH here is not meant to refer only to the artifactual component of the rate heterogeneity generated by recombination; it is the observed rate heterogeneity (i.e., the estimate of α in a particular likelihood model), which may or may not have a component produced by recombination. In the face of recombination, the ARH is not an estimate of the “real” rate heterogeneity (RRH, i.e., the true, underlying variation among sites in their rate of point substitutions); it is an estimate of the combined effects of both the RRH and recombination.
Importantly, the ARH on its own is of little value in detecting recombination if its constituents are not known: a low value of α may be the result of recombination, or RRH, or some combination of the two. Here, a new method, the informative-sites test, is proposed that exploits the relationship between recombination and apparent rate heterogeneity to detect and measure recombination from nucleotide sequence data and to test whether recombination has contributed to the ARH. The approach is first introduced with a simple example, then applied to both simulated and real examples.
The Method
Rate Heterogeneity and the Informative-Sites Test
Consider the simple example outlined in figure 1 , which demonstrates the impact of recombination on ARH. Here, four 500-nt alignments supporting various topologies among taxa A, B, C, and D were concatenated to create a “recombinant” alignment, 2,000 nt in length. The procedure was as follows. The alignment for the first 500-nt region (1–500 in fig. 1 ) was generated with the program Seq-Gen (Rambaut and Grassly 1997 ) from the starting tree shown. It was produced under the model described in the next section, Analysis of Simulated Data, with equal rates for all sites. Next, the sequences in this alignment were relabeled to produce the subsequent 500-nt regions (501–1000 and 1001–1500). Note, for example, that in the 501–1000 region, taxon D corresponded to taxon 2 (not 4) from the starting tree, while B corresponded with 3, and C corresponded with 4 (fig. 1 ). The final region, 1501–2000, was identical to the first. The overall alignment, therefore, comprised regions of distinct ancestry, typical of recombination, and contained mosaic sequences. Taxon D, for instance, included sequence regions corresponding to taxa 4, 2, 3, then 4 again, of the starting tree.
Not surprisingly, an ML search on the 1–500 alignment recovered the correct tree topology (fig. 1 ), with no evidence for site-specific rate heterogeneity (α = ∞). The results for the subsequent regions were identical in tree shape and parameter estimates but reflected the relabeling described above. However, analysis of the concatenated alignment revealed a different picture. Here, the estimate of α dropped to just 0.53, indicating a high degree of ARH due solely to the impact of recombination. Moreover, while the estimated tree topology was accurate for the flanking regions, it was consequently incorrect with respect to the other half of the alignment. Many of the polymorphic sites from the two middle regions that supported different topologies had to be accounted for by extra changes at the tips of the tree. The resulting elongation of the terminal branches in the overall pedigree gave it a more starlike shape than the trees reconstructed from the nonrecombinant regions. This example demonstrates that recombination (1) influences the shape of phylogenetic trees (tending to make them more starlike) and (2) affects inferences about evolutionary process (inflating the observed degree of rate heterogeneity) (Schierup and Hein2000) . These two observations form the foundation of the informative-sites test.
The rationale for the method is simple. The branches of a true “star” phylogeny emanate from a single node. In the absence of recombination, sequence alignments that yield starlike trees will tend to exhibit relatively numerous (parsimony) uninformative polymorphic sites (e.g., singletons) and few informative sites (i.e., polymorphic sites where a minority nucleotide is present in at least two taxa). However, as figure 1 demonstrates, starlike trees can also arise from the strong but conflicting phylogenetic signal generated by recombination. The 2,000-nt alignment contained four distinct regions with well-supported partitions of taxa. However, the informative sites for each region defined different partitions of taxa. The result was a relatively starlike phylogenetic tree, deceptively similar to what might be expected if there were actually minimal phylogenetic signal throughout the entire alignment. Recombination produces trees that are more starlike than expected given the composition of their polymorphic sites.
To put it another way, recombination gives rise to phylogenetic trees that are unexpectedly rich in (conflicting) phylogenetic information given their shape. The informative-sites test uses a Monte Carlo approach to simulate nucleotide sequence evolution under the constraint of clonal descent (i.e., no recombination) and then to test whether the proportion of informative sites in the real data is higher than the clonal expectation. The procedure is as follows.
To begin, assume that the sequences in question evolved clonally. Estimate the ML tree and substitution model parameters (transition/transversion ratio, base frequencies, α) using the original data.
Rerun evolution many times (e.g., n = 1,000) using the estimated tree and model parameters found in the first step, but under the constraint of clonality. Clonality is enforced by evolving sequences on a single tree (specifically, the one estimated in step 1) instead of a network or series of trees. In effect, any ARH observed in the original data is at this point converted entirely to RRH, whether or not it had a component due to recombination. This step produces a large number of clonal data sets that match the observed data in terms of tree shape and ARH.
Test the hypothesis that the original alignment evolved clonally by comparing its pattern of polymorphic sites with the expectation for clonal data. Perform a significance test comparing the observed proportion of two-state parsimony-informative sites to all polymorphic sites (q) against the same ratio calculated for each of the clonally simulated alignments (qc). A P value is defined as the proportion of simulated alignments that satisfy qc > q.
For instance, if the observed proportion of informative sites is greater than any out of 1,000 clonal simulations (P < 0.001), significant elongation of the terminal branches of the overall tree is inferred, and a significant pattern of recombination is concluded. This is equivalent to testing whether recombination is at least partially responsible for the ARH in the original data. If, however, the level of phylogenetic signal in the data, as measured by the proportion of informative sites, is typical of clonally evolved data sets (e.g., P = 0.511), then the hypothesis of clonality cannot be rejected.
In alignments of just four taxa, all of the parsimony-informative sites will include exactly two of the four possible nucleotides. With added taxa, informative sites exhibiting more than two states will sometimes arise, especially in saturated data sets. However, it is a matter of empirical observation that nonreciprocal recombination tends to inflate the proportion of two-state informative sites versus all other sorts of polymorphic sites, including three- and four-state parsimony-informative sites (data not shown). Hence, the measure of phylogenetic signal used for the informative-sites test, q, is defined as the proportion of two-state parsimony-informative sites among the polymorphic sites as a whole.
The example in figure 1 illustrates the approach. The value of q is shown below the ML tree found for the first 500-nt region. Since this alignment was generated without recombination, q was not expected to be significantly greater than q̂c, the average proportion of two-state informative sites calculated from the clonal null distribution. Indeed, for this data set, the observed proportion of informative sites was identical to the clonal expectation, with q = q̂c = 0.36. Accordingly, there was no statistical evidence for recombination (P = 0.511; i.e., q was less than qc in 511 out of 1,000 clonally generated alignments).
On the other hand, when the informative-sites test was applied to the 2,000-nt recombinant alignment, it strongly rejected the clonal model. Although the value of q remained at 0.36, q̂c dropped to 0.21, reflecting the relatively starlike shape of the estimated tree for the overall alignment (fig. 1 ). In fact, for the 2,000-nt alignment, q was greater than any qc from 1,000 clonally evolved data sets (P < 0.001), strong evidence of its recombinant origin.
The Informative-Sites Index

Software to run the informative-sites test is available at http://evolve.zoo.ox.ac.uk/software.
Analysis of Simulated Data Sets
Nonreciprocal Recombination Simulations
In addition to those described in figure 1 , several simulated nucleotide alignments were used to evaluate the performance of the method, using clonal populations as well as populations subject to a wide range of recombination rates. To begin with, 100 alignments—each 500 nt in length—were evolved from the 16-taxon starting tree shown in figure 2 . These simulations were carried out in Seq-Gen (Rambaut and Grassly 1997 ) under an HKY model of sequence substitution (Hasegawa, Kishino, and Yano 1985 ) with equal base frequencies, a transition/transversion ratio of 2.0 (κ = 4.0), and rate homogeneity of sites. These 100 clonal data sets were then subjected to 20, 50, 200, or 500 rounds of nonreciprocal recombination, producing 100 new alignments in each case, using code from PAL (Phylogenetic Analysis Library, A. Drummond and K. Strimmer, http://www.pal-project.org). Every recombination event saw a 10-nt fragment from an “acceptor” sequence replaced by the homologous region from a nonidentical “donor,” with all fragments, acceptors, and donors randomly selected.
The first step in the analysis of each alignment was to estimate its ML parameters and phylogenetic tree. Using the MPT as the starting tree, an ML heuristic search with tree bisection-reconnection (TBR) branch swapping was conducted under an HKY+gamma substitution model as implemented in PAUP* (Swofford2000) . The base frequencies were empirically estimated from the data, and the transition/transversion ratio and α parameter of the gamma distribution (discrete approximation with eight rate categories) were initially estimated on the MPT and then reestimated on the topology found by the heuristic search.
Table 1 summarizes the results of the informative-sites test for the clonal and recombinant alignments. The mean (or median) values for the various statistics were calculated from the results of the 100 replicates in each group (0, 20, 50, 200, or 500 recombination events).
First, note the striking effect that recombination had on the apparent rate heterogeneity of the data. The 100 clonal alignments returned a median α value of infinity, as expected since they were all generated without rate heterogeneity. However, after just 20 small recombination events, the tendency for recombination to produce artifactual rate heterogeneity was already clear, with α = 6.58. In fact, α declined steadily with increasing levels of recombination, down to a median value of just 0.42 for the set of alignments most influenced by recombination. Contrast this with the very minimal effect recombination had on the transition/transversion rate bias, κ, and on the observed number of polymorphic sites, v, compared with the clonal value, v̂c.
A comparison of the mean values of q and q̂c for each group captures the essence of the method. For the clonal data sets (no recombination events), q and q̂c were nearly identical, as anticipated. No clonal alignment gave a statistically significant result, and the average ISI for these data sets, at 0.02, was near 0, reflecting their clonal history. The pattern for the recombinant alignments was very different. Here, the disparity between q and q̂c grew ever larger with increasing recombination. The trend was clear even after 20 recombination events, although with only 14 out of the 100 in this group proving significant, the test was fairly conservative. The tendency for recombination to generate two-state informative sites, moreover, was plainly illustrated by the increasing value of q associated with every successive jump in recombination rate. The average value of q after 500 rounds of recombination, for instance, was 0.64—up from 0.52. Nevertheless, for this group, which predictably gave rise to the most starlike trees and the lowest estimate of α, the clonal expectation for the proportion of informative sites was the lowest of all at just 0.27. With t close to t̂r and an average ISI of 0.89, these alignments were evidently approaching complete linkage equilibrium. (See fig. 2 for representative results at various recombination levels.)
To investigate how robust the test was to uncertainty in the likelihood estimation of model parameters used for generating the null data, 10 alignments from each recombination level (0 through 500) were reexamined. This time, approximate 95% confidence limits were obtained for each parameter (i.e., transition/transversion ratio and α) using the likelihood ratio test. These confidence limits were then specified—instead of the ML estimates—as the model parameters when generating the clonal, null data sets for the test. All four combinations of the extreme values of the two parameters were tried. Comparison of the results obtained using the ML estimates of the parameters versus the 95% confidence limits revealed virtually no difference. Using the confidence limits, no false positives (i.e., type I errors) were generated from the data sets with 0 recombination events, and no false negatives (i.e., type II errors) were observed in the data sets with 200 and 500 recombination events. At the lower levels of recombination, all data sets with significant results using ML estimates were significant in some or all of the combinations of 95% confidence limit parameters. Data sets that were not significant using ML estimates were similarly not significant when the confidence limits were used instead. These findings indicate that the informative-sites test is very robust to error in the estimation of parameter values and that such error is unlikely to greatly bias the results of the method.
Comparisons with the Homoplasy Test
A subset of the alignments from each of the groups listed in table 1 was evaluated by both the informative-sites test and the homoplasy test in order to compare their performances in detecting and quantifying recombination. The homoplasy test uses the presence of excessive homoplasy as an indication of recombination and, like the informative-sites test, permits the calculation of an index, the “homoplasy ratio,” that measures the extent of recombination (Maynard Smith and Smith 1998 ). Like the ISI, the homoplasy ratio is expected to be about 0 for clonal data and 1 for data at complete linkage equilibrium.
Briefly, 10 randomly chosen alignments from each recombination level listed in table 1 were subjected to both tests, and the numbers of statistically significant results (0.01 level) and the range of index values were compared. Next, a representative likelihood tree from each group served as the template in Seq-Gen to generate 10 new clonal alignments using the corresponding α and κ recorded for each group in table 1 . Thus, for every original alignment, a parallel alignment was produced that mimicked its phylogenetic tree, α, and κ but was generated without recombination. This resulted in five new groups, with 10 alignments each, that were characterized by their rate heterogeneity—with the new, clonal “α = 0.76” group, for example, corresponding to the original “200 recombination events” group.
The results of the comparisons are illustrated in figure 3 . Notably, the tests gave very similar results for the original data sets (fig. 3a and b ), which were all simulated without any RRH. Neither test returned any false positives in the first (clonal) group, and both tests detected recombination in all alignments with 200 or more events and showed comparable sensitivity to one another at lower levels. Furthermore, their respective index values traced very similar paths from near 0 for the clonal data to near 1 at the highest level of recombination.
The two tests gave very different results from each other, however, given the parallel set of alignments which were all clonal but were generated with varying degrees of RRH (fig. 3c and d ). While the informative-sites test correctly detected no evidence for recombination, the homoplasy test produced several false positives. This tendency, particularly strong at higher levels of site-specific rate heterogeneity, was apparent even at low levels of RRH (e.g., α = 2.52). The results of the homoplasy test were virtually identical for the recombinant data sets and their clonal counterparts simulated with rate heterogeneity (fig. 3b and d ).
Although the homoplasy test includes techniques designed to account for rate heterogeneity and thus avoid false positives (Maynard Smith and Smith 1998 ), some important conclusions can be drawn from the comparisons here. First, the informative-sites test clearly benefits by accommodating any apparent rate heterogeneity as an integral part of the test itself. Since it does not rely on ad hoc methods to account for site-specific rate heterogeneity, the test does not appear to be prone to mistaking site-specific rate heterogeneity for recombination. Second, because the homoplasy test can evidently give misleading results in the face of even mild unaccounted-for rate heterogeneity, extremely reliable methods must be used to measure its extent.
The results of two further comparisons of the informative-sites test and the homoplasy test are shown in figures 4 and 5 . In the first of these, 10 clonal data sets were generated using the same starting tree and model of evolution as for the data in table 1 , except that a transition/transversion ratio of 20.0 (κ = 40.0) was specified. These data sets were then subjected to increasing levels of nonreciprocal recombination using the procedure outlined previously. While the power of the homoplasy test was unaffected by extreme transition/transversion rate bias, the informative-sites test appeared to become more conservative under these circumstances (fig. 4 ). Although the results of the informative-sites test should thus be interpreted with caution for data sets with unusually strong transition/transversion rate bias, this finding highlights the observation that the method appears to be a “safe” test for recombination: it is unlikely to produce false-positive results. Indeed, the simulations in this study suggested no circumstances under which the method could be biased toward type I error.
In the next comparison (fig. 5 ), 10 clonal data sets were generated under the same likelihood model as the data in table 1 , but on a different tree. In this case, a tree with all branch lengths four times longer than those of the starting tree in figure 2 was used to produce a highly saturated alignment, as might be encountered in some viral data sets. Under these circumstances, the homoplasy test appeared to lose power, while the informative-sites test behaved as expected. With saturated data sets that were clonal or had low levels of recombination, the homoplasy ratio was clearly biased toward negative values (fig. 5 ). Mild saturation in the other simulations may underlie the slightly negative average values for the homoplasy ratio consistently observed in the clonal cases (figs. 3b, 3d, and 4b ).
Additional Analyses
Several other simulated sequence alignments were used to explore the performance of the informative-sites test, with different transition/transversion biases, base composition biases, sequence lengths, numbers of taxa, recombination fragment lengths, and numbers of polymorphic sites. Although the sensitivity of the test appeared to improve with greater sequence length, number of polymorphic sites, and number of taxa, there was no indication that the method was invalidated by any of these factors (data not shown). Moreover, the results of the test on the simulated sequence alignments were almost identical whether the tree was estimated using the heuristic search procedure outlined above, found with an exhaustive ML search, or obtained by optimizing the branch lengths of the MPT topology. Based on these observations, it seems reasonable, especially for data sets with many taxa and long sequences, to obtain the likelihood tree and model parameters used for the test simply by optimizing on the MPT.
In addition to the techniques already described, recombination was also simulated using the program Treevolve (N. Grassly and A. Rambaut, http://evolve.zoo.ox.ac.uk/software), which implements a coalescent model that can incorporate recombination as well as exponential population growth, a more widely recognized cause of starlike phylogenies (Slatkin and Hudson 1991 ). The informative-sites test reliably identified recombination in this context too (data not shown). This was not surprising, since this approach to recombination simulation is essentially the same as that used in figure 1 in that different regions of an alignment are allowed to evolve on different trees. Importantly, the coalescent simulations showed that the test was able to distinguish between the effects of recombination and exponential population growth. Because population growth had no influence on ARH, its effects were not mistakenly interpreted as evidence for recombination by the informative-sites test.
Analysis of Real Data
Seven real sequence data sets, from viruses, bacteria, and human mitochondria, were also examined with the informative-sites test. Influenza C virus (ICV), a negative-strand RNA virus, and hepatitis C virus (HCV) were chosen because they are thought to evolve clonally (Muerhoff et al. 1997 ; Worobey and Holmes 1999 ). The others—dengue virus type 1 (DEN-1 virus), GB virus C (GBV-C), Helicobacter pylori, and human mitochondrial DNA (mtDNA)—have all previously been reported to exhibit evidence of recombination (Suerbaum et al. 1998 ; Eyre-Walker, Smith, and Maynard Smith 1999a, 1999b ; Holmes, Worobey, and Rambaut 1999 ; Worobey, Rambaut, and Holmes 1999 ; Worobey and Holmes 2001 ). All of the alignments were of third-codon-position nucleotides except for H. pylori and mtDNA, for which synonymous third sites were used in keeping with previous studies (Suerbaum et al. 1998 ; Eyre-Walker, Smith, and Maynard Smith 1999a ).
The ICV alignment, 642 third sites in length, included 16 sequences from the haemagglutinin-esterase gene with the GenBank accession numbers D63467–D63470, D63472, D28967, D28969–D28971, M11637, M11639–M11643, and M17868. The intergenotype HCV alignment consisted of six sequences from the complete coding region (2,971 third sites) with the accession numbers D50409, D00944, D63821, D28917, D17763, and Y13184. The DEN-1 virus data set (seven taxa, 774 third sites from three genes) is described in Worobey, Rambaut, and Holmes (1999) . The H. pylori alignment (144 synonymous third sites of the flaA gene from 33 Canadian isolates) is described in Suerbaum et al. (1998) . The GBV-C type 2 alignment (nine taxa, 2,841 third sites from entire coding region) and GBV-C type 3 alignment (16 taxa, 2,836 third sites from entire coding region) are both described in Worobey and Holmes (2001) . Finally, the mtDNA alignment (40 taxa, 3,561 synonymous third sites from entire coding region) was modified from the data set described in Eyre-Walker, Smith, and Maynard Smith (1999b) by removing identical sequences, eliminating one incomplete sequence, and then removing sites with gaps. All seven alignments are available from the author on request. The heuristic search procedure that was applied to the simulated data sets listed in table 1 was also followed with these alignments except for H. pylori. Unusually, in this case, the likelihood topology required substantially more steps than the MPT. Since the ISI is calculated using the value of t from the MPT, that topology was chosen for the subsequent analysis.
The results were largely as expected except for the mtDNA data set that exhibited a slightly smaller value of q than the null expectation, a pattern not suggestive of recombination but consistent with a clonal history for this population (table 2 ). This was in contrast to the results of the homoplasy test, which rejected the clonal model when applied to the same sequences (Eyre-Walker, Smith, and Maynard Smith 1999a, 1999b ). The two viral examples that were assumed to be clonal indeed appeared to be so on the basis of the informative-sites test. For both ICV and HCV, the observed proportion of informative sites was almost exactly that expected under clonality. Their ISI values were close to 0, and the null hypothesis of clonality could not be rejected. Helicobacter pylori, DEN-1 virus, and the two GBV-C data sets, on the other hand, all exhibited values of q substantially larger than q̂c, along with ISI values suggestive of a large role for recombination, supported by highly significant P values (table 2 ). Interestingly, the high ISI value for H. pylori, 0.85, was very similar to the homoplasy ratio of 0.8 calculated using the homoplasy test on the same data (Suerbaum et al. 1998 ). The DEN-1 data, with ISI = 0.49, appeared to be somewhat less affected by recombination.
However, perhaps the most remarkable results were for GBV-C. The two GBV-C data sets showed strikingly similar measures of ARH, transition/transversion bias, and recombination, despite representing separate populations of the virus from different parts of the world (Worobey and Holmes2001) . Both gave highly significant P values strongly rejecting the clonal model. Moreover, they shared the same ISI value, 0.82, indicating that very similar processes may shape the evolution of distinct populations of GBV-C. These results establish that recombination can cause viruses, as well as bacteria (Suerbaum et al. 1998 ), to approach complete linkage equilibrium.
Discussion
The informative-sites test is a useful new procedure for testing the assumption of clonality that underlies phylogenetic trees and the inferences made from them. Because it works by teasing apart the processes contributing to apparent rate heterogeneity, it simultaneously provides a means of determining whether the observed rate heterogeneity is real or is at least partly an artifact of recombination. It is recommended that this method be applied to a gap-free nucleotide sequence alignment of third-codon-position sites from nonoverlapping reading frames. The majority of changes at such sites are silent, and confining analysis to them may improve precision, since they tend to show relatively less site-specific rate heterogeneity than, for example, first- or second-codon-position sites. Examination of many real data sets, in addition to simulated ones, indicates that the site-specific rate heterogeneity generated by mutation bias or selective constraints at third sites can be adequately accounted for by the method described here and that the informative-sites test applied to such alignments is very unlikely to produce false positives. For instance, the value of q for the HCV data set analyzed here matched the predicted clonal value very closely even though HCV is thought to experience strong selective pressure (Manzin et al.2000) .
If recombination has significantly influenced current genetic diversity, the test should be appropriate whether the events have been ancient, recent, rare, or frequent and whether or not clear mosaic sequences are evident. Thus, it is particularly relevant for those populations where recombination may be so common, or sequences so similar, that methods that rely on mosaic detection (reviewed in Maynard Smith 1999 ) will be inadequate. Although it may be convenient, it is probably unwise to treat as clonal any data set that passes through the relatively coarse filter imposed by such tests.
While the informative-sites test gave results very similar to those of the homoplasy test for the H. pylori data set, the two methods differed when applied to the mtDNA data. One possible explanation is that the informative-sites test suffered a type II error—a false negative—in this case. In light of figure 4 , and given that these data were marked by considerable transition/transversion rate bias as well as high base composition bias (κ = 45.3; table 2 ), it is difficult to rule this possibility out. However, it is interesting, although not necessarily indicative of clonality, that the value of q in the mtDNA example did not just fall short of significance, but was slightly lower than the clonal expectation (table 2 ).
Another possibility is that the homoplasy test generated a type I error, or false positive. Given the results presented in figure 3 , it is worth noting that when the homoplasy test was applied to the mtDNA, the data were assumed to be free of site-specific rate heterogeneity (Eyre-Walker, Smith, and Maynard Smith 1999a, 1999b ). Hypervariable sites due to selective constraints were ruled out by comparing the observed divergence of mtDNA sequences between different primate species with that expected, at saturation, in the absence of selective constraints (Eyre-Walker, Smith, and Maynard Smith 1999a ). However, this method is suitable for detecting site-specific rate heterogeneity only in the biologically unlikely form of “constrained” versus “hypervariable” sites, where one class of sites cannot change and the other changes at a single rate. If rates among sites actually vary over a range of values, and if changes between nucleotides at a given site are symmetric, such a method will not be capable of detecting among-sites rate heterogeneity, since any site with a nonzero rate will eventually reach saturation.
In addition, though, Eyre-Walker, Smith, and Maynard Smith (1999a) examined the number of variable third sites shared between human and other primate mtDNA and found no evidence for an excess. Since elevated substitution rates at some third sites might cause those that are hypervariable in humans to also appear in other primates, this was taken as evidence against site-specific rate heterogeneity. Therefore, if the homoplasy test has produced a false positive in this case due to undetected rate heterogeneity, and if the high degree of ARH in these mtDNA data (table 2 ) actually reflects RRH in a clonal population (as the informative-sites test suggests), then the constraints producing rate heterogeneity at third sites in mtDNA may be inconsistent across species.
In other cases, the evidence for recombination is overwhelming, so its implications need to be very carefully considered (see Schierup and Hein [2000] and Worobey and Holmes [2001] for a discussion of many of these implications). For example, the notion that phylogenetic trees reconstructed from recombinant data will systematically underestimate divergence times appears to be a misconception. The example in figure 1 is sufficient to show that this is not always the case. In this instance, the branch lengths of the tree for the 2,000-nt alignment, once corrected for the considerable apparent rate heterogeneity caused by recombination, implied a deceptively long genetic distance/time to the common ancestor of the four taxa. In fact, recombinant data analyzed by ML models that include rate heterogeneity will give rise to two competing effects: a tree-shortening tendency due to the homogenizing effects of recombination, and a tree-lengthening tendency due to the inflated ARH generated by recombination. Figure 1 shows that this tree-lengthening effect can result in overestimation of the time to most recent common ancestor (TMRCA) when ML models incorporating rate heterogeneity are naïvely used on data sets that have a recombinant history. Interestingly, Schierup and Hein (2000) recently concluded that recombination could give rise to underestimation of the TMRCA when using distance methods but to unbiased estimates when using ML methods. However, an important point to consider in this context is that data sets with higher levels of recombination will also show higher levels of ARH. If this recombination-generated ARH had been accounted for during tree construction in Schierup and Hein's (2000) simulation study, the ML approach may well have indicated a bias toward overestimation of TMRCA, as suggested by figure 1 here. While further work will be required to understand the relative strengths of the conflicting effects that might bias dating, it is clear from these studies that phylogenetic inference in the face of recombination is much more complicated than is currently appreciated.
For any recombining population, a key question is the following: If the assumption of clonality is not valid, at what level of recombination is the convenient inference of a single phylogenetic tree no longer useful? Limited recombination may sometimes have insignificant effects and be ignored without consequence. Obvious recombinants can be detected and removed in other instances. However, in cases like that of the GBV-C subtypes analyzed here, the most appropriate use of a phylogenetic tree may be to show that a phylogenetic tree is not of much use. In such circumstances, it might be worth searching for small genomic regions that are less likely to be profoundly affected by recombination but which may contain sufficient phylogenetic signal to address the question at hand.
Note Added in Proof
The informative-sites test was also applied to another, larger, human mtDNA data set. This new alignment (Ingman, M., H. Kaessmann, S. Pääbo, and U. Gyllensten. 2000. Mitochondrial genome variation and the origin of modern humans. Nature 408:708–713) contained 53 isolates for which full-length coding region sequences were available (3750 third sites analyzed). The hypothesis of clonality could not be rejected with the informative-sites test (P = 0.599). Indeed, while it exhibited a fairly high degree of site-specific rate heterogeneity at third sites (α = 0.61—a potential danger for the homoplasy test) this data set fit the clonal expectation very closely under the informative-sites test (ISI = −0.01). It would appear that the ARH in human mtDNA reflects “real” subsititution rate variation among sites, not recombination.
Antony Dean, Reviewing Editor
Abbreviations: ARH, apparent rate heterogeneity; DEN-1, dengue virus type 1; GBV-C, GB virus C; HCV, hepatitis C virus; ICV, influenza C virus; ISI, informative-sites index; ML, maximum likelihood; MPT, maximum-parsimony tree; mtDNA, mitochondrial DNA; nt, nucleotide; RRH, real rate heterogeneity; TMRCA, time to most recent common ancestor.
Address for correspondence and reprints: Michael Worobey, Department of Zoology, University of Oxford, South Parks Road, Oxford OX1 3PS, United Kingdom. [email protected].
Keywords: recombination GB virus C mitochondria maximum likelihood rate heterogeneity clonal
Table 1 Results of the Informative-Sites Test for Clonal and Recombinant Simulated Data
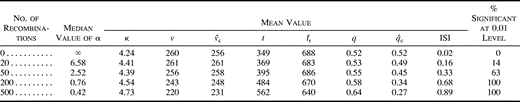
Table 1 Results of the Informative-Sites Test for Clonal and Recombinant Simulated Data
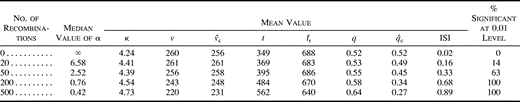
Table 2 Results of the Informative Sites Test for a Variety of Real Data Sets

Table 2 Results of the Informative Sites Test for a Variety of Real Data Sets

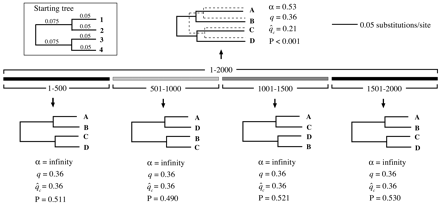
Fig. 1.—Demonstration of the relationship between recombination and rate heterogeneity, and the elements of the informative-sites test. Branch lengths on all the trees are drawn to the scale shown. The estimated maximum-likelihood tree, α, q, and q̂c are shown below each 500-nt region. Compared with those of the clonally generated 500-nt regions, the estimated trees for the recombinant 2,000-nt alignment were more starlike. (The branch lengths of the solid tree at the top have been corrected for the apparent rate heterogeneity; those of the dashed tree have not.) The concatenated alignment showed evidence of considerable recombination-generated apparent rate heterogeneity and a highly significant excess of informative sites compared with the clonal expectation. Accommodating the apparent rate heterogeneity in the overall alignment gave rise to a tree with greater root-to-tip distances than obtained for the clonal regions
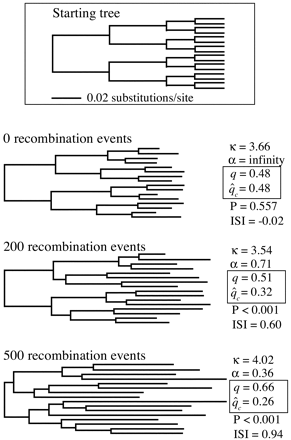
Fig. 2.—The starting tree and some examples of estimated maximum-likelihood trees at various levels of recombination for the simulation study summarized in table 1 . The branch lengths on all trees are drawn to the same scale. The trees below the starting tree are those estimated for one randomly chosen representative of the original 100 replicates over various levels of recombination. As the number of recombination events increased, the trees became more starlike. After 500 recombination events, the starting topology was no longer obtained, and the estimated tree was dominated by long terminal branches. Although there was no ARH in the clonal data set, the ARH increased with recombination rate, as did the disparity between q and q̂c
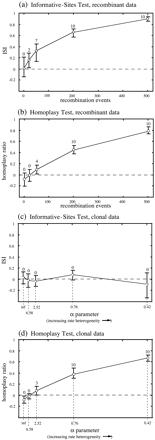
Fig. 3.—Comparison of the informative-sites test and the homoplasy test. The horizontal axes in a and b show the number of recombination events experienced by each set of 10 alignments. The points represent the average index value (ISI or homoplasy ratio) at each level, and the bars mark the maximum and minimum values observed for that group. Above each bar is the number of significant results (0.01 level) out of the 10 alignments. The results for the two methods were very similar for the recombinant data (a and b). The methods gave divergent results in c and d. In these two plots, the horizontal axes represent the degree of rate heterogeneity under which these clonal alignments were evolved. While the informative-sites test readily distinguished between recombinant data and clonal data with matching rate heterogeneity (a vs. c), the homoplasy test did not (b vs. d)
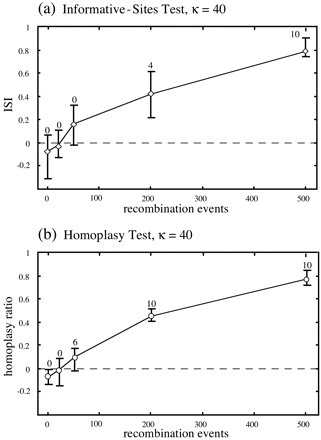
Fig. 4.—Comparison of the informative-sites test and the homoplasy test for the data with extreme transition/transversion rate bias, with axes and labels as described in the legend to figure 3 . The informative-sites test appeared to underestimate the extent of recombination compared with the homoplasy test, which was more sensitive than the informative-sites test under these conditions
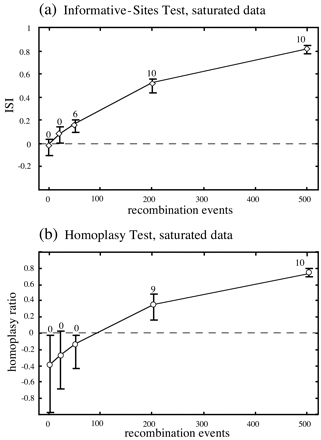
Fig. 5.—Comparison of the informative-sites test and the homoplasy test for the saturated data, with axes and labels as described in the legend to figure 3 . Under these conditions, the homoplasy test appeared to be less sensitive than the informative-sites test in detecting recombination
I gratefully acknowledge Andrew Rambaut (who kindly wrote the C code for the informative-sites test), Eddie Holmes, Rob Freckleton, David Posada, Mike Charleston, Paul Harvey, Korbinian Strimmer, Oliver Pybus, David Robertson, Adam Eyre-Walker, Philip Awadalla, and John Maynard Smith for stimulating discussions. The comments and criticisms of one very insightful anonymous reviewer were much appreciated. This work was supported by the Rhodes Trust, the Natural Sciences and Engineering Research Council of Canada, and St. John's College, Oxford.
References
Eyre-Walker A., N. H. Smith, J. Maynard Smith,
———.
Hasegawa M., H. Kishino, T. Yano,
Holmes E. C., M. Worobey, A. Rambaut,
Manzin A., L. Solforosi, M. Debiaggi, F. Zara, E. Tanzi, L. Romano, A. R. Zanetti, M. Clementi,
Maynard Smith J.,
Maynard Smith J., N. H. Smith,
Maynard Smith J., N. H. Smith, M. O'Rourke, B. G. Spratt,
Muerhoff A. S., D. B. Smith, T. P. Leary, J. C. Erker, S. M. Desai, I. K. Mushahwar,
Rambaut A., N. C. Grassly,
Schierup M. H., J. Hein,
Sharp P. M., D. L. Robertson, B. H. Hahn,
Slatkin M., R. R. Hudson,
Suerbaum S., J. Maynard Smith, K. Bapumia, G. Morelli, N. H. Smith, E. Kunstmann, I. Dyrek, M. Achtman,
Sullivan J., K. E. Holsinger, C. Simon,
Swofford D. L.,
Worobey M., E. C. Holmes,
Worobey M., A. Rambaut, E. C. Holmes,
Yang Z.,



