-
PDF
- Split View
-
Views
-
Cite
Cite
Matthew O Jackson, Yiqing Xing, The Incentive Complementarity Between Formal and Informal Enforcement, Journal of the European Economic Association, Volume 22, Issue 5, October 2024, Pages 2294–2328, https://doi.org/10.1093/jeea/jvae009
Close - Share Icon Share
Abstract
We introduce a model in which people exchange some goods and services informally in their community and others formally on a market. We show that enforcement by informal communities and a formal market are complements: If communities ostracize individuals who are caught cheating on the market, this bolsters incentives to comply with exchanges in both settings. Although transactions within a community generate lower gains from trade than those on the wider market, the enhanced incentives from simultaneously transacting in communities and on the overall market can be welfare-enhancing compared with either extreme. We discuss the implications of informal community exchanges in a country’s development as well as how moral or religious beliefs enhance the complementarity between community and formal enforcement.
A set of Teaching Slides to accompany this article is available online as Supplementary Data.
1. Introduction
The key to successful economic exchanges here is not necessarily an impartial and efficient third-party enforcing agency, but the existence of a level of trust or other self-enforcing institutions in relevant networks of commerce, credit, wage-labor, and other contractual relations that support free market activities. In other words, the state is neither necessary nor sufficient. The simple model in which it is only the state and threat of its justice and police systems that makes people behave cooperatively seems a poor description of any known situation.
Joel Mokyr (2008), page 71
The above quote makes clear the importance of incentives beyond state punishment. Yet, despite the extensive evidence that reputations matter, we still know little about how informal social relationships interact with formal institutions in the enforcement of norms and contracts. Why and when does one form of enforcement enhance the effectiveness of the other?
We answer this question by characterizing the complementarity between “formal enforcement” by a market and “informal enforcement” (e.g., threats of ostracism) by communities. We explore (i) why and when these two forms of enforcement coexist, (ii) why using both forms of enforcement improves incentives, and (iii) the impact of morality (e.g., anticipated guilt from having done something deemed morally wrong, or supernatural punishment for having committed a sin).
In our model, a household’s tasks and goods can be exchanged with others in their community or with others in the general economy through trade in markets. The gains from trade increase with the number of people with whom a household can potentially trade: Autarky is less efficient than conducting exchanges in a community and the latter is less efficient than doing exchanges in the whole economy. People who cheat in their part of an exchange in their community are ostracized: They can no longer exchange tasks/goods that are normally exchanged in the community. People who cheat in their part of an exchange in the formal market are caught and convicted with some probability, depending on the enforcement system, and face formal punishment (e.g., fines for damages, jail time for fraud, etc.), and their names are made public.
Although exchanges on the open market substitute for exchanges in one’s own community, there is also an important incentive complementarity. When people are caught cheating on the formal market and their names become public, people in their communities can also ostracize them. For instance, someone caught embezzling and cheating on a contract risks being ostracized by their neighbors. As a result, the punishment from being caught by the police is more than the fine itself as it also includes the loss of reputation and community interaction. Government enforcement is, thus, more effective and less costly when there is more community interaction as there is a greater cost associated with the loss of reputation. Thus, there is an interesting trade-off: having more community interaction leads to lower gains from trade, but it can offer greater incentives to follow through with market exchanges and, thus, an optimum can involve a mixture of both forms of exchange.1
Although some instances of publicizing crimes and court cases are not intended to be public shamings (others may be for public safety, as in the registration of sex offenders or malpractice suits), they still have the same consequence of making the offender’s transgressions known to their community. For these people, this not only leads to difficulties in obtaining future employment (e.g., see the discussion and references in Ahmed and Lång 2017), but it also leads to other more direct ostracism by members of their community (e.g., Winnick and Bodkin 2008). These social sanctions have a significant deterrent effect on crime (e.g., Buonanno, Pasini, and Vanin 2012). Thus, the complementarity that we analyze here is not simply a theoretical construct: The difficulties faced by ex-convicts or people accused of malpractice, among others, are substantial and costly to them. In some cases, the loss of reputation and ostracism by an offender’s community can be as costly or even more costly than any fine or nominal punishment meted out by a court and have been found to have significant deterrent effects for first offenders.
We characterize the optimal (welfare-maximizing and self-enforcing) enforcement system and highlight how the optimal mixture of formal and informal enforcement depends on the cost of formal enforcement. At one extreme, when governments are fully effective and formal enforcement of market exchanges is cheap, the optimal system is “all market”—no community exchange is needed. At the other extreme, where formal enforcement is very expensive, “all community” is the optimal system. If the cost of formal enforcement is intermediate, the optimal system features a mixture of both community and market exchanges. This mixture is possible only when the incentive complementarity is above a certain threshold. This intermediate range involves discontinuities on both ends. The first discontinuity is that the amount of community exchanges in any optimal system is either zero or bounded away from zero, as informal enforcement is self-enforcing and needs some critical level of interaction in order to function. The second discontinuity comes from the fact that formal enforcement must occur at some minimum level in order to make the market function and this does not rely on any fixed-cost of formal enforcement.
Our model sheds light on economic development and the growth of government. Given the complementarity that we outline, a strong community system can enhance, rather than impede, government and legal enforcement. In order to modernize most effectively, it can be beneficial for governments to maintain and leverage a certain level of community rather than abandon it. Ultimately, even at high levels of development, there are exchanges that are shared among friends and in the community and these relationships and reputations bolster market incentives.
We also discuss the impact of people either having a moral code that they find internally costly to break (e.g., via feelings of “guilt”) or believing that supernatural forces will punish them if they fail to obey norms of behavior. Such moral reasoning itself is not complementary to the other forms of enforcement as it is present regardless of whether one is punished by their community or through law enforcement. As we show, however, it can enhance the complementarity between formal and informal enforcement by relaxing both incentive constraints. By contrast, errors in formal enforcement—for example, from corruption—break the informational linkage and the complementarity between formal and informal enforcement. Sufficient errors in enforcement (false positives) can cause a community to lose trust in law enforcement and, consequently, to no longer ostracize community members who are “caught,” thereby destroying the complementarity between government and community. Small changes in errors or corruption can lead to discontinuous declines in the effectiveness of enforcement and welfare.
Related Literature.
A key ingredient of our analysis is the importance of reputation and enforcement in communities, which is the subject of much study.2 There is an abundance of empirical examples in which community reputations help sustain honest behavior on a market, even without formal legal enforcement.3 We put a model of community enforcement to work as a complement to formal legal enforcement.
Early papers studying the coexistence of formal and informal exchange generally take a substitute perspective (Kranton 1996; Dixit 2003a, b; Greif and Tabellini 2010, 2017). Other papers focus on culture (norms, beliefs, and values) and show that it can either enhance or hinder institutions.4 The key way in which our work differs from the previous literature is that we analyze the complementarity between the community and the formal government and the importance of using them together rather than looking at the circumstances under which either or both thrive. This echoes the empirical findings that communities and local elites can facilitate formal institutions.5
A comparative static that more-developed societies (which have lower law enforcement costs c) rely more on the market and less on their communities is consistent with many empirical and anecdotal findings (McCleary and Barro 2006; Lowes et al. 2017; Banerjee et al. 2018), and is the subject of much of the previous literature (e.g., Kranton 1996; Gagnon and Goyal 2017; Dixit 2003a). This mechanical substitution does not preclude the simultaneous use of formal and informal enforcement being more powerful combined than when used alone—that is, in the sense of a complementarity that enhances incentives. The increased use of one makes the other more effective, so they are substitutes in terms of task provision but at the same time complements in terms of incentive provision.
There are recent papers that have complementarities between formal and informal enforcement. Acemoglu and Wolitzky (2020) analyze an environment where community enforcement incentivizes formal enforcers who, in turn, discipline regular agents. Ali and Miller (2022) show that better formal enforcement promotes community enforcement by incentivizing agents to truthfully communicate who has cheated in informal interactions.6 Our paper, by contrast, highlights a different channel: the fear of subsequent loss of reputation, where the value in community exchanges increases the costs associated with formal detection.7 We formally define and prove an “incentive complementarity” between formal and informal enforcement. We also analyze how the strength of this complementarity determines the optimal combination of formal and informal enforcement and, thus, how it determines the optimal level of social welfare.
2. The Model
2.1. The Setting
Communities, Actions, and Payoffs.
A finite population of agents, denoted by N, is partitioned among multiple communities, each having at least two agents.
Time proceeds in discrete periods |$\tau \in \lbrace 1,2,\ldots \rbrace$| and agents discount utility according to a discount factor |$\delta \in (0,1)$|.
In each period, |$\tau$|, agents exchange goods either in the market or in their community. All agents are matched the same way, either in their community or on the market in any period.8 Let |$e^\tau \in \lbrace {\textit {community, market}}\rbrace$| denote the type of exchange in period |$\tau$|, and let q denote the probability that |$e^\tau = {\textit {community}}$| and |$1-q$| denote the probability that |$e^\tau = {\textit {market}}$|, independent across periods.
Community Exchanges and Informal Enforcement.
When |$e^\tau = {\textit {community}}$|, agents exchanging tasks or goods are randomly matched in their community.9 Agents simultaneously choose an action |$a_i \in \lbrace {\textit {abide, deviate}}\rbrace$|. When an agent “abides,” they deliver their task/good for their exchange and incur a cost, |$t_c$|. If they “deviate,” they do not deliver their task/good and incur no cost. An agent obtains a benefit |$v> t_c$| if the agent who is matched with them abides. Thus, the payoffs for the community exchange have a prisoner’s dilemma-like structure as seen in Table 1.10
| . | Partner’s Action . | |
|---|---|---|
| . | abide . | deviate . |
| Abide | |$v-t_c$| | |$-t_c$| |
| Deviate | v | 0 |
| . | Partner’s Action . | |
|---|---|---|
| . | abide . | deviate . |
| Abide | |$v-t_c$| | |$-t_c$| |
| Deviate | v | 0 |
| . | Partner’s Action . | |
|---|---|---|
| . | abide . | deviate . |
| Abide | |$v-t_c$| | |$-t_c$| |
| Deviate | v | 0 |
| . | Partner’s Action . | |
|---|---|---|
| . | abide . | deviate . |
| Abide | |$v-t_c$| | |$-t_c$| |
| Deviate | v | 0 |
If some agents deviate while others (at least one) abide in a community, then the deviating agents are ostracized. This means that in any future periods in which these agents would normally have been matched in their community, they are no longer matched and instead receive an autarchic payoff of 0 for those periods.11
Also, ostracism only applies when agents are being hurt; it is not applied when all of the agents in a community deviate in some period. This allows us to model equilibria in which community exchanges cannot be supported and all of the agents deviate without being punished, so the community is effectively closed. If there is only one remaining agent, then there is no matching and the community closes.
Market Exchanges and Formal Enforcement.
When |$e^\tau = {\textit {market}}$|, agents simultaneously choose an action |$a_i \in \lbrace {\textit {abide, deviate}}\rbrace$| for their market exchanges. The cost is |$t_m$| if an agent abides in the market and is 0 if they deviate, where |$t_c> t_m> 0$|. Thus, market exchanges are less costly and generate more gains from trade than community exchanges.
Market exchanges are monitored and guaranteed by a third party, for example, a clearing house such as the NYSE, or a governmental organization, platform, and so forth. Thus, an agent engaging in a market exchange obtains v regardless of the other agents’ actions.12 Therefore, an agent’s payoff from an exchange is |$u^{\tau }_i = v-t_m$| if they abide and is |$u^{\tau }_i =v$| if they deviate.13
If an agent i deviates, then they are caught and convicted with a probability |$\phi$| in which case the following occur:
i pays a fine|$f > 0$| (which encompasses legal costs, damages, loss of license, monetary fines, jail time, etc.), denoted by |$f^{\tau }_i = f$|;
With a probability |$\psi$|, the news that agent i has been caught is learned by i’s community; this leads to agent i’s ostracism from their community.
If an agent deviates but is not caught/convicted by the enforcer (with probability |$1-\phi$|), then there are no consequences for that agent.
The formal market keeps a list of the agents who have been ostracized by their communities up through period |$\tau$|, |$O^{\tau }$|. Any agent on that list, |$i \in O^{\tau }$|, is monitored in every market exchange in the future |$(\forall \tau ^{\prime } > \tau )$|, and if they deviate again then they pay a larger fine |$F > t_m$| (large enough to incentivize them to sustain market exchanges).
Finally, the market closes if its operator expects to incur losses. In particular, the market becomes unavailable if some agents are expected to deviate with a positive probability in some period on the equilibrium path. When the market is unavailable (denoted as |$z = 0$|), everyone’s payoff on the market is 0, regardless of their action, and no one is convicted. The market status (|$z =0$| or 1) is chosen once and for all before the agents play the game and is commonly observed by all.
In summary, there are two differences between community and market enforcement: First, community punishment is informal and through ostracism, while market enforcement is formal and via a fine. Second, communities are small and deviators are always caught, while the market is large and deviators are only convicted with some probability. One could also allow markets to ostracize agents, but given the imperfect enforcement, the complementarities and results below would still exist—the key difference is that deviators are more easily caught/convicted in communities than in the market.
Histories.
An agent’s history consists of the public history and their private history, |$h^\tau _{i} = (h^\tau _{{\textit {public}}}, h^\tau _{{\textit {private,i}}})$|, specified as follows.
The public history includes an indicator of whether the market is available (|$z = 1$|) or not (|$z = 0$|), a list of whether their past exchanges took place in the community or the market, and which agents have been ostracized (which are in an autarchy).
where |$O^\tau$| denotes the list of agents who have been ostracized by their communities by the end of period |$\tau$| (so this is a non-shrinking set over time).
An agent’s private history at the end of period |$\tau$| also includes their past actions, payoffs, and fines.
This includes agent i’s own action, |$a^{\tau }_i$|, their payoff from the exchange, |$u^{\tau }_i$|, and any fine that was imposed by the formal enforcer |$f^{\tau }_i \in \lbrace \emptyset , f, F\rbrace$|.14
Let |$h_i^{0}= \emptyset$| so that histories are well defined for the initial period. Let |$\mathcal {H}_i \equiv \lbrace (h_{{\textit {public}}}^{\tau }, h_{{\textit {private,i}}}^{\tau })\rbrace _{\tau }$| denote the set of all possible histories for agent i, and |$\mathcal {H}_{{\textit {public}}} \equiv \lbrace h_{{\textit {public}}}^{\tau }\rbrace _{\tau }$| be the set of all finite public histories.
Strategies and Equilibrium.
A strategy |$\sigma _i: \mathcal {H}_i \times \lbrace {\textit {community, market}}\rbrace \rightarrow \Delta (\lbrace {\textit {abide, deviate}}\rbrace )$| is a function that maps every possible history of agent i to an action, |$\sigma _i(h^{\tau -1}_{i},e^\tau )\in \Delta (\lbrace {\textit {abide, deviate}}\rbrace )$|.15 Let |$\sigma$| denote a profile (of strategies) for all agents.
We call |$\sigma$| a public strategy profile if, for every i, |$\sigma _i$| depends only on the public history, |$h_{{\textit {public}}}^{\tau -1}$|, and the current matching type, |$e^\tau$|, (which is also public); thus, |$\sigma _i(h^{\tau -1}_{{\textit {public}}}, h^{\tau -1}_{{\textit {private,i}}}, e^\tau )=\sigma _i(h^{\tau -1}_{{\textit {public}}}, \tilde{h}^{{\tau -1}}_{{\textit {private,i}}}, e^\tau )$| for all |$\tilde{h}^{{\tau -1}}_{{\textit {private,i}}}$|.
A strategy profile |$\sigma ^{*}$| is a perfect public equilibrium (given an enforcement system |$(\phi , q)$|) if |$\sigma ^{*}$| is a public strategy profile and a Nash equilibrium at every |$(h^{\tau -1}_{{\textit {public}}},e^\tau )$| and all corresponding possible private histories.16
We also require that the market status is consistent with the equilibrium profile: the market closes (|$z = 0$|) if some agents deviate with a positive probability in some period on the equilibrium path.
2.2. Exchange Systems and Incentive Compatibility
An exchange system for a society is a list |$(\phi , q; z, \sigma )$|, such that the strategy profile |$\sigma$| is a perfect public equilibrium, given the enforcement system |$(\phi , q)$| and the market status z, which is consistent with the equilibrium. There can be multiple equilibria: for instance, if nobody expects anyone to abide in community exchanges, then it can be a best response not to abide either, but if one expects everyone to abide, then abiding can be an equilibrium; similarly, it is always consistent to have the market closed (|$z=0$|) and all of the agents deviating on the market.
Let |$V(\delta , v, t_c) \equiv {\delta (v - t_c) }/({1-\delta })$| denote the discounted sum of the future values of community exchanges, when |$q = 1$|. The following three incentive constraints are useful in characterizing various equilibrium possibilities:
The community (ICcom) requires that the cost of abiding in an exchange in one’s community, |$t_c$|, does not exceed the future value of holding community membership, |$qV$|, and only applies when |$q> 0$|.
The market-only (ICmark-only) requires that the cost of abiding in a market exchange, |$t_m$|, does not exceed the first-time expected punishment and can only apply when |$q<1$|. This condition is useful in characterizing the cases where agents only abide on the market.
When agents abide in their community, the extra term, |$-\psi q V$| in the denominator of the market (ICmark), captures the complementarity between community and market enforcement. A larger fraction of community exchanges, q, results in a higher value of community membership, which enhances the complementarity.
An equilibrium, |$\sigma$|, is said to be fully exchanging if all agents abide at all histories on the equilibrium path. This implies that the market is available (|$z = 1$|), for consistency. A (formal and informal) enforcement system, |$(\phi , q)$|, is incentive compatible if the system admits a fully exchanging equilibrium. A lemma characterizes incentive-compatible enforcement systems.
(Incentive compatible enforcement systems). An enforcement system, |$(\phi , q)$|, is incentive compatible if and only if |$(IC^{\textit{com}})$| and |$(IC^{\textit{mark}})$| both hold.
To further prepare for a formal definition of social welfare, we also need to analyze enforcement systems that are not incentive compatible (i.e., fully exchanging equilibria do not exist). In particular, we define an equilibrium, |$\sigma$|, to be
community-exchanging if all agents abide in all community exchanges on the equilibrium path but in none of the market exchanges (and the market closes) and
market-exchanging if all agents abide in all market exchanges on the equilibrium path (and, hence, the market is open) but in none of the community exchanges.
The next lemma provides conditions for the enforcement systems to support these equilibria.
An enforcement system, |$(\phi , q)$|, permits
a community-exchanging equilibrium if and only if |$(IC^{\textit{com}})$| holds, and
a market-exchanging equilibrium if and only if |$(IC^{\textit{mark-only}})$| holds.
Figure 1 plots the incentive compatibility constraints and the enforcement systems |$(\phi ,q)$| that support different equilibria.
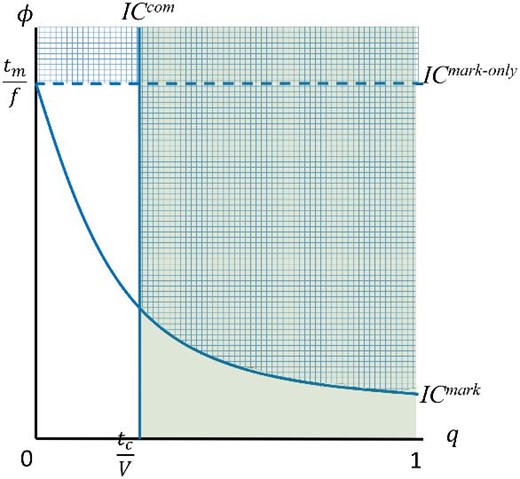
The incentive constraints. The regions in which the enforcement systems support, respectively, the market-exchanging equilibria (in the grid area), the community-exchanging equilibria (in the shaded area), and the fully exchanging equilibria (in the grid and the shaded areas).
Throughout our analysis, we consider the case in which
The former inequality is the condition that |$V(\delta , v, t_c) > t_c$| and, therefore, allows for a nondegenerate set of q’s such that the community incentive constraints are met; otherwise, the model becomes degenerate and the only possible incentive-compatible system is all market. The latter condition allows for the existence of a nondegenerate set of |$\phi$|’s for which abiding in a market exchange can be made incentive compatible: If a person knows that they will be caught with certainty, then deviation does not pay.
2.3. Welfare and Incentive Complementarity
Social Welfare.
Our interest is in characterizing the welfare associated with different enforcement systems and in identifying those that are welfare-maximizing. Welfare includes not only the payoffs from exchanges but also the costs of maintaining the formal market. Ostracism, on the other hand, is only costly in terms of lost payoffs and has no additional costs.
The per-capita per-period cost of formal enforcement is denoted by |$C(\phi ,q)$|, which applies only when the market is available. Two canonical examples are
|$C(\phi , q) = c\phi$| where |$c> 0$| is a scalar so that the cost is per probability of detection per capita, and
|$C(\phi , q) = c\phi (1-q)$| so that the cost is per probability of detection per market exchange.
From Lemma 1 and 2, the welfare |$\Pi (\phi ,q)$| associated with equilibria in which agents fully abide in whichever of community and market are open is:
Incentive Complementarity.
A key concept is the incentive complementarity in enforcement: The interaction between different types of enforcement in that the increased use of one increases the incentives associated with the other. We formalize this with standard increasing differences conditions, as follows:
There are weak increasing differences relative to some |$\lbrace (\phi ,q), (\phi ^{\prime },q^{\prime })\rbrace$| s.t. |$q^{\prime }<q, \phi ^{\prime } <\phi$| if
and there are strict increasing differences if
We say that informal and formal enforcements are incentive complements at |$(\phi _0, q_0)$| if
(|$\textit{WID}$|) holds for every |$\lbrace (\phi _0, q_0), (\phi ^{\prime },q^{\prime })\rbrace$| such that |$q^{\prime } < q_0, \phi ^{\prime }< \phi _0$|, and |$\lbrace (\phi ,q),(\phi _0, q_0)\rbrace$| s.t. |$q > q_0, \phi > \phi _0$|, and
for every neighborhood of |$(\phi _0, q_0)$|, (|$\textit{SID}$|) holds for some |$\lbrace (\phi _0, q_0), (\phi ^{\prime },q^{\prime })\rbrace$| s.t. |$q^{\prime } < q_0, \phi ^{\prime }< \phi _0$|, or some |$\lbrace (\phi ,q),(\phi _0, q_0)\rbrace$| s.t. |$q > q_0, \phi > \phi _0$|, within that neighborhood.
Incentive complementarity requires that using more formal enforcement becomes weakly more effective at higher rates of q and strictly for some points in each neighborhood of q. It requires weakly increasing differences for all monotone comparisons around the point |$(\phi _0, q_0)$| and strictly increasing differences for some monotone comparisons around the point |$(\phi _0, q_0)$| (including arbitrarily close comparisons).
Key Parameters.
Throughout the paper, we characterize the properties of a formal and informal enforcement system by |$(\phi , q)$|, where recall that |$\phi$| is the probability of catching agents in market deviations and q is the probability of community exchanges. We treat |$(\phi ,q)$| as (possibly being) endogenous and analyze, for instance, whether an enforcement system is incentive compatible and/or welfare-maximizing.17
We also examine the effects of two exogenous parameters, c and |$\psi$|. The former measures the cost of formal enforcement and the latter measures the linkage between formal and informal enforcement. Comparative statics for other exogenous parameters, |$\delta , v, t_c, t_m, f$|, are provided in an online appendix.18
3. Analysis with Linear Costs
We begin by analyzing a linear cost function for enforcement,
so that the amount of enforcement is per probability of detection per capita.
We characterize the optimal enforcement system, analyze incentive complementarity, and provide a series of comparative statics results. The linear cost function admits simpler figures and expressions. Most results extend readily to general cost functions, as shown in Section 4.1.
3.1. The Optimal Enforcement System
We now characterize the welfare-maximizing incentive-compatible enforcement system, |$(\phi , q)$|.
It follows from Lemma 1 and the definition of welfare (equation 1) that the optimal enforcement system solves the following problem:
Given any q, the optimal level of formal enforcement, |$\phi$|, is pinned down as the lowest level that satisfies the applicable incentive constraint(s) (if feasible). Therefore, we characterize the potential optima in terms of q.
The optimal enforcement system, |$(\phi , q)$|, belongs to one of the following four possible regimes (characterized by q, with |$\bar{q} = {t_c}/{V}$| and |$\bar{q} = {(\psi V - f)}/{2\psi V}$|):
all community, |$q = 1$|,
mix high—a mixed regime with a high community level, |$q \in (\bar{q}, \bar{q}]$|,
mix minimal—a mixed regime with the minimal community level that allows for the incentive compatibility of community exchange, |$q = \bar{q}$|, and
all market, |$q = 0$|.
A full characterization of the optimal enforcement system is provided in Proposition 1.
Let |$\bar{\psi } = {f}/{(V-t_c)}$| and |$\bar{\psi } = {f}/{(V-2t_c)}$|.
(The Optimal Mixture of Informal and Formal Enforcement). The optimal enforcement system is characterized as follows:
If the information spread from market to community is low, |$\psi <\bar{\psi }$|, then the optimum is one of the two extremes all community or all market, separated by a threshold |$c^{*} = {(t_c - t_m)f}/{t_m}$|, such that the optimum is:
all community, if |$c > c^{*}$|, and
all market, if |$c < c^{*}$|.
If the information spread is intermediate |$\psi \in (\bar{\psi }, \bar{\psi }]$|, then there are three potentially optimal regimes, separated by two thresholds |$c^{{\textit {mark}}} < c^{{\textit {com}}}$|, as follows:19
all community, if |$c> c^{{\textit {com}}}$|,
mix minimal, if |$c \in (c^{{\textit {mark}}}, c^{{\textit {com}}})$|, and
all market, if |$c< c^{{\textit {mark}}}$|.
If the information spread is high |$\psi > \bar{\psi }$|, then any of the four regimes can be optimal, separated by three thresholds |$c^{{\textit {mark}}} < c^{{\textit {mix-high}}} < c^{{\textit {com}}}$|, as follows:
all community, if |$c> c^{{\textit {com}}}$|,
mix high, if |$c \in (c^{{\textit {mix-high}}}, c^{{\textit {com}}})$|,20
mix minimal, if |$c \in (c^{{\textit {mark}}}, c^{{\textit {mix-high}}})$|, and
all market, if |$c< c^{{\textit {mark}}}$|.
Figure 2 depicts cases 1 and 3.
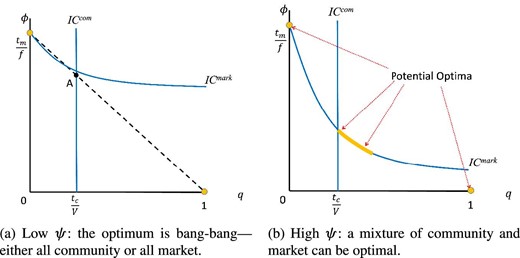
The two cases from Proposition 1. Case 1 (the left-hand panel) emerges when |$\psi < \underline{\psi }$| so that (|$IC^{\textit{mark}}$|) is above point A. Case 3 (the right-hand panel) occurs when |$\psi > \bar{\psi }$|.
When |$\psi$| is large enough (|$\psi > \bar{\psi }$|, case 3), there are four potential optimal regimes, plotted in Figure 3. In particular, mixed regimes, where community and formal enforcement are used simultaneously, can be optimal (3(b) and 3(c)).
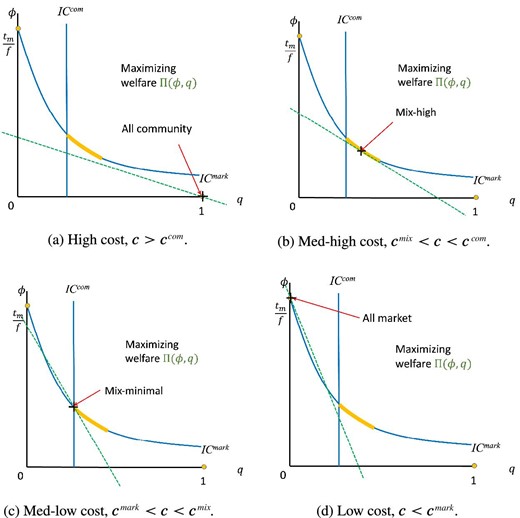
The four regimes of optimal enforcement systems (Case 3, Proposition 1) are presented in descending order of c. The green dotted line is an iso-welfare line, |$\Pi (\phi , q) = q (v-t_c) +(1-q) (v-t_m) - c\phi$|, where lines closer to the origin have higher welfare.
The Effects of Reducing the Cost of Formal Enforcement
As presented in Proposition 1, a reduction in the cost of formal enforcement, c,21 has important global impacts, in terms of shifting the optimal regimes—from those that rely more on community to those that rely more on formal enforcement. The same trend also applies locally, within each regime. This is summarized in the next proposition.
(Comparative Statics in c). As the cost of formal enforcement, c, increases,
the use of the community weakly increases and the optimal probability of enforcement, |$\phi$|, weakly decreases; in addition,
welfare weakly decreases (and strictly decreases whenever formal enforcement is used).
In Online Appendix Section E, we present a numerical example that illustrates the above comparative statics.
We conclude the analysis of optimal enforcement systems with two remarks.
First, the optimality of a mixture of formal and informal enforcement is made possible through strong enough complementarity (cases 2 or 3): the concern of losing one’s reputation in the community provides an extra incentive to behave well on the market. In contrast, when |$\psi$| is zero or relatively small, the complementarity is so low that just using one or the other exchange option is always better than having both. We further illustrate this point in Section 3.2.
Second, equilibria never involve small amounts of either type of enforcement. If both are used, then they are both used in amounts above a threshold: |$q^{*} \ge \bar{q} > 0$| and |$1- q^{*} > 1 - \bar{q} > 0$|. This holds even though we have not assumed any fixed costs.22 The first discontinuous jump in community use comes from the fact that community enforcement requires a minimal threshold in order for future reciprocation to outweigh current temptation. The second discontinuous jump also does not involve any fixed costs but occurs since market incentives require a sufficient probability of being caught and thus a sufficient expenditure on law enforcement. This is a direct corollary to Proposition 1 and is formally presented as Corollary A.1 in OnlineAppendix A.1.
3.2. The Incentive Complementarity Between Informal and Formal Enforcement
Next, we analyze the incentive complementarity between informal and formal enforcement, according to the characterization of social welfare (equation 1) and the definition of incentive complementarity (from Section 2.3).
We remark that the simple cost function, |$c\phi$|, has the merit that there is no inherent complementarity between |$\phi$| and q in the cost function. Therefore, the complementarity that we analyze is a result of the interactions between the two forms of enforcement in providing incentives.
(The Incentive Complementarity). Informal and formal enforcement are incentive complements whenever they are both active in an optimal enforcement system. That is, if |$(\phi ^{*},q^{*})$| is optimal and |$0<q^{*}<1$|, then the incentive complementarity holds at |$(\phi ^{*},q^{*})$|.
Thus, informal and formal enforcement are incentive complements at any interior optimum, |$(\phi ^{*}, q^{*}) \in (0,1)^2$|. Recall that the necessary and sufficient condition for the existence of such interior optima is that |$\psi$| is above some minimal level, |$\psi > \bar{\psi }$| (cases 2 or 3, Proposition 1).
The incentive complementarity comes from an informational linkage—the chance that the community learns that one of their members has been arrested and consequently then ostracizes them. Thus, having more community interaction makes formal enforcement more effective as the cost of being caught is higher due to the community’s reaction in ostracizing members who cheat on the market.
On the other hand, when the informational linkage is too small, there is not enough incentive complementarity and the optimal enforcement system is either all market or all community (case 1, Proposition 1, as plotted in Figure 2(a)).23
The Effects of Better Information Linkage
The above discussion already clarifies that the informational linkage, indexed by |$\psi$|, is the source of the complementarity between informal and formal enforcement. Proposition 1 highlights the key global impact of the complementarity: A large enough |$\psi > \bar{\psi }$| enables there to be mixed regimes where the community and the market are both active—this switches the environment from case 1 to case 2 (and further to case 3 when |$\psi > \bar{\psi }$|).
Here, we further highlight the parameter’s more-local impacts. In particular, recall that the optimal enforcement system consists of both informal and formal enforcement when |$c \in (c^{{\textit {mark}}}, c^{{\textit {com}}})$|.
An increase in |$\psi$| expands this region, as stated in the following proposition:
(Comparative Statics in |$\psi$|). An increase in the information linkage, |$\psi$|, expands the region of complementarity: |$c^{{\textit {mark}}}$| is decreasing and |$c^{{\textit {com}}}$| is increasing in |$\psi$|.
Figure 4 illustrates Proposition 4. An increase in |$\psi$| relaxes the market incentive constraint (which is lowered in the figure) and, therefore, enlarges the range of the set of potential optimal mixes of community and formal enforcement (depicted as the yellow part of the curve).
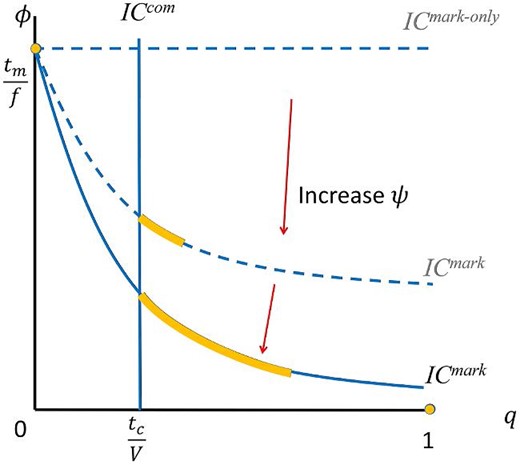
Comparative statics in |$\psi$|. As |$\psi$| increases, the market incentive constraint is easier to satisfy. A larger set of community and formal enforcement becomes potentially optimal.
The benefits from increasing |$\psi$| clarify why there are so many instances in which authorities publicize convictions, such as those referred to in the introduction. This can be a relatively cheap way of improving enforcement. In fact, even if the fine, f, is 0, a high |$\psi$| can make formal enforcement very effective: an authority does not formally punish the person but does publicize their misbehavior through the reaction of their community.24
We explore the comparative statics in other parameters in the Online Appendix Section D.25
The complementarity in incentives implies that when one develops formal institutions (a market and legal enforcement), nurturing and maintaining some community interactions can be vital to the successful growth of formal institutions. We discuss this topic next.
4. Extensions and Further Implications
4.1. Discussions of General Cost Functions
We now discuss conditions on general cost functions that ensure that the results of the paper still hold (except the expressions for |$\bar{\psi }$|, |$\bar{\psi }$|, and the cost thresholds in Proposition 1).
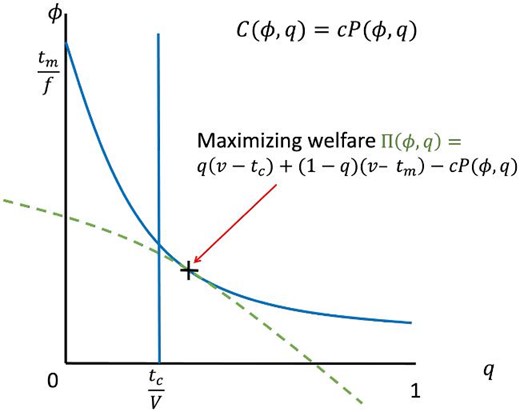
Recall that |$C(\phi ,q)$| is the (per-capita) cost of formal enforcement to support a probability |$\phi$| of catching a deviator on the market, when the market is available. Without loss of generality, we rewrite C as
This parametrization enables the comparative statics in c (Proposition 2). We interpret |$P(\phi ,q)$| as the size of the formal apparatus needed to obtain a probability of enforcement |$\phi$| on a market of size |$1-q$|, and |$c > 0$| to be a unit cost of (formal) enforcement. We assume
|$P(0,q) = 0$|, |$P(\phi , q) > 0$| whenever |$\phi > 0$| and |$q < 1$|;
|$P(\phi ,q)$| is strictly increasing in |$\phi$| when |$q<1$|, non-increasing in q;
|$P(\phi ,q)$| is quasi-convex in |$(\phi , q)$| and differentiable in both arguments when |$\phi > 0$|; and
the “iso-welfare” curves, |$\Pi (\phi ,q) = {\textit {const}}$|, are downward sloping in |$(\phi ,q)$| space and, in particular, |$P_q({t_m}/{f},0)> -P({t_m}/{f},0)$|.
Condition 1 requires that the cost of formal enforcement is positive at any positive detection probability (|$\phi > 0$|) when market exchanges are possible |$(q < 1)$|. Condition 2 is a standard monotonicity condition. Conditions 3 and 4 imply smooth, concave, and downward-sloping iso-welfare curves, which guarantee the existence of solutions in maximizing welfare. We note that differentiability is only required for |$\phi > 0$|, which still allows for a discontinuity when |$\phi =0$| as there can be a fixed cost of formal enforcement. In addition, the condition |$P_q({t_m}/{f},0)> -P({t_m}/{f},0)$| guarantees that the iso-cost curve that goes through the two extreme points, all community, |$(\phi ,q) = (0,1)$|, and all market, |$(\phi ,q) = ({t_m}/{f},0)$|, is downward sloping.
Under these conditions, the problem of solving welfare-maximizing incentive-compatible enforcement systems is illustrated in Figure 5.
4.2. Community-Poverty Traps and Other Development Implications
The incentive complementarity identified in this paper also provides some key insights into how a nation can grow, or fail, as we now briefly discuss.
Building institutions for formal enforcement tends to involve large up-front investments. This is exacerbated by the fact that, as we have seen, formal enforcement is used discontinuously and so to be welfare-enhancing it should be used above a minimum scale. This makes it difficult for a society to transition from local community enforcement to having a market economy. This is especially true if the society must pay for investments out of its current consumption. Growth and future prosperity may depend on having some market interactions, and the costs of transition can be prohibitive to a given society.
In particular, we explore the effects of the fundamental parameters on two sets of outcome variables. First, we consider |$c^{{\textit {com}}}$|, the threshold cost of legal enforcement at which the market emerges; recall that an all-community regime is optimal iff |$c \ge c^{{\textit {com}}}$|. Thus a higher |$c^{{\textit {com}}}$| implies that it is more attractive to adopt some market/legal enforcement. Second, we consider |$\bar{q}$| and |$\bar{q}$|, the lower and upper bounds of the proportion of community exchanges, q, that could be part of an optimal mixture of market and community exchanges (as defined in Lemma A.1 in the appendix).
Consider the threshold cost level at which the market emerges, |$c^{{\textit {com}}}$|, and the region of interior levels of community exchanges in potential optima, |$[\bar{q}, \bar{q}]$|.
As |$\delta$| increases, v increases, or |$t_c$| decreases: |$c^{{\textit {com}}}$| increases, |$\bar{q}$| decreases and |$\bar{q}$| increases.
As |$\psi$| increases: |$c^{{\textit {com}}}$| increases, |$\bar{q}$| remains constant and |$\bar{q}$| increases.
Thus, the region |$[\bar{q}, \bar{q}]$| expands with a larger |$\delta$|, v, or |$\psi$|, and shrinks with a larger |$t_c$|.
A strong community value (resulting from a large |$\delta$|, v or a small |$t_c$|) and a community closely attuned to law enforcement (a large |$\psi$|), each makes law enforcement more effective and cheaper. Therefore, states with strong community bases can modernize faster and more effectively. That is, given the complementarity, a strong community can actually help the transition to formal enforcement, rather than delaying it. With appropriate measures of key variables, one could examine this result both cross-sectionally and dynamically. The key variables to measure would be to estimate the economic values of |$t_c$| and |$t_m$| and, thus, the advantages of moving to a well-functioning market, and then also to have a measure of how well a country enforces its laws (a basis for estimating C).
We remark that although productivity can be enhanced through the complementarity of community and formal enforcement, it can be that community leaders deliberately block this complementarity and the development of markets. Such leaders may benefit from community power and be threatened by formal institutional growth. By breaking this complementarity, a leader can impede the functioning of formal institutions and ensure that the community remains the central provider. This can be done by discrediting formal institutions, breaking the information conduit between formal misbehavior and informal punishments, refusing to ostracize, or even by sheltering or rewarding criminals. All such actions would diminish |$\psi$| (the probability that an agent is ostracized conditional on cheating on the market) and, thus, make it harder for the market to function. History is full of such roadblocks to development, from medieval Europe to modern Egypt; this often involves conflicts between states trying to gain formal power and religious and other community leaders who are reluctant to relinquish it.26 Such attempts to prevent members from interacting outside of the community are not only driven by leaders but can also be part of a system that becomes self-perpetuating: such as gang members who are marked by deliberate crimes or tattoos that make it impossible for them to interact outside of their community, or even aspects of the “Acting White” phenomenon analyzed by Austen-Smith and Fryer (2005) where individuals who attempt to gain the skills needed to transact outside of the community are ostracized just for attempting to reach outside of the community.
Our model also provides other predictions for productivity. In OnlineAppendix Section C, we provide a preliminary empirical analysis based on cross-country correlations of overall production (log GDP) with the strength of community and formal enforcement. Although such correlations cannot be taken to be causal, they show facts that are consistent with the model’s predictions.
Some basic correlations are consistent with findings in some of the previous literature: GDP is positively correlated with formal enforcement (rule of law) and positively correlated with a measure of community enforcement—how much one believes they can count on other members of one’s community for help. The more novel relationship that we document is an interaction effect: GDP is positively correlated with the product of community and formal enforcement. Thus, the correlation of GDP with the rule of law is increasing in the perceived strength of the community. In other words, community and formal enforcement are complements in predicting productive outcomes.
4.3. The Impacts of Morality, Religion, and Corruption
Finally, we highlight how guilt costs associated with cheating enhance the complementarity between formal and informal enforcement and, hence, boost social welfare. Corruption or errors in formal enforcement, on the other hand, reduce the complementarity.
Guilt costs for cheating can result from various sources, such as moral or other psychological factors,27 supernatural punishment for bad behaviors,28 and other religious beliefs.29 We model this as an intrinsic disutility, |$S\ge 0$|, that an agent suffers when they deviate. This term enters the incentive constraints in both the market and the community and, therefore, relaxes both incentive constraints and changes the optimal enforcement system. A full analysis appears in Online Appendix Section E.1. As we show (in Proposition E.1), an increase in morality increases social welfare (a higher |$\Pi$|) and promotes the emergence of formal enforcement (a higher |$c^{{\textit {com}}}$|). More importantly, morality enhances the complementarity between formal and informal enforcement (i.e., the region of the mixed regimes, |$[\bar{q}, \bar{q}]$|, expands).
While morality enhances this complementarity, corruption can impede it. A simple effect of corruption is to decrease the efficiency of enforcement and, thus, to raise the cost of enforcement. This can be analyzed as in the comparative statics above (lowering |$\phi$|).
It might also be that enforcement is less efficient. In particular, law enforcement can make both type I and type II errors: not identifying cheating as well as falsely identifying innocent people as cheaters. This can occur for many reasons, and is just one facet of corruption. In particular, the probability |$\phi$| of being caught now happens |$\\gtrsimmma$| of the time when the person is innocent and |$1-\\gtrsimmma$| of the time when the person is guilty. So, |$\\gtrsimmma$| captures the level of corruption. We provide details in Online Appendix Section E.2.
In addition, if false arrests erode a community’s trust in the outcomes of formal enforcement, then essentially there is no complementarity (|$\psi = 0$|).30 As previously discussed (Figure 2(a)), the equilibrium is then bang–bang: either all community or all market. Consequently, corruption can force a society to choose all community or all market and, therefore, can lead to a discontinuous drop in welfare. This sort of discontinuity may be at work in many societies in which local communities have lost faith in their formal enforcement agencies.31
5. Concluding Remarks
We have analyzed a complementarity between formal enforcement by a market and informal enforcement by communities. Our model sheds light on why and when these two forms of enforcement coexist and why using both of them promotes incentives and welfare. It also provides new insights on economic development, poverty traps, and the ongoing role of informal enforcement in a society’s transition to a modern economy, as well as the impacts of morality, religion, and corruption.
Our analysis has focused on one “market,” while in practice people are often interacting across many. This leads to interesting questions as to what happens when there are several competing markets or platforms: does that change their incentives to police their users? Moreover, people can also change or hide their identity, so it can be hard for one market or platform to publicize bad behavior in a way that reaches appropriate communities. This can give rise to economies of scope and scale as a single platform covering many different markets (e.g., WeChat) can internalize more of the complementarities than separate platforms. Further study of such phenomena could provide new insights into the functioning of online platforms.
There are also community reputations that our model could be used to further study. An agent can identify their counterparty’s community, then knowing whether that community follows through with ostracizing cheaters tells the agent whether they can trust the counterparty. This provides incentives for communities to maintain their reputations (c.f. Greif 1989; Richman 2006; Deb 2020).
Our analysis also has implications for issues such as privacy on online platforms, which one can think of as a formal market. If a platform allows people to have anonymous identities, then that is effectively setting |$\psi =0$| in the model. Instead, having an identity that can be recognized by one’s community outside of the platform provides incentives to behave on the platform. Privacy is an important issue with many aspects, but the results here provide one angle on how a public persona can provide incentives.32
Acknowledgments
Jackson and Xing contributed equally to this paper. We thank the editor, three anonymous referees, Daron Acemoglu, Alberto Alesina, Nageeb Ali, Marcus Berliant, Tim Besley, Yi Chen, Chen Cheng, Mauricio Drelichman, Georgy Egorov, Hülya Eraslan, Tom Gresik, Bård Harstad, Alessandro Lizzeri, David McAdams, Joel Mokyr, Jonathan Moreno Medina, Maggie Penn, and participants at the Decentralization Conference, IOG meetings of CIFAR, ThReD, Wallis annual conference, CCERSI, HUST, NBER, PKU, Princeton, and Yale Law School for helpful comments. We gratefully acknowledge financial support under ARO MURI Award No. W911NF-12-1-0509 and NSF grants SES-1629446, SES-2018554 (Jackson).
Notes
The editor in charge of this paper was Vasiliki Skreta.
Appendix: Omitted Proofs
This appendix includes omitted proofs: A.1 for the main results and A.2 for the complementarity with more general functional forms.33
A.1 Omitted Proofs of the Main Results
Recall that |$qV(\delta , v, t_c) = q \delta (v-t_c)/(1-\delta )$| is the discounted sum of future values one receives from community exchanges. We drop the parameters, |$(\delta , v, t_c)$|, to simplify notations.
“Only if”. We prove the contrapositive statement. Suppose there is a fully exchanging equilibrium, |$\sigma$|; that is, all agents abide at all histories on path. We show that both (|$IC^{\textit{com}}$|) and (|$IC^{\textit{mark}}$|) hold.
The above condition must hold for any |$q > 0$| (when |$e^1 = c$| is possible). Thus, (|$IC^{\textit{com}}$|) holds.
The above condition must hold for any |$q <1$| (when |$e^1 = m$| is possible). Thus, (|$IC^{\textit{mark}}$|) holds.
“If”. Suppose (|$IC^{\textit{com}}$|) and (|$IC^{\textit{mark}}$|) both hold, consider the strategy profile in which all agents abide at all histories. It is fully exchanging and we show that it is an equilibrium. We show that no one strictly benefits from deviating, in any period |$\tau$| and any history in which |$O^{\tau -1} = \emptyset$|: If an agent deviates on the market (|$e^{\tau } = m$|), with a probability |$\phi$| they are caught and pay a fine f and with a (total) probability |$\phi \psi$| they are ostracized by their community and, thus, lose the future value |$qV$|. (|$IC^{\textit{mark}}$|) implies that |$t_m \le \phi (f + \psi q V)$|, the gain by deviating in the current exchange does not exceed the expected loss and, hence, deviating on the market is not rewarding. If an agent deviates in the community (|$e^{\tau } = c$|), they are automatically ostracized and thus lose the future value |$qV$|.34 (|$IC^{\textit{com}}$|) implies that |$t_c \le \phi (f + \psi q V)$| and, hence, deviating in the community is not rewarding. In sum, no agent prefers to deviate either on the market or in the community; hence, the strategy profile being considered is a fully exchanging equilibrium.
This proof applies the one-shot deviation principle, which is valid for perfect public equilibria.
Statement 1. Since the market closes (|$z = 0$|), everyone always receives 0 when |$e^{\tau } = {\textit {market}}$|, regardless of their choices. This also implies that no agents strictly prefer to switch to abiding when |$e^{\tau } = {\textit {market}}$|. Consider any community exchange on-path, where (a one-shot) deviation leads to ostracism, which results in a payoff of 0 when |$e^{\tau } = {\textit {community}}$|. Thus, deviating leads to a current payoff of |$v + 0$| while abiding leads to a payoff of |$v - t_c + {\delta q(v-t_c)}/{(1-\delta )} = v-t_c + qV$|. Deviating is not strictly profitable if and only if |$qV(\delta , v, t_c) \ge t_c$|; that is, (|$IC^{\textit{com}}$|) holds.
Statement 2. Firstly, it is not rewarding for anyone to switch to abide in their community, given that the rest of the community always deviate in any community exchanges. Now consider a one-shot deviation by someone in a market exchange: Doing so results in an expected payoff of |$v - \phi f + {\delta (1-q)(v-t_m)}/{(1-\delta )}$| (and recall that the payoff is 0 in any community exchange). One’s on-path payoff, on the other hand, is |$v - t_m + {\delta (1-q)(v-t_m)}/{(1-\delta )}$|. Deviating is not strictly profitable if and only if |$\phi f \ge t_m$|, that is, (|$IC^{\textit{mark-only}}$|) holds.
Proofs of Propositions 1, 2, 4, and 5.
Before going into any specific proofs, we first provide a detailed analysis for the baseline case, |$C = c \phi$|. One could easily extend these to any linear cost function |$C(\phi ,q) = c_0 + c_1 \phi + c_2 q,$| for which |$c_1> 0$|, with more complicated expressions. The proofs under more general cost functions appear in Online Appendix B.
One may refer to Figure 3 for graphical illustrations of the four potential optimal regimes.
To simplify notation, we define the following welfare cost function:
Easy to see that maximizing welfare is equivalent to minimizing the welfare cost, subject to the two incentive constraints.
We first analyze the optimal |$\phi$| for different regions of q and then optimize it globally.
When |$q = 1$| (all community), |$\phi =0,$| and, hence the welfare cost is
When |$q = 0$| (all market), binding (|$IC^{\textit{mark}}$|) implies |$\phi ^{{\textit {all-mark}}} = {t_m}/{f}$| and, hence, the welfare cost is
When |$q \in (0,1)$|, both the community and the market are active. This includes two regimes, depending on whether (|$IC^{\textit{com}}$|) binds.
The mix-minimal, |$(\phi ^{{\textit {mix-minimal}}}, q^{{\textit {mix-minimal}}})$|, is such that (|$IC^{\textit{com}}$|) and (|$IC^{\textit{mark}}$|) both bind. Hence, |$q^{{\textit {mix-minimal}}} = \bar{q} = {t_c}/{V}$| and |$\phi ^{{\textit {mix-minimal}}} = {t_m}/{(f+\psi t_c)}$|. Therefore, the welfare cost is
Finally, a “mixed regime a high community level occurs when |$q > \bar{q}$| and, hence, only (|$IC^{\textit{mark}}$|) binds. In this case, minimizing H subject to (|$IC^{\textit{mark}}$|) has a local minimizer
which corresponds to the following (local minimal) welfare cost:
Finally, the (globally) optimal regime is one that minimizes the welfare cost:
For the purpose of this proof, we treat both |$H^{{\textit {mix}}}(c)$| and |$H^{{\textit {all-mark}}}(c)$| as functions of c. Recall |$H^{{\textit {all-com}}} = t_c - t_m$| is invariant in c.
If |$\psi < \bar{\psi } \equiv {f}/{(V-t_c)}$| (Case 1), the intersection of the two incentive constraints, |$(\phi ^{{\textit {mix-minimal}}}, q^{{\textit {mix-minimal}}}) = \left({t_m}/{(f+\psi t_c)}, {t_c}/{V}\right)$|, is strictly above the straight line that connects |$(0, t_m/f)$| (all market) and (1,0) (all-community) (see Figure 2 for a graphical illustration). |$H^{{\textit {mix-minimal}}} > \max \lbrace H^{{\textit {all-mark}}}, H^{{\textit {all-com}}}\rbrace$|, therefore, a mixed regime is never optimal. All market is optimal for |$c < c^{*} \equiv {(t_c - t_m)f}/{t_m}$| and, otherwise, all community is optimal.
If |$\psi > \bar{\psi }$|, |$(\phi ^{{\textit {mix-minimal}}}, q^{{\textit {mix-minimal}}})$| is below the straight line that connects |$(0, t_m/f)$| and (1, 0). Hence, some mixed regimes can be potentially optimal.
At |$c = 0$|, |$H^{{\textit {all-mark}}}(0) = 0$| achieves the lowest possible welfare cost; hence, the optimal system starts with all market (at |$c = 0)$|.
Next, as we further increase the cost, the mix-minimal becomes optimal.
To further analyze the mixed regime(s), consider the following two c’s:
It is easy to verify that |$c^{{\textit {tangent}}} > c^{{\textit {intersection}}}$| iff |$\bar{q} > \bar{q}$|; that is, |$\psi > \bar{\psi } = {f}/{(V-2t_c)}$|. Thus, we have35
If |$\bar{q} < \bar{q}$|; that is, |$\psi < \bar{\psi }$|, then we have Case 2. In this case, |$c^{{\textit {com}}} = c^{{\textit {tangent}}}$| such that the mix-minimal is optimal for |$c \in (c^{{\textit {mark}}}, c^{{\textit {com}}})$|, and the all market is optimal otherwise.
- If |$\bar{q} > \bar{q}$|; that is, |$\psi > \bar{\psi }$|, then we have Case 3. In this case, |$c^{{\textit {com}}} = c^{{\textit {intersection}}}$|. In addition, let |$c^{{\textit {mix-high}}}$| solve$$\begin{eqnarray} \frac{t_c}{V} = q^{{\textit {mix-high}}}(c) = \sqrt{\frac{ct_m}{(t_c - t_m) \psi V}} - \frac{ f}{ \psi V}; \end{eqnarray}$$that is, the point of tangency to (|$IC^{\textit{mark}}$|) is exactly the intersection of the two IC’s. We have$$\begin{eqnarray} c^{{\textit {mix-high}}} = \left(t_c + \frac{f}{\psi } \right)^2 \cdot \frac{(t_c - t_m) \psi }{V t_m}. \end{eqnarray}$$
Then, the mix-minimal regime (|$q = \bar{q}$|) is optimal for |$c \in (c^{{\textit {mark}}}, c^{{\textit {mix-high}}})$| and the mix-high regime (with some |$q \in (\bar{q}, \bar{q})$|) is optimal for |$c \in (c^{{\textit {mix-high}}}, c^{{\textit {com}}})$|.
Finally, all community is optimal for |$c > c^{{\textit {com}}}$|.
Proposition 1 and its proof imply the comparative statics across regimes; that is, when an increase in c alters the optimal regime. It remains to show the results within each regime.
For the comparative statics w.r.t. the welfare, it follows from Envelope Theorem that |${\mathbf {d}\Pi }/{\mathbf {d} c} = - \phi \le 0$|. Therefore, |$\Pi$| decreases in c and strictly so when |$\phi > 0$|.
Now we turn to comparative statics w.r.t. |$\phi$| and q.
In the all community regime, the welfare cost |$t_c - t_m$|, |$q = 1$|, and |$\phi = 0$| are all constant in c, so the stated results are trivial.
In the all market regime, both q and |$\phi$| are constant in c, and, hence, the welfare cost strictly increases in c.
Finally, in the mix- regimes, the binding (|$IC^{\textit{mark}}$|) implies that |$\phi$| is a (strictly decreasing) function of q, |$\phi (q) = {t_m}/{(f + \psi q V)}$|; hence, the optimization problem becomes |$\min _{q \ge t_c / V} H(q; c) = q(t_c - t_m) + cq.$| Consequently, the optimal q increases in c and the optimal |$\phi$| decreases in c.
Hence, |$c^{{\textit {mark}}}$| decreases in |$\psi$|.
As for |$c^{{\textit {com}}}$|, we have that |$c^{{\textit {tangent}}}$| and |$c^{{\textit {intersection}}}$| both increase in |$\psi$| (equation A.3 and A.5); hence, |$c^{{\textit {com}}} \equiv \max \lbrace c^{{\textit {tangent}}}, c^{{\textit {intersection}}}\rbrace$| increases in |$\psi$|.
|$c^{{{{\textit {com}}}}}$|, |$\bar{q}$|, and |$\bar{q}$| are defined in Proposition 1 and Lemma A.1.
Recall that |$\bar{q}$| is determined by (|$IC^{\textit{com}}$|) so that |$\bar{q} = {t_c}/{V} = {(1-\delta )t_c}/({\delta (v-t_c)})$|. Thus, it decreases in |$\delta$| and v, increases in |$t_c$| and remains constant in |$\psi$|.
Next, we turn to |$c^{{\textit {com}}}$| and |$\bar{q}$|. Recall that |$c^{{\textit {com}}} \equiv \max \lbrace c^{{\textit {tangent}}}, c^{{\textit {{{intersection}}}}}\rbrace$| in which |$c^{{\textit {tangent}}}$| and |$c^{{\textit {intersection}}}$| are provided in (equation A.3 and A.5). It is easy to verify that |$c^{{\textit {tangent}}}$| and |$c^{{\textit {intersection}}}$| both increase in |$\psi$| and V; hence, |$c^{{\textit {com}}} \equiv \max \lbrace c^{{\textit {tangent}}}, c^{{\textit {intersection}}}\rbrace$| increases in |$\psi$| and V.
In addition, |$\bar{q}$| (equation A.4) also increases in |$\psi$| and V.
Finally, it follows from the expression |$V = {\delta (v-t_c)}/{(1-\delta )}$| that, as |$\delta$| increases, v increases, or as |$t_c$| decreases, |$V = {\delta (v-t_c)}/{(1-\delta )}$| increases, hence, |$\bar{q}$| and |$c^{{\textit {com}}}$| both increase.
Formal Statement of the Discontinuities.
(Discontinuities). The level of community exchanges in an optimal enforcement system, |$q^{*}$|, is such that |$q^{*} \in [\bar{q}, \bar{q}]$|, or |$q^{*} = 0$|, or |$q^{*} = 1$|, where |$\bar{q} > 0$| and |$\bar{q} < 1$|.
A.2 Proof of Proposition 3 and General Results concerning the Incentive Complementarity.
We provide some more general results, to which Proposition 3 is a corollary.
We begin with a characterization of when strict increasing differences is satisfied.
(Strictly increasing differences). Consider a cost function |$C(\phi ,q) = c_0 + c_1 \phi + c_2 q,$| for some scalars, for which |$c_1> 0$|.
Strict increasing differences holds for some |$\lbrace (q, \phi ), (q^{\prime }, \phi ^{\prime })\rbrace$|, such that |$q^{\prime }<q, \phi ^{\prime } <\phi$| if and only if |$\psi > 0$|, |$q \in (0,1)$|, |$(1-q) (v-t_m) > c_1\phi ^{\prime }$|, and the community and outside incentive constraints are satisfied at |$(q,\phi )$|. |$(IC^{\textit{mark}})$| fails at each of the other three combinations (or |$(IC^{\textit{mark-only}})$| fails in case that |$q^{\prime }$| also fails to satisfy |$(IC^{\textit{com}})$|).
More generally, if |$C(\phi ,q)$| is such that |$-C(\phi ,q)$| satisfies weak increasing differences (relative to any |$q^{\prime }<q, \phi ^{\prime } <\phi$|), then strict increasing differences holds for some |$\lbrace (q, \phi ), (q^{\prime }, \phi ^{\prime })\rbrace$| such that |$q^{\prime }<q, \phi ^{\prime } <\phi$| if |$\psi > 0$|, |$q \in (0,1)$|, |$(1-q) (v-t_m) > C(\phi ^{\prime },q)$|, and the community and outside incentive constraints are satisfied at |$(q,\phi )$| and |$(IC^{\textit{mark}})$| fails at each of the other three combinations (or |$(IC^{\textit{mark-only}})$| fails in case that |$q^{\prime }$| also fails to satisfy |$(IC^{\textit{com}})$|).
is the outside incentive constraint that covers the case in which |$(IC^{\textit{com}})$| fails to hold (which also means that |$q<1$|).
It follows directly that |$(IC^{\textit{com}})$| is independent of |$\phi$|. Therefore, from the definition of |$\Pi (\phi ,q)$| it follows that there are two possible cases for |$\Pi (\phi ,q) - \Pi (\phi ^{\prime },q)$|, depending on whether the status of the market IC constraint differs at |$\phi$| and |$\phi ^{\prime }$|:
if the change in |$\phi$| does not alter the status of the market IC; in particular,
1. |$(IC^{\textit{com}})$| holds for q and |$(IC^{\textit{mark}})$| holds at both |$q, \phi$| and |$q,\phi ^{\prime }$|,
2. |$(IC^{\textit{com}})$| holds for q and |$(IC^{\textit{mark}})$| fails at both |$q, \phi$| and |$q,\phi ^{\prime }$|,
3. |$(IC^{\textit{com}})$| fails for q and |$(IC^{\textit{mark-only}})$| holds at both |$\phi$| and |$\phi ^{\prime }$|, or
4. |$(IC^{\textit{com}})$| fails for q and |$(IC^{\textit{mark-only}})$| fails at both |$\phi$| and |$\phi ^{\prime }$|.
if the market IC holds at the higher |$\phi$| but not at the lower one, |$\phi ^{\prime }$|, (the latter of which implies that market closes, hence, the cost does not apply); in particular,
5. |$(IC^{\textit{com}})$| holds for q and |$(IC^{\textit{mark}})$| holds at |$q,\phi$| but not at |$q,\phi ^{\prime }$|, or
6. |$(IC^{\textit{com}})$| fails for q and |$(IC^{\textit{mark-only}})$| holds at |$\phi$| but not at |$\phi ^{\prime }$|.
Given that |$q> q^{\prime }$| and |$\phi > \phi ^{\prime }$|, some possible combinations are ruled out. For instance (1) for |$q^{\prime }$| implies that it holds for q too, and (6) for q implies that (6) holds for |$q^{\prime }$| too. Thus, we are left for one of (2)–(4) for |$q^{\prime }$| and (5) for q. Note that (5) rules out (3).
Thus, we are left with (2) or (4) at |$q^{\prime }$| (and |$\phi , \phi ^{\prime }$|) and (1) at q (and |$\phi , \phi ^{\prime }$|). In addition, this situation requires that |$(IC^{\textit{mark}})$| and |$(IC^{\textit{mark-only}})$| differ; that is, |$\psi > 0$|.
Thus, we can conclude that |$(\textit{SID})$| holds if and only if|$(1-q) (v-t_m) > c_1\phi ^{\prime }$|, |$\psi > 0$|; in addition, |$(IC^{\textit{com}})$| holds for q and |$(IC^{\textit{mark}})$| holds at |$q,\phi$| but not at |$q,\phi ^{\prime }$|, while either |$(IC^{\textit{com}})$| fails for |$q^{\prime }$| and |$(IC^{\textit{mark-only}})$| fails at both |$\phi$| and |$\phi ^{\prime }$|, or |$(IC^{\textit{com}})$| holds for |$q^{\prime }$| and |$(IC^{\textit{mark}})$| fails at both |$\phi$| and |$\phi ^{\prime }$|.
By the weak increasing differences condition of |$-C$|, it then follows that
|$\Pi (\phi ,q) - \Pi (\phi ^{\prime },q) - (\Pi (\phi ,q^{\prime }) - \Pi (\phi ^{\prime },q^{\prime })) = - (C(\phi ,q) - C(\phi ^{\prime },q) - (C(\phi ,q^{\prime })- C(\phi ^{\prime },q^{\prime }))) - C(\phi ^{\prime },q)+ (1-q) (v-t_m) \ge - C(\phi ^{\prime },q)+ (1-q) (v-t_m) > 0,$| when |$(1-q) (v-t_m) > C(\phi ^{\prime },q)$|, as claimed.
Next, to prove Proposition 3, we first establish the following properties.
(SID and WID around the Optima). Consider any |$q^{*},\phi ^{*}$| with |$q^{*}\in (0,1)$| that are optimal enforcement systems. We have
for every |$(q, \phi )$| such that |$q > q^{*}, \phi > \phi ^{*}$|, |$(WID)$| holds, and
for every |$(q, \phi )$| such that |$q < q^{*}, \phi < \phi ^{*}$|, |$(SID)$| holds.
Statement |${1}$|. |$(q^{*},\phi ^{*})$| being optimal implies that |$(IC^{\textit{mark}})$| must be binding and |$(IC^{\textit{com}})$| must hold. Therefore, both |$(IC^{\textit{mark}})$| and |$(IC^{\textit{com}})$| must also hold for any |$q > q^{*}, \phi > \phi ^{*}$|. It then implies
|$\Pi (\phi ,q) - \Pi (\phi ^{*},q) = C(\phi ^{*},q) - C(\phi ,q) \ge C(\phi ^{*},q^{*}) - C(\phi ,q^{*}) = \Pi (\phi ,q^{*}) - \Pi (\phi ^{*},q^{*}), \forall q > q^{*}, \phi > \phi ^{*},$| in which “|$\ge$|” follows the assumption that |$-C(\phi ,q)$| has weak increasing differences.
Statement |${2}$|. Consider any |$(q, \phi )$| such that |$q < q^{*}, \phi < \phi ^{*}$|, then |$(IC^{\textit{com}})$| holds for |$q^{*}$| and |$(IC^{\textit{mark}})$| holds at |$(q^{*},\phi ^{*})$| but not at |$(q^{*},\phi )$| (since |$(IC^{\textit{mark}})$| is binding at |$(q^{*},\phi ^{*}))$|. Therefore, situation (5) in the proof of Lemma A.1 holds for |$q^{*}$| and any |$\phi <\phi ^{*}$|. □
Next, we show (2) or (4) is satisfied for q|$(< q^{*})$| and any |$\phi <\phi ^{*}$|: If |$(IC^{\textit{com}})$| holds for q, then since |$(IC^{\textit{mark}})$| is binding at |$q^{*},\phi ^{*}$| and |$\psi > 0$|, it must fail at |$q,\phi ^{*}$| and |$q,\phi$|. If |$(IC^{\textit{com}})$| fails for |$q^{\prime }$|, then since |$\psi > 0$| and |$(IC^{\textit{mark}})$| is binding at |$q^{*},\phi ^{*}$|, it must be that |$(IC^{\textit{mark-only}})$| (a stronger constraint) fails at both |$q^{\prime },\phi ^{*}$| and |$q^{\prime },\phi ^{\prime }$|.
“|$> $|” follows from C being strictly increasing in |$\phi$|. The first “|$\ge$|” follows from |$-C(\phi ,q)$| having weak increasing differences. The second “|$\ge$|” follows from |$(\phi ^{*},q^{*})$| being optimal (and, hence, its welfare is at least the welfare for the all-community case).
Proposition 3 is an immediate corollary to the following result, which is stated for more general cost functions.
(Complements). Suppose |$-C(\phi ,q)$| satisfies weak increasing differences. Then informal and formal enforcement are incentive complements at |$(\phi ^{*},q^{*})$| s.t. |$0<q^{*}<1$|if and only if|$\psi > 0$| and |$(IC^{\textit{mark}})$| is binding and |$(IC^{\textit{com}})$| holds at |$(\phi ^{*},q^{*})$|.
We first observe that the “if” part is a corollary to Lemma A.2, given the definition of incentive complementarity (Section 2.3). What is left is the “only if” part; that is, complementarity does not hold at any |$(q_0, \phi _0)$| such that
|$(IC^{\textit{com}})$| fails, or
|$(IC^{\textit{com}})$| holds, but |$(IC^{\textit{mark}})$| fails, or
|$(IC^{\textit{com}})$| and |$(IC^{\textit{mark}})$| both hold, but |$(IC^{\textit{mark}})$| is slack.
We show that the |$(\textit{SID})$| part of the definition of complementarity fails in any of the above cases. To do so, we apply the proof of Lemma A.1.
For (a), there exists some small enough neighborhood of |$(q_0, \phi _0)$| such that |$(IC^{\textit{com}})$| also fails for every |$(q,\phi )$| in the neighborhood. So |$(IC^{\textit{mark-only}})$| shall be considered and it is independent of q. Therefore, the same situation (3), (4), or (6) in the proof of Lemma A.1) must apply to both q and |$q_0$| (and |$\phi , \phi _0$|), hence, |$(\textit{SID})$| fails.
For (b), that |$(IC^{\textit{mark}})$| fails for |$(q_0, \phi _0)$| implies the existence of some small enough neighborhood of |$(q_0, \phi _0)$| such that |$(IC^{\textit{mark}})$| also fails for every |$(q, \phi )$| in the neighborhood. Moreover, in the same neighborhood, if |$q < q_0$| and |$(IC^{\textit{com}})$| fails for q, |$(IC^{\textit{mark-only}})$| would also fail for |$\phi < \phi _0$| since |$(IC^{\textit{mark-only}})$| is more demanding than |$(IC^{\textit{mark}})$|. As a result, either (2) or (4) applies to q and |$q_0$| (which could be different). In either case, |$(\textit{SID})$| fails.
For (c), there exists some small enough neighborhood of |$(q_0, \phi _0)$| such that for every |$(q, \phi )$| in the neighborhood, |$(IC^{\textit{mark}})$| holds for both |$(q^{\prime }, \phi _0)$| and |$(q^{\prime }, \phi )$| in which |$q^{\prime } \equiv \max (q_0, q)$|. Therefore, (1) or (3) holds for |$q^{\prime }$| (and |$\phi , \phi _0$|), which implies |$(\textit{SID})$| does not hold.
Footnotes
Instances of making criminals known to their communities have been prevalent throughout history and are still pervasive today. During the Spanish Inquisition in both Spain and Portugal, people sentenced for crimes were subjected to the auto-da-fé, which was a public parading and shaming of the convicted (fewer than 5% were executed, e.g., see Henningsen 1993). In ancient China, among “the five punishments,” mo, also known as qing, was a punishment where the offender would be tattooed on the face or forehead with indelible ink. The quote from Mokyr (2008) above refers to the importance of sustaining economic exchanges through reputations. As Mokyr states (pp. 79–80): “In Britain during the Industrial Revolution, the social norms of what was perceived to be a gentlemanly culture with an emphasis on honesty and meeting one’s obligations, supported cooperative equilibria that allowed commercial and credit transactions to be consummated and partnerships to survive without overly concern about possible defections and other forms of opportunistic behavior. Gentlemen (or those who aspired to become gentlemen) moved in similar circles and faced one another in a variety of linked contexts. [...] The prevalence of a social convention that defined “gentlemanly” or “polite” behavior and penalized serious deviations from it through irreparable damage to one’s reputation, supplemented formal (legal) relations with a moral code that enabled an effective mode of transacting without relying on the State except in extremis.” In modern settings, there are public databases on malpractice suits in medicine and law, public listings of court cases as well as lists of ex-convicts and their various crimes, required registration of sex offenders, and police logs of crimes being published in local newspapers and on websites. There are also many websites that rate providers of various goods and services.
Other authors have made the point that contracts are necessarily incomplete and so some things have to be handled outside of formal contracting: That is, there are situations in which both formal and informal enforcement are needed (e.g., see Bohnet, Frey, and Huck 2001; Poppo and Zenger 2002; Lazzarini, Miller, and Zenger 2004 and Holmstrom and Tirole 1989; Dixit 2011; Bodoh-Creed 2019 for surveys and recent results). Others (e.g., Balmaceda 2023) point out how improved borrowing that loosens credit constraints can lead to complementarities between formal and informal exchange. Although the basic point that having more arenas of interaction can help with incentives is similar, the setting and the way in which the complementarity works is very different.
The basic logic resembles that of the multi-market contact literature, pioneered by Bernheim and Whinston (1990), which, in a completely different context, highlights that collusion between firms in repeated interactions could be easier to sustain if they interact in multiple markets.
This simplifies the notation and avoids a situation where only one agent is on the market or inside the community and, hence, is unable to find a match, but one can easily extend the model to allow for a probability of failing to match.
Agents can be matched in pairs or cycles of more than two, each providing a good/task to the next agent in the cycle. What is important here is that each agent expects to give something up and get something of higher value.
If the agents are matched in a cycle of more than two, then the “partner” is the agent who is to deliver the good or service to the agent in question.
In our study, ostracism is an automatic part of the matching process. One could model this explicitly by having a community chief who observes all past community behavior and only matches those agents who have never cheated on an exchange (for instance having the chief receive a strictly dominant payoff for exactly matching those agents who have never cheated). One could, instead, model matching and ostracism as decentralized choices of the agents in the community, but this would come with additional notation and equilibria as well as further questions regarding what is consistent with equilibrium. For comprehensive discussions of incentives in ostracism and the changes that modeling them can introduce; see, for example, Ali and Miller (2016, 2022).
One can also have the case in which the value v is higher for market exchanges than for community exchanges, with additional notation but without any change in the structure of the results that follow.
A deviation, although not affecting other agents’ payoffs, brings a loss of v to social welfare (formally defined below).
The history does not explicitly include whether they have been ostracized, since that can be deduced from their actions and the public history.
To simplify notation, we allow ostracized agents to choose an action in each community exchange but that action is payoff-irrelevant for everyone. Similarly, when the market is unavailable |$(z=0)$|, agents still choose actions in market exchanges even though they are payoff irrelevant.
For detailed discussions of perfect public equilibrium, see Ch. 7 in Mailath and Samuelson (2006).
It could be that a society optimizes its formal/informal exchange structure. As societies develop, markets often initially have some particular days and locations at which they bring people together. For instance, in medieval Europe, market towns and market rights were often granted by royal charters and often were close to fortifications (e.g., the Domesday Book of 1086 listed 50 markets throughout England, and see Dyer 2000 for some discussion). The prevalence of market transactions can grow, becoming more frequent as enforcement grows. Generally, we think of q as being nonzero, as even in the most developed modern societies, there are still many informal exchanges of favors, loans, and other goods and services. In some societies, history and culture can prevent the market/community mix from being optimal. Regardless of whether |$(\phi , q)$| is optimized or evolves suboptimally, it is important to characterize the welfare associated with different combinations in order to understand the possibilities.
Throughout the paper, we take it as given that f is a finite exogenous number; otherwise, with an arbitrarily huge fine, one can always ensure that incentives come with small formal detection rates. There are (at least) four reasons this is not done in practice. First, a breach of contract is generally pursued through civil courts and the payments that are in question are often limited to the provable damages incurred. In some egregious cases, this might involve punitive damages or a criminal case (e.g., for fraud). Second, there is a moral concept of “cruel and unusual punishment” or that the “punishment should fit the crime.” For instance, the Eighth Amendment to the U.S. Constitution states that “Excessive bail shall not be required, neither excessive fines imposed nor cruel and unusual punishment inflicted,” and such policies date back to English Law in 1689. The UN’s Universal Declaration of Human Rights states that “No one shall be subjected to torture or to cruel, inhuman or degrading treatment or punishment.” This concept has a long history, for instance, Hamarabi’s code states: “If a man destroys the eye of another man, they shall destroy his eye. If one breaks a man’s bone, they shall break his bone. If one destroys the eye of a freeman or breaks the bone of a freeman he shall pay one gold mina. If one destroys the eye of a man’s slave or breaks a bone of a man’s slave he shall pay one-half his price.” Third, there may be errors made in which case huge fines for small offenses are not welfare maximizing. A fourth reason is that it can be costly for a government to punish people who cannot afford to pay a fine—especially when this involves imprisonment. In short, a fine shall be “commensurate” with the offense.
See the proof for the explicit expressions.
This regime disappears when |$c^{\textit{mix-high}} = c^{\textit {com}}$|.
This parameter can be interpreted in various ways. First, a larger c corresponds to a more costly, or relatively labor-intensive, legal enforcement technology. Thus, rural, poor, or less developed societies tend to have large cs. In addition, c captures the effective cost in the sense that in a corrupt system it is more costly to deliver the same probability of enforcement due to moral hazard on the part of the judges and others involved in enforcement, hence, corruption can be partly captured by a larger c (see Sections 4.3 and Online Appendix E.2 for a more extensive look at corruption).
This is in contrast to the argument in, for instance, Casari (2007) in which fixed costs play an important role in the adoption of a formal institution (charters).
To further illustrate that the information linkage between community and formal enforcement is the driving force, we remark that that fines, f, are not incentive complements with q. To see this, it follows from |$(IC^{\textit{mark}})$| that |$f = {t_m}/{\phi } - \psi V q$| and, thus, f and q are substitutes, even for providing incentives.
This is, in part, the way the enforcement of the Gentleman’s rules worked as described by Mokyr (2008)—news of the person’s misbehavior and their subsequent loss of reputation and standing in their clubs and society were strong punishments and worked well, even in the face of relatively ineffective fines and courts.
Another interesting set of comparative statics concerns changes in |$t_m-t_c$|. As a country industrializes and urbanizes, the relative gains from trade on an open market compared to doing everything in the community increase. This tilts the objective function and benefits to society toward the market. At the same time, a decrease in |$t_m$| also makes the formal incentive constraint easier to satisfy. These combined forces tend to lower the optimal amount of community exchanges, which is consistent with what is seen in many settings as an economy grows. However, this does not always cut that amount to zero, as the level of complementarity from the community can still be very large and useful (see Online Appendix Section D.3).
A state can also underestimate the importance of informal community cooperation in sustaining their formal institutions.
There is a behavioral theory literature that addresses guilt aversion and the cost of cheating (Battigalli and Dufwenberg 2007; Ellingsen and Johannesson 2008; Gneezy, Kajackaite, and Sobel 2018). Relatedly, an experimental literature, pioneered by Mazar, Amir, and Ariely (2008) and Fischbacher and Föllmi-Heusi (2013), conducts lab experiments to disentangle the impact of morality from that of formal sanctions.
For instance, Christianity, Islam, and Judaism specify punishments for sins. Hinduism and several branches of Buddhism emphasize rewards and/or punishments through reincarnation and rebirth. Chinese traditional religion emphasizes moral reciprocity (“bao ying”) and also the veneration of ancestors in not having them feel shamed because of their offspring’s misbehaviors. Finally, many religions envision a heaven, and punishment from the difference between what happens if one behaves or not.
Empirical studies show that supernatural beliefs facilitate cooperation in human groups (Atkinson and Bourrat 2011) and serve as a costly signaling device that helps to strengthen communities (Power 2017), that church attendance reduces crime (Moreno 2018) and can be positively correlated with economic growth (Barro and McCleary 2003) and growth-promoting economic attitudes (Guiso, Sapienza, and Zingales 2003).
We still consider the simple case where there are no bad or dishonest types and, hence, every guilty person is a result of false arrests. To further investigate this point, one could include some bad types who always deviate (Sugaya and Wolitzky 2020), which in the face of false arrests can lead normal types to deviate.
For instance, “Black Youth Project 100” worked to undo the New York City Housing Authority’s “permanent exclusion” policy, which ostracizes criminals and does not allow them to live in or visit housing projects. Activists in Chicago worked to eliminate the city’s gang database, arguing that criteria for inclusion were vague. For more on both of these; see “Black Lives Matter Is Democracy in Action” by Barbara Ransby, Oct 21, 2017, New York Times.
This is consistent with analyses in other settings that also point out that publicity can provide incentives that result in higher levels of public good provision, better electoral accountability, and political compliance, among others. See, for instance, Gavazza and Lizzeri (2009); Daughety and Reinganum (2010); Forssbaeck and Oxelheim (2014); Acquisti, Taylor, and Wagman (2016); Ali and Bénabou (2020); Tirole (2021), and the papers cited therein.
For additional online appendices, see https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3153842.
Their future value from market exchanges remains unchanged since they would abide the exchanges, which is incentivized by the enlarged fine that they would face.
Intuitively, |$\bar{q} > \bar{q}$| implies that the tangential point (in q-|$\phi$| space) is on the right side of |$(IC^{\textit{com}})$| (or the intersection point of the two IC’s), which further implies a bigger cost parameter, |$c^{{\textit {tangent}}}$|, that corresponds to the tangential line (flatter in q–|$\phi$| space).



