-
PDF
- Split View
-
Views
-
Cite
Cite
Xavier Gabaix, Marshall Lecture 2023: Behavioral Macroeconomics via Sparse Dynamic Programming, Journal of the European Economic Association, Volume 21, Issue 6, December 2023, Pages 2327–2376, https://doi.org/10.1093/jeea/jvad057
Close - Share Icon Share
Abstract
This paper proposes a tractable way to model boundedly rational dynamic programming. The agent uses an endogenously simplified, or “sparse,” model of the world and the consequences of his actions and acts according to a behavioral Bellman equation. The framework yields a behavioral version of some of the canonical models in macroeconomics and finance. In the life-cycle model, the agent initially does not pay much attention to retirement and undersaves; late in life, he progressively saves more, generating realistic dynamics. In the consumption-savings model, the consumer decides to pay little or no attention to the interest rate and more attention to his income. Ricardian equivalence and the Lucas critique partially fail because the consumer may not pay full attention to taxes and policy changes. In a Merton-style dynamic portfolio choice problem, the agent endogenously pays limited or no attention to the varying equity premium and hedging demand terms. Finally, in the neoclassical growth model, agents act on a simplified model of the macroeconomy; in equilibrium, fluctuations are larger and more persistent.
1. Introduction
In economics, we build a simplified model of the world—we select “important” dimensions of the world, and know that the model is not literally the true world. However, we assume that agents in our model are not like us: that they comprehend the full complexity of their world. This asymmetry is of course a bit odd. In contrast, in the present paper, agents behave like us economists: They build a simplified model of the (model) world they live in, and use it to act.
This paper shows a tractable way to model such behavioral agents, in a fairly general class of dynamic problems. Those agents tend to be more realistic than rational agents, and their bounded rationality has important policy consequences.
I show how the framework applies to some of the canonical models in macro-finance, in partial and general equilibrium: consumption-saving problems, the baseline neoclassical growth model (the Cass–Koopmans model), general linear-quadratic problems, and dynamic investment in risky assets (Merton’s problem). The upshot is that we have a portable, fairly general structure that applies to some core machines of macroeconomics and allows to see where bounded rationality (BR) is important in those situations.
One of the persistent criticisms of traditional economics is the unrealism of the infinitely forward-looking agent who computes the whole equilibrium in her own head. This lack of realism has long been suspected to be the cause of some counterfactual predictions that we will review below. Behavioral economics aims to provide an alternative. The greatest successes of behavioral economics in the literature so far change the agents’ tastes (e.g. prospect theory or hyperbolic discounting) or their beliefs (e.g. overconfidence), while keeping the assumption of rationality. When tackling the rationality assumption, there is much less agreement, and the modeling of bounded rationally is much more piecemeal, different from one situation to the next.
This paper proposes a compromise that keeps much of the generality of the rational approach and injects some of the wisdom of the behavioral approach, mostly inattention and simplification. It does so by proposing a way to insert some BR into a large class of problems, the “recursive” contexts, that is, with dynamic programming around a dynamic steady state.
To illustrate these ideas, let us consider a canonical consumption-savings problem. The agent maximizes utility from consumption, subject to a budget constraint, with a stochastic interest rate and stochastic income. In the rational model, the agent solves a complex dynamic programming (DP) problem with three state variables (wealth, income, and the interest rate). This is a complex problem that requires a computer to solve.
How will a boundedly rational agent behave? I assume that the agent starts with a much simpler model, where the interest rate and income are constant—this is the agent’s “default” model. Only one state variable remains, his wealth. He knows what to do then (consume a certain fraction of his wealth, and permanent income), but what will he do in a more complex environment, with stochastic interest rate and stochastic income? In the sparse version, he considers parsimonious enrichments to the value function, as in a Taylor expansion. He asks, for each component, whether it will matter enough for his decision. If a given feature (say, the interest rate) is small enough compared to some threshold (taken to be a fraction of standard deviation of consumption), then he drops the feature or partially attenuates it. The result is a consumption policy that pays partial attention to income and possibly no attention at all to the interest rate. This seems realistic.1
The result is a sparse version of the traditional permanent-income model. We see that it is often simpler than the traditional model. Indeed, the agent typically ends up using a rule which is simpler (e.g. not paying attention to the interest rate).
I also present a behavioral version of a large class of models and work out, in detail, a BR version of most canonical of them, the neoclassical growth model of Cass–Koopmans. In this version, agents pay of lot of attention to their own variables, less to aggregate variables. One upshot is that with BR, macroeconomic fluctuations are larger and more persistent. I illustrate this proposition, and qualify it, as it appears to hold for most reasonable values of the parameters, but can be overturned for extreme values. To understand the simple idea, imagine first an economy with only one state variable, capital. It starts with a steady state amount of capital. Then, there is a positive shock to the endowment of capital. In a rational economy, agents would consume a certain fraction of it, say 6%, every period. That will lead the capital stock to revert quickly to its mean. However, in an economy with sparse agents, investors will not pay full attention to the additional capital. They will consume less of it than a rational agent would. Hence, capital will be depleted more slowly and will mean-revert more slowly. The shock has more persistent effects. Given that shocks are more persistent, past shocks accumulate more. Mechanically, this leads to larger average deviations of capital from its trend. As a consequence, the interest rate and gross domestic product (GDP) also have larger, and more persistent, deviations from trend.
The model allows us to express those ideas in simple, quantitative ways. It also allows us to explore them in rich environments.
Here are some conclusions for individual decision-making in macroeconomic contexts:2
Agents react more to near, rather than future, shocks. For instance, the (finitely lived) consumer has a higher marginal propensity to consume (MPC) for current and near payments, rather than distant payments.
The Euler equation fails (under the objective model of the world). However, it holds under the agent’s subjective, sparse model.
Agents start saving “too late” for retirement, and expenditure falls in the years before retirement (as the agent scrambles to save more for retirement).
Agents accumulate a too small buffer of savings, as they are (partially) inattentive to the risk of income fluctuations.
Agents do not react much or at all to the interest rate, at least when small purchases are concerned. However, they tolerate a non-smooth consumption profiles. Note that in the rational model, the first fact would require a low intertemporal elasticity of substitution (IES), while the second fact would require a high IES.
The agent doesn’t need to the whole actual macro equilibrium in his head before acting; he just uses a simplified model of the world, leading to simple policies, for example, partially forward-looking consumption functions.
When choosing their portfolio, agents pay less attention to the hedging demand motive.
Here are some conclusions for aggregate macroeconomics:
Fiscal policy is more powerful because Ricardian equivalence partly fails. If the government gives a dollar today and takes it back later (plus interest), consumption today increases—though it should not react in the simplest rational model.3
The Lucas critique has less, or zero, bite. When policy changes are small and temporary, sparse agents’ policy functions do not change, or change little.
GDP fluctuations are amplified and more persistent in the most basic dynamic stochastic general equilibrium (DSGE) model (compared to the rational benchmark).
This perspective revives the “old Keynesian” agent. The agent here looks like a hybrid between a neoclassical agent and an old Keynesian agent,4 in the sense that he’s myopic and adopts simple decision rules. However, unlike the truly old Keynesian agent, those decision rules are microfounded—as policies that are optimal under a simplified model of the world. Unlike the neoclassical and New Keynesian agent, this sparse agent is partially myopic and does not react to all things.
Those substantive conclusions are, I hope, of some interest. Still, the main contribution of this paper is its methodology. It develops a procedure that allows an economist to continuously transform a rational agent into a boundedly rational one. This leads to further substantive conclusions about the impact of BR on economic life, such as the ones above.
This paper is indebted to a series of ideas in behavioral modeling in micro and macro contexts. This literature will be discussed in Section 8, after the model is clear to the reader. The rest of the paper is as follows. Section 2 gives an elementary, but substantive, example—a behavioral version the life cycle model. Section 3 presents the general procedure. Then, we apply it to a variety of canonical examples. Section 4 presents basic partial-equilibrium building blocks with behavioral agents: the basic consumption–savings problem, including variants such as the failure of Ricardian equivalence. Section 5 works out the baseline neoclassical growth model. Section 6 develops other models. Section 7 proposes discusses variants, and frequently asked questions. Section 8 contains the literature review. Section 9 concludes. The online appendix contain further proofs and extensions.
Notations. I will use superscript r for the traditional or rational model, d for the default model, and s for the sparse or behavioral model. I will call |$a\odot b {:\!}= (a_{i}b_{i})_{i=1...n}$| the component-wise product.
2. Behavioral Life-Cycle Model: A Gentle Introduction
As a simple introduction, I give a behavioral version of the most basic life-cycle model (Modigliani and Brumberg 1954).5 The agent works for the first L periods of his life, then retires, and dies at period T. His utility is
The interest rate and the subjective discount rate are both 0. He receives income |$y_{t}=\bar{y}$| when working (|$t\in [0,L)$|), and |$y_{t}=\bar{y}+\hat{y}$| when retired (|$t\in [L,T)$|). Here |$\hat{y}<0$| captures the income loss during retirement. Income corresponds to the dotted line in Figure 1. Financial wealth |$w_{t}$| evolves as |$w_{t+1}=w_{t}+y_{t}-c_{t}$|, and the terminal condition is |$w_{T}=0$|.
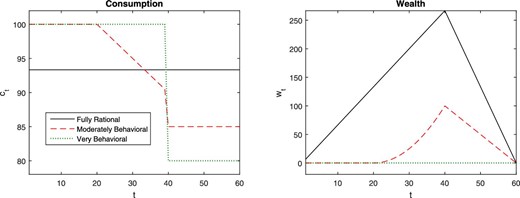
Consumption and wealth of behavioral life-cycle agents. Income is plotted in the dotted line—it is also the very behavioral agent’s consumption. The agent starts life at time 0, receives income |$\bar{y}=100$| while working (until period 40), and receives |$\bar{y}+\hat{y}=80$| in retirement (period 40–60). The solid line represents a fully rational agent (i.e. |$\bar{\kappa }=0$|), the dashed line a moderately behavioral agent (|$0<\bar{\kappa }<\bar{\kappa }^{\ast }$|, for a finite |$\bar{\kappa }^{\ast }=|\hat{y}|$|), and the dotted line a very behavioral agent (|$\bar{\kappa } \ge \bar{\kappa }^{\ast }$|), who just consumes current income. The moderately behavioral agent does not save for retirement at first, but starts saving before retirement. The right panel plots the wealth accumulated by the agent.
Let us first analyze a rational agent. At time 0, his resources are |$\Omega _{0} {:\!}= w_{0}+\sum _{\tau =0}^{T-1}y_{\tau }=w_{0}+T\bar{y}-x$|, where |$x {:\!}= -(T-L)\hat{y}>0$| is the total income loss due to retirement. His consumption problem is |$\max _{(c_{t})_{0\le t<T}}\sum _{t=0}^{T-1}u(c_{t})$| s.t. |$\sum _{t=0}^{T-1}c_{t}=\Omega _{0}$|, with |$u^{\prime }>0,u^{\prime \prime }<0$|. So he consumes a constant amount at all periods:|$\ c_{t}={\Omega _{0}}/{T}={(w_{0}-x)}/{T}+\bar{y}$|. In particular:
The same reasoning holds starting at a date |$t\le L$|. Then, there are only |$T-t$| periods remaining, so the policy becomes:
That policy guarantees a constant consumption |$c_{t}=c_{0}$| over his lifetime.
There is a dynamic programming formulation that will be useful in the behavioral model. At time t, the remaining lifetime utility is |$(T-t)u(c_{t})$|. So, the value function is (for |$t\le L$|)
where superscript r denotes the rational agent. This rational agent (1) satisfies the Bellman equation:6|$c_{t}={arg\, max}_{c}v(c,w_{t},x,t)$|, where we define:
Let us now consider the behavioral agent. I want to capture the idea that he does not fully perceive income loss associated with retirement. The systematic procedure will be justified and explained in the body of this paper, but here I just show how it applies in this case. The behavioral agent will consume:
where |$m_{t}\in [0,1]$| denotes an (endogenous) attention to future retirement. If |$m_{t}=1$|, the agent is fully rational. However, if |$m_{t}=0$|, the agent doesn’t see retirement at all: he behaves as if there was no income loss from retirement in the future. The general model allows for partial attention |$m_{t}$|. Given |$m_{t}$|, the solution of (4) is:7
In the full model developed soon, attention |$m_{t}$| will come from the costs and benefits of attention, and will be expressed as follows. Calling |$c_{t}(m_{t})={(w_{t}-m_{t}x}/{(T-t))}+\bar{y}$|, we define |$c_{t}^{d}=c_{t}(0)={(w_{t}}/{(T-t))}+\bar{y}$|, the “default” policy that corresponds to no attention to retirement; |$c_{t}^{\prime }(0)={-x}/{(T-t)}$| the marginal impact of attention; and |$v_{cc}^{t}=v_{cc}(c_{t}^{d},w_{t},0,t)=(1+{1}/{(T-t-1)})u^{\prime \prime }(c_{t}^{d})$| the curvature of the objective function. The general procedure will give the attention at time t to the income loss during retirement:
for an attention function |$\mathcal {A}$| with values in |$[0,1]$| and a cost of cognition |$\kappa _{t}$| discussed soon.8 A little more calculation gives the value of attention as follows.
Hence, when |$\kappa _{t}>0$|, consumption weakly falls over time, and discretely falls at retirement. After retirement, consumption is constant.
I next present a numerical illustration. I use the attention function |$\mathcal {A}(v)=\max (1-{1}/{|v|},0)$| from (15). I assume the following scaling of the cost: |$\kappa _{t}=\bar{\kappa }^{2}|u^{\prime \prime }(c_{t}^{d})|$| with |$c_{t}^{d}={(w_{t}}/{(T-t))}+\bar{y}$|. This is largely for convenience, and it corresponds to a constant cost when utility is linear-quadratic. This simplifies the expressions without changing the economics much. Then (using continuous time to make expressions neat), the agent thinks about retirement as soon as |$({x}/{(T-t)})\ge \bar{\kappa }$|, that is, at a time |$s=\max (0,\min (L,T-{x}/{\bar{\kappa }}))$|. Solving for wealth, the value of consumption is (when |$s\in (0,L)$|; Section E in the online appendix describes the whole solution, including in discrete time):9
where |$w_{L}=(1-{L}/{T})w_{0}+(\bar{\kappa }^{2}/{x})(L-s)^{2}$|.
Figure 1 plots the resulting consumption and wealth (|$w_{0}=0$|, |$\bar{y}=100$|) for different levels of the cost of rationality |$\kappa$|. The solid line represents a fully rational agent (i.e. |$\bar{\kappa }=0$|): he fully smooths consumption. The dotted line shows a very behavioral agent, who simply consumes current income (|$\bar{\kappa }\ge \bar{\kappa }^{\ast } {:\!}= {x}/{(T-L)}=|\hat{y}|$|). The dashed line shows a moderately boundedly rational agent (|$0<\bar{\kappa }<\bar{\kappa }^{\ast }$|).
At first, he does not save for retirement. He’s thinking “let me not think about that future loss of income at retirement, it’s so remote than it’s not worth it”. However, he does start saving at some point before retirement—at period 20 in this calibration. This is because in (5), |$|{\partial c_{t}}/{\partial m_{t}}|={m_{t}x}/{(T-t)}$|, so that thinking more about retirement is more important as time goes by. So, at period 21, he thinks “OK, I should start thinking a bit about that retirement, and saves a bit”: Over time he thinks more about retirement, and saves more. At retirement, his consumption drops as he fully realizes that his income has fallen. This illustrates the smooth, partial myopia of this agent.
This paper is mostly theoretical, but it is worth asking the following question.
Is it indeed the case that people tend to save “too late” for retirement? The issue is still controversial, but let us consider three salient facts.
Expenditure declines after the age of 45 (Aguiar and Hurst 2013, Figure 1, for expenditures without housing services)—much like the behavioral agent of Figure 1.
There is a fall in expenditure when income predictably falls, again like in Figure 1:
People say that they plan for retirement late in their working life, or not at all. For instance, 23% of the 18–29 year old say that have “figured out how much they need to save for retirement”, while 51% of the 45–59 year old say they have done so (Lusardi and Mitchell 2011).11
Facts 1–3 arise naturally from the behavior as described in Figure 1. For Fact 3, if agents indeed have a |$\kappa$| too large, they don’t plan for retirement at all, even right before it.
Facts 1–3 are each inconsistent with the plainest rational model.
Facts 1–2a can be made consistent with an enriched rational model. Fact 1 can be explained by introducing credit constraints and income risk (Gourinchas and Parker (2002)). Facts 1 and 2a can be explained by observing that retired consumers buy more efficiently or buy fewer non-work goods (Aguiar and Hurst 2013). Fact 2b is harder to reconcile with fully forward-looking models, though qualitatively consistent with Figure 1. Fact 3 is not consistent with a rational model, but one could dismiss it by stating that agents’ reports of what they think about are meaningless—a point of view I do not share.12
Though these facts are not dispositive, they form, I submit, reasonable presumptive evidence for the idea that people are not fully far-sighted, even for retirement savings. The present framework could help write enriched empirical models allowing for both traditional factors and myopia, where the above-mentioned evidence could be systematically assessed.
This example illustrates the behavior and mechanics of the sparse agent. I now move on to a systematic formulation of that agent, which applies to much more general problems.
3. General Framework
3.1. The Sparse Max for Static Problems: Quick Review
To think about BR, the tractable dynamic framework laid out here is possible because it rests on a tractable static framework I laid out in previous work (Gabaix 2014, 2019). I review it in this subsection. There, the core is a sparse max or |${smax}$| operator, which is a generalized, behavioral version of the traditional |$\max$| operator of maximization under constraints.
Let us review the sparse max when there is no budget constraint. The agent faces a maximization problem which is, in its rational version, |$\max _{a}v(a,x)$|, where a is an action and x a state variable.13 There is an attention vector, m, and an attention-dependent extension of the utility function, |$v(a,x,m)$|. For instance, we will typically take
to be the perceived utility function when the consumer is partially inattentive to |$x_{i}$|. When |$m_{i}=1$|, the agent fully perceives dimension i; when |$m_{i}=0\,$|, the agent is fully inattentive to it. Attention generates an action, |$a(x,m) {:\!}= {arg\, max}_{a}v(a,x,m)$|. There is a default attention vector |$m^{d}$|, taken to be 0 in most applications, and a default action |$a^{d} {:\!}= {arg\, max}_{a}v(a,x,m^{d})$|. I call |$a_{m_{i}}={\partial a}/{\partial m_{i}}$|, evaluated at |$(a,m)=(a^{d},m^{d})$|, the normative impact on the action of a change in attention. Hence, |$a_{m_{i}}=-v_{aa}^{-1}v_{am_{i}}$|. When (7) holds, |$a_{m_{i}}=a_{x_{i}}(x,m)_{|m=(1,...,1),x=0}x_{i}$|.
There is a nonnegative parameter |$\kappa$|, which is a cognition cost—formally, a taste for sparsity. When |$\kappa =0$|, the agent is the traditional agent.14 The |$x_{i}$| are viewed by the agent as being drawn from a distribution with standard deviation |$\sigma _{i}$|.
(Sparse max operator, without a budget constraint) The sparse max, |${smax}_{a;m\mid m^{d}}v(a,x,m)$|, is defined by the following procedure.
with the cost-of-inattention factors |$\Lambda _{ii} {:\!}= -\mathbb {E}[a_{m_{i}}v_{aa}a_{m_{i}}]$|, |$g^{\prime }>0$|.
and set the resulting utility to be |$v^{s}=v(a^{s},x)$|. In the expressions above, derivatives are evaluated at |$m=m^{d}$| and |$a^{d}={arg\, max}_{a}v(a,x,m^{d})$|.
In other terms, the agent solves for the optimal |$m^{\ast }$| that trades off a proxy for the utility losses (the first term in the right-hand side of equation (8)) and a psychological penalty for deviations from a sparse model (the second term on the right-hand side of equation (8)).15 Then, the agent maximizes over the action a, as if |$m^{\ast }$| were the true model. The problem is solved by backward induction.
This leads to define the attention function:16
This represents the optimal attention to a variable with variance |$|v|$|, normalizing other factors to 1. Figure 2 plots typical shapes.
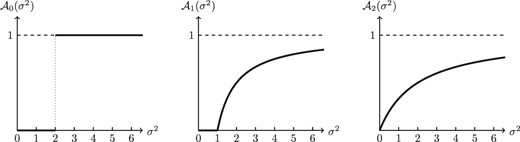
Three attention functions |$\mathcal {A}_{0},\mathcal {A}_{1}$|, and |$\mathcal {A}_{2}$|, corresponding to fixed cost, linear cost, and quadratic cost, respectively. We see that |$\mathcal {A}_{0}$| and |$\mathcal {A}_{1}$| induce sparsity—that is, a range where attention is exactly 0. |$\mathcal {A}_{1}$| and |$\mathcal {A}_{2}$| induce a continuous reaction function. |$\mathcal {A}_{1}$| alone induces sparsity and continuity.
Then, the value of attention to dimension i is given by the key relation:
This formula gives a simple “plug and play” solution for the (potentially very complex) attention problem: to allocate attention to dimension i, just use (10). There is no need to come back (except for generalizations) to the background problem (8). The following Lemma derives a typical case.
with |$a_{x_{i}}={\partial a}/{\partial x_{i}}=-v_{aa}^{-1}\cdot v_{a,x_{i}}$|. In the expressions above, derivatives are evaluated at |$x=0$| and |$a^{d}={arg\, max}_{a}v(a,0)$|.
The intuition is that the |$x_{i}$|’s are truncated. If |$|a_{x_{i}}|$| is small enough, so that |$x_{i}$| shouldn’t matter much anyway, then |$m_{i}^{\ast }=0$|, and the agent doesn’t pay attention to |$x_{i}$| (if |$m_{i}^{d}=0$|).
This leads to the defining the truncation function, with b the coefficient on the state variable x in a linear policy function:
It is the coefficient b, times the attention to the coefficient, divided by the scaled cognition cost k.
The following lemma gives a more explicit version of the action.
with |$\kappa _{a} {:\!}= (\kappa /|v_{aa}|)^{1/2}$|.
When attention is chosen after seeing x (“ex post” ), we use the same expressions, with |$\sigma _{i} {:\!}= |x_{i}|$|. For instance, the ex-post action becomes:
In the “ex ante” procedure, the slope is chosen before seeing |$x_{i}$|. Hence, the policy is still linear in |$x_{i}$|, which makes that procedure useful in macro. In the “ex post” procedure, the truncation is chosen after seeing the |$x_{i}$|, and the policy is non-linear in |$x_{i}$|.
Attention and Truncation Functions. Here are some good truncation functions. In Gabaix (2014), I study attention functions |$\mathcal {A}_{\alpha }(\sigma ^{2})$| corresponding to |$g(m)=m^{\alpha }1_{m>0}$|. For instance, for the values |$\alpha =0,1,2$|, we have:
The truncation functions |$\tau _{\alpha }(b,k)$| is then (using (12)):17
Figure 2 plots the attention functions, and Figure 3 the corresponding truncation functions.
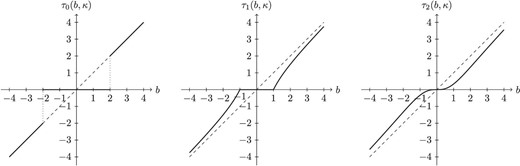
Three truncation functions. Because it gives sparsity and continuity, the |$\tau _{1}$| function is recommended.
3.2. Dynamic Programming: A Motivating Example
To motivate the general structure, let us start with a basic example, the consumption-savings problem. The agent has utility |$\mathbb {E}\sum _{t=0}^{\infty }\beta ^{t}c_{t}^{1-\gamma }/(1-\gamma )$|. Wealth |$w_{t}$|, and the state variables evolve as:
That is, wealth at |$t+1$| is savings at t, |$w_{t}-c_{t}$|, invested at rate |$r_{t}=\bar{r}+\hat{r}_{t}$|, plus current income, |$y_{t}=\bar{y}+\hat{y}_{t}$|. Here, |$\hat{r}_{t}$| and |$\hat{y}_{t}$| are deviations of the interest rate and income from their means, respectively, and follow AR(1) processes, where |$\varepsilon _{t+1}^{r}$| and |$\varepsilon _{t+1}^{y}$| are disturbances with mean zero and no correlation across periods. For simplicity, assume here that |$\beta R=1$|, where |$R {:\!}= 1+\bar{r}$|.
This is a complex problem, with 3 state variables
This is also a metaphor for a more complex model, which could have 30 or 300 state variables. What will the agent do at time 0?18
One thing I wish to capture is “the agent may not want to think about the interest rate”. The reader can introspect: when most people plan their vacation, do they think “now interest rates are high, so it’s a makes good sense to spend little this summer, and more next summer; this way we’ll respect our Euler equation, and will make sure that our consumption growth is high, in congruence with the current high interest rate?” Most people, and the reader, I imagine, do not do that (by the way, econometric evidence confirms that they don’t, see, for example, Hall 1988). Non-economists would find that depiction of them ludicrous. Accordingly, the sparse agent will be allowed not to think about the interest rate—though he will think about it, say when buying a house, or when interest rates are very volatile.
Second, “the agent may wish to imagine simplified dynamics for the process”, for example, he may replace the dynamics of this income, for instance, by a simpler process, for example, imagine it will be roughly constant—without paying attention to the detailed stochasticity of the income process.
Before showing the equations, I propose an intuitive picture of what the agent’s world view is. I posit that the agent knows what to do in a simpler, default model. That is, he assumes that future interest rate and income will be constant. Then, the optimal consumption is
and the value function is
Then, the agent decides whether to enrich his very model where everything is constant. He asks “is it worth thinking about the interest rate?” To do so, he contemplates a one-variable enrichment, with the interest rate, and sees whether it’s worth it. If it isn’t, he settles for a model where the interest rate is constant. If it is, he enriches his model, with a non-constant interest rates.
Here is how I propose to capture those ideas. I posit that the agent contemplates a “simplifiable meta-model”. In our example, this is a transition function |$F(c_{t},z_{t},m)$|, whose components are (with |$F=(F^{w},F^{r},F^{y})$|):19
where |$\rho _{r}(m) {:\!}= m_{\rho _{r}}\rho _{r}+(1-m_{\rho _{r}})\rho _{r}^{d}$| and |$\rho _{y} (m) {:\!}= m_{\rho _{y}}\rho _{y}+(1-m_{\rho _{y}})\rho _{y}^{d}$|.
For instance, when |$m_{r}=0$|, the agent doesn’t pay attention to the interest rate, while if |$m_{r}=1$|, he will pay attention to 1. Likewise, |$m_{y}$| represents the agent’s attention to future income shocks: if |$m_{y}<1$| the agent pays little attention to future income streams—he is myopic toward them. Parameter |$m_{\sigma _{y}}$| in (22) represents the attention to noise: when |$m_{\sigma _{y}}=0$|, the agent doesn’t pay attention to the stochasticity of the income—which will lead the agent to accumulate a too small buffer of savings and be vulnerable to shocks.20 Parameter |$m_{\rho }$| represents the attention to the fine structure of the income process: when |$m_{\rho _{y}}\!=\!0$|, agent replaces the true autocorrelation |$\rho _{y}$| by another one, |$\rho _{y}^{d}$|, for example, if |$\rho _{y}^{d}>\rho _{y}$| and |$m_{\rho _{y}}\!<\!1$|, the agent will think that income shocks are more persistent than they are.
Here,
is the subjective parametrization of the world, and |$\mu =(1,1,1,1,1,1)$| is the objective parametrization. Instead of thinking that the transition function is |$z_{t+1}=F(c_{t},z_{t},\mu )$|, the agent will decide to imagine that it is |$z_{t+1}=F(c_{t},z_{t},m)$|.
So far, we have described a structure. The next section defines the sparse max. In particular, what does it mean to “use a simplified model”, what’s the agent’s anticipation of his future actions, so we have a well-defined notion of dynamic programming? Next, how will attention be allocated? Then, we will study consequences of this behavior for classic macro questions.
3.3. Sparse Dynamic Programming: Basic Definition
The state |$z_{t}$|, the action |$a_{t}$| and the i.i.d. innovation |$\varepsilon _{t+1}$| are vectors. There are T periods, where T could be infinite.
The rational problem. The agent’s rational problem is:
and a terminal condition |$z_{T}\in \mathcal {F}^{T}$| for a given set |$\mathcal {F}^{T}$|.21
The rational version of the DP problem is a series of value functions |$V^{r,t}$| satisfying the Bellman equation:
for |$t=0,...,T-1$|, and with |$V^{r,T}(z)=0$|. A policy is then a function |$a(z)$|. Actually, one can drop the index t in the explicit formulation of (24), if state vector includes the calendar date t, for example, if we can write |$z_{t}=(w,x,t)$| and V depends on that calendar date component. This way, the traditional Bellman equation can be simply written without explicit t superscript:
The sparse max version. In the |${smax}$| version, we are given attention-augmented utility and transition functions in a way that will be illustrated later, for example, in Proposition 2:22
We are also given a “default proxy value function”, |$V^{p}(z)$|. Typically, it is just the rational value function (|$V^{p}=V^{r}$|), that is, the function assuming that the agent will behave rationally afterwards—in the simplified model contemplated by the agent (this will be very clear in the 3-period example of Proposition 6).23 We could also have |$V^{p}$| to be the objective value function (where the agent has rational expectations about his own boundedly rational behavior—something I derive in Section 3.4). But, the two differ only by second order terms (see Proposition 4), so this assumption makes materially little difference. Since it is simpler, and (I will argue) more realistic, I recommend taking |$V^{p}=V^{r}$|.
The agent’s action is as follows.24
Hence, the agent maximizes his perceived flow utility function, and his perceived continuity value function. The degree of sophistication in those perceptions is controlled by vector m. When the cost of rationality |$\kappa$| is 0 (and |$m=(1,...1)$|), and |$V^{p}=V^{r}$|, the agent is just the rational agent.
3.4. More Advanced Notion: Iterated Dynamic Sparse Max
The rest of this section examines advanced notions, so the reader is encouraged to skip it in the first reading.
Given the decision function |$a(z) {:\!}= a(z,V^{p})$| from Definition 2, the agent obtains an objective value function |$V^{o}(z)$|, which satisfies:
Does this equation admit a well-defined solution |$V^{o}$|? This is not problematic with a finite-horizon (it is calculated by backwards induction). With an infinite horizon, we adapt the machinery of Bellman operators. It uses some technical assumptions, made throughout this section. Formally, we assume that in this section, and in particular in Definition 3, u, |$V,$| and |$V^p$| are bounded functions, so that the operator |$\mathcal {T}$| maps pairs of bounded functions into bounded functions. We also make the very mild assumption that the expectation in (29) is well-defined—which is true under weak technical conditions.25
Given this, (28) can be written as:
This operator |$\mathcal {T}\,(V,V^{p})$| has the usual good properties, recorded in the following lemma.26
(Monotone contraction) The operator |$\mathcal {T}\,(V,V^{p})$| is a monotone |$\beta -$|contraction as a function of V. More explicitly: for any bounded functions |$V,\widetilde{V}$| (i) |$\Vert \mathcal {T}\,(V,V^{p})-\mathcal {T}(\widetilde{V},V^{p})\Vert _{\infty }\le \beta \Vert V-\widetilde{V}\Vert _{\infty }$|; (ii) if |$V(z)\le \widetilde{V}(z)$| for all z, then |$\mathcal {T}\,(V,V^{p})(z)\le \mathcal {T}(\widetilde{V},V^{p})(z)$| for all z.
This implies that a solution to (30) exists.
The objective value function is the a unique fixed point |$V^{o}$| of the equation |$V^{o}= \mathcal {T}\,(V^{o},V^{p})$|.
Hence, so far, given an original proxy value |$V^{p}$|, we defined a policy |$a(z,V^{p})$|, which generates a new value function |$V^{o}$|. We can iterate the process. This generates the “|$q-$|iterated” |${smax}$| action.
(Action in sparse dynamic programming, |$q-$|iterated) The basic (|$0-$|iterated) dynamic |${smax}$| action is the action |$a(z,V^{p})$| from Definition 2. The |$q-$|iterated dynamic |${smax}$| action is |$a(z,V^{(q)})$|, where |$V^{(0)}=V^{p}$|, and for |$q>1$|, |$V^{(q)}$| is characterized by |$V^{(q)}= \mathcal {T}\,(V^{(q)},V^{(q-1)})$|.
In some sense, the basic sparse max agent is naive about his future actions, while the |$q-$|iterated agent is more sophisticated. In practice, we will just take the basic action of Definition 2 in most problems of interest: this captures the essence of the economics, while keeping the model quite easy to use. Working through examples below will suggest that the higher-iterations are quite demanding in rationality.
With a finite horizon when |$q\ge T-1$|, the |$q-$|iterated value |$V^{(q)}$| satisfies:
That is, we obtain the agent’s full value function. This is the same formulation as in the rational version, but with a |${smax}$| rather than a |$\max$| operator. In that formulation, the BR agent is very sophisticated (perhaps too much so) about his own future behavior: he sees how much he will see how much he will see (etc. – iterated q times) future inattention.
With finite horizon, the definition gives a construction of the value function by backward induction: starting from |$V^{T}=0$|, we successively calculate |$V^{T-1}$|,..., |$V^{0}$| (note that the time t is inside vector z).27
3.5. Some General Features of Sparse Dynamic Programming
This subsection presents some general features of sparse dynamic programming, including tools to compute it easily, and derives quite systematically the difference between the actions of a sparse agent and of a rational agent. It derives the general form of predictions (e.g. in Proposition 2) that appear in the rest of the paper. Still, as this section is a bit dry, the reader may wish to skim it, read the main examples shown later, and then come back to it with those examples in mind.
The results are proven for finite-horizon problems. I conjecture that they hold for infinite-horizon problems under some reasonable assumptions.28
Taylor expansion of policy and value functions. We decompose the vector of state variables into: |$z=(w,x)$|, where w is a vector of variables that are fully taken into account in the default model (including possibly calendar time), while x is a vector of variables not taken into account in the default model. To capture this, I assume throughout the paper that |$u(a,w,x,m)$| and|$F(a,w,x,m)$|are independent of mwhen|$x=0$|. I also assume throughout the paper that |$F^{x}(a,w,x,m)=0$| when |$x=0$|, so small x’s at t generate small x’s at |$t+1$|.
I will frequently assume the following “local autonomy of the disturbance” condition:
where |$F_{a}^{x}$| is derivative with respect to a of the law of motion of x. This says that when |$x=0$|, a small change in action a doesn’t affect it directly, that is, x is locally independent of the agent’s actions. This is for instance the case for macroeconomic disturbances, for example, if |$x_{t+1}=\rho _{x}x_{t}+\varepsilon _{t+1}^{x}$|, as we postulated for some variables above (e.g. (17)). This decoupling of the change in the variable |$x_t$| from action |$a_t$| brings a lot of tractability to the system—otherwise things would much more complicated (a matrix Ricatti equation would need to be solved for, see Section A.1 in online appendix).
For simplicity, I assume that the functions are infinitely differentiable, and so is the attention function (the Online Appendix weakens those conditions in Section G.1; the exposition is then heavier).
The main tools are the following.
This proposition will be quite useful. To derive policies, first we can simply do a Taylor expansion of the rational policy around the default model, and then truncate term by term.
The following proposition indicates that to calculate the leading terms of the sparse policy, one can do a simple Taylor expansion around the default model, |$V^{d}(w)$|. One does not need to calculate explicitly the full rational policy |$V^{r}(w,x)$|.
(Simple procedure to calculate the rational or sparse policy, to the first order) Assume the local autonomy condition (32). To calculate the policies |$a^{s}(w,x)$| and |$a^{r}(w,x)$| up to second order terms, one can simply do a Taylor expansion around the default model with value function |$V^{d}(w)$| (which gives |$V_{x}$| and |$V_{wx}$|), following the procedure outlined in Section A.1 in online appendix. In particular, one does not need to fully solve the rational model.
I now present some basic facts that are helpful in thinking about those policy functions. The first three (Proposition 4 and Lemmas 5–6) are very simple—basically they rely on the envelope theorem—and would apply any other “reasonable” models of misoptimization where the behavioral action differs from the rational action by some small term (order |$O(\Vert x\Vert )$|).29
For small x, we have: |$V(w,x)=V^{r}(w,x)+\mathsf {R}(w,x)$|, where the residual |$\mathsf {R}(w,x)=O(\Vert x\Vert ^{2})$| for x close to 0. In other words, the sparse value function and the rational value functions differ only by second order terms in x.
This implies that, at |$x=0:$|
Typically |$V_{xx}\ne V_{xx}^{r}$|, however.
We have the following Lemma.30
(Close policies give very close value functions) Suppose a policy |$a(w,x)$| such that |$a(w,x)=a^{d}(w)+O(\Vert x\Vert)$|. Then, |$V^{o}(w,x|a(\cdot ))=V^{r}(w,x)+O(\Vert x\Vert ^{2})$|.
This means that if the policy is approximately correct, up to first order terms, then the value function is approximated by the correct optimal policy, up to second order terms. This is again the envelope theorem.
(Close proxy value functions give close policies) Consider two proxy value functions |$V^{p},V^{p^{\prime }}$|such that, |$V^{p}(w,x)=V^{p^{\prime }}(w,x)+O(\Vert x\Vert ^{2})$|, and assume (32). Then, |$a(w,x,V^{p})=a(w,x,V^{p^{\prime }})+O(\Vert x\Vert ^{2})$|.
This lemma means that to know the optimal policy up to second order terms, we just need to have a proxy value function that is accurate up to second order terms. This is intuitive, but the proof reveals that condition (32) is required.
The above two lemmas imply that sophistication versus naiveté lead to the same policies, up to second order terms. Given also the naive / basic action (|$q=0$|) is simpler, this is another reason for modeling agents with the basic policy.31
(Sophistication versus Naiveté makes only a second order difference in actions) Consider the |$q-$|iterated agent of Definition (4). Suppose that the level 0 agent used a proxy value function |$V^{p}$| such that |$V^{p}(w,x)=V^{r}(w,x)+O(\Vert x\Vert ^{2})$|. Then, the actions at higher levels of sophistication |$q\ge 0$| differ only by second order terms from the naive action: |$a(Z,V^{(q)})=a(Z,V^{(0)})+O(\Vert x\Vert ^{2})$|.
For instance, in the life-cycle model of Section 2, I assumed basic |$(q=0)$| agents, who project them selves are rational. If I had assumed partially (low |$q>0$|) or fully sophisticated agents (|$q\ge T-1$|), who keenly understand their future BR, Proposition 5 says that the consumption would have been the same, up to |$O(x^{2})$| terms.
4. Intertemporal Consumption: Behavioral Version
I now work out a few explicit examples, starting from very simple ones to build the intuition.
4.1. The Life-Cycle Problem Revisited
4.1.1. Detailed Analysis with Three Periods
Here I revisit the life-cycle model of Section 2, in more detail. I take a 3-period version (|$L=2$|, |$T=3$|).32 Utility is |$\sum _{t=0}^{2}u(c_{t})$|, and there is no discounting (|$R=\beta =1$|). The agent starts with an endowment |$w_{0}$|, has no regular income (|$\bar{y}=0$|) and receives x at time 2; x is known at time 0, but the agent “may not think about it”. For instance, x could represent a negative income shock, such as a tax to pay, or a decrease in income as retirement. Calling |$w_{t}$| the wealth at the beginning of period t, the budget constraints at times |$t=0,1,2$| are: |$w_{1}=w_{0}-c_{0}$|, |$w_{2}=w_{1}-c_{1}$|, |$0=w_{2}+x-c_{2}$|.
How much attention will the agent pay to time-2 payment x? First, let us observe that a rational agent smooths consumption: lifetime resources are |$w_{0}+x$| (initial wealth |$w_{0}$| and time-2 payment x), and they should be consumed equally in the three periods:
The corresponding dynamic policy (expressed with |$w_{t}$| rather than |$w_{0}$|) is:
For example, at time 1, the life-time remaining resources (|$w_{1}+x$|) should be divided equally among the two remaining periods.
I first state the behavioral policy, then derive it. The derivation is instructive.33
If |$|x|$| is not too large, they satisfy |$m_{0}\le m_{1}\le 1$|, that is, the agent reacts more to near variables than distant variables.
Derivation of Proposition 6. We apply the smax procedure of Definition 2, using backward induction.
At time 2, the agent consumes all his disposable wealth:
At time 1, the agent’s problem is:
The FOC |$v_{c_{1}}^{1}=0$| reads: |$u^{\prime }(c_{1})=V_{w}^{2}(w_{1}-c_{1},m_{1}x)=u^{\prime }(w_{1}-c_{1}+m_{1}x)$|, so |$c_{1}=w_{1}-c_{1}+m_{1}x$|, and
The agent pays partial attention |$m_{1}$| to the time-2 income x.
To calculate attention |$m_{1}$|, we apply (11). Noting that |$v_{cc}^{2}(c,x,m_{1})_{\mid m_{1}=0}=2u^{\prime \prime }(c_{1}^{d})$|, where |$c^{d}={w_{1}}/{2}$| is the optimal consumption with |$m_{1}=0$|, we have
so
At time 0, the agent does |${smax}_{c_{0};m}v^{0}(c_{0},x,m_{0})$|, with
where I use Definition 2, with |$V^{p}=V^{r}$|, the value function where the agent projects that he will be rational in the future:34
The FOC is |$v_{c_{0}}^{0}=0$| with, that is,
and
To determine attention |$m_{0}$|, we again use (11); we calculate:
so that |$m_{0}=\mathcal {A}(\frac{1}{\kappa }v_{cc}^{0}\operatorname{var}(\partial _{m_{0}}c_{0}))=\mathcal {A}(\frac{1}{\kappa }\frac{3}{2}u^{\prime \prime }(c^{d})\operatorname{var}(\frac{x}{3}))$|, that is,
The consumptions are:
Comparing (37) and (42), we see that
When |$x=0$|, this is automatically verified, as |${w_{0}}/{3}={w_{1}}/{2}$|. Hence, we have |$m_{0}\le m_{1}$| iff x is not too large.35|$\square$|
4.1.2. A few Features of a Sparse Agent
This example and the life-cycle model of Section 2 illustrates a few general features.
Sparse agents are globally patient like rational agents, but still myopic to a variety of small future shocks. Indeed, agents here invest their wealth |$w_{t}$| very patiently, exactly like rational agents: they fully smooth it over the horizon. At the same time, they tend to be myopic about future small shocks (the time-2 shock x). In other terms, in the present model, agents are only partially myopic (e.g. don’t react to a scheduled increase in taxes). This behavior cannot be captured with a model simply assuming a low discount factor |$\beta$|.
The Euler equation fails. The Euler equation holds under the BR-perceived consumption, but not under the actual consumption. For instance, at time 1, if |$m_{1}=0$|, then the agent expects to consume |$(c_{1},c_{2})=({w_{1}}/{2},{w_{1}}/{2})$|, but actually consumes |$(c_{1},c_{2})=({w_{1}}/{2},{w_{1}}/{2}+x)$|. The traditional Euler equation basically only holds if agents are exactly rational (Hall 1988), so it is a fragile way to model agents. In contrast, sparse consumption functions are a more robust way of modeling them.
The first and second welfare theorems fail. This 3-period example features a simple economy, “production” being the linear storage technology allowing to transfer the good 1-for-1 across periods. Here, we do not have a Pareto-optimum, as the agent fails to maximize.36 Likewise, if the first welfare theorem fails, typically the second welfare theorem fails. However, some optimum tax policy can generally restore efficiency.
Agents react more to “near” shocks than to “distant” shocks (in math, |$m_{0}\le m_{1}$|). The main reason is that, normatively, the shock x should impact |$c_{0}$| as
while it should impact |$c_{1}$| as
Hence, attention to the last period shock x is lower at earlier dates |$(t=0$|) than at late dates |$(t=1$|).
This example suggests a few interesting variants. I discuss some of them in Section 7.1.
4.2. Consumption-Savings with Infinite Horizon
Here, I propose a version of the permanent income consumption problem of Section 3.2.
Formalism. We have |$x_{t}$| the state vector of disturbances, which follows a process: |$x_{t+1}=F^{x}(x_{t},\varepsilon _{t+1}^{x})$|. The interest rate and income deviations from their means are a linear function of that state vector: |$\hat{r}_{t}=k^{r}\cdot x_{t},\ \hat{y}_{t}=k^{y}\cdot x_{t}$| for some vectors |$k^{r},k^{y}$|. The perceived law of motion for wealth is kept throughout as (20). However, the perceived law of motion for |$x_{t}$| can be very general, for example, |$x_{t+1}=A(m)x_{t}+\sigma (m)\varepsilon _{t+1}$| for some parametrizations of the matrix and stochasticity.
As a concrete example, let us review the basic example with the full formalism (which the reader is encouraged to skip at first). The state vector is:37
Here |$\sigma ^{y}$| parametrizes the stochasticity of income, which may be set to zero in a simplified model. The simplifiable meta-model is: |$\hat{z}_{t+1}=F^{z}(c_{t},z_{t},\varepsilon _{t+1},m)$|, where the components are: for wealth, (20):
for the interest rate and income, using the notation X a shorthand for r or y,
for parameters |$z_{i}=\rho _{r},\sigma _{r},\rho _{y},\sigma _{y}$|,
For instance, if |$m_{\sigma ^{y}}=0$|, the agent projects income to have 0 stochasticity in the future.
Results. I start with a simple lemma describing the rational policy, using Taylor expansions.38 To signify “up to second order term”, I use the notation |$O(\Vert x\Vert ^{2})$|, where |$\Vert x\Vert ^{2} {:\!}= \mathbb {E}[\hat{y}_{\tau }^{2}]/\bar{y}^{2}+\mathbb {E}[\hat{r}_{\tau }^{2}]/\bar{r}^{2}$| (the constants |$\bar{y},\bar{r}$| are just here to keep valid units). Recall that |$R {:\!}= 1+\bar{r}$|.
Consumption reacts to future interest rates and income changes, according to the usual income and substitutions effects (multiplied by |$\psi$|).39
The behavioral policy is then as follows.
where |$\mathbb {E}_{t}^{s}$| is the expectation taken with respect to the agent’s beliefs under the subjective model.
The policy of the behavioral agent is the policy of a rational agent, under a subjective model, and with partial inattention to income and interest rate.
Now, I record the important case of AR(1) processes.
with |$B_{r}^{s}(w_{t})=\frac{b_{r}(w_{t})m_{r}}{R-\rho _{r}(m)}$| and |$B_{y}^{s}=\frac{b_{y}m_{y}}{R-\rho _{y}(m)}$|.
Endogenizing attention, we have
This shows a “feature-by-feature” truncation. It is useful because it embodies in a compact way the policy of a sparse agent in quite a complicated world. Note that the agent can solve this problem without solving the 3-dimensional (and potentially 21-dimensional, say, if there are 20 state variables besides wealth) problem. Only local expansions and truncations are necessary.41 Attention to the interest will become higher if the interest rate is very volatile (|$\sigma _{r}$| high, e.g. as in hyperinflations).42
Numerical illustration. To get a feel for the effects, consider a calibration with (using annual units): |$\gamma =1$|, |$\bar{r}=5\%$|, |$w_{t}=2c_{t}^{d}$|, |$c_{t}^{d}=1$|, |$\sigma _{r}=0.8\%$|, |$\sigma _{y}=0.2$|, |$\rho _{y}=0.95$|, |$\rho _{r}=0.7$|: as income shocks (roughly corresponding to “carrier risk”) are persistent, they are important to the consumer’s welfare.43 I use the |$\tau _{1}$| truncation function. I parametrize |$\kappa =\bar{\kappa }^{2}|u^{\prime \prime }(c_{t}^{d})|$|, as in Section 2 (see also Section A.2.2 in online appendix).
Figure 4 shows the attention to the interest rate and income. At |$\kappa =0$|, the agent is fully rational, attention is 1. For higher |$\bar{\kappa }$|, attention drops, more so for the interest rate. For |$\bar{\kappa }$| above 0.02, the agent stops thinking about the interest rate. Because the interest rate makes him change his consumption by less than 2% on average, it’s optimal for him not to think about the interest rate. Still, he thinks a lot about his income. Attention to current income falls when |$\bar{\kappa }\simeq 0.1$|, that is, then the agent truncates features that make him change his consumption by less than 10%. Note that this “source-specific” selective attention could not be rationalized by just a fixed adjustment cost to consumption, which affect all causes of consumption change equally.
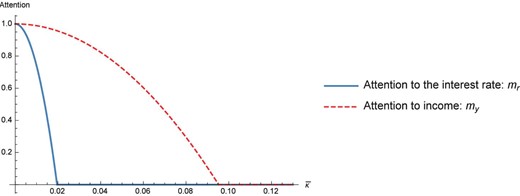
This figure shows the attention to the interest rate (|$m_{r}$|) and to income (|$m_{y}$|) as a function of the cost of thinking, |$\bar{\kappa }$|.
The same reasoning holds in every period. The above describes a practical way to do sparse dynamic programming. In some cases, this is simpler than the rational way (as the agent does not need to solve for the equilibrium), and it may also be more sensible.
This section has developed the sparsely behavioral version of a basic machine of macroeconomics: the consumption function of an agent in a world of dynamic interest rates and income shocks. This is useful, because from this machine can be used in a host of situations. I turn to two such situations before turning its use in general equilibrium (Section 5).
4.3. Application: Ricardian Equivalence
Intuitively, a sparse agent will violate Ricardian equivalence as he is partially myopic. To see more precisely, I keep interest rates constant, and call |$\hat{g}_{t}$| the transfers from the government to the agent at time t. To see this, call |$w_{t^{-}}$| the financial wealth at the beginning of the period (before government transfers) and specialize Proposition 7, setting |$\hat{y}_{\tau } {:\!}= \hat{g}_{\tau +1}$|. We obtain the consumption:
Suppose that the government gives |$\hat{g}$|to the agent at t, and |$-\hat{g}R^{T}$| in T periods. A rational consumer would not change consumption, as the present value is unchanged (Barro 1974). However, a BR consumer increases consumption by |$({\bar{r}}/{R})(1-m_{g})\hat{g}$|: the positive shock increases it by |$({\bar{r}}/{R})\hat{g}$|, and the negative shock decreases is by |$({\bar{r}}/{R})m_{g} \hat{g}$|.
(Failure of Ricardian equivalence) A behavioral consumer increases consumption at t by |$({\bar{r}}/{R})(1-m_{g})\hat{g}$|. This way, Ricardian equivalence does not hold, unless attention is full. The further away the increase in taxes (keeping their present value constant), the lower the reaction.
Section C.6 in online appendix develops in details the dynamics of attention to future taxes: in particular, how attention becomes higher close to the tax hike.
4.4. Application: Lucas Critique
With sparse agents, the Lucas (1976) critique stops applying—or at least applies less. Lucas’ critique is that if the parameters of the world (e.g. tax) change, people’s reactions functions will change. However, with sparse agents, this is it not true: when changes are small, agents choose keep their default “policy functions”. For instance, suppose that there is a small, temporary consumption tax |$\mathcal {T}_{t}$|, in the permanent income model above, so that the perceived law of motion for wealth becomes:
If the tax is small, agent will pay 0 attention to it (|$m_{\mathcal {T}}=0$|), and their policy function will not change. The aggregate outcome will change, because agents will be poorer —but the policy function will not change.
5. Neoclassical Growth Model: A Behavioral Version
I now move on to general equilibrium, and study a behavioral version of the baseline neoclassical growth model, the Cass–Koopmans model.44
5.1. Setup
The utility function is still |$\mathbb {E}\sum _{t=0}^{\infty }\beta ^{t}({C_{t}^{1-\gamma }}/{1-\gamma })$|, and we again call |$\psi ={1}/{\gamma }$|. The aggregate capital stock follows:
where |$\varepsilon _{t+1}$| are mean-zero shocks. This way, there is just one state variable in the economy, the capital stock. In the most basic neoclassical model, |$\varepsilon _{t+1}$| is always 0, and L is fixed.45 I define |$f(K) {:\!}= \mathsf {f}(K,L)-\delta K$|, which is output net of the capital depreciation at the fixed labor supply, so that |$K_{t+1}=$| |$f(K)+K_{t}-C_{t}+\varepsilon _{t+1}$|.
This is a textbook example, which introduces generations of students to macroeconomics (Blanchard and Fisher 1989 (chapter 2), Acemoglu 2008 (Chapter 8), Romer 2018). In that tradition, we have infinitely-rational forward looking agents that calculate the whole macroeconomic equilibrium in their heads. They are supposed to use the dynamics:
and given |$K_{0}$|, find the unique |$c_{0}$| that leads to a non-explosive path (the saddle path, see Figure 5). The psychology of that is arguably quite alien to any human’s intuition. Still, it’s on that strange core model that much of dynamic macroeconomics rests. Hence, it is useful to develop an alternative to that model, something I now do.
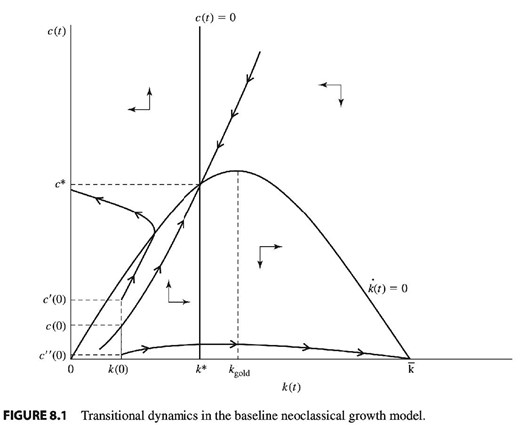
This figure shows the traditional approach to the neoclassical growth model. The agent is supposed to find the unique saddle path leading to non-explosive dynamics. Arguably, this is psychologically quite absurd. The present paper proposes a more behavioral approach. Source: Acemoglu (2008).
Let us first review the mechanics of convergence. If there were no shocks, the economy would be at the steady state, with capital stock |$K^{\ast }$|. I use the hat notation for deviations from the mean, e.g. |$\hat{K}_{t}=K_{t}-K^{\ast }$|. The law of motion for capital (55) is, in linearized form:
where r is the steady state interest rate, |$1+r=f^{\prime }(K_{\ast })$|.
As there is one state variable, the linear policy function of the agent (rational or not) is:
for some constant b to be determined.
Plugging this into (56), we obtain: |$\hat{K}_{t+1}=(1+r-b)\hat{K}_{t}+\varepsilon _{t+1}$|, that is,
where |$\phi$| is the speed of mean-reversion:
When agents are more reactive to shocks (when b is higher), the economy mean-reverts faster to the steady state (|$\phi$| is higher).
Squaring equation (58), we obtain: |$\operatorname{var}\hat{K}_{t+1}=(1-\phi )^{2}\operatorname{var}\hat{K}_{t}+\sigma _{\varepsilon }^{2}$|. As in the steady state, |$\operatorname{var}\hat{K}_{t+1}=\operatorname{var}\hat{K}_{t}$|, |$\operatorname{var}\hat{K}_{t}=({\sigma _{\varepsilon }^{2}}/{1-(1-\phi )^{2}})$|, that is, in the limit of small time intervals:
When shocks mean-revert more slowly (lower |$\phi$|), the average deviation of the stock price from trend is higher (shocks “pile up” more).
The steady state. Rational agent. The rational agent has a value function |$V(K_{t})$|, which satisfies:
The steady state is at |$K=K_{\ast }$|, |$C_{t}=C_{\ast }$| with:46
which determines |$K_{\ast }$|, the gross interest rate |$1+\bar{r}=f^{\prime }(K_{\ast })$| and consumption is |$C_{\ast }=F(K_{\ast })$|.
Behavioral agent. I consider here the decentralized approach. In a population with mass 1 and aggregate capital stock |$K_{t}$|, I consider an individual represent agent, who has his own wealth |$k_{t}$|, under control. In equilibrium |$k_{t}=K_{t}$|. But when deciding on his own consumption, and agent is an infinitesimal price taker, and takes the macro variables (|$K_{t}$|) as unaffected by his own actions.
Suppose that the agent has a consumption rule that’s consistent with a steady state growth, that is, |$c_{t}=\bar{y}+\mu k_{t}$|, where the MPC is |$\mu =1-\beta$|. By the analytics above (equation (19)), this is the optimal policy in the steady state.47 Then, wealth evolves as |$k_{t+1}=(1+\bar{r})(k_{t}+\bar{y}-c_{t})=(1+\bar{r})(1-\mu )k_{t}$|. So, at a steady state, |$\bar{r}$| adjusts so that |$1=(1+\bar{r})(1-\mu )=(1+\bar{r})\beta$|. This gives the same condition (62), hence the same steady state as in the rational case.
The behavioral agent here inherits the same steady state as the neoclassical agent, with |$\beta (1+\bar{r})=1$| at the steady state. Only the dynamics around the steady state are different. I now turn to them. For simplicity, I use the notation r for the steady state interest rate |$\bar{r}$|.
5.2. Convergence: Boundedly Rational Version
The agent’s wealth evolves as:
where |$y_{t}=f(K_{t})-K_{t}f^{\prime }(K_{t})$| is labor income, and |$r_{t}=f^{\prime }(K_{t})$| is the interest rate. Taylor expansions around the steady state yield:
Rather than positing that the agent correctly sees a whole saddle path, I posit that in the agent’s model, capital evolves with a subjective speed of mean-reversion |$\phi ^{s}$|: |$\mathbb {E}_{t}[\hat{K}_{t+1}]=(1-\phi ^{s})\hat{K}_{t}$|. I again parametrize it as:
where |$\phi$| is the true speed of mean-reversion (which will be determined as an endogenous outcome) and |$\phi ^{d}$| is a default value—perhaps coming from some empirical experience, saying for instance that “business cycles” have a half-life of a few years.
For simplicity, I posit that the agent pays the same attention |$m_{K}$| to all macro variables.48 Lemma 8 reads here (using the continuous time notation):
and using (63) and (65) we obtain:
that is, as |$k^{\ast }=K^{\ast }$|,
with
Hence, in the aggregate |$\hat{C}_{t}=b\hat{K}_{t}$| with
and using (59) we obtain the actual speed of mean-reversion of the economy:
Rational agent. The rational agent has a correct model (|$\phi ^{s}=\phi$|, |$m_{K}=1$|). So the speed of mean-reversion is |$\phi =\phi ^{r}$|; (66) gives
whose solution is |$\phi ^{r}=\frac{-r+\sqrt{r^{2}+4\xi }}{2}$|.
Behavioral agent. Let us now endogenize |$m_{\phi }$| and |$m_{K}$|.
at the default model, he doesn’t react to |$\phi$|, the speed of mean reversion of aggregate variables, given he’s not even thinking about aggregate variables (here, just capital). This means (using equation (11)) that |$m_{\phi }=0$|: the optimal refinement in thinking about the speed of mean reversion is 0. Hence, |$\phi ^{s}=\phi ^{d}$|, the projected speed of mean-reversion (|$\phi ^{s}$|) is the default one (|$\phi ^{d}$|).49 Given (66), this implies that the actual speed of mean-reversion is:
Note that in the rational expectations case |$\phi ^{d}=\phi$|, which remains a useful benchmark. The next Proposition studies the more general case, in which |$\phi ^{d}\ge \min (\phi ,\phi ^{r})$|.
(Fluctuations are larger and more persistent with sparse agents) Suppose that |$\phi ^{d}\ge \min (\phi ,\phi ^{r})$| and |$\kappa >0$|. Then |$\phi <\phi ^{r}$|: in the sparse economy, GDP fluctuations have slower mean-reversion and higher variance than in the rational economy.
Consumption is less volatile in the sparse than in the rational economy, if |$\phi \ge r$|, which seems empirically valid.
To get a quantitative expression for |$\phi$|, I use the attention function |$\mathcal {A}_{1}(v)=\max (1-{1}/{v},0)$| from (15).
It is lower (and aggregate fluctuations are larger) when agents’ bounded rationality |$\kappa$| is stronger.
There are two conclusions from this analysis.
First, bounded rationality generates more volatile and persistent fluctuations.
Second, and more importantly, we have a structure that gives an alternative to the rational general equilibrium model. In addition, the worldview of the agent is arguably more sensible. In the behavioral model, the agent pays only partial attention to aggregate state variables and has a simplified understanding of their dynamics: this is, arguably, how most people orient themselves, without a full, structural of model of the causes of aggregate dynamics (which no one knows anyway, including economists). For instance, they say “healthy business cycles typical mean-revert in about 4 years” (which corresponds here to taking |$\phi ^{d}={1}/{4}$|), and they forecast based on that benchmark. People can act with that simplified understanding.
Of course, this does not say that the model does make better predictions—though the generation of higher volatility of GDP is intriguing. It does mean that we have a modeling structure that could be promising in future quantitative work. Acemoglu and Jensen (2023) propose a further analysis of the neoclassical growth model with behavioral features.
5.3. Generalization: Recursive Competitive Equilibrium with Behavioral Agents
Here, I define the behavioral extension of the Prescott and Mehra (1980) recursive competitive equilibrium—which is a formalization of the intuitive concept of dynamic equilibrium. It formalizes what we did in Section 5.2. It is more of methodological interest. It shows the “template” of dynamic equilibrium with behavioral in other contexts. The key issue is that the agents’ behavior affect aggregate future outcomes, but agents may have only a simplified understanding of that.
We are given a steady state capital |$\bar{K}$|, a default law of motion |$K^{\prime }=G^{d}(K)$|, with |$G^{d}(K)=\bar{K}+\phi ^{d}(K-\bar{K})$|. A given m gives perceived laws of motions for private wealth |$k^{\prime }=F^{k}(c,k,K,m)$| and for the aggregate variables |$K^{\prime }=G(K,m)$|.50 In turn, they generate a default value function |$V^{r}(k,K\mid F^{k}(\cdot ,m),G(\cdot ,m))$|, which is the rational value function under those laws of motion. The proxy value function chosen is then: |$V^{p}=V^{r}$| or, depending on the context, a second-order approximation of it.51
In the context of the Cass–Koopmans above the definition is as follows. This template can be generalized quite easily to more state variables, several types, flexible labor supply etc. This mostly just takes more space (see Ljungqvist and Sargent 2012, Chapter 12).
(Behavioral recursive competitive equilibrium) A behavioral recursive competitive equilibrium is
- A set of prices |$r(K),\omega (K)$|, and perceived prices |$r(K,m),\omega (K,m)$| with |$m {:\!}= (m_{K},m_{K}^{2},m_{K^{\prime }},m_{\varepsilon })$|, with:and the same for |$\omega (K,m)$|.(69)$$\begin{eqnarray} r\left(K,m\right)=\bar{r}+m_{K}r^{\prime }\left(\bar{K}\right)\left(K-\bar{K}\right)+m_{K^{2}}\left[r\left(K\right)-\bar{r}-r^{\prime }\left(\bar{K}\right)\left(K-\bar{K}\right)\right] \end{eqnarray}$$
A set of policies: consumption |$c(k,K)$| and firms’s factor demand: |$k^{D}(K),L^{D}(K)$|.
- A perceived law of motion for private capital:|$\ k^{\prime }=F^{k}(c,k,K,m)$|$$\begin{eqnarray} F^{k}\left(c,k,K,m\right) {:\!}= \left(1+r\left(K,m\right)\right)\left(k-c+\omega \left(K,m\right)\bar{L}\right)+m_{\varepsilon }\varepsilon _{t+1}. \end{eqnarray}$$
An actual law of motion for the aggregate capital:|$\ K^{\prime }=G(K)$|.
A perceived law of motion for aggregate capital:|$\ K^{\prime }=G(K,m)=m_{K^{\prime }}G(K)+(1-m_{K^{\prime }})G^{d}(K)$|
such that
- The agent chooses consumption |$c(k,K,m)$| sparsely and optimally as:where |$V^{r}(k,K\mid F^{k}(\cdot ,m),G(\cdot ,m))$| is the rational value function associated with the perceived law of motions |$F^{k}$| and G.$$\begin{align*} \begin{split} & \quad\quad \quad\quad \quad\quad \\ & = {arg\, smax}_{c;m}\big \lbrace u\left(c\right) +\beta V^{r}\big(F^{k}\left(c,k,K,m\right),G\left(K,m\right)\mid F^{k}\left(\cdot ,m\right),G\left(\cdot ,m\right)\big)\big \rbrace , \end{split} \end{align*}$$
Firms maximize profit: |$k^{D},L^{D}\in {arg\, max}_{k^{D},L^{D}}\lbrace \mathsf {f}(k^{D},L^{D})-r(K)k^{D}-\omega (K)L^{D}\rbrace$|.
Markets clear: |$k^{D}(K)=K$|, |$L^{D}(K)=\bar{L}$|.
The actual law of motion is consistent with individual choice: |$G(K)=\mathsf {f}(K,\bar{L})-c(K,K)+\varepsilon _{K}$|.
To interpret (69), consider the case where the agent doesn’t pay attention to nonlinear terms (|$m_{K^{2}}=0$|),52 doesn’t pay attention to stochastic noise in the future (|$m_{\varepsilon }=0$|) and uses a simplified, AR(1) view of aggregate dynamics (|$m_{K^{\prime }}=0$|). Then, his model of the world is exactly as in Section 5.2. His proxy value function |$V^{r}(k,K\mid F^{k}(\cdot ,m),G(\cdot ,m))$| is the proxy value function under that simplified model, where everything is an AR(1). The value function was already calculated in Lemma 8, using |$\rho _{r}=\rho _{y}=1-\phi$|.
6. Behavioral Version of a Few Other Models
To make sure that the model is widely applicable, I developed a behavioral version of a few other important machines of dynamic economics. I summarize them here, while the Online Appendix has the specifics. I start with the Merton problem, which illustrates a case where risk matters for the agent’s decision.
6.1. Merton Portfolio Choice Model
A core model is dynamic finance is the Merton (1971) portfolio choice problem.53 The agent’s utility is:
and his wealth |$w_{t}$| evolves according to:
where |$\theta _{t}$| is the allocation to equities. The equity premium |$\pi _{t}=\bar{\pi }+\hat{\pi }_{t}$| has a variable part |$\hat{\pi }_{t}$|, which follows
where the return is |$d\tilde{r}_{t}=(r_{t}+\pi _{t})dt+\sigma dZ_{t}^{1}$|. The parameter |$\chi _{t}\ge 0$| indicates that equity returns mean-revert: good returns today lead to lower returns tomorrow. That will create a hedging demand term. I again call |$\psi ={1}/{\gamma }$| the IES.
So, in theory, the agent should take into account both the variable equity premium |$\hat{\pi }_{t}$| and also the “hedging demand,” the demand due to the fact that equity returns mean-revert.
Proposition 12 describes the action of a sparse agent. When |$\kappa =0$|, we recover the fully rational agent, as in Barberis (2000), Campbell and Viceira (2002), and Wachter and Yogo (2010), with the notoriously sophisticated hedging demand term |$H_{t}$|. When |$\kappa >0$| increases, portfolio choice becomes insensitive to the change in the equity premium, |$\hat{\pi }_{t}$|, and the agent thinks less about the mean-reversion of asset, the |$H_{t}$| terms. The fact that people are relatively insensitive to the changes in the risk premium is a empirical central finding in Giglio et al. (2021). It also means that people’s demand for stocks is inelastic, so that flows in the stock markets have a large impact on prices (see Gabaix and Koijen 2022 and the references therein). Hence, a simple model of inattention is useful to model basic facts of economic life.
In addition, the agent is here allowed to be “schizophrenic:” he pays attention to different things as a consumer than as an investor.54 For instance, suppose that the price-earnings ratio of equities is very high and expected equity returns are very low; then, the agent will decrease her exposure to equities (|$\theta <\theta _{\ast }$|), but not reduce her consumption (|$\mu _{t}^{s}=\mu _{\ast }$|). The Online Appendix (Section C.1) develops the Merton portfolio choice model in much greater generality, with many assets and factors.
6.2. Other Models
Linear quadratic models. Many economic problems can be conveniently expressed as linear-quadratic models (Ljungqvist and Sargent 2012). Section C.2 in online appendix derives how to systematically derive a BR version of those models. The models are very tractable (there is no matrix Ricatti equation to solve). Hence, the model offers a way to quite generally have behavioral version of linear-quadratic problems.
Precautionary savings. The consumer may save more when the future is uncertain, a phenomenon known as “precautionary savings” (e.g. Carroll and Samwick 1997). However, a BR consumer may not think much or at all about the stochasticity of his income and under-accumulate a buffer of savings. This is developed in Section C.3 in online appendix.
Real Investment Model. In macro-style investment models, the firm optimizes on investment, with adjustment costs. A behavioral version of this problem is in Section C.5 in online appendix. The firm uses a simplified model of future profits, which can lead it astray (see Greenwood and Hanson 2015).
The Becker–Murphy model of rational addiction. The Becker and Murphy (1988) model of rational addiction is a peak of the use of rationality in economics. Section C.5 in online appendix gives a behavioral version of it. Qualitative evidence in favor of the model (the fact that future increase in prices lower consumption today) are also consistent with this BR version—it shows that agent are at least partially rational (as in the present model), not that they are fully rational (as assumed by Becker–Murphy). This distinction is important: If people are BR enough, they’d be better off under a high tax, or a ban, of the addictive substance—while the optimal tax is 0 in the Becker–Murphy model.55
7. Discussion
7.1. Model Enrichments
Here, I discuss different potential enrichments of the model; the Online Appendix (Section F) discusses more. I discuss them at first in the context of the 3-period model of Section 4.1.
What happens if the agent takes into account the future costs of thinking?
One could imagine that the agent will take into consideration the future costs of thinking in this decision, and in the value function. Of course, this becomes a very sophisticated agent then—far from a BR agent. However, for completeness, I explore this direction in the Online Appendix, Section F.3. The consequences are very minor.56 This is why I don’t incorporate this feature in the basic model.
More sophisticated behavioral agents. We can illustrate the degrees of sophistication of Definition 4 in the 3-period model of Section 4.1. In the basic smax |$(q=0$|), the time-1 value function is |$V^{t=1,(q=0)}(w_{1},x)=2u({w_{1}+x}/{2})$|. With one iteration, the time-1 value function is:
which gives the agent a more sophisticated understanding of his future actions.
The value functions using |$q=1$| or |$q=0$| are the same, up to second order terms, and so are all consumptions. In addition, |$m_{0}^{\ast }$| is the same under both models. Hence, as in Proposition 5, the naive / sophisticated difference changes only second order terms. This is why I have selected the naive case |$(q=0$| iterations) as the baseline case. It is simpler, more plausible cognitively, and yields the same result as the sophisticated case, up to second order terms.57
Enriched models of attention. Suppose that x is very negative, and the agent doesn’t see it at first (still |$w_{0}+x>0$|, so the agent can avoid starvation). Will the agent detect the starvation that menaces him? Section F.1 of the Online Appendix gives a simple fix, in which the attention at time 1 becomes:
for some |$K>1$|. In the second term of the max, the agent takes into account the extra income x. One could imagine other variants as well, which are discussed in Section F of the Online Appendix.
7.2. Frequently Asked Questions
How do markets clear? They clear as usual: prices adjust so that supply equals demand.58 We need at least one agent, in each market, to pay some attention to the price. For instance, in the Cass–Koopmans model of Section 5, firms pay attention to the interest rate (in their loan demand), even though consumers might potentially not pay attention to the interest rate (in their loan supply). So, |$r_{t}=f^{\prime }(K_{t})$| survives, but the Euler equation doesn’t.
Does the model only generate underreaction? The model most directly gives underreaction, but can indirectly generate overreaction.59 Suppose that an analyst sees a company C with a surge in profits. She’ll increase her estimate of its value. However, suppose that she forgets that the competitors of company C will try to imitate it, this way eroding C’s future profit (see Greenwood and Hanson 2015). The analyst overreacts to the surge in profits because she neglected the competition’s response. More generally neglecting mitigating factors (i.e. negatively correlated additional effects) leads to overreaction. Likewise, a consumer overreacts to an income shock if she underpays attention to the fact than that shock is very transitory.
What about other types of dynamic problems, with discrete actions?
To have a viable path to bounded rationality, or artificial intelligence, we need environments with enough structure.60 Here, I rely a particular structure: “smooth” environments, where actions and variables are continuous, functions are smooth, and the world lives close to a well-understood steady state. This means that this theory—in its present form—does not have much to say about discrete environments with essentially no structure, like the traveling-salesman problem.61 Fortunately, worlds with smooth structure are very relevant in economics, especially macro-finance, and the present framework allows us to make progress on those.
What happens with developed financial markets? For instance, in the life-cycle problem of Section 2, what would happen if the x was securitized (so that not just bonds, but also claims on x can be traded)? Here are some short remarks—I plan to offer a serious treatment of sparse finance in a future paper. First, all basic arbitrages are excluded: as x is deterministic, if x is not priced at its fair value, there’s an infinite payoff from trading it: so, agent will pay attention to that arbitrage, and x will be traded at its fair value, x. Second, even though the agent as an investor may fully take x into account, as a consumer he might not fully take it into account.62
Can’t one explain anything with bounded rationality? Let us observe that traditional economics models, when free, can “explain almost anything”. For instance, the Arrow–Debreu model has a great many degrees of freedom. However, there are two disciplines (besides intuition, a soft form of empirical knowledge): hard empirical constraints on the parameters (e.g. on the production functions) and constraints on the number of free parameters that can be tuned around an agreed-upon baseline model.
I adopt the same attitude here. Take the life-cycle model of Figure 1. There is one free parameter (|$\bar{\kappa }$|) to fit a whole lifetime: the model is parsimonious. Next, the model is tightly constrained in its prediction: it can only give shapes similar to the ones in the Figure 1: first consumption is flat, then declines before retirement, drops at retirement, and is flat thereafter.
This said, there are many extensions that one can think about to enrich the sparse agent (e.g. varying defaults, persistence in attention, heterogeneity in rationality etc.). It means that it’s a framework with intriguing features worth exploring. However, to keep the parsimony, I think it is useful to coalesce around a very simple default structure. Here, I reported a minimalist one with I found useful across a range of problems.
Isn’t there much arbitrariness in terms of the “default”, and what can non-attended to? The Bayesian counterpart of the “default” is the “prior.”63 There is no good theory of the “prior,” but researchers still move on with “reasonable” priors. Likewise, in information economics researchers posit what is known to the agent and what information requires a mental cost.
The situation with sparsity and its default is very similar. I use “reasonable” default and try to make “reasonable” assumptions about what is perfectly perceived (e.g. time t) and is not (income after retirement).
An open question for much of economics is a way to systematize such “intuitively reasonable” choices. In the meantime, despite the fact that the model needs inputs, the model produces a good amount of value added, for example, in Figure 1.
As there is one way to be rational, and many ways to be boundedly in rational theory, how do we know how to proceed? It is true that there are many ways to deviate from pure rationality, but some are much more important than others (perhaps they are on a power law, like so many things). Here, I focus of one feature: people use a simplify their picture of the world. There are others (e.g. loss aversion, hyperbolic discounting) and together they constitute a useful account of major deviations from pure rationality.
This agent is quite sophisticated —almost Bayesian. How do we account for big mistakes then? We can try to account for big mistakes and miscalibrations in at least two ways. First, agents don’t have good priors (“hyperparameters” in hierarchical Bayes models) on which information is useful. For instance, they (ex post faultily) don’t think that thinking about future retirement will help them much, that “it’s just too hard”.64 Second, they could have a high cost of cognition in some domains: in the “proportional thinking” specification of Section A.2.2 in online appendix, agent eliminate considerations that matter for less than 5% of the decision (|$\bar{\kappa }=5\%$| then). A medium-run research goal is to measure more systematically attention and costs of cognition, informed by models such as the present one.65
Furthermore, sparse agents display only intermediate sophistication. This paper differs from models that demand Bayesian updating, with optimal use of information (and agents pay optimal costs to acquire it, for example, as in Van Nieuwerburgh and Veldkamp 2010). Behavioral agents like my sparse agents do not do Bayesian updating.66 For instance, if they see their income go up, Bayesian agents should infer “probably, the interest rate is high” (as income and interest rates tend to have positive correlation), but sparse agents don’t do that inference.
Are those agents easier or more complex to use than rational agents? Historically, behaviorally agents have often been more difficult to use (for the economist deriving their actions) than rational agents. However, sparse agents are often easier to use. For instance, they don’t need to solve the full equilibrium in their head—they use a sensible consumption rule (e.g. (53)), which may not be exactly optimum in their context, but does guide them through life. Also, they may use a reduced number of variables (e.g. their decision depends on two variables rather than 20). Hence, they are easier to use.
8. Literature Review
This paper builds on two strands of the literature: on a relatively recent strand of basic behavioral modeling and on an older set of ideas tailored to specific macroeconomic contexts.
One key difference here is that the model is quite systematic. It applies, in a unified manner, to a wide class of models. This generality is possible because I build on earlier work (Gabaix 2014) that developed a quite systematic way to think about boundedly rational optimization in static contexts. There, I proposed a “sparse max”, a behavioral, less than fully rational and attentive version of the traditional max operator. That paper was concerned with static cases, while here I explore dynamic ones. That paper allows to give a behavioral formulation of some basic chapters of the microeconomic textbooks (consumer theory, equilibrium theory, Arrow–Debreu). The present paper gives a behavioral version of basic chapters of the macroeconomics textbook. A companion piece, Gabaix (2020), uses ideas in this paper to propose a behavioral version of the New Keynesian model. A related paper, Farhi and Gabaix (2020), proposes a behavioral version of textbook taxation theory. Hence, we have a more unified view of bounded rationality in micro and macro. In Gabaix (2019), which is a survey/manifesto, I try to convey how this and related approach to behavioral inattention unify tractably many behavioral biases, and mesh well with normal economics.
The “micro” sparse max relies on a strand of paper thinking about basic behavioral modeling, in particular inattention, salience. See, for instance, Bordalo, Gennaioli, and Shleifer (BGS) (2018), Chetty, Looney, and Kroft (2009), Gabaix and Laibson (2006), Khaw, Li, and Woodford (2021), Kőszegi and Szeidl (2013), Lian (2021), and Schwartzstein (2014).
Since this paper circulated (in the Spring 2012), a number of “behavioral macro” papers have been written. One particularly fruitful theme has been the application to monetary policy, including the “forward guidance puzzle” (McKay, Nakamura, and Steinsson 2016, Del Negro, Giannoni, and Patterson 2023). In Gabaix (2020), I proposed a tractable approach, building on the present paper: the inattention is there on the dynamics of the state vector, that is, shrinking the |$\rho _{r}$| and |$\rho _{y}$| in (16)-16), and all similar variables, by a “cognitive discounting” multiplicative factor |$\bar{m}$| (so that |$\rho _{r}^{s}=\bar{m}\rho _{r}$|). This makes agents dampened a bit the immediate future, and a lot the distant future. This proves useful to offer a unified treatment of agent’s myopia for monetary and fiscal policy, as well as optimal reaction by the government. Other approaches are incomplete information Angeletos and Lian (2018), and level-k thinking (Farhi and Werning 2019), limited planning horizons (Woodford 2019), and credit constraints (Bilbiie 2021). While those approaches differ in a variety of small ways, Meggiorini (2023) notes that the sparsity approach is indeed particularly tractable, which allows her, using it (especially in the “cognitive discounting” version) to develop a behavioral enrichment of the Smets and Wouters (2007) model, which widely used for policy analysis. This brings us closer to behavioral macro for usable for policy analysis.
The “macro” dimension of the sparse max relates to papers which offer a variety of devices to model some form of bounded rationality and are tailored to macro contexts (see Veldkamp 2011 and Woodford 2013). To examine the pros and cons of models, I use the following criteria in Table 1:
Do the models also apply to bounded rationality in static contexts? If the goal (which is mine, at least) is to have a quite unified way of talking about bounded rationality in both static (e.g. doing static consumer theory with n goods) and dynamic contexts, this is a desirable property.
Can the model keep a representative agent? This is very desirable, as most clean theory keeps the representative agent (or at most a small number of types of agents).
Do we keep deterministic actions, or do actions have to be random?
Do we have source-dependent inattention?
Is the model Bayesian? Most economists would think it’s a good feature. As the goal is to explore bounded rationality, I submit that it is worthwhile to entertain non-Bayesian models.
Can the model handle a tractable behavioral version of a general textbook static problems, like |$\max _{c_{1},...,c_{n}}u(c_{1},...,c_{n})$| s.t. |$\sum _{i}p_{i}c_{i}=w$|? A tractable dynamic model handling general problems such as (23) should a fortiori be able to work in static context. Only the sparse max is—so far—able to do that. Other approaches might do that, but now they appear too complicated to do so.
| . | BR in . | Rep. . | . | Source . | . | . |
|---|---|---|---|---|---|---|
| . | static . | agent . | Determ. . | dependent . | . | Textbook . |
| . | contexts . | allowed . | actions . | attention . | Bayesian . | micro . |
| Rule-of-thumb | |$\checkmark$| | |$\checkmark$| | ||||
| Hyperbolics | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | |||
| Credit constraints | |$\checkmark$| | |$\checkmark$| | ||||
| Imperfectly updated info. | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | |||
| Noisy info. | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | |||
| Entropy penalty | |$\checkmark$| | |$\checkmark$| | ||||
| BGS/salience | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | ||
| Sparsity | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| |
| . | BR in . | Rep. . | . | Source . | . | . |
|---|---|---|---|---|---|---|
| . | static . | agent . | Determ. . | dependent . | . | Textbook . |
| . | contexts . | allowed . | actions . | attention . | Bayesian . | micro . |
| Rule-of-thumb | |$\checkmark$| | |$\checkmark$| | ||||
| Hyperbolics | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | |||
| Credit constraints | |$\checkmark$| | |$\checkmark$| | ||||
| Imperfectly updated info. | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | |||
| Noisy info. | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | |||
| Entropy penalty | |$\checkmark$| | |$\checkmark$| | ||||
| BGS/salience | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | ||
| Sparsity | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| |
| . | BR in . | Rep. . | . | Source . | . | . |
|---|---|---|---|---|---|---|
| . | static . | agent . | Determ. . | dependent . | . | Textbook . |
| . | contexts . | allowed . | actions . | attention . | Bayesian . | micro . |
| Rule-of-thumb | |$\checkmark$| | |$\checkmark$| | ||||
| Hyperbolics | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | |||
| Credit constraints | |$\checkmark$| | |$\checkmark$| | ||||
| Imperfectly updated info. | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | |||
| Noisy info. | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | |||
| Entropy penalty | |$\checkmark$| | |$\checkmark$| | ||||
| BGS/salience | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | ||
| Sparsity | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| |
| . | BR in . | Rep. . | . | Source . | . | . |
|---|---|---|---|---|---|---|
| . | static . | agent . | Determ. . | dependent . | . | Textbook . |
| . | contexts . | allowed . | actions . | attention . | Bayesian . | micro . |
| Rule-of-thumb | |$\checkmark$| | |$\checkmark$| | ||||
| Hyperbolics | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | |||
| Credit constraints | |$\checkmark$| | |$\checkmark$| | ||||
| Imperfectly updated info. | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | |||
| Noisy info. | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | |||
| Entropy penalty | |$\checkmark$| | |$\checkmark$| | ||||
| BGS/salience | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | ||
| Sparsity | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| | |$\checkmark$| |
Rule-of-thumb consumers. Campbell and Mankiw (1989) assume that a fraction |$\lambda$| are “rule-of-thumb” consumers who just consume their current income, |$c_{t}=\bar{y}+\hat{y}_{t}$|. Those agents could be interpreted as “super-sparse,” and pay attention to no other variables, while perceiving income shocks as being fully persistent.67 In a sense, this research vastly generalizes the Campbell and Mankiw (1989), which have proved a useful benchmark. Hence, aggregate consumption is
and we do obtain the higher MPC for current income than for discounted future income.
Hyperbolic consumers. Laibson (1997) models hyperbolic consumers (fully rational or fully naive), and O’Donoghue and Rabin (2001) model partially naive consumers. There are some key differences. One is that a hyperbolic consumer is still a wealth-maximizer, so his consumption function depends only on the present value of future income, without a higher marginal propensity to consume out of current rather than future income Barro (1999)—unless they are credit constrained (then hyperbolicity amplifies the effect of credit constraints). Another is that sparse agents have source-dependent myopia, unlike (the most common) hyperbolic consumers.
Credit constrained consumers. Those consumers are rational, but credit constrained now or in the near future. As a result, their MPC out of current income is higher than out of future income (e.g. Kaplan, Moll, and Violante 2018). A big difference with sparse agents is that again sparse agents have source-dependent myopia. Hsieh (2003) provides evidence for source-dependent myopia: his consumers consume “regularly arriving” government transfers (from the Alaskan oil fund) rationally (see however Kueng 2018), but react in a myopic way (high MPC) to other transitory income shocks.
Imperfectly updated information. Agents update their information set every now and then, for example, when hitting a threshold, at fixed or random time intervals (Caballero 1995; Gabaix and Laibson 2002;Mankiw and Reis 2002; Reis 2006; Abel, Eberly, and Panageas 2013) or in other imperfect ways (Sargent et al. 1993; Fuster, Hebert, and Laibson 2012; Schwartzstein 2014; Bushong, Rabin, and Schwartzstein 2021). This captures a real phenomenon, but does not apply to the most basic setup, for example, static ones. Those models are also very complex in rich environments, though some pockets of tractability are being elaborated (Angeletos and Huo 2021).
Other behavioral models of salience. Bordalo, Gennaioli, and Shleifer (2013, 2018) are pursuing an influential research program modeling the impact of “salience” in a vast number of settings (see also Kőszegi and Szeidl 2013). In a rough sense, their salience transforms initial variables |$x_{i}$| into salience-adjusted variables |$m_{i}x_{i}$|, with a salience function different determining the |$m_{i}$| (which can be greater than 1) in a way different from the sparsity setup, but related to it (also, sparsity concentrates on continuous actions, BGS on discrete choices). Modulo this change, and the current proposal should apply to BGS’ setup, making it dynamic.
Entropy penalty. In the Sims (2003) approach to inattention, the penalty is an entropy penalty, which results in parsimonious (but very complex to solve, see Jung et al. 2019) models, which do not allow for source-dependent inattention. Other papers (Maćkowiak and Wiederholt 2015; Woodford 2020) deviate from this doctrine by accepting source-dependent inattention. Even though there are many differences of details, there is a common spirit. In noisy-signal theory actions are stochastic: the same problems lead to stochastic actions by agents. As a result, we lose the representative agent in the noisy-signals models. It can be recovered by taking linear approximations. In contrast, in sparsity theory actions are deterministic, which is one factor making this model easier to analyze. In addition, and relatedly, the sparsity model applies well to basic micro (Gabaix 2014), which is so far too difficult for noisy-signal models.
Near rational approach. The “near rational” approach says that agents will lose at most |$\varepsilon$| utils: it is often useful (Akerlof and Yellen 1985; Chetty 2012; Kueng 2018), but it does not offer a precise model of which actions people will take. The statistics used by the sparsity model are those of the near rational approach (utility losses as in (10)), but sparsity makes a definite prediction about agents’ actions.
The Hansen and Sargent (2008) robustness framework generates distorted subjective beliefs; they exhibit a sophisticated form of risk aversion and pessimism, but not myopia and simplification per se.
9. Conclusion
I presented a practical way to do boundedly rational dynamic programming. It is portable and tractable and sheds light on a number of puzzles reviewed in the introduction. Given that it is easy to use and sensible, this model is likely useful to study other issues in macroeconomics and finance. One limitation of the proposed approach is its reliance on linearization and small deviations from the steady state. Overcoming this limitation would be a fruitful research challenge.
Acknowledgments
This paper was a background paper for my Marshall Lecture at the EEA meetings in August 2023. First draft: March 2012. I thank David Laibson for a great many enlightening conversations about behavioral economics. For useful comments I also thank Adrien Auclert, Robert Barro, John Campbell, John Cochrane, Emmanuel Farhi, Drew Fudenberg, Peter Ganong, Mark Gertler, David Hirshleifer, Bentley MacLeod, Matteo Maggiori, Jonathan Parker, Nicola Pavoni, Zhaonan Qu, Michael Rockinger, Thomas Sargent, Josh Schwarzstein, Andrei Shleifer, Joel Sobel, Bruno Strulovici, Richard Thaler, Jessica Wachter, Michael Woodford, seminar participants at various seminars and conferences, and my discussants: Andrew Abel, Nick Barberis, Thomas Chaney, Harrison Hong, Jennifer La’O, Ali Lazrak, Ricardo Reis, Alp Simsek, Alexis Toda. I thank Wu Di, Lilian Hartmann, Chenxi Wang, and Jerome Williams for very good research assistance. I am grateful to the Dauphine-CAM foundation, the Ferrante Fund at Harvard, the Institute for New Economic Thinking, the NSF (SES-1325181), and the Sloan Foundation for financial support.
Notes
The editor in charge of this paper was Nicola Pavoni.
Footnotes
In the language of Kahneman (2011) (chapter 8), the agent “substitutes” a complex problem by a simpler one—decision-making in a simplified world.
The rest of the paper will give references about those stylized facts.
In Gabaix (2020), I also find that monetary policy, especially forward guidance, is less powerful. I do so in writing a behavioral version of the New Keynesian model, applying the techniques of the present paper.
The canonical New Keynesian agent is basically the neoclassical agent, in a world of sticky prices. He’s fully rational.
It is a bit unusual to start a framework with an example, but this example will useful to illustrate modeling choices.
Here, I use the basic sparse max of Definition 2, where the agent uses a simplified model of his own future actions. If the agent has a “sophisticated” understanding of this future actions (as in the iterated procedure developed in Definition 4, the decision would be the same to the first order, that is, up to |$O(x^{2})$| terms (see Section 3.5).
Proof: the first order condition (FOC) of (4) is: |$u^{\prime }(c_{t})=V_{w}^{r}=u^{\prime }(\frac{w_{t}+\bar{y}-c_{t}-m_{t}x}{T-t-1}+\bar{y})$|, that is, |$c_{t}=\frac{w_{t}+\bar{y}-c_{t}-m_{t}x}{T-t-1}+\bar{y}$|, that is, |$c_{t}=\frac{w_{t}-m_{t}x}{T-t}+\bar{y}$|.
As we will see below, the numerator inside (6) represents the utility gains from optimizing (up to a factor of two), which are related to the curvature of the value function, |$v_{cc}^{t}$|, and how much the agent’s consumption changes when she is more attentive, |$c_{t}^{\prime }(0)$|.
With this scaling for |$\kappa _{t}$|, the expression for consumption is independent of the concave utility function u.
In addition, Bernheim, Skinner, and Weinberg (2001) (Figure 4) find that the drop is more pronounced for individuals with low wealth. This is what the present model predicts: controlling for lifetime incomes, agents with higher BR (higher |$\kappa$|) accumulate fewer assets and have a bigger drop in consumption at retirement. See also Kueng (2018).
More indirectly, a whole literature on retirement plans supports the notion of inert decision-making for retirement. For instance, Beshears et al. (2015) find that the potency of framing and defaults is reduced as people approach retirement, consistent with the notion they think more carefully about retirement as they are near it.
Note that a simple hyperbolic agent (Laibson 1997, O’Donoghue and Rabin 2001) would not behave this way. That agent has full foresight of future income flows, and sees equally perfectly pre- and post-retirement income. For instance, the policy of the log agent is |$c_{t}=\frac{w_{t}+x+(T-t-1)\bar{y}}{1+\beta (T-t-1)}$|. However, with uncertainty and credit constraints, the hyperbolic agent can look closer to the one with the above behavior (Harris and Laibson 2001), though with much complexity and not because of limited foresight about future income.
This utility may be a value function, as in (3).
This is true unless the matrix |$\Lambda$| of Definition 1 is singular—in that case, the iterated sparse max of Definition F.1 helps.
In Gabaix (2014), I sum over all terms |$\sum _{i,j}(1-m_{i})\Lambda _{ij}(1-m_{j})$|, with |$\Lambda _{ij} := -\mathbb {E}[a_{m_{i}}u_{aa}a_{m_{j}}]$|. Here, I streamline the procedure, and let the agent consider only the diagonal terms. This is inessential, but is simpler.
Also, if there are more than one optimum m’s, we take the largest one.
Another useful cost function is |$g_{L_{1}}(m)=-\ln (1-m)$|, which generates |$\mathcal {A}_{L_{1}}(\sigma ^{2})=\max (1-\frac{1}{|\sigma |},0)$|, and |$\tau _{L_{1}}(b,k)=\textit {sign}(b)\max (|b|-|k|,0)$|. The subscript |$L_{1}$| denotes that it often arises when doing an |$L_{1}$| regularization, as in the sparsity literature in statistics (Tibshirani 1996, Candes and Tao 2006).
This is related to the “perceived law of motion” of the literature on learning (Evans and Honkapohja 2001; Evans and Honkapohja 2013). There are important differences: the concept of a simplified model also holds in static contexts, without learning; the procedure is not about learning, but rather about the simplification of a known (but complex) already-learned model; and in dynamic programming the sparse agent needs to have a model of his own future actions.
Section C.3 of the Online Appendix develops this. See Lusardi et al. (2011) for evidence of an insufficient buffer stock of saving. If agents underperceive the risks to income, that motivates policy of extra assistance, for example, extra unemployment benefits.
With infinite horizon, the transversality condition is typically |$\lim \sup _{T \rightarrow \infty }Z_{T}\in \mathcal {F}^{T}$|.
One can take |$u(a,z;m)=u(a,m\odot z,t)$| and for the kth component of vector |$F^{z}$|
It could also be some approximation of the objective value function—much like in chess, people and computers use something akin to proxy value functions, that encode distant behavior. See Gabaix et al. (2006) for an algorithm using an early version of this idea of proxy value function.
If there are domain conditions for |$a(Z,V^{p})$|, we just add them to the definition of |$a(Z,V^{p})$|, as in the static smax with budget constraints Gabaix (2014).
The simplest would be to assume a finite number of potential values for the noise z, for instance.
It is tempting to define |$V=\mathcal {T}\,(V,V)$|, but the operator |$V\mapsto \mathcal {T}\,(V,V)$| does not (prima facie at least) satisfy the good properties of Lemma 3. Only |$V\mapsto \mathcal {T}\,(V,V^{p})$| does.
I contemplated taking (31) as a starting point for dynamic programming, but it proved psychologically too complicated, and mathematically hard to handle, due to the unusual fixed point in V.
See Harris and Laibson (2001, 2013) for a related analysis showing the ty of the mathematics of infinite horizon dynamic programming when the agents misoptimize. Fortunately, those difficulties dissolve with a finite horizon. Still, extending the analysis here to an infinite horizon seems like an interesting, difficult problem. Zhaonan Qu and I have results along those lines, but they is quite involved, and too technical for the present paper.
The intuition is that as x is small, and the action is close to the optimum, we get only second order losses |$O(\Vert x\Vert ^{2})$| from misoptimization.
Here, |$V^{o}(w,x|a(\cdot ))$| is the policy induced by a, closely along the lines of Lemma 4.
Hyperbolic discounting naive and sophisticated agents often act quite differently (Laibson 1997, O’Donoghue and Rabin 2001). However, in simple consumption-savings problems, the discrepancy between the two types’ consumption is still |$O((1-\beta )^{2})$|, where |$\beta$| is the hyperbolicity parameter, so quite modest if |$\beta$| is close to 1.
Section A.3 in Online Appendix gives more complements for the T period model.
I use the notation |$\sigma _{x}^{2}=\mathbb {E}[x^{2}]$| to indicate the prospective magnitude of x; with ex post attention, we simplify have |$\sigma _{x}^{2}=x^{2}.$|
In terms of the iterated sparse max of Definition 4, this is the value function under procedure with |$q=0$| iteration, t. If we used the procedure with |$q=1-$|iteration, the agent uses the objective value function, which is:
If x was very large and positive, we could have the following effect: the agent realizes at time 1 that he’s actually quite wealthy, so pays less attention. This effect needs a very large x, so is not operative in most situations.
In Gabaix (2014) (Proposition 8) the first welfare theorem (in a static economy) does hold if agents have the same misperceptions: the reason is that in that setup, the agent is assumed to fully perceive consumptions (a defensible assumption in a static context)—whereas in the present model he doesn’t. For instance, at time 1 the fully naive agent projects that |$c_{1}=c_{2}={w_{1}}/{2}$|, whereas in fact |$c_{2}={w_{1}}/{2}+x$|.
If |$\rho _{r},\sigma _{r},\rho _{y},\sigma _{y}$| are correctly perceived, then we can just take |$z_{t}=(w_{t},\hat{r}_{t},\hat{y}_{t})$|.
In independent work, Auclert (2019) contains a similar Taylor expansion for the rational case, with more general assets.
The term |$\mu _{t}$| is the MPC, and contains substitutions and income effects from wealth before receiving the innovation in income, |$w_{t}-\bar{y}$|. The term |$\nu _{t}$| contains the baseline income |$\bar{y}$|, expected value of future income |$\hat{y}_{\tau }$|, and and substitution effects interest rates associated with the income stream of |$\bar{y}$| per period. There is no income effect for |$\bar{y}$|, as no interest rate was going to accrue to |$\bar{y}$|.
Call |$v(c)=u(c)+V^r((1+\bar{r}+\hat{r}_t)(w_t-c)+\bar{y}+\hat{y}_t)$|. I use the well-known fact that in the limit of small-time intervals |$v_{cc}=u_{cc}$|. See Section D.1 in online appendix.
Note here that the active decision is that of consumption, not savings. For most variables (except current income), it does not matter: the impact of interest rates, future taxes, future income shocks, etc. are the same whether a sparse agent uses the consumption frame or saving frame. See Section C.7 in Online Appendix for a discussion: the consumption frame is arguably better, as it yields great utility when |$\phi _{y}>r$|, income shocks are less than extremely persistent.
Likewise, in the model, a wealthy rentier, with much financial wealth but little labor or state income, will endogenously pay more attention to the interest rate, as it is more important for her consumption (and will bemoan at low interest rates, which lead her to cut on consumption).
This numerical example is a rough AR(1) rendition of the “permanent-transitory models” in the literature.
For simplicity, I remove here the “growth” part, but it is straightforward to add.
I keep the noise |$\varepsilon _{t+1}$| because it makes the model a true DSGE model, and because it yields a scale for typical business-cycle fluctuations that it useful to determine attention.
The traditional proof is by taking the derivative w.r.t. K in (61), so |$V^{\prime }(K_{\ast })=\beta (1+F^{\prime }(K_{\ast }))V^{\prime }(K_{\ast })$|.
Here, wealth is taken at the beginning of the period, before receiving labor income.
It is easy to generalize to the case where people’s attention to income and the interest rate differ.
With the iterated sparse max of Definition F.1 of the Online Appendix, we can have |$m_{\phi }>0$|.
The present paper offers a systematic way in which agents simplify the moments they use to think about general equilibrium. This could be useful to systematize procedures such as the one in Krusell and Smith (1998). See also Barberis, Shleifer, and Vishny (1998) and Hong, Stein, and Yu (2007) for an early analyses of financial equilibrium when agents use a simplified model.
That is, |$V^{p}(k,K|F(\cdot ,m),G(\cdot ,m))=V^{r}(k,K|F(\cdot ,m),G(\cdot ,m))+O(|K-\bar{K}|^{2})$|.
Here, |$m_{K^{2}}$| is the attention to non-linear terms. If |$m_{K^{2}}=0$|, the agent simply linearizes the impact of the state variable on the interest rate. When using the plain sparse max (as opposed to the iterated sparse max of Definition F.1 of Online Appendix), the algorithm will select |$m_{K^{2}}=0$|, that is, remove the nonlinear terms.
Section C.1 of the Online Appendix studies a more general Merton’s problem with many assets and factors.
To do that, formally, I use the variant of sparse max specified in Gabaix (2014) (Section XV.D of the Online Appendix), which specifies a different attention for each type of action (formally, for each coordinate of the action vector).
This analysis is in the spirit of Gruber and Kőszegi (2001), who study a hyperbolic discounting addict, rather than a boundedly rational one in the sense of this paper.
First, the basic smax agent does not change his action at all. What changes is on the the |$q-$|iterated agent with |$q\ge 1$|. Second, in accordance with Section 3.5, this change makes only a second order change in the action.
Why not model iterated expectations, such as the agent’s perception at time 0 of his perception at time 2 of his perception at time 5? The short answer is that this leads to a combinatorial explosion of the complexity of the model. See Section F.7.1 in Online Appendix.
See Gabaix (2014) (Section IV) for a systematic analysis in static contexts.
There is no known good general-purpose algorithm for worlds with no structure and high dimensionality. There may not be any, if |$P\ne NP$|. Also, one will never be able to calculate the cognitive cost of the “rational limit” while problem |$P\ne ^{?}NP$| is open; most experts think it is likely to remain open for decades.
One could imagine that some variant could be helpful, for example, by smoothing or doing a convex relation of discrete problems.
See Proposition 12 and its discussion.
The default is a deterministic point estimate (which is useful to model bounded rationality), the prior is a probabilistic distribution.
Farhi and Gabaix (2020), (Section 6.1) discusses models with suboptimal allocation of attention.
It would be interesting to formalize systematically a form of “lazy pseudo-Bayesian updating”, but I differ that to future research.
Actually, the “fully” persistent part is not necessary. It is enough that the agent’s consumption is an affine function of their current income (and perhaps wealth), to the exemption of forward-looking variables.



