Self-Esteem, Moral Capital, and Wrongdoing Free

Abstract

1. Introduction

Norms defining socially acceptable behavior play a large role in socioeconomic outcomes by discouraging opportunistic behavior. But what determines adherence to received social norms such as moral rules? If norms are inculcated as a stable part of tastes, Beckerian models of crime will predict an individual’s adherence to norms to depend steadily on variations in the extrinsic payoffs to opportunism. However, the propensity for opportunistic behavior may change with a personal history of misbehavior due to changes in intrinsic motivation. If personal history matters to individual incentives for observing norms, then variation in “cultures of corruption” across countries or organizations may reflect adverse shocks to past behavior, rather than just deep moral fundamentals.¹ For example, an individual who becomes corrupt during an economic crisis may persist in corrupt tendencies even after the economy has recovered. Conversely, someone who has behaved well may have more of a stake in maintaining good conduct.

We propose a theory focused on the dynamics of virtue and corruption and study the possibility of persistent patterns of self-reinforcing behavior. The theory also helps understand how the power of extrinsic incentives (e.g., law enforcement) depends on timing, and how small differences in the environment may lead to large differences in behavior. In our model an individual lives for ever and faces in each period a stochastic “temptation”, which we think of as an opportunity to increase consumption utility by dishonest means. For concreteness, think of a policeman who in each period faces a bribe offer of random size. The officer receives utility from consumption goods bought with bribe money, but he also values the possibility of maintaining the notion of having “a good heart”—that is, that he is the kind of a person whose nature steers him towards honesty. Another example fitting the model is the Weberian account of the Calvinist Ethic. In that account, a person who does not know his predestination status (saved or doomed) may enjoy being profligate but would also like to maintain or even increase his confidence of having been born saved.

We use a planner–doer model à la Shefrin and Thaler (1981) with a few modifications. The planner is the only deliberate decision maker, and believes the doer to have one of two types, “good” or “bad”, each with a hardwired tendency for either a “good” or a “bad” action (e.g., reject or accept the bribe, respectively). The type of the doer is unknown to the planner, but the planner cares directly about it—a form of self-esteem tied to received values or norms. The planner must then decide in each period whether to attempt to steer the doer towards the good action or to give up and let the doer alone drive behavior; the planner makes this decision knowing that he will rationally update his beliefs about the doer’s type upon observing behavior. As done in earlier work (Bénabou and Pycia 2002; Fudenberg and Levine 2006) we conceptualize the planner as the conscious element in the mind, usually linked to the notion of “executive function” and the top-down coordinating role of the prefrontal cortex (PFC). The doer captures subcortical parts of the brain that exert subconscious influences on behavior.

There are several precedents in the literature of linking the emergence of self-discipline to self-image management. Economic theory has incorporated the idea that people care about self-image (e.g., Rabin 2000; Brekke, Kverndokk, and Nyborg 2000; Kőszegi 2006; Bénabou and Tirole 2006, 2011; Cervellati, Esteban, and Kranich 2006), and there is experimental evidence that self-concept maintenance limits dishonesty (Fischbacher and Heusi 2008). Economics has also incorporated the notion that behavior is influenced by subconscious impulses (e.g., Bénabou and Pycia 2002, Prelec and Bodner 2003, and Berhneim and Rangel 2004), and that past actions may contain information about the self, creating a role for introspective reputation (Prelec and Bodner 2003; Bénabou and Tirole 2002, 2004, 2011).

Two factors enable past actions to contain information about the doer’s type in our model. First, the planner’s control over the doer is imperfect, meaning that the planner’s attempt to steer the doer towards a “good” action may not succeed. This is consistent with work in neuroscience showing that the PFC carries out its tasks by “biasing signals” that enhance some impulses and inhibit others (Miller and Cohen 2001). This function is not perfect nor acts unopposed; other areas also affect the signals available to circuits that implement actions.² Second, the planner has imperfect information regarding the “authorship” of actions: if the action taken by the doer matches the planner’s override, the planner cannot be sure whether this was due to the override or to the doer’s own drive. The inability of an individual to assign authorship over his externally observable action is consistent with work in psychology and neuroscience. It may appear obvious that we do things “because we want to”. However, determining the causal role of conscious deliberation and cognitive override in the actions we take is a formidable inference process for the planner (Wegner and Wheatley 1999). After reviewing the various ways in which the mind may frame its control over actions (and be variably successful), Vallacher and Wegner (1987) conclude that exact attribution of “this simple input for self-conception—action—is inherently uncertain”.³

Given these ingredients, our first step is to study conditions for the self-esteem motive to induce adherence to a received moral norm for a single decision-maker with time-consistent preferences in a stationary, infinite horizon environment. In our model an override by the planner lowers the variance over future self-image. Thus, a planner with concave self-esteem payoffs will want to override the doer if temptations are low enough. This emergence of self-restraint mirrors results in Kőszegi (2006) (see also Bénabou and Tirole 2002). But it is not obvious how virtue is to respond to the presence of a future comprising an ongoing learning and decision-making process. We show that the presence of a future increases incentives to resist temptations. We then move on to ask whether good behavior will build its own demise, or whether good acts, by improving self-image, will lead to ever stronger incentives to do good. Such a persistently self-reinforcing path would lend support to the Weberian account of the Calvinist ethic as an explanation for sustained good behavior.

The key contribution in our paper is to show that, under certain assumptions, a stationary environment must result in a (literally) virtuous circle: good actions improve the self-image, and this in turn further strengthens incentives to resist temptations.⁴ This resembles Aristotle’s description of virtue as a process of habituation through action. As the beliefs about the self enter the problem as a state variable that is costly to improve (it requires forgoing temptations), they act as a form of capital, which we term “moral capital”. We explore the limits of our virtuous circle result. We show that moral capital has nonmonotonic effects on behavior when the environment is not stationary due to a finite horizon, or when doers can tremble and as a result changes in moral capital affect the informational content of actions.

A key mechanism in our model is that the incentive to adhere to a social norm stems from a desire to diminish the arrival of information. An individual cannot change his beliefs in expectation, but an attempt to override the doer diminishes the variance of future self-image.⁵ The concept of self-esteem utility closest to ours is found in the task choice model of Kőszegi (2006), where individuals derive utility from the self-image of being a highly productive type and where individuals may be risk averse with respect to that self-image.

We offer three applications. One shows how the distribution of moral capital has an impact on aggregate outcomes. In particular, in a society in demographic steady state, shocks in the distant past have long-lasting effects on wrongdoing by affecting the polarization of individual beliefs. In another extension we show that the presence of moral capital affects optimal deterrence schemes through channels absent from traditional models of crime, à la Becker (1968), where “moral costs” are a constant taste parameter. Since individuals with lost self-esteem no longer have an intrinsic motive to self-deter, a myopic social planner will select harsher punishments for repeat offenders. In another extension we study how individuals with different levels of self-image sort themselves into activities with different levels of temptation. We show that high temptation activities (e.g., politics) display more prevalent wrongdoing than low temptation activities (e.g., academia) not only due to the higher temptations but also because they attract those least equipped to resist temptations.

We take both self-esteem and temptations to be genuine sources of utility, unlike the subconscious elements that may alter externally observed actions. This mirrors the approach in Bernheim and Rangel (2004), as does our view that subconscious factors affect actions in ways that are independent of consciously perceived utility.⁶ Observable actions may constitute a mistake from the perspective of the planner, placing limits on a revealed preference approach. One implication is that nonchoice data (from the neuroscientific to happiness reports) may be relevant to the study of adherence to moral norms. In an Online Appendix we offer foundations for our model through a more general framework of (imperfect) conscious control over actions that is related to Bernheim and Rangel’s (2004) set up.

2. The Model

2.1. Basic Setup

An individual lives in an infinite horizon world with discrete time, and discounts the future by a factor |$\lambda \in (0,1)$|⁠. The conscious aspect of the individual is referred to as the “planner”, and the subconscious part as the “doer”. The planner is the only decision maker in the model, and the one whose welfare we equate with that of the individual. The doer is the default driver of externally observable actions by the individual, but the planner has the (imperfect) ability to override the doer. The planner’s override decision entails choosing a value for the control |${a_t} \in [0,1]$|⁠; we will be interested in whether |${a_t}$| takes the value of 0, in which case we will say the planner “gives up”, or 1, in which case we will say the planner attempts to override the doer. It is technically convenient to allow for mixing and let |${a_t}$| take any value in the unit interval. The doer is characterized by a type |$\theta \in \{ {\theta _g},{\theta _b}\} $|⁠, good or bad, and we will refer to the type of the doer as that of the individual, in the understanding that the type characterizes the doer only. The individual is born with an initial belief that her type is good with probability |${\mu _0}$|⁠.

In each period t the individual faces a nonnegative temptation |${x_t}$|⁠, drawn independently from a distribution with cumulative density F in the nonnegative real numbers. We assume that F is continuous and strictly increasing with |$Ex \lt \infty $|⁠. For example, think of a bureaucrat facing an opportunity for taking a bribe each period. The temptation is the additional consumption utility obtained by consuming the bribe. Given the lack of restrictions on the shape of F, we can assume without loss of generality that utility is linear in x. To see what our reduced-form temptation means, denote the consumption utility function by v, the consumption available by honest means by |${c_h}$|⁠, and the additional consumption available by dishonest means by |${c_d}$|⁠. Then |$x \equiv v({c_h} + {c_d}) - v({c_h})$| measures the additional utility from the bribe that is tempting the individual. For example, a period when |${c_h}$| is lower—say because an inflationary shock lowers real wages in the public sector—results in a higher x due to concave v. A shift in the distribution towards higher temptations reflects an environment where wrongdoing opportunities are relatively more attractive, but not necessarily one where total consumption (including that bought with bribe money) is higher.

The planner consciously perceives an additively separable payoff comprising both the utility from temptations |${x_t}$| and a utility from beliefs for being good (self-esteem). A planner holding a belief |$\mu $| by the end of a period enjoys a self-esteem utility |$u(\mu )$| in that period. We assume that u is concave, strictly increasing, and bounded for |$\mu \in [0,1]$|⁠. This formulation where the individual obtains utility from beliefs in a direct way follows an ego-utility formulation as in Kőszegi (2006). This differs from the usual expected utility formulation where individuals have a von Neumann–Morgenstern utility from outcomes and where beliefs only count as weights associated with different outcome realizations. Beliefs may affect utility directly because they yield a sense of self-worth, or because the person derives utility from anticipatory feelings about future outcomes. Consumption utility |${x_t}$| is not dependent on type: individuals realize that goods obtained by dishonest means would yield as much consumption utility as those gained honestly. Thus, while individuals enjoy the thought of being good, they draw utility from temptations consumed.

An individual can take one of two externally observable actions in a given period: yield to the temptation |$({r_t} = 0)$|⁠, or resist |$({r_t} = 1)$|⁠. We now explain how externally observable actions are determined.⁷ If, after observing the temptation |${x_t}$| the planner gives up |$({a_t} = 0)$| the doer is left to drive behavior alone, and behavior will match the doer’s type: resist if good (⁠|${r_t} = 1$| if |$\theta = {\theta _g}$|⁠), give in if bad (⁠|${r_t} = 0$| if |$\theta = {\theta _b}$|⁠).⁸ If the planner attempts an override |$({a_t} = 1)$|⁠, then this increases the probability, from zero to |$\varphi \gt 0$|⁠, that when the doer is bad the externally observable action is resistance. (The override is inconsequential if the doer is good, because the good doer resists for sure.) The parameter |$\varphi $| is the probability that the override attempted by the planner overcomes the tendencies of the doer.⁹ It captures a causal effect of a deliberate choice by the planner on the action taken externally, and as such it is a manifestation of free will as defined by some psychologists (e.g., Vallacher and Wegner 1987). We will refer to |$\varphi $| as the “free will” parameter.

The timing of the problem is depicted in Figure 1.

Figure 1

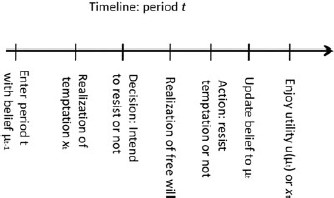
At the start of period t planner has prior |${\mu _{t - 1}}$| and observes temptation |${x_t}$|⁠. He then decides whether to attempt override |$({a_t} = 1)$|⁠, or not |$({a_t} = 0)$|⁠. The externally observable action |${r_t}$| is then determined. Under |${a_t} = 0$|⁠, the doer alone determines |${r_t}$|⁠, so |${r_t} = 1$| if |$\theta = {\theta _g}$| and |${r_t} = 0$| if |$\theta = {\theta _b}$|⁠. Under |${a_t} = 1,\;{r_t} = 1$| for sure if |$\theta = {\theta _g}$| and with probability |$\varphi $| if |$\theta = {\theta _b}$|⁠. At the end of period t, knowing |${a_t}$| and |${r_t}$|⁠, the planner updates belief to |${\mu _t}$|⁠.

Open in new tabDownload slide

2.2. One-Period Problem

First consider an individual who lives only for one period and faces a temptation of size x. If the planner chooses to give up, the temptation is taken only if the doer is bad and resisted only if the doer is good. The externally observable action r will then fully reveal the doer’s type. With probability |${\mu _0}$| the individual will become certain of having a good type |$({\mu _1} = 1)$|⁠, and with complementary probability |$ 1 - {\mu _0}$| certain of having a bad type |$({\mu _1} = 0)$|⁠. The expected posterior is, of course, equal to the prior |${\mu _0}$|⁠.

The expected belief when attempting an override is also, of course, equal to the prior, so attempting an override cannot improve the expected posterior. Although the expected belief cannot be manipulated, expected utility can be, because an override attempt yields a “gamble” over future self-image that is less risky. Attempting an override results in a lower variance over posterior beliefs, |$\mu _0^2(1 - {\mu _0})(1 - \varphi )/[{\mu _0} + (1 - {\mu _0})\varphi ]$|⁠, than leaving the doer alone, in which case the variance is |${\mu _0}(1 - {\mu _0})$|⁠.

The idea that individuals may want to manipulate the higher moments of a distribution of beliefs has emerged in various settings. In Carrillo and Mariotti (2000) an individual has commitment problems and knows that her behavior, current and future, depends on beliefs about the level of future costs that current consumption creates. This individual cannot alter her expected beliefs, but changing the distribution of beliefs may be beneficial when actions depend on the position of beliefs relative to specific, decision-relevant, thresholds. Related ideas emerge in Kamenica and Gentzkow’s (2011) study of persuasion. In Kőszegi’s (2006) paper on overconfidence and task choice the individual manipulates the arrival of information for intrinsic reasons. Risk aversion over future beliefs about competence drives incentives for information manipulation. In Kőszegi’s study the objective is to understand the emergence of overconfidence, while we study adherence to norms. In addition, we assume a smoothly concave ego-utility rather than a step function. The link between risk aversion and the demand for information is present also in Bénabou and Tirole 2002 (see especially p. 906–907). The known insight that risk aversion leads to information aversion foretells the driving force behind our result that the shape of self-esteem utility drives adherence to norms. But the question remains open as to whether the insight remains valid in the dynamic version of our problem, where the future matters in nontrivial ways.

Does the presence of a future affect current adherence to norms, and is adherence necessarily strengthened by the accumulation of moral capital? We study this problem with a dynamic model. We show later that a finite horizon confounds the effect of changes in the individual’s beliefs with those of an approaching terminal date. Therefore we use an infinite horizon model for the main analysis.

2.3. Repeated Problem

It is straightforward to show that the map in (9) satisfies the conditions for existence of a unique (continuous) value function.¹⁰ This dynamic formulation yields the first result as follows.

The cutoff |${x^*}\left( \mu \right)$| is strictly positive if the lower risk gamble (over both the current and the continuation payoff) stemming from the override attempt yields strictly higher expected utility. In the one-period problem (captured by the first line in equation (10)) the cutoff is, as shown before, positive whenever u is concave. If the value function V were concave it would be immediate that cutoffs must be positive in the dynamic problem as well, since the added term (captured by the second line in equation (10)) is isomorphic to the one expressing the static trade-off. However, the map in equation (9) does not preserve concavity, so we rely on an alternative argument based on the sequential optimality of cutoffs to obtain the following proposition.

While the planner remains uncertain he attempts an override to resist every temptation |${x_t}$| such that |${x_t} \le {x^*}({\mu _t})$|⁠. If the individual is risk averse over beliefs about type, then as long as he remains uncertain the personal history of cutoffs or “moral standards” will evolve according to |${x^*}\left( {{\mu _0}} \right),{x^*}\left( {{\mu _1}} \right),....$| The resistance continues until the first time he either faces a temptation above |${x^*}\left( {{\mu _t}} \right)$| or, if the doer is bad, the first time the override fails, which has the independent probability |$1 - \varphi $| every period.

Note that we did not assume that larger temptations are harder to resist: the probability of successful override is independent of the size of the temptation. The fact that individuals are more likely to resist small temptations is entirely due to their optimization behavior.

Three additional observations are in order. First, wrongdoing provides conclusive evidence of bad type, so the stochastic process for beliefs differs from many learning setups where revisions become smaller as more information is obtained. Here, as long as there is any uncertainty over the type, a sudden and ever higher “fall from grace” always remains a possibility, although such a fall keeps getting more unlikely as the record of good behavior gets longer.

Second, in a world where the average temptation is sufficiently high, having a good type is bad news for expected utility. The benefit of having a good type is the self-esteem, but having a bad type has the benefit of increasing the opportunities for consumption. Thus, both period utility and present value V may be increasing or decreasing in |$\mu $|⁠, depending on whether the average temptation |$Ex$| is large or small relative to the maximum utility gain from self-esteem, |$u(1) - u(0)$|⁠.

Third, further characterizing the policy function in the context of the recursive formulation is hard. In addition to the map in (9) not preserving concavity, intuitive approaches that could help characterize the optimal policy in the context of dynamic programming are not applicable to our problem.¹¹ Therefore, our strategy for analyzing the optimal policy will rely on the less elegant approach of dealing with discounted sums of utility flows. We relegate the proofs to the Appendix.

2.3.1. Optimal Policy

This result can be understood by considering how the expected costs and benefits of attempted resistance vary with |$\mu $|⁠, while holding x fixed. The benefit–cost ratio can be seen in equation (10), separately (but in the same functional form) for current and future periods. Given that the uncertain planner faces qualitatively the same problem every period, the intuition is best explained by reference to the trade-off in current period alone. The benefit of override is the expected utility gain from risk reduction, as reflected in the numerator of the benefit-cost ratio for the current period—see the first line in equation (10). This benefit is at first increasing, but eventually decreases in |$\mu $|⁠, because uncertainty is highest at intermediate values of |$\mu $|⁠. The cost, in turn, is proportional to the probability |$\varphi \left( {1 - \mu } \right)$| that the attempt to resist causes the individual to forgo the temptation. This cost is reflected in the denominator of the benefit–cost ratio, and is linearly decreasing in |$\mu $|⁠. For low values of |$\mu $| the result is obvious: higher |$\mu $| means higher benefit (more risk reduction) and lower cost (fewer forgone temptations), so the benefit–cost ratio of an override can only increase. Eventually both benefits and costs are decreasing in |$\mu $|⁠, so the result is non-obvious. The proof shows that the rate |$\varphi $| at which cost decrease is faster than the rate at which the benefits of risk reduction can decrease for all values of |$\mu $|⁠.

While the optimal policy |${x^*}\left( \mu \right)$| is stationary, the temporal evolution of personal standards has a direction. As long as the planner remains uncertain of the doer’s type, the belief |${\mu _t}$| will keep increasing according to (1), so, by virtue of Proposition 2, the effective cutoff |${x^*}\left( {{\mu _t}} \right)$| will also increase over time. This yields the following remark.

This implication of Proposition 2 echoes Aristotle’s characterization of virtue as a process of habituation through action, where the exercise of virtue makes it more likely that virtuous behavior obtains subsequently (see Aristotle 1998); a literal virtuous circle. The chronological age implications of the result should not be taken literally—age in our model reflects the number of temptations a person has faced before, so the interpretation of periods as calendar time implicitly assumes that temptations arrive at the same rate during the lifetime.

Note that the result in Proposition 2 obtains regardless of whether the value function is increasing or even monotonic. The top panel of Figure 2 depicts the expected value function, |$V(\mu ) \equiv {E_x}V\left( {\mu ,x} \right)$|⁠, and the associated optimal policy function, for three cases.¹² In the first case temptations are relatively small, so good types have a higher expected utility than bad types, |${V_1} \gt {V_0}$|⁠. The resulting value function is increasing. The second case is the opposite, with relatively high temptations, |${V_1} \lt {V_0}$|⁠. This case results in a decreasing value function. In the third case expected utilities are balanced, |${V_1} = {V_0}$|⁠. In this case the value function is nonmonotonic, with an interior maximum (the same is true for the roughly balanced case, |${V_1} \approx {V_0}$|⁠). The bottom panel of Figure 2 depicts the (always increasing) policy function |${x^*}$| for the same cases.

Figure 2

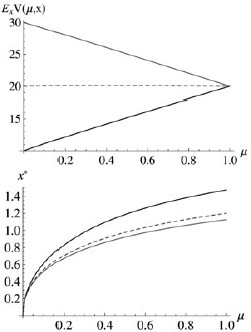
Expected value function |$V(\mu ) \equiv \;{E_x}V\left( {x,\mu } \right)$| and optimal policy |${x^*}\left( \mu \right)$| function under three different cases. The case with a benign environment, where full self-esteem offers significantly more utility than the average temptation, results when |$u(1) - u(0) \gt \gt Ex$|⁠; it is depicted in black. The opposite case of a harsh environment is depicted in grey, and the balanced case is depicted with dashed curves. (The relatively flat value function of the balanced case is also strictly concave value, with a maximum at |$\mu = 0.294$|⁠.) Parameters: |$\rho = 0.5,\;\varphi = 0.75,\;\lambda = 0.9$|⁠, and x is distributed exponentially with |$Ex = 1$|⁠, 3, and 2 respectively.

Open in new tabDownload slide

It is worth noting the role of the assumption of imperfect override. With perfect override |$(\varphi = 1)$| beliefs do not change |$(b\left( \mu \right) = \mu )$| and there can be no moral growth. However, the planner would still attempt to override the doer when the temptation is low enough, due to the risk aversion over beliefs. The individual would keep resisting until a sufficiently high temptation is encountered, at which point the planner accepts the “final gamble” and finds out the doer’s true type.

2.3.2. Comparative Statics

Next we study the dependence of the optimal policy on the level of anticipated temptations and on individual time preference. To introduce higher anticipated temptations, consider a uniformly shifted distribution such that |${F_\varepsilon }\left( x \right) = F\left( {x - \varepsilon } \right)$| for |$x \ge \varepsilon $| and zero otherwise. The parameter |$\varepsilon $| defines an increase in temptations that implies a shift in the sense of first order stochastic dominance.

When the planner expects higher temptations in the future he will choose less stringent moral standards today. This is because falling to a temptation today would wipe out the person’s moral capital and direct him to “a life of crime”. The higher the distribution of temptations, the more attractive is that life relative to slowing learning for the sake of self-esteem.

Note that a more benign environment in the sense of lower temptations will impact behavior in two ways. A direct effect is that, given the individual’s cutoffs, a less tempting environment makes it less likely that a high enough temptation will materialize so as to induce the planner to give up. The indirect effect is that the expectation of a more benign environment leads the individual to resist even larger shocks, complementing the direct effect. This positive feedback suggests that small differences in the environment can generate larger departures in the overall level of wrongdoing.

Higher moral standards can be interpreted as a type of investment; hence the term “moral capital”. The temptation would be available immediately, but a successful resistance improves (in expectation) the entire future path of self-esteem utility flows. It is therefore natural that a higher discount factor increases cutoffs.¹³

By contrast, the relation of the efficacy of the planner’s intervention |$\varphi $| and moral standards is not clear cut. On the one hand, if the planner attempts an override, then a higher |$\varphi $| reduces the probability of finding out the true type this period, thus reducing the variance of updated beliefs. On the other hand, there is also an effect in the opposite direction, because the attempt is now more likely to preclude the enjoyment of a temptation.

2.4. Finite Horizon

We now explore forces that may create nonmonotonic effects of moral capital on individual moral standards. Consider a finite horizon setting. Figure 3 shows the numerically obtained optimal policy for the last three periods of a life with a known end period. (The one period case can be interpreted as the last period of a finite horizon life.) Just like in the infinite horizon case, the optimal cutoff is monotonic increasing in beliefs in any given period. At the same time, the cutoff is higher the longer is the remaining lifetime, for any given level of beliefs |$\mu $|⁠. This is consistent with our comparative static result on time preference.

Now let us consider how moral standards may evolve as we follow an individual who remains uncertain and keeps resisting temptations during the final periods of a finite life. As he moves forward in time, a shrinking horizon reduces the relative weight of the future, and this induces a weakening in personal moral standards for any given level of beliefs. At the same time, his consistent rejection of temptations increases his confidence in having a good type, and this works towards higher standards. With t closer to final period T, |$x_t^*\left( \mu \right)$| is lower at any |$\mu $|⁠, but |${\mu _t}$| is higher than |${\mu _{t - 1}}$|⁠. The direction of the temporal change in moral standards is therefore ambiguous. Figure 3 shows two examples for the evolution of beliefs, in accordance with (1), depicted by the successive vertical dashed lines. For the individual who enters the final three periods with a relatively low initial belief the impact of “Aristotelian” moral growth dominates at first, and the effective cutoff |$x_t^*\left( {{\mu _t}} \right)$| is at first increasing. For another individual, who enters with a relatively high belief, the impact of the shrinking horizon dominates and the cutoff is decreasing over time.

Figure 3

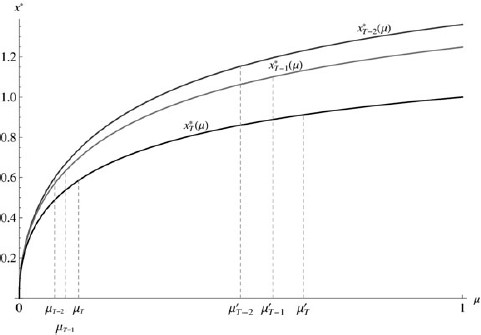
Optimal policy and histories of beliefs for the last three periods of a finite horizon (⁠|$T - 2,\;T - 1$|⁠, and T), conditional on successful override. Same parameters as in Figure 2, with |$Ex = 3$|⁠. For the individual with low initial beliefs |${\mu _{T - 2}}$|⁠, moral standards increase in |$T - 1$| (due to “Aristotelian” moral growth) then decrease in the last period due to the finite horizon effect. For high initial beliefs |$\mu _{T - 2}^\prime $|⁠, the finite horizon effect dominates and moral standards decrease over time.

Open in new tabDownload slide

In sum, the stationary environment offered by the infinite horizon is crucial for obtaining unambiguous results about personal moral growth, because adherence to standards is an investment in moral capital that yields returns in the future. The effect of an approaching terminal date reduces the return to such investment and acts as a confounder.

2.5. Fallible Types

So far we have assumed that individuals have a dichotomous and absolute view of the nature of good and bad: they do not believe that it is possible for a person to be “a little bit corrupt”. This implies that wrongdoing, if observed even once, provides conclusive evidence of a bad type. This Manichaean interpretation of good and bad is not just a useful simplifying assumption (which it also is) but has a long history in religion and philosophy. In this section we investigate the impact of allowing for a less stark formulation, by assuming that individuals believe that types are fallible: under no override, bad types may take good actions, and good types may take bad actions.

In particular, we now assume that in the absence of a successful override by the planner, the good doer selects the good action with some probability |${\gamma _g} \lt 1$| and the bad type takes the good action with a lower probability |${\gamma _b} \in [0,{\gamma _g})$|⁠. Thus |$1 - {\gamma _g}$| and |${\gamma _b}$| are “error rates” for the good and bad doers, respectively. We assume that the deviations from typical behavior are independent across time and that the planner’s override prevails independently with probability |$\varphi $|⁠. Thus, when the planner selects |$a = 1$| then the probability of a type |$j \in \{ g,b\} $| doer taking the good action is |${\gamma _j} + (1 - {\gamma _j})a\varphi $|⁠. The planner’s override increases the probability of a good action.

The updating rules become slightly more complicated. No evidence is conclusive of either type, but bad actions will cause the beliefs to be revised downwards, and good actions upward, and revisions are larger when the error rates are smaller.¹⁴ This expanded model nests our baseline model as a special case where |${\gamma _g} = 1$| and |${\gamma _b} = 0$|⁠. In any case, beliefs will eventually converge to be arbitrarily close to the truth.

Figure 4 shows the numerically obtained optimal policy when individuals believe that good types can “tremble”, for several cases of the “error rate”. The policy functions reveal that when the belief in one’s goodness gets sufficiently close to certainty, then the cutoff selected by the planner begins to decrease. The reason is intuitive. If the planner is almost certain that the doer is good, but also believes that the good doer can make mistakes, then the planner also anticipates that after observing a bad action he will attribute the bad action to a mistake by the good doer rather than to the doer being bad. This plausible deniability reduces the incentives to maintain adherence to high standards. However, if good types are believed to make mistakes very rarely (⁠|${\gamma _g}$| close to one) then the optimal policy is close to that of the basic model, and the level of beliefs beyond which moral standards begin to decrease gets very close to one. Interpreting the discount factor as including a hazard rate for survival, a good type following such a policy could have a very low chance of ever making it to the decreasing part of the policy function.

Figure 4

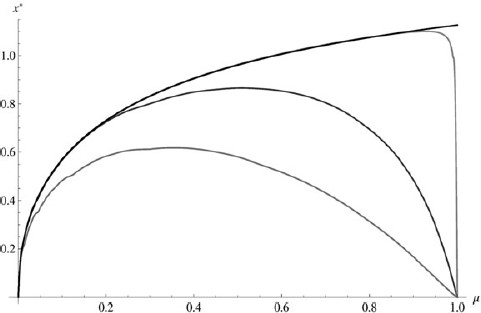
Optimal policy for fallible types, under different values of symmetric error rate, |$\varepsilon = 1 - {\gamma _g} = {\gamma _b}$|⁠. The lowest curve corresponds to the highest error rate |$\varepsilon = 0.25$|⁠. The following two curves in grey have |$\varepsilon = 0.1$|⁠, and |$\varepsilon = 0.001$|⁠. The highest values of |${x^*}$| obtain in the infallible case |$\varepsilon = 0$|⁠, which is the basic model (in black). Other parameters are as in Figure 2, with |${E_x} = 3$|⁠.

Open in new tabDownload slide

It is worth noting that very high self-confidence may also lead to more lax moral standards for reasons other than those captured here, but which have received attention in psychology, such as feelings of invincibility or a loss of perspective.

2.6. Discussion

By focusing on conditions that ensure stationarity, we are able to isolate a result where moral capital always reinforces intrinsic motivation. That result breaks down with a finite horizon or due to factors that alter the informational content of actions. With fallible types, changes in moral capital change the relative role the planner assigns to luck versus the doer’s type. This complements the recent analysis of “beliefs as assets” by Bénabou and Tirole (2011). We now discuss other implications of our model and further discuss related literature.

2.6.1. Rationalizing the Calvinist Ethic

The Weberian account of the Calvinist Ethic (Weber 1905) has been extremely influential at shaping views on differential socioeconomic performance, and been called “the most important sociological thesis of all time” (Rubinstein 1999).

In the Weberian account, a person not knowing his predestination status (saved or doomed, the types of the doer) may enjoy being profligate but would also like to maintain or even increase his confidence of having been born saved. The presumably inevitable consequence is that everyone has an incentive to try and live like a saved person would. There are two problems with that account. The first is that, if anyone can mimic a “saved” person, it is unclear how a good introspective reputation can be developed. The second problem is that if past good actions can improve self-image, but a better self-image could weaken the incentives to adhere to norms, then it is difficult to explain sustained good behavior. The study of the Calvinist Ethic from a modeling perspective was pioneered by Prelec and Bodner (2003) and Bénabou and Tirole (2004), in papers where individual behavior results from noncooperative interactions between fully strategic temporal selves. They study conditions under which the person may improve his confidence of being saved even when knowing that he has a motive to try to act like one.

Our model allows an interpretation of the Calvinist ethic from a dynamic perspective, based on different assumptions about the sources of impulse control. Our approach involves a single decision-maker whose visceral impulses are captured as behavioral types with no strategic intent. Our approach can explain the possibility of increased confidence in salvation through the planner’s imperfect override capability and inability to assign authorship to actions. But where our model helps more distinctly is with the second problem—when do gains in moral capital reinforce good behavior—which is eminently dynamic, and which requires a clean isolation of the effects of moral capital.

Our analysis shows that the reinforcing effects can be persistent rather than self-defeating. The self-reinforcement of virtue is more likely with a longer time horizon and with a lower chance that a bad action can be attributed to a “mistake” by the good type. When the environment is stationary (infinite horizon) and when the informational content of actions remains constant across levels of the state variable (infallible good types), then moral capital has unambiguously reinforcing effects. Thus, the improvement in introspective reputation following good actions, and the reinforcing effect of introspective reputation on further incentives to behave like a “saved” type would, provide a way to understand how the Calvinist ethic could yield sustained good behavior.

2.6.2. Introspective Reputation, Time Consistency, and Planner–Doer Approaches

Our model joins various others in the study of introspective reputation. Learning about some aspect of the self is possible when the person updates by conditioning on an “incomplete” set of events. In Bénabou and Tirole’s (2004) model, for instance, the individual forgets the motivations that led to an act. For updating purposes, this has the same effect as the planner not knowing whether an override attempt has worked. In their model, the person forgets, but made a fully conscious decision that reveals the person’s preference at the point in time when the decision was made. In our case, as in Bernheim and Rangel (2004), externally observable actions may constitute a mistake from the person’s perspective, which places limits on a revealed preference approach to study motivation.

It is worth remarking that in our model preferences are time consistent. Planner–doer models with time-consistent preferences can generate behavior that resembles what obtains in models where time inconsistency is built-in by assumption, a point made by Bénabou and Pycia (2002) and Fudenberg and Levine (2006). Not all predictions will be similar however. Settings where time-inconsistency is assumed tend to generate a demand for commitment. The individual would typically like to face lower temptations or have a lower vulnerability to them. This is not necessarily true in our set up. First, when the expected value of temptations is sufficiently high, then having a good type (which is good for “commitment”) results in lower expected utility. Second, in our model the induced preferences over environments are different. For example, if two activities entail different parameters for the salience of the present, as captured by the hyperbolic discounting parameter |$\beta $|⁠, then individuals with time-inconsistent preferences would always choose the activity with the higher |$\beta $|⁠. Another possibility, in the context of Bénabou and Tirole (2004), is to capture temptations with the cost of forgoing a craving. In their model individuals would always prefer those costs to be lower, while in our model individuals may prefer the distribution of temptations to be higher. As we will discuss later in the career choice application, it is precisely the individuals who are less confident of having a good type (and who should have the stronger demand for commitment) who turn out to have a stronger preference for a high temptation activity.

The modeling approach closest to ours in the literature is perhaps that in Bernheim and Rangel (2004), so it may be helpful to further clarify the connections between our theory and theirs. Bernheim and Rangel posit an individual who faces cues from the environment, and has a level of susceptibility M to these cues. When M lies above a given threshold |${M^T}$| the individual falls in a “hot” state where he consumes a substance regardless of any conscious attempts to do otherwise. The susceptibility M in each period depends on a probabilistic state |$\omega $| as well as on a “lifestyle” action |${a_t}$| taken at the beginning of each period. The essential role of the lifestyle action |${a_t}$| is to shift susceptibility and make it less likely that the individual enters the hot state. In their model, override fails completely in the hot state. With this similarity comes a related difference: in their model the override failure (having entered a hot state) is known to the individual while in ours it is beyond the reach of consciousness.¹⁵ Thus, the individual in our model is less cognizant of the possible values of each argument affecting M, although he does know his own choice of a. Conditional on that difference, our action a can also be interpreted as a lifestyle choice.¹⁶ The most obvious difference is that the history of consumption plays no role in our model, and we focus instead on belief-driven sources of persistence. (This also sets our theory apart from early models of addiction like that by Becker and Murphy (1988) where past consumption alters future marginal utilities). A less obvious, but important, difference is that in Bernheim and Rangel’s theory the individual lacks any power to select his desired action in the hot state, but has full power in the cold state. But this does not address the question of how we ever select actions. In the Online Appendix we show in more detail what it means to choose an externally observable action, by conceptualizing the initial, and in our model unobservable, action a, as an exertion of the will aimed at overriding impulses. This helps rationalize the role of the types and override invoked in our basic model.

3. Applications

3.1. Wrongdoing in the Aggregate

Now we want to study the effect on aggregate wrongdoing of past shocks to the distribution of temptations. As time goes by, however, two things occur simultaneously: shocks recede in the past, and individuals age. To isolate the role of past shocks it is necessary to approximate an “ageless” cohort, and to achieve this we consider a society made of infinitely many generations in demographic steady state. Assume that the discount factor reflects a constant death rate, and that there is a constant birth rate of new uncertain individuals. As we show in our working paper, there exists a demographic steady state in which older cohorts have exponentially smaller population shares. With finite lifespans (of uncertain length) a substantial fraction of bad types never fall, because they die first.

Now consider two societies with the same fundamentals (⁠|$\mu ,\;\varphi ,\;\lambda $|⁠, F), one of which suffers an unexpected shock to the distribution of temptations for one period. For example, a macroeconomic shock lowers baseline consumption and thereby increases the additional consumption utility from any given stealing opportunity. In our setup this means that the distribution of temptations is higher, in the sense of stochastic dominance. The immediate impact of the shock is that an unusually large fraction of each living cohort encounters a temptation above their cutoff. The bad types who fall because of the shock lose their moral capital and do not return to good ways after the shock is over. Bad shocks that caused a higher share of people to give in to temptations in one period yield higher wrongdoing rates for every subsequent period in finite time. Wrongdoing rates in the shocked society only converge to the baseline levels of the “normal” society in infinite time, once all cohorts alive at the time of the shock are replaced. Thus, discrepancies in wrongdoing across societies reflect bad luck in the past, rather than differences in moral fundamentals.

If the birth prior |${\mu _0}$| equals the true probability of having a good type, a bad shock does not affect the average belief, but makes its distribution more polarized for all subsequent periods in finite time—thus, the higher wrongdoing rate in the shocked society is related to the higher second moment of the distribution of individual moral capital.

According to Proposition 2, higher initial beliefs lead to stronger resistance to temptations, which suggests a useful social role for indoctrination. Suppose the aim is to minimize wrongdoing. The strength of individual resistance to temptations is increasing in the confidence of having a good type, so inculcating a high initial belief |${\mu _0}$| on the youth would reduce the aggregate wrongdoing rate regardless of the true |$\mu $|⁠. It is obvious that wrongdoing would be reduced by a reduction in the available temptations, but, more surprisingly, wrongdoing rates could also be reduced by introducing an additional contrived temptation on the youth. Suppose that the society is able to label some consumption opportunity as a temptation to be avoided (i.e., a taboo good). To be useful in building moral capital, the size of this temptation has to be below the cutoff of the inexperienced individual |${x^*}\left( {{\mu _0}} \right)$|⁠, and be socially innocuous in the sense that consuming it does not constitute part of the wrongdoing that is being minimized. The benefit of this contrived temptation is that those who successfully resist it will be stronger when they meet their first real temptation (they have a cutoff |${x^*}\left( {{\mu _1}} \right) \gt {x^*}\left( {{\mu _0}} \right)$|⁠). The cost is that some bad types now fall earlier than they otherwise would have. Depending on parameters, this can reduce the steady state wrongdoing rate in the society.¹⁷

3.2. Punishing Repeat Offenders

We now investigate whether and how the presence of moral capital may affect optimal extrinsic deterrence schemes. The main idea is that the presence of endogenous moral capital affects the effectiveness of deterrence depending on its timing relative to criminal history, so optimal deterrence will vary with individuals’ criminal record; in addition, and perhaps more interestingly, the effect depends on the time horizon of the social planner. In order to get the essential message across as cleanly as possible, we impose a number of simplifications.

Consider a social planner facing a single cohort of a given age, the members of which survive from one period to the next with probability |$\lambda \in (0,1)$|⁠. The planner knows the past behavior by all agents and wants to minimize aggregate wrongdoing going forward. The planner has a one-time capability to impose punishment on those who do wrong in the current period, an event that is detectable with some probability. Should the social planner make punishments contingent on the offender’s personal history?

For simplicity, we subsume the probability of detection and the intensity of punishment in a composite expected punishment variable that the planner controls. |${N_r}$| and |${N_f}$| denote the expected punishment to be imposed respectively on the repeat and the first-time offenders that seize a temptation in the current period. The net expected return from seizing a temptation x is therefore |$x - {N_r}$| for the repeat offender and |$x - {N_f}$| for the first time offender. Note that a repeat offender is already certain of having a bad type, while the first time offender is, before committing a crime, uncertain. Making punishment contingent on an offense being the first is equivalent to making it contingent on the offender being uncertain. We restrict attention to bad types (the only ones that do wrong) and normalize their mass to 1.

To make things interesting, assume that raising expected punishments is costly to the social planner, as captured by an increasing and convex function |$c({N_r} + {N_f})$|⁠. This captures a world where threatening with more likely and intense punishment is costly because it requires stronger detection and punishment capabilities.¹⁸ To cleanly separate the time preference of the planner from that of the population, we assume that the planner discounts the future according to the factor |$\delta \lt 1$|⁠, while individuals have a survival rate |$\lambda $| and (to save on notation) do not further discount time. Also, for technical reasons, we assume here that larger temptations are less common than small ones—namely, that |$f\left( x \right)$| is decreasing.¹⁹

To construct the objective of the social planner, we first characterize the impact of punishment on wrongdoing. We know from previous sections that, absent punishment, those who are certain of being bad give up and do wrong for sure. Threatened with a punishment |${N_r}$| they would attempt to resist whenever the realized temptation is smaller than the punishment—that is, whenever |$x \lt {N_r}$|⁠, and in that case resist with probability |$\varphi $|⁠. Therefore, given a punishment |${N_r}$|⁠, the rate of wrongdoing among the certain will be |$1 - \varphi F\left( {{N_r}} \right)$|⁠. That means the punishment on repeat offenders obtains a reduction in wrongdoing of exactly |$\varphi F\left( {{N_r}} \right)$| in the current period. As punishment applies in the current period only, and the certain learn nothing regardless of their action, |${N_r}$| has no further impact on wrongdoing.

Recall that |$x_t^* = {x^*}\left( {{\mu _t}} \right)$|⁠, and set the current period to |$t = 1$|⁠. The impact of current period punishment on wrongdoing by first-time offenders is then captured by the following lemma.

The proof shows that under punishment |${N_f}$| the current cutoff is |$x_1^{*p} = x_1^* + {N_f}$| (the superscript “p” denotes a solution under the punishment regime), so current punishment raises the current optimal cutoff of the uncertain one for one. So punishment achieves a reduction in current wrongdoing equal to |$\varphi (F(x_1^* + {N_f}) - F(x_1^*))$|⁠, and raises the share of individuals who resist and remain uncertain of their type, leading to lower wrongdoing in future periods. Specifically, of those who are saved from temptation in the current period, |$\varphi \lambda F(x_2^*)$| are saved again in period 2, and |${(\varphi \lambda )^2}F(x_2^*)F(x_3^*)$| in period 3, and so on, explaining the expression in the last lemma, where the summation captures the present and future (discounted) reductions in wrongdoing. All future cutoffs are unchanged by the one-time punishment.

3.2.1. Social Planner’s Problem

An intrinsic disposition to resist temptations allows individuals to behave honestly even when there are no extrinsic incentives in place. But extrinsic incentives can obviously help keep individuals behaving honestly. Proposition 4 tells us that the design of extrinsic incentives should reflect the strength of intrinsic dispositions to avoid wrongdoing. An optimizing social planner spends less resources trying to deter agents that already have intrinsic self-deterrent motives, and chooses to punish more harshly those who have lost their moral capital and are willing to take any temptation that comes their way.²⁰ This design resembles the very common penal profile of heavier sentences on wrongdoers with a criminal record, and rules such as the “three strikes and you are out” that apply in many US states. Notably, in California there is a second strike provision according to which a second felony triggers a sentence twice as heavy (Clark, Austin, and Henry 1997). Note however that our last proposition does not support those institutions in an unconditional way—harsher punishment for repeat offenders may not make sense if the planning horizon is long, which can occur either because the planner is patient, or because agents live for a long time. In this case there is an option value to keeping the uncertain honest, in order to preserve their self-deterrence for the future. Under a long horizon, this effect may dominate and the planner would prefer to use resources to deter crime by first time offenders.²¹

3.3. Career Choice, Moral Capital, and Moral Adverse Selection

We have shown that wrongdoing rates will be higher when individuals are impatient, when their confidence of having the good type is low, and when temptations are higher. The latter feature induces both a mechanical increase in wrongdoing through higher temptations being drawn, as well as a decrease in the endogenous resistance threshold chosen by individuals. But these effects could be mitigated if individuals who are less confident about being good were to optimally select low-temptation environments. But how do individuals select into careers in an economy where individual beliefs vary and different careers offer different distributions of temptations?

For concreteness, consider two occupations, “politics” and “academia”. Assume that a person who enters politics faces a higher distribution of temptations, in the sense of first-order stochastic dominance. The population consists of a continuum of individuals with heterogeneous initial beliefs |$\mu \in [0,1]$|⁠. We want to know how individuals self-select into different occupations depending on |$\mu $|⁠. One might imagine that individuals with a low prior |$\mu $| may have an incentive to choose a low temptation activity, given that they have lower cutoffs and therefore a higher chance of giving up. Indeed, as mentioned earlier, “shelter-seeking” behavior can arise in models with time-inconsistent preferences.

Assume the economy needs workers in both careers, so compensation adjusts to ensure both careers attract a positive measure of types. The mechanism of this adjustment is immaterial for our exercise; what matters is that in equilibrium individuals who require a lower compensating differential will enter the low-temptation career. To isolate the effect of interest in the simplest way, suppose individuals live for one period. We then have the following proposition.

Rather than seek “shelter” in the low-temptation occupation, individuals who are more vulnerable to temptation choose activities with higher temptations. This is a moral adverse selection pattern whereby the activities with temptations attract those least equipped to resist them. In the extreme case of one activity with temptations and one without, this sorting must lead to an increase in wrongdoing. This result informs the literature on political selection which is concerned with the incentives of able and honest individuals to enter a public life where corruption opportunities may abound.²²

For individuals who know their type the selection incentives are clear: if we abstract from wages, an individual with |$\mu = 1$| will obtain u(1) in either occupation and be indifferent between the two careers. It follows he will prefer the low-temptation career under any positive compensating differential favoring that career. On the other end of the type spectrum, an individual with |$\mu = 0$| only cares about temptations and will choose the high-temptation activity unless there is a fairly large compensating differential in favor of the low-temptation activity. In between, the result is not obvious, because of the said incentive facing the uncertain types to protect their self-image by choosing a low-temptation activity. Moreover, as shown before, for a given distribution of temptations the value function is not necessarily monotonic in |$\mu $|⁠, nor is it clear which types would place more value in a given shift in temptations. The value added of the last proposition (and the nontrivial aspect of the proof) is that the compensating differential that must be paid to attract a type |$\mu $| into the low temptation activity is monotonically decreasing in |$\mu $|⁠. Therefore, the population can always be divided into just two segments by their beliefs |$\mu $| so that types in the lower segment of self-image will enter the high-temptation profession.

Are politicians more corrupt than academics because they are inherently less moral or because they have more opportunities for corrupt behavior? In our model both arguments are correct. Even if people were divided randomly between occupations, the higher temptations would cause there to be more wrongdoing in the high-temptation sector, because of the forces highlighted by the main model: a mechanical effect and, in a dynamic setting, because cutoffs are endogenously lower when expected temptations are higher. But a third effect is present: the high-temptation activity will attract the weakest types: so they will choose even lower cutoffs, and even holding fixed the temptations, fall more often.

4. Conclusion

We propose a planner–doer model of endogenous moral standards rooted in three ideas: that actions depend partly on unconscious drives subsumed in the doer, that the planner cannot easily attribute authorship of actions between himself and the doer, and that people prefer to think they have a good type of doer—namely that their unconscious drives are geared towards a received morality of resisting temptations. We characterize conditions under which self-restraint will emerge endogenously in the form of passing on enjoyable temptations for the sake of keeping a good introspective reputation. Our emphasis is on studying a stationary dynamic environment in order to identify conditions for persistently self-reinforcing patterns of virtue and corruption.

When conscious intent as captured by the planner’s attempts to override the doer does not fully determine actions, a history of resistance improves self-image and increases the disposition to resist temptations, yielding a view of morality as a cumulative process of habituation through action. This view of morality parallels Aristotle’s account of the development of virtue. We view the improvement of the individual’s self-image as a process of moral capital formation. When individuals perform actions that damage their self-image, durable damage is also done to their willingness to resist such actions in the future, creating hysteresis in wrongdoing at the individual level.

Stronger initial beliefs about having a good type, lower expected temptations and a lower discount rate increase endogenous adherence to moral standards. At the societal level, the wrongdoing rate is determined not just by the average self-image but more generally by its distribution across individuals. Societies with the same distribution of types but with histories involving larger temptation shocks will have a more polarized distribution of individual self-images and higher wrongdoing. Therefore, cross-country measures of wrongdoing and cultures of corruption may not reflect differences in deep moral fundamentals but simply different shock histories.

A valid critique of our basic model, and of other models in the literature where changing higher moments of a distribution is valuable, is that these models are not fully identified empirically. The general point is made in a perceptive paper by Eliaz and Spiegler (2006), and the implication for our setup is that one could obtain a positive function |${x^*}\left( \mu \right)$| if postulating (in a suitable manner) that the planner has a self-esteem that decreases in |$\mu $|⁠. This does not render these theories vacuous—they may be rooted in the behaviorally correct notions but often fail to make predictions that are distinct enough. To be sure, more needs to be done to further validate these theories, for example by deriving, and empirically examining, auxiliary predictions. Hopefully, our extensions and applications represent useful steps in that direction. An additional critique is that the model focuses exclusively in ex-ante incentives to manipulate information under the assumption that the individual is fully Bayesian afterwards, when in reality individuals may engage in actions to protect their self-concept ex post, for example by not updating in a Bayesian manner after doing something immoral.

Our model offers some detail about the workings of identity (see also Bénabou and Tirole 2004). Akerlof and Kranton (2000) posit that identity affects behavior because it poses costs to an individual doing things deemed inappropriate for people with that identity. Our model suggests that “identity-based costs” may not be constant, but respond to past actions and to the person’s beliefs that such identity (e.g., that of a good person) is still hers. The model can also rationalize why societies may prefer to punish repeat offenders more harshly–showing that the optimal design of deterrence schemes may change when the disposition toward wrongdoing is endogenized–, and also why high temptation activities such as politics attract the individuals least equipped to resist. We call this the moral adverse selection effect, and we show that it magnifies wrongdoing.

Acknowledgments

We thank Roland Bénabou, Jeremy Bulow, Pedro Dal Bó, Erik Eyster, Mitri Kitti, Botond Kőszegi, Keith Krehbiel, Don Moore, John Morgan, Santiago Oliveros, Demian Pouzo, Matt Rabin, Tim Williamson, and seminar participants at Arizona State, Berkeley, Birmingham, Essex, HECER, Princeton, Stanford, UCSD, and Universidad de San Andrés for useful conversations and comments. Juan Escobar provided excellent research assistance. Dal Bó is a Research Associate at NBER. Marko Terviö received funding from the European Research Council (ERC Grant Agreement n. 240970).

Appendix: A.1. The (Non-Recursive) Infinite Horizon Formulation

A.2. Proof of Proposition 2: Policy Monotonicity

A.2.1. Monotonicity

A.2.2. Finite Limit of Policy Function

It is sufficient to show that, for every |$\mu \lt 1$|⁠, a sufficiently large temptation makes it optimal to give up. The continuation value of an uncertain individual is bounded above by the present value of getting the highest possible expected period utility forever, which is finite since |$\lambda \lt 1,\;u(1) \lt 1$|⁠, and |$Ex \lt \infty $|⁠. Therefore |${E_x}V\left( {b\left( {{\mu _t}} \right),{x_{t + 1}}} \right),$| with V(.) given by equation (8), is bounded above. By contrast, the current period temptation on offer, |${x_t}$|⁠, enters linearly in |$U(0,{x_t},{\mu _t})$|⁠. Thus, a sufficiently high temptation at hand in the current period will make giving up |$({a_t} = 0)$| optimal.

A.3. Proof of Proposition 3: Comparative Statics

The result for |$\lambda $| is clear by inspection of equation (A.13); all partial derivatives are either positive or vanish by the envelope theorem.

References

Supporting Information

Additional Supporting Information may be found in the online version of this article at the publisher’s website:

Appendix B:

Author notes