-
PDF
- Split View
-
Views
-
Cite
Cite
Xinguang Yuan, Gang Hu, Jingyu Zhong, Guo Wei, HBWO-JS: jellyfish search boosted hybrid beluga whale optimization algorithm for engineering applications, Journal of Computational Design and Engineering, Volume 10, Issue 4, August 2023, Pages 1615–1656, https://doi.org/10.1093/jcde/qwad060
Close - Share Icon Share
Abstract
Beluga whale optimization (BWO) algorithm is a recently proposed population intelligence algorithm. Inspired by the swimming, foraging, and whale falling behaviors of beluga whale populations, it shows good competitive performance compared to other state-of-the-art algorithms. However, the original BWO faces the challenges of unbalanced exploration and exploitation, premature stagnation of iterations, and low convergence accuracy in high-dimensional complex applications. Aiming at these challenges, a hybrid BWO based on the jellyfish search optimizer (HBWO-JS), which combines the vertical crossover operator and Gaussian variation strategy with a fusion of jellyfish search (JS) optimizer, is developed for solving global optimization in this paper. First, the BWO algorithm is fused with the JS optimizer to improve the problem that BWO tends to fall into the best local solution and low convergence accuracy in the exploitation stage through multi-stage exploration and collaborative exploitation. Then, the introduced vertical cross operator solves the problem of unbalanced exploration and exploitation processes by normalizing the upper and lower bounds of two stochastic dimensions of the search agent, thus further improving the overall optimization capability. In addition, the introduced Gaussian variation strategy forces the agent to explore the minimum neighborhood, extending the entire iterative search process and thus alleviating the problem of premature stagnation of the algorithm. Finally, the superiority of the proposed HBWO-JS is verified in detail by comparing it with basic BWO and eight state-of-the-art algorithms on the CEC2019 and CEC2020 test suites, respectively. Also, the scalability of HBWO-JS is evaluated in three dimensions (10D, 30D, 50D), and the results show the stable performance of the proposed algorithm in terms of dimensional scalability. In addition, three practical engineering designs and two Truss topology optimization problems demonstrate the practicality of HBWO-JS. The optimization results show that HBWO-JS has a strong competitive ability and broad application prospects.
Proposing a hybrid beluga whale optimization algorithm termed HBWO-JS for global optimization.
Introducing jellyfish search, vertical crossover operator, and Gaussian variation in HBWO-JS.
The proposed HBWO-JS is tested on CEC2019 and CEC2020 test suites as well as five engineering design problems.
The superiority and validity of HBWO-JS are verified by comparing with state-of-the-art algorithms.
1. Introduction
Optimization problems are an unavoidable area of research in science and engineering, as many practical applications require optimization solutions (Yildiz et al., 2022; Hu et al., 2023c). Furthermore, as real-world problems become complex, optimization requirements become sophisticated and tricky (Hu et al., 2022f). Correspondingly, researchers have developed the Meta–Heuristic (NH) algorithms with different requirements to solve complex optimization problems in various domains, such as curve and surface optimization (Hu et al., 2021, 2022c, e), travelling salesman problem (Gezici & Livatyali, 2022; Gharehchopogh & Abdollahzadeh, 2022), high-dimensional feature selection problems (Awadallah et al., 2022; Hu et al., 2022a; Hu et al., 2022d), wireless sensor network energy consumption (Hu et al., 2022b; Li et al., 2022; Ma et al., 2023), the medical image segmentation problem (He et al., 2021; Nama, 2022; Zhao et al., 2023), job shop scheduling problems (Gao et al., 2020; He & Huang, 2020), and others (Zheng et al., 2022). These NH or hybrid algorithms have been shown to have many advantages in solving realistic complex optimization problems.
With the development of metaheuristic algorithms, the use of classification methods based on the source of inspiration has become increasingly common in the relevant literature. Akyol & Alatas (2017) classified algorithms into nine categories based on the source of their design: biology-based, physics-based, social-based, mathematics-based, music-based, chemistry-based, motion-based, population-based, and mixed methods. Alatas & Bingöl (2020) added three new categories to the nine classifications, plant-based, light-based, and water-based approaches. Abualigah et al. (2021a, 2021b) then simplified the metaheuristic algorithms into four types: evolutionary-based, population-based, human behavior-based, and physics- and chemistry-based. Evolutionary-based algorithms were the first metaheuristic techniques to emerge. They are based on an in-depth understanding of the potential relationship between biological evolution and algorithmic optimization, linking natural and artificial evolution and considering the independent optimization variables as genes in biology. Evolution-based algorithms are inspired by natural evolution and mimic crossover, mutation, and selection biologically driven. The traditional evolutionary algorithm is the genetic algorithm (GA), which is inspired by Darwinian evolutionary ideas (Chen et al., 2022). Differential evolution (DE; Storn & Price, 1997), as a common evolutionary-based algorithm, is influenced by GA update rules. Population-based algorithms simulate the division of labor and collaborative behavior among groups of organisms during predation and drive the progress of the entire population through the interaction of information between individuals (Hu et al., 2023d). Particle Swarm Optimization (PSO; Shu et al., 2023) is the best-known population-based algorithm. The algorithm is inspired by the collaborative operation of individuals and groups of birds in a flock. The Artificial Hummingbird Algorithm (AHA; Zhao et al., 2022b) is a new and popular population-based algorithm. It is influenced by artificial hummingbirds that accomplish foraging through an information exchange process. Human behavior-based algorithms simulate human community cooperation and communication processes. The Group Teaching Optimization Algorithm (GTOA; Zhang & Jin, 2020) is a typical human behavior-based algorithm. GTOA simulates the behavior of a teacher in a class (community) to develop a specific teaching method based on the differences of students (communication process). Physics- and chemistry-based algorithms are inspired by scientific phenomena such as electromagnetic forces, gravitational forces, magnetic fields, and chemical reactions. The Gravity Search Algorithm (GSA; Rashedi et al., 2009) is one of the most common and well-known physics- and chemistry-based algorithms. It is inspired by the laws of gravity and motion based on Newton. Atomic Search Optimization (ASO; Zhao et al., 2019) is an emerging physics- and chemistry-based algorithm that simulates the interactions of atoms in nature. The crystal structure algorithm (CryStAl; Talatahari et al., 2021) is chiefly inspired by the principles underlying the formation of crystal structures from the addition of the basis to the lattice points, which is a natural phenomenon that can be seen in the symmetric arrangement of constituents in crystalline minerals such as quartz.
According to the “No Free Lunch” theorem (Griffiths & Orponen, 2005), no single optimization algorithm can effectively solve all optimization problems. A certain algorithm tends to provide a better solution only in some specific optimization problems. Different NH algorithms are often proposed for solving optimization problems in specific contexts. At the same time, researchers tend to migrate NH algorithms to solve other types of optimization problems. Then, due to the differences in constraints, modalities, concavity, etc., of different types of optimization problems. Therefore, NH algorithms are often accompanied by many potential problems that affect the performance of the algorithm when solving different optimization problems, such as local capture of optimal values, premature convergence, slow convergence, and exploration-utilization imbalance (Shan et al., 2023; Su et al., 2023). However, these potential problems during optimization can lead to unsuitable solutions obtained by the algorithm that do not obtain optimal solutions (Hu et al., 2023d). Therefore, in order to ensure the broad adaptability and generality of the NH algorithm in solving optimization problems (Premkumar et al., 2022; Yu et al., 2022), researchers have attempted to enhance and improve the NH algorithm in a variety of ways in the context of multiple optimization applications. Such behavior can significantly improve the NH algorithm’s ability to solve multiple types of optimization problems and make it potentially highly adaptable (Qi et al., 2022a; Qiao et al., 2022).
From the related literature, it can be found that researchers have improved the performance of metaheuristic algorithms and applied them to realistic optimization problems by two forms of modifications: (i) proposing improvement strategies and introducing existing strategies to mitigate and solve the performance deficiencies of the algorithms locally (Hu et al., 2023b). For example, Hu et al. (2022d) addressed the problems of low accuracy and slow convergence of the black widow optimization algorithm by proposing three improved strategies: mate selection strategy, mutation operator for differential evolution, and adaptive parameter strategy. Yang et al. (2022) proposed a multi-strategy whale optimization algorithm. The four strategies include chaotic logic mapping, adaptive weights and dynamic convergence factors, the Lévy flight mechanism, and the introduction of an evolutionary population dynamics mechanism to solve the problems of local optimum and slow convergence of the whale optimization algorithm. Mohammad introduced the multi-trial vector (MTV) method for diversity components to the differential evolutionary algorithm. The improved algorithm alleviated premature convergence and increased population diversity (Nadimi-Shahraki & Zamani, 2022). In addition, researchers have studied many examples of algorithm improvement by introducing strategies (Saha, 2022; Qi et al., 2022b). (ii) To integrate the algorithm with other NH algorithms to draw on the algorithm’s ability to solve different problems (Zhou et al., 2022). For example, Rohit et al. proposed a hybrid version of the Marine Predator Algorithm (MPA) and the Naked Mole Rat Algorithm (NMRA) to combine the advantages of both algorithms (Salgotra et al., 2023). Seyyedabbasi (2022) combined the WOA algorithm with the Sine Cosine Algorithm (SCA) to fuse the advantages of both exploration and exploitation. Saafan & El-Gendy (2021) combined the Whale Optimization Algorithm (WOA) with the Salp Swarm algorithm (SSA) for the tuning of adaptive PID controllers. Chakraborty et al. (2021) mixed adaptive differential evolution (SHADE) with an improved WOA to reduce the cases of falling into local optimum and stagnation.
However, large-scale application processes have revealed that the NH algorithms in the two modified forms mentioned above sometimes suffer from unbalanced exploration and exploitation processes and unstable optimization when used for optimization problems. The introduction of multiple operators and strategies will improve the optimization performance of the algorithm in some aspects, but in this case, the mutual interference and influence of multiple strategies may indirectly harm the performance of the algorithm in other aspects. In addition, for the fusion form of multiple algorithms, the original NH algorithm absorbs the process of fusion algorithms with significant optimization performance. However, the performance deficiencies of the fusion algorithm in the face of other optimization problems are retained throughout the optimization process of the algorithm. Therefore, the improved NH algorithm combining the two modified forms demonstrates better convergence and optimization performance in solving optimization problems than the fusion strategy or algorithm alone. For example, Hu et al. (2022d) proposed a hybrid modified arithmetic optimization algorithm (CSOAOA) that introduces two strategies, the good point set and the optimal neighborhood, and then fuses the modified arithmetic optimization algorithm with the crisscross optimization algorithm. The algorithm successfully solved some numerical cases and engineering optimization problems. A new hybrid PSO based on the sine cosine algorithm and Levy flight is proposed by Chegini et al. (2018). This algorithm combines the sine cosine algorithm and PSO. Then, the Levy flight strategy is introduced to improve exploration capability. Yu et al. (2023) proposed a grey wolf optimizer-based chaotic GSA for global optimization. The proposed algorithm improves the exploration efficiency by embedding a chaotic map. Then, a hunting mechanism based on the gray wolf optimizer is introduced to the improved GSA for improving the exploitation process.
BWO is a swarm intelligence algorithm that simulates the swim, prey, and whale-falling behavior of beluga whales. It has successfully solved the truss structure optimization problem due to its fast search speed, few control parameters, and strong global search capability. In addition, the results of the BWO algorithm on 75 test functions show that the BWO algorithm is competitive and effective compared with some well-known algorithms. This study still introduces the hybrid BWO based on the jellyfish search (JS) optimizer (HBWO-JS) algorithm for solving engineering optimization problems. There are three main motivations and implications: (i) BWO is considered an effective algorithm for solving engineering optimization (Zhong et al., 2022). However, it tends to fall into the best local solution and low convergence accuracy at the exploitation stage. This result has led to BWO producing unsatisfactory optimization results in solving engineering optimization problems. Therefore, the BWO algorithm is improved to address the shortcomings of the algorithm by combining two modified forms to solve high-complexity and high-dimensional engineering optimization problems that meet realistic requirements. (ii) The JS optimizer is structurally sound, and the introduction of the ocean flow process ensures a reasonable exploitation phase and the ability to jump out of local solutions (Chou & Truong, 2021). The JS optimizer successfully solves the structural optimization problem. JS may be an effective metaheuristic algorithm for solving optimization problems. Furthermore, since the JS optimizer was proposed, it has gained wide attention and application in various fields, for example, hyperparameters of the stacking system (Truong & Chou, 2022), income forecast of rural residents (Lei et al., 2022), global optimization with applications to cloud task scheduling (Attiya et al., 2022), optimal management of coastal aquifers (Ezzeldin et al., 2022), parameter Identification of photovoltaic models (Abdel-Basset et al., 2021), multi-level threshold image segmentation (Zheng et al., 2023), and achieved good optimization results. (iii) The fusion of BWO algorithm and JS algorithm can significantly improve the optimization performance of the algorithm in the exploitation stage. However, there is a possibility of indirectly depleting the performance of other aspects. Therefore, multiple enhancement strategies for different aspects are introduced to improve the performance loss caused by algorithm fusion.
Therefore, this paper first integrates the BWO algorithm with the JS algorithm to improve the problem that BWO tends to fall into the best local solution and low convergence accuracy during the exploitation phase through multi-stage exploration and collaborative exploitation. The BWO algorithm borrows and absorbs the JS algorithm’s ability to efficiently solve truss structure optimization problems by relying on active and passive motion behaviors. However, enhancing the exploitation throughout the iteration may unbalance the exploration and exploitation process in order to cause premature stagnation and thus reduce the optimization capability of BWO. For this reason, the vertical crossover operator is introduced in this paper to alleviate the problem of an unbalanced exploration and exploitation process, thus further improving the optimization capability of the algorithm. The vertical crossover operator normalizes the upper and lower bounds of two stochastic dimensions of the same search agent, ensuring that the dimension that may be optimal is not destroyed. Then, the introduced Gaussian variation strategy forces the agents to explore their minimal neighborhoods, extending the whole iterative search process, thus enhancing the algorithm’s ability to jump out of local premature stagnation. The BWO algorithm is able to effectively solve complex high-dimensional engineering optimization problems through the combination of vertical crossover operator, Gaussian variation strategy, and fusion JS algorithm. To verify the optimization capability of the proposed HBWO-JS, the effectiveness of the HBWO-JS combining the two modified forms is verified using the CEC2019 test suites. The dimensional scalability of the proposed HBWO-JS is investigated on CEC2020, including 30, 50, and 100 dimensions. Secondly, the proposed HBWO-JS is compared with other recently proposed algorithms, and its quality is evaluated using the Wilcoxon rank sum and Friedman test. In addition, engineering optimization and truss topology optimization problems are used to verify the practicality of the proposed algorithm.
There are three main contributions of this study:
A hierarchical search algorithm for hybrid JS and BWO is proposed, which improves the problem of easily falling into local solutions during exploitation by multi-stage exploration and cooperative exploitation well and overcomes the problem that the exploitation process of BWO may regress to exploration.
The vertical crossover operator is introduced, considering the existence of dimensions where the optimal search agent is not the optimal case. The vertical crossover operator selects the same search agent as the pivot point of the exploration region and chooses two random dimensions to normalize the upper and lower bounds. The vertical crossover operation produces a descendant search agent that does not destroy the dimension that may be optimal. The vertical crossover operator overcomes the problem of fusing BWO and JS exploration and exploitation imbalances.
Based on the current position information of the search region of each agent, the agents are forced to explore their very small neighborhood search region by Gaussian variation to avoid exploring the possible better positions of the agents ignoring the neighborhood. Thus, the Gaussian variation strategy extends the search agents’ exploration regions and helps the algorithm to jump out of local stagnation more easily.
The rest of this paper is structured as follows: Section 2 explains the BWO algorithm and the JS algorithm in basic terms. The vertical crossover operator and Gaussian variation strategy are described and the proposed HBWO-JS algorithm is presented in detail in Section 3. Section 4 is dedicated to numerical experiments and results from the analysis, including the comparison of HBWO-JS with other state-of-the-art algorithms on CEC2019 and CEC2020. Section 5 evaluates the effectiveness of the proposed HBWO-JS in solving practical problems using three real engineering design problems. Finally, the proposed HBWO-JS is applied to the truss topology optimization problem. The conclusions of this paper are presented in Section 7.
2. Fundamentals
This section explains the fundamentals of the meta-heuristics that need to be fused in order to propose a hybrid multi-strategy metaheuristic algorithm for solving engineering problems. The following paragraphs outline the BWO and JS algorithms.
2.1. The beluga whale optimization
Beluga whale optimization (BWO) algorithm (Zhong et al., 2022) is a proposed NH algorithm based on the behavior of beluga whales, which mainly simulates the swimming, feeding and whale falling behavior of beluga whale populations in nature. Based on the mechanism of population, the beluga whale population is considered as a search agent in the BWO algorithm, and each beluga whale is a candidate solution, and its position is continuously updated during the optimization phase. The advantages of the original BWO algorithm are a simple optimization structure, few parameters, and easy implementation. The whole process of BWO includes the exploration and exploitation phase, the whale landing phase, and specific implementation steps as follows.
2.1.1. Initialization
Suppose the whole population of beluga whales (as shown in Equation 2.1) has N individual beluga whales and is randomly initialized in the dim dimensional search space.
2.1.2. The swim behavior (exploration phase)
Some beluga whales will perform social behaviors through different postures when moving, such as two belugas swimming closely together in a synchronized or mirrored manner. This unique population behavior provides a direction for modeling swim behavior strategies. Beluga whales will effectively explore the solution space through different swim behaviors. The swimming behavior (exploration phase) defines the balance factor in addition to the position update formulation.
2.1.2.1. The balancing factor Bf
The balancing factor Bf is proposed to help the BWO algorithm move efficiently from the exploration to the exploitation phase, and the corresponding model is shown below.
where t denotes the iteration of the current situation, T represents the maximum number of iterations, and Br is an arbitrary number between (0, 1) that varies randomly with the iterations. The value of Bf influences the choice of the update strategy. If Bf is greater than 0.5, the strategy of the exploration phase is employed to update the beluga whale’s location. Conversely, the strategy in the exploitation phase is employed to update the beluga whale’s position. From Fig. 1, it can be found that the fluctuation range of Bf is gradually decreasing from (0, 1) to (0, 0.5) as the number of iterations T increases, indicating that the probabilities of the mining and exploration phases have changed, specifically the probability of the mining phase is significantly increasing.

2.1.2.2. Update location of the swim behavior
The exploratory behavior of the BWO algorithm is referenced to the swim activity of beluga whales. Therefore, the location of the search agents is determined by the paired swimming between belugas, which is updated as follows:
where Xi,j (t+1) is the new position of the ith beluga whale in the jth dimension for t+1 iterations. prand is a randomly selected dimension from the dim dimensions. Xi,prand (t) is the position of the ith beluga at the time of the prand dimension. Xrand,p1(t) is a randomly selected position in the jth dimension different from the ith beluga whale. r1 and r2 are random numbers between 0 and 1. The formula for updating the position of the beluga whale is chosen based on the parity of the jth dimension, and the updated position of the beluga whale reflects the synchronized or mirrored behavior of the beluga while swimming or diving.
2.1.3. The feeding behavior (exploitation phase)
Beluga whales will seek the collaboration of the positions of nearby belugas when foraging. Thus, beluga whales accomplish foraging through the information provided by the beluga whales in the best position and the beluga whales in other positions. At the same time, this beluga whale also provides location information to other beluga whales. The foraging behavior (exploitation phase) defines the Levy operator in addition to the representation of position updates.
2.1.2.1. The defined of the Levy operator
Levy operator Levyf is the Levy function and the main formula is shown below:
where U and V represent normally distributed random numbers. α is chosen with reference to the original BWO (Zhong et al., 2022) and is a default constant equal to 1.5.
2.1.2.2. Update location of the feeding behavior
The exploitation phase of BWO mimics the feeding behavior of beluga whales. Beluga whales forage or move by cooperating with nearby belugas whales. Therefore, the exploitation phase of the BWO algorithm is based on sharing optimal location information and other location information. The introduction of the Levy flight strategy in the update formula (Equation 2.6) enhances the convergence and convergence of the BWO algorithm. The mathematical model of the exploitation phase is represented as follows:
where Xi(t) and Xrand(t) are the positions of the ith beluga whale and random beluga whales at t iterations, and Xi(t+1) is the new position of the ith beluga at t+1 iterations. Xbest(t) is the best-positioned individual of all beluga whales. r3 and r4 are random numbers between (0, 1). C1 is a factor of arbitrary jump strength to adjust the power of the Levy flight, and C1 = 2·r4·(1- t / T).
2.1.4. The behavior of whale falls
During movement and foraging, a few beluga whales are subjected to a predatory minority of prey and do not survive, thus falling to the bottom. Therefore, the information about the location of the beluga whale fall can help other beluga whales to avoid the threat. Also, a whale fall probability is set to simulate the small changes in the population from beluga whale falls.
2.1.4.1. The defined of the the probability of whale fall Wf
The linear calculation of the probability of whale fall (Wf) during the whale fall is given by
Figure 2 provides the variation of Bf and Wf. The probability of whale fall gradually decreases from 0.1 to 0.05 as the iteration proceeds, implying that beluga whale mortality may be lower when they are closer to the food source during the exploitation phase. Algorithm 1 shows the pseudo-code of BWO.

2.1.4.2. Update location of the whale falls
The behavior of whale falls simulates the process of beluga whale mortality. To ensure that the population size remains N after the whale fall process, the position of the beluga whale and the step size of the whale fall are used to determine the updated position. The associated mathematical model is expressed as follows:
where r5, r6 and r7 are random numbers that lie between 0 and 1, and XStep is the step size of the whale fall, as follows:
where C2 is the parameter factor related to whale falling probability, and C2 =2Wf × N. ub and lb are the upper and lower boundaries of the independent variables, respectively.

2.2. JS optimizer
JS is a population-based NH algorithm proposed by Chou & Truong (2021), inspired by the behavior of jellyfish in the ocean. Like standard NH algorithms, JS starts with a random solution and iteratively optimizes through the effects of ocean currents, passive motion and active motion to find a solution close to the optimal solution.
The following three equations are given to update the position of the solution to a near-optimal solution [Equations (2.10)–(2.12)], representing current influence, passive motion, and active motion, respectively. The average vector of all jellyfish usually specifies the current direction in the oceanic population to the jellyfish currently in the optimal state. Passive motion is the motion of a jellyfish in the vicinity of its position. Active motion relies on comparing the amount of food of two jellyfish to determine if there is relative motion. Where XMean is the average of all jellyfish and rand is a random number at (0, 1). α is the distribution factor, which is set to 3 in the original JS algorithm (Chou & Truong, 2021). Where γ is a shift factor that determines the length of the jellyfish movement in the nearby position. In the original JS algorithm, it is usually taken as γ = 0.1 (Chou & Truong, 2021). The definition of direction (DT) is given in Equation (2.13). Where k is the randomly determined position of the jellyfish.
The Temporal control Tool (CoT) was used to control the trend between the observed currents and the inward travel of the jellyfish population, and the related definition is shown in Equation (2.14). Where, when CoT (t) ≥ 0.5, the jellyfish move their position according to the direction of the current. Suppose CoT (t) < 0.5, then the relationship between (1-CoT (t)) and the rand is considered. If rand < (1-CoT (t)), the jellyfish update their position l0 by the formula of active movement. Otherwise, the jellyfish update their position by the correlation formula of passive movement.
3. HBWO-JS
Falling into the optimal local solution and poor convergence accuracy are the drawbacks of the BWO algorithm. In order to solve the above problems and improve the performance of the algorithm, a multi-strategy hybrid HBWO-JS algorithm is proposed. In the HBWO-JS algorithm, the BWO algorithm is integrated with the JS algorithm. The problems that BWO tends to fall into the best local solution and low convergence accuracy in the exploitation stage are improved by multi-stage exploration and collaborative exploitation. In addition, the introduction of a vertical crossover operator and Gaussian variation strategy alleviates the problems of an unbalanced exploration and exploitation process and the tendency to fall into local stagnation. In this section, the introduced vertical crossover operator and Gaussian variation strategy are first introduced. Then, the proposed HBWO-JS algorithm is introduced, and pseudo-code and flowchart are provided.
3.1. Vertical crossover operator
The vertical crossover operation originates from the crossover factor in the crisscross optimization algorithm (Meng et al., 2014). Considering the existence of dimensions where the optimal search agent is not the optimal case, the vertical crossover operator is introduced. The vertical crossover operator selects the same search agent as the pivot point of the exploration region and chooses two random dimensions to normalize the upper and lower bounds. The vertical crossover operation produces a descendant search agent that does not destroy the dimension that may be optimal. The better-performing solution will replace the obtained best solution and become the parent of HBWO-JS. Vertical crossover updates the new beluga position by performing a dimensional crossover between any two dimensions of the beluga whale position. The vertical crossover operation is used to update the position of the d1th dimension by the relationship between the d1th and d2th dimensions. After generating the new beluga positions for the next iteration, they must compete with the corresponding belugas at the positions of t iterations. The specific formula for updating the position is shown below.
where |$X_{i,{d_1}}^{vc}(t)$| is the new position of the ith beluga whale in the d1th dimension at t+1th iteration by the vertical crossover operator, both d1 and d2 belong to (1, ..., dim). F represents the objective function to be optimized.
3.2. Gaussian variation strategy
The Gaussian variation strategy simulates the process by which the beluga at the optimal position guides the other belugas to update their positions (Sultan et al., 2020). Based on information about the current position of each agent's search region, the agents are forced to explore their very small neighborhood search region by Gaussian variation to avoid exploring possible better positions in the neighborhood that the agents ignore. The Gaussian variation strategy helps the beluga at the optimal position to further explore the nearby positions of the optimal beluga, providing the possibility of finding the optimal solution. The position of the optimally located beluga whale is updated with other beluga whales’ positions by comparing them, guiding other beluga whales to find prey and escape from natural enemies. The Gaussian variant is always able to retain the better position in the iterations. The Gaussian variant strategy fully exploits the optimal beluga ground guidance, thus improving the convergence accuracy of the algorithm. The formula for the probability density function of Gaussian distribution is shown below.
where μ is the mean and σ implies the standard deviation.
The improved update strategy by the Gaussian variation operator is shown in Equation (3.4).
where φ is a random integer in the range of 0 and 1, GF is defined as shown in Equation (3.3), and Xbest,j is the new position of the best beluga whale in the jth dimension at t+1th iteration.
3.3. Proposed algorithm (HBWO-JS)
It is in this section of the paper that the proposed HBWO-JS algorithm is described. The BWO algorithm has some drawbacks when it comes to optimization. Although it is effective in finding the best solution and simple to implement, it tends to fall into optimal local solutions in the exploitation phase. To improve the convergence accuracy and avoid local optima, the exploration phase plays an important role in the algorithm performance. Meanwhile, the exploitation phase also affects the convergence performance of the algorithm. The JS algorithm gives the basic description of the algorithm in the previous section and is used as the basic part of the HBWO-JS algorithm. The JS algorithm completes the exploration and exploitation through two strategies, passive motion, and active motion. In addition, the introduction of the current ocean strategy ensures the ability of JS to search for optimal solutions in the exploration phase. The JS algorithm attempts to find efficient solutions in the sub-optimal region of the search space. Although the JS algorithm is generally simple to implement and has fewer parameters, it demonstrates weak capabilities in the exploitation phase of solution space exploration. Therefore, by fusing the BWO and JS algorithms, the proposed HBWO-JS algorithm guarantees an efficient exploration process and discovers optimal and suitable solutions throughout the search region. However, there are some limitations in the exploitation phase. The HBWO-JS hybrid algorithm improves the convergence accuracy by adding vertical crossover operators to alleviate the problem of premature stagnation in the exploitation phase. In addition, the introduction of the Gaussian variation strategy extends the search for the optimal solution during the exploitation process, thus ensuring that the algorithm finds the optimal solution. Thus, the proposed fusion improvement algorithm balances exploration and exploitation in an orderly manner and improves the algorithm’s performance.
In the optimization process of the proposed HBWO-JS algorithm, the swim behavior of BWO and the passive motion of JS algorithm are executed first, as well as the foraging behavior and active motion in the exploitation phase. Then, the introduction of the falling whale process, the vertical cross operator and the Gaussian variation strategy help the algorithm to jump out of the local solution effectively and improve the convergence performance in the exploitation phase. The following section provides the detailed steps of the proposed HBWO-JS.
Step 1: The parameters of the algorithm are set, including the overall size N and the maximum number of iterations T, the distribution factor α. The initial positions of all beluga whales are randomly generated in the solution space, and the fitness value is given based on the optimization function;
Step 2: Each beluga is decided to enter the exploration or exploitation phase according to the Bf balance factor. Suppose Bf > 0.5 for the iterative process, the position of the beluga is updated based on Equation (2.3) for the exploration phase. Suppose Bf < 0.5, the position of the beluga is updated based on Equation (2.6) for the exploitation phase.
Step 3: Calculate the probability Wf of the whale falling and update the position of the beluga whale according to Equation (2.7).
Step 4: The position of the beluga whales in the pairwise dimension is updated by Equation (3.1) and Equation (3.2) of the vertical cross operator.
Step 5: The Gaussian variation strategy based on Equation (3.4) updates the position of the beluga whale by the neighborhood of the optimal beluga whale position.
Step 6: Calculate CoT (t) according to Equation (2.14). If c(t) ≥ 0.5, the beluga will follow the current and update its position by Equation (2.10).
Step 7: If CoT (t) < 0.5, consider further that if the random number rand > (1 - CoT (t)), then the beluga whales will update its position by the passive motion of Equation (2.11); otherwise, the position of the beluga whales will be updated by the active motion according to Equation (2.12).
Step 8: Determine whether the new position of the updated white whale crosses the upper and lower boundaries. Then find the optimal beluga whale position location best*. Update the number of iterations t, and determine the iteration termination condition.
If t iterations are greater than the maximum number of iterations T, the HBWO-JS algorithm stops the optimization process. Otherwise, Step 2 is repeated.
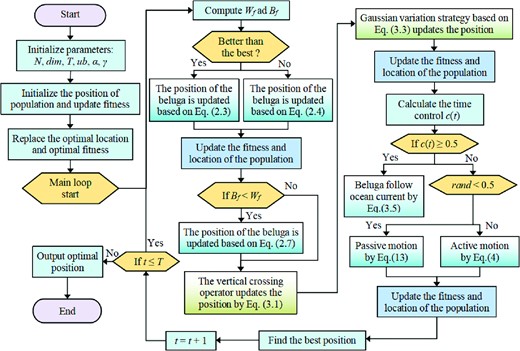
In addition, to show the HBWO-JS algorithm more clearly, Fig. 3 provides the flowchart of the proposed HBWO-JS. The updates to the positions and the vertical crossover operator, and Gaussian variation strategy are marked in the figure for the exploration and exploitation phases of the BWO algorithm and JS algorithm, respectively. In addition, the figure first defines the relevant parameters and initialization. Then the position update process is executed until the termination requirement is satisfied, and then the loop is skipped.

Algorithm 2 provides the pseudo-code of the proposed HBWO-JS. Lines 3-16 are the exploration and exploitation process of the original BWO algorithm. Lines 17-25 are the whale fall phase. Lines 27-38 give the update process of the vertical crossover operator and Gaussian variation strategy. Lines 39-54 update the position by active and passive motion of the JS algorithm.

3.4. The algorithm complexity of HBWO-JS
The computational complexity of the algorithm is an essential indicator of understanding its performance of the algorithm. The HBWO-JS algorithm consists of five related processes: initialization, fitness evaluation, update of the beluga whale, modified BWO vertical crossover operator and Gaussian variation operator, and fusion of the JS algorithm. First, the initialization is targeted to all beluga whales in the population and the process does not count in the iteration cycle. Therefore, the computational complexity of the initialization process is O(N). Secondly, the fitness evaluation is influenced by the complexity of the target problem, and different optimization problems will lead to different complexities, so the complexity of the fitness evaluation is not considered. In addition, for the location update process of beluga, the exploration and exploitation phases are affected by Bf(t). Therefore, the computational complexity is calculated as O(T·N). In the whale fall phase, the beluga whale position is updated only when Bf(t)≤Wf. Therefore, the literature related to the original BWO algorithm (Zhong et al., 2022) approximates the complexity of this part as O(N·0.1·T). Vertical crossover considers the communication between two individual beluga whales. Therefore, the strategy will simultaneously update the positions of both beluga whales during one cycle. The Gaussian variation operator is targeted at all beluga whales in the population algorithm. Therefore, the overall complexity of both is O(N·T·3/2). Finally, the active and passive motions of the JS algorithm are influenced by the time control function. Therefore, the complexity update position of the JS algorithm is O(T·N), where T is the maximum number of iterations and N is the number of belugas. Therefore, the computational complexity of HBWO-JS is O(N·(1+3.6·T)).
4. Application of the HBWO-JS on Benchmark Functions
This section applies the proposed IWOSSA algorithm to a series of test experiments to verify its various performances. All experimental simulations are performed using Matlab-2019b, Intel(R) Core(TM) i5-9300H CPU @ 2.40 GHz 8.00 GB.
4.1. Algorithm and experimental parameter settings
To examine the performance of the proposed HBWO-JS algorithm, it was compared with the CEC winner and well-known algorithms. Experiments were conducted on the CEC2017 test suite (see Table A1) using three different CEC winners and four well-known algorithms. In addition, to investigate the performance of the HBWO-JS algorithm for different test functions, the CEC2019 benchmark problem is tested in numerical experiments. Table A2 provides the CEC2019 test function details in Appendix. In addition, to study the dimensional scalability of the proposed HBWO-JS algorithm, the CEC2020 benchmark suite in 10, 30, 50, and 100 dimensions is tested in numerical experiments. Table A3 provides the CEC2020 test function details in Appendix. The algorithms compared include, three different CEC winners, four well-known algorithms and eight recently proposed intelligent algorithms. The specific algorithms are shown below:
JS optimizer (2021; Chou & Truong, 2021),
BWO (2022; Zhong et al., 2022),
AHA (2022; Zhao et al., 2022b),
Artificial rabbits optimization (ARO; 2022; Wang et al., 2022)
Dandelion optimizer (DO; 2022; Zhao et al., 2022a),
Snake optimizer (SO; 2022; Hashim & Hussien, 2022),
White shark optimizer (WSO; 2022; Braik et al., 2022),
Reptile search algorithm (RSA; 2022; Abualigah et al., 2022),
L-SHADE (2014; Tanabe & Fukunaga, 2014),
LSHADE-cnEpSin (2016; Awad et al., 2016),
LSHADE-SPACMA (2017; Mohamed et al., 2017).
PSO (1995; Kennedy & Eberhart, 1995),
GA (1975; Chen et al., 2022),
WOA (2016; Mirjalili & Lewis, 2016),
Grey wolf optimizer (GWO; 2014; Mirjalili et al., 2014),
Artificial bee colony (ABC; 2005; Karaboga & Akay, 2009).
The parameter settings of the above latest algorithms are summarized in Table 1. To eliminate the randomness of the experiments, 30 independent runs are performed times. The maximum number of iterations and population size of all algorithms are 500 and 30, respectively. This paper evaluated the performance of algorithms based on the following criteria to analyse the performance of the algorithms.
where NE is the number of executions and whaleend is the result of the last iteration of each run. In this study, algorithms with smaller Best, Worst, Mean, and Std are more stable.
| Methods . | Year . | Related parameter settings . |
|---|---|---|
| JS | 2021 | β = 3, γ = 0.1. |
| BWO | 2022 | Probability of whale fall decreased at interval Wf [0.1, 0.05] |
| AHA | 2022 | Migration coefficient = 2n |
| WSO | 2022 | fmin = 0.07, fmax = 0.75, τ = 4.125, a0 = 6.25, a1 = 100, a2 = 0.0005. |
| DO | 2022 | α ∈ [0, 1], k ∈ [0, 1]. |
| PSO | 1997 | Cognitive coefficient and Social coefficient = 2, Inertia constant: decreased in [0.9–0]. |
| WOA | 2016 | Fluctuation range: Reduced in [2, 0], coefficient of the logarithmic spiral shape = 1. |
| GWO | 2014 | Convergence parameter (a) : Linear reduction from 2 to 0. |
| GA | 1975 | Type: real coded, selection: roulette wheel, crossover = 0.8, mutation = Gaussian. |
| L-SHADE | 2014 | Crossover rate MCR = 0.5, scaling factor MF = 0.5. |
| LSHADE-EpSin | 2016 | H = 5, NPmin = 4, pbest rate = 0.11, arc rate = 1.4, ps = 0.5, pc =0.4. |
| Methods . | Year . | Related parameter settings . |
|---|---|---|
| JS | 2021 | β = 3, γ = 0.1. |
| BWO | 2022 | Probability of whale fall decreased at interval Wf [0.1, 0.05] |
| AHA | 2022 | Migration coefficient = 2n |
| WSO | 2022 | fmin = 0.07, fmax = 0.75, τ = 4.125, a0 = 6.25, a1 = 100, a2 = 0.0005. |
| DO | 2022 | α ∈ [0, 1], k ∈ [0, 1]. |
| PSO | 1997 | Cognitive coefficient and Social coefficient = 2, Inertia constant: decreased in [0.9–0]. |
| WOA | 2016 | Fluctuation range: Reduced in [2, 0], coefficient of the logarithmic spiral shape = 1. |
| GWO | 2014 | Convergence parameter (a) : Linear reduction from 2 to 0. |
| GA | 1975 | Type: real coded, selection: roulette wheel, crossover = 0.8, mutation = Gaussian. |
| L-SHADE | 2014 | Crossover rate MCR = 0.5, scaling factor MF = 0.5. |
| LSHADE-EpSin | 2016 | H = 5, NPmin = 4, pbest rate = 0.11, arc rate = 1.4, ps = 0.5, pc =0.4. |
| Methods . | Year . | Related parameter settings . |
|---|---|---|
| JS | 2021 | β = 3, γ = 0.1. |
| BWO | 2022 | Probability of whale fall decreased at interval Wf [0.1, 0.05] |
| AHA | 2022 | Migration coefficient = 2n |
| WSO | 2022 | fmin = 0.07, fmax = 0.75, τ = 4.125, a0 = 6.25, a1 = 100, a2 = 0.0005. |
| DO | 2022 | α ∈ [0, 1], k ∈ [0, 1]. |
| PSO | 1997 | Cognitive coefficient and Social coefficient = 2, Inertia constant: decreased in [0.9–0]. |
| WOA | 2016 | Fluctuation range: Reduced in [2, 0], coefficient of the logarithmic spiral shape = 1. |
| GWO | 2014 | Convergence parameter (a) : Linear reduction from 2 to 0. |
| GA | 1975 | Type: real coded, selection: roulette wheel, crossover = 0.8, mutation = Gaussian. |
| L-SHADE | 2014 | Crossover rate MCR = 0.5, scaling factor MF = 0.5. |
| LSHADE-EpSin | 2016 | H = 5, NPmin = 4, pbest rate = 0.11, arc rate = 1.4, ps = 0.5, pc =0.4. |
| Methods . | Year . | Related parameter settings . |
|---|---|---|
| JS | 2021 | β = 3, γ = 0.1. |
| BWO | 2022 | Probability of whale fall decreased at interval Wf [0.1, 0.05] |
| AHA | 2022 | Migration coefficient = 2n |
| WSO | 2022 | fmin = 0.07, fmax = 0.75, τ = 4.125, a0 = 6.25, a1 = 100, a2 = 0.0005. |
| DO | 2022 | α ∈ [0, 1], k ∈ [0, 1]. |
| PSO | 1997 | Cognitive coefficient and Social coefficient = 2, Inertia constant: decreased in [0.9–0]. |
| WOA | 2016 | Fluctuation range: Reduced in [2, 0], coefficient of the logarithmic spiral shape = 1. |
| GWO | 2014 | Convergence parameter (a) : Linear reduction from 2 to 0. |
| GA | 1975 | Type: real coded, selection: roulette wheel, crossover = 0.8, mutation = Gaussian. |
| L-SHADE | 2014 | Crossover rate MCR = 0.5, scaling factor MF = 0.5. |
| LSHADE-EpSin | 2016 | H = 5, NPmin = 4, pbest rate = 0.11, arc rate = 1.4, ps = 0.5, pc =0.4. |
4.2. Ablation analysis of multi-strategy fusion BWO
Ablation analysis of multiple strategies is done to verify the improvement of the proposed strategies on the performance of BWO and to verify the impact of the collaborative strategies on the performance of the algorithm. In order to improve the drawbacks of BWO, which is easy to fall into local solutions and low convergence accuracy, and to improve the optimization performance of the algorithm, three fusion strategies are introduced in the proposed HBWO-JS algorithm, including the vertical cross (VC) operator, Gaussian variation (GV) strategy, and JS optimizer. The variant BWO algorithm with one or more fusion strategies is given in Table 2. Where 1 indicates that the strategy is introduced and 0 indicates that the strategy is not introduced. The performance of the BWO algorithm with multiple variants of fusion was analysed in the CEC2019 test suite. The experimental results of multiple BWO variants in the CEC2019 test suite are given in Table 3, which includes the mean, standard value, and ranking. Where the maximum number of iterations is 500, and the number of populations is 30. All algorithms are run 30 times.
| Strategies . | VCBWO . | GVBWO . | BWO-JS . | VCGBWO . | VCBWO-JS . | GVBWO-JS . | HBWO-JS . |
|---|---|---|---|---|---|---|---|
| VC operator | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| GV strategy | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| JS optimizer | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| Strategies . | VCBWO . | GVBWO . | BWO-JS . | VCGBWO . | VCBWO-JS . | GVBWO-JS . | HBWO-JS . |
|---|---|---|---|---|---|---|---|
| VC operator | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| GV strategy | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| JS optimizer | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| Strategies . | VCBWO . | GVBWO . | BWO-JS . | VCGBWO . | VCBWO-JS . | GVBWO-JS . | HBWO-JS . |
|---|---|---|---|---|---|---|---|
| VC operator | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| GV strategy | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| JS optimizer | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| Strategies . | VCBWO . | GVBWO . | BWO-JS . | VCGBWO . | VCBWO-JS . | GVBWO-JS . | HBWO-JS . |
|---|---|---|---|---|---|---|---|
| VC operator | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| GV strategy | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| JS optimizer | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| Function . | Index . | VCBWO . | GVBWO . | BWO-JS . | VCGBWO . | VCBWO-JS . | GVBWO-JS . | HBWO-JS . |
|---|---|---|---|---|---|---|---|---|
| cec01 | Mean | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Std | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Rank | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| cec02 | Mean | 4.9355 | 4.8391 | 4.2545 | 4.4379 | 4.2530 | 4.3753 | 4.2956 |
| Std | 0.1057 | 0.2351 | 0.0218 | 0.2107 | 0.0244 | 0.2701 | 0.1350 | |
| Rank | 7 | 6 | 2 | 5 | 1 | 4 | 3 | |
| cec03 | Mean | 1.5186 | 4.7697 | 2.9326 | 1.5379 | 1.4588 | 2.4477 | 1.4407 |
| Std | 0.1947 | 0.7478 | 0.9471 | 0.3201 | 0.2376 | 0.6221 | 0.2172 | |
| Rank | 3 | 7 | 6 | 4 | 2 | 5 | 1 | |
| cec04 | Mean | 19.9451 | 62.5346 | 23.5441 | 17.4045 | 17.6106 | 20.7087 | 16.2736 |
| Std | 5.9921 | 12.9445 | 8.2295 | 5.6700 | 6.9618 | 7.2957 | 4.7905 | |
| Rank | 4 | 7 | 6 | 2 | 3 | 5 | 1 | |
| cec05 | Mean | 5.9789 | 28.9367 | 1.1146 | 1.7274 | 1.0591 | 1.1021 | 1.0149 |
| Std | 3.4240 | 12.0086 | 0.0477 | 0.1383 | 0.0348 | 0.0560 | 0.0336 | |
| Rank | 6 | 7 | 4 | 5 | 2 | 3 | 1 | |
| cec06 | Mean | 4.5496 | 9.0390 | 3.2280 | 3.7285 | 2.3042 | 3.0224 | 1.7047 |
| Std | 0.9632 | 1.0891 | 1.1071 | 0.8793 | 1.1065 | 1.0899 | 0.7570 | |
| Rank | 6 | 7 | 4 | 5 | 2 | 3 | 1 | |
| cec07 | Mean | 581.3652 | 1498.3475 | 910.7788 | 481.9452 | 524.7422 | 852.2646 | 484.5589 |
| Std | 146.0901 | 185.9660 | 338.9622 | 149.1909 | 160.9474 | 268.0498 | 158.9041 | |
| Rank | 4 | 7 | 6 | 1 | 3 | 5 | 2 | |
| cec08 | Mean | 3.8119 | 4.5207 | 3.9995 | 3.7101 | 3.7076 | 3.8685 | 3.4773 |
| Std | 0.2722 | 0.2300 | 0.3018 | 0.2420 | 0.2224 | 0.3583 | 0.3336 | |
| Rank | 4 | 7 | 6 | 3 | 2 | 5 | 1 | |
| cec09 | Mean | 1.2720 | 2.2206 | 1.2419 | 1.2639 | 1.2379 | 1.3179 | 1.2026 |
| Std | 0.0636 | 0.6949 | 0.0762 | 0.0707 | 0.0661 | 0.0918 | 0.0581 | |
| Rank | 5 | 7 | 3 | 4 | 2 | 6 | 1 | |
| cec10 | Mean | 20.2651 | 21.3527 | 20.5005 | 18.0535 | 18.0260 | 19.0130 | 17.9548 |
| Std | 2.5348 | 0.1678 | 3.4343 | 6.1666 | 7.3379 | 5.7405 | 6.9747 | |
| Rank | 5 | 7 | 6 | 3 | 2 | 4 | 1 | |
| Average rank | 4.5 | 6.3 | 4.4 | 3.3 | 2 | 4.1 | 1.3 | |
| Finally rank | 6 | 7 | 5 | 3 | 2 | 4 | 1 | |
| Function . | Index . | VCBWO . | GVBWO . | BWO-JS . | VCGBWO . | VCBWO-JS . | GVBWO-JS . | HBWO-JS . |
|---|---|---|---|---|---|---|---|---|
| cec01 | Mean | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Std | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Rank | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| cec02 | Mean | 4.9355 | 4.8391 | 4.2545 | 4.4379 | 4.2530 | 4.3753 | 4.2956 |
| Std | 0.1057 | 0.2351 | 0.0218 | 0.2107 | 0.0244 | 0.2701 | 0.1350 | |
| Rank | 7 | 6 | 2 | 5 | 1 | 4 | 3 | |
| cec03 | Mean | 1.5186 | 4.7697 | 2.9326 | 1.5379 | 1.4588 | 2.4477 | 1.4407 |
| Std | 0.1947 | 0.7478 | 0.9471 | 0.3201 | 0.2376 | 0.6221 | 0.2172 | |
| Rank | 3 | 7 | 6 | 4 | 2 | 5 | 1 | |
| cec04 | Mean | 19.9451 | 62.5346 | 23.5441 | 17.4045 | 17.6106 | 20.7087 | 16.2736 |
| Std | 5.9921 | 12.9445 | 8.2295 | 5.6700 | 6.9618 | 7.2957 | 4.7905 | |
| Rank | 4 | 7 | 6 | 2 | 3 | 5 | 1 | |
| cec05 | Mean | 5.9789 | 28.9367 | 1.1146 | 1.7274 | 1.0591 | 1.1021 | 1.0149 |
| Std | 3.4240 | 12.0086 | 0.0477 | 0.1383 | 0.0348 | 0.0560 | 0.0336 | |
| Rank | 6 | 7 | 4 | 5 | 2 | 3 | 1 | |
| cec06 | Mean | 4.5496 | 9.0390 | 3.2280 | 3.7285 | 2.3042 | 3.0224 | 1.7047 |
| Std | 0.9632 | 1.0891 | 1.1071 | 0.8793 | 1.1065 | 1.0899 | 0.7570 | |
| Rank | 6 | 7 | 4 | 5 | 2 | 3 | 1 | |
| cec07 | Mean | 581.3652 | 1498.3475 | 910.7788 | 481.9452 | 524.7422 | 852.2646 | 484.5589 |
| Std | 146.0901 | 185.9660 | 338.9622 | 149.1909 | 160.9474 | 268.0498 | 158.9041 | |
| Rank | 4 | 7 | 6 | 1 | 3 | 5 | 2 | |
| cec08 | Mean | 3.8119 | 4.5207 | 3.9995 | 3.7101 | 3.7076 | 3.8685 | 3.4773 |
| Std | 0.2722 | 0.2300 | 0.3018 | 0.2420 | 0.2224 | 0.3583 | 0.3336 | |
| Rank | 4 | 7 | 6 | 3 | 2 | 5 | 1 | |
| cec09 | Mean | 1.2720 | 2.2206 | 1.2419 | 1.2639 | 1.2379 | 1.3179 | 1.2026 |
| Std | 0.0636 | 0.6949 | 0.0762 | 0.0707 | 0.0661 | 0.0918 | 0.0581 | |
| Rank | 5 | 7 | 3 | 4 | 2 | 6 | 1 | |
| cec10 | Mean | 20.2651 | 21.3527 | 20.5005 | 18.0535 | 18.0260 | 19.0130 | 17.9548 |
| Std | 2.5348 | 0.1678 | 3.4343 | 6.1666 | 7.3379 | 5.7405 | 6.9747 | |
| Rank | 5 | 7 | 6 | 3 | 2 | 4 | 1 | |
| Average rank | 4.5 | 6.3 | 4.4 | 3.3 | 2 | 4.1 | 1.3 | |
| Finally rank | 6 | 7 | 5 | 3 | 2 | 4 | 1 | |
| Function . | Index . | VCBWO . | GVBWO . | BWO-JS . | VCGBWO . | VCBWO-JS . | GVBWO-JS . | HBWO-JS . |
|---|---|---|---|---|---|---|---|---|
| cec01 | Mean | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Std | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Rank | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| cec02 | Mean | 4.9355 | 4.8391 | 4.2545 | 4.4379 | 4.2530 | 4.3753 | 4.2956 |
| Std | 0.1057 | 0.2351 | 0.0218 | 0.2107 | 0.0244 | 0.2701 | 0.1350 | |
| Rank | 7 | 6 | 2 | 5 | 1 | 4 | 3 | |
| cec03 | Mean | 1.5186 | 4.7697 | 2.9326 | 1.5379 | 1.4588 | 2.4477 | 1.4407 |
| Std | 0.1947 | 0.7478 | 0.9471 | 0.3201 | 0.2376 | 0.6221 | 0.2172 | |
| Rank | 3 | 7 | 6 | 4 | 2 | 5 | 1 | |
| cec04 | Mean | 19.9451 | 62.5346 | 23.5441 | 17.4045 | 17.6106 | 20.7087 | 16.2736 |
| Std | 5.9921 | 12.9445 | 8.2295 | 5.6700 | 6.9618 | 7.2957 | 4.7905 | |
| Rank | 4 | 7 | 6 | 2 | 3 | 5 | 1 | |
| cec05 | Mean | 5.9789 | 28.9367 | 1.1146 | 1.7274 | 1.0591 | 1.1021 | 1.0149 |
| Std | 3.4240 | 12.0086 | 0.0477 | 0.1383 | 0.0348 | 0.0560 | 0.0336 | |
| Rank | 6 | 7 | 4 | 5 | 2 | 3 | 1 | |
| cec06 | Mean | 4.5496 | 9.0390 | 3.2280 | 3.7285 | 2.3042 | 3.0224 | 1.7047 |
| Std | 0.9632 | 1.0891 | 1.1071 | 0.8793 | 1.1065 | 1.0899 | 0.7570 | |
| Rank | 6 | 7 | 4 | 5 | 2 | 3 | 1 | |
| cec07 | Mean | 581.3652 | 1498.3475 | 910.7788 | 481.9452 | 524.7422 | 852.2646 | 484.5589 |
| Std | 146.0901 | 185.9660 | 338.9622 | 149.1909 | 160.9474 | 268.0498 | 158.9041 | |
| Rank | 4 | 7 | 6 | 1 | 3 | 5 | 2 | |
| cec08 | Mean | 3.8119 | 4.5207 | 3.9995 | 3.7101 | 3.7076 | 3.8685 | 3.4773 |
| Std | 0.2722 | 0.2300 | 0.3018 | 0.2420 | 0.2224 | 0.3583 | 0.3336 | |
| Rank | 4 | 7 | 6 | 3 | 2 | 5 | 1 | |
| cec09 | Mean | 1.2720 | 2.2206 | 1.2419 | 1.2639 | 1.2379 | 1.3179 | 1.2026 |
| Std | 0.0636 | 0.6949 | 0.0762 | 0.0707 | 0.0661 | 0.0918 | 0.0581 | |
| Rank | 5 | 7 | 3 | 4 | 2 | 6 | 1 | |
| cec10 | Mean | 20.2651 | 21.3527 | 20.5005 | 18.0535 | 18.0260 | 19.0130 | 17.9548 |
| Std | 2.5348 | 0.1678 | 3.4343 | 6.1666 | 7.3379 | 5.7405 | 6.9747 | |
| Rank | 5 | 7 | 6 | 3 | 2 | 4 | 1 | |
| Average rank | 4.5 | 6.3 | 4.4 | 3.3 | 2 | 4.1 | 1.3 | |
| Finally rank | 6 | 7 | 5 | 3 | 2 | 4 | 1 | |
| Function . | Index . | VCBWO . | GVBWO . | BWO-JS . | VCGBWO . | VCBWO-JS . | GVBWO-JS . | HBWO-JS . |
|---|---|---|---|---|---|---|---|---|
| cec01 | Mean | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Std | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Rank | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| cec02 | Mean | 4.9355 | 4.8391 | 4.2545 | 4.4379 | 4.2530 | 4.3753 | 4.2956 |
| Std | 0.1057 | 0.2351 | 0.0218 | 0.2107 | 0.0244 | 0.2701 | 0.1350 | |
| Rank | 7 | 6 | 2 | 5 | 1 | 4 | 3 | |
| cec03 | Mean | 1.5186 | 4.7697 | 2.9326 | 1.5379 | 1.4588 | 2.4477 | 1.4407 |
| Std | 0.1947 | 0.7478 | 0.9471 | 0.3201 | 0.2376 | 0.6221 | 0.2172 | |
| Rank | 3 | 7 | 6 | 4 | 2 | 5 | 1 | |
| cec04 | Mean | 19.9451 | 62.5346 | 23.5441 | 17.4045 | 17.6106 | 20.7087 | 16.2736 |
| Std | 5.9921 | 12.9445 | 8.2295 | 5.6700 | 6.9618 | 7.2957 | 4.7905 | |
| Rank | 4 | 7 | 6 | 2 | 3 | 5 | 1 | |
| cec05 | Mean | 5.9789 | 28.9367 | 1.1146 | 1.7274 | 1.0591 | 1.1021 | 1.0149 |
| Std | 3.4240 | 12.0086 | 0.0477 | 0.1383 | 0.0348 | 0.0560 | 0.0336 | |
| Rank | 6 | 7 | 4 | 5 | 2 | 3 | 1 | |
| cec06 | Mean | 4.5496 | 9.0390 | 3.2280 | 3.7285 | 2.3042 | 3.0224 | 1.7047 |
| Std | 0.9632 | 1.0891 | 1.1071 | 0.8793 | 1.1065 | 1.0899 | 0.7570 | |
| Rank | 6 | 7 | 4 | 5 | 2 | 3 | 1 | |
| cec07 | Mean | 581.3652 | 1498.3475 | 910.7788 | 481.9452 | 524.7422 | 852.2646 | 484.5589 |
| Std | 146.0901 | 185.9660 | 338.9622 | 149.1909 | 160.9474 | 268.0498 | 158.9041 | |
| Rank | 4 | 7 | 6 | 1 | 3 | 5 | 2 | |
| cec08 | Mean | 3.8119 | 4.5207 | 3.9995 | 3.7101 | 3.7076 | 3.8685 | 3.4773 |
| Std | 0.2722 | 0.2300 | 0.3018 | 0.2420 | 0.2224 | 0.3583 | 0.3336 | |
| Rank | 4 | 7 | 6 | 3 | 2 | 5 | 1 | |
| cec09 | Mean | 1.2720 | 2.2206 | 1.2419 | 1.2639 | 1.2379 | 1.3179 | 1.2026 |
| Std | 0.0636 | 0.6949 | 0.0762 | 0.0707 | 0.0661 | 0.0918 | 0.0581 | |
| Rank | 5 | 7 | 3 | 4 | 2 | 6 | 1 | |
| cec10 | Mean | 20.2651 | 21.3527 | 20.5005 | 18.0535 | 18.0260 | 19.0130 | 17.9548 |
| Std | 2.5348 | 0.1678 | 3.4343 | 6.1666 | 7.3379 | 5.7405 | 6.9747 | |
| Rank | 5 | 7 | 6 | 3 | 2 | 4 | 1 | |
| Average rank | 4.5 | 6.3 | 4.4 | 3.3 | 2 | 4.1 | 1.3 | |
| Finally rank | 6 | 7 | 5 | 3 | 2 | 4 | 1 | |
As can be seen from Table 3, the BWO variants improved by a single strategy exhibit relatively unstable and poor performance compared to the multi-strategy BWO variants. The three single-strategy improved BWO variants, including VCBWO, GVBWO, and BWO-JS, are ranked as the last three. The performance of VCBWO-JS in the cec02 test function outperforms that of the proposed HBWO-JS. The performance of VCGBWO in the cec07 test function outperforms the proposed HBWO-JS. The experimental results show that the introduction of the two fusion strategies is useful to improve the performance of the original algorithm, especially the introduced VC operator strategy, but it lacks robustness. Moreover, the experimental results show that VCGBWO, VCBWO-JS, and GVBWO-JS have average rankings of 2, 3, and 4, respectively, which outperform the single-strategy improved VCBWO, GVBWO, and BWO-JS in terms of overall optimization performance, and this situation indicates that the collaborative effect of multiple strategies has a great impact on the improvement of algorithm performance. VC operator requires the BWO algorithm to focus more on balanced exploration and exploitation, as well as avoiding local optima. At the same time, the GV strategy leads the algorithm to search more deeply for the optimal solution and continuously update the optimal position. In addition, the proposed HBWO-JS fuses three related strategies and obtains the best average ranking. In addition, the proposed HBWO-JS obtains the best ranking and the best average value in all eight test functions. The experimental conclusion shows that cooperation among multiple strategies can balance the advantages and disadvantages among strategies. Compared with BWO, the proposed HBWO-JS mainly improves the exploration and balancing ability and the ability to jump out of local solutions. Thus, the combination of the VC operator, GV strategy, and JS optimizer leads the BWO algorithm to the optimal solution.
4.3. Comparison with the CEC winners and famous algorithm on CEC2017 suite
The experimental results obtained in the CEC2017 test suite HBWO-JS and the CEC winners, and the well-known algorithms are shown in Table 4, where the data in bold are the best case of the mean value under the same benchmark functions. From the numerical results in the table, it can be found that HBWO-JS succeeded in finding the mean best value for all the compared algorithms for 10 tested functions (cec01, cec04, cec06, cec10, cec11, cec20, cec22, cec28, cec29, and cec30). Furthermore, LSHADE-cnEpSin and L-SHADE successfully found eight and seven optimal mean values, respectively. In addition, the proposed HBWO-JS obtained the best average ranking of 2.1. The average rankings of HBWO-JS and L-SHADE are closer. Then, the best algorithms in order are the three CEC winners, L-SHADE, LSHADE-cnEpSin, and LSHADE-SPACMA, respectively. The PSO, GA, ABC, GWO, and WOA algorithms have relatively poor performance in the CEC2017 test functions. This situation may be due to their early proposal and the simplicity of the algorithm principle. For the single-peaked functions (cec01 and cec03), HBWO-JS obtained the optimal results in both cec01. For multimodal functions (cec04-cec16), HBWO-JS does not optimize as well as the CEC champion algorithm, except for cec04, cec06, cec10, and cec11. For hybrid and composite functions (F17-F30), the overall optimization performance of HBWO-JS is also better than the other algorithms.
Comparison between HBWO-JS and CEC winners and classical algorithms in the CEC2017 test suite.
| Function . | Index . | Algorithms . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HBWO-JS . | L-SHADE . | LSHADE-cnEpSin . | LSHADE-SPACMA . | PSO . | GA . | ABC . | GWO . | WOA . | ||
| cec01 | Mean | 5.02E+03 | 5.51E+03 | 1.44E+06 | 4.26E+06 | 4.15E+09 | 3.15E+10 | 7.68E+07 | 2.47E+09 | 1.70E+09 |
| Std | 3.26E+03 | 5.89E+03 | 7.91E+05 | 2.03E+06 | 3.30E+09 | 1.13E+10 | 9.33E+07 | 1.44E+09 | 6.54E+08 | |
| Rank | 1 | 2 | 3 | 4 | 8 | 9 | 5 | 7 | 6 | |
| cec03 | Mean | 2.27E+04 | 3.46E+04 | 1.13E+04 | 1.47E+04 | 1.19E+05 | 2.70E+05 | 4.07E+05 | 5.63E+04 | 2.62E+05 |
| Std | 5.41E+03 | 4.81E+04 | 1.83E+04 | 7.97E+03 | 8.17E+04 | 9.24E+04 | 1.57E+05 | 1.28E+04 | 6.44E+04 | |
| Rank | 3 | 4 | 1 | 2 | 6 | 8 | 9 | 5 | 7 | |
| cec04 | Mean | 4.86E+02 | 4.90E+02 | 4.97E+02 | 5.03E+02 | 9.78E+02 | 7.43E+03 | 5.58E+02 | 6.13E+02 | 8.62E+02 |
| Std | 3.51E+01 | 2.88E+01 | 9.16E+00 | 1.13E+01 | 5.43E+02 | 3.12E+03 | 5.69E+01 | 5.81E+01 | 1.71E+02 | |
| Rank | 1 | 2 | 3 | 4 | 8 | 9 | 5 | 6 | 7 | |
| cec05 | Mean | 6.23E+02 | 5.44E+02 | 5.21E+02 | 6.61E+02 | 7.47E+02 | 8.49E+02 | 7.61E+02 | 6.32E+02 | 8.20E+02 |
| Std | 2.96E+01 | 8.10E+00 | 6.38E-02 | 1.69E+01 | 4.03E+01 | 5.21E+01 | 1.28E+01 | 4.37E+01 | 5.43E+01 | |
| Rank | 3 | 2 | 1 | 5 | 6 | 9 | 7 | 4 | 8 | |
| cec06 | Mean | 6.00E+02 | 6.01E+02 | 6.02E+02 | 6.03E+02 | 6.47E+02 | 6.70E+02 | 6.14E+02 | 6.11E+02 | 6.81E+02 |
| Std | 1.39E-01 | 6.00E-01 | 4.85E-01 | 6.37E-01 | 1.22E+01 | 1.83E+01 | 4.80E+00 | 3.47E+00 | 1.13E+01 | |
| Rank | 1 | 2 | 3 | 4 | 7 | 8 | 6 | 5 | 9 | |
| cec07 | Mean | 8.78E+02 | 7.97E+02 | 9.24E+02 | 9.07E+02 | 1.07E+03 | 1.66E+03 | 1.00E+03 | 8.97E+02 | 1.29E+03 |
| Std | 3.93E+01 | 1.90E+01 | 1.14E+01 | 1.91E+01 | 5.13E+01 | 2.23E+02 | 1.45E+01 | 5.77E+01 | 6.68E+01 | |
| Rank | 2 | 1 | 5 | 4 | 7 | 9 | 6 | 3 | 8 | |
| cec08 | Mean | 8.98E+02 | 8.48E+02 | 9.74E+02 | 9.60E+02 | 9.97E+02 | 1.09E+03 | 1.06E+03 | 9.05E+02 | 1.04E+03 |
| Std | 1.23E+01 | 9.42E+00 | 1.40E+01 | 1.45E+01 | 3.70E+01 | 4.29E+01 | 1.21E+01 | 2.16E+01 | 5.14E+01 | |
| Rank | 2 | 1 | 5 | 4 | 6 | 9 | 8 | 3 | 7 | |
| cec09 | Mean | 3.12E+03 | 1.12E+03 | 9.12E+02 | 9.28E+02 | 4.74E+03 | 1.07E+04 | 6.15E+03 | 2.48E+03 | 1.07E+04 |
| Std | 1.25E+03 | 1.36E+02 | 6.25E+00 | 1.67E+01 | 1.52E+03 | 2.47E+03 | 1.12E+03 | 1.03E+03 | 4.42E+03 | |
| Rank | 5 | 3 | 1 | 2 | 6 | 9 | 7 | 4 | 8 | |
| cec10 | Mean | 3.55E+03 | 3.75E+03 | 7.60E+03 | 7.20E+03 | 6.68E+03 | 6.54E+03 | 9.34E+03 | 4.60E+03 | 6.75E+03 |
| Std | 3.01E+02 | 3.95E+02 | 6.19E+02 | 7.08E+02 | 6.32E+02 | 5.51E+02 | 2.70E+02 | 1.05E+03 | 7.76E+02 | |
| Rank | 1 | 2 | 8 | 7 | 5 | 4 | 9 | 3 | 6 | |
| cec11 | Mean | 1.19E+03 | 1.25E+03 | 1.26E+03 | 1.26E+03 | 2.04E+03 | 1.84E+04 | 1.49E+04 | 1.91E+03 | 6.80E+03 |
| Std | 3.08E+01 | 5.01E+01 | 3.14E+01 | 2.53E+01 | 7.67E+02 | 8.79E+03 | 3.40E+03 | 8.35E+02 | 3.05E+03 | |
| Rank | 1 | 2 | 4 | 3 | 6 | 9 | 8 | 5 | 7 | |
| cec12 | Mean | 6.78E+05 | 8.75E+04 | 1.20E+03 | 8.13E+05 | 6.88E+08 | 4.34E+09 | 7.35E+08 | 9.70E+07 | 2.40E+08 |
| Std | 3.61E+05 | 6.51E+04 | 7.52E-01 | 5.58E+05 | 1.59E+09 | 2.17E+09 | 2.44E+08 | 8.87E+07 | 1.58E+08 | |
| Rank | 3 | 2 | 1 | 4 | 7 | 9 | 8 | 5 | 6 | |
| cec13 | Mean | 5.93E+03 | 1.02E+04 | 1.31E+03 | 3.58E+04 | 1.05E+08 | 5.69E+09 | 2.73E+05 | 8.14E+06 | 2.07E+06 |
| Std | 5.46E+03 | 1.14E+04 | 6.71E-01 | 8.84E+03 | 3.99E+08 | 5.43E+09 | 2.55E+05 | 2.50E+07 | 3.34E+06 | |
| Rank | 2 | 3 | 1 | 4 | 8 | 9 | 5 | 7 | 6 | |
| cec14 | Mean | 1.17E+04 | 1.56E+03 | 1.53E+03 | 1.60E+03 | 3.95E+05 | 1.02E+07 | 4.95E+05 | 3.53E+05 | 2.46E+06 |
| Std | 8.61E+03 | 5.82E+01 | 1.65E+01 | 4.29E+01 | 8.38E+05 | 8.81E+06 | 2.01E+05 | 5.35E+05 | 3.15E+06 | |
| Rank | 4 | 2 | 1 | 3 | 6 | 9 | 7 | 5 | 8 | |
| cec15 | Mean | 3.64E+03 | 1.90E+03 | 5.20E+03 | 8.11E+03 | 3.31E+04 | 1.20E+09 | 1.43E+06 | 6.10E+05 | 2.63E+06 |
| Std | 2.74E+03 | 2.25E+02 | 1.63E+03 | 4.39E+03 | 3.43E+04 | 2.02E+09 | 1.22E+06 | 8.15E+05 | 7.41E+06 | |
| Rank | 2 | 1 | 3 | 4 | 5 | 9 | 7 | 6 | 8 | |
| cec16 | Mean | 2.32E+03 | 2.35E+03 | 1.61E+03 | 3.02E+03 | 3.53E+03 | 3.92E+03 | 3.99E+03 | 2.58E+03 | 4.05E+03 |
| Std | 1.84E+02 | 2.16E+02 | 1.55E-01 | 1.92E+02 | 5.44E+02 | 4.59E+02 | 2.30E+02 | 2.93E+02 | 5.46E+02 | |
| Rank | 2 | 3 | 1 | 5 | 6 | 7 | 8 | 4 | 9 | |
| cec17 | Mean | 1.95E+03 | 1.90E+03 | 2.22E+03 | 2.13E+03 | 2.67E+03 | 3.39E+03 | 2.92E+03 | 2.05E+03 | 2.58E+03 |
| Std | 1.57E+02 | 1.13E+02 | 1.14E+02 | 1.20E+02 | 3.55E+02 | 1.22E+03 | 1.66E+02 | 1.56E+02 | 2.48E+02 | |
| Rank | 2 | 1 | 5 | 4 | 7 | 9 | 8 | 3 | 6 | |
| cec18 | Mean | 3.57E+05 | 2.67E+04 | 1.13E+04 | 1.72E+04 | 1.29E+07 | 3.54E+07 | 1.83E+07 | 9.82E+05 | 8.69E+06 |
| Std | 3.14E+05 | 1.84E+04 | 7.24E+03 | 7.89E+03 | 2.50E+07 | 4.21E+07 | 7.07E+06 | 1.13E+06 | 8.17E+06 | |
| Rank | 4 | 3 | 1 | 2 | 7 | 9 | 8 | 5 | 6 | |
| cec19 | Mean | 2.94E+03 | 2.07E+03 | 2.38E+03 | 3.77E+03 | 4.30E+06 | 6.45E+08 | 1.84E+04 | 1.91E+06 | 1.13E+07 |
| Std | 1.23E+03 | 8.55E+01 | 2.79E+02 | 1.97E+03 | 1.72E+07 | 6.92E+08 | 4.25E+04 | 2.64E+06 | 1.51E+07 | |
| Rank | 3 | 1 | 2 | 4 | 7 | 9 | 5 | 6 | 8 | |
| cec20 | Mean | 2.26E+03 | 2.28E+03 | 2.66E+03 | 2.64E+03 | 2.76E+03 | 3.11E+03 | 3.08E+03 | 2.48E+03 | 2.84E+03 |
| Std | 8.68E+01 | 1.19E+02 | 1.19E+02 | 1.05E+02 | 2.38E+02 | 2.85E+02 | 1.15E+02 | 2.29E+02 | 1.96E+02 | |
| Rank | 1 | 2 | 5 | 4 | 6 | 9 | 8 | 3 | 7 | |
| cec21 | Mean | 2.38E+03 | 2.35E+03 | 2.47E+03 | 2.46E+03 | 2.52E+03 | 2.63E+03 | 2.56E+03 | 2.41E+03 | 2.62E+03 |
| Std | 4.58E+01 | 8.13E+00 | 1.36E+01 | 1.50E+01 | 4.48E+01 | 7.92E+01 | 1.34E+01 | 4.25E+01 | 6.09E+01 | |
| Rank | 2 | 1 | 5 | 4 | 6 | 9 | 7 | 3 | 8 | |
| cec22 | Mean | 2.30E+03 | 2.68E+03 | 2.32E+03 | 2.32E+03 | 7.55E+03 | 8.26E+03 | 1.05E+04 | 5.38E+03 | 6.56E+03 |
| Std | 1.65E+00 | 1.00E+03 | 2.49E+00 | 4.32E+00 | 2.46E+03 | 1.09E+03 | 3.41E+02 | 2.45E+03 | 2.63E+03 | |
| Rank | 1 | 4 | 2 | 3 | 7 | 8 | 9 | 5 | 6 | |
| cec23 | Mean | 2.73E+03 | 2.70E+03 | 2.82E+03 | 2.81E+03 | 3.33E+03 | 3.25E+03 | 2.92E+03 | 2.79E+03 | 3.10E+03 |
| Std | 1.71E+01 | 1.33E+01 | 1.41E+01 | 1.93E+01 | 1.90E+02 | 1.17E+02 | 1.58E+01 | 4.65E+01 | 6.84E+01 | |
| Rank | 2 | 1 | 5 | 4 | 9 | 8 | 6 | 3 | 7 | |
| cec24 | Mean | 2.91E+03 | 2.87E+03 | 2.80E+03 | 2.97E+03 | 3.59E+03 | 3.57E+03 | 3.11E+03 | 2.96E+03 | 3.23E+03 |
| Std | 2.27E+01 | 1.57E+01 | 3.58E+01 | 8.71E+00 | 2.37E+02 | 1.44E+02 | 1.33E+01 | 6.32E+01 | 8.84E+01 | |
| Rank | 3 | 2 | 1 | 5 | 9 | 8 | 6 | 4 | 7 | |
| cec25 | Mean | 2.89E+03 | 2.89E+03 | 2.87E+03 | 2.89E+03 | 3.10E+03 | 5.32E+03 | 2.96E+03 | 2.98E+03 | 3.11E+03 |
| Std | 7.48E+00 | 7.07E+00 | 2.57E+01 | 6.44E+00 | 8.57E+01 | 1.19E+03 | 3.14E+01 | 3.49E+01 | 5.40E+01 | |
| Rank | 3 | 2 | 1 | 4 | 7 | 9 | 5 | 6 | 8 | |
| cec26 | Mean | 3.91E+03 | 4.20E+03 | 2.71E+03 | 5.17E+03 | 6.80E+03 | 8.75E+03 | 5.91E+03 | 4.87E+03 | 7.99E+03 |
| Std | 1.03E+03 | 1.62E+02 | 6.81E-01 | 1.47E+02 | 1.61E+03 | 1.00E+03 | 1.92E+02 | 3.06E+02 | 1.04E+03 | |
| Rank | 2 | 3 | 1 | 5 | 7 | 9 | 6 | 4 | 8 | |
| cec27 | Mean | 3.20E+03 | 3.23E+03 | 3.22E+03 | 3.22E+03 | 3.61E+03 | 3.94E+03 | 3.20E+03 | 3.26E+03 | 3.45E+03 |
| Std | 7.56E-05 | 1.58E+01 | 5.52E+00 | 6.09E+00 | 1.79E+02 | 2.42E+02 | 6.88E-05 | 3.21E+01 | 1.15E+02 | |
| Rank | 2 | 5 | 4 | 3 | 8 | 9 | 1 | 6 | 7 | |
| cec28 | Mean | 3.24E+03 | 3.24E+03 | 3.24E+03 | 3.25E+03 | 3.75E+03 | 6.15E+03 | 3.30E+03 | 3.44E+03 | 3.55E+03 |
| Std | 1.63E+01 | 2.74E+01 | 1.71E+01 | 1.65E+01 | 4.31E+02 | 1.25E+03 | 1.27E-01 | 6.44E+01 | 1.04E+02 | |
| Rank | 1 | 2 | 3 | 4 | 8 | 9 | 5 | 6 | 7 | |
| cec29 | Mean | 3.57E+03 | 3.60E+03 | 3.95E+03 | 3.88E+03 | 4.81E+03 | 6.07E+03 | 5.01E+03 | 3.81E+03 | 5.36E+03 |
| Std | 1.16E+02 | 1.08E+02 | 1.24E+02 | 1.32E+02 | 5.53E+02 | 6.86E+02 | 2.58E+02 | 1.98E+02 | 3.94E+02 | |
| Rank | 1 | 2 | 5 | 4 | 6 | 9 | 7 | 3 | 8 | |
| cec30 | Mean | 8.81E+03 | 1.08E+04 | 3.33E+04 | 4.51E+04 | 1.81E+07 | 1.65E+08 | 7.11E+05 | 8.39E+06 | 4.06E+07 |
| Std | 1.98E+03 | 3.24E+03 | 1.64E+04 | 2.58E+04 | 4.94E+07 | 1.91E+08 | 5.88E+05 | 6.50E+06 | 3.86E+07 | |
| Rank | 1 | 2 | 3 | 4 | 7 | 9 | 5 | 6 | 8 | |
| Mean rank | 2.10 | 2.17 | 2.90 | 3.90 | 6.83 | 8.59 | 6.59 | 4.66 | 7.28 | |
| Final ranking | 1 | 2 | 3 | 4 | 7 | 9 | 6 | 5 | 8 | |
| Function . | Index . | Algorithms . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HBWO-JS . | L-SHADE . | LSHADE-cnEpSin . | LSHADE-SPACMA . | PSO . | GA . | ABC . | GWO . | WOA . | ||
| cec01 | Mean | 5.02E+03 | 5.51E+03 | 1.44E+06 | 4.26E+06 | 4.15E+09 | 3.15E+10 | 7.68E+07 | 2.47E+09 | 1.70E+09 |
| Std | 3.26E+03 | 5.89E+03 | 7.91E+05 | 2.03E+06 | 3.30E+09 | 1.13E+10 | 9.33E+07 | 1.44E+09 | 6.54E+08 | |
| Rank | 1 | 2 | 3 | 4 | 8 | 9 | 5 | 7 | 6 | |
| cec03 | Mean | 2.27E+04 | 3.46E+04 | 1.13E+04 | 1.47E+04 | 1.19E+05 | 2.70E+05 | 4.07E+05 | 5.63E+04 | 2.62E+05 |
| Std | 5.41E+03 | 4.81E+04 | 1.83E+04 | 7.97E+03 | 8.17E+04 | 9.24E+04 | 1.57E+05 | 1.28E+04 | 6.44E+04 | |
| Rank | 3 | 4 | 1 | 2 | 6 | 8 | 9 | 5 | 7 | |
| cec04 | Mean | 4.86E+02 | 4.90E+02 | 4.97E+02 | 5.03E+02 | 9.78E+02 | 7.43E+03 | 5.58E+02 | 6.13E+02 | 8.62E+02 |
| Std | 3.51E+01 | 2.88E+01 | 9.16E+00 | 1.13E+01 | 5.43E+02 | 3.12E+03 | 5.69E+01 | 5.81E+01 | 1.71E+02 | |
| Rank | 1 | 2 | 3 | 4 | 8 | 9 | 5 | 6 | 7 | |
| cec05 | Mean | 6.23E+02 | 5.44E+02 | 5.21E+02 | 6.61E+02 | 7.47E+02 | 8.49E+02 | 7.61E+02 | 6.32E+02 | 8.20E+02 |
| Std | 2.96E+01 | 8.10E+00 | 6.38E-02 | 1.69E+01 | 4.03E+01 | 5.21E+01 | 1.28E+01 | 4.37E+01 | 5.43E+01 | |
| Rank | 3 | 2 | 1 | 5 | 6 | 9 | 7 | 4 | 8 | |
| cec06 | Mean | 6.00E+02 | 6.01E+02 | 6.02E+02 | 6.03E+02 | 6.47E+02 | 6.70E+02 | 6.14E+02 | 6.11E+02 | 6.81E+02 |
| Std | 1.39E-01 | 6.00E-01 | 4.85E-01 | 6.37E-01 | 1.22E+01 | 1.83E+01 | 4.80E+00 | 3.47E+00 | 1.13E+01 | |
| Rank | 1 | 2 | 3 | 4 | 7 | 8 | 6 | 5 | 9 | |
| cec07 | Mean | 8.78E+02 | 7.97E+02 | 9.24E+02 | 9.07E+02 | 1.07E+03 | 1.66E+03 | 1.00E+03 | 8.97E+02 | 1.29E+03 |
| Std | 3.93E+01 | 1.90E+01 | 1.14E+01 | 1.91E+01 | 5.13E+01 | 2.23E+02 | 1.45E+01 | 5.77E+01 | 6.68E+01 | |
| Rank | 2 | 1 | 5 | 4 | 7 | 9 | 6 | 3 | 8 | |
| cec08 | Mean | 8.98E+02 | 8.48E+02 | 9.74E+02 | 9.60E+02 | 9.97E+02 | 1.09E+03 | 1.06E+03 | 9.05E+02 | 1.04E+03 |
| Std | 1.23E+01 | 9.42E+00 | 1.40E+01 | 1.45E+01 | 3.70E+01 | 4.29E+01 | 1.21E+01 | 2.16E+01 | 5.14E+01 | |
| Rank | 2 | 1 | 5 | 4 | 6 | 9 | 8 | 3 | 7 | |
| cec09 | Mean | 3.12E+03 | 1.12E+03 | 9.12E+02 | 9.28E+02 | 4.74E+03 | 1.07E+04 | 6.15E+03 | 2.48E+03 | 1.07E+04 |
| Std | 1.25E+03 | 1.36E+02 | 6.25E+00 | 1.67E+01 | 1.52E+03 | 2.47E+03 | 1.12E+03 | 1.03E+03 | 4.42E+03 | |
| Rank | 5 | 3 | 1 | 2 | 6 | 9 | 7 | 4 | 8 | |
| cec10 | Mean | 3.55E+03 | 3.75E+03 | 7.60E+03 | 7.20E+03 | 6.68E+03 | 6.54E+03 | 9.34E+03 | 4.60E+03 | 6.75E+03 |
| Std | 3.01E+02 | 3.95E+02 | 6.19E+02 | 7.08E+02 | 6.32E+02 | 5.51E+02 | 2.70E+02 | 1.05E+03 | 7.76E+02 | |
| Rank | 1 | 2 | 8 | 7 | 5 | 4 | 9 | 3 | 6 | |
| cec11 | Mean | 1.19E+03 | 1.25E+03 | 1.26E+03 | 1.26E+03 | 2.04E+03 | 1.84E+04 | 1.49E+04 | 1.91E+03 | 6.80E+03 |
| Std | 3.08E+01 | 5.01E+01 | 3.14E+01 | 2.53E+01 | 7.67E+02 | 8.79E+03 | 3.40E+03 | 8.35E+02 | 3.05E+03 | |
| Rank | 1 | 2 | 4 | 3 | 6 | 9 | 8 | 5 | 7 | |
| cec12 | Mean | 6.78E+05 | 8.75E+04 | 1.20E+03 | 8.13E+05 | 6.88E+08 | 4.34E+09 | 7.35E+08 | 9.70E+07 | 2.40E+08 |
| Std | 3.61E+05 | 6.51E+04 | 7.52E-01 | 5.58E+05 | 1.59E+09 | 2.17E+09 | 2.44E+08 | 8.87E+07 | 1.58E+08 | |
| Rank | 3 | 2 | 1 | 4 | 7 | 9 | 8 | 5 | 6 | |
| cec13 | Mean | 5.93E+03 | 1.02E+04 | 1.31E+03 | 3.58E+04 | 1.05E+08 | 5.69E+09 | 2.73E+05 | 8.14E+06 | 2.07E+06 |
| Std | 5.46E+03 | 1.14E+04 | 6.71E-01 | 8.84E+03 | 3.99E+08 | 5.43E+09 | 2.55E+05 | 2.50E+07 | 3.34E+06 | |
| Rank | 2 | 3 | 1 | 4 | 8 | 9 | 5 | 7 | 6 | |
| cec14 | Mean | 1.17E+04 | 1.56E+03 | 1.53E+03 | 1.60E+03 | 3.95E+05 | 1.02E+07 | 4.95E+05 | 3.53E+05 | 2.46E+06 |
| Std | 8.61E+03 | 5.82E+01 | 1.65E+01 | 4.29E+01 | 8.38E+05 | 8.81E+06 | 2.01E+05 | 5.35E+05 | 3.15E+06 | |
| Rank | 4 | 2 | 1 | 3 | 6 | 9 | 7 | 5 | 8 | |
| cec15 | Mean | 3.64E+03 | 1.90E+03 | 5.20E+03 | 8.11E+03 | 3.31E+04 | 1.20E+09 | 1.43E+06 | 6.10E+05 | 2.63E+06 |
| Std | 2.74E+03 | 2.25E+02 | 1.63E+03 | 4.39E+03 | 3.43E+04 | 2.02E+09 | 1.22E+06 | 8.15E+05 | 7.41E+06 | |
| Rank | 2 | 1 | 3 | 4 | 5 | 9 | 7 | 6 | 8 | |
| cec16 | Mean | 2.32E+03 | 2.35E+03 | 1.61E+03 | 3.02E+03 | 3.53E+03 | 3.92E+03 | 3.99E+03 | 2.58E+03 | 4.05E+03 |
| Std | 1.84E+02 | 2.16E+02 | 1.55E-01 | 1.92E+02 | 5.44E+02 | 4.59E+02 | 2.30E+02 | 2.93E+02 | 5.46E+02 | |
| Rank | 2 | 3 | 1 | 5 | 6 | 7 | 8 | 4 | 9 | |
| cec17 | Mean | 1.95E+03 | 1.90E+03 | 2.22E+03 | 2.13E+03 | 2.67E+03 | 3.39E+03 | 2.92E+03 | 2.05E+03 | 2.58E+03 |
| Std | 1.57E+02 | 1.13E+02 | 1.14E+02 | 1.20E+02 | 3.55E+02 | 1.22E+03 | 1.66E+02 | 1.56E+02 | 2.48E+02 | |
| Rank | 2 | 1 | 5 | 4 | 7 | 9 | 8 | 3 | 6 | |
| cec18 | Mean | 3.57E+05 | 2.67E+04 | 1.13E+04 | 1.72E+04 | 1.29E+07 | 3.54E+07 | 1.83E+07 | 9.82E+05 | 8.69E+06 |
| Std | 3.14E+05 | 1.84E+04 | 7.24E+03 | 7.89E+03 | 2.50E+07 | 4.21E+07 | 7.07E+06 | 1.13E+06 | 8.17E+06 | |
| Rank | 4 | 3 | 1 | 2 | 7 | 9 | 8 | 5 | 6 | |
| cec19 | Mean | 2.94E+03 | 2.07E+03 | 2.38E+03 | 3.77E+03 | 4.30E+06 | 6.45E+08 | 1.84E+04 | 1.91E+06 | 1.13E+07 |
| Std | 1.23E+03 | 8.55E+01 | 2.79E+02 | 1.97E+03 | 1.72E+07 | 6.92E+08 | 4.25E+04 | 2.64E+06 | 1.51E+07 | |
| Rank | 3 | 1 | 2 | 4 | 7 | 9 | 5 | 6 | 8 | |
| cec20 | Mean | 2.26E+03 | 2.28E+03 | 2.66E+03 | 2.64E+03 | 2.76E+03 | 3.11E+03 | 3.08E+03 | 2.48E+03 | 2.84E+03 |
| Std | 8.68E+01 | 1.19E+02 | 1.19E+02 | 1.05E+02 | 2.38E+02 | 2.85E+02 | 1.15E+02 | 2.29E+02 | 1.96E+02 | |
| Rank | 1 | 2 | 5 | 4 | 6 | 9 | 8 | 3 | 7 | |
| cec21 | Mean | 2.38E+03 | 2.35E+03 | 2.47E+03 | 2.46E+03 | 2.52E+03 | 2.63E+03 | 2.56E+03 | 2.41E+03 | 2.62E+03 |
| Std | 4.58E+01 | 8.13E+00 | 1.36E+01 | 1.50E+01 | 4.48E+01 | 7.92E+01 | 1.34E+01 | 4.25E+01 | 6.09E+01 | |
| Rank | 2 | 1 | 5 | 4 | 6 | 9 | 7 | 3 | 8 | |
| cec22 | Mean | 2.30E+03 | 2.68E+03 | 2.32E+03 | 2.32E+03 | 7.55E+03 | 8.26E+03 | 1.05E+04 | 5.38E+03 | 6.56E+03 |
| Std | 1.65E+00 | 1.00E+03 | 2.49E+00 | 4.32E+00 | 2.46E+03 | 1.09E+03 | 3.41E+02 | 2.45E+03 | 2.63E+03 | |
| Rank | 1 | 4 | 2 | 3 | 7 | 8 | 9 | 5 | 6 | |
| cec23 | Mean | 2.73E+03 | 2.70E+03 | 2.82E+03 | 2.81E+03 | 3.33E+03 | 3.25E+03 | 2.92E+03 | 2.79E+03 | 3.10E+03 |
| Std | 1.71E+01 | 1.33E+01 | 1.41E+01 | 1.93E+01 | 1.90E+02 | 1.17E+02 | 1.58E+01 | 4.65E+01 | 6.84E+01 | |
| Rank | 2 | 1 | 5 | 4 | 9 | 8 | 6 | 3 | 7 | |
| cec24 | Mean | 2.91E+03 | 2.87E+03 | 2.80E+03 | 2.97E+03 | 3.59E+03 | 3.57E+03 | 3.11E+03 | 2.96E+03 | 3.23E+03 |
| Std | 2.27E+01 | 1.57E+01 | 3.58E+01 | 8.71E+00 | 2.37E+02 | 1.44E+02 | 1.33E+01 | 6.32E+01 | 8.84E+01 | |
| Rank | 3 | 2 | 1 | 5 | 9 | 8 | 6 | 4 | 7 | |
| cec25 | Mean | 2.89E+03 | 2.89E+03 | 2.87E+03 | 2.89E+03 | 3.10E+03 | 5.32E+03 | 2.96E+03 | 2.98E+03 | 3.11E+03 |
| Std | 7.48E+00 | 7.07E+00 | 2.57E+01 | 6.44E+00 | 8.57E+01 | 1.19E+03 | 3.14E+01 | 3.49E+01 | 5.40E+01 | |
| Rank | 3 | 2 | 1 | 4 | 7 | 9 | 5 | 6 | 8 | |
| cec26 | Mean | 3.91E+03 | 4.20E+03 | 2.71E+03 | 5.17E+03 | 6.80E+03 | 8.75E+03 | 5.91E+03 | 4.87E+03 | 7.99E+03 |
| Std | 1.03E+03 | 1.62E+02 | 6.81E-01 | 1.47E+02 | 1.61E+03 | 1.00E+03 | 1.92E+02 | 3.06E+02 | 1.04E+03 | |
| Rank | 2 | 3 | 1 | 5 | 7 | 9 | 6 | 4 | 8 | |
| cec27 | Mean | 3.20E+03 | 3.23E+03 | 3.22E+03 | 3.22E+03 | 3.61E+03 | 3.94E+03 | 3.20E+03 | 3.26E+03 | 3.45E+03 |
| Std | 7.56E-05 | 1.58E+01 | 5.52E+00 | 6.09E+00 | 1.79E+02 | 2.42E+02 | 6.88E-05 | 3.21E+01 | 1.15E+02 | |
| Rank | 2 | 5 | 4 | 3 | 8 | 9 | 1 | 6 | 7 | |
| cec28 | Mean | 3.24E+03 | 3.24E+03 | 3.24E+03 | 3.25E+03 | 3.75E+03 | 6.15E+03 | 3.30E+03 | 3.44E+03 | 3.55E+03 |
| Std | 1.63E+01 | 2.74E+01 | 1.71E+01 | 1.65E+01 | 4.31E+02 | 1.25E+03 | 1.27E-01 | 6.44E+01 | 1.04E+02 | |
| Rank | 1 | 2 | 3 | 4 | 8 | 9 | 5 | 6 | 7 | |
| cec29 | Mean | 3.57E+03 | 3.60E+03 | 3.95E+03 | 3.88E+03 | 4.81E+03 | 6.07E+03 | 5.01E+03 | 3.81E+03 | 5.36E+03 |
| Std | 1.16E+02 | 1.08E+02 | 1.24E+02 | 1.32E+02 | 5.53E+02 | 6.86E+02 | 2.58E+02 | 1.98E+02 | 3.94E+02 | |
| Rank | 1 | 2 | 5 | 4 | 6 | 9 | 7 | 3 | 8 | |
| cec30 | Mean | 8.81E+03 | 1.08E+04 | 3.33E+04 | 4.51E+04 | 1.81E+07 | 1.65E+08 | 7.11E+05 | 8.39E+06 | 4.06E+07 |
| Std | 1.98E+03 | 3.24E+03 | 1.64E+04 | 2.58E+04 | 4.94E+07 | 1.91E+08 | 5.88E+05 | 6.50E+06 | 3.86E+07 | |
| Rank | 1 | 2 | 3 | 4 | 7 | 9 | 5 | 6 | 8 | |
| Mean rank | 2.10 | 2.17 | 2.90 | 3.90 | 6.83 | 8.59 | 6.59 | 4.66 | 7.28 | |
| Final ranking | 1 | 2 | 3 | 4 | 7 | 9 | 6 | 5 | 8 | |
Comparison between HBWO-JS and CEC winners and classical algorithms in the CEC2017 test suite.
| Function . | Index . | Algorithms . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HBWO-JS . | L-SHADE . | LSHADE-cnEpSin . | LSHADE-SPACMA . | PSO . | GA . | ABC . | GWO . | WOA . | ||
| cec01 | Mean | 5.02E+03 | 5.51E+03 | 1.44E+06 | 4.26E+06 | 4.15E+09 | 3.15E+10 | 7.68E+07 | 2.47E+09 | 1.70E+09 |
| Std | 3.26E+03 | 5.89E+03 | 7.91E+05 | 2.03E+06 | 3.30E+09 | 1.13E+10 | 9.33E+07 | 1.44E+09 | 6.54E+08 | |
| Rank | 1 | 2 | 3 | 4 | 8 | 9 | 5 | 7 | 6 | |
| cec03 | Mean | 2.27E+04 | 3.46E+04 | 1.13E+04 | 1.47E+04 | 1.19E+05 | 2.70E+05 | 4.07E+05 | 5.63E+04 | 2.62E+05 |
| Std | 5.41E+03 | 4.81E+04 | 1.83E+04 | 7.97E+03 | 8.17E+04 | 9.24E+04 | 1.57E+05 | 1.28E+04 | 6.44E+04 | |
| Rank | 3 | 4 | 1 | 2 | 6 | 8 | 9 | 5 | 7 | |
| cec04 | Mean | 4.86E+02 | 4.90E+02 | 4.97E+02 | 5.03E+02 | 9.78E+02 | 7.43E+03 | 5.58E+02 | 6.13E+02 | 8.62E+02 |
| Std | 3.51E+01 | 2.88E+01 | 9.16E+00 | 1.13E+01 | 5.43E+02 | 3.12E+03 | 5.69E+01 | 5.81E+01 | 1.71E+02 | |
| Rank | 1 | 2 | 3 | 4 | 8 | 9 | 5 | 6 | 7 | |
| cec05 | Mean | 6.23E+02 | 5.44E+02 | 5.21E+02 | 6.61E+02 | 7.47E+02 | 8.49E+02 | 7.61E+02 | 6.32E+02 | 8.20E+02 |
| Std | 2.96E+01 | 8.10E+00 | 6.38E-02 | 1.69E+01 | 4.03E+01 | 5.21E+01 | 1.28E+01 | 4.37E+01 | 5.43E+01 | |
| Rank | 3 | 2 | 1 | 5 | 6 | 9 | 7 | 4 | 8 | |
| cec06 | Mean | 6.00E+02 | 6.01E+02 | 6.02E+02 | 6.03E+02 | 6.47E+02 | 6.70E+02 | 6.14E+02 | 6.11E+02 | 6.81E+02 |
| Std | 1.39E-01 | 6.00E-01 | 4.85E-01 | 6.37E-01 | 1.22E+01 | 1.83E+01 | 4.80E+00 | 3.47E+00 | 1.13E+01 | |
| Rank | 1 | 2 | 3 | 4 | 7 | 8 | 6 | 5 | 9 | |
| cec07 | Mean | 8.78E+02 | 7.97E+02 | 9.24E+02 | 9.07E+02 | 1.07E+03 | 1.66E+03 | 1.00E+03 | 8.97E+02 | 1.29E+03 |
| Std | 3.93E+01 | 1.90E+01 | 1.14E+01 | 1.91E+01 | 5.13E+01 | 2.23E+02 | 1.45E+01 | 5.77E+01 | 6.68E+01 | |
| Rank | 2 | 1 | 5 | 4 | 7 | 9 | 6 | 3 | 8 | |
| cec08 | Mean | 8.98E+02 | 8.48E+02 | 9.74E+02 | 9.60E+02 | 9.97E+02 | 1.09E+03 | 1.06E+03 | 9.05E+02 | 1.04E+03 |
| Std | 1.23E+01 | 9.42E+00 | 1.40E+01 | 1.45E+01 | 3.70E+01 | 4.29E+01 | 1.21E+01 | 2.16E+01 | 5.14E+01 | |
| Rank | 2 | 1 | 5 | 4 | 6 | 9 | 8 | 3 | 7 | |
| cec09 | Mean | 3.12E+03 | 1.12E+03 | 9.12E+02 | 9.28E+02 | 4.74E+03 | 1.07E+04 | 6.15E+03 | 2.48E+03 | 1.07E+04 |
| Std | 1.25E+03 | 1.36E+02 | 6.25E+00 | 1.67E+01 | 1.52E+03 | 2.47E+03 | 1.12E+03 | 1.03E+03 | 4.42E+03 | |
| Rank | 5 | 3 | 1 | 2 | 6 | 9 | 7 | 4 | 8 | |
| cec10 | Mean | 3.55E+03 | 3.75E+03 | 7.60E+03 | 7.20E+03 | 6.68E+03 | 6.54E+03 | 9.34E+03 | 4.60E+03 | 6.75E+03 |
| Std | 3.01E+02 | 3.95E+02 | 6.19E+02 | 7.08E+02 | 6.32E+02 | 5.51E+02 | 2.70E+02 | 1.05E+03 | 7.76E+02 | |
| Rank | 1 | 2 | 8 | 7 | 5 | 4 | 9 | 3 | 6 | |
| cec11 | Mean | 1.19E+03 | 1.25E+03 | 1.26E+03 | 1.26E+03 | 2.04E+03 | 1.84E+04 | 1.49E+04 | 1.91E+03 | 6.80E+03 |
| Std | 3.08E+01 | 5.01E+01 | 3.14E+01 | 2.53E+01 | 7.67E+02 | 8.79E+03 | 3.40E+03 | 8.35E+02 | 3.05E+03 | |
| Rank | 1 | 2 | 4 | 3 | 6 | 9 | 8 | 5 | 7 | |
| cec12 | Mean | 6.78E+05 | 8.75E+04 | 1.20E+03 | 8.13E+05 | 6.88E+08 | 4.34E+09 | 7.35E+08 | 9.70E+07 | 2.40E+08 |
| Std | 3.61E+05 | 6.51E+04 | 7.52E-01 | 5.58E+05 | 1.59E+09 | 2.17E+09 | 2.44E+08 | 8.87E+07 | 1.58E+08 | |
| Rank | 3 | 2 | 1 | 4 | 7 | 9 | 8 | 5 | 6 | |
| cec13 | Mean | 5.93E+03 | 1.02E+04 | 1.31E+03 | 3.58E+04 | 1.05E+08 | 5.69E+09 | 2.73E+05 | 8.14E+06 | 2.07E+06 |
| Std | 5.46E+03 | 1.14E+04 | 6.71E-01 | 8.84E+03 | 3.99E+08 | 5.43E+09 | 2.55E+05 | 2.50E+07 | 3.34E+06 | |
| Rank | 2 | 3 | 1 | 4 | 8 | 9 | 5 | 7 | 6 | |
| cec14 | Mean | 1.17E+04 | 1.56E+03 | 1.53E+03 | 1.60E+03 | 3.95E+05 | 1.02E+07 | 4.95E+05 | 3.53E+05 | 2.46E+06 |
| Std | 8.61E+03 | 5.82E+01 | 1.65E+01 | 4.29E+01 | 8.38E+05 | 8.81E+06 | 2.01E+05 | 5.35E+05 | 3.15E+06 | |
| Rank | 4 | 2 | 1 | 3 | 6 | 9 | 7 | 5 | 8 | |
| cec15 | Mean | 3.64E+03 | 1.90E+03 | 5.20E+03 | 8.11E+03 | 3.31E+04 | 1.20E+09 | 1.43E+06 | 6.10E+05 | 2.63E+06 |
| Std | 2.74E+03 | 2.25E+02 | 1.63E+03 | 4.39E+03 | 3.43E+04 | 2.02E+09 | 1.22E+06 | 8.15E+05 | 7.41E+06 | |
| Rank | 2 | 1 | 3 | 4 | 5 | 9 | 7 | 6 | 8 | |
| cec16 | Mean | 2.32E+03 | 2.35E+03 | 1.61E+03 | 3.02E+03 | 3.53E+03 | 3.92E+03 | 3.99E+03 | 2.58E+03 | 4.05E+03 |
| Std | 1.84E+02 | 2.16E+02 | 1.55E-01 | 1.92E+02 | 5.44E+02 | 4.59E+02 | 2.30E+02 | 2.93E+02 | 5.46E+02 | |
| Rank | 2 | 3 | 1 | 5 | 6 | 7 | 8 | 4 | 9 | |
| cec17 | Mean | 1.95E+03 | 1.90E+03 | 2.22E+03 | 2.13E+03 | 2.67E+03 | 3.39E+03 | 2.92E+03 | 2.05E+03 | 2.58E+03 |
| Std | 1.57E+02 | 1.13E+02 | 1.14E+02 | 1.20E+02 | 3.55E+02 | 1.22E+03 | 1.66E+02 | 1.56E+02 | 2.48E+02 | |
| Rank | 2 | 1 | 5 | 4 | 7 | 9 | 8 | 3 | 6 | |
| cec18 | Mean | 3.57E+05 | 2.67E+04 | 1.13E+04 | 1.72E+04 | 1.29E+07 | 3.54E+07 | 1.83E+07 | 9.82E+05 | 8.69E+06 |
| Std | 3.14E+05 | 1.84E+04 | 7.24E+03 | 7.89E+03 | 2.50E+07 | 4.21E+07 | 7.07E+06 | 1.13E+06 | 8.17E+06 | |
| Rank | 4 | 3 | 1 | 2 | 7 | 9 | 8 | 5 | 6 | |
| cec19 | Mean | 2.94E+03 | 2.07E+03 | 2.38E+03 | 3.77E+03 | 4.30E+06 | 6.45E+08 | 1.84E+04 | 1.91E+06 | 1.13E+07 |
| Std | 1.23E+03 | 8.55E+01 | 2.79E+02 | 1.97E+03 | 1.72E+07 | 6.92E+08 | 4.25E+04 | 2.64E+06 | 1.51E+07 | |
| Rank | 3 | 1 | 2 | 4 | 7 | 9 | 5 | 6 | 8 | |
| cec20 | Mean | 2.26E+03 | 2.28E+03 | 2.66E+03 | 2.64E+03 | 2.76E+03 | 3.11E+03 | 3.08E+03 | 2.48E+03 | 2.84E+03 |
| Std | 8.68E+01 | 1.19E+02 | 1.19E+02 | 1.05E+02 | 2.38E+02 | 2.85E+02 | 1.15E+02 | 2.29E+02 | 1.96E+02 | |
| Rank | 1 | 2 | 5 | 4 | 6 | 9 | 8 | 3 | 7 | |
| cec21 | Mean | 2.38E+03 | 2.35E+03 | 2.47E+03 | 2.46E+03 | 2.52E+03 | 2.63E+03 | 2.56E+03 | 2.41E+03 | 2.62E+03 |
| Std | 4.58E+01 | 8.13E+00 | 1.36E+01 | 1.50E+01 | 4.48E+01 | 7.92E+01 | 1.34E+01 | 4.25E+01 | 6.09E+01 | |
| Rank | 2 | 1 | 5 | 4 | 6 | 9 | 7 | 3 | 8 | |
| cec22 | Mean | 2.30E+03 | 2.68E+03 | 2.32E+03 | 2.32E+03 | 7.55E+03 | 8.26E+03 | 1.05E+04 | 5.38E+03 | 6.56E+03 |
| Std | 1.65E+00 | 1.00E+03 | 2.49E+00 | 4.32E+00 | 2.46E+03 | 1.09E+03 | 3.41E+02 | 2.45E+03 | 2.63E+03 | |
| Rank | 1 | 4 | 2 | 3 | 7 | 8 | 9 | 5 | 6 | |
| cec23 | Mean | 2.73E+03 | 2.70E+03 | 2.82E+03 | 2.81E+03 | 3.33E+03 | 3.25E+03 | 2.92E+03 | 2.79E+03 | 3.10E+03 |
| Std | 1.71E+01 | 1.33E+01 | 1.41E+01 | 1.93E+01 | 1.90E+02 | 1.17E+02 | 1.58E+01 | 4.65E+01 | 6.84E+01 | |
| Rank | 2 | 1 | 5 | 4 | 9 | 8 | 6 | 3 | 7 | |
| cec24 | Mean | 2.91E+03 | 2.87E+03 | 2.80E+03 | 2.97E+03 | 3.59E+03 | 3.57E+03 | 3.11E+03 | 2.96E+03 | 3.23E+03 |
| Std | 2.27E+01 | 1.57E+01 | 3.58E+01 | 8.71E+00 | 2.37E+02 | 1.44E+02 | 1.33E+01 | 6.32E+01 | 8.84E+01 | |
| Rank | 3 | 2 | 1 | 5 | 9 | 8 | 6 | 4 | 7 | |
| cec25 | Mean | 2.89E+03 | 2.89E+03 | 2.87E+03 | 2.89E+03 | 3.10E+03 | 5.32E+03 | 2.96E+03 | 2.98E+03 | 3.11E+03 |
| Std | 7.48E+00 | 7.07E+00 | 2.57E+01 | 6.44E+00 | 8.57E+01 | 1.19E+03 | 3.14E+01 | 3.49E+01 | 5.40E+01 | |
| Rank | 3 | 2 | 1 | 4 | 7 | 9 | 5 | 6 | 8 | |
| cec26 | Mean | 3.91E+03 | 4.20E+03 | 2.71E+03 | 5.17E+03 | 6.80E+03 | 8.75E+03 | 5.91E+03 | 4.87E+03 | 7.99E+03 |
| Std | 1.03E+03 | 1.62E+02 | 6.81E-01 | 1.47E+02 | 1.61E+03 | 1.00E+03 | 1.92E+02 | 3.06E+02 | 1.04E+03 | |
| Rank | 2 | 3 | 1 | 5 | 7 | 9 | 6 | 4 | 8 | |
| cec27 | Mean | 3.20E+03 | 3.23E+03 | 3.22E+03 | 3.22E+03 | 3.61E+03 | 3.94E+03 | 3.20E+03 | 3.26E+03 | 3.45E+03 |
| Std | 7.56E-05 | 1.58E+01 | 5.52E+00 | 6.09E+00 | 1.79E+02 | 2.42E+02 | 6.88E-05 | 3.21E+01 | 1.15E+02 | |
| Rank | 2 | 5 | 4 | 3 | 8 | 9 | 1 | 6 | 7 | |
| cec28 | Mean | 3.24E+03 | 3.24E+03 | 3.24E+03 | 3.25E+03 | 3.75E+03 | 6.15E+03 | 3.30E+03 | 3.44E+03 | 3.55E+03 |
| Std | 1.63E+01 | 2.74E+01 | 1.71E+01 | 1.65E+01 | 4.31E+02 | 1.25E+03 | 1.27E-01 | 6.44E+01 | 1.04E+02 | |
| Rank | 1 | 2 | 3 | 4 | 8 | 9 | 5 | 6 | 7 | |
| cec29 | Mean | 3.57E+03 | 3.60E+03 | 3.95E+03 | 3.88E+03 | 4.81E+03 | 6.07E+03 | 5.01E+03 | 3.81E+03 | 5.36E+03 |
| Std | 1.16E+02 | 1.08E+02 | 1.24E+02 | 1.32E+02 | 5.53E+02 | 6.86E+02 | 2.58E+02 | 1.98E+02 | 3.94E+02 | |
| Rank | 1 | 2 | 5 | 4 | 6 | 9 | 7 | 3 | 8 | |
| cec30 | Mean | 8.81E+03 | 1.08E+04 | 3.33E+04 | 4.51E+04 | 1.81E+07 | 1.65E+08 | 7.11E+05 | 8.39E+06 | 4.06E+07 |
| Std | 1.98E+03 | 3.24E+03 | 1.64E+04 | 2.58E+04 | 4.94E+07 | 1.91E+08 | 5.88E+05 | 6.50E+06 | 3.86E+07 | |
| Rank | 1 | 2 | 3 | 4 | 7 | 9 | 5 | 6 | 8 | |
| Mean rank | 2.10 | 2.17 | 2.90 | 3.90 | 6.83 | 8.59 | 6.59 | 4.66 | 7.28 | |
| Final ranking | 1 | 2 | 3 | 4 | 7 | 9 | 6 | 5 | 8 | |
| Function . | Index . | Algorithms . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HBWO-JS . | L-SHADE . | LSHADE-cnEpSin . | LSHADE-SPACMA . | PSO . | GA . | ABC . | GWO . | WOA . | ||
| cec01 | Mean | 5.02E+03 | 5.51E+03 | 1.44E+06 | 4.26E+06 | 4.15E+09 | 3.15E+10 | 7.68E+07 | 2.47E+09 | 1.70E+09 |
| Std | 3.26E+03 | 5.89E+03 | 7.91E+05 | 2.03E+06 | 3.30E+09 | 1.13E+10 | 9.33E+07 | 1.44E+09 | 6.54E+08 | |
| Rank | 1 | 2 | 3 | 4 | 8 | 9 | 5 | 7 | 6 | |
| cec03 | Mean | 2.27E+04 | 3.46E+04 | 1.13E+04 | 1.47E+04 | 1.19E+05 | 2.70E+05 | 4.07E+05 | 5.63E+04 | 2.62E+05 |
| Std | 5.41E+03 | 4.81E+04 | 1.83E+04 | 7.97E+03 | 8.17E+04 | 9.24E+04 | 1.57E+05 | 1.28E+04 | 6.44E+04 | |
| Rank | 3 | 4 | 1 | 2 | 6 | 8 | 9 | 5 | 7 | |
| cec04 | Mean | 4.86E+02 | 4.90E+02 | 4.97E+02 | 5.03E+02 | 9.78E+02 | 7.43E+03 | 5.58E+02 | 6.13E+02 | 8.62E+02 |
| Std | 3.51E+01 | 2.88E+01 | 9.16E+00 | 1.13E+01 | 5.43E+02 | 3.12E+03 | 5.69E+01 | 5.81E+01 | 1.71E+02 | |
| Rank | 1 | 2 | 3 | 4 | 8 | 9 | 5 | 6 | 7 | |
| cec05 | Mean | 6.23E+02 | 5.44E+02 | 5.21E+02 | 6.61E+02 | 7.47E+02 | 8.49E+02 | 7.61E+02 | 6.32E+02 | 8.20E+02 |
| Std | 2.96E+01 | 8.10E+00 | 6.38E-02 | 1.69E+01 | 4.03E+01 | 5.21E+01 | 1.28E+01 | 4.37E+01 | 5.43E+01 | |
| Rank | 3 | 2 | 1 | 5 | 6 | 9 | 7 | 4 | 8 | |
| cec06 | Mean | 6.00E+02 | 6.01E+02 | 6.02E+02 | 6.03E+02 | 6.47E+02 | 6.70E+02 | 6.14E+02 | 6.11E+02 | 6.81E+02 |
| Std | 1.39E-01 | 6.00E-01 | 4.85E-01 | 6.37E-01 | 1.22E+01 | 1.83E+01 | 4.80E+00 | 3.47E+00 | 1.13E+01 | |
| Rank | 1 | 2 | 3 | 4 | 7 | 8 | 6 | 5 | 9 | |
| cec07 | Mean | 8.78E+02 | 7.97E+02 | 9.24E+02 | 9.07E+02 | 1.07E+03 | 1.66E+03 | 1.00E+03 | 8.97E+02 | 1.29E+03 |
| Std | 3.93E+01 | 1.90E+01 | 1.14E+01 | 1.91E+01 | 5.13E+01 | 2.23E+02 | 1.45E+01 | 5.77E+01 | 6.68E+01 | |
| Rank | 2 | 1 | 5 | 4 | 7 | 9 | 6 | 3 | 8 | |
| cec08 | Mean | 8.98E+02 | 8.48E+02 | 9.74E+02 | 9.60E+02 | 9.97E+02 | 1.09E+03 | 1.06E+03 | 9.05E+02 | 1.04E+03 |
| Std | 1.23E+01 | 9.42E+00 | 1.40E+01 | 1.45E+01 | 3.70E+01 | 4.29E+01 | 1.21E+01 | 2.16E+01 | 5.14E+01 | |
| Rank | 2 | 1 | 5 | 4 | 6 | 9 | 8 | 3 | 7 | |
| cec09 | Mean | 3.12E+03 | 1.12E+03 | 9.12E+02 | 9.28E+02 | 4.74E+03 | 1.07E+04 | 6.15E+03 | 2.48E+03 | 1.07E+04 |
| Std | 1.25E+03 | 1.36E+02 | 6.25E+00 | 1.67E+01 | 1.52E+03 | 2.47E+03 | 1.12E+03 | 1.03E+03 | 4.42E+03 | |
| Rank | 5 | 3 | 1 | 2 | 6 | 9 | 7 | 4 | 8 | |
| cec10 | Mean | 3.55E+03 | 3.75E+03 | 7.60E+03 | 7.20E+03 | 6.68E+03 | 6.54E+03 | 9.34E+03 | 4.60E+03 | 6.75E+03 |
| Std | 3.01E+02 | 3.95E+02 | 6.19E+02 | 7.08E+02 | 6.32E+02 | 5.51E+02 | 2.70E+02 | 1.05E+03 | 7.76E+02 | |
| Rank | 1 | 2 | 8 | 7 | 5 | 4 | 9 | 3 | 6 | |
| cec11 | Mean | 1.19E+03 | 1.25E+03 | 1.26E+03 | 1.26E+03 | 2.04E+03 | 1.84E+04 | 1.49E+04 | 1.91E+03 | 6.80E+03 |
| Std | 3.08E+01 | 5.01E+01 | 3.14E+01 | 2.53E+01 | 7.67E+02 | 8.79E+03 | 3.40E+03 | 8.35E+02 | 3.05E+03 | |
| Rank | 1 | 2 | 4 | 3 | 6 | 9 | 8 | 5 | 7 | |
| cec12 | Mean | 6.78E+05 | 8.75E+04 | 1.20E+03 | 8.13E+05 | 6.88E+08 | 4.34E+09 | 7.35E+08 | 9.70E+07 | 2.40E+08 |
| Std | 3.61E+05 | 6.51E+04 | 7.52E-01 | 5.58E+05 | 1.59E+09 | 2.17E+09 | 2.44E+08 | 8.87E+07 | 1.58E+08 | |
| Rank | 3 | 2 | 1 | 4 | 7 | 9 | 8 | 5 | 6 | |
| cec13 | Mean | 5.93E+03 | 1.02E+04 | 1.31E+03 | 3.58E+04 | 1.05E+08 | 5.69E+09 | 2.73E+05 | 8.14E+06 | 2.07E+06 |
| Std | 5.46E+03 | 1.14E+04 | 6.71E-01 | 8.84E+03 | 3.99E+08 | 5.43E+09 | 2.55E+05 | 2.50E+07 | 3.34E+06 | |
| Rank | 2 | 3 | 1 | 4 | 8 | 9 | 5 | 7 | 6 | |
| cec14 | Mean | 1.17E+04 | 1.56E+03 | 1.53E+03 | 1.60E+03 | 3.95E+05 | 1.02E+07 | 4.95E+05 | 3.53E+05 | 2.46E+06 |
| Std | 8.61E+03 | 5.82E+01 | 1.65E+01 | 4.29E+01 | 8.38E+05 | 8.81E+06 | 2.01E+05 | 5.35E+05 | 3.15E+06 | |
| Rank | 4 | 2 | 1 | 3 | 6 | 9 | 7 | 5 | 8 | |
| cec15 | Mean | 3.64E+03 | 1.90E+03 | 5.20E+03 | 8.11E+03 | 3.31E+04 | 1.20E+09 | 1.43E+06 | 6.10E+05 | 2.63E+06 |
| Std | 2.74E+03 | 2.25E+02 | 1.63E+03 | 4.39E+03 | 3.43E+04 | 2.02E+09 | 1.22E+06 | 8.15E+05 | 7.41E+06 | |
| Rank | 2 | 1 | 3 | 4 | 5 | 9 | 7 | 6 | 8 | |
| cec16 | Mean | 2.32E+03 | 2.35E+03 | 1.61E+03 | 3.02E+03 | 3.53E+03 | 3.92E+03 | 3.99E+03 | 2.58E+03 | 4.05E+03 |
| Std | 1.84E+02 | 2.16E+02 | 1.55E-01 | 1.92E+02 | 5.44E+02 | 4.59E+02 | 2.30E+02 | 2.93E+02 | 5.46E+02 | |
| Rank | 2 | 3 | 1 | 5 | 6 | 7 | 8 | 4 | 9 | |
| cec17 | Mean | 1.95E+03 | 1.90E+03 | 2.22E+03 | 2.13E+03 | 2.67E+03 | 3.39E+03 | 2.92E+03 | 2.05E+03 | 2.58E+03 |
| Std | 1.57E+02 | 1.13E+02 | 1.14E+02 | 1.20E+02 | 3.55E+02 | 1.22E+03 | 1.66E+02 | 1.56E+02 | 2.48E+02 | |
| Rank | 2 | 1 | 5 | 4 | 7 | 9 | 8 | 3 | 6 | |
| cec18 | Mean | 3.57E+05 | 2.67E+04 | 1.13E+04 | 1.72E+04 | 1.29E+07 | 3.54E+07 | 1.83E+07 | 9.82E+05 | 8.69E+06 |
| Std | 3.14E+05 | 1.84E+04 | 7.24E+03 | 7.89E+03 | 2.50E+07 | 4.21E+07 | 7.07E+06 | 1.13E+06 | 8.17E+06 | |
| Rank | 4 | 3 | 1 | 2 | 7 | 9 | 8 | 5 | 6 | |
| cec19 | Mean | 2.94E+03 | 2.07E+03 | 2.38E+03 | 3.77E+03 | 4.30E+06 | 6.45E+08 | 1.84E+04 | 1.91E+06 | 1.13E+07 |
| Std | 1.23E+03 | 8.55E+01 | 2.79E+02 | 1.97E+03 | 1.72E+07 | 6.92E+08 | 4.25E+04 | 2.64E+06 | 1.51E+07 | |
| Rank | 3 | 1 | 2 | 4 | 7 | 9 | 5 | 6 | 8 | |
| cec20 | Mean | 2.26E+03 | 2.28E+03 | 2.66E+03 | 2.64E+03 | 2.76E+03 | 3.11E+03 | 3.08E+03 | 2.48E+03 | 2.84E+03 |
| Std | 8.68E+01 | 1.19E+02 | 1.19E+02 | 1.05E+02 | 2.38E+02 | 2.85E+02 | 1.15E+02 | 2.29E+02 | 1.96E+02 | |
| Rank | 1 | 2 | 5 | 4 | 6 | 9 | 8 | 3 | 7 | |
| cec21 | Mean | 2.38E+03 | 2.35E+03 | 2.47E+03 | 2.46E+03 | 2.52E+03 | 2.63E+03 | 2.56E+03 | 2.41E+03 | 2.62E+03 |
| Std | 4.58E+01 | 8.13E+00 | 1.36E+01 | 1.50E+01 | 4.48E+01 | 7.92E+01 | 1.34E+01 | 4.25E+01 | 6.09E+01 | |
| Rank | 2 | 1 | 5 | 4 | 6 | 9 | 7 | 3 | 8 | |
| cec22 | Mean | 2.30E+03 | 2.68E+03 | 2.32E+03 | 2.32E+03 | 7.55E+03 | 8.26E+03 | 1.05E+04 | 5.38E+03 | 6.56E+03 |
| Std | 1.65E+00 | 1.00E+03 | 2.49E+00 | 4.32E+00 | 2.46E+03 | 1.09E+03 | 3.41E+02 | 2.45E+03 | 2.63E+03 | |
| Rank | 1 | 4 | 2 | 3 | 7 | 8 | 9 | 5 | 6 | |
| cec23 | Mean | 2.73E+03 | 2.70E+03 | 2.82E+03 | 2.81E+03 | 3.33E+03 | 3.25E+03 | 2.92E+03 | 2.79E+03 | 3.10E+03 |
| Std | 1.71E+01 | 1.33E+01 | 1.41E+01 | 1.93E+01 | 1.90E+02 | 1.17E+02 | 1.58E+01 | 4.65E+01 | 6.84E+01 | |
| Rank | 2 | 1 | 5 | 4 | 9 | 8 | 6 | 3 | 7 | |
| cec24 | Mean | 2.91E+03 | 2.87E+03 | 2.80E+03 | 2.97E+03 | 3.59E+03 | 3.57E+03 | 3.11E+03 | 2.96E+03 | 3.23E+03 |
| Std | 2.27E+01 | 1.57E+01 | 3.58E+01 | 8.71E+00 | 2.37E+02 | 1.44E+02 | 1.33E+01 | 6.32E+01 | 8.84E+01 | |
| Rank | 3 | 2 | 1 | 5 | 9 | 8 | 6 | 4 | 7 | |
| cec25 | Mean | 2.89E+03 | 2.89E+03 | 2.87E+03 | 2.89E+03 | 3.10E+03 | 5.32E+03 | 2.96E+03 | 2.98E+03 | 3.11E+03 |
| Std | 7.48E+00 | 7.07E+00 | 2.57E+01 | 6.44E+00 | 8.57E+01 | 1.19E+03 | 3.14E+01 | 3.49E+01 | 5.40E+01 | |
| Rank | 3 | 2 | 1 | 4 | 7 | 9 | 5 | 6 | 8 | |
| cec26 | Mean | 3.91E+03 | 4.20E+03 | 2.71E+03 | 5.17E+03 | 6.80E+03 | 8.75E+03 | 5.91E+03 | 4.87E+03 | 7.99E+03 |
| Std | 1.03E+03 | 1.62E+02 | 6.81E-01 | 1.47E+02 | 1.61E+03 | 1.00E+03 | 1.92E+02 | 3.06E+02 | 1.04E+03 | |
| Rank | 2 | 3 | 1 | 5 | 7 | 9 | 6 | 4 | 8 | |
| cec27 | Mean | 3.20E+03 | 3.23E+03 | 3.22E+03 | 3.22E+03 | 3.61E+03 | 3.94E+03 | 3.20E+03 | 3.26E+03 | 3.45E+03 |
| Std | 7.56E-05 | 1.58E+01 | 5.52E+00 | 6.09E+00 | 1.79E+02 | 2.42E+02 | 6.88E-05 | 3.21E+01 | 1.15E+02 | |
| Rank | 2 | 5 | 4 | 3 | 8 | 9 | 1 | 6 | 7 | |
| cec28 | Mean | 3.24E+03 | 3.24E+03 | 3.24E+03 | 3.25E+03 | 3.75E+03 | 6.15E+03 | 3.30E+03 | 3.44E+03 | 3.55E+03 |
| Std | 1.63E+01 | 2.74E+01 | 1.71E+01 | 1.65E+01 | 4.31E+02 | 1.25E+03 | 1.27E-01 | 6.44E+01 | 1.04E+02 | |
| Rank | 1 | 2 | 3 | 4 | 8 | 9 | 5 | 6 | 7 | |
| cec29 | Mean | 3.57E+03 | 3.60E+03 | 3.95E+03 | 3.88E+03 | 4.81E+03 | 6.07E+03 | 5.01E+03 | 3.81E+03 | 5.36E+03 |
| Std | 1.16E+02 | 1.08E+02 | 1.24E+02 | 1.32E+02 | 5.53E+02 | 6.86E+02 | 2.58E+02 | 1.98E+02 | 3.94E+02 | |
| Rank | 1 | 2 | 5 | 4 | 6 | 9 | 7 | 3 | 8 | |
| cec30 | Mean | 8.81E+03 | 1.08E+04 | 3.33E+04 | 4.51E+04 | 1.81E+07 | 1.65E+08 | 7.11E+05 | 8.39E+06 | 4.06E+07 |
| Std | 1.98E+03 | 3.24E+03 | 1.64E+04 | 2.58E+04 | 4.94E+07 | 1.91E+08 | 5.88E+05 | 6.50E+06 | 3.86E+07 | |
| Rank | 1 | 2 | 3 | 4 | 7 | 9 | 5 | 6 | 8 | |
| Mean rank | 2.10 | 2.17 | 2.90 | 3.90 | 6.83 | 8.59 | 6.59 | 4.66 | 7.28 | |
| Final ranking | 1 | 2 | 3 | 4 | 7 | 9 | 6 | 5 | 8 | |
4.4. Result analysis for the CEC2019 benchmark functions
The test results of the 10 benchmark functions of the CEC2019 test set are shown in Table 5, where the data in bold are the best cases of the average values of all nine methods under the same benchmark functions. From the numerical results in Table 5, it can be found that HBWO-JS shows significant competitiveness and stability on all 10 tested functions, especially in cec01, cec02, cec03, cec04, cec06, cec07, cec08, cec10, finding the best value of theoretical extremes and ranking first among all the algorithms. Furthermore, the Std of HBWO-JS outperformed all other algorithms on other functions, cec05, and cec09. In the Friedman test, HBWO-JS has an average rank of 1.3 and finally ranks first, followed by AHA in second place. In addition, for the cec01 test function, the proposed HBWO-JS and BWO, AHA, and RSA all find optimal results. Table 6 provides the results of the Wilcoxon rank sum test for all methods, where “+” indicates that the different algorithms outperform the proposed HBWO-JS algorithm in the selected test problem; “−” in contrast to “+”, indicates that the proposed HBWO-JS outperforms the other algorithms in the selected test problem. “=” indicates that the other algorithms do not differ significantly from the proposed HBWO-JS in handling the selected test problem. The table shows that only AHA outperforms the proposed HBWO-JS on one test function (cec09). The JS, BWO, AHA, ARO, DO, SO, WSO, and RSA has rank sum test results of 0/0/10, 0/0/10, 1/4/5, 0/3/7, 0/1/9, 0/1/9, 0/2/8, and 0/0/10.
Experimental outcomes attained by nine algorithms on the CEC2019 test suite.
| Function . | Index . | Algorithms . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HBWO-JS . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . | ||
| cec01 | Best | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 44.94 | 1.00 | 735.42 | 1.00 |
| Worst | 1.00 | 190141.86 | 1.00 | 1.00 | 1.00 | 637364.83 | 120136.89 | 459567.07 | 1.00 | |
| Mean | 1.00 | 10160.76 | 1.00 | 1.00 | 1.00 | 101629.23 | 32535.10 | 60505.64 | 1.00 | |
| Std | 0.00 | 35652.04 | 0.00 | 0.00 | 0.00 | 143909.25 | 36735.19 | 105878.90 | 0.00 | |
| Rank | 1 | 6 | 1 | 1 | 5 | 9 | 7 | 8 | 1 | |
| cec02 | Best | 4.2334 | 4.2298 | 4.9988 | 4.2172 | 4.2096 | 315.7346 | 5.0000 | 62.9354 | 4.8744 |
| Worst | 5.0000 | 112.2304 | 5.0000 | 5.0000 | 5.0000 | 2080.1800 | 753.1927 | 1168.7727 | 5.0000 | |
| Mean | 4.2956 | 17.3165 | 5.0000 | 4.5216 | 4.3548 | 786.7426 | 243.6912 | 235.7905 | 4.9957 | |
| Std | 0.1350 | 23.0445 | 0.0002 | 0.3491 | 0.2127 | 481.4622 | 164.5665 | 206.7904 | 0.0229 | |
| Rank | 1 | 6 | 5 | 3 | 2 | 9 | 8 | 7 | 4 | |
| cec03 | Best | 1.0149 | 2.9486 | 2.7012 | 1.0005 | 1.4137 | 1.4092 | 1.4174 | 1.1589 | 6.5512 |
| Worst | 1.9884 | 6.4529 | 7.2032 | 4.5752 | 5.4525 | 10.7110 | 7.7199 | 4.9906 | 10.0138 | |
| Mean | 1.4407 | 4.9440 | 5.0638 | 1.7294 | 2.4667 | 6.9114 | 4.7468 | 2.7067 | 8.0420 | |
| Std | 0.2172 | 1.0121 | 0.9607 | 0.6914 | 1.0301 | 3.0731 | 2.0816 | 0.9892 | 0.8531 | |
| Rank | 1 | 6 | 7 | 2 | 3 | 8 | 5 | 4 | 9 | |
| cec04 | Best | 9.5187 | 9.9776 | 63.8525 | 8.9597 | 4.9811 | 8.9606 | 7.9866 | 8.1256 | 55.8445 |
| Worst | 29.1260 | 33.2841 | 106.7514 | 44.7780 | 45.7730 | 74.6266 | 34.8326 | 41.6974 | 119.1290 | |
| Mean | 16.2736 | 19.2218 | 82.4830 | 21.6973 | 17.8702 | 36.0170 | 17.6244 | 19.5944 | 87.0995 | |
| Std | 4.7905 | 5.2342 | 10.4289 | 9.4409 | 8.2538 | 16.7931 | 5.7783 | 9.2821 | 12.7096 | |
| Rank | 1 | 4 | 8 | 6 | 3 | 7 | 2 | 5 | 9 | |
| cec05 | Best | 1.0123 | 1.0158 | 29.2699 | 1.0174 | 1.0154 | 1.0703 | 1.0473 | 1.0579 | 44.2344 |
| Worst | 1.1452 | 1.2914 | 85.0071 | 1.2730 | 1.4435 | 1.9158 | 1.2173 | 3.4134 | 113.2750 | |
| Best | 1.0149 | 2.9486 | 2.7012 | 1.0005 | 1.4137 | 1.4092 | 1.4174 | 1.1589 | 79.9990 | |
| Std | 0.0336 | 0.0775 | 12.9365 | 0.0671 | 0.0852 | 0.1490 | 0.0485 | 0.6368 | 18.0103 | |
| Rank | 2 | 8 | 7 | 1 | 5 | 4 | 6 | 3 | 9 | |
| cec06 | Best | 1.0246 | 1.0620 | 9.4502 | 1.0892 | 1.0980 | 1.6778 | 1.2576 | 1.3408 | 8.5339 |
| Worst | 3.5445 | 4.7492 | 11.5440 | 4.8924 | 4.6538 | 8.3538 | 6.6065 | 5.0093 | 12.5887 | |
| Mean | 1.7047 | 2.3351 | 10.5720 | 2.5376 | 2.2508 | 4.8321 | 3.7391 | 3.1198 | 10.7489 | |
| Std | 0.7570 | 0.9096 | 0.6035 | 1.1507 | 0.9774 | 1.7159 | 1.3485 | 1.0463 | 0.9784 | |
| Rank | 1 | 3 | 8 | 4 | 2 | 7 | 6 | 5 | 9 | |
| cec07 | Best | 242.6790 | 317.8746 | 916.9078 | 238.4547 | 230.0355 | 491.1312 | 253.3952 | 477.9319 | 1287.2425 |
| Worst | 771.4527 | 1796.6636 | 2101.6793 | 1093.2275 | 1124.3791 | 1485.9684 | 1101.6897 | 1779.1404 | 2246.4237 | |
| Mean | 484.5589 | 1101.5621 | 1718.2096 | 648.1085 | 642.3277 | 973.4150 | 687.8904 | 1169.7182 | 1841.0866 | |
| Std | 158.9041 | 371.6299 | 256.9217 | 238.8129 | 209.6633 | 250.7041 | 246.9875 | 386.9086 | 209.4990 | |
| Rank | 1 | 6 | 8 | 3 | 2 | 5 | 4 | 7 | 9 | |
| cec08 | Best | 2.8343 | 3.4969 | 4.0801 | 2.5995 | 2.8274 | 3.6995 | 2.7865 | 2.9969 | 4.4430 |
| Worst | 4.0614 | 4.6721 | 5.0310 | 4.2040 | 4.3917 | 4.8536 | 4.3974 | 4.7245 | 5.2382 | |
| Mean | 3.4773 | 4.0735 | 4.7669 | 3.5125 | 3.7319 | 4.2205 | 3.9045 | 3.8995 | 4.9456 | |
| Std | 0.3336 | 0.2953 | 0.2097 | 0.4043 | 0.3941 | 0.3095 | 0.4008 | 0.4063 | 0.1920 | |
| Rank | 1 | 6 | 8 | 2 | 3 | 7 | 5 | 4 | 9 | |
| cec09 | Best | 1.1133 | 1.1371 | 2.3118 | 1.0607 | 1.0542 | 1.0857 | 1.1223 | 1.1146 | 2.4667 |
| Worst | 1.3044 | 1.4226 | 3.9506 | 1.4011 | 1.3629 | 1.6413 | 1.5933 | 1.6641 | 4.3532 | |
| Mean | 1.2026 | 1.2561 | 3.3861 | 1.1818 | 1.1847 | 1.3023 | 1.3529 | 1.2319 | 3.1237 | |
| Std | 0.0581 | 0.0657 | 0.3782 | 0.0930 | 0.0728 | 0.1230 | 0.1206 | 0.1159 | 0.5021 | |
| Rank | 3 | 5 | 9 | 1 | 2 | 6 | 7 | 4 | 8 | |
| cec10 | Best | 1.0224 | 9.6265 | 21.1911 | 2.6493 | 1.0570 | 21.0006 | 21.2267 | 5.0012 | 21.1799 |
| Worst | 21.0870 | 21.6237 | 21.6119 | 21.0868 | 21.1032 | 21.1284 | 21.7000 | 21.7063 | 21.6700 | |
| Mean | 17.9548 | 20.6938 | 21.4494 | 20.3907 | 20.3527 | 21.0191 | 21.5034 | 20.0372 | 21.4743 | |
| Std | 6.9747 | 2.9991 | 0.0888 | 3.3512 | 3.6445 | 0.0313 | 0.1079 | 4.5363 | 0.1201 | |
| Rank | 1 | 5 | 7 | 4 | 3 | 6 | 9 | 2 | 8 | |
| Mean rank | 1.3 | 5.5 | 6.8 | 2.7 | 3 | 6.8 | 5.9 | 4.9 | 7.5 | |
| Final ranking | 1 | 5 | 7 | 2 | 3 | 7 | 6 | 4 | 9 | |
| Function . | Index . | Algorithms . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HBWO-JS . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . | ||
| cec01 | Best | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 44.94 | 1.00 | 735.42 | 1.00 |
| Worst | 1.00 | 190141.86 | 1.00 | 1.00 | 1.00 | 637364.83 | 120136.89 | 459567.07 | 1.00 | |
| Mean | 1.00 | 10160.76 | 1.00 | 1.00 | 1.00 | 101629.23 | 32535.10 | 60505.64 | 1.00 | |
| Std | 0.00 | 35652.04 | 0.00 | 0.00 | 0.00 | 143909.25 | 36735.19 | 105878.90 | 0.00 | |
| Rank | 1 | 6 | 1 | 1 | 5 | 9 | 7 | 8 | 1 | |
| cec02 | Best | 4.2334 | 4.2298 | 4.9988 | 4.2172 | 4.2096 | 315.7346 | 5.0000 | 62.9354 | 4.8744 |
| Worst | 5.0000 | 112.2304 | 5.0000 | 5.0000 | 5.0000 | 2080.1800 | 753.1927 | 1168.7727 | 5.0000 | |
| Mean | 4.2956 | 17.3165 | 5.0000 | 4.5216 | 4.3548 | 786.7426 | 243.6912 | 235.7905 | 4.9957 | |
| Std | 0.1350 | 23.0445 | 0.0002 | 0.3491 | 0.2127 | 481.4622 | 164.5665 | 206.7904 | 0.0229 | |
| Rank | 1 | 6 | 5 | 3 | 2 | 9 | 8 | 7 | 4 | |
| cec03 | Best | 1.0149 | 2.9486 | 2.7012 | 1.0005 | 1.4137 | 1.4092 | 1.4174 | 1.1589 | 6.5512 |
| Worst | 1.9884 | 6.4529 | 7.2032 | 4.5752 | 5.4525 | 10.7110 | 7.7199 | 4.9906 | 10.0138 | |
| Mean | 1.4407 | 4.9440 | 5.0638 | 1.7294 | 2.4667 | 6.9114 | 4.7468 | 2.7067 | 8.0420 | |
| Std | 0.2172 | 1.0121 | 0.9607 | 0.6914 | 1.0301 | 3.0731 | 2.0816 | 0.9892 | 0.8531 | |
| Rank | 1 | 6 | 7 | 2 | 3 | 8 | 5 | 4 | 9 | |
| cec04 | Best | 9.5187 | 9.9776 | 63.8525 | 8.9597 | 4.9811 | 8.9606 | 7.9866 | 8.1256 | 55.8445 |
| Worst | 29.1260 | 33.2841 | 106.7514 | 44.7780 | 45.7730 | 74.6266 | 34.8326 | 41.6974 | 119.1290 | |
| Mean | 16.2736 | 19.2218 | 82.4830 | 21.6973 | 17.8702 | 36.0170 | 17.6244 | 19.5944 | 87.0995 | |
| Std | 4.7905 | 5.2342 | 10.4289 | 9.4409 | 8.2538 | 16.7931 | 5.7783 | 9.2821 | 12.7096 | |
| Rank | 1 | 4 | 8 | 6 | 3 | 7 | 2 | 5 | 9 | |
| cec05 | Best | 1.0123 | 1.0158 | 29.2699 | 1.0174 | 1.0154 | 1.0703 | 1.0473 | 1.0579 | 44.2344 |
| Worst | 1.1452 | 1.2914 | 85.0071 | 1.2730 | 1.4435 | 1.9158 | 1.2173 | 3.4134 | 113.2750 | |
| Best | 1.0149 | 2.9486 | 2.7012 | 1.0005 | 1.4137 | 1.4092 | 1.4174 | 1.1589 | 79.9990 | |
| Std | 0.0336 | 0.0775 | 12.9365 | 0.0671 | 0.0852 | 0.1490 | 0.0485 | 0.6368 | 18.0103 | |
| Rank | 2 | 8 | 7 | 1 | 5 | 4 | 6 | 3 | 9 | |
| cec06 | Best | 1.0246 | 1.0620 | 9.4502 | 1.0892 | 1.0980 | 1.6778 | 1.2576 | 1.3408 | 8.5339 |
| Worst | 3.5445 | 4.7492 | 11.5440 | 4.8924 | 4.6538 | 8.3538 | 6.6065 | 5.0093 | 12.5887 | |
| Mean | 1.7047 | 2.3351 | 10.5720 | 2.5376 | 2.2508 | 4.8321 | 3.7391 | 3.1198 | 10.7489 | |
| Std | 0.7570 | 0.9096 | 0.6035 | 1.1507 | 0.9774 | 1.7159 | 1.3485 | 1.0463 | 0.9784 | |
| Rank | 1 | 3 | 8 | 4 | 2 | 7 | 6 | 5 | 9 | |
| cec07 | Best | 242.6790 | 317.8746 | 916.9078 | 238.4547 | 230.0355 | 491.1312 | 253.3952 | 477.9319 | 1287.2425 |
| Worst | 771.4527 | 1796.6636 | 2101.6793 | 1093.2275 | 1124.3791 | 1485.9684 | 1101.6897 | 1779.1404 | 2246.4237 | |
| Mean | 484.5589 | 1101.5621 | 1718.2096 | 648.1085 | 642.3277 | 973.4150 | 687.8904 | 1169.7182 | 1841.0866 | |
| Std | 158.9041 | 371.6299 | 256.9217 | 238.8129 | 209.6633 | 250.7041 | 246.9875 | 386.9086 | 209.4990 | |
| Rank | 1 | 6 | 8 | 3 | 2 | 5 | 4 | 7 | 9 | |
| cec08 | Best | 2.8343 | 3.4969 | 4.0801 | 2.5995 | 2.8274 | 3.6995 | 2.7865 | 2.9969 | 4.4430 |
| Worst | 4.0614 | 4.6721 | 5.0310 | 4.2040 | 4.3917 | 4.8536 | 4.3974 | 4.7245 | 5.2382 | |
| Mean | 3.4773 | 4.0735 | 4.7669 | 3.5125 | 3.7319 | 4.2205 | 3.9045 | 3.8995 | 4.9456 | |
| Std | 0.3336 | 0.2953 | 0.2097 | 0.4043 | 0.3941 | 0.3095 | 0.4008 | 0.4063 | 0.1920 | |
| Rank | 1 | 6 | 8 | 2 | 3 | 7 | 5 | 4 | 9 | |
| cec09 | Best | 1.1133 | 1.1371 | 2.3118 | 1.0607 | 1.0542 | 1.0857 | 1.1223 | 1.1146 | 2.4667 |
| Worst | 1.3044 | 1.4226 | 3.9506 | 1.4011 | 1.3629 | 1.6413 | 1.5933 | 1.6641 | 4.3532 | |
| Mean | 1.2026 | 1.2561 | 3.3861 | 1.1818 | 1.1847 | 1.3023 | 1.3529 | 1.2319 | 3.1237 | |
| Std | 0.0581 | 0.0657 | 0.3782 | 0.0930 | 0.0728 | 0.1230 | 0.1206 | 0.1159 | 0.5021 | |
| Rank | 3 | 5 | 9 | 1 | 2 | 6 | 7 | 4 | 8 | |
| cec10 | Best | 1.0224 | 9.6265 | 21.1911 | 2.6493 | 1.0570 | 21.0006 | 21.2267 | 5.0012 | 21.1799 |
| Worst | 21.0870 | 21.6237 | 21.6119 | 21.0868 | 21.1032 | 21.1284 | 21.7000 | 21.7063 | 21.6700 | |
| Mean | 17.9548 | 20.6938 | 21.4494 | 20.3907 | 20.3527 | 21.0191 | 21.5034 | 20.0372 | 21.4743 | |
| Std | 6.9747 | 2.9991 | 0.0888 | 3.3512 | 3.6445 | 0.0313 | 0.1079 | 4.5363 | 0.1201 | |
| Rank | 1 | 5 | 7 | 4 | 3 | 6 | 9 | 2 | 8 | |
| Mean rank | 1.3 | 5.5 | 6.8 | 2.7 | 3 | 6.8 | 5.9 | 4.9 | 7.5 | |
| Final ranking | 1 | 5 | 7 | 2 | 3 | 7 | 6 | 4 | 9 | |
Experimental outcomes attained by nine algorithms on the CEC2019 test suite.
| Function . | Index . | Algorithms . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HBWO-JS . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . | ||
| cec01 | Best | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 44.94 | 1.00 | 735.42 | 1.00 |
| Worst | 1.00 | 190141.86 | 1.00 | 1.00 | 1.00 | 637364.83 | 120136.89 | 459567.07 | 1.00 | |
| Mean | 1.00 | 10160.76 | 1.00 | 1.00 | 1.00 | 101629.23 | 32535.10 | 60505.64 | 1.00 | |
| Std | 0.00 | 35652.04 | 0.00 | 0.00 | 0.00 | 143909.25 | 36735.19 | 105878.90 | 0.00 | |
| Rank | 1 | 6 | 1 | 1 | 5 | 9 | 7 | 8 | 1 | |
| cec02 | Best | 4.2334 | 4.2298 | 4.9988 | 4.2172 | 4.2096 | 315.7346 | 5.0000 | 62.9354 | 4.8744 |
| Worst | 5.0000 | 112.2304 | 5.0000 | 5.0000 | 5.0000 | 2080.1800 | 753.1927 | 1168.7727 | 5.0000 | |
| Mean | 4.2956 | 17.3165 | 5.0000 | 4.5216 | 4.3548 | 786.7426 | 243.6912 | 235.7905 | 4.9957 | |
| Std | 0.1350 | 23.0445 | 0.0002 | 0.3491 | 0.2127 | 481.4622 | 164.5665 | 206.7904 | 0.0229 | |
| Rank | 1 | 6 | 5 | 3 | 2 | 9 | 8 | 7 | 4 | |
| cec03 | Best | 1.0149 | 2.9486 | 2.7012 | 1.0005 | 1.4137 | 1.4092 | 1.4174 | 1.1589 | 6.5512 |
| Worst | 1.9884 | 6.4529 | 7.2032 | 4.5752 | 5.4525 | 10.7110 | 7.7199 | 4.9906 | 10.0138 | |
| Mean | 1.4407 | 4.9440 | 5.0638 | 1.7294 | 2.4667 | 6.9114 | 4.7468 | 2.7067 | 8.0420 | |
| Std | 0.2172 | 1.0121 | 0.9607 | 0.6914 | 1.0301 | 3.0731 | 2.0816 | 0.9892 | 0.8531 | |
| Rank | 1 | 6 | 7 | 2 | 3 | 8 | 5 | 4 | 9 | |
| cec04 | Best | 9.5187 | 9.9776 | 63.8525 | 8.9597 | 4.9811 | 8.9606 | 7.9866 | 8.1256 | 55.8445 |
| Worst | 29.1260 | 33.2841 | 106.7514 | 44.7780 | 45.7730 | 74.6266 | 34.8326 | 41.6974 | 119.1290 | |
| Mean | 16.2736 | 19.2218 | 82.4830 | 21.6973 | 17.8702 | 36.0170 | 17.6244 | 19.5944 | 87.0995 | |
| Std | 4.7905 | 5.2342 | 10.4289 | 9.4409 | 8.2538 | 16.7931 | 5.7783 | 9.2821 | 12.7096 | |
| Rank | 1 | 4 | 8 | 6 | 3 | 7 | 2 | 5 | 9 | |
| cec05 | Best | 1.0123 | 1.0158 | 29.2699 | 1.0174 | 1.0154 | 1.0703 | 1.0473 | 1.0579 | 44.2344 |
| Worst | 1.1452 | 1.2914 | 85.0071 | 1.2730 | 1.4435 | 1.9158 | 1.2173 | 3.4134 | 113.2750 | |
| Best | 1.0149 | 2.9486 | 2.7012 | 1.0005 | 1.4137 | 1.4092 | 1.4174 | 1.1589 | 79.9990 | |
| Std | 0.0336 | 0.0775 | 12.9365 | 0.0671 | 0.0852 | 0.1490 | 0.0485 | 0.6368 | 18.0103 | |
| Rank | 2 | 8 | 7 | 1 | 5 | 4 | 6 | 3 | 9 | |
| cec06 | Best | 1.0246 | 1.0620 | 9.4502 | 1.0892 | 1.0980 | 1.6778 | 1.2576 | 1.3408 | 8.5339 |
| Worst | 3.5445 | 4.7492 | 11.5440 | 4.8924 | 4.6538 | 8.3538 | 6.6065 | 5.0093 | 12.5887 | |
| Mean | 1.7047 | 2.3351 | 10.5720 | 2.5376 | 2.2508 | 4.8321 | 3.7391 | 3.1198 | 10.7489 | |
| Std | 0.7570 | 0.9096 | 0.6035 | 1.1507 | 0.9774 | 1.7159 | 1.3485 | 1.0463 | 0.9784 | |
| Rank | 1 | 3 | 8 | 4 | 2 | 7 | 6 | 5 | 9 | |
| cec07 | Best | 242.6790 | 317.8746 | 916.9078 | 238.4547 | 230.0355 | 491.1312 | 253.3952 | 477.9319 | 1287.2425 |
| Worst | 771.4527 | 1796.6636 | 2101.6793 | 1093.2275 | 1124.3791 | 1485.9684 | 1101.6897 | 1779.1404 | 2246.4237 | |
| Mean | 484.5589 | 1101.5621 | 1718.2096 | 648.1085 | 642.3277 | 973.4150 | 687.8904 | 1169.7182 | 1841.0866 | |
| Std | 158.9041 | 371.6299 | 256.9217 | 238.8129 | 209.6633 | 250.7041 | 246.9875 | 386.9086 | 209.4990 | |
| Rank | 1 | 6 | 8 | 3 | 2 | 5 | 4 | 7 | 9 | |
| cec08 | Best | 2.8343 | 3.4969 | 4.0801 | 2.5995 | 2.8274 | 3.6995 | 2.7865 | 2.9969 | 4.4430 |
| Worst | 4.0614 | 4.6721 | 5.0310 | 4.2040 | 4.3917 | 4.8536 | 4.3974 | 4.7245 | 5.2382 | |
| Mean | 3.4773 | 4.0735 | 4.7669 | 3.5125 | 3.7319 | 4.2205 | 3.9045 | 3.8995 | 4.9456 | |
| Std | 0.3336 | 0.2953 | 0.2097 | 0.4043 | 0.3941 | 0.3095 | 0.4008 | 0.4063 | 0.1920 | |
| Rank | 1 | 6 | 8 | 2 | 3 | 7 | 5 | 4 | 9 | |
| cec09 | Best | 1.1133 | 1.1371 | 2.3118 | 1.0607 | 1.0542 | 1.0857 | 1.1223 | 1.1146 | 2.4667 |
| Worst | 1.3044 | 1.4226 | 3.9506 | 1.4011 | 1.3629 | 1.6413 | 1.5933 | 1.6641 | 4.3532 | |
| Mean | 1.2026 | 1.2561 | 3.3861 | 1.1818 | 1.1847 | 1.3023 | 1.3529 | 1.2319 | 3.1237 | |
| Std | 0.0581 | 0.0657 | 0.3782 | 0.0930 | 0.0728 | 0.1230 | 0.1206 | 0.1159 | 0.5021 | |
| Rank | 3 | 5 | 9 | 1 | 2 | 6 | 7 | 4 | 8 | |
| cec10 | Best | 1.0224 | 9.6265 | 21.1911 | 2.6493 | 1.0570 | 21.0006 | 21.2267 | 5.0012 | 21.1799 |
| Worst | 21.0870 | 21.6237 | 21.6119 | 21.0868 | 21.1032 | 21.1284 | 21.7000 | 21.7063 | 21.6700 | |
| Mean | 17.9548 | 20.6938 | 21.4494 | 20.3907 | 20.3527 | 21.0191 | 21.5034 | 20.0372 | 21.4743 | |
| Std | 6.9747 | 2.9991 | 0.0888 | 3.3512 | 3.6445 | 0.0313 | 0.1079 | 4.5363 | 0.1201 | |
| Rank | 1 | 5 | 7 | 4 | 3 | 6 | 9 | 2 | 8 | |
| Mean rank | 1.3 | 5.5 | 6.8 | 2.7 | 3 | 6.8 | 5.9 | 4.9 | 7.5 | |
| Final ranking | 1 | 5 | 7 | 2 | 3 | 7 | 6 | 4 | 9 | |
| Function . | Index . | Algorithms . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HBWO-JS . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . | ||
| cec01 | Best | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 44.94 | 1.00 | 735.42 | 1.00 |
| Worst | 1.00 | 190141.86 | 1.00 | 1.00 | 1.00 | 637364.83 | 120136.89 | 459567.07 | 1.00 | |
| Mean | 1.00 | 10160.76 | 1.00 | 1.00 | 1.00 | 101629.23 | 32535.10 | 60505.64 | 1.00 | |
| Std | 0.00 | 35652.04 | 0.00 | 0.00 | 0.00 | 143909.25 | 36735.19 | 105878.90 | 0.00 | |
| Rank | 1 | 6 | 1 | 1 | 5 | 9 | 7 | 8 | 1 | |
| cec02 | Best | 4.2334 | 4.2298 | 4.9988 | 4.2172 | 4.2096 | 315.7346 | 5.0000 | 62.9354 | 4.8744 |
| Worst | 5.0000 | 112.2304 | 5.0000 | 5.0000 | 5.0000 | 2080.1800 | 753.1927 | 1168.7727 | 5.0000 | |
| Mean | 4.2956 | 17.3165 | 5.0000 | 4.5216 | 4.3548 | 786.7426 | 243.6912 | 235.7905 | 4.9957 | |
| Std | 0.1350 | 23.0445 | 0.0002 | 0.3491 | 0.2127 | 481.4622 | 164.5665 | 206.7904 | 0.0229 | |
| Rank | 1 | 6 | 5 | 3 | 2 | 9 | 8 | 7 | 4 | |
| cec03 | Best | 1.0149 | 2.9486 | 2.7012 | 1.0005 | 1.4137 | 1.4092 | 1.4174 | 1.1589 | 6.5512 |
| Worst | 1.9884 | 6.4529 | 7.2032 | 4.5752 | 5.4525 | 10.7110 | 7.7199 | 4.9906 | 10.0138 | |
| Mean | 1.4407 | 4.9440 | 5.0638 | 1.7294 | 2.4667 | 6.9114 | 4.7468 | 2.7067 | 8.0420 | |
| Std | 0.2172 | 1.0121 | 0.9607 | 0.6914 | 1.0301 | 3.0731 | 2.0816 | 0.9892 | 0.8531 | |
| Rank | 1 | 6 | 7 | 2 | 3 | 8 | 5 | 4 | 9 | |
| cec04 | Best | 9.5187 | 9.9776 | 63.8525 | 8.9597 | 4.9811 | 8.9606 | 7.9866 | 8.1256 | 55.8445 |
| Worst | 29.1260 | 33.2841 | 106.7514 | 44.7780 | 45.7730 | 74.6266 | 34.8326 | 41.6974 | 119.1290 | |
| Mean | 16.2736 | 19.2218 | 82.4830 | 21.6973 | 17.8702 | 36.0170 | 17.6244 | 19.5944 | 87.0995 | |
| Std | 4.7905 | 5.2342 | 10.4289 | 9.4409 | 8.2538 | 16.7931 | 5.7783 | 9.2821 | 12.7096 | |
| Rank | 1 | 4 | 8 | 6 | 3 | 7 | 2 | 5 | 9 | |
| cec05 | Best | 1.0123 | 1.0158 | 29.2699 | 1.0174 | 1.0154 | 1.0703 | 1.0473 | 1.0579 | 44.2344 |
| Worst | 1.1452 | 1.2914 | 85.0071 | 1.2730 | 1.4435 | 1.9158 | 1.2173 | 3.4134 | 113.2750 | |
| Best | 1.0149 | 2.9486 | 2.7012 | 1.0005 | 1.4137 | 1.4092 | 1.4174 | 1.1589 | 79.9990 | |
| Std | 0.0336 | 0.0775 | 12.9365 | 0.0671 | 0.0852 | 0.1490 | 0.0485 | 0.6368 | 18.0103 | |
| Rank | 2 | 8 | 7 | 1 | 5 | 4 | 6 | 3 | 9 | |
| cec06 | Best | 1.0246 | 1.0620 | 9.4502 | 1.0892 | 1.0980 | 1.6778 | 1.2576 | 1.3408 | 8.5339 |
| Worst | 3.5445 | 4.7492 | 11.5440 | 4.8924 | 4.6538 | 8.3538 | 6.6065 | 5.0093 | 12.5887 | |
| Mean | 1.7047 | 2.3351 | 10.5720 | 2.5376 | 2.2508 | 4.8321 | 3.7391 | 3.1198 | 10.7489 | |
| Std | 0.7570 | 0.9096 | 0.6035 | 1.1507 | 0.9774 | 1.7159 | 1.3485 | 1.0463 | 0.9784 | |
| Rank | 1 | 3 | 8 | 4 | 2 | 7 | 6 | 5 | 9 | |
| cec07 | Best | 242.6790 | 317.8746 | 916.9078 | 238.4547 | 230.0355 | 491.1312 | 253.3952 | 477.9319 | 1287.2425 |
| Worst | 771.4527 | 1796.6636 | 2101.6793 | 1093.2275 | 1124.3791 | 1485.9684 | 1101.6897 | 1779.1404 | 2246.4237 | |
| Mean | 484.5589 | 1101.5621 | 1718.2096 | 648.1085 | 642.3277 | 973.4150 | 687.8904 | 1169.7182 | 1841.0866 | |
| Std | 158.9041 | 371.6299 | 256.9217 | 238.8129 | 209.6633 | 250.7041 | 246.9875 | 386.9086 | 209.4990 | |
| Rank | 1 | 6 | 8 | 3 | 2 | 5 | 4 | 7 | 9 | |
| cec08 | Best | 2.8343 | 3.4969 | 4.0801 | 2.5995 | 2.8274 | 3.6995 | 2.7865 | 2.9969 | 4.4430 |
| Worst | 4.0614 | 4.6721 | 5.0310 | 4.2040 | 4.3917 | 4.8536 | 4.3974 | 4.7245 | 5.2382 | |
| Mean | 3.4773 | 4.0735 | 4.7669 | 3.5125 | 3.7319 | 4.2205 | 3.9045 | 3.8995 | 4.9456 | |
| Std | 0.3336 | 0.2953 | 0.2097 | 0.4043 | 0.3941 | 0.3095 | 0.4008 | 0.4063 | 0.1920 | |
| Rank | 1 | 6 | 8 | 2 | 3 | 7 | 5 | 4 | 9 | |
| cec09 | Best | 1.1133 | 1.1371 | 2.3118 | 1.0607 | 1.0542 | 1.0857 | 1.1223 | 1.1146 | 2.4667 |
| Worst | 1.3044 | 1.4226 | 3.9506 | 1.4011 | 1.3629 | 1.6413 | 1.5933 | 1.6641 | 4.3532 | |
| Mean | 1.2026 | 1.2561 | 3.3861 | 1.1818 | 1.1847 | 1.3023 | 1.3529 | 1.2319 | 3.1237 | |
| Std | 0.0581 | 0.0657 | 0.3782 | 0.0930 | 0.0728 | 0.1230 | 0.1206 | 0.1159 | 0.5021 | |
| Rank | 3 | 5 | 9 | 1 | 2 | 6 | 7 | 4 | 8 | |
| cec10 | Best | 1.0224 | 9.6265 | 21.1911 | 2.6493 | 1.0570 | 21.0006 | 21.2267 | 5.0012 | 21.1799 |
| Worst | 21.0870 | 21.6237 | 21.6119 | 21.0868 | 21.1032 | 21.1284 | 21.7000 | 21.7063 | 21.6700 | |
| Mean | 17.9548 | 20.6938 | 21.4494 | 20.3907 | 20.3527 | 21.0191 | 21.5034 | 20.0372 | 21.4743 | |
| Std | 6.9747 | 2.9991 | 0.0888 | 3.3512 | 3.6445 | 0.0313 | 0.1079 | 4.5363 | 0.1201 | |
| Rank | 1 | 5 | 7 | 4 | 3 | 6 | 9 | 2 | 8 | |
| Mean rank | 1.3 | 5.5 | 6.8 | 2.7 | 3 | 6.8 | 5.9 | 4.9 | 7.5 | |
| Final ranking | 1 | 5 | 7 | 2 | 3 | 7 | 6 | 4 | 9 | |
Wilcoxon rank sum test results (p-values) for HBWO-JS and other algorithm in the CEC2019 test suite.
| Functions . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . |
|---|---|---|---|---|---|---|---|---|
| cec01 | 4.57E-12/– | NaN/= | NaN/= | NaN/= | 1.21E-12/– | 4.57E-12/– | 1.21E-12/– | NaN/= |
| cec02 | 8.89E-10/– | 7.04E-11/– | 0.17480/= | 0.18574/– | 3.02E-11/– | 3.02E-11/– | 3.02E-11/– | 3.52E-11/– |
| cec03 | 3.02E-11/– | 3.02E-11/– | 0.16238/= | 1.09E-05/– | 1.73E-07/– | 2.44E-09/– | 4.57E-09/– | 3.02E-11/– |
| cec04 | 0.01273/– | 3.02E-11/– | 0.04676/– | 0.68432/= | 1.16E-07/– | 0.42039/= | 0.27719/= | 3.02E-11/– |
| cec05 | 0.01076/– | 3.02E-11/– | 0.00238/– | 0.00042/– | 1.33E-10/– | 1.87E-05/– | 1.46E-10/– | 3.02E-11/– |
| cec06 | 0.00227/– | 3.02E-11/– | 0.00095/– | 0.00762/– | 2.92E-09/– | 4.31E-08/– | 8.20E-07/– | 3.02E-11/– |
| cec07 | 3.35E-08/– | 3.02E-11/– | 0.00486/– | 0.00350/– | 3.82E-09/– | 0.00152/– | 2.92E-09/– | 3.02E-11/– |
| cec08 | 3.35E-08/– | 3.02E-11/– | 0.62040/= | 0.01327/– | 1.17E-09/– | 2.96E-05/– | 4.08E-05/– | 3.02E-11/– |
| cec09 | 0.00350/– | 3.02E-11/– | 0.03147/+ | 0.29727/= | 0.00047/– | 9.53E-07/– | 0.64142/= | 3.02E-11/– |
| cec10 | 3.50E-09/– | 3.02E-11/– | 0.07978/= | 0.42896/= | 0.20095/= | 3.02E-11/– | 2.03E-07/– | 3.02E-11/– |
| +/=/– | 0/0/10 | 0/0/10 | 1/4/5 | 0/3/7 | 0/1/9 | 0/1/9 | 0/2/8 | 0/0/10 |
| Functions . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . |
|---|---|---|---|---|---|---|---|---|
| cec01 | 4.57E-12/– | NaN/= | NaN/= | NaN/= | 1.21E-12/– | 4.57E-12/– | 1.21E-12/– | NaN/= |
| cec02 | 8.89E-10/– | 7.04E-11/– | 0.17480/= | 0.18574/– | 3.02E-11/– | 3.02E-11/– | 3.02E-11/– | 3.52E-11/– |
| cec03 | 3.02E-11/– | 3.02E-11/– | 0.16238/= | 1.09E-05/– | 1.73E-07/– | 2.44E-09/– | 4.57E-09/– | 3.02E-11/– |
| cec04 | 0.01273/– | 3.02E-11/– | 0.04676/– | 0.68432/= | 1.16E-07/– | 0.42039/= | 0.27719/= | 3.02E-11/– |
| cec05 | 0.01076/– | 3.02E-11/– | 0.00238/– | 0.00042/– | 1.33E-10/– | 1.87E-05/– | 1.46E-10/– | 3.02E-11/– |
| cec06 | 0.00227/– | 3.02E-11/– | 0.00095/– | 0.00762/– | 2.92E-09/– | 4.31E-08/– | 8.20E-07/– | 3.02E-11/– |
| cec07 | 3.35E-08/– | 3.02E-11/– | 0.00486/– | 0.00350/– | 3.82E-09/– | 0.00152/– | 2.92E-09/– | 3.02E-11/– |
| cec08 | 3.35E-08/– | 3.02E-11/– | 0.62040/= | 0.01327/– | 1.17E-09/– | 2.96E-05/– | 4.08E-05/– | 3.02E-11/– |
| cec09 | 0.00350/– | 3.02E-11/– | 0.03147/+ | 0.29727/= | 0.00047/– | 9.53E-07/– | 0.64142/= | 3.02E-11/– |
| cec10 | 3.50E-09/– | 3.02E-11/– | 0.07978/= | 0.42896/= | 0.20095/= | 3.02E-11/– | 2.03E-07/– | 3.02E-11/– |
| +/=/– | 0/0/10 | 0/0/10 | 1/4/5 | 0/3/7 | 0/1/9 | 0/1/9 | 0/2/8 | 0/0/10 |
Wilcoxon rank sum test results (p-values) for HBWO-JS and other algorithm in the CEC2019 test suite.
| Functions . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . |
|---|---|---|---|---|---|---|---|---|
| cec01 | 4.57E-12/– | NaN/= | NaN/= | NaN/= | 1.21E-12/– | 4.57E-12/– | 1.21E-12/– | NaN/= |
| cec02 | 8.89E-10/– | 7.04E-11/– | 0.17480/= | 0.18574/– | 3.02E-11/– | 3.02E-11/– | 3.02E-11/– | 3.52E-11/– |
| cec03 | 3.02E-11/– | 3.02E-11/– | 0.16238/= | 1.09E-05/– | 1.73E-07/– | 2.44E-09/– | 4.57E-09/– | 3.02E-11/– |
| cec04 | 0.01273/– | 3.02E-11/– | 0.04676/– | 0.68432/= | 1.16E-07/– | 0.42039/= | 0.27719/= | 3.02E-11/– |
| cec05 | 0.01076/– | 3.02E-11/– | 0.00238/– | 0.00042/– | 1.33E-10/– | 1.87E-05/– | 1.46E-10/– | 3.02E-11/– |
| cec06 | 0.00227/– | 3.02E-11/– | 0.00095/– | 0.00762/– | 2.92E-09/– | 4.31E-08/– | 8.20E-07/– | 3.02E-11/– |
| cec07 | 3.35E-08/– | 3.02E-11/– | 0.00486/– | 0.00350/– | 3.82E-09/– | 0.00152/– | 2.92E-09/– | 3.02E-11/– |
| cec08 | 3.35E-08/– | 3.02E-11/– | 0.62040/= | 0.01327/– | 1.17E-09/– | 2.96E-05/– | 4.08E-05/– | 3.02E-11/– |
| cec09 | 0.00350/– | 3.02E-11/– | 0.03147/+ | 0.29727/= | 0.00047/– | 9.53E-07/– | 0.64142/= | 3.02E-11/– |
| cec10 | 3.50E-09/– | 3.02E-11/– | 0.07978/= | 0.42896/= | 0.20095/= | 3.02E-11/– | 2.03E-07/– | 3.02E-11/– |
| +/=/– | 0/0/10 | 0/0/10 | 1/4/5 | 0/3/7 | 0/1/9 | 0/1/9 | 0/2/8 | 0/0/10 |
| Functions . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . |
|---|---|---|---|---|---|---|---|---|
| cec01 | 4.57E-12/– | NaN/= | NaN/= | NaN/= | 1.21E-12/– | 4.57E-12/– | 1.21E-12/– | NaN/= |
| cec02 | 8.89E-10/– | 7.04E-11/– | 0.17480/= | 0.18574/– | 3.02E-11/– | 3.02E-11/– | 3.02E-11/– | 3.52E-11/– |
| cec03 | 3.02E-11/– | 3.02E-11/– | 0.16238/= | 1.09E-05/– | 1.73E-07/– | 2.44E-09/– | 4.57E-09/– | 3.02E-11/– |
| cec04 | 0.01273/– | 3.02E-11/– | 0.04676/– | 0.68432/= | 1.16E-07/– | 0.42039/= | 0.27719/= | 3.02E-11/– |
| cec05 | 0.01076/– | 3.02E-11/– | 0.00238/– | 0.00042/– | 1.33E-10/– | 1.87E-05/– | 1.46E-10/– | 3.02E-11/– |
| cec06 | 0.00227/– | 3.02E-11/– | 0.00095/– | 0.00762/– | 2.92E-09/– | 4.31E-08/– | 8.20E-07/– | 3.02E-11/– |
| cec07 | 3.35E-08/– | 3.02E-11/– | 0.00486/– | 0.00350/– | 3.82E-09/– | 0.00152/– | 2.92E-09/– | 3.02E-11/– |
| cec08 | 3.35E-08/– | 3.02E-11/– | 0.62040/= | 0.01327/– | 1.17E-09/– | 2.96E-05/– | 4.08E-05/– | 3.02E-11/– |
| cec09 | 0.00350/– | 3.02E-11/– | 0.03147/+ | 0.29727/= | 0.00047/– | 9.53E-07/– | 0.64142/= | 3.02E-11/– |
| cec10 | 3.50E-09/– | 3.02E-11/– | 0.07978/= | 0.42896/= | 0.20095/= | 3.02E-11/– | 2.03E-07/– | 3.02E-11/– |
| +/=/– | 0/0/10 | 0/0/10 | 1/4/5 | 0/3/7 | 0/1/9 | 0/1/9 | 0/2/8 | 0/0/10 |
Table 7 gives the running times of all nine methods for 30 runs on the 10 test functions of CEC2019. From the table, it can be found that the running time of HBWO-JS is only less than that of the RSA algorithm on all the test functions except for the cec06 test function. For the cec06 test function, the proposed algorithm took the longest run time, but the run times of all algorithms generally improved for this problem. In addition, the running times of the DO algorithm and HBWO-JS are almost the same. In terms of the computational cost of all methods, JS has the shortest execution time. Compared to the original BWO algorithm, the running time of the proposed HBWO-JS algorithm increased, and this situation is mainly due to the fact that the improved strategy introduced by the proposed algorithm increased the complexity of the algorithm. At the same time, the introduction of the strategy also improves the optimization performance of the algorithm. Moreover, to show the results more clearly, Fig. 4 gives the average running times for more than 10 tested functions in the CEC2019 benchmark test. From the figure, it can be found that the SO algorithm has the shortest average running time of 3.2633 seconds for the 10 test functions, followed by the JS algorithm. Furthermore, the average running time of the proposed HBWO-JS is only smaller than the RSA algorithm and higher than the other seven algorithms.

The average running time of 10 test functions of different algorithms for the CEC 2019 benchmark.
CPU runtime of HBWO-JS and the newly proposed algorithms in the CEC2019 test suite.
| Functions . | HBWO-JS . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . |
|---|---|---|---|---|---|---|---|---|---|
| cec01 | 9.69163 | 2.70215 | 4.09707 | 4.02892 | 4.04357 | 7.36717 | 3.01663 | 4.38286 | 13.32446 |
| cec02 | 7.28288 | 1.61482 | 3.32729 | 3.95625 | 3.32750 | 6.70642 | 1.76909 | 3.03638 | 20.15202 |
| cec03 | 7.38374 | 1.95221 | 3.42876 | 3.38365 | 3.14041 | 6.87973 | 1.72712 | 2.75874 | 22.62053 |
| cec04 | 7.17492 | 1.77633 | 3.19970 | 3.58559 | 3.18401 | 6.23587 | 1.65159 | 2.77246 | 13.23679 |
| cec05 | 7.72200 | 1.77085 | 3.21667 | 4.44779 | 3.16879 | 6.20414 | 1.73030 | 2.91507 | 13.77346 |
| cec06 | 49.08469 | 14.64674 | 17.37629 | 17.09916 | 16.19378 | 19.89825 | 15.37619 | 19.30107 | 25.89622 |
| cec07 | 8.89141 | 2.45879 | 3.37873 | 3.39919 | 3.30066 | 6.67244 | 1.82688 | 3.23606 | 12.99641 |
| cec08 | 7.57456 | 2.07446 | 3.23915 | 3.12214 | 3.13018 | 6.18207 | 1.94390 | 2.77391 | 13.79860 |
| cec09 | 7.07422 | 1.60859 | 3.08642 | 2.76952 | 2.96914 | 6.25181 | 1.53776 | 2.76261 | 13.04697 |
| cec10 | 8.35921 | 2.39725 | 3.24218 | 2.95944 | 3.12323 | 6.44863 | 2.05308 | 2.72623 | 14.43542 |
| Functions . | HBWO-JS . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . |
|---|---|---|---|---|---|---|---|---|---|
| cec01 | 9.69163 | 2.70215 | 4.09707 | 4.02892 | 4.04357 | 7.36717 | 3.01663 | 4.38286 | 13.32446 |
| cec02 | 7.28288 | 1.61482 | 3.32729 | 3.95625 | 3.32750 | 6.70642 | 1.76909 | 3.03638 | 20.15202 |
| cec03 | 7.38374 | 1.95221 | 3.42876 | 3.38365 | 3.14041 | 6.87973 | 1.72712 | 2.75874 | 22.62053 |
| cec04 | 7.17492 | 1.77633 | 3.19970 | 3.58559 | 3.18401 | 6.23587 | 1.65159 | 2.77246 | 13.23679 |
| cec05 | 7.72200 | 1.77085 | 3.21667 | 4.44779 | 3.16879 | 6.20414 | 1.73030 | 2.91507 | 13.77346 |
| cec06 | 49.08469 | 14.64674 | 17.37629 | 17.09916 | 16.19378 | 19.89825 | 15.37619 | 19.30107 | 25.89622 |
| cec07 | 8.89141 | 2.45879 | 3.37873 | 3.39919 | 3.30066 | 6.67244 | 1.82688 | 3.23606 | 12.99641 |
| cec08 | 7.57456 | 2.07446 | 3.23915 | 3.12214 | 3.13018 | 6.18207 | 1.94390 | 2.77391 | 13.79860 |
| cec09 | 7.07422 | 1.60859 | 3.08642 | 2.76952 | 2.96914 | 6.25181 | 1.53776 | 2.76261 | 13.04697 |
| cec10 | 8.35921 | 2.39725 | 3.24218 | 2.95944 | 3.12323 | 6.44863 | 2.05308 | 2.72623 | 14.43542 |
CPU runtime of HBWO-JS and the newly proposed algorithms in the CEC2019 test suite.
| Functions . | HBWO-JS . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . |
|---|---|---|---|---|---|---|---|---|---|
| cec01 | 9.69163 | 2.70215 | 4.09707 | 4.02892 | 4.04357 | 7.36717 | 3.01663 | 4.38286 | 13.32446 |
| cec02 | 7.28288 | 1.61482 | 3.32729 | 3.95625 | 3.32750 | 6.70642 | 1.76909 | 3.03638 | 20.15202 |
| cec03 | 7.38374 | 1.95221 | 3.42876 | 3.38365 | 3.14041 | 6.87973 | 1.72712 | 2.75874 | 22.62053 |
| cec04 | 7.17492 | 1.77633 | 3.19970 | 3.58559 | 3.18401 | 6.23587 | 1.65159 | 2.77246 | 13.23679 |
| cec05 | 7.72200 | 1.77085 | 3.21667 | 4.44779 | 3.16879 | 6.20414 | 1.73030 | 2.91507 | 13.77346 |
| cec06 | 49.08469 | 14.64674 | 17.37629 | 17.09916 | 16.19378 | 19.89825 | 15.37619 | 19.30107 | 25.89622 |
| cec07 | 8.89141 | 2.45879 | 3.37873 | 3.39919 | 3.30066 | 6.67244 | 1.82688 | 3.23606 | 12.99641 |
| cec08 | 7.57456 | 2.07446 | 3.23915 | 3.12214 | 3.13018 | 6.18207 | 1.94390 | 2.77391 | 13.79860 |
| cec09 | 7.07422 | 1.60859 | 3.08642 | 2.76952 | 2.96914 | 6.25181 | 1.53776 | 2.76261 | 13.04697 |
| cec10 | 8.35921 | 2.39725 | 3.24218 | 2.95944 | 3.12323 | 6.44863 | 2.05308 | 2.72623 | 14.43542 |
| Functions . | HBWO-JS . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . |
|---|---|---|---|---|---|---|---|---|---|
| cec01 | 9.69163 | 2.70215 | 4.09707 | 4.02892 | 4.04357 | 7.36717 | 3.01663 | 4.38286 | 13.32446 |
| cec02 | 7.28288 | 1.61482 | 3.32729 | 3.95625 | 3.32750 | 6.70642 | 1.76909 | 3.03638 | 20.15202 |
| cec03 | 7.38374 | 1.95221 | 3.42876 | 3.38365 | 3.14041 | 6.87973 | 1.72712 | 2.75874 | 22.62053 |
| cec04 | 7.17492 | 1.77633 | 3.19970 | 3.58559 | 3.18401 | 6.23587 | 1.65159 | 2.77246 | 13.23679 |
| cec05 | 7.72200 | 1.77085 | 3.21667 | 4.44779 | 3.16879 | 6.20414 | 1.73030 | 2.91507 | 13.77346 |
| cec06 | 49.08469 | 14.64674 | 17.37629 | 17.09916 | 16.19378 | 19.89825 | 15.37619 | 19.30107 | 25.89622 |
| cec07 | 8.89141 | 2.45879 | 3.37873 | 3.39919 | 3.30066 | 6.67244 | 1.82688 | 3.23606 | 12.99641 |
| cec08 | 7.57456 | 2.07446 | 3.23915 | 3.12214 | 3.13018 | 6.18207 | 1.94390 | 2.77391 | 13.79860 |
| cec09 | 7.07422 | 1.60859 | 3.08642 | 2.76952 | 2.96914 | 6.25181 | 1.53776 | 2.76261 | 13.04697 |
| cec10 | 8.35921 | 2.39725 | 3.24218 | 2.95944 | 3.12323 | 6.44863 | 2.05308 | 2.72623 | 14.43542 |
The convergence curves are a visual representation to evaluate the performance and iteration speed of the method search development. The convergence curves of HBWO-JS and the other eight methods on all the 10 CEC2019 benchmark functions are shown in Fig. 5. As shown in Fig. 5, HBWO-JS converges significantly faster than the other algorithms on most of the functions (cec01, cec02, cec06, cec09, cec10) and has the best convergence accuracy. According to the analysis of the iteration diagram of the HBWO-JS algorithm, the HBWO-JS algorithm tends to converge to the near-optimal solution in the first and middle of the iterations. It then gradually approaches the optimal solution and updates the solution in the number of iterations to confirm the previous search results. This result shows that the HBWO-JS algorithm is able to balance the two phases of exploration and exploitation well. This result may be because the optimal neighborhood update strategy helps the algorithm explore potentially better solutions near the leading individuals in the population. Conversely, the vertical crossover operator and Gaussian variation strategy alleviate the problem of premature stagnation of BWO, thus improving the iterative accuracy of the original BWO during the iterative process.

Convergence trends of the CEC2019 test suite with the HBWO-JS, JS, BWO, AHA, ARO, DO, SO, WSO, RSA algorithm.
The box plot is a visual representation to assess the stability and robustness of the algorithm operation. Figure 6 provides the box plots for all 10 CEC2019s of the search algorithms. From the plots, it can be explored that in most cases, the distribution of the iterative final adaptation values of the HBWO-JS algorithm is smaller than that of the other compared algorithms, which can indicate that the HBWO-JS algorithm has good operational stability and robustness in solving the CEC2019 test problem. The final results show that the HBWO-JS algorithm can solve the optimization problem more stably and with high convergence speed and accuracy. Figure 7 shows the radar plots of the HBWO-JS algorithm and the other eight search algorithms. It can be intuitively explored that HBWO-JS has the smallest radar plot area, which indicates that HBWO-JS ranks better than the other algorithms and reflects the efficient optimization capability of HBWO-JS.

Box plot of the HBWO-JS, JS, BWO, AHA, ARO, DO, SO, WSO, RSA algorithm for CEC2019 test suite (red minus → Median; red plus → Outlier).

Radar plots of the HBWO-JS, JS, BWO, AHA, ARO, DO, SO, WSO, RSA algorithm for CEC2019 test suite.
4.5. Result analysis for the CEC2020 benchmark functions
This section still presents the results obtained by HBWO-JS at CEC2020 with the eight latest algorithms (JS, BWO, AHA, ARO, DO, SO, WSO, RSA), where numerical experiments include four different dimensions (10, 30, 50, and 100 dimensions). The data in bold are the best-case average of all nine methods under the same benchmark function.
Tables 8, 9, 10, and 11 provide the numerical results of HBWO-JS experiments in three different dimensions (10, 30, 50, and 100 dimensions), respectively. The table shows that the average Friedman ranking results of HBWO-JS in the four dimensions are 1.4, 1.3, 1.8, and 1.5, respectively. Figure 8 shows the cumulative average ranking of all algorithms in the three dimensions. The histogram in the figure shows that the proposed HBWO-JS algorithm has the smallest objective function value and the smallest cumulative average ranking. Therefore, HBWO-JS demonstrates excellent performance in all dimensions. According to the experimental statistics, HBWO-JS can successfully optimize six test functions (cec01-cec04, cec06, cec08), seven test functions (cec01-cec04, cec06, cec08, cec09), four test functions (cec02, cec04, cec06, cec08), and five test functions (cec04, cec06, cec07, cec08, and cec09). For the cec04 test function, the optimal values are found for HBWO-JS and BWO, AHA, ARO, SO, and RSA in four dimensions: 10, 30, 50, and 100 dimensions. In addition, for the cec04, cec06, and cec08 test functions, the proposed HBWO-JS algorithm can find the best case in all four dimensions, so for these four test functions, HBWO-JS is dimensionally extensible. The statistical results prove that HBWO-JS can provide excellent output results in three different dimensions, and the exploitation advantages are consistent when dealing with optimization tasks in different dimensions. As the number of dimensions increases, HBWO-JS still demonstrates excellent competitiveness. The ARO algorithm is second to the second-ranked algorithm that proposes the HBWO-JS algorithm. At 100 dimensions, the DO algorithm has the second-lowest average ranking. In summary, it can be seen that HBWO-JS eliminates the problem of difficult and inefficient optimization of BWO as the dimensional increases due to the integration with another excellent algorithm JS. Also, the vertical crossover operator and Gaussian variation operator better help the HBWO-JS algorithm to alleviate the slow iteration and easily fall into the local solution problem, thus improving the convergence accuracy of the algorithm.

Cumulative average ranking of all algorithms in 10, 30, 50, and 100 dimensions.
The results of HBWO-JS and other algorithms for CEC2020 test functions (the dimension dim = 10).
| Function . | Index . | Algorithms . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HBWO-JS . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . | ||
| cec01 | Best | 1.01E+02 | 1.05E+02 | 5.35E+09 | 1.01E+02 | 1.23E+02 | 2.96E+02 | 1.30E+02 | 3.25E+03 | 3.72E+09 |
| Worst | 5.17E+03 | 3.19E+03 | 1.24E+10 | 7.37E+03 | 9.66E+03 | 1.68E+04 | 1.44E+04 | 8.75E+07 | 1.74E+10 | |
| Mean | 1.04E+03 | 1.18E+03 | 8.63E+09 | 1.92E+03 | 2.69E+03 | 5.74E+03 | 2.49E+03 | 8.84E+06 | 1.05E+10 | |
| Std | 1.21E+03 | 9.42E+02 | 2.01E+09 | 1.90E+03 | 2.38E+03 | 4.12E+03 | 2.99E+03 | 2.18E+07 | 3.67E+09 | |
| Rank | 1 | 2 | 8 | 3 | 5 | 6 | 4 | 7 | 9 | |
| cec02 | Best | 1.14E+03 | 1.24E+03 | 2.21E+03 | 1.12E+03 | 1.23E+03 | 1.35E+03 | 1.22E+03 | 1.13E+03 | 2.28E+03 |
| Worst | 1.71E+03 | 2.46E+03 | 2.95E+03 | 2.00E+03 | 2.00E+03 | 2.51E+03 | 2.27E+03 | 2.72E+03 | 3.16E+03 | |
| Mean | 1.36E+03 | 1.95E+03 | 2.60E+03 | 1.54E+03 | 1.51E+03 | 1.87E+03 | 1.60E+03 | 1.89E+03 | 2.80E+03 | |
| Std | 1.22E+02 | 3.40E+02 | 2.00E+02 | 2.07E+02 | 1.98E+02 | 2.89E+02 | 2.15E+02 | 5.09E+02 | 2.11E+02 | |
| Rank | 1 | 7 | 8 | 3 | 2 | 5 | 4 | 6 | 9 | |
| cec03 | Best | 7.18E+02 | 7.20E+02 | 7.86E+02 | 7.22E+02 | 7.18E+02 | 7.28E+02 | 7.19E+02 | 7.21E+02 | 7.89E+02 |
| Worst | 7.41E+02 | 7.60E+02 | 8.22E+02 | 7.87E+02 | 7.60E+02 | 7.94E+02 | 7.69E+02 | 7.61E+02 | 8.32E+02 | |
| Mean | 2.30E+03 | 2.30E+03 | 2.73E+03 | 2.30E+03 | 2.30E+03 | 2.40E+03 | 2.30E+03 | 2.31E+03 | 3.10E+03 | |
| Std | 5.32E+00 | 1.15E+01 | 9.69E+00 | 1.54E+01 | 8.54E+00 | 1.83E+01 | 1.30E+01 | 1.01E+01 | 1.20E+01 | |
| Rank | 1 | 4 | 8 | 2 | 3 | 7 | 5 | 6 | 9 | |
| cec04 | Best | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 |
| Worst | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | |
| Mean | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | |
| Std | 0.00E+00 | 1.02E-01 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 9.41E-01 | 7.18E-02 | 8.15E-01 | 0.00E+00 | |
| Rank | 1 | 6 | 1 | 1 | 1 | 8 | 7 | 9 | 1 | |
| cec05 | Best | 1.98E+03 | 2.67E+03 | 1.35E+05 | 1.92E+03 | 1.80E+03 | 2.38E+03 | 2.68E+03 | 1.84E+03 | 3.13E+05 |
| Worst | 9.68E+03 | 1.74E+04 | 4.88E+05 | 2.94E+05 | 3.93E+04 | 3.83E+04 | 5.39E+05 | 2.63E+03 | 7.69E+05 | |
| Mean | 3.96E+03 | 5.35E+03 | 3.15E+05 | 1.82E+04 | 5.60E+03 | 8.18E+03 | 3.06E+04 | 2.05E+03 | 5.26E+05 | |
| Std | 1.97E+03 | 2.79E+03 | 1.00E+05 | 5.28E+04 | 7.36E+03 | 8.75E+03 | 9.96E+04 | 1.83E+02 | 8.28E+04 | |
| Rank | 2 | 3 | 8 | 6 | 4 | 5 | 7 | 1 | 9 | |
| cec06 | Best | 5.32E+00 | 1.15E+01 | 9.69E+00 | 1.54E+01 | 8.54E+00 | 1.83E+01 | 1.30E+01 | 1.01E+01 | 1.20E+01 |
| Worst | 1.72E+03 | 1.76E+03 | 2.16E+03 | 1.90E+03 | 1.84E+03 | 1.94E+03 | 1.85E+03 | 1.84E+03 | 2.60E+03 | |
| Mean | 1.62E+03 | 1.65E+03 | 1.99E+03 | 1.72E+03 | 1.69E+03 | 1.77E+03 | 1.69E+03 | 1.69E+03 | 2.18E+03 | |
| Std | 4.05E+01 | 5.79E+01 | 9.39E+01 | 9.82E+01 | 6.56E+01 | 9.80E+01 | 8.08E+01 | 8.25E+01 | 1.78E+02 | |
| Rank | 1 | 2 | 8 | 6 | 3 | 7 | 4 | 5 | 9 | |
| cec07 | Best | 2.14E+03 | 2.23E+03 | 9.61E+03 | 2.10E+03 | 2.12E+03 | 2.49E+03 | 2.60E+03 | 2.11E+03 | 1.45E+04 |
| Worst | 2.98E+03 | 4.48E+03 | 5.52E+05 | 2.23E+04 | 8.39E+03 | 2.63E+04 | 1.02E+04 | 2.59E+03 | 6.09E+06 | |
| Mean | 2.37E+03 | 2.90E+03 | 1.07E+05 | 4.58E+03 | 3.47E+03 | 9.27E+03 | 4.77E+03 | 2.23E+03 | 7.34E+05 | |
| Std | 2.11E+02 | 5.54E+02 | 1.23E+05 | 5.02E+03 | 1.97E+03 | 7.12E+03 | 2.56E+03 | 8.96E+01 | 1.28E+06 | |
| Rank | 2 | 3 | 8 | 5 | 4 | 7 | 6 | 1 | 9 | |
| cec08 | Best | 2.22E+03 | 2.30E+03 | 2.33E+03 | 2.23E+03 | 2.23E+03 | 2.24E+03 | 2.30E+03 | 2.22E+03 | 2.60E+03 |
| Worst | 2.30E+03 | 2.30E+03 | 3.17E+03 | 2.31E+03 | 2.30E+03 | 3.87E+03 | 2.31E+03 | 2.35E+03 | 3.56E+03 | |
| Mean | 2.30E+03 | 2.30E+03 | 2.73E+03 | 2.30E+03 | 2.30E+03 | 2.40E+03 | 2.30E+03 | 2.31E+03 | 3.10E+03 | |
| Std | 2.13E+01 | 5.02E-01 | 2.18E+02 | 1.33E+01 | 1.26E+01 | 3.69E+02 | 1.26E+00 | 1.83E+01 | 2.49E+02 | |
| Rank | 1 | 4 | 8 | 2 | 3 | 7 | 5 | 6 | 9 | |
| cec09 | Best | 2.50E+03 | 2.53E+03 | 2.65E+03 | 2.50E+03 | 2.50E+03 | 2.50E+03 | 2.63E+03 | 2.51E+03 | 2.81E+03 |
| Worst | 2.75E+03 | 2.76E+03 | 2.86E+03 | 2.77E+03 | 2.78E+03 | 2.82E+03 | 2.77E+03 | 2.79E+03 | 2.99E+03 | |
| Mean | 2.62E+03 | 2.71E+03 | 2.78E+03 | 2.60E+03 | 2.72E+03 | 2.76E+03 | 2.75E+03 | 2.72E+03 | 2.89E+03 | |
| Std | 1.21E+02 | 7.12E+01 | 7.46E+01 | 1.25E+02 | 7.52E+01 | 7.36E+01 | 2.47E+01 | 8.13E+01 | 5.26E+01 | |
| Rank | 2 | 3 | 8 | 1 | 5 | 7 | 6 | 4 | 9 | |
| cec10 | Best | 2.90E+03 | 2.90E+03 | 2.98E+03 | 2.90E+03 | 2.90E+03 | 2.90E+03 | 2.90E+03 | 2.90E+03 | 3.13E+03 |
| Worst | 2.95E+03 | 2.95E+03 | 3.42E+03 | 2.95E+03 | 2.95E+03 | 2.95E+03 | 2.95E+03 | 2.99E+03 | 3.69E+03 | |
| Mean | 2.92E+03 | 2.92E+03 | 3.24E+03 | 2.93E+03 | 2.92E+03 | 2.92E+03 | 2.93E+03 | 2.93E+03 | 3.34E+03 | |
| Std | 2.28E+01 | 2.41E+01 | 1.02E+02 | 2.09E+01 | 2.36E+01 | 2.38E+01 | 2.18E+01 | 2.47E+01 | 9.41E+01 | |
| Rank | 2 | 4 | 8 | 6 | 1 | 3 | 5 | 7 | 9 | |
| Mean rank | 1.4 | 3.8 | 7.3 | 3.5 | 3.1 | 6.2 | 5.3 | 5.2 | 8.2 | |
| Final ranking | 1 | 4 | 8 | 3 | 2 | 7 | 6 | 5 | 9 | |
| +/=/– | –/–/– | 0/3/7 | 0/1/9 | 1/3/6 | 0/4/6 | 0/1/9 | 0/0/10 | 2/0/8 | 0/1/9 | |
| Function . | Index . | Algorithms . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HBWO-JS . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . | ||
| cec01 | Best | 1.01E+02 | 1.05E+02 | 5.35E+09 | 1.01E+02 | 1.23E+02 | 2.96E+02 | 1.30E+02 | 3.25E+03 | 3.72E+09 |
| Worst | 5.17E+03 | 3.19E+03 | 1.24E+10 | 7.37E+03 | 9.66E+03 | 1.68E+04 | 1.44E+04 | 8.75E+07 | 1.74E+10 | |
| Mean | 1.04E+03 | 1.18E+03 | 8.63E+09 | 1.92E+03 | 2.69E+03 | 5.74E+03 | 2.49E+03 | 8.84E+06 | 1.05E+10 | |
| Std | 1.21E+03 | 9.42E+02 | 2.01E+09 | 1.90E+03 | 2.38E+03 | 4.12E+03 | 2.99E+03 | 2.18E+07 | 3.67E+09 | |
| Rank | 1 | 2 | 8 | 3 | 5 | 6 | 4 | 7 | 9 | |
| cec02 | Best | 1.14E+03 | 1.24E+03 | 2.21E+03 | 1.12E+03 | 1.23E+03 | 1.35E+03 | 1.22E+03 | 1.13E+03 | 2.28E+03 |
| Worst | 1.71E+03 | 2.46E+03 | 2.95E+03 | 2.00E+03 | 2.00E+03 | 2.51E+03 | 2.27E+03 | 2.72E+03 | 3.16E+03 | |
| Mean | 1.36E+03 | 1.95E+03 | 2.60E+03 | 1.54E+03 | 1.51E+03 | 1.87E+03 | 1.60E+03 | 1.89E+03 | 2.80E+03 | |
| Std | 1.22E+02 | 3.40E+02 | 2.00E+02 | 2.07E+02 | 1.98E+02 | 2.89E+02 | 2.15E+02 | 5.09E+02 | 2.11E+02 | |
| Rank | 1 | 7 | 8 | 3 | 2 | 5 | 4 | 6 | 9 | |
| cec03 | Best | 7.18E+02 | 7.20E+02 | 7.86E+02 | 7.22E+02 | 7.18E+02 | 7.28E+02 | 7.19E+02 | 7.21E+02 | 7.89E+02 |
| Worst | 7.41E+02 | 7.60E+02 | 8.22E+02 | 7.87E+02 | 7.60E+02 | 7.94E+02 | 7.69E+02 | 7.61E+02 | 8.32E+02 | |
| Mean | 2.30E+03 | 2.30E+03 | 2.73E+03 | 2.30E+03 | 2.30E+03 | 2.40E+03 | 2.30E+03 | 2.31E+03 | 3.10E+03 | |
| Std | 5.32E+00 | 1.15E+01 | 9.69E+00 | 1.54E+01 | 8.54E+00 | 1.83E+01 | 1.30E+01 | 1.01E+01 | 1.20E+01 | |
| Rank | 1 | 4 | 8 | 2 | 3 | 7 | 5 | 6 | 9 | |
| cec04 | Best | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 |
| Worst | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | |
| Mean | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | |
| Std | 0.00E+00 | 1.02E-01 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 9.41E-01 | 7.18E-02 | 8.15E-01 | 0.00E+00 | |
| Rank | 1 | 6 | 1 | 1 | 1 | 8 | 7 | 9 | 1 | |
| cec05 | Best | 1.98E+03 | 2.67E+03 | 1.35E+05 | 1.92E+03 | 1.80E+03 | 2.38E+03 | 2.68E+03 | 1.84E+03 | 3.13E+05 |
| Worst | 9.68E+03 | 1.74E+04 | 4.88E+05 | 2.94E+05 | 3.93E+04 | 3.83E+04 | 5.39E+05 | 2.63E+03 | 7.69E+05 | |
| Mean | 3.96E+03 | 5.35E+03 | 3.15E+05 | 1.82E+04 | 5.60E+03 | 8.18E+03 | 3.06E+04 | 2.05E+03 | 5.26E+05 | |
| Std | 1.97E+03 | 2.79E+03 | 1.00E+05 | 5.28E+04 | 7.36E+03 | 8.75E+03 | 9.96E+04 | 1.83E+02 | 8.28E+04 | |
| Rank | 2 | 3 | 8 | 6 | 4 | 5 | 7 | 1 | 9 | |
| cec06 | Best | 5.32E+00 | 1.15E+01 | 9.69E+00 | 1.54E+01 | 8.54E+00 | 1.83E+01 | 1.30E+01 | 1.01E+01 | 1.20E+01 |
| Worst | 1.72E+03 | 1.76E+03 | 2.16E+03 | 1.90E+03 | 1.84E+03 | 1.94E+03 | 1.85E+03 | 1.84E+03 | 2.60E+03 | |
| Mean | 1.62E+03 | 1.65E+03 | 1.99E+03 | 1.72E+03 | 1.69E+03 | 1.77E+03 | 1.69E+03 | 1.69E+03 | 2.18E+03 | |
| Std | 4.05E+01 | 5.79E+01 | 9.39E+01 | 9.82E+01 | 6.56E+01 | 9.80E+01 | 8.08E+01 | 8.25E+01 | 1.78E+02 | |
| Rank | 1 | 2 | 8 | 6 | 3 | 7 | 4 | 5 | 9 | |
| cec07 | Best | 2.14E+03 | 2.23E+03 | 9.61E+03 | 2.10E+03 | 2.12E+03 | 2.49E+03 | 2.60E+03 | 2.11E+03 | 1.45E+04 |
| Worst | 2.98E+03 | 4.48E+03 | 5.52E+05 | 2.23E+04 | 8.39E+03 | 2.63E+04 | 1.02E+04 | 2.59E+03 | 6.09E+06 | |
| Mean | 2.37E+03 | 2.90E+03 | 1.07E+05 | 4.58E+03 | 3.47E+03 | 9.27E+03 | 4.77E+03 | 2.23E+03 | 7.34E+05 | |
| Std | 2.11E+02 | 5.54E+02 | 1.23E+05 | 5.02E+03 | 1.97E+03 | 7.12E+03 | 2.56E+03 | 8.96E+01 | 1.28E+06 | |
| Rank | 2 | 3 | 8 | 5 | 4 | 7 | 6 | 1 | 9 | |
| cec08 | Best | 2.22E+03 | 2.30E+03 | 2.33E+03 | 2.23E+03 | 2.23E+03 | 2.24E+03 | 2.30E+03 | 2.22E+03 | 2.60E+03 |
| Worst | 2.30E+03 | 2.30E+03 | 3.17E+03 | 2.31E+03 | 2.30E+03 | 3.87E+03 | 2.31E+03 | 2.35E+03 | 3.56E+03 | |
| Mean | 2.30E+03 | 2.30E+03 | 2.73E+03 | 2.30E+03 | 2.30E+03 | 2.40E+03 | 2.30E+03 | 2.31E+03 | 3.10E+03 | |
| Std | 2.13E+01 | 5.02E-01 | 2.18E+02 | 1.33E+01 | 1.26E+01 | 3.69E+02 | 1.26E+00 | 1.83E+01 | 2.49E+02 | |
| Rank | 1 | 4 | 8 | 2 | 3 | 7 | 5 | 6 | 9 | |
| cec09 | Best | 2.50E+03 | 2.53E+03 | 2.65E+03 | 2.50E+03 | 2.50E+03 | 2.50E+03 | 2.63E+03 | 2.51E+03 | 2.81E+03 |
| Worst | 2.75E+03 | 2.76E+03 | 2.86E+03 | 2.77E+03 | 2.78E+03 | 2.82E+03 | 2.77E+03 | 2.79E+03 | 2.99E+03 | |
| Mean | 2.62E+03 | 2.71E+03 | 2.78E+03 | 2.60E+03 | 2.72E+03 | 2.76E+03 | 2.75E+03 | 2.72E+03 | 2.89E+03 | |
| Std | 1.21E+02 | 7.12E+01 | 7.46E+01 | 1.25E+02 | 7.52E+01 | 7.36E+01 | 2.47E+01 | 8.13E+01 | 5.26E+01 | |
| Rank | 2 | 3 | 8 | 1 | 5 | 7 | 6 | 4 | 9 | |
| cec10 | Best | 2.90E+03 | 2.90E+03 | 2.98E+03 | 2.90E+03 | 2.90E+03 | 2.90E+03 | 2.90E+03 | 2.90E+03 | 3.13E+03 |
| Worst | 2.95E+03 | 2.95E+03 | 3.42E+03 | 2.95E+03 | 2.95E+03 | 2.95E+03 | 2.95E+03 | 2.99E+03 | 3.69E+03 | |
| Mean | 2.92E+03 | 2.92E+03 | 3.24E+03 | 2.93E+03 | 2.92E+03 | 2.92E+03 | 2.93E+03 | 2.93E+03 | 3.34E+03 | |
| Std | 2.28E+01 | 2.41E+01 | 1.02E+02 | 2.09E+01 | 2.36E+01 | 2.38E+01 | 2.18E+01 | 2.47E+01 | 9.41E+01 | |
| Rank | 2 | 4 | 8 | 6 | 1 | 3 | 5 | 7 | 9 | |
| Mean rank | 1.4 | 3.8 | 7.3 | 3.5 | 3.1 | 6.2 | 5.3 | 5.2 | 8.2 | |
| Final ranking | 1 | 4 | 8 | 3 | 2 | 7 | 6 | 5 | 9 | |
| +/=/– | –/–/– | 0/3/7 | 0/1/9 | 1/3/6 | 0/4/6 | 0/1/9 | 0/0/10 | 2/0/8 | 0/1/9 | |
The results of HBWO-JS and other algorithms for CEC2020 test functions (the dimension dim = 10).
| Function . | Index . | Algorithms . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HBWO-JS . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . | ||
| cec01 | Best | 1.01E+02 | 1.05E+02 | 5.35E+09 | 1.01E+02 | 1.23E+02 | 2.96E+02 | 1.30E+02 | 3.25E+03 | 3.72E+09 |
| Worst | 5.17E+03 | 3.19E+03 | 1.24E+10 | 7.37E+03 | 9.66E+03 | 1.68E+04 | 1.44E+04 | 8.75E+07 | 1.74E+10 | |
| Mean | 1.04E+03 | 1.18E+03 | 8.63E+09 | 1.92E+03 | 2.69E+03 | 5.74E+03 | 2.49E+03 | 8.84E+06 | 1.05E+10 | |
| Std | 1.21E+03 | 9.42E+02 | 2.01E+09 | 1.90E+03 | 2.38E+03 | 4.12E+03 | 2.99E+03 | 2.18E+07 | 3.67E+09 | |
| Rank | 1 | 2 | 8 | 3 | 5 | 6 | 4 | 7 | 9 | |
| cec02 | Best | 1.14E+03 | 1.24E+03 | 2.21E+03 | 1.12E+03 | 1.23E+03 | 1.35E+03 | 1.22E+03 | 1.13E+03 | 2.28E+03 |
| Worst | 1.71E+03 | 2.46E+03 | 2.95E+03 | 2.00E+03 | 2.00E+03 | 2.51E+03 | 2.27E+03 | 2.72E+03 | 3.16E+03 | |
| Mean | 1.36E+03 | 1.95E+03 | 2.60E+03 | 1.54E+03 | 1.51E+03 | 1.87E+03 | 1.60E+03 | 1.89E+03 | 2.80E+03 | |
| Std | 1.22E+02 | 3.40E+02 | 2.00E+02 | 2.07E+02 | 1.98E+02 | 2.89E+02 | 2.15E+02 | 5.09E+02 | 2.11E+02 | |
| Rank | 1 | 7 | 8 | 3 | 2 | 5 | 4 | 6 | 9 | |
| cec03 | Best | 7.18E+02 | 7.20E+02 | 7.86E+02 | 7.22E+02 | 7.18E+02 | 7.28E+02 | 7.19E+02 | 7.21E+02 | 7.89E+02 |
| Worst | 7.41E+02 | 7.60E+02 | 8.22E+02 | 7.87E+02 | 7.60E+02 | 7.94E+02 | 7.69E+02 | 7.61E+02 | 8.32E+02 | |
| Mean | 2.30E+03 | 2.30E+03 | 2.73E+03 | 2.30E+03 | 2.30E+03 | 2.40E+03 | 2.30E+03 | 2.31E+03 | 3.10E+03 | |
| Std | 5.32E+00 | 1.15E+01 | 9.69E+00 | 1.54E+01 | 8.54E+00 | 1.83E+01 | 1.30E+01 | 1.01E+01 | 1.20E+01 | |
| Rank | 1 | 4 | 8 | 2 | 3 | 7 | 5 | 6 | 9 | |
| cec04 | Best | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 |
| Worst | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | |
| Mean | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | |
| Std | 0.00E+00 | 1.02E-01 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 9.41E-01 | 7.18E-02 | 8.15E-01 | 0.00E+00 | |
| Rank | 1 | 6 | 1 | 1 | 1 | 8 | 7 | 9 | 1 | |
| cec05 | Best | 1.98E+03 | 2.67E+03 | 1.35E+05 | 1.92E+03 | 1.80E+03 | 2.38E+03 | 2.68E+03 | 1.84E+03 | 3.13E+05 |
| Worst | 9.68E+03 | 1.74E+04 | 4.88E+05 | 2.94E+05 | 3.93E+04 | 3.83E+04 | 5.39E+05 | 2.63E+03 | 7.69E+05 | |
| Mean | 3.96E+03 | 5.35E+03 | 3.15E+05 | 1.82E+04 | 5.60E+03 | 8.18E+03 | 3.06E+04 | 2.05E+03 | 5.26E+05 | |
| Std | 1.97E+03 | 2.79E+03 | 1.00E+05 | 5.28E+04 | 7.36E+03 | 8.75E+03 | 9.96E+04 | 1.83E+02 | 8.28E+04 | |
| Rank | 2 | 3 | 8 | 6 | 4 | 5 | 7 | 1 | 9 | |
| cec06 | Best | 5.32E+00 | 1.15E+01 | 9.69E+00 | 1.54E+01 | 8.54E+00 | 1.83E+01 | 1.30E+01 | 1.01E+01 | 1.20E+01 |
| Worst | 1.72E+03 | 1.76E+03 | 2.16E+03 | 1.90E+03 | 1.84E+03 | 1.94E+03 | 1.85E+03 | 1.84E+03 | 2.60E+03 | |
| Mean | 1.62E+03 | 1.65E+03 | 1.99E+03 | 1.72E+03 | 1.69E+03 | 1.77E+03 | 1.69E+03 | 1.69E+03 | 2.18E+03 | |
| Std | 4.05E+01 | 5.79E+01 | 9.39E+01 | 9.82E+01 | 6.56E+01 | 9.80E+01 | 8.08E+01 | 8.25E+01 | 1.78E+02 | |
| Rank | 1 | 2 | 8 | 6 | 3 | 7 | 4 | 5 | 9 | |
| cec07 | Best | 2.14E+03 | 2.23E+03 | 9.61E+03 | 2.10E+03 | 2.12E+03 | 2.49E+03 | 2.60E+03 | 2.11E+03 | 1.45E+04 |
| Worst | 2.98E+03 | 4.48E+03 | 5.52E+05 | 2.23E+04 | 8.39E+03 | 2.63E+04 | 1.02E+04 | 2.59E+03 | 6.09E+06 | |
| Mean | 2.37E+03 | 2.90E+03 | 1.07E+05 | 4.58E+03 | 3.47E+03 | 9.27E+03 | 4.77E+03 | 2.23E+03 | 7.34E+05 | |
| Std | 2.11E+02 | 5.54E+02 | 1.23E+05 | 5.02E+03 | 1.97E+03 | 7.12E+03 | 2.56E+03 | 8.96E+01 | 1.28E+06 | |
| Rank | 2 | 3 | 8 | 5 | 4 | 7 | 6 | 1 | 9 | |
| cec08 | Best | 2.22E+03 | 2.30E+03 | 2.33E+03 | 2.23E+03 | 2.23E+03 | 2.24E+03 | 2.30E+03 | 2.22E+03 | 2.60E+03 |
| Worst | 2.30E+03 | 2.30E+03 | 3.17E+03 | 2.31E+03 | 2.30E+03 | 3.87E+03 | 2.31E+03 | 2.35E+03 | 3.56E+03 | |
| Mean | 2.30E+03 | 2.30E+03 | 2.73E+03 | 2.30E+03 | 2.30E+03 | 2.40E+03 | 2.30E+03 | 2.31E+03 | 3.10E+03 | |
| Std | 2.13E+01 | 5.02E-01 | 2.18E+02 | 1.33E+01 | 1.26E+01 | 3.69E+02 | 1.26E+00 | 1.83E+01 | 2.49E+02 | |
| Rank | 1 | 4 | 8 | 2 | 3 | 7 | 5 | 6 | 9 | |
| cec09 | Best | 2.50E+03 | 2.53E+03 | 2.65E+03 | 2.50E+03 | 2.50E+03 | 2.50E+03 | 2.63E+03 | 2.51E+03 | 2.81E+03 |
| Worst | 2.75E+03 | 2.76E+03 | 2.86E+03 | 2.77E+03 | 2.78E+03 | 2.82E+03 | 2.77E+03 | 2.79E+03 | 2.99E+03 | |
| Mean | 2.62E+03 | 2.71E+03 | 2.78E+03 | 2.60E+03 | 2.72E+03 | 2.76E+03 | 2.75E+03 | 2.72E+03 | 2.89E+03 | |
| Std | 1.21E+02 | 7.12E+01 | 7.46E+01 | 1.25E+02 | 7.52E+01 | 7.36E+01 | 2.47E+01 | 8.13E+01 | 5.26E+01 | |
| Rank | 2 | 3 | 8 | 1 | 5 | 7 | 6 | 4 | 9 | |
| cec10 | Best | 2.90E+03 | 2.90E+03 | 2.98E+03 | 2.90E+03 | 2.90E+03 | 2.90E+03 | 2.90E+03 | 2.90E+03 | 3.13E+03 |
| Worst | 2.95E+03 | 2.95E+03 | 3.42E+03 | 2.95E+03 | 2.95E+03 | 2.95E+03 | 2.95E+03 | 2.99E+03 | 3.69E+03 | |
| Mean | 2.92E+03 | 2.92E+03 | 3.24E+03 | 2.93E+03 | 2.92E+03 | 2.92E+03 | 2.93E+03 | 2.93E+03 | 3.34E+03 | |
| Std | 2.28E+01 | 2.41E+01 | 1.02E+02 | 2.09E+01 | 2.36E+01 | 2.38E+01 | 2.18E+01 | 2.47E+01 | 9.41E+01 | |
| Rank | 2 | 4 | 8 | 6 | 1 | 3 | 5 | 7 | 9 | |
| Mean rank | 1.4 | 3.8 | 7.3 | 3.5 | 3.1 | 6.2 | 5.3 | 5.2 | 8.2 | |
| Final ranking | 1 | 4 | 8 | 3 | 2 | 7 | 6 | 5 | 9 | |
| +/=/– | –/–/– | 0/3/7 | 0/1/9 | 1/3/6 | 0/4/6 | 0/1/9 | 0/0/10 | 2/0/8 | 0/1/9 | |
| Function . | Index . | Algorithms . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HBWO-JS . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . | ||
| cec01 | Best | 1.01E+02 | 1.05E+02 | 5.35E+09 | 1.01E+02 | 1.23E+02 | 2.96E+02 | 1.30E+02 | 3.25E+03 | 3.72E+09 |
| Worst | 5.17E+03 | 3.19E+03 | 1.24E+10 | 7.37E+03 | 9.66E+03 | 1.68E+04 | 1.44E+04 | 8.75E+07 | 1.74E+10 | |
| Mean | 1.04E+03 | 1.18E+03 | 8.63E+09 | 1.92E+03 | 2.69E+03 | 5.74E+03 | 2.49E+03 | 8.84E+06 | 1.05E+10 | |
| Std | 1.21E+03 | 9.42E+02 | 2.01E+09 | 1.90E+03 | 2.38E+03 | 4.12E+03 | 2.99E+03 | 2.18E+07 | 3.67E+09 | |
| Rank | 1 | 2 | 8 | 3 | 5 | 6 | 4 | 7 | 9 | |
| cec02 | Best | 1.14E+03 | 1.24E+03 | 2.21E+03 | 1.12E+03 | 1.23E+03 | 1.35E+03 | 1.22E+03 | 1.13E+03 | 2.28E+03 |
| Worst | 1.71E+03 | 2.46E+03 | 2.95E+03 | 2.00E+03 | 2.00E+03 | 2.51E+03 | 2.27E+03 | 2.72E+03 | 3.16E+03 | |
| Mean | 1.36E+03 | 1.95E+03 | 2.60E+03 | 1.54E+03 | 1.51E+03 | 1.87E+03 | 1.60E+03 | 1.89E+03 | 2.80E+03 | |
| Std | 1.22E+02 | 3.40E+02 | 2.00E+02 | 2.07E+02 | 1.98E+02 | 2.89E+02 | 2.15E+02 | 5.09E+02 | 2.11E+02 | |
| Rank | 1 | 7 | 8 | 3 | 2 | 5 | 4 | 6 | 9 | |
| cec03 | Best | 7.18E+02 | 7.20E+02 | 7.86E+02 | 7.22E+02 | 7.18E+02 | 7.28E+02 | 7.19E+02 | 7.21E+02 | 7.89E+02 |
| Worst | 7.41E+02 | 7.60E+02 | 8.22E+02 | 7.87E+02 | 7.60E+02 | 7.94E+02 | 7.69E+02 | 7.61E+02 | 8.32E+02 | |
| Mean | 2.30E+03 | 2.30E+03 | 2.73E+03 | 2.30E+03 | 2.30E+03 | 2.40E+03 | 2.30E+03 | 2.31E+03 | 3.10E+03 | |
| Std | 5.32E+00 | 1.15E+01 | 9.69E+00 | 1.54E+01 | 8.54E+00 | 1.83E+01 | 1.30E+01 | 1.01E+01 | 1.20E+01 | |
| Rank | 1 | 4 | 8 | 2 | 3 | 7 | 5 | 6 | 9 | |
| cec04 | Best | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 |
| Worst | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | |
| Mean | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | |
| Std | 0.00E+00 | 1.02E-01 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 9.41E-01 | 7.18E-02 | 8.15E-01 | 0.00E+00 | |
| Rank | 1 | 6 | 1 | 1 | 1 | 8 | 7 | 9 | 1 | |
| cec05 | Best | 1.98E+03 | 2.67E+03 | 1.35E+05 | 1.92E+03 | 1.80E+03 | 2.38E+03 | 2.68E+03 | 1.84E+03 | 3.13E+05 |
| Worst | 9.68E+03 | 1.74E+04 | 4.88E+05 | 2.94E+05 | 3.93E+04 | 3.83E+04 | 5.39E+05 | 2.63E+03 | 7.69E+05 | |
| Mean | 3.96E+03 | 5.35E+03 | 3.15E+05 | 1.82E+04 | 5.60E+03 | 8.18E+03 | 3.06E+04 | 2.05E+03 | 5.26E+05 | |
| Std | 1.97E+03 | 2.79E+03 | 1.00E+05 | 5.28E+04 | 7.36E+03 | 8.75E+03 | 9.96E+04 | 1.83E+02 | 8.28E+04 | |
| Rank | 2 | 3 | 8 | 6 | 4 | 5 | 7 | 1 | 9 | |
| cec06 | Best | 5.32E+00 | 1.15E+01 | 9.69E+00 | 1.54E+01 | 8.54E+00 | 1.83E+01 | 1.30E+01 | 1.01E+01 | 1.20E+01 |
| Worst | 1.72E+03 | 1.76E+03 | 2.16E+03 | 1.90E+03 | 1.84E+03 | 1.94E+03 | 1.85E+03 | 1.84E+03 | 2.60E+03 | |
| Mean | 1.62E+03 | 1.65E+03 | 1.99E+03 | 1.72E+03 | 1.69E+03 | 1.77E+03 | 1.69E+03 | 1.69E+03 | 2.18E+03 | |
| Std | 4.05E+01 | 5.79E+01 | 9.39E+01 | 9.82E+01 | 6.56E+01 | 9.80E+01 | 8.08E+01 | 8.25E+01 | 1.78E+02 | |
| Rank | 1 | 2 | 8 | 6 | 3 | 7 | 4 | 5 | 9 | |
| cec07 | Best | 2.14E+03 | 2.23E+03 | 9.61E+03 | 2.10E+03 | 2.12E+03 | 2.49E+03 | 2.60E+03 | 2.11E+03 | 1.45E+04 |
| Worst | 2.98E+03 | 4.48E+03 | 5.52E+05 | 2.23E+04 | 8.39E+03 | 2.63E+04 | 1.02E+04 | 2.59E+03 | 6.09E+06 | |
| Mean | 2.37E+03 | 2.90E+03 | 1.07E+05 | 4.58E+03 | 3.47E+03 | 9.27E+03 | 4.77E+03 | 2.23E+03 | 7.34E+05 | |
| Std | 2.11E+02 | 5.54E+02 | 1.23E+05 | 5.02E+03 | 1.97E+03 | 7.12E+03 | 2.56E+03 | 8.96E+01 | 1.28E+06 | |
| Rank | 2 | 3 | 8 | 5 | 4 | 7 | 6 | 1 | 9 | |
| cec08 | Best | 2.22E+03 | 2.30E+03 | 2.33E+03 | 2.23E+03 | 2.23E+03 | 2.24E+03 | 2.30E+03 | 2.22E+03 | 2.60E+03 |
| Worst | 2.30E+03 | 2.30E+03 | 3.17E+03 | 2.31E+03 | 2.30E+03 | 3.87E+03 | 2.31E+03 | 2.35E+03 | 3.56E+03 | |
| Mean | 2.30E+03 | 2.30E+03 | 2.73E+03 | 2.30E+03 | 2.30E+03 | 2.40E+03 | 2.30E+03 | 2.31E+03 | 3.10E+03 | |
| Std | 2.13E+01 | 5.02E-01 | 2.18E+02 | 1.33E+01 | 1.26E+01 | 3.69E+02 | 1.26E+00 | 1.83E+01 | 2.49E+02 | |
| Rank | 1 | 4 | 8 | 2 | 3 | 7 | 5 | 6 | 9 | |
| cec09 | Best | 2.50E+03 | 2.53E+03 | 2.65E+03 | 2.50E+03 | 2.50E+03 | 2.50E+03 | 2.63E+03 | 2.51E+03 | 2.81E+03 |
| Worst | 2.75E+03 | 2.76E+03 | 2.86E+03 | 2.77E+03 | 2.78E+03 | 2.82E+03 | 2.77E+03 | 2.79E+03 | 2.99E+03 | |
| Mean | 2.62E+03 | 2.71E+03 | 2.78E+03 | 2.60E+03 | 2.72E+03 | 2.76E+03 | 2.75E+03 | 2.72E+03 | 2.89E+03 | |
| Std | 1.21E+02 | 7.12E+01 | 7.46E+01 | 1.25E+02 | 7.52E+01 | 7.36E+01 | 2.47E+01 | 8.13E+01 | 5.26E+01 | |
| Rank | 2 | 3 | 8 | 1 | 5 | 7 | 6 | 4 | 9 | |
| cec10 | Best | 2.90E+03 | 2.90E+03 | 2.98E+03 | 2.90E+03 | 2.90E+03 | 2.90E+03 | 2.90E+03 | 2.90E+03 | 3.13E+03 |
| Worst | 2.95E+03 | 2.95E+03 | 3.42E+03 | 2.95E+03 | 2.95E+03 | 2.95E+03 | 2.95E+03 | 2.99E+03 | 3.69E+03 | |
| Mean | 2.92E+03 | 2.92E+03 | 3.24E+03 | 2.93E+03 | 2.92E+03 | 2.92E+03 | 2.93E+03 | 2.93E+03 | 3.34E+03 | |
| Std | 2.28E+01 | 2.41E+01 | 1.02E+02 | 2.09E+01 | 2.36E+01 | 2.38E+01 | 2.18E+01 | 2.47E+01 | 9.41E+01 | |
| Rank | 2 | 4 | 8 | 6 | 1 | 3 | 5 | 7 | 9 | |
| Mean rank | 1.4 | 3.8 | 7.3 | 3.5 | 3.1 | 6.2 | 5.3 | 5.2 | 8.2 | |
| Final ranking | 1 | 4 | 8 | 3 | 2 | 7 | 6 | 5 | 9 | |
| +/=/– | –/–/– | 0/3/7 | 0/1/9 | 1/3/6 | 0/4/6 | 0/1/9 | 0/0/10 | 2/0/8 | 0/1/9 | |
The results of HBWO-JS and other algorithms for CEC2020 test functions (the dimension dim = 30).
| Function . | Index . | Algorithms . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HBWO-JS . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . | ||
| cec01 | Best | 1.77E+05 | 3.08E+07 | 4.50E+10 | 7.09E+06 | 6.41E+06 | 2.73E+05 | 7.88E+05 | 5.88E+09 | 2.97E+10 |
| Worst | 1.66E+06 | 3.83E+09 | 5.99E+10 | 4.42E+08 | 8.80E+07 | 2.72E+06 | 6.39E+07 | 2.15E+10 | 6.39E+10 | |
| Mean | 6.01E+05 | 2.98E+08 | 5.30E+10 | 6.02E+07 | 2.88E+07 | 9.07E+05 | 9.75E+06 | 1.28E+10 | 4.74E+10 | |
| Std | 3.55E+05 | 6.87E+08 | 4.17E+09 | 8.70E+07 | 1.76E+07 | 6.27E+05 | 1.22E+07 | 4.16E+09 | 6.65E+09 | |
| Rank | 1 | 6 | 9 | 5 | 4 | 2 | 3 | 7 | 8 | |
| cec02 | Best | 2.54E+03 | 5.27E+03 | 7.97E+03 | 3.19E+03 | 3.22E+03 | 3.13E+03 | 2.88E+03 | 4.95E+03 | 7.18E+03 |
| Worst | 4.73E+03 | 9.03E+03 | 9.37E+03 | 5.42E+03 | 5.21E+03 | 6.22E+03 | 7.04E+03 | 8.90E+03 | 8.53E+03 | |
| Mean | 4.02E+03 | 8.12E+03 | 8.67E+03 | 4.31E+03 | 4.21E+03 | 4.94E+03 | 4.07E+03 | 7.59E+03 | 7.94E+03 | |
| Std | 4.67E+02 | 8.88E+02 | 3.51E+02 | 5.16E+02 | 5.27E+02 | 7.08E+02 | 8.17E+02 | 1.06E+03 | 4.24E+02 | |
| Rank | 1 | 8 | 9 | 4 | 3 | 5 | 2 | 6 | 7 | |
| cec03 | Best | 8.48E+02 | 8.61E+02 | 1.34E+03 | 8.82E+02 | 8.47E+02 | 8.71E+02 | 7.86E+02 | 1.03E+03 | 1.32E+03 |
| Worst | 1.22E+03 | 1.20E+03 | 1.47E+03 | 1.32E+03 | 1.22E+03 | 1.11E+03 | 1.05E+03 | 1.37E+03 | 1.48E+03 | |
| Mean | 9.09E+02 | 9.86E+02 | 1.40E+03 | 1.05E+03 | 9.52E+02 | 1.01E+03 | 9.11E+02 | 1.14E+03 | 1.40E+03 | |
| Std | 6.83E+01 | 7.21E+01 | 3.33E+01 | 1.07E+02 | 8.78E+01 | 6.11E+01 | 5.00E+01 | 8.98E+01 | 3.80E+01 | |
| Rank | 1 | 4 | 9 | 6 | 3 | 5 | 2 | 7 | 8 | |
| cec04 | Best | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.91E+03 | 1.90E+03 |
| Worst | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.92E+03 | 1.90E+03 | 1.99E+03 | 1.90E+03 | |
| Mean | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.91E+03 | 1.90E+03 | 1.94E+03 | 1.90E+03 | |
| Std | 0.00E+00 | 4.12E-03 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 4.60E+00 | 1.34E-01 | 1.45E+01 | 0.00E+00 | |
| Rank | 1 | 6 | 1 | 1 | 1 | 8 | 7 | 9 | 1 | |
| cec05 | Best | 1.02E+05 | 1.10E+05 | 2.48E+07 | 3.41E+05 | 4.12E+05 | 1.26E+05 | 6.62E+04 | 7.56E+04 | 2.62E+07 |
| Worst | 2.91E+06 | 2.55E+06 | 1.31E+08 | 5.27E+06 | 3.95E+06 | 6.65E+06 | 4.20E+06 | 1.96E+07 | 1.51E+08 | |
| Mean | 9.02E+05 | 7.99E+05 | 7.32E+07 | 2.41E+06 | 1.55E+06 | 1.71E+06 | 1.63E+06 | 2.67E+06 | 8.25E+07 | |
| Std | 7.19E+05 | 5.12E+05 | 2.33E+07 | 1.44E+06 | 1.02E+06 | 1.33E+06 | 1.12E+06 | 4.07E+06 | 3.39E+07 | |
| Rank | 2 | 1 | 8 | 6 | 3 | 5 | 4 | 7 | 9 | |
| cec06 | Best | 1.74E+03 | 1.80E+03 | 4.13E+03 | 1.76E+03 | 1.81E+03 | 1.86E+03 | 1.76E+03 | 1.90E+03 | 3.44E+03 |
| Worst | 2.07E+03 | 2.79E+03 | 5.85E+03 | 2.56E+03 | 2.52E+03 | 2.80E+03 | 2.69E+03 | 3.03E+03 | 6.91E+03 | |
| Mean | 1.92E+03 | 2.21E+03 | 5.07E+03 | 2.13E+03 | 2.15E+03 | 2.28E+03 | 2.17E+03 | 2.36E+03 | 4.71E+03 | |
| Std | 8.38E+01 | 2.49E+02 | 3.82E+02 | 2.01E+02 | 1.91E+02 | 2.49E+02 | 2.26E+02 | 2.84E+02 | 7.84E+02 | |
| Rank | 1 | 5 | 9 | 2 | 3 | 6 | 4 | 7 | 8 | |
| cec07 | Best | 1.85E+04 | 2.75E+04 | 3.63E+06 | 5.18E+04 | 5.91E+04 | 4.58E+04 | 1.92E+04 | 6.04E+03 | 5.78E+06 |
| Worst | 8.13E+05 | 9.05E+05 | 6.08E+07 | 1.61E+06 | 3.17E+06 | 2.02E+06 | 1.10E+06 | 2.73E+06 | 9.49E+07 | |
| Mean | 2.48E+05 | 2.39E+05 | 3.03E+07 | 5.18E+05 | 5.17E+05 | 6.41E+05 | 5.07E+05 | 2.88E+05 | 4.40E+07 | |
| Std | 1.85E+05 | 1.96E+05 | 1.51E+07 | 3.78E+05 | 6.08E+05 | 4.63E+05 | 3.25E+05 | 5.19E+05 | 2.57E+07 | |
| Rank | 2 | 1 | 8 | 6 | 5 | 7 | 4 | 3 | 9 | |
| cec08 | Best | 2.30E+03 | 2.34E+03 | 7.64E+03 | 2.32E+03 | 2.32E+03 | 2.30E+03 | 2.33E+03 | 3.16E+03 | 6.89E+03 |
| Worst | 2.31E+03 | 2.70E+03 | 9.97E+03 | 7.18E+03 | 2.43E+03 | 7.65E+03 | 7.45E+03 | 7.45E+03 | 1.03E+04 | |
| Mean | 2.31E+03 | 2.43E+03 | 8.91E+03 | 2.65E+03 | 2.34E+03 | 5.93E+03 | 4.28E+03 | 5.05E+03 | 8.57E+03 | |
| Std | 2.24E+00 | 1.01E+02 | 5.87E+02 | 1.19E+03 | 2.04E+01 | 1.90E+03 | 1.70E+03 | 1.21E+03 | 9.31E+02 | |
| Rank | 1 | 3 | 9 | 4 | 2 | 7 | 5 | 6 | 8 | |
| cec09 | Best | 2.88E+03 | 2.94E+03 | 3.45E+03 | 2.96E+03 | 2.89E+03 | 2.95E+03 | 2.88E+03 | 3.17E+03 | 3.30E+03 |
| Worst | 3.00E+03 | 3.12E+03 | 3.91E+03 | 3.29E+03 | 3.06E+03 | 3.26E+03 | 3.08E+03 | 3.66E+03 | 4.46E+03 | |
| Mean | 2.94E+03 | 3.01E+03 | 3.60E+03 | 3.06E+03 | 2.96E+03 | 3.10E+03 | 2.96E+03 | 3.36E+03 | 3.53E+03 | |
| Std | 3.01E+01 | 4.89E+01 | 9.03E+01 | 6.53E+01 | 4.90E+01 | 7.97E+01 | 4.70E+01 | 1.21E+02 | 2.63E+02 | |
| Rank | 1 | 4 | 9 | 5 | 2 | 6 | 3 | 7 | 8 | |
| cec10 | Best | 2.89E+03 | 2.95E+03 | 4.21E+03 | 2.89E+03 | 2.92E+03 | 2.88E+03 | 2.89E+03 | 3.08E+03 | 3.95E+03 |
| Worst | 2.96E+03 | 3.08E+03 | 4.69E+03 | 3.02E+03 | 3.05E+03 | 2.97E+03 | 2.97E+03 | 3.82E+03 | 6.12E+03 | |
| Mean | 2.91E+03 | 3.00E+03 | 4.45E+03 | 2.96E+03 | 2.96E+03 | 2.91E+03 | 2.93E+03 | 3.32E+03 | 5.02E+03 | |
| Std | 1.82E+01 | 3.34E+01 | 1.37E+02 | 3.31E+01 | 3.20E+01 | 2.14E+01 | 2.36E+01 | 1.88E+02 | 6.18E+02 | |
| Rank | 2 | 6 | 8 | 4 | 5 | 1 | 3 | 7 | 9 | |
| Mean rank | 1.3 | 4.4 | 7.9 | 4.3 | 3.1 | 5.2 | 3.7 | 6.6 | 7.5 | |
| Final ranking | 1 | 5 | 9 | 4 | 2 | 6 | 3 | 7 | 8 | |
| +/=/– | –/–/– | 0/2/8 | 0/1/9 | 0/1/9 | 0/3/7 | 0/2/8 | 0/3/7 | 0/2/8 | 0/1/9 | |
| Function . | Index . | Algorithms . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HBWO-JS . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . | ||
| cec01 | Best | 1.77E+05 | 3.08E+07 | 4.50E+10 | 7.09E+06 | 6.41E+06 | 2.73E+05 | 7.88E+05 | 5.88E+09 | 2.97E+10 |
| Worst | 1.66E+06 | 3.83E+09 | 5.99E+10 | 4.42E+08 | 8.80E+07 | 2.72E+06 | 6.39E+07 | 2.15E+10 | 6.39E+10 | |
| Mean | 6.01E+05 | 2.98E+08 | 5.30E+10 | 6.02E+07 | 2.88E+07 | 9.07E+05 | 9.75E+06 | 1.28E+10 | 4.74E+10 | |
| Std | 3.55E+05 | 6.87E+08 | 4.17E+09 | 8.70E+07 | 1.76E+07 | 6.27E+05 | 1.22E+07 | 4.16E+09 | 6.65E+09 | |
| Rank | 1 | 6 | 9 | 5 | 4 | 2 | 3 | 7 | 8 | |
| cec02 | Best | 2.54E+03 | 5.27E+03 | 7.97E+03 | 3.19E+03 | 3.22E+03 | 3.13E+03 | 2.88E+03 | 4.95E+03 | 7.18E+03 |
| Worst | 4.73E+03 | 9.03E+03 | 9.37E+03 | 5.42E+03 | 5.21E+03 | 6.22E+03 | 7.04E+03 | 8.90E+03 | 8.53E+03 | |
| Mean | 4.02E+03 | 8.12E+03 | 8.67E+03 | 4.31E+03 | 4.21E+03 | 4.94E+03 | 4.07E+03 | 7.59E+03 | 7.94E+03 | |
| Std | 4.67E+02 | 8.88E+02 | 3.51E+02 | 5.16E+02 | 5.27E+02 | 7.08E+02 | 8.17E+02 | 1.06E+03 | 4.24E+02 | |
| Rank | 1 | 8 | 9 | 4 | 3 | 5 | 2 | 6 | 7 | |
| cec03 | Best | 8.48E+02 | 8.61E+02 | 1.34E+03 | 8.82E+02 | 8.47E+02 | 8.71E+02 | 7.86E+02 | 1.03E+03 | 1.32E+03 |
| Worst | 1.22E+03 | 1.20E+03 | 1.47E+03 | 1.32E+03 | 1.22E+03 | 1.11E+03 | 1.05E+03 | 1.37E+03 | 1.48E+03 | |
| Mean | 9.09E+02 | 9.86E+02 | 1.40E+03 | 1.05E+03 | 9.52E+02 | 1.01E+03 | 9.11E+02 | 1.14E+03 | 1.40E+03 | |
| Std | 6.83E+01 | 7.21E+01 | 3.33E+01 | 1.07E+02 | 8.78E+01 | 6.11E+01 | 5.00E+01 | 8.98E+01 | 3.80E+01 | |
| Rank | 1 | 4 | 9 | 6 | 3 | 5 | 2 | 7 | 8 | |
| cec04 | Best | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.91E+03 | 1.90E+03 |
| Worst | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.92E+03 | 1.90E+03 | 1.99E+03 | 1.90E+03 | |
| Mean | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.91E+03 | 1.90E+03 | 1.94E+03 | 1.90E+03 | |
| Std | 0.00E+00 | 4.12E-03 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 4.60E+00 | 1.34E-01 | 1.45E+01 | 0.00E+00 | |
| Rank | 1 | 6 | 1 | 1 | 1 | 8 | 7 | 9 | 1 | |
| cec05 | Best | 1.02E+05 | 1.10E+05 | 2.48E+07 | 3.41E+05 | 4.12E+05 | 1.26E+05 | 6.62E+04 | 7.56E+04 | 2.62E+07 |
| Worst | 2.91E+06 | 2.55E+06 | 1.31E+08 | 5.27E+06 | 3.95E+06 | 6.65E+06 | 4.20E+06 | 1.96E+07 | 1.51E+08 | |
| Mean | 9.02E+05 | 7.99E+05 | 7.32E+07 | 2.41E+06 | 1.55E+06 | 1.71E+06 | 1.63E+06 | 2.67E+06 | 8.25E+07 | |
| Std | 7.19E+05 | 5.12E+05 | 2.33E+07 | 1.44E+06 | 1.02E+06 | 1.33E+06 | 1.12E+06 | 4.07E+06 | 3.39E+07 | |
| Rank | 2 | 1 | 8 | 6 | 3 | 5 | 4 | 7 | 9 | |
| cec06 | Best | 1.74E+03 | 1.80E+03 | 4.13E+03 | 1.76E+03 | 1.81E+03 | 1.86E+03 | 1.76E+03 | 1.90E+03 | 3.44E+03 |
| Worst | 2.07E+03 | 2.79E+03 | 5.85E+03 | 2.56E+03 | 2.52E+03 | 2.80E+03 | 2.69E+03 | 3.03E+03 | 6.91E+03 | |
| Mean | 1.92E+03 | 2.21E+03 | 5.07E+03 | 2.13E+03 | 2.15E+03 | 2.28E+03 | 2.17E+03 | 2.36E+03 | 4.71E+03 | |
| Std | 8.38E+01 | 2.49E+02 | 3.82E+02 | 2.01E+02 | 1.91E+02 | 2.49E+02 | 2.26E+02 | 2.84E+02 | 7.84E+02 | |
| Rank | 1 | 5 | 9 | 2 | 3 | 6 | 4 | 7 | 8 | |
| cec07 | Best | 1.85E+04 | 2.75E+04 | 3.63E+06 | 5.18E+04 | 5.91E+04 | 4.58E+04 | 1.92E+04 | 6.04E+03 | 5.78E+06 |
| Worst | 8.13E+05 | 9.05E+05 | 6.08E+07 | 1.61E+06 | 3.17E+06 | 2.02E+06 | 1.10E+06 | 2.73E+06 | 9.49E+07 | |
| Mean | 2.48E+05 | 2.39E+05 | 3.03E+07 | 5.18E+05 | 5.17E+05 | 6.41E+05 | 5.07E+05 | 2.88E+05 | 4.40E+07 | |
| Std | 1.85E+05 | 1.96E+05 | 1.51E+07 | 3.78E+05 | 6.08E+05 | 4.63E+05 | 3.25E+05 | 5.19E+05 | 2.57E+07 | |
| Rank | 2 | 1 | 8 | 6 | 5 | 7 | 4 | 3 | 9 | |
| cec08 | Best | 2.30E+03 | 2.34E+03 | 7.64E+03 | 2.32E+03 | 2.32E+03 | 2.30E+03 | 2.33E+03 | 3.16E+03 | 6.89E+03 |
| Worst | 2.31E+03 | 2.70E+03 | 9.97E+03 | 7.18E+03 | 2.43E+03 | 7.65E+03 | 7.45E+03 | 7.45E+03 | 1.03E+04 | |
| Mean | 2.31E+03 | 2.43E+03 | 8.91E+03 | 2.65E+03 | 2.34E+03 | 5.93E+03 | 4.28E+03 | 5.05E+03 | 8.57E+03 | |
| Std | 2.24E+00 | 1.01E+02 | 5.87E+02 | 1.19E+03 | 2.04E+01 | 1.90E+03 | 1.70E+03 | 1.21E+03 | 9.31E+02 | |
| Rank | 1 | 3 | 9 | 4 | 2 | 7 | 5 | 6 | 8 | |
| cec09 | Best | 2.88E+03 | 2.94E+03 | 3.45E+03 | 2.96E+03 | 2.89E+03 | 2.95E+03 | 2.88E+03 | 3.17E+03 | 3.30E+03 |
| Worst | 3.00E+03 | 3.12E+03 | 3.91E+03 | 3.29E+03 | 3.06E+03 | 3.26E+03 | 3.08E+03 | 3.66E+03 | 4.46E+03 | |
| Mean | 2.94E+03 | 3.01E+03 | 3.60E+03 | 3.06E+03 | 2.96E+03 | 3.10E+03 | 2.96E+03 | 3.36E+03 | 3.53E+03 | |
| Std | 3.01E+01 | 4.89E+01 | 9.03E+01 | 6.53E+01 | 4.90E+01 | 7.97E+01 | 4.70E+01 | 1.21E+02 | 2.63E+02 | |
| Rank | 1 | 4 | 9 | 5 | 2 | 6 | 3 | 7 | 8 | |
| cec10 | Best | 2.89E+03 | 2.95E+03 | 4.21E+03 | 2.89E+03 | 2.92E+03 | 2.88E+03 | 2.89E+03 | 3.08E+03 | 3.95E+03 |
| Worst | 2.96E+03 | 3.08E+03 | 4.69E+03 | 3.02E+03 | 3.05E+03 | 2.97E+03 | 2.97E+03 | 3.82E+03 | 6.12E+03 | |
| Mean | 2.91E+03 | 3.00E+03 | 4.45E+03 | 2.96E+03 | 2.96E+03 | 2.91E+03 | 2.93E+03 | 3.32E+03 | 5.02E+03 | |
| Std | 1.82E+01 | 3.34E+01 | 1.37E+02 | 3.31E+01 | 3.20E+01 | 2.14E+01 | 2.36E+01 | 1.88E+02 | 6.18E+02 | |
| Rank | 2 | 6 | 8 | 4 | 5 | 1 | 3 | 7 | 9 | |
| Mean rank | 1.3 | 4.4 | 7.9 | 4.3 | 3.1 | 5.2 | 3.7 | 6.6 | 7.5 | |
| Final ranking | 1 | 5 | 9 | 4 | 2 | 6 | 3 | 7 | 8 | |
| +/=/– | –/–/– | 0/2/8 | 0/1/9 | 0/1/9 | 0/3/7 | 0/2/8 | 0/3/7 | 0/2/8 | 0/1/9 | |
The results of HBWO-JS and other algorithms for CEC2020 test functions (the dimension dim = 30).
| Function . | Index . | Algorithms . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HBWO-JS . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . | ||
| cec01 | Best | 1.77E+05 | 3.08E+07 | 4.50E+10 | 7.09E+06 | 6.41E+06 | 2.73E+05 | 7.88E+05 | 5.88E+09 | 2.97E+10 |
| Worst | 1.66E+06 | 3.83E+09 | 5.99E+10 | 4.42E+08 | 8.80E+07 | 2.72E+06 | 6.39E+07 | 2.15E+10 | 6.39E+10 | |
| Mean | 6.01E+05 | 2.98E+08 | 5.30E+10 | 6.02E+07 | 2.88E+07 | 9.07E+05 | 9.75E+06 | 1.28E+10 | 4.74E+10 | |
| Std | 3.55E+05 | 6.87E+08 | 4.17E+09 | 8.70E+07 | 1.76E+07 | 6.27E+05 | 1.22E+07 | 4.16E+09 | 6.65E+09 | |
| Rank | 1 | 6 | 9 | 5 | 4 | 2 | 3 | 7 | 8 | |
| cec02 | Best | 2.54E+03 | 5.27E+03 | 7.97E+03 | 3.19E+03 | 3.22E+03 | 3.13E+03 | 2.88E+03 | 4.95E+03 | 7.18E+03 |
| Worst | 4.73E+03 | 9.03E+03 | 9.37E+03 | 5.42E+03 | 5.21E+03 | 6.22E+03 | 7.04E+03 | 8.90E+03 | 8.53E+03 | |
| Mean | 4.02E+03 | 8.12E+03 | 8.67E+03 | 4.31E+03 | 4.21E+03 | 4.94E+03 | 4.07E+03 | 7.59E+03 | 7.94E+03 | |
| Std | 4.67E+02 | 8.88E+02 | 3.51E+02 | 5.16E+02 | 5.27E+02 | 7.08E+02 | 8.17E+02 | 1.06E+03 | 4.24E+02 | |
| Rank | 1 | 8 | 9 | 4 | 3 | 5 | 2 | 6 | 7 | |
| cec03 | Best | 8.48E+02 | 8.61E+02 | 1.34E+03 | 8.82E+02 | 8.47E+02 | 8.71E+02 | 7.86E+02 | 1.03E+03 | 1.32E+03 |
| Worst | 1.22E+03 | 1.20E+03 | 1.47E+03 | 1.32E+03 | 1.22E+03 | 1.11E+03 | 1.05E+03 | 1.37E+03 | 1.48E+03 | |
| Mean | 9.09E+02 | 9.86E+02 | 1.40E+03 | 1.05E+03 | 9.52E+02 | 1.01E+03 | 9.11E+02 | 1.14E+03 | 1.40E+03 | |
| Std | 6.83E+01 | 7.21E+01 | 3.33E+01 | 1.07E+02 | 8.78E+01 | 6.11E+01 | 5.00E+01 | 8.98E+01 | 3.80E+01 | |
| Rank | 1 | 4 | 9 | 6 | 3 | 5 | 2 | 7 | 8 | |
| cec04 | Best | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.91E+03 | 1.90E+03 |
| Worst | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.92E+03 | 1.90E+03 | 1.99E+03 | 1.90E+03 | |
| Mean | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.91E+03 | 1.90E+03 | 1.94E+03 | 1.90E+03 | |
| Std | 0.00E+00 | 4.12E-03 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 4.60E+00 | 1.34E-01 | 1.45E+01 | 0.00E+00 | |
| Rank | 1 | 6 | 1 | 1 | 1 | 8 | 7 | 9 | 1 | |
| cec05 | Best | 1.02E+05 | 1.10E+05 | 2.48E+07 | 3.41E+05 | 4.12E+05 | 1.26E+05 | 6.62E+04 | 7.56E+04 | 2.62E+07 |
| Worst | 2.91E+06 | 2.55E+06 | 1.31E+08 | 5.27E+06 | 3.95E+06 | 6.65E+06 | 4.20E+06 | 1.96E+07 | 1.51E+08 | |
| Mean | 9.02E+05 | 7.99E+05 | 7.32E+07 | 2.41E+06 | 1.55E+06 | 1.71E+06 | 1.63E+06 | 2.67E+06 | 8.25E+07 | |
| Std | 7.19E+05 | 5.12E+05 | 2.33E+07 | 1.44E+06 | 1.02E+06 | 1.33E+06 | 1.12E+06 | 4.07E+06 | 3.39E+07 | |
| Rank | 2 | 1 | 8 | 6 | 3 | 5 | 4 | 7 | 9 | |
| cec06 | Best | 1.74E+03 | 1.80E+03 | 4.13E+03 | 1.76E+03 | 1.81E+03 | 1.86E+03 | 1.76E+03 | 1.90E+03 | 3.44E+03 |
| Worst | 2.07E+03 | 2.79E+03 | 5.85E+03 | 2.56E+03 | 2.52E+03 | 2.80E+03 | 2.69E+03 | 3.03E+03 | 6.91E+03 | |
| Mean | 1.92E+03 | 2.21E+03 | 5.07E+03 | 2.13E+03 | 2.15E+03 | 2.28E+03 | 2.17E+03 | 2.36E+03 | 4.71E+03 | |
| Std | 8.38E+01 | 2.49E+02 | 3.82E+02 | 2.01E+02 | 1.91E+02 | 2.49E+02 | 2.26E+02 | 2.84E+02 | 7.84E+02 | |
| Rank | 1 | 5 | 9 | 2 | 3 | 6 | 4 | 7 | 8 | |
| cec07 | Best | 1.85E+04 | 2.75E+04 | 3.63E+06 | 5.18E+04 | 5.91E+04 | 4.58E+04 | 1.92E+04 | 6.04E+03 | 5.78E+06 |
| Worst | 8.13E+05 | 9.05E+05 | 6.08E+07 | 1.61E+06 | 3.17E+06 | 2.02E+06 | 1.10E+06 | 2.73E+06 | 9.49E+07 | |
| Mean | 2.48E+05 | 2.39E+05 | 3.03E+07 | 5.18E+05 | 5.17E+05 | 6.41E+05 | 5.07E+05 | 2.88E+05 | 4.40E+07 | |
| Std | 1.85E+05 | 1.96E+05 | 1.51E+07 | 3.78E+05 | 6.08E+05 | 4.63E+05 | 3.25E+05 | 5.19E+05 | 2.57E+07 | |
| Rank | 2 | 1 | 8 | 6 | 5 | 7 | 4 | 3 | 9 | |
| cec08 | Best | 2.30E+03 | 2.34E+03 | 7.64E+03 | 2.32E+03 | 2.32E+03 | 2.30E+03 | 2.33E+03 | 3.16E+03 | 6.89E+03 |
| Worst | 2.31E+03 | 2.70E+03 | 9.97E+03 | 7.18E+03 | 2.43E+03 | 7.65E+03 | 7.45E+03 | 7.45E+03 | 1.03E+04 | |
| Mean | 2.31E+03 | 2.43E+03 | 8.91E+03 | 2.65E+03 | 2.34E+03 | 5.93E+03 | 4.28E+03 | 5.05E+03 | 8.57E+03 | |
| Std | 2.24E+00 | 1.01E+02 | 5.87E+02 | 1.19E+03 | 2.04E+01 | 1.90E+03 | 1.70E+03 | 1.21E+03 | 9.31E+02 | |
| Rank | 1 | 3 | 9 | 4 | 2 | 7 | 5 | 6 | 8 | |
| cec09 | Best | 2.88E+03 | 2.94E+03 | 3.45E+03 | 2.96E+03 | 2.89E+03 | 2.95E+03 | 2.88E+03 | 3.17E+03 | 3.30E+03 |
| Worst | 3.00E+03 | 3.12E+03 | 3.91E+03 | 3.29E+03 | 3.06E+03 | 3.26E+03 | 3.08E+03 | 3.66E+03 | 4.46E+03 | |
| Mean | 2.94E+03 | 3.01E+03 | 3.60E+03 | 3.06E+03 | 2.96E+03 | 3.10E+03 | 2.96E+03 | 3.36E+03 | 3.53E+03 | |
| Std | 3.01E+01 | 4.89E+01 | 9.03E+01 | 6.53E+01 | 4.90E+01 | 7.97E+01 | 4.70E+01 | 1.21E+02 | 2.63E+02 | |
| Rank | 1 | 4 | 9 | 5 | 2 | 6 | 3 | 7 | 8 | |
| cec10 | Best | 2.89E+03 | 2.95E+03 | 4.21E+03 | 2.89E+03 | 2.92E+03 | 2.88E+03 | 2.89E+03 | 3.08E+03 | 3.95E+03 |
| Worst | 2.96E+03 | 3.08E+03 | 4.69E+03 | 3.02E+03 | 3.05E+03 | 2.97E+03 | 2.97E+03 | 3.82E+03 | 6.12E+03 | |
| Mean | 2.91E+03 | 3.00E+03 | 4.45E+03 | 2.96E+03 | 2.96E+03 | 2.91E+03 | 2.93E+03 | 3.32E+03 | 5.02E+03 | |
| Std | 1.82E+01 | 3.34E+01 | 1.37E+02 | 3.31E+01 | 3.20E+01 | 2.14E+01 | 2.36E+01 | 1.88E+02 | 6.18E+02 | |
| Rank | 2 | 6 | 8 | 4 | 5 | 1 | 3 | 7 | 9 | |
| Mean rank | 1.3 | 4.4 | 7.9 | 4.3 | 3.1 | 5.2 | 3.7 | 6.6 | 7.5 | |
| Final ranking | 1 | 5 | 9 | 4 | 2 | 6 | 3 | 7 | 8 | |
| +/=/– | –/–/– | 0/2/8 | 0/1/9 | 0/1/9 | 0/3/7 | 0/2/8 | 0/3/7 | 0/2/8 | 0/1/9 | |
| Function . | Index . | Algorithms . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HBWO-JS . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . | ||
| cec01 | Best | 1.77E+05 | 3.08E+07 | 4.50E+10 | 7.09E+06 | 6.41E+06 | 2.73E+05 | 7.88E+05 | 5.88E+09 | 2.97E+10 |
| Worst | 1.66E+06 | 3.83E+09 | 5.99E+10 | 4.42E+08 | 8.80E+07 | 2.72E+06 | 6.39E+07 | 2.15E+10 | 6.39E+10 | |
| Mean | 6.01E+05 | 2.98E+08 | 5.30E+10 | 6.02E+07 | 2.88E+07 | 9.07E+05 | 9.75E+06 | 1.28E+10 | 4.74E+10 | |
| Std | 3.55E+05 | 6.87E+08 | 4.17E+09 | 8.70E+07 | 1.76E+07 | 6.27E+05 | 1.22E+07 | 4.16E+09 | 6.65E+09 | |
| Rank | 1 | 6 | 9 | 5 | 4 | 2 | 3 | 7 | 8 | |
| cec02 | Best | 2.54E+03 | 5.27E+03 | 7.97E+03 | 3.19E+03 | 3.22E+03 | 3.13E+03 | 2.88E+03 | 4.95E+03 | 7.18E+03 |
| Worst | 4.73E+03 | 9.03E+03 | 9.37E+03 | 5.42E+03 | 5.21E+03 | 6.22E+03 | 7.04E+03 | 8.90E+03 | 8.53E+03 | |
| Mean | 4.02E+03 | 8.12E+03 | 8.67E+03 | 4.31E+03 | 4.21E+03 | 4.94E+03 | 4.07E+03 | 7.59E+03 | 7.94E+03 | |
| Std | 4.67E+02 | 8.88E+02 | 3.51E+02 | 5.16E+02 | 5.27E+02 | 7.08E+02 | 8.17E+02 | 1.06E+03 | 4.24E+02 | |
| Rank | 1 | 8 | 9 | 4 | 3 | 5 | 2 | 6 | 7 | |
| cec03 | Best | 8.48E+02 | 8.61E+02 | 1.34E+03 | 8.82E+02 | 8.47E+02 | 8.71E+02 | 7.86E+02 | 1.03E+03 | 1.32E+03 |
| Worst | 1.22E+03 | 1.20E+03 | 1.47E+03 | 1.32E+03 | 1.22E+03 | 1.11E+03 | 1.05E+03 | 1.37E+03 | 1.48E+03 | |
| Mean | 9.09E+02 | 9.86E+02 | 1.40E+03 | 1.05E+03 | 9.52E+02 | 1.01E+03 | 9.11E+02 | 1.14E+03 | 1.40E+03 | |
| Std | 6.83E+01 | 7.21E+01 | 3.33E+01 | 1.07E+02 | 8.78E+01 | 6.11E+01 | 5.00E+01 | 8.98E+01 | 3.80E+01 | |
| Rank | 1 | 4 | 9 | 6 | 3 | 5 | 2 | 7 | 8 | |
| cec04 | Best | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.91E+03 | 1.90E+03 |
| Worst | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.92E+03 | 1.90E+03 | 1.99E+03 | 1.90E+03 | |
| Mean | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.91E+03 | 1.90E+03 | 1.94E+03 | 1.90E+03 | |
| Std | 0.00E+00 | 4.12E-03 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 4.60E+00 | 1.34E-01 | 1.45E+01 | 0.00E+00 | |
| Rank | 1 | 6 | 1 | 1 | 1 | 8 | 7 | 9 | 1 | |
| cec05 | Best | 1.02E+05 | 1.10E+05 | 2.48E+07 | 3.41E+05 | 4.12E+05 | 1.26E+05 | 6.62E+04 | 7.56E+04 | 2.62E+07 |
| Worst | 2.91E+06 | 2.55E+06 | 1.31E+08 | 5.27E+06 | 3.95E+06 | 6.65E+06 | 4.20E+06 | 1.96E+07 | 1.51E+08 | |
| Mean | 9.02E+05 | 7.99E+05 | 7.32E+07 | 2.41E+06 | 1.55E+06 | 1.71E+06 | 1.63E+06 | 2.67E+06 | 8.25E+07 | |
| Std | 7.19E+05 | 5.12E+05 | 2.33E+07 | 1.44E+06 | 1.02E+06 | 1.33E+06 | 1.12E+06 | 4.07E+06 | 3.39E+07 | |
| Rank | 2 | 1 | 8 | 6 | 3 | 5 | 4 | 7 | 9 | |
| cec06 | Best | 1.74E+03 | 1.80E+03 | 4.13E+03 | 1.76E+03 | 1.81E+03 | 1.86E+03 | 1.76E+03 | 1.90E+03 | 3.44E+03 |
| Worst | 2.07E+03 | 2.79E+03 | 5.85E+03 | 2.56E+03 | 2.52E+03 | 2.80E+03 | 2.69E+03 | 3.03E+03 | 6.91E+03 | |
| Mean | 1.92E+03 | 2.21E+03 | 5.07E+03 | 2.13E+03 | 2.15E+03 | 2.28E+03 | 2.17E+03 | 2.36E+03 | 4.71E+03 | |
| Std | 8.38E+01 | 2.49E+02 | 3.82E+02 | 2.01E+02 | 1.91E+02 | 2.49E+02 | 2.26E+02 | 2.84E+02 | 7.84E+02 | |
| Rank | 1 | 5 | 9 | 2 | 3 | 6 | 4 | 7 | 8 | |
| cec07 | Best | 1.85E+04 | 2.75E+04 | 3.63E+06 | 5.18E+04 | 5.91E+04 | 4.58E+04 | 1.92E+04 | 6.04E+03 | 5.78E+06 |
| Worst | 8.13E+05 | 9.05E+05 | 6.08E+07 | 1.61E+06 | 3.17E+06 | 2.02E+06 | 1.10E+06 | 2.73E+06 | 9.49E+07 | |
| Mean | 2.48E+05 | 2.39E+05 | 3.03E+07 | 5.18E+05 | 5.17E+05 | 6.41E+05 | 5.07E+05 | 2.88E+05 | 4.40E+07 | |
| Std | 1.85E+05 | 1.96E+05 | 1.51E+07 | 3.78E+05 | 6.08E+05 | 4.63E+05 | 3.25E+05 | 5.19E+05 | 2.57E+07 | |
| Rank | 2 | 1 | 8 | 6 | 5 | 7 | 4 | 3 | 9 | |
| cec08 | Best | 2.30E+03 | 2.34E+03 | 7.64E+03 | 2.32E+03 | 2.32E+03 | 2.30E+03 | 2.33E+03 | 3.16E+03 | 6.89E+03 |
| Worst | 2.31E+03 | 2.70E+03 | 9.97E+03 | 7.18E+03 | 2.43E+03 | 7.65E+03 | 7.45E+03 | 7.45E+03 | 1.03E+04 | |
| Mean | 2.31E+03 | 2.43E+03 | 8.91E+03 | 2.65E+03 | 2.34E+03 | 5.93E+03 | 4.28E+03 | 5.05E+03 | 8.57E+03 | |
| Std | 2.24E+00 | 1.01E+02 | 5.87E+02 | 1.19E+03 | 2.04E+01 | 1.90E+03 | 1.70E+03 | 1.21E+03 | 9.31E+02 | |
| Rank | 1 | 3 | 9 | 4 | 2 | 7 | 5 | 6 | 8 | |
| cec09 | Best | 2.88E+03 | 2.94E+03 | 3.45E+03 | 2.96E+03 | 2.89E+03 | 2.95E+03 | 2.88E+03 | 3.17E+03 | 3.30E+03 |
| Worst | 3.00E+03 | 3.12E+03 | 3.91E+03 | 3.29E+03 | 3.06E+03 | 3.26E+03 | 3.08E+03 | 3.66E+03 | 4.46E+03 | |
| Mean | 2.94E+03 | 3.01E+03 | 3.60E+03 | 3.06E+03 | 2.96E+03 | 3.10E+03 | 2.96E+03 | 3.36E+03 | 3.53E+03 | |
| Std | 3.01E+01 | 4.89E+01 | 9.03E+01 | 6.53E+01 | 4.90E+01 | 7.97E+01 | 4.70E+01 | 1.21E+02 | 2.63E+02 | |
| Rank | 1 | 4 | 9 | 5 | 2 | 6 | 3 | 7 | 8 | |
| cec10 | Best | 2.89E+03 | 2.95E+03 | 4.21E+03 | 2.89E+03 | 2.92E+03 | 2.88E+03 | 2.89E+03 | 3.08E+03 | 3.95E+03 |
| Worst | 2.96E+03 | 3.08E+03 | 4.69E+03 | 3.02E+03 | 3.05E+03 | 2.97E+03 | 2.97E+03 | 3.82E+03 | 6.12E+03 | |
| Mean | 2.91E+03 | 3.00E+03 | 4.45E+03 | 2.96E+03 | 2.96E+03 | 2.91E+03 | 2.93E+03 | 3.32E+03 | 5.02E+03 | |
| Std | 1.82E+01 | 3.34E+01 | 1.37E+02 | 3.31E+01 | 3.20E+01 | 2.14E+01 | 2.36E+01 | 1.88E+02 | 6.18E+02 | |
| Rank | 2 | 6 | 8 | 4 | 5 | 1 | 3 | 7 | 9 | |
| Mean rank | 1.3 | 4.4 | 7.9 | 4.3 | 3.1 | 5.2 | 3.7 | 6.6 | 7.5 | |
| Final ranking | 1 | 5 | 9 | 4 | 2 | 6 | 3 | 7 | 8 | |
| +/=/– | –/–/– | 0/2/8 | 0/1/9 | 0/1/9 | 0/3/7 | 0/2/8 | 0/3/7 | 0/2/8 | 0/1/9 | |
The results of HBWO-JS and other algorithms for CEC2020 test functions (the dimension dim = 50).
| Function . | Index . | Algorithms . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HBWO-JS . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . | ||
| cec01 | Best | 1.81E+07 | 2.04E+09 | 9.57E+10 | 6.56E+08 | 4.07E+08 | 4.75E+06 | 2.03E+08 | 2.80E+10 | 8.41E+10 |
| Worst | 7.73E+07 | 2.11E+10 | 1.16E+11 | 2.12E+10 | 5.67E+09 | 4.33E+07 | 1.85E+09 | 7.20E+10 | 1.12E+11 | |
| Mean | 4.28E+07 | 9.40E+09 | 1.07E+11 | 4.22E+09 | 2.48E+09 | 1.83E+07 | 6.80E+08 | 5.24E+10 | 9.84E+10 | |
| Std | 1.76E+07 | 4.79E+09 | 4.52E+09 | 4.68E+09 | 1.35E+09 | 9.99E+06 | 4.15E+08 | 1.03E+10 | 7.28E+09 | |
| Rank | 2 | 6 | 9 | 5 | 4 | 1 | 3 | 7 | 8 | |
| cec02 | Best | 6.04E+03 | 1.28E+04 | 1.43E+04 | 6.19E+03 | 6.20E+03 | 7.35E+03 | 6.20E+03 | 9.76E+03 | 1.31E+04 |
| Worst | 9.12E+03 | 1.60E+04 | 1.62E+04 | 1.03E+04 | 1.03E+04 | 1.10E+04 | 1.52E+04 | 1.62E+04 | 1.61E+04 | |
| Mean | 7.49E+03 | 1.52E+04 | 1.53E+04 | 8.10E+03 | 8.31E+03 | 8.75E+03 | 9.55E+03 | 1.49E+04 | 1.47E+04 | |
| Std | 7.89E+02 | 7.57E+02 | 4.77E+02 | 9.50E+02 | 9.09E+02 | 1.05E+03 | 2.29E+03 | 1.13E+03 | 7.23E+02 | |
| Rank | 1 | 8 | 9 | 2 | 3 | 4 | 5 | 7 | 6 | |
| cec03 | Best | 1.10E+03 | 1.18E+03 | 1.84E+03 | 1.15E+03 | 1.10E+03 | 1.14E+03 | 1.06E+03 | 1.45E+03 | 1.86E+03 |
| Worst | 1.74E+03 | 1.69E+03 | 2.05E+03 | 1.76E+03 | 1.61E+03 | 1.75E+03 | 1.35E+03 | 2.07E+03 | 2.04E+03 | |
| Mean | 1.26E+03 | 1.42E+03 | 1.99E+03 | 1.51E+03 | 1.36E+03 | 1.38E+03 | 1.21E+03 | 1.69E+03 | 1.96E+03 | |
| Std | 1.55E+02 | 1.26E+02 | 4.22E+01 | 1.78E+02 | 1.30E+02 | 1.27E+02 | 8.94E+01 | 1.15E+02 | 4.46E+01 | |
| Rank | 2 | 5 | 9 | 6 | 3 | 4 | 1 | 7 | 8 | |
| cec04 | Best | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.91E+03 | 1.90E+03 | 1.95E+03 | 1.90E+03 |
| Worst | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.94E+03 | 1.90E+03 | 2.06E+03 | 1.90E+03 | |
| Mean | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.92E+03 | 1.90E+03 | 1.99E+03 | 1.90E+03 | |
| Std | 0.00E+00 | 4.45E-02 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 6.98E+00 | 9.32E-02 | 2.81E+01 | 0.00E+00 | |
| Rank | 1 | 6 | 1 | 1 | 1 | 8 | 7 | 9 | 1 | |
| cec05 | Best | 1.43E+06 | 3.87E+05 | 1.82E+08 | 3.46E+06 | 1.54E+06 | 1.66E+06 | 1.14E+06 | 6.09E+06 | 1.55E+08 |
| Worst | 7.09E+06 | 7.65E+06 | 7.85E+08 | 2.40E+07 | 1.46E+07 | 7.39E+06 | 2.47E+07 | 7.39E+07 | 1.29E+09 | |
| Mean | 3.80E+06 | 3.63E+06 | 5.24E+08 | 1.05E+07 | 6.19E+06 | 3.74E+06 | 7.42E+06 | 2.32E+07 | 4.65E+08 | |
| Std | 1.79E+06 | 1.81E+06 | 1.40E+08 | 4.80E+06 | 3.47E+06 | 1.43E+06 | 5.30E+06 | 1.38E+07 | 2.46E+08 | |
| Rank | 3 | 1 | 9 | 6 | 4 | 2 | 5 | 7 | 8 | |
| cec06 | Best | 2.23E+03 | 2.63E+03 | 6.92E+03 | 2.36E+03 | 2.56E+03 | 2.88E+03 | 2.57E+03 | 2.80E+03 | 6.03E+03 |
| Worst | 3.08E+03 | 3.93E+03 | 1.04E+04 | 3.50E+03 | 4.29E+03 | 4.59E+03 | 3.91E+03 | 4.70E+03 | 1.02E+04 | |
| Mean | 2.69E+03 | 3.48E+03 | 8.65E+03 | 2.85E+03 | 3.23E+03 | 3.72E+03 | 3.13E+03 | 3.85E+03 | 8.14E+03 | |
| Std | 2.22E+02 | 3.18E+02 | 8.23E+02 | 2.89E+02 | 4.44E+02 | 4.56E+02 | 3.20E+02 | 4.61E+02 | 9.33E+02 | |
| Rank | 1 | 5 | 9 | 2 | 4 | 6 | 3 | 7 | 8 | |
| cec07 | Best | 2.89E+05 | 3.17E+05 | 1.77E+07 | 1.24E+06 | 7.07E+05 | 3.89E+05 | 5.67E+05 | 2.89E+05 | 2.98E+07 |
| Worst | 7.73E+06 | 4.11E+06 | 1.49E+08 | 9.70E+06 | 1.07E+07 | 9.19E+06 | 1.03E+07 | 7.57E+06 | 1.86E+08 | |
| Mean | 1.84E+06 | 1.82E+06 | 7.60E+07 | 4.49E+06 | 3.88E+06 | 2.85E+06 | 3.42E+06 | 2.61E+06 | 8.22E+07 | |
| Std | 1.46E+06 | 9.75E+05 | 3.09E+07 | 2.09E+06 | 2.22E+06 | 2.14E+06 | 2.42E+06 | 1.48E+06 | 3.83E+07 | |
| Rank | 2 | 1 | 8 | 7 | 6 | 4 | 5 | 3 | 9 | |
| cec08 | Best | 2.35E+03 | 4.41E+03 | 1.49E+04 | 2.51E+03 | 2.88E+03 | 8.59E+03 | 7.60E+03 | 6.07E+03 | 1.65E+04 |
| Worst | 1.06E+04 | 1.74E+04 | 1.80E+04 | 1.22E+04 | 1.25E+04 | 1.25E+04 | 1.63E+04 | 1.64E+04 | 1.83E+04 | |
| Mean | 8.30E+03 | 1.34E+04 | 1.67E+04 | 9.47E+03 | 9.16E+03 | 1.03E+04 | 1.16E+04 | 1.22E+04 | 1.75E+04 | |
| Std | 2.45E+03 | 3.94E+03 | 6.15E+02 | 2.00E+03 | 1.83E+03 | 9.45E+02 | 2.50E+03 | 1.98E+03 | 5.14E+02 | |
| Rank | 1 | 7 | 8 | 3 | 2 | 4 | 5 | 6 | 9 | |
| cec09 | Best | 3.13E+03 | 3.26E+03 | 4.15E+03 | 3.30E+03 | 3.17E+03 | 3.23E+03 | 3.12E+03 | 3.81E+03 | 3.80E+03 |
| Worst | 3.44E+03 | 3.63E+03 | 4.71E+03 | 3.80E+03 | 3.35E+03 | 3.74E+03 | 3.38E+03 | 4.60E+03 | 6.17E+03 | |
| Mean | 3.28E+03 | 3.41E+03 | 4.51E+03 | 3.47E+03 | 3.26E+03 | 3.48E+03 | 3.23E+03 | 4.16E+03 | 4.48E+03 | |
| Std | 6.82E+01 | 8.31E+01 | 1.38E+02 | 1.15E+02 | 5.21E+01 | 1.21E+02 | 7.30E+01 | 2.03E+02 | 6.64E+02 | |
| Rank | 3 | 4 | 9 | 5 | 2 | 6 | 1 | 7 | 8 | |
| cec10 | Best | 3.12E+03 | 3.41E+03 | 1.27E+04 | 3.22E+03 | 3.19E+03 | 3.05E+03 | 3.16E+03 | 5.31E+03 | 9.66E+03 |
| Worst | 3.37E+03 | 4.35E+03 | 1.56E+04 | 4.22E+03 | 3.88E+03 | 3.23E+03 | 3.56E+03 | 8.96E+03 | 1.59E+04 | |
| Mean | 3.20E+03 | 3.79E+03 | 1.44E+04 | 3.57E+03 | 3.52E+03 | 3.15E+03 | 3.36E+03 | 7.43E+03 | 1.33E+04 | |
| Std | 5.35E+01 | 2.25E+02 | 7.31E+02 | 2.38E+02 | 1.59E+02 | 4.25E+01 | 1.13E+02 | 1.07E+03 | 1.54E+03 | |
| Rank | 2 | 6 | 9 | 5 | 4 | 1 | 3 | 7 | 8 | |
| Mean rank | 1.8 | 4.9 | 8 | 4.2 | 3.3 | 4 | 3.8 | 6.7 | 7.3 | |
| Final ranking | 1 | 6 | 9 | 5 | 2 | 4 | 3 | 7 | 8 | |
| +/=/– | –/–/– | 0/2/8 | 0/1/9 | 0/1/9 | 0/3/7 | 2/2/6 | 1/2/7 | 0/0/10 | 0/1/9 | |
| Function . | Index . | Algorithms . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HBWO-JS . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . | ||
| cec01 | Best | 1.81E+07 | 2.04E+09 | 9.57E+10 | 6.56E+08 | 4.07E+08 | 4.75E+06 | 2.03E+08 | 2.80E+10 | 8.41E+10 |
| Worst | 7.73E+07 | 2.11E+10 | 1.16E+11 | 2.12E+10 | 5.67E+09 | 4.33E+07 | 1.85E+09 | 7.20E+10 | 1.12E+11 | |
| Mean | 4.28E+07 | 9.40E+09 | 1.07E+11 | 4.22E+09 | 2.48E+09 | 1.83E+07 | 6.80E+08 | 5.24E+10 | 9.84E+10 | |
| Std | 1.76E+07 | 4.79E+09 | 4.52E+09 | 4.68E+09 | 1.35E+09 | 9.99E+06 | 4.15E+08 | 1.03E+10 | 7.28E+09 | |
| Rank | 2 | 6 | 9 | 5 | 4 | 1 | 3 | 7 | 8 | |
| cec02 | Best | 6.04E+03 | 1.28E+04 | 1.43E+04 | 6.19E+03 | 6.20E+03 | 7.35E+03 | 6.20E+03 | 9.76E+03 | 1.31E+04 |
| Worst | 9.12E+03 | 1.60E+04 | 1.62E+04 | 1.03E+04 | 1.03E+04 | 1.10E+04 | 1.52E+04 | 1.62E+04 | 1.61E+04 | |
| Mean | 7.49E+03 | 1.52E+04 | 1.53E+04 | 8.10E+03 | 8.31E+03 | 8.75E+03 | 9.55E+03 | 1.49E+04 | 1.47E+04 | |
| Std | 7.89E+02 | 7.57E+02 | 4.77E+02 | 9.50E+02 | 9.09E+02 | 1.05E+03 | 2.29E+03 | 1.13E+03 | 7.23E+02 | |
| Rank | 1 | 8 | 9 | 2 | 3 | 4 | 5 | 7 | 6 | |
| cec03 | Best | 1.10E+03 | 1.18E+03 | 1.84E+03 | 1.15E+03 | 1.10E+03 | 1.14E+03 | 1.06E+03 | 1.45E+03 | 1.86E+03 |
| Worst | 1.74E+03 | 1.69E+03 | 2.05E+03 | 1.76E+03 | 1.61E+03 | 1.75E+03 | 1.35E+03 | 2.07E+03 | 2.04E+03 | |
| Mean | 1.26E+03 | 1.42E+03 | 1.99E+03 | 1.51E+03 | 1.36E+03 | 1.38E+03 | 1.21E+03 | 1.69E+03 | 1.96E+03 | |
| Std | 1.55E+02 | 1.26E+02 | 4.22E+01 | 1.78E+02 | 1.30E+02 | 1.27E+02 | 8.94E+01 | 1.15E+02 | 4.46E+01 | |
| Rank | 2 | 5 | 9 | 6 | 3 | 4 | 1 | 7 | 8 | |
| cec04 | Best | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.91E+03 | 1.90E+03 | 1.95E+03 | 1.90E+03 |
| Worst | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.94E+03 | 1.90E+03 | 2.06E+03 | 1.90E+03 | |
| Mean | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.92E+03 | 1.90E+03 | 1.99E+03 | 1.90E+03 | |
| Std | 0.00E+00 | 4.45E-02 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 6.98E+00 | 9.32E-02 | 2.81E+01 | 0.00E+00 | |
| Rank | 1 | 6 | 1 | 1 | 1 | 8 | 7 | 9 | 1 | |
| cec05 | Best | 1.43E+06 | 3.87E+05 | 1.82E+08 | 3.46E+06 | 1.54E+06 | 1.66E+06 | 1.14E+06 | 6.09E+06 | 1.55E+08 |
| Worst | 7.09E+06 | 7.65E+06 | 7.85E+08 | 2.40E+07 | 1.46E+07 | 7.39E+06 | 2.47E+07 | 7.39E+07 | 1.29E+09 | |
| Mean | 3.80E+06 | 3.63E+06 | 5.24E+08 | 1.05E+07 | 6.19E+06 | 3.74E+06 | 7.42E+06 | 2.32E+07 | 4.65E+08 | |
| Std | 1.79E+06 | 1.81E+06 | 1.40E+08 | 4.80E+06 | 3.47E+06 | 1.43E+06 | 5.30E+06 | 1.38E+07 | 2.46E+08 | |
| Rank | 3 | 1 | 9 | 6 | 4 | 2 | 5 | 7 | 8 | |
| cec06 | Best | 2.23E+03 | 2.63E+03 | 6.92E+03 | 2.36E+03 | 2.56E+03 | 2.88E+03 | 2.57E+03 | 2.80E+03 | 6.03E+03 |
| Worst | 3.08E+03 | 3.93E+03 | 1.04E+04 | 3.50E+03 | 4.29E+03 | 4.59E+03 | 3.91E+03 | 4.70E+03 | 1.02E+04 | |
| Mean | 2.69E+03 | 3.48E+03 | 8.65E+03 | 2.85E+03 | 3.23E+03 | 3.72E+03 | 3.13E+03 | 3.85E+03 | 8.14E+03 | |
| Std | 2.22E+02 | 3.18E+02 | 8.23E+02 | 2.89E+02 | 4.44E+02 | 4.56E+02 | 3.20E+02 | 4.61E+02 | 9.33E+02 | |
| Rank | 1 | 5 | 9 | 2 | 4 | 6 | 3 | 7 | 8 | |
| cec07 | Best | 2.89E+05 | 3.17E+05 | 1.77E+07 | 1.24E+06 | 7.07E+05 | 3.89E+05 | 5.67E+05 | 2.89E+05 | 2.98E+07 |
| Worst | 7.73E+06 | 4.11E+06 | 1.49E+08 | 9.70E+06 | 1.07E+07 | 9.19E+06 | 1.03E+07 | 7.57E+06 | 1.86E+08 | |
| Mean | 1.84E+06 | 1.82E+06 | 7.60E+07 | 4.49E+06 | 3.88E+06 | 2.85E+06 | 3.42E+06 | 2.61E+06 | 8.22E+07 | |
| Std | 1.46E+06 | 9.75E+05 | 3.09E+07 | 2.09E+06 | 2.22E+06 | 2.14E+06 | 2.42E+06 | 1.48E+06 | 3.83E+07 | |
| Rank | 2 | 1 | 8 | 7 | 6 | 4 | 5 | 3 | 9 | |
| cec08 | Best | 2.35E+03 | 4.41E+03 | 1.49E+04 | 2.51E+03 | 2.88E+03 | 8.59E+03 | 7.60E+03 | 6.07E+03 | 1.65E+04 |
| Worst | 1.06E+04 | 1.74E+04 | 1.80E+04 | 1.22E+04 | 1.25E+04 | 1.25E+04 | 1.63E+04 | 1.64E+04 | 1.83E+04 | |
| Mean | 8.30E+03 | 1.34E+04 | 1.67E+04 | 9.47E+03 | 9.16E+03 | 1.03E+04 | 1.16E+04 | 1.22E+04 | 1.75E+04 | |
| Std | 2.45E+03 | 3.94E+03 | 6.15E+02 | 2.00E+03 | 1.83E+03 | 9.45E+02 | 2.50E+03 | 1.98E+03 | 5.14E+02 | |
| Rank | 1 | 7 | 8 | 3 | 2 | 4 | 5 | 6 | 9 | |
| cec09 | Best | 3.13E+03 | 3.26E+03 | 4.15E+03 | 3.30E+03 | 3.17E+03 | 3.23E+03 | 3.12E+03 | 3.81E+03 | 3.80E+03 |
| Worst | 3.44E+03 | 3.63E+03 | 4.71E+03 | 3.80E+03 | 3.35E+03 | 3.74E+03 | 3.38E+03 | 4.60E+03 | 6.17E+03 | |
| Mean | 3.28E+03 | 3.41E+03 | 4.51E+03 | 3.47E+03 | 3.26E+03 | 3.48E+03 | 3.23E+03 | 4.16E+03 | 4.48E+03 | |
| Std | 6.82E+01 | 8.31E+01 | 1.38E+02 | 1.15E+02 | 5.21E+01 | 1.21E+02 | 7.30E+01 | 2.03E+02 | 6.64E+02 | |
| Rank | 3 | 4 | 9 | 5 | 2 | 6 | 1 | 7 | 8 | |
| cec10 | Best | 3.12E+03 | 3.41E+03 | 1.27E+04 | 3.22E+03 | 3.19E+03 | 3.05E+03 | 3.16E+03 | 5.31E+03 | 9.66E+03 |
| Worst | 3.37E+03 | 4.35E+03 | 1.56E+04 | 4.22E+03 | 3.88E+03 | 3.23E+03 | 3.56E+03 | 8.96E+03 | 1.59E+04 | |
| Mean | 3.20E+03 | 3.79E+03 | 1.44E+04 | 3.57E+03 | 3.52E+03 | 3.15E+03 | 3.36E+03 | 7.43E+03 | 1.33E+04 | |
| Std | 5.35E+01 | 2.25E+02 | 7.31E+02 | 2.38E+02 | 1.59E+02 | 4.25E+01 | 1.13E+02 | 1.07E+03 | 1.54E+03 | |
| Rank | 2 | 6 | 9 | 5 | 4 | 1 | 3 | 7 | 8 | |
| Mean rank | 1.8 | 4.9 | 8 | 4.2 | 3.3 | 4 | 3.8 | 6.7 | 7.3 | |
| Final ranking | 1 | 6 | 9 | 5 | 2 | 4 | 3 | 7 | 8 | |
| +/=/– | –/–/– | 0/2/8 | 0/1/9 | 0/1/9 | 0/3/7 | 2/2/6 | 1/2/7 | 0/0/10 | 0/1/9 | |
The results of HBWO-JS and other algorithms for CEC2020 test functions (the dimension dim = 50).
| Function . | Index . | Algorithms . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HBWO-JS . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . | ||
| cec01 | Best | 1.81E+07 | 2.04E+09 | 9.57E+10 | 6.56E+08 | 4.07E+08 | 4.75E+06 | 2.03E+08 | 2.80E+10 | 8.41E+10 |
| Worst | 7.73E+07 | 2.11E+10 | 1.16E+11 | 2.12E+10 | 5.67E+09 | 4.33E+07 | 1.85E+09 | 7.20E+10 | 1.12E+11 | |
| Mean | 4.28E+07 | 9.40E+09 | 1.07E+11 | 4.22E+09 | 2.48E+09 | 1.83E+07 | 6.80E+08 | 5.24E+10 | 9.84E+10 | |
| Std | 1.76E+07 | 4.79E+09 | 4.52E+09 | 4.68E+09 | 1.35E+09 | 9.99E+06 | 4.15E+08 | 1.03E+10 | 7.28E+09 | |
| Rank | 2 | 6 | 9 | 5 | 4 | 1 | 3 | 7 | 8 | |
| cec02 | Best | 6.04E+03 | 1.28E+04 | 1.43E+04 | 6.19E+03 | 6.20E+03 | 7.35E+03 | 6.20E+03 | 9.76E+03 | 1.31E+04 |
| Worst | 9.12E+03 | 1.60E+04 | 1.62E+04 | 1.03E+04 | 1.03E+04 | 1.10E+04 | 1.52E+04 | 1.62E+04 | 1.61E+04 | |
| Mean | 7.49E+03 | 1.52E+04 | 1.53E+04 | 8.10E+03 | 8.31E+03 | 8.75E+03 | 9.55E+03 | 1.49E+04 | 1.47E+04 | |
| Std | 7.89E+02 | 7.57E+02 | 4.77E+02 | 9.50E+02 | 9.09E+02 | 1.05E+03 | 2.29E+03 | 1.13E+03 | 7.23E+02 | |
| Rank | 1 | 8 | 9 | 2 | 3 | 4 | 5 | 7 | 6 | |
| cec03 | Best | 1.10E+03 | 1.18E+03 | 1.84E+03 | 1.15E+03 | 1.10E+03 | 1.14E+03 | 1.06E+03 | 1.45E+03 | 1.86E+03 |
| Worst | 1.74E+03 | 1.69E+03 | 2.05E+03 | 1.76E+03 | 1.61E+03 | 1.75E+03 | 1.35E+03 | 2.07E+03 | 2.04E+03 | |
| Mean | 1.26E+03 | 1.42E+03 | 1.99E+03 | 1.51E+03 | 1.36E+03 | 1.38E+03 | 1.21E+03 | 1.69E+03 | 1.96E+03 | |
| Std | 1.55E+02 | 1.26E+02 | 4.22E+01 | 1.78E+02 | 1.30E+02 | 1.27E+02 | 8.94E+01 | 1.15E+02 | 4.46E+01 | |
| Rank | 2 | 5 | 9 | 6 | 3 | 4 | 1 | 7 | 8 | |
| cec04 | Best | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.91E+03 | 1.90E+03 | 1.95E+03 | 1.90E+03 |
| Worst | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.94E+03 | 1.90E+03 | 2.06E+03 | 1.90E+03 | |
| Mean | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.92E+03 | 1.90E+03 | 1.99E+03 | 1.90E+03 | |
| Std | 0.00E+00 | 4.45E-02 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 6.98E+00 | 9.32E-02 | 2.81E+01 | 0.00E+00 | |
| Rank | 1 | 6 | 1 | 1 | 1 | 8 | 7 | 9 | 1 | |
| cec05 | Best | 1.43E+06 | 3.87E+05 | 1.82E+08 | 3.46E+06 | 1.54E+06 | 1.66E+06 | 1.14E+06 | 6.09E+06 | 1.55E+08 |
| Worst | 7.09E+06 | 7.65E+06 | 7.85E+08 | 2.40E+07 | 1.46E+07 | 7.39E+06 | 2.47E+07 | 7.39E+07 | 1.29E+09 | |
| Mean | 3.80E+06 | 3.63E+06 | 5.24E+08 | 1.05E+07 | 6.19E+06 | 3.74E+06 | 7.42E+06 | 2.32E+07 | 4.65E+08 | |
| Std | 1.79E+06 | 1.81E+06 | 1.40E+08 | 4.80E+06 | 3.47E+06 | 1.43E+06 | 5.30E+06 | 1.38E+07 | 2.46E+08 | |
| Rank | 3 | 1 | 9 | 6 | 4 | 2 | 5 | 7 | 8 | |
| cec06 | Best | 2.23E+03 | 2.63E+03 | 6.92E+03 | 2.36E+03 | 2.56E+03 | 2.88E+03 | 2.57E+03 | 2.80E+03 | 6.03E+03 |
| Worst | 3.08E+03 | 3.93E+03 | 1.04E+04 | 3.50E+03 | 4.29E+03 | 4.59E+03 | 3.91E+03 | 4.70E+03 | 1.02E+04 | |
| Mean | 2.69E+03 | 3.48E+03 | 8.65E+03 | 2.85E+03 | 3.23E+03 | 3.72E+03 | 3.13E+03 | 3.85E+03 | 8.14E+03 | |
| Std | 2.22E+02 | 3.18E+02 | 8.23E+02 | 2.89E+02 | 4.44E+02 | 4.56E+02 | 3.20E+02 | 4.61E+02 | 9.33E+02 | |
| Rank | 1 | 5 | 9 | 2 | 4 | 6 | 3 | 7 | 8 | |
| cec07 | Best | 2.89E+05 | 3.17E+05 | 1.77E+07 | 1.24E+06 | 7.07E+05 | 3.89E+05 | 5.67E+05 | 2.89E+05 | 2.98E+07 |
| Worst | 7.73E+06 | 4.11E+06 | 1.49E+08 | 9.70E+06 | 1.07E+07 | 9.19E+06 | 1.03E+07 | 7.57E+06 | 1.86E+08 | |
| Mean | 1.84E+06 | 1.82E+06 | 7.60E+07 | 4.49E+06 | 3.88E+06 | 2.85E+06 | 3.42E+06 | 2.61E+06 | 8.22E+07 | |
| Std | 1.46E+06 | 9.75E+05 | 3.09E+07 | 2.09E+06 | 2.22E+06 | 2.14E+06 | 2.42E+06 | 1.48E+06 | 3.83E+07 | |
| Rank | 2 | 1 | 8 | 7 | 6 | 4 | 5 | 3 | 9 | |
| cec08 | Best | 2.35E+03 | 4.41E+03 | 1.49E+04 | 2.51E+03 | 2.88E+03 | 8.59E+03 | 7.60E+03 | 6.07E+03 | 1.65E+04 |
| Worst | 1.06E+04 | 1.74E+04 | 1.80E+04 | 1.22E+04 | 1.25E+04 | 1.25E+04 | 1.63E+04 | 1.64E+04 | 1.83E+04 | |
| Mean | 8.30E+03 | 1.34E+04 | 1.67E+04 | 9.47E+03 | 9.16E+03 | 1.03E+04 | 1.16E+04 | 1.22E+04 | 1.75E+04 | |
| Std | 2.45E+03 | 3.94E+03 | 6.15E+02 | 2.00E+03 | 1.83E+03 | 9.45E+02 | 2.50E+03 | 1.98E+03 | 5.14E+02 | |
| Rank | 1 | 7 | 8 | 3 | 2 | 4 | 5 | 6 | 9 | |
| cec09 | Best | 3.13E+03 | 3.26E+03 | 4.15E+03 | 3.30E+03 | 3.17E+03 | 3.23E+03 | 3.12E+03 | 3.81E+03 | 3.80E+03 |
| Worst | 3.44E+03 | 3.63E+03 | 4.71E+03 | 3.80E+03 | 3.35E+03 | 3.74E+03 | 3.38E+03 | 4.60E+03 | 6.17E+03 | |
| Mean | 3.28E+03 | 3.41E+03 | 4.51E+03 | 3.47E+03 | 3.26E+03 | 3.48E+03 | 3.23E+03 | 4.16E+03 | 4.48E+03 | |
| Std | 6.82E+01 | 8.31E+01 | 1.38E+02 | 1.15E+02 | 5.21E+01 | 1.21E+02 | 7.30E+01 | 2.03E+02 | 6.64E+02 | |
| Rank | 3 | 4 | 9 | 5 | 2 | 6 | 1 | 7 | 8 | |
| cec10 | Best | 3.12E+03 | 3.41E+03 | 1.27E+04 | 3.22E+03 | 3.19E+03 | 3.05E+03 | 3.16E+03 | 5.31E+03 | 9.66E+03 |
| Worst | 3.37E+03 | 4.35E+03 | 1.56E+04 | 4.22E+03 | 3.88E+03 | 3.23E+03 | 3.56E+03 | 8.96E+03 | 1.59E+04 | |
| Mean | 3.20E+03 | 3.79E+03 | 1.44E+04 | 3.57E+03 | 3.52E+03 | 3.15E+03 | 3.36E+03 | 7.43E+03 | 1.33E+04 | |
| Std | 5.35E+01 | 2.25E+02 | 7.31E+02 | 2.38E+02 | 1.59E+02 | 4.25E+01 | 1.13E+02 | 1.07E+03 | 1.54E+03 | |
| Rank | 2 | 6 | 9 | 5 | 4 | 1 | 3 | 7 | 8 | |
| Mean rank | 1.8 | 4.9 | 8 | 4.2 | 3.3 | 4 | 3.8 | 6.7 | 7.3 | |
| Final ranking | 1 | 6 | 9 | 5 | 2 | 4 | 3 | 7 | 8 | |
| +/=/– | –/–/– | 0/2/8 | 0/1/9 | 0/1/9 | 0/3/7 | 2/2/6 | 1/2/7 | 0/0/10 | 0/1/9 | |
| Function . | Index . | Algorithms . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HBWO-JS . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . | ||
| cec01 | Best | 1.81E+07 | 2.04E+09 | 9.57E+10 | 6.56E+08 | 4.07E+08 | 4.75E+06 | 2.03E+08 | 2.80E+10 | 8.41E+10 |
| Worst | 7.73E+07 | 2.11E+10 | 1.16E+11 | 2.12E+10 | 5.67E+09 | 4.33E+07 | 1.85E+09 | 7.20E+10 | 1.12E+11 | |
| Mean | 4.28E+07 | 9.40E+09 | 1.07E+11 | 4.22E+09 | 2.48E+09 | 1.83E+07 | 6.80E+08 | 5.24E+10 | 9.84E+10 | |
| Std | 1.76E+07 | 4.79E+09 | 4.52E+09 | 4.68E+09 | 1.35E+09 | 9.99E+06 | 4.15E+08 | 1.03E+10 | 7.28E+09 | |
| Rank | 2 | 6 | 9 | 5 | 4 | 1 | 3 | 7 | 8 | |
| cec02 | Best | 6.04E+03 | 1.28E+04 | 1.43E+04 | 6.19E+03 | 6.20E+03 | 7.35E+03 | 6.20E+03 | 9.76E+03 | 1.31E+04 |
| Worst | 9.12E+03 | 1.60E+04 | 1.62E+04 | 1.03E+04 | 1.03E+04 | 1.10E+04 | 1.52E+04 | 1.62E+04 | 1.61E+04 | |
| Mean | 7.49E+03 | 1.52E+04 | 1.53E+04 | 8.10E+03 | 8.31E+03 | 8.75E+03 | 9.55E+03 | 1.49E+04 | 1.47E+04 | |
| Std | 7.89E+02 | 7.57E+02 | 4.77E+02 | 9.50E+02 | 9.09E+02 | 1.05E+03 | 2.29E+03 | 1.13E+03 | 7.23E+02 | |
| Rank | 1 | 8 | 9 | 2 | 3 | 4 | 5 | 7 | 6 | |
| cec03 | Best | 1.10E+03 | 1.18E+03 | 1.84E+03 | 1.15E+03 | 1.10E+03 | 1.14E+03 | 1.06E+03 | 1.45E+03 | 1.86E+03 |
| Worst | 1.74E+03 | 1.69E+03 | 2.05E+03 | 1.76E+03 | 1.61E+03 | 1.75E+03 | 1.35E+03 | 2.07E+03 | 2.04E+03 | |
| Mean | 1.26E+03 | 1.42E+03 | 1.99E+03 | 1.51E+03 | 1.36E+03 | 1.38E+03 | 1.21E+03 | 1.69E+03 | 1.96E+03 | |
| Std | 1.55E+02 | 1.26E+02 | 4.22E+01 | 1.78E+02 | 1.30E+02 | 1.27E+02 | 8.94E+01 | 1.15E+02 | 4.46E+01 | |
| Rank | 2 | 5 | 9 | 6 | 3 | 4 | 1 | 7 | 8 | |
| cec04 | Best | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.91E+03 | 1.90E+03 | 1.95E+03 | 1.90E+03 |
| Worst | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.94E+03 | 1.90E+03 | 2.06E+03 | 1.90E+03 | |
| Mean | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.92E+03 | 1.90E+03 | 1.99E+03 | 1.90E+03 | |
| Std | 0.00E+00 | 4.45E-02 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 6.98E+00 | 9.32E-02 | 2.81E+01 | 0.00E+00 | |
| Rank | 1 | 6 | 1 | 1 | 1 | 8 | 7 | 9 | 1 | |
| cec05 | Best | 1.43E+06 | 3.87E+05 | 1.82E+08 | 3.46E+06 | 1.54E+06 | 1.66E+06 | 1.14E+06 | 6.09E+06 | 1.55E+08 |
| Worst | 7.09E+06 | 7.65E+06 | 7.85E+08 | 2.40E+07 | 1.46E+07 | 7.39E+06 | 2.47E+07 | 7.39E+07 | 1.29E+09 | |
| Mean | 3.80E+06 | 3.63E+06 | 5.24E+08 | 1.05E+07 | 6.19E+06 | 3.74E+06 | 7.42E+06 | 2.32E+07 | 4.65E+08 | |
| Std | 1.79E+06 | 1.81E+06 | 1.40E+08 | 4.80E+06 | 3.47E+06 | 1.43E+06 | 5.30E+06 | 1.38E+07 | 2.46E+08 | |
| Rank | 3 | 1 | 9 | 6 | 4 | 2 | 5 | 7 | 8 | |
| cec06 | Best | 2.23E+03 | 2.63E+03 | 6.92E+03 | 2.36E+03 | 2.56E+03 | 2.88E+03 | 2.57E+03 | 2.80E+03 | 6.03E+03 |
| Worst | 3.08E+03 | 3.93E+03 | 1.04E+04 | 3.50E+03 | 4.29E+03 | 4.59E+03 | 3.91E+03 | 4.70E+03 | 1.02E+04 | |
| Mean | 2.69E+03 | 3.48E+03 | 8.65E+03 | 2.85E+03 | 3.23E+03 | 3.72E+03 | 3.13E+03 | 3.85E+03 | 8.14E+03 | |
| Std | 2.22E+02 | 3.18E+02 | 8.23E+02 | 2.89E+02 | 4.44E+02 | 4.56E+02 | 3.20E+02 | 4.61E+02 | 9.33E+02 | |
| Rank | 1 | 5 | 9 | 2 | 4 | 6 | 3 | 7 | 8 | |
| cec07 | Best | 2.89E+05 | 3.17E+05 | 1.77E+07 | 1.24E+06 | 7.07E+05 | 3.89E+05 | 5.67E+05 | 2.89E+05 | 2.98E+07 |
| Worst | 7.73E+06 | 4.11E+06 | 1.49E+08 | 9.70E+06 | 1.07E+07 | 9.19E+06 | 1.03E+07 | 7.57E+06 | 1.86E+08 | |
| Mean | 1.84E+06 | 1.82E+06 | 7.60E+07 | 4.49E+06 | 3.88E+06 | 2.85E+06 | 3.42E+06 | 2.61E+06 | 8.22E+07 | |
| Std | 1.46E+06 | 9.75E+05 | 3.09E+07 | 2.09E+06 | 2.22E+06 | 2.14E+06 | 2.42E+06 | 1.48E+06 | 3.83E+07 | |
| Rank | 2 | 1 | 8 | 7 | 6 | 4 | 5 | 3 | 9 | |
| cec08 | Best | 2.35E+03 | 4.41E+03 | 1.49E+04 | 2.51E+03 | 2.88E+03 | 8.59E+03 | 7.60E+03 | 6.07E+03 | 1.65E+04 |
| Worst | 1.06E+04 | 1.74E+04 | 1.80E+04 | 1.22E+04 | 1.25E+04 | 1.25E+04 | 1.63E+04 | 1.64E+04 | 1.83E+04 | |
| Mean | 8.30E+03 | 1.34E+04 | 1.67E+04 | 9.47E+03 | 9.16E+03 | 1.03E+04 | 1.16E+04 | 1.22E+04 | 1.75E+04 | |
| Std | 2.45E+03 | 3.94E+03 | 6.15E+02 | 2.00E+03 | 1.83E+03 | 9.45E+02 | 2.50E+03 | 1.98E+03 | 5.14E+02 | |
| Rank | 1 | 7 | 8 | 3 | 2 | 4 | 5 | 6 | 9 | |
| cec09 | Best | 3.13E+03 | 3.26E+03 | 4.15E+03 | 3.30E+03 | 3.17E+03 | 3.23E+03 | 3.12E+03 | 3.81E+03 | 3.80E+03 |
| Worst | 3.44E+03 | 3.63E+03 | 4.71E+03 | 3.80E+03 | 3.35E+03 | 3.74E+03 | 3.38E+03 | 4.60E+03 | 6.17E+03 | |
| Mean | 3.28E+03 | 3.41E+03 | 4.51E+03 | 3.47E+03 | 3.26E+03 | 3.48E+03 | 3.23E+03 | 4.16E+03 | 4.48E+03 | |
| Std | 6.82E+01 | 8.31E+01 | 1.38E+02 | 1.15E+02 | 5.21E+01 | 1.21E+02 | 7.30E+01 | 2.03E+02 | 6.64E+02 | |
| Rank | 3 | 4 | 9 | 5 | 2 | 6 | 1 | 7 | 8 | |
| cec10 | Best | 3.12E+03 | 3.41E+03 | 1.27E+04 | 3.22E+03 | 3.19E+03 | 3.05E+03 | 3.16E+03 | 5.31E+03 | 9.66E+03 |
| Worst | 3.37E+03 | 4.35E+03 | 1.56E+04 | 4.22E+03 | 3.88E+03 | 3.23E+03 | 3.56E+03 | 8.96E+03 | 1.59E+04 | |
| Mean | 3.20E+03 | 3.79E+03 | 1.44E+04 | 3.57E+03 | 3.52E+03 | 3.15E+03 | 3.36E+03 | 7.43E+03 | 1.33E+04 | |
| Std | 5.35E+01 | 2.25E+02 | 7.31E+02 | 2.38E+02 | 1.59E+02 | 4.25E+01 | 1.13E+02 | 1.07E+03 | 1.54E+03 | |
| Rank | 2 | 6 | 9 | 5 | 4 | 1 | 3 | 7 | 8 | |
| Mean rank | 1.8 | 4.9 | 8 | 4.2 | 3.3 | 4 | 3.8 | 6.7 | 7.3 | |
| Final ranking | 1 | 6 | 9 | 5 | 2 | 4 | 3 | 7 | 8 | |
| +/=/– | –/–/– | 0/2/8 | 0/1/9 | 0/1/9 | 0/3/7 | 2/2/6 | 1/2/7 | 0/0/10 | 0/1/9 | |
The results of HBWO-JS and other algorithms for CEC2020 test functions (the dimension dim = 100).
| Function . | Index . | Algorithms . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HBWO-JS . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . | ||
| cec01 | Best | 1.31E+09 | 5.78E+10 | 2.48E+11 | 3.71E+10 | 3.58E+10 | 3.66E+08 | 9.68E+09 | 1.46E+11 | 2.05E+11 |
| Worst | 3.79E+09 | 1.06E+11 | 2.70E+11 | 8.91E+10 | 7.55E+10 | 1.34E+09 | 2.38E+10 | 2.08E+11 | 2.61E+11 | |
| Mean | 2.34E+09 | 7.83E+10 | 2.59E+11 | 6.65E+10 | 5.23E+10 | 7.30E+08 | 1.44E+10 | 1.73E+11 | 2.47E+11 | |
| Std | 6.43E+08 | 1.28E+10 | 6.03E+09 | 1.31E+10 | 1.05E+10 | 2.46E+08 | 3.55E+09 | 1.53E+10 | 9.84E+09 | |
| Rank | 2 | 6 | 9 | 5 | 4 | 1 | 3 | 7 | 8 | |
| cec02 | Best | 1.29E+04 | 2.37E+04 | 3.14E+04 | 1.49E+04 | 1.75E+04 | 1.47E+04 | 2.34E+04 | 2.14E+04 | 3.11E+04 |
| Worst | 2.05E+04 | 3.32E+04 | 3.37E+04 | 1.94E+04 | 2.28E+04 | 2.21E+04 | 3.34E+04 | 3.31E+04 | 3.41E+04 | |
| Mean | 1.73E+04 | 3.18E+04 | 3.28E+04 | 1.71E+04 | 2.01E+04 | 1.89E+04 | 3.09E+04 | 2.83E+04 | 3.25E+04 | |
| Std | 1.65E+03 | 1.74E+03 | 5.70E+02 | 1.36E+03 | 1.35E+03 | 1.89E+03 | 2.07E+03 | 3.86E+03 | 7.65E+02 | |
| Rank | 2 | 7 | 9 | 1 | 4 | 3 | 6 | 5 | 8 | |
| cec03 | Best | 2.03E+03 | 2.55E+03 | 3.68E+03 | 2.59E+03 | 2.48E+03 | 2.31E+03 | 1.98E+03 | 3.31E+03 | 3.73E+03 |
| Worst | 3.17E+03 | 3.52E+03 | 4.05E+03 | 3.39E+03 | 3.41E+03 | 3.32E+03 | 2.47E+03 | 4.15E+03 | 4.12E+03 | |
| Mean | 2.54E+03 | 3.11E+03 | 3.89E+03 | 3.08E+03 | 2.93E+03 | 2.81E+03 | 2.25E+03 | 3.65E+03 | 3.90E+03 | |
| Std | 2.93E+02 | 2.70E+02 | 9.31E+01 | 2.00E+02 | 2.05E+02 | 2.73E+02 | 1.19E+02 | 2.24E+02 | 8.96E+01 | |
| Rank | 2 | 6 | 8 | 5 | 4 | 3 | 1 | 7 | 9 | |
| cec04 | Best | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.96E+03 | 1.90E+03 | 2.07E+03 | 1.90E+03 |
| Worst | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 2.09E+03 | 1.90E+03 | 2.76E+03 | 1.90E+03 | |
| Mean | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 2.01E+03 | 1.90E+03 | 2.24E+03 | 1.90E+03 | |
| Std | 0.00E+00 | 9.14E-02 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 3.17E+01 | 0.00E+00 | 1.39E+02 | 0.00E+00 | |
| Rank | 1 | 7 | 1 | 1 | 1 | 8 | 1 | 9 | 1 | |
| cec05 | Best | 2.02E+07 | 3.55E+07 | 1.11E+09 | 3.60E+07 | 3.01E+07 | 1.62E+07 | 2.06E+07 | 4.00E+07 | 7.17E+08 |
| Worst | 7.07E+07 | 8.60E+07 | 1.89E+09 | 1.72E+08 | 1.04E+08 | 4.99E+07 | 1.12E+08 | 5.58E+08 | 2.01E+09 | |
| Mean | 4.21E+07 | 6.06E+07 | 1.62E+09 | 8.95E+07 | 6.32E+07 | 2.98E+07 | 6.05E+07 | 2.18E+08 | 1.29E+09 | |
| Std | 1.22E+07 | 1.16E+07 | 1.91E+08 | 3.63E+07 | 2.12E+07 | 9.38E+06 | 2.24E+07 | 1.21E+08 | 3.66E+08 | |
| Rank | 2 | 4 | 9 | 6 | 5 | 1 | 3 | 7 | 8 | |
| cec06 | Best | 5.61E+03 | 7.09E+03 | 2.39E+04 | 5.48E+03 | 5.65E+03 | 6.51E+03 | 5.46E+03 | 9.45E+03 | 1.99E+04 |
| Worst | 8.41E+03 | 1.22E+04 | 3.21E+04 | 8.65E+03 | 9.47E+03 | 1.02E+04 | 7.93E+03 | 1.71E+04 | 3.54E+04 | |
| Mean | 6.65E+03 | 9.44E+03 | 2.90E+04 | 6.84E+03 | 7.78E+03 | 8.20E+03 | 6.67E+03 | 1.25E+04 | 2.81E+04 | |
| Std | 6.79E+02 | 1.23E+03 | 1.99E+03 | 7.07E+02 | 1.11E+03 | 8.68E+02 | 5.24E+02 | 1.64E+03 | 4.16E+03 | |
| Rank | 1 | 6 | 9 | 3 | 4 | 5 | 2 | 7 | 8 | |
| cec07 | Best | 2.82E+06 | 1.02E+07 | 2.40E+08 | 1.07E+07 | 1.07E+07 | 6.26E+06 | 5.55E+06 | 1.74E+07 | 2.12E+08 |
| Worst | 1.68E+07 | 4.25E+07 | 3.96E+08 | 5.85E+07 | 5.04E+07 | 2.44E+07 | 4.97E+07 | 1.34E+08 | 7.34E+08 | |
| Mean | 9.61E+06 | 1.85E+07 | 3.44E+08 | 3.20E+07 | 2.36E+07 | 1.18E+07 | 2.52E+07 | 6.35E+07 | 4.40E+08 | |
| Std | 3.06E+06 | 6.48E+06 | 3.56E+07 | 1.24E+07 | 9.43E+06 | 4.24E+06 | 1.10E+07 | 3.34E+07 | 1.28E+08 | |
| Rank | 1 | 3 | 8 | 6 | 4 | 2 | 5 | 7 | 9 | |
| cec08 | Best | 1.74E+04 | 2.50E+04 | 3.39E+04 | 1.75E+04 | 2.01E+04 | 1.88E+04 | 2.48E+04 | 2.32E+04 | 3.38E+04 |
| Worst | 2.33E+04 | 3.55E+04 | 3.60E+04 | 2.49E+04 | 2.63E+04 | 2.35E+04 | 3.57E+04 | 3.50E+04 | 3.58E+04 | |
| Mean | 2.09E+04 | 3.22E+04 | 3.50E+04 | 2.15E+04 | 2.29E+04 | 2.13E+04 | 3.29E+04 | 2.86E+04 | 3.48E+04 | |
| Std | 1.44E+03 | 3.10E+03 | 4.53E+02 | 1.80E+03 | 1.49E+03 | 1.22E+03 | 2.40E+03 | 3.77E+03 | 5.88E+02 | |
| Rank | 1 | 6 | 9 | 3 | 4 | 2 | 7 | 5 | 8 | |
| cec09 | Best | 4.26E+03 | 4.38E+03 | 8.45E+03 | 4.51E+03 | 4.62E+03 | 4.34E+03 | 4.31E+03 | 6.78E+03 | 7.22E+03 |
| Worst | 4.57E+03 | 5.99E+03 | 1.03E+04 | 5.24E+03 | 5.21E+03 | 5.68E+03 | 5.33E+03 | 1.02E+04 | 1.46E+04 | |
| Mean | 4.36E+03 | 5.38E+03 | 9.37E+03 | 4.82E+03 | 4.94E+03 | 4.79E+03 | 4.79E+03 | 7.83E+03 | 9.71E+03 | |
| Std | 7.54E+01 | 3.23E+02 | 4.56E+02 | 1.61E+02 | 1.67E+02 | 2.73E+02 | 2.23E+02 | 6.71E+02 | 2.60E+03 | |
| Rank | 1 | 6 | 8 | 4 | 5 | 3 | 2 | 7 | 9 | |
| cec10 | Best | 3.94E+03 | 5.70E+03 | 2.65E+04 | 5.27E+03 | 5.07E+03 | 3.74E+03 | 4.50E+03 | 1.19E+04 | 2.05E+04 |
| Worst | 4.68E+03 | 1.05E+04 | 3.04E+04 | 1.01E+04 | 7.65E+03 | 3.94E+03 | 7.69E+03 | 2.13E+04 | 2.89E+04 | |
| Mean | 4.16E+03 | 7.96E+03 | 2.82E+04 | 7.55E+03 | 6.48E+03 | 3.84E+03 | 5.37E+03 | 1.61E+04 | 2.54E+04 | |
| Std | 1.64E+02 | 1.21E+03 | 9.97E+02 | 1.20E+03 | 6.23E+02 | 5.87E+01 | 6.73E+02 | 2.19E+03 | 1.85E+03 | |
| Rank | 2 | 6 | 9 | 5 | 4 | 1 | 3 | 7 | 8 | |
| Mean rank | 1.5 | 5.7 | 7.9 | 3.9 | 3.9 | 2.9 | 3.3 | 6.8 | 7.6 | |
| Final ranking | 1 | 6 | 9 | 4 | 4 | 2 | 3 | 7 | 8 | |
| +/=/– | –/–/– | 0/0/10 | 0/1/9 | 0/4/6 | 0/1/9 | 2/2/5 | 1/2/7 | 0/0/10 | 0/1/9 | |
| Function . | Index . | Algorithms . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HBWO-JS . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . | ||
| cec01 | Best | 1.31E+09 | 5.78E+10 | 2.48E+11 | 3.71E+10 | 3.58E+10 | 3.66E+08 | 9.68E+09 | 1.46E+11 | 2.05E+11 |
| Worst | 3.79E+09 | 1.06E+11 | 2.70E+11 | 8.91E+10 | 7.55E+10 | 1.34E+09 | 2.38E+10 | 2.08E+11 | 2.61E+11 | |
| Mean | 2.34E+09 | 7.83E+10 | 2.59E+11 | 6.65E+10 | 5.23E+10 | 7.30E+08 | 1.44E+10 | 1.73E+11 | 2.47E+11 | |
| Std | 6.43E+08 | 1.28E+10 | 6.03E+09 | 1.31E+10 | 1.05E+10 | 2.46E+08 | 3.55E+09 | 1.53E+10 | 9.84E+09 | |
| Rank | 2 | 6 | 9 | 5 | 4 | 1 | 3 | 7 | 8 | |
| cec02 | Best | 1.29E+04 | 2.37E+04 | 3.14E+04 | 1.49E+04 | 1.75E+04 | 1.47E+04 | 2.34E+04 | 2.14E+04 | 3.11E+04 |
| Worst | 2.05E+04 | 3.32E+04 | 3.37E+04 | 1.94E+04 | 2.28E+04 | 2.21E+04 | 3.34E+04 | 3.31E+04 | 3.41E+04 | |
| Mean | 1.73E+04 | 3.18E+04 | 3.28E+04 | 1.71E+04 | 2.01E+04 | 1.89E+04 | 3.09E+04 | 2.83E+04 | 3.25E+04 | |
| Std | 1.65E+03 | 1.74E+03 | 5.70E+02 | 1.36E+03 | 1.35E+03 | 1.89E+03 | 2.07E+03 | 3.86E+03 | 7.65E+02 | |
| Rank | 2 | 7 | 9 | 1 | 4 | 3 | 6 | 5 | 8 | |
| cec03 | Best | 2.03E+03 | 2.55E+03 | 3.68E+03 | 2.59E+03 | 2.48E+03 | 2.31E+03 | 1.98E+03 | 3.31E+03 | 3.73E+03 |
| Worst | 3.17E+03 | 3.52E+03 | 4.05E+03 | 3.39E+03 | 3.41E+03 | 3.32E+03 | 2.47E+03 | 4.15E+03 | 4.12E+03 | |
| Mean | 2.54E+03 | 3.11E+03 | 3.89E+03 | 3.08E+03 | 2.93E+03 | 2.81E+03 | 2.25E+03 | 3.65E+03 | 3.90E+03 | |
| Std | 2.93E+02 | 2.70E+02 | 9.31E+01 | 2.00E+02 | 2.05E+02 | 2.73E+02 | 1.19E+02 | 2.24E+02 | 8.96E+01 | |
| Rank | 2 | 6 | 8 | 5 | 4 | 3 | 1 | 7 | 9 | |
| cec04 | Best | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.96E+03 | 1.90E+03 | 2.07E+03 | 1.90E+03 |
| Worst | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 2.09E+03 | 1.90E+03 | 2.76E+03 | 1.90E+03 | |
| Mean | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 2.01E+03 | 1.90E+03 | 2.24E+03 | 1.90E+03 | |
| Std | 0.00E+00 | 9.14E-02 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 3.17E+01 | 0.00E+00 | 1.39E+02 | 0.00E+00 | |
| Rank | 1 | 7 | 1 | 1 | 1 | 8 | 1 | 9 | 1 | |
| cec05 | Best | 2.02E+07 | 3.55E+07 | 1.11E+09 | 3.60E+07 | 3.01E+07 | 1.62E+07 | 2.06E+07 | 4.00E+07 | 7.17E+08 |
| Worst | 7.07E+07 | 8.60E+07 | 1.89E+09 | 1.72E+08 | 1.04E+08 | 4.99E+07 | 1.12E+08 | 5.58E+08 | 2.01E+09 | |
| Mean | 4.21E+07 | 6.06E+07 | 1.62E+09 | 8.95E+07 | 6.32E+07 | 2.98E+07 | 6.05E+07 | 2.18E+08 | 1.29E+09 | |
| Std | 1.22E+07 | 1.16E+07 | 1.91E+08 | 3.63E+07 | 2.12E+07 | 9.38E+06 | 2.24E+07 | 1.21E+08 | 3.66E+08 | |
| Rank | 2 | 4 | 9 | 6 | 5 | 1 | 3 | 7 | 8 | |
| cec06 | Best | 5.61E+03 | 7.09E+03 | 2.39E+04 | 5.48E+03 | 5.65E+03 | 6.51E+03 | 5.46E+03 | 9.45E+03 | 1.99E+04 |
| Worst | 8.41E+03 | 1.22E+04 | 3.21E+04 | 8.65E+03 | 9.47E+03 | 1.02E+04 | 7.93E+03 | 1.71E+04 | 3.54E+04 | |
| Mean | 6.65E+03 | 9.44E+03 | 2.90E+04 | 6.84E+03 | 7.78E+03 | 8.20E+03 | 6.67E+03 | 1.25E+04 | 2.81E+04 | |
| Std | 6.79E+02 | 1.23E+03 | 1.99E+03 | 7.07E+02 | 1.11E+03 | 8.68E+02 | 5.24E+02 | 1.64E+03 | 4.16E+03 | |
| Rank | 1 | 6 | 9 | 3 | 4 | 5 | 2 | 7 | 8 | |
| cec07 | Best | 2.82E+06 | 1.02E+07 | 2.40E+08 | 1.07E+07 | 1.07E+07 | 6.26E+06 | 5.55E+06 | 1.74E+07 | 2.12E+08 |
| Worst | 1.68E+07 | 4.25E+07 | 3.96E+08 | 5.85E+07 | 5.04E+07 | 2.44E+07 | 4.97E+07 | 1.34E+08 | 7.34E+08 | |
| Mean | 9.61E+06 | 1.85E+07 | 3.44E+08 | 3.20E+07 | 2.36E+07 | 1.18E+07 | 2.52E+07 | 6.35E+07 | 4.40E+08 | |
| Std | 3.06E+06 | 6.48E+06 | 3.56E+07 | 1.24E+07 | 9.43E+06 | 4.24E+06 | 1.10E+07 | 3.34E+07 | 1.28E+08 | |
| Rank | 1 | 3 | 8 | 6 | 4 | 2 | 5 | 7 | 9 | |
| cec08 | Best | 1.74E+04 | 2.50E+04 | 3.39E+04 | 1.75E+04 | 2.01E+04 | 1.88E+04 | 2.48E+04 | 2.32E+04 | 3.38E+04 |
| Worst | 2.33E+04 | 3.55E+04 | 3.60E+04 | 2.49E+04 | 2.63E+04 | 2.35E+04 | 3.57E+04 | 3.50E+04 | 3.58E+04 | |
| Mean | 2.09E+04 | 3.22E+04 | 3.50E+04 | 2.15E+04 | 2.29E+04 | 2.13E+04 | 3.29E+04 | 2.86E+04 | 3.48E+04 | |
| Std | 1.44E+03 | 3.10E+03 | 4.53E+02 | 1.80E+03 | 1.49E+03 | 1.22E+03 | 2.40E+03 | 3.77E+03 | 5.88E+02 | |
| Rank | 1 | 6 | 9 | 3 | 4 | 2 | 7 | 5 | 8 | |
| cec09 | Best | 4.26E+03 | 4.38E+03 | 8.45E+03 | 4.51E+03 | 4.62E+03 | 4.34E+03 | 4.31E+03 | 6.78E+03 | 7.22E+03 |
| Worst | 4.57E+03 | 5.99E+03 | 1.03E+04 | 5.24E+03 | 5.21E+03 | 5.68E+03 | 5.33E+03 | 1.02E+04 | 1.46E+04 | |
| Mean | 4.36E+03 | 5.38E+03 | 9.37E+03 | 4.82E+03 | 4.94E+03 | 4.79E+03 | 4.79E+03 | 7.83E+03 | 9.71E+03 | |
| Std | 7.54E+01 | 3.23E+02 | 4.56E+02 | 1.61E+02 | 1.67E+02 | 2.73E+02 | 2.23E+02 | 6.71E+02 | 2.60E+03 | |
| Rank | 1 | 6 | 8 | 4 | 5 | 3 | 2 | 7 | 9 | |
| cec10 | Best | 3.94E+03 | 5.70E+03 | 2.65E+04 | 5.27E+03 | 5.07E+03 | 3.74E+03 | 4.50E+03 | 1.19E+04 | 2.05E+04 |
| Worst | 4.68E+03 | 1.05E+04 | 3.04E+04 | 1.01E+04 | 7.65E+03 | 3.94E+03 | 7.69E+03 | 2.13E+04 | 2.89E+04 | |
| Mean | 4.16E+03 | 7.96E+03 | 2.82E+04 | 7.55E+03 | 6.48E+03 | 3.84E+03 | 5.37E+03 | 1.61E+04 | 2.54E+04 | |
| Std | 1.64E+02 | 1.21E+03 | 9.97E+02 | 1.20E+03 | 6.23E+02 | 5.87E+01 | 6.73E+02 | 2.19E+03 | 1.85E+03 | |
| Rank | 2 | 6 | 9 | 5 | 4 | 1 | 3 | 7 | 8 | |
| Mean rank | 1.5 | 5.7 | 7.9 | 3.9 | 3.9 | 2.9 | 3.3 | 6.8 | 7.6 | |
| Final ranking | 1 | 6 | 9 | 4 | 4 | 2 | 3 | 7 | 8 | |
| +/=/– | –/–/– | 0/0/10 | 0/1/9 | 0/4/6 | 0/1/9 | 2/2/5 | 1/2/7 | 0/0/10 | 0/1/9 | |
The results of HBWO-JS and other algorithms for CEC2020 test functions (the dimension dim = 100).
| Function . | Index . | Algorithms . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HBWO-JS . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . | ||
| cec01 | Best | 1.31E+09 | 5.78E+10 | 2.48E+11 | 3.71E+10 | 3.58E+10 | 3.66E+08 | 9.68E+09 | 1.46E+11 | 2.05E+11 |
| Worst | 3.79E+09 | 1.06E+11 | 2.70E+11 | 8.91E+10 | 7.55E+10 | 1.34E+09 | 2.38E+10 | 2.08E+11 | 2.61E+11 | |
| Mean | 2.34E+09 | 7.83E+10 | 2.59E+11 | 6.65E+10 | 5.23E+10 | 7.30E+08 | 1.44E+10 | 1.73E+11 | 2.47E+11 | |
| Std | 6.43E+08 | 1.28E+10 | 6.03E+09 | 1.31E+10 | 1.05E+10 | 2.46E+08 | 3.55E+09 | 1.53E+10 | 9.84E+09 | |
| Rank | 2 | 6 | 9 | 5 | 4 | 1 | 3 | 7 | 8 | |
| cec02 | Best | 1.29E+04 | 2.37E+04 | 3.14E+04 | 1.49E+04 | 1.75E+04 | 1.47E+04 | 2.34E+04 | 2.14E+04 | 3.11E+04 |
| Worst | 2.05E+04 | 3.32E+04 | 3.37E+04 | 1.94E+04 | 2.28E+04 | 2.21E+04 | 3.34E+04 | 3.31E+04 | 3.41E+04 | |
| Mean | 1.73E+04 | 3.18E+04 | 3.28E+04 | 1.71E+04 | 2.01E+04 | 1.89E+04 | 3.09E+04 | 2.83E+04 | 3.25E+04 | |
| Std | 1.65E+03 | 1.74E+03 | 5.70E+02 | 1.36E+03 | 1.35E+03 | 1.89E+03 | 2.07E+03 | 3.86E+03 | 7.65E+02 | |
| Rank | 2 | 7 | 9 | 1 | 4 | 3 | 6 | 5 | 8 | |
| cec03 | Best | 2.03E+03 | 2.55E+03 | 3.68E+03 | 2.59E+03 | 2.48E+03 | 2.31E+03 | 1.98E+03 | 3.31E+03 | 3.73E+03 |
| Worst | 3.17E+03 | 3.52E+03 | 4.05E+03 | 3.39E+03 | 3.41E+03 | 3.32E+03 | 2.47E+03 | 4.15E+03 | 4.12E+03 | |
| Mean | 2.54E+03 | 3.11E+03 | 3.89E+03 | 3.08E+03 | 2.93E+03 | 2.81E+03 | 2.25E+03 | 3.65E+03 | 3.90E+03 | |
| Std | 2.93E+02 | 2.70E+02 | 9.31E+01 | 2.00E+02 | 2.05E+02 | 2.73E+02 | 1.19E+02 | 2.24E+02 | 8.96E+01 | |
| Rank | 2 | 6 | 8 | 5 | 4 | 3 | 1 | 7 | 9 | |
| cec04 | Best | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.96E+03 | 1.90E+03 | 2.07E+03 | 1.90E+03 |
| Worst | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 2.09E+03 | 1.90E+03 | 2.76E+03 | 1.90E+03 | |
| Mean | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 2.01E+03 | 1.90E+03 | 2.24E+03 | 1.90E+03 | |
| Std | 0.00E+00 | 9.14E-02 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 3.17E+01 | 0.00E+00 | 1.39E+02 | 0.00E+00 | |
| Rank | 1 | 7 | 1 | 1 | 1 | 8 | 1 | 9 | 1 | |
| cec05 | Best | 2.02E+07 | 3.55E+07 | 1.11E+09 | 3.60E+07 | 3.01E+07 | 1.62E+07 | 2.06E+07 | 4.00E+07 | 7.17E+08 |
| Worst | 7.07E+07 | 8.60E+07 | 1.89E+09 | 1.72E+08 | 1.04E+08 | 4.99E+07 | 1.12E+08 | 5.58E+08 | 2.01E+09 | |
| Mean | 4.21E+07 | 6.06E+07 | 1.62E+09 | 8.95E+07 | 6.32E+07 | 2.98E+07 | 6.05E+07 | 2.18E+08 | 1.29E+09 | |
| Std | 1.22E+07 | 1.16E+07 | 1.91E+08 | 3.63E+07 | 2.12E+07 | 9.38E+06 | 2.24E+07 | 1.21E+08 | 3.66E+08 | |
| Rank | 2 | 4 | 9 | 6 | 5 | 1 | 3 | 7 | 8 | |
| cec06 | Best | 5.61E+03 | 7.09E+03 | 2.39E+04 | 5.48E+03 | 5.65E+03 | 6.51E+03 | 5.46E+03 | 9.45E+03 | 1.99E+04 |
| Worst | 8.41E+03 | 1.22E+04 | 3.21E+04 | 8.65E+03 | 9.47E+03 | 1.02E+04 | 7.93E+03 | 1.71E+04 | 3.54E+04 | |
| Mean | 6.65E+03 | 9.44E+03 | 2.90E+04 | 6.84E+03 | 7.78E+03 | 8.20E+03 | 6.67E+03 | 1.25E+04 | 2.81E+04 | |
| Std | 6.79E+02 | 1.23E+03 | 1.99E+03 | 7.07E+02 | 1.11E+03 | 8.68E+02 | 5.24E+02 | 1.64E+03 | 4.16E+03 | |
| Rank | 1 | 6 | 9 | 3 | 4 | 5 | 2 | 7 | 8 | |
| cec07 | Best | 2.82E+06 | 1.02E+07 | 2.40E+08 | 1.07E+07 | 1.07E+07 | 6.26E+06 | 5.55E+06 | 1.74E+07 | 2.12E+08 |
| Worst | 1.68E+07 | 4.25E+07 | 3.96E+08 | 5.85E+07 | 5.04E+07 | 2.44E+07 | 4.97E+07 | 1.34E+08 | 7.34E+08 | |
| Mean | 9.61E+06 | 1.85E+07 | 3.44E+08 | 3.20E+07 | 2.36E+07 | 1.18E+07 | 2.52E+07 | 6.35E+07 | 4.40E+08 | |
| Std | 3.06E+06 | 6.48E+06 | 3.56E+07 | 1.24E+07 | 9.43E+06 | 4.24E+06 | 1.10E+07 | 3.34E+07 | 1.28E+08 | |
| Rank | 1 | 3 | 8 | 6 | 4 | 2 | 5 | 7 | 9 | |
| cec08 | Best | 1.74E+04 | 2.50E+04 | 3.39E+04 | 1.75E+04 | 2.01E+04 | 1.88E+04 | 2.48E+04 | 2.32E+04 | 3.38E+04 |
| Worst | 2.33E+04 | 3.55E+04 | 3.60E+04 | 2.49E+04 | 2.63E+04 | 2.35E+04 | 3.57E+04 | 3.50E+04 | 3.58E+04 | |
| Mean | 2.09E+04 | 3.22E+04 | 3.50E+04 | 2.15E+04 | 2.29E+04 | 2.13E+04 | 3.29E+04 | 2.86E+04 | 3.48E+04 | |
| Std | 1.44E+03 | 3.10E+03 | 4.53E+02 | 1.80E+03 | 1.49E+03 | 1.22E+03 | 2.40E+03 | 3.77E+03 | 5.88E+02 | |
| Rank | 1 | 6 | 9 | 3 | 4 | 2 | 7 | 5 | 8 | |
| cec09 | Best | 4.26E+03 | 4.38E+03 | 8.45E+03 | 4.51E+03 | 4.62E+03 | 4.34E+03 | 4.31E+03 | 6.78E+03 | 7.22E+03 |
| Worst | 4.57E+03 | 5.99E+03 | 1.03E+04 | 5.24E+03 | 5.21E+03 | 5.68E+03 | 5.33E+03 | 1.02E+04 | 1.46E+04 | |
| Mean | 4.36E+03 | 5.38E+03 | 9.37E+03 | 4.82E+03 | 4.94E+03 | 4.79E+03 | 4.79E+03 | 7.83E+03 | 9.71E+03 | |
| Std | 7.54E+01 | 3.23E+02 | 4.56E+02 | 1.61E+02 | 1.67E+02 | 2.73E+02 | 2.23E+02 | 6.71E+02 | 2.60E+03 | |
| Rank | 1 | 6 | 8 | 4 | 5 | 3 | 2 | 7 | 9 | |
| cec10 | Best | 3.94E+03 | 5.70E+03 | 2.65E+04 | 5.27E+03 | 5.07E+03 | 3.74E+03 | 4.50E+03 | 1.19E+04 | 2.05E+04 |
| Worst | 4.68E+03 | 1.05E+04 | 3.04E+04 | 1.01E+04 | 7.65E+03 | 3.94E+03 | 7.69E+03 | 2.13E+04 | 2.89E+04 | |
| Mean | 4.16E+03 | 7.96E+03 | 2.82E+04 | 7.55E+03 | 6.48E+03 | 3.84E+03 | 5.37E+03 | 1.61E+04 | 2.54E+04 | |
| Std | 1.64E+02 | 1.21E+03 | 9.97E+02 | 1.20E+03 | 6.23E+02 | 5.87E+01 | 6.73E+02 | 2.19E+03 | 1.85E+03 | |
| Rank | 2 | 6 | 9 | 5 | 4 | 1 | 3 | 7 | 8 | |
| Mean rank | 1.5 | 5.7 | 7.9 | 3.9 | 3.9 | 2.9 | 3.3 | 6.8 | 7.6 | |
| Final ranking | 1 | 6 | 9 | 4 | 4 | 2 | 3 | 7 | 8 | |
| +/=/– | –/–/– | 0/0/10 | 0/1/9 | 0/4/6 | 0/1/9 | 2/2/5 | 1/2/7 | 0/0/10 | 0/1/9 | |
| Function . | Index . | Algorithms . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HBWO-JS . | JS . | BWO . | AHA . | ARO . | DO . | SO . | WSO . | RSA . | ||
| cec01 | Best | 1.31E+09 | 5.78E+10 | 2.48E+11 | 3.71E+10 | 3.58E+10 | 3.66E+08 | 9.68E+09 | 1.46E+11 | 2.05E+11 |
| Worst | 3.79E+09 | 1.06E+11 | 2.70E+11 | 8.91E+10 | 7.55E+10 | 1.34E+09 | 2.38E+10 | 2.08E+11 | 2.61E+11 | |
| Mean | 2.34E+09 | 7.83E+10 | 2.59E+11 | 6.65E+10 | 5.23E+10 | 7.30E+08 | 1.44E+10 | 1.73E+11 | 2.47E+11 | |
| Std | 6.43E+08 | 1.28E+10 | 6.03E+09 | 1.31E+10 | 1.05E+10 | 2.46E+08 | 3.55E+09 | 1.53E+10 | 9.84E+09 | |
| Rank | 2 | 6 | 9 | 5 | 4 | 1 | 3 | 7 | 8 | |
| cec02 | Best | 1.29E+04 | 2.37E+04 | 3.14E+04 | 1.49E+04 | 1.75E+04 | 1.47E+04 | 2.34E+04 | 2.14E+04 | 3.11E+04 |
| Worst | 2.05E+04 | 3.32E+04 | 3.37E+04 | 1.94E+04 | 2.28E+04 | 2.21E+04 | 3.34E+04 | 3.31E+04 | 3.41E+04 | |
| Mean | 1.73E+04 | 3.18E+04 | 3.28E+04 | 1.71E+04 | 2.01E+04 | 1.89E+04 | 3.09E+04 | 2.83E+04 | 3.25E+04 | |
| Std | 1.65E+03 | 1.74E+03 | 5.70E+02 | 1.36E+03 | 1.35E+03 | 1.89E+03 | 2.07E+03 | 3.86E+03 | 7.65E+02 | |
| Rank | 2 | 7 | 9 | 1 | 4 | 3 | 6 | 5 | 8 | |
| cec03 | Best | 2.03E+03 | 2.55E+03 | 3.68E+03 | 2.59E+03 | 2.48E+03 | 2.31E+03 | 1.98E+03 | 3.31E+03 | 3.73E+03 |
| Worst | 3.17E+03 | 3.52E+03 | 4.05E+03 | 3.39E+03 | 3.41E+03 | 3.32E+03 | 2.47E+03 | 4.15E+03 | 4.12E+03 | |
| Mean | 2.54E+03 | 3.11E+03 | 3.89E+03 | 3.08E+03 | 2.93E+03 | 2.81E+03 | 2.25E+03 | 3.65E+03 | 3.90E+03 | |
| Std | 2.93E+02 | 2.70E+02 | 9.31E+01 | 2.00E+02 | 2.05E+02 | 2.73E+02 | 1.19E+02 | 2.24E+02 | 8.96E+01 | |
| Rank | 2 | 6 | 8 | 5 | 4 | 3 | 1 | 7 | 9 | |
| cec04 | Best | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.96E+03 | 1.90E+03 | 2.07E+03 | 1.90E+03 |
| Worst | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 2.09E+03 | 1.90E+03 | 2.76E+03 | 1.90E+03 | |
| Mean | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 1.90E+03 | 2.01E+03 | 1.90E+03 | 2.24E+03 | 1.90E+03 | |
| Std | 0.00E+00 | 9.14E-02 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 3.17E+01 | 0.00E+00 | 1.39E+02 | 0.00E+00 | |
| Rank | 1 | 7 | 1 | 1 | 1 | 8 | 1 | 9 | 1 | |
| cec05 | Best | 2.02E+07 | 3.55E+07 | 1.11E+09 | 3.60E+07 | 3.01E+07 | 1.62E+07 | 2.06E+07 | 4.00E+07 | 7.17E+08 |
| Worst | 7.07E+07 | 8.60E+07 | 1.89E+09 | 1.72E+08 | 1.04E+08 | 4.99E+07 | 1.12E+08 | 5.58E+08 | 2.01E+09 | |
| Mean | 4.21E+07 | 6.06E+07 | 1.62E+09 | 8.95E+07 | 6.32E+07 | 2.98E+07 | 6.05E+07 | 2.18E+08 | 1.29E+09 | |
| Std | 1.22E+07 | 1.16E+07 | 1.91E+08 | 3.63E+07 | 2.12E+07 | 9.38E+06 | 2.24E+07 | 1.21E+08 | 3.66E+08 | |
| Rank | 2 | 4 | 9 | 6 | 5 | 1 | 3 | 7 | 8 | |
| cec06 | Best | 5.61E+03 | 7.09E+03 | 2.39E+04 | 5.48E+03 | 5.65E+03 | 6.51E+03 | 5.46E+03 | 9.45E+03 | 1.99E+04 |
| Worst | 8.41E+03 | 1.22E+04 | 3.21E+04 | 8.65E+03 | 9.47E+03 | 1.02E+04 | 7.93E+03 | 1.71E+04 | 3.54E+04 | |
| Mean | 6.65E+03 | 9.44E+03 | 2.90E+04 | 6.84E+03 | 7.78E+03 | 8.20E+03 | 6.67E+03 | 1.25E+04 | 2.81E+04 | |
| Std | 6.79E+02 | 1.23E+03 | 1.99E+03 | 7.07E+02 | 1.11E+03 | 8.68E+02 | 5.24E+02 | 1.64E+03 | 4.16E+03 | |
| Rank | 1 | 6 | 9 | 3 | 4 | 5 | 2 | 7 | 8 | |
| cec07 | Best | 2.82E+06 | 1.02E+07 | 2.40E+08 | 1.07E+07 | 1.07E+07 | 6.26E+06 | 5.55E+06 | 1.74E+07 | 2.12E+08 |
| Worst | 1.68E+07 | 4.25E+07 | 3.96E+08 | 5.85E+07 | 5.04E+07 | 2.44E+07 | 4.97E+07 | 1.34E+08 | 7.34E+08 | |
| Mean | 9.61E+06 | 1.85E+07 | 3.44E+08 | 3.20E+07 | 2.36E+07 | 1.18E+07 | 2.52E+07 | 6.35E+07 | 4.40E+08 | |
| Std | 3.06E+06 | 6.48E+06 | 3.56E+07 | 1.24E+07 | 9.43E+06 | 4.24E+06 | 1.10E+07 | 3.34E+07 | 1.28E+08 | |
| Rank | 1 | 3 | 8 | 6 | 4 | 2 | 5 | 7 | 9 | |
| cec08 | Best | 1.74E+04 | 2.50E+04 | 3.39E+04 | 1.75E+04 | 2.01E+04 | 1.88E+04 | 2.48E+04 | 2.32E+04 | 3.38E+04 |
| Worst | 2.33E+04 | 3.55E+04 | 3.60E+04 | 2.49E+04 | 2.63E+04 | 2.35E+04 | 3.57E+04 | 3.50E+04 | 3.58E+04 | |
| Mean | 2.09E+04 | 3.22E+04 | 3.50E+04 | 2.15E+04 | 2.29E+04 | 2.13E+04 | 3.29E+04 | 2.86E+04 | 3.48E+04 | |
| Std | 1.44E+03 | 3.10E+03 | 4.53E+02 | 1.80E+03 | 1.49E+03 | 1.22E+03 | 2.40E+03 | 3.77E+03 | 5.88E+02 | |
| Rank | 1 | 6 | 9 | 3 | 4 | 2 | 7 | 5 | 8 | |
| cec09 | Best | 4.26E+03 | 4.38E+03 | 8.45E+03 | 4.51E+03 | 4.62E+03 | 4.34E+03 | 4.31E+03 | 6.78E+03 | 7.22E+03 |
| Worst | 4.57E+03 | 5.99E+03 | 1.03E+04 | 5.24E+03 | 5.21E+03 | 5.68E+03 | 5.33E+03 | 1.02E+04 | 1.46E+04 | |
| Mean | 4.36E+03 | 5.38E+03 | 9.37E+03 | 4.82E+03 | 4.94E+03 | 4.79E+03 | 4.79E+03 | 7.83E+03 | 9.71E+03 | |
| Std | 7.54E+01 | 3.23E+02 | 4.56E+02 | 1.61E+02 | 1.67E+02 | 2.73E+02 | 2.23E+02 | 6.71E+02 | 2.60E+03 | |
| Rank | 1 | 6 | 8 | 4 | 5 | 3 | 2 | 7 | 9 | |
| cec10 | Best | 3.94E+03 | 5.70E+03 | 2.65E+04 | 5.27E+03 | 5.07E+03 | 3.74E+03 | 4.50E+03 | 1.19E+04 | 2.05E+04 |
| Worst | 4.68E+03 | 1.05E+04 | 3.04E+04 | 1.01E+04 | 7.65E+03 | 3.94E+03 | 7.69E+03 | 2.13E+04 | 2.89E+04 | |
| Mean | 4.16E+03 | 7.96E+03 | 2.82E+04 | 7.55E+03 | 6.48E+03 | 3.84E+03 | 5.37E+03 | 1.61E+04 | 2.54E+04 | |
| Std | 1.64E+02 | 1.21E+03 | 9.97E+02 | 1.20E+03 | 6.23E+02 | 5.87E+01 | 6.73E+02 | 2.19E+03 | 1.85E+03 | |
| Rank | 2 | 6 | 9 | 5 | 4 | 1 | 3 | 7 | 8 | |
| Mean rank | 1.5 | 5.7 | 7.9 | 3.9 | 3.9 | 2.9 | 3.3 | 6.8 | 7.6 | |
| Final ranking | 1 | 6 | 9 | 4 | 4 | 2 | 3 | 7 | 8 | |
| +/=/– | –/–/– | 0/0/10 | 0/1/9 | 0/4/6 | 0/1/9 | 2/2/5 | 1/2/7 | 0/0/10 | 0/1/9 | |
In addition, this study provides the Wilcoxon rank sum test results in the last row of Tables 8, 9, 10, and 11. In the face of the 10D problem, only two algorithms, JS and SO, exist that perform better than the proposed HBWO-JS algorithm for the test problems, one and two test functions, respectively, and the rest perform worse than the proposed algorithm. Furthermore, in 30D problems, the HBWO-JS algorithm is not worse than the other algorithms in all problems. In the face of 50D problems, only two algorithms, ARO and DO, have test problems with better performance than the proposed HBWO-JS algorithm, two and one test functions, respectively, and the rest have worse performance than the proposed algorithm. Also, when facing the 100D problem, only two algorithms, DO and SO, perform better than the proposed HBWO-JS algorithm on the test problems, two and one test functions, respectively, and the rest of the algorithms perform worse than the proposed algorithm.
In addition, Figs 9, 10, 11, and 12 provide the results of running the HBWO-JS algorithm and other algorithms for CEC2020 in dimensions 10, 30, 50, and 100, respectively. The HBWO-JS algorithm finds the near-optimal solution in the middle of each iteration and then gradually approaches the optimal solution in subsequent iterations. This convergence behavior proves that the HBWO-JS algorithm is efficiently convergent. In addition, the proposed HBWO-JS algorithm obtains optimal solutions on most of the tested functions and converges quickly on almost all functions. As can be seen from the figure, HBWO-JS converges to the optimal solution value at a gradually slowing rate. The convergence rate of SO and ARO is comparable to that of the HBWO-JS algorithm. In addition, the slope of the convergence curve of the earlier HBWO-JS algorithm is very large and almost vertical, which indicates the high sensitivity of the proposed HBWO-JS algorithm, as seen from the figure. Also, the continuity of global and local optima can be continuously maintained and developed in the middle and later iterations. In addition, for some functions, a random mutation process of HBWO-JS can be found during the iterations, which also demonstrates the ability of HBWO-JS to track the optimal solution for an optimization. Finally, the observed experimental results show that HBWO-JS can be considered a reliable, efficient, and stable algorithm. Also, Figs 13, 14, 15, and 16 provide box plots four dimensions in all test problems, from which it can be observed that the narrow shape of the box and the overall smaller average value also show the stability and robustness of HBWO-JS.

Convergence trends of the CEC2020 test suite with the HBWO-JS, JS, BWO, AHA, ARO, DO, SO, WSO, RSA algorithm (the dimension dim = 10).
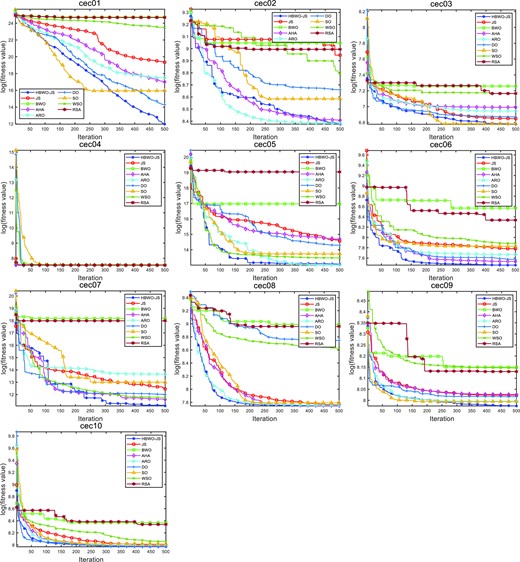
Convergence trends of the CEC2020 test suite with the HBWO-JS, JS, BWO, AHA, ARO, DO, SO, WSO, RSA algorithm (the dimension dim = 30).

Convergence trends of the CEC2020 test suite with the HBWO-JS, JS, BWO, AHA, ARO, DO, SO, WSO, RSA algorithm (the dimension dim = 50).

Convergence trends of the CEC2020 test suite with the HBWO-JS, JS, BWO, AHA, ARO, DO, SO, WSO, RSA algorithm (the dimension dim = 10).
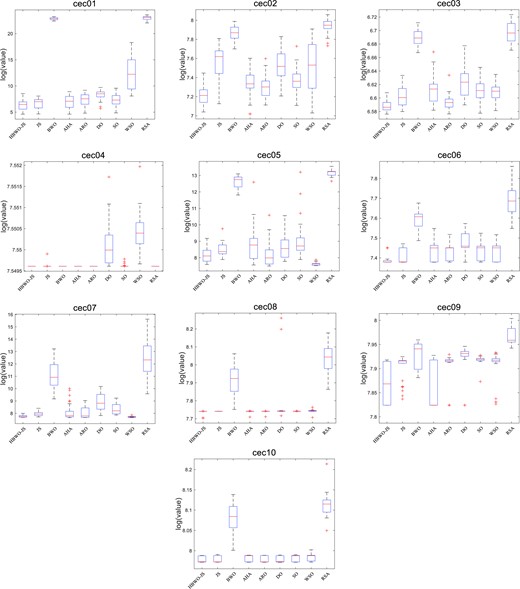
Box plot of the HBWO-JS, JS, BWO, AHA, ARO, DO, SO, WSO, RSA algorithm for CEC2020 test suite (the dimension dim = 10; red minus → Median; red plus → Outlier).

Box plot of the HBWO-JS, JS, BWO, AHA, ARO, DO, SO, WSO, RSA algorithm for CEC2020 test suite (the dimension dim = 30; red minus → Median; red plus → Outlier).

Box plot of the HBWO-JS, JS, BWO, AHA, ARO, DO, SO, WSO, RSA algorithm for CEC2020 test suite (the dimension dim = 50; red minus → Median; red plus → Outlier).

Box plot of the HBWO-JS, JS, BWO, AHA, ARO, DO, SO, WSO, RSA algorithm for CEC2020 test suite (the dimension dim = 100; red minus → Median; red plus → Outlier).
5. HBWO-JS Applied to Engineering Problems
All problems in which constraints are satisfied by choosing a specific range of parameters are defined as optimization problems. In most cases, finding the global optimum over the whole exploration area is difficult. And for some problems with inequality constraints, the global optimum is located in a large range of the search area. In this section, three engineering problems, including the piston lever design problem (PLD), car side impact design (CSID) problem, and single-stage cylindrical gear problem, are utilized to evaluate the efficiency of the HBWO-JS algorithm. All algorithms are run with a uniformly guaranteed maximum number of iterations of 500 and a population size of 30. Each algorithm is executed 30 times in different optimization problems to prevent chance.
5.1. PLD
The optimal requirement for the PLD problem is to locate the four components of the piston, as shown schematically in Fig. 17. The whole optimization process is to ensure that the oil volume is reduced to the minimum case during the lifting of the piston rod from 0° to 45° (Bayzidi et al., 2021). The specific formulation of the PLD problem is shown as follows:

Suppose:
Minimize:
Subject to:
where,
Variable range:
The optimization results of the proposed HBWO-JS algorithm are compared with WSO, SO, RSA, DO, ARO, AHA, and JS for experiments. The optimization results of the independent variables are provided in Table 12. the statistical results of the relevant runs 30 times are given in Table 13. According to Table 12, the amount of the fitness function of PLV obtained by HBWO-JS (8.41270) is smaller than the values obtained by the other seven methods. In general, HBWO-JS did an excellent job of balancing exploration and exploration search. In addition, the experimental results show that HBWO-JS is able to satisfy the optimization impact of engineering difficulties and significantly reduce manufacturing costs.
Optimal construction variables of HBWO-JS and other algorithms for solving PLD problem.
| Algorithms . | Variables . | Minimum case . | |||
|---|---|---|---|---|---|
| x1 . | x2 . | x3 . | x4 . | ||
| WSO | 425.00702 | 425.30713 | 68.99431 | 2.49231 | 143.62339 |
| SO | 364.03909 | 375.51431 | 75.00001 | 2.70673 | 129.73742 |
| RSA | 90.64241 | 90.99491 | 100.26755 | 3.86125 | 112.13276 |
| DO | 274.98346 | 275.91753 | 87.00008 | 3.05352 | 95.90068 |
| ARO | 250.09972 | 251.02479 | 89.88845 | 3.14648 | 88.65433 |
| AHA | 100.03534 | 101.63386 | 107.92718 | 3.71004 | 40.23778 |
| JS | 0.05947 | 2.38286 | 101.62895 | 4.57692 | 13.06635 |
| HBWO-JS | 0.05000 | 2.04151 | 120.00000 | 4.08303 | 8.41270 |
| Algorithms . | Variables . | Minimum case . | |||
|---|---|---|---|---|---|
| x1 . | x2 . | x3 . | x4 . | ||
| WSO | 425.00702 | 425.30713 | 68.99431 | 2.49231 | 143.62339 |
| SO | 364.03909 | 375.51431 | 75.00001 | 2.70673 | 129.73742 |
| RSA | 90.64241 | 90.99491 | 100.26755 | 3.86125 | 112.13276 |
| DO | 274.98346 | 275.91753 | 87.00008 | 3.05352 | 95.90068 |
| ARO | 250.09972 | 251.02479 | 89.88845 | 3.14648 | 88.65433 |
| AHA | 100.03534 | 101.63386 | 107.92718 | 3.71004 | 40.23778 |
| JS | 0.05947 | 2.38286 | 101.62895 | 4.57692 | 13.06635 |
| HBWO-JS | 0.05000 | 2.04151 | 120.00000 | 4.08303 | 8.41270 |
Optimal construction variables of HBWO-JS and other algorithms for solving PLD problem.
| Algorithms . | Variables . | Minimum case . | |||
|---|---|---|---|---|---|
| x1 . | x2 . | x3 . | x4 . | ||
| WSO | 425.00702 | 425.30713 | 68.99431 | 2.49231 | 143.62339 |
| SO | 364.03909 | 375.51431 | 75.00001 | 2.70673 | 129.73742 |
| RSA | 90.64241 | 90.99491 | 100.26755 | 3.86125 | 112.13276 |
| DO | 274.98346 | 275.91753 | 87.00008 | 3.05352 | 95.90068 |
| ARO | 250.09972 | 251.02479 | 89.88845 | 3.14648 | 88.65433 |
| AHA | 100.03534 | 101.63386 | 107.92718 | 3.71004 | 40.23778 |
| JS | 0.05947 | 2.38286 | 101.62895 | 4.57692 | 13.06635 |
| HBWO-JS | 0.05000 | 2.04151 | 120.00000 | 4.08303 | 8.41270 |
| Algorithms . | Variables . | Minimum case . | |||
|---|---|---|---|---|---|
| x1 . | x2 . | x3 . | x4 . | ||
| WSO | 425.00702 | 425.30713 | 68.99431 | 2.49231 | 143.62339 |
| SO | 364.03909 | 375.51431 | 75.00001 | 2.70673 | 129.73742 |
| RSA | 90.64241 | 90.99491 | 100.26755 | 3.86125 | 112.13276 |
| DO | 274.98346 | 275.91753 | 87.00008 | 3.05352 | 95.90068 |
| ARO | 250.09972 | 251.02479 | 89.88845 | 3.14648 | 88.65433 |
| AHA | 100.03534 | 101.63386 | 107.92718 | 3.71004 | 40.23778 |
| JS | 0.05947 | 2.38286 | 101.62895 | 4.57692 | 13.06635 |
| HBWO-JS | 0.05000 | 2.04151 | 120.00000 | 4.08303 | 8.41270 |
Comparisons of statistical results using reported algorithms in literature for solving PLD problem.
| Algorithms . | Best . | Worst . | Mean . | Std . |
|---|---|---|---|---|
| WSO | 8.41279 | 167.47457 | 143.62339 | 58.24871 |
| SO | 8.41270 | 207.12686 | 129.73742 | 72.29369 |
| RSA | 9.15003 | 370.62462 | 112.13276 | 144.20465 |
| DO | 8.41272 | 167.53892 | 95.90068 | 81.19134 |
| ARO | 8.41272 | 167.47421 | 88.65433 | 80.92348 |
| AHA | 8.41271 | 167.48083 | 40.23778 | 65.27261 |
| JS | 8.41269834 | 22.35084689 | 13.06635215 | 5.3254216 |
| HBWO-JS | 8.41269832 | 8.41269832 | 8.41269832 | 4.35E-11 |
| Algorithms . | Best . | Worst . | Mean . | Std . |
|---|---|---|---|---|
| WSO | 8.41279 | 167.47457 | 143.62339 | 58.24871 |
| SO | 8.41270 | 207.12686 | 129.73742 | 72.29369 |
| RSA | 9.15003 | 370.62462 | 112.13276 | 144.20465 |
| DO | 8.41272 | 167.53892 | 95.90068 | 81.19134 |
| ARO | 8.41272 | 167.47421 | 88.65433 | 80.92348 |
| AHA | 8.41271 | 167.48083 | 40.23778 | 65.27261 |
| JS | 8.41269834 | 22.35084689 | 13.06635215 | 5.3254216 |
| HBWO-JS | 8.41269832 | 8.41269832 | 8.41269832 | 4.35E-11 |
Comparisons of statistical results using reported algorithms in literature for solving PLD problem.
| Algorithms . | Best . | Worst . | Mean . | Std . |
|---|---|---|---|---|
| WSO | 8.41279 | 167.47457 | 143.62339 | 58.24871 |
| SO | 8.41270 | 207.12686 | 129.73742 | 72.29369 |
| RSA | 9.15003 | 370.62462 | 112.13276 | 144.20465 |
| DO | 8.41272 | 167.53892 | 95.90068 | 81.19134 |
| ARO | 8.41272 | 167.47421 | 88.65433 | 80.92348 |
| AHA | 8.41271 | 167.48083 | 40.23778 | 65.27261 |
| JS | 8.41269834 | 22.35084689 | 13.06635215 | 5.3254216 |
| HBWO-JS | 8.41269832 | 8.41269832 | 8.41269832 | 4.35E-11 |
| Algorithms . | Best . | Worst . | Mean . | Std . |
|---|---|---|---|---|
| WSO | 8.41279 | 167.47457 | 143.62339 | 58.24871 |
| SO | 8.41270 | 207.12686 | 129.73742 | 72.29369 |
| RSA | 9.15003 | 370.62462 | 112.13276 | 144.20465 |
| DO | 8.41272 | 167.53892 | 95.90068 | 81.19134 |
| ARO | 8.41272 | 167.47421 | 88.65433 | 80.92348 |
| AHA | 8.41271 | 167.48083 | 40.23778 | 65.27261 |
| JS | 8.41269834 | 22.35084689 | 13.06635215 | 5.3254216 |
| HBWO-JS | 8.41269832 | 8.41269832 | 8.41269832 | 4.35E-11 |
5.2. CSID
Based on the European Enhanced Vehicle Safety Council (EEVC) procedure, this study investigates the optimization problem of a car subjected to a side impact, which is optimally required to achieve the minimum case of the weight of the door by adjusting nine impact parameters. Figure 18 shows the model of the car side impact problem. According to the simplified optimization model of Youn et al. (Youn & Choi, 2004), the specific formulation of the CSID problem is shown below.

Minimize:
Subject to:
Variable range:
The optimization results of the proposed HBWO-JS algorithm for CSID are compared with WSO, SO, RSA, DO, ARO, AHA, and JS for the experiments. The optimization results of the independent variables are provided in Table 14; the statistical results of the relevant runs 30 times are given in Table 15. According to Table 14, the amount of fitness function of CSID obtained by HBWO-JS (22.8452536) is smaller than the results of optimization by the other seven methods. In general, HBWO-JS does a good job in global search. In addition, the experimental results show that HBWO-JS is able to satisfy the optimization impact of engineering difficulties and significantly find the door weight for the minimum case.
Optimal construction variables of HBWO-JS and other algorithms for solving CSID problem.
| Algorithms . | Variables . | |||||
|---|---|---|---|---|---|---|
| z1 . | z2 . | z3 . | z4 . | z5 . | z6 . | |
| RSA | 0.5582391 | 1.2510718 | 0.5553102 | 1.2858772 | 0.6058203 | 1.2508719 |
| AHA | 0.5357509 | 1.1755893 | 0.5223455 | 1.2246030 | 0.5197215 | 1.3372923 |
| DO | 0.5000233 | 1.2206681 | 0.5000134 | 1.2325457 | 0.5173562 | 1.2927733 |
| WSO | 0.5098872 | 1.1833252 | 0.5150247 | 1.2475072 | 0.5325131 | 1.2370275 |
| ARO | 0.5056171 | 1.1858457 | 0.5055551 | 1.2306904 | 0.5193284 | 1.3442855 |
| SO | 0.5150859 | 1.1761861 | 0.5035944 | 1.2313418 | 0.5017206 | 1.2941253 |
| JS | 0.5006119 | 1.1651128 | 0.5001726 | 1.2514078 | 0.5005317 | 1.4792699 |
| HBWO-JS | 0.5000000 | 1.1196305 | 0.5000000 | 1.2973362 | 0.5000000 | 1.4998457 |
| Variables | Minimum weight | |||||
| z7 | z8 | z9 | z10 | z11 | ||
| 0.5906219 | 0.6202851 | 0.4431583 | −3.8282799 | 3.6443327 | 24.7832110 | |
| 0.5003422 | 0.6426417 | 0.5525141 | −5.2445401 | 2.8725694 | 23.2940282 | |
| 0.5000331 | 0.5874500 | 0.2246874 | −7.1445584 | 4.0793353 | 23.2905574 | |
| 0.5025410 | 0.7479548 | 0.4647983 | −7.3707008 | 4.0923118 | 23.2884132 | |
| 0.5007215 | 0.7262638 | 0.4336405 | −6.4414053 | 3.0481084 | 23.1223322 | |
| 0.5004893 | 0.7313767 | 0.5100820 | −7.5488568 | 4.0425995 | 23.0612498 | |
| 0.5002164 | 0.7167913 | 0.4833567 | −10.8718732 | 0.3965207 | 22.9701882 | |
| 0.5000000 | 0.8645165 | 0.3540178 | −18.9940358 | 0.0810628 | 22.8452536 | |
| Algorithms . | Variables . | |||||
|---|---|---|---|---|---|---|
| z1 . | z2 . | z3 . | z4 . | z5 . | z6 . | |
| RSA | 0.5582391 | 1.2510718 | 0.5553102 | 1.2858772 | 0.6058203 | 1.2508719 |
| AHA | 0.5357509 | 1.1755893 | 0.5223455 | 1.2246030 | 0.5197215 | 1.3372923 |
| DO | 0.5000233 | 1.2206681 | 0.5000134 | 1.2325457 | 0.5173562 | 1.2927733 |
| WSO | 0.5098872 | 1.1833252 | 0.5150247 | 1.2475072 | 0.5325131 | 1.2370275 |
| ARO | 0.5056171 | 1.1858457 | 0.5055551 | 1.2306904 | 0.5193284 | 1.3442855 |
| SO | 0.5150859 | 1.1761861 | 0.5035944 | 1.2313418 | 0.5017206 | 1.2941253 |
| JS | 0.5006119 | 1.1651128 | 0.5001726 | 1.2514078 | 0.5005317 | 1.4792699 |
| HBWO-JS | 0.5000000 | 1.1196305 | 0.5000000 | 1.2973362 | 0.5000000 | 1.4998457 |
| Variables | Minimum weight | |||||
| z7 | z8 | z9 | z10 | z11 | ||
| 0.5906219 | 0.6202851 | 0.4431583 | −3.8282799 | 3.6443327 | 24.7832110 | |
| 0.5003422 | 0.6426417 | 0.5525141 | −5.2445401 | 2.8725694 | 23.2940282 | |
| 0.5000331 | 0.5874500 | 0.2246874 | −7.1445584 | 4.0793353 | 23.2905574 | |
| 0.5025410 | 0.7479548 | 0.4647983 | −7.3707008 | 4.0923118 | 23.2884132 | |
| 0.5007215 | 0.7262638 | 0.4336405 | −6.4414053 | 3.0481084 | 23.1223322 | |
| 0.5004893 | 0.7313767 | 0.5100820 | −7.5488568 | 4.0425995 | 23.0612498 | |
| 0.5002164 | 0.7167913 | 0.4833567 | −10.8718732 | 0.3965207 | 22.9701882 | |
| 0.5000000 | 0.8645165 | 0.3540178 | −18.9940358 | 0.0810628 | 22.8452536 | |
Optimal construction variables of HBWO-JS and other algorithms for solving CSID problem.
| Algorithms . | Variables . | |||||
|---|---|---|---|---|---|---|
| z1 . | z2 . | z3 . | z4 . | z5 . | z6 . | |
| RSA | 0.5582391 | 1.2510718 | 0.5553102 | 1.2858772 | 0.6058203 | 1.2508719 |
| AHA | 0.5357509 | 1.1755893 | 0.5223455 | 1.2246030 | 0.5197215 | 1.3372923 |
| DO | 0.5000233 | 1.2206681 | 0.5000134 | 1.2325457 | 0.5173562 | 1.2927733 |
| WSO | 0.5098872 | 1.1833252 | 0.5150247 | 1.2475072 | 0.5325131 | 1.2370275 |
| ARO | 0.5056171 | 1.1858457 | 0.5055551 | 1.2306904 | 0.5193284 | 1.3442855 |
| SO | 0.5150859 | 1.1761861 | 0.5035944 | 1.2313418 | 0.5017206 | 1.2941253 |
| JS | 0.5006119 | 1.1651128 | 0.5001726 | 1.2514078 | 0.5005317 | 1.4792699 |
| HBWO-JS | 0.5000000 | 1.1196305 | 0.5000000 | 1.2973362 | 0.5000000 | 1.4998457 |
| Variables | Minimum weight | |||||
| z7 | z8 | z9 | z10 | z11 | ||
| 0.5906219 | 0.6202851 | 0.4431583 | −3.8282799 | 3.6443327 | 24.7832110 | |
| 0.5003422 | 0.6426417 | 0.5525141 | −5.2445401 | 2.8725694 | 23.2940282 | |
| 0.5000331 | 0.5874500 | 0.2246874 | −7.1445584 | 4.0793353 | 23.2905574 | |
| 0.5025410 | 0.7479548 | 0.4647983 | −7.3707008 | 4.0923118 | 23.2884132 | |
| 0.5007215 | 0.7262638 | 0.4336405 | −6.4414053 | 3.0481084 | 23.1223322 | |
| 0.5004893 | 0.7313767 | 0.5100820 | −7.5488568 | 4.0425995 | 23.0612498 | |
| 0.5002164 | 0.7167913 | 0.4833567 | −10.8718732 | 0.3965207 | 22.9701882 | |
| 0.5000000 | 0.8645165 | 0.3540178 | −18.9940358 | 0.0810628 | 22.8452536 | |
| Algorithms . | Variables . | |||||
|---|---|---|---|---|---|---|
| z1 . | z2 . | z3 . | z4 . | z5 . | z6 . | |
| RSA | 0.5582391 | 1.2510718 | 0.5553102 | 1.2858772 | 0.6058203 | 1.2508719 |
| AHA | 0.5357509 | 1.1755893 | 0.5223455 | 1.2246030 | 0.5197215 | 1.3372923 |
| DO | 0.5000233 | 1.2206681 | 0.5000134 | 1.2325457 | 0.5173562 | 1.2927733 |
| WSO | 0.5098872 | 1.1833252 | 0.5150247 | 1.2475072 | 0.5325131 | 1.2370275 |
| ARO | 0.5056171 | 1.1858457 | 0.5055551 | 1.2306904 | 0.5193284 | 1.3442855 |
| SO | 0.5150859 | 1.1761861 | 0.5035944 | 1.2313418 | 0.5017206 | 1.2941253 |
| JS | 0.5006119 | 1.1651128 | 0.5001726 | 1.2514078 | 0.5005317 | 1.4792699 |
| HBWO-JS | 0.5000000 | 1.1196305 | 0.5000000 | 1.2973362 | 0.5000000 | 1.4998457 |
| Variables | Minimum weight | |||||
| z7 | z8 | z9 | z10 | z11 | ||
| 0.5906219 | 0.6202851 | 0.4431583 | −3.8282799 | 3.6443327 | 24.7832110 | |
| 0.5003422 | 0.6426417 | 0.5525141 | −5.2445401 | 2.8725694 | 23.2940282 | |
| 0.5000331 | 0.5874500 | 0.2246874 | −7.1445584 | 4.0793353 | 23.2905574 | |
| 0.5025410 | 0.7479548 | 0.4647983 | −7.3707008 | 4.0923118 | 23.2884132 | |
| 0.5007215 | 0.7262638 | 0.4336405 | −6.4414053 | 3.0481084 | 23.1223322 | |
| 0.5004893 | 0.7313767 | 0.5100820 | −7.5488568 | 4.0425995 | 23.0612498 | |
| 0.5002164 | 0.7167913 | 0.4833567 | −10.8718732 | 0.3965207 | 22.9701882 | |
| 0.5000000 | 0.8645165 | 0.3540178 | −18.9940358 | 0.0810628 | 22.8452536 | |
Comparisons of statistical results using reported algorithms in literature for solving CSID problem.
| Algorithms . | Best . | Worst . | Mean . | Std . |
|---|---|---|---|---|
| RSA | 23.90374445 | 25.80341649 | 24.783211 | 0.457309119 |
| AHA | 22.88597103 | 23.92931122 | 23.29402815 | 0.277195485 |
| DO | 22.84963807 | 23.9773463 | 23.29055741 | 0.380845363 |
| WSO | 22.87044815 | 23.88332683 | 23.28841321 | 0.313219992 |
| ARO | 22.87901425 | 23.74793418 | 23.12233217 | 0.231916421 |
| SO | 22.84374882 | 23.90906827 | 23.06124984 | 0.272873687 |
| JS | 22.86161303 | 23.26402502 | 22.97018823 | 0.127257418 |
| HBWO-JS | 22.8435394 | 22.84742107 | 22.8452536 | 0.001220161 |
| Algorithms . | Best . | Worst . | Mean . | Std . |
|---|---|---|---|---|
| RSA | 23.90374445 | 25.80341649 | 24.783211 | 0.457309119 |
| AHA | 22.88597103 | 23.92931122 | 23.29402815 | 0.277195485 |
| DO | 22.84963807 | 23.9773463 | 23.29055741 | 0.380845363 |
| WSO | 22.87044815 | 23.88332683 | 23.28841321 | 0.313219992 |
| ARO | 22.87901425 | 23.74793418 | 23.12233217 | 0.231916421 |
| SO | 22.84374882 | 23.90906827 | 23.06124984 | 0.272873687 |
| JS | 22.86161303 | 23.26402502 | 22.97018823 | 0.127257418 |
| HBWO-JS | 22.8435394 | 22.84742107 | 22.8452536 | 0.001220161 |
Comparisons of statistical results using reported algorithms in literature for solving CSID problem.
| Algorithms . | Best . | Worst . | Mean . | Std . |
|---|---|---|---|---|
| RSA | 23.90374445 | 25.80341649 | 24.783211 | 0.457309119 |
| AHA | 22.88597103 | 23.92931122 | 23.29402815 | 0.277195485 |
| DO | 22.84963807 | 23.9773463 | 23.29055741 | 0.380845363 |
| WSO | 22.87044815 | 23.88332683 | 23.28841321 | 0.313219992 |
| ARO | 22.87901425 | 23.74793418 | 23.12233217 | 0.231916421 |
| SO | 22.84374882 | 23.90906827 | 23.06124984 | 0.272873687 |
| JS | 22.86161303 | 23.26402502 | 22.97018823 | 0.127257418 |
| HBWO-JS | 22.8435394 | 22.84742107 | 22.8452536 | 0.001220161 |
| Algorithms . | Best . | Worst . | Mean . | Std . |
|---|---|---|---|---|
| RSA | 23.90374445 | 25.80341649 | 24.783211 | 0.457309119 |
| AHA | 22.88597103 | 23.92931122 | 23.29402815 | 0.277195485 |
| DO | 22.84963807 | 23.9773463 | 23.29055741 | 0.380845363 |
| WSO | 22.87044815 | 23.88332683 | 23.28841321 | 0.313219992 |
| ARO | 22.87901425 | 23.74793418 | 23.12233217 | 0.231916421 |
| SO | 22.84374882 | 23.90906827 | 23.06124984 | 0.272873687 |
| JS | 22.86161303 | 23.26402502 | 22.97018823 | 0.127257418 |
| HBWO-JS | 22.8435394 | 22.84742107 | 22.8452536 | 0.001220161 |
5.3 Single stage cylindrical gear
The optimization objective of the single stage cylindrical gear (SSCG) problem is to find the lightest reducer weight and to satisfy sixteen difficult mechanical optimization constraints (Cheng et al., 2022). A diagrammatic representation of the single-stage cylindrical gear reducer problem is given in Fig. 19. Based on the general model of the optimization model, the optimization model of the SSCG problem is provided below.

Suppose:
Minimize:
Subject to:
Variable range:
|$50 \le {t_4} \le 150,$||$50 \le {t_5} \le 200,$||$15 \le {t_6} \le 30,$|and t4, t5, t6 are integers.
The optimization results of the proposed HBWO-JS algorithm for SSCG are experimentally compared with WSO, SO, RSA, DO, ARO, AHA, and JS. The optimization results for the independent variables are provided in Table 16. The statistical results for the relevant runs of 30 times are given in Table 17. According to Table 16, the amount of fitness function of SSCG obtained by HBWO-JS (1.42E+07) is smaller than the optimization results of the other seven methods. In general, HBWO-JS does a good job in global search. In addition, the experimental results show that HBWO-JS can satisfy the optimization influence of engineering difficulty and find the minimum weight significantly.
Optimal construction variables of HBWO-JS and other algorithms for solving SSCG problem.
| Algorithms . | Variables . | Minimum weight . | |||||
|---|---|---|---|---|---|---|---|
| z1 . | z2 . | z3 . | z4 . | z5 . | z6 . | ||
| RSA | 85.87450 | 163.76939 | 6 | 65 | 79 | 20 | 2.72E+06 |
| WSO | 53.42474 | 150.01887 | 6 | 68 | 84 | 29 | 4.68E+05 |
| AHA | 63.98859 | 150.00000 | 8 | 68 | 84 | 22 | 1.96E+05 |
| ARO | 60.27978 | 150.00002 | 8 | 68 | 84 | 22 | 1.71E+05 |
| DO | 50.48122 | 150.00000 | 10 | 68 | 84 | 18 | 1.35E+05 |
| JS | 65.01274 | 150.00000 | 8 | 68 | 84 | 24 | 1.57E+05 |
| SO | 53.38515 | 150.00000 | 10 | 68 | 84 | 20 | 2.33E+05 |
| HBWO-JS | 50.00000 | 150.00000 | 10 | 68 | 84 | 18 | 0.00E+00 |
| Algorithms . | Variables . | Minimum weight . | |||||
|---|---|---|---|---|---|---|---|
| z1 . | z2 . | z3 . | z4 . | z5 . | z6 . | ||
| RSA | 85.87450 | 163.76939 | 6 | 65 | 79 | 20 | 2.72E+06 |
| WSO | 53.42474 | 150.01887 | 6 | 68 | 84 | 29 | 4.68E+05 |
| AHA | 63.98859 | 150.00000 | 8 | 68 | 84 | 22 | 1.96E+05 |
| ARO | 60.27978 | 150.00002 | 8 | 68 | 84 | 22 | 1.71E+05 |
| DO | 50.48122 | 150.00000 | 10 | 68 | 84 | 18 | 1.35E+05 |
| JS | 65.01274 | 150.00000 | 8 | 68 | 84 | 24 | 1.57E+05 |
| SO | 53.38515 | 150.00000 | 10 | 68 | 84 | 20 | 2.33E+05 |
| HBWO-JS | 50.00000 | 150.00000 | 10 | 68 | 84 | 18 | 0.00E+00 |
Optimal construction variables of HBWO-JS and other algorithms for solving SSCG problem.
| Algorithms . | Variables . | Minimum weight . | |||||
|---|---|---|---|---|---|---|---|
| z1 . | z2 . | z3 . | z4 . | z5 . | z6 . | ||
| RSA | 85.87450 | 163.76939 | 6 | 65 | 79 | 20 | 2.72E+06 |
| WSO | 53.42474 | 150.01887 | 6 | 68 | 84 | 29 | 4.68E+05 |
| AHA | 63.98859 | 150.00000 | 8 | 68 | 84 | 22 | 1.96E+05 |
| ARO | 60.27978 | 150.00002 | 8 | 68 | 84 | 22 | 1.71E+05 |
| DO | 50.48122 | 150.00000 | 10 | 68 | 84 | 18 | 1.35E+05 |
| JS | 65.01274 | 150.00000 | 8 | 68 | 84 | 24 | 1.57E+05 |
| SO | 53.38515 | 150.00000 | 10 | 68 | 84 | 20 | 2.33E+05 |
| HBWO-JS | 50.00000 | 150.00000 | 10 | 68 | 84 | 18 | 0.00E+00 |
| Algorithms . | Variables . | Minimum weight . | |||||
|---|---|---|---|---|---|---|---|
| z1 . | z2 . | z3 . | z4 . | z5 . | z6 . | ||
| RSA | 85.87450 | 163.76939 | 6 | 65 | 79 | 20 | 2.72E+06 |
| WSO | 53.42474 | 150.01887 | 6 | 68 | 84 | 29 | 4.68E+05 |
| AHA | 63.98859 | 150.00000 | 8 | 68 | 84 | 22 | 1.96E+05 |
| ARO | 60.27978 | 150.00002 | 8 | 68 | 84 | 22 | 1.71E+05 |
| DO | 50.48122 | 150.00000 | 10 | 68 | 84 | 18 | 1.35E+05 |
| JS | 65.01274 | 150.00000 | 8 | 68 | 84 | 24 | 1.57E+05 |
| SO | 53.38515 | 150.00000 | 10 | 68 | 84 | 20 | 2.33E+05 |
| HBWO-JS | 50.00000 | 150.00000 | 10 | 68 | 84 | 18 | 0.00E+00 |
Comparisons of statistical results using reported algorithms in literature for solving SSCG problem.
| Algorithms . | Best . | Worst . | Mean . | Std . |
|---|---|---|---|---|
| RSA | 1.03E+07 | 1.97E+07 | 1.46E+07 | 2.72E+06 |
| WSO | 1.36E+07 | 1.47E+07 | 1.43E+07 | 4.68E+05 |
| AHA | 1.55E+07 | 1.62E+07 | 1.57E+07 | 1.96E+05 |
| ARO | 1.55E+07 | 1.62E+07 | 1.57E+07 | 1.71E+05 |
| DO | 1.57E+07 | 1.62E+07 | 1.61E+07 | 1.35E+05 |
| JS | 1.54E+07 | 1.62E+07 | 1.57E+07 | 1.57E+05 |
| SO | 1.56E+07 | 1.62E+07 | 1.61E+07 | 2.33E+05 |
| HBWO-JS | 1.42E+07 | 1.42E+07 | 1.42E+07 | 0.00E+00 |
| Algorithms . | Best . | Worst . | Mean . | Std . |
|---|---|---|---|---|
| RSA | 1.03E+07 | 1.97E+07 | 1.46E+07 | 2.72E+06 |
| WSO | 1.36E+07 | 1.47E+07 | 1.43E+07 | 4.68E+05 |
| AHA | 1.55E+07 | 1.62E+07 | 1.57E+07 | 1.96E+05 |
| ARO | 1.55E+07 | 1.62E+07 | 1.57E+07 | 1.71E+05 |
| DO | 1.57E+07 | 1.62E+07 | 1.61E+07 | 1.35E+05 |
| JS | 1.54E+07 | 1.62E+07 | 1.57E+07 | 1.57E+05 |
| SO | 1.56E+07 | 1.62E+07 | 1.61E+07 | 2.33E+05 |
| HBWO-JS | 1.42E+07 | 1.42E+07 | 1.42E+07 | 0.00E+00 |
Comparisons of statistical results using reported algorithms in literature for solving SSCG problem.
| Algorithms . | Best . | Worst . | Mean . | Std . |
|---|---|---|---|---|
| RSA | 1.03E+07 | 1.97E+07 | 1.46E+07 | 2.72E+06 |
| WSO | 1.36E+07 | 1.47E+07 | 1.43E+07 | 4.68E+05 |
| AHA | 1.55E+07 | 1.62E+07 | 1.57E+07 | 1.96E+05 |
| ARO | 1.55E+07 | 1.62E+07 | 1.57E+07 | 1.71E+05 |
| DO | 1.57E+07 | 1.62E+07 | 1.61E+07 | 1.35E+05 |
| JS | 1.54E+07 | 1.62E+07 | 1.57E+07 | 1.57E+05 |
| SO | 1.56E+07 | 1.62E+07 | 1.61E+07 | 2.33E+05 |
| HBWO-JS | 1.42E+07 | 1.42E+07 | 1.42E+07 | 0.00E+00 |
| Algorithms . | Best . | Worst . | Mean . | Std . |
|---|---|---|---|---|
| RSA | 1.03E+07 | 1.97E+07 | 1.46E+07 | 2.72E+06 |
| WSO | 1.36E+07 | 1.47E+07 | 1.43E+07 | 4.68E+05 |
| AHA | 1.55E+07 | 1.62E+07 | 1.57E+07 | 1.96E+05 |
| ARO | 1.55E+07 | 1.62E+07 | 1.57E+07 | 1.71E+05 |
| DO | 1.57E+07 | 1.62E+07 | 1.61E+07 | 1.35E+05 |
| JS | 1.54E+07 | 1.62E+07 | 1.57E+07 | 1.57E+05 |
| SO | 1.56E+07 | 1.62E+07 | 1.61E+07 | 2.33E+05 |
| HBWO-JS | 1.42E+07 | 1.42E+07 | 1.42E+07 | 0.00E+00 |
6. Truss Topology Optimization Design
Ensuring the minimization of structural weight under a given constraint is the most important goal of all Truss Topology Optimization Design (TTOD). Since many unnecessary members and nodes may be present in a complete truss structure, topology optimization provides the opportunity to remove unnecessary members and nodes. Topology optimization will be particularly advantageous in this regard when the nodes under study require relatively high costs. TTOD usually considers a combination of stress, displacement, buckling, and frequency constraints. These complex constraints make it not an easy task to accomplish such optimization, mainly because of the large search space, non-linearity, and non-convexity. As an emerging optimization algorithm, the NH algorithm can effectively solve the complex constraint problem because it does not require gradient information. And the ability of the NH algorithm to find the global optimum for TTOD (Hare et al., 2013) has been demonstrated. This section uses the proposed HBWO-JS algorithm to verify the optimization efficiency in solving truss topology optimization problems under complex constraints. The experimental simulations give two specific cases, including 24-truss topology optimization and 72-truss topology optimization.
6.1. Introduction to the optimization model of TTOD
The ultimate goal of TTOD is to find the truss structure and layout that makes the ground structure the lightest load-bearing (Kaveh & Zolghadr, 2013). Two types of nodes are included in the ground structure: essential nodes and optional nodes. Among them, the nodes that quickly carry structural, load, and nodal loads are called mandatory nodes. On the other hand, the optional nodes represent nodes that are not compulsorily required and are present to help better distribute the stresses in the members. This section gives the main constraints of relevance, including those subject to static and dynamic constrained by natural frequency, element stress, node displacement, Euler buckling, and motion stability (Tejani et al., 2019). The optimization algorithm chosen, on the other hand, determines the problem of the removal of structural reinforcement that forms the layout or topology of the structure through the optimization process. The mathematical optimization model of TTOD is shown below.
Suppose:
Minimize:
where p represents the number of component elements, q is the number of constituent elements and nodes, and X denotes the set of independent variables. In addition, Li, ρi, and Ai denote the element length, density, and cross-sectional area of the ith component element, respectively. cj is the mass of node j.
Subject to:
where the constraint represents the stress constraint and the stress is denoted as σi.
where the constraint represents the displacement constraint, and δj is the displacement of node j.
where the above equation can give the Eulerian buckling equation, and the definition of σiE is given below.
The below equation can give the inherent frequency constraint, and fr is the inherent frequency of the structure in the rth mode.
The equation representing the cross-section’s upper and lower limits is given below.
The optimization process requires a penalty function to be applied to the constraints to guarantee the optimization conditions (Tejani et al., 2018). The penalty term will become zero if the constraints are not violated. Otherwise, the constraint violation will be penalized by a positive penalty term. The specific penalty function is as follows.
where
where p represents the degree of constraint violation and is limited by p*i, n represents the active constraint. ε is assigned equal to 2 to ensure the balance between exploitation and exploration during experimental validation.
6.2. 24-truss topology optimization
The topology of the 24-bar truss is shown in Fig. 20, where the structure consists of 24 members and eight nodes. In addition, six nodes must be present in the structure. The 24-bar truss problem has various loading conditions: (1) F1 = 5×104 N, F2 = 0 N. (2) F1 = 0 N, F2 = 5×104 N. The concentrated mass on node 3 is 500kg. In addition, the stress and displacement constraints are 173.43 MPa and 10 mm, respectively. The intrinsic frequency constraint f1 ≥ 30 Hz. the critical in the continuous cross-sectional area. The material properties E = 6.9 × 1010 Pa and ρ = 2740 kg m−3. Table 18 provides the results for 30 independent runs, and the best results for the average values are highlighted in bold. “Remove” indicates the deletion of the corresponding component.

Optimal construction variables and best weight of HBWO-JS and other algorithms for solving 24-bar truss structure problem (without lumped mass).
| Variables . | HBWO-JS . | JS . | AHA . | ARO . | DO . | SO . | WSO . | RSA . |
|---|---|---|---|---|---|---|---|---|
| A1(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | 7.20578 |
| A2(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | 1.16156 |
| A3(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| A4(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| A5(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| A6(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| A7(cm2) | 19.34440 | 26.96870 | 21.86849 | 24.48660 | 19.10780 | 18.75999 | 19.21593 | 21.84101 |
| A8(cm2) | 8.31023 | 8.97423 | 7.63422 | 13.14203 | 7.05513 | 2.62543 | 3.24392 | 8.51581 |
| A9(cm2) | Removed | 3.35920 | 9.51430 | Removed | Removed | Removed | Removed | 21.46295 |
| A10(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| A11(cm2) | Removed | Removed | Removed | Removed | 3.81133 | Removed | Removed | Removed |
| A12(cm2) | 4.57058 | 12.56140 | 9.88465 | 11.73777 | Removed | 4.06399 | 2.47841 | 14.22146 |
| A13(cm2) | 17.15647 | Removed | Removed | Removed | 15.05648 | 19.67481 | 25.12797 | Removed |
| A14(cm2) | 1.43340 | 10.06953 | 8.54674 | 18.43253 | 4.63104 | Removed | Removed | Removed |
| A15(cm2) | 5.60960 | 6.48394 | 9.40339 | 4.07311 | Removed | 3.65589 | 4.00197 | 21.88813 |
| A16(cm2) | 23.69792 | 24.18504 | 24.00292 | 24.13453 | 12.03459 | 24.08025 | 23.01496 | 28.35124 |
| A17(cm2) | Removed | Removed | Removed | Removed | 11.10583 | 1.49481 | 5.21012 | Removed |
| A18(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | 5.05067 | 14.03055 |
| A19(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| A20(cm2) | Removed | Removed | Removed | Removed | 9.10922 | Removed | Removed | 14.75830 |
| A21(cm2) | Removed | Removed | Removed | Removed | 13.52817 | 6.93141 | 3.99957 | 10.69145 |
| A22(cm2) | Removed | 7.11151 | 4.54303 | Removed | 6.18288 | 1.87872 | 10.04527 | 9.29453 |
| A23(cm2) | 2.23298 | Removed | Removed | 9.69296 | 7.77161 | Removed | Removed | 5.41125 |
| A24(cm2) | 2.24076 | 2.32557 | 8.45219 | 10.53789 | Removed | Removed | Removed | Removed |
| Best weight | 133.49913 | 137.70058 | 149.56415 | 150.17416 | 154.19145 | 140.01922 | 161.05027 | 234.38332 |
| Variables . | HBWO-JS . | JS . | AHA . | ARO . | DO . | SO . | WSO . | RSA . |
|---|---|---|---|---|---|---|---|---|
| A1(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | 7.20578 |
| A2(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | 1.16156 |
| A3(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| A4(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| A5(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| A6(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| A7(cm2) | 19.34440 | 26.96870 | 21.86849 | 24.48660 | 19.10780 | 18.75999 | 19.21593 | 21.84101 |
| A8(cm2) | 8.31023 | 8.97423 | 7.63422 | 13.14203 | 7.05513 | 2.62543 | 3.24392 | 8.51581 |
| A9(cm2) | Removed | 3.35920 | 9.51430 | Removed | Removed | Removed | Removed | 21.46295 |
| A10(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| A11(cm2) | Removed | Removed | Removed | Removed | 3.81133 | Removed | Removed | Removed |
| A12(cm2) | 4.57058 | 12.56140 | 9.88465 | 11.73777 | Removed | 4.06399 | 2.47841 | 14.22146 |
| A13(cm2) | 17.15647 | Removed | Removed | Removed | 15.05648 | 19.67481 | 25.12797 | Removed |
| A14(cm2) | 1.43340 | 10.06953 | 8.54674 | 18.43253 | 4.63104 | Removed | Removed | Removed |
| A15(cm2) | 5.60960 | 6.48394 | 9.40339 | 4.07311 | Removed | 3.65589 | 4.00197 | 21.88813 |
| A16(cm2) | 23.69792 | 24.18504 | 24.00292 | 24.13453 | 12.03459 | 24.08025 | 23.01496 | 28.35124 |
| A17(cm2) | Removed | Removed | Removed | Removed | 11.10583 | 1.49481 | 5.21012 | Removed |
| A18(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | 5.05067 | 14.03055 |
| A19(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| A20(cm2) | Removed | Removed | Removed | Removed | 9.10922 | Removed | Removed | 14.75830 |
| A21(cm2) | Removed | Removed | Removed | Removed | 13.52817 | 6.93141 | 3.99957 | 10.69145 |
| A22(cm2) | Removed | 7.11151 | 4.54303 | Removed | 6.18288 | 1.87872 | 10.04527 | 9.29453 |
| A23(cm2) | 2.23298 | Removed | Removed | 9.69296 | 7.77161 | Removed | Removed | 5.41125 |
| A24(cm2) | 2.24076 | 2.32557 | 8.45219 | 10.53789 | Removed | Removed | Removed | Removed |
| Best weight | 133.49913 | 137.70058 | 149.56415 | 150.17416 | 154.19145 | 140.01922 | 161.05027 | 234.38332 |
Optimal construction variables and best weight of HBWO-JS and other algorithms for solving 24-bar truss structure problem (without lumped mass).
| Variables . | HBWO-JS . | JS . | AHA . | ARO . | DO . | SO . | WSO . | RSA . |
|---|---|---|---|---|---|---|---|---|
| A1(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | 7.20578 |
| A2(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | 1.16156 |
| A3(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| A4(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| A5(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| A6(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| A7(cm2) | 19.34440 | 26.96870 | 21.86849 | 24.48660 | 19.10780 | 18.75999 | 19.21593 | 21.84101 |
| A8(cm2) | 8.31023 | 8.97423 | 7.63422 | 13.14203 | 7.05513 | 2.62543 | 3.24392 | 8.51581 |
| A9(cm2) | Removed | 3.35920 | 9.51430 | Removed | Removed | Removed | Removed | 21.46295 |
| A10(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| A11(cm2) | Removed | Removed | Removed | Removed | 3.81133 | Removed | Removed | Removed |
| A12(cm2) | 4.57058 | 12.56140 | 9.88465 | 11.73777 | Removed | 4.06399 | 2.47841 | 14.22146 |
| A13(cm2) | 17.15647 | Removed | Removed | Removed | 15.05648 | 19.67481 | 25.12797 | Removed |
| A14(cm2) | 1.43340 | 10.06953 | 8.54674 | 18.43253 | 4.63104 | Removed | Removed | Removed |
| A15(cm2) | 5.60960 | 6.48394 | 9.40339 | 4.07311 | Removed | 3.65589 | 4.00197 | 21.88813 |
| A16(cm2) | 23.69792 | 24.18504 | 24.00292 | 24.13453 | 12.03459 | 24.08025 | 23.01496 | 28.35124 |
| A17(cm2) | Removed | Removed | Removed | Removed | 11.10583 | 1.49481 | 5.21012 | Removed |
| A18(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | 5.05067 | 14.03055 |
| A19(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| A20(cm2) | Removed | Removed | Removed | Removed | 9.10922 | Removed | Removed | 14.75830 |
| A21(cm2) | Removed | Removed | Removed | Removed | 13.52817 | 6.93141 | 3.99957 | 10.69145 |
| A22(cm2) | Removed | 7.11151 | 4.54303 | Removed | 6.18288 | 1.87872 | 10.04527 | 9.29453 |
| A23(cm2) | 2.23298 | Removed | Removed | 9.69296 | 7.77161 | Removed | Removed | 5.41125 |
| A24(cm2) | 2.24076 | 2.32557 | 8.45219 | 10.53789 | Removed | Removed | Removed | Removed |
| Best weight | 133.49913 | 137.70058 | 149.56415 | 150.17416 | 154.19145 | 140.01922 | 161.05027 | 234.38332 |
| Variables . | HBWO-JS . | JS . | AHA . | ARO . | DO . | SO . | WSO . | RSA . |
|---|---|---|---|---|---|---|---|---|
| A1(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | 7.20578 |
| A2(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | 1.16156 |
| A3(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| A4(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| A5(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| A6(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| A7(cm2) | 19.34440 | 26.96870 | 21.86849 | 24.48660 | 19.10780 | 18.75999 | 19.21593 | 21.84101 |
| A8(cm2) | 8.31023 | 8.97423 | 7.63422 | 13.14203 | 7.05513 | 2.62543 | 3.24392 | 8.51581 |
| A9(cm2) | Removed | 3.35920 | 9.51430 | Removed | Removed | Removed | Removed | 21.46295 |
| A10(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| A11(cm2) | Removed | Removed | Removed | Removed | 3.81133 | Removed | Removed | Removed |
| A12(cm2) | 4.57058 | 12.56140 | 9.88465 | 11.73777 | Removed | 4.06399 | 2.47841 | 14.22146 |
| A13(cm2) | 17.15647 | Removed | Removed | Removed | 15.05648 | 19.67481 | 25.12797 | Removed |
| A14(cm2) | 1.43340 | 10.06953 | 8.54674 | 18.43253 | 4.63104 | Removed | Removed | Removed |
| A15(cm2) | 5.60960 | 6.48394 | 9.40339 | 4.07311 | Removed | 3.65589 | 4.00197 | 21.88813 |
| A16(cm2) | 23.69792 | 24.18504 | 24.00292 | 24.13453 | 12.03459 | 24.08025 | 23.01496 | 28.35124 |
| A17(cm2) | Removed | Removed | Removed | Removed | 11.10583 | 1.49481 | 5.21012 | Removed |
| A18(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | 5.05067 | 14.03055 |
| A19(cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| A20(cm2) | Removed | Removed | Removed | Removed | 9.10922 | Removed | Removed | 14.75830 |
| A21(cm2) | Removed | Removed | Removed | Removed | 13.52817 | 6.93141 | 3.99957 | 10.69145 |
| A22(cm2) | Removed | 7.11151 | 4.54303 | Removed | 6.18288 | 1.87872 | 10.04527 | 9.29453 |
| A23(cm2) | 2.23298 | Removed | Removed | 9.69296 | 7.77161 | Removed | Removed | 5.41125 |
| A24(cm2) | 2.24076 | 2.32557 | 8.45219 | 10.53789 | Removed | Removed | Removed | Removed |
| Best weight | 133.49913 | 137.70058 | 149.56415 | 150.17416 | 154.19145 | 140.01922 | 161.05027 | 234.38332 |
The numerical results in Table 18 show the minimum mass values obtained by all algorithms when the structural constraints are satisfied. The population of all algorithms is 30, and the maximum number of iterations is 500. The minimum mass obtained by HBWO-JS is 133.49913 kg. The results obtained by HBWO-JS outperform the other seven compared algorithms. The best results for JS, AHA, ARO, DO, SO, WSO, and RSA is 137.70058, 149.56415, 150.17416, 154.19145, 140.01922, 161.05027, and 234.38332 kg. The second-ranking is JS. Figure 21 provides the relative virtual effect plots for different algorithms after removing the unwanted structures. The JS and AHA have the same structure. At the same time, the other algorithms have different topological shapes. However, the proposed HBWO-JS requires nine building blocks (Fig. 21a), but many have a cross-section of only 1 cm2.

24-bar truss topology optimization structure: (a) HBWO-JS; (b) JS; (c) AHA; (d) ARO; (e) DO; (f) SO; (g) WSO; (h) RSA.
Figure 22 provides the convergence plots of all algorithms for the 24-truss optimization problem. The convergence plots show that HGWO-JS converges comparably to the other algorithms in the early stages, while RSA converges more slowly. After the 250th iteration, HGWO-JS, ARO, DO, and AHA converges to the vicinity of the local solution. The experimental conclusion shows that HGWO-JS has good convergence performance and optimization effect.

Convergence trends of the 24-bar truss structure optimization problem with the HBWO-JS, JS, AHA, ARO, DO, SO, WSO, RSA algorithm.
6.3. 72-truss topology optimization
The topology of the 72-bar truss is shown in Fig. 23. The structure consists of 72 members and 20 nodes. 72-bar truss problem has various loading conditions: (1) F1x= F1y = 22.25kN and F1z = −22.25kN. (2) F1z = F2z = F3z = F4z = −22.25KN. The concentrated masses on nodes 1, 2, 3, and 4 are 2270 kg. In addition, the stress and displacement constraints are σmaxi = 172.375 MPa and δ1x&1y&2x&2y&3x&3y&4x&4y = 6.35 mm. Natural frequency constraints are f1 ≥ 4 Hz and f3 ≥ 6 Hz. The critical area is 1 cm2. Material properties E = 6.895×1010Pa and ρ = 2767.99 kg m−3. Table 19 provides the results of 30 independent runs, and the best results of the average values are marked in bold. “Remove” indicates the deletion of the corresponding component.

Optimal construction variables and best weight of HBWO-JS and other algorithms for solving 72-bar truss structure problem (without lumped mass).
| Variables . | HBWO-JS . | JS . | AHA . | ARO . | DO . | SO . | WSO . | RSA . |
|---|---|---|---|---|---|---|---|---|
| Group1 A1∼A4 (cm2) | 4.59446 | 5.35270 | 6.39851 | 5.10661 | 5.07816 | 5.99714 | 7.43496 | 13.27162 |
| Group2 A5∼A12 (cm2) | 8.71029 | 9.24390 | 12.05449 | 10.88687 | 10.94558 | 10.96412 | 8.25410 | 7.39752 |
| Group3 A13∼A16 (cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | 6.36611 |
| Group4 A17∼A18 (cm2) | 9.12775 | 10.34671 | Removed | Removed | Removed | Removed | 10.02505 | 9.82170 |
| Group5 A19∼A22 (cm2) | 10.15482 | 8.53522 | 10.38949 | 10.19986 | 9.13551 | 5.98834 | 11.92909 | 12.88030 |
| Group6 A23∼A30 (cm2) | 8.21962 | 9.14798 | 7.97586 | 6.06223 | 9.18191 | 7.88126 | 8.11222 | 10.10056 |
| Group7 A31∼A34 (cm2) | 3.25743 | Removed | 3.49691 | 3.33075 | 3.27975 | 2.61536 | Removed | 10.07807 |
| Group8 A35∼A36 (cm2) | Removed | Removed | 6.38376 | 6.32638 | 5.98996 | 5.56496 | Removed | Removed |
| Group9 A37∼A40 (cm2) | 12.53245 | 15.79730 | 10.89588 | 13.18683 | 13.65711 | 15.22403 | 6.81452 | 9.63412 |
| Group10 A41∼A48 (cm2) | 8.42090 | 8.18269 | 6.77067 | 9.04570 | 7.44328 | 8.77231 | 8.48838 | 8.50997 |
| Group11 A49∼A52 (cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| Group12 A53∼A54 (cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| Group13 A55∼A58 (cm2) | 15.32671 | 13.78927 | 17.06051 | 15.01429 | 14.90610 | 17.01520 | 26.43803 | 15.06306 |
| Group14 A59∼A66 (cm2) | 7.75289 | 7.39692 | 7.47352 | 8.28850 | 6.55719 | 6.18966 | 12.27899 | 9.06675 |
| Group15 A67∼A70 (cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| Group16 A71∼A72 (cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | 6.06917 |
| Best weight (kg) | 453.18004 | 460.62844 | 455.25465 | 453.56728 | 453.56728 | 455.25465 | 479.89210 | 542.34685 |
| Variables . | HBWO-JS . | JS . | AHA . | ARO . | DO . | SO . | WSO . | RSA . |
|---|---|---|---|---|---|---|---|---|
| Group1 A1∼A4 (cm2) | 4.59446 | 5.35270 | 6.39851 | 5.10661 | 5.07816 | 5.99714 | 7.43496 | 13.27162 |
| Group2 A5∼A12 (cm2) | 8.71029 | 9.24390 | 12.05449 | 10.88687 | 10.94558 | 10.96412 | 8.25410 | 7.39752 |
| Group3 A13∼A16 (cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | 6.36611 |
| Group4 A17∼A18 (cm2) | 9.12775 | 10.34671 | Removed | Removed | Removed | Removed | 10.02505 | 9.82170 |
| Group5 A19∼A22 (cm2) | 10.15482 | 8.53522 | 10.38949 | 10.19986 | 9.13551 | 5.98834 | 11.92909 | 12.88030 |
| Group6 A23∼A30 (cm2) | 8.21962 | 9.14798 | 7.97586 | 6.06223 | 9.18191 | 7.88126 | 8.11222 | 10.10056 |
| Group7 A31∼A34 (cm2) | 3.25743 | Removed | 3.49691 | 3.33075 | 3.27975 | 2.61536 | Removed | 10.07807 |
| Group8 A35∼A36 (cm2) | Removed | Removed | 6.38376 | 6.32638 | 5.98996 | 5.56496 | Removed | Removed |
| Group9 A37∼A40 (cm2) | 12.53245 | 15.79730 | 10.89588 | 13.18683 | 13.65711 | 15.22403 | 6.81452 | 9.63412 |
| Group10 A41∼A48 (cm2) | 8.42090 | 8.18269 | 6.77067 | 9.04570 | 7.44328 | 8.77231 | 8.48838 | 8.50997 |
| Group11 A49∼A52 (cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| Group12 A53∼A54 (cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| Group13 A55∼A58 (cm2) | 15.32671 | 13.78927 | 17.06051 | 15.01429 | 14.90610 | 17.01520 | 26.43803 | 15.06306 |
| Group14 A59∼A66 (cm2) | 7.75289 | 7.39692 | 7.47352 | 8.28850 | 6.55719 | 6.18966 | 12.27899 | 9.06675 |
| Group15 A67∼A70 (cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| Group16 A71∼A72 (cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | 6.06917 |
| Best weight (kg) | 453.18004 | 460.62844 | 455.25465 | 453.56728 | 453.56728 | 455.25465 | 479.89210 | 542.34685 |
Optimal construction variables and best weight of HBWO-JS and other algorithms for solving 72-bar truss structure problem (without lumped mass).
| Variables . | HBWO-JS . | JS . | AHA . | ARO . | DO . | SO . | WSO . | RSA . |
|---|---|---|---|---|---|---|---|---|
| Group1 A1∼A4 (cm2) | 4.59446 | 5.35270 | 6.39851 | 5.10661 | 5.07816 | 5.99714 | 7.43496 | 13.27162 |
| Group2 A5∼A12 (cm2) | 8.71029 | 9.24390 | 12.05449 | 10.88687 | 10.94558 | 10.96412 | 8.25410 | 7.39752 |
| Group3 A13∼A16 (cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | 6.36611 |
| Group4 A17∼A18 (cm2) | 9.12775 | 10.34671 | Removed | Removed | Removed | Removed | 10.02505 | 9.82170 |
| Group5 A19∼A22 (cm2) | 10.15482 | 8.53522 | 10.38949 | 10.19986 | 9.13551 | 5.98834 | 11.92909 | 12.88030 |
| Group6 A23∼A30 (cm2) | 8.21962 | 9.14798 | 7.97586 | 6.06223 | 9.18191 | 7.88126 | 8.11222 | 10.10056 |
| Group7 A31∼A34 (cm2) | 3.25743 | Removed | 3.49691 | 3.33075 | 3.27975 | 2.61536 | Removed | 10.07807 |
| Group8 A35∼A36 (cm2) | Removed | Removed | 6.38376 | 6.32638 | 5.98996 | 5.56496 | Removed | Removed |
| Group9 A37∼A40 (cm2) | 12.53245 | 15.79730 | 10.89588 | 13.18683 | 13.65711 | 15.22403 | 6.81452 | 9.63412 |
| Group10 A41∼A48 (cm2) | 8.42090 | 8.18269 | 6.77067 | 9.04570 | 7.44328 | 8.77231 | 8.48838 | 8.50997 |
| Group11 A49∼A52 (cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| Group12 A53∼A54 (cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| Group13 A55∼A58 (cm2) | 15.32671 | 13.78927 | 17.06051 | 15.01429 | 14.90610 | 17.01520 | 26.43803 | 15.06306 |
| Group14 A59∼A66 (cm2) | 7.75289 | 7.39692 | 7.47352 | 8.28850 | 6.55719 | 6.18966 | 12.27899 | 9.06675 |
| Group15 A67∼A70 (cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| Group16 A71∼A72 (cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | 6.06917 |
| Best weight (kg) | 453.18004 | 460.62844 | 455.25465 | 453.56728 | 453.56728 | 455.25465 | 479.89210 | 542.34685 |
| Variables . | HBWO-JS . | JS . | AHA . | ARO . | DO . | SO . | WSO . | RSA . |
|---|---|---|---|---|---|---|---|---|
| Group1 A1∼A4 (cm2) | 4.59446 | 5.35270 | 6.39851 | 5.10661 | 5.07816 | 5.99714 | 7.43496 | 13.27162 |
| Group2 A5∼A12 (cm2) | 8.71029 | 9.24390 | 12.05449 | 10.88687 | 10.94558 | 10.96412 | 8.25410 | 7.39752 |
| Group3 A13∼A16 (cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | 6.36611 |
| Group4 A17∼A18 (cm2) | 9.12775 | 10.34671 | Removed | Removed | Removed | Removed | 10.02505 | 9.82170 |
| Group5 A19∼A22 (cm2) | 10.15482 | 8.53522 | 10.38949 | 10.19986 | 9.13551 | 5.98834 | 11.92909 | 12.88030 |
| Group6 A23∼A30 (cm2) | 8.21962 | 9.14798 | 7.97586 | 6.06223 | 9.18191 | 7.88126 | 8.11222 | 10.10056 |
| Group7 A31∼A34 (cm2) | 3.25743 | Removed | 3.49691 | 3.33075 | 3.27975 | 2.61536 | Removed | 10.07807 |
| Group8 A35∼A36 (cm2) | Removed | Removed | 6.38376 | 6.32638 | 5.98996 | 5.56496 | Removed | Removed |
| Group9 A37∼A40 (cm2) | 12.53245 | 15.79730 | 10.89588 | 13.18683 | 13.65711 | 15.22403 | 6.81452 | 9.63412 |
| Group10 A41∼A48 (cm2) | 8.42090 | 8.18269 | 6.77067 | 9.04570 | 7.44328 | 8.77231 | 8.48838 | 8.50997 |
| Group11 A49∼A52 (cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| Group12 A53∼A54 (cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| Group13 A55∼A58 (cm2) | 15.32671 | 13.78927 | 17.06051 | 15.01429 | 14.90610 | 17.01520 | 26.43803 | 15.06306 |
| Group14 A59∼A66 (cm2) | 7.75289 | 7.39692 | 7.47352 | 8.28850 | 6.55719 | 6.18966 | 12.27899 | 9.06675 |
| Group15 A67∼A70 (cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | Removed |
| Group16 A71∼A72 (cm2) | Removed | Removed | Removed | Removed | Removed | Removed | Removed | 6.06917 |
| Best weight (kg) | 453.18004 | 460.62844 | 455.25465 | 453.56728 | 453.56728 | 455.25465 | 479.89210 | 542.34685 |
The numerical results in Table 19 show the minimum mass values obtained by all algorithms when the structural constraints are satisfied. The population of all algorithms is 30, and the maximum number of iterations is 500. the minimum mass obtained by HBWO-JS is 453.18004 kg. The results obtained by HBWO-JS outperform the other seven compared algorithms. The best results for JS, AHA, ARO, DO, SO, WSO, and RSA are 460.62844, 455.25465, 453.56728, 453.56728, 455.25465, 479.89210, 542.34685 kg. The second-ranked algorithms are ARO and DO, both obtaining a minimum weight of 453.56728 kg. Figure 24 provides a plot of the relative virtual effects of the different algorithms after removing the unwanted structures. JS and WSO have the same structure. AHA, ARO, DO, and SO have the same results. In addition, the topology shapes of HBWO-JS and RSA are different. However, the proposed HBWO-JS requires 10 building blocks (Fig. 24a).

72-bar truss topology structure: (a) HBWO-JS; (b) JS, WSO; (c) AHA, ARO, DO, SO; (d) RSA.
Figure 25 provides the convergence plots of all algorithms for the 72 truss optimization problems. The convergence plots show that HGWO-JS has a high-speed convergence rate in the early stage, which is significantly faster than the other algorithms. In contrast, RSA and WSO converge slower. After the 150th iteration, HGWO-JS converges to the vicinity of the local solution and gradually approaches the optimal solution. The experimental conclusion shows that HGWO-JS has good convergence performance and optimization effect in solving the 72-truss topology optimization problem.

Convergence trends of the 72-bar truss structure optimization problem with the HBWO-JS, JS, AHA, ARO, DO, SO, WSO, RSA algorithm.
7. Conclusions
A HBWO-JS is introduced in this study. The proposed HBWO-JS integrates the BWO algorithm with the JS algorithm to improve the problem that BWO tends to fall into the best local solution and low convergence accuracy in the exploitation phase through multi-stage exploration and collaborative exploitation. Then, the introduced vertical crossover operator ensures that the dimension that may be optimal is not destroyed by normalizing the upper and lower bounds of two stochastic dimensions of the same search agent. The vertical crossover operator alleviates the problem of an unbalanced exploration and exploitation process, thus further improving the optimization capability of the algorithm. The introduced Gaussian variation strategy then forces the agents to explore their minimal neighborhoods, extending the entire iterative search process and thus enhancing the algorithm’s ability to jump out of local premature stagnation. The BWO algorithm provides a framework for efficiently solving complex, high-dimensional engineering optimization problems through the combined action of the vertical crossover operator, Gaussian variation strategy, and JS algorithm. To demonstrate the efficiency of the proposed HBWO-JS, which is compared with the eight latest proposed algorithms on two widely used benchmark suites (CEC2019, CEC2020). The experimental results confirm that HBWO-JS can obtain better results than other search algorithms on most tested problems. In addition, this paper evaluates the scalability of HBWO-JS in different dimensions. The numerical results show that the algorithm is relatively stable in dimensional scalability. Then, the proposed HBWO-JS is employed to solve three real engineering problems, and the optimization results also validate the competitive performance of the proposed HBWO-JS. Finally, the proposed HBWO-JS is used to solve the truss topology optimization problem and the HBWO-JS obtains a lighter truss structure than the existing solutions.
HBWO-JS performs well in dealing with global optimization problems and practical engineering applications, but some of its solutions sometimes need to be closer to the global optimum. In addition, the introduction of Gaussian variation strategies increases the time cost, a problem that can be found in the results in Table 5. Therefore, it is our future work further to enhance HBWO-JS in a low time cost way to obtain a solution that is as close to the global optimum as possible.
Code availability
The Matlab source code of the HBWO-JS related to this article can be found online at https://www.researchgate.net/publication/370262520_HBWO-JS_Code.
Acknowledgement
This work is supported by the National Natural Science Foundation of China (Grant Nos. 51875454).
Conflict of interest statement
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Data availability
All data generated or analysed during this study are included in this published article.
References
Appendix A
| Function type . | No. . | Function name . | Optimal value . |
|---|---|---|---|
| Unimodal functions | 1 | Shifted and Rotated Bent Cigar Function | 100 |
| 3 | Shifted and Rotated Zakharov Function | 300 | |
| Multimodal functions | 4 | Shifted and Rotated Rosenbrock’s Function | 400 |
| 5 | Shifted and Rotated Rastrigin’s Function | 500 | |
| 6 | Shifted and Rotated Expanded Scaffer’s F6 Function | 600 | |
| 7 | Shifted and Rotated Lunacek Bi_Rastrigin Function | 700 | |
| 8 | Shifted and Rotated Non-Continuous Rastrigin’s Function | 800 | |
| 9 | Shifted and Rotated Levy Function | 900 | |
| 10 | Shifted and Rotated Schwefel’s Function | 1000 | |
| Hybrid functions | 11 | Hybrid Function 1 (N = 3) | 1100 |
| 12 | Hybrid Function 2 (N = 3) | 1200 | |
| 13 | Hybrid Function 3 (N = 3) | 1300 | |
| 14 | Hybrid Function 4 (N = 4) | 1400 | |
| 15 | Hybrid Function 5 (N = 4) | 1500 | |
| 16 | Hybrid Function 6 (N = 4) | 1600 | |
| 17 | Hybrid Function 7 (N = 5) | 1700 | |
| 18 | Hybrid Function 8 (N = 5) | 1800 | |
| 19 | Hybrid Function 9 (N = 5) | 1900 | |
| 20 | Hybrid Function 10 (N = 6) | 2000 | |
| Composition functions | 21 | Composition Function 1 (N = 3) | 2100 |
| 22 | Composition Function 2 (N = 3) | 2200 | |
| 23 | Composition Function 3 (N = 4) | 2300 | |
| 24 | Composition Function 4 (N = 4) | 2400 | |
| 25 | Composition Function 5 (N = 5) | 2500 | |
| 26 | Composition Function 6 (N = 5) | 2600 | |
| 27 | Composition Function 7 (N = 6) | 2700 | |
| 28 | Composition Function 8 (N = 6) | 2800 | |
| 29 | Composition Function 9 (N = 3) | 2900 | |
| 30 | Composition Function 10 (N = 3) | 3000 | |
| Search range: [−100,100]D | |||
| Function type . | No. . | Function name . | Optimal value . |
|---|---|---|---|
| Unimodal functions | 1 | Shifted and Rotated Bent Cigar Function | 100 |
| 3 | Shifted and Rotated Zakharov Function | 300 | |
| Multimodal functions | 4 | Shifted and Rotated Rosenbrock’s Function | 400 |
| 5 | Shifted and Rotated Rastrigin’s Function | 500 | |
| 6 | Shifted and Rotated Expanded Scaffer’s F6 Function | 600 | |
| 7 | Shifted and Rotated Lunacek Bi_Rastrigin Function | 700 | |
| 8 | Shifted and Rotated Non-Continuous Rastrigin’s Function | 800 | |
| 9 | Shifted and Rotated Levy Function | 900 | |
| 10 | Shifted and Rotated Schwefel’s Function | 1000 | |
| Hybrid functions | 11 | Hybrid Function 1 (N = 3) | 1100 |
| 12 | Hybrid Function 2 (N = 3) | 1200 | |
| 13 | Hybrid Function 3 (N = 3) | 1300 | |
| 14 | Hybrid Function 4 (N = 4) | 1400 | |
| 15 | Hybrid Function 5 (N = 4) | 1500 | |
| 16 | Hybrid Function 6 (N = 4) | 1600 | |
| 17 | Hybrid Function 7 (N = 5) | 1700 | |
| 18 | Hybrid Function 8 (N = 5) | 1800 | |
| 19 | Hybrid Function 9 (N = 5) | 1900 | |
| 20 | Hybrid Function 10 (N = 6) | 2000 | |
| Composition functions | 21 | Composition Function 1 (N = 3) | 2100 |
| 22 | Composition Function 2 (N = 3) | 2200 | |
| 23 | Composition Function 3 (N = 4) | 2300 | |
| 24 | Composition Function 4 (N = 4) | 2400 | |
| 25 | Composition Function 5 (N = 5) | 2500 | |
| 26 | Composition Function 6 (N = 5) | 2600 | |
| 27 | Composition Function 7 (N = 6) | 2700 | |
| 28 | Composition Function 8 (N = 6) | 2800 | |
| 29 | Composition Function 9 (N = 3) | 2900 | |
| 30 | Composition Function 10 (N = 3) | 3000 | |
| Search range: [−100,100]D | |||
| Function type . | No. . | Function name . | Optimal value . |
|---|---|---|---|
| Unimodal functions | 1 | Shifted and Rotated Bent Cigar Function | 100 |
| 3 | Shifted and Rotated Zakharov Function | 300 | |
| Multimodal functions | 4 | Shifted and Rotated Rosenbrock’s Function | 400 |
| 5 | Shifted and Rotated Rastrigin’s Function | 500 | |
| 6 | Shifted and Rotated Expanded Scaffer’s F6 Function | 600 | |
| 7 | Shifted and Rotated Lunacek Bi_Rastrigin Function | 700 | |
| 8 | Shifted and Rotated Non-Continuous Rastrigin’s Function | 800 | |
| 9 | Shifted and Rotated Levy Function | 900 | |
| 10 | Shifted and Rotated Schwefel’s Function | 1000 | |
| Hybrid functions | 11 | Hybrid Function 1 (N = 3) | 1100 |
| 12 | Hybrid Function 2 (N = 3) | 1200 | |
| 13 | Hybrid Function 3 (N = 3) | 1300 | |
| 14 | Hybrid Function 4 (N = 4) | 1400 | |
| 15 | Hybrid Function 5 (N = 4) | 1500 | |
| 16 | Hybrid Function 6 (N = 4) | 1600 | |
| 17 | Hybrid Function 7 (N = 5) | 1700 | |
| 18 | Hybrid Function 8 (N = 5) | 1800 | |
| 19 | Hybrid Function 9 (N = 5) | 1900 | |
| 20 | Hybrid Function 10 (N = 6) | 2000 | |
| Composition functions | 21 | Composition Function 1 (N = 3) | 2100 |
| 22 | Composition Function 2 (N = 3) | 2200 | |
| 23 | Composition Function 3 (N = 4) | 2300 | |
| 24 | Composition Function 4 (N = 4) | 2400 | |
| 25 | Composition Function 5 (N = 5) | 2500 | |
| 26 | Composition Function 6 (N = 5) | 2600 | |
| 27 | Composition Function 7 (N = 6) | 2700 | |
| 28 | Composition Function 8 (N = 6) | 2800 | |
| 29 | Composition Function 9 (N = 3) | 2900 | |
| 30 | Composition Function 10 (N = 3) | 3000 | |
| Search range: [−100,100]D | |||
| Function type . | No. . | Function name . | Optimal value . |
|---|---|---|---|
| Unimodal functions | 1 | Shifted and Rotated Bent Cigar Function | 100 |
| 3 | Shifted and Rotated Zakharov Function | 300 | |
| Multimodal functions | 4 | Shifted and Rotated Rosenbrock’s Function | 400 |
| 5 | Shifted and Rotated Rastrigin’s Function | 500 | |
| 6 | Shifted and Rotated Expanded Scaffer’s F6 Function | 600 | |
| 7 | Shifted and Rotated Lunacek Bi_Rastrigin Function | 700 | |
| 8 | Shifted and Rotated Non-Continuous Rastrigin’s Function | 800 | |
| 9 | Shifted and Rotated Levy Function | 900 | |
| 10 | Shifted and Rotated Schwefel’s Function | 1000 | |
| Hybrid functions | 11 | Hybrid Function 1 (N = 3) | 1100 |
| 12 | Hybrid Function 2 (N = 3) | 1200 | |
| 13 | Hybrid Function 3 (N = 3) | 1300 | |
| 14 | Hybrid Function 4 (N = 4) | 1400 | |
| 15 | Hybrid Function 5 (N = 4) | 1500 | |
| 16 | Hybrid Function 6 (N = 4) | 1600 | |
| 17 | Hybrid Function 7 (N = 5) | 1700 | |
| 18 | Hybrid Function 8 (N = 5) | 1800 | |
| 19 | Hybrid Function 9 (N = 5) | 1900 | |
| 20 | Hybrid Function 10 (N = 6) | 2000 | |
| Composition functions | 21 | Composition Function 1 (N = 3) | 2100 |
| 22 | Composition Function 2 (N = 3) | 2200 | |
| 23 | Composition Function 3 (N = 4) | 2300 | |
| 24 | Composition Function 4 (N = 4) | 2400 | |
| 25 | Composition Function 5 (N = 5) | 2500 | |
| 26 | Composition Function 6 (N = 5) | 2600 | |
| 27 | Composition Function 7 (N = 6) | 2700 | |
| 28 | Composition Function 8 (N = 6) | 2800 | |
| 29 | Composition Function 9 (N = 3) | 2900 | |
| 30 | Composition Function 10 (N = 3) | 3000 | |
| Search range: [−100,100]D | |||
| No. . | Functions . | |$F_i^* = {F_i}({x^*})$| . | Dim . | Search range . |
|---|---|---|---|---|
| cec01 | Storn’s Chebyshev Polynomial Fitting Problem | 1 | 9 | [−8192,8192] |
| cec02 | Inverse Hilbert Matrix Problem | 1 | 16 | [−16384,16 384] |
| cec03 | Lennard–Jones Minimum Energy Cluster | 1 | 18 | [−4,4] |
| cec04 | Rastrigin’s Function | 1 | 10 | [−100,100] |
| cec05 | Griewangk’s Function | 1 | 10 | [−100,100] |
| cec06 | Weierstrass Function | 1 | 10 | [−100,100] |
| cec07 | Modified Schwefel’s Function | 1 | 10 | [−100,100] |
| cec08 | Expanded Schaffer’s F6 Function | 1 | 10 | [−100,100] |
| cec09 | Happy Cat Function | 1 | 10 | [−100,100] |
| cec10 | Ackley Function | 1 | 10 | [−100,100] |
| No. . | Functions . | |$F_i^* = {F_i}({x^*})$| . | Dim . | Search range . |
|---|---|---|---|---|
| cec01 | Storn’s Chebyshev Polynomial Fitting Problem | 1 | 9 | [−8192,8192] |
| cec02 | Inverse Hilbert Matrix Problem | 1 | 16 | [−16384,16 384] |
| cec03 | Lennard–Jones Minimum Energy Cluster | 1 | 18 | [−4,4] |
| cec04 | Rastrigin’s Function | 1 | 10 | [−100,100] |
| cec05 | Griewangk’s Function | 1 | 10 | [−100,100] |
| cec06 | Weierstrass Function | 1 | 10 | [−100,100] |
| cec07 | Modified Schwefel’s Function | 1 | 10 | [−100,100] |
| cec08 | Expanded Schaffer’s F6 Function | 1 | 10 | [−100,100] |
| cec09 | Happy Cat Function | 1 | 10 | [−100,100] |
| cec10 | Ackley Function | 1 | 10 | [−100,100] |
| No. . | Functions . | |$F_i^* = {F_i}({x^*})$| . | Dim . | Search range . |
|---|---|---|---|---|
| cec01 | Storn’s Chebyshev Polynomial Fitting Problem | 1 | 9 | [−8192,8192] |
| cec02 | Inverse Hilbert Matrix Problem | 1 | 16 | [−16384,16 384] |
| cec03 | Lennard–Jones Minimum Energy Cluster | 1 | 18 | [−4,4] |
| cec04 | Rastrigin’s Function | 1 | 10 | [−100,100] |
| cec05 | Griewangk’s Function | 1 | 10 | [−100,100] |
| cec06 | Weierstrass Function | 1 | 10 | [−100,100] |
| cec07 | Modified Schwefel’s Function | 1 | 10 | [−100,100] |
| cec08 | Expanded Schaffer’s F6 Function | 1 | 10 | [−100,100] |
| cec09 | Happy Cat Function | 1 | 10 | [−100,100] |
| cec10 | Ackley Function | 1 | 10 | [−100,100] |
| No. . | Functions . | |$F_i^* = {F_i}({x^*})$| . | Dim . | Search range . |
|---|---|---|---|---|
| cec01 | Storn’s Chebyshev Polynomial Fitting Problem | 1 | 9 | [−8192,8192] |
| cec02 | Inverse Hilbert Matrix Problem | 1 | 16 | [−16384,16 384] |
| cec03 | Lennard–Jones Minimum Energy Cluster | 1 | 18 | [−4,4] |
| cec04 | Rastrigin’s Function | 1 | 10 | [−100,100] |
| cec05 | Griewangk’s Function | 1 | 10 | [−100,100] |
| cec06 | Weierstrass Function | 1 | 10 | [−100,100] |
| cec07 | Modified Schwefel’s Function | 1 | 10 | [−100,100] |
| cec08 | Expanded Schaffer’s F6 Function | 1 | 10 | [−100,100] |
| cec09 | Happy Cat Function | 1 | 10 | [−100,100] |
| cec10 | Ackley Function | 1 | 10 | [−100,100] |
| Type . | No. . | Functions . | |$F_i^* = {F_i}({x^*})$| . |
|---|---|---|---|
| Unimodal function | cec01 | Shifted and Rotated Bent Cigar Function (CEC2017 F1) | 100 |
| Basic functions | cec02 | Shifted and Rotated Schwefel’s Function (CEC2014 F11) | 1100 |
| cec03 | Shifted and Rotated Lunacek bi-Rastrigin Function (CEC2017 F7) | 700 | |
| cec04 | Expanded Rosenbrock’s plus Griewangk's Function (CEC2017 F19) | 1900 | |
| Hybrid functions | cec05 | Hybrid Function 1 (N = 3) (CEC2014 F17) | 1700 |
| cec06 | Hybrid Function 2 (N = 4) (CEC2017 F16) | 1600 | |
| cec07 | Hybrid Function 3 (N = 5) (CEC2014 F21) | 2100 | |
| Composition functions | cec08 | Composition Function 1 (N = 3) (CEC2017 F22) | 2200 |
| cec09 | Composition Function 2 (N = 4) (CEC2017 F24) | 2400 | |
| cec10 | Composition Function 3 (N = 5) (CEC 017 F25) | 2500 | |
| Search range: [−100,100]D | |||
| Type . | No. . | Functions . | |$F_i^* = {F_i}({x^*})$| . |
|---|---|---|---|
| Unimodal function | cec01 | Shifted and Rotated Bent Cigar Function (CEC2017 F1) | 100 |
| Basic functions | cec02 | Shifted and Rotated Schwefel’s Function (CEC2014 F11) | 1100 |
| cec03 | Shifted and Rotated Lunacek bi-Rastrigin Function (CEC2017 F7) | 700 | |
| cec04 | Expanded Rosenbrock’s plus Griewangk's Function (CEC2017 F19) | 1900 | |
| Hybrid functions | cec05 | Hybrid Function 1 (N = 3) (CEC2014 F17) | 1700 |
| cec06 | Hybrid Function 2 (N = 4) (CEC2017 F16) | 1600 | |
| cec07 | Hybrid Function 3 (N = 5) (CEC2014 F21) | 2100 | |
| Composition functions | cec08 | Composition Function 1 (N = 3) (CEC2017 F22) | 2200 |
| cec09 | Composition Function 2 (N = 4) (CEC2017 F24) | 2400 | |
| cec10 | Composition Function 3 (N = 5) (CEC 017 F25) | 2500 | |
| Search range: [−100,100]D | |||
| Type . | No. . | Functions . | |$F_i^* = {F_i}({x^*})$| . |
|---|---|---|---|
| Unimodal function | cec01 | Shifted and Rotated Bent Cigar Function (CEC2017 F1) | 100 |
| Basic functions | cec02 | Shifted and Rotated Schwefel’s Function (CEC2014 F11) | 1100 |
| cec03 | Shifted and Rotated Lunacek bi-Rastrigin Function (CEC2017 F7) | 700 | |
| cec04 | Expanded Rosenbrock’s plus Griewangk's Function (CEC2017 F19) | 1900 | |
| Hybrid functions | cec05 | Hybrid Function 1 (N = 3) (CEC2014 F17) | 1700 |
| cec06 | Hybrid Function 2 (N = 4) (CEC2017 F16) | 1600 | |
| cec07 | Hybrid Function 3 (N = 5) (CEC2014 F21) | 2100 | |
| Composition functions | cec08 | Composition Function 1 (N = 3) (CEC2017 F22) | 2200 |
| cec09 | Composition Function 2 (N = 4) (CEC2017 F24) | 2400 | |
| cec10 | Composition Function 3 (N = 5) (CEC 017 F25) | 2500 | |
| Search range: [−100,100]D | |||
| Type . | No. . | Functions . | |$F_i^* = {F_i}({x^*})$| . |
|---|---|---|---|
| Unimodal function | cec01 | Shifted and Rotated Bent Cigar Function (CEC2017 F1) | 100 |
| Basic functions | cec02 | Shifted and Rotated Schwefel’s Function (CEC2014 F11) | 1100 |
| cec03 | Shifted and Rotated Lunacek bi-Rastrigin Function (CEC2017 F7) | 700 | |
| cec04 | Expanded Rosenbrock’s plus Griewangk's Function (CEC2017 F19) | 1900 | |
| Hybrid functions | cec05 | Hybrid Function 1 (N = 3) (CEC2014 F17) | 1700 |
| cec06 | Hybrid Function 2 (N = 4) (CEC2017 F16) | 1600 | |
| cec07 | Hybrid Function 3 (N = 5) (CEC2014 F21) | 2100 | |
| Composition functions | cec08 | Composition Function 1 (N = 3) (CEC2017 F22) | 2200 |
| cec09 | Composition Function 2 (N = 4) (CEC2017 F24) | 2400 | |
| cec10 | Composition Function 3 (N = 5) (CEC 017 F25) | 2500 | |
| Search range: [−100,100]D | |||


