An inequality-constrained regularized inversion of slip distributions on multiple faults with applications to the 2016 Kumamoto Mw 7.0 earthquake

Xu, Peiliang

doi:10.1093/gji/ggac437

SUMMARY

Although slip inversion has been almost always reported to be inherently non-unique, we prove that Fredholm integral equations of the first kind for slip inversion are mathematically of a unique solution, theoretically assuring that earthquake rupture can be properly reconstructed if there exist a sufficiently large number of measurements. The statement about non-uniqueness of slip inversion can be misleading and misunderstanding, since it is theoretically not true but simply caused by a practical issue of lack of measurements. We propose an inequality-constrained regularized inversion of slip distributions on multiple faults. The method implements a physically more general inequality constraint to accommodate more complex dislocation models and allows reconstructing a complex earthquake mechanism on multiple faults from measurements. The corresponding inequality constraints are a natural extension of positivity constraints proposed by Olson & Apsel and Hartzell & Heaton, or the equivalent inequality constraints that only allow slips to take place between −45° and 45° around the main rupture direction. The regularization parameter is chosen by minimizing the mean squared errors of inverted slip solutions. The proposed method is applied to the 2016 Kumamoto M_w 7.0 earthquake with GNSS measurements. Our slip inversion results show that the 2016 Kumamoto earthquake is only of magnitude M_w 6.7 and ruptures shallowly up to 10 km under the surface. More precisely, about 94 and 88 per cent of the energy released from Hinagu and Futagawa faults take place up to this depth, with the maximum slips of 4.81 and 7.89 m on each fault, respectively.

Geophysical methods, Inverse theory, Tomography, Seismology, Inequality constraints, Multiple faults

Subject

Seismology

Issue Section:

Seismology

1 INTRODUCTION

Reconstruction of slip distributions on faults is essential for earthquake engineering and to understand source mechanics of earthquakes (see e.g. Aki & Richards 1980; Lay & Wallace 1995). Slip distributions have often been determined from seismic recordings (Olson & Apsel 1982; Hartzell & Heaton 1983), terrestrial geodetic measurements (Savage & Hastie 1966; Ando 1975; Ward & Barrientos 1986), global navigation satellite systems (GNSS) (Freymueller et al. 1994; Cambiotti et al. 2017) and/or interferometric synthetic aperture radar (InSAR) imaging (Lohman & Barnhart 2010; Yang et al. 2022). These different types of measurements have their own advantages and disadvantages. For example, seismic measurements are much more sensitive than geodetic measurements. Modern seismometers with micro-electro–mechanical systems are required to respond to seismic motion of acceleration at the noise level of 10⁻⁵ to $10^{- 7} m \cdot s^{- 2} (\sqrt{Hz})^{- 1}$ (D’Alessandro et al. 2019), while GNSS and InSAR can only detect movements larger than a few mm. However, seismometers are subject to instrumental drifts, tilts and saturations and can be numerically unreliable in the case of high sampling rates (Xu 2021a). Conventional terrestrial geodetic measurements are not always available for earthquake research, unless specially designed along certain faults, which can now be fully overcome by using space geodesy such as GNSS and InSAR. Although GNSS can now be routinely used to study earthquakes, its spatial resolution is much lower than InSAR. As a result, to take full advantages of different types of seismic and geodetic measurements, they have now been often combined together for reconstruction of slip distributions.

A number of methods can be used for inversion of slip distributions, including least squares (see e.g. Savage & Hastie 1966; Ando 1975; Olson & Apsel 1982; Tarantola & Valette 1982), generalized inverse of matrices (see e.g. Menke 1984; Segall & Harris 1986; Barrientos & Ward 1990), regularization (see e.g. Freymueller et al. 1994; Lohman & Barnhart 2010; Gallovič et al. 2015) and Bayesian inversion (Tarantola 1987; Cambiotti et al. 2017; Benavente et al. 2019). Due to measurement errors and likely model limitations, these inversion methods can result in negative slips that are against the main direction of rupture on a fault, which are believed to be physically not acceptable. To make inversion results of slip distributions physically reasonable, Olson & Apsel (1982) first proposed imposing the positivity constraints on slip components (see also Hartzell & Heaton 1983) and applied the method to study the 1979 Imperial Valley earthquake. The positivity constraints, also referred improperly to as and treated as no-back slip constraints in the seismological literature, have since been widely applied in seismology, in particular, for inversion of slip distributions (see e.g. Du et al. 1992; Courboulex et al. 1997; Cambiotti et al. 2017; Benavente et al. 2019; Ortega-Culaciati et al. 2021), for inversion of moment and slip rates (see e.g. Das & Kostrov 1997; Bindi & Caponnetto 2001; Lindsey et al. 2021) and for determination of source time functions (see e.g. Zollo et al. 1995; Chu et al. 2009; Plourde & Bostock 2017). The positivity constraints for inversion of slip distributions have also been modified to allow slips to take place between −45° and 45° around the main rupture vector on the fault plane (see e.g. Asano & Iwata 2016), which are mathematically equivalent to positivity constraints from the solution point of view. For simplicity, we will refer to these particular inequality constraints as the 45° positivity constraints in the remainder of this paper.

The positivity constraints on slip distributions may imply a physically simplified model of rupture, since the slips of rupture are only allowed to point within a quarter of arc. An earthquake may be physically more complex in terms of a combination of edge, screw and plastic dislocations and can involve multiple faults. From this point of view, we should better not impose too strict constraints to inattentively eliminate such a possible complexity of rupture in advance. Thus, it may be more appropriate to relax the positivity constraints so that we can reconstruct more complex slip distributions on the fault planes of earthquakes from measured data. A reasonable physical assumption would be that no projected component of a slip is permitted to move against the main rupture direction on a fault. As a result of this relaxed assumption, we expect to physically reconstruct and better understand a more complex source of earthquake (if any). In this paper, we will reformulate this relaxed condition as a set of inequality constraints to reconstruct slip distributions. On the other hand, both the positivity constraints and the 45° positivity constraints can only be applied on a single fault. Although they can be applied to an earthquake involved with different faults, this can only be possible, if the main ruptures on all these faults are of the same rake angle, as can be seen in the literature (see e.g. Asano & Iwata 2016; Yue et al. 2017). We will show later in this paper that our new formulation is free of this restriction on the same rake angle and can readily be applied to study a large earthquake with the ruptures taking place on multiple faults with different rake angles. From this point of view, our new approach is theoretically more advantageous. More specifically, we will propose and formulate a new inequality-constrained regularized inversion method in Section 2. We will then simulate examples in Section 3 to demonstrate how the method works and to show the effect of positivity constraints on slip inversion. Finally, we will apply the proposed inversion method to the 2016 Kumamoto M_w 7.0 earthquake with the ruptures on both Hinagu and Futagawa faults from GNSS measurements in Section 4.

2 AN INEQUALITY-CONSTRAINED REGULARIZED SLIP INVERSION METHOD FOR MULTIPLE FAULTS

According to the dislocation theory (Steketee 1958; Okada 1985), a dislocation function

U (ξ)

on a fault surface S buried in a semi-infinite elastic medium generates a static displacement field

u (x)

at the point

x

⁠, which can be written symbolically after Steketee (1958) in the following integral equations:

\begin{array}{r} u_{i} (x) = \frac{1}{8 π μ} \int \int_{S} U^{T} (ξ) τ^{i} (x, ξ) n (ξ) d S (ξ), (i = 1, 2, 3), \end{array}

(1)

where

n (ξ)

is the unit vector of direction cosines normal to the fault surface element

d S (ξ)

⁠,

τ^{i} (x, ξ)

is the Green's stress tensor at

ξ

on the surface element

d S (ξ)

due to the force

8 π μ e_{i}

at

x

and μ is a Lamé’s elastic constant or the modulus of rigidity and

e_{i}

is the ith natural basis.

The displacement field

u_{i} (x)

of (1) in a semi-infinite isotropic elastic medium can also be alternatively expressed in the following integral equations (Okada 1985):

\begin{array}{rcl} u_{i} (x) & = & \int \int_{S} \sum_{j = 1}^{3} \sum_{k = 1}^{3} U_{j} (ξ) {λ δ_{j k} \frac{\partial u_{i}^{n}}{\partial ξ_{n}} + μ (\frac{\partial u_{i}^{j}}{\partial ξ_{k}} + \frac{\partial u_{i}^{k}}{\partial ξ_{j}})} \\ n_{k} (ξ) d S (ξ), (i = 1, 2, 3), \end{array}

(2)

where

U_{j} (ξ)

is the jth component of the dislocations

U (ξ)

⁠, δ_jk is the Kronecker delta, λ is a Lamé’s elastic constant,

n_{k} (ξ)

is the kth component of the direction cosine vector

n (ξ)

and

u_{i}^{j}

is the ith component of the displacements at

x

due to the jth direction unit point force at

ξ

⁠. Based on Steketee (1958) and Press (1965), Okada (1985) worked out all the analytical expressions to explicitly compute the surface displacements, strains and tilts due to a rectangular dislocation buried in a half-space of isotropic medium. These analytical formulae have since been widely applied in seismology.

If the fault geometry is defined, the displacement fields (1) and (2) are actually Fredholm integral equations of the first kind with the unknown dislocation functions (see e.g. Kondo 1991; Hackbusch 1995). Given the fault plane S and the surface P of a half-space of isotropic elastic medium where the displacements

u_{i} (x) (i = 1, 2, 3)

are collected and

x \in P

⁠, it can be proved that there intuitively exists a unique solution to the 2-D slip function

U (ξ)

on the fault plane, namely,

ξ \in S

from the surface displacement measurements

u_{i} (x \in P) (i = 1, 2, 3)

⁠. Actually, if there would exist a different solution, say

V (ξ) (ξ \in S)

⁠, then we have

\begin{array}{r} u_{i} (x) = \frac{1}{8 π μ} \int \int_{S} V^{T} (ξ) τ^{i} (x, ξ) n (ξ) d S (ξ), (i = 1, 2, 3) . \end{array}

(3)

The difference between (1) and (3) yields:

\begin{array}{r} 0 = \frac{1}{8 π μ} \int \int_{S} d U^{T} (ξ) τ^{i} (x, ξ) n (ξ) d S (ξ), (i = 1, 2, 3), \end{array}

(4)

where

d U (ξ) = U (ξ) - V (ξ)

⁠. (4) implies that there is a slip distribution that generates no displacements anywhere in the semi-infinite isotropic medium outside the fault plane. From the physical point of view, since the fundamental (Green's) stress tensor

τ^{i} (x, ξ)

results from a force

8 π μ e_{i}

at

x

⁠, which, in turn, generates the displacements at

x

⁠, for (4) to hold everywhere on P,

d U (ξ)

must be equal to zero.

In this study, we assume surface displacement measurements, which can be either computed with seismic data or measured with GNSS and/or InSAR, and use them to invert for the coseismic slip distribution on an earthquake fault. We use Okada’s (1985) analytical formulae to connect the slip distribution on a fault plane to the displacement measurements on surface. More precisely, if we divide a fault plane into t elementary patches and discretize the integral equation (1) or (2), we obtain the corresponding discretized observational equations, which can be symbolically written as follows:

\begin{array}{r} y = A m + ϵ, \end{array}

(5)

where

y

is an n-dimensional displacement vector,

A

is a coefficient matrix,

m

is the unknown vector of slips on the fault to be estimated and

ϵ

is the random error vector of the displacements

y

⁠.

ϵ

is often assumed to be of zero mean and variance–covariance matrix

D (ϵ) = W^{- 1} σ^{2}

⁠, where

W

is the weight matrix of

y

and σ² is an unknown or given variance of unit weight. If the stochastic model is only known up to a few unknown parameters in inverse problems, one will have to estimate the stochastic model as well (Xu et al. 2006; Xu 2009). In case that an earthquake involves multiple faults, we can repeat the same procedure for one fault to connect the measured data to the slip unknowns on all the faults. We gratefully use the open source matlab codes by Beauducel (2014) to compute the coefficient matrix

A

⁠.

Before we go on to present our inequality-constrained regularized inversion method, some remarks about existence, uniqueness and stability of inverting slip distributions would be useful and helpful.

Remark 1. Since the integral equation (1) or (2) is physically motivated and mathematically formulated, the existence of solution is warranted. Given the geometry of a fault and the displacement functions on the surface of the semi-infinite elastic medium, the uniqueness of solution should also become clear, as demonstrated in the above. Nevertheless, slip/rupture inversion has often been stated to be inherently non-unique in the seismological literature (see e.g. Olson & Apsel 1982; Olson & Anderson 1988; Das & Kostrov 1994; Beresnov 2003; Mai et al. 2016), a statement of this kind is misleading. Actually, the slip/rupture solution to the integral equation (1) or (2) is mathematically unique. In seismology, what we really encounter is more practical. We can never have all the displacement functions $u_{i} (x) (i = 1, 2, 3)$ on the whole surface. Instead, we always only have a limited number of measurements, which can certainly not be able to reconstruct the continuous (or infinitely dimensional) dislocation functions $U (ξ)$ on the fault plane. Thus, when the non-uniqueness of slip/rupture inversion is mentioned in the seismological literature, such a non-uniqueness is more of a practical issue solely due to the lack of data. This latter practical meaning cannot be overemphasized as if it were theoretically true, since it is equivalent to saying that reconstructing the slip distribution on a fault could never be possible physically, irrelevant of whether we have an infinite number of measured data.

Remark 2. Seismologists often use a limited number of geodetic/seismic data to compute a much larger number of slip/rupture unknowns. In other words, the total number of geodetic/seismic data is smaller than that of unknown slip components, namely, n < 2t in the case of static slip inversion or at each epoch of sampling in the case of kinematic slip inversion, as can routinely be seen, for example, in Olson & Anderson (1988), Das & Kostrov (1994), Reilinger et al. (2000), Sekiguchi et al. (2000), Bouchon et al. (2002), Custódio & Archuleta (2007), Hao et al. (2017), Hallo & Gallovič (2020) and Asano & Iwata (2021). In this case of n < 2t, the consequences of such a common practice of inversion are straightforward and direct. Different research groups worldwide reported almost completely different slip distributions for the same earthquakes. Two of such examples are the 17 August 1999 Izmit earthquake M 7.5 (compare e.g. Reilinger et al. 2000; Feigl et al. 2002; Gülen et al. 2002; Li et al. 2002; Bouchon et al. 2002; Sekiguchi & Iwata 2002; Delouis et al. 2002; Beresnov 2003) and the 1992 Landers, California earthquake M_w 7.3 (compare e.g. Cohee & Beroza 1994; Freymueller et al. 1994; Wald & Heaton 1994; Cotton & Campillo 1995; Hartzell & Liu 1996; Hernandez et al. 1999; Minson et al. 2013; Xu et al. 2016; Gombert et al. 2018; Wang et al. 2022). In fact, even different types of data and/or different inversion methods have been well known to produce significantly different slip models (see e.g. Olson & Apsel 1982; Feigl et al. 2002). Confusing situations of this kind should clearly indicate that there is still a long way to correctly image what really happens on the fault during an earthquake. Fundamental understanding and correct knowledge of data and inversion methods are critical for properly recovering physical information on slips to advance seismological science or understanding of faulting mechanics.

Remark 3. If n < 2t, the discretized inverse model (5) has an infinite number of mathematically equivalent solutions, which fit the data equally well. No single solution is better than any others in the solution set, as mathematically explained in Xu (1997). There is no extra information to decide which solution should dominate physically either. A common practice in seismology is to obtain a unique solution in this case by applying minimum norm, regularization and/or Bayesian methods to (5). Although the minimum norm, regularization and Bayesian methods can produce a unique solution to (5), they are mathematically equivalent to defining a different mathematical datum for the rank-deficient model (5). However, such a datum is not better than any other constraints mathematically and is not physically justified. Thus, such a unique solution is simply superficially the best. Even worse, since any unique solution to the rank-deficient model (5) contains artificial information, any geophysical interpretation of the solution is very likely biased and not physically supported, which can only add one more element of confusion to slip imaging. We should emphasize that mathematics can only provide a tool to help extract physical information from measurements. It cannot create physical information that does not exist. Incorrect prior assumption behind Bayesian inference is of consequences. We may like to note: (i) Bayesian inference in the geophysical literature always implicitly assumes zero prior mean, which means that we implicitly assume that there are no slips on the fault. Slips do occur on faults during earthquakes. Thus, this implicit assumption of zero prior mean is clearly not true, whose implications have been either mentioned in statistics (see e.g. Akaike 1980) or well addressed in geodesy (see e.g. Xu 1992a, 2021b; Xu & Rummel 1994); (ii) no matter whether the number of data is sufficient, if the prior information used in Bayesian seismology is subjective, the error evaluation of the estimated parameters is not correct either, as demonstrated from the statistical point of view by Xu (1992a, 2021b). The concept of mean squared errors (MSE) should apply; and (iii) a popular opinion exists in the seismological community that Bayesian inference solves this type of problems, since it explores a huge number of candidate models. Such an advantage is superficial as well, in particular, for inverse ill-posed problems. Given a Gaussian random variable, as often used in slip inversion, it is essentially equivalent mathematically to represent this random variable in a probability density, in a set of mean and variance, or in a large number of samplings. The last representation does not have any advantage than the former two representations. In fact, unless the number of samplings is sufficiently large, it is less efficient to report the full information on the random variable.

Based on these remarks, and bearing in mind that the integral equations (1) and (2) are of the first kind and their solutions are inherently very sensitive to small errors of measurements, all what we can do is to find a best balance among a limited number of data, modelling, solution stability and quality (in terms of MSE). If the number of data is small, we should reduce the resolution of slip distributions by increasing the size of patch, no matter whether we like it or not. Let measurements speak for themselves and let them decide to what extent we can extract physical information from a limited number of measurements. Even though the resolution is lowered, at the very least, we are sure that this is the only physical information we can derive from the measurements. It is more realistic and closer to the truth, since it honestly reflects the real situation without use of any subjective or superficial information. It can avoid any potential arbitrary and possibly misleading interpretation of faulting mechanics for earthquakes, due to superficial fine resolution of slips on a fault. Therefore, we will assume n > 2t throughout this work.

The positivity constraints proposed by Olson & Apsel (1982) (see also Hartzell & Heaton 1983) limit the slips at all the elementary cells/patches to move or point within a quarter of arc. If a large earthquake involves multiple faults with different rake angles, the positivity constraints, or equivalently, the 45° positivity constraints are not linear any more and the popular solution algorithm of Lawson & Hanson (1974) under non-negative linear constraints cannot be applied, as otherwise most often used in the seismological inversion of kinematic and static rupture. Thus, we will relax the positivity constraints and allow the slips to move in the half-space defined by the main rupture directions on the faults of an earthquake. In other words, no projected component of any slip at any patch can be allowed to move in the opposite direction of the main rupture direction on each fault. Assuming that a large earthquake involves multiple faults and denoting the directional unit vector of the main rupture on each fault by

n_{j} (j = 1, 2, . . ., l)

⁠, we can then mathematically represent our assumption of slip movements in the following system of inequalities for each fault involved:

\begin{array}{r} n_{j}^{T} m_{i}^{j} \geq 0, (i = 1, 2, . . ., t_{j}), \end{array}

(6)

where the script j stands for the jth fault (j = 1, 2,.., l),

m_{i}^{j}

is the slip vector at the ith patch on the jth fault. The inequality constraints (6) can be equivalently rewritten in matrix form as follows:

\begin{array}{r} B_{j} m^{j} \geq 0, \end{array}

(7)

where

m^{j}

stands for the unknown vector of all the slips on the jth fault, and the matrix

B_{j}

is given below:

\begin{array}{r} B_{j} = [\begin{array}{c} n_{j}^{T} & 0_{2} & 0_{2} & \dots & 0_{2} \\ 0_{2} & n_{j}^{T} & 0_{2} & \dots & 0_{2} \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ 0_{2} & 0_{2} & 0_{2} & \dots & n_{j}^{T} \end{array}], \end{array}

and

0_{2}

is a 2-D zero row vector. By collecting the inequality constraints (7) together for all the faults involved, we finally have the following inequality constraints:

\begin{array}{r} B m \geq 0, \end{array}

(8)

where

B

is a block-diagonal matrix with its jth block being equal to

B_{j}

⁠, and

m

consists of all the unknown slips arranged one fault after another for the earthquake. The formulation of constraints (8) is theoretically significant in three aspects: (i) it mathematically allows the reconstruction of more complex rupture of an earthquake (if any); (ii) it can be applied to a large earthquake involving multiple faults with different rake angles; and (iii) it is a natural extension of the positivity constraints (or equivalently, the 45° positivity constraints) proposed by Olson & Apsel (1982) (see also Hartzell & Heaton 1983) for a single fault.

Applying the weighted least squares (LS) principle to the observational equation (5) under the inequality constraints (8), we have the inequality-constrained optimization problem as follows:

\begin{array}{r} min: (y - A m)^{T} W (y - A m), \end{array}

(9)

subject to the inequality constraints (8). If the inequality constraints (8) are not applied, the weighted LS solution of slips is given as follows:

\begin{array}{r} {\hat{m}}_{l s} = N^{- 1} W A^{T} y, \end{array}

(10)

where the normal matrix

N

is given by

\begin{array}{r} N = A^{T} W A . \end{array}

The variance–covariance matrix of the weighted LS estimate

{\hat{m}}_{l s}

is readily given as follows:

\begin{array}{r} D ({\hat{m}}_{l s}) = N^{- 1} σ^{2} . \end{array}

(11)

If σ² is unknown and if the number of measurements is sufficiently large, σ² of (11) should be replaced with its weighted LS estimate. Since the model (5) is ill-posed in nature, the diagonal elements of

D ({\hat{m}}_{l s})

can be very large, implying that

{\hat{m}}_{l s}

is poorly estimated. One approach to obtain a unique and stable solution is to discard some smallest eigenvalues of

N

⁠, which is better known as the truncated singular value decomposition (SVD) method. Nevertheless, the solution quality by applying the truncated SVD method depends on how small eigenvalues are cut off (Xu 1998).

Because (5) is a discretized version of the integral equations of the first kind and inherently ill-posed, the inequality-constrained weighted LS solution can still be unstable numerically and can be very poor in accuracy. We apply regularization to obtain a stable and accurate solution of

m

⁠. More precisely, we will solve the following inequality-constrained regularization problem:

\begin{array}{r} min: (y - A m)^{T} W (y - A m) + κ m^{T} S m, \end{array}

(12)

subject to the inequality constraints (8), where κ is a regularization parameter,

S

is a given positive definite or semi-positive definite smoothness matrix, which can be constructed either by setting

S

to an identity matrix (see e.g. Hoerl & Kennard 1970) or by requiring the smoothness of the first and/or second derivatives (see e.g. Wahba 1992).

The smoothness matrix with the derivative information can become important in high resolution of inversion. In the case of slip inversion, the size of a patch is generally not small and imposing the smoothness constraints of derivatives such as the Laplacian operator may not help too much. Therefore, we will limit ourselves to the ordinary ridge in this paper, namely with

S

being set to an identity matrix. Accordingly, the optimization model (12) can be simplified as follows:

\begin{array}{r} min: (y - A m)^{T} W (y - A m) + κ m^{T} m . \end{array}

(13)

If the inequality constraints (8) are not imposed, we obtain the regularized solution as follows:

\begin{array}{r} {\hat{m}}_{0} = N_{κ}^{- 1} A^{T} W y, \end{array}

(14a)

where

\begin{array}{r} N_{κ} = A^{T} W A + κ I, \end{array}

(14b)

with

I

being an identity matrix.

Before a solution of slips is made physically meaningful via the inequality-constraints, we should first make sure that it is of the best quality by choosing the optimal regularization parameter κ on the basis of a certain optimality criterion. Since regularization is a mathematical tool to stabilize a solution of slips to the ill-posed problem (5), it will create some bias in

{\hat{m}}_{0}

of (14a) from the frequentist point of view (see e.g. Hoerl & Kennard 1970; Xu 1992b). The bias of

{\hat{m}}_{0}

is denoted by

bias ({\hat{m}}_{0})

and given by:

\begin{array}{r} bias ({\hat{m}}_{0}) = E ({\hat{m}}_{0}) - m = - κ N_{κ}^{- 1} m . \end{array}

(15)

Thus, we can write the MSE of

{\hat{m}}_{0}

as follows:

\begin{array}{r} MSE ({\hat{m}}_{0}) = tr {D ({\hat{m}}_{0})} + [bias ({\hat{m}}_{0})]^{T} bias ({\hat{m}}_{0}), \end{array}

(16)

where

MSE ({\hat{m}}_{0})

stands for the MSE of

{\hat{m}}_{0}

⁠, tr{ · } is the operator of trace of a square matrix and

D ({\hat{m}}_{0})

is the variance–covariance matrix of

{\hat{m}}_{0}

⁠. By minimizing the MSE criterion (16), we can iteratively determine the optimal regularization parameter κ (Xu 1992b; Xu et al. 2021). It is easy to prove that

\begin{array}{r} {E ({\hat{m}}_{0})}^{T} E ({\hat{m}}_{0}) < m^{T} m, \end{array}

(17)

implying that the regularized inversion of slips is of less power and always shrunken towards zero. Actually, this point applies to all inversion methods for ill-posed problems, no matter whether stabilization is materialized through regularization with a positive definite or semi-positive definite matrix

S

under the Bayesian or frequentist’s framework of statistics or by discarding some smallest eigenvalues. If interpreted in terms of earthquakes, a direct implication of the inequality (17) could be that the seismic moment and earthquake magnitude computed with the inverted slips could be theoretically underestimated in its long-term statistical performance. We should also note, however, that if too small a regularization is used, the corresponding regularized solution can still be substantially unstable and inaccurate. If such an unstable and inaccurate solution is used to compute the released energy, the power and moment can be probably overestimated instead of underestimated.

Following van de Panne (1975) (see also Xu et al. 1999), if the physical inequality-constraints (8) are imposed, we can directly write the solution to the inequality-constrained regularization problem (13) as follows:

\begin{array}{r} \hat{m} = {\hat{m}}_{0} + N_{κ}^{- 1} B^{T} q, \end{array}

(18)

where

{\hat{m}}_{0}

and

N_{κ}

are given by (14a) and (14b), respectively. Here, the vector

q

is the solution to the following linear complementarity problem (LCP):

\begin{array}{r} h = B N_{κ}^{- 1} B^{T} q + B {\hat{m}}_{0}, \end{array}

(19a)

where

\begin{array}{r} h^{T} q = 0, h \geq 0, q \geq 0 . \end{array}

(19b)

The LCP (19) is of a unique solution and can be solved by using either the interior point approach or the parametric method. For more details on the LCP solution, the reader can refer to Xu et al. (1999).

3 SYNTHETIC SIMULATED EXAMPLES

The purpose of this section is fourfold: (i) to demonstrate the proposed inequality-constrained inversion of slip distributions; (ii) to show the effect of positivity constraints in the case of a more complex slip distribution on a fault; (iii) to compare the results with the proposed inequality constraints in this paper and those with the positivity constraints and the 45° positivity constraints; and (iv) to show the consequences of an insufficient number of measurements in slip inversion. To make sure that the simulated results are statistically significant and that numerical comparisons are scientifically sound for the first three purposes, we will assume a sufficiently large number of surface displacement measurements, even though we know that the number of geodetic measurements such as GNSS stations is often quite limited in reality. Nevertheless, InSAR indeed could provide us with far more displacement measurements on the surface.

We use Matlab (R2021a, ver.9.10) to simulate a complex slip distribution on a fault (length 44.88 km, width 30.00 km, strike 55.0° and dip 66.0°), which is divided into 7 × 6 patches, though the simulated slip distribution may be apparently different from results of slip inversion in the seismological literature. The true slips simulated on the patches are shown in Fig. 1, which range from 0.14 to 3.56 m in magnitude and from –81.82° to 86.25° in rake, with a mean slip value of 0.97 m and a mean rake angle of 5.42°, respectively. The total release of energy through slips on the fault is equivalent to an earthquake of M_w 7.0. The example is simulated to clearly demonstrate that complex slips cannot be correctly reconstructed and will be precluded, if inversion is not properly constrained, as will be illustrated in the cases of the positivity constraints and the equivalent 45° positivity constraints. Actually, we do not know whether complex slip patterns of this kind can be physically possible/feasible. Thus, it is interesting to see whether the inequality-constrained regularized inversion proposed in this paper can reconstruct such a complex slip distribution.

Figure 1.

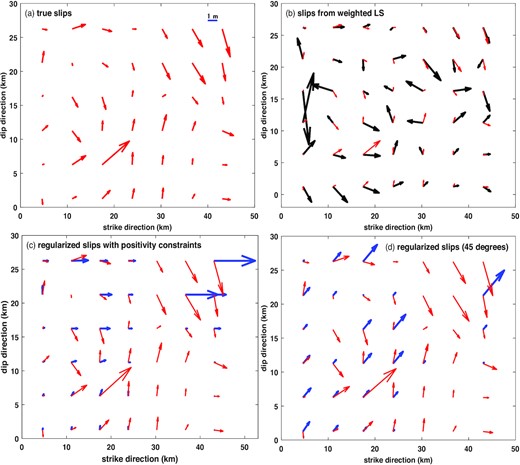
The simulated true slips and the results of slip inversion with a less number of measurements than that of unknown slip components on the fault, computed with the minimum norm weighted LS method and the regularization method with either the positivity constraints or the 45° positivity constraints. Panel (a): the simulated true slips; panel (b): the inverted slips with the minimum norm weighted LS method; panel (c): the inverted slips by applying the regularization method with the positivity constraints; and panel (d): the inverted slips by applying the regularization method with the 45° positivity constraints. For convenience of comparison, we also show the simulated true slips in red in all the other three panels of inverted slip solutions.

Open in new tab Download slide

3.1 Consequences of slip inversion with an insufficient number of measurements

Many seismological inversions of slip distributions have been carried out with an insufficient number of measurements, as can be seen in, for example, Olson & Anderson (1988), Das & Kostrov (1994), Reilinger et al. (2000), Bouchon et al. (2002), Custódio & Archuleta (2007), Hao et al. (2017) and Hallo & Gallovič (2020). In other words, we will have to invert for more unknown slip parameters from a less number of measurements. In this case, the simplest method is to apply the pseudo-inverse of the normal matrix $N$ and solve for the slip unknown parameters $m$ (see e.g. Menke 1984), which is also well known as the minimum norm weighted LS solution (see e.g. Rao & Mitra 1972; Grafarend & Schaffrin 1993, chapter 1(b)). The other routine practice is most often to apply regularization and/or so-called Bayesian framework to the observational model (5), with extra constraints of positivity or equivalently, the 45° positivity constraints. Thus, we would like to first briefly demonstrate the consequences of inversion with an insufficient number of measurements through the simulated example.

For this purpose, we simulate 15 GNSS stations, which are uniformly distributed symmetrically on the surface above the fault in an area of 40 km by 20 km. We then like to invert for 84 slip components on the fault from the 45 components of displacements at these 15 GNSS stations. Since GNSS precise point positioning (PPP) does not require a reference datum and is advantageous for seismological applications, we assume that the displacements from these 15 GNSS stations are all obtained with GNSS PPP. One more important advantage of PPP over the relative GNSS positioning method is that if the latter is used to process GNSS data, we can only obtain the relative displacements for slip inversion, which will theoretically weaken the geometry of measurements, in particular, those important GNSS stations in the epicentre of a large earthquake. As for the random errors of the measured displacements, although PPP has often been reported to be of a few cm accuracy, this level of accuracy is only true to give a statistical image of PPP long-term performance. In seismological applications, we are more concerned with a short term performance of PPP over a few minutes. Xu et al. (2013) reported that the accuracy of PPP over a short period can reach 3–4 mm in the horizontal components and subcentimetre in the vertical component. More theoretical and practical confirmations can be found in Shu et al. (2017) and Xu et al. (2019a,b). Thus, the displacements are simulated with a 4 mm accuracy for the horizontal components and 8 mm for the vertical component. The inversion results of slips on the fault with the minimum norm weighted LS method are shown in Fig. 1, which is equivalent to an earthquake of M_w 7.24. Although the value of moment magnitude is only slightly larger than the true value of M_w 7.00, it is rather clear from the upper-right panel of the figure that the minimum norm weighted LS slips are not physically acceptable in the sense that the slips apparently move arbitrarily around the clock of 24 hr and are significantly different from the simulated true values both in the magnitudes and directions of slips.

Following the standard practice of slip inversion in the seismological community, although there are an insufficient number of measurements, we go ahead by using regularization and/or Bayesian method to determine the optimal regularization parameter as if the unknown parameters $m$ could be unbiasedly estimated with a statistical variance–covariance matrix. As a result, we additionally obtain two slip inversion results by naïvely imposing the positivity constraints or by constraining the slips to take place between −45° and 45° around the mean rupture direction (namely the 45° positivity constraints), though we know the simulated true slips do not satisfy these two types of positivity constraints; the corresponding inverted slips are shown in the two lower panels of Fig. 1, respectively. Both of the constrained regularized slip solutions completely fail to reconstruct the true slip distribution, both in sizes and patterns, by comparing the recovered slips with the simulated true values (also shown in red), as is clear in the two lower panels of Fig. 1. Nevertheless, they do satisfy the pre-imposed directions of slips as a direct consequence of the positivity constraints or the 45° positivity constraints. The corresponding moment magnitudes are equal to M_w 6.80 and M_w 6.77, respectively, which are slightly smaller than the simulated true magnitude M_w 7.00.

To conclude, if there are an insufficient number of measurements, none of the methods in the above, namely, the minimum norm weighted LS method and the two variants of regularization with either the positivity constraints or the 45° positivity constraints, can correctly reconstruct the complex (true) slip distribution for the simulated example, though the moment magnitudes computed with these results of slips are not very different from the simulated true value M_w 7.00.

3.2 Slip reconstruction with more measurements than the slip unknowns

We will now simulate more displacement measurements than necessary to invert for the slip distribution with the new proposed inversion method. In total, we simulate 29 403 displacements in an area of 60 km by 40 km above the fault, with half of them on one side of the strike and the other half on the other side. As in Section 3.1, we will invert for the same 84 slip components on the fault. The simulated standard deviation σ is set to 0.004 m. Although this example is only of 84 slip unknowns to be determined from a very large number of 29 403 displacements, its condition number still reaches a very high value of 3.38E+10, with the smallest eigenvalue of 8.83E-10. The eigenvalues of the example are shown in Fig. 2. To validate the correctness of the forward modelling, we assume no modelling errors and reconstruct the 84 slips with the weighted LS method from the true values of 29 403 displacements, namely, the simulated measurements without adding any random errors, which are shown in the right-hand panel of Fig. 2, together with the true values of slips. It is clear that if the measurements are error-free, the slips are perfectly recovered, with the maximum error of 8.91E-07 m.

Figure 2.

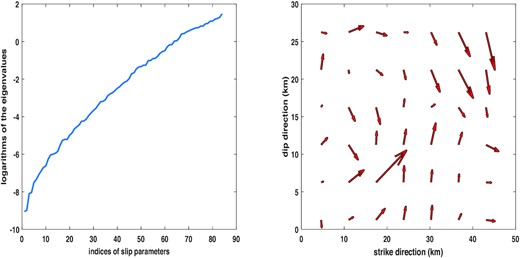
The eigenvalues of the simulated example to reconstruct the slip distribution (left-hand panel) and the weighted LS reconstruction of the slip distribution from the measurements free of random errors (right-hand panel). In this right-hand panel, the slips reconstructed with the weighted LS method from the error-free measurements are shown in black and the simulated true slips in red, which completely overlap each other.

Open in new tab Download slide

We apply four inversion methods to invert for the slip distribution on the fault, namely, the inequality-constrained regularization method, the minimum norm weighted LS method and the two variants of regularization with either the positivity constraints or the 45° positivity constraints.

Before we discuss the inversion results of slips, we would like to note that the minimum norm weighted LS method and regularization fit the data very well. In fact, they exactly recover the true value of the standard deviation, namely, $\hat{σ} = 0.004$ m, though the inverted slip distributions can be almost completely different. In other words, fitting data well cannot be used to judge whether a solution is physically meaningful/reasonable for inverse ill-posed problems, which is certainly always true for rank-deficient problems as a mathematical limit (of inverse ill-posed problems) in terms of matrix rank. Following Xu et al. (2021), we obtain the optimal regularization parameter κ = 0.0011 by minimizing the MSE (16) of the estimated slips. The seismic moment magnitudes computed with the four methods under study are equal to M_w 7.60 for the minimum norm weighted LS method, M_w 6.87 for regularization with the positivity constraints, M_w 6.81 for regularization with the 45° positivity constraints, and finally M_w 6.98 for our inequality-constrained regularization method, respectively. It is clear that: (i) the weighted LS method leads to an overestimate of the true value of magnitude, because its slip solution is rather unstable and noisy due to the ill-posed nature of (5); (ii) both variants of regularization with the positivity constraints and the 45° positivity constraints tend to underestimate the seismic moment magnitude; and (iii) the inequality-constrained regularization method proposed in this paper produces the best estimate of the seismic moment magnitude, which is the closest to its true value M_w 7.00 in these simulations.

For a detailed analysis and comparison of the four inversion methods, we plot the corresponding reconstructed slip distributions in Fig. 3. Although the minimum norm weighted LS method is well known to lead to unstable and unreliable estimates, we still show its estimated slips here mainly for a quick comparison. It is clear from Fig. 3 that the minimum norm weighted LS method and the two variants of regularization with either the positivity constraints or the 45° positivity constraints result in almost completely incorrect reconstructions of the slip distribution in both sizes and directions of slips. The failure of these three methods is likely due to the fact that the simulated true slip distribution is physically complex. From this point of view, it is not appropriate to impose strong inequality constraints on slip inversion, in particular, since we indeed do not know whether dislocations associated with a certain earthquake are simple or complex. The inequality-constrained regularization method proposed in this paper can be generally said to be very successful to accurately reconstruct the simulated complex slip distribution. Most of the slips on the fault are correctly reconstructed, since the reconstructed and true vectors of slips almost exactly overlap, as can be seen from the lower-right panel. Nevertheless, the largest slip vector has been underestimated.

Figure 3.

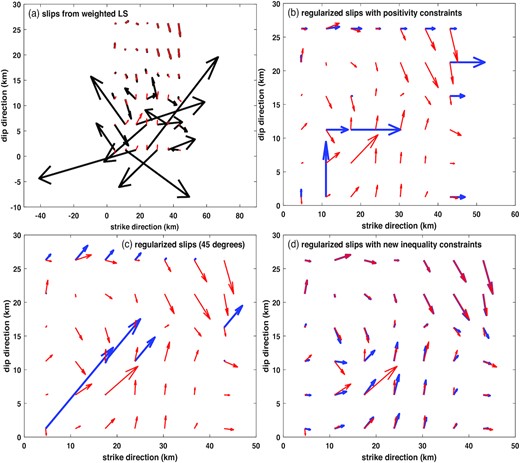
The slips on the fault reconstructed with the minimum norm weighted LS method, the two variants of regularization with either the positivity constraints or the 45° positivity constraints, and our inequality-constrained regularization method. Panel (a): the inverted slips with the minimum norm weighted LS method (black arrows); panel (b): the inverted slips by applying the regularization method with the positivity constraints (blue arrows); panel (c): the inverted slips by applying the regularization method with the 45° positivity constraints (blue arrows); and panel (d): the inverted slips by applying our inequality-constrained regularization method (blue arrows). For convenience of comparison, we also show the simulated true slips in red in all these four panels of inverted slip solutions.

Open in new tab Download slide

Bearing in mind that the smoothness constraints of derivatives with the Laplacian operator are commonly used in slip inversion, we compute the Laplacian-based smoothness matrix $S$ in (12), apply the MSE criterion to determine the optimal regularization parameter κ and reconstruct the slip distribution from the simulated displacements. The slip results are shown in Fig. 4, together with the regularized slip solution with the identity matrix for convenience of comparison. We summarize the major results for this simulated example in the following: (i) the data fitting with the Laplacian smoothness matrix $S$ is basically the same as all the other methods tested in this section. The optimal regularization parameter is equal to 0.0007, which is slightly smaller than 0.0011 with the identity matrix; (ii) the slip distribution reconstructed with the Laplacian smoothness matrix $S$ is only slightly different from that with the identity matrix, as can be clearly seen from Fig. 4. Both of the slip distributions produce the moment magnitude M_w 6.98; and (iii) the Laplacian smoothness matrix $S$ results in two slip vectors with a component on the opposite side of the main rupture direction. No such opposite slip vectors appear in the inequality-constrained regularized solution of slips.

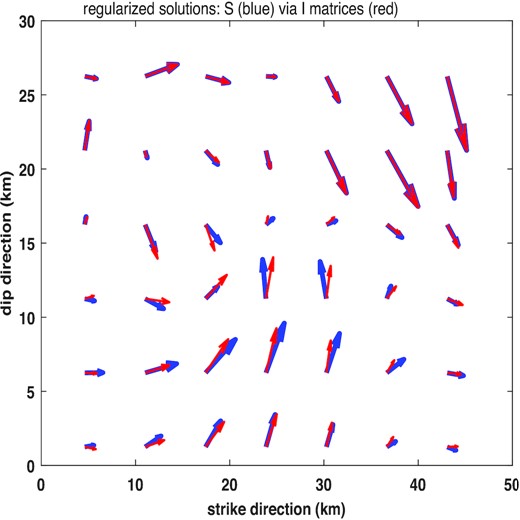
$The slip distributions reconstructed by using regularization with the Laplacian-based smoothness matrix $\mathbf {S}$ (the blue arrows) and an identity matrix $\mathbf {I}$ (the red arrows), respectively.$

Figure 4.

The slip distributions reconstructed by using regularization with the Laplacian-based smoothness matrix $S$ (the blue arrows) and an identity matrix $I$ (the red arrows), respectively.

Open in new tab Download slide

4 APPLICATIONS TO THE 2016 KUMAMOTO M_W 7.0 EARTHQUAKE FROM GNSS MEASUREMENTS

A moment magnitude M_w 7.0 earthquake hit Kumamoto, Japan, at 01:25 am in the early morning of 16 April 2016 (Japan local time) according to Japan Meteorological Agency (JMA) (https://www.data.jma.go.jp/svd/eqev/data/2016_04_14_kumamoto/index.html), which involved the two fault systems of Futagawa and Hinagu (see e.g. Asano & Iwata 2016, 2021; Fukahata & Hashimoto 2016; Scott et al. 2019; Hallo & Gallovič 2020). The earthquake was reported to start on Hinagu fault, reach the intersection of Hinagu and Futagawa faults and then continue the rupture onto Futagawa fault (Asano & Iwata 2021). As in the case of all other large earthquakes in Japan, this earthquake was well recorded by the excellent, continuous monitoring seismological infrastructure of Japan such as the strong motion monitoring networks ‘K-NET/KiK-net’ (see e.g. Kinoshita 1998; Aoi et al. 2004, 2020) and the continuous GNSS monitoring network ‘GEONET’ (see e.g. Tsuji et al. 2013; Tsuji & Hatanaka 2018). It was also well mapped by geodetic imaging satellites such as the ALOS-2 satellite and Sentinel-1 satellite (see e.g. Fukahata & Hashimoto 2016; He et al. 2020; Yang et al. 2021).

A number of kinematic and static rupture models for the earthquake have been published with different types of data and different solution methods. These models are derived either purely by using interferometric synthetic aperture radar (InSAR) data from the ALOS-2 satellite (see e.g. Fukahata & Hashimoto 2016; Yang et al. 2021), teleseismic and strong motion data (see e.g. Asano & Iwata 2016, 2021; Yagi et al. 2016; Hao et al. 2017; Hallo & Gallovič 2020), GEONET GPS data (see e.g. Tanaka et al. 2019) or by combining InSAR, GPS, seismic and light-detection-and-ranging (LiDAR) data (see e.g. Yue et al. 2017; Scott et al. 2019; He et al. 2020). Almost all researchers obtained a moment magnitude M_w 7.0 or slightly larger for this earthquake (see e.g. Fukahata & Hashimoto 2016; Yagi et al. 2016; Hao et al. 2017; Yue et al. 2017; Scott et al. 2019; Tanaka et al. 2019; He et al. 2020; Hallo & Gallovič 2020; Yang et al. 2021; Asano & Iwata 2021). The maximum slip can range from about 5 m (see e.g. Fukahata & Hashimoto 2016; Asano & Iwata 2016, 2021; Yang et al. 2021) or about 6 m (see e.g. Yagi et al. 2016; Hao et al. 2017; Tanaka et al. 2019) up to 8 m (see e.g. Hallo & Gallovič 2020) or even 10 m (Yue et al. 2017). In most cases, the maximum slip was reported to take place on Futagawa fault. Nevertheless, inconsistent results were also mentioned by Scott et al. (2019), who reported that LiDAR-optical-InSAR and optical-InSAR inversions ended up with the maximum slip on Hinagu and Futagawa faults, respectively. Overparametrization is obvious in the case of slip inversion with seismic or GPS data. For example, Asano & Iwata (2016) divided Hinagu and Futagawa faults into 189 patches of size 2 km by 2 km, and used only 15 strong motion stations to reconstruct the kinematic rupture process. A further investigation was reported recently by Asano & Iwata (2021) to refine the kinematic rupture process with 220 patches from 20 strong motion stations. Yagi et al. (2016) tried to recover the slip distribution on 290 patches with teleseismic P-wave data at 27 broad-band seismic stations. Hao et al. (2017) used 32 teleseismic and 29 long-period waveforms to invert for slips on 290 patches. Hallo & Gallovič (2020) chose 29 strong motion stations to recover slips on 234 patches. In the synthetic tests, they tried to invert for slips on 720 patches with strong motion data of 40 stations. In the case of GEONET GPS data, Tanaka et al. (2019) determined static slips on 126 patches from only 20 GEONET stations. Positivity constraints are also imposed to avoid physically unacceptable slip solutions (see e.g. Asano & Iwata 2016; Yue et al. 2017; Scott et al. 2019).

A major purpose of this section is to demonstrate our inequality-constrained regularized inversion method with a real example of earthquakes involved with multiple faults. The 2016 Kumamoto M_w 7.0 earthquake with two faults of Hinagu and Futagawa is one of such best examples. So far as data and modelling are concerned, we will limit ourselves to GNSS data and avoid the issue of modelling deficiency of slip inversion in the first instant by directly using a larger size of patch under the reality of a limited number of measurements. Although InSAR could provide many more measurements, the problem is that geodetic InSAR imaging can only repeat itself after almost 1 month in the case of the ALOS-2 satellite (see e.g. He et al. 2020; Yang et al. 2021) or about two weeks in the case of the Sentinel-1A satellite (He et al. 2020). Unless post-seismic slips, major foreshocks and aftershocks are properly taken into account, the factors of these kinds can affect inverted slip distributions of the main shock, because they all contribute to measured displacements due to poor temporal resolution inherent to InSAR. On the other hand, seismic inversion of slip distributions is often underdetermined with more unknowns than measurements (see e.g. Yagi et al. 2016; Asano & Iwata 2016; Hao et al. 2017; Tanaka et al. 2019; Hallo & Gallovič 2020) and (implicitly) requires arbitrary (artificial) information to find a unique solution. Seismometers are also well known to be inherently subject to instrumental drift, tilts and clipping. Even more, accelerograms have been found to be numerically unreliable in the case of high sampling rates and technological innovation of accelerometers is now under development (Xu 2021a). Thus, we will refrain ourselves from using seismic data on this earthquake.

4.1 Fault geometry and test computation

We use Okada’s elastic half-space model to compute displacements by using the Matlab codes of Beauducel (2014), with a Poisson’s ratio of 0.25 and a rigidity modulus of 30 GPa. Before we start the slip inversion, we make several test computations. We first follow Asano & Iwata (2016) and set the length and width of Hinagu fault to 15 and 18 km, and those of Futagawa fault to 27 and 18 km, respectively. The test computation shows that the length of Hinagu fault is somehow too short to accommodate the coseismic displacements of the GEONET stations. As a result, we extend the length of Hinagu fault to 24 km. We should like to note, however, that their slip results tended to satisfy a shorter length for Hinagu fault, while our test computation does require the extension of length from those used, for example, in Asano & Iwata (2016) and Yagi et al. (2016). Our test computation is satisfactory with the length of Futagawa fault used by Asano & Iwata (2016), though other researches used a length of up to about 40 km for this part of the fault (see e.g. Fukahata & Hashimoto 2016; Hao et al. 2017).

The second test computation is to see what resolution of slip inversion may be expected with the GEONET displacements (to be explained later). Although a very fine resolution of 2 km by 2 km patch size has been reported in the literature (see e.g. Yagi et al. 2016; Asano & Iwata 2016; Hao et al. 2017; Hallo & Gallovič 2020), the GEONET stations that can be used to study this earthquake are obviously not sufficient to support this fine resolution of slip inversion without imposing more or less arbitrary and superficial information that cannot be checked independently. We will avoid this situation of having more unknowns than measurements in the first instant. As a result, we start with a patch size of 3 km by 3 km but find that the corresponding formulation is still too ill-posed to handle, since our computer fails to correctly compute the condition number of the normal matrix $N$ ⁠. Thus, we will limit ourselves to the patch size of 4 km by 4 km in this study and actually have 65 patches in total to model Hinagu and Futagawa faults, or more precisely, 30 for Hinagu fault and 35 for Futagawa fault. We will also include the inversion results with a patch size of 5 km by 5 km for the purpose of comparison.

As for the parameters of fault geometry, different researchers obtained or used different strike and dip angles for both faults (see e.g. Asano & Iwata 2016, 2021; Fukahata & Hashimoto 2016; Yue et al. 2017; Hao et al. 2017; He et al. 2020; Hallo & Gallovič 2020; Yang et al. 2021). We will just take the reported strike/dip/rake angles from the above publications, compute the average values of these angles and use them as the fault parameters in our inversion of slip distributions. The mean strike, dip and rake angles are equal to 204.33°, 73.82° and –169.68° for Hinagu fault and 233.61°, 65.60° and –158.50° for Futagawa fault, respectively. We select the GEONET data in the Kyushu area but limit ourselves to those stations whose coseismic displacements are statistically significant with a probability of 95 per cent, based on the standard deviations of 0.004 m for the horizontal components and 0.008 m for the vertical component (see e.g. Xu et al. 2013; Shu et al. 2017). We finally have three component ENU displacements at 123 GEONET stations, whose horizontal displacements are shown in Fig. 5, together with the main shock and Hinagu/Futagawa faults. Among these 123 GEONET stations, only 13 stations are of horizontal displacements larger than 0.1 m. The maximum coseismic horizontal displacement is 1.018 m, with the maximum coseismic vertical displacement of 0.251 m at the same GEONET station.

Figure 5.

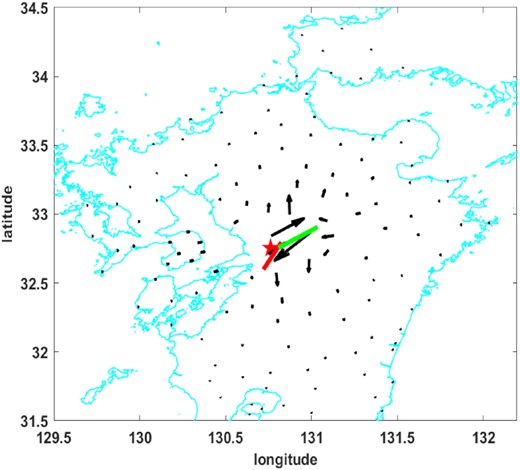
The horizontal displacements at the 123 GEONET stations (black arrows), the JMA epicentre of the 2016 Kumamoto M_w 7.0 earthquake (red star) and the involved Hinagu (red line) and Futagawa (green line) faults. The largest horizontal displacement is 1.018 m.

Open in new tab Download slide

Using the combined geometry of the specified fault parameters and the 123 GEONET stations, we can readily obtain the coefficient matrix $A$ in (5) and accordingly compute the eigenvalues of the normal matrix $N$ in (10), which are shown in Fig. 6. The minimum and maximum eigenvalues and the condition number are equal to 1.6460E-20, 0.0975 and 5.9219E+18, respectively. Bearing in mind that we have totally only 130 slip unknowns, this very large condition number indicates that a direct minimum norm weighted LS reconstruction of slips is almost impossible at this patch size of 4 km by 4 km, since a small error can be amplified to an extremely large extent. Actually, if the minimum norm weighted LS slips are used to compute the moment magnitude as if they were fine, we would obtain a completely incorrect large value of M_w 10.15, implying that the moment magnitude could be overestimated if the high instability is not properly controlled, for example, due to use of too small a regularization parameter, as theoretically expected in Section 2. In order to find a relatively stable and high quality solution of slips, we obtain the optimal regularization parameter κ of 1.5296E-04 by minimizing the MSE objective function (16). To give the reader an impression of how the MSE values change with different values of regularization parameter κ, we also show the MSE curve in Fig. 6.

Figure 6.

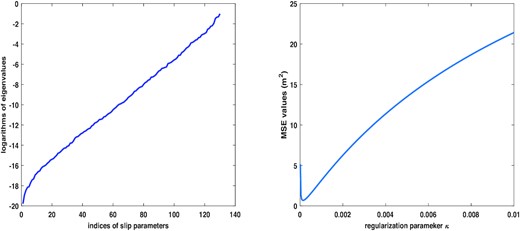
The eigenvalues of the slip inversion with a patch size of 4 km by 4 km (left-hand panel) and the MSE values with different values of regularization parameter κ (right-hand panel).

Open in new tab Download slide

4.2 Inversion results of slip distributions

The regularized reconstructions of slip distributions on Hinagu and Futagawa faults without imposing the physical inequality-constraints (8) are shown in Fig. 7, which are equivalent to an earthquake magnitude M_w 7.1. The basic features of both slip patterns on Hinagu and Futagawa faults are that large ruptures take place shallowly at the depth less than 10 km. This is particularly true on Hinagu fault up to a few km beneath the surface. Nevertheless, it is clear that because the inversion of slips is highly ill-posed with a very large condition number, the naïve regularized inversion results in some unreasonable slips, in particular, in the southwest end of Hinagu fault and roughly right under Aso volcano in the eastern end of Futagawa fault, as can be seen in Fig. 7. Thus, we apply the inequality-constrained regularization to invert for the static slips, which are plotted in Fig. 8 and are equivalent to an earthquake magnitude M_w 6.6. Our moment magnitude M_w 6.6 is slightly smaller than almost all other researches (see e.g. Yagi et al. 2016; Asano & Iwata 2016, 2021; Fukahata & Hashimoto 2016; Yue et al. 2017; Hao et al. 2017; He et al. 2020; Hallo & Gallovič 2020; Yang et al. 2021). The physically constrained regularized slips in Fig. 8 remain the basic feature of rupture that major ruptures take place shallowly on both Hinagu and Futagawa faults. All the physically unreasonable slips disappear on both faults. The largest slips are 4.11 m on Hinagu fault and 6.93 m on Futagawa fault, respectively; both of them take place less than 5 km in depth under the surface. More precisely, about 82 and 78 per cent of energy are released by the large ruptures taking place up to about 8 km right below the surface on Hinagu and Futagawa faults, respectively, which will readily generate large horizontal displacements on the surface. These results may be highly related to and explain well the largest damage of Mashiki city roughly at the corner of intersection of Hinagu and Futagawa faults (see e.g. Kawase et al. 2017), even though we only obtain a moment magnitude M_w 6.6 for the 2016 Kumamoto earthquake. we may like to note that the 45° positivity constraints result in about the same magnitude M_w 6.6 but with apparently unacceptable slip distributions, which are shown in Fig. S1 in the electronic supplementary materials.

Figure 7.

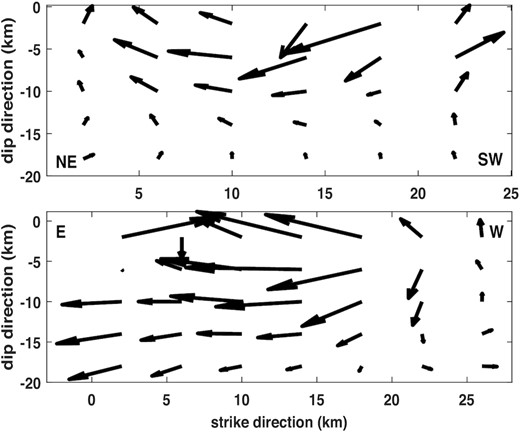
The regularized reconstructions of static slips on Hinagu (upper panel) and Futagawa (lower panel) faults with a patch size of 4 km by 4 km.

Open in new tab Download slide

Figure 8.

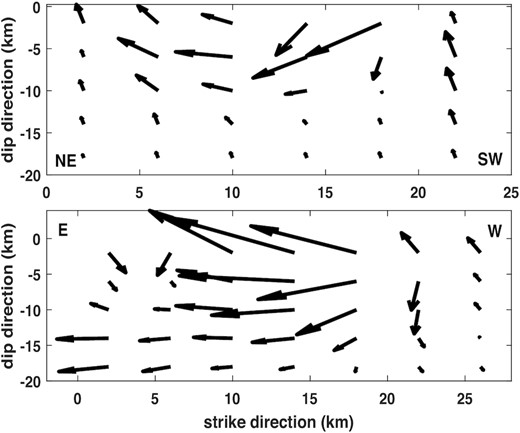
The inequality-constrained regularized solutions of static slips on Hinagu (upper panel) and Futagawa (lower panel) faults with a patch size of 4 km by 4 km. The maximum slips on Hinagu and Futagawa faults are 4.11 and 6.93 m, respectively.

Open in new tab Download slide

To show the effect of regularization parameter κ on slip inversion, we increase the regularization parameter from its optimal value 1.5296E-04 to 0.01. In this case, the condition number is sufficiently small, implying that we can readily obtain a stable inversion of slips. The inverted slip distributions derived from the regularized reconstructions without and with the inequality-constraints (8) are shown in Figs S2 and S3, respectively. The regularized slips are equivalent to a moment magnitude M_w 6.8. It is clear by comparing these two figures that all the ruptures slip along almost the same direction on both Hinagu and Futagawa faults, no matter whether the inequality-constraints (8) are applied. Nevertheless, at the very least, a closer look has consistently shown that about 76 and 79 per cent of energy release take place shallowly up to less than 10 km under the surface on Hinagu and Futagawa faults. We should point out, however, that the reconstructions of slips with the regularization parameter 0.01 are oversmoothed and largely biased, as can be seen from the MSE values on the right-hand panel of Fig. 6.

To further demonstrate the importance of physical inequality constraints, we now show the slip distribution in Fig. 9, which is obtained by applying regularization only with the Laplacian smoothness matrix $S$ without any of the inequality constraints, namely, the positivity constraints, the 45° positivity constraints or our new inequality constraints. First of all, we like to report: (i) the Laplacian smoothness matrix $S$ results in a slightly worse fitting of data (⁠ $\hat{σ} = 0.028$ m), a slightly smaller regularization parameter (κ = 1.1962E-04) and a slightly larger seismic moment magnitude M_w 7.31 than the identity matrix $I$ (⁠ $\hat{σ} = 0.026$ m, κ = 1.5296E-04 and M_w 7.13). Actually, we observed a slightly smaller regularization parameter with the Laplacian smoothness matrix $S$ in the simulated example as well; (ii) however, it is surprised to see from Fig. 9 that the slip distributions on both Hinagu and Futagawa faults reconstructed with the Laplacian smoothness matrix $S$ look physically completely unacceptable and much worse than those with the identity matrix. This becomes obvious when we compare the slip distributions in Fig. 7 with those in Fig. 9, though the Laplacian smoothness matrix $S$ and the identity matrix are found to produce almost the same results in the simulated example. The reason may be attributed to a very large condition number here due to the limited number of GNSS stations with a weak geometrical constraint on the slips, which is much larger than that in the simulated example by more than eight orders of magnitude. On the other hand, the smallest eigenvalue of $(N + κ S)$ is smaller than that of $N_{κ}$ by a factor of 15.86, which makes the Laplacian-based inversion more unstable and noisier; and finally (iii) we should like to note that the Laplacian smoothness matrix $S$ results in 19 slip vectors on Hinagu fault and 10 slip vectors on Futagawa fault with the projected components against the main rupture directions of both faults, respectively. In other words, the regularized slip distributions with only the Laplacian smoothness matrix $S$ but without physical inequality constraints are not acceptable in this example. Again, our inequality-constrained regularized slip distributions satisfy the no-back slip conditions (8).

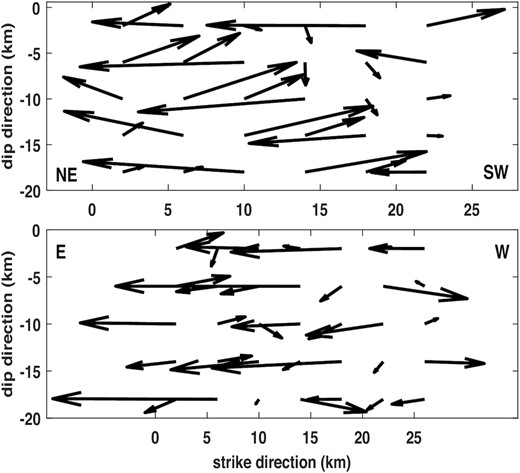
$The regularized solutions of static slips on Hinagu (upper panel) and Futagawa (lower panel) faults with the Laplacian smoothness matrix $\mathbf {S}$ with a patch size of 4 km by 4 km.$

Figure 9.

The regularized solutions of static slips on Hinagu (upper panel) and Futagawa (lower panel) faults with the Laplacian smoothness matrix $S$ with a patch size of 4 km by 4 km.

Open in new tab Download slide

Up to the present, we have not touched too much on the data fitting. The reasons are threefold: (i) good fitting of data does not mean good solutions for inverse ill-posed problems, as mentioned in Remark 3. The weighted LS solution is an extreme example, which attains the best fitting of data but is the least accurate and almost always physically meaningless; (ii) the most important and most difficult aspect of inverse ill-posed problem theory is to accurately reconstruct the unknown function of interest; and (iii) it is clear from (12) or (13) that the basic objective function of all regularization methods is involved with two terms: one responsible for data fitting and the other for regularization. Unless the regularization parameter κ is incorrectly selected, regularization methods and the weighted LS method would generally result in a similar performance of data fitting. Nevertheless, since people seem to care much about data fitting in seismic inversion, we plot the original GEONET horizontal displacements in Figs S4–S7, together with their LS and regularized counterparts with different regularization methods. As theoretically expected, the data fittings from different regularization methods in this paper are not very different.

Since the measured GEONET displacements, the weighted LS estimates and their corresponding regularized displacements almost overlap each other in Figs S4 and S6, we further locally amplify the large displacements in the epicentre area and show the data fitting for each of the weighted LS and regularization methods in Figs S5 and S7. We can intuitively see from the panels in Figs S5 and S7 that the weighted LS method fits the data best, as theoretically expected. The regularization method without any constraints performs better than that with our new inequality constraints. The method with the 45° constraints is of the worst performance of data fitting. For more details, the reader is referred to the electronic supplementary materials.

Bearing in mind that a patch size of 4 km by 4 km leads to a very large condition number of 5.9219E+18, we would like to investigate the effect of patch size on slip inversion by increasing the patch size to 5 km by 5 km. In this case, we only have 40 patches, or more precisely, 20 patches on Hinagu fault and another 20 patches on Futagawa fault. The eigenvalues of the normal matrix $N$ and the MSE values with different regularization parameters are shown in Fig. S8. Although the patch size has been increased to 5 km by 5 km, the maximum eigenvalue does not change significantly. However, the minimum eigenvalue has substantially increased to 3.2802E-14, which is about six orders of magnitude larger than that with a patch size of 4 km by 4 km. As a result, the condition number accordingly decreases from 5.9219E+18 to 2.4911E+12.

The 5 km by 5 km patch size leads to the optimal regularization parameter of 1.5960E-04, which is basically the same as in the case of 4 km by 4 km patch size. The regularized model with the 5 km by 5 km patch size fits the GEONET displacements with a fitting error of 0.0229 m, which is slightly better than that of 0.0258 m with the 4 km by 4 km patch size. The inequality-constrained regularized reconstructions of slips are shown in Fig. 10, with an equivalent moment magnitude M_w 6.7. Comparing the inverted slips on both Figs 8 and 10, we can find that the feature of major rupture in the very shallow parts of Hinagu and Futagawa faults remains unchanged, with the maximum slips of 4.81 and 7.89 m on Hinagu and Futagawa faults, respectively. More precisely, about 94 and 88 per cent of the energy release from the rupture on each of Hinagu and Futagawa faults take place up to the depth of 10 km, respectively; this may again be highly related to the largest damage observed in Mashiki town. The maximum slip of 4.81 m on Hinagu fault is much larger than most researches on the earthquake but may still be reasonable. Actually, Scott et al. (2019) even found the largest slip on Hinagu fault from the LiDAR-optical-InSAR data. The inversion results with the 5 km by 5 km patch size may be more preferable in terms of a smaller fitting error and model simplicity, in particular, bearing in mind that the number of the GEONET stations with a sufficient large displacement in Kyushu area is limited to study this earthquake.

Figure 10.

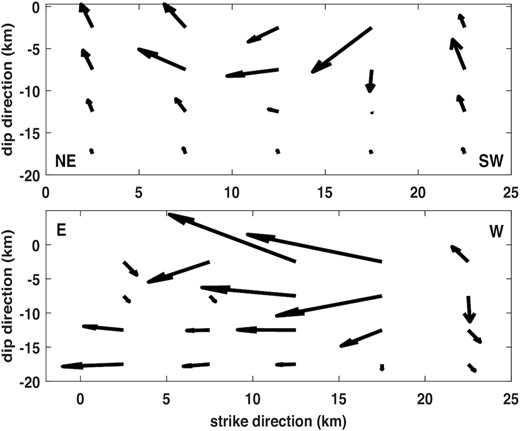
The inequality-constrained regularized solutions of static slips on Hinagu (upper panel) and Futagawa (lower panel) faults with a patch size of 5 km by 5 km. The maximum slips on Hinagu and Futagawa faults are 4.81 and 7.89 m, respectively.

Open in new tab Download slide

Based on the reconstructed slip distributions in Figs 7–10, we may like to summarize that: (i) due to the limited data with a weak geometrical constraint on the fault slips, the regularized slip results without the inequality constraints can be physically unreasonable; (ii) because of a very large condition number with only the GNSS displacements, we could likely only be able to obtain the basic pattern of slip distributions on Hinagu and Futagawa faults. The detailed results of slips, in particular, those right under the Aso volcano in the eastern part of Futagawa fault, may very likely be unreliable and inaccurate, again, due to a very large condition number, or equivalently, the weak geometrical constraint of the limited number of GNSS data. Any geophysical interpretation of the detailed results of slips should be exercised with great care; and (iii) it is hard to judge whether the slight reverse components on both Hinagu and Futagawa faults could be real in terms of the very large condition number, though the inequality-constrained regularized slip distributions fit the vertical GNSS displacements well. We obtain a small fitting error of 0.005 m for the largest vertical displacement of 0.251 m. With the largest vertical uplift displacement of 0.251 m near the Futagawa fault in mind, such slight reverse components might be physically possible to help release the earthquake energy with a very severe rupture in the very shallow parts of the faults. A slight reverse component can also be observed on Hinagu fault from InSAR (Hallo and Gallovič 2020; Yang et al. 2021) and on Futagawa fault from InSAR (compare the left part of slip inversion results of figs 4 and 6 in Fukahata & Hashimoto 2016). Nevertheless, even if InSAR data are used, different researchers could obtain inconsistent results about the possibility of a slight reverse component, as can be inferred by comparing fig. 8 in Yang et al. (2021) with fig. 6 in Fukahata & Hashimoto (2016).

5 CONCLUSION

Slip inversion is essential to understand source mechanics of earthquakes. Problems of inverting for static and/or kinematic rupture from surface measurements have been almost always stated to be inherently non-unique in the seismological literature (see e.g. Olson & Apsel 1982; Olson & Anderson 1988; Das & Kostrov 1994; Beresnov 2003; Mai et al. 2016). Statements of this kind mathematically imply that slip/rupture could have never been correctly recovered, because there exist an infinite number of mathematically equivalent solutions to any problem that is inherently non-unique, irrelevant of whether we would have an infinite number of geometrically best possible measurements on any earthquake. Given the geometry of a fault and the displacement functions on the surface of the semi-infinite elastic medium, the slip function on the fault is defined by Fredholm integral equation (1) or (2) of the first kind. We prove that Fredholm integral equation (1) or (2) of the first kind for slip inversion is mathematically of a unique solution, which is a theoretical guarantee that earthquake slip/rupture can be properly reconstructed if there exist a sufficiently large number of measurements. The non-uniqueness issue of slip inversion in the seismological literature is not mathematically true but is practically caused due to lack of measurements. This practical aspect of non-uniqueness due to lack of data should not be overemphasized to avoid any potential misunderstanding that reconstructing the slip distribution on a fault could never be possible, physically and mathematically.

We have proposed an inequality-constrained regularized inversion of slip distributions on multiple faults. The method implements physically more general inequality constraints to accept more complex dislocation models and/or a combination of complex dislocation models. The formulation of constraints (8) is theoretically significant in three aspects: (i) it mathematically allows the reconstruction of more complex slip/rupture of an earthquake (if any) from measurements; (ii) it can be applied to a large earthquake involving multiple faults with different rake angles; and (iii) the corresponding inequality constraints (8) can be thought of as a natural extension of the positivity constraints, or equivalently, the 45° positivity constraints, as first proposed by Olson & Apsel (1982) and Hartzell & Heaton (1983) for a single fault or multiple faults with a single rake angle. The regularization parameter is chosen by minimizing the mean squared errors of the inverted slip solution.

The proposed method is applied to the 2016 Kumamoto M_w 7.0 earthquake with GNSS measurements. We have limited the number of patches to avoid the rank-deficiency (or non-uniqueness) of the linearized version (5) of Fredholm integral equation (1) or (2) of the first kind due to lack of data in the first instant, since a rank-deficient linear system of equations can only produce a set of mathematically equivalent solutions with an infinite number of elements. Although the number of GEONET stations in the study area allows a maximum number of about 180 patches for both Hinagu and Futagawa faults, test computations have shown that with a patch size of 3 km by 3 km, the model (5) is extremely ill-conditioned. Physically reasonable solutions could hardly be expected. Therefore, we have focused on investigating two patch sizes, namely, one with the size of 4 km by 4 km and the other with the size of 5 km by 5 km. The inequality-constrained regularized inversions with both sizes of patches have resulted in a similar pattern of slip distributions on both Hinagu and Futagawa faults. The ruptures of the earthquake take place shallowly up to 10 km under the surface of Hinagu and Futagawa faults. The inverted slips with the patch size of 5 km by 5 km are preferable in terms of model simplicity and a smaller fitting error, and since there are only a limited number of GEONET displacements larger than 10 cm. The inversion results of slips have shown that: (i) the 2016 Kumamoto earthquake is only of magnitude M_w 6.6-6.7. Nevertheless, if the inequality constraints are not imposed on the slips of Hinagu and Futagawa faults, namely, slips are allowed to move freely around the clock, then the seismic moment magnitude we obtained for the 2016 Kumamoto earthquake is equal to M_w 7.13 with a patch size of 4 km by 4 km (or M_w 7.16 with a patch size of 5 km by 5 km), which is comparable with what has been reported in the literature, though physically apparently not feasible; and (ii) about 80–94 percent of the energy release takes place up to the depth of 10 km or even shallower on Hinagu and Futagawa faults, with the maximum slips of 4.11–4.81 m on Hinagu fault and 6.93–7.89 m on Futagawa fault, respectively, which may be highly related to the largest damage in Mashiki town observed by Kawase et al. (2017).

Finally, we may also like to note that obtaining a unique solution to a rank-deficient linearized model due to lack of data could not make us closer to the truth of an earthquake, since such a unique solution involves subjective or artificial information. We can never know whether such artificial information is correct or not. Instead, it is highly recommended to use a rougher patch in this case, which may seemingly prevent us from a fine (but arbitrary) imaging of an earthquake; but at the very least, we could get some more or less close-to-true information on the earthquake. Much more effort should be made to advance seismological infrastructures, in particular, innovations of seismometers and space geodesy imaging, for more useful and real-time data on large earthquakes.

SUPPORTING INFORMATION

Figure S1. The regularized slip distributions with the 45° positivity constraints: the upper panel—Hinagu fault; the lower panel—Futagawa fault.

Figure S2. The regularized slip distributions with a 0.01 regularization parameter without the inequality-constraints: the upper panel—Hinagu fault; the lower panel—Futagawa fault.

Figure S3. The regularized slip distributions with a 0.01 regularization parameter with the inequality-constraints: the upper panel—Hinagu fault; the lower panel—Futagawa fault.

Figure S4. The horizontal displacements at the 123 GEONET stations (black arrows), their weighted LS estimates (red arrows), the estimates regularized respectively with the 45° positivity constraints (cyan arrows) and our own new inequality constraints (green arrows) and the ordinary regularized estimates without inequality constraints (blue arrows). The largest horizontal displacement is 1.018 m.

Figure S5. The GEONET horizontal displacements, the weighted LS estimates and the regularized estimates with the identity smoothness matrix shown inside the box with red dashed line in Fig. S4. Panel A: the GEONET displacements (black arrows) and the weighted LS estimates (red arrows); panel B: the GEONET displacements (black arrows) and the regularized estimates (blue arrows); panel C: the GEONET displacements (black arrows) and the regularized estimates with the 45° positivity constraints (cyan arrows); and panel D: the GEONET displacements (black arrows) and the regularized estimates with our own new inequality constraints (green arrows). The largest GEONET horizontal displacement is 1.018 m.

Figure S6. The horizontal displacements at the 123 GEONET stations (black arrows), the estimates regularized, respectively, with the 45° positivity constraints (cyan arrows) and our own new inequality constraints (green arrows) and the ordinary regularized estimates without inequality constraints (blue arrows). The largest horizontal displacement is 1.018 m. This figure is different from Fig. S4 in that the Laplacian smoothness matrix is implemented in regularization instead of an identity smoothness matrix.

Figure S7. The horizontal displacements and the regularized estimates with the Laplacian smoothness matrix shown inside the box with red dashed line in Fig. S6. Panel A: the GEONET displacements (black arrows) and the regularized estimates without any constraints (blue arrows); panel B: the GEONET displacements (black arrows) and the regularized estimates with the 45° positivity constraints (cyan arrows); and panel C: the GEONET displacements (black arrows) and the regularized estimates with our own new inequality constraints (green arrows).

Figure S8. The eigenvalues of the slip inversion with a patch size of 5 km by 5 km (left-hand panel) and the MSE values with different values of regularization parameter k (right-hand panel).

Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the paper.

ACKNOWLEDGEMENTS

I thank Prof K. Heki for suggesting making Figs S4 and S6 more reader-friendly, which results in two more locally amplified figures, namely, Figs S5 and S7. I also thank an anonymous reviewer very much for the constructive comments, which have helped improve the manuscript.

DATA AVAILABILITY

I acknowledge the Geospatial Information Authority (GSI) of Japan for the GEONET displacement data and thank Prof Y. Fukahata very much for making the data available to me. Hinagu and Futagawa faults are shown on the basis of the active fault bank in Japan at the link https://gbank.gsj.jp/activefault/search.

REFERENCES

Akaike

H.

,

1980

.

Likelihood and the Bayes procedure

, in

Bayesian Statistics

, pp.

1

–

13

., eds

Bernardo

J.M.

,

de Groot

M.H.

,

Lindley

D.V.

,

Smith

A.F.M.

,

University Press

.

Aki

K.

,

Richards

P.

,

1980

.

Quantitative Seismology: Theory and Methods

,

WH Freeman and Company

.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Ando

M.

,

1975

.

Source mechanisms and tectonic significance of historical earthquakes along the Nankai trough, Japan

,

Tectonophysics

,

27

,

119

–

140

.

10.1016/0040-1951(75)90102-X

Aoi

S.

et al. ,

2020

.

MOWLAS: NIED observation network for earthquake, tsunami and volcano

,

Earth Planets Space

,

72

,

doi: 10.1186/s40623-020-01250-x

.

10.1186/s40623-020-01250-x

Google Scholar

OpenURL Placeholder Text

WorldCat

Crossref

Aoi

S.

,

Kugugi

T.

,

Fujiwara

H.

,

2004

.

Strong-motion seismograph network operated by NIED: K-NET and KiK-net

,

J. Assoc. Earthq. Eng.

,

4

,

65

–

74

.

Asano

K.

,

Iwata

T.

,

2016

.

Source rupture processes of the foreshock and mainshock in the 2016 Kumamoto earthquake sequence estimated from the kinematic waveform inversion of strong motion data

,

Earth Planets Space

,

68

,

doi: 10.1186/s40623-016-0519-9

.

10.1186/s40623-016-0519-9

Google Scholar

OpenURL Placeholder Text

WorldCat

Crossref

Asano

K.

,

Iwata

T.

,

2021

.

Revisiting the source rupture process of the mainshock of the 2016 Kumamoto earthquake and implications for the generation of near-fault ground motions and forward-directivity pulse

,

Bull. seism. Soc. Am.

,

111

,

2426

–

2440

.

Barrientos

S.E.

,

Ward

S.N.

,

1990

.

The 1960 Chile earthquake: inversion for slip distribution from surface deformation

,

Geophys. J. Int.

,

103

,

589

–

598

.

10.1111/j.1365-246X.1990.tb05673.x

Beauducel

F.

,

2014

.

Matlab/Octave tools for geophysical studies: deformation analytical models

,

Available at: https://github.com/IPGP/deformations-matlab

.

Benavente

R.

,

Dettmer

J.

,

Cummins

P.R.

,

Sambridge

M.

,

2019

.

Efficient Bayesian uncertainty estimation in linear finite fault inversion with positivity constraints by employing a log-normal prior

,

Geophys. J. Int.

,

217

,

469

–

484

.

Beresnov

I.

,

2003

.

Uncertainties in finite-fault slip inversions: to what extent to believe? (A critical review)

,

Bull. seism. Soc. Am.

,

93

,

2445

–

2458

.

Bindi

D.

,

Caponnetto

A.

,

2001

.

Tomographic imaging of the earthquake source: numerical validation in two-dimensional approximation

,

J. geophys. Res.

,

106

,

6643

–

6656

.

Bouchon

M.

,

Toksöz

M.N.

,

Karabulut

H.

,

Bouin

M.

,

Dietrich

M.

,

Aktar

M.

,

Edie

M.

,

2002

.

Space and time evolution of rupture and faulting during the 1999 Izmit (Turkey) earthquake

,

Bull. seism. Soc. Am.

,

92

,

256

–

266

.

Cambiotti

G.

,

Zhou

X.

,

Sparacino

F.

,

Sabadini

R.

,

Sun

W.

,

2017

.

Joint estimate of the rupture area and slip distribution of the 2009 L’Aquila earthquake by a Bayesian inversion of GPS data

,

Geophys. J. Int.

,

209

,

992

–

1003

.

Chu

R.

,

Zhu

L.

,

Helmberger

D.V.

,

2009

.

Determination of earthquake focal depths and source time functions in central Asia using teleseismic P waveforms

,

Geophys. Res. Lett.

,

36

(

17

),

doi: 10.1029/2009GL039494

.

10.1029/2009GL039494

Google Scholar

OpenURL Placeholder Text

WorldCat

Crossref

Cohee

B.P.

,

Beroza

G.C.

,

1994

.

Slip distribution of the 1992 Landers earthquake and its implications for earthquake source mechanics

,

Bull. seism. Soc. Am

.,

84

,

692

–

712

.

10.1016/0148-9062(95)94486-9

Cotton

F.

,

Campillo

M.

,

1995

.

Frequency domain inversion of strong motions: application to the 1992 Landers earthquake

,

J. geophys. Res.

,

100

,

3961

–

3975

.

Courboulex

F.

,

Santoyo

M.A.

,

Pacheco

J.F.

,

Singh

S.K.

,

1997

.

The 14 September 1995 (M = 7.3) Copala, Mexico, earthquake: a source study using, teleseismic, regional, and local data

,

Bull. seism. Soc. Am.

,

87

,

99

–

1010

.

10.1785/BSSA0870040999

Custódio

S.

,

Archuleta

R.J.

,

2007

.

Parkfield earthquakes: characteristic or complementary?

,

J. geophys. Res.

,

112

(

B5

),

doi: 10.1029/2006JB004617

.

10.1029/2006JB004617

Google Scholar

OpenURL Placeholder Text

WorldCat

Crossref

D’Alessandro

A.

,

Scudero

S.

,

Vitale

G.

,

2019

.

Review of the capacitive MEMS for seismology

,

Sensors

,

19

(

4

),

doi: 10.3390/s19143093

.

10.3390/s19143093

Google Scholar

OpenURL Placeholder Text

WorldCat

Crossref

Das

S.

,

Kostrov

B.V.

,

1994

.

Diversity of solutions of the problem of earthquake faulting inversion. Application to SH waves for the great Macquarie Ridge earthquake

,

Phys. Earth planet. Inter.

,

85

,

293

–

318

.

10.1016/0031-9201(94)90119-8

Das

S.

,

Kostrov

B.V.

,

1997

.

Determination of the polynomial moments of the seismic moment rate density distribution with positivity constraints

,

Geophys. J. Int.

,

131

,

115

–

126

.

10.1111/j.1365-246X.1997.tb00598.x

Delouis

B.

,

Giardini

D.

,

Lundgren

P.

,

Salichon

J.

,

2002

.

Joint inversion of InSAR, GPS, teleseismic, and strong-motion data for the spatial and temporal distribution of earthquake slip: application to the 1999 İzmit mainshock

,

Bull. seism. Soc. Am.

,

92

,

278

–

299

.

Du

Y.

,

Aydin

A.

,

Segall

P.

,

1992

.

Comparison of various inversion techniques as applied to the determination of a geophysical deformation model for the 1983 Borah Peak earthquake

,

Bull. seism. Soc. Am.

,

82

,

1840

–

1866

.

10.1785/BSSA0820041840

Feigl

K.

et al. ,

2002

.

Estimating slip distribution for the Izmit mainshock from coseismic GPS, ERS-1, RADARSAT, and SPOT measurements

,

Bull. seism. Soc. Am.

,

92

,

138

–

160

.

Freymueller

J.

,

King

N.E.

,

Segall

P.

,

1994

.

The co-seismic slip distribution of the Landers earthquake

,

Bull. seism. Soc. Am.

,

84

,

646

–

659

.

10.1785/BSSA0840030646

Fukahata

Y.

,

Hashimoto

M.

,

2016

.

Simultaneous estimation of the dip angles and slip distribution on the faults of the 2016 Kumamoto earthquake through a weak nonlinear inversion of InSAR data

,

Earth Planets Space

,

68

,

doi: 10.1186/s40623-016-0580-4

.

10.1186/s40623-016-0580-4

Google Scholar

OpenURL Placeholder Text

WorldCat

Crossref

Gallovič

F.

,

Imperatori

W.

,

Mai

P.

,

2015

.

Effects of three-dimensional crustal structureand smoothing constraint on earthquake slipinversions: Case study of the Mw6.3 2009 L’Aquila earthquake

,

J. geophys. Res.: Solid Earth

,

120

,

428

–

449

.

Gombert

B.

,

Duputel

Z.

,

Jolivet

R.

,

Doubre

C.

,

Rivera

L.

,

Simons

M.

,

2018

.

Revisiting the 1992 Landers earthquake: a Bayesian exploration of co-seismic slip and off-fault damage

,

Geophys. J. Int.

,

212

,

839

–

852

.

Grafarend

E.

,

Schaffrin

B.

,

1993

.

Ausgleichung in linearen Modellen

,

BI Wissenschaftsverlag

.

Gülen

L.

,

Pinar

A.

,

Kalafat

D.

,

Özel

N.

,

Horasan

G.

,

Yilmazer

M.

,

Isikara

A.M.

,

2002

.

Surface fault breaks, aftershock distribution, and rupture process of the 17 August 1999 İzmit, Turkey, earthquake

,

Bull. seism. Soc. Am.

,

92

,

230

–

244

.

Hackbusch

W.

,

1995

.

Integral Equations: Theory and Numerical Treatment

,

Birkhäuser Verlag

.

Hallo

M.

,

Gallovič

F.

,

2020

.

Bayesian self-adapting fault slip inversion with Green’s functions uncertainty and application on the 2016 M_w7.1 Kumamoto earthquake

,

J. geophys. Res.

,

125

,

e2019JB018703

,

doi: 10.1029/2019JB018703

.

Hao

J.

,

Ji

C.

,

Yao

Z.

,

2017

.

Slip history of the 2016 Mw 7.0 Kumamoto earthquake: intraplate rupture in complex tectonic environment

,

Geophys. Res. Lett.

,

44

,

743

–

750

.

Hartzell

S.

,

Liu

P.

,

1996

.

Calculation of earthquake rupture histories using a hybrid global search algorithm: application to the 1992 Landers, California, earthquake

,

Phys. Earth planet. Inter.

,

95

,

79

–

99

.

10.1016/0031-9201(95)03108-1

Hartzell

S.H.

,

Heaton

T.H.

,

1983

.

Inversion of strong ground motion and teleseismic waveform data for the fault rupture history of the 1979 Imperial, V.alley., California, earthquake

,

Bull. seism. Soc. Am

,

73

,

1553

–

1583

.

10.1785/BSSA07306A1553

He

Z.

,

Chen

T.

,

Wang

M.

,

Li

Y.

,

2020

.

Multi-segment rupture model of the 2016 Kumamoto Earthquake revealed by InSAR and GPS data

,

Remote Sens.

,

12

(

22

),

doi: 10.3390/rs12223721

.

10.3390/rs12223721

Google Scholar

OpenURL Placeholder Text

WorldCat

Crossref

Hernandez

B.

,

Cotton

F.

,

Campillo

M.

,

1999

.

Contribution of radar interferometry to a two-step inversion of the kinematic process of the 1992 Landers earthquake

,

J. geophys. Res.

,

104

,

13 083

–

13 099

.

Hoerl

A.E.

,

Kennard

R.W.

,

1970

.

Ridge regression: biased estimation for nonorthogonal problems

,

Technometrics

,

12

,

55

–

67

.

10.1080/00401706.1970.10488634

Kawase

H.

,

Matsushima

S.

,

Nagashima

F.

,

Baoyintu d Kenichi Nakano

K.

,

2017

.

The cause of heavy damage concentration in downtown Mashiki inferred from observed data and field survey of the 2016 Kumamoto earthquake

,

Earth, Planets Space

,

69

,

doi: 10.1186/s40623-016-0591-1

.

10.1186/s40623-016-0591-1

Google Scholar

OpenURL Placeholder Text

WorldCat

Crossref

Kinoshita

S.

,

1998

.

Kyoshin net (K-NET)

,

Seismol. Res. Lett.

,

69

,

309

–

332

.

10.1785/gssrl.69.4.309

Kondo

J.

,

1991

.

Integral Equations

,

Clarendon Press

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Lawson

C.L.

,

Hanson

R.J.

,

1974

.

Solving Least Squares Problems

,

Prentice-Hall

.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Lay

T.

,

Wallace

T.C.

,

1995

.

Modern Global Seismology

,

Academic Press

.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Li

X.

,

Cormier

V.F.

,

Toksöz

M.N.

,

2002

.

Complex source process of the 17 August 1999 İzmit, Turkey, earthquake

,

Bull. seism. Soc. Am.

,

92

,

267

–

277

.

Lindsey

E.O.

,

Mallick

R.

,

Hubbard

J.A.

,

Bradley

K.E.

,

Almeida

R.V.

,

Moore

J.

,

Bürgmann

R.

,

Hill

E.M.

,

2021

.

Slip rate deficit and earthquake potential on shallow megathrusts

,

Nat. Geosci.

,

14

,

321

–

326

.

10.1038/s41561-021-00736-x

Lohman

R.B.

,

Barnhart

W.D.

,

2010

.

Evaluation of earthquake triggering during the 2005.2008 earthquake sequence on Qeshm Island, Iran

,

J. geophys. Res.

,

115

(

B12

),

doi: 10.1029/2010JB007710

.

10.1029/2010JB007710

Google Scholar

OpenURL Placeholder Text

WorldCat

Crossref

Mai

P.M.

et al. ,

2016

.

The earthquake-source inversion validation (SIV) project

,

Seismol. Res. Lett.

,

87

,

690

–

708

.

Menke

W.

,

1984

.

Geophysical Data Analysis: Discrete Inverse Theory

,

Academic Press

.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Minson

S.E.

,

Simons

M.

,

Beck

J.L.

,

2013

.

Bayesian inversion for finite fault earthquake source models I–theory and algorithm

,

Geophys. J. Int.

,

194

,

1701

–

1726

.

Okada

Y.

,

1985

.

Surface deformation due to shear and tensile faults in a half-space

,

Bull. seism. Soc. Am.

,

75

,

1135

–

1154

.

10.1785/BSSA0750041135

Olson

A.H.

,

Anderson

J.G.

,

1988

.

Implications of frequency-domain inversion of earthquake ground motions for resolving the space-time dependence of slip on an extended fault

,

Geophys. J.

,

94

,

443

–

455

.

10.1111/j.1365-246X.1988.tb02267.x

Olson

A.H.

,

Apsel

R.J.

,

1982

.

Finite faults and inverse theory with applications to the 1979 Imperial Valley earthquake

,

Bull. seism. Soc. Am.

,

72

,

1969

–

2001

.

10.1785/BSSA07206A1969

Ortega-Culaciati

F.

,

Simons

M.

,

Ruiz

J.

,

Rivera

L.

,

Díz-Salazar

N.

,

2021

.

An EPIC Tikhonov regularization: application to quasi-static fault slip inversion

,

J. geophys. Res.

,

126

,

e2020JB021141

,

doi: 10.1029/2020JB021141

.

Plourde

A.P.

,

Bostock

M.G.

,

2017

.

Multichannel deconvolution for earthquake apparent source time functions

,

Bull. seism. Soc. Am.

,

107

,

1904

–

1913

.

Press

F.

,

1965

.

Displacements, strains, and tilts at teleseismic distances

,

J. geophys. Res.

,

70

,

2395

–

2412

.

10.1029/JZ070i010p02395

Rao

C.R.

,

Mitra

S.K.

,

1972

.

Generalized inverse of a matrix and its applications

, in

Proceedings of the Sixth Berkeley Symp Math Stat Prob

,

Vol. 1: Theory of Statistics

, pp.

601

–

620

., eds

Le Cam

L.M.

,

Neyman

J.

,

Scott

E.L.

,

Univ. California Press

.

Reilinger

R.E.

et al. ,

2000

.

Coseismic and postseismic fault slip for the 17 August 1999, M = 7.5, Izmit, Turkey earthquake

,

Science

,

289

,

1519

–

1524

.

10.1126/science.289.5484.1519

Savage

J.C.

,

Hastie

L.M.

,

1966

.

Surface deformation associated with dip-slip faulting

,

J. geophys. Res.

,

71

,

4897

–

4904

.

10.1029/JZ071i020p04897

Scott

C.

,

Champenois

J.

,

Klinger

Y.

,

Nissen

E.

,

Maruyama

T.

,

Chiba

T.

,

Arrowsmith

R.

,

2019

.

The 2016 M7 Kumamoto, Japan, earthquake slip field derived from a joint inversion of differential lidar topography, optical correlation, and InSAR surface displacements

,

Geophys. Res. Lett.

,

46

,

6341

–

6351

.

Segall

P.

,

Harris

R.

,

1986

.

Slip deficit on the San Andreas fault at, P.arkfield., California, as revealed by inversion of geodetic data

,

Science

,

233

,

1409

–

1413

.

10.1126/science.233.4771.1409

Sekiguchi

H.

,

Irikura

K.

,

Iwata

T.

,

2000

.

Fault geometry at the rupture termination of the 1995 Hyogo-ken Nanbu earthquake

,

Bull. seism. Soc. Am.

,

90

,

117

–

133

.

Sekiguchi

H.

,

Iwata

T.

,

2002

.

Rupture process of the 1999 Kocaeli, Turkey, earthquake estimated from strong-motion waveforms

,

Bull. seism. Soc. Am.

,

92

,

300

–

311

.

Shu

Y.M.

,

Shi

Y.

,

Xu

P.L.

,

Niu

X.J.

,

Liu

J.N.

,

2017

.

Error analysis of high-rate GNSS precise point positioning for seismic wave measurement

,

Adv. Space Res.

,

59

,

2691

–

2713

.

10.1016/j.asr.2017.02.006

Steketee

J.A.

,

1958

.

On Volterra’s dislocation in a semi-infinite elastic medium

,

Can. J. Phys.

,

36

,

192

–

205

.

Tanaka

Y.

,

Ohta

Y.

,

Miyazaki

S.

,

2019

.

Real-time coseismic slip estimation via the GNSS carrier phase to fault slip approach: a case study of the 2016 Kumamoto earthquake

,

Geophys. Res. Lett.

,

46

,

1367

–

1374

.

Tarantola

A.

,

1987

.

Inverse Problem Theory: Methods for Data Fitting and Model Parameter Estimation

,

Elsevier

.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Tarantola

A.

,

Valette

B.

,

1982

.

Generalized nonlinear inverse problems solved using the least squares criterion

,

Rev. Geophys.

,

20

,

219

–

232

.

10.1029/RG020i002p00219

Tikhonov

A.N.

,

Arsenin

V.Y.

,

1977

.

Solutions of Ill-Posed Problem

,

John Wiley & Sons

.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Tsuji

H.

,

Hatanaka

Y.

,

2018

.

GEONET as infrastructure for disaster mitigation

,

J. Disaster Res.

,

13

(

3

),

424

–

432

.

10.20965/jdr.2018.p0424

Tsuji

H.

,

Miyagawa

K.

,

Yamaguchi

K.

,

Yahagi

T.

,

Oshima

K.

,

Yamao

H.

,

Furuya

T.

,

2013

.

Modernization of GEONET from GPS to GNSS

,

Bull. Geospat. Inf. Auth. Japan

,

61

,

9

–

20

.

Google Scholar

OpenURL Placeholder Text

WorldCat

van de Panne

C.

,

1975

.

Methods for Linear and Quadratic Programming

,

North-Holland

.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Wahba

G.

,

1992

.

Spline Models for Observational Data

,

Capital City Press

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Wald

D.J.

,

Heaton

T.H.

,

1994

.

Spatial and temporal distribution of slip for the 1992 Landers, California, earthquake

,

Bull. seism. Soc. Am.

,

84

,

668

–

691

.

10.1785/BSSA0840030668

Wang

X.

,

Wang

J.T.

,

Zhang

C.H.

,

2022

.

A broadband kinematic source inversion method considering realistic Earth models and its application to the 1992 Landers earthquake

,

J. geophys. Res.

,

127

,

e2021JB023216

,

doi: 10.1029/2021JB023216

.

Ward

S.N.

,

Barrientos

S.E.

,

1986

.

An inversion for slip distribution and fault shape from geodetic observations of the 1983, Borah, Peak., Idaho, earthquake

,

J. geophys. Res.

,

91

,

4909

–

4919

.

10.1029/JB091iB05p04909

Xu

P.

,

Cannon

E.

,

Lachapelle

G.

,

1999

.

Stabilizing ill-conditioned linear complementarity problems

,

J. Geod.

,

73

,

204

–

213

.

10.1007/s001900050237

Xu

P.L.

,

1992a

.

The value of minimum norm estimation of geopotential fields

,

Geophys. J. Int.

,

111

,

170

–

178

.

10.1111/j.1365-246X.1992.tb00563.x

Xu

P.L.

,

1992b

.

Determination of surface gravity anomalies using gradiometric observables

,

Geophys. J. Int.

,

110

,

321

–

332

.

10.1111/j.1365-246X.1992.tb00877.x

Xu

P.L.

,

1997

.

A general solution in nonlinear rank-defect geodetic models

,

Boll. Geod. Sci. Aff.

,

56

,

1

–

25

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Xu

P.L.

,

1998

.

Truncated SVD methods for linear discrete ill-posed problems

,

Geophys. J. Int.

,

135

,

505

–

514

.

10.1046/j.1365-246X.1998.00652.x

Xu

P.L.

,

2009

.

Iterative generalized cross-validation for fusing heteroscedastic data of inverse ill-posed problems

,

Geophys. J. Int.

,

179

,

182

–

200

.

10.1111/j.1365-246X.2009.04280.x

Xu

P.L.

,

2021a

.

Technological revolution of accelerometers: a regularization method to compute accelerations

, in

iPoster presented online at AGU Fall Meeting

,

New Orleans, LA and Online Everywhere, 13–17 December

.

Xu

P.L.

,

2021b

.

A new look at Akaike’s Bayesian information criterion for inverse ill-posed problems

,

J. Frankl. Inst.-Eng. Appl. Math.

,

358

,

4077

–

4102

.

10.1016/j.jfranklin.2021.03.003

Xu

P.L.

,

Du

F.

,

Shu

Y.M.

,

Zhang

H.P.

,

Shi

Y.

,

2021

.

Regularized reconstruction of peak ground velocity and acceleration from very high-rate GNSS precise point positioning with applications to the 2013 Lushan M_w6.6 earthquake

,

J. Geod.

,

95

,

doi: 10.1007/s00190-020-01449-6

.

10.1007/s00190-004-0386-1

Google Scholar

OpenURL Placeholder Text

WorldCat

Crossref

Xu

P.L.

,

Rummel

R.

,

1994

.

Generalized ridge regression with applications in determination of potential fields

,

Manuscr. Geod.

,

20

,

8

–

20

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Xu

P.L.

,

Shen

Y.Z.

,

Fukuda

Y.

,

Liu

Y.M.

,

2006

.

Variance component estimation in inverse ill-posed linear models

,

J. Geod.

,

80

,

69

–

81

.

10.1007/s00190-006-0032-1

Xu

P.L.

,

Shi

C.

,

Fang

R.

,

Liu

J.N.

,

Niu

X.J.

,

Zhang

Q.

,

Yanagidani

T.

,

2013

.

High-rate precise point positioning (PPP) to measure seismic wave motions: an experimental comparison of GPS PPP with inertial measurement units

,

J. Geod.

,

87

,

361

–

372

.

10.1007/s00190-012-0606-z

Xu

P.L.

,

Shu

Y.M.

,

Liu

J.N.

,

Nishimura

T.

,

Shi

Y.

,

Freymueller

J.T.

,

2019a

.

A large scale of apparent sudden movements in Japan detected by high-rate GPS after the 2011 Tohoku Mw9.0 earthquake: Physical signals or unidentified artifacts?

,

Earth, Planets Space

,

71

,

doi: 10.1186/s40623-019-1023-9

.

10.1186/s40623-019-1023-9

Google Scholar

OpenURL Placeholder Text

WorldCat

Crossref

Xu

P.L.

,

Shu

Y.

,

Niu

X.

,

Liu

J.N.

,

Yao

W.

,

Chen

Q.

,

2019b

.

High-rate multi-GNSS attitude determination: experiments, comparisons with inertial measurement units and applications of GNSS rotational seismology to the 2011 Tohoku M_w9.0 earthquake

,

Meas. Sci. Technol.

,

30

,

024003

.

Xu

X.H.

,

Tong

X.P.

,

Sandwell

D.T.

,

Milliner

C.

,

Dolan

J.F.

,

Hollingsworth

J.

,

Leprince

S.

,

Ayoub

F.

,

2016

.

Refining the shallow slip deficit

,

Geophys. J. Int.

,

204

,

1867

–

1886

.

Yagi

Y.

,

Okuwaki

R.

,

Enescu

B.

,

Kasahara

A.

,

Miyakawa

A.

,

Otsubo

M.

,

2016

.

Rupture process of the 2016 Kumamoto earthquake in relation to the thermal structure around Aso volcano

,

Earth, Planets Space

,

68

,

doi: 10.1186/s40623-016-0492-3

.

10.1186/BF03353057

Google Scholar

OpenURL Placeholder Text

WorldCat

Crossref

Yang

J.Y.

,

Xu

C.J.

,

Wen

Y.M.

,

Xu

G.Y.

,

2022

.

The July 2020 M-w 6.3 Nima earthquake, Central Tibet: a shallow normal-faulting event rupturing in a stepover zone

,

Seism. Res. Lett.

,

93

,

45

–

55

.

Yang

Y.

,

Chen

Q.

,

Xu

Q.

,

Zhao

J.

,

Hu

J.

,

Li

H.

,

Xu

L.

,

2021

.

Comprehensive investigation of capabilities of the left-looking InSAR observations in coseismic surface deformation mapping and faulting model estimation using multi-pass measurements: an example of the 2016 Kumamoto, Japan earthquake

,

Remote Sens.

,

13

,

doi: 10.3390/rs13112034

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Yue

H.

,

Ross

Z.E.

,

Liang

C.

,

Michel

S.

,

Fattahi

H.

,

Fielding

E.

,

Jia

B.

,

2017

.

The 2016 Kumamoto M_w = 7.0 earthquake: a significant event in a fault-volcano system

,

J. geophys. Res.

,

122

,

9166

–

9183

.

Zollo

A.

,

Capuano

P.

,

Singh

S.K.

,

1995

.

Use of small earthquake records to determine the source time functions of larger earthquakes: an alternative method and an application

,

Bull. seism. Soc. Am.

,

85

,

1249

–

1256

.

Google Scholar

OpenURL Placeholder Text

WorldCat

This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)

Download all slides

Month:	Total Views:
November 2022	87
December 2022	29
January 2023	11
February 2023	18
March 2023	18
April 2023	24
May 2023	21
June 2023	5
July 2023	11
August 2023	4
September 2023	5
October 2023	6
November 2023	3
December 2023	5
January 2024	38
February 2024	9
March 2024	19
April 2024	11
May 2024	22
June 2024	9
July 2024	14
August 2024	15
September 2024	12
October 2024	6
November 2024	10
December 2024	6
January 2025	19
February 2025	8
March 2025	11
April 2025	15
May 2025	3

Article Contents

An inequality-constrained regularized inversion of slip distributions on multiple faults with applications to the 2016 Kumamoto M_w 7.0 earthquake

SUMMARY

1 INTRODUCTION

2 AN INEQUALITY-CONSTRAINED REGULARIZED SLIP INVERSION METHOD FOR MULTIPLE FAULTS

3 SYNTHETIC SIMULATED EXAMPLES

3.1 Consequences of slip inversion with an insufficient number of measurements

3.2 Slip reconstruction with more measurements than the slip unknowns

4 APPLICATIONS TO THE 2016 KUMAMOTO M_W 7.0 EARTHQUAKE FROM GNSS MEASUREMENTS

4.1 Fault geometry and test computation

4.2 Inversion results of slip distributions

5 CONCLUSION

SUPPORTING INFORMATION

ACKNOWLEDGEMENTS

DATA AVAILABILITY

REFERENCES

Supplementary data

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

An inequality-constrained regularized inversion of slip distributions on multiple faults with applications to the 2016 Kumamoto Mw 7.0 earthquake

SUMMARY

1 INTRODUCTION

2 AN INEQUALITY-CONSTRAINED REGULARIZED SLIP INVERSION METHOD FOR MULTIPLE FAULTS

3 SYNTHETIC SIMULATED EXAMPLES

3.1 Consequences of slip inversion with an insufficient number of measurements

3.2 Slip reconstruction with more measurements than the slip unknowns

4 APPLICATIONS TO THE 2016 KUMAMOTO MW 7.0 EARTHQUAKE FROM GNSS MEASUREMENTS

4.1 Fault geometry and test computation

4.2 Inversion results of slip distributions

5 CONCLUSION

SUPPORTING INFORMATION

ACKNOWLEDGEMENTS

DATA AVAILABILITY

REFERENCES

Supplementary data

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

An inequality-constrained regularized inversion of slip distributions on multiple faults with applications to the 2016 Kumamoto M_w 7.0 earthquake

4 APPLICATIONS TO THE 2016 KUMAMOTO M_W 7.0 EARTHQUAKE FROM GNSS MEASUREMENTS