Skin effect in generalized radial flow model in fractured media

Summary

1 Introduction

Models for describing groundwater flow in fractured media have been developed for several decades (e.g. Gringarten & Witherspoon 1972; Cinco-Ley & Samaniego 1981; Jenkins & Prentice 1982). The model of generalized radial flow (GRF) proposed by Barker (1988) introduces a new parameter, flow dimension, to conceptualize the channelized geometry of flow in fractured media. Barker's (1988) model allows the flow dimension to be an arbitrary number which ranges from one to three. The value of flow dimension is unity for a parallel flow, two for a cylindrical flow and three for a spherical flow. The flow, for example, in a vertical fracture intercepted by a pumping well can be regarded as 1-D. On the other hand, it will be considered to be 2-D when the well completely penetrates the homogeneous porous aquifer. In addition, the flow in the case of pumping concentrated within a fracture connected to a dense and extended network is expected to be -3-D (Lods & Gouze 2008).

The GRF model has been widely used for interpreting interference pumping tests (e.g. Leveinen 2000; Walker & Roberts 2003; Kuusela-Lahtinen et al. 2003; Le Borgne et al. 2004) and has been extended to develop solutions for different circumstances. A skin zone around the wellbore may be produced by well construction or development. The formation properties of the skin zone are significantly different from the original ones. The well skin might have some effects upon the flow in fractured media (Kabala & Cassiani 1997; Park & Zhan 2002). Mathematically, the skin can be described in two ways. One is to treat the skin as a different formation and solve the flow system of the skin zone. The other is to represent the skin as a skin factor by lumping all properties of the skin together as an energy loss term for the fracture system. Hamm & Bidaux (1996) proposed a Laplace-domain solution for double-porosity systems that consider transient flow, well storage capacity and skin effect for constant-rate tests. Leveinen (2000) formulated a composite analytical solution which allows the flow dimension to be fractional for a fractured-zone aquifer under a constant pumping rate. Instead of treating the skin as a factor, his model assumes a composite structure representing the fractures intersecting the pumping well and the fracture system comprising the actual aquifer. Audouin & Bodin (2008) further extended the Barker's work to develop analytical solutions for the cross-borehole slug tests in fractured media. It is worth noting that the solutions proposed by Hamm & Bidaux (1996), Leveinen (2000) and Audouin & Bodin (2008) are all in the Laplace domain. Based on Barker's model (1988), Rehbinder (2010) solved the generalized flow equation with both Dirichlet and Neumann conditions and presented analytical solutions in the time domain. However, the skin effect is not considered in his model. If a skin factor is used to represent the skin effect in the fracture flow model, the boundary condition at the rim of wellbore will become the Robin condition for constant-head tests.

In this paper, we first present a mathematical model describing the flow behaviour under the Robin type of boundary condition with the consideration of the skin effect in a fractured aquifer. We then develop the analytical solution for the head distribution of the model by the methods of Laplace transform and Bromwich integral. Moreover, the solution for the wellbore flux is also developed analytically based on the head solution and Darcy's law. These solutions constitute extensions of the Rehbinder's (2010) accounting for the well skin effect. Rehbinder (1999) proposed two methods, simple and complicated inversions, to invert the Laplace-domain solutions into time-domain solutions. The analysis demonstrated that the solution inverted by the complicated inversion converges more rapidly, while the approach using simple inversion method is easier to follow. The simple inversion method will be utilized in this study because it is relatively straightforward. The presence of skin generally has a significant effect on the flow behaviour near the well and therefore the issue of well skin effect on the flow behaviour deserves more attention. Since the developed solutions can be applied to delineate the spatial and temporal head distribution and wellbore flux for flow in fractured media with various dimensions, it has practical use in site characterization for fractured media.

2 Methodology

2.1 GRF model

According to Barker (1988), the GRF model for fractured media reads

1

where h is the hydraulic head, r_w is the radius of the source, κ=K/S_s is the hydraulic diffusivity, K is the hydraulic conductivity, S_s is the specific storage, r is the radial distance from the centre of the source, t is the discharge (or recharge) time and n is an integer or non-integer dimensionality of the fracture system ranging from one to three, for example, 1 ≤n≤ 3. Compared to the thickness of the aquifer, a well skin around the source is extremely small and therefore can be treated as a skin factor in the fracture flow model. The boundary condition at radius r_w under a constant-head test becomes the Robin's type and is expressed as:

2

where H(t) is Heaviside's step function, s_f=Kd_s/(K_sr_w) is the skin factor, d_s is the skin thickness and K_s is the hydraulic conductivity of the skin. Note that the initial condition must be compatible with the boundary condition (i.e. eq. 2). Thus, h₀ (0) = 0. In addition, the condition that | h₀ (t)| is limited (Rehbinder 2010) should also behold. The introduction of dimensionless variables ϕ=h/h_r, ϕ₀=h₀/h_r, τ=κt/r²_w and ξ=r/r_w leads to the following governing equation and associated boundary and initial conditions:

3

4

5

and

6

By means of Laplace transform with variable p, the partial differential eq. (3) can be transformed into an ordinary one subject to the initial condition (6):

7

8

and

9

Eq. (7) can then be solved with boundary conditions (8) and (9). The Laplace-domain solution of dimensionless hydraulic head is found as

10

where K_ν (·) is the modified Bessel functions of the second kinds of order ν= 1 −n/2. Based on the convolution theorem and eq. (10), the time-domain solution of dimensionless hydraulic head can be expressed as

11

where the Laplace transform of f(ξ, τ) is

12

Based on Darcy's law, the dimensionless flux leaving the well can be expressed as

13

According to the simple inversion approach in Rehbinder (1999), eq. (12) can be rewritten as

14

which gives

15

and

16

For the special case that the head is constant at the boundary, ϕ₀ (τ) equals H(τ). Eq. (11) can then be further expressed as

17

The inverse Laplace transform of eq. (17) can be obtained via the Bromwich integral method (e.g. Davies 2002; Yeh & Yang 2006). As such,

18

and

19

where η is a dummy variable, A(η) =J_ν (η) −s_fηJ_ν−1(η), B(η) =Y_ν (η) −s_fηY_ν−1(η) and J_ν (·) and Y_ν (·) are the Bessel functions of the first and second kind of order ν, respectively. The detailed development of eq. (18) is listed in the Appendix.

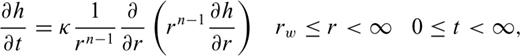
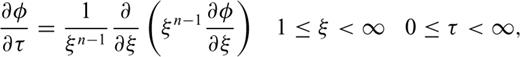
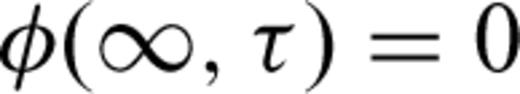
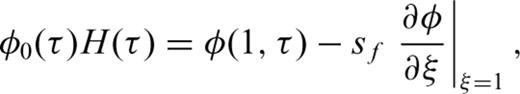
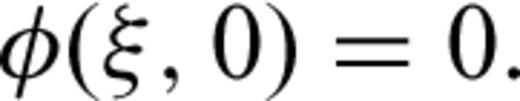
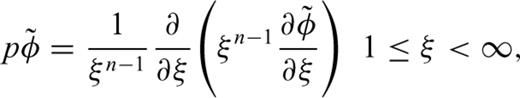
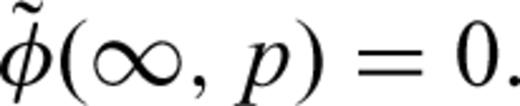
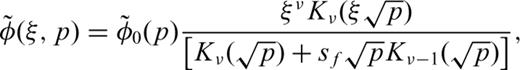
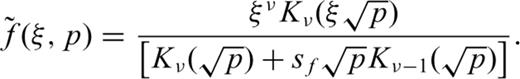
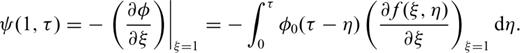
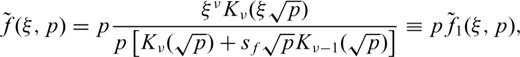
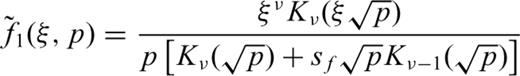
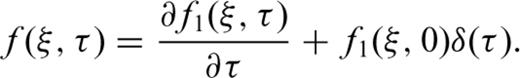
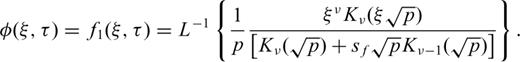
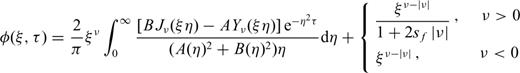
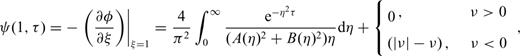
2.2 Removal of the singularity of integrand at the origin

The integration with respect to η in eq. (19) is evaluated numerically. The problem of singularity at η= 0 for the integral should be solved first. The integral range of eq. (19) can be split into two regions, that is, [0, a] and [a, ∞], as

20

The exponential function in the integration can be expended to a series as (Peng et al. 2002)

21

Substituting eq. (21) into eq. (20), the first integral on the right-hand side (RHS) is then written as

22

where a is extremely small and β= 4s_fν− 2. Eq. (22) is further rearranged to

23

The first term on the RHS of eq. (23) can be calculated using the differentiation formula for the arctangent function (Abramowitz & Stegun, 1970, p. 82, eq. 4.4.53) and yields

24

Note that A(0)/B(0) = 0 when η= 0; therefore tan⁻¹[A(0)/B(0)] equals zero. According to the relationships of eqs (20)–(24), the singularity of the integration in eq. (19) can be removed using the following equation after some algebraic manipulations:

25

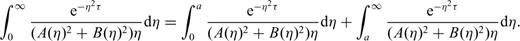
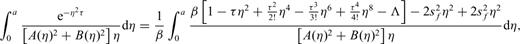
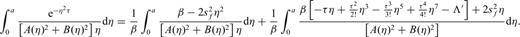
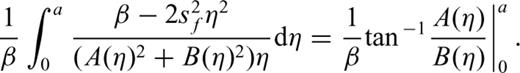
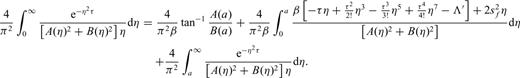
3 Results

The dimensionless wellbore flux decreases with increasing skin factor for various flow dimensions (Fig. 1). The curves of dimensionless wellbore flux for s_f= 0 and s_f= 0.5 for different n are distinctly different at early times. This discrepancy of these curves indicates that the skin has substantial impact on the dimensionless wellbore flux and the effect of well skin reaches its maximum for n= 3 at early times. In contrary, the differences between these curves decrease at late times. The results indicate that the early time data are better to use for determining the value of the skin factor than the late time data. However, the skin effect might not be observed at late time data especially for n= 1 since it vanishes at late times.

Figure 1

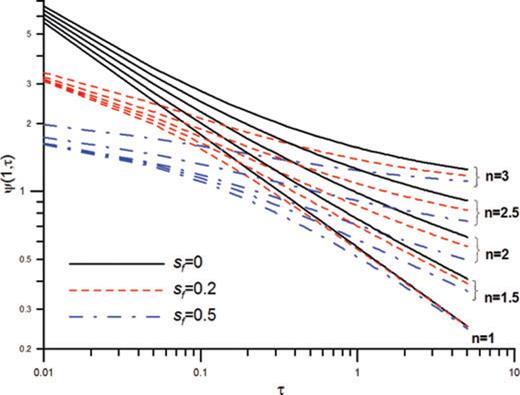
The well skin effect on the dimensionless wellbore flux as a function of dimensionless time for various values of skin factor s_f (i.e. 0, 0.2 and 0.5) and flow dimension n (i.e. 1, 1.5, 2, 2.5 and 3).

Open in new tabDownload slide

4 Discussion

As shown in Fig. 1, the differences in wellbore flux among the curves of various dimensionality are small when τ is small for s_f= 0, 0.2 and 0.5. In other words, the wellbore flux is independent of the dimensionality n when τ is small as indicated in Rehbinder (2010). This phenomenon can be demonstrated from the analysis of eq. (19) when τ is small. Using the asymptotic expansion of the Bessel function in eq. (17) for a large value of p, it yields the following equation:

26

It would be expected from eq. (26) that the flow is only affected by the skin at early times. The influence of the dimensionality on wellbore flux becomes considerable when τ increases because the exponential term on the RHS of eq. (19) becomes less important as τ increases. It is worth mentioning that the effect of dimensionality on wellbore flux becomes less important since the solution of wellbore flux in eq. (19) for τ→∞ is zero when n≤ 2. However, the zero wellbore flux is physically impossible because of the presence of pumping. In addition, eq. (26) is identical to the small-time solution of eq. (44) in Rehbinder (2010) when s_f= 0.

Solutions developed in this study are based on the GRF model, and therefore the use of these solutions may also be restricted by the limitations of the GRF model. Eqs (18) and (19) are adequate for describing the flow behaviour in continuous media since the GRF model is a continuum in which the flow is not necessarily 2-D during the pumping test (Rafini & Larocque 2009). As demonstrated above, the influence of dimensionality on the wellbore flux is important in a fracture system. Therefore, a careful treatment of the dimensionality is required when the scale of the fracture flow system increases as indicated in Barker (1988).

5 Concluding Remarks

The GRF equation, describing the transient head distribution of flow with arbitrary dimensionality in fractured media, has been solved with the considering the well skin effect. The boundary condition around the source under a constant-head test will become the Robin condition if the well skin effect is taken into account. The Laplace transform is applied to solve the partial differential equation under the Robin type of boundary condition. The solution in Laplace domain is further transformed into time domain via the method of Bromwich integral. Furthermore, based on the head solution and Darcy's law, the time-domain solution for wellbore flux is developed to investigate the well skin effect. Results of this study indicate that the influence of skin on wellbore flux is significant for various flow dimensions and the skin effect should be taken into account in characterizing fracture aquifers. The newly developed solutions are helpful for determining the values of the skin factor and hydraulic parameters from the analysis of the field data obtained from constant-head tests in fractured media.

Acknowledgments

We are grateful to the editor, Dr Jörg Renner, and two anonymous reviewers for their thoughtful comments and guidance. Research leading to this work has been partially supported by the grants from Taiwan National Science Council under the contract numbers NSC99-2221-E-009-062-MY3 and NSC 99-NU-E-009-001.

Appendix

To invert the Laplace-domain solution, eq. (10) into the time-domain solution, the Bromwich integral (Davies 2002) is applied as

(A1)

where p is a complex variable and c is a large, real, positive constant so that all the poles lie to the left of line (c− i∞, c+ i∞). The closed contour with a branch point at p= 0 for the integral is shown in Fig. A1 and the integral is expressed as

(A2)

Figure A1

The closed contour used in the Bromwich integral.

Open in new tabDownload slide

The closed contour consists of the part C₀ of the Bromwich line from −∞ to ∞, semicircles C₁ and C₅, lines C₂ and C₄ parallel to the real axis and a circle C₃ of radius ɛ around the origin. As one would expect, the integrals taken along C₁ and C₅ vanish when R tends to infinity. Consequently, the calculation of the integral along the path C₀ yields the inversion in eq. (A1) and it is written as

(A3)

Assume p=η² e^iπ and apply the formulae (Abramowitz & Stegun 1970)

(A4)

The integral along the path C₂ can be obtained as

(A5)

Similarly, the integral along the path C₄ is calculated by introducing p=η² e^−iπas

(A6)

For the integral along the small circle C₃, we define p as p=ɛ e^iθ and use the approximated form

(A7)

The integral leads to

(A8)

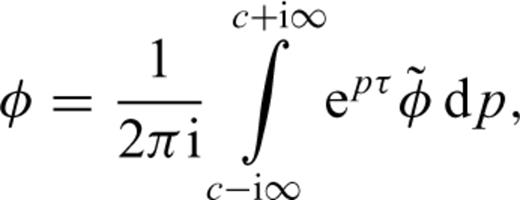
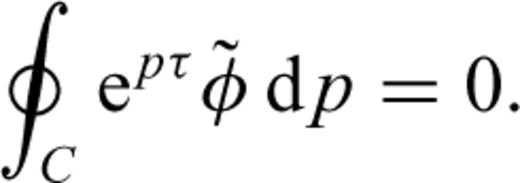
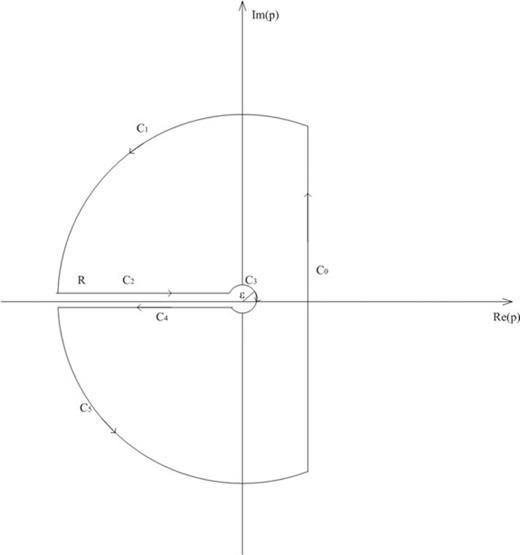
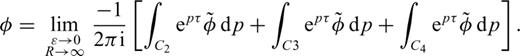
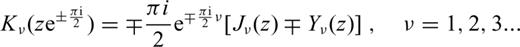
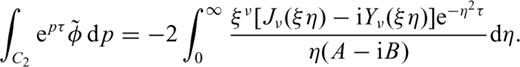
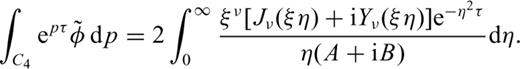
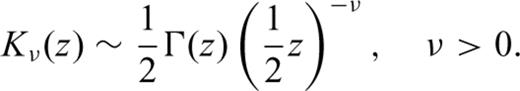
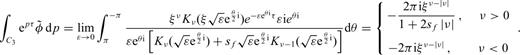
Combining eqs (A5), (A6) and (A8) and substituting into eq. (A2) yields the solution of eq. (11).

References