-
PDF
- Split View
-
Views
-
Cite
Cite
Vincent Jacquemet, Nathalie Virag, Lukas Kappenberger, Wavelength and vulnerability to atrial fibrillation: Insights from a computer model of human atria, EP Europace, Volume 7, Issue s2, 2005, Pages S83–S92, https://doi.org/10.1016/j.eupc.2005.03.017
Close - Share Icon Share
Abstract
To explain the contradictory results related to the concept of critical cardiac wavelength in the initiation and perpetuation of atrial fibrillation (AF).
A biophysically based computer model was used to: (1) study the relationship between wavelength and AF perpetuation in the presence of multiple re-entrant wavelets, (2) evaluate the performance of different existing methods for wavelength estimation in the presence of different arrhythmogenic substrates, and (3) document the impact of either heterogeneities in refractoriness or the presence of a mother rotor on wavelength estimation.
The simulations confirmed that the wavelength must be below a critical value for AF to be sustained, when the perpetuation mechanism relies on multiple re-entrant wavelets. The estimated value of wavelength was not the same for all methods tested and depended in part on the nature of the spatio-temporal organization of the AF dynamics.
A priori information about the underlying wavelet dynamics is needed for a correct interpretation of the cardiac wavelength as estimated by the current clinical methods.
Introduction
Atrial fibrillation (AF) is the most frequent type of arrhythmia, often leading to severe clinical complications. However, its underlying electrophysiological mechanisms are not as yet fully understood, this being partly due to the various aetiologies of AF. Furthermore, progression from paroxysmal to permanent AF involves functional changes in the atrial cells (i.e. electrical remodelling) or structural changes in the atrial tissue (e.g. increased spatial heterogeneities, dilatation of atria, etc.) [1]. The state of the atria during AF may be characterized by the number and spatial extent of small wave fronts (wavelets) that propagate and interact in a random fashion over the atrial surface.
The multiple wavelets hypothesis is a conceptual description of AF, postulating that the maintenance of AF relies on the presence of a sufficient number of such wavelets while undergoing fractionation, collisions and coalescence [2]. In one of the first computer models of AF, Moe et al. demonstrated the importance of a critical mass and a short refractory period in the perpetuation of AF [3]. This theory was also supported by human experimental mapping studies during type III AF, showing the presence of multiple wavelets, with areas of slow conduction and conduction block [4]. Allessie et al. [5] estimated that at least 3–6 wavelets are required for the perpetuation of AF. Arrhythmogenic factors are expected to increase the number of wavelets, while therapeutic interventions are intended to reduce the number. For example, Wang et al. [6] showed that during pharmacological treatment of AF, the actual termination of AF was preceded by a reduction of the average number of wavelets.
Cardiac wavelength is defined as the distance travelled by the depolarization wave during the functional refractory period [7]. A direct local estimate of the wavelength WL is obtained by the product of conduction velocity (CV) and effective refractory period (ERP): WL=CV×ERP. The number of wavelets that fit onto the atrial surface at any given time clearly depends on atrial size, CV and ERP[3]. A decrease in wavelength, either by ERP shortening or by a decrease in CV may, therefore, increase the vulnerability to AF. For instance, in the study of Ravelli et al. [8], vagal stimulation and increase in atrial pressure, resulting in atrial stretch and reduction of ERP, facilitated the initiation of AF by premature stimuli. Rensma et al. also demonstrated the importance of wavelength in the induction of AF [9].
Wavelength is difficult to measure in patients, especially during permanent AF because of limited spatial sampling over the atrial surface. As a result, several indirect techniques for wavelength estimation have been developed that require only a limited number of atrial electrograms [10]. These measures of wavelength and the correlation with AF inducibility and perpetuation are not consistent. For example, Graux et al. proposed an endocavitary approach to calculate wavelength in patients with paroxysmal AF and found a (negative) correlation between wavelength and the occurrence of spontaneous or induced atrial arrhythmias [7]. In contrast, Fareh et al. measured wavelength in dogs subject to rapid atrial pacing and found that ERP and wavelength were not significant determinants of AF inducibility [22], while the presence of heterogeneities appeared to be a key factor. The apparent contradiction between these results might be related to the difficulty in reliably estimating wavelength experimentally and to create comparable and reproducible substrates for AF.
In this paper, biophysical models with different arrhythmogenic substrates are used to study: (1) the critical wavelength for AF initiation in the framework of the multiple wavelets hypothesis, (2) different existing methods for wavelength estimation, and (3) the effect of the AF substrate (such as the presence of heterogeneities) on wavelength estimation. An advantage of computer modelling over clinical studies is that the full spatio-temporal development of wavelets may be studied, since the time course of transmembrane potentials is available at any location.
Methods
Computer models of AF
Biophysical models of AF with an identical anatomical structure but with three different types of AF substrate were used: (A) a substrate in which the perpetuation of AF results exclusively from multiple re-entrant wavelets, (B) a substrate entailing a mother rotor, and (C) a model of AF with multiple wavelets in the presence of heterogeneities in refractoriness. The first model was used to investigate the concept of critical wavelength in a simple, homogeneous substrate. The two other models involve clear inhomogeneities. They served to evaluate wavelength estimation techniques in cases where the nature of the wavelet dynamics is drastically different.
All models had a common geometry, derived from magnetic resonance images of human atria, in which the atria were represented by a monolayer in 3-D space [11]. The geometry contained holes at sites of the entries and exits of the vessels as well as at the locations of the valves connecting the atria to the ventricles. It included a gross fibre structure based on human histological data [12]. The resulting atrial surface was meshed with triangular elements and electrical propagation was solved in the mono-domain framework [12]. At each of the 100 000 nodes of the mesh, a cell model was implemented, based on either the Luo–Rudy [13] or the Courtemanche membrane kinetics model [14], depending on the substrate studied. Transmembrane potentials, ionic currents, and unipolar or bipolar electrograms could be generated at any point of the atrial surface [12].
Substrate A
The tissue substrate of the first model of AF was homogeneous, based on Luo–Rudy membrane kinetics [13], with some of its parameters adjusted to the specific atrial cellular properties [15]. More precisely, the channel conductances GNa, GK and Gsi were set to 16, 0.423 and 0.085 mS/cm2, respectively [11]. During sinus rhythm, the CV was 70 cm/s and the ERP was 260 ms. This set of parameters constituted the baseline model, which forms a suitable paradigm for the study of the multiple wavelets hypothesis, because its perpetuation mechanisms only rely on multiple wavelets undergoing functional and anatomical re-entries and wave breaks [11]. For this substrate, AF was initiated in the baseline model by 2 to 5 s of 20-Hz burst pacing applied near the sino-atrial node.
Interventions altering wavelength
In order to investigate the arrhythmogenic effect of changes in electrophysiological and conduction properties (remodelling), a set of experiments was performed in which the tissue properties were altered in such a way that variations of wavelength could be expected. Some seconds after AF initiation in the baseline model, a combination of the following interventions was applied abruptly: (a) reduction of the ERP down to the range 177–260 ms by adjusting the parameter Gsi as shown in Virag et al. [11], (b) modification of the CV value in the range 50–120 cm/s, and (c) increasing the ratio of longitudinal to transverse fibre conductivity from 1:1 (isotropic) to 9:1, implemented by decreasing the transverse conductivity. For each of the interventions, eight AF episodes were simulated, each differing in the moment of application of the intervention only. In some episodes, all having identical tissue properties, AF terminated due to random interactions of wave fronts with other wave fronts and boundaries. For each episode, AF duration (time from intervention to AF termination) was documented. If AF duration was more than 20 s, the simulated fibrillation was considered to be sustained, and the experiment was stopped.
Substrate B
Evidence of spatio-temporal organization and even periodicity in experimental models of AF [16,,17] has suggested another mechanism for AF perpetuation: the mother rotor hypothesis, in which a single source (or possibly a small number of sources) of stable re-entrant wave fronts, presumably located in the left atrium, maintain the fibrillatory activity [18].
In order to assess wavelength estimation techniques for this type of AF dynamics, a mathematical model of cholinergic AF based on the Courtemanche kinetics, adapted from Kneller et al. [19] and Vigmond et al. [20], was developed, as described in Jacquemet et al. [21]. The inclusion of a vagal action resulted in a significant ERP shortening and a complete loss of rate adaptation. Patchy heterogeneities (characteristic length scale: 2 cm) in this vagal action, representing a heterogeneous concentration of acetylcholine, led to a distribution of ERP values ranging from 50 to 100 ms. During sinus rhythm, the CV was 90 cm/s. The initiation of AF was accomplished by premature stimuli in the left atrium.
Substrate C
The effect of refractoriness heterogeneity on AF vulnerability shown in the dog model of Fareh et al. [22] led us to consider a third type of AF dynamics, involving heterogeneities in action potential duration (APD). Patchy heterogeneities with a characteristic length scale of 2 cm (see [12]) were introduced by modifying the local membrane properties of the Courtemanche cell model. The channel conductances associated with the ionic currents Ito, ICaL, IKur, IKr were altered by a factor 0.2, 0.7, 0.1, 1.5 (respectively) in the patches and by a factor 3, 0.5, 1, 3 elsewhere. This resulted in an APD dispersion of 195±15 ms (range 150–230 ms) and a CV of 70 cm/s during normal rhythm. AF was induced by rapid pacing in the left atrium appendage.
Wavelength measures
Three measures of wavelength were studied: (1) a direct local estimate obtained from dense activation maps over large parts of the atria, (2) the approach proposed by Graux et al. [7] to be applied in patients with paroxysmal AF using just two electrodes during sinus and paced rhythm, and (3) the method developed by Botteron and Smith [10], an indirect method yielding a measure of spatial organization, requiring decapolar catheter electrode recordings. The basic characteristics of these methods are summarized in Table 1.
| . | Direct method . | Graux et al. . | Botteron and Smith . |
|---|---|---|---|
| Physical interpretation | Dynamical estimate of average wavelength | Assessment of the substrate | Measure of organization |
| Scope | Local/global in space and time | Local (right atrium) | Global (right atrium) |
| Rhythm | Both paced rhythm and AF | Paced rhythm only | AF only |
| Clinical facility | Currently not applicable | EP lab | EP lab |
| Data acquisition | Mapping system capable of measuring membrane potential | Two catheter electrodes | Decapolar catheter electrode |
| Data processing | Geometrical computations and estimation of ERP from APD | Straightforward | Basic signal processing tools |
| . | Direct method . | Graux et al. . | Botteron and Smith . |
|---|---|---|---|
| Physical interpretation | Dynamical estimate of average wavelength | Assessment of the substrate | Measure of organization |
| Scope | Local/global in space and time | Local (right atrium) | Global (right atrium) |
| Rhythm | Both paced rhythm and AF | Paced rhythm only | AF only |
| Clinical facility | Currently not applicable | EP lab | EP lab |
| Data acquisition | Mapping system capable of measuring membrane potential | Two catheter electrodes | Decapolar catheter electrode |
| Data processing | Geometrical computations and estimation of ERP from APD | Straightforward | Basic signal processing tools |
ERP, effective refractory period; APD, action potential duration; EP, electrophysiology; AF, atrial fibrillation.
| . | Direct method . | Graux et al. . | Botteron and Smith . |
|---|---|---|---|
| Physical interpretation | Dynamical estimate of average wavelength | Assessment of the substrate | Measure of organization |
| Scope | Local/global in space and time | Local (right atrium) | Global (right atrium) |
| Rhythm | Both paced rhythm and AF | Paced rhythm only | AF only |
| Clinical facility | Currently not applicable | EP lab | EP lab |
| Data acquisition | Mapping system capable of measuring membrane potential | Two catheter electrodes | Decapolar catheter electrode |
| Data processing | Geometrical computations and estimation of ERP from APD | Straightforward | Basic signal processing tools |
| . | Direct method . | Graux et al. . | Botteron and Smith . |
|---|---|---|---|
| Physical interpretation | Dynamical estimate of average wavelength | Assessment of the substrate | Measure of organization |
| Scope | Local/global in space and time | Local (right atrium) | Global (right atrium) |
| Rhythm | Both paced rhythm and AF | Paced rhythm only | AF only |
| Clinical facility | Currently not applicable | EP lab | EP lab |
| Data acquisition | Mapping system capable of measuring membrane potential | Two catheter electrodes | Decapolar catheter electrode |
| Data processing | Geometrical computations and estimation of ERP from APD | Straightforward | Basic signal processing tools |
ERP, effective refractory period; APD, action potential duration; EP, electrophysiology; AF, atrial fibrillation.
Direct measure
The first measure yields a time-varying estimate of the wavelength during any type of atrial rhythm. It requires high-resolution electrical mapping for simultaneous CV and ERP estimation, from which the spatio-temporal behaviour of wavelength can be computed as the product CV×ERP. Such data can only be obtained under experimental conditions where a large number of electrodes are used to map AF [22] or from computer simulations. Applying this technique to patients with permanent AF is currently not practical. The results of the direct method, however, can serve as a gold standard when evaluating the methods that can be clinically employed. The computer-based application allows local depolarization and repolarization to be tracked over the entire atria. This results in accurate estimates of wave front location, CV and APD. In experimental set-ups, the APD values are more difficult to obtain since repolarization can only be indirectly inferred.
In this study, 1300 of the 100 000 computed transmembrane potentials at points that were regularly distributed over the atrial surface were used to construct activation maps. Along each detected wave front, the APD (measured at 90% repolarization) and the CV values were determined. Since ERP cannot be directly measured without additional stimulation protocol, it was approximated as the sum of APD and a correction constant computed during paced rhythm. This correction, estimated as the quantity ERP−APD averaged over 10 pacing rates with a diastolic interval <50 ms, was in the range 15–20 ms, depending on the tissue substrate. The product ERP×CV was then averaged over all the wave fronts present within an interval of 100 ms around any time instant considered.
Graux's measure
The measure proposed by Graux et al. can be used prior to AF initiation only. The involved protocol prescribes the use of two electrodes placed in the free wall of the right atrium [7].
In our application, ERP and CV were determined during stable paced rhythm (cycle length 460 ms) and their product provided the wavelength. The ERP was measured using premature stimuli. In the presence of anisotropy, the geometrical mean of transverse CV (across fibres) and longitudinal CV (along fibres) was used. In heterogeneous tissues, the ERP values listed in the results section were the mean of results obtained from several electrode pairs, randomly distributed over the right atrial surface.
Botteron's measure
The measure by Botteron and Smith is an indirect technique, prompted by the difficulty of measuring wavelength during permanent AF. The correlation over time between bipolar atrial electrograms recorded at different locations in the right atrium was shown to decrease with the inter-electrode distance, following an approximately exponential curve [10]. The space constant δ extracted from this exponential decay characterizes the disorganization and the complexity of the activation patterns. Assuming re-entrant wavelets travelling randomly over the atrial tissue, the space constant δ computed during AF is related to the average wavelength [10]. However, during periodic rhythms, like sinus rhythm or flutter, activation sequences measured at distant locations are delayed but otherwise identical, resulting in a perfect correlation of the electrograms, and wavelength cannot be inferred from the organization measure.
In our application, this measure was applied to electrograms simulated at an 8-by-8 grid of bipolar electrodes located on the right atrial free wall.
Results
Critical wavelength for the self-perpetuation of multiple wavelets: the direct method
As described for substrate A, a model with homogeneous tissue properties, three interventions were applied to provide a basis for studying the basic concept of critical wavelength as observable from the direct measure applied to our computer model. The results are shown in Fig. 1. Note that wavelength shortening was consistently associated with a prolongation of the mean AF duration.
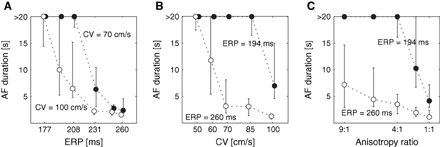
Atrial fibrillation (AF) duration as a function of (A) the refractory period (ERP), (B) the conduction velocity (CV) and (C) the anisotropy ratio. The circles represent the median of AF duration and the error bars are associated with the first and the third quartile.
All episodes of AF were found to be sustained, indicating that the substrate was vulnerable to AF, if the wavelength was shorter than approximately 5 cm.
Critical wavelength for the self-perpetuation of multiple wavelets: the clinical measures
In order to test the critical wavelength concept as obtained from clinically applied methods, the Graux's and Botteron's measures were implemented using data from the simulated AF. Fig. 2 displays the pooled results for mean AF duration as a function of the wavelength resulting from using Botteron's measure. These results may be compared directly with the results of published clinical application [10]. Fig. 2 shows that AF was sustained (i.e. AF duration was >20 s) when the wavelength was below a critical value of 10±1 cm.
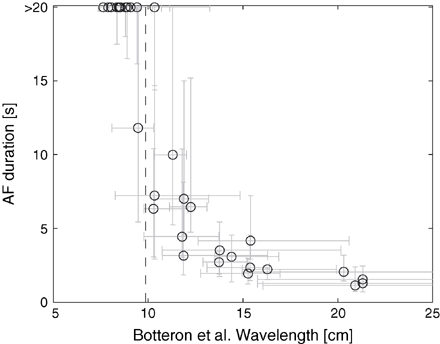
Critical wavelength. Atrial fibrillation (AF) duration as a function of the wavelength estimated using Botteron's method. The vertical dashed line indicates the critical wavelength.
The wavelength estimates of Graux et al. and Botteron–Smith rely on a different characterization of AF. The former gives information about the electrical substrate while the latter measures the degree of organization during AF. A comparison of the results obtained by using Graux's and Botteron's measures applied to the data presented in Fig. 1 is shown in Fig. 3. Their relationship was found to be approximately linear (correlation coefficient: 0.91), with the Botteron-based wavelength estimates being shorter than those based on the Graux's measure.
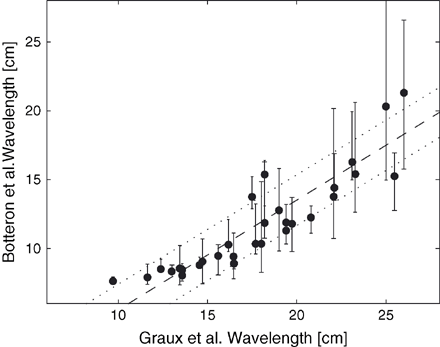
Comparison between Graux et al. and Botteron and Smith approaches for wavelength estimation. A regression line is superimposed (dashed line), as well as a confidence interval (dotted lines).
Effect of the AF substrate on wavelength
The evolution in time of the multiple wavelets observed for each of the three substrates studied was found to be clearly different. This is illustrated in the panels shown in the right hand column of Fig. 4. These are maps of the instantaneous transmembrane potentials, from which the progression of the wave fronts can be followed. The corresponding evolutions in time of the mean wavelength computed using the direct method is shown on the left in this figure.
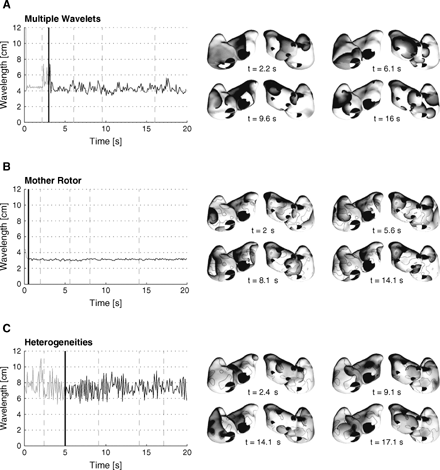
Wavelength during AF initiation and perpetuation estimated using the direct method for the substrate A, B and C. The thick vertical lines indicate the end of the initiation protocol. The right panels display transmembrane potential maps, grey-level coded from white (resting potential) to black (excited tissue). Thick black lines represent propagating wave fronts. For each space plot, an anterior view (on the left) and a posterior view (on the right) are shown.
During the initiation phase (rapid pacing protocol), wavelength was stable until the first wave break marking the onset of AF. Then, oscillations in average wavelength were observed, reflecting the progressive disorganization of the dynamics. During sustained AF, stationary fluctuations around a stable value were observed. The mean and standard deviation of the spatially averaged wavelength differed significantly in the three models. In the model of multiple wavelets (Fig. 4A), the wavelength was 4.3±0.5 cm. Since the tissue properties were uniform in this case, the variations over time were due to dynamic instabilities arising from the involvement of ERP restitution [11]. In the model of a mother rotor (Fig. 4B), the wavelength was very short and stable (3.1±0.1 cm). The wavelets mostly propagated in the regions of shorter ERP, around islands of longer ERP. The stability of the wavelength reflected the organization (or even quasi-periodicity) of the underlying wavelet dynamics. In the last model including heterogeneities in refractoriness (Fig. 4C), the large variations in wavelength (7.6±1.2 cm) were related to the range of ERP values at the wave fronts propagating throughout the atrial tissue.
Effect of the AF substrate on wavelength estimation
The estimated values of wavelength depended significantly on the method used and on the type of AF dynamics. Table 2 summarizes the wavelength obtained by using each of the three estimation techniques applied to the three episodes of AF presented in Fig. 4. In addition, the results pertaining to the non-sustained situation for substrate A are listed. These results indicate that the direct method tends to lead to shorter wavelength measures than Botteron's method, which in turns gives smaller values than the protocol from Graux et al. An exception is the model of a mother rotor (Fig. 4B), in which Botteron's wavelength was 26.5 cm, although a visual inspection of the membrane potential maps showed that 4–6 small wavelets were present in the tissue.
| Substrate . | Model of AF . | Direct method . | Graux et al. . | Botteron and Smith . |
|---|---|---|---|---|
| A | Multiple wavelets (unsustained) | 6.5±1.3 cm | 16.2 cm | 12.4 cm |
| A | Multiple wavelets (sustained) | 4.3±0.5 cm | 13.0 cm | 8.2 cm |
| B | Mother rotor (vagal) | 3.1±0.1 cm | 5.3±2 cm | 26.5 cm |
| C | Re-entries (heterogeneities) | 7.6±1.2 cm | 13.6±1 cm | 9.7 cm |
| Substrate . | Model of AF . | Direct method . | Graux et al. . | Botteron and Smith . |
|---|---|---|---|---|
| A | Multiple wavelets (unsustained) | 6.5±1.3 cm | 16.2 cm | 12.4 cm |
| A | Multiple wavelets (sustained) | 4.3±0.5 cm | 13.0 cm | 8.2 cm |
| B | Mother rotor (vagal) | 3.1±0.1 cm | 5.3±2 cm | 26.5 cm |
| C | Re-entries (heterogeneities) | 7.6±1.2 cm | 13.6±1 cm | 9.7 cm |
AF, atrial fibrillation.
| Substrate . | Model of AF . | Direct method . | Graux et al. . | Botteron and Smith . |
|---|---|---|---|---|
| A | Multiple wavelets (unsustained) | 6.5±1.3 cm | 16.2 cm | 12.4 cm |
| A | Multiple wavelets (sustained) | 4.3±0.5 cm | 13.0 cm | 8.2 cm |
| B | Mother rotor (vagal) | 3.1±0.1 cm | 5.3±2 cm | 26.5 cm |
| C | Re-entries (heterogeneities) | 7.6±1.2 cm | 13.6±1 cm | 9.7 cm |
| Substrate . | Model of AF . | Direct method . | Graux et al. . | Botteron and Smith . |
|---|---|---|---|---|
| A | Multiple wavelets (unsustained) | 6.5±1.3 cm | 16.2 cm | 12.4 cm |
| A | Multiple wavelets (sustained) | 4.3±0.5 cm | 13.0 cm | 8.2 cm |
| B | Mother rotor (vagal) | 3.1±0.1 cm | 5.3±2 cm | 26.5 cm |
| C | Re-entries (heterogeneities) | 7.6±1.2 cm | 13.6±1 cm | 9.7 cm |
AF, atrial fibrillation.
Discussion
Critical wavelength for multiple wavelets re-entry
The need for a critical wavelength for AF to be sustained is well established in the literature. Allessie et al. estimated this critical wavelength in humans to be 12 cm [2]. In a clinical study on the disorganization of the atrial electrical activity during human AF, Botteron and Smith found a critical wavelength of 13±3.6 cm [10]. Graux et al. reported a high vulnerability to spontaneous and induced AF in patients whose cardiac wavelength was shorter than 12 cm during paced rhythm [7]. Other studies based on a wavelength index qualitatively confirmed these findings [23,,24].
In our computer model of AF based on multiple wavelets, the successful induction of sustained AF required a wavelength shorter than 10±1 cm (Fig. 2) as computed with the Botteron and Smith method, in agreement with the clinical data cited above. Furthermore, a shortening of the wavelength, either by a reduction of the ERP or by a decrease of the longitudinal or transverse CV, resulted in an increase of the vulnerability to AF (Fig. 1). The critical wavelength, obtained using exactly the same method as Botteron and Smith, is nevertheless slightly shorter than those estimated in clinical experiments. One reason for this discrepancy is that sustained AF is more ‘difficult’ to initiate in this idealized, uniform, model than in diseased human atria. This is consistent with experimental studies showing that anatomical structures such as the pectinate muscles [25] and heterogeneities in refractoriness [22] may play an important role in the vulnerability to AF. These features, not present in our model, are expected to enable sustained AF with a longer wavelength.
Comparison of the wavelength estimates
Despite the good correspondence between the simulated and experimental critical wavelengths calculated using Botteron and Smith method, these values differed significantly from those obtained in the model of multiple wavelets by the direct method (approximately 5 cm, see Table 2), which served as a gold standard. One reason for this difference is that the direct method involves a spatial averaging of the local wavelength over all the wave fronts. For wave fronts propagating across fibre, near the tip of the spirals or near pivoting points, and close to lines of block, the local wavelength can be very small, tending to reduce the wavelength estimate. Another reason for the difference is that both the Botteron and Smith and the Graux et al. techniques tend to overestimate the wavelength.
The mathematical derivation by Botteron and Smith of the wavelength estimate from their measure of organization, relying on the leading circle hypothesis [26], assumes that the ERP can by approximated by the mean AF cycle length, i.e. the excitable gap is neglected. Since the excitable gap can lie in the range of 20–30% of the AF cycle length [27], this results in an overestimation of the wavelength for both the simulated and the clinical data. The wavelength estimate of Graux et al. is obtained during paced rhythm (cycle length ≥460 ms), prior to AF initiation. Thus, this estimate was not designed to take into account the changes in ERP and CV due to rate adaptation during an episode of AF or (reversible) remodelling after a long period of AF.
A comparison of these measures in the case of the model of multiple wavelets (Fig. 3) suggests a linear correlation between the Graux wavelength (measured during pacing and characterizing the substrate) and the Botteron wavelength (measured during AF and characterizing the wavelet dynamics), the former being consistently larger than the latter.
Importance of the underlying wavelet dynamics
The results showed that the estimates of wavelengths also depended on the type of AF (see Table 2). Three different dynamics of AF were considered in the study: a model of multiple wavelets undergoing re-entries and wave breaks, a model of a mother rotor, and a model of AF dynamics based on multiple wavelets perpetuated by heterogeneities in refractoriness.
In the first model, only dynamical heterogeneities (beat-to-beat variations in APD and in local cycle length) can produce wave breaks and maintain the fibrillatory activity. In this particular case, the wavelength was a critical parameter for the initiation of sustained AF as it defines the minimal spatial extent of the re-entrant circuits, in qualitative agreement with the clinical studies of Botteron and Smith [10] and Graux et al. [7].
In the second model, stable spirals (rotors) were moving around regions with longer APD values. As demonstrated by Kneller et al. [19] in their computer model of cholinergic AF on which our model is based, the maintenance of AF is ensured by just one or a few rotors whose lifetime goes beyond 10 rotations, while most of the spirals are short-lived. Although a short wavelength remains a necessary condition for AF vulnerability, the spatial scale of the heterogeneities also plays a crucial role [19]. The spatio-temporal organization of the resulting dynamics has an impact on the wavelength estimates. The direct method gives a short wavelength that is very stable over time (see Fig. 4C). This value is shorter than the Graux estimate (see Table 2), because most of the wave fronts are found in the regions with shorter APD values during AF, while the slow pacing protocol proposed by Graux et al. initiates broad wave fronts propagating continuously throughout the whole tissue. The Botteron estimate, on the other hand, leads to large values (> 25 cm) during AF. The hypothesis of multiple wavelets randomly travelling over the atrial surface assumed by Botteron is not present in this model of AF, thus confounding the wavelength estimate. Wavelength can, therefore, not always be derived from a measure of organization.
In the third model, both heterogeneities in refractoriness and dynamical heterogeneities due to the local rate adaptation were at the origin of the wave breaks and the perpetuation of AF. The wavelength obtained by the direct method was larger than the corresponding critical wavelength computed in a homogeneous tissue with the model of multiple wavelets, suggesting that the heterogeneities tend to extend the range of wavelength for which the tissue may be vulnerable to AF. The Botteron wavelength, however, was shorter than the critical wavelength, indicating that the presence of heterogeneities may lead to the same degree of disorganization despite a longer wavelength. Fareh et al. performed a similar study in dogs subjected to rapid pacing and found only a weak correlation between vulnerability to AF and wavelength, while the correlation with ERP heterogeneity was strong [22]. Wavelength is, therefore, not the only marker of vulnerability to AF.
Limitations
In this study, idealized tissue conditions have been investigated, representing paradigms of AF dynamics that correspond to the main hypotheses about the mechanisms underlying AF. In particular: only homogeneous tissue or simple forms of heterogeneity have been implemented; the model was lacking 3D structures like fibre bundles or variations in tissue thickness; tissue conductivity was either isotropic or based on a gross representation of the fibre structure.
Substrate A generated a larger variability in local cycle length than observed in patients [11]; the very short APD values of substrate B were closer to the values measured in animal models than to clinical data [19]. In contrast, in patients, atrial tissues may include several of the different arrhythmogenic factors simultaneously, making it more difficult to identify the key factors responsible for the vulnerability to AF.
No electrophysiological difference between the left and the right atrium was included, although left–right differences were observed in the wavelets dynamics, due to differences in the anatomical obstacles and the location of the heterogeneities contained within them. Experimental evidence of left-right differences have been found [15], as well as the occurrence of ectopic beats originating from the pulmonary veins [28]. These specificities of each atrium may have an impact on the relevance of the clinical estimates of wavelength, since they use only recordings from the right atrium.
Conclusion
In our model of AF based on multiple re-entrant wavelets, the simulations confirm the notion that wavelength needs to be below the critical value of 9–11 cm for AF to be sustained, in agreement with clinical data from human atria. The results also indicate that wavelength is difficult to assess using data from a small number of recording sites. The existing techniques for wavelength estimation do not apply to all types of atrial rhythms (sinus rhythm, flutter, paroxysmal AF, permanent AF) and are not appropriate for all forms of AF dynamics (random propagation of multiple re-entrant wavelets, organized activity perpetuated by a few sources of wavelets).
The simulations suggest that a priori information about the underlying wavelet dynamics is needed to extract an accurate measure of wavelength in patients. Computer modelling may help develop new methods for wavelength estimation since it enables the comparison with direct computation of wavelength in models with different substrates and AF dynamics, even during long episodes of AF.
This study was made possible through grants from the Theo-Rossi-Di-Montelera Foundation, Medtronic Europe, the Swiss Governmental Commission of Innovative Technologies (CTI), and the Swiss National Science Foundation (SNSF). The authors wish to thank Ryan Lahm, Drs. Josée Morisette and Arthur Stillman who kindly furnished the atrial geometry surface model. The authors also would like to thank Professor A. van Oosterom for helpful discussions and suggestions.



