-
PDF
- Split View
-
Views
-
Cite
Cite
Laurence Mangin, Alain Vinet, Pierre Pagé, Leon Glass, Effects of antiarrhythmic drug therapy on atrioventricular nodal function during atrial fibrillation in humans, EP Europace, Volume 7, Issue s2, 2005, Pages S71–S82, https://doi.org/10.1016/j.eupc.2005.03.016
Close - Share Icon Share
Abstract
To assess the effects of metoprolol and amiodarone on atrial and ventricular activity during atrial fibrillation (AF) in post-surgical patients, and to develop and use a mathematical model of the atrioventricular (AV) node during AF that incorporates parameters describing the properties of the AV node to evaluate the physiological basis of the drug effects.
Ten post-surgical patients were evaluated where three received no medical therapy, three received metoprolol, three received amiodarone, and one received both metoprolol and amiodarone. The medications led to increases of 37–310 ms in the mean VV interval in treated patients, but much smaller changes in the mean AA intervals in the right and left atria. The mathematical model incorporating a random influence of the concealed conduction parameter was capable of reproducing the histograms of the VV intervals based on the input from the right atrium by systematically searching parameter space.
Changes in the ventricular rate are mainly due to the alteration in the AV nodal properties rather than changes in the atrial rhythm. The medications can display differential effects on the physiological properties of the AV node, and therefore the mathematical model may help to identify novel pharmacological targets.
Introduction
One of the major medical problems facing cardiologists is the treatment of paroxysmal and chronic atrial fibrillation (AF) [1–7]. Despite major advances in therapies involving ablation of regions of the heart implicated in the initiation and maintenance of AF [8], in the majority of patients, medical therapies remain the treatment of choice. There is a long-standing debate on the relative efficacy of maintaining sinus rhythm vs the control of the ventricular rate. Although from a physiological perspective it is appealing to maintain sinus rhythm, recent clinical studies have demonstrated similar clinical outcomes for strategies involving either maintenance of sinus rhythm or control of the ventricular rhythm [4]. Since it is often easier to control the ventricular rate than maintain sinus rhythm, rate control of AF is an extremely important treatment option. Yet, our physiological understanding of the effects of pharmacological agents on the AV node is still limited [6,,9,11]. The current paper deals with mathematical aspects of modelling of the atrioventricular (AV) node which are relevant to the determinants of ventricular response during AF. The long range goal of this approach is to develop sufficient information about the role of pharmacological agents on AV nodal physiology during AF, so that choice of therapy could be optimized based on physiological properties of the AV node.
Mathematical modelling based on physiological studies of the AV node has had a rich history [12–19] (for review of early papers see [20]), but only relatively few papers deal with modelling of the AV node during AF [21–27]. During rapid atrial pacing in normal individuals, or during normal sinus rates in individuals with compromised AV function, the ventricular response may display variety of regular Wenckebach coupling patterns between the atrial and ventricular rates. Theoretical models have been able to predict both qualitative and quantitative aspects of AV nodal conduction, as a function of stimulation frequency [14,,15,,20] and there is some limited knowledge of the effects of pharmacological agents on mathematical models of the AV node [9,,10]. In view of the success of these mathematical models in predicting the AV node response during regular atrial and ventricular activity, it seems reasonable to assume that the same models will be successful in predicting the ventricular response during AF. However, Jorgensen et al. found that the earlier models could not reproduce statistical features of the ventricular response based on atrial activity unless an additional term representing concealed conduction was added to the model [22]. Concealed conduction refers to a physiological effect by which a blocked beat leads to increased refractoriness of the AV node, so that the conduction time through the node is elevated relative to what it would have been if the blocked beat had not occurred [11,,16,21,28–,34]. During AF, the atrial activity is typically rapid so that a large fraction of the atrial activations is blocked in the AV node, and consequently the effects of concealed conduction are significant.
In the current paper we study the ventricular response during AF in 10 post-surgical patients both prior to and following the administration of medications (metoprolol and amiodarone) that are used clinically to control the ventricular response. The data collected from atrial and ventricular activity provide a unique insight into the response of the atrial and ventricular activity to drugs during AF. By developing a mathematical model for the AV node during AF, we analyze how drug therapy differentially affects the parameters describing AV nodal function.
Methods
Clinical data
Unipolar epicardial recordings were carried out in 10 patients experiencing paroxysmal AF after open-heart bypass surgery at the Hôpital du Sacré-Cœur, Montréal. The baseline clinical characteristics of the patients are shown in Table 1. After surgery, all patients had three temporary unipolar epicardial wire electrodes (Model 6492, Medtronic Inc, Minneapolis, MN, USA) attached to the muscular part of the atrium: two on the right atrium (one in the mid right atrial free wall in the sinus node region and the other in the lower third of the right atrial free wall) and one on the left atrium near the left inferior pulmonary vein. Patients were monitored continuously for four days post-operatively with a Holter device (Spacelab Burdick, Model 6632, Dallas, TX, USA). Data were downloaded each day to a CD-ROM. Recordings began 24 h after heart surgery. The selected 10 patients had several episodes of AF that ended before 48 h. Every patient gave informed written consent for the test protocol, which was approved by the Ethics Committee of the Hôpital du Sacré-Cœur, Montréal.
| Patient . | Age (yr)/gender . | LVEF (%) . | Preoperative medication . | Medical history . | Perioperative data CAB (number of vessels grafted)/VR . |
|---|---|---|---|---|---|
| 1 | 78/M | 50 | Calcium antagonist | Hypertension, myocardial infarction, diabetes, stroke | 3/0 |
| 2 | 70/M | 50 | 0 | 0 | 1/1 |
| 3 | 64/F | 40 | 0 | Myocardial infarction | 2/0 |
| 4 | 78/F | 40 | β-Blocker ACEI | Myocardial infarction | 1/1 |
| 5 | 60/M | 45 | 0 | 0 | 3/0 |
| 6 | 55/M | 40 | 0 | 0 | 2/0 |
| 7 | 65/M | 60 | 0 | 0 | 2/0 |
| 8 | 77/M | 65 | 0 | Hypertension | 1/1 |
| 9 | 65/M | 45 | 0 | Hypertension | 1/1 |
| 10 | 71/M | 25 | Nitrates ACEI | Hypertension, myocardial infarction | 3/0 |
| Patient . | Age (yr)/gender . | LVEF (%) . | Preoperative medication . | Medical history . | Perioperative data CAB (number of vessels grafted)/VR . |
|---|---|---|---|---|---|
| 1 | 78/M | 50 | Calcium antagonist | Hypertension, myocardial infarction, diabetes, stroke | 3/0 |
| 2 | 70/M | 50 | 0 | 0 | 1/1 |
| 3 | 64/F | 40 | 0 | Myocardial infarction | 2/0 |
| 4 | 78/F | 40 | β-Blocker ACEI | Myocardial infarction | 1/1 |
| 5 | 60/M | 45 | 0 | 0 | 3/0 |
| 6 | 55/M | 40 | 0 | 0 | 2/0 |
| 7 | 65/M | 60 | 0 | 0 | 2/0 |
| 8 | 77/M | 65 | 0 | Hypertension | 1/1 |
| 9 | 65/M | 45 | 0 | Hypertension | 1/1 |
| 10 | 71/M | 25 | Nitrates ACEI | Hypertension, myocardial infarction | 3/0 |
LVEF: left ventricular ejection fraction, ACEI: angiotensin converting enzyme inhibitor, CAB: coronary artery bypass, VR: valve replacement. Preoperative medication was stopped one day before surgery.
| Patient . | Age (yr)/gender . | LVEF (%) . | Preoperative medication . | Medical history . | Perioperative data CAB (number of vessels grafted)/VR . |
|---|---|---|---|---|---|
| 1 | 78/M | 50 | Calcium antagonist | Hypertension, myocardial infarction, diabetes, stroke | 3/0 |
| 2 | 70/M | 50 | 0 | 0 | 1/1 |
| 3 | 64/F | 40 | 0 | Myocardial infarction | 2/0 |
| 4 | 78/F | 40 | β-Blocker ACEI | Myocardial infarction | 1/1 |
| 5 | 60/M | 45 | 0 | 0 | 3/0 |
| 6 | 55/M | 40 | 0 | 0 | 2/0 |
| 7 | 65/M | 60 | 0 | 0 | 2/0 |
| 8 | 77/M | 65 | 0 | Hypertension | 1/1 |
| 9 | 65/M | 45 | 0 | Hypertension | 1/1 |
| 10 | 71/M | 25 | Nitrates ACEI | Hypertension, myocardial infarction | 3/0 |
| Patient . | Age (yr)/gender . | LVEF (%) . | Preoperative medication . | Medical history . | Perioperative data CAB (number of vessels grafted)/VR . |
|---|---|---|---|---|---|
| 1 | 78/M | 50 | Calcium antagonist | Hypertension, myocardial infarction, diabetes, stroke | 3/0 |
| 2 | 70/M | 50 | 0 | 0 | 1/1 |
| 3 | 64/F | 40 | 0 | Myocardial infarction | 2/0 |
| 4 | 78/F | 40 | β-Blocker ACEI | Myocardial infarction | 1/1 |
| 5 | 60/M | 45 | 0 | 0 | 3/0 |
| 6 | 55/M | 40 | 0 | 0 | 2/0 |
| 7 | 65/M | 60 | 0 | 0 | 2/0 |
| 8 | 77/M | 65 | 0 | Hypertension | 1/1 |
| 9 | 65/M | 45 | 0 | Hypertension | 1/1 |
| 10 | 71/M | 25 | Nitrates ACEI | Hypertension, myocardial infarction | 3/0 |
LVEF: left ventricular ejection fraction, ACEI: angiotensin converting enzyme inhibitor, CAB: coronary artery bypass, VR: valve replacement. Preoperative medication was stopped one day before surgery.
Data analysis
Epicardial signals were acquired at 500 Hz. Left and right atrial electrograms were analyzed in segments of 3 min intervals during AF. Custom written software in MATLAB 6.5 (Mathworks, USA) was developed to detect the activation times from the electrograms. Automatic detection of the ventricular activation times was performed using the fact that the ventricular activity is synchronous on the three electrodes. Briefly, the waveforms of the channels were baseline-corrected with a polynomial fit, then summed, squared and passed through a threshold to detect the ventricular activations, which were then verified visually. Electrogram signals coming from the inferior free wall of the right atrium and near the inferior pulmonary vein of the left atrium were chosen for subsequent analysis. After applying a derivative filter, the atrial activation times were determined manually. The timing procedure was repeated three times with a change in rate of detection less than 5%. Based on these data, for each 3 min period during AF, we determined the mean interatrial activation times, ?> and ?> in the right and left atria, respectively, and the mean interventricular activation times ?> Histograms showing the distribution of the atrial and ventricular interbeat intervals were also computed.
Finite difference equation model of AV nodal function during AF
AV nodal recovery curve
Previous studies on AV nodal conduction have shown that AV nodal conduction time is a function of the preceding recovery (VA) interval, a longer recovery interval leading to a shorter conduction time. This relationship, called the AV nodal recovery curve, can be approximated by an exponential function [14,,17,,28]. ?> where AVmin is the minimum conduction time corresponding to propagation in a fully recovered tissue, α and τ are positive constants and VA is any recovery interval that exceeds the effective refractory period (θ) of the AV node.
The conducted beat is thus preceded by (k − 1) blocked activations. The procedure is iterated to determine the successive activation times.
Model of AV nodal function incorporating concealed conduction
where Ωi is a normally distributed random number with mean zero and standard deviation 1. Following a conducted beat, the refractory period is reset to θ and subsequent blocked beats again lead to a prolongation of the refractory period.
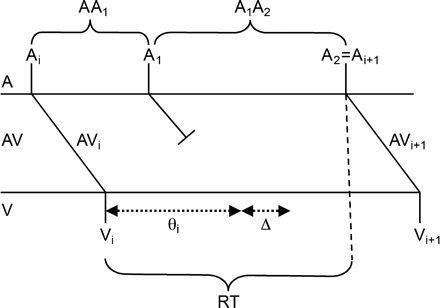
Schematic representation of the model. An atrial impulse arriving at the AV node at Ti is conducted to the ventricles with an AV nodal conduction time of AVi leading to a ventricular beat at time Vi. The refractory time following this beat is initially θi. An atrial impulse, A1, arriving at the AV node at a time interval AA1 following the first beat is blocked leading to a prolongation of the refractory period to θi + Δ, where Δ = ΩΔstd + Δmean and Ω is a normally distributed random number. The next atrial event A2 comes in after the expiration of the new refractory period, and it is thus conducted through the AV node to the ventricles with a conduction time AVi + 1, which is a function of the recovery time RT = AA1 + A1A2 − AVi.
Model assessment and sensitivity analysis
Starting with the experimental atrial input time series AAexp and an initial ventricular activation, a sequence of computed ventricular activations VVmodel is generated iteratively for each set of parameter values. We assessed the similarity of the distributions of VVmodel and VVexp by applying the Kolmogorov-Smirnov test which nonparametrically tests against the null hypothesis that the distributions of the VVmodel and VVexp are the same. The result of the Kolmogorov-Smirnov test P is the significance level for the null hypothesis. A small probability value P means that the cumulative distribution function of VVmodel has a low probability of being the same as VVexp, such that the null hypothesis is rejected. A high P value means that null hypothesis cannot be rejected.
The mathematical model has six parameters and it is difficult to determine the values of all six parameters. This is because the six dimensional parameter space is large, several of the parameters have a similar effect on the global dynamics and for the values of some parameters there is a weak dependence on other parameters. Consequently, except where noted otherwise, we have fixed the values of three parameters at approximately the midpoint of their physiological values determined in previous studies [9,,14,,18], α = 200 ms, τ = 100 ms, Δstd = 50 ms, and varied the remaining parameters over their physiological ranges 0 ≤ θ ≤ 300 ms, 0 ≤ Δmean ≤ 150 ms, 0 ≤ AVmin ≤ 300 ms. Increases in each of these parameters would be associated with depressed conduction through the AV node. However, the model allows for quantifying the mechanism of depressed conduction – e.g. increased θ will give different effects from increasing Δmean or the minimum conduction time AVmin.
To quantify the relative importance of the refractoriness θ and concealed conduction Δmean, a sensitivity analysis of the model using a 3-dimensional representation was performed by fixing AVmin, α, τ, Δstd while the refractory period and concealed conduction parameters were varied. The P value for each parameter combination was determined. This 3-D [P, θ, Δmean] representation allowed us to explore the parameter space of the model. The AV nodal recovery curve with the estimated AVmin and α, τ parameters was also computed in order to describe the properties of the AV node during AF. The inputs to the AV node are usually assumed to come primarily from the pathways in the right atrium. Consequently, the electrode closest to the AV node in the right atrium was used as the input.
Effects of antiarrhythmic drug therapy
Epicardial recordings from 10 patients before and 1 h after antiarrhythmic drug therapy were studied. Patients 1–3 did not receive any antiarrhythmic drug. Patients 4–6 received a 24-h infusion of amiodarone (20 mg/kg). Patients 7–9 received an intravenous injection (IV) of the β1 adrenoreceptor blocking agent metoprolol (0.2 mg/kg) and patient 10 received a combination of IV metoprolol (0.2 mg/kg) + oral amiodarone (300 mg).
Statistical analysis
MATLAB 6.5 (Mathworks, USA) software was used for the statistical analyses and for the simulations.
Results
Clinical data
Fig. 2 shows the electrograms of patient 10 from the right (c1) and left (c2) atria during sinus rhythm (panel A), during AF before administration of metoprolol + amiodarone (panel B), and after administration of medication (panel C). The times of the atrial activation are indicated by dots above the complexes, and the times of the ventricular activation are indicated by a V. The left fibrillatory activity is extremely regular before (B-c2) and after (C-c2) the drug. Furthermore, the right-to-left atrial period ratio is above one (236 ms/177 ms) and increases after the drug (266 ms/172 ms, panel C).
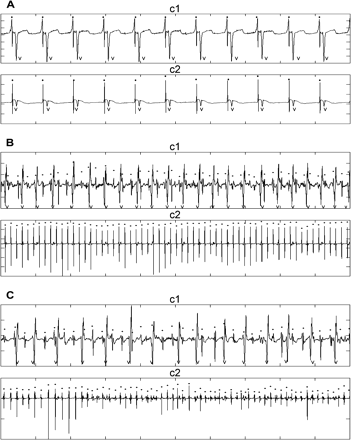
Epicardial atrial signals during sinus rhythm panel (A) and AF before panel (B) and after amiodarone + metoprolol in patient 10 panel (C). Traces labeled c1 are recorded from the right atrial inferior free wall, and traces labeled c2 are recorded from the left atrium near the left inferior pulmonary vein. Ten second data segments are shown. The left fibrillatory activity is regular before (B-c2) and after (C-c2) the drug.
Fig. 3 shows ?> and ?> (top panel) and ?> (lower panel) during AF before and after the administration of medication. In patients 1–3, who did not receive medication, the only significant changes observed were in patient 2 in whom there was a decrease in ?> from 160 to 154 ms, and an increase in ?> from 441 to 467 ms. Following medication, in patients 4, 7, 9, 10, ?> increased by more than 20 ms whereas the changes in ?> were always less than 20 ms, the two largest changes being 19 and 18 ms in patients 7 and 9, respectively. Furthermore in all patients receiving medication, ?> markedly increased (Fig. 3, bottom panel). Since we find negligible changes in the atrial activity but a marked increase in the mean ?> in patients 5, 6, and 8, the changes in ventricular activity in these patients must be associated with changes in the properties of the AV node rather than changes in the atrial activity. In patients 4, 7, 9 and 10 after medication, there are changes in both the atrial and ventricular activity. In these patients the changes in the ventricular rate arise as a consequence of the changes induced by the medication in the atria and/or in the AV node.
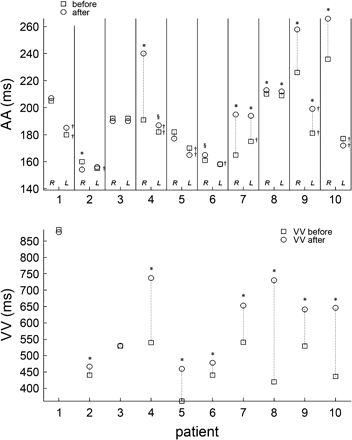
Top panel shows ?> and ?> during AF before and after the administration of medication in all the patients. *P < 0.001, §P < 0.05 after vs before medication; †P < 0.001 LA vs RA. Bottom panel shows the VV interval ?> in all patients before and after medication. See text for comments.
The physiology of atrial and nodal activities is reflected in the ratios ?> and ?> In Fig. 4 we display these ratios for all patients, both before and after pharmacological therapy. For the patients in whom the ratio ?> is approximately 1.0 and in whom the standard deviations of the mean atrial activation rates are comparatively small (Table 2), it is likely that there is a well-organized reentrant (or perhaps focal) activity in either the left or right atrium that serves to entrain the activity in the atria. For the patients in whom ?> is greater than 1.0, it is likely that there is either a focal or reentrant regular activity in the left atrium that breaks up during propagation in the right atrium, similar to what has been observed recently in sheep [35–37].
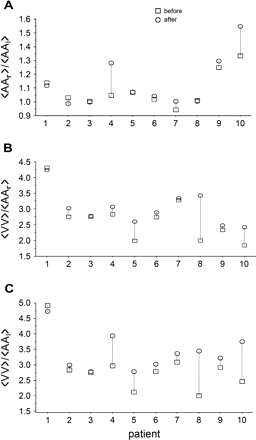
Ratio of ?> (panel A), ?> (panel B) and ?> (panel C) before and after medication in all patients. See text for comments.
Mean right/left (RA/LA) atrial, and observed/simulated ventricular (VV) activation time with parameters estimation in patients 1–10
| Patient . | . | RA . | LA . | VV . | Simulated VV . | Parameters evaluation . |
|---|---|---|---|---|---|---|
| 1 | Before | 205 ± 28 (1009) | 180 ± 27 (1009)† | 885 ± 91 (199) | 823 ± 105 (220) | P = 0.6, θ = 270, Δmean = 45, AVmin = 330 |
| After | 207 ± 40 (864) | 185 ± 29 (953)† | 877 ± 154 (209) | 888 ± 101 (203) | P = 0.85, θ = 340, Δmean = 25, AVmin = 350 | |
| 2 | Before | 160 ± 33 (1074) | 155 ± 35 (1101)† | 441 ± 83 (387) | 444 ± 88 (386) | P = 0.7, θ = 140, Δmean = 50, AVmin = 135 |
| After | 154 ± 32 (1127)* | 156 ± 31 (1108) | 467 ± 81 (385)* | 468 ± 86 (370) | P = 0.9, θ = 200, Δmean = 30, AVmin = 120 | |
| 3 | Before | 192 ± 31 (950) | 192 ± 26 (949) | 529 ± 104 (344) | 521 ± 97 (346) | P = 0.6, θ = 110, Δmean = 65, AVmin = 210 |
| After | 190 ± 33 (939) | 190 ± 32 (907) | 530 ± 75 (393) | 535 ± 98 (338) | P = 0.6, θ = 115, Δmean = 50, AVmin = 225 | |
| 4 | Before A | 191 ± 36 (880) | 182 ± 34 (922)† | 540 ± 101 (330) | 545 ± 112 (309) | P = 0.95, θ = 195, Δmean = 65, AVmin = 140 |
| After A | 240 ± 30 (812)* | 187 ± 25 (972)†§ | 737 ± 100 (254)* | 741 ± 104 (263) | P = 0.6, θ = 200, Δmean = 75, AVmin = 380 | |
| 5 | Before A | 182 ± 32 (1003) | 170 ± 27 (1007)† | 362 ± 51 (496) | 363 ± 53 (504) | P = 0.9, θ = 110, Δmean = 30, AVmin = 105 |
| After A | 177 ± 36 (970) | 165 ± 35 (1043)† | 460 ± 109 (394)* | 466 ± 115 (369) | P = 0.8, θ = 200, Δmean = 65, AVmin = 80 | |
| 6 | Before A | 161 ± 31 (1113) | 158 ± 33 (1140) | 441 ± 83 (371) | 446 ± 92 (403) | P = 0.8, θ = 115, Δmean = 55, AVmin = 150 |
| After A | 165 ± 39 (1296)§ | 158 ± 38 (1308)† | 478 ± 82 (372)* | 499 ± 86 (432) | P = 0.85, θ = 190, Δmean = 60, AVmin = 130 | |
| 7 | Before M | 165 ± 23 (1070) | 175 ± 36 (1056)† | 541 ± 85 (332) | 548 ± 86 (334) | P = 0.6, θ = 220, Δmean = 20, AVmin = 190 |
| After M | 195 ± 35 (900)* | 194 ± 33 (907)* | 653 ± 113 (269)* | 656 ± 116 (268) | P = 0.95, θ = 230, Δmean = 60, AVmin = 210 | |
| 8 | Before M | 210 ± 18 (856) | 209 ± 9 (851) | 420 ± 22 (390) | 419 ± 33 (429) | P = 0.95, θ = 105, Δmean = 55, AVmin = 125 |
| After M | 213 ± 17 (847)* | 212 ± 12 (848)* | 730 ± 74 (138)* | 727 ± 90 (249) | P = 0.6, θ = 245, Δmean = 15, AVmin = 325 | |
| 9 | Before M | 226 ± 52 (804) | 181 ± 46 (1002)† | 529 ± 126 (339) | 528 ± 117 (344) | P = 0.75, θ = 200, Δmean = 100, AVmin = 100 |
| After M | 258 ± 65 (704)* | 199 ± 61 (919)†* | 641 ± 144 (279)* | 651 ± 156 (278) | P = 0.6, θ = 220, Δmean = 125, AVmin = 145 | |
| 10 | Before M + A | 236 ± 44 (778) | 177 ± 29 (1027)† | 437 ± 70 (279) | 437 ± 65 (320) | P = 0.75, θ = 80, Δmean = 50, AVmin = 175 |
| After M + A | 266 ± 42 (688)* | 172 ± 29 (1082)† | 646 ± 113 (279)* | 646 ± 110 (283) | P = 0.75, θ = 165, Δmean = 80, AVmin = 260 |
| Patient . | . | RA . | LA . | VV . | Simulated VV . | Parameters evaluation . |
|---|---|---|---|---|---|---|
| 1 | Before | 205 ± 28 (1009) | 180 ± 27 (1009)† | 885 ± 91 (199) | 823 ± 105 (220) | P = 0.6, θ = 270, Δmean = 45, AVmin = 330 |
| After | 207 ± 40 (864) | 185 ± 29 (953)† | 877 ± 154 (209) | 888 ± 101 (203) | P = 0.85, θ = 340, Δmean = 25, AVmin = 350 | |
| 2 | Before | 160 ± 33 (1074) | 155 ± 35 (1101)† | 441 ± 83 (387) | 444 ± 88 (386) | P = 0.7, θ = 140, Δmean = 50, AVmin = 135 |
| After | 154 ± 32 (1127)* | 156 ± 31 (1108) | 467 ± 81 (385)* | 468 ± 86 (370) | P = 0.9, θ = 200, Δmean = 30, AVmin = 120 | |
| 3 | Before | 192 ± 31 (950) | 192 ± 26 (949) | 529 ± 104 (344) | 521 ± 97 (346) | P = 0.6, θ = 110, Δmean = 65, AVmin = 210 |
| After | 190 ± 33 (939) | 190 ± 32 (907) | 530 ± 75 (393) | 535 ± 98 (338) | P = 0.6, θ = 115, Δmean = 50, AVmin = 225 | |
| 4 | Before A | 191 ± 36 (880) | 182 ± 34 (922)† | 540 ± 101 (330) | 545 ± 112 (309) | P = 0.95, θ = 195, Δmean = 65, AVmin = 140 |
| After A | 240 ± 30 (812)* | 187 ± 25 (972)†§ | 737 ± 100 (254)* | 741 ± 104 (263) | P = 0.6, θ = 200, Δmean = 75, AVmin = 380 | |
| 5 | Before A | 182 ± 32 (1003) | 170 ± 27 (1007)† | 362 ± 51 (496) | 363 ± 53 (504) | P = 0.9, θ = 110, Δmean = 30, AVmin = 105 |
| After A | 177 ± 36 (970) | 165 ± 35 (1043)† | 460 ± 109 (394)* | 466 ± 115 (369) | P = 0.8, θ = 200, Δmean = 65, AVmin = 80 | |
| 6 | Before A | 161 ± 31 (1113) | 158 ± 33 (1140) | 441 ± 83 (371) | 446 ± 92 (403) | P = 0.8, θ = 115, Δmean = 55, AVmin = 150 |
| After A | 165 ± 39 (1296)§ | 158 ± 38 (1308)† | 478 ± 82 (372)* | 499 ± 86 (432) | P = 0.85, θ = 190, Δmean = 60, AVmin = 130 | |
| 7 | Before M | 165 ± 23 (1070) | 175 ± 36 (1056)† | 541 ± 85 (332) | 548 ± 86 (334) | P = 0.6, θ = 220, Δmean = 20, AVmin = 190 |
| After M | 195 ± 35 (900)* | 194 ± 33 (907)* | 653 ± 113 (269)* | 656 ± 116 (268) | P = 0.95, θ = 230, Δmean = 60, AVmin = 210 | |
| 8 | Before M | 210 ± 18 (856) | 209 ± 9 (851) | 420 ± 22 (390) | 419 ± 33 (429) | P = 0.95, θ = 105, Δmean = 55, AVmin = 125 |
| After M | 213 ± 17 (847)* | 212 ± 12 (848)* | 730 ± 74 (138)* | 727 ± 90 (249) | P = 0.6, θ = 245, Δmean = 15, AVmin = 325 | |
| 9 | Before M | 226 ± 52 (804) | 181 ± 46 (1002)† | 529 ± 126 (339) | 528 ± 117 (344) | P = 0.75, θ = 200, Δmean = 100, AVmin = 100 |
| After M | 258 ± 65 (704)* | 199 ± 61 (919)†* | 641 ± 144 (279)* | 651 ± 156 (278) | P = 0.6, θ = 220, Δmean = 125, AVmin = 145 | |
| 10 | Before M + A | 236 ± 44 (778) | 177 ± 29 (1027)† | 437 ± 70 (279) | 437 ± 65 (320) | P = 0.75, θ = 80, Δmean = 50, AVmin = 175 |
| After M + A | 266 ± 42 (688)* | 172 ± 29 (1082)† | 646 ± 113 (279)* | 646 ± 110 (283) | P = 0.75, θ = 165, Δmean = 80, AVmin = 260 |
All values are in ms. Data are given mean ± SD, N: number of events of the time series, VV: ventricular time series; M: metoprolol, A: amiodarone, M + A: metoprolol + amiodarone; *P < 0.001, §p < 0.05 after vs before medication, †P < 0.001 RA vs LA, parametric t-test. P: probability value. Three parameters are fixed: Δstd = 50 ms, α = 200 ms and τ = 100 ms.
Mean right/left (RA/LA) atrial, and observed/simulated ventricular (VV) activation time with parameters estimation in patients 1–10
| Patient . | . | RA . | LA . | VV . | Simulated VV . | Parameters evaluation . |
|---|---|---|---|---|---|---|
| 1 | Before | 205 ± 28 (1009) | 180 ± 27 (1009)† | 885 ± 91 (199) | 823 ± 105 (220) | P = 0.6, θ = 270, Δmean = 45, AVmin = 330 |
| After | 207 ± 40 (864) | 185 ± 29 (953)† | 877 ± 154 (209) | 888 ± 101 (203) | P = 0.85, θ = 340, Δmean = 25, AVmin = 350 | |
| 2 | Before | 160 ± 33 (1074) | 155 ± 35 (1101)† | 441 ± 83 (387) | 444 ± 88 (386) | P = 0.7, θ = 140, Δmean = 50, AVmin = 135 |
| After | 154 ± 32 (1127)* | 156 ± 31 (1108) | 467 ± 81 (385)* | 468 ± 86 (370) | P = 0.9, θ = 200, Δmean = 30, AVmin = 120 | |
| 3 | Before | 192 ± 31 (950) | 192 ± 26 (949) | 529 ± 104 (344) | 521 ± 97 (346) | P = 0.6, θ = 110, Δmean = 65, AVmin = 210 |
| After | 190 ± 33 (939) | 190 ± 32 (907) | 530 ± 75 (393) | 535 ± 98 (338) | P = 0.6, θ = 115, Δmean = 50, AVmin = 225 | |
| 4 | Before A | 191 ± 36 (880) | 182 ± 34 (922)† | 540 ± 101 (330) | 545 ± 112 (309) | P = 0.95, θ = 195, Δmean = 65, AVmin = 140 |
| After A | 240 ± 30 (812)* | 187 ± 25 (972)†§ | 737 ± 100 (254)* | 741 ± 104 (263) | P = 0.6, θ = 200, Δmean = 75, AVmin = 380 | |
| 5 | Before A | 182 ± 32 (1003) | 170 ± 27 (1007)† | 362 ± 51 (496) | 363 ± 53 (504) | P = 0.9, θ = 110, Δmean = 30, AVmin = 105 |
| After A | 177 ± 36 (970) | 165 ± 35 (1043)† | 460 ± 109 (394)* | 466 ± 115 (369) | P = 0.8, θ = 200, Δmean = 65, AVmin = 80 | |
| 6 | Before A | 161 ± 31 (1113) | 158 ± 33 (1140) | 441 ± 83 (371) | 446 ± 92 (403) | P = 0.8, θ = 115, Δmean = 55, AVmin = 150 |
| After A | 165 ± 39 (1296)§ | 158 ± 38 (1308)† | 478 ± 82 (372)* | 499 ± 86 (432) | P = 0.85, θ = 190, Δmean = 60, AVmin = 130 | |
| 7 | Before M | 165 ± 23 (1070) | 175 ± 36 (1056)† | 541 ± 85 (332) | 548 ± 86 (334) | P = 0.6, θ = 220, Δmean = 20, AVmin = 190 |
| After M | 195 ± 35 (900)* | 194 ± 33 (907)* | 653 ± 113 (269)* | 656 ± 116 (268) | P = 0.95, θ = 230, Δmean = 60, AVmin = 210 | |
| 8 | Before M | 210 ± 18 (856) | 209 ± 9 (851) | 420 ± 22 (390) | 419 ± 33 (429) | P = 0.95, θ = 105, Δmean = 55, AVmin = 125 |
| After M | 213 ± 17 (847)* | 212 ± 12 (848)* | 730 ± 74 (138)* | 727 ± 90 (249) | P = 0.6, θ = 245, Δmean = 15, AVmin = 325 | |
| 9 | Before M | 226 ± 52 (804) | 181 ± 46 (1002)† | 529 ± 126 (339) | 528 ± 117 (344) | P = 0.75, θ = 200, Δmean = 100, AVmin = 100 |
| After M | 258 ± 65 (704)* | 199 ± 61 (919)†* | 641 ± 144 (279)* | 651 ± 156 (278) | P = 0.6, θ = 220, Δmean = 125, AVmin = 145 | |
| 10 | Before M + A | 236 ± 44 (778) | 177 ± 29 (1027)† | 437 ± 70 (279) | 437 ± 65 (320) | P = 0.75, θ = 80, Δmean = 50, AVmin = 175 |
| After M + A | 266 ± 42 (688)* | 172 ± 29 (1082)† | 646 ± 113 (279)* | 646 ± 110 (283) | P = 0.75, θ = 165, Δmean = 80, AVmin = 260 |
| Patient . | . | RA . | LA . | VV . | Simulated VV . | Parameters evaluation . |
|---|---|---|---|---|---|---|
| 1 | Before | 205 ± 28 (1009) | 180 ± 27 (1009)† | 885 ± 91 (199) | 823 ± 105 (220) | P = 0.6, θ = 270, Δmean = 45, AVmin = 330 |
| After | 207 ± 40 (864) | 185 ± 29 (953)† | 877 ± 154 (209) | 888 ± 101 (203) | P = 0.85, θ = 340, Δmean = 25, AVmin = 350 | |
| 2 | Before | 160 ± 33 (1074) | 155 ± 35 (1101)† | 441 ± 83 (387) | 444 ± 88 (386) | P = 0.7, θ = 140, Δmean = 50, AVmin = 135 |
| After | 154 ± 32 (1127)* | 156 ± 31 (1108) | 467 ± 81 (385)* | 468 ± 86 (370) | P = 0.9, θ = 200, Δmean = 30, AVmin = 120 | |
| 3 | Before | 192 ± 31 (950) | 192 ± 26 (949) | 529 ± 104 (344) | 521 ± 97 (346) | P = 0.6, θ = 110, Δmean = 65, AVmin = 210 |
| After | 190 ± 33 (939) | 190 ± 32 (907) | 530 ± 75 (393) | 535 ± 98 (338) | P = 0.6, θ = 115, Δmean = 50, AVmin = 225 | |
| 4 | Before A | 191 ± 36 (880) | 182 ± 34 (922)† | 540 ± 101 (330) | 545 ± 112 (309) | P = 0.95, θ = 195, Δmean = 65, AVmin = 140 |
| After A | 240 ± 30 (812)* | 187 ± 25 (972)†§ | 737 ± 100 (254)* | 741 ± 104 (263) | P = 0.6, θ = 200, Δmean = 75, AVmin = 380 | |
| 5 | Before A | 182 ± 32 (1003) | 170 ± 27 (1007)† | 362 ± 51 (496) | 363 ± 53 (504) | P = 0.9, θ = 110, Δmean = 30, AVmin = 105 |
| After A | 177 ± 36 (970) | 165 ± 35 (1043)† | 460 ± 109 (394)* | 466 ± 115 (369) | P = 0.8, θ = 200, Δmean = 65, AVmin = 80 | |
| 6 | Before A | 161 ± 31 (1113) | 158 ± 33 (1140) | 441 ± 83 (371) | 446 ± 92 (403) | P = 0.8, θ = 115, Δmean = 55, AVmin = 150 |
| After A | 165 ± 39 (1296)§ | 158 ± 38 (1308)† | 478 ± 82 (372)* | 499 ± 86 (432) | P = 0.85, θ = 190, Δmean = 60, AVmin = 130 | |
| 7 | Before M | 165 ± 23 (1070) | 175 ± 36 (1056)† | 541 ± 85 (332) | 548 ± 86 (334) | P = 0.6, θ = 220, Δmean = 20, AVmin = 190 |
| After M | 195 ± 35 (900)* | 194 ± 33 (907)* | 653 ± 113 (269)* | 656 ± 116 (268) | P = 0.95, θ = 230, Δmean = 60, AVmin = 210 | |
| 8 | Before M | 210 ± 18 (856) | 209 ± 9 (851) | 420 ± 22 (390) | 419 ± 33 (429) | P = 0.95, θ = 105, Δmean = 55, AVmin = 125 |
| After M | 213 ± 17 (847)* | 212 ± 12 (848)* | 730 ± 74 (138)* | 727 ± 90 (249) | P = 0.6, θ = 245, Δmean = 15, AVmin = 325 | |
| 9 | Before M | 226 ± 52 (804) | 181 ± 46 (1002)† | 529 ± 126 (339) | 528 ± 117 (344) | P = 0.75, θ = 200, Δmean = 100, AVmin = 100 |
| After M | 258 ± 65 (704)* | 199 ± 61 (919)†* | 641 ± 144 (279)* | 651 ± 156 (278) | P = 0.6, θ = 220, Δmean = 125, AVmin = 145 | |
| 10 | Before M + A | 236 ± 44 (778) | 177 ± 29 (1027)† | 437 ± 70 (279) | 437 ± 65 (320) | P = 0.75, θ = 80, Δmean = 50, AVmin = 175 |
| After M + A | 266 ± 42 (688)* | 172 ± 29 (1082)† | 646 ± 113 (279)* | 646 ± 110 (283) | P = 0.75, θ = 165, Δmean = 80, AVmin = 260 |
All values are in ms. Data are given mean ± SD, N: number of events of the time series, VV: ventricular time series; M: metoprolol, A: amiodarone, M + A: metoprolol + amiodarone; *P < 0.001, §p < 0.05 after vs before medication, †P < 0.001 RA vs LA, parametric t-test. P: probability value. Three parameters are fixed: Δstd = 50 ms, α = 200 ms and τ = 100 ms.
Following administration of medication, the ratios ?> and ?> tended to increase, (Fig. 4B,C) indicating that the number of atrial activations that are blocked in the AV node increased following medication. It is therefore important to develop better ways to analyze the effects of blocked beats on AV nodal properties.
Mathematical quantification of AV nodal properties, refractoriness and concealed conduction during AF
The data described above document the effects of drugs on atrial and ventricular activities during AF. One of our goals is to use these data to obtain insight into the quantitative functional properties of the AV node. In contrast to electrophysiological studies, in which properties of the AV node can be directly assessed using programmed stimulation, we use the fluctuating properties of the atrial and ventricular activities to determine the most appropriate parameters for the AV node functional properties in the context of our theoretical model.
In order to clarify our procedures, and to demonstrate the limitations of previous models that have been used to model the AV node, we first present the results of simulations using three different models of the AV node. These models are: (i) Eq. (2) without concealed conduction as proposed by Shrier et al. [14]; (ii) Eq. (2) plus concealed conduction where Δstd = 0, so that each concealed beat leads to an equal increment in the refractory time, as proposed by Jorgensen et al. [22]; (iii) Eq. (2) plus concealed conduction where Δstd is a positive number, so that each concealed beat leads to a variable increment in the refractory time. The model proposed by Shrier et al. gives good predictions of the ventricular response during atrial stimulation for a variety of fixed rates [14]. However, this model does not give good agreement with the observed ventricular activity in patients with AF. This is illustrated by applying the model to patient 5 after medication. The best agreement that we obtained is shown in Fig. 5B. The shape of the histogram of the VV intervals computed from the simulated time series does not agree with the observed VV distribution (Fig. 5A). Now consider the addition of concealed conduction using the model of Jorgensen et al. [22]. The best agreement is found with θ = 110 ms, Δmean = 120 ms, AVmin = 70 ms, α = 240 ms, τ = 195 ms. The probability value P is higher but the histogram is multi-modal (Fig. 5C). However, when we allow the concealed beats to have varying effects by assuming Δstd is finite, we find excellent agreement between the observed and simulated histograms (Fig. 5D, P = 0.95). In the analysis reported below, in order to avoid problems associated with overfitting the data, we fix the values of Δstd, α, τ and allow the other parameters to vary. We obtain good agreement between the data and simulated results (Table 2). Patients treated with amiodarone had increased refractoriness, i.e. θ, and concealed conduction, Δmean. Patients treated with β-blockers had an increase in θ and the minimum conduction time AVmin.
![Observed histograms of VV intervals in patient 5 after medication. (B) Best fit using the AV nodal recovery curve without concealed conduction in the model of Shrier et al. [14]. (C) Best fit with the inclusion of the concealed conduction Δmean in the theoretical model of Jorgensen et al. [22]. (D) Best fit using the current model.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/europace/7/s2/10.1016_j.eupc.2005.03.016/4/m_s71_5.gif?Expires=1750343031&Signature=Omn2y4YPw5CzgtAxoUKTU4b90Hvutkz6dCkJmxKQKlvKxb5W0atIl70mmavPGZdTnSOeDDAFUaH~KF8a6UJszrLJrJJaFdMrPXe89Nhm~Mj0Mrb7vt0owHSdmadxFY9ctvfDzKnXqQr1GULI-h9ea4pbyXuOUzk34Wy3P2FPKfBOjkPG0uSlAQJ4ci5W1z8X6cnONodCFRxxPoHfqri9mn283P72M2rpAaGlPsyRuHzdd7nDrKj37O2wvSEBAJiGXyz0r-J0Hl0V7m6WiT1Wr5x9tl6hHlvtkJ442XBJAeT2rdblKcTyt0VJkAfnfX-4wAjVdbXHturwjSUhjpV6ug__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Observed histograms of VV intervals in patient 5 after medication. (B) Best fit using the AV nodal recovery curve without concealed conduction in the model of Shrier et al. [14]. (C) Best fit with the inclusion of the concealed conduction Δmean in the theoretical model of Jorgensen et al. [22]. (D) Best fit using the current model.
Sensitivity analysis of the model
Fig. 6 explores the performance of the model for patient 5 upon variation of the refractory period θ and Δmean. A good agreement between the simulated and observed ventricular RR interval is found over a particular range of θ and Δmean. The best agreement between the computed and observed distribution of RR intervals is observed for a ridge on which θ is remarkably constant (Fig. 6 top). Therefore, the concealed conduction parameter plays a major role in determining the best agreement between the observed and simulated ventricular time series. After amiodarone (Fig. 6 bottom), there is a strong shift of the parameters towards larger values of θ and Δmean. There is now a ridge of values along which θ and Δmean simultaneously vary with many different combinations giving good agreement of the model with the clinical data.

Sensitivity analysis of the model illustrated by a three-dimensional representation which explores the parameter space of the model (refractory period and concealed conduction parameters) of patient 5 during AF, before the medication (top) and after 1 h of amiodarone (bottom). Δstd, AVmin, α and τ are fixed while θ and Δmean are varied. The best agreement between the computed and observed distribution of RR intervals is observed for a ridge on which θ is constant (top). The concealed conduction parameter Δmean plays a major role in determining the ventricular response. After amiodarone, the parameter space of the model is shifted towards more refractoriness.
Discussion
The current work provides a unique opportunity to analyze the determinants of the ventricular response during AF using a clinical and mathematical modelling approach. Left, right atrial, and ventricular activities were simultaneously recorded before and after administration of amiodarone and/or metoprolol in conscious post-operative patients. The drugs lead to a prolongation of the inter-activation time in the right atrium from 3 to 49 ms in 5/7 treated patients, have less effects on the left atrium, but prolong much more the ventricular period. To define the effects of medication on the AV node during AF, we developed a mathematical model that includes concealed conduction. Using this model, it is possible to evaluate the role of the drugs in modifying the properties of the AV node during AF.
Pathophysiological mechanisms and effects of antiarrhythmic drugs during AF
The underlying mechanisms involved in the genesis and maintenance of AF are multiple. In patients experiencing paroxysmal AF, the mechanism may be a focal source localized usually in one of the pulmonary veins [38]. In chronic AF, the prevailing theory is that multiple random wavelets of activation coexist to create a disorganized cardiac rhythm [39]. Recent experimental data indicate that AF may be organized by one, or a small number of high frequency reentrant sources in the LA, with fibrillatory conduction toward the RA [36,,37]. Optical mapping studies in the isolated sheep heart demonstrated that during AF there were steep activation frequency gradients between the LA and the RA [37]. Mansour et al. also showed a left-to-right gradient of atrial frequencies during AF in sheep [37]. In the 10 post-operative patients experiencing paroxysmal AF, the ratio ?> is greater than 1.0, for all cases except one before and one after drug (Fig. 4A).
Little information is available on the precise mechanisms of the acute effects of the drug on atrial tissue. The different actions of amiodarone at the atrial level in patients 4–6 and 10 may be related to significant intrinsic differences in the action potential duration between the LA and RA myocytes. Regional action potential variability is associated with distinctive patterns of repolarization and ionic current density [40]. Action potential duration and refractory period are shorter in the LA than in the RA free wall due to differences in the IKr current [40]. One possible explanation is that amiodarone lengthens the refractory period differently depending on the atrial area. The target ionic current responsible for such interatrial differences remains to be determined.
AV nodal function during AF
The rate-dependent conduction of the AV node depends on the complex anatomical structure of the node involving multiple cell types and both fast and slow pathways [41,,42]. Nevertheless, the recovery of excitability of the ICaL calcium current is among the major determinants of the dynamics. β-Adrenergic stimulation of the AV nodal tissue increases both ICaL and IK currents. These act together to produce a shorter effective refractory period as well as faster AV conduction speed, thus promoting a higher ventricular activation rate during AF. These physiological actions provide a foundation for the use of blockers such metoprolol, or antiarrhythmic drugs with class IV and class III actions as amiodarone to help control the ventricular rate during AF.
Previous studies developed a theoretical model of the AV node based on independent tests of AV nodal function during atrial pacing [10,,14,,15,,19]. The current work combined with earlier studies demonstrates that the mathematical models developed in these studies cannot be used to compute the ventricular response during spontaneous AF [23]. We developed a model during AF that allows us to set parameters based on comparisons between the experimental and simulated histograms. Although ideally we would have liked to predict the time of occurrence of every ventricular contraction, this was not possible, likely because of the stochastic nature of the penetration of atrial activity into the AV node during AF. However, by attempting to simulate the statistical features of the histogram of VV intervals during AF, we were able to demonstrate that many plausible models of AV nodal function, are not adequate to model the AV node during AF.
The irregular ventricular rhythm that accompanies AF has been explained in terms of concealed conduction within the AV node [11,,16,,21,,28–,32]. The exact mechanism of concealed conduction remains controversial, but is thought to involve both conduction in the AV nodal slow pathway and electrotonic inhibition. It is important to understand the role of concealed conduction in determining the ventricular response rhythm during AF [29–31]. In the current model, each blocked beat leads to an increase in the refractory period of the AV node by an amount Δ that follows a Gaussian distribution. Since the atrial activity is quite regular in several of the subjects, other models in which each blocked beat has an identical effect did not lead to broad unimodal histograms similar to what was observed in most of the patients, but rather led to multi-modal histograms reflecting the variable conduction ratios between atrial and ventricular activity, see Fig. 5. The accuracy of the parameter estimation is evaluated by the sensitivity analysis exploring the parameter space of the model. Such an analysis confirms that the concealed conduction parameter Δmean plays a major role in determining the agreement between the simulated and observed VV time series, for example see Fig. 6.
Our data raises the important question of the relative roles of the medications on the atrial activity, the refractory time, and the concealed conduction. An earlier study in a porcine model of AF [11] assessed the role of metoprolol on concealed conduction. In this experiment AF was induced by delivering premature stimuli with the presence of metacholine. Metoprolol led to a significant increase in the mean interatrial activation times in the right atrium and also led to a reduced ventricular activation rate. Since the lower atrial activation rate would be expected to lead to reduced concealed conduction, [32] van den Berg et al. concluded that concealed conduction was not a significant contributor to the pharmacological effects of metoprolol but that it acted by increasing the refractory time of the AV node [11]. However, since the parameters describing concealed conduction can also be affected by the medication, it is possible that a smaller number of blocked atrial activations would lead to an increased slowing of ventricular response. Although no direct measure of concealed conduction is possible during AF, the mathematical model suggests that changes in concealed conduction might be affected by the medication differently from changes in other physiological properties of the AV node, and, thus, might constitute distinct targets for medication.
Limitations
The main limitation of the current study is that the mathematical model of the AV node is approximate, and it is not easy to estimate the magnitude of the errors of the derived parameters. In this context, the decreased conduction through the AV node can be associated with an increase in the refractory period, an increase in the minimum conduction time, or an increase in the parameter that accounts for the concealed conduction (Fig. 5 bottom). To some extent, similar quantitative changes in the dynamics can result from an increase in any of those parameters. Thus, without a method to measure directly the magnitude of concealed conduction, definitive statements of the magnitude of the effects on the functional properties of the AV node cannot be made. Furthermore, each simulation is stochastic since Δstd is a parameter that controls a random distribution. As an example, we performed for patient 5 before treatment, 10 trials of simulations to evaluate the mean and standard deviation of the three main parameters. We found that the range for those parameters as well as for the probability value is narrow: P = 0.79 ± 0.06, θ = 110 ± 5 ms, Δmean = 28 ± 8 ms, AVmin = 110 ± 5 ms.
Neither fatigue, nor facilitation has been incorporated in the model [18,,43]. Whereas such contributions can account for the AV nodal response during a variety of pacing protocols, their contribution during AF are not known. To date, fatigue and facilitation have been invoked to describe observed dynamics during rapid activation in which each atrial stimulus is conducted to the ventricles or when a small fraction of atrial activations are blocked in the AV node [15]. Further limitations arise from the difficulty of assessing atrial electrical activity during AF. Because of technical limitations necessitated by the surgical protocol, the positioning of the leads was not in the direct vicinity of the AV node. However, since in many of the patients, the activities in the right and left atria were quite regular with very similar frequencies, in many instances our measured atrial rate likely does reflect the rate impinging on the AV node. Finally, AV nodal electrophysiological properties during post-operative AF may be different than the properties during chronic AF. Catecholamine release is enhanced and autonomic regulation is altered after heart surgery [7,,44]. Therefore, the current results may not be extrapolated to other types of AF.
Despite these limitations, the current study demonstrates that medications might have differential effects on various parameters describing AV nodal physiology during AF and that mathematical modelling should be able to help decipher these complex phenomena. We hope that the current study helps to stimulate further research into these clinically important phenomena.
We thank Eric Libby, Pierre Rocque and Yalin Yin for their excellent technical assistance and Dr. S. Nattel for helpful conversations.
References
Author notes
*This work was supported by the Simone and Cino Del Duca Foundation, Paris, France, the CIHR, MITACS and the Research Resource for Complex Physiologic Signals (NIH).



