-
PDF
- Split View
-
Views
-
Cite
Cite
Maohua Yang, Zonghua Bo, Tao Xu, Bo Xu, Dongdong Wang, Hang Zheng, Uni-GBSA: an open-source and web-based automatic workflow to perform MM/GB(PB)SA calculations for virtual screening, Briefings in Bioinformatics, Volume 24, Issue 4, July 2023, bbad218, https://doi.org/10.1093/bib/bbad218
Close - Share Icon Share
Abstract
Binding free energy calculation of a ligand to a protein receptor is a fundamental objective in drug discovery. Molecular mechanics/Generalized-Born (Poisson–Boltzmann) surface area (MM/GB(PB)SA) is one of the most popular methods for binding free energy calculations. It is more accurate than most scoring functions and more computationally efficient than alchemical free energy methods. Several open-source tools for performing MM/GB(PB)SA calculations have been developed, but they have limitations and high entry barriers to users. Here, we introduce Uni-GBSA, a user-friendly automatic workflow to perform MM/GB(PB)SA calculations, which can perform topology preparation, structure optimization, binding free energy calculation and parameter scanning for MM/GB(PB)SA calculations. It also offers a batch mode that evaluates thousands of molecules against one protein target in parallel for efficient application in virtual screening. The default parameters are selected after systematic testing on the PDBBind-2011 refined dataset. In our case studies, Uni-GBSA produced a satisfactory correlation with the experimental binding affinities and outperformed AutoDock Vina in molecular enrichment. Uni-GBSA is available as an open-source package at https://github.com/dptech-corp/Uni-GBSA. It can also be accessed for virtual screening from the Hermite web platform at https://hermite.dp.tech. A free Uni-GBSA web server of a lab version is available at https://labs.dp.tech/projects/uni-gbsa/. This increases user-friendliness because the web server frees users from package installations and provides users with validated workflows for input data and parameter settings, cloud computing resources for efficient job completions, a user-friendly interface and professional support and maintenance.
INTRODUCTION
In drug discovery, one of the most important objectives in drug discovery is finding a novel hit compound that binds a protein receptor, and the binding affinity of a drug molecule to a protein receptor is commonly assessed using the binding free energy [1]. Computational approaches can drastically cut the time and expense of designing new drug molecules as compared with experimental methods at some points in drug discovery. One of the most widely used computational methods in virtual screening is docking based on scoring function [2]. Many scoring functions have been developed, such as Vina score [3], X-Score [4] and GlideScore [5]. They are frequently calculated as weighted sums of some empirical energy terms. Due to the simple analytical functional forms of the empirical energy terms, docking calculation based on scoring functions is very efficient but leads to relatively large errors [6], which makes its binding affinity estimation unreliable. Theoretically accurate methods, such as free energy perturbation (FEP) [7] and thermodynamic integration (TI) [8], have been developed to calculate binding free energy. They are pathway methods, in which the initial state and the final state of the system interconvert via infinitesimal alchemical changes in its energy function. Although they are more accurate, they suffer from slow convergence of the free energy differences and, thus, have high computational cost, making them not suitable for virtual screening. Molecular mechanics/Generalized-Born (Poisson–Boltzmann) surface area (MM/GB(PB)SA) [9], which balances computational cost and accuracy, has become a popular method for binding free energy calculations in virtual screening. Many computational tools used to perform MM/GB(PB)SA calculations have been developed and released over the years, both commercially and in open-source formats. Open-source tools represented by MMPBSA.py [10], g_mmpbsa [11], GMXPBSA2.1 [12], CaFE [13] and gmx_MMPBSA [14] are free to access but have several limitations, such as the number of calculations that can be performed and various compatibility issues. In addition, because these tools are mostly available as packages or plugins, they also suffer from several user-friendliness issues: (1) Installation and configuration: Users need to install and configure on their own computers, which can be a difficult task for those without technical expertise. (2) Input preparation: users need to prepare input data independently, which may require installation and usage of other packages. This can make the initial setup difficult and lead to errors in results, especially for new users. (3) Limited computing resources: users need to perform calculations on their own computers or computing resources, which can be a limitation for computationally intensive tasks. (4) Command line input: These packages usually require users to use command line inputs to navigate and perform tasks. This can be challenging for users who are not familiar with the syntax and structure of command line commands. (5) Support and maintenance: These open-source packages usually do not have professional support and maintenance team. When there are bugs and security vulnerabilities, users may need to rely on the community to get help.
Here, we present an automatic user-friendly end-to-end workflow, named Uni-GBSA, to lower the entry barrier to MM/GB(PB)SA calculations. Uni-GBSA can accommodate users with different needs and levels of skills and experience. In addition to an open-source package (documentation, test files and tutorials included) at https://github.com/dptech-corp/Uni-GBSA, it is available on the Hermite web platform at https://hermite.dp.tech. A free lab version of the Uni-GBSA web server is also available at https://labs.dp.tech/projects/uni-gbsa/. This significantly improves accessibility and usability of the workflow because the web platform (1) frees users from package installations, (2) provides validated workflows for input data and parameter settings, (3) offers users access to cloud computing resources to complete their jobs efficiently, (4) provides a user-friendly interface that is easy to navigate and (5) is maintained by a professional tea to provide users with better support and maintenance.
Several functions can be performed with Uni-GBSA, including (1) topology preparation with different force fields and charge methods, (2) molecular dynamics (MD) simulations, (3) binding free energy calculations with different solvent models (GB and PB), (4) binding free energy decomposition and (4) parameter scanning for MM/GB(PB)SA calculations. For application in virtual screening, we developed a batch mode to allow efficient evaluation of thousands of ligands against one protein receptor in parallel. We also conducted two case studies on the scoring (i.e. the ability of a method to produce binding scores in a linear correlation with experimental binding data) and ranking power (i.e. the ability of a method to correctly rank the known ligands of a certain target).
THEORY
In the MM/GB(PB)SA approach [15, 16], the binding free energy for a protein–ligand complex (|$\Delta $|G) can be estimated using Eq. 1:
|$\Delta{G}$| can also be expressed as follows:
|$\Delta{H}$| is the change of enthalpy, which can be decomposed into contributions of the molecular mechanics (MM) energy changes(|$\Delta E_{MM}$|) in the gas phase and the solvation free energy (|$\Delta G_{SOLV}$|) as shown in equation (3). –T|$\Delta S$| is the conformational entropy upon ligand binding, where T is the absolute temperature. –T|$\Delta S$| is usually neglected due to the expensive computational cost. The effective free energy is sufficient for comparing relative binding free energies of related ligands. [17]
|$\Delta E_{MM}$| and |$\Delta G_{SOLV}$| can be further decomposed into contributions of different interactions as expressed in Eq.4 and Eq.5:
|$\Delta E_{INT}$| is the change in internal energies, which includes the bond, angle and dihedral energies. |$\Delta E_{ELE}$| and |$\Delta E_{VDW}$| are the electrostatic energies and the van der Waals energies, respectively. |$\Delta E_{ELE}$| is usually calculated using Coulomb’s law with atomic charges from the MM force field, so the values depend on the charges used for the protein and the ligand.
|$\Delta G_{SOLV}$| is the sum of the polar contribution |$\Delta G_{GB/PB}$| and the nonpolar contribution |$\Delta G_{SA}$|. The polar contribution |$\Delta G_{GB/PB}$| represents the electrostatic interaction between the solute and the continuum solvent. It is calculated using the PB or GB model. The GB method can provide an analytical expression for |$\Delta G_{SOLV}$| and is thus much faster than the PB method.
The nonpolar contribution results from cavitation (i.e. the cost of making a cavity within the solvent) and van der Waals interactions between the solute and the solvent around the cavity. It is typically assumed to be proportional to the total solvent-accessible surface area (SASA) of the solute and calculated using Eq.6, where |$\gamma $| is the surface tension constant and b is a correction constant.
MATERIALS AND METHODS
Workflow
Uni-GBSA is an automatic workflow to perform MM/GB(PB)SA calculations from force field building, structure optimization free energy calculation. There are four main steps in the Uni-GBSA workflow as shown in Figure 1:
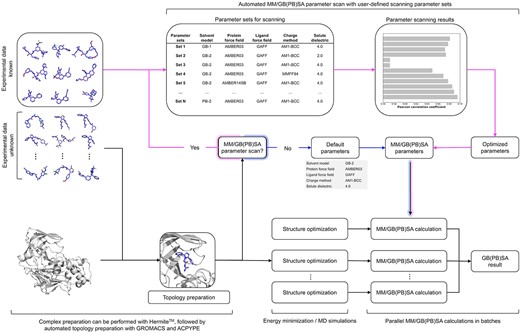
(1) Topology preparation
Uni-GBSA uses the GROMACS software package [18–20], which supports various molecular force fields, for protein parametrization. The open-source software acpype (or AnteChamber PYthon Parser interfacE) [21], a wrapper script around the ANTECHAMBER software [22, 23], is used for force field parameterization of ligands.
(2) Structure optimization
Obtaining reliable binding poses between proteins and ligands is crucial for MM/GB(PB)SA calculations [17]. Here, we introduced a structure optimization step to the traditional MM/GB(PB)SA calculation process. Binding poses can be optimized with either energy minimization or MD simulation methods, which are chosen by the user.
(3) MM/GB(PB)SA calculation
Uni-GBSA can perform MM/GB(PB)SA calculation with a set of user-defined parameters, obtained from the parameter scanning step or otherwise. When parameters are not provided by the user, Uni-GBSA performs MM/GB(PB)SA calculations with the default parameters: implicit solvent model: GB-OBC1 [24], protein force field: AMBER03 [25], ligand force field: general AMBER force field (GAFF) [23], ligand charge method: AM1-BCC [26] and solute dielectric constant (|$\varepsilon _{in}$|): 4.0. The default parameters were selected after systematic parameter testing on 1864 protein–ligand complexes from the PDBBind-2011 refined dataset [27–29]. Details on parameter testing are explained below.
(4) MM/GB(PB)SA parameter scan (optional)
The accuracy of MM/GB(PB)SA calculations is system-dependent and can vary depending on choices of parameters such as the force field, charge model, solvation method and solvent dielectric constant. [17]. For instance, Hou et al. [17] found that the AMBER03 force field performed better with MD simulations of less than 1 ns for both MM/GBSA and MM/PBSA. For MD simulations of 2-4 ns, MM/GBSA performed the best with AMBER99, while MM/PBSA performs the best with AMBER99SB. Therefore, it is crucial to fine-tune the parameters specific to the system of interest before M/GB(PB)SA calculations due to the system dependence of parameters for MM/GB(PB)SA calculations.
To address this issue, we introduce the parameter scan function. If the user has experimental binding data on the system of interest, Uni-GBSA can perform an automatic parameter optimization prior to production MM/GB(PB)SA calculation. In this step, the user needs to provide a small dataset of protein–ligand complexes, their corresponding experimental binding data and the parameters the user wishes to scan. A series of MM/GB(PB)SA calculations are performed using different sets of parameters chosen by users. The correlation between binding free energies calculated by the MM/GB(PB)SA approach and the experimental data for each set of parameters are automatically calculated and ranked. Finally, a set of optimized parameters for this system are returned, which can be used in the subsequent MM/GB(PB)SA calculations for the larger dataset.
If there is no available experimental data, a possible solution is to use a small set of theoretical data (e.g. from FEP calculations) to perform the parameter scan.
In the absence of theoretical data, the default parameters can be used. Our default parameters have already been systematically tested and validated (discussed in detail in Results and Discussion), and are likely to provide reasonable performance.
Batch mode
For application in virtual screening, Uni-GBSA offers a batch mode to evaluate the binding free energy of many ligands to one protein target. The force field parameterization processes for protein and ligands are performed separately. As the protein target is the same for all ligands, force field parameterization of the protein is performed only once, which is then concatenated with each ligand. This greatly reduces computational time and cost. The parallel feature in the batch mode, making full use of CPU resources, greatly improves the calculation efficiency.
Uni-GBSA open-source package
Uni-GBSA is freely available as an open-source package (documentation, test files and tutorials included) at https://github.com/dptech-corp/Uni-GBSA. The package includes seven tools: unigbsa-buildtop, unigbsa-buildsys, unigbsa-md, unigbsa-pbc, unigbsa-scan, unigbsa-traj, unigbsa-pipeline. All tools can be executed using the command line.
unigbsa-buildtop is an automatic GROMACS topology generation tool. Given a protein file in the PDB format and a ligand file in the MOL or SDF format, it generates GROMACS topology files for both the protein and the ligand. The protein force field, ligand force field and ligand charge method parameters can be specified by the user using the command line. If not specified, default parameters are used.
unigbsa-buildsys builds the GROMACS simulation systems for the protein–ligand complexes. It places the protein and ligand into a periodic box (default: triclinic) and solvates the system with a salt concentration of 0.15 mol L|$^{-1}$|. The simulation box type and the salt concentration can be changed by the user using the command line.
unigbsa-md performs MD simulations on the protein–ligand complexes. It contains four steps: simulation system preparation, energy minimization, equilibration simulation with position restraints on the heavy atoms (100 ps NVT and 100 ps NPT equilibration simulations) and production simulations. Simulation steps (default: 2500 steps, 2 fs timestep) and the number of frames to save for the trajectory file (default: 100) can be specified by the user.
unigbsa-pbc processes the periodic boundary condition of a GROMACS trajectory file.
unigbsa-traj then calculates the MM/GB(PB)SA from the MD trajectory. An index file, containing two groups named ’RECEPTOR’ and ’LIGAND’, for the protein and ligand, respectively, is required.
unigbsa-pipeline automates all the individual tools mentioned above. Users only need to provide input files for both proteins and ligands.
unigbsa-scan scans for the best parameters for MM/GB(PB)SA calculations for a given set of experimental data. In addition to the protein and ligands input files, the corresponding experimental data in the CSV format are also required to perform the scan.
Uni-GBSA on web platforms
In addition to the open-source package, Uni-GBSA is also available on the Hermite web platform. Hermite (https://hermite.dp.tech) is a new-generation Drug Design Platform powered by AI, Physics and Computing. As a web-based software as a service (SaaS) solution, Hermite possesses the power of structure modeling, virtual screening, binding affinity evaluations, etc. Currently, Uni-GBSA has been integrated into the Hermite platform, which not only frees users from the tedious work of package installations but also provides validated workflows for input data and parameter settings. In addition, as running a number of MM/GB(PB)SA jobs simultaneously can be computationally demanding, the Hermite SaaS platform offers users access to sufficient or even unlimited computing resources to complete their jobs efficiently.
Input interface
MM/GB(PB)SA calculations can be implemented via our user-friendly input interface, as shown in Figure 2A).
A protein structure in the PDB format is required. The user can either upload the protein structure in the PDB format or obtain it directly from the Research Collaboratory for Structural Bioinformatics PDB (RCSB) using the PDB code, for example, 10GS. The platform then performs an automatic structure check to identify any issues, such as missing residues. If the check fails, the user can directly repair the structure using the ‘Protein Preparation’ function provided on the platform or upload a new protein structure prepared by the users themselves.
A ligand structure in the MOL or SDF formats is also required. The user can either upload files or select them interactively from the 3D Workspace. An automatic structure check is also performed on the ligand structure. If needed, the ligand structure can be repaired using the ‘Ligand Preparation’ function provided on the platform.
The default parameters are automatically inputted. If ‘Total Decomposition Contribution Analysis’ is selected, energy decomposition by residue will be calculated and the job completion time will be longer.
Optional: The user can define a job name. This is recommended for easier identification in the job list.

Demonstration of using Uni-GBSA on the Hermite web platform. (A) Example of the input interface. The input protein and ligand structure files are required. The default parameters are automatically inputted, as shown on the right. (B) Example of the output interface. The result is shown in tabulated form, but can also be shown as a horizontal bar plot for easy visualization. If total decomposition contribution analysis is selected, energy decomposition by residue will be presented as a table.
Once the protein and ligand structure files are provided and parameters for MM/GB(PB)SA calculations are set, the user can submit the job to our cloud platform.
Output interface
After completion, job results are sent back to the website and the job status changes from ‘Running’ to ‘Finished’. The user can access the result from the ‘Show’ icon in the job list. The output interface, by default, shows the energy terms from the MM/GB(PB)SA calculation in tabulated form (Figure 2B). These can also be visualized as a horizontal bar plot for easier interpretation. If total decomposition contribution analysis is selected, the result can be accessed via the ‘Decomposition’ tab as a table. All job files, including input protein and ligand structure files (original and, if requested, processed by ‘Protein/Ligand Preparation), MM/GB(PB)SA calculation parameters and results and the job log files, can be downloaded as a ZIP file.
Online documentations
User manual for the Hermite web platform and the MM/GB (PB)SA function is available online (https://hermite-doc.dp.tech/docs/) and can be easily accessed from the ‘Help Center’ icon on the side menu. It contains detailed instructions with visual aids explaining how to set up a calculation and access the resulting data. The online manual is updated regularly based on user needs, feedback or method improvements.
Run-time and data availability
A typical ‘Protein Preparation’ step takes about no more than 5 min per protein structure on the Hermite web platform. A typical ‘Ligand Preparation’ step takes from several minutes to dozens of minutes depending on the number of ligands. MM/GB(PB)SA job runs could take from minutes to hours, which is affected by both the number of ligands as well as the job settings. For virtual screening, 3000 ligands can be uploaded at once in a single job for MM/GB(PB)SA calculations. There is no limit on the number of jobs submitted per day or the size of uploaded data. Job results are saved on the server permanently and can be accessed anytime.
Lab version
A free Uni-GBSA web server of a lab version is available at https://labs.dp.tech/projects/uni-gbsa/. The lab version supports two modes for task submission: (1) Guest (non-registered) task submission: All tasks are publicly visible and can be downloaded by anyone. (2) User (registered) task submission: Tasks submitted by users are only visible and downloadable by the submitting user. On this free lab web server, for each guest/user, there is a limit of 10 Uni-GBSA tasks per day, with a maximum of 100 ligands per task.
RESULTS AND DISCUSSION
Parameter testing on PDBBind-2011 refined dataset
We carried out parameter testing on the PDBBind-2011 refined dataset [27–29] containing 1864 protein–ligand complexes. The dataset has been studied in previous work [29]. During our study, apart from the variable of investigation, default parameters were used in the calculations. All the protein and ligand structures were prepared on the Hermite web platform (https://hermite.dp.tech).
(1) Effect of structure optimization methods
The structure of the binding pose plays an important role in the results of MM/PB(GB)SA calculations [17]. We conducted a comparative study of binding free energy calculations using 10 different structure optimization methods: energy minimization (EM), and MD simulations of 100 ps, 200 ps, 500 ps, 800 ps, 1 ns, 2 ns, 3 ns, 4 ns and 5 ns. For the MD simulations, 50-ps NVT and 50-ps NPT equilibration simulations with positional restraints on heavy atoms were first performed. The restraints were then released for the MD production simulations. For each system, the binding free energy was averaged over 10 snapshots evenly spaced along the trajectory. The correlations between the experimental binding free energies and the calculated values are summarized in Figure 3A. A higher Pearson correlation coefficient (r|$_{p}$|) indicates better performance.
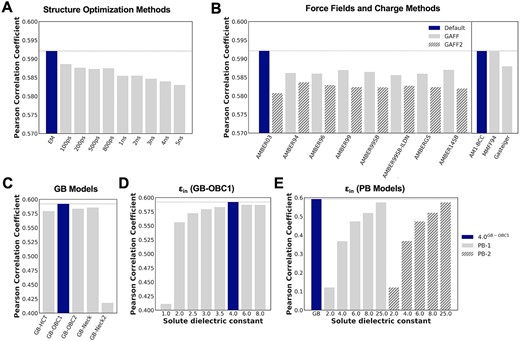
The effects of (A) structure optimization methods, (B) protein force fields, ligand force fields (GAFF: without stripes, GAFF2: with stripes) and charge models, (C) GB models, solute dielectric constants with (D) GB-OBC1 model and (E) PB models (PB-1: without stripes, PB-2:with stripes) on the correlation between the free energy values calculated by MM/GB(PB)SA and the experimental values of the PDBBind-2011 refined dataset. The default parameter is shown in dark blue and the other parameters are shown in gray. The Pearson correlation coefficient for the default parameter is shown with a horizontal dashed line. Specific numbers for the Pearson correlation coefficients are documented in SI Section 1.
When no structural optimization was performed (i.e. the structures from the PDBBind-2011 refined dataset were used directly as input poses), the correlation with experimental data was, as expected, very poor (r|$_{p}$| = 0.005). When a simple energy minimization was performed on the protein–ligand complexes before MM/GBSA calculations, the correlation was significantly improved (r|$_{p}$| = 0.592). This could be attributed to the removal of clashes between atoms in the complexes in energy minimization. When MD simulations were performed, we found that the binding free energy calculations worsened with longer MD simulations. Similar observations have been reported previously, where MM/GB(PB)SA calculations on energy-minimized conformations frequently yielded results as good as or better than those from MD [30–33], while the impact of the length MD simulations on binding free energy calculations may be system-dependent [34–36]. For example, Johnson et al. [34] found that MM/PBSA calculations on conformations from MD simulations ranging from 0.25 to 2 ns provided satisfactory results, but the accuracy decreased when the MD simulations were longer than 2 ns [34]. Wang et al. [35] observed that longer MD simulations (ranging from 0.4 to 4.8 ns) did not necessarily give better results. However, Virtanen et al. [36] showed that the length of the MD simulations was not critical to the accuracy of the binding free energy calculations. In summary, it is beneficial to perform an energy minimization on the protein–ligand complexes before MM/GB(PB)SA calculations, and MD simulations may not be essential for binding free energy calculations.
(2) Effect of force fields and charge models
The force fields and ligand charge models are crucial in the performance of MM/GB(PB)SA calculations as they determine all of the interactions in a system [29]. We studied the effects of force fields on the binding free energies calculated by MM/GBSA using eight different versions of the nonpolarizable AMBER force fields (AMBER94 [37], AMBER96 [38], AMBER99 [39], AMBER99SB [40], AMBER99SB-ILDN [41], AMBER03 [25], AMBER14SB [42] and AMBERGS [43]) for proteins and the general AMBER force fields (GAFF [23] and GAFF2 [44]) for ligands with the AM1-BCC charge method [26]. In addition, we also tested the MMFF94 [45] and Gasteiger [46] charge models in conjunction with the AMBER03 force field for proteins and the GAFF force field for ligands. The correlations between the experimental binding free energies and the calculated values are shown in Figure 3B.
The best result was obtained when the AMBER03 force field for proteins and GAFF for ligands were used. For the same ligand force field, except for AMBER03, all other protein force fields gave similar performances. When the same protein force field was used, the results of MM/GBSA calculations were consistently better when the ligands were parametrized with GAFF than with GAFF2. For the charge methods, AM1-BCC and MMFF94 produced similar results. The Gasteiger charge model had the poorest performance (r|$_{p}$| = 0.588), but the differences were very small (<0.005).
(3) Effect of solvent models and solute dielectric constants
Solvent models and solute dielectric constants also have great influences on the performance of MM/GB(PB)SA calculations [29]. We tested seven solvation models, provided in the AMBER software package. These include five GB models (GB-HCT, GB-OBC1, GB-OBC2, GB-Neck and GB-Neck2) [24, 47, 48] and two PB models (PB-1 and PB-2) [49, 50]. We also performed a systematic scanning of the solute dielectric |$\varepsilon _{in}$| ranging from 1 to 25 with the solvent models GB-OBC1, PB-1 and PB-2.
Except for GB-Neck2 (r|$_{p}$| = 0.418), differences in the performance of MM/GBSA calculations between the different GB models were very small (Figure 3C). For GB-OBC1, performance improved significantly when solute dielectric increased from 1.0 (r|$_{p}$| = 0.411) to 2.0 (r|$_{p}$| = 0.556). The best performance (r|$_{p}$| = 0.592) was achieved when |$\varepsilon _{in}$| = 4.0 (Figure 3D). For the PB models, both PB-1 and PB-2 showed similarly poor performances with |$\varepsilon _{in}$| ranging from 2.0 to 8.0. A much higher solute dielectric (|$\varepsilon _{in}$| = 25.0) was needed to obtain comparable performance (r|$_{p}$| = 0.574) (Figure 3E). In summary, PB models were more strongly influenced by solute dielectric constants than the GB models. A systematic scanning of solute dielectric constants may be helpful as the best dielectric constant is system-dependent.
After parameter testing on the PDBBind-2011 refined dataset. We used the PDBBind-2020 refined dataset containing 5316 protein–ligand complexes, an updated version of PDBBind-2011, to validate the correlation between the binding free energy evaluated by Uni-GBSA and the experimental binding affinity. We then compared Uni-GBSA with Autodock Vina [3] using the BACE-1 dataset [51] containing 1547 molecules against BACE-1 protein target to validate the enrichment power for bio-active molecules of Uni-GBSA.
Scoring power of Uni-GBSA on PDBBind datasets
We evaluated the scoring power [52], i.e. the ability of a method to produce binding scores in a linear correlation with experimental binding data, of Uni-GBSA on the PDBBind-2020 refined dataset. We calculated the Pearson correlation coefficient between the binding free energy calculated by Uni-GBSA and the experimental results as the metric using the default parameters (i.e. solvation mode: GB-OBC1 [24], protein force field: AMBER03 [25], ligand force field: GAFF [23], ligand charge method: AM1-BCC [26], dielectric constant: 4.0) and workflow (i.e. topology preparation, structure optimization by energy minimization, MM/GB(PB)SA calculation) of Uni-GBSA. The results are shown in Figure 4.
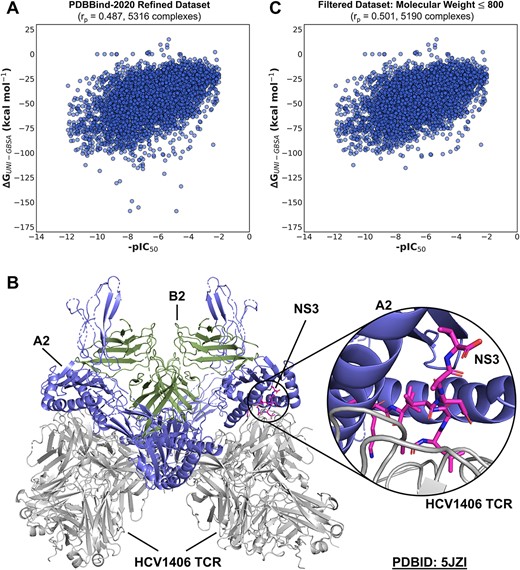
Scoring power of Uni-GBSA on PDBBind-2020 refined dataset. (A) Correlations between binding free energy calculated by Uni-GBSA and experimental binding affinity on the PDBBind-2020 refined dataset. r|$_{p}$| refers to the Pearson correlation coefficient. (B) Structure of the T-cell receptor (TCR) variable domains relative to the peptide-MHC complex. The complex composes of the peptide nonstructural protein 3 (NS3) and the human leukocyte antigen class I histocompatibility antigen A-2 alpha chain (A2). B2 refers to beta-2-microglobulin. (C) Correlation between binding free energy calculated by Uni-GBSA and experimental binding affinity on the PDBBind-2020 filtered dataset after removal of ligands with molecular weights greater than 800 g mol|$^{-1}$|.
On the PDBBind-2011 refined dataset, the binding free energies calculated using the MM/GBSA approach showed a good correlation with the experimental data (r|$_{p}$| = 0.592), which is comparable with the r|$_{p}$| = 0.579 reported previously [29]. In comparison, the correlation on the full PDBBind-2020 refined dataset (r|$_{p}$| = 0.487) was weaker (Figure 4A). We noted that the binding free energies of several ligands were significantly overestimated (<150 kcal M|$^{-1}$|). These were found to be large ligands with molecular weights (MW) greater than 800 g mol|$^{-1}$|. The five most overestimated complexes were found to be the major histocompatibility complex class I (MHC-I) systems (PDB ID: 5JZI and 5ISZ) which are known to bind peptides of length 8–11 [53] and MHC-I like systems (PDB ID: 6MJA, 6MJI and 6MJ4). We also found some inconsistencies between the binding affinities documented in the PDBBind-2020 refined dataset and their corresponding literature sources for these larger ligands. For example, the experimental binding affinity for 5JZI (|$16 \pm 1 \mu $|M) was measured between the HCV1406 T-cell receptor (TCR) and the NS3/A2 complex, composed of the peptide nonstructural protein 3 (NS3) and the human leukocyte antigen class I histocompatibility antigen A-2 alpha chain (A2) [54] (Figure 4B). However, the ligand was given solely as NS3 in the PDBBind-2020 refined dataset, so the binding free energy estimated by Uni-GBSA was of a different system than the experimental value.
As a result, we filtered the ligands with MW >800 g mol|$^{-1}$| which removed 129 complexes from the dataset. The filtered dataset yielded a better correlation with experimental data (r|$_{p}$| = 0.501) (Figure 4C). However, this was still worse than the performance on the PDBBind-2011 refined dataset. We attribute this to the increased diversity and complexity of the protein–ligand complexes in the PDBBind-2020 refined dataset, which is an updated version of the PDBBind-2011 refined dataset. Because parameters for MM/GB(PB)SA calculations depend on the studied system, it is difficult to select a set of parameters that is suitable for all systems in a dataset [17]. For example, ligand charge has a critical effect on the binding of a protein–ligand complex. Hou et al. found that the performances of MM/GBSA and MM/PBSA are worse in the binding free energy calculations of ligands with high formal charges; the uncertainty in the accuracy of MM/GB(PB)SA calculations increased on an enlarged dataset with unbalanced samples (e.g. ligands containing five and six formal charges only have 10 and 13 occurrences in the dataset). [29]. Because of the system dependence of parameters for MM/GB(PB)SA calculations, we speculate that the default parameters used might not be suitable for all systems in the PDBBind-2020 refined dataset and led to larger uncertainties.
Ranking power of Uni-GBSA on BACE-1 dataset
To demonstrate the applicability of Uni-GBSA, we also evaluated the ranking power [52], i.e. the ability of a method to correctly rank the known ligands of a certain target protein by their binding affinities, on the well-studied BACE-1 dataset [51]. We took the widely used metric, enrichment factor (EF), to evaluate the ranking power. EF is defined as the following equation:
Here we calculated the EF under different sampling ratios (1%, 5%, 10%, 15%, 20%) from the top ranking results to compare the ranking power of the Vina scoring function [3] and Uni-GBSA’s MM/GB(PB)SA calculations on the top-1 binding poses predicted by molecular docking software Uni-Dock [55], respectively. The true binders were screened out for both methods.
For the Uni-GBSA method, we performed parameter scanning on a subset of 273 BACE-1 complexes with known crystal structures (Figure 5A). We scanned four GB models (GB-HCT, GB-OBC1, GB-OBC2 and GB-Neck) [24, 47, 48] and two PB models (PB-1 and PB-2) [49, 50] with the default solute dielectric |$\varepsilon _{in}$| of 4.0. For the default solvent model GB-OBC1, we also scanned solute dielectric |$\varepsilon _{in}$| ranging from 2.0 to 8.0. The optimized parameters were found to be |$\varepsilon _{in}$| = 8.0 with all other parameters being the default. These parameters then were used in the subsequent MM/GB(PB)SA calculations.
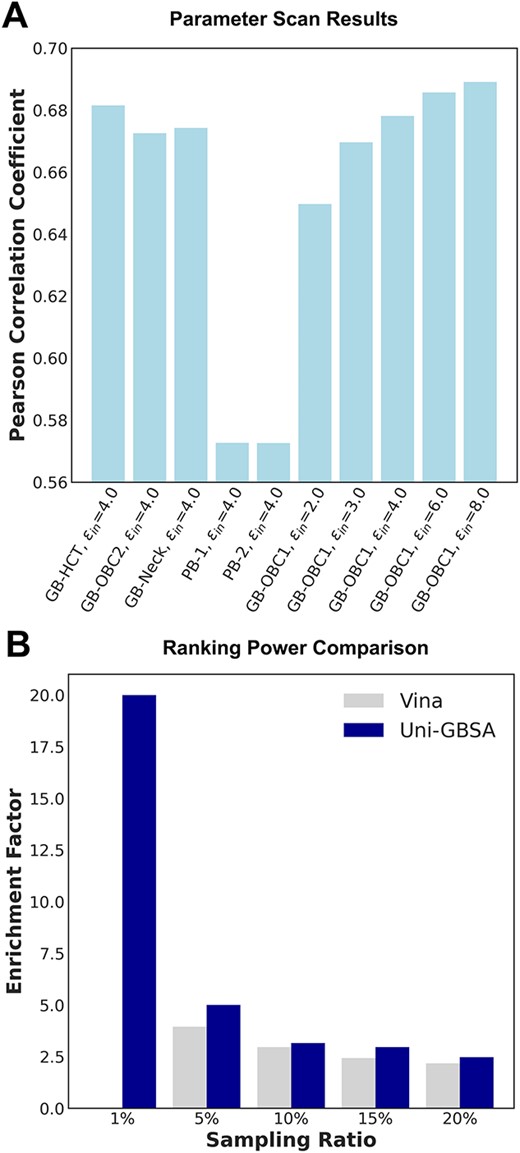
Ranking power of Uni-GBSA on BACE-1 dataset. (A) Results from parameter scan for MM/GB(PB)SA calculations using Uni-GBSA. (B) Comparison of enrichment factor results by Vina and Uni-GBSA methods. Specific numbers for the Pearson correlation coefficients and enrichment factors are documented in SI Section 2.
We found that the number of true positive molecules picked using Uni-GBSA is consistently higher than that picked using the Vina scoring function in all sampling ratios (Figure 5B). This suggests that Uni-GBSA has a better performance for molecular enrichment in virtual screening.
CONCLUSION
Uni-GBSA is an automatic workflow, which can perform topology preparation, structure optimization, parameter scanning and binding free energy calculation. We systematically tested different parameters, including structure optimization methods, force fields, ligand charge methods, solvent models and solute dielectric constants, on the PDBBind-2011 refined dataset. A set of optimal parameters was selected as the default for Uni-GBSA, which produced a satisfactory correlation with the experimental binding affinities. The applicability of Uni-GBSA in virtual screening was then tested on the BACE-1 dataset. We used optimized parameters obtained from parameter scanning and the batch mode to calculate the binding free energies using Uni-GBSA. Uni-GBSA consistently was found to outperform AutoDock Vina in molecular enrichment for all sampling ratios tested.
Uni-GBSA is accessible and usable by users with different needs and levels of IT skills. It is freely available as an open-source package (documentation, test files and tutorials included) at https://github.com/dptech-corp/Uni-GBSA. It can also be accessed from the Hermite web platform at https://hermite.dp.tech. A free Uni-GBSA web server of a lab version is available at https://labs.dp.tech/projects/uni-gbsa/. This web server implementation significantly lowers the entry barrier to MM/GB(PB)SA calculations because of the following reasons: (1) No installation required: With a web server, users do not need to install any software or packages on their own computers. This eliminates the need for users to have technical expertise in installation and configuration and can save time and reduce the risk of installation errors. (2) Validated workflows: The web server provides users with validated workflows for input data and parameter settings, which can be easier to set up than using an open-source package. (3) Access to resources: The web server offers users access to cloud computing resources, which can be more powerful and efficient than the resources available on the users’ own computers. This can be particularly useful for computationally intensive tasks. (4) User-friendly interface: The web server often provides a user-friendly interface that is easy to navigate, which can be more convenient for users. (5) Support and maintenance: The web server is maintained by a professional team, which can provide users with better support and maintenance, and can ensure that the server is always up-to-date and working efficiently. We expect Uni-GBSA to be widely applied in virtual screening.
We note that the MM/GB(PB)SA approach still has limitations. For example, although much faster and less computationally costly than the more rigorous alchemical methods (such as FEP and TI), MM/PB(GB)SA approach is less accurate [56, 57]. To improve the accuracy of MM/GB(PB)SA calculations, we plan to improve the force field, for example, using the Differentiable Molecular Force Field (DMFF) [58], an open-source molecular force field development tool that utilizes the automatic differentiation technique.
Uni-GBSA is a user-friendly automatic workflow, which can perform topology preparation, structure optimization, binding free energy calculation and parameter scanning for MM/GB(PB)SA calculations. For the application of virtual screening, Uni-GBSA also has a batch mode that evaluates thousands of molecules against one protein target in parallel.
We performed systematic parameter testing on the PDBBind-2011 refined dataset and selected the parameters that produced a satisfactory correlation with the experimental binding affinity as the default parameters for Uni-GBSA.
In our case studies, the binding free energy calculations by Uni-GBSA are in good agreement with experimental values, and the ranking power of Uni-GBSA outperformed AutoDock Vina on the BACE-1 dataset.
Uni-GBSA is available as an open-source package at https://github.com/dptech-corp/Uni-GBSA. It can also be accessed from the Hermite web platform at https://hermite.dp.tech. A free Uni-GBSA web server of a lab version is available at https://labs.dp.tech/projects/uni-gbsa/.
ACKNOWLEDGEMENTS
This work was supported by National Key R&D Program of China (2022YFA1004300). All experiments were carried out on the cloud platform Bohrium (https://bohrium.dp.tech).
DATA AVAILABILITY
The data and source code are available at https://github.com/dptech-corp/Uni-GBSA.
Author Biographies
Maohua Yang is a CADD Researcher at DP Technology. His research focuses on developing and utilizing computational tools for drug designing.
Zonghua Bo is a Researcher at DP Technology. Her research focuses on developing and utilizing computational tools for drug discovery, such as virtual screening and molecular generation.
Tao Xu is currently the product director at DP Technology. His research interests include CADD, bioinformatics, cheminformatics, R&D informatics as well as synthetic biology.
Bo Xu is CPO at DP Technology, in charge of Product Design and Management. She has 19 years of experience in Produce Management for CADD, Search and Recommendation, Business-to-Business electronic commerce, wholesales and supply chain systems.
Dongdong Wang is a Senior Researcher at DP Technology. His research focuses on computational simulations and drug design for proteins such as intrinsically disordered proteins (IDPs) and membrane proteins.
Hang Zheng is a Senior Researcher at DP Technology, specializing in the emerging paradigm of AI for Science. His research interests lie in utilizing physics-based models and artificial intelligence algorithms to address challenges in drug discovery, such as virtual screening, free energy calculations, QSAR modeling, and molecular generation.
REFERENCES
Author notes
Maohua Yang and Zonghua Bo contributed equally.


