-
PDF
- Split View
-
Views
-
Cite
Cite
Lun Hu, Xiaojuan Wang, Yu-An Huang, Pengwei Hu, Zhu-Hong You, A survey on computational models for predicting protein–protein interactions, Briefings in Bioinformatics, Volume 22, Issue 5, September 2021, bbab036, https://doi.org/10.1093/bib/bbab036
Close - Share Icon Share
Abstract
Proteins interact with each other to play critical roles in many biological processes in cells. Although promising, laboratory experiments usually suffer from the disadvantages of being time-consuming and labor-intensive. The results obtained are often not robust and considerably uncertain. Due recently to advances in high-throughput technologies, a large amount of proteomics data has been collected and this presents a significant opportunity and also a challenge to develop computational models to predict protein–protein interactions (PPIs) based on these data. In this paper, we present a comprehensive survey of the recent efforts that have been made towards the development of effective computational models for PPI prediction. The survey introduces the algorithms that can be used to learn computational models for predicting PPIs, and it classifies these models into different categories. To understand their relative merits, the paper discusses different validation schemes and metrics to evaluate the prediction performance. Biological databases that are commonly used in different experiments for performance comparison are also described and their use in a series of extensive experiments to compare different prediction models are discussed. Finally, we present some open issues in PPI prediction for future work. We explain how the performance of PPI prediction can be improved if these issues are effectively tackled.
Introduction
As one of the most common molecules found in cells, proteins are essential to regulate a variety of biological processes in living organisms. Instead of acting independently, proteins interact with each other to function well. In this regard, protein–protein interactions (PPIs) are of great significance to provide mechanistic insights into a better understanding for the functional organization of proteome. Moreover, from a practical perspective, the monitoring and study of PPIs is able to provide interesting and significant candidates for both diagnostic and therapeutic targets with medical applicability, thus facilitating the design of novel drugs [5, 68]. Hence, the problem of predicting PPIs is a fundamental research topic in system biology and has thus attracted more attention in recent years. Currently available PPI prediction methods can be generally classified into either laboratory-based or computational-based.
In the field of traditional biology, the collection of PPI data is achieved mainly by laboratory-based methods, such as yeast two-hybrid [28, 48, 79, 93], TAP-tagging [15, 39, 61, 94], protein chips [90, 107], synthetic lethal analysis [91] and correlated mRNA expression profile [32]. However, laboratory-based methods suffer from several disadvantages. First of all, laboratory experiments are normally time-consuming and labor-intensive, thus resulting in an inefficient identification of PPIs. Secondly, the PPI data generated by laboratory-based methods is not complete due to the constraints of laboratory experiments [76, 80]. Lastly, it has been verified that high ratios of false positives and false negatives are frequently observed in the prediction results [33, 46, 84]. To overcome these disadvantages, a variety of computational models have been proposed such that interacting pairs of proteins can be identified systematically.
As an intuitive way to predict PPIs, link prediction models are widely adopted by following the evidence that proteins interact if one of them is similar to the other’s partners [53]. Given a PPI network, this kind of prediction models target to design different topological similarity measures to quantify the possibility of being interacted for pairs of query proteins based on their connections in the network. However, the performances of link prediction models heavily rely on the reliability of PPI networks, which is not always the case at present due to the considerable number of false-positive and false-negative PPIs. Moreover, regarding the scale-free property of PPI networks [45, 56], only a few proteins are densely connected while the connections in the rest of the proteins are much sparser. Obviously, for sparsely connected proteins, the predictive power of link prediction models is not as promising as that for densely connected proteins. Benefited from the development of high-throughput technologies, a vast amount of biological information from genomics, transcriptomics and proteomics fields has been generated. Thus, computational models that additionally make use of biological information of proteins have been proposed to predict PPIs.
In living organisms, interacting proteins tend to possess similar evolutionary histories [62]. It is for this reason that most of computational models are interested in extracting homogeneous features from different sources of biological information, such as protein sequences, structures, genomic information and GO terms. On the other hand, the consideration of biological information is able to minimize the negative influence caused by the existence of false-positive and false-negative PPIs in the network, thus improving the performance of PPI prediction. Once homogeneous features are obtained, feature vectors can thus be constructed for pairs of proteins and then integrated into popular classifiers to accomplish the prediction task. Hence, for computational models making use of PPI networks and biological information of proteins, their performances are determined by two aspects, feature extraction and classifier selection. Moreover, another point worth noting is the imbalance between interacting proteins and non-interacting proteins, as the number of interacting proteins is far less than that of non-interacting proteins in a PPI network. Such imbalance could also yield certain bias against the existence of interaction between pairwise proteins. Nevertheless, the additional consideration of biological information offers an alternative view to address the problem of PPI prediction and can help us to further study the functional homogeneity of proteins.
In this review, we present a comprehensive survey of the recent efforts that have been made towards the development of effective computational models for PPI prediction. To provide a big picture about the development of laboratory-based and computational-based models, publication statistics as of December 2020 is presented in Figure 1, where we record the number of publications that feature the search strings ‘protein–protein interaction’ and ‘protein interaction’ and specific techniques either in the title or as the topic by using the Thomson Reuters Web of Science database. Obviously, the use of computational models appears to have outstripped the laboratory-based methods. At the early stage of computational models, the genomic information of proteins is the main source adopted for PPI prediction. Due to the development of high-throughput techniques, a vast amount of PPI data and biological data have become available and easy-to-access, and thus the publications of computational models for PPI prediction are undergoing a rapid growth since 2005. The ever-increasing PPI data further raises new challenges for large-scale prediction and also provides an opportunity of applying deep learning techniques for solving the problem of PPI prediction as indicated by Figure 1B.
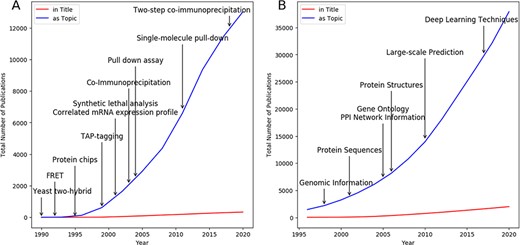
A and B present the publication statistics on laboratory-based and computational-based models, respectively, as of December 2020. Vertical arrows mark important techniques mentioned in this review and their first publication date by year.
Different from previous reviews [25, 92], we provide an up-to-date and systematic review of all the recent prediction models developed in the past decade, current challenges and prospects of future work. Moreover, in addition to the common categories used to group computational models for PPI prediction, this survey puts emphasis on discussing the new categories of deep learning-based and large-scale models. The issues related to experimental data preparation, validation schemes, evaluation metrics and online tools are also involved to present a comprehensive survey about PPI prediction. The rest of this survey is organized as follows. In Section 2, biological databases that are widely used to predict PPIs are introduced. In Section 3, representative works in two kinds of computational models mentioned above are presented with an in-depth discussion about their advantages and disadvantages. After that, several evaluation metrics are explained in Section 4, following which we introduce available online tools to predict PPIs in Section 5. Finally, challenges and future work are discussed in Section 6.
PPI networks and related biological information
Due to the development of high-throughput technologies, a large amount of PPI data has been extracted and formatted in a easy-to-access manner. Several databases are established to make these PPI data available for academic researchers. Regarding the classification of PPI prediction models, it is possible to classify them into two major categories: one is network-based and the other is the integration of PPI data and the biological information of proteins. In particular, for network-based computational models, their prediction tasks are mainly achieved by solely taking into account of PPI networks, where proteins are denoted as nodes and their interactions are the edges. In addition to the PPI data, integrated computational models make use of different biological information of proteins, including but not limited to protein sequences, protein structures, genomic information and gene ontology (GO), for an improved accuracy of PPI prediction. Such biological information of proteins is normally processed to construct feature vectors of PPIs such that conventional classification techniques can be applied. In the remaining part of this section, we describe the PPI data and related biological information of proteins in more details and also introduce the related databases where these data are readily made available. For the sake of clarity, a brief description of related biological databases is given in Table 1.
| . | Databases . | Description . | URL . | Last Update . | References . |
|---|---|---|---|---|---|
| PPI networks | BIND | PPIs collected from the species of humans, fruit flies, yeast, nematodes, etc. | http://download.baderlab.org/BINDTranslation/ | 2005 | [4] |
| DIP | Experimentally curated PPI database including biological information of proteins, PPIs and experimental techniques for detecting interactions | http://dip.doe-mbi.ucla.edu/dip/Main.cgi | 2020 | [97] | |
| MINT | Experimentally curated PPI database that covers about 117001 PPIs from 607 different species | https://mint.bio.uniroma2.it/ | 2012 | [59] | |
| Biogrid | Composed of proteins, and their genetic and chemical interactions, currently has more than 1.5 million interactions obtained from high-throughput experiments | http://www.thebiogrid.org | 2020 | [16] | |
| HPRD | The largest human PPI database including protein annotation, PPIs, post-transcriptional modification, subcellular location and other information | http://www.hprd.org | 2010 | [51] | |
| IntAct | Approximately 275000 curated binary interaction evidences from more than 5000 publications | http://www.ebi.ac.uk/intact | 2014 | [70] | |
| STRING | Functional associations between protein pairs and covers 2031 species, 9643763 proteins and a total of 1380838440 PPIs | https://string-db.org/STRING | 2019 | [87] | |
| Protein sequences | UniProt | A collection of protein sequences and their annotations with three major components including UniProtKB, UniParc and UniRef | http://www.uniprot.org | 2020 | [20] |
| PIR | Protein sequences and high-quality annotations by integrating more than 90 biological databases | http://pir.georgetown.edu | 2020 | [7] | |
| SWISS-PROT | A database composed of protein sequences and detailed annotations and it has been merged into the UniProt and maintained by EBI now | http://www.expasy.ch/sport | 2020 | [13] | |
| NRL3D | Primary structures of proteins with known three-dimensional structures | http://www.ncifcrf.gov/NRL-3D | 2020 | [29] | |
| TrEMBL | Computer-annotated protein sequences complementary to SWISS-PORT | http://www.expasy.ch/ | 2020 | [13] | |
| Higher-level structures | PDB | Experimentally determined 3D structures of proteins , nucleic acids and sugar | http://www.rcsb.org/ | 2020 | [96] |
| SCOP | Proteins and their classifications with known structures, and also describes the functions and evolutionary relationships between them in details | http://scop.mrc-lmb.cam.ac.uk/scop | 2020 | [2] | |
| Genomic information | MIPS | Homology data of mammalian proteins, mainly including human, rat, mouse and other species | http://mips.gsf.de/proj/ppi/ | 2005 | [71] |
| CGD | Phylogeny and gene similarity information for proteins. | http://www.candidagenome.org/ | 2014 | [9] | |
| Gene ontology | GO Database | The world’s largest source of information on the functions of genes ranging from the molecular to the organism level | http://www.geneontology.org | 2020 | [19] |
| QuickGO | A fast web-based browser of the GO and GO annotation data | http://www.ebi.ac.uk/QuickGO | 2020 | [10] |
| . | Databases . | Description . | URL . | Last Update . | References . |
|---|---|---|---|---|---|
| PPI networks | BIND | PPIs collected from the species of humans, fruit flies, yeast, nematodes, etc. | http://download.baderlab.org/BINDTranslation/ | 2005 | [4] |
| DIP | Experimentally curated PPI database including biological information of proteins, PPIs and experimental techniques for detecting interactions | http://dip.doe-mbi.ucla.edu/dip/Main.cgi | 2020 | [97] | |
| MINT | Experimentally curated PPI database that covers about 117001 PPIs from 607 different species | https://mint.bio.uniroma2.it/ | 2012 | [59] | |
| Biogrid | Composed of proteins, and their genetic and chemical interactions, currently has more than 1.5 million interactions obtained from high-throughput experiments | http://www.thebiogrid.org | 2020 | [16] | |
| HPRD | The largest human PPI database including protein annotation, PPIs, post-transcriptional modification, subcellular location and other information | http://www.hprd.org | 2010 | [51] | |
| IntAct | Approximately 275000 curated binary interaction evidences from more than 5000 publications | http://www.ebi.ac.uk/intact | 2014 | [70] | |
| STRING | Functional associations between protein pairs and covers 2031 species, 9643763 proteins and a total of 1380838440 PPIs | https://string-db.org/STRING | 2019 | [87] | |
| Protein sequences | UniProt | A collection of protein sequences and their annotations with three major components including UniProtKB, UniParc and UniRef | http://www.uniprot.org | 2020 | [20] |
| PIR | Protein sequences and high-quality annotations by integrating more than 90 biological databases | http://pir.georgetown.edu | 2020 | [7] | |
| SWISS-PROT | A database composed of protein sequences and detailed annotations and it has been merged into the UniProt and maintained by EBI now | http://www.expasy.ch/sport | 2020 | [13] | |
| NRL3D | Primary structures of proteins with known three-dimensional structures | http://www.ncifcrf.gov/NRL-3D | 2020 | [29] | |
| TrEMBL | Computer-annotated protein sequences complementary to SWISS-PORT | http://www.expasy.ch/ | 2020 | [13] | |
| Higher-level structures | PDB | Experimentally determined 3D structures of proteins , nucleic acids and sugar | http://www.rcsb.org/ | 2020 | [96] |
| SCOP | Proteins and their classifications with known structures, and also describes the functions and evolutionary relationships between them in details | http://scop.mrc-lmb.cam.ac.uk/scop | 2020 | [2] | |
| Genomic information | MIPS | Homology data of mammalian proteins, mainly including human, rat, mouse and other species | http://mips.gsf.de/proj/ppi/ | 2005 | [71] |
| CGD | Phylogeny and gene similarity information for proteins. | http://www.candidagenome.org/ | 2014 | [9] | |
| Gene ontology | GO Database | The world’s largest source of information on the functions of genes ranging from the molecular to the organism level | http://www.geneontology.org | 2020 | [19] |
| QuickGO | A fast web-based browser of the GO and GO annotation data | http://www.ebi.ac.uk/QuickGO | 2020 | [10] |
| . | Databases . | Description . | URL . | Last Update . | References . |
|---|---|---|---|---|---|
| PPI networks | BIND | PPIs collected from the species of humans, fruit flies, yeast, nematodes, etc. | http://download.baderlab.org/BINDTranslation/ | 2005 | [4] |
| DIP | Experimentally curated PPI database including biological information of proteins, PPIs and experimental techniques for detecting interactions | http://dip.doe-mbi.ucla.edu/dip/Main.cgi | 2020 | [97] | |
| MINT | Experimentally curated PPI database that covers about 117001 PPIs from 607 different species | https://mint.bio.uniroma2.it/ | 2012 | [59] | |
| Biogrid | Composed of proteins, and their genetic and chemical interactions, currently has more than 1.5 million interactions obtained from high-throughput experiments | http://www.thebiogrid.org | 2020 | [16] | |
| HPRD | The largest human PPI database including protein annotation, PPIs, post-transcriptional modification, subcellular location and other information | http://www.hprd.org | 2010 | [51] | |
| IntAct | Approximately 275000 curated binary interaction evidences from more than 5000 publications | http://www.ebi.ac.uk/intact | 2014 | [70] | |
| STRING | Functional associations between protein pairs and covers 2031 species, 9643763 proteins and a total of 1380838440 PPIs | https://string-db.org/STRING | 2019 | [87] | |
| Protein sequences | UniProt | A collection of protein sequences and their annotations with three major components including UniProtKB, UniParc and UniRef | http://www.uniprot.org | 2020 | [20] |
| PIR | Protein sequences and high-quality annotations by integrating more than 90 biological databases | http://pir.georgetown.edu | 2020 | [7] | |
| SWISS-PROT | A database composed of protein sequences and detailed annotations and it has been merged into the UniProt and maintained by EBI now | http://www.expasy.ch/sport | 2020 | [13] | |
| NRL3D | Primary structures of proteins with known three-dimensional structures | http://www.ncifcrf.gov/NRL-3D | 2020 | [29] | |
| TrEMBL | Computer-annotated protein sequences complementary to SWISS-PORT | http://www.expasy.ch/ | 2020 | [13] | |
| Higher-level structures | PDB | Experimentally determined 3D structures of proteins , nucleic acids and sugar | http://www.rcsb.org/ | 2020 | [96] |
| SCOP | Proteins and their classifications with known structures, and also describes the functions and evolutionary relationships between them in details | http://scop.mrc-lmb.cam.ac.uk/scop | 2020 | [2] | |
| Genomic information | MIPS | Homology data of mammalian proteins, mainly including human, rat, mouse and other species | http://mips.gsf.de/proj/ppi/ | 2005 | [71] |
| CGD | Phylogeny and gene similarity information for proteins. | http://www.candidagenome.org/ | 2014 | [9] | |
| Gene ontology | GO Database | The world’s largest source of information on the functions of genes ranging from the molecular to the organism level | http://www.geneontology.org | 2020 | [19] |
| QuickGO | A fast web-based browser of the GO and GO annotation data | http://www.ebi.ac.uk/QuickGO | 2020 | [10] |
| . | Databases . | Description . | URL . | Last Update . | References . |
|---|---|---|---|---|---|
| PPI networks | BIND | PPIs collected from the species of humans, fruit flies, yeast, nematodes, etc. | http://download.baderlab.org/BINDTranslation/ | 2005 | [4] |
| DIP | Experimentally curated PPI database including biological information of proteins, PPIs and experimental techniques for detecting interactions | http://dip.doe-mbi.ucla.edu/dip/Main.cgi | 2020 | [97] | |
| MINT | Experimentally curated PPI database that covers about 117001 PPIs from 607 different species | https://mint.bio.uniroma2.it/ | 2012 | [59] | |
| Biogrid | Composed of proteins, and their genetic and chemical interactions, currently has more than 1.5 million interactions obtained from high-throughput experiments | http://www.thebiogrid.org | 2020 | [16] | |
| HPRD | The largest human PPI database including protein annotation, PPIs, post-transcriptional modification, subcellular location and other information | http://www.hprd.org | 2010 | [51] | |
| IntAct | Approximately 275000 curated binary interaction evidences from more than 5000 publications | http://www.ebi.ac.uk/intact | 2014 | [70] | |
| STRING | Functional associations between protein pairs and covers 2031 species, 9643763 proteins and a total of 1380838440 PPIs | https://string-db.org/STRING | 2019 | [87] | |
| Protein sequences | UniProt | A collection of protein sequences and their annotations with three major components including UniProtKB, UniParc and UniRef | http://www.uniprot.org | 2020 | [20] |
| PIR | Protein sequences and high-quality annotations by integrating more than 90 biological databases | http://pir.georgetown.edu | 2020 | [7] | |
| SWISS-PROT | A database composed of protein sequences and detailed annotations and it has been merged into the UniProt and maintained by EBI now | http://www.expasy.ch/sport | 2020 | [13] | |
| NRL3D | Primary structures of proteins with known three-dimensional structures | http://www.ncifcrf.gov/NRL-3D | 2020 | [29] | |
| TrEMBL | Computer-annotated protein sequences complementary to SWISS-PORT | http://www.expasy.ch/ | 2020 | [13] | |
| Higher-level structures | PDB | Experimentally determined 3D structures of proteins , nucleic acids and sugar | http://www.rcsb.org/ | 2020 | [96] |
| SCOP | Proteins and their classifications with known structures, and also describes the functions and evolutionary relationships between them in details | http://scop.mrc-lmb.cam.ac.uk/scop | 2020 | [2] | |
| Genomic information | MIPS | Homology data of mammalian proteins, mainly including human, rat, mouse and other species | http://mips.gsf.de/proj/ppi/ | 2005 | [71] |
| CGD | Phylogeny and gene similarity information for proteins. | http://www.candidagenome.org/ | 2014 | [9] | |
| Gene ontology | GO Database | The world’s largest source of information on the functions of genes ranging from the molecular to the organism level | http://www.geneontology.org | 2020 | [19] |
| QuickGO | A fast web-based browser of the GO and GO annotation data | http://www.ebi.ac.uk/QuickGO | 2020 | [10] |
PPI networks
PPI networks are constructed by PPI data, and they are capable of revealing the structural characteristics of proteins. As has been pointed out by Newman, two proteins are more likely to interact with each other if they have more common interacting partners. In the context of PPI networks, such viewpoint can be intuitively interpreted by the number of common adjacent nodes, thus providing certain evidence to predict the likelihood of being interacting. Currently, there are several known databases that provide PPIs to construct networks, such as BIND [4], DIP [97], MINT [59], BioGRID [16], HPRD [51], IntAct [70] and STRING [87]. Among them, the BIND database is rarely used at present, as it has not been updated and maintained after 2005. Since PPIs provided by these databases are verified through experiments, they are eligible to be used as the ground truth data to evaluate the prediction results. Moreover, among these databases, STRING, IntAct and MINT additionally provide the scores of PPIs obtained from different sources to indicate their reliability. Hence, a more reliable PPI network can thus be constructed by disregarding PPIs with smaller scores.
Biological information of proteins
The biological information of proteins reveals the properties of proteins from a biological perspective and it is for this reason that such information is commonly used by integrated computational models to perform their prediction tasks. At present, the biological information of proteins include protein sequences, protein structures, genomic information and GO.
Protein sequences
As the primary structures of proteins, protein sequences are composed of amino acids, and each protein has unique sequence information that plays a significant role in determining high-level structures and biological characteristics. It has been pointed out by [3] that the knowledge extracted from protein sequences could be sufficient to estimate the interacting likelihood between pairwise proteins. Thus, a variety of sequential features, such as hydrophobicity, evolutionary profiles and amino acid compositions, are proposed to indicate the similarity between the sequences of two proteins, thus improving the prediction accuracy of PPIs. The information of protein sequences can be obtained from UniProt [20], PIR [7], SWISS-PROT [13], NRL3D [29] and TrEMBL [13] databases.
Higher-level structures
In addition to the primary structures of proteins, there are also another three higher-level structures including secondary, tertiary and quarternary structures. In particular, the secondary structures of proteins are alpha helix and beta sheet. When compared with secondary structures, tertiary and quarternary structures are 3D. Since these higher-level structures are determined by the primary structures, it is also possible for us to make use of them for the purpose of predicting PPIs. However, when compared with protein sequences, higher-level structure s information of proteins has a limited impact to the prediction of PPIs, as there is a considerably large difference between the number of proteins with known sequences and those with experimentally verified structures. Regarding the secondary structures, existing prediction algorithms develop different computational models to identify specific spatial structures that frequently appear on protein-protein binding motif regions. But when predicting PPIs based on 3D structures, we intend to identify the best compatibility of interacting regions in 3D structures and proteins are likely to be interacting if they are compatible. Higher-level protein structure s information can be obtained from PDB [96] and SCOP [2].
Genomic information
Due to the development of whole-genome sequencing technology, genomic-based computational models perform their prediction tasks based on the observation that interactions are existed between proteins encoded by conserved gene pairs. Obviously, the conservation knowledge of genes, such as gene fusion, gene order and phylogenetic profile, are relevant to the evolution of the genome across different species and hints at how gene-encoding proteins interact with each other. For example, gene fusion is adopted to predict the interacting proteins by following the observation that a part of single-domain protein in one organism is able to be fused into a multiple-domain protein in some other organisms; computational models using the phylogenetic profile are developed based on the hypothesis that the respective phylogenetic trees of interacting proteins are more similar due to the co-evolution. Genomic information can be obtained in MIPS [71] and The Candida Genome Database (CGD) [9].
Gene ontology
GO is a well-established universal vocabulary that describes the functions and connections of genes and their products, and it is composed of three categories including cellular components, molecular functions and biological processes. In particular, cellular components are the cellular structural positions where gene products perform functions, such as mitochondria and ribosomes. Since proteins with similar functions are more likely to interact with each other for functioning well, the semantic similarity in GO between protein pairs can be a promising indicator for the functional similarity of proteins, thus revealing the possibility of being interacting. The GO data can be downloaded from the GO database [19] and QuickGO [10].
Computational models of PPI prediction
As a complementary approach to predict PPIs, computational models have been undergoing a rapid development due to the wide availability of experimentally curated PPI data over the past few years. As mentioned before, the main idea behind these models is to make use of biological knowledge that is verified to be able to determine previously known interactions, thus providing valuable insights into designing new experiments for confirming PPIs from proteins of interest. As presented in Figure 2, existing computational models of PPI prediction can be classified into two major categories, one is network-based models that solely rest on PPI network data and the other is integrated models that consider the biological information of proteins extracted from different sources. Moreover, certain attempts have been made recently by using deep learning algorithms for PPI prediction and they are also introduced in this section. Specific computational models that fall within these categories are listed in Table 2. Moreover, the advantages and disadvantages of significant models are briefly described in Table 3.
| Category . | Representative model . | Description . | Reference . |
|---|---|---|---|
| Network-based models | Zeng et al. | Zeng et al. design an integrated local similarity index by comining common neighbors and preferential attachment. | [103] |
| SFCN | SFCN accurately identifies all the future common neighbors in addition to those in the PPI network. | [57] | |
| Sim | Sim predicts PPIs from the perspectives of complementary protein interfaces and gene duplication. | [18] | |
| L3 | L3 follows the observation that proteins tend to interact not if they are similar to each other, but if one of them is similar to the other’s partners. | [53] | |
| Wang et al. | Wang et al. design a novel stochastic block model to predict PPIs based on the latent structural features of proteins in the PPI network. | [95] | |
| SpectralLink | SpectralLink captures the topological affinity of proteins using a multi-way spectral clustering method. | [86] | |
| RWS | RWS makes use of a random walk-based procedure to compute the higher-order topological similarities shared by two proteins. | [54] | |
| IRAP | IRAP assesses the reliability of protein interactions by considering the alternative path of PPIs in the underlying PPI network. | [17] | |
| You et al. | You et al. employ a manifold embedding technique purely based on topological information of PPI network. | [99] | |
| Huang et al. | Huang et al. incorporate evolutionary information into geometric space to improve the accuracy of PPI prediction. | [47] | |
| Xiao et al. | Xiao et al. combine graph convolutional network and PageRank method to predict PPIs. | [98] | |
| Sequence-based models | Bock and Gough | Bock and Gough integrate protein primary structures and associated physicochemical properties with SVM for PPI prediction. | [12] |
| PPIevo | PPIevo develops a novel evolutionary-based feature extraction algorithm to compose feature vectors of proteins. | [102] | |
| VLASPD | VLASPD takes variable-length segments of protein sequences into account for PPI prediction. | [41] | |
| CD | CD reasons that protein pairs with similar substitution rates are likely to interact with each other. | [40] | |
| CoFex | CoFex predicts PPIs based on protein sequence and extracts features from both sequences in a protein pair instead of a single protein. | [42] | |
| Structure-based models | PrePPI | PrePPI applies Bayesian statistics with the information of structure and non-structure interactions to predict PPIs. | [104] |
| MEGADOCK | MEGDOCK is a docking-based model to predict PPIs using decoy similarity. | [69] | |
| InterPred | InterPred combines massive structural comparisons and molecular docking with a random forest classifier. | [66] | |
| UniAlign | UniAlign follows the idea that proteins with similar interface architecture share similar interaction partners. | [106] | |
| Planas et al. | The motivation of Planas et al. is that the balance between interacting and non-interacting structural features determines if a protein pairs interact or not. | [77] | |
| Genomic-based models | Enright et al. | Enright et al. identify gene-fusion events based on sequence comparison for PPI prediction. | [26] |
| Dandekar et al. | Dankekar et al. recognize that proteins encoded by conserved gene pairs appear to interact physically. | [22] | |
| Pazos et al. | Pazos et al. predict PPIs based on the comparison of the evolutionary distances between the sequences of associated protein families. | [73] | |
| Pellegriniet et al. | Pellegrinet et al. develop a phylogenetic profiling method for PPI prediction. | [75] | |
| GO-based models | Bandyopadhyay et al. | Bandyopadhyay et al. use a novel set of features to represent a protein pair based on their annotated GO terms. | [6] |
| TCSS | TCSS predict s PPIs based on the similarity of GO terms and it also considers unequal depth of biological knowledge representation in different branches of the GO graph. | [49] | |
| Deep learning-based models | SAE | SAE combines stacked autoencoder with protein sequence to predict PPIs | [85] |
| DPPI | DPPI construct s a deep learning framework using sequence information alone. | [34] | |
| DNN-PPI | DNN-PPI exploits the features learned automatically only from protein primary sequence to predict PPI. | [55] | |
| Large-scale models | LDA-RF | LDA-RF obtains low dimensional latent topic features from protein sequences and then adopts the scalable random forest model for prediction. | [72] |
| You et al. | You et al. adopt a parallel SVM model to predict PPIs in a distributed manner. | [100] | |
| pVLASPD | pVLASPD integrates VLASPD with the MapReduce framework for large-scale PPI prediction. | [44] | |
| Ji et al. | Ji et al. makes use of a distributed implementation of random forest with protein feature vectors. | [50] |
| Category . | Representative model . | Description . | Reference . |
|---|---|---|---|
| Network-based models | Zeng et al. | Zeng et al. design an integrated local similarity index by comining common neighbors and preferential attachment. | [103] |
| SFCN | SFCN accurately identifies all the future common neighbors in addition to those in the PPI network. | [57] | |
| Sim | Sim predicts PPIs from the perspectives of complementary protein interfaces and gene duplication. | [18] | |
| L3 | L3 follows the observation that proteins tend to interact not if they are similar to each other, but if one of them is similar to the other’s partners. | [53] | |
| Wang et al. | Wang et al. design a novel stochastic block model to predict PPIs based on the latent structural features of proteins in the PPI network. | [95] | |
| SpectralLink | SpectralLink captures the topological affinity of proteins using a multi-way spectral clustering method. | [86] | |
| RWS | RWS makes use of a random walk-based procedure to compute the higher-order topological similarities shared by two proteins. | [54] | |
| IRAP | IRAP assesses the reliability of protein interactions by considering the alternative path of PPIs in the underlying PPI network. | [17] | |
| You et al. | You et al. employ a manifold embedding technique purely based on topological information of PPI network. | [99] | |
| Huang et al. | Huang et al. incorporate evolutionary information into geometric space to improve the accuracy of PPI prediction. | [47] | |
| Xiao et al. | Xiao et al. combine graph convolutional network and PageRank method to predict PPIs. | [98] | |
| Sequence-based models | Bock and Gough | Bock and Gough integrate protein primary structures and associated physicochemical properties with SVM for PPI prediction. | [12] |
| PPIevo | PPIevo develops a novel evolutionary-based feature extraction algorithm to compose feature vectors of proteins. | [102] | |
| VLASPD | VLASPD takes variable-length segments of protein sequences into account for PPI prediction. | [41] | |
| CD | CD reasons that protein pairs with similar substitution rates are likely to interact with each other. | [40] | |
| CoFex | CoFex predicts PPIs based on protein sequence and extracts features from both sequences in a protein pair instead of a single protein. | [42] | |
| Structure-based models | PrePPI | PrePPI applies Bayesian statistics with the information of structure and non-structure interactions to predict PPIs. | [104] |
| MEGADOCK | MEGDOCK is a docking-based model to predict PPIs using decoy similarity. | [69] | |
| InterPred | InterPred combines massive structural comparisons and molecular docking with a random forest classifier. | [66] | |
| UniAlign | UniAlign follows the idea that proteins with similar interface architecture share similar interaction partners. | [106] | |
| Planas et al. | The motivation of Planas et al. is that the balance between interacting and non-interacting structural features determines if a protein pairs interact or not. | [77] | |
| Genomic-based models | Enright et al. | Enright et al. identify gene-fusion events based on sequence comparison for PPI prediction. | [26] |
| Dandekar et al. | Dankekar et al. recognize that proteins encoded by conserved gene pairs appear to interact physically. | [22] | |
| Pazos et al. | Pazos et al. predict PPIs based on the comparison of the evolutionary distances between the sequences of associated protein families. | [73] | |
| Pellegriniet et al. | Pellegrinet et al. develop a phylogenetic profiling method for PPI prediction. | [75] | |
| GO-based models | Bandyopadhyay et al. | Bandyopadhyay et al. use a novel set of features to represent a protein pair based on their annotated GO terms. | [6] |
| TCSS | TCSS predict s PPIs based on the similarity of GO terms and it also considers unequal depth of biological knowledge representation in different branches of the GO graph. | [49] | |
| Deep learning-based models | SAE | SAE combines stacked autoencoder with protein sequence to predict PPIs | [85] |
| DPPI | DPPI construct s a deep learning framework using sequence information alone. | [34] | |
| DNN-PPI | DNN-PPI exploits the features learned automatically only from protein primary sequence to predict PPI. | [55] | |
| Large-scale models | LDA-RF | LDA-RF obtains low dimensional latent topic features from protein sequences and then adopts the scalable random forest model for prediction. | [72] |
| You et al. | You et al. adopt a parallel SVM model to predict PPIs in a distributed manner. | [100] | |
| pVLASPD | pVLASPD integrates VLASPD with the MapReduce framework for large-scale PPI prediction. | [44] | |
| Ji et al. | Ji et al. makes use of a distributed implementation of random forest with protein feature vectors. | [50] |
| Category . | Representative model . | Description . | Reference . |
|---|---|---|---|
| Network-based models | Zeng et al. | Zeng et al. design an integrated local similarity index by comining common neighbors and preferential attachment. | [103] |
| SFCN | SFCN accurately identifies all the future common neighbors in addition to those in the PPI network. | [57] | |
| Sim | Sim predicts PPIs from the perspectives of complementary protein interfaces and gene duplication. | [18] | |
| L3 | L3 follows the observation that proteins tend to interact not if they are similar to each other, but if one of them is similar to the other’s partners. | [53] | |
| Wang et al. | Wang et al. design a novel stochastic block model to predict PPIs based on the latent structural features of proteins in the PPI network. | [95] | |
| SpectralLink | SpectralLink captures the topological affinity of proteins using a multi-way spectral clustering method. | [86] | |
| RWS | RWS makes use of a random walk-based procedure to compute the higher-order topological similarities shared by two proteins. | [54] | |
| IRAP | IRAP assesses the reliability of protein interactions by considering the alternative path of PPIs in the underlying PPI network. | [17] | |
| You et al. | You et al. employ a manifold embedding technique purely based on topological information of PPI network. | [99] | |
| Huang et al. | Huang et al. incorporate evolutionary information into geometric space to improve the accuracy of PPI prediction. | [47] | |
| Xiao et al. | Xiao et al. combine graph convolutional network and PageRank method to predict PPIs. | [98] | |
| Sequence-based models | Bock and Gough | Bock and Gough integrate protein primary structures and associated physicochemical properties with SVM for PPI prediction. | [12] |
| PPIevo | PPIevo develops a novel evolutionary-based feature extraction algorithm to compose feature vectors of proteins. | [102] | |
| VLASPD | VLASPD takes variable-length segments of protein sequences into account for PPI prediction. | [41] | |
| CD | CD reasons that protein pairs with similar substitution rates are likely to interact with each other. | [40] | |
| CoFex | CoFex predicts PPIs based on protein sequence and extracts features from both sequences in a protein pair instead of a single protein. | [42] | |
| Structure-based models | PrePPI | PrePPI applies Bayesian statistics with the information of structure and non-structure interactions to predict PPIs. | [104] |
| MEGADOCK | MEGDOCK is a docking-based model to predict PPIs using decoy similarity. | [69] | |
| InterPred | InterPred combines massive structural comparisons and molecular docking with a random forest classifier. | [66] | |
| UniAlign | UniAlign follows the idea that proteins with similar interface architecture share similar interaction partners. | [106] | |
| Planas et al. | The motivation of Planas et al. is that the balance between interacting and non-interacting structural features determines if a protein pairs interact or not. | [77] | |
| Genomic-based models | Enright et al. | Enright et al. identify gene-fusion events based on sequence comparison for PPI prediction. | [26] |
| Dandekar et al. | Dankekar et al. recognize that proteins encoded by conserved gene pairs appear to interact physically. | [22] | |
| Pazos et al. | Pazos et al. predict PPIs based on the comparison of the evolutionary distances between the sequences of associated protein families. | [73] | |
| Pellegriniet et al. | Pellegrinet et al. develop a phylogenetic profiling method for PPI prediction. | [75] | |
| GO-based models | Bandyopadhyay et al. | Bandyopadhyay et al. use a novel set of features to represent a protein pair based on their annotated GO terms. | [6] |
| TCSS | TCSS predict s PPIs based on the similarity of GO terms and it also considers unequal depth of biological knowledge representation in different branches of the GO graph. | [49] | |
| Deep learning-based models | SAE | SAE combines stacked autoencoder with protein sequence to predict PPIs | [85] |
| DPPI | DPPI construct s a deep learning framework using sequence information alone. | [34] | |
| DNN-PPI | DNN-PPI exploits the features learned automatically only from protein primary sequence to predict PPI. | [55] | |
| Large-scale models | LDA-RF | LDA-RF obtains low dimensional latent topic features from protein sequences and then adopts the scalable random forest model for prediction. | [72] |
| You et al. | You et al. adopt a parallel SVM model to predict PPIs in a distributed manner. | [100] | |
| pVLASPD | pVLASPD integrates VLASPD with the MapReduce framework for large-scale PPI prediction. | [44] | |
| Ji et al. | Ji et al. makes use of a distributed implementation of random forest with protein feature vectors. | [50] |
| Category . | Representative model . | Description . | Reference . |
|---|---|---|---|
| Network-based models | Zeng et al. | Zeng et al. design an integrated local similarity index by comining common neighbors and preferential attachment. | [103] |
| SFCN | SFCN accurately identifies all the future common neighbors in addition to those in the PPI network. | [57] | |
| Sim | Sim predicts PPIs from the perspectives of complementary protein interfaces and gene duplication. | [18] | |
| L3 | L3 follows the observation that proteins tend to interact not if they are similar to each other, but if one of them is similar to the other’s partners. | [53] | |
| Wang et al. | Wang et al. design a novel stochastic block model to predict PPIs based on the latent structural features of proteins in the PPI network. | [95] | |
| SpectralLink | SpectralLink captures the topological affinity of proteins using a multi-way spectral clustering method. | [86] | |
| RWS | RWS makes use of a random walk-based procedure to compute the higher-order topological similarities shared by two proteins. | [54] | |
| IRAP | IRAP assesses the reliability of protein interactions by considering the alternative path of PPIs in the underlying PPI network. | [17] | |
| You et al. | You et al. employ a manifold embedding technique purely based on topological information of PPI network. | [99] | |
| Huang et al. | Huang et al. incorporate evolutionary information into geometric space to improve the accuracy of PPI prediction. | [47] | |
| Xiao et al. | Xiao et al. combine graph convolutional network and PageRank method to predict PPIs. | [98] | |
| Sequence-based models | Bock and Gough | Bock and Gough integrate protein primary structures and associated physicochemical properties with SVM for PPI prediction. | [12] |
| PPIevo | PPIevo develops a novel evolutionary-based feature extraction algorithm to compose feature vectors of proteins. | [102] | |
| VLASPD | VLASPD takes variable-length segments of protein sequences into account for PPI prediction. | [41] | |
| CD | CD reasons that protein pairs with similar substitution rates are likely to interact with each other. | [40] | |
| CoFex | CoFex predicts PPIs based on protein sequence and extracts features from both sequences in a protein pair instead of a single protein. | [42] | |
| Structure-based models | PrePPI | PrePPI applies Bayesian statistics with the information of structure and non-structure interactions to predict PPIs. | [104] |
| MEGADOCK | MEGDOCK is a docking-based model to predict PPIs using decoy similarity. | [69] | |
| InterPred | InterPred combines massive structural comparisons and molecular docking with a random forest classifier. | [66] | |
| UniAlign | UniAlign follows the idea that proteins with similar interface architecture share similar interaction partners. | [106] | |
| Planas et al. | The motivation of Planas et al. is that the balance between interacting and non-interacting structural features determines if a protein pairs interact or not. | [77] | |
| Genomic-based models | Enright et al. | Enright et al. identify gene-fusion events based on sequence comparison for PPI prediction. | [26] |
| Dandekar et al. | Dankekar et al. recognize that proteins encoded by conserved gene pairs appear to interact physically. | [22] | |
| Pazos et al. | Pazos et al. predict PPIs based on the comparison of the evolutionary distances between the sequences of associated protein families. | [73] | |
| Pellegriniet et al. | Pellegrinet et al. develop a phylogenetic profiling method for PPI prediction. | [75] | |
| GO-based models | Bandyopadhyay et al. | Bandyopadhyay et al. use a novel set of features to represent a protein pair based on their annotated GO terms. | [6] |
| TCSS | TCSS predict s PPIs based on the similarity of GO terms and it also considers unequal depth of biological knowledge representation in different branches of the GO graph. | [49] | |
| Deep learning-based models | SAE | SAE combines stacked autoencoder with protein sequence to predict PPIs | [85] |
| DPPI | DPPI construct s a deep learning framework using sequence information alone. | [34] | |
| DNN-PPI | DNN-PPI exploits the features learned automatically only from protein primary sequence to predict PPI. | [55] | |
| Large-scale models | LDA-RF | LDA-RF obtains low dimensional latent topic features from protein sequences and then adopts the scalable random forest model for prediction. | [72] |
| You et al. | You et al. adopt a parallel SVM model to predict PPIs in a distributed manner. | [100] | |
| pVLASPD | pVLASPD integrates VLASPD with the MapReduce framework for large-scale PPI prediction. | [44] | |
| Ji et al. | Ji et al. makes use of a distributed implementation of random forest with protein feature vectors. | [50] |
| Category . | Representative model . | Advantages . | Disadvantages . |
|---|---|---|---|
| Network-based models | L3 [53] | L3 argues that proteins interact if one of them is similar to the other’s partners instead of being similar to each other. | L3 is incapable of predicting PPIs between proteins that are distantly located away from each other without any common neighbors. |
| SpectralLink [86] | SpectralLink considers the global network structures of PPI network. | Many complex structural properties in real networks are simply ignored. | |
| RWS [54] | RWS can effectively overcome the high level of noise, sparseness and highly skewed degree distribution of PPI networks. | The robustness of RWS could be decreased by the simple cut-off-based strategy used to maintain the number of edges in |$G$|. | |
| You et al. [99] | This model can work on a sparse PPI network with only topological information. | The number of dimensions used by manifold embedding may influence the prediction accuracy. | |
| Huang et al. [47] | This model integrates evolutionary information into |$G$| and obtains a better performance. | This model heavily rests on the completeness of |$G$|, which is difficult to be satisfied in practical PPI networks. | |
| Sequence-based models | Bock and Gough [12] | This work provides a theoretical and systematic analysis on how to perform the PPI prediction explicitly based on primary structures of proteins. | The generalization to other species, such as bacteria or archea, is problematic. |
| VLASPD [41] | VLASPD takes variable-length segments of protein sequences into account for PPI prediction. | The vast amount of variable-length patterns may confuse the classifiers to accurately predict PPIs. | |
| CD [40] | The substitution rate estimation proposed by the CD model is more informative. | It fails to infer specific features of PPIs, such as the interacting residues in the interfaces. | |
| Structure-based models | PrePPI [104] | PrePPI can identify unexpected PPIs of significant biological interest by using three-dimensional structural information. | PrePPI is incapable of predicting PPIs for proteins whose 3D structures are not experimentally determined. |
| InterPred [66] | The consideration of close and remote structural interaction templates improves the prediction accuracy. | The steps of structural template searching and docking are time-consuming. | |
| Genomic-based models | Enright et al. [26] | This model makes use of gene fusion events to predict PPIs. | Interactions where fusion events are not covered through the analysis of genomic sequencing are not able to be predicted. |
| Dandekar et al. [22] | Conserved gene pairs are used to predict PPIs. | This model fails to predict PPIs composed of proteins whose conservation of gene-order is missed. | |
| Pellegriniet et al. [75] | This model explores the possibility of using a phylogenetic profiling method for PPI prediction. | It is inefficient for PPI prediction when the number of profile patterns grows exponentially. | |
| GO-based models | Bandyopadhyay et al. [6] | This model demonstrates that GO-based features have a better performance than sequence-based spectrum count features. | The inherent directed acyclic graph structure of GO is ignored. |
| TCSS [49] | TCSS considers unequal depth of biological knowledge representation in different GO categories. | The proposed similarity measure may be overestimated in some scenarios. | |
| Deep learning-based models | Sun et al. [85] | This model is able to learn the hidden interaction features due to the powerful generalization capacity of deep learning. | The unbalance situation between interacting and non-interacting proteins could possibly degrade the accuracy. |
| DNN-PPI [55] | DNN-PPI does not need to extract features from protein sequences. | The number of layers for convolution neural network has to be determined carefully. | |
| Large-scale models | LDA-RF [6] | LDA-RF converts the hidden internal structures in low dimensional latent semantic space for large-scale PPI prediction. | The inference procedure of latent dirichlet allocation is not scalable. |
| You et al. [100] | A parallel SVM model is adopted to decompose the prediction task into many tiny subtasks. | The extraction of local sequential features is not designed for parallelization. |
| Category . | Representative model . | Advantages . | Disadvantages . |
|---|---|---|---|
| Network-based models | L3 [53] | L3 argues that proteins interact if one of them is similar to the other’s partners instead of being similar to each other. | L3 is incapable of predicting PPIs between proteins that are distantly located away from each other without any common neighbors. |
| SpectralLink [86] | SpectralLink considers the global network structures of PPI network. | Many complex structural properties in real networks are simply ignored. | |
| RWS [54] | RWS can effectively overcome the high level of noise, sparseness and highly skewed degree distribution of PPI networks. | The robustness of RWS could be decreased by the simple cut-off-based strategy used to maintain the number of edges in |$G$|. | |
| You et al. [99] | This model can work on a sparse PPI network with only topological information. | The number of dimensions used by manifold embedding may influence the prediction accuracy. | |
| Huang et al. [47] | This model integrates evolutionary information into |$G$| and obtains a better performance. | This model heavily rests on the completeness of |$G$|, which is difficult to be satisfied in practical PPI networks. | |
| Sequence-based models | Bock and Gough [12] | This work provides a theoretical and systematic analysis on how to perform the PPI prediction explicitly based on primary structures of proteins. | The generalization to other species, such as bacteria or archea, is problematic. |
| VLASPD [41] | VLASPD takes variable-length segments of protein sequences into account for PPI prediction. | The vast amount of variable-length patterns may confuse the classifiers to accurately predict PPIs. | |
| CD [40] | The substitution rate estimation proposed by the CD model is more informative. | It fails to infer specific features of PPIs, such as the interacting residues in the interfaces. | |
| Structure-based models | PrePPI [104] | PrePPI can identify unexpected PPIs of significant biological interest by using three-dimensional structural information. | PrePPI is incapable of predicting PPIs for proteins whose 3D structures are not experimentally determined. |
| InterPred [66] | The consideration of close and remote structural interaction templates improves the prediction accuracy. | The steps of structural template searching and docking are time-consuming. | |
| Genomic-based models | Enright et al. [26] | This model makes use of gene fusion events to predict PPIs. | Interactions where fusion events are not covered through the analysis of genomic sequencing are not able to be predicted. |
| Dandekar et al. [22] | Conserved gene pairs are used to predict PPIs. | This model fails to predict PPIs composed of proteins whose conservation of gene-order is missed. | |
| Pellegriniet et al. [75] | This model explores the possibility of using a phylogenetic profiling method for PPI prediction. | It is inefficient for PPI prediction when the number of profile patterns grows exponentially. | |
| GO-based models | Bandyopadhyay et al. [6] | This model demonstrates that GO-based features have a better performance than sequence-based spectrum count features. | The inherent directed acyclic graph structure of GO is ignored. |
| TCSS [49] | TCSS considers unequal depth of biological knowledge representation in different GO categories. | The proposed similarity measure may be overestimated in some scenarios. | |
| Deep learning-based models | Sun et al. [85] | This model is able to learn the hidden interaction features due to the powerful generalization capacity of deep learning. | The unbalance situation between interacting and non-interacting proteins could possibly degrade the accuracy. |
| DNN-PPI [55] | DNN-PPI does not need to extract features from protein sequences. | The number of layers for convolution neural network has to be determined carefully. | |
| Large-scale models | LDA-RF [6] | LDA-RF converts the hidden internal structures in low dimensional latent semantic space for large-scale PPI prediction. | The inference procedure of latent dirichlet allocation is not scalable. |
| You et al. [100] | A parallel SVM model is adopted to decompose the prediction task into many tiny subtasks. | The extraction of local sequential features is not designed for parallelization. |
| Category . | Representative model . | Advantages . | Disadvantages . |
|---|---|---|---|
| Network-based models | L3 [53] | L3 argues that proteins interact if one of them is similar to the other’s partners instead of being similar to each other. | L3 is incapable of predicting PPIs between proteins that are distantly located away from each other without any common neighbors. |
| SpectralLink [86] | SpectralLink considers the global network structures of PPI network. | Many complex structural properties in real networks are simply ignored. | |
| RWS [54] | RWS can effectively overcome the high level of noise, sparseness and highly skewed degree distribution of PPI networks. | The robustness of RWS could be decreased by the simple cut-off-based strategy used to maintain the number of edges in |$G$|. | |
| You et al. [99] | This model can work on a sparse PPI network with only topological information. | The number of dimensions used by manifold embedding may influence the prediction accuracy. | |
| Huang et al. [47] | This model integrates evolutionary information into |$G$| and obtains a better performance. | This model heavily rests on the completeness of |$G$|, which is difficult to be satisfied in practical PPI networks. | |
| Sequence-based models | Bock and Gough [12] | This work provides a theoretical and systematic analysis on how to perform the PPI prediction explicitly based on primary structures of proteins. | The generalization to other species, such as bacteria or archea, is problematic. |
| VLASPD [41] | VLASPD takes variable-length segments of protein sequences into account for PPI prediction. | The vast amount of variable-length patterns may confuse the classifiers to accurately predict PPIs. | |
| CD [40] | The substitution rate estimation proposed by the CD model is more informative. | It fails to infer specific features of PPIs, such as the interacting residues in the interfaces. | |
| Structure-based models | PrePPI [104] | PrePPI can identify unexpected PPIs of significant biological interest by using three-dimensional structural information. | PrePPI is incapable of predicting PPIs for proteins whose 3D structures are not experimentally determined. |
| InterPred [66] | The consideration of close and remote structural interaction templates improves the prediction accuracy. | The steps of structural template searching and docking are time-consuming. | |
| Genomic-based models | Enright et al. [26] | This model makes use of gene fusion events to predict PPIs. | Interactions where fusion events are not covered through the analysis of genomic sequencing are not able to be predicted. |
| Dandekar et al. [22] | Conserved gene pairs are used to predict PPIs. | This model fails to predict PPIs composed of proteins whose conservation of gene-order is missed. | |
| Pellegriniet et al. [75] | This model explores the possibility of using a phylogenetic profiling method for PPI prediction. | It is inefficient for PPI prediction when the number of profile patterns grows exponentially. | |
| GO-based models | Bandyopadhyay et al. [6] | This model demonstrates that GO-based features have a better performance than sequence-based spectrum count features. | The inherent directed acyclic graph structure of GO is ignored. |
| TCSS [49] | TCSS considers unequal depth of biological knowledge representation in different GO categories. | The proposed similarity measure may be overestimated in some scenarios. | |
| Deep learning-based models | Sun et al. [85] | This model is able to learn the hidden interaction features due to the powerful generalization capacity of deep learning. | The unbalance situation between interacting and non-interacting proteins could possibly degrade the accuracy. |
| DNN-PPI [55] | DNN-PPI does not need to extract features from protein sequences. | The number of layers for convolution neural network has to be determined carefully. | |
| Large-scale models | LDA-RF [6] | LDA-RF converts the hidden internal structures in low dimensional latent semantic space for large-scale PPI prediction. | The inference procedure of latent dirichlet allocation is not scalable. |
| You et al. [100] | A parallel SVM model is adopted to decompose the prediction task into many tiny subtasks. | The extraction of local sequential features is not designed for parallelization. |
| Category . | Representative model . | Advantages . | Disadvantages . |
|---|---|---|---|
| Network-based models | L3 [53] | L3 argues that proteins interact if one of them is similar to the other’s partners instead of being similar to each other. | L3 is incapable of predicting PPIs between proteins that are distantly located away from each other without any common neighbors. |
| SpectralLink [86] | SpectralLink considers the global network structures of PPI network. | Many complex structural properties in real networks are simply ignored. | |
| RWS [54] | RWS can effectively overcome the high level of noise, sparseness and highly skewed degree distribution of PPI networks. | The robustness of RWS could be decreased by the simple cut-off-based strategy used to maintain the number of edges in |$G$|. | |
| You et al. [99] | This model can work on a sparse PPI network with only topological information. | The number of dimensions used by manifold embedding may influence the prediction accuracy. | |
| Huang et al. [47] | This model integrates evolutionary information into |$G$| and obtains a better performance. | This model heavily rests on the completeness of |$G$|, which is difficult to be satisfied in practical PPI networks. | |
| Sequence-based models | Bock and Gough [12] | This work provides a theoretical and systematic analysis on how to perform the PPI prediction explicitly based on primary structures of proteins. | The generalization to other species, such as bacteria or archea, is problematic. |
| VLASPD [41] | VLASPD takes variable-length segments of protein sequences into account for PPI prediction. | The vast amount of variable-length patterns may confuse the classifiers to accurately predict PPIs. | |
| CD [40] | The substitution rate estimation proposed by the CD model is more informative. | It fails to infer specific features of PPIs, such as the interacting residues in the interfaces. | |
| Structure-based models | PrePPI [104] | PrePPI can identify unexpected PPIs of significant biological interest by using three-dimensional structural information. | PrePPI is incapable of predicting PPIs for proteins whose 3D structures are not experimentally determined. |
| InterPred [66] | The consideration of close and remote structural interaction templates improves the prediction accuracy. | The steps of structural template searching and docking are time-consuming. | |
| Genomic-based models | Enright et al. [26] | This model makes use of gene fusion events to predict PPIs. | Interactions where fusion events are not covered through the analysis of genomic sequencing are not able to be predicted. |
| Dandekar et al. [22] | Conserved gene pairs are used to predict PPIs. | This model fails to predict PPIs composed of proteins whose conservation of gene-order is missed. | |
| Pellegriniet et al. [75] | This model explores the possibility of using a phylogenetic profiling method for PPI prediction. | It is inefficient for PPI prediction when the number of profile patterns grows exponentially. | |
| GO-based models | Bandyopadhyay et al. [6] | This model demonstrates that GO-based features have a better performance than sequence-based spectrum count features. | The inherent directed acyclic graph structure of GO is ignored. |
| TCSS [49] | TCSS considers unequal depth of biological knowledge representation in different GO categories. | The proposed similarity measure may be overestimated in some scenarios. | |
| Deep learning-based models | Sun et al. [85] | This model is able to learn the hidden interaction features due to the powerful generalization capacity of deep learning. | The unbalance situation between interacting and non-interacting proteins could possibly degrade the accuracy. |
| DNN-PPI [55] | DNN-PPI does not need to extract features from protein sequences. | The number of layers for convolution neural network has to be determined carefully. | |
| Large-scale models | LDA-RF [6] | LDA-RF converts the hidden internal structures in low dimensional latent semantic space for large-scale PPI prediction. | The inference procedure of latent dirichlet allocation is not scalable. |
| You et al. [100] | A parallel SVM model is adopted to decompose the prediction task into many tiny subtasks. | The extraction of local sequential features is not designed for parallelization. |
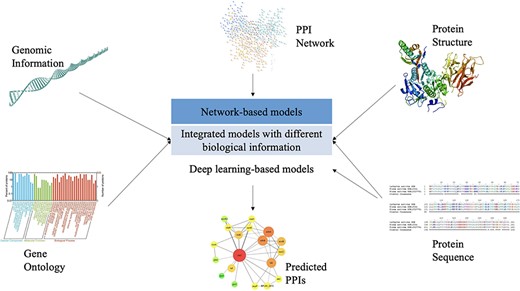
An illustration of biological knowledge used by different computational models for PPI prediction.
Network-based computational models
With the increase in the coverage of the interactome, network-based computational models have been developed to take advantage of connectivity patterns characterizing known PPIs in a given PPI network to predict missing PPIs. Although network-based link prediction algorithms rooted in social network analysis can be applied to address the problem of PPI prediction, they fail to capture the connectivity patterns that govern the construction of PPI networks, as two proteins interact if one of them is similar to the interacting partners of the other. In this regard, given two query proteins, their connectivity situations are closely related to the existence of an interaction between them. Network-based computational models intend to score protein pairs by their connectivities in the PPI network, thus determining whether these pairwise proteins are interacting or not.
Generally, a PPI network can be represented by a two-element tuple |$G=\lbrace V,E\rbrace $|, where |$V=\lbrace v_i\rbrace (1\leq i\leq n_V)$| is a set of |$n_V$| proteins and |$E=\lbrack e_{ij}\rbrack (1\leq i,j\leq n_V)$| is a |$n_V\times n_V$| adjacency matrix of |$G$|. Given two protein s |$v_i$| and |$v_j$|, |$e_{ij}=1$| if |$v_i$| and |$v_j$| are interacting, otherwise |$e_{ij}=0$|. Representative works in the category of network-based computational models are introduced in the rest of this section.
Common neighbors
As one of the most intuitive strategies for link prediction, the criterion of common neighbors has attracted much attention in developing computation models for PPI prediction. In [103], an integrated local similarity index combining common neighbors and preferential attachment is presented to estimate the likelihood of the existence of a PPI between two proteins based on local information of nearest neighbors. Due to the simple format, this similarity index provides competitively accurate prediction with less computational complexity. However, it only utilizes the current common neighbors and is not eligible to obtain promising prediction accuracy in evolving networks. Hence, Li et al. [57] propose the similarity-based future common neighbors (SFCN) model for PPI prediction, which accurately identify all the future common neighbors in addition to the current ones in the PPI network. The SFCN model has demonstrated a better accuracy performance and provided a more reliable robustness, as future common neighbors make more contributions than the current common neighbors in predicting PPIs from a given PPI network.
By incorporating the biological information of proteins, the Sim model could further improve the prediction accuracy when compared with many other network-based models, but the sparseness of PPI networks make it fail to predict the interaction between two proteins located in disjointed parts.
Network path
In (3), |$d_x=\sum _{z=1}^{n_V}e_{xz}$| and |$d_y=\sum _{z=1}^{n_V}e_{yz}$| are the degrees of |$v_x$| and |$v_y,$| respectively.
Experiment results demonstrate that L3 significantly outperforms all existing link prediction methods, including TCP. However, constrained by the specified of network paths, L3 is incapable of predicting PPIs between proteins that are far away from each other without any common neighbors. To address this problem, Wang et al. [95] design a novel stochastic block model for predicting PPIs without determining the length of network paths in advance. By simulating the generative process of a PPI network, the proposed model can capture the latent structural features of proteins according to their likelihoods of being grouped in the same protein complex, thus verifying whether two proteins interact with each other or not.
Global network structure
In |$G$|, local network structures refer to the neighboring information of proteins. In this regard, most of aforementioned computational models for PPI prediction only consider the local structures when performing their prediction tasks. In contrast to local network structures, global network structures are used to describe the topological information of an entire network, which may provide more comprehensive evidence to verify the existence of PPIs. As such, SpectralLink [86] is proposed by using a multi-way spectral clustering method to capture the topological affinity of proteins in a PPI network. By constructing the normalized Laplacian matrix from a given PPI network, SpectralLink makes use of the top-|$K$| eigenvectors to produce a less noisy matrix and selects the well-known Bray-Curtis coefficient to measure the topological similarity between two proteins from a global perspective. SpectralLink then uses the similarity score to indicate the probability of being interacting for two given proteins. A major disadvantage of SpectralLink is that many complex structural properties are not taken into account, such as degree heterogeneity and rich-club phenomenon. In order to assess the reliability of PPIs, Chen et al. [17] propose a novel measure, namely IRAP, to indicate the functional linkage between two proteins by considering the alternative path of PPIs in the underlying PPI network. IRAP adopts the weight of the strongest alternative path to assess the reliability of PPIs. Compared with the other reliability measures such as IG [81, 82], IRAP is more promising, as it is a global system-wide measure by considering the entire PPI network instead of merely local neighbors. Lei et al. [54] hypothesize that two proteins having similar distances to all other proteins in the PPI network can potentially interact with each other. To implement this hypothesis, a random walk with resistance model, denoted as RWS, is developed to measure the distances between a target protein and all other proteins by applying a novel random walk procedure to each protein. After that, similarities of topological profiles can be obtained for each pair of proteins. In the final step, novel PPIs are predicted to connect proteins that are topologically similar. Although the high level of noise, sparseness and highly skewed degree distribution of PPI networks have negative impacts to the performance of PPI prediction, RWS can effectively overcome these disadvantages by reconstructing PPI network. But the cut-off-based strategy adopted by RWS to maintain the number of edges in |$G$| is simple, and thus may degrade the robustness of RWS.
Geometric embedding
Geometric embedding aims to formulate a new representation for a given PPI network in a geometric space. Each protein can be considered as a point in this geometric space and thus the spatial distance between pairwise proteins can be computed using their corresponding coordinates. You et al. [99] develop a robust manifold embedding technique for predicting new interactions by only using the topological information of PPI networks. In particular, a given PPI network is first transformed into a low-dimensional geometric space based on isometric feature mapping, and then the solution of predicting protein interactions is to measure the similarity between proteins in this embedded space. In contrast to most of aforementioned models whose performance is heavily impacted by the sparseness of |$G$|, this model can work on a sparse PPI network without considering additional information. However, when computing the reliable index, the scoring function is designed in a rather simple form and thus the number of dimensions used by manifold embedding may influence the prediction accuracy. Huang et al. [47] apply an evolutionary model to simulate the evolutionary process of a given PPI network, and then embed the evolved network into a geometric space. When assigning geometric coordinates to proteins, Multi-dimensional Scaling (MDS) [89], which is a classical nonlinear dimensionality reduction algorithm, is used. In doing so, the Euclidean distance between protein pairs can be computed and used to determine whether there is an interaction between a pair of proteins. The integration of evolutionary information into |$G$| certainly improves the performance of PPI prediction, but this evolutionary model heavily rests on the completeness of |$G$|, which is difficult to be satisfied in practical PPI networks. Xiao et al. [98] propose a novel protein embedding method by combining graph convolutional network (GCN) and PageRank to better explore the topological information of PPI networks across higher-order neighborhoods of each protein. A higher-order GCN variational auto-encoder architecture is then developed to jointly represent both higher-order local and global PPI network topology for novel PPI prediction. By adopting a co-training technique according to the L3 principle, this model considers both local and global structures of |$G$|, thus presenting a more robust performance against the noise and incompleteness of |$G$|.
Sequence-based computational models
The basic components of proteins are amino acids. For each protein, its sequence of amino acids determines its primary structure. Since there is a lot of useful information carried by protein sequences, several attempts have been made to develop different computational models based on protein sequences. Before introducing some representative works in this direction, we first give the mathematical notations about the protein sequence information.
Given an alphabet set |$\Gamma =\lbrace \gamma _i\rbrace $| consisting of total |$n_\Gamma $| different amino acids, a protein sequence |$S$| with length |$n_S$| is represented as |$S=(s_t)$|, where |$1\leq s_t\leq n_S$| and |$s_t\in \Gamma $|. Therefore, a |$k$|-mer segment starting from the position |$t$| in |$s$| is denoted as |$S_{t,k}=(s_t,s_{t+1},\dots ,s_{t+k-1})$|, where |$1\leq t\leq n_S-k+1$|. Some representative works in this direction are introduced as follows.
Sequence similarity
In general, most of sequence-based computational models consider the similarity in the sequence between pairs of proteins and then take advantage of the learning ability of traditional classifiers, such as support vector machine (SVM) [21] and random forest [14], to perform the prediction task. These computational models can be distinguished by the way they use to extract feature vectors from protein sequences and also by the design of kernel function to concatenate the feature vectors of individual proteins.
Bock and Gough [12] construct the feature vector for each protein sequence based on the residue properties of amino acids, such as charge, hydrophobicity and surface tension. A concatenation operation is then applied to transform these variable-length vectors into fixed-length ones, several SVMs with different standard kernel functions are trained to perform the prediction task. As the first attempt in this direction, this work provides a theoretical and systematic analysis on how to perform the PPI prediction explicitly based on primary structures of proteins. But the generalization to other species, such as bacteria or archea, is problematic, as the SVM classifiers trained are mainly focused on proteins predominantly representing eukaryotes.
In addition to explicitly compose feature vectors of proteins from their sequences, PPIevo [102] has been developed to extract the feature vectors from Position-Specific Scoring Matrix for individual proteins based on their sequences. To represent a protein pair, PPIevo combines some statistics of the feature vectors of proteins in this pair, and adopts Random Forest to build classifiers for the prediction of PPIs. It is also argued that the construction of non-interacting proteins could lead a severe performance overestimation. Instead of composing feature vectors of proteins with fix-length |$k$|-mers, VLASPD [41] intends to identify variable-length |$k$|-mers that are capable of providing certain evidence in support or reject the interaction between two proteins. The experimental results demonstrate that the consideration of variable-length patterns provide more valuable insights into capturing the latent characteristics in the sequence information of interacting proteins. However, the vast amount of variable-length patterns may confuse the classifiers to accurately predict PPIs and it is for this reason that feature reduction techniques are suggested to be incorporated into VLASPD for achieving an improved performance.
Co-evolutionary analysis
In (5), |$o(\gamma _i,*)_k = \sum _{j=1}^{n_\Gamma }o(\gamma _i,\gamma _j)_k$| and |$o(*,\gamma _j)_k=\sum _{i=1}^{n_\Gamma }o(\gamma _i,\gamma _j)_k$|. |$(\gamma _i,\gamma _j)_k$| are determined as a co-evolutionary pattern if |$p\big ((\gamma _i,\gamma _j)_k\big )$| is significantly larger than the product of |$p\big ((\gamma _i,*)_k\big )$| and |$p\big ((*,\gamma _j)_k\big )$| at a confidence level of 95%. Based on the presence and absence of co-evolutionary patterns in the sequences of two proteins, co-evolutionary feature vectors can be composed for protein pairs rather than individual proteins. There are two major disadvantages of CoFex when we apply it to predict PPIs. First of all, it is yet unknown how to determine a proper range of |$k$|. A larger range of |$k$| could result in more co-evolutionary patterns, thus confusing the classifiers, while a smaller range of |$k$| may miss many useful co-evolutionary patterns. Secondly, CoFex is not able to predict the interactions for proteins whose sequences do not contain any of co-evolutionary patterns.
Structure-based computational models
In addition to protein sequences, protein structures also contain useful information related to the functions and biological processes of proteins, thus leading to an accurate PPI prediction.
As a well-known structure-based computational model, PrePPI [104] demonstrates that three-dimensional structural information is also applicable to predict PPIs with an accuracy and coverage better than predictions based on non-structural information. To do so, PrePPI first integrates both structural and non-structural interaction evidences using Bayesian statistics. Five empirical scores can thus be computed and then combined using a Bayesian network to yield a likelihood of being interacting. The experimental results show that PrePPI is comparable in accuracy to high-throughput experiments and it can identify unexpected PPIs of significant biological interest. However, PrePPI is incapable of predicting PPIs for proteins whose 3D structures are not experimentally determined. Ohue et al. [69] develop a docking system, namely MEGADOCK, that can sample an extremely large number of protein dockings at a relative high speed. When applied to predict PPIs, MEGADOCK first calculates the energy score for each decoy and perform s a clustering process for the proteins according to their similarity in decoy. WIth the cluste ring result, affinity scores can be obtained for PPI prediction. To address the heavy computing load required when calculating the three-dimensional structures at interactome scale, MEGADOCK is particularly designed to work in a large-scale parallelized computing environment, which in return makes it possible to predict PPIs in an acceptable time.
Mirabello et al. [66] present a fully automated pipeline, namely InterPred, to predict PPIs. In particular, several structural features are extracted by combing structural modeling, massive structural comparisons and molecular docking and then InterPred makes use of a random forest classifier to distinguish correct PPIs from incorrect data. A major factor contributing to the promising performance of InterPred is the consideration of close and remote structural interaction templates, which is regarded as a significant improvement when comparing to sequence-based models. Concerning the efficiency of InterPred, the steps of structural template searching and docking are time-consuming, thus decreasing the efficiency of InterPred. Zhao et al. [106] introduce the UniAlign model to predict the interactions between HIV-1 and human proteins based on the assumption that proteins with similar interface architecture share more common interaction partners. Hence, UniAlign calculates the similarity between two protein interface architectures and trains a SVM classifier with Gaussian kernel for binary classification of interactions. The main contribution of UniAlign is that it provides the first structural evidence regarding the formation of PPIs. It is for this reason that we may consider the results of UniAlign as an additional information source and integrate it into an integrative computational framework for predicting novel PPIs based on multiple sources.
Furthermore, in [77], structural features, such as loops and domains, have been verified to provide valuable insights into the molecular mechanisms of PPIs. That is to say, both the interacting region and the rest of protein surface are important for PPI prediction. With this argument in mind, a prediction model is proposed in [77] by combining the favoring and disfavoring structural features of proteins. The experiment results on several sets with unbalanced ratios of interactions and non-interactions indicate that the accuracy could be improved by more than 25% in the most unfavorable circumstances. Moreover, the conclusion made in this work is also consistent with the funnel-like intermolecular energy landscape theory when used to describe the formation of PPIs.
Genomic-based computational models
Regarding the genomic information used for PPI prediction, existing computational models mainly consider three sources of genomic information including gene fusion, gene-order and phylogenetic relationship. With these genomic information, the functional similarity between proteins can be computed and used to predict PPIs.
Gene fusion plays an essential role in the evolution of gene architecture. Two proteins are interacting with each other if they are found to have homologs in another genome where they are fused into a single protein.In this regard, Enright et al. [26] have developed a computational model to discover fusion events in different genomes. With this mode, proteins that are involved in a fusion event are more likely to interact with each other. However, the disadvantage of using gene fusion is that for proteins where fusion events are not covered through the analysis of genomic sequencing, their interactions are not able to be predicted.
It has been pointed out by [22] that proteins encoded by conversed gene pairs have a better chance of being interacted with each other. Since conserved gene pairs are within a low level conservation of gene-order, the conservation of gene-order can be exploited to help predict PPIs. Though promising, the use of gene-order cannot predict PPIs composed of proteins whose conservation of gene-order is missed, such as those encoded by distantly located genes.
Phylogenetic relationships refer to the evolutionary history among proteins and they are often presented within a phylogenetic tree. Proteins that have similar phylogenetic relationships are functionally related and they tend to be interacting in order to perform the same molecular functions. In contrary of [40, 42] that obtain evolutionary information indirectly from protein sequences, phylogenetic relationships provide an explicit way to make use of evolutionary information of proteins for PPI prediction. Pellegriniet et al. [75] make use of phylogenetic profiles to predict PPIs. In particular, the co-evolution history of proteins is characterized by the use of phylogenetic profiles and proteins with similar profiles are strongly expected to interact. As the first attempt in this direction, this work demonstrates that the comparison between phylogenetic profiles of proteins is also a useful tool for PPI prediction. However, constrained by the amount of fully sequenced genomes at that time, the data adopted to construct the profiles of proteins is rather small, thus degrading the applicability. Pazos et al. [73] design a distance-based measure to compute the similarity between the phylogenetic trees of proteins, and whether there is a possible interaction between them can thus be determined. Covering a significant number the potential interactions, this model is applicable to a large-scale prediction of PPIs, but since the distance matrices are not a perfect representation of corresponding phylogenetic trees, it is prone to false positives and false negatives.
GO-based computational models
Motivated by the intuition that interacting proteins are more likely to be located in similar locations or participate in similar biological processes, GO-based computational models make use of different semantic similarity measures to quantify the similarities between proteins based on their function, thus assessing the physiological relevance between pairwise proteins. This kind of computational models normally target to construct feature vectors for pairs of protein, which are then integrated with traditional classifiers for PPI prediction.
Given a pair of proteins, Bandyopadhyay et al. [6] consider it as a document composed of words, and each word is one of common GO terms shared by these two proteins. Each unique word is taken as a feature to construct the feature vectors for protein pairs. The value of each feature is calculated using information content of the corresponding term multiplied by a coefficient, which represents the weight of that term inside a document. Although the experiment results show that GO-based features have a better performance than sequence-based spectrum count features, the inherent directed acyclic graph structure of GO is ignored. Hence, it is possible to improve the prediction accuracy by considering all relationships existed among GO terms. Since most of semantic similarity measures used for assessing the confidence of PPIs fail to consider the different GO terms related to cell positions and also ignore the unequal depth in the hierarchy of GO categories, the similarity results may be overestimated or underestimated. Hence, an improved topological clustering semantic similarity is adopted by TCSS [49] and it takes into consideration the unequal depth of biological knowledge representation in different branches of the GO hierarchy. However, the use of the similarity function to assess PPIs may be overestimated in some scenarios, such as computing the functional similarity in a more general manner.
Deep learning-based computational models
In recent years, due to the strong ability of unsupervised feature learning, deep learning has attracted much attention from researchers in a variety of computational fields, such as natural language understanding, machine learning and image processing. There also have been certain attempts made to apply deep learning techniques for PPI prediction and they are briefly introduced as follows.
Sun et al. [85] make use of stacked autoencoder (SAE) composed of multiple layers of autoencoders to predict PPIs based on protein sequences. Regarding the input of SAE, two methods including the autocovariance method and the conjoint triad method are adopted to encode the protein sequences. Benefited from the powerful generalization capacity provided by deep learning in learning hidden interaction features, the best model achieves an average accuracy of 97.19% with 10-fold cross-validation (CV), thus demonstrating the superiority of deep learning in predicting PPIs. However, the performance of this model is subject to the quality of training data, as the unbalance situation between interacting and non-interacting proteins could possibly degrade the accuracy. As another attempt of applying deep learning based on protein sequences, DPPI [34] first constructs a profile representation for the sequence of each protein based on a large amount of unsupervised data. After that, a Siamese-like convolutional neural network architecture is employed by DPPI to learn the complex interaction relationship between pairwise proteins. Lastly, DPPI randomly projects the values of the last convolutional module into a subspace to calculate the interaction probability for prediction. By incorporating random projection and data augmentation into the convolutional neural network, the predictive power and computational efficiency of DPPI can be improved, thus making DPPI outperforms a few recent sequence-based models on several benchmarks in terms of PR-AUC. Moreover, DPPI is scalable with respect to the increase in the size of training data and is also applicable to many other biological problems, such as predicting cytokine-receptor binding affinities, without significant parameter tuning.
To investigate the over-fitting and generalization of deep learning models in predicting PPIs, Li et al [55] propose a deep neural network framework, namely DNN-PPI, based on features automatically obtained from protein sequences. DNN-PPI explicitly take s the sequences of two interacting proteins as the input and feed s them into the encoding, embedding, convolution neural network, and long short-term memory neural network layers in a sequential manner. Then, DNN-PPI concatenates the two outputs from the previous layer into a single vector, which is wired as the input of the fully connected neural network. Finally, DNN-PPI adopts the Adam optimizer to learn the network weights for predicting PPIs. The major difference between DNN-PPI and the previous deep learning-based models is that the operation of feature extraction is not applied by DNN-PPI to preprocess protein sequences. In doing so, the sequence information can be fully exploited by DNN-PPI for an improved performance in PPI prediction. Moreover, the adoption of a simple one-hot encoding allows DNN-PPI to be with more competitive generalization capability for predicting PPIs. When compared with the model proposed by Sun et al. [85], DNN-PPI demonstrates its superiority, as it performs better by 3.4%. However, the number of layers for convolution neural network has to be determined carefully for achieving a desired performance level.
Computational models for large-scale PPI prediction
At present, the amount of protein interactions that have been identified is less than 20% of the whole interactome [101]. With the development of high-throughput technologies, the size and complexity of protein interaction data have also increased significantly. A new challenge is thus raised for large-scale PPI prediction. Recently, several attempts have been made in this field and representative works are introduced as below.
The LDA-RF model [72] is developed to predict human PPIs explicitly from protein sequences, and it is able to handle large-scale datasets by converting the hidden internal structures in low dimensional latent semantic space. In LDA-RF, Although random forest has a good performance to the large-scale prediction task, the inference procedure of latent dirichlet allocation is inefficient [43], and thus constrains the scalability of LDA-RF. To achieve the purpose of effectively and accurately predicting large-scale PPIs, You et al. [100] propose a parallel SVM model by only requiring the use of protein sequence information for large-scale PPI prediction. First, the autocorrelation descriptor method is adopted to extract local sequential features from protein sequences. Then distributed SVM classifiers are trained under the MapReduce framework such that the training time can be considerably reduced. An efficiency bottleneck of this model is that the extraction of local sequential features is not designed for parallelization. To overcome this problem, Hu et al. [44] later propose a large-scale protein interaction prediction algorithm, namely pVLASPD, by parallelizing all steps of VLASPD. pVLASPD first extracts amino acid fragments from sequences of proteins for statistical analysis, and then constructs the corresponding feature vectors of proteins to train the classifier models. These tasks are further decomposed into tiny tasks each of which is executed in a different thread. As a recent attempt in this direction, Ji et al. [50] employ the Moran autocorrelation descriptor method to convert the protein feature vectors into uniform matrices and then make use of a distributed implementation of random forest to make the prediction of PPIs. However, the scalability of the Moran autocorrelation descriptor method is yet to be verified especially for a huge amount of protein sequence information.
Performance evaluation
As an essential step to verify the superiority of computational models, performance evaluation involves several aspects, including experimental data preparation, validation scheme and evaluation metrics. The rest of this section is unfolded with an detailed description for each of these aspects.
Experimental data preparation
In order to achieve an accurate PPI prediction, existing computation models normally follow a supervised learning framework to prepare experimental data composed of interacting and non-interacting pairs of proteins. Interacting proteins are positive samples and can be explicitly extracted from the aforementioned PPI databases. However, the preparation of negative samples, i.e., non-interacting proteins, is not as straightforward as that of interacting proteins. Since the knowledge of non-interacting proteins also plays a critical role in training computational models for PPI prediction, different strategies have been designed to construct non-interacting proteins. As an intuitive and simple strategy, randomly generating non-interacting proteins from positive samples is widely adopted by most of computational models, but its applicability is heavily subject to the quality of interacting proteins. Due to the fact that PPI networks are far from being complete at present, the set of non-interacting proteins generated by the random strategy is possible contaminated by interacting proteins not reported before, thus affecting the assessment of computation models. Hence, to obtain high quality of non-interacting proteins, the second strategy takes into account the difference in cellular localization between proteins. For example, in [40], two proteins are non-interacting if they are observed from plasma membrane and nuclear respectively, and thus a total of |$2750990$| protein pairs are selected as a standard negative dataset. Regarding the features extracted for training, the strategy of random selection from interacting proteins obviously is able to estimate the distribution of features without any bias, but the constraint of not being co-localized intentionally imposes certain bias to the distribution of features that is different from the true one, thus leading to an inaccurate assessment about the prediction performance of computational models [8]. Recently, the release of Negatome 2.0 [11] provides an alternative way to obtain non-interacting proteins by considering both text mining and literature curation with protein structure analyses. The amount of manual and structure-based non-interacting protein pairs is 6532 in Negatome 2.0. After removing non-interacting proteins that are reported as interacting in the IntAct database, a more stringent dataset containing 6136 non-interacting protein pairs is also provided by Negatome 2.0.
CV schemes
Once the experimental data is readily available, the next step is to select an appropriate CV scheme for performance evaluation. In the context of CV, experimental data is normally divided into two parts, one is training data and the other is testing data. The purpose of using training data is to train the computational models by tuning their performance. For the testing data, its interacting and non-interacting proteins are not existed in the training data and hence we can use it to unbiasedly evaluate the performance of computational models for unknown protein pairs. The popular CV schemes contain held-out validation, |$K$|-fold CV and leave-one-out CV. and their details are introduced as follows.
Held-out validation
As the simplest implementation of CV, held-out validation randomly divides the experimental data into training and testing data, and a common split is using 80% of experimental data for training and the remaining 20% for testing. However, the evaluation obtained from held-out validation can have a considerably large variance, as the performance of computational models is heavily determined by protein pairs in the training and testing data, and it could be significantly different according to the division made by held-out validation.
|$K$|-fold CV
To overcome the disadvantages of hold-out validation, |$K$|-fold CV first divides the experimental data into |$K$| groups, and then repeats the hold-out validation |$K$| times. For each time, one of |$K$| groups is used as the testing data and the other |$K-1$| groups are merged together to form a training data. When compared with hold-out validation, the advantage of |$K$|-fold CV is that its dependency on the division of experimental data is much less that that of hold-out validation. Moreover, each protein pair in the experimental data is able to be divided into the test data exactly once. In doing so, the variance of evaluation results is reduced. The disadvantage of |$K$|-fold CV is the computational time of |$K$|-fold CV is |$K$| times as much as that of hold-out validation.
Leave-one-out CV
As the extreme case of |$K$|-fold CV, leave-one-out CV (LOOCV) is |$K$|-fold CV where |$K$| is equal to the number of protein pairs in the experimental data. That is to say, under the LOOCV scheme, the computational models are trained on all experimental data except for one protein pair for which a prediction is made. The advantage of LOOCV is that the distribution of features in the training data is much closer to the truth and hence the evaluation results are more reliable. However, the computational cost of LOOCV increases dramatically when the experimental data is large-scale.
Evaluation metrics
To quantitatively evaluate the PPIs predicted by computational models, several evaluation metrics can be used and they are Matthew correlation coefficient (MCC) [63], F1-score [78, 83], Area Under Receiver Operating Characteristic Curve (AUC) [27, 65] and Precision-Recall AUC (PR AUC) [23]. Before introducing these evaluation metrics, we introduce the terms involved as follows.
True Positive (TP): the number of interacting protein pairs predicted correctly;
True Negative (TN): the number of non-interacting protein pairs predicted correctly;
False Positive (FP): the number of non-interacting protein pairs predicted as interacting;
False Negative (FN): the number of interacting protein pairs predicted as non-interacting.
Matthew correlation coefficient
F1-score
In (7), |$Precision$| is the proportion of correctly predicted interacting protein pairs to all protein pairs predicted to be interacting pairs, and |$Recall$| is the proportion of correctly predicted interacting protein pairs to all the protein pairs in the data set.
Area under receiver
Precision-recall AUC
As has been pointed out in [23], ROC curves and the corresponding AUC scores can present an overly optimistic impression about the performance of computational models if there is a large imbalance between the numbers of interacting and non-interacting proteins. Hence, for imbalanced experimental data, it is improper to make use of AUC for measuring the prediction accuracy. To overcome this problem, Presion-Recall ROC curves (PR-ROC) could be considered as an promising alternative to ROC curves. PR-AUC is able to computed by trapezoidal integral for the area under PR-ROC curves. The scores of PR-AUC are also within the range |$\lbrack 0,1\rbrack $| and a larger score of PR-AUC indicates that the computational model involved has a stronger ability to separate interacting and non-interacting protein pairs.
Tools and applications
To facilitate the use of computational models in PPI prediction, many easy-to-access tools have been developed. In this section, we briefly introduce several representative tools that either integrate multiple sources of protein information or provide a more comprehensive analysis to the predicted PPIs. The details of these tools are given in Table 4.
| Tool . | Features . | Availability . | Website . | Input Format . | Limitations . |
|---|---|---|---|---|---|
| BIPS | Predict PPIs based on GO terms and clusters of orthologous proteins | Online | http://sbi.imim.es/BIPS.php | A list of sequences or protein identifiers | heavily relied on the BIANA framework [30] |
| OpenPPI predictor | Predict PPIs using interactome data from related organisms | Standalone | http://tools.neb.com/∼posfai/ | Sequences of proteins | Subject to the amount of orthologous proteins |
| PrePPI | Predict PPIs with 3D structural information | Online | http://bhapp.c2b2.columbia.edu/PrePPI | UniProt accession number, gene name or protein name | May appear physically unrealistic in many cases |
| PIPs | Predict PPIs based on the topology of network and other biological information | Online | http://www.compbio.dundee.ac.uk/www-pips | IPI, RefSeq and UniProt identifiers of proteins | Only 10% of the human interactome have been identified |
| PSOPIA | Predict unknown PPIs with known homologous PPIs | Online | http://mizuguchilab.org/PSOPIA | A pair of protein sequences in a FASTA format | Not support batch processing |
| HIPPIE | Predict PPIs based on different types of experimental information of proteins | Online | http://cbdm.uni-mainz.de/hippie/ | A single UniProt identifier, gene symbol or Entrez gene id | Biased training data |
| MEGADOCK-Web | Predict with protein chain structures | Online | http://www.bi.cs.titech.ac.jp/megadock-web/ | PDB ID, UniProt identifier, protein name or gene name | Only applicable to human species |
| Tool . | Features . | Availability . | Website . | Input Format . | Limitations . |
|---|---|---|---|---|---|
| BIPS | Predict PPIs based on GO terms and clusters of orthologous proteins | Online | http://sbi.imim.es/BIPS.php | A list of sequences or protein identifiers | heavily relied on the BIANA framework [30] |
| OpenPPI predictor | Predict PPIs using interactome data from related organisms | Standalone | http://tools.neb.com/∼posfai/ | Sequences of proteins | Subject to the amount of orthologous proteins |
| PrePPI | Predict PPIs with 3D structural information | Online | http://bhapp.c2b2.columbia.edu/PrePPI | UniProt accession number, gene name or protein name | May appear physically unrealistic in many cases |
| PIPs | Predict PPIs based on the topology of network and other biological information | Online | http://www.compbio.dundee.ac.uk/www-pips | IPI, RefSeq and UniProt identifiers of proteins | Only 10% of the human interactome have been identified |
| PSOPIA | Predict unknown PPIs with known homologous PPIs | Online | http://mizuguchilab.org/PSOPIA | A pair of protein sequences in a FASTA format | Not support batch processing |
| HIPPIE | Predict PPIs based on different types of experimental information of proteins | Online | http://cbdm.uni-mainz.de/hippie/ | A single UniProt identifier, gene symbol or Entrez gene id | Biased training data |
| MEGADOCK-Web | Predict with protein chain structures | Online | http://www.bi.cs.titech.ac.jp/megadock-web/ | PDB ID, UniProt identifier, protein name or gene name | Only applicable to human species |
| Tool . | Features . | Availability . | Website . | Input Format . | Limitations . |
|---|---|---|---|---|---|
| BIPS | Predict PPIs based on GO terms and clusters of orthologous proteins | Online | http://sbi.imim.es/BIPS.php | A list of sequences or protein identifiers | heavily relied on the BIANA framework [30] |
| OpenPPI predictor | Predict PPIs using interactome data from related organisms | Standalone | http://tools.neb.com/∼posfai/ | Sequences of proteins | Subject to the amount of orthologous proteins |
| PrePPI | Predict PPIs with 3D structural information | Online | http://bhapp.c2b2.columbia.edu/PrePPI | UniProt accession number, gene name or protein name | May appear physically unrealistic in many cases |
| PIPs | Predict PPIs based on the topology of network and other biological information | Online | http://www.compbio.dundee.ac.uk/www-pips | IPI, RefSeq and UniProt identifiers of proteins | Only 10% of the human interactome have been identified |
| PSOPIA | Predict unknown PPIs with known homologous PPIs | Online | http://mizuguchilab.org/PSOPIA | A pair of protein sequences in a FASTA format | Not support batch processing |
| HIPPIE | Predict PPIs based on different types of experimental information of proteins | Online | http://cbdm.uni-mainz.de/hippie/ | A single UniProt identifier, gene symbol or Entrez gene id | Biased training data |
| MEGADOCK-Web | Predict with protein chain structures | Online | http://www.bi.cs.titech.ac.jp/megadock-web/ | PDB ID, UniProt identifier, protein name or gene name | Only applicable to human species |
| Tool . | Features . | Availability . | Website . | Input Format . | Limitations . |
|---|---|---|---|---|---|
| BIPS | Predict PPIs based on GO terms and clusters of orthologous proteins | Online | http://sbi.imim.es/BIPS.php | A list of sequences or protein identifiers | heavily relied on the BIANA framework [30] |
| OpenPPI predictor | Predict PPIs using interactome data from related organisms | Standalone | http://tools.neb.com/∼posfai/ | Sequences of proteins | Subject to the amount of orthologous proteins |
| PrePPI | Predict PPIs with 3D structural information | Online | http://bhapp.c2b2.columbia.edu/PrePPI | UniProt accession number, gene name or protein name | May appear physically unrealistic in many cases |
| PIPs | Predict PPIs based on the topology of network and other biological information | Online | http://www.compbio.dundee.ac.uk/www-pips | IPI, RefSeq and UniProt identifiers of proteins | Only 10% of the human interactome have been identified |
| PSOPIA | Predict unknown PPIs with known homologous PPIs | Online | http://mizuguchilab.org/PSOPIA | A pair of protein sequences in a FASTA format | Not support batch processing |
| HIPPIE | Predict PPIs based on different types of experimental information of proteins | Online | http://cbdm.uni-mainz.de/hippie/ | A single UniProt identifier, gene symbol or Entrez gene id | Biased training data |
| MEGADOCK-Web | Predict with protein chain structures | Online | http://www.bi.cs.titech.ac.jp/megadock-web/ | PDB ID, UniProt identifier, protein name or gene name | Only applicable to human species |
BIPS [31] provides a web-based interface to predict PPI according to the interolog information by integrating several PPI-related databases and it also considers additional biological information,such as GO terms and clusters of orthologous proteins, to further improve the reliability of predicted PPIs. As an open source program module, OpenPPI_predictor [74] is able to generate a putative PPI network for given proteins by using orthologous interactome data obtained from a related and experimentally studied organism. To construct a database of predicted and experimentally determined PPIs, PrePPI [105] predict PPIs using a Bayesian framework that combines structural, functional, evolutionary and expression information for the human proteome. As another database of predicted PPIs for human, PIPs [64] calculates the probability of interaction by combining different features including gene co-expression, orthology, domain co-occurrence, co-localization, post translational modification and transitive network analysis. PSOPIA [67] provides a web-based tool for predicting PPIs based on three sequence-based features, including the sequence similarities to a known PPI, statistical propensities of domain pairs observed in PPIs, and a sum of edge weights along the shortest path between homologous proteins in a PPI network. To be a one-stop resource for generating reliable PPI networks, HIPPIE [1] uses information from experiments performed to compute a confidence score for a pair of proteins, and this score is half manual and half computationally optimized based on the amount and quality of experimental evidence. MEGADOCK-Web [36] provides a web-based interface to predict PPIs based on protein-protein docking, and furthermore it is able to visualize the candidates that may interact with the input of protein pairs from the perspective of biochemical pathways.
Challenges and future work
PPIs are crucial for understanding the mechanisms of most biological processes, and also play a significant role in organismal development and function from a molecular perspective. Since the laboratory-based approaches suffer from the disadvantages of being time-consuming and labor-intensive, a variety of computational models have thus been developed to facilitate the prediction of PPIs. In this paper, a comprehensive survey is summarized to introduce the recent efforts made to development of effective prediction models. The challenges and future work are presented as below.
Most of computational models are proposed by following the paradigm of supervised learning, and accordingly the quality of training data is a key issue determining the accuracy performance of PPI prediction. However, concerning the high false-positive and false-negative ratios observed in PPIs generated by high-throughput technologies, there is a necessity for us to pre-process the PPI data such that the quality of training data could be improved and more appropriate to evaluate the performances of prediction models. Meanwhile, in addition to the PPI data, other sources of biological information of proteins are taken into account to compensate for the negative influences resulted from the problematic reliability of PPI data. Hence, how to effectively integrate multiple sources of biological information for PPI prediction is still one of major challenges that need to be resolved as one of future work.
Due to the spatial and temporal regulations in the cell type and cell cycle phase, PPIs are dynamic in cells, but scientific explorations of capturing dynamics of PPIs between physiological and disease conditions are limited [58]. It is for this reason that few computational models have been proposed for predicting dynamic PPIs. Recent advances in quantitative proteomics offer a technique, namely thermal proximity coaggregation (TPCA), to infer the dynamics of PPIs according to the melting curves of proteins during denaturation [88]. In this regard, the future work should be focused on the development of new computational models that use TPCA features extracted from the melting curves to predict PPIs in different tissues or cell lines. Moreover, the development of next-generation sequencing technologies, such as RNA-seq, provides us a more comprehensive gene expression map, we could design new dynamic prediction models according to RNA-seq time series data. Lastly, since the dynamic changes of PPIs are also observed in different tissues or subcellular locations, this would be especially useful by considering the spatial information for predicting dynamic PPIs.
The accuracy performance of computational models is normally evaluated with the PPI data collected from the yeast or human species. But few of existing computational models have conducted experiments to analyze their performance when predicting PPIs from other species, such as plants and oviparous animals. Whether the performance of computational models is still promising in the species other than yeast or human species is yet to be determined. Furthermore, co-evolutionary evidences report that certain evolutionary patterns of PPIs are conserved across different species. The future work would be focused on predicting PPIs in different species according to the evolutionary patterns.
Because of the development of high-throughput technologies, a vast amount of functional genomic data across multiple omics has been accumulated by several large-scale projects, thus providing an alternative view to systematically infer PPIs within the context of specific multi-omics data [35]. However, although the integration of these data may provide extra evidence on the prediction of PPIs, the relationship between PPIs and multi-omics data is still to be thoroughly investigated. In this regard, how to effectively integrate multi-omics data with machine learning techniques is a crucial step for the successful prediction of PPIs.
When predicting PPIs based on PPI networks, local and global network structures are verified to be useful for improving the prediction accuracy. However, few of existing network-based models take into account the complementarity of these two kinds of structure information. Furthermore, how to incorporate biological information of proteins into PPI networks remains a challenging problem to be solved for PPI prediction. Recently, as an important task in network analysis, attributed graph clustering (AGC) has been attracting much attention and many effective clustering algorithms [37, 38] are proposed by jointly modelling graph structures and node attributes. Thus, it is possible for us to firstly apply the AGC algorithms such that proteins that are more likely to be interact are grouped into the same clusters. After that, a number of local structure-based similarity measures, such as Sim [18] and L3 [53], can be used to compute the possibility of proteins in the same cluster. In this regard, combining local and global network structures with AGC may be the focus of future work for PPI prediction.
This article summarizes available biological databases related to the prediction of PPIs, and also presents the popular online tools.
Computational models commonly used for PPI prediction are classified into several categories including network-based models, integrated models of protein interaction networks and biological information of proteins, deep learning-based models and large-scale models. In addition to the details of these models, their differences are also discussed.
A number of evaluation metrics can be taken to obtain more reliable estimates of the performance of computational models, but most of them are not sufficiently account for the heavy biases found in the protein interaction networks and biological data utilized for training and testing.
Increasing amount of functional genomic data is believed to hold the potential to improve the effectiveness of computational models.
Data Availability Statement
No new data were generated or analysed in support of this research.
Funding
This work has been supported by the National Natural Science Foundation of China (NSFC; grant number 61602352), the Pioneer Hundred Talents Program of Chinese Academy of Sciences and the NSFC Excellent Young Scholars Program (grant number 61722212).
Lun Hu. He received the B.Eng. degree from the Department of Control Science and Engineering, Huazhong University of Science and Technology, Wuhan, China, in 2006, and the M.Sc. and Ph.D. degrees from the Department of Computing, The Hong Kong Polytechnic University, Hong Kong, in 2008 and 2015, respectively. He joined the Xinjiang Technical Institute of Physics and Chemistry, Chinese Academy of Sciences, Urumqi, China, in 2020 as a professor of computer science. His research interests include machine learning, complex network analytics and their applications in bioinformatics.
Xiaojuan Wang. She received the B.Eng. degree from the Department of Control Science and Engineering, Anhui University, Hefei, China, in 2018. She is pursuing the M.Sc. degree with the School of Computer Science and Technology, Wuhan University of Technology, Wuhan, China.
Yu-An Huang. He received the M.S. degree in computer and software engineering from Shenzhen University, Shenzhen, China, in 2015, and the Ph.D. degree from the Department of Computing, The Hong Kong Polytechnic University, Hong Kong, in 2020. He is currently an assistant professor in the College of Computer Science and Software Engineering, Shenzhen University. His current research interests mainly focus on machine learning, artificial intelligence and bioinformatics.
Pengwei Hu. He is a Research Scientist in the IBM, China for AI Healthcare. He received his Ph.D. from the Department of Computing, The Hong Kong Polytechnic University in 2018, advised by Prof. Keith C.C. Chan. During the Ph.D. study, he also worked as a visiting research student at the University of Calgary supervised by Prof. Henry Leung. Dr. Hu’s main research interest is in machine learning, including AI for healthcare, automation and social media. He is editor of Frontiers in Artificial Intelligence, Frontiers in Neurorobotics.
Zhu-Hong You. He received his B.E. degree in Electronic Information Science and Engineering from Hunan Normal University, Changsha, China, in 2005. He obtained his Ph.D. degree in control science and engineering from University of Science and Technology of China (USTC), Hefei, China, in 2010. From June 2008 to November 2009, he was a visiting research fellow at the Center of Biotechnology and Information, Cornell University. He is currently a professor with Northwestern Polytechnical University, Xi'an, China. His current research interests include neural networks, intelligent information processing, sparse representation, and its applications in bioinformatics.
References
David Binns, Emily Dimmer, Rachael Huntley, Daniel Barrell,
Brigitte Boeckmann, Amos Bairoch, Rolf Apweiler, Marie-Claude Blatter, Anne Estreicher, Elisabeth Gasteiger,
Jin Chen, Wynne Hsu,
Thomas Dandekar, Berend Snel,
David De Juan, Florencio Pazos, and
Hui Ge, Zhihua Liu,
Anne-Claude Gingras, Matthias Gstaiger,
Somaye Hashemifar, Behnam Neyshabur,
Takanori Hayashi, Yuri Matsuzaki, Keisuke Yanagisawa, Masahito Ohue, and
Tiantian He, Yang Liu,
Yuen Ho, Albrecht Gruhler,
Lun Hu, Keith CC Chan, Xiaohui Yuan, and
Lun Hu, Xiaohui Yuan,
Lun Hu, Jun Zhang, Xiangyu Pan, Hong Yan, and
Lei Huang, Li Liao, and
TS Keshava Prasad, Renu Goel, Kumaran Kandasamy, Shivakumar Keerthikumar, Sameer Kumar, Suresh Mathivanan, Deepthi Telikicherla, Rajesh Raju, Beema Shafreen, Abhilash Venugopal, et al. Human protein reference database-
Ozlem Keskin, Nurcan Tuncbag, and
Min Li, Hao Gao,
Shibao Li, Junwei Huang, Zhigang Zhang, Jianhang Liu,
Guillaume Marmier, Martin Weigt, and
Masahito Ohue, Yuri Matsuzaki, Nobuyuki Uchikoga, Takashi Ishida, and
Philipp Pagel, Stefan Kovac, Matthias Oesterheld, Barbara Brauner,
Xiao-Yong Pan, Ya-Nan Zhang, and
Rintaro Saito, Harukazu Suzuki, and
Rintaro Saito, Harukazu Suzuki, and
Tanlin Sun, Bo Zhou,
Panagiotis Symeonidis, Nantia Iakovidou,
Amy Hin Yan Tong, Becky Drees, Giuliano Nardelli, Gary D Bader, Barbara Brannetti, Luisa Castagnoli, Marie Evangelista, Silvia Ferracuti, Bryce Nelson, Serena Paoluzi, et al. A combined experimental and computational strategy to define protein interaction networks for peptide recognition modules. Science, 295(5553):321–324,
Amy Hin Yan Tong, Marie Evangelista, Ainslie B Parsons, Hong Xu, Gary D Bader, Nicholas Pagé, Mark Robinson, Sasan Raghibizadeh, Christopher WV Hogue, Howard Bussey, et al. Systematic genetic analysis with ordered arrays of yeast deletion mutants. Science, 294(5550):2364–2368,
Nurcan Tuncbag, Gozde Kar, Ozlem Keskin, Attila Gursoy, and
Ioannis Xenarios, Lukasz Salwinski,
Zhu-Hong You, Ying-Ke Lei, Jie Gui, De-Shuang Huang, and
Haiyuan Yu, Pascal Braun,
Javad Zahiri, Omid Yaghoubi,
Qiangfeng Cliff Zhang, Donald Petrey, Lei Deng, Li Qiang, Yu Shi, Chan Aye Thu, Brygida Bisikirska, Celine Lefebvre, Domenico Accili, Tony Hunter, et al. Structure-based prediction of protein–protein interactions on a genome-wide scale. Nature, 490(7421):556–560,


