Search
Close
Search
Advanced Search
Search Menu
AI Discovery Assistant

Abstract

Heterophylly, i.e. morphological changes in leaves along the axis of an individual plant, is regarded as a strategy used by plants to cope with environmental change. However, little is known of the extent to which heterophylly is controlled by genes and how each underlying gene exerts its effect on heterophyllous variation. We described a geometric morphometric model that can quantify heterophylly in plants and further constructed an R-based computing platform by integrating this model into a genetic mapping and association setting. The platform, named HpQTL, allows specific quantitative trait loci mediating heterophyllous variation to be mapped throughout the genome. The statistical properties of HpQTL were examined and validated via computer simulation. Its biological relevance was demonstrated by results from a real data analysis of heterophylly in a wood plant, mei (Prunus mume). HpQTL provides a powerful tool to analyze heterophylly and its underlying genetic architecture in a quantitative manner. It also contributes a new approach for genome-wide association studies aimed to dissect the programmed regulation of plant development and evolution.

heterophylly, QTL, leaf shape, geometric morphometrics, shape mapping, woody plant

Introduction

The shoot of a plant grows by adding new metamers at its apex that form internodes, leaves and buds. These shoot components display gradual or disrupt transitions along the shoot, even in a constant environment, a phenomenon observed pervasively in most land plants [1–4]. Shape variation in leaves produced on the same shoot, particularly called heterophylly, is a concept that has received a great deal of attention during the past centuries [5–10]. It has been widely accepted that heterophylly is of ecological and evolutionary significance because it is adaptive and functional under particular environmental conditions [8, 11, 12]. Heterophyllous characteristics have well been described from morphological, anatomical and physiological aspects [13, 14]. Several studies have revealed the biochemical mechanisms underlying heterophylly, identifying various hormones, such as ethylene and abscisic acid (ABA), involved in the sequential alteration of leaf form [15, 16].

More recently, many studies have begun to characterize the mechanistic link between gene expression, hormonal action and heterophylly [4, 17]. It has been observed that KNOTTED1-like homeobox orthologs participate in regulating heterophyllous expression for Rorippa aquatica (Brassicaceae), through the accumulation of gibberellin in the leaf primordia [17]. In the aquatic fern Marsilea quadrifolia, plant hormone ABA-responsive heterophylly genes were identified, showing diverse patterns of expression during heterophyllous induction [18]. The transcriptomic analysis of RNA-seq data identified the key role of SQUAMOSA promoter-binding protein like, NAC and YUCCA genes in the heterophyllous variation of Gevuina avellana, a temperate rainforest tree [19]. Despite extensive efforts to link gene expression with heterophylly, however, little is known about the genetic architecture of heterophyllous variation, including the number of genes involved, their genomic locations and the magnitudes of their genetic effects.

Genetic mapping or association studies built on artificial or natural populations provide a powerful tool to dissect the genetic control of heterophylly and relate this knowledge with the environmental adaptation of plants. To perform genetic mapping, heterrophylly is treated as a phenotypic trait that is defined quantitatively. Traditional approaches for defining leaf shape are based on the measurements of leaf traits, such as length, width, angle and ratio of length to width, analyzed by multivariate morphometric methods [20, 21], but these approaches are not precise, as they contain little information about the spatial distribution of shape change. As a result of this drawback, geometric morphometrics (GM) that can precisely characterize shape variation has arisen as a useful approach for shape analysis in the past two decades [22, 23]. Two GM approaches based on landmarks and outlines have been developed [24, 25] and, more recently, integrated into genetic mapping, aimed to map specific shape quantitative trait loci (QTLs) for a variety of organs [26–28].

Current models for shape mapping were designed to characterize shape variation on a single position of organisms at a time, but fail to capture the differentiation of organ shape on multiple positions, such as heterophylly, limiting their applications to addressing more complex biological questions. The motivations of this article are to expand the principle of GM-based shape mapping to map QTLs for multiple shapes and detail a statistical procedure of testing how a shape QTL contributes to heterophyllous variation within a plant. The statistical method was packed as an R platform, allowing the new method to be used freely by other researchers interested in studying the genetic architecture of heterophylly. The new method was applied to analyze mapping data of heterophylly in a woody plant, mei (Prunus mume), leading to the identification of key QTLs correlated with the capacity of plants to alter their leaf shape in response to environmental perturbations.

Model

Genetic design

A segregating population is prerequisite for mapping QTLs. Consider a mapping population that contains n plants all genotyped for a panel of molecular markers throughout the genome. Different from traditional strategies that measure and map a single phenotype, the new model allows high-dimensional phenotypic data to be mapped at the same time. Assume that J leaves, labeled as 1, … , J in order from bottom to top, located along the axis of a shoot are photoed for each plant. The contour of each leaf is delineated by choosing a finite number of semilandmarks (say L) on its boundary. These semilandmarks are spaced clockwise at equally spaced radii, having each point described by x and y coordinates, representing the shape of a leaf. Let t0, t1, … , tL denote the accumulated length of step segments from semilandmark 1, … , L, respectively.

Let zi1 = (xi1, yi1), … , ziJ = (xiJ, yiJ) denote x- and y-coordinate vectors on the curvatures of J sequential leaves from plant i, where xij = (xij(t0), xij(t1), … , xij(tL)) and yij = (yij(t0), yij(t1), … , yij(tL)) are the phenotypic values of L semilandmarks for leaf j from plant i, respectively. Consider a SNP whose three genotypes are AA with n1 observations, Aa with n2 observations and aa with n3 observations. The likelihood of coordinate values at the given SNP is expressed as
(1)
where fk(zi1, … , ziJ|φk,η) is a multivariate normal distribution of x- and y-coordinate shape phenotypes for J sequential leaves from plant i with SNP genotype k (k = 1 for AA, 2 for Aa and 3 for aa), φk is a set of parameters that describe a vector of expectation values specific to SNP genotype k, and η is a set of parameters that model the covariance structure common to all genotype groups. In fk(zi1, … , ziJ|φk,η), we will model genotyped-specific mean vectors (using parameters φk) and covariance structure (using parameters η). Mean vectors of x- and y-coordinates for SNP genotype k over L semilandmarks are expressed as:
(2)
The matrix of residual covariances of x- and y-coordinates among L semilandmarks for J leaves is expressed as:
where Σj on-diagonal is a (2L × 2L)-dimensional longitudinal matrix of variance–covariance between x- and y-coordinates for leaf j, and Σjj′=Σj′j off-diagonal is a (2L × 2L)-dimensional matrix of covariance between x- and y-coordinates of leaf j and j′. It is not unreasonable to assume that x- and y-coordinates at one leaf are independent of those at other leaves, suggesting that Σjj′ and Σj′j are zero matrices. Thus, we have
where Σj=[ΣjxΣjxyΣjyxΣjy]⁠, with
(3a)
(3b)
(3c)
It can be seen that overall matrix (3a) is composed of semilandmark-dependent residual variances for each coordinate, σxj2(l) and σyj2(l)⁠, residual covariances of each coordinate between different semilandmarks, σxj(l,l′) and σyj(l,l′) (l, l′ = 1, … , L), residual covariances between different coordinates at the same semilandmark, σjxy(l)⁠, and residual covariances between different coordinates over different semilandmarks, σjxy(xl,yl′)⁠. Next, we will show how to model the structures of matrices (3a)–(3c) by time-series statistical approaches.

Fourier modeling of the mean vectors

Outline-based shape mapping proposed by Bo et al. [28] models the mean vectors for each genotype by Elliptic Fourier (EF) analysis. EF capitalizes on a ‘Fourier series’ of ellipses to approximate an object’s outline through semilandmarks [29–31]. A periodic function, expressed as a weighted sum of simpler sinusoidal component functions, derived from the discrete Fourier transform was used to fit sampled semilandmarks along the outline. Denote the perimeter of the outline by T, which is equivalent to the period of the signal. Thus, for leaf j from plants of genotype k, we use the EF expansion to describe the coordinate sequences x and y at a random semilandmark, l (l = 1, … , L), with curvilinear abscissa of tl (tl = 0, … , T), expressed as:
(4a)
(4b)
where r is the number of harmonics, tl is the accumulated length of step segments at point l, T = tL is the perimeter expressed as the sum of lengths of all steps around the outline and a0kj and b0kj are the x- and y-coordinates of the centroid of the configuration for leaf j from genotype k estimated by:
(5a)
(5a)
arkj and brkj are Fourier coefficients of the rth harmonics for coordinate x of leaf j from genotype k, expressed as:
(6a)
(6b)
crkj and drkj are Fourier coefficients of the rth harmonics for coordinate y of leaf j from genotype k, expressed as:
(7a)
(7b)
Note that (a0ij, arij, brij, crij and drij) are the EF coefficients of leaf shape for individual plants, Δxijl=xij(tl+1)−xij(tl) and Δyijl=yij(tl+1)−yij(tl) are the displacements of leaf j from plant i between semilandmarks l and l + 1 along the x and y axis, respectively, and Δtl is the length of step l and l + 1. It can be seen that the characteristic of heterophylly for genotype k is determined jointly by parameter vectors:
(8a)
and
(8b)
which are expressed as φk = (⁠φkx⁠,φky⁠), describing the size and shape of J leaves using R harmonics. In practice, the number of desired harmonics R needed for reconstructing the outline is usually fewer than half the number of original sampled points, to fit a given outline with some reliability. However, the optimal number of harmonics can be determined by the goodness-of-fit using the sum of squared distances between the original data and reconstructed outline.

The shapes of all leaves from the same metamer on a shoot need to be aligned among different plants, to minimize variation caused by position, scale and rotation [32]. However, as heterophylly contains within-plant variation not only in leaf shape but also in leaf size, a Procrustes alignment is made for outlines of leaves from different metamers on the same shoot, by adjusting for variation only because of position and rotation but not because of scale. Giardina and Kuhl [33] proposed a direct procedure for normalizing the EF analysis coefficients calculated from raw outlines to remove the position and rotation effects. This procedure that was integrated into Bo et al.’s shape mapping can be used directly in the current model for mapping heterophylly.

Autoregressive modeling of the covariance matrix

The covariance matrices (3a)–(3c) are each composed of residual variances and covariances among spatially connected semilandmarks. Thus, time-series approaches can be used to model the structure of these covariance matrices. Let eijx(l) = xij(l)−μkjx(l) and eijy(l) = yij(l)− μkjy(l) denote residual errors of x- and y-coordinates at semilandmark tl on leaf j from plant i. To structure these residual matrices, we implement a bivariate first-order autoregressive model [34], which suggests the following relationships:
(9a)
(9b)
where pjx and pjy are the antedependent coefficients that describe the correlations between errors at two consecutive semilandmarks for leaf j within coordinates x and y, respectively, pjx←y and pjy←x are the antedependent coefficients that describe the impact of y- or x-coordinate at the previous semilandmark on x- or y-coordinate at the current semilandmark for leaf j, respectively, and εijx(l) and εijy(l) are the white noises of x- and y-coordinates that are independent across different semilandmarks, respectively, satisfying var(⁠εijx(l)⁠) = δxj2 and var(⁠εijy(l)⁠) = δyj2⁠, which are called the nugget (nonspatial variance).
By considering spatial covariance because of autocorrelation, the residual matrices (3a) and (3b) are rewritten as:
(10a)
(10b)
where σxj2 and σyj2 are the partial sills (spatial variances), and Rx and Ry are the spatial autocorrelation matrices for x- and y-coordinates, respectively. The autocorrelations can be modeled by a function, such as the exponential correlation rll′ = exp (–Dll′⁠), where Dll′ is the Mahalanobis distance between two semilandmarks l and l′ (l, l′ = 1, … , L). The residual matrix (3c) that models the interdependence of x- and y-coordinates is expressed as:
(10c)
where ρj and ψj are the nonspatial and spatial correlations between the two coordinates, respectively, and Rxy is the spatial autocorrelation between x- and y-coordinates from different semilandmarks.

Taken together, model parameters contained in Equations (10a–)–(10c), arrayed in η, were used to model the structure of residual covariance matrices for x- and y-coordinates. Based on such structural modeling, the closed forms of the determinants and inverses for the residual matrix, Σj⁠, can be derived. By implementing these closed forms into the solving procedure of likelihood (1), the computational efficient of residual covariance matrices can be enhanced.

Hypothesis tests

The existence of a QTL that determines heterophylly can be assessed by formulating hypotheses tests. These hypotheses from Equation (8a) and (8b) are expressed as:
(11)
where the H0 corresponds to the reduced model, in which there is no QTL, and the H1 corresponds to the full model, in which there is a QTL. The test statistics for the aforementioned hypotheses are calculated as the log-likelihood ratio of the reduced to the full model, which is compared with the critical threshold.
If a significant QTL is detected, we need to test whether this QTL controls heterophylly, and it can be tested by using the following hypotheses:

Under the null hypothesis, genotype-specific EF parameters can be estimated with the implementation of the EM algorithm with constraints.

Different components of Fourier series show different properties of leaf shape. The sine components in Equations (4a) and (4b) are related with the asymmetry of a leaf, whereas the cosine components are related with the symmetry of a leaf. Thus, by testing these two components separately, we can examine how a QTL affects the symmetry and asymmetry of a leaf.

We implemented the model of mapping heterophylly into an R-based platform, HpQTL, for its broad use by other interesting researchers. The package lists several functions for shape QTL mapping, including shape alignment and digitizing, EF curve fitting and QTL mapping.

A worked example

Plant material

The biological usefulness of the new model was validated by analyzing a mapping data about heterophylly in mei (P. mume), a woody plant species. By crossing two cultivars, P. mume ‘Fenban’ (BJFU1210120013) as the female parent and P. mume ‘Kouzi Yudie’ (BJFU1210120022) as the male parent, both from Qingdao Mei Garden, Qingdao, China, we obtained a segregating F1 population of 228 progeny [35, 36]. The population was genotyped for 1484 SNP markers and InDels. For a full-sib family derived from two heterozygous parents, a marker may be segregating according to either F2-like intercross or backcross-like testcross [37–39]. The markers genotyped include 271 intercross markers and 1213 testcross markers. Of these testcross markers, 620 and 593 are segregating because of the heterozygosity of parents Fenban and Kouzi Yudie, respectively. JoinMap version 4 [40] was used to construct a genetic linkage map from SSR and SNP markers. The map is composed of eight linkage groups corresponding to mei’s eight haploid chromosomes. The total length of the map is 670 cm, with an average marker distance of 0.5 cm.

All the F1 hybrids and their parents were grown in the Xiao Tangshan Horticultural Trial, Beijing, China [35, 36]. All F1 hybrids were cut off after 1 year of growth in the field. In the next spring, new shoots sprouted from 1 year rooting systems. During the end of July, the fast-growing season of mei, we chose three equally spaced leaves on the main stem to study the genetic control of heterophylly in woody plants. The shape of the three chosen leaves was measured by their digital images. The two parents, Fenban (female) and Kouzi Yudie (male), differ in leaf shape, with former having a more rounded leaf blade while the latter having a longer tip (Figure 1) The F1 genotypes derived from these two parents display considerable variation in leaf shape.

Differences in leaf shape between two parents, Fenban (female parent) and Kouzi Yudie (male parent), used to generate an F1 full-sib family. Three leaves, labeled as 1, 2 and 3, from the shoot tip, were sampled to show heterophylly.
Figure 1

Differences in leaf shape between two parents, Fenban (female parent) and Kouzi Yudie (male parent), used to generate an F1 full-sib family. Three leaves, labeled as 1, 2 and 3, from the shoot tip, were sampled to show heterophylly.

Open in new tabDownload slide

Mapping heterophylly QTLs

The R package implementing the new mapping model, i.e HpQTL, was used to analyze the heterophylly data of mei. Leaf image data were loaded in R, from which to discern the object and background and translate the images to black and white based on 600 × 900 pixels from a leaf digital image (Figure 2). Next, we marked a set of semilandmarks on the boundary of each leaf spaced at an equal radial angle (Figure 2) and get the coordinates of each point in a two-dimensional matrix, from which we can obtain the shape of each leaf in terms of x- and y-coordinates. It can be seen that there is great variability in x- and y-coordinates among the F1 hybrids, which can be compared with the difference in leaf shape between the two parents.

The procedure of extracting leaf boundary from a leaf image. (A) Original color images. (B) Black and white images translated from color images. (C) Shape alignment by filtering out the position, scale and rotation effects. (D) A set of points on the boundary spaced at an equal radial angle.
Figure 2

The procedure of extracting leaf boundary from a leaf image. (A) Original color images. (B) Black and white images translated from color images. (C) Shape alignment by filtering out the position, scale and rotation effects. (D) A set of points on the boundary spaced at an equal radial angle.

Open in new tabDownload slide

Normalized EF analysis aimed to remove the position and rotation effects of raw outlines [33] was used to fit curves to the outlines of leaf shape. The goodness-of-fit of the original data to normalized outlines depends on the choice of the number of harmonics in contour analysis. An optimal number of harmonics were determined by information criterion AIC. AIC suggests that four is an optimal number of harmonics, with the first four harmonics explaining nearly 95% of leaf shape information (Figure 3). The estimates of EF coefficients under the first nine harmonics are given in Supplementary Table S1. By reading marker data, we used HpQTL to perform QTL mapping for heterophylly described by Fourier functions, obtaining a plot of log-likelihood ratio values that reflect the significance of marker associations over the genome. Through a multiple comparison, we identified five significant QTLs associated with heterophyllous variation (Figure 4).

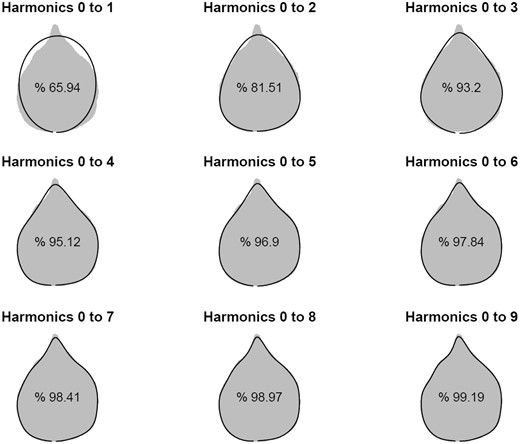
Outline reconstruction from EF analysis applied to the outline coordinates of a random leaf. The original outline corresponds to the gray shape, while reconstructed leaves are solid black outlines. The percentage of an actual leaf shape explained by the reconstructed shape, as seen in the leaf shape, increases with the harmonic order of EF function.
Figure 3

Outline reconstruction from EF analysis applied to the outline coordinates of a random leaf. The original outline corresponds to the gray shape, while reconstructed leaves are solid black outlines. The percentage of an actual leaf shape explained by the reconstructed shape, as seen in the leaf shape, increases with the harmonic order of EF function.

Open in new tabDownload slide
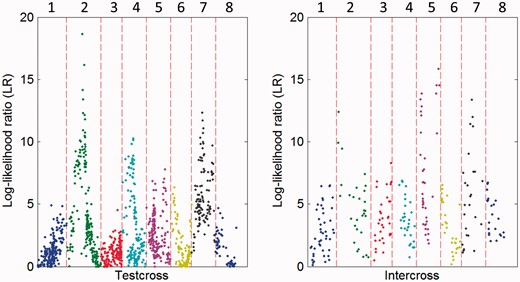
The genetic map locations of QTLs that control Fourier parameters throughout eight linkage groups of the P. mume genome. The cases for testcross markers and intercross markers are given, respectively, because they have different critical thresholds (15.0 for testcross markers and 14.8 for intercross markers at a marginal significance level) determined from permutation tests.
Figure 4

The genetic map locations of QTLs that control Fourier parameters throughout eight linkage groups of the P. mume genome. The cases for testcross markers and intercross markers are given, respectively, because they have different critical thresholds (15.0 for testcross markers and 14.8 for intercross markers at a marginal significance level) determined from permutation tests.

Open in new tabDownload slide

To show how a QTL controls heterophylly, we picked up the most significant QTL hk_hk1742 on chromosome 2 to explain its spatial pattern of genetic effect. Three genotypes of this QTL well explain the variation of leaf shape from each of three positions among F1 hybrids in terms of x- and y-coordinate values (Figure 5). By translating EF curves back to leaf shape, we can visualize in which part of leaf shape the three genotypes differ. For example, for the top leaf (Leaf 1), two homozygotes tend to be similar to each another, but both of which are different dramatically from the heterozygote. The heterozygote is relatively more ovate than the homozygotes.

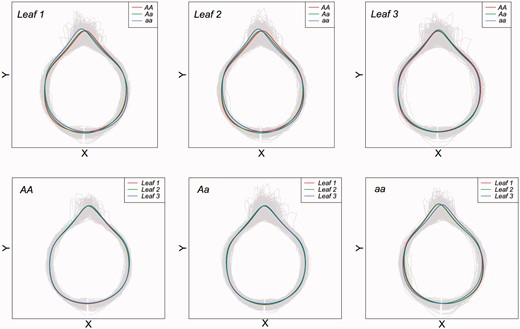
Visualized variation in the shape of three heterophyllous leaves in P. mume at an intercross QTL of the largest test statistic (hk_hk1742 on chromosome 2). The upper panel shows genotypic variation among three genotypes AA, Aa and aa for each leaf, whereas the lower panel shows heterophyllous variation for each genotype.
Figure 5

Visualized variation in the shape of three heterophyllous leaves in P. mume at an intercross QTL of the largest test statistic (hk_hk1742 on chromosome 2). The upper panel shows genotypic variation among three genotypes AA, Aa and aa for each leaf, whereas the lower panel shows heterophyllous variation for each genotype.

Open in new tabDownload slide

It is interesting to note that this QTL affects leaf shape in different ways depending on where a leaf is located on the main stem. Overall, the QTL displays an increased effect on leaf shape with an increasing leaf position according to hypothesis tests (11) (Figure 5), which suggests that this is a heterophyllous QTL.<AQ5/> Of three genotypes, the two homozygotes tend to be stable over different positions, but the heterozygote alters its leaf shape strikingly from the bottom to top. This result suggests that the dominant effect of this QTL produces an important role in regulating the heterophylly of mei trees.

Computer simulation

HpQTL was equipped with a functionality to perform Monte Carlo simulation studies which test the statistical power of the model and the precision of its parameter estimation. Here, we present an example to show the statistical property of HpQTL. The simulation mimicked the working example of mei, assuming a segregating population of 250 individuals in which a QTL exists to affect heterophylly. For each genotype of the QTL, we hypothesized a set of EF parameters from a Fourier series function with four harmonics for three heterophyllous leaves located on the same shoot. The phenotypic values of x- and y-coordinates for these three leaves were simulated by genotypic values of the QTL plus residual errors whose covariance structure follow the antedependence model.

Supplementary Table S2 gives the results about the maximum likelihood estimates of genotype-specific EE parameters from the assumed mapping population under 0.1 heritability of heterophylly. Overall, HpQTL provides reasonably accurate and precise estimates of all Fourier parameters for three heterophyllous leaves at different QTLs genotypes. By using these estimated parameters, we reconstructed the shape of each leaf at a different shoot position for the three genotypes (Figure 6). All leaf shapes can be well estimated, suggesting the statistical efficacy of HpQTL. We conducted an additional simulation study to investigate the power of heterophylly QTL detection by simulating the phenotypic data of a mapping population of 250 individuals containing a single group. It was found that the empirical power of QTL detection by HpQTL is beyond 0.95. Also, HpQTL can well estimate the genetic effect of the QTL on the heterophyllous differentiation of leaf shape among different shoot positions.

Comparison of estimated leaf shape with actual leaf shape for different genotypes and different heterophyllous leaves from simulated data.
Figure 6

Comparison of estimated leaf shape with actual leaf shape for different genotypes and different heterophyllous leaves from simulated data.

Open in new tabDownload slide

Discussion

A central question in developmental biology is how cells and tissues properly alter their performances over time to best adapt to endogenous and exogenous environments. One of the most pronounced examples of this phenomenon in plants is heterophylly that involves the transition of leaf size and shape from one position to next on the same shoot [11]. How heterophylly takes place, how it plays a role in ecological and evolutionary processes and, more importantly, what is its genetic signature have been an interesting subject of attention for centuries, and these questions have continued to intrigue modern biologists [5–10].

This study presented a quantitative description of heterophylly by implementing GM, overcoming the inaccuracy of traditional shape analysis purely relying on length, width, angle and ratio [32]. Although heterophyllous plants offer fascinating opportunities to study developmental questions related to plant adaptation and speciation, the previous description of heterophyllous changes in plants has developed in an inconsistent way, which prevents the extraction of useful information from this phenomenon. The GM-based approach developed can precisely characterize the subtle variation of leaf morphologies and their developmental changes over time and space. First, it quantifies the outline of leaf shape by fitting EF functions [29–31] and uses EF parameters to capture the origin and sources of shape variation. In plants, the place of leaves that exhibit phenotypic variation may be related to the plant’s capacity to respond to light irradiation. For example, more ovate leaves are thought to be able to capture more light than more lanceolate leaves [9]; thus, the detailed characterization of shape variation in different positions is of use to address key ecological questions in plants.

Second, we implemented EF functions into a genetic mapping or association study framework, allowing the underlying genetic control by individual QTLs to be characterized. This implementation leads to a so-called HpQTL R platform, which has multiple functionalities. It can test whether there is specific QTL that controls heterophylly in plant, followed by a testing procedure of how the QTL regulates heterophyllous change and how each QTL genotype changes its expression of leaf shape from the bottom to up position in plants. HpQTL can help users to calculate the power of QTL detection, assess the precision of parameter estimation and determine the sample size optimally used for QTL detection.

HpQTL may be modified in several aspects. First, the model should be able to model the allometric relationship of leaf size and shape [9]. The current version identifies leaf shape variation that may be partly because of size by not adjusting for the scale effect. By calculating a position-varying single measure of leaf shape from x- and y-coordinates, we may draw a curve over leaf boundary. Thus, the area under curve (AUC) can be used to specify the size of a leaf. By mapping the AUC, we can judge how size QTLs are consistent with shape QTLs from which a network of pleiotropic control over leaf size and shape can be charted.

As heterophylly may be the consequence of plant adaptation, HpQTL should be modified to model the environmental components of heterophyllous variation. By planting the mapping population in multiple environments with recombinant inbred lines or clonal replicates [41], heterophylly and its environment-dependent variation can be characterized. The phenotypic changes of the same genotype over different environment can be termed environment-induced phenotypic plasticity (EiPH) [41–44], whereas the changes of the same phenotype within a plant, such as heterophylly, termed development-induced phenotypic plasticity (DiPH) [11]. The extended HpQTL model will not only characterize the genetic control of EiPH and DiPH, respectively, but also the pleiotropic control network of both of these features, better charting a comprehensive picture of the genetic architecture of heterophylly. HpQTL can be freely downloaded by other researchers at http://ccb.bjfu.edu.cn/program.html or can be requested from the corresponding author.

Key Points

  • Morphological variation in leaf size and shape within a single plant is termed heterophylly, regarded as the plant’s adaptation to surrounding environmental conditions.

  • The biochemical and molecular mechanisms underlying heterophyllic alteration have been investigated increasingly in the community of plant biological research.

  • Despite its fundamental importance, the genetic architecture of heterophyllous variation has not been systematically explored because of unavailability of the software that can precisely quantify within-plant variation in leaf shape.

  • We described and assessed a geometric morphometric approach for mapping QTLs that affect heterophyllous variation and packed this approach into an R-based platform for public use.

Supplementary Data

Supplementary data are available online at http://bib.oxfordjournals.org/.

Funding

The Beijing Nova program (grant number Z161100004916074), the Medium and Long Scientific Research Project for Young Teachers in Beijing Forestry University (grant number 2016ZCQ02), National Natural Science Foundation of China (grant number 31401900), Special Fund for Forest Scientific Research in the Public Welfare (grant number 201404102) and ‘One-thousand Person Plan’ Award.

Lidan Sun is a lecturer in Ornamental Genetics in Beijing Key Laboratory of Ornamental Plants Germplasm Innovation and Molecular Breeding, National Engineering Research Center for Floriculture at Beijing Forestry University.

Jing Wang is a doctoral student in Computational Genetics in the Center for Computational Biology at Beijing Forestry University.

Xuli Zhu is a doctoral student in Computational Genetics in the Center for Computational Biology at Beijing Forestry University.

Libo Jiang is a doctoral student in Computational Genetics in the Center for Computational Biology at Beijing Forestry University.

Kirk Gosik is a PhD candidate in Statistical Genetics in the Department of Public Health Sciences at Pennsylvania State University.

Mengmeng Sang is a doctoral student in Computational Genetics in the Center for Computational Biology at Beijing Forestry University.

Fengsuo Sun a doctoral student in Computational Genetics in the Center for Computational Biology at Beijing Forestry University.

Tangren Cheng is an associate professor of Ornamental Genetics and the executive director of National Engineering Research Center for Floriculture at Beijing Forestry University.

Qixiang Zhang is a professor of ornamental genetics and the director of National Engineering Research Center for Floriculture at Beijing Forestry University.

Rongling Wu founded the Center for Computational Biology at Beijing Forestry University. He is distinguished professor of Statistics and director of the Center for Statistical Genetics at Pennsylvania State University.

References

1

Poethig
RS.
Phase change and the regulation of shoot morphogenesis in plants
.
Science
1990
;
250
:
923
–
30
.

Google Scholar

Crossref
Search ADS
PubMed

 
2

Poethig
RS.
The past, present, and future of vegetative phase change
.
Plant Physiol
2010
;
154
:
541
–
4
.

Google Scholar

Crossref
Search ADS
PubMed

 
3

Wanke
D.
The ABA-mediated switch between submersed and emersed life-styles in aquatic macrophytes
.
J Plant Res
2011
;
124
:
467
–
75
.

Google Scholar

Crossref
Search ADS
PubMed

 
4

Nakayama
H
,
Nakayama
N
,
Nakamasu
A
, et al.
Toward elucidating the mechanisms that regulate heterophylly
.
Plant Morphol
2012
;
24
:
57
–
63
.

Google Scholar

Crossref
Search ADS

 
5

Goebel
K.
Ueber die Jugendzustände der Pflanzen
.
Flora
1889
;
72
:
1
–
44
.

Google Scholar

OpenURL Placeholder Text

 
6

Arber
A.
On heterophylly in water plants
.
Am Nat
1919
;
53
:
272
–
8
.

Google Scholar

Crossref
Search ADS

 
7

Fassett
NC
,
A Manual of Aquatic Plants
.
Madison, WI
:
The University of Wisconsin Press
,
1930
.

Google Scholar

OpenURL Placeholder Text

 
8

Cook
SA
,
Johnson
MP.
Adaptation to heterogenous environments I. Variation in heterophylly in Ranunculus flammula L
.
Evolution
1968
;
22
:
496
–
516
.

Google Scholar

PubMed
OpenURL Placeholder Text

 
9

Costa
MMR
,
Yang
SX
,
Critchley
J
, et al.
The genetic basis for natural variation in heteroblasty in Antirrhinum
.
New Phytol
2012
;
196
:
1251
–
9
.

Google Scholar

Crossref
Search ADS
PubMed

 
10

Nakayama
H
,
Kimura
S.
Leaves may function as temperature sensors in the heterophylly of Rorippa aquatica (Brassicaceae)
.
Plant Signal Behav
2015
;
10
:
e1091909.

Google Scholar

Crossref
Search ADS
PubMed

 
11

Zotz
G
,
Wilhelm
K
,
Becker
A.
Heteroblasty: a review
.
Bot Rev
2011
;
77
:
109
–
51
.

Google Scholar

Crossref
Search ADS

 
12

Winn
AA.
The functional significance and fitness consequences of heterophylly
.
Intl J Plant Sci
1999
;
160
:
S113
–
21
.

Google Scholar

Crossref
Search ADS

 
13

Kaplan
DR.
Heteroblastic leaf development in Acacia—morphological and morphogenetic implications
.
La Cellule
1980
;
73
:
135
–
203
.

Google Scholar

OpenURL Placeholder Text

 
14

Lee
DW
,
Richards
JH.
 Heteroblastic development in vines. In:
Putz
FE
,
Mooney
HA
 (eds).
The Biology of Vines
.
Cambridge
:
Cambridge University Press
,
1991
,
205
–
43
.

Google Scholar

OpenURL Placeholder Text

 
15

Kuwabara
A
,
Ikegami
K
,
Koshiba
T
, et al.
Effects of ethylene and abscisic acid upon heterophylly in Ludwigia arcuata (Onagraceae)
.
Planta
2003
;
217
:
880
–
7
.

Google Scholar

Crossref
Search ADS
PubMed

 
16

Iida
S
,
Miyagi
A
,
Aoki
S
, et al.
Molecular adaptation of rbcL in the heterophyllous aquatic plant Potamogeton
.
PLoS One
2009
;
4
:
e4633.

Google Scholar

Crossref
Search ADS
PubMed

 
17

Nakayama
H
,
Nakayama
N
,
Seiki
S
, et al.
Regulation of the KNOX-GA gene module induces heterophyllic alteration in North American lake cress
.
Plant Cell
2014
;
26
:
4733
–
48
.

Google Scholar

Crossref
Search ADS
PubMed

 
18

Hsu
TC
,
Liu
HC
,
Wang
JS
, et al.
Early genes responsive to abscisic acid during heterophyllous induction in Marsilea quadrifolia
.
Plant Mol Biol
2001
;
47
:
703
–
15
.

Google Scholar

Crossref
Search ADS
PubMed

 
19

Ostria-Gallardo
E
,
Ranjan
A
,
Chitwood
DH
, et al.
Transcriptomic analysis suggests a key role for SQUAMOSA PROMOTER BINDING PROTEIN LIKE, NAC and YUCCA genes in the heteroblastic development of the temperate rainforest tree Gevuina avellana (Proteaceae)
.
New Phytol
2016
;
210
:
 694
–
708
.

Google Scholar

Crossref
Search ADS
PubMed

 
20

Bookstein
FL.
The Measurement of Biological Shape and Shape Change
.
New York, NY
:
Springer-Verlag
,
1978
.

Google Scholar

Crossref
Search ADS

 
21

Slice
DE.
Geometric morphometrics
.
Ann Rev Anthropol
2007
;
36
:
261
–
81
.

Google Scholar

Crossref
Search ADS

 
22

Bookstein
FL.
Morphometric Tools for Landmark Data: Geometry and Biology
.
New York, NY
:
Cambridge University Press
,
1991
.

Google Scholar

OpenURL Placeholder Text

 
23

Adams
DC
,
Rohlf
FJ
,
Slice
DE.
A field comes of age: geometric morphometrics in the 21st century
.
Hystrix
2013
;
24
:
7
–
14
.

Google Scholar

OpenURL Placeholder Text

 
24

Adams
DC
,
Otárola-Castillo
E.
geomorph: an R package for the collection and analysis of geometric morphometric shape data
.
Methods Ecol Evol
2013
;
4
:
393
–
9
.

Google Scholar

Crossref
Search ADS

 
25

Crampton
JS.
Elliptic Fourier shape analysis of fossil bivalves: some practical considerations
.
Lethaia
1995
;
28
:
179
–
86
.

Google Scholar

Crossref
Search ADS

 
26

Fu
G
,
Berg
A
,
Das
K
, et al.
A statistical model for mapping morphological shape
.
Theor Biol Med Model
2010
;
7
:
28.

Google Scholar

Crossref
Search ADS
PubMed

 
27

Fu
GF
,
Bo
WB
,
Pang
XM
, et al.
Mapping shape QTLs using a radius-centroid-contour model
.
Heredity
2013
;
110
:
511
–
19
.

Google Scholar

Crossref
Search ADS
PubMed

 
28

Bo
WH
,
Wang
Z
,
Xu
F
, et al.
Shape mapping: genetic mapping meets geometric morphometrics
.
Brief Bioinform
2014
;
15
:
 571
–
81
.

Google Scholar

Crossref
Search ADS
PubMed

 
29

Kaesler
RL
,
Waters
JA.
Fourier analysis of the ostracode margin
.
Geol Soc Am Bull
1972
;
83
:
1169
–
78
.

Google Scholar

Crossref
Search ADS

 
30

Kuhl
FP
,
Giardina
CR.
Elliptic Fourier features of a closed contour
.
Comput Graph Image Proc
1982
;
9
:
236
–
58
.

Google Scholar

Crossref
Search ADS

 
31

Rohlf
FJ
,
Archie
J.
A comparison of Fourier methods for the description of wing shape in mosquitos (Diptera: Culicidae)
.
Syst Zool
1984
;
33
:
302
–
17
.

Google Scholar

Crossref
Search ADS

 
32

Kendall
DG.
Shape manifolds, procrustean metrics, and complex projective spaces
.
Bull London Math Soc
1984
;
16
:
81
–
121
.

Google Scholar

Crossref
Search ADS

 
33

Giardina
CR
,
Kuhl
FP.
Accuracy of curve approximation by harmonically related vectors with elliptical loci
.
Comput Graph Image Process
1977
;
6
:
277
–
85
.

Google Scholar

Crossref
Search ADS

 
34

Li
N
,
McMurry
T
,
Berg
A
, et al.
Functional clustering of periodic transcriptional profiles through ARMA(p,q)
.
PLoS ONE
2010
;
5
(
4
):
e9894.

Google Scholar

Crossref
Search ADS
PubMed

 
35

Sun
L
,
Wang
Y
,
Yan
X
, et al.
Genetic control of juvenile growth and botanical architecture in an ornamental woody plant, Prunus mume Sieb. et Zucc. as revealed by a high-density linkage map
.
BMC Genet
2014
;
15
:
S1.

Google Scholar

Crossref
Search ADS
PubMed

 
36

Sun
L
,
Yang
W
,
Zhang
Q
, et al.
Genome-wide characterization and linkage mapping of simple sequence repeats in mei (Prunus mume Sieb. et Zucc.)
.
PLoS ONE
2013
;
8
:
e59562.

Google Scholar

Crossref
Search ADS
PubMed

 
37

Wu
R
,
Ma
CX
,
Painter
I
, et al.
Simultaneous maximum likelihood estimation of linkage and linkage phases in outcrossing species
.
Theor Popul Biol
2002
;
61
:
349
–
63
.

Google Scholar

Crossref
Search ADS
PubMed

 
38

Lu
Q
,
Cui
Y
,
Wu
R.
A multilocus likelihood approach to joint modeling of linkage, parental diplotype and gene order in a full-sib family
.
BMC Gent
2004
;
5
:
1.

Google Scholar

OpenURL Placeholder Text

 
39

Tong
C
,
Wang
Z
,
Zhang
B
, et al.
3FunMap: full-sib family functional mapping of dynamic traits
.
Bioinformatics
2011
;
27
:
2006
–
8
.

Google Scholar

Crossref
Search ADS
PubMed

 
40

Van Ooijen
J.
JoinMap®4, Software for the Calculation of Genetic Linkage Maps in Experimental Populations
.,
Wageningen
:
Kyazma BV
,
2006
.

Google Scholar

OpenURL Placeholder Text

 
41

Jiang
LB
,
Clavijo
JA
,
Sun
LD
, et al.
Plastic expression of heterochrony quantitative trait loci (hQTL) for leaf growth in the common bean (Phaseolus vulgaris L.)
.
New Phytol
2015
;
207
:
872
–
82
.

Google Scholar

Crossref
Search ADS
PubMed

 
42

Wu
R.
The detection of plasticity genes in heterogeneous environments
.
Evolution
1998
;
54
:
967
–
77
.

Google Scholar

Crossref
Search ADS

 
43

Donohue
K.
Development in the wild: phenotypic plasticity
.
Ann Plant Rev
2013
;
45
:
321
–
56
.

Google Scholar

OpenURL Placeholder Text

 
44

Wang
Z
,
Pang
XM
,
Wu
WM
, et al.
Modeling phenotypic plasticity in growth trajectories: a statistical framework
.
Evolution
2014
;
68
:
81
–
91
.

Google Scholar

Crossref
Search ADS
PubMed

 

Author notes

These authors Lidan Sun, Jing Wang, Xuli Zhu and Libo Jiang contributed equally to this work.

© The Author 2017. Published by Oxford University Press. All rights reserved. For Permissions, please email: [email protected]
This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)
Issue Section:
Paper
Download all slides
  • Supplementary data

    • Supplementary data

    Supplementary Data - doc file