-
PDF
- Split View
-
Views
-
Cite
Cite
Giobbe Forni, Jacopo Martelossi, Pablo Valero, Frank H Hennemann, Oskar Conle, Andrea Luchetti, Barbara Mantovani, Macroevolutionary Analyses Provide New Evidence of Phasmid Wings Evolution as a Reversible Process, Systematic Biology, Volume 71, Issue 6, November 2022, Pages 1471–1486, https://doi.org/10.1093/sysbio/syac038
Close - Share Icon Share
Abstract
The concept that complex ancestral traits can never be recovered after their loss is still widely accepted, despite phylogenetic and molecular approaches suggest instances where phenotypes may have been lost throughout the evolutionary history of a clade and subsequently reverted back in derived lineages. One of the first and most notable examples of such a process is wing evolution in phasmids; this polyneopteran order of insects, which comprises stick and leaf insects, has played a central role in initiating a long-standing debate on the topic. In this study, a novel and comprehensive time tree including over 300 Phasmatodea species is used as a framework for investigating wing evolutionary patterns in the clade. Despite accounting for several possible biases and sources of uncertainty, macroevolutionary analyses consistently revealed multiple reversals to winged states taking place after their loss, and reversibility is coupled with higher species diversification rates. Our findings support a loss of or reduction in wings that occurred in the lineage leading to the extant phasmid most recent common ancestor, and brachyptery is inferred to be an unstable state unless co-opted for nonaerodynamic adaptations. We also explored how different assumptions of wing reversals probability could impact their inference: we found that until reversals are assumed to be over 30 times more unlikely than losses, they are consistently inferred despite uncertainty in tree and model parameters. Our findings demonstrate that wing evolution is a reversible and dynamic process in phasmids and contribute to our understanding of complex trait evolution. [Dollo’s law; Phasmatodea; phylogenetic comparative methods; polyneoptera; reversals; wing.]
Traits are commonly lost during evolution, and although some changes can be easily reverted in the short term (Rebolleda-Gómez et al. 2019; Teotónio and Rose 2000), it can be argued that complex structures lost in the line of evolution cannot revert back to their former state over long time spans. This concept is often referred to as Dollo’s law (Dollo 1893), although in its original conception, reversals of complex traits were considered possible as secondary convergence events (i.e., homoplasies, Gould 1970). This evolutionary principle has become popular due to the intuitive examples supporting it and is still commonly accepted, despite a large number of cases where it is apparently violated have been proposed (Collin and Miglietta 2008).
Most evidence of the reversible evolution of complex traits comes from phylogenetic comparative approaches and includes a large number of examples, such as shell coiling in limpets (Collin and Cipriani 2003), compound eyes in ostracods (Syme and Oakley 2012), sex and parasitism in mites (Domes et al. 2007; Klimov and O’Connor 2013), mandibular teeth in frogs (Wiens 2011), limb evolution (Kohlsdorf and Wagner 2006), and eggshells and oviparity (Lynch and Wagner 2010; Recknagel et al. 2018; Esquerré et al. 2019) in Squamata. At the same time, several possible mechanisms underlying the reversible evolution of complex traits have been suggested, including phenotypic plasticity (Parker et al. 2021; Visser et al. 2021) and reticulate evolution (Horreo et al. 2020). Examples of compensatory mutations that have been able to rescue the once-lost functionality of genes have also been found (Esfeld et al. 2018), and it has been observed that a reversal to a lost ancestral state could happen through changes in relatively few genes (Seher et al. 2012). Moreover, some observations suggest that the molecular blueprint associated with a trait could be preserved even in its phenotypical absence (e.g., Carlini et al. 2013; Leal and Cohn 2016) due to chance (Marshall et al. 1994; Lynch 2021) or pleiotropic constraints (Lammers et al. 2019).
Among the many examples of the reversibility of complex traits, i.e., those made by several integrated components, the evolution of wings in phasmids stands as one of the first and most iconic examples (Whiting et al. 2003) and played a central role in initiating a long-standing debate on this topic (Collin and Miglietta 2008). This polyneopteran order of insects includes over 450 genera and 3300 described species, of which 40|$\%$|circa are macropterous, whereas the remaining are either brachypterous or apterous (Brock et al. 2021). As shown in Figure 1, the wings of phasmids present a high level of anatomical disparity, and differences can be found at all taxonomic levels, including between congeneric species (Zeng et al. 2020). Macropterous phasmid species present wings that can sustain flight or control free-fall descent from tree canopies, depending on the wing-to-body size ratio (Maginnis 2006). Some lineages have also evolved nonaerodynamic adaptations for wings, such as aposematic coloration or stridulation capacity, which are typical of brachypterous forms.
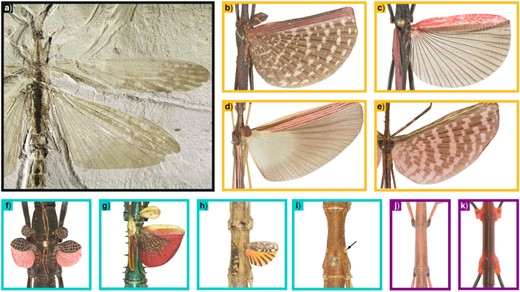
Wing disparity among extinct and extant Phasmatodea. a) Aclistophasma echinulatum (Yang, Engel & Gao 2021); b) Pterinoxylus crassus Kirby 1889; c) Orthomeria kangi (Vallotto, Bresseel, Heitzmann & Gottardo, 2016); d) Parastratocles fuscomarginatus (Conle, Hennemann, Bellanger, Lelong, Jourdan & Valero, 2020); e) Diesbachia tamyris (Westwood 1859); f) Peruphasma schultei Conle and Hennemann 2005; g) Achrioptera manga (Glaw, Hawlitschek, Dunz, Goldberg & Bradler 2019); h) Phaenopharos struthioneus (Westwood 1859); i) Hypocyrtus ornatissimus (Brunner von Wattenwyl 1907); j) Bacillus atticus Brunner von Wattenwyl 1882; k) Oreophoetes peruana (Saussure 1868). Boxes are colored according to the trait state: gold |$=$| macroptery, turquoise |$=$| brachyptery, and violet |$=$| aptery. All photographs were taken by Pablo Valero, with the exception of A. echinulatum, which was provided by Hongru Yang.
Wings emerged early in the diversification of insects, with frequent losses occurring during their evolutionary history (Wipfler et al. 2019). In 2003, Whiting et al. proposed that wings disappeared in the lineage that led to extant phasmids, and subsequent reversals restored the lost structures throughout the evolutionary history of the clade. Shortly after this claim, several comments followed (Stone and French 2003; Trueman et al. 2004) and, even with a growing consensus that lost traits can be recovered (Porter and Crandall 2003; Wiens 2011), several possible weak arguments have been exposed in the paper by Whiting et al.; concurrently, many approaches have been proposed to avoid the incorrect rejection of traits irreversible loss. Root prior probability (Goldberg and Igić 2008; Sauquet et al. 2017), trait-dependent diversification rates (Goldberg and Igić 2008; Holland et al. 2020), and tree uncertainty (Bollback 2006; Rangel et al. 2015) must all be carefully considered when testing for the irreversible evolution of a trait.
Phylogenetic tests of irreversible trait evolution are frequently misled by inappropriate assignment of the character state distribution at the root, which should be avoided unless unequivocal evidence is available. Extinct phasmatodean clades such as Gallophasmatidae, Pterophasmatidae and Susumanioidea are thought to represent stem groups of modern stick and leaf insects, and they do not allow us to make conclusive considerations of the wing status of the most recent common ancestor (MRCA) of the extant species (Yang et al. 2019, 2021). Nonetheless, a stark difference can be observed between the wings of extinct stem phasmids and those of extant species: the latter have either reduced or absent tegmina (hardened forewings), whereas stem fossil specimens present both pairs of full-sized wings. This is the case for the fossil specimen Aclistophasma echinulatum, which is shown in Figure 1a. In insects, wings confer a plethora of potential advantages, such as evading predators, dispersal, and mate-finding (Goldsworthy and Wheeler 1989). However, partial reduction or complete loss can have adaptive value as well: wing loss has been related to increased female fecundity (Roff 1994) and cryptic capacity (Whiting et al. 2003) and to trade-offs in resource allocation between different anatomical structures (Maginnis 2006). In several insect clades, different flight capabilities are associated with different diversification rates and both dispersal reduction and increases can act as possible drivers of diversification (Ikeda et al. 2012; Misof et al. 2014; Waters et al. 2020). Other than flight, different nonaerodynamics adaptations can be associated to wings and can drive species diversification dynamics (e.g., features under sexual selection; Singh and Singh 2014; Hawkes et al. 2019). When the state of a trait affects species diversification rates, it can drive its distribution along a clade phylogeny; in this context, traits that are irreversibly lost and are expected to become less frequent throughout the evolution of a clade can instead be widespread if they drive species diversification dynamics (Goldberg and Igić 2008). This phenomenon can lead to strong biases in transition rate estimation and ancestral state inference reconstruction when common MK models, which assume that the state of the trait does not influence the probability of extinction or speciation, are used (Holland et al. 2020). Even if there is contrasting evidence regarding the interaction between phasmid wings and clade diversification dynamics (Zeng et al. 2020; Bank and Bradler 2022), this aspect needs to be carefully considered when testing for irreversible trait evolution. Approaches that model the relationships among character states and diversification rates (*SSE models; State Speciation and Extinction) can perform well even in such scenarios; moreover, this framework can be further expanded to include “hidden states” (Hidden State Speciation and Extinction [HiSSE]; Beaulieu and O’Meara 2016), which can avoid spurious correlations (Rabosky and Goldberg 2015) and account for heterogeneity over time and across lineages. An additional obstacle in elucidating wing evolutionary patterns comes from phylogenetic uncertainty, which is often associated with Euphasmatodea (i.e., all Phasmatodea excluding Timematodea, which include the single genus Timema). Although a recent phylotranscriptomic sequencing effort shows fundamental progress for understanding the systematic relationships of the major clades of Euphasmatodea (Simon et al. 2019; further refined in Tihelka et al. 2020), the clade still presents uncertain instances in both systematic relationships and divergence times (e.g., Robertson et al. 2018). As such, this kind of uncertainty cannot be disregarded when studying macroevolutionary patterns in the clade.
In this study, we reconstructed a comprehensive time tree of over 300 phasmid species and leveraged it to explore the evolutionary patterns of wings in the clade. We tested the hypothesis that reversals could restore a trait to its former state subsequently to its loss by taking advantage of multiple approaches, including different trait-coding strategies along with global (model-fitting) and local (ancestral state reconstruction; ASRs) approaches. We considered common biases in phylogenetic comparative analyses and implemented all possible recommendations proposed for testing reversible trait evolution, such as trait-dependent diversification rates and phylogenetic uncertainty. Furthermore, we tested the impact of different assumptions about the probability of wing losses and reversals on our findings. By addressing these questions relative to the phasmid wing, we used an iconic case to test to what extent the evolution of a complex trait can be a dynamic and reversible process.
Materials and Methods
Phylogenetic Data Set
Samples were collected, morphologically identified, and preserved dry or in ethanol until molecular analyses were carried out. Genomic DNA was extracted from leg tissues of 111 individuals (Supplementary Table S1 available on Dryad at https://doi.org/10.5061/dryad.9kd51c5k2) using the “Smarter Nucleic Acid Preparation” (Stratec) protocol. Eight molecular markers were amplified, consisting of two mitochondrial (two fragments of cytochrome oxidase subunit I; one of cytochrome oxidase subunit II) and one nuclear (histone subunit 3) protein-coding gene (PCG) along with two mitochondrial (12S; 16S) and two nuclear (28S; 18S) ribosomal RNAs (rRNAs). PCRs were carried out according to standard protocols; primer sequences and annealing conditions can be found in Supplementary Table S2 available on Dryad. PCR products were screened through 1|$\%$| agarose gel electrophoresis and purified using ExoSAP PCR Product Cleanup Reagent (Thermo Fisher). Amplicons were Sanger sequenced by Macrogen Europe Lab. Chromatograms were inspected with SeqTrace 0.9.0 (Stucky 2012), and the resulting sequences were visualized using Aliview v1.26 (Larsson 2014). BLASTn (Zhang and Madden 1997) on the NCBI GenBank database was used to search for potential contaminants. Additional sequences were obtained from unpublished in-house projects on Euphasmatodea systematics (GenBank accession numbers MN449491-MN449962 and MT077516-MT077845) and from all specimens for which species-level identification was available from the following papers: Whiting et al. (2003), Buckley et al. (2009, 2010), Bradler et al. (2014, 2015), Goldberg et al. (2015), Robertson et al. (2018), and Glaw et al. (2019). As outgroups, we included sequences of 23 Notoptera species (Grylloblattodea |$+$| Mantophasmatodea; Jarvis and Whiting 2006; Damgaard et al. 2008). Taxonomic annotation is provided in Supplementary Table S1 available on Dryad. We did not consider Embioptera, which would represent the true sister group of Phasmatodea, as both previously published (Song et al. 2016) and our own exploratory analyses showed that their inclusion introduces long-branch attraction artifacts.
Rogue Taxa Removal and Time-Tree Inference
All sequences were aligned using Mafft 7.402 (Katoh and Standley 2013): PCGs were translated into amino acids using AliView v1.26, aligned using the “L-INS-i” algorithm, and subsequently retrotranslated into nucleotides. rRNAs were aligned using the “–X-INS-i” algorithm to consider their secondary structure. Gblock v. 0.91b (Castresana 2000) was used to exclude possible misaligned positions, selecting the codon flag for PCGs and the nucleotide flag for rRNAs. Other parameters were set as follows: the minimum number of sequences for a conserved position was 50|$\%$| (PCGs and rRNA) of the sequences included in the alignment; the minimum number of sequences for a flanking position was 70|$\%$| for PCGs and 60|$\%$| for rRNAs; the maximum number of contiguous nonconserved positions was 8 for PCGs and 10 for rRNAs; the minimum length of a block was 10 for PCGs and 5 for rRNAs; and the allowed gap position was all for PCGs and with half for rRNAs. Each alignment was then concatenated using Phyutility v. 2.2 (Smith and Dunn 2008).
Maximum likelihood inference was performed using IQ-TREE 1.6.12 (Nguyen et al. 2015), and the concatenated alignment was partitioned a priori into 12 subsets consisting of four rRNA genes (12S, 16S, 18S, and 28S) and the three codon positions of the three protein-coding genes (COI, COII, and H3). The best-fit partitioning scheme and evolutionary model were chosen using ModelFinder (Kalyaanamoorthy et al. 2017) according to the BIC score (Supplementary Table S3 available on Dryad). Branch support was estimated with 1000 UltraFast parametric bootstrap replicates (Minh et al. 2013). RogueNaRok (Aberer et al. 2013) was used to identify and remove rogue taxa until no rogue taxa were found.
We carried out two Bayesian inferences with Beast 2.6.3 (Bouckaert et al. 2014): a first one using only the monophyletic constraints associated with fossil calibrations (Supplementary Table S4 available on Dryad) and a second one including additional monophyletic constraints to match the phylogenomic resolution of Tihelka et al. (2020) (Supplementary Materials available on Dryad). In both instances, divergence times estimation, tree inference, and model averaging were jointly performed with the bModelTest package (Bouckaert and Drummond 2017) using a fully Bayesian framework. The concatenated alignment was partitioned a priori by gene with unlinked site models and linked tree and clock models; a relaxed clock with a lognormal distribution and a birth–death model were used as clock and tree priors, respectively. An exponential distribution was chosen as the prior distribution with a minimum hard bound set to the age of the fossil and a soft maximum bound 410 million years ago (Ma), which is the estimated age of the oldest hexapod fossil (the Rhynie Chert Rhyniella praecursor;Hirst and Maulik 1926; Wolfe et al. 2016). Two independent chains were run for 400 million generations and sampled every 5000 states. After convergence and adequate ESS were assessed (|$>$|200) with Tracer v.1.7.1 (Rambaut et al. 2018), log files and tree files were combined with LogCombiner v. 2.6.2, and a 25|$\%$| conservative burn-in was used. For subsequent macroevolutionary analyses, we used (1) a random sampling of 1000 trees from the posterior distribution of the BI inference that leveraged only the monophyletic constraints associated with fossil calibrations (Fossils-Constrained trees or FC-Trees) or (2) the maximum clade credibility tree derived from the BI that leverages phylogenomic constraints (Phylogenomic-Constrained tree or PC-Tree); for the latter, trees were summarized retaining the median node heights in TreeAnnotator v. 2.4.2. Analyses using FC-Trees allowed us to take into consideration the impact of uncertainty in systematic relationships and divergence times, whereas analyses with the PC-Tree leveraged the current best single hypothesis for the evolutionary history of Phasmatodea.
Morphological Data Sets
The morphological data sets of wing states were compiled from all available sources, including collected specimens and images on the Phasmida Species File portal (http://phasmida.speciesfile.org; last accessed in July 2020). We considered wings to be a species-level trait, and in the case of sexual dimorphism, the more “complex” structure between the two sexes was considered (e.g., a species with apterous females and brachypterous males was considered brachypterous). In the first coding scheme, wing morphology was coded as a 2-states trait, with presence as 1 (including both macroptery and brachyptery) and absence as 0 (aptery). An alternative 3-states coding scheme considered macroptery and brachyptery as different states, so that 0 was aptery, 1 was brachyptery, and 2 was macroptery. Brachypterous species were defined as having alae reaching up to the posterior margin of abdominal tergum II, whereas we considered macropterous species as having alae projecting over the posterior margin of tergum II. All coding schemes are provided in Supplementary Table S1 available on Dryad.
For both the FC-Trees and the PC-Tree, we pruned all outgroup species and a single ingroup species, Dimorphodes prostasis, Westwood 1859, for which no conclusive morphological information was available.
MK Models Considering Two States (Winged and Apterous)
We initially used a model comparison approach that evaluated three common MK models through the fitDiscrete function of the R package geiger v2.0 (Pennell et al. 2014). These models included (1) equal rates (ER), (2) all rates different (ARD), and (3) loss only (LO). All the models were fitted on the PC-Tree, and their resulting corrected Akaike Information Criterion (AICc) scores were compared. To consider tree uncertainty in model selection and parameter estimations, we used the influ_discrete function from the R package sensiPhy v0.8.5 (Paterno et al. 2018) and fit all aforementioned models to the 1000 FC-Trees.
ASRs were performed on the PC-Tree with the best-fit model of evolution and other models. The rayDISC function and a prior root probability weighted according to the methods of Maddison et al. (2007) and FitzJohn et al. (2009) were used so that root state probability was weighted according to their conditional probability given the data (ER-MADDFITZ and ARD-MADDFITZ).
As this assumption can greatly influence ASR and parameter estimation (Goldberg and Igić 2008; Sauquet et al. 2017), to test the sensitivity of our results, we performed two additional ASRs with ER and ARD models and a flat prior so that the root state is equally likely to be in states 0 and 1 (ER-FLAT and ARD-FLAT). We also performed two additional ASRs assuming a winged MRCA (by fixing the root state to 1) and assuming either a loss-only (LO) model or allowing for reversals (ER-WR and ARD-WR).
To take into account parameter and tree uncertainty in ASR, we performed stochastic character mapping (SCM) using the make.simmap function, implemented in Phytools (Revell 2012), under the best-fit model on the PC-Tree with 100 simulations (100Sim) and across 100 randomly sampled FC-Trees with one simulation (100Trees).
MK Models Considering Three States (Macropterous, Brachypterous, and Apterous)
When considering brachyptery, our comparative analyses followed the same approach used with the 2-states character-coding scheme but took into account a wider range of evolutionary models. We fitted the three unordered MK models previously used: (1) ER, (2) ARD, and (3) LO, and added a (4) symmetrical model (SYM). We also took into consideration additional biologically meaningful custom MK models, in which one or more transitions were fixed to 0: (5) ordered loss only (O-LO), in which only losses between proximal states were allowed; (6) partial reversal brachyptery, where all losses and transitions from brachypterous to macropterous forms were allowed; (7) partial reversal of aptery to brachyptery (PR-AB), where all losses and transitions from apterous to brachypterous were allowed; (8) ordered complete gain, with all losses allowed plus transitions from apterous to brachypterous and from brachypterous to macropterous; and (9) ordered full model (O-FM), where only transitions between proximal states were allowed. A graphical representation of these models can be found in Supplementary Figure S1 available on Dryad. As before, this model-fitting approach was carried out on both the PC-Tree and the 1000 randomly sampled FC-Trees. In the latter case, for simplicity and due to computational limits, we excluded from these analyses the O-LO and PR-AB models (see Results for justification). As sensiPhy can handle only binary characters, we used a custom script to run the fitDiscrete function on the 1000 FC-Trees.
As the outcome of model-fitting analyses was quite conclusive (see Results), we conducted the ASRs on the PC-Tree using rayDISC with the best-fit model only and a maddfitz or flat prior (ARD-MADDFITZ and ARD-FLAT). Unlike the analyses carried out with the 2-states coding, the transition rates inferred by rayDISC and fitDiscrete were different, so we also carried out an additional ASR to mirror previous model selection analyses with fitDiscrete (forcing transition rates calculated by fitDiscrete and a maddfitz root prior; ARD-FIXED). As for the 2-states coding analyses, we performed an ASR with an ARD model and fixed the root state to be macropterous (ARD-WR).
Additionally, tree and parameter uncertainty in ASR was taken into consideration by carrying out two SCM analyses with 100 simulations on the PC-Tree (100Sim) and 100 randomly sampled FC-Trees with one simulation (100Trees).
Analyses in a HiSSE Framework
To assess whether trait-dependent diversification rates could bias our previous analyses and to consider a heterogeneous evolutionary process across different parts of the phylogeny, we relied on the HiSSE framework in R (Beaulieu and O’Meara 2016). The association between shifts in phasmid diversification rates and the evolution of wings and flight capabilities was tested using 2-states character coding (macroptery and brachyptery as 1; aptery as 0; Supplementary Table S1 available on Dryad and Supplementary Materials available on Dryad). We tested a wide range of possible macroevolutionary scenarios on the PC-Tree: in addition to standard Binary State Speciation and Extinction (BiSSE) and HiSSE models, where all transitions between observed and hidden states were allowed, we took advantage of the HiSSE framework to test four classes of biologically meaningful custom models with two hidden states and different assumptions on the possible transitions between observed and hidden states. Specifically, we tested models assuming the reversibility between apterous and winged states only in hidden state A and (1) a full reversible hidden state B; (2) a hidden state B that is reversible only in the winged state; (3) a hidden state B that is reversible only in the apterous state; and (4) a hidden state B that is irreversible in both observed states. We also built null versions separately for each model, including custom versions, to test the interaction between wing states and diversification dynamics (i.e., fixing diversification rates to be equal between winged and apterous species and to vary only between hidden states, including multiple CID-2 and CID-4 models). All models were fitted multiple times with different numbers of free parameters (i.e., equal or different extinction fractions and/or forcing multiple transition rates between both observed and hidden states to be equal and/or different). In total, 43 models were tested: a graphical overview of transition rates allowed between the observed and hidden states in the different custom models can be found in Supplementary Figure S2 available on Dryad. To account for incomplete taxon sampling, in all analyses, the sampling fraction of winged and wingless species was set to 0.1 and 0.09, respectively, considering that of the |$\sim$|3300 described species, |$\sim$|45|$\%$| presented wings (either macropterous or brachypterous). This estimate represents a middle ground between what was reported by Brock et al. 2021 (40|$\%$| of winged species) and by Zeng et al. 2020 (in 51|$\%$| of species, males are winged/brachypterous, but the authors acknowledge that their taxon sampling may be biased toward winged species).
All macroevolutionary scenarios were compared through AICc and model averaged with the GetModelAveRates and GetAICWeights functions from the Hisse package. Inferred net diversification rates of winged and apterous species were then compared with a two-sided Wilcoxon rank sum test in R.
Impact of Different Assumptions Regarding Wing Reversal Probability on Their Inference
As previous approaches leveraged no information on transition rates between different states other than the trait distribution on the tips of the tree and the tree itself, we explored the impact of different assumptions of the probability of wing reversals on our analyses. We assumed a diminishing probability of reversals compared with losses (from 1:1 to 1:500 with an interval of 10, corresponding to an ER model and an approximation of an LO model) in conjunction with loss rates between 0.001 and 0.02, with an interval of 0.001. These rates were chosen to reflect the optimized values found in previous analyses (0.00350 for the ER model and 0.00886 for the LO model; see Results). We carried out SCM using the Phytools function using either 100 simulations on the PC-Tree (100Sim) or 100 random FC-Trees with one simulation (100Trees) for each combination of reversal relative probability and model rate.
Results
Data Sets and Time-Tree Inference
The concatenated alignment resulted in 4112 positions and included 345 taxa, 322 of which were phasmids (Supplementary Materials available on Dryad: https://doi.org/10.5061/dryad.9kd51c5k2). Of the 322 phasmid taxa, 92 represented new specimens, and 230 were obtained from NCBI. We were able to obtain information about the wing state for all Phasmatodea species except for Dimorphodes prostasis Westwood 1859, which was excluded from comparative analyses. Overall, 180 species were identified as apterous (56|$\%$|), 33 as brachypterous (10|$\%$|), and 108 as macropterous (34|$\%$|) (Supplementary Table S1 available on Dryad). The 1000 randomly sampled FC-Trees presented a wide range of arrangements among the major clades of phasmids, yet major and established phasmid clades were found to be monophyletic (see Supplementary Materials available on Dryad). The constrained PC-Tree (Supplementary Fig. S3 available on Dryad) found the divergence between the two suborders Timematodea and Euphasmatodea at 180 Ma (95|$\%$| High Posterior Density, HPD |$=$| 122–249 Ma), with the Euphasmatodea radiation beginning 108 Ma (95|$\%$| HPD |$=$| 75–148 Ma) and the diversification of major lineages occurring in the subsequent 30 million years.
MK Models Analyses Considering Two States (Winged and Apterous)
For the 2-states character-coding scheme, the best fit on the PC-Tree resulted to be the ER model (AICc |$=$| 276.5326, Supplementary Table S5A available on Dryad) with a transition rate between the two states equal to 0.00350 (Supplementary Fig. S1 available on Dryad), followed by the ARD model (AICc |$=$| 278.1931), with transition rates similar to those of the ER model. The LO model had a |$\Delta$|AICc |$=$| 28.894.
For all ASRs in which the root was not constrained to the winged states (ARD-FLAT; ARD-MADDFITZ; ER-FLAT; ER-MADDFITZ), we always found high support for an apterous MRCA (PP |$>$| 0.88). Under an ER-MADDFITZ model, the root of the PC-Tree was reconstructed as apterous with the maximum posterior probability (PP); 23 reversals of wings were inferred (9 along internal branches and 14 along terminal branches), whereas wing losses were inferred 15 times (5 along internal branches and 10 along terminal branches) (total number of transitions: 38; Fig. 2a; Supplementary Fig. S4 available on Dryad). Similar results were obtained when the ASR was carried out under the ARD model due to the similar inferred transition rates (ARD-MADDFITZ; Supplementary Fig. S4 available on Dryad). Instead, in a scenario consistent with irreversible wing loss, 61 independent losses (34 on terminal branches and 27 on internal branches) of wings were necessary to explain the distribution of the trait throughout the tree (LO; Supplementary Fig. S4 available on Dryad). Even when using a flat prior (ER-FLAT and ARD-FLAT), the root was recovered as apterous for both ER and ARD models (PP |$>$| 75), with transition rates and overall ASRs approximately equal to those obtained in previous analyses (Supplementary Table S6A available on Dryad and Supplementary Fig. S4 available on Dryad). When fixing the root state to the winged states (ARD-WR and ER-WR ASRs), multiple reversals of wings were inferred (Supplementary Fig. S4 available on Dryad): along terminal branches only and with a winged Euphasmatodea backbone with ARD-WR; along both internal and terminal branches and with an apterous Euphasmatodea backbone in ER-WR.
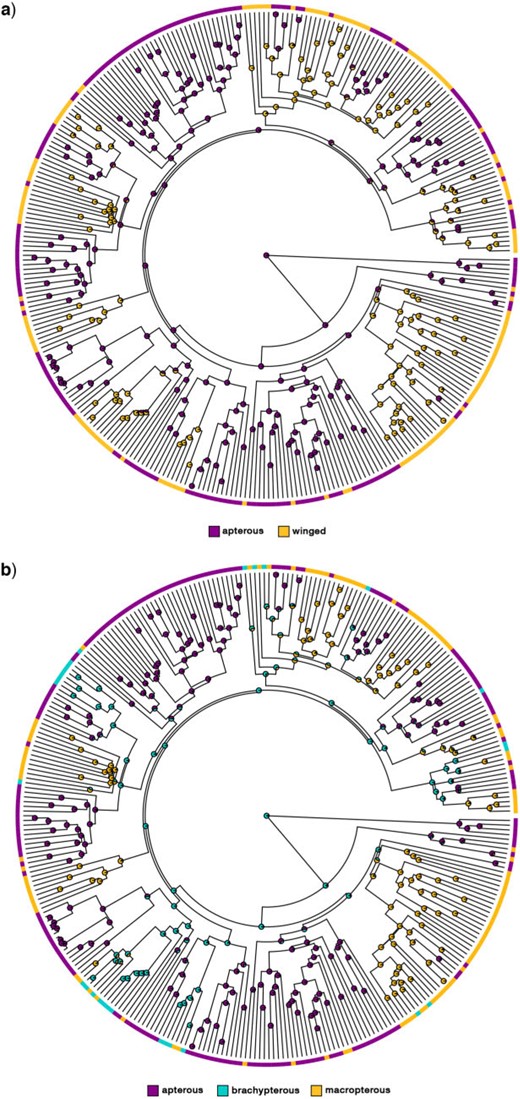
Phasmatodea wing ancestral state reconstruction on the “Phylogenomic-Constrained” maximum clade credibility tree obtained from the Bayesian inference (PC-Tree). a) Leverages a 2-states character-coding schemes with an equal rates (ER) and a maddfitz root prior. b) Leverages a 3-states character-coding schemes with an all rates different (ARD) model, fixed transition rates, and a maddfitz root prior. Additional ASRs using different root priors can be found in Supplementary Figures S4 and S5 available on Dryad.
Sensitivity analyses highlighted a strong preference for the ER model (Fig. 3a): it was recovered as the best fit for 993 trees out of the 1000 taken from the BEAST posterior distribution, and its AICc distribution was significantly lower than all the others (Kruskal–Wallis test, |$P < 0.001$|; post hoc pairwise Wilcoxon test with Bonferroni correction, |$P < 0.001$|). For the remaining seven trees, the ARD model was found to have the best fit.
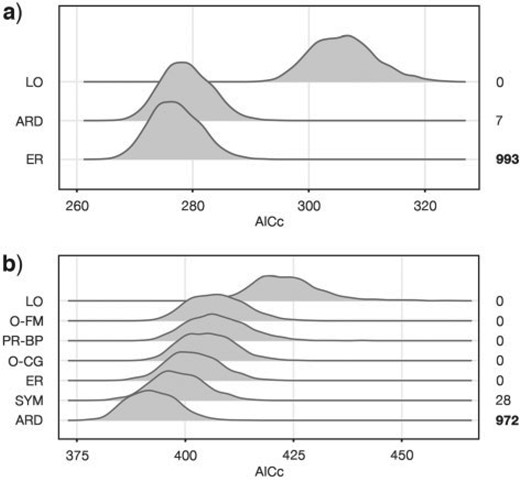
Markov evolutionary models fitting considering uncertainty in tree topology and branch lengths. Analyses were performed on the 2-states a) and 3-states b) character-coding schemes for 1000 trees randomly sampled from the posterior distribution of the “Fossil-Constrained” Bayesian inference (FC-Trees). On the right side, the number of trees for which each model resulted in the best fit is reported, with the more frequent ones (ER and ARD) highlighted in bold. Graphic visualization of 2-states and 3-states models can be found in Supplementary Figure S2 available on Dryad. Model abbreviations are ARD |$=$| all rates different; ER |$=$| equal rates; LO |$=$| loss only; O-CG |$=$| ordered complete gain, with all losses allowed plus transitions from apterous to brachypterous and from brachypterous to macropterous; O-FM |$=$| ordered full model, where only transitions between proximal states were allowed; PR-BP |$=$| partial reversal brachyptery, where all losses and transitions from brachypterous to macropterous forms were allowed; SYM |$=$| symmetrical. A graphic representation of the models can be found in Supplementary Figure S1 available on Dryad.
SCM highlights a weak impact of parameter, topology, and branch lengths: both 100Sim and 100Trees analyses showed a high preference for an apterous root (Fig. 4a) and a higher number of reversals than losses (Fig. 4b). An average of 46.27 and 48.01 changes between states were inferred for the 100Sim and 100Tree analyses, respectively, with averages of 27.23 and 27.14 for reversals to winged forms.
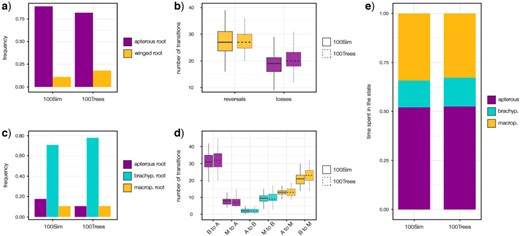
Stochastic character mapping leveraging 2-states and 3-states coding schemes: the frequency of the root state is represented in a) and c). b) and d) describe the average number of inferred transitions. e) Represents the time spent in each state for the 3-states character-coding scheme. In b) and d), boxplots are colored according to transition end states: color codes related to wing conditions as in a) and c) 100Sim refers to stochastic character mapping analyses with 100 simulations on the PC-Tree; 100Trees refers to the same analyses on 100 randomly sampled FC-Trees with a single simulation.
MK Models Considering Three States (Macropterous, Brachypterous and Apterous)
When implementing brachyptery as a third state, ARD resulted in the best-fitting model (AICc |$= 389.5214$|) on the PC-Tree, followed by SYM (|$\Delta$|AICc |$= 3.744$|) and ER (|$\Delta$|AICc |$= 6.597$|) (Supplementary Table S5B available on Dryad). Again, the LO model was rejected with a |$\Delta$|AICc |$= 33.12$|. The two models O-LO and PR-AB were less supported, with |$\Delta$|AICc values of 33.671 and 43.408, respectively; therefore, we discarded them from subsequent analyses. The transition rates of the ARD model are shown in Supplementary Figure S1 available on Dryad. The highest transition rates are those that describe the shifts from brachyptery to either macropterous (0.01117) or apterous (0.0169) forms, whereas the rates from apterous to fully macropterous forms and vice versa were closely matched (0.00181 and 0.00166).
The ASRs carried out on the PC-Tree under the ARD model resulted in different outcomes depending on the parameters used (Supplementary Fig. S5 available on Dryad; Fig. 2b), but in all reconstructions, reversals to macropterous or brachypterous forms from apterous ancestors were inferred. Under a flat root prior or a maddfitz one with fixed rates, the root was reconstructed as apterous and brachypterous with PP values of 0.84 and 0.91, respectively (ARD-FLAT and ARD-FIXED; Supplementary Fig. S5 available on Dryad; Supplementary Table S6b available on Dryad). Using a maddfitz prior with transition rates inferred directly by rayDISC, the root was recovered again as apterous with a PP of 0.74 (ARD-MADDFITZ; Supplementary Fig. S5 available on Dryad). The ASR that assumed a fixed macropterous root (ARD-WR) presented multiple reversals of both macropterous and brachypterous wings (Supplementary Fig. S5 available on Dryad). In two models (ARD-FIXED and ARD-WR), reversals from apterous to brachypterous or macropterous forms were present only on terminal branches and a brachypterous Euphasmatodea backbone was inferred. A large number of transitions from brachyptery to both macroptery and aptery was found, reflecting the low rates between apterous and macropterous forms and the high rates for moving away from the partially developed wing.
Sensitivity analyses highlight a strong preference of the ARD model, which was recovered as the best fit for 972 of the 1000 randomly sampled FC-Trees, with an AICc distribution significantly lower than that of all others (Kruskal–Wallis test, |$P < 0.001$|; post hoc pairwise Wilcoxon test with Bonferroni correction, |$P < 0.001$|), whereas the SYM model was preferred for the remaining 28 trees (Fig. 3b).
Regarding SCMs, a brachypterous root was preferred in both analyses (Fig. 4c), and an average of 84.79 and 87.76 changes between states were inferred for the 100Sim and 100Trees analyses, respectively. In both of them, the highest average number of transitions was found for brachypterous to apterous forms (31.19 for the 100Sim analysis and 31.94 for the 100Trees analysis), followed by the transition from brachypterous to fully macropterous (21.05 and 23.05, respectively) (Fig. 4d). The same results are reflected by the mean total time spent in each state, with brachyptery being the least represented (14|$\%$| for both analyses; Fig. 4e).
Analyses in a HiSSE Framework
When wing evolution was modeled in a more complex framework that accounted for state-dependent diversification and different kinds of reversible and irreversible hidden states, AICc model selection favored models with hidden state A, which allows for transitions between apterous and winged states, and hidden state B, which does not allow transitions between the observed states either directly or globally (models 27, 29, 43, 35, 27, 33, 25 and 39; Supplementary Table S7a available on Dryad). In these models, hidden state A, which allows direct transitions between winged and apterous states, is always associated with a higher net diversification rate compared with hidden state B, which does not allow direct transitions between observed states (Supplementary Fig. S2 available on Dryad). All top eight ranking models assume such a scenario (Supplementary Table S7b available on Dryad) and the highest-ranking one assumes the reversibility of apterous and winged states only when in hidden state A, whereas hidden state B is irreversible only in combination with the winged state; in this model, diversification rates differ across hidden states but not observed states (Fig. 5a; Model 37 in Supplementary Fig. S2 available on Dryad and Supplementary Table S7 available on Dryad). A similar model with an equal extinction fraction between all states but different net diversification rates was the second more supported model with a |$\Delta$|AICc of 1.83 (Model 29). In this case, the net diversification rates for winged and apterous species were equal when in hidden state A (even if left free to vary; 0.081), whereas they were inferred to be lower and different when in irreversible hidden state B, with a higher value for winged species (0.019 vs. 0.048). The third, fourth, and fifth models also assume reversibility between apterous and winged states only in hidden state A but assume full reversibility between hidden states: among them, the first two are models which consider diversification rates that are independent from wing states, whereas the third model assumes diversification rates that are dependent on wing states only in combination with hidden states (Models 43, 35, and 27 with |$\Delta$|AICc values of 2.2, 3.99, and 4.51, respectively). Models that support reversibility between apterous and winged states only in a hidden state and where another hidden state in which both apterous and winged states are irreversible “dead-ends” are weakly supported: among those, the highest ranking model that assumes that diversification rates are independent from wing states is ranked sixth with a |$\Delta$|AICc of 4.87 (Model 33). Models that assume reversibility of apterous and winged states only when in hidden state A and with hidden state B, which is irreversible only for apterous states, are also weakly supported (Model 39; |$\Delta$|AICc |$= 7$|). The sum of the AICc weights of these first six models (which assume the full reversibility of wings in both hidden states) sums up to 0.91 and among them, the first two (assuming an irreversible winged hidden state) account for the 68|$\%$| of the total AICc weights, whereas the last one only for the 4|$\%$|. Our results unexpectedly provide stronger support for instances of irreversible evolution of wings than their irreversible loss. At the same time, our analyses support a marginal yet consistent increase in diversification rates associated with wing presence (Fig. 5b and d; two-sided Wilcoxon rank sum test; |$P < 0.001$|). Throughout the 43 models considered, the MRCA of extant Phasmatodea was reconstructed as wingless with high support in all but three models (Supplementary Table S7 available on Dryad), and the model-averaged ASR largely agrees with the one obtained leveraging the MK models (Fig. 5c): an apterous root and backbone are inferred, whereas multiple transitions from apterous to winged forms are found after the diversification of major Euphasmatodea clades.
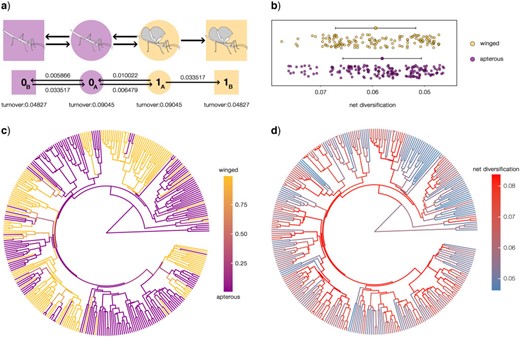
Ancestral state reconstruction in a HiSSE framework. a) The best fit model out of the 43 tested and the inferred transition rates; b) scatterplots of net diversification rates across winged (macropterous and brachypterous) and apterous branches; the two distributions are significantly different (Wilcoxon test |$P < 0.001$|); c) wing ancestral state reconstruction using model averaging; d) ancestral state reconstruction of net diversification rates using model averaging. A description of the models is available in Supplementary Table S7 available on Dryad; the custom-designed HiSSE models are also represented graphically in Supplementary Figure S2 available on Dryad.
Impact of Different Assumptions Regarding Win Reversal Probability on Their Inference
When different assumptions on the relative probability of reversals (ratio of wing reversals to loss rates) are tested in an SCM framework, it can be observed that up to a ratio of 1:30, reversals are consistently inferred in both the 100Sim and 100Trees analyses (at least one reversal is inferred in each of the 100 SCM analyses) independently from the absolute values of the evolutionary model parameters (Fig. 6; Supplementary Fig. S6 available on Dryad). The latter strongly affects the consistency of reversal inference when the ratio of reversals to losses is assumed to be lower than 1:30; at low model rates, reversals are inferred even when they are assumed to be 500 times less likely than losses. Remarkably, no evolutionary model considered in this analysis consistently rules out the possibility of reversals, which are always inferred under certain tree and model parameter conditions.
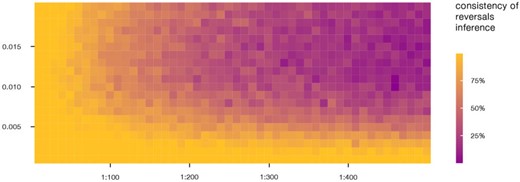
Impact of different assumptions regarding wing reversal probability on their inference. Tile coloring represents the consistency of reversal inference on the PC-Tree when different model rate (|$x$|-axis) and relative probability of reversal (|$y$|-axis) combinations are assumed. When consistency equals 100|$\%$|, at least one reversal is inferred in each of the 100 simulations of the stochastic character mapping analysis performed using the relative model parameter combination; if consistency |$<$|100|$\%$| and |$>$|0|$\%$|, reversals are inferred only on a fraction of the considered trees and character histories.
Discussion
Our comprehensive phylogenetic reconstruction of Phasmatodea evolution highlighted once more the difficulties in finding a stable and supported backbone for Euphasmatodea phylogeny using a handful of gene fragments due to the scarce phylogenetic signal associated with their rapid evolutionary radiation (e.g., Robertson et al. 2018; Glaw et al. 2019). Moreover, in phasmids, uncertainty is not only limited to systematic relationships but also found in the timing of their evolution. In previous studies, the split between Euphasmatodea and Timematodea ranged between |$\sim$|95 Ma and |$\sim$|270 Ma (Buckley et al. 2009; Forni et al. 2021), whereas our estimate set it at |$\sim$|174.5 Ma (95|$\%$| HPD: 122.63–249.1 Ma); this date falls between those inferred in the recent phylogenomic efforts by Simon et al. (2019) and Tihelka et al. (2020) (|$\sim$|121 and |$\sim$|250 Ma, respectively). The same holds true for the Euphasmatodea crown node, which is found to be in the Mid-Cretaceous at |$\sim$|105 Ma (95|$\%$| HPD: 75–148 Ma) in this study, whereas in phylogenomic analyses, it ranges from |$\sim$|80 Ma to |$\sim$|150 Ma. Such striking incongruences are also found at lower taxonomic levels (Bank et al. 2021a) and can be largely explained by the different choices and/or usages of fossil calibration; our approach has been to include in our analyses only fossils that are deemed uncontroversial in their placement (Bradler and Buckley 2011) and to implement wide upper boundaries of prior distribution to avoid forcing any specific hypothesis. Paleontological evidence (Yang et al. 2019) is consistent with our results, indicating that the Mid-Cretaceous was an important period of phasmid diversification that is possibly related to the contemporary rapid diversification of angiosperms (Peris et al. 2017). Throughout this article, we carefully considered uncertainty in phasmid systematic relationships and divergence times by leveraging two kinds of analyses: one relying on the single best phylogenetic hypothesis currently available (PC-Tree) and another that allowed us to consider extensive uncertainty in topology and branch lengths (FC-Trees).
The first evidence of the reversible evolution of phasmid wings is simply provided by the distribution of the trait states across the phylogeny (Fig. 2). Although many apterous, brachypterous, and macropterous species form well-supported clades, others include a mixture of different states; e.g., several macropterous species, such as Bacteria ploiaria (Westwood 1859), Cranidium gibbosum (Burmeister 1838), and Lobofemora bidoupensis (Bresseel and Constant 2015), are found in clades mainly including apterous species. This is also the case for some winged Heteropterygidae species that—as recently corroborated by Bank et al. (2021b)—are found nested in a largely brachypterous/apterous clade. This kind of pattern appears to be consistent with shallow morphological taxonomy, and it has to be considered that we carefully excluded any rogue taxa from our analyses.
Model selection strongly supported models in which reversals occurred (i.e., from apterous to winged forms in the 2-states analyses and from apterous to brachypterous and macropterous forms in the 3-states analyses; Fig. 3). These outcomes were consistent for both the PC-Tree and FC-Trees analyses, whereas a model consistent with irreversible wing loss, e.g., LO, was never supported. Interestingly, brachyptery was the most unstable state, showing the highest rates of transition departing from it compared with other states. Similar outcomes are provided by SCM analyses (both 100Sim and 100Trees): reversals are consistently inferred, and brachyptery is recovered as the state with the greatest number of transitions moving away from it and with the least time spent within this state (Fig. 4). This evidence may reflect the results obtained by Zeng et al. (2020), who proposed a fitness valley of intermediate size wings between two adaptive peaks represented by apterous and macropterous taxa (Stroud and Losos 2016). Complete development or complete loss of wings conveys direct benefits by themselves, such as dispersal and defensive capability, increased mimicry capacity, or increased fecundity in females (Roff 1994; Whiting et al. 2003; Zeng et al. 2020), whereas brachypterous wings may be positively selected and maintained only when co-opted for nonaerodynamic purposes. For all the brachypterous species we considered, wings are associated with functions such as aposematism or stridulation, with very few exceptions, such as Hypocyrtus ornatissimus (Brunner von Wattenwyl 1907). In the ground-dwelling Heteropterygidae, acoustic adaptations have been proposed as an initial driver of brachypterous wing reversal, with macroptery secondarily restored in species that adopted an arboreal lifestyle (Bank et al. 2021b).
When phasmid wing evolution is modeled in a more complex framework that accounts for state-dependent diversification and different kinds of reversible and irreversible states, aptery is again found to be fully reversible. Interestingly, wings are inferred as an irreversible phenotypic endpoint in some instances: this may reflect historical constraints acting on wing developmental mechanisms (Bull and Charnov 1985) or selective pressures shared by clades with similar ecological niches (Mena et al. 2020). The trait-dependent diversification analyses presented here reject the hypothesis that wings represent major drivers of shifts in diversification rates in phasmids (Fig. 5b), consistently with other studies (Bank and Bradler 2022). As we relied on a straightforward trait coding scheme that does not consider the different adaptations that wings underlie (e.g., flight capabilities, mating, crypsis, and defense), we cannot rule out the effect of some of them on phasmid diversification dynamics. Yet, wings presence and absence do not appear to bias their reversals inference and the state of extant Phasmatodea MRCA. It is interesting to note how all eight top-ranking *SSE models assume a hidden state that allows for reversibility between apterous and winged forms and is characterized by higher net diversification rates. In our opinion, this correlation between diversification rates and wing reversibility can be explained by at least two hypotheses: (1) wing reversibility may allow for broader ecological opportunities and thus cause an increase in species diversification (Yoder et al. 2010), or conversely, (2) rapid diversification events may facilitate the shift between different states due to the associated demographic dynamics (Nevado et al. 2019).
Extinct species representing the stem group of all extant Phasmatodea (e.g., Susumanioidea, Archipseudophasma, and Pterophasmatidae; Yang et al. 2019, 2021; e.g., A. echinulatum in Fig. 1a) present fully developed tegmina, whereas all other extinct (e.g., Eophyllium messelense; Wedmann et al. 2007) and extant taxa have reduced ones (when present; Fig. 1b–h). Long tegmina are considered the plesiomorphic state of Polyneoptera (Wipfler et al. 2019) and it is therefore possible to hypothesize that also the ancestor lineage of extant Phasmatodea presented two fully developed wing pairs and experienced either a reduction or a loss of wings. Reversals that subsequently happened in the lineages leading to extant forms restored the structure in a partially different form; such differences between the ancestral (elongated tegmina) and derived (reduced tegmina) morphologies may represent evidence of its reversals (Cronk 2009; Recknagel et al. 2018). Despite the known limitations of ASR in inferring the precise number and position of transitions (Goldberg and Igić 2008; Duchêne and Lanfear 2015), our analyses support the aforementioned hypothesis and consistently reject a macropterous MRCA of extant Phasmatodea. ASRs on the PC-Tree inferred the root as apterous using the 2-states character-coding scheme (even when considering different root prior probabilities) and either as apterous or brachypterous using the 3-states coding scheme (depending on the combination of transition rates and root assumptions). Moreover, these results are closely matched by *SSE and SCM reconstructions. No known fossil has been confidently placed in the stem lineage of extant Euphasmatodea (or Timematodea) leaving a gap of knowledge on their wings morphology that span over 100 Myr. Yet, a macropterous MRCA of extant Phasmatodea cannot be entirely ruled out given that—as highlighted before—all Phasmatodea stem fossils are macropterous. When forcing a macropterous root in combination with the 2-states and 3-states character-coding schemes: (1) in one ASR, Euphasmatodea backbone is recovered as macropterous, with all reversal to the winged state inferred on terminal branches; (2) in two ASRs, losses of fully developed wings are inferred in the branches immediately after the root (leading to Euphasmatodea and Timematodea).
Standard approaches do not consider any prior assumptions on the mechanism of evolution and leverage transition rates estimated on the basis of trait distribution at the tips of the phylogeny and the tree itself. When there are no particular expectations on the relative probability of transitions between states, this seems to be a valid approach. However, the majority of our analyses found comparable rates of losses and reversals and an equal probability of losing and reverting back to a complex structure: this represents a strong deviation from common expectations and assumptions. Genomic and transcriptomic studies are contributing to elucidate possible mechanisms associated with trait reversal (Seher et al. 2012; Carlini et al. 2013; Esfeld et al. 2018; Lammers et al. 2019), which can be theoretically used as informative priors to be applied in the framework of comparative methods. As this insight is not available for phasmid wings, we tested the impact of different assumptions on the relative probability of wing reversal compared with wing loss (reversal:loss ratios from 1:10 up to 1:500; Fig. 6). Although a large effect of the absolute values of the model parameter can be observed, until a relative probability of 1:30 is assumed, reversals are consistently inferred. When reversals are assumed to be more unlikely events, they are no longer inferred consistently; however, even when reversals are considered highly unlikely, a scenario of irreversible evolution is never consistently supported. Previous debates on the possible reversible evolution of phasmid wings found very contrasting results, with the absolute values of the evolutionary model parameters playing a major role in defining a probability threshold above which the reversible evolution scenario is no longer supported (Whiting et al. 2003, p. 1:1500; Trueman et al. 2004, p. 1:13). Although there is no approach to determining such a threshold (Stone and French 2003), our findings are robust to the intuitive expectation of reversals being more unlikely events than losses.
The wings of extant phasmids present the same morphology as those of other insects, including the same arrangement of veins and cross veins (Whiting et al. 2003; Engel et al. 2013), associated thoracic modifications (i.e., muscles and innervations; Kutsch and Kittmann 1991) and wing bases (Yoshizawa 2011). This evidence intuitively suggests that in extant species these structures might be generated by the same developmental program found in their ancestor; yet a thorough understanding of phasmid wings developmental program is essential for the interpretation of the process leading to the observed phylogenetic pattern of their reversals. The repeated recruitment of the same genetical developmental program that specifies wing identity would explain the similarity between ancestral and derived wings and would allow us to consider the ancestral and derived structures as homologous (Wagner 2007). Differences and similarities in derived traits with respect to their ancestral form could be explained by the possible co-option of some genes and the decay of others, along with the general preservation of the gene regulatory network responsible for trait expression due to pleiotropic constraints (i.e., selection for traits other than the lost one; van der Kooi and Schwander 2014; Lammers et al. 2019). Wings share part of their developmental program with other insect structures (Prud’homme et al. 2011; Almudi et al. 2020). For example, wings and legs are tightly linked from a developmental perspective: their imaginal discs are generated from the same group of cells, and the genetic pathway that guides the development of both structures is largely shared (Cohen et al. 1993; Kim et al. 1996). Moreover, it has been observed that leg regeneration during phasmid development leads to a smaller wing and weaker flight capability (Maginnis 2006). Extensive developmental, morphological, genomic, and transcriptomic studies are necessary to unravel the relationship among phasmid wings and with other polyneopteran insects: these approaches would allow a better understanding of the mechanisms underlying reversals and can provide a more appropriate framework to test for Dollo’s law rejection. Nonetheless, the results presented here, along with a growing body of research (Zeng et al. 2020; Bank and Bradler 2022), strongly support reversible wing evolution in phasmids.
Conclusions
Altogether, the findings presented here support a dynamic and reversible evolution of wings in Phasmatodea: our analyses inferred either the absence or an extreme reduction of wings in the MRCA of extant species, with multiple reversals subsequently restoring the once lost structure. Moreover, our findings suggest that brachyptery is an unstable state unless co-opted for nonaerodynamic adaptations and that the reversibility of wing states is coupled with an increase in species diversification rates. The consistency observed with multiple complementary approaches and the scarce impact of different topological arrangements and divergence times allow us to hypothesize that our findings will not be easily challenged by future phylogenetic hypotheses or comparative approaches. Yet, the evidence presented here is limited to a macroevolutionary framework, and complementary developmental, morphological, genomic, and transcriptomic approaches will be necessary to understand the relationship between derived and ancestral trait states. Nonetheless, phasmid wings represent an extraordinary example of the dynamic and reversible evolution of complex traits.
Supplementary Material
Data available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.9kd51c5k2.
Funding
This work was supported by Canziani Funding to A.L. and B.M.
Acknowledgments
The authors would like to thank Mattia Ragazzini for help in revising the character-coding tables. We also wish to thank Taiping Gao and Hongru Yang for permitting the usage of the photo of the Aclistophasma echinulatum fossil.
Data Deposition
All sequences produced have been submitted to GenBank under the accession numbers MN449491–MN449962, MT077516–MT077845, MW089913–MW090026, MW138438–MW138572, MW138575–MW138724, MW528968–MW529005, and MW530366–MW530419.
Data Availability
The data associated with this article are available for review via Dryad. The following is a temporary direct download link. Please copy and paste it directly into a web browser to download the data files to your computer (unfortunately this may not work as a link to click on) https://datadryad.org/stash/share/dLF-WIhmAufxYD8UFdGS9Wc4Y42M6afHE6TqDpJoe4w.
References
Author notes
Giobbe Forni and Jacopo Martelossi contributed equally to this article



