-
PDF
- Split View
-
Views
-
Cite
Cite
Shoto Aoki, Hidenori Fukaya, Naoto Kan, A Lattice Formulation of Weyl Fermions on a Single Curved Surface, Progress of Theoretical and Experimental Physics, Volume 2024, Issue 4, April 2024, 043B05, https://doi.org/10.1093/ptep/ptae041
Close - Share Icon Share
Abstract
In the standard lattice domain-wall fermion formulation, one needs two flat domain-walls where both of the left- and right-handed massless modes appear. In this work we investigate a single domain-wall system with a nontrivial curved background. Specifically we consider a massive fermion on a 3D square lattice, whose domain-wall is a 2D sphere. In the free theory, we find that a single Weyl fermion is localized at the wall and it feels gravity through the induced spin connection. With a topologically nontrivial U(1) link gauge field, however, we find a zero mode with the opposite chirality localized at the center where the gauge field is singular. In the latter case, the low-energy effective theory is not chiral but vectorlike. We discuss how to circumvent this obstacle in formulating lattice chiral gauge theory in the single domain-wall fermion system.
1. Introduction
Lattice gauge theory has been successful in understanding and computing nonperturbative dynamics of particle physics. Numerical simulation of quantum chromodynamics (QCD) on a flat Euclidean lattice has been an essential tool for examining the standard model in various hadronic processes. Domain-wall fermions, in particular, defined on a five-dimensional square lattice, achieve a good control of chiral symmetry, where the unwanted mixing between the left- and right-handed quarks is well suppressed.
In the standard domain-wall fermion formulation [1–3] on a flat five-dimensional lattice, we need at least two domain-walls where the left- and right-handed massless fermions are localized. If one of them is decoupled from the gauge fields, the system may enable formulation of a chiral gauge theory on a lattice [4–7].1 In order to decouple the unwanted modes, a smooth elimination of gauge fields has been considered in Refs. [11,12] but it turned out that this task is not that easy. For instance, the cobordism invariance of the instanton background forces the two domain-walls to have the same number of zero modes [13] (see also related works [14–17]). This indicates that the low-energy theory has both of the left- and right-handed modes. Another approach is the so-called symmetric mass generation [18–31], which gaps out the unwanted chiral modes by generating mass without breaking the chiral symmetry. This, however, requires a highly nonperturbative dynamics.
In our recent works [32,33] we have been studying a massive fermion system with a nonflat single domain-wall. In the case with an S1 domain-wall embedded into a flat 2D square lattice, we observed that ma assless Dirac fermion appears on the wall, having a definite eigenvalue of the gamma matrix perpendicular to the domain-wall. Similarly, we observed that a two-flavor massive fermion, which respects the time-reversal symmetry, yields a massless Dirac fermion on the S2 domain-wall embedded in flat three dimensions. Also in this case, the edge-localized modes are the eigenstates of the gamma matrix accompanied by an operator exchanging the flavor index.
Moreover, it was found through the Dirac operator spectrum that the edge-localized modes feel gravity via the induced spin connection on the curved domain-wall. This is a realization of the Einstein equivalence principle, which tells that any acceleration is indistinguishable from gravity. We have numerically confirmed that the rotational symmetry is monotonically recovered toward the classical continuum limit of the higher-dimensional square lattice. The limit of the Dirac operator eigenvalue spectrum is consistent with that in the continuum theory, which has a manifest gauge symmetry under the general coordinate transformation.
In this work, we extend our study on the curved domain-wall fermions in two new directions. One is to employ Shamir’s formulation [2,3]. We consider a 2D spherical domain-wall embedded into a 3D square lattice, but we ignore the lattice points outside of the domain-wall, which is equivalent to taking the fermion mass to +∞. The second is to consider a single-flavor fermion, which loses the time-reversal symmetry in three dimensions. Then the edge-localized modes should represent not Dirac but Weyl fermions. From the Dirac operator spectrum, we investigate the gravity induced on the wall, and examine its continuum limit. A preliminary result of this work was presented in Ref. [34].
In this setup, a single massless fermion with a definite chirality is localized on a single domain-wall. Namely, it looks as if a Weyl fermion on an S2 surface is nonperturbatively regularized on a lattice. In recent publications [35,36] this single-domain-wall system was proposed as a lattice regularization of chiral gauge theories.
Contrary to expectation, when it is coupled to the U(1) gauge field, we observe a nontrivial dynamics where the low-energy theory becomes not chiral but rather vectorlike. This happens when the gauge field on the S2 has a nontrivial topological charge. The Gauss law in three dimensions requires a singular source of the gauge flux inside the spherical domain-wall. This configuration is an analog of a magnetic monopole in three spatial dimensions, whose magnetic flux penetrates the S2 surface. The additive mass renormalization through the Wilson term due to the singular gauge field becomes strong enough to flip the sign of the effective mass of the fermion, and another domain-wall is created around the singularity. The dynamically created domain-wall captures a single-fermion zero mode with the opposite chirality to the original edge modes on the S2. This dynamical creation of domain-walls was already reported in our previous work on the Dirac fermion system [37,38], which gives a microscopic description of the Witten effect [39]: the magnetic monopole gains an electric charge because the electron zero mode is bound to the small but finite spherical domain-wall around the monopole. We discuss how to circumvent this obstacle in formulating chiral gauge theory.
The rest of this paper is organized as follows. In Sect. 2 we show that the edge-localized modes generally exist and they feel the induced gravity. In Sect. 3 we analyze the lattice domain-wall fermion system numerically. Our result shows that a Weyl fermion appears on the S2 domain-wall, as is expected. In Sect. 4, however, we show that an oppositely chiral zero mode appears when the gauge field has a point-like singularity. We discuss in Sect. 5 how to avoid the unwanted zero modes with the opposite chirality. A summary is given in Sect. 6.
2. Continuum analysis of 3D Shamir domain-wall fermion with a single S2 boundary
We first consider a Dirac fermion action in a 3D flat continuum spacetime |$\mathbb {R}^3$|,
where the Dirac operator with a position-dependent mass m(x) is given by
Here we have introduced a background U(1) gauge field Ai(x) and σi denote the Pauli matrices representing the gamma matrices in three dimensions.
We assume that the mass function m(x) has a spherical domain-wall structure:
where we assume m > 0, M > 0. In order to obtain the Shamir domain-wall fermion Dirac operator, we take the M → +∞ limit, which is equivalent to imposing a boundary condition
Here the chirality operator σr is given by
which is well-defined at any point on the S2 surface |x| = r0. In the same way, the conjugate operator D† requires the boundary condition with the opposite chirality σr = −1.
We show below that the chiral edge-localized modes generally exist on the curved spherical domain-wall, at least approximately in Sect. 2.1. We also derive in Sect. 2.2 an exact eigenfunction when the gauge field configuration respects the rotational symmetry.
2.1. Edge-localized modes in general background gauge field
First, let us confirm the existence of the edge-localized modes in a general U(1) gauge field background. Here we assume that the gauge field is smooth everywhere without any singularity.
In the polar coordinates and taking the radial gauge condition Ar = 0, the Dirac operator inside the domain-wall |x| ≤ r0 is expressed by
where the Hermitian operator |$iD^{S^2}$| is defined by
Here we have introduced the dimensionless vector potentials: |$\hat{A}_\theta :=r A_\theta$| and |$\hat{A}_\phi :=r \sin \theta A_\phi$|.
In fact, we can identify |$D^{S^2}$| as the effective Dirac operator on S2 for the low-energy edge-localized modes. Taking a gauge transformation or the Euclidean version of the local Lorentz transformation,
as well as a U(1) gauge transformation, we obtain the 2D massless Dirac operator:
We can see that the spin connection σ3cos θ/2 is induced.2 It is also important to note that the rotated 2D Dirac operator anticommutes with the chirality operator R(θ, ϕ)σrR(θ, ϕ)−1 = σ3.
Let χ(θ, ϕ) be a function in the domain of |$iD^{S^2}$| at r = r0. Then we can construct an edge-localized mode
in relation to which the Dirac operator effectively acts as
with the chiral projection operators P± ≔ (1 + σr)/2. Here we have used an approximation in the large-m limit,
Thus, the edge-localized mode |$\psi _+^e$| represents one massless fermion with positive chirality on the single S2 surface with radius r0.
When we take M in Eq. (3) to negative infinity keeping the sign of m unchanged, the boundary condition requires the negative chirality at r = r0, which prohibits the edge-localized modes. If we take both m and M to be negative, the negatively chiral edge-mode
appears. The case with mM < 0 is analogous to a normal insulator where no edge-localized mode appears, and mM > 0 corresponds to a topological insulator where the existence of the edge excitation is topologically protected. Thus, our curved domain-wall fermion system with mM > 0 has the edge-localized modes, which describe a single Weyl fermion on a single curved surface.
The edge-localized Weyl fermion feels inertial force resulting from the constrained motion. As explicitly shown in Eq. (9), this force can be identified as gravity through the induced spin connection. This is consistent with Einstein’s equivalence principle, which indicates that any constraint force can be identified as gravity. Since the edge modes are constrained on the curved S2 surface, gravity is naturally induced on them. Interestingly, the induced gravity reflects only intrinsic geometry and the extrinsic information is invisible. This is not special for S2 but true on general curved domain-walls as discussed in Ref. [40]. The extrinsic curvature contribution is suppressed exponentially in the large-m limit.
2.2. Exact edge-localized modes with rotational symmetry
Next we exactly solve the eigenproblem of the curved domain-wall fermion Dirac operator in the case where the system has a rotational symmetry. Let us take the radial gauge Ar = 0 and assume that the field strength Fμν perpendicular to the domain-wall is uniformly distributed. Such U(1) backgrounds are classified by the topological charge,
Our target gauge field background in the whole 3D space is achieved by putting a “monopole” at the origin.3 The vector potential generated by the monopole is
where qm is the magnetic charge of the monopole, which satisfies Dirac’s quantization condition |$q_m=\frac{n}{2}~(n\in \mathbb {Z})$|. To be precise, this expression has a singularity at x = y = 0 and z < 0, which is the so-called Dirac string. In order to eliminate the Dirac string, we need another set of gauge potentials in the z ≤ 0 region but here we simply ignore the neighborhood of the string. In fact, the Dirac string automatically disappears in the lattice regularization that we will discuss in the next section. The field strength we have obtained is
With the above spherically symmetric gauge field background, the effective 2D Dirac operator |$iD^{S^2}$| can be written as
where Li is the orbital angular momentum operator in the presence of the monopole,
Instead of D itself, let us solve the eigenproblem of the Hermitian operator D†D. Note that D†D commutes with the total angular momentum operators Ji = Li + σi/2 as well as |$D^{S^2}$| so that it is convenient to consider the simultaneous eigenstates of |$\boldsymbol {J}^2=\sum _i(J^i)^2$|, J3, and |$D^{S^2}$|. Let j be the highest weight of |$\boldsymbol {J}$|, which takes discrete values:4
with a constraint j ≥ 0. The eigenfunction denoted by |$\chi _{j,j_3, \pm }$| satisfies
Here we have used the facts that |$(D^{S^2})^2$| is written as a linear combination of |$\boldsymbol {J}^2$|, σr, and identity, and that |$D^{S^2}$| anticommutes with σr. As will be shown below, the edge-localized eigenvalue of D†D depends only on j. Therefore, the degeneracy of the eigenvalue is 2(2j + 1) [37,41].
Since the chirality operator σr, which determines the boundary condition at r = r0, anticommutes with |$D^{S^2}$|, the eigenstate ψ of D†D is written by a linear combination of |$\chi _{j,j_3 ,\pm }$|:
Substituting this into the equation D†Dψ = E2ψ, where we assume m2 > E2, we find that the functions g±(r) satisfy the modified Bessel equations with a rescaled variable z = κr where |$\kappa =\sqrt{m^2-E^2}$|,
From the regularity condition at r = 0, we find the solutions in terms of the modified Bessel function of the first kind: g+(r) = AIν − 1/2(κr) and g−(r) = BIν + 1/2(κr) with numerical constants A and B, respectively. Since Iμ(z) are an exponentially increasing function of z, the solutions are exponentially localized at the edge, r = r0.
The boundary condition at r = r0: σrψ = +ψ and σrDψ = −Dψ, leads to two equations:
which determine the coefficients A, B up to normalization, and the eigenvalue E2. According to the asymptotic form |$I_\mu (z)\sim \frac{e^z}{ \sqrt{2\pi z} } \left( 1- \frac{4\mu ^2-1}{8z} \right)$|, the eigenvalue converges to
in the large-κr0 limit, which is independent of the mass parameter m. Moreover, the eigenvalue is shared with that of the massless 2D Dirac operator |$(iD^{S^2})^2$| shown in Eq. (22). It is important to remark in the free case with n = 0 that the eigenvalue is gapped from zero, which is a gravitational effect [32,42].
The case of |$j=\frac{{\left |n \right|}-1}{2}$| with n ≠ 0 is qualitatively different from the above result. Let |$\chi _{j,j_3,0}$| be an eigenstate satisfying
Assuming the edge-localized mode has the following form,
we find that f(r) satisfies the same equation as Eq. (25), but with ν = 0, and thus we obtain
with a normalization constant C.
It is interesting to note that the chiral boundary condition σrψ0(r = r0) = +ψ0(r = r0) is never satisfied with n < 0. Also, another boundary condition σrDψ0(r = r0) = −Dψ0(r = r0) is only satisfied by Dψ0(r = r0) = 0 when we take the m → ∞ limit. This reflects the Atiyah–Singer (AS) index theorem [43] on the sphere S2,
The Weyl fermion with positive chirality cannot give a negative contribution to the index when n < 0. Only in the m → ∞ limit do we have an exactly chiral zero mode of both D†D and |$iD^{S^2}$|.
Thus, we have obtained the exact massless edge-localized modes with the positive chirality, describing a Weyl fermion on the sphere with radius r0. Their existence is guaranteed even in the presence of a nontrivial gauge field background. This single domain-wall fermion system looks a good candidate for nonperturbatively formulating chiral gauge theory on a lattice. Note, however, that the chirality is not perfect unless we take the mr0 → ∞ limit. In particular, it is not obvious in the above analysis what will happen to the chiral zero mode when mr0 is finite. So far we have ignored the short-distance singularity at the location of the monopole. As will be seen below, a highly nonperturbative and careful short-distance analysis is needed to understand this problem.
3. Lattice analysis in free theory
In this section we discuss a lattice regularization of the curved domain-wall fermion system. In the free fermion theory with trivial link variables we show that a single Weyl fermion appears on a single spherical domain-wall. We also discuss its continuum and finite volume systematics.
For discretization of the Dirac operator, we employ the Wilson Dirac operator
where the lattice spacing is denoted by a, and we assume that m > 0. The difference operator in the i-direction for a spinor field located at the lattice site x is defined by
with the unit vector |$\hat{i}$| in the corresponding direction. As the standard choice, we take the coefficient of the Wilson term w = 1. With this choice, the Dirac operator can be written as
It was shown by Shamir [2] in the standard flat domain-wall fermion that there is no need to impose a chiral boundary condition on the lattice but it is enough simply to set ψx = 0 outside the domain-wall. The same is true for our curved case. As shown in Fig. 1 where a 2D slice at z = 1/2 is drawn, we impose
where the center of the domain-wall is put at the origin x0 = (0, 0, 0). Note that our lattice sites are put at half-integral points: x = ((2n1 − 1)/2, (2n2 − 1)/2, (2n3 − 1)/2) with integer values ni. Put x at one of the inner nearest-neighbor sites of the domain-wall, where |$x+\hat{j}$| is put outside of the wall. Then the Dirac operator acts as
which imposes the boundary condition |$P^j_-\psi _x=0$| in the continuum limit a → 0, while |$P^j_+\psi _x$| can be taken arbitrarily, as far as |$\psi _x-\psi _{x-\hat{j}} \sim O(a)$|. With this simple boundary condition, the Hermitian conjugate of the Wilson Dirac operator |$D^\dagger _W$| is canonically defined.
![A 2D slice at z = 1/2 of the spherical domain-wall in our lattice space. The hopping to the outside of the sphere r = r0 is cut off. Adapted from [34].](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/ptep/2024/4/10.1093_ptep_ptae041/1/m_ptae041fig1.jpeg?Expires=1750206833&Signature=rYSjGaZWUh6Vnifmr9Zes5dR8bqpYafuLjyX085iUVt3dvDllUAPu8w7n-aKGpXeYR3fuUaypUAeFFhN328fVPrhA9pcffCrXFFqGDc-MHG-KgN9L1ASq7~pyNYTkWmTmxCL6d1LoFXEE~FQT5K9zcHdRff2velkgLUlmk4MnYegmXP3Zde-ItVDLG24cGqXStq~vMb1uyYl-RG2IO9J2YpcyxJiL3Y4zlHd7UP7g3oTLNDl0COiTLplQxTYhEsME3UkrhnwTIXnXVQ16hIWDxMaVuOvSMnQ9GGn~KeXQQR13PQHyzKPzES38phfnEfl1GRLe-jq5N3NcZ5elJJIIw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
A 2D slice at z = 1/2 of the spherical domain-wall in our lattice space. The hopping to the outside of the sphere r = r0 is cut off. Adapted from [34].
To be precise, our domain-wall is not a smooth sphere but a rather digitized zigzag surface like a block toy as depicted in Fig. 1. It is, therefore, important to check if the rotational symmetry is recovered in the continuum limit. In our previous work on Dirac fermions [42], we already obtained positive numerical evidence. The rotational symmetry of the lowest eigenmodes was almost linearly recovered in the a → 0 limit. We will address this issue for the Weyl fermion at the end of this section.
We numerically solve the eigenproblem of |$D_W^\dagger D_W$| as well as |$D_W D_W^\dagger$|, which are both Hermitian. With the obtained normalized eigenfunction ϕk(x), where k is the label for the low-lying modes, we measure the expectation value
where the chirality operator σr(x) = ∑iσixi/|x| is unambiguously defined at all our half-integral lattice sites. We also scan the local chirality, defined by
for each lattice site x in order to study its spatial distribution. This turns out to be useful in analyzing the case with a nontrivial U(1) gauge field background in the next section.
In Fig. 2, we plot the eigenvalue spectrum of |$D_W^\dagger D_W$| at r0 = 24a and ma = 0.35. Solving |$D_W^\dagger D_W \phi _k =E_k^2\phi _k$|, its square root normalized by r0: r0|E| is plotted by filled circle symbols. The color gradation shows the chirality expectation value. We can see that the low-lying modes below mr0, shown by the dotted horizontal line, have the positive chirality. The obtained eigenvalues agree with the continuum prediction marked by cross symbols in which the finite volume correction to the infinite volume value r0|E| = ν = 1, 2, 3, ⋅⋅⋅ in Eq. (28) is taken into account. The 2(j + 1/2) (or 2ν in this case) degeneracy with j = 1/2, 3/2, ⋅⋅⋅ also looks consistent. The gravitational effect through the induced spin connection, or the gap from zero, is clearly seen.
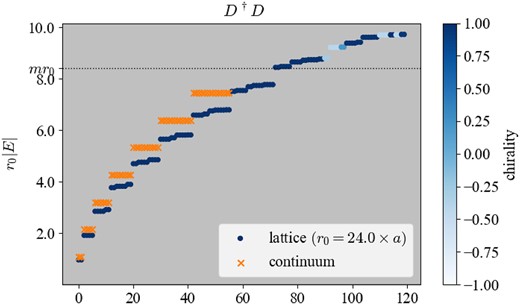
The spectrum of |$D_W^\dagger D_W$| at r0 = 24a and ma = 0.35. The square-rooted value r0|E| is plotted. The color gradation shows the chirality expectation value. The dotted horizontal line indicates the value of mass mr0, above which the eigenmodes are extended to the bulk. Our low-lying eigenvalues below mr0 of the edge-localized modes agree well with the continuum prediction marked by cross symbols.
We also plot the eigenvalue spectrum of |$D_WD_W^\dagger$| on the same lattice in Fig. 3. The spectrum is the same as that of |$D_W^\dagger D_W$| but the chirality is opposite.
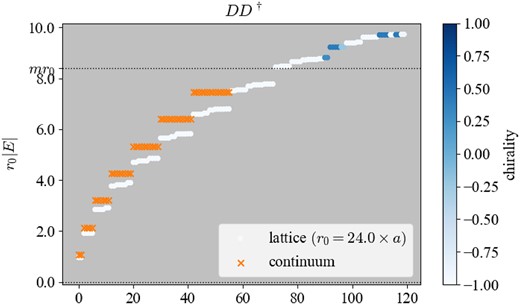
The spectrum of |$D_WD_W^\dagger$|. The lattice setup is the same as in Fig. 2.
Figure 4 presents the amplitude of the lowest eigenmode at the z = 1/2 slice of |$D_W^\dagger D_W$| (left panel) and that of |$D_WD_W^\dagger$| (right). The color gradation indicates the local chirality defined by Eq. (42). As is expected, these eigenmodes are localized at the domain-wall r = r0 and have a uniform distribution of the chirality.
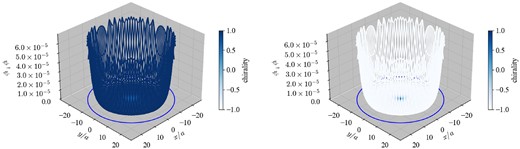
The amplitude of the lowest eigenstate of |$D_W^\dagger D_W$| at r0 = 24a and ma = 0.35 (left) and that of |$D_WD_W^\dagger$| (right). The color gradation shows the local chirality.
In order to estimate the systematic error due to the lattice discretization, we vary the lattice spacing keeping the dimensionless quantity mr0 = 8.4 fixed. In Fig. 5, we plot the relative ratio of the first eigenvalue,
where |$E_j^{\rm con.}$| is the corresponding continuum prediction obtained by numerically solving Eq. (26). We can see that our lattice values are linearly approaching the continuum limit with the lattice spacing a.
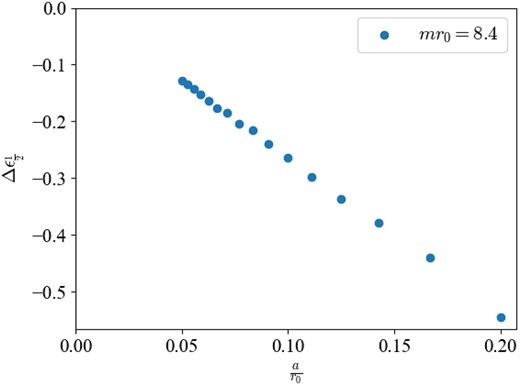
The relative deviation of the eigenvalue E1/2 as a function of the lattice spacing a with mr0 = 8.4.
In Fig. 6, we plot r0|E1/2| with a fixed lattice spacing ma = 0.35, as a function of r0/a. The lattice results marked by lower triangle symbols are consistent with the continuum prediction given by the solid curve, which is
in the large-mr0 expansion. Note that the finite volume correction is not an exponential but a power function of r0, since the propagating fermion at the edge is massless.
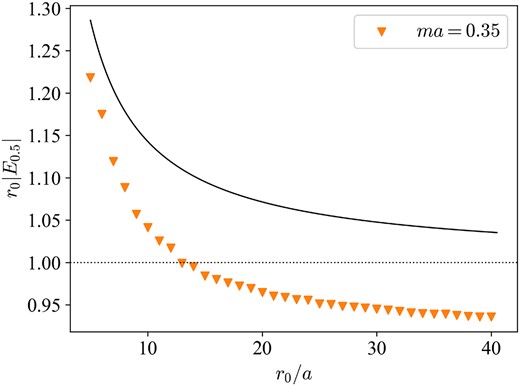
The finite volume effect on the eigenvalue of the lowest mode as a function of the radius of the sphere at ma = 0.35. The solid line represents the continuum prediction Er0 = 1 + 1/2mr0.
Finally, let us examine the rotational symmetry in the continuum limit. The three plots in Fig. 7 show the same eigenfunction with j = 1/2 with three different lattice spacings a/r0 = 1/16, 1/24, and 1/32. The finer the lattice spacing, the better the rotational symmetry looks. The symmetry can be quantified by taking the standard deviation σ of the amplitude peaks at the nearest-neighbor points to the domain-wall r = r0 normalized by their average μ as presented in Fig. 8. The result is not monotonic but still shows a reasonable convergence to zero in the a → 0 limit. This supports that our digitized surface is a good regularization of the 2D sphere.
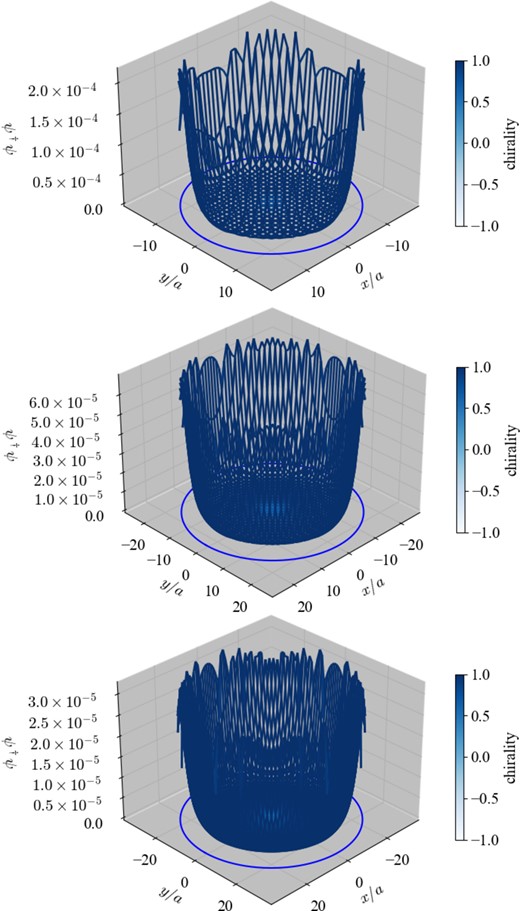
(Top) The amplitude of the lowest eigenstate of |$D_W^\dagger D_W$| at mr0 = 8.4 and a/r0 = 1/16. (Middle) That at a/r0 = 1/24. (Bottom) That at a/r0 = 1/32.
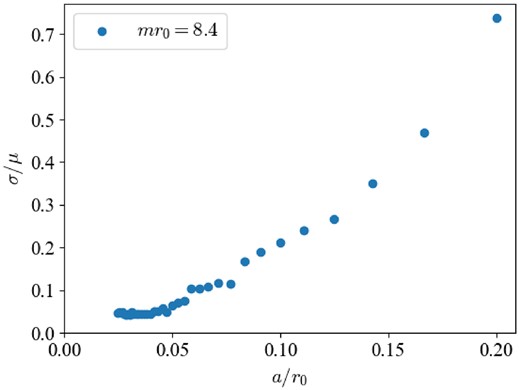
The standard deviation σ divided by the average μ of the peaks as a function of the lattice spacing a with mr0 = 8.4.
The above numerical evidence in the free case shows that we can formulate a single Weyl fermion by this single curved domain-wall fermion on a square lattice. In the large-mr0 limit, the finite volume effect is suppressed by 1/mr0 and the chirality becomes exact. But below we will see that the system shows a nontrivial behavior when a gauge field is turned on.
4. With nontrivial U(1) gauge fields
Next we set nontrivial U(1) gauge link variables,
where the vector potential Aj(x) is defined in Eq. (15). The covariant difference operator in the Wilson Dirac operator acts as
With these link variables, the Dirac string has no physical effect. In other words, the singularity of the continuum gauge field is automatically canceled by the multivaluedness of the U(1) link variables. To confirm this, let us compare the values of the two plaquettes p+ and p− in the x-y plane whose centers are located at x+ = (0, 0, 1/2) and x− = (0, 0, −1/2), respectively. If the Dirac string is physical, the plaquette values should be asymmetric since the string intersects the plaquette at x− but does not for the one at x+. But this is not true: by a direct computation, we obtain the symmetric result:
which indicates that the magnetic flux from the monopole penetrating the two plaquettes at x± is the same. On this lattice, the total magnetic flux from the monopole is nonzero, which allows violation of the Bianchi identity in the continuum limit.
In Fig. 9, we plot the eigenvalue spectrum of |$D_W^\dagger D_W$| with the monopole charge n = 1 (top panel) and that with n = −1 (bottom). The lattice setup is the same as in Fig. 2. For n = +1, the lattice result is consistent with the continuum prediction marked by cross symbols. The low-lying modes with r0|E| < mr0 have ∼+1 chirality as the color gradation indicates. For n = −1, however, we find one near-zero mode with the opposite chirality σr = −1, which does not exist in the continuum analysis.
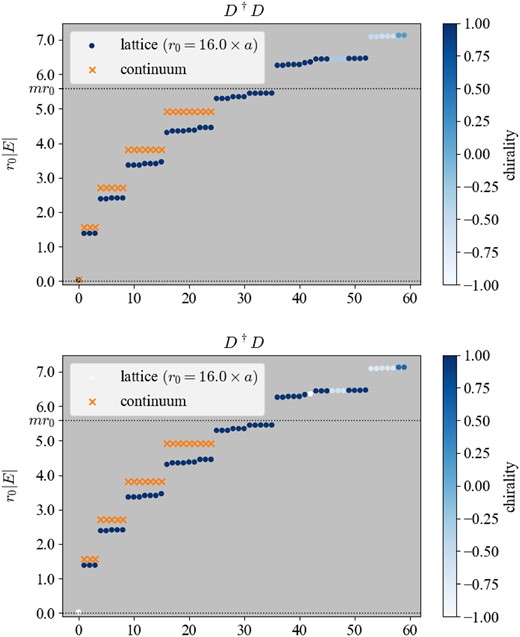
(Top) The eigenvalue spectrum of |$D_W^\dagger D_W$| with the monopole charge n = 1. Otherwise, the lattice setup is the same as in Fig. 2. (Bottom) The same but with n = −1. We can see a near-zero mode, which does not exist in the continuum prediction.
The amplitude of the oppositely chiral near-zero mode at the z = 1/2 slice is plotted in Fig. 10. This mode is not located at the domain-wall but localized at the center where the monopole sits.
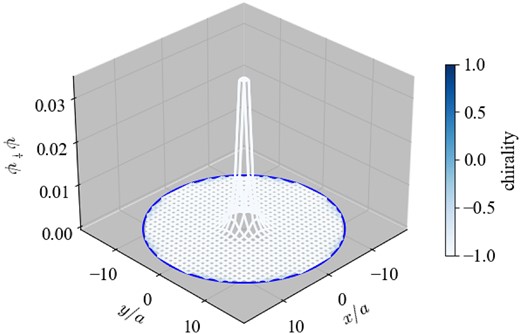
The amplitude of the zero mode of |$D_W^\dagger D_W$| at r0 = 16a, ma = 0.35, and n = −1.
What is the origin of the new center-localized zero mode with the opposite chirality? In fact, in our previous work [37], we observed a similar phenomenon in the four-spinor system where a zero Dirac spinor mode appears in the vicinity of the monopole. Our microscopic analysis revealed that the additive mass renormalization from the Wilson term becomes strong enough at the singularity of the gauge field to flip the sign of the effective mass, which creates another small but finite domain-wall near the origin. This dynamically created domain-wall captures one edge-localized zero mode (of the electron), which explains why the monopole becomes a dyon in topological insulators [39].
In the top panel of Fig. 11, we present the distribution in the z = 1/2 slice of the effective mass defined by
where ϕ0 denotes the center-localized zero mode with n = −1. We can see that an island of the positive mass region whose edge is another domain-wall is created. For comparison, we also plot the same quantity but with the lowest eigenmode with n = 0 in the bottom panel of Fig. 11, where the mass is negative everywhere except for the edge r = r0. Thus, we can identify the center-localized zero mode as the edge mode of the new domain-wall near the monopole.
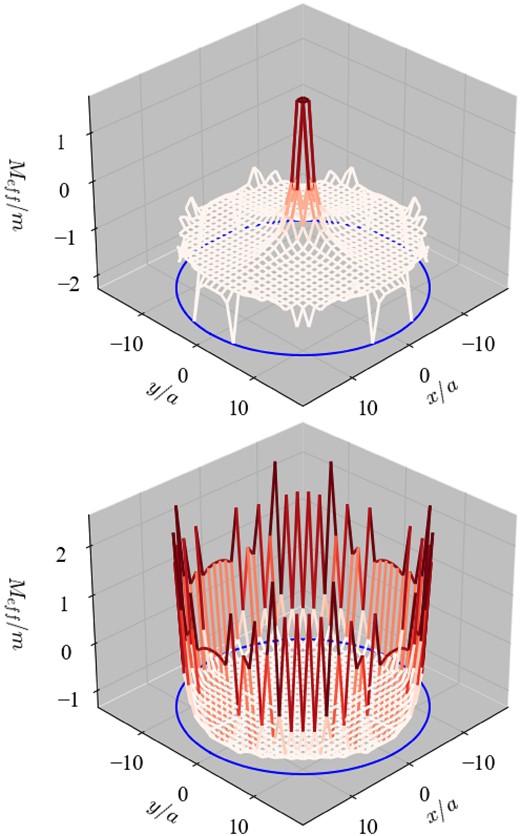
(Top) The effective mass of the zero mode at n = −1. (Bottom) That of the lowest mode at n = 0. The red–white color gradation expresses the sign of the effective mass.
Figure 12 shows the eigenvalue distribution of |$D_WD_W^\dagger$|. A similar center-localized mode with positive chirality, which is opposite to that localized at r = r0, appears when n = +1.
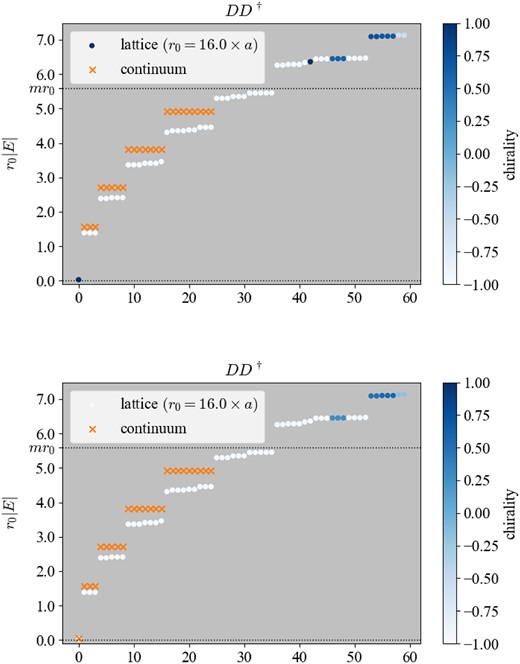
(Top) The eigenvalue spectrum of |$D_W D_W^\dagger$| with the monopole charge n = 1. Otherwise, the lattice setup is the same as in Fig. 2. (Bottom) The same but with n = −1.
The appearance of another domain-wall and the opposite chiral zero mode on it may indicate that the low-energy theory is not a simple chiral theory with a single Weyl fermion on a single domain-wall but a nontrivial vectorlike theory on the two domain-walls.
5. How to avoid opposite chiral modes
In this section we show in continuum analysis that the center-localized mode is stable against perturbation of the background gauge and gravity field since it is topologically protected. It is, therefore, crucial for constructing a chiral gauge theory in this setup to find a formulation which eliminates such oppositely chiral zero modes.
In order to make the problem explicit, let us consider a Hermitian operator in continuum
where the domain-wall Dirac operator D is defined as per Eq. (2) but with two domain-walls:
where we assume that r1 is put in the vicinity of the monopole at the inverse of the cutoff scale.
In the M → +∞ limit, the edge-localized states are the eigenmode of
The positive γ modes are located at the outer domain-wall at r = r0, whereas the negative γ modes are at r = r1. At the outer domain-wall, the Dirac operator acts as the 2D massless operator in Eq. (17), and the same is true for r = r1 but with a different scale:
It is not difficult to see that the two massless Dirac operators |$D^{S^2}$| at r = r0 and |$\bar{D}^{S^2}$| at r = r1 share the same index:
Namely, the existence of the zero modes at the two spherical domain-walls is topologically guaranteed by the AS index on them. For n > 0, the two zero modes with σr = sgn(n) appear for D on the r = r0 domain-wall and another for D† is localized at r = r1. For n < 0, there are also two zero modes but the roles of the r0 and r1 are flipped.
The above equivalence |${\rm Ind}D^{S^2} ={\rm Ind}\bar{D}^{S^2}$| is a consequence of cobordism invariance of the AS index. Since the two spheres at r = r0 and r = r1 share the same bulk region in r1 < r < r0, they are cobordant and must have the same index.
Therefore, the opposite chiral zero modes are as stable as those localized at the edge r = r0 against any perturbative deformation of the configuration. Their existence in this continuum analysis looks like a serious obstacle in constructing a chiral gauge theory. The situation is apparently the same as the flat two domain-wall system where it is difficult to decouple the unwanted opposite chiral modes from the theory. Some time ago a promising proposal was made, to use the Yang–Mills gradient flow to turn off the gauge interaction for one of the chiral modes in the two domain-wall fermion system [11,12]. However, it was pointed out in Ref. [13] (see also related works [14–17]) that a topologically nontrivial gauge background cannot eliminate the zero modes that originated from the AS index. This is also a consequence of the cobordism invariance of the index.
Note, however, that the situation on the lattice is not exactly the same as in the continuum analysis above. First, the inner domain-wall is not fixed but can appear only with a singular gauge field configuration. Second, the center-localized mode is effectively a zero-dimensional object, having no θ and ϕ dependence on the small sphere, which is isolated from the bulk modes. Taking these differences from the flat two-domain-wall case into account, we would like to propose two ideas which may be useful to avoid the appearance of the opposite chiral modes.
One is to impose the admissibility condition [44] or a smoothness condition for every plaquette on the lattice. Under this condition, the only admissible link gauge fields, satisfying
with some small real number ϵ are taken to construct the theory. Then, singular configurations are not allowed in the theory. In the continuum limit, the condition is equivalent to imposing the Bianchi identity.
Under the admissibility condition, we cannot put a monopole on the lattice. If ϵ is small enough, we will be able to limit the additive mass renormalization through the Wilson term and avoid dynamical creation of the domain-walls. However, this would restrict the surface theory to be fixed in a topologically trivial sector where the instanton number is forced to be zero. By enlarging the gauge symmetry, which is a well-known prescription by ’t Hooft and Polyakov [45,46], this fixing topology problem may be circumvented but the discussion is beyond the scope of this work.
The second proposal is to resort to the so-called symmetric mass generation. Recently many studies [18–31] have discussed the possibility of gapping out the edge-localized modes for special combinations of Weyl fermions by nontrivial interactions such as four-Fermi vertices, without breaking the chiral symmetry. This is possible only when both their perturbative and nonperturbative gauge anomalies are canceled. Since the unwanted center-localized modes in our system are essentially zero-dimensional, the analysis may be a lot easier than for those in general dimensions. Once the center-localized zero modes were gapped out, they would have an eigenvalue which scales as 1/r1, and we will be able to show that they are decoupled from the low-energy dynamics and the total system is essentially chiral.
6. Summary and discussion
In this work, we have investigated a Shamir lattice domain-wall fermion system with a single curved surface. We have embedded a 2D spherical domain-wall into a 3D flat square lattice ignoring fermion hopping to the outside of the domain-wall. Solving the Dirac equation of the 3D negatively massive Wilson fermion in this system, we have examined the existence of massless chiral edge-localized modes and the gravity they feel through the induced spin connections.
In the free fermion theory with trivial gauge link variables, we have verified the existence of the edge-localized modes on the surface. Moreover, we have shown that these edge modes are almost chiral and massless. We have also identified the effect of the induced gravity as a gap in the Dirac eigenvalue spectrum. The continuum extrapolation and large volume limit are well under control, including recovery of the rotational symmetry. Our single domain-wall fermion system thus describes a single Weyl fermion in the low-energy limit.
With nontrivial U(1) gauge link variables, however, it has turned out that the system shows a dramatic change. With the magnetic monopole-like configuration, we have observed that a center-localized zero mode appears in the vicinity of the monopole, having the opposite chirality to that of the edge modes. This was not expected in the continuum analysis, under a condition where the eigenfunctions are smooth everywhere. We have found that the singularity of the gauge field creates another small but finite domain-wall via additive mass renormalization near the origin, which makes the massless zero mode localized at the wall.
We have discussed the stability of the dynamically created domain-wall and the center-localized zero mode on it and shown that they are topologically protected by the AS index theorem on the sphere. We have then made two proposals to avoid the appearance of these opposite chiral zero modes. One is to impose the admissibility condition, and another is the use of symmetric mass generation. The smallness of the domain-wall radius may help in the analysis of the center-localized mode as it is essentially a zero-dimensional object, which is greatly isolated from the massive bulk modes.
Acknowledgement
We thank S. Aoki, M. Furuta, S. Iso, D.B. Kaplan, Y. Kikukawa, M. Koshino, Y. Matsuki, S. Matsuo, T. Onogi, S. Yamaguchi, M. Yamashita, and R. Yokokura for useful discussions. In particular, we thank Y. Kikukawa for his instruction regarding technical details on the symmetric mass generation.
Funding
Open Access funding: SCOAP3.
Footnotes
Instead of directly using the domain-wall fermions, the effective four-dimensional Dirac operator (also known as the overlap Dirac operator [8]) was used to formulate some successful examples of nonperturbative formulation of lattice chiral gauge theory. See Refs. [7,9,10] and the references therein.
To be precise, the induced connection is spin-c with an additional U(1) part |$\frac{i}{2}$|, which, however, can be eliminated by the gauge transformation. We keep this unphysical U(1) part nonzero to make the analysis simpler, since otherwise, the gauge transformation requires multiple-patch covering of |$\mathbb {R}^3$| to avoid multivaluedness of the gauge transformation with respect to θ.
It may not be adequate to name this configuration a “monopole” since our gauge potential is considered not in 3D space but in 2 + 1-dimensional spacetime. But the computation is completely parallel to the case with the monopole in three spatial dimensions that we discussed in Ref. [37].
The lower bound of j comes from the nontrivial contribution from the monopole, which is proportional to n.



