Feasibility study of the K⁺d → K⁰pp reaction for the Θ⁺ pentaquark

Abstract

1. Introduction

The physics of pentaquarks, which are baryons consisting of four valence quarks and one antiquark, has been renewed very recently, as the LHCb Collaboration announced new findings of three heavy pentaquarks, |$P_c$| [1–4]. The LHCb Collaboration also found five excited |$\Omega_c$| in the channel of the |$\Xi_c^+ K^-$| invariant mass [5]. Four of them were confirmed by the Belle Collaboration [6]. Since these newly found excited |$\Omega_c$| have very small decay widths, several theoretical works have suggested that at least some of them may be identified as singly heavy pentaquarks [7–10]. On the other hand, discussion of light pentaquarks, which was once triggered by the theoretical prediction [11] and the first measurement of the |$\Theta^+$| [12], has become dormant since the null results of the |$\Theta^+$| baryon were reported by the CLAS Collaboration [13–15]. Moreover, both the KEK-PS E533 Collaboration [16] and the J-PARC E19 Collaboration [17,18] searched for the “|$\Theta^+$|” using the pion beam but found no significant peak corresponding to the “|$\Theta^+$|” pentaquark. The Belle Collaboration looked for isospin partners of the “|$\Theta^+$|” in the first observed process |$\gamma \gamma \to p \bar{p} K^+ K^-$| but again found no significant evidence for them [19]. All these negative results make the existence of the “|$\Theta^+$|” rather unlikely, so that both experimental and theoretical investigations on the “|$\Theta^+$|” ebbed away.

Meanwhile, the LEPS Collaboration and DIANA Collaboration continued to report evidence for the existence of the “|$\Theta^+$|” [20–23]. Some years ago, Amaryan et al. analyzed the data from the CLAS Collaboration [24], using the interference method with |$\phi$|-meson photoproduction. They found a peak around |$\sim 1.54$| GeV, which corresponds to the “|$\Theta^+$|”. The statistical significance of this peak was |$5.3\sigma$| [24]. In Ref. [25], the SELEX data on hadro-nucleus collisions at Fermilab were analyzed in the search for formation of the “|$\Theta^+$|”. A narrow enhancement near 1539 MeV was observed in the mass spectrum of the |$pK_S^0$| system emitted at small |$x_F$| from hadron collisions with copper nuclei, where |$x_F$| denotes the Feynman variable defined as the ratio of the momentum |$p_L^*/p_{\mathrm{max}}^*$| (for details see Ref. [25]). However, the results from Ref. [25] show definite dependence on the kinematics.

After the LHCb Collaboration reported the existence of heavy pentaquarks, interest in light pentaquarks seems to have been renewed. For example, the existence of a narrow nucleon resonance |$N^*(1685)$| has been announced by a series of experiments in |$\eta$| photoproduction off the quasi-neutron [26–35]. More recently, a similar narrow peak was observed in the |$\gamma p \to p\pi^0 \eta$| reaction [36]. Though the identification of this narrow resonance is still under debate, one possible interpretation is that it can be regarded as a pentaquark nucleon, which is a member of the baryon antidecuplet [37–39].

Based on previous experimental studies on the “|$\Theta^+$|”, we could draw at least one conclusion: the “|$\Theta^+$|” is most unlikely to exist. Even though it might exist, it is elusive. However, we want to mention that almost all previous experiments have utilized indirect methods such as photon and pion beams, which suffer from large backgrounds [40,41]. Moreover, we know that the “|$\Theta^+$|”, if it exists, decays into |$K^{0} p$| or |$K^{+} n$| and hence couples to them. In particular, the |$K^+ n$| channel may be the most probable one to search for the “|$\Theta^+$|”. In fact, the DIANA Collaboration used the low-energy |$K^+ \mathrm{Xe}$| reaction in the xenon bubble chamber [22,23,42–44], though there is also a theoretical criticism of the DIANA results in 2003 [45]. Nevertheless, the |$K^+$| beam may provide an ultimate smoking gun to whether the “|$\Theta^+$|” exists or not, since it will create the “|$\Theta^+$|” by direct formation and it will be seen in the differential and total cross sections if it exists. There is also a discussion on |$K^+N$| reactions in a nucleus [46]. Thus, measuring the |$K^+ d \to K^0 pp$| reaction is the simplest and final experiment to put a period to the existence of the “|$\Theta^+$|” pentaquark. This process, compared with other reactions such as photoproduction and |$\pi$|-induced productions, is not hampered by significant backgrounds. This means that the experiment of |$K^+d \to K^0 pp$| will clearly assess the existence of the “|$\Theta^+$|”.

The |$K^+ d \to K^0 pp$| reaction has already been investigated theoretically [47] with the width of the “|$\Theta^+$|” being assumed to be |$1$|–|$20 \text{ MeV}$|⁠. Simulations were also performed for experiments proposed at J-PARC [48,49]. In Ref. [47] Sibirtsev et al. considered the single-step process or the impulse scattering process in which the proton in the deuteron was regarded as a spectator and the neutron interacts with the |$K^+$| to produce a proton and a neutral kaon. When the |$K^+$| momentum lies in the range of |$0.47$|–|$0.64 \text{ GeV} / c$|⁠, the peak corresponding to the “|$\Theta^+$|” was seen in the |$K^0 p$| invariant mass spectra. In the vicinity of |$0.47 \text{ GeV} / c$|⁠, the “|$\Theta^+$|” peak was also shown in the total cross sections. In the present work, we include both the single-step and double-step processes and scrutinize the feasibility of the |$K^+ d \to K^0 pp$| reaction in observing the “|$\Theta^+$|” pentaquark. The use of the double-step process was also proposed in Ref. [50]. In the double-step processes, a kaon is exchanged in the course of the interaction between the proton and the neutron. We will show that in the present work the single-step process can cover the energy region corresponding to the “|$\Theta^+$|” peak with an initial kaon momentum |$k_{\mathrm{lab}}\approx 0.4 \text{ GeV} /c$| in the laboratory frame while the double-step processes provide a potential possibility to reach the “|$\Theta^+$|” energy region with a higher kaon momentum |$k_{\mathrm{lab}}\approx 1 \text{ GeV} /c$|⁠. In the present work, therefore, we will carefully investigate the |$K^+d\to K^0 pp$| reaction in the context of the possible existence of the “|$\Theta^+$|”, considering both the single- and double-step processes.

This paper is organized as follows. In Sect. 2, we formulate the cross section of the |$K^{+} d \to K^{0} p p$| reaction. The |$K N \to K N$| scattering amplitude is also shown in this section. In Sect. 3, we give numerical results on the cross section of the |$K^{+} d \to K^{0} p p$| reaction and investigate the strength of a peak signal in the |$K^{0} p$| spectrum, which will provide a good guideline to conclude whether the “|$\Theta ^{+}$|” exists or not. Section 4 is devoted to the summary of this study.

2. Formulation

2.1. Cross section of the |$K^{+} d \to K^{0} p p$| reaction

2.2. Scattering amplitude of the |$K^{+} d \to K^{0} p p$| reaction

Fig. 1.

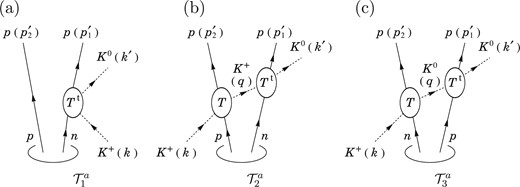
Diagrams for the |$K^{+} d \to K^{0} p p$| reaction. Momenta of particles are shown in parentheses.

Open in new tabDownload slide

2.3. Scattering amplitude of the |$K N \to K N$| reaction

We turn to the |$K N \to K N$| scattering amplitude |$T_{K N \to K N}$|⁠, which is expressed in terms of a |$2 \times 2$| matrix. In the present work, we first present the |$K N \to K N$| amplitude in terms of the partial waves in the CM frame of the |$K N$| system, and then transform it to that in the target-baryon rest frame, taking the method in Ref. [58].

Since we need the |$K N$| amplitudes in the energy range from its threshold to |$w \sim 2 \text{ GeV}$|⁠, we utilize the on-shell |$K N$| amplitude developed in the SAID program [59], in which they provide the on-shell |$K N$| amplitude in various partial waves. We here take the SAID partial-wave amplitudes up to the |$D$| waves and calculate the off-shell amplitudes by using Eq. (17).

The “|$\Theta ^{+}$|” contributions to the |$K^{+} n \to K^{0} p$| and |$K^{0} p \to K^{0} p$| amplitudes are evaluated with the isospin relation |$T_{K^{+} n \to K^{0} p}^{( \Theta )} = - T_{K^{0} p \to K^{0} p}^{( \Theta )} = - T_{K^{+} n \to K^{+} n}^{( \Theta )}$|⁠.

3. Numerical results and discussion

We are now in a position to present the numerical results and discuss their physical implications, in particular how the signal of the “|$\Theta ^{+}$|” pentaquark, if it exists, emerges in the |$K^{0} p$| spectrum.

3.1. Two mechanisms to reach the “|$\Theta ^{+}$|” energy

Before we discuss the details of the |$K^{0} p$| spectrum, we first examine which conditions are better to reach the “|$\Theta ^{+}$|” energy region and to search for its peak. To this end, we calculate the |$K^{0} p$| invariant mass of the |$K^{+} d \to K^{0} p p$| reaction, assuming that the nucleon Fermi motion is zero and that the reaction takes place only in the impulse scattering process. In this case, one proton is produced from a zero-momentum neutron in the initial state of the |$K^{+} n \to K^{0} p$| reaction, while the other proton comes out just as a spectator. Then, we can calculate the |$K^{0} p$| invariant mass in two ways: combining |$K^{0}$| with the produced proton in the impulse scattering process, and |$K^{0}$| with the spectator proton. Namely, in terms of the formulation in Sect. 2.1, the former (latter) case means that the produced proton is the “first” (“second”) proton while the spectator is the “second” (“first”) proton.

The |$K^{0} p$| invariant mass of these two methods is plotted in Fig. 2 in terms of the square boxes (former) and curves (latter), respectively. We note that, in general, the possible |$K^{0} p$| invariant mass discussed here is slightly smeared compared with those in Fig. 2 due to the Fermi motion of the nucleons inside a deuteron. As one can see, on the one hand, the square boxes in Fig. 2 reach around the “|$\Theta ^{+}$|” energy region |$\sim 1.52 \text{ GeV}$| with the initial kaon momentum |$k_{\rm lab} \approx 0.40 \text{ GeV} /c$|⁠. This means that one can investigate the “|$\Theta ^{+}$|” energy region directly in the impulse scattering process with the initial kaon momentum |$k_{\rm lab} \approx 0.40 \text{ GeV} /c$| and with the backward “second” proton. On the other hand, the curves in Fig. 2 suggest that even with higher kaon momenta one can reach the “|$\Theta ^{+}$|” energy region by observing the forward “second” proton. In this case, although the impulse scattering process cannot produce the “|$\Theta ^{+}$|”, double-step scattering can do it, where the intermediate kaon may lead to the formation of the “|$\Theta ^{+}$|”, being combined with the “first” proton.

Fig. 2.

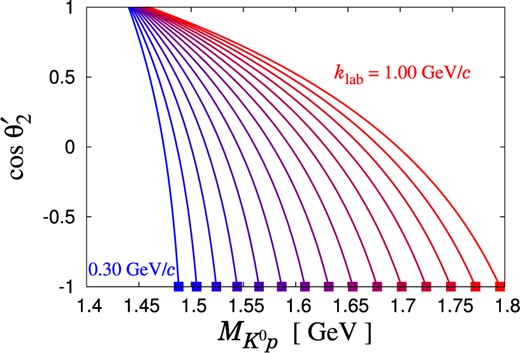
Possible |$K^{0} p$| invariant mass of the |$K^{+} d \to K^{0} p p$| reaction with the impulse scattering process as a function of the scattering angle for the “second” proton in the global CM frame |$\theta _{2}^{\prime}$|⁠. The initial kaon momentum in the laboratory frame |$k_{\rm lab}$| is taken from |$0.30 \text{ GeV} /c$| to |$1.00 \text{ GeV} /c$| in intervals of |$0.05 \text{ GeV} /c$|⁠. We assume zero Fermi motion. The square boxes represent the invariant mass of |$K^{0}$| and the proton produced in the impulse process, while the lines represent that of |$K^{0}$| and the spectator proton.

Open in new tabDownload slide

Therefore, the present study is two-fold. Firstly, we check whether a possible “|$\Theta ^{+}$|” signal will appear in the impulse scattering process with lower kaon momenta |$k_{\rm lab} \approx 0.40 \text{ GeV} /c$|⁠. In fact, Ref. [47] already carried this out. Thus, in the first part of the present work, we extend Ref. [47] and perform a more detailed analysis of the study. Secondly, we investigate whether the double-step scattering contribution with higher kaon momenta |$k_{\rm lab} \sim 1 \text{ GeV} /c$| can generate the “|$\Theta ^{+}$|” in the |$K^{+} d \to K^{0} p p$| reaction.

3.2. Lower kaon momentum

Let us first consider the case of lower kaon momenta. In this case, we expect that the impulse scattering process dominates the |$K^{+} d \to K^{0} p p$| reaction. Indeed, we will see that this is the case at lower kaon momenta, since the double-step processes give only a few % contribution to the differential cross section. In the following discussions for lower momentum we examine the impulse scattering process only, unless explicitly mentioned. This allows one to check how the results of the cross section for the |$K^{+} d \to K^{0} p p$| reaction are affected when the “|$\Theta ^{+}$|” is taken into account.

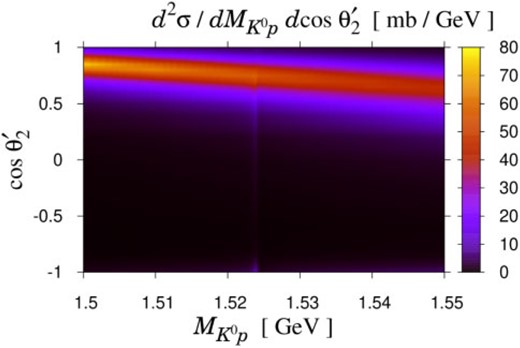
In order to see how the “|$\Theta ^{+}$|” influences the cross section, we show in Fig. 3 the results for the differential cross section |$d^{2} \sigma / d M_{K^{0} p} \cos \theta _{2}^{\prime}$| with the initial kaon momentum |$k_{\rm lab} = 0.45 \text{ GeV} /c$|⁠. The “|$\Theta ^{+}$|” with |$J^{P} = 1/2^{+}$| is taken into account. Here we show only the region |$\cos \theta _{2}^{\prime} \le - 0.9$| because there is no significant structure in the region |$\cos \theta _{2}^{\prime} > 0.9$|⁠. We find two structures in the contour plot of Fig. 3: a sharp peak at |$M_{K^{0} p} = 1.524 \text{ GeV}$| as a “|$\Theta ^{+}$|” signal and a broad bump at |$M_{K^{0} p} = 1.54 \text{ GeV}$| and |$\cos \theta _{2}^{\prime} = -1$| corresponding to the square boxes in Fig. 2, arising from the kinematical effects. The Fermi motion of the bound neutron due to the deuteron wave function, on the one hand, makes the peak at |$( M_{K^{0} p} , \, \cos \theta _{2}^{\prime} ) = ( 1.54 \text{ GeV} , \, -1)$| broad. On the other hand, thanks to the same Fermi motion of the bound neutron, we can reach the “|$\Theta ^{+}$|” energy in the impulse scattering process even when the initial kaon momentum does not exactly match the kaon momentum that generates the two-body CM energy |$1.524 \text{ GeV}$| with a free nucleon at rest, i.e., the kaon momentum |$k_{\rm lab} \approx 0.40 \text{ GeV} /c$|⁠. Therefore, we can observe the “|$\Theta ^{+}$|” signal with |$k_{\rm lab} = 0.45 \text{ GeV} /c$| as in the left panel of Fig. 3.

Fig. 3.

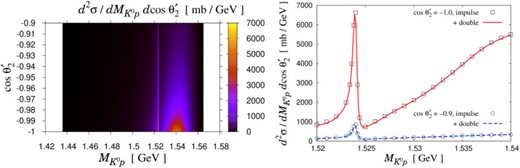
Results for the differential cross section of the |$K^{+} d \to K^{0} p p$| reaction in the impulse scattering process (left) and a comparison of the differential cross section with and without the double-step processes at |$\cos \theta _{2}^{\prime} = -1.0$| and |$-0.9$| (right). The initial kaon momentum is fixed as |$k_{\rm lab} = 0.45 \text{ GeV} /c$|⁠. The “|$\Theta^{+}$|” with |$J^{P} = 1/2^{+}$| is taken into account.

Open in new tabDownload slide

To confirm that the impulse scattering process dominates the |$K^{+} d \to K^{0} p p$| reaction in the lower kaon momentum case, we compare in the right panel of Fig. 3 the differential cross section |$d^{2} \sigma / d M_{K^{0} p} \cos \theta _{2}^{\prime}$| only with the impulse scattering (points) and that with the double-step processes (lines). The initial kaon momentum is |$k_{\rm lab} = 0.45 \text{ GeV} /c$|⁠, the spin/parity of the “|$\Theta ^{+}$|” is |$J^{P} = 1/2^{+}$|⁠, and the scattering angles |$\cos \theta _{2}^{\prime} = -1.0$| and |$-0.9$| are considered. From the right panel of Fig. 3 we can see that the contributions from the double-step processes are indeed negligible in the lower kaon momentum case. Indeed, the double-step processes give only a few % contribution to the differential cross section. The same behavior is observed at other angles |$\cos \theta _{2}^{\prime}$| and other (but lower) kaon momenta. Therefore, we can safely concentrate on the impulse scattering process in this subsection.

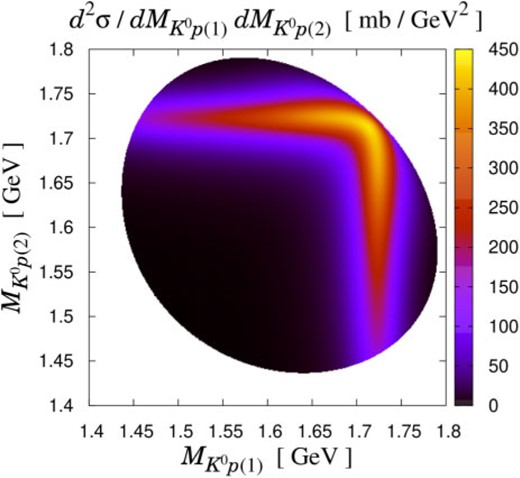
We discuss the same reaction with the Dalitz plot |$d^{2} \sigma / d M_{K^{0} p (1)} d M_{K^{0} p (2)}$|⁠. In Fig. 4 we show the Dalitz plot with |$k_{\rm lab} = 0.45 \text{ GeV} / c$| and the “|$\Theta ^{+}$|” with spin and parity |$J^{P} = 1/2 ^{+}$|⁠. Broad structures around |$M_{K^{0} p (1)} \sim 1.54$| in the vertical direction and |$M_{K^{0} p (2)} \sim 1.54$| in the horizontal direction originate from the kinematical effects, which correspond to the square boxes in Fig. 2. In addition, sharp structures at |$M_{K^{0} p (1)} = 1.524$| in the vertical direction and |$M_{K^{0} p(2)} = 1.524$| in the horizontal direction indicate the “|$\Theta^{+}$|” signal.

Fig. 4.

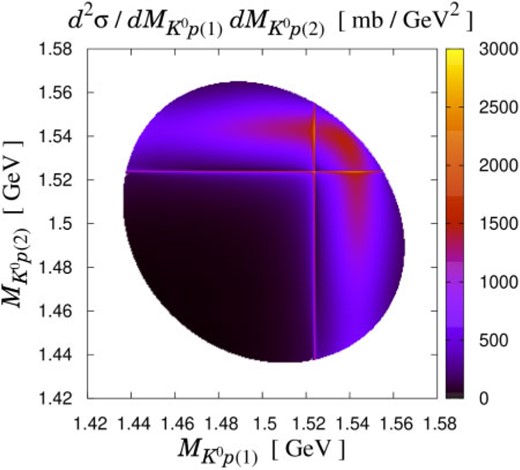
Dalitz plot of the |$K^{+} d \to K^{0} p p$| reaction in the impulse scattering process. The initial kaon momentum is fixed as |$k_{\rm lab} = 0.45 \text{ GeV} /c$|⁠. The “|$\Theta^{+}$|” with |$J^{P} = 1/2^{+}$| is taken into account.

Open in new tabDownload slide

In Fig. 5 we plot the |$K^{0} p$| invariant mass spectra of the |$K^{+} d \to K^{0} p p$| reaction with three initial kaon momenta |$k_{\rm lab} = 0.40 \text{ GeV} /c$|⁠, |$0.45 \text{ GeV} / c$|⁠, and |$0.50 \text{ GeV} /c$|⁠. Here we take into account the “|$\Theta ^{+}$|” contribution with |$J^{P} = 1/2^{+}$|⁠, and we integrate with respect to the scattering angle in the range |$-1 < \cos \theta _{2}^{\prime} < -0.8$|⁠. As one can see from Fig. 5, on the one hand, the broad-peak structure, which corresponds to impulse scattering of the initial kaon and almost on-shell bound neutron, moves upward as |$k_{\rm lab}$| increases, as expected from the square boxes in Fig. 2. On the other hand, the “|$\Theta ^{+}$|” signal stays at |$1.524 \text{ GeV}$| with different values of |$k_{\rm lab}$|⁠. Among the three values of the kaon momenta, |$k_{\rm lab} = 0.40 \text{ GeV} / c$| yields the highest peak at |$M_{K^{0} p} = 1.524 \text{ GeV}$| for the “|$\Theta ^{+}$|” signal on top of the broad peak. This is a consequence of the momentum matching in Fig. 2.

Fig. 5.

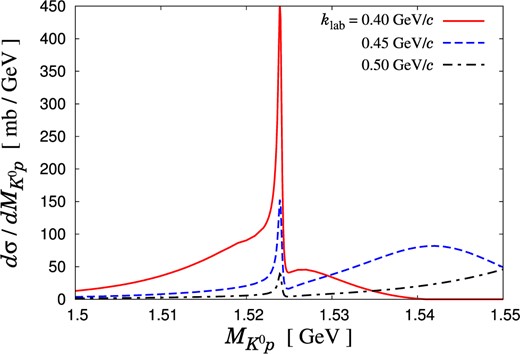
|$K^{0} p$| invariant mass spectrum of the |$K^{+} d \to K^{0} p p$| reaction with initial kaon momenta |$k_{\rm lab} = 0.40 \text{ GeV} /c$|⁠, |$0.45 \text{ GeV} /c$|⁠, and |$0.50 \text{ GeV} / c$| in the impulse scattering process. The integral range of the scattering angle is |$-1 < \cos \theta _{2}^{\prime} < -0.8$|⁠. The “|$\Theta ^{+}$|” with |$J^{P} = 1/2^{+}$| is taken into account.

Open in new tabDownload slide

We then examine other spin/parity combinations of the “|$\Theta ^{+}$|” pentaquark: |$J^{P} = 1/2^{-}$|⁠, |$3/2^{+}$|⁠, and |$3/2^{-}$|⁠. In Fig. 6 we show the |$K^{0} p$| invariant mass spectrum of the |$K^{+} d \to K^{0} p p$| reaction with the initial kaon momentum |$k_{\rm lab} = 0.40 \text{ GeV} / c$| and with the “|$\Theta ^{+}$|” of |$J^{P} = 1/2^{\pm}$| and |$3/2^{\pm}$|⁠. The integral range of the scattering angle is |$-1 < \cos \theta _{2}^{\prime} < -0.8$|⁠. Figure 6 indicates that the peak heights for the “|$\Theta ^{+}$|” signal in different quantum numbers are similar to each other. These peaks generate the “|$\Theta ^{+}$|” production cross section |$\sim$| several hundred |$\mu \text{b}$| to |$1 \text{ mb}$| with |$k_{\rm lab} \approx 0.40 \text{ GeV} / c$|⁠.

Fig. 6.

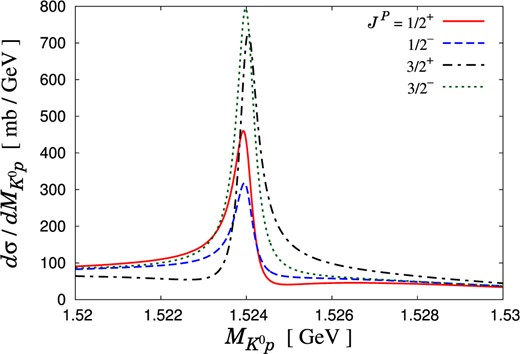
|$K^{0} p$| invariant mass spectrum of the |$K^{+} d \to K^{0} p p$| reaction in the impulse scattering process with the “|$\Theta ^{+}$|” spin/parity |$J^{P} = 1/2^{\pm}$| and |$3/2^{\pm}$|⁠. The initial kaon momentum is fixed as |$k_{\rm lab} = 0.40 \text{ GeV} /c$|⁠. The integral range of the scattering angle is |$-1 < \cos \theta _{2}^{\prime} < -0.8$|⁠.

Open in new tabDownload slide

Finally we calculate the total cross section of the |$K^{+} d \to K^{0} p p$| reaction with the “|$\Theta ^{+}$|” contribution of spin/parity |$J^{P} = 1/2^{\pm}$| and |$3/2^{\pm}$|⁠. The result is shown in Fig. 7 together with the old experimental data on |$K^+d\to K^0pp$| scattering [61–64]. Note that similar results were already obtained in Ref. [47], in which, however, the width of the “|$\Theta^+$|” was taken to be |$1$|–|$20 \text{ MeV}$|⁠. As shown in Fig. 7, even if the decay width of the “|$\Theta ^{+}$|” is as small as |$\Gamma _{\Theta} = 0.5 \text{ MeV}$|⁠, which is approximately 2–40 times smaller than those in Ref. [47], one can observe a bump structure around the initial kaon momentum in the laboratory frame |$k_{\rm lab} = 0.4 \text{ GeV} / c$|⁠. The height of the bump gives indeed a few hundred |$\mu \text{b}$| to |$1 \text{ mb}$|⁠. While the old experiments lack data in the vicinity of |$k_{\mathrm{lab}} \approx 0.4\,\text{ GeV}/c$|⁠, new experiments at the J-PARC, if performed exclusively near this value of the initial kaon momentum in the near future, will be able to assess the existence of the “|$\Theta^+$|”, because the size of the bump structure (a few hundred |$\mu \text{b}$| to |$1 \text{ mb}$|⁠) is still strong enough to be seen. In order to check a bump structure in the total cross section in Fig. 7, the required resolution of the initial kaon momentum is about several tens of MeV|$/ c$|⁠, while one can observe the “|$\Theta ^{+}$|” peak, if it exists, in the |$K^{0} p$| invariant mass spectrum as in Fig. 6 with the resolution of the |$K^{0} p$| invariant mass |$\sim 1 \text{ MeV}$|⁠.

Fig. 7.

Total cross section of the |$K^{+} d \to K^{0} p p$| reaction as a function of the initial kaon momentum in the laboratory frame |$k_{\rm lab}$|⁠. We take into account only the impulse scattering. The experimental data are taken from Refs. [61–64].

Open in new tabDownload slide

3.3. Higher kaon momentum

We now focus on the case of higher kaon momenta. To reach the “|$\Theta ^{+}$|” energy region with higher kaon momenta, we need to consider the double-step scattering process where the initial |$K^+$| produces a proton from the deuteron in the first collision, losing some of its momentum. Then, it interacts with the other nucleon in the second collision. In this process, the first collision corresponds to the |$K^{+} p \to K^{+} p$| or |$K^{+} n \to K^{0} p$| reaction of the forward proton emission. In this sense, the initial kaon momentum should be chosen such that the forward proton emission efficiently takes place in the first collision. In other words, we require a specific initial kaon momentum in such a way that the |$K^{+} p \to K^{+} p$| and |$K^{+} n \to K^{0} p$| cross sections with the forward proton emission should be large. In fact, this strategy was employed to search for a |$\bar{K} N N$| quasi-bound state in the |$K^{-} {}^{3}\text{He} \to \Lambda p n$| reaction in the J-PARC E15 experiment [65,66]. In the J-PARC E15 experiment, to generate a |$\bar{K} N N$| quasi-bound state, they planned to prepare a slow antikaon and two of the three bound nucleons in |${}^{3} \text{He}$| by using the |$K^{-} n \to K^{-} n$| or |$K^{-} p \to \bar{K}^{0} n$| reaction with the fast forward neutron emission as the first collision, which eventually leads to the |$\bar{K} N N$| quasi-bound state (see also the theoretical calculation of the |$K^{-}{}^{3}\text{He} \to \Lambda p n$| reaction in Ref. [67]). To prepare a slow antikaon and fast forward neutron emission as much as possible, the initial |$K^{-}$| momentum |$k_{\rm lab} = 1.0 \text{ GeV} /c$| was selected in Refs. [65,66].

As shown in the top panels of Fig. 8 for the differential cross sections of the |$\bar{K} N \to \bar{K} N$| reaction as functions of the initial antikaon momentum |$k_{\rm lab}$| and antikaon scattering angle |$\theta _{K}$|⁠, the |$\bar{K} N \to \bar{K} N$| differential cross section indeed reveals a peak structure at |$k_{\rm lab} \approx 1 \text{ GeV} / c$| and |$\cos _{K} \approx -1$|⁠, which is essential to obtain a slow antikaon with the forward neutron emission.

Fig. 8.

Differential cross sections of the |$K^{-} n \to K^{-} n$| (top left), |$K^{-} p \to \bar{K}^{0} n$| (top right), |$K^{+} p \to K^{+} p$| (bottom left), and |$K^{+} n \to K^{0} p$| (bottom right) reactions. The |$\bar{K} N \to \bar{K} N$| cross sections are taken from a dynamical coupled-channels model, and the |$K N \to K N$| cross sections are calculated with the SAID amplitudes [59].

Open in new tabDownload slide

When it comes to the |$K N \to K N$| case, the bottom panels of Fig. 8 illustrate the |$K^{+} p \to K^{+} p$| and |$K^{+} n \to K^{0} p$| reaction cross sections, which indicates that |$k_{\rm lab} = 0.8$|–|$0.9 \text{ GeV} /c$| are the best values for the present study of the |$K^{+} d \to K^{0} p p$| reaction. With these kaon momenta, we obtain the largest cross sections of the |$K^{+} n \to K^{0} p$| and |$K^{+} p \to K^{+} p$| reactions at |$\cos \theta _{K} \approx -1$|⁠, which corresponds to the forward proton emission. Thus, we fix the initial kaon momentum to be |$k_{\rm lab} = 0.85 \text{ GeV} / c$| and compute the |$K^{0} p$| invariant mass spectrum of the |$K^{+} d \to K^{0} p p$| reaction. Note that we take into account here both the double-step scattering process and the impulse scattering one.

In Fig. 9, we show the results of the differential cross section in the “|$\Theta ^{+}$|” energy region including the “|$\Theta ^{+}$|” with |$J^{P} = 1/2^{+}$|⁠. Figure 9 exhibits three structures: a band at |$\cos \theta _{2}^{\prime} \gtrsim 0.5$|⁠, a thin line at |$M_{K^{0} p} = 1.524 \text{ GeV}$|⁠, and a sharp peak at |$( M_{K^{0} p} , \, \cos \theta _{2}^{\prime} ) = ( 1.524 \text{ GeV} , \, -1 )$|⁠. The first band structure corresponds to the line in Fig. 2 and originates from the impulse scattering contribution. Note, however, that it was parametrized in terms of the invariant mass of |$K^{0}$| and spectator proton. The second one, the line structure, represents a signal of the “|$\Theta ^{+}$|”. The impulse scattering process cannot generate the line structure because in such a case a highly off-shell neutron is required. Therefore, we can conclude that this line structure is given by the double-step scattering process. The third one, which corresponds to the sharp peak around 1.524 GeV and |$\cos \theta _{2}^{\prime} = -1$|⁠, arises from the “|$\Theta ^{+}$|” production in the impulse scattering process with a highly off-shell bound nucleon. This contribution, however, depends on the tail of the deuteron wave function in momentum space and thus contains large theoretical uncertainty. Therefore, we do not regard this third sharp-peak structure at |$( M_{K^{0} p} , \, \cos \theta _{2}^{\prime} ) = ( 1.524 \text{ GeV} , \, -1 )$| as an important one.

Fig. 9.

Differential cross section of the |$K^{+} d \to K^{0} p p$| reaction in the impulse plus double scattering processes. The initial kaon momentum is fixed as |$k_{\rm lab} = 0.85 \text{ GeV} /c$|⁠. The “|$\Theta ^{+}$|” with |$J^{P} = 1/2^{+}$| is taken into account.

Open in new tabDownload slide

As in the lower kaon momentum case, we can discuss the same reaction with the Dalitz plot |$d^{2} \sigma / d M_{K^{0} p (1)} d M_{K^{0} p (2)}$|⁠. In Fig. 10 we show the Dalitz plot with |$k_{\rm lab} = 0.85 \text{ GeV} / c$| and the “|$\Theta ^{+}$|” spin/parity |$J^{P} = 1/2 ^{+}$|⁠. We can hardly distinguish the “|$\Theta ^{+}$|” signal around |$M_{K^{0} p (1)} = 1.524$| in the vertical direction and |$M_{K^{0} p (2)} = 1.524$| in the horizontal direction because the impulse scattering process dominates the reaction as a whole. Nevertheless, if we enlarge the Dalitz plot, we can observe small sharp structures at |$M_{K^{0} p (1)} = 1.524$| in the vertical direction and |$M_{K^{0} p (2)} = 1.524$| in the horizontal direction as the “|$\Theta ^{+}$|” signal.

Fig. 10.

Dalitz plot of the |$K^{+} d \to K^{0} p p$| reaction in the impulse plus double scattering processes. The initial kaon momentum is fixed as |$k_{\rm lab} = 0.85 \text{ GeV} /c$|⁠. The “|$\Theta^{+}$|” with |$J^{P} = 1/2^{+}$| is taken into account.

Open in new tabDownload slide

Now the very important task is to answer how significant the signal of the “|$\Theta ^{+}$|” in the double-step scattering process, i.e., the thin line structure in Fig. 9, is compared to the impulse scattering contribution parametrized in terms of the invariant mass of |$K^{0}$| and spectator proton band in Fig. 9. To do that, we integrate the differential cross section of Fig. 9 with the integral range |$0 < \cos \theta _{2}^{\prime} < 1$|⁠, which results in the |$K^{0} p$| invariant mass spectrum in Fig. 11. Here we have introduced the “|$\Theta ^{+}$|” contribution of spin/parity |$J^{P} = 1/2^{\pm}$| and |$3/2^{\pm}$|⁠. As shown in Fig. 11, with every spin/parity of the “|$\Theta ^{+}$|”, a small “|$\Theta ^{+}$|” signal exists on a smooth background. The smooth background out of the “|$\Theta ^{+}$|” energy comes from the broad band at |$\cos \theta _{2}^{\prime} \gtrsim 0.5$| in Fig. 9, so we can see that the background originates from the impulse scattering contribution. This dominates the cross section (i.e., the integral of the mass spectrum) of the reaction. Nevertheless, the small “|$\Theta ^{+}$|” signal is not invisible owing to the double-step processes. By calculating the excess area of the spectrum in Fig. 11 on top of the background from the impulse scattering contribution, we find that the “|$\Theta^{+}$|” production cross section turns out to be about |$0.9 ~\mu \text{b}$|⁠, |$0.4 ~\mu \text{b}$|⁠, |$1 ~\mu \text{b}$|⁠, and |$3 ~\mu \text{b}$| for the spin/parity of the “|$\Theta ^{+}$|” |$J^{P} = 1/2^{+}$|⁠, |$J^{P} = 1/2^{-}$|⁠, |$J^{P} = 3/2^{+}$|⁠, and |$J^{P} = 3/2^{-}$|⁠, respectively. Therefore, we expect that in the |$K^{+} d \to K^{0} p p$| reaction with higher kaon momenta |$k_{\rm lab} \approx 0.85 \text{ GeV} / c$| a measurement of the production cross section |$\lesssim 1 ~\mu \text{b}$| is required to save the “|$\Theta ^{+}$|” pentaquark. One can experimentally assess the existence of such a narrow peak in the |$K^{0} p$| spectrum with the resolution of the |$K^{0} p$| invariant mass |$\sim 1 \text{ MeV}$|⁠.

Fig. 11.

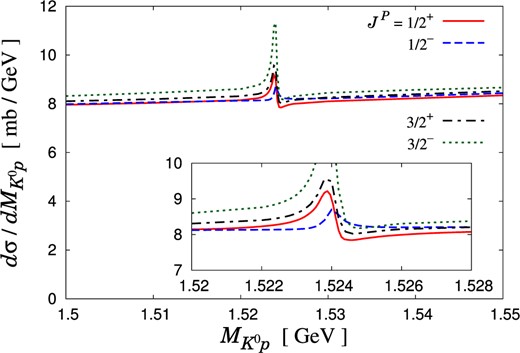
|$K^{0} p$| invariant mass spectrum of the |$K^{+} d \to K^{0} p p$| reaction in the impulse and double-step scattering processes with the “|$\Theta ^{+}$|” spin/parity |$J^{P} = 1/2^{\pm}$| and |$3/2^{\pm}$|⁠. The initial kaon momentum is fixed to be |$k_{\rm lab} = 0.85 \text{ GeV} /c$|⁠. The integral range of the scattering angle is given as |$0 < \cos \theta _{2}^{\prime} < 1$|⁠. The inset represents an enlarged figure.

Open in new tabDownload slide

4. Summary and outlook

In the present work, we have investigated the |$K^+ d \to K^0 pp$| reaction as a feasibility study to suggest the kinematical conditions for the most probable range of the initial kaon momentum and to assess the existence of the “|$\Theta^+$|” pentaquark in this reaction. We consider two different dynamical processes for the |$K^+ d \to K^0 pp$| reaction, i.e., the single-step or impulse scattering process and the double-step scattering process. While the first was already considered in a previous study, the latter was ignored. In the present work, we took into account both the processes and scrutinized the kinematical conditions relevant to each process and their relevances in the production of the “|$\Theta^+$|” pentaquark. We showed explicitly that, to produce the “|$\Theta ^{+}$|”, the impulse scattering process is dominant over the double-step scattering process in lower-momentum regions (⁠|$k_{\mathrm{lab}}\approx 0.40 \text{ GeV} /c$|⁠), whereas the double-step one overtakes the impulse one in higher-momentum regions (⁠|$k_{\mathrm{lab}}\approx 0.85 \text{ GeV} /c$|⁠). We found that the strength of the bump structure corresponding to the “|$\Theta^+$|” is about a few hundred |$\mu\mathrm{b}$| to 1 mb in the lower-momentum region, while it is about 1 |$\mu\mathrm{b}$| in the higher-momentum region.

The |$K^+$| beam has a unique feature in investigating the existence of the “|$\Theta^+$|”, compared with almost all experiments done previously. This tentative pentaquark state “|$\Theta^+$|” is strongly coupled to either |$K^+ n$| or |$K^0 p$|⁠. This implies that the charged |$K^+$| beam provides a chance to produce the “|$\Theta^+$|” by direct formation. Thus, it is not necessary to resort to any complicated methods of experimental analysis to observe the “|$\Theta^+$|”, if it exists. In this sense, J-PARC is the best place to perform the ultimate experiments with the |$K^+$| beam to put a final period to the matter of the “|$\Theta^+$|” existence. It is physically worthwhile to carry out such experiments in the future. If the experiments at J-PARC find that “|$\Theta^+$|” does not exist, it will bring any debate on the existence of the “|$\Theta^+$|” to an end. However, if the experiments yield any evidence for its existence, it will reignite interest in the physics of light pentaquarks.

Acknowledgements

The authors want to express their gratitude to M. Oka and K. Tanida for useful discussions. H.-Ch.K. is also grateful to M. V. Polyakov and Gh.-S. Yang for valuable discussions and comments. He is also very grateful to the members of the Advanced Science Research Center (ASRC), Japan Atomic Energy Agency (JAEA), where part of the work was carried out, for the hospitality and support. H.-Ch.K. is supported by the Basic Science Research Program through the National Research Foundation of Korea funded by the Ministry of Education, Science and Technology (2018R1A2B2001752 and 2018R1A5A1025563). A.H. is supported in part by JSPS KAKENHI No. JP17K05441 (C) and Grants-in-Aid for Scientific Research on Innovative Areas (No. 18H05407).

Funding

Open Access funding: SCOAP|$^3$|⁠.

Footnotes

References