Θ+ baryon, N* (1685) resonance, and πN sigma term reexamined within the framework of a chiral soliton model

Abstract

We reexamine the properties of the baryon antidecuplet Θ⁺ and N*, and the πN sigma term within the framework of a chiral soliton model, focusing on their dependence on the Θ⁺ mass. It turns out that the measured value of the N* mass, M_N* = 1686 MeV, is consistent with that of the Θ⁺ mass M_Θ⁺ = 1524 MeV by the LEPS collaboration [T. Nakano et al. [LEPS Collaboration], Phys. Rev. C 79, 025210 (2009)]. The N*→Nγ magnetic transition moments are almost independent of the Θ⁺ mass. The ratio of the radiative decay width Γ_nn* to Γ_pp* turns out to be around 5. The decay width for Θ⁺→NK is studied in the context of the LEPS and DIANA experiments. When the LEPS value of the Θ⁺ mass is employed, we obtain Γ_ΘNK = (0.5 ± 0.1) MeV. The πN sigma term is found to be almost independent of the Θ⁺ mass. In addition, we derive a new expression for the πN sigma term in terms of the isospin mass splittings of the hyperon octet as well as that of the antidecuplet N*.

1. Introduction

The baryon antidecuplet is the first excitation consisting of exotic pentaquark baryons [1; 2; 3]. Since the LEPS collaboration reported the first measurement of the pentaquark baryon Θ⁺ [4], pentaquark baryons attracted a great deal of attention, before a series of CLAS experiments announced null results for Θ⁺ [5; 6; 7; 8], which cast doubt on the existence of pentaquarks [9; 10]. On the other hand, the DIANA collaboration has continued searching for Θ⁺ [11; 12] and observed the formation of a narrow pK⁰ peak with a mass of 1538 ± 2 MeV/c² and a width of Γ = 0.39 ± 0.10 MeV in the |$K^{+}n\rightarrow K^{0}p$| reaction with higher statistical significance (6 σ−8 σ) [12]. The decay width was more precisely measured in comparision with the former DIANA measurement [13], the statistics being doubled. The SVD experiment has also found a narrow peak with the mass (1523 ± 2_stat. ± 3_syst.) MeV in the inclusive reaction

$$pA\to pK_s^0+X$$

[14; 15]. In 2009, the LEPS collaboration again announced evidence for Θ⁺ [16]: The mass of Θ⁺ was found to be M_Θ = 1524 ± 2 ± 3 MeV/c² and the statistical significance of the peak turned out to be 5.1 σ. The differential cross section was estimated to be (12 ± 2) nb/sr in the photon energy ranging from 2.0 GeV to 2.4 GeV in the LEPS angular range. While the statistics of the new LEPS data has been improved by a factor of 8 over the previous measurement [4], Ref. [17] has raised doubts about the Θ⁺ peak found by the LEPS collaboration. Very recently, Amaryan et al. reported a narrow structure around 1.54 GeV in the process γ+p→pK_SK_L via interference with ϕ-meson production with the statistical significance 5.9 σ [18], though the CLAS collaboration has not officially approved their analysis [19].

In addition to the Θ⁺ baryon, Kuznetsov et al. [20] have observed a new nucleon-like resonance around 1.67 GeV from η photoproduction off the deutron in the neutron channel. The decay width was measured to be around 40 MeV, the effects of the Fermi motion being not excluded [21]. On the other hand, this narrow resonant structure was not seen in the quasi-free proton channel [20]. The findings of Ref. [20] are consistent with the theoretical predictions [22; 23] of non-strange exotic baryons. Moreover, the narrow width and isospin asymmetry in the initial states, also called the neutron anomaly [24], are typical characteristics for photoexcitation of the non-strange antidecuplet pentaquark [25; 26]. New analyses of the free proton GRAAL data [24; 27; 28; 29; 30] have revealed a resonance structure with a mass around 1685 MeV and width Γ≤15 MeV, though the data of Ref. [31] do not agree with those of Ref. [27]. For a detailed discussion of this discrepancy, we refer to Ref. [28]. The CB-ELSA collaboration [32; 33; 34] has also confirmed evidence for this N* resonance in line with that of GRAAL. Very recently, Kuznetsov and Polyakov have extracted a new result for the narrow peak: M_N* = 1686 ± 7 ± 5 MeV with the decay width Γ≈28 ± 12 MeV [35]. All these experimental facts are compatible with the results for transition magnetic moments in the chiral quark–soliton model (χQSM) [25; 26] and the phenomenological analysis of non-strange pentaquark baryons [36]. The γN→ηN reaction was studied within an effective Lagrangian approach [37; 38] that has described qualitatively well the GRAAL data. The present status of N*(1685) is summarized in Ref. [39], in which the reason why N*(1685) can be most probably identified as a baryon antidecuplet member was discussed in detail.

In the present work, we want to examine the relation between the Θ⁺ mass and other observables such as the mass of the N* (M_N*), N*→Nγ transition magnetic moments (μ_NN*), the decay width of Θ⁺ (Γ_Θ⁺), and the πN sigma term (σ_πN), in the context of the LEPS and DIANA experiments. In particular, we will regard the N*(1685) resonance with the narrow width as a member of the antidecuplet in this work. The mass splittings of the SU(3) baryons within a chiral soliton model (χSM) were reinvestigated with all parameters fixed unequivocally [40]. Since the mass of Θ⁺ observed by the LEPS collaboration is different from that observed by the DIANA collaboration, it is of great importance to examine carefully the relevance of the analysis in Ref. [40] with regard to the LEPS and DIANA experiments. We will show in this work that the decay width Γ_Θ obtained from the χSM [40] is consistent with these two experiments. We will also study the dependence of the N* mass on M_Θ⁺, which turns out to be compatible with the LEPS data. In addition, we also investigate the dependence of the N*→N magnetic transition moment on M_Θ⁺, which is shown to be almost insensitive to the Θ⁺ mass. Finally, σ_πN will be examined; this becomes one of the essential quantities in the physics of dark matter [41; 42]. Motivated by its relevance in dark matter, a great amount of effort has gone into the evaluation of σ_πN. For example, there are now various results from lattice QCD [43; 44; 45; 46]. However, the value of σ_πN still does not converge, but is known only with a wide range of uncertantities: 35–75 MeV. Thus, we will discuss σ_πN in connection with the baryon antidecuplet and will show that it is rather stable with respect to the Θ⁺ mass. Moreover, its predicted value is smaller than that used in previous analyses [2; 47; 48].

The present work is organized as follows: In Sect. 22, the pertinent formulae for the baryon antidecuplet within a chiral soliton model are compiled. In Sect. 3, we discuss the results. The final section is devoted to a summary and a conclusion.

2. Baryon antidecuplet from a chiral soliton model

We first recapitulate briefly the formulae of mass splittings, magnetic moments, and axial-vector constants within the framework of the χSM. We begin with the collective Hamiltonian of chiral solitons, which have been thoroughly studied within various versions of the χSM, such as the chiral quark–soliton model [49; 50], the Skyrme model [51], and the chiral hyperbag model [52]. The most general form of the collective Hamiltonian in the SU(3) χSM can be written as follows:

\begin{equation} H = M_{{\rm cl}} + H_{{\rm rot}} + H_{{\rm sb}}, \label{eq2.1} \end{equation}

(2.1)

where M_cl denotes the classical soliton mass. H_rot and H_sb respectively stand for the 1/N_c rotational and symmetry-breaking corrections with the effects of isospin and SU(3) flavor symmetry breakings included [53]:

\begin{align} H_{{\rm rot}} & = \frac{1}{2I_{1}}\sum_{i=1}^{3}\hat{J}_{i}^{2} + \frac{1}{2I_{2}}\sum_{p=4}^{7}\hat{J}_{p}^{2}, \label{eq2.2}\\ H_{{\rm sb}} & = (m_{{\rm d}}-m_{{\rm u}}) \left(\frac{\sqrt{3}}{2} \alpha D_{38}^{(8)}(A) + \beta\,\hat{T_{3}} + \frac{1}{2} \gamma\sum_{i=1}^{3}D_{3i}^{(8)}(A)\, \hat{J}_{i}\right)\notag\\ & \quad + (m_{{\rm s}}-\bar{m}) \left(\alpha\, D_{88}^{(8)}(A) + \beta\,\hat{Y} + \frac{1}{\sqrt{3}} \gamma \sum_{i=1}^{3}D_{8i}^{(8)}(A)\,\hat{J}_{i}\right) \end{align}

(2.2)

\begin{align} \quad - (m_{{\rm u}}+m_{{\rm d}}+m_{{\rm s}}) (\alpha+\beta), \label{eq2.3} \end{align}

(2.3)

where I_1,2 represent the soliton moments of inertia that depend on the dynamics of specific formulations of the χSM. However, they will be determined by the masses of the baryon octet, Ω mass, and Θ⁺ mass. The J_i denote the generators of the SU(3) group. The m_u, m_d, and m_s designate the up, down, and strange current quark masses, respectively. The |$\bar {m}$| is the average of the up and down quark masses. We want to mention that we do not need to know each current quark mass separately but only the ratio of them, i.e., |$m_{{\mathrm {s}}}/\bar {m}$|⁠, to determine the sigma πN term. The |$D_{ab}^{(\mathcal {R})}(A)$| indicate the SU(3) Wigner D functions. The |$\hat {Y}$| and |$\hat {T_{3}}$| are the operators of the hypercharge and isospin third component, respectively. The α, β, and γ are given in terms of the σ_πN and soliton moments of inertia I_1,2 and K_1,2 as follows:

\begin{equation} \alpha=-\left(\frac{\sigma_{\pi N}}{3 \bar{m}}-\frac{K_{2}}{I_{2}}\right), \quad \beta=-\frac{K_{2}}{I_{2}},\quad \gamma=2\left(\frac{K_{1}}{I_{1}}-\frac{K_{2}}{I_{2}}\right). \label{eq2.4} \end{equation}

(2.4)

Since α, β, and γ depend on the moments of inertia and σ_πN, they are also related to the details of the specific dynamics of the χSM. Note that α, β, and γ defined in the present work do not contain the strange quark mass, while those in Refs. [2; 47] include it.

In the χSM, we have the following constraint for J₈:

\begin{equation} J_{8} = -\frac{N_{c}}{2\sqrt{3}}B = -\frac{\sqrt{3}}{2},\quad Y' = \frac{2}{\sqrt{3}}J_{8} = -\frac{N_{c}}{3} = -1,\label{eq2.5} \end{equation}

(2.5)

where B represents the baryon number. It is related to the eighth component of the soliton angular velocity, which is due to the presence of the discrete valence quark level in the Dirac-sea spectrum in the SU(3) χQSM [49; 54], while it arises from the Wess–Zumino term in the SU(3) Skyrme model [55; 56; 57]. Its presence has no effect on the chiral soliton but allows us to take only the SU(3) irreducible representations with zero triality. Thus, the allowed SU(3) multiplets are the baryon octet (J = 1/2), decuplet (J = 3/2), and antidecuplet (J = 1/2), etc.

The baryon collective wave functions of H are written as SU(3) Wigner D functions in the representation |$\mathcal {R}$|⁠:

\begin{align} \langle A|\mathcal{R}, B(Y\,T\,T_{3},\; Y^{\prime}\,J\,J_{3}) \rangle & = \Psi_{(\mathcal{R}^{*} ; Y^{\prime}\,J\, J_{3})}^{(\mathcal{R};\, Y\,T\,T_{3})}(A) \notag\\ & = \sqrt{{\mathrm{dim}}(\mathcal{R})} (-)^{J_{3} + Y^{\prime}/2}\,D_{(Y,\, T,\, T_{3})(-Y^{\prime},\, J,\,-J_{3})}^{(\mathcal{R})*}(A), \label{eq2.6} \end{align}

(2.6)

where |$\mathcal {R}$| stands for the allowed irreducible representations of the SU(3) group, i.e. |$\mathcal {R}=8, 10, \overline {10},\ldots $| and Y,T,T₃ are the corresponding hypercharge, isospin, and its third component, respectively. The constraint of the right hypercharge Y^′ = 1 selects a tower of allowed SU(3) representations: the lowest ones, i.e., the baryon octet and decuplet, coincide with those of the quark model. This has been considered as a success of collective quantization and as a sign of certain duality between a rigidly rotating heavy soliton and a constituent quark model. The third lowest representation is the antidecuplet [2], which includes the Θ⁺ and N* baryons.

Different SU(3) representations get mixed in the presence of the symmetry-breaking term H_sb of the collective Hamiltonian in Eq. (2.3), so that the collective wave functions are no longer in pure states but are given as the following linear combinations [49; 58]:

\begin{align} |B_{8}\rangle & = |8_{1/2},B\rangle + c_{\overline{10}}^{B}|\overline{10}_{1/2},B\rangle + c_{27}^{B}|27_{1/2},B\rangle ,\notag\\ |B_{10}\rangle & = |10_{3/2},B\rangle + a_{27}^{B}|27_{3/2},B\rangle + a_{35}^{B}|35_{3/2},B\rangle, \notag\\ |B_{\overline{10}}\rangle & = |\overline{10}_{1/2},B\rangle + d_{8}^{B}|8_{1/2},B\rangle + d_{27}^{B}|27_{1/2},B\rangle + d_{\overline{35}}^{B} |\overline{35}_{1/2},B\rangle.\label{eq2.7} \end{align}

(2.7)

Detailed expressions for the coefficients in Eq. (2.7) can be found in Refs. [47; 49].

Since we take into account the effects of isospin symmetry breaking, we also have to introduce the EM mass corrections to the mass splitting of the SU(3) baryons, which are equally important. The EM corrections to the baryon masses can be derived from the baryonic two-point correlation functions. The corresponding collective operator has already been derived in Ref. [59]:

\begin{equation} M_{B}^{{\rm EM}} = \langle B|\mathcal{O}^{{\rm EM}}|B\rangle, \label{eq2.8} \end{equation}

(2.8)

where

\begin{equation} \mathcal{O}^{{\rm EM}} = c^{(1)} D_{\Lambda\Lambda}^{(1)} + c^{(8)} (\sqrt{3}D_{\Sigma^{0}\Lambda}^{(8)} +D_{\Lambda\Lambda}^{(8)}) + c^{(27)} (\sqrt{5}D_{\Sigma_{2}^{0}\Lambda_{27}}^{(27)} +\sqrt{3} D_{\Sigma_{1}^{0}\Lambda_{27}}^{(27)} + D_{\Lambda_{27}\Lambda_{27}}^{(27)}). \label{eq2.9} \end{equation}

(2.9)

The unknown parameters c⁽⁸⁾ and c⁽²⁷⁾ are determined by the experimental data for the EM mass splittings of the baryon octet, while c⁽¹⁾ can be absorbed in the center of baryon masses. The values of c⁽⁸⁾ and c⁽²⁷⁾ have been obtained as

\begin{equation} c^{(8)} = -0.15\pm 0.23,\quad c^{(27)} = 8.62\pm 2.39 \label{eq2.10} \end{equation}

(2.10)

in units of MeV [59].

The final expressions for the masses of Θ⁺ and N* are given as

\begin{align} M_{\Theta^+} &= \overline{M}_{\overline{\textbf{10}}} + \frac{1}{4} \left(c^{(8)} - \frac{4}{21} c^{(27)}\right) - 2(m_{{\mathrm{s}}} - \bar{m}) \delta, \notag\\ M_{N^*} &= \overline{M}_{\overline{\textbf{10}}} +\frac{1}{4}\left(c^{(8)} - \frac{32}{63} c^{(27)} \right) T_3 + \frac{1}{4} \left(c^{(8)} + \frac{8}{63} c^{(27)} \right) \left(T_3^2 + \frac{1}{4}\right)\notag\\ & \quad - (m_{{\rm d}}-m_{{\rm u}}) T_3\,\delta - (m_{{\rm s}} - \bar{m}) \delta, \label{eq2.11} \end{align}

(2.11)

where |$\overline {M}_{\overline {\textbf {10}}}$| denotes the center of the mass splittings of the baryon antidecuplet and δ is a parameter defined as

\begin{equation} \delta = -\frac{1}{8} \alpha - \beta + \frac1{16}\gamma. \label{eq2.12} \end{equation}

(2.12)

The collective operators for the magnetic moments and axial-vector constants can respectively be parameterized by six parameters that can be treated as free [60; 61; 62]:

\begin{align} \hat{\mu} & = w_{1}D_{X3}^{(8)}+w_{2}d_{pq3}D_{Xp}^{(8)}\cdot \hat{J}_{q}+\frac{w_{3}}{\sqrt{3}}D_{X8}^{(8)}\hat{J}_{3} \notag\\ & \quad + \frac{w_{4}}{\sqrt{3}}d_{pq3}D_{Xp}^{(8)}D_{8q}^{(8)} + w_{5}(D_{X3}^{(8)}D_{88}^{(8)}+D_{X8}^{(8)}D_{83}^{(8)}) +w_{6}(D_{X3}^{(8)}D_{88}^{(8)}-D_{X8}^{(8)}D_{83}^{(8)}),\notag\\ \hat{g}_A &= a_1 D_{X3}^{(8)} + a_2d_{pq3}D_{Xp}^{(8)}\,\hat{J}_q + \frac{a_3}{\sqrt{3}} D_{X8}^{(8)}\,\hat{J}_3 \notag\\ & \quad + \frac{a_4}{\sqrt{3}}d_{pq3} D_{Xp}^{(8)}\,D_{8q}^{(8)} + a_5 (D_{X3}^{(8)}\,D_{88}^{(8)}+D_{X8}^{(8)}\,D_{83}^{(8)}) + a_6(D_{X3}^{(8)}\,D_{88}^{(8)}-D_{X8}^{(8)}\,D_{83}^{(8)}), \label{eq2.13} \end{align}

(2.13)

where |$\hat {J}_q$| (⁠|$\hat {J}_3$|⁠) stand for the qth (third) component of the spin operator of the baryons. The parameters w_i and a_i can be unambiguously fixed by using the magnetic moments and semileptonic decay constants of the baryon octet (Ref. [63] and G.-S. Yang and H.-Ch. Kim, manuscript in preparation). We refer to Ref. [63] for detailed expressions for the N*→N transition magnetic moments and for the Θ⁺ magnetic moment and axial-vector constants for Θ→KN decay.

3. Results and discussion

In order to find the masses of the baryon antidecuplet, we need to fix the relevant parameters. There are several ways to fix them. For example, Diakonov et al. [2] use the mass splittings of the baryon octet and decuplet, πN sigma term, and the N* mass that was then taken to be around 1710 MeV. The πN sigma term was taken from Ref. [64], i.e. σ_πN≈45 MeV. In addition, the ratio of the current quark mass m_s/(m_u+m_d)≈12.5 was quoted from Ref. [65] to determine the parameters:

\begin{equation} m_{{\rm s}} \alpha\approx -218\,{\rm MeV}, \quad m_{{\rm s}} \beta\approx-156\,{\rm MeV}, \quad m_{{\rm s}} \gamma \approx-107\,{\rm MeV}.\label{eq3.1} \end{equation}

(3.1)

On the other hand, Ellis et al. [47] carried out the analysis for the mass splittings of the baryon antidecuplet, based on the experimental data of the Θ⁺ and Ξ⁻⁻ masses together with those of the baryon octet and decuplet. They predicted the πN sigma term σ_πN = 73 MeV from the fitted values of the parameters:

\begin{equation} I_2 = 0.49\,{\rm fm},\quad m_{{\rm s}} \alpha=-605\,{\rm MeV},\quad m_{{\rm s}} \beta=-23\,{\rm MeV}, \quad m_{{\rm s}}\gamma=152\,{\rm MeV}. \label{eq3.2} \end{equation}

(3.2)

Very recently, Ref. [40] reanalyzed the mass splittings of the SU(3) baryons within a χSM, employing isospin symmetry breaking. An obvious advantage of including the effects of isospin symmetry breaking is that one can fully utilize the whole experimental data of the octet masses to fix the parameters. Using the baryon octet masses, the Ω⁻ mass (1672.45 ± 0.29) MeV [66] and the Θ⁺ mass (1524 ± 5) MeV [16], both of which are isosinglet baryons, the key parameters were found to be:

\begin{align} I_2& = (0.420\pm 0.006)\,{\mathrm{fm}},\quad m_{{\rm s}} \alpha=(-262.9\pm5.9)\,{\rm MeV},\notag\\ m_{{\rm s}} \beta &= (-144.3\pm3.2)\,{\rm MeV},\quad m_{{\rm s}} \gamma = (-104.2\pm2.4)\,{\rm MeV}. \label{eq3.3} \end{align}

(3.3)

In addition, the πN sigma term was predicted as σ_πN = (36.4 ± 3.9) MeV. Since δ is defined in Eq. (2.12), let us compare its values from each piece of work mentioned above. The corresponding results are given, respectively, as follows:

\begin{align} m_{{\mathrm{s}}} \delta &= 177\,{\rm MeV}\ (\hbox{Diakonov et al.}), \quad m_{{\rm s}} \delta= 108\,{\rm MeV}\ (\hbox{Ellis et al.}),\notag\\ m_{{\rm s}} \delta & = 171\,{\rm MeV}\ (\hbox{present work}), \label{eq3.4} \end{align}

(3.4)

with isospin symmetry breaking switched off. If we use the LEPS experimental data [16] for M_Θ⁺, we can immediately obtain the corresponding masses for N*, respectively:

\begin{align} M_{N^*} & = 1700\,{\mathrm{MeV}}\ (\hbox{Diakonov et al.}),\quad M_{N^*} = 1631\,{\rm MeV}\ (\hbox{Ellis et al.}), \notag\\ M_{N^*} & = 1694\,{\rm MeV}\ (\hbox{present work}). \label{eq3.5} \end{align}

(3.5)

If one employs the DIANA data [12], the N* mass is given as

\begin{align} M_{N^*} & = 1715\,{\mathrm{MeV}}\ (\hbox{Diakonov et al.}),\quad M_{N^*} = 1646\,{\rm MeV}\ (\hbox{Ellis et al.}), \notag\\ M_{N^*} & = 1708\,{\rm MeV}\ (\hbox{present work}). \label{eq3.6} \end{align}

(3.6)

The comparison made above already indicates that the predicted masses of the N*(1685) resonance from the previous analyses deviate from the experimental data. Moreover, it is essential to take into account the effects of isospin symmetry breaking, in order to produce the mass of the N* resonance quantitatively [40]. Since there are, however, two different experimental values for the Θ⁺ mass from the LEPS and DIANA collaborations, it is necessary to examine carefully the dependence of the relevant observables on that of the Θ⁺ baryon rather than choosing one specific value of M_Θ⁺ to fit the parameters. Thus, in the present section, we discuss the dependence of relevant observables on M_Θ⁺, taking it as a free parameter.

In Fig. 1, we show the N* mass as a function of M_Θ⁺. The vertical shaded bars bounded with solid and dashed lines denote the measured values of the Θ⁺ mass with uncertainties from the LEPS and DIANA collaborations, respectively. The horizontal shaded region denotes the values of the N* mass with an uncertainty taken from Ref. [24]. The sloping shaded region shows the dependence of the N* mass on M_Θ⁺. The N* mass increases monotonically as M_Θ⁺ increases. This behavior can be easily understood from Eq. (2.11): the mass of the N* resonance depends linearly on the parameter δ. Interestingly, if we take the M_Θ⁺ value of the LEPS experiment, i.e., M_Θ⁺ = 1524 MeV, we obtain M_N*≃1690 MeV, which is in good agreement with the experimental data: M_N* = (1685 ± 12) MeV [24]. On the other hand, if we use the value of M_Θ⁺ measured by the DIANA collaboration, the N* mass turns out to be larger than 1690 MeV. This implies that the Θ⁺ mass reported by the LEPS collaboration [16] is consistent with that of N*(1685) from recent experiments [20; 32; 33; 34; 35]—at least, in the present framework of a χSM with isospin symmetry breaking [40].

Fig. 1.

The dependence of the N* mass on M_Θ⁺. The vertical shaded bars bounded with solid and dashed lines denote the measured values of the Θ⁺ mass with uncertainties from the LEPS and DIANA collaborations, respectively. The horizontal shaded region shows the values of the N* mass with the uncertainty taken from Ref. [24]. The sloping shaded region represents the present results of the M_Θ⁺ dependence of the N* mass.

Open in new tab Download slide

The parameters w_i in Eq. (2.13) can be fitted by the magnetic moments of the baryon octet [60; 61; 62]. However, since the mixing coefficients appearing in Eq. (2.7) depend explicitly on α and γ, the parameters w_i are also given as functions of σ_πN through α and γ, as shown in Ref. [26]. As previously mentioned, since the mass parameters α and γ as well as σ_πN were unambiguously fixed in Ref. [40], we can derive the transition magnetic moments for the N*→Nγ decay unequivocally. Explicitly, the transition magnetic moments μ_pp* and μ_nn* are recapitulated, respectively, as follows [26]:

\begin{align} \mu_{pp^{\ast}}^{(0)} & = 0, \notag\\ \mu_{pp^{\ast}}^{({\mathrm{op}})} & = -\frac{1}{27\sqrt{5}}w_{4}-\frac{1}{18\sqrt{5}}\left(w_{5} +\frac{3}{2}w_{6}\right),\notag\\ \mu_{pp^{\ast}}^{({\rm wf})} & = -\frac{5}{24\sqrt{5}}\left(w_{1} +\frac{5}{2}w_{2}-\frac{1}{2}w_{3}\right)c_{\overline{10}} -\frac{35}{72\sqrt{5}}\left(w_{1}-\frac{11}{14}w_{2} -\frac{3}{14}w_{3}\right)c_{27}\notag\\ & \quad +\left[\frac{1}{2\sqrt{5}}\left(w_{1} -\frac{1}{2}w_{2}+\frac{1}{6}w_{3}\right) -\frac{7}{6\sqrt{5}}\left(w_{1}-\frac{1}{2}w_{2} -\frac{1}{14}w_{3}\right)\right]d_{8}\notag\\ & \quad -\frac{1}{45\sqrt{5}}\left(w_{1}+2w_{2} -\frac{3}{2}w_{3}\right)d_{27}, \notag\\ \mu_{nn^{\ast}}^{(0)} & = \frac{1}{6\sqrt{5}}\left(w_{1}+w_{2}+\frac{w_{3}}{2}\right),\notag\\ \mu_{nn^{\ast}}^{({\rm op})} & = -\frac{1}{54\sqrt{5}}w_{4} +\frac{1}{18\sqrt{5}}\left(w_{5}+\frac{3}{2}w_{6}\right),\notag\\ \mu_{nn^{\ast}}^{({\rm wf})} & = \frac{7}{36\sqrt{5}}\left(w_{1}-\frac{11}{14}w_{2}-\frac{3}{14}w_{3}\right)c_{27} +\frac{1}{2\sqrt{5}}\left(w_{1}-\frac{1}{2}w_{2}+\frac{1}{6}w_{3}\right)d_{8}\notag\\ & \quad -\frac{1}{90\sqrt{5}}\left(w_{1}+2w_{2}-\frac{3}{2}w_{3}\right)d_{27}. \label{eq3.7} \end{align}

(3.7)

As already discussed in Ref. [26], μ_pp* vanishes in the SU(3) symmetric case. Thus, μ_pp* is only finite with the effects of SU(3) symmetry breaking included.

Figure 2 shows the transition magnetic moments for the N*→Nγ decay as functions of M_Θ⁺. While μ_pp* is almost independent of M_Θ⁺, μ_nn* decreases slowly as M_Θ⁺ increases. On the other hand, the magnitude of μ_nn* turns out to be larger than that of μ_pp*, as has already been pointed out in Refs. [25; 26; 36].

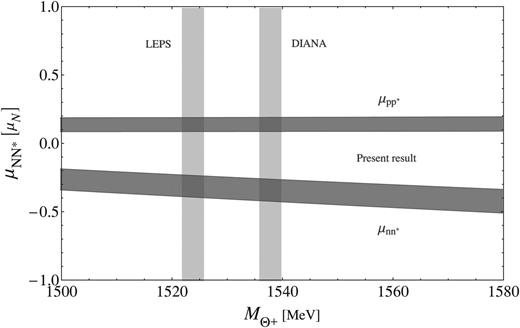
Fig. 2.

The dependence of the transition magnetic moments for the N*→Nγ decay on M_Θ⁺. The vertical shaded bars bounded with solid and dashed lines denote the measured values of the Θ⁺ mass with uncertainties from the LEPS and DIANA collaborations, respectively. The horizontal shaded regions stand for the present results of the M_Θ⁺ dependence of the transition magnetic moments μ_p*p and μ_n*n.

Open in new tab Download slide

In Table 1, we list each contribution to μ_NN* as well as the radiative decay widths for N*→Nγ using the mass of Θ⁺ from the LEPS experiment. Note that the sign of μ_nn* is negative whereas that of μ_pp* is positive. However, the previous result for μ_nn* was positive [26]. The reason for this can be found in the different values of w_i. Let us compare closely the present results with those of Ref. [26], considering only the SU(3) symmetric part without loss of generality. In fact, w_i derived in Ref. [26] depends on σ_πN:

\begin{equation} w_1^{{\mathrm{old}}} = -3.736-0.107\, \sigma_{\pi N},\quad w_2^{{\rm old}} = 24.37-0.21\,\sigma_{\pi N},\quad w_3^{{\rm old}} = 7.547. \label{eq3.8} \end{equation}

(3.8)

If one takes the value of the πN sigma terms as σ_πN≈40 MeV (70 MeV), one gets

\begin{equation} w_1^{{\mathrm{old}}} = -8.14 (-11.44),\quad w_2^{{\rm old}} = 15.97 (9.67),\quad w_3^{{\rm old}} = 7.547, \label{eq3.9} \end{equation}

(3.9)

while the results in this work use the newly obtained values of w_i (G.-S. Yang and H.-Ch. Kim, manuscript in preparation):

\begin{equation} w_1 = -12.95\pm 0.10,\quad w_2 = 5.388\pm 0.933, \quad w_3 = 8.354\pm 0.861. \label{eq3.10} \end{equation}

(3.10)

Thus, the magnitude of the present w₁ is larger than those of

$$w_1^{{\mathrm {old}}}$$

⁠, whereas that of w₂ turns out to be smaller than those of w^old₂. Since w₁ and w₂ have different signs, as in Eq. (3.7), they destructively interfere eath other, so that the sign of μ_nn* becomes negative in the present case but is positive in Ref. [26]. However, the magnetic properties of the octet and decuplet baryons are almost intact because of the constructive interference of w₁ and w₂, even though we have different values of w_i. The ratios of the transition magnetic moments and of the radiative decay widths are obtained as

\begin{equation} \left|\frac{\mu_{nn^{\ast}}}{\mu_{pp^{\ast}}}\right| = 2.08\pm 0.97,\quad \frac{\Gamma_{nn^{\ast}}}{\Gamma_{pp^{\ast}}} = 4.36\pm 1.02. \label{eq3.11} \end{equation}

(3.11)

Table 1.

Open in new tab

The results of the N*→N transition magnetic moments in units of the nuclear magneton μ_N and of the radiative decay widths in units of keV. The mass M_Θ⁺ = (1524 ± 5) MeV is used as an input.

μ_NN*

|$\mu _{NN^*}^{(0)}$|

|$\mu _{NN^*}^{({\mathrm {op}})}$|

|$\mu _{NN^*}^{({\mathrm {wf}})}$|

|$\mu _{NN^*}^{({\mathrm {total}})}$|

Γ_NN* (keV)

μ_pp*

0.272 ± 0.051

−0.125 ± 0.013

0.146 ± 0.053

17.7 ± 3.2

μ_nn*

−0.252 ± 0.077

−0.159 ± 0.042

0.107 ± 0.003

−0.304 ± 0.089

77.1 ± 11.3

The narrowness of the decay width is one of the peculiar characteristics of pentaquark baryons. For example, the decay width of Θ⁺→KN vanishes in the nonrelativistic limit [67]. The decay width Γ_ΘNK has already been studied in chiral soliton models with SU(3) symmetry breaking taken into account. We refer to Refs. [69; 70] for details. In Fig. 3, we examine the dependence of the decay width Γ_NΘ for Θ⁺→KN on the Θ⁺ mass. Being different from the N* mass and the transition magnetic moments, the decay width Γ_Θ⁺N increases almost quadratically as M_Θ⁺ increases. This can be understood from the fact that the decay width is proportional to the square of the g_NKΘ⁺ coupling constant, which depends linearly on M_Θ⁺. When the Θ⁺ mass is the same as the value measured by the LEPS collaboration, Γ_NΘ⁺ turns out to be about 0.5 MeV. However, at the value M_Θ⁺≈1540 MeV, corresponding to that of the DIANA experiment, the decay width Γ_NΘ⁺ is close to 1 MeV. We want to emphasize that the decay width of Θ⁺ is still below 1 MeV in the range of M_Θ⁺: 1520−1540 MeV. When we use the measured value of M_Θ⁺ from the LEPS collaboration, we obtain Γ_Θ⁺→NK = 0.5 ± 0.1 MeV.

Fig. 3.

The dependence of the decay width Γ_NΘ⁺ for the Θ⁺→KN decay on M_Θ⁺. The vertical shaded bars bounded with solid and dashed lines denote the measured values of the Θ⁺ mass with uncertainties from the LEPS and DIANA collaborations, respectively. The horizontal shaded region shows the values of the N* mass with an uncertainty taken from Ref. [24]. The sloping shaded region represents the present results of the M_Θ⁺ dependence of Γ_NΘ⁺.

Open in new tab Download slide

Figure 4 depicts the predicted values of the πN sigma term as a function of the Θ⁺ mass. At first sight, the result is rather surprising. Firstly, it is almost insensitive to the Θ⁺ mass. Secondly, the value of σ_πN is fairly small compared to those known from previous work on the baryon antidecuplet [47; 48]. In order to understand the reason for this difference, we want to examine in detail the πN sigma term in comparison with those discussed in previous work, in particular, with Ref. [48], where the πN sigma term was extensively studied within the same framework. Since σ_πN is expressed as

\begin{equation} \sigma_{\pi N} = -3 \bar{m} (\alpha + \beta), \label{eq3.12} \end{equation}

(3.12)

we need to scrutinize the dependence of |$\bar {m}\alpha $| and |$\bar {m}\beta $| on M_Θ⁺.

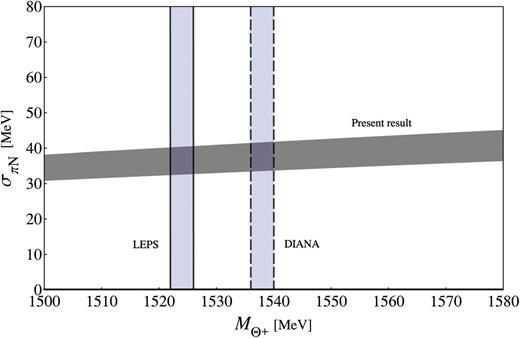
Fig. 4.

The dependence of σ_πN on the Θ⁺ mass. The vertical shaded bars bounded with solid and dashed lines denote the measured values of the Θ⁺ mass with uncertainties from the LEPS and DIANA collaborations, respectively. The sloping shaded region represents the present results of the M_Θ⁺ dependence of σ_πN.

Open in new tab Download slide

Figure 5 depicts the results of the parameters |$-3\bar {m}\alpha $| and |$-3\bar {m}\beta $| as functions of M_Θ⁺. Interestingly, while |$-3\bar {m}\alpha $| increases monotonically as M_Θ⁺ increases, |$-3\bar {m}\beta $| decreases at almost the same rate as |$-3\bar {m}\alpha $|⁠. Consequently, σ_πN remains rather stable. On the other hand, Schweitzer [48] expressed σ_πN in terms of the mass splittings of each representation:

\begin{equation} \frac{m_{{\mathrm{s}}}}{\bar{m}} \sigma_{\pi N} = 3(4 M_{\Sigma} - 3 M_\Lambda - M_N) + 4(M_\Omega - M_\Delta) -4(M_{\Xi_{3/2}} - M_{\Theta^+}), \label{eq3.13} \end{equation}

(3.13)

and determined it to be σ_πN = (74 ± 12) MeV , taking the experimental values of M_Θ⁺ = 1540 MeV and M_{Ξ_3/2} = 1862 MeV [68] for granted at that time, and using the ratio of the current quark mass |$m_{{\mathrm {s}}}/\bar {m} =25.9$|⁠. However, using the predicted value of M_{Ξ_3/2}≈2020 MeV in Ref. [40], we get σ_πN≈45 MeV . Thus, the present result is not in contradiction with that of Ref. [48].

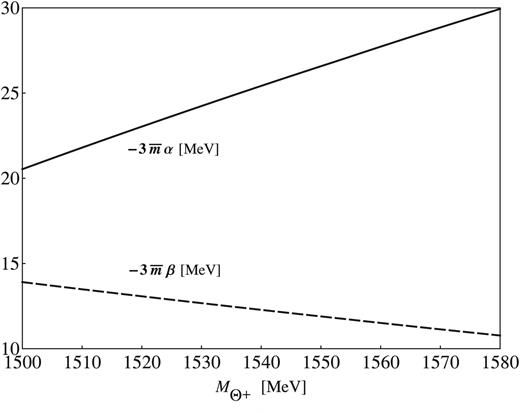
$The results of the parameters $-3\bar {m}\alpha $ and $-3\bar {m}\beta $ as functions of MΘ+.$

Fig. 5.

The results of the parameters |$-3\bar {m}\alpha $| and |$-3\bar {m}\beta $| as functions of M_Θ⁺.

Open in new tab Download slide

Taking the effects of isospin symmetry breaking into account, however, we can rewrite σ_πN in terms of the mass splittings of the isospin multiplets

\begin{equation} \sigma_{\pi N} = \frac{3\bar{m}}{m_{{\mathrm{d}}} - m_{{\rm u}}}\left[\frac{10}{3}(M_{\Sigma^0} - M_{\Sigma^+}) + \frac53(M_{\Xi^-} - M_{\Xi^0}) - 4(M_{n^*} - M_{p^*}) \right]. \label{eq3.14} \end{equation}

(3.14)

Plugging the ratio (m_d−m_u)/(m_u+m_d) = 0.28 ± 0.03 [71] into Eq. (3.14), considering the experimental data for the corresponding baryon octet masses [66], and using the values of M_n* and M_p* predicted in Ref. [40], we obtain σ_πN≈34 MeV , which is almost the same as that of Ref. [40].

4. Summary and conclusion

In the present work, we aimed to investigate various observables of the baryon antidecuplet Θ⁺ and N*, emphasizing their dependence on the Θ⁺ mass within a chiral soliton model. We utilized the mass parameters α, β, and γ, derived unequivocally in Ref. [40]. We first compared the present result of the N* mass with those predicted by previous analyses [2; 47]. We then examined the dependence of the N* mass on the Θ⁺ one. We found that the measured value of the Θ⁺ mass by the LEPS collaboration turned out to be consistent with that of the N* mass by Kuznetsov and Polyakov [24] within the present framework. We then scrutinized the transition magnetic moments of the radiative decay N*→Nγ. While μ_pp* is almost independent of the Θ⁺ mass, μ_nn* decreases slowly as M_Θ⁺ increases. We also discussed the results of the N*→Nγ transition magnetic moments with those of previous work. The decay width of Θ⁺ was studied and was found to be 0.5 ± 0.1 MeV when the LEPS data for M_Θ⁺ were employed, which is compatible with the corresponding measured decay width from the DIANA collaboration. Finally, we analyzed the πN sigma term within the present framework. It turned out that σ_πN was almost independent of the Θ⁺ mass. We explained the reason why it was smaller than those in previous analyses, in particular, in Ref. [48]. In addition, we found a new expression for the πN sigma term in terms of the isospin mass splittings of the hyperon octet as well as that of the antidecuplet N*.

Acknowledgements

We are grateful to T. Nakano for suggesting the analysis of the Θ⁺ mass dependence of relevant observables. The present work was supported by a National Research Foundation of Korea (NRF) grant funded by the Korean government (MEST) (No. 2012001083).

References

Praszałowicz

Jezabek

Praszałowicz

in Proceedings of the Workshop on Skyrmions and Anomalies, Kraköw, Poland

1987

(World Scientific, Singapore)

Diakonov

Petrov

Polyakov

M. V.

Z. Phys. A

1997

, vol.

359

pg.

305

Month:	Total Views:
November 2016	1
January 2017	5
February 2017	6
April 2017	1
May 2017	1
June 2017	5
September 2017	3
November 2017	1
December 2017	6
January 2018	5
February 2018	12
March 2018	5
April 2018	6
May 2018	1
June 2018	6
July 2018	12
August 2018	4
September 2018	2
October 2018	2
November 2018	4
December 2018	2
January 2019	3
February 2019	6
March 2019	8
April 2019	7
May 2019	4
June 2019	5
July 2019	7
August 2019	7
September 2019	5
October 2019	5
November 2019	10
December 2019	2
January 2020	10
February 2020	3
March 2020	1
April 2020	2
May 2020	4
June 2020	3
July 2020	2

Article Contents

Θ+ baryon, N* (1685) resonance, and πN sigma term reexamined within the framework of a chiral soliton model Open Access

Abstract

1. Introduction

2. Baryon antidecuplet from a chiral soliton model

3. Results and discussion

4. Summary and conclusion

Acknowledgements

References

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Θ⁺ baryon, N* (1685) resonance, and πN sigma term reexamined within the framework of a chiral soliton model