-
PDF
- Split View
-
Views
-
Cite
Cite
Pavel A Andreev, L S Kuz’menkov, On the equation of state for the “thermal” part of the spin current: The Pauli principle contribution in the spin wave spectrum in a cold fermion system, Progress of Theoretical and Experimental Physics, Volume 2019, Issue 5, May 2019, 053J01, https://doi.org/10.1093/ptep/ptz029
Close - Share Icon Share
Abstract
Spin evolution opened a large field in quantum plasma research. The spin waves in plasmas were considered among new phenomena in spin-1/2 quantum plasmas. The spin density evolution equation found by means of many-particle quantum hydrodynamics shows the existence of a “thermal” part of the spin current which is an analog of the thermal pressure, or the Fermi pressure for a degenerate electron gas, existing in the Euler equation. However, this term has been dropped, since no equation of state for the thermal part of the spin current (TPSC), like the one we have for the pressure, has been found. In this paper we derive the equation of state for the TPSC and apply it for the study of the spectrum of collective excitations in spin-1/2 quantum plasmas. We focus our research on the spectrum of spin waves, since this spectrum is affected by the TPSC. We consider two kinds of plasmas: electron–ion plasma with motionless ions and degenerate electrons, and degenerate electron–positron plasmas. We also present the nonlinear Pauli equation with the spinor pressure term containing the described effects. The thermal part of the spin current flux existing in the spin current evolution equation is also derived. We also consider the contribution of the TPSC in the grand generalized vorticity evolution.
1. Introduction
For almost 15 years, spin-1/2 quantum plasmas have been in the center of active consideration. Starting from the explicit derivation of the continuity, Euler, and magnetic moment evolution equations from the many-particle Pauli equation in 2001 [1,2], which contains the derivation of the Coulomb and spin–spin exchange correlations, analyses of many collective phenomena have been performed. The contributions of the spin dynamics to plasma properties have been calculated during such research. First of all, the spin contribution in plasma dynamics arises via the force of the spin–spin interaction.
Along the way, the following have been studied: the shift of the electromagnetic wave frequency [3], the increase of the fast magnetosonic mode frequency and the decrease of the slow magnetosonic mode frequency [4,5], the interaction of the magnetosonic waves in spin-1/2 quantum plasmas [6], the reduction of the energy transport in quantum spin-1/2 plasmas due to the modification of the group velocity of the extraordinary wave at a certain range of wave numbers [7], the widening of the solitary magnetosonic waves by a pressure-like term with a negative sign caused by the spin–spin interaction force [8], the nonlinear whistlers in strongly magnetized high-density plasmas forming large-scale density fluctuations [9], investigation of magnetic diffusivity and the obtained results that it plays a dominant role in the transition from a solitary wave to a shock wave for arbitrary-amplitude magnetosonic waves [10], detailed analysis of the small and arbitrary shock structures in spin-1/2 quantum plasma [11], the composite nonlinear structures within magnetosonic soliton interactions [12], the dynamics of small but finite amplitude magnetosonic waves exhibiting both oscillatory and monotonic shock-like perturbations significantly affected by the spin–spin interaction [13], circularly polarized Alfvén solitary waves with Gaussian form surrounded by smaller sinusoidal variations in the density envelope [14], and modification of the Rayleigh–Taylor instability [15].
The described phenomena exist, in some form, in spinless plasmas, while there are some plasma effects requiring the spin of particles. Here, the following purely spin plasma phenomena have been found: spin-plasma waves [3,16–22]; spin-electron acoustic waves [23–25], which are possibly related to high-temperature superconductivity [26]; the spin-electron acoustic soliton [27]; spin (quantum) vorticity [22,28,29]; the spin-caused modulational instability of magnetosonic waves in dense quantum plasma [30]; spin instabilities caused by specific equilibrium distribution functions [31]; and the instability of plasma and spin-plasma waves at the propagation of a spin-polarized neutron beam through magnetized spin-1/2 plasmas arising due to the spin–spin and spin–current interactions [19,32]. Some effects are reviewed in Ref. [33].
Moreover, spin contributes to plasma dynamics via modification of the Fermi pressure [23,34] and due to spin current evolution [35].
The magnetization enters the spectrum of Langmuir waves propagating parallel to the external magnetic field due to the modification of the Fermi pressure [23,34]. The increase in the spin polarization of electrons increases the Fermi pressure up to 60%. The contribution of this phenomenon can also be found in many other plasma effects.
The spin current (SC) tensor arises in the Bloch equation. Usually, we present it in terms of other hydrodynamical variables, applying Takabayasi’s results for single-particle hydrodynamics [36] to truncate the set of quantum hydrodynamic (QHD) equations by dropping its thermal part. However, we can find an equation for the dynamical evolution of the SC under the influence of the electromagnetic field [35,37–40], but it does not give the thermal part of the spin current (TPSC). In the general form, the SC evolution equation contains a pressure-like term (the TPSC flux), but no explicit form for this term has been found. Therefore, this term has been dropped in earlier research. Let us mention now that in this paper we present the TPSC and the thermal spin current flux for the degenerate electron gas, where the described quantities are caused by the Pauli blocking principle like the Fermi pressure in the Euler equation.
The SC plays an important role in quantum plasma physics. However, it is also the center of attention in condensed matter physics, especially when applying it to spintronics. Spintronics is related to spin-dependent electron transport phenomena [41]. To model effects related to the SCs, the analytical definition of the SC in terms of an effective single-particle wave function is developed in Refs. [42–45]. The necessity of applying the full current composed of the spin and the orbital currents is suggested in Ref. [46]. The methodology of such research differs from quantum hydrodynamics, where the SC arises as a part of the hydrodynamic variable set to describe collective phenomena.
A special case of spin-1/2 quantum plasma modeling is the separate description of spin-up and spin-down electrons. In this picture we do not consider electrons as a single fluid [1,3,47], but we consider them as two interacting fluids [23,48–50]. Since the Fermi pressures of the spin-up and spin-down magnetized electrons are different, the two-fluid model gives extra longitudinal waves in the electron gas [23,24]. These waves are related to the relative motion of the spin-up and spin-down electrons, and are called spin-electron acoustic waves (SEAWs). If we consider wave propagation parallel or perpendicular to the external magnetic field we find a single SEAW [23], while for oblique propagation we find two branches of SEAWs [24]. These modes are affected by the Coulomb exchange interaction [27]. The nonlinear SEAWs propagating parallel to the external magnetic field were considered, and the existence of the spin electron acoustic soliton was demonstrated [27]. It was shown that the interaction of electrons via spelnons (the quantum of the SEAWs) gives a mechanism for Cooper pair formation [26]. This kind of Cooper pair gives a mechanism for high-temperature superconductivity [26]. The TPSC also contributes to the separate spin evolution quantum hydrodynamics. Thus, its derivation is essential for all forms of spin-1/2 quantum hydrodynamics.
The QHD models are related to the specific form of the wave equation (Schrödinger, Pauli, or Dirac). A general first-principle theory of resonant nondissipative vector waves assuming no specific wave equation is developed in Ref. [51].
The quantum properties of plasmas are also caused by the exchange interaction, but we do not consider it here. Descriptions of the exchange interaction in plasmas are presented in Refs. [2,27,34,52–56]. The methodology of many-particle quantum hydrodynamics can be applied to the derivation of the quantum kinetic equations for spinning particles [57], which is analogous to the Wigner function method [58].
The majority of effects in spin quantum plasma and the spin-related effects in condensed matter physics can be affected by the TPSC. Thus, we obtain it here for the degenerate electron gas, so the TPSC is related to the particle distribution under the Fermi step. It arises from the magnetic moment evolution equation. In its nature, it is not related to the interparticle interaction. If one considers spin-1/2 quantum plasmas with the spin–orbit interaction, when the spin current tensor arises in the force field in the Euler equation and the spin torque in the magnetic moment evolution equation [19], the TPSC also arises there. Applying the TPSC to different quantum plasma phenomena, we consider spin-plasma waves propagating parallel and perpendicular to the external field in electron–ion and electron–positron plasmas, the TPSC in quantum vorticity, and calculate the thermal part of the spin current flux existing in the SC evolution equation.
This paper is organized as follows. In Sect. 2 we present the nonlinear Pauli equation with the spinor pressure. We also describe the derivation of the QHD equations from the microscopic model. In Sect. 3 we introduce the velocity field and show the existence of the TPSC in the Bloch equation. In Sect. 4 we present the explicit form of the TPSC for the degenerate electron gas arising from the nonlinear Pauli equation. The corresponding modification of the quantum vorticity evolution equation is also described in Sect. 4. In Sect. 5, we present the thermal part of the spin current flux existing in the SC evolution equation. In Sect. 6 and beyond we apply the obtained model to the wave properties in plasmas: in Sect. 6 we consider the contribution of the TPSC to the spectrum of plasma waves; in Sect. 7 we show the contribution of the TPSC to the QHD model of electron–positron plasmas; and in Sect. 8 we consider the wave spectrum of electron–positron plasmas. In Sect. 9, a summary of the obtained results is presented.
2. Model: QHD equations
2.1. Non-linear Pauli equation
The equations of spin-1/2 quantum hydrodynamics can be represented as the nonlinear Pauli equation [1]. It is similar to the spinless case, where the continuity and Euler equations can be represented as the single-fluid effective nonlinear Schrödinger equation (NLSE) [54]. Even the spin–orbit interaction [19] and other relativistic effects [22,59] can be included in the nonlinear effective equations. The nonlinearity is caused by different factors: the many-particle interaction effect and the pressure, particularly the Fermi pressure. The NLSE for two- and three-dimensional degenerate electron gases containing the Fermi pressure and the Coulomb exchange interaction for partially polarized electron gas are obtained in Ref. [34]. However, the partial spin polarization in the Fermi pressure is presented in scalar form. If we want to include the spin separation effect revealed in the two-fluid model of electrons [23,24,50], we can construct the nonlinear Pauli equation containing the pressure in spinor form,
In accordance with the Fermi pressures for the spin-up and spin-down electrons, |$\pi_{s}$|, with |$s=\uparrow, \downarrow$|, has the following explicit form: |$\pi_{s}=(6\pi^{2})^{2/3}\hbar^{2}n_{s}^{2/3}/2m$|. Here, we have the mass of particles |$m$|, the reduced Planck constant |$\hbar$|, and the concentrations of spin-1/2 particles with different spin projections on a chosen direction |$n_{s}$|.
Equation (1) is actually in partial agreement with Ref. [23]. It corresponds to Ref. [23] in the separate descriptions of the spin-up and spin-down fermions and the appearance of partial Fermi pressures for each species of electron. However, Eq. (1) leads to a TPSC which was not presented in Ref. [23]. The NLSE, Eq. (1), can be represented as a single-fluid quantum hydrodynamics of electrons or as a two-fluid model with separate spin evolution, at our choice.
In the context of the model in Eq. (1) we need to mention an excellent example of NLSEs applying to the study of Bose–Einstein condensates (BECs): the well-known Gross–Pitaevskii equation. Its traditional form allows us to model the behavior of scalar particles (particles with zero spin or located in a single hyperfine state). However, generalization of the Gross–Pitaevskii equation was suggested for spinor BECs (the spin-1 and spin-2 bosons) with evolving occupations of three or five hyperfine states [60–64]. The evolution of the occupations leads to the appearance of spin waves. These waves are similar to the spin-plasma waves found for magnetized spin-1/2 plasmas [3,16,17]. For the neutral bosons, the nonlinearity in the NLSE is caused by the short-range interaction [60–64], while in plasmas it is related to the Fermi pressure and the electromagnetic interaction.
The derivation of the separate spin evolution quantum hydrodynamic (SSE-QHD) model is presented in Ref. [23] for the simple case of single-particle motion for methodological reasons. So, readers can easily understand the derivation method and the main structure of the new terms. However, the final equations, Eqs. (8)–(15), in Ref. [23] are presented for many-particle systems. These equations can be found by a similar derivation based on the many-particle model in accordance with the general scheme of many-particle quantum hydrodynamics (MPQHD).
2.2. First-principle derivation of many-particle QHD equations
Applying the microscopic concentration in classical physics allows us to derive a set of hydrodynamic-like equations [65,66]. An explicit averaging of the microscopic concentration allows us to obtain hydrodynamic equations for smooth functions describing the macro behavior of mediums [67–70]. Similarly, an appropriate definition of the quantum many-particle concentration allows us to derive the set of QHD equations with a truncation at a necessary step.
The quantum mechanical definition of the concentration is constructed in accordance with the basic principles of quantum theory. We take the microscopic concentration existing in classical mechanics, where particles are point-like objects. Each classical particle has zero volume along with finite characteristics, such as mass or charge. Hence, they are modeled as delta functions moving in three-dimensional physical space: |$n(\textbf{r},t)=\sum_{i=1}^{N}\delta(\textbf{r}-\textbf{r}_{i}(t))$|, where |$N$| is the number of particles, |$\textbf{r}_{i}(t)$| is the coordinate of the |$i$|th particle as a function of time, and |$\textbf{r}$| is the field of coordinates giving arithmetization of the physical space.
In quantum mechanics, we construct corresponding operators by replacing the dynamical functions |$\textbf{r}_{i}(t)$| by corresponding operators |$\hat{\textbf{r}}_{i}$|: |$\hat{\textbf{r}}_{i}\psi=\textbf{r}_{i}\psi$| (for the coordinate representation of quantum mechanics), where |$\psi$| is an arbitrary wave function. Finally, the operator of the concentration arises as |$\hat{n}=\sum_{i=1}^{N}\delta(\textbf{r}-\textbf{r}_{i})$|. A function of the concentration is the quantum mechanical average of the operator |$\hat{n}$| on the many-particle wave function presented by Eq. (2). Note that the delta function is an object existing in the spirit of quantum mechanics. For instance, the eigenfunction of the coordinate (the momentum) operator |$\hat{\textbf{r}}$| (|$\hat{\textbf{p}}$|) in the coordinate (the momentum) representation is proportional to the delta function |$\psi(\textbf{r})=C\delta (\textbf{r})$| (|$\psi(\textbf{p})=C\delta (\textbf{p})$|).
The subscripts |$i$| and |$j$| are the numbers of particles. The Green functions of the Coulomb and spin–spin interactions have the following forms: |$\textrm{G}_{ij}=1/r_{ij}$|, |$\textrm{G}^{\alpha\beta}_{ij}=4\pi\delta^{\alpha\beta}\delta(\textbf{r}_{ij})+\partial^{\alpha}_{i}\partial^{\beta}_{i}(1/r_{ij})$|, where |$\delta^{\alpha\beta}$| is the Kronecker symbol.
As the first step, differentiating the particle concentration in Eq. (2) with respect to time and applying the Schrödinger equation with the Hamiltonian of Eq. (3), we find the continuity equation |$\partial_{t}n+\nabla \textbf{j}=0$|.
Next, we differentiate the particle current |$\textbf{j}$| with respect to time and find the momentum balance equation |$\partial_{t}\textrm{j}^{\alpha}+\partial^{\beta}\Pi^{\alpha\beta}/m=\textrm{F}^{\alpha}/m$|, where |$\Pi^{\alpha\beta}$| is the momentum flux and |$\textbf{F}$| is the force field. The force field consists of two parts, |$\textbf{F}=\textbf{F}_{\rm ext}+\textbf{F}_{\rm int}$|. The explicit form of the momentum flux arises at the derivation of the Euler equation in the following forms: |$\Pi^{\alpha\beta}=\langle\delta(\textbf{r}-\textbf{r}_{i})\hat{\textrm{D}}_{i}^{\beta}\hat{\textrm{D}}_{i}^{\alpha}/m_{i}\rangle$|.
The first term in the force field is the force of the particle interaction with the external field, |$\textbf{F}_{\rm ext}=qn\textbf{E}_{\rm ext}+\frac{q}{c}\textbf{j}\times \textbf{B}_{\rm ext}+\textrm{M}^{\beta}\nabla\textrm{B}^{\beta}_{\rm ext}$|. The force field |$\textbf{F}_{\rm ext}$| contains an extra function. In the last term we meet the magnetic moment density, |$\textbf{M}(\textbf{r},t)=\langle\gamma_{i}\widehat{\boldsymbol {\sigma}}_{i}\delta(\textbf{r}-\textbf{r}_{i})\rangle$|.
We have presented a general derivation of the Euler equation beyond the self-consistent field approximation from the many-particle Schrödinger equation. Below, we consider the self-consistent field approximation. Hence, we consider the two-particle concentration as the product of the particle concentrations, |$n_{2}(\textbf{r},\textbf{r}',t)=n(\textbf{r},t)n(\textbf{r}',t)$|, and the two-particle magnetization as the product of the magnetization, |$\textrm{M}^{\alpha\beta}_{2}(\textbf{r},\textbf{r}',t)=\textrm{M}^{\alpha}(\textbf{r},t)\textrm{M}^{\beta}(\textbf{r}',t)$|. The exchange interaction in terms of MPQHD is considered in Refs. [2,27,34].
We can include the exchange interaction in accordance with the cited papers. The exchange interaction is calculated rigorously in terms of MPQHD in Ref. [34]. In the case of the single-fluid model of electrons, it is included in the nonlinear Schrödinger equation in Ref. [34]. The exchange interaction in SSE-QHD is considered in Ref. [27], where it is shown that the exchange interaction gives a contribution in the Fermi pressure of the spin-down electrons. If we include it, the pressure term in Eq. (1) appears as
The inner electric and magnetic fields in Eqs. (6) and (7) satisfy the quasi-static Maxwell equations |$\nabla \cdot\textbf{E}=4\pi\rho$|, |$\nabla \times\textbf{E}=0$|, |$\nabla \times\textbf{B}=4\pi\nabla \times\textbf{M}$|, and |$\nabla \cdot\textbf{B}=0$|, where |$\rho$| is the charge density. In the self-consistent field approximation, the full force field can be presented as follows: |$\textbf{F}=qn\textbf{E}+\frac{q}{c}n\textbf{v}\times\textbf{B}+\textrm{M}^{\beta}\nabla \textrm{B}^{\beta}$|.
Considering the time evolution of the magnetic moment density and applying the Pauli equation with the Hamiltonian in Eq. (3), we find, in the self-consistent field approximation, the magnetic moment evolution equation |$\partial_{t}\textrm{M}^{\alpha}+\nabla^{\beta}\textrm{J}^{\alpha\beta} =\frac{2\gamma}{\hbar}\varepsilon^{\alpha\beta\gamma}\textrm{M}^{\beta}\textrm{B}^{\gamma}$| containing the SC tensor |$\textrm{J}^{\alpha\beta}=\langle \gamma_{i}\delta(\textbf{r}-\textbf{r}_{i})\hat{\textrm{D}}_{i}^{\beta}\widehat{\sigma}_{i}^{\alpha}/m_{i}\rangle$|. The general form of the magnetic moment evolution equation can be found in Ref. [1]— see Eq. (30) therein.
3. Introduction of the velocity field
This spinor satisfies the condition |$\phi^{+}\phi=1$|. The generalized Madelung decomposition contains |$a$| and |$S$|, which are the amplitude and the phase of the wave function, respectively. A similar representation can be applied to the macroscopic wave function obeying the NLSE in Eq. (1) and to the microscopic many-particle wave function obeying the Schrödinger equation with the Hamiltonian in Eq. (3).
The second term is the quantum part of the SC, which is an analog of the quantum Bohm potential being the quantum part of the pressure. The last term is related to incoherent motion of spinning particles and presents the TPSC.
The application of the generalized Madelung decomposition to the momentum flux tensor |$\Pi^{\alpha\beta}$| in the many-particle Euler equation gives the following result: |$\Pi^{\alpha\beta}=mnv^{\alpha}v^{\beta}+\textrm{P}^{\alpha\beta}+\textrm{T}^{\alpha\beta}$|, where |$\textrm{P}^{\alpha\beta}$| is the thermal pressure, and |$\textrm{T}^{\alpha\beta}$| is the quantum part giving the quantum Bohm potential. A similar picture arises for the SC in Eq. (9) [1,72].
Here, we refer to the single-fluid model of electrons, while all plasma is considered as a many-fluid liquid and each species is considered as a fluid. Recently, a two-fluid model of spin-1/2 fermions was developed [23,24,50], where the spin-up and spin-down electrons are considered as two different fluids.
To the best of our knowledge, it is impossible to give a straightforward derivation of the NLSE in Eq. (1) from single-fluid quantum hydrodynamics, as was done for the spinless regime [54]. However, we can justify the NLSE deriving the QHD equations from the NLSE as was done in Ref. [1].
The energy evolution in many-particle quantum systems was considered in Refs. [54] (for the spinless case) and [1] (for spin-1/2 particles). The energy evolution equation was explicitly derived there.
Our brief discussion in Sects. 2.2 and 3, together with earlier works [1,54] shows that an explicit account of the microscopic dynamics of |$N$| quantum particles leads to the derivation of the thermal pressure, the thermal spin current, and the vector of the thermal current existing in the energy evolution equation (see Refs. [1,54]) from the many-particle pure quantum states described by the many-particle wave function or the many-particle wave spinor for spin-1/2 particles. This derivation does not require any statistical assumptions or averaging. The derivation requires the correct choice of collective variables obeying the microscopic evolution.
4. Equation of state for the thermal part of the spin current
In the previous section, we have demonstrated the existence of the TPSC and formulated the problem of finding an equation of state for the TPSC.
Due to its nature, we can also call it the Fermi SC.
The Landau–Lifshitz–Gilbert (LLG) equation does not include the quantum part of the SC [73,74]. The convective part of the SC is sometimes included in the LLG equation— it is included, for instance, in Refs. [22,74]. For a recent example of the LLG equation without the convective part of the SC, see Ref. [73]. Some generalizations of the LLG equation are presented in the literature. For instance, a nutation term is introduced in Ref. [73], where it is substituted in the atomistic LLG equation [75]. The LLG equation successfully describes the magnetic moment precession around and its relaxation toward the effective field acting on the magnetization for time scales down to femtoseconds [76,77].
Traditionally, hydrodynamic models give us an unclosed set of equations that can contain the thermal pressure, the thermal current vector (if we consider the energy evolution equation), the thermal part of the spin current (if we consider the spin evolution), etc. Therefore, we need to use other methods to get a closed set of equations. One such is the application of the kinetic model (the model from Ref. [57] can be used in our case), which is closely related to MPQHD. In terms of the kinetic model, the thermal pressure is the second moment of the distribution function on the momentum (considered in the local rest frame). If we aim to consider small perturbations of the equilibrium state we can use the equilibrium distribution function (the Maxwell distribution function or the Fermi–Dirac distribution function) to calculate the form of the pressure foe the process close to equilibrium. One of the ways to treat the TPSC is to find an appropriate equilibrium spin distribution function. In this case, the spin current is the first moment of the spin distribution function [57] on the momentum. Another way, which is used in this paper, is to derive the TPSC from the NLPE derived from the Euler equations of SSE-QHD: |$\Pi^{\alpha\beta}\rightarrow p^{\alpha\beta}=(1/m)\int p^{\alpha}p^{\beta}f_{0}(p)d\textbf{p}$|. For an isotropic distribution function we find |$p^{\alpha\beta}=p \delta^{\alpha\beta}$|, which includes |$p=p^{zz}$|, where |$p^{zz}=(2\pi/m)\int p_{z}^{2}p^{2} [2\vartheta(p-p_{Fe})/(2\pi\hbar)^{3}]\sin\theta d\theta dp$| for degenerate electrons with no external fields. Calculation gives |$p^{zz}=(3\pi^{2})^{\frac{2}{3}}n_{0}^{\frac{5}{3}}\hbar^{2}/5m$|. Changing the distribution function to |$f_{0}(p)=[\vartheta(p-p_{Fu})+\vartheta(p-p_{Fd})]/(2\pi\hbar)^{3}$| for a magnetized degenerate electron gas, we obtain the formula in Eq. (13).
Application of the equation of state for the pressure in the form of the Fermi pressure assumes that the medium is uniform. However, it gives relatively good results with the following limitations. A qualitative description of small perturbations is found in the spectrum up to the second order on the wave vector. However, quantitative accuracy requires an account of the pressure evolution equation [78,79]. Hydrodynamics describes a plasma as a continuous medium. Consequently, the wavelength of the perturbations should be considerably larger then the average interparticle distance, |$k\sqrt[3]{n_{0}}\ll 1$|.
Our model is based on a consistent account of the “thermal” pressure and the “thermal” spin current. Therefore, our model inherits the limitations described above.
4.1. Contribution of the TPSC in quantum vorticity
Considering the quantum vorticity caused by the spin of particles, the quantum vorticity evolution equation has been found—see Eq. (13) in Ref. [28] and Eq. (4.6) in Ref. [80]. The quantum vorticity has been combined with the classical vorticity to obtain the grand generalized vorticity [28]. In this section, we consider the contribution of the TPSC |${\boldsymbol {\Im}}$| in the grand generalized vorticity dynamics.
The first two terms in Eq. (19) give the canonical form of the vorticity evolution equation leading to helicity conservation. The last term describes the contribution of the TPSC. It is a generalization of the equation obtained in Ref. [80]— see Eq. (4.7) therein.
Takabayasi’s works [81–84] provide us with quantum vorticity research. The quantum relativistic vorticity (see Eq. (II) on p. 17) and the corresponding four-vector Clebsch potential (the last relation in Eq. (f) on p. 26) can be found in Ref. [85]. A recent study of the vorticity structures can be found in Ref. [29]. The quantum spirals explicitly arising from the Pauli equation are considered in Ref. [86].
5. Thermal part of the flux of the spin current
The quantum hydrodynamic equations, belonging to classical hydrodynamics, are not restricted by the continuity, Euler, or magnetic moment evolution equations. They can include energy, pressure, and thermal flux evolution equations, as is well known from the classical five- and thirteen-moment models. In spin-1/2 quantum plasmas we can derive the SC evolution equation [35]. This equation can be derived directly from the many-particle Schrödinger (Pauli) equation [35], or we can calculate moments of the distribution functions [20,38,39,57]. However, the earlier derivations have not presented the thermal part of the spin current flux, which exists in the SC evolution equation. In this section we present a derivation of the thermal part of the spin current flux applying the NLSE of Eq. (1).
The term obtained is nonzero in the linear regime for magnetized plasmas or magnetized dielectrics. Consequently, it gives a contribution to the wave dispersion.
If we want to derive an extended set of QHD equations containing the energy evolution [1,54], the pressure evolution, and the SC evolution, we do not have to use kinetic equations [20,38,39], but we can derive the hydrodynamic equations directly from the microscopic Schrödinger equation [1,35,54] or using some other method [87]. The explicit contribution of the quantum Bohm potential to the energy evolution of spin-1/2 particles was derived in Ref. [88].
6. Spin waves in electron–ion plasmas
The presence of spin waves in plasmas and their dispersion was found in 2006 in Ref. [16] by application of the hybrid kinetic–hydrodynamic method, where particle motion was described by the Vlasov equation and the spin dynamics was described by the hydrodynamic-like magnetic moment evolution equation. Waves propagating perpendicular to the external field were found there, as was the necessity for the anomalous magnetic moment of the electron. A similar solution in terms of a purely hydrodynamic description was found in Ref. [3]. Since the hydrodynamic description does not show cyclotron resonances, the anomalous magnetic moment was not included to distinguish the spin mode from the charge waves. The kinetics in the extended phase space, including two extra dimensions, caused by spin direction evolution was applied in Ref. [17]. A spin wave similar to that described above was obtained there. The contribution of the quantum Bohm potential existing in the magnetic moment evolution equation [36] to the spectrum of spin waves was later found in Ref. [21]. The features of spin-plasma waves in electron–positron plasmas arising due to the annihilation interaction in the presence of the quantum Bohm potential were considered in Ref. [22].
The spin also gives a contribution to the longitudinal waves. For instance, it arises in the spectrum of Langmuir waves via the spin–orbit interaction [89].
We consider high-frequency oscillations, and hence we assume that ions are motionless. We consider the located in an external magnetic field |$\textbf{B}_{0}=\textrm{B}_{0}\textbf{e}_{z}$|. We are going to calculate the dispersion of small-amplitude wave excitations. The equilibrium state is a macroscopically motionless uniform system of electrons described by the equilibrium constant concentration |$n_{0e}$|, which is equal to the concentration of ions |$n_{0i}$|, a zero velocity field |$\textbf{v}_{0e}=0$|, a zero electric field |$\textbf{E}_{0}=0$|, and equilibrium magnetization. If the magnetization is caused by the external magnetic field, we can write |$\textbf{M}_{0}=n_{0}{\boldsymbol {\mu}}_{0}=\chi \textbf{B}_{0}$|, where |$\chi$| is the ratio between the equilibrium magnetic susceptibility and the equilibrium magnetic permeability. Small perturbations are described by |$\delta n_{e}$|, |$\delta \textbf{v}_{e}$|, |$\delta \textbf{E}$|, |$\delta{\boldsymbol {\mu}}_{e}$|, and |$\delta \textbf{B}$|.
After Fourier transformation of the linearized set of QHD equations in Eqs. (10)–(14) we find a set of algebraic equations. We express all hydrodynamic variables via the amplitude of the electric field perturbation |$\textbf{E}_{A}$| and obtain a set of three algebraic equations, |$\Lambda^{\alpha\beta}\textrm{E}_{A}^{\beta}=0$|.
Our analysis is dedicated to point-like objects. The model of finite-radius ions in electron–ion plasmas was considered in Ref. [90].
6.1. Propagation parallel to the external field
Nonzero perturbations exist if the determinant of the matrix |$\Lambda^{\alpha\beta}$| is equal to zero: |$\det\hat{\Lambda}=0$|. This condition gives the dispersion dependencies of wave perturbations. The general dispersion equation splits into two equations. One of them is for the longitudinal perturbations |$\textbf{k}\parallel \textbf{e}_{z}\parallel\delta \textbf{E}$|, and the other is for the transverse perturbations |$\textbf{k}\perp\delta \textbf{E}$|.

The ratio between the TSCF and the Langmuir frequency, |$\chi=\textrm{w}/\omega_{Le}$|, as a function of the equilibrium concentration |$\lg n_{0}$|, measured in cm|$^{-3}$|, and the external magnetic field |$\lg \textrm{B}_{0}$|, measured in G.
As follows from Fig. 1, for large concentrations |$n_{0}\sim 10^{23}$| cm|$^{-3}$| and average magnetic fields |$\textrm{B}_{0}<10^7$|, the Larmor frequency is negligible compared to the TSCF. Moreover, the TSCF is comparable with the Langmuir frequency, but the Langmuir frequency is larger than the TSCF, |$\omega_{Le}>\textrm{w}$|. Hence, Eq. (25) can be simplified to |$\omega=\textrm{w} -\omega_{\mu}k_{z}^{2}c^{2}/(k_{z}^{2}c^{2}+\omega_{Le}^{2}-\textrm{w}^{2})$|. If we do not make any assumptions about the magnitude of the last term, which is caused by spin evolution, in the dispersion equation we need to solve it numerically. The solutions are presented in Figs. 3 and 4.
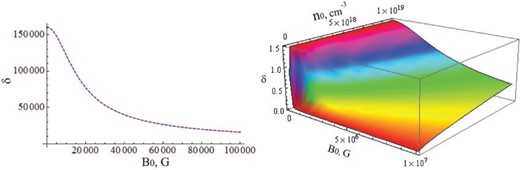
The ratio between the TSCF and the Larmor frequency, |$\delta=\textrm{w}/|\Omega_{e}|$|. The upper figure describes |$\delta$| as a function of the magnetic field at a fixed equilibrium concentration |$n_{0}=10^{23}$| cm|$^{-3}$|. The lower figure presents |$\delta$| as a function of the external magnetic field (large magnetic field) and the equilibrium concentration (small concentration).
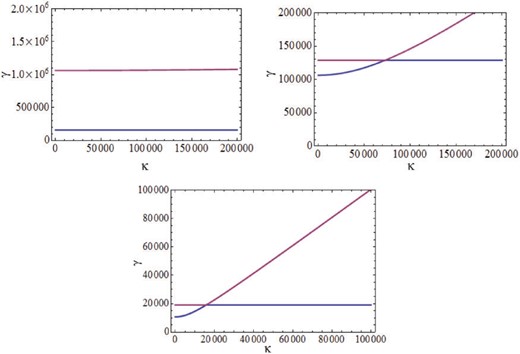
Solutions of Eq. (22) giving the frequency |$\gamma=\omega/|\Omega_{e}|$| as a function of the dimensionless wave vector |$\kappa=k_{z}c/|\Omega_{e}|=mc^{2}k_{z}/(eB_{0})$|. Equation (22) gives two solutions: the ordinary (electromagnetic) wave and the spin-plasma wave. At the equilibrium concentration |$n_{0}=10^{23}$| cm|$^{-3}$| and several values of the magnetic field (|$\textrm{B}_{0}=10^{3}$| G, |$\textrm{B}_{0}=10^{4}$| G, |$\textrm{B}_{0}=10^{5}$| G) we consider the frequency of these waves as a function of the wave vector. The upper (lower) line in the upper figure describes the ordinary (spin-plasma) wave. For the larger magnetic fields these dispersion dependencies cross each other. Hence we have hybridization of these waves.
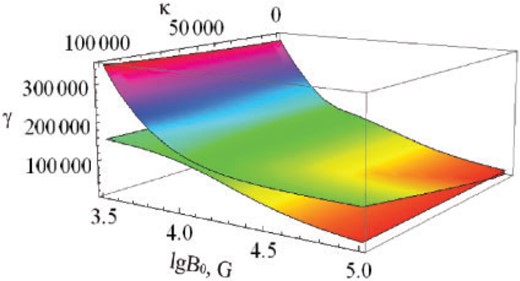
Solutions of Eq. (22) |$\omega(k_{z})$| at the equilibrium concentration |$n_{0}=10^{23}$| cm|$^{-3}$| and continuously changing small magnetic field |$\textrm{B}_{0}$|. Here we use the dimensionless wave vector |$\kappa=k_{z}c/|\Omega_{e}|=mc^{2}k_{z}/(eB_{0})$|. It shows the hybridization of the ordinary electromagnetic and spin-plasma waves.
For small wave vectors |$k$|, the frequency of the ordinary wave is comparable with the Langmuir frequency. If the TSCF is comparable, we find hybridization of the ordinary wave and the spin-plasma wave depicted in Figs. 3 and 4. In the middle and the lower pictures in Fig. 3 we see crossing of the dispersion dependencies of the ordinary wave and the spin-plasma wave. To see the hybridization, we need to decrease the frequency scale, as shown in Fig. 5, to |$\textrm{B}_{0}=10^{4}$| G.
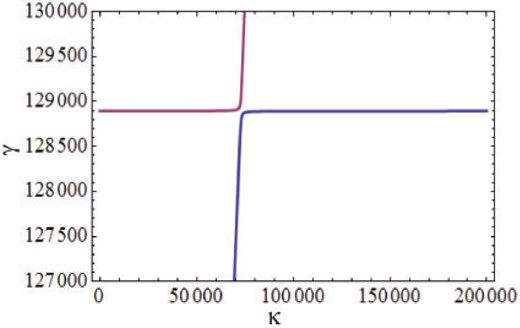
More detail of the hybridization of the ordinary and spin-plasma waves at |$\textrm{B}_{0}=10^{4}$| G and |$n_{0}=10^{23}$| cm|$^{-3}$| presented in the middle picture of Fig. 3.
To conclude this subsection, we note that if we do not account for the TPSC, or assume it to be rather small, we find the spin-plasma wave as part of the right circularly polarized wave spectrum. If the TPSC dominates over the Larmor frequency and the quantum part of the SC, the right circularly polarized spin-plasma wave does not exist, but we find a left circularly polarized spin-plasma wave. For large enough TPSC we find hybridization of the spin-plasma wave and the ordinary electromagnetic wave.
The left and right circularly polarized modes are different in the classical picture. However, the spin dynamics modifies the spectrum in the vicinity of the Larmor frequency (or the generalized Larmor frequency after accounting for the TPSC) due to the existence of the spin wave. Moreover, the generalized Larmor frequency changes under the influence of the parameters of the system. Therefore, the area of the spectrum modification also changes. The spin wave is a fine effect since it is created by the spin in a charge-dominated system. Hence, the large change of the spin wave spectrum under the TPSC effect, which is created by deformation or splitting (there are two Fermi surfaces for the spin-up and spin-down electrons) of the Fermi surface, is a possible effect.
6.2. Propagation perpendicular to the external field
With the generalization of spin-1/2 quantum hydrodynamics developed in 2001 [1], we are going to generalize the spin plasma wave spectrum calculated in Refs. [3,16].
Using the representation |$\omega_{\mu}=4\pi\Omega_{e}\chi_{e}$|, as in Ref. [3], the numerator can be rewritten as |$4\pi\Omega^{2}_{e}k_{\perp}^{2}\chi_{e}$|.
The solutions in Eqs. (29) and (30) generalize the solutions in Eqs. (8) and (9) of Ref. [3].
The TSCF can dominate in |$\widetilde{\Omega}_{\gamma}$| in the regime of perpendicular propagation. It reveals a spectrum similar to the spectrum found and described for parallel propagation.
The TPSC modifies the Larmor frequency arising from the magnetic moment precession. Therefore, the effects described in the previous paragraph can also be affected by the TPSC.
7. Features of the QHD model for spin-1/2 electron–positron plasmas
The model of spin-1/2 electron–positron plasmas differs from the model of spin-1/2 electron–ion plasmas due to the existence of the additional annihilation interaction between electrons and positrons. The corresponding hydrodynamic and kinetic models were recently derived in Ref. [22]. In this paper, we generalize the hydrodynamic model developed there, including the TPSC.
8. Spin waves in electron–positron plasmas
The spin-plasma waves in electron–positron plasmas show some similarity to the electron–ion spin-plasma waves. A principal difference is in the existence of the annihilation interaction.
Considering the propagation of waves parallel to the external field, we see that for electron–positron plasmas the nondiagonal elements disappear, since the contributions of the electrons and positrons cancel each other. Therefore, the circularly polarized waves in electron–ion plasmas are linearly polarized in electron–positron plasmas, and taking account of the spin dynamics does not change it. Nevertheless, the spin gives a contribution to the dispersion of the electromagnetic linearly polarized waves. Moreover, the spin leads to spin-plasma waves similar to the electron–ion plasmas described above.
The contribution of the TPSC in the resonance frequency for electron–ion plasmas is described above. Electron–positron plasmas differ in the presence of the annihilation interaction, which increases the frequency |$\Theta$| by a constant |$\Lambda$|.
The frequency of the spin-plasma wave is close to the resonance frequency |$\omega_{R}=\sqrt{\Theta^{2}-\Lambda^{2}}$|. Let us consider this frequency in more detail. The annihilation interaction arises in the resonance frequency |$\sqrt{\Theta^{2}-\Lambda^{2}}$| twice. These contributions partially cancel each other. Considering the square of |$\Theta$| explicitly, we have |$\sqrt{\Theta^{2}-\Lambda^{2}}= \sqrt{(\frac{2\gamma}{\hbar}B_{0}+\frac{\hbar\mu_{0}}{2m\gamma}k_{z}^{2}+\textrm{w}) (\frac{2\gamma}{\hbar}B_{0}+\frac{\hbar\mu_{0}}{2m\gamma}k_{z}^{2}+\textrm{w}+2\Lambda)}$|. This shows that the annihilation interaction increases the resonance frequency, while the TPSC decreases it, as has been demonstrated in more detail for electron–ion plasmas.
The last term in Eq. (35) arises due to the spin of the electrons and positrons. It increases the degree of the dispersion equation and leads to the appearance of the spin-plasma wave, as was also demonstrated in Sect. 6.2 for electron–ion plasmas.
This is an analog of the solution in Eq. (30) found for electron–ion plasmas.
For both parallel and perpendicular propagation of spin-plasma waves, we have the same resonance frequency: |$\sqrt{\Theta^{2}-\Lambda^{2}}$|.
This solution includes the hybridization of two branches studied numerically for waves propagating parallel to the external field in electron–ion plasmas and presented in Figs. 4 and 5.
9. Conclusion
The thermal part of the spin current has not been considered in condensed matter physics and the physics of quantum plasmas. In this paper, we have improved the magnetic moment evolution equation for degenerate electrons and applied it to spin-1/2 quantum plasma phenomena.
The explicit forms of the TPSC and the TPSC flux have been derived for degenerate electrons. A corresponding modification of the quantum vorticity evolution equation has been found. The TPSC has been applied to find the spectra of transverse waves, focusing on spin-plasma waves, in electron–ion and electron–positron plasmas. It has been demonstrated that the TPSC decreases the frequencies of the spin-plasma waves with right circular polarization propagating parallel and perpendicular to the external magnetic field. We have found that for large enough TPSC, spin-plasma waves with right circular polarization propagating parallel to the external magnetic field disappear, but right circularly polarized spin-plasma waves arise at a frequency close to the TSCF. If the TSCF and the Langmuir frequency are approximately equal to each other, we have obtained hybridization of the spin-plasma wave and the ordinary electromagnetic wave and their spectra.
All these effects have been found as applications of the generalized nonlinear Pauli equation with the spinor pressure term suggested in this paper.
Acknowledgements
The work of P.A. was supported by the Russian Foundation for Basic Research (grant no. 16-32-00886) and the Dynasty foundation.



