Abstract
The warping effect on the fractional quantum Hall (FQH) states in topological insulators is studied theoretically. Based on the perturbed wavefunctions, which include contributions from the warping term, analytical expressions for Haldane's pseudopotentials are obtained. We show that the warping term does not break the symmetry of the pseudopotentials for |$n={\pm }1$| Landau levels (LLs). On increasing the warping strength of the Fermi surface, our results indicate that the stability of the FQH states for LL |$n=0$| (LLs |$n={\pm }1$|) becomes stronger (weaker), and the excitation gap at the |$\nu =1/3$| FQH state for LL |$n=0$| also increases while the gaps for LLs |$n={\pm }1$| are unchanged.
1. Introduction
Topological insulators (TIs) as a new phase of quantum matter, which cannot be adiabatically connected to conventional insulators and semiconductors, have been intensively studied in recent years [1–10]. TIs are characterized by a full insulating gap in the bulk and protected gapless edge or surface states. Near the Fermi level the low-energy dispersion of the TI surface states shows a Dirac linear behavior. However, the recent angle-resolved photoemission spectroscopy experiments show that the Fermi surface in Bi2Te3 [9,10], a typical TI, is a snowflake shape rather than a circle one. The origin of this snowflake-like Fermi surface has been confirmed to arise from an unconventional hexagonal warping term [11]. It is this warping term that brings about many unique physical phenomena [12–14], which cannot be observed in other systems, including the extensively studied graphene and the conventional 2D electron gas.
More recently, increasing attention has been paid to the interactions of the Dirac-type quasiparticles and their strong correlation effects in TI, especially the TI fractional quantum Hall (TIFQH) states. Despite no undeniable experimental observation of the TIFQH states heretofore, some theoretical studies have been undertaken. For example, DaSilva [15] predicted the stability of the TIFQH states for Landau levels (LLs) with index |$n=0$| and ±1 in TIs. Apalkov and Chakraborty studied the finite thickness effect on the TIFQH states [16]. Also, the present authors investigated the influences of the Zeeman splitting and the tilted strong magnetic field on the stability of the TIFQH states [17,18] with large g factor. However, many important and interesting open questions, such as the warping effect, the spin excitations, and the subband–LL coupling, have not been discussed in the TIFQH regime.
In this paper we theoretically study the warping effect on the TIFQH states. Here the warping term is perturbatively treated. With the help of the numerical calculations, we show that the warping term cannot break the symmetry of Haldane's pseudopotentials for |$n={\pm }1$| LLs, which differs from the role of the spin splitting [17]. Moreover, our results indicate that, with an increase in the warping strength of the Fermi surface, the stability of the TIFQH states for LL |$n=0$| (LLs |$n={\pm }1$|) become stronger (weaker), and the excitation gap at |$\nu =1/3$| filling for LL |$n=0$| (gaps for LLs |$n={\pm }1$|) also increases (remains unchanged).
2. Model and results
Figure 1 plots Haldane's pseudopotentials of Coulomb interaction |$V^{(n,m)}$| for (a) |$n = 0$| and (b) |$n = 1$| LLs as functions of the relative angular momentum m. Comparing these with the results in the absence of the warping term (black dots in Fig. 1), one can clearly see that, in the presence of the warping term, the magnitude of the pseudopotentials increases (red stars in Fig. 1).
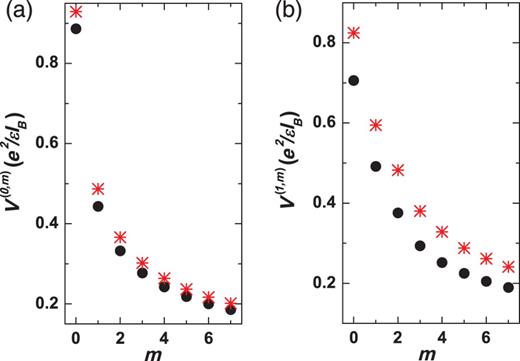
The effective pseudopotentials of the Coulomb interaction |$V^{(n,m)}$| between two electrons at (a) |$n = 0$| and (b) |$n = 1$| LLs as functions of the relative angular momentum with different warping strengths, |$\zeta = 0$| (circles) and |$\zeta = 0.2$| (stars).
Subsequently, the stability of the TIFQH states should also be modified by the warping term. The typical results of |$V^{(n,1)}/V^{(n,3)}$| (|$n = 0$| and |$n = \pm 1$|) are shown in Fig. 2 as a function of the warping parameter ζ. One can see that, with increasing ζ, |$V^{(0,1)}/V^{(0,3)}$| increases while |$V^{(\pm 1, 1)}/V^{(\pm 1, 3)}$| decreases. According to the composite fermion theory, the larger the value of |$V^{(n,1)}/V^{(n,3)}$| is, the more stable are the fractional quantum Hall states. Therefore, the remarkable warping term results in the composite fermions at fractional filling for LL |$n = 0$| (LLs |$n = \pm 1$|) becoming more stable (unstable). This result suggests that on the surface of a TI material with strong (weak) warping strength, such as Bi2Te3 (Bi2Se3), the TIFQH states for LLs |$n = 0$||$(n = \pm 1)$| may be observed much more easily under a perpendicular magnetic field. We hope that this prediction will be detected in future experiments.
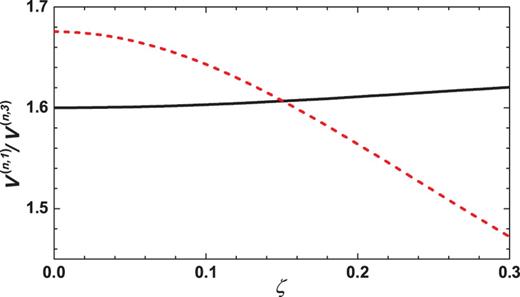
The ratio of the first and third relative angular momentum pseudopotentials for LLs |$n = 0$| (black solid line) and |$n = \pm 1$| (red dashed line) as a function of the warping term ζ.
In what follows, by using the exact diagonalization method in the spherical geometry, we investigate the system with the fractional filling factor |$\nu = 1/(2p + 1)$|, where p is an integer. For briefness we only illustrate the |$\nu = 1/3$| TIFQH state, which is realized at |$S=\frac {3}{2}(N - 1)$| in the spherical geometry, with N being the electron number. Under this configuration, the perpendicular magnetic field is equivalent to a fictitious radial magnetic field produced by a magnetic monopole at the center of a sphere of radius |$R=\sqrt {S}l_{B}$| (in units of flux quanta), and the many-body states can be described by the total angular momentum L and its z component |$L_{z}$|.
We show in Fig. 3 the energy spectra of the many-body states at |$\nu = 1/3$| filling for |$N = 7$| electrons. Comparing the two cases with |$(\zeta = 0.2)$| and without |$(\zeta = 0)$| warping term, one can see from Fig. 3 that the gap width at |$n = 0$| LL between the ground state and the first excited state has a visible increment, while those at |$n = \pm 1$| LL remain unchanged. Furthermore, we calculate the corresponding excitation gap width |$E_{\mathrm {gap}}^{n} (\zeta)$| by increasing the warping term from |$\zeta = 0$| to |$\zeta = 0.3$|. The variations |$\Delta E_{\mathrm {gap}} = E_{\rm gap}^{n} (\zeta) - E_{\rm gap}^{n} (\zeta = 0)$| as a function of ζ are plotted in Fig. 4, which shows that the TIFQH gap between the ground state and the lowest excited state at |$n = 0$| LL (solid line) is sensitively dependent on the warping term while the |$\Delta E_{\mathrm {gap}}$| at |$n = \pm 1$| LLs (dashed line) remains constant no matter whether the warping term is included or not. This also implies that the warping term is different from the Zeeman splitting and the tilted magnetic field, which will induce a change in the gap of the TIFQH states at LLs |$n = \pm 1$| [17,18].
Exact energies versus the angular momentum L for |$N = 7$| electrons at the |$\nu = \frac {1}{3}$| TIFQH state. The warping strength is chosen as |$\zeta = 0$| (circles) and |$\zeta = 0.2$| (stars).
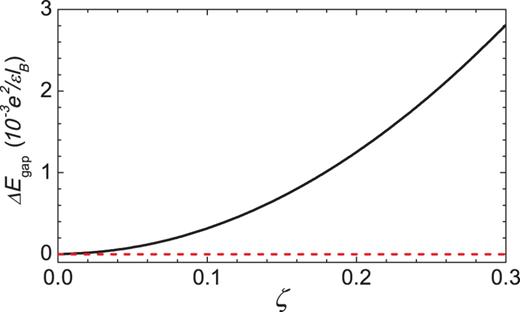
The increment of the gap width as a function of the warping term ζ for |$N = 7$| electrons at |$\nu = \frac {1}{3}$| TIFQH states for LLs |$n = 0$| (black solid line) and |$n = \pm 1$| (red dashed line).
3. Conclusion
In summary, we have perturbatively studied the effect of the warping term on the TIFQH states. It was found that, unlike the role of the Zeeman splitting and the tilted magnetic field, the warping term does not break the symmetry of Haldane's pseudopotentials for |$n = \pm 1$| LLs. Our results showed, on one hand, that the stability of the |$\nu = 1/3$| TIFQH states for LL |$n = 0$| (LLs |$n = \pm 1$|) becomes stronger (weaker) by increasing the warping strength of the Fermi surface. On the other hand, the excitation gap for LL |$n = 0$| increases on increasing the strength of the warping term; the gaps for LLs |$n = \pm 1$| are insensitive to this term.
Acknowledgements
This work was supported by the Natural Science Foundation of China under Grant Nos. 11274049, 10904005, 11004013, and by the the National Basic Research Program of China (973 Program) under Grant No. 2009CB929103.
References
