-
PDF
- Split View
-
Views
-
Cite
Cite
Liat Levavi, Benny Bar-On, How do roses build failure-resistant anchoring tools?, PNAS Nexus, Volume 3, Issue 12, December 2024, pgae501, https://doi.org/10.1093/pnasnexus/pgae501
Close - Share Icon Share
Abstract
Rose prickles are small-scale, plant-based anchoring tools of multifunctional biomechanical roles, combining physical defense against herbivores and growth support on surrounding objects. By employing multiscale structural observations, nanomechanical characterizations, and finite-element simulations, we unveil that the dog rose (Rosa canina Linnaeus) prickle incorporates structural–mechanical modifications at different length scales, resulting in macroscopic stress-locking effects that provide the prickle extreme damage-resistant capabilities and secure its functional form against catastrophic failures. These functional design strategies, unique to plant-based biomechanical tools, may promote futuristic micro-engineered anchoring platforms for micro-robotics locomotion, biomedical microinjection, and micromechanical systems.
Rose shrubs possess miniature epidermal appendages (prickles) that provide them with crucial biomechanical capabilities (physical defense and growth support). The dog rose prickles (Rosa Canina Linnaeus) incorporate intimate relationships between their geometrical shape, microstructural density, and nanomechanical properties, making them multifunctional anchoring tools with outstanding resistance to mechanical failures. This unusual “design solution” of biomechanical tools in the plant kingdom may promote the development of innovative micro-anchoring platforms for diverse applications.
Introduction
Plants possess a variety of small-scaled, curve-shaped, and sharp-edged anchoring tools in the forms of spines, thorns, and prickle, providing them essential biomechanical functions, including physical defense against herbivores and frictional contact for growth support (1–4). Among these, rose prickles are specifically recognized by their hard and sharp tips that easily puncture and tear softer target objects alongside their overall high rigidity and damage resistance that preserve their shapes mostly undeformed and undamaged even upon significant mechanical loadings (5). While the botanical aspects of rose prickles, e.g. formation process, morphological characteristics, and anatomical composition, have been extensively studied over the years (6–10), their hierarchical structures and biomechanical load-bearing characteristics are still largely unexplored. Identifying the structural mechanics principles of rose prickles is a critical milestone toward understanding how plants evolve and adapt their anchoring tools to promote their herbivory defense and growth support functions; practically, these insights may open new horizons for advanced engineering developments of miniature, high-performance anchoring platforms for various applications (11, 12).
Rose prickles integrate distinct structural characteristics at different length scales. On the macroscopic level, their geometrical shapes exhibit pronounced widening from their sharp tip toward the underlying stem with different aspect ratios along the stem axis and at the stem circumference, which globally links to a universal geometrical law of various nonplant sharped-edge biomechanical tools of different sizes and shapes (e.g. stingers, fangs, and teeth) (13). On the material level, the prickles are fundamentally biological composites made of highly lignified cellular tissues (exterior epidermis and interior cortical) of spatially varying microstructural characteristics (i.e. sizes, shapes, and cell wall thicknesses) (5, 7). The composite characteristics of the prickles are specifically modified near their tip and close to their exterior surface—analogously to various anchoring tools in nonplant systems, such as arthropod claws, squid beaks, and worm jaws (14, 15)—which implies their mechanical adaptation in terms of functional load bearing. Indeed, extensive mechanical experiments on rose prickles shed light on their significant damage resistance, where overload failures never occurred within the bulk prickle but only at its connection site with the stem (5, 16). To the best of our knowledge, the origins of these damage-resistant characteristics have yet to be discovered, and more broadly, the fundamental load-bearing characteristics of the prickles and their relationships to their diverse biomechanical functions have yet to be explored.
The failure process of load-bearing plant organs is inherently complex due to their internal composite architectures and pronounced microstructural anisotropy. These characteristics give rise to various, nonclassical, toughening mechanics that detain, direct, and even prevent their fracture paths (17, 18). For example, basal failure of rose prickles is a priori unpredictable, which may occur within the directional tissue of the prickle itself, below the prickle, above or beneath the interfacial cork layer, or at nondirectional cortical parenchyma of the stem. Each failure type incorporates distinct fractured surfaces with different fracture paths and follows different force–displacement trends until complete failure (5, 7). Although a profound failure criterion is currently not in hand, the von Mises stress and the principle tensile stress may be considered as possible indicators for the onset of mechanical damage and a failure sequence within the prickle. The von Mises stress indicator corresponds to a distortion-driven failure, suitable for ductile engineering materials and conventionally employed, experimentally supported, in various biomechanical elements (19–23). The principal tensile stress indicator corresponds to a stretching failure, suitable for brittle engineering materials and, thus, for dry plant parts. Specifically, the local orientation of the principal stress represents a critical stretching-failure axis within the plant part, which is commonly resisted by the local microstructural anisotropy of the underlying tissues (24, 25).
In this study, we employ multiscale structural observations, nanomechanical experiments, and numerical simulations to disclose the fundamental structure–mechanics–function relationships of rose prickles, focusing on the prickles of the Rosa canina Linnaeus (dog rose) shrub as a model system of our analysis. To this end, we employ macroscale and microscale computed tomography (CT) and scanning electron microscopy (SEM) to characterize the hierarchical structure of the prickle across the millimeter-to-micrometer length scales and nanoindentation experiments to identify nanomechanical properties of its basic microstructural materials. Then, we integrate these findings into finite-element (FE) simulations on the native structural forms of the prickles, disclose their stress morphologies at puncturing, hanging, and anchoring functional states, and unveil how the geometrical and material characteristics of the prickle reciprocally evolved, and possibly adapted, to promote its biomechanical load bearing and to secure its form against catastrophic failure.
Materials and methods
Samples
Dry samples of Rosa canina L. branches, coated with prickles, were received from the “Wahl Rose Garden” in Jerusalem, Israel. The prickles were cut from the stem by a scalpel and stored at room temperature.
Computed tomography
CT scans of the prickles were conducted with SkyScan (Bruker, MA). For low-resolution CT scans of the whole prickle, a SkyScan-1072 scanner was used with the following parameters: voxel size 6–9 µm3, voltage 40 kW, current 100 µA, and exposure time 3,000 ms. For high-resolution CT (μCT) scans of local regions within the prickle, a SkyScan-1272 scanner was used with the following parameters: voxel size 0.8 μm3, voltage 40 kV, current 100 µA, and exposure time 2,000 ms. The images were reconstructed with NRecon 1.7.5.9 and DataViewer 1.6 software (Bruker). Volume fraction analyses, visualizations (artificially colored), and segmentation for the FE model were conducted with Avizo 9.3 software (Thermo Fisher Scientific, Germany).
Scanning electron microscopy
SEM observations were conducted with either (ⅰ) FEI Phenom XL G2 (Thermo Fisher Scientific) with secondary electron (SE) and backscatter electron detectors, 5–10 kV, or (ⅱ) FEI Verios 460L (Thermo Fisher Scientific) at SE mode, using an Elstar in-lens and Everhart–Thornley detectors, 3 kV, 25 pA. Both free-fractured and embedded–polished samples were analyzed after a 15 nm gold coating.
Image analysis
Geometrical and cross-sectional image analysis was conducted by built-in algorithms in MATLAB 2021b. The geometrical shape and ventral edge characterizations were conducted by using Kirsch's compass masks algorithm on lateral images of the prickle. The cross-sectional analysis was conducted by using regionprops algorithm for edge detection and axes measurements of the oval cross-sections. Volume fraction analysis of the microtubular arrays within the different regions of the prickle was conducted by using ImageJ (v1.54f) and Fiji (ImageJ2) open-source software tools (imagej.net) on SEM and CT images.
Nanoindentation experiments
Indentation experiments were conducted with the Hysitron Triboindenter-950 (Bruker) with a Berkovich tip. Prior to the experiments, samples were embedded in cold mounting epoxy and then cut-polished. The nanoindentation experiments were conducted on cross-sections of the samples following a load-control protocol: linear loading for 5 s and up to a maximal force of 70 µN, a constant maximal force for 2 s, and then linear unloading for 5 s. The nanoindentation analysis followed the Oliver–Pharr method and yielded the indentation modulus and indentation hardness (26).
Statistical analysis
Statistical tests for the measured indentation modulus, indentation hardness, and contact resistance were performed in MATLAB 2021b. Nonparametric Mann–Whitney U test or Kruskal–Wallis test was used for comparison between two or three groups, respectively, with Tukey's post hoc test. The statistical distributions of the measured parameters were extracted by a standard transformation of Weibull's coordinates, yielding Weibull's cumulative distribution function for each parameter, namely
FE simulations
FE simulations were conducted with commercial software (ABAQUS/standard 6.14). The analysis was carried out on reconstructed geometrical models from the CT analysis segmented by four-node, 3D linear-elastic tetrahedral elements (C3D4, ABAQUS element library). The simulation models included overall
Results
Hierarchical structure and material characteristics
Structural parts
The geometrical shape of the R. canina prickle resembles a sickle with a tapered structure that expands from the tip toward the stem (Fig. 1A–B). The total length of the ventral edge of the prickle is
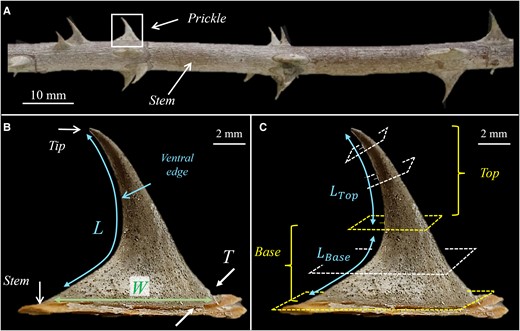
Geometrical shape of the Rosa canina L. prickle. A) A stem with several prickles. B) A single prickle. L is the overall length of the ventral edge of the prickle from tip to base. W and T are the maximal width and thickness of the prickle at the connection site of the prickle and the stem. W spans along the stem axis, and T spans along stem circumference. C) The local normal cross-sections at the top part of the prickle are locally parallel to the ventral edge; the local normal cross-sections at the base part of the prickle are globally parallel to the surface of the stem. The ventral lengths of the top and base parts of the prickle are
The cross-sections of the prickle are oval shaped of local width
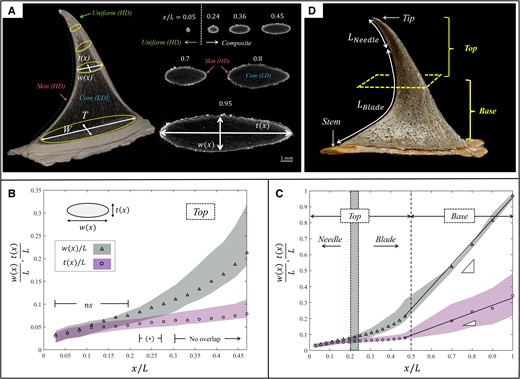
Cross-sectional geometry of the Rosa canina L. prickle. A) µCT image of the prickle with x indicating the location along the ventral edge (left) and selected cross-sectional images of the prickle in different locations (right). The cross-sectional shape is oval, with width
Accordingly, the overall shape of the prickle incorporates two distinct structural parts: (i) an initial sharpened needle-like part that is located close to the tip (ventral length
Material characteristics
The prickle incorporates distinct regions of higher-density (HD) and lower-density (LD) materials, represented by the bright and dark areas of the CT imaging (Fig. 2A). Cross-sections close to the tip include a uniform (HD) material (ventral length

Cross-sectional material of the Rosa canina L. prickle. A) µCT image of the prickle. The green shaded region indicates the uniform region close to the tip; the red shaded region and blue shaded regions indicate the skin and core regions of the prickle.
All material regions of the prickle are internally architected as microtubular arrays of a few micrometer-thick cell walls that enclose hollow interiors (Fig. 3B–D). At the top part of the prickle, these microtubular arrays are locally parallel to the ventral edge (i.e. normal to the cross-section). At the base part of the prickle, the microtubular arrays within the core region are globally normal to the surface of the stem (i.e. normal to the cross-section), whereas the microtubular arrays within the skin region are locally parallel to the exterior surface of the prickle (Fig. 3A, E–G). µCT-based and SEM-based volumetric analysis of the cell walls indicated high microtubular density within uniform and skin regions (∼80%) and low microtubular density within the core region (∼50%) (Table S2). Notably, the microtubular density is locally extreme at the apex of the prickle (∼95%), i.e. close to that of a bulk solid.
Nanomechanical characteristics
Nanoindentation measurements on the cell walls yielded the indentation modulus (E) and hardness (H) of the microtubular arrays at the different material regions within the prickle (Fig. 4, Table S2). The results for both E and H are significantly different between the uniform, skin, and core regions, and their statistical CDFs tightly follow Weibull's form. The uniform region exhibits the highest hardness (H), the skin region exhibits the highest modulus (E), and the core region exhibits the lowest nanomechanical characteristics (both H and E). The ratio
![Nanoindentation results for the cell walls of the prickle. A–C) Bar plots for the indentation modulus (E), indentation hardness (H), and contact-damage resistance (H3/E2) of the cell walls within the different material regions of the prickle. The upper and lower edges indicate the upper and lower quartiles, and the horizontal lines indicate the medians. The whiskers indicate the dataset range, and the circles indicate the outliers. D–F) Statistical representations of the datasets in (A–C) via Weibull's CDF. E0, H0, and [H3/E2]0 are the corresponding Weibull's scale parameter, κ are their corresponding shape parameters, and R2 are the coefficient of determination to Weibull's coordinates of each dataset.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/pnasnexus/3/12/10.1093_pnasnexus_pgae501/15/m_pgae501f4.jpeg?Expires=1748446165&Signature=GbR2IuIYOOvCzEeWxC~VPZ3ImXnxs5MbOIegD56w4aSFvSWmpsUoGjqg8n06DJRwk8nWeQ7kVoaYwsP1TPvBjWNZGmeLr1cVtU~ILhJCGlPdYZWMXFPjDpaxv9UlInbVjuRcixyOtl2FQtqo1Hw7CnAy2WwzISYMq44zkDrnRIeeXOm-QChzmomgkwh2-BbfaGdhydQ4wAkiPvhHulQqOBGriTnHl2O66X93ClMYt53Skxy0-7C08mbp3dHoPyQj2gqdbhZugdc~k9eHU31CKhAt4ASXniZG6fe-E2L3Nh~N9BkkhcW3q1eS-qWV8VCnuWjK-T5hdKrg6Bho1O902A__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Nanoindentation results for the cell walls of the prickle. A–C) Bar plots for the indentation modulus (E), indentation hardness (H), and contact-damage resistance (
A summary of the hierarchical structure and material characteristics of the R. canina prickle is shown in Fig. 5. These results are integrated next into FE simulations to analyze the biomechanical load-bearing characteristics at different functional states.
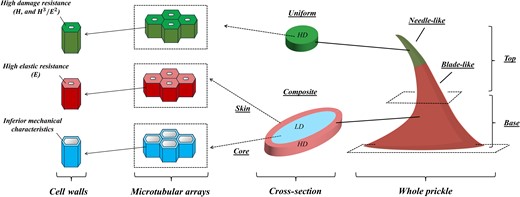
Schematic illustration for the hierarchical structure of the R. canina prickle. The uppermost needle-like structure of the prickle includes a uniform, high-density microtubular material of high abrasion resistance. The subsequent blade-like structure of the prickle is a skin–core composite. The skin comprises a high-density microtubular material of high elastic resistance, and the core is a low-density microtubular material with inferior mechanical properties.
Biomechanical load bearing
The biomechanical load-bearing analysis of the prickle was carried out via FE simulations, focusing on its typical functional states: (i) puncturing of the prickle into target mediums (herbivory defense function) (Fig. 6A), (ii) local hanging of the prickle on surrounding objects (growth support function) (Fig. 6B), and (iii) anchoring of the prickle on rough surfaces or tearing through target mediums (growth support and herbivory defense functions, respectively) (Fig. 6C).
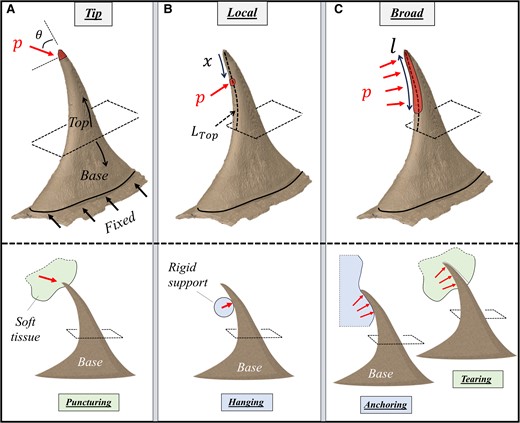
Models for the biomechanical analysis of the R. canina prickle. A) Tip loading represents the puncturing of the prickle into target mediums (herbivory defense); B) local ventral loadings represent the leaning of the prickle on surrounding objects (growth support); C) broad ventral loadings represent tearing of the prickle throughout target mediums (herbivory defense) or anchoring of the prickle on rough surfaces (growth support). In (A), a directed pressure p (i.e. traction) is applied on the apex of the prickle at different orientations (θ) within the sagittal plane of the prickle. In (B), a local normal pressure p is applied at different ventral locations (x) along the top part of the prickle (length
Puncturing
In the puncturing state, the apex of the prickle incorporated a directed pressure (i.e. traction) at different orientations (θ) within the sagittal plane—spanning between locally parallel ventral edge at the tip (
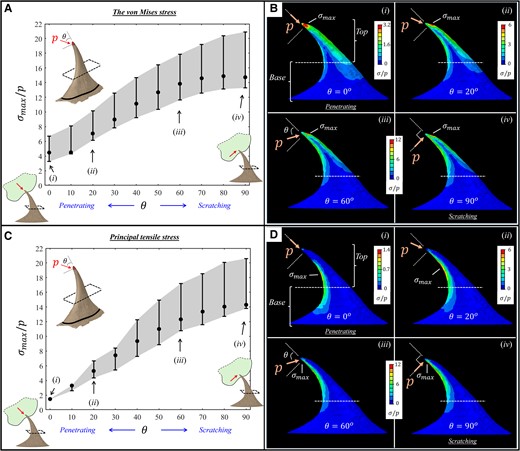
FE results for the stresses (
Hanging
In the hanging state, the ventral edge of the prickle incorporated local normal pressure at different positions along the top part of the prickle (
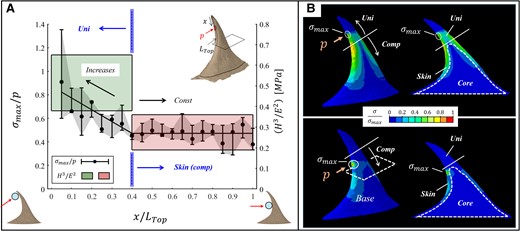
FE results for the stresses (
Anchoring–tearing
In the anchoring–tearing state, the ventral edge of the prickle incorporated normal pressure loading spanning from the tip over a certain ventral length along the top part of the prickle (
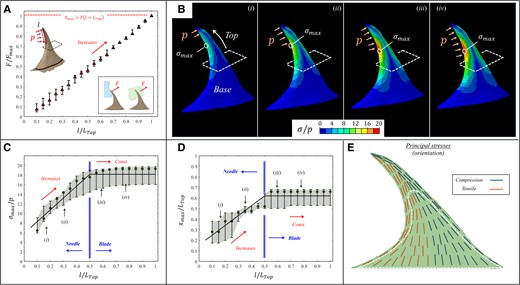
FE results for the stresses (
Base widening
The base part of the prickle serves as a bridging region that gradually reduces the stresses within the prickle toward its mechanically weakened connection site with the stem (Figs. 9 and 10). The stress reduction effect is especially pronounced for long-range loadings, which yield broad stress morphologies throughout the majority of the prickle. To demonstrate the stress reduction effect, we modified the FE model with full-length pressure loadings by artificially excluding portions of the base part and observed the stress variations at the bottom surface of the model that correspond to the modified prickle–stem connection site. In the absence of the base part, the top part of the prickle directly connects to the stem, forming a sharp geometrical transition, of approximately right angle, between the ventral edge of the prickle and the long axis of the stem (Fig. 10A). This sharp geometrical transition yields stress intensification effects that produce extreme stress values at the prickle–stem connection site, which offends the load-bearing efficiency of the prickle and promotes its overloading catastrophic failure (i.e. complete traction). Notably, sharp transitions in cross-section cause stress concentrations is a central result of classical elasticity. The stresses at the connection site rapidly decrease, by a power low, while including larger portions of the base part (Fig. 10B–C)—both by blunting the prickle–stem geometrical transition and by expanding the total area of the connection site that decrease its effective force-to-area ratio. Notably, the connection stresses diminish by three orders of magnitude and become practically insignificant for the native prickle (i.e. with the whole base part) (Fig. 10D)—securing its weakened connection site with the stem against mechanical failure.
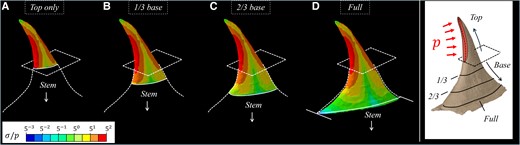
FE results for the stresses (
Discussion
The rose prickles belong to a large group of functional epidermal appendages located on the stems of various shrubs and even on the trunks of some tree species. Despite their miniature sizes and minor mass portions, rose prickles provide the shrub significant functional capabilities—by forming mechanical growth support for its flexible stems via hanging on neighboring plants or anchoring into rough surrounding objects (e.g. rocks) and by deterring herbivores via puncturing, scratching, and tearing their mouthpart tissues. The multiple functions of the rose prickle intimately link to the overall load-bearing characteristics of its hierarchical structure—originated from the nanomechanical characteristics of its cell walls, upscaled through density-induced modifications of its microtubular arrays at different regions of the prickle, and finalized by graded geometrical characteristics of its macroscopic shape.
Failure resistance strategies of rose prickles
The rose prickle incorporates various structural–mechanical strategies to promote its failure resistance against diverse functional–mechanical loading states. In the puncturing state, the minimal stress for loadings close-to-parallel to the tip direction indicates that the prickle is primarily adapted to sustain penetration-dominant loadings, and its load-to-failure capabilities at this state are about two to three times greater than at the combined penetration–scratching and the scratching-dominant states. Moreover, the persistent near-tip location of the maximal stress for all loading states corresponds well to the extreme microtubular density at this region, providing the prickle with enhanced damage resistance to puncturing loadings. In the hanging state, the apparent correlation between the variations in the maximal stress and the contact resistance of the underlying material indicates a preannounced load-bearing adaptation that facilitates the hanging function of the prickle at different ventral positions. In the anchoring–tearing state, the maximal stress-locking effect promotes the load-bearing efficiency of the prickle by allowing it to magnify, and even double, the anchoring–tearing forces on target objects without increasing the maximal stress. Complementarily, the locking effect of the location of the maximal stress secures the prickle against catastrophic failures by confining its potential damage to the needle–blade connection site—preventing its further propagation within the blade-like part or downward to the prickle–stem connection site (i.e. blade fracture or prickle traction, respectively). The correspondence between the local orientations of the principal stresses and the material anisotropy by the microtubular orientations gives rise to toughening mechanisms that resist mechanical failure within the bulk prickle, which is in line with previous experimental observations that failure typically occurs at the basal region below the prickle—either in the vicinity of the cork layer or within the stem tissue. Such basal failure is further detained by the gradual base widening of the prickle, which prevents the emergence of stress concentrations due to sharp geometrical transitions between the prickle and the stem.
Links between rose prickles and other load-bearing biomechanical elements
The basic nanomechanical characteristics (E and H) of the cell walls comprising the rose prickle correspond well to those of plant tissues of pronounced mechanical roles (secondary xylem, sclerenchyma, and collenchyma), present in diverse types of load-bearing plant parts, including various of woods (30–33), nutshells (34), leaves (35), and winged seeds (36). The nanomechanical contact resistance (
The high-density uniform and skin regions of the prickle effectively upscale the nanomechanical characteristics of their microtubular arrays into the material level—forming mechanically enhanced functional regions. The uniform region equips the prickle with a hard and contact-resistant tip that facilitates its puncturing capabilities into target mediums by generating stress concentrations and micro-damage effects that reduce their overall work-to-puncture (44–48). The exterior skin region equips the prickle with a stiff and hard coating that sustains its direct and indirect mechanical loadings, transmits their resultant stresses toward the stem, and promotes the overall structural resistance of the prickle to flexural deformations (49). Notably, the density-induced modifications of the rose prickle are analogous to chemical-induced and compositional-induced modifications found in various other nonplant biomechanical elements, e.g. metal-ion deposition that modifies the cutting edges of arthropod cuticular tools and marine worm jaws, and chitin content and alignment modification that reinforces the exocuticle parts of spider fangs and claws, and scorpion pincers (50–55).
The gradual morphological changes in the geometrical shape of the prickle form three distinct structural parts that fulfill different mechanical functions. The uppermost, puncturing, needle-like part of the prickle includes a semi-circular, slightly expanding cross-sectional shape that facilitates its puncturing efficiency by decreasing frictional loss (48, 56), enhancing its buckling stability (57, 58), and confining its puncturing stress-to-failure to the apex region (22, 59). Contrary to injection-related biomechanical elements that typically preserve their expanding semi-circular shapes throughout most of their structures (e.g. stingers, fangs, and spines (49, 58, 60–62)), the rose prickle breaks its axisymmetric expansion after a certain distance from the tip—modifying its remaining underlying into a flattened blade-like part that corresponds to miniature anchoring tools (e.g. insect claws, ant mandibles, and radular teeth (55, 63–65)). The oval cross-sectional expansion of the blade-like part facilitates the flexural rigidity of the prickle parallel to the stem axis, eliminates the evolution of significant bending stresses far from the tip, and confines the extreme stress states within the prickle to its near-tip region, which does not exceed the needle–blade connection site (49, 59). The final geometrical modification arises at the base part of the prickle, in which all cross-sections lay parallel to the stem axis, and their oval shapes exhibit pronounced aspect ratios that rapidly expand toward the connection site of the prickle with the stem. While such basal modification is typically absent in nonplant biomechanical elements (or very minimal, e.g. in some snake fangs (22, 62)), its presence is very dominant in rose prickles and apparently in various other plant anchoring elements (e.g. spines, thorns, trichomes, and fruit hooks) (5, 39, 40, 66). Evidently, the base part plays a significant role in protecting the weakened connection site of the prickle with the stem, thus securing the prickle against catastrophic traction failure.
Macroscopically, the stress morphologies within the prickle and the local orientation of the principal stresses closely follow the classical beam theory. This observation allows approaching the mechanical behavior of rose prickles and other sharp-edge biomechanical tools via analytical modeling tools of structural composites (67). Such models would possibly provide new insights into stress-to-failure characteristics of diverse forms of biomechanical tools and disclose other load-bearing aspects, such as graded deformation patterns, optimal structural stiffness, and puncture mechanics (68, 69), which may play critical roles in their functional capabilities.
Conclusions
The natural design principles of the rose prickle as a natural, plant-form anchoring tool demonstrate complementary structural and material adaptations that promote its load-bearing capabilities for multiple biomechanical functions. These design principles may open new horizons for developing advanced engineering forms for miniature anchoring platforms for diverse applications (70–73).
Acknowledgments
The authors acknowledge the generous support of the Pearlstone Center for Aeronautical Engineering Studies, the scientific support from the Ilse Katz Institute for Nanoscale Science and Technology, and the valuable support of the Wahl Rose Garden (Jerusalem, Israel).
Supplementary Material
Supplementary material is available at PNAS Nexus online.
Funding
The authors declare no funding.
Author Contributions
L.L. carried out the structural observations, nanomechanical measurements, and FE simulations. B.B.-O. designed the research, and carried out the structural and mechanical modeling. All authors analyzed the data, discussed the results, and wrote the manuscript.
Data Availability
All data are available in the main text or the supplementary materials.
References
Author notes
Competing Interest: The authors declare no competing interests.


