-
PDF
- Split View
-
Views
-
Cite
Cite
H Z Zhong, C W Li, R Das, J F Gu, M Qian, Post-yield softening of bending-dominated metal metamaterials, PNAS Nexus, Volume 2, Issue 3, March 2023, pgad075, https://doi.org/10.1093/pnasnexus/pgad075
Close - Share Icon Share
Abstract
Post-yield softening (PYS) plays an important role in guiding the design of high-performance energy-absorbing lattice materials. PYS is usually restricted to lattice materials that are stretching dominated according to the Gibson–Ashby model. Contrary to this long-held assumption, this work shows that PYS can also occur in various bending-dominated Ti-6Al-4V lattices with increasing relative density. The underlying mechanism for this unusual property is elucidated using the Timoshenko beam theory. It is attributed to the increase in stretching and shear deformation with increasing relative density, thereby increasing the tendency towards PYS. The finding of this work extends perspectives on PYS for the design of high-performance energy-absorbing lattice materials.
One of the most fascinating developments enabled by additive manufacturing is intricate lattice materials. PYS plays an important role in guiding the design of high-performance energy-absorbing lattices. Contrary to the long-held assumption that PYS is restricted to stretching-dominated lattices, this work shows that PYS also occurs in various bending-dominated lattices with high relative densities. This is because deformation by stretching and shear in bending-dominated lattices increases with increasing relative density, thereby increasing the tendency towards PYS. This finding helps to improve the design of high-performance bend-dominated lattices for energy absorption applications.
Introduction
Lattice materials are cellular materials that consist of interconnected struts organized into repeating unit cells (1, 2). They can be used for diverse applications, including light-weight structures, orthopedic implants, filters, heat exchangers, catalyst platforms, battery electrodes, and sound or energy absorbers. Powder bed fusion (PBF) additive manufacturing (AM) has revolutionized their design and fabrication, leading to important applications of these novel cellular materials in various industrial sectors.
The concept of post-yield softening (PYS) was proposed by Ashby (1). In the Gibson–Ashby classification of cellular materials, according to the Maxwell criterion (3), bending-dominated lattice materials require , where b and j are the number of lattice struts and nodes, respectively, while stretching-dominated lattice materials require (1, 4). Figure 1 shows the characteristic compression stress–strain curves for both types of lattice structures [1], with PYS restricted to stretching-dominated lattices (Fig. 1a) according to Ashby (1). The occurrence of PYS is due to the sudden release of the significant elastic strain energy stored in the stretching-dominated lattice struts at the onset of plasticity (yielding), or crushing, or buckling (Fig. 1a). In contrast, the elastic strain energy stored in the bending-dominated lattice struts is much lower at the onset of plasticity (yielding), or crushing, or buckling (Fig. 1b), and thus, the release is negligible, resulting in a smooth transition from the peak stress to the plateau stress (5, 6). Although it is referred to as PSY, the first peak stress point in Fig. 1a or Fig. 1b includes the case of crushing or buckling according to Ashby.
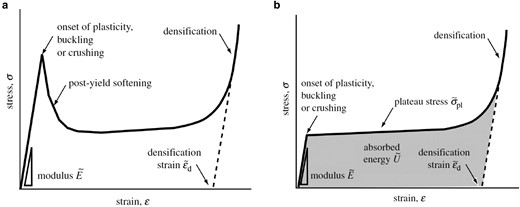
Characteristic compression stress–strain curves for (a) stretching-dominated lattices with PYS and (b) bending-dominated lattices, adapted from Ref. (1).
Although Ashby emphasized that bending-dominated lattices are better suited to absorb energy than stretching-dominated lattices (1), unfortunately, bending-dominated lattices have poor yield strength, corresponding to low energy absorption (the region below the curve in Fig. 1b). Therefore, in practice, stretching-dominated lattices can instead provide higher energy absorption. Mitigating the PYS can further improve this ability. Thus, many efforts have been made in this regard, including the introduction of irregular (7), heterogeneous (8), or hybrid structures (9) in stretching-dominated lattices. These measures are effective in reducing the PYS to some extent, but often at the expense of yield strength. Other efforts have focused on microstructural control to improve the yield strength, including through the selection of base alloys (10), the use of reinforcement phases (11), and heat treatments (12–14). They are all widely used in practice.
The Gibson–Ashby model predicts that the yield strength of a cellular material () is proportional to its relative density by an exponential relationship , where n is a scaling exponent (≥1). Therefore, an effective way to increase the yield strength is to increase the for both stretching-dominated (n = 1) and bending-dominated (n = 1.5) lattices (1, 15–18). In this work, we show that bending-dominated lattices with a high ρRD can also exhibit PYS. The underlying mechanism is elucidated, allowing effective control of the PYS phenomenon in bend-dominated lattices for energy absorption.
Identification of the PYS phenomena in bending-dominated lattices
Figure 2a shows five body-centered cubic (BCC) lattice designs with ρRD = 0.02, 0.06, 0.13, 0.17, and 0.25. They were printed in Ti-6Al-4V using laser PBF (LPBF) for evaluation. Figure 2b shows the failure mode of each LPBF-printed lattice design after compression. At low relative densities (0.02 and 0.06), the lattice samples exhibited noticeable densification, as highlighted by the first two red rectangles in Fig. 2b. However, at higher relative densities (0.13–0.25), the failure mode changed to 45°-oriented crushing due to high localized shear deformation, as shown by the three inclined red rectangles in Fig. 2b.
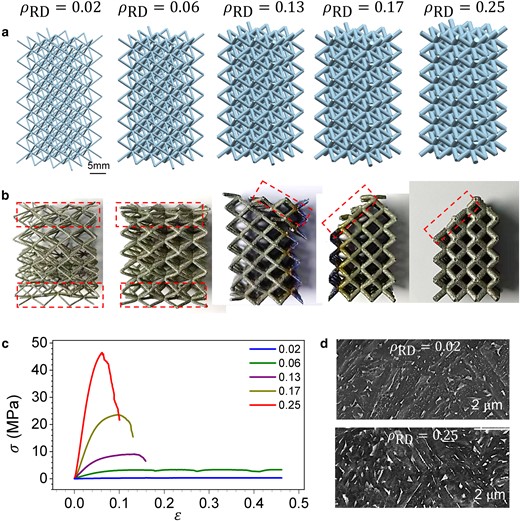
(a) Computer-aided design (CAD) models of BCC lattices with five relative densities. (b) Failure modes of each BCC Ti-6Al-4V lattice after compression. (c) Representative compressive stress–strain curves for each BCC Ti-6Al-4V lattice. PYS occurred with . (d) Microstructures of lattice struts with and .
Figure 2c shows representative compressive stress–strain (σ−ɛ) curves obtained from each BCC Ti-6Al-4V lattice. PYS occurred in lattices with ρRD = 0.13, 0.17, and 0.25, but not in lattices with ρRD = 0.02 and 0.06. This is consistent with the failure modes shown in Fig. 2b. At ρRD = 0.02 or 0.06, the slope of the compressive stress–strain curve after yielding is close to zero over a wide range of strain up to 0.45, in line with Fig. 1b. However, at higher relative densities (0.13, 0.17, and 0.25), all BCC Ti-6Al-4V lattices exhibited obvious PYS, akin to Fig. 1a instead. Furthermore, the occurrence of PYS in these BCC lattices intensified with increasing relative density.
Since the deformation behavior is affected by microstructure, we examined the lattice microstructures with and . As shown in Fig. 2d, very similar microstructures were observed (α′/α + β, where the bright phase is β). Furthermore, μ-CT characterization found no detectable difference in defects (the strut relative density is about 99.95% by μ-CT). Therefore, it can be concluded that the PYS observed in Fig. 2c is due to the increase in lattice . This is contractionary to the long-held assumption that PYS does not occur in bending-dominated lattices (Fig. 1).
To confirm the generality of the PYS phenomenon observed above, we designed and printed two additional bending-dominated Ti-6Al-4V lattices with high values, rhombic dodecahedron (), and diamond (). The observations are summarized in Fig. 3. PYS occurred in both lattices due to their high values. The failure modes, i.e. 45°-oriented crushing due to highly localized shear deformation, are also similar.
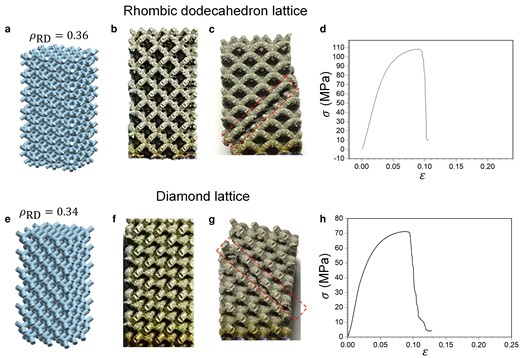
PYS in bending-dominated rhombic dodecahedron and diamond Ti-6Al-4V lattices. (a, e) CAD models. (b, f) As-printed samples. (c, g) After compression. (d, h) Compressive stress–strain curves.
The underlying mechanism
The Gibson–Ashby model considers lattice deformation by only stretching or bending based on the Euler–Bernoulli beam theory (19). In contrast, the Timoshenko beam theory (20) considers deformation by concurrent bending, stretching, and shear. For a comprehensive analysis of the lattice deformation behavior, especially when the lattice relative density is no longer sufficiently low, it is necessary to employ the Timoshenko beam theory. The analytical method used below is similar to that used in Ref. (21).
Figure 4a illustrates a BCC lattice structure consisting of uniform cylindrical struts of length and diameter under uniaxial compression by an applied force . This applied force is shared by each BCC unit cell as (Fig. 4b). Since each BCC unit cell contains four equally inclined long struts, we have , where is the force applied to each strut (Fig. 4c-d). The force component causes stretching deformation along the strut axis with the displacement (Fig. 4e), while the force component results in bending deformation with the displacement (Fig. 4f) and shear deformation with the displacement (Fig. 4g). Since each BCC cell is not shared with any neighboring cells, the displacement of each cell can be regarded as that of the lattice.
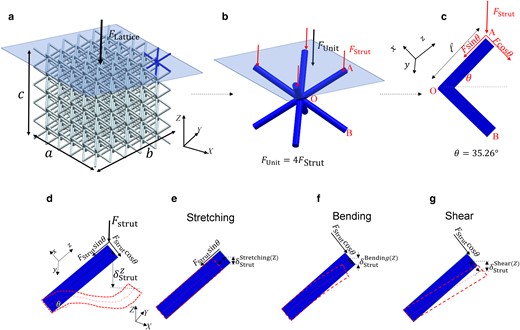
Deformation by concurrent stretching, bending, and shear in a BCC lattice. (a) A BCC lattice under compression by . (b) A BCC unit cell in (a) under compression by . (c) The force applied to strut AO in (b), where . (d) Strut AO before and after deformation by concurrent stretching (e), bending (f), and shear (g). (e–g) illustrate the force components responsible for stretching along the strut axis () (e), bending () (f), and shear () (g). Figure 4 is adapted from Ref. (21).
By definition (19, 22), the resulting displacement by each deformation mechanism in the local coordinate x-y-z, where z is along the strut axis, can be written as follows:
In these equations, is the elastic modulus of the strut material; is Poisson’s ratio, is a shear coefficient, where for cylindrical struts (23), and θ is the strut inclination angle ( for BCC lattice struts). For Ti-6Al-4V, , , and GPa.
The contribution of each deformation mechanism in a lattice structure can be evaluated by the elastic strain energy through simulations (24–26). The elastic strain energy (U) is the product of the applied force multiplied by half of the displacement (27–29). Letting , , and denote the elastic strain energies of a lattice strut caused by stretching, bending, and shear, respectively, we have
The total elastic strain energy stored in such a strut can be written as follows (26, 28):
Note that the of a BCC lattice can be written as (neglecting the lattice nodal effect) follows:
Using Eqs. 1–8, we can calculate the percentage of each form of elastic strain energy (). For example, for deformation by bending, we obtain
Figure 5a plots versus (the blue line). The trend is clear, namely, decreases with increasing , while (the red line in Fig. 5a), where increases with increasing . In other words, for bending-dominated BCC lattices, deformation by stretching and shear increases with increasing while deformation by bending decreases with increasing . However, it should be noted that is still much larger than (Fig. 5a).
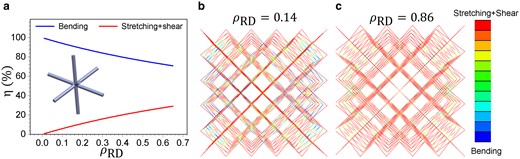
(a) Distribution of elastic strain energy in BCC lattices caused by bending and stretching + shear based on Eq. 5. (b, c) FEM of the distribution of elastic strain energy in two BCC lattices ( and 0.86) caused by bending and stretching + shear. Deformation by stretching and shear (light-green to red) increases with increasing while deformation by bending (light-blue to blue) decreases.
The trends revealed by Fig. 5a are confirmed by our finite-element modeling (FEM) results, which are displayed in Fig. 5b-c through two BCC lattices, one with and the other with . Stretching and shear (light-green to red) increased with increasing , accompanied by a decrease in bending (light-blue to blue). This visualization reaffirms that deformation by stretching and shear becomes more important in a bending-dominated lattice with increasing lattice , thereby increasing the tendency towards PYS.
Conclusion
PYS was found to occur in “bending-dominated” BCC, rhombic dodecahedron, and diamond Ti-6Al-4V lattices with a high relative density, contrary to the long-held assumption that PYS is generally absent in bending-dominated lattices. This unusual property is rationalized by their deformation mechanisms using the Timoshenko beam theory, where “bending-dominated” lattices exhibit an increase in stretching and shear deformation with increasing relative density, thereby increasing the tendency towards PYS.
Materials and methods
Design of lattice samples
BCC lattices (Maxwell number m = −13, connectivity Z = 8 (4)) are classical bending-dominated lattices. Therefore, they are chosen as the main lattice topology for this study. The BCC lattice samples are designed with five relative densities (ρRD): 0.02, 0.06, 0.13, 0.17, and 0.25. Each BCC lattice sample consists of unit cells, and the unit cell size is 5.77 × 5.77 × 5.77 mm3, with the strut length being fixed at 5 mm. In addition, we have considered two other bending-dominated lattice topologies, rhombic dodecahedron (RHD), and diamond lattices with ρRD = 0.36 or 0.34. Each lattice sample similarly comprises unit cells with a unit cell size of 3 × 3 × 3 mm3 and a strut length of 5 mm.
AM of lattice samples by laser PBF
A Farsoon LPBF system was used to print all lattice samples with a laser power of 95 W, a layer thickness of 20 μm, a scan speed of 1,200 mm/s, and a hatch spacing of 80 μm. The threshold for the hatch vector filter is 0.1 μm. Argon gas-atomized Ti-6Al-4V powder (size range: 15–40 μm) was used. A 15 mm-thick Ti-6Al-4V build plate was used, preheated to 100°C. A zig zag hatch style was adopted (67°), rotated at 90° between layers.
Lattice characterization and mechanical testing
The lattice microstructure was studied using a scanning electron microscope (SEM, TESCAN LYRA3, TESCAN ORSAY HOLDING, a.m.). The internal defects of lattices were characterized using a computed tomography scanner (ZEISS Radial 520 Versa), which has a microfocus X-ray tube (μ-CT), operated at the voltage of and power of .
Uniaxial compression tests were conducted using a calibrated SANS electromechanical Universal Testing Machine (capacity:100 KN, model: 5105, power: 1.5 kW, and voltage: 380 V) at the speed of 1 mm/min (strain rate: 4.8 × 10−4 s−1). The load was measured through a load cell in the system. The compressive stress was calculated from the compressive load and initial lattice cross-section area perpendicular to the loading direction, rather than the cross-section area of the struts. The strain was obtained from the compressive displacement, divided by the initial height (gauge length) of the lattice specimen.
Finite-element modeling
To quantify lattice deformation caused by bending, stretching, and shear, ABAQUS\Standard (version: 2021, Dassault Systèmes Simulia Corp.) was used to perform FEM. All FE models were meshed with two-node beam elements. Titanium alloy Ti-6Al-4V was used as the constituent material, which has a theoretical density of 4.43 g/cm3, Poisson’s ratio of 0.3, and elastic modulus of 110 GPa, assumed to be linearly elastic, isotropic, and homogeneous.
To simulate the boundary conditions in the compression tests, encastre boundary conditions (30) were applied to all “bottom” nodes of each lattice sample. The “top” nodes of each lattice sample were attached to a rigid shell, which was subjected to an applied displacement up to 10% of the lattice height (simulating a compression test). To reduce the computational time, each lattice comprised 125 unit cells (5 × 5 × 5).
The axial force (), bending moment (M), and shear force () were all obtained from the output of NFORCSO in ABAQUS (NFORCSO: nodal forces in beam section orientation). The elastic strain energy components of each lattice sample due to deformation by stretching (), bending (), and shear () were also obtained from the NFORCSO output. The percentage of each form of elastic strain energy was then calculated as , , and , where custom-developed scripts were coupled with ABAQUS for these calculations.
Funding
This study was funded by the National Natural Science Foundation of China (Grant 51971145) and the Australian Research Council (DP200102666).
Author contributions
H.Z.Z. and M.Q. conceived the idea and designed the experiments. H.Z.Z. printed all samples, completed essential characterization, and performed FEM. C.W.L. and R.D. reviewed the results, provided supervision, and edited the manuscript. J.F.G. acquired funding, provided supervision, managed the project, analyzed the results, and edited the manuscript. M.Q. acquired funding, provided supervision, critically analyzed the results, and finalized the manuscript with H.Z.Z.
Data availability
All data are included in the manuscript and/or supporting information.
References
Author notes
Competing interest: The authors declare no competing interest.


