Abstract
The microstructural and textural characteristics of a spinel corona that formed around a faceted corundum xenocrystal by reaction with the hosting basaltic melt in the Siebengebirge volcanic field demonstrate that the crystallographic and shape preferred orientation of spinel is influenced by the orientation of the reaction interface with respect to the corundum crystal lattice. The spinel roughly shows the common topotactic orientation relationships with corundum, where one of the planes is parallel to the (0001) plane, and three of the planes are parallel to the planes. In detail, there are subtle but systematic deviations from this topotactic relationship due to small rotations about the c-axis and/or an a-axis of corundum. The former is observed when the corundum c-axis is closely parallel to the interface plane, while the latter require a corundum a-axis orientation perpendicular to the interface. In this case, the preferred sense of rotation depends on the sign of the a-axis direction, irrespective of the spinel growth direction being parallel or antiparallel to this axis. Additionally, the selection of either one or both of two spinel twin variants that equally fulfill the topotactic orientation relationship depends on the orientation of the corundum-spinel interface with respect to the lattices of both the corundum and the spinel. Finally, also the grain boundary character is controlled by the interface orientation and the corundum lattice. Despite the differences between corona segments, the nature of these textures are persistent along and across each segment. We emphasize that all these microstructural and textural features are ascribed to the period of spinel growth in magmatic environment. The extent to which prominent slip planes in spinel are aligned parallel with the corundum-spinel interface seems to be of crucial importance for the nature of the spinel texture and microstructure, indicating that the activity of dislocations pertaining to these slip systems ease the accommodation of lattice misfit across the corundum-spinel interface. By comparison with experimentally grown spinel layers, we infer predominantly interface reaction controlled growth of the studied spinel corona.
INTRODUCTION
Reaction between two mutually incompatible phases producing a layer of a new phase or a sequence of layers of multiple new phases at their interface is a common phenomenon in rocks (Gaidies et al., 2017), ceramics (Schmalzried, 1962), and metals (Bouché et al., 1998; Springer et al., 1999). In mineral and rock systems, the resulting microstructures are referred to as reaction rims, reaction bands, or corona microstructures. Reaction rim growth requires transport of chemical components across the newly forming mineral layer(s), which can only occur by diffusion unless migration of fluid or melt is involved. In addition, the reaction interfaces on either side of the reaction rim need to propagate into the reactant phases. Both processes are time and temperature dependent, and together determine the growth rate and the microstructure of the corona. Corona microstructures thus bear information on the conditions, duration, and mechanisms of corona growth. Extracting this information requires independently calibrated material parameters and kinetic laws coupled with a detailed understanding of the processes underlying corona formation.
The formation of spinel reaction rims is of particular interest in ceramics (Yamaguchi & Tokuda, 1967; Mackenzie & Ryan, 1981). For the binary MgO–AlO system, the equilibrium phase relations are well constrained (Sack, 1982; Sack & Ghiorso, 1991; Hallstedt, 1992; Jung et al., 2004; Zienert & Fabrichnaya, 2013). Kinetic experiments revealed that the growth of thick polycrystalline magnesio–aluminate spinel reaction rims follows a parabolic rate law (Carter, 1961; Whitney II & Stubican, 1971; Schmalzried, 1981; Dybkov, 1986; Zhang et al., 1996; Ting & Lu, 1999; Watson & Price, 2002; Götze et al., 2014, 2016), indicating diffusion controlled growth. Bulk material transport has been shown to occur by a combination of grain boundary and volume diffusion, where Mg and Al ions migrate through a sublattice of largely immobile oxygen (Carter, 1961; Rossi
& Fulrath, 1963; Whitney II & Stubican, 1971; Zhang et al., 1996; Watson & Price, 2002; Liu et al., 2005; Götze et al., 2010). However, for very thin rims, diffusion is sufficiently fast so that rim growth becomes interface reaction controlled instead, leading to a linear rate law (Götze et al., 2014). Bulk diffusivities and, hence, the rate of diffusion controlled reaction rim growth depend on the microstructural and textural characteristics of the newly forming polycrystalline spinel layer including both the abundance and character of spinel grain boundaries (Götze et al., 2010; Keller et al., 2010). Grain boundary character refers to the crystallographic misorientation between the grains as well as the orientation of the grain boundary plane with respect to the lattices of both adjacent grains sharing the grain boundary, which has a strong effect on grain boundary diffusivity. Keller et al. (2010) applied uniaxial loads to tune the grain boundary character distribution of a polycrystalline spinel layer growing at the interface between periclase and corundum and found a substantial effect of grain boundary character distribution on rim growth rate in the diffusion-controlled growth regime.
The spinel of reaction rims forming between periclase and corundum usually shows systematic crystallographic orientation relationships (CORs) with the reactant phases (Rossi & Fulrath, 1963; Li et al., 1992; Hesse et al., 1995; Sieber et al., 1996; Liu et al., 2005, 2006; Götze et al., 2010; Keller et al., 2010; Jeřábek et al., 2014). The layer of newly forming spinel usually grows from the original corundum-periclase interface into both directions. Spinel replacing periclase typically inherits the fcc oxygen sublattice from the reactant periclase leading to a cube to cube COR (Sieber et al., 1996; Keller et al., 2010; Götze et al., 2010; Jeřábek et al., 2014; Li et al., 2016). At the spinel-corundum interface, the fcc oxygen sublattice of spinel develops from the hcp oxygen sub-lattice of corundum. When spinel layers grow at periclase-corundum contacts parallel to the corundum basal plane under hydrostatic conditions, topotactic CORs with and are formed (Rossi & Fulrath, 1963; Li et al., 1992; Götze et al., 2010; Keller et al., 2010; Jeřábek et al., 2014; Li et al., 2018). In thin film settings, growth of spinel on a surface yielded the COR and (Li et al., 1992), whereas growth on a surface yielded and (Hesse et al., 1994; Sieber et al., 1996).
Therefore, it appears that the CORs developed in spinel rims may depend on the orientation of the reaction interface with respect to the crystal lattice of corundum. However, very few reaction interface orientations have so far been investigated. Furthermore, this hypothesis relies on comparing thin film and thick rim experiments. It is unclear, whether the CORs observed in thin film experiments are affected by the interface-controlled nature of the reaction, and whether these CORs would persist to larger rim thicknesses, especially given the expected change of growth regime from interface reaction controlled to diffusion controlled (Abart & Petrishcheva, 2011).
In this study, we use scanning electron microscopy (SEM), electron backscatter diffraction (EBSD) analysis, micro-X-ray computed tomography (-CT), and electron probe microanalysis (EPMA) to investigate a spinel corona that formed at the interface between basaltic melt and an initially faceted corundum single crystal in a magmatic environment pertaining to the Siebengebirge Volcanic Field (Baldwin & Ballhaus, 2018). There, a corona of ferromagnesio–aluminate spinel (Mg,Fe)AlO formed by reaction of the corundum with the basaltic melt under isostatic conditions at pressures in the GPa range (Baldwin et al., 2017). The investigated material provides an ideal opportunity to address a number of outstanding questions regarding the growth of spinel reaction rims on corundum in particular, and reaction rims in general:
(1) What is the effect of different orientations of the reaction interface with respect to the lattice of the reactant corundum on the microstructure, texture, and grain boundary character distribution of spinel rims?
(2) If variations in microstructure, texture, and/or grain boundary character are present, how do they correlate with the mechanisms and/or rates of rim formation?
(3) How do observations made on natural rims grown under high-pressure, isostatic conditions in the presence of melt and volatiles conform with or differ from results of rim-growth experiments involving exclusively solid phases?
MATERIAL AND METHODS
Sample
We studied sample PE21 from Baldwin et al. (2017), which is an about 2 cm-sized pale blue to milky white corundum xenocrystal enclosed in an alkali basalt from the Siebengebirge Volcanic Field, Germany. The sample is a polished rock slab with a random cross section of the corundum exposed on the polished sample surface. The corundum crystal has an elongated rhombohedral shape with a brownish colored central growth sector parallel to the elongation direction (Fig. 1). The overall geometry suggests that the corundum was euhedral, when it came into contact with the alkali basalt melt. The corundum is surrounded by a continuous about 200 micrometers wide dark layer of spinel separating the corundum from the dark green host basalt. We may safely assume that all corona segments corresponding to the different facets of the corundum crystal formed at the same time and under the same physico-chemical conditions. The basalt features phenocrystals of pyroxene (augite and pigeonite), plagioclase (An), and olivine. The basalt is enriched in plagioclase in an about 200 micrometers wide zone adjacent to the spinel corona. The -CT image shown in Figure 1 displays an overall spinel-plagioclase double-layer structure. Similar microstructures were described from corundum xenocrysts in alkaline basalt from Changle in China (Dong et al., 2007).
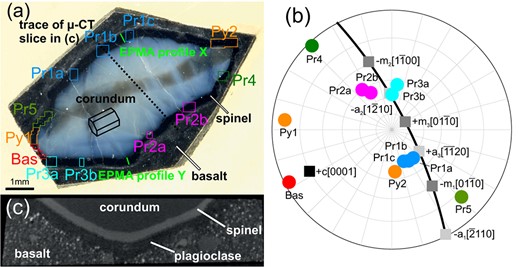
Fig. 1
(a) Rock slab with polished cross section of the corundum xenocrystal; the central brownish zone extending from the lower left to the upper right edge of the pale blue corundum corresponds to a growth sector with abundant sub- sized Ti-oxide inclusions. The dark corona around the corundum crystal is comprised of spinel; the outermost surrounding material consists of the plagioclase enriched outer corona and the host basalt. The rectangles indicate areas from which crystal orientation data were collected by EBSD. The green solid lines mark the positions of the compositional profiles collected by EPMA. The dotted line indicates the trace of the slice of the -CT scan shown in (c). (b) Upper hemisphere stereographic projection showing the poles of the corundum facets captured in the scan areas indicated by the circles with numerical labels. In addition, the poles of important lattice planes of corundum are indicated by squares, and the basal plane is shown as a thick line. (c) Slice of the -CT scan normal to the investigated 2D section; the angle between the investigated 2D section and the interface in the center of the region mapped by scan Pr1b can be seen on the left.
Instrumentation
The FEI Quanta 3D Field Emission Gun SEM at the Faculty of Earth Sciences, Geography and Astronomy at the University of Vienna (Austria) used for EBSD analysis as well as BSE and FSE imaging is equipped with an EDAX Pegasus Apex 4 system consisting of an EDAX DigiView IV EBSD camera. The sample surface was chemo-mechanically polished to ultra-high quality using colloidal silica suspension (SytonTM). To establish electrical conductivity, the sample was carbon coated using a single carbon thread evaporated at high vacuum (< 1 10 mbar). EBSD data were collected using the OIM Data Collection software v7.3. EBSD analyses were performed at 13 or 14 mm working distance and 70 stage tilt resulting in a beam incidence angle of 20 with respect to the sample surface. The electron beam conditions were at 15 or 20 kV acceleration voltage and 2–4 nA probe current using a 1 mm SEM aperture in analytic beam mode. In order to obtain representative information on the microstructure and texture of the whole spinel corona, 12 EBSD-COM (crystallographic orientation mapping) data sets, corresponding to interface segments with different interface orientations, were collected at step sizes between 0.1 and 0.7 . The Matlab toolbox MTEX version 4.1.4 (Bachmann et al., 2010) was used to calculate orientation distribution functions (ODFs) for spinel crystal orientation data and the mean crystallographic orientation of the corundum single crystal from each individual scan. The ODF calculations were performed using a de La Vallée Poussin kernel with a half-width of 1.5. The software ‘Fityk’ was used to fit grain boundary trace orientation distribution profiles for the individual scans (Wojdyr, 2010).
Mineral chemical analyses were performed on a Cameca SXFiveFE electron probe micro analyzer at the Department of Lithospheric Research, University of Vienna (Austria). Two compositional profiles across the spinel rim were analyzed at step sizes of 10 in the inner part, and 2 in the outer part, according to the different grain sizes in these two domains.
The 3D geometry of the concentric layers constituting the corona structure was determined by X-ray micro computed tomography (-CT) using a Bruker Skyscan 1173 instrument at the Department of Paleontology at the University of Vienna (Austria). Details on EBSD collection parameters and the data clean up procedure can be found in the supplementary material together with the parameters for EPMA and -CT.
RESULTS
General microstructure and corundum spinel interface orientation
Based on its internal microstructure, the spinel corona is subdivided into an inner layer, which is exclusively comprised of spinel, and a thinner outer layer, which is comprised of an intimate intergrowth of spinel and plagioclase. The boundary between the two spinel layers is marked by a zone of relatively small, equant spinel grains with diameters of about 2 (Fig. 2). This zone extends parallel to the perimeter of the corundum crystal and is interpreted as the trace of the original corundum-melt interface. The boundary between the outer spinel layer and the surrounding basalt has a complex geometry due to intimately intergrown, 10–30 sized plagioclase and spinel grains. Nevertheless, the outer spinel layer can be traced as an up to 40 thick zone all around the corundum xenocrystal. On its outer side, the spinel corona is further accompanied by an about 200 wide zone, where the basalt is enriched in plagioclase. In the following, we focus on the internal microstructures and textures of the inner spinel layer, which grew into the corundum crystal.
The present interface between the inner spinel layer and the corundum appears smooth when observed at the millimeter and 100 micrometer scale. At the tens of micrometer scale, the trace of the interface shows cusps at intersections with spinel grain boundaries, or isolated steps seemingly following certain lattice planes of corundum and/or spinel (Fig. 2). The forthcoming discussion refers to the mm scale structure reflecting the former corundum growth facets, which separate the inner spinel layer into distinct segments.
The orientations of the corundum facets were determined by combining BSE images with -CT data and crystal orientation data (Fig. 1). For each corona segment, the orientation of the interface was constructed from its trace on the sample surface as observed on the BSE image, on the one hand, and its trace in a slice of the -CT reconstruction taken perpendicular to the trace in the BSE image, on the other hand. From these two traces and the corundum crystal orientation, the interface plane orientation relative to the lattice of corundum was determined. Due to the limited spatial resolution of the -CT scan (ca. 9 m pixel width) and the presence of micrometer scale irregularities of the corundum spinel interface the reconstruction bears some inaccuracy. Nevertheless, the basic character could be well discerned, and facets corresponding to prismatic, pyramidal, and basal planes of corundum were identified. Most of the investigated segments cover corundum facets at low angles (up to 17°) to a prism plane (scans Pr1a-c, Pr2a-b, Pr3a-b, Pr4, and Pr5; Fig. 1). They are therefore denoted as (sub)prismatic segments. Segments Pr1, Pr2, and Pr3 are located along elongated straight corundum facets, while Pr4 and Pr5 are located in considerably concave sections between corundum crystal edges. The corundum facets of all subprismatic segments except for Pr5 are close to one of the planes. Scan Bas corresponds to a relatively short convex segment where the corundum-spinel interface is subparallel to the corundum basal plane with an angular deviation of about 12. The interfaces of scans Py1 and Py2 correspond to obtuse pyramidal planes.
In the 2D section of the polished sample surface, the apparent thickness of the segments of the inner spinel layer ranges from 110 to 280 . For most segments, this is larger than the true thickness due to oblique cut. Only a few short segments show the true thickness in the 2D section (Fig. 1). As determined by combining -CT data with BSE images, the true thickness of the inner spinel layer ranges from 130 to 160 for most corona segments, yielding 150 on average. Only the particular segments associated with scans Bas and Pr5 deviate from this range, the former being somewhat thicker, the latter thinner. For all other segments, minor thickness variations between the different segments are below the precision of the determination. Within each segment, the thickness of the inner spinel layer is quite uniform.

Fig. 2
Forward Scatter Electron (FSE) images of corona segments corresponding to EBSD data sets (a) Py1, (b) Pr1b, and (c) Py2 showing the polycrystalline nature of the spinel layer, the presence of very fine grained equant spinel grains close to the initial corundum/basalt interface, and the different microstructures of the inner and outer spinel layer. Note the micrometer scale cusps and steps of the final spinel/corundum interface indicated by arrows. White line markers in (b) highlight the position of the initial interface between corundum and melt (dotted line), the inner corona (dash-dotted line) and the outer corona (dashed line). The black rectangle in (c) highlights a wedge-shaped, basalt filled gap in the spinel rim.
Mineral compositions
The corundum xenocryst has a composition of >98 wt % AlO with about 0.9 wt % FeO and 0.8 wt % TiO, where most of the titanium is carried by sub-micron sized Ti-oxide inclusions (Baldwin et al., 2017). The spinel mineral formula was calculated assuming perfect stoichiometry according to the structural formula , where A and B denote di- and trivalent cations, and superscripts IV and VI indicate tetrahedral and octahedral coordination by oxygen, respectively, and is the inversion parameter. The spinel may be described as a solid solution of intermediate composition between spinel s.str. (MgAlO) and hercynite (FeAlO) with the average composition SpHc. Magnetite (FeO) and ulvöspinel (FeTiO) are present as minor phase components (X < 0.02; X < 0.002). A subtle compositional zoning exists from the outer spinel layer towards the corundum-spinel interface with a slight increase of the spinel mole fraction from X = 0.538 to 0.542 and of the hercynite mole fraction from X = 0.445 to 0.455 compensated by a concomitant decrease of X from 0.014 to 0.002 and of X from 0.005 to 0.003 (Fig. 3). Plagioclase in domains next to the spinel layer has labradorite composition.
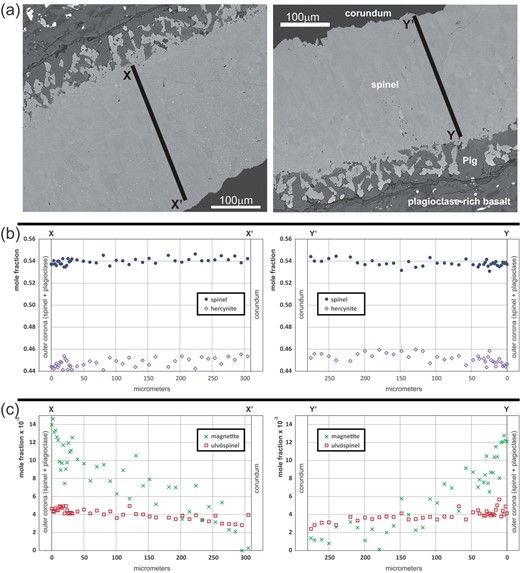
Fig. 3
(a) BSE images showing the location of the EPMA profiles indicated in Fig. 1a. (b) EPMA compositional profiles showing spinel s.str and hercynite fractions. (c) Profiles of minor components magnetite and ulvöspinel.
Microstructure and texture of inner spinel layer
Microstructure
For quantitative microstructure and texture analysis, only data from the innermost 80% of the inner spinel layer were considered, in order to avoid potential effects by contribution of adjacent grains from the outer corona and the surrounding basalt. In FSE orientation contrast images (Fig. 2), the inner spinel layer has a polycrystalline appearance resulting from several to some 10’s of sized domains with different crystallographic orientations. In most corona segments, three types of grain boundaries dominate, namely (i) low-angle grain boundaries, (ii) 3 boundaries, and (iii) high-angle boundaries with misorientation angles >45, which result from low-angle deviations from 3 misorientations. The spinel domains thus represent twin variants with subgrains. Some segments of the inner spinel layer (scans Pr1-3) show a palisade like microstructure defined by perfectly straight twin boundaries, which are oriented (sub)parallel to the corundum basal plane. In these corona segments, the subgrains appear roughly equant with curved boundaries (e.g. scan Pr1b in Fig. 2b). In other segments (scans Py1, Pr4), subgrains show a palisade structure although twin boundaries are rare (scan Py1 in Fig. 2a). In these segments, the pronounced shape preferred orientation is perpendicular to the corundum-spinel interface, which is interpreted as the spinel growth direction. Scan Py2 is special as it is located at a strongly outwards convex portion of the corona, where a wedge-shaped, basalt filled gap in the spinel rim is observed (Fig. 2c). Scan Py2 shows a peculiar internal microstructure of spinel, being the only segment, where the inner corona contains some plagioclase. Scans Bas and Pr5 also have special microstructural features, which are addressed below.
Crystallographic orientation relationships
In Fig. 4, the crystallographic orientation data of spinel from three representative segments, two prismatic and one pyramidal, of the inner spinel layer are illustrated using and pole figures calculated from the respective orientation distribution functions (Fig. 4, left side). To show the CORs between corundum and spinel, the and (0001) plane poles of the corundum crystal were plotted as black filled circles in cropped areas of the corresponding spinel and pole figures (Fig. 4, right side). In the inner spinel layer, the spinel exhibits two prominent texture components, which are dominant in all corona segments. Both texture components cluster around the previously described commonly observed topotactic COR with the precursor corundum, where one of the and three of the (Rossi & Fulrath, 1963; Li et al., 1992; Götze et al., 2010; Keller et al., 2010; Jeřábek et al., 2014; Li et al., 2018). The orientations of the two texture components are related by the spinel twin law, which corresponds to 3 fcc twinning and is generated by a mutual rotation of the two twin variants over 60 about a common axis. In the case at hand, the that is common to both twin variants is parallel to . We denote one of the two twin variants as twin t (red in Figs 5 and 6), which is represented by the spinel domains with orientations that deviate no more than 15 from , , , . The other texture component is referred to as twin t (blue in Figs 5 and 6) and is defined as spinel with orientations that do not deviate by more than 15 from , , , . In all scans except for scans Bas and Py2, more than 90% of the spinel data points in the inner spinel layer pertain to either t or t. Within the individual corona segments, the quality of topotactic match between spinel and corundum varies, but neither a systematic change of the quality of match across the thickness of the corona, nor differences between the two spinel twin variants are observed (Fig. 5).
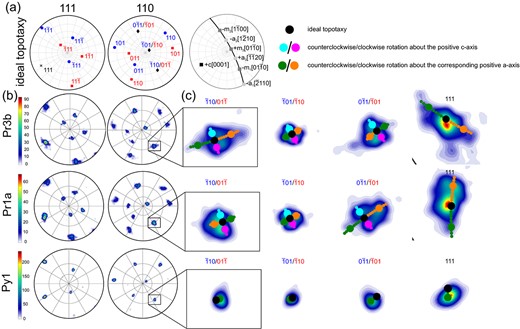
Fig. 4
Pole figures (equal angle upper hemisphere projection) showing (a) the position of the and poles for the perfectly topotactic t and t orientations as well as the position of the c-axis and the and directions of the corundum single crystal. (b) and pole figures of the prismatic segments covered by scans Pr3b and Pr1a and the pyramidal segment covered by scan Py1. (c) Close-ups of the poles poles and the pole .

Fig. 5
Twin variant distribution in corona segments; (a) scan Pr1b exhibits about equal proportions of t and t; (b) scan Py1 shows pronounced selection of the t variant; (c) scan Bas has a significant share of spinel not pertaining to either variant.
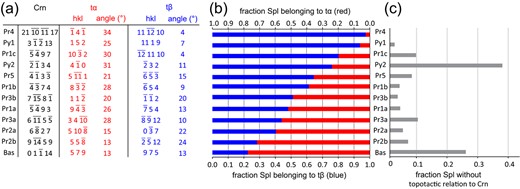
Fig. 6
(a) Lattice planes parallel to the corundum-spinel interface for the corundum single crystal and for the ideal orientations of t and t for the spinel layer segments investigated by EBSD. The angles show the rotation of the t and t planes from the nearest or plane of spinel. (b) Relative fraction of t and t among spinel pertaining to either variant for all investigated scans. (c) Fraction of spinel not pertaining to either variant for all investigated scans.
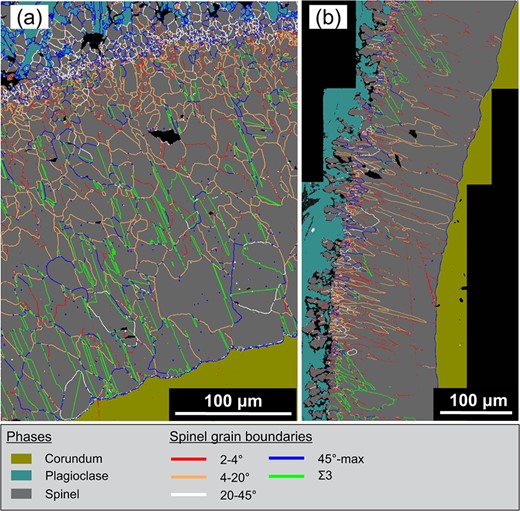
Fig. 7
Distribution of GB types in (a) the prismatic segment corresponding to scan Pr1c and (b) the pyramidal segment corresponding to scan Py1. Significant densities of GBs with misorientation angles between 20 and 45 occur only in the vicinity of the original contact between corundum and melt.
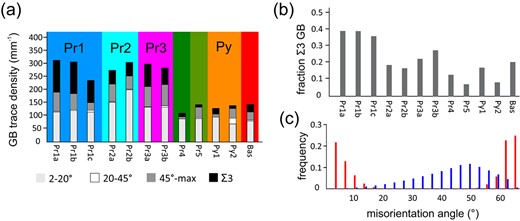
Fig. 8
(a) Densities of GB types in the inner spinel corona. (b) Fraction of 3 boundaries among all GB types. (c) Misorientation angle distribution of scan Pr1a in red and theoretical misorientation angle distribution for cubic polycrystals with random texture in blue.
Dispersion of spinel crystal orientations
While the topotactic relationship is approximately fulfilled in all studied corona segments, the CORs between spinel and corundum show both statistical dispersion and systematic deviations from the ideal topotactic orientation relationship, which differ for the different corona segments. In the segment captured by scan Py1, which corresponds to a pyramidal plane of corundum, the CORs show the least dispersion. About 85% of the spinel deviates less than 5 from one of the two ideal topotactic CORs. For the other corona segments, this fraction ranges from 25 to 55%. Scan Bas features a particularly wide dispersion, and only 75% of the spinel data points pertain to t or t with a tolerance of 15°. However, setting the misorientation tolerance to 20 increases this fraction to 95%. Only in the segment covered by scan Py2 a significant fraction of spinel does not show any topotactic relationship to the precursor corundum. Even when allowing for a 20 misorientation tolerance, only 65% of the spinel data points fall into the orientation range of the topotactic CORs (Fig. 6).
Apart from the statistical dispersion, the orientation distributions in the different corona segments exhibit systematic deviations from ideal topotaxy. In the pole figures of all studied corona segments, except for scans Bas, Py1, and Py2, the maxima that correspond to the orientations of the two texture components consist of several, up to four, sub-maxima. In the corona segments that roughly correspond to corundum prism facets (scans Pr1–5) the spinel exhibits characteristic rotations of 3 about , which produces two about equally pronounced sub-maxima lying on a large circle perpendicular to slightly off the ideal topotactic orientation relationship (Fig. 4). In the corona segments that roughly correspond to the prism planes, these are the prism planes that are perpendicular to one of the crystallographic -axes of corundum, the spinel may, in addition, be rotated by up to 7 about the corresponding -axis. Interestingly, rotations about an -axis have a preferred sense of rotation, leading to a deviation of the mean orientation of spinel from the ideal topotactic orientation relationship. More specifically, for the corona segments covered by scans Pr1, the spinel growth direction is sub-parallel to the positive axis, which corresponds to the direction, and the rotation about this axis is predominantly clockwise (Fig. 4). Similarly, for the corona segments covered by scans Pr2–3, the growth direction is sub-parallel to the negative axis, that is the direction, and the rotation of spinel is primarily counterclockwise about the negative axis and the growth direction. For the prism facets, this rotation is thus always clockwise when viewed along the corresponding positive -axis, irrespective of whether the spinel growth direction is (sub-)parallel or antiparallel to the positive -axis. In scans Pr4 and Pr5, the spinel exhibits only rotations of approximately 3 about the axis that is parallel to , without significant deviation of the mean orientation from ideal topotactic match.
The spinel from scan Py1 shows only a single orientation maximum of the predominant t twin variant. This maximum deviates from the ideal topotactic orientation by a clockwise rotation of 3 about the positive direction viewed in this particular direction of corundum. Scans Bas and Py2 show a larger orientation dispersion and no clear (sub)maxima of the spinel orientations are developed.
Relative abundances of twin variants
While the t and t orientations are crystallographically equivalent with respect to the ideal topotaxy to corundum, their relative abundances vary in a systematic manner between the different corona segments (Figs 5 and 6). In some segments (scans Pr1a, Pr2a, Pr3a, and Pr3b), both twin variants are about equally frequent. Other segments show a predominance of one variant, where >75% of topotactic spinel corresponds to one twin variant. For scan Bas t is predominant, while for scans Pr1c, Pr4, and Py1 t predominates. The relative abundance of the twin variants correlates with their crystallographic orientations relative to the corundum-spinel interface (Fig. 6). When one of the or one of the planes of one twin variant is oriented close to parallel to the corundum-spinel interface plane, while for the other twin variant these lattice planes enclose a high angle to the interface, the former dominates over the latter. For example, in scans Pr1c and Pr4, one of the lattice planes of t is rotated by only 4 from the corundum spinel interface, while no such parallel alignment exists for t leading to a strong prevalence of the t variant. Similarly, for scan Py1, one of the lattice planes of twin variant t is rotated by only 7 from the corundum spinel interface with no such parallel alignment for t leading to a prevalence of t. When the or the planes have about equal inclination angles relative to the corundum-spinel interface for both twin variants, both variants occur with about equal frequency such as in scan Pr3b. Similarly, when neither twin variant has or oriented closely parallel to the corundum-spinel interface, both variants occur with roughly similar frequency such as in scans Pr1a, Pr2a, and Pr3a. Only scans Bas and Py2 deviate from this general pattern. In these segments, a large fraction of spinel (25 and 38%, respectively) does not pertain to any of the t or t twin variants. Scans Pr4 and Py1 show roughly the same abundance of t and t close to the original corundum-basalt interface but feature exclusively t orientation near the spinel-corundum interface. All other segments show quite uniform distribution of the twin variants across the inner layer of the corona (Fig. 5).
Types of spinel grain boundaries
All segments of the inner corona exhibit general grain boundaries (GBs) as well as fcc boundaries (Figs 7 and 8). Except for scan Bas, the boundaries predominantly are coherent twin boundaries (TB), where the trace of a plane in each of the two neighboring twin individuals is within 2 parallel to the trace of the boundary plane.
All corona segments (except for scans Bas and Py2) exhibit similar distributions of the GB misorientation angles, which significantly deviate from a random distribution for polycrystalline materials comprised of cubic crystals (Fig. 8c). Based on this distribution, four main types of GBs can be distinguished: (i) Boundaries with up to about 20 misorientation are henceforth referred to as low-angle boundaries (LAB). Their frequency shows a distinct minimum at 4 misorientation. The measured frequency of misorientation angles of up to 4 may be influenced by imperfections in the quality of the specimen surface such as scratches. This is why only GBs with misorientation angles of 4–20 are henceforth considered as LAB. (ii) General high-angle GBs (HAGB) have misorientation angles >45, boundaries are excluded from this group. (iii) boundaries including TBs. (iv) GBs with misorientation angles between 20 and 45. These GBs are largely restricted to the area close to the position of the original interface between corundum and melt (Fig. 7). An exception is scan Py2, where these GBs constitute 16% of all GBs.
The HAGB traces consistently form triple junctions with one boundary and one LAB. The combination of misorientations of twins (60 about ) and LABs (up to 20) lead to misorientation angles between about 45 and 62, i.e. the maximum possible for cubic crystals. This interval also corresponds to the observed elevated boundary frequency of HAGBs compared to GBs with 20–45 misorientation, which are very rare in the inner spinel corona at some distance from the initial interface of corundum and melt. HAGBs are thus regarded as combinations of and LABs. While the misorientation axes of the LABs are randomly distributed, the misorientation axes of the HAGBs inherit a preferred orientation around from the associated boundaries, where the preferred orientation of the axes becomes successively weaker with increasing deviation from the misorientation (see supplementary material for the distribution of the misorientation axes). Any significant deviation (>2) of the alignment of the traces of the TBs with the trace of the corundum basal plane that can be seen e.g. in Fig. 7 is due to the deviation from the ideal topotactic orientation of the spinel, which leads to a rotation of the (111) planes of both t and t away from the corundum basal plane.
Area density of spinel grain boundaries
The different GB types exhibit characteristic variations in their area density, that is the total length of the respective GB traces per area, and in the preferred orientation of the respective GB traces (Fig. 8a). Based on the overall area density of general GBs, the data set can be divided into two broad categories characterized by relatively low area densities of 110–140 per mm (scans Bas, Pr4, Pr5, Py1, and Py2) and by relatively high area densities of 240–310 per mm (scans Pr1–3). Segments of the latter category show curved general GBs with a comparatively weak preferred orientation of the GB traces (Fig. 2b). Still an SPO is produced by the presence of TBs. The majority of TB traces are subparallel to the trace of the corundum basal plane, whereas those parallel to other equivalent plane traces are subordinate. Segments showing the highest fraction of TBs are associated with subprismatic corundum facets (sub)perpendicular to (scans Pr1a-c and Pr3b). There, nearly 40% of the GB traces correspond to TBs, and approximately the same fraction is represented by LABs. The corona segments covered by scans Pr2a-b are dominated by LABs accounting for 56 and 66% of the traces, respectively, and have a moderate fraction of HAGBs between 19 and 17%. Scans Pr3a-b show rather high interaction between LABs and TBs leading to a high fraction of HAGBs, which constitute 23 to 28%.
Contrastingly, the segments with lower GB area densities are largely dominated by general GBs with a strongly preferred orientation approximately perpendicular to the corundum-spinel interface, while TBs are rare (e.g. Fig. 2a). Scans Py1 and Pr4 are dominated by LABs (74 to 81%, respectively), and TBs make up only 15 and 20%, respectively, whereas the HAGB fraction is negligible. The corona segment covered by scan Pr5 has similarities to scans Py1 and Pr4, but shows a significantly weaker preferred orientation of the GB traces. Scan Pr5 shows strong interaction between LABs and TBs and therefore exhibits an appreciable fraction of HAGBs along with lower fractions of both LABs and TBs. The corona segments covered by scans Bas and Py2 show exceptional microstructural features that are unique for each of the segments. There, spinel has relatively coarse, nearly equidimensional subgrains without SPO. Scan Bas has a relatively high fraction of boundaries (20%) that are not coherent TBs. In this segment, grain boundaries are mostly curved and boundaries are partly serrated. Scan Py2 represents the only investigated corona segment that has a significant fraction of GBs with misorientation angles > 20 that are not related to interactions between LABs and TBs. This segment also features a large number of grains that lack topotaxy with corundum.
Preferred orientation of spinel grain boundary traces
The orientation distribution of the GB traces with respect to the orientation of the trace of the corundum-spinel interface shows systematic differences between the different segments of the inner spinel layer. In all corona segments, except for scan Bas, the traces of the TBs are (sub)parallel to the trace of the corundum basal plane, irrespective of the orientation of the corundum-spinel interface. In contrast, the orientations of the general GBs show a unimodal distribution, which depends on both the orientation of the corundum-spinel interface and on the orientation of the corundum basal plane.
We define as the angle enclosed by the outward pointing normal of the trace of the corundum-spinel interface and the GB trace, where = 0 corresponds to GB traces that are normal to the trace of the corundum-spinel interface. Positive values of represent GB traces that are rotated counterclockwise from the normal to the trace of the interface, and negative values correspond to GB traces that are rotated clockwise (Fig. 9). The interval of possible values spans 180.
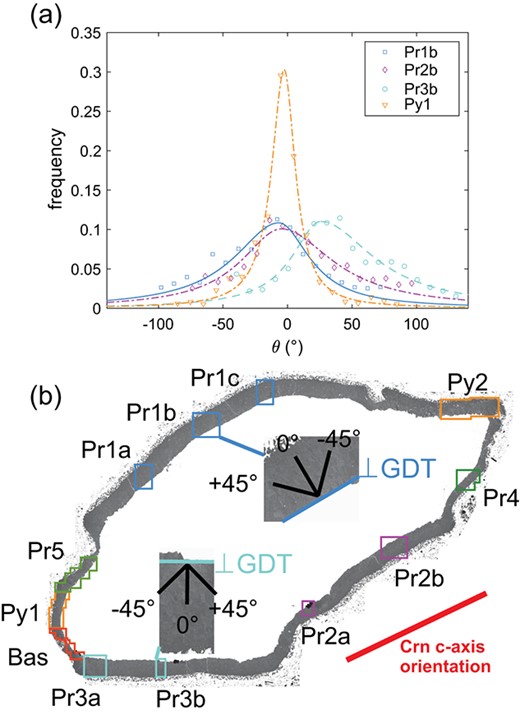
Fig. 9
(a) Orientation distributions of the GB traces for scans Pr1b, Pr2b, and Pr3b corresponding to prismatic facets and for scan Py1 corresponding to a pyramidal facet of corundum. Symbols represent the measured length fractions and lines are fitted asymmetric Lorentzian functions. The trace of the growth direction (GDT) corresponds to = 0. (b) Stitched BSED images of the spinel rim with inverted grey values, showing the position of EBSD scans Pr1b and Pr3b and the corresponding orientation of the GDT with respect to the corundum c-axis projected to the sample surface.
The orientation distribution of the length fractions of GB traces except for the
boundaries were quantified for all scans with a binning of 10
using the OIM Analysis Software. For each scan area, the measured GB distributions were quantified by fitting an asymmetric Lorentzian function of the form
to the data, where
and F
are the position and height of the mode and
represents the half widths at half maximum to the left and right side of the mode. For
,
=
and for
,
=
. The results from fitting are listed in Table
1, exemplary fits for scans Pr1b, Pr2b, Pr3b, and Py1 are shown in
Fig. 9a alongside the data.
Table 1Grain boundary orientation distribution fitting parameters
| Scan
. |
. | F
. |
. |
. | R
. |
|---|
| Pr1a | 11 | 0.106 | 58 | 22 | 0.93 |
| Pr1b | -3 | 0.104 | 54 | 29 | 0.94 |
| Pr1c | -1 | 0.085 | 65 | 53 | 0.9 |
| Pr2a | -9 | 0.14 | 18 | 37 | 0.89 |
| Pr2b | -4 | 0.101 | 25 | 43 | 0.89 |
| Pr3a | 21 | 0.098 | 36 | 59 | 0.86 |
| Pr3b | 21 | 0.110 | 27 | 49 | 0.9 |
| Pr4 | -5 | 0.243 | 14 | 15 | 0.98 |
| Pr5 | -1 | 0.13 | 29 | 33 | 0.96 |
| Py1 | 4 | 0.3 | 12 | 10 | 0.98 |
| Py2 | 12 | 0.081 | 71 | 58 | 0.68 |
| Bas | 64 | 0.09 | 65 | 43 | 0.53 |
| Scan
. |
. | F
. |
. |
. | R
. |
|---|
| Pr1a | 11 | 0.106 | 58 | 22 | 0.93 |
| Pr1b | -3 | 0.104 | 54 | 29 | 0.94 |
| Pr1c | -1 | 0.085 | 65 | 53 | 0.9 |
| Pr2a | -9 | 0.14 | 18 | 37 | 0.89 |
| Pr2b | -4 | 0.101 | 25 | 43 | 0.89 |
| Pr3a | 21 | 0.098 | 36 | 59 | 0.86 |
| Pr3b | 21 | 0.110 | 27 | 49 | 0.9 |
| Pr4 | -5 | 0.243 | 14 | 15 | 0.98 |
| Pr5 | -1 | 0.13 | 29 | 33 | 0.96 |
| Py1 | 4 | 0.3 | 12 | 10 | 0.98 |
| Py2 | 12 | 0.081 | 71 | 58 | 0.68 |
| Bas | 64 | 0.09 | 65 | 43 | 0.53 |
Table 1Grain boundary orientation distribution fitting parameters
| Scan
. |
. | F
. |
. |
. | R
. |
|---|
| Pr1a | 11 | 0.106 | 58 | 22 | 0.93 |
| Pr1b | -3 | 0.104 | 54 | 29 | 0.94 |
| Pr1c | -1 | 0.085 | 65 | 53 | 0.9 |
| Pr2a | -9 | 0.14 | 18 | 37 | 0.89 |
| Pr2b | -4 | 0.101 | 25 | 43 | 0.89 |
| Pr3a | 21 | 0.098 | 36 | 59 | 0.86 |
| Pr3b | 21 | 0.110 | 27 | 49 | 0.9 |
| Pr4 | -5 | 0.243 | 14 | 15 | 0.98 |
| Pr5 | -1 | 0.13 | 29 | 33 | 0.96 |
| Py1 | 4 | 0.3 | 12 | 10 | 0.98 |
| Py2 | 12 | 0.081 | 71 | 58 | 0.68 |
| Bas | 64 | 0.09 | 65 | 43 | 0.53 |
| Scan
. |
. | F
. |
. |
. | R
. |
|---|
| Pr1a | 11 | 0.106 | 58 | 22 | 0.93 |
| Pr1b | -3 | 0.104 | 54 | 29 | 0.94 |
| Pr1c | -1 | 0.085 | 65 | 53 | 0.9 |
| Pr2a | -9 | 0.14 | 18 | 37 | 0.89 |
| Pr2b | -4 | 0.101 | 25 | 43 | 0.89 |
| Pr3a | 21 | 0.098 | 36 | 59 | 0.86 |
| Pr3b | 21 | 0.110 | 27 | 49 | 0.9 |
| Pr4 | -5 | 0.243 | 14 | 15 | 0.98 |
| Pr5 | -1 | 0.13 | 29 | 33 | 0.96 |
| Py1 | 4 | 0.3 | 12 | 10 | 0.98 |
| Py2 | 12 | 0.081 | 71 | 58 | 0.68 |
| Bas | 64 | 0.09 | 65 | 43 | 0.53 |
In segments where the projection of the spinel growth direction onto the section surface is subparallel to the trace of the corundum basal plane (scans Pr1a-c, Pr2a-b), the mode of the GB orientation distribution closely conforms with these two directions. Still, the distribution skews left () for scans Pr1 and right for scans Pr2. For scans Pr3, the mode of the distribution lies between the projection of the spinel growth direction and the trace of the corundum basal plane and is skewed right towards the trace of the corundum basal plane. By contrast, scans Py1, Pr4, and Pr5 exhibit symmetrical GB orientation distributions with Lorentzian shape centered around the projection of the growth direction, seemingly unaffected by the orientation of the corundum basal plane. The corona segment, where the projection of the spinel growth direction is close to perpendicular to the trace of the corundum basal plane (scan Bas), shows a random grain boundary structure. There, the distribution has a broad maximum and does not show a Lorentzian shape. Similarly, the distribution of the GB traces from scan Py2 does not have a clear maximum.
Diffuse orientation transition zones in spinel
Some spinel grains contain grain-internal domains with mutual misorientations of up to 4 that are separated from one another by spatially diffuse, up to 500 nm wide, though localized orientation transition zones (Fig. 10). Along profiles across such orientation transition zones, the point-to-point misorientations (green dotted line in Fig. 10d) are only slightly elevated as compared to the random misorientation between data points in the homogeneously oriented domain interiors. Still, the cumulative point-to-origin misorientation (green solid line in Fig. 10d) amounts to a total misorientation of about 3. Contrastingly, in a profile across a regular GB (purple dotted line in Fig. 10d), the misorientation angles show a distinct peak at a single data point, which coincides with the position of the GB and constitutes the total misorientation of the GB. At some locations, the orientation transition zones laterally pass into regular GBs, whereas in other places they are spatially unrelated to any other microstructural feature. Twin boundaries either crosscut or fade out where they encounter an orientation transition zone. The orientation transition zones are present in all corona segments irrespective of whether the spinel grains pertain to one of the two main texture components or not.
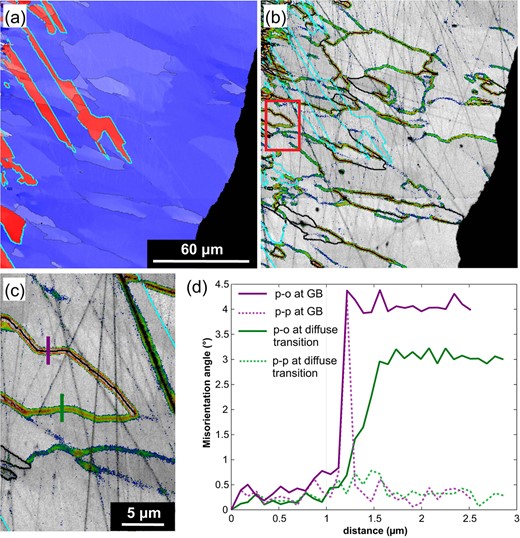
Fig. 10
(a) Orientation map showing t (red) and t (blue) in a section of scan Py1. Crystal orientations are colored as in Fig. 5, 3 boundaries are marked in cyan and LABs are marked in black. Domains with moderately different orientations are frequently separated by diffuse transition zones. (b) Fifth neighbor kernel average misorientation maps using rainbow colors for the angular interval between 0.7 (blue) and 1.8 (red) of the same section as in a highlighting the diffuse transition zones and LABs (black solid lines). (c) Close-up of b showing the position of two orientation profiles in d. (d) Misorientation profiles showing point to origin (p-o) and point to point (p-p) misorientations for an LAB (purple) and a diffuse transition zone (green). The misorientation over the LAB is restricted to distances smaller than the step size of the scan of 100 nm. The cumulative p-o misorientation reaches 3 over a distance of about 500 nm across the diffuse transition zone while the p-p misorientation remains below 1.
DISCUSSION
Formation of the spinel corona
Diffusion of Al, Mg, and Fe
The spinel corona formed by reaction between the corundum xenocrystal and the basaltic melt at a temperature of 1250 and a pressure of >1 GPa (Baldwin et al., 2017). Corundum is not a liquidus phase in alkaline basalt implying that the melt was undersaturated with respect to corundum. Apparently, the corundum crystal was accidentally entrained in the alkali basalt melt as a xenocrystal and reacted with the melt producing spinel and plagioclase, which now constitute the double layer corona.
Formation of spinel along the original corundum-melt contact supposedly started with the heterogeneous nucleation of spinel on the corundum surface. Once a continuous layer of spinel had formed, further growth of the spinel corona required that Mg and Fe components were transferred from the basalt melt to the corundum-spinel interface, where these components were used for the formation of spinel. Mass balance at the corundum-spinel interface may be written as: 1 AlO(s) + (Fe,Mg)O(m) = (Fe,Mg)AlO(s) + () AlO(m), where ‘(s)’ and ‘(m)’ refer to solid and mobile, respectively, and is a stoichiometric coefficient with . AlO(s) and (Fe,Mg)AlO(s) denote reactant corundum and product spinel, respectively, and (Fe,Mg)O(m) as well as AlO(m) are mobile components. It must be noted that AlO(m) and (Fe,Mg)O(m) are used here in the sense of system components, chemical entities that suffice to describe the chemical compositions of interest, but they do not necessarily represent the diffusing species.
The spinel formed in this reaction grew from the original corundum-melt contact into the corundum xenocrystal and now constitutes the inner spinel layer. The reaction equation is written so that only the fraction of the AlO contained in the original corundum is incorporated into the spinel forming at the corundum-spinel interface. The remaining fraction () of the AlO is regarded to diffuse from the corundum-spinel interface outwards. The outwards diffusion of AlO is driven by the AlO chemical potential difference that prevails between the corundum-spinel interface and the basalt, which is undersaturated with respect to corundum. Once it passed through the layer of spinel, this mobile AlO component reacted with the FeO and MgO components of the basalt to form spinel according to the reaction () AlO(m) + (Mg,Fe)O(m) = (Fe,Mg)AlO(s) + () AlO(m), where the reaction equation is written so that out of the () moles of AlO(m) arriving from the corundum-spinel interface only the fraction moles AlO(m) reacted with (Mg,Fe)O of the melt at the spinel-melt interface, and the remaining () moles AlO(m) were released into the alkali basalt melt. The spinel formed by this reaction constitutes the spinel of the outer layer of the spinel corona. It has first been argued on theoretical grounds (Wagner, 1936) and later demonstrated in experiment (Carter, 1961; Greskovich & Stubican, 1969; Sockel & Schmalzried, 1966; Hesse, 1987; Nagata et al., 1991; Hesse et al., 1994; Götze et al., 2010; Keller et al., 2010; Jeřábek et al., 2014) that , which corresponds to the interdiffusion of 2 Al versus 3 (Fe,Mg) in an otherwise largely immobile oxygen sublattice. Thus, if the entire fraction of () moles AlO(m) arriving at the outer border of the inner spinel layer were used for producing the spinel of the outer spinel layer, that is if , then the volume of the spinel constituting the inner spinel layer would have to be three times the volume of the spinel in the outer spinel layer. In the corona studied here, the volume of spinel in the outer spinel layer is generally less than 1/3 of the volume of spinel in the inner layer, indicating that . This implies that a fraction moles of the mobile AlO(m) diffused beyond the domain occupied by the newly formed spinel and reacted with the basalt melt to produce plagioclase, which is intimately intergrown with spinel in the outer spinel layer and which is the volumetrically dominant phase in the plagioclase-rich outer corona.
Transformation strain and reaction induced deformation
Growth of the inner spinel layer by the in-diffusion of Fe and Mg through a sublattice of largely immobile oxygen implies a volume increase of 17% at the corundum-spinel interface. Thus, when one unit volume of corundum is consumed in the course of the propagation of the reaction interface, 1.17 unit volumes of spinel are generated. Given the single crystal nature of the reactant corundum and the closed envelope 3D geometry of the corona, this transformation strain caused an outward movement of the newly formed spinel relative to the reactant corundum (Abart et al., 2016; Gaidies et al., 2017; Kuleci et al., 2016). The outward movement of material points in a concentric spinel layer inevitably leads to internal deformation of the spinel corona with shortening perpendicular to the reaction interface and extension parallel to it, or by the formation of tensile cracks perpendicular to the corundum-spinel interface in the outermost portions of the corona (Kuleci et al., 2017). The internal deformation and the formation of tensile cracks is expected to be particularly pronounced at the edges where two differently oriented corona segments form a projecting corner. A wedge shaped gap in the spinel corona is indeed observed at the projecting corner close to scan Py2 (Fig. 2c) testifying to tensile fracturing of the spinel corona. In the corona segment next to this gap spinel shows a peculiar microstructure and texture and, unlike all other corona segments, here, the inner corona layer contains plagioclase. Internal crystal plastic deformation of spinel associated with fracturing is supposed to have obliterated the typical topotactic COR between corundum and spinel, producing a microstructure with a significant fraction of high-angle GBs unrelated to TBs.
Effect of corundum facets on spinel microstructure and texture
At the time of corona growth, the basalt matrix was largely in the liquid state, so that the externally imposed stress state was close to isostatic. Therefore, only the interface orientation and reaction induced deformation are considered as potential controls on the microstructures and textures of the different corona segments, where the latter influence is particularly pronounced at strongly outwards convex corona segments as in the case of scan Py2.
Controls on twin variant selection
For a given corona segment, out of the two twin variants t and t, the one that has a or a lattice plane oriented close to parallel with the corundum spinel interface is preferentially selected. Noting that is the most densely packed plane in spinel, and is the most densely packed plane of the oxygen sublattice, the observed variant selection appears to be related to the close alignment of densely packed planes of the spinel with the reaction interface. It is interesting to note that the and planes are the most important slip planes in spinel, where and are the corresponding slip systems (Hornstra, 1960; Hwang et al., 1975). It is hypothesized that parallel alignment of an important spinel slip plane with the reaction interface allows for efficient accommodation of lattice misfit between spinel and corundum and eases propagation of the reaction interface. This view is corroborated by findings of Li et al. (2018), who inferred that edge dislocations and the associated glissile partial dislocations provide the means for an energetically favorable accommodation of the misfit between the corundum and spinel lattices. In addition, these partial dislocations allow for efficient propagation of the corundum-spinel interface by their glide along . The observed twin variant selection is consistent with such a transformation mechanism.
Controls on the deviations from ideal topotaxy
The orientation of the corundum-spinel interface with respect to the lattice of corundum influences the deviations of the spinel orientations from the perfect topotactic orientation relationship with corundum. In all corona segments that correspond to prismatic facets of corundum, a significant fraction of spinel is rotated away from the ideal topotactic orientation by about 3 around . Thus, the rotation axis lies in the plane of the corundum-spinel interface or at a very shallow angle with respect to the interface. In the corona segments corresponding to corundum prismatic planes, a significant fraction of spinel may also be rotated by up to 7 around the specific -axis, which is (sub)perpendicular to the interface. Interestingly, the sense of rotation is predominantly clockwise if viewed along the positive direction of the corresponding corundum -axis, irrespective of whether the spinel growth direction is parallel or antiparallel to this -axis.
In the literature, small but systematic deviations from ideal topotatactic relationships between various substrates and thin spinel films have been reported (Carter & Schmalzried, 1985; Hesse et al., 1994; Sieber et al., 1996; Li et al., 2018). The rotation away from ideal topotactic match was interpreted as a mechanism for the accommodation of the lattice misfit between spinel and the substrate material through the introduction of misfit dislocations at interface steps. Carter & Schmalzried (1985) ascribed angular deviations of up to 5 between the (111) plane of Co-Al spinel and planes to minimizing lattice misfit along the interface plane. Li et al. (2018) reported misorientations of up to 7 from magnesio–aluminate spinel that formed during early stages of rim growth in thin-film experiments. These latter authors noted that, in addition to misorientations, edge dislocations are required in combination with interface ledges to accommodate the calculated oxygen sublattice misfit of 3.76% between the parallel directions and lying in the corundum-spinel interface plane, which was parallel to in their case.
For the natural corona under study, the fact that particular rotation axes are active in some segments but not in others, depending on the orientation of the corundum-spinel interface relative to the lattice of corundum, suggests that the interface structure has a significant impact on the phase transformation. This is corroborated by the fact that the selection of the spinel twin variants depends on the orientation of the important spinel slip planes relative to the corundum-spinel interface.
The nature of the topotactic orientation relationships at the advanced rim growth stage, as observed in the natural spinel corona under study, differs markedly from that in spinel reaction rims grown experimentally at corundum-periclase contacts. For the latter, deviations of spinel orientations from perfect topotaxy with corundum hardly ever exceed 2 and are restricted to domains close to the position of the original periclase-corundum interface (Jeřábek et al., 2014). The spinel formed during the late growth stages of the experimentally produced reaction rims shows perfect topotactic match with corundum.
Li et al. (2018) attributed differences in the quality of corundum-spinel topotactic orientation relationships between thin films and thick diffusion couples to a change in the mechanisms of interface motion between the early and the late stages of layer growth. These authors argued that the development towards ideal topotaxy correlates with a change in the structure of misfit dislocations and, thus, in the mechanisms of interface motion. During early growth stages, the corundum-spinel interface propagates by the gliding of edge-dislocations combined with step-edge growth in a poorly organized interface. During advanced growth stages, the corundum-spinel interface becomes progressively more organized, and the reaction front propagates exclusively via the glide of partial dislocations parallel to the corundum basal plane, leading to perfectly aligned corundum and spinel crystal orientations. The change in transformation mechanism is supposed to correlate with the transition from interface-reaction controlled to diffusion controlled growth, which inevitably occurs with increasing thickness of the spinel layer (Abart & Petrishcheva, 2011, Abart et al., 2016).
It is hypothesized that the rotations away from the ideal topotactic orientation relationships observed in our study are related to misfit dislocations. If the rotations were caused by edge dislocations, the Burgers vectors would be normal, if they were generated by a single set of screw dislocations, the Burgers vectors would be parallel to the rotation axis. Edge dislocations with Burgers vectors associated with the dominant slip systems in spinel s.str are consistent with both rotations about the direction, which is parallel to and rotations about the directions that are parallel to the directions. By contrast, dislocations with Burgers vectors parallel to have not been identified in spinel. Therefore, the activation of multiple sets of screw dislocations with strain fields adding up to rotations about would be necessary to generate the required rotation. For this reason and because misfit dislocations with screw character are generally rare, whereas misfit dislocations between corundum and spinel with edge character were observed by Li et al. (2018), we infer an edge character of potential misfit dislocations for this rotation axis. Dislocations with Burgers vector parallel to may dissociate into Shockley partial dislocations with Burgers vectors parallel to . However, the total rotation produced by these partial dislocations would correspond to the rotation produced by full dislocations. In previous studies, both full dislocations with Burgers vectors parallel to and the associated Shockley partial dislocations with Burgers vectors parallel to have been reported as predominant misfit dislocations at interfaces that are parallel to corundum (0001) and spinel (Li et al., 2018). The rotations causing the observed deviations from perfect topotaxy must originate in properties of the corundum lattice, as the associated directions in spinel are crystallographically equivalent, and both spinel twin variants largely reflect identical orientation variations. Yunin & Drozdov (2018) demonstrated that even though corundum has a centrosymmetric trigonal symmetry, + facets can be distinguished from the obverse - facets by XRD techniques e.g. by the positions of the basal plane and the cleavage planes. This is in contrast to the basal facets and the prismatic facets, which are not distinguishable from the respective obverse facets. The difference between the positive and negative a facets is thought to influence epitaxial growth on such facets (Yunin & Drozdov, 2018; Grundmann & Lorenz, 2021) and may likewise be connected to the selection of one sense of rotation for the orientation dispersion about the -axes. The latter is restricted to corona segments where the corundum spinel interface is subparallel to an a plane. This influence of the corundum crystallography on the orientation dispersion further corroborates the interface controlled nature of spinel growth in the studied sample.
Controls on spinel grain boundary characteristics and grain morphology
The density and characteristics of both general GBs as well as boundaries depend on the orientation of the spinel-corundum interface with respect to the lattice of corundum. The boundaries with misorientation predominantly constitute TBs, the traces of which follow the plane that is (sub)parallel to the trace of in all parts of the corona. Scan Bas, where the corundum-spinel interface is subparallel to the corundum basal plane, is a notable exception. Small rotations of the TB orientation from the orientation of are caused by deviations from the ideal topotaxy of the t and t grains with respect to corundum. The fraction of TBs and the related HAGBs depends on the extent of twin variant selection. Naturally, segments with one predominant twin variant have a rather small fraction of these boundaries both overall as well as in relation to LABs. For example, scan Pr1c, which exhibits a predominance of t, has a significantly smaller fraction of TBs and HAGBs than otherwise similar segments such as scans Pr1a and Pr1b that have a more balanced variant fraction. Accordingly, segments with a high proportion of spinel that does not pertain to one of the variants have a small fraction of TBs both overall as well as in relation to LABs.
The variations in grain boundary area density are also connected with the nature of the grain boundary orientation distribution. Segment Py1 and the subprismatic segments Pr4 and Pr5 located close to intercepts between segments, where the interface has a strong curvature, exhibit a grain boundary orientation distribution that is independent of the orientation of the corundum basal plane and rather follows the spinel growth direction. The resulting palisade microstructure is primarily due to LABs. TBs and HAGBs with orientations controlled by the crystallographic orientation of corundum are rare in these corona segments. This grain boundary microstructure produces highly elongated 2D grain sections in cuts perpendicular to the corundum-spinel interface, and equant polygonal 2D sections in cuts parallel to the corundum-spinel interface. Similar palisade microstructures have been observed in reaction layers formed in nature and experiments (Milke & Wirth, 2003; Keller et al., 2010; Götze et al., 2010; Jeřábek et al., 2014).
The microstructure is different in the corona segments that formed at (sub)prismatic facets of corundum. These segments show high fractions of TBs and HAGBs. The latter have traces with preferred orientations lying between the growth direction projected into the 2D section and the trace of the corundum basal plane (scans Pr3). Considering that HAGBs represent angular deviations of up to 20 from TB misorientations, a weak preferred orientation parallel to the corundum basal plane may result. Depending on the relative orientation of the spinel growth direction and the corundum basal plane, the orientations of the HAGB traces deviate to different extent from the normal direction of the corundum-spinel interface trace towards the orientation of the trace of the Crn basal plane. This feature is not visible in 2D sections where the trace of the spinel growth direction projected into the plane of the polished section, and the trace of the corundum basal plane coincide (scans Pr1 and Pr2). Contrary to HAGBs, the orientation distribution of the LAB traces in segments associated with corundum prism facets are consistent with a palisade or polygonal microstructure in 2D sections depending on the cut perpendicular or parallel to the corundum-spinel interface.
Since only the traces of the GBs and not the full orientation of the GB planes are accessible through 2D microscopy, cutting effects need to be taken into account. It was shown based on geometrical arguments that sectioning effects may change the skewness of the orientation distribution of grain boundary traces, but they do not affect the mode (Harker & Parker, 1945; Smith, 1948). More specifically, if the grain boundaries of the spinel palisade microstructure are perpendicular to the corundum-spinel interface, the mode of the orientation distribution is at = 0 irrespective of the orientation of the 2D cut, while the skewness depends on the orientation of the cut. In particular, this cutting effect is consistent with a left skew of the measured GB trace distribution in the case of scans Pr1 and with a right skew in the case of scans Pr2 and Pr3. Contrastingly, in the corona segments covered by scans Py1, Pr4, and Pr5, where the corundum-spinel interface is close to perpendicular to the 2D cut, the orientation distribution of the grain boundary traces is symmetrical about the mode. Here the mode of the distribution closely follows the growth direction, and no influence of the corundum crystal orientation can be observed.
For all corona segments we can infer that (i) the relative abundances of the different grain-boundary types depend on the orientation of the corundum-spinel interface with respect to corundum and the associated quality of topotactic match between spinel and corundum and the twin variant selection, and (ii) the preferred orientation of TBs follows the orientation of the corundum basal plane, the preferred orientation of LABs is parallel to the spinel growth direction and the orientation of HAGBs lies between these two directions. The dependence of LAB orientation on the spinel growth direction and the nature of the orientation transition zones that interact with LABs indicate that the spinel (sub)grain microstructure is an original growth feature of the spinel layer.
Previous experimental work by Keller et al. (2010) and Jeřábek et al. (2014) showed that for spinel rims grown under uniaxial load at the contact between corundum and periclase single crystal reactants the GB character of the spinel rim as well as the GB area density strongly influence rim growth rate. This was taken as an indication that GB diffusion contributes considerably to the necessary chemical mass transfer. Keller et al. (2010) inferred that the efficiency of GB diffusion depends on the GB character, that is the misorientation across the GB in combination with the orientation of the GB plane. These latter authors found diffusion along 3 GBs to be only slightly enhanced as compared to volume diffusion and the diffusivities along GBs with <15 GB misorientation to be one order of magnitude lower than along high angle GBs with misorientations of 15-55. Interestingly, in the natural corona under study, the rim thickness is quite uniform over all corona segments, except for those associated with scans Bas and Pr5. The two segments with deviating rim thicknesses can be explained with their specific locations in the corona. The segment covered by scan Bas is located close to the tip of the corundum crystal, where the corona is strongly convex and has somewhat above average rim thickness. The segment covered by scan Pr5 is located in a reentrant corner of the corona and has somewhat below average rim thickness. Despite markedly different microstructures, all other segments of the corona have thicknesses that are similar within the accuracy of the determination. Therefrom we infer that the observed microstructural variations do not significantly affect the rim thickness.
Characteristics of the interface orientation subparallel to the corundum basal plane
In earlier experimental studies, spinel layers were grown on specific corundum surfaces. For example, spinel layers grown on the corundum basal plane (Keller et al., 2010; Jeřábek et al., 2014; Li et al., 2018) show similar topotactic COR as observed in the present study. Spinel grown on a pyramidal surface (Hesse et al., 1994) or on a prism plane (Li et al., 1992) shows different CORs with respect to corundum, an effect that was probably imposed from periclase, the second reactant phase. The corona segment covered by scan Bas is the only investigated part of the corona that is subparallel to the corundum basal plane. The plane parallel to the corundum-spinel interface at this segment was determined as , which is rotated 12 from the basal plane. The microstructural and textural characteristics of this segment differ strongly from the ones of the other corona segments and rather resemble those of spinel grown experimentally on facets. For this particular interface orientation, the grain boundaries in spinel are strongly curved and lobate at the micrometer scale. Results from atomic scale investigations of experimental samples showed segments of incoherent grain boundaries alternating with coherent twin boundaries parallel to the (111) that is parallel to the corundum basal plane (Li et al., 2018). The preferred orientation of the TBs parallel to the corundum basal plane is consistent with our observations in the natural sample. However, Li et al. (2018) found that in order to accomplish growth of two neighboring twin individuals in a direction perpendicular to an interface that is parallel to the corundum basal plane, the boundary between the two spinel twin individuals must propagate out of the interface plane. This produces curved boundary segments that are highly stepped on the nanometer scale, and also yield highly serrated and lobate boundary microstructures at the scale of several micrometers (Li et al., 2018). In the natural corona, such a microstructure is only observed in the corona segment captured by scan Bas. Therefore, the particular microstructures of experimental samples with the interface orientation parallel to the corundum basal plane are not representative for most of the segments of the natural corona, where segments corresponding to prismatic and pyramidal facets of corundum dominate (Dobrovinskaya et al., 2009).
Implications
The systematic microstructural differences between the natural spinel corona and synthetic rims imply different growth mechanisms. Firstly, the persistent systematic deviations from ideal topotactic COR between spinel and corundum correspond to features that are commonly associated with the early stages of layer growth in experiments (Sieber et al., 1996; Li et al., 2018). Secondly, the relatively uniform thickness of the different corona segments despite markedly different microstructural characteristics is at odds with the strong microstructural and textural dependence of rim growth rates in experiment (Keller et al., 2010). Noting that in experiment the microstructural and textural control on rim growth rates is probably due to the effect of the grain boundary character on grain boundary diffusion, the lack of systematic thickness variations in the natural corona suggests that chemical mass transfer was not rate limiting. Instead, the overall growth rate probably was controlled by the processes that are localized at the corundum-spinel interface, and corona growth was rather interface reaction controlled than diffusion controlled. This view is corroborated by the fact that the microstructural and textural differences between the corona segments, like the activity of different rotation axes, point to an influence of the particular interface structure on the crystallization of spinel.
It was argued on theoretical grounds (Abart & Petrishcheva, 2011, Abart et al., 2016), and was shown experimentally (Götze et al., 2014) that rim growth tends to be interface reaction controlled during the early growth stages, when the rim of the newly formed phase is still thin. In this case, diffusion distances are short and diffusion is very efficient. As a consequence, the driving force for interface motion that are the chemical potential jumps across the corundum-spinel interface are large, and the corundum-spinel interface organizes itself so that its mobility is maximized at the expense of an energetically unfavorable interface structure. When the diffusion distances increase with layer growth, diffusion becomes successively less efficient and may become rate limiting. During advanced growth stages the driving force for interface motion decreases, and consequently, the interface organizes itself into an energetically more favorable configuration at the expense of a lower mobility. Both interface reaction controlled (Götze et al., 2014; Li et al., 2016) and diffusion controlled (Keller et al., 2010; Götze et al., 2010; Jeřábek et al., 2014) growth of spinel reaction rims have been documented in thin film and thick diffusion couple experiments. For spinel layers grown between corundum single crystals and amorphous MgO films, the change from interface-reaction controlled to diffusion controlled growth was estimated to occur at about 1 rim thickness (Götze et al., 2014).
Contrasting with the corresponding microstructural and textural transition observed in experiment, the natural corona shows characteristics consistent with interface-reaction controlled growth throughout the entire inner spinel corona. This, in turn, suggests that the diffusivities of Al, Mg, and Fe species were higher in the natural corona than during experimental layer growth. This can be well explained by the presence of a silicate melt and volatile species including HO at pressures in the GPa range during corona formation in nature, whereas the experiments were all performed in vacuum or under an inert gas atmosphere. Another fundamental difference between experimental and natural corona formation is that both reactant phases are solid in the rim growth experiments, while for the natural corona the source of the Mg and Fe required for the growth of spinel from corundum is a basaltic melt. Thus, while some solid state reactions were performed under uniaxial load (Keller et al., 2010; Götze et al., 2010; Jeřábek et al., 2014) the natural corona grew under isostatic stress conditions.
Furthermore, the transformation strain at the corundum-spinel interface, which leads to dilation perpendicular to the interface, can be accommodated without shape change of the specimen in the plan-parallel geometry of the rim growth experiments. In contrast, this transformation strain inevitably causes deformation in the closed envelope geometry of the natural corona. Deformation is indeed evident at the strongly convex section of the corona covered by scan Py2. The presence of LABs and orientation transition zones in the inner corona of the natural sample could possibly be related to crystal-plastic deformation and subgrain formation due to yielding of the material to deviatoric stress. Externally imposed stress can be ruled out, as the surrounding basaltic melt cannot transmit deviatoric stress to an extent that could cause crystal-plastic deformation of spinel. Thus, deviatoric stress related to the transformation strain at the corundum-spinel interface must be invoked. The intimate association and observed intersections of low-angle grain boundaries and spinel TBs point to a co-genetic origin. These features may have formed either during spinel rim growth, or later during cooling from magmatic temperatures. The latter would have also affected the basaltic rock matrix and is ruled out due to the absence of deformation features in the host rock. It is therefore inferred that twinning and the formation of low-angle GBs represent growth features. The presence of orientation transition zones demonstrates that the corona retained its original microstructures and textures, because these transition zones would have recovered to low-angle GBs, if subsequent recrystallization had occurred.
Lastly, the layer growth rates obtained from experimental spinel layer growth on a surface (Götze et al., 2010; Jeřábek et al., 2014; Li et al., 2018) are not necessarily representative for spinel layer growth on corundum with other facets. These experiments rather address a special case, where a plane is parallel to the reaction interface for both twin variants, allowing for efficient dislocation glide parallel to the reaction interface (Li et al., 2018). The kinetics of reaction rim growth always involve both material transport across the growing reaction rim, and structural transformation at the reaction interfaces (Abart et al., 2016). Depending on the relative rates of the two processes, either one can be rate limiting. Our findings suggest that finite mobility of the corundum-spinel interface, and thus processes localized at this interface, were a limiting factor for spinel layer growth throughout its entire growth history. This result has important implications for studies that derive reaction rates from reaction rim thicknesses in natural rocks. For example, when deriving crystal residence time in a comparable magmatic system, a linear dependence of the growth rate with time may have to be applied even when rim thicknesses exceed several hundred micrometers. Furthermore, any petrogenetic interpretation of microstructures and textures of reaction product phases requires consideration of the particular reaction interface orientation with respect to the reactant and product crystal(s).
CONCLUSIONS
The microstructural and textural characteristics of a spinel corona that formed at the contact between a centimeter sized, faceted corundum xenocrystal and a basaltic host melt in the Siebengebirge volcanic field show remarkable differences and similarities between the corona segments corresponding to different corundum facets and with respect to experimentally grown spinel reaction rims. In general, spinel follows the well known topotactic orientation relationship with one of the and three . This orientation relationship ensures alignment of close packed planes in both phases and is typical for the transformation of phases with hcp stacked oxygen sublattice to phases with fcc stacking. The crystal orientation relationship is fulfilled by two twin variants related by a 60 rotation about the common . In detail, the CORs of the spinel corona show statistical dispersion around the ideal topotactic relationship and systematic deviations, which differ among the corona segments. For segments corresponding to prismatic corundum facets the crystal orientation relationships form up to four clusters a few degrees off the ideal topotactic relationship. The deviations can be explained by rotations about the direction that is parallel to the axis and, in addition, for specific prism planes that are perpendicular to the corundum -axis by rotations about the respective -axis. Both rotations can be linked to edge dislocations at the corundum-spinel interfaces that are associated with the and slip systems. The degree of parallel alignment of the respective glide planes with the corundum-spinel interface controls the selection of twin variants. Out of the two twin variants fulfilling the general topotactic orientation relationship, the one that has a or a lattice plane oriented close to parallel with the corundum spinel interface is preferentially selected.
Spinel grain boundaries show pronounced preferential orientations in most corona segments. Twin boundaries almost always follow the orientation of the corundum basal plane and are more frequent in segments with an about equal share of the twin variants. General low and high angle boundaries preferentially follow the spinel growth direction or the corundum basal plane. The degree of preferential alignment of general boundaries with either the growth direction or the basal plane differs between corona segments. Therefore, the preferred orientation of spinel boundaries is controlled by orientation of the growth direction, the CORs, and the degree of twin variant selection, and thus it is also controlled by the interface orientation with respect to the corundum lattice.
The fact that, despite markedly different microstructural characteristics, the spinel corona has quite uniform thickness over all segments indicates that chemical mass transfer by diffusion was not rate limiting. Instead, localized processes underlying interface motion appear to have been rate limiting through the entire growth history of the spinel corona. This is corroborated by the systematic differences in microstructural and textural characteristics between the different corona segments, which indicate that the specific interface structures prevailing in the different segments strongly influenced the mechanisms of topotactic spinel growth.
Acknowledgments
The authors acknowledge -CT data collection by Dr Sebastian Stumpf at the -CT Facility at the Department of Paleontology (University of Vienna). We highly appreciate the very constructive reviews by Florian Heidelbach, Tomo Morishita, and Chris Ballhaus.
Funding
R. Schuster, L. Baldwin, and G. Habler acknowledge funding by the Austrian Science Fund (FWF): I1704-N19. R. Abart was supported by the European Union's Horizon 2020 research and innovation programme, Marie Sklodowska-Curie grant No. 656378, Interfacial Reactions. During the period of manuscript preparation, R. Schuster received financial support by the Austrian Federal Ministry for Digital and Economic Affairs and the National Foundation for Research, Technology and Development.
REFERENCES
Abart
,
R.
&
Petrishcheva
, E.
(
2011
).
Thermodynamic model for reaction rim growth: interface reaction and diffusion control
.
American Journal of Science
311
(
6
),
517
–
527
.
Abart
,
R.
,
Svoboda
, J.
,
Jeřábek
, P.
,
Povoden-Karadeniz
, E.
&
Habler
, G.
(
2016
).
Interlayer growth kinetics of a binary solid-solution based on the thermodynamic extremal principle: application to the formation of spinel at periclase-corundum contacts
.
American Journal of Science
316
(
4
),
309
–
328
.
Bachmann
,
F.
,
Hielscher
, R.
&
Schaeben
, H.
(
2010
)
Texture analysis with MTEX- Free and open source software toolbox
. In:
Solid State Phenomena
, Vol.
160
.
Trans Tech Publications Ltd
, pp.
63
–
68
.
Baldwin
,
L. C.
&
Ballhaus
, C.
(
2018
).
Experimental investigation of the reaction between corundum xenocrysts and alkaline basaltic host magma: constraints on magma residence times of basalt-hosted sapphires
.
Lithos
302–303
,
447
–
454
.
Baldwin
,
L. C.
,
Tomaschek
, F.
,
Ballhaus
, C.
,
Gerdes
, A.
,
Fonseca
, R. O. C.
,
Wirth
, R.
,
Geisler
, T.
&
Nagel
, T.
(
2017
).
Petrogenesis of alkaline basalt-hosted sapphire megacrysts. Petrological and geochemical investigations of in situ sapphire occurrences from the Siebengebirge Volcanic Field, Germany
.
Contributions to Mineralogy and Petrology
172
(
6
),
43
.
Bouché
,
K.
,
Barbier
, F.
&
Coulet
, A.
(
1998
).
Intermetallic compound layer growth between solid iron and molten aluminium
.
Materials Science and Engineering: A
249
(
1–2
),
167
–
175
.
http://10.1016/S0921-5093(98)00573-5.
Carter
,
C. B.
and
Schmalzried
, H
. (
1985
).
The growth of spinel into
Al
.
Philosophical Magazine A: Physics of Condensed Matter, Structure, Defects and Mechanical Properties
,
52
(
2
),
207
–
224
.
Carter
,
R. E.
(
1961
).
Mechanism of solid-state reaction between magnesium oxide and aluminum oxide and between magnesium oxide and ferric oxide
.
Journal of the American Ceramic Society
44
(
3
),
116
–
120
.
Dobrovinskaya
,
E. R.
,
Lytvynov
, L. A.
&
Pishchik
, V.
(
2009
)
Properties of sapphire
. In: (eds)
Sapphire
.
Boston, MA
:
Springer
, pp.
55
–
176
.
Dong
,
Z. L.
,
Chen
, X. M.
,
Hu
, W. X.
,
Wang
, R. C.
&
Zhao
, M.
(
2007
).
Coronas of corundum megacrysts in the Neogene Changle basalt and its forming model
.
Acta Petrologica Sinica
23
,
805
–
816
.
Dybkov
,
V. I.
(
1986
).
Reaction diffusion in heterogeneous binary systems—Part 1 Growth of the chemical compound layers at the interface between two elementary substances: one compound layer
.
Journal of Materials Science
21
(
9
),
3078
–
3084
.
Gaidies
,
F.
,
Milke
, R.
,
Heinrich
, W.
, and
Abart
, R.
(
2017
).
Metamorphic mineral reactions: porphyroblast, corona and symplectite growth
.
EMU Notes in Mineralogy
,
16
,
469
–
540
.,
http://10.1180/EMU-notes.16.14
Götze
,
L. C.
,
Abart
, R.
,
Milke
, R.
,
Schorr
, S.
,
Zizak
, I.
,
Dohmen
, R.
&
Wirth
, R.
(
2014
).
Growth of magnesio–aluminate spinel in thin-film geometry: in situ monitoring using synchrotron X-ray diffraction and thermodynamic model
.
Physics and Chemistry of Minerals
41
(
9
),
681
–
693
.
Götze
,
L. C.
,
Abart
, R.
,
Rybacki
, E.
,
Keller
, L. M.
,
Petrishcheva
, E.
&
Dresen
, G.
(
2010
).
Reaction rim growth in the system MgO–Al–SiO under uniaxial stress
.
Mineralogy and Petrology
99
(
3–4
),
263
–
277
.
Götze
,
L. C.
,
Milke
, R.
,
Zizak
, I.
&
Wirth
, R.
(
2016
).
In situ monitoring and ex situ TEM analyses of spinel (MgAl) growth between (111)-oriented periclase (MgO) substrates and Al thin films
.
Journal of Materials Science
51
(
19
),
8824
–
8844
.
Greskovich
,
C.
and
Stubican
, V. S.
(
1969
).
Interdiffusion studies in the system
MgO–Cr
.
Journal of Physics and Chemistry of Solids
,
30
(
4
),
909
–
917
.
Grundmann
,
M.
&
Lorenz
, M.
(
2021
).
Azimuthal anisotropy of rhombohedral (Corundum Phase) heterostructures
.
Physica Status Solidi (b)
258
(
7
), .
http://10.1002/pssb.202100104.
Hallstedt
,
B
. (
1992
).
Thermodynamic assessment of the system MgO–Al
.
Journal of the American Ceramic Society
,
75
(
6
),
1497
–
1507
.
Harker
,
D.
&
Parker
, E. R.
(
1945
).
Grain shape and grain growth
.
Transactions of the American Society for Metals
34
,
156
–
201
.
Hesse
,
D.
(
1987
).
Formation of ceramic thin films by solid-state interface reactions
.
Journal of Vacuum Science & Technology A: Vacuum, Surfaces, and Films
5
(
4
),
1696
–
1702
.
http://10.1116/1.574556.
Hesse
,
D.
,
Scholz
, R.
,
Senz
, S.
,
Sieber
, H.
,
Werner
, P.
&
Heydenreich
, J.
(
1994
).
The structure of spinel/oxide reaction fronts during spinel-forming solid state reactions
.
MRS Online Proceedings Library Archive
357
.
Hesse
,
D.
,
Senz
, S.
,
Scholz
, R.
,
Werner
, P.
&
Heydenreich
, J.
(
1995
).
Structure and morphology of the reaction fronts during the formation of MgAl thin films by solid state reaction between R-cut sapphire substrates and MgO films
.
Interface Science
2
(
3
),
221
–
237
.
Hornstra
,
J.
(
1960
).
Dislocations, stacking faults and twins in the spinel structure
.
Journal of Physics and Chemistry of Solids
15
(
3–4
),
311
–
323
.
Hwang
,
L.
,
Heuer
, A. H.
&
Mitchell
, T. E.
(
1975
)
Slip systems in stoichiometric MgAl spinel
. In:
Deformation of Ceramic Materials
.
US
:
Springer
, pp.
257
–
270
.
Jeřábek
,
P.
,
Abart
, R.
,
Rybacki
, E.
&
Habler
, G.
(
2014
).
Microstructure and texture evolution during growth of magnesio–aluminate spinel at corundum-periclase interfaces under uniaxial load: the effect of stress concentration on reaction progress
.
American Journal of Science
314
(
5
),
940
–
965
.
Jung
,
I. H.
,
Decterov
, S. A.
&
Pelton
, A. D.
(
2004
).
Critical thermodynamic evaluation and optimization of the MgO–Al, CaO–MgO–Al, and MgO–Al–SiO Systems
.
Journal of Phase Equilibria and Diffusion
25
(
4
),
329
–
345
.
Keller
,
L. M.
,
Götze
, L. C.
,
Rybacki
, E.
,
Dresen
, G.
&
Abart
, R.
(
2010
).
Enhancement of solid-state reaction rates by non-hydrostatic stress effects on polycrystalline diffusion kinetics
.
American Mineralogist
95
(
10
),
1399
–
1407
.
Kuleci
,
H.
,
Schmidt
, C.
,
Rybacki
, E.
,
Petrishcheva
, E.
&
Abart
, R.
(
2016
).
Hydration of periclase at 350°C to 620°C and 200 MPa: experimental calibration of reaction rate
.
Mineralogy and Petrology
110
(
1
),
1
–
10
.
Kuleci
,
H.
,
Ulven
, O. I.
,
Rybacki
, E.
,
Wunder
, B.
&
Abart
, R.
(
2017
).
Reaction-induced fracturing in a hot pressed calcite-periclase aggregate
.
Journal of Structural Geology
94
,
116
–
135
.
Li
,
C.
,
Griffiths
, T.
,
Pennycook
, T. J.
,
Mangler
, C.
,
Jeřábek
, P.
,
Meyer
, J.
,
Habler
, G.
&
Abart
, R.
(
2016
).
The structure of a propagating MgAl/MgO interface: linked atomic- and m-scale mechanisms of interface motion
.
Philosophical Magazine
96
(
23
),
2488
–
2503
.
Li
,
C.
,
Habler
, G.
,
Griffiths
, T.
,
Rečnik
, A.
,
Jeřábek
, P.
,
Götze
, L. C.
,
Mangler
, C.
,
Pennycook
, T. J.
,
Meyer
, J.
&
Abart
, R.
(
2018
).
Structure evolution of hcp/ccp metal oxide interfaces in solid-state reactions
.
Acta Crystallographica Section A: Foundations and Advances
74
(
5
),
466
–
480
.
Li
,
D. X.
,
Pirouz
, P.
,
Heuer
, A. H.
,
Yadavalli
, S.
&
Flynn
, C. P.
(
1992
).
A high-resolution electron microscopy study of MgO/Al interfaces and MgAl spinel formation
.
Philosophical Magazine A: Physics of Condensed Matter, Structure, Defects and Mechanical Properties
65
(
2
),
403
–
425
.
Liu
,
C. M.
,
Chen
, J. C.
&
Chen
, C. J.
(
2005
).
The growth of an epitaxial Mg-Al spinel layer on sapphire by solid-state reactions
.
Journal of Crystal Growth
285
(
1–2
),
275
–
283
.
Liu
,
C. M.
,
Chen
, J. C.
&
Chen
, C. J.
(
2006
).
The morphology of an epitaxial Mg–Al spinel layer on a sapphire surface
.
Journal of Crystal Growth
292
(
2
),
302
–
305
.
Mackenzie
,
K. J. D.
&
Ryan
, M. J.
(
1981
).
Effect of electric fields on solid-state reactions between oxides
.
Journal of Materials Science
16
(
3
),
579
–
588
.
Milke
,
R.
&
Wirth
, R.
(
2003
).
The formation of columnar fiber texture in wollastonite rims by induced stress and implications for diffusion-controlled corona growth
.
Physics and Chemistry of Minerals
30
(
4
),
230
–
242
.
Nagata
,
K.
,
Nishiwaki
, R.
,
Nakamura
, Y.
&
Maruyama
, T.
(
1991
).
Kinetic mechanisms of the formations of MgCr and FeCr spinels from their metal oxides
.
Solid State Ionics
49
(
C
),
161
–
166
.
Rossi
,
R. C.
&
Fulrath
, R. M.
(
1963
).
Epitaxial growth of spinel by reaction in the solid state
.
Journal of the American Ceramic Society
46
(
3
),
145
–
149
.
Sack
,
R. O.
(
1982
).
Spinels as petrogenetic indicators: activity-composition relations at low pressures
.
Contributions to Mineralogy and Petrology
79
(
2
),
169
–
186
.
Sack
,
R. O.
&
Ghiorso
, M. S.
(
1991
).
An internally consistent model for the thermodynamic properties of Fe–Mg–titanomagnetite–aluminate spinels
.
Contributions to Mineralogy and Petrology
106
(
4
),
474
–
505
.
Schmalzried
,
H.
(
1962
).
Reaktionsmechanismen der Spinellbildung im festen Zustand
.
Zeitschrift fur Physikalische Chemie
33
(
1–4
),
111
–
128
.
Schmalzried
,
H.
(
1981
).
Solid State Reactions, 2nd edn. Verlag Chemie
,
Weinheim
.
Sieber
,
H.
,
Hesse
, D.
,
Pan
, X.
,
Senz
, S.
, and
Heydenreich
, J.
(
1996
).
TEM investigations of spinel-forming solid state reactions: reaction mechanism, film orientation, and interface structure during MgAl formation on MgO (001) and Al2O3 (11.2) single crystal substrates
.
Zeitschrift fuer Anorganische und Allgemeine Chemie
,
622
(
10
),
1658
–
1666
.
Smith
,
C. S.
(
1948
).
Grains, phases, and interfaces: an introduction of microstructure
.
Transactions of the Metallurgical Society of AIME
,
175
,
15
–
51
.
Sockel
,
H. G.
&
Schmalzried
, H.
(
1966
)
The role of phase boundaries during reaction between single crystals of various oxides
. In:
The Role of Grain Boundaries and Surfaces in Ceramics
.
US
:
Springer
,
61
–
73
.
Springer
,
H.
,
Kostka
, A.
,
Payton
, E. J.
,
Raabe
, D.
,
Kaysser-Pyzalla
, A.
&
Eggeler
, G.
(
2011
).
On the formation and growth of intermetallic phases during interdiffusion between low-carbon steel and aluminum alloys
.
Acta Materialia
59
(
4
),
1586
–
1600
.
10.1016/j.actamat.2010.11.023.
Ting
,
C. J.
&
Lu
, H. Y.
(
1999
).
Defect reactions and the controlling mechanism in the sintering of magnesium aluminate spinel
.
Journal of the American Ceramic Society
82
(
4
),
841
–
848
.
Wagner
,
C.
(
1936
).
The mechanism of formation of ionic compounds of higher order (Double salts, spinel, silicates)
.
Zeitschrift fur Physikalische Chemie
34
,
209
–
316
.
Watson
,
E. B.
&
Price
, J. D.
(
2002
).
Kinetics of the reaction MgO + Al MgAl and Al–Mg interdiffusion in spinel at 1200 to 2000°C and 1.0 to 4.0 GPa
.
Geochimica et Cosmochimica Acta
66
(
12
),
2123
–
2138
.
Whitney II
, W. P. and
Stubican
, V. S
. (
1971
).
Interdiffusion studies in the system
MgO–Al
.
Journal of Physics and Chemistry of Solids
,
32
(
2
),
305
–
312
.
Yamaguchi
,
G.
&
Tokuda
, T.
(
1967
).
Some aspects of solid state reactions between oxides
.
Bulletin of the Chemical Society of Japan
40
(
4
),
843
–
851
.
Yunin
,
P. A.
&
Drozdov
, Y. N.
(
2018
).
How to distinguish between opposite faces of an a-plane sapphire wafer
.
Journal of Applied Crystallography
51
(
2
),
549
–
551
.
Zhang
,
P.
,
Debroy
, T.
&
Seetharaman
, S.
(
1996
).
Interdiffusion in the MgO–Al spinel with or without some dopants
.
Metallurgical and materials transactions A
27
(
8
),
2105
–
2114
.
Zienert
,
T.
and
Fabrichnaya
, O
. (
2013
).
Thermodynamic assessment and experiments in the system MgO–Al
.
Calphad: Computer Coupling of Phase Diagrams and Thermochemistry
,
40
,
1
–
9
.
© The Author(s) 2023. Published by Oxford University Press.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (
https://creativecommons.org/licenses/by/4.0/), which permits unrestricted reuse, distribution, and reproduction in any medium, provided the original work is properly cited.
PDF












