-
PDF
- Split View
-
Views
-
Cite
Cite
Sang-Hyeon Ahn, Precision of measurements and the biases due to the geomagnetic declination in the Korean observations of the comet C/1723 T1, Publications of the Astronomical Society of Japan, Volume 73, Issue 6, December 2021, Pages 1615–1630, https://doi.org/10.1093/pasj/psab099
Close - Share Icon Share
Abstract
Positions of the comet C/1723 T1 recorded in Korean historical resources are analysed to estimate the precision of measurements and the bias due to the geomagnetic declination at Seoul. We calculate the ephemeris of the comet by adopting the orbital elements determined by Gustav Spörer in 1843 based upon the Bradley’s telescopic observations in 1723. We confirm that the Bradley’s observations have a measurement error of 25″. The positions of the comet recorded in the Korean manuscripts are compared with the modern ephemeris. We find that there are misalignments in the instrument’s polar axis with Earth’s rotation axis: if the measurements were rounded up, there are alignment errors of 0.°0 ± 0.°2 in elevation and |$-{0{_{.}^{\circ}}3}\pm {0{_{.}^{\circ}}3}$| in azimuth (to 1σ); if the measurements were rounded down, there are alignment errors of −0.°5 ± 0.°4 in elevation and +0.°5 ± 0.°6 in azimuth (to 1σ). Assuming that the instrument’s polar axis was aligned with a magnetic compass, we can regard the misalignment of the polar axis in azimuth as the geomagnetic declination at Seoul in 1723. We find that the geomagnetic declination obtained is in agreement with the recent models of the historical geomagnetic fields. We also obtain the one-time measurement error of |${0{_{.}^{\circ}}25}$|, which is not different from the one-time measurement error of |${0{_{.}^{\circ}}3}$| obtained from the observational data of Mars in 1491.
1 Introduction
A comet appeared on the October sky in 1723. The comet is called C/1723 T1. Astronomical telescopes were being used in astronomical observations in the eighteenth century in Europe. In particular, James Bradley of England made use of a micrometer to measure precise positions of the comet relative to the background stars, as well as using a seven-foot focal length telescope (Bradley 1724).
Although the first telescope for watching landscapes was brought to Korea in 1631, telescopes could not have been utilized for astronomical observations until the latter period of the 18th century. Thus, it is thought that the Korean astronomers in 1723 observed the comet with an aid of traditional armilla, such as the small abridged armilla (often called Soganui in Korean) that was first developed in the Joseon dynasty by court officials and engineers at the order of King Sejong in the 15th century, and bare eyes. The armilla had been a major instrument for measuring positions of astronomical objects, as can be deduced from observations of Mars in 1491 (Lee 2012; Ahn 2021).
An instrument called Gyugwan1 appeared in literatures as being used to observe celestial phenomena after the latter period of the 17th century. Thus the positions of the comet C/1723 T1 might have been measured with it. It is an interesting matter whether the precision of such observational instruments had been improved. However, the real instrument, having been used for observing the comet, does not exist now. Instead, we have only the observational records that had been made with the instrument. Thus, analysing the observational data may give us some information on the instrument. For example, we can check if there had been any change in the precision of measurements. Ahn (2021) analysed the observational data for the retrograde motion of Mars in 1491 to find that the observational precision was |${0{_{.}^{\circ}}3}$| in the 15th century. However, we need more cases to test any existence of such change in the precision of measurements.
Hence, in this paper, we analyse the observational data for a comet C/1723 T1 that are recorded in the observational reports written the court astronomers of the Joseon dynasty, complemented by the astronomical records in official history books such as the Daily Records of Royal Secretariat of Joseon Dynasty (hereafter called “the Diary,” for convenience) and the Annals of the Joseon Dynasty (hereafter the Sillok, for convenience). The orbital elements of C/1723 T1 were determined from precise telescopic observations made by European astronomers. The Korean observations are less precise, and so they may be less useful for the orbit determination. Nevertheless, the coordinate data can be used to estimate the precision of measurements in 18th-century Korea. The data and the analysis method will be described in section 2. The results will be presented in section 3. Lastly, we discuss the implication of the results on the archaeo-historical geomagnetic fields in section 4.
2 Data
2.1 European records
The observational results of the comet C/1723 T1 were compiled in a few literatures (e.g., Vsekhsvyatskii 1964; Kronk 1999). It was independently discovered at such remote sites as Peking in China by the Chinese court astronomers and a Jesuit called Ignatius Kögler on 1723 October 10.8, Cayenne in French Guiana by another Jesuit called Crossat on 1723 October 15.9, and Mumbai in India by William Saunderson on 1723 October 16.7 (Jenniskens 2006). In particular, James Bradley was informed of the appearance of the comet by Edmond Halley, and began to observe the comet on 1723 October 21 (Bradley 1724). Halley continued to observe the comet until the end of November. They made the final observation on December 1, when moonlight prevented them from detecting the comet. Bradley made his final observation on December 18.78 at Winstead, England (Bradley 1724). We list his observations in table 1. The positions of the comet observed by Bradley are given in equatorial coordinates. The first entry on the position of the comet on October 20 is that given by Halley in ecliptic coordinates, and so it is converted into the equatorial coordinates.
| Date . | Time . | JD . | RA (αB) . | RA (αE) . | αB − αE . | Dec (δB) . | Dec (δE) . | δB − δE . | . |
|---|---|---|---|---|---|---|---|---|---|
| (month dd) . | (hh:mm) . | −2350662 . | (°) . | (°) . | (′) . | (°) . | (°) . | (′) . | Observer . |
| October 20 | 20:05 | 3.33682 | 308.46252 | 308.41088 | 3.098 | −13.60611 | −13.55332 | −3.167 | Halley |
| October 21 | 18:21 | 4.26460 | 307.11111 | 307.09433 | 1.007 | −11.13750 | −11.13303 | −0.268 | Bradley |
| October 23 | 19:22 | 6.30696 | 305.11221 | 305.09902 | 0.792 | −7.31778 | −7.31362 | −0.249 | Bradley |
| 20:50 | 6.36807 | 305.06000 | 305.05268 | 0.439 | −7.22222 | −7.22236 | 0.008 | Bradley | |
| October 24 | 18:58 | 7.29029 | 304.37778 | 304.42153 | −2.625 | −6.16667 | −5.96508 | −12.095 | Bradley |
| October 25 | 20:57 | 8.37293 | 303.81944 | 303.81609 | 0.201 | −4.73167 | −4.72849 | −0.191 | Bradley |
| October 26 | 18:35 | 9.27432 | 303.41111 | 303.39876 | 0.741 | −3.85083 | −3.85296 | 0.128 | Bradley |
| November 01 | 18:22 | 15.26529 | 301.80639 | 301.79725 | 0.548 | −0.10000 | −0.10177 | 0.106 | Bradley |
| November 02 | 18:24 | 16.26668 | 301.65472 | 301.65197 | 0.165 | +0.31667 | 0.31418 | 0.149 | Bradley |
| November 04 | 20:02 | 18.33473 | 301.42611 | 301.41950 | 0.397 | +1.06944 | 1.06209 | 0.441 | Bradley |
| November 09 | 20:56 | 23.37223 | 301.12222 | 301.12900 | −0.407 | +2.45556 | 2.45207 | 0.209 | Bradley |
| November 10 | 18:20 | 24.26390 | 301.10556 | 301.10792 | −0.142 | +2.65750 | 2.65354 | 0.238 | Bradley |
| November 16 | 17:53 | 30.24515 | 301.13333 | 301.13217 | 0.070 | +3.79389 | 3.78930 | 0.275 | Bradley |
| November 19 | 19:06 | 33.29585 | 301.23056 | 301.23194 | −0.083 | +4.26028 | 4.26764 | −0.442 | Bradley |
| November 25 | 18:20 | 39.26390 | 301.54583 | 301.55213 | −0.378 | +5.09167 | 5.08888 | 0.167 | Bradley |
| December 01 | 19:45 | 45.32293 | 301.99722 | 302.00681 | −0.575 | +5.81528 | 5.83260 | −1.039 | Halley |
| December 18 | 18:45 | 62.28126 | 303.70972 | 303.70706 | 0.160 | +7.77500 | 7.77310 | 0.114 | Bradley |
| |$\langle {\Delta \alpha }\rangle = {0.20\prime }$| | |$\langle {\Delta \delta }\rangle = -{0.02\prime }$| | ||||||||
| |$S_{\Delta \alpha }={0.47\prime }$| | |$S_{\Delta \delta }={0.37\prime }$| | ||||||||
| Date . | Time . | JD . | RA (αB) . | RA (αE) . | αB − αE . | Dec (δB) . | Dec (δE) . | δB − δE . | . |
|---|---|---|---|---|---|---|---|---|---|
| (month dd) . | (hh:mm) . | −2350662 . | (°) . | (°) . | (′) . | (°) . | (°) . | (′) . | Observer . |
| October 20 | 20:05 | 3.33682 | 308.46252 | 308.41088 | 3.098 | −13.60611 | −13.55332 | −3.167 | Halley |
| October 21 | 18:21 | 4.26460 | 307.11111 | 307.09433 | 1.007 | −11.13750 | −11.13303 | −0.268 | Bradley |
| October 23 | 19:22 | 6.30696 | 305.11221 | 305.09902 | 0.792 | −7.31778 | −7.31362 | −0.249 | Bradley |
| 20:50 | 6.36807 | 305.06000 | 305.05268 | 0.439 | −7.22222 | −7.22236 | 0.008 | Bradley | |
| October 24 | 18:58 | 7.29029 | 304.37778 | 304.42153 | −2.625 | −6.16667 | −5.96508 | −12.095 | Bradley |
| October 25 | 20:57 | 8.37293 | 303.81944 | 303.81609 | 0.201 | −4.73167 | −4.72849 | −0.191 | Bradley |
| October 26 | 18:35 | 9.27432 | 303.41111 | 303.39876 | 0.741 | −3.85083 | −3.85296 | 0.128 | Bradley |
| November 01 | 18:22 | 15.26529 | 301.80639 | 301.79725 | 0.548 | −0.10000 | −0.10177 | 0.106 | Bradley |
| November 02 | 18:24 | 16.26668 | 301.65472 | 301.65197 | 0.165 | +0.31667 | 0.31418 | 0.149 | Bradley |
| November 04 | 20:02 | 18.33473 | 301.42611 | 301.41950 | 0.397 | +1.06944 | 1.06209 | 0.441 | Bradley |
| November 09 | 20:56 | 23.37223 | 301.12222 | 301.12900 | −0.407 | +2.45556 | 2.45207 | 0.209 | Bradley |
| November 10 | 18:20 | 24.26390 | 301.10556 | 301.10792 | −0.142 | +2.65750 | 2.65354 | 0.238 | Bradley |
| November 16 | 17:53 | 30.24515 | 301.13333 | 301.13217 | 0.070 | +3.79389 | 3.78930 | 0.275 | Bradley |
| November 19 | 19:06 | 33.29585 | 301.23056 | 301.23194 | −0.083 | +4.26028 | 4.26764 | −0.442 | Bradley |
| November 25 | 18:20 | 39.26390 | 301.54583 | 301.55213 | −0.378 | +5.09167 | 5.08888 | 0.167 | Bradley |
| December 01 | 19:45 | 45.32293 | 301.99722 | 302.00681 | −0.575 | +5.81528 | 5.83260 | −1.039 | Halley |
| December 18 | 18:45 | 62.28126 | 303.70972 | 303.70706 | 0.160 | +7.77500 | 7.77310 | 0.114 | Bradley |
| |$\langle {\Delta \alpha }\rangle = {0.20\prime }$| | |$\langle {\Delta \delta }\rangle = -{0.02\prime }$| | ||||||||
| |$S_{\Delta \alpha }={0.47\prime }$| | |$S_{\Delta \delta }={0.37\prime }$| | ||||||||
Bradley observed the comet at Wanstead in Essex, after he was alerted by Edmond Halley to the appearance of the comet. He used a telescope with a focal length of seven feet, equipped with a micrometer, which results in a sub-arcminute precision.
| Date . | Time . | JD . | RA (αB) . | RA (αE) . | αB − αE . | Dec (δB) . | Dec (δE) . | δB − δE . | . |
|---|---|---|---|---|---|---|---|---|---|
| (month dd) . | (hh:mm) . | −2350662 . | (°) . | (°) . | (′) . | (°) . | (°) . | (′) . | Observer . |
| October 20 | 20:05 | 3.33682 | 308.46252 | 308.41088 | 3.098 | −13.60611 | −13.55332 | −3.167 | Halley |
| October 21 | 18:21 | 4.26460 | 307.11111 | 307.09433 | 1.007 | −11.13750 | −11.13303 | −0.268 | Bradley |
| October 23 | 19:22 | 6.30696 | 305.11221 | 305.09902 | 0.792 | −7.31778 | −7.31362 | −0.249 | Bradley |
| 20:50 | 6.36807 | 305.06000 | 305.05268 | 0.439 | −7.22222 | −7.22236 | 0.008 | Bradley | |
| October 24 | 18:58 | 7.29029 | 304.37778 | 304.42153 | −2.625 | −6.16667 | −5.96508 | −12.095 | Bradley |
| October 25 | 20:57 | 8.37293 | 303.81944 | 303.81609 | 0.201 | −4.73167 | −4.72849 | −0.191 | Bradley |
| October 26 | 18:35 | 9.27432 | 303.41111 | 303.39876 | 0.741 | −3.85083 | −3.85296 | 0.128 | Bradley |
| November 01 | 18:22 | 15.26529 | 301.80639 | 301.79725 | 0.548 | −0.10000 | −0.10177 | 0.106 | Bradley |
| November 02 | 18:24 | 16.26668 | 301.65472 | 301.65197 | 0.165 | +0.31667 | 0.31418 | 0.149 | Bradley |
| November 04 | 20:02 | 18.33473 | 301.42611 | 301.41950 | 0.397 | +1.06944 | 1.06209 | 0.441 | Bradley |
| November 09 | 20:56 | 23.37223 | 301.12222 | 301.12900 | −0.407 | +2.45556 | 2.45207 | 0.209 | Bradley |
| November 10 | 18:20 | 24.26390 | 301.10556 | 301.10792 | −0.142 | +2.65750 | 2.65354 | 0.238 | Bradley |
| November 16 | 17:53 | 30.24515 | 301.13333 | 301.13217 | 0.070 | +3.79389 | 3.78930 | 0.275 | Bradley |
| November 19 | 19:06 | 33.29585 | 301.23056 | 301.23194 | −0.083 | +4.26028 | 4.26764 | −0.442 | Bradley |
| November 25 | 18:20 | 39.26390 | 301.54583 | 301.55213 | −0.378 | +5.09167 | 5.08888 | 0.167 | Bradley |
| December 01 | 19:45 | 45.32293 | 301.99722 | 302.00681 | −0.575 | +5.81528 | 5.83260 | −1.039 | Halley |
| December 18 | 18:45 | 62.28126 | 303.70972 | 303.70706 | 0.160 | +7.77500 | 7.77310 | 0.114 | Bradley |
| |$\langle {\Delta \alpha }\rangle = {0.20\prime }$| | |$\langle {\Delta \delta }\rangle = -{0.02\prime }$| | ||||||||
| |$S_{\Delta \alpha }={0.47\prime }$| | |$S_{\Delta \delta }={0.37\prime }$| | ||||||||
| Date . | Time . | JD . | RA (αB) . | RA (αE) . | αB − αE . | Dec (δB) . | Dec (δE) . | δB − δE . | . |
|---|---|---|---|---|---|---|---|---|---|
| (month dd) . | (hh:mm) . | −2350662 . | (°) . | (°) . | (′) . | (°) . | (°) . | (′) . | Observer . |
| October 20 | 20:05 | 3.33682 | 308.46252 | 308.41088 | 3.098 | −13.60611 | −13.55332 | −3.167 | Halley |
| October 21 | 18:21 | 4.26460 | 307.11111 | 307.09433 | 1.007 | −11.13750 | −11.13303 | −0.268 | Bradley |
| October 23 | 19:22 | 6.30696 | 305.11221 | 305.09902 | 0.792 | −7.31778 | −7.31362 | −0.249 | Bradley |
| 20:50 | 6.36807 | 305.06000 | 305.05268 | 0.439 | −7.22222 | −7.22236 | 0.008 | Bradley | |
| October 24 | 18:58 | 7.29029 | 304.37778 | 304.42153 | −2.625 | −6.16667 | −5.96508 | −12.095 | Bradley |
| October 25 | 20:57 | 8.37293 | 303.81944 | 303.81609 | 0.201 | −4.73167 | −4.72849 | −0.191 | Bradley |
| October 26 | 18:35 | 9.27432 | 303.41111 | 303.39876 | 0.741 | −3.85083 | −3.85296 | 0.128 | Bradley |
| November 01 | 18:22 | 15.26529 | 301.80639 | 301.79725 | 0.548 | −0.10000 | −0.10177 | 0.106 | Bradley |
| November 02 | 18:24 | 16.26668 | 301.65472 | 301.65197 | 0.165 | +0.31667 | 0.31418 | 0.149 | Bradley |
| November 04 | 20:02 | 18.33473 | 301.42611 | 301.41950 | 0.397 | +1.06944 | 1.06209 | 0.441 | Bradley |
| November 09 | 20:56 | 23.37223 | 301.12222 | 301.12900 | −0.407 | +2.45556 | 2.45207 | 0.209 | Bradley |
| November 10 | 18:20 | 24.26390 | 301.10556 | 301.10792 | −0.142 | +2.65750 | 2.65354 | 0.238 | Bradley |
| November 16 | 17:53 | 30.24515 | 301.13333 | 301.13217 | 0.070 | +3.79389 | 3.78930 | 0.275 | Bradley |
| November 19 | 19:06 | 33.29585 | 301.23056 | 301.23194 | −0.083 | +4.26028 | 4.26764 | −0.442 | Bradley |
| November 25 | 18:20 | 39.26390 | 301.54583 | 301.55213 | −0.378 | +5.09167 | 5.08888 | 0.167 | Bradley |
| December 01 | 19:45 | 45.32293 | 301.99722 | 302.00681 | −0.575 | +5.81528 | 5.83260 | −1.039 | Halley |
| December 18 | 18:45 | 62.28126 | 303.70972 | 303.70706 | 0.160 | +7.77500 | 7.77310 | 0.114 | Bradley |
| |$\langle {\Delta \alpha }\rangle = {0.20\prime }$| | |$\langle {\Delta \delta }\rangle = -{0.02\prime }$| | ||||||||
| |$S_{\Delta \alpha }={0.47\prime }$| | |$S_{\Delta \delta }={0.37\prime }$| | ||||||||
Bradley observed the comet at Wanstead in Essex, after he was alerted by Edmond Halley to the appearance of the comet. He used a telescope with a focal length of seven feet, equipped with a micrometer, which results in a sub-arcminute precision.
A parabolic orbit of C/1723 T1 was computed by several researchers including Bradley (1724) and Spörer (1843). In particular, Gustav Spörer computed the orbit as his doctoral dissertation with his advisor Johann Encke. The orbit is also listed in Winlock (1896). It was adopted by the NASA JPL Horizons On-Line System to generate the ephemeris of the comet. Table 2 shows the orbital elements determined by Bradley and by Spörer.
| Designation . | Bradley . | Spörer . | NASA JPL Horizons . | Meaning of the terms . |
|---|---|---|---|---|
| T0 | 1723 September 24.6 | 1723 September 28.128 | 1723 September 28.128 | Time of perihelion passage |
| ω | |${331.4\circ }$| | |${331.380\circ }$| | |${331.380\circ }$| | Argument of periapsis |
| Ω (J2000.0) | |${14.2\circ }$| | |${18.102\circ }$| | |${18.102\circ }$| | Longitude of ascending node |
| i | |${130.0\circ }$| | |${130.028\circ }$| | |${132.028\circ }$| | Inclination |
| q | 0.999 | 0.99879 | 0.99879 | Distance of periapsis |
| e | 1.0 | 1.0 | 1.0 | Eccentricity |
| Designation . | Bradley . | Spörer . | NASA JPL Horizons . | Meaning of the terms . |
|---|---|---|---|---|
| T0 | 1723 September 24.6 | 1723 September 28.128 | 1723 September 28.128 | Time of perihelion passage |
| ω | |${331.4\circ }$| | |${331.380\circ }$| | |${331.380\circ }$| | Argument of periapsis |
| Ω (J2000.0) | |${14.2\circ }$| | |${18.102\circ }$| | |${18.102\circ }$| | Longitude of ascending node |
| i | |${130.0\circ }$| | |${130.028\circ }$| | |${132.028\circ }$| | Inclination |
| q | 0.999 | 0.99879 | 0.99879 | Distance of periapsis |
| e | 1.0 | 1.0 | 1.0 | Eccentricity |
The NASA JPL Horizons System adopted the results of Spörer.
| Designation . | Bradley . | Spörer . | NASA JPL Horizons . | Meaning of the terms . |
|---|---|---|---|---|
| T0 | 1723 September 24.6 | 1723 September 28.128 | 1723 September 28.128 | Time of perihelion passage |
| ω | |${331.4\circ }$| | |${331.380\circ }$| | |${331.380\circ }$| | Argument of periapsis |
| Ω (J2000.0) | |${14.2\circ }$| | |${18.102\circ }$| | |${18.102\circ }$| | Longitude of ascending node |
| i | |${130.0\circ }$| | |${130.028\circ }$| | |${132.028\circ }$| | Inclination |
| q | 0.999 | 0.99879 | 0.99879 | Distance of periapsis |
| e | 1.0 | 1.0 | 1.0 | Eccentricity |
| Designation . | Bradley . | Spörer . | NASA JPL Horizons . | Meaning of the terms . |
|---|---|---|---|---|
| T0 | 1723 September 24.6 | 1723 September 28.128 | 1723 September 28.128 | Time of perihelion passage |
| ω | |${331.4\circ }$| | |${331.380\circ }$| | |${331.380\circ }$| | Argument of periapsis |
| Ω (J2000.0) | |${14.2\circ }$| | |${18.102\circ }$| | |${18.102\circ }$| | Longitude of ascending node |
| i | |${130.0\circ }$| | |${130.028\circ }$| | |${132.028\circ }$| | Inclination |
| q | 0.999 | 0.99879 | 0.99879 | Distance of periapsis |
| e | 1.0 | 1.0 | 1.0 | Eccentricity |
The NASA JPL Horizons System adopted the results of Spörer.
We generate the ephemeris of the comet C/1723 T1 using the NASA/JPL Horizons On-Line Ephemeris System.2 We obtain the topocentric apparent airless positions of the comet at Seoul (|${127.05\circ }$|E, |${37.58\circ }$|N). The positions of the Earth and the Sun are calculated using DE431, and the dates are given in the Gregorian calendar. HORIZONS adopts the UT1 and the ΔT table given by the Stephenson/Morrison spline (Stephenson & Morrison 1984; Stephenson 1997; Morrison & Stephenson 2004), and adjusts the UT values prior to 1962 for compatibility with the Horizons DE431 planetary ephemeris lunar tidal acceleration |$\dot{n}=-{25.8^{\prime \prime }}/cy^2$|. We also adopt the same ΔT table for the PC planetarium software Stellarium in this study.
The calculated equatorial coordinates of the comet are shown in table 1. We see that the observed positions of the comet on October 20 and October 24 have large errors. The position on October 20 was observed by Halley. Bradley could not measure the position of a reference star due to cloudy weather on October 24, but he estimated the position of the reference star to obtain the coordinate of the comet. The large error must have originated from this estimation. Thus we discard these two data and obtain the statistical quantities. We can see in table 1 that Bradley’s observations are in good agreement with the ephemeris generated by adopting Spörer’s orbital elements. The right ascensions of the comet measured by Bradley have the mean and the standard deviation of errors |$\langle {\Delta \alpha }\rangle \pm S_{\Delta \alpha }={0.20^{\prime }}\pm {0.47^{\prime }}$|, and the declinations have the mean and the standard deviation of errors |$\langle {\Delta \delta }\rangle \pm S_{\Delta \delta }=-{0.02^{\prime }}\pm {0.37^{\prime }}$|.
2.2 Korean records
Whenever a special celestial object, either a comet or a guest star, appeared, continuous and intensive observations were made by teams of court astronomers in the Joseon dynasty. They wrote daily reports, called Seong-Byeon Cheuku Danja in Korean, to inform the monarch and the court of the observational results. (Hereafter, the reports are denoted by “the Reports,” for convenience.) After the celestial phenomenon disappeared, these Reports were collected, copied, and bound into a manuscript book called the Astronomical Registry, or Cheon-Byeon Deungnok in Korean, for preservation in the Royal Astronomical Bureau. They are called the Registry of Comet, the Registry of Guest Star, or the Registry of Stellar Phenomenon in accordance with the kinds of celestial phenomena. (We call these books “the Registries” in this paper for convenience.) Moreover, the astronomers in the Royal Astronomical Bureau compiled observational Reports every six months to be bound into manuscript books called the Extracts of Celestial Phenomena, or Cheon-Byeon Chochul in Korean (Sekiguti 1917a). We call these books the “Extracts” in this paper for convenience.)
Wada (1917) reported his inspection of the observational documents that had been piled up in a storage building of the Royal Astronomical Bureau of the Joseon dynasty. However, only 12 volumes of them, including eight Registries and four Extracts, were saved by his colleagues (Sekiguti 1917a, 1917b; Ahn 2013). Currently, the whereabouts of only six volumes of the Registries are known (Nha 1982; Nha et al. 2012; Ahn 2013), and one of them is the Astronomical Registries of the comet C/1723 T1.
In addition, we have other data sources that can be complementary to the first-hand records in the Registries. During the Joseon dynasty, the observational records documented in the Reports were submitted to the Royal Secretariats and then reported to the monarch. The Royal Secretariats kept documenting those records into a Diary called Seungjeongwon Ilgi. Moreover, after a monarch died, all the official documents, including astronomical Reports, that had been generated during their reign were collected to be used as historical sources for editing the official chronicle, called the Sillok, of the monarch. Thus, we can now seethe observational data for the comet C/1723 T1 in the Diary and the Sillok as well. In this paper, we analyze the observational records written in the Astronomical Registry of the comet C/1723 T1, whose Chinese letters were deciphered and listed in Nha (1982). Moreover, we cross-check the observational records written in these literatures, translate them into English, and show them in appendix 2.
A typical observational record for C/1723 T1 is “The 27th day of the 9th month in the 3rd reign year of King Gyeongjong: During the 1st watch of the night, the comet had moved to be seen at 3 du of (the lunar lodge) Niu and a polar angle of 98 du.” From these records, we have information such as dates/times of observation and lodge/polar angles. The time system used in 1723 is different from the modern system. The lodge and polar angles are defined in a different way from the modern equatorial coordinates. Hence, these data must be converted into modern values.
First, the dates and times must be converted into the modern system. The dates are given in the lunar calendar, and so it can be converted into the Gregorian calendar using the date conversion table given by Han (1987). Here, we have to be cautious in the date conversion. The dates in the records are different from the observational dates. If the observation was made after midnight, the observational date is the same as the date of the record; but if the observation was made before midnight, the observational date should be one day earlier than the date of record. For example, the record described above was recorded on 1723 October 25, but the observational date should be 1723 October 24, because the observation was made during the 1st watch of the previous night, i.e., before midnight.
The time system that was used in the records needs to be explained in more detail. According to the previous research on the time systems used in the Joseon dynasty (Saito 1994; Ahn et al. 2006; Hahn & Nam 2008), the night-watch system was established in 1434 or the 16th reign year of King Sejong when the automated clepsydra called Jagyeongnu was developed and began to be operated. The night-watch system adopted at that time was the Shoushi or Datong system.3
In 1653, the Joseon dynasty adopted the new night-watch system defined in accordance with the Xixian calendar system that had already been adopted by the Qing dynasty in 1645. In the Xixian system, one day was divided into 96 equal segments of time, and the twilight time span is defined as the time span between the sunset/sunrise and the time when the altitude of the Sun becomes −18°, which is the same as the definition of astronomical twilight in modern astronomy. However, according to a record in the Sillok, it is certain that the old-fashioned Shoushi/Datong system had still been in use in astronomical observations in 1754 CE (Lee et al. 2011). It was in 1789 when the new time system in the Xixian system began to be used in reality (Seo et al. 1796).
Considering these historical facts, it is certain that the observing times recorded in the records of C/1723 T1 can be calculated with the Shoushi/Datong system. In the Shoushi/Datong system, one day is segmented into 100 equal parts called ge, and the duration of night is defined as a time span between the evening twilight time to the morning twilight time. Here, the evening twilight time is defined as the time 2.5 ge after the sunset of the day, and the morning twilight time is defined as the time 2.5 ge before the sunrise of the next day. The time of 2.5 ge is called the twilight time span. The duration of night is divided into five equal segments. Each time segment is called a watch (or geng in Chinese, gyeong in Korean). The twilight time span, Δtwi, is defined to be Δtwi = 2.5 ge or 36 min for either the evening twilight or the morning twilight. When a sunset time, tset, and a sunrise time, trise, are given, the night duration, τ, will be τ = (trise − Δtwi) − (tset + Δtwi), and the interval for one watch is obtained by τ/5. The first watch will then be from (tset + Δtwi) to (tset + Δtwi) + τ/5, and the mid-first-watch will be (tset + Δtwi) + τ/10. We convert the observational time into the Julian day (JD). The third column of table 3 presents the observational times calculated in accordance with the Shoushi/Datong system.
Observational data for C/1723 T1 made by the court astronomers of the Joseon dynasty.*
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . | (13) . | . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Record . | Obs. . | Obs. . | TJD . | H.A. . | RA . | L.A. . | L.A. . | Error . | Dec . | P.A. . | P.A. . | Error . | . |
| dates . | dates . | times . | . | h . | αE . | Aobs . | Acal . | eA . | δE . | Δobs . | Δcal . | |$e_\Delta$| . | . |
| (lunar) . | (Greg.) . | geng/hh:mm . | (d) . | (°) . | (°) . | (du) . | (du) . | (du) . | (°) . | (du) . | (du) . | (du) . | . |
| 09.25 | October 20 | 2/21:57 | 3.04 | 40.78 | 308.91 | 7 | 7.65 | −14.46 | 105 | 105.99 | A | ||
| October 21 | 2/21:54 | 4.04 | 42.54 | 307.38 | 7 | 6.11 | −11.68 | 105 | 103.17 | B | |||
| October 22 | 2/21:56 | 5.04 | 9.49 | 306.22 | 7 | 4.92 | 2.08 | −9.68 | 105 | 100.94 | 4.06 | C | |
| 09.26 | October 22 | 1/19:34 | 4.94 | 9.49 | 306.32 | 4 | 5.03 | −9.68 | 101 | 101.14 | |$\bigcirc{1}$| | ||
| October 23 | 1/19:33 | 5.94 | 11.16 | 305.39 | 4 | 4.09 | −0.09 | −7.89 | 101 | 99.32 | 1.68 | |$\bigcirc{2}$| | |
| 09.27 | October 24 | 1/19:32 | 6.94 | 12.64 | 304.65 | 3 | 3.33 | −0.33 | −6.42 | 98 | 97.83 | 0.17 | |
| 09.28 | October 25 | 1/19:31 | 7.94 | 13.98 | 304.04 | 2 | 2.72 | −0.72 | −5.20 | 96 | 96.59 | −0.59 | |
| 09.30 | October 27 | 1/19:29 | 9.94 | 16.36 | 303.13 | 1 | 1.79 | −0.79 | −3.28 | 95 | 94.65 | 0.35 | |
| 10.01 | October 28 | 1/19:28 | 10.94 | 17.44 | 302.78 | 1 | 1.44 | −0.44 | −2.52 | 94 | 93.87 | 0.13 | |
| 10.02 | October 29 | 1/19:26 | 11.93 | 18.22 | 302.49 | 1 | 1.14 | −0.14 | −1.85 | 93 | 93.19 | −0.19 | |
| 10.03 | October 30 | 1/19:26 | 12.93 | 19.45 | 302.24 | 1 | 0.89 | 0.11 | −1.25 | 92.5 | 92.59 | −0.09 | |
| 10.04 | October 31 | 1/19:25 | 13.93 | 20.40 | 302.03 | 1 | 0.68 | 0.32 | −0.73 | 92 | 92.05 | −0.05 | |
| 10.05 | November 01 | 1/19:24 | 14.93 | 21.32 | 301.85 | 1 | 0.49 | 0.51 | −0.25 | 91.5 | 91.55 | −0.05 | |
| Statistics for full data | 〈eA〉 = +0.05 | |$\langle {e_\Delta }\rangle =+0.5$| | |||||||||||
| |$\langle {S_{e_{\rm A}}}\rangle \simeq 0.8$| | |$\langle {S_{e_\Delta }}\rangle \simeq 1.4$| | ||||||||||||
| Statistics for records except for the records of 09.25 and 09.26 | 〈eA〉 ≃ −0.2 | |$\langle {e_\Delta }\rangle =-0.04$| | |||||||||||
| |$\langle {S_{e_{\rm A}}}\rangle \simeq 0.5$| | |$\langle {S_{e_\Delta }}\rangle \simeq 0.3$| | ||||||||||||
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . | (13) . | . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Record . | Obs. . | Obs. . | TJD . | H.A. . | RA . | L.A. . | L.A. . | Error . | Dec . | P.A. . | P.A. . | Error . | . |
| dates . | dates . | times . | . | h . | αE . | Aobs . | Acal . | eA . | δE . | Δobs . | Δcal . | |$e_\Delta$| . | . |
| (lunar) . | (Greg.) . | geng/hh:mm . | (d) . | (°) . | (°) . | (du) . | (du) . | (du) . | (°) . | (du) . | (du) . | (du) . | . |
| 09.25 | October 20 | 2/21:57 | 3.04 | 40.78 | 308.91 | 7 | 7.65 | −14.46 | 105 | 105.99 | A | ||
| October 21 | 2/21:54 | 4.04 | 42.54 | 307.38 | 7 | 6.11 | −11.68 | 105 | 103.17 | B | |||
| October 22 | 2/21:56 | 5.04 | 9.49 | 306.22 | 7 | 4.92 | 2.08 | −9.68 | 105 | 100.94 | 4.06 | C | |
| 09.26 | October 22 | 1/19:34 | 4.94 | 9.49 | 306.32 | 4 | 5.03 | −9.68 | 101 | 101.14 | |$\bigcirc{1}$| | ||
| October 23 | 1/19:33 | 5.94 | 11.16 | 305.39 | 4 | 4.09 | −0.09 | −7.89 | 101 | 99.32 | 1.68 | |$\bigcirc{2}$| | |
| 09.27 | October 24 | 1/19:32 | 6.94 | 12.64 | 304.65 | 3 | 3.33 | −0.33 | −6.42 | 98 | 97.83 | 0.17 | |
| 09.28 | October 25 | 1/19:31 | 7.94 | 13.98 | 304.04 | 2 | 2.72 | −0.72 | −5.20 | 96 | 96.59 | −0.59 | |
| 09.30 | October 27 | 1/19:29 | 9.94 | 16.36 | 303.13 | 1 | 1.79 | −0.79 | −3.28 | 95 | 94.65 | 0.35 | |
| 10.01 | October 28 | 1/19:28 | 10.94 | 17.44 | 302.78 | 1 | 1.44 | −0.44 | −2.52 | 94 | 93.87 | 0.13 | |
| 10.02 | October 29 | 1/19:26 | 11.93 | 18.22 | 302.49 | 1 | 1.14 | −0.14 | −1.85 | 93 | 93.19 | −0.19 | |
| 10.03 | October 30 | 1/19:26 | 12.93 | 19.45 | 302.24 | 1 | 0.89 | 0.11 | −1.25 | 92.5 | 92.59 | −0.09 | |
| 10.04 | October 31 | 1/19:25 | 13.93 | 20.40 | 302.03 | 1 | 0.68 | 0.32 | −0.73 | 92 | 92.05 | −0.05 | |
| 10.05 | November 01 | 1/19:24 | 14.93 | 21.32 | 301.85 | 1 | 0.49 | 0.51 | −0.25 | 91.5 | 91.55 | −0.05 | |
| Statistics for full data | 〈eA〉 = +0.05 | |$\langle {e_\Delta }\rangle =+0.5$| | |||||||||||
| |$\langle {S_{e_{\rm A}}}\rangle \simeq 0.8$| | |$\langle {S_{e_\Delta }}\rangle \simeq 1.4$| | ||||||||||||
| Statistics for records except for the records of 09.25 and 09.26 | 〈eA〉 ≃ −0.2 | |$\langle {e_\Delta }\rangle =-0.04$| | |||||||||||
| |$\langle {S_{e_{\rm A}}}\rangle \simeq 0.5$| | |$\langle {S_{e_\Delta }}\rangle \simeq 0.3$| | ||||||||||||
The dates in the lunar calendar are given in the first column. For example, 09.21 means the 21st day of the 9th month (of the 3rd reign year of King Gyeongjong, or 1723). The second column represents the dates of observations in the Gregorian calendar. The third column represents the observing times, where the first numbers are the times in watches or geng, and the final numbers are the mid-watch times. The fourth column represents the dates and times, TJD, in Julian days of J1723.0 counted after JD =2350662. The fifth column is the hour angle of the comet at the observing time. The sixth, seventh, and eighth columns represent the right ascensions, the observed lodge angles, and the ephemeris lodge angles of the comet, respectively. The lodge angles are referenced to the lunar lodge of Niu or Quanniu (β Cap), whose right ascension was |$\alpha _0={301.36\circ }$| during this period. The ninth column represents the errors in the lodge angles |$e_{\rm A}=A_{\rm obs}-A_{\rm cal}$|. The 10th, 11th, and 12th columns represent the ephemeris declinations, the observed polar angles, and the ephemeris polar angles of the comet, respectively. The 13th column represents the errors in the polar angles |$e_\Delta=\Delta_{\rm obs}-\Delta_{\rm cal}$|. We do not show the observational data that do not have measurements.
Observational data for C/1723 T1 made by the court astronomers of the Joseon dynasty.*
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . | (13) . | . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Record . | Obs. . | Obs. . | TJD . | H.A. . | RA . | L.A. . | L.A. . | Error . | Dec . | P.A. . | P.A. . | Error . | . |
| dates . | dates . | times . | . | h . | αE . | Aobs . | Acal . | eA . | δE . | Δobs . | Δcal . | |$e_\Delta$| . | . |
| (lunar) . | (Greg.) . | geng/hh:mm . | (d) . | (°) . | (°) . | (du) . | (du) . | (du) . | (°) . | (du) . | (du) . | (du) . | . |
| 09.25 | October 20 | 2/21:57 | 3.04 | 40.78 | 308.91 | 7 | 7.65 | −14.46 | 105 | 105.99 | A | ||
| October 21 | 2/21:54 | 4.04 | 42.54 | 307.38 | 7 | 6.11 | −11.68 | 105 | 103.17 | B | |||
| October 22 | 2/21:56 | 5.04 | 9.49 | 306.22 | 7 | 4.92 | 2.08 | −9.68 | 105 | 100.94 | 4.06 | C | |
| 09.26 | October 22 | 1/19:34 | 4.94 | 9.49 | 306.32 | 4 | 5.03 | −9.68 | 101 | 101.14 | |$\bigcirc{1}$| | ||
| October 23 | 1/19:33 | 5.94 | 11.16 | 305.39 | 4 | 4.09 | −0.09 | −7.89 | 101 | 99.32 | 1.68 | |$\bigcirc{2}$| | |
| 09.27 | October 24 | 1/19:32 | 6.94 | 12.64 | 304.65 | 3 | 3.33 | −0.33 | −6.42 | 98 | 97.83 | 0.17 | |
| 09.28 | October 25 | 1/19:31 | 7.94 | 13.98 | 304.04 | 2 | 2.72 | −0.72 | −5.20 | 96 | 96.59 | −0.59 | |
| 09.30 | October 27 | 1/19:29 | 9.94 | 16.36 | 303.13 | 1 | 1.79 | −0.79 | −3.28 | 95 | 94.65 | 0.35 | |
| 10.01 | October 28 | 1/19:28 | 10.94 | 17.44 | 302.78 | 1 | 1.44 | −0.44 | −2.52 | 94 | 93.87 | 0.13 | |
| 10.02 | October 29 | 1/19:26 | 11.93 | 18.22 | 302.49 | 1 | 1.14 | −0.14 | −1.85 | 93 | 93.19 | −0.19 | |
| 10.03 | October 30 | 1/19:26 | 12.93 | 19.45 | 302.24 | 1 | 0.89 | 0.11 | −1.25 | 92.5 | 92.59 | −0.09 | |
| 10.04 | October 31 | 1/19:25 | 13.93 | 20.40 | 302.03 | 1 | 0.68 | 0.32 | −0.73 | 92 | 92.05 | −0.05 | |
| 10.05 | November 01 | 1/19:24 | 14.93 | 21.32 | 301.85 | 1 | 0.49 | 0.51 | −0.25 | 91.5 | 91.55 | −0.05 | |
| Statistics for full data | 〈eA〉 = +0.05 | |$\langle {e_\Delta }\rangle =+0.5$| | |||||||||||
| |$\langle {S_{e_{\rm A}}}\rangle \simeq 0.8$| | |$\langle {S_{e_\Delta }}\rangle \simeq 1.4$| | ||||||||||||
| Statistics for records except for the records of 09.25 and 09.26 | 〈eA〉 ≃ −0.2 | |$\langle {e_\Delta }\rangle =-0.04$| | |||||||||||
| |$\langle {S_{e_{\rm A}}}\rangle \simeq 0.5$| | |$\langle {S_{e_\Delta }}\rangle \simeq 0.3$| | ||||||||||||
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . | (13) . | . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Record . | Obs. . | Obs. . | TJD . | H.A. . | RA . | L.A. . | L.A. . | Error . | Dec . | P.A. . | P.A. . | Error . | . |
| dates . | dates . | times . | . | h . | αE . | Aobs . | Acal . | eA . | δE . | Δobs . | Δcal . | |$e_\Delta$| . | . |
| (lunar) . | (Greg.) . | geng/hh:mm . | (d) . | (°) . | (°) . | (du) . | (du) . | (du) . | (°) . | (du) . | (du) . | (du) . | . |
| 09.25 | October 20 | 2/21:57 | 3.04 | 40.78 | 308.91 | 7 | 7.65 | −14.46 | 105 | 105.99 | A | ||
| October 21 | 2/21:54 | 4.04 | 42.54 | 307.38 | 7 | 6.11 | −11.68 | 105 | 103.17 | B | |||
| October 22 | 2/21:56 | 5.04 | 9.49 | 306.22 | 7 | 4.92 | 2.08 | −9.68 | 105 | 100.94 | 4.06 | C | |
| 09.26 | October 22 | 1/19:34 | 4.94 | 9.49 | 306.32 | 4 | 5.03 | −9.68 | 101 | 101.14 | |$\bigcirc{1}$| | ||
| October 23 | 1/19:33 | 5.94 | 11.16 | 305.39 | 4 | 4.09 | −0.09 | −7.89 | 101 | 99.32 | 1.68 | |$\bigcirc{2}$| | |
| 09.27 | October 24 | 1/19:32 | 6.94 | 12.64 | 304.65 | 3 | 3.33 | −0.33 | −6.42 | 98 | 97.83 | 0.17 | |
| 09.28 | October 25 | 1/19:31 | 7.94 | 13.98 | 304.04 | 2 | 2.72 | −0.72 | −5.20 | 96 | 96.59 | −0.59 | |
| 09.30 | October 27 | 1/19:29 | 9.94 | 16.36 | 303.13 | 1 | 1.79 | −0.79 | −3.28 | 95 | 94.65 | 0.35 | |
| 10.01 | October 28 | 1/19:28 | 10.94 | 17.44 | 302.78 | 1 | 1.44 | −0.44 | −2.52 | 94 | 93.87 | 0.13 | |
| 10.02 | October 29 | 1/19:26 | 11.93 | 18.22 | 302.49 | 1 | 1.14 | −0.14 | −1.85 | 93 | 93.19 | −0.19 | |
| 10.03 | October 30 | 1/19:26 | 12.93 | 19.45 | 302.24 | 1 | 0.89 | 0.11 | −1.25 | 92.5 | 92.59 | −0.09 | |
| 10.04 | October 31 | 1/19:25 | 13.93 | 20.40 | 302.03 | 1 | 0.68 | 0.32 | −0.73 | 92 | 92.05 | −0.05 | |
| 10.05 | November 01 | 1/19:24 | 14.93 | 21.32 | 301.85 | 1 | 0.49 | 0.51 | −0.25 | 91.5 | 91.55 | −0.05 | |
| Statistics for full data | 〈eA〉 = +0.05 | |$\langle {e_\Delta }\rangle =+0.5$| | |||||||||||
| |$\langle {S_{e_{\rm A}}}\rangle \simeq 0.8$| | |$\langle {S_{e_\Delta }}\rangle \simeq 1.4$| | ||||||||||||
| Statistics for records except for the records of 09.25 and 09.26 | 〈eA〉 ≃ −0.2 | |$\langle {e_\Delta }\rangle =-0.04$| | |||||||||||
| |$\langle {S_{e_{\rm A}}}\rangle \simeq 0.5$| | |$\langle {S_{e_\Delta }}\rangle \simeq 0.3$| | ||||||||||||
The dates in the lunar calendar are given in the first column. For example, 09.21 means the 21st day of the 9th month (of the 3rd reign year of King Gyeongjong, or 1723). The second column represents the dates of observations in the Gregorian calendar. The third column represents the observing times, where the first numbers are the times in watches or geng, and the final numbers are the mid-watch times. The fourth column represents the dates and times, TJD, in Julian days of J1723.0 counted after JD =2350662. The fifth column is the hour angle of the comet at the observing time. The sixth, seventh, and eighth columns represent the right ascensions, the observed lodge angles, and the ephemeris lodge angles of the comet, respectively. The lodge angles are referenced to the lunar lodge of Niu or Quanniu (β Cap), whose right ascension was |$\alpha _0={301.36\circ }$| during this period. The ninth column represents the errors in the lodge angles |$e_{\rm A}=A_{\rm obs}-A_{\rm cal}$|. The 10th, 11th, and 12th columns represent the ephemeris declinations, the observed polar angles, and the ephemeris polar angles of the comet, respectively. The 13th column represents the errors in the polar angles |$e_\Delta=\Delta_{\rm obs}-\Delta_{\rm cal}$|. We do not show the observational data that do not have measurements.
For a given time of observation, the right ascension of the comet, αE, is calculated using the NASA JPL Horizons system based on the orbital elements determined by Spörer, and the right ascension of the determinative star of the lunar lodge Quanniu (β Cap), α0, is obtained using Stellarium. Here, it is well-known that the determinative star of the lunar lodge Niu is identified with β Cap, which can be confirmed in many literatures (e.g., Pan 1984; Sun 1997; Ahn et al. 2006; Cullen 1996, etc.). The ephemeris lodge angle of the comet, Acal, is then calculated by Acal = αE − α0. If the comet is located within another lunar lodge, then the determinative star of that lunar lodge must be used as a reference star. The ephemeris polar angle of the comet, Δcal, is calculated by Δcal = 90° − δE, where δE is the ephemeris declination of the comet obtained using the NASA JPL Horizons system. Both lodge and polar angles are in Babylonian degrees, and so they are converted into the Chinese degrees by considering the fact that 360° in Babylonian degrees are equivalent to 365.2575 du in Chinese degrees following the Chiljeongsan system or, equivalently, the Shoushi/Datong system (Lee et al. 2010).
We calculate both lodge and polar angles for all the observational data recorded in the Astronomical Registry for C/1723, and show them in table 3. The errors in the lodge and polar angles are shown in the ninth and 13th columns, respectively. Their means and the sample standard deviations are shown in the second line from the bottom. We see that the errors can be statistically considered as agreeing with zero within the sample standard deviations. However, the two data for the dates of 09.25 and 09.26 seem to be rather far from the zero error, even within the obtained sample standard deviations. Hence, we obtain the means and the sample standard deviations for a sample excluding the data for 09.25 and 09.26. We see that the errors in this case can also be regarded as being zero within the sample standard deviations. Morever, the sample standard deviations are acceptable because the graduations of the presumed observing instrument (such as the Small armilla) are thought to have been graduated by a quarter du (at least one du). We know that the other instruments developed and used during the Joseon dynasty had been graduated as such.
In order to see how far the data of 09.25 and 09.25 are from the actual orbit of the comet, we show in figure 1 the positions of the comet measured by the Korean observers as well as those calculated from the known orbital elements. The white dots linked by a solid line are the positions of the comet calculated using the NASA JPL Horizons system for every day at 00:00 Local Standard Time. Here, the times are given in Local Standard Time (LST) for convenience. The numbers attached to the white dots in figure 1 represent the ephemeris dates, and the numbers attached to the stars represent the dates of observations. The numbers in the squared brackets are the observational dates in the lunar calendar, which are also given in the first column of table 3.
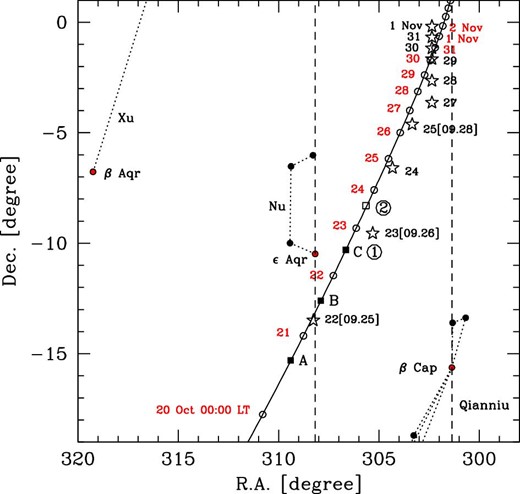
Apparent motion of the comet C/1723 T1 and the positions of the comet measured by the court astronomers of the Joseon dynasty. The white dots linked by a curve represent the apparent motion of the comet calculated with the orbital elements determined by Spörer, which can be regarded as being the true positions. The numbers attached to the dots means the observing date at the Local Standard Time 00 : 00 for every day in Seoul. The stars represent the positions of the comet measured by the court astronomers. The observational dates are tagged to the stars. The observed position on October 22 can be chosen among A, B, and C, while the observed position on October 23 can be chosen between |$\bigcirc{1}\,\,$| and |$\bigcirc{2}\,\,$|. (Color online)
In figure 1 we see that all records but three are in agreement with the ephemeris positions. The three exceptions are the observational records of 09.25, 09.26, and 09.28 in lunar dates, as shown in figure 1. The observation of 09.28 (or October 26) was actually observed in the evening of October 25, but the observed coordinate angles indicate that the comet was located on the position of October 26. There must be some confusion in date-keeping, but we may neglect this difference because the comet moved slowly during this period.
The observed positions of 09.25 and 09.26 seem to be much further from the actual orbit of the comet. The lunar date of 09.25 is converted to October 23 in the record date. The actual observation must have been made in the evening of October 22. However, the observed position of the comet on that date is too far from the ephemeris position, which is located at the position plotted by a black square and labelled as C in figure 1. There must be some errors in the record, and so we can make a choice for the correct observational date from three possibilities. We designate the three possibilities by black squares labelled as A, B, and C in figure 1 and in the right-most column of table 3. Similarly, the lunar date of 09.26 is converted to be October 24 in record date. The actual observation must have been made in the evening of October 23. However, the observed position of the comet is between the two nearby ephemeris positions, which are labelled with |$\bigcirc{1}$| and |$\bigcirc{2}$| in figure 1 and in the right-most column of table 3. Thus we have two choices for the identification of the 09.26 record. In this paper, we define data sets labelled by A1, A2, B1, B2, and C2 by combinations of the choices {A, B, C} for the record of 09.25 and the choices|$\lbrace \bigcirc{1}\,\,,\ \bigcirc{2}\,\,\rbrace$| for the record of 09.26.
On the other hand, it is natural that all the observational Reports were bound into a book in a proper sequence of observational dates. We have no reason to doubt the integrity of the dates of records written in the Registry. Moreover, according to the report of 09.25, lightning struck before the observation and the altitude of the comet was relatively low during the observation. Hence it is likely that the observation has peculiarly large errors. Therefore, it would be better to discard the record of 09.25. By discarding the record of 09.25, we form the CS data set that is composed of nine observations. Furthermore, discarding one more record of 09.26, we form the CC data set composed of eight observations.
In addition, analysing the observational data for the retrograde motion of Mars in 1491 CE (Ahn 2021), we have seen that some court astronomers rounded up their measurements while some others rounded down their measurements. Similarly, we do not know whether the court astronomers in 1723 rounded up or rounded down their measurements from the first decimal place. Hence, we are to consider the two possibilities together in this paper. Meanwhile, we see in table 3 that two polar angles have angles of half du. Thus, for consistency, we form the CR data set that is identical to the CC data set except that the two polar angles with half-du are forced to be rounded up; while the CR′ data set is identical to the CC data set except that the two polar angles with half-du are forced to be rounded down. Assuming that the recorded angles were rounded up, we conducted the χ2 minimizations to obtain the misalignment corrections and the measurement errors for the data sets of A1, A2, B1, B2, C2, CS, CC, and CR. After that, assuming that the recorded angles were rounded down, we performed the same analyses for A1, A2, B1, B2, C2, CS, CC, and CR′.
3 Results
The device for measuring positions of the comet must have been a small meridian device whose axis of rotation should be aligned with the axis of the Earth’s rotation. There should be alignment errors in elevation and azimuth of the polar axis. We denote the alignment error in elevation by De and the alignment error in azimuth by Da. The polar alignment error in elevation is defined in such a way that its positive value means that the polar axis of the device is pointing to the south of the north celestial pole. A positive error in azimuth means that the polar axis of the armilla is pointing to the east of the northern celestial pole.
We describe how to obtain De and Da such that the χ2 value of observational errors is minimized. We consider a sufficiently large domain of (De, Da), for example De ∈ (−5°, 5°) and Da ∈ (−5°, 5°). For each grid value of (De, Da), we obtain both the polar alignment error for the ith lodge angle, |$D_A^i=D_\alpha ^i$|, and the polar alignment error in the ith polar angle, |$D_\Delta ^i=-D_\delta ^i$|, by plugging the declination (δi) and hour angle (hi) of the comet at the time of the ith observation into equation (1). Here, the hour angles and declinations of the comet are calculated using NASA JPL Horizons for the observing times corresponding to the mid-watch times. We list the mid-watch times, the hour angles, and the declinations in the third, fifth, and ninth columns of table 3, respectively. We note that the errors in the hour angles are roughly ±15°, because the observing times are given in a time unit of “watch” that is roughly two hours.
We will then calculate the measurement errors in lodge and polar angles. If the court astronomers rounded up their measurements from the first decimal place, we will get the misaligned lodge angles |$\lfloor (A_{\rm cal}^i)^*+1/2\rfloor$| and the misaligned polar angle |$\lfloor (\Delta _{\rm cal}^i)^*+1/2\rfloor$|; if court astronomers rounded down their measurements from the first decimal place, then we would get the lodge angles |$\lfloor (A_{\rm cal}^i)^*\rfloor$| and the polar angle |$\lfloor (\Delta _{\rm cal}^i)^*\rfloor$|. Here, ⌊x⌋ is a floor function of x. In principle, we should calculate the measurement errors in this way. However, the rounding up/down of measured angles from the first decimal place gives rise to integral contributions to χ2 values, and the number of data is not sufficiently large. Hence, the resultant χ2 statistic maps are not smooth but patched, such that the minimum |$\chi _{\rm min}^2$| cannot be well constrained. We describe this problem in appendix 1 in detail, and we present an alternative method to mitigate this problem.
Lodge angles are obtained by measuring the positions of both the comet and the determinative star (or the reference star of the lunar lodge), while polar angles are obtained by measuring the object once with one end of the graduations fixed at the rotation axis of the armilla. Moreover, the measured angles can be either rounded up or rounded down during the measurements. For these cases, the statistical properties of observational errors in angles are investigated by Ahn (2021).
Whether the measured lodge/polar angles were rounded up or down, the variance of observational errors in lodge angles is |$(\sigma _{\rm e_{\rm A}}^i)^2=2(\sigma _{\rm m}^i)^2+1/12$| and the variance of observational errors in polar angles is |$(\sigma _{{\rm e}_\Delta }^i)^2=(\sigma _{\rm m}^i)^2+1/12$|, where |$\sigma _{\rm m}^i$| is the single measurement error for the ith observation, meaning the measurement error associated with reading the position once in the graduations. A detailed discussion on this can be found in Ahn (2021). Furthermore, we assume that each measurement of lodge angles has the same variance or |$(\sigma _{\rm e_{\rm A}}^i)^2=\sigma _{\rm e_{\rm A}}^2=2\sigma _{\rm m}^2+1/12$| for all i = 1, 2, 3, ..., nA. We also assume that each measurement of polar angles has the same variance or |$(\sigma _{{\rm e}_\Delta }^i)^2=\sigma _{{\rm e}_\Delta }^2=\sigma _{\rm m}^2+1/12$| for all |$i=1, 2, 3, ..., n_\Delta$|. Here, nA is the number of lodge angles, and |$n_\Delta$| is the number of polar angles. Since the measurements must have been made with the same instrument, there is no reason that the one-time measurement errors for each observation are different from one another. Thus we assume that |$\sigma _{\rm m}^i=\sigma _{\rm m}$| for every observation.
Now, we conduct χ2 minimizations for the data sets denoted by A1, A2, B1, B2, C2, CS, CC, and CR, assuming that the observed angles were rounded up. For example, for the case of A1, we have 10 lodge angles and 10 polar angles; that is, nA = 10 and |$n_\Delta =10$|. We know that the two means |$\langle e_{\rm A}\rangle =\langle e_\Delta \rangle =0$| because we assume that all measurements were rounded up. We have two unknowns, De and Da, with the single measurement error σm being a free parameter. Thus, the degrees of freedom become |$\nu =n_{\rm A}+n_\Delta -2=18$|. If the model is correct, we expect |$\chi _{\rm min}^2\simeq \nu \pm \sqrt{2\nu }$|. Hence, we search for a proper model or unknowns (De, Da) to give |$\chi _{\rm min}^2\simeq \nu$|.
Figure 2 shows the χ2 statistic map for the A1 data set. We find that the model with the misalignment of the polar axis amounting to |$(D_{\rm e}, D_{\rm a})=(+{0.24\circ }, -{0.38\circ })$| is the proper model that minimizes the χ2 statistic. Moreover, it should be |$\sigma _{\rm m}={0.29\circ }\simeq {0{_{.}^{\circ}}3}$| in order for |$\chi _{\rm min}^2=\nu =18$|.

χ2 statistic map for alignment errors of the polar axis for the data set A1 that best fits the observed lodge and polar angles, assuming that the angles were rounded up. The contours for the 1σ, 2σ, and 3σ χ2 values are drawn. The best-fitting values are the polar alignment error in elevation |$D_{\rm e}=+{0{_{.}^{\circ}}24}$| and the polar alignment error in azimuth |$D_{\rm a}=-{0{_{.}^{\circ}}38}$|, with the one-time measurement error being |$\sigma _{\rm m}={0{_{.}^{\circ}}29}$|.
For the case of two variables, a joint confidence region for (De, Da) is defined by the zone which satisfies |$\chi ^2<\chi _{\rm min}^2+\Delta \chi ^2$|, where Δχ2 = 2.30 for the |$68.27\%$| confidence level (1σ), Δχ2 = 6.17 for the |$95.45\%$| confidence level (2σ), and Δχ2 = 11.8 for the |$99.73\%$| confidence level (3σ). We obtain the |$68\%$| confidence interval |$D_{\rm e}=[+{0.03\circ }, +{0.45\circ }]$| and the |$99.7\%$| confidence interval |$D_{\rm e}=[-{0.23\circ }, +{0.71\circ }]$| with |$D_{\rm a}=-{0.38\circ }$| fixed. We also obtain the |$68\%$| confidence interval |$D_{\rm a}=[-{0.71\circ },-{0.38\circ }]$| and the |$99.7\%$| confidence interval |$D_{\rm a}=[-{1.11\circ }, +{0.34\circ }]$| with |$D_{\rm e}=+{0.24\circ }$| fixed. Therefore, we conclude that |$D_{\rm e}=+{0.24\circ }\pm {0.21\circ }\simeq +{0.2\circ }\pm {0.2\circ }$| and |$D_{\rm a}=-{0.38\circ }\pm {0.32\circ }\simeq -{0.4\circ }\pm {0.3\circ }$| (to 1σ) and |$D_{\rm e}=+{0.24\circ }\pm {0.47\circ }\simeq +{0.2\circ }\pm {0.5\circ }$| and |$D_{\rm a}=-{0.38\circ }\pm {0.73\circ }\simeq -{0.4\circ }\pm {0.7\circ }$| (to 3σ).
Similarly to the case of the data set of A1, we conduct the χ2 minimization scheme to each data set of A2, B1, B2, C2, CS, CC, and CR. In table 4 the entire results assuming that the measured angles in the records were rounded up are shown. We note that if the records of 09.25 and 09.26 were measured in the evenings of the day prior to the date in the record, which is the C2 data set in this paper, the one-time measurement error is quite large, amounting to 1°, which is comparable to the results obtained by Lee (2012). If we assume that there was confusion in keeping the observational dates, we find that the A1 set among the data sets has the minimal σm. It is notable that the one-time measurement error σm for the A1 set is comparable to the value obtained from the positional data of Mars measured in 1491 (Ahn 2021).
Alignment errors and one-time measurement errors in the lodge and polar angles of C/1723 T1.*
| . | Numbers . | DoF . | De . | C.I. . | C.I. . | Da . | C.I . | C.I. . | σm . | |
|---|---|---|---|---|---|---|---|---|---|---|
| Data . | nA . | |$n_\Delta$| . | ν . | (°) . | |$68\%$| . | |$99.7\%$| . | (°) . | |$68\%$| . | |$99.7\%$| . | (°) . |
| A1 | 10 | 10 | 18 | +0.24 | [+0.03, +0.45] | [−0.23, +0.71] | −0.38 | [−0.71,−0.06] | [−1.11, +0.34] | 0.29 |
| A2 | 10 | 10 | 18 | −0.01 | [−0.30, +0.27] | [−0.65, +0.62] | −0.17 | [−0.62, +0.29] | [−1.20, +0.87] | 0.47 |
| B1 | 10 | 10 | 18 | +0.01 | [−0.26, +0.29] | [−0.61, +0.64] | −0.47 | [−0.91,−0.02] | [−1.48, +0.54] | 0.46 |
| B2 | 10 | 10 | 18 | −0.24 | [−0.56, +0.08] | [−0.96, +0.48] | −0.26 | [−0.79, +0.26] | [−1.45, +0.93] | 0.55 |
| C2 | 10 | 10 | 18 | −0.37 | [−0.91, +0.17] | [−1.59, +0.85] | −0.46 | [−1.37, +0.45] | [−2.52, +1.60] | 1.01 |
| CS | 9 | 9 | 16 | −0.11 | [−0.37, +0.16] | [−0.71, +0.50] | −0.42 | [−0.68,0.24] | [−1.26, +0.81] | 0.41 |
| CC | 8 | 8 | 14 | +0.12 | [−0.08, +0.31] | [−0.32, +0.56] | −0.30 | [−0.60,0.00] | [−0.98, +0.38] | 0.19 |
| CR | 8 | 8 | 14 | −0.004 | [−0.21, +0.20] | [−0.47, +0.46] | −0.32 | [−0.65,0.01] | [−1.07, +0.42] | 0.23 |
| . | Numbers . | DoF . | De . | C.I. . | C.I. . | Da . | C.I . | C.I. . | σm . | |
|---|---|---|---|---|---|---|---|---|---|---|
| Data . | nA . | |$n_\Delta$| . | ν . | (°) . | |$68\%$| . | |$99.7\%$| . | (°) . | |$68\%$| . | |$99.7\%$| . | (°) . |
| A1 | 10 | 10 | 18 | +0.24 | [+0.03, +0.45] | [−0.23, +0.71] | −0.38 | [−0.71,−0.06] | [−1.11, +0.34] | 0.29 |
| A2 | 10 | 10 | 18 | −0.01 | [−0.30, +0.27] | [−0.65, +0.62] | −0.17 | [−0.62, +0.29] | [−1.20, +0.87] | 0.47 |
| B1 | 10 | 10 | 18 | +0.01 | [−0.26, +0.29] | [−0.61, +0.64] | −0.47 | [−0.91,−0.02] | [−1.48, +0.54] | 0.46 |
| B2 | 10 | 10 | 18 | −0.24 | [−0.56, +0.08] | [−0.96, +0.48] | −0.26 | [−0.79, +0.26] | [−1.45, +0.93] | 0.55 |
| C2 | 10 | 10 | 18 | −0.37 | [−0.91, +0.17] | [−1.59, +0.85] | −0.46 | [−1.37, +0.45] | [−2.52, +1.60] | 1.01 |
| CS | 9 | 9 | 16 | −0.11 | [−0.37, +0.16] | [−0.71, +0.50] | −0.42 | [−0.68,0.24] | [−1.26, +0.81] | 0.41 |
| CC | 8 | 8 | 14 | +0.12 | [−0.08, +0.31] | [−0.32, +0.56] | −0.30 | [−0.60,0.00] | [−0.98, +0.38] | 0.19 |
| CR | 8 | 8 | 14 | −0.004 | [−0.21, +0.20] | [−0.47, +0.46] | −0.32 | [−0.65,0.01] | [−1.07, +0.42] | 0.23 |
The minimized χ2 values for various sets of data, assuming that the measurements were rounded up. The sets A1, CC, and CR seems to be better fits.
Alignment errors and one-time measurement errors in the lodge and polar angles of C/1723 T1.*
| . | Numbers . | DoF . | De . | C.I. . | C.I. . | Da . | C.I . | C.I. . | σm . | |
|---|---|---|---|---|---|---|---|---|---|---|
| Data . | nA . | |$n_\Delta$| . | ν . | (°) . | |$68\%$| . | |$99.7\%$| . | (°) . | |$68\%$| . | |$99.7\%$| . | (°) . |
| A1 | 10 | 10 | 18 | +0.24 | [+0.03, +0.45] | [−0.23, +0.71] | −0.38 | [−0.71,−0.06] | [−1.11, +0.34] | 0.29 |
| A2 | 10 | 10 | 18 | −0.01 | [−0.30, +0.27] | [−0.65, +0.62] | −0.17 | [−0.62, +0.29] | [−1.20, +0.87] | 0.47 |
| B1 | 10 | 10 | 18 | +0.01 | [−0.26, +0.29] | [−0.61, +0.64] | −0.47 | [−0.91,−0.02] | [−1.48, +0.54] | 0.46 |
| B2 | 10 | 10 | 18 | −0.24 | [−0.56, +0.08] | [−0.96, +0.48] | −0.26 | [−0.79, +0.26] | [−1.45, +0.93] | 0.55 |
| C2 | 10 | 10 | 18 | −0.37 | [−0.91, +0.17] | [−1.59, +0.85] | −0.46 | [−1.37, +0.45] | [−2.52, +1.60] | 1.01 |
| CS | 9 | 9 | 16 | −0.11 | [−0.37, +0.16] | [−0.71, +0.50] | −0.42 | [−0.68,0.24] | [−1.26, +0.81] | 0.41 |
| CC | 8 | 8 | 14 | +0.12 | [−0.08, +0.31] | [−0.32, +0.56] | −0.30 | [−0.60,0.00] | [−0.98, +0.38] | 0.19 |
| CR | 8 | 8 | 14 | −0.004 | [−0.21, +0.20] | [−0.47, +0.46] | −0.32 | [−0.65,0.01] | [−1.07, +0.42] | 0.23 |
| . | Numbers . | DoF . | De . | C.I. . | C.I. . | Da . | C.I . | C.I. . | σm . | |
|---|---|---|---|---|---|---|---|---|---|---|
| Data . | nA . | |$n_\Delta$| . | ν . | (°) . | |$68\%$| . | |$99.7\%$| . | (°) . | |$68\%$| . | |$99.7\%$| . | (°) . |
| A1 | 10 | 10 | 18 | +0.24 | [+0.03, +0.45] | [−0.23, +0.71] | −0.38 | [−0.71,−0.06] | [−1.11, +0.34] | 0.29 |
| A2 | 10 | 10 | 18 | −0.01 | [−0.30, +0.27] | [−0.65, +0.62] | −0.17 | [−0.62, +0.29] | [−1.20, +0.87] | 0.47 |
| B1 | 10 | 10 | 18 | +0.01 | [−0.26, +0.29] | [−0.61, +0.64] | −0.47 | [−0.91,−0.02] | [−1.48, +0.54] | 0.46 |
| B2 | 10 | 10 | 18 | −0.24 | [−0.56, +0.08] | [−0.96, +0.48] | −0.26 | [−0.79, +0.26] | [−1.45, +0.93] | 0.55 |
| C2 | 10 | 10 | 18 | −0.37 | [−0.91, +0.17] | [−1.59, +0.85] | −0.46 | [−1.37, +0.45] | [−2.52, +1.60] | 1.01 |
| CS | 9 | 9 | 16 | −0.11 | [−0.37, +0.16] | [−0.71, +0.50] | −0.42 | [−0.68,0.24] | [−1.26, +0.81] | 0.41 |
| CC | 8 | 8 | 14 | +0.12 | [−0.08, +0.31] | [−0.32, +0.56] | −0.30 | [−0.60,0.00] | [−0.98, +0.38] | 0.19 |
| CR | 8 | 8 | 14 | −0.004 | [−0.21, +0.20] | [−0.47, +0.46] | −0.32 | [−0.65,0.01] | [−1.07, +0.42] | 0.23 |
The minimized χ2 values for various sets of data, assuming that the measurements were rounded up. The sets A1, CC, and CR seems to be better fits.
In table 4 we see that the data sets of A1, CC, and CR have relatively small one-time measurement errors. However, we select the result for the CR data set as the most probable one, for the following reasons. One reason is that there is no explicit evidence for the existence of confusion in keeping the observational dates. The other reason is that the polar alignment error in elevation, De, for the data set CR is quite small. The latter criterion can be justified as follows. The lodge/polar angles of C/1723 must have been measured with a meridian equatorial instrument such as the small abridged armilla. The polar axis of the small abridged armilla is cast in such a way that it makes a specific angle with respect to the pillar pointing to the zenith, which can be seen in figure1 of Ahn (2021). The specific angle was to be 90° − φ, where the latitude of the observing site, φ, must have been accurately determined with another large and precise instrument. The small abridged armilla was detachable from the stem pillar that had already been erected on the water-levelled ground and accurately adjusted to be normal to the ground and pointing to the zenith. When an observation was made, the instrument was plugged in to the stem pillar. The observer had only to align the azimuthal direction of the polar axis using a magnetic compass. The polar alignment error in elevation will then be quite small.
In conclusion, the polar alignment error in elevation for the CR data set |$D_{\rm e}\approx {0.0\circ }\pm {0.2\circ }$| (to 1σ) and |$D_{\rm e}\approx {0.0\circ }\pm {0.5\circ }$| (to 3σ), the polar alignment error in azimuth |$D_{\rm a}\simeq -{0{_{.}^{\circ}}3}\pm {0{_{.}^{\circ}}3}$| (to 1σ) and |$D_{\rm a}\simeq -{0{_{.}^{\circ}}3}\pm {0.7\circ }$| (to 3σ), and the one-time measurement error is |$\sigma _{\rm m}\simeq {0.23\circ }\approx {0.2\circ }$|.
In table 5 we show the results of the χ2 minimizations when we assume that the angles in the records were rounded down. Similarly to the rounding-up cases described above, the A1 data set gives the minimum one-time measurement error when only the recorded dates were confused. The results obtained for the A1 data set gives us the polar alignment error in elevation |$D_{\rm e}\simeq -{0.35\circ }\pm {0.47\circ }$| (to 3σ), the polar alignment error in azimuth |$D_{\rm a}\simeq +{0.28\circ }\pm {0.72\circ }$| (to 3σ), and the one-time measurement error |$\sigma _{\rm m}\simeq {0.29\circ }$|. However, similarly to the rounded-up case, we may just as well discard the outliers as presume the existence of confusion in keeping the observational dates. Thus, the CR′ data set is thought to be most proper one. The results for the CR′ set give us the smallest σm, and also De ≈ 0 within the 3σ confidence interval.
Alignment errors and one-time measurement errors in the lodge and polar angles of C/1723 T1.*
| . | Numbers . | DoF . | De . | C.I. . | C.I. . | Da . | C.I . | C.I. . | σm . | |
|---|---|---|---|---|---|---|---|---|---|---|
| Data . | nA . | |$n_\Delta$| . | ν . | (°) . | |$68\%$| . | |$99.7\%$| . | (°) . | |$68\%$| . | |$99.7\%$| . | (°) . |
| A1 | 10 | 10 | 18 | −0.35 | [−0.56, −0.15] | [−0.82, +0.11] | +0.28 | [−0.03, +0.60] | [−0.43, +1.01] | 0.29 |
| A2 | 10 | 10 | 18 | −0.71 | [−0.89, −0.33] | [−1.24, +0.02] | +0.50 | [+0.05, +0.96] | [−0.52, +1.53] | 0.46 |
| B1 | 10 | 10 | 18 | −0.58 | [−0.90, −0.26] | [−1.31, +0.15] | +0.19 | [−0.34, +0.72] | [−1.01, +1.39] | 0.56 |
| B2 | 10 | 10 | 18 | −0.84 | [−1.20, −0.48] | [−1.65, −0.02] | +0.40 | [−0.20, +1.00] | [−0.96, +1.76] | 0.64 |
| C2 | 10 | 10 | 18 | −1.29 | [−1.77, −0.80] | [−2.38, −0.19] | +0.98 | [+0.11, +1.86] | [−1.00, +2.97] | 0.92 |
| CS | 9 | 9 | 16 | −0.69 | [−1.08, −0.30] | [−1.38, +0.01] | +0.53 | [−0.14, +1.21] | [−0.67, +1.74] | 0.45 |
| CC | 8 | 8 | 14 | −0.58 | [−0.91, −0.25] | [−1.10, −0.06] | +0.44 | [−0.08, +0.96] | [−0.38, +1.26] | 0.21 |
| CR′ | 8 | 8 | 14 | −0.46 | [−0.82, −0.11] | [−1.02, +0.10] | +0.46 | [−0.11, +1.04] | [−0.45, +1.37] | 0.25 |
| . | Numbers . | DoF . | De . | C.I. . | C.I. . | Da . | C.I . | C.I. . | σm . | |
|---|---|---|---|---|---|---|---|---|---|---|
| Data . | nA . | |$n_\Delta$| . | ν . | (°) . | |$68\%$| . | |$99.7\%$| . | (°) . | |$68\%$| . | |$99.7\%$| . | (°) . |
| A1 | 10 | 10 | 18 | −0.35 | [−0.56, −0.15] | [−0.82, +0.11] | +0.28 | [−0.03, +0.60] | [−0.43, +1.01] | 0.29 |
| A2 | 10 | 10 | 18 | −0.71 | [−0.89, −0.33] | [−1.24, +0.02] | +0.50 | [+0.05, +0.96] | [−0.52, +1.53] | 0.46 |
| B1 | 10 | 10 | 18 | −0.58 | [−0.90, −0.26] | [−1.31, +0.15] | +0.19 | [−0.34, +0.72] | [−1.01, +1.39] | 0.56 |
| B2 | 10 | 10 | 18 | −0.84 | [−1.20, −0.48] | [−1.65, −0.02] | +0.40 | [−0.20, +1.00] | [−0.96, +1.76] | 0.64 |
| C2 | 10 | 10 | 18 | −1.29 | [−1.77, −0.80] | [−2.38, −0.19] | +0.98 | [+0.11, +1.86] | [−1.00, +2.97] | 0.92 |
| CS | 9 | 9 | 16 | −0.69 | [−1.08, −0.30] | [−1.38, +0.01] | +0.53 | [−0.14, +1.21] | [−0.67, +1.74] | 0.45 |
| CC | 8 | 8 | 14 | −0.58 | [−0.91, −0.25] | [−1.10, −0.06] | +0.44 | [−0.08, +0.96] | [−0.38, +1.26] | 0.21 |
| CR′ | 8 | 8 | 14 | −0.46 | [−0.82, −0.11] | [−1.02, +0.10] | +0.46 | [−0.11, +1.04] | [−0.45, +1.37] | 0.25 |
The minimized χ2 values for various sets of data, assuming that the measurements were rounded down. The sets A1 and CR′ seems to be better fits.
Alignment errors and one-time measurement errors in the lodge and polar angles of C/1723 T1.*
| . | Numbers . | DoF . | De . | C.I. . | C.I. . | Da . | C.I . | C.I. . | σm . | |
|---|---|---|---|---|---|---|---|---|---|---|
| Data . | nA . | |$n_\Delta$| . | ν . | (°) . | |$68\%$| . | |$99.7\%$| . | (°) . | |$68\%$| . | |$99.7\%$| . | (°) . |
| A1 | 10 | 10 | 18 | −0.35 | [−0.56, −0.15] | [−0.82, +0.11] | +0.28 | [−0.03, +0.60] | [−0.43, +1.01] | 0.29 |
| A2 | 10 | 10 | 18 | −0.71 | [−0.89, −0.33] | [−1.24, +0.02] | +0.50 | [+0.05, +0.96] | [−0.52, +1.53] | 0.46 |
| B1 | 10 | 10 | 18 | −0.58 | [−0.90, −0.26] | [−1.31, +0.15] | +0.19 | [−0.34, +0.72] | [−1.01, +1.39] | 0.56 |
| B2 | 10 | 10 | 18 | −0.84 | [−1.20, −0.48] | [−1.65, −0.02] | +0.40 | [−0.20, +1.00] | [−0.96, +1.76] | 0.64 |
| C2 | 10 | 10 | 18 | −1.29 | [−1.77, −0.80] | [−2.38, −0.19] | +0.98 | [+0.11, +1.86] | [−1.00, +2.97] | 0.92 |
| CS | 9 | 9 | 16 | −0.69 | [−1.08, −0.30] | [−1.38, +0.01] | +0.53 | [−0.14, +1.21] | [−0.67, +1.74] | 0.45 |
| CC | 8 | 8 | 14 | −0.58 | [−0.91, −0.25] | [−1.10, −0.06] | +0.44 | [−0.08, +0.96] | [−0.38, +1.26] | 0.21 |
| CR′ | 8 | 8 | 14 | −0.46 | [−0.82, −0.11] | [−1.02, +0.10] | +0.46 | [−0.11, +1.04] | [−0.45, +1.37] | 0.25 |
| . | Numbers . | DoF . | De . | C.I. . | C.I. . | Da . | C.I . | C.I. . | σm . | |
|---|---|---|---|---|---|---|---|---|---|---|
| Data . | nA . | |$n_\Delta$| . | ν . | (°) . | |$68\%$| . | |$99.7\%$| . | (°) . | |$68\%$| . | |$99.7\%$| . | (°) . |
| A1 | 10 | 10 | 18 | −0.35 | [−0.56, −0.15] | [−0.82, +0.11] | +0.28 | [−0.03, +0.60] | [−0.43, +1.01] | 0.29 |
| A2 | 10 | 10 | 18 | −0.71 | [−0.89, −0.33] | [−1.24, +0.02] | +0.50 | [+0.05, +0.96] | [−0.52, +1.53] | 0.46 |
| B1 | 10 | 10 | 18 | −0.58 | [−0.90, −0.26] | [−1.31, +0.15] | +0.19 | [−0.34, +0.72] | [−1.01, +1.39] | 0.56 |
| B2 | 10 | 10 | 18 | −0.84 | [−1.20, −0.48] | [−1.65, −0.02] | +0.40 | [−0.20, +1.00] | [−0.96, +1.76] | 0.64 |
| C2 | 10 | 10 | 18 | −1.29 | [−1.77, −0.80] | [−2.38, −0.19] | +0.98 | [+0.11, +1.86] | [−1.00, +2.97] | 0.92 |
| CS | 9 | 9 | 16 | −0.69 | [−1.08, −0.30] | [−1.38, +0.01] | +0.53 | [−0.14, +1.21] | [−0.67, +1.74] | 0.45 |
| CC | 8 | 8 | 14 | −0.58 | [−0.91, −0.25] | [−1.10, −0.06] | +0.44 | [−0.08, +0.96] | [−0.38, +1.26] | 0.21 |
| CR′ | 8 | 8 | 14 | −0.46 | [−0.82, −0.11] | [−1.02, +0.10] | +0.46 | [−0.11, +1.04] | [−0.45, +1.37] | 0.25 |
The minimized χ2 values for various sets of data, assuming that the measurements were rounded down. The sets A1 and CR′ seems to be better fits.
In conclusion, for the rounded-down case, the CR′ set gives us the polar alignment error in elevation |$D_{\rm e}\simeq -{0.46\circ }\pm {0.36\circ }$| (to 1σ) and |$D_{\rm e}\simeq -{0.46\circ }\pm {0.56\circ }$| (to 3σ), the polar alignment error in azimuth |$D_{\rm a}\simeq +{0.46\circ }\pm {0.57\circ }$| (to 1σ) and |$D_{\rm a}\simeq +{0.46\circ }\pm {0.91\circ }$| (to 3σ), and the one-time measurement error |$\sigma _{\rm m}\simeq {0{_{.}^{\circ}}25}$|.
Note that the one-time measurement error is estimated from the observational data for the motion of Mars in 1491 to be |$\sigma _{\rm m}={0.3^{\prime }}$| (Ahn 2021). Comparing this error with that estimated in this paper for the comet C/1723, we see that the precisions of measurements have little difference. It is inferred that the meridian instrument for observing the comet C/1723 might have little technical improvement compared with the small abridged armilla that had been used to observed the retrograde motion of Mars in 1491.
4 Conclusions
In this paper, we analysed the positional data of a comet called C/1723 T1 observed and recorded by the court astronomers of the Joseon dynasty. Bradley (1724) measured the coordinates of this comet precisely with the aid of a telescope equipped with a micrometer. His coordinate data were used to determine the orbital elements of the comet (Spörer 1843, for example). We generated an ephemeris using the NASA JPL Horizons system and adopting Spörer’s orbital elements. By comparing the ephemeris with Bradley’s observational data, we found that the measurement error of the observations is 30″ in right ascension, 20″ in declination, and 25″ on average.
The ephemeris coordinates were compared with the Korean data recorded in observational reports in a book called the Astronomical Registry. We found a couple of records showing large deviations, which can be attributed to either the confusion in dates of observations or the bad weather. Hence, considering these possibilities, we formed a number of data sets. Moreover, since the observations must have been made using a sort of meridian and equatorial instrument, they should inevitably be affected by the misalignments of the polar axis with respect to the Earth’s rotation axis. In addition, it is not certain whether the court astronomers rounded up their measurements or rounded them down. Thus, we applied a χ2 minimization scheme for the various sets of data to find the most probable values of polar alignment errors in elevation/azimuth for rounded-up/rounded-down assumptions.
As results, we found that, assuming the measurements were rounded up, the alignment error in elevation |$D_{\rm e}\simeq {0.00\circ }\pm {0.47\circ }\approx {0.0\circ }\pm {0.5\circ }$| (to 3σ) and the alignment error in azimuth |$D_{\rm a}=-{0.32\circ }\pm {0.75\circ }\approx -{0{_{.}^{\circ}}3}\pm {0.8\circ }$| (to 3σ), and the one-time measurement error |$\sigma _{\rm m}\simeq {0.23\circ }\approx {0.2\circ }$| for the positional data for the comet C/1723 T1. On the other hand, assuming the measurements were rounded down, the alignment error in elevation |$D_{\rm e}\simeq -{0.46\circ }\pm {0.56\circ }\approx -{0.5\circ }\pm {0.6\circ }$|, the alignment error in the azimuthal direction |$D_{\rm a}=+{0.46\circ }\pm {0.91\circ }\approx +{0.5\circ }\pm {0.9\circ }$| (to 3σ), and the one-time measurement error is |$\sigma _{\rm m}\simeq {0{_{.}^{\circ}}25}\approx {0{_{.}^{\circ}}3}$|.
According to chronicles, it is explicitly said that the polar axis of the observing instrument was aligned using a magnetic compass in 1491. In this case, we can regard the alignment error in azimuth as being equivalent to the geomagnetic declination at the observing site in the observing time. Similarly, we postulate that a magnetic compass was also used for aligning the polar axis during the observations of C/1723 T1.
Among the geomagnetic models that give long-term variations of geomagnetic fields, we introduced two recent models that are based on a vast amount of archaeological and historical data and are valid at the relevant epoch of 1723. One model is the geomagnetic field model called arhimag1k (Senftleben 2020), and the other model is the geomagnetic field model called BIGMUDI4K.1 (Arneitz et al. 2019). Figure 3 shows the temporal variations of geomagnetic declination of these models at Seoul (|${37.58\circ }\:$|N latitude and |${126.99\circ }\:$|E longitude). The solid curve in the lower panel of figure 3 represents the geomagnetic declinations that are calculated using the geomagnetic field model called arhimag1k,5 and the solid curve in the upper panel of figure 3 represents the geomagnetic declinations that are calculated using the BIGMUDI4K.1 model.6 The dotted and the dashed lines in both panels represent their 1σ and 2σ uncertainties, respectively.
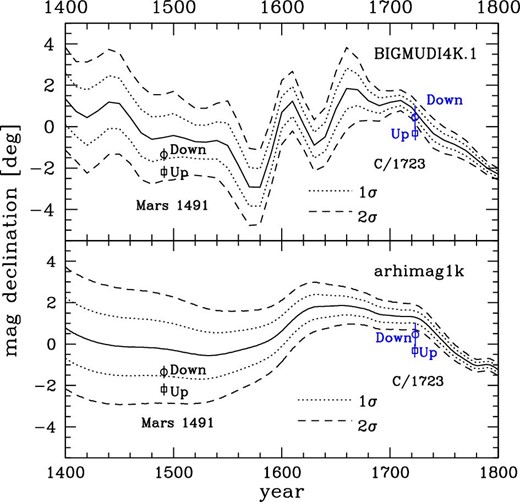
Temporal variations of geomagnetic declination at Seoul (|${37{_{.}^{\circ}}58}$|N latitude and |${126{_{.}^{\circ}}99}$|E longitude). The solid curve in the lower panel represents the temporal variations of geomagnetic declinations calculated using the arhimag1k model (Senftleben 2020), and the solid curve in the upper panel represents the temporal variations of geomagnetic declinations calculated using the BIGMUD4K.1 model (Arneitz et al. 2019). The dotted curves and the dashed curves represent their 1σ and 2σ errors, respectively. The white dot with error bars and the white square with error bars at the right-hand side represent our results for rounded-down and rounded-up angles, respectively; those on the left-hand side represent the results for the motion of Mars in 1491 (Ahn 2021). (Color online)
In the right-hand part of figure 3, we plot the geomagnetic declinations at Seoul in 1723 obtained from the observational data of the comet C/1723. We also plot the geomagnetic declinations at Seoul in 1491 obtained from the observational data of Mars (Ahn 2021). For both sets of results, the white dots with error bars in both panels represent the rounded-down cases, while the white squares with error bars in both panels represent the rounded-up cases. We see in the figure that the geomagnetic declination obtained for rounded-down cases is in agreement with the geomagnetic model of BIGMUDI4K.1 within the 1σ uncertainties of the model. The geomagnetic declination is also in rough agreement with the geomagnetic model of arhimag1k, within the 2σ uncertainties of the model. However, strictly speaking, the geomagnetic declination obtained for rounded-up cases is not in agreement with both models within the 2σ uncertainties. We can also see in the left-hand part of figure 3 that the geomagnetic declination estimated from the rounded-down coordinates of Mars in 1491 is in better agreement with the models. It is also noteworthy that our results show better agreement with the BIGMUDI4K.1 model than with the arhimag1k model. However, in order to strengthen the findings, we need more observational data from historical resources.
It is also noteworthy that the one-time measurement error is estimated to have been |$\sim {0{_{.}^{\circ}}25}$|, which is rather similar to that obtained from the positional data of Mars in 1491 by Ahn (2021). That is to say, the observational precision does not show conspicuous improvement during the 230 years. This also implies that there is no great improvement in astrometric technology. It may indicate that the observing devices had not been improved in either size or precision. However, in order to make a firm conclusion, we also need more observational data that has preserved in historical resources.
Acknowledgements
The author is grateful to Dr. Monika Kortes for providing the geomagnetic field data at Seoul in 1723 using the Arhimag1k model. This work is supported by the Korea Research Foundation through grant NRF-2021R1F1A1057571.
Appendix 1. Methodology for χ2 minimizations
A lodge angle is determined by two measurements, while a polar angle is determined by one single measurement. Hence, Ahn (2021) shows that the measurement errors in lodge angles have a mean of 〈eA〉 = 0 and the variance of |$\sigma _{\rm e_{\rm A}}^2=2\sigma _{\rm m}^2+1/12$| for rounded-up measurements; the measurement errors in lodge angles have a mean of 〈eA〉 = −1/2 and the variance of |$\sigma _{\rm e_{\rm A}}^2=2\sigma _{\rm m}^2+1/12$| for rounded-down measurements, where σm is one-time measurement error. He also shows that the measurement errors in polar angles have a mean of |$\langle e_\Delta \rangle =0$| and the variance of |$\sigma _{{\rm e}_\Delta }^2=\sigma _{\rm m}^2+1/12$| for rounded-up measurements, while the measurement errors in lodge angles have a mean of |$\langle e_\Delta \rangle =-1/2$| and the variance of |$\sigma _{{\rm e}_\Delta }^2=\sigma _{\rm m}^2+1/12$| for rounded-down measurements.
For example, we are now to apply the χ2 minimization scheme for the data sets A1 and CR′, assuming that the measured angles were rounded down. The resultant χ2 maps are shown in the left-hand panels of figures 4 and 5. We see that the maps seem to have a minimum, but they are not smooth but patched. This is not only because the number of data is small but also because rounded angles will contribute discontinuously to the χ2 value.
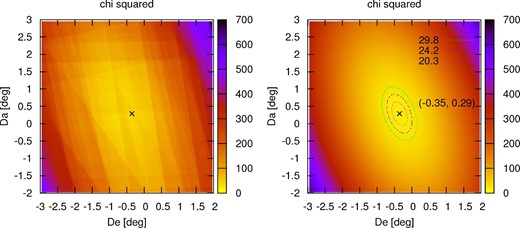
χ2 statistic maps for the polar alignment errors of the data set A1. The panel on the left shows the χ2 map when we assume that all the observed angles were rounded down from the first decimal place. Since the rounding-down for a measured angle makes the contribution of the ith angle to the |$\chi^2$| statistic, by an integer amount, the χ2-map looks descrete and discontinuous. In addition, the number of data is not large enough. On the other hand, the panel on the right-hand side shows the equivalent χ2-map for the same CR′ data set but assuming that the rounding-down effect is compensated for. The contours represent the 1σ, 2σ, and 3σ values, respectively. We obtain the best-fitting values of De = −0.35°, Da = 0.29°, and σm = 0.29°. We confirm that the χ2 maps for both calculations look similar. (Color online)
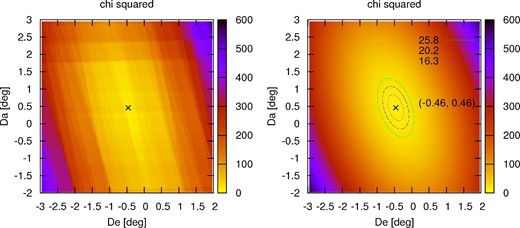
χ2 statistic map for the alignment errors of the polar axis for the data set CR′. We obtain similar results to those in figure 4. The best-fitting values are De = −0.46°, Da = 0.46°, and |$\sigma _{\rm m}={0{_{.}^{\circ}}25}$|. (Color online)
We perform the χ2 minimization for the data sets A1 and CR′, assuming that the measured angles were rounded down. The resultant χ2 maps are shown in the right-hand panels of figures 4 and 5. We can see that the χ2 maps are smooth and that they are similar to their counterparts in the left-hand panels. Therefore, in this paper we will obtain the most probable values of alignment errors in elevation and azimuth using the latter simplified method.
Appendix 2. Translation of observational records
Registry: 1723 October 19 [18]:7 The 21st day of the 9th month in the 3rd reign year of King Gyeongjong, the day of Dingyou; During the 1st watch of the night, a celestial object appeared within the angular span of the lunar lodge Nu. It seemed to have a tail.
Sillok: During the 1st watch of the night, a comet appeared within the angular span of the lunar lodge Nu. It was whitish, and it seemed to have a tail. It disappeared 15 days later.
Registry: 1723 October 20 [19]: The 22nd day of the 9th month in the 3rd reign year of King Gyeongjong, the day of Wuxu; During the 1st watch of the night, the celestial object that appeared in the previous night had moved northwestward by 1 du. It was as big (or bright) as the big star in the Qianniu (β Cap). It was whitish. Its tail was (....missing letters...).
Registry: 1723 October 21 [20]: The 23rd day of the 9th month in the 3rd reign year of King Gyeongjong, the day of Jihai; During the night, the celestial object that had been seen in the previous night could not be observed due to heavy clouds.
Registry: 1723 October 22 [21]: The 24th day of the 9th month in the 3rd reign year of King Gyeongjong, the day of Gengzi; During the 1st watch of the night, the comet had moved northwestward. Its tail pointed to the big star of the lunar lodge Nu (ε Aqr). It must be a comet.
Diary: In the evening twilight, it thundered and lightning struck. During the 1st watch of the night, the comet had moved northwestward to be seen. Its tail pointed to the big star of the lunar lodge Nu (or ε Aqr). It must be a comet. During the 2nd and 3rd watches, lightning struck.
Sillok: In the evening twilight, there were thunder and lightning. During the 2nd and 3rd watches, lightning struck.
Registry: 1723 October 23 [A: October 20, B: October 21, C: October 22]: The 25th day of the 9th month in the 3rd reign year of King Gyeongjong, the day of Xinchou; During the 2nd watch of the night, the comet had moved to be seen at 7 du of (the lunar lodge) Niu (β Cap) and the polar angle of 105 du. Its shape was comparable to the big star of Qianniu (β Cap). The tail was approximately 5 or 6 cun long.8 It was whitish.
Diary: During the 1st watch of the night, there was lightning. During the 2nd watch, the comet had moved to be seen within the angular span of the lunar lodge Niu. The tail was approximately 5 or 6 cun long. It was whitish. During the time of wei (or 13:00–15:00 LT), it snowed.
Sillok: During the 1st watch, lightning struck. During the 2nd watch, the comet had moved to be seen within the angular span of the lunar lodge Niu. During the time of wei, it snowed.
Registry: 1723 October 24 [|$\bigcirc{1}\,$|: October 22, |$\bigcirc{2}\,$|: October 23]: The 26th day of the 9th month in the 3rd reign year of King Gyeongjong, the day of Renyin; During the 1st watch of the night, the comet had moved to be seen at 4 du of (the lunar lodge) Niu and a polar angle of 101 du. Its shape, colour, and tail were not changed compared to the previous night.
Diary: During the 1st watch, the comet had moved to be seen within the angular span of the lunar lodge Niu. Its tail was approximately 5 or 6 cun long. It was whitish.
Registry: 1723 October 25 [24]: The 27th day of the 9th month in the 3rd reign year of King Gyeongjong, the day of Guimao; During the 1st watch of the night, the comet had moved to be seen at 3 du of (the lunar lodge) Niu and a polar angle of 98 du. Its shape, colour, and tail were not changed compared to the previous night.
Diary: During the 1st watch, the comet was seen within the angular span of the lunar lodge Niu. Its tail was approximately 5 or 6 cun long. It was whitish. During the 2nd and 3rd watches, lightning struck.
Sillok: During the 2nd and 3rd watches, lightning struck.
Registry: 1723 October 26 [25]: The 28th day of the 9th month in the 3rd reign year of King Gyeongjong, the day of Jiachen; During the 1st watch of the night, the comet had moved and was seen at 2 du of (the lunar lodge) Niu and a polar angle of 96 du. Its shape and colour were not changed compared to the previous night. The tail was slightly shorter than the previous night.
Diary: During the 1st watch of the night, the comet had moved to be seen within the angular span of the lunar lodge Niu. Its tail was approximately 4 or 5 chi long. It was whitish.
Registry: 1723 October 27 [26]: The 29th day of the 9th month in the 3rd reign year of King Gyeongjong, the day of Yisi; During the night, the comet could not be observed due to heavy clouds.
Registry: 1723 October 28 [27]: The 30th day of the 9th month in the 3rd reign year of King Gyeongjong, the day of Bingwu; During the 1st watch of the night, the comet had moved to be seen at 1 du of (the lunar lodge) Niu and its polar angle of 95 du. Its shape and tail became still smaller than it had been the night before last night.
Diary: During the 1st watch of the night, the comet was seen within the angular span of the lunar lodge Niu. Its shape became smaller than before. Its tail was approximately 2 or 3 cun long. It was whitish. Hail as big as soy beans fell, and lightning struck. During the 2nd and 3rd watches, it thundered and lightning struck.
Sillok: During the 1st watch of the night, hail as big as soy beans fell, and lightning struck. During the 2nd and 3rd watches, it thundered and lightning struck.
Registry: 1723 October 29 [28]: The 1st day of the 10th month in the 3rd reign year of King Gyeongjong, the day of Dingwei; During the 1st watch of the night, the comet had moved to be seen at 1 du of (the lunar lodge) Niu and a polar angle of 94 du. Its shape and tail became still smaller than the previous night.
Diary: During the 1st watch of the night, the comet was seen within the angular span of the lunar lodge Niu. Its shape became still smaller than the previous night. Its tail was approximately 1 cun long. It was whitish. During the 4th watch, lightning struck.
Sillok: During the 2nd and 3rd watches, lightning struck.
Registry: 1723 October 30 [29]: The 2nd day of the 10th month in the 3rd reign year of King Gyeongjong, the day of Wushen; During the 1st watch of the night, the comet had moved to be seen at 1 du of (the lunar lodge) Niu and a polar angle of 93 du. Its shape and tail showed no difference from what it had been in the previous night.
Diary: During the 1st watch of the night, the comet was seen within the angular span of the lunar lodge Niu. Its shape and tail showed no difference from what it had been in the previous night. It was whitish.
Registry: 1723 October 31 [30]: The 3rd day of the 10th month in the 3rd reign year of King Gyeongjong, the day of Jiyou; During the 1st watch of the night, the comet had moved to be seen at 1 du of (the lunar lodge) Niu and a polar angle of 92.5 du. Its shape and tail were diminishing gradually day by day.
Diary: During the 1st watch of the night, the comet had moved to be seen within the angular span of the lunar lodge Niu. Its shape and tail were diminishing gradually day by day. It was whitish.
Registry: 1723 November 1 [October 31]: The 4th day of the 10th month in the 3rd reign year of King Gyeongjong, the day of Gengxu; During the 1st watch of the night, the comet had moved to be seen at 1 du of (the lunar lodge) Niu and a polar angle of 92 du. Its shape and tail became still smaller than it had been in the previous night.
Diary: During the 1st watch of the night, the comet was seen within the angular span of the lunar lodge Niu. Its shape and tail became smaller to be almost exhausted. It was whitish. From the 2nd watch to the 5th watch, lightning struck.
Sillok: From the 2nd watch to the 5th watch, lightning struck.
Registry: 1723 November 2 [1]: The 5th day of the 10th month in the 3rd reign year of King Gyeongjong, the day of Xinhai; During the 1st watch of the night, the comet had moved to be seen at 1 du of (the lunar lodge) Niu and a polar angle of 91.5 du. Its shape and tail became smaller to be almost exhausted.
Diary: During the time of Mao (or 05:00 to 07:00 LT), it thundered. During the 1st watch of the night, the comet was seen within the angular span of Niu. Its shape and tail became smaller to be almost exhausted. During the 2nd watch, a meteor appeared below Tianjin (Cygnus) and disappeared into the western horizon. It was as big as a fist. Its tail was approximately 3 or 4 chi long and red in colour. Lightning struck. During the 3rd watch, lightning struck.
Sillok: During the time of Mao, it thundered. During the 2nd watch of the night, a meteor appeared below Tianjin and disappeared into the western horizon. It was as big as a fist. Its tail was 3 or 4 chi long and red in colour. Lightning struck. During the 3rd watch, lightning struck.
Registry: 1723 November 3 [2]: The 6th day of the 10th month in the 3rd reign year of King Gyeongjong, the day of Renzi; During the 1st watch of the night, the moonlight shone on the comet. The shape and tail was hard to see.
Diary: During the 1st watch of the night, the moonlight shone on the comet. The shape and tail was hard to see. It was foggy. During the 5th watch, a meteor appeared below the lunar lodge of Kui and disappeared to the North. It was as big as a fist, and approximately 2 or 3 chi long. It was red in colour. It was foggy.
Sillok: During the 1st watch of the night, it was foggy. During the 5th watch, a meteor appeared below the lunar lodge of Kui and disappeared to the North. It was as big as a fist, and approximately 2 or 3 chi long. It was red in colour. It was foggy.
Registry: 1723 November 4 [3]: The 7th day of the 10th month in the 3rd reign year of King Gyeongjong, the day of Guichou; During the 1st watch of the night, the moonlight shone on the comet, and so the comet could not be observed.
Diary: From the morning twilight to the time of chen (from 07:00 to 09:00 LT), it was foggy.
Sillok: From the morning twilight to the time of chen, it was foggy.
Registry: 1723 November 5 [4]: The 8th day of the 10th month in the 3rd reign year of King Gyeongjong, the day of Jiayin; During the 1st watch of the night, the moonlight shone on the comet, and so the comet could not be observed.
Diary: During the 2nd watch of the night, a meteor appeared below Zuoqi and disappeared to the Western horizon. It was as big as a fist, approximately 3 or 4 chi long, and red in colour. Its light shone on the ground. From the 3rd watch to the 5th watch, lightning struck.
Sillok: During the 2nd watch of the night, a meteor appeared below Zuoqi and disappeared to the Western horizon. It was as big as a fist, approximately 3 or 4 chi long, and red in colour. Its light shone on the ground. From the 3rd watch to the 5th watch, there was lightning.
Registry: 1723 November 6 [5]: The 9th day of the 10th month in the 3rd reign year of King Gyeongjong, the day of Yimao; During the 1st watch of the night, the moon shone on the comet, and so the comet could not be observed.]
Registry: 1723 November 7 [6]: The 10th day of the 10th month in the 3rd reign year of King Gyeongjong, the day of Bingchen; During the 1st watch of the night, the moonlight shone on the comet, and so the comet could not be observed.
Diary: The Royal Astronomical Bureau reported that lightning struck during the 4th and 5th watches of the night.
Sillok: From the 4th watch to the 5th watch, lightning struck.
Registry: 1723 November 8 [7]: The 11th day of the 10th month in the 3rd reign year of King Gyeongjong, the day of Dingsi; During the 1st watch of the night, the moon shone on the comet, and so the comet could not be observed.
Registry: 1723 November 9 [8]: The 12th day of the 10th month in the 3rd reign year of King Gyeongjong, the day of Wuwu; During the 1st watch of the night, the moonlight shone on the comet, and so the comet could not be observed.
Registry: 1723 November 10 [9]: The 13th day of the 10th month in the 3rd reign year of King Gyeongjong, the day of Jiwei; During the 1st watch of the night, the moonlight shone on the comet, and so the comet could not be observed.
Registry: 1723 November 11 [10]: The 14th day of the 10th month in the 3rd reign year of King Gyeongjong, the day of Gengshen; During the 1st watch of the night, the moonlight shone on the comet, and so the comet could not be observed.
Diary: During the 1st watch of the night, a white vapour appeared from the northwest, passed by the side of the moon, and pointed directly to the southeast. It covers the whole sky, and its width was approximately 1 chi. Its inside was red and the outside was blue. It disappeared before long. During the 5th watch, a lunar halo appeared.
Sillok: During the 1st watch of the night, a white vapour appeared from the northwest, passed by the side of the moon, and pointed directly to the southeast. It covers the whole sky, and its width was approximately 1 chi. Its inside was red and the outside was blue. It disappeared before long.
Registry: 1723 November 12 [11]: The 15th day of the 10th month in the 3rd reign year of King Gyeongjong, the day of Xinyou; During the 1st watch of the night, the moonlight shone on the comet, and so the comet could not be observed.
Registry: 1723 November 13 [12]: The 16th day of the 10th month in the 3rd reign year of King Gyeongjong, the day of Renxu; During the 1st watch of the night, the moonlight shone on the comet, and so the comet could not be observed.
Diary: The Royal Astronomical Bureau reported that a lunar halo appeared during the 3rd and 4th watches.
Sillok: During the 3rd and 4th watches, a lunar halo appeared.
Registry: 1723 November 14 [13]: The 17th day of the 10th month in the 3rd reign year of King Gyeongjong, the day of Guihai; During the 1st watch of the night, it was clear, and stars appeared. However, the comet, having been observed before, was not observed at any effort. There was no doubt in its disappearance.
Diary: During the 4th watch of the night, a lunar halo embraced the Mars.
Sillok: During the 4th watch of the night, a lunar halo embraced the Mars.
Footnotes
Gyu-gwan means a sighting tube, which had been used as a name of an aiming-bar in armillary instruments. During the Yuan dynasty, Guo Shoujing renamed it as Gyu-hyeong after improving it (Lee et al. 2016).
Since the time system of the Datong system succeeded that of the Shuoshi system, the time system reformed in 1434 can also be called the Shoushi system.
R. Pass 2003, Two star polar alignment 〈http://rppass.com/align.pdf〉.
The geomagnetic declination values and their errors at Seoul are generated using the arhimag1k model and kindly provided by Dr. Monika Kortes.
The geomagnetic declination values and errors at Seoul were generated using the BIGMUDI4K.1 model kindly provided at the website 〈https://cobs.zamg.ac.at/data/index.php/de/models-and-databases/geomagnetic-model〉.
The date of record is October 19, while the date of observation is October 18.
In premodern Chinese length units, 10 fen is equivalent to 1 cun, which is roughly one inch. 10 cun is equivalent to 1 chi, which is roughly one foot. 10 chi is equivalent to 1 zhang. Analyses of observational records for the angular distance between Mars and nearby stars in 1491 revealed that 1 chi in length units is roughly equivalent to 1 Chinese degree or 1 du (Ahn 2021).



