An analytical density profile of dense circumstellar medium in Type II supernovae

Properties of the progenitor stars adopted in this work to calculate the numerical CSM profile.*

Model	M_ZAMS [M_⊙]	Z [Z_⊙]	R [R_⊙]	T_eff [K]	M_He,core	M_H,env
R15	15	1	670	4000	4.9	7.9
R20	20	1	840	4000	6.7	11.6
B20	20	10⁻²	130	9900	8.9	11.0

Model	M_ZAMS [M_⊙]	Z [Z_⊙]	R [R_⊙]	T_eff [K]	M_He,core	M_H,env
R15	15	1	670	4000	4.9	7.9
R20	20	1	840	4000	6.7	11.6
B20	20	10⁻²	130	9900	8.9	11.0

*

The first two are red supergiants, and the last is a blue supergiant. The columns are: model name, ZAMS mass, metallicity, radius, effective temperature, mass within helium core, and mass of hydrogen envelope (total mass minus M_He,core).

Table 1.

Properties of the progenitor stars adopted in this work to calculate the numerical CSM profile.*

Model	M_ZAMS [M_⊙]	Z [Z_⊙]	R [R_⊙]	T_eff [K]	M_He,core	M_H,env
R15	15	1	670	4000	4.9	7.9
R20	20	1	840	4000	6.7	11.6
B20	20	10⁻²	130	9900	8.9	11.0

Model	M_ZAMS [M_⊙]	Z [Z_⊙]	R [R_⊙]	T_eff [K]	M_He,core	M_H,env
R15	15	1	670	4000	4.9	7.9
R20	20	1	840	4000	6.7	11.6
B20	20	10⁻²	130	9900	8.9	11.0

*

The first two are red supergiants, and the last is a blue supergiant. The columns are: model name, ZAMS mass, metallicity, radius, effective temperature, mass within helium core, and mass of hydrogen envelope (total mass minus M_He,core).

Table 2.

Models of the CSM, and results of fitting for the numerical CSM profile with our analytical model.*

Model	E_inj [10⁴⁷ erg]	t_stop	R_in,CSM [cm]	M_CSM [M_⊙]	r_* [cm]	ρ_* [g cm⁻³]	y
R15f0.3	1.4	4 yr	5.0 × 10¹³	0.11	6.4 × 10¹⁴	2.7 × 10⁻¹⁴	2.6
R15f0.5	2.4	4 yr	7.0 × 10¹³	0.49	9.5 × 10¹⁴	4.9 × 10⁻¹⁴	1.7
R20f0.3	2.2	5 yr	9.1 × 10¹³	0.13	8.5 × 10¹⁴	1.1 × 10⁻¹⁴	2.8
R20f0.5	3.7	5 yr	9.5 × 10¹³	0.62	1.2 × 10¹⁵	3.2 × 10⁻¹⁴	1.7
B20f0.3	54	15 d	7.2 × 10¹²	0.30	5.5 × 10¹³	8.7 × 10⁻¹¹	3.6
B20f0.5	91	15 d	7.0 × 10¹²	0.79	6.7 × 10¹³	9.5 × 10⁻¹¹	3.8

Model	E_inj [10⁴⁷ erg]	t_stop	R_in,CSM [cm]	M_CSM [M_⊙]	r_* [cm]	ρ_* [g cm⁻³]	y
R15f0.3	1.4	4 yr	5.0 × 10¹³	0.11	6.4 × 10¹⁴	2.7 × 10⁻¹⁴	2.6
R15f0.5	2.4	4 yr	7.0 × 10¹³	0.49	9.5 × 10¹⁴	4.9 × 10⁻¹⁴	1.7
R20f0.3	2.2	5 yr	9.1 × 10¹³	0.13	8.5 × 10¹⁴	1.1 × 10⁻¹⁴	2.8
R20f0.5	3.7	5 yr	9.5 × 10¹³	0.62	1.2 × 10¹⁵	3.2 × 10⁻¹⁴	1.7
B20f0.3	54	15 d	7.2 × 10¹²	0.30	5.5 × 10¹³	8.7 × 10⁻¹¹	3.6
B20f0.5	91	15 d	7.0 × 10¹²	0.79	6.7 × 10¹³	9.5 × 10⁻¹¹	3.8

*

The first five columns are model name, injected energy, time that we stop our simulation, and the innermost radius and total mass of the region that we define as CSM. The last three columns are the results of the least-squares fitting, with fitted parameters (r_*, ρ_*, y).

Table 2.

Open in new tab Download slide

Models of the CSM, and results of fitting for the numerical CSM profile with our analytical model.*

Model	E_inj [10⁴⁷ erg]	t_stop	R_in,CSM [cm]	M_CSM [M_⊙]	r_* [cm]	ρ_* [g cm⁻³]	y
R15f0.3	1.4	4 yr	5.0 × 10¹³	0.11	6.4 × 10¹⁴	2.7 × 10⁻¹⁴	2.6
R15f0.5	2.4	4 yr	7.0 × 10¹³	0.49	9.5 × 10¹⁴	4.9 × 10⁻¹⁴	1.7
R20f0.3	2.2	5 yr	9.1 × 10¹³	0.13	8.5 × 10¹⁴	1.1 × 10⁻¹⁴	2.8
R20f0.5	3.7	5 yr	9.5 × 10¹³	0.62	1.2 × 10¹⁵	3.2 × 10⁻¹⁴	1.7
B20f0.3	54	15 d	7.2 × 10¹²	0.30	5.5 × 10¹³	8.7 × 10⁻¹¹	3.6
B20f0.5	91	15 d	7.0 × 10¹²	0.79	6.7 × 10¹³	9.5 × 10⁻¹¹	3.8

Model	E_inj [10⁴⁷ erg]	t_stop	R_in,CSM [cm]	M_CSM [M_⊙]	r_* [cm]	ρ_* [g cm⁻³]	y
R15f0.3	1.4	4 yr	5.0 × 10¹³	0.11	6.4 × 10¹⁴	2.7 × 10⁻¹⁴	2.6
R15f0.5	2.4	4 yr	7.0 × 10¹³	0.49	9.5 × 10¹⁴	4.9 × 10⁻¹⁴	1.7
R20f0.3	2.2	5 yr	9.1 × 10¹³	0.13	8.5 × 10¹⁴	1.1 × 10⁻¹⁴	2.8
R20f0.5	3.7	5 yr	9.5 × 10¹³	0.62	1.2 × 10¹⁵	3.2 × 10⁻¹⁴	1.7
B20f0.3	54	15 d	7.2 × 10¹²	0.30	5.5 × 10¹³	8.7 × 10⁻¹¹	3.6
B20f0.5	91	15 d	7.0 × 10¹²	0.79	6.7 × 10¹³	9.5 × 10⁻¹¹	3.8

*

The first five columns are model name, injected energy, time that we stop our simulation, and the innermost radius and total mass of the region that we define as CSM. The last three columns are the results of the least-squares fitting, with fitted parameters (r_*, ρ_*, y).

Plugging |$v=f(X)\sqrt{GM_*/r}$| into the continuity equation

$$\begin{eqnarray} \frac{\partial \rho }{\partial t}+\frac{1}{r^2}\frac{\partial }{\partial r}(r^2\rho v) =0, \end{eqnarray}$$

(10)

we convert it to a differential equation with respect to r and X:

$$\begin{eqnarray} -\frac{2}{3}\frac{X^{3/2}}{f}\frac{\partial \ln \rho }{\partial \ln X} + \frac{\partial \ln \rho }{\partial \ln r} + \frac{\partial \ln \rho }{\partial \ln X} + \frac{3}{2} + \frac{\partial \ln f}{\partial \ln X} = 0. \end{eqnarray}$$

(11)

Comparing this with the total derivative of the density,

$$\begin{eqnarray} d\ln \rho = \frac{\partial \ln \rho }{\partial \ln r} d\ln r + \frac{\partial \ln \rho }{\partial \ln X} d \ln X, \end{eqnarray}$$

(12)

we obtain

$$\begin{eqnarray} \frac{d\ln \rho }{-\frac{3}{2}-\frac{\partial \ln f}{\partial \ln X}} = \frac{d\ln X}{1-\frac{2X^{3/2}}{3f}} = d\ln r. \end{eqnarray}$$

(13)

Substitution of f(X) in equation (8) into these equations yields

$$\begin{eqnarray} \frac{d\ln \rho }{dX} &=& \frac{-4.5X^3+30.047X^{3/2}-12.247}{X^4-5.828X^{5/2}+8.165X}, \end{eqnarray}$$

(14)

$$\begin{eqnarray} \frac{d\ln r}{dX} &=& \frac{X^3-10.016X^{3/2}+8.165}{X^4-5.828X^{5/2}+8.165X}. \end{eqnarray}$$

(15)

We solve for ρ and r as a function of X. After some algebra,

$$\begin{eqnarray} \rho &=& FX^{-3/2}\frac{(3.485-X^{3/2})^{6.334}}{(2.343-X^{3/2})^{8.334}}\equiv Fg(X) , \end{eqnarray}$$

(16)

$$\begin{eqnarray} r &=& BX\left(\frac{2.343-X^{3/2}}{3.485-X^{3/2}}\right)^{2.445}\equiv Bh(X). \end{eqnarray}$$

(17)

We note that X^3/2 < (6^2/3/2)^3/2 ≈ 2.12 < 2.343. Since the initial conditions give a relation between F and B as F = F(B), the general solution for ρ can be written as

$$\begin{eqnarray} \rho (r,X) = F\left[\frac{r}{h(X)}\right]g(X). \end{eqnarray}$$

(18)

Although the exact functional form of F is uncertain, we can still obtain the profile at the limit of small r and t ≫ t₀. For X → X_in,CSM ≪ 1, we find that r/h(X) becomes independent of r and g(X) ∝ r^−3/2. Thus, regardless of the exact form of the function F, we expect that the profile follows ρ ∝ r^−3/2 when we are looking at the region where X ∼ X_in,CSM. This asymptotic behaviour is analogous to spherical Bondi accretion (Bondi 1952), which solves the spherical steady-state accretion flow onto a central object. In fact, these two settings are essentially the same in the region where X ≪ 1, i.e., where t_fb ≪ t and the steady-state assumption is valid.

2.2 Connection to the unbound CSM

At large r, the effect of gravity is usually negligible and the density profile is expected to be similar to that of the outer ejecta in normal SNe. The profile changes according to whether the outer envelope is convective or radiative, but is generally steep, with ρ ∝ r⁻¹² for red supergiants (RSGs) and ρ ∝ r⁻¹⁰ for blue supergiants (BSGs) (Matzner & McKee 1999). We consider an interpolation of the inner and outer power-law limits, with a harmonic mean inspired by Matzner and McKee (1999),

$$\begin{eqnarray} \rho _{\rm CSM}(r) = \rho _* \left[\frac{(r/r_*)^{1.5/y}+(r/r_*)^{n_{\rm max}/y}}{2}\right]^{(-y)}, \end{eqnarray}$$

(19)

where r_* and ρ_* are the transition radius and density, n_max = 12 (= 10) for RSGs (BSGs), and y is a parameter that controls the curvature (smaller y gives a sharper transition).

3 Comparison with numerical results

To assess the reliability of our analytical model, we also numerically calculate the CSM profile using radiation hydrodynamics code developed by Kuriyama and Shigeyama (2020). We fit the numerical profile with the function in equation (19) using the least-squares method, with (r_*, ρ_*, y) as fitting parameters.

We prepare three hydrogen-rich progenitors, two RSGs with zero-age main sequence (ZAMS) mass of 15 and 20 M_⊙, and a BSG with ZAMS mass of 20 M_⊙. The stars are generated by the MESA code (Paxton et al. 2011, 2013, 2015, 2018, 2019) version 12778, using the example_make_pre_ccsn test suite. For the former two RSGs the default parameters are used and solar metallicity assumed. To obtain the BSG progenitor we change the metallicity to 10⁻² Z_⊙, and adopt a thermohaline efficiency parameter of 1 for semiconvection with the Ledoux criterion [the default value is 0; for a discussion of this parameter see Paxton et al. (2013) and references therein]. As the structure of the envelope does not change in the last decades of its life, we use the stars evolved up to core collapse for the input of the simulation. The properties of the progenitors are summarized in table 1.

As in Kuriyama and Shigeyama (2020), we inject some energy at the base of the hydrogen envelope and follow the response of the envelope. The injected energy is comparable to the envelope’s binding energy E_bind and thus parameterized as E_inj = f_injE_bind. We adopt the values f_inj = {0.3, 0.5}, which results in a range of CSM masses in line with what is usually considered to reproduce Type IIn SNe (Kuriyama & Shigeyama 2020).

The simulation gives a density profile of the entire matter that was originally the hydrogen-rich envelope of the progenitor. This means that we need to define the interface between the star (which eventually becomes the SN ejecta) and the CSM. As can be seen in the density profiles of figure 1, there is ubiquitously a density jump, which can be ascribed to the infalling CSM crashing the stellar envelope. We thus assume that the smooth profile outside this density jump is the CSM, and fit this region with the analytical profile. The number of cells used for the fit is of order 1000. As r and ρ span more than an order of magnitude, we fit the function log ρ[log (r)] to ensure contributions over the entire fitting region.

Fig. 1.

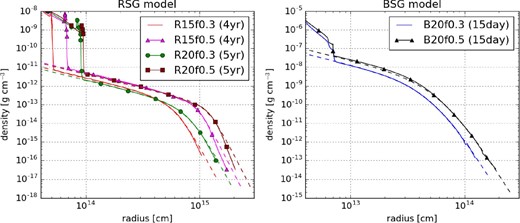
CSM density profiles obtained by numerical simulations (solid lines) compared with our analytical fit (dashed lines). The left panel is for the RSG progenitors, while the right panel is for the BSG progenitors. (Color online)

The time dependence of the profile can be easily derived once the fluid element at r = r_* starts to expand homologously. During this phase the value of the curvature parameter y is expected to be unchanged. This is because y is governed only by the CSM in the vicinity of r = r_* that should also be homologously expanding. Taking into account the time evolution of the CSM mass, the parameters evolve as r_* ∝ t, and ρ_* as given in equation (A6) in the Appendix. This homologous phase sets in from when the specific kinetic energy of the CSM at the transition radius, |$\approx r_*^2/2t^2$|⁠, is much larger than the gravitational potential at that radius, GM_*/r_*. Setting a parameter v_* = r_*/t, which is constant with respect to time in the homologous phase, the ratio of the two energies is

$$\begin{eqnarray} \frac{v_*^2/2}{GM_*/(tv_*)} \sim 12\left(\frac{t}{1\, {\rm yr}}\right)\left(\frac{M_*}{10\, {M}_{\odot }}\right)^{-1}\left(\frac{v_*}{10^7\, {\rm cm\, s^{-1}}}\right)^3. \end{eqnarray}$$

(20)

After this ratio becomes much larger than 1, the above simple scaling can be used when considering the future evolution of the profile. Thus we stop the simulations at the time t_stop (defined as the epoch from energy injection) when this ratio is ≳5, for the sake of computational cost. The value of t_stop for BSGs is much shorter than that for RSGs due to the larger v_* (see table 2).

Table 2 shows our fitting results, and figure 1 shows the corresponding fits. We find that our analytical profile produces good fits to the numerical results, although we find discrepancies in the tails of the RSG models. A similar discrepancy is seen in Matzner and McKee (1999), which they ascribe to the presence of the superadiabatic gradient close to the surface of RSGs. We presume the same physics operate in our models, but this difference in the tail, which carries negligible mass in the CSM, will likely not affect the observational properties of interaction-powered SNe.

4 Discussions

4.1 Implication for the bolometric light curve

We consider the implications of our density profile model by comparing our profile with the commonly adopted “wind profile” of ρ ∝ r⁻². As an example, we compare the bolometric light curves from ejecta–CSM interaction, using a numerical model by Takei and Shigeyama (2020).

We consider CSM with our analytical profile of equation (19) with parameters r_* = 3.4 × 10¹⁵ cm, y = 2.8, and total CSM mass of 0.13 M_⊙, and compare this against the wind profile. Our parameters correspond to the R20f0.3 model, but assuming that the energy was injected 20 yr before core collapse. For the wind profile we use a similar function to equation (19), but change the inner power-law index to asymptotically be −2 instead of −1.5. We use the same r_* and y for the two profiles, but use a different value for ρ_* so that the two CSMs have the same total mass. We show the density profiles in the left panel of figure 2.

Fig. 2.

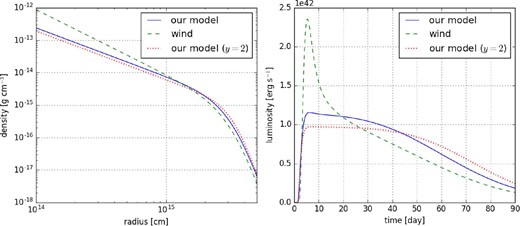
Comparison of our profile with a wind profile at the inner edge. The left panel shows the assumed CSM profiles for input to the light curve model, all having a total mass of 0.13 M_⊙ in the range 10¹⁴ cm < r < 10¹⁶ cm. The right panel shows the bolometric light curves for the profiles. (Color online)

Open in new tab Download slide

For the ejecta we adopt mass and energy of M_ej = 15 M_⊙ and E_ej = 10⁵¹ erg, respectively. We assume homologous ejecta with a density profile (Matzner & McKee 1999)

$$\begin{eqnarray} \rho _{\rm ej} (r,t) &=& \left\lbrace \begin{array}{ll}t^{-3}\left[r/(gt)\right]^{-n} &\quad (r/t > v_t),\\ t^{-3}(v_t/g)^{-n} \left[r/(tv_t)\right]^{-\delta } &\quad (r/t < v_t), \end{array}\right. \end{eqnarray}$$

(21)

where we adopt n = 12 and δ = 1. The factors g and v_t are constants determined from M_ej and E_ej. We refer to Takei and Shigeyama (2020) for the details of the light curve model.

The right panel of figure 2 shows the resulting bolometric light curves. We find that the bolometric light curve from our shallower profile displays a much flatter shape than that from the wind profile. The flat light curve is due to the constant kinetic energy dissipation rate for n = 12 and CSM with power-law index −1.5 (Moriya et al. 2013). However the plateau may not be universal, since the light curve would depend on the diffusion timescale in the CSM and the time for the shock to reach r_*. It would be interesting to do a more exhaustive parameter study and compare the light curve models with observations of interaction-powered SNe. We plan to do this in future work.

4.2 A guide for modelling our CSM profile

An important application of our model would be to compare with observations of interaction-powered SNe to extract the parameters of the CSM. As observed data also depend on other parameters such as the ejecta’s kinetic energy and radiation conversion efficiency, we are usually only interested in a rough inference of the radius and mass of the CSM, which relate to the epoch and strength of the mass loss. Here we show that in this case only r_* and ρ_* are important, and y is not such an important factor.

In figure 2 we also show the difference in the light curve if we change from our fiducial case of y = 2.8 (solid line) to y = 2 (dotted line), with the total CSM mass remaining the same. We find that while the shape of the light curve becomes slightly modified, the overall luminosity and timescale is similar. We conclude that while varying y can make slight changes to observables, it is relatively less important than the other two parameters r_*, ρ_*.

The total CSM mass calculated from the analytical profile is |$M_{\rm CSM} \approx \int _0^\infty 4\pi r^2\rho _{\rm CSM} dr \equiv 4\pi r_*^3\rho _* \eta (y)$|⁠, where

$$\begin{eqnarray} \eta (y)&\equiv & \int _0^\infty dx\, x^2\left(\frac{x^{1.5/y}+x^{{n_{\rm max}}/y}}{2}\right)^{(-y)},\quad x\equiv r/r_*. \end{eqnarray}$$

(22)

We find that in the range 1 ≤ y ≤ 4, η varies by a factor of ∼3. Fixing y ≈ 2 (y ≈ 4) for RSGs (BSGs), and modelling the CSM by just two parameters (r_*, ρ_* or r_*, M_CSM) should be sufficient if one is interested in order-of-magnitude estimates of the extent and mass of the CSM. We therefore recommend the density profiles

$$\begin{eqnarray} \rho _{\rm CSM}(r) &=& \left\lbrace \begin{array}{ll}\rho _* \left[\frac{(r/r_*)^{0.75}+(r/r_*)^{6}}{2}\right]^{-2} &\quad ({\rm RSGs}) ,\\ \rho _* \left[\frac{(r/r_*)^{0.375}+(r/r_*)^{2.5}}{2}\right]^{-4} &\quad ({\rm BSGs}). \end{array}\right. \end{eqnarray}$$

(23)

This two-parameter modelling is complementary to the commonly used power-law profile ρ_CSM(r) = qr^−s that also has two parameters: index s and normalization q.

5 Conclusions

In this work we have derived an analyical density profile of CSM created from a single mass eruption event years to decades before core collapse. We find that the density profile is well described by a double power-law, reflecting the bound and unbound limits of the CSM under the influence of gravitational pull from the central star. Using numerical simulations of Kuriyama and Shigeyama (2020), we verified that our profile is in good agreement with that numerically obtained from radiation hydrodynamical calculations.

We have shown that the radius and density at the transition are the two important parameters of our model that one should vary when trying to reproduce observations. We encourage future works attempting to model observations (e.g., light curves, spectra) of interaction-powered SNe to include our profile as input if possible.

The main conclusion of our model is that the inner part of the double power-law density profile follows ρ ∝ r^−1.5, shallower than the wind profile. This flat profile is consistent with that reported for the Type IIn SN 2006jd (Chandra et al. 2012). An independent study that modelled the optical light curve of SN 2006jd (Moriya et al. 2014) confirms this, while it finds steeper CSM for many of the other samples. We note, however, that light curve modelling can be subject to various systematic uncertainties, with different models disagreeing on the inferred density profile; see, e.g., the discussion in Takei and Shigeyama (2020) for SN 2005kj.

We mention a few possible caveats to our model. First, our model assumes a single mass eruption, while multiple mass eruptions are observed for some Type IIn SNe, the representative being SN 2009ip (Smith et al. 2010; Pastorello et al. 2013). Though Type IIn SNe with signatures of multiple mass eruptions with a short interval (within years) are likely rare (Nyholm et al. 2020), for such cases the density profile can be different from our simple profile (see, e.g., figure 12 of Kuriyama & Shigeyama 2021).

Second, our model reproduces well CSM that expands homologously at the outermost radius. For lower f_inj, or shorter interval from expansion to core collapse (comparable to or less than the progenitor’s dynamical timescale), the outermost CSM would not be homologous and the profile can be more complex. However, these cases would lead to a much smaller extent of the CSM and/or much lighter CSM mass, which may not reproduce the features of the CSM in observed interaction-powered SNe.

Funding

This work is supported by Japan Society for the Promotion of Science KAKENHI Grant Numbers JP19J21578, JP16H06341, and JP20H05639, Ministry of Education, Culture, Sports, Science and Technology, Japan.

Acknowledgements

DT is supported by the Advanced Leading Graduate Course for Photon Science (ALPS) at the University of Tokyo. YT is supported by the RIKEN Junior Research Associate Program.

Appendix. Homologous expansion phase

After the CSM at r = r_* reaches the homologous phase, the velocity v_* and curvature parameter y are expected to be constant. At the innermost region, the CSM plunges into the star with a negative velocity, which reduces the mass of the CSM. In this section we first derive the total CSM mass and the density normalization parameter ρ_* as a function of time, and compare this time evolution with the numerical results.

The mass inflow (loss) rate of CSM from the innermost radius R_in,CSM is

$$\begin{eqnarray} \frac{dM_{\rm CSM}}{dt}&=&(4\pi r^2\rho v)_{r=R_{\rm in, CSM}} \nonumber \\ &\approx & -4\pi \sqrt{2GM_*R_{\rm in, CSM}^3}\times \rho (R_{\rm in, CSM}), \end{eqnarray}$$

(A1)

where we have used the free-fall approximation |$v\approx -\sqrt{2GM_*/r}$|⁠. From the analytical profile,

$$\begin{eqnarray} \rho (R_{\rm in, CSM}) &=& \rho _*\left[\frac{(R_{\rm in, CSM}/r_*)^{1.5/y}+(R_{\rm in, CSM}/r_*)^{n_{\rm max}/y}}{2}\right]^{-y} \nonumber \\ &\approx & 2^y\rho _*\left(\frac{R_{\rm in, CSM}}{r_*}\right)^{-1.5}, \end{eqnarray}$$

(A2)

where we used |$(R_{\rm in, CSM}/r_*)^{n_{\rm max}-1.5}\ll 1$|⁠. Using the relation |$M_{\rm CSM}\approx 4\pi r_*^3\rho _*\eta (y)$| in section 4 with η(y) defined in equation (22), we obtain the following differential equation:

$$\begin{eqnarray} \frac{dM_{\rm CSM}}{dt}&\approx & -\frac{2^{y+0.5}}{\eta (y)}\sqrt{\frac{GM_*}{v_*^3}}M_{\rm CSM}t^{-3/2}. \end{eqnarray}$$

(A3)

The solution to this equation is

$$\begin{eqnarray} M_{\rm CSM} = M_{\rm stop}\exp \left[\frac{2^{y+1.5}}{\eta (y)}\sqrt{\frac{GM_*}{v_*^3}}(t^{-1/2}-t_{\rm stop}^{-1/2})\right], \end{eqnarray}$$

(A4)

where t_stop is the time when the fluid at r = r_* enters a homologous expansion phase, and the constant M_stop is the total CSM mass at t = t_stop. We note that while this solution diverges at t → 0, it is not valid at t → 0 because the homologous phase is yet to be achieved. This expression can be rewritten as M_CSM ∝ exp [(t/t_c)^−1/2 − (t_stop/t_c)^−1/2], where

$$\begin{eqnarray} t_\mathrm{c} = \frac{2^{2y+3}}{\eta (y)^2}\frac{GM_*}{v_*^3} \sim 1\, {\rm yr} \left(\frac{M_*}{10\, {M}_{\odot }}\right)\left(\frac{v_*}{100\, {\rm km\, s^{-1}}}\right)^{-3}. \end{eqnarray}$$

(A5)

The latter scaling is for a reference value y = 2. The numerical factor 2^2y+3/η(y)² is a monotonically increasing function of y, ranging from 23 to 88 for 1 ≤ y ≤ 4 and n_max = 12. The time dependence of ρ_* is then

$$\begin{eqnarray} \rho _*(t) \propto t^{-3}\exp \left[\left(\frac{t}{t_{\rm c}}\right)^{-1/2}\right]. \end{eqnarray}$$

(A6)

To test this solution, we carry out the numerical simulation up to 10 yr for Model R15f0.3. Then, in addition to t = 4 yr presented in the main text, we fit the CSM profile at t = 2, 7, 10 yr, with the same fitting parameters (r_*, ρ_*, y). The fitting results are shown in figure 3 and table 3. The analytical profile fits the numerically obtained profile well at all times. We find that the value of y is nearly converged at t = t_stop = 4 yr, with future change within only ∼6%. We note that this small difference in y has a tiny effect on the observables, such as the light curve discussed in section 4.

Fig. 3.

Time evolution of the CSM density profile (left panel). The density profiles obtained by numerical simulations (solid lines) compared with our analytical fit (dashed lines) for various ages from 2 to 10 yr. The black dotted line is the CSM profile at t = 10 yr obtained from using the parameters fitted with equation (23) for t = 4 yr and the scaling of r_* and ρ_* formulated in the Appendix. (Right panel) Values of ρ_* obtained from fitting for the four values of t, compared with the analytical formula in equation (A6) shown as a dashed line. The normalization of the two lines is set to cross the point at t = 4 yr. (Color online)

Open in new tab Download slide

Table 3.

Results of fitting for the numerical CSM profile with our analytical model for different epochs for the R15f0.3 model.*

t	R_in,CSM	r_*	ρ_*	y
[yr]	[cm]	[cm]	[g cm⁻³]
2	5.0 × 10¹³	3.1 × 10¹⁴	5.5 × 10⁻¹³	2.08
4	5.9 × 10¹³	6.4 × 10¹⁴	2.7 × 10⁻¹⁴	2.61
7	6.6 × 10¹³	1.1 × 10¹⁵	2.9 × 10⁻¹⁵	2.77
10	8.2 × 10¹³	1.6 × 10¹⁵	7.7 × 10⁻¹⁶	2.78

t	R_in,CSM	r_*	ρ_*	y
[yr]	[cm]	[cm]	[g cm⁻³]
2	5.0 × 10¹³	3.1 × 10¹⁴	5.5 × 10⁻¹³	2.08
4	5.9 × 10¹³	6.4 × 10¹⁴	2.7 × 10⁻¹⁴	2.61
7	6.6 × 10¹³	1.1 × 10¹⁵	2.9 × 10⁻¹⁵	2.77
10	8.2 × 10¹³	1.6 × 10¹⁵	7.7 × 10⁻¹⁶	2.78

*

The columns are age, the innermost radius that we define as CSM, and the fitted parameters (r_*, ρ_*, y). The value for t = 4 yr is the same as that in table 2.

Table 3.

Results of fitting for the numerical CSM profile with our analytical model for different epochs for the R15f0.3 model.*

t	R_in,CSM	r_*	ρ_*	y
[yr]	[cm]	[cm]	[g cm⁻³]
2	5.0 × 10¹³	3.1 × 10¹⁴	5.5 × 10⁻¹³	2.08
4	5.9 × 10¹³	6.4 × 10¹⁴	2.7 × 10⁻¹⁴	2.61
7	6.6 × 10¹³	1.1 × 10¹⁵	2.9 × 10⁻¹⁵	2.77
10	8.2 × 10¹³	1.6 × 10¹⁵	7.7 × 10⁻¹⁶	2.78

t	R_in,CSM	r_*	ρ_*	y
[yr]	[cm]	[cm]	[g cm⁻³]
2	5.0 × 10¹³	3.1 × 10¹⁴	5.5 × 10⁻¹³	2.08
4	5.9 × 10¹³	6.4 × 10¹⁴	2.7 × 10⁻¹⁴	2.61
7	6.6 × 10¹³	1.1 × 10¹⁵	2.9 × 10⁻¹⁵	2.77
10	8.2 × 10¹³	1.6 × 10¹⁵	7.7 × 10⁻¹⁶	2.78

*

The columns are age, the innermost radius that we define as CSM, and the fitted parameters (r_*, ρ_*, y). The value for t = 4 yr is the same as that in table 2.

Using the fitting parameters at t = 4 yr and equation (A6), we analytically calculate the density profile at t = 10 yr. The value of t_c for this model is obtained from the fitting parameters as t_c ≈ 11 yr. The result of using this scaling is shown as black dotted lines in the left panel of figure 3. We find that the density profile matches the numerical results well, which validates the analytical evolution and our assumption on transition to homologous flow at t = t_stop. The right panel of figure 3 shows the value of ρ_* at the four epochs, compared with the analytical curve of equation (A6). We confirm that the analytical model gives a good match to the numerical results.

Footnotes

1

The exact border where the fallback starts is found to be at X ≈ 0.93.

References

Bondi

H.

1952

,

MNRAS

,

112

,

195

Bruch

R. J.

et al.

2021

,

ApJ

,

912

,

46

Chandra

P.

,

Chevalier

R. A.

,

Chugai

N.

,

Fransson

C.

,

Irwin

C. M.

,

Soderberg

A. M.

,

Chakraborti

S.

,

Immler

S.

2012

,

ApJ

,

755

,

110

Chatzopoulos

E.

,

Wheeler

J. C.

,

Vinko

J.

2012

,

ApJ

,

746

,

121

Chevalier

R. A.

,

Irwin

C. M.

2011

,

ApJ

,

729

,

L6

Ginzburg

S.

,

Balberg

S.

2012

,

ApJ

,

757

,

178

Grasberg

E. K.

,

Nadyozhin

D. K.

1987

,

Astron. Zh.

,

64

,

1199

Kuriyama

N.

,

Shigeyama

T.

2020

,

A&A

,

635

,

A127

Kuriyama

N.

,

Shigeyama

T.

2021

,

A&A

,

646

,

A118

Matzner

C. D.

,

McKee

C. F.

1999

,

ApJ

,

510

,

379

Moriya

T.

,

Tominaga

N.

,

Blinnikov

S. I.

,

Baklanov

P. V.

,

Sorokina

E. I.

2011

,

MNRAS

,

415

,

199

Moriya

T. J.

,

Maeda

K.

,

Taddia

F.

,

Sollerman

J.

,

Blinnikov

S. I.

,

Sorokina

E. I.

2013

,

MNRAS

,

435

,

1520

Moriya

T. J.

,

Maeda

K.

,

Taddia

F.

,

Sollerman

J.

,

Blinnikov

S. I.

,

Sorokina

E. I.

2014

,

MNRAS

,

439

,

2917

Moriya

T. J.

,

Sorokina

E. I.

,

Chevalier

R. A.

2018

,

Space Sci. Rev.

,

214

,

59

Morozova

V.

,

Piro

A. L.

,

Valenti

S.

2018

,

ApJ

,

858

,

15

Murase

K.

,

Franckowiak

A.

,

Maeda

K.

,

Margutti

R.

,

Beacom

J. F.

2019

,

ApJ

,

874

,

80

Nyholm

A.

et al.

2020

,

A&A

,

637

,

A73

Pastorello

A.

et al.

2013

,

ApJ

,

767

,

1

Paxton

B.

et al.

2013

,

ApJS

,

208

,

4

Paxton

B.

et al.

2015

,

ApJS

,

220

,

15

Paxton

B.

et al.

2018

,

ApJS

,

234

,

34

Paxton

B.

et al.

2019

,

ApJS

,

243

,

10

Paxton

B.

,

Bildsten

L.

,

Dotter

A.

,

Herwig

F.

,

Lesaffre

P.

,

Timmes

F.

2011

,

ApJS

,

192

,

3

Smith

N.

et al.

2010

,

AJ

,

139

,

1451

Soker

N.

2021

,

ApJ

,

906

,

1

Suzuki

A.

,

Moriya

T. J.

,

Takiwaki

T.

2020

,

ApJ

,

899

,

56

Svirski

G.

,

Nakar

E.

,

Sari

R.

2012

,

ApJ

,

759

,

108

Takei

Y.

,

Shigeyama

T.

2020

,

PASJ

,

72

,

67

Tsuna

D.

,

Ishii

A.

,

Kuriyama

N.

,

Kashiyama

K.

,

Shigeyama

T.

2020

,

ApJ

,

897

,

L44

Tsuna

D.

,

Kashiyama

K.

,

Shigeyama

T.

2019

,

ApJ

,

884

,

87

Yaron

O.

et al.

2017

,

Nature Phys.

,

13

,

510