-
PDF
- Split View
-
Views
-
Cite
Cite
Yohei Koizumi, Masayuki Kuzuhara, Masashi Omiya, Teruyuki Hirano, John Wisniewski, Wako Aoki, Bun’ei Sato, Characterization of M dwarfs using optical mid-resolution spectra for exploration of small exoplanets, Publications of the Astronomical Society of Japan, Volume 73, Issue 1, February 2021, Pages 154–173, https://doi.org/10.1093/pasj/psaa112
Close - Share Icon Share
Abstract
We present the optical spectra of 338 nearby M dwarfs, and compute their spectral types, effective temperatures (Teff), and radii. Our spectra were obtained using several optical spectrometers with spectral resolutions that range from 1200 to 10000. As many as 97% of the observed M-type dwarfs have a spectral type of M3–M6, with a typical error of 0.4 subtype, among which the spectral types M4–M5 are the most common. We infer the Teff of our sample by fitting our spectra with theoretical spectra from the PHOENIX model. Our inferred Teff is calibrated with the optical spectra of M dwarfs whose Teff have been well determined with the calibrations that are supported by previous interferometric observations. Our fitting procedures utilize the VO absorption band (7320–7570 Å) and the optical region (5000–8000 Å), yielding typical errors of 128 K (VO band) and 85 K (optical region). We also determine the radii of our sample from their spectral energy distributions. We find most of our sample stars have radii of <0.6 R⊙, with the average error being 3%. Our catalog enables efficient sample selection for exoplanet surveys around nearby M-type dwarfs.
1 Introduction
In recent years, M dwarfs have been gathering attention as attractive targets to detect Earth-mass planets in habitable zones. M dwarfs are main-sequence stars with effective temperatures (Teff) ranging from 2300 to 3900 K (e.g., Rajpurohit et al. 2013) and approximate masses ranging from 0.09 to 0.6 M⊙ (e.g., Kraus & Hillenbrand 2007). The low temperatures cause the habitable zones around these stars to be located closer to the central stars compared to hotter stars. Combining the small orbital distance and the low stellar mass, the stellar radial velocity variations caused by an Earth-mass planet in the habitable zone have an amplitude comparable to ∼1 m s−1, which is ten times larger than that of a solar-mass star hosting an Earth-mass planet in the habitable zone (e.g., Burke & McCullough 2014). Therefore, it is easier to detect Earth-mass planets in the habitable zones around M dwarfs than around Sun-like stars.
Rocky planets are expected to be more common around M dwarfs as compared to Sun-like stars (Dressing & Charbonneau 2013), and M dwarfs comprise more than 70% of stars in the solar neighborhood (Henry et al. 1994; Reid et al. 2004). This enhances the probability of detecting habitable planets around M dwarfs in the solar neighborhood. For these reasons, several groups are planning planet-search programs targeting M dwarfs using state-of-the-art high-dispersion spectrographs such as IRD (Kotani et al. 2018), SPIRou (Artigau et al. 2014), HPF (Mahadevan et al. 2012), and CARMENES (Quirrenbach et al. 2014).
Accurate characterization of fundamental stellar properties is very important for planet-search programs because the estimation of planetary physical properties such as mass and radius directly depend on these stellar properties. These fundamental stellar properties are also crucial when we compare the properties of planetary systems between various types of stars. For example, it is known that the occurrence rate of giant planets is correlated with the stellar mass (e.g., Johnson et al. 2010; Gaidos et al. 2013), and that of small planets increases as the stellar temperature decreases (Howard et al. 2012). It should be stressed here that stellar properties such as mass, radius, and luminosity are all correlated with the stellar Teff (e.g., Mann et al. 2013b, 2015). Therefore, the precise determination of stellar temperatures is necessary in exoplanet surveys.
It is more challenging, however, to determine the stellar temperatures of M dwarfs than those of solar-type stars. For M dwarfs, molecular absorption bands (mainly metal oxides and hydrides such as TiO and CaH) are dominant in their optical and near-infrared spectra because of their low Teff (Bessell 1991; Kirkpatrick et al. 1991). Figure 1 shows typical molecular absorption features in the optical spectra of M dwarfs. For solar-type stars, their physical properties can be determined by using equivalent widths of atomic absorption lines. However, the continuum region in M dwarf spectra cannot be accurately determined because of strong and complex absorption bands (see figure 1). It is then notable that the synthetic model atmosphere for low-mass stars is still incomplete, as discussed in Veyette et al. (2017), making it more difficult to characterize those cool dwarfs. Hence, it is crucial to validate how synthetic model atmospheres are applied to observed spectra of M dwarfs given the model uncertainties. Actually, the empirically calibrated methods to constrain the properties of M dwarfs were provided by Mann, Gaidos, and Ansdell (2013b) and Mann et al. (2015). They also applied their methods to a lot of M dwarfs by comparing their optical and near-infrared medium-resolution spectra to synthetic model spectra, providing Teff over a range of 2600–4200 K with a precision of ∼60 K.
Regardless of the improvements in synthetic model spectra, there are still some wavelength regions that are not suitable for estimation of stellar properties (e.g., Reylé et al. 2011). Furthermore, it is possible that the existing techniques of stellar characterization are not suited for the specifications of the available instruments (e.g., narrow wavelength coverage). We thus need to develop the techniques that can be applied to different instrumental specifications, so that various telecopes and instruments can be applied to a variety of M dwarfs, such as distant ones.
The radii of bright and nearby M dwarfs can be determined using their parallaxes and angular diameters measured by interferometric observations, as shown by Boyajian et al. (2012), who measured the stellar radii of a set of early M dwarfs. In the same work, they also determined stellar luminosities by combining bolometric fluxes with parallaxes. Stellar masses have also been determined from the empirical relations between the absolute K magnitudes and masses (e.g., Henry & McCarthy 1993; Delfosse et al. 2000). Mann, Gaidos, and Ansdell (2013b) and Mann et al. (2015) derived the relations between Teff and stellar properties (radius, mass, and luminosity) by using the measurements of Boyajian et al. (2012). However, M dwarfs are generally small and faint, which makes direct radius measurements using interferometry difficult for most of them.
The radii of M dwarfs are also measured by observations of eclipsing binary stars; however, these radii are 5%–15% larger than predicted by theory (e.g., Torres & Ribas 2002; Kraus et al. 2011). The lack of precise measurements of parallaxes for M dwarfs was one of the major sources of error when estimating their properties. Because Gaia (Gaia Collaboration 2018) now provides precise parallaxes of nearby M dwarfs, we can improve the estimation of radii.
In this paper we determine the Teff of M dwarfs by using medium-resolution optical spectra, which are more readily available than their infrared spectra, and determine their radii using photometric data and parallaxes. Our method is calibrated with M dwarfs whose Teff are well determined by previous studies that employed interferometric observations. For spectra with limited or narrow wavelength coverages, we find that the Teff estimation is refined by utilizing only VO absorption features if available. Compared with TiO absorption, this absorption can reproduce well the temperatures determined in Mann et al. (2015). This method makes it possible to estimate the properties of many M dwarfs relatively easily with sufficient precision, and enables us to efficiently select M dwarfs that are suitable for large exoplanet surveys. We also provide the spectral types of our sample.
The rest of the paper is organized as follows. In section 2 we describe our sample and observations. Section 3 details our analysis. Our results are summarized in section 4. We discuss the validity of our results, and compare them with the other studies, in section 5. We conclude the paper in section 6 with a summary of our study.
2 Data
2.1 Target sample
Our target sample was drawn from the LSPM catalog (Lépine & Shara 2005), which comprises stars with annual proper motions larger than |${0{^{\prime \prime }_{.}}15}$|. We attempted to exclude binaries and multiple-star systems from the sample for our spectroscopic characterizations. We then used the SIMBAD database to identify eclipsing binaries, double or multiple stars, and spectroscopic binaries. Based on the Washington Double Star catalog (WDS; Mason et al. 2001, 2014), we also avoided stars from which companion candidates are located at projected separations smaller than 1000 au.1 In spite of these attempts, our sample still includes some known multiple-star systems, which are marked in table 9 if they are found in the WDS catalog.
Our sample consists of 338 M dwarfs. Their brightness and parallaxes (plx) lie in the ranges 7 < J < 11.5 and |${0{^{\prime \prime }_{.}}02}<\rm {plx}<{0{^{\prime \prime }_{.}}13}$|. The J magnitudes were drawn from the Two Micron All Sky Survey (2MASS; Cutri et al. 2003), and parallaxes were drawn from Gaia DR2 (Gaia Collaboration 2018) or MEarth observations (Dittmann et al. 2014).2 The fraction of stars with Gaia DR2 parallaxes is 92%. Figure 2 shows histograms of our sample.
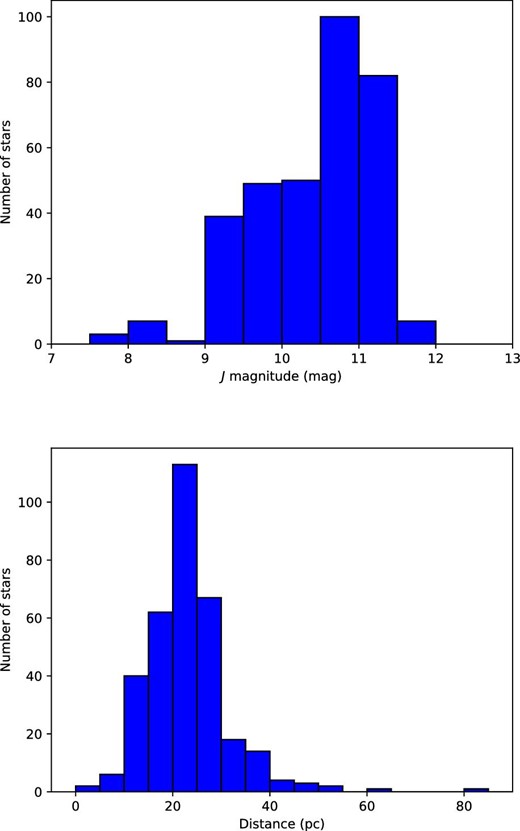
Histograms of our samples: J-band magnitudes (top), distances (bottom). (Color online)
2.2 Observations
The majority (N = 249) of the spectra of our sample were obtained using the Kyoto Okayama Optical Low-dispersion Spectrograph (KOOLS; Yoshida 2005) mounted on the 188 cm telescope at Okayama Astrophysical Observatory (OAO) and the Bench spectrograph (Bershady et al. 2008; Knezek et al. 2010) mounted on the 3.5 m telescope of the WYIN observatory.3 The KOOLS observations were conducted from 2014 August to 2016 April, and the Bench spectrograph observations were performed in 2016 November and 2017 May. In addition, only 21 samples were observed with the Medium And Low-dispersion Long-slit Spectrograph (MALLS; Ozaki & Tokimasa 2005) mounted on the 2 m telescope at Nishi-Harima Astronomical Observatory (NHAO) from 2016 December to 2017 July and the Calar Alto Faint Object Spectrograph (CAFOS; Meisenheimer 1994) mounted on the 2.2 m telescope at Calar Alto Observatory (CAO)4 in 2016 October. Finally, the Dual Imaging Spectrograph (DIS)5 mounted on the ARC 3.5 m telescope at Apache Point Observatory (APO)6 from 2016 November to 2018 March were utilized to take the spectra of 70 stars. KOOLS was upgraded to KOOLS-IFU (Matsubayashi et al. 2019) in 2016 February, but the spectrograph itself did not change. Slit widths were set to |${1{^{\prime \prime }_{.}}0}$| for KOOLS, |${1{^{\prime \prime }_{.}}2}$| for MALLS, |${1{^{\prime \prime }_{.}}2}$| for CAFOS, and |${1{^{\prime \prime }_{.}}5}$| for DIS. The KOOLS-IFU have fiber arrays on their focal planes, whose widths were set to |${1{^{\prime \prime }_{.}}8}$| for KOOLS-IFU. We adopted ∇Pak7 (Eigenbrot & Bershady 2018), which has rectangular arrays with rows of fibers whose fields of view (FoVs) vary from |${1{^{\prime \prime }_{.}}87}$| to |${5{^{\prime \prime }_{.}}62}$|, to inject the lights from our targets into the Bench spectrograph. We then used the smallest-FoV fiber in our observations. Table 1 shows the details of the instruments we used, and our observations are summarized in table 8. Our spectra have typical signal-to-noise ratios at 7400 Å of ∼80 for KOOLS, ∼36 for KOOLS-IFU, and ∼100 for the other instruments. The noise values are just based on the photon noise of each obtained spectrum. We note that the CCD of KOOLS had bad pixels in the range 6675–6715 Å, and therefore we did not use this area in our analysis.
| Instrument and telescope . | Wavelength . | Disperser . | Resolution . | Num. . | Num. . |
|---|---|---|---|---|---|
| . | (Å) . | . | (R ∼ λ/Δλ) . | stars . | nights . |
| KOOLS/OAO 188 cm | 6400–7600 | VPH683 | 2000 | 91 | 17 |
| KOOLS-IFU/OAO 188 cm | 6400–7600 | VPH683 | 2000 | 33 | 6 |
| MALLS/NHAO 2 m | 5200–8200 | 300 l/mm | 1200 | 18 | 8 |
| Bench spectrograph/WIYN 3.5 m | 5000–7900 | [email protected] | 1700 | 125 | 9 |
| CAFOS/CAO 2.2 m | 4200–8300 | G-100 | 1700 | 3 | 2 |
| DIS/APO 3.5 m | 4160–5430, 6100–7300 | B1200, R1200 | 10000 | 68 | 7 |
| Instrument and telescope . | Wavelength . | Disperser . | Resolution . | Num. . | Num. . |
|---|---|---|---|---|---|
| . | (Å) . | . | (R ∼ λ/Δλ) . | stars . | nights . |
| KOOLS/OAO 188 cm | 6400–7600 | VPH683 | 2000 | 91 | 17 |
| KOOLS-IFU/OAO 188 cm | 6400–7600 | VPH683 | 2000 | 33 | 6 |
| MALLS/NHAO 2 m | 5200–8200 | 300 l/mm | 1200 | 18 | 8 |
| Bench spectrograph/WIYN 3.5 m | 5000–7900 | [email protected] | 1700 | 125 | 9 |
| CAFOS/CAO 2.2 m | 4200–8300 | G-100 | 1700 | 3 | 2 |
| DIS/APO 3.5 m | 4160–5430, 6100–7300 | B1200, R1200 | 10000 | 68 | 7 |
The KOOLS-IFU and Bench spectrograph transfer object light to their spectrographs through fibers of widths |${1{^{\prime \prime }_{.}}8}$| (KOOLS-IFU) and |${1{^{\prime \prime }_{.}}87}$| (Bench spectrograph).
| Instrument and telescope . | Wavelength . | Disperser . | Resolution . | Num. . | Num. . |
|---|---|---|---|---|---|
| . | (Å) . | . | (R ∼ λ/Δλ) . | stars . | nights . |
| KOOLS/OAO 188 cm | 6400–7600 | VPH683 | 2000 | 91 | 17 |
| KOOLS-IFU/OAO 188 cm | 6400–7600 | VPH683 | 2000 | 33 | 6 |
| MALLS/NHAO 2 m | 5200–8200 | 300 l/mm | 1200 | 18 | 8 |
| Bench spectrograph/WIYN 3.5 m | 5000–7900 | [email protected] | 1700 | 125 | 9 |
| CAFOS/CAO 2.2 m | 4200–8300 | G-100 | 1700 | 3 | 2 |
| DIS/APO 3.5 m | 4160–5430, 6100–7300 | B1200, R1200 | 10000 | 68 | 7 |
| Instrument and telescope . | Wavelength . | Disperser . | Resolution . | Num. . | Num. . |
|---|---|---|---|---|---|
| . | (Å) . | . | (R ∼ λ/Δλ) . | stars . | nights . |
| KOOLS/OAO 188 cm | 6400–7600 | VPH683 | 2000 | 91 | 17 |
| KOOLS-IFU/OAO 188 cm | 6400–7600 | VPH683 | 2000 | 33 | 6 |
| MALLS/NHAO 2 m | 5200–8200 | 300 l/mm | 1200 | 18 | 8 |
| Bench spectrograph/WIYN 3.5 m | 5000–7900 | [email protected] | 1700 | 125 | 9 |
| CAFOS/CAO 2.2 m | 4200–8300 | G-100 | 1700 | 3 | 2 |
| DIS/APO 3.5 m | 4160–5430, 6100–7300 | B1200, R1200 | 10000 | 68 | 7 |
The KOOLS-IFU and Bench spectrograph transfer object light to their spectrographs through fibers of widths |${1{^{\prime \prime }_{.}}8}$| (KOOLS-IFU) and |${1{^{\prime \prime }_{.}}87}$| (Bench spectrograph).
We used IRAF8 for the data reduction, which included bias subtraction, flat-fielding, sky-background subtraction, aperture extraction, wavelength calibration, and instrumental response correction. We also used the data-reduction software9 for KOOLS and the pipelines10 developed for KOOLS-IFU. Our wavelength calibrations were based on a Fe-Ne-Ar lamp for KOOLS, KOOLS-IFU, and MALLS, a Cu-Ar lamp for the Bench spectrograph, and a Hg-He-Rb lamp for CAFOS. On each night, we observed some spectrophotometric standards listed in Oke (1990) to correct the instrumental responses of the telescopes and instruments. Examples of the reduced spectra are shown in figure 3.
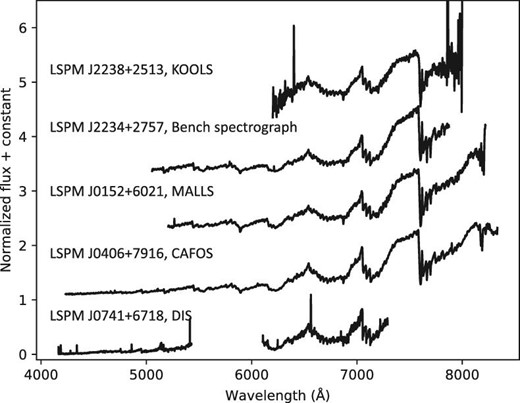
Examples of our samples. The top one is LSPM J2238+2513 obtained by KOOLS, the second from the top is LSPM J2234+2757 obtained by the Bench spectrograph, the third from the top is LSPM J0152+6021 obtained by MALLS, the fourth from the top is LSPM J0406+7916 obtained by CAFOS, and the bottom sample is LSPM J0741+6718 obtained by DIS. We note that the CCD of KOOLS had bad pixels in 6675–6715 Å, which were excluded in this study.
2.3 Data from other literature
We also analyzed the data of Mann et al. (2015) to calibrate the stellar properties derived from our observed spectra. They obtained 183 optical and near-infrared spectra of nearby K7–M7 single dwarfs from the CONCH-SHELL catalog (Gaidos et al. 2014) and Lépine and Gaidos (2011), using the SuperNova Integral Field Spectrograph (SNIFS; Aldering et al. 2002; Lantz et al. 2004) mounted on the University of Hawaii 2.2 m telescope at Mauna Kea. Their spectra covered the wavelength range 3200–9700 Å with a wavelength resolution of R ∼ 1000. The median distance of their sample was ∼10 pc, and their |$[\rm {Fe/H}]$| ranged from −0.60 to +0.53. Mann et al. (2015) derived Teff for their sample by fitting the CFIST suite11 of the BT-Settl version of the PHOENIX model (Allard et al. 2013) to the observed spectra, using the method detailed in Mann, Gaidos, and Ansdell (2013b), and achieved a Teff precision of ∼60 K.
3 Analysis
In this section we explain our method of determining stellar Teff, radii, and spectral types. The calculation of Teff is based on synthetic spectra, and the radii are estimated from photometric magnitudes and the Gaia parallaxes, while we determined the spectral types from molecular absorption features. The Teff are calibrated with the optical spectra of the M dwarfs in Mann et al. (2015). Our methods are based on those used by Mann et al. (2015) and the references therein, which provide the well-calibrated Teff estimates. We expand their approach to include different wavelength regimes, and note that our methodology is even applicable to datasets having relatively narrow wavelength coverage, such as KOOLS.
3.1 Temperature
3.1.1 Temperature from optical spectra
We obtained Teff, |$[\rm {Fe/H}]$|, and log g of the synthetic spectra range from 2300 to 4500 K in increments of 100 K, from −1.0 to 1.0 in increments of 0.1, and 4.5 or 5.0, respectively. We note that the original grid interval of the model for log g and metallicity were 0.5, which we interpolated linearly to obtain an interval of 0.1. A synthetic model spectrum was convolved with a Gaussian whose width corresponds to the wavelength resolution of each instrument. We discarded the wavelength ranges affected by telluric absorptions and possible |$\rm {H_\alpha }$| emissions. Additionally, we omitted the region of 6400–6600 Å, in which there is a TiO absorption that remains poorly modeled (Reylé et al. 2011)—this was also omitted in the analysis of Lépine et al. (2013) and Mann, Gaidos, and Ansdell (2013b). One should note there is still the inaccuracy of TiO line lists, as seen in the comparison of high-resolution spectroscopy of M dwarfs to the modeled TiO spectra (Hoeijmakers et al. 2015; McKemmish et al. 2019).
First, we calculated χ2 values for the spaced model grid to get a rough global minimum. After determining the best-fitting model from all models sampled with the Teff interval of 100 K, we further explored a better fit around the initial best-fitting model as below. We selected two additional models: one has a higher Teff than the best-fitting model by 100 K, and the other has a lower Teff by 100 K. For the stars observed with KOOLS or KOOLS-IFU, we also selected two models, one of which has a higher Teff than the best-fitting model by 200 K, and the other has a lower Teff by 200 K. Then, these models and the initial best-fitting model (i.e., Teff = best − 100 K, best, best + 100 K) were linearly interpolated, from which we further sought the final best-fitting model spectrum. The metallicity and log g were also optimized again, with the same interpolations as described above. Next, we generated 1000 mock datasets by adding artificial noise to the best-fitting spectrum, and repeated our model fitting procedure. The metallicity and log g were fixed at the best-fitting values. In this step, artificial noise was extracted from a Gaussian distribution whose standard deviation is equal to a value large enough to scale the reduced χ2 of the best fit to unity. Thus, we repeated the optimizations for the 1000 mock datasets, and we calculated the average and standard deviation of 1000 Teff optimizations, which were accepted as the final estimate of a stellar Teff and its error value.
3.1.2 Calibration using the literature data
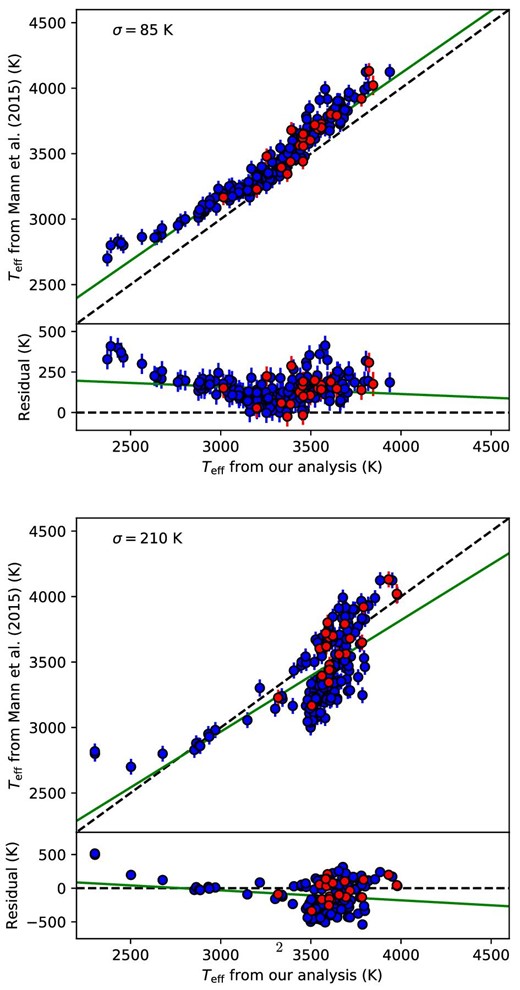
Comparison of our method with Mann et al. (2015). The top panel is the result for 5000–8000 Å, and bottom is for 6600–7500 Å. The green lines in the figure represent linear functions fitted to the data. The red points represent stars which have interferometric observations (Lane et al. 2001; Ségransan et al. 2003; Berger et al. 2006; Kervella et al. 2008; Demory et al. 2009; von Braun et al. 2011, 2012, 2014; Boyajian et al. 2012). (Color online)
The narrow wavelength coverage of KOOLS and KOOLS-IFU prevents us from accurately determining stellar Teff (see the top panel of figure 4). To improve the precision of our Teff estimation with the wavelength range of 6600–7500 Å, we focus on the wavelength ranges of the three molecular absorption bands listed in table 2 rather than using the whole wavelength range. These three regions are less affected by telluric absorptions in the spectra obtained by KOOLS or KOOLS-IFU (see figure 6). We reanalyzed the data of Mann et al. (2015) using these three bands, and the results for each band are shown in figure 5. The green lines in figure 5 represent the linear functions that were fitted to the relations between our re-analysis of the data in Mann et al. (2015) and the original analysis of Mann et al. (2015). The VO band was the most sensitive to Teff (see figure 6). The best-fitting linear functions have residual scatters of 239 K for the fit using TiO band1, 177 K for the fit using TiO band2, and 103 K for the fit using the VO band. Therefore, we used the VO band for the data obtained by KOOLS in calculating Teff.
![Synthetic spectra of Husser et al. (2013), which we used for fits to estimate stellar Teff. The metallicity was fixed as $\rm {[Fe/H]}=0.0$ in this plot. The VO band is a region in 7320–7570 Å. (Color online)](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/pasj/73/1/10.1093_pasj_psaa112/2/m_psaa112fig6.jpeg?Expires=1749236902&Signature=y7uv3DSaLxKfqcta~GNrbRlyoypRs27ZWiekqw2H7er9~22k5AAcaoUlxP5Udvbm-8DBzBJ79jpBZo01WMQyFbQ0C~ZxlGVF0NkSHJg8kpiMJphtI13wzfOQ98e9KX9QNoaNNHZxQ2K0WxO00SsHR5xXFX3ablckPfUHOHzvbJKCgbOygP4EfbrJ3A6jzsajocGIyBPNcTWqn2clLdf~cr2qM55m7xY96hkw4fKZIEOXc8Vx1ASnhhDzSSkw6ek5tNsnEniufglsM98OIQxS8UCv-j9yHtqknUOp~FkKDymNccAE6Rhte~BA4qxUJyn0moh7KWdM32vZQXLvIfQqEw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Synthetic spectra of Husser et al. (2013), which we used for fits to estimate stellar Teff. The metallicity was fixed as |$\rm {[Fe/H]}=0.0$| in this plot. The VO band is a region in 7320–7570 Å. (Color online)
Molecular absorption bands used in synthetic spectra fitting for KOOLS spectra.
| Band . | Wavelength range (Å) . |
|---|---|
| TiO band1 | 6600–6850 |
| TiO band2 | 6960–7160 |
| VO band | 7320–7570 |
| Band . | Wavelength range (Å) . |
|---|---|
| TiO band1 | 6600–6850 |
| TiO band2 | 6960–7160 |
| VO band | 7320–7570 |
Molecular absorption bands used in synthetic spectra fitting for KOOLS spectra.
| Band . | Wavelength range (Å) . |
|---|---|
| TiO band1 | 6600–6850 |
| TiO band2 | 6960–7160 |
| VO band | 7320–7570 |
| Band . | Wavelength range (Å) . |
|---|---|
| TiO band1 | 6600–6850 |
| TiO band2 | 6960–7160 |
| VO band | 7320–7570 |
3.1.3 Estimation of temperature for our data
We fitted PHOENIX model spectra to our data, and estimated their Teff. As mentioned above, the fit used the VO band for the data obtained by KOOLS and full spectral ranges for the data obtained by the other instruments. Figure 7 shows examples of optical spectra and best-fitting synthetic spectra.
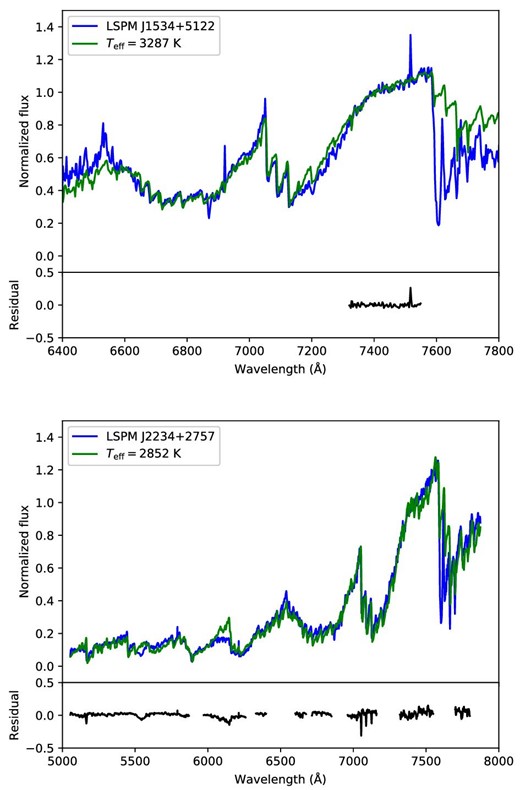
Examples of optical spectra (blue) and the best-fitted synthetic spectra (green). The top panel is LSPM J1534+5122 obtained by KOOLS, and bottom panel is LSPM J2234+2757 obtained by Bench spectrograph. The wavelength ranges of residuals in both panels correspond to the wavelengths that were utilized in our fitting analyses. As in figure 3, we removed KOOLS CCD bad pixels in this plot. (Color online)
We then applied linear corrections derived by comparison with Mann et al. (2015) [equation (2)]. The coefficients of linear corrections are listed in table 3. We implemented the linear correction error in the total Teff uncertainty by calculating |$\sigma _{\rm {Total}} = \sqrt{\sigma ^2_{\rm {fit}} + \sigma ^2_{\rm {corr}}}$|, where σfit is the fit error and σcorr is the linear correction error (see table 3). The standard deviations of residuals in the linear function fitting (see sub-subsection 3.1.2) were taken to be the linear correction errors. We did not calculate Teff for stars observed by DIS because their wavelength range was not suitable for our analysis.
| Band . | a . | b . | σcorr (K) . |
|---|---|---|---|
| VO band | 1.405 | −1449.9 | 103 |
| 5000–8000 Å | 0.954 | 296.6 | 85 |
| Band . | a . | b . | σcorr (K) . |
|---|---|---|---|
| VO band | 1.405 | −1449.9 | 103 |
| 5000–8000 Å | 0.954 | 296.6 | 85 |
| Band . | a . | b . | σcorr (K) . |
|---|---|---|---|
| VO band | 1.405 | −1449.9 | 103 |
| 5000–8000 Å | 0.954 | 296.6 | 85 |
| Band . | a . | b . | σcorr (K) . |
|---|---|---|---|
| VO band | 1.405 | −1449.9 | 103 |
| 5000–8000 Å | 0.954 | 296.6 | 85 |
3.2 Radii from spectral energy distribution
We determined the stellar radii and Teff from the spectral energy distribution (SED), the distribution of the flux density in wavelength or frequency units used to characterize stellar parameters (e.g., Teff, radius, and interstellar extinction). Such stellar properties can be calculated by comparing photometric magnitudes with synthetic stellar spectra.
For each star, we retrieved the V magnitudes from the fourth US Naval Observatory CCD Astrograph Catalog (UCAC4; Zacharias et al. 2012) and Lépine & Shara (2005); Gaia G, GBP, and GRP magnitudes from Gaia DR2 (Gaia Collaboration 2018); J, H, and K magnitudes from 2MASS (Cutri et al. 2003; Skrutskie et al. 2006); and W1, W2, W3, and W4 magnitudes from the Wide-field Infrared Survey Explorer (WISE; Wright et al. 2010). The photometric measurements used for our SED analysis are provided in tables 10 and 11. All the photometric systems used and their effective wavelengths are shown in table 4. We compiled the flux zero points for the V band from Mann and von Braun (2015), Gaia bands from Evans et al. (2018), JHK bands from Cohen, Wheaton, and Megeath (2003), and Wise bands from Wright et al. (2010). The instrument response curves were drawn from Mann and von Braun (2015) for V band, Evans et al. (2018) for the Gaia bands, Cohen, Wheaton, and Megeath (2003) for the JHK bands, and Jarrett et al. (2011) for the Wise bands.
| Band . | Effective wavelength (μm) . | Reference . |
|---|---|---|
| V | 0.5477 | UCAC4 and LSPM |
| G | 0.6405 | Gaia DR2 |
| G BP | 0.5131 | Gaia DR2 |
| G RP | 0.7778 | Gaia DR2 |
| J | 1.235 | 2MASS |
| H | 1.662 | 2MASS |
| K | 2.195 | 2MASS |
| W1 | 3.368 | WISE |
| W2 | 4.618 | WISE |
| W3 | 12.082 | WISE |
| W4 | 22.194 | WISE |
| Band . | Effective wavelength (μm) . | Reference . |
|---|---|---|
| V | 0.5477 | UCAC4 and LSPM |
| G | 0.6405 | Gaia DR2 |
| G BP | 0.5131 | Gaia DR2 |
| G RP | 0.7778 | Gaia DR2 |
| J | 1.235 | 2MASS |
| H | 1.662 | 2MASS |
| K | 2.195 | 2MASS |
| W1 | 3.368 | WISE |
| W2 | 4.618 | WISE |
| W3 | 12.082 | WISE |
| W4 | 22.194 | WISE |
| Band . | Effective wavelength (μm) . | Reference . |
|---|---|---|
| V | 0.5477 | UCAC4 and LSPM |
| G | 0.6405 | Gaia DR2 |
| G BP | 0.5131 | Gaia DR2 |
| G RP | 0.7778 | Gaia DR2 |
| J | 1.235 | 2MASS |
| H | 1.662 | 2MASS |
| K | 2.195 | 2MASS |
| W1 | 3.368 | WISE |
| W2 | 4.618 | WISE |
| W3 | 12.082 | WISE |
| W4 | 22.194 | WISE |
| Band . | Effective wavelength (μm) . | Reference . |
|---|---|---|
| V | 0.5477 | UCAC4 and LSPM |
| G | 0.6405 | Gaia DR2 |
| G BP | 0.5131 | Gaia DR2 |
| G RP | 0.7778 | Gaia DR2 |
| J | 1.235 | 2MASS |
| H | 1.662 | 2MASS |
| K | 2.195 | 2MASS |
| W1 | 3.368 | WISE |
| W2 | 4.618 | WISE |
| W3 | 12.082 | WISE |
| W4 | 22.194 | WISE |
We used the PHOENIX BT-SETTL version (Allard et al. 2011) in our SED analysis. We note that the model grid is different from that in the model fitting for optical spectra. The synthetic spectra of Husser et al. (2013) cover the wavelength range from 0.5 to 5.5 |$\rm {\mu m}$|. However, the effective wavelengths of W3 and W4 are longer than 5.5 |$\rm {\mu m}$|, so we could not use the synthetic spectra of Husser et al. (2013) in the SED analysis.
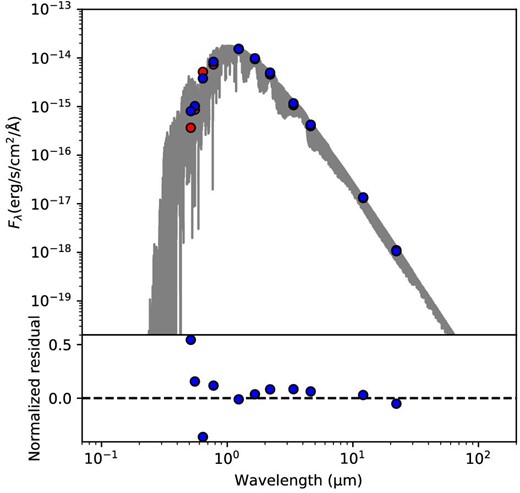
Example of spectral energy distribution. This is a plot of LSPM J1502+7527. Blue points represent photometry, red points represent photometry calculated from synthetic spectra, and the gray line is the best-fitting synthetic spectrum in the SED calculation. Each axis uses the logarithmic scale. Teff for the synthetic spectrum is 2837 K, and that for the optical spectrum is 2802 K. (Color online)
3.3 Spectral type
| Index . | Δλnum (Å) . | Δλden (Å) . | Reference . |
|---|---|---|---|
| CaH2 | 6814–6846 | 7042–7046 | Reid, Hawley, and Gizis (1995) |
| Ratio A (CaH) | 7020–7050 | 6960–6990 | Kirkpatrick, Henry, and McCarthy (1991) |
| CaH Narr | 7044–7049 | 6972.5–6977.5 | Shkolnik, Liu, and Reid (2009) |
| TiO3 | 7092–7097 | 7079–7084 | Reid, Hawley, and Gizis (1995) |
| TiO5 | 7126–7135 | 7042–7046 | Reid, Hawley, and Gizis (1995) |
| VO | ∑ 7385–7395, 7505–7515 | 7445–7460 | Kirkpatrick, Henry, and Simons (1995) |
| Index . | Δλnum (Å) . | Δλden (Å) . | Reference . |
|---|---|---|---|
| CaH2 | 6814–6846 | 7042–7046 | Reid, Hawley, and Gizis (1995) |
| Ratio A (CaH) | 7020–7050 | 6960–6990 | Kirkpatrick, Henry, and McCarthy (1991) |
| CaH Narr | 7044–7049 | 6972.5–6977.5 | Shkolnik, Liu, and Reid (2009) |
| TiO3 | 7092–7097 | 7079–7084 | Reid, Hawley, and Gizis (1995) |
| TiO5 | 7126–7135 | 7042–7046 | Reid, Hawley, and Gizis (1995) |
| VO | ∑ 7385–7395, 7505–7515 | 7445–7460 | Kirkpatrick, Henry, and Simons (1995) |
Indices were calculated as i = Fnum/Fden. The regions near 7040, 7400, and 7510 Å are continuum regions.
| Index . | Δλnum (Å) . | Δλden (Å) . | Reference . |
|---|---|---|---|
| CaH2 | 6814–6846 | 7042–7046 | Reid, Hawley, and Gizis (1995) |
| Ratio A (CaH) | 7020–7050 | 6960–6990 | Kirkpatrick, Henry, and McCarthy (1991) |
| CaH Narr | 7044–7049 | 6972.5–6977.5 | Shkolnik, Liu, and Reid (2009) |
| TiO3 | 7092–7097 | 7079–7084 | Reid, Hawley, and Gizis (1995) |
| TiO5 | 7126–7135 | 7042–7046 | Reid, Hawley, and Gizis (1995) |
| VO | ∑ 7385–7395, 7505–7515 | 7445–7460 | Kirkpatrick, Henry, and Simons (1995) |
| Index . | Δλnum (Å) . | Δλden (Å) . | Reference . |
|---|---|---|---|
| CaH2 | 6814–6846 | 7042–7046 | Reid, Hawley, and Gizis (1995) |
| Ratio A (CaH) | 7020–7050 | 6960–6990 | Kirkpatrick, Henry, and McCarthy (1991) |
| CaH Narr | 7044–7049 | 6972.5–6977.5 | Shkolnik, Liu, and Reid (2009) |
| TiO3 | 7092–7097 | 7079–7084 | Reid, Hawley, and Gizis (1995) |
| TiO5 | 7126–7135 | 7042–7046 | Reid, Hawley, and Gizis (1995) |
| VO | ∑ 7385–7395, 7505–7515 | 7445–7460 | Kirkpatrick, Henry, and Simons (1995) |
Indices were calculated as i = Fnum/Fden. The regions near 7040, 7400, and 7510 Å are continuum regions.
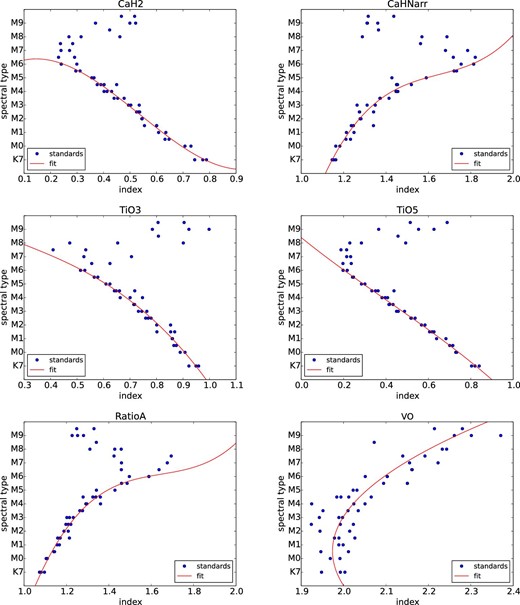
Relations between index values and spectral types (SpTs). Blue points represent the spectral standard stars listed in table 7, and red lines are the polynomial functions fitted to the index–SpT relations. (Color online)
| Index . | a . | b . | c . | d . |
|---|---|---|---|---|
| CaH2 | 34.39 | −55.22 | 13.96 | 5.415 |
| Ratio A | 31.41 | −155.3 | 258.6 | −138.8 |
| CaH Narr | 33.50 | −165.5 | 276.7 | −151.2 |
| TiO3 | −12.12 | 7.889 | −9.272 | 10.26 |
| TiO5 | −3.700 | 4.478 | −12.59 | 8.399 |
| Index . | a . | b . | c . | d . |
|---|---|---|---|---|
| CaH2 | 34.39 | −55.22 | 13.96 | 5.415 |
| Ratio A | 31.41 | −155.3 | 258.6 | −138.8 |
| CaH Narr | 33.50 | −165.5 | 276.7 | −151.2 |
| TiO3 | −12.12 | 7.889 | −9.272 | 10.26 |
| TiO5 | −3.700 | 4.478 | −12.59 | 8.399 |
| Index . | a . | b . | c . | d . |
|---|---|---|---|---|
| CaH2 | 34.39 | −55.22 | 13.96 | 5.415 |
| Ratio A | 31.41 | −155.3 | 258.6 | −138.8 |
| CaH Narr | 33.50 | −165.5 | 276.7 | −151.2 |
| TiO3 | −12.12 | 7.889 | −9.272 | 10.26 |
| TiO5 | −3.700 | 4.478 | −12.59 | 8.399 |
| Index . | a . | b . | c . | d . |
|---|---|---|---|---|
| CaH2 | 34.39 | −55.22 | 13.96 | 5.415 |
| Ratio A | 31.41 | −155.3 | 258.6 | −138.8 |
| CaH Narr | 33.50 | −165.5 | 276.7 | −151.2 |
| TiO3 | −12.12 | 7.889 | −9.272 | 10.26 |
| TiO5 | −3.700 | 4.478 | −12.59 | 8.399 |
Second, we computed each index value for our samples, and applied equations (5) and (8) to them. If stars were judged to be early or middle types (K7–M6) from the VO index, the median of the spectral types derived from the five indices (CaH2, Ratio A, CaH Narr, TiO3, and TiO5) was adopted as their best spectral type, and the error was identical to the standard deviation. If stars turned out to be later types (M6–9), we adopted the spectral types obtained from the VO index.
4 Result
4.1 Temperature
We show Teff for our samples determined by using optical spectra in table 9, and a histogram of Teff in the top panel of figure 10. The stars observed by the Bench spectrograph/WIYN are dominant in the lower-temperature regime. Because the WIYN telescope aperture is larger than that of the other telescopes, it enables us to observe fainter stars.
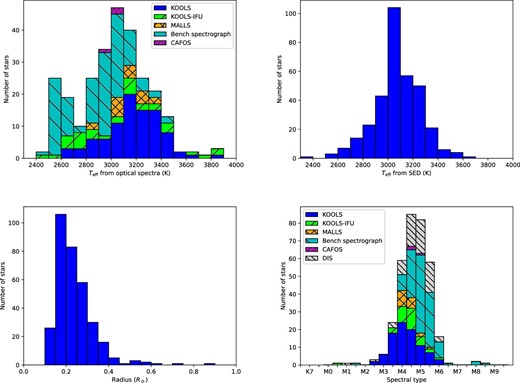
Histograms of our stellar parameter derivations. The top left panel is a histogram of Teff derived from optical spectra, the top right is that of Teff derived from SED, the bottom left panel shows radii, and the bottom right panel shows spectral types. (Color online)
The typical errors in Teff are 128 K for KOOLS and KOOLS-IFU, and 85 K for the other instruments. We note that the spectra observed with KOOLS-IFU have low S/N (average S/N at 7400 Å ∼ 36) and it results in larger errors for KOOLS-IFU. In other studies, Teff for M dwarfs has been determined with a precision of approximately 100 K or less. Mann, Gaidos, and Ansdell (2013b) and Mann et al. (2015) determined Teff for M dwarfs from optical and near-infrared spectra with a precision of approximately 60 K. Using a wider wavelength coverage among our adopted ranges, we can determine Teff with a precision similar to other studies. We note that our linear correction that is applied to the temperature estimates for the wavelengths of 5000–8000 Å has larger uncertainties in the Teff range <2600 K, suggesting that one needs to notice the derived temperatures of those (see also sub-subsection 3.1.2).
We also obtained Teff for our M dwarfs by SED fitting, and the error in Teff obtained from SED fitting is ∼40 K on average. We note that the errors should be underestimated, because we did not reflect the various uncertainties of the model spectra in our analysis. The Teff measured from SED are also summarized in figure 10 and table 9. In table 9, there are some stars whose Teff was not calculated from SED, because we calculated the Teff for the stars whose photometric magnitudes and parallaxes are available.
4.2 Radii
We also obtained the stellar radii of our samples from the SED calculations. Stars with approximately 0.2 R⊙ are the most common in our sample (see figure 10). The relative average error in radii is 3%.
There are some stars whose radii are larger than 0.6 R⊙. LSPM J0919+6203 has a radius of R = 0.88 R⊙. However, its spectral type is estimated as M1 V and the parallax is 18.8578 mas, which is relatively small in our samples (the median of the parallaxes is 44.4032 mas). LSPM J1334+2011 also has a large radius (0.72 R⊙) and its parallax is 18.2323 mas. Therefore, these stars may have large radii.
LSPM J1914+1919 also has a large radius (0.61 R⊙). Our Teff estimation from its SED suggested Teff = 3367 K, which is applied to the empirical relation in Mann et al. (2015). As a result, the radius of LSPM J1914+1919 was inferred to be 0.32 R⊙; this implies that we overestimated the radius of this object. LSPM J1914+1919 was reported as a multiple-star system in WDS (Mason et al. 2001, 2014), likely leading to an overestimatation of the radius.
As in our Teff estimation, we did not consider the incompleteness of the model spectrum in our analysis. Therefore, the errors on radii should also be underestimated. In addition, our result may be biased by unresolved binaries.
4.3 Spectral type
We show the histogram of the spectral types in the bottom panel of figure 10. Our results are also summarized in table 9. M4–M5 stars are dominant in our samples, and there are 17 late M dwarfs (later than M6) in our samples. The average error is 0.4 subtype, and it indicates that we can determine spectral types with high precision.
5 Discussion
5.1 Temperature estimation for the KOOLS spectra
In our analysis, we utilized the VO band to determine Teff with the PHOENIX-ACES model grid (Husser et al. 2013). We also repeated our analysis for the spectra of Mann et al. (2015) with the PHOENIX BT-Settl version (Allard et al. 2011). We found that the resulting scatters of linear correction were 154 K for TiO band1, 161 K for TiO band2, and 88 K for the VO band (see figure 11). Again, the VO band gives the best-fitting results, though we employed different models. We therefore concluded that TiO band1 would be useless for estimation of Teff in spite of the differences of model spectra, with the caveat that our two adopted models are both based on the scheme of the PHOENIX group. This may be because the absorption of this band is shallow and has been poorly constrained with respect to its line list, as briefly described in sub-subsection 3.1.1.
5.2 Comparison between Teff from optical spectra and from SED
We compare the Teff from optical spectra with those from SED in figure 12. In this comparison, we exclude the stars with S/N at 7400 Å < 50. The standard deviation of the difference between the Teff derived by the two methods is 165 K. Most of our results follow the 1 : 1 relation. However, we found a trend towards higher Teff. In the lower-Teff region, Teff from optical spectra tend to have smaller values than those from SED. Our linear correction for the wavelength range 5000–8000 Å has a larger deviation in the lower Teff region (see the top panel of figure 4). This deviation could be attributed to the larger deviations of our derived Teff from those in Mann et al. 2015, see sub-subsection 3.1.2, or a general incompleteness of modeling such cool atmospheres. The removal of stars with Teff < 2600 K yields a standard deviation of 130 K in the differences of the spectrum-based and SED-based Teff. We cannot find a clear reason for the trend towards higher Teff and outliers. Unlike methods which utilize high-resolution spectroscopy, we do not fit the continuum level. Accuracy of flux calibration is vital for the determination of Teff. Thus, there might be some incompleteness of flux calibration in our spectra.
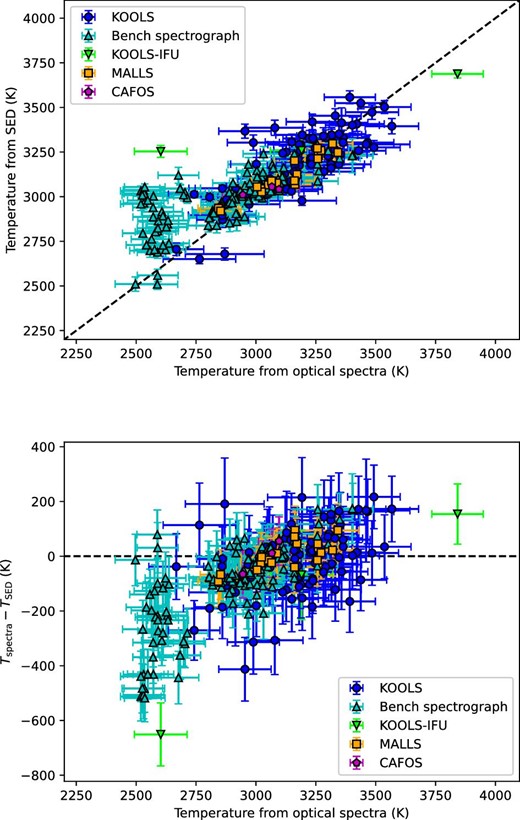
Comparison between Teff from optical spectra and from SED. In the top panel, the vertical axis shows Teff from SED and the horizontal axis shows Teff from optical spectra. The bottom panel shows the residual of Teff. (Color online)
5.3 Comparison with other studies
5.3.1 Temperature
We compare our results with Terrien et al. (2015) using the 62 common stars. They derived the Teff of M dwarfs from the spectral features in the near-infrared using the methods of Mann, Gaidos, and Ansdell (2013b). We show the comparison in figure 13. In Mann, Gaidos, and Ansdell (2013b), the relations are derived between Teff and molecular absorption features in the JHK bands: Teff is expressed as a quadratic polynomial of the absorption lines in each band. However, their relations are based on stars with 3200–5000 K, and therefore Teff below 3200 K may not be calculated. We conclude that our result is more accurate and that our methods are applicable to a wider Teff range.
5.3.2 Radii
We compared our radii with the empirical radii. Gaia provides accurate trigonometric parallaxes for our samples. Therefore, we could obtain the luminosities in the K band by combining the Gaia parallaxes and 2MASS observations. Mann et al. (2019) derived an empirical relation between the mass and K-band absolute magnitude. Rabus et al. (2019) obtained an empirical mass–radius relation for low-mass stars. From these two empirical relations, the radii of our samples were calculated. The comparison is shown in figure 14, and our radii are on average 3% larger than the empirical radii. We also found larger disagreements for larger radii (>0.6 R⊙). However, their radii are overestimated (see subsection 4.2). We also compared our results with the stellar evolution model. Figure 14 shows a comparison of the radii and luminosities of our samples with the Dartmouth Stellar Evolution Database (Dotter et al. 2008). The |$[\rm {Fe/H}]$| of the evolution model is fixed at the solar value, and we set the stellar age to be 1 Gyr. We found that our radii are also approximately 9% larger than those from the stellar evolution model. Although it is unclear and beyond the scope of this paper why the radii of our samples were overestimated relative to the predictions from stellar evolution models, the reason might be the absence of strong magnetic fields in the models. Mullan and MacDonald (2001) proposed that inhibition of convection in stars with strong magnetic activities makes their radii larger. Strong magnetic fields should be produced in rapidly rotating stars, and close binary systems are tidally locked and rapidly rotating (Chabrier et al. 2007; Kesseli et al. 2018; and references therein). However, Kesseli et al. (2018) inferred the radii of rapidly rotating mid-to-late M dwarfs with inflations compared with the model predictions but without significant inflations compared with slowly rotating stars, concluding that their overestimated radii were not due to rapid rotation (and binarity). Our overestimation is about 9%, which is close to the 10%–15% in Kesseli et al. (2018). Assuming most of our samples to be slowly rotating inactive stars, we also find that rapid rotation (i.e., strong magnetic field) should not be the main reason for their overestimated radii. This means that stellar evolutionary models can underpredict the radii of inactive M dwarfs, consistent with the finding of Mann et al. (2015) that radius underpredictions of evolution models do not correlate with activity indicators.
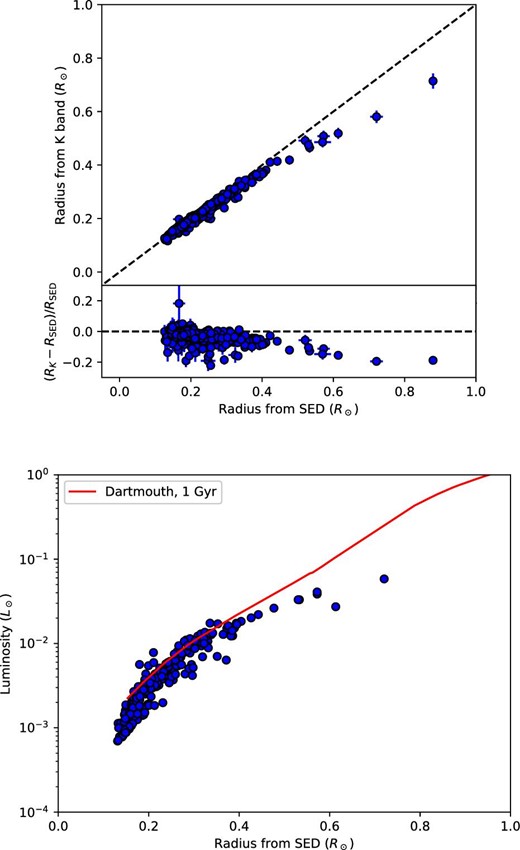
Comparisons with empirical radius (top) and the Dartmouth Stellar Evolution Database (bottom). The empirical radius is calculated from the mass–luminosity relation of Mann et al. (2019) and the mass–radius relation of Rabus et al. (2019). In the bottom panel, the solid line represents the 1 Gyr Dartmouth evolution model (Dotter et al. 2008). (Color online)
5.3.3 Spectral type
We compared our results with PMSU using 79 common stars. In figure 15, we show that our results are in agreement with PMSU. The standard deviation of the difference between the spectral types derived by us and by PMSU is 0.4 subtype. The average error in our result is 0.4 subtype, and we can derive the spectral types with the same precision as in previous research (e.g., Alonso-Floriano et al. 2015). Thus, we conclude that our results are reliable.
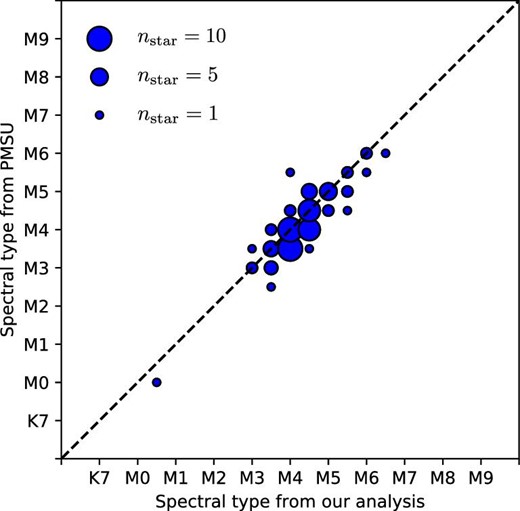
Comparison of our results with PMSU. The vertical axis shows spectral types from PMSU and the horizontal axis shows spectral types from our analysis. The larger a circle, the greater the number of stars at a data point. (Color online)
5.4 Effect of metallicity
Metallicities have been estimated from optical spectra for early M dwarfs, and from infrared spectra for mid-to-late M dwarfs (e.g., Mann et al. 2013a, 2014). We used the VO band to determine Teff for the data of KOOLS and KOOLS-IFU, but the VO band is also known to be sensitive to metallicity (Mann et al. 2013a). In figure 16, we show the PHOENIX model spectra that were used in sub-subsection 3.1.1. As can be seen in figure 16, VO absorption appears as the metallicity increases. Therefore, our Teff may be affected by metallicity. We recalculated the Teff from optical spectra, fixing |$[\rm {Fe/H}]$| at 0.0. For the KOOLS and KOOLS-IFU data, the Teff of 37% of the stars changed by ≤100 K, and that of 13% of the stars changed by ≥300 K. The mean change in the data of KOOLS and KOOLS-IFU is 179 K. For the stars observed with the other instruments, the Teff of the 76% changed by ≤100 K, and the mean change is 89 K. Teff can be changed on the order of 100 K, and the influence of metallicity can be mitigated if a wider wavelength range is available. As demonstrated, e.g., in Mann et al. (2013a, 2014), molecular absorption features in near-infrared spectra should be more adequate for an M dwarf with respect to its metallicity estimation. Once such a method restricts the metallicity of our sample, its stellar properties can be improved by combining the metallicity restriction and our observed spectrum.
![Synthetic spectra of $[\rm {Fe/H}]$ = 0.0, 0.5, and −1.0, taken from Husser et al. (2013), that we used in our Teff estimations. Teff is fixed as T = 3000 K in this plot. The VO band is a region in 7320–7570 Å. (Color online)](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/pasj/73/1/10.1093_pasj_psaa112/2/m_psaa112fig16.jpeg?Expires=1749236902&Signature=4uobtMkQVlKuf4Aa5CQq~Yydtj6KNV9dq~W8zT7kF6R9dYRlJE9PWmgY8-AzBMtxnE~5YQ8Hi-fPUIH9BBW~GXcJtjLwPy5C5d9onNOLWKjL9fRPtUs3nA~XHAh44njaBgFXDeVe3Q6oMs2kV62Z-icPqTpRUSJoixZucBZ43~ETzryyDivfQLnixjfT-msp8t1q8lTKyhzulnKZSq~ZjHFgmJ-nDE9Se66APSatx5mwmuproieLg33jQImznzYXmCTBTtKGsg~CbeGNieHUcum-fIXfnITts0RDNLS9Yr8b988hb49ncIfnalUPL-zrDguzVa~WglJGcLW4wK-cIQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Synthetic spectra of |$[\rm {Fe/H}]$| = 0.0, 0.5, and −1.0, taken from Husser et al. (2013), that we used in our Teff estimations. Teff is fixed as T = 3000 K in this plot. The VO band is a region in 7320–7570 Å. (Color online)
6 Conclusion and summary
We determined the Teff, radii, and spectral types of 338 M dwarfs. The Teff were calculated by comparing their optical spectra with the synthetic spectra of Husser et al. (2013). To estimate more precise Teff, we calibrated our method using the data of Mann et al. (2015), which have well-determined Teff values. Some of our spectra have a narrow-wavelength region (6400–7600 Å), for which we found that it is better to focus on one of three molecular absorption bands than using the entire wavelength regions; the VO band is the most sensitive to Teff. The typical errors were 128 K for KOOLS and KOOLS-IFU, and 85 K for the other instruments. Although the use of a wider wavelength coverage makes it more accurate and precise to estimate Teff from optical spectra, we demonstrated that it is possible to reproduce Teff by selecting a suitable region even if only narrow wavelength coverage is available. This helps to infer the temperature of M dwarfs when one can use only spectrographs with narrow wavelength coverage including VO absorption on 7320–7570 Å. For the stars with Teff < 2600 K, we note that our linear correction for 5000–8000 Å has larger deviations and thus our method would fail to estimate correct Teff. We tested the effect of metallicity, and found that our Teff estimates can change on the order of 100 K. The effect of metallicity is important if one hopes to estimate the Teff of an M dwarf with a precision better than 100 K, and it can be mitigated given a wider wavelength range. Near-infrared spectra can restrict the metallicity of M dwarfs (e.g., Mann et al. 2013a, 2014). If near-infrared spectra can be combined with the optical spectra in this paper, more robust Teff estimates are available.
We also calculated Teff from SED with a typical error of 40 K. In the comparison between the Teff from optical spectra and those from SED, we found deviations in the higher-Teff region. Although we cannot find any clear reasons, the deviations arise at the spectral types of M4–M5.5; one needs to take care of the possibility that our Teff estimates from optical spectra may be overestimated for these spectral types. We also obtained the radii of our samples by SED calculation. Stars with approximately 0.2 R⊙ are the most common in our sample. The average error in the radii is 3%. Comparing our results with the empirical radii and the stellar evolution model, we found that our radii are larger than the empirical and theoretical predictions. Finally, we determined the spectral types of our samples, which are consistent with the results of previous studies, and the errors of those spectral types are as small as in Alonso-Floriano et al. (2015).
Any exoplanet surveys infer the properties of identified planets, such as mass, Teff, and habitability. Those characterizations depend on the properties of their parent stars. In addition, the formation and evolution history of planets are expected to be dependent on the properties of their host stars. Accordingly, it is essential to obtain more precise and robust stellar parameters. Also, the stellar parameters have to be well constrained before the start of surveys, since target selection plays an important role in the strategy of an exoplanet survey.
Our results can help to determine the stellar properties of M dwarfs that have been observed in exoplanet surveys, as well as their target selection. Furthermore, we provide a method that enables us to infer the Teff of M dwarfs over limited wavelengths of optical spectra, based on the samples well calibrated by Mann et al. (2015). Our developed methods can be applied to the optical spectra of M dwarfs that have similar wavelength ranges to ours, to infer their Teff with a precision of ∼100 K. We also note that Teff can be determined with a precision of 128 K based on VO absorption around ∼7500 Å if the wavelength coverage is not the same as Mann et al. (2015). Currently, M dwarfs are one of the primary targets not only in radial velocity surveys as described in section 1 but also in transit surveys (e.g., Delrez et al. 2018). It is hoped that this work can help those surveys efficiently perform target selection and well constrain the parameters of their discovered planets.
Supplementary data
The following supplementary data is available at PASJ online.
A complete listing of tables 7–11 (see the appendices).
| Spectral type . | Object . | Reference . |
|---|---|---|
| K7 | BD +33 1505 | PMSU |
| K7 | HD 79210 | PMSU |
| K7 | HD 79211 | PMSU |
| M0.0 | BD +45 2743 | PMSU |
| M0.0 | HD 209290 | PMSU |
| M0.5 | BD +44 2051 A | PMSU |
| M0.5 | LHS 1747 | PMSU |
| M1.0 | BD +36 2219 | PMSU |
| M1.0 | GX And | PMSU |
| M1.5 | G 242-048 | PMSU |
| Spectral type . | Object . | Reference . |
|---|---|---|
| K7 | BD +33 1505 | PMSU |
| K7 | HD 79210 | PMSU |
| K7 | HD 79211 | PMSU |
| M0.0 | BD +45 2743 | PMSU |
| M0.0 | HD 209290 | PMSU |
| M0.5 | BD +44 2051 A | PMSU |
| M0.5 | LHS 1747 | PMSU |
| M1.0 | BD +36 2219 | PMSU |
| M1.0 | GX And | PMSU |
| M1.5 | G 242-048 | PMSU |
| Spectral type . | Object . | Reference . |
|---|---|---|
| K7 | BD +33 1505 | PMSU |
| K7 | HD 79210 | PMSU |
| K7 | HD 79211 | PMSU |
| M0.0 | BD +45 2743 | PMSU |
| M0.0 | HD 209290 | PMSU |
| M0.5 | BD +44 2051 A | PMSU |
| M0.5 | LHS 1747 | PMSU |
| M1.0 | BD +36 2219 | PMSU |
| M1.0 | GX And | PMSU |
| M1.5 | G 242-048 | PMSU |
| Spectral type . | Object . | Reference . |
|---|---|---|
| K7 | BD +33 1505 | PMSU |
| K7 | HD 79210 | PMSU |
| K7 | HD 79211 | PMSU |
| M0.0 | BD +45 2743 | PMSU |
| M0.0 | HD 209290 | PMSU |
| M0.5 | BD +44 2051 A | PMSU |
| M0.5 | LHS 1747 | PMSU |
| M1.0 | BD +36 2219 | PMSU |
| M1.0 | GX And | PMSU |
| M1.5 | G 242-048 | PMSU |
| Object . | Date . | Exposure time (s) . | Instruments . |
|---|---|---|---|
| EPIC 248536375 | 2018-01-26 | 2000 | DIS/APO 3.5 m |
| GJ 1002 | 2018-01-25 | 600 | DIS/APO 3.5 m |
| GJ 2005 | 2018-01-25 | 300 | DIS/APO 3.5 m |
| GJ 3707 | 2016-04-15 | 600 | KOOLS-IFU/OAO 188 cm |
| GJ 592 | 2016-04-15 | 900 | KOOLS-IFU/OAO 188 cm |
| LEHPM 2-174 | 2017-05-05 | 1800 | Bench spectrograph/WIYN 3.5 m |
| LP 851-346 | 2017-05-05 | 1800 | Bench spectrograph/WIYN 3.5 m |
| LSPM J0020+3305 | 2016-11-20 | 400 | Bench spectrograph/WIYN 3.5 m |
| LSPM J0027+4941 | 2014-09-22 | 600 | KOOLS/OAO 188 cm |
| LSPM J0030+7742 | 2016-11-19 | 1140 | Bench spectrograph/WIYN 3.5 m |
| Object . | Date . | Exposure time (s) . | Instruments . |
|---|---|---|---|
| EPIC 248536375 | 2018-01-26 | 2000 | DIS/APO 3.5 m |
| GJ 1002 | 2018-01-25 | 600 | DIS/APO 3.5 m |
| GJ 2005 | 2018-01-25 | 300 | DIS/APO 3.5 m |
| GJ 3707 | 2016-04-15 | 600 | KOOLS-IFU/OAO 188 cm |
| GJ 592 | 2016-04-15 | 900 | KOOLS-IFU/OAO 188 cm |
| LEHPM 2-174 | 2017-05-05 | 1800 | Bench spectrograph/WIYN 3.5 m |
| LP 851-346 | 2017-05-05 | 1800 | Bench spectrograph/WIYN 3.5 m |
| LSPM J0020+3305 | 2016-11-20 | 400 | Bench spectrograph/WIYN 3.5 m |
| LSPM J0027+4941 | 2014-09-22 | 600 | KOOLS/OAO 188 cm |
| LSPM J0030+7742 | 2016-11-19 | 1140 | Bench spectrograph/WIYN 3.5 m |
| Object . | Date . | Exposure time (s) . | Instruments . |
|---|---|---|---|
| EPIC 248536375 | 2018-01-26 | 2000 | DIS/APO 3.5 m |
| GJ 1002 | 2018-01-25 | 600 | DIS/APO 3.5 m |
| GJ 2005 | 2018-01-25 | 300 | DIS/APO 3.5 m |
| GJ 3707 | 2016-04-15 | 600 | KOOLS-IFU/OAO 188 cm |
| GJ 592 | 2016-04-15 | 900 | KOOLS-IFU/OAO 188 cm |
| LEHPM 2-174 | 2017-05-05 | 1800 | Bench spectrograph/WIYN 3.5 m |
| LP 851-346 | 2017-05-05 | 1800 | Bench spectrograph/WIYN 3.5 m |
| LSPM J0020+3305 | 2016-11-20 | 400 | Bench spectrograph/WIYN 3.5 m |
| LSPM J0027+4941 | 2014-09-22 | 600 | KOOLS/OAO 188 cm |
| LSPM J0030+7742 | 2016-11-19 | 1140 | Bench spectrograph/WIYN 3.5 m |
| Object . | Date . | Exposure time (s) . | Instruments . |
|---|---|---|---|
| EPIC 248536375 | 2018-01-26 | 2000 | DIS/APO 3.5 m |
| GJ 1002 | 2018-01-25 | 600 | DIS/APO 3.5 m |
| GJ 2005 | 2018-01-25 | 300 | DIS/APO 3.5 m |
| GJ 3707 | 2016-04-15 | 600 | KOOLS-IFU/OAO 188 cm |
| GJ 592 | 2016-04-15 | 900 | KOOLS-IFU/OAO 188 cm |
| LEHPM 2-174 | 2017-05-05 | 1800 | Bench spectrograph/WIYN 3.5 m |
| LP 851-346 | 2017-05-05 | 1800 | Bench spectrograph/WIYN 3.5 m |
| LSPM J0020+3305 | 2016-11-20 | 400 | Bench spectrograph/WIYN 3.5 m |
| LSPM J0027+4941 | 2014-09-22 | 600 | KOOLS/OAO 188 cm |
| LSPM J0030+7742 | 2016-11-19 | 1140 | Bench spectrograph/WIYN 3.5 m |
| Object . | Spectral type . | T spec (K) . | T SED (K) . | Radius (R⊙) . |
|---|---|---|---|---|
| EPIC 248536375 | M2.5 ± 0.4 | — | — | — |
| GJ 1002 | M5.5 ± 0.3 | — | 2929 ± 24 | 0.1433 ± 0.0048 |
| GJ 2005* | M6 | — | — | — |
| GJ 3707 | M4 ± 0.4 | 3620 ± 119 | 3237 ± 37 | 0.4107 ± 0.0081 |
| GJ 592 | M4 ± 0.3 | 2603 ± 110 | 3254 ± 33 | 0.3459 ± 0.0059 |
| LEHPM 2-174 | M8.5 | 2588 ± 85 | 2509 ± 29 | 0.1863 ± 0.0093 |
| LP 851-346 | M8 | 2497 ± 85 | 2511 ± 40 | 0.1281 ± 0.0087 |
| LSPM J0020+3305 | M5.5 ± 0.3 | 2631 ± 85 | 2847 ± 36 | 0.1464 ± 0.0068 |
| LSPM J0027+4941 | M4 ± 0.2 | 3346 ± 133 | 3181 ± 40 | 0.3043 ± 0.0082 |
| LSPM J0030+7742 | M6 ± 0.4 | 2558 ± 85 | 2698 ± 37 | 0.1616 ± 0.009 |
| LSPM J0032+5429 | M4 ± 0.2 | 3313 ± 141 | 3182 ± 41 | 0.3174 ± 0.0088 |
| LSPM J0035+0233* | M5.5 ± 0.3 | — | 2886 ± 40 | 0.2782 ± 0.0153 |
| LSPM J0040+3122 | M4 ± 0.3 | 3305 ± 123 | 3223 ± 44 | 0.3383 ± 0.0099 |
| LSPM J0044+0907 | M4 ± 0.2 | 3314 ± 134 | 3160 ± 38 | 0.4042 ± 0.0103 |
| LSPM J0046+4851 | M4.5 ± 0.4 | — | 3029 ± 25 | 0.2817 ± 0.0096 |
| LSPM J0049+6205 | M5.5 ± 0.5 | 2520 ± 85 | 3032 ± 27 | 0.1714 ± 0.0065 |
| LSPM J0051+4531 | M4.5 ± 0.3 | 3405 ± 85 | 3235 ± 46 | 0.303 ± 0.0097 |
| LSPM J0055+1439 | M4 ± 0.4 | — | 3193 ± 40 | 0.3287 ± 0.0083 |
| LSPM J0100+6656 | M4 ± 0.4 | 3188 ± 114 | 3291 ± 43 | 0.3664 ± 0.009 |
| LSPM J0101+3832 | M5 ± 0.3 | 3320 ± 85 | 3298 ± 41 | 0.3726 ± 0.0085 |
| LSPM J0102+1009W* | M1 ± 0.3 | — | 3593 ± 55 | 0.5209 ± 0.0184 |
| Object . | Spectral type . | T spec (K) . | T SED (K) . | Radius (R⊙) . |
|---|---|---|---|---|
| EPIC 248536375 | M2.5 ± 0.4 | — | — | — |
| GJ 1002 | M5.5 ± 0.3 | — | 2929 ± 24 | 0.1433 ± 0.0048 |
| GJ 2005* | M6 | — | — | — |
| GJ 3707 | M4 ± 0.4 | 3620 ± 119 | 3237 ± 37 | 0.4107 ± 0.0081 |
| GJ 592 | M4 ± 0.3 | 2603 ± 110 | 3254 ± 33 | 0.3459 ± 0.0059 |
| LEHPM 2-174 | M8.5 | 2588 ± 85 | 2509 ± 29 | 0.1863 ± 0.0093 |
| LP 851-346 | M8 | 2497 ± 85 | 2511 ± 40 | 0.1281 ± 0.0087 |
| LSPM J0020+3305 | M5.5 ± 0.3 | 2631 ± 85 | 2847 ± 36 | 0.1464 ± 0.0068 |
| LSPM J0027+4941 | M4 ± 0.2 | 3346 ± 133 | 3181 ± 40 | 0.3043 ± 0.0082 |
| LSPM J0030+7742 | M6 ± 0.4 | 2558 ± 85 | 2698 ± 37 | 0.1616 ± 0.009 |
| LSPM J0032+5429 | M4 ± 0.2 | 3313 ± 141 | 3182 ± 41 | 0.3174 ± 0.0088 |
| LSPM J0035+0233* | M5.5 ± 0.3 | — | 2886 ± 40 | 0.2782 ± 0.0153 |
| LSPM J0040+3122 | M4 ± 0.3 | 3305 ± 123 | 3223 ± 44 | 0.3383 ± 0.0099 |
| LSPM J0044+0907 | M4 ± 0.2 | 3314 ± 134 | 3160 ± 38 | 0.4042 ± 0.0103 |
| LSPM J0046+4851 | M4.5 ± 0.4 | — | 3029 ± 25 | 0.2817 ± 0.0096 |
| LSPM J0049+6205 | M5.5 ± 0.5 | 2520 ± 85 | 3032 ± 27 | 0.1714 ± 0.0065 |
| LSPM J0051+4531 | M4.5 ± 0.3 | 3405 ± 85 | 3235 ± 46 | 0.303 ± 0.0097 |
| LSPM J0055+1439 | M4 ± 0.4 | — | 3193 ± 40 | 0.3287 ± 0.0083 |
| LSPM J0100+6656 | M4 ± 0.4 | 3188 ± 114 | 3291 ± 43 | 0.3664 ± 0.009 |
| LSPM J0101+3832 | M5 ± 0.3 | 3320 ± 85 | 3298 ± 41 | 0.3726 ± 0.0085 |
| LSPM J0102+1009W* | M1 ± 0.3 | — | 3593 ± 55 | 0.5209 ± 0.0184 |
| Object . | Spectral type . | T spec (K) . | T SED (K) . | Radius (R⊙) . |
|---|---|---|---|---|
| EPIC 248536375 | M2.5 ± 0.4 | — | — | — |
| GJ 1002 | M5.5 ± 0.3 | — | 2929 ± 24 | 0.1433 ± 0.0048 |
| GJ 2005* | M6 | — | — | — |
| GJ 3707 | M4 ± 0.4 | 3620 ± 119 | 3237 ± 37 | 0.4107 ± 0.0081 |
| GJ 592 | M4 ± 0.3 | 2603 ± 110 | 3254 ± 33 | 0.3459 ± 0.0059 |
| LEHPM 2-174 | M8.5 | 2588 ± 85 | 2509 ± 29 | 0.1863 ± 0.0093 |
| LP 851-346 | M8 | 2497 ± 85 | 2511 ± 40 | 0.1281 ± 0.0087 |
| LSPM J0020+3305 | M5.5 ± 0.3 | 2631 ± 85 | 2847 ± 36 | 0.1464 ± 0.0068 |
| LSPM J0027+4941 | M4 ± 0.2 | 3346 ± 133 | 3181 ± 40 | 0.3043 ± 0.0082 |
| LSPM J0030+7742 | M6 ± 0.4 | 2558 ± 85 | 2698 ± 37 | 0.1616 ± 0.009 |
| LSPM J0032+5429 | M4 ± 0.2 | 3313 ± 141 | 3182 ± 41 | 0.3174 ± 0.0088 |
| LSPM J0035+0233* | M5.5 ± 0.3 | — | 2886 ± 40 | 0.2782 ± 0.0153 |
| LSPM J0040+3122 | M4 ± 0.3 | 3305 ± 123 | 3223 ± 44 | 0.3383 ± 0.0099 |
| LSPM J0044+0907 | M4 ± 0.2 | 3314 ± 134 | 3160 ± 38 | 0.4042 ± 0.0103 |
| LSPM J0046+4851 | M4.5 ± 0.4 | — | 3029 ± 25 | 0.2817 ± 0.0096 |
| LSPM J0049+6205 | M5.5 ± 0.5 | 2520 ± 85 | 3032 ± 27 | 0.1714 ± 0.0065 |
| LSPM J0051+4531 | M4.5 ± 0.3 | 3405 ± 85 | 3235 ± 46 | 0.303 ± 0.0097 |
| LSPM J0055+1439 | M4 ± 0.4 | — | 3193 ± 40 | 0.3287 ± 0.0083 |
| LSPM J0100+6656 | M4 ± 0.4 | 3188 ± 114 | 3291 ± 43 | 0.3664 ± 0.009 |
| LSPM J0101+3832 | M5 ± 0.3 | 3320 ± 85 | 3298 ± 41 | 0.3726 ± 0.0085 |
| LSPM J0102+1009W* | M1 ± 0.3 | — | 3593 ± 55 | 0.5209 ± 0.0184 |
| Object . | Spectral type . | T spec (K) . | T SED (K) . | Radius (R⊙) . |
|---|---|---|---|---|
| EPIC 248536375 | M2.5 ± 0.4 | — | — | — |
| GJ 1002 | M5.5 ± 0.3 | — | 2929 ± 24 | 0.1433 ± 0.0048 |
| GJ 2005* | M6 | — | — | — |
| GJ 3707 | M4 ± 0.4 | 3620 ± 119 | 3237 ± 37 | 0.4107 ± 0.0081 |
| GJ 592 | M4 ± 0.3 | 2603 ± 110 | 3254 ± 33 | 0.3459 ± 0.0059 |
| LEHPM 2-174 | M8.5 | 2588 ± 85 | 2509 ± 29 | 0.1863 ± 0.0093 |
| LP 851-346 | M8 | 2497 ± 85 | 2511 ± 40 | 0.1281 ± 0.0087 |
| LSPM J0020+3305 | M5.5 ± 0.3 | 2631 ± 85 | 2847 ± 36 | 0.1464 ± 0.0068 |
| LSPM J0027+4941 | M4 ± 0.2 | 3346 ± 133 | 3181 ± 40 | 0.3043 ± 0.0082 |
| LSPM J0030+7742 | M6 ± 0.4 | 2558 ± 85 | 2698 ± 37 | 0.1616 ± 0.009 |
| LSPM J0032+5429 | M4 ± 0.2 | 3313 ± 141 | 3182 ± 41 | 0.3174 ± 0.0088 |
| LSPM J0035+0233* | M5.5 ± 0.3 | — | 2886 ± 40 | 0.2782 ± 0.0153 |
| LSPM J0040+3122 | M4 ± 0.3 | 3305 ± 123 | 3223 ± 44 | 0.3383 ± 0.0099 |
| LSPM J0044+0907 | M4 ± 0.2 | 3314 ± 134 | 3160 ± 38 | 0.4042 ± 0.0103 |
| LSPM J0046+4851 | M4.5 ± 0.4 | — | 3029 ± 25 | 0.2817 ± 0.0096 |
| LSPM J0049+6205 | M5.5 ± 0.5 | 2520 ± 85 | 3032 ± 27 | 0.1714 ± 0.0065 |
| LSPM J0051+4531 | M4.5 ± 0.3 | 3405 ± 85 | 3235 ± 46 | 0.303 ± 0.0097 |
| LSPM J0055+1439 | M4 ± 0.4 | — | 3193 ± 40 | 0.3287 ± 0.0083 |
| LSPM J0100+6656 | M4 ± 0.4 | 3188 ± 114 | 3291 ± 43 | 0.3664 ± 0.009 |
| LSPM J0101+3832 | M5 ± 0.3 | 3320 ± 85 | 3298 ± 41 | 0.3726 ± 0.0085 |
| LSPM J0102+1009W* | M1 ± 0.3 | — | 3593 ± 55 | 0.5209 ± 0.0184 |
| Object . | Parallax (mas) . | V (mag) . | G (mag) . | G BP (mag) . | G RP (mag) . | J (mag) . |
|---|---|---|---|---|---|---|
| EPIC 248536375 | — | — | — | — | — | — |
| GJ 1002 | 206.213 ± 0.128 | 13.837 ± 0.030 | 11.7804 ± 0.0008 | 14.0961 ± 0.0024 | 10.4046 ± 0.0023 | 8.323 ± 0.019 |
| GJ 2005 | — | 15.301 ± 0.030 | 13.0942 ± 0.0038 | 15.5725 ± 0.0063 | 11.6056 ± 0.0137 | 9.254 ± 0.034 |
| GJ 3707 | 81.552 ± 0.104 | 12.083 ± 0.040 | 10.7352 ± 0.0010 | 12.3571 ± 0.0020 | 9.5251 ± 0.0010 | 7.768 ± 0.029 |
| GJ 592 | 71.655 ± 0.080 | 12.726 ± 0.050 | 11.3527 ± 0.0017 | 12.9767 ± 0.0034 | 10.1587 ± 0.0017 | 8.432 ± 0.021 |
| LEHPM 2-174 | 56.081 ± 0.252 | — | 15.3726 ± 0.0010 | 18.5729 ± 0.0250 | 13.8258 ± 0.0097 | 11.160 ± 0.023 |
| LP 851-346 | 91.595 ± 0.154 | — | 15.1217 ± 0.0009 | 18.4005 ± 0.0222 | 13.5791 ± 0.0058 | 10.930 ± 0.023 |
| LSPM J0020+3305 | 81.631 ± 0.117 | 15.900 ± 0.500 | 13.9610 ± 0.0005 | 16.4199 ± 0.0043 | 12.5380 ± 0.0030 | 10.284 ± 0.021 |
| LSPM J0027+4941 | 44.804 ± 0.065 | 14.192 ± 0.050 | 12.7892 ± 0.0003 | 14.4785 ± 0.0022 | 11.5369 ± 0.0012 | 9.733 ± 0.021 |
| LSPM J0030+7742 | 76.000 ± 4.000 | 16.630 ± 0.500 | 14.3528 ± 0.0013 | 17.1088 ± 0.0064 | 12.8778 ± 0.0027 | 10.458 ± 0.023 |
| LSPM J0032+5429 | 50.070 ± 0.062 | 13.859 ± 0.030 | 12.4587 ± 0.0003 | 14.1399 ± 0.0019 | 11.2063 ± 0.0010 | 9.387 ± 0.022 |
| LSPM J0035+0233 | 38.127 ± 0.373 | 16.360 ± 0.500 | 14.2090 ± 0.0035 | 16.4858 ± 0.0056 | 12.7269 ± 0.0036 | 10.517 ± 0.023 |
| LSPM J0040+3122 | 44.403 ± 0.070 | 13.798 ± 0.040 | 12.4890 ± 0.0005 | 14.0960 ± 0.0030 | 11.2642 ± 0.0012 | 9.491 ± 0.022 |
| LSPM J0044+0907 | 37.572 ± 0.345 | 14.080 ± 0.030 | 12.6048 ± 0.0004 | 14.3415 ± 0.0024 | 11.3358 ± 0.0016 | 9.501 ± 0.026 |
| LSPM J0046+4851 | 25.184 ± 0.352 | 16.590 ± 0.500 | 14.5870 ± 0.0007 | 16.5068 ± 0.0080 | 13.2723 ± 0.0023 | 11.339 ± 0.021 |
| LSPM J0049+6205 | 37.893 ± 0.059 | 16.960 ± 0.500 | 14.7747 ± 0.0005 | 16.7483 ± 0.0054 | 13.4538 ± 0.0020 | 11.474 ± 0.021 |
| LSPM J0051+4531 | 28.079 ± 0.066 | 15.007 ± 0.040 | 13.6986 ± 0.0009 | 15.2859 ± 0.0062 | 12.4728 ± 0.0021 | 10.715 ± 0.022 |
| LSPM J0055+1439 | 24.769 ± 0.080 | 15.306 ± 0.060 | 13.8806 ± 0.0007 | 15.5607 ± 0.0039 | 12.6269 ± 0.0028 | 10.804 ± 0.022 |
| LSPM J0100+6656 | 44.299 ± 0.038 | 13.425 ± 0.020 | 12.1603 ± 0.0004 | 13.6628 ± 0.0022 | 10.9736 ± 0.0009 | 9.408 ± 0.029 |
| LSPM J0101+3832 | 26.570 ± 0.076 | 14.483 ± 0.030 | 13.2271 ± 0.0013 | 14.7573 ± 0.0051 | 12.0182 ± 0.0036 | 10.312 ± 0.025 |
| LSPM J0102+1009W | 18.858 ± 0.045 | 15.210 ± 0.500 | 12.6121 ± 0.0006 | 13.7365 ± 0.0031 | 11.5568 ± 0.0016 | 10.153 ± 0.027 |
| Object . | Parallax (mas) . | V (mag) . | G (mag) . | G BP (mag) . | G RP (mag) . | J (mag) . |
|---|---|---|---|---|---|---|
| EPIC 248536375 | — | — | — | — | — | — |
| GJ 1002 | 206.213 ± 0.128 | 13.837 ± 0.030 | 11.7804 ± 0.0008 | 14.0961 ± 0.0024 | 10.4046 ± 0.0023 | 8.323 ± 0.019 |
| GJ 2005 | — | 15.301 ± 0.030 | 13.0942 ± 0.0038 | 15.5725 ± 0.0063 | 11.6056 ± 0.0137 | 9.254 ± 0.034 |
| GJ 3707 | 81.552 ± 0.104 | 12.083 ± 0.040 | 10.7352 ± 0.0010 | 12.3571 ± 0.0020 | 9.5251 ± 0.0010 | 7.768 ± 0.029 |
| GJ 592 | 71.655 ± 0.080 | 12.726 ± 0.050 | 11.3527 ± 0.0017 | 12.9767 ± 0.0034 | 10.1587 ± 0.0017 | 8.432 ± 0.021 |
| LEHPM 2-174 | 56.081 ± 0.252 | — | 15.3726 ± 0.0010 | 18.5729 ± 0.0250 | 13.8258 ± 0.0097 | 11.160 ± 0.023 |
| LP 851-346 | 91.595 ± 0.154 | — | 15.1217 ± 0.0009 | 18.4005 ± 0.0222 | 13.5791 ± 0.0058 | 10.930 ± 0.023 |
| LSPM J0020+3305 | 81.631 ± 0.117 | 15.900 ± 0.500 | 13.9610 ± 0.0005 | 16.4199 ± 0.0043 | 12.5380 ± 0.0030 | 10.284 ± 0.021 |
| LSPM J0027+4941 | 44.804 ± 0.065 | 14.192 ± 0.050 | 12.7892 ± 0.0003 | 14.4785 ± 0.0022 | 11.5369 ± 0.0012 | 9.733 ± 0.021 |
| LSPM J0030+7742 | 76.000 ± 4.000 | 16.630 ± 0.500 | 14.3528 ± 0.0013 | 17.1088 ± 0.0064 | 12.8778 ± 0.0027 | 10.458 ± 0.023 |
| LSPM J0032+5429 | 50.070 ± 0.062 | 13.859 ± 0.030 | 12.4587 ± 0.0003 | 14.1399 ± 0.0019 | 11.2063 ± 0.0010 | 9.387 ± 0.022 |
| LSPM J0035+0233 | 38.127 ± 0.373 | 16.360 ± 0.500 | 14.2090 ± 0.0035 | 16.4858 ± 0.0056 | 12.7269 ± 0.0036 | 10.517 ± 0.023 |
| LSPM J0040+3122 | 44.403 ± 0.070 | 13.798 ± 0.040 | 12.4890 ± 0.0005 | 14.0960 ± 0.0030 | 11.2642 ± 0.0012 | 9.491 ± 0.022 |
| LSPM J0044+0907 | 37.572 ± 0.345 | 14.080 ± 0.030 | 12.6048 ± 0.0004 | 14.3415 ± 0.0024 | 11.3358 ± 0.0016 | 9.501 ± 0.026 |
| LSPM J0046+4851 | 25.184 ± 0.352 | 16.590 ± 0.500 | 14.5870 ± 0.0007 | 16.5068 ± 0.0080 | 13.2723 ± 0.0023 | 11.339 ± 0.021 |
| LSPM J0049+6205 | 37.893 ± 0.059 | 16.960 ± 0.500 | 14.7747 ± 0.0005 | 16.7483 ± 0.0054 | 13.4538 ± 0.0020 | 11.474 ± 0.021 |
| LSPM J0051+4531 | 28.079 ± 0.066 | 15.007 ± 0.040 | 13.6986 ± 0.0009 | 15.2859 ± 0.0062 | 12.4728 ± 0.0021 | 10.715 ± 0.022 |
| LSPM J0055+1439 | 24.769 ± 0.080 | 15.306 ± 0.060 | 13.8806 ± 0.0007 | 15.5607 ± 0.0039 | 12.6269 ± 0.0028 | 10.804 ± 0.022 |
| LSPM J0100+6656 | 44.299 ± 0.038 | 13.425 ± 0.020 | 12.1603 ± 0.0004 | 13.6628 ± 0.0022 | 10.9736 ± 0.0009 | 9.408 ± 0.029 |
| LSPM J0101+3832 | 26.570 ± 0.076 | 14.483 ± 0.030 | 13.2271 ± 0.0013 | 14.7573 ± 0.0051 | 12.0182 ± 0.0036 | 10.312 ± 0.025 |
| LSPM J0102+1009W | 18.858 ± 0.045 | 15.210 ± 0.500 | 12.6121 ± 0.0006 | 13.7365 ± 0.0031 | 11.5568 ± 0.0016 | 10.153 ± 0.027 |
| Object . | Parallax (mas) . | V (mag) . | G (mag) . | G BP (mag) . | G RP (mag) . | J (mag) . |
|---|---|---|---|---|---|---|
| EPIC 248536375 | — | — | — | — | — | — |
| GJ 1002 | 206.213 ± 0.128 | 13.837 ± 0.030 | 11.7804 ± 0.0008 | 14.0961 ± 0.0024 | 10.4046 ± 0.0023 | 8.323 ± 0.019 |
| GJ 2005 | — | 15.301 ± 0.030 | 13.0942 ± 0.0038 | 15.5725 ± 0.0063 | 11.6056 ± 0.0137 | 9.254 ± 0.034 |
| GJ 3707 | 81.552 ± 0.104 | 12.083 ± 0.040 | 10.7352 ± 0.0010 | 12.3571 ± 0.0020 | 9.5251 ± 0.0010 | 7.768 ± 0.029 |
| GJ 592 | 71.655 ± 0.080 | 12.726 ± 0.050 | 11.3527 ± 0.0017 | 12.9767 ± 0.0034 | 10.1587 ± 0.0017 | 8.432 ± 0.021 |
| LEHPM 2-174 | 56.081 ± 0.252 | — | 15.3726 ± 0.0010 | 18.5729 ± 0.0250 | 13.8258 ± 0.0097 | 11.160 ± 0.023 |
| LP 851-346 | 91.595 ± 0.154 | — | 15.1217 ± 0.0009 | 18.4005 ± 0.0222 | 13.5791 ± 0.0058 | 10.930 ± 0.023 |
| LSPM J0020+3305 | 81.631 ± 0.117 | 15.900 ± 0.500 | 13.9610 ± 0.0005 | 16.4199 ± 0.0043 | 12.5380 ± 0.0030 | 10.284 ± 0.021 |
| LSPM J0027+4941 | 44.804 ± 0.065 | 14.192 ± 0.050 | 12.7892 ± 0.0003 | 14.4785 ± 0.0022 | 11.5369 ± 0.0012 | 9.733 ± 0.021 |
| LSPM J0030+7742 | 76.000 ± 4.000 | 16.630 ± 0.500 | 14.3528 ± 0.0013 | 17.1088 ± 0.0064 | 12.8778 ± 0.0027 | 10.458 ± 0.023 |
| LSPM J0032+5429 | 50.070 ± 0.062 | 13.859 ± 0.030 | 12.4587 ± 0.0003 | 14.1399 ± 0.0019 | 11.2063 ± 0.0010 | 9.387 ± 0.022 |
| LSPM J0035+0233 | 38.127 ± 0.373 | 16.360 ± 0.500 | 14.2090 ± 0.0035 | 16.4858 ± 0.0056 | 12.7269 ± 0.0036 | 10.517 ± 0.023 |
| LSPM J0040+3122 | 44.403 ± 0.070 | 13.798 ± 0.040 | 12.4890 ± 0.0005 | 14.0960 ± 0.0030 | 11.2642 ± 0.0012 | 9.491 ± 0.022 |
| LSPM J0044+0907 | 37.572 ± 0.345 | 14.080 ± 0.030 | 12.6048 ± 0.0004 | 14.3415 ± 0.0024 | 11.3358 ± 0.0016 | 9.501 ± 0.026 |
| LSPM J0046+4851 | 25.184 ± 0.352 | 16.590 ± 0.500 | 14.5870 ± 0.0007 | 16.5068 ± 0.0080 | 13.2723 ± 0.0023 | 11.339 ± 0.021 |
| LSPM J0049+6205 | 37.893 ± 0.059 | 16.960 ± 0.500 | 14.7747 ± 0.0005 | 16.7483 ± 0.0054 | 13.4538 ± 0.0020 | 11.474 ± 0.021 |
| LSPM J0051+4531 | 28.079 ± 0.066 | 15.007 ± 0.040 | 13.6986 ± 0.0009 | 15.2859 ± 0.0062 | 12.4728 ± 0.0021 | 10.715 ± 0.022 |
| LSPM J0055+1439 | 24.769 ± 0.080 | 15.306 ± 0.060 | 13.8806 ± 0.0007 | 15.5607 ± 0.0039 | 12.6269 ± 0.0028 | 10.804 ± 0.022 |
| LSPM J0100+6656 | 44.299 ± 0.038 | 13.425 ± 0.020 | 12.1603 ± 0.0004 | 13.6628 ± 0.0022 | 10.9736 ± 0.0009 | 9.408 ± 0.029 |
| LSPM J0101+3832 | 26.570 ± 0.076 | 14.483 ± 0.030 | 13.2271 ± 0.0013 | 14.7573 ± 0.0051 | 12.0182 ± 0.0036 | 10.312 ± 0.025 |
| LSPM J0102+1009W | 18.858 ± 0.045 | 15.210 ± 0.500 | 12.6121 ± 0.0006 | 13.7365 ± 0.0031 | 11.5568 ± 0.0016 | 10.153 ± 0.027 |
| Object . | Parallax (mas) . | V (mag) . | G (mag) . | G BP (mag) . | G RP (mag) . | J (mag) . |
|---|---|---|---|---|---|---|
| EPIC 248536375 | — | — | — | — | — | — |
| GJ 1002 | 206.213 ± 0.128 | 13.837 ± 0.030 | 11.7804 ± 0.0008 | 14.0961 ± 0.0024 | 10.4046 ± 0.0023 | 8.323 ± 0.019 |
| GJ 2005 | — | 15.301 ± 0.030 | 13.0942 ± 0.0038 | 15.5725 ± 0.0063 | 11.6056 ± 0.0137 | 9.254 ± 0.034 |
| GJ 3707 | 81.552 ± 0.104 | 12.083 ± 0.040 | 10.7352 ± 0.0010 | 12.3571 ± 0.0020 | 9.5251 ± 0.0010 | 7.768 ± 0.029 |
| GJ 592 | 71.655 ± 0.080 | 12.726 ± 0.050 | 11.3527 ± 0.0017 | 12.9767 ± 0.0034 | 10.1587 ± 0.0017 | 8.432 ± 0.021 |
| LEHPM 2-174 | 56.081 ± 0.252 | — | 15.3726 ± 0.0010 | 18.5729 ± 0.0250 | 13.8258 ± 0.0097 | 11.160 ± 0.023 |
| LP 851-346 | 91.595 ± 0.154 | — | 15.1217 ± 0.0009 | 18.4005 ± 0.0222 | 13.5791 ± 0.0058 | 10.930 ± 0.023 |
| LSPM J0020+3305 | 81.631 ± 0.117 | 15.900 ± 0.500 | 13.9610 ± 0.0005 | 16.4199 ± 0.0043 | 12.5380 ± 0.0030 | 10.284 ± 0.021 |
| LSPM J0027+4941 | 44.804 ± 0.065 | 14.192 ± 0.050 | 12.7892 ± 0.0003 | 14.4785 ± 0.0022 | 11.5369 ± 0.0012 | 9.733 ± 0.021 |
| LSPM J0030+7742 | 76.000 ± 4.000 | 16.630 ± 0.500 | 14.3528 ± 0.0013 | 17.1088 ± 0.0064 | 12.8778 ± 0.0027 | 10.458 ± 0.023 |
| LSPM J0032+5429 | 50.070 ± 0.062 | 13.859 ± 0.030 | 12.4587 ± 0.0003 | 14.1399 ± 0.0019 | 11.2063 ± 0.0010 | 9.387 ± 0.022 |
| LSPM J0035+0233 | 38.127 ± 0.373 | 16.360 ± 0.500 | 14.2090 ± 0.0035 | 16.4858 ± 0.0056 | 12.7269 ± 0.0036 | 10.517 ± 0.023 |
| LSPM J0040+3122 | 44.403 ± 0.070 | 13.798 ± 0.040 | 12.4890 ± 0.0005 | 14.0960 ± 0.0030 | 11.2642 ± 0.0012 | 9.491 ± 0.022 |
| LSPM J0044+0907 | 37.572 ± 0.345 | 14.080 ± 0.030 | 12.6048 ± 0.0004 | 14.3415 ± 0.0024 | 11.3358 ± 0.0016 | 9.501 ± 0.026 |
| LSPM J0046+4851 | 25.184 ± 0.352 | 16.590 ± 0.500 | 14.5870 ± 0.0007 | 16.5068 ± 0.0080 | 13.2723 ± 0.0023 | 11.339 ± 0.021 |
| LSPM J0049+6205 | 37.893 ± 0.059 | 16.960 ± 0.500 | 14.7747 ± 0.0005 | 16.7483 ± 0.0054 | 13.4538 ± 0.0020 | 11.474 ± 0.021 |
| LSPM J0051+4531 | 28.079 ± 0.066 | 15.007 ± 0.040 | 13.6986 ± 0.0009 | 15.2859 ± 0.0062 | 12.4728 ± 0.0021 | 10.715 ± 0.022 |
| LSPM J0055+1439 | 24.769 ± 0.080 | 15.306 ± 0.060 | 13.8806 ± 0.0007 | 15.5607 ± 0.0039 | 12.6269 ± 0.0028 | 10.804 ± 0.022 |
| LSPM J0100+6656 | 44.299 ± 0.038 | 13.425 ± 0.020 | 12.1603 ± 0.0004 | 13.6628 ± 0.0022 | 10.9736 ± 0.0009 | 9.408 ± 0.029 |
| LSPM J0101+3832 | 26.570 ± 0.076 | 14.483 ± 0.030 | 13.2271 ± 0.0013 | 14.7573 ± 0.0051 | 12.0182 ± 0.0036 | 10.312 ± 0.025 |
| LSPM J0102+1009W | 18.858 ± 0.045 | 15.210 ± 0.500 | 12.6121 ± 0.0006 | 13.7365 ± 0.0031 | 11.5568 ± 0.0016 | 10.153 ± 0.027 |
| Object . | H (mag) . | K (mag) . | W1 (mag) . | W2 (mag) . | W3 (mag) . | W4 (mag) . |
|---|---|---|---|---|---|---|
| EPIC 248536375 | — | — | — | — | — | — |
| GJ 1002 | 7.792 ± 0.034 | 7.439 ± 0.021 | 7.176 ± 0.028 | 6.993 ± 0.020 | 6.860 ± 0.016 | 6.766 ± 0.080 |
| GJ 2005 | 8.547 ± 0.036 | 8.241 ± 0.030 | 7.836 ± 0.023 | 7.620 ± 0.021 | 7.353 ± 0.017 | 7.184 ± 0.103 |
| GJ 3707 | 7.137 ± 0.040 | 6.863 ± 0.024 | 6.712 ± 0.037 | 6.555 ± 0.020 | 6.490 ± 0.016 | 6.384 ± 0.054 |
| GJ 592 | 7.871 ± 0.036 | 7.572 ± 0.023 | 7.386 ± 0.025 | 7.252 ± 0.021 | 7.149 ± 0.016 | 7.066 ± 0.098 |
| LEHPM 2-174 | 10.550 ± 0.023 | 10.128 ± 0.021 | 9.889 ± 0.023 | 9.678 ± 0.021 | 9.380 ± 0.029 | 8.857 ± 0.332 |
| LP 851-346 | 10.295 ± 0.023 | 9.881 ± 0.019 | 9.646 ± 0.021 | 9.448 ± 0.019 | 9.235 ± 0.030 | — |
| LSPM J0020+3305 | 9.691 ± 0.022 | 9.330 ± 0.018 | 9.092 ± 0.023 | 8.901 ± 0.020 | 8.724 ± 0.024 | 8.227 ± 0.189 |
| LSPM J0027+4941 | 9.160 ± 0.021 | 8.852 ± 0.018 | 8.665 ± 0.022 | 8.522 ± 0.019 | 8.376 ± 0.019 | 8.317 ± 0.168 |
| LSPM J0030+7742 | 9.891 ± 0.027 | 9.562 ± 0.021 | 9.317 ± 0.023 | 9.115 ± 0.019 | 8.832 ± 0.022 | 9.036 ± 0.378 |
| LSPM J0032+5429 | 8.827 ± 0.016 | 8.570 ± 0.014 | 8.406 ± 0.022 | 8.223 ± 0.020 | 8.118 ± 0.018 | 8.229 ± 0.177 |
| LSPM J0035+0233 | 9.933 ± 0.025 | 9.543 ± 0.021 | 9.309 ± 0.023 | 9.110 ± 0.021 | 8.959 ± 0.030 | 8.845 ± 0.448 |
| LSPM J0040+3122 | 8.864 ± 0.030 | 8.592 ± 0.020 | 8.419 ± 0.024 | 8.293 ± 0.021 | 8.158 ± 0.019 | 7.936 ± 0.158 |
| LSPM J0044+0907 | 8.957 ± 0.030 | 8.621 ± 0.020 | 8.434 ± 0.024 | 8.273 ± 0.019 | 8.145 ± 0.020 | 8.105 ± 0.228 |
| LSPM J0046+4851 | 10.733 ± 0.019 | 10.432 ± 0.018 | 10.234 ± 0.022 | 10.052 ± 0.020 | 9.858 ± 0.031 | — |
| LSPM J0049+6205 | 10.897 ± 0.026 | 10.620 ± 0.020 | — | — | — | — |
| LSPM J0051+4531 | 10.165 ± 0.023 | 9.912 ± 0.020 | 9.763 ± 0.024 | 9.579 ± 0.020 | 9.448 ± 0.027 | — |
| LSPM J0055+1439 | 10.216 ± 0.030 | 9.934 ± 0.019 | 9.785 ± 0.024 | 9.631 ± 0.020 | 9.531 ± 0.035 | — |
| LSPM J0100+6656 | 8.726 ± 0.031 | 8.484 ± 0.023 | 8.262 ± 0.022 | 8.140 ± 0.021 | 8.054 ± 0.020 | 8.629 ± 0.370 |
| LSPM J0101+3832 | 9.729 ± 0.030 | 9.475 ± 0.018 | 9.310 ± 0.023 | 9.172 ± 0.020 | 9.065 ± 0.023 | 8.872 ± 0.318 |
| LSPM J0102+1009W | 9.525 ± 0.102 | 9.312 ± 0.027 | 8.315 ± 0.023 | 8.277 ± 0.020 | 8.261 ± 0.021 | 8.031 ± 0.222 |
| Object . | H (mag) . | K (mag) . | W1 (mag) . | W2 (mag) . | W3 (mag) . | W4 (mag) . |
|---|---|---|---|---|---|---|
| EPIC 248536375 | — | — | — | — | — | — |
| GJ 1002 | 7.792 ± 0.034 | 7.439 ± 0.021 | 7.176 ± 0.028 | 6.993 ± 0.020 | 6.860 ± 0.016 | 6.766 ± 0.080 |
| GJ 2005 | 8.547 ± 0.036 | 8.241 ± 0.030 | 7.836 ± 0.023 | 7.620 ± 0.021 | 7.353 ± 0.017 | 7.184 ± 0.103 |
| GJ 3707 | 7.137 ± 0.040 | 6.863 ± 0.024 | 6.712 ± 0.037 | 6.555 ± 0.020 | 6.490 ± 0.016 | 6.384 ± 0.054 |
| GJ 592 | 7.871 ± 0.036 | 7.572 ± 0.023 | 7.386 ± 0.025 | 7.252 ± 0.021 | 7.149 ± 0.016 | 7.066 ± 0.098 |
| LEHPM 2-174 | 10.550 ± 0.023 | 10.128 ± 0.021 | 9.889 ± 0.023 | 9.678 ± 0.021 | 9.380 ± 0.029 | 8.857 ± 0.332 |
| LP 851-346 | 10.295 ± 0.023 | 9.881 ± 0.019 | 9.646 ± 0.021 | 9.448 ± 0.019 | 9.235 ± 0.030 | — |
| LSPM J0020+3305 | 9.691 ± 0.022 | 9.330 ± 0.018 | 9.092 ± 0.023 | 8.901 ± 0.020 | 8.724 ± 0.024 | 8.227 ± 0.189 |
| LSPM J0027+4941 | 9.160 ± 0.021 | 8.852 ± 0.018 | 8.665 ± 0.022 | 8.522 ± 0.019 | 8.376 ± 0.019 | 8.317 ± 0.168 |
| LSPM J0030+7742 | 9.891 ± 0.027 | 9.562 ± 0.021 | 9.317 ± 0.023 | 9.115 ± 0.019 | 8.832 ± 0.022 | 9.036 ± 0.378 |
| LSPM J0032+5429 | 8.827 ± 0.016 | 8.570 ± 0.014 | 8.406 ± 0.022 | 8.223 ± 0.020 | 8.118 ± 0.018 | 8.229 ± 0.177 |
| LSPM J0035+0233 | 9.933 ± 0.025 | 9.543 ± 0.021 | 9.309 ± 0.023 | 9.110 ± 0.021 | 8.959 ± 0.030 | 8.845 ± 0.448 |
| LSPM J0040+3122 | 8.864 ± 0.030 | 8.592 ± 0.020 | 8.419 ± 0.024 | 8.293 ± 0.021 | 8.158 ± 0.019 | 7.936 ± 0.158 |
| LSPM J0044+0907 | 8.957 ± 0.030 | 8.621 ± 0.020 | 8.434 ± 0.024 | 8.273 ± 0.019 | 8.145 ± 0.020 | 8.105 ± 0.228 |
| LSPM J0046+4851 | 10.733 ± 0.019 | 10.432 ± 0.018 | 10.234 ± 0.022 | 10.052 ± 0.020 | 9.858 ± 0.031 | — |
| LSPM J0049+6205 | 10.897 ± 0.026 | 10.620 ± 0.020 | — | — | — | — |
| LSPM J0051+4531 | 10.165 ± 0.023 | 9.912 ± 0.020 | 9.763 ± 0.024 | 9.579 ± 0.020 | 9.448 ± 0.027 | — |
| LSPM J0055+1439 | 10.216 ± 0.030 | 9.934 ± 0.019 | 9.785 ± 0.024 | 9.631 ± 0.020 | 9.531 ± 0.035 | — |
| LSPM J0100+6656 | 8.726 ± 0.031 | 8.484 ± 0.023 | 8.262 ± 0.022 | 8.140 ± 0.021 | 8.054 ± 0.020 | 8.629 ± 0.370 |
| LSPM J0101+3832 | 9.729 ± 0.030 | 9.475 ± 0.018 | 9.310 ± 0.023 | 9.172 ± 0.020 | 9.065 ± 0.023 | 8.872 ± 0.318 |
| LSPM J0102+1009W | 9.525 ± 0.102 | 9.312 ± 0.027 | 8.315 ± 0.023 | 8.277 ± 0.020 | 8.261 ± 0.021 | 8.031 ± 0.222 |
| Object . | H (mag) . | K (mag) . | W1 (mag) . | W2 (mag) . | W3 (mag) . | W4 (mag) . |
|---|---|---|---|---|---|---|
| EPIC 248536375 | — | — | — | — | — | — |
| GJ 1002 | 7.792 ± 0.034 | 7.439 ± 0.021 | 7.176 ± 0.028 | 6.993 ± 0.020 | 6.860 ± 0.016 | 6.766 ± 0.080 |
| GJ 2005 | 8.547 ± 0.036 | 8.241 ± 0.030 | 7.836 ± 0.023 | 7.620 ± 0.021 | 7.353 ± 0.017 | 7.184 ± 0.103 |
| GJ 3707 | 7.137 ± 0.040 | 6.863 ± 0.024 | 6.712 ± 0.037 | 6.555 ± 0.020 | 6.490 ± 0.016 | 6.384 ± 0.054 |
| GJ 592 | 7.871 ± 0.036 | 7.572 ± 0.023 | 7.386 ± 0.025 | 7.252 ± 0.021 | 7.149 ± 0.016 | 7.066 ± 0.098 |
| LEHPM 2-174 | 10.550 ± 0.023 | 10.128 ± 0.021 | 9.889 ± 0.023 | 9.678 ± 0.021 | 9.380 ± 0.029 | 8.857 ± 0.332 |
| LP 851-346 | 10.295 ± 0.023 | 9.881 ± 0.019 | 9.646 ± 0.021 | 9.448 ± 0.019 | 9.235 ± 0.030 | — |
| LSPM J0020+3305 | 9.691 ± 0.022 | 9.330 ± 0.018 | 9.092 ± 0.023 | 8.901 ± 0.020 | 8.724 ± 0.024 | 8.227 ± 0.189 |
| LSPM J0027+4941 | 9.160 ± 0.021 | 8.852 ± 0.018 | 8.665 ± 0.022 | 8.522 ± 0.019 | 8.376 ± 0.019 | 8.317 ± 0.168 |
| LSPM J0030+7742 | 9.891 ± 0.027 | 9.562 ± 0.021 | 9.317 ± 0.023 | 9.115 ± 0.019 | 8.832 ± 0.022 | 9.036 ± 0.378 |
| LSPM J0032+5429 | 8.827 ± 0.016 | 8.570 ± 0.014 | 8.406 ± 0.022 | 8.223 ± 0.020 | 8.118 ± 0.018 | 8.229 ± 0.177 |
| LSPM J0035+0233 | 9.933 ± 0.025 | 9.543 ± 0.021 | 9.309 ± 0.023 | 9.110 ± 0.021 | 8.959 ± 0.030 | 8.845 ± 0.448 |
| LSPM J0040+3122 | 8.864 ± 0.030 | 8.592 ± 0.020 | 8.419 ± 0.024 | 8.293 ± 0.021 | 8.158 ± 0.019 | 7.936 ± 0.158 |
| LSPM J0044+0907 | 8.957 ± 0.030 | 8.621 ± 0.020 | 8.434 ± 0.024 | 8.273 ± 0.019 | 8.145 ± 0.020 | 8.105 ± 0.228 |
| LSPM J0046+4851 | 10.733 ± 0.019 | 10.432 ± 0.018 | 10.234 ± 0.022 | 10.052 ± 0.020 | 9.858 ± 0.031 | — |
| LSPM J0049+6205 | 10.897 ± 0.026 | 10.620 ± 0.020 | — | — | — | — |
| LSPM J0051+4531 | 10.165 ± 0.023 | 9.912 ± 0.020 | 9.763 ± 0.024 | 9.579 ± 0.020 | 9.448 ± 0.027 | — |
| LSPM J0055+1439 | 10.216 ± 0.030 | 9.934 ± 0.019 | 9.785 ± 0.024 | 9.631 ± 0.020 | 9.531 ± 0.035 | — |
| LSPM J0100+6656 | 8.726 ± 0.031 | 8.484 ± 0.023 | 8.262 ± 0.022 | 8.140 ± 0.021 | 8.054 ± 0.020 | 8.629 ± 0.370 |
| LSPM J0101+3832 | 9.729 ± 0.030 | 9.475 ± 0.018 | 9.310 ± 0.023 | 9.172 ± 0.020 | 9.065 ± 0.023 | 8.872 ± 0.318 |
| LSPM J0102+1009W | 9.525 ± 0.102 | 9.312 ± 0.027 | 8.315 ± 0.023 | 8.277 ± 0.020 | 8.261 ± 0.021 | 8.031 ± 0.222 |
| Object . | H (mag) . | K (mag) . | W1 (mag) . | W2 (mag) . | W3 (mag) . | W4 (mag) . |
|---|---|---|---|---|---|---|
| EPIC 248536375 | — | — | — | — | — | — |
| GJ 1002 | 7.792 ± 0.034 | 7.439 ± 0.021 | 7.176 ± 0.028 | 6.993 ± 0.020 | 6.860 ± 0.016 | 6.766 ± 0.080 |
| GJ 2005 | 8.547 ± 0.036 | 8.241 ± 0.030 | 7.836 ± 0.023 | 7.620 ± 0.021 | 7.353 ± 0.017 | 7.184 ± 0.103 |
| GJ 3707 | 7.137 ± 0.040 | 6.863 ± 0.024 | 6.712 ± 0.037 | 6.555 ± 0.020 | 6.490 ± 0.016 | 6.384 ± 0.054 |
| GJ 592 | 7.871 ± 0.036 | 7.572 ± 0.023 | 7.386 ± 0.025 | 7.252 ± 0.021 | 7.149 ± 0.016 | 7.066 ± 0.098 |
| LEHPM 2-174 | 10.550 ± 0.023 | 10.128 ± 0.021 | 9.889 ± 0.023 | 9.678 ± 0.021 | 9.380 ± 0.029 | 8.857 ± 0.332 |
| LP 851-346 | 10.295 ± 0.023 | 9.881 ± 0.019 | 9.646 ± 0.021 | 9.448 ± 0.019 | 9.235 ± 0.030 | — |
| LSPM J0020+3305 | 9.691 ± 0.022 | 9.330 ± 0.018 | 9.092 ± 0.023 | 8.901 ± 0.020 | 8.724 ± 0.024 | 8.227 ± 0.189 |
| LSPM J0027+4941 | 9.160 ± 0.021 | 8.852 ± 0.018 | 8.665 ± 0.022 | 8.522 ± 0.019 | 8.376 ± 0.019 | 8.317 ± 0.168 |
| LSPM J0030+7742 | 9.891 ± 0.027 | 9.562 ± 0.021 | 9.317 ± 0.023 | 9.115 ± 0.019 | 8.832 ± 0.022 | 9.036 ± 0.378 |
| LSPM J0032+5429 | 8.827 ± 0.016 | 8.570 ± 0.014 | 8.406 ± 0.022 | 8.223 ± 0.020 | 8.118 ± 0.018 | 8.229 ± 0.177 |
| LSPM J0035+0233 | 9.933 ± 0.025 | 9.543 ± 0.021 | 9.309 ± 0.023 | 9.110 ± 0.021 | 8.959 ± 0.030 | 8.845 ± 0.448 |
| LSPM J0040+3122 | 8.864 ± 0.030 | 8.592 ± 0.020 | 8.419 ± 0.024 | 8.293 ± 0.021 | 8.158 ± 0.019 | 7.936 ± 0.158 |
| LSPM J0044+0907 | 8.957 ± 0.030 | 8.621 ± 0.020 | 8.434 ± 0.024 | 8.273 ± 0.019 | 8.145 ± 0.020 | 8.105 ± 0.228 |
| LSPM J0046+4851 | 10.733 ± 0.019 | 10.432 ± 0.018 | 10.234 ± 0.022 | 10.052 ± 0.020 | 9.858 ± 0.031 | — |
| LSPM J0049+6205 | 10.897 ± 0.026 | 10.620 ± 0.020 | — | — | — | — |
| LSPM J0051+4531 | 10.165 ± 0.023 | 9.912 ± 0.020 | 9.763 ± 0.024 | 9.579 ± 0.020 | 9.448 ± 0.027 | — |
| LSPM J0055+1439 | 10.216 ± 0.030 | 9.934 ± 0.019 | 9.785 ± 0.024 | 9.631 ± 0.020 | 9.531 ± 0.035 | — |
| LSPM J0100+6656 | 8.726 ± 0.031 | 8.484 ± 0.023 | 8.262 ± 0.022 | 8.140 ± 0.021 | 8.054 ± 0.020 | 8.629 ± 0.370 |
| LSPM J0101+3832 | 9.729 ± 0.030 | 9.475 ± 0.018 | 9.310 ± 0.023 | 9.172 ± 0.020 | 9.065 ± 0.023 | 8.872 ± 0.318 |
| LSPM J0102+1009W | 9.525 ± 0.102 | 9.312 ± 0.027 | 8.315 ± 0.023 | 8.277 ± 0.020 | 8.261 ± 0.021 | 8.031 ± 0.222 |
Acknowledgements
We would like to thank Andrew Mann for providing their spectra and Hiroki Ishikawa for helping us with observations. We also thank Diane Harmer, Susan Ridgway, and the telescope operator for helping us with observations at WIYN. This work was supported by JSPS KAKENHI Grant Numbers 16K17660, 19K14783, and 8H05442A. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. This research has made use of the VizieR catalog access tool, CDS, Strasbourg, France (DOI: 10.26093/cds/vizier). The original description of the VizieR service was published in Bogdan and Schlickeiser (1985). This research has made use of the Washington Double Star Catalog maintained at the U.S. Naval Observatory. This research is based on observations at Okayama Astrophysical Observatory (OAO), which is operated by the National Astronomical Observatory of Japan, Nishi-Harima Astronomical Observatory, which is operated by the Center for Astronomy of University of Hyogo, Centro Astronómico Hispano Alemán (CAHA) at Calar Alto, which is operated jointly by the Max-Planck Institut für Astronomie and the Instituto de Astrofísica de Andalucía, and the Apache Point Observatory 3.5 m telescope, which is owned and operated by the Astrophysical Research Consortium. Data presented herein were obtained at the WIYN Observatory from telescope time allocated to NN-EXPLORE through the scientific partnership of the National Aeronautics and Space Administration, the National Science Foundation, and NSF’s NOIRLab. The WIYN observing nights were obtained through NOAO proposals with IDs 16B-0275 and 17A-0380 (PI: Masashi Omiya). NOAO is operated by the Association of Universities for Research in Astronomy (AURA) under a cooperative agreement with the National Science Foundation. GradPak was made possible by the U.S. National Science Foundation (NSF) grants ATI-0804576, AST-1009471, and AST-1517006, as well as gift funds from the UW-Madison Department of Astronomy. The APO observations were in part performed with observing time that we purchased with financial support from the Astrobiology Center, NINS. We appreciate our anonymous referee, whose comments and suggestions significantly improved the quality of this paper.
Appendix 1. Flux normalization for temperature estimation
In equation (1), we considered constant, linear, quadratic, or cubic normalization. We adopted constant normalization since it provides the smallest residuals (a standard deviation of 85 K) in the fit of the linear correction equation (2) to the relations of our obtained Teff and the Teff from Mann et al. (2015) (see figure 17). In other words, constant normalization provides the highest accuracy in the reproduction of well-calibrated Teff estimates from Mann et al. (2015).
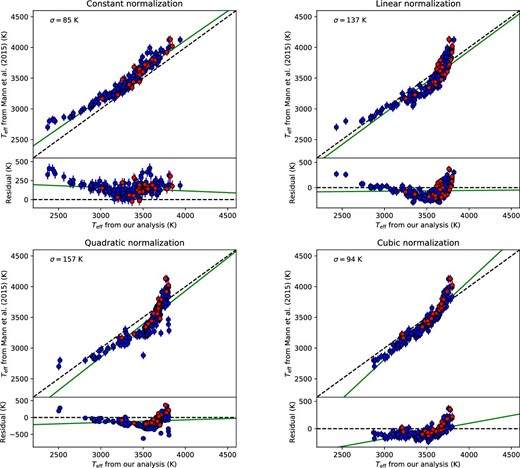
As figure 4, but only the wavelength range of 5000–8000 Å is compared and the four types of normalizations are adopted in the optimizations of equation (1). The top left panel is the result for constant, top right for linear, bottom left for quadratic, and bottom right for cubic normalization. The green lines in the figure represent linear correction functions (see sub-subsection 3.1.2), and σ is the standard deviation of the residual of the best-fitting linear function. (Color online)
Appendix 2. Spectral standard stars
The spectral standard stars that we used are listed in table 7.14
Appendix 3. Our samples
The star names, observation date, exposure times, and spectrographs are listed in table 8.14
Appendix 4. Results and stellar parameters
We summarize our results and stellar parameters in tables 9–11.14Tspec is the temperature obtained from optical spectra. We note that the wavelength range of DIS is 6100–7300 Å, and we did not consider the VO index for
the spectra obtained by DIS. Therefore, the spectral types of DIS data may be earlier than they actually are.
Footnotes
This work made use of the spectra which were obtained in the IRD target selection. They applied a 1000 au threshold for their sample selection. See the IRD proposal https://www.naoj.org/Science/SACM/Senryaku/IRD_180520235849.pdf for details.
We also partially used the Hipparcos (van Leeuwen 2007) parallaxes for the selection of targets in this study, but those parallaxes were not finally adopted in the analysis below.
The WIYN Observatory is a joint facility of the University of Wisconsin-Madison, Indiana University, the National Optical Astronomy Observatory, and the University of Missouri.
Based on observations collected at the Centro Astronómico Hispano Alemán (CAHA) at Calar Alto, operated jointly by the Max-Planck Institut für Astronomie and the Instituto de Astrofísica de Andalucía (CSIC).
Based on observations obtained with the Apache Point Observatory 3.5 m telescope, which is owned and operated by the Astrophysical Research Consortium.
Pronounced “GradPak.”
IRAF is distributed by the National Optical Astronomy Observatories, which is operated by the Association of Universities for Research in Astronomy, Inc. under cooperative agreement with the National Science Foundation, USA.
References







